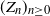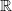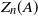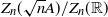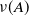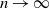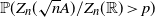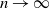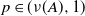1. Introduction and main results
1.1. Introduction
We consider a branching random walk (BRW) model, which is governed by a probability distribution
![]() $\{p_k\}_{k\geq 0}$
on the natural numbers (called the offspring distribution) and a real-valued random variable X (called the step size or displacement). This model is defined as follows. At time 0, there is one particle located at the origin. The particle dies and produces offspring according to the offspring distribution
$\{p_k\}_{k\geq 0}$
on the natural numbers (called the offspring distribution) and a real-valued random variable X (called the step size or displacement). This model is defined as follows. At time 0, there is one particle located at the origin. The particle dies and produces offspring according to the offspring distribution
![]() $\{p_k\}_{k\geq 0}$
. Afterwards, the offspring particles move independently according to the law of X. This forms a process
$\{p_k\}_{k\geq 0}$
. Afterwards, the offspring particles move independently according to the law of X. This forms a process
![]() $Z_1$
. For any point process
$Z_1$
. For any point process
![]() $Z_n$
,
$Z_n$
,
![]() $n\geq 2$
, we define it by the iteration
$n\geq 2$
, we define it by the iteration
![]() $Z_n=\sum_{x\in Z_{n-1}}\tilde{Z}_1^{x}$
, where
$Z_n=\sum_{x\in Z_{n-1}}\tilde{Z}_1^{x}$
, where
![]() $\tilde{Z}_1^{x}$
has the same distribution as
$\tilde{Z}_1^{x}$
has the same distribution as
![]() $Z_1(\cdot-S_x)$
, and
$Z_1(\cdot-S_x)$
, and
![]() $\{\tilde{Z}_1^{x}\,{:}\, x\in Z_{n-1}\}$
(conditioned on
$\{\tilde{Z}_1^{x}\,{:}\, x\in Z_{n-1}\}$
(conditioned on
![]() $Z_{n-1}$
) are independent. Here and later, for a point process (also for a point measure)
$Z_{n-1}$
) are independent. Here and later, for a point process (also for a point measure)
![]() $\xi$
,
$\xi$
,
![]() $x\in\xi$
means x is an atom of
$x\in\xi$
means x is an atom of
![]() $\xi$
, and
$\xi$
, and
![]() $S_x$
is the position of x (i.e.
$S_x$
is the position of x (i.e.
![]() $\xi=\sum_{x\in\xi}\delta_{S_x}$
).
$\xi=\sum_{x\in\xi}\delta_{S_x}$
).
We are interested here in the large-deviation probabilities of the corresponding empirical distribution, which is defined as
According to [Reference Biggins7, Theorem 6]: if
![]() $\mathbb{E}[X]=0$
,
$\mathbb{E}[X]=0$
,
![]() $\mathbb{E}\big[X^2\big]=1$
,
$\mathbb{E}\big[X^2\big]=1$
,
![]() $\mathbb{E}[Z_1(\mathbb{R})\log Z_1(\mathbb{R})]<\infty$
, and
$\mathbb{E}[Z_1(\mathbb{R})\log Z_1(\mathbb{R})]<\infty$
, and
![]() $\mathbb{E}[Z_1(\mathbb{R})]>1$
, then, for any Borel-measurable set
$\mathbb{E}[Z_1(\mathbb{R})]>1$
, then, for any Borel-measurable set
![]() $A\subset\mathbb{R}$
,
$A\subset\mathbb{R}$
,
![]() $\bar{Z}_n(\sqrt n A)\rightarrow \nu(A)$
$\bar{Z}_n(\sqrt n A)\rightarrow \nu(A)$
![]() $\mathbb{P}$
-a.s. (almost surely) on non-extinction, where
$\mathbb{P}$
-a.s. (almost surely) on non-extinction, where
![]() $\nu$
is the standard Gaussian measure. So, it is natural to study the decay rate of
$\nu$
is the standard Gaussian measure. So, it is natural to study the decay rate of
![]() $\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)$
as
$\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)$
as
![]() $n\rightarrow\infty$
, where
$n\rightarrow\infty$
, where
![]() $p\in(\nu(A),1)$
.
$p\in(\nu(A),1)$
.
In fact, this question was considered in [Reference Louidor and Perkins32] under the assumption that
![]() $p_0=p_1=0$
and
$p_0=p_1=0$
and
![]() $\mathbb{P}(X=1)=\mathbb{P}(X=-1)$
. Later, [Reference Chen and He13] further investigated the problem for unbounded displacements; see also [Reference Louidor and Tsairi33]. However, they always assumed that the offspring law and step size have an exponential moment (or that the step size has a stretched exponential moment). So, we shall deal here with the case that the offspring law or step size has a heavy tail (i.e.
$\mathbb{P}(X=1)=\mathbb{P}(X=-1)$
. Later, [Reference Chen and He13] further investigated the problem for unbounded displacements; see also [Reference Louidor and Tsairi33]. However, they always assumed that the offspring law and step size have an exponential moment (or that the step size has a stretched exponential moment). So, we shall deal here with the case that the offspring law or step size has a heavy tail (i.e.
![]() $\mathbb{E}[\textrm{e}^{\theta Z_1(\mathbb{R})}]=+\infty$
or
$\mathbb{E}[\textrm{e}^{\theta Z_1(\mathbb{R})}]=+\infty$
or
![]() $\mathbb{E}[\textrm{e}^{\theta X}]=+\infty$
for any
$\mathbb{E}[\textrm{e}^{\theta X}]=+\infty$
for any
![]() $\theta>0$
). We will see that the strategy for studying this problem and the answers obtained will be very different from theirs.
$\theta>0$
). We will see that the strategy for studying this problem and the answers obtained will be very different from theirs.
We also mention here that the BRW model has been extensively studied in recent decades due to its connection to many fields, such as Gaussian multiplicative chaos, random walks in random environments, random polymers, random algorithms, discrete Gaussian free field, etc; see [Reference Aïdékon, Hu and Shi1, Reference Bramson, Ding and Zeitouni9, Reference Hu and Shi27, Reference Liu30, Reference Liu31] and references therein, and refer to [Reference Shi38] for a more detailed overview. The large-deviation probabilities (LDP) for BRW and branching Brownian motion (BBM) on the real line have attracted the attention of many researchers. For example, [Reference Chen and He14, Reference Gantert and Höfelsauer22, Reference Hu26] considered the LDP and the moderate deviation of BRW’s maximum (for BBM’s maximum, see [Reference Chauvin and Rouault11, Reference Derrida and Shi17–Reference Derrida and Shi19]); [Reference Öz36] studied the lower deviation of BBM’s local mass. See also [Reference Aïdékon, Hu and Shi1] for the upper deviation of BBM’s level sets. Some other related works include [Reference Bhattacharya6, Reference Buraczewski and Maślanka10, Reference Rouault37].
The a.s. behaviour of
![]() $\bar{Z}_n(\sqrt nA)$
has been considered by many researchers, e.g. [Reference Asmussen and Kaplan2, Reference Biggins7, Reference Harris25, Reference Klebaner28]. Moreover, that the a.s. convergence rate of
$\bar{Z}_n(\sqrt nA)$
has been considered by many researchers, e.g. [Reference Asmussen and Kaplan2, Reference Biggins7, Reference Harris25, Reference Klebaner28]. Moreover, that the a.s. convergence rate of
![]() $\bar{Z}_n(\sqrt nA)-\nu(A)$
tends to zero has also been well studied recently: [Reference Chen12] considered the branching Wiener process; [Reference Gao and Liu23] generalized Chen’s results to the BRW, but a kind of Cramér’s condition is needed for the step size; [Reference Grübel and Kabluchko24] studied the case when the step size of the BRW is lattice. These results show that
$\bar{Z}_n(\sqrt nA)-\nu(A)$
tends to zero has also been well studied recently: [Reference Chen12] considered the branching Wiener process; [Reference Gao and Liu23] generalized Chen’s results to the BRW, but a kind of Cramér’s condition is needed for the step size; [Reference Grübel and Kabluchko24] studied the case when the step size of the BRW is lattice. These results show that
![]() $\sqrt n(\bar{Z}_n(\sqrt n A)-\nu(A))$
converges almost surely to a non-degenerate limit.
$\sqrt n(\bar{Z}_n(\sqrt n A)-\nu(A))$
converges almost surely to a non-degenerate limit.
1.2. Main results
Before giving our results, we first introduce some notation. Let
![]() $\mathcal{A}$
be the algebra generated by
$\mathcal{A}$
be the algebra generated by
![]() $\{(-\infty,x],x\in\mathbb{R}\}$
. For a non-empty set
$\{(-\infty,x],x\in\mathbb{R}\}$
. For a non-empty set
![]() $A\in\mathcal{A}$
and
$A\in\mathcal{A}$
and
![]() $p\in\left(\nu(A),1\right)$
, define
$p\in\left(\nu(A),1\right)$
, define
![]() $I_A(p)=\inf\left\{\left|x\right|\,{:}\,\nu\left(A-x\right)\geq p\right\}$
,
$I_A(p)=\inf\left\{\left|x\right|\,{:}\,\nu\left(A-x\right)\geq p\right\}$
,
![]() $J_A(p)=\inf\big\{r\,{:}\,\sup_{x\in\mathbb{R}}\nu\left(\left(A-x\right)/\sqrt{1-r}\right)\geq p$
,
$J_A(p)=\inf\big\{r\,{:}\,\sup_{x\in\mathbb{R}}\nu\left(\left(A-x\right)/\sqrt{1-r}\right)\geq p$
,
![]() $r\in\left[0,1\right)\big\}$
. Let
$r\in\left[0,1\right)\big\}$
. Let
![]() $|Z_n|\,{:\!=}\,Z_n(\mathbb{R})$
,
$|Z_n|\,{:\!=}\,Z_n(\mathbb{R})$
,
![]() $m\,{:\!=}\,\mathbb{E}[|Z_1|]$
, and
$m\,{:\!=}\,\mathbb{E}[|Z_1|]$
, and
![]() $b\,{:\!=}\,\min\{k\geq 0\,{:}\, p_k>0\}\leq B\,{:\!=}\,\sup\{k\geq 0: p_k>0\}\leq+\infty$
. Recall that
$b\,{:\!=}\,\min\{k\geq 0\,{:}\, p_k>0\}\leq B\,{:\!=}\,\sup\{k\geq 0: p_k>0\}\leq+\infty$
. Recall that
![]() $\{p_k\}_{k\geq 0}$
is the offspring law, and X is the step size. In the remainder of this work we always need the following assumptions.
$\{p_k\}_{k\geq 0}$
is the offspring law, and X is the step size. In the remainder of this work we always need the following assumptions.
Assumption 1.
-
(i)
 $p_0=0$
,
$p_0=0$
,
 $p_1<1$
.
$p_1<1$
. -
(ii) X is symmetric and
 $\mathbb{E}\big[X^2\big]=1$
.
$\mathbb{E}\big[X^2\big]=1$
. -
(iii) A is a no-empty set in
 $\mathcal{A}$
.
$\mathcal{A}$
.
Remark 1. In Assumption 1(i),
![]() $p_0=0$
is made for convenience. If not, we can condition on non-extinction to obtain analogous results. Assumption 1(ii) is not essential either, but simplifies the proof. Assumption 1(iii) is crucial to our main results, and if
$p_0=0$
is made for convenience. If not, we can condition on non-extinction to obtain analogous results. Assumption 1(ii) is not essential either, but simplifies the proof. Assumption 1(iii) is crucial to our main results, and if
![]() $A\notin\mathcal{A}$
, then the situation would be very different (see [Reference Louidor and Perkins32, Proposition 1.3]).
$A\notin\mathcal{A}$
, then the situation would be very different (see [Reference Louidor and Perkins32, Proposition 1.3]).
Now we are ready to state our main results. The first theorem concerns the case that the offspring law has a Pareto tail. Let
![]() $\Lambda(a)\,{:\!=}\,\sup_{t\in\mathbb{R}}\{at-\log\mathbb{E}[\textrm{e}^{tX}]\}$
be the rate function in Cramér’s theorem; see [Reference Dembo and Zeitouni15, Section 2.2].
$\Lambda(a)\,{:\!=}\,\sup_{t\in\mathbb{R}}\{at-\log\mathbb{E}[\textrm{e}^{tX}]\}$
be the rate function in Cramér’s theorem; see [Reference Dembo and Zeitouni15, Section 2.2].
Theorem 1. Take
![]() $p\in(\nu(A),1)$
such that
$p\in(\nu(A),1)$
such that
![]() $I_A(\!\cdot\!)$
is continuous at p and
$I_A(\!\cdot\!)$
is continuous at p and
![]() $I_A(p)<\infty$
. Suppose
$I_A(p)<\infty$
. Suppose
![]() $\mathbb{P}(|Z_1|>x)=\Theta(1)x^{-\beta}$
as
$\mathbb{P}(|Z_1|>x)=\Theta(1)x^{-\beta}$
as
![]() $x\rightarrow+\infty$
for some constant
$x\rightarrow+\infty$
for some constant
![]() $\beta>1$
. Assume
$\beta>1$
. Assume
![]() $\mathbb{E}\left[\textrm{e}^{\theta X}\right]<\infty$
for some
$\mathbb{E}\left[\textrm{e}^{\theta X}\right]<\infty$
for some
![]() $\theta>0$
.
$\theta>0$
.
-
(i) If
 $0<\beta-1<-\frac{\log {p_1}}{\log m}$
, then where
$0<\beta-1<-\frac{\log {p_1}}{\log m}$
, then where \begin{align} -\inf_{h>0}\Phi_1(h) & \leq\liminf_{n\rightarrow\infty}\frac{1}{\sqrt{n}\,}\log\mathbb{P}\big(\bar{Z}_n(\sqrt nA)\geq p\big)\\[2pt] & \leq\limsup_{n\rightarrow\infty}\frac{1}{\sqrt{n}\,}\log\mathbb{P}\big(\bar{Z}_n(\sqrt nA)\geq p\big)\leq-\sup_{h>0}\Phi^{\prime}_1(h),\nonumber \end{align}
\begin{align} -\inf_{h>0}\Phi_1(h) & \leq\liminf_{n\rightarrow\infty}\frac{1}{\sqrt{n}\,}\log\mathbb{P}\big(\bar{Z}_n(\sqrt nA)\geq p\big)\\[2pt] & \leq\limsup_{n\rightarrow\infty}\frac{1}{\sqrt{n}\,}\log\mathbb{P}\big(\bar{Z}_n(\sqrt nA)\geq p\big)\leq-\sup_{h>0}\Phi^{\prime}_1(h),\nonumber \end{align}
 $\Phi_1(h)\,{:\!=}\,h(\beta-1)\log m+ \Lambda\big(\frac{I_A(p)}{h}\big)h$
,
$\Phi_1(h)\,{:\!=}\,h(\beta-1)\log m+ \Lambda\big(\frac{I_A(p)}{h}\big)h$
,
 $\Phi^{\prime}_1(h)\,{:\!=}\,(h(\beta-1)\log m)\wedge \big(\Lambda\big(\frac{I_A(p)}{h}\big)h\big)$
, and we make the convention that
$\Phi^{\prime}_1(h)\,{:\!=}\,(h(\beta-1)\log m)\wedge \big(\Lambda\big(\frac{I_A(p)}{h}\big)h\big)$
, and we make the convention that
 $-\log{p_1}=+\infty$
if
$-\log{p_1}=+\infty$
if
 $p_1=0$
.
$p_1=0$
.
-
(ii) If
 $\beta-1\geq -\frac{\log {p_1}}{\log m}$
, then where
$\beta-1\geq -\frac{\log {p_1}}{\log m}$
, then where \begin{align} -\inf_{h>0}\Phi_2(h) & \leq\liminf_{n\rightarrow\infty}\frac{1}{\sqrt{n}\,}\log\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)\\[2pt] & \leq\limsup_{n\rightarrow\infty}\frac{1}{\sqrt{n}\,}\log\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p) \leq-\sup_{h>0}\Phi^{\prime}_2(h),\nonumber \end{align}
\begin{align} -\inf_{h>0}\Phi_2(h) & \leq\liminf_{n\rightarrow\infty}\frac{1}{\sqrt{n}\,}\log\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)\\[2pt] & \leq\limsup_{n\rightarrow\infty}\frac{1}{\sqrt{n}\,}\log\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p) \leq-\sup_{h>0}\Phi^{\prime}_2(h),\nonumber \end{align}
 $\Phi_2(h)\,{:\!=}\,-h\log{p_1}+\Lambda\big(\frac{I_A(p)}{h}\big)h$
,
$\Phi_2(h)\,{:\!=}\,-h\log{p_1}+\Lambda\big(\frac{I_A(p)}{h}\big)h$
,
 $\Phi^{\prime}_2(h)\,{:\!=}\,(-h\log{p_1})\wedge\big(\Lambda\big(\frac{I_A(p)}{h}\big)h\big)$
.
$\Phi^{\prime}_2(h)\,{:\!=}\,(-h\log{p_1})\wedge\big(\Lambda\big(\frac{I_A(p)}{h}\big)h\big)$
.
Remark 2. If
![]() $p_1>0$
,
$p_1>0$
,
![]() $-\log{p_1}/\log m$
is the so-called Schröder constant, which determines the asymptotic behaviour of the harmonic moments of
$-\log{p_1}/\log m$
is the so-called Schröder constant, which determines the asymptotic behaviour of the harmonic moments of
![]() $|Z_n|$
(see Lemma 2). Furthermore, we will see that the asymptotic behaviour of
$|Z_n|$
(see Lemma 2). Furthermore, we will see that the asymptotic behaviour of
![]() $\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)$
mainly depends on the harmonic moments.
$\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)$
mainly depends on the harmonic moments.
Remark 3. If
![]() $\beta\in(0,1)$
, [Reference Athreya and Hong3] showed that
$\beta\in(0,1)$
, [Reference Athreya and Hong3] showed that
![]() $\bar{Z}_n(\sqrt n(-\infty,y])$
converges in distribution to a Bernoulli random variable.
$\bar{Z}_n(\sqrt n(-\infty,y])$
converges in distribution to a Bernoulli random variable.
The next theorem considers the case that the offspring law has a Weibull tail. As we can see in the following, the decay scales are the same as when that offspring law has an exponential moment. However, the Böttcher constant appears in the rate function.
Theorem 2. Take
![]() $p\in(\nu(A),1)$
such that
$p\in(\nu(A),1)$
such that
![]() $I_A(\!\cdot\!)$
is continuous at p and
$I_A(\!\cdot\!)$
is continuous at p and
![]() $I_A(p)<\infty$
. Suppose
$I_A(p)<\infty$
. Suppose
![]() $\mathbb{P}(|Z_1|>x)\sim l_1\textrm{e}^{-l x^{\beta}}$
as
$\mathbb{P}(|Z_1|>x)\sim l_1\textrm{e}^{-l x^{\beta}}$
as
![]() $x\rightarrow\infty$
for some constants
$x\rightarrow\infty$
for some constants
![]() $\beta\in(0,1)$
and
$\beta\in(0,1)$
and
![]() $l_1, l\in(0,+\infty)$
. Assume
$l_1, l\in(0,+\infty)$
. Assume
![]() $p_1=0$
.
$p_1=0$
.
-
(i) If
 $\textrm{ess} \, \sup X=L\in(0,+\infty)$
, then (1)where
$\textrm{ess} \, \sup X=L\in(0,+\infty)$
, then (1)where \begin{equation} \lim_{n\rightarrow\infty}\frac{1}{\sqrt{n}\,}\log\left[-\log \mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)\right]=\frac{I_A(p)}{L} \frac{\rho\beta}{\beta+\rho-\beta\rho}\log m, \end{equation}
\begin{equation} \lim_{n\rightarrow\infty}\frac{1}{\sqrt{n}\,}\log\left[-\log \mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)\right]=\frac{I_A(p)}{L} \frac{\rho\beta}{\beta+\rho-\beta\rho}\log m, \end{equation}
 $\rho$
is the so-called Böttcher constant such that
$\rho$
is the so-called Böttcher constant such that
 $b=m^{\rho}$
.
$b=m^{\rho}$
.
-
(ii) If
 $\mathbb{P}(X>x)=\Theta(1)\textrm{e}^{-\lambda x^{\alpha}}$
as
$\mathbb{P}(X>x)=\Theta(1)\textrm{e}^{-\lambda x^{\alpha}}$
as
 $x\rightarrow\infty$
for some constants
$x\rightarrow\infty$
for some constants
 $\alpha\in(0,\infty)$
and
$\alpha\in(0,\infty)$
and
 $\lambda>0$
, then (2)
$\lambda>0$
, then (2) \begin{equation} \lim\limits_{n\rightarrow\infty}\frac{(\log n)^{(\alpha-1)\vee 0}}{n^{\alpha/2}} \log\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)= -\lambda {I_A(p)}^{\alpha}\left(\frac{2\beta\rho\log m}{\alpha(\beta+\rho-\beta\rho)}\right)^{(\alpha-1)\vee 0}. \end{equation}
\begin{equation} \lim\limits_{n\rightarrow\infty}\frac{(\log n)^{(\alpha-1)\vee 0}}{n^{\alpha/2}} \log\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)= -\lambda {I_A(p)}^{\alpha}\left(\frac{2\beta\rho\log m}{\alpha(\beta+\rho-\beta\rho)}\right)^{(\alpha-1)\vee 0}. \end{equation}
Remark 4. For the Schröder case (i.e.
![]() $p_1>0$
), we can check that, combining the proof of [Reference Chen and He13, Theorem 1.1] and Lemma 5, we can generalize [Reference Chen and He13, Theorem 1.1] to the case that
$p_1>0$
), we can check that, combining the proof of [Reference Chen and He13, Theorem 1.1] and Lemma 5, we can generalize [Reference Chen and He13, Theorem 1.1] to the case that
![]() $|Z_1|$
has a Weibull tail.
$|Z_1|$
has a Weibull tail.
As we can see in the above, when the step size has an exponential moment, the decay rate is very sensitive to the tail of the offspring law. However, in the next theorem we will see that when the step size has a Pareto tail, the offspring law seems to have little effect on the decay rate.
Theorem 3. Take
![]() $p\in(\nu(A),1)$
such that
$p\in(\nu(A),1)$
such that
![]() $I_A(\!\cdot\!)$
is continuous at p and
$I_A(\!\cdot\!)$
is continuous at p and
![]() $I_A(p)<\infty$
. Suppose
$I_A(p)<\infty$
. Suppose
![]() $\mathbb{E}\big[|Z_1|^{\beta}\big]<\infty$
for some
$\mathbb{E}\big[|Z_1|^{\beta}\big]<\infty$
for some
![]() $\beta>1$
and
$\beta>1$
and
![]() $b<B$
. Assume
$b<B$
. Assume
![]() $\mathbb{P}(X>x)\sim \kappa x^{-\alpha}$
as
$\mathbb{P}(X>x)\sim \kappa x^{-\alpha}$
as
![]() $x\rightarrow\infty$
for some constants
$x\rightarrow\infty$
for some constants
![]() $\kappa>0$
and
$\kappa>0$
and
![]() $\alpha>2$
. Then
$\alpha>2$
. Then
Remark 5. If
![]() $b=B$
, the above result is still true provided A is unbounded and
$b=B$
, the above result is still true provided A is unbounded and
![]() $p\in\big(\nu(A),\nu(A)+b^{-1}(1-\nu(A))\big)$
.
$p\in\big(\nu(A),\nu(A)+b^{-1}(1-\nu(A))\big)$
.
The above theorems all assume that
![]() $I_A(p)<\infty$
, and we have seen that in this case the law of step size plays an important role in the decay rate. However, in the following we will see that if
$I_A(p)<\infty$
, and we have seen that in this case the law of step size plays an important role in the decay rate. However, in the following we will see that if
![]() $I_A(p)=\infty$
, the decay rate mainly depends on the offspring law.
$I_A(p)=\infty$
, the decay rate mainly depends on the offspring law.
Theorem 4. Suppose
![]() $I_A(p)=\infty$
and
$I_A(p)=\infty$
and
![]() $J_A(\!\cdot\!)$
is continuous at p for
$J_A(\!\cdot\!)$
is continuous at p for
![]() $p\in(\nu(A),1)$
.
$p\in(\nu(A),1)$
.
-
(i) If
 $\mathbb{P}(|Z_1|>x)=\Theta(1)x^{-\beta}$
as
$\mathbb{P}(|Z_1|>x)=\Theta(1)x^{-\beta}$
as
 $x\rightarrow+\infty$
for some constant
$x\rightarrow+\infty$
for some constant
 $\beta>1$
, then
$\beta>1$
, then  \begin{equation*} \lim\limits_{n\rightarrow\infty}\frac{1}{n}\log\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p) =\begin{cases} -J_A(p)(\beta-1)\log m, &0<\beta-1<-\frac{\log{p_1}}{\log m}; \\ \\[-7pt] J_A(p)\log{p_1}, &\beta-1\geq -\frac{\log{p_1}}{\log m}. \end{cases} \end{equation*}
\begin{equation*} \lim\limits_{n\rightarrow\infty}\frac{1}{n}\log\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p) =\begin{cases} -J_A(p)(\beta-1)\log m, &0<\beta-1<-\frac{\log{p_1}}{\log m}; \\ \\[-7pt] J_A(p)\log{p_1}, &\beta-1\geq -\frac{\log{p_1}}{\log m}. \end{cases} \end{equation*}
-
(ii) Assume
 $\mathbb{P}(|Z_1|>x)\sim l_1\textrm{e}^{-l x^{\beta}}$
as
$\mathbb{P}(|Z_1|>x)\sim l_1\textrm{e}^{-l x^{\beta}}$
as
 $x\rightarrow\infty$
for some constants
$x\rightarrow\infty$
for some constants
 $\beta\in(0,1)$
and
$\beta\in(0,1)$
and
 $l_1, l\in(0,+\infty)$
.
$l_1, l\in(0,+\infty)$
.-
(a) If
 $p_1>0$
, then
$p_1>0$
, then
 $\lim\limits_{n\rightarrow\infty}\frac{1}{n}\log\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)=J_A(p)\log{p_1}$
.
$\lim\limits_{n\rightarrow\infty}\frac{1}{n}\log\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)=J_A(p)\log{p_1}$
. -
(b) If
 $p_1=0$
, then
$p_1=0$
, then  \begin{equation*}\lim_{n\rightarrow\infty}\frac{1}{n}\log\left[-\log \mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)\right]=J_A(p) \frac{\rho\beta}{\beta+\rho-\beta\rho}\log m. \end{equation*}
\begin{equation*}\lim_{n\rightarrow\infty}\frac{1}{n}\log\left[-\log \mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)\right]=J_A(p) \frac{\rho\beta}{\beta+\rho-\beta\rho}\log m. \end{equation*}
-
Remark 6. In fact, Theorems 3 and 4 can also be generalized to the case that the step size X is in the domain of attraction of an
![]() $\alpha$
-stable law with
$\alpha$
-stable law with
![]() $\alpha\in(0,2]$
. The results and proofs are similar; the main changes are to replace
$\alpha\in(0,2]$
. The results and proofs are similar; the main changes are to replace
![]() $\nu$
with the
$\nu$
with the
![]() $\alpha$
-stable law and replace
$\alpha$
-stable law and replace
![]() $\sqrt n$
with
$\sqrt n$
with
![]() $\inf\{x\,{:}\,\mathbb{P}(|X|>x)<n^{-1}\}$
(which is a regular variation sequence with index
$\inf\{x\,{:}\,\mathbb{P}(|X|>x)<n^{-1}\}$
(which is a regular variation sequence with index
![]() $1/\alpha$
).
$1/\alpha$
).
Although, the proofs of the above four theorems differ from case to case, the basic strategy behind each of them is the same. If
![]() $I_A(p)<\infty$
, we let x be the number realizing the infimum in the definition of
$I_A(p)<\infty$
, we let x be the number realizing the infimum in the definition of
![]() $I_A(p)$
, otherwise we let x realize the supremum in the definition of
$I_A(p)$
, otherwise we let x realize the supremum in the definition of
![]() $J_A(p)$
. The lower bound aims at achieving the event
$J_A(p)$
. The lower bound aims at achieving the event
![]() $\{\bar{Z}_n(\sqrt nA)\geq p)\}$
in the most effortless way. For Theorems 1, 2, and 4, our strategy is to let one particle reach around
$\{\bar{Z}_n(\sqrt nA)\geq p)\}$
in the most effortless way. For Theorems 1, 2, and 4, our strategy is to let one particle reach around
![]() $x\sqrt n$
at some intermediate generation
$x\sqrt n$
at some intermediate generation
![]() $t_n$
, and then force its children to dominate the population size at time
$t_n$
, and then force its children to dominate the population size at time
![]() $t_n+1$
(since in these theorems the offspring law has a heavy tail, this can be done with relatively high probability). Finally, optimizing for
$t_n+1$
(since in these theorems the offspring law has a heavy tail, this can be done with relatively high probability). Finally, optimizing for
![]() $t_n$
yields the desired lower bound. For Theorem 3 the step size has a heavy tail, so particles can reach a high position in a short time. Therefore, in order to achieve
$t_n$
yields the desired lower bound. For Theorem 3 the step size has a heavy tail, so particles can reach a high position in a short time. Therefore, in order to achieve
![]() $\{\bar{Z}_n(\sqrt nA)\geq p)\}$
, we can let one particle reach around
$\{\bar{Z}_n(\sqrt nA)\geq p)\}$
, we can let one particle reach around
![]() $x\sqrt n$
in the first generation and other particles stay around the origin.
$x\sqrt n$
in the first generation and other particles stay around the origin.
For the upper bound all the theorems use a similar idea, which is borrowed from [Reference Louidor and Perkins32]. Our main tasks are to generalize their [Reference Louidor and Perkins32, Lemma 2.4] in the heavy-tail case and to study the asymptotic behaviours of the harmonic moments and stretched exponential moments of
![]() $|Z_n|$
.
$|Z_n|$
.
The rest of this paper is organised as follows. In Section 2 we present some preliminary results that are frequently used in our proofs. We consider the offspring law with a Pareto tail in Section 3, and a Weibull tail in Section 4. Section 5 is devoted to studying the case that the step size has a Pareto tail. The last section considers the case that
![]() $I_A(p)=+\infty$
. We always use C, C
$I_A(p)=+\infty$
. We always use C, C
![]() $^{\prime}$
,
$^{\prime}$
,
![]() $C_0$
,
$C_0$
,
![]() $C_1$
, … and
$C_1$
, … and
![]() $c_1$
,
$c_1$
,
![]() $c_2$
, … to denote positive constants. As usual, we denote by
$c_2$
, … to denote positive constants. As usual, we denote by
![]() $C(\epsilon,M)$
(or
$C(\epsilon,M)$
(or
![]() $C_{\epsilon,M}$
) a positive constant depending only on
$C_{\epsilon,M}$
) a positive constant depending only on
![]() $\epsilon$
and M. And, by convention,
$\epsilon$
and M. And, by convention,
![]() $f(x)=\Theta(1)g(x)$
as
$f(x)=\Theta(1)g(x)$
as
![]() $x\rightarrow+\infty$
means there exist constants
$x\rightarrow+\infty$
means there exist constants
![]() $C\geq C'>0$
such that
$C\geq C'>0$
such that
![]() $C'\leq|f(x)/g(x)|\leq C$
for all
$C'\leq|f(x)/g(x)|\leq C$
for all
![]() $x>1$
, and
$x>1$
, and
![]() $f(x)\sim g(x)$
means
$f(x)\sim g(x)$
means
![]() $\lim\limits_{x\rightarrow\infty} f(x)/g(x)=1$
.
$\lim\limits_{x\rightarrow\infty} f(x)/g(x)=1$
.
2. Preliminaries
In the following, we mainly concentrate on the offspring law
![]() $|Z_1|$
(or step size X) having one of the two typical heavy tails: Weibull or Pareto. For convenience, we write
$|Z_1|$
(or step size X) having one of the two typical heavy tails: Weibull or Pareto. For convenience, we write
![]() $|Z_1|\sim \textrm{Pareto}(\beta)$
if
$|Z_1|\sim \textrm{Pareto}(\beta)$
if
![]() $\mathbb{P}(|Z_1|>x)=\Theta(1)x^{-\beta}$
as
$\mathbb{P}(|Z_1|>x)=\Theta(1)x^{-\beta}$
as
![]() $x\rightarrow+\infty$
for some constant
$x\rightarrow+\infty$
for some constant
![]() $\beta>1$
, and
$\beta>1$
, and
![]() $|Z_1|\sim \textrm{Weibull}(\beta)$
if
$|Z_1|\sim \textrm{Weibull}(\beta)$
if
![]() $\mathbb{P}(|Z_1|>x)\sim l_1\textrm{e}^{-l x^{\beta}}$
as
$\mathbb{P}(|Z_1|>x)\sim l_1\textrm{e}^{-l x^{\beta}}$
as
![]() $x\rightarrow\infty$
for some constants
$x\rightarrow\infty$
for some constants
![]() $\beta\in(0,1)$
and
$\beta\in(0,1)$
and
![]() $l_1, l\in(0,+\infty)$
. We denote by
$l_1, l\in(0,+\infty)$
. We denote by
![]() $\nu_n$
the distribution of
$\nu_n$
the distribution of
![]() $S_n\,{:\!=}\,\sum^n_{i=1}X_i$
, where
$S_n\,{:\!=}\,\sum^n_{i=1}X_i$
, where
![]() $\{X_i\}_{i\geq 1}$
are independent and identically distributed (i.i.d.) copies of the step size X. We write
$\{X_i\}_{i\geq 1}$
are independent and identically distributed (i.i.d.) copies of the step size X. We write
![]() $W_n\,{:\!=}\,|Z_n|/m^n$
. From [Reference Denisov, Korshunov and Wachtel16, Theorems 1 and 3] and [Reference Liang and Liu29, Theorem 1], we have the following uniform bounds for
$W_n\,{:\!=}\,|Z_n|/m^n$
. From [Reference Denisov, Korshunov and Wachtel16, Theorems 1 and 3] and [Reference Liang and Liu29, Theorem 1], we have the following uniform bounds for
![]() $W_n$
.
$W_n$
.
Lemma 1.
-
(i) If
 $|Z_1|\sim \textrm{Pareto}(\beta)$
for some
$|Z_1|\sim \textrm{Pareto}(\beta)$
for some
 $\beta>1$
then there exist constants
$\beta>1$
then there exist constants
 $0<c_1<c_2<\infty$
such that
$0<c_1<c_2<\infty$
such that
 $c_1x^{-\beta}\leq\mathbb{P}(W_n>x)\leq c_2x^{-\beta}$
for all
$c_1x^{-\beta}\leq\mathbb{P}(W_n>x)\leq c_2x^{-\beta}$
for all
 $x>1$
and
$x>1$
and
 $n\geq 1$
. Hence, for
$n\geq 1$
. Hence, for
 $\alpha\in[1,\beta)$
,
$\alpha\in[1,\beta)$
,
 $\sup_{n\geq1}\mathbb{E}[W^{\alpha}_n]<\infty$
.
$\sup_{n\geq1}\mathbb{E}[W^{\alpha}_n]<\infty$
. -
(ii) If
 $|Z_1|\sim \textrm{Weibull}(\beta)$
for some
$|Z_1|\sim \textrm{Weibull}(\beta)$
for some
 $\beta\in(0,1)$
then, for every
$\beta\in(0,1)$
then, for every
 $\epsilon\in(0,1)$
, there exist constants
$\epsilon\in(0,1)$
, there exist constants
 $c_{\epsilon}>c^{\prime}_{\epsilon}>0$
depending only on
$c_{\epsilon}>c^{\prime}_{\epsilon}>0$
depending only on
 $\epsilon$
such that
$\epsilon$
such that
 $ c^{\prime}_{\epsilon}\textrm{e}^{-l((m+\epsilon)x)^\beta}\leq\mathbb{P}(W_n>x)\leq c_{\epsilon}\textrm{e}^{-l\left((m-\epsilon)x\right)^\beta}$
for all
$ c^{\prime}_{\epsilon}\textrm{e}^{-l((m+\epsilon)x)^\beta}\leq\mathbb{P}(W_n>x)\leq c_{\epsilon}\textrm{e}^{-l\left((m-\epsilon)x\right)^\beta}$
for all
 $x>0$
and
$x>0$
and
 $n\geq 1$
. Hence, for
$n\geq 1$
. Hence, for
 $\alpha\in(0,\beta)$
and
$\alpha\in(0,\beta)$
and
 $\theta>0$
,
$\theta>0$
,
 $\sup_{n\geq1}\mathbb{E}\left[\textrm{e}^{\theta W_n^{\alpha}}\right]<\infty$
.
$\sup_{n\geq1}\mathbb{E}\left[\textrm{e}^{\theta W_n^{\alpha}}\right]<\infty$
. -
(ii) If
 $\mathbb{E}[|Z_1|^{\beta}]<\infty$
for some
$\mathbb{E}[|Z_1|^{\beta}]<\infty$
for some
 $\beta>1$
then (3)
$\beta>1$
then (3) \begin{equation} \mathbb{E}\Big[\sup_{n\geq 1}W^{\beta}_n\Big]<\infty. \end{equation}
\begin{equation} \mathbb{E}\Big[\sup_{n\geq 1}W^{\beta}_n\Big]<\infty. \end{equation}
The following lemma gives the asymptotic behaviour of harmonic moments; see [Reference Ney and Vidyashankar35, Theorem 1].
Lemma 2. If
![]() $\mathbb{E}[|Z_1|]<\infty$
and
$\mathbb{E}[|Z_1|]<\infty$
and
![]() $r>0$
then
$r>0$
then
![]() $\lim_{n\rightarrow\infty}\mathbb{E}\left[{|Z_n|^{-r}}\right]{A_n(r)}=C_0$
, where
$\lim_{n\rightarrow\infty}\mathbb{E}\left[{|Z_n|^{-r}}\right]{A_n(r)}=C_0$
, where
![]() $C_0\in(0,+\infty)$
is a constant depending only on
$C_0\in(0,+\infty)$
is a constant depending only on
![]() $\{p_k\}_{k\geq0}$
and r, and
$\{p_k\}_{k\geq0}$
and r, and
 \begin{equation*} A_n(r)=\left\{ \begin{array}{lcl} p^{-n}_1,&& {r>-\dfrac{\log{p_1}}{\log m}};\\ \\[-7pt] np^{-n}_1,&& {r=-\dfrac{\log{p_1}}{\log m}};\\ \\[-7pt] m^{nr},&& {r<-\dfrac{\log{p_1}}{\log m}}. \end{array}\right. \end{equation*}
\begin{equation*} A_n(r)=\left\{ \begin{array}{lcl} p^{-n}_1,&& {r>-\dfrac{\log{p_1}}{\log m}};\\ \\[-7pt] np^{-n}_1,&& {r=-\dfrac{\log{p_1}}{\log m}};\\ \\[-7pt] m^{nr},&& {r<-\dfrac{\log{p_1}}{\log m}}. \end{array}\right. \end{equation*}
The next lemma considers the asymptotic behaviour of stretched exponential moments, and we will see that it is related to the LDP of
![]() $\bar{Z}_n(\sqrt nA)$
when
$\bar{Z}_n(\sqrt nA)$
when
![]() $|Z_1|$
has a Weibull tail. Recall that
$|Z_1|$
has a Weibull tail. Recall that
![]() $\rho$
is the Böttcher constant such that
$\rho$
is the Böttcher constant such that
![]() $b=m^{\rho}$
.
$b=m^{\rho}$
.
Lemma 3. Assume that
![]() $\mathbb{E}[|Z_1|\log |Z_1|]<\infty$
. For any
$\mathbb{E}[|Z_1|\log |Z_1|]<\infty$
. For any
![]() $\beta\in(0,1),\ l\in(0,\infty)$
,
$\beta\in(0,1),\ l\in(0,\infty)$
,
 \begin{alignat*}{2} \lim_{n\rightarrow\infty}\frac{1}{n}{\log \mathbb{E}\left[\textrm{e}^{-l|Z_n|^{\beta}}\right]} & = p_1 , & {if}\ p_1 & > 0; \\[3pt] \lim_{n\rightarrow\infty}\frac{1}{n}{\log\left[-\log \mathbb{E}\left[\textrm{e}^{-l|Z_n|^{\beta}}\right]\right]} & = \frac{\beta\rho}{\beta+\rho-\beta\rho}\log m , \quad & {if}\ p_1 & = 0. \end{alignat*}
\begin{alignat*}{2} \lim_{n\rightarrow\infty}\frac{1}{n}{\log \mathbb{E}\left[\textrm{e}^{-l|Z_n|^{\beta}}\right]} & = p_1 , & {if}\ p_1 & > 0; \\[3pt] \lim_{n\rightarrow\infty}\frac{1}{n}{\log\left[-\log \mathbb{E}\left[\textrm{e}^{-l|Z_n|^{\beta}}\right]\right]} & = \frac{\beta\rho}{\beta+\rho-\beta\rho}\log m , \quad & {if}\ p_1 & = 0. \end{alignat*}
Proof. We first consider the case
![]() $p_1=0$
. Let d be the greatest common divisor of
$p_1=0$
. Let d be the greatest common divisor of
![]() $\{j-k\,{:}\,j\neq k,\ p_j p_k>0\}$
. According the proof of [Reference Fleischmann and Wachtel20, Theorem 6], for any fixed
$\{j-k\,{:}\,j\neq k,\ p_j p_k>0\}$
. According the proof of [Reference Fleischmann and Wachtel20, Theorem 6], for any fixed
![]() $\varepsilon\in(0,1)$
there exist constants
$\varepsilon\in(0,1)$
there exist constants
![]() $c_3\geq c_4>0$
such that, for any
$c_3\geq c_4>0$
such that, for any
![]() $b^n\leq k\leq \lfloor m^{(1-\varepsilon)n}\rfloor$
,
$b^n\leq k\leq \lfloor m^{(1-\varepsilon)n}\rfloor$
,
![]() $k=b^n\ (\textrm{mod}\ d)$
, and
$k=b^n\ (\textrm{mod}\ d)$
, and
![]() $n\geq 1$
,
$n\geq 1$
,
 \begin{equation} \exp\left[ -c_3\left(\frac{k}{m^n}\right)^{-\frac{\rho}{1-\rho}}\right]\leq m^n\mathbb{P}(|Z_n|=k)\leq\exp\left[ -c_4 \left(\frac{k}{m^n}\right)^{-\frac{\rho}{1-\rho}}\right].\end{equation}
\begin{equation} \exp\left[ -c_3\left(\frac{k}{m^n}\right)^{-\frac{\rho}{1-\rho}}\right]\leq m^n\mathbb{P}(|Z_n|=k)\leq\exp\left[ -c_4 \left(\frac{k}{m^n}\right)^{-\frac{\rho}{1-\rho}}\right].\end{equation}
Hence, for the upper bound, we have
 \begin{align} \mathbb{E}\left[\textrm{e}^{-l|Z_n|^{\beta}}\right] & \leq \mathbb{E}\left[\textrm{e}^{-l|Z_n|^{\beta}}\textbf{1}_{\{|Z_n|\leq m^{(1-\varepsilon)n}\}}\right]+\textrm{e}^{-lm^{\beta(1-\varepsilon)n}}\nonumber\\ & \leq m^{-n} \!\!\!\!\! \sum_{\scriptsize\begin{array}{c}b^n\leq k\leq \lfloor m^{(1-\varepsilon)n}\rfloor \\ k=b^n(\textrm{mod}\ d)\end{array}} \!\!\!\!\! \exp(-lk^{\beta}) \exp\left[ -c_4 \left(\frac{k}{m^n}\right)^{-\frac{\rho}{1-\rho}}\right]+\textrm{e}^{-lm^{\beta(1-\varepsilon)n}}.\end{align}
\begin{align} \mathbb{E}\left[\textrm{e}^{-l|Z_n|^{\beta}}\right] & \leq \mathbb{E}\left[\textrm{e}^{-l|Z_n|^{\beta}}\textbf{1}_{\{|Z_n|\leq m^{(1-\varepsilon)n}\}}\right]+\textrm{e}^{-lm^{\beta(1-\varepsilon)n}}\nonumber\\ & \leq m^{-n} \!\!\!\!\! \sum_{\scriptsize\begin{array}{c}b^n\leq k\leq \lfloor m^{(1-\varepsilon)n}\rfloor \\ k=b^n(\textrm{mod}\ d)\end{array}} \!\!\!\!\! \exp(-lk^{\beta}) \exp\left[ -c_4 \left(\frac{k}{m^n}\right)^{-\frac{\rho}{1-\rho}}\right]+\textrm{e}^{-lm^{\beta(1-\varepsilon)n}}.\end{align}
Note that there exists a positive constant T depending only on l,
![]() $c_4$
,
$c_4$
,
![]() $\rho$
, and
$\rho$
, and
![]() $\beta$
such that, for n large enough,
$\beta$
such that, for n large enough,
As a consequence, if
![]() $1-\varepsilon>\frac{\rho }{\beta+\rho-\beta\rho}$
then
$1-\varepsilon>\frac{\rho }{\beta+\rho-\beta\rho}$
then
 \begin{align*} \mathbb{E}\left[\textrm{e}^{-l|Z_n|^{\beta}}\right]& \leq m^{\varepsilon n}\exp\left(-Tm^\frac{\beta\rho n}{\beta+\rho-\beta\rho}\right)+\textrm{e}^{-lm^{\beta(1-\varepsilon)n}}\\ &\leq2m^{\varepsilon n}\exp\left(-(T\wedge l)m^\frac{\beta\rho n}{\beta+\rho-\beta\rho}\right),\nonumber \end{align*}
\begin{align*} \mathbb{E}\left[\textrm{e}^{-l|Z_n|^{\beta}}\right]& \leq m^{\varepsilon n}\exp\left(-Tm^\frac{\beta\rho n}{\beta+\rho-\beta\rho}\right)+\textrm{e}^{-lm^{\beta(1-\varepsilon)n}}\\ &\leq2m^{\varepsilon n}\exp\left(-(T\wedge l)m^\frac{\beta\rho n}{\beta+\rho-\beta\rho}\right),\nonumber \end{align*}
which yields
For the lower bound, similarly, using the left-hand side of (4) we have, for n large enough,
 \begin{align*} \mathbb{E}\left[\textrm{e}^{-l|Z_n|^{\beta}}\right]&\geq m^{-n}\sum_{\scriptsize\begin{array}{c}b^n\leq k\leq \lfloor m^{(1-\varepsilon)n}\rfloor \\ k=b^n(\textrm{mod}\ d)\end{array}}\exp(-lk^{\beta}) \exp\left[ -c_3 \left(\frac{k}{m^n}\right)^{-\frac{\rho}{1-\rho}}\right]\\ &\geq m^{-n}\exp\left(-T'm^\frac{\beta\rho n}{\beta+\rho-\beta\rho}\right),\nonumber \end{align*}
\begin{align*} \mathbb{E}\left[\textrm{e}^{-l|Z_n|^{\beta}}\right]&\geq m^{-n}\sum_{\scriptsize\begin{array}{c}b^n\leq k\leq \lfloor m^{(1-\varepsilon)n}\rfloor \\ k=b^n(\textrm{mod}\ d)\end{array}}\exp(-lk^{\beta}) \exp\left[ -c_3 \left(\frac{k}{m^n}\right)^{-\frac{\rho}{1-\rho}}\right]\\ &\geq m^{-n}\exp\left(-T'm^\frac{\beta\rho n}{\beta+\rho-\beta\rho}\right),\nonumber \end{align*}
where
![]() $T'>0$
depends on l,
$T'>0$
depends on l,
![]() $c_3$
,
$c_3$
,
![]() $\rho$
,
$\rho$
,
![]() $\beta$
, and d. Taking limits yields
$\beta$
, and d. Taking limits yields
For
![]() $p_1>0$
, by [Reference Fleischmann and Wachtel21, Lemma 13] there exists a universal constant
$p_1>0$
, by [Reference Fleischmann and Wachtel21, Lemma 13] there exists a universal constant
![]() $c>0$
such that, for any
$c>0$
such that, for any
![]() $k,n\geq1$
,
$k,n\geq1$
,
![]() $\mathbb{P}(|Z_n|=k)\leq cp^n_1k^{-(\log p_1/\log m)-1}$
. Thus,
$\mathbb{P}(|Z_n|=k)\leq cp^n_1k^{-(\log p_1/\log m)-1}$
. Thus,
![]() $p^n_1e^{-l}\leq\mathbb{E}\big[\textrm{e}^{-l|Z_n|^{\beta}}\big]\leq cp^n_1\sum_{k\geq1} k^{-(\log p_1/\log m)-1}\textrm{e}^{-lk^{\beta}}$
, which implies the desired result.
$p^n_1e^{-l}\leq\mathbb{E}\big[\textrm{e}^{-l|Z_n|^{\beta}}\big]\leq cp^n_1\sum_{k\geq1} k^{-(\log p_1/\log m)-1}\textrm{e}^{-lk^{\beta}}$
, which implies the desired result.
The following two lemmas are analogous results to [Reference Louidor and Perkins32, Lemma 2.4]. In the following, we denote by
![]() $\mathcal{M}$
the collection of all local finite point measures on
$\mathcal{M}$
the collection of all local finite point measures on
![]() $\mathbb{R}$
. Recall that for
$\mathbb{R}$
. Recall that for
![]() $\xi\in\mathcal{M}$
,
$\xi\in\mathcal{M}$
,
![]() $x\in\xi$
means x is an atom of
$x\in\xi$
means x is an atom of
![]() $\xi$
, and
$\xi$
, and
![]() $S_x$
is the position of x (i.e.
$S_x$
is the position of x (i.e.
![]() $\xi=\sum_{x\in\xi}\delta_{S_x}$
).
$\xi=\sum_{x\in\xi}\delta_{S_x}$
).
![]() $|\xi|$
represents the total number of its atoms. Let
$|\xi|$
represents the total number of its atoms. Let
![]() $Z^{\xi}_n$
be the branching random walk started from
$Z^{\xi}_n$
be the branching random walk started from
![]() $Z^{\xi}_0=\xi$
; for simplicity, we write
$Z^{\xi}_0=\xi$
; for simplicity, we write
![]() $Z^{x}_n\,{:\!=}\,Z^{\delta_{S_x}}_n$
. Denote by
$Z^{x}_n\,{:\!=}\,Z^{\delta_{S_x}}_n$
. Denote by
![]() $\bar{Z}^{\xi}_n(\!\cdot\!)$
the corresponding empirical distribution of
$\bar{Z}^{\xi}_n(\!\cdot\!)$
the corresponding empirical distribution of
![]() $Z^{\xi}_n$
. Let
$Z^{\xi}_n$
. Let
![]() $W^x_n\,{:\!=}\,|Z^{x}_n|/m^n$
.
$W^x_n\,{:\!=}\,|Z^{x}_n|/m^n$
.
Lemma 4. Assume
![]() $\mathbb{E}[|Z_1|^{\beta}]<\infty$
or
$\mathbb{E}[|Z_1|^{\beta}]<\infty$
or
![]() $|Z_1|\sim \textrm{Pareto}(\beta)$
for some
$|Z_1|\sim \textrm{Pareto}(\beta)$
for some
![]() $\beta>1$
. Then, for every
$\beta>1$
. Then, for every
![]() $\epsilon\in\big(0,\frac{1}{3}\big)$
, there exists a constant
$\epsilon\in\big(0,\frac{1}{3}\big)$
, there exists a constant
![]() $C_{1}>0$
depending on
$C_{1}>0$
depending on
![]() $\epsilon$
and
$\epsilon$
and
![]() $\beta$
such that, for any
$\beta$
such that, for any
![]() $\xi\in\mathcal{M}$
,
$\xi\in\mathcal{M}$
,
![]() $n\geq 1$
, and
$n\geq 1$
, and
![]() $A\subset\mathbb{R}$
,
$A\subset\mathbb{R}$
,
 \begin{equation} \mathbb{P}\Bigg(\bar{Z}^{\xi}_n(A)\geq \frac{1}{|\xi|}\sum_{x\in\xi}\nu_n\left(A-S_x\right)+\epsilon\Bigg)\leq C_{1}|\xi|^{1-\beta}.\end{equation}
\begin{equation} \mathbb{P}\Bigg(\bar{Z}^{\xi}_n(A)\geq \frac{1}{|\xi|}\sum_{x\in\xi}\nu_n\left(A-S_x\right)+\epsilon\Bigg)\leq C_{1}|\xi|^{1-\beta}.\end{equation}
The same holds if
![]() $>$
and
$>$
and
![]() $+\epsilon$
are replaced by
$+\epsilon$
are replaced by
![]() $<$
,
$<$
,
![]() $-\epsilon$
.
$-\epsilon$
.
Proof. We first consider the case
![]() $\mathbb{E}\big[|Z_1|^{\beta}\big]<\infty$
for some
$\mathbb{E}\big[|Z_1|^{\beta}\big]<\infty$
for some
![]() $\beta>1$
. By the branching property, for any
$\beta>1$
. By the branching property, for any
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $\epsilon\in(0,\frac{1}{3})$
, we have
$\epsilon\in(0,\frac{1}{3})$
, we have
 \begin{align} \mathbb{P}\Bigg(\bar{Z}^{\xi}_n(A) & \geq \frac{1}{|\xi|}\sum_{x\in\xi}\nu_n\left(A-S_x\right)+\epsilon\Bigg)\nonumber\\ & = \mathbb{P}\Bigg(\frac{\frac{1}{|\xi|}\sum_{x\in\xi}{Z}^{x}_n(A)/m^n}{\frac{1}{|\xi|}\sum_{x\in\xi}{Z}^{x}_n/m^n}\geq\frac{1}{|\xi|}\sum_{x\in\xi}\nu_n(A-S_x)+\epsilon\Bigg)\nonumber\\ & \leq \mathbb{P}\Bigg(\sum_{x\in\xi}{W}^{x}_n<|\xi|(1-\epsilon/2)\Bigg)+\mathbb{P}\Bigg(\sum_{x\in\xi}\left({W}^{x}_n(A)-\nu_n\left(A-S_x\right)\right)>|\xi|\epsilon/3\Bigg)\nonumber\\ & \leq \mathbb{P}\Bigg(\sum_{x\in\xi}(1-W^x_n)>\frac{\epsilon}{3}{|\xi|}\Bigg)+\mathbb{P}\Bigg(\sum_{x\in\xi}\left({W}^{x}_n(A)-\nu_n\left(A-S_x\right)\right)>|\xi|\epsilon/3\Bigg)\nonumber\\ &\,{=\!:}\,I_1+I_2,\end{align}
\begin{align} \mathbb{P}\Bigg(\bar{Z}^{\xi}_n(A) & \geq \frac{1}{|\xi|}\sum_{x\in\xi}\nu_n\left(A-S_x\right)+\epsilon\Bigg)\nonumber\\ & = \mathbb{P}\Bigg(\frac{\frac{1}{|\xi|}\sum_{x\in\xi}{Z}^{x}_n(A)/m^n}{\frac{1}{|\xi|}\sum_{x\in\xi}{Z}^{x}_n/m^n}\geq\frac{1}{|\xi|}\sum_{x\in\xi}\nu_n(A-S_x)+\epsilon\Bigg)\nonumber\\ & \leq \mathbb{P}\Bigg(\sum_{x\in\xi}{W}^{x}_n<|\xi|(1-\epsilon/2)\Bigg)+\mathbb{P}\Bigg(\sum_{x\in\xi}\left({W}^{x}_n(A)-\nu_n\left(A-S_x\right)\right)>|\xi|\epsilon/3\Bigg)\nonumber\\ & \leq \mathbb{P}\Bigg(\sum_{x\in\xi}(1-W^x_n)>\frac{\epsilon}{3}{|\xi|}\Bigg)+\mathbb{P}\Bigg(\sum_{x\in\xi}\left({W}^{x}_n(A)-\nu_n\left(A-S_x\right)\right)>|\xi|\epsilon/3\Bigg)\nonumber\\ &\,{=\!:}\,I_1+I_2,\end{align}
where
![]() $\epsilon\in\big(0,\frac{1}{3}\big)$
is used in the first inequality.
$\epsilon\in\big(0,\frac{1}{3}\big)$
is used in the first inequality.
We first consider
![]() $I_2$
. By [Reference Nagaev34, Corollary 1.6], we know that if
$I_2$
. By [Reference Nagaev34, Corollary 1.6], we know that if
![]() $Y_x$
,
$Y_x$
,
![]() $x\in\xi$
, are independent random variables with zero mean, and
$x\in\xi$
, are independent random variables with zero mean, and
![]() $A^+_t=\sum_{x\in\xi}\mathbb{E}\big[Y^t_x \textbf{1}_{\{Y_x\geq 0\}}\big]<\infty$
for some
$A^+_t=\sum_{x\in\xi}\mathbb{E}\big[Y^t_x \textbf{1}_{\{Y_x\geq 0\}}\big]<\infty$
for some
![]() $1\leq t\leq 2$
, then, for
$1\leq t\leq 2$
, then, for
![]() $y^t\geq 4A^+_t$
and
$y^t\geq 4A^+_t$
and
![]() $z>y$
,
$z>y$
,
 \begin{equation} \mathbb{P}\Bigg(\sum\limits_{x\in\xi} Y_x\geq z\Bigg)\leq\sum\limits_{x\in\xi}\mathbb{P}(Y_x>y)+\left(\textrm{e}^2A^+_t/zy^{t-1}\right)^{z/2y}.\end{equation}
\begin{equation} \mathbb{P}\Bigg(\sum\limits_{x\in\xi} Y_x\geq z\Bigg)\leq\sum\limits_{x\in\xi}\mathbb{P}(Y_x>y)+\left(\textrm{e}^2A^+_t/zy^{t-1}\right)^{z/2y}.\end{equation}
So, if we choose
![]() $t=1+\frac{\beta-1}{2\beta}$
,
$t=1+\frac{\beta-1}{2\beta}$
,
![]() $y=\frac{1}{4\beta}z$
, and
$y=\frac{1}{4\beta}z$
, and
![]() $z=|\xi|\epsilon/3$
, then
$z=|\xi|\epsilon/3$
, then
![]() $t\in(1,2\wedge\beta]$
. Let
$t\in(1,2\wedge\beta]$
. Let
![]() $Y_x={W}^{x}_n(A)-\nu_n(A-S_x)$
. Note that by (3), there exists a constant
$Y_x={W}^{x}_n(A)-\nu_n(A-S_x)$
. Note that by (3), there exists a constant
![]() $C_{\beta}>0$
such that
$C_{\beta}>0$
such that
Therefore,
![]() $A^+_t<\infty$
. Furthermore, by (9), there exists a constant
$A^+_t<\infty$
. Furthermore, by (9), there exists a constant
![]() $C_{\epsilon,\beta}>0$
such that, for all
$C_{\epsilon,\beta}>0$
such that, for all
![]() $|\xi|>C_{\epsilon,\beta}$
and
$|\xi|>C_{\epsilon,\beta}$
and
![]() $n\geq1$
,
$n\geq1$
,
 \begin{equation*}y^t=\left(\frac{\epsilon|\xi|}{12\beta}\right)^t\geq 4|\xi|C_{\beta}\geq 4|\xi|\mathbb{E}[W^t_n]\geq 4\sum\limits_{x\in\xi}\mathbb{E}[Y^t_x \textbf{1}_{\{Y_x\geq 0\}}].\end{equation*}
\begin{equation*}y^t=\left(\frac{\epsilon|\xi|}{12\beta}\right)^t\geq 4|\xi|C_{\beta}\geq 4|\xi|\mathbb{E}[W^t_n]\geq 4\sum\limits_{x\in\xi}\mathbb{E}[Y^t_x \textbf{1}_{\{Y_x\geq 0\}}].\end{equation*}
So, by (8), it follows that, for all
![]() $|\xi|>C_{\epsilon,\beta}$
,
$|\xi|>C_{\epsilon,\beta}$
,
![]() $n\geq 1$
, and
$n\geq 1$
, and
![]() $A\subset\mathbb{R}$
,
$A\subset\mathbb{R}$
,
 \begin{align}I_2&\leq|\xi|\mathbb{P}\bigg({W}^{x}_n(A)-\nu_n(A-S_x)>\frac{\epsilon|\xi|}{12\beta}\bigg)+\bigg(\frac{\textrm{e}^2C_{\beta}3^{t}}{(4\beta)^{1-t}\epsilon^t}\bigg)^{2\beta}|\xi|^{(1-t)2\beta}\nonumber\\ &\leq|\xi|\mathbb{P}\bigg({W}_n>\frac{\epsilon|\xi|}{12\beta}\bigg)+\bigg(\frac{\textrm{e}^2C_{\beta}3^{t}}{(4\beta)^{1-t}\epsilon^t}\bigg)^{2\beta}|\xi|^{1-\beta}.\end{align}
\begin{align}I_2&\leq|\xi|\mathbb{P}\bigg({W}^{x}_n(A)-\nu_n(A-S_x)>\frac{\epsilon|\xi|}{12\beta}\bigg)+\bigg(\frac{\textrm{e}^2C_{\beta}3^{t}}{(4\beta)^{1-t}\epsilon^t}\bigg)^{2\beta}|\xi|^{(1-t)2\beta}\nonumber\\ &\leq|\xi|\mathbb{P}\bigg({W}_n>\frac{\epsilon|\xi|}{12\beta}\bigg)+\bigg(\frac{\textrm{e}^2C_{\beta}3^{t}}{(4\beta)^{1-t}\epsilon^t}\bigg)^{2\beta}|\xi|^{1-\beta}.\end{align}
By (3) and the Markov inequality, there exists a constant
![]() $C^{\prime}_{\epsilon,\beta}>0$
such that, for all
$C^{\prime}_{\epsilon,\beta}>0$
such that, for all
![]() $n\geq1$
,
$n\geq1$
,
Plugging (11) into (10) yields, for all
![]() $|\xi|>C_{\epsilon,\beta}$
,
$|\xi|>C_{\epsilon,\beta}$
,
![]() $n\geq 1$
, and
$n\geq 1$
, and
![]() $A\subset\mathbb{R}$
,
$A\subset\mathbb{R}$
,
For
![]() $I_1$
, using (8) again and letting
$I_1$
, using (8) again and letting
![]() $Y_x=1-W^x_n$
, we have, for all
$Y_x=1-W^x_n$
, we have, for all
![]() $|\xi|>\frac{12\beta}{\epsilon}$
and
$|\xi|>\frac{12\beta}{\epsilon}$
and
![]() $n\geq1$
,
$n\geq1$
,
Plugging the above two inequalities into (7) means that there exists a constant
![]() $T(\epsilon,\beta)>0$
such that, for
$T(\epsilon,\beta)>0$
such that, for
![]() $|\xi|>C_{\epsilon,\beta}\vee\frac{12\beta}{\epsilon}$
,
$|\xi|>C_{\epsilon,\beta}\vee\frac{12\beta}{\epsilon}$
,
 \begin{equation*}\mathbb{P}\Bigg(\bar{Z}^{\xi}_n(A)\geq \frac{1}{|\xi|}\sum_{x\in\xi}\nu_n\left(A-S_x\right)+\epsilon\Bigg)\leq T(\epsilon,\beta)|\xi|^{1-\beta}.\end{equation*}
\begin{equation*}\mathbb{P}\Bigg(\bar{Z}^{\xi}_n(A)\geq \frac{1}{|\xi|}\sum_{x\in\xi}\nu_n\left(A-S_x\right)+\epsilon\Bigg)\leq T(\epsilon,\beta)|\xi|^{1-\beta}.\end{equation*}
Hence, to obtain (6), we can take
![]() $C_1\,{:\!=}\,\big(C_{\epsilon,\beta}\vee\frac{12\beta}{\epsilon}\big)^{\beta-1}\vee T(\epsilon,\beta)$
. For the case
$C_1\,{:\!=}\,\big(C_{\epsilon,\beta}\vee\frac{12\beta}{\epsilon}\big)^{\beta-1}\vee T(\epsilon,\beta)$
. For the case
![]() $\mathbb{P}(|Z_1|>x)\sim \Theta(1)x^{-\beta}$
, as a consequence of Lemma 1 we only need to replace (11) by
$\mathbb{P}(|Z_1|>x)\sim \Theta(1)x^{-\beta}$
, as a consequence of Lemma 1 we only need to replace (11) by
Replacing A with
![]() $A^\textrm{c}$
, we obtain (6) with
$A^\textrm{c}$
, we obtain (6) with
![]() $>$
and
$>$
and
![]() $+\epsilon$
replaced by
$+\epsilon$
replaced by
![]() $<$
,
$<$
,
![]() $-\epsilon$
.
$-\epsilon$
.
Remark 7. We can check that if
![]() $\xi$
is a point process with a fixed number of atoms the result is similar, with
$\xi$
is a point process with a fixed number of atoms the result is similar, with
![]() $\mathbb{E}[\nu_n(A-S_x)]$
replacing
$\mathbb{E}[\nu_n(A-S_x)]$
replacing
![]() $\nu_n(A-S_x)$
.
$\nu_n(A-S_x)$
.
Lemma 5. If
![]() $|Z_1|\sim \textrm{Weibull}(\beta)$
for some
$|Z_1|\sim \textrm{Weibull}(\beta)$
for some
![]() $\beta\in(0,1)$
then, for every
$\beta\in(0,1)$
then, for every
![]() $\epsilon>0$
small enough, there exist positive constants
$\epsilon>0$
small enough, there exist positive constants
![]() $C_2$
and
$C_2$
and
![]() $C_3$
depending on
$C_3$
depending on
![]() $\epsilon$
and
$\epsilon$
and
![]() $\beta$
such that, for any
$\beta$
such that, for any
![]() $\xi\in\mathcal{M}$
,
$\xi\in\mathcal{M}$
,
![]() $n\geq 1$
, and any
$n\geq 1$
, and any
![]() $A\subset\mathbb{R}$
,
$A\subset\mathbb{R}$
,
 \begin{equation} \mathbb{P}\Bigg(\bar{Z}^{\xi}_n(A)\geq \frac{1}{|\xi|}\sum_{x\in\xi}\nu_n(A-S_x)+\epsilon\Bigg)\leq C_2\textrm{e}^{-C_3|\xi|^{\beta}}. \end{equation}
\begin{equation} \mathbb{P}\Bigg(\bar{Z}^{\xi}_n(A)\geq \frac{1}{|\xi|}\sum_{x\in\xi}\nu_n(A-S_x)+\epsilon\Bigg)\leq C_2\textrm{e}^{-C_3|\xi|^{\beta}}. \end{equation}
The same holds if
![]() $>$
and
$>$
and
![]() $+\epsilon$
are replaced by
$+\epsilon$
are replaced by
![]() $<$
,
$<$
,
![]() $-\epsilon$
.
$-\epsilon$
.
Proof. From (7), for every
![]() $\epsilon\in\left(0,\frac{1}{3}\right)$
we have
$\epsilon\in\left(0,\frac{1}{3}\right)$
we have
 \begin{align} \mathbb{P}\Bigg(\bar{Z}^{\xi}_n(A) & \geq \frac{1}{|\xi|}\sum_{x\in\xi}\nu_n(A-S_x)+\epsilon\Bigg)\nonumber\\ & \leq \mathbb{P}\Bigg(\sum_{x\in\xi}(1-W^x_n)>\frac{\epsilon}{3}{|\xi|}\Bigg) + \mathbb{P}\Bigg(\sum_{x\in\xi}{W}^{x}_n(A)>\sum_{x\in\xi}\nu_n(A-S_x)+|\xi|\epsilon/3\Bigg)\nonumber\\ & \,{=\!:}\, I_1 + I_2. \end{align}
\begin{align} \mathbb{P}\Bigg(\bar{Z}^{\xi}_n(A) & \geq \frac{1}{|\xi|}\sum_{x\in\xi}\nu_n(A-S_x)+\epsilon\Bigg)\nonumber\\ & \leq \mathbb{P}\Bigg(\sum_{x\in\xi}(1-W^x_n)>\frac{\epsilon}{3}{|\xi|}\Bigg) + \mathbb{P}\Bigg(\sum_{x\in\xi}{W}^{x}_n(A)>\sum_{x\in\xi}\nu_n(A-S_x)+|\xi|\epsilon/3\Bigg)\nonumber\\ & \,{=\!:}\, I_1 + I_2. \end{align}
For
![]() $I_1$
, note that
$I_1$
, note that
![]() $\sup\limits_{x,n}\mathbb{E}\left[\textrm{e}^{1-W^x_n}\right]<\infty$
. Furthermore, by Lemma 1,
$\sup\limits_{x,n}\mathbb{E}\left[\textrm{e}^{1-W^x_n}\right]<\infty$
. Furthermore, by Lemma 1,
![]() $\mathbb{E}\left[((1-W^x_n)^-)^2\right]\leq 3+\sup_n\mathbb{E}\left[W^2_n\right]<\infty$
. Hence, by [Reference Louidor and Perkins32, Lemma 2.3], there exists a constant
$\mathbb{E}\left[((1-W^x_n)^-)^2\right]\leq 3+\sup_n\mathbb{E}\left[W^2_n\right]<\infty$
. Hence, by [Reference Louidor and Perkins32, Lemma 2.3], there exists a constant
![]() $c_5>0$
such that, for all n,
$c_5>0$
such that, for all n,
![]() $\xi$
, and
$\xi$
, and
![]() $\epsilon$
small enough,
$\epsilon$
small enough,
 \begin{equation} I_1=\mathbb{P}\Bigg(\sum_{x\in\xi}(1-W^x_n)>\frac{\epsilon}{3}{|\xi|}\Bigg) \leq \textrm{e}^{-c_5\epsilon^2|\xi|}. \end{equation}
\begin{equation} I_1=\mathbb{P}\Bigg(\sum_{x\in\xi}(1-W^x_n)>\frac{\epsilon}{3}{|\xi|}\Bigg) \leq \textrm{e}^{-c_5\epsilon^2|\xi|}. \end{equation}
For
![]() $I_2$
, by Lemma 1 there exists a constant
$I_2$
, by Lemma 1 there exists a constant
![]() $c_6>0$
such that, for all
$c_6>0$
such that, for all
![]() $y>0$
and
$y>0$
and
![]() $n\geq1$
,
$n\geq1$
,
![]() $\mathbb{P}({W}^{x}_n(A)>y)\leq\mathbb{P}(W_n>y)\leq c_6\exp[-l(m-1)^{\beta}y^\beta]$
. Let
$\mathbb{P}({W}^{x}_n(A)>y)\leq\mathbb{P}(W_n>y)\leq c_6\exp[-l(m-1)^{\beta}y^\beta]$
. Let
![]() $X_i$
,
$X_i$
,
![]() $i\geq 1$
, be i.i.d. copies of
$i\geq 1$
, be i.i.d. copies of
![]() ${W}^{x}_n(A)$
, and
${W}^{x}_n(A)$
, and
 \begin{equation*} a_i(|\xi|)= \begin{cases} \Big(|\xi|\epsilon/3+\sum_{x\in\xi}\nu_n(A-S_x)\Big)^{-1}, & 1\leq i\leq |\xi|; \\ \\[-7pt] 0 , & i > |\xi|. \end{cases} \end{equation*}
\begin{equation*} a_i(|\xi|)= \begin{cases} \Big(|\xi|\epsilon/3+\sum_{x\in\xi}\nu_n(A-S_x)\Big)^{-1}, & 1\leq i\leq |\xi|; \\ \\[-7pt] 0 , & i > |\xi|. \end{cases} \end{equation*}
Then, by slight modifications of the proof of the upper bound [Reference Aurzada5, Theorem 2.1], there exist positive constants T, T
![]() $^{\prime}$
depending on
$^{\prime}$
depending on
![]() $\epsilon$
and
$\epsilon$
and
![]() $\beta$
such that, for any
$\beta$
such that, for any
![]() $|\xi|>T$
,
$|\xi|>T$
,
![]() $n\geq 1$
, and any
$n\geq 1$
, and any
![]() $A\subset\mathbb{R}$
,
$A\subset\mathbb{R}$
,
 \begin{equation} I_2=\mathbb{P}\Bigg(\sum_{x\in\xi}{W}^{x}_n(A)>\sum_{x\in\xi}\nu_n(A-S_x)+|\xi|\epsilon/3\Bigg)\leq \textrm{e}^{-T'|\xi|^{\beta}}. \end{equation}
\begin{equation} I_2=\mathbb{P}\Bigg(\sum_{x\in\xi}{W}^{x}_n(A)>\sum_{x\in\xi}\nu_n(A-S_x)+|\xi|\epsilon/3\Bigg)\leq \textrm{e}^{-T'|\xi|^{\beta}}. \end{equation}
Plugging (14) and (15) into (13) concludes the proof of this lemma with
![]() $C_2\,{:\!=}\,\textrm{e}^{T'T^{\beta}}$
and
$C_2\,{:\!=}\,\textrm{e}^{T'T^{\beta}}$
and
![]() $C_3\,{:\!=}\,T'\wedge(c_5\epsilon^2)$
.
$C_3\,{:\!=}\,T'\wedge(c_5\epsilon^2)$
.
The following lemma concerns LDP of sums of i.i.d. Weibull-tail random variables.
Lemma 6. Suppose
![]() $\{X_i\}_{i\geq 1}$
is a sequence of i.i.d. random variables having the same distribution as X. Assume that
$\{X_i\}_{i\geq 1}$
is a sequence of i.i.d. random variables having the same distribution as X. Assume that
![]() $\mathbb{P}(X>x)=\Theta(1)\textrm{e}^{-\lambda x^{\alpha}}$
as
$\mathbb{P}(X>x)=\Theta(1)\textrm{e}^{-\lambda x^{\alpha}}$
as
![]() $x\rightarrow\infty$
with some
$x\rightarrow\infty$
with some
![]() $\alpha\in(1,\infty)$
and
$\alpha\in(1,\infty)$
and
![]() $\lambda>0$
,
$\lambda>0$
,
![]() $t_n=o(n^{1/3}),$
and
$t_n=o(n^{1/3}),$
and
![]() $t_n\rightarrow\infty$
. For any
$t_n\rightarrow\infty$
. For any
![]() $0<a<b\leq+\infty$
, we have
$0<a<b\leq+\infty$
, we have
 \begin{equation*}\lim\limits_{n\rightarrow\infty}\frac{{t_n}^{\alpha-1}}{n^{\alpha/2}}\log\mathbb{P}\left(\sum^{t_n}_{i=1}X_i\in(a\sqrt n,b\sqrt n)\right)= -\lambda a^{\alpha}.\end{equation*}
\begin{equation*}\lim\limits_{n\rightarrow\infty}\frac{{t_n}^{\alpha-1}}{n^{\alpha/2}}\log\mathbb{P}\left(\sum^{t_n}_{i=1}X_i\in(a\sqrt n,b\sqrt n)\right)= -\lambda a^{\alpha}.\end{equation*}
Proof. The upper bound can be found in [Reference Chen and He13, Lemma B.1]. For the lower bound, since
![]() $C\textrm{e}^{-\lambda x^{\alpha}}\leq\mathbb{P}(X>x)\leq C'\textrm{e}^{-\lambda x^{\alpha}}$
for some constants
$C\textrm{e}^{-\lambda x^{\alpha}}\leq\mathbb{P}(X>x)\leq C'\textrm{e}^{-\lambda x^{\alpha}}$
for some constants
![]() $C'>C>0$
, we have, for n large enough,
$C'>C>0$
, we have, for n large enough,
 \begin{align*} \mathbb{P}\left(\sum^{t_n}_{i=1}X_i\in(a\sqrt n,b\sqrt n)\right) & \geq \mathbb{P}\left(X_i\in\left(\frac{a\sqrt n}{t_n},\frac{b\sqrt n}{t_n} \right), \textrm{ for all } 1\leq i\leq t_n\right) \\[4pt] & \geq \left(C\exp\left[-\lambda\left(\frac{a\sqrt n}{t_n}\right)^{\alpha}\right]-C'\exp\left[-\lambda\left(\frac{b\sqrt n}{t_n}\right)^{\alpha}\right]\right)^{t_n} \\[4pt] & \geq C^{t_n}\exp\left[-\lambda a^{\alpha}\frac{n^{\alpha/2}}{t^{\alpha-1}_n}\right]. \end{align*}
\begin{align*} \mathbb{P}\left(\sum^{t_n}_{i=1}X_i\in(a\sqrt n,b\sqrt n)\right) & \geq \mathbb{P}\left(X_i\in\left(\frac{a\sqrt n}{t_n},\frac{b\sqrt n}{t_n} \right), \textrm{ for all } 1\leq i\leq t_n\right) \\[4pt] & \geq \left(C\exp\left[-\lambda\left(\frac{a\sqrt n}{t_n}\right)^{\alpha}\right]-C'\exp\left[-\lambda\left(\frac{b\sqrt n}{t_n}\right)^{\alpha}\right]\right)^{t_n} \\[4pt] & \geq C^{t_n}\exp\left[-\lambda a^{\alpha}\frac{n^{\alpha/2}}{t^{\alpha-1}_n}\right]. \end{align*}
Then, the desired lower bound follows, provided
![]() $t_n=o(\sqrt n)$
.
$t_n=o(\sqrt n)$
.
3. Proof of Theorem 1
In this section we assume that
![]() $|Z_1|\sim \textrm{Pareto}(\beta)$
for some
$|Z_1|\sim \textrm{Pareto}(\beta)$
for some
![]() $\beta\in(1,+\infty)$
, and
$\beta\in(1,+\infty)$
, and
![]() $\mathbb{E}[\textrm{e}^{\theta X}]<\infty$
for some
$\mathbb{E}[\textrm{e}^{\theta X}]<\infty$
for some
![]() $\theta>0$
. We also assume that
$\theta>0$
. We also assume that
![]() $I_A(p)<\infty$
and
$I_A(p)<\infty$
and
![]() $I_A(\!\cdot\!)$
is continuous at p.
$I_A(\!\cdot\!)$
is continuous at p.
Proof. We start with the lower bound. Fix
![]() $\epsilon>0$
. By the continuity of
$\epsilon>0$
. By the continuity of
![]() $I_A(\!\cdot\!)$
at p, there exist some
$I_A(\!\cdot\!)$
at p, there exist some
![]() $\delta>0$
and
$\delta>0$
and
![]() $|x|<I_A(p)+\epsilon$
such that, for any small
$|x|<I_A(p)+\epsilon$
such that, for any small
![]() $\eta>0$
,
$\eta>0$
,
![]() $\inf_{y\in[x-\eta,x+\eta]}\nu(A-y)\geq p+\delta$
. Consequently, we can choose
$\inf_{y\in[x-\eta,x+\eta]}\nu(A-y)\geq p+\delta$
. Consequently, we can choose
![]() $M>1$
large enough that
$M>1$
large enough that
![]() $\frac{1}{1+M^{-1}}\inf_{y\in[x-\eta,x+\eta]}\nu(A-y)\geq p+\frac{\delta}{2}$
. Let
$\frac{1}{1+M^{-1}}\inf_{y\in[x-\eta,x+\eta]}\nu(A-y)\geq p+\frac{\delta}{2}$
. Let
![]() $t_n\,{:\!=}\,\lfloor h\sqrt n\rfloor$
with some
$t_n\,{:\!=}\,\lfloor h\sqrt n\rfloor$
with some
![]() $h>0$
, and
$h>0$
, and
![]() $|v|$
be the generation of particle v. Set
$|v|$
be the generation of particle v. Set
![]() $Z^v_{k} \,{:\!=}\, \sum_ {u\in Z_{|v|+k},u\textrm{ is a descent of }v}\delta_{S_u-S_v}$
;
$Z^v_{k} \,{:\!=}\, \sum_ {u\in Z_{|v|+k},u\textrm{ is a descent of }v}\delta_{S_u-S_v}$
;
![]() $H(u) \,{:\!=}\, \{w\in Z_{t_n+1} : w\notin Z^u_{1}\}$
for
$H(u) \,{:\!=}\, \{w\in Z_{t_n+1} : w\notin Z^u_{1}\}$
for
![]() $u\in Z_{t_n}$
;
$u\in Z_{t_n}$
;
![]() $\mathcal{E} \,{:\!=}\, \{(\xi,k,r)\in \mathcal{M}\times\mathbb{N^+}\times\mathbb{N^+} \,{:}\, \xi$
has exactly one atom z such that
$\mathcal{E} \,{:\!=}\, \{(\xi,k,r)\in \mathcal{M}\times\mathbb{N^+}\times\mathbb{N^+} \,{:}\, \xi$
has exactly one atom z such that
![]() $S_z \in [(x-\eta)\sqrt n,(x+\eta)\sqrt n];\ k>2Mr\}$
;
$S_z \in [(x-\eta)\sqrt n,(x+\eta)\sqrt n];\ k>2Mr\}$
;
![]() $E \,{:\!=}\, \big\{Z_{t_n}$
has exactly one particle u such that
$E \,{:\!=}\, \big\{Z_{t_n}$
has exactly one particle u such that
![]() $S_u \in [(x-\eta)\sqrt n,(x+\eta)\sqrt n]$
and
$S_u \in [(x-\eta)\sqrt n,(x+\eta)\sqrt n]$
and
![]() $|Z^u_1|>2M\sum_{v\neq u,v\in Z_{t_n}}|Z^v_1|\big\}$
. Namely,
$|Z^u_1|>2M\sum_{v\neq u,v\in Z_{t_n}}|Z^v_1|\big\}$
. Namely,
![]() $Z^v_{k}$
is the kth generation of the sub-BRW emanating from particle v, and H(u) represents a collection of particles at time
$Z^v_{k}$
is the kth generation of the sub-BRW emanating from particle v, and H(u) represents a collection of particles at time
![]() $t_n+1$
who are not the children of u. The proof of the lower bound is divided into two main steps.
$t_n+1$
who are not the children of u. The proof of the lower bound is divided into two main steps.
For the first step, we will show that there exists a constant
![]() $C_M>0$
such that, for n large enough,
$C_M>0$
such that, for n large enough,
![]() $\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)\geq C_M\mathbb{P}(E)$
. Let
$\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)\geq C_M\mathbb{P}(E)$
. Let
![]() $\{Z^{i}_n\}_{n\geq 0}$
,
$\{Z^{i}_n\}_{n\geq 0}$
,
![]() $i\geq 1$
, be i.i.d. copies of
$i\geq 1$
, be i.i.d. copies of
![]() $\{Z_n\}_{n\geq 0}$
and
$\{Z_n\}_{n\geq 0}$
and
![]() $W^{v}_{n-t_n-1}\,{:\!=}\,|Z^{v}_{n-t_n-1}|m^{-(n-t_n-1)}$
, and let
$W^{v}_{n-t_n-1}\,{:\!=}\,|Z^{v}_{n-t_n-1}|m^{-(n-t_n-1)}$
, and let
![]() $x_v$
be the displacement of particle v. By the Markov property, we have
$x_v$
be the displacement of particle v. By the Markov property, we have
 \begin{align*} & \mathbb{P}\big(\bar{Z}_n(\sqrt nA)\geq p\big)\nonumber \\[4pt] & \geq \mathbb{P}\left(\vphantom{\frac{\sum\limits_{v\in Z^u_{1}}|Z^{v}_{n-t_n-1}|}{\sum\limits_{w\in H(u)}|Z^{w}_{n-t_n-1}|}}\textrm{there exists } u\in Z_{t_n} \textrm{ such that} \right. \nonumber \\[4pt] & \qquad \qquad \frac{\sum\limits_{v\in Z^u_{1}}Z^{v}_{n-t_n-1}(\sqrt nA-x_v-S_u)+\sum\limits_{w\in H(u)}Z^{w}_{n-t_n-1}(\sqrt nA-S_w)}{\sum\limits_{v\in Z^u_{1}}|Z^{v}_{n-t_n-1}|+\sum\limits_{w\in H(u)}|Z^{w}_{n-t_n-1}|}\geq p \textrm{ and} \nonumber \\[4pt] & \left. \qquad \qquad \frac{\sum\limits_{v\in Z^u_{1}}|Z^{v}_{n-t_n-1}|}{\sum\limits_{w\in H(u)}|Z^{w}_{n-t_n-1}|}>M \right) \nonumber \\ \end{align*}
\begin{align*} & \mathbb{P}\big(\bar{Z}_n(\sqrt nA)\geq p\big)\nonumber \\[4pt] & \geq \mathbb{P}\left(\vphantom{\frac{\sum\limits_{v\in Z^u_{1}}|Z^{v}_{n-t_n-1}|}{\sum\limits_{w\in H(u)}|Z^{w}_{n-t_n-1}|}}\textrm{there exists } u\in Z_{t_n} \textrm{ such that} \right. \nonumber \\[4pt] & \qquad \qquad \frac{\sum\limits_{v\in Z^u_{1}}Z^{v}_{n-t_n-1}(\sqrt nA-x_v-S_u)+\sum\limits_{w\in H(u)}Z^{w}_{n-t_n-1}(\sqrt nA-S_w)}{\sum\limits_{v\in Z^u_{1}}|Z^{v}_{n-t_n-1}|+\sum\limits_{w\in H(u)}|Z^{w}_{n-t_n-1}|}\geq p \textrm{ and} \nonumber \\[4pt] & \left. \qquad \qquad \frac{\sum\limits_{v\in Z^u_{1}}|Z^{v}_{n-t_n-1}|}{\sum\limits_{w\in H(u)}|Z^{w}_{n-t_n-1}|}>M \right) \nonumber \\ \end{align*}
 \begin{align} \nonumber\\[-30pt] & \geq \int_{\mathcal{E}}\mathbb{P}\left(\frac{\sum^k\limits_{i=1}Z^{i}_{n-t_n-1}(\sqrt nA-x_v-S_z)}{\sum^k\limits_{i=1}|Z^{i}_{n-t_n-1}|+\sum^r\limits_{j=1}|Z^{j}_{n-t_n-1}|}\geq p \textrm{ and} \right. \nonumber \\ & \left. \qquad \qquad \frac{\sum^k\limits_{i=1}|Z^{i}_{n-t_n-1}|}{\sum^r\limits_{j=1}|Z^{j}_{n-t_n-1}|}>M \right) \mathbb{P}(Z_{t_n}\in \textrm{d}\xi, \, |Z^{z}_{1}|\in \textrm{d} k, \, |H(z)|\in \textrm{d} r)\nonumber \\ & \geq \int_{\mathcal{E}}\mathbb{P}\left(\frac{\sum^k\limits_{i=1}Z^{i}_{n-t_n-1}(\sqrt nA-x_v-S_z)}{(1+M^{-1})\sum^k\limits_{i=1}|Z^{i}_{n-t_n-1}|}\geq p \textrm{ and} \right. \nonumber \\ & \left. \qquad \qquad \frac{\sum^k\limits_{i=1}{W^{i}_{n-t_n-1}}}{\sum^r\limits_{j=1}W^{j}_{n-t_n-1}}>M \right) \mathbb{P}\left(Z_{t_n}\in \textrm{d}\xi, \, |Z^{z}_{1}|\in \textrm{d} k, \, |H(z)|\in \textrm{d} r\right)\nonumber \\ & \,{=\!:}\, \int_{\mathcal{E}} P_n(\xi,k,r)\mathbb{P}(Z_{t_n}\in \textrm{d}\xi, \, |Z^{z}_{1}|\in \textrm{d} k, \, |H(z)|\in \textrm{d} r),\end{align}
\begin{align} \nonumber\\[-30pt] & \geq \int_{\mathcal{E}}\mathbb{P}\left(\frac{\sum^k\limits_{i=1}Z^{i}_{n-t_n-1}(\sqrt nA-x_v-S_z)}{\sum^k\limits_{i=1}|Z^{i}_{n-t_n-1}|+\sum^r\limits_{j=1}|Z^{j}_{n-t_n-1}|}\geq p \textrm{ and} \right. \nonumber \\ & \left. \qquad \qquad \frac{\sum^k\limits_{i=1}|Z^{i}_{n-t_n-1}|}{\sum^r\limits_{j=1}|Z^{j}_{n-t_n-1}|}>M \right) \mathbb{P}(Z_{t_n}\in \textrm{d}\xi, \, |Z^{z}_{1}|\in \textrm{d} k, \, |H(z)|\in \textrm{d} r)\nonumber \\ & \geq \int_{\mathcal{E}}\mathbb{P}\left(\frac{\sum^k\limits_{i=1}Z^{i}_{n-t_n-1}(\sqrt nA-x_v-S_z)}{(1+M^{-1})\sum^k\limits_{i=1}|Z^{i}_{n-t_n-1}|}\geq p \textrm{ and} \right. \nonumber \\ & \left. \qquad \qquad \frac{\sum^k\limits_{i=1}{W^{i}_{n-t_n-1}}}{\sum^r\limits_{j=1}W^{j}_{n-t_n-1}}>M \right) \mathbb{P}\left(Z_{t_n}\in \textrm{d}\xi, \, |Z^{z}_{1}|\in \textrm{d} k, \, |H(z)|\in \textrm{d} r\right)\nonumber \\ & \,{=\!:}\, \int_{\mathcal{E}} P_n(\xi,k,r)\mathbb{P}(Z_{t_n}\in \textrm{d}\xi, \, |Z^{z}_{1}|\in \textrm{d} k, \, |H(z)|\in \textrm{d} r),\end{align}
where
![]() $\mathbb{P}(Z_{t_n}\in \textrm{d}\xi)$
represents the distribution of the point process
$\mathbb{P}(Z_{t_n}\in \textrm{d}\xi)$
represents the distribution of the point process
![]() $Z_{t_n}$
(for a serious definition of a point process’s distribution, see [Reference Bovier8, Section 2.1]). To finish the first step, it suffices to show that
$Z_{t_n}$
(for a serious definition of a point process’s distribution, see [Reference Bovier8, Section 2.1]). To finish the first step, it suffices to show that
Since
![]() $A\in\mathcal{A}$
(see Assumption 1), we can write
$A\in\mathcal{A}$
(see Assumption 1), we can write
![]() $A=\sum^l_{i=1}(a_i,b_i]$
for some natural number l, where
$A=\sum^l_{i=1}(a_i,b_i]$
for some natural number l, where
![]() $-\infty\leq a_i<b_i\leq+\infty$
. Let
$-\infty\leq a_i<b_i\leq+\infty$
. Let
![]() $A(x,\eta)\,{:\!=}\,\sum^l_{i=1}\left(a_i-x+\eta,b_i-x-\eta\right)$
. Since
$A(x,\eta)\,{:\!=}\,\sum^l_{i=1}\left(a_i-x+\eta,b_i-x-\eta\right)$
. Since
![]() $S_z\in[(x-\eta)\sqrt n,(x+\eta)\sqrt n]$
, we can choose
$S_z\in[(x-\eta)\sqrt n,(x+\eta)\sqrt n]$
, we can choose
![]() $\eta$
small enough such that
$\eta$
small enough such that
Thus, by the central limit theorem, there exists a constant
![]() $C(M,h,x,\eta,\delta)>0$
such that, for
$C(M,h,x,\eta,\delta)>0$
such that, for
![]() $n>C(M,h,x,\eta,\delta)$
,
$n>C(M,h,x,\eta,\delta)$
,
Recall that
![]() $Z^{i}_{n-t_n-1}$
,
$Z^{i}_{n-t_n-1}$
,
![]() $W^{i}_{n-t_n-1}$
, and
$W^{i}_{n-t_n-1}$
, and
![]() $X_i$
,
$X_i$
,
![]() $1\leq i\leq k$
, are respectively i.i.d. copies of
$1\leq i\leq k$
, are respectively i.i.d. copies of
![]() $Z_{n-t_n-1}$
,
$Z_{n-t_n-1}$
,
![]() $W_{n-t_n-1}$
, and X. Since
$W_{n-t_n-1}$
, and X. Since
![]() $\sqrt nA(x,\eta)\subset \sqrt nA-S_z$
, by (16), we have
$\sqrt nA(x,\eta)\subset \sqrt nA-S_z$
, by (16), we have
 \begin{align*}P_n(\xi,k,m)&\geq \mathbb{P}\left(\frac{\sum\limits^k_{i=1}Z^{i}_{n-t_n-1}(\sqrt nA(x,\eta)-X_i)}{(1+M^{-1})\sum\limits^k_{i=1}|Z^{i}_{n-t_n-1}|}\geq p \textrm{ and } \frac{\sum\limits^k_{i=1}{W^{i}_{n-t_n-1}}}{\sum\limits^{\lfloor\frac{k}{2M}\rfloor}_{j=1}W^{j}_{n-t_n-1}}>M\right)\\[3pt] &\,{=\!:}\,\mathbb{E}\left[{\bf 1}_{\{A_{n,k}\geq p\}}{\bf 1}_{\{B_{n,k}\geq M\}}\right].\nonumber\end{align*}
\begin{align*}P_n(\xi,k,m)&\geq \mathbb{P}\left(\frac{\sum\limits^k_{i=1}Z^{i}_{n-t_n-1}(\sqrt nA(x,\eta)-X_i)}{(1+M^{-1})\sum\limits^k_{i=1}|Z^{i}_{n-t_n-1}|}\geq p \textrm{ and } \frac{\sum\limits^k_{i=1}{W^{i}_{n-t_n-1}}}{\sum\limits^{\lfloor\frac{k}{2M}\rfloor}_{j=1}W^{j}_{n-t_n-1}}>M\right)\\[3pt] &\,{=\!:}\,\mathbb{E}\left[{\bf 1}_{\{A_{n,k}\geq p\}}{\bf 1}_{\{B_{n,k}\geq M\}}\right].\nonumber\end{align*}
Fix
![]() $k> 2M$
(since
$k> 2M$
(since
![]() $(\xi,k,r)\in\mathcal{E}$
) and
$(\xi,k,r)\in\mathcal{E}$
) and
![]() $\epsilon'\in(0,\eta)$
. A random variable
$\epsilon'\in(0,\eta)$
. A random variable
![]() $N(\epsilon', k)>0$
exists such that, for
$N(\epsilon', k)>0$
exists such that, for
![]() $n>N(\epsilon', k)$
and
$n>N(\epsilon', k)$
and
![]() $1\leq i\leq k$
,
$1\leq i\leq k$
,
![]() $\sqrt nA(x,\eta+\epsilon')\subset\sqrt nA(x,\eta)-X_i\subset \sqrt nA(x,\eta-\epsilon')$
. Thus,
$\sqrt nA(x,\eta+\epsilon')\subset\sqrt nA(x,\eta)-X_i\subset \sqrt nA(x,\eta-\epsilon')$
. Thus,
 \begin{align*} &\frac{\sum\limits^k_{i=1}m^{-(n-t_n-1)}Z^{i}_{n-t_n-1}(\sqrt nA(x,\eta+\epsilon'))}{(1+M^{-1})\sum\limits^k_{i=1}m^{-(n-t_n-1)}|Z^{i}_{n-t_n-1}|}\leq A_{n,k} \\[3pt] &\quad \leq \frac{\sum\limits^k_{i=1}m^{-(n-t_n-1)}Z_{n-t_n-1}^{i}(\sqrt nA(x,\eta-\epsilon'))}{(1+M^{-1})\sum\limits^k_{i=1}m^{-(n-t_n-1)}|Z^{i}_{n-t_n-1}|}.\end{align*}
\begin{align*} &\frac{\sum\limits^k_{i=1}m^{-(n-t_n-1)}Z^{i}_{n-t_n-1}(\sqrt nA(x,\eta+\epsilon'))}{(1+M^{-1})\sum\limits^k_{i=1}m^{-(n-t_n-1)}|Z^{i}_{n-t_n-1}|}\leq A_{n,k} \\[3pt] &\quad \leq \frac{\sum\limits^k_{i=1}m^{-(n-t_n-1)}Z_{n-t_n-1}^{i}(\sqrt nA(x,\eta-\epsilon'))}{(1+M^{-1})\sum\limits^k_{i=1}m^{-(n-t_n-1)}|Z^{i}_{n-t_n-1}|}.\end{align*}
Since
![]() $\bar{Z}_n(\sqrt nA)\rightarrow\nu(A)$
and
$\bar{Z}_n(\sqrt nA)\rightarrow\nu(A)$
and
![]() $W_n\rightarrow W$
, the above implies that
$W_n\rightarrow W$
, the above implies that
![]() $\lim_{n\rightarrow \infty}A_{n,k}= \frac{1}{1+M^{-1}}\nu(A(x,\eta))$
,
$\lim_{n\rightarrow \infty}A_{n,k}= \frac{1}{1+M^{-1}}\nu(A(x,\eta))$
,
![]() $\mathbb{P}$
-a.s. On the other hand, it is easy to see that
$\mathbb{P}$
-a.s. On the other hand, it is easy to see that
 \begin{equation*}\lim\limits_{n\rightarrow\infty}B_{n,k}= {\sum\limits^k_{i=1}{W^{i}}} \Big / {\sum\limits^{\lfloor\frac{k}{2M}\rfloor}_{j=1}W^{j}} \,{=\!:}\,B_k \qquad \mathbb{P}\textrm{{-}a.s.},\end{equation*}
\begin{equation*}\lim\limits_{n\rightarrow\infty}B_{n,k}= {\sum\limits^k_{i=1}{W^{i}}} \Big / {\sum\limits^{\lfloor\frac{k}{2M}\rfloor}_{j=1}W^{j}} \,{=\!:}\,B_k \qquad \mathbb{P}\textrm{{-}a.s.},\end{equation*}
where
![]() $W^i$
and
$W^i$
and
![]() $W^j$
are i.i.d. copies of
$W^j$
are i.i.d. copies of
![]() $W\,{:\!=}\,\lim_{n\rightarrow\infty}|Z_n|/m^n$
. Hence, by the dominated convergence theorem and (18), for any fixed
$W\,{:\!=}\,\lim_{n\rightarrow\infty}|Z_n|/m^n$
. Hence, by the dominated convergence theorem and (18), for any fixed
![]() $k>2M$
we have
$k>2M$
we have
So, to achieve (17), it suffices to show that
and
By the strong law of large numbers, we can easily obtain
![]() $\inf_{k>2M}\mathbb{P}\left(B_k>M\right)>0$
. For (20), observe that
$\inf_{k>2M}\mathbb{P}\left(B_k>M\right)>0$
. For (20), observe that
For the first term on the right-hand side of (23), let
![]() $\xi=\sum^k_{i=1}\delta_{X_i}$
be a point process (recall that the
$\xi=\sum^k_{i=1}\delta_{X_i}$
be a point process (recall that the
![]() $X_i$
,
$X_i$
,
![]() $i\geq 1$
, are i.i.d. copies of X). By Remark 7 and (19), there exists a constant
$i\geq 1$
, are i.i.d. copies of X). By Remark 7 and (19), there exists a constant
![]() $C_1>0$
depending on
$C_1>0$
depending on
![]() $\delta$
and
$\delta$
and
![]() $\beta$
such that, for
$\beta$
such that, for
![]() $n>C(M,h,x,\eta,\delta)$
,
$n>C(M,h,x,\eta,\delta)$
,
 \begin{align*}\mathbb{P}(A_{n,k}<p) &=\mathbb{P}\left(\frac{\sum\limits^k_{i=1}Z^{i}_{n-t_n-1}(\sqrt nA(x,\eta)-X_i)}{(1+M^{-1})\sum\limits^k_{i=1}|Z^{i}_{n-t_n-1}|}<p \right)\nonumber \\ &=\mathbb{P}\left(\bar{Z}^{\xi}_{n-t_n-1}(\sqrt nA(x,\eta))<p\big(1+M^{-1}\big)\right)\nonumber \\ &\leq \mathbb{P}\left(\bar{Z}^{\xi}_{n-t_n-1}(\sqrt nA(x,\eta))<\nu_{n-t_n}(\sqrt nA(x,\eta))-\frac{\delta}{8}\right)\nonumber \end{align*}
\begin{align*}\mathbb{P}(A_{n,k}<p) &=\mathbb{P}\left(\frac{\sum\limits^k_{i=1}Z^{i}_{n-t_n-1}(\sqrt nA(x,\eta)-X_i)}{(1+M^{-1})\sum\limits^k_{i=1}|Z^{i}_{n-t_n-1}|}<p \right)\nonumber \\ &=\mathbb{P}\left(\bar{Z}^{\xi}_{n-t_n-1}(\sqrt nA(x,\eta))<p\big(1+M^{-1}\big)\right)\nonumber \\ &\leq \mathbb{P}\left(\bar{Z}^{\xi}_{n-t_n-1}(\sqrt nA(x,\eta))<\nu_{n-t_n}(\sqrt nA(x,\eta))-\frac{\delta}{8}\right)\nonumber \end{align*}
 \begin{align} \nonumber\\[-40pt] &=\mathbb{P}\left(\bar{Z}^{\xi}_{n-t_n-1}(\sqrt nA(x,\eta))<\mathbb{E}\left[\frac{1}{|\xi|}\sum_{z\in\xi}\nu_{n-t_n-1}(\sqrt nA(x,\eta)-S_z)\right]-\frac{\delta}{8}\right)\nonumber \\ &\leq C_1k^{1-\beta},\end{align}
\begin{align} \nonumber\\[-40pt] &=\mathbb{P}\left(\bar{Z}^{\xi}_{n-t_n-1}(\sqrt nA(x,\eta))<\mathbb{E}\left[\frac{1}{|\xi|}\sum_{z\in\xi}\nu_{n-t_n-1}(\sqrt nA(x,\eta)-S_z)\right]-\frac{\delta}{8}\right)\nonumber \\ &\leq C_1k^{1-\beta},\end{align}
where the third equality holds since
For the second term on the right-hand side of (23), by the strong law of large numbers we have
For the third term on the right-hand side of (23), there exists a constant
![]() $C(M,\beta)>0$
such that, for any
$C(M,\beta)>0$
such that, for any
![]() $k>2M$
and
$k>2M$
and
![]() $n\geq1$
,
$n\geq1$
,
 \begin{align}\mathbb{P}(B_{n,k}<M & , B_k\geq M)\nonumber \\ &\leq\mathbb{P}(B_{n,k}<M)\nonumber \\ &=\mathbb{P}\left(\frac{\sum\limits^k_{i=1}{W^{i}_{n-t_n-1}}}{\sum\limits^{\lfloor\frac{k}{2M}\rfloor}_{j=1}W^{j}_{n-t_n-1}}<M\right)\nonumber \\ &\leq\mathbb{P}\left(\sum\limits^k_{i=1}W^{i}_{n-t_n-1}<M\sum\limits^{\lfloor\frac{k}{2M}\rfloor}_{j=1}W^{j}_{n-t_n-1},\sum\limits^{\lfloor\frac{k}{2M}\rfloor}_{j=1}W^{j}_{n-t_n-1}<\frac{k}{2M}\frac{3}{2}\right) \nonumber \\ & \quad + \mathbb{P}\left(\sum\limits^{\lfloor\frac{k}{2M}\rfloor}_{j=1}W^{j}_{n-t_n-1}\geq\frac{k}{2M}\frac{3}{2}\right)\nonumber \\ &\leq\mathbb{P}\left(\sum\limits^k_{i=1}W^{i}_{n-t_n-1}<\frac{3k}{4}\right)+\mathbb{P}\left(\sum\limits^{\lfloor\frac{k}{2M}\rfloor}_{j=1}W^{j}_{n-t_n-1}\geq\frac{k}{2M}\frac{3}{2}\right)\nonumber \\ &\leq\mathbb{P}\left(\sum\limits^k_{i=1}\left(1-W^{i}_{n-t_n-1}\right)>\frac{k}{4}\right)+\mathbb{P}\left(\sum\limits^{\lfloor\frac{k}{2M}\rfloor}_{j=1}\left(W^{j}_{n-t_n-1}-1\right)\geq\frac{k}{2M}\frac{1}{2}\right)\nonumber \\ &\leq C(M,\beta)k^{1-\beta},\end{align}
\begin{align}\mathbb{P}(B_{n,k}<M & , B_k\geq M)\nonumber \\ &\leq\mathbb{P}(B_{n,k}<M)\nonumber \\ &=\mathbb{P}\left(\frac{\sum\limits^k_{i=1}{W^{i}_{n-t_n-1}}}{\sum\limits^{\lfloor\frac{k}{2M}\rfloor}_{j=1}W^{j}_{n-t_n-1}}<M\right)\nonumber \\ &\leq\mathbb{P}\left(\sum\limits^k_{i=1}W^{i}_{n-t_n-1}<M\sum\limits^{\lfloor\frac{k}{2M}\rfloor}_{j=1}W^{j}_{n-t_n-1},\sum\limits^{\lfloor\frac{k}{2M}\rfloor}_{j=1}W^{j}_{n-t_n-1}<\frac{k}{2M}\frac{3}{2}\right) \nonumber \\ & \quad + \mathbb{P}\left(\sum\limits^{\lfloor\frac{k}{2M}\rfloor}_{j=1}W^{j}_{n-t_n-1}\geq\frac{k}{2M}\frac{3}{2}\right)\nonumber \\ &\leq\mathbb{P}\left(\sum\limits^k_{i=1}W^{i}_{n-t_n-1}<\frac{3k}{4}\right)+\mathbb{P}\left(\sum\limits^{\lfloor\frac{k}{2M}\rfloor}_{j=1}W^{j}_{n-t_n-1}\geq\frac{k}{2M}\frac{3}{2}\right)\nonumber \\ &\leq\mathbb{P}\left(\sum\limits^k_{i=1}\left(1-W^{i}_{n-t_n-1}\right)>\frac{k}{4}\right)+\mathbb{P}\left(\sum\limits^{\lfloor\frac{k}{2M}\rfloor}_{j=1}\left(W^{j}_{n-t_n-1}-1\right)\geq\frac{k}{2M}\frac{1}{2}\right)\nonumber \\ &\leq C(M,\beta)k^{1-\beta},\end{align}
where, for the last inequality, we used exactly the same arguments as for bounding
![]() $I_1$
and
$I_1$
and
![]() $I_2$
in Lemma 4. Plugging (25), (26), and (27) into (23), we obtain that for every
$I_2$
in Lemma 4. Plugging (25), (26), and (27) into (23), we obtain that for every
![]() $\epsilon>0$
there exists a constant
$\epsilon>0$
there exists a constant
![]() $C(\epsilon,M,\beta,\delta)$
such that, for
$C(\epsilon,M,\beta,\delta)$
such that, for
![]() $k>C(\epsilon,M,\beta,\delta)$
and
$k>C(\epsilon,M,\beta,\delta)$
and
![]() $n>C(M,h,x,\eta,\delta)$
,
$n>C(M,h,x,\eta,\delta)$
,
![]() $\left|\mathbb{E}\left[{\bf 1}_{\{A_{n,k}\geq p\}}{\bf 1}_{\{B_{n,k}\geq M\}}\right]-\mathbb{P}\left(B_k\geq M\right)\right|<\epsilon$
. Combining this with (20), there exists some large constant
$\left|\mathbb{E}\left[{\bf 1}_{\{A_{n,k}\geq p\}}{\bf 1}_{\{B_{n,k}\geq M\}}\right]-\mathbb{P}\left(B_k\geq M\right)\right|<\epsilon$
. Combining this with (20), there exists some large constant
![]() $C(\epsilon,M,\beta,h,x,\eta,\delta,p)$
such that, for
$C(\epsilon,M,\beta,h,x,\eta,\delta,p)$
such that, for
![]() $n>C(\epsilon,M,\beta,h,x,\eta,\delta,p)$
and
$n>C(\epsilon,M,\beta,h,x,\eta,\delta,p)$
and
![]() $k>2M$
,
$k>2M$
,
![]() $\left|\mathbb{E}\left[{\bf 1}_{\{A_{n,k}\geq p\}}{\bf 1}_{\{B_{n,k}\geq M\}}\right]-\mathbb{P}\left(B_k\geq M\right)\right|<\epsilon$
. Thus, (21) holds. This, combined with (22) and (16), implies that there exist positive constants
$\left|\mathbb{E}\left[{\bf 1}_{\{A_{n,k}\geq p\}}{\bf 1}_{\{B_{n,k}\geq M\}}\right]-\mathbb{P}\left(B_k\geq M\right)\right|<\epsilon$
. Thus, (21) holds. This, combined with (22) and (16), implies that there exist positive constants
![]() $C_M$
and
$C_M$
and
![]() $C(M,\beta,h,x,\eta,\delta,p)$
such that, for
$C(M,\beta,h,x,\eta,\delta,p)$
such that, for
![]() $n>C(M,\beta,h,x,\eta,\delta,p)$
,
$n>C(M,\beta,h,x,\eta,\delta,p)$
,
![]() $\mathbb{P}\big(\bar{Z}_n(\sqrt nA)\geq p\big)\geq C_M\mathbb{P}(E)$
, which completes the first step.
$\mathbb{P}\big(\bar{Z}_n(\sqrt nA)\geq p\big)\geq C_M\mathbb{P}(E)$
, which completes the first step.
For the second step, we will give a lower bound of
![]() $\mathbb{P}(E)$
. Define
$\mathbb{P}(E)$
. Define
![]() $\mathcal{F}_{t_n}\,{:\!=}\,\sigma(Z_{i}$
,
$\mathcal{F}_{t_n}\,{:\!=}\,\sigma(Z_{i}$
,
![]() $1\leq i\leq t_n)$
. By the first step, for
$1\leq i\leq t_n)$
. By the first step, for
![]() $n>C(M,\beta,h,x,\eta,\delta,p)$
,
$n>C(M,\beta,h,x,\eta,\delta,p)$
,
 \begin{align}&\mathbb{P}\left(\bar{Z}_n(\sqrt nA)\geq p\right)\nonumber \\ &\geq C_M\mathbb{P}\left(\!\textrm{there exists }u\in Z_{t_n} \textrm{ such that } S_u\in[(x-\eta)\sqrt n,(x+\eta)\sqrt n],|Z^{u}_{1}|>2M\!\!\sum_{\scriptsize\begin{array}{c}v\neq u\, v\in Z_{t_n}\end{array}}\!\!\!|Z^{v}_{1}|\right)\nonumber \\ &=C_M\mathbb{E}\Bigg[\sum_{u\in Z_{t_n}}{\bf 1}_{\{S_u\in[(x-\eta)\sqrt n,(x+\eta)\sqrt n]\}}{\bf 1}_{\{|Z^{u}_{1}|>2M\sum\limits_{v\neq u, v\in Z_{t_n}}|Z^{v}_{1}|\}}\Bigg]\nonumber \\ &=C_M\mathbb{E}\Bigg[\sum_{u\in Z_{t_n}}{\bf 1}_{\{S_u\in[(x-\eta)\sqrt n,(x+\eta)\sqrt n]\}}\mathbb{E}\left[{\bf 1}_{\{|Z^{u}_{1}|>2M\sum\limits_{v\neq u, v\in Z_{t_n}}|Z^{v}_{1}|\}} \ \Big| \ \mathcal{F}_{t_n}\right]\Bigg],\end{align}
\begin{align}&\mathbb{P}\left(\bar{Z}_n(\sqrt nA)\geq p\right)\nonumber \\ &\geq C_M\mathbb{P}\left(\!\textrm{there exists }u\in Z_{t_n} \textrm{ such that } S_u\in[(x-\eta)\sqrt n,(x+\eta)\sqrt n],|Z^{u}_{1}|>2M\!\!\sum_{\scriptsize\begin{array}{c}v\neq u\, v\in Z_{t_n}\end{array}}\!\!\!|Z^{v}_{1}|\right)\nonumber \\ &=C_M\mathbb{E}\Bigg[\sum_{u\in Z_{t_n}}{\bf 1}_{\{S_u\in[(x-\eta)\sqrt n,(x+\eta)\sqrt n]\}}{\bf 1}_{\{|Z^{u}_{1}|>2M\sum\limits_{v\neq u, v\in Z_{t_n}}|Z^{v}_{1}|\}}\Bigg]\nonumber \\ &=C_M\mathbb{E}\Bigg[\sum_{u\in Z_{t_n}}{\bf 1}_{\{S_u\in[(x-\eta)\sqrt n,(x+\eta)\sqrt n]\}}\mathbb{E}\left[{\bf 1}_{\{|Z^{u}_{1}|>2M\sum\limits_{v\neq u, v\in Z_{t_n}}|Z^{v}_{1}|\}} \ \Big| \ \mathcal{F}_{t_n}\right]\Bigg],\end{align}
where the first equality follows from the fact that the random variable inside the expectation can only be 0 or 1 (since there exists at most one individual satisfying
![]() $|Z^{u}_{1}|>2M\sum_{v\neq u, v\in Z_{t_n}}|Z^{v}_{1}|$
for
$|Z^{u}_{1}|>2M\sum_{v\neq u, v\in Z_{t_n}}|Z^{v}_{1}|$
for
![]() $u\in Z_{t_n}$
). Let
$u\in Z_{t_n}$
). Let
![]() $k_i$
,
$k_i$
,
![]() $i\geq 0$
, be i.i.d. copies of
$i\geq 0$
, be i.i.d. copies of
![]() $|Z_1|$
, and independent of
$|Z_1|$
, and independent of
![]() $Z_{t_n}$
. Since
$Z_{t_n}$
. Since
![]() $|Z_1|\sim \textrm{Pareto}(\beta)$
, there exists a constant
$|Z_1|\sim \textrm{Pareto}(\beta)$
, there exists a constant
![]() $C_4>0$
such that
$C_4>0$
such that
![]() $\mathbb{P}(|Z_1|>x)>C_4 x^{-\beta}$
for all
$\mathbb{P}(|Z_1|>x)>C_4 x^{-\beta}$
for all
![]() $x>1$
. Recall the well-known fact that if U and V are independent random variables then, for any bounded measurable function F(x,y), we have
$x>1$
. Recall the well-known fact that if U and V are independent random variables then, for any bounded measurable function F(x,y), we have
![]() $\mathbb{E}[F(U,V) \mid \sigma(V)]=\mathbb{E}[F(U,v)]\big|_{v=V}$
. Using this fact, we have
$\mathbb{E}[F(U,V) \mid \sigma(V)]=\mathbb{E}[F(U,v)]\big|_{v=V}$
. Using this fact, we have
 \begin{align}\mathbb{E}\left[{\bf 1}_{\{|Z^{u}_{1}|>2M\sum\limits_{\scriptsize\begin{array}{c}v\neq u \\ v\in Z_{t_n}\end{array}}|Z^{v}_{1}|\}} \ \big| \ \mathcal{F}_{t_n}\right]&=\mathbb{E}\left[{\bf 1}_{\{k_0>2M\sum^{|Z_{t_n}|-1}_{i=1}k_i\}} \ \Big | \ \mathcal{F}_{t_n}\right]\nonumber \\ &=\mathbb{E}\left[{\bf 1}_{\{k_0>2M\sum^{j}_{i=1}k_i\}}\right]\Big{|}_{j=|Z_{t_n}|-1}\nonumber \\ &=\mathbb{E}\left[\mathbb{E}\left[{\bf 1}_{\{k_0>2M\sum^{j}_{i=1}k_i\}}\Big{|}\sigma(k_1,\ldots,k_j)\right]\right]\Big{|}_{j=|Z_{t_n}|-1}\nonumber \\ &\geq C_4\mathbb{E}\left[\left(2M\sum^{j}_{i=1}k_i\right)^{-\beta}\right]\Bigg{|}_{j=|Z_{t_n}|-1}\nonumber \\ &= C_4\mathbb{E}\left[\left(2M\sum^{|Z_{t_n}|-1}_{i=1}k_i\right)^{-\beta} \ \Big | \ \sigma(|Z_{t_n}|)\right]\nonumber \\ &\geq C_4(2M)^{-\beta}\mathbb{E}\left[ |Z_{t_n+1}|^{-\beta} \ \big | \ \mathcal{F}_{t_n}\right].\end{align}
\begin{align}\mathbb{E}\left[{\bf 1}_{\{|Z^{u}_{1}|>2M\sum\limits_{\scriptsize\begin{array}{c}v\neq u \\ v\in Z_{t_n}\end{array}}|Z^{v}_{1}|\}} \ \big| \ \mathcal{F}_{t_n}\right]&=\mathbb{E}\left[{\bf 1}_{\{k_0>2M\sum^{|Z_{t_n}|-1}_{i=1}k_i\}} \ \Big | \ \mathcal{F}_{t_n}\right]\nonumber \\ &=\mathbb{E}\left[{\bf 1}_{\{k_0>2M\sum^{j}_{i=1}k_i\}}\right]\Big{|}_{j=|Z_{t_n}|-1}\nonumber \\ &=\mathbb{E}\left[\mathbb{E}\left[{\bf 1}_{\{k_0>2M\sum^{j}_{i=1}k_i\}}\Big{|}\sigma(k_1,\ldots,k_j)\right]\right]\Big{|}_{j=|Z_{t_n}|-1}\nonumber \\ &\geq C_4\mathbb{E}\left[\left(2M\sum^{j}_{i=1}k_i\right)^{-\beta}\right]\Bigg{|}_{j=|Z_{t_n}|-1}\nonumber \\ &= C_4\mathbb{E}\left[\left(2M\sum^{|Z_{t_n}|-1}_{i=1}k_i\right)^{-\beta} \ \Big | \ \sigma(|Z_{t_n}|)\right]\nonumber \\ &\geq C_4(2M)^{-\beta}\mathbb{E}\left[ |Z_{t_n+1}|^{-\beta} \ \big | \ \mathcal{F}_{t_n}\right].\end{align}
Plugging (28) into (27) yields, for
![]() $n>C(M,\beta,h,x,\eta,\delta,p)$
,
$n>C(M,\beta,h,x,\eta,\delta,p)$
,
 \begin{align}&\mathbb{P}\left(\bar{Z}_n(\sqrt nA)\geq p\right)\nonumber \\ &\geq C_MC_4(2M)^{-\beta}\mathbb{E}\left[\mathbb{E}\left[\sum_{u\in Z_{t_n}}{\bf 1}_{\{S_u\in[(x-\eta)\sqrt n,(x+\eta)\sqrt n]\}} |Z_{t_n+1}|^{-\beta} \ \Big | \ \mathcal{F}_{t_n}\right]\right]\nonumber \\ &= C_MC_4(2M)^{-\beta}\mathbb{E}\left[\frac{|Z_{t_n}|}{|Z_{t_n+1}|^{\beta}}\right]\nu_{t_n}\left([(x-\eta)\sqrt n,(x+\eta)\sqrt n]\right),\end{align}
\begin{align}&\mathbb{P}\left(\bar{Z}_n(\sqrt nA)\geq p\right)\nonumber \\ &\geq C_MC_4(2M)^{-\beta}\mathbb{E}\left[\mathbb{E}\left[\sum_{u\in Z_{t_n}}{\bf 1}_{\{S_u\in[(x-\eta)\sqrt n,(x+\eta)\sqrt n]\}} |Z_{t_n+1}|^{-\beta} \ \Big | \ \mathcal{F}_{t_n}\right]\right]\nonumber \\ &= C_MC_4(2M)^{-\beta}\mathbb{E}\left[\frac{|Z_{t_n}|}{|Z_{t_n+1}|^{\beta}}\right]\nu_{t_n}\left([(x-\eta)\sqrt n,(x+\eta)\sqrt n]\right),\end{align}
where the last equality follows from the fact that the branching and motion are independent. By Fatou’s lemma, for n large enough,
Plugging (30) into (29) yields the existence of a constant
![]() $C'(\epsilon,M,\beta,h,x,\eta,\delta,p)$
such that, for
$C'(\epsilon,M,\beta,h,x,\eta,\delta,p)$
such that, for
![]() $n>C'(\epsilon,M,\beta,h,x,\eta,\delta,p)$
,
$n>C'(\epsilon,M,\beta,h,x,\eta,\delta,p)$
,
 \begin{align*}\mathbb{P}(\bar{Z}_n&(\sqrt nA)\geq p) \\[3pt] &\geq C_MC_4(2M)^{-\beta}0.9m^{-\beta}\mathbb{E}\left[W^{1-\beta}\right]m^{-(\beta-1)t_n}\nu_{t_n}\big([(x-\eta)\sqrt n,(x+\eta)\sqrt n]\big)\\[3pt] &\geq C_MC_4(2M)^{-\beta}0.9m^{-\beta}\mathbb{E}\left[W^{1-\beta}\right] m^{-(\beta-1)h\sqrt n}\exp\bigg[{-}\bigg(\Lambda\bigg(\frac{x-\eta}{h}\bigg)+\epsilon\bigg)h\sqrt n\bigg],\nonumber\end{align*}
\begin{align*}\mathbb{P}(\bar{Z}_n&(\sqrt nA)\geq p) \\[3pt] &\geq C_MC_4(2M)^{-\beta}0.9m^{-\beta}\mathbb{E}\left[W^{1-\beta}\right]m^{-(\beta-1)t_n}\nu_{t_n}\big([(x-\eta)\sqrt n,(x+\eta)\sqrt n]\big)\\[3pt] &\geq C_MC_4(2M)^{-\beta}0.9m^{-\beta}\mathbb{E}\left[W^{1-\beta}\right] m^{-(\beta-1)h\sqrt n}\exp\bigg[{-}\bigg(\Lambda\bigg(\frac{x-\eta}{h}\bigg)+\epsilon\bigg)h\sqrt n\bigg],\nonumber\end{align*}
where the last inequality follows by Cramér’s theorem. Hence, for every
![]() $\epsilon$
,
$\epsilon$
,
![]() $\eta$
small enough and
$\eta$
small enough and
![]() $h>0$
, the above yields
$h>0$
, the above yields
First, let
![]() $\epsilon\rightarrow 0$
, and then maximize the lower bound with h, to finally obtain
$\epsilon\rightarrow 0$
, and then maximize the lower bound with h, to finally obtain
which concludes the desired lower bound for the case of
![]() $\beta-1<\frac{-\log{p_1}}{\log m}$
. For
$\beta-1<\frac{-\log{p_1}}{\log m}$
. For
![]() $\beta-1\geq \frac{-\log{p_1}}{\log m}$
, [Reference Chen and He13, Lemma 3.1] gives
$\beta-1\geq \frac{-\log{p_1}}{\log m}$
, [Reference Chen and He13, Lemma 3.1] gives
We next consider the upper bound in Theorem 1. By the definition of
![]() $I_A(p)$
, for every
$I_A(p)$
, for every
![]() $\eta\in(0,I_A(p))$
there exists
$\eta\in(0,I_A(p))$
there exists
![]() $\delta>0$
such that
$\delta>0$
such that
Set
![]() $B_n\,{:\!=}\,[(-I_A(p)+\eta)\sqrt n,(I_A(p)-\eta)\sqrt n]$
,
$B_n\,{:\!=}\,[(-I_A(p)+\eta)\sqrt n,(I_A(p)-\eta)\sqrt n]$
,
![]() $\mathcal{M}_1\,{:\!=}\,\big\{\xi\in \mathcal{M}:\frac{\xi(B_n^\textrm{c})}{|\xi|}\leq \frac{\delta}{2}\big\}$
, and
$\mathcal{M}_1\,{:\!=}\,\big\{\xi\in \mathcal{M}:\frac{\xi(B_n^\textrm{c})}{|\xi|}\leq \frac{\delta}{2}\big\}$
, and
![]() $t_n\,{:\!=}\,\lfloor h\sqrt n\rfloor$
for some
$t_n\,{:\!=}\,\lfloor h\sqrt n\rfloor$
for some
![]() $h>0$
. For every
$h>0$
. For every
![]() $\xi\in\mathcal{M}_1$
and n large enough, we have
$\xi\in\mathcal{M}_1$
and n large enough, we have
 \begin{align*} &\frac{1}{|\xi|}\sum\limits_{z\in\xi}\nu_{n-{t_n}}(\sqrt n A-S_z)+\frac{\delta}{4} \\[2pt]& \leq \frac{1}{|\xi|}\sum\limits_{\scriptsize\begin{array}{c}z\in\xi \\ z\in B^\textrm{c}_n \end{array}}\nu_{n-{t_n}}(\sqrt n A-S_z) + \frac{1}{|\xi|}\sum\limits_{\scriptsize\begin{array}{c}z\in\xi \\ z\in B_n \end{array}}\nu_{n-{t_n}}(\sqrt n A-S_z)+\frac{\delta}{4}\\[2pt] & \leq \frac{\xi(B_n^\textrm{c})}{|\xi|}+\sup_{|z|\leq I_A(p)-\eta}\nu_{n-{t_n}}(\sqrt {n} (A-z))+\frac{\delta}{4}\\[2pt] & \leq \frac{\delta}{2}+p-\frac{3\delta}{4}+\frac{\delta}{4}\\[2pt] & = p,\nonumber\end{align*}
\begin{align*} &\frac{1}{|\xi|}\sum\limits_{z\in\xi}\nu_{n-{t_n}}(\sqrt n A-S_z)+\frac{\delta}{4} \\[2pt]& \leq \frac{1}{|\xi|}\sum\limits_{\scriptsize\begin{array}{c}z\in\xi \\ z\in B^\textrm{c}_n \end{array}}\nu_{n-{t_n}}(\sqrt n A-S_z) + \frac{1}{|\xi|}\sum\limits_{\scriptsize\begin{array}{c}z\in\xi \\ z\in B_n \end{array}}\nu_{n-{t_n}}(\sqrt n A-S_z)+\frac{\delta}{4}\\[2pt] & \leq \frac{\xi(B_n^\textrm{c})}{|\xi|}+\sup_{|z|\leq I_A(p)-\eta}\nu_{n-{t_n}}(\sqrt {n} (A-z))+\frac{\delta}{4}\\[2pt] & \leq \frac{\delta}{2}+p-\frac{3\delta}{4}+\frac{\delta}{4}\\[2pt] & = p,\nonumber\end{align*}
where the third inequality follows by the generalized central limit theorem (see [Reference Louidor and Perkins32, Lemma 2.2]) and (31). Hence, by Lemma 4 and the Markov inequality, for n large enough,
 \begin{align}&\mathbb{P}\left(\bar{Z}_{n}(\sqrt n A)\geq p\right)\nonumber \\ &\leq \mathbb{P}\left(\bar{Z}_{t_n}(B_n^\textrm{c})\geq \frac{\delta}{2}\right)+\mathbb{P}\left(\bar{Z}_{t_n}(B_n^\textrm{c})\leq \frac{\delta}{2},\bar{Z}_{n}(\sqrt n A)\geq p\right)\nonumber \\ &\leq \mathbb{E}\left[\frac{2}{\delta}\frac{Z_{t_n}(B_n^\textrm{c})}{|Z_{t_n}|}\right]+\int_{\mathcal{M}_1}\!\!\!\!\mathbb{P}\Bigg(\bar{Z}^\xi_{n-t_n}(\sqrt nA)\geq \frac{1}{|\xi|}\sum_{z\in\xi}\nu_{n-t_n}(\sqrt nA-S_z)+\frac{\delta}{4}\Bigg)\mathbb{P}(Z_{t_n}\in \textrm{d}\xi)\nonumber \\ &\leq \mathbb{E}\left[\frac{2}{\delta}\frac{Z_{t_n}(B_n^\textrm{c})}{|Z_{t_n}|}\right]+C_1\mathbb{E}\big[|Z_{t_n}|^{-(\beta-1)}\big].\end{align}
\begin{align}&\mathbb{P}\left(\bar{Z}_{n}(\sqrt n A)\geq p\right)\nonumber \\ &\leq \mathbb{P}\left(\bar{Z}_{t_n}(B_n^\textrm{c})\geq \frac{\delta}{2}\right)+\mathbb{P}\left(\bar{Z}_{t_n}(B_n^\textrm{c})\leq \frac{\delta}{2},\bar{Z}_{n}(\sqrt n A)\geq p\right)\nonumber \\ &\leq \mathbb{E}\left[\frac{2}{\delta}\frac{Z_{t_n}(B_n^\textrm{c})}{|Z_{t_n}|}\right]+\int_{\mathcal{M}_1}\!\!\!\!\mathbb{P}\Bigg(\bar{Z}^\xi_{n-t_n}(\sqrt nA)\geq \frac{1}{|\xi|}\sum_{z\in\xi}\nu_{n-t_n}(\sqrt nA-S_z)+\frac{\delta}{4}\Bigg)\mathbb{P}(Z_{t_n}\in \textrm{d}\xi)\nonumber \\ &\leq \mathbb{E}\left[\frac{2}{\delta}\frac{Z_{t_n}(B_n^\textrm{c})}{|Z_{t_n}|}\right]+C_1\mathbb{E}\big[|Z_{t_n}|^{-(\beta-1)}\big].\end{align}
For the first term on the right-hand side of (32), define
![]() $\mathcal{G}_{t_n}\,{:\!=}\,\sigma(|Z_i|, 1\leq i\leq t_n)$
. Since the branching and motion are independent we have, for n large enough,
$\mathcal{G}_{t_n}\,{:\!=}\,\sigma(|Z_i|, 1\leq i\leq t_n)$
. Since the branching and motion are independent we have, for n large enough,
 \begin{align}\mathbb{E}\left[\frac{2}{\delta}\frac{Z_{t_n}(B_n^\textrm{c})}{|Z_{t_n}|}\right]&=\mathbb{E}\left[\mathbb{E}\left[\frac{2}{\delta}\frac{Z_{t_n}(B_n^\textrm{c})}{|Z_{t_n}|}\ \big| \ \mathcal{G}_{t_n}\right]\right] \nonumber \\ &= \frac{4}{\delta}\nu_{t_n}\left((I_A(p)-\eta)\sqrt n\right)\nonumber \\ &\leq\frac{4}{\delta} \exp\bigg[{-}\left(\Lambda\left(\frac{I_A(p)-\eta}{h}\right)-\epsilon\right)h\sqrt n\bigg],\end{align}
\begin{align}\mathbb{E}\left[\frac{2}{\delta}\frac{Z_{t_n}(B_n^\textrm{c})}{|Z_{t_n}|}\right]&=\mathbb{E}\left[\mathbb{E}\left[\frac{2}{\delta}\frac{Z_{t_n}(B_n^\textrm{c})}{|Z_{t_n}|}\ \big| \ \mathcal{G}_{t_n}\right]\right] \nonumber \\ &= \frac{4}{\delta}\nu_{t_n}\left((I_A(p)-\eta)\sqrt n\right)\nonumber \\ &\leq\frac{4}{\delta} \exp\bigg[{-}\left(\Lambda\left(\frac{I_A(p)-\eta}{h}\right)-\epsilon\right)h\sqrt n\bigg],\end{align}
where the second equality comes from the symmetry of the step size, and the last inequality follows by Cramér’s theorem. For the second term on the right-hand side of (32), by Lemma 2, for n large enough,
 \begin{equation}\mathbb{E}\left[|Z_{t_n}|^{-(\beta-1)}\right]\leq\begin{cases}2C_0 m^{-(\beta-1)h\sqrt n}, &\beta-1\geq \dfrac{-\log{p_1}}{\log m}; \\ \\[-7pt] 2C_0 p_1^{h\sqrt n}, &0<\beta-1<\dfrac{-\log{p_1}}{\log m}.\end{cases}\end{equation}
\begin{equation}\mathbb{E}\left[|Z_{t_n}|^{-(\beta-1)}\right]\leq\begin{cases}2C_0 m^{-(\beta-1)h\sqrt n}, &\beta-1\geq \dfrac{-\log{p_1}}{\log m}; \\ \\[-7pt] 2C_0 p_1^{h\sqrt n}, &0<\beta-1<\dfrac{-\log{p_1}}{\log m}.\end{cases}\end{equation}
Plugging (33) and (34) into (32) yields that if
![]() $\beta-1\geq \frac{-\log{p_1}}{\log m}$
then
$\beta-1\geq \frac{-\log{p_1}}{\log m}$
then
and if
![]() $0<\beta-1<\frac{\log \frac{1}{p_1}}{\log m}$
then
$0<\beta-1<\frac{\log \frac{1}{p_1}}{\log m}$
then
So, the upper bound follows by optimizing h on
![]() $(0,+\infty)$
.
$(0,+\infty)$
.
4. Proof of Theorem 2
In this section we consider the case that the offspring law has a Weibull tail, i.e.
![]() $\mathbb{P}(|Z_1|>x)\sim l_1\textrm{e}^{-l x^{\beta}}$
as
$\mathbb{P}(|Z_1|>x)\sim l_1\textrm{e}^{-l x^{\beta}}$
as
![]() $x\rightarrow\infty$
for some constants
$x\rightarrow\infty$
for some constants
![]() $\beta\in(0,1)$
and
$\beta\in(0,1)$
and
![]() $l_1, l\in(0,+\infty)$
. We assume that
$l_1, l\in(0,+\infty)$
. We assume that
![]() $I_A(p)<\infty$
and
$I_A(p)<\infty$
and
![]() $I_A(\!\cdot\!)$
is continuous at p. Comparing with the case where the offspring law has exponential moment, the results and proofs do not change in the Schröder case. However, in the Böttcher case things become different: the Böttcher constant will appear in the rate function. So, in this section we further assume
$I_A(\!\cdot\!)$
is continuous at p. Comparing with the case where the offspring law has exponential moment, the results and proofs do not change in the Schröder case. However, in the Böttcher case things become different: the Böttcher constant will appear in the rate function. So, in this section we further assume
![]() $p_1=0$
. Moreover, unlike the Pareto case, the tail of the step size matters for the decay scale of LDP. To show this, we will investigate two types of step size: bounded step size and Weibull-tail step size.
$p_1=0$
. Moreover, unlike the Pareto case, the tail of the step size matters for the decay scale of LDP. To show this, we will investigate two types of step size: bounded step size and Weibull-tail step size.
4.1. Proof of (1)
In this subsection we assume that
![]() $p_1=0$
and
$p_1=0$
and
![]() $0<\textrm{ess}\sup X=L<\infty$
. We are going to show that
$0<\textrm{ess}\sup X=L<\infty$
. We are going to show that
Proof. We start with the lower bound. By the continuity of
![]() $I_A(\!\cdot\!)$
at p, for every
$I_A(\!\cdot\!)$
at p, for every
![]() $\varepsilon>0$
there exists
$\varepsilon>0$
there exists
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $|I_A(p+2\delta)-I_A(p)|<\varepsilon$
. Furthermore, it is easy to see that there exists
$|I_A(p+2\delta)-I_A(p)|<\varepsilon$
. Furthermore, it is easy to see that there exists
![]() $x\in\mathbb{R}$
such that
$x\in\mathbb{R}$
such that
![]() $\nu(A-x)=p+2\delta$
. So, by the continuity of
$\nu(A-x)=p+2\delta$
. So, by the continuity of
![]() $\nu(A-\cdot)$
, there exists some
$\nu(A-\cdot)$
, there exists some
![]() $\eta>0$
such that
$\eta>0$
such that
![]() $\inf_{z\in\left(x,x+\frac{2\eta x}{L}\right)}\nu(A-z)\geq p+\delta$
, where
$\inf_{z\in\left(x,x+\frac{2\eta x}{L}\right)}\nu(A-z)\geq p+\delta$
, where
![]() $(b,a)\,{:\!=}\,(a,b)$
, if
$(b,a)\,{:\!=}\,(a,b)$
, if
![]() $a<b$
. Let
$a<b$
. Let
![]() $t_n\,{:\!=}\,\left\lceil\frac{|x|\sqrt n}{(L-\eta)}\right\rceil$
and
$t_n\,{:\!=}\,\left\lceil\frac{|x|\sqrt n}{(L-\eta)}\right\rceil$
and
 \begin{equation*}E\,{:\!=}\,\Bigg\{\textrm{there exists } u\in Z_{t_n} \textrm{ such that } S_u\in\bigg(x\sqrt n,x\sqrt n+\frac{2\eta x\sqrt n}{L}\bigg), |Z^{u}_{1}|>2M\!\!\sum_{\scriptsize\begin{array}{c}v\neq u \\ v\in Z_{t_n}\end{array}}\!\!|Z^{v}_{1}|\Bigg\}.\end{equation*}
\begin{equation*}E\,{:\!=}\,\Bigg\{\textrm{there exists } u\in Z_{t_n} \textrm{ such that } S_u\in\bigg(x\sqrt n,x\sqrt n+\frac{2\eta x\sqrt n}{L}\bigg), |Z^{u}_{1}|>2M\!\!\sum_{\scriptsize\begin{array}{c}v\neq u \\ v\in Z_{t_n}\end{array}}\!\!|Z^{v}_{1}|\Bigg\}.\end{equation*}
Since
![]() $|Z_1|\sim \textrm{Weibull}(\beta)$
, there exist constants
$|Z_1|\sim \textrm{Weibull}(\beta)$
, there exist constants
![]() $c_7>0$
and
$c_7>0$
and
![]() $l>0$
such that
$l>0$
such that
![]() $\mathbb{P}(|Z_1|>y)>c_7\textrm{e}^{-ly^\beta}$
for all
$\mathbb{P}(|Z_1|>y)>c_7\textrm{e}^{-ly^\beta}$
for all
![]() $y>0$
. By similar arguments for the lower bound in Theorem 1, there exist constants
$y>0$
. By similar arguments for the lower bound in Theorem 1, there exist constants
![]() $C_M>0$
and
$C_M>0$
and
![]() $T(\eta,x)>0$
such that, for n large enough,
$T(\eta,x)>0$
such that, for n large enough,
 \begin{align}\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)&\geq C_M\mathbb{P}(E)\nonumber\\[3pt] &=C_M\mathbb{P}\bigg(S_{t_n}\in\bigg(x\sqrt n,x\sqrt n+\frac{2\eta x\sqrt n}{L}\bigg)\bigg)c_7\mathbb{E}\left[|Z_{t_n}|\textrm{e}^{-l(2M)^{\beta}|Z_{t_n+1}|^{\beta}}\right]\nonumber\\[3pt] &\geq C_M\textrm{e}^{-T(\eta,x)t_n}\mathbb{E}\left[\textrm{e}^{-l(2M)^{\beta}|Z_{t_n+1}|^{\beta}}\right],\end{align}
\begin{align}\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)&\geq C_M\mathbb{P}(E)\nonumber\\[3pt] &=C_M\mathbb{P}\bigg(S_{t_n}\in\bigg(x\sqrt n,x\sqrt n+\frac{2\eta x\sqrt n}{L}\bigg)\bigg)c_7\mathbb{E}\left[|Z_{t_n}|\textrm{e}^{-l(2M)^{\beta}|Z_{t_n+1}|^{\beta}}\right]\nonumber\\[3pt] &\geq C_M\textrm{e}^{-T(\eta,x)t_n}\mathbb{E}\left[\textrm{e}^{-l(2M)^{\beta}|Z_{t_n+1}|^{\beta}}\right],\end{align}
where the last inequality follows by Cramér’s theorem and the fact that
![]() $|x\sqrt n|\leq \left\lceil\frac{|x|\sqrt n}{(L-\eta)}\right\rceil L$
. Hence, by Lemma 3, we have
$|x\sqrt n|\leq \left\lceil\frac{|x|\sqrt n}{(L-\eta)}\right\rceil L$
. Hence, by Lemma 3, we have
Finally, by letting
![]() $\eta\rightarrow0$
and
$\eta\rightarrow0$
and
![]() $\varepsilon\rightarrow0$
, we obtain the desired lower bound.
$\varepsilon\rightarrow0$
, we obtain the desired lower bound.
Then, for the upper bound, for any
![]() $\varepsilon\in(0,I_A(p))$
set
$\varepsilon\in(0,I_A(p))$
set
![]() $t_n\,{:\!=}\,\lfloor (I_A(p)-\varepsilon)\sqrt n/L\rfloor$
. By Lemma 5 and arguments from [Reference Louidor and Perkins32, (2.30)–(2.33)], there exists
$t_n\,{:\!=}\,\lfloor (I_A(p)-\varepsilon)\sqrt n/L\rfloor$
. By Lemma 5 and arguments from [Reference Louidor and Perkins32, (2.30)–(2.33)], there exists
![]() $\delta>0$
such that, for n large enough,
$\delta>0$
such that, for n large enough,
 \begin{align*}\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)&\leq \int_{\mathcal{M}}\mathbb{P}\bigg(\bar{Z}^\xi_{n-t_n}(\sqrt nA)\geq \frac{1}{|\xi|}\sum_{z\in\xi}\nu_{n-t_n}(\sqrt nA-S_z)+\frac{\delta}{3}\bigg)\mathbb{P}(Z_{t_n}\in \textrm{d}\xi)\\[3pt] &\leq C_2\mathbb{E}\big[\textrm{e}^{-C_3|Z_{t_n}|^{\beta}}\big].\nonumber\end{align*}
\begin{align*}\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)&\leq \int_{\mathcal{M}}\mathbb{P}\bigg(\bar{Z}^\xi_{n-t_n}(\sqrt nA)\geq \frac{1}{|\xi|}\sum_{z\in\xi}\nu_{n-t_n}(\sqrt nA-S_z)+\frac{\delta}{3}\bigg)\mathbb{P}(Z_{t_n}\in \textrm{d}\xi)\\[3pt] &\leq C_2\mathbb{E}\big[\textrm{e}^{-C_3|Z_{t_n}|^{\beta}}\big].\nonumber\end{align*}
Thus, by Lemma 3, we have
Finally, the desired upper bound follows by letting
![]() $\varepsilon\rightarrow 0$
.
$\varepsilon\rightarrow 0$
.
4.2. Proof of (2)
In this subsection we consider the case where the step size X satisfies
![]() $\mathbb{P}(X>x)=\Theta(1)\textrm{e}^{-\lambda x^{\alpha}}$
as
$\mathbb{P}(X>x)=\Theta(1)\textrm{e}^{-\lambda x^{\alpha}}$
as
![]() $x\rightarrow\infty$
for some
$x\rightarrow\infty$
for some
![]() $\alpha\in(0,\infty)$
,
$\alpha\in(0,\infty)$
,
![]() $\lambda>0$
. We are going to show that if
$\lambda>0$
. We are going to show that if
![]() $\alpha>1$
, then
$\alpha>1$
, then
For
![]() $\alpha\in(0,1]$
, using the same arguments as [Reference Chen and He13, Section 4.1.1] and Lemma 5, we can easily obtain
$\alpha\in(0,1]$
, using the same arguments as [Reference Chen and He13, Section 4.1.1] and Lemma 5, we can easily obtain
![]() $\lim_{n\rightarrow\infty}\frac{1}{n^{\alpha/2}}\log\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)= -\lambda {I_A(p)}^{\alpha}$
, so we feel free to omit its proof here.
$\lim_{n\rightarrow\infty}\frac{1}{n^{\alpha/2}}\log\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)= -\lambda {I_A(p)}^{\alpha}$
, so we feel free to omit its proof here.
Proof. For the lower bound, we start by fixing
![]() $\epsilon>0$
. There exist some
$\epsilon>0$
. There exist some
![]() $\eta,\delta>0$
and
$\eta,\delta>0$
and
![]() $|x|<I_A(p)+\epsilon$
such that
$|x|<I_A(p)+\epsilon$
such that
![]() $\inf_{y\in(x-\eta,x+\eta)}\nu(A-y)\geq p+\delta$
. Let
$\inf_{y\in(x-\eta,x+\eta)}\nu(A-y)\geq p+\delta$
. Let
![]() $E\,{:\!=}\,\big\{$
there exists
$E\,{:\!=}\,\big\{$
there exists
![]() $u\in Z_{t_n}$
such that
$u\in Z_{t_n}$
such that
![]() $S_u\in\left((x-\eta)\sqrt n,(x+\eta)\sqrt n\right)$
,
$S_u\in\left((x-\eta)\sqrt n,(x+\eta)\sqrt n\right)$
,
![]() $|Z^{u}_{1}|>2M\sum_{v\neq u,v\in Z_{t_n}}|Z^{v}_{1}|\big\}$
, where
$|Z^{u}_{1}|>2M\sum_{v\neq u,v\in Z_{t_n}}|Z^{v}_{1}|\big\}$
, where
![]() $t_n\,{:\!=}\,\lfloor t\log n\rfloor$
for some
$t_n\,{:\!=}\,\lfloor t\log n\rfloor$
for some
![]() $0<t<\frac{\alpha(\beta+\rho-\beta\rho)}{2\log(m+\epsilon)\beta\rho}$
. Similar to (35), we have, for n large enough,
$0<t<\frac{\alpha(\beta+\rho-\beta\rho)}{2\log(m+\epsilon)\beta\rho}$
. Similar to (35), we have, for n large enough,
 \begin{align*}\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)&\geq C_M\mathbb{P}(E)\\[3pt] &=C_M\mathbb{P}\left(S_{t_n}\in\left((x-\eta)\sqrt n,(x+\eta)\sqrt n\right)\right)c_7\mathbb{E}\left[|Z_{t_n}|\textrm{e}^{-l(2M)^{\beta}|Z_{t_n+1}|^{\beta}}\right]\\[3pt] &\geq c_7C_M\exp\left\{-(\lambda+\epsilon)|x-\eta|^{\alpha}\frac{n^{\alpha/2}}{(t\log n)^{\alpha-1}}\right\}\mathbb{E}\left[\textrm{e}^{-l(2M)^{\beta}|Z_{t_n+1}|^{\beta}}\right]\\[3pt] &\geq c_7C_M\exp\left\{-(\lambda+\epsilon)|x-\eta|^{\alpha}\frac{n^{\alpha/2}}{(t\log n)^{\alpha-1}}\right\}\exp\left(-n^\frac{\beta\rho t\log (m+\epsilon)}{\beta+\rho-\beta\rho}\right)\\[3pt] &\geq c_7C_M\exp\left\{-(\lambda+2\epsilon) |x-\eta|^{\alpha}\frac{n^{\alpha/2}}{(t\log n)^{\alpha-1}}\right\},\nonumber\end{align*}
\begin{align*}\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)&\geq C_M\mathbb{P}(E)\\[3pt] &=C_M\mathbb{P}\left(S_{t_n}\in\left((x-\eta)\sqrt n,(x+\eta)\sqrt n\right)\right)c_7\mathbb{E}\left[|Z_{t_n}|\textrm{e}^{-l(2M)^{\beta}|Z_{t_n+1}|^{\beta}}\right]\\[3pt] &\geq c_7C_M\exp\left\{-(\lambda+\epsilon)|x-\eta|^{\alpha}\frac{n^{\alpha/2}}{(t\log n)^{\alpha-1}}\right\}\mathbb{E}\left[\textrm{e}^{-l(2M)^{\beta}|Z_{t_n+1}|^{\beta}}\right]\\[3pt] &\geq c_7C_M\exp\left\{-(\lambda+\epsilon)|x-\eta|^{\alpha}\frac{n^{\alpha/2}}{(t\log n)^{\alpha-1}}\right\}\exp\left(-n^\frac{\beta\rho t\log (m+\epsilon)}{\beta+\rho-\beta\rho}\right)\\[3pt] &\geq c_7C_M\exp\left\{-(\lambda+2\epsilon) |x-\eta|^{\alpha}\frac{n^{\alpha/2}}{(t\log n)^{\alpha-1}}\right\},\nonumber\end{align*}
where the second inequality follows from Lemma 3, the third inequality comes from Lemma 3, and the last inequality follows from the fact that
![]() $t<\frac{\alpha(\beta+\rho-\beta\rho)}{2\log(m+\epsilon)\beta\rho}$
. Hence, for any
$t<\frac{\alpha(\beta+\rho-\beta\rho)}{2\log(m+\epsilon)\beta\rho}$
. Hence, for any
![]() $\epsilon>0$
, some
$\epsilon>0$
, some
![]() $\eta>0$
,
$\eta>0$
,
![]() $|x|<I_A(p)+\epsilon$
, and any
$|x|<I_A(p)+\epsilon$
, and any
![]() $0<t<\frac{\alpha(\beta+\rho-\beta\rho)}{2\log(m+\epsilon)\beta\rho}$
, we have
$0<t<\frac{\alpha(\beta+\rho-\beta\rho)}{2\log(m+\epsilon)\beta\rho}$
, we have
Finally, by letting
![]() $\epsilon\rightarrow 0$
,
$\epsilon\rightarrow 0$
,
![]() $t\rightarrow \frac{\alpha(\beta+\rho-\beta\rho)}{2\log m\beta\rho}$
gives the desired lower bound.
$t\rightarrow \frac{\alpha(\beta+\rho-\beta\rho)}{2\log m\beta\rho}$
gives the desired lower bound.
For the upper bound, set
![]() $t_n\,{:\!=}\, \lfloor t\log n\rfloor$
for
$t_n\,{:\!=}\, \lfloor t\log n\rfloor$
for
![]() $t>\frac{\alpha(\beta+\rho-\beta\rho)}{2\beta\rho\log(m-\epsilon)}$
, and
$t>\frac{\alpha(\beta+\rho-\beta\rho)}{2\beta\rho\log(m-\epsilon)}$
, and
![]() $B_n\,{:\!=}\,[(-I_A(p)+\eta)\sqrt n,(I_A(p)-\eta)\sqrt n]$
. Using the arguments from (31) to (32), there exists some
$B_n\,{:\!=}\,[(-I_A(p)+\eta)\sqrt n,(I_A(p)-\eta)\sqrt n]$
. Using the arguments from (31) to (32), there exists some
![]() $\delta>0$
such that, for n large enough,
$\delta>0$
such that, for n large enough,
 \begin{align*}&\mathbb{P}\left(\bar{Z}_{n}(\sqrt n A)\geq p\right) \\[3pt] &\leq \mathbb{E}\left[\frac{2}{\delta}\frac{Z_{t_n}(B_n^\textrm{c})}{|Z_{t_n}|}\right]+\int_{\mathcal{M}_1}\!\!\!\mathbb{P}\bigg(\bar{Z}^\xi_{n-t_n}(\sqrt nA)\geq \frac{1}{|\xi|}\sum_{z\in\xi}\nu_{n-t_n}(\sqrt nA-S_z)+\frac{\delta}{4}\bigg)\mathbb{P}(Z_{t_n}\in \textrm{d}\xi) \\[3pt] &\leq \frac{2}{\delta}\mathbb{P}(S_{t_n}\in B^\textrm{c}_n)+C_2\mathbb{E}\left[\textrm{e}^{-C_3|Z_{t_n}|^{\beta}}\right], \end{align*}
\begin{align*}&\mathbb{P}\left(\bar{Z}_{n}(\sqrt n A)\geq p\right) \\[3pt] &\leq \mathbb{E}\left[\frac{2}{\delta}\frac{Z_{t_n}(B_n^\textrm{c})}{|Z_{t_n}|}\right]+\int_{\mathcal{M}_1}\!\!\!\mathbb{P}\bigg(\bar{Z}^\xi_{n-t_n}(\sqrt nA)\geq \frac{1}{|\xi|}\sum_{z\in\xi}\nu_{n-t_n}(\sqrt nA-S_z)+\frac{\delta}{4}\bigg)\mathbb{P}(Z_{t_n}\in \textrm{d}\xi) \\[3pt] &\leq \frac{2}{\delta}\mathbb{P}(S_{t_n}\in B^\textrm{c}_n)+C_2\mathbb{E}\left[\textrm{e}^{-C_3|Z_{t_n}|^{\beta}}\right], \end{align*}
where the last inequality follows from Lemma 5. As a consequence, by Lemmas 6 and 3, for n large enough,
 \begin{align*}\mathbb{P}\left(\bar{Z}_{n}(\sqrt n A)\geq p\right)&\leq \exp\left\{-\lambda (I_A(p)-\eta-\epsilon)^{\alpha}\frac{n^{\alpha/2}}{(t\log n)^{\alpha-1}}\right\}+C_2\exp\left(-n^\frac{\beta\rho t\log (m-\epsilon)}{\beta+\rho-\beta\rho}\right)\\[3pt] &\leq \exp\left\{-(\lambda-2\epsilon)(I_A(p)-\eta)^{\alpha}\frac{n^{\alpha/2}}{(t\log n)^{\alpha-1}}\right\},\nonumber\end{align*}
\begin{align*}\mathbb{P}\left(\bar{Z}_{n}(\sqrt n A)\geq p\right)&\leq \exp\left\{-\lambda (I_A(p)-\eta-\epsilon)^{\alpha}\frac{n^{\alpha/2}}{(t\log n)^{\alpha-1}}\right\}+C_2\exp\left(-n^\frac{\beta\rho t\log (m-\epsilon)}{\beta+\rho-\beta\rho}\right)\\[3pt] &\leq \exp\left\{-(\lambda-2\epsilon)(I_A(p)-\eta)^{\alpha}\frac{n^{\alpha/2}}{(t\log n)^{\alpha-1}}\right\},\nonumber\end{align*}
where the last inequality follows from
![]() $t>\frac{\alpha(\beta+\rho-\beta\rho)}{2\beta\rho\log(m-\epsilon)}$
. So, for any
$t>\frac{\alpha(\beta+\rho-\beta\rho)}{2\beta\rho\log(m-\epsilon)}$
. So, for any
![]() $\epsilon, \eta>0$
small enough and
$\epsilon, \eta>0$
small enough and
![]() $t>\frac{\alpha(\beta+\rho-\beta\rho)}{2\beta\rho\log(m-\epsilon)}$
, we have
$t>\frac{\alpha(\beta+\rho-\beta\rho)}{2\beta\rho\log(m-\epsilon)}$
, we have
which implies the upper bound by letting
![]() $\epsilon, \eta\rightarrow 0$
and
$\epsilon, \eta\rightarrow 0$
and
![]() $t\rightarrow \frac{\alpha(\beta+\rho-\beta\rho)}{2\beta\rho\log m}$
.
$t\rightarrow \frac{\alpha(\beta+\rho-\beta\rho)}{2\beta\rho\log m}$
.
5. Proof of Theorem 3
In this section we assume
![]() $\mathbb{E}[|Z_1|^{\beta}]<\infty$
for some
$\mathbb{E}[|Z_1|^{\beta}]<\infty$
for some
![]() $\beta>1$
, and
$\beta>1$
, and
![]() $I_A(\!\cdot\!)$
is continuous at p for some
$I_A(\!\cdot\!)$
is continuous at p for some
![]() $p\in(\nu(A),1-\nu(A))$
. Here, we consider the step size to have a Pareto tail, i.e.
$p\in(\nu(A),1-\nu(A))$
. Here, we consider the step size to have a Pareto tail, i.e.
![]() $\mathbb{P}(X>x)\sim \kappa x^{-\alpha}$
as
$\mathbb{P}(X>x)\sim \kappa x^{-\alpha}$
as
![]() $x\rightarrow\infty$
for some constants
$x\rightarrow\infty$
for some constants
![]() $\kappa>0$
and
$\kappa>0$
and
![]() $\alpha>2$
. We are going to show that if
$\alpha>2$
. We are going to show that if
![]() $b<B$
then
$b<B$
then
![]() $\lim_{n\rightarrow\infty}\frac{1}{\log n}\log\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)=-\frac{\alpha}{2}$
. Furthermore, if
$\lim_{n\rightarrow\infty}\frac{1}{\log n}\log\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)=-\frac{\alpha}{2}$
. Furthermore, if
![]() $b=B$
and A is an unbounded set, the above still holds provided that
$b=B$
and A is an unbounded set, the above still holds provided that
![]() $0<p-\nu(A)<(1-\nu(A))/b$
.
$0<p-\nu(A)<(1-\nu(A))/b$
.
Proof. We start with the lower bound. By the continuity of
![]() $I_A(\!\cdot\!)$
at p, for every
$I_A(\!\cdot\!)$
at p, for every
![]() $\epsilon>0$
there exist
$\epsilon>0$
there exist
![]() $\eta, \delta>0$
such that, for some
$\eta, \delta>0$
such that, for some
![]() $|x|\leq I_A(p)+\epsilon$
,
$|x|\leq I_A(p)+\epsilon$
,
![]() $\inf_{y\in[x-\eta,x+\eta]}\nu(A-y)\geq p+\delta$
. Without loss of generality, we write
$\inf_{y\in[x-\eta,x+\eta]}\nu(A-y)\geq p+\delta$
. Without loss of generality, we write
![]() $A=\sum^h_{j=1}(a_j,b_j]$
. Set
$A=\sum^h_{j=1}(a_j,b_j]$
. Set
![]() $A(x,\eta)\,{:\!=}\,\sum^h_{j=1}\left(a_j-(x-\eta),b_j-(x+\eta)\right)$
,
$A(x,\eta)\,{:\!=}\,\sum^h_{j=1}\left(a_j-(x-\eta),b_j-(x+\eta)\right)$
,
![]() $A(\epsilon)\,{:\!=}\,\sum^h_{j=1}\left(a_j+\epsilon,b_j-\epsilon\right)$
. Obviously, we can choose
$A(\epsilon)\,{:\!=}\,\sum^h_{j=1}\left(a_j+\epsilon,b_j-\epsilon\right)$
. Obviously, we can choose
![]() $\epsilon, \eta$
small enough such that
$\epsilon, \eta$
small enough such that
![]() $\nu(A(x,\eta))>p+\frac{\delta}{2}$
,
$\nu(A(x,\eta))>p+\frac{\delta}{2}$
,
![]() $\nu(A(\epsilon))>\nu(A)-\frac{\delta}{2}$
. Set
$\nu(A(\epsilon))>\nu(A)-\frac{\delta}{2}$
. Set
![]() $\mathcal{E}\,{:\!=}\,\big\{\xi\in\mathcal{M} \,{:}\, \xi=\sum^b_{i=1}\delta_{{x_i}\sqrt{n}}$
, where
$\mathcal{E}\,{:\!=}\,\big\{\xi\in\mathcal{M} \,{:}\, \xi=\sum^b_{i=1}\delta_{{x_i}\sqrt{n}}$
, where
![]() $x_1\in(x-\eta,x+\eta)$
,
$x_1\in(x-\eta,x+\eta)$
,
![]() $x_i\in(-\epsilon,\epsilon)$
,
$x_i\in(-\epsilon,\epsilon)$
,
![]() $i=2, \ldots, b\big\}$
. By the Markov property,
$i=2, \ldots, b\big\}$
. By the Markov property,
![]() $\mathbb{P}(\bar{Z}_{n}(\sqrt n A)\geq p)\geq\int_\mathcal{E} \mathbb{P}\big(\bar{Z}^{\xi}_{n-1}(\sqrt n A)\geq p\big)\mathbb{P}(Z_1\in \textrm{d}\xi)$
. For every
$\mathbb{P}(\bar{Z}_{n}(\sqrt n A)\geq p)\geq\int_\mathcal{E} \mathbb{P}\big(\bar{Z}^{\xi}_{n-1}(\sqrt n A)\geq p\big)\mathbb{P}(Z_1\in \textrm{d}\xi)$
. For every
![]() $\xi\in \mathcal{E}$
, it is easy to see that
$\xi\in \mathcal{E}$
, it is easy to see that
![]() $A-x_1\supset A(x,\eta)$
,
$A-x_1\supset A(x,\eta)$
,
![]() $A-x_i\supset A(\epsilon)$
,
$A-x_i\supset A(\epsilon)$
,
![]() $i=2, \ldots, b$
. Hence,
$i=2, \ldots, b$
. Hence,
 \begin{align} \mathbb{P}(\bar{Z}_{n}&(\sqrt n A) \geq p) \geq \int_\mathcal{E}\mathbb{P}\left(\bar{Z}^{\xi}_{n-1}(\sqrt nA)\geq p\right)\mathbb{P}(Z_1\in \textrm{d}\xi)\nonumber\\[2pt] & \geq \int_\mathcal{E} \mathbb{P}\left(\frac{Z^{1}_{n-1}(\sqrt n A(x,\eta))+\sum^b_{i=2}Z^{i}_{n-1}(\sqrt n A(\epsilon))}{\sum^b_{i=1}|Z^{i}_{n-1}|}\geq p\right)\mathbb{P}(Z_1\in \textrm{d}\xi)\nonumber\\[2pt] & = \mathbb{P}\left(\frac{Z^{1}_{n-1}(\sqrt n A(x,\eta))+\sum^b_{i=2}Z^{i}_{n-1}(\sqrt n A(\epsilon))}{\sum^b_{i=1}|Z^{i}_{n-1}|}\geq p\right)\mathbb{P}(Z_1\in \mathcal{E}), \end{align}
\begin{align} \mathbb{P}(\bar{Z}_{n}&(\sqrt n A) \geq p) \geq \int_\mathcal{E}\mathbb{P}\left(\bar{Z}^{\xi}_{n-1}(\sqrt nA)\geq p\right)\mathbb{P}(Z_1\in \textrm{d}\xi)\nonumber\\[2pt] & \geq \int_\mathcal{E} \mathbb{P}\left(\frac{Z^{1}_{n-1}(\sqrt n A(x,\eta))+\sum^b_{i=2}Z^{i}_{n-1}(\sqrt n A(\epsilon))}{\sum^b_{i=1}|Z^{i}_{n-1}|}\geq p\right)\mathbb{P}(Z_1\in \textrm{d}\xi)\nonumber\\[2pt] & = \mathbb{P}\left(\frac{Z^{1}_{n-1}(\sqrt n A(x,\eta))+\sum^b_{i=2}Z^{i}_{n-1}(\sqrt n A(\epsilon))}{\sum^b_{i=1}|Z^{i}_{n-1}|}\geq p\right)\mathbb{P}(Z_1\in \mathcal{E}), \end{align}
where
![]() $Z^{i}_{n-1}(\!\cdot\!)$
,
$Z^{i}_{n-1}(\!\cdot\!)$
,
![]() $1\leq i\leq b$
, are i.i.d. copies of
$1\leq i\leq b$
, are i.i.d. copies of
![]() $Z_{n-1}(\!\cdot\!)$
. Since
$Z_{n-1}(\!\cdot\!)$
. Since
![]() $\bar{Z}_{n}(\sqrt n A)\rightarrow \nu(A)$
and
$\bar{Z}_{n}(\sqrt n A)\rightarrow \nu(A)$
and
![]() $|Z_n|m^{-n}\rightarrow W$
almost surely, we have, as
$|Z_n|m^{-n}\rightarrow W$
almost surely, we have, as
![]() $n\to\infty$
,
$n\to\infty$
,
 \begin{align} & \frac{Z^{1}_{n-1}(\sqrt n A(x,\eta))+\sum^b_{i=2}Z^{i}_{n-1}(\sqrt n A(\epsilon))}{\sum^b_{i=1}|Z^{i}_{n-1}|}\nonumber\\[2pt] &\qquad\qquad\qquad\qquad\qquad \longrightarrow \frac{\sum^b_{i=2}\nu(A(\epsilon))W_i+\nu(A(x,\eta))W_1}{\sum^b_{i=1}W_i} \qquad \mathbb{P}\textrm{-a.s.}, \end{align}
\begin{align} & \frac{Z^{1}_{n-1}(\sqrt n A(x,\eta))+\sum^b_{i=2}Z^{i}_{n-1}(\sqrt n A(\epsilon))}{\sum^b_{i=1}|Z^{i}_{n-1}|}\nonumber\\[2pt] &\qquad\qquad\qquad\qquad\qquad \longrightarrow \frac{\sum^b_{i=2}\nu(A(\epsilon))W_i+\nu(A(x,\eta))W_1}{\sum^b_{i=1}W_i} \qquad \mathbb{P}\textrm{-a.s.}, \end{align}
where
![]() $W_i$
,
$W_i$
,
![]() $1\leq i\leq b$
, are i.i.d. copies of W. If
$1\leq i\leq b$
, are i.i.d. copies of W. If
![]() $b<B$
, then
$b<B$
, then
![]() $W_i$
has a continuous density on
$W_i$
has a continuous density on
![]() $(0,+\infty)$
(see [Reference Athreya and Ney4, Chapter II, Lemma 2]). In this case, by the dominated convergence theorem and (37),
$(0,+\infty)$
(see [Reference Athreya and Ney4, Chapter II, Lemma 2]). In this case, by the dominated convergence theorem and (37),
 \begin{equation} \lim\limits_{n\rightarrow\infty}\mathbb{P}\left(\frac{Z^{1}_{n-1}(\sqrt n A(x,\eta))+\sum^b_{i=2}Z^{i}_{n-1}(\sqrt n A(\epsilon))}{\sum^b_{i=1}|Z^{i}_{n-1}|}\geq p\right)\,{=\!:}\,C(\epsilon,\eta,x)>0. \end{equation}
\begin{equation} \lim\limits_{n\rightarrow\infty}\mathbb{P}\left(\frac{Z^{1}_{n-1}(\sqrt n A(x,\eta))+\sum^b_{i=2}Z^{i}_{n-1}(\sqrt n A(\epsilon))}{\sum^b_{i=1}|Z^{i}_{n-1}|}\geq p\right)\,{=\!:}\,C(\epsilon,\eta,x)>0. \end{equation}
Since
![]() $\mathbb{P}(X>x)\sim\kappa x^{-\alpha}$
, there exists a constant
$\mathbb{P}(X>x)\sim\kappa x^{-\alpha}$
, there exists a constant
![]() $C(\kappa,x,\epsilon,\eta)\,{=\!:}\, C_7>0$
such that, for n large enough,
$C(\kappa,x,\epsilon,\eta)\,{=\!:}\, C_7>0$
such that, for n large enough,
Plugging (38) and (39) into (36) yields, for n large enough,
![]() $\mathbb{P}(\bar{Z}_{n}(\sqrt n A)\geq p)\geq 0.9C(\epsilon,\eta,x)C_7p_bn^{-\alpha/2}$
, which implies the desired lower bound if
$\mathbb{P}(\bar{Z}_{n}(\sqrt n A)\geq p)\geq 0.9C(\epsilon,\eta,x)C_7p_bn^{-\alpha/2}$
, which implies the desired lower bound if
![]() $b<B$
.
$b<B$
.
If
![]() $b=B$
and A is unbounded, without loss of generality we assume
$b=B$
and A is unbounded, without loss of generality we assume
![]() $A=(a,+\infty)$
. Set
$A=(a,+\infty)$
. Set
![]() $\mathcal{E'}\,{:\!=}\,\big\{\xi\in\mathcal{M} \,{:}\, \xi=\sum^b_{i=1}\delta_{{x_i}\sqrt{n}}$
, where
$\mathcal{E'}\,{:\!=}\,\big\{\xi\in\mathcal{M} \,{:}\, \xi=\sum^b_{i=1}\delta_{{x_i}\sqrt{n}}$
, where
![]() $x_1\in[t\sqrt n,+\infty)$
,
$x_1\in[t\sqrt n,+\infty)$
,
![]() $x_i\in(-\epsilon,\epsilon)$
,
$x_i\in(-\epsilon,\epsilon)$
,
![]() $i=2, \ldots, b\big\}$
, where t is some positive constant. Using similar arguments to above, we obtain
$i=2, \ldots, b\big\}$
, where t is some positive constant. Using similar arguments to above, we obtain
 \begin{equation*} \mathbb{P}(\bar{Z}_{n}(\sqrt n A)\geq p)\geq\mathbb{P}\left(\frac{Z^{1}_{n-1}(\sqrt n(a-t,+\infty))+\sum^b_{i=2}Z^{i}_{n-1}(\sqrt n A(\epsilon))}{\sum^b_{i=1}Z^{i}_{n-1}}\geq p\right)\mathbb{P}(Z_1\in \mathcal{E'}). \end{equation*}
\begin{equation*} \mathbb{P}(\bar{Z}_{n}(\sqrt n A)\geq p)\geq\mathbb{P}\left(\frac{Z^{1}_{n-1}(\sqrt n(a-t,+\infty))+\sum^b_{i=2}Z^{i}_{n-1}(\sqrt n A(\epsilon))}{\sum^b_{i=1}Z^{i}_{n-1}}\geq p\right)\mathbb{P}(Z_1\in \mathcal{E'}). \end{equation*}
For any
![]() $p\in\big(\nu(A),\nu(A)+\frac{1-\nu(A)}{b}\big)$
, there exists
$p\in\big(\nu(A),\nu(A)+\frac{1-\nu(A)}{b}\big)$
, there exists
![]() $\delta'>0$
such that
$\delta'>0$
such that
If we choose
![]() $\epsilon$
small enough and t large enough, then
$\epsilon$
small enough and t large enough, then
![]() $\nu(A(\epsilon))\geq \nu(A)-\delta'$
,
$\nu(A(\epsilon))\geq \nu(A)-\delta'$
,
![]() $\nu((a-t,+\infty))>1-\delta'$
. This, together with (37) and (40), shows that, almost surely,
$\nu((a-t,+\infty))>1-\delta'$
. This, together with (37) and (40), shows that, almost surely,
 \begin{equation*}\frac{Z^{1}_{n-1}(\sqrt n(a-t,+\infty))+\sum^b_{i=2}Z^{i}_{n-1}(\sqrt n A(\epsilon))}{\sum^b_{i=1}|Z^{i}_{n-1}|}\rightarrow \frac{(b-1)\nu(A(\epsilon))+\nu((a-t,+\infty))}{b}>p,\end{equation*}
\begin{equation*}\frac{Z^{1}_{n-1}(\sqrt n(a-t,+\infty))+\sum^b_{i=2}Z^{i}_{n-1}(\sqrt n A(\epsilon))}{\sum^b_{i=1}|Z^{i}_{n-1}|}\rightarrow \frac{(b-1)\nu(A(\epsilon))+\nu((a-t,+\infty))}{b}>p,\end{equation*}
which implies the desired lower bound.
For the upper bound, set
![]() $t_n\,{:\!=}\,\lfloor c\log n\rfloor$
for some
$t_n\,{:\!=}\,\lfloor c\log n\rfloor$
for some
![]() $c>0$
. By copying the arguments from (31) to (32), there exist constants
$c>0$
. By copying the arguments from (31) to (32), there exist constants
![]() $\delta, \eta >0$
such that, for n large enough,
$\delta, \eta >0$
such that, for n large enough,
![]() $\mathbb{P}\left(\bar{Z}_{n}(\sqrt n A)\geq p\right)\leq \frac{4}{\delta}\mathbb{P}\left(S_{t_n}\geq(I_A(p)-\eta)\sqrt n\right)+ C_1\mathbb{E}\big[|Z_{t_n}|^{-(\beta-1)}\big]$
, where the last inequality follows from Lemma 4. For the first term of the right-hand side of the latter inequality, by (8), there exists a constant
$\mathbb{P}\left(\bar{Z}_{n}(\sqrt n A)\geq p\right)\leq \frac{4}{\delta}\mathbb{P}\left(S_{t_n}\geq(I_A(p)-\eta)\sqrt n\right)+ C_1\mathbb{E}\big[|Z_{t_n}|^{-(\beta-1)}\big]$
, where the last inequality follows from Lemma 4. For the first term of the right-hand side of the latter inequality, by (8), there exists a constant
![]() $C_8>0$
depending on c,
$C_8>0$
depending on c,
![]() $\kappa$
,
$\kappa$
,
![]() $\alpha$
, and
$\alpha$
, and
![]() $\eta$
such that, for n large enough,
$\eta$
such that, for n large enough,
![]() $\frac{4}{\delta}\mathbb{P}\left(S_{t_n}\geq(I_A(p)-\eta)\sqrt n\right) \leq C_8 n^{-\frac{\alpha}{2}}\log n$
. For the second term, by Lemma 2, for n large enough,
$\frac{4}{\delta}\mathbb{P}\left(S_{t_n}\geq(I_A(p)-\eta)\sqrt n\right) \leq C_8 n^{-\frac{\alpha}{2}}\log n$
. For the second term, by Lemma 2, for n large enough,
![]() $\mathbb{E}\left[|Z_{t_n}|^{-(\beta-1)}\right]\leq 2C_0\left(m^{-t_n(\beta-1)}+p_1^{t_n}\right)$
. Hence, for n large enough,
$\mathbb{E}\left[|Z_{t_n}|^{-(\beta-1)}\right]\leq 2C_0\left(m^{-t_n(\beta-1)}+p_1^{t_n}\right)$
. Hence, for n large enough,
![]() $\mathbb{P}\left(\bar{Z}_{n}(\sqrt n A)\geq p\right)\leq C_8n^{-\frac{\alpha}{2}}\log n+2C_0\left(m^{-t_n(\beta-1)}+p_1^{t_n}\right)$
. Since
$\mathbb{P}\left(\bar{Z}_{n}(\sqrt n A)\geq p\right)\leq C_8n^{-\frac{\alpha}{2}}\log n+2C_0\left(m^{-t_n(\beta-1)}+p_1^{t_n}\right)$
. Since
![]() $t_n=\lfloor c\log n\rfloor$
, if we choose
$t_n=\lfloor c\log n\rfloor$
, if we choose
![]() $c>\frac{\alpha}{2(\beta-1)\log m}\vee\frac{\alpha}{-2\log p_1}$
then, for large n,
$c>\frac{\alpha}{2(\beta-1)\log m}\vee\frac{\alpha}{-2\log p_1}$
then, for large n,
![]() $\mathbb{P}\left(\bar{Z}_{n}(\sqrt n A)\geq p\right)\leq 2C_8n^{-\frac{\alpha}{2}}\log n$
. Thus, we have
$\mathbb{P}\left(\bar{Z}_{n}(\sqrt n A)\geq p\right)\leq 2C_8n^{-\frac{\alpha}{2}}\log n$
. Thus, we have
6. Proof of Theorem 4
In this subsection we assume that
![]() $I_A(p)=\infty$
,
$I_A(p)=\infty$
,
![]() $J_A(p)$
is continuous at p, and
$J_A(p)$
is continuous at p, and
![]() $\mathbb{E}\big[X^2\big]<\infty$
. We are going to prove that if
$\mathbb{E}\big[X^2\big]<\infty$
. We are going to prove that if
![]() $|Z_1|\sim \textrm{Pareto}(\beta)$
with some
$|Z_1|\sim \textrm{Pareto}(\beta)$
with some
![]() $\beta>1$
, then
$\beta>1$
, then
 \begin{equation*}\lim\limits_{n\rightarrow\infty}\frac{1}{n}\log\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)=\begin{cases}-J_A(p)(\beta-1)\log m, &0<\beta-1<\dfrac{-\log p_1}{\log m}; \\ \\[-7pt] J_A(p)\log{p_1}, &\beta-1\geq \dfrac{-\log p_1}{\log m},\end{cases}\end{equation*}
\begin{equation*}\lim\limits_{n\rightarrow\infty}\frac{1}{n}\log\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)=\begin{cases}-J_A(p)(\beta-1)\log m, &0<\beta-1<\dfrac{-\log p_1}{\log m}; \\ \\[-7pt] J_A(p)\log{p_1}, &\beta-1\geq \dfrac{-\log p_1}{\log m},\end{cases}\end{equation*}
and if
![]() $|Z_1|\sim \textrm{Weibull}(\beta)$
with some
$|Z_1|\sim \textrm{Weibull}(\beta)$
with some
![]() $\beta\in(0,1)$
, then
$\beta\in(0,1)$
, then
![]() $\lim_{n\rightarrow\infty}\frac{1}{n}\log\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)=J_A(p)\log{p_1}$
for
$\lim_{n\rightarrow\infty}\frac{1}{n}\log\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)=J_A(p)\log{p_1}$
for
![]() $p_1>0$
, and
$p_1>0$
, and
Proof. Considering the lower bound, we first examine
![]() $|Z_1|$
with a Pareto tail. If
$|Z_1|$
with a Pareto tail. If
![]() $\beta-1\geq \frac{-\log{p_1}}{\log m}$
then from [Reference Chen and He13, Lemma 3.4] we have
$\beta-1\geq \frac{-\log{p_1}}{\log m}$
then from [Reference Chen and He13, Lemma 3.4] we have
![]() $\liminf_{n\rightarrow\infty}\frac{1}{n}\log\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)\geq J_A(p)\log{p_1}$
. Now we shall consider the case of
$\liminf_{n\rightarrow\infty}\frac{1}{n}\log\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)\geq J_A(p)\log{p_1}$
. Now we shall consider the case of
![]() $0<\beta-1<\frac{-\log{p_1}}{\log m}$
. Since
$0<\beta-1<\frac{-\log{p_1}}{\log m}$
. Since
![]() $J_A(p)$
is continuous at p, for any
$J_A(p)$
is continuous at p, for any
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $\delta>0$
such that, for
$\delta>0$
such that, for
![]() $r\,{:\!=}\,J_A(p+2\delta)\in(0,1)$
, we have
$r\,{:\!=}\,J_A(p+2\delta)\in(0,1)$
, we have
![]() $|r-J_A(p)|<\epsilon$
. Moreover, by the definition of
$|r-J_A(p)|<\epsilon$
. Moreover, by the definition of
![]() $J_A(p)$
, there exists
$J_A(p)$
, there exists
![]() $x\in\mathbb{R}$
such that
$x\in\mathbb{R}$
such that
So, for any small
![]() $\eta>0$
,
$\eta>0$
,
 \begin{equation} \nu\left(\bigcap\limits_{y\in[x-\eta,x+\eta]}\frac{A-y}{\sqrt{1-r}\,}\right)\geq p+\delta. \end{equation}
\begin{equation} \nu\left(\bigcap\limits_{y\in[x-\eta,x+\eta]}\frac{A-y}{\sqrt{1-r}\,}\right)\geq p+\delta. \end{equation}
Set
![]() $t_n\,{:\!=}\,\lfloor rn\rfloor$
, and for large M set
$t_n\,{:\!=}\,\lfloor rn\rfloor$
, and for large M set
![]() $E\,{:\!=}\,\big\{$
there exists
$E\,{:\!=}\,\big\{$
there exists
![]() $u\in Z_{t_n}$
such that
$u\in Z_{t_n}$
such that
![]() $S_u\in[(x-\eta)\sqrt n,(x+\eta)\sqrt n]$
,
$S_u\in[(x-\eta)\sqrt n,(x+\eta)\sqrt n]$
,
![]() $|Z^{u}_{1}|>2M\sum_{v\neq u,v\in Z_{t_n}}|Z^{v}_{1}|\big\}$
. Similar to (18), from (41) and
$|Z^{u}_{1}|>2M\sum_{v\neq u,v\in Z_{t_n}}|Z^{v}_{1}|\big\}$
. Similar to (18), from (41) and
![]() $S_u\in[(x-\eta)\sqrt n,(x+\eta)\sqrt n]$
, we can choose
$S_u\in[(x-\eta)\sqrt n,(x+\eta)\sqrt n]$
, we can choose
![]() $\eta$
small enough such that
$\eta$
small enough such that
where
![]() $A(x,\eta)\,{:\!=}\,\sum^l_{i=1}\left(a_i-x+\eta,b_i-x-\eta\right).$
By [Reference Louidor and Perkins32, Lemma 2.2], it follows that
$A(x,\eta)\,{:\!=}\,\sum^l_{i=1}\left(a_i-x+\eta,b_i-x-\eta\right).$
By [Reference Louidor and Perkins32, Lemma 2.2], it follows that
This, combined with (42), shows that there exists a constant
![]() $C(M,r,x,\eta,\delta)>0$
such that, for
$C(M,r,x,\eta,\delta)>0$
such that, for
![]() $n>C(M,r,x,\eta,\delta)>0$
,
$n>C(M,r,x,\eta,\delta)>0$
,
![]() $\frac{1}{1+M^{-1}}\nu_{n-t_n}(\sqrt nA(x,\eta))>p+\frac{\delta}{8}$
, which plays the same role in this proof as (19) in Theorem 1. Using similar arguments to the proof of the lower bound in Theorem 1, there exists a constant
$\frac{1}{1+M^{-1}}\nu_{n-t_n}(\sqrt nA(x,\eta))>p+\frac{\delta}{8}$
, which plays the same role in this proof as (19) in Theorem 1. Using similar arguments to the proof of the lower bound in Theorem 1, there exists a constant
![]() $C_M>0$
such that, for n large enough,
$C_M>0$
such that, for n large enough,
 \begin{align} \mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p) &\geq C_M\mathbb{P}\left(E\right) \nonumber\\[3pt] &\geq C_M 0.9C_0m^{-t_n(\beta-1)}\nu_{t_n}\left([(x-\eta)\sqrt n,(x+\eta)\sqrt n]\right)\nonumber\\[3pt] &\geq 0.9^2C_MC_0C_9m^{-t_n(\beta-1)}, \end{align}
\begin{align} \mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p) &\geq C_M\mathbb{P}\left(E\right) \nonumber\\[3pt] &\geq C_M 0.9C_0m^{-t_n(\beta-1)}\nu_{t_n}\left([(x-\eta)\sqrt n,(x+\eta)\sqrt n]\right)\nonumber\\[3pt] &\geq 0.9^2C_MC_0C_9m^{-t_n(\beta-1)}, \end{align}
where the last inequality holds since
![]() $\lim_{n\rightarrow\infty}\nu_{t_n}\left([(x-\eta)\sqrt n,(x+\eta)\sqrt n]\right){=}C(r,x,\eta)\,{=\!:}\,C_9{>}0$
. Taking limits in (43) yields
$\lim_{n\rightarrow\infty}\nu_{t_n}\left([(x-\eta)\sqrt n,(x+\eta)\sqrt n]\right){=}C(r,x,\eta)\,{=\!:}\,C_9{>}0$
. Taking limits in (43) yields
![]() $\liminf_{n\rightarrow\infty}\frac{1}{n}\log\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)\geq-(J_A(p)+\epsilon)(\beta-1)\log m$
. Then, the desired lower bound follows by letting
$\liminf_{n\rightarrow\infty}\frac{1}{n}\log\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)\geq-(J_A(p)+\epsilon)(\beta-1)\log m$
. Then, the desired lower bound follows by letting
![]() $\epsilon \rightarrow 0$
.
$\epsilon \rightarrow 0$
.
We now consider the upper bound. For
![]() $\epsilon \in(0,J_A(p))$
, set
$\epsilon \in(0,J_A(p))$
, set
![]() $t_n\,{:\!=}\,\lfloor(J_A(p)-\epsilon)n\rfloor$
. By the definition of
$t_n\,{:\!=}\,\lfloor(J_A(p)-\epsilon)n\rfloor$
. By the definition of
![]() $J_A(p)$
there exists
$J_A(p)$
there exists
![]() $\delta>0$
such that, for
$\delta>0$
such that, for
![]() $\epsilon'\in[\epsilon,2\epsilon]$
,
$\epsilon'\in[\epsilon,2\epsilon]$
,
 \begin{equation} \sup_{y\in\mathbb{R}}\nu\left(\frac{A-y}{\sqrt{1-J_A(p)+\epsilon'}\,}\right)\leq p-\delta. \end{equation}
\begin{equation} \sup_{y\in\mathbb{R}}\nu\left(\frac{A-y}{\sqrt{1-J_A(p)+\epsilon'}\,}\right)\leq p-\delta. \end{equation}
Thus, for any
![]() $\xi\in\mathcal{M}$
,
$\xi\in\mathcal{M}$
,
 \begin{align*} \frac{1}{|\xi|}\sum_{y\in\xi}\nu_{n-t_n}(\sqrt nA-S_y)+\frac{\delta}{2}&\leq\frac{1}{|\xi|}\sum_{y\in\xi}\nu\left(\frac{\sqrt n}{\sqrt{n-t_n}\,}A-\frac{S_y}{\sqrt{n-t_n}\,}\right)+\frac{3\delta}{4}\\ &\leq p-\frac{3\delta}{4}+\frac{3\delta}{4} =p,\nonumber \end{align*}
\begin{align*} \frac{1}{|\xi|}\sum_{y\in\xi}\nu_{n-t_n}(\sqrt nA-S_y)+\frac{\delta}{2}&\leq\frac{1}{|\xi|}\sum_{y\in\xi}\nu\left(\frac{\sqrt n}{\sqrt{n-t_n}\,}A-\frac{S_y}{\sqrt{n-t_n}\,}\right)+\frac{3\delta}{4}\\ &\leq p-\frac{3\delta}{4}+\frac{3\delta}{4} =p,\nonumber \end{align*}
where the first inequality follows from the generalized central limit theorem, and the second inequality follows from (44) and the fact that
![]() $g(u,v)=\nu(uA+v)$
is a continuous function on
$g(u,v)=\nu(uA+v)$
is a continuous function on
![]() $\mathbb{R}^2$
. Thus, for n large enough,
$\mathbb{R}^2$
. Thus, for n large enough,
Hence, by Lemma 4, there exists
![]() $C_1>0$
such that, for large n,
$C_1>0$
such that, for large n,
![]() $\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)\leq C_1\mathbb{E}\left[|Z_{t_n}|^{-(\beta-1)}\right]$
. As a consequence, the upper bound follows by Lemma 2.
$\mathbb{P}(\bar{Z}_n(\sqrt nA)\geq p)\leq C_1\mathbb{E}\left[|Z_{t_n}|^{-(\beta-1)}\right]$
. As a consequence, the upper bound follows by Lemma 2.
If
![]() $|Z_1|$
has a Weibull tail, similar arguments to those above, together with Lemmas 3 and 5, get the desired results.
$|Z_1|$
has a Weibull tail, similar arguments to those above, together with Lemmas 3 and 5, get the desired results.
Acknowledgement
I would like to thank my supervisor Hui He for useful discussions and advice while working on this subject.
Funding Information
There are no funding bodies to thank relating to the creation of this article.
Competing Interests
There were no competing interests to declare which arose during the preparation or publication process of this article.