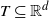1. Introduction
Let
![]() $X=\{ X_t, t\in T \}$
be a stationary random field on an unbounded index subset T of
$X=\{ X_t, t\in T \}$
be a stationary random field on an unbounded index subset T of
![]() $\mathbb{R}^d$
,
$\mathbb{R}^d$
,
![]() $d\ge 1$
, defined on an abstract probability space
$d\ge 1$
, defined on an abstract probability space
![]() $(\Omega, \mathcal{F}, \mathbb P)$
. If
$(\Omega, \mathcal{F}, \mathbb P)$
. If
![]() $X_0$
is square-integrable then the classical definition of long range dependence is
$X_0$
is square-integrable then the classical definition of long range dependence is
where
![]() $C_X(t)=\textrm{cov}(X_0, X_t)$
,
$C_X(t)=\textrm{cov}(X_0, X_t)$
,
![]() $t\in T$
. There are also other definitions, for example in terms of spectral density of X being unbounded at zero, growth comparison of partial sums (Allan sample variance), the order of the variance of sums going to infinity, etc.; see the recent reviews [Reference Giraitis, Koul and Surgailis15], [Reference Beran, Feng, Ghosh and Kulik5], and [Reference Samorodnitsky35] for processes and [Reference Lavancier20] for random fields. These approaches are not equivalent.
$t\in T$
. There are also other definitions, for example in terms of spectral density of X being unbounded at zero, growth comparison of partial sums (Allan sample variance), the order of the variance of sums going to infinity, etc.; see the recent reviews [Reference Giraitis, Koul and Surgailis15], [Reference Beran, Feng, Ghosh and Kulik5], and [Reference Samorodnitsky35] for processes and [Reference Lavancier20] for random fields. These approaches are not equivalent.
More importantly, there is no unified approach to defining the long memory property if X is heavy-tailed, i.e. with infinite variance. Many authors use the phenomenon of phase transition in certain parameters of the field (such as the stability index, Hurst index, heaviness of the tails, etc.) to consider the different limiting behaviour. To give just a few examples, we mention [Reference Sly and Heyde40] for the subordinated heavy-tailed Gaussian time series whereas [Reference Samorodnitsky34], [Reference Roy and Samorodnitsky32], [Reference Roy31], [Reference Owada and Samorodnitsky27], and [Reference Samorodnitsky and Wang37] consider the extreme value behaviour of partial maxima of stable random processes and fields and a connection with their ergodic properties. In [Reference Dehling and Philipp12, page 76], the short or long memory for stationary time series is defined by using different limits in functional limit theorems. The papers [Reference Damarackas and Paulauskas10] and [Reference Paulauskas28] analyse different measures of dependence (such as
![]() $\alpha$
-spectral covariance) for linear random fields with infinite variance lying in the domain of attraction of a stable law. These are used to define various types of memory and prove corresponding limit theorems for partial sums.
$\alpha$
-spectral covariance) for linear random fields with infinite variance lying in the domain of attraction of a stable law. These are used to define various types of memory and prove corresponding limit theorems for partial sums.
The main goal of our paper is to give a simple, uniform view of long range dependence that applies to any stationary (light- or heavy-tailed) random field X; see Definition 1. In Section 3.2 we show that all rapidly mixing random fields are short range dependent in the sense of the new definition. No moment assumptions are needed there. In Section 3.3 we give sufficient conditions for a subordinated Gaussian (possibly heavy-tailed) random field to be short or long range dependent. We show that the transition from short to long memory occurs at the same boundary for both finite and infinite variance random fields; see Theorem 2 and Example 1. This cannot be achieved using the classical definitions based on second-order properties. In the next section the same is done for stochastic volatility random fields of the form
![]() $X_t=G(Y_t)Z_t$
. Different sources of long range dependence are described. Conditions for long or short memory of
$X_t=G(Y_t)Z_t$
. Different sources of long range dependence are described. Conditions for long or short memory of
![]() $\alpha$
-stable moving averages and certain max-stable processes are discussed in the forthcoming paper [Reference Makogin, Oesting, Rapp and Spodarev25].
$\alpha$
-stable moving averages and certain max-stable processes are discussed in the forthcoming paper [Reference Makogin, Oesting, Rapp and Spodarev25].
As indicated above, one can approach long memory from two different perspectives: through the distributional properties of the process or the limiting behaviour of suitable statistics. Our definition falls into the first category. Thus, as the next step, we attempt to link the definition with limit theorems. In this context, the appropriate statistic to study appears to be the volume of level sets of the field. This is done in Section 4. First, we consider subordinated Gaussian random fields and show the agreement between our definition and the limiting behaviour. See Section 4.1.1. In the following section we indicate that our definition is not suitable for capturing the limiting behaviour of the empirical mean. In Section 4.2 we consider the corresponding problems for random volatility models. In order to do so, we have to develop limiting theory for integral functionals of random volatility models, including the case of limit theorems for the volume of level sets of X. These results are of independent interest.
For better readability, proofs of the most of results are moved to the Appendix.
2. Preliminaries
Recall that T is an unbounded subset of
![]() $\mathbb{R}^d$
. Let
$\mathbb{R}^d$
. Let
![]() $\mathbb N_0=\mathbb N\cup \{ 0 \}$
, and let
$\mathbb N_0=\mathbb N\cup \{ 0 \}$
, and let
![]() $\nu_d(\cdot)$
be the d-dimensional Lebesgue measure. We let
$\nu_d(\cdot)$
be the d-dimensional Lebesgue measure. We let
![]() $\mathbb{R}_\pm$
denote either
$\mathbb{R}_\pm$
denote either
![]() $\mathbb{R}_+=[0,+\infty)$
or
$\mathbb{R}_+=[0,+\infty)$
or
![]() $\mathbb{R}_-=(-\infty,0]$
, depending on the context. For instance,
$\mathbb{R}_-=(-\infty,0]$
, depending on the context. For instance,
![]() $G\colon \mathbb{R}\to \mathbb{R}_\pm$
means that G maps
$G\colon \mathbb{R}\to \mathbb{R}_\pm$
means that G maps
![]() $\mathbb{R}$
either to
$\mathbb{R}$
either to
![]() $\mathbb{R}_+$
or to
$\mathbb{R}_+$
or to
![]() $\mathbb{R}_-$
. Let
$\mathbb{R}_-$
. Let
![]() $\|\cdot\|$
be a norm in the Euclidean space
$\|\cdot\|$
be a norm in the Euclidean space
![]() $\mathbb{R}^d$
. For two functions
$\mathbb{R}^d$
. For two functions
![]() $f,g\colon \mathbb{R}\to \mathbb{R} $
we write
$f,g\colon \mathbb{R}\to \mathbb{R} $
we write
![]() $f(x) \sim g(x)$
,
$f(x) \sim g(x)$
,
![]() $x\to a$
if
$x\to a$
if
![]() $\lim_{x\to a} f(x)/g(x)=1$
, where
$\lim_{x\to a} f(x)/g(x)=1$
, where
![]() $g(x)\neq 0$
in a neighbourhood of a. Let
$g(x)\neq 0$
in a neighbourhood of a. Let
![]() $\langle f, g\rangle = \int_{\mathbb{R}} f(x)g(x) \, {\textrm{d}} x$
be the inner product in the space
$\langle f, g\rangle = \int_{\mathbb{R}} f(x)g(x) \, {\textrm{d}} x$
be the inner product in the space
![]() $L^2(\mathbb{R})$
of square-integrable functions. Further, we shall make use of the inner product
$L^2(\mathbb{R})$
of square-integrable functions. Further, we shall make use of the inner product
![]() $\langle f, g\rangle_{\varphi} = \int_{\mathbb{R}} f(x)g(x)\varphi(x) \, {\textrm{d}} x$
in the space
$\langle f, g\rangle_{\varphi} = \int_{\mathbb{R}} f(x)g(x)\varphi(x) \, {\textrm{d}} x$
in the space
![]() $L^2_{\varphi}(\mathbb{R})$
of functions which are square-integrable with the weight
$L^2_{\varphi}(\mathbb{R})$
of functions which are square-integrable with the weight
![]() $\varphi$
, where
$\varphi$
, where
![]() $\varphi$
is the standard normal density. For a finite measure
$\varphi$
is the standard normal density. For a finite measure
![]() $\mu$
on
$\mu$
on
![]() $\mathbb{R}$
, let
$\mathbb{R}$
, let
![]() $\textrm{supp} (\mu)$
be its support, i.e. the complement of the largest measurable subset of
$\textrm{supp} (\mu)$
be its support, i.e. the complement of the largest measurable subset of
![]() $\mu$
-measure zero in
$\mu$
-measure zero in
![]() $\mathbb{R}$
.
$\mathbb{R}$
.
Let
![]() $(\Omega, \mathcal{F}, \mathbb P)$
be a probability space. We say that
$(\Omega, \mathcal{F}, \mathbb P)$
be a probability space. We say that
![]() $\{ X_t, \; t\in T \}$
is white noise if it consists of independent and identically distributed (i.i.d.) random variables
$\{ X_t, \; t\in T \}$
is white noise if it consists of independent and identically distributed (i.i.d.) random variables
![]() $X_t$
.
$X_t$
.
For any random variable X, let
![]() $F_X(x)=\mathbb P(X\le x)$
and
$F_X(x)=\mathbb P(X\le x)$
and
![]() $\bar{F}_X(x)=1-F_X(x)$
be the cumulative distribution function and the tail distribution function of X, respectively. Let
$\bar{F}_X(x)=1-F_X(x)$
be the cumulative distribution function and the tail distribution function of X, respectively. Let
![]() $F_{X,Y}(x,y)=\mathbb P(X\le x, Y\le y)$
,
$F_{X,Y}(x,y)=\mathbb P(X\le x, Y\le y)$
,
![]() $x,y\in \mathbb{R}$
be the bivariate distribution function of a random vector (X,Y). Later on we make use of the formula
$x,y\in \mathbb{R}$
be the bivariate distribution function of a random vector (X,Y). Later on we make use of the formula
for any
![]() $\sigma$
-algebra
$\sigma$
-algebra
![]() $\mathcal{A}\subset \mathcal{F}$
.
$\mathcal{A}\subset \mathcal{F}$
.
A random field
![]() $X=\{X_t,t\in T\}$
is called associated (A) if
$X=\{X_t,t\in T\}$
is called associated (A) if
for any finite subset
![]() $I\subset T$
and for any bounded coordinate-wise non-decreasing Borel functions
$I\subset T$
and for any bounded coordinate-wise non-decreasing Borel functions
![]() $f,g\colon \mathbb{R}^{|I|}\rightarrow\mathbb{R}$
, where
$f,g\colon \mathbb{R}^{|I|}\rightarrow\mathbb{R}$
, where
![]() $X_I=\{X_t,t\in I \}$
. X is called positively associated (PA) or negatively associated (NA) if
$X_I=\{X_t,t\in I \}$
. X is called positively associated (PA) or negatively associated (NA) if
respectively, for all finite disjoint subsets
![]() $I,J\subset T$
, and for any bounded coordinate-wise non-decreasing Borel functions
$I,J\subset T$
, and for any bounded coordinate-wise non-decreasing Borel functions
![]() $f\colon \mathbb{R}^{|I|}\rightarrow\mathbb{R}$
,
$f\colon \mathbb{R}^{|I|}\rightarrow\mathbb{R}$
,
![]() $g\colon \mathbb{R}^{|J|}\rightarrow\mathbb{R}$
; see e.g. [Reference Bulinski and Shashkin7].
$g\colon \mathbb{R}^{|J|}\rightarrow\mathbb{R}$
; see e.g. [Reference Bulinski and Shashkin7].
We use the notation
![]() $B\sim S_{\alpha} (\sigma,1,0 ) $
for an
$B\sim S_{\alpha} (\sigma,1,0 ) $
for an
![]() $\alpha$
-stable subordinator B with scale parameter
$\alpha$
-stable subordinator B with scale parameter
![]() $\sigma>0$
; see [Reference Samorodnitsky and Taqqu36].
$\sigma>0$
; see [Reference Samorodnitsky and Taqqu36].
3. Long range dependence
Consider a real-valued stationary random field
![]() $X=\{X_t,t\in T\}$
. Introduce
$X=\{X_t,t\in T\}$
. Introduce
It is always defined, as the indicators involved are bounded functions.
Definition 1. A random field
![]() $X=\{X_t,t\in T\}$
is called short range dependent (s.r.d.) if, for any finite measure
$X=\{X_t,t\in T\}$
is called short range dependent (s.r.d.) if, for any finite measure
![]() $\mu$
on
$\mu$
on
![]() $\mathbb{R}$
,
$\mathbb{R}$
,
X is long range dependent (l.r.d.) if there exists a finite measure
![]() $\mu$
on
$\mu$
on
![]() $\mathbb{R}$
such that
$\mathbb{R}$
such that
![]() $\sigma^2_{\mu,X}=+\infty.$
For discrete parameter random fields (say, if
$\sigma^2_{\mu,X}=+\infty.$
For discrete parameter random fields (say, if
![]() $T\subseteq \mathbb Z^d$
), the
$T\subseteq \mathbb Z^d$
), the
![]() $\int_T \,{\textrm{d}} t$
above should be replaced by
$\int_T \,{\textrm{d}} t$
above should be replaced by
![]() $\sum_{t\in T\colon t\neq 0}$
.
$\sum_{t\in T\colon t\neq 0}$
.
3.1. Motivation
Assume that X is stationary with marginal distribution function
![]() $F_X(x)=\mathbb P(X_0\le x)$
,
$F_X(x)=\mathbb P(X_0\le x)$
,
![]() $x\in\mathbb{R}$
, covariance function
$x\in\mathbb{R}$
, covariance function
![]() $C(t)=\textrm{cov}(X_0, X_t)$
,
$C(t)=\textrm{cov}(X_0, X_t)$
,
![]() $t\in T$
, and moreover
$t\in T$
, and moreover
Examples of X with this property are all PA or NA random functions. Applying [Reference Lehmann21, Lemma 2], we have (the equality is originally attributed to Hoeffding (1940))
Then X is long range dependent if
which agrees with the classical definition.
However, in Definition 1 we integrate
![]() $|\textrm{cov}_X(t,u,v)|$
with respect to a finite measure
$|\textrm{cov}_X(t,u,v)|$
with respect to a finite measure
![]() $\mu\times\mu$
instead of Lebesgue measure
$\mu\times\mu$
instead of Lebesgue measure
![]() ${\textrm{d}} u \, {\textrm{d}} v$
. First, for infinite variance the right-hand side of (4) is often infinite, regardless of any dependence structure. As such, the classical definition of long memory is irrelevant in the infinite variance case. Second, our definition will have a natural link with the asymptotic behaviour of volumes of excursions of X above levels u, v. Recall the functional central limit theorem (CLT) for normed volumes of excursion sets of X at level u proved in [Reference Meschenmoser and Shashkin26] (see also [Reference Spodarev41, Theorem 9] for a generalization of this result to fields without a finite second moment). Namely, for a large class of weakly dependent stationary random fields X on
${\textrm{d}} u \, {\textrm{d}} v$
. First, for infinite variance the right-hand side of (4) is often infinite, regardless of any dependence structure. As such, the classical definition of long memory is irrelevant in the infinite variance case. Second, our definition will have a natural link with the asymptotic behaviour of volumes of excursions of X above levels u, v. Recall the functional central limit theorem (CLT) for normed volumes of excursion sets of X at level u proved in [Reference Meschenmoser and Shashkin26] (see also [Reference Spodarev41, Theorem 9] for a generalization of this result to fields without a finite second moment). Namely, for a large class of weakly dependent stationary random fields X on
![]() $\mathbb{R}^d$
, the function
$\mathbb{R}^d$
, the function
is the covariance function of the centred Gaussian process which appears as a limit of
in
![]() $\mathcal{D}(\mathbb{R})$
equipped with the
$\mathcal{D}(\mathbb{R})$
equipped with the
![]() $J_1$
Skorokhod topology. If, in particular, the random field is PA or NA, then by the continuous mapping theorem we have
$J_1$
Skorokhod topology. If, in particular, the random field is PA or NA, then by the continuous mapping theorem we have
as
![]() $n\to\infty$
for any finite measure
$n\to\infty$
for any finite measure
![]() $\mu$
with
$\mu$
with
![]() $\sigma^2_{\mu,X} $
as in Definition 1. So X is s.r.d. if the asymptotic covariance
$\sigma^2_{\mu,X} $
as in Definition 1. So X is s.r.d. if the asymptotic covariance
![]() $\sigma^2_{\mu,X} $
in the central limit theorem (6) is finite for any finite integration measure
$\sigma^2_{\mu,X} $
in the central limit theorem (6) is finite for any finite integration measure
![]() $\mu$
prescribing the choice of levels u. In contrast,
$\mu$
prescribing the choice of levels u. In contrast,
for
![]() $\mu=\delta_{\{ u_0 \}}$
means that a different normalization is needed in (5) and a non-Gaussian limit may arise.
$\mu=\delta_{\{ u_0 \}}$
means that a different normalization is needed in (5) and a non-Gaussian limit may arise.
Let us point out one possible interpretation of Definition 1 in a financial context. Assume
![]() $X=\{ X_t, t\in \mathbb Z\}$
to be a time series representing the stock price for which an American option at price
$X=\{ X_t, t\in \mathbb Z\}$
to be a time series representing the stock price for which an American option at price
![]() $u_0>0$
,
$u_0>0$
,
![]() $t\in [0,n]$
,
$t\in [0,n]$
,
![]() $n\in\mathbb N$
is issued. The customer may buy a call at price
$n\in\mathbb N$
is issued. The customer may buy a call at price
![]() $u_0$
whenever
$u_0$
whenever
![]() $X_t>u_0$
for some
$X_t>u_0$
for some
![]() $t\in[0,n]$
. Relation (6) with
$t\in[0,n]$
. Relation (6) with
![]() $\mu=\delta_{\{ u_0 \}}$
is written as
$\mu=\delta_{\{ u_0 \}}$
is written as
Then the long range dependence in the sense of Definition 1 of the stock price X (i.e.
![]() $\sigma^2_{\delta_{\{ u_0 \}},X} =+\infty$
) means that the amount of time within [0,n] at which the option may be exercised is not asymptotically normal for large time horizons n. In contrast, the short range dependence of stock X means asymptotic normality of this time span for any price
$\sigma^2_{\delta_{\{ u_0 \}},X} =+\infty$
) means that the amount of time within [0,n] at which the option may be exercised is not asymptotically normal for large time horizons n. In contrast, the short range dependence of stock X means asymptotic normality of this time span for any price
![]() $u_0$
for which the option was issued, provided that X satisfies the conditions of [Reference Meschenmoser and Shashkin26] or [Reference Spodarev41].
$u_0$
for which the option was issued, provided that X satisfies the conditions of [Reference Meschenmoser and Shashkin26] or [Reference Spodarev41].
In terms of potential theory, the value
![]() $\sigma^2_{\mu,X}$
in Definition 1 is the energy of measure
$\sigma^2_{\mu,X}$
in Definition 1 is the energy of measure
![]() $\mu$
with symmetric kernel
$\mu$
with symmetric kernel
![]() $K(u,v)=\int_T |\textrm{cov}_X(t,u,v)|\,{\textrm{d}} t$
; see [Reference Landkof19, page 77 ff.].
$K(u,v)=\int_T |\textrm{cov}_X(t,u,v)|\,{\textrm{d}} t$
; see [Reference Landkof19, page 77 ff.].
Self-similar random fields. We conclude this section with the formulation of long range dependence in a special case of self-similarity.
Let
![]() $X=\{X_t,t\in \mathbb{R}^d_+\}$
be a real-valued multi-self-similar random field. By definition, it is stochastically continuous and there exist numbers
$X=\{X_t,t\in \mathbb{R}^d_+\}$
be a real-valued multi-self-similar random field. By definition, it is stochastically continuous and there exist numbers
![]() $H_1,\ldots,H_d>0$
such that, for a diagonal matrix
$H_1,\ldots,H_d>0$
such that, for a diagonal matrix
![]() $A=\mbox{diag}(a_1,\ldots,a_d)$
with
$A=\mbox{diag}(a_1,\ldots,a_d)$
with
![]() $a_1,\ldots,a_d>0$
, we have
$a_1,\ldots,a_d>0$
, we have
Introduce the notation
![]() ${\bf 1}=(1,\ldots, 1)\in\mathbb{R}^d_+$
and
${\bf 1}=(1,\ldots, 1)\in\mathbb{R}^d_+$
and
![]() ${\textrm{e}}^s=({\textrm{e}}^{s_1}, \ldots, {\textrm{e}}^{s_d} )$
for
${\textrm{e}}^s=({\textrm{e}}^{s_1}, \ldots, {\textrm{e}}^{s_d} )$
for
![]() $s=(s_1,\ldots, s_d)\in\mathbb{R}^d$
. By [Reference Davydov and Paulauskas11, Proposition 6], the field
$s=(s_1,\ldots, s_d)\in\mathbb{R}^d$
. By [Reference Davydov and Paulauskas11, Proposition 6], the field
is stationary. Using Definition 1 for Y together with the substitution
![]() $t_i={\textrm{e}}^{s_i}$
,
$t_i={\textrm{e}}^{s_i}$
,
![]() $i=1,\ldots, d$
, we say that X is s.r.d. if, for any finite measure
$i=1,\ldots, d$
, we say that X is s.r.d. if, for any finite measure
![]() $\mu$
on
$\mu$
on
![]() $\mathbb{R}$
,
$\mathbb{R}$
,
 \[\int_{\mathbb{R}^d_+}\int_{\mathbb{R}^2} \biggl| {\textrm{cov}}\biggl({\bf 1} (X_{\bf 1}>u),{\bf 1}\biggl(X_{\bf t}>v\cdot \prod_{j=1}^d t_j^{H_j}\biggr) \biggr) \biggr|\, \dfrac{\mu({\textrm{d}} u)\, \mu({\textrm{d}} v)\, {\textrm{d}} t}{\prod_{j=1}^d t_j } <+\infty,\]
\[\int_{\mathbb{R}^d_+}\int_{\mathbb{R}^2} \biggl| {\textrm{cov}}\biggl({\bf 1} (X_{\bf 1}>u),{\bf 1}\biggl(X_{\bf t}>v\cdot \prod_{j=1}^d t_j^{H_j}\biggr) \biggr) \biggr|\, \dfrac{\mu({\textrm{d}} u)\, \mu({\textrm{d}} v)\, {\textrm{d}} t}{\prod_{j=1}^d t_j } <+\infty,\]
where
![]() ${\textrm{d}} t={\textrm{d}} t_1\ldots {\textrm{d}} t_d$
means integration with respect to Lebesgue measure in
${\textrm{d}} t={\textrm{d}} t_1\ldots {\textrm{d}} t_d$
means integration with respect to Lebesgue measure in
![]() $\mathbb{R}^d_+$
. Conversely, X is l.r.d. if the above integral is infinite for some finite measure
$\mathbb{R}^d_+$
. Conversely, X is l.r.d. if the above integral is infinite for some finite measure
![]() $\mu$
on
$\mu$
on
![]() $\mathbb{R}$
.
$\mathbb{R}$
.
3.2. Checking the short or long range dependence
Let
![]() $\mathbb P_{\mu}(\cdot)=\mu(\cdot)/\mu(\mathbb{R})$
denote the probability measure associated with the finite measure
$\mathbb P_{\mu}(\cdot)=\mu(\cdot)/\mu(\mathbb{R})$
denote the probability measure associated with the finite measure
![]() $\mu$
on
$\mu$
on
![]() $\mathbb{R}$
. Let U,V be two independent random variables with distribution
$\mathbb{R}$
. Let U,V be two independent random variables with distribution
![]() $\mathbb P_\mu$
. Then the variance
$\mathbb P_\mu$
. Then the variance
![]() $\sigma^2_{\mu,X}$
from Definition 1 becomes
$\sigma^2_{\mu,X}$
from Definition 1 becomes
This relation is useful for checking the short range dependence of X by showing the finiteness of
![]() $\sigma^2_{\mu,X}$
for any i.i.d. random variables U and V. Definition 1 is equivalent to the following lemma.
$\sigma^2_{\mu,X}$
for any i.i.d. random variables U and V. Definition 1 is equivalent to the following lemma.
Lemma 1. A stationary real-valued random field X with marginal distribution function
![]() $F_X$
is s.r.d. in the sense of Definition 1 if
$F_X$
is s.r.d. in the sense of Definition 1 if
for any probability measure
![]() $\mathbb P_0$
on
$\mathbb P_0$
on
![]() ${\operatorname{Im} F_X}$
, where
${\operatorname{Im} F_X}$
, where
![]() $C_{0,t}$
is the copula of the bivariate distribution of
$C_{0,t}$
is the copula of the bivariate distribution of
![]() $(X_0, X_t)$
,
$(X_0, X_t)$
,
![]() $t\in T$
, and
$t\in T$
, and
![]() $\operatorname{Im} F_X=F_X(\bar{\mathbb{R}})\subseteq [0,1]$
is the range of
$\operatorname{Im} F_X=F_X(\bar{\mathbb{R}})\subseteq [0,1]$
is the range of
![]() $F_X$
on
$F_X$
on
![]() $\bar{\mathbb{R}}=\mathbb{R}\cup\{+\infty\}\cup\{-\infty\}$
; X is l.r.d. in the sense of Definition 1 if there exists a probability measure
$\bar{\mathbb{R}}=\mathbb{R}\cup\{+\infty\}\cup\{-\infty\}$
; X is l.r.d. in the sense of Definition 1 if there exists a probability measure
![]() $\mathbb P_0$
on
$\mathbb P_0$
on
![]() $\operatorname{Im} F_X$
such that the above integral is infinite.
$\operatorname{Im} F_X$
such that the above integral is infinite.
Proof. By relation (7) and Sklar’s theorem (see e.g. [Reference Durante and Sempi14, Theorem 2.2.1]) we have, for any definite measure
![]() $\mu$
on
$\mu$
on
![]() $\mathbb{R}$
,
$\mathbb{R}$
,
The choice of
![]() $C_{0,t}$
is unique on
$C_{0,t}$
is unique on
![]() $\operatorname{Im} F_X$
; see [Reference Durante and Sempi14, Lemma 2.2.9]. Applying the substitution
$\operatorname{Im} F_X$
; see [Reference Durante and Sempi14, Lemma 2.2.9]. Applying the substitution
![]() $x=F_X(u)$
,
$x=F_X(u)$
,
![]() $y=F_X(v)$
, we get
$y=F_X(v)$
, we get
where the probability measure
![]() $ \mathbb P_0$
has a cumulative distribution function
$ \mathbb P_0$
has a cumulative distribution function
![]() $\mu ( (-\infty, F_X^-(x)) ) $
,
$\mu ( (-\infty, F_X^-(x)) ) $
,
![]() $x\in[0,1]$
, and
$x\in[0,1]$
, and
![]() $F_X^-$
is the generalized inverse for
$F_X^-$
is the generalized inverse for
![]() $F_X$
.
$F_X$
.
![]()
Lemma 1 implies that the new definition of memory is marginal-free, i.e. independent of the distribution of marginals
![]() $F_X$
if
$F_X$
if
![]() $\operatorname{Im} F_X=[0,1]$
, which is the case for absolutely continuous
$\operatorname{Im} F_X=[0,1]$
, which is the case for absolutely continuous
![]() $F_X$
. It essentially involves only the bivariate dependence structure encoded in the copula
$F_X$
. It essentially involves only the bivariate dependence structure encoded in the copula
![]() $C_{0,t}$
.
$C_{0,t}$
.
If condition (3) holds, then application of the Fubini–Tonelli theorem leads to
where
![]() $F_\mu (x)=\mathbb P_\mu((-\infty, x))$
is the (left-side continuous) distribution function of probability measure
$F_\mu (x)=\mathbb P_\mu((-\infty, x))$
is the (left-side continuous) distribution function of probability measure
![]() $\mathbb P_\mu$
. In this case the s.r.d. condition
$\mathbb P_\mu$
. In this case the s.r.d. condition
![]() $\sigma^2_{\mu,X}<+\infty$
reads as a classical covariance summability property of the subordinated random field
$\sigma^2_{\mu,X}<+\infty$
reads as a classical covariance summability property of the subordinated random field
![]() $Y_t=F_\mu (X_t)$
,
$Y_t=F_\mu (X_t)$
,
![]() $t\in T$
.
$t\in T$
.
By stationarity of X, we have
![]() $\textrm{cov}_X(t,u,v)=\textrm{cov}_X(-t,u,v)$
for any
$\textrm{cov}_X(t,u,v)=\textrm{cov}_X(-t,u,v)$
for any
![]() $t,-t\in T$
,
$t,-t\in T$
,
![]() $u,v\in\mathbb{R}$
. Hence, in order to show long range dependence for
$u,v\in\mathbb{R}$
. Hence, in order to show long range dependence for
![]() $T=\mathbb{R}$
, it is enough to check that
$T=\mathbb{R}$
, it is enough to check that
for some
![]() $u_0\in\mathbb{R}$
. For
$u_0\in\mathbb{R}$
. For
![]() $T=\mathbb Z$
it is sufficient to consider
$T=\mathbb Z$
it is sufficient to consider
![]() $\sum_{t=1}^\infty |\textrm{cov}_X(t,u_0,u_0)| =+\infty. $
$\sum_{t=1}^\infty |\textrm{cov}_X(t,u_0,u_0)| =+\infty. $
3.2.1. Short range dependence for mixing random fields
Let
![]() $\mathcal{U}, \mathcal{V}$
be two sub-
$\mathcal{U}, \mathcal{V}$
be two sub-
![]() $\sigma$
-algebras of
$\sigma$
-algebras of
![]() $\mathcal{F}$
. Introduce the z-mixing coefficient
$\mathcal{F}$
. Introduce the z-mixing coefficient
![]() $z(\mathcal{U},\mathcal{V})$
(where
$z(\mathcal{U},\mathcal{V})$
(where
![]() $z\in\{\alpha,\beta,\phi, \psi, \rho \}$
) as in [Reference Doukhan13, page 3]. For instance, it is given for
$z\in\{\alpha,\beta,\phi, \psi, \rho \}$
) as in [Reference Doukhan13, page 3]. For instance, it is given for
![]() $z=\alpha$
by
$z=\alpha$
by
Let
![]() $X=\{X_t, t\in T\}$
be a random field. Let
$X=\{X_t, t\in T\}$
be a random field. Let
![]() $X_C=\{X_t, t\in C\}$
,
$X_C=\{X_t, t\in C\}$
,
![]() $C\subset T$
, and let
$C\subset T$
, and let
![]() $\sigma_{X_\mathcal{C}}$
be the
$\sigma_{X_\mathcal{C}}$
be the
![]() $\sigma$
-algebra generated by
$\sigma$
-algebra generated by
![]() $X_C$
. If
$X_C$
. If
![]() $|C|$
is the cardinality of a finite set C, then the z-mixing coefficient of X is given by
$|C|$
is the cardinality of a finite set C, then the z-mixing coefficient of X is given by
where
![]() $ u,v \in \mathbb N $
and d(A,B) is the Hausdorff distance between finite subsets A and B generated by the metric on
$ u,v \in \mathbb N $
and d(A,B) is the Hausdorff distance between finite subsets A and B generated by the metric on
![]() $\mathbb{R}^d$
. The interrelations between different mixing coefficients
$\mathbb{R}^d$
. The interrelations between different mixing coefficients
![]() $z_X$
,
$z_X$
,
![]() $z\in\{\alpha,\beta,\phi, \psi, \rho \}$
are given in [Reference Doukhan13, Proposition 1], for example.
$z\in\{\alpha,\beta,\phi, \psi, \rho \}$
are given in [Reference Doukhan13, Proposition 1], for example.
We state the result that links mixing properties and the short range dependence. The field X may be non-Gaussian and have infinite variance.
Theorem 1. Let
![]() $X = \{X_t, t\in T\}$
be a stationary random field with z-mixing rate satisfying
$X = \{X_t, t\in T\}$
be a stationary random field with z-mixing rate satisfying
![]() $\int_T z_X(\|t\|,1,1) \, {\textrm{d}} t < +\infty$
, where
$\int_T z_X(\|t\|,1,1) \, {\textrm{d}} t < +\infty$
, where
![]() $z\in\{\alpha,\beta,\phi, \psi, \rho \}$
. Then X is s.r.d. in the sense of Definition 1 with
$z\in\{\alpha,\beta,\phi, \psi, \rho \}$
. Then X is s.r.d. in the sense of Definition 1 with
Proof. Without loss of generality, we prove the result for
![]() $\alpha$
-mixing X. Introduce random variables
$\alpha$
-mixing X. Introduce random variables
![]() $\xi(u)={\bf 1}(X_0>u)$
,
$\xi(u)={\bf 1}(X_0>u)$
,
![]() $\eta(v)={\bf 1}(X_t>v)$
, where
$\eta(v)={\bf 1}(X_t>v)$
, where
![]() $t \in T$
,
$t \in T$
,
![]() $u,v \in \mathbb{R}.$
Then, by the covariance inequality in [Reference Doukhan13, Theorem 3] connecting the covariance of random variables with their mixing rates, we have
$u,v \in \mathbb{R}.$
Then, by the covariance inequality in [Reference Doukhan13, Theorem 3] connecting the covariance of random variables with their mixing rates, we have
 \begin{align*} &\int_T\int_{\mathbb{R}^2} |\textrm{cov}_X(t, u, v)| \mu(\textrm{d} u) \mu( \textrm{d} v) \,\textrm{d} t = \int_T\int_{\mathbb{R}^2} |\textrm{cov}(\xi(u), \eta(v))| \mu(\textrm{d} u) \mu( \textrm{d} v) \,\textrm{d} t \\[3pt] &\quad \le 8 \int_T \alpha (\sigma_{X_0},\sigma_{X_t})\,\textrm{d} t \int_{\mathbb{R}^2 } \| \xi(u) \|_{\infty} \| \eta(v)\|_{\infty} \mu ({\textrm{d}} u) \mu ({\textrm{d}} v) \\[3pt] &\quad \leq 8\int_T \alpha_X(\|t\|,1,1)\,\textrm{d} t \cdot \mu^2(\mathbb{R})
< +\infty,\end{align*}
\begin{align*} &\int_T\int_{\mathbb{R}^2} |\textrm{cov}_X(t, u, v)| \mu(\textrm{d} u) \mu( \textrm{d} v) \,\textrm{d} t = \int_T\int_{\mathbb{R}^2} |\textrm{cov}(\xi(u), \eta(v))| \mu(\textrm{d} u) \mu( \textrm{d} v) \,\textrm{d} t \\[3pt] &\quad \le 8 \int_T \alpha (\sigma_{X_0},\sigma_{X_t})\,\textrm{d} t \int_{\mathbb{R}^2 } \| \xi(u) \|_{\infty} \| \eta(v)\|_{\infty} \mu ({\textrm{d}} u) \mu ({\textrm{d}} v) \\[3pt] &\quad \leq 8\int_T \alpha_X(\|t\|,1,1)\,\textrm{d} t \cdot \mu^2(\mathbb{R})
< +\infty,\end{align*}
where
![]() $ \| Y \|_{\infty} = \mbox{Ess-sup} (Y)$
.
$ \| Y \|_{\infty} = \mbox{Ess-sup} (Y)$
.
![]()
To illustrate the above theorem, we let
![]() $Y=\{ Y_t, \, t\in \mathbb N \}$
denote a stationary almost surely (a.s.) non-negative
$Y=\{ Y_t, \, t\in \mathbb N \}$
denote a stationary almost surely (a.s.) non-negative
![]() $\psi$
-mixing random sequence with univariate cumulative distribution function
$\psi$
-mixing random sequence with univariate cumulative distribution function
![]() $F_Y$
and
$F_Y$
and
![]() $\int_{\mathbb{R}^d} \psi_Y(\|t\|,1,1) \, {\textrm{d}} t < +\infty.$
Examples of
$\int_{\mathbb{R}^d} \psi_Y(\|t\|,1,1) \, {\textrm{d}} t < +\infty.$
Examples of
![]() $\psi$
-mixing random sequences can be found for example in [Reference Doukhan13, Example 4] (see also references therein), [Reference Heinrich16, Theorem 2.2], [Reference Rapaport29, Proof of Claim 2.5], [Reference Bradley6], and [Reference Samur38, pages 54–55]. Let
$\psi$
-mixing random sequences can be found for example in [Reference Doukhan13, Example 4] (see also references therein), [Reference Heinrich16, Theorem 2.2], [Reference Rapaport29, Proof of Claim 2.5], [Reference Bradley6], and [Reference Samur38, pages 54–55]. Let
![]() $F^{-1}_Z$
be the quantile function of a random variable Z with
$F^{-1}_Z$
be the quantile function of a random variable Z with
![]() $\mathbb E Z^2=+\infty$
. Set
$\mathbb E Z^2=+\infty$
. Set
![]() $G(x)=F^{-1}_Z(F_Y(x))$
,
$G(x)=F^{-1}_Z(F_Y(x))$
,
![]() $x\ge 0$
; then
$x\ge 0$
; then
![]() $X_t=G(Y_t)$
,
$X_t=G(Y_t)$
,
![]() $t\in \mathbb N$
is
$t\in \mathbb N$
is
![]() $\psi$
-mixing as well. Moreover, it is s.r.d. by the last theorem and has infinite variance because of
$\psi$
-mixing as well. Moreover, it is s.r.d. by the last theorem and has infinite variance because of
![]() $X_0\stackrel{d}{=} Z$
.
$X_0\stackrel{d}{=} Z$
.
Remark 1. For a Gaussian
![]() $\phi$
-mixing random field X, the statement of Theorem 1 is trivial, since such an X is m-dependent [Reference Ibragimov and Linnik17, Theorem 17.3.2], and the integral
$\phi$
-mixing random field X, the statement of Theorem 1 is trivial, since such an X is m-dependent [Reference Ibragimov and Linnik17, Theorem 17.3.2], and the integral
![]() $\int_0^\infty |\textrm{cov}_X(t,u,v)|\,{\textrm{d}} t$
in Definition 1 is bounded by 2m for any
$\int_0^\infty |\textrm{cov}_X(t,u,v)|\,{\textrm{d}} t$
in Definition 1 is bounded by 2m for any
![]() $u,v\in\mathbb{R}$
.
$u,v\in\mathbb{R}$
.
3.3. Subordinated Gaussian random fields
Recall that
![]() $\varphi(x) $
is the density of the standard normal law. We use the notation
$\varphi(x) $
is the density of the standard normal law. We use the notation
![]() $\Phi(x)$
for its cumulative distribution function. Introduce the Hermite polynomials
$\Phi(x)$
for its cumulative distribution function. Introduce the Hermite polynomials
![]() $H_n$
of degree
$H_n$
of degree
![]() $n\in \mathbb N_0$
by
$n\in \mathbb N_0$
by
where
![]() $\varphi^{(n)}$
is the nth derivative of
$\varphi^{(n)}$
is the nth derivative of
![]() $\varphi$
. Clearly
$\varphi$
. Clearly
For even orders n, Hermite polynomials are even functions, whereas for odd n they are odd functions. It is well known that Hermite polynomials form an orthogonal basis in
![]() $L^2_{\varphi}(\mathbb{R})$
. For any function
$L^2_{\varphi}(\mathbb{R})$
. For any function
![]() $f\in L^2_{\varphi}(\mathbb{R})$
with
$f\in L^2_{\varphi}(\mathbb{R})$
with
![]() $\langle f, 1\rangle_{\varphi} = 0$
, let
$\langle f, 1\rangle_{\varphi} = 0$
, let
be the Hermite rank of f. Furthermore, the Hermite rank can also be defined for functions
![]() $f\not\in L^2_{\varphi}(\mathbb{R})$
, as long as
$f\not\in L^2_{\varphi}(\mathbb{R})$
, as long as
![]() $\langle |f|^{1+\theta}, \varphi\rangle<\infty$
for some
$\langle |f|^{1+\theta}, \varphi\rangle<\infty$
for some
![]() $\theta\in (0,1)$
; see [Reference Sly and Heyde40] or [Reference Beran, Feng, Ghosh and Kulik5, Section 4.3.5].
$\theta\in (0,1)$
; see [Reference Sly and Heyde40] or [Reference Beran, Feng, Ghosh and Kulik5, Section 4.3.5].
Let
![]() $Y = \{Y_t, t\in T\}$
be a stationary centred Gaussian real-valued random field with
$Y = \{Y_t, t\in T\}$
be a stationary centred Gaussian real-valued random field with
![]() $\textrm{var}\, Y_t=1$
and
$\textrm{var}\, Y_t=1$
and
![]() $C_Y(t)=\textrm{cov}(Y_0,Y_t)$
,
$C_Y(t)=\textrm{cov}(Y_0,Y_t)$
,
![]() $t\in T$
. The subordinated Gaussian random field X is defined by
$t\in T$
. The subordinated Gaussian random field X is defined by
![]() $X_t=G(Y_t)$
,
$X_t=G(Y_t)$
,
![]() $ t\in T$
, where
$ t\in T$
, where
![]() $G\colon \mathbb{R}\rightarrow \operatorname{Im}(G)\subseteq\mathbb{R}$
is a measurable function.
$G\colon \mathbb{R}\rightarrow \operatorname{Im}(G)\subseteq\mathbb{R}$
is a measurable function.
Assume first that X is square-integrable. The following lemma is proved in [Reference Rozanov33, Lemma 10.2].
Lemma 2. Let
![]() $Z_1, Z_2$
be standard normal random variables with
$Z_1, Z_2$
be standard normal random variables with
![]() $\rho = \textrm{cov}(Z_1,Z_2)$
, and let F, G be functions satisfying
$\rho = \textrm{cov}(Z_1,Z_2)$
, and let F, G be functions satisfying
![]() $\mathbb E F^2(Z_1), \mathbb E G^2(Z_1) < +\infty$
. Then
$\mathbb E F^2(Z_1), \mathbb E G^2(Z_1) < +\infty$
. Then
Let
![]() $C_X(t)=\textrm{cov}(X_0,X_t)$
,
$C_X(t)=\textrm{cov}(X_0,X_t)$
,
![]() $t\in T$
. Assuming
$t\in T$
. Assuming
![]() $C_Y(t)\ge 0$
for all
$C_Y(t)\ge 0$
for all
![]() $t\in T$
and applying this lemma to our subordinated process
$t\in T$
and applying this lemma to our subordinated process
![]() $X=G(Y)$
we get that it is s.r.d. in the sense of Definition 1 if
$X=G(Y)$
we get that it is s.r.d. in the sense of Definition 1 if
 \begin{equation} \int_T|C_X(t)| \, {\textrm{d}} t = \sum_{k=1}^{\infty}\dfrac{\langle G, H_k\rangle_{\varphi}^2}{k!}\int_T C_Y^k(t)\, {\textrm{d}} t <+\infty.\end{equation}
\begin{equation} \int_T|C_X(t)| \, {\textrm{d}} t = \sum_{k=1}^{\infty}\dfrac{\langle G, H_k\rangle_{\varphi}^2}{k!}\int_T C_Y^k(t)\, {\textrm{d}} t <+\infty.\end{equation}
We shall see that an analogous result holds also if X has no finite second moment. Introduce the condition
(
![]() $\boldsymbol{\rho}$
)
$\boldsymbol{\rho}$
)
![]() $ |C_Y(t)|<1$
for all
$ |C_Y(t)|<1$
for all
![]() $t\neq 0$
if T is countable, and for
$t\neq 0$
if T is countable, and for
![]() $\nu_d$
-almost every
$\nu_d$
-almost every
![]() $t\in T$
if T is uncountable.
$t\in T$
if T is uncountable.
The following result gives the conditions for short range dependence of a subordinated Gaussian random field, without a moment assumption. Its proof is given in the Appendix.
Theorem 2. Let Y be the Gaussian random field introduced above. Let X be a subordinated Gaussian random field defined by
![]() $X_t=G(Y_t)$
,
$X_t=G(Y_t)$
,
![]() $t\in T$
, where G is a right-continuous strictly monotone (increasing or decreasing) function. Assume that condition (
$t\in T$
, where G is a right-continuous strictly monotone (increasing or decreasing) function. Assume that condition (
![]() $\boldsymbol{\rho}$
) holds. Let
$\boldsymbol{\rho}$
) holds. Let
where
![]() $G^-$
is the generalized inverse of G if G is increasing or the generalized inverse of
$G^-$
is the generalized inverse of G if G is increasing or the generalized inverse of
![]() $-G$
if G is decreasing. Then X is s.r.d. in the sense of Definition 1 if and only if
$-G$
if G is decreasing. Then X is s.r.d. in the sense of Definition 1 if and only if
for any finite measure
![]() $\mu$
on
$\mu$
on
![]() $\mathbb{R}$
.
$\mathbb{R}$
.
Corollary 1. Assume that the conditions of Theorem 2 hold.
-
(i) Let
 $\mu({\textrm{d}} x)=f(x) \, {\textrm{d}} x$
for
$\mu({\textrm{d}} x)=f(x) \, {\textrm{d}} x$
for
 $f\in L^1(\mathbb{R})$
such that
$f\in L^1(\mathbb{R})$
such that
 $f(x)\ge 0$
for all
$f(x)\ge 0$
for all
 $x\in\mathbb{R}$
. If
$x\in\mathbb{R}$
. If
 $G\in C^1(\mathbb{R})$
and
$G\in C^1(\mathbb{R})$
and
 $\operatorname{Im}(G)=\mathbb{R}$
, then
$\operatorname{Im}(G)=\mathbb{R}$
, then
 $b_k (\mu)= \langle G^\prime f(G), H_k\rangle_{\varphi}^2$
,
$b_k (\mu)= \langle G^\prime f(G), H_k\rangle_{\varphi}^2$
,
 $k\in \mathbb N$
. In this case all coefficients
$k\in \mathbb N$
. In this case all coefficients
 $b_k(\mu)$
are finite if, for some
$b_k(\mu)$
are finite if, for some
 $\theta \in (0,1)$
, we have
$\theta \in (0,1)$
, we have
 $E[|G^\prime (Y_0)f(G(Y_0))|^{1+\theta}] < +\infty.$
If
$E[|G^\prime (Y_0)f(G(Y_0))|^{1+\theta}] < +\infty.$
If
 $G^\prime f(G)$
is an even function then
$G^\prime f(G)$
is an even function then
 $b_k(\mu)=0$
for all natural odd k.
$b_k(\mu)=0$
for all natural odd k. -
(ii) If
 $X_t=G(|Y_t|)$
,
$X_t=G(|Y_t|)$
,
 $t\in T$
, then the s.r.d. condition (10) simplifies to
(11)
$t\in T$
, then the s.r.d. condition (10) simplifies to
(11) \begin{equation}\sum_{k=1}^{\infty}\dfrac{b_{2k-1}(\mu)}{(2k)!} \int_T C_Y^{2k}(t) \, {\textrm{d}} t <+\infty.\end{equation}
\begin{equation}\sum_{k=1}^{\infty}\dfrac{b_{2k-1}(\mu)}{(2k)!} \int_T C_Y^{2k}(t) \, {\textrm{d}} t <+\infty.\end{equation}
Remark 2. Based on Theorem 2 and Corollary 1, the long range dependence in the sense of Definition 1 can also be formulated as follows.
-
(i)
 $X=G(Y)$
is l.r.d. if there exists
$X=G(Y)$
is l.r.d. if there exists
 $ u_0\in\mathbb{R}$
such that
$ u_0\in\mathbb{R}$
such that
 $ b_k(\delta_{\{u_0\}})<+\infty$
for all k and the series (10) diverges to
$ b_k(\delta_{\{u_0\}})<+\infty$
for all k and the series (10) diverges to
 $+\infty$
.
$+\infty$
. -
(ii) If the initial process Y is s.r.d. then all powers of
 $C_Y$
are integrable on T and the long memory of
$C_Y$
are integrable on T and the long memory of
 $X=G(|Y|)$
can only come from function G. This can happen, for example, if its coefficients
$X=G(|Y|)$
can only come from function G. This can happen, for example, if its coefficients
 $b_k(\mu)$
decrease to zero slowly enough. Conversely, assume that Y is l.r.d.,
$b_k(\mu)$
decrease to zero slowly enough. Conversely, assume that Y is l.r.d.,
 $ 0 < b_{2k-1}(\mu)< +\infty$
for all
$ 0 < b_{2k-1}(\mu)< +\infty$
for all
 $k \in \mathbb{N}$
and some finite measure
$k \in \mathbb{N}$
and some finite measure
 $\mu$
. If there exists
$\mu$
. If there exists
 $ k\in \mathbb{N}$
such that
$ k\in \mathbb{N}$
such that
 $\int_T C_Y^{2k}(t) \, {\textrm{d}} t = +\infty $
, then X is l.r.d.
$\int_T C_Y^{2k}(t) \, {\textrm{d}} t = +\infty $
, then X is l.r.d.
Let us illustrate the last point of Remark 2 with an example.
Example 1. Let
![]() $G(x)={\textrm{e}}^{x^2/(2\alpha)}$
,
$G(x)={\textrm{e}}^{x^2/(2\alpha)}$
,
![]() $\alpha>0$
,
$\alpha>0$
,
![]() $T=\mathbb{R}^d$
. Then it is easy to see that
$T=\mathbb{R}^d$
. Then it is easy to see that
where
![]() $L(x)=\sqrt{ 2/(\pi \log x) } $
. For
$L(x)=\sqrt{ 2/(\pi \log x) } $
. For
![]() $\alpha\in(1,2]$
,
$\alpha\in(1,2]$
,
![]() $\mathbb E \, X_0<\infty$
,
$\mathbb E \, X_0<\infty$
,
![]() $\mathbb E \, X_0^2=+\infty$
.
$\mathbb E \, X_0^2=+\infty$
.
To compute
![]() $b_{2k-1}(\mu)$
, we notice that
$b_{2k-1}(\mu)$
, we notice that
Using the upper bound
![]() $ | H_{2k-1}(x) | \le x \,{\textrm{e}}^{x^2/4} (2k-1)!! /4$
,
$ | H_{2k-1}(x) | \le x \,{\textrm{e}}^{x^2/4} (2k-1)!! /4$
,
![]() $x\ge 0$
from [Reference Abramowitz and Stegun1, page 787], one can show that
$x\ge 0$
from [Reference Abramowitz and Stegun1, page 787], one can show that
 \begin{align*}b_{2k-1}(\mu) &\le \dfrac{ \alpha}{16\pi} [(2k-1)!!]^2 \biggl( \int_1^\infty u^{-\alpha/2} \sqrt{\log u} \, \mu({\textrm{d}} u) \biggr)^2 \\[3pt] &\le \dfrac{ \alpha }{ 4\pi } \mu^2 ([1,+\infty)) [ (2k-1)!!]^2 \\[3pt] &<+\infty\end{align*}
\begin{align*}b_{2k-1}(\mu) &\le \dfrac{ \alpha}{16\pi} [(2k-1)!!]^2 \biggl( \int_1^\infty u^{-\alpha/2} \sqrt{\log u} \, \mu({\textrm{d}} u) \biggr)^2 \\[3pt] &\le \dfrac{ \alpha }{ 4\pi } \mu^2 ([1,+\infty)) [ (2k-1)!!]^2 \\[3pt] &<+\infty\end{align*}
for all
![]() $ k\in\mathbb N.$
$ k\in\mathbb N.$
We note that the use of the finite measure
![]() $\mu$
is crucial here, since for the Lebesgue measure the integral
$\mu$
is crucial here, since for the Lebesgue measure the integral
![]() $\int_1^\infty u^{-\alpha/2} \sqrt{\log u} \, \mu({\textrm{d}} u)$
is infinite for
$\int_1^\infty u^{-\alpha/2} \sqrt{\log u} \, \mu({\textrm{d}} u)$
is infinite for
![]() $\alpha\leq2$
.
$\alpha\leq2$
.
Now, by Stirling’s formula [Reference Andrews, Askey and Roy4, Theorem 1.4.2], we get
for
![]() $c_3>0$
, so
$c_3>0$
, so
Assume that
![]() $C_Y(t)\sim \|t\|^{-\eta}$
as
$C_Y(t)\sim \|t\|^{-\eta}$
as
![]() $\|t\|\to +\infty$
,
$\|t\|\to +\infty$
,
![]() $\eta>0$
. Then
$\eta>0$
. Then
![]() $X={\textrm{e}}^{Y^2/(2\alpha)}$
,
$X={\textrm{e}}^{Y^2/(2\alpha)}$
,
![]() $\alpha >0$
, is
$\alpha >0$
, is
-
• l.r.d. if
 $\eta\in (0, d/2]$
, since then
$\eta\in (0, d/2]$
, since then
 \begin{equation*}\sum_{k=1}^{\infty}\dfrac{b_{2k-1}(\mu)}{(2k)!} \int_T C_Y^{2k}(t) \, {\textrm{d}} t =+\infty;\end{equation*}
\begin{equation*}\sum_{k=1}^{\infty}\dfrac{b_{2k-1}(\mu)}{(2k)!} \int_T C_Y^{2k}(t) \, {\textrm{d}} t =+\infty;\end{equation*}
-
• s.r.d. if
 $\eta> d/2$
, since then we have
and the series (11) behaves like
$\eta> d/2$
, since then we have
and the series (11) behaves like \[\int_{\mathbb{R}^d} C_Y^{2k}(t)\, {\textrm{d}} t =O(k^{-1}) \quad \text{as } k\to +\infty,\]
\[\int_{\mathbb{R}^d} C_Y^{2k}(t)\, {\textrm{d}} t =O(k^{-1}) \quad \text{as } k\to +\infty,\]
 ${\sum_{k=1}^\infty k^{-3/2} <+\infty.}$
${\sum_{k=1}^\infty k^{-3/2} <+\infty.}$
Here the source of long memory of X is the l.r.d. field Y. If
![]() $\alpha>2$
the variance of
$\alpha>2$
the variance of
![]() $X_0$
is finite, and our results agree with the definition in (1) by relation (8) if we note that
$X_0$
is finite, and our results agree with the definition in (1) by relation (8) if we note that
![]() $\operatorname{rank} (G)=2$
. However, the main point of this example is that we have the same transition from short to long memory (i.e.
$\operatorname{rank} (G)=2$
. However, the main point of this example is that we have the same transition from short to long memory (i.e.
![]() $\eta=d/2$
) for both finite and infinite variance fields.
$\eta=d/2$
) for both finite and infinite variance fields.
Note that for
![]() $\eta\in (d/2, d)$
the Gaussian field Y is l.r.d. but the subordinated field
$\eta\in (d/2, d)$
the Gaussian field Y is l.r.d. but the subordinated field
![]() $X={\textrm{e}}^{Y^2/(2\alpha)}$
is s.r.d. This agrees with the classical theory for finite variance, but is novel for infinite variance.
$X={\textrm{e}}^{Y^2/(2\alpha)}$
is s.r.d. This agrees with the classical theory for finite variance, but is novel for infinite variance.
3.4. Stochastic volatility models
We present a way of constructing random fields with long memory by introducing a random volatility
![]() $G(Y_t)$
(being a deterministic function of a random scaling field
$G(Y_t)$
(being a deterministic function of a random scaling field
![]() $Y=\{ Y_t, t\in T \}$
) of a random field
$Y=\{ Y_t, t\in T \}$
) of a random field
![]() $Z=\{ Z_t, t\in T \}$
. We assume that Y and Z are independent. An overview of random volatility models and their applications in finance can be found in [Reference Shephard39] and [Reference Andersen, Davis and Mikosch3, Part II], for example. For each
$Z=\{ Z_t, t\in T \}$
. We assume that Y and Z are independent. An overview of random volatility models and their applications in finance can be found in [Reference Shephard39] and [Reference Andersen, Davis and Mikosch3, Part II], for example. For each
![]() $t\in T$
,
$t\in T$
,
![]() $X_t=G(Y_t)Z_t$
is a scale mixture of
$X_t=G(Y_t)Z_t$
is a scale mixture of
![]() $G(Y_t)$
and
$G(Y_t)$
and
![]() $Z_t$
; see [Reference Steutel and van Harn42, Chapter VI, page 345]. Let
$Z_t$
; see [Reference Steutel and van Harn42, Chapter VI, page 345]. Let
![]() $\bar{F}_Z=1-F_Z$
be the marginal tail distribution function of
$\bar{F}_Z=1-F_Z$
be the marginal tail distribution function of
![]() $Z_t$
for stationary Z.
$Z_t$
for stationary Z.
For a finite measure
![]() $\mu$
, introduce the functional
$\mu$
, introduce the functional
The next lemma follows trivially from relation (2), independence of Y and Z, and Tonelli’s theorem.
Lemma 3. Let a random field
![]() $X=\{ X_t, t\in T \}$
be given by
$X=\{ X_t, t\in T \}$
be given by
![]() $X_t=G(Y_t)Z_t$
, where
$X_t=G(Y_t)Z_t$
, where
![]() $Y=\{ Y_t, t\in T \}$
and
$Y=\{ Y_t, t\in T \}$
and
![]() $Z=\{ Z_t, t\in T \}$
are independent stationary random fields, Z has property (3),
$Z=\{ Z_t, t\in T \}$
are independent stationary random fields, Z has property (3),
![]() $G\colon \mathbb{R}\to\mathbb{R}_{\pm}$
and
$G\colon \mathbb{R}\to\mathbb{R}_{\pm}$
and
![]() $\mathbb P (G(Y_t)=0)=0$
for all
$\mathbb P (G(Y_t)=0)=0$
for all
![]() $t\in T$
. Then
$t\in T$
. Then
 \begin{align}&\int_T \int_{\mathbb{R}^2}\textrm{cov}_X(t,u,v)\, \mu({\textrm{d}} u)\,\mu({\textrm{d}} v)\,{\textrm{d}} t \notag\\[3pt] &\quad = D_{\mu} (G(Y),Z_0) + \int_T \int_{\mathbb{R}^2}\mathbb E [ \textrm{cov}_Z(t,u/G(Y_0),v/G(Y_t))]\, \mu({\textrm{d}} u)\,\mu({\textrm{d}} v)\,{\textrm{d}} t.\end{align}
\begin{align}&\int_T \int_{\mathbb{R}^2}\textrm{cov}_X(t,u,v)\, \mu({\textrm{d}} u)\,\mu({\textrm{d}} v)\,{\textrm{d}} t \notag\\[3pt] &\quad = D_{\mu} (G(Y),Z_0) + \int_T \int_{\mathbb{R}^2}\mathbb E [ \textrm{cov}_Z(t,u/G(Y_0),v/G(Y_t))]\, \mu({\textrm{d}} u)\,\mu({\textrm{d}} v)\,{\textrm{d}} t.\end{align}
Let us illustrate the use of Lemma 3.
Corollary 2. Let the random field X be given by
![]() $X_t=A Z_t$
,
$X_t=A Z_t$
,
![]() $t\in T$
,
$t\in T$
,
![]() $|T|=+\infty$
, where
$|T|=+\infty$
, where
![]() $A>0$
a.s., A and Z are independent, and
$A>0$
a.s., A and Z are independent, and
![]() $$Z \in {\bf{PA}}$$
is stationary. Then X is l.r.d. in the sense of Definition 1 if there exists
$$Z \in {\bf{PA}}$$
is stationary. Then X is l.r.d. in the sense of Definition 1 if there exists
![]() $u_0\in \mathbb{R}$
such that
$u_0\in \mathbb{R}$
such that
![]() $\bar{F}_Z (u_0/A)\neq \textrm{const.}$
a.s.
$\bar{F}_Z (u_0/A)\neq \textrm{const.}$
a.s.
The above corollary evidently holds true if, for example,
![]() $Z_0\sim \textrm{Exp}(\lambda)$
,
$Z_0\sim \textrm{Exp}(\lambda)$
,
![]() $$A \sim $$
Fréchet(1) for any
$$A \sim $$
Fréchet(1) for any
![]() $\lambda>0$
. It also clearly applies to a sub-Gaussian random field X, where
$\lambda>0$
. It also clearly applies to a sub-Gaussian random field X, where
![]() $A=\sqrt{B}$
,
$A=\sqrt{B}$
,
![]() $B\sim S_{\alpha/2} ( ( \cos {{\pi\alpha}/{\pi\alpha}}) ^{2/\alpha},1,0 ) $
,
$B\sim S_{\alpha/2} ( ( \cos {{\pi\alpha}/{\pi\alpha}}) ^{2/\alpha},1,0 ) $
,
![]() $\alpha \in (0,2)$
, and Z is a centred stationary Gaussian random field with covariance function
$\alpha \in (0,2)$
, and Z is a centred stationary Gaussian random field with covariance function
![]() $C(t)\ge 0$
for all
$C(t)\ge 0$
for all
![]() $t\in T$
and a non-degenerate tail
$t\in T$
and a non-degenerate tail
![]() $\bar{F}_Z$
.
$\bar{F}_Z$
.
The following corollary describes the situation where a light-tailed Y is responsible for the long range dependence of X while Z is responsible for heavy tails.
Corollary 3. For the random field
![]() $X=\{ X_t, t\in T\}$
given by
$X=\{ X_t, t\in T\}$
given by
![]() $X_t=Y_t Z_t$
,
$X_t=Y_t Z_t$
,
![]() $t\in T$
, assume that random fields
$t\in T$
, assume that random fields
![]() $Y=\{ Y_t, t\in T\}$
and
$Y=\{ Y_t, t\in T\}$
and
![]() $Z=\{ Z_t, t\in T\}$
are stationary and independent. Assume that
$Z=\{ Z_t, t\in T\}$
are stationary and independent. Assume that
![]() $Z_0$
has a regularly varying tail, that is,
$Z_0$
has a regularly varying tail, that is,
![]() $\mathbb P(Z_0>x)\sim L(x)/x^\alpha$
as
$\mathbb P(Z_0>x)\sim L(x)/x^\alpha$
as
![]() $x\to +\infty$
for some
$x\to +\infty$
for some
![]() $\alpha>0$
, where the function L is slowly varying at
$\alpha>0$
, where the function L is slowly varying at
![]() $+\infty$
. For
$+\infty$
. For
![]() $Y_0>0$
a.s. assume that
$Y_0>0$
a.s. assume that
![]() $\mathbb E Y_0^{\delta}<\infty$
and
$\mathbb E Y_0^{\delta}<\infty$
and
![]() $\mathbb E ( Y_0^{\delta}Y_t^{\delta} ) <\infty$
for some
$\mathbb E ( Y_0^{\delta}Y_t^{\delta} ) <\infty$
for some
![]() $\delta>\alpha$
and all
$\delta>\alpha$
and all
![]() $t\in T$
. Let
$t\in T$
. Let
![]() $Y, Z\in$
PA(NA). Then X is l.r.d. if
$Y, Z\in$
PA(NA). Then X is l.r.d. if
![]() $Y^\alpha=\{Y_t^\alpha, \,t\in T\}$
is l.r.d.
$Y^\alpha=\{Y_t^\alpha, \,t\in T\}$
is l.r.d.
Now we scale a l.r.d. (possibly heavy-tailed) random field Z by a random volatility G(Y) being a subordinated Gaussian random field.
Lemma 4. Let
![]() $X_t=G(Y_t) Z_t$
be a random field as in Lemma 3. Assume further that Y is a centred Gaussian random field with unit variance and covariance function
$X_t=G(Y_t) Z_t$
be a random field as in Lemma 3. Assume further that Y is a centred Gaussian random field with unit variance and covariance function
![]() $\rho(t)\ge 0$
satisfying condition (
$\rho(t)\ge 0$
satisfying condition (
![]() $\boldsymbol{\rho}$
). Then
$\boldsymbol{\rho}$
). Then
 \begin{equation*}D_{\mu} (G(Y),Z_0) = \sum_{k=1}^\infty \dfrac{ \bigl( \int_{\mathbb{R}} \langle \bar{F}_Z (u/G(\cdot)), H_k(\cdot) \rangle_\varphi \, \mu({\textrm{d}} u) \bigr)^2 }{k!}\int_T \rho^k(t) \, {\textrm{d}} t .\end{equation*}
\begin{equation*}D_{\mu} (G(Y),Z_0) = \sum_{k=1}^\infty \dfrac{ \bigl( \int_{\mathbb{R}} \langle \bar{F}_Z (u/G(\cdot)), H_k(\cdot) \rangle_\varphi \, \mu({\textrm{d}} u) \bigr)^2 }{k!}\int_T \rho^k(t) \, {\textrm{d}} t .\end{equation*}
The following example illustrates our definition of long range dependence in the context of a popular long memory stochastic volatility model that is used in econometrics to model log-returns of stocks; see [Reference Beran, Feng, Ghosh and Kulik5, page 70 ff.] and references therein.
Example 2. Assume that
![]() $X=\{X_t,t\in\mathbb Z\}$
has a form
$X=\{X_t,t\in\mathbb Z\}$
has a form
![]() $X_t={\textrm{e}}^{Y_t^2 /4}Z_t$
, where
$X_t={\textrm{e}}^{Y_t^2 /4}Z_t$
, where
![]() $Z_t$
is a sequence of i.i.d. random variables with finite moment of order
$Z_t$
is a sequence of i.i.d. random variables with finite moment of order
![]() $2+\delta$
for some
$2+\delta$
for some
![]() $\delta>0$
, while
$\delta>0$
, while
![]() $Y_t$
is a centred stationary Gaussian PA long memory sequence with unit variance and covariance function
$Y_t$
is a centred stationary Gaussian PA long memory sequence with unit variance and covariance function
![]() $C_Y$
satisfying condition (
$C_Y$
satisfying condition (
![]() $\boldsymbol{\rho}$
). Both sequences
$\boldsymbol{\rho}$
). Both sequences
![]() $Z_t$
and
$Z_t$
and
![]() $Y_t$
are assumed to be independent of each other. From Example 1 we know that
$Y_t$
are assumed to be independent of each other. From Example 1 we know that
![]() ${\textrm{e}}^{Y_0^2 /4}$
is regularly varying with index
${\textrm{e}}^{Y_0^2 /4}$
is regularly varying with index
![]() $\alpha=2$
. By Breiman’s lemma the tail distribution function of
$\alpha=2$
. By Breiman’s lemma the tail distribution function of
![]() $|X_0|$
is also regularly varying with index
$|X_0|$
is also regularly varying with index
![]() $\alpha =2$
, and hence
$\alpha =2$
, and hence
![]() $X_0$
has infinite variance. Choose
$X_0$
has infinite variance. Choose
![]() $\mu=\delta_{\{ u_0\}} $
for some
$\mu=\delta_{\{ u_0\}} $
for some
![]() $u_0\in\mathbb{R}$
. Lemmas 3 and 4 yield
$u_0\in\mathbb{R}$
. Lemmas 3 and 4 yield
 \begin{equation}\sum_{t=1}^{\infty} \int_{\mathbb{R}^2} {\textrm{cov}}_X(t,u,v) \mu({\textrm{d}} u)\mu({\textrm{d}} v) = \sum_{k=1}^\infty \dfrac{ \langle \bar{F}_Z(u_0/G), H_k\rangle_\varphi^2 }{k!} \sum_{t=1}^{\infty} C_Y^k(t) ,\end{equation}
\begin{equation}\sum_{t=1}^{\infty} \int_{\mathbb{R}^2} {\textrm{cov}}_X(t,u,v) \mu({\textrm{d}} u)\mu({\textrm{d}} v) = \sum_{k=1}^\infty \dfrac{ \langle \bar{F}_Z(u_0/G), H_k\rangle_\varphi^2 }{k!} \sum_{t=1}^{\infty} C_Y^k(t) ,\end{equation}
where
![]() $G(x)={\textrm{e}}^{x^2/4}$
. Since
$G(x)={\textrm{e}}^{x^2/4}$
. Since
![]() $\bar{F}_Z(u_0/G)$
is symmetric, monotone non-decreasing, and bounded, we get
$\bar{F}_Z(u_0/G)$
is symmetric, monotone non-decreasing, and bounded, we get
![]() $\langle \bar{F}_Z(u_0/G), H_{k}\rangle_\varphi=0$
for all odd k, and it is finite for all even
$\langle \bar{F}_Z(u_0/G), H_{k}\rangle_\varphi=0$
for all odd k, and it is finite for all even
![]() $k\in\mathbb N$
. Moreover, by Lemma 5(ii) we have
$k\in\mathbb N$
. Moreover, by Lemma 5(ii) we have
![]() $\operatorname{rank}(\bar{F}_Z(u_0/G) )=2$
. It is clear that X is l.r.d. if
$\operatorname{rank}(\bar{F}_Z(u_0/G) )=2$
. It is clear that X is l.r.d. if
![]() $\sum_{t=1}^\infty\rho^2(t)=+\infty$
. In particular, if
$\sum_{t=1}^\infty\rho^2(t)=+\infty$
. In particular, if
![]() $C_Y(t)\sim |t|^{-\eta}$
as
$C_Y(t)\sim |t|^{-\eta}$
as
![]() $|t|\to\infty$
, then long range dependence occurs if
$|t|\to\infty$
, then long range dependence occurs if
![]() $\eta\in (0,1/2]$
. Again, similarly to Example 1, the point here is that we obtain long memory for both finite and infinite variance.
$\eta\in (0,1/2]$
. Again, similarly to Example 1, the point here is that we obtain long memory for both finite and infinite variance.
4. Limit theorems
In this section we investigate connections between Definition 1 and limit theorems for random volatility and subordinated Gaussian random fields. In order to do so, we have to specify the statistic whose limiting behaviour we consider. We focus on the volume of the excursion sets.
In Section 4.1 we consider subordinated Gaussian random fields. In Section 4.1.1 we show by a natural example that our definition of long memory is in agreement with the existing limiting behaviour of the volume of excursions of X over some levels u. On the other hand, in Section 4.1.2 we will indicate that the limiting behaviour of the empirical mean cannot be directly related to our definition. The latter is not surprising.
In Section 4.2 we consider related problems for stochastic volatility random fields.
From now on we assume the random field X to be measurable. In what follows, L will indicate a slowly varying function at infinity, that can be different at each of its occurrences.
We start with the following lemma, which will play a major role.
Lemma 5. Let Y, Z be independent random variables such that
![]() $Y\sim N(0,1)$
. For any monotone right-continuous non-constant function
$Y\sim N(0,1)$
. For any monotone right-continuous non-constant function
![]() $G\colon \mathbb{R}\to\mathbb{R}_\pm$
with
$G\colon \mathbb{R}\to\mathbb{R}_\pm$
with
![]() $\nu_1 (\{x\in\mathbb{R}\colon G(x)=0\} ) =0 $
, consider the functions
$\nu_1 (\{x\in\mathbb{R}\colon G(x)=0\} ) =0 $
, consider the functions
![]() $\widetilde{G}(y)=G(|y|)$
and
$\widetilde{G}(y)=G(|y|)$
and
for a fixed
![]() $u> 0$
if
$u> 0$
if
![]() $G\ge 0$
and
$G\ge 0$
and
![]() $u<0$
if
$u<0$
if
![]() $G\le 0$
. Then the following hold.
$G\le 0$
. Then the following hold.
-
(i) Let
 $G\colon \mathbb{R}\to\mathbb{R}_\pm$
be as above such that
$G\colon \mathbb{R}\to\mathbb{R}_\pm$
be as above such that
 $\mathbb E |G(Y)|^{1+\theta}<+\infty $
for some
$\mathbb E |G(Y)|^{1+\theta}<+\infty $
for some
 $\theta\in(0,1]$
. Then
$\theta\in(0,1]$
. Then
 \[ \operatorname{rank} (G)= \operatorname{rank}( \zeta_{G,1,u}) = \operatorname{rank}( \zeta_{G,Z,u})=1. \]
\[ \operatorname{rank} (G)= \operatorname{rank}( \zeta_{G,1,u}) = \operatorname{rank}( \zeta_{G,Z,u})=1. \]
-
(ii) Let
 $G\colon \mathbb{R}_+\to\mathbb{R}_\pm$
be as above such that
$G\colon \mathbb{R}_+\to\mathbb{R}_\pm$
be as above such that
 $\mathbb E |\widetilde{G}(Y)|^{1+\theta}<+\infty $
for some
$\mathbb E |\widetilde{G}(Y)|^{1+\theta}<+\infty $
for some
 $\theta\in(0,1]$
,
$\theta\in(0,1]$
,
 $G^-(u)\neq 0$
, where
$G^-(u)\neq 0$
, where
 $G^{-}$
is the generalized inverse of G. Then
$G^{-}$
is the generalized inverse of G. Then
 \[ \operatorname{rank} (\widetilde{G})=\operatorname{rank}( {\zeta}_{\widetilde{G},1,u})= \operatorname{rank}( {\zeta}_{\widetilde{G},Z,u})=2. \]
\[ \operatorname{rank} (\widetilde{G})=\operatorname{rank}( {\zeta}_{\widetilde{G},1,u})= \operatorname{rank}( {\zeta}_{\widetilde{G},Z,u})=2. \]
Remark 3.
-
(i) If
 $Z\equiv 1$
, then the assertion of Lemma 5(i) holds under milder assumptions on G and u. Thus let
$Z\equiv 1$
, then the assertion of Lemma 5(i) holds under milder assumptions on G and u. Thus let
 $G\colon \mathbb{R}\to\mathbb{R}$
be a monotone right-continuous non-constant function such that
$G\colon \mathbb{R}\to\mathbb{R}$
be a monotone right-continuous non-constant function such that
 $\mathbb E |G(Y)|^{1+\theta}<+\infty $
for some
$\mathbb E |G(Y)|^{1+\theta}<+\infty $
for some
 $\theta\in(0,1]$
. Then, for any
$\theta\in(0,1]$
. Then, for any
 $u\in\mathbb{R}$
,
$u\in\mathbb{R}$
,
 $\operatorname{rank} ( G) =\operatorname{rank} ( \zeta_{G,1,u})=1$
.
$\operatorname{rank} ( G) =\operatorname{rank} ( \zeta_{G,1,u})=1$
. -
(ii) The assumption of non-negative or non-positive G is essential to the rank condition
 $ \operatorname{rank} ( \zeta_{G,Z,u})=1$
of Lemma 5(i), since for
$ \operatorname{rank} ( \zeta_{G,Z,u})=1$
of Lemma 5(i), since for
 $G(y)=y$
and symmetric Z we have
$G(y)=y$
and symmetric Z we have
 $\mathbb E[Y {\bf 1} \{ YZ >u \}] =0,$
so the Hermite rank of
$\mathbb E[Y {\bf 1} \{ YZ >u \}] =0,$
so the Hermite rank of
 $\zeta_{G,Z,u} $
is greater than 1. Similarly, one can construct examples of functions G with
$\zeta_{G,Z,u} $
is greater than 1. Similarly, one can construct examples of functions G with
 $\operatorname{rank} ( \zeta_{\widetilde{G},Z,u})>2$
for some
$\operatorname{rank} ( \zeta_{\widetilde{G},Z,u})>2$
for some
 $u\in\mathbb{R}$
if the assumptions of Lemma 5(ii) do not hold. For instance,
$u\in\mathbb{R}$
if the assumptions of Lemma 5(ii) do not hold. For instance,
 $G^-(u)=0$
means that
$G^-(u)=0$
means that
 $\operatorname{rank} ( \zeta_{\widetilde{G},Z,u})\ge 4$
.
$\operatorname{rank} ( \zeta_{\widetilde{G},Z,u})\ge 4$
. -
(iii) If G is non-negative or non-positive and
 $u=0$
, then it is easily seen that
$u=0$
, then it is easily seen that
 $\zeta_{G,Z,0}\equiv 0$
and, formally speaking, its Hermite rank is infinite.
$\zeta_{G,Z,0}\equiv 0$
and, formally speaking, its Hermite rank is infinite.
4.1. Limit theorems for subordinated Gaussian processes
Let
![]() $X=\{ X_t, t\in\mathbb{R}^d \}$
, where
$X=\{ X_t, t\in\mathbb{R}^d \}$
, where
![]() $X_t= G(Y_t)$
and
$X_t= G(Y_t)$
and
![]() $Y=\{ Y_t, t\in \mathbb{R}^d \}$
is a stationary isotropic l.r.d. centred Gaussian random field with covariance function
$Y=\{ Y_t, t\in \mathbb{R}^d \}$
is a stationary isotropic l.r.d. centred Gaussian random field with covariance function
![]() $C_Y(t)= \|t\|^{-\eta}L(\|t\|)$
,
$C_Y(t)= \|t\|^{-\eta}L(\|t\|)$
,
![]() $\eta\in (0,d/q)$
(see [Reference Ivanov and Leonenko18], [Reference Leonenko22], and [Reference Leonenko and Olenko23]). Here
$\eta\in (0,d/q)$
(see [Reference Ivanov and Leonenko18], [Reference Leonenko22], and [Reference Leonenko and Olenko23]). Here
![]() $\mathbb E G^2(Y_0)<+\infty$
and q is the Hermite rank of G. Under some technical assumptions on the spectral density
$\mathbb E G^2(Y_0)<+\infty$
and q is the Hermite rank of G. Under some technical assumptions on the spectral density
![]() $f(\lambda)$
of Y (see [Reference Leonenko and Olenko23, Assumption 2]),
$f(\lambda)$
of Y (see [Reference Leonenko and Olenko23, Assumption 2]),
where
 \begin{align} R &= ( \gamma(d,\eta) ) ^{q/2}\int^\prime_{\mathbb{R}^{dq}} \int_W \,{\textrm{e}}^{{\textrm{i}}\langle \lambda_1+\ldots+\lambda_q,u\rangle} \,{\textrm{d}} u \dfrac{\tilde{B}(d\lambda_1) \ldots \tilde{B} (d\lambda_q)}{ ( \| \lambda_1\| \cdot \ldots \cdot \| \lambda_q\| ) ^{(d-\eta)/2}},\nonumber\\[3pt] \gamma(d,\eta) &=\dfrac{\Gamma ( (d-\eta)/2 ) }{2^\eta \pi^{d/2} \Gamma(\eta/2)},\end{align}
\begin{align} R &= ( \gamma(d,\eta) ) ^{q/2}\int^\prime_{\mathbb{R}^{dq}} \int_W \,{\textrm{e}}^{{\textrm{i}}\langle \lambda_1+\ldots+\lambda_q,u\rangle} \,{\textrm{d}} u \dfrac{\tilde{B}(d\lambda_1) \ldots \tilde{B} (d\lambda_q)}{ ( \| \lambda_1\| \cdot \ldots \cdot \| \lambda_q\| ) ^{(d-\eta)/2}},\nonumber\\[3pt] \gamma(d,\eta) &=\dfrac{\Gamma ( (d-\eta)/2 ) }{2^\eta \pi^{d/2} \Gamma(\eta/2)},\end{align}
and
![]() $\int^\prime_{\mathbb{R}^{dq}} $
is the multiple Wiener–ItÔ integral with respect to a complex Gaussian white noise measure
$\int^\prime_{\mathbb{R}^{dq}} $
is the multiple Wiener–ItÔ integral with respect to a complex Gaussian white noise measure
![]() $\tilde{B}$
(with structural measure being the spectral measure of Y; see [Reference Ivanov and Leonenko18, Section 2.9]). It is easy to see that for
$\tilde{B}$
(with structural measure being the spectral measure of Y; see [Reference Ivanov and Leonenko18, Section 2.9]). It is easy to see that for
![]() $q=1$
the distribution of R is Gaussian. However, the normalization
$q=1$
the distribution of R is Gaussian. However, the normalization
![]() $n^{\eta/2-d} L^{-1/2}(n)$
differs from the usual CLT normalizing factor
$n^{\eta/2-d} L^{-1/2}(n)$
differs from the usual CLT normalizing factor
![]() $n^{-d/2}$
, which agrees with the fact that X is l.r.d. in the sense of the usual definition as in (1). For
$n^{-d/2}$
, which agrees with the fact that X is l.r.d. in the sense of the usual definition as in (1). For
![]() $q\ge 2$
, we get a q-Rosenblatt-type distribution for R; see [Reference Veillette and Taqqu43] and [Reference Leonenko, Ruiz-Medina and Taqqu24] and references therein for its properties in the case
$q\ge 2$
, we get a q-Rosenblatt-type distribution for R; see [Reference Veillette and Taqqu43] and [Reference Leonenko, Ruiz-Medina and Taqqu24] and references therein for its properties in the case
![]() $q=2$
.
$q=2$
.
4.1.1 Volume of level sets
We apply the above observations to level sets. Assume
![]() $G\colon \mathbb{R}\to\mathbb{R}$
to be a monotone right-continuous function such that
$G\colon \mathbb{R}\to\mathbb{R}$
to be a monotone right-continuous function such that
![]() $\mathbb E |G(Y)|^{1+\theta}<+\infty $
with
$\mathbb E |G(Y)|^{1+\theta}<+\infty $
with
![]() $\theta\in(0,1)$
. Let the variance of
$\theta\in(0,1)$
. Let the variance of
![]() $X_0$
be infinite. For any
$X_0$
be infinite. For any
![]() $u\in\mathbb{R}$
introduce the function
$u\in\mathbb{R}$
introduce the function
![]() $g_u(x)=\zeta_{G,1,u} (x)$
, where
$g_u(x)=\zeta_{G,1,u} (x)$
, where
![]() $\zeta_{G,1,u} $
is given in (15). By Remark 3(i), the Hermite ranks of G and
$\zeta_{G,1,u} $
is given in (15). By Remark 3(i), the Hermite ranks of G and
![]() $g_u$
are equal to one. If
$g_u$
are equal to one. If
![]() $\eta\in (0,d)$
then
$\eta\in (0,d)$
then
as
![]() $n\to+\infty$
, where R is given in (16). The normalization in this limit theorem is not of CLT type
$n\to+\infty$
, where R is given in (16). The normalization in this limit theorem is not of CLT type
![]() $n^{-d/2}$
, which should be attributed to the l.r.d. case. Let us compare this behaviour with Definition 1. As an example, we consider
$n^{-d/2}$
, which should be attributed to the l.r.d. case. Let us compare this behaviour with Definition 1. As an example, we consider
for some
![]() $\beta>\sqrt{2(1+\theta)}$
. Note that it is possible that the variance of
$\beta>\sqrt{2(1+\theta)}$
. Note that it is possible that the variance of
![]() $X=G(Y)$
is infinite. Set
$X=G(Y)$
is infinite. Set
![]() $\mu=\delta_{\{ 0 \} }$
. By Remark 2(i) we get
$\mu=\delta_{\{ 0 \} }$
. By Remark 2(i) we get
![]() $b_k(\mu)=H_k^2(0)/(2\pi)<+\infty$
for any
$b_k(\mu)=H_k^2(0)/(2\pi)<+\infty$
for any
![]() $k\ge 0$
,
$k\ge 0$
,
![]() $b_0>0$
,
$b_0>0$
,
![]() $b_1= 0$
, etc. By the choice
$b_1= 0$
, etc. By the choice
![]() $ C_Y(t)= \|t\|^{-\eta}L(\|t\|)$
,
$ C_Y(t)= \|t\|^{-\eta}L(\|t\|)$
,
![]() $\eta\in (0,d)$
we get that
$\eta\in (0,d)$
we get that
![]() $\int_{\mathbb{R}^d} |C_Y(t)|\, {\textrm{d}} t = +\infty$
, and the series (10) diverges. Then X is l.r.d. in the sense of Definition 1 for
$\int_{\mathbb{R}^d} |C_Y(t)|\, {\textrm{d}} t = +\infty$
, and the series (10) diverges. Then X is l.r.d. in the sense of Definition 1 for
![]() $\eta\in (0,d)$
, which is in accordance with the above limit theorem.
$\eta\in (0,d)$
, which is in accordance with the above limit theorem.
4.1.2. Empirical mean: infinite variance case
In this section we show that Definition 1 cannot be linked to the behaviour of integrals or partial sums of the field X if X has infinite variance. For that, we use the framework of time series
![]() $X=\{ X_t, \ t\in\mathbb Z \}$
, where many more models have been widely explored, as compared to (continuous-time) random fields.
$X=\{ X_t, \ t\in\mathbb Z \}$
, where many more models have been widely explored, as compared to (continuous-time) random fields.
Consider (as in Section 3.3) a subordinated time series
![]() $X_t=G(|Y_t|)$
,
$X_t=G(|Y_t|)$
,
![]() $t\in\mathbb Z$
, where
$t\in\mathbb Z$
, where
![]() $\{Y_t, \: t\in\mathbb Z\}$
is a centred Gaussian long memory linear time series with non-decreasing covariance function
$\{Y_t, \: t\in\mathbb Z\}$
is a centred Gaussian long memory linear time series with non-decreasing covariance function
![]() $C_Y(t)=\textrm{cov}(Y_0,Y_t)\sim |t|^{-\eta}L(t) $
,
$C_Y(t)=\textrm{cov}(Y_0,Y_t)\sim |t|^{-\eta}L(t) $
,
![]() $t\to+\infty$
,
$t\to+\infty$
,
![]() $\eta\in(0,1)$
, and such that
$\eta\in(0,1)$
, and such that
![]() $\mathbb P(|X_0|>x)\sim x^{-\alpha}L(x)$
,
$\mathbb P(|X_0|>x)\sim x^{-\alpha}L(x)$
,
![]() $\alpha\in (0,2)$
. It is further assumed that G has Hermite rank q. By Corollary 1(ii), X is short range dependent in the sense of Definition 1 whenever, for any finite measure
$\alpha\in (0,2)$
. It is further assumed that G has Hermite rank q. By Corollary 1(ii), X is short range dependent in the sense of Definition 1 whenever, for any finite measure
![]() $\mu$
on
$\mu$
on
![]() $\mathbb{R}$
,
$\mathbb{R}$
,
We note that
where
![]() $\delta>0$
is arbitrary and
$\delta>0$
is arbitrary and
![]() $c_0, c_1>0$
are some constants. The second inequality holds since
$c_0, c_1>0$
are some constants. The second inequality holds since
![]() $L(t)\le c_2 t^\delta$
for
$L(t)\le c_2 t^\delta$
for
![]() $t\ge t_0$
, where
$t\ge t_0$
, where
![]() $t_0>0$
is large enough and
$t_0>0$
is large enough and
![]() $c_2=c_2(\delta,t_0)=(1+\delta) L(t_0)/t_0^\delta \le 1$
for large
$c_2=c_2(\delta,t_0)=(1+\delta) L(t_0)/t_0^\delta \le 1$
for large
![]() $t_0$
; see [Reference Resnick30, Proposition 2.6]. The right-hand side of (17) is finite and equal to
$t_0$
; see [Reference Resnick30, Proposition 2.6]. The right-hand side of (17) is finite and equal to
![]() $O(1/k)$
whenever
$O(1/k)$
whenever
![]() $\eta\in(1/2,1)$
, since
$\eta\in(1/2,1)$
, since
![]() $\delta>0$
can be chosen arbitrarily small. The series in (17) diverges if
$\delta>0$
can be chosen arbitrarily small. The series in (17) diverges if
![]() $\eta\in (0,1/2)$
. If
$\eta\in (0,1/2)$
. If
![]() $\eta=1/2$
, the summability of the series in (17) depends on the particular form of the slowly varying function L and will not be discussed here.
$\eta=1/2$
, the summability of the series in (17) depends on the particular form of the slowly varying function L and will not be discussed here.
Thus, for
![]() $\eta\in(1/2,1)$
, X is s.r.d. whenever
$\eta\in(1/2,1)$
, X is s.r.d. whenever
for any finite measure
![]() $\mu$
.
$\mu$
.
Now we have to consider a special example of function G in order to get more explicit results for the s.r.d. case. As in Example 1, set
![]() $G(x)={\textrm{e}}^{x^2/(2\alpha)}$
,
$G(x)={\textrm{e}}^{x^2/(2\alpha)}$
,
![]() $\alpha\in(0,2]$
. By relation (12), condition (18) is satisfied for
$\alpha\in(0,2]$
. By relation (12), condition (18) is satisfied for
![]() $\eta\in(1/2,1)$
, hence X is s.r.d. in the sense of Definition 1 if
$\eta\in(1/2,1)$
, hence X is s.r.d. in the sense of Definition 1 if
![]() $\eta\in(1/2,1)$
and l.r.d. if
$\eta\in(1/2,1)$
and l.r.d. if
![]() $\eta\in (0,1/2)$
.
$\eta\in (0,1/2)$
.
Let us compare this result with the limiting behaviour of the partial sums
![]() $S_n=\sum_{t=1}^n (X_t-\mathbb E[X_t])$
as given in [Reference Sly and Heyde40] and [Reference Beran, Feng, Ghosh and Kulik5, Section 4.3.5]; see Table 1. There some discrepancies are seen, that is, Definition 1 does not agree with the asymptotic behaviour of
$S_n=\sum_{t=1}^n (X_t-\mathbb E[X_t])$
as given in [Reference Sly and Heyde40] and [Reference Beran, Feng, Ghosh and Kulik5, Section 4.3.5]; see Table 1. There some discrepancies are seen, that is, Definition 1 does not agree with the asymptotic behaviour of
![]() $S_n$
.
$S_n$
.
Table 1. Short or long memory of
![]() $X_t={\textrm{e}}^{Y_t^2/(2\alpha)}$
in the infinite variance case
$X_t={\textrm{e}}^{Y_t^2/(2\alpha)}$
in the infinite variance case
![]() $\alpha\in(1,2)$
depending on the long memory parameter
$\alpha\in(1,2)$
depending on the long memory parameter
![]() $\eta$
of Y according to [Reference Sly and Heyde40].
$\eta$
of Y according to [Reference Sly and Heyde40].

4.2. Limit theorems for the integrals of functionals of l.r.d. random volatility fields
In this section we will justify that our definition of long range dependence is in agreement with limit theorems for volumes of level sets for random volatility models. Unlike the subordinated Gaussian case, where the limiting results are known, a general asymptotic theory has to be developed.
Let X be a random volatility field of the form
![]() $X_t=G(Y_t)Z_t$
,
$X_t=G(Y_t)Z_t$
,
![]() $t\in \mathbb Z^d$
, where
$t\in \mathbb Z^d$
, where
-
•
 $\{G(Y_t),t\in \mathbb{R}^d\}$
is a subordinated Gaussian measurable random field, which is sampled at points
$\{G(Y_t),t\in \mathbb{R}^d\}$
is a subordinated Gaussian measurable random field, which is sampled at points
 $t\in\mathbb Z^d$
,
$t\in\mathbb Z^d$
, -
•
 $\{Z_t,t\in \mathbb Z^d\}$
is white noise,
$\{Z_t,t\in \mathbb Z^d\}$
is white noise, -
• the random fields Y and Z are independent.
Our goal is to prove limit theorems for
![]() $\sum_{t\in W_n}g(X_t)$
as
$\sum_{t\in W_n}g(X_t)$
as
![]() $n\to\infty$
, where
$n\to\infty$
, where
![]() $W_n=[-n,n]^d \cap \mathbb Z^d$
and g is a real-valued Borel-measurable function such that
$W_n=[-n,n]^d \cap \mathbb Z^d$
and g is a real-valued Borel-measurable function such that
Introduce the function
It follows from (19) that for
![]() $\nu_1$
-almost every
$\nu_1$
-almost every
![]() $y\in \mathbb{R}$
$y\in \mathbb{R}$
By (19) we also have
![]() $\mathbb E[\xi(Y_0)]=0$
. Let
$\mathbb E[\xi(Y_0)]=0$
. Let
be the mth Hermite coefficient of
![]() $\xi$
. We recall that a sufficient condition for the finiteness of J(m) is
$\xi$
. We recall that a sufficient condition for the finiteness of J(m) is
for some
![]() $\theta\in(0,1]$
, where
$\theta\in(0,1]$
, where
![]() $\mathcal{Y}$
is a sigma-field generated by the entire sequence Y. Let
$\mathcal{Y}$
is a sigma-field generated by the entire sequence Y. Let
![]() $\operatorname{rank} (\xi)= q$
. Furthermore, set
$\operatorname{rank} (\xi)= q$
. Furthermore, set
which is almost everywhere finite by (20), and
![]() $\chi(y)=\mathbb E[m^2(y,Z_0)].$
We also assume
$\chi(y)=\mathbb E[m^2(y,Z_0)].$
We also assume
Note that under (22), using the Lyapunov inequality on a space of finite measure and the stationarity of
![]() $Y_t$
, we have for any finite subset
$Y_t$
, we have for any finite subset
![]() $I\subset \mathbb Z^d$
$I\subset \mathbb Z^d$
 \begin{align*}\mathbb E\biggl[\biggl(\sum_{t\in I}\chi(Y_t)\biggr)^3\biggr]<\infty.\end{align*}
\begin{align*}\mathbb E\biggl[\biggl(\sum_{t\in I}\chi(Y_t)\biggr)^3\biggr]<\infty.\end{align*}
The following result shows that the limiting behaviour is primarily determined by the function
![]() $\xi$
, with
$\xi$
, with
![]() $\xi\equiv 0$
being the boundary case.
$\xi\equiv 0$
being the boundary case.
Theorem 3. Assume that the random field
![]() $X_t=G(Y_t)Z_t$
,
$X_t=G(Y_t)Z_t$
,
![]() $t\in\mathbb Z^d$
, is as above, and satisfies the following:
$t\in\mathbb Z^d$
, is as above, and satisfies the following:
-
• Y is a homogeneous isotropic centred Gaussian random field with the covariance function
 $C_Y(t)=\mathbb E [Y_0Y_t]= \|t\|^{-\eta}L(\|t\|)$
,
$C_Y(t)=\mathbb E [Y_0Y_t]= \|t\|^{-\eta}L(\|t\|)$
,
 $\eta\in (0,d/q)$
and L is slowly varying at infinity,
$\eta\in (0,d/q)$
and L is slowly varying at infinity, -
• Y has a spectral density
 $f(\lambda)$
which is continuous for all
$f(\lambda)$
which is continuous for all
 $\lambda\neq 0$
and decreasing in a neighbourhood of 0.
$\lambda\neq 0$
and decreasing in a neighbourhood of 0.
Assume that (19), (21) with
![]() $\theta=1$
, and (22) hold.
$\theta=1$
, and (22) hold.
-
(i) If
 $\xi(y)\equiv 0$
, then
(23)where
$\xi(y)\equiv 0$
, then
(23)where \begin{align}n^{-d/2}\sum_{t\in W_n}g(X_t) \stackrel{d}{\longrightarrow} \mathcal{N}(0,\sigma^2), \quad n\to+\infty,\end{align}
\begin{align}n^{-d/2}\sum_{t\in W_n}g(X_t) \stackrel{d}{\longrightarrow} \mathcal{N}(0,\sigma^2), \quad n\to+\infty,\end{align}
 $\sigma^2=\mathbb E[g^2(X_0)] 2^d>0$
.
$\sigma^2=\mathbb E[g^2(X_0)] 2^d>0$
.
-
(ii) If
 $\xi(y)\not\equiv 0$
, then
(24)where the random variable R is given in (16) with
$\xi(y)\not\equiv 0$
, then
(24)where the random variable R is given in (16) with \begin{align}n^{q\eta/2-d}L^{-q/2}(n)\sum_{t\in W_n} g(X_t) \stackrel{d}{\longrightarrow} R, \quad n\to+\infty,\end{align}
\begin{align}n^{q\eta/2-d}L^{-q/2}(n)\sum_{t\in W_n} g(X_t) \stackrel{d}{\longrightarrow} R, \quad n\to+\infty,\end{align}
 $W=[-1,1]^d$
.
$W=[-1,1]^d$
.
Example 3. Assume that
![]() $g(y)=y$
,
$g(y)=y$
,
![]() $\mathbb E[G^2(Y_0)]<\infty$
, and
$\mathbb E[G^2(Y_0)]<\infty$
, and
![]() $\mathbb E[Z_0]=0$
. Then
$\mathbb E[Z_0]=0$
. Then
![]() $\xi(y)=G(y) \mathbb E[Z_0]= 0$
and (23) always holds. In this case there is no contribution from the long memory of the random field
$\xi(y)=G(y) \mathbb E[Z_0]= 0$
and (23) always holds. In this case there is no contribution from the long memory of the random field
![]() $Y_t$
.
$Y_t$
.
Example 4. Assume that
![]() $g(y)=y-\mathbb E[G(Y_0)Z_0]$
and
$g(y)=y-\mathbb E[G(Y_0)Z_0]$
and
![]() $\mathbb E[Z_0]\not=0$
. Then
$\mathbb E[Z_0]\not=0$
. Then
![]() $\xi(y)=\mathbb E[Z_0]\{ G(y)- \mathbb E[G(Y_0)]\}$
. Condition (22) is satisfied if
$\xi(y)=\mathbb E[Z_0]\{ G(y)- \mathbb E[G(Y_0)]\}$
. Condition (22) is satisfied if
![]() $\mathbb E[|Z_0|^3]<+\infty$
and
$\mathbb E[|Z_0|^3]<+\infty$
and
![]() $\mathbb E[G^4(Y_0)]<+\infty$
. In this case
$\mathbb E[G^4(Y_0)]<+\infty$
. In this case
![]() $\xi(y)\not\equiv 0$
, and (24) always holds.
$\xi(y)\not\equiv 0$
, and (24) always holds.
Example 5. Assume that
![]() $g(y)=g_u(y)={\bf 1} \{y>u\}-\mathbb P ( G(Y_0)Z_0>u) $
, where G is non-negative or non-positive
$g(y)=g_u(y)={\bf 1} \{y>u\}-\mathbb P ( G(Y_0)Z_0>u) $
, where G is non-negative or non-positive
![]() $\nu_1$
-a.e. Then
$\nu_1$
-a.e. Then
if
![]() $u\neq 0$
, so case (24) applies. If
$u\neq 0$
, so case (24) applies. If
![]() $u=0$
, then
$u=0$
, then
![]() $\xi(y)\equiv 0$
(compare Remark 3(iii)), so case (23) holds true.
$\xi(y)\equiv 0$
(compare Remark 3(iii)), so case (23) holds true.
Example 6. Let the random volatility field
![]() $X_t=G(|Y_t|)Z_t$
,
$X_t=G(|Y_t|)Z_t$
,
![]() $t\in\mathbb Z^d$
be as in Lemma 4, where
$t\in\mathbb Z^d$
be as in Lemma 4, where
![]() $\{ Z_t\}$
is heavy-tailed white noise,
$\{ Z_t\}$
is heavy-tailed white noise,
![]() $\mathbb E Z_0^2=+\infty$
. Let Y satisfy the assumptions of Theorem 3. Choose
$\mathbb E Z_0^2=+\infty$
. Let Y satisfy the assumptions of Theorem 3. Choose
![]() $G(x)\ge 0$
as in Lemma 5(ii), and let
$G(x)\ge 0$
as in Lemma 5(ii), and let
![]() $C_Y(t)\sim \|t\|^{-\eta}$
as
$C_Y(t)\sim \|t\|^{-\eta}$
as
![]() $ \|t\|\to+\infty$
be non-negative. Similarly to Example 2, an analogue of relation (14) holds true: for
$ \|t\|\to+\infty$
be non-negative. Similarly to Example 2, an analogue of relation (14) holds true: for
![]() $\mu=\delta_{\{u_0\}}$
,
$\mu=\delta_{\{u_0\}}$
,
![]() $u_0>0$
we have
$u_0>0$
we have
 \begin{equation*}\sum_{t\in \mathbb Z^d, \, t\neq 0}\int_{\mathbb{R}^2} {\textrm{cov}}_X(t,u,v) \mu({\textrm{d}} u)\mu({\textrm{d}} v) = \sum_{k=1}^\infty \dfrac{ \langle \bar{F}_Z(u_0/\widetilde{G}), H_k\rangle_\varphi^2 }{k!} \sum_{t\in \mathbb Z^d, \, t\neq 0}\ C_Y^k(t) ,\end{equation*}
\begin{equation*}\sum_{t\in \mathbb Z^d, \, t\neq 0}\int_{\mathbb{R}^2} {\textrm{cov}}_X(t,u,v) \mu({\textrm{d}} u)\mu({\textrm{d}} v) = \sum_{k=1}^\infty \dfrac{ \langle \bar{F}_Z(u_0/\widetilde{G}), H_k\rangle_\varphi^2 }{k!} \sum_{t\in \mathbb Z^d, \, t\neq 0}\ C_Y^k(t) ,\end{equation*}
where
![]() $\widetilde{G}(y)=G(|y|)$
,
$\widetilde{G}(y)=G(|y|)$
,
![]() $y\in\mathbb{R}$
. Since
$y\in\mathbb{R}$
. Since
![]() $\operatorname{rank} (\bar{F}_Z(u_0/\widetilde{G}) )=2$
, X is l.r.d. in the sense of Definition 1 if
$\operatorname{rank} (\bar{F}_Z(u_0/\widetilde{G}) )=2$
, X is l.r.d. in the sense of Definition 1 if
![]() $\sum_{t\in \mathbb Z^d, \, t\neq 0} C_Y^{2}(t) =+\infty$
, i.e. if
$\sum_{t\in \mathbb Z^d, \, t\neq 0} C_Y^{2}(t) =+\infty$
, i.e. if
![]() $\eta<d/2$
.
$\eta<d/2$
.
Consider function
![]() $\xi $
from Example 5 with
$\xi $
from Example 5 with
![]() $u=u_0>0$
and
$u=u_0>0$
and
![]() $\widetilde{G}$
instead of G. By Lemma 5(ii),
$\widetilde{G}$
instead of G. By Lemma 5(ii),
![]() $\operatorname{rank} (\xi )=2$
. By Theorem 3 and Example 5, the asymptotic behaviour of the cardinality of the level sets of X at level
$\operatorname{rank} (\xi )=2$
. By Theorem 3 and Example 5, the asymptotic behaviour of the cardinality of the level sets of X at level
![]() $u_0$
is of l.r.d. type if
$u_0$
is of l.r.d. type if
![]() $\eta\in(0,d/2)$
, which is in agreement with our definition.
$\eta\in(0,d/2)$
, which is in agreement with our definition.
Remark 4. We would like to connect the assumption
![]() $\xi\equiv 0$
to our definition. Let g,h be functions such that
$\xi\equiv 0$
to our definition. Let g,h be functions such that
![]() $\mathbb E[g(X_0)]=\mathbb E[h(X_0)]=0$
. If
$\mathbb E[g(X_0)]=\mathbb E[h(X_0)]=0$
. If
![]() $\mathbb E [g(X_0)h(X_t)]<\infty$
for all t, and
$\mathbb E [g(X_0)h(X_t)]<\infty$
for all t, and
![]() $\mathbb E[g(G(y)Z_0)]=\mathbb E[h(G(y)Z_0)]=0$
for all y, then for
$\mathbb E[g(G(y)Z_0)]=\mathbb E[h(G(y)Z_0)]=0$
for all y, then for
![]() $t\not=0$
$t\not=0$
where
![]() $\mathbb P_{Y_0,Y_t}$
is the joint law of
$\mathbb P_{Y_0,Y_t}$
is the joint law of
![]() $(Y_0,Y_t)$
. In particular, take
$(Y_0,Y_t)$
. In particular, take
Then
and the random field X is s.r.d. according to Definition 1 for
![]() $\xi\equiv 0$
.
$\xi\equiv 0$
.
5. Summary and outlook
We proposed a new definition of long memory for stationary random fields X indexed by any set
![]() $T\subset \mathbb{R}^d$
, which works also for heavy-tailed X. We showed that this definition is a good fit to the asymptotic behaviour of the volume of the excursion set of X at a level
$T\subset \mathbb{R}^d$
, which works also for heavy-tailed X. We showed that this definition is a good fit to the asymptotic behaviour of the volume of the excursion set of X at a level
![]() $u\in\mathbb{R}$
in an unboundedly growing observation window
$u\in\mathbb{R}$
in an unboundedly growing observation window
![]() $W_n$
. This connection to non-central limit theorems was proved for a class of random volatility fields with subordinated l.r.d. Gaussian volatility.
$W_n$
. This connection to non-central limit theorems was proved for a class of random volatility fields with subordinated l.r.d. Gaussian volatility.
Appendix A Proofs
Proof of Theorem 2. If X is a centred stationary unit variance Gaussian random field with covariance function
![]() $C_Y(t)$
,
$C_Y(t)$
,
see [Reference Bulinski, Spodarev and Timmermann8, Lemma 2].
Consider representation (25). Since the density
![]() $f_{(U,V)}$
of a bivariate normal distribution with zero mean, unit variances, and correlation coefficient
$f_{(U,V)}$
of a bivariate normal distribution with zero mean, unit variances, and correlation coefficient
![]() $\mp r$
equals
$\mp r$
equals
then it is easy to see that
Since G is strictly monotone, by properties of the generalized inverse of G we have
 \begin{align*} &\int_T\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}|\textrm{cov}_X(t, u, v)| \mu(\textrm{d} u) \mu (\textrm{d} v) \,\textrm{d} t \\[3pt]&\quad = \int_T\!\!\! \int_{(\operatorname{Im}(G))^2} |\textrm{cov}_Y(t, G^-(u), G^-(v))| \mu(\textrm{d} u) \mu (\textrm{d} v) \,\textrm{d} t \\[3pt] &\quad = \int_T\!\!\! \int_{(\operatorname{Im}(G))^2} \!\!\! \int_{0}^{|C_Y(t)|} \exp\biggl( -\dfrac{(G^-(u))^2-2\operatorname{sign}(C_Y(t))rG^-(u)G^-(v)+(G^-(v))^2}{2(1-r^2)}\biggr)\\[3pt] &\quad \quad\ \dfrac{\textrm{d} r \mu(\textrm{d} u) \mu (\textrm{d} v) \,\textrm{d} t}{2\pi \sqrt{1-r^2}}.\end{align*}
\begin{align*} &\int_T\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}|\textrm{cov}_X(t, u, v)| \mu(\textrm{d} u) \mu (\textrm{d} v) \,\textrm{d} t \\[3pt]&\quad = \int_T\!\!\! \int_{(\operatorname{Im}(G))^2} |\textrm{cov}_Y(t, G^-(u), G^-(v))| \mu(\textrm{d} u) \mu (\textrm{d} v) \,\textrm{d} t \\[3pt] &\quad = \int_T\!\!\! \int_{(\operatorname{Im}(G))^2} \!\!\! \int_{0}^{|C_Y(t)|} \exp\biggl( -\dfrac{(G^-(u))^2-2\operatorname{sign}(C_Y(t))rG^-(u)G^-(v)+(G^-(v))^2}{2(1-r^2)}\biggr)\\[3pt] &\quad \quad\ \dfrac{\textrm{d} r \mu(\textrm{d} u) \mu (\textrm{d} v) \,\textrm{d} t}{2\pi \sqrt{1-r^2}}.\end{align*}
By [Reference CramÉr9, formula (21.12.5)] for the density
![]() $f_{(U,V)}$
with correlation coefficient
$f_{(U,V)}$
with correlation coefficient
![]() $\operatorname{sign}(C_Y(t))r\in(-1,1)$
, we have
$\operatorname{sign}(C_Y(t))r\in(-1,1)$
, we have
By condition
![]() $\nu_d(\{t\in T\colon |C_Y(t)|=1\})=0$
, the above series converges uniformly for
$\nu_d(\{t\in T\colon |C_Y(t)|=1\})=0$
, the above series converges uniformly for
![]() $r \in (-1,1)$
, so integration over
$r \in (-1,1)$
, so integration over
![]() $r\in [0; |C_Y(t)|]$
and summation with respect to k can be interchanged. Then the above triple integral reads
$r\in [0; |C_Y(t)|]$
and summation with respect to k can be interchanged. Then the above triple integral reads
 \begin{align*}& \int_T\int_{\operatorname{Im}(G)^2}\int_{0}^{|C_Y(t)|}\sum_{k=0}^{\infty}\dfrac{\Phi^{(k+1)}(G^-(u))\Phi^{(k+1)}(G^-(v))}{k!}(\operatorname{sign}(C_Y(t))r)^k \,\textrm{d} r\mu(\textrm{d} u) \mu (\textrm{d} v) \,\textrm{d} t\\[3pt] &\quad = \int_T\int_{\operatorname{Im}(G)^2}\varphi(G^-(u))\varphi(G^-(v))\sum_{k=0}^{\infty}\dfrac{H_k(G^-(u))H_k(G^-(v))}{k!}\operatorname{sign}(C_Y(t))^k \\[3pt] &\quad\quad \times \dfrac{|C_Y(t)|^{k+1}}{k+1} \mu(\textrm{d} u) \mu (\textrm{d} v) \,\textrm{d} t\\[3pt] &\quad =\int_T\int_{\operatorname{Im}(G)^2} |C_Y(t)|\varphi(G^-(u))\varphi(G^-(v))\sum_{k=0}^{\infty}\dfrac{H_k(G^-(u))H_k(G^-(v))}{(k+1)k!}C_Y(t)^k \mu(\textrm{d} u) \mu (\textrm{d} v) \,\textrm{d} t.\end{align*}
\begin{align*}& \int_T\int_{\operatorname{Im}(G)^2}\int_{0}^{|C_Y(t)|}\sum_{k=0}^{\infty}\dfrac{\Phi^{(k+1)}(G^-(u))\Phi^{(k+1)}(G^-(v))}{k!}(\operatorname{sign}(C_Y(t))r)^k \,\textrm{d} r\mu(\textrm{d} u) \mu (\textrm{d} v) \,\textrm{d} t\\[3pt] &\quad = \int_T\int_{\operatorname{Im}(G)^2}\varphi(G^-(u))\varphi(G^-(v))\sum_{k=0}^{\infty}\dfrac{H_k(G^-(u))H_k(G^-(v))}{k!}\operatorname{sign}(C_Y(t))^k \\[3pt] &\quad\quad \times \dfrac{|C_Y(t)|^{k+1}}{k+1} \mu(\textrm{d} u) \mu (\textrm{d} v) \,\textrm{d} t\\[3pt] &\quad =\int_T\int_{\operatorname{Im}(G)^2} |C_Y(t)|\varphi(G^-(u))\varphi(G^-(v))\sum_{k=0}^{\infty}\dfrac{H_k(G^-(u))H_k(G^-(v))}{(k+1)k!}C_Y(t)^k \mu(\textrm{d} u) \mu (\textrm{d} v) \,\textrm{d} t.\end{align*}
Abel’s uniform convergence test allows us to interchange the sum and the integral over
![]() $\operatorname{Im}(G)^2 $
. Since
$\operatorname{Im}(G)^2 $
. Since
![]() $b_k\geq 0$
, we get
$b_k\geq 0$
, we get
 \begin{align*} & \int_T\sum_{k=0}^{\infty}\int_{\operatorname{Im}(G)^2} \varphi(G^-(u))\varphi(G^-(v))\dfrac{H_k(G^-(u))H_k(G^-(v))}{(k+1)!}|C_Y(t)|C_Y(t)^k \,\textrm{d} r \mu(\textrm{d} u) \mu (\textrm{d} v) \,\textrm{d} t \nonumber \\[3pt] &\quad =\int_T\sum_{k=0}^{\infty}\dfrac{1}{(k+1)!}\biggl(\int_{\operatorname{Im}(G)}\varphi(G^-(u))H_k(G^-(u)) \mu(\textrm{d} u)\biggr)^2 |C_Y(t)|C_Y(t)^k \,\textrm{d} t\nonumber \\[3pt] &\quad = \int_T\sum_{k=0}^{\infty}\dfrac{b_k(\mu)}{(k+1)!}|C_Y(t)|C_Y(t)^k \,\textrm{d} t = \sum_{k=1}^{\infty}\dfrac{b_{k-1}(\mu)}{k!}\int_{T}|C_Y(t)|\rho^{k-1}(t)\,\textrm{d} t ,\end{align*}
\begin{align*} & \int_T\sum_{k=0}^{\infty}\int_{\operatorname{Im}(G)^2} \varphi(G^-(u))\varphi(G^-(v))\dfrac{H_k(G^-(u))H_k(G^-(v))}{(k+1)!}|C_Y(t)|C_Y(t)^k \,\textrm{d} r \mu(\textrm{d} u) \mu (\textrm{d} v) \,\textrm{d} t \nonumber \\[3pt] &\quad =\int_T\sum_{k=0}^{\infty}\dfrac{1}{(k+1)!}\biggl(\int_{\operatorname{Im}(G)}\varphi(G^-(u))H_k(G^-(u)) \mu(\textrm{d} u)\biggr)^2 |C_Y(t)|C_Y(t)^k \,\textrm{d} t\nonumber \\[3pt] &\quad = \int_T\sum_{k=0}^{\infty}\dfrac{b_k(\mu)}{(k+1)!}|C_Y(t)|C_Y(t)^k \,\textrm{d} t = \sum_{k=1}^{\infty}\dfrac{b_{k-1}(\mu)}{k!}\int_{T}|C_Y(t)|\rho^{k-1}(t)\,\textrm{d} t ,\end{align*}
where the integral over T and the sum are interchangeable by Tonelli’s theorem subdividing T into parts
![]() $T^+ = \{t\in T\colon C_Y(t)\geq 0\}$
and
$T^+ = \{t\in T\colon C_Y(t)\geq 0\}$
and
![]() $T^- = \{t\in T\colon C_Y(t)< 0\}.$
Then
$T^- = \{t\in T\colon C_Y(t)< 0\}.$
Then
![]() $X=G(Y)$
has short memory if
$X=G(Y)$
has short memory if
for any finite measure
![]() $\mu$
on
$\mu$
on
![]() $\mathbb{R}$
.
$\mathbb{R}$
.
![]()
Proof of Corollary 1. (i) It follows from relation (9) using the change of variables
![]() $u=G(x)$
and by [Reference Beran, Feng, Ghosh and Kulik5, Lemma 4.21].
$u=G(x)$
and by [Reference Beran, Feng, Ghosh and Kulik5, Lemma 4.21].
(ii) Without loss of generality, assume G is an increasing function. Since the probability density of the centred univariate and bivariate Gaussian distribution is invariant under transformation
![]() $x\longmapsto-x,y\longmapsto-y$
, we get
$x\longmapsto-x,y\longmapsto-y$
, we get
 \begin{align*} \textrm{cov}_X(t, u, v) & = \mathbb P(|Y_0|>G^{-}(u),|Y_t|>G^{-}(v)) -\mathbb P(|Y_0|>G^{-}(u))\mathbb P(|Y_t|>G^{-}(v))\\[3pt] &= 2 ( \mathbb P(Y_0>G^{-}(u),Y_t>G^{-}(v))-\mathbb P(Y_0>G^{-}(u))\mathbb P(Y_t>G^{-}(v))\\[3pt] &\quad + \mathbb P(Y_0>G^{-}(u),Y_t<-G^{-}(v))-\mathbb P(Y_0>G^{-}(u))\mathbb P(Y_t<-G^{-}(v)) ) .\end{align*}
\begin{align*} \textrm{cov}_X(t, u, v) & = \mathbb P(|Y_0|>G^{-}(u),|Y_t|>G^{-}(v)) -\mathbb P(|Y_0|>G^{-}(u))\mathbb P(|Y_t|>G^{-}(v))\\[3pt] &= 2 ( \mathbb P(Y_0>G^{-}(u),Y_t>G^{-}(v))-\mathbb P(Y_0>G^{-}(u))\mathbb P(Y_t>G^{-}(v))\\[3pt] &\quad + \mathbb P(Y_0>G^{-}(u),Y_t<-G^{-}(v))-\mathbb P(Y_0>G^{-}(u))\mathbb P(Y_t<-G^{-}(v)) ) .\end{align*}
Let
![]() $Z=-Y_t$
,
$Z=-Y_t$
,
![]() $x=G^-(u)$
, and
$x=G^-(u)$
, and
![]() $y=G^-(v)$
. Thus
$y=G^-(v)$
. Thus
Since
![]() $\textrm{cov}(Y_0,Z) = -C_Y(t) $
and
$\textrm{cov}(Y_0,Z) = -C_Y(t) $
and
![]() $xy=G^{-}(u)G^{-}(v)\ge 0$
, we have by formula (25) that
$xy=G^{-}(u)G^{-}(v)\ge 0$
, we have by formula (25) that
 \begin{align*} & |\textrm{cov}_X(t, u, v)| \\[3pt] & \quad =\dfrac{2}{2\pi} \biggl|\int_{0}^{C_Y(t)}\dfrac{1}{\sqrt{1-r^2}}\exp\biggl(-\dfrac{x^2-2rxy+y^2}{2(1-r^2)}\biggr) \,\textrm{d} r \\[3pt] &\quad\quad + \int_{0}^{-C_Y(t)}\dfrac{1}{\sqrt{1-r^2}}\exp\biggl(-\dfrac{x^2-2rxy+y^2}{2(1-r^2)}\biggr) \,\textrm{d} r \biggr| \\[3pt] & \quad = \int_{0}^{|C_Y(t)|} \biggl(\exp\biggl(-\dfrac{x^2-2rxy+y^2}{2(1-r^2)}\biggr) - \exp\biggl(-\dfrac{x^2+2rxy+y^2}{2(1-r^2)}\biggr)\biggr) \dfrac{\textrm{d} r}{\pi \sqrt{1-r^2}}.\end{align*}
\begin{align*} & |\textrm{cov}_X(t, u, v)| \\[3pt] & \quad =\dfrac{2}{2\pi} \biggl|\int_{0}^{C_Y(t)}\dfrac{1}{\sqrt{1-r^2}}\exp\biggl(-\dfrac{x^2-2rxy+y^2}{2(1-r^2)}\biggr) \,\textrm{d} r \\[3pt] &\quad\quad + \int_{0}^{-C_Y(t)}\dfrac{1}{\sqrt{1-r^2}}\exp\biggl(-\dfrac{x^2-2rxy+y^2}{2(1-r^2)}\biggr) \,\textrm{d} r \biggr| \\[3pt] & \quad = \int_{0}^{|C_Y(t)|} \biggl(\exp\biggl(-\dfrac{x^2-2rxy+y^2}{2(1-r^2)}\biggr) - \exp\biggl(-\dfrac{x^2+2rxy+y^2}{2(1-r^2)}\biggr)\biggr) \dfrac{\textrm{d} r}{\pi \sqrt{1-r^2}}.\end{align*}
Similarly to the proof of Theorem 2, we use representation (26) to write
 \begin{align*} & \int_T\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty} |\textrm{cov}_X(t, u, v)| \mu(\textrm{d} u) \mu( \textrm{d} v) \,\textrm{d} t \\[3pt] &\quad = 2\int_T\int_{\operatorname{Im}(G)^2} \sum_{k=0}^{\infty}\dfrac{1-(-1)^k}{(k+1)!}H_{k}(x)H_{k}(y)\varphi(x)\varphi(y)|C_Y(t)|^{k+1} \mu(\textrm{d} u) \mu( \textrm{d} v) \,\textrm{d} t\\[3pt] &\quad =\int_T \sum_{k=1}^{\infty}\dfrac{4}{(2k)!}\biggl(\int_{\operatorname{Im}(G)}H_{2k-1}(G^-(u))\varphi(G^-(u)) \mu(\textrm{d} u) \biggr)^2|C_Y(t)|^{2k} \,\textrm{d} t \\[3pt] &\quad =4\sum_{k=1}^{\infty}\dfrac{b_{2k-1}(\mu)}{(2k)!}\int_T \rho^{2k}(t) \,\textrm{d} t.\end{align*}
\begin{align*} & \int_T\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty} |\textrm{cov}_X(t, u, v)| \mu(\textrm{d} u) \mu( \textrm{d} v) \,\textrm{d} t \\[3pt] &\quad = 2\int_T\int_{\operatorname{Im}(G)^2} \sum_{k=0}^{\infty}\dfrac{1-(-1)^k}{(k+1)!}H_{k}(x)H_{k}(y)\varphi(x)\varphi(y)|C_Y(t)|^{k+1} \mu(\textrm{d} u) \mu( \textrm{d} v) \,\textrm{d} t\\[3pt] &\quad =\int_T \sum_{k=1}^{\infty}\dfrac{4}{(2k)!}\biggl(\int_{\operatorname{Im}(G)}H_{2k-1}(G^-(u))\varphi(G^-(u)) \mu(\textrm{d} u) \biggr)^2|C_Y(t)|^{2k} \,\textrm{d} t \\[3pt] &\quad =4\sum_{k=1}^{\infty}\dfrac{b_{2k-1}(\mu)}{(2k)!}\int_T \rho^{2k}(t) \,\textrm{d} t.\end{align*}
![]()
Proof of Corollary 2. Choose
![]() $\mu=\delta_{\{ u_0\}}$
,
$\mu=\delta_{\{ u_0\}}$
,
![]() $u_0\in\mathbb{R}$
and write
$u_0\in\mathbb{R}$
and write
 \begin{align*}& \int_T\int_{\mathbb{R}^2}\textrm{cov}_X(t,u,v)\, \mu({\textrm{d}} u)\,\mu({\textrm{d}} v)\,{\textrm{d}} t \\[3pt] &\quad = \int_T\textrm{cov} ( \bar{F}_Z(u_0/A),\bar{F}_Z(u_0/A) ) \,{\textrm{d}} t + \int_T \mathbb E [ \textrm{cov}_Z(t,u_0/A,u_0/A)] \,{\textrm{d}} t\\[3pt] &\quad \ge \int_T \textrm{var}( \bar{F}_Z (u_0/A)) \,{\textrm{d}} t\\[3pt] &\quad = +\infty ,\end{align*}
\begin{align*}& \int_T\int_{\mathbb{R}^2}\textrm{cov}_X(t,u,v)\, \mu({\textrm{d}} u)\,\mu({\textrm{d}} v)\,{\textrm{d}} t \\[3pt] &\quad = \int_T\textrm{cov} ( \bar{F}_Z(u_0/A),\bar{F}_Z(u_0/A) ) \,{\textrm{d}} t + \int_T \mathbb E [ \textrm{cov}_Z(t,u_0/A,u_0/A)] \,{\textrm{d}} t\\[3pt] &\quad \ge \int_T \textrm{var}( \bar{F}_Z (u_0/A)) \,{\textrm{d}} t\\[3pt] &\quad = +\infty ,\end{align*}
since
![]() $$Z \in {\bf{PA}}$$
,
$$Z \in {\bf{PA}}$$
,
![]() $\bar{F}_Z (u_0/A)$
is non-degenerate and bounded.
$\bar{F}_Z (u_0/A)$
is non-degenerate and bounded.
![]()
Proof of Corollary \refcor:rvt0. Without loss of generality assume
![]() $Z, Y\in$
PA. Then
$Z, Y\in$
PA. Then
![]() $Y^\alpha\in$
PA too, and the second term in (13) is non-negative. Let
$Y^\alpha\in$
PA too, and the second term in (13) is non-negative. Let
Since
![]() $Y\in$
PA and the function
$Y\in$
PA and the function
![]() $\bar{F}_Z(u/\cdot)$
is bounded and non-decreasing for
$\bar{F}_Z(u/\cdot)$
is bounded and non-decreasing for
![]() $u>0$
, we get
$u>0$
, we get
![]() $A_{u,v}(t)\ge 0$
for all
$A_{u,v}(t)\ge 0$
for all
![]() $u,v\in\mathbb{R}_+$
,
$u,v\in\mathbb{R}_+$
,
![]() $t\in T .$
Using the regular variation of the tail of
$t\in T .$
Using the regular variation of the tail of
![]() $Z_0$
, the independence of Y and Z, and Potter’s bound [Reference Resnick30, Proposition 2.6], one can easily show that under the above assumptions on the integrability of Y we obtain
$Z_0$
, the independence of Y and Z, and Potter’s bound [Reference Resnick30, Proposition 2.6], one can easily show that under the above assumptions on the integrability of Y we obtain
for any
![]() $t\in T$
. Then, for sufficiently large
$t\in T$
. Then, for sufficiently large
![]() $N>0$
, there exists
$N>0$
, there exists
![]() $u_0>N$
such that for the Dirac measure
$u_0>N$
such that for the Dirac measure
![]() $\mu=\delta_{\{ u_0 \}}$
and some
$\mu=\delta_{\{ u_0 \}}$
and some
![]() $\varepsilon\in(0,1)$
, we have
$\varepsilon\in(0,1)$
, we have
which is infinite if
![]() $Y^\alpha$
is l.r.d. Thus
$Y^\alpha$
is l.r.d. Thus
![]() $X=Y Z$
is l.r.d. if
$X=Y Z$
is l.r.d. if
![]() $Y^\alpha$
is l.r.d.
$Y^\alpha$
is l.r.d.
![]()
Proof of Lemma 4. Without loss of generality, assume G is non-negative. By Lemma 2, and the Fubini and Tonelli theorems for
![]() $G_u(y)=\bar{F}_Z (u/G(y)) $
, we get
$G_u(y)=\bar{F}_Z (u/G(y)) $
, we get
 \begin{align*}D_{\mu} (G(Y),Z_0) &=\int_T\int_{\mathbb{R}^2} \textrm{cov} ( G_u(Y_0), G_v(Y_t)) \mu({\textrm{d}} u) \mu({\textrm{d}} v) \, {\textrm{d}} t \\[3pt] &= \sum_{k=1}^\infty \dfrac{\bigl( \int_\mathbb{R} \langle G_u, H_k\rangle_\varphi \, \mu({\textrm{d}} u) \bigr)^2 }{k!}\int_T \rho^k(t) \, {\textrm{d}} t .\end{align*}
\begin{align*}D_{\mu} (G(Y),Z_0) &=\int_T\int_{\mathbb{R}^2} \textrm{cov} ( G_u(Y_0), G_v(Y_t)) \mu({\textrm{d}} u) \mu({\textrm{d}} v) \, {\textrm{d}} t \\[3pt] &= \sum_{k=1}^\infty \dfrac{\bigl( \int_\mathbb{R} \langle G_u, H_k\rangle_\varphi \, \mu({\textrm{d}} u) \bigr)^2 }{k!}\int_T \rho^k(t) \, {\textrm{d}} t .\end{align*}
The change of order of the sum and integrals is justified by the Weierstrass uniform convergence test since, for almost all
![]() $t\in T$
,
$t\in T$
,
 \[\sum_{k=1}^\infty \dfrac{| \langle G_u, H_k\rangle_\varphi \langle G_v, H_k\rangle_\varphi | }{k!}\rho^k(t) \le\sum_{k=1}^\infty \dfrac{ \langle 1, |H_k|\rangle_\varphi^2 }{k!}\rho^k(t) \le\sum_{k=1}^\infty \rho^k(t) <\infty\]
\[\sum_{k=1}^\infty \dfrac{| \langle G_u, H_k\rangle_\varphi \langle G_v, H_k\rangle_\varphi | }{k!}\rho^k(t) \le\sum_{k=1}^\infty \dfrac{ \langle 1, |H_k|\rangle_\varphi^2 }{k!}\rho^k(t) \le\sum_{k=1}^\infty \rho^k(t) <\infty\]
due to
![]() $\langle 1, |H_k|\rangle_\varphi \le \sqrt{k!}$
, by the Cauchy–Schwarz inequality and due to condition (
$\langle 1, |H_k|\rangle_\varphi \le \sqrt{k!}$
, by the Cauchy–Schwarz inequality and due to condition (
![]() $\boldsymbol{\rho}$
).
$\boldsymbol{\rho}$
).
![]()
Proof of Lemma 5. (i) If
![]() $G\colon \mathbb{R}\to\mathbb{R} $
is monotone, then
$G\colon \mathbb{R}\to\mathbb{R} $
is monotone, then
![]() $\operatorname{rank} (G)=1$
due to
$\operatorname{rank} (G)=1$
due to
What is the Hermite rank of
![]() $\zeta_{G,Z,u} $
? First consider
$\zeta_{G,Z,u} $
? First consider
![]() $Z\equiv 1$
. Since the Hermite rank of
$Z\equiv 1$
. Since the Hermite rank of
![]() $y\mapsto {\bf 1} \{ y>u \} - \bar{F}_Y(u)$
is one, we can write
$y\mapsto {\bf 1} \{ y>u \} - \bar{F}_Y(u)$
is one, we can write
where G is non-decreasing without loss of generality. Hence
![]() $\operatorname{rank} ( \zeta_{G,1,u})=1 $
for any
$\operatorname{rank} ( \zeta_{G,1,u})=1 $
for any
![]() $u\in \mathbb{R}$
. Now let
$u\in \mathbb{R}$
. Now let
![]() $G\colon \mathbb{R}\to\mathbb{R}_\pm$
and Z be arbitrary. Without loss of generality, assume G is non-negative. Then
$G\colon \mathbb{R}\to\mathbb{R}_\pm$
and Z be arbitrary. Without loss of generality, assume G is non-negative. Then
since for any
![]() $u\neq 0$
the function
$u\neq 0$
the function
![]() $y\mapsto \bar{F}_Z (u/G(y)) $
is monotone, and we can use the reasoning (27). For non-positive G replace
$y\mapsto \bar{F}_Z (u/G(y)) $
is monotone, and we can use the reasoning (27). For non-positive G replace
![]() $ \bar{F}_Z$
above with
$ \bar{F}_Z$
above with
![]() $ {F}_Z$
.
$ {F}_Z$
.
(ii)Without loss of generality, assume that G is non-negative and non-decreasing. We prove that
![]() $\operatorname{rank} (\widetilde{G})=2$
.
$\operatorname{rank} (\widetilde{G})=2$
.
Clearly, since
![]() $y\mapsto G(|y|)$
is even, we have
$y\mapsto G(|y|)$
is even, we have
![]() $\mathbb E[Y G(|Y|)]=0$
. Now
$\mathbb E[Y G(|Y|)]=0$
. Now
We note that
and hence by symmetry
Also, by the mean value theorem, due to monotonicity of non-constant G, there exists
![]() $y_0\in [0,1)$
such that
$y_0\in [0,1)$
such that
Therefore
 \begin{align*}& \int_0^\infty G(y)(y^2-1)\varphi(y)\,{\textrm{d}} y \\[3pt] &\quad \geq G(y_0) \int_0^1 (y^2-1)\varphi(y)\,{\textrm{d}} y + G(1)\int_1^\infty (y^2-1)\varphi(y)\,{\textrm{d}} y\\[3pt] &\quad = -G(y_0) \int_1^\infty (y^2-1)\varphi(y)\,{\textrm{d}} y +G(1)\int_1^\infty (y^2-1)\varphi(y)\,{\textrm{d}} y\\[3pt] &\quad =(G(1)-G(y_0)) \int_1^\infty (y^2-1)\varphi(y)\,{\textrm{d}} > 0.\end{align*}
\begin{align*}& \int_0^\infty G(y)(y^2-1)\varphi(y)\,{\textrm{d}} y \\[3pt] &\quad \geq G(y_0) \int_0^1 (y^2-1)\varphi(y)\,{\textrm{d}} y + G(1)\int_1^\infty (y^2-1)\varphi(y)\,{\textrm{d}} y\\[3pt] &\quad = -G(y_0) \int_1^\infty (y^2-1)\varphi(y)\,{\textrm{d}} y +G(1)\int_1^\infty (y^2-1)\varphi(y)\,{\textrm{d}} y\\[3pt] &\quad =(G(1)-G(y_0)) \int_1^\infty (y^2-1)\varphi(y)\,{\textrm{d}} > 0.\end{align*}
For non-negative non-increasing G, we can use the estimate
 \begin{align*}\int_0^\infty G(y)(y^2-1)\varphi(y)\,{\textrm{d}} y & \leq G(y_0) \int_0^1 (y^2-1)\varphi(y)\,{\textrm{d}} y + G(1)\int_1^\infty (y^2-1)\varphi(y)\,{\textrm{d}} y\\[3pt] & =(G(y_0)-G(1)) \int_0^1 (y^2-1)\varphi(y)\,{\textrm{d}} y < 0.\end{align*}
\begin{align*}\int_0^\infty G(y)(y^2-1)\varphi(y)\,{\textrm{d}} y & \leq G(y_0) \int_0^1 (y^2-1)\varphi(y)\,{\textrm{d}} y + G(1)\int_1^\infty (y^2-1)\varphi(y)\,{\textrm{d}} y\\[3pt] & =(G(y_0)-G(1)) \int_0^1 (y^2-1)\varphi(y)\,{\textrm{d}} y < 0.\end{align*}
If
![]() $G(y)\le 0$
just multiply it by
$G(y)\le 0$
just multiply it by
![]() $-1$
. This proves that the Hermite rank of
$-1$
. This proves that the Hermite rank of
![]() $G(|y|)$
is 2.
$G(|y|)$
is 2.
Now compute the Hermite rank of
![]() $\zeta_{\widetilde{G},1,u} $
for any
$\zeta_{\widetilde{G},1,u} $
for any
![]() $u\in\mathbb{R}$
. Since
$u\in\mathbb{R}$
. Since
![]() $\zeta_{\widetilde{G},1,u} $
is even,
$\zeta_{\widetilde{G},1,u} $
is even,
![]() $\operatorname{rank} (\zeta_{\widetilde{G},1,u})>1$
. Assuming without loss of generality that G is non-negative and non-decreasing, we calculate
$\operatorname{rank} (\zeta_{\widetilde{G},1,u})>1$
. Assuming without loss of generality that G is non-negative and non-decreasing, we calculate
 \begin{align*}\langle \zeta_{\widetilde{G},1,u}, H_2 \rangle_\varphi & =\mathbb E[(Y^2-1){\bf 1} \{G(|Y|)>u\}] \\[3pt] &= \int_{\mathbb{R}}(y^2-1){\bf 1} \{|y|>G^-(u)\} \varphi(y)\, {\textrm{d}} y\\[3pt] & =2\int_{G^-(u)}^\infty (y^2-1) \varphi(y)\, {\textrm{d}} y \neq 0\end{align*}
\begin{align*}\langle \zeta_{\widetilde{G},1,u}, H_2 \rangle_\varphi & =\mathbb E[(Y^2-1){\bf 1} \{G(|Y|)>u\}] \\[3pt] &= \int_{\mathbb{R}}(y^2-1){\bf 1} \{|y|>G^-(u)\} \varphi(y)\, {\textrm{d}} y\\[3pt] & =2\int_{G^-(u)}^\infty (y^2-1) \varphi(y)\, {\textrm{d}} y \neq 0\end{align*}
due to (28) and
![]() $G^-(u)\neq 0$
. So
$G^-(u)\neq 0$
. So
![]() $\operatorname{rank} \zeta_{\widetilde{G},1,u}=2$
. For general Z, we note that
$\operatorname{rank} \zeta_{\widetilde{G},1,u}=2$
. For general Z, we note that
![]() $\zeta_{\widetilde{G},Z,u}$
is even, so
$\zeta_{\widetilde{G},Z,u}$
is even, so
![]() $\operatorname{rank} (\zeta_{\widetilde{G},Z,u})>1$
. If G is non-negative, then
$\operatorname{rank} (\zeta_{\widetilde{G},Z,u})>1$
. If G is non-negative, then
by the first part of the proof of (ii), since
![]() $\bar{F}_Z( u/G(|y|))$
is a monotone even function of y. Modifications of the proof for
$\bar{F}_Z( u/G(|y|))$
is a monotone even function of y. Modifications of the proof for
![]() $G\le 0 $
or G non-increasing are obvious.
$G\le 0 $
or G non-increasing are obvious.
![]()
Proof of Theorem 3. Let
![]() $\mathcal{Y}$
be the
$\mathcal{Y}$
be the
![]() $\sigma$
-algebra generated by the entire random field
$\sigma$
-algebra generated by the entire random field
![]() $\{Y_t,t\in \mathbb Z^d\}$
. Then
$\{Y_t,t\in \mathbb Z^d\}$
. Then
where
and
The above decomposition is allowed by (20). The limiting behaviour of the sum depends on interplay between
![]() $M_n$
and
$M_n$
and
![]() $K_n$
. First we state the limiting results for
$K_n$
. First we state the limiting results for
![]() $M_n$
and
$M_n$
and
![]() $K_n$
separately.
$K_n$
separately.
Lemma 6. Under the assumptions of Theorem 3,
where
![]() $\sigma^2=\mathbb E[\chi(Y_0)]2^d>0$
.
$\sigma^2=\mathbb E[\chi(Y_0)]2^d>0$
.
Proof. We calculate
where
![]() $V_{t}=m(Y_t,Z_t).$
Note that, due to stationarity of Y and Z, the random variables
$V_{t}=m(Y_t,Z_t).$
Note that, due to stationarity of Y and Z, the random variables
![]() $V_{t}$
are identically distributed and conditionally independent, given
$V_{t}$
are identically distributed and conditionally independent, given
![]() $\mathcal{Y}$
. Therefore
$\mathcal{Y}$
. Therefore
The standard inequality,
yields
 \begin{align*}\biggl|\mathbb E\biggl[\exp\biggl\{\dfrac{{\textrm{i}} z }{n^{d/2}} V_{t}\biggr\}\mid {\mathcal Y}\biggr]-\mathbb E\biggl[\biggl(1+\dfrac{{\textrm{i}} z V_t}{n^{d/2}}-\dfrac{1}{2}\dfrac{z^2V_t}{n^d}\biggr)\mid {\mathcal Y}\biggr]\biggr|&\leq \mathbb E\biggl[\min\biggl\{\dfrac{|z|^2V_t^2}{n^d}, \dfrac{|z|^3|V_t|^3}{n^{3d/2}} \biggr\}\mid {\mathcal Y}\biggr]\\[3pt] &=:\mathbb E[V_{t,n}\mid {\mathcal Y}].\end{align*}
\begin{align*}\biggl|\mathbb E\biggl[\exp\biggl\{\dfrac{{\textrm{i}} z }{n^{d/2}} V_{t}\biggr\}\mid {\mathcal Y}\biggr]-\mathbb E\biggl[\biggl(1+\dfrac{{\textrm{i}} z V_t}{n^{d/2}}-\dfrac{1}{2}\dfrac{z^2V_t}{n^d}\biggr)\mid {\mathcal Y}\biggr]\biggr|&\leq \mathbb E\biggl[\min\biggl\{\dfrac{|z|^2V_t^2}{n^d}, \dfrac{|z|^3|V_t|^3}{n^{3d/2}} \biggr\}\mid {\mathcal Y}\biggr]\\[3pt] &=:\mathbb E[V_{t,n}\mid {\mathcal Y}].\end{align*}
For complex numbers
![]() $z_1,\ldots,z_m$
,
$z_1,\ldots,z_m$
,
![]() $w_1,\ldots,w_m$
of modulus at most 1, we have
$w_1,\ldots,w_m$
of modulus at most 1, we have
Hence
 \begin{align*}A_n({\mathcal Y})& :=\biggl|\prod_{t\in W_n}\mathbb E\biggl[\exp\biggl\{\dfrac{{\textrm{i}} z }{n^{d/2}} V_{t}\biggr\}\mid \mathcal{Y}\biggr]-\prod_{t\in W_n}\mathbb E\biggl[\biggl(1+\dfrac{{\textrm{i}} z V_t}{n^{d/2}}-\dfrac{1}{2}\dfrac{z^2V_t^2}{n^d}\biggr)\mid {\mathcal Y}\biggr]\biggr|\\[3pt] &\leq \sum_{t\in W_n}\biggl|\mathbb E\biggl[\exp\biggl\{\dfrac{{\textrm{i}} z }{n^{d/2}} V_{t}\biggr\}\mid \mathcal{Y}\biggr]-\mathbb E\biggl[\biggl(1+\dfrac{{\textrm{i}} z V_t}{n^{d/2}}-\dfrac{1}{2}\dfrac{z^2V_t^2}{n^d}\biggr)\mid {\mathcal Y}\biggr]\biggr|\\[3pt] &\leq \sum_{t\in W_n}\mathbb E[V_{t,n}\mid {\mathcal Y}].\end{align*}
\begin{align*}A_n({\mathcal Y})& :=\biggl|\prod_{t\in W_n}\mathbb E\biggl[\exp\biggl\{\dfrac{{\textrm{i}} z }{n^{d/2}} V_{t}\biggr\}\mid \mathcal{Y}\biggr]-\prod_{t\in W_n}\mathbb E\biggl[\biggl(1+\dfrac{{\textrm{i}} z V_t}{n^{d/2}}-\dfrac{1}{2}\dfrac{z^2V_t^2}{n^d}\biggr)\mid {\mathcal Y}\biggr]\biggr|\\[3pt] &\leq \sum_{t\in W_n}\biggl|\mathbb E\biggl[\exp\biggl\{\dfrac{{\textrm{i}} z }{n^{d/2}} V_{t}\biggr\}\mid \mathcal{Y}\biggr]-\mathbb E\biggl[\biggl(1+\dfrac{{\textrm{i}} z V_t}{n^{d/2}}-\dfrac{1}{2}\dfrac{z^2V_t^2}{n^d}\biggr)\mid {\mathcal Y}\biggr]\biggr|\\[3pt] &\leq \sum_{t\in W_n}\mathbb E[V_{t,n}\mid {\mathcal Y}].\end{align*}
We argue that
![]() \begin{align*} A_n({\mathcal Y})\to 0\end{align*}
in probability. If this is the case, then the conditional characteristic function
\begin{align*} A_n({\mathcal Y})\to 0\end{align*}
in probability. If this is the case, then the conditional characteristic function
and
have the same limit in probability. Applying the
![]() $\log$
to the above expression and
$\log$
to the above expression and
![]() $\log(1-x)=-x+O(x^3)$
, we have
$\log(1-x)=-x+O(x^3)$
, we have
 \begin{align*}\log B_n({\mathcal Y}) & =\sum_{t\in W_n}\log\mathbb E\biggl[1+\dfrac{{\textrm{i}} z V_{t}}{n^{d/2}}- \dfrac{z^2 V_{t}^2}{2 n^{d}}\mid \mathcal{Y}\biggr]\\[3pt] & =\dfrac{{\textrm{i}} z }{n^{d/2}}\sum_{t\in W_n}\mathbb E[V_t\mid {\mathcal Y}]-\dfrac{z^2}{2n^{d}}\sum_{t\in W_n} \mathbb E[V_{t}^2\mid \mathcal{Y}]\\[3pt] &\quad + O(1)\dfrac{|z|^3}{n^{3d/2}}\sum_{t\in W_n} (|\mathbb E[V_t\mid {\mathcal Y}]|) ^3+O(1)\dfrac{z^6}{n^{3d}}\sum_{t\in W_n} (\mathbb E[V_{t}^2\mid \mathcal{Y}]) ^3.\end{align*}
\begin{align*}\log B_n({\mathcal Y}) & =\sum_{t\in W_n}\log\mathbb E\biggl[1+\dfrac{{\textrm{i}} z V_{t}}{n^{d/2}}- \dfrac{z^2 V_{t}^2}{2 n^{d}}\mid \mathcal{Y}\biggr]\\[3pt] & =\dfrac{{\textrm{i}} z }{n^{d/2}}\sum_{t\in W_n}\mathbb E[V_t\mid {\mathcal Y}]-\dfrac{z^2}{2n^{d}}\sum_{t\in W_n} \mathbb E[V_{t}^2\mid \mathcal{Y}]\\[3pt] &\quad + O(1)\dfrac{|z|^3}{n^{3d/2}}\sum_{t\in W_n} (|\mathbb E[V_t\mid {\mathcal Y}]|) ^3+O(1)\dfrac{z^6}{n^{3d}}\sum_{t\in W_n} (\mathbb E[V_{t}^2\mid \mathcal{Y}]) ^3.\end{align*}
The expression in the last line is
![]() $o_P(1)$
by (22). By the definition,
$o_P(1)$
by (22). By the definition,
![]() $\mathbb E[m(y,Z_t)]=0$
and hence
$\mathbb E[m(y,Z_t)]=0$
and hence
![]() $\mathbb E[V_{t}\mid \mathcal{Y}]=0$
. We have
$\mathbb E[V_{t}\mid \mathcal{Y}]=0$
. We have
![]() $\mathbb E[V_{t}^2\mid \mathcal{Y}]=\chi(Y_t)$
and therefore
$\mathbb E[V_{t}^2\mid \mathcal{Y}]=\chi(Y_t)$
and therefore
Since
![]() $\chi$
is measurable, the ergodic theorem [Reference Yaglom44, page 339] implies that
$\chi$
is measurable, the ergodic theorem [Reference Yaglom44, page 339] implies that
whenever the covariance of the field
![]() $\chi(Y_t)$
goes to zero as
$\chi(Y_t)$
goes to zero as
![]() $\|t\|\to +\infty$
. To check the latter property, we use Lemma 2 to conclude
$\|t\|\to +\infty$
. To check the latter property, we use Lemma 2 to conclude
as
![]() $\|t\|\to +\infty$
, since the infinite series in the last expression is finite due to
$\|t\|\to +\infty$
, since the infinite series in the last expression is finite due to
![]() $\textrm{var}(\chi(Y_0))<\infty$
; see (22). Hence
$\textrm{var}(\chi(Y_0))<\infty$
; see (22). Hence
![]() $\log B_n(\mathcal{Y})\to -z^2\sigma^2/2$
in probability. By the continuous mapping theorem,
$\log B_n(\mathcal{Y})\to -z^2\sigma^2/2$
in probability. By the continuous mapping theorem,
Since
![]() $| \mathbb E[\exp\{{\textrm{i}} z \tilde{M}_n\}\mid \mathcal{Y}] |\le 1$
for all
$| \mathbb E[\exp\{{\textrm{i}} z \tilde{M}_n\}\mid \mathcal{Y}] |\le 1$
for all
![]() $n\in\mathbb N$
, this sequence is uniformly integrable. Using the property of
$n\in\mathbb N$
, this sequence is uniformly integrable. Using the property of
![]() $L^1$
-convergence of uniformly integrable sequences, we get
$L^1$
-convergence of uniformly integrable sequences, we get
and we are done.
![]()
Lemma 7. Under the assumptions of Theorem 3,
Proof. Consider the random variable
According to [Reference Leonenko and Olenko23, Theorem 4] and [Reference Alodat and Olenko2, Theorem 4.3], the random variables
have the same limiting distributions as
![]() $n\to+\infty$
. Furthermore, if
$n\to+\infty$
. Furthermore, if
![]() $\eta\in (0,d/q)$
we have by [Reference Leonenko and Olenko23, Theorem 5] that
$\eta\in (0,d/q)$
we have by [Reference Leonenko and Olenko23, Theorem 5] that
converges in distribution to random variable R.
![]()
If
![]() $\xi(y)\equiv 0$
, the long memory part
$\xi(y)\equiv 0$
, the long memory part
![]() $K_n$
is not present and we apply Lemma 6. If
$K_n$
is not present and we apply Lemma 6. If
![]() $\xi(y)\not\equiv 0$
, we note that the rate of convergence in Lemma 7 is slower than in Lemma 6, whenever
$\xi(y)\not\equiv 0$
, we note that the rate of convergence in Lemma 7 is slower than in Lemma 6, whenever
![]() $\eta\in (0,d/q)$
.
$\eta\in (0,d/q)$
.
Acknowledgements
We thank P. Doukhan for his remarks on
![]() $\psi$
-mixing. E. Spodarev is grateful to the German Academic Exchange Service (DAAD) for supporting his research visit to Ottawa in late 2015.
$\psi$
-mixing. E. Spodarev is grateful to the German Academic Exchange Service (DAAD) for supporting his research visit to Ottawa in late 2015.