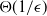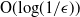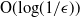1. Introduction
Resource allocation and load balancing problems arise frequently in a wide variety of applications such as wireless networks, data centers, ride hailing systems (e.g. Uber and Lyft), routeing and congestion control of traffic, manufacturing, telecommunications, etc. Performance analysis of these systems is frequently addressed by modeling them as stochastic processing networks (SPNs) [Reference Williams12], and essential performance measures are delay and queue lengths. Exact analysis of these measures usually becomes intractable, so a common practice is to study asymptotic regimes. Heavy traffic is a popular regime, where one studies the behavior of the system as the load grows to the maximum capacity. The heavy traffic limit of queue lengths and delay provides meaningful insights about the actual performance of the systems, but an essential question is whether the limiting behavior is close to the behavior in all traffic. In [Reference Eryilmaz and Srikant2], [Reference Hurtado-Lange and Maguluri4], and [Reference Maguluri and Srikant7], Eryilmaz, Hurtado-Lange, Maguluri, and Srikant obtain the heavy traffic limit of linear combinations of the expected queue lengths. However, the rate of convergence to this limit is not studied. In other words, they compute error bounds on the queue lengths that vanish in heavy traffic, but they are not optimized. In this paper we show that these error bounds grow logarithmically, as opposed to the polynomial bounds obtained in [Reference Eryilmaz and Srikant2], [Reference Hurtado-Lange and Maguluri4], and [Reference Maguluri and Srikant7].
Most of the literature on heavy traffic analysis is for systems that satisfy the so-called complete resource pooling (CRP) condition. Under this condition, the system exhibits state space collapse (SSC) onto a line, and hence it behaves as a single-server queue in the heavy traffic limit. There are several methodologies to study systems that satisfy CRP, such as diffusion limits [Reference Stolyar11], transform methods [Reference Hurtado-Lange and Maguluri5], and Lyapunov drift-based arguments [Reference Eryilmaz and Srikant2]. The latter has also been used to show that the steady-state mean of a linear combination of the queue lengths is of the form
![]() ${K_1}/{\epsilon}+\textrm{o}({1}/{\epsilon})$
, where
${K_1}/{\epsilon}+\textrm{o}({1}/{\epsilon})$
, where
![]() $K_1$
is an appropriately defined constant and
$K_1$
is an appropriately defined constant and
![]() $\epsilon$
is a parameter representing how far away the arrival rate vector is from the boundary of the capacity region.
$\epsilon$
is a parameter representing how far away the arrival rate vector is from the boundary of the capacity region.
In this paper we study a generalized switch model, which was first introduced in [Reference Stolyar11] to study several SPNs with control on the service process, such as input-queued switches, ad hoc wireless networks, cloud computing, data centers, etc. We consider the MaxWeight algorithm, and, using a tighter variant of the drift argument in [Reference Eryilmaz and Srikant2], [Reference Hurtado-Lange and Maguluri4], and [Reference Maguluri and Srikant7], we show that MaxWeight is within
![]() $K_2\,{\log}({1}/{\epsilon})$
of the optimal policy under the CRP condition (see Corollary 2.1). This is the first contribution of this paper.
$K_2\,{\log}({1}/{\epsilon})$
of the optimal policy under the CRP condition (see Corollary 2.1). This is the first contribution of this paper.
We also study a generalized switch without assuming that the CRP condition is satisfied, and we improve the bounds presented in [Reference Hurtado-Lange and Maguluri4] without adding any assumption. Specifically, we compute an upper bound of the form
![]() ${K_1}/{\epsilon}+K_2\,{\log}({1}/{\epsilon})$
for linear combinations of the expected queue lengths (see Theorem 2.1). This establishes a logarithmically growing error bound with respect to the limiting queue length, which is of the form
${K_1}/{\epsilon}+K_2\,{\log}({1}/{\epsilon})$
for linear combinations of the expected queue lengths (see Theorem 2.1). This establishes a logarithmically growing error bound with respect to the limiting queue length, which is of the form
![]() ${K_1}/{\epsilon}$
. This is the second contribution of this paper.
${K_1}/{\epsilon}$
. This is the second contribution of this paper.
In addition to systems where the service is controlled, we look at load balancing systems, where the control is on the arrivals. We consider the popular ‘join the shortest queue’ (JSQ) algorithm, which is known to exhibit a one-dimensional SSC [Reference Eryilmaz and Srikant2]. We show that the mean sum of the queue lengths is
![]() ${K^{\prime}_1}/{\epsilon}+K^{\prime}_2\,{\log}({1}/{\epsilon})$
(see Theorem 3.1) which, in conjunction with the universal lower bound (ULB) shown in [Reference Eryilmaz and Srikant2], establishes that JSQ is within
${K^{\prime}_1}/{\epsilon}+K^{\prime}_2\,{\log}({1}/{\epsilon})$
(see Theorem 3.1) which, in conjunction with the universal lower bound (ULB) shown in [Reference Eryilmaz and Srikant2], establishes that JSQ is within
![]() $K^{\prime}_2\,{\log}({1}/{\epsilon})$
of the optimal routeing policy. This is the third contribution of this paper. Similar results can be obtained for other routeing algorithms, such as power-of-d choices. However, we focus on JSQ in this paper, for brevity.
$K^{\prime}_2\,{\log}({1}/{\epsilon})$
of the optimal routeing policy. This is the third contribution of this paper. Similar results can be obtained for other routeing algorithms, such as power-of-d choices. However, we focus on JSQ in this paper, for brevity.
1.1. Literature review
The work closest to ours in the literature is that of Meyn [Reference Meyn8], who studied a general resource allocation problem under the CRP condition. Meyn showed that a variation of the MaxWeight algorithm, called h-MaxWeight, achieves logarithmic optimality. Our result is similar in flavor but has two main distinctions. Firstly, our result is valid for the non-CRP case as well. Secondly, in [Reference Meyn8] Meyn worked with h-MaxWeight, where h is a function that needs to be computed by analyzing the first-order approximation of the system. In this paper we use drift-based arguments that are easier to generalize to other SPNs. We showcase this generalization by analyzing the load balancing system under JSQ. Singh and Stolyar [Reference Singh and Stolyar10] and Sharifnassab, Tsitsiklis, and Golestani [Reference Sharifnassab, Tsitsiklis and Golestani9] studied systems where the CRP condition is not satisfied. In particular, Singh and Stolyar [Reference Singh and Stolyar10] also studied a generalized switch operating under the MaxWeight algorithm in heavy traffic. However, in contrast to the present work, the focus in [Reference Singh and Stolyar10] is to show that the service provided to each of the queues is smooth across time, i.e. there are not large gaps in service. This is done by characterizing the deviations of the queue lengths from the region of SSC. While we also obtain a bound on such deviations, the motivation, technique, and results are different.
Sharifnassab, Tsitsiklis, and Golestani [Reference Sharifnassab, Tsitsiklis and Golestani9] studied the more general setting of a multi-hop switched network with a general arrival process, operating under the MaxWeight scheduling algorithm. They analyzed the first-order approximation of the system (typically known as the ‘fluid model’) and bounded the gap between the fluid and the stochastic model in terms of the arrival process. Their results are applicable to a broader class of systems than the current paper, but they did not study the heavy traffic steady-state behavior.
1.2. Notation
We denote the set of integers from 1 to n by [n]. We denote the set of real and integer numbers by
![]() $\mathbb{R}$
and
$\mathbb{R}$
and
![]() $\mathbb{Z}$
, respectively, and we add a subscript
$\mathbb{Z}$
, respectively, and we add a subscript
![]() $+$
to denote the subset of non-negative numbers. We define the greatest integer smaller than or equal to
$+$
to denote the subset of non-negative numbers. We define the greatest integer smaller than or equal to
![]() $x \in \mathbb{R}_+$
by
$x \in \mathbb{R}_+$
by
![]() $\lfloor x \rfloor$
. All the vectors in the paper are boldface. The sets of n-dimensional vectors with real components and non-negative real components are denoted by
$\lfloor x \rfloor$
. All the vectors in the paper are boldface. The sets of n-dimensional vectors with real components and non-negative real components are denoted by
![]() $\mathbb{R}^n$
and
$\mathbb{R}^n$
and
![]() $\mathbb{R}_+^n$
, respectively. We denote the dot product between two vectors by
$\mathbb{R}_+^n$
, respectively. We denote the dot product between two vectors by
![]() $\langle {\boldsymbol{{x}}},{\boldsymbol{{y}}} \rangle$
and the Euclidean norm of a vector by
$\langle {\boldsymbol{{x}}},{\boldsymbol{{y}}} \rangle$
and the Euclidean norm of a vector by
![]() $\|{\boldsymbol{{x}}}\|$
. We denote the ith canonical vector by
$\|{\boldsymbol{{x}}}\|$
. We denote the ith canonical vector by
![]() ${\boldsymbol{{e}}}^{(i)}$
, the vector of ones by
${\boldsymbol{{e}}}^{(i)}$
, the vector of ones by
![]() $\textbf{1}$
, and the vector of zeros by
$\textbf{1}$
, and the vector of zeros by
![]() $\textbf{0}$
. We denote the transpose of a matrix by
$\textbf{0}$
. We denote the transpose of a matrix by
![]() $A^\top$
, and the Hadamard product between two matrices by
$A^\top$
, and the Hadamard product between two matrices by
![]() $A \circ B$
. The expectation and variance of a random variable X are given by
$A \circ B$
. The expectation and variance of a random variable X are given by
![]() $\mathbb{E}[X]$
and
$\mathbb{E}[X]$
and
![]() $\text{Var}[{X}]$
, respectively, and the covariance between two random variables X and Y by
$\text{Var}[{X}]$
, respectively, and the covariance between two random variables X and Y by
![]() ${\textrm{Cov}}(X,Y)$
. The probability of an event E is denoted by
${\textrm{Cov}}(X,Y)$
. The probability of an event E is denoted by
![]() $\mathbb{P}[E]$
, and the indicator function of an event E by
$\mathbb{P}[E]$
, and the indicator function of an event E by
![]() ${\unicode{x1D7D9}_{\{{E} \}}}$
. For a set S we use
${\unicode{x1D7D9}_{\{{E} \}}}$
. For a set S we use
![]() $\textrm{Int}(S)$
and
$\textrm{Int}(S)$
and
![]() $\textrm{Bo}(S)$
to denote its relative interior and its relative boundary, respectively.
$\textrm{Bo}(S)$
to denote its relative interior and its relative boundary, respectively.
2. Logarithmic error bounds in the generalized switch
2.1. Model
In this section we present the generalized switch model in detail. Consider n queues operating in discrete time, with time indexed by
![]() $k \in \mathbb{Z}_+$
. A pictorial example is presented in Figure 1.
$k \in \mathbb{Z}_+$
. A pictorial example is presented in Figure 1.

Figure 1. Generalized switch model.
2.1.1. Arrival process.
We define a sequence of i.i.d. random variables
![]() $\{a_i(k) \colon k \in \mathbb{Z}_+ \}$
for all
$\{a_i(k) \colon k \in \mathbb{Z}_+ \}$
for all
![]() $i \in [n]$
, where
$i \in [n]$
, where
![]() $a_i(k)$
denotes the number of jobs that arrive at the ith queue at time k. Denote the mean arrival rate vector by
$a_i(k)$
denotes the number of jobs that arrive at the ith queue at time k. Denote the mean arrival rate vector by
![]() $\boldsymbol{\lambda}\stackrel{\triangle}{=} \mathbb{E}[{{\boldsymbol{{a}}}(1)}]$
and the covariance matrix of the random vector
$\boldsymbol{\lambda}\stackrel{\triangle}{=} \mathbb{E}[{{\boldsymbol{{a}}}(1)}]$
and the covariance matrix of the random vector
![]() ${\boldsymbol{{a}}}(1)$
by
${\boldsymbol{{a}}}(1)$
by
![]() $\Sigma_a$
. Assume
$\Sigma_a$
. Assume
![]() $a_i(1) \leq A_{\max}$
with probability 1 for all
$a_i(1) \leq A_{\max}$
with probability 1 for all
![]() $i \in [n]$
, where
$i \in [n]$
, where
![]() $A_{\max}$
is a finite constant.
$A_{\max}$
is a finite constant.
2.1.2. Service process.
Let
![]() $s_i(k)$
be the potential service that can be offered by server i in time slot k. If there are not enough jobs to serve in the queue, there is unused service in that time slot, and we denote it by
$s_i(k)$
be the potential service that can be offered by server i in time slot k. If there are not enough jobs to serve in the queue, there is unused service in that time slot, and we denote it by
![]() $u_i(k)$
. Then the actual number of served jobs in queue i at time k is
$u_i(k)$
. Then the actual number of served jobs in queue i at time k is
![]() $s_i(k)-u_i(k)$
. We allow interference among the servers, which requires them to satisfy a set of feasibility constraints in each time slot. The scheduler is allowed to pick any service rate vector that satisfies these constraints in each time slot. Additionally, the environment of the servers can affect the interference constraints. We capture this by a sequence of i.i.d. random variables
$s_i(k)-u_i(k)$
. We allow interference among the servers, which requires them to satisfy a set of feasibility constraints in each time slot. The scheduler is allowed to pick any service rate vector that satisfies these constraints in each time slot. Additionally, the environment of the servers can affect the interference constraints. We capture this by a sequence of i.i.d. random variables
![]() $\{M(k)\colon k \in \mathbb{Z}_+\}$
, where M(k) is the ‘channel state’ in time slot k. We assume that the channel state has a finite state space, denoted by
$\{M(k)\colon k \in \mathbb{Z}_+\}$
, where M(k) is the ‘channel state’ in time slot k. We assume that the channel state has a finite state space, denoted by
![]() $\mathcal{M}$
, and that the interference constraints in time slot k are completely determined by the value of M(k). Let the pmf of M(1) be
$\mathcal{M}$
, and that the interference constraints in time slot k are completely determined by the value of M(k). Let the pmf of M(1) be
![]() $\psi_m\stackrel{\triangle}{=}\mathbb{P}[M(1)=m]$
for all
$\psi_m\stackrel{\triangle}{=}\mathbb{P}[M(1)=m]$
for all
![]() $m \in \mathcal{M}$
. Finally,
$m \in \mathcal{M}$
. Finally,
![]() $\mathcal{S}^{(m)}$
denotes the set of feasible service rate vectors in channel state m. Observe that
$\mathcal{S}^{(m)}$
denotes the set of feasible service rate vectors in channel state m. Observe that
![]() $\mathcal{S}^{(m)}$
contains the potential (not necessarily actual) service rates that satisfy the interference constraints in channel state m and, therefore, for any
$\mathcal{S}^{(m)}$
contains the potential (not necessarily actual) service rates that satisfy the interference constraints in channel state m and, therefore, for any
![]() ${\boldsymbol{{x}}}\in\mathcal{S}^{(m)}$
, all the non-negative vectors that are dominated by
${\boldsymbol{{x}}}\in\mathcal{S}^{(m)}$
, all the non-negative vectors that are dominated by
![]() ${\boldsymbol{{x}}}$
are also feasible. In other words, if
${\boldsymbol{{x}}}$
are also feasible. In other words, if
![]() $\textbf{0}\leq{\boldsymbol{{y}}}\leq{\boldsymbol{{x}}}$
, then
$\textbf{0}\leq{\boldsymbol{{y}}}\leq{\boldsymbol{{x}}}$
, then
![]() ${\boldsymbol{{y}}}$
is also a feasible service rate vector. For simplicity, we only consider maximal feasible service rate vectors in each set
${\boldsymbol{{y}}}$
is also a feasible service rate vector. For simplicity, we only consider maximal feasible service rate vectors in each set
![]() $\mathcal{S}^{(m)}$
and their projection on the coordinate axes, and we assume that
$\mathcal{S}^{(m)}$
and their projection on the coordinate axes, and we assume that
![]() $\mathcal{S}^{(m)}$
is a finite set for each
$\mathcal{S}^{(m)}$
is a finite set for each
![]() $m\in\mathcal{M}$
. Thus there exists a finite constant
$m\in\mathcal{M}$
. Thus there exists a finite constant
![]() $S_{\max}$
such that
$S_{\max}$
such that
![]() $s_i(1) \leq S_{\max}$
with probability 1 for all
$s_i(1) \leq S_{\max}$
with probability 1 for all
![]() $i\in[n]$
.
$i\in[n]$
.
2.1.3. Queueing process.
The following steps are followed in each time slot (in this order).
-
• Observe the channel state and queue length vector.
-
• A scheduling problem is solved to determine which queues are served and the service rates are determined according to the channel state.
-
• Arrivals occur in the system.
-
• Jobs are processed according to the selected schedule.
Then the queue dynamics follow the recursion
Thus
![]() $\{{\boldsymbol{{q}}}(k)\colon k\in\mathbb{Z}_+ \}$
is a discrete-time Markov chain with countable state space. If the unused service is positive, then the queue length at the start of the next time slot should be zero and vice versa. Thus we have
$\{{\boldsymbol{{q}}}(k)\colon k\in\mathbb{Z}_+ \}$
is a discrete-time Markov chain with countable state space. If the unused service is positive, then the queue length at the start of the next time slot should be zero and vice versa. Thus we have
The scheduling problem is solved using the MaxWeight scheduling algorithm, which selects the schedule with the maximum total weighted queue length. Mathematically, provided that
![]() $M(k)=m$
, we have
$M(k)=m$
, we have
and the ties are broken randomly. Observe that, unless there are ties, the potential service vector is deterministic after observing the channel state and the queue length vector.
2.1.4. Capacity region.
It is proved in [Reference Eryilmaz and Srikant2] that the capacity region of this system is
![]() $ \mathcal{C}= \sum_{m\in \mathcal{M}} \psi_m\,\textrm{ConvexHull}(\mathcal{S}^{(m)} )$
. Thus it is a coordinate convex polytope. We describe it as the intersection of finitely many half-spaces, i.e. we write
$ \mathcal{C}= \sum_{m\in \mathcal{M}} \psi_m\,\textrm{ConvexHull}(\mathcal{S}^{(m)} )$
. Thus it is a coordinate convex polytope. We describe it as the intersection of finitely many half-spaces, i.e. we write
Without loss of generality, we assume
![]() ${\boldsymbol{{c}}}^{(\ell)} \geq \textbf{0}$
,
${\boldsymbol{{c}}}^{(\ell)} \geq \textbf{0}$
,
![]() $\|{\boldsymbol{{c}}}^{(\ell)}\|=1$
and
$\|{\boldsymbol{{c}}}^{(\ell)}\|=1$
and
![]() $b^{(\ell)}>0$
for all
$b^{(\ell)}>0$
for all
![]() $\ell \in [L]$
. We also denote the
$\ell \in [L]$
. We also denote the
![]() $\ell$
th facet as
$\ell$
th facet as
![]() $\mathcal{F}^{(\ell)} \stackrel{\triangle}{=}\bigl\{{\boldsymbol{{x}}}\in\mathcal{C}\colon \bigl\langle{\boldsymbol{{c}}}^{(\ell)},{\boldsymbol{{x}}}\bigr\rangle=b^{(\ell)} \bigr\}$
. In addition, we denote the maximum
$\mathcal{F}^{(\ell)} \stackrel{\triangle}{=}\bigl\{{\boldsymbol{{x}}}\in\mathcal{C}\colon \bigl\langle{\boldsymbol{{c}}}^{(\ell)},{\boldsymbol{{x}}}\bigr\rangle=b^{(\ell)} \bigr\}$
. In addition, we denote the maximum
![]() ${\boldsymbol{{c}}}^{(\ell)}$
-weighted service rate by
${\boldsymbol{{c}}}^{(\ell)}$
-weighted service rate by
![]() $b^{(m,\ell)}$
. Mathematically, we have
$b^{(m,\ell)}$
. Mathematically, we have
To capture the randomness in the service process due to the channel state, we define a sequence of i.i.d. random variables
![]() $\{B_\ell(k)\colon k \in \mathbb{Z}_+\}$
(independent of queue lengths and arrival process) with pmf given by
$\{B_\ell(k)\colon k \in \mathbb{Z}_+\}$
(independent of queue lengths and arrival process) with pmf given by
![]() $\mathbb{P}\bigl[B_\ell(1)=b^{(m,\ell)}\bigr]=\psi_m$
. Let the covariance matrix of the vector
$\mathbb{P}\bigl[B_\ell(1)=b^{(m,\ell)}\bigr]=\psi_m$
. Let the covariance matrix of the vector
![]() $\{B_\ell(1)\}_{\ell \in [L]}$
be
$\{B_\ell(1)\}_{\ell \in [L]}$
be
![]() $\Sigma_B$
.
$\Sigma_B$
.
2.1.5. Heavy traffic and state space collapse.
In heavy traffic, we take the limit as the vector of arrival rates approaches the boundary of the capacity region. Formally, we fix a vector
![]() $\boldsymbol{\nu}$
on the boundary of
$\boldsymbol{\nu}$
on the boundary of
![]() $\mathcal{C}$
. For
$\mathcal{C}$
. For
![]() $\epsilon\in(0,1)$
, we let
$\epsilon\in(0,1)$
, we let
![]() $\boldsymbol{\lambda}^{\!(\epsilon)}\stackrel{\triangle}{=} (1-\epsilon)\boldsymbol{\nu}$
be the mean arrival rate vector, and we take the limit as
$\boldsymbol{\lambda}^{\!(\epsilon)}\stackrel{\triangle}{=} (1-\epsilon)\boldsymbol{\nu}$
be the mean arrival rate vector, and we take the limit as
![]() $\epsilon\downarrow 0$
. Specifically, we analyze a sequence of generalized switches parametrized by
$\epsilon\downarrow 0$
. Specifically, we analyze a sequence of generalized switches parametrized by
![]() $\epsilon$
and denote the queue length, arrival process, service process, and unused service for the
$\epsilon$
and denote the queue length, arrival process, service process, and unused service for the
![]() $\epsilon$
th system by
$\epsilon$
th system by
![]() $\bigl\{{\boldsymbol{{q}}}^{(\epsilon)}(k)\colon k \in \mathbb{Z}_+\bigr\}$
,
$\bigl\{{\boldsymbol{{q}}}^{(\epsilon)}(k)\colon k \in \mathbb{Z}_+\bigr\}$
,
![]() $\bigl\{{\boldsymbol{{a}}}^{(\epsilon)}(k)\colon k \in \mathbb{Z}_+\bigr\}$
,
$\bigl\{{\boldsymbol{{a}}}^{(\epsilon)}(k)\colon k \in \mathbb{Z}_+\bigr\}$
,
![]() $\bigl\{{\boldsymbol{{s}}}^{(\epsilon)}(k)\colon k \in \mathbb{Z}_+\bigr\}$
, and
$\bigl\{{\boldsymbol{{s}}}^{(\epsilon)}(k)\colon k \in \mathbb{Z}_+\bigr\}$
, and
![]() $\bigl\{{\boldsymbol{{u}}}^{(\epsilon)}(k)\colon k \in \mathbb{Z}_+\bigr\}$
, respectively. The parametrization is such that
$\bigl\{{\boldsymbol{{u}}}^{(\epsilon)}(k)\colon k \in \mathbb{Z}_+\bigr\}$
, respectively. The parametrization is such that
![]() $\mathbb{E}\bigl[{{\boldsymbol{{a}}}^{(\epsilon)}(1)}\bigr]=\boldsymbol{\lambda}^{\!(\epsilon)}$
. Then the heavy traffic regime is observed as
$\mathbb{E}\bigl[{{\boldsymbol{{a}}}^{(\epsilon)}(1)}\bigr]=\boldsymbol{\lambda}^{\!(\epsilon)}$
. Then the heavy traffic regime is observed as
![]() $\epsilon\downarrow 0$
.
$\epsilon\downarrow 0$
.
For every
![]() $\epsilon\in(0,1)$
, observe that
$\epsilon\in(0,1)$
, observe that
![]() $\boldsymbol{\lambda}^{\!(\epsilon)} \in \textrm{Int}(\mathcal{C})$
and therefore the queue length process
$\boldsymbol{\lambda}^{\!(\epsilon)} \in \textrm{Int}(\mathcal{C})$
and therefore the queue length process
![]() $\bigl\{{\boldsymbol{{q}}}^{(\epsilon)}(k)\colon k\in\mathbb{Z}_+\bigr\}$
of the generalized switch operating under MaxWeight is a positive recurrent discrete-time Markov chain. Thus the steady-state vector of queue lengths is well-defined. A proof of positive recurrence is presented in [Reference Eryilmaz and Srikant2]. We denote all the steady-state vectors with a bar on top of the variable. In particular,
$\bigl\{{\boldsymbol{{q}}}^{(\epsilon)}(k)\colon k\in\mathbb{Z}_+\bigr\}$
of the generalized switch operating under MaxWeight is a positive recurrent discrete-time Markov chain. Thus the steady-state vector of queue lengths is well-defined. A proof of positive recurrence is presented in [Reference Eryilmaz and Srikant2]. We denote all the steady-state vectors with a bar on top of the variable. In particular,
![]() $\overline{{\boldsymbol{{q}}}}^{(\epsilon)}$
is a steady-state random vector that is the limit in distribution of
$\overline{{\boldsymbol{{q}}}}^{(\epsilon)}$
is a steady-state random vector that is the limit in distribution of
![]() ${\boldsymbol{{q}}}^{(\epsilon)}(k)$
as
${\boldsymbol{{q}}}^{(\epsilon)}(k)$
as
![]() $k \rightarrow \infty$
. In addition, let
$k \rightarrow \infty$
. In addition, let
![]() $\overline{{\boldsymbol{{a}}}}^{(\epsilon)}$
,
$\overline{{\boldsymbol{{a}}}}^{(\epsilon)}$
,
![]() $\overline{M}$
,
$\overline{M}$
,
![]() $\overline{B}_\ell$
be the steady-state random vector/variable with the same distribution as
$\overline{B}_\ell$
be the steady-state random vector/variable with the same distribution as
![]() ${\boldsymbol{{a}}}^{(\epsilon)}(1)$
, M(1),
${\boldsymbol{{a}}}^{(\epsilon)}(1)$
, M(1),
![]() $B_\ell(1)$
, respectively. We have
$B_\ell(1)$
, respectively. We have
![]() $\mathbb{E}\bigl[{\overline{{\boldsymbol{{a}}}}^{(\epsilon)}}\bigr]=\boldsymbol{\lambda}^{\!(\epsilon)}$
, and denote the covariance matrix of
$\mathbb{E}\bigl[{\overline{{\boldsymbol{{a}}}}^{(\epsilon)}}\bigr]=\boldsymbol{\lambda}^{\!(\epsilon)}$
, and denote the covariance matrix of
![]() $\overline{{\boldsymbol{{a}}}}^{(\epsilon)}$
by
$\overline{{\boldsymbol{{a}}}}^{(\epsilon)}$
by
![]() $\Sigma_a^{(\epsilon)}$
. Also, denote the steady-state offered service by
$\Sigma_a^{(\epsilon)}$
. Also, denote the steady-state offered service by
![]() $\overline{{\boldsymbol{{s}}}}^{(\epsilon)}$
and the steady-state unused service by
$\overline{{\boldsymbol{{s}}}}^{(\epsilon)}$
and the steady-state unused service by
![]() $\overline{{\boldsymbol{{u}}}}^{(\epsilon)}$
. Finally, let
$\overline{{\boldsymbol{{u}}}}^{(\epsilon)}$
. Finally, let
![]() $\bigl(\overline{{\boldsymbol{{q}}}}^{(\epsilon)}\bigr)^+\stackrel{\triangle}{=} \overline{{\boldsymbol{{q}}}}^{(\epsilon)}+\overline{{\boldsymbol{{a}}}}^{(\epsilon)}-\overline{{\boldsymbol{{s}}}}^{(\epsilon)}+\overline{{\boldsymbol{{u}}}}^{(\epsilon)}$
be the vector of queue lengths one time slot after
$\bigl(\overline{{\boldsymbol{{q}}}}^{(\epsilon)}\bigr)^+\stackrel{\triangle}{=} \overline{{\boldsymbol{{q}}}}^{(\epsilon)}+\overline{{\boldsymbol{{a}}}}^{(\epsilon)}-\overline{{\boldsymbol{{s}}}}^{(\epsilon)}+\overline{{\boldsymbol{{u}}}}^{(\epsilon)}$
be the vector of queue lengths one time slot after
![]() $\overline{{\boldsymbol{{q}}}}^{(\epsilon)}$
.
$\overline{{\boldsymbol{{q}}}}^{(\epsilon)}$
.
Define the cone
![]() $\mathcal{K}$
spanned by the normal to the facets
$\mathcal{K}$
spanned by the normal to the facets
![]() $\mathcal{F}^{(\ell)}$
that intersect at
$\mathcal{F}^{(\ell)}$
that intersect at
![]() $\boldsymbol{\nu}$
, i.e. the facets such that
$\boldsymbol{\nu}$
, i.e. the facets such that
![]() $\boldsymbol{\nu} \in \mathcal{F}^{(\ell)}$
. Let
$\boldsymbol{\nu} \in \mathcal{F}^{(\ell)}$
. Let
![]() $P\stackrel{\triangle}{=} \bigl\{\ell\in[L]\colon \boldsymbol{\nu}\in\mathcal{F}^{(\ell)}\bigr\}$
. It was shown in [Reference Hurtado-Lange and Maguluri4] that, as
$P\stackrel{\triangle}{=} \bigl\{\ell\in[L]\colon \boldsymbol{\nu}\in\mathcal{F}^{(\ell)}\bigr\}$
. It was shown in [Reference Hurtado-Lange and Maguluri4] that, as
![]() $\epsilon$
decreases to zero, the vector of queue lengths concentrates around the cone
$\epsilon$
decreases to zero, the vector of queue lengths concentrates around the cone
![]() $\mathcal{K}$
. In other words, it was shown that the projection of the vector of queue lengths on the cone
$\mathcal{K}$
. In other words, it was shown that the projection of the vector of queue lengths on the cone
![]() $\mathcal{K}$
approximates the actual vector of queue lengths, and the error of approximation is bounded by a finite (but unknown) constant. Therefore this result is a notion of SSC. In Proposition 2.1 we prove an explicit expression for this upper bound. Observe that the cone
$\mathcal{K}$
approximates the actual vector of queue lengths, and the error of approximation is bounded by a finite (but unknown) constant. Therefore this result is a notion of SSC. In Proposition 2.1 we prove an explicit expression for this upper bound. Observe that the cone
![]() $\mathcal{K}$
can also be represented as
$\mathcal{K}$
can also be represented as
 \begin{equation*} \mathcal{K}=\Biggl\{{\boldsymbol{{x}}}\in\mathbb{R}^n_+\colon {\boldsymbol{{x}}}=\sum_{\ell\in P}\xi_\ell {\boldsymbol{{c}}}^{(\ell)}\;, \;\xi_\ell\geq 0 \ \text{{for all} $ \ell\in P$} \Biggr\}.\end{equation*}
\begin{equation*} \mathcal{K}=\Biggl\{{\boldsymbol{{x}}}\in\mathbb{R}^n_+\colon {\boldsymbol{{x}}}=\sum_{\ell\in P}\xi_\ell {\boldsymbol{{c}}}^{(\ell)}\;, \;\xi_\ell\geq 0 \ \text{{for all} $ \ell\in P$} \Biggr\}.\end{equation*}
In addition, define
![]() $\mathcal{H}$
as the affine hull of
$\mathcal{H}$
as the affine hull of
![]() $\mathcal{K}$
, and let
$\mathcal{K}$
, and let
![]() $\tilde{P} \subset P$
be the maximal set of indices in P such that
$\tilde{P} \subset P$
be the maximal set of indices in P such that
![]() $\bigl\{{\boldsymbol{{c}}}^{(\ell)} \colon \ell \in \tilde{P}\bigr\}$
is a set of linearly independent vectors. Let
$\bigl\{{\boldsymbol{{c}}}^{(\ell)} \colon \ell \in \tilde{P}\bigr\}$
is a set of linearly independent vectors. Let
![]() $C\stackrel{\triangle}{=} \bigl[{\boldsymbol{{c}}}^{(\ell)}\bigr]_{\ell \in \tilde{P}}$
be a matrix with columns
$C\stackrel{\triangle}{=} \bigl[{\boldsymbol{{c}}}^{(\ell)}\bigr]_{\ell \in \tilde{P}}$
be a matrix with columns
![]() ${\boldsymbol{{c}}}^{(\ell)}$
with
${\boldsymbol{{c}}}^{(\ell)}$
with
![]() $\ell\in\tilde{P}$
, and observe that
$\ell\in\tilde{P}$
, and observe that
![]() $\mathcal{H}$
is the column space of C.
$\mathcal{H}$
is the column space of C.
2.2. Logarithmic error bounds
In this section we present the main result of this paper. Specifically, we provide error bounds of linear combinations of the expected queue lengths as
![]() $\epsilon \downarrow 0$
. After stating the result, we discuss two applications of the result. Then in Section 2.3 we prove SSC, which is an essential step in the proof of Theorem 2.1, and in Section 2.4 we prove the theorem.
$\epsilon \downarrow 0$
. After stating the result, we discuss two applications of the result. Then in Section 2.3 we prove SSC, which is an essential step in the proof of Theorem 2.1, and in Section 2.4 we prove the theorem.
Theorem 2.1. Consider a set of generalized switches operating under the MaxWeight scheduling policy, parametrized by the heavy traffic parameter
![]() $\epsilon \in (0,1)$
as described in Section 2.1. Then there exists
$\epsilon \in (0,1)$
as described in Section 2.1. Then there exists
![]() $\epsilon_0\in(0,1)$
such that for any
$\epsilon_0\in(0,1)$
such that for any
![]() $\epsilon<\epsilon_0$
and any vector
$\epsilon<\epsilon_0$
and any vector
![]() ${\boldsymbol{{w}}} \in \bigcap_{\ell \in P} \mathcal{F}^{(\ell)}$
, we have
${\boldsymbol{{w}}} \in \bigcap_{\ell \in P} \mathcal{F}^{(\ell)}$
, we have
where
![]() $H\stackrel{\triangle}{=} C(C^\top C)^{-1}C^\top $
is the projection matrix into
$H\stackrel{\triangle}{=} C(C^\top C)^{-1}C^\top $
is the projection matrix into
![]() $\mathcal{H}$
and
$\mathcal{H}$
and
![]() $\beta$
is a constant independent of
$\beta$
is a constant independent of
![]() $\epsilon$
and
$\epsilon$
and
![]() ${\boldsymbol{{w}}}$
.
${\boldsymbol{{w}}}$
.
A similar result establishing the heavy traffic behavior of a generalized switch when the CRP condition is not necessarily satisfied, was presented in [Reference Hurtado-Lange and Maguluri4]. The main difference is that the result in [Reference Hurtado-Lange and Maguluri4] shows that the right-hand side term in (2.4) is
![]() $\textrm{o}({1}/{\epsilon})$
, and we obtain a tighter bound.
$\textrm{o}({1}/{\epsilon})$
, and we obtain a tighter bound.
Theorem 2.1 presents a logarithmic error bound of the queue length behavior in light traffic (positive
![]() $\epsilon$
) with respect to the heavy traffic behavior. However, the result is not sufficient to claim optimality of MaxWeight because we are not comparing MaxWeight against any other scheduling policy in this paper. One way to prove such a result for a scheduling algorithm
$\epsilon$
) with respect to the heavy traffic behavior. However, the result is not sufficient to claim optimality of MaxWeight because we are not comparing MaxWeight against any other scheduling policy in this paper. One way to prove such a result for a scheduling algorithm
![]() $\mathcal{A}$
would be to obtain a ULB (i.e. a lower bound for the linear combination of queue lengths that is satisfied by all scheduling policies), and then prove that this ULB is achieved by the generalized switch operating under
$\mathcal{A}$
would be to obtain a ULB (i.e. a lower bound for the linear combination of queue lengths that is satisfied by all scheduling policies), and then prove that this ULB is achieved by the generalized switch operating under
![]() $\mathcal{A}$
. One can compute such a ULB for the generalized switch [Reference Hurtado-Lange and Maguluri4, Proposition 1], but this ULB is not necessarily for the same linear combination of queue lengths as presented in Theorem 2.1. Hence we cannot conclude optimality of MaxWeight. Further, there are counterexamples that prove that MaxWeight is not optimal. In [Reference Lu, Maguluri, Squillante, Suk and Wu6], Lu et al. show the existence of a gap between the performance of a
$\mathcal{A}$
. One can compute such a ULB for the generalized switch [Reference Hurtado-Lange and Maguluri4, Proposition 1], but this ULB is not necessarily for the same linear combination of queue lengths as presented in Theorem 2.1. Hence we cannot conclude optimality of MaxWeight. Further, there are counterexamples that prove that MaxWeight is not optimal. In [Reference Lu, Maguluri, Squillante, Suk and Wu6], Lu et al. show the existence of a gap between the performance of a
![]() $2\times 2$
switch (which is a particular case of the generalized switch) and the ULB computed in [Reference Maguluri and Srikant7] (which is a particular case of the ULB computed in [Reference Hurtado-Lange and Maguluri4]). Specifically, they show that the ULB and the performance of MaxWeight differ by a multiplicative constant. Hence, in general, MaxWeight need not be within an additive error of
$2\times 2$
switch (which is a particular case of the generalized switch) and the ULB computed in [Reference Maguluri and Srikant7] (which is a particular case of the ULB computed in [Reference Hurtado-Lange and Maguluri4]). Specifically, they show that the ULB and the performance of MaxWeight differ by a multiplicative constant. Hence, in general, MaxWeight need not be within an additive error of
![]() $\textrm{O}(\!\log\!({1}/{\epsilon}))$
from the optimal policy.
$\textrm{O}(\!\log\!({1}/{\epsilon}))$
from the optimal policy.
Such a logarithmic optimality of MaxWeight can be obtained from Theorem 2.1 when the CRP condition is satisfied and SSC occurs in a one-dimensional subspace. In this case the heavy traffic limit is known to be the same as the ULB of the scaled expected linear combination of the queue length. Specifically, if we fix
![]() $\ell\in[L]$
and assume
$\ell\in[L]$
and assume
![]() $\boldsymbol{\nu}\in \textrm{Int}\bigl(\mathcal{F}^{(\ell)}\bigr)$
, the CRP condition is satisfied and SSC occurs in the line generated by
$\boldsymbol{\nu}\in \textrm{Int}\bigl(\mathcal{F}^{(\ell)}\bigr)$
, the CRP condition is satisfied and SSC occurs in the line generated by
![]() ${\boldsymbol{{c}}}^{(\ell)}$
. Then, as shown in [Reference Hurtado-Lange and Maguluri4, Proposition 1], for any scheduling algorithm, we have
${\boldsymbol{{c}}}^{(\ell)}$
. Then, as shown in [Reference Hurtado-Lange and Maguluri4, Proposition 1], for any scheduling algorithm, we have
where
![]() $b_{\max}\stackrel{\triangle}{=} \max_{m\in\mathcal{M},\ell\in[L]}\bigl\{b^{(m,\ell)}\bigr\}$
and
$b_{\max}\stackrel{\triangle}{=} \max_{m\in\mathcal{M},\ell\in[L]}\bigl\{b^{(m,\ell)}\bigr\}$
and
![]() $\sigma_{B_\ell}^2\stackrel{\triangle}{=} (\Sigma_B)_{\ell,\ell}$
. By Theorem 2.1, we know that MaxWeight approaches the above lower bound as
$\sigma_{B_\ell}^2\stackrel{\triangle}{=} (\Sigma_B)_{\ell,\ell}$
. By Theorem 2.1, we know that MaxWeight approaches the above lower bound as
![]() $\epsilon \downarrow 0$
. Thus Theorem 2.1 establishes that MaxWeight is within
$\epsilon \downarrow 0$
. Thus Theorem 2.1 establishes that MaxWeight is within
![]() $\textrm{O}(\!\log\!({1}/{\epsilon}))$
of the optimal policy under the CRP condition. We formally present this result in the next corollary.
$\textrm{O}(\!\log\!({1}/{\epsilon}))$
of the optimal policy under the CRP condition. We formally present this result in the next corollary.
Corollary 2.1. For the generalized switch operating under MaxWeight, as described in Theorem 2.1, fix
![]() $\ell\in[L]$
and assume
$\ell\in[L]$
and assume
![]() $\boldsymbol{\nu}\in \textrm{Int}\bigl(\mathcal{F}^{(\ell)}\bigr)$
. Then, for any
$\boldsymbol{\nu}\in \textrm{Int}\bigl(\mathcal{F}^{(\ell)}\bigr)$
. Then, for any
![]() $\epsilon<\epsilon_0$
, we have
$\epsilon<\epsilon_0$
, we have
where
![]() $\tilde{\beta}$
is a constant independent of
$\tilde{\beta}$
is a constant independent of
![]() $\epsilon$
, which we compute in (A.2). Hence the MaxWeight algorithm is heavy traffic optimal and the error bound to the optimal value is
$\epsilon$
, which we compute in (A.2). Hence the MaxWeight algorithm is heavy traffic optimal and the error bound to the optimal value is
![]() $\textrm{O}(\!\log\!({1}/{\epsilon} ))$
.
$\textrm{O}(\!\log\!({1}/{\epsilon} ))$
.
We present the proof of Corollary 2.1 in Appendix A. An immediate corollary of Theorem 2.1 is to compute the bounds in the case of an input-queued switch. An input-queued switch is a generalized switch where the number of queues is a perfect square, say
![]() $n=N^2$
, the channel state is fixed over time, and the feasibility constraints are known. Specifically, the input-queued switch can be thought of as an
$n=N^2$
, the channel state is fixed over time, and the feasibility constraints are known. Specifically, the input-queued switch can be thought of as an
![]() $N\times N$
matrix, where the (i, j)th component of the matrix is the queue of packets at ith input port, waiting to be processed at the jth output port. Thus rows are queues at input ports and columns are queues at output ports. All jobs take exactly one time slot to be processed and, in each time slot, at most one input/output pair can be served in each row and column. Then the set of feasible service rate vectors is the set of
$N\times N$
matrix, where the (i, j)th component of the matrix is the queue of packets at ith input port, waiting to be processed at the jth output port. Thus rows are queues at input ports and columns are queues at output ports. All jobs take exactly one time slot to be processed and, in each time slot, at most one input/output pair can be served in each row and column. Then the set of feasible service rate vectors is the set of
![]() $N\times N$
permutation matrices. In Figure 2 we present a pictorial example of a
$N\times N$
permutation matrices. In Figure 2 we present a pictorial example of a
![]() $2\times 2$
switch (Figure 2a) and a
$2\times 2$
switch (Figure 2a) and a
![]() $3\times 3$
switch (Figure 2b).
$3\times 3$
switch (Figure 2b).

Figure 2. Illustration of queue length vector in input-queued switch.
Below we present the performance bound for this system under the assumption that the arrival rate to all of the queues is
![]() ${(1-\epsilon)}/{N}$
, and hence all the queues are saturated in the heavy traffic limit.
${(1-\epsilon)}/{N}$
, and hence all the queues are saturated in the heavy traffic limit.
Corollary 2.2. For the input-queued switch defined above with independent arrivals, heavy traffic parameter
![]() $\epsilon \in (0,1)$
, and
$\epsilon \in (0,1)$
, and
![]() $\bigl(\sigma_{a_i}^{(\epsilon)}\bigr)^2\stackrel{\triangle}{=} \Sigma_{i,i}^{(\epsilon)}$
, there exists a constant
$\bigl(\sigma_{a_i}^{(\epsilon)}\bigr)^2\stackrel{\triangle}{=} \Sigma_{i,i}^{(\epsilon)}$
, there exists a constant
![]() $\overline{\beta}$
and
$\overline{\beta}$
and
![]() $\epsilon_0\in(0,1)$
such that for all
$\epsilon_0\in(0,1)$
such that for all
![]() $\epsilon<\epsilon_0$
$\epsilon<\epsilon_0$
 \begin{equation*} \Biggl|\mathbb{E}\Biggl[{\sum_{i=1}^{N^2} \overline{q}^{(\epsilon)}_i}\Biggr]- \biggl(\dfrac{1}{\epsilon}-\dfrac{1}{2N\epsilon}\biggr)\sum_{i=1}^{N^2}\bigl(\sigma_{a_i}^{(\epsilon)}\bigr)^2\Biggr| \leq \overline{\beta} \log\biggl(\dfrac{1}{\epsilon}\biggr). \end{equation*}
\begin{equation*} \Biggl|\mathbb{E}\Biggl[{\sum_{i=1}^{N^2} \overline{q}^{(\epsilon)}_i}\Biggr]- \biggl(\dfrac{1}{\epsilon}-\dfrac{1}{2N\epsilon}\biggr)\sum_{i=1}^{N^2}\bigl(\sigma_{a_i}^{(\epsilon)}\bigr)^2\Biggr| \leq \overline{\beta} \log\biggl(\dfrac{1}{\epsilon}\biggr). \end{equation*}
The proof involves simplifying the left-hand side of (2.4) and is omitted as it is similar to [Reference Hurtado-Lange and Maguluri4, Corollary 1].
2.3. State space collapse
We start by introducing some notation. For each
![]() $\epsilon\in(0,1)$
, let
$\epsilon\in(0,1)$
, let
![]() ${\boldsymbol{{q}}}_{\parallel \mathcal{K}}^{(\epsilon)}(k)$
and
${\boldsymbol{{q}}}_{\parallel \mathcal{K}}^{(\epsilon)}(k)$
and
![]() ${\boldsymbol{{q}}}_{\parallel \mathcal{H}}^{(\epsilon)}(k)$
be the projection of
${\boldsymbol{{q}}}_{\parallel \mathcal{H}}^{(\epsilon)}(k)$
be the projection of
![]() ${\boldsymbol{{q}}}^{(\epsilon)}(k)$
on
${\boldsymbol{{q}}}^{(\epsilon)}(k)$
on
![]() $\mathcal{K}$
and
$\mathcal{K}$
and
![]() $\mathcal{H}$
respectively, and
$\mathcal{H}$
respectively, and
Finally, we denote the steady-state vectors by
![]() $\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{K}}^{(\epsilon)}$
,
$\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{K}}^{(\epsilon)}$
,
![]() $\overline{{\boldsymbol{{q}}}}_{\perp \mathcal{K}}^{(\epsilon)}$
,
$\overline{{\boldsymbol{{q}}}}_{\perp \mathcal{K}}^{(\epsilon)}$
,
![]() $\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}^{(\epsilon)}$
, and
$\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}^{(\epsilon)}$
, and
![]() $\overline{{\boldsymbol{{q}}}}_{\perp \mathcal{H}}^{(\epsilon)}$
, which are the limit in distribution of
$\overline{{\boldsymbol{{q}}}}_{\perp \mathcal{H}}^{(\epsilon)}$
, which are the limit in distribution of
![]() ${\boldsymbol{{q}}}_{\parallel \mathcal{K}}^{(\epsilon)}(k)$
,
${\boldsymbol{{q}}}_{\parallel \mathcal{K}}^{(\epsilon)}(k)$
,
![]() ${\boldsymbol{{q}}}_{\perp \mathcal{K}}^{(\epsilon)}(k)$
,
${\boldsymbol{{q}}}_{\perp \mathcal{K}}^{(\epsilon)}(k)$
,
![]() ${\boldsymbol{{q}}}_{\parallel \mathcal{H}}^{(\epsilon)}(k)$
, and
${\boldsymbol{{q}}}_{\parallel \mathcal{H}}^{(\epsilon)}(k)$
, and
![]() ${\boldsymbol{{q}}}_{\perp \mathcal{H}}^{(\epsilon)}(k)$
as
${\boldsymbol{{q}}}_{\perp \mathcal{H}}^{(\epsilon)}(k)$
as
![]() $k\to\infty$
, respectively. The steady-state vectors are well-defined as the above Markov chains are positive recurrent by the definition of projection and by the fact that
$k\to\infty$
, respectively. The steady-state vectors are well-defined as the above Markov chains are positive recurrent by the definition of projection and by the fact that
![]() $\bigl\{{\boldsymbol{{q}}}^{(\epsilon)}(k)\colon k\in\mathbb{Z}_+\bigr\}$
is positive recurrent for all
$\bigl\{{\boldsymbol{{q}}}^{(\epsilon)}(k)\colon k\in\mathbb{Z}_+\bigr\}$
is positive recurrent for all
![]() $\epsilon\in(0,1)$
[Reference Stolyar11, Proposition 2].
$\epsilon\in(0,1)$
[Reference Stolyar11, Proposition 2].
It was proved in [Reference Hurtado-Lange and Maguluri4] that
![]() $\|\overline{{\boldsymbol{{q}}}}_{\perp \mathcal{K}}\|$
has bounded moments, where the bounds do not depend on
$\|\overline{{\boldsymbol{{q}}}}_{\perp \mathcal{K}}\|$
has bounded moments, where the bounds do not depend on
![]() $\epsilon$
. Here we explicitly compute a bound, and later we use it to obtain the heavy traffic error bounds.
$\epsilon$
. Here we explicitly compute a bound, and later we use it to obtain the heavy traffic error bounds.
Proposition 2.1. For the generalized switch model operating under MaxWeight parametrized by
![]() $\epsilon\in(0,1)$
described in Section 2.1, consider a vector
$\epsilon\in(0,1)$
described in Section 2.1, consider a vector
![]() $\boldsymbol{\nu}\in\textrm{Bo}(\mathcal{C})$
. Let
$\boldsymbol{\nu}\in\textrm{Bo}(\mathcal{C})$
. Let
![]() $\delta>0$
be such that
$\delta>0$
be such that
![]() $\delta\leq b^{(\ell)} - \bigl\langle {\boldsymbol{{c}}}^{(\ell)},\boldsymbol{\nu}\bigr\rangle$
for all
$\delta\leq b^{(\ell)} - \bigl\langle {\boldsymbol{{c}}}^{(\ell)},\boldsymbol{\nu}\bigr\rangle$
for all
![]() $\ell\in[L]\setminus P$
if
$\ell\in[L]\setminus P$
if
![]() $P\subsetneq [L]$
and
$P\subsetneq [L]$
and
![]() $\delta=1$
if
$\delta=1$
if
![]() $P=[L]$
. Let
$P=[L]$
. Let
![]() $\alpha\stackrel{\triangle}{=} \max\{A_{\max},S_{\max}\}$
. If
$\alpha\stackrel{\triangle}{=} \max\{A_{\max},S_{\max}\}$
. If
![]() $\epsilon<{\delta}/{(2\|\boldsymbol{\nu}\|)}$
, then for each
$\epsilon<{\delta}/{(2\|\boldsymbol{\nu}\|)}$
, then for each
![]() $r=1,2,\ldots$
we have
$r=1,2,\ldots$
we have
We present the proof in Appendix B.
2.4. Proof of Theorem 2.1.
The first part of our proof is similar to the proof of [Reference Hurtado-Lange and Maguluri4, Theorem 1], so we omit some steps. In the second part we show how to obtain logarithmic error bounds with respect to the heavy traffic limit. These bounds are tighter than the bounds presented in [Reference Hurtado-Lange and Maguluri4, Theorem 1].
Proof of Theorem 2.1.We omit the dependence on
![]() $\epsilon$
of the variables for ease of exposition.
$\epsilon$
of the variables for ease of exposition.
It suffices to show the result for
![]() ${\boldsymbol{{w}}}=\boldsymbol{\nu}$
, for the following reason. For any
${\boldsymbol{{w}}}=\boldsymbol{\nu}$
, for the following reason. For any
![]() ${\boldsymbol{{w}}}\in\bigcap_{\ell\in P}\mathcal{F}^{(\ell)}$
, let
${\boldsymbol{{w}}}\in\bigcap_{\ell\in P}\mathcal{F}^{(\ell)}$
, let
![]() ${\boldsymbol{{w}}}_\perp = {\boldsymbol{{w}}}-\boldsymbol{\nu}$
. Then for every
${\boldsymbol{{w}}}_\perp = {\boldsymbol{{w}}}-\boldsymbol{\nu}$
. Then for every
![]() $\ell\in P$
we have
$\ell\in P$
we have
![]() $\bigl\langle {\boldsymbol{{c}}}^{(\ell)},{\boldsymbol{{w}}}_\perp\bigr\rangle=0$
. Hence, since
$\bigl\langle {\boldsymbol{{c}}}^{(\ell)},{\boldsymbol{{w}}}_\perp\bigr\rangle=0$
. Hence, since
![]() $\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}=\sum_{\ell\in P}\tilde{\xi}_\ell {\boldsymbol{{c}}}^{(\ell)}$
for some
$\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}=\sum_{\ell\in P}\tilde{\xi}_\ell {\boldsymbol{{c}}}^{(\ell)}$
for some
![]() $\tilde{\xi}_\ell\in\mathbb{R}$
by definition of the subspace
$\tilde{\xi}_\ell\in\mathbb{R}$
by definition of the subspace
![]() $\mathcal{H}$
, we have
$\mathcal{H}$
, we have
We start by defining the Lyapunov function
![]() $V_{\parallel \mathcal{H}}({\boldsymbol{{q}}})\stackrel{\triangle}{=}\| {\boldsymbol{{q}}}_{\parallel \mathcal{H}}\|^2$
. To set the drift of this Lyapunov function to zero in the steady state, we first verify that
$V_{\parallel \mathcal{H}}({\boldsymbol{{q}}})\stackrel{\triangle}{=}\| {\boldsymbol{{q}}}_{\parallel \mathcal{H}}\|^2$
. To set the drift of this Lyapunov function to zero in the steady state, we first verify that
![]() $\mathbb{E}\bigl[{\| \overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}\|^2}\bigr]<\infty$
. We omit this step for brevity, but it can be shown using the moment bounds obtained from the Foster–Lyapunov theorem [Reference Hajek3, Proposition 6.16] with Lyapunov function
$\mathbb{E}\bigl[{\| \overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}\|^2}\bigr]<\infty$
. We omit this step for brevity, but it can be shown using the moment bounds obtained from the Foster–Lyapunov theorem [Reference Hajek3, Proposition 6.16] with Lyapunov function
![]() $V({\boldsymbol{{q}}})=\|{\boldsymbol{{q}}}\|^2$
, and non-expansivity of the projection onto a convex set. Setting the drift of
$V({\boldsymbol{{q}}})=\|{\boldsymbol{{q}}}\|^2$
, and non-expansivity of the projection onto a convex set. Setting the drift of
![]() $V_{\parallel \mathcal{H}}({\boldsymbol{{q}}})$
to zero in the steady state, we obtain
$V_{\parallel \mathcal{H}}({\boldsymbol{{q}}})$
to zero in the steady state, we obtain
 \begin{align}0 &= \mathbb{E}\bigl[{\|\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}^+ \|^2 - \|\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}} \|^2}\bigr] \notag \\&= \mathbb{E}\bigl[{\|\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}^+ -\overline{{\boldsymbol{{u}}}}_{\parallel \mathcal{H}}+\overline{{\boldsymbol{{u}}}}_{\parallel \mathcal{H}} \|^2 - \|\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}} \|^2}\bigr] \notag \\&= \mathbb{E}\bigl[{\|\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}^+ -\overline{{\boldsymbol{{u}}}}_{\parallel \mathcal{H}} \|^2 +\|\overline{{\boldsymbol{{u}}}}_{\parallel \mathcal{H}} \|^2 +2\big\langle \overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}^+-\overline{{\boldsymbol{{u}}}}_{\parallel \mathcal{H}},\,\overline{{\boldsymbol{{u}}}}_{\parallel \mathcal{H}} \big\rangle - \|\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}} \|^2}\bigr] \notag \\&\stackrel{(a)}{=} \mathbb{E}\bigl[{\|\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}+\overline{{\boldsymbol{{a}}}}_{\parallel \mathcal{H}}-\overline{{\boldsymbol{{s}}}}_{\parallel \mathcal{H}} \|^2 -\|\overline{{\boldsymbol{{u}}}}_{\parallel \mathcal{H}}\|^2 +2\big\langle\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}^+,\overline{{\boldsymbol{{u}}}}_{\parallel \mathcal{H}} \big\rangle- \|\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}} \|^2}\bigr] \notag \\&\stackrel{(b)}{=}\underbrace{\mathbb{E}\bigl[{\|\overline{{\boldsymbol{{a}}}}_{\parallel \mathcal{H}} - \overline{{\boldsymbol{{s}}}}_{\parallel \mathcal{H}}\|^2}\bigr]}_{\mathcal{T}_2} +\underbrace{2\mathbb{E}\bigl[{\big\langle \overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}},\, \overline{{\boldsymbol{{a}}}}_{\parallel \mathcal{H}}-\overline{{\boldsymbol{{s}}}}_{\parallel \mathcal{H}} \big\rangle}\bigr]}_{-\mathcal{T}_1}-\underbrace{\mathbb{E}\bigl[{\|\overline{{\boldsymbol{{u}}}}_{\parallel \mathcal{H}} \|^2}\bigr]}_{\mathcal{T}_3} \notag \\& \quad\, + \underbrace{2\mathbb{E}\bigl[{\big\langle\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}^+,\, \overline{{\boldsymbol{{u}}}}_{\parallel \mathcal{H}}\big\rangle}\bigr]}_{\mathcal{T}_4}, \end{align}
\begin{align}0 &= \mathbb{E}\bigl[{\|\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}^+ \|^2 - \|\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}} \|^2}\bigr] \notag \\&= \mathbb{E}\bigl[{\|\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}^+ -\overline{{\boldsymbol{{u}}}}_{\parallel \mathcal{H}}+\overline{{\boldsymbol{{u}}}}_{\parallel \mathcal{H}} \|^2 - \|\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}} \|^2}\bigr] \notag \\&= \mathbb{E}\bigl[{\|\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}^+ -\overline{{\boldsymbol{{u}}}}_{\parallel \mathcal{H}} \|^2 +\|\overline{{\boldsymbol{{u}}}}_{\parallel \mathcal{H}} \|^2 +2\big\langle \overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}^+-\overline{{\boldsymbol{{u}}}}_{\parallel \mathcal{H}},\,\overline{{\boldsymbol{{u}}}}_{\parallel \mathcal{H}} \big\rangle - \|\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}} \|^2}\bigr] \notag \\&\stackrel{(a)}{=} \mathbb{E}\bigl[{\|\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}+\overline{{\boldsymbol{{a}}}}_{\parallel \mathcal{H}}-\overline{{\boldsymbol{{s}}}}_{\parallel \mathcal{H}} \|^2 -\|\overline{{\boldsymbol{{u}}}}_{\parallel \mathcal{H}}\|^2 +2\big\langle\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}^+,\overline{{\boldsymbol{{u}}}}_{\parallel \mathcal{H}} \big\rangle- \|\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}} \|^2}\bigr] \notag \\&\stackrel{(b)}{=}\underbrace{\mathbb{E}\bigl[{\|\overline{{\boldsymbol{{a}}}}_{\parallel \mathcal{H}} - \overline{{\boldsymbol{{s}}}}_{\parallel \mathcal{H}}\|^2}\bigr]}_{\mathcal{T}_2} +\underbrace{2\mathbb{E}\bigl[{\big\langle \overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}},\, \overline{{\boldsymbol{{a}}}}_{\parallel \mathcal{H}}-\overline{{\boldsymbol{{s}}}}_{\parallel \mathcal{H}} \big\rangle}\bigr]}_{-\mathcal{T}_1}-\underbrace{\mathbb{E}\bigl[{\|\overline{{\boldsymbol{{u}}}}_{\parallel \mathcal{H}} \|^2}\bigr]}_{\mathcal{T}_3} \notag \\& \quad\, + \underbrace{2\mathbb{E}\bigl[{\big\langle\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}^+,\, \overline{{\boldsymbol{{u}}}}_{\parallel \mathcal{H}}\big\rangle}\bigr]}_{\mathcal{T}_4}, \end{align}
where (a) holds by definition of norm and dot product, and by the queue dynamics in (2.1), and (b) holds by expanding the first norm square and reorganizing terms. Thus we have
Observe that in the computation of (2.5) we only used properties of the Euclidean norm, the dot product, and the dynamics of the queues (2.1). Then (2.5) is valid for any SPN that satisfies (2.1).
We compute each
![]() $\mathcal{T}_i$
for
$\mathcal{T}_i$
for
![]() $i=1,2,3,4$
separately. The terms
$i=1,2,3,4$
separately. The terms
![]() $\mathcal{T}_1$
and
$\mathcal{T}_1$
and
![]() $\mathcal{T}_4$
are the bottlenecks for the optimal error bounds, so we compute them at the end of this proof. We start with
$\mathcal{T}_4$
are the bottlenecks for the optimal error bounds, so we compute them at the end of this proof. We start with
![]() $\mathcal{T}_2$
and
$\mathcal{T}_2$
and
![]() $\mathcal{T}_3$
, which we borrow from [Reference Hurtado-Lange and Maguluri4].
$\mathcal{T}_3$
, which we borrow from [Reference Hurtado-Lange and Maguluri4].
The term
![]() $\mathcal{T}_2$
is related to the square of the arrivals and services, and therefore the covariance matrix of both processes is involved. Also, the arrival and service rate vectors are projected on
$\mathcal{T}_2$
is related to the square of the arrivals and services, and therefore the covariance matrix of both processes is involved. Also, the arrival and service rate vectors are projected on
![]() $\mathcal{H}$
. Then, using the least-squares problem, we can compute the desired norm. The details of this computation can be verified in [Reference Hurtado-Lange and Maguluri4, equations (38)–(42)], and we omit them for brevity. We obtain that there exists a constant
$\mathcal{H}$
. Then, using the least-squares problem, we can compute the desired norm. The details of this computation can be verified in [Reference Hurtado-Lange and Maguluri4, equations (38)–(42)], and we omit them for brevity. We obtain that there exists a constant
![]() $\beta_1$
such that
$\beta_1$
such that
Now we compute
![]() $\mathcal{T}_3$
. Observe that the unused service vector is bounded, because the potential service rate vector is also bounded. Additionally, the more loaded the system, the least unused service we should expect. Translating these intuitions into mathematics yields (2.8), where
$\mathcal{T}_3$
. Observe that the unused service vector is bounded, because the potential service rate vector is also bounded. Additionally, the more loaded the system, the least unused service we should expect. Translating these intuitions into mathematics yields (2.8), where
![]() $\beta_2$
is a positive constant. A formal proof can be found in [Reference Hurtado-Lange and Maguluri4, equations (43)–(44)]. We omit the details for brevity:
$\beta_2$
is a positive constant. A formal proof can be found in [Reference Hurtado-Lange and Maguluri4, equations (43)–(44)]. We omit the details for brevity:
Now we focus on the terms
![]() $\mathcal{T}_1$
and
$\mathcal{T}_1$
and
![]() $\mathcal{T}_4$
. We start with
$\mathcal{T}_4$
. We start with
![]() $\mathcal{T}_1$
:
$\mathcal{T}_1$
:
where (a) follows by first using the orthogonality principle and then substituting
![]() $\mathbb{E}[{\overline{{\boldsymbol{{a}}}}}]=$
$\mathbb{E}[{\overline{{\boldsymbol{{a}}}}}]=$
![]() $(1-\epsilon)\boldsymbol{\nu}$
and observing that
$(1-\epsilon)\boldsymbol{\nu}$
and observing that
![]() $\overline{{\boldsymbol{{a}}}}$
is independent of
$\overline{{\boldsymbol{{a}}}}$
is independent of
![]() $\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}$
. Observe that the first term is part of (2.4), which is the expression we want to obtain. Then we only need to bound the second term. We present the result in Claim 2.1, and we prove it at the end of the section.
$\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}$
. Observe that the first term is part of (2.4), which is the expression we want to obtain. Then we only need to bound the second term. We present the result in Claim 2.1, and we prove it at the end of the section.
Claim 2.1. Consider the system described in Theorem 2.1. Then there exist
![]() $\epsilon^{\prime}_0>0$
and a finite constant
$\epsilon^{\prime}_0>0$
and a finite constant
![]() $\beta_3$
such that
$\beta_3$
such that
For
![]() $\mathcal{T}_4$
we have the following result.
$\mathcal{T}_4$
we have the following result.
Claim 2.2. Consider the system described in Theorem 2.1. Then there exist
![]() $\epsilon^{\prime\prime}_0>0$
and a finite constant
$\epsilon^{\prime\prime}_0>0$
and a finite constant
![]() $\beta_4$
such that
$\beta_4$
such that
The proofs of both claims are presented at the end of the section. Now, using (2.7), (2.8), and Claims 2.1, 2.2 in (2.6), we obtain that for any
![]() $\epsilon<\epsilon_0\stackrel{\triangle}{=} \min\{\epsilon^{\prime}_0,\epsilon^{\prime\prime}_0\}$
$\epsilon<\epsilon_0\stackrel{\triangle}{=} \min\{\epsilon^{\prime}_0,\epsilon^{\prime\prime}_0\}$
where
![]() $\beta\stackrel{\triangle}{=}\max\{\beta_1,\beta_2,\beta_3,\beta_4\}$
.
$\beta\stackrel{\triangle}{=}\max\{\beta_1,\beta_2,\beta_3,\beta_4\}$
.
Now we prove the claims. The main idea is to use Hölder’s inequality and Proposition 2.1 with the right choice of the parameter r. We additionally use the following result, which is proved in [Reference Hurtado-Lange and Maguluri4, Lemmas 2 and 3], and we intuitively explain below.
Lemma 2.1. Let
![]() $\ell\in P$
and
$\ell\in P$
and
![]() $m\in\mathcal{M}$
.
$m\in\mathcal{M}$
.
-
(i) Then there exists
 $\boldsymbol{\nu}^{(m)}\in \mathcal{S}^{(m)}$
such that
$\boldsymbol{\nu}^{(m)}\in \mathcal{S}^{(m)}$
such that
 $b^{(m,\ell)}=\bigl\langle {\boldsymbol{{c}}}^{(\ell)},\boldsymbol{\nu}^{(m)}\bigr\rangle$
. This implies that, for each
$b^{(m,\ell)}=\bigl\langle {\boldsymbol{{c}}}^{(\ell)},\boldsymbol{\nu}^{(m)}\bigr\rangle$
. This implies that, for each
 $\ell\in P$
,
$\ell\in P$
,  \begin{equation*} b^{(\ell)}=\mathbb{E}\bigl[{\overline{B}_\ell}\bigr]=\sum_{m\in\mathcal{M}}\psi_m b^{(m,\ell)}. \end{equation*}
\begin{equation*} b^{(\ell)}=\mathbb{E}\bigl[{\overline{B}_\ell}\bigr]=\sum_{m\in\mathcal{M}}\psi_m b^{(m,\ell)}. \end{equation*}
-
(ii) Define
 $\pi^{(m,\ell)}\stackrel{\triangle}{=} \,\mathbb{P}\bigl[{\bigl\langle {\boldsymbol{{c}}}^{(\ell)},\overline{{\boldsymbol{{s}}}}\bigr\rangle =b^{(m,\ell)}\mid \overline{M}=m }\bigr]$
. Then
$\pi^{(m,\ell)}\stackrel{\triangle}{=} \,\mathbb{P}\bigl[{\bigl\langle {\boldsymbol{{c}}}^{(\ell)},\overline{{\boldsymbol{{s}}}}\bigr\rangle =b^{(m,\ell)}\mid \overline{M}=m }\bigr]$
. Then
 $1-\pi^{(m,\ell)} \leq \epsilon b^{(m,l)}/\gamma^{(m)}$
, where is positive and finite.
$1-\pi^{(m,\ell)} \leq \epsilon b^{(m,l)}/\gamma^{(m)}$
, where is positive and finite. \begin{equation*} \gamma^{(m)}\stackrel{\triangle}{=} \min\bigl\{b^{(m,\ell)}-\bigl\langle{\boldsymbol{{c}}}^{(\ell)},{\boldsymbol{{x}}}\bigr\rangle\colon \bigl\langle {\boldsymbol{{c}}}^{(\ell)},{\boldsymbol{{x}}}\bigr\rangle<b^{(m,\ell)} ,\,\ell\in P,\, {\boldsymbol{{x}}}\in\mathcal{S}^{(m)} \bigr\} \end{equation*}
\begin{equation*} \gamma^{(m)}\stackrel{\triangle}{=} \min\bigl\{b^{(m,\ell)}-\bigl\langle{\boldsymbol{{c}}}^{(\ell)},{\boldsymbol{{x}}}\bigr\rangle\colon \bigl\langle {\boldsymbol{{c}}}^{(\ell)},{\boldsymbol{{x}}}\bigr\rangle<b^{(m,\ell)} ,\,\ell\in P,\, {\boldsymbol{{x}}}\in\mathcal{S}^{(m)} \bigr\} \end{equation*}
One difficulty of the generalized switch model is that the vector of potential service rates obtained from MaxWeight (see (2.3)) does not necessarily belong to the capacity region
![]() $\mathcal{C}$
. Given the channel state
$\mathcal{C}$
. Given the channel state
![]() $\overline{M}=m$
, we know that the vector of potential service satisfies
$\overline{M}=m$
, we know that the vector of potential service satisfies
![]() $\overline{{\boldsymbol{{s}}}}\in \mathcal{S}^{(m)}$
. However, the capacity region
$\overline{{\boldsymbol{{s}}}}\in \mathcal{S}^{(m)}$
. However, the capacity region
![]() $\mathcal{C}$
is a convex combination of the sets
$\mathcal{C}$
is a convex combination of the sets
![]() $\textrm{ConvexHull}(\mathcal{S}^{(m)})$
for all
$\textrm{ConvexHull}(\mathcal{S}^{(m)})$
for all
![]() $m\in\mathcal{M}$
. Hence there is no guarantee that the feasible service rate vectors belong to
$m\in\mathcal{M}$
. Hence there is no guarantee that the feasible service rate vectors belong to
![]() $\mathcal{C}$
.
$\mathcal{C}$
.
The first part of the lemma shows that the location parameter
![]() $b^{(\ell)}$
of each facet of
$b^{(\ell)}$
of each facet of
![]() $\mathcal{C}$
is a convex combination of the location parameter of hyperplanes that pass through the boundary of each set
$\mathcal{C}$
is a convex combination of the location parameter of hyperplanes that pass through the boundary of each set
![]() $\textrm{ConvexHull}(\mathcal{S}^{(m)})$
, and the weights associated to this convex combinations correspond to the probability of observing each channel state, i.e.
$\textrm{ConvexHull}(\mathcal{S}^{(m)})$
, and the weights associated to this convex combinations correspond to the probability of observing each channel state, i.e.
![]() $\psi_m$
. The second part of the lemma shows that, given the channel state, the feasible service vector selected by the MaxWeight algorithm achieves the maximum
$\psi_m$
. The second part of the lemma shows that, given the channel state, the feasible service vector selected by the MaxWeight algorithm achieves the maximum
![]() ${\boldsymbol{{c}}}^{(\ell)}$
weighted service rate,
${\boldsymbol{{c}}}^{(\ell)}$
weighted service rate,
![]() $b^{(m,\ell)}$
, with high probability. These results are important because in the proof of Theorem 2.1 we work with
$b^{(m,\ell)}$
, with high probability. These results are important because in the proof of Theorem 2.1 we work with
![]() $\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}$
, and by definition,
$\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}$
, and by definition,
![]() $\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}$
is a linear combination of the vectors
$\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}$
is a linear combination of the vectors
![]() ${\boldsymbol{{c}}}^{(\ell)}$
with
${\boldsymbol{{c}}}^{(\ell)}$
with
![]() $\ell\in P$
. These two results imply that, intuitively, the expected vector of potential service rate behaves as if it belonged to the capacity region.
$\ell\in P$
. These two results imply that, intuitively, the expected vector of potential service rate behaves as if it belonged to the capacity region.
Proof of Claim 2.1.Conditioning on the channel state, we get
where
![]() $\boldsymbol{\nu}^{(m)}$
is defined as in Lemma 2.1 and (a) follows from Lemma 2.1 part (i), and because
$\boldsymbol{\nu}^{(m)}$
is defined as in Lemma 2.1 and (a) follows from Lemma 2.1 part (i), and because
![]() $\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}$
is a linear combination of the vectors
$\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}$
is a linear combination of the vectors
![]() ${\boldsymbol{{c}}}^{(\ell)}$
with
${\boldsymbol{{c}}}^{(\ell)}$
with
![]() ${\boldsymbol{{c}}}^{(\ell)}\in \tilde{P}$
. It remains to show that
${\boldsymbol{{c}}}^{(\ell)}\in \tilde{P}$
. It remains to show that
![]() ${\mathbb{E}_m\bigl[{ \bigl\langle \overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}, \overline{{\boldsymbol{{s}}}}-\boldsymbol{\nu}^{(m)}\bigr\rangle {\unicode{x1D7D9}_{\{{\langle{\boldsymbol{{c}}}^{(\ell)},\overline{{\boldsymbol{{s}}}}\rangle\neq b^{(m,\ell)}} \}}}}\bigr]}$
is
${\mathbb{E}_m\bigl[{ \bigl\langle \overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}, \overline{{\boldsymbol{{s}}}}-\boldsymbol{\nu}^{(m)}\bigr\rangle {\unicode{x1D7D9}_{\{{\langle{\boldsymbol{{c}}}^{(\ell)},\overline{{\boldsymbol{{s}}}}\rangle\neq b^{(m,\ell)}} \}}}}\bigr]}$
is
![]() $\textrm{O}(\epsilon\log\!({1}/{\epsilon}))$
.
$\textrm{O}(\epsilon\log\!({1}/{\epsilon}))$
.
Observe that
![]() $\overline{{\boldsymbol{{q}}}}=\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}+\overline{{\boldsymbol{{q}}}}_{\perp \mathcal{H}} = \overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{K}}+\overline{{\boldsymbol{{q}}}}_{\perp \mathcal{K}}$
, and thus
$\overline{{\boldsymbol{{q}}}}=\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}+\overline{{\boldsymbol{{q}}}}_{\perp \mathcal{H}} = \overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{K}}+\overline{{\boldsymbol{{q}}}}_{\perp \mathcal{K}}$
, and thus
 \begin{align}&{\mathbb{E}_m\bigl[{ \bigl\langle \overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}, \overline{{\boldsymbol{{s}}}}-\boldsymbol{\nu}^{(m)}\bigr\rangle {\unicode{x1D7D9}_{\{{\langle{\boldsymbol{{c}}}^{(\ell)},\overline{{\boldsymbol{{s}}}}\rangle\neq b^{(m,\ell)}} \}}}}\bigr]} \notag \\[6pt]&\quad ={\mathbb{E}_m\bigl[{\bigl\langle \overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{K}},\overline{{\boldsymbol{{s}}}}-\boldsymbol{\nu}^{(m)} \bigr\rangle{\unicode{x1D7D9}_{\{{\langle{\boldsymbol{{c}}}^{(\ell)},\overline{{\boldsymbol{{s}}}}\rangle\neq b^{(m,\ell)}}\}}}}\bigr]} \end{align}
\begin{align}&{\mathbb{E}_m\bigl[{ \bigl\langle \overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{H}}, \overline{{\boldsymbol{{s}}}}-\boldsymbol{\nu}^{(m)}\bigr\rangle {\unicode{x1D7D9}_{\{{\langle{\boldsymbol{{c}}}^{(\ell)},\overline{{\boldsymbol{{s}}}}\rangle\neq b^{(m,\ell)}} \}}}}\bigr]} \notag \\[6pt]&\quad ={\mathbb{E}_m\bigl[{\bigl\langle \overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{K}},\overline{{\boldsymbol{{s}}}}-\boldsymbol{\nu}^{(m)} \bigr\rangle{\unicode{x1D7D9}_{\{{\langle{\boldsymbol{{c}}}^{(\ell)},\overline{{\boldsymbol{{s}}}}\rangle\neq b^{(m,\ell)}}\}}}}\bigr]} \end{align}
Now we show that the terms in (2.9) and (2.10) are
![]() $\textrm{O}(\epsilon\log\!({1}/{\epsilon}))$
. From (2.9), we have
$\textrm{O}(\epsilon\log\!({1}/{\epsilon}))$
. From (2.9), we have
by the definition of projection on the cone
![]() $\mathcal{K}$
and by definition of
$\mathcal{K}$
and by definition of
![]() $\boldsymbol{\nu}^{(m)}$
and
$\boldsymbol{\nu}^{(m)}$
and
![]() $b^{(m,\ell)}$
in Lemma 2.1 part (i). Now we have
$b^{(m,\ell)}$
in Lemma 2.1 part (i). Now we have
 \begin{align}0&\geq {\mathbb{E}_m\bigl[{\bigl\langle \overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{K}},\overline{{\boldsymbol{{s}}}}-\boldsymbol{\nu}^{(m)} \bigr\rangle{\unicode{x1D7D9}_{\{{\langle{\boldsymbol{{c}}}^{(\ell)},\overline{{\boldsymbol{{s}}}}\rangle\neq b^{(m,\ell)}}\}}}}\bigr]} \notag \\[3pt]&\stackrel{(a)}{\geq} - {\mathbb{E}_m\bigl[{\bigl\langle\overline{{\boldsymbol{{q}}}}_{\perp \mathcal{K}}, \overline{{\boldsymbol{{s}}}}-\boldsymbol{\nu}^{(m)}\bigr\rangle {\unicode{x1D7D9}_{\{{\langle{\boldsymbol{{c}}}^{(\ell)},\overline{{\boldsymbol{{s}}}}\rangle\neq b^{(m,\ell)}}\}}}}\bigr]} \notag \\[3pt]&\stackrel{(b)}{\geq} - \mathbb{E}\bigl[{\|\overline{{\boldsymbol{{q}}}}_{\perp \mathcal{K}} \|^r}\bigr]^{{1}/{r}} {\mathbb{E}_m\bigl[{\| \overline{{\boldsymbol{{s}}}}-\boldsymbol{\nu}^{(m)} \|^p {\unicode{x1D7D9}_{\{{\langle{\boldsymbol{{c}}}^{(\ell)},\overline{{\boldsymbol{{s}}}}\rangle\neq b^{(m,\ell)}}\}}}}\bigr]}^{{1}/{p}} \notag \\[3pt]&\stackrel{(c)}{\geq} -R_r^{{1}/{r}}\, {\mathbb{E}_m\bigl[{\| \overline{{\boldsymbol{{s}}}}-\boldsymbol{\nu}^{(m)} \|^p {\unicode{x1D7D9}_{\{{\langle{\boldsymbol{{c}}}^{(\ell)},\overline{{\boldsymbol{{s}}}}\rangle\neq b^{(m,\ell)}}\}}}}\bigr]}^{{1}/{p}}, \notag\end{align}
\begin{align}0&\geq {\mathbb{E}_m\bigl[{\bigl\langle \overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{K}},\overline{{\boldsymbol{{s}}}}-\boldsymbol{\nu}^{(m)} \bigr\rangle{\unicode{x1D7D9}_{\{{\langle{\boldsymbol{{c}}}^{(\ell)},\overline{{\boldsymbol{{s}}}}\rangle\neq b^{(m,\ell)}}\}}}}\bigr]} \notag \\[3pt]&\stackrel{(a)}{\geq} - {\mathbb{E}_m\bigl[{\bigl\langle\overline{{\boldsymbol{{q}}}}_{\perp \mathcal{K}}, \overline{{\boldsymbol{{s}}}}-\boldsymbol{\nu}^{(m)}\bigr\rangle {\unicode{x1D7D9}_{\{{\langle{\boldsymbol{{c}}}^{(\ell)},\overline{{\boldsymbol{{s}}}}\rangle\neq b^{(m,\ell)}}\}}}}\bigr]} \notag \\[3pt]&\stackrel{(b)}{\geq} - \mathbb{E}\bigl[{\|\overline{{\boldsymbol{{q}}}}_{\perp \mathcal{K}} \|^r}\bigr]^{{1}/{r}} {\mathbb{E}_m\bigl[{\| \overline{{\boldsymbol{{s}}}}-\boldsymbol{\nu}^{(m)} \|^p {\unicode{x1D7D9}_{\{{\langle{\boldsymbol{{c}}}^{(\ell)},\overline{{\boldsymbol{{s}}}}\rangle\neq b^{(m,\ell)}}\}}}}\bigr]}^{{1}/{p}} \notag \\[3pt]&\stackrel{(c)}{\geq} -R_r^{{1}/{r}}\, {\mathbb{E}_m\bigl[{\| \overline{{\boldsymbol{{s}}}}-\boldsymbol{\nu}^{(m)} \|^p {\unicode{x1D7D9}_{\{{\langle{\boldsymbol{{c}}}^{(\ell)},\overline{{\boldsymbol{{s}}}}\rangle\neq b^{(m,\ell)}}\}}}}\bigr]}^{{1}/{p}}, \notag\end{align}
where (a) holds because
![]() $\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{K}}=\overline{{\boldsymbol{{q}}}}-\overline{{\boldsymbol{{q}}}}_{\perp \mathcal{K}}$
, and because
$\overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{K}}=\overline{{\boldsymbol{{q}}}}-\overline{{\boldsymbol{{q}}}}_{\perp \mathcal{K}}$
, and because
![]() $\bigl\langle\overline{{\boldsymbol{{q}}}},\overline{{\boldsymbol{{s}}}}-\boldsymbol{\nu}^{(m)}\bigr\rangle\geq 0$
by the definition of MaxWeight in (2.3) and since
$\bigl\langle\overline{{\boldsymbol{{q}}}},\overline{{\boldsymbol{{s}}}}-\boldsymbol{\nu}^{(m)}\bigr\rangle\geq 0$
by the definition of MaxWeight in (2.3) and since
![]() $\boldsymbol{\nu}^{(m)}\in\mathcal{S}^{(m)}$
, (b) holds using Hölder’s inequality for some
$\boldsymbol{\nu}^{(m)}\in\mathcal{S}^{(m)}$
, (b) holds using Hölder’s inequality for some
![]() $p,r>1$
such that
$p,r>1$
such that
![]() ${1}/{p}+{1}/{r}=1$
, and (c) holds by SSC in Proposition 2.1. Now, by the definition of
${1}/{p}+{1}/{r}=1$
, and (c) holds by SSC in Proposition 2.1. Now, by the definition of
![]() $R_r$
, we have
$R_r$
, we have
where
Here (a) follows from Stirling’s approximation for the factorial.
Now we bound the remaining term
![]() ${\mathbb{E}_m\bigl[{\| \overline{{\boldsymbol{{s}}}}-\boldsymbol{\nu}^{(m)} \|^p {\unicode{x1D7D9}_{\{{\langle{\boldsymbol{{c}}}^{(\ell)},\overline{{\boldsymbol{{s}}}}\rangle\neq b^{(m,\ell)}}\}}}}\bigr]}^{{1}/{p}}$
as follows:
${\mathbb{E}_m\bigl[{\| \overline{{\boldsymbol{{s}}}}-\boldsymbol{\nu}^{(m)} \|^p {\unicode{x1D7D9}_{\{{\langle{\boldsymbol{{c}}}^{(\ell)},\overline{{\boldsymbol{{s}}}}\rangle\neq b^{(m,\ell)}}\}}}}\bigr]}^{{1}/{p}}$
as follows:
 \begin{align}0 & \leq {\mathbb{E}_m\bigl[{\| \overline{{\boldsymbol{{s}}}}-\boldsymbol{\nu}^{(m)} \|^p {\unicode{x1D7D9}_{\{{\langle{\boldsymbol{{c}}}^{(\ell)},\overline{{\boldsymbol{{s}}}}\rangle\neq b^{(m,\ell)}}\}}}}\bigr]}^{{1}/{p}} \notag \\&\stackrel{(a)}{=} {\mathbb{E}_m\bigl[{\| \overline{{\boldsymbol{{s}}}}-\boldsymbol{\nu}^{(m)} \|^p \mid \bigl\langle{\boldsymbol{{c}}}^{(\ell)},\overline{{\boldsymbol{{s}}}}\bigr\rangle\neq b^{(m,\ell)}}\bigr]}^{{1}/{p}}\bigl(1-\pi^{(m,\ell)} \bigr)^{{1}/{p}} \notag \\&\stackrel{(b)}{\leq} n\bigl(S_{\max} + V_{\max}\bigr)\bigl(1-\pi^{(m,\ell)} \bigr)^{{1}/{p}} \stackrel{(c)}{=} \beta_6\epsilon^{{1}/{p}} ,\end{align}
\begin{align}0 & \leq {\mathbb{E}_m\bigl[{\| \overline{{\boldsymbol{{s}}}}-\boldsymbol{\nu}^{(m)} \|^p {\unicode{x1D7D9}_{\{{\langle{\boldsymbol{{c}}}^{(\ell)},\overline{{\boldsymbol{{s}}}}\rangle\neq b^{(m,\ell)}}\}}}}\bigr]}^{{1}/{p}} \notag \\&\stackrel{(a)}{=} {\mathbb{E}_m\bigl[{\| \overline{{\boldsymbol{{s}}}}-\boldsymbol{\nu}^{(m)} \|^p \mid \bigl\langle{\boldsymbol{{c}}}^{(\ell)},\overline{{\boldsymbol{{s}}}}\bigr\rangle\neq b^{(m,\ell)}}\bigr]}^{{1}/{p}}\bigl(1-\pi^{(m,\ell)} \bigr)^{{1}/{p}} \notag \\&\stackrel{(b)}{\leq} n\bigl(S_{\max} + V_{\max}\bigr)\bigl(1-\pi^{(m,\ell)} \bigr)^{{1}/{p}} \stackrel{(c)}{=} \beta_6\epsilon^{{1}/{p}} ,\end{align}
where (a) holds by definition of
![]() $\pi^{(m,\ell)}$
in Lemma 2.1 part (ii), (b) holds with
$\pi^{(m,\ell)}$
in Lemma 2.1 part (ii), (b) holds with
![]() $V_{\max} = \max_{m\in \mathcal{M}, i\in[n]}\nu^{(m)}_i$
, and (c) holds by Lemma 2.1 part (ii) for
$V_{\max} = \max_{m\in \mathcal{M}, i\in[n]}\nu^{(m)}_i$
, and (c) holds by Lemma 2.1 part (ii) for
Putting everything together, we obtain
 \begin{align*} 0&\geq {\mathbb{E}_m\bigl[{\bigl\langle \overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{K}},\overline{{\boldsymbol{{s}}}}-\boldsymbol{\nu}^{(m)} \bigr\rangle{\unicode{x1D7D9}_{\{{\langle{\boldsymbol{{c}}}^{(\ell)},\overline{{\boldsymbol{{s}}}}\rangle\neq b^{(m,\ell)}}\}}}}\bigr]} \notag \\ &\geq -\beta_5\beta_6{\textrm{e}}^{{1}/{r}-1}r^{1+{1}/{2r}}\epsilon^{{1}/{p}} \notag \\ &\stackrel{(a)}{=} -\beta_5\beta_6{\textrm{e}}^{\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}-1}\biggl\lfloor\log\biggl(\dfrac{1}{\epsilon}\biggr)\biggr\rfloor^{1+{{1}/{2\lfloor\log\!({{1}/{\epsilon}})\rfloor}}}\epsilon^{-\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}}\epsilon \notag \\ &\stackrel{(b)}{\geq} -2\beta_5\beta_6 \epsilon\log\biggl(\dfrac{1}{\epsilon}\biggr) \quad \text{{for all} $ \epsilon<\epsilon^{\prime}_0$,}\end{align*}
\begin{align*} 0&\geq {\mathbb{E}_m\bigl[{\bigl\langle \overline{{\boldsymbol{{q}}}}_{\parallel \mathcal{K}},\overline{{\boldsymbol{{s}}}}-\boldsymbol{\nu}^{(m)} \bigr\rangle{\unicode{x1D7D9}_{\{{\langle{\boldsymbol{{c}}}^{(\ell)},\overline{{\boldsymbol{{s}}}}\rangle\neq b^{(m,\ell)}}\}}}}\bigr]} \notag \\ &\geq -\beta_5\beta_6{\textrm{e}}^{{1}/{r}-1}r^{1+{1}/{2r}}\epsilon^{{1}/{p}} \notag \\ &\stackrel{(a)}{=} -\beta_5\beta_6{\textrm{e}}^{\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}-1}\biggl\lfloor\log\biggl(\dfrac{1}{\epsilon}\biggr)\biggr\rfloor^{1+{{1}/{2\lfloor\log\!({{1}/{\epsilon}})\rfloor}}}\epsilon^{-\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}}\epsilon \notag \\ &\stackrel{(b)}{\geq} -2\beta_5\beta_6 \epsilon\log\biggl(\dfrac{1}{\epsilon}\biggr) \quad \text{{for all} $ \epsilon<\epsilon^{\prime}_0$,}\end{align*}
where (a) holds after choosing
![]() $r\stackrel{\triangle}{=}\lfloor\log\!({1}/{\epsilon})\rfloor$
, and (b) follows for
$r\stackrel{\triangle}{=}\lfloor\log\!({1}/{\epsilon})\rfloor$
, and (b) follows for
![]() $\epsilon^{\prime}_0$
as defined below, and because by the definition of floor function we have
$\epsilon^{\prime}_0$
as defined below, and because by the definition of floor function we have
 \begin{align*} &\lim_{\epsilon \downarrow 0} {\textrm{e}}^{\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}-1}\biggl\lfloor\log\biggl(\dfrac{1}{\epsilon}\biggr)\biggr\rfloor^{\tfrac{1}{2\lfloor\log\!({1}/{\epsilon})\rfloor}}\epsilon^{-\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}}\notag \\ &\quad \leq \lim_{\epsilon \downarrow 0} {\textrm{e}}^{\tfrac{1}{\log\!({1}/{\epsilon})-1}-1} \lim_{\epsilon \downarrow 0} \log\biggl(\dfrac{1}{\epsilon}\biggr)^{\tfrac{1}{2\log\!({1}/{\epsilon})-2}}\lim_{\epsilon \downarrow 0} \epsilon^{-\tfrac{1}{\log\!({1}/{\epsilon})}} = \dfrac{1}{e} \times 1 \times e=1.\end{align*}
\begin{align*} &\lim_{\epsilon \downarrow 0} {\textrm{e}}^{\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}-1}\biggl\lfloor\log\biggl(\dfrac{1}{\epsilon}\biggr)\biggr\rfloor^{\tfrac{1}{2\lfloor\log\!({1}/{\epsilon})\rfloor}}\epsilon^{-\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}}\notag \\ &\quad \leq \lim_{\epsilon \downarrow 0} {\textrm{e}}^{\tfrac{1}{\log\!({1}/{\epsilon})-1}-1} \lim_{\epsilon \downarrow 0} \log\biggl(\dfrac{1}{\epsilon}\biggr)^{\tfrac{1}{2\log\!({1}/{\epsilon})-2}}\lim_{\epsilon \downarrow 0} \epsilon^{-\tfrac{1}{\log\!({1}/{\epsilon})}} = \dfrac{1}{e} \times 1 \times e=1.\end{align*}
By definition of limit, there exists
![]() $\epsilon^{\prime}_0>0$
such that for all
$\epsilon^{\prime}_0>0$
such that for all
![]() $\epsilon<\epsilon^{\prime}_0$
we have
$\epsilon<\epsilon^{\prime}_0$
we have
 \begin{equation*} {\textrm{e}}^{\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}-1}\biggl\lfloor\log\biggl(\dfrac{1}{\epsilon}\biggr)\biggr\rfloor^{\tfrac{1}{2\lfloor\log\!({1}/{\epsilon})\rfloor}}\epsilon^{-\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}} \leq 2.\end{equation*}
\begin{equation*} {\textrm{e}}^{\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}-1}\biggl\lfloor\log\biggl(\dfrac{1}{\epsilon}\biggr)\biggr\rfloor^{\tfrac{1}{2\lfloor\log\!({1}/{\epsilon})\rfloor}}\epsilon^{-\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}} \leq 2.\end{equation*}
The proof that the term (2.10) is
![]() $\textrm{O}(\epsilon\log\!({1}/{\epsilon}))$
follows similarly by linearity of dot product, Hölder’s inequality with
$\textrm{O}(\epsilon\log\!({1}/{\epsilon}))$
follows similarly by linearity of dot product, Hölder’s inequality with
![]() $r=\lfloor\log\!({1}/{\epsilon})\rfloor$
and (2.11). We omit the details for brevity.
$r=\lfloor\log\!({1}/{\epsilon})\rfloor$
and (2.11). We omit the details for brevity.
We end this section with the proof of Claim 2.2.
Proof of Claim 2.2.In this proof we use ideas and notation from [Reference Eryilmaz and Srikant2, equation (56)]. For each
![]() $\ell\in P$
, let
$\ell\in P$
, let
![]() $\mathcal{L}_+^{(\ell)}\stackrel{\triangle}{=} \bigl\{i\in[n]\colon c_i^{(\ell)}>0 \bigr\}$
and define
$\mathcal{L}_+^{(\ell)}\stackrel{\triangle}{=} \bigl\{i\in[n]\colon c_i^{(\ell)}>0 \bigr\}$
and define
Then
where (a) follows using the definition of projection on the subspace to substitute
then the key property (2.2), and that
Then (b) holds by Hölder’s inequality with
![]() $p,r>1$
integers such that
$p,r>1$
integers such that
![]() ${1}/{r}+{1}/{p}=1$
.
${1}/{r}+{1}/{p}=1$
.
Now we bound each of the terms. For the first term we use Proposition 2.1, and we obtain
where (a) holds by Stirling’s approximation for the factorial. For the second term we obtain
 \begin{equation*}0 \leq \mathbb{E}\bigl[{\bigl\|\widetilde{\overline{{\boldsymbol{{u}}}}}^{(\ell)}\bigr\|^p}\bigr]\stackrel{(a)}{\leq} \sum_{\ell\in P}\sum_{i\in \mathcal{L}_+^{(\ell)}} \dfrac{\tilde{c}^{(\ell)}_i}{\tilde{c}^{(\ell)}_i} \mathbb{E}\bigl[{\widetilde{u}_i^p}\bigr]\stackrel{(b)}{\leq} \dfrac{S_{\max}^{p-1}}{\widetilde{c}_{\min}} \sum_{\ell\in P} \mathbb{E}\bigl[{\bigl\langle\widetilde{{\boldsymbol{{c}}}}^{(\ell)},\,\widetilde{\overline{{\boldsymbol{{u}}}}}^{(\ell)}\bigr\rangle}\bigr]\stackrel{(c)}{\leq} \beta_7 |P| \frac{S_{\max}^{p-1}}{\tilde{c}_{\min}} \epsilon,\end{equation*}
\begin{equation*}0 \leq \mathbb{E}\bigl[{\bigl\|\widetilde{\overline{{\boldsymbol{{u}}}}}^{(\ell)}\bigr\|^p}\bigr]\stackrel{(a)}{\leq} \sum_{\ell\in P}\sum_{i\in \mathcal{L}_+^{(\ell)}} \dfrac{\tilde{c}^{(\ell)}_i}{\tilde{c}^{(\ell)}_i} \mathbb{E}\bigl[{\widetilde{u}_i^p}\bigr]\stackrel{(b)}{\leq} \dfrac{S_{\max}^{p-1}}{\widetilde{c}_{\min}} \sum_{\ell\in P} \mathbb{E}\bigl[{\bigl\langle\widetilde{{\boldsymbol{{c}}}}^{(\ell)},\,\widetilde{\overline{{\boldsymbol{{u}}}}}^{(\ell)}\bigr\rangle}\bigr]\stackrel{(c)}{\leq} \beta_7 |P| \frac{S_{\max}^{p-1}}{\tilde{c}_{\min}} \epsilon,\end{equation*}
where (a) follows as all the terms in the summation are non-negative, (b) holds by defining
![]() $\widetilde{c}_{\min}=\min_{\ell\in P, i\in[n]}\bigl\{\tilde{c}^{(\ell)}_i\bigr\}$
and by definition of dot product, and (c) follows from [Reference Hurtado-Lange and Maguluri4, equation (43)] for a finite constant
$\widetilde{c}_{\min}=\min_{\ell\in P, i\in[n]}\bigl\{\tilde{c}^{(\ell)}_i\bigr\}$
and by definition of dot product, and (c) follows from [Reference Hurtado-Lange and Maguluri4, equation (43)] for a finite constant
![]() $\beta_7$
, using a similar argument to the properties used to obtain (2.8). Now pick
$\beta_7$
, using a similar argument to the properties used to obtain (2.8). Now pick
![]() $r \stackrel{\triangle}{=} \lfloor\log\!({1}/{\epsilon})\rfloor$
to get
$r \stackrel{\triangle}{=} \lfloor\log\!({1}/{\epsilon})\rfloor$
to get
 \begin{align*} 0 &\leq \biggl|\dfrac{\mathcal{T}_4}{2} \biggr| \notag \\ & \leq \beta_5\beta_7^{1/p}\dfrac{S_{\max}^{1-{1}/{p}}}{\widetilde{c}_{\min}^{{1}/{p}}}|P|^{{1}/{p}} {\textrm{e}}^{{1}/{r}-1} r^{1+{1}/{2r}} \epsilon^{{1}/{p}} \\ &= \beta_5\beta_7^{1/p} S_{\max}^{\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}}\biggl(\dfrac{|P|}{\widetilde{c}_{\min}}\biggr)^{1-\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}} {\textrm{e}}^{\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}-1}\biggl\lfloor\log\biggl(\dfrac{1}{\epsilon}\biggr)\biggr\rfloor^{1+\tfrac{1}{2\lfloor\log\!({1}/{\epsilon})\rfloor}} \epsilon^{-\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}}\epsilon \notag \\ &\overset{(a)}{\leq} 2\beta_5 \max { \beta_7, 1 }\, \dfrac{|P|}{\widetilde{c}_{\min}}\epsilon \log\biggl(\dfrac{1}{\epsilon}\biggr) \quad \text{{for all} $\epsilon<\epsilon^{\prime\prime}_0$,}\end{align*}
\begin{align*} 0 &\leq \biggl|\dfrac{\mathcal{T}_4}{2} \biggr| \notag \\ & \leq \beta_5\beta_7^{1/p}\dfrac{S_{\max}^{1-{1}/{p}}}{\widetilde{c}_{\min}^{{1}/{p}}}|P|^{{1}/{p}} {\textrm{e}}^{{1}/{r}-1} r^{1+{1}/{2r}} \epsilon^{{1}/{p}} \\ &= \beta_5\beta_7^{1/p} S_{\max}^{\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}}\biggl(\dfrac{|P|}{\widetilde{c}_{\min}}\biggr)^{1-\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}} {\textrm{e}}^{\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}-1}\biggl\lfloor\log\biggl(\dfrac{1}{\epsilon}\biggr)\biggr\rfloor^{1+\tfrac{1}{2\lfloor\log\!({1}/{\epsilon})\rfloor}} \epsilon^{-\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}}\epsilon \notag \\ &\overset{(a)}{\leq} 2\beta_5 \max { \beta_7, 1 }\, \dfrac{|P|}{\widetilde{c}_{\min}}\epsilon \log\biggl(\dfrac{1}{\epsilon}\biggr) \quad \text{{for all} $\epsilon<\epsilon^{\prime\prime}_0$,}\end{align*}
where (a) follows as
 \begin{align*} \lim_{\epsilon \downarrow 0} &S_{\max}^{\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}}\biggl(\dfrac{|P|}{e\widetilde{c}_{\min}}\biggr)^{1-\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}} \biggl\lfloor\log\biggl(\dfrac{1}{\epsilon}\biggr)\biggr\rfloor^{\tfrac{1}{2\lfloor\log\!({1}/{\epsilon})\rfloor}}\epsilon^{-\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}} \notag \\ & \leq1 \times \dfrac{|P|}{e\widetilde{c}_{\min}} \times 1 \times e=\dfrac{|P|}{\widetilde{c}_{\min}}.\end{align*}
\begin{align*} \lim_{\epsilon \downarrow 0} &S_{\max}^{\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}}\biggl(\dfrac{|P|}{e\widetilde{c}_{\min}}\biggr)^{1-\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}} \biggl\lfloor\log\biggl(\dfrac{1}{\epsilon}\biggr)\biggr\rfloor^{\tfrac{1}{2\lfloor\log\!({1}/{\epsilon})\rfloor}}\epsilon^{-\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}} \notag \\ & \leq1 \times \dfrac{|P|}{e\widetilde{c}_{\min}} \times 1 \times e=\dfrac{|P|}{\widetilde{c}_{\min}}.\end{align*}
Thus there exists
![]() $\epsilon^{\prime\prime}_0>0$
such that for all
$\epsilon^{\prime\prime}_0>0$
such that for all
![]() $\epsilon<\epsilon^{\prime\prime}_0$
we have
$\epsilon<\epsilon^{\prime\prime}_0$
we have
 \begin{equation*} S_{\max}^{\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}}\biggl(\dfrac{|P|}{e\widetilde{c}_{\min}}\biggr)^{1-\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}} \biggl\lfloor\log\biggl(\dfrac{1}{\epsilon}\biggr)\biggr\rfloor^{\tfrac{1}{2\lfloor\log\!({1}/{\epsilon})\rfloor}} \epsilon^{-\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}}\leq \dfrac{2|P|}{\widetilde{c}_{\min}}. \end{equation*}
\begin{equation*} S_{\max}^{\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}}\biggl(\dfrac{|P|}{e\widetilde{c}_{\min}}\biggr)^{1-\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}} \biggl\lfloor\log\biggl(\dfrac{1}{\epsilon}\biggr)\biggr\rfloor^{\tfrac{1}{2\lfloor\log\!({1}/{\epsilon})\rfloor}} \epsilon^{-\tfrac{1}{\lfloor\log\!({1}/{\epsilon})\rfloor}}\leq \dfrac{2|P|}{\widetilde{c}_{\min}}. \end{equation*}
The key idea in obtaining a logarithmic error bound is in picking the right exponent r in Hölder’s inequality while bounding terms
![]() $\mathcal{T}_1$
and
$\mathcal{T}_1$
and
![]() $\mathcal{T}_4$
. We do this by minimizing the upper bound over r (for a fixed
$\mathcal{T}_4$
. We do this by minimizing the upper bound over r (for a fixed
![]() $\epsilon$
), which gives
$\epsilon$
), which gives
![]() $r = \lfloor\log\!({1}/{\epsilon} )\rfloor$
. The idea of optimizing over the exponent in Hölder’s inequality is motivated by the paper [Reference Chen, Maguluri, Shakkottai and Shanmugam1].
$r = \lfloor\log\!({1}/{\epsilon} )\rfloor$
. The idea of optimizing over the exponent in Hölder’s inequality is motivated by the paper [Reference Chen, Maguluri, Shakkottai and Shanmugam1].
3. Logarithmic error bounds in the load balancing system
While the generalized switch models many different SPNs with control on the service process, there are many systems where the control is on the arrivals, such as the load balancing system. In this section we show that a similar methodology to the proof of Theorem 2.1 can be used in load balancing systems. Specifically, we study a load balancing system operating under ‘join the shortest queue’ (JSQ) as an illustrative example. Similar results can be obtained for other routeing algorithms such as power-of-d choices. We first define the model.
3.1. Load balancing model
Consider an SPN with n queues, each of them with a separate server. Arrivals occur in a single stream, and a dispatcher routes them according to JSQ (i.e. to the server with the smallest number of jobs in line). After routeing, jobs cannot commute lines. We model the system in discrete time, and we track the number of jobs in each queue. Then the service policy is irrelevant. In each time slot, all the arrivals are routed to the same queue.
Let
![]() $\{a(k)\colon k\in\mathbb{Z}_+\}$
be the arrival process to the system, which is a sequence of i.i.d. random variables, and let
$\{a(k)\colon k\in\mathbb{Z}_+\}$
be the arrival process to the system, which is a sequence of i.i.d. random variables, and let
![]() ${\boldsymbol{{a}}}(k)$
be the vector of arrivals to the queues after routeing at time k. By definition of JSQ, we have
${\boldsymbol{{a}}}(k)$
be the vector of arrivals to the queues after routeing at time k. By definition of JSQ, we have
If there are multiple minimizers, any can be chosen at random. Note that
![]() $a(k)=\sum_{i=1}^n a_i(k)$
by definition. The potential service is a sequence of i.i.d. random vectors, which we denote by
$a(k)=\sum_{i=1}^n a_i(k)$
by definition. The potential service is a sequence of i.i.d. random vectors, which we denote by
![]() $\{{\boldsymbol{{s}}}(k)\colon k\in\mathbb{Z}_+\}$
, and it is independent of the arrival and queue length processes. We assume there exist finite constants
$\{{\boldsymbol{{s}}}(k)\colon k\in\mathbb{Z}_+\}$
, and it is independent of the arrival and queue length processes. We assume there exist finite constants
![]() $A_{\max}$
and
$A_{\max}$
and
![]() $S_{\max}$
such that
$S_{\max}$
such that
![]() $a(1)\leq A_{\max}$
and
$a(1)\leq A_{\max}$
and
![]() $s_i(1)\leq S_{\max}$
for all
$s_i(1)\leq S_{\max}$
for all
![]() $i\in[n]$
with probability 1. We use
$i\in[n]$
with probability 1. We use
![]() ${\boldsymbol{{u}}}(k)$
to denote the unused service vector in time slot k, which is defined similarly to the generalized switch model. The dynamics of the queues occur according to (2.1), and (2.2) is satisfied for all
${\boldsymbol{{u}}}(k)$
to denote the unused service vector in time slot k, which is defined similarly to the generalized switch model. The dynamics of the queues occur according to (2.1), and (2.2) is satisfied for all
![]() $i\in[n]$
.
$i\in[n]$
.
Let
![]() $\boldsymbol{\mu}\stackrel{\triangle}{=} \mathbb{E}[{{\boldsymbol{{s}}}(1)}]$
,
$\boldsymbol{\mu}\stackrel{\triangle}{=} \mathbb{E}[{{\boldsymbol{{s}}}(1)}]$
,
![]() $\sigma_{s_i}^2\stackrel{\triangle}{=} \text{Var}[{s_i(1)}]$
for each
$\sigma_{s_i}^2\stackrel{\triangle}{=} \text{Var}[{s_i(1)}]$
for each
![]() $i\in[n]$
, and let
$i\in[n]$
, and let
![]() $\mu_\Sigma \stackrel{\triangle}{=} \sum_{i=1}^n \mu_i$
. We assume
$\mu_\Sigma \stackrel{\triangle}{=} \sum_{i=1}^n \mu_i$
. We assume
![]() $\mu_i>0$
for all
$\mu_i>0$
for all
![]() $i\in[n]$
because otherwise the jobs routed to the server with zero service rate will never be processed. It is well known that the capacity region of the load balancing model is
$i\in[n]$
because otherwise the jobs routed to the server with zero service rate will never be processed. It is well known that the capacity region of the load balancing model is
![]() $\mathcal{C}=\{\lambda\in\mathbb{R}_+\colon \lambda\leq \mu_\Sigma \}$
, and that JSQ is a throughput optimal routeing algorithm [Reference Eryilmaz and Srikant2, Lemma 2]. Then, to model heavy traffic, we parametrize the arrival process by
$\mathcal{C}=\{\lambda\in\mathbb{R}_+\colon \lambda\leq \mu_\Sigma \}$
, and that JSQ is a throughput optimal routeing algorithm [Reference Eryilmaz and Srikant2, Lemma 2]. Then, to model heavy traffic, we parametrize the arrival process by
![]() $\epsilon\in(0,\mu_\Sigma )$
, letting
$\epsilon\in(0,\mu_\Sigma )$
, letting
![]() $\lambda^{(\epsilon)}\stackrel{\triangle}{=} \mathbb{E}\bigl[{a^{(\epsilon)}(1)}\bigr]=\mu_\Sigma-\epsilon$
and
$\lambda^{(\epsilon)}\stackrel{\triangle}{=} \mathbb{E}\bigl[{a^{(\epsilon)}(1)}\bigr]=\mu_\Sigma-\epsilon$
and
![]() $\bigl(\sigma_a^{(\epsilon)}\bigr)^2\stackrel{\triangle}{=} \text{Var}\bigl[{a^{(\epsilon)}(1)}\bigr]$
.
$\bigl(\sigma_a^{(\epsilon)}\bigr)^2\stackrel{\triangle}{=} \text{Var}\bigl[{a^{(\epsilon)}(1)}\bigr]$
.
It is also known that SSC occurs in the line where all the queues are equally long. Specifically, denoting
 \begin{equation*}\overline{{\boldsymbol{{q}}}}^{(\epsilon)}_{\parallel} \stackrel{\triangle}{=} \Biggl(\dfrac{1}{n}\sum_{i=1}^n \overline{q}^{(\epsilon)}_i\Biggr)\textbf{1}\quad\text{and}\quad \overline{{\boldsymbol{{q}}}}^{(\epsilon)}_\perp\stackrel{\triangle}{=} \overline{{\boldsymbol{{q}}}}^{(\epsilon)}-\overline{{\boldsymbol{{q}}}}^{(\epsilon)}_{\parallel},\end{equation*}
\begin{equation*}\overline{{\boldsymbol{{q}}}}^{(\epsilon)}_{\parallel} \stackrel{\triangle}{=} \Biggl(\dfrac{1}{n}\sum_{i=1}^n \overline{q}^{(\epsilon)}_i\Biggr)\textbf{1}\quad\text{and}\quad \overline{{\boldsymbol{{q}}}}^{(\epsilon)}_\perp\stackrel{\triangle}{=} \overline{{\boldsymbol{{q}}}}^{(\epsilon)}-\overline{{\boldsymbol{{q}}}}^{(\epsilon)}_{\parallel},\end{equation*}
we have that
![]() $\mathbb{E}\bigl[{\|\overline{{\boldsymbol{{q}}}}^{(\epsilon)}_\perp \|^r}\bigr]$
is bounded for all
$\mathbb{E}\bigl[{\|\overline{{\boldsymbol{{q}}}}^{(\epsilon)}_\perp \|^r}\bigr]$
is bounded for all
![]() $r\geq 1$
, as proved in [Reference Eryilmaz and Srikant2, Proposition 1]. Recall that we add a bar on top of the variables to denote steady state.
$r\geq 1$
, as proved in [Reference Eryilmaz and Srikant2, Proposition 1]. Recall that we add a bar on top of the variables to denote steady state.
3.2. Logarithmic error bounds
The goal of this section is to prove the following result.
Theorem 3.1. Consider a set of load balancing systems operating under JSQ, parametrized by the heavy traffic parameter
![]() $\epsilon\in(0,\mu_\Sigma)$
, as described above. Then there exists a constant
$\epsilon\in(0,\mu_\Sigma)$
, as described above. Then there exists a constant
![]() $\beta_{\textrm{JSQ}}$
and
$\beta_{\textrm{JSQ}}$
and
![]() $\epsilon_0\in(0,\mu_\Sigma)$
such that for all
$\epsilon_0\in(0,\mu_\Sigma)$
such that for all
![]() $\epsilon<\epsilon_0$
$\epsilon<\epsilon_0$
 \begin{equation*} \Biggl|\mathbb{E}\Biggl[{\sum_{i=1}^n \overline{q}^{(\epsilon)}_i }\Biggr] -\dfrac{1}{2\epsilon}\Biggl( \bigl(\sigma_a^{(\epsilon)}\bigr)^2 + \sum_{i=1}^n\sigma_{s_i}^2 \Biggr) \Biggr|\leq \beta_{\textrm{JSQ}}\log\biggl(\dfrac{1}{\epsilon} \biggr). \end{equation*}
\begin{equation*} \Biggl|\mathbb{E}\Biggl[{\sum_{i=1}^n \overline{q}^{(\epsilon)}_i }\Biggr] -\dfrac{1}{2\epsilon}\Biggl( \bigl(\sigma_a^{(\epsilon)}\bigr)^2 + \sum_{i=1}^n\sigma_{s_i}^2 \Biggr) \Biggr|\leq \beta_{\textrm{JSQ}}\log\biggl(\dfrac{1}{\epsilon} \biggr). \end{equation*}
Similarly to the generalized switch, an essential step in the proof of Theorem 3.1 is to find explicit upper bounds for the moments of
![]() $\|\overline{{\boldsymbol{{q}}}}^{(\epsilon)}_\perp \|$
. We present them in the next proposition.
$\|\overline{{\boldsymbol{{q}}}}^{(\epsilon)}_\perp \|$
. We present them in the next proposition.
Proposition 3.1. For the load balancing system operating under JSQ, parametrized by
![]() $\epsilon\in(0,\mu_\Sigma)$
as described in Section 3.1, let
$\epsilon\in(0,\mu_\Sigma)$
as described in Section 3.1, let
Then, for any choice of
![]() $\epsilon\in(0,(\mu_{\min}-\delta)n)$
, and all
$\epsilon\in(0,(\mu_{\min}-\delta)n)$
, and all
![]() $r=1,2,\ldots,$
we have
$r=1,2,\ldots,$
we have
The proof of Proposition 3.1 is very similar to the proof of [Reference Eryilmaz and Srikant2, Proposition 1], so we omit it.
The proof of Theorem 3.1 follows from the computation of the upper bound in [Reference Eryilmaz and Srikant2], similarly to the proof of Theorem 2.1. We include a sketch proof for completeness.
Proof of Theorem 3.1.In this proof we omit the dependence on
![]() $\epsilon$
of the variables, for ease of exposition. We set the drift of
$\epsilon$
of the variables, for ease of exposition. We set the drift of
![]() $V_\parallel({\boldsymbol{{q}}})\stackrel{\triangle}{=} \| {\boldsymbol{{q}}}_\parallel\|^2$
to zero. First observe that in the computation of (2.5) we only use properties of projection and norm, and we did not use properties of the generalized switch itself. Therefore the same steps can be followed for the load balancing system. We obtain
$V_\parallel({\boldsymbol{{q}}})\stackrel{\triangle}{=} \| {\boldsymbol{{q}}}_\parallel\|^2$
to zero. First observe that in the computation of (2.5) we only use properties of projection and norm, and we did not use properties of the generalized switch itself. Therefore the same steps can be followed for the load balancing system. We obtain
 \begin{align*} 0 &= \mathbb{E}\bigl[{\|\overline{{\boldsymbol{{q}}}}_\parallel^+\|^2 - \|\overline{{\boldsymbol{{q}}}}_\parallel\|^2 }\bigr] \\ &= \underbrace{\mathbb{E}\bigl[{\|\overline{{\boldsymbol{{a}}}}_\parallel - \overline{{\boldsymbol{{s}}}}_\parallel\|^2}\bigr]}_{\mathcal{T}_2} +\underbrace{2\mathbb{E}\bigl[{\big\langle \overline{{\boldsymbol{{q}}}}_\parallel,\, \overline{{\boldsymbol{{a}}}}_\parallel-\overline{{\boldsymbol{{s}}}}_\parallel \big\rangle} \bigr]}_{-\mathcal{T}_1}-\underbrace{\mathbb{E}\bigl[{\|\overline{{\boldsymbol{{u}}}}_\parallel \|^2}\bigr]}_{\mathcal{T}_3} + \underbrace{2\mathbb{E}\bigl[{\big\langle\overline{{\boldsymbol{{q}}}}_\parallel^+,\, \overline{{\boldsymbol{{u}}}}_\parallel\big\rangle} \bigr]}_{\mathcal{T}_4}. \end{align*}
\begin{align*} 0 &= \mathbb{E}\bigl[{\|\overline{{\boldsymbol{{q}}}}_\parallel^+\|^2 - \|\overline{{\boldsymbol{{q}}}}_\parallel\|^2 }\bigr] \\ &= \underbrace{\mathbb{E}\bigl[{\|\overline{{\boldsymbol{{a}}}}_\parallel - \overline{{\boldsymbol{{s}}}}_\parallel\|^2}\bigr]}_{\mathcal{T}_2} +\underbrace{2\mathbb{E}\bigl[{\big\langle \overline{{\boldsymbol{{q}}}}_\parallel,\, \overline{{\boldsymbol{{a}}}}_\parallel-\overline{{\boldsymbol{{s}}}}_\parallel \big\rangle} \bigr]}_{-\mathcal{T}_1}-\underbrace{\mathbb{E}\bigl[{\|\overline{{\boldsymbol{{u}}}}_\parallel \|^2}\bigr]}_{\mathcal{T}_3} + \underbrace{2\mathbb{E}\bigl[{\big\langle\overline{{\boldsymbol{{q}}}}_\parallel^+,\, \overline{{\boldsymbol{{u}}}}_\parallel\big\rangle} \bigr]}_{\mathcal{T}_4}. \end{align*}
We analyze term by term. For
![]() $\mathcal{T}_1$
we obtain
$\mathcal{T}_1$
we obtain
 \begin{equation} \dfrac{\mathcal{T}_1}{2} = \mathbb{E}\bigl[{\big\langle \overline{{\boldsymbol{{q}}}}_\parallel,\overline{{\boldsymbol{{s}}}}_\parallel-\overline{{\boldsymbol{{a}}}}_\parallel\big\rangle}\bigr] \stackrel{(a)}{=} \dfrac{1}{n}\mathbb{E}\Biggl[{\sum_{i=1}^n \overline{q}_i}\Biggr] \mathbb{E}\Biggl[{\sum_{i=1}^n \overline{s}_i-\overline{a}}\Biggr] \stackrel{(b)}{=} \dfrac{\epsilon}{n}\mathbb{E}\Biggl[{\sum_{i=1}^n \overline{q}_i}\Biggr], \end{equation}
\begin{equation} \dfrac{\mathcal{T}_1}{2} = \mathbb{E}\bigl[{\big\langle \overline{{\boldsymbol{{q}}}}_\parallel,\overline{{\boldsymbol{{s}}}}_\parallel-\overline{{\boldsymbol{{a}}}}_\parallel\big\rangle}\bigr] \stackrel{(a)}{=} \dfrac{1}{n}\mathbb{E}\Biggl[{\sum_{i=1}^n \overline{q}_i}\Biggr] \mathbb{E}\Biggl[{\sum_{i=1}^n \overline{s}_i-\overline{a}}\Biggr] \stackrel{(b)}{=} \dfrac{\epsilon}{n}\mathbb{E}\Biggl[{\sum_{i=1}^n \overline{q}_i}\Biggr], \end{equation}
where (a) follows by definition of the projection, because the total arrivals and the potential service are independent of the queue lengths, and rearranging terms, and (b) holds by definition of
![]() $\epsilon$
. For
$\epsilon$
. For
![]() $\mathcal{T}_2$
we obtain
$\mathcal{T}_2$
we obtain
 \begin{align} \mathcal{T}_2 = \mathbb{E}\bigl[{\| \overline{{\boldsymbol{{a}}}}_\parallel-\overline{{\boldsymbol{{s}}}}_\parallel\|^2}\bigr] &\stackrel{(a)}{=} \dfrac{1}{n}\Biggl(\mathbb{E}\bigl[{\overline{a}^2}\bigr] + \mathbb{E}\Biggl[{\Biggl(\sum_{i=1}^n \overline{s}_i \Biggr)^2}\Biggr] - 2\mathbb{E}[{\overline{a}}]\mathbb{E}\Biggl[{\sum_{i=1}^n \overline{s}_i}\Biggr] \Biggr) \notag \\ &\stackrel{(b)}{=} \dfrac{1}{n}\Biggl( \bigl(\sigma_a^{(\epsilon)}\bigr)^2 + \sum_{i=1}^n \sigma_{s_i}^2+ \epsilon^2 \Biggr), \end{align}
\begin{align} \mathcal{T}_2 = \mathbb{E}\bigl[{\| \overline{{\boldsymbol{{a}}}}_\parallel-\overline{{\boldsymbol{{s}}}}_\parallel\|^2}\bigr] &\stackrel{(a)}{=} \dfrac{1}{n}\Biggl(\mathbb{E}\bigl[{\overline{a}^2}\bigr] + \mathbb{E}\Biggl[{\Biggl(\sum_{i=1}^n \overline{s}_i \Biggr)^2}\Biggr] - 2\mathbb{E}[{\overline{a}}]\mathbb{E}\Biggl[{\sum_{i=1}^n \overline{s}_i}\Biggr] \Biggr) \notag \\ &\stackrel{(b)}{=} \dfrac{1}{n}\Biggl( \bigl(\sigma_a^{(\epsilon)}\bigr)^2 + \sum_{i=1}^n \sigma_{s_i}^2+ \epsilon^2 \Biggr), \end{align}
where (a) holds by definition of the projection and Euclidean norm, and (b) holds by the definition of variance and of
![]() $\epsilon$
. For
$\epsilon$
. For
![]() $\mathcal{T}_3$
we obtain
$\mathcal{T}_3$
we obtain
 \begin{equation} |\mathcal{T}_3| = \mathbb{E}\bigl[{\|\overline{{\boldsymbol{{u}}}}_\parallel \|^2}\bigr] = \dfrac{1}{n}\mathbb{E}\Biggl[{\Biggl(\sum_{i=1}^n \overline{u}_i\Biggr)^2 }\Biggr] \stackrel{(a)}{\leq} S_{\max} \mathbb{E}\Biggl[{\sum_{i=1}^n \overline{u}_i}\Biggr] \stackrel{(b)}{=} S_{\max} \epsilon, \end{equation}
\begin{equation} |\mathcal{T}_3| = \mathbb{E}\bigl[{\|\overline{{\boldsymbol{{u}}}}_\parallel \|^2}\bigr] = \dfrac{1}{n}\mathbb{E}\Biggl[{\Biggl(\sum_{i=1}^n \overline{u}_i\Biggr)^2 }\Biggr] \stackrel{(a)}{\leq} S_{\max} \mathbb{E}\Biggl[{\sum_{i=1}^n \overline{u}_i}\Biggr] \stackrel{(b)}{=} S_{\max} \epsilon, \end{equation}
where (a) holds because, by definition of unused service, we have
![]() $\overline{u}_i\leq \overline{s}_i\leq S_{\max}$
with probability 1 for all
$\overline{u}_i\leq \overline{s}_i\leq S_{\max}$
with probability 1 for all
![]() $i\in[n]$
, and (b) holds because
$i\in[n]$
, and (b) holds because
![]() $\mathbb{E}\bigl[{\sum_{i=1}^n\overline{u}_i}\bigr]=\epsilon$
, which can be easily proved by setting the drift of the function
$\mathbb{E}\bigl[{\sum_{i=1}^n\overline{u}_i}\bigr]=\epsilon$
, which can be easily proved by setting the drift of the function
![]() $V_\ell({\boldsymbol{{q}}})=\sum_{i=1}^n q_i$
to zero. A proof of this fact can be found in [Reference Hurtado-Lange and Maguluri5, Lemma 5].
$V_\ell({\boldsymbol{{q}}})=\sum_{i=1}^n q_i$
to zero. A proof of this fact can be found in [Reference Hurtado-Lange and Maguluri5, Lemma 5].
For the term
![]() $\mathcal{T}_4$
we follow a similar approach to the proof of Theorem 2.1. We obtain
$\mathcal{T}_4$
we follow a similar approach to the proof of Theorem 2.1. We obtain
 \begin{align} \biggl|\dfrac{\mathcal{T}_4}{2}\biggr| = \mathbb{E}\bigl[{\big\langle\overline{{\boldsymbol{{q}}}}_\parallel^+, \overline{{\boldsymbol{{u}}}}_\parallel\big\rangle}\bigr] &\stackrel{(a)}{=} -\mathbb{E}\bigl[{\big\langle \overline{{\boldsymbol{{q}}}}_\perp^+,\overline{{\boldsymbol{{u}}}}\big\rangle}\bigr] \notag \\ & \stackrel{(b)}{\leq} \mathbb{E}\bigl[{\|\overline{{\boldsymbol{{q}}}}_\perp^+\|^r}\bigr]^{{1}/{r}} \mathbb{E}\bigl[{\|\overline{{\boldsymbol{{u}}}}\|^p} \bigr]^{{1}/{p}} \notag \\ & \stackrel{(c)}{\leq} \bigl(R_r^{(\textrm{JSQ})}\bigr)^{{1}/{r}} S_{\max}^{{1}/{r}}\epsilon^{1-{1}/{r}}, \end{align}
\begin{align} \biggl|\dfrac{\mathcal{T}_4}{2}\biggr| = \mathbb{E}\bigl[{\big\langle\overline{{\boldsymbol{{q}}}}_\parallel^+, \overline{{\boldsymbol{{u}}}}_\parallel\big\rangle}\bigr] &\stackrel{(a)}{=} -\mathbb{E}\bigl[{\big\langle \overline{{\boldsymbol{{q}}}}_\perp^+,\overline{{\boldsymbol{{u}}}}\big\rangle}\bigr] \notag \\ & \stackrel{(b)}{\leq} \mathbb{E}\bigl[{\|\overline{{\boldsymbol{{q}}}}_\perp^+\|^r}\bigr]^{{1}/{r}} \mathbb{E}\bigl[{\|\overline{{\boldsymbol{{u}}}}\|^p} \bigr]^{{1}/{p}} \notag \\ & \stackrel{(c)}{\leq} \bigl(R_r^{(\textrm{JSQ})}\bigr)^{{1}/{r}} S_{\max}^{{1}/{r}}\epsilon^{1-{1}/{r}}, \end{align}
where (a) holds by definition of the projection, and reorganizing terms, (b) holds by Hölder’s inequality with
![]() $p,r>1$
integers such that
$p,r>1$
integers such that
![]() ${1}/{r}+{1}/{p}=1$
, and (c) holds by Proposition 3.1, because
${1}/{r}+{1}/{p}=1$
, and (c) holds by Proposition 3.1, because
![]() $\overline{{\boldsymbol{{u}}}}\leq \overline{{\boldsymbol{{s}}}} \leq S_{\max}\textbf{1}$
component-wise with probability 1, and because
$\overline{{\boldsymbol{{u}}}}\leq \overline{{\boldsymbol{{s}}}} \leq S_{\max}\textbf{1}$
component-wise with probability 1, and because
![]() $\mathbb{E}\bigl[{\sum_{i=1}^n \overline{u}_i}\bigr]=\epsilon$
.
$\mathbb{E}\bigl[{\sum_{i=1}^n \overline{u}_i}\bigr]=\epsilon$
.
Then, putting (3.1), (3.2), (3.3), and (3.4) together, and letting
![]() $r=\lceil\log\!({1}/{\epsilon}) \rceil$
, we obtain the result.
$r=\lceil\log\!({1}/{\epsilon}) \rceil$
, we obtain the result.
4. Conclusions
In this paper we study the performance of generalized switch operating under MaxWeight both when the CRP condition is satisfied and when it is not. We show that MaxWeight is within
![]() $\textrm{O}(\!\log\!({1}/{\epsilon}))$
from its heavy traffic performance. Additionally, when the CRP condition is satisfied, we show that it is within
$\textrm{O}(\!\log\!({1}/{\epsilon}))$
from its heavy traffic performance. Additionally, when the CRP condition is satisfied, we show that it is within
![]() $\textrm{O}(\!\log\!({1}/{\epsilon}))$
from the optimal policy.
$\textrm{O}(\!\log\!({1}/{\epsilon}))$
from the optimal policy.
We also analyze the load balancing system operating under JSQ and prove that the rate of convergence of JSQ to the optimal heavy traffic performance under heavy traffic is
![]() $\textrm{O}(\!\log\!({1}/{\epsilon}))$
. Similar results can be obtained for other routeing algorithms.
$\textrm{O}(\!\log\!({1}/{\epsilon}))$
. Similar results can be obtained for other routeing algorithms.
A possible line of future work is to explore if the
![]() $\textrm{O}(\!\log\!({1}/{\epsilon}))$
error is tight. At this point it is not known if the log error is an artifact of our proof or if there is indeed a log error in the heavy traffic prelimit.
$\textrm{O}(\!\log\!({1}/{\epsilon}))$
error is tight. At this point it is not known if the log error is an artifact of our proof or if there is indeed a log error in the heavy traffic prelimit.
Appendix A. Proof of Corollary 2.1
Proof.In this case we have
![]() $\mathcal{K}=\bigl\{\xi {\boldsymbol{{c}}}^{(\ell)}\colon \xi\geq 0 \bigr\}$
, i.e. the cone
$\mathcal{K}=\bigl\{\xi {\boldsymbol{{c}}}^{(\ell)}\colon \xi\geq 0 \bigr\}$
, i.e. the cone
![]() $\mathcal{K}$
is a half-line. This implies that
$\mathcal{K}$
is a half-line. This implies that
![]() $\mathcal{H}$
is the entire line defined by
$\mathcal{H}$
is the entire line defined by
![]() ${\boldsymbol{{c}}}^{(\ell)}$
. Then in Theorem 2.1 we can take
${\boldsymbol{{c}}}^{(\ell)}$
. Then in Theorem 2.1 we can take
![]() ${\boldsymbol{{w}}}=b^{(\ell)}{\boldsymbol{{c}}}^{(\ell)}$
, and we have
${\boldsymbol{{w}}}=b^{(\ell)}{\boldsymbol{{c}}}^{(\ell)}$
, and we have
![]() $H={\boldsymbol{{c}}}^{(\ell)} \bigl({\boldsymbol{{c}}}^{(\ell)}\bigr)^\top $
because we assumed
$H={\boldsymbol{{c}}}^{(\ell)} \bigl({\boldsymbol{{c}}}^{(\ell)}\bigr)^\top $
because we assumed
![]() $\|{\boldsymbol{{c}}}^{(\ell)}\|=1$
. Then we obtain
$\|{\boldsymbol{{c}}}^{(\ell)}\|=1$
. Then we obtain
where
![]() $\sigma_{B_\ell}^2\stackrel{\triangle}{=} (\Sigma_B)_{\ell,\ell}$
and
$\sigma_{B_\ell}^2\stackrel{\triangle}{=} (\Sigma_B)_{\ell,\ell}$
and
![]() $\beta$
is a constant that does not depend on
$\beta$
is a constant that does not depend on
![]() $\epsilon$
.
$\epsilon$
.
To obtain a ULB, we use [Reference Hurtado-Lange and Maguluri4, Proposition 1]. We obtain that, under any scheduling algorithm (not necessarily MaxWeight), the expected queue length vector in the steady state satisfies
where
![]() $b_{\max}\stackrel{\triangle}{=} \max_{m\in\mathcal{M},\ell\in[L]}\bigl\{b^{(m,\ell)}\bigr\}$
. Then, putting the two results together, we obtain
$b_{\max}\stackrel{\triangle}{=} \max_{m\in\mathcal{M},\ell\in[L]}\bigl\{b^{(m,\ell)}\bigr\}$
. Then, putting the two results together, we obtain
 \begin{align*}\mathbb{E}\bigl[{\bigl\langle\overline{{\boldsymbol{{q}}}}^{(\epsilon)}, {\boldsymbol{{c}}}^{(\ell)}\bigr\rangle}\bigr]& \leq \textrm{ULB} + \biggl(\dfrac{b_{\max}(1-\epsilon)}{2} + \beta \log\biggl(\dfrac{1}{\epsilon} \biggr) \biggr) \\ &\stackrel{(a)}{\leq} \textrm{ULB} + \biggl(\dfrac{b_{\max}}{2}+\beta \biggr)\log\biggl(\dfrac{1}{\epsilon} \biggr),\end{align*}
\begin{align*}\mathbb{E}\bigl[{\bigl\langle\overline{{\boldsymbol{{q}}}}^{(\epsilon)}, {\boldsymbol{{c}}}^{(\ell)}\bigr\rangle}\bigr]& \leq \textrm{ULB} + \biggl(\dfrac{b_{\max}(1-\epsilon)}{2} + \beta \log\biggl(\dfrac{1}{\epsilon} \biggr) \biggr) \\ &\stackrel{(a)}{\leq} \textrm{ULB} + \biggl(\dfrac{b_{\max}}{2}+\beta \biggr)\log\biggl(\dfrac{1}{\epsilon} \biggr),\end{align*}
where (a) holds because
![]() $1-x\leq \log\!({1}/{x})$
for all
$1-x\leq \log\!({1}/{x})$
for all
![]() $x>0$
. Therefore, defining
$x>0$
. Therefore, defining
and using (A.1), we obtain
Appendix B. Proof of Proposition 2.1
Proof of Proposition 2.1.The proof is similar to [Reference Hurtado-Lange and Maguluri4, Proposition 2], so we only present a sketch. The first inequality holds because
![]() $\mathcal{K}\subset \mathcal{H}$
and by definition of
$\mathcal{K}\subset \mathcal{H}$
and by definition of
![]() $\overline{{\boldsymbol{{q}}}}_{\perp\mathcal{K}}$
and
$\overline{{\boldsymbol{{q}}}}_{\perp\mathcal{K}}$
and
![]() $\overline{{\boldsymbol{{q}}}}_{\perp \mathcal{H}}$
. Now we bound the second inequality. From the definition of projection, the triangle inequality and the queue dynamics presented in (2.2), we obtain
$\overline{{\boldsymbol{{q}}}}_{\perp \mathcal{H}}$
. Now we bound the second inequality. From the definition of projection, the triangle inequality and the queue dynamics presented in (2.2), we obtain
with probability 1, and that for all
![]() ${\boldsymbol{{q}}}$
such that
${\boldsymbol{{q}}}$
such that
![]() $\|{\boldsymbol{{q}}}_{\perp\mathcal{K}}\|\geq {(4n\alpha)}/{\delta}$
we have
$\|{\boldsymbol{{q}}}_{\perp\mathcal{K}}\|\geq {(4n\alpha)}/{\delta}$
we have
Using these results in [Reference Maguluri and Srikant7, Lemma 3], we obtain the result.
Funding information
This work was partially supported by the National Science Foundation grants CCF-1850439 and EPCN-2144316. Daniela Hurtado-Lange has partial funding from the Chilean National Agency for Research and Development ANID/DOCTORADO BECAS CHILE/2018-72190413.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.