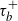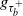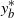1. Introduction
Last exit times have received increasing attention in theoretical and applied probability. For example, [Reference Getoor and Sharpe14] studied the joint distribution of the last exit time of a standard Markov process from a transient set and its location at that time, and [Reference Salminen22] studied the last passage times of linear diffusions and proposed the h-transform method. Recently, this work was extended in [Reference Egami and Kevkhishvili13] to a general setting and an application in credit risk management considered. In line with the recent trend of studies on quantitative risk management, it is natural to study the last exit time for a stochastic process X below level zero, i.e.
\begin{equation} g=\sup\{s \geq 0\colon X_s\leq 0 \},\end{equation}
where X can be interpreted as a firm value process and the distributional study of g can provide valuable information on the duration of financial distress (i.e. the period with negative firm value). We follow the convention that
$\sup\emptyset=0$
. The distribution of g for a spectrally negative Lévy process (SNLP) was first solved in [Reference Chiu and Yin10].
A more general form is given by
$g_{t}=\sup\{0 \leq s \leq t \colon X_s\leq 0 \}$
, which denotes the last time below zero until time t. When X is a Brownian motion, it is known from [Reference Chung11] that
$g_t$
follows the arcsine distribution. Apart from Brownian motions, there are few explicit results on the distribution of
$g_{t}$
for more general processes, and the main challenge is the lack of mathematical tractability in this finite-horizon setting. A notable breakthrough in [Reference Baurdoux2] is to replace the finite horizon t by a random horizon
$e_q$
, independent and exponentially distributed, and consider
$g_{e_q}=\sup\{0 \leq s \leq e_q \colon X_s\leq 0 \}$
. The Laplace transform of
$g_{e_q}$
was solved in [Reference Baurdoux2] for SNLPs. Later, [Reference Cai and Li8, Reference Li, Yin and Zhou20] studied the occupation times until
$g_{e_q}$
for SNLPs. It is worth noting that this technique of horizon randomization is commonly adopted in the finance literature; see the seminal work [Reference Carr9] on the application to option pricing.
The last exit times are not stopping times, meaning that the past history of the process is insufficient to determine whether or not last exit times have been realized. As such, for the purpose of decision making, another line of study is to optimally predict last exit times by stopping times. The optimal prediction of the last zero of Brownian motion with drift was studied in [Reference Du Toit, Peskir and Shiryaev12], while [Reference Glover and Hulley15] generalizes the prediction of last passage times to a transient diffusion. Under the framework of SNLPs, [Reference Baurdoux and Pedraza3] studied the optimal prediction of g, defined in (1.1), in
$L_1$
-distance. It was extended by [Reference Baurdoux and Pedraza5] to the much more challenging
$L_p$
-distance. Also, the prediction of
$g_{e_q}$
was recently considered in [Reference Baurdoux and Pedraza4] in
$L_1$
-distance.
One shortcoming of the last exit time g is that it is an infinite-horizon measure in the sense that its distributional study and applications are based on the assumption that the model for the underlying process X is unchanged and valid forever. This is a rather strong assumption from the model risk perspective. In this sense,
$g_t$
and
$g_{e_q}$
weaken the assumption as the model validation is only required to hold up to a finite or random horizon.
Our motivation for this paper is along the same lines but with the major difference that we intend to reduce the model validation assumption at the state level (instead of the time level as for
$g_t$
and
$g_{e_q}$
). More specifically, we consider the last exit time that X is below zero until it reaches a level
$b>0$
, i.e.
$g_{\tau_b^+}=\sup\{0 \leq s\leq \tau_b^+ \colon X_s\leq 0 \}$
, where
$\tau_b^+=\inf\{ t>0\colon X_t>b\}$
, in which we follow the convention that
$\inf\emptyset=\infty$
. Within the realm of corporate risk management, this extension is a logical progression since a firm’s capital structure and profitability are prone to shift as the firm expands. In this context, the parameter b can be interpreted as a critical threshold of the firm’s value. Once this threshold is surpassed, the company may proceed to hire additional employees, distribute dividends to shareholders, and venture into new business areas, rendering the previous model obsolete.
The contribution of this paper is twofold. In the first part, we derive the joint Laplace transform of
$g_{{\tau}_b^+}$
and
${\tau}_b^+$
for SNLPs. It should be noted that the method employed in [Reference Baurdoux2, Reference Chiu and Yin10] to study g and
$g_{e_q}$
cannot be directly applied to analyze
$g_{{\tau}_b^+}$
. To overcome this challenge, we adopt a hybrid observation scheme approach proposed in [Reference Li, Willmot and Wong19]. The merit of this approach is to unify the cases with bounded or unbounded variation sample paths. Furthermore, by letting
$b\rightarrow \infty$
, we can recover the distribution of g as obtained in [Reference Chiu and Yin10], but with the added benefit of offering an alternative proof that is significantly simpler.
In the second part, we study the optimal prediction problem for
$g_{\tau_b^+}$
in
$L_1$
-distance, that is,
$\inf_{\tau \in \mathcal{T} } \mathbb{E}_x[|g_{\tau_b^+}-\tau|]$
, where
$\mathcal{T}$
is the set of all stopping times of the process X. We find that the optimal stopping time is the first time that the process X hits a fixed level, denoted by
$y_b^*\in [0,b]$
. The optimal stopping boundary
$y_b^*$
is explicitly derived and it is closely related to the value of b and the cumulative distribution function of
$\underline{X}_{\infty}\,:\!=\,\inf_{t\geq 0} X_t$
. At the end, examples of Brownian motion with drift and the Cramér–Lundberg model with exponential jumps are considered to demonstrate the optimal boundary.
Our motivation to examine the optimal prediction problem for
$g_{\tau_b^+}$
also comes from a theoretical point of view. It is seen in [Reference Baurdoux and Pedraza3] that the optimal prediction of g boils down to an optimal stopping problem with an infinite time horizon, and hence the solution is a fixed boundary. However, surprisingly, in [Reference Baurdoux and Pedraza4] it is shown that the optimal prediction of
$g_{e_q}$
is equivalent to a finite-horizon optimal stopping problem, and the optimal solution depends on a non-negative curve which is killed at the moment the mean of the exponential time is reached. Hence, unlike the Canadisation of American-type options (see [Reference Carr9]), optimal prediction problems with exponential time horizon do not necessarily result in infinite-horizon optimal stopping problems. With this in mind, we see that predicting
$g_{\tau_b^+}$
, i.e. the first exit time type of random horizon, effectively maintains the problem’s infinite-horizon setting, resulting in a fixed boundary solution.
The rest of the paper is organized as follows. Section 2 provides some preliminary results concerning SNLPs. Section 3 derives an explicit expression for the joint distribution of
$g_{{\tau}_b^+}$
and
${\tau}_b^+$
. Section 4 formulates the optimal prediction problem and provides the solution, while the proofs are deferred to Section 5.
2. Preliminaries
In this section we provide some preliminaries on spectrally negative Lévy processes, including scale functions and some fluctuation identities. More information on Lévy processes can be found in [Reference Bertoin6, Reference Kyprianou17, Reference Sato23] for interested readers.
Let X be a spectrally negative Lévy process defined on the filtered probability space
$(\Omega,\mathcal{F}, \mathbb{F}, \mathbb{P})$
, where
$\mathbb{F}=\{\mathcal{F}_t,t\geq 0 \}$
is the filtration generated by X which is naturally enlarged (see [Reference Bichteler7, Definition 1.3.38]), and we exclude the case where X has monotone paths. We assume that X is given on the canonical space
$\Omega$
, which consists of all functions
$\omega\colon [0,\infty)\mapsto \mathbb{R}$
that are right-continuous and have left limits, and that
$X_t(\omega)=\omega_t$
. We then introduce the shift operator
$\theta_t$
, acting on the elements of
$\Omega$
, defined by
$X_s\circ \theta_t(\omega)=X_s(\theta_t(\omega))=X_{t+s}(\omega)$
, for any
$s,t\geq 0$
.
Throughout this paper, for all
$x\in \mathbb{R}$
, denote by
$\mathbb{P}_x$
the law of X when started at the point
$x\in \mathbb{R}$
, and the associated expectation by
$\mathbb{E}_x$
. For simplicity, we write
$\mathbb{P}=\mathbb{P}_0$
and
$\mathbb{E}=\mathbb{E}_0$
.
The distribution of X is characterized by its Lévy triplet
$(\mu,\sigma, \Pi)$
, where
$\mu \in \mathbb{R}$
,
$\sigma\geq 0$
, and
$\Pi$
is the Lévy measure concentrated on
$({-}\infty,0)$
with the property
$\int_{({-}\infty,0)} (1\wedge y^2)\,\Pi(\text{d}y)<\infty$
. The Laplace exponent of X is defined by
$\psi(\theta)=\log(\mathbb{E}[\mathrm{e}^{\theta X_1}])$
. It is a strictly convex and infinitely differentiable function on
$\mathbb{R}_+$
with
$\psi(0)=0$
and
$\psi(\infty)=\infty$
. We know from the Lévy–Khintchine formula that
$\psi$
is of the form
\begin{align*}\psi(\theta)=-\mu \theta +\frac{1}{2} \sigma^2 \theta^2 + \int_{({-}\infty,0)}\big(\mathrm{e}^{\theta y}-1-\theta y \mathbf{1}_{\{ y>-1\}}\big)\,\Pi(\text{d}y)\end{align*}
for all
$\theta\geq 0$
. For any
$q\geq 0$
, the right inverse of
$\psi$
is defined as
$\Phi_q=\sup\{ \theta \geq 0\colon \psi(\theta)=q \}$
. It is known that the behaviour of X at infinity is determined by the sign of
$\psi^{\prime}(0{+})$
. Indeed, if
$\psi^{\prime}(0{+})> 0$
we have that X drifts to infinity, that is,
$\lim_{t\rightarrow \infty}X_t =\infty$
almost surely; in this case,
${\Phi}_q=0$
if and only if
$q=0$
. If
$\psi^{\prime}(0{+})<0$
, the process X drifts to minus infinity, that is,
$\lim_{t\rightarrow \infty}X_t ={-}\infty$
almost surely, and the process oscillates, i.e.
$\limsup_{t\rightarrow\infty} X_t=\infty=-\liminf_{t\rightarrow\infty}X_t$
whenever
$\psi^{\prime}(0{+})=0$
.
The sample paths of X are of bounded variation if and only if
$\sigma=0$
and
$$\int_{(-1,0)}(-y)\,\Pi(\text{d}y)<\infty.$$
For this particular case, we write
$\psi(\theta)=\delta \theta -\int_{({-}\infty,0)}(1-\mathrm{e}^{\theta y})\,\Pi(\text{d}y)$
, where
$\delta=-\mu-\int_{(-1,0)}y\,\Pi(\text{d}y)$
. Note that monotone processes are excluded from the definition of spectrally negative Lévy processes, so we assume that
$\delta>0$
when X is of bounded variation.
We now introduce scale functions, which play an essential role in the derivation of fluctuation identities for spectrally negative Lévy processes. For
$q\geq 0$
, the q-scale function is such that
$W^{(q)}=0$
for
$x<0$
, and is uniquely characterised on
$[0,\infty)$
as the only right-continuous function with Laplace transform
\begin{equation} \int_0^{\infty}\mathrm{e}^{-\theta x} W^{(q)}(x)\,\text{d}x = \frac{1}{\psi_q(\theta)} \quad \text{for } \theta>\Phi_q,\end{equation}
where
$\psi_q(\theta)=\psi(\theta)-q$
. We have that
$W^{(q)}$
is strictly increasing and continuous on
$(0,\infty)$
. For ease of notation we assume that
$\Pi$
has no atoms when X is of bounded variation, which guarantees that
$W\in C^1(0,\infty)$
. When
$q=0$
, we write
$W=W^{(0)}$
. The value of
$W^{(q)}$
at zero depends on the path variation of X. To be more precise,
\begin{equation} W^{(q)}(0) = \left\{ \begin{array}{ll} {1}/{\delta}, &\,\,\, \sigma=0\ \text{and}\ \int_{(-1,0)}{(-y)}{\Pi}\,(\text{d}y)<\infty ; \\ 0, & \,\,\,\text{otherwise}. \end{array} \right.\end{equation}
Furthermore, it is established that
\begin{equation} \lim_{x\rightarrow\infty}\mathrm{e}^{-{\Phi}_qx}W^{(q)}(x)={\Phi}^{\prime}_q,\end{equation}
where
${\Phi}^{\prime}_q={\partial\Phi_q}/{\partial q}$
. Moreover, from [Reference Kyprianou17, (8.22)], it is known that there exists a non-increasing function g such that, for any
$a>x$
,
\begin{equation} \log(W(x))=\log(W(a))-\int_x^a g(t)\,\text{d}t.\end{equation}
Another class of scale function is defined by
\begin{equation} Z^{(q)}(x,\theta) = \mathrm{e}^{{\theta}x}\bigg(1-{\psi}_q(\theta) \int_{0}^{x}\mathrm{e}^{-{\theta}y}W^{(q)}(y)\,\text{d}y\bigg), \quad x\in \mathbb{R}.\end{equation}
We note that
$Z^{(q)}(x,\theta)=\mathrm{e}^{{\theta}x}$
for all
$x\leq 0$
, and
$Z^{(q)}(b,\Phi_q)=\mathrm{e}^{\Phi_q b}$
for all
$b\in \mathbb{R}$
and
$q\geq 0$
. When
$\theta=0$
,
$Z^{(q)}(x,\theta)$
reduces to
$Z^{(q)}(x)$
as defined in [Reference Kyprianou17]. By using (2.1), we can rewrite (2.5) as
\begin{equation} Z^{(q)}(x,\theta) = {\psi}_q(\theta)\int_{0}^{\infty}\mathrm{e}^{-{\theta}y}W^{(q)}(x+y)\,\text{d}y, \quad x\geq 0,\ \theta>{\Phi}_q.\end{equation}
We then introduce some results on the first passage time. For any
$a\geq 0$
, the Laplace transform of
$\tau_a^+$
is given by
\begin{equation} \mathbb{E}\big[\mathrm{e}^{-q\tau_a^+}\mathbf{1}_{\{\tau_a^+<\infty \}}\big]=\mathrm{e}^{-{\Phi}_qa}.\end{equation}
Denote by
$\tau_0^-$
the first time X drops below the level zero, that is,
$\tau_0^-=\inf\{t>0\colon X_t<0\}$
. The Laplace transform of
$\tau_a^+$
on the event that X crosses above the level a before dropping below the level zero is given by
\begin{equation} \mathbb{E}_x\big[\mathrm{e}^{-q\tau_a^+} \mathbf{1}_{\{\tau_a^+ <\tau_0^-\}}\big]=\frac{W^{(q)}(x)}{W^{(q)}(a)}\end{equation}
for all
$q\geq 0$
and
$x\leq a$
. Moreover, whenever
$\psi^{\prime}(0{+})\geq 0$
, the probability of never entering the set
$({-}\infty,0]$
is given by
$\mathbb{P}_x(\tau_0^-=\infty)=\psi^{\prime}(0{+})W(x)$
for any
$x\geq 0$
. Hence, by writing
$\underline{X}_{t}=\inf_{0\leq s\leq t}X_s$
for
$t\geq 0$
, we deduce that the cumulative distribution function of
$-\underline{X}_{\infty}$
when X drifts to infinity is given by
\begin{equation} F(x)\,:\!=\,\mathbb{P}(-\underline{X}_{\infty}\leq x)=\mathbb{P}_x(\tau_0^-=\infty)=\psi^{\prime}(0{+})W(x)\end{equation}
for any
$x\in \mathbb{R}$
. For any
$a \in \mathbb{R}$
and
$q\geq 0$
, the q-potential measure of X killed upon entering the set
$[a,\infty)$
is absolutely continuous with respect to the Lebesgue measure, leading to
\begin{equation} \int_0^{\infty}\mathrm{e}^{-qt}\mathbb{P}_x\big(X_t\in\text{d}y,t<\tau_a^+\big)\,\text{d}t = \big[\mathrm{e}^{-\Phi_q(a-x)}W^{(q)}(a-y)-W^{(q)}(x-y) \big]\,\text{d}y\end{equation}
for all
$x,y\leq a$
.
3. Joint distribution of
$g_{{\tau}_b^+}$
and
${\tau}_b^+$
In this section we derive the joint distribution of the first passage time
${\tau}_b^+$
and the last passage time
$g_{\tau_b^+}=\sup\{0 \leq s \leq \tau_b^+ \colon X_s\leq 0 \}$
, where
$b>0$
is a fixed positive level. The results generalize [Reference Chiu and Yin10] by letting b go to infinity. It is worth noting that the approach used in [Reference Baurdoux2, Reference Chiu and Yin10] are not directly applicable in our case. As such, we adopt the hybrid observation scheme approach proposed in [Reference Li, Willmot and Wong19] to study the joint distribution of
${\tau}_b^+$
and
$g_{\tau_b^+}$
. The merit of this approach is that the two cases of the underlying process with bounded or unbounded variation paths can be treated in a unified way, and the proof is significantly simplified.
We then introduce the hybrid observation scheme. Briefly speaking, we observe the underlying process discretely (with independent exponential time increments) when it is non-negative, and then switch to continuous observation when it becomes negative. It will be switched back to discrete observation once it recovers the level 0. Formally, we first define the following sequence of time nodes
$\{{\xi}_n\}_{n\in\mathbb{N}}$
. Let
$\xi_0=0$
, and
\begin{equation*} {\xi}_n-{\xi}_{n-1}=\left\{ \begin{array}{ll} e_n^{\lambda} &\,\,\, \text{if}\ X_{{\xi}_{n-1}}\geq0,\\ {\tau}_0^+\circ{\theta}_{{\xi}_{n-1}}+e_n^{\lambda} &\,\,\, \text{if}\ X_{{\xi}_{n-1}}<0, \end{array} \right.\end{equation*}
where
$\{e_n^{\lambda}\}_{n{\in}\mathbb{N}}$
is a sequence of independent and identically distributed (i.i.d.) exponential random variables with mean
$1/{\lambda}>0$
, and we recall that
$\theta$
is the Markov shift operator and satisfies
$X_t\circ{\theta}_s=X_{s+t}$
.
Under this hybrid observation scheme, we define the first time the process is observed below level 0 by
$T_0^{\lambda,-}=\inf\{{\xi}_n\colon X_{{\xi}_n}<0,\, n\in \mathbb{N}\}$
. Note that
$T_0^{\lambda,-}$
is identical to the first time below level 0 under the so-called Poissonian observation scheme; see, e.g., [Reference Albrecher, Ivanovs and Zhou1, Reference Landriault, Li, Wong and Xu18]. We recall the following two formulas from the literature ([Reference Albrecher, Ivanovs and Zhou1, (15)] and [Reference Landriault, Li, Wong and Xu18, (3.5)]). For
$q,\theta\geq0$
and
$x\ {\leq}\ b$
,
\begin{align} \mathbb{E}_x\big[\exp\big\{{-}q{T_0^{\lambda,-}}+{\theta}X_{T_0^{\lambda,-}}\big\} \mathbf{1}_{\{ T_0^{\lambda,-} \lt {\tau}_b^+\}}\big] & = \frac{\lambda}{\lambda-{\psi}_q(\theta)} \bigg(Z^{(q)}(x,\theta) \nonumber \\ & \qquad\qquad\qquad - Z^{(q)}(b,\theta)\frac{Z^{(q)}(x,{\Phi}_{\lambda+q})}{Z^{(q)}(b,{\Phi}_{\lambda+q})}\bigg), \end{align}
\begin{align} \mathbb{E}_x\big[\mathrm{e}^{-q{\tau}_b^+}\mathbf{1}_{\{{\tau}_b^+ \lt T_0^{\lambda,-}\}}\big] & = \frac{Z^{(q)}(x,{\Phi}_{\lambda+q})}{Z^{(q)}(b,{\Phi}_{\lambda+q})}.\qquad\quad\qquad \end{align}
The last zero of X (under the hybrid observation scheme) before crossing above level b (under the continuous observation scheme) is defined by
\begin{equation*} g^{\lambda}_{\tau_b^+} \,:\!=\, \sup\{{\xi}_n+{\tau}_0^+\circ{\theta}_{{\xi}_n}\colon X_{{\xi}_n}<0,\, {\xi}_n<\tau_b^+,\, n\in\mathbb{N}\}.\end{equation*}
Since the hybrid observation scheme reduces to continuous observation when the intensity
$\lambda$
goes to infinity, we have, for any
$x\in \mathbb{R}$
,
$\lim_{\lambda\uparrow\infty} g^{\lambda}_{{\tau}_b^+}=g_{{\tau}_b^+}$
$\mathbb{P}_x$
-almost surely. See Figure 1 for an illustration of the hybrid observation scheme as well as the two last passage times
$g^{\lambda}_{\tau_b^+}$
and
$g_{\tau_b^+}$
.
FIGURE 1. Illustration of the hybrid observation scheme,
$g^{\lambda}_{\tau_b^+}$
, and
$g_{\tau_b^+}$
.
The following theorem presents the joint distribution of
$g_{{\tau}_b^+}$
and
${\tau}_b^+-g_{{\tau}_b^+}$
.
Theorem 3.1.
For
$p, q\geq0$
,
$x<b$
, and
$b>0$
,
\begin{equation} \mathbb{E}_x\big[\exp\big\{{-}{p}g_{{\tau}_b^+}-{q}({\tau}_b^+-g_{{\tau}_b^+})\big\} \mathbf{1}_{\{\tau_b^+<\infty\}}\big] = \mathrm{e}^{-{\Phi}_{p}(b-x)}\frac{W^{(p)}(b)}{W^{(q)}(b)}+\frac{W^{(q)}(x)}{W^{(q)}(b)}-\frac{W^{(p)}(x)}{W^{(q)}(b)}. \end{equation}
Proof. We first derive
$f(x)\,:\!=\,\mathbb{E}_x\big[\exp\big\{{-}{p}g^{\lambda}_{{\tau}_b^+}-{q}({\tau}_b^+-g^{\lambda}_{{\tau}_b^+})\big\} \mathbf{1}_{\{\tau_b^+<\infty \}}\big]$
,
$x<b$
. For
$x<0$
, it follows from the spatial homogeneity and (2.7) that
\begin{equation} f(x) =\mathbb{E}_x\big[\mathrm{e}^{-p{\tau}_0^+}\mathbf{1}_{\{{\tau}_0^+<\infty\}}\big]f(0) = \mathrm{e}^{{\Phi}_{p}x}f(0). \end{equation}
Note that, conditional on the values
$\{e_n^{\lambda}\}_{n{\in}\mathbb{N}}$
, the times
$\{\xi_n\}_{n\in \mathbb{N}}$
and
$T_0^{\lambda,-}$
are stopping times of X. Hence, by conditioning on
$\{e_n^{\lambda}\}_{n{\in}\mathbb{N}}$
, further conditioning on
$T_{0}^{\lambda,-}$
, and applying the strong Markov property of X, we obtain that, for any
$0 \leq x< b$
,
\begin{align} f(x) & = \int_{{-}\infty}^{0}\mathbb{E}_x\big[\mathrm{e}^{-{p}T_0^{\lambda,-}} \mathbf{1}_{\{X_{T_0^{\lambda,-}}\in \text{d} u,\,T_0^{\lambda,-} \lt {\tau}_b^+\}}\big]f(u) + \mathbb{E}_x\big[\mathrm{e}^{-{q}{\tau}_b^+}\mathbf{1}_{\{{\tau}_b^+ \lt T_0^{\lambda,-}\}}\big] \nonumber \\ & = \int_{{-}\infty}^{0}\mathbb{E}_x\big[\mathrm{e}^{-{p}T_0^{\lambda,-}} \mathbf{1}_{\{X_{T_0^{\lambda,-}}\in \text{d} u,\,T_0^{\lambda,-} \lt {\tau}_b^+\}}\big]e^{{\Phi}_{p}u}f(0) + \mathbb{E}_x\big[\mathrm{e}^{-{q}{\tau}_b^+}\mathbf{1}_{\{{\tau}_b^+ \lt T_0^{\lambda,-}\}}\big] \nonumber \\ & = \mathbb{E}_x\big[\exp\big\{{-}{p}T_0^{\lambda,-}+{{\Phi}_{p}}X_{T_0^{\lambda,-}}\big\} \mathbf{1}_{\{T_0^{\lambda,-}\lt{\tau}_b^+\}}\big]f(0) + \mathbb{E}_x\big[\mathrm{e}^{-{q}{\tau}_b^+}\mathbf{1}_{\{{\tau}_b^+\lt T_0^{\lambda,-}\}}\big], \end{align}
where we used (3.4) in the second identity. By letting
$x=0$
in (3.5), we can solve f(0) and obtain
\begin{align} f(0) = \frac{\mathbb{E}\big[\mathrm{e}^{-{q}{\tau}_b^+}\mathbf{1}_{\{{\tau}_b^+\lt T_0^{\lambda,-}\}}\big]} {1-\mathbb{E}\big[\exp\big\{{-}{p}T_0^{\lambda,-}+{{\Phi}_{p}}X_{T_0^{\lambda,-}}\big\} \mathbf{1}_{\{T_0^{\lambda,-}<{\tau}_b^+\}}\big]} & = \frac{Z^{(q)}(0,{\Phi}_{\lambda+q})/Z^{(q)}(b,{\Phi}_{\lambda+q})} {\mathrm{e}^{{\Phi}_{p}b}Z^{(p)}(0,{\Phi}_{\lambda+p})/Z^{(p)}(b,{\Phi}_{\lambda+p})} \nonumber \\ & = \mathrm{e}^{-{\Phi}_{p}b}\frac{Z^{(p)}(b,{\Phi}_{\lambda+p})}{Z^{(q)}(b,{\Phi}_{\lambda+q})}, \end{align}
where we used (3.1) and (3.2) in the second identity, and
$Z^{(q)}(0,\theta)=1$
in the last identity. Substituting (3.6) into (3.4), for
$x<0$
,
\begin{equation} f(x) = \mathrm{e}^{-{\Phi}_{p}(b-x)}\frac{Z^{(p)}(b,{\Phi}_{\lambda+p})}{Z^{(q)}(b,{\Phi}_{\lambda+q})}. \end{equation}
Then, substituting (3.6) into (3.5), and using (3.1) and (3.2) again, for
$0 \leq x \lt b$
we have
\begin{equation} f(x) = \mathrm{e}^{-{\Phi}_{p}(b-x)}\frac{Z^{(p)}(b,{\Phi}_{\lambda+p})}{Z^{(q)}(b,{\Phi}_{\lambda+q})} + \frac{Z^{(q)}(x,{\Phi}_{\lambda+q})}{Z^{(q)}(b,{\Phi}_{\lambda+q})} - \frac{Z^{(p)}(x,{\Phi}_{\lambda+p})}{Z^{(q)}(b,{\Phi}_{\lambda+q})}. \end{equation}
We furthermore unify (3.7) and (3.8) into one expression for
$x \lt b$
:
\begin{equation} f(x) = \mathrm{e}^{-{\Phi}_{p}(b-x)}\frac{Z^{(p)}(b,{\Phi}_{\lambda+p})}{Z^{(q)}(b,{\Phi}_{\lambda+q})} + \bigg(\frac{Z^{(q)}(x,{\Phi}_{\lambda+q})}{Z^{(q)}(b,{\Phi}_{\lambda+q})} - \frac{Z^{(p)}(x,{\Phi}_{\lambda+p})}{Z^{(q)}(b,{\Phi}_{\lambda+q})}\bigg)\mathbf{1}_{\{0 \leq x\lt b\}}. \end{equation}
By (2.6) and the fact that
$Z^{(q)}(0,\cdot)=1$
, we have
\begin{align*} \lim_{\lambda\rightarrow\infty}\frac{{\Phi}_{\lambda+q}}{{\Phi}_{\lambda+p}} = \lim_{\lambda\rightarrow\infty}\frac{{\Phi}_{\lambda+q}[{Z^{(q)}(0,{\Phi}_{\lambda+q})}]/{\lambda}} {{\Phi}_{\lambda+p}[{Z^{(p)}(0,{\Phi}_{\lambda+p})}]/{\lambda}} & = \lim_{\lambda\rightarrow\infty}\frac{{\Phi}_{\lambda+q} \int_{0}^{\infty}\mathrm{e}^{-{\Phi}_{\lambda+q}y}W^{(q)}(y)\,\text{d}y} {{\Phi}_{\lambda+p}\int_{0}^{\infty}\mathrm{e}^{-{\Phi}_{\lambda+p}y}W^{(p)}(y)\,\text{d}y} \\ & = \lim_{y\rightarrow 0+}\frac{W^{(q)}(y)}{W^{(p)}(y)} = 1, \end{align*}
where the third equality is by the initial value theorem and the last limit can be found in [Reference Albrecher, Ivanovs and Zhou1, p. 1373]. This, together with (2.6), yields
\begin{align} \lim_{\lambda\rightarrow\infty}\frac{Z^{(p)}(x,{\Phi}_{\lambda+p})}{Z^{(q)}(b,{\Phi}_{\lambda+q})} & = \lim_{\lambda\rightarrow\infty}\frac{{\psi}_p({\Phi}_{\lambda+p})}{{\psi}_q({\Phi}_{\lambda+q})} \frac{\int_{0}^{\infty}\mathrm{e}^{-{\Phi}_{\lambda+p}u}W^{(p)}(x+u)\,\text{d}u} {\int_{0}^{\infty}\mathrm{e}^{-{\Phi}_{\lambda+q}u}W^{(q)}(b+u)\,\text{d}u} \nonumber \\ & = \lim_{\lambda\rightarrow\infty}\frac{\int_{0}^{\infty}\mathrm{e}^{-{\Phi}_{\lambda+p}u}W^{(p)}(x+u)\,\text{d}u} {\int_{0}^{\infty}\mathrm{e}^{-{\Phi}_{\lambda+q}u}W^{(q)}(b+u)\,\text{d}u} \nonumber \\ & = \lim_{\lambda\rightarrow\infty}\frac{{\Phi}_{\lambda+q}}{{\Phi}_{\lambda+p}} \frac{{\Phi}_{\lambda+p}\int_{0}^{\infty}\mathrm{e}^{-{\Phi}_{\lambda+p}u}W^{(p)}(x+u)\,\text{d}u} {{\Phi}_{\lambda+q}\int_{0}^{\infty}\mathrm{e}^{-{\Phi}_{\lambda+q}u}W^{(q)}(b+u)\,\text{d}u} = \frac{W^{(p)}(x)}{W^{(q)}(b)}. \end{align}
By taking the limit
$\lambda\uparrow\infty$
in (3.9) and using (3.10), we can conclude that
\begin{align*} & \mathbb{E}_x\big[\exp\big\{{-}{p}g_{{\tau}_b^+}-{q}({\tau}_b^+-g_{{\tau}_b^+})\big\}\big] \\ & = \lim_{\lambda\rightarrow\infty} \mathbb{E}_x\big[\exp\big\{{-}{p}g^{\lambda}_{{\tau}_b^+}-{q}({\tau}_b^+-g^{\lambda}_{{\tau}_b^+})\big\}\big] \\ & = \lim_{\lambda\rightarrow\infty}\bigg(\mathrm{e}^{-{\Phi}_{p}(b-x)} \frac{Z^{(p)}(b,{\Phi}_{\lambda+p})}{Z^{(q)}(b,{\Phi}_{\lambda+q})} + \bigg(\frac{Z^{(q)}(x,{\Phi}_{\lambda+q})}{Z^{(q)}(b,{\Phi}_{\lambda+q})} - \frac{Z^{(p)}(x,{\Phi}_{\lambda+p})}{Z^{(q)}(b,{\Phi}_{\lambda+q})}\bigg)\mathbf{1}_{\{0 \leq x \lt b\}}\bigg) \\ & = \mathrm{e}^{-{\Phi}_{p}(b-x)}\frac{W^{(p)}(b)}{W^{(q)}(b)} + \frac{W^{(q)}(x)}{W^{(q)}(b)} - \frac{W^{(p)}(x)}{W^{(q)}(b)}, \end{align*}
where in the last equality we used that
$W^{(q)}$
and
$W^{(p)}$
vanish on
$({{-}\infty} ,0)$
.
Remark 3.1. It is worth noting that an alternative approach to proving Theorem 3.1 is to modify the roadmap proposed in [Reference Kyprianou17, exercise in 8.10].
By letting
$b\rightarrow\infty$
in (3.3), using (2.3) and the fact that
$\lim_{b\uparrow\infty}W(b)=1/\psi^{\prime}(0{+})$
when X drifts to infinity (see [Reference Kuznetsov, Kyprianou and Rivero16, Lemma 3.3]), we obtain the Laplace transform of the last zero g, which recovers [Reference Chiu and Yin10, Theorem 3.1] and [Reference Baurdoux2, Theorem 1].
Corollary 3.1.
Suppose that
$\psi^{\prime}(0{+})>0$
. For
$p \geq 0$
,
\begin{align*} \mathbb{E}_x[\mathrm{e}^{-{p}g}]=\psi^{\prime}(0{+})\big({\Phi}^{\prime}_{p}\mathrm{e}^{{\Phi}_{p}x}+W(x)-W^{(p)}(x)\big). \end{align*}
Example 3.1. Suppose that X is a Brownian motion with drift, i.e.
$X_t={\mu}t+{\sigma}B_t$
, where
$\mu\in\mathbb{R}$
,
$\sigma>0$
, and
$\{B_t\}_{t\geq0}$
is a standard Brownian motion. It follows that
$\psi(\theta)={\mu}{\theta}+\frac{1}{2}{\sigma}^2{\theta}^2$
. The two roots of
$\psi(\theta)-q=0$
are given by
${\Phi}_q=(\sqrt{{\mu}^2+2q{\sigma}^2}-{\mu})/\sigma^{2}$
and
$-{\rho}_q=-(\sqrt{{\mu}^2+2q{\sigma}^2}+{\mu})/\sigma^{2}$
. The q-scale function is given by
\begin{equation} W^{(q)}(x) = \frac{\exp\!({\Phi}_qx)-\exp\!{({-}{\rho}_qx)}}{\sqrt{{\mu}^2+2q{\sigma}^2}}. \end{equation}
It follows from Theorem 3.1 that
\begin{align*} & \mathbb{E}_x\big[\exp\big\{{-}{p}g_{{\tau}_b^+}-{q}({\tau}_b^+-g_{{\tau}_b^+})\big\}\big] \\ & = \frac{\exp\!({\Phi}_qx)-\exp\!({-}{\rho}_qx)}{\exp\!({\Phi}_qb)-\exp\!({-}{\rho}_qb)} \\ &\quad- \frac{\sqrt{{\mu}^2+2q{\sigma}^2}}{\sqrt{{\mu}^2+2p{\sigma}^2}\,} \frac{\big(\exp\!({\Phi}_px-({2b\sqrt{{\mu}^2+2p{\sigma}^2}}/{{\sigma}^2})) - \exp\!({-}{\rho}_px)\big)} {\exp\!({\Phi}_qb)-\exp\!({-}{\rho}_qb)}. \end{align*}
Example 3.2. Suppose that X follows the Cramér–Lundberg model with exponential jumps, i.e.
$X_t={\mu}t-\sum_{i=1}^{N_t}C_i$
, where
$\mu\in\mathbb{R}$
,
$\{N_t\}_{t\geq0}$
is a Poisson process with intensity
$\eta>0$
, and
$\{C_i\}_{i\in\mathbb{N}}$
are i.i.d. exponential random variables with parameter
$\alpha>0$
, which are independent of
$N_t$
. It is known that
$\psi(\theta)=\mu{\theta}-{\eta}+({{\alpha}{\eta}}/({\theta+\alpha}))$
. The two roots of
$\psi(\theta)-q=0$
are given by
\begin{align*} {\Phi}_{q} & = \frac{1}{2\mu}(\sqrt{(q+\eta-{\alpha}\mu)^{2}+4\mu{\alpha}{q}}+(q+\eta-{\alpha}\mu)), \\ -{\rho}_{q} & = -\frac{1}{2\mu}(\sqrt{(q+\eta-{\alpha}\mu)^{2}+4\mu{\alpha}{q}}-(q+\eta-{\alpha}\mu)). \end{align*}
The q-scale function is given by
\begin{equation} W^{(q)}(x)={\Phi}^{\prime}_q\exp\!({\Phi}_qx)-{\rho}^{\prime}_q\exp\!({-}{\rho}_qx), \end{equation}
where
$$ {\Phi}^{\prime}_q=\frac{1}{2\mu}\left(\frac{q+\eta+{\alpha}\mu}{\sqrt{(q+\eta-{\alpha}\mu)^2+4\mu{\alpha}q}\,}+1\right), \qquad \!\!\!\! {\rho}^{\prime}_q=\frac{1}{2\mu}\left(\frac{q+\eta+{\alpha}\mu}{\sqrt{(q+\eta-{\alpha}\mu)^2+4c{\alpha}q}\,}-1\right). $$
It follows from Theorem 3.1 that
\begin{align*} \mathbb{E}_x\big[\exp&\big\{{-}{p}g_{{\tau}_b^+}-{q}({\tau}_b^+-g_{{\tau}_b^+})\big\}\big] \\ & = \frac{{\Phi}^{\prime}_q\exp\!({\Phi}_qx)-{\rho}^{\prime}_q\exp\!({-}{\rho}_qx)} {{\Phi}^{\prime}_q\exp\!({\Phi}_qb)-{\rho}^{\prime}_q\exp\!({-}{\rho}_qb)} \\ & \quad - \frac{{\rho}^{\prime}_p\big(\exp\!({\Phi}_px-({b}/{\mu}){\sqrt{(p+\eta-\alpha\mu)^2+4{\mu}{\alpha}p}}) - \exp\!({-}{\rho}_px)\big)}{{\Phi}^{\prime}_q\exp\!({\Phi}_qb)-{\rho}^{\prime}_q\exp\!({-}{\rho}_qb)}. \end{align*}
4. Optimal prediction of
$g_{\tau_b^+}$
In this section, we consider the optimal prediction problem for
$g_{\tau_b^+}$
, that is, for fixed
$b> 0$
and
$x\in \mathbb{R}$
,
\begin{equation} \inf_{\tau \in \mathcal{T} } \mathbb{E}_x\big[\big|g_{\tau_b^+}-\tau\big|\big],\end{equation}
where
$\mathcal{T}$
is the set of all stopping times. To avoid triviality (i.e. the mean of
$g_{\tau_b^+}$
being infinite), we assume that X drifts to infinity. Indeed, if X does not drift to infinity, we obtain from Theorem 3.1 that
$\mathbb{E}_x\big[g_{\tau_b^+}\big]=\infty$
. Thus, for any stopping time
$\tau$
with finite mean,
\begin{equation*} \mathbb{E}\big[\big|g_{\tau_b^+}-\tau\big|\big] \geq \mathbb{E}\big[g_{\tau_b^+}\big]-\mathbb{E}[\tau ]=\infty.\end{equation*}
Hence, in the context of a minimization problem with stopping times that have a finite mean, any stopping time can provide a solution.
The following theorem presents the solution to the optimal prediction problem (4.1). Its proof is postponed to Section 5. Recall from (2.9) that
$F(x)=\psi^{\prime}(0{+})W(x)$
is the cumulative distribution function of
$-\underline{X}_{\infty}$
, and it is continuous and strictly increasing in
$x\in(0,\infty)$
. From (2.2), we know that
$F(0)=0$
if X is of unbounded variation, and
$F(0)=\psi^{\prime}(0{+})/\delta\in (0,1)$
when X is of bounded variation.
Theorem 4.1. Suppose that X is a spectrally negative Lévy process that drifts to infinity. We define
\begin{equation*} y_b^* = \inf\bigg\{y\in[0,b]\colon\int_{[0,y]}F(y-z)\,F(\text{d}z) \geq \frac{F(b)}{2}\bigg\}, \end{equation*}
where we follow the convention that
$\inf \emptyset =b$
. Then the stopping time
$\tau_{y_b^*}=\inf\{t\geq 0\colon X_t\geq y_b^* \}$
is optimal for (4.1) for any
$x\in \mathbb{R}$
. More specifically:
-
(i) If
$F(0)\geq\sqrt{\frac12}$
,
$y_b^*=0$
for all
$b>0$
. -
(ii) If
$\frac12\leq F(0)<\sqrt{\frac12}$
then, for
$ b\leq F^{-1}(2F(0)^2)$
,
$y^*_b=0$
. For
$b> F^{-1}(2F(0)^2)$
, the value
$y_b^*\in (0,b)$
is the unique solution to
\begin{equation*} \int_{[0,y]}F(y-z)\,F(\text{d}z) - \frac{F(b)}{2} = 0. \end{equation*}
-
(iii) If
$F(0)<\frac12$
, let
$b_0>0$
be the unique solution to For
\begin{equation*} \int_{[0,b]}F(b-z)\,F(\text{d}z) - \frac{F(b)}{2} = 0. \end{equation*}
$ b\leq b_0$
,
$y^*_b=b$
. For
$b>b_0$
,
$y_b^*\in (0,b)$
is the unique solution to
\begin{equation*} \int_{[0,y]}F(y-z)\,F(\text{d}z) - \frac{F(b)}{2} = 0. \end{equation*}
Remark 4.1. Since F is the cumulative distribution function of
$-\underline{X}_{\infty}$
, the function
$y\mapsto \int_{[0,y]}F(y-z)\,F(\text{d}z)$
is actually the cumulative distribution function of
$-\underline{X}_{\infty}-\underline{Y}_{\infty}$
, where
$\underline{Y}_{\infty}$
is an independent copy of
$\underline{X}_{\infty}$
. Therefore, Theorem 4.1 indicates that the optimal stopping boundary
$y_b^{*}$
corresponds to the minimum in between b and the
$F(b)/2$
-quantile of the random variable
$-\underline{X}_{\infty}-\underline{Y}_{\infty}$
.
In [Reference Baurdoux and Pedraza3], the optimally predicting problem for the last zero
$g=\sup\{t\geq 0 \colon X_t\leq 0 \}$
, i.e.
\begin{equation} \inf_{\tau \in \mathcal{T} } \mathbb{E}_x[|g-\tau|],\end{equation}
is solved when X is a spectrally negative Lévy process. Upon assuming that the Lévy measure
$\Pi$
satisfies
$\int_{({-}\infty,-1)} y^2 \,\Pi(\text{d} y) < \infty$
, which ensures the existence of the first moment of g, the stopping time
$\tau_{a^*}=\inf\{t\geq 0\colon X_t\geq a^* \}$
is optimal for (4.2), where
\begin{equation*} a^*=\inf\bigg\{y\geq 0\colon\int_{[0,y]} F(y-z)\,F(\text{d}z)\geq \frac12\bigg\}.\end{equation*}
Since
$\lim_{b\rightarrow\infty} F(b)=1$
, we obtain the following corollary which verifies the convergence of the optimal stopping boundary.
Corollary 4.1.
$\lim_{b\rightarrow \infty} y_b^*=a^*$
.
Example 4.1. Suppose that X is a Brownian motion with positive drift, i.e.
$X_t=\mu t+\sigma B_t$
, where
$\mu>0$
,
$\sigma>0$
, and
$\{B_t\}_{t\geq0}$
is a standard Brownian motion. It is known from (3.11) and
$F(x)=\psi^{\prime}(0{+})W(x)=\mu W(x)$
that
$F(x)=1-\exp\!({-}{2\mu x}/{\sigma^2})$
,
$x\geq 0$
. That is,
$-\underline{X}_{\infty} \sim \text{Exp}(2\mu /\sigma^2)$
, which implies that
$\int_{[0,y]}F(y-z)\,F(\text{d}z)$
corresponds to the cumulative distribution function of a
$\text{Gamma}(2,2 \mu/\sigma^2)$
random variable given by
\begin{equation*} \int_{[0,y]}F(y-z)\,F(\text{d}z) = 1 - \frac{2\mu y}{\sigma^2}\exp\bigg({-}\frac{2\mu y}{\sigma^2}\bigg) - \exp\bigg({-}\frac{2\mu y}{\sigma^2}\bigg), \quad y\geq 0. \end{equation*}
Hence, it follows from Theorem 4.1 that the optimal stopping boundary is
\begin{equation*} y_b^* = \inf\bigg\{y\in[0,b]\colon 1 - \frac{2\mu y}{\sigma^2}\exp\bigg({-}\frac{2\mu y}{\sigma^2}\bigg) - \exp\bigg({-}\frac{2\mu y}{\sigma^2}\bigg) \geq \frac{1-\exp\!({-}{2\mu b}/{\sigma^2})}{2}\bigg\}. \end{equation*}
Figure 2 plots the mapping
$b\mapsto y_b^*$
with
$\mu=1=\sigma$
. Note that X is of unbounded variation with
$F(0)=0$
. Consistent with Theorem 4.1(iii) and Corollary 4.1, it can be seen that
$y_b^*$
increases linearly for
$b<b_0$
, and
$y_b^*$
converges to the value
$a^*\approx 0.8391$
when
$b\rightarrow\infty$
.
FIGURE 2. Optimal stopping boundary
$y_b^*$
for the drifted Brownian motion model with
$\mu=1=\sigma$
.
Example 4.2. Suppose that X follows a Cramér–Lundberg model with exponential jumps, i.e.
$X_t={\mu}t-\sum_{i=1}^{N_t}C_i$
, where
$\mu>0$
,
$\{N_t\}_{\{t\geq0\}}$
is a Poisson process with intensity
$\eta>0$
, and
$\{C_i\}_{i\in\mathbb{N}}$
are i.i.d. exponential random variables with parameter
$\alpha>0$
, which are independent of
$N_t$
. In this case, X is a spectrally negative Lévy process drifting to infinity by assuming
$\psi^{\prime}(0{+})=\mu-({\eta}/{\alpha})>0$
. It follows from (3.12) and
$F(x)=\psi^{\prime}(0{+})W(x)=(\mu-({\eta}/{\alpha})) W(x)$
that
\begin{equation*} F(x) = 1 - \frac{\eta}{{\alpha}{\mu}}\exp\bigg({-}\bigg(\alpha-\frac{\eta}{\mu}\bigg)x\bigg), \quad x\geq0. \end{equation*}
In particular,
$F(0)=1-({\eta}/{{\alpha}{\mu}})>0$
. Hence
\begin{align*} \int_{[0,y]}F(y-z)\,F(\text{d}z) & = 1 + \frac{\eta}{\alpha\mu}\bigg(\frac{\eta}{\alpha\mu}-2\bigg) \exp\bigg({-}\bigg(\alpha-\frac{\eta}{\mu}\bigg)y\bigg) \\ & \quad - \bigg(\frac{\eta}{\alpha\mu}\bigg)^2\bigg(\alpha-\frac{\eta}{\mu}\bigg)y \exp\bigg({-}\bigg(\alpha-\frac{\eta}{\mu}\bigg)y\bigg), \quad y\geq 0. \end{align*}
The optimal boundary follows from Theorem 4.1:
\begin{equation*} y_b^* = \inf\bigg\{y\in[0,b]\colon\int_{[0,y]}F(y-z)\,F(\text{d}z) \geq \frac{1-({\eta}/{{\alpha}{\mu}})\exp\!({-}(\alpha-({\eta}/{\mu}))b)}{2}\bigg\}. \end{equation*}
Figure 3 depicts the mapping
$b\mapsto y_b^*$
under the Cramér–Lundberg model for the three cases in Theorem 4.1. Note that in this case X is of bounded variation with
$F(0)=1-({\eta}/{\alpha \mu})>0$
. The parameters in Figure 3(a) are set to
$\mu=1$
,
$\eta=\frac12$
,
$\alpha=2$
, which implies
$F(0)=\frac34$
. From Theorem 4.1(i),
$y_b^*=0$
for any
$b>0$
. In Figure 3(b), we set
$\mu=1$
,
$\eta=1$
,
$\alpha=3$
, which implies
$F(0)=\frac23\in\big[\frac12,\sqrt{\frac12}\big)$
. From Theorem 4.1(ii),
$y_b^*=0$
for
$b<F^{-1}(2F(0)^2)$
, and then increases with b. It converges to
$a^*\approx 0.0656$
as
$b\rightarrow\infty$
according to Corollary 4.1. In Figure 3(c), we set
$\mu=1$
,
$\eta=2$
,
$\alpha=3$
, which implies
$F(0)=\frac13$
. From Theorem 4.1(iii) and Corollary 4.1, we see that
$y_b^*=b$
for
$b<b_0$
, and
$y_b^*$
converges to the value
$a^*\approx 0.9711$
when
$b\rightarrow\infty$
.
FIGURE 3. Optimal stopping boundary
$y_b^*$
for the Cramér–Lundberg model with exponential jumps.
5. Proof of Theorem 4.1
Since the random time
$g_{\tau_b^+}$
is only
$\mathbb{F}$
-measurable, we first use the following lemma to establish an equivalence between the optimal prediction problem (4.1) and an optimal stopping problem.
Lemma 5.1.
For any
$\tau \in \mathcal{ T}$
,
$\mathbb{E}_x\big[\big|g_{\tau_b^+}-\tau\big|\big] = \mathbb{E}_x\big[g_{\tau_b^+}\big] + \mathbb{E}_x\big[\int_0^{\tau}G_b(s,X_s)\,\text{d}s\big]$
, where
$G_b(s,x):\!=2\big[\mathbf{1}_{\{\tau_b^+\leq s\}}+\mathbf{1}_{\{\tau_b^+>s\}}{W(x)}/{W(b)}\big]-1$
. Then the optimal prediction problem (4.1) is equivalent to the optimal stopping problem
\begin{equation} V_b(x) = \inf_{\tau\in\mathcal{T}}\mathbb{E}_x\bigg[\int_0^{\tau}G_b(s,X_s)\,\text{d}s\bigg]. \end{equation}
Proof. For any stopping time
$\tau\in\mathcal{T}$
and
$x\in\mathbb{R}$
,
$|g_{\tau_b^+}-\tau| = \int_0^{\tau}(2\mathbf{1}_{\{g_{\tau_b^+}\leq s\}}-1)\,\text{d}s + g_{\tau_b^+}$
. From Fubini’s theorem and the tower property of conditional expectations, it follows that
\begin{align} \mathbb{E}_{x}\big[\big|g_{\tau _{b}^{+}}-\tau\big|\big] & = \mathbb{E}_{x}\bigg[\int_{0}^{\tau}(2\mathbf{1}_{\{g_{\tau_{b}^{+}}\leq s\}}-1)\,\text{d}s\bigg] + \mathbb{E}_{x}\big[g_{\tau _{b}^{+}}\big] \nonumber \\ & = \mathbb{E}_{x}\bigg[\int_{0}^{\infty}\mathbf{1}_{\{s<\tau\}} \big(2\mathbb{E}_{x}\big[\mathbf{1}_{\{g_{\tau_{b}^{+}}\leq s\}}\mid\mathcal{F}_{s}\big]-1\big)\,\text{d}s\bigg] + \mathbb{E}_{x}\big[g_{\tau_{b}^{+}}\big] \nonumber \\ & = \mathbb{E}_{x}\bigg[\int_{0}^{\tau}(2\mathbb{P}_{x}\big(g_{\tau_{b}^{+}}\leq s\mid\mathcal{F}_{s}\big)-1)\, \text{d}s\bigg] + \mathbb{E}_{x}\big[g_{\tau _{b}^{+}}\big]. \end{align}
Note that in the event of
$\big\{\tau_b^+\leq s\big\}$
we have
$g_{\tau_b^+}\leq \tau_b^+ \leq s$
and thus
\begin{equation} \mathbb{P}_x\big(g_{\tau_b^+}\leq s\mid\mathcal{F}_s\big) = \mathbf{1}_{\{\tau_b^+\leq s\}} + \mathbb{P}_x\big(g_{\tau_b^+}\leq s,\tau_b^+>s\mid\mathcal{F}_s\big). \end{equation}
Further, the event
$\big\{g_{\tau_b^+}\leq s,\tau_b^+>s\big\}$
is equal to
$\{ X_u \geq 0 \text{ for all } u\in [s,\tau_b^+],\tau_b^+>s\}$
(up to a
$\mathbb{P}$
-null set). Hence, for all
$s\geq 0$
,
\begin{align*} \mathbb{P}_x\big(g_{\tau_b^+}\leq s, \tau_b^+>s\mid\mathcal{F}_s\big) & = \mathbb{P}_x(X_u \geq 0 \text{ for all } u\in [s,\tau_b^+],\tau_b^+>s\mid\mathcal{F}_s ) \\ & = \mathbf{1}_{\{\tau_b^+>s\}}\mathbb{P}_{x}\Big(\inf_{0\leq u\leq\tau_b^+-s}X_{u+s} \geq 0\mid\mathcal{F}_s\Big) \\ & = \mathbf{1}_{\{\tau_b^+>s\}}\mathbb{P}_{X_s}\big(\underline{X}_{\tau_b^+} \geq 0\big) \\ & = \mathbf{1}_{\{\tau_b^+>s\}}\mathbb{P}_{X_s}\big(\tau_b^+<\tau_0^-\big) = \mathbf{1}_{\{\tau_b^+>s\}}\frac{W(X_s)}{W(b)}, \end{align*}
where we recall that
$\underline{X}_t=\inf_{0\leq s\leq t} X_s$
, and the last equality follows from the Markov property of X and (2.8). Substituting into (5.3) yields
\begin{equation*} \mathbb{P}_x\big(g_{\tau_b^+}\leq s\mid\mathcal{F}_s\big) = \mathbf{1}_{\{\tau_b^+\leq s\}} + \mathbf{1}_{\{\tau_b^+>s\}}\frac{W(X_s)}{W(b)}. \end{equation*}
Further, substituting this expression into (5.2) yields, for any
$x\in\mathbb{R}$
,
\begin{equation*} \inf_{\tau\in\mathcal{T}}\mathbb{E}_x\big[\big|g_{\tau_b^+}-\tau\big|\big] = \mathbb{E}_x\big[g_{\tau_b^+}\big] + \inf_{\tau\in\mathcal{T}}\mathbb{E}_x\bigg[ \int_0^{\tau}\bigg(2\bigg[\mathbf{1}_{\{\tau_b^+\leq s\}}+\mathbf{1}_{\{\tau_b^+>s\}}\frac{W(X_s)}{W(b)}\bigg] - 1\bigg)\,\text{d}s\bigg], \end{equation*}
completing the assertion of the proof.
We then focus on the optimal stopping problem (5.1). The next lemma provides some basic properties of the value function
$V_b$
.
Lemma 5.2.
-
(i)
$V_b(x)$
is non-decreasing in x.
-
(ii)
$V_b(x)\in ({-}\infty,0]$
for all
$x\in \mathbb{R}$
. In particular,
$V_b(x)=0$
for all
$x\geq b$
. -
(iii) For any
$x\in \mathbb{R}$
and
$b>0$
, we can write (5.4)
\begin{equation} V_b(x) = \inf_{\tau\in\mathcal{T}}\mathbb{E}_x\bigg[\int_0^{\tau\wedge\tau_b^+}\bigg(2\frac{W(X_s)}{W(b)}-1\bigg)\, \text{d}s\bigg]. \end{equation}
-
(iv) Fix
$b>0$
. Let
$D=\{x\in\mathbb{R}\colon V_b(x)=0\}$
and
$\tau_{D}=\inf\{t\geq 0\colon X_t\in D\}$
. Then D is a closed set and
$\tau_D$
is an optimal stopping time for (5.1).
Proof. (i). For
$x\in \mathbb{R}$
and
$b>0$
, by the spatial homogeneity of X,
\begin{equation*} V_b(x) = \inf_{\tau\in\mathcal{T}}\mathbb{E}\bigg[\int_0^{\tau}\bigg(2\left[\mathbf{1}_{\{\tau_{b-x}^+\leq s\}} + \mathbf{1}_{\{\tau_{b-x}^+>s\}}\frac{W(X_s+x)}{W(b)}\right]-1\bigg)\,\text{d}s\bigg]. \end{equation*}
Fix
$s\geq 0$
. We define the auxiliary function
\begin{equation*} F_s(x,b)=\mathbf{1}_{\{ \tau_{b-x}^+\leq s\}}+\mathbf{1}_{\{\tau_{b-x}^+>s \}} \frac{W(X_s+x)}{W(b)}. \end{equation*}
We then show that, for fixed
$b>0$
, the mapping
$x\mapsto F_s(x,b)$
is non-decreasing. Take
$x_1\leq x_2$
, then
$\tau_{b-x_2}^+\leq \tau_{b-x_1}^+$
. First, if
$\omega\in \big\{s<\tau_{b-x_2}^+\big\}$
, then we have
$\omega\in\big\{s<\tau_{b-x_1}^+\big\}$
and
\begin{equation*} F_s(x_1,b)(\omega) = \frac{W(X_s+x_1)}{W(b)}\leq \frac{W(X_s+x_2)}{W(b)}=F_s(x_2,b)(\omega), \end{equation*}
where we used that W is increasing. Second, if
$\omega\in\big\{\tau_{b-x_2}^+\leq s<\tau_{b-x_1}^+\big\}$
, we have
$X_s(\omega)\leq b-x_1$
and then
\begin{equation*} F_s(x_1,b)(\omega)= \frac{W(X_s+x_1)}{W(b)}\leq 1=F_s(x_2,b)(\omega). \end{equation*}
Lastly, if
$\omega\in\big\{\tau_{b-x_2}^+<\tau_{b-x_1}^+\leq s\big\}$
, we have
$F_s(x_1,b)(\omega)=1=F_s(x_2,b)(\omega)$
. Therefore, by integrating
$2F_s(x,b)-1$
with respect to
$\text{d}s\times\mathbb{P}$
, and taking the infimum upon all stopping times, we deduce that
$x\mapsto V_b(x)$
is non-decreasing.
(ii) and (iii). By taking
$\tau\equiv 0$
in the definition of
$V_b$
(see (5.1)), we deduce that
$V_b(x)\leq 0$
for all
$x\in \mathbb{R}$
. Moreover, for
$x\geq b$
, it is obvious that
$\inf_{\tau\in\mathcal{T}}\mathbb{E}_x\big[\big|g_{\tau_b^+}-\tau\big|\big] = \inf_{\tau\in\mathcal{T}}\mathbb{E}_x[\tau]=0$
, where the infimum is attained by
$\tau \equiv 0$
. It follows from Lemma 5.1 that the stopping time
$\tau \equiv 0$
is also optimal for (5.1), and then
$V_b(x)=0$
when
$x\geq b$
.
Next, we proceed to show that (5.4) holds. By (5.1),
\begin{align*} V_b(x) & = \inf_{\tau\in\mathcal{T}}\mathbb{E}_x\bigg[\int_0^{\tau}\bigg(2\left[\mathbf{1}_{\{\tau_{b}^+\leq s\}} + \mathbf{1}_{\{\tau_{b}^+>s\}}\frac{W(X_s)}{W(b)}\right] - 1\bigg)\,\text{d}s\bigg] \\ & = \inf_{\tau\in\mathcal{T}}\mathbb{E}_x\bigg[\int_0^{\tau}\bigg(\mathbf{1}_{\{\tau_{b}^+\leq s\}} + \mathbf{1}_{\{\tau_{b}^+>s\}}\bigg[2\frac{W(X_s)}{W(b)}-1\bigg]\bigg)\,\text{d}s\bigg] \\ & \geq \inf_{\tau\in\mathcal{T}}\mathbb{E}_x\bigg[\int_0^{\tau\wedge\tau_b^+}\bigg(2\frac{W(X_s)}{W(b)}-1\bigg)\, \text{d}s\bigg]. \end{align*}
On the other hand, from the definition of
$V_b(x)$
in (5.1), for an arbitrary stopping time
$\tau$
and any
$x\in \mathbb{R}$
,
\begin{equation*} V_b(x) \leq \mathbb{E}_x\bigg[\int_0^{\tau\wedge\tau_b^+}\bigg(2\bigg[\mathbf{1}_{\{\tau_{b}^+\leq s\}} + \mathbf{1}_{\{\tau_{b}^+>s\}}\frac{W(X_s)}{W(b)}\bigg]-1\bigg)\,\text{d}s\bigg] = \mathbb{E}_x\bigg[\int_0^{\tau\wedge\tau_b^+}\bigg(2\frac{W(X_s)}{W(b)}-1\bigg)\,\text{d}s\bigg]. \end{equation*}
Thus, we deduce that, for any
$x\in \mathbb{R}$
,
\begin{equation*} V_b(x) \leq \inf_{\tau\in\mathcal{T}}\mathbb{E}_x\bigg[\int_0^{\tau\wedge\tau_b^+}\bigg(2\frac{W(X_s)}{W(b)}-1\bigg)\, \text{d}s\bigg]. \end{equation*}
The claim then follows.
It remains to show that
$V_b(x)>{-}\infty$
for all
$x\in \mathbb{R}$
. For all
$s<\tau_b^+$
, because W is increasing and non-negative,
\begin{equation*} -1\leq 2 \frac{W(X_s)}{W(b)}-1\leq 1. \end{equation*}
Thus, by differentiating (2.7) and setting
$q=0$
, we deduce that, for all
$x\in \mathbb{R}$
and
$b>0$
,
\begin{align*} \mathbb{E}_x\bigg[{\sup}_{t\geq 0}\bigg|\int_0^{t\wedge\tau_b^+} \bigg(2\frac{W(X_s)}{W(b)}-1\bigg)\,\text{d}s\bigg|\bigg] \leq \mathbb{E}_x[\tau_b^+]=\frac{b-x}{\psi^{\prime}(0{+})}<\infty, \end{align*}
where we used that
$\psi(\Phi_q)=q$
so that
$\Phi^{\prime}_q=1/\psi^{\prime}(\Phi_{q})$
. Therefore,
$V_b(x)>{-}\infty$
for all
$x\in \mathbb{R}$
.
(iv). First, we show that
$x\mapsto V_b(x)$
is upper semicontinuous. Note that it suffices to take the infimum in the definition of
$V_b$
over stopping times with finite mean. Indeed, for any stopping time
$\tau$
with
$\mathbb{E}[\tau]=\infty$
, since
$\mathbb{E}[\tau_b^+]<\infty$
, we have that
\begin{equation*} \mathbb{E}_x\bigg[\int_0^{\tau}\bigg(\mathbf{1}_{\{\tau_{b}^+\leq s\}} + \mathbf{1}_{\{\tau_{b}^+>s\}}\bigg[2\frac{W(X_s)}{W(b)}-1\bigg]\bigg)\,\text{d}s\bigg] \geq -\mathbb{E}\big[\tau\wedge\tau_b^+\big] + \mathbb{E}\big[\tau-\big(\tau\wedge\tau_b^+\big)\big]=\infty. \end{equation*}
Due to the fact that the infimum of an upper semicontinuous function is upper semicontinuous, it suffices to show that, for each
$\tau \in \mathcal{T}$
with finite mean, the mapping
\begin{equation} x \mapsto \mathbb{E}\bigg[\int_0^{\tau}(2F_s(x,b)-1)\,\text{d}s\bigg] \end{equation}
is upper semicontinuous. Since
$x\mapsto F_s(x,b)$
is non-decreasing as shown in part (i), the upper semicontinuity follows if the mapping given in (5.5) is right-continuous. We then show the right continuity of (5.5). Note that the stochastic process
$\{\tau_t^+\colon t\geq0\}$
is a subordinator (see, e.g., [Reference Kyprianou17, Corollary 3.14]) and thus stochastically continuous. Indeed, the stochastic continuity of
$\{\tau_t^+,t\geq 0\}$
implies that, for any
$h>0$
,
$y>0$
, and
$\varepsilon>0$
,
$\lim_{h\downarrow 0}\mathbb{P}\big(\big|\tau_{y-h}^+-\tau_y^+\big|>\varepsilon\big)=0$
. In other words,
$\tau_{y-h}^+$
converges in probability to
$\tau_y^+$
when
$h\downarrow 0$
. Moreover, since the mapping
$h\mapsto \tau_{y-h}^+$
is decreasing, we deduce that the convergence holds almost surely. Thus, we obtain, by the right continuity of W,
\begin{align*} \lim_{h\downarrow 0}F_s(x+h,b) & = \lim_{h\downarrow 0}\bigg[\mathbf{1}_{\{\tau_{b-x-h}^+\leq s\}} + \mathbf{1}_{\{\tau_{b-x-h}^+>s\}}\frac{W(X_s+x+h)}{W(b)}\bigg] \\ & = \bigg[\mathbf{1}_{\{\tau_{b-x}^+\leq s\}} + \mathbf{1}_{\{\tau_{b-x}^+>s\}}\frac{W(X_s+x)}{W(b)}\bigg] = F_s(x,b) \end{align*}
almost surely. Hence, from the dominated convergence theorem we deduce that, for any stopping time
$\tau$
with finite mean,
\begin{equation*} \lim_{h \downarrow 0}\mathbb{E}\bigg[\int_0^{\tau}(2F_s(x+h,b)-1)\,\text{d}s\bigg] = \mathbb{E}\bigg[\int_0^{\tau}(2F_s(x,b)-1)\,\text{d}s\bigg]. \end{equation*}
Therefore, the mapping
$x\mapsto\mathbb{E}\big[\int_0^{\tau}(2F_s(x,b)-1)\,\text{d}s\big]$
is right-continuous and thus upper semicontinuous as claimed. Hence, we have that D is a closed set.
Next, we proceed to show that
$\tau_D$
is optimal for
$V_b$
. For
$a\in \mathbb{R}$
,
$y>0$
, and
$x \leq y$
, we define the stochastic process
$\{ L_t^{a,y,x}, t \geq 0\}$
as follows:
\begin{equation*} L_t^{a,y,x} = a + \int_0^t\mathbf{1}_{\{y\vee(\overline{X}_s+x)\lt b\}}\bigg(2\frac{W(X_s+x)}{W(b)}-1\bigg)\,\text{d}s, \end{equation*}
where
$\overline{X}_t=\sup_{0\leq r \leq t } X_r$
. For any
$t\geq 0$
, we simply write
$L_t=L_t^{0,0,0}$
. It can be seen that the family of probability measures
$\mathbb{P}_{a,y,x}=\text{Law}((L^{a,y,x},y\vee (\overline{X}+x), X+x)\mid\mathbb{P} )$
is Markovian (see [Reference Peskir and Shiryaev21, Section III.6]). Then we have that, for any
$a\in \mathbb{R}$
,
$y>0$
, and
$x\leq y$
,
\begin{align*} \widetilde{V}(a,y,x) \,:\!=\, \inf_{\tau\in\mathcal{T}}\mathbb{E}_{a,y,x}[L_{\tau}] & = \inf_{\tau\in\mathcal{T}}\mathbb{E}\big[L_{\tau}^{a,y,x}\big] \\ & = a + \inf_{\tau\in\mathcal{T}}\mathbb{E}\bigg[\int_0^\tau\mathbf{1}_{\{y\vee(\overline{X}_s+x)\lt b\}} \bigg(2\frac{W(X_s+x)}{W(b)}-1\bigg)\,\text{d}s\bigg] \\ & = a + \inf_{\tau\in\mathcal{T}}\mathbb{E}\bigg[\int_0^\tau\mathbf{1}_{\{y\lt b\}}\mathbf{1}_{\{\overline{X}_s+x\lt b\}} \bigg(2\frac{W(X_s+x)}{W(b)}-1\bigg)\,\text{d}s\bigg] \\ & = a + \mathbf{1}_{\{y\lt b\}}\inf_{\tau\in\mathcal{T}}\mathbb{E}_x\bigg[\int_0^\tau\mathbf{1}_{\{\overline{X}_s\lt b\}} \bigg(2\frac{W(X_s)}{W(b)}-1\bigg)\,\text{d}s\bigg] \\ & = a + \mathbf{1}_{\{y\lt b\}}V_b(x). \end{align*}
Since
$V_b(x)$
is non-positive and upper semicontinuous, it follows that
$\widetilde{V}$
is upper semicontinuous. From the general theory of optimal stopping (see, e.g., [Reference Peskir and Shiryaev21, Corollary 2.9]), we deduce that an optimal stopping time for
$\widetilde{V}$
, and hence also optimal for
$V_b$
, is given by
\begin{equation*} \inf\{t\geq 0\colon\widetilde{V}(L_t,\overline{X}_t,X_t)=L_t\} = \inf\{t\geq 0\colon L_t+\mathbf{1}_{\{\overline{X}_t\lt b\}}V_b(X_t)=L_t\} = \tau_D\wedge\tau_b^+ = \tau_D, \end{equation*}
where in the last equality we used that
$V_b(x)=0$
for all
$x\geq b$
, so then
$[b,\infty)\subset D$
. The proof is now complete.
Since
$V_b$
is a non-decreasing function and D is a closed set we deduce that
$D=[y_b^*,\infty)$
for some value
$y_b^*$
to be determined. Moreover, since W vanishes on
$({-}\infty,0)$
, we deduce from (5.4) that, for any
$x<0$
,
\begin{equation*} V_b(x) \leq \mathbb{E}_x\bigg[\int_0^{\tau_{0}^+}\bigg(2\frac{W(X_s)}{W(b)}-1\bigg)\,\text{d}s\bigg] = -\mathbb{E}_x[\tau_0^+]<0.\end{equation*}
This implies that
$y_b^*\geq 0$
, and then
$y_b^*\in [0,b]$
. Hence, we deduce that
$\tau_D\leq \tau_b^+$
and, from (5.4),
\begin{equation} V_b(x) = \inf_{ y\in[0,b]} V_{b,y}(x)=V_{b,y_b^*}(x)\end{equation}
for all
$x\in \mathbb{R}$
and
$b>0$
, where
\begin{equation*} V_{b,y}(x) \,:\!=\, \mathbb{E}_x\bigg[\int_0^{\tau_{y}^+}\bigg(2\frac{W(X_s)}{W(b)}-1\bigg)\,\text{d}s\bigg].\end{equation*}
The following lemma ensures that the convolution of W with W (and W ′) is sufficiently smooth. These facts will be helpful in the upcoming lemmas.
Lemma 5.3.
Let
$f\colon\mathbb{R}\mapsto\mathbb{R}^+$
be any non-negative function such that
$\int_0^{y}f(z)\,\text{d}z<\infty$
for any
$y\geq 0$
. Further assume that
$W\in C^{1}(0,\infty)$
and
$f\in C(0,\infty)$
. Then, the convolution function
$J(y)\,:\!=\,\int_{0}^{y}W(y-z)f(z)\,\text{d}z$
,
$y\geq 0$
, belongs to
$ C^{1}(0,\infty)$
and
\begin{equation*} \frac{\text{d}}{\text{d}y}J(y) = W(0)f(y) + \int_{0}^{y}W{^{\prime}}(y-z)f(z)\,\text{d}z. \end{equation*}
Proof. For any
$u\geq 0$
and
$y>0$
we define the auxiliary function
\begin{equation*} T(u,y)\,:\!=\,\int_{0}^{y}W{^{\prime}}(y-z+u)f(z)\,\text{d}z. \end{equation*}
We first prove that T is continuous in each argument. That is, for fixed
$u\geq 0$
, the mapping
$y\mapsto T(u,y)$
is continuous on
$(0,\infty)$
and, for fixed
$y>0$
, the mapping
$u\mapsto T(u,y)$
is continuous on
$[0,\infty)$
. For arbitrarily fixed
$y>0$
and
$u\geq 0$
, let
$\delta \gt 0$
and
$\varepsilon>0$
be such that
$\delta\lt y$
and
$u<\varepsilon$
. Then, for any
$z\in (0,\delta]$
,
\begin{align*} W{^{\prime}}(y-z+u)f(z) & \leq f(z)\,{{\sup}_{v\in[y-\delta+u,y+u]}}W^{\prime}(v) \\ & \leq f(z)\,{\sup}_{v\in[y-\delta,y+\varepsilon]}W^{\prime}(v) = C_1f(z), \end{align*}
where
$ C_1\,:\!=\,\sup_{u\in [y-\delta, y+\varepsilon]}W{^{\prime}}(u)$
. It follows from the continuity of W
′ on
$[y-\delta, y+\varepsilon]$
that
$0\lt C_1<\infty$
. On the other hand, for any
$z\in (\delta,y]$
we see that
\begin{equation*} W{^{\prime}}(y-z+u)f(z) \leq W{^{\prime}}(y-z+u) \,{\sup}_{v \in [\delta,y] } f(v) = C_2 W{^{\prime}}(y-z+u), \end{equation*}
where
$ C_2\,:\!=\,\sup_{v \in [\delta,y] } f(v)$
and we used that
$W^{\prime}(x)>0$
for all
$x>0$
. Since f is a non-negative and continuous function in
$(0,\infty)$
,
$0\lt C_2<\infty$
. Hence, since W
′ and f are non-negative we obtain that, for any
$z\in (0,y)$
,
\begin{equation*} 0\leq W{^{\prime}}(y-z+u)f(z) \leq C_1f(z)+C_2 W{^{\prime}}(y-z+u). \end{equation*}
Moreover,
\begin{equation*} \int_0^{y}[C_1f(z)+C_2 W{^{\prime}}(y-z+u)]\,\text{d}z = C_1\int_0^{y}f(z)\,\text{d}z + C_2[W(y+u)-W(u)] < \infty. \end{equation*}
Therefore, since W
′ is continuous on
$(0,\infty)$
, we deduce from the extended dominated convergence theorem that T is continuous in each argument.
Next, for any
$y>0$
, we prove
\begin{equation*} \lim_{h\downarrow0}\frac{1}{h} [J(y+h)-J(y)]=W(0)f(y)+\int_{0}^{y}W{^{\prime}}(y-z)f(z)\,\text{d}z. \end{equation*}
For any
$h>0$
and
$y>0$
, it follows that
\begin{align} & \frac{1}{h}[J(y+h)-J(y)] \nonumber \\ & \qquad = \frac{1}{h}\bigg(\int_{0}^{y+h}W(y+h-z)f(z)\,\text{d}z - \int_{0}^{y}W(y-z)f(z)\,\text{d}z\bigg) \nonumber \\ & \qquad = \frac{1}{h}\bigg(\int_{0}^{y}[W(y+h-z)-W(y-z)]f(z)\,\text{d}z + \int_{y}^{y+h}W(y+h-z)f(z)\,\text{d}z\bigg). \end{align}
For the first term on the right-hand side we see from Fubini’s theorem that
\begin{align*} \frac{1}{h}\int_{0}^{y}[W(y+h-z)-W(y-z)]f(z)\,\text{d}z & = \frac{1}{h}\int_{0}^{y}\int_{0}^{h}W^{\prime}(y-z+u)f(z)\,\text{d}u\,\text{d}z \\ & = \frac{1}{h}\int_{0}^{h} T(u,y)\,\text{d}u. \end{align*}
Therefore, by the fundamental theorem of calculus we see that, for any
$y>0$
,
\begin{equation*} \lim_{h\downarrow0}\frac{1}{h}\int_{0}^{y}[W(y+h-z)-W(y-z)]f(z)\,\text{d}z = T(0,y) = \int_0^y W^{\prime}(y-z)f(z)\,\text{d}z. \end{equation*}
For the second term on the right-hand side of (5.7), since W is strictly increasing on
$[0,\infty)$
, we have
\begin{align*} \frac{1}{h}\int_{y}^{y+h}W(y+h-z)f(z)\,\text{d}z & \leq \frac{1}{h}W(h)\int_{y}^{y+h}f(z)\,\text{d}z, \\ \frac{1}{h}\int_{y}^{y+h}W(y+h-z)f(z)\,\text{d}z & \geq W(0)\frac{1}{h}\int_{y}^{y+h}f(z)\,\text{d}z. \end{align*}
Thus, we can deduce from the fact that f and W are continuous on
$(0,\infty)$
and the fundamental theorem of calculus that
\begin{equation*} \lim_{h\downarrow0}\frac{1}{h}\int_{y}^{y+h}W(y+h-z)f(z)\,\text{d}z = W(0)f(y). \end{equation*}
Therefore, we conclude that, for any
$y>0$
,
\begin{equation*} \lim_{h\downarrow0}\frac{1}{h}[J(y+h)-J(y)] = W(0)f(y) + \int_{0}^{y}W{^{\prime}}(y-z)f(z)\,\text{d}z. \end{equation*}
Using similar arguments we can show that, for any
$y>0$
,
\begin{equation*} \lim_{h\downarrow0}\frac{1}{h}[J(y)-J(y-h)] = f(y)W(0) + \int_{0}^{y}W{^{\prime}}(y-z)f(z)\,\text{d}z. \end{equation*}
Finally, the continuity of
$({\text{d}}/{\text{d}y})J(y)$
on
$(0,\infty)$
follows by the continuity of f and T(0, y).
The next lemma provides an analytical expression for the function
$V_{b,y}$
in terms of the scale function W. We recall that
$F(x)=\psi^{\prime}(0{+})W(x)$
is the cumulative distribution function of
$-\underline{X}_{\infty}$
.
Lemma 5.4.
For any
$b>0$
,
$y\geq 0$
, and
$x\leq y$
,
\begin{equation} V_{b,y}(x)=H_b(y)-H_b(x), \end{equation}
where
$H_b(y)=({2}/{W(b)})\int_{0}^{y}W(z)W(y-z)\,\text{d}z-({y}/{\psi^{\prime}(0{+})})$
. Moreover,
$V_b(x)=V_{b,y_b^*}(x)$
, where
$y_b^*$
is given by
\begin{equation} y_b^*=\inf\bigg\{y\in[0,b]\colon\int_{[0,y]}F(y-z)\,F(\text{d}z) \geq \frac{F(b)}{2}\bigg\}. \end{equation}
Proof. Fix
$y\geq 0$
. For any
$x\leq y$
, it follows from (2.10) that
\begin{align*} V_{b,y}(x) & = \mathbb{E}_{x}\bigg[\int_{0}^{\tau_{y}^{+}}\bigg( 2\frac{W(X_{s})}{W(b)}-1\bigg)\,\text{d}s\bigg] \\ & = \int_{{-}\infty}^{y}2\frac{W(z)}{W(b)} \int_{0}^{\infty}\mathbb{P}_{x}(X_{s}\in \text{d}z,s<\tau _{y}^{+})\,\text{d}s - \mathbb{E}_{x}[\tau _{y}^{+}] \\ & = \frac{2}{W(b)}\int_{{-}\infty}^{y}W(z)[W(y-z)-W(x-z)]\,\text{d}z - \frac{y-x}{\psi {\prime}(0{+})} = H_{b}(y)-H_{b}(x), \end{align*}
where in the last equality we used that W vanishes on
$({-}\infty ,0)$
.
Let
$y_{b}^{\ast}$
be such that
$\inf_{y\in [0,b]}H_{b}(y)=H_{b}(y_{b}^{\ast})$
. We then show that
$y_{b}^{\ast }$
is given by (5.9). For
$y\geq 0$
, by Lemma 5.3, we have
\begin{align*} {H_{b}^{\prime}}(y) & = \frac{2}{W(b)}W(y)W(0)+\frac{2}{W(b)}\int_{0}^{y}W(z){W^{\prime}}(y-z)\,\text{d}z - \frac{1}{\psi{\prime}(0{+})} \\ & = \frac{2}{W(b)}W(y)W(0)+\frac{2}{W(b)}\int_{0}^{y}W(y-z){W^{\prime}}(z)\,\text{d}z - \frac{1}{\psi{\prime}(0{+})}. \end{align*}
Since W is non-negative and strictly increasing, we deduce that
$H_{b}^{\prime }(y)$
is strictly increasing. Thus, the function
$H_{b}(y)$
attains its infimum on [0, b] at the point
\begin{align*} \inf\bigg\{y&\in[0,b]\colon\frac{2}{W(b)}W(y)W(0) + \frac{2}{W(b)}\int_{0}^{y}W(y-z){W^{\prime}}(z)\,\text{d}z - \frac{1}{\psi{\prime}(0{+})} \geq 0\bigg\} \\ & = \inf\bigg\{y\in[0,b]\colon\int_{[0,y]}F(y-z)\,F(\text{d}z) \geq \frac{F(b)}{2}\bigg\} = y_{b}^{\ast}, \end{align*}
where we used
$F(z)=\psi ^{\prime }(0{+})W(z)$
for all
$z\geq 0$
, and that the measure
$F(\text{d}z)=\psi{\prime}(0{+})\,W(\text{d}z)$
may have an atom at zero (when X is of bounded variation). Since
$y_b^*$
is defined within [0, b], we follow the convention that
$\inf\emptyset=b$
.
It remains to verify that
$V_{b}(x)=V_{b,y_{b}^{\ast }}(x)$
. Since
$V_{b,y}(x)=0$
for
$x>y$
, we obtain from (5.6) and (5.8) that
\begin{align*} V_{b}(x) = \inf_{y\in[0,b]}V_{b,y}(x) = 0\wedge\inf_{y\in[x,b]}V_{b,y}(x) & = 0\wedge\Big(\inf_{y\in[x,b]}H_{b}(y)-H_{b}(x)\Big) \\ & = \inf_{y\in[x,b]}H_{b}(y)-H_{b}(x). \end{align*}
If
$x\leq y_{b}^{\ast }$
, it is clear that
$V_{b}(x)=H_{b}(y_{b}^{\ast})-H_{b}(x)=V_{b,y_{b}^{\ast }}(x)$
. If
$x>y_{b}^{\ast }$
, we have
$V_{b,y_{b}^{\ast }}(x)=0$
. Further, since
$H_{b}(y)$
is strictly increasing for
$y\in[y_{b}^{\ast },b]$
and
$x>y_{b}^{\ast }$
, we have
$\inf_{y\in[x,b]}H_{b}(y)=H_{b}(x)$
and thus
$V_{b}(x)=0$
.
Before we give a more explicit characterization of the optimal stopping boundary
$y_b^*$
, we introduce some auxiliary results. For
$a\geq 0$
, we define
\begin{equation*} K(a)=\int_{[0,a]}F(a-z)\,F(\text{d}z) - \frac{F(a)}{2}.\end{equation*}
Lemma 5.5. We have the following results for the auxiliary function K(a):
-
(i) If
$F(0)\geq \frac12$
,
$K(0)\geq 0$
and
$K(a)>0$
for all
$a> 0$
. -
(ii) If
$F(0)<\frac12$
, the equation
$K(a)=0$
has a unique solution
$b_0\in (0,\infty)$
with
$K(a)<0$
for all
$a\in [0,b_0)$
and
$K(a)> 0$
for all
$a\in (b_0,\infty)$
.
Proof. First, since both
$y\mapsto \int_{[0,y]}F(y-z)\,F(\text{d}z)$
and F are cumulative distribution functions, it can be seen that
$\lim_{a\rightarrow\infty}K(a)=\frac12$
. Hence, there exists
$N>0$
sufficiently large that
$[N,\infty)\subset\{a\geq 0\colon K(a)\geq 0\}$
.
From (2.4), we deduce that
${F^{\prime}}(x)/F(x)$
is non-increasing. Therefore, for any
$a>0$
, it follows from Lemma 5.3 that
\begin{align*} {K^{\prime}}(a) & = 2F(0){F^{\prime}}(a) + \int_{0}^{a}{F^{\prime}}(a-z){F^{\prime}}(z)\,\text{d}z - \frac{{F^{\prime}}(a)}{2} \\ & = 2F(0){F^{\prime}}(a) + \int_{0}^{a}\frac{{F^{\prime}}(a-z)}{F(a-z)}F(a-z){F^{\prime}}(z)\,\text{d}z - \frac{{F^{\prime}}(a)}{2} \\ & \geq 2F(0){F^{\prime}}(a) + \frac{{F^{\prime}}(a)}{F(a)}\int_{0}^{a}F(a-z){F^{\prime}}(z)\,\text{d}z - \frac{{F^{\prime}}(a)}{2} \\ & = \frac{{F^{\prime}}(a)}{F(a)}[F(a)F(0)+K(a)]. \end{align*}
In fact, this inequality is strict when X is of unbounded variation. If not, we have
\begin{equation*} \int_{0}^{a}\frac{{F^{\prime}}(a-z)}{F(a-z)}F(a-z){F^{\prime}}(z)\,\text{d}z = \frac{{F^{\prime}}(a)}{F(a)}\int_{0}^{a}F(a-z){F^{\prime}}(z)\,\text{d}z, \end{equation*}
for some
$a\geq 0$
. Since F and
${F^{\prime}}$
are strictly positive on
$(0,\infty)$
, we deduce that
${F^{\prime}}(y)/F(y)=C$
for some
$C\geq 0$
and all
$y\in (0,a)$
. This implies that
$F(y)=B\mathrm{e}^{Cy}$
for some
$B\geq 0$
and any
$y\in(0,a)$
. Using the fact that X is of unbounded variation, so then
$F(0{+})=\psi ^{\prime }(0{+})W(0{+})=0$
, we deduce that
$B=0$
. This contradicts the fact that F is strictly increasing. Hence, when X is of unbounded variation, we have
\begin{equation} {K^{\prime}}(a) > \frac{{F^{\prime}}(a)}{F(a)}K(a). \end{equation}
Since
$F(0)>0$
when X is of bounded variation, the strict inequality (5.10) holds regardless of the path variation of X.
Further, it is easy to show from (5.10), the continuity of K and
${K^{\prime}}$
, and the behaviour of K near 0 and at infinity that there exists a value
$b_{0}\geq 0$
such that
$\{a\geq0\colon K(a)\geq0\}=[b_{0},\infty)$
. Moreover,
$K(a)<0$
for all
$a\in[0,b_{0})$
, and
$K(a)> 0$
for all
$a\in(b_{0},\infty)$
. In particular, if
$F(0)\geq\frac12$
,
$K(0)=F(0)^{2}-{F(0)}/{2}=F(0)\big(F(0)-\frac{1}{2}\big) \geq 0$
, so that
$b_{0}=0$
. Otherwise, if
$F(0)<\frac12$
, by the continuity of K and (5.10), we deduce that
$b_{0}>0$
and
$b_{0}$
is the unique solution to the equation
$K(a)=0$
.
The following lemma provides a more explicit characterization of the optimal stopping boundary
$y_b^*$
.
Lemma 5.6.
-
(i) If
$F(0)\geq\sqrt{\frac12}$
,
$y_b^*=0$
for all
$b>0$
. -
(ii) If
$\frac12\leq F(0)<\sqrt{\frac12}$
, then for
$b\leq F^{-1}(2F(0)^2)$
,
$y^*_b=0$
. For
$b> F^{-1}(2F(0)^2)$
, the value
$y_b^*\in (0,b)$
is the unique solution to
$\int_{[0,y]}F(y-z)\,F(\text{d}z) - \frac12{F(b)} = 0$
. -
(iii) If
$F(0)<\frac12$
, let
$b_0>0$
be the unique solution to
$\int_{[0,b]}F(b-z)\,F(\text{d}z) = \frac12{F(b)}$
. For
$b\leq b_0$
,
$y^*_b=b$
. For
$b>b_0$
,
$y_b^*\in (0,b)$
is the unique solution to
\begin{equation*} \int_{[0,y]}F(y-z)\,F(\text{d}z) - \frac{F(b)}{2} = 0. \end{equation*}
Proof. We define the function
$P_b(y) = \int_{[0,y]}F(y-z)\,F(\text{d}z) - \frac12{F(b)}$
for
$y\geq 0$
and
$b> 0$
. Hence,
$P_b(b)=K(b)$
and
$y_b^*=\inf\{y\in[0,b]\colon P_b(y)\geq 0\}$
.
-
(i). If
$F(0)\geq \sqrt{\frac12}$
,
$P_b(0)= F(0)^2-\frac12{F(b)} \geq \frac12({1-F(b)})\geq 0$
for all
$b> 0$
. Since
$P_b$
is strictly increasing, and from the definition of
$y_b^*$
, we deduce that
$y_b^*=0$
for any
$b> 0$
. -
(ii). Suppose that
$\frac12\leq F(0)<\sqrt{\frac12}$
. From Lemma 5.5 we know that
$K(a)> 0$
for all
$a> 0$
. This implies that
$y_b^*<b$
for all
$b>0$
. Note that
$F^{-1}(2F(0)^2)$
is well defined since
$2F(0)^2\geq F(0)$
. For
$b\leq F^{-1}(2F(0)^2)$
, for any
$y\in (0,b]$
,
$P_b(y)> P_b(0)=F(0)^2-\frac12{F(b)}\geq 0$
. Thus, we deduce that
$y^*_b=0$
. On the other hand, for
$b> F^{-1}(2F(0)^2)$
,
$P_b(0)< 0$
. This, together with
$P_b(b)=K(b)>0$
and
$P_b(y)$
being strictly increasing on
$(0,\infty)$
, mean we can deduce that
$y_b^*$
is the unique solution to the equation
$P_b(y)=0$
. -
(iii). Suppose that
$F(0)<\frac12$
. From Lemma 5.5, we know that the value
$b_0$
is such that
$K(a)\leq 0$
for all
$a\leq b_0$
and
$K(a)>0$
for all
$a>b_0$
. Hence, for
$b\leq b_0$
,
$P_b(y)\leq P_b(b)=K(b)\leq 0$
for all
$y\leq b$
. Thus,
$y_b^*=b$
. Otherwise, for
$b>b_0$
, and
\begin{equation*} P_b(0)=F(0)^2-\frac{F(b)}{2}<\frac{F(0)-F(b)}{2}\leq 0, \end{equation*}
$P_b(b)=K(b)>0$
. Thus, the value
$y_b^*$
is the unique solution to the equation
$P_b(y)=0$
.
Acknowledgements
We would like to thank two anonymous referees for their helpful comments and suggestions.
Funding information
Xiaofeng Yang is supported by the China Scholarship Council (No. CSC202206370081) and Hunan Provincial Innovation Foundation for Postgraduate (No. CX20220247). Bin Li gratefully acknowledges support from the Natural Sciences and Engineering Research Council of Canada (No. 04338).
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.
