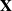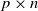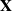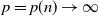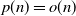1. Introduction
1.1. Background
For any two positive integers
![]() $p,n\geq2$
, let us define a
$p,n\geq2$
, let us define a
![]() $p\times n$
random matrix
$p\times n$
random matrix
![]() $\mathbf{X}_{p\times n}$
whose entries
$\mathbf{X}_{p\times n}$
whose entries
![]() $X_{ij}$
,
$X_{ij}$
,
![]() $1\leq i\leq p$
,
$1\leq i\leq p$
,
![]() $1\leq j\leq n$
, are independent and identically distributed (i.i.d.) real random variables satisfying
$1\leq j\leq n$
, are independent and identically distributed (i.i.d.) real random variables satisfying
where
![]() $\mathbb{E}$
denotes the expectation and
$\mathbb{E}$
denotes the expectation and
![]() $\mathbb{V}$
the variance. Then the 2-norm condition number k(p,n) of
$\mathbb{V}$
the variance. Then the 2-norm condition number k(p,n) of
![]() $\mathbf{X}_{p\times n}$
is defined as
$\mathbf{X}_{p\times n}$
is defined as
![]() $k(p,n)=\sigma_{\max}/\sigma_{\min}$
, with
$k(p,n)=\sigma_{\max}/\sigma_{\min}$
, with
![]() $\sigma_{\max}$
and
$\sigma_{\max}$
and
![]() $\sigma_{\min}$
denoting the maximal and minimal singular values of
$\sigma_{\min}$
denoting the maximal and minimal singular values of
![]() $\mathbf{X}_{p\times n}$
. The name ‘2-norm’ comes from the fact that the maximal singular value
$\mathbf{X}_{p\times n}$
. The name ‘2-norm’ comes from the fact that the maximal singular value
![]() $\sigma_{\max}$
coincides with the norm
$\sigma_{\max}$
coincides with the norm
![]() $||\mathbf{X}||_2=\sup\big\{||\mathbf{X}x||_2\;:\;x\in \mathbb{R}^n \text{ with }||x||_2=1\big\}$
, where the 2-norm of a vector
$||\mathbf{X}||_2=\sup\big\{||\mathbf{X}x||_2\;:\;x\in \mathbb{R}^n \text{ with }||x||_2=1\big\}$
, where the 2-norm of a vector
![]() $x\in \mathbb{R}^n$
is the Euclidean norm defined as
$x\in \mathbb{R}^n$
is the Euclidean norm defined as
![]() $||x||_2=\big(\sum_{i=1}^nx_i^2\big)^{1/2}$
(for simplicity,
$||x||_2=\big(\sum_{i=1}^nx_i^2\big)^{1/2}$
(for simplicity,
![]() $||x||_2$
will be written as
$||x||_2$
will be written as
![]() $||x||$
). In numerical linear algebra and the theory of probability in Banach spaces, condition numbers play an important role (cf. [Reference Rudelson17, Reference Trefethen and Bau23]). In statistics, if we define a square matrix
$||x||$
). In numerical linear algebra and the theory of probability in Banach spaces, condition numbers play an important role (cf. [Reference Rudelson17, Reference Trefethen and Bau23]). In statistics, if we define a square matrix
![]() $\mathbf{W}_{p\times p}:=\mathbf{X}\mathbf{X}^\top/n$
, then
$\mathbf{W}_{p\times p}:=\mathbf{X}\mathbf{X}^\top/n$
, then
![]() $\mathbf{W}$
is usually called a sample covariance matrix in the framework of estimating the population covariance matrix given vanishing population mean, where p denotes the dimension of the population and n is the sample size. In this setting the condition number has the equivalent form
$\mathbf{W}$
is usually called a sample covariance matrix in the framework of estimating the population covariance matrix given vanishing population mean, where p denotes the dimension of the population and n is the sample size. In this setting the condition number has the equivalent form
![]() $k(p,n)=\sigma_{\max}/\sigma_{\min}=(\lambda_{\max}/\lambda_{\min})^{1/2}$
, with
$k(p,n)=\sigma_{\max}/\sigma_{\min}=(\lambda_{\max}/\lambda_{\min})^{1/2}$
, with
![]() $\lambda_{\max}$
and
$\lambda_{\max}$
and
![]() $\lambda_{\min}$
denoting the maximal and minimal eigenvalues of
$\lambda_{\min}$
denoting the maximal and minimal eigenvalues of
![]() $\mathbf{W}_{p\times p}$
.
$\mathbf{W}_{p\times p}$
.
One specific application of using condition numbers in statistics, which is also our main motivation, is to test the null hypothesis that the population covariance is a scalar multiple of identity. The union-intersection test method in [Reference Srivastava and Khatri20, Section 7.4] suggests that the null hypothesis is rejected for large values of the condition number. To achieve this, we often need to study the null distribution of the sample condition number. For instance, in order to find the corresponding p-value, it is necessary to investigate the probability
![]() $\mathbb{P}(k(p,n)\geq c)$
with
$\mathbb{P}(k(p,n)\geq c)$
with
![]() $c\geq1$
. Unfortunately, so far in the literature there is no efficient way to evaluate such a probability. In Section 5 we present an easy and efficient way to control such a probability in order to feasibly perform the hypotheses test using the union-intersection test method. Another interesting aspect of condition numbers is that they have one=to-one correspondence with the so-called first anti-eigenvalues defined as
$c\geq1$
. Unfortunately, so far in the literature there is no efficient way to evaluate such a probability. In Section 5 we present an easy and efficient way to control such a probability in order to feasibly perform the hypotheses test using the union-intersection test method. Another interesting aspect of condition numbers is that they have one=to-one correspondence with the so-called first anti-eigenvalues defined as
![]() $2(\lambda_{\max}\lambda_{\min})^{1/2}/(\lambda_{\max}+\lambda_{\min})$
, which can be found in many applications (cf. [Reference Gustafson9]). Since the condition number k(p,n) of
$2(\lambda_{\max}\lambda_{\min})^{1/2}/(\lambda_{\max}+\lambda_{\min})$
, which can be found in many applications (cf. [Reference Gustafson9]). Since the condition number k(p,n) of
![]() $\,\mathbf{X}_{p\times n}$
is invariant under matrix transpose, we shall in this paper always assume that
$\,\mathbf{X}_{p\times n}$
is invariant under matrix transpose, we shall in this paper always assume that
![]() $2\leq p\leq n$
. When the entries
$2\leq p\leq n$
. When the entries
![]() $X_{ij}$
are i.i.d. real standard normal random variables,
$X_{ij}$
are i.i.d. real standard normal random variables,
![]() $\mathbf{W}_{p\times p}$
is called a real central Wishart matrix and denoted as
$\mathbf{W}_{p\times p}$
is called a real central Wishart matrix and denoted as
![]() $W_p(n, n^{-1}\mathbf{I})$
, with
$W_p(n, n^{-1}\mathbf{I})$
, with
![]() $\mathbf{I}=\mathbf{I}_{p\times p}$
being an identity matrix.
$\mathbf{I}=\mathbf{I}_{p\times p}$
being an identity matrix.
From the matrix size point of view, the various studies of condition numbers of random matrices in the literature can be classified into two categories: for rectangular random matrices (i.e.
![]() $p<n$
; see, for example, [Reference Anderson and Wells1, Reference Chen and Dongarra4, Reference Edelman and Sutton7, Reference Litvak, Pajor, Rudelson and Tomczak-Jaegermann13]) and for square random matrices (i.e.
$p<n$
; see, for example, [Reference Anderson and Wells1, Reference Chen and Dongarra4, Reference Edelman and Sutton7, Reference Litvak, Pajor, Rudelson and Tomczak-Jaegermann13]) and for square random matrices (i.e.
![]() $p=n$
; see, for example, [Reference Edelman6, Reference Rudelson17, Reference Tao and Vu21]). Results concerning lower/upper bounds of the minimal singular value
$p=n$
; see, for example, [Reference Edelman6, Reference Rudelson17, Reference Tao and Vu21]). Results concerning lower/upper bounds of the minimal singular value
![]() $\sigma_{\min}$
can be found, for instance, in [Reference Litvak, Tikhomirov, Tomczak-Jaegermann, Klartag and Milman14, Reference Rudelson17–Reference Rudelson and Vershynin19], while results on limiting distributions of
$\sigma_{\min}$
can be found, for instance, in [Reference Litvak, Tikhomirov, Tomczak-Jaegermann, Klartag and Milman14, Reference Rudelson17–Reference Rudelson and Vershynin19], while results on limiting distributions of
![]() $\sigma_{\min}$
and k(p,n) as n tends to infinity are contained in [6, Section 3] and [Reference Tao and Vu22], among others. From the distribution (of entries) point of view, we can also classify the results on condition numbers of random matrices in two categories: entries being standard normal random variables (see, for example, [Reference Anderson and Wells1, Reference Chen and Dongarra4, Reference Edelman6, Reference Edelman and Sutton7]) and entries being other (especially discrete) random variables (see, for example, [Reference Litvak, Pajor, Rudelson and Tomczak-Jaegermann13, Reference Rudelson17, Reference Tao and Vu21]). In general it is easier to study random matrices with standard normal entries (i.e. Wishart matrices
$\sigma_{\min}$
and k(p,n) as n tends to infinity are contained in [6, Section 3] and [Reference Tao and Vu22], among others. From the distribution (of entries) point of view, we can also classify the results on condition numbers of random matrices in two categories: entries being standard normal random variables (see, for example, [Reference Anderson and Wells1, Reference Chen and Dongarra4, Reference Edelman6, Reference Edelman and Sutton7]) and entries being other (especially discrete) random variables (see, for example, [Reference Litvak, Pajor, Rudelson and Tomczak-Jaegermann13, Reference Rudelson17, Reference Tao and Vu21]). In general it is easier to study random matrices with standard normal entries (i.e. Wishart matrices
![]() $W_p(n, n^{-1}\mathbf{I})$
) since there is an explicit (even though involved to some extent) joint distribution of the eigenvalues of
$W_p(n, n^{-1}\mathbf{I})$
) since there is an explicit (even though involved to some extent) joint distribution of the eigenvalues of
![]() $W_p(n, n^{-1}\mathbf{I})$
, and it is not available for discrete random matrices. Also note that if the distribution of the entries is sub-Gaussian (see Section 1.2 for a detailed definition; cf. [Reference Litvak, Pajor, Rudelson and Tomczak-Jaegermann13, Reference Rudelson17, Reference Vershynin24]), then all its moments, tail estimates, and moment-generating function can be controlled explicitly, which are in turn used to derive results on condition numbers.
$W_p(n, n^{-1}\mathbf{I})$
, and it is not available for discrete random matrices. Also note that if the distribution of the entries is sub-Gaussian (see Section 1.2 for a detailed definition; cf. [Reference Litvak, Pajor, Rudelson and Tomczak-Jaegermann13, Reference Rudelson17, Reference Vershynin24]), then all its moments, tail estimates, and moment-generating function can be controlled explicitly, which are in turn used to derive results on condition numbers.
The aim of this paper is to investigate limiting behaviors of the condition number k(p,n) in terms of large deviations for large n (and possibly for large p at the same time as well), for rectangular random matrices (i.e.
![]() $p<n$
) and for entries being i.i.d. sub-Gaussian random variables satisfying the conditions in (1). It turns out that such investigation heavily depends on the relation between p and n, and in this paper we will only focus on the case when p is fixed or
$p<n$
) and for entries being i.i.d. sub-Gaussian random variables satisfying the conditions in (1). It turns out that such investigation heavily depends on the relation between p and n, and in this paper we will only focus on the case when p is fixed or
![]() $p=p(n)=o(n)$
as
$p=p(n)=o(n)$
as
![]() $n\rightarrow\infty$
. Despite being in the framework of such a classical setting (i.e. one dimension of a random matrix is fixed or negligible with respect to the other one), large deviations of k(p,n) have not appeared in the literature so far. Throughout the paper
$n\rightarrow\infty$
. Despite being in the framework of such a classical setting (i.e. one dimension of a random matrix is fixed or negligible with respect to the other one), large deviations of k(p,n) have not appeared in the literature so far. Throughout the paper
![]() $f(n)=o(n)$
means
$f(n)=o(n)$
means
![]() $\lim_{n\rightarrow\infty}f(n)/n=0$
, and
$\lim_{n\rightarrow\infty}f(n)/n=0$
, and
![]() $f(n)=O(n)$
stands for
$f(n)=O(n)$
stands for
![]() $0<c_1\leq f(n)/n\leq c_2<\infty$
for all n and some positive constants
$0<c_1\leq f(n)/n\leq c_2<\infty$
for all n and some positive constants
![]() $c_1$
and
$c_1$
and
![]() $c_2$
independent of n.
$c_2$
independent of n.
Laws of large numbers of the extreme eigenvalues
![]() $\lambda_{\max}$
and
$\lambda_{\max}$
and
![]() $\lambda_{\min}$
of the sample covariance matrices
$\lambda_{\min}$
of the sample covariance matrices
![]() $\mathbf{W}_{p\times p}$
have been obtained in the forms
$\mathbf{W}_{p\times p}$
have been obtained in the forms
![]() $\lambda_{\max}\rightarrow(1+\kappa^{1/2})^2$
and
$\lambda_{\max}\rightarrow(1+\kappa^{1/2})^2$
and
![]() $\lambda_{\min}\rightarrow(1-\kappa^{1/2})^2$
in probability under the assumption
$\lambda_{\min}\rightarrow(1-\kappa^{1/2})^2$
in probability under the assumption
![]() $p/n\rightarrow \kappa\in [0,1]$
as
$p/n\rightarrow \kappa\in [0,1]$
as
![]() $n\rightarrow\infty$
(see, for instance, [Reference Edelman6, Lemma 4.1] for Wishart matrices and [Reference Bai, Silverstein and Yin2, Reference Bai and Yin3] for general matrices). Therefore, when p is either fixed or
$n\rightarrow\infty$
(see, for instance, [Reference Edelman6, Lemma 4.1] for Wishart matrices and [Reference Bai, Silverstein and Yin2, Reference Bai and Yin3] for general matrices). Therefore, when p is either fixed or
![]() $p(n)=o(n)$
(i.e.
$p(n)=o(n)$
(i.e.
![]() $\kappa=0$
), it always holds that
$\kappa=0$
), it always holds that
![]() $k(p,n)\rightarrow1$
in probability. Then, a large-deviation probability of k(p,n) takes the form
$k(p,n)\rightarrow1$
in probability. Then, a large-deviation probability of k(p,n) takes the form
![]() $\mathbb{P}(k(p,n)\geq c)$
with
$\mathbb{P}(k(p,n)\geq c)$
with
![]() $c \geq 1$
. The specific aim of the paper is to study the limiting behaviors of
$c \geq 1$
. The specific aim of the paper is to study the limiting behaviors of
![]() $\mathbb{P}(k(p,n)\geq c)$
for large n.
$\mathbb{P}(k(p,n)\geq c)$
for large n.
The asymptotics of
![]() $\mathbb{P}(k(p,n)\geq c)$
with
$\mathbb{P}(k(p,n)\geq c)$
with
![]() $c\geq1$
as
$c\geq1$
as
![]() $n\rightarrow\infty$
cannot be readily obtained from the existing literature. To see this, we first note that for Wishart matrices an exact expression of the density function of the condition number k(p,n) was derived in [Reference Anderson and Wells1] for all
$n\rightarrow\infty$
cannot be readily obtained from the existing literature. To see this, we first note that for Wishart matrices an exact expression of the density function of the condition number k(p,n) was derived in [Reference Anderson and Wells1] for all
![]() $2\leq p\leq n$
. However, some complicated zonal polynomials appeared in the density function, which prevents us obtaining any useful asymptotics as
$2\leq p\leq n$
. However, some complicated zonal polynomials appeared in the density function, which prevents us obtaining any useful asymptotics as
![]() $n\rightarrow\infty$
. In [Reference Chen and Dongarra4, Reference Edelman and Sutton7], lower and upper bounds of
$n\rightarrow\infty$
. In [Reference Chen and Dongarra4, Reference Edelman and Sutton7], lower and upper bounds of
![]() $\mathbb{P}(k(p,n)\geq c)$
were given (again only for Wishart matrices) for the purpose of studying tails of the condition number (i.e. for large c). Despite the tight bounds as
$\mathbb{P}(k(p,n)\geq c)$
were given (again only for Wishart matrices) for the purpose of studying tails of the condition number (i.e. for large c). Despite the tight bounds as
![]() $c\rightarrow\infty$
(with fixed p and n), the asymptotics with fixed c as
$c\rightarrow\infty$
(with fixed p and n), the asymptotics with fixed c as
![]() $n\rightarrow\infty$
turn out to be very inaccurate. For general sample covariance matrices, large-deviation asymptotics for
$n\rightarrow\infty$
turn out to be very inaccurate. For general sample covariance matrices, large-deviation asymptotics for
![]() $\lambda_{\max}$
and
$\lambda_{\max}$
and
![]() $\lambda_{\min}$
(individually and jointly) as
$\lambda_{\min}$
(individually and jointly) as
![]() $n\rightarrow\infty$
were established in [Reference Fey, van der Hofstad and Klok8]. But the condition number cannot be precisely controlled by
$n\rightarrow\infty$
were established in [Reference Fey, van der Hofstad and Klok8]. But the condition number cannot be precisely controlled by
![]() $\lambda_{\max}$
or/and
$\lambda_{\max}$
or/and
![]() $\lambda_{\min}$
, and the contraction principle cannot be readily applied.
$\lambda_{\min}$
, and the contraction principle cannot be readily applied.
In this paper, while we employ the proof ideas in [Reference Fey, van der Hofstad and Klok8], we adopt several new strategies in order to improve certain restrictions and obtain non-asymptotic bounds. More specifically, in [Reference Fey, van der Hofstad and Klok8] the results were derived under the assumption
![]() $p=o(n/\ln\ln n)$
, and in this paper we adopt the concentration inequality for the maximal eigenvalue (see Lemma 5) and have improved the assumption to
$p=o(n/\ln\ln n)$
, and in this paper we adopt the concentration inequality for the maximal eigenvalue (see Lemma 5) and have improved the assumption to
![]() $p=o(n)$
; the employment of such concentration inequality also enables us to consider quite general distribution of the entries (namely sub-Gaussian distribution), improving the results in [Reference Fey, van der Hofstad and Klok8] where the entries are assumed to be symmetric and bounded (except for normal entries). Furthermore, the strategy of using two independent
$p=o(n)$
; the employment of such concentration inequality also enables us to consider quite general distribution of the entries (namely sub-Gaussian distribution), improving the results in [Reference Fey, van der Hofstad and Klok8] where the entries are assumed to be symmetric and bounded (except for normal entries). Furthermore, the strategy of using two independent
![]() $\chi^2$
random variables to control the condition number enables us to obtain non-asymptotic bounds for the distribution function of the condition number. To state the main result of the paper, let us introduce several notations/definitions.
$\chi^2$
random variables to control the condition number enables us to obtain non-asymptotic bounds for the distribution function of the condition number. To state the main result of the paper, let us introduce several notations/definitions.
1.2. Sub-Gaussian distribution
A random variable X is said to be sub-Gaussian if it satisfies one of the following three equivalent properties with parameters
![]() $K_i$
,
$K_i$
,
![]() $1\leq i\leq 3$
, differing from each other by at most an absolute constant factor (cf. [Reference Vershynin24, Lemma 5.5]):
$1\leq i\leq 3$
, differing from each other by at most an absolute constant factor (cf. [Reference Vershynin24, Lemma 5.5]):
-
(i) Tails:
 $\mathbb{P}(|X|>t)\leq \exp\{1-t^2/K_1^2\}$
for all
$\mathbb{P}(|X|>t)\leq \exp\{1-t^2/K_1^2\}$
for all
 $t\geq0$
.
$t\geq0$
. -
(ii) Moments:
 $(\mathbb{E}|X|^p)^{1/p}\leq K_2\sqrt{p}$
for all
$(\mathbb{E}|X|^p)^{1/p}\leq K_2\sqrt{p}$
for all
 $p\geq1$
.
$p\geq1$
. -
(iii) Super-exponential moment:
 $\mathbb{E}\exp\{X^2/K_3^2\}\leq \mathrm{e}$
. If, further,
$\mathbb{E}\exp\{X^2/K_3^2\}\leq \mathrm{e}$
. If, further,
 $\mathbb{E}(X)=0$
, then (i)–(iii) are also equivalent to the following:
$\mathbb{E}(X)=0$
, then (i)–(iii) are also equivalent to the following: -
(iv) Moment-generating function:
 $\mathbb{E}\exp\{tX\}\leq \exp\{t^2K_4^2\}$
for all
$\mathbb{E}\exp\{tX\}\leq \exp\{t^2K_4^2\}$
for all
 $t\in \mathbb{R}$
for some constant
$t\in \mathbb{R}$
for some constant
 $K_4$
.
$K_4$
.
Furthermore, the sub-Gaussian norm of X is defined as
![]() $\sup_{p\geq1}p^{-1/2}(\mathbb{E}|X|^p)^{1/p}$
, namely the smallest
$\sup_{p\geq1}p^{-1/2}(\mathbb{E}|X|^p)^{1/p}$
, namely the smallest
![]() $K_2$
in (ii). It is noted that normal (or Gaussian), Bernoulli, and bounded random variables are all sub-Gaussian.
$K_2$
in (ii). It is noted that normal (or Gaussian), Bernoulli, and bounded random variables are all sub-Gaussian.
1.3. Rate functions
To state large deviations, we need to introduce rate functions. In each Euclidean space
![]() $\mathbb{R}^p$
with
$\mathbb{R}^p$
with
![]() $p\geq2$
, the Euclidean norm is, as before, written as
$p\geq2$
, the Euclidean norm is, as before, written as
![]() $||x||$
, and the inner product of x and y is written as
$||x||$
, and the inner product of x and y is written as
![]() $x\cdot y=x_1y_1+\cdots+x_py_p$
. For any
$x\cdot y=x_1y_1+\cdots+x_py_p$
. For any
![]() $\alpha,c\in \mathbb{R}$
, we define
$\alpha,c\in \mathbb{R}$
, we define
where
![]() $S_{x,i}=\sum_{k=1}^px_k X_{ki}$
for
$S_{x,i}=\sum_{k=1}^px_k X_{ki}$
for
![]() $x=(x_1,\ldots, x_p)\in \mathbb{R}^p$
,
$x=(x_1,\ldots, x_p)\in \mathbb{R}^p$
,
![]() $1\leq i\leq n$
. Notice that
$1\leq i\leq n$
. Notice that
![]() $I_{p,\alpha}(c)$
is non-increasing in p for each fixed
$I_{p,\alpha}(c)$
is non-increasing in p for each fixed
![]() $\alpha$
and c, and therefore the limit
$\alpha$
and c, and therefore the limit
![]() $I_{\infty,\alpha}(c):=\lim_{p\rightarrow\infty}I_{p,\alpha}(c)$
exists.
$I_{\infty,\alpha}(c):=\lim_{p\rightarrow\infty}I_{p,\alpha}(c)$
exists.
1.4. Main result
Theorem 1. Suppose that the entries
![]() $X_{ij}$
,
$X_{ij}$
,
![]() $1\leq i\leq p$
,
$1\leq i\leq p$
,
![]() $1\leq j\leq n$
, are i.i.d. sub-Gaussian satisfying (1). Then, for any
$1\leq j\leq n$
, are i.i.d. sub-Gaussian satisfying (1). Then, for any
![]() $c\geq 1$
we have, for fixed p,
$c\geq 1$
we have, for fixed p,
and, for
![]() $p=p(n)\rightarrow\infty$
with
$p=p(n)\rightarrow\infty$
with
![]() $p(n)=o(n)$
,
$p(n)=o(n)$
,
Since the standard normal distribution is sub-Gaussian, a very special case of Theorem 1 is the real central Wishart matrix
![]() $W_p(n, n^{-1}\mathbf{I})$
for which the entries
$W_p(n, n^{-1}\mathbf{I})$
for which the entries
![]() $X_{ij}$
,
$X_{ij}$
,
![]() $1\leq i\leq p$
,
$1\leq i\leq p$
,
![]() $1\leq j\leq n$
, are i.i.d. standard normal N(0,1).
$1\leq j\leq n$
, are i.i.d. standard normal N(0,1).
Corollary 1. Suppose that the entries
![]() $X_{ij}$
,
$X_{ij}$
,
![]() $1\leq i\leq p$
,
$1\leq i\leq p$
,
![]() $1\leq j\leq n$
, are i.i.d. standard normal N(0,1). Then, for any
$1\leq j\leq n$
, are i.i.d. standard normal N(0,1). Then, for any
![]() $c\geq 1$
,
$c\geq 1$
,
![]() $\lim_{n\rightarrow\infty}n^{-1}\ln \mathbb{P}(k^2(p,n)\geq c)=-2^{-1}\ln[(c+1)^2/(4c)]$
when p is fixed or
$\lim_{n\rightarrow\infty}n^{-1}\ln \mathbb{P}(k^2(p,n)\geq c)=-2^{-1}\ln[(c+1)^2/(4c)]$
when p is fixed or
![]() $p=p(n)\rightarrow\infty$
with
$p=p(n)\rightarrow\infty$
with
![]() $p(n)=o(n)$
.
$p(n)=o(n)$
.
In order to carry out a specific application of Corollary 1 in statistics (namely the union-intersection test method mentioned above), in Section 3 we prove a somewhat interesting result specified in Lemma 3: the upper tail of
![]() $k^2(p,n)=\lambda_{\max}/\lambda_{\min}$
can be controlled by the upper tails of ratios of two independent
$k^2(p,n)=\lambda_{\max}/\lambda_{\min}$
can be controlled by the upper tails of ratios of two independent
![]() $\chi^2$
random variables. This in turn yields an independent concise proof of Corollary 1 (under the assumption that p is fixed or
$\chi^2$
random variables. This in turn yields an independent concise proof of Corollary 1 (under the assumption that p is fixed or
![]() $p(n)=o(n/\ln n)$
). Note that individually
$p(n)=o(n/\ln n)$
). Note that individually
![]() $\lambda_{\max}$
and
$\lambda_{\max}$
and
![]() $\lambda_{\min}$
for Wishart matrices
$\lambda_{\min}$
for Wishart matrices
![]() $W_p(n, n^{-1}\mathbf{I})$
are not
$W_p(n, n^{-1}\mathbf{I})$
are not
![]() $\chi^2$
random variables (actually, the exact evaluation of the distributions of
$\chi^2$
random variables (actually, the exact evaluation of the distributions of
![]() $\lambda_{\max}$
and
$\lambda_{\max}$
and
![]() $\lambda_{\min}$
is difficult, involving hypergeometric functions; see [Reference Muirhead15, Section 9.7]). Furthermore, it is clear that
$\lambda_{\min}$
is difficult, involving hypergeometric functions; see [Reference Muirhead15, Section 9.7]). Furthermore, it is clear that
![]() $\lambda_{\max}$
and
$\lambda_{\max}$
and
![]() $\lambda_{\min}$
are not independent. From this point of view, to control
$\lambda_{\min}$
are not independent. From this point of view, to control
![]() $k^2(p,n)$
using ratios of two independent
$k^2(p,n)$
using ratios of two independent
![]() $\chi^2$
random variables is kind of unexpected. Such an application is formulated in detail in Section 5.
$\chi^2$
random variables is kind of unexpected. Such an application is formulated in detail in Section 5.
It should be mentioned in Theorem 1 that
![]() $I_{p,0}(1)=0$
,
$I_{p,0}(1)=0$
,
![]() $I_{\infty,0}(1)=0$
, and both
$I_{\infty,0}(1)=0$
, and both
![]() $0<I_{p,0}(c)<\infty$
and
$0<I_{p,0}(c)<\infty$
and
![]() $0<I_{\infty,0}(c)<\infty$
for all
$0<I_{\infty,0}(c)<\infty$
for all
![]() $c>1$
(see Lemma 7). To find explicit expressions for
$c>1$
(see Lemma 7). To find explicit expressions for
![]() $I_{p,0}(c)$
is in general not easy because of the infimum; however, for some special cases it is feasible to compute
$I_{p,0}(c)$
is in general not easy because of the infimum; however, for some special cases it is feasible to compute
![]() $I_{p,0}(c)$
. One particular example is, as we have seen, Corollary 1 for which
$I_{p,0}(c)$
. One particular example is, as we have seen, Corollary 1 for which
![]() $I_{p,0}(c)$
can be explicitly written (and turns out to be independent of p). Below is another example.
$I_{p,0}(c)$
can be explicitly written (and turns out to be independent of p). Below is another example.
Example 1. Let
![]() $p=2$
and the entries
$p=2$
and the entries
![]() $X_{ij}$
be
$X_{ij}$
be
![]() $\mathbb{P}(X_{ij}=-1)=\mathbb{P}(X_{ij}=1)=1/2.$
Then
$\mathbb{P}(X_{ij}=-1)=\mathbb{P}(X_{ij}=1)=1/2.$
Then
![]() $I_{2,0}(c)=\ln(2c^{c/(c+1)}/(c+1))$
. To see this, note that the matrix
$I_{2,0}(c)=\ln(2c^{c/(c+1)}/(c+1))$
. To see this, note that the matrix
![]() $\mathbf{W}_{2\times 2}:=\mathbf{X}\mathbf{X}^\top/n$
can be explicitly written as
$\mathbf{W}_{2\times 2}:=\mathbf{X}\mathbf{X}^\top/n$
can be explicitly written as
 \begin{equation*}\mathbf{W}=\frac{1}{n}\begin{bmatrix} n\;\;\;\;\;\;\;\; & \sum_{j=1}^nX_{1j}X_{2j} \\[5pt] \sum_{j=1}^nX_{1j}X_{2j}\;\;\;\;\;\;\;\; & n\end{bmatrix}.\end{equation*}
\begin{equation*}\mathbf{W}=\frac{1}{n}\begin{bmatrix} n\;\;\;\;\;\;\;\; & \sum_{j=1}^nX_{1j}X_{2j} \\[5pt] \sum_{j=1}^nX_{1j}X_{2j}\;\;\;\;\;\;\;\; & n\end{bmatrix}.\end{equation*}
Therefore,
![]() $\lambda_{\max}=\big(n+\big|\sum_{j=1}^nX_{1j}X_{2j}\big|\big)/n$
and
$\lambda_{\max}=\big(n+\big|\sum_{j=1}^nX_{1j}X_{2j}\big|\big)/n$
and
![]() $\lambda_{\min}=\big(n-\big|\sum_{j=1}^nX_{1j}X_{2j}\big|\big)/n$
. Hence,
$\lambda_{\min}=\big(n-\big|\sum_{j=1}^nX_{1j}X_{2j}\big|\big)/n$
. Hence,
![]() $\mathbb{P}(k^2(p,n)\geq c)=\mathbb{P}\big(\big|\sum_{j=1}^nX_{1j}X_{2j}\big|\geq (c-1)n/(c+1)\big)$
. Notice that
$\mathbb{P}(k^2(p,n)\geq c)=\mathbb{P}\big(\big|\sum_{j=1}^nX_{1j}X_{2j}\big|\geq (c-1)n/(c+1)\big)$
. Notice that
![]() $\{X_{1j}X_{2j},\ 1\leq j\leq n\}$
are i.i.d. random variables with a common distribution
$\{X_{1j}X_{2j},\ 1\leq j\leq n\}$
are i.i.d. random variables with a common distribution
![]() $\mathbb{P}(X_{1j}X_{2j}=-1)=\mathbb{P}(X_{1j}X_{2j}=1)=1/2$
; then Cramér’s theorem yields
$\mathbb{P}(X_{1j}X_{2j}=-1)=\mathbb{P}(X_{1j}X_{2j}=1)=1/2$
; then Cramér’s theorem yields
 \begin{equation*}\lim_{n\rightarrow\infty} n^{-1}\ln \mathbb{P}\Bigg(\bigg|\sum_{j=1}^nX_{1j}X_{2j}\bigg|\geq (c-1)n/(c+1)\Bigg)=-\ln(2c^{c/(c+1)}/(c+1)),\end{equation*}
\begin{equation*}\lim_{n\rightarrow\infty} n^{-1}\ln \mathbb{P}\Bigg(\bigg|\sum_{j=1}^nX_{1j}X_{2j}\bigg|\geq (c-1)n/(c+1)\Bigg)=-\ln(2c^{c/(c+1)}/(c+1)),\end{equation*}
so
![]() $I_{2,0}(c)=\ln(2c^{c/(c+1)}/(c+1))$
.
$I_{2,0}(c)=\ln(2c^{c/(c+1)}/(c+1))$
.
A full proof of Theorem 1 will be given in Section 4. It would be interesting to investigate explicit expressions of
![]() $I_{\infty,0}(c)$
as well. However, a major difficulty comes from the infimum over all
$I_{\infty,0}(c)$
as well. However, a major difficulty comes from the infimum over all
![]() $x,y\in \mathbb{R}^p$
with
$x,y\in \mathbb{R}^p$
with
![]() $||x||=||y||=1$
and
$||x||=||y||=1$
and
![]() $x\cdot y=0$
as
$x\cdot y=0$
as
![]() $p\rightarrow\infty$
. If we can show that, under suitable additional assumptions,
$p\rightarrow\infty$
. If we can show that, under suitable additional assumptions,
then we prove an elegant universality result: the large-deviation asymptotics of the condition number of a sub-Gaussian random matrix coincide with those of a standard normal random matrix as
![]() $n\rightarrow\infty$
. We note that (4) cannot hold in general only under the assumptions of Theorem 1. For instance, if
$n\rightarrow\infty$
. We note that (4) cannot hold in general only under the assumptions of Theorem 1. For instance, if
![]() $\mathbb{P}(X_{ij}=-1)=\mathbb{P}(X_{ij}=1)=1/2$
, then
$\mathbb{P}(X_{ij}=-1)=\mathbb{P}(X_{ij}=1)=1/2$
, then
![]() $\mathbb{P}(\lambda_{\min}=0)\geq \mathbb{P}(X_{ij}=1$
,
$\mathbb{P}(\lambda_{\min}=0)\geq \mathbb{P}(X_{ij}=1$
,
![]() $1\leq i\leq 2$
,
$1\leq i\leq 2$
,
![]() $1\leq j\leq n)=2^{-2n}$
. This implies that, for any
$1\leq j\leq n)=2^{-2n}$
. This implies that, for any
![]() $c\geq1$
,
$c\geq1$
,
 \begin{align*}I_{\infty,0}(c)&=-\lim_{n\rightarrow\infty}n^{-1}\ln \mathbb{P}\left(k^2(p,n)\geq c\right)\\&\leq -\lim_{n\rightarrow\infty}n^{-1}\ln \mathbb{P}\left(\lambda_{\min}=0\right)\leq 2\ln 2,\end{align*}
\begin{align*}I_{\infty,0}(c)&=-\lim_{n\rightarrow\infty}n^{-1}\ln \mathbb{P}\left(k^2(p,n)\geq c\right)\\&\leq -\lim_{n\rightarrow\infty}n^{-1}\ln \mathbb{P}\left(\lambda_{\min}=0\right)\leq 2\ln 2,\end{align*}
and in this case (4) does not hold. Therefore, to show (4) it is likely that some regularity assumptions should be imposed on the distribution of
![]() $X_{ij}$
. Furthermore, if we are able to manage to prove that for each
$X_{ij}$
. Furthermore, if we are able to manage to prove that for each
![]() $p=p(n)$
the minimizing couple
$p=p(n)$
the minimizing couple
![]() $(x,y)=((x_1,\ldots,x_p),(y_1,\ldots,y_p))$
in
$(x,y)=((x_1,\ldots,x_p),(y_1,\ldots,y_p))$
in
![]() $I_{p,0}(c)$
satisfies the condition
$I_{p,0}(c)$
satisfies the condition
![]() $\lim_{n\rightarrow\infty}\max(|x_1|,\ldots,|x_p|)=0$
and
$\lim_{n\rightarrow\infty}\max(|x_1|,\ldots,|x_p|)=0$
and
![]() $\lim_{n\rightarrow\infty}\max(|y_1|,\ldots,|y_p|)=0,$
then according to [Reference Kevei12, Theorem 1] both
$\lim_{n\rightarrow\infty}\max(|y_1|,\ldots,|y_p|)=0,$
then according to [Reference Kevei12, Theorem 1] both
![]() $S_{x,1}$
and
$S_{x,1}$
and
![]() $S_{y,1}$
converge to N(0,1) in distribution and (4) very likely holds. However, the minimizing couple seems to be very challenging to obtain explicitly, even for the simplest case described in Example 1 with
$S_{y,1}$
converge to N(0,1) in distribution and (4) very likely holds. However, the minimizing couple seems to be very challenging to obtain explicitly, even for the simplest case described in Example 1 with
![]() $p=2$
.
$p=2$
.
At the end of this section, we make an observation. Because of the finiteness of the rate function at each
![]() $c\geq1$
in Theorem 1, it follows that
$c\geq1$
in Theorem 1, it follows that
![]() $\mathbb{P}(k^2(p,n)\geq c)>0$
for n large enough (strictly positive), which is a non-trivial fact. On the other hand, because of the positivity of the rate function at each
$\mathbb{P}(k^2(p,n)\geq c)>0$
for n large enough (strictly positive), which is a non-trivial fact. On the other hand, because of the positivity of the rate function at each
![]() $c>1$
,
$c>1$
,
![]() $\mathbb{P}(k^2(p,n)\geq c)$
tends to zero exponentially fast as
$\mathbb{P}(k^2(p,n)\geq c)$
tends to zero exponentially fast as
![]() $n\rightarrow\infty$
.
$n\rightarrow\infty$
.
2. Proof outlines
Overall, the proof ideas are based on the ones in [Reference Fey, van der Hofstad and Klok8] which were used to study
![]() $\lambda_{\max}$
and
$\lambda_{\max}$
and
![]() $\lambda_{\min}$
individually and jointly. More precisely, for the lower bounds in (2) and (3), we relate the condition number probability to that involving n i.i.d. random variables so that the classical Cramér’s theorem can be used.
$\lambda_{\min}$
individually and jointly. More precisely, for the lower bounds in (2) and (3), we relate the condition number probability to that involving n i.i.d. random variables so that the classical Cramér’s theorem can be used.
Lemma 1. For any
![]() $2\leq p\leq n$
and
$2\leq p\leq n$
and
![]() $c\geq1$
, the set
$c\geq1$
, the set
![]() $\{k^2(p,n)\geq c\}$
is equal to the set
$\{k^2(p,n)\geq c\}$
is equal to the set
![]() $\{x,y\in\mathbb{R}^p \text{ s.t. }||x||=||y||=1,\ x\cdot y=0, \text{ and }(x\cdot\mathbf{W}x)/(y\cdot\mathbf{W}y)\geq c\}.$
$\{x,y\in\mathbb{R}^p \text{ s.t. }||x||=||y||=1,\ x\cdot y=0, \text{ and }(x\cdot\mathbf{W}x)/(y\cdot\mathbf{W}y)\geq c\}.$
Proof of Lemma 1. If
![]() $\omega\in\{\omega:k^2(p,n)\geq c\}$
, then let us take x = the eigenvector of
$\omega\in\{\omega:k^2(p,n)\geq c\}$
, then let us take x = the eigenvector of
![]() $\lambda_{\max}$
and y = the eigenvector of
$\lambda_{\max}$
and y = the eigenvector of
![]() $\lambda_{\min}$
. We can think of x and y as normalized vectors so that
$\lambda_{\min}$
. We can think of x and y as normalized vectors so that
![]() $||x||=||y||=1$
and
$||x||=||y||=1$
and
![]() $x\cdot y=0$
. Furthermore,
$x\cdot y=0$
. Furthermore,
![]() $(x\cdot\mathbf{W}x)/(y\cdot\mathbf{W}y)=k^2(p,n)\geq c$
. To see the other direction, let us take
$(x\cdot\mathbf{W}x)/(y\cdot\mathbf{W}y)=k^2(p,n)\geq c$
. To see the other direction, let us take
![]() $\omega\in\{(x\cdot\mathbf{W}x)/(y\cdot\mathbf{W}y)\geq c\}$
for some
$\omega\in\{(x\cdot\mathbf{W}x)/(y\cdot\mathbf{W}y)\geq c\}$
for some
![]() $||x||=||y||=1$
and
$||x||=||y||=1$
and
![]() $x\cdot y=0$
. Since
$x\cdot y=0$
. Since
![]() $\lambda_{\max}\geq z\cdot\mathbf{W}z$
and
$\lambda_{\max}\geq z\cdot\mathbf{W}z$
and
![]() $\lambda_{\min}\leq z\cdot\mathbf{W}z$
for all
$\lambda_{\min}\leq z\cdot\mathbf{W}z$
for all
![]() $z\in \mathbb{R}^p$
with
$z\in \mathbb{R}^p$
with
![]() $||z||=1$
, it follows that
$||z||=1$
, it follows that
![]() $k^2(p,n)\geq (x\cdot\mathbf{W}x)/$
$k^2(p,n)\geq (x\cdot\mathbf{W}x)/$
![]() $(y\cdot\mathbf{W}y)\geq c$
.
$(y\cdot\mathbf{W}y)\geq c$
.
![]()
With the help of Lemma 1, we can take any two fixed points
![]() $x,y\in\mathbb{R}^p$
with
$x,y\in\mathbb{R}^p$
with
![]() $||x||=||y||=1$
and
$||x||=||y||=1$
and
![]() $x\cdot y=0$
, and obtain
$x\cdot y=0$
, and obtain
 \begin{equation}\begin{aligned}\mathbb{P}\left(k^2(p,n)\geq c\right)\geq \mathbb{P}\left((x\cdot\mathbf{W}x)/(y\cdot\mathbf{W}y)\geq c\right)=\mathbb{P}\left(\sum_{i=1}^n(S_{x,i}^2-cS_{y,i}^2)/n\geq0\right).\end{aligned}\end{equation}
\begin{equation}\begin{aligned}\mathbb{P}\left(k^2(p,n)\geq c\right)\geq \mathbb{P}\left((x\cdot\mathbf{W}x)/(y\cdot\mathbf{W}y)\geq c\right)=\mathbb{P}\left(\sum_{i=1}^n(S_{x,i}^2-cS_{y,i}^2)/n\geq0\right).\end{aligned}\end{equation}
Now the classical Cramér’s theorem applied to the n i.i.d. random variables
![]() $(S_{x,i}^2-cS_{y,i}^2)$
,
$(S_{x,i}^2-cS_{y,i}^2)$
,
![]() $1\leq i\leq n$
, gives the lower bounds.
$1\leq i\leq n$
, gives the lower bounds.
The upper bounds in (2) and (3) are more complicated. In order to be able to still make use of Lemma 1, we need to divide the surface
![]() $S:=\{x\in \mathbb{R}^p:||x||=1\}$
of the p-dimensional sphere of unit radius into smaller pieces, and then take approximations.
$S:=\{x\in \mathbb{R}^p:||x||=1\}$
of the p-dimensional sphere of unit radius into smaller pieces, and then take approximations.
Lemma 2. For any
![]() $0<d<1/2$
, let
$0<d<1/2$
, let
![]() $N_d$
denote the minimal number of spherical caps of chord
$N_d$
denote the minimal number of spherical caps of chord
![]() $2d\sqrt{1-d^2/4}$
needed in order to cover S, and
$2d\sqrt{1-d^2/4}$
needed in order to cover S, and
![]() $\{x^{(i)},1\leq i\leq N_d\}$
be the centers of these spherical caps. Then, any two points
$\{x^{(i)},1\leq i\leq N_d\}$
be the centers of these spherical caps. Then, any two points
![]() $x,y\in S$
with
$x,y\in S$
with
![]() $x\cdot y=0$
can be approximated in the following way: there exist
$x\cdot y=0$
can be approximated in the following way: there exist
![]() $1\leq i,j\leq N_d$
such that
$1\leq i,j\leq N_d$
such that
![]() $||x-x^{(i)}||\leq d$
,
$||x-x^{(i)}||\leq d$
,
![]() $||y-y^{(i,j)}||\leq 2d$
,
$||y-y^{(i,j)}||\leq 2d$
,
![]() $||y^{(i,j)}-x^{(j)}||\leq d$
, and
$||y^{(i,j)}-x^{(j)}||\leq d$
, and
![]() $x^{(i)}\cdot y^{(i,j)}=0$
.
$x^{(i)}\cdot y^{(i,j)}=0$
.
The proof of Lemma 2 is given in [Reference Fey, van der Hofstad and Klok8, p. 1056], and the total number of pairs
![]() $\{x^{(i)},y^{(i,j)}\}_{i,j\geq1}$
is bounded by
$\{x^{(i)},y^{(i,j)}\}_{i,j\geq1}$
is bounded by
![]() $N_d^2$
. Thanks to Lemma 2, the probability
$N_d^2$
. Thanks to Lemma 2, the probability
![]() $\mathbb{P}\left(k^2(p,n)\geq c\right)$
essentially has an upper bound
$\mathbb{P}\left(k^2(p,n)\geq c\right)$
essentially has an upper bound
in an appropriate form for some
![]() $c_d$
depending on d (see estimates (9) below for a precise formulation of such an upper bound). However, estimating this upper bound requires subtle relations among
$c_d$
depending on d (see estimates (9) below for a precise formulation of such an upper bound). However, estimating this upper bound requires subtle relations among
![]() $N_d, p$
, and n, and it turns out that the desired upper bounds in (2) and (3) can be derived in this way only for fixed p or
$N_d, p$
, and n, and it turns out that the desired upper bounds in (2) and (3) can be derived in this way only for fixed p or
![]() $p=p(n)\rightarrow\infty$
with
$p=p(n)\rightarrow\infty$
with
![]() $p(n)=o(n)$
; see Section 4 for the proof details.
$p(n)=o(n)$
; see Section 4 for the proof details.
In order to achieve an application in statistics using Wishart matrices, some non-asymptotic estimates will be derived for the distribution function of the condition number using ratios of two independent
![]() $\chi^2$
random variables; see Lemma 3 for a precise formulation. To this end, we decompose the joint probability density function of the ordered p eigenvalues.
$\chi^2$
random variables; see Lemma 3 for a precise formulation. To this end, we decompose the joint probability density function of the ordered p eigenvalues.
The non-trivial proofs of the positivity
![]() $I_{p,0}(c)>0$
and
$I_{p,0}(c)>0$
and
![]() $I_{\infty,0}(c)>0$
with
$I_{\infty,0}(c)>0$
with
![]() $c>1$
and of the finiteness
$c>1$
and of the finiteness
![]() $I_{p,0}(c)<\infty$
and
$I_{p,0}(c)<\infty$
and
![]() $I_{\infty,0}(c)<\infty$
with
$I_{\infty,0}(c)<\infty$
with
![]() $c\geq1$
are given in Lemma 7.
$c\geq1$
are given in Lemma 7.
3. Wishart matrices
In this section we restrict ourselves to real central Wishart matrices
![]() $\mathbf{W}_{p\times p}=\mathbf{X}\mathbf{X}^\top/n$
. The condition number k(p,n) of
$\mathbf{W}_{p\times p}=\mathbf{X}\mathbf{X}^\top/n$
. The condition number k(p,n) of
![]() $\mathbf{W}$
does not depend on the scaling parameter
$\mathbf{W}$
does not depend on the scaling parameter
![]() $1/n$
, so throughout this section for simplicity the non-negative real eigenvalues
$1/n$
, so throughout this section for simplicity the non-negative real eigenvalues
![]() $\lambda_i\geq0$
,
$\lambda_i\geq0$
,
![]() $1\leq i\leq p$
, of
$1\leq i\leq p$
, of
![]() $\mathbf{X}\mathbf{X}^\top$
are considered. In this setting, let us denote
$\mathbf{X}\mathbf{X}^\top$
are considered. In this setting, let us denote
![]() $\lambda=(\lambda_1,\ldots,\lambda_p)$
; then, the probability density function of
$\lambda=(\lambda_1,\ldots,\lambda_p)$
; then, the probability density function of
![]() $\lambda$
can be written as (cf. [Reference James10])
$\lambda$
can be written as (cf. [Reference James10])
 \begin{equation*}f_{p,n}(\lambda)=c(p,n)\cdot \exp\left\{-\sum_{i=1}^p\lambda_i/2\right\}\cdot\prod_{1\leq i<j\leq p}|\lambda_i-\lambda_j|\cdot \prod_{i=1}^p\lambda_i^{(n-p-1)/2},\end{equation*}
\begin{equation*}f_{p,n}(\lambda)=c(p,n)\cdot \exp\left\{-\sum_{i=1}^p\lambda_i/2\right\}\cdot\prod_{1\leq i<j\leq p}|\lambda_i-\lambda_j|\cdot \prod_{i=1}^p\lambda_i^{(n-p-1)/2},\end{equation*}
where
![]() $c(p,n)=(\pi^{p/2}/2^{(n+2)p/2})\prod_{i=1}^p\left(\Gamma(1+i/2)\Gamma((n-p+i)/2)\right)^{-1}$
. Hence, the probability density function
$c(p,n)=(\pi^{p/2}/2^{(n+2)p/2})\prod_{i=1}^p\left(\Gamma(1+i/2)\Gamma((n-p+i)/2)\right)^{-1}$
. Hence, the probability density function
![]() $g_{p,n}(\lambda_\mathrm{ord})$
of the ordered eigenvalues
$g_{p,n}(\lambda_\mathrm{ord})$
of the ordered eigenvalues
![]() $\lambda_\mathrm{ord}=(\lambda_{(1)},\ldots,\lambda_{(p)})$
with
$\lambda_\mathrm{ord}=(\lambda_{(1)},\ldots,\lambda_{(p)})$
with
![]() $\lambda_{(1)}\geq \lambda_{(2)}\geq\cdots\geq \lambda_{(p)}\geq0$
is
$\lambda_{(1)}\geq \lambda_{(2)}\geq\cdots\geq \lambda_{(p)}\geq0$
is
![]() $g_{p,n}(\lambda_\mathrm{ord})=p!f_{p,n}(\lambda_\mathrm{ord})$
on
$g_{p,n}(\lambda_\mathrm{ord})=p!f_{p,n}(\lambda_\mathrm{ord})$
on
![]() $\lambda_{(1)}\geq \lambda_{(2)}\geq\cdots\geq \lambda_{(p)}\geq0$
. The main result of this section is to control the condition number using ratios of two independent
$\lambda_{(1)}\geq \lambda_{(2)}\geq\cdots\geq \lambda_{(p)}\geq0$
. The main result of this section is to control the condition number using ratios of two independent
![]() $\chi^2$
random variables.
$\chi^2$
random variables.
Lemma 3. For any
![]() $c\geq1$
and
$c\geq1$
and
![]() $2\leq p\leq n$
,
$2\leq p\leq n$
,
where
![]() $U_1\sim \chi^2(n)$
,
$U_1\sim \chi^2(n)$
,
![]() $U_2\sim \chi^2(n)$
,
$U_2\sim \chi^2(n)$
,
![]() $U_3\sim \chi^2(n+3p-5)$
, and
$U_3\sim \chi^2(n+3p-5)$
, and
![]() $U_4\sim \chi^2(n-p+1)$
are four independent
$U_4\sim \chi^2(n-p+1)$
are four independent
![]() $\chi^2$
random variables, and
$\chi^2$
random variables, and
Proof. The lower bound follows from (5). More specifically, in the summation
![]() $\sum_{i=1}^n(S_{x,i}^2-cS_{y,i}^2)$
, each
$\sum_{i=1}^n(S_{x,i}^2-cS_{y,i}^2)$
, each
![]() $S_{x,i}=\sum_{k=1}^px_k X_{ki}\sim N(0,1)$
and
$S_{x,i}=\sum_{k=1}^px_k X_{ki}\sim N(0,1)$
and
![]() $S_{y,i}=\sum_{k=1}^py_k X_{ki}\sim N(0,1)$
. Furthermore,
$S_{y,i}=\sum_{k=1}^py_k X_{ki}\sim N(0,1)$
. Furthermore,
![]() $S_{x,i}$
and
$S_{x,i}$
and
![]() $S_{y,j}$
are independent since
$S_{y,j}$
are independent since
![]() $\mathbb{E}(S_{x,i}S_{y,j})=x\cdot y=0$
. Therefore,
$\mathbb{E}(S_{x,i}S_{y,j})=x\cdot y=0$
. Therefore,
![]() $\sum_{i=1}^nS_{x,i}^2\sim \chi^2(n)$
, which is independent of
$\sum_{i=1}^nS_{x,i}^2\sim \chi^2(n)$
, which is independent of
![]() $\sum_{i=1}^nS_{y,i}^2\sim \chi^2(n)$
.
$\sum_{i=1}^nS_{y,i}^2\sim \chi^2(n)$
.
For the upper bound, we decompose the density function
![]() $g_{p,n}(\lambda_\mathrm{ord})$
of the ordered eigenvalues
$g_{p,n}(\lambda_\mathrm{ord})$
of the ordered eigenvalues
![]() $\lambda_{(1)}\geq \lambda_{(2)}\geq\cdots\geq \lambda_{(p)}\geq0$
as follows:
$\lambda_{(1)}\geq \lambda_{(2)}\geq\cdots\geq \lambda_{(p)}\geq0$
as follows:
 \begin{align*}g_{p,n}(\lambda_\mathrm{ord}) & = p!f_{p,n}(\lambda_\mathrm{ord}) \\ & = p!c(p,n)\cdot \exp\left\{-\sum_{i=1}^p\lambda_{(i)}/2\right\}\cdot\prod_{1\leq i<j\leq p}(\lambda_{(i)}-\lambda_{(j)})\cdot \prod_{i=1}^p\lambda_{(i)}^{(n-p-1)/2} \\ & = C(p,n)\cdot \bigg[(\lambda_{(1)}\lambda_{(p)})^{(n-p-1)/2}\mathrm{e}^{-(\lambda_{(1)}+\lambda_{(p)})/2}\prod_{2\leq i\leq p}(\lambda_{(1)}-\lambda_{(i)}) \\ & \qquad\qquad\qquad\prod_{2\leq i\leq p-1}(\lambda_{(i)}-\lambda_{(p)})\bigg]\cdot h_{p,n}(\lambda_{(2)},\ldots,\lambda_{(p-1)}),\end{align*}
\begin{align*}g_{p,n}(\lambda_\mathrm{ord}) & = p!f_{p,n}(\lambda_\mathrm{ord}) \\ & = p!c(p,n)\cdot \exp\left\{-\sum_{i=1}^p\lambda_{(i)}/2\right\}\cdot\prod_{1\leq i<j\leq p}(\lambda_{(i)}-\lambda_{(j)})\cdot \prod_{i=1}^p\lambda_{(i)}^{(n-p-1)/2} \\ & = C(p,n)\cdot \bigg[(\lambda_{(1)}\lambda_{(p)})^{(n-p-1)/2}\mathrm{e}^{-(\lambda_{(1)}+\lambda_{(p)})/2}\prod_{2\leq i\leq p}(\lambda_{(1)}-\lambda_{(i)}) \\ & \qquad\qquad\qquad\prod_{2\leq i\leq p-1}(\lambda_{(i)}-\lambda_{(p)})\bigg]\cdot h_{p,n}(\lambda_{(2)},\ldots,\lambda_{(p-1)}),\end{align*}
where
![]() $C(p,n)=(p!c(p,n))/((p-2)!c(p-2,n-2))$
, and
$C(p,n)=(p!c(p,n))/((p-2)!c(p-2,n-2))$
, and
![]() $h_{p,n}$
is another density function given by
$h_{p,n}$
is another density function given by
![]() $h_{p,n}(\lambda_{(2)},\ldots,\lambda_{(p-1)})=(p-2)!c(p-2,n-2)\cdot \exp\big\{{-}\sum_{i=2}^{p-1}\lambda_{(i)}/2\big\}\cdot\prod_{2\leq i<j\leq p-1}(\lambda_{(i)}-\lambda_{(j)})\cdot \prod_{i=2}^{p-1}\lambda_{(i)}^{(n-p-1)/2}$
. If one applies the bound
$h_{p,n}(\lambda_{(2)},\ldots,\lambda_{(p-1)})=(p-2)!c(p-2,n-2)\cdot \exp\big\{{-}\sum_{i=2}^{p-1}\lambda_{(i)}/2\big\}\cdot\prod_{2\leq i<j\leq p-1}(\lambda_{(i)}-\lambda_{(j)})\cdot \prod_{i=2}^{p-1}\lambda_{(i)}^{(n-p-1)/2}$
. If one applies the bound
![]() $\prod_{2\leq i\leq p}(\lambda_{(1)}-\lambda_{(i)})\prod_{2\leq i\leq p-1}(\lambda_{(i)}-\lambda_{(p)})\leq \lambda_{(1)}^{(p-1)+(p-2)}$
on
$\prod_{2\leq i\leq p}(\lambda_{(1)}-\lambda_{(i)})\prod_{2\leq i\leq p-1}(\lambda_{(i)}-\lambda_{(p)})\leq \lambda_{(1)}^{(p-1)+(p-2)}$
on
![]() $\lambda_{(1)}\geq \lambda_{(2)}\geq\cdots\geq \lambda_{(p)}\geq0$
, then
$\lambda_{(1)}\geq \lambda_{(2)}\geq\cdots\geq \lambda_{(p)}\geq0$
, then
![]() $g_{p,n}(\lambda_\mathrm{ord})\leq C(p,n)\cdot \lambda_{(1)}^{(n+3p-7)/2}\cdot \lambda_{(p)}^{(n-p-1)/2}\cdot \mathrm{e}^{-(\lambda_{(1)}+\lambda_{(p)})/2}\cdot h_{p,n}(\lambda_{(2)},\ldots,\lambda_{(p-1)})$
. Hence,
$g_{p,n}(\lambda_\mathrm{ord})\leq C(p,n)\cdot \lambda_{(1)}^{(n+3p-7)/2}\cdot \lambda_{(p)}^{(n-p-1)/2}\cdot \mathrm{e}^{-(\lambda_{(1)}+\lambda_{(p)})/2}\cdot h_{p,n}(\lambda_{(2)},\ldots,\lambda_{(p-1)})$
. Hence,
 \begin{align*} \mathbb{P}(k^2(p,n)\geq c) & = \int_{\lambda_{(1)}/\lambda_{(p)}\geq c, \lambda_{(1)}\geq\cdots\geq\lambda_{(p)}\geq0} g_{p,n}(\lambda_\mathrm{ord}) \, \mathrm{d} \lambda_{(1)}\cdots \mathrm{d} \lambda_{(p)} \\ & \leq \int_{\lambda_{(1)}/\lambda_{(p)}\geq c}\int_{\lambda_{(2)}\geq\cdots\geq\lambda_{(p-1)}\geq0} g_{p,n}(\lambda_\mathrm{ord}) \, \mathrm{d}\lambda_{(1)}\cdots \mathrm{d}\lambda_{(p)} \\ & \leq C(p,n)\int_{\lambda_{(1)}/\lambda_{(p)}\geq c} \!\!\! \lambda_{(1)}^{(n+3p-7)/2}\cdot \lambda_{(p)}^{(n-p-1)/2}\cdot \mathrm{e}^{-(\lambda_{(1)}+\lambda_{(p)})/2} \, \mathrm{d}\lambda_{(1)}\mathrm{d}\lambda_{(p)} \\ & = a(p,n)\cdot \mathbb{P}(U_3/U_4\geq c),\end{align*}
\begin{align*} \mathbb{P}(k^2(p,n)\geq c) & = \int_{\lambda_{(1)}/\lambda_{(p)}\geq c, \lambda_{(1)}\geq\cdots\geq\lambda_{(p)}\geq0} g_{p,n}(\lambda_\mathrm{ord}) \, \mathrm{d} \lambda_{(1)}\cdots \mathrm{d} \lambda_{(p)} \\ & \leq \int_{\lambda_{(1)}/\lambda_{(p)}\geq c}\int_{\lambda_{(2)}\geq\cdots\geq\lambda_{(p-1)}\geq0} g_{p,n}(\lambda_\mathrm{ord}) \, \mathrm{d}\lambda_{(1)}\cdots \mathrm{d}\lambda_{(p)} \\ & \leq C(p,n)\int_{\lambda_{(1)}/\lambda_{(p)}\geq c} \!\!\! \lambda_{(1)}^{(n+3p-7)/2}\cdot \lambda_{(p)}^{(n-p-1)/2}\cdot \mathrm{e}^{-(\lambda_{(1)}+\lambda_{(p)})/2} \, \mathrm{d}\lambda_{(1)}\mathrm{d}\lambda_{(p)} \\ & = a(p,n)\cdot \mathbb{P}(U_3/U_4\geq c),\end{align*}
where the last equality comes from identifying the density functions of the corresponding two independent
![]() $\chi^2$
random variables. We remark that similar decompositions were used for
$\chi^2$
random variables. We remark that similar decompositions were used for
![]() $\lambda_{\max}$
and
$\lambda_{\max}$
and
![]() $\lambda_{\min}$
individually in [Reference Jiang and Li11].
$\lambda_{\min}$
individually in [Reference Jiang and Li11].
![]()
As mentioned earlier, the upper tail controls specified in Lemma 3 yield an independent concise proof of Corollary 1 (with
![]() $p=o(n/\ln n)$
), which is presented here for the sake of completeness.
$p=o(n/\ln n)$
), which is presented here for the sake of completeness.
Proof of Corollary 1. It suffices to prove the upper bound for
![]() $c>1$
. Lemma 3 yields
$c>1$
. Lemma 3 yields
We shall first prove
![]() $\lim_{n\rightarrow\infty}n^{-1}\ln a(p,n)=0$
under
$\lim_{n\rightarrow\infty}n^{-1}\ln a(p,n)=0$
under
![]() $p=o(n/\ln n)$
. If p is fixed, then, as
$p=o(n/\ln n)$
. If p is fixed, then, as
![]() $n\rightarrow\infty$
,
$n\rightarrow\infty$
,
 \begin{align*}\ln a(p,n)&=\ln\left[\frac{\pi\Gamma((n+3p-5)/2)\Gamma((n-p+1)/2)}{\Gamma(p/2)\Gamma(n/2)\Gamma((p-1)/2)\Gamma((n-1)/2)}\right]\\&=\ln\Gamma((n+3p-5)/2)+\ln\Gamma((n-p+1)/2)\\&\,\,\,\,\,\,-\ln\Gamma(n/2)-\ln\Gamma((n-1)/2)+o(n).\end{align*}
\begin{align*}\ln a(p,n)&=\ln\left[\frac{\pi\Gamma((n+3p-5)/2)\Gamma((n-p+1)/2)}{\Gamma(p/2)\Gamma(n/2)\Gamma((p-1)/2)\Gamma((n-1)/2)}\right]\\&=\ln\Gamma((n+3p-5)/2)+\ln\Gamma((n-p+1)/2)\\&\,\,\,\,\,\,-\ln\Gamma(n/2)-\ln\Gamma((n-1)/2)+o(n).\end{align*}
It follows from Stirling’s approximation that
![]() $\ln \Gamma(x)=x\ln x-x+o(x)$
as
$\ln \Gamma(x)=x\ln x-x+o(x)$
as
![]() $x\rightarrow\infty$
, so
$x\rightarrow\infty$
, so
![]() $\ln a(p,n)$
becomes
$\ln a(p,n)$
becomes
![]() $(n/2)\ln((n+3p-5)/n)+(n/2)\ln((n-p+1)/(n-1))+o(n)=o(n)$
, which proves the limit
$(n/2)\ln((n+3p-5)/n)+(n/2)\ln((n-p+1)/(n-1))+o(n)=o(n)$
, which proves the limit
![]() $\lim_{n\rightarrow\infty}n^{-1}\ln a(p,n)=0$
. When
$\lim_{n\rightarrow\infty}n^{-1}\ln a(p,n)=0$
. When
![]() $p=p(n)\rightarrow\infty$
with
$p=p(n)\rightarrow\infty$
with
![]() $p(n)=o(n/\ln n)$
as
$p(n)=o(n/\ln n)$
as
![]() $n\rightarrow\infty$
, similar arguments to those above yield
$n\rightarrow\infty$
, similar arguments to those above yield
![]() $\ln a(p,n)=(n/2)\ln((n+3p-5)/n)+(n/2)\ln((n-p+1)/(n-1))+O(1)p\ln n+o(n)$
, and this again implies the limit
$\ln a(p,n)=(n/2)\ln((n+3p-5)/n)+(n/2)\ln((n-p+1)/(n-1))+O(1)p\ln n+o(n)$
, and this again implies the limit
![]() $\lim_{n\rightarrow\infty}n^{-1}\ln a(p,n)=0$
.
$\lim_{n\rightarrow\infty}n^{-1}\ln a(p,n)=0$
.
Next, we shall prove the following estimate:
To this end, let us first rewrite the ratio of the two independent
![]() $\chi^2$
random variables as summations of squares of independent standard normal random variables,
$\chi^2$
random variables as summations of squares of independent standard normal random variables,
 \begin{align*}\mathbb{P}(U_3/U_4\geq c)=\mathbb{P}\left(\sum_{i=1}^{n+3p-5}\xi_i^2-c\sum_{i=1}^{n-p+1}\eta_i^2\geq0\right),\end{align*}
\begin{align*}\mathbb{P}(U_3/U_4\geq c)=\mathbb{P}\left(\sum_{i=1}^{n+3p-5}\xi_i^2-c\sum_{i=1}^{n-p+1}\eta_i^2\geq0\right),\end{align*}
where
![]() $\xi_i$
and
$\xi_i$
and
![]() $\eta_i$
are independent standard normal random variables. However, the two degrees of freedom
$\eta_i$
are independent standard normal random variables. However, the two degrees of freedom
![]() $n+3p-5$
and
$n+3p-5$
and
![]() $n-p+1$
are different, so Cramér’s theorem cannot be readily applied. To achieve the large-deviation asymptotics, we make use of the Gärtner–Ellis theorem [Reference Dembo and Zeitouni5, Section 2.3]. To this end, let us define
$n-p+1$
are different, so Cramér’s theorem cannot be readily applied. To achieve the large-deviation asymptotics, we make use of the Gärtner–Ellis theorem [Reference Dembo and Zeitouni5, Section 2.3]. To this end, let us define
 \begin{equation*}Z_n=\left(\sum_{i=1}^{n+3p-5}\xi_i^2-c\sum_{i=1}^{n-p+1}\eta_i^2\right)/n,\end{equation*}
\begin{equation*}Z_n=\left(\sum_{i=1}^{n+3p-5}\xi_i^2-c\sum_{i=1}^{n-p+1}\eta_i^2\right)/n,\end{equation*}
and consider the logarithmic moment-generating function of
![]() $Z_n$
defined as
$Z_n$
defined as
![]() $\Lambda_n(\theta)=\ln \mathbb{E}\exp\{\theta Z_n\}.$
By using the fact that
$\Lambda_n(\theta)=\ln \mathbb{E}\exp\{\theta Z_n\}.$
By using the fact that
![]() $\mathbb{E}\exp\{\theta\xi_i^2\}=(1-2\theta)^{-1/2}$
for
$\mathbb{E}\exp\{\theta\xi_i^2\}=(1-2\theta)^{-1/2}$
for
![]() $\theta<1/2$
, one can establish the limit, for
$\theta<1/2$
, one can establish the limit, for
![]() $-1/(2c)<\theta<1/2$
and
$-1/(2c)<\theta<1/2$
and
![]() $p=o(n)$
,
$p=o(n)$
,
If one defines the Fenchel–Legendre transform of
![]() $\Lambda(\theta)$
as
$\Lambda(\theta)$
as
![]() $\Lambda^*(\alpha)=\sup_{\theta \in \mathbb{R}}[\theta\cdot \alpha-\Lambda(\theta)]$
,
$\Lambda^*(\alpha)=\sup_{\theta \in \mathbb{R}}[\theta\cdot \alpha-\Lambda(\theta)]$
,
![]() $\alpha\in \mathbb{R}$
, then the Gärtner–Ellis theorem says that, for any closed set F,
$\alpha\in \mathbb{R}$
, then the Gärtner–Ellis theorem says that, for any closed set F,
Now we take
![]() $F=[0,\infty)$
, and we claim that, for any
$F=[0,\infty)$
, and we claim that, for any
![]() $\alpha\geq0$
,
$\alpha\geq0$
,
![]() $\Lambda^*(\alpha)=\sup_{\theta \geq 0}[\theta\cdot \alpha-\Lambda(\theta)].$
This comes from the fact that
$\Lambda^*(\alpha)=\sup_{\theta \geq 0}[\theta\cdot \alpha-\Lambda(\theta)].$
This comes from the fact that
![]() $\Lambda(\theta)=\ln \mathbb{E}\exp\{\theta\xi_i^2-c\theta\eta_i^2\}\geq\theta(1-c),$
thus implying
$\Lambda(\theta)=\ln \mathbb{E}\exp\{\theta\xi_i^2-c\theta\eta_i^2\}\geq\theta(1-c),$
thus implying
![]() $\theta\cdot \alpha-\Lambda(\theta)\leq \theta(\alpha+(c-1))\leq0$
for any
$\theta\cdot \alpha-\Lambda(\theta)\leq \theta(\alpha+(c-1))\leq0$
for any
![]() $\theta\leq0.$
Therefore,
$\theta\leq0.$
Therefore,
![]() $\Lambda^*(\alpha)$
is non-decreasing in
$\Lambda^*(\alpha)$
is non-decreasing in
![]() $\alpha$
for
$\alpha$
for
![]() $\alpha\geq0$
. Hence, in (7) we have
$\alpha\geq0$
. Hence, in (7) we have
![]() $\inf_{\alpha\in F}\Lambda^*(\alpha)=\Lambda^*(0)=2^{-1}\ln\left[(c+1)^2/(4c)\right]$
, so (6) now follows from (7).
$\inf_{\alpha\in F}\Lambda^*(\alpha)=\Lambda^*(0)=2^{-1}\ln\left[(c+1)^2/(4c)\right]$
, so (6) now follows from (7).
![]()
4. Random matrices with sub-Gaussian entries
In this section we consider sub-Gaussian random matrices
![]() $\mathbf{X}$
with i.i.d. entries
$\mathbf{X}$
with i.i.d. entries
![]() $X_{ij}$
being sub-Gaussian satisfying (1). To establish large-deviation asymptotics for the condition numbers in Theorem 1, we handle the two cases p being fixed and p(n) being dependent on n separately since there are more subtle relations among
$X_{ij}$
being sub-Gaussian satisfying (1). To establish large-deviation asymptotics for the condition numbers in Theorem 1, we handle the two cases p being fixed and p(n) being dependent on n separately since there are more subtle relations among
![]() $N_d$
(which appeared in Lemma 2), d, p, and n when
$N_d$
(which appeared in Lemma 2), d, p, and n when
![]() $p(n)\rightarrow\infty$
. To avoid triviality let us focus on the case
$p(n)\rightarrow\infty$
. To avoid triviality let us focus on the case
![]() $c>1$
.
$c>1$
.
Since the lower bounds have already been proved in Section 2, we focus here on the upper bounds. In the spirit of Lemmas 1 and 2, the set
![]() $\{k^2(p,n)\geq c\}$
can be rewritten and estimated as follows (for notational simplicity, all points x, y,
$\{k^2(p,n)\geq c\}$
can be rewritten and estimated as follows (for notational simplicity, all points x, y,
![]() $x^{(i)}$
, and
$x^{(i)}$
, and
![]() $y^{(i,j)}$
below will be on S, and we will not write this explicitly):
$y^{(i,j)}$
below will be on S, and we will not write this explicitly):
 \begin{equation} \begin{aligned} \{k^2(p,n)\geq c\} & = \{ x,y \text{ s.t. }x\cdot y=0 \text{ and }(x\cdot\mathbf{W}x)/(y\cdot\mathbf{W}y)\geq c\}\\ & \subseteq \{ x^{(i)},y^{(i,j)} \text{ s.t. }x^{(i)}\cdot y^{(i,j)}=0 \text{ and }\\ & \qquad x^{(i)}\cdot\mathbf{W}x^{(i)}-cy^{(i,j)}\cdot\mathbf{W}y^{(i,j)}\geq -2\lambda_{\max}d(2c+1)\},\end{aligned}\end{equation}
\begin{equation} \begin{aligned} \{k^2(p,n)\geq c\} & = \{ x,y \text{ s.t. }x\cdot y=0 \text{ and }(x\cdot\mathbf{W}x)/(y\cdot\mathbf{W}y)\geq c\}\\ & \subseteq \{ x^{(i)},y^{(i,j)} \text{ s.t. }x^{(i)}\cdot y^{(i,j)}=0 \text{ and }\\ & \qquad x^{(i)}\cdot\mathbf{W}x^{(i)}-cy^{(i,j)}\cdot\mathbf{W}y^{(i,j)}\geq -2\lambda_{\max}d(2c+1)\},\end{aligned}\end{equation}
where the inclusion
![]() $\subseteq$
comes from Lemma 2 and the fact
$\subseteq$
comes from Lemma 2 and the fact
![]() $|x\cdot\mathbf{W}x-x^{(i)}\cdot\mathbf{W}x^{(i)}|\leq (||x||+||x^{(i)}||)||W||||x-x^{(i)}||\leq 2 \lambda_{\max}d.$
$|x\cdot\mathbf{W}x-x^{(i)}\cdot\mathbf{W}x^{(i)}|\leq (||x||+||x^{(i)}||)||W||||x-x^{(i)}||\leq 2 \lambda_{\max}d.$
4.1. Fixed dimension p
When p is fixed, the number
![]() $N_d$
of spherical caps of chord
$N_d$
of spherical caps of chord
![]() $2d\sqrt{1-d^2/4}$
needed to cover S can be chosen fixed as well, and the exact expression of
$2d\sqrt{1-d^2/4}$
needed to cover S can be chosen fixed as well, and the exact expression of
![]() $N_d$
is not important. To analyze the probability of the latter set in (8), we further consider two disjoint sets
$N_d$
is not important. To analyze the probability of the latter set in (8), we further consider two disjoint sets
![]() $\{\lambda_{\max}\leq p K\}$
and
$\{\lambda_{\max}\leq p K\}$
and
![]() $\{\lambda_{\max}> p K\}$
for some large K which will be specified later. Since
$\{\lambda_{\max}> p K\}$
for some large K which will be specified later. Since
![]() $\lambda_{\max}\leq \mathrm{tr}(\mathbf{W})$
, with
$\lambda_{\max}\leq \mathrm{tr}(\mathbf{W})$
, with
![]() $\mathrm{tr}(\mathbf{W})$
denoting the trace of
$\mathrm{tr}(\mathbf{W})$
denoting the trace of
![]() $\mathbf{W}$
, it then follows from (8) that
$\mathbf{W}$
, it then follows from (8) that
 \begin{equation} \begin{aligned} \mathbb{P}(k^2(p,n)\geq c) & \leq \mathbb{P}\big(\text{there exists } x^{(i)},y^{(i,j)} \text{ s.t. }x^{(i)}\cdot y^{(i,j)}=0 \text{ and }\\ &\qquad\,\,\, x^{(i)}\cdot\mathbf{W}x^{(i)}-cy^{(i,j)}\cdot\mathbf{W}y^{(i,j)}\geq -2pKd(2c+1)\big)\\ &\quad+\mathbb{P}\big(\mathrm{tr}(\mathbf{W})>pK\big)\\ &\leq \sum_{1\leq i,j\leq N_d}\mathbb{P}\big(x^{(i)}\cdot\mathbf{W}x^{(i)}-cy^{(i,j)}\cdot\mathbf{W}y^{(i,j)}\geq -2pKd(2c+1)\big)\\ &\quad+\mathbb{P}\big(\mathrm{tr}(\mathbf{W})>pK\big).\end{aligned}\end{equation}
\begin{equation} \begin{aligned} \mathbb{P}(k^2(p,n)\geq c) & \leq \mathbb{P}\big(\text{there exists } x^{(i)},y^{(i,j)} \text{ s.t. }x^{(i)}\cdot y^{(i,j)}=0 \text{ and }\\ &\qquad\,\,\, x^{(i)}\cdot\mathbf{W}x^{(i)}-cy^{(i,j)}\cdot\mathbf{W}y^{(i,j)}\geq -2pKd(2c+1)\big)\\ &\quad+\mathbb{P}\big(\mathrm{tr}(\mathbf{W})>pK\big)\\ &\leq \sum_{1\leq i,j\leq N_d}\mathbb{P}\big(x^{(i)}\cdot\mathbf{W}x^{(i)}-cy^{(i,j)}\cdot\mathbf{W}y^{(i,j)}\geq -2pKd(2c+1)\big)\\ &\quad+\mathbb{P}\big(\mathrm{tr}(\mathbf{W})>pK\big).\end{aligned}\end{equation}
Therefore, denoting
![]() $\varepsilon:=2pKd(2c+1)$
with
$\varepsilon:=2pKd(2c+1)$
with
![]() $-\varepsilon>1-c$
for small d, Cramér’s theorem yields
$-\varepsilon>1-c$
for small d, Cramér’s theorem yields
 \begin{align*}\limsup_{n\rightarrow\infty}n^{-1}\ln & \sum_{1\leq i,j\leq N_d}\mathbb{P}\big(x^{(i)}\cdot\mathbf{W}x^{(i)}-cy^{(i,j)}\cdot\mathbf{W}y^{(i,j)}\geq -\varepsilon\big)\\&=\max_{1\leq i,j\leq N_d}\limsup_{n\rightarrow\infty}n^{-1}\ln \mathbb{P}\big(x^{(i)}\cdot\mathbf{W}x^{(i)}-cy^{(i,j)}\cdot\mathbf{W}y^{(i,j)}\geq -\varepsilon\big)\\&\leq \max_{1\leq i,j\leq N_d} -\sup_{\theta\in\mathbb{R}}\big[-\varepsilon\theta-\ln \mathbb{E}\exp\big\{\theta\big(S_{x^{(i)},1}^2-cS_{y^{(i,j)},1}^2\big)\big\}\big]\\&\leq -I_{p,-\varepsilon}(c).\end{align*}
\begin{align*}\limsup_{n\rightarrow\infty}n^{-1}\ln & \sum_{1\leq i,j\leq N_d}\mathbb{P}\big(x^{(i)}\cdot\mathbf{W}x^{(i)}-cy^{(i,j)}\cdot\mathbf{W}y^{(i,j)}\geq -\varepsilon\big)\\&=\max_{1\leq i,j\leq N_d}\limsup_{n\rightarrow\infty}n^{-1}\ln \mathbb{P}\big(x^{(i)}\cdot\mathbf{W}x^{(i)}-cy^{(i,j)}\cdot\mathbf{W}y^{(i,j)}\geq -\varepsilon\big)\\&\leq \max_{1\leq i,j\leq N_d} -\sup_{\theta\in\mathbb{R}}\big[-\varepsilon\theta-\ln \mathbb{E}\exp\big\{\theta\big(S_{x^{(i)},1}^2-cS_{y^{(i,j)},1}^2\big)\big\}\big]\\&\leq -I_{p,-\varepsilon}(c).\end{align*}
On the other hand, it follows from Cramér’s theorem again that, with
![]() $K>1$
,
$K>1$
,
 \begin{align*}\limsup_{n\rightarrow\infty}n^{-1}\ln \mathbb{P}\big(\mathrm{tr}(\mathbf{W})>pK\big) &=\limsup_{n\rightarrow\infty}n^{-1}\ln \mathbb{P}\left(\sum_{i=1}^p\sum_{j=1}^nX_{ij}^2/(np)>K\right)\\&\leq -p I_{X^2}(K),\end{align*}
\begin{align*}\limsup_{n\rightarrow\infty}n^{-1}\ln \mathbb{P}\big(\mathrm{tr}(\mathbf{W})>pK\big) &=\limsup_{n\rightarrow\infty}n^{-1}\ln \mathbb{P}\left(\sum_{i=1}^p\sum_{j=1}^nX_{ij}^2/(np)>K\right)\\&\leq -p I_{X^2}(K),\end{align*}
where
![]() $I_{X^2}(K)=\sup_{\theta\in\mathbb{R}}\big[\theta K-\ln \mathbb{E}\exp\big\{\theta X_{11}^2\big\}\big]$
. We now apply the following fact, whose proof will be presented in Section 6.
$I_{X^2}(K)=\sup_{\theta\in\mathbb{R}}\big[\theta K-\ln \mathbb{E}\exp\big\{\theta X_{11}^2\big\}\big]$
. We now apply the following fact, whose proof will be presented in Section 6.
Lemma 4. Under the assumptions of Theorem 1 with a fixed p, for any
![]() $c>1$
we have
$c>1$
we have
![]() $\lim_{\varepsilon\rightarrow0^-}I_{p,\varepsilon}(c)=I_{p,0}(c)<\infty$
and
$\lim_{\varepsilon\rightarrow0^-}I_{p,\varepsilon}(c)=I_{p,0}(c)<\infty$
and
![]() $\lim_{K\rightarrow\infty}I_{X^2}(K)=\infty$
.
$\lim_{K\rightarrow\infty}I_{X^2}(K)=\infty$
.
Taking into account all these observations, we obtain, from (9),
By sending
![]() $d\rightarrow0^+$
(equivalently
$d\rightarrow0^+$
(equivalently
![]() $\varepsilon\rightarrow0^+$
), it follows that
$\varepsilon\rightarrow0^+$
), it follows that
![]() $I_{p,-\varepsilon}(c)\rightarrow I_{p,0}(c)$
. Furthermore, by taking large K, it is clear that
$I_{p,-\varepsilon}(c)\rightarrow I_{p,0}(c)$
. Furthermore, by taking large K, it is clear that
![]() $I_{X^2}(K)>I_{p,0}(c)$
. Therefore,
$I_{X^2}(K)>I_{p,0}(c)$
. Therefore,
4.2. High dimension
 $${\bf{p}}\; = \;{\bf{p}}({\bf{n}})$$
$${\bf{p}}\; = \;{\bf{p}}({\bf{n}})$$
We note that the arguments in Section 4.1 do not go through when
![]() $p=p(n)\rightarrow\infty$
as
$p=p(n)\rightarrow\infty$
as
![]() $n\rightarrow\infty$
since, when we take the limit
$n\rightarrow\infty$
since, when we take the limit
![]() $n\rightarrow\infty$
, the parameter
$n\rightarrow\infty$
, the parameter
![]() $\varepsilon\rightarrow\infty$
as well. Furthermore, the number
$\varepsilon\rightarrow\infty$
as well. Furthermore, the number
![]() $N_d$
of spherical caps of chord
$N_d$
of spherical caps of chord
![]() $2\tilde{d}:=2d\sqrt{1-d^2/4}$
needed to cover S is important and an explicit expression for this in terms of d is needed. According to [Reference Rogers16],
$2\tilde{d}:=2d\sqrt{1-d^2/4}$
needed to cover S is important and an explicit expression for this in terms of d is needed. According to [Reference Rogers16],
![]() $N_d=4p(n)^{3/2}\tilde{d}^{-p(n)}(\ln p(n)+\ln\ln p(n)-\ln \tilde{d})(1+O(1/\ln p(n)))$
for all
$N_d=4p(n)^{3/2}\tilde{d}^{-p(n)}(\ln p(n)+\ln\ln p(n)-\ln \tilde{d})(1+O(1/\ln p(n)))$
for all
![]() $d<1/2$
and large p(n). The main ingredient of the proof in the high dimension setting is the following concentration inequality for the maximal singular value of the matrix
$d<1/2$
and large p(n). The main ingredient of the proof in the high dimension setting is the following concentration inequality for the maximal singular value of the matrix
![]() $\mathbf{X}_{p\times n}$
.
$\mathbf{X}_{p\times n}$
.
Lemma 5. [Reference Vershynin24, Theorem 5.39] With
![]() $p\leq n$
, suppose that the entries
$p\leq n$
, suppose that the entries
![]() $X_{ij}$
,
$X_{ij}$
,
![]() $1\leq i\leq p$
,
$1\leq i\leq p$
,
![]() $1\leq j\leq n$
are i.i.d. sub-Gaussian. Then, for any
$1\leq j\leq n$
are i.i.d. sub-Gaussian. Then, for any
![]() $\gamma\geq0$
,
$\gamma\geq0$
,
![]() $\mathbb{P}(\lambda_{\max}>(1+\kappa_1+\gamma)^2)\leq 2\exp\{-\kappa_2\gamma^2n\}$
, where
$\mathbb{P}(\lambda_{\max}>(1+\kappa_1+\gamma)^2)\leq 2\exp\{-\kappa_2\gamma^2n\}$
, where
![]() $\kappa_1,\kappa_2>0$
are two constants depending only on the sub-Gaussian norm of
$\kappa_1,\kappa_2>0$
are two constants depending only on the sub-Gaussian norm of
![]() $X_{ij}$
.
$X_{ij}$
.
With such a concentration inequality, we estimate as follows:
![]() $\mathbb{P}(k^2(p,n)\geq c)\leq \mathbb{P}(k^2(p,n)\geq c,\lambda_{\max}\leq (1+\kappa_1+\gamma)^2)+\mathbb{P}(\lambda_{\max}>(1+\kappa_1+\gamma)^2)$
. For the term
$\mathbb{P}(k^2(p,n)\geq c)\leq \mathbb{P}(k^2(p,n)\geq c,\lambda_{\max}\leq (1+\kappa_1+\gamma)^2)+\mathbb{P}(\lambda_{\max}>(1+\kappa_1+\gamma)^2)$
. For the term
![]() $\mathbb{P}(k^2(p,n)\geq c,\lambda_{\max}\leq (1+\kappa_1+\gamma)^2)$
we can employ the idea used to prove (9) to obtain
$\mathbb{P}(k^2(p,n)\geq c,\lambda_{\max}\leq (1+\kappa_1+\gamma)^2)$
we can employ the idea used to prove (9) to obtain
 \begin{multline*} \mathbb{P}\big(k^2(p,n)\geq c,\lambda_{\max}\leq (1+\kappa_1+\gamma)^2\big)\\ \leq N_d^2\max_{1\leq i,j\leq N_d}\mathbb{P}\big(x^{(i)}\cdot\mathbf{W}x^{(i)}-cy^{(i,j)}\cdot\mathbf{W}y^{(i,j)}\geq -2(1+\kappa_1+\gamma)^2d(2c+1)\big).\end{multline*}
\begin{multline*} \mathbb{P}\big(k^2(p,n)\geq c,\lambda_{\max}\leq (1+\kappa_1+\gamma)^2\big)\\ \leq N_d^2\max_{1\leq i,j\leq N_d}\mathbb{P}\big(x^{(i)}\cdot\mathbf{W}x^{(i)}-cy^{(i,j)}\cdot\mathbf{W}y^{(i,j)}\geq -2(1+\kappa_1+\gamma)^2d(2c+1)\big).\end{multline*}
It now follows again from Cramér’s theorem that, with
![]() $\varepsilon=2(1+\kappa_1+\gamma)^2d(2c+1)$
,
$\varepsilon=2(1+\kappa_1+\gamma)^2d(2c+1)$
,
 \begin{align*}n^{-1}\ln \mathbb{P}&(k^2(p,n)\geq c,\lambda_{\max}\leq (1+\kappa_1+\gamma)^2)\\&\leq (2/n)\ln N_d-\min_{1\leq i,j\leq N_d}\sup_{\theta\in\mathbb{R}}\big[-\varepsilon\theta-\ln \mathbb{E}\exp\big\{\theta\big(S_{x^{(i)},1}^2-cS_{y^{(i,j)},1}^2\big)\big\}\big]\\&\leq (2/n)\ln N_d- I_{p(n),-\varepsilon}(c)\\&\leq (2/n)\ln N_d- I_{\infty,-\varepsilon}(c),\end{align*}
\begin{align*}n^{-1}\ln \mathbb{P}&(k^2(p,n)\geq c,\lambda_{\max}\leq (1+\kappa_1+\gamma)^2)\\&\leq (2/n)\ln N_d-\min_{1\leq i,j\leq N_d}\sup_{\theta\in\mathbb{R}}\big[-\varepsilon\theta-\ln \mathbb{E}\exp\big\{\theta\big(S_{x^{(i)},1}^2-cS_{y^{(i,j)},1}^2\big)\big\}\big]\\&\leq (2/n)\ln N_d- I_{p(n),-\varepsilon}(c)\\&\leq (2/n)\ln N_d- I_{\infty,-\varepsilon}(c),\end{align*}
where the last inequality comes from the fact that
![]() $I_{p,-\varepsilon}\geq I_{\infty,-\varepsilon}(c)$
for small enough
$I_{p,-\varepsilon}\geq I_{\infty,-\varepsilon}(c)$
for small enough
![]() $\varepsilon.$
The assumption
$\varepsilon.$
The assumption
![]() $p=p(n)=o(n)$
implies that
$p=p(n)=o(n)$
implies that
![]() $\lim_{n\rightarrow\infty} (2/n)\ln N_d=0$
for each fixed d. Therefore,
$\lim_{n\rightarrow\infty} (2/n)\ln N_d=0$
for each fixed d. Therefore,
![]() $\limsup_{n\rightarrow\infty}n^{-1}\ln \mathbb{P}(k^2(p,n)\geq c,\lambda_{\max}\leq (1+\kappa_1+\gamma)^2)\leq - I_{\infty,-\varepsilon}(c)$
. Taking the limit
$\limsup_{n\rightarrow\infty}n^{-1}\ln \mathbb{P}(k^2(p,n)\geq c,\lambda_{\max}\leq (1+\kappa_1+\gamma)^2)\leq - I_{\infty,-\varepsilon}(c)$
. Taking the limit
![]() $d\rightarrow0^+$
implies that
$d\rightarrow0^+$
implies that
![]() $\limsup_{n\rightarrow\infty}n^{-1}\ln \mathbb{P}(k^2(p,n)\geq c,\lambda_{\max}\leq (1+\kappa_1+\gamma)^2)\leq - I_{\infty,0}(c)$
. The limit
$\limsup_{n\rightarrow\infty}n^{-1}\ln \mathbb{P}(k^2(p,n)\geq c,\lambda_{\max}\leq (1+\kappa_1+\gamma)^2)\leq - I_{\infty,0}(c)$
. The limit
![]() $\lim_{\varepsilon\rightarrow0^-}I_{\infty,\varepsilon}(c)=I_{\infty,0}(c)$
is established in Lemma 6. In summary,
$\lim_{\varepsilon\rightarrow0^-}I_{\infty,\varepsilon}(c)=I_{\infty,0}(c)$
is established in Lemma 6. In summary,
![]() $\limsup_{n\rightarrow\infty}n^{-1}\ln \mathbb{P}(k^2(p,n)\geq c)\leq \max(-I_{\infty,0}(c),-\kappa_2 \gamma^2)$
, and the proof is completed by sending
$\limsup_{n\rightarrow\infty}n^{-1}\ln \mathbb{P}(k^2(p,n)\geq c)\leq \max(-I_{\infty,0}(c),-\kappa_2 \gamma^2)$
, and the proof is completed by sending
![]() $\gamma\rightarrow\infty$
.
$\gamma\rightarrow\infty$
.
Lemma 6. Under the assumptions of Theorem 1 with
![]() $p=p(n)\rightarrow\infty$
and
$p=p(n)\rightarrow\infty$
and
![]() $p(n)=o(n)$
, we have, for any
$p(n)=o(n)$
, we have, for any
![]() $c>1$
,
$c>1$
,
![]() $\lim_{\varepsilon\rightarrow0^-}I_{\infty,\varepsilon}(c)=I_{\infty,0}(c)<\infty$
.
$\lim_{\varepsilon\rightarrow0^-}I_{\infty,\varepsilon}(c)=I_{\infty,0}(c)<\infty$
.
Proof. Since
![]() $I_{p,\varepsilon}(c)$
is non-increasing in p, the arguments leading to (10) still work in this case. Therefore, by taking
$I_{p,\varepsilon}(c)$
is non-increasing in p, the arguments leading to (10) still work in this case. Therefore, by taking
![]() $p(n)\rightarrow\infty$
we obtain
$p(n)\rightarrow\infty$
we obtain
![]() $2(N+1)\varepsilon/\varepsilon_0\leq I_{\infty,\varepsilon}(c)-I_{\infty,0}(c)\leq 0$
, and complete the proof by sending
$2(N+1)\varepsilon/\varepsilon_0\leq I_{\infty,\varepsilon}(c)-I_{\infty,0}(c)\leq 0$
, and complete the proof by sending
![]() $\varepsilon\rightarrow0^-$
.
$\varepsilon\rightarrow0^-$
.
![]()
5. Application: The union-intersection test method
In this section, suppose that a population is p-variate normal with a zero mean vector and covariance matrix
![]() $\Sigma_{p\times p}$
. The sphericity test deals with the hypotheses
$\Sigma_{p\times p}$
. The sphericity test deals with the hypotheses
![]() $H_0: \Sigma_{p\times p}=\sigma^2 I_{p\times p}$
for some
$H_0: \Sigma_{p\times p}=\sigma^2 I_{p\times p}$
for some
![]() $\sigma>0$
,
$\sigma>0$
,
![]() $H_1: \Sigma_{p\times p}\neq\sigma^2 I_{p\times p}$
. Among others, the union-intersection test method [Reference Srivastava and Khatri20, Section 7.4] suggests that
$H_1: \Sigma_{p\times p}\neq\sigma^2 I_{p\times p}$
. Among others, the union-intersection test method [Reference Srivastava and Khatri20, Section 7.4] suggests that
![]() $H_0$
is rejected if
$H_0$
is rejected if
![]() $k^2(p,n) \geq c$
, where c is determined from
$k^2(p,n) \geq c$
, where c is determined from
![]() $\mathbb{P}(k^2(p,n) \geq c)=\alpha$
with a given significance level
$\mathbb{P}(k^2(p,n) \geq c)=\alpha$
with a given significance level
![]() $\alpha$
. Unfortunately, so far in the literature there is no efficient way to evaluate the probability
$\alpha$
. Unfortunately, so far in the literature there is no efficient way to evaluate the probability
![]() $\mathbb{P}(k^2(p,n) \geq c)$
under the hypothesis
$\mathbb{P}(k^2(p,n) \geq c)$
under the hypothesis
![]() $H_0$
. We remark here (again) that an exact expression for
$H_0$
. We remark here (again) that an exact expression for
![]() $\mathbb{P}(k^2(p,n) \geq c)$
was derived in [Reference Anderson and Wells1] with
$\mathbb{P}(k^2(p,n) \geq c)$
was derived in [Reference Anderson and Wells1] with
![]() $\Sigma_{p\times p}=I_{p\times p}$
for all
$\Sigma_{p\times p}=I_{p\times p}$
for all
![]() $2\leq p\leq n$
involving complicated zonal polynomials which prevents us efficiently obtaining the probability
$2\leq p\leq n$
involving complicated zonal polynomials which prevents us efficiently obtaining the probability
![]() $\mathbb{P}(k^2(p,n) \geq c)$
(especially for large n). In this section we aim to control the probability
$\mathbb{P}(k^2(p,n) \geq c)$
(especially for large n). In this section we aim to control the probability
![]() $\mathbb{P}(k^2(p,n) \geq c)$
(under
$\mathbb{P}(k^2(p,n) \geq c)$
(under
![]() $\Sigma_{p\times p}=I_{p\times p}$
in which we choose, without loss of generality,
$\Sigma_{p\times p}=I_{p\times p}$
in which we choose, without loss of generality,
![]() $\sigma=1$
since the condition number does not depend on
$\sigma=1$
since the condition number does not depend on
![]() $\sigma$
) using the upper bound in Lemma 3 which is easy and efficient, and then apply it to test the above hypotheses using the union-intersection test method.
$\sigma$
) using the upper bound in Lemma 3 which is easy and efficient, and then apply it to test the above hypotheses using the union-intersection test method.
Recall the upper bound of
![]() $\mathbb{P}(k^2(p,n) \geq c)$
in Lemma 3:
$\mathbb{P}(k^2(p,n) \geq c)$
in Lemma 3:
![]() $\mathbb{P}(k^2(p,n)\geq c)\leq a(p,n)\cdot \mathbb{P}(U_3/U_4\geq c)$
, where
$\mathbb{P}(k^2(p,n)\geq c)\leq a(p,n)\cdot \mathbb{P}(U_3/U_4\geq c)$
, where
![]() $U_3\sim \chi^2(n+3p-5)$
and
$U_3\sim \chi^2(n+3p-5)$
and
![]() $U_4\sim \chi^2(n-p+1)$
are two independent
$U_4\sim \chi^2(n-p+1)$
are two independent
![]() $\chi^2$
random variables. With such an upper bound, we are able to control the p-value for the above hypotheses test. More specifically, let
$\chi^2$
random variables. With such an upper bound, we are able to control the p-value for the above hypotheses test. More specifically, let
![]() $k^2_\mathrm{obs}(p,n)$
denote the observed condition number for data simulated with
$k^2_\mathrm{obs}(p,n)$
denote the observed condition number for data simulated with
![]() $\Sigma_{p\times p}=I_{p\times p}$
; then, the p-value has an upper bound
$\Sigma_{p\times p}=I_{p\times p}$
; then, the p-value has an upper bound
![]() $p_\mathrm{upp}$
defined as
$p_\mathrm{upp}$
defined as
![]() $p_\mathrm{upp}= a(p,n)\cdot \mathbb{P}(U_3/U_4\geq k^2_\mathrm{obs}(p,n))$
. The null hypothesis
$p_\mathrm{upp}= a(p,n)\cdot \mathbb{P}(U_3/U_4\geq k^2_\mathrm{obs}(p,n))$
. The null hypothesis
![]() $H_0$
is then rejected if
$H_0$
is then rejected if
![]() $p_\mathrm{upp}<\alpha$
. Based on these, the simulated powers
$p_\mathrm{upp}<\alpha$
. Based on these, the simulated powers
![]() $\hat{h}$
of the hypotheses are obtained for various
$\hat{h}$
of the hypotheses are obtained for various
![]() $\Sigma_{p\times p}$
through computer simulations (performed
$\Sigma_{p\times p}$
through computer simulations (performed
![]() $N=10\,000$
times); see Tables 1 and 2.
$N=10\,000$
times); see Tables 1 and 2.
Table 1. Simulated powers when
![]() $p=2$
, for
$p=2$
, for
![]() $\Sigma_{p\times p}= \begin{bmatrix}
1\;\;\;\; & 0.5\\
0.5\;\;\;\; & 1
\end{bmatrix} $
,
$\Sigma_{p\times p}= \begin{bmatrix}
1\;\;\;\; & 0.5\\
0.5\;\;\;\; & 1
\end{bmatrix} $
,
![]() $p=2$
, and
$p=2$
, and
![]() $\alpha=0.05$
.
$\alpha=0.05$
.

Table 2. Simulated powers when
![]() $p=4$
, for
$p=4$
, for
 $\Sigma_{p\times p}= \begin{bmatrix} 1\;\;\;\;\;\; & 0.25\;\;\;\;\;\; & 0.25\;\;\;\;\;\; & 0.4 \\ 0.25\;\;\;\;\;\; & 1\;\;\;\;\;\; & 0.1\;\;\;\;\;\; & 0.2 \\ 0.25\;\;\;\;\;\; & 0.1\;\;\;\;\;\; & 1\;\;\;\;\;\; & 0.3 \\ 0.4\;\;\;\;\;\; & 0.2\;\;\;\;\;\; & 0.3\;\;\;\;\;\; & 1 \end{bmatrix} $
,
$\Sigma_{p\times p}= \begin{bmatrix} 1\;\;\;\;\;\; & 0.25\;\;\;\;\;\; & 0.25\;\;\;\;\;\; & 0.4 \\ 0.25\;\;\;\;\;\; & 1\;\;\;\;\;\; & 0.1\;\;\;\;\;\; & 0.2 \\ 0.25\;\;\;\;\;\; & 0.1\;\;\;\;\;\; & 1\;\;\;\;\;\; & 0.3 \\ 0.4\;\;\;\;\;\; & 0.2\;\;\;\;\;\; & 0.3\;\;\;\;\;\; & 1 \end{bmatrix} $
,
![]() $p=4$
, and
$p=4$
, and
![]() $\alpha=0.05$
.
$\alpha=0.05$
.

These simulated powers suggest that when n is large, it is easy to make a correct conclusion that the population covariance matrix is not an identity matrix. Here we also note that if one uses the above procedures to simulate the type-I error
![]() $\alpha$
(under the setting that the population covariance matrix is an identity matrix), it can happen that the simulated type-I error is much smaller than
$\alpha$
(under the setting that the population covariance matrix is an identity matrix), it can happen that the simulated type-I error is much smaller than
![]() $\alpha$
since an upper bound of the p-value is used during the procedures. For instance, with
$\alpha$
since an upper bound of the p-value is used during the procedures. For instance, with
![]() $p=4$
,
$p=4$
,
![]() $n=100$
,
$n=100$
,
![]() $N=10\,000$
, and
$N=10\,000$
, and
![]() $\alpha=0.05$
, the simulated type-I error is around
$\alpha=0.05$
, the simulated type-I error is around
![]() $10^{-4}$
.
$10^{-4}$
.
6. Other detailed proofs
This section contains proofs of the facts and the auxiliary lemmas used in previous sections.
Proof of Lemma 4. We first prove that
![]() $\lim_{K\rightarrow\infty}I_{X^2}(K)=\infty$
. Since
$\lim_{K\rightarrow\infty}I_{X^2}(K)=\infty$
. Since
![]() $X_{ij}$
are sub-Gaussian, it follows from the super-exponential moment that
$X_{ij}$
are sub-Gaussian, it follows from the super-exponential moment that
![]() $\mathbb{E}\exp\{t X_{11}^2\}<\infty$
for some
$\mathbb{E}\exp\{t X_{11}^2\}<\infty$
for some
![]() $t>0$
(actually, one can take
$t>0$
(actually, one can take
![]() $t=1/K_3^2$
). Therefore,
$t=1/K_3^2$
). Therefore,
We then prove that
![]() $I_{p,0}(c)<\infty$
for all
$I_{p,0}(c)<\infty$
for all
![]() $p\geq2$
and
$p\geq2$
and
![]() $c\geq1$
. It suffices to just prove the case
$c\geq1$
. It suffices to just prove the case
![]() $p=2$
since
$p=2$
since
![]() $0\leq I_{p,0}(c)\leq I_{2,0}(c)$
. To show this, we take
$0\leq I_{p,0}(c)\leq I_{2,0}(c)$
. To show this, we take
![]() $x^*=(x_1,x_2)=(1/\sqrt{2},1/\sqrt{2})$
and
$x^*=(x_1,x_2)=(1/\sqrt{2},1/\sqrt{2})$
and
![]() $y^*=(y_1,y_2)=(1/\sqrt{2},-1/\sqrt{2})$
. Hence,
$y^*=(y_1,y_2)=(1/\sqrt{2},-1/\sqrt{2})$
. Hence,
 \begin{align*}S_{x^*,1}^2-cS_{y^*,1}^2&=\big(X_{11}/\sqrt{2}+X_{21}/\sqrt{2}\big)^2-c\big(X_{11}/\sqrt{2}-X_{21}/\sqrt{2}\big)^2\\&=(1-c)\big(X_{11}^2+X_{21}^2\big)/2+(1+c)X_{11}X_{21}.\end{align*}
\begin{align*}S_{x^*,1}^2-cS_{y^*,1}^2&=\big(X_{11}/\sqrt{2}+X_{21}/\sqrt{2}\big)^2-c\big(X_{11}/\sqrt{2}-X_{21}/\sqrt{2}\big)^2\\&=(1-c)\big(X_{11}^2+X_{21}^2\big)/2+(1+c)X_{11}X_{21}.\end{align*}
If everything is restricted to the set
![]() $\{X_{21}+\varepsilon_1\geq X_{11}\geq X_{21}\geq \varepsilon_2\geq0\}$
for some
$\{X_{21}+\varepsilon_1\geq X_{11}\geq X_{21}\geq \varepsilon_2\geq0\}$
for some
![]() $\varepsilon_1,\varepsilon_2\geq0$
, then
$\varepsilon_1,\varepsilon_2\geq0$
, then
 \begin{align*}S_{x^*,1}^2-cS_{y^*,1}^2&\geq(1-c)X_{11}^2+(1+c)X_{11}(X_{11}-\varepsilon_1)\\&=X_{11}(2X_{11}-(1+c)\varepsilon_1)\\&\geq X_{11}(2\varepsilon_2-(1+c)\varepsilon_1)\\&\geq 0 \quad \text{ if }(1+c)\varepsilon_1\leq 2\varepsilon_2.\end{align*}
\begin{align*}S_{x^*,1}^2-cS_{y^*,1}^2&\geq(1-c)X_{11}^2+(1+c)X_{11}(X_{11}-\varepsilon_1)\\&=X_{11}(2X_{11}-(1+c)\varepsilon_1)\\&\geq X_{11}(2\varepsilon_2-(1+c)\varepsilon_1)\\&\geq 0 \quad \text{ if }(1+c)\varepsilon_1\leq 2\varepsilon_2.\end{align*}
Therefore, for
![]() $(1+c)\varepsilon_1\leq 2\varepsilon_2$
,
$(1+c)\varepsilon_1\leq 2\varepsilon_2$
,
 \begin{align*}I_{2,0}(c)&=\inf_{x,y\in \mathbb{R}^2,||x||=||y||=1,x\cdot y=0} \, \sup_{\theta\in\mathbb{R}}\left[-\ln \mathbb{E}\exp\{\theta(S_{x,1}^2-cS_{y,1}^2)\}\right]\\&=\inf_{x,y\in \mathbb{R}^2,||x||=||y||=1,x\cdot y=0}\, \sup_{\theta\geq0}\left[-\ln \mathbb{E}\exp\{\theta(S_{x,1}^2-cS_{y,1}^2)\}\right]\\&\leq \sup_{\theta\geq0}\left[-\ln \mathbb{E}\exp\{\theta(S_{x^*,1}^2-cS_{y^*,1}^2)\}\right]\\&\leq -\ln \mathbb{P}(X_{21}+\varepsilon_1\geq X_{11}\geq X_{21}\geq \varepsilon_2\geq0).\end{align*}
\begin{align*}I_{2,0}(c)&=\inf_{x,y\in \mathbb{R}^2,||x||=||y||=1,x\cdot y=0} \, \sup_{\theta\in\mathbb{R}}\left[-\ln \mathbb{E}\exp\{\theta(S_{x,1}^2-cS_{y,1}^2)\}\right]\\&=\inf_{x,y\in \mathbb{R}^2,||x||=||y||=1,x\cdot y=0}\, \sup_{\theta\geq0}\left[-\ln \mathbb{E}\exp\{\theta(S_{x,1}^2-cS_{y,1}^2)\}\right]\\&\leq \sup_{\theta\geq0}\left[-\ln \mathbb{E}\exp\{\theta(S_{x^*,1}^2-cS_{y^*,1}^2)\}\right]\\&\leq -\ln \mathbb{P}(X_{21}+\varepsilon_1\geq X_{11}\geq X_{21}\geq \varepsilon_2\geq0).\end{align*}
We now claim that, for any entries
![]() $X_{ij}$
satisfying the assumptions of Theorem 1, there always exist
$X_{ij}$
satisfying the assumptions of Theorem 1, there always exist
![]() $\varepsilon_1$
and
$\varepsilon_1$
and
![]() $\varepsilon_2$
with
$\varepsilon_2$
with
![]() $(1+c)\varepsilon_1\leq 2\varepsilon_2$
such that
$(1+c)\varepsilon_1\leq 2\varepsilon_2$
such that
![]() $\mathbb{P}(X_{21}+\varepsilon_1\geq X_{11}\geq X_{21}\geq \varepsilon_2\geq0)>0$
. Here we chose the right side of zero without loss of generality because
$\mathbb{P}(X_{21}+\varepsilon_1\geq X_{11}\geq X_{21}\geq \varepsilon_2\geq0)>0$
. Here we chose the right side of zero without loss of generality because
![]() $\mathbb{E}(X_{ij}=0)$
, but if needed the left side of zero can be chosen. To see this claim, let us first look at the case when the distribution of
$\mathbb{E}(X_{ij}=0)$
, but if needed the left side of zero can be chosen. To see this claim, let us first look at the case when the distribution of
![]() $X_{ij}$
has a pure discrete part on
$X_{ij}$
has a pure discrete part on
![]() $\mathbb{R}^+$
, and in this case we can simply take
$\mathbb{R}^+$
, and in this case we can simply take
![]() $\varepsilon_1=\varepsilon_2=0$
since
$\varepsilon_1=\varepsilon_2=0$
since
![]() $\mathbb{P}(X_{11}=X_{21}\geq0)>0$
. If the distribution of
$\mathbb{P}(X_{11}=X_{21}\geq0)>0$
. If the distribution of
![]() $X_{ij}$
does not contain a pure discrete part, then there must exist
$X_{ij}$
does not contain a pure discrete part, then there must exist
![]() $0<c_1<c_2<c_3$
with
$0<c_1<c_2<c_3$
with
![]() $c_3=c_1+2c_1/(1+c)$
(here it is stressed again that, without loss of generality, we only consider the distribution on
$c_3=c_1+2c_1/(1+c)$
(here it is stressed again that, without loss of generality, we only consider the distribution on
![]() $\mathbb{R}^+$
) such that
$\mathbb{R}^+$
) such that
![]() $\mathbb{P}(X_{ij}\in(c_1,c_2))>0$
and
$\mathbb{P}(X_{ij}\in(c_1,c_2))>0$
and
![]() $\mathbb{P}(X_{ij}\in(c_2,c_3))>0$
. Setting
$\mathbb{P}(X_{ij}\in(c_2,c_3))>0$
. Setting
![]() $\varepsilon_1=c_3-c_1$
and
$\varepsilon_1=c_3-c_1$
and
![]() $\varepsilon_2=c_1$
, it follows that
$\varepsilon_2=c_1$
, it follows that
![]() $(1+c)\varepsilon_1= 2\varepsilon_2$
and
$(1+c)\varepsilon_1= 2\varepsilon_2$
and
This proves
![]() $I_{2,0}(c)<\infty$
for any
$I_{2,0}(c)<\infty$
for any
![]() $c\geq1$
. Next, we shall prove that, for
$c\geq1$
. Next, we shall prove that, for
![]() $c>1$
,
$c>1$
,
![]() $\lim_{\varepsilon\rightarrow0^+}I_{p,-\varepsilon}(c)=I_{p,0}(c)$
. To achieve this limit, first note that we can actually prove a stronger finiteness result:
$\lim_{\varepsilon\rightarrow0^+}I_{p,-\varepsilon}(c)=I_{p,0}(c)$
. To achieve this limit, first note that we can actually prove a stronger finiteness result:
![]() $I_{2,\varepsilon_0}(c)<\infty$
for some small
$I_{2,\varepsilon_0}(c)<\infty$
for some small
![]() $\varepsilon_0>0$
. (‘Stronger’ here refers to the fact that
$\varepsilon_0>0$
. (‘Stronger’ here refers to the fact that
![]() $I_{2,\alpha}(c)$
is non-decreasing in
$I_{2,\alpha}(c)$
is non-decreasing in
![]() $\alpha$
for all
$\alpha$
for all
![]() $\alpha\geq 1-c$
.) By taking the same
$\alpha\geq 1-c$
.) By taking the same
![]() $x^*$
and
$x^*$
and
![]() $y^*$
as in the above arguments, we obtain
$y^*$
as in the above arguments, we obtain
 \begin{align*}\mathbb{E}\exp\big\{\theta&\big(S_{x^*,1}^2-cS_{y^*,1}^2\big)\big\}\geq\\&\begin{cases}\exp\{\theta\varepsilon_2(2\varepsilon_2-(1+c)\varepsilon_1)\}\mathbb{P}(X_{21}+\varepsilon_1\geq X_{11}\geq X_{21}\geq \varepsilon_2\geq0),& \mathrm{(I)} \\\exp\{\theta 2\varepsilon_2^2\}\mathbb{P}(X_{11}=X_{21}\geq \varepsilon_2\geq0),& \mathrm{(II)}\end{cases}\end{align*}
\begin{align*}\mathbb{E}\exp\big\{\theta&\big(S_{x^*,1}^2-cS_{y^*,1}^2\big)\big\}\geq\\&\begin{cases}\exp\{\theta\varepsilon_2(2\varepsilon_2-(1+c)\varepsilon_1)\}\mathbb{P}(X_{21}+\varepsilon_1\geq X_{11}\geq X_{21}\geq \varepsilon_2\geq0),& \mathrm{(I)} \\\exp\{\theta 2\varepsilon_2^2\}\mathbb{P}(X_{11}=X_{21}\geq \varepsilon_2\geq0),& \mathrm{(II)}\end{cases}\end{align*}
where (I) represents the case when the distribution of
![]() $X_{ij}$
has no pure discrete part, and (II) means that the distribution has a pure discrete part. If in the above arguments we take
$X_{ij}$
has no pure discrete part, and (II) means that the distribution has a pure discrete part. If in the above arguments we take
![]() $c_3=c_1+1.5c_1/(1+c)$
(everything else will be kept the same), then
$c_3=c_1+1.5c_1/(1+c)$
(everything else will be kept the same), then
![]() $(1+c)\varepsilon_1=1.5c_1\leq 2\varepsilon_2$
. Hence,
$(1+c)\varepsilon_1=1.5c_1\leq 2\varepsilon_2$
. Hence,
![]() $I_{2,\varepsilon_0}(c)<\infty$
for any
$I_{2,\varepsilon_0}(c)<\infty$
for any
![]() $\varepsilon_0\leq \min\{\varepsilon_2(2\varepsilon_2-(1+c)\varepsilon_1),2\varepsilon_2^2\}$
, implying that
$\varepsilon_0\leq \min\{\varepsilon_2(2\varepsilon_2-(1+c)\varepsilon_1),2\varepsilon_2^2\}$
, implying that
![]() $I_{p,\varepsilon_0}(c)<\infty$
for any
$I_{p,\varepsilon_0}(c)<\infty$
for any
![]() $p\geq2$
.
$p\geq2$
.
If we denote
![]() $g_{x,y}(\alpha)=\sup_{\theta\in\mathbb{R}}\big[\theta \alpha-\ln \mathbb{E}\exp\big\{\theta\big(S_{x,1}^2-cS_{y,1}^2\big)\big\}\big]$
, then it is clear that
$g_{x,y}(\alpha)=\sup_{\theta\in\mathbb{R}}\big[\theta \alpha-\ln \mathbb{E}\exp\big\{\theta\big(S_{x,1}^2-cS_{y,1}^2\big)\big\}\big]$
, then it is clear that
![]() $I_{p,\alpha}(c)=\inf_{x,y\in \mathbb{R}^p,||x||=||y||=1,x\cdot y=0}g_{x,y}(\alpha)$
. Since
$I_{p,\alpha}(c)=\inf_{x,y\in \mathbb{R}^p,||x||=||y||=1,x\cdot y=0}g_{x,y}(\alpha)$
. Since
![]() $0\leq I_{p,\varepsilon}(c)\leq I_{p,\varepsilon_0}(c):=N<\infty$
for all
$0\leq I_{p,\varepsilon}(c)\leq I_{p,\varepsilon_0}(c):=N<\infty$
for all
![]() $1-c\leq \varepsilon\leq \varepsilon_0$
, it suffices to consider
$1-c\leq \varepsilon\leq \varepsilon_0$
, it suffices to consider
![]() $A:=\{(x,y)\in \mathbb{R}^{2p}: ||x||=||y||=1,x\cdot y=0, g_{x,y}(\varepsilon_0)\leq N+1\}$
, that is,
$A:=\{(x,y)\in \mathbb{R}^{2p}: ||x||=||y||=1,x\cdot y=0, g_{x,y}(\varepsilon_0)\leq N+1\}$
, that is,
![]() $I_{p,\varepsilon}(c)=\inf_{x,y\in A}g_{x,y}(\varepsilon)$
for all
$I_{p,\varepsilon}(c)=\inf_{x,y\in A}g_{x,y}(\varepsilon)$
for all
![]() $1-c\leq \varepsilon\leq \varepsilon_0$
. Then, for any
$1-c\leq \varepsilon\leq \varepsilon_0$
. Then, for any
![]() $(x,y)\in A$
, the convexity of
$(x,y)\in A$
, the convexity of
![]() $g_{x,y}(\varepsilon)$
in
$g_{x,y}(\varepsilon)$
in
![]() $\varepsilon\in (1-c,0)$
yields
$\varepsilon\in (1-c,0)$
yields
This gives us the following nice bounds (with
![]() $g_{x,y}(0)\geq 0$
in mind):
$g_{x,y}(0)\geq 0$
in mind):
Hence,
 \begin{equation}\begin{aligned}(N+1)\varepsilon/\varepsilon_0&\leq \inf_{(x,y)\in A}\left(g_{x,y}(\varepsilon)-g_{x,y}(0)\right)\\&\leq \inf_{(x,y)\in A}g_{x,y}(\varepsilon)-\inf_{(x,y)\in A}g_{x,y}(0)\\&=I_{p,\varepsilon}(c)-I_{p,0}(c)\leq 0.\end{aligned}\end{equation}
\begin{equation}\begin{aligned}(N+1)\varepsilon/\varepsilon_0&\leq \inf_{(x,y)\in A}\left(g_{x,y}(\varepsilon)-g_{x,y}(0)\right)\\&\leq \inf_{(x,y)\in A}g_{x,y}(\varepsilon)-\inf_{(x,y)\in A}g_{x,y}(0)\\&=I_{p,\varepsilon}(c)-I_{p,0}(c)\leq 0.\end{aligned}\end{equation}
Sending
![]() $\varepsilon\rightarrow0^-$
in (10) completes the proof.
$\varepsilon\rightarrow0^-$
in (10) completes the proof.
![]()
Lemma 7. The functions
![]() $I_{p,0}(c)$
and
$I_{p,0}(c)$
and
![]() $I_{\infty,0}(c)$
in Theorem 1 satisfy
$I_{\infty,0}(c)$
in Theorem 1 satisfy
![]() $I_{p,0}(1)=0$
and
$I_{p,0}(1)=0$
and
![]() $0<I_{p,0}(c)<\infty$
for
$0<I_{p,0}(c)<\infty$
for
![]() $c>1$
,
$c>1$
,
![]() $I_{\infty,0}(1)=0$
and
$I_{\infty,0}(1)=0$
and
![]() $0<I_{\infty,0}(c)<\infty$
for
$0<I_{\infty,0}(c)<\infty$
for
![]() $c>1$
.
$c>1$
.
Proof. The proof of the finiteness of
![]() $I_{p,0}(c)$
and
$I_{p,0}(c)$
and
![]() $I_{\infty,0}(c)$
has been done separately in Lemmas 4 and 6. Here we prove the rest.
$I_{\infty,0}(c)$
has been done separately in Lemmas 4 and 6. Here we prove the rest.
Jensen’s inequality yields
![]() $\ln \mathbb{E}\exp\{\theta(S_{x,1}^2-S_{y,1}^2)\}\geq \mathbb{E}(\theta(S_{x,1}^2-S_{y,1}^2))=0$
. Therefore,
$\ln \mathbb{E}\exp\{\theta(S_{x,1}^2-S_{y,1}^2)\}\geq \mathbb{E}(\theta(S_{x,1}^2-S_{y,1}^2))=0$
. Therefore,
![]() $\sup_{\theta\in\mathbb{R}}\big[-\ln \mathbb{E}\exp\big\{\theta\big(S_{x,1}^2-S_{y,1}^2\big)\big\}\big]\leq0$
, implying that
$\sup_{\theta\in\mathbb{R}}\big[-\ln \mathbb{E}\exp\big\{\theta\big(S_{x,1}^2-S_{y,1}^2\big)\big\}\big]\leq0$
, implying that
![]() $I_{p,0}(1)\leq 0$
. Taking
$I_{p,0}(1)\leq 0$
. Taking
![]() $\theta=0$
gives
$\theta=0$
gives
![]() $I_{p,0}(1)= 0$
. The term
$I_{p,0}(1)= 0$
. The term
![]() $I_{\infty,0}(1)$
as the limit of
$I_{\infty,0}(1)$
as the limit of
![]() $I_{p,0}(1)$
must also satisfy
$I_{p,0}(1)$
must also satisfy
![]() $I_{\infty,0}(1)=0$
.
$I_{\infty,0}(1)=0$
.
Now we prove that
![]() $I_{p,0}(c)>0$
and
$I_{p,0}(c)>0$
and
![]() $I_{\infty,0}(c)>0$
for
$I_{\infty,0}(c)>0$
for
![]() $c>1$
; this will be done in three steps.
$c>1$
; this will be done in three steps.
Step 1 We claim that, for any
![]() $c\geq1,p\geq2$
,
$c\geq1,p\geq2$
,
To see (11), it suffices to notice that
Step 2 For
![]() $c>1$
and fixed
$c>1$
and fixed
![]() $p\geq2$
, it will be proved that
$p\geq2$
, it will be proved that
![]() $I_{p,0}(c)>0$
. To this end, let us first note that, because of
$I_{p,0}(c)>0$
. To this end, let us first note that, because of
![]() $\mathbb{E}\exp\{tX_{11}^2\}<\infty$
for some
$\mathbb{E}\exp\{tX_{11}^2\}<\infty$
for some
![]() $t>0$
(as remarked in the proof of Lemma 4),
$t>0$
(as remarked in the proof of Lemma 4),
 \begin{align}\mathbb{E}\exp\{t S_{x,1}^2\}\leq \mathbb{E}\exp\left\{t\sum_{i=1}^pX_{i1}^2\right\}=\left(\mathbb{E}\exp\{tX_{11}^2\}\right)^p<\infty.\end{align}
\begin{align}\mathbb{E}\exp\{t S_{x,1}^2\}\leq \mathbb{E}\exp\left\{t\sum_{i=1}^pX_{i1}^2\right\}=\left(\mathbb{E}\exp\{tX_{11}^2\}\right)^p<\infty.\end{align}
Then, it follows from
![]() $\mathrm{e}^x=1+x+x^2/2+\mathrm{e}^{\alpha x}x^3/6$
for some
$\mathrm{e}^x=1+x+x^2/2+\mathrm{e}^{\alpha x}x^3/6$
for some
![]() $\alpha\in[0,1]$
that
$\alpha\in[0,1]$
that
for small
![]() $0\leq s\leq \varepsilon_0$
. The term
$0\leq s\leq \varepsilon_0$
. The term
![]() $\mathbb{E}(S_{x,1}^4)$
can be bounded as
$\mathbb{E}(S_{x,1}^4)$
can be bounded as
 \begin{equation*}\mathbb{E}(S_{x,1}^4)=\mathbb{E}(X_{11}^4)\sum_{i=1}^px_i^4+6\mathbb{E}(X_{11}^2)\sum_{1\leq i<j\leq p}x_i^2x_j^2\leq 16K_2^4+12pK_2^2,\end{equation*}
\begin{equation*}\mathbb{E}(S_{x,1}^4)=\mathbb{E}(X_{11}^4)\sum_{i=1}^px_i^4+6\mathbb{E}(X_{11}^2)\sum_{1\leq i<j\leq p}x_i^2x_j^2\leq 16K_2^4+12pK_2^2,\end{equation*}
and the term
for some
![]() $K>0$
and
$K>0$
and
![]() $\varepsilon$
with
$\varepsilon$
with
![]() $\varepsilon_0+\varepsilon\leq t$
, where the finiteness comes from (12). Therefore, we can rewrite, for small
$\varepsilon_0+\varepsilon\leq t$
, where the finiteness comes from (12). Therefore, we can rewrite, for small
![]() $0\leq s\leq\varepsilon_0$
,
$0\leq s\leq\varepsilon_0$
,
 \begin{align*}\mathbb{E}\exp\{sS_{x,1}^2\}&=1+s+s^2\cdot c_1+s^3\cdot c_2(s),\\\mathbb{E}\exp\{sS_{y,1}^2\}&=1+s+s^2\cdot c_1^{'}+s^3\cdot c_2^{'}(s),\end{align*}
\begin{align*}\mathbb{E}\exp\{sS_{x,1}^2\}&=1+s+s^2\cdot c_1+s^3\cdot c_2(s),\\\mathbb{E}\exp\{sS_{y,1}^2\}&=1+s+s^2\cdot c_1^{'}+s^3\cdot c_2^{'}(s),\end{align*}
where
![]() $0<c_1,c_1^{'}<\infty$
and
$0<c_1,c_1^{'}<\infty$
and
![]() $0<c_2(s), c_2^{'}(s)<\infty$
for all
$0<c_2(s), c_2^{'}(s)<\infty$
for all
![]() $0\leq s\leq \varepsilon_0$
. Now we apply the estimate
$0\leq s\leq \varepsilon_0$
. Now we apply the estimate
![]() $\ln(1+x)\leq x-x^2/4$
for all
$\ln(1+x)\leq x-x^2/4$
for all
![]() $|x|<1$
and obtain
$|x|<1$
and obtain
 \begin{align*}\ln \mathbb{E}\exp\{\theta S_{x,1}^2\}&\leq (\theta+\theta^2\cdot c_1+\theta^3\cdot c_2(\theta))-o(\theta),\\\ln \mathbb{E}\exp\{-\theta cS_{y,1}^2\}&\leq(-\theta c+(\theta c)^2\cdot c_1^{'}-(\theta c)^3\cdot c_2^{'}(\theta))-o(\theta) \end{align*}
\begin{align*}\ln \mathbb{E}\exp\{\theta S_{x,1}^2\}&\leq (\theta+\theta^2\cdot c_1+\theta^3\cdot c_2(\theta))-o(\theta),\\\ln \mathbb{E}\exp\{-\theta cS_{y,1}^2\}&\leq(-\theta c+(\theta c)^2\cdot c_1^{'}-(\theta c)^3\cdot c_2^{'}(\theta))-o(\theta) \end{align*}
for small
![]() $\theta$
. Hence, for small enough
$\theta$
. Hence, for small enough
![]() $\theta$
, uniform in x and y,
$\theta$
, uniform in x and y,
Taking this inequality back to (11), we get, for small
![]() $\theta\leq \epsilon$
,
$\theta\leq \epsilon$
,
 \begin{align*}I_{p,0}(c)&\geq 1/2\,\,\cdot\inf_{x,y\in \mathbb{R}^p,||x||=||y||=1,x\cdot y=0} \, \sup_{\theta\leq \epsilon}\left[-\ln \left(\mathbb{E}\exp\{\theta S_{x,1}^2\}\mathbb{E}\exp\{-\theta cS_{y,1}^2\}\right)\right]\\&\geq \sup_{\theta\leq \epsilon}[\theta(c-1)+o(\theta)]>0.\end{align*}
\begin{align*}I_{p,0}(c)&\geq 1/2\,\,\cdot\inf_{x,y\in \mathbb{R}^p,||x||=||y||=1,x\cdot y=0} \, \sup_{\theta\leq \epsilon}\left[-\ln \left(\mathbb{E}\exp\{\theta S_{x,1}^2\}\mathbb{E}\exp\{-\theta cS_{y,1}^2\}\right)\right]\\&\geq \sup_{\theta\leq \epsilon}[\theta(c-1)+o(\theta)]>0.\end{align*}
Step 3 For
![]() $c>1$
, we prove that
$c>1$
, we prove that
![]() $I_{\infty,0}(c)>0$
. The proof will be identical to the one in Step 2 if we one can show, instead of using (12), that
$I_{\infty,0}(c)>0$
. The proof will be identical to the one in Step 2 if we one can show, instead of using (12), that
![]() $\mathbb{E}\exp\{t S_{x,1}^2\}\leq C<\infty$
for some
$\mathbb{E}\exp\{t S_{x,1}^2\}\leq C<\infty$
for some
![]() $t>0$
and some constant
$t>0$
and some constant
![]() $C>0$
which is independent of p and x. To this end, we use the moment-generating function upper bound in the definition of a sub-Gaussian random variable:
$C>0$
which is independent of p and x. To this end, we use the moment-generating function upper bound in the definition of a sub-Gaussian random variable:
Now we apply (13) and the fact that
![]() $\mathbb{E}\exp\{t Z\}=\exp\{t^2/2\}$
for all
$\mathbb{E}\exp\{t Z\}=\exp\{t^2/2\}$
for all
![]() $t\in\mathbb{R}$
, where
$t\in\mathbb{R}$
, where
![]() $Z\sim N(0,1)$
, which is independent of the entries, and derive, for any
$Z\sim N(0,1)$
, which is independent of the entries, and derive, for any
![]() $0\leq t\leq 1/(8K_4^2)$
, that
$0\leq t\leq 1/(8K_4^2)$
, that
 \begin{align*}\mathbb{E}\exp\{t S_{x,1}^2\} & = \mathbb{E}\big(\mathbb{E}\big(\exp\big\{tS_{x,1}^2\big\} \mid S_{x,1}\big)\big)=\mathbb{E}\big(\mathbb{E}\big(\mathbb{E}\big(\exp\big\{\sqrt{2t}S_{x,1}Z\big\} \mid S_{x,1}\big) \mid S_{x,1}\big)\big) \\&=\mathbb{E}\big(\mathbb{E}\big(\exp\big\{\sqrt{2t}S_{x,1}Z\big\} \mid S_{x,1}\big)\big)=\mathbb{E}\exp\big\{\sqrt{2t}S_{x,1}Z\big\} \\ & =\mathbb{E}\big(\mathbb{E}\big(\exp\big\{\sqrt{2t}S_{x,1}Z\big\} \mid Z\big)\big)\\&=\mathbb{E}\left(\mathbb{E}\left(\prod_{i=1}^p\mathbb{E}\exp\big\{\sqrt{2t}x_iX_{i1}Z\big\} \mid Z\right)\right)\leq \mathbb{E}\left(\prod_{i=1}^p\exp\big\{2tx_i^2Z^2K_4^2\big\}\right)\\&=\mathbb{E}\exp\big\{2tZ^2K_4^2\big\}=\big(1-4tK_4^2\big)^{-1/2}\leq \sqrt{2}.\end{align*}
\begin{align*}\mathbb{E}\exp\{t S_{x,1}^2\} & = \mathbb{E}\big(\mathbb{E}\big(\exp\big\{tS_{x,1}^2\big\} \mid S_{x,1}\big)\big)=\mathbb{E}\big(\mathbb{E}\big(\mathbb{E}\big(\exp\big\{\sqrt{2t}S_{x,1}Z\big\} \mid S_{x,1}\big) \mid S_{x,1}\big)\big) \\&=\mathbb{E}\big(\mathbb{E}\big(\exp\big\{\sqrt{2t}S_{x,1}Z\big\} \mid S_{x,1}\big)\big)=\mathbb{E}\exp\big\{\sqrt{2t}S_{x,1}Z\big\} \\ & =\mathbb{E}\big(\mathbb{E}\big(\exp\big\{\sqrt{2t}S_{x,1}Z\big\} \mid Z\big)\big)\\&=\mathbb{E}\left(\mathbb{E}\left(\prod_{i=1}^p\mathbb{E}\exp\big\{\sqrt{2t}x_iX_{i1}Z\big\} \mid Z\right)\right)\leq \mathbb{E}\left(\prod_{i=1}^p\exp\big\{2tx_i^2Z^2K_4^2\big\}\right)\\&=\mathbb{E}\exp\big\{2tZ^2K_4^2\big\}=\big(1-4tK_4^2\big)^{-1/2}\leq \sqrt{2}.\end{align*}
This completes the proof.
![]()
7. Open problems and future work
In this paper we have only considered condition numbers for some special rectangular random matrices (i.e.
![]() $p<n$
with
$p<n$
with
![]() $p=o(n)$
). It would be interesting and challenging to study large-deviation probabilities of condition numbers for square random matrices with
$p=o(n)$
). It would be interesting and challenging to study large-deviation probabilities of condition numbers for square random matrices with
![]() $p=n$
(and also for almost square random matrices with
$p=n$
(and also for almost square random matrices with
![]() $n=p+b$
for b fixed or
$n=p+b$
for b fixed or
![]() $b=o(n)$
). The main difficulty lies in the fact that the various estimates used throughout the paper become imprecise when
$b=o(n)$
). The main difficulty lies in the fact that the various estimates used throughout the paper become imprecise when
![]() $p=n$
(or
$p=n$
(or
![]() $n=p+b$
).
$n=p+b$
).
Another rectangular case we have not touched on here is when
![]() $p/n\rightarrow \kappa\in (0,1)$
, and in this case
$p/n\rightarrow \kappa\in (0,1)$
, and in this case
![]() $k^2(p,n)\rightarrow(1+\kappa^{1/2})^2/(1-\kappa^{1/2})^2$
in probability. With this law of large numbers it is also natural to study the corresponding large-deviation asymptotics of k(p,n) for large n.
$k^2(p,n)\rightarrow(1+\kappa^{1/2})^2/(1-\kappa^{1/2})^2$
in probability. With this law of large numbers it is also natural to study the corresponding large-deviation asymptotics of k(p,n) for large n.
The last open problem is about a universality result (mentioned in (4)): under what assumptions on the distribution of the entries does
![]() $I_{\infty,0}(c)=2^{-1}\ln\left[(c+1)^2/(4c)\right]$
? If the assumptions can be specified, then the large-deviation asymptotics of condition numbers for all such distributions coincide with those for Wishart matrices.
$I_{\infty,0}(c)=2^{-1}\ln\left[(c+1)^2/(4c)\right]$
? If the assumptions can be specified, then the large-deviation asymptotics of condition numbers for all such distributions coincide with those for Wishart matrices.
Acknowledgements
The authors are truly grateful to the two referees who carefully read the paper and provided constructive and essential comments which have led to an improved version of the paper, and to the Editor for help throughout the whole process.