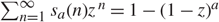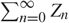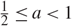1 Introduction
1.1 Progeny of a branching process
If p is a distribution on the set ℕ of nonnegative integers with generating function
\[f_p(z)=\sum_{n=0}^{\infty}p_nz^{\,n} ,\]
consider the branching process 
$$(Z_n )_{n = 0}^\infty$$ governed by p It is easily seen that
\begin{equation}\Pr(S=n)=s_a(n)=\frac{1}{n!}a(1-a)(2-a)\cdots (n-1-a)=\frac{-(\!-a)_n}{n!}.\end{equation}
It is well known that Pr (there exists n: Zn = 0) = 1 if and only if 
$$m = \sum\nolimits_{n = 0}^\infty np_n \le 1$$. Under these circumstances, the random variable
S=\sum_{n=0}^{\infty}Z_n
is finite. Its distribution q is called the progeny of p and we have the following link between the generating functions of p and q. For all z such that |z| ≤ 1 the following holds:
\begin{equation}f_q(z)=zf_p(\,f_q(z)).\end{equation}
Since Z 0 =1, the sum S is concentrated on ℕ+ Given p, the calculation of q, or of fq, is not easy in general. It can be done using the Lagrange–Bürmann formula (see [Reference Whittaker and Watson7, p. 129]). To compute q, the only simple case is when fp is a fractional linear function (also called the Möbius or homographic function); see [Reference Toulouse6, p.~266]. Surprisingly enough, given fq, computing fp is easier. In fact, the function 
$$z = g(u) = f_q^{(- 1)} (u)$$ valued in [0,1] is well defined for u ∈ [0, 1] by u= fq(z) and (1) leads to
\begin{equation}f_p(u)=\frac{u}{g(u)}.\end{equation}
Although the correspondence p ↦ q is one-to-one, clearly not all distributions q on ℕ+ can be the progeny of some p. For instance, q cannot have a bounded support, except in the degenerate case where p0 =1. Another necessary condition for q to be a progeny is 
$$q_1 = f'_q (0) > 0$$. If that were not true, the reciprocal function g of fq would not be analytic at 0. In general, given a probability q on ℕ+, no necessary and sufficient condition for q to be a progeny is known. Two classical treatises on these subjects are [Reference Harris3] and [Reference Athreya and Ney1].
1.2 Sibuya distribution
In the remainder of this paper, we use the Pochhammer symbol (x)n= x(x + 1) · · · (x + n−1). The Sibuya distribution sa with parameter a ∈ (0, 1) is a probability on positive integers ℕ+ = {1, 2, …} such that if S ∼sa then
\begin{equation}f_{s_a}(z)=\E(z^S)=1-(1-z)^a.\end{equation}
It is easily seen that, for n ≥ 1,
\begin{equation}\Pr(S=n)=s_a(n)=\frac{1}{n!}a(1-a)(2-a)\cdots (n-1-a)=\frac{-(\!-a)_n}{n!}.\end{equation}
Although this law sa has been considered before, traditionally one refers to [Reference Sibuya5] for its study. In the latter, sa appears as a particular case of what Sibuya calls a digamma law: Equations (16) and (28) of that paper for γ =−α = a yield (4) above. Surprisingly, (3) does not appear in the paper. If S ∼ s 1/2, the distribution of 2S is well known as the law of first return to 0 of a simple random walk. Another probabilistic interpretation of S ∼ sa is S(w) = min{n: w ∈ An}, where (An)n≥1 is a sequence of independent events such that Pr (An) = a/n. Kozubowski and Podgórski [Reference Kozubowski and Podgórski4] provided numerous observations and a rich set of references about sa.
The most interesting feature of the Sibuya law from the point of view of branching processes is the semigroup property 
$$f_{s_a } \circ f_{s_{a'} } = f_{s_{aa'} } .$$ This implies that if the branching process 
$$(Z_n )_{n = 0}^\infty$$ is governed by sa then the law of Zn is quite explicit and is equal to 
$$s_{a^n } .$$ This distribution is an example of an embeddable law in a continuous semigroup for composition. See [Reference Grey2] for instance. There are other variations of this distribution, sometimes informally called Sibuya distributions. One is the mixture of sa with the Dirac measure at 0, (1−λ)δ 0 + λsa, where 0 < λ ≤ 1, which has generating function
\begin{equation}f_{(1-\lambda)\delta_0+\lambda\ s_a}(u)=1-\lambda (1-u)^a.\end{equation}
Another one is the natural exponential family extension of the Sibuya distribution, say 
$$s_a^{(\rho )},$$ defined for 0 < ρ ≤ 1 by its generating function
\begin{equation}f_{ s_a^{(\rho)}}(u)=c(1- (1-\rho u)^a),\qquad c=\frac{1}{1- (1-\rho)^a}.\end{equation}
However, in the present paper ‘Sibuya law’ will mean sa for some 0 < a < only.
1.3 When is the Sibuya distribution a progeny?
Since the Sibuya distribution is concentrated on ℕ+, has an unbounded support, and satisfies q 1 = a > 0, the natural question is the following: given a ∈ (0, 1), does there exist p such that q = sa? The following proposition gives the answer and constitutes the aim of the present paper.
Proposition 1. The Sibuya distribution sa is a progeny if and only if 
$${\textstyle{1 \over 2}} \le a < 1.$$
Note that the question is a natural question, since we can compute g explicitly. One should not wonder whether (5) is a progeny, since it has an atom at 0. Case (6) is more interesting.
Corollary 1. For ρ ∈ (0, 1), the distribution 
$$s_a^{(\rho )}$$ is a progeny if and only if 
$${\textstyle{1 \over 2}} \le a < 1.$$
2 Proofs
Proof of Proposition 1. For simplicity, we let b = 1/a >1. Calculating the function g which appears in (2) is easy since, if u ∈ [0, 1], the only solution z ∈ [0, 1] of the equation u = (1 − (1 − z)1/b is g(u) = 1 − (1 − u)b. We therefore have to prove that the function
u \mapsto h_b(u)=\frac{u}{1-(1-u)^b}
has a power series expansion with nonnegative coefficients if and only if 1 ≤ b ≤ 2.
We let B denote the set of b > 1 such that s 1/b is a progeny. The case b = 1 is degenerate.
Step (i): 2 is in B, 3 is not in B We have
h_2(u)=\half\frac{1}{1-u/2}=\sum_{n=0}^{\infty}\frac{1}{2^{n+1}}u^n
and we obtain the well-known fact that s 1/2 is the progeny of a geometric distribution starting at 0. For b = 3, we have
\ h_3(u)=\frac{1}{3}\times \frac{1}{1-u+{u^2}/{3}}=\frac{1}{3}\sum_{n=0}^{\infty}r^n \frac{\sin(n+1)\theta}{\sin \theta}u^n,
where 
$$r^{ \pm \theta } = {1 \over 2}(3 \pm \sqrt 3 )$$ are the complex roots of the polynomial 1 — u + u2/3 In fact, 
$$r = \sqrt 3$$ and θ = ± π/6 Clearly, sin (n + 1)θ / sin θ ≥ 0 for all n is impossible and therefore 3 is not in B
Step (ii): b is in B if 1 < b < 2 Using the Pochhammer symbol, we can write
(1-u)^b=\sum_{n=0}^{\infty}\frac{(\!-b)_n}{n!}u^n.
Let
H(u)=\frac{1}{bu^2}(\!-1+bu+(1-u)^b)=\frac{b-1}{2}+\sum_{n=1}^{\infty}(b\,{-}\,1)(2\,{-}\,b)(3\,{-}\,b)\cdots(n\,{+}\,1\,{-}\,b)\frac{u^n}{(n\,{+}\,2)!}.
Since 1 < b < 2, all the coefficients of H are positive. As a consequence of the definition of H,
h_b(u)=\frac{1}{b}\frac{1}{1-uH(u)} = \frac{1}{b}\sum_{n=0}^{\infty}u^nH(u)^n,
and, since the coefficients of H are positive, this implies that b ∈ B.
Step (ii): b is not in B if b > 3. Consider the numbers (Pn)n≥2 defined by
\begin{equation}\frac{bu}{1-(1-u)^b}=1+\frac{b-1}{2}u+\sum_{n=2}^{\infty}P_nu^n.\end{equation}
A simple calculation shows that
\begin{align*}P_2=\frac{b^2-1}{6},\quad P_3=\frac{b^2-1}{4},\quad P_4=\frac{(19-b^2)(b^2-1)}{30},\quad P_5=\frac{(9-b^2)(b^2-1)}{4}.\end{align*}
Therefore, P 5 < 0 if b > 3.
Step (iv): b is not in B if 2 < b < 3. This point is more difficult. Let us introduce the numbers (pn)n≥2 defined by
\begin{align}\frac{1-(1-u)^b}{bu}&= \int_0^1(1-ux)^{b-1} \sd x\nonumber\\ &= 1-\frac{b-1}{2}u+\sum_{n=2}^{\infty}\frac{(1-b)_n}{(n+1)!}u^n \nonumber \\& =1-\frac{b-1}{2}u+\sum_{n=2}^{\infty}p_nu^n ,\end{align}
where
\begin{align}p_n=\frac{1}{(n+1)!}(b-1)(b-2)(3-b)\cdots (n-b).\\[-14pt]\nonumber\end{align}
The radius of convergence of power series (8) is 1. Observe that, since n ≥ 2, from (9), we have pn >0 if 2 < b < 3. To simplify, we now let
v=\frac{b-1}{2}u,\qquad u=\frac{2}{b-1}v,\qquad A_n=P_n\frac{2^n}{(b-1)^n},\qquad a_n=p_n\frac{2^n}{(b-1)^n},
where Pn was defined in (7). With this notation, equalities (7) and (8) become
\begin{align}\frac{2b}{b-1} \frac{v}{1-\left(1-{2v}/{(b-1)}\right)^b}&=1+v+\sum_{n=2}^{\infty}A_nv^n ,\end{align}
\begin{align}\frac{b-1}{2b}\frac{1-\left(1-{2v}/{(b-1)}\right)^b}{v}&= 1-v+\sum_{n=2}^{\infty}a_nv^n.\end{align}
Since 2 < b < 3, the radius of convergence of the power series on the right-hand side of (11) is (b − 1)/2< 1. Because an > 0, this remark implies that
\begin{equation}\sum_{n=2}^{\infty}a_n=\infty.\end{equation}
Now we multiply the right-hand sides of (11) and (10). Their product is 1. We obtain
\begin{gather*}\sum_{n=2}^{\infty}(a_n+A_n)v^n+\sum_{n=2}^{\infty}(a_n-A_n) v^{n+1}+\Bigg(\sum_{n=2}^{\infty}a_nv^n\Bigg)\Bigg(\sum_{n=2}^{\infty}A_nv^n\Bigg) = v^2 ,\\ \sum_{n=2}^{\infty}(a_n+A_n)v^n+\sum_{n=3}^{\infty}(a_{n-1}-A_{n-1})v^{n}+\sum_{n=4}^{\infty}\Bigg(\sum_{k=2}^{n-2}A_{n-k}a_k\Bigg)v^n=v^2 .\end{gather*}
From this last equality, watching the coefficient on νn for n ≥ 4, we obtain
\begin{equation}a_n+a_{n-1}+\sum_{k=2}^{n-2}A_{n-k}a_k=A_{n-1}-A_n .\end{equation}
Now assume that An ≥ 0 for all n ≥ 2, which is equivalent to assuming that b ∈ B. Then (13) implies that an ≤ An −1 −An. Summing from n = 4 to N we obtain, for all N,
\sum_{n=4}^Na_n\leq A_3-A_N\leq A_3,
which contradicts (12). Therefore, there exists at least one n such that An < 0 and the proposition is proved.
Proof of Corollary 1. If fq(z) = c(1 − (1 − ρz)1/b) then
g(u)=\frac{1}{\rho}\Big(1-\left(1-\frac{u}{c}\right)^b\Big).
From the proposition, the corresponding fecundity distribution p does exist if and only if 1< b ≤ 2, since
\begin{equation*}\frac{f_p(cu)}{c\rho}=\frac{u}{1-(1-u)^b}.\tag*{$\square$}\end{equation*}
Acknowledgements
I thank the referee for several useful remarks. I am deeply indebted to ‘jandri’, an anonymous contributor of the Internet site ‘les-mathematiques.net’ (http://www.les-mathematiques.net/phorum/read.php?4,1628022,1671930), where I raised the question of the positivity of the coefficients (Pn) in (7) for the first time. He suggested the possibility that the Pn are all positive if and only if 1 < b ≤ 2. He observed that P 5 < 0 if b > 3 and even pointed out that, for b = 2 + 10−9, the first negative Pn occurs for n = 45, which strongly suggested that Proposition 1 was correct.
