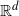1. Introduction
Ever since the seminal papers of Rényi and Sulanke [Reference Rényi and Sulanke20, Reference Rényi and Sulanke21, Reference Rényi and Sulanke22], the approximation of convex bodies by random polytopes has been a much-studied branch of stochastic geometry. A typical object of investigation is the convex hull of n independent, identically distributed random points in a given convex body in
![]() ${\mathbb R}^d$
. A typical question concerns the asymptotic behavior of a geometric functional of this convex hull, as the number n of random points tends to infinity. Surveys at least partially devoted to this topic include [Reference Bárány2,Reference Bárány3], [Reference Buchta and Hlawka8], [Reference Hug and Spodarev13] , [Reference Reitzner, Kendall and Molchanov19], [Reference Schneider24, Reference Schneider, Goodman, O’Rourke and Tóth26], [Reference Schneider and Weil27, Section 8.2], and [Reference Weil, Wieacker, Gruber and Wills29]. The precise asymptotic formulas that have been obtained usually require that the convex body K under consideration is either sufficiently smooth (where sometimes the existence of freely rolling balls may be sufficient) or a polytope. For general convex bodies, one has a precise asymptotic formula for the volume, denoted by V. Let
${\mathbb R}^d$
. A typical question concerns the asymptotic behavior of a geometric functional of this convex hull, as the number n of random points tends to infinity. Surveys at least partially devoted to this topic include [Reference Bárány2,Reference Bárány3], [Reference Buchta and Hlawka8], [Reference Hug and Spodarev13] , [Reference Reitzner, Kendall and Molchanov19], [Reference Schneider24, Reference Schneider, Goodman, O’Rourke and Tóth26], [Reference Schneider and Weil27, Section 8.2], and [Reference Weil, Wieacker, Gruber and Wills29]. The precise asymptotic formulas that have been obtained usually require that the convex body K under consideration is either sufficiently smooth (where sometimes the existence of freely rolling balls may be sufficient) or a polytope. For general convex bodies, one has a precise asymptotic formula for the volume, denoted by V. Let
![]() $K\subset
{\mathbb R}^d$
be a convex body with
$K\subset
{\mathbb R}^d$
be a convex body with
![]() $V(K)=1$
(say), and let
$V(K)=1$
(say), and let
![]() $K_n$
denote the convex hull of n independent random points in K with uniform distribution. Then, as shown in [Reference Schütt28],
$K_n$
denote the convex hull of n independent random points in K with uniform distribution. Then, as shown in [Reference Schütt28],
with an explicit constant c(d), where
![]() ${{\mathbb E}}$
denotes mathematical expectation. Here
${{\mathbb E}}$
denotes mathematical expectation. Here
![]() $\kappa$
is the generalized Gauss –Kronecker curvature (which exists almost everywhere on
$\kappa$
is the generalized Gauss –Kronecker curvature (which exists almost everywhere on
![]() $\partial K$
) and
$\partial K$
) and
![]() ${\mathcal{H}}^{d-1}$
is the
${\mathcal{H}}^{d-1}$
is the
![]() $(n-1)$
-dimensional Hausdorff measure. However, for most convex bodies (in the sense of Baire category : see [Reference Zamfirescu30]) the right-hand side of (1) is zero, so (1) gives only partial information on the order of
$(n-1)$
-dimensional Hausdorff measure. However, for most convex bodies (in the sense of Baire category : see [Reference Zamfirescu30]) the right-hand side of (1) is zero, so (1) gives only partial information on the order of
![]() $V(K)-{{\mathbb E}} V(K_n)$
. Additional information for all convex bodies is provided by a result in [Reference Bárány and Larman4], which says that
$V(K)-{{\mathbb E}} V(K_n)$
. Additional information for all convex bodies is provided by a result in [Reference Bárány and Larman4], which says that
Here the notation
![]() $f(n)\ll g(n)$
means that there exists a constant
$f(n)\ll g(n)$
means that there exists a constant
![]() $c>0$
such that
$c>0$
such that
![]() $f(n)\le cg(n)$
for all sufficiently large
$f(n)\le cg(n)$
for all sufficiently large
![]() $n\in {\mathbb N}$
. The constant c has to be independent of n, but it may depend on the dimension d, the convex body K, and later on the given measure
$n\in {\mathbb N}$
. The constant c has to be independent of n, but it may depend on the dimension d, the convex body K, and later on the given measure
![]() $\varphi$
. For the mean width W, it was shown in [Reference Schneider23] that
$\varphi$
. For the mean width W, it was shown in [Reference Schneider23] that
The orders are best possible; they are attained by sufficiently smooth bodies on the right side of (2) and the left side of (3), and by polytopes on the left side of (2) and the right side of (3). This change of optimality makes it difficult to conjecture how a common generalization of (2) and (3) to general intrinsic volumes might look. Although a guess has been formulated in [1, p. 675], this has remained one of the major mysteries in this area.
It should be mentioned that it follows from [Reference Gruber11] that for most convex bodies (in the sense of Baire category) the middle terms in (2) and (3) oscillate, as
![]() $n\to\infty$
, between the orders given by the left and right sides. More precise formulations are found in [Reference Bárány and Larman4, Theorem 5] and [Reference Schneider23, p. 305]. This shows that, for general convex bodies, two-sided inequalities of type (Reference Bárány2, Reference Bárány3) with optimal orders are the best one can expect (up to the involved constants).
$n\to\infty$
, between the orders given by the left and right sides. More precise formulations are found in [Reference Bárány and Larman4, Theorem 5] and [Reference Schneider23, p. 305]. This shows that, for general convex bodies, two-sided inequalities of type (Reference Bárány2, Reference Bárány3) with optimal orders are the best one can expect (up to the involved constants).
Vaguely ‘dual’ to the preceding are questions about the approximation of a convex body by the intersection of random closed half-spaces containing the body. Such questions have been treated in the plane in [Reference Rényi and Sulanke22] and in higher dimensions in [Reference Böröczky and Schneider6], [Reference Böröczky, Fodor and Hug7], [Reference Fodor, Hug and Ziebarth10], and [Reference Kaltenbach15].
A common feature of these investigations is that a fixed number n of independent random objects, points, or hyperplanes is considered, and in the end this number n tends to infinity. In the case of hyperplanes, the underlying model, for example in [Reference Rényi and Sulanke22], and [Reference Böröczky and Schneider6], may seem a bit artificial, since the hyperplanes must be restricted so that they intersect a region close to the convex body under consideration.
Another model, which in the case of hyperplanes seems more natural, starts with a stationary Poisson process, either of points or of hyperplanes, which is then restricted, either to the points contained in the considered convex body or to the hyperplanes not intersecting the body. The intensity of the Poisson process is finally assumed to increase to infinity. For point processes, relevant investigations are [Reference Bárány and Reitzner5], [Reference Calka and Yukich9], [Reference Pardon16, Reference Pardon17], and hyperplane processes are considered in [Reference Kaltenbach15].
The setting in this paper consists in a stationary Poisson hyperplane process X and a convex body K with interior points in
![]() ${\mathbb R}^d$
. The K-cell of X is the random polytope defined by
${\mathbb R}^d$
. The K-cell of X is the random polytope defined by
where
![]() $H^-(K)$
denotes the closed half-space bounded by H that contains K. If the intensity of X tends to infinity, the K-cell
$H^-(K)$
denotes the closed half-space bounded by H that contains K. If the intensity of X tends to infinity, the K-cell
![]() $Z_K$
may or may not approximate K, depending on the directional distribution of X (an even probability measure on the unit sphere) in relation to properties of K. In [Reference Hug and Schneider14], the approximation was measured in terms of the Hausdorff metric, and various situations of good approximation were investigated. For example,
$Z_K$
may or may not approximate K, depending on the directional distribution of X (an even probability measure on the unit sphere) in relation to properties of K. In [Reference Hug and Schneider14], the approximation was measured in terms of the Hausdorff metric, and various situations of good approximation were investigated. For example,
![]() $Z_K$
converges almost surely to K in the Hausdorff metric as the intensity of X tends to infinity, if and only if the support of the directional distribution of X contains the support of the area measure of K.
$Z_K$
converges almost surely to K in the Hausdorff metric as the intensity of X tends to infinity, if and only if the support of the directional distribution of X contains the support of the area measure of K.
The majority of investigations on random approximation deals with the asymptotic behavior of geometric functionals, such as volume, mean width, number of k-faces, of the approximating random polytopes. In the present setting, a first result of this type was proved in [Reference Kaltenbach15]. We assume now that the stationary Poisson hyperplane process X has intensity
![]() $n\in{\mathbb N}$
, and we denote the corresponding K-cell by
$n\in{\mathbb N}$
, and we denote the corresponding K-cell by
![]() $Z_K^{(n)}$
. It is assumed further that the directional distribution
$Z_K^{(n)}$
. It is assumed further that the directional distribution
![]() $\varphi$
of X has a positive, continuous density with respect to spherical Lebesgue measure. Under these assumptions, Kaltenbach [Reference Kaltenbach15] proved that
$\varphi$
of X has a positive, continuous density with respect to spherical Lebesgue measure. Under these assumptions, Kaltenbach [Reference Kaltenbach15] proved that
The proof can be considered as a ‘dualization’ (in a non-precise sense) of that of (3) and an extension to Poisson processes.
The purpose of this note is to obtain a similar counterpart to (2), and thus a result of type (5) with the volume replaced by the mean width W (observe that under dualization, volume and mean width interchange their roles, roughly). We have to assume now that the stationary Poisson hyperplane process X is also isotropic, that is, its distribution is invariant under rotations.
Theorem 1. Let X be a stationary and isotropic Poisson hyperplane process in
![]() ${\mathbb R}^d$
of intensity n. Let
${\mathbb R}^d$
of intensity n. Let
![]() $K\subset {\mathbb R}^d$
be a convex body with interior points, and let
$K\subset {\mathbb R}^d$
be a convex body with interior points, and let
![]() $Z_K^{(n)}$
denote the K-cell of X. Then
$Z_K^{(n)}$
denote the K-cell of X. Then
For random polytopes generated by finitely many independent hyperplanes with a suitable distribution, depending on K, a similar result was proved in [Reference Böröczky and Schneider6]. Some ideas used there can be employed in the following. It turned out, however, that a proof for Poisson hyperplane processes is not straightforward and requires additional arguments. These will be presented in this note.
That the orders in (6) are best possible can be seen from extensions, to Poisson hyperplane processes, of precise asymptotic formulas that have been obtained for a finite number of independent random hyperplanes with a suitable distribution. These formulas are, on the one hand, Theorem 1.3 in [Reference Böröczky and Schneider6], which holds for simple polytopes, and on the other hand Theorem 5.2 in [Reference Böröczky, Fodor and Hug7], which yields the exact order on the right side of (6) if applied to a convex body of class
![]() $C^2$
. The extension, which we do not carry out here, would require a dual version of the argument sketched in [Reference Reitzner18] (proof of Lemma 1) and an estimate of the type provided by Lemma 1 below.
$C^2$
. The extension, which we do not carry out here, would require a dual version of the argument sketched in [Reference Reitzner18] (proof of Lemma 1) and an estimate of the type provided by Lemma 1 below.
2. Preliminaries
The standard scalar product of
![]() ${\mathbb R}^d$
is denoted by
${\mathbb R}^d$
is denoted by
![]() $\langle\cdot\,,\cdot\rangle$
, and the induced norm by
$\langle\cdot\,,\cdot\rangle$
, and the induced norm by
![]() $\|\cdot\|$
. The unit ball of
$\|\cdot\|$
. The unit ball of
![]() ${\mathbb R}^d$
is
${\mathbb R}^d$
is
![]() $B^d$
, and the unit sphere is
$B^d$
, and the unit sphere is
![]() ${{\mathbb S}^{d-1}}$
. Lebesgue measure on
${{\mathbb S}^{d-1}}$
. Lebesgue measure on
![]() ${{\mathbb R}^d}$
is denoted by
${{\mathbb R}^d}$
is denoted by
![]() $\lambda_d$
.
$\lambda_d$
.
Hyperplanes and closed half-spaces of
![]() ${\mathbb R}^d$
are written in the form
${\mathbb R}^d$
are written in the form
respectively, with
![]() $u\in{{\mathbb S}^{d-1}}$
and
$u\in{{\mathbb S}^{d-1}}$
and
![]() $\tau\in{\mathbb R}$
. Let
$\tau\in{\mathbb R}$
. Let
![]() ${\mathcal{H}}$
be the space of hyperplanes in
${\mathcal{H}}$
be the space of hyperplanes in
![]() ${\mathbb R}^d$
with its usual topology. For a subset
${\mathbb R}^d$
with its usual topology. For a subset
![]() $M\subset{\mathbb R}^d$
, we write
$M\subset{\mathbb R}^d$
, we write
We let
![]() ${{\mathcal K}}_d$
denote the space of d-dimensional convex bodies (compact, convex sets with interior points) in
${{\mathcal K}}_d$
denote the space of d-dimensional convex bodies (compact, convex sets with interior points) in
![]() ${\mathbb R}^d$
. As usual, it is equipped with the Hausdorff metric. For
${\mathbb R}^d$
. As usual, it is equipped with the Hausdorff metric. For
![]() $K\in{{\mathcal K}}_d$
, let
$K\in{{\mathcal K}}_d$
, let
![]() $R_o(K)$
be the radius of the smallest ball with center at the origin o of
$R_o(K)$
be the radius of the smallest ball with center at the origin o of
![]() ${\mathbb R}^d$
that contains K.
${\mathbb R}^d$
that contains K.
For our notation concerning point processes, we refer to [Reference Schneider and Weil27, Sections 3.1 and 3.2]. In particular, given a locally compact topological space E, we let
![]() $({\sf N}_s(E), {\mathcal N}_s(E))$
denote the measurable space of simple, locally finite counting measures on E. We often identify a simple counting measure
$({\sf N}_s(E), {\mathcal N}_s(E))$
denote the measurable space of simple, locally finite counting measures on E. We often identify a simple counting measure
![]() $\eta\in {\sf N}_s(E)$
with its support, using
$\eta\in {\sf N}_s(E)$
with its support, using
![]() $\eta(\{x\})=1$
and
$\eta(\{x\})=1$
and
![]() $x\in\eta$
synonymously. A (simple) point process in E is a mapping
$x\in\eta$
synonymously. A (simple) point process in E is a mapping
![]() $X \colon (\Omega,{A},{\mathbb P})\to ({N}_s(E), {\mathcal
N}_s(E))$
, where
$X \colon (\Omega,{A},{\mathbb P})\to ({N}_s(E), {\mathcal
N}_s(E))$
, where
![]() $(\Omega,{A},{\mathbb P})$
is some probability space, such that
$(\Omega,{A},{\mathbb P})$
is some probability space, such that
![]() $\{X(C)=0\}$
is measurable for all compact sets
$\{X(C)=0\}$
is measurable for all compact sets
![]() $C\subset E$
. We let
$C\subset E$
. We let
![]() $\Theta={{\mathbb E}\,} X$
denote the intensity measure of X. The point process X is a Poisson process if
$\Theta={{\mathbb E}\,} X$
denote the intensity measure of X. The point process X is a Poisson process if
for
![]() $k\in {\mathbb N}_0$
and each Borel set
$k\in {\mathbb N}_0$
and each Borel set
![]() $A\subset E$
with
$A\subset E$
with
![]() $\Theta(A)<\infty$
. For the independence properties of (simple) Poisson processes, we refer to [Reference Schneider and Weil27, Theorem 3.2.2]. A stationary Poisson hyperplane process in
$\Theta(A)<\infty$
. For the independence properties of (simple) Poisson processes, we refer to [Reference Schneider and Weil27, Theorem 3.2.2]. A stationary Poisson hyperplane process in
![]() ${\mathbb R}^d$
is a Poisson process X in the space
${\mathbb R}^d$
is a Poisson process X in the space
![]() ${\mathcal{H}}$
of hyperplanes whose intensity measure (and hence whose distribution) is invariant under translations. The intensity measure of such a process, assumed to be non-zero, is of the form
${\mathcal{H}}$
of hyperplanes whose intensity measure (and hence whose distribution) is invariant under translations. The intensity measure of such a process, assumed to be non-zero, is of the form
for Borel sets
![]() $A\subset {\mathcal{H}}$
. Here
$A\subset {\mathcal{H}}$
. Here
![]() $\gamma>0$
is the intensity of X and
$\gamma>0$
is the intensity of X and
![]() $\varphi$
is an even probability measure on the sphere
$\varphi$
is an even probability measure on the sphere
![]() ${{\mathbb S}^{d-1}}$
, the spherical directional distribution of X.
${{\mathbb S}^{d-1}}$
, the spherical directional distribution of X.
We assume now that X is a stationary Poisson hyperplane process in
![]() ${\mathbb R}^d$
of intensity
${\mathbb R}^d$
of intensity
![]() $\gamma>0$
and with a non-degenerate spherical directional distribution
$\gamma>0$
and with a non-degenerate spherical directional distribution
![]() $\varphi$
. Here, ‘non-degenerate’ means that
$\varphi$
. Here, ‘non-degenerate’ means that
![]() $\varphi$
is not concentrated on any great subsphere.
$\varphi$
is not concentrated on any great subsphere.
For
![]() $K\in{{\mathcal K}}_d$
, we let
$K\in{{\mathcal K}}_d$
, we let
![]() $Z_K$
denote the K-cell defined by X and K, as above. This is a random polytope, since it is almost surely bounded. More precisely, we show the following estimate, which later on, when the intensity tends to infinity, will allow us to restrict ourselves to K-cells contained in a sufficiently large fixed ball.
$Z_K$
denote the K-cell defined by X and K, as above. This is a random polytope, since it is almost surely bounded. More precisely, we show the following estimate, which later on, when the intensity tends to infinity, will allow us to restrict ourselves to K-cells contained in a sufficiently large fixed ball.
Lemma 1. Let
![]() $K\in{{\mathcal K}}_d$
. There are constants
$K\in{{\mathcal K}}_d$
. There are constants
![]() $a,b>0$
, depending only on
$a,b>0$
, depending only on
![]() $\varphi$
, such that
$\varphi$
, such that
Proof. Since
![]() ${\textrm{supp}}\,\varphi$
, the support of the even measure
${\textrm{supp}}\,\varphi$
, the support of the even measure
![]() $\varphi$
, is not contained in a great subsphere, we can choose vectors
$\varphi$
, is not contained in a great subsphere, we can choose vectors
![]() $\pm e_1,\dots,\pm e_d\in {\textrm{supp}}\,\varphi$
positively spanning
$\pm e_1,\dots,\pm e_d\in {\textrm{supp}}\,\varphi$
positively spanning
![]() ${\mathbb R}^d$
. In the following, we write
${\mathbb R}^d$
. In the following, we write
![]() $e_{d+i}\colon=-e_i$
for
$e_{d+i}\colon=-e_i$
for
![]() $i=1,\dots,d$
. We can choose a sufficiently large constant b and sufficiently small, pairwise disjoint neighborhoods
$i=1,\dots,d$
. We can choose a sufficiently large constant b and sufficiently small, pairwise disjoint neighborhoods
![]() $U_i\subset {{\mathbb S}^{d-1}}$
of
$U_i\subset {{\mathbb S}^{d-1}}$
of
![]() $e_i$
,
$e_i$
,
![]() $i=1,\dots,2d$
, such that each intersection
$i=1,\dots,2d$
, such that each intersection
 $$\label{2.2}
P\colon= \bigcap_{i=1}^{2d} H^-(u_i,1) \quad \mbox{with }u_i\in U_i,\,i=1,\dots,2d,
$$
$$\label{2.2}
P\colon= \bigcap_{i=1}^{2d} H^-(u_i,1) \quad \mbox{with }u_i\in U_i,\,i=1,\dots,2d,
$$
is a polytope with
![]() $R_o(P)\le b$
. Let
$R_o(P)\le b$
. Let
![]() $x\ge 0$
. If the numbers
$x\ge 0$
. If the numbers
![]() $\tau_i$
are such that
$\tau_i$
are such that
![]() $R_o(K)\le \tau_i\le R_o(K)+x$
and if
$R_o(K)\le \tau_i\le R_o(K)+x$
and if
![]() $u_i\in U_i$
for
$u_i\in U_i$
for
![]() $i=1,\dots,2d$
, then
$i=1,\dots,2d$
, then
 $$R_o\bigg(\bigcap_{i=1}^{2d} H^-(u_i,\tau_i)\bigg) \le R_o((R_o(K)+x)P)=(R_o(K)+x)R_o(P)\le b(R_o(K)+x).$$
$$R_o\bigg(\bigcap_{i=1}^{2d} H^-(u_i,\tau_i)\bigg) \le R_o((R_o(K)+x)P)=(R_o(K)+x)R_o(P)\le b(R_o(K)+x).$$
The sets of hyperplanes
are pairwise disjoint. If
![]() $X(A_i(x)) >0$
for
$X(A_i(x)) >0$
for
![]() $i=1,\dots,2d$
, then
$i=1,\dots,2d$
, then
![]() $R_o(Z_K)\le b(R_o(K)+x)$
. Therefore, observing that
$R_o(Z_K)\le b(R_o(K)+x)$
. Therefore, observing that
![]() $\Theta(A_i(x)) = \gamma x\varphi(U_i)$
and choosing
$\Theta(A_i(x)) = \gamma x\varphi(U_i)$
and choosing
![]() $0<a\le\varphi(U_i)$
for
$0<a\le\varphi(U_i)$
for
![]() $i=1,\dots,2d$
, we get
$i=1,\dots,2d$
, we get
 \begin{align*}
&{\mathbb P}(R_o(Z_K) > b(R_o(K)+x))\\
&\qquad \le {\mathbb P}( X(A_i(x))=0\mbox{ for at least one } i\in \{1,\dots,2d\})\\
&\qquad = 1-\prod_{i=1}^{2d} (1-{\mathbb P}( X(A_i(x))=0))\\
&\qquad = 1-\prod_{i=1}^{2d} (1- {\textrm{e}}^{-\gamma\varphi(U_i)x})\\
&\qquad \le 1-(1- {\textrm{e}}^{- \gamma ax})^{2d}\\
&\qquad \le 2d \,{\textrm{e}}^{-\gamma ax},
\end{align*}
\begin{align*}
&{\mathbb P}(R_o(Z_K) > b(R_o(K)+x))\\
&\qquad \le {\mathbb P}( X(A_i(x))=0\mbox{ for at least one } i\in \{1,\dots,2d\})\\
&\qquad = 1-\prod_{i=1}^{2d} (1-{\mathbb P}( X(A_i(x))=0))\\
&\qquad = 1-\prod_{i=1}^{2d} (1- {\textrm{e}}^{-\gamma\varphi(U_i)x})\\
&\qquad \le 1-(1- {\textrm{e}}^{- \gamma ax})^{2d}\\
&\qquad \le 2d \,{\textrm{e}}^{-\gamma ax},
\end{align*}
by Bernoulli’s inequality. This was the assertion.
3. Proof of the upper bound
The approach to proving the right-hand estimate of (6) consists in establishing an extremal property of balls and then finding a connection to a known result on approximation of balls by convex hulls of finitely many random points. Since we are dealing with Poisson processes, this requires extra arguments in either step.
Let X be a stationary Poisson hyperplane process in
![]() ${\mathbb R}^d$
, with a non-degenerate spherical directional distribution
${\mathbb R}^d$
, with a non-degenerate spherical directional distribution
![]() $\varphi$
and with intensity
$\varphi$
and with intensity
![]() $\gamma$
. If a convex body
$\gamma$
. If a convex body
![]() $K\in{{\mathcal K}}_d$
is given, we let
$K\in{{\mathcal K}}_d$
is given, we let
![]() $Z_K$
denote the K-cell defined by X and K, as in (4). In order to be able to compare
$Z_K$
denote the K-cell defined by X and K, as in (4). In order to be able to compare
![]() $Z_K$
and
$Z_K$
and
![]() $Z_L$
for different
$Z_L$
for different
![]() $K,L\in {{\mathcal K}}_d$
, we use an auxiliary Poisson process. For this, we consider the product space
$K,L\in {{\mathcal K}}_d$
, we use an auxiliary Poisson process. For this, we consider the product space
![]() $E\colon={{\mathbb S}^{d-1}}\times[0,\infty)$
with the product measure
$E\colon={{\mathbb S}^{d-1}}\times[0,\infty)$
with the product measure
![]() $\varphi\otimes \lambda_+$
, where
$\varphi\otimes \lambda_+$
, where
![]() $\lambda_+$
is the Lebesgue measure on
$\lambda_+$
is the Lebesgue measure on
![]() $[0,\infty)$
. Let Y be the Poisson process on E with intensity measure
$[0,\infty)$
. Let Y be the Poisson process on E with intensity measure
![]() $2\gamma\varphi\otimes\lambda_+$
. (Its existence and uniqueness up to stochastic equivalence follows, for example, from [Reference Schneider and Weil27, Theorem 3.2.1].) Let M(E) denote the set of all locally finite subsets
$2\gamma\varphi\otimes\lambda_+$
. (Its existence and uniqueness up to stochastic equivalence follows, for example, from [Reference Schneider and Weil27, Theorem 3.2.1].) Let M(E) denote the set of all locally finite subsets
![]() $S\subset E$
with the property that the set
$S\subset E$
with the property that the set
![]() $\{u\in{{\mathbb S}^{d-1}} \colon (u,t)\in S \mbox{ for some }t\ge 0\}$
positively spans
$\{u\in{{\mathbb S}^{d-1}} \colon (u,t)\in S \mbox{ for some }t\ge 0\}$
positively spans
![]() ${\mathbb R}^d$
. For
${\mathbb R}^d$
. For
![]() $\eta\in{N}_s(E)$
with support in M(E), we define
$\eta\in{N}_s(E)$
with support in M(E), we define
for
![]() $K\in{{\mathcal K}}_d$
, where
$K\in{{\mathcal K}}_d$
, where
![]() $h(K,\cdot)\colon=\max\{\langle x,\cdot\rangle \colon x\in K\}$
denotes the support function of K. This is a polytope containing K. We shall see below that the random polytope P(Y,K) is stochastically equivalent to the K-cell
$h(K,\cdot)\colon=\max\{\langle x,\cdot\rangle \colon x\in K\}$
denotes the support function of K. This is a polytope containing K. We shall see below that the random polytope P(Y,K) is stochastically equivalent to the K-cell
![]() $Z_K$
defined by the hyperplane process X. We use the random polytopes P(Y,K) to show that the function
$Z_K$
defined by the hyperplane process X. We use the random polytopes P(Y,K) to show that the function
![]() $K\mapsto {{\mathbb E}} W(Z_K)$
is concave and continuous on
$K\mapsto {{\mathbb E}} W(Z_K)$
is concave and continuous on
![]() ${{\mathcal K}}_d$
. Here a function
${{\mathcal K}}_d$
. Here a function
![]() $f \colon {{\mathcal K}}_d\to{\mathbb R}$
is called concave if
$f \colon {{\mathcal K}}_d\to{\mathbb R}$
is called concave if
for
![]() $K,L\in{{\mathcal K}}_d$
and
$K,L\in{{\mathcal K}}_d$
and
![]() $\alpha\in[0,1]$
, where
$\alpha\in[0,1]$
, where
![]() $K+L\colon=\{x+y \colon x\in K,\,y\in L\}$
and
$K+L\colon=\{x+y \colon x\in K,\,y\in L\}$
and
![]() $\beta K\colon=\{\beta x \colon x\in K\}$
for
$\beta K\colon=\{\beta x \colon x\in K\}$
for
![]() $K,L\in {{\mathcal K}}_d$
and
$K,L\in {{\mathcal K}}_d$
and
![]() $\beta\ge 0$
.
$\beta\ge 0$
.
Lemma 2. For
![]() $K,L\in{{\mathcal K}}_d$
and
$K,L\in{{\mathcal K}}_d$
and
![]() $\alpha\in[0,1]$
,
$\alpha\in[0,1]$
,
The functional
![]() $K\mapsto {{\mathbb E}} W(Z_K)$
is continuous on
$K\mapsto {{\mathbb E}} W(Z_K)$
is continuous on
![]() ${{\mathcal K}}_d$
.
${{\mathcal K}}_d$
.
Proof. For
![]() $\eta\in{N}_s(E)$
we have
$\eta\in{N}_s(E)$
we have
as follows immediately from the definition of
![]() $P(\eta,K)$
and the linearity properties of the support function. The monotonicity and linearity properties of the mean width yield
$P(\eta,K)$
and the linearity properties of the support function. The monotonicity and linearity properties of the mean width yield
Here we can replace
![]() $\eta$
with Y. Then linearity and monotonicity of the expectation yield
$\eta$
with Y. Then linearity and monotonicity of the expectation yield
We define the Poisson hyperplane process
![]() $X_K$
by
$X_K$
by
for Borel sets
![]() $A\subset{\mathcal{H}}$
. Its intensity measure is given by
$A\subset{\mathcal{H}}$
. Its intensity measure is given by
 \begin{align*}
{{\mathbb E}\,} X_K(A) &= \Theta(A\setminus {\mathcal{H}}_{{\textrm{int}}\,K})\\
&= \gamma\int_{{{\mathbb S}^{d-1}}} \int_{-\infty}^\infty {\bf 1}\{H(u,\tau)\in A\}{\bf 1}\{H(u,\tau)\cap{\textrm{int}}\,K=\emptyset\}\,{\textrm{d}}\tau\,\varphi({\textrm{d}} u)\\
&= \gamma\int_{{{\mathbb S}^{d-1}}} \int_{-\infty}^{-h(K,-u)} {\bf 1}\{H(u,\tau)\in A\}\,{\textrm{d}}\tau\,\varphi({\textrm{d}} u)\\
&\quad\, + \gamma\int_{{{\mathbb S}^{d-1}}} \int_{h(K,u)}^{\infty} {\bf 1}\{H(u,\tau)\in A\}\,{\textrm{d}}\tau\,\varphi({\textrm{d}} u)\\
&= 2\gamma\int_{{{\mathbb S}^{d-1}}} \int_{h(K,u)}^{\infty} {\bf 1}\{H(u,\tau)\in A\}\,{\textrm{d}}\tau\,\varphi({\textrm{d}} u),
\end{align*}
\begin{align*}
{{\mathbb E}\,} X_K(A) &= \Theta(A\setminus {\mathcal{H}}_{{\textrm{int}}\,K})\\
&= \gamma\int_{{{\mathbb S}^{d-1}}} \int_{-\infty}^\infty {\bf 1}\{H(u,\tau)\in A\}{\bf 1}\{H(u,\tau)\cap{\textrm{int}}\,K=\emptyset\}\,{\textrm{d}}\tau\,\varphi({\textrm{d}} u)\\
&= \gamma\int_{{{\mathbb S}^{d-1}}} \int_{-\infty}^{-h(K,-u)} {\bf 1}\{H(u,\tau)\in A\}\,{\textrm{d}}\tau\,\varphi({\textrm{d}} u)\\
&\quad\, + \gamma\int_{{{\mathbb S}^{d-1}}} \int_{h(K,u)}^{\infty} {\bf 1}\{H(u,\tau)\in A\}\,{\textrm{d}}\tau\,\varphi({\textrm{d}} u)\\
&= 2\gamma\int_{{{\mathbb S}^{d-1}}} \int_{h(K,u)}^{\infty} {\bf 1}\{H(u,\tau)\in A\}\,{\textrm{d}}\tau\,\varphi({\textrm{d}} u),
\end{align*}
where we have used the fact that
![]() $\varphi$
is an even measure. Next, we define a mapping
$\varphi$
is an even measure. Next, we define a mapping
![]() $F_K \colon E\to {\mathcal{H}}$
by
$F_K \colon E\to {\mathcal{H}}$
by
and denote for
![]() $\eta\in{N}_s(E)$
by
$\eta\in{N}_s(E)$
by
![]() $F_K(\eta)$
the pushforward of
$F_K(\eta)$
the pushforward of
![]() $\eta$
under
$\eta$
under
![]() $F_K$
. Then
$F_K$
. Then
![]() $F_K(Y)$
is a Poisson hyperplane process. For its intensity measure we obtain, for Borel sets
$F_K(Y)$
is a Poisson hyperplane process. For its intensity measure we obtain, for Borel sets
![]() $A\subset{\mathcal{H}}$
,
$A\subset{\mathcal{H}}$
,
 \begin{align*}
{{\mathbb E}\,}(F_K(Y))(A) &= {{\mathbb E}} Y(F_K^{-1}(A))\\
&= 2\gamma \int_{{{\mathbb S}^{d-1}}} \int_0^\infty {\bf 1}\{(u,t)\in F_K^{-1}(A)\}\,{\textrm{d}} t\,\varphi({\textrm{d}} u)\\
&= 2\gamma \int_{{{\mathbb S}^{d-1}}} \int_0^\infty {\bf 1}\{H(u,h(K,u)+t)\in A\}\,{\textrm{d}} t\,\varphi({\textrm{d}} u)\\
&= 2\gamma \int_{{{\mathbb S}^{d-1}}} \int_{h(K,u)}^\infty {\bf 1}\{H(u,\tau)\in A\}\,{\textrm{d}} \tau\,\varphi({\textrm{d}} u).
\end{align*}
\begin{align*}
{{\mathbb E}\,}(F_K(Y))(A) &= {{\mathbb E}} Y(F_K^{-1}(A))\\
&= 2\gamma \int_{{{\mathbb S}^{d-1}}} \int_0^\infty {\bf 1}\{(u,t)\in F_K^{-1}(A)\}\,{\textrm{d}} t\,\varphi({\textrm{d}} u)\\
&= 2\gamma \int_{{{\mathbb S}^{d-1}}} \int_0^\infty {\bf 1}\{H(u,h(K,u)+t)\in A\}\,{\textrm{d}} t\,\varphi({\textrm{d}} u)\\
&= 2\gamma \int_{{{\mathbb S}^{d-1}}} \int_{h(K,u)}^\infty {\bf 1}\{H(u,\tau)\in A\}\,{\textrm{d}} \tau\,\varphi({\textrm{d}} u).
\end{align*}
Thus,
![]() $X_K$
and
$X_K$
and
![]() $F_K(Y)$
have the same intensity measure. Since either of them is a Poisson process, they are stochastically equivalent. It follows that the zero cell
$F_K(Y)$
have the same intensity measure. Since either of them is a Poisson process, they are stochastically equivalent. It follows that the zero cell
![]() $Z_K$
is stochastically equivalent to the random polytope P(Y,K). Therefore, (8) yields the assertion (7).
$Z_K$
is stochastically equivalent to the random polytope P(Y,K). Therefore, (8) yields the assertion (7).
To prove the continuity assertion, let
![]() $K,K_i\in{{\mathcal K}}_d$
for
$K,K_i\in{{\mathcal K}}_d$
for
![]() $i\in{\mathbb N}$
and suppose that
$i\in{\mathbb N}$
and suppose that
![]() $K_i\to K$
in the Hausdorff metric, as
$K_i\to K$
in the Hausdorff metric, as
![]() $i\to\infty$
. If
$i\to\infty$
. If
![]() $\varepsilon_0>0$
is small enough, then
$\varepsilon_0>0$
is small enough, then
is a convex body for any
![]() $\varepsilon >-\varepsilon_0$
. Clearly,
$\varepsilon >-\varepsilon_0$
. Clearly,
![]() $K_\varepsilon\to K$
as
$K_\varepsilon\to K$
as
![]() $\varepsilon\to 0$
. For given
$\varepsilon\to 0$
. For given
![]() $\varepsilon>0$
, let i be so large that
$\varepsilon>0$
, let i be so large that
![]() $K_{-\varepsilon}\subset K_i\subset K_\varepsilon$
. Observe also that
$K_{-\varepsilon}\subset K_i\subset K_\varepsilon$
. Observe also that
![]() $X({\mathcal{H}}_{K_i}\triangle{\mathcal{H}}_K)=0$
(where
$X({\mathcal{H}}_{K_i}\triangle{\mathcal{H}}_K)=0$
(where
![]() $\triangle$
denotes the symmetric difference) implies that
$\triangle$
denotes the symmetric difference) implies that
![]() $Z_{K_i}=Z_K$
. Therefore,
$Z_{K_i}=Z_K$
. Therefore,
 \begin{align*}
|{{\mathbb E}} W(Z_{K_i})-{{\mathbb E}} W(Z_K)| &\le {{\mathbb E}}|W(Z_{K_i}) - W(Z_K)|\\
&\le {\mathbb P}(X({\mathcal{H}}_{K_i}\triangle {\mathcal{H}}_K)>0){{\mathbb E}} W(Z_{K_{\varepsilon}})\\
&\le {\mathbb P}(X({\mathcal{H}}_{K_\varepsilon}\setminus{\mathcal{H}}_{K_{-\varepsilon}})>0){{\mathbb E}} W(Z_{K_{\varepsilon_0}})\\
& \to 0
\end{align*}
\begin{align*}
|{{\mathbb E}} W(Z_{K_i})-{{\mathbb E}} W(Z_K)| &\le {{\mathbb E}}|W(Z_{K_i}) - W(Z_K)|\\
&\le {\mathbb P}(X({\mathcal{H}}_{K_i}\triangle {\mathcal{H}}_K)>0){{\mathbb E}} W(Z_{K_{\varepsilon}})\\
&\le {\mathbb P}(X({\mathcal{H}}_{K_\varepsilon}\setminus{\mathcal{H}}_{K_{-\varepsilon}})>0){{\mathbb E}} W(Z_{K_{\varepsilon_0}})\\
& \to 0
\end{align*}
as
![]() $\varepsilon\to 0$
. The limit follows from the fact that
$\varepsilon\to 0$
. The limit follows from the fact that
as
![]() $\varepsilon\to 0$
, by monotone convergence. This proves the continuity assertion.
$\varepsilon\to 0$
, by monotone convergence. This proves the continuity assertion.
From now on, we assume that the stationary Poisson hyperplane process X is isotropic and has intensity n. Then its intensity measure is given by
![]() $\Theta=n\mu$
with
$\Theta=n\mu$
with
where
![]() $\sigma$
is the normalized spherical Lebesgue measure. For convex bodies
$\sigma$
is the normalized spherical Lebesgue measure. For convex bodies
![]() $K,L\in{{\mathcal K}}_d$
with
$K,L\in{{\mathcal K}}_d$
with
![]() $K\subset L$
, we have
$K\subset L$
, we have
 \begin{align}
\mu({\mathcal{H}}_L\setminus{\mathcal{H}}_K) &= \int_{{\mathcal{H}}\setminus{\mathcal{H}}_K} {\bf 1}\{H\cap L\not=\emptyset\}\,\mu({\textrm{d}} H)\nonumber\\
&= \int_{{{\mathbb S}^{d-1}}} \int_{-\infty}^\infty {\bf 1}\{H(u,\tau)\cap L\not=\emptyset\}{\bf 1}\{H(u,\tau)\cap K=\emptyset\}\,{\textrm{d}}\tau\,\sigma({\textrm{d}} u)\nonumber\\
&= 2\int_{{{\mathbb S}^{d-1}}}[h(L,u)-h(K,u)]\,\sigma({\textrm{d}} u)\nonumber\\
&= W(L)-W(K).
\label{eqn10}\end{align}
\begin{align}
\mu({\mathcal{H}}_L\setminus{\mathcal{H}}_K) &= \int_{{\mathcal{H}}\setminus{\mathcal{H}}_K} {\bf 1}\{H\cap L\not=\emptyset\}\,\mu({\textrm{d}} H)\nonumber\\
&= \int_{{{\mathbb S}^{d-1}}} \int_{-\infty}^\infty {\bf 1}\{H(u,\tau)\cap L\not=\emptyset\}{\bf 1}\{H(u,\tau)\cap K=\emptyset\}\,{\textrm{d}}\tau\,\sigma({\textrm{d}} u)\nonumber\\
&= 2\int_{{{\mathbb S}^{d-1}}}[h(L,u)-h(K,u)]\,\sigma({\textrm{d}} u)\nonumber\\
&= W(L)-W(K).
\label{eqn10}\end{align}
Lemma 3. If X is isotropic, then the functional
attains its maximum at balls.
Proof. If X is isotropic, then the functional
![]() $K\mapsto {{\mathbb E}} W(Z_K)$
is invariant under rigid motions. Since by Lemma 2 it is concave and continuous on
$K\mapsto {{\mathbb E}} W(Z_K)$
is invariant under rigid motions. Since by Lemma 2 it is concave and continuous on
![]() ${{\mathcal K}}_d$
, it is well known that on the set of convex bodies
${{\mathcal K}}_d$
, it is well known that on the set of convex bodies
![]() $K\in {{\mathcal K}}_d$
with given mean width W(K) it attains its maximum at balls. The proof, which uses Hadwiger’s ‘Zweites Kugelungstheorem’ ([Reference Hadwiger12, pp. 170–171], reproduced in [Reference Schneider25, Theorem 3.3.5]), is carried out in [Reference Böröczky and Schneider6, p. 621].
$K\in {{\mathcal K}}_d$
with given mean width W(K) it attains its maximum at balls. The proof, which uses Hadwiger’s ‘Zweites Kugelungstheorem’ ([Reference Hadwiger12, pp. 170–171], reproduced in [Reference Schneider25, Theorem 3.3.5]), is carried out in [Reference Böröczky and Schneider6, p. 621].
To take advantage of the preceding lemma, we connect this to a known asymptotic result about convex hulls of i.i.d. random points in a ball. First we write the result of Lemma 3 in the form
We recall that here
![]() $Z_K=Z_K^{(n)}$
and
$Z_K=Z_K^{(n)}$
and
![]() $Z_{B^d}=Z_{B^d}^{(n)}$
and that we intend to let n tend to infinity. In view of this, we choose a number
$Z_{B^d}=Z_{B^d}^{(n)}$
and that we intend to let n tend to infinity. In view of this, we choose a number
![]() $R>b$
, where b is the constant appearing in Lemma 1 for
$R>b$
, where b is the constant appearing in Lemma 1 for
![]() $K=B^d$
, and state that
$K=B^d$
, and state that
as
![]() $n\to \infty$
(where the constant involved in
$n\to \infty$
(where the constant involved in
![]() ${\textrm{O}}$
depends on R). For the proof, we note that the left side of (12) can be estimated by
${\textrm{O}}$
depends on R). For the proof, we note that the left side of (12) can be estimated by
 \begin{align*}
{{\mathbb E}\,} [W(Z_{B^d}){\bf 1}\{R_o(Z_{B^d})\ge R\}] & \le {{\mathbb E}\,} [2R_o(Z_{B^d}){\bf 1}\{R_o(Z_{B^d})\ge R\}]\\
&= 2\int_\Omega R_o(Z_{B^d}){\bf 1}\{R_o(Z_{B^d})\ge R\}\,{\textrm{d}}{\mathbb P}\\
&= 2\int_0^\infty {\mathbb P}(R_o(Z_{B^d}){\bf 1}\{R_o(Z_{B^d})\ge R\}>t)\,{\textrm{d}} t\\
&= 2R\,{\mathbb P}(R_o(Z_{B^d})\ge R) + 2\int_R^\infty {\mathbb P}(R_o(Z_{B^d})>t)\,{\textrm{d}} t.
\end{align*}
\begin{align*}
{{\mathbb E}\,} [W(Z_{B^d}){\bf 1}\{R_o(Z_{B^d})\ge R\}] & \le {{\mathbb E}\,} [2R_o(Z_{B^d}){\bf 1}\{R_o(Z_{B^d})\ge R\}]\\
&= 2\int_\Omega R_o(Z_{B^d}){\bf 1}\{R_o(Z_{B^d})\ge R\}\,{\textrm{d}}{\mathbb P}\\
&= 2\int_0^\infty {\mathbb P}(R_o(Z_{B^d}){\bf 1}\{R_o(Z_{B^d})\ge R\}>t)\,{\textrm{d}} t\\
&= 2R\,{\mathbb P}(R_o(Z_{B^d})\ge R) + 2\int_R^\infty {\mathbb P}(R_o(Z_{B^d})>t)\,{\textrm{d}} t.
\end{align*}
Lemma 1 provides an estimate for
![]() ${\mathbb P}(R_o(Z_{B^d})\ge b(1+x))$
. Using this with
${\mathbb P}(R_o(Z_{B^d})\ge b(1+x))$
. Using this with
![]() $b(1+x)=R$
for the first summand and with
$b(1+x)=R$
for the first summand and with
![]() $b(1+x)=t$
for the second summand (and observing that now
$b(1+x)=t$
for the second summand (and observing that now
![]() $\gamma=n$
), we obtain (12).
$\gamma=n$
), we obtain (12).
We use the bijective mapping
Let
![]() $\kappa_0$
be the pushforward of the measure
$\kappa_0$
be the pushforward of the measure
![]() $\mu$
, restricted to
$\mu$
, restricted to
![]() ${\mathcal{H}}\setminus {\mathcal{H}}_{B^d}$
, under
${\mathcal{H}}\setminus {\mathcal{H}}_{B^d}$
, under
![]() $\xi$
. Then
$\xi$
. Then
for Borel sets
![]() $A\subset B^d\setminus\{o\}$
, where
$A\subset B^d\setminus\{o\}$
, where
![]() $\omega_d$
is the surface area of the unit sphere. The measure
$\omega_d$
is the surface area of the unit sphere. The measure
![]() $\kappa_0$
is infinite, but finite on compact subsets of
$\kappa_0$
is infinite, but finite on compact subsets of
![]() $B^d\setminus\{o\}$
.
$B^d\setminus\{o\}$
.
Let
![]() $Y_n$
denote the Poisson point process in
$Y_n$
denote the Poisson point process in
![]() ${\mathbb R}^d$
with intensity measure
${\mathbb R}^d$
with intensity measure
![]() $n\kappa_0$
. Let
$n\kappa_0$
. Let
![]() $Q_n$
be the convex hull of
$Q_n$
be the convex hull of
![]() $Y_n$
. Then
$Y_n$
. Then
![]() $Q_n$
is a random polytope, which is stochastically equivalent to the polar of
$Q_n$
is a random polytope, which is stochastically equivalent to the polar of
![]() $Z_{B^d}$
. With the constant
$Z_{B^d}$
. With the constant
![]() $R>b$
chosen above, we set
$R>b$
chosen above, we set
![]() $r=1/R$
and
$r=1/R$
and
![]() $B_r= rB^d$
. By (10), we have
$B_r= rB^d$
. By (10), we have
hence
Now it follows from (11) and (12) that
To express the latter expectation in a suitable way, we note that
![]() $Q_n$
is almost surely a simplicial polytope, hence each of its facets is the convex hull of d points of
$Q_n$
is almost surely a simplicial polytope, hence each of its facets is the convex hull of d points of
![]() $Y_n$
. For any d points
$Y_n$
. For any d points
![]() $x_1,\dots,x_d\in Y_n$
(almost surely, they are affinely independent and their affine hull does not contain o), we define
$x_1,\dots,x_d\in Y_n$
(almost surely, they are affinely independent and their affine hull does not contain o), we define
where
![]() $H^-(x_1,\dots,x_d)$
is the closed half-space bounded by
$H^-(x_1,\dots,x_d)$
is the closed half-space bounded by
![]() ${\textrm{aff}}\{x_1,\dots,x_d\}$
that contains o. Further, we define
${\textrm{aff}}\{x_1,\dots,x_d\}$
that contains o. Further, we define
Then we have
 \begin{align*}
& \kappa_0(B^d\setminus Q_n){\bf 1}\{B_r\subset Q_n\} \\
& \qquad
= \dfrac{1}{d!}\sum_{(x_1,\dots,x_d)\in (Y_n)^d_{\not=}} {\bf 1}\{Y_n(S(x_1,\dots,x_d))=0\}\kappa_0(T(x_1,\dots,x_d)){\bf 1}\{B_r\subset Q_n\},
\end{align*}
\begin{align*}
& \kappa_0(B^d\setminus Q_n){\bf 1}\{B_r\subset Q_n\} \\
& \qquad
= \dfrac{1}{d!}\sum_{(x_1,\dots,x_d)\in (Y_n)^d_{\not=}} {\bf 1}\{Y_n(S(x_1,\dots,x_d))=0\}\kappa_0(T(x_1,\dots,x_d)){\bf 1}\{B_r\subset Q_n\},
\end{align*}
where
![]() $\eta^d_{\not=}$
denotes the set of ordered d-tuples of pairwise different elements from the support of
$\eta^d_{\not=}$
denotes the set of ordered d-tuples of pairwise different elements from the support of
![]() $\eta$
. We note that if
$\eta$
. We note that if
![]() $B_r\subset Q_n$
, then points
$B_r\subset Q_n$
, then points
![]() $x_1,\dots,x_d\in Y_n$
with
$x_1,\dots,x_d\in Y_n$
with
![]() $Y_n(S(x_1,\dots,x_d))=0$
automatically satisfy
$Y_n(S(x_1,\dots,x_d))=0$
automatically satisfy
![]() $x_1,\dots,x_d\in B^d\setminus B_r$
and
$x_1,\dots,x_d\in B^d\setminus B_r$
and
![]() ${\textrm{aff}}\{x_1,\dots,x_d\}\cap B_r=\emptyset$
a.s. Therefore,
${\textrm{aff}}\{x_1,\dots,x_d\}\cap B_r=\emptyset$
a.s. Therefore,
 \begin{align*}
& \kappa_0(B^d\setminus Q_n){\bf 1}\{B_r\subset Q_n\}\\
&\qquad = \dfrac{1}{d!}\sum_{(x_1,\dots,x_d)\in (Y_n)^d_{\not=}} {\bf 1}\{Y_n(S(x_1,\dots,x_d))=0,\,B_r\subset Q_n\}\kappa_0(T(x_1,\dots,x_d))\\
&\qquad\quad\, \times\,{\bf 1}\{x_1,\dots,x_d\in B^d\setminus B_r\}{\bf 1}\{{\textrm{aff}}\{x_1,\dots,x_d\}\cap B_r=\emptyset\}.
\end{align*}
\begin{align*}
& \kappa_0(B^d\setminus Q_n){\bf 1}\{B_r\subset Q_n\}\\
&\qquad = \dfrac{1}{d!}\sum_{(x_1,\dots,x_d)\in (Y_n)^d_{\not=}} {\bf 1}\{Y_n(S(x_1,\dots,x_d))=0,\,B_r\subset Q_n\}\kappa_0(T(x_1,\dots,x_d))\\
&\qquad\quad\, \times\,{\bf 1}\{x_1,\dots,x_d\in B^d\setminus B_r\}{\bf 1}\{{\textrm{aff}}\{x_1,\dots,x_d\}\cap B_r=\emptyset\}.
\end{align*}
Using the Slivnyak–Mecke formula (see e.g. [Reference Schneider and Weil27, Corollary 3.2.3]) and noting that
![]() $n\kappa_0$
is the intensity measure of
$n\kappa_0$
is the intensity measure of
![]() $Y_n$
, we obtain
$Y_n$
, we obtain
 \begin{align*}
& {{\mathbb E}\,}[\kappa_0(B^d\setminus Q_n){\bf 1}\{B_r\subset Q_n\}]\\
&\qquad = \dfrac{n^d}{d!}\int_{B^d\setminus B_r}\dots\int_{B^d\setminus B_r} {{\mathbb E}} {\bf 1}\{Y_n(S(x_1,\dots,x_d))=0,\,B_r\subset {\textrm{conv}}(Y_n\cup\{x_1,\dots,x_d\})\}\\
&\qquad\quad\, \times \kappa_0(T(x_1,\dots,x_d)){\bf 1}\{{\textrm{aff}}\{x_1,\dots,x_d\}\cap B_r=\emptyset\}\,\kappa_0({\textrm{d}} x_1)\cdots\kappa_0({\textrm{d}} x_d).
\end{align*}
\begin{align*}
& {{\mathbb E}\,}[\kappa_0(B^d\setminus Q_n){\bf 1}\{B_r\subset Q_n\}]\\
&\qquad = \dfrac{n^d}{d!}\int_{B^d\setminus B_r}\dots\int_{B^d\setminus B_r} {{\mathbb E}} {\bf 1}\{Y_n(S(x_1,\dots,x_d))=0,\,B_r\subset {\textrm{conv}}(Y_n\cup\{x_1,\dots,x_d\})\}\\
&\qquad\quad\, \times \kappa_0(T(x_1,\dots,x_d)){\bf 1}\{{\textrm{aff}}\{x_1,\dots,x_d\}\cap B_r=\emptyset\}\,\kappa_0({\textrm{d}} x_1)\cdots\kappa_0({\textrm{d}} x_d).
\end{align*}
Let
![]() $\lambda_0\colon= (2/\omega_d)\lambda_d$
. For Borel sets
$\lambda_0\colon= (2/\omega_d)\lambda_d$
. For Borel sets
![]() $A\subset B^d\setminus B_r$
we have
$A\subset B^d\setminus B_r$
we have
For fixed
![]() $x_1,\dots,x_d\in B^d\setminus B_r$
with
$x_1,\dots,x_d\in B^d\setminus B_r$
with
![]() ${\textrm{aff}}\{x_1,\dots,x_d\}\cap B_r=\emptyset$
, we have
${\textrm{aff}}\{x_1,\dots,x_d\}\cap B_r=\emptyset$
, we have
 \begin{align*}
& {{\mathbb E}} {\bf 1}\{Y_n(S(x_1,\dots,x_d))=0,\,B_r\subset {\textrm{conv}}(Y_n\cup\{x_1,\dots,x_d\}\}\\
&\qquad \le {{\mathbb E}} {\bf 1}\{Y_n(S(x_1,\dots,x_d))=0\}\\
&\qquad = {\textrm{e}}^{-n\kappa_0(S(x_1,\dots,x_d))}\\
&\qquad \le {\textrm{e}}^{-n\lambda_0(S(x_1,\dots,x_d))}.
\end{align*}
\begin{align*}
& {{\mathbb E}} {\bf 1}\{Y_n(S(x_1,\dots,x_d))=0,\,B_r\subset {\textrm{conv}}(Y_n\cup\{x_1,\dots,x_d\}\}\\
&\qquad \le {{\mathbb E}} {\bf 1}\{Y_n(S(x_1,\dots,x_d))=0\}\\
&\qquad = {\textrm{e}}^{-n\kappa_0(S(x_1,\dots,x_d))}\\
&\qquad \le {\textrm{e}}^{-n\lambda_0(S(x_1,\dots,x_d))}.
\end{align*}
Therefore, we can estimate
 \begin{align*}
& {{\mathbb E}\,}[\kappa_0(B^d\setminus Q_n){\bf 1}\{B_r\subset Q_n\}] \\
&\qquad
\ll n^d\int_{B^d}\dots\int_{B^d} \,{\textrm{e}}^{-n\lambda_0(S(x_1,\dots,x_d))} \,\lambda_0(T(x_1,\dots,x_d))\,\lambda_0({\textrm{d}} x_1)\cdots\lambda_0({\textrm{d}} x_d).
\end{align*}
\begin{align*}
& {{\mathbb E}\,}[\kappa_0(B^d\setminus Q_n){\bf 1}\{B_r\subset Q_n\}] \\
&\qquad
\ll n^d\int_{B^d}\dots\int_{B^d} \,{\textrm{e}}^{-n\lambda_0(S(x_1,\dots,x_d))} \,\lambda_0(T(x_1,\dots,x_d))\,\lambda_0({\textrm{d}} x_1)\cdots\lambda_0({\textrm{d}} x_d).
\end{align*}
Let
![]() $\widetilde Y_n$
be a Poisson point process in
$\widetilde Y_n$
be a Poisson point process in
![]() ${\mathbb R}^d$
with intensity measure
${\mathbb R}^d$
with intensity measure
![]() $n\lambda_0$
, and let
$n\lambda_0$
, and let
Using the Slivnyak–Mecke formula as above yields that
 \begin{align*}
& {{\mathbb E}}\lambda_0(B^d\setminus \Pi_n)\\
&\qquad = n^d \int_{B^d}\dots\int_{B^d} \,{\textrm{e}}^{-n\lambda_0(S(x_1,\dots,x_d))}
\lambda_0(T(x_1,\dots,x_d))\,\lambda_0({\textrm{d}} x_1)\cdots\lambda_0({\textrm{d}} x_d).
\end{align*}
\begin{align*}
& {{\mathbb E}}\lambda_0(B^d\setminus \Pi_n)\\
&\qquad = n^d \int_{B^d}\dots\int_{B^d} \,{\textrm{e}}^{-n\lambda_0(S(x_1,\dots,x_d))}
\lambda_0(T(x_1,\dots,x_d))\,\lambda_0({\textrm{d}} x_1)\cdots\lambda_0({\textrm{d}} x_d).
\end{align*}
We conclude that
It follows from Lemma 1 in [Reference Reitzner18] that
4. Proof of the lower bound
The proof of the left-hand estimate of (6) requires only a few changes in the proof of the corresponding inequality in [Reference Böröczky and Schneider6, (1.3)].
Let
![]() $K\in{{\mathcal K}}_d$
. For
$K\in{{\mathcal K}}_d$
. For
![]() $x\in{\mathbb R}^d\setminus K$
, we define
$x\in{\mathbb R}^d\setminus K$
, we define
![]() $K^x\colon= {\textrm{conv}}(K\cup \{x\})$
and set
$K^x\colon= {\textrm{conv}}(K\cup \{x\})$
and set
for hyperplanes
![]() $H\in{\mathcal{H}}\setminus {\mathcal{H}}_K$
. For
$H\in{\mathcal{H}}\setminus {\mathcal{H}}_K$
. For
![]() $t> 0$
we define
$t> 0$
we define
We assume now, as in Theorem 1, that X is a stationary and isotropic Poisson hyperplane process in
![]() ${\mathbb R}^d$
of intensity
${\mathbb R}^d$
of intensity
![]() $n\in {\mathbb N}$
. Let
$n\in {\mathbb N}$
. Let
![]() $H\in{\mathcal{H}}\setminus{\mathcal{H}}_K$
, and let
$H\in{\mathcal{H}}\setminus{\mathcal{H}}_K$
, and let
![]() $z\in H$
be such that
$z\in H$
be such that
![]() $m(H)= W(K^{z})-W(K)$
(clearly, such a point exists). If no hyperplane of X separates z and K, then
$m(H)= W(K^{z})-W(K)$
(clearly, such a point exists). If no hyperplane of X separates z and K, then
![]() $z\in Z_K^{(n)}$
and hence
$z\in Z_K^{(n)}$
and hence
![]() $H\cap Z_K^{(n)}\not=\emptyset$
. It follows that
$H\cap Z_K^{(n)}\not=\emptyset$
. It follows that
 \begin{align*}
{\mathbb P} (H\cap Z_K^{(n)}\not=\emptyset ) &\ge {\mathbb P}(X({\mathcal{H}}_{K^{z}}\setminus{\mathcal{H}}_K)=0)\\
&={\rm exp}\, [-\Theta({\mathcal{H}}_{K^{z}}\setminus{\mathcal{H}}_K)]\\
& = {\textrm{e}}^{-nm(H)},
\end{align*}
\begin{align*}
{\mathbb P} (H\cap Z_K^{(n)}\not=\emptyset ) &\ge {\mathbb P}(X({\mathcal{H}}_{K^{z}}\setminus{\mathcal{H}}_K)=0)\\
&={\rm exp}\, [-\Theta({\mathcal{H}}_{K^{z}}\setminus{\mathcal{H}}_K)]\\
& = {\textrm{e}}^{-nm(H)},
\end{align*}
where (10) was used. Therefore, we obtain (using (10) again and Fubini’s theorem)
 \begin{align*}
{{\mathbb E}} W(Z_K^{(n)})-W(K) &{} = \int_\Omega\int_{{\mathcal{H}}\setminus{\mathcal{H}}_K} {\bf 1}\{H\cap Z_K^{(n)}\not=\emptyset\}\,\mu({\textrm{d}} H)\,{\textrm{d}}{\mathbb P}\\
&= \int_{{\mathcal{H}}\setminus{\mathcal{H}}_K} {\mathbb P}(H\cap Z_K^{(n)}\not=\emptyset)\,\mu({\textrm{d}} H)\\
&\ge \int_{{\mathcal{H}}\setminus{\mathcal{H}}_K} \,{\textrm{e}}^{-nm(H)}\,\mu({\textrm{d}} H)\\
&\ge \int_{{\mathcal{H}}\setminus {\mathcal{H}}_K} {\bf 1}\{m(H)\le t\} \,{\textrm{e}}^{-nt}\,\mu({\textrm{d}} H)\\
&= {\textrm{e}}^{-nt}\mu({\mathcal{H}}_K(t)),
\end{align*}
\begin{align*}
{{\mathbb E}} W(Z_K^{(n)})-W(K) &{} = \int_\Omega\int_{{\mathcal{H}}\setminus{\mathcal{H}}_K} {\bf 1}\{H\cap Z_K^{(n)}\not=\emptyset\}\,\mu({\textrm{d}} H)\,{\textrm{d}}{\mathbb P}\\
&= \int_{{\mathcal{H}}\setminus{\mathcal{H}}_K} {\mathbb P}(H\cap Z_K^{(n)}\not=\emptyset)\,\mu({\textrm{d}} H)\\
&\ge \int_{{\mathcal{H}}\setminus{\mathcal{H}}_K} \,{\textrm{e}}^{-nm(H)}\,\mu({\textrm{d}} H)\\
&\ge \int_{{\mathcal{H}}\setminus {\mathcal{H}}_K} {\bf 1}\{m(H)\le t\} \,{\textrm{e}}^{-nt}\,\mu({\textrm{d}} H)\\
&= {\textrm{e}}^{-nt}\mu({\mathcal{H}}_K(t)),
\end{align*}
where
![]() $t> 0$
can be any number. The choice
$t> 0$
can be any number. The choice
![]() $t=1/n$
gives
$t=1/n$
gives
The remainder of the proof is similar to that in [6, p. 619]. For the reader’s convenience, we adapt the argument to the present case. The idea is to use a result from Bárány and Larman [Reference Bárány and Larman4], together with polarity.
We translate K so that (say) its centroid is at the origin. Let
![]() $K^\circ$
be the polar body of K. For
$K^\circ$
be the polar body of K. For
![]() $x\in K^\circ$
, let v(x) denote the minimal volume that a closed half-space containing x cuts off from
$x\in K^\circ$
, let v(x) denote the minimal volume that a closed half-space containing x cuts off from
![]() $K^\circ$
, and define
$K^\circ$
, and define
for
![]() $t> 0$
. We can choose
$t> 0$
. We can choose
![]() $\rho,t_0>0$
such that
$\rho,t_0>0$
such that
![]() $\rho B^d\subset K^\circ(t)$
for
$\rho B^d\subset K^\circ(t)$
for
![]() $0<t\le t_0$
.
$0<t\le t_0$
.
Let
![]() $\psi{\colon} {\mathbb R}^d\setminus\{o\}\to {\mathcal{H}}\setminus{\mathcal{H}}_{\{o\}}$
be the inverse of the map
$\psi{\colon} {\mathbb R}^d\setminus\{o\}\to {\mathcal{H}}\setminus{\mathcal{H}}_{\{o\}}$
be the inverse of the map
![]() $\xi$
defined by (13) ; thus
$\xi$
defined by (13) ; thus
Let
![]() $\nu$
denote the pushforward of the Lebesgue measure
$\nu$
denote the pushforward of the Lebesgue measure
![]() $\lambda_d$
under
$\lambda_d$
under
![]() $\psi$
; thus
$\psi$
; thus
for Borel sets
![]() $A\subset {\mathcal{H}}\setminus{\mathcal{H}}_{\{o\}}$
.
$A\subset {\mathcal{H}}\setminus{\mathcal{H}}_{\{o\}}$
.
Let
![]() $H(u,\tau)$
be a hyperplane contained in
$H(u,\tau)$
be a hyperplane contained in
![]() ${\mathcal{H}}_{\rho^{-1}B^d}\setminus {\mathcal{H}}_K$
. Since
${\mathcal{H}}_{\rho^{-1}B^d}\setminus {\mathcal{H}}_K$
. Since
![]() $H(u,\tau)\cap K=\emptyset$
, we have
$H(u,\tau)\cap K=\emptyset$
, we have
![]() $\tau\ge h(K,u)$
, which is bounded from below by a positive constant depending only on K. Since
$\tau\ge h(K,u)$
, which is bounded from below by a positive constant depending only on K. Since
![]() $H(u,\tau)\cap \rho^{-1}B^d\not=\emptyset$
, we have
$H(u,\tau)\cap \rho^{-1}B^d\not=\emptyset$
, we have
![]() $\tau\le \rho^{-1}$
. Now comparison of (16) and (9) yields the existence of constants
$\tau\le \rho^{-1}$
. Now comparison of (16) and (9) yields the existence of constants
![]() $c_1,c_2>0$
, depending only on d and K, such that
$c_1,c_2>0$
, depending only on d and K, such that
Let
![]() $0<t\le t_0$
and
$0<t\le t_0$
and
![]() $x\in K^\circ(t)\setminus\partial K^\circ$
. There is a hyperplane E through x that bounds a closed half-space
$x\in K^\circ(t)\setminus\partial K^\circ$
. There is a hyperplane E through x that bounds a closed half-space
![]() $E^+$
not containing o, such that
$E^+$
not containing o, such that
![]() $\lambda_d(K^\circ\cap E^+)\le t$
. If
$\lambda_d(K^\circ\cap E^+)\le t$
. If
![]() $H\colon=\psi(x)$
and
$H\colon=\psi(x)$
and
![]() $y \colon=\psi^{-1}(E)$
, then
$y \colon=\psi^{-1}(E)$
, then
![]() $y\in H\in {\mathcal{H}}_{\rho^{-1}B^d}\setminus {\mathcal{H}}_K$
. The mapping
$y\in H\in {\mathcal{H}}_{\rho^{-1}B^d}\setminus {\mathcal{H}}_K$
. The mapping
![]() $\psi$
maps the cap
$\psi$
maps the cap
![]() $K^\circ\cap E^+$
bijectively onto the set of hyperplanes (weakly) separating y and K. We denote this set by
$K^\circ\cap E^+$
bijectively onto the set of hyperplanes (weakly) separating y and K. We denote this set by
![]() ${\mathcal{H}}^y_K$
. It follows that
${\mathcal{H}}^y_K$
. It follows that
hence
![]() $H\in {\mathcal{H}}_K(c_2t)$
. Since
$H\in {\mathcal{H}}_K(c_2t)$
. Since
![]() $x\in K^\circ(t)\setminus\partial K^\circ$
was arbitrary, this shows that
$x\in K^\circ(t)\setminus\partial K^\circ$
was arbitrary, this shows that
![]() $\psi(K^\circ(t)) \subset {\mathcal{H}}_K(c_2t)$
. Therefore,
$\psi(K^\circ(t)) \subset {\mathcal{H}}_K(c_2t)$
. Therefore,
If we choose
![]() $t=1/(c_2n)$
, then this inequality together with (15) shows that
$t=1/(c_2n)$
, then this inequality together with (15) shows that
Theorem 2 of [Reference Bárány and Larman4] says that
for sufficiently small
![]() $\varepsilon>0$
, with some constant c depending only on K. It follows that
$\varepsilon>0$
, with some constant c depending only on K. It follows that
for all sufficiently large n, where
![]() $c_3$
is a constant depending only on d and K. By adapting the constant, we can assume that this holds for all
$c_3$
is a constant depending only on d and K. By adapting the constant, we can assume that this holds for all
![]() $n\in {\mathbb N}$
. This completes the proof of the lower bound in (6).
$n\in {\mathbb N}$
. This completes the proof of the lower bound in (6).
Acknowledgement
Thanks are due to the referees, whose comments have led to corrections, clarifications, and simplifications.