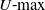1. Introduction
U-statistics were introduced in probability by Halmos [Reference Halmos3] and Hoeffding [Reference Hoeffding4] in the mid-1940s as a functional generalization of sample mean. Let
$ \xi_1, \xi_2, \dots $
be a sequence of independent identically distributed random elements taking values in a measurable space
$(\mathfrak{X}, \mathfrak{A})$
. We define a real-valued symmetric Borel function
$ f(x_1, \dots, x_m) $
on the space
$ {\mathfrak{X}}^m, $
which we call a kernel of degree
$ m. $
U-statistics are defined as follows:
\begin{equation}U_n = {\binom{n}{m}}^{-1}\sum_J f(\xi_{i_1}, \ldots, \xi_{i_m}),\end{equation}
where
$n \ge m$
and the set
\begin{equation*}J = \{(i_1, \ldots , i_m) \colon 1 \le i_1 < \cdots < i_m \le n\}.\end{equation*}
Over the past few decades, U-statistics have been studied in detail in many publications, and the state of the art is presented in the monographs [Reference Korolyuk and Borovskikh7] and [Reference Lee11].
In 2008 Lao and Meyer [Reference Lao9, Reference Lao and Mayer10, Reference Mayer14] independently considered the so-called
$U{\hbox{-}}\textrm{max}$
statistics, which are obtained from (1.1) by removing the normalizing factor and replacing the sum with the maximum over the set
$J\colon $
\begin{equation}M_n = \max_J f(\xi_{i_1}, \ldots, \xi_{i_m}).\end{equation}
The
$U{\hbox{-}}\textrm{min}$
statistics
$M^{\prime}_n$
are defined in a similar way by replacing max with min.
Lao and Mayer mainly studied the limit behavior of maximal and minimal distances, areas and perimeters of sets formed by random points on a circle or a sphere. They used the Poisson approximation from the monograph [Reference Barbour, Holst and Janson2] and the paper [Reference Silverman and Brown16], and proved a number of theorems on convergence to a Weibull distribution.
Lao and Mayer studied the kernels of low degrees, for example the area and perimeter of random triangles (see [Reference Lao and Mayer10]). Koroleva and Nikitin considered
$U{\hbox{-}}\textrm{max}$
statistics of a more complicated nature (see [Reference Koroleva and Nikitin6]). In particular, they considered the maximal perimeter among all perimeters of convex m-gons, where random vertices are chosen from n independent points uniformly distributed on a circle. This was generalized in another direction in the papers [Reference Simarova17] and [Reference Simarova18], where a generalized perimeter of a random convex polygon was considered.
These papers considered the uniform distribution of points on the unit circle. More general distributions were used by Lao and Mayer for some particular two-dimensional kernels, namely for the distances between points and the scalar product of two position vectors in [Reference Lao9], [Reference Lao and Mayer10], and [Reference Mayer14]. More complicated kernels were studied in [Reference Polevaya and Nikitin15], namely the areas and perimeters of inscribed polygons with more general conditions on the distribution of vertices. A common feature of all papers was that they investigated specific particular cases of
$ U{\hbox{-}}\textrm{max}$
statistics and U-min statistics.
This paper is devoted to a significant generalization of known limit theorems for
$U{\hbox{-}}\textrm{max}$
and
$U{\hbox{-}}\textrm{min}$
statistics. We consider an almost arbitrary distribution of points on a circle, as well as a wide and general class of smooth kernels with a natural structure of the set of extreme points. In this formulation, the limit behavior is determined by the degree of the kernel f, by the Hessian of the kernel at the maximal points, and also by the distribution of the points on the circle. The general formulas are used for kernels of a special type with convexity properties. Most of the previously known results can be deduced from Theorem 3.1 but we also provide some new examples.
Our paper consists of several parts. First, in Section 2, we introduce the basic notation and restrictions, and then in Section 3 we formulate the general limit relations we have obtained. Further, in Sections 4 and 5 we apply our results to some specific classes of kernels. For these classes, more explicit and relatively simple limit theorems for
$ U{\hbox{-}}\textrm{max}$
statistics of geometric nature are obtained. Some interesting examples are also given. A detailed proof of the main result of Section 3 is rather painstaking and is of considerable length. Therefore we place it at the end of the paper; it occupies Sections 6 and 7.
2. Preliminaries
In this section we introduce necessary conditions and definitions. We consider
$ U{\hbox{-}}\textrm{max}$
statistics with a fixed kernel f depending on m points
$ V_1,\ldots, V_m $
lying on the unit circle
$ S^1 $
with center O at the origin, that is,
\begin{equation*}f\colon (S^1)^m \rightarrow \mathbb{R}.\end{equation*}
Further, we always assume that
$m \ge 2.$
Let
$ \beta_i $
denote the angle between the vectors
$ OV_1 $
and
$ OV_{i + 1} $
(taken counterclockwise). We call such angles central. In this way,
\begin{equation}\beta_i=\angle V_{1}OV_{i+1}.\end{equation}
Sometimes for the sake of brevity we will use the notation
\begin{equation}\beta=(\beta_1, \ldots, \beta_{m-1}) \in [0, 2\pi)^{m-1}.\end{equation}
All angles that appear in this paper are considered modulo
$ 2 \pi. $
All algebraic operations involving several angles are also considered modulo
$ 2 \pi, $
unless otherwise stated.
Now we give some conditions that will be used below.
A. Conditions on the kernel f
-
A1. The function f is invariant with respect to rotations. Equivalently, this means that the function f can be written in the form
(2.3)where
\begin{equation} f(V_1, \ldots, V_m)= h(\beta_1, \ldots, \beta_{m-1})=h(\beta), \end{equation}
$\beta_i$
are central angles, and
$h\colon [0,2\pi)^{m-1} \rightarrow \mathbb{R}$
is a function.
-
A2. The function f cannot be changed after any permutation of the points
$ V_1, \ldots, V_m. $
Therefore the function h is also a symmetric function of its arguments. -
A3. The function h is continuous and can be continuously extended to a function
$h\colon [0,2\pi]^{m-1} \rightarrow \mathbb{R}.$
-
A4. The function h reaches its maximal value M and this maximum is realized only at a finite number of points
$ W_1, \ldots, W_k \in [0, 2 \pi]^{m-1}. $
It is assumed that none of these points lie on the boundary of the domain of definition of the function h. In other words,
$ W^j_i \in (0, 2 \pi) $
for all
$ i \in \{1, \ldots, k\}, j \in \{1, \ldots, m-1\}, $
where
$ W ^ j_i $
is the jth component of the point
$ W_i. $
Condition A4 together with condition A2 allows us to make the following conclusion about the structure of the maxima of the function f: there is only a finite number of points (up to rotations) where the maximal value of the function f is attained. Moreover, none of these points have matching components.
-
A5. There exists
$ \delta> 0 $
such that the function h is three-times continuously differentiable in the
$ \delta$
-neighborhood of any maximum point
$ W_i, $
$ i \in \{1, \ldots, k \} $
. -
A6. Consider the Hessian matrix
$ G_i $
of the form
\begin{equation*}G_i=\begin{pmatrix}\dfrac{\partial^2 h(W_i)}{\partial^2 x_1} & \quad\dfrac{\partial^2 h(W_i)}{\partial x_1 \partial x_2 } & \quad\ldots & \quad\dfrac{\partial^2 h(W_i)}{\partial x_1 \partial x_{m-1}} \\[15pt]\dfrac{\partial^2 h(W_i)}{\partial x_1 \partial x_2} & \quad \dfrac{\partial^2 h(W_i)}{\partial^2 x_2 } & \quad \ldots & \quad \dfrac{\partial^2 h(W_i)}{\partial x_2 \partial x_{m-1}} \\[4pt]\vdots & \quad \vdots & \quad \ddots & \quad \vdots \\[4pt]\dfrac{\partial^2 h(W_i)}{\partial x_{m-1} \partial x_1} & \quad \dfrac{\partial^2 h(W_i)}{ \partial x_{m-1}\partial x_2 } & \quad \ldots & \quad \dfrac{\partial^2 h(W_i)}{\partial^2 x_{m-1}} \\\end{pmatrix}\!. \end{equation*}
We require that the condition
\begin{equation*} \det\!(G_i) \ne 0 \end{equation*}
holds for all
$ i \in \{1, \ldots, k \} $
.
B. Conditions on the distribution of points
-
B1. The random points
$ V_1, \ldots, V_n $
are independently distributed on the unit circle
$ S^1 $
with the same probability density function
$ p(x). $
-
B2. The density function p is continuous (therefore it can be considered as a non-negative continuous
$ 2 \pi $
-periodic function
$p\colon \mathbb{R} \rightarrow \mathbb{R_{+}}$
such that
$ \int _0^{2 \pi} p(x){\textrm{d}} x = 1 $
). -
B3. There exists at least one maximal point of the kernel (which we denote by
$W_*$
) such that
\begin{equation*}\int_{0}^{2\pi} \Biggl[p(x)\prod_{l=1}^{m-1} p\bigl(x+W_{*}^l\bigr)\Biggr] {\textrm{d}} x \ne 0.\end{equation*}
Similar conditions on p(x) arose in [Reference Polevaya and Nikitin15].
Remark 2.1. The conditions imposed on the density p are not too restrictive. For example, continuous densities separated from zero or continuous densities taking the value 0 only on a set of measure less than
$ {2 \pi}/{m} $
are suitable for these conditions. A useful example of non-uniform distribution is the von Mises distribution (see e.g. [Reference Mardia and Jupp13]).
3. Main results
Now we state the main result of this paper.
Theorem 3.1. (General theorem.) Suppose that a kernel f and points
$V_1, \ldots, V_n$
satisfy all conditions A and B. Let
$M_n$
be the
$U{\hbox{-}}\textrm{max}$
statistic constructed by a kernel f, that is,
$ M_n = \max_{1 \le i_1< \ldots <i_m \le n} f(V_{i_1}, \ldots, V_{i_m}).$
Then for every
$t>0$
the following relation holds true:
\begin{equation*}\lim_{n \rightarrow \infty} \mathbb{P}\bigl\lbrace n^{{2m}/{(m-1)}} (M-M_n)\le t\bigr\rbrace=1 -\exp\biggl({-\dfrac{t^{{(m-1)}/{2}}K_m}{m!}}\biggr),\end{equation*}
where
\begin{equation*}K_m=\dfrac{(2\pi)^{{(m-1)}/{2}}}{\Gamma\bigl(\frac{m+1}{2}\bigr)}\sum_{i=1}^k \biggl( \dfrac{1}{\sqrt{\det\!({-}G_i)}} \int_0^{2\pi} p(x) \prod_{l=1}^{m-1} p\bigl(x+W_i^l\bigr) \,{\textrm{d}} x \biggr)\end{equation*}
and M is from condition A4. The rate of convergence is
${\textrm{O}}\bigl(n^{-{1}/{(m-1)}}\bigr).$
Theorem 3.1 immediately implies several simple but very useful consequences. As far as we know, these consequences are new. First of all, Theorem 3.1 can be modified slightly for
$ U{\hbox{-}}\textrm{min}$
statistics.
Corollary 3.1. Let us replace the maximum M with the minimum
$ \mu $
and consider the points of minimum in conditions A4, A5, A6, and B3. Let
$M^{\prime}_n$
denote the
$U{\hbox{-}}\textrm{min}$
statistic constructed by a kernel f, i.e.
$ M^{\prime}_n = \min_{1 \le i_1< \ldots <i_m \le n} f(V_{i_1}, \ldots, V_{i_m}).$
Then for each
$t>0$
we have
\begin{equation*}\lim_{n \rightarrow \infty} \mathbb{P}\bigl\{ n^{{2m}/{(m-1)}} (M^{\prime}_n-\mu)\le t \bigr\}=1 -\exp\biggl({-\dfrac{t^{{(m-1)}/{2}}K_m}{m!}}\biggr),\end{equation*}
where
\begin{equation*}K_m=\dfrac{(2\pi)^{{(m-1)}/{2}}}{\Gamma\bigl(\frac{m+1}{2}\bigr)}\sum_{i=1}^k\biggl( \dfrac{1}{\sqrt{\det\!(G_i)}} \int_0^{2\pi} p(x) \prod_{l=1}^{m-1} p\bigl(x+W_i^l\bigr) \,{\textrm{d}} x\biggr) .\end{equation*}
Corollary 3.2. (Particular case.) If p is the uniform density, then the constant
$K_m$
from Theorem 3.1 has the following form:
\begin{equation*}K_m=\dfrac{1}{(2\pi)^{{(m-1)}/{2}}\Gamma\bigl(\frac{m+1}{2}\bigr)} \sum_{i=1}^k \dfrac{1}{\sqrt{ \det\!({-}G_i)}}.\end{equation*}
Remark 3.1. Theorem 3.1 may be applied to a rather wide class of kernels from stochastic geometry but of course not to all of them. In [Reference Simarova18] the definition of a generalized perimeter was introduced. It is the sum of the yth degrees of the side lengths of a polygon constructed on m given points on a circle. It is shown that for
$ y>1 $
and
$m > 1+\pi/(\!\arccos{{1}/{\sqrt{y}}})$
, the generalized perimeter attains its maximum on the configuration of points in which some of them coincide. This shows that our result cannot be applied to this rather simple variant of the problem. In this case the limit relation is still an open question.
Remark 3.2. Note that condition A3 may be replaced with the following one: the function h is continuous and can be continuously extended to a function
$h\colon [0,2\pi]^{m-1} \rightarrow \mathbb{R} \cup \{-\infty\}.$
It follows from the fact that the function
$\hat{h}(x)=\max{\!(h(x), M-1)},$
where M is from condition A4 and
$\hat{f}$
constructed from
$\hat{h}$
by (2.3), satisfies Theorem 3.1. The limiting relation does not change after replacing
$\hat{f}$
with f.
In the following sections we give limit theorems for
$ U{\hbox{-}}\textrm{max}$
statistics generated by kernels of a special form that attain their maximum only at the vertices of a regular polygon. This special case covers a large number of standard geometric characteristics.
4. Limit behavior of U-max statistics for several functions depending on the side lengths of the polygon
Suppose that
$V_1, \ldots, V_m$
and
$\beta_1, \ldots, \beta_{m-1}$
are as introduced earlier, and also for a moment assume that
$0=\beta_0 \le \beta_1 \le \ldots \le \beta_{m-1}\le \beta_m=2\pi.$
We construct functions f and h via the following formula:
\begin{equation}f(V_1, \ldots, V_m)=h(\beta_1, \ldots, \beta_{m-1}) = \sum_{i=1}^{m}g(\beta_i-\beta_{i-1}),\end{equation}
where
$g\colon [0, 2\pi] \rightarrow \mathbb{R}$
is continuous and three-times continuously differentiable in some neighborhood of the point
$ {2 \pi}/{m}. $
We also require
$g^{\prime\prime}({2\pi}/{m}) \ne 0.$
Further, we define the function h on
$ [0, 2 \pi]^{m-1} $
so that it is symmetric and corresponds to the function f by (2.3). Such a function f satisfies conditions A1 and A3. Condition A2 also holds since the function f depends only on the angles between neighboring vectors
$ OV_1, \ldots, OV_m. $
Under additional restrictions we get the following statement.
Theorem 4.1. Suppose that the points
$ V_1, \ldots, V_n $
are independently distributed on
$ S^1 $
with a common continuous density p(x) such that
\begin{equation*} \int_{0}^{2\pi} \prod_{l=0}^{m-1} p\biggl(x+\dfrac{2\pi l}{m}\biggr){\textrm{d}} x >0. \end{equation*}
Consider the
$ U{\hbox{-}}\textrm{max}$
statistic
$ M_n $
with a kernel f of the form (4.1). Suppose that this kernel attains its maximum only at the vertices of a regular m-gon.
Then for any
$ t>0 $
the following limit relation holds:
\begin{equation}\lim_{n \rightarrow \infty} \mathbb{P}\biggl\lbrace n^{{2m}/{(m-1)}} \biggl(mg\biggl(\dfrac{2\pi}{m}\biggr)-M_n\biggr)\le t\biggr\rbrace=1 -\exp\biggl({-\dfrac{t^{{(m-1)}/{2}}K_m}{m}}\biggr),\end{equation}
where
\begin{equation*}K_m=\dfrac{(2\pi)^{{(m-1)}/{2}}\bigl[\int_{0}^{2\pi} \prod_{l=0}^{m-1} p\bigl(x+\frac{2\pi l}{m}\bigr){\textrm{d}} x \bigr]}{ \bigl({-}g^{\prime\prime}\bigl(\frac{2\pi}{m}\bigr)\bigr)^{{(m-1)}/{2}}\Gamma\bigl(\frac{m+1}{2}\bigr)\sqrt{m}}.\end{equation*}
Proof. Let us first prove that the function f and density p satisfy conditions A and B from Section 3. It was established above that conditions A1, A2, and A3 are met. The fulfillment of condition A4 follows from the fact that a regular polygon is the only maximal point of the function
$ f. $
Condition A5 follows from formula (4.1) and the differentiability assumption. Conditions B1 and B2 are obviously satisfied (they are assumed in the statement of the theorem). It remains to check the properties A6 and B3; then we can use Theorem 3.1.
By (2.2), a regular m-gon corresponds to some permutation of the angles in
$W^*=(W^1, \ldots, W^{m-1}),$
where
$ W^i = {2 \pi i }/{m} $
. Thus there are
$(m-1)!$
maxima of the corresponding function h, and the Hessian determinants of the function h at all these points are the same. It allows us to restrict ourselves to the case
$0\le \beta_1\le \ldots\le \beta_{m-1}\le 2\pi.$
Thus the condition that the maximum of the function f is attained only on a regular m-gon means that the point
$ W^* $
is the maximum of the function h among all points with ordered angles. Together with the condition
\begin{equation*}\int_{0}^{2\pi} \prod_{l=0}^{m-1} p\biggl(x+\dfrac{2\pi l}{m}\biggr){\textrm{d}} x >0,\end{equation*}
it implies the validity of condition B3. Next we obtain an explicit formula for the determinant of the Hessian matrix of the function h at the point
$ W^* $
and make sure that it is not equal to zero. This fact implies the fulfillment of condition A6, and then an application of Theorem 3.1 finishes the proof of Theorem 4.1.
By simple calculations, we get
\begin{equation*}\dfrac{\partial^2 h}{\partial x_i \partial x_j} (W^*) = \begin{cases}0& \text{if $ |i-j|>1$,}\\[5pt]2g^{\prime\prime}\biggl(\dfrac{2\pi}{m}\biggr)& \text{if $ i=j$,}\\[13pt]-g^{\prime\prime}\biggl(\dfrac{2\pi}{m}\biggr)& \text{if $ |i-j|=1$.}\end{cases}\end{equation*}
Therefore the Hessian matrix at the point
$ W^* $
is
\begin{align*}G(W^*) = g^{\prime\prime}\biggl(\dfrac{2\pi}{m}\biggr) \begin{pmatrix}2 & \quad -1 & \quad 0 & \quad 0 & \quad \ldots & \quad 0\\[3pt]-1 & \quad 2 & \quad -1 & \quad 0 & \quad \ldots & \quad 0\\[3pt]0 & \quad -1 & \quad 2 & \quad -1 & \quad \ldots & \quad 0\\[3pt]\vdots & \quad \vdots & \quad \vdots & \quad \vdots & \quad \ddots & \quad \vdots \\[3pt]0 & \quad 0 & \quad 0 & \quad 0 & \quad \ldots & \quad 2\\\end{pmatrix} = g^{\prime\prime}\biggl(\dfrac{2\pi}{m}\biggr)B_{m -1}.\end{align*}
The determinant of the tridiagonal Toeplitz matrix
$ B_{m-1}$
is well known: it is equal to m. Hence
\begin{equation*}\det\!({-}G(W^*))=m\cdot\biggl({-}g^{\prime\prime}\biggl(\dfrac{2\pi}{m}\biggr)\biggr)^{m-1} \ne 0,\end{equation*}
and the conditions of Theorem 3.1 are satisfied. Recalling the fact that there are
$(m-1)!$
maxima of the function h with the same determinant of the Hessian matrix and the same integral, we obtain the desired limit relation.
Lemma 4.1. For strictly concave functions
$g\colon [0,2\pi] \rightarrow \mathbb{R},$
the maximum of the function f defined by (4.1) is attained only at the vertices of a regular m -gon.
Proof. We assume that
$0 \le \beta_1 \le \ldots \le \beta_{m-1} \le 2\pi.$
Let us prove that the point
$W^*=(W^1, \ldots, W^{m-1}),$
where
$ W^i = {2 \pi i}/{m}, $
is the only maximum of the function f among all points with ordered angles. Due to Jensen’s inequality we have
\begin{align}f(V_1, \ldots, V_m) = \sum_{i=1}^{m}g(\beta_i-\beta_{i-1}) \le m g\biggl(\dfrac{\beta_m-\beta_0}{m}\biggr) =mg\biggl(\dfrac{2\pi}{m}\biggr) =\sum_{i=1}^{m}g\bigl(W^i-W^{i-1}\bigr).\end{align}
The function g is strictly concave; therefore, if the arguments of the function g are not all equal, inequality in (4.3) is strict.
By combining Theorem 4.1 and Lemma 4.1, we obtain the following corollary.
Corollary 4.1. Suppose that a function
$g\colon [0, 2\pi] \rightarrow \mathbb{R}$
is continuous, strictly concave, three-times continuously differentiable in a neighborhood of the point
$ {2 \pi}/{m} $
and
$ g^{\prime\prime} ({2 \pi}/{m}) \ne 0. $
Let the function f be defined by (4.1). Then the
$ U{\hbox{-}}\textrm{max}$
statistic with a kernel f satisfies relation (4.2) of Theorem 4.1.
Corollary 4.2. In Theorem 4.1 we may consider functions f for which a regular polygon is the only point of minimum. Then, for the
$ U{\hbox{-}}\textrm{min}$
statistic
$ M^{\prime}_n $
generated by a kernel f, the following limit relation holds for any
$t>0$
(similarly to (4.2)):
\begin{equation*}\lim_{n \rightarrow \infty} \mathbb{P}\biggl\lbrace n^{{2m}/{(m-1)}} \biggl(M^{\prime}_n-mg\biggl(\dfrac{2\pi}{m}\biggr)\biggr)\le t\biggr\rbrace=1 -\exp\biggl({-\dfrac{t^{{(m-1)}/{2}}K_m}{m}}\biggr),\end{equation*}
where
\begin{equation*}K_m=\dfrac{(2\pi)^{{(m-1)}/{2}}\bigl[\int_{0}^{2\pi} \prod_{l=0}^{m-1} p\bigl(x+\frac{2\pi l}{m}\bigr){\textrm{d}} x \bigr]}{ \bigl(g^{\prime\prime}\bigl(\frac{2\pi}{m}\bigr)\bigr)^{{(m-1)}/{2}}\Gamma\bigl(\frac{m+1}{2}\bigr)\sqrt{m}}.\end{equation*}
In particular, this is the case when we consider the strictly convex functions g in Corollary 4.1 instead of strictly concave ones.
Remark 4.1. If p is the uniform density, then the constant
$K_m$
from Theorem 4.1 satisfies
\begin{equation}K_m=\dfrac{1}{ \bigl({-}2\pi g^{\prime\prime}\bigl(\frac{2\pi}{m}\bigr)\bigr)^{{(m-1)}/{2}}\Gamma\bigl(\frac{m+1}{2}\bigr)\sqrt{m}}.\end{equation}
Example 4.1. (Maximal perimeter of inscribed polygon.) Let us consider the maximal perimeter of an inscribed convex m-gon with random vertices on a circle with
$m \ge 3$
. This is the
$ U{\hbox{-}}\textrm{max}$
statistic with a kernel f of the form (4.1), where
$ g(x) = 2 \sin\!{{({x}/{2})}}. $
This function is strictly concave, hence the results follow from Theorem 4.1. The limit behavior of the
$ U{\hbox{-}}\textrm{max}$
statistic with such a kernel in the case of the uniform distribution of points may be found in [Reference Koroleva and Nikitin6]; the result coincides with Remark 4.1 with this function g, so the result [Reference Koroleva and Nikitin6] is a simple special case of our results.
Example 4.2. (Maximal area of inscribed polygon.) Another
$ U{\hbox{-}}\textrm{max}$
statistic considered in [Reference Koroleva and Nikitin6] was the area of an inscribed convex m-gon with
$m \ge 3$
. It is generated by a kernel f of the form (4.1), where
$ g(x) = \frac12 \sin{x}. $
The maximum of the function f is attained only on a regular m-gon; see e.g. [Reference Yaglom and Boltyanskii20, problem 57a]. Therefore the limit theorem for this
$ U{\hbox{-}}\textrm{max}$
statistic follows directly from Theorem 4.1 and Remark 4.1. The results of [Reference Koroleva and Nikitin6] and more general results of [Reference Polevaya and Nikitin15] again follow from ours as simple special cases. Similar statements hold for the areas and perimeters of the described random polygons considered in [Reference Koroleva and Nikitin6]; they also follow from Theorem 4.1 with some g(x).
Example 4.3. (Sum of the distances from the center to the vertices of described polygon.) Let us now consider the example of a kernel that did not arise earlier in the literature on the limit behavior of
$ U{\hbox{-}}\textrm{max}$
statistics. We define a kernel
$f\colon (S^1)^m \rightarrow \mathbb{R} \cup \{+\infty\}$
with
$m \ge 3$
as follows: construct the described convex m-gon with vertices at points
$ A_1, \ldots, A_m $
such that its sides touch the circle
$ S^1 $
at points
$ U_1, \ldots, U_m. $
Define the function
\begin{equation*} f(V_1, \ldots, V_m) = \sum _{i = 1}^m |OA_i| \end{equation*}
as the sum of distances from the center to the vertices of the described m-gon. It is possible that some vertex
$ A_i $
goes to infinity; in this case we define
$ f(V_1, \ldots, V_m) = + \infty. $
The function f can be written in the form (4.1) when
$g(x)=(\!\cos{{({x}/{2})}})^{-1},$
if
$ 0 \le x <\pi, $
and
$ g(x) = + \infty $
otherwise. The case
$ g(x) = + \infty $
can occur if some vertex
$ A_i $
goes to infinity. Note that
\begin{equation*}g^{\prime\prime}(x)=\dfrac{1+\sin^2{{({x}/{2})}}}{4\cos^3{{({x}/{2})}}} >0 \quad \text{for $ x \in [0, \pi)$,}\end{equation*}
so the function is strictly convex on
$ [0, \pi). $
By Corollary 4.2, the minimum will be attained at the vertices of a regular m-gon, and for the
$ U{\hbox{-}}\textrm{min}$
statistic
$ M^{\prime}_n $
generated by a kernel f we have for any
$ t> 0 $
\begin{equation*}\lim_{n \rightarrow \infty} \mathbb{P}\biggl\lbrace n^{{2m}/{(m-1)}} \biggl(M^{\prime}_n-\dfrac{m}{\cos{\frac{\pi}{m}}}\biggr)\le t \biggr\rbrace=1 -\exp\biggl({-\dfrac{t^{{(m-1)}/{2}}K_m}{m}}\biggr),\end{equation*}
where
\begin{equation*}K_m=\dfrac{\bigl(8\pi \cos^3{\frac{\pi}{m}} \bigr)^{{(m-1)}/{2}}\bigl[\int_{0}^{2\pi} \prod_{l=0}^{m-1} p\bigl(x+\frac{2\pi l}{m}\bigr) \,{\textrm{d}} x \bigr]}{ \bigl(1+\sin^2{\frac{\pi}{m}}\bigr)^{{(m-1)}/{2}}\Gamma\bigl(\frac{m+1}{2}\bigr)\sqrt{m}}.\end{equation*}
Example 4.4. (Generalized perimeter of the polygon.) In [Reference Simarova17, Reference Simarova18] a definition of a generalized perimeter was introduced. A generalized perimeter of order y is the sum of the yth degrees of the side lengths of a convex inscribed polygon constructed on m given points. This function may also be written as
\begin{equation*} f(V_1, \ldots, V_m)=\sum_{i=1}^mg(\beta_i-\beta_{i-1}), \end{equation*}
where
$g(x)=2^y\sin^y{({x}/{2})}.$
The function g is convex for negative y and concave for
$ y \in (0,1] $
, so the limit relation obtained in these cases for
$ U{\hbox{-}}\textrm{min}$
and
$ U{\hbox{-}}\textrm{max}$
statistics, respectively, is also a special case of the equality (4.4) (see [Reference Simarova17]).
For
$ y \in (1,2]$
and
$m = 3 $
, the function g is not concave but the function f also attains its maximum only on the vertices of regular triangle, so relation (4.2) with constant (4.4) from Theorem 4.1 also holds true in this case. This was shown in [Reference Simarova18].
Example 4.5. (Further generalization of the perimeter.) The concept of a generalized perimeter introduced in [Reference Simarova17] may be generalized further. Suppose that a kernel f is given by
\begin{equation}f(V_1, \ldots, V_m)=\sum_{i=1}^m r(|V_iV_{i+1}|),\end{equation}
where
$r\colon [0,2] \rightarrow \mathbb{R}$
is a function and the points
$ V_1, \ldots, V_m $
are ordered counterclockwise, and we also assume that the kernel is symmetric. By
$|V_{i}V_{i+1}|$
we denote the length of the side of the polygon. The generalized perimeter introduced in [Reference Simarova17] and [Reference Simarova18] corresponds to the function
$ r (x) = x^y. $
If the function r is continuous, strictly concave, increasing, three-times continuously differentiable in some neighborhood of the point
$2\sin\!{{({\pi}/{m})}}$
and
$r^{\prime\prime}(2\sin\!{{({\pi}/{m})}}) \ne 0,$
then the function
$g(x) = r(2\sin\!{{({x}/{2})}})$
is strictly concave. By Corollary 4.1, we can write the limit relation for
$ U{\hbox{-}}\textrm{max}$
statistics from Theorem 4.1. It is also possible to replace the conditions of strict concavity and increasing with the conditions of concavity and strict increasing.
Similarly, if r is a continuous strictly convex decreasing function which is three-times continuously differentiable in some neighborhood of the point
$2\sin\!{{({\pi}/{m})}},$
and
$r^{\prime\prime}(2\sin\!{{({\pi}/{m})}}) \ne 0,$
then the function
$g(x) = r(2\sin\!{{({x}/{2})}})$
is strictly convex. By Corollary 4.2, we can write the limit relation for
$ U{\hbox{-}}\textrm{min}$
statistics. The condition of strict convexity and decreasing may be replaced by the condition of convexity and strict decreasing.
In particular, let us use the function
$r(x)={\textrm{e}}^{-ax}x^b (\!\ln{({x}/{2})})^c$
. Such functions were considered by Alexander and Stolarsky in [Reference Alexander and Stolarsky1]. Let
$ \tau(a, b, c) $
denote the function that is equal to 1 if the function r is strictly concave and increasing, and equal to
$-1$
if the function r is strictly convex and decreasing. Then the following equality from [Reference Alexander and Stolarsky1] is true:
\begin{equation*}\tau(a,b,c)=\begin{cases}({-}1)^c &\text{if $ a \ge 0, b \le 0$, $c \in \mathbb{N}$,}\\[3pt]-1 &\text{if $ a \ge 0$, $b \le 0$, $c=0$, $a^2+b^2 \ne 0$,}\\[3pt]1 &\text{if $ a=0$, $0<b \le 1$, $c=0$.}\end{cases}\end{equation*}
We may study the limit behavior of
$ U{\hbox{-}}\textrm{max}$
(resp.
$ U{\hbox{-}}\textrm{min}$
) statistics
$ M_n $
(resp.
$M^{\prime}_n$
) with a kernel f constructed by (4.5) in the case when
$ \tau = 1 \,$
(resp.
$\tau = -1$
). It can be simply done by using
$ g(x) = r (2 \sin\!{{({x}/{2})}} )$
in Theorem 4.1.
5. Limit behavior of U-max statistics for several functions depending on the side lengths and diagonals of a polygon
In this section the arguments are very similar to those in Section 4. We define a kernel f and the corresponding function h by the set of angles
$(\beta_1, \ldots\beta_{m-1})$
introduced in (2.2). The connection between f and h is given by (2.3). We again define the function h using a continuous function
$ g\colon [0, 2 \pi] \rightarrow \mathbb{R}$
, but in a different way. The restrictions on the function g will be different, and the function h itself is defined via the following analogue of (4.1):
\begin{equation}f(V_1, \ldots, V_m) =h(\beta_1, \ldots, \beta_{m-1}) = \sum_{0 \le i<j \le m-1}g(|\beta_j-\beta_{i}|), \quad \text{where $ \beta_0=0$.}\end{equation}
In other words, in this section we consider functions depending on the angles between any pairs of points
$ V_i $
and
$ V_j, $
but not only on the angles between adjacent points, as was done in the previous section.
We state an analogue of Theorem 4.1 for a kernel f of the form (5.1).
Theorem 5.1. Suppose that the points
$ V_1, \ldots, V_n $
are independently distributed on
$ S^1 $
with a common continuous density function p(x) such that
\begin{equation*} \int_{0}^{2\pi} \prod_{l=0}^{m-1} p\biggl(x+\dfrac{2\pi l}{m}\biggr){\textrm{d}} x >0. \end{equation*}
Consider a continuous function
$g\colon[0, 2\pi] \rightarrow \mathbb{R}$
which is three-times continuously differentiable in the neighborhoods of points
$ {2 \pi s}/{m} $
for all
$ s \in \{1, \ldots, m-1 \}$
and such that
$ g(x) = g(2 \pi-x). $
We construct a function f by (5.1) and suppose that it attains its maximum only at the vertices of a regular m-gon. Let
$ M_n $
be the
$ U{\hbox{-}}\textrm{max}$
statistic with a kernel
$ f. $
Consider the symmetric matrix
$G=(g_{i,j})_{i,j=1}^{m-1},$
where
\begin{equation} g_{i,j}=\begin{cases}-g^{\prime\prime}\biggl(\dfrac{2\pi|i-j|}{m}\biggr)& \text{if $ i \ne j$,}\\[12pt]\displaystyle \sum_{s=1}^{m-1}g^{\prime\prime}\biggl(\dfrac{2\pi s}{m}\biggr)& \text{if $ i=j$.}\end{cases} \end{equation}
If
$\det{G}\ne 0,$
then, for any
$ t>0, $
the following limit relation holds:
\begin{equation}\lim_{n \rightarrow \infty} \mathbb{P}\biggl\lbrace n^{{2m}/{(m-1)}} \biggl(\dfrac{1}{2}\sum_{s=1}^{m-1}mg\biggl(\dfrac{2\pi s}{m}\biggr)-M_n\biggr)\le t\biggr\rbrace=1 -\exp\biggl({-\dfrac{t^{{(m-1)}/{2}}K_m}{m}}\biggr),\end{equation}
where
\begin{equation*}K_m=\dfrac{(2\pi)^{{(m-1)}/{2}}\bigl[\int_{0}^{2\pi} \prod_{l=0}^{m-1} p\bigl(x+\frac{2\pi l}{m}\bigr){\textrm{d}} x \bigr]}{ \sqrt{\det\!({-}G)}\Gamma\bigl(\frac{m+1}{2}\bigr)}.\end{equation*}
The proof of this theorem is similar to the proof of Theorem 4.1 and therefore omitted.
Remark 5.1. If the values of second derivatives at the points
$ {2 \pi s}/{m} $
are negative for all
$ s \in \{1, \ldots, m-1 \}, $
then
\begin{equation*} g_{i,i}>\sum_{j=1 \\i \ne j}^{m-1} |g_{i,j}|. \end{equation*}
Matrices with such a property are called diagonally dominant, and according to [Reference Horn and Johnson5, Chapter 6, § 1, p. 392, Th. 6.1.10] the determinants of such matrices are non-zero.
Now we describe the extreme points of the function f for concave g having some symmetry property. This is an analogue of Lemma 4.1.
Lemma 5.1. Suppose that a function
$ g\colon [0, 2 \pi] \rightarrow \mathbb{R}$
is a continuous and strictly concave function such that
$ g(x) = g (2\pi-x). $
Then the function f defined by (5.1) attains its maximum only at the vertices of a regular m -gon, and its maximal value is equal to
\begin{equation*}\dfrac{1}{2} \sum_ {s = 1}^{m-1} mg \biggl(\dfrac{2 \pi s}{m} \biggr).\end{equation*}
Proof. Without loss of generality, we assume that the vertices
$ V_1, \ldots, V_m $
are ordered counterclockwise. Let
$P(k, V_1, \ldots, V_m)$
denote the sum
$\sum_{i=1}^{m} g(\beta_{i+k}-\beta_i)$
assuming that
$\beta_0=0, \beta_{m+s}=2\pi+\beta_s$
for
$ s \in \{0, \ldots, m-1 \}. $
Then
\begin{equation*}f(V_1, \ldots, V_m)=\dfrac{1}{2}\sum_{i=1}^{m-1} P(i,V_1, \ldots, V_m).\end{equation*}
We prove that the maximum of
$ P (k, V_1, \ldots, V_m) $
is attained only on a regular m-gon.
Due to strict concavity,
\begin{equation*}P(k, V_1, \ldots, V_m)=\sum_{i=1}^{m} g(\beta_{i+k}-\beta_i) \le m g\biggl(\dfrac{2\pi k}{m}\biggr),\end{equation*}
and equality is achieved only when
$ \beta_{i + k} - \beta_i = {2 \pi k}/{m} $
for all i and k. Therefore the maximal value is attained only at the vertices of a regular polygon.
Combining the results of Theorem 5.1 and Lemma 5.1, we obtain the following corollary.
Corollary 5.1. If a function
$g\colon [0, 2\pi] \rightarrow \mathbb{R}$
is continuous, strictly concave, three-times continuously differentiable in the neighborhoods of points
$ {2 \pi s}/{m} $
for all
$ s \in \{1, \ldots, m-1 \}, $
and also has the property
$ g(x) = g(2 \pi-x), $
and if the probability density function p is continuous and
\begin{equation*} \int_{0}^{2\pi} \prod_{l=0}^{m-1} p\biggl(x+\dfrac{2\pi l}{m}\biggr){\textrm{d}} x >0, \end{equation*}
then for the
$ U{\hbox{-}}\textrm{max}$
statistic
$ M_n $
with a kernel f of the form (5.1), relation (5.3) of Theorem 5.1 holds.
Similarly to Section 4, this statement can be reformulated for
$ U{\hbox{-}}\textrm{min}$
statistics and strictly convex functions
$ g. $
Remark 5.2. One of the main differences between Sections 5 and 4 is the condition
$ g(x) = g (2 \pi-x),$
which was not involved in Section 4. It gives the equality of elements on the main diagonal of the matrix G introduced in Theorem 5.1. This condition also implies that
$ g (| \beta_i- \beta_j |) = r (| V_iV_ {j} |), $
where
$ | V_iV_{j} | $
is the length of the segment
$ V_iV_j. $
Thus, by analogy with Example 4.5, we may say that all the functions f satisfying (5.1) are the generalized sums of pairwise distances between points. This shows that the functions g from Examples 4.1 and 4.3 cannot be used to construct the functions f in (5.1). This property holds for the function g from Examples 4.1, 4.4, and 4.5. Such functions g are also differentiable on
$ (0, 2 \pi), $
and Remark 5.1 holds for them. Therefore the functions f constructed in these examples by (5.1) satisfy Theorem 5.1.
Example 5.1. As already mentioned, the function g(x) introduced in Example 4.5 may be used in this case as well.
Example 5.2. (Sum of pairwise distances between vertices.) Consider the simple case where g(x) is defined in Example 4.1, and the resulting function
$ f (V_1, \ldots, V_m) $
is the sum of the pairwise distances between points
$ V_1, \ldots, V_m $
with
$m \ge 3.$
According to [Reference Toth19], the maximum is attained only at the vertices of a regular polygon and is equal to
$ m \cot\!{{({\pi}/{2m})}}.$
The limit relation (5.3) holds but we did not manage to calculate the exact constant
$K_m$
in it for an arbitrary
$ m.$
The elements of the matrix G involved in Theorem 5.1 have the following form:
\begin{equation*}g_{i,j}=\begin{cases}\dfrac{1}{2}\sin{\dfrac{|i-j|\pi}{m}}& \text{if $ i \ne j$,}\\[12pt]-\dfrac{1}{2} \cot{ \dfrac{\pi}{2m}}& \text{if $ i=j$.}\end{cases} \end{equation*}
Example 5.3. (Pairwise sum of inverse distances between vertices.) Let
$g(x)=(2\sin\! {({x}/{2})})^{-1}$
and construct a kernel f using formula (5.1) with
$m \ge 3.$
It is easy to see that the constructed kernel f is equal to
\begin{equation*} f(V_1, \ldots, V_m) = \sum_{j> i} \dfrac{1}{| V_iV_j |}, \end{equation*}
that is, the sum of the inverse distances between the vertices
$ V_1, \ldots, V_m, $
where
$m \ge 3.$
This example was considered by Toth [Reference Toth19].
The minimal value of a kernel f is attained only at the vertices of a regular polygon and is equal to
\begin{equation*}\dfrac{m}{4} \sum_{k=1}^{m-1}\dfrac{1}{\sin\!{\bigl(\frac{\pi k}{m}\bigr)}}\end{equation*}
(see [Reference Toth19]). The second derivative of the function g is equal to
\begin{equation*}g^{\prime\prime}(x)=\dfrac{2-\sin^2{\frac{x}{2}}}{8\sin^3{\frac{x}{2}}},\end{equation*}
so the elements of the matrix G defined by (5.2) have the following form:
\begin{equation*}g_{i,j}=\begin{cases}-\dfrac{2-\sin^2\!{\bigl(\frac{\pi |i-j|}{m}\bigr)}}{8\sin^3\!{\bigl(\frac{\pi |i-j|}{m}\bigr)}} & \text{if $ i \ne j$,}\\[17pt]\displaystyle\sum_{s=1}^{m-1} \dfrac{2-\sin^2\!{\bigl(\frac{\pi s}{m}\bigr)}}{8\sin^3\!{\bigl(\frac{\pi s}{m}\bigr)}}& \text{if $ i=j$.}\end{cases} \end{equation*}
6. Proof of Theorem 3.1: part 1
We return to the proof of our general Theorem 3.1. It can be divided into two parts. The first part takes the form of the following statement.
Theorem 6.1. Suppose that a kernel f and points
$V_1, \ldots, V_n$
satisfy conditions A and B from Section 2. Let
$M_n$
be the
$U{\hbox{-}}\textrm{max}$
statistic constructed via a kernel f, that is,
\begin{equation*}M_n = \max_{1 \le i_1< \ldots <i_m \le n} f(V_{i_1}, \ldots, V_{i_m}).\end{equation*}
Then the following two statements are true.
-
(i) There exist constants
$C>0$
and
$D>0 $
such that, for any number
$\varepsilon$
,
$0<\varepsilon<C,$
if
$f(V_1, \ldots, V_m) \ge M-\varepsilon,$
then
$\min_{1\le i \le k}{\|W_i-\beta\|}\le D\sqrt{\varepsilon},$
where
$ \beta $
is defined by (2.2) and (2.1), and
$W_i$
is defined by condition A4. -
(ii) The following relation holds true:
where
\begin{equation*}\lim_{\varepsilon \rightarrow 0+} \varepsilon^{-{(m-1)}/{2}} \mathbb{P}\lbrace f(V_1, \ldots, V_m) \ge M-\varepsilon \rbrace = K_m,\end{equation*}
\begin{equation*} K_m=\dfrac{(2\pi)^{{(m-1)}/{2}}}{\Gamma\bigl(\frac{m+1}{2}\bigr)}\sum_{i=1}^k \Biggl( \dfrac{1}{\sqrt{\det\!({-}G_i)}} \int_0^{2\pi} \Biggl(p(x) \prod_{l=1}^{m-1} p\bigl(x+W_i^l\bigr) \Biggr){\textrm{d}} x\Biggr). \end{equation*}
Proof.It is clear that
\begin{equation*}\mathbb{P}\{f(V_1, \ldots, V_m)>z\} = \mathbb{P}\{h(\beta_1, \ldots, \beta_{m-1})>z\},\end{equation*}
where
$ \beta_i $
are random angles defined by (2.1). Further, we deal with the function h only.
Let us define, for every
$ \varepsilon> 0 $
, the number
\begin{equation} \hat{S}(\varepsilon) = \min\lbrace s \ge 0 \mid \forall x \in [0,2\pi]^{m-1}\colon M-f(x) \le \varepsilon \Rightarrow \exists i\colon \|x-W_i\| \le s \rbrace. \end{equation}
In other words
$ \hat{S}(\varepsilon) $
is the minimal radius of balls with centers in
$ W_i, i = 1,\ldots, k, $
such that if the value of the function differs from the maximum value by less than
$ \varepsilon, $
then the argument of the function must lie in one of the balls. For any
$ \varepsilon> 0 $
, this minimal radius obviously exists. Also, let us define for any
$\varepsilon>0$
\begin{equation}S(\varepsilon)=\max\bigl(\hat{S}(\varepsilon), \varepsilon^{{1}/{3}}\bigr).\end{equation}
It is easy to show that
\begin{equation} \lim_{\varepsilon \rightarrow 0+}S(\varepsilon) =0. \end{equation}
Indeed, (6.3) is equivalent to the limit relation
$ \lim_{\varepsilon \rightarrow 0+}\hat{S}(\varepsilon) =0. $
The function
$ \hat{S}(x) $
is non-decreasing and non-negative, so the limit
$\lim_{\varepsilon \rightarrow 0+}\hat{S}(\varepsilon)$
exists and is non-negative. We denote it by a and suppose that
$a>0$
(otherwise (6.3) is proved). Then for any
$\varepsilon>0$
there exists
$x_{\varepsilon} \in [0,2\pi]^{m-1}$
such that
$\min_{1 \le i \le k}\|W_i-x_{\varepsilon}\| \ge a $
and
$|h(x_{\varepsilon})-M|\le \varepsilon.$
Let
$\varepsilon_n = {1}/{n}.$
Then the infinite sequence
$x_{\varepsilon_n}, $
which belongs to the compact set
$[0,2\pi]^{m-1}, $
has a convergent subsequence with some limit
$x^{*}.$
By construction,
$x^{*} \ne W_i$
for any i, and the continuity of h implies that
$ h(x^{*}) = M. $
This contradiction proves (6.3).
Equation (6.3) implies that, for sufficiently small
$ \varepsilon,$
$ S (\varepsilon)$
-neighborhoods of points
$ V_1, \ldots, V_k $
have empty intersection. Hence, by definitions (6.1) and (6.2), for sufficiently small
$ \varepsilon $
the following equality is valid:
\begin{equation}\mathbb{P}\{h(\beta)\ge M-\varepsilon\} =\sum_{i=1}^k \mathbb{P}\{h(\beta) \ge M-\varepsilon, \|W_i-\beta\|\le S(\varepsilon) \}.\end{equation}
Let us fix some
$i \in \{1, \ldots, k\}.$
Assume that the following event happens for some
$\varepsilon>0$
:
\begin{equation}h(\beta)=h(\beta_1, \ldots, \beta_{m-1}) \ge M-\varepsilon,\, \|W_i-\beta\|\le S(\varepsilon).\end{equation}
By (6.3) there exists
$ \varepsilon_0> 0 $
such that
$ S(\varepsilon_0) <{\delta}/{2}, $
where
$ \delta $
is the number from condition A5. The function
$ S(\varepsilon) $
is non-decreasing, so for any positive
$ \varepsilon<\varepsilon_0 $
we have
\begin{equation}S(\varepsilon)<\dfrac{\delta}{2}.\end{equation}
Below we deal with
$ \varepsilon<\varepsilon_0 $
only. Since the function h is three-times continuously differentiable in the
$ \delta$
-neighborhood of any maximal point, in this neighborhood we consider the Taylor expansion of the function h at the point
$ W_i $
with the third-order remainder. For this purpose we introduce the notation
\begin{equation}\alpha_j = \beta_j-W_i^j \quad\text{and}\quad \alpha=(\alpha_1, \ldots, \alpha_{m-1}).\end{equation}
It is clear that
\begin{equation*}\|\alpha\|=\|\beta-W_i\| < \dfrac{\delta}{2}.\end{equation*}
Here
$ \alpha $
is an element of
$ \mathbb {R}^{m-1} $
which is considered as a difference of two elements of
$ \mathbb{R}^{m-1} $
and not as the difference of two sets of angles. By (6.3) and condition A4 it is the same for small
$ \varepsilon. $
We write the Taylor expansion of the function h at the point
$ W_i.$
Then we have
\begin{align} h(\beta)&=h(\beta_1, \ldots, \beta_{m-1})\notag \\ &=h\bigl(W_i^1+\alpha_1, W_i^2+\alpha_2, \ldots, W_i^{m-1}+\alpha_{m-1}\bigr) \notag \\&=h(W_i)+\sum_{j=1}^{m-1} \dfrac{\partial h(W_i)}{\partial x_j}\, \alpha_j + \sum_{1 \le l,s \le m-1}\dfrac{1}{2} \dfrac{\partial^2 h(W_i)}{\partial x_l\partial x_s} \, \alpha_l\alpha_s \notag \\ &\quad +\sum_{1 \le l,s,t \le m-1}\dfrac{1}{6} \dfrac{\partial^3 h(W_i+r_{(l,s,t)})}{\partial x_l \partial x_s \partial x_t}\, \alpha_l \alpha_s \alpha_t,\end{align}
where
$r_{(l,s,t)} =c_{(l,s,t)} \cdot (\alpha_1, \ldots,\alpha_{m-1}),$
and
$c_{(l,s,t)} \in (0,1)$
are constants depending on indices l, s, t and on the function h. According to condition A4,
$ W_i $
does not lie on the boundary of the definition domain of the continuous function h, so
${\partial h(W_i)}/{\partial x_j} =0$
for all
$ j \in \{1, \ldots, m-1 \}. $
Hence the linear term in expansion (6.8) is equal to 0.
Consider the matrix
\begin{equation} A^i=\dfrac{1}{2}G_i,\end{equation}
where the
$G_i$
are the same as in condition A6. It is clear that the coefficient before
$ \alpha_l \alpha_s $
in (6.8) is
$ a^i_{l, s} $
(the element of the matrix
$ A^i$
). Thus
\begin{equation*}h(\beta)=M+\sum_{1 \le l,s \le m-1}a^i_{l,s} \alpha_l\alpha_s+\dfrac{1}{6}\sum_{1 \le l,s,t \le m-1} \dfrac{\partial^3 h (W_i+r_{(l,s,t)})}{\partial x_l \partial x_s \partial x_t} \alpha_l \alpha_s \alpha_t.\end{equation*}
Therefore condition (6.5) is equivalent to
\begin{equation}-\sum_{1 \le l,s \le m-1}a^i_{l,s} \alpha_l\alpha_s-\dfrac{1}{6}\sum_{1 \le l,s,t \le m-1} \dfrac{\partial^3 h(W_i+r_{(l,s,t)})}{\partial x_l \partial x_s \partial x_t} \alpha_l \alpha_s \alpha_t \le \varepsilon.\end{equation}
Under conditions (6.5) and (6.6), we estimate the third-order terms in this formula. Since the functions
\begin{equation*}\dfrac{\partial^3 h(W_i+r)}{\partial x_l \partial x_s \partial x_t}\end{equation*}
are continuous for
$|r| \le {\delta}/{2},$
there exists
$ L_1>0 $
such that
\begin{equation*}\biggl|\dfrac{\partial^3 h(W_i+r)}{\partial x_l \partial x_s \partial x_t}\biggr|\end{equation*}
does not exceed
$ L_1 $
for all
$ |r| \le {\delta}/{2}. $
Therefore the following inequality holds true:
\begin{equation}\biggl|\dfrac{1}{6} \dfrac{\partial^3 h (W_i+r_{(l,s,t)})}{\partial x_l \partial x_s \partial x_t} \alpha_l \alpha_s \alpha_t\biggr| \le L_1 |\alpha_l \alpha_s \alpha_t|\le L_1 \dfrac{|\alpha_l|^3+|\alpha_s|^3+|\alpha_t|^3}{3} \le L_1 \dfrac{\alpha_l^2+\alpha_s^2+\alpha_t^2}{3} S(\varepsilon).\end{equation}
The last inequality follows from
$ \| \alpha \| < S(\varepsilon). $
Summing (6.11) over all triplets (l, s, t), we get the inequality
\begin{equation*}\Biggl|\dfrac{1}{6}\sum_{1 \le l,s,t \le m-1} \dfrac{\partial^3 h(W_i+r_{(l,s,t)})}{\partial x_l \partial x_s \partial x_t} \alpha_l \alpha_s \alpha_t\Biggr| \le m^2L_1 S(\varepsilon)\sum_{s=1}^{m-1}\alpha_s^2 =L_2S(\varepsilon) \sum_{s=1}^{m-1}\alpha_s^2.\end{equation*}
Therefore the following estimate is valid for all
$\|\alpha\|<S(\varepsilon)$
:
\begin{align}L_2S(\varepsilon) \sum_{s=1}^{m-1}\alpha_s^2 -\sum_{1 \le l,s \le m-1}a^i_{l,s} \,\alpha_l\alpha_s &\ge M-h (W_i+\alpha)\notag \\& \ge -L_2S(\varepsilon) \sum_{s=1}^{m-1}\alpha_s^2 -\sum_{1 \le l,s \le m-1}a^i_{l,s}\, \alpha_l\alpha_s.\end{align}
Collecting the results of (6.5), (6.10), and (6.12), we obtain
\begin{align}&\mathbb{P}\Biggl\lbrace \Biggl({-}\sum_{1 \le l,s \le m-1}a^i_{l,s} \alpha_l \alpha_s -L_2 S(\varepsilon)\sum_{s=1}^{m-1}\alpha_s^2\Biggr) \le \varepsilon, \|\alpha\|<S(\varepsilon) \Biggr\rbrace \notag \\&\quad \ge \mathbb{P}\lbrace h(\beta) >M-\varepsilon, \|W_i-\beta\| \le S(\varepsilon)\rbrace \notag \\&\quad \ge \mathbb{P}\Biggl\lbrace \Biggl({-}\sum_{1 \le l,s \le m-1}a^i_{l,s}\alpha_l \alpha_s +L_2 S(\varepsilon)\sum_{s=1}^{m-1}\alpha_s^2 \Biggr)\le \varepsilon, \|\alpha\|<S(\varepsilon) \Biggr\rbrace.\end{align}
Denote
\begin{equation*}A^i (\varepsilon)=\begin{cases}A^i+L_2 S(\varepsilon)I_{m-1} &\text{for $ \varepsilon \ge 0$,} \\[4pt]A^i -L_2 S({-}\varepsilon)I_{m-1} & \text{for $ \varepsilon \le 0$,}\end{cases}\end{equation*}
where
$ A^{i} $
is the same as in (6.9), and
$ I_{m-1} $
is the identity matrix of size
$ (m-1)\times (m-1). $
Then inequality (6.13) may be rewritten using the scalar product
$ \langle \, \cdot\, ,\, \cdot\, \rangle $
as
\begin{align} \mathbb{P}\lbrace -\langle A^i(\varepsilon)\alpha, \alpha \rangle \le \varepsilon, \|\alpha\|<S(\varepsilon)\,\rbrace & \ge \mathbb{P}\lbrace h(\beta) \ge M-\varepsilon, \|W_i-\beta\|\le S(\varepsilon)\rbrace \notag \\& \ge \mathbb{P}\lbrace -\langle A^i ({-}\varepsilon)\alpha, \alpha \rangle \le \varepsilon, \|\alpha\|<S(\varepsilon)\rbrace.\end{align}
Next we need the following lemma.
Lemma 6.1. There exist constants
$ \varepsilon_1> 0 $
and
$ \lambda> 0 $
such that for any
$ | \varepsilon | <\varepsilon_1 $
the matrix
$ A^i(\varepsilon) $
is negative definite, and none of its eigenvalues exceed
$ - \lambda. $
Proof.It is well known that a symmetric real-valued matrix B is negative definite if and only if all the eigenvalues of the matrix B are negative (see e.g. [Reference Horn and Johnson5, §4.1, p. 231, Th. 4.1.10]). Therefore, to prove Lemma 6.1, it is enough to show that none of the eigenvalues of the matrix
$A^i(\varepsilon)$
exceed some
$-\gamma<0$
, for small
$\varepsilon.$
Let
\begin{equation}\lambda_1(B) \le \ldots \le \lambda_{s}(B)\end{equation}
denote the eigenvalues of the Hermitian matrix B of size
$s \times s$
. The matrix
$ A^i $
is negative semidefinite (see e.g. [Reference Zorich21, §4.5, p. 563]). By condition A6 and (6.9),
$\det\!(A^i) \ne 0, $
hence the matrix
$A^i$
is negative definite. Using (6.15) it is equivalent to
$\lambda_{m-1}(A^i)<0.$
In what follows, we will need the Weyl theorem formulated below. It may be found in [Reference Horn and Johnson5, §4.3, p. 239, Th. 4.3.1], for example.
Theorem 6.2. (Weyl.) Let A, B be Hermitian matrices of size
$s \times s$
. Then, using (6.15), we have
\begin{equation*}\lambda_i(A+B) \le \lambda_{i+j}(A)+\lambda_{s-j}(B) \end{equation*}
for all
$i \in \{1, \ldots, s\}, \, j \in \{0, \ldots, s-i\}.$
Due to the Weyl theorem the eigenvalues of
$A^i(\varepsilon)$
do not exceed
$\lambda_{m-1}(A^i)+L_2S(|\varepsilon|).$
Therefore we can put
\begin{equation*}\gamma=\dfrac{|\lambda_{m-1}(A^i)|}{2}\end{equation*}
and
$\varepsilon_0$
such that
\begin{equation*}S(\varepsilon_0)< \dfrac{|\lambda_{m-1}(A^i)|}{2L_2}.\end{equation*}
By (6.3) such
$\gamma$
and
$\varepsilon_0$
satisfy the conditions of Lemma 6.1.
Remark 6.1. Obviously,
\begin{equation*}\lim_{\varepsilon \rightarrow 0} \det\!(A^i(\varepsilon)) = \det\!(A^i)>0. \end{equation*}
Lemma 6.2. There exist constants
$ C, D> 0 $
such that if, for some
$ \varepsilon> 0 $
and
$ \beta $
, the conditions
-
(i)
$h(\beta) > M - \varepsilon,$
-
(ii)
$\|\alpha\|=\|W_i-\beta\|<S(\varepsilon),$
-
(iii)
$\varepsilon<C,$
are satisfied, then
$ \| \alpha \| \le D \sqrt{\varepsilon}. $
The notation
$ \alpha $
and
$ \beta $
are the same as above.
Proof. Let
$ C = \min\!(\varepsilon_1, \varepsilon_0), $
where
$ \varepsilon_1 $
is from Lemma 6.1 and
$ \varepsilon_0 $
is from (6.6). According to the Rayleigh theorem (see e.g. [Reference Horn and Johnson5, §4.2, p. 234, Th. 4.2.2]) the inequality
$\langle Bx,x \rangle \le \lambda_s(B) \|x\|^2,$
where
$\lambda_s(B)$
is from (6.15), holds for every Hermitian matrix B of size
$s \times s$
. Then for any
$ | \varepsilon | <C $
we have
$ \langle A^i (\varepsilon) x, x \rangle \le -\gamma \| x \|^2, $
where
$ \gamma $
is also from Lemma 6.1. Note that by (6.12) the following inequality is valid for positive
$\varepsilon$
:
\begin{equation*} M + \langle A^i (\varepsilon) \alpha, \alpha \rangle \ge h(W_i + \alpha) > M - \varepsilon. \end{equation*}
Therefore
$ \varepsilon \ge -\langle A^i(\varepsilon)\alpha,\alpha\rangle \ge \gamma\|\alpha\|^2.$
Hence
$ \| \alpha \|$
is less than
${\sqrt{\varepsilon}}/{\sqrt{ \gamma}}. $
The next corollary follows from the proof of Lemma 6.2.
Corollary 6.1. If
$ \varepsilon \ge - \langle A^i (\varepsilon) \alpha, \alpha \rangle $
and
$ 0 <\varepsilon <C, $
then
$ \| \alpha \| \le D \sqrt{\varepsilon}. $
Lemma 6.2 completely proves assertion (i) of Theorem 6.1. It remains to prove the second one. For this purpose we need to calculate
\begin{equation*}\mathbb{P}\lbrace\langle-A^i(\!\pm\varepsilon) \alpha, \alpha\rangle \le \varepsilon, \|\alpha\|<S(\varepsilon) \rbrace\end{equation*}
for small
$ \varepsilon. $
By Corollary 6.1 condition
$\|\alpha\|<S(\varepsilon),$
where
$S(\varepsilon)$
is defined by (6.3), follows from the inequality
$\langle -A^i(\!\pm\varepsilon) \alpha, \alpha\rangle \le \varepsilon$
for sufficiently small
$\varepsilon.$
Therefore
\begin{equation*}\mathbb{P}\lbrace\langle-A^i(\!\pm\varepsilon) \alpha, \alpha\rangle \le \varepsilon, \|\alpha\|<S(\varepsilon) \rbrace = \mathbb{P}\lbrace\langle-A^i(\!\pm\varepsilon) \alpha, \alpha\rangle \le \varepsilon \rbrace.\end{equation*}
Below we assume that
$ 0 <\varepsilon <C, $
where C is the same as in Lemma 6.2.
Lemma 6.3. For sufficiently small
$ \varepsilon $
there exists
$x^{*}(\varepsilon)\in [0,2\pi]^{m-1}$
such that the following equality holds:
\begin{equation*}\mathbb{P}\lbrace\langle-A^i(\!\pm\varepsilon) \alpha, \alpha\rangle \le \varepsilon \rbrace = \dfrac{(\pi \varepsilon)^{{(m-1)}/{2}}}{\Gamma\bigl(\frac{m+1}{2}\bigr)\sqrt{\det\!({-}A^i(\varepsilon))}} \cdot \int_0^{2\pi} \Biggl[p(y) \prod_{l=1}^{m-1} p\bigl(y +W_i^l+x^{*}_l(\varepsilon)\bigr) \Biggr]\,{\textrm{d}} y,\end{equation*}
where
$\|x^{*}(\varepsilon)\|\le D\sqrt{\varepsilon},$
and the constant D is introduced in Lemma 6.2.
Proof. In order to simplify the formulas, we put
\begin{equation*} B=-A^i(\varepsilon)=(b_{i,j})_{i, j=1}^{m-1, m-1}. \end{equation*}
We also introduce
$ \beta_0 = \angle xOV_1 $
to be the angle between the axis Ox and the vector
$ OV_1, $
taken counterclockwise. We have
\begin{align}&\mathbb{P}\lbrace\langle-A^i(\!\pm\varepsilon) \alpha, \alpha\rangle \le \varepsilon \rbrace =\mathbb{P} \{\langle B\alpha, \alpha\rangle \le \varepsilon \} =\mathbb{P}\Biggl\lbrace\sum_{1 \le s,t \le m-1} b_{s, t} \alpha_s \alpha_t \le \varepsilon \Biggr \rbrace \notag \\&\quad =\int_{0}^{2\pi} p(y) \int_{\mathbb{R}^{m-1}} {\bf 1} \Biggl\lbrace \sum_{1 \le s,t \le m-1} b_{s, t} x_s x_t \le\varepsilon \Biggr \rbrace \prod_{l=1}^{m-1}\rho_l(x_l\mid \beta_0=y) \,{\textrm{d}} x_1 \cdots \,{\textrm{d}} x_{m-1} \,{\textrm{d}} y,\end{align}
where
$\rho_l(x_l\mid \beta_0=y)$
is the conditional density of
$ \alpha_l=x_l $
given
$\beta_0=y. $
Taking into account that
$ V_1, \ldots, V_m $
are independent random variables and using (6.7), we obtain
$\rho_l(x_l\mid \beta_0=y)=p\bigl(y+W_i^l+x_l\bigr).$
Also note that in the general case the second integral is taken not over
$ \mathbb{R}^{m-1} $
but over quotient space
$ \mathbb{R}^{m-1}/_\sim, $
where
$ x, y \in \mathbb{R}^{m-1} $
and
$ x \sim y $
if, for any
$ i \in \{1, \ldots, m-1 \} $
, we have
$ x^i- y^i = 2 \pi r $
for some
$ r \in \mathbb{Z}. $
The reason is that the values of
$\alpha$
which differ by
$2\pi r$
correspond to the same angle
$\beta.$
But by Corollary 6.1, inequality
$ \langle B \alpha, \alpha \rangle \le \varepsilon $
implies
$ \| \alpha \| \le D \sqrt{\varepsilon}. $
Therefore, for small
$ \varepsilon, $
all the
$ \alpha \in \mathbb{R}^{m-1} $
satisfying this inequality correspond to different
$ \beta. $
Hence, for sufficiently small
$ \varepsilon $
, we may indeed integrate over
$ \mathbb{R}^{m-1}. $
Using these facts, we continue (6.16):
\begin{align}& \mathbb{P}\lbrace\langle-A^i(\!\pm\varepsilon) \alpha, \alpha\rangle \le \varepsilon \rbrace \notag \\&\quad =\int_{0}^{2\pi} p(y) \int_{\mathbb{R}^{m-1}} {\bf 1} \Biggl \lbrace \sum_{1 \le s,t \le m-1} b_{s, t} x_s x_t \le\varepsilon \Biggr \rbrace \prod_{l=1}^{m-1}p\bigl(y+W_i^l+x_l\bigr){\textrm{d}} x_1 \cdots \,{\textrm{d}} x_{m-1} \,{\textrm{d}} y \notag \\&\quad =\int_{\mathbb{R}^{m-1}} {\bf 1} \Biggl\lbrace \sum_{1 \le s,t \le m-1} b_{s, t} x_s x_t \le\varepsilon \Biggr \rbrace\int_{0}^{2\pi} p(y) \prod_{l=1}^{m-1}p\bigl(y+W_i^l+x_l\bigr){\textrm{d}} y \,{\textrm{d}} x_1 \cdots \,{\textrm{d}} x_{m-1}.\end{align}
This formula is obtained just by switching the integration order. In order to calculate this integral we define the set
\begin{equation} T=\Biggl\lbrace x \in \mathbb{R}^{m-1}\colon \sum_{1 \le s,t \le m-1} b_{s, t} x_s x_t \le \varepsilon \Biggr\rbrace= \lbrace x \in \mathbb{R}^{m-1}\colon \langle x, Bx \rangle \le \varepsilon \rbrace. \end{equation}
The set T is an ellipsoid with center 0 and configuration matrix
$({1}/{\varepsilon}\cdot B)^{-1}$
; see [Reference Kurzhanski and Valyi8, p. 97]. It is well known that the ellipsoid with center 0 and symmetric positive semidefinite configuration matrix Q is defined by
$\{x \in \mathbb{R}^{p}\colon \langle x, Q^{-1}x \rangle \le 1\}$
and its volume is equal to
\begin{equation*}\dfrac{\pi^{{p}/{2}}}{\Gamma({p}/{2}+1)\sqrt{\det{Q}}}.\end{equation*}
It is mentioned in [Reference Kurzhanski and Valyi8, p. 103], for example. Therefore the Lebesgue measure of the set T satisfies the equality
\begin{equation} \operatorname{meas}\!(T)=\dfrac{(\varepsilon \pi)^{{(m-1)}/{2}}}{\sqrt{\det\!(B)}\Gamma\bigl(\frac{m+1}{2}\bigr)}. \end{equation}
In what follows, we will need a mean value theorem (see e.g. [Reference Makarov and Podkorytov12]). Using this theorem we obtain the equality
\begin{align}& \int_{\mathbb{R}^{m-1}} {\bf 1}\Biggl \lbrace \sum_{1 \le s,t \le m-1} b_{s, t} x_s x_t \le \varepsilon \Biggr \rbrace \int_{0}^{2\pi} p(y) \prod_{l=1}^{m-1}p\bigl(y+W^i_l+x_l\bigr){\textrm{d}} y \, \,{\textrm{d}} x_1 \cdots \,{\textrm{d}} x_{m-1} \notag \\ & \quad =\int_{0}^{2\pi} p(y) \prod_{l=1}^{m-1}p\bigl(y+W^i_l+x^{*}_l(\varepsilon)\bigr){\textrm{d}} y \cdot \operatorname{meas}\!(T),\quad \text{where $ x^{*}(\varepsilon) \in T$.}\end{align}
Recall that the set T is defined by (6.18). The condition
$x^{*}(\varepsilon) \in T$
together with (6.18) implies
\begin{equation*}\sum_{1 \le s,t \le m-1} b_{s, t} x^{*}_s(\varepsilon) x^{*}_t(\varepsilon) \le \varepsilon.\end{equation*}
Therefore Corollary 6.1 implies inequality
$\|x^{*}(\varepsilon)\|\le D\sqrt{\varepsilon},$
where the constant D is introduced in Lemma 6.2. Hence, collecting formulas (6.17), (6.19), (6.20), we finish the proof.
Substituting the result of Lemma 6.3 into inequality (6.14), for small
$ \varepsilon $
we get the relation
\begin{align*}&\dfrac{(\pi \varepsilon)^{{(m-1)}/{2}}}{\Gamma\bigl(\frac{m+1}{2}\bigr)\sqrt{\det\!({-}A^i(\varepsilon))}} \cdot \int_0^{2\pi} \Biggl[p(y) \prod_{l=1}^{m-1} p\bigl(y+W_i^l+x^{*}_l(\varepsilon)\bigr) \Biggr]{\textrm{d}} y \\&\quad \ge \mathbb{P}\{h(\beta) \ge M-\varepsilon, \|W_i-\beta\| \le S(\varepsilon )\} \\& \quad \ge\dfrac{(\pi \varepsilon)^{{(m-1)}/{2}}}{\Gamma\bigl(\frac{m+1}{2}\bigr)\sqrt{\det\!({-}A^i({-}\varepsilon))}} \cdot \int_0^{2\pi} \Biggl[p(y) \prod_{l=1}^{m-1} p\bigl(y+W_i^l+x^{*}_l({-}\varepsilon)\bigr) \Biggr]{\textrm{d}} y.\end{align*}
Dividing both sides of this inequality by
$ \varepsilon^{{(m-1)}/{2}} $
and tending
$ \varepsilon $
to 0, we get
\begin{align}&\lim_{\varepsilon \rightarrow 0+}\dfrac{\pi^{{(m-1)}/{2}}}{\Gamma\bigl(\frac{m+1}{2}\bigr)\sqrt{\det\!({-}A^i(\varepsilon))}} \cdot \int_0^{2\pi} \Biggl[p(y) \prod_{l=1}^{m-1} p\bigl(y+W_i^l+x^{*}_l(\varepsilon)\bigr) \Biggr]{\textrm{d}} y\notag \\&\quad \ge \lim_{\varepsilon \rightarrow 0+}\varepsilon^{-{(m-1)}/{2}}\mathbb{P}\{h(\beta) \ge M-\varepsilon, \|W_i-\beta\|\le S(\varepsilon)\} \notag \\&\quad \ge \lim_{\varepsilon \rightarrow 0+} \dfrac{\pi^{{(m-1)}/{2}}}{\Gamma\bigl(\frac{m+1}{2}\bigr)\sqrt{\det\!({-}A^i({-}\varepsilon))}} \cdot \int_0^{2\pi} \Biggl[p(y) \prod_{l=1}^{m-1} p\bigl(y+W_i^l+x^{*}_l({-}\varepsilon)\bigr) \Biggr]\, {\textrm{d}}\beta_0.\end{align}
Using
\begin{align*} \lim_{\varepsilon \rightarrow 0} \det\!(A^i(\varepsilon)) &=\det\!(A^i),\\ \lim_{\varepsilon \rightarrow 0} \int_0^{2\pi} \Biggl[p(y) \prod_{l=1}^{m-1} p\bigl(y+W_i^l+x^{*}_l(\varepsilon)\bigr) \Biggr]{\textrm{d}} y & = \int_0^{2\pi} \Biggl[p(y) \prod_{l=1}^{m-1} p\bigl(y+W_i^l\bigr) \Biggr]{\textrm{d}} y,\end{align*}
we pass to the limit in (6.21) and obtain
\begin{align}&\lim_{\varepsilon \rightarrow 0+}\varepsilon^{-{(m-1)}/{2}}\mathbb{P}\{h(\beta) \ge M-\varepsilon, \|W_i-\beta\| \le S(\varepsilon)\} \notag \\ &\quad =\dfrac{\pi^{{(m-1)}/{2}}}{\Gamma\bigl(\frac{m+1}{2}\bigr)\sqrt{\det\!({-}A^i)}} \cdot \int_0^{2\pi} \Biggl[p(y) \prod_{l=1}^{m-1} p\bigl(y+W_i^l\bigr) \Biggr]{\textrm{d}} y.\end{align}
From (6.9) we may conclude that
\begin{equation}\det\!({-}A^i)=\dfrac{\det\!({-}G_i)}{2^{m-1}}.\end{equation}
Now, using (6.4), (6.22), and (6.23), we obtain
\begin{align*}\lim_{\varepsilon \rightarrow 0+}\varepsilon^{-{(m-1)}/{2}}\mathbb{P}\{h(\beta) \ge M-\varepsilon\}& = \dfrac{\pi^{{(m-1)}/{2}}}{\Gamma\bigl(\frac{m+1}{2}\bigr)}\sum_{i=1}^k \dfrac{\int_0^{2\pi} \bigl[p(y) \prod_{l=1}^{m-1} p\bigl(y+W_i^l\bigr) \bigr] {\textrm{d}} y}{\sqrt{\det\!({-}A^i)}} \\&=\dfrac{(2\pi)^{{(m-1)}/{2}}}{\Gamma\bigl(\frac{m+1}{2}\bigr)}\sum_{i=1}^k \dfrac{\int_0^{2\pi} \bigl[p(y) \prod_{l=1}^{m-1} p\bigl(y+W_i^l\bigr) \bigr]\,{\textrm{d}} y}{\sqrt{\det\!({-}G_i)}},\end{align*}
and Theorem 6.1 is proved.
7. Proof of Theorem 3.1: part 2
In this section we prove the second part of Theorem 3.1.
Theorem 7.1. Suppose that a kernel f and points
$V_1, \ldots, V_n$
satisfy conditions A and B, which are listed in Section 2. Let
$M_n$
be the
$U{\hbox{-}}\textrm{max}$
statistic constructed via kernel f, that is,
$ M_n = \max_{1 \le i_1< \ldots <i_m \le n} f(V_{i_1}, \ldots, V_{i_m}).$
Then for every
$t>0$
the following relation holds true:
\begin{equation*}\lim_{n \rightarrow \infty} \mathbb{P}\bigl\lbrace n^{{2m}/{(m-1)}} (M-M_n)\le t)\bigr\rbrace=1 - \exp\biggl({-\dfrac{t^{{(m-1)}/{2}}K_m}{m!}}\biggr),\end{equation*}
where the constant
$ K_m $
is introduced in condition (ii) of Theorem 6.1. The rate of convergence is
$O\bigl(n^{-{1}/{(m-1)}}\bigr).$
Before proving Theorem 7.1, let us mention two theorems that play a key role in studying the limit behavior of
$U{\hbox{-}}\textrm{max}$
statistics. The first theorem is taken from [Reference Lao and Mayer10], where Lao and Mayer applied the Poisson approximation from the monograph [Reference Barbour, Holst and Janson2]. This is still the main research method in this field.
Theorem 7.2. ([Reference Lao and Mayer10].) Let
$ \xi_1, \xi_2, \dots, \xi_n $
be a sequence of independent identically distributed random elements taking values in a measurable space
$(\mathfrak{X}, \mathfrak{A})$
, and let the function
$f(x_1, \dots, x_m)$
be a real-valued symmetric Borel function,
$f \colon {\mathfrak{X}}^m\rightarrow\mathbb{R}.$
Let
$M_n=\max_J h(\xi_{i_1}, \ldots, \xi_{i_m})$
be the
$U{\hbox{-}}\textrm{max}$
statistic introduced in (1.2), and define, for any
$z \in \mathbb{R}$
, the following quantities:
\begin{align*}p_{n,z}&=\mathbb{P}\{f(\xi_1,\ldots,\xi_m)>z\}, \quad\lambda_{n,z}=\left(\begin{array}{c}n\\m\end{array}\right) p_{n,z},\\\tau_{n,z}(r)&=\dfrac{\mathbb{P}\{f(\xi_1, \ldots,\xi_m)>z, f(\xi_{1+m-r},\xi_{2+m-r}, \ldots, \xi_{2m-r})>z\}}{p_{n,z}}.\end{align*}
Then, for all
$n \ge m$
and for each
$z \in \mathbb{R}$
, we have
\begin{align} & |\mathbb{P}(M_n \le z)-{\textrm{e}}^{-\lambda_{n,z}}| \notag \\&\quad \le \bigl( 1- {\textrm{e}}^{-\lambda_{n,z}} \bigr) \cdot \Biggl[ p_{n,z}\biggl(\left(\begin{array}{c}n\\m\end{array}\right) - \left(\begin{array}{c}n-m\\m\end{array}\right) \biggr)+\sum_{r=1}^{m-1}\left(\begin{array}{c}m\\r\end{array}\right) \left(\begin{array}{c}n-m\\m-r\end{array}\right) \tau_{n,z}(r) \Biggr].\end{align}
Remark 7.1. ([Reference Lao and Mayer10].) If the sample size n tends to infinity, then the right-hand side of (7.1) is of asymptotic order
\begin{equation*}{\textrm{O}}\Biggl(p_{n,z}n^{m-1}+\sum_{r=1}^{m-1}\tau_{n,z}(r)n^{m-r}\Biggr),\end{equation*}
where for
$m>1$
the first term is negligibly small with respect to the sum.
Silverman and Brown [Reference Silverman and Brown16] have found the conditions for a general theorem used in [Reference Barbour, Holst and Janson2] yielding a non-trivial Weibull law in the limit.
Theorem 7.3. ([Reference Silverman and Brown16].) Let the conditions of Theorem 7.2 be satisfied. If, for some sequence of transformations
$z_n\colon T \rightarrow \mathbb{R},\, T \subset \mathbb{R},$
the equalities
\begin{align}&\lim_{n \rightarrow \infty}\lambda_{n, z_n(t)} = \lambda_t >0,\end{align}
\begin{align} & \lim_{n \rightarrow \infty} n^{2m-1} p_{n,z_n(t)}\tau_{n,z_n(t)}(m-1)=0\end{align}
hold, for each
$t \in T$
, then
\begin{equation} \lim_{n \rightarrow \infty} \mathbb{P}(M_n \le z_n(t))={\textrm{e}}^{-\lambda_t}\end{equation}
for all
$t \in T.$
Remark 7.2. ([Reference Lao and Mayer10].) Condition (7.2) implies
$p_{n,z}={\textrm{O}}(n^{-m}).$
Therefore, according to Remark 7.1, the rate of convergence in (7.4) is
\begin{equation*}{\textrm{O}}\Biggl(n^{-1}+\sum_{r=1}^{m-1}n^{2m-r}p_{n,z}\tau_{n,z}(r)\Biggr).\end{equation*}
Hence, for
$m \ge 2$
, condition (7.3) can be replaced by
\begin{equation}\lim_{n \rightarrow \infty}n^{2m-r}p_{n,z}\tau_{n,z}(r)=0 \quad \text{for any $ r \in \{1, \ldots, m-1\}$.}\end{equation}
Now we will use the above assertions to prove Theorem 7.1.
Proof.For any
$ t> 0 $
we define the transformation
\begin{equation*} z_n(t)=M-tn^{-{2m}/{(m-1)}} .\end{equation*}
Let us consider
$\lambda_{n, z_n(t)}$
defined in Theorem 7.2. Then
\begin{equation*}\lambda_{n,z_n(t)} =\dfrac{n!}{m! (n-m)!}\mathbb{P}\{f(V_1, \ldots, V_m)>z_n(t)\}.\end{equation*}
We put
$\varepsilon=tn^{-{2m}/{(m-1)}}, $
then
$n^m \varepsilon^{{(m-1)}/{2}} = t^{{(m-1)}/{2}}.$
Let us prove the fulfillment of condition (7.2) of Theorem 7.3. We write
\begin{align*}\lim_{n \rightarrow \infty} \lambda_{n,z_n(t)}& = \lim_{n \rightarrow \infty} \dfrac{n!}{m! (n-m)!}\mathbb{P}\{f(V_1, \ldots, V_m)>z_n(t)\} \\& =\dfrac{1}{m!} \lim_{n \rightarrow \infty} \dfrac{n!}{n^m (n-m)!} n^m \varepsilon^{{(m-1)}/{2}} \varepsilon^{-{(m-1)}/{2}} \mathbb{P}\{f(V_1, \ldots, V_m)>M-\varepsilon\} \\& =\dfrac{1}{m!} t^{{(m-1)}/{2}} \lim_{n \rightarrow \infty} \bigl(tn^{-{2m}/{(m-1)}}\bigr)^{-{(m-1)}/{2}}\mathbb{P}\bigl\{f(V_1, \ldots, V_m)>M-tn^{-{2m}/{(m-1)}}\bigr\}\\& =\dfrac{t^{{(m-1)}/{2}}K_m}{m!} \\&=\!:\, \lambda_t>0.\end{align*}
In the last line we used statement (ii) of Theorem 6.1. Now we will prove condition (7.5) of Remark 7.2. We formulate this statement as a separate lemma.
Lemma 7.1. For each
$r \in \{1, \ldots, m-1 \}$
we have the following relation:
\begin{equation*}\lim_{n \rightarrow \infty}n^{2m-r}\mathbb{P}\{f(V_1, \ldots, V_m)>z_n(t), f(V_{1+m-r}, \ldots, V_{2m-r})>z_n(t)\}=0.\end{equation*}
Proof. Let us introduce the following notation:
$\beta_i=\angle V_1OV_{i+1}$
for
$i \in \{1, \ldots, 2m-r-1\}$
,
$\gamma_i=\angle V_{m-r+1}OV_{i+1}$
for
$i \in \{m-r, \ldots, 2m-r-1\}.$
Such notation corresponds to (2.1) and (2.2) for each
$i \in \{1, \ldots, m-1\}.$
It is clear that
$\gamma_i=(\beta_i-\beta_{m-r})\ \operatorname{mod}{2\pi}$
for any
$i \ge m.$
We introduce the events
\begin{equation*}Q_{i,j}= \bigl\{\|W_i- (\beta_1, \ldots, \beta_{m-1})\| \le D\sqrt{\varepsilon},\ \|W_j- (\gamma_{m-r}, \ldots, \gamma_{2m-r-1})\| \le D\sqrt{\varepsilon}\bigr\},\end{equation*}
where
$W_i$
is the same as in condition A4 and the constant D is introduced in Theorem 6.1. It follows from Lemma 6.2 that for small
$ z_n (t) $
the following equality holds true:
\begin{align}& \{ f(V_1, \ldots, V_m)\ge z_n(t)\cap f(V_{1+m-r}, \ldots, V_{2m-r})\ge z_n(t) \}\notag \\&\quad =\cup_{ 1\le i,j \le k} \bigl([f(V_1, \ldots, V_m)\ge z_n(t)\cap f(V_{1+m-r}, \ldots, V_{2m-r})\ge z_n(t)] \cap Q_{i,j}\bigr).\end{align}
Next we estimate the probability
\begin{equation}\mathbb{P} \{[f(V_1, \ldots, V_m)\ge z_n(t)\cap f(V_{1+m-r}, \ldots, V_{2m-r})\ge z_n(t)] \cap Q_{i,j} \}.\end{equation}
By the definition for all elements
$V_i$
from
$Q_{i,j}$
we have the following bounds for
$\beta_i$
and
$\gamma_i$
:
$ \|\beta_{l}-W_i^l\| \le D\sqrt{\varepsilon}$
for each
$i<m,$
and
$\|\gamma_{l}-W_j^{l-m+r}\|\le D\sqrt{\varepsilon}.$
For
$ l \ge m $
we obtain
\begin{equation*}\bigl\|\beta_l-W_i^{m-r}-W_j^{l-m+r}\bigr\| \le \bigl\|\beta_l-\beta_{m-r}-W_j^{l-m+r}\bigr\|+\bigl\|\beta_{m-r}-W_i^{m-r}\bigr\| \le 2D\sqrt{\varepsilon}.\end{equation*}
Let
$ L_p $
denote the maximal value of density
$p(x).$
Using the properties of distribution of
$\beta_l,$
we can estimate the upper bound of probability from (7.7) by
\begin{equation*}\bigl(2DL_p\sqrt{\varepsilon}\bigr)^{m-1} \bigl(4DL_p\sqrt{\varepsilon}\bigr)^{m-r}.\end{equation*}
Using formula (7.6) and substituting
$\varepsilon=tn^{-{2m}/{(m-1)}}$
in the estimate of (7.7), we obtain the inequality
\begin{align*}&n^{2m-r}\mathbb{P}\{f(V_1, \ldots, V_m)\ge z_n(t), f(V_{1+m-r}, \ldots, V_{2m-r})\ge z_n(t)\}\\&\quad \le n^{2m-r} k^2 \Bigl(2DL_p\sqrt{tn^{-{2m}/{(m-1)}}}\Bigr)^{m-1} \Bigl(4DL_p\sqrt{tn^{-{2m}/{(m-1)}}}\Bigr)^{m-r}\\ &\quad ={\textrm{O}}\bigl(n^{-{(m-r)}/{(m-1)}}\bigr)\\ &\quad ={\textrm{o}}(1).\end{align*}
Let us return to the proof of Theorem 7.1. Now we may use Theorem 7.3, since all its conditions are verified. Then according to (7.4) we obtain
\begin{equation*}\lim_{n \rightarrow \infty} \mathbb{P}(M_n \le z_n(t))={\textrm{e}}^{-\lambda_t}\end{equation*}
for any
$t \in T.$
Hence
\begin{equation*}\lim_{n \rightarrow \infty} \mathbb{P}\bigl(M_n \le M-t n^{-{2m}/{(m-1)}}\bigr)= \exp\biggl({-\dfrac{t^{{(m-1)}/{2}} K_m}{m!}}\biggr).\end{equation*}
Therefore, for any
$ t> 0 $
, the following relation is valid:
\begin{equation*}\lim_{n \rightarrow \infty} \mathbb{P}\bigl\{ n^{{2m}/{(m-1)}} (M-M_n)\le t) \bigr\}=1 - \exp\biggl({-\dfrac{t^{{(m-1)}/{2}}K_m}{m!}}\biggr).\end{equation*}
According to Remark 7.2, the convergence rate is
\begin{equation*}{\textrm{O}}\Biggl(n^{-1}+\sum_{r=1}^{m-1}p_{n,z_n(t)}\tau_{n,z_n(t)}(r)n^{2m-r}\Biggr).\end{equation*}
From the proof of Lemma 7.1, it follows that
\begin{equation*}{\textrm{O}}\bigl(p_{n,z_n(t)}\tau_{n,z_n(t)}(r)n^{2m-r}\bigr)={\textrm{O}}\bigl(n^{-{(m-r)}/{(m-1)}}\bigr),\end{equation*}
therefore it is
${\textrm{O}}\bigl(n^{-{1}/{(m-1)}}\bigr)$
for
$ m> 1.$
Hence Theorem 7.1 is proved.
The combination of Theorems 6.1 and 7.1 implies Theorem 3.1.
Acknowledgements
The authors would like to thank Dr Andrei Zaitsev and Dr Dmitry Zaporozhets for their invaluable help concerning this paper. We would like to thank the referees for their careful reading of our manuscript and especially for the helpful comments and suggestions.
Funding information
The work of Ekaterina Simarova was supported by the Ministry of Science and Higher Education of the Russian Federation, agreement no. 075-15-2019-1619. The work of Yakov Nikitin was supported by joint grant RFBR-DFG no. 20-51-12004.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.
