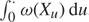1. Introduction
Below we will write Q[W] for EQ[W], Q[W; A] for EQ[W 1A], and Q[W|G] for EQ[W|G]. Given an expression ℛ(x) defined for x ∈ R, R being understood from the context, we will write ℛ(⋅) for the function (R ∋ x ↦ ℛ (x)).
1.1. Problem delineation
Let X = (X t)t∈[0,∞) be a spectrally negative Lévy process (SNLP) under the probabilities (Px)x∈ℝ. This means that X is a cádlá, real-valued process with no positive jumps and non-monotone paths that has stationary independent increments and, under P0, almost surely (a.s.) vanishes at zero; furthermore, for each x ∈ ℝ, the law of X under Px is that of x + X under P0. We refer to [Reference Bertoin1], [Reference Doney and Picard4], [Reference Kyprianou11], and [Reference Sato18] for the general background on (the fluctuation theory of) Lévy processes, and to [Reference Bertoin1, Chapter VII], [11, Chapter 8], [Reference Doney and Picard4, Chapter 9], and [Reference Sato18, Section 9.46] for SNLP in particular. As usual we set P ≔ P0. The expression ‘a.s.’ without further qualification is to be understood as ‘Px a.s. for all x ∈ ℝ’; similarly for ‘distributed’, ‘independent’, and so on.
For c ∈ ℝ, we next denote by ![]() $$\tau _c^+ := \inf \{ t \in (0,\infty ):{X_t} > c\} $$ the first hitting time of the set (c, ∞ ) by the process X. Further, let q ∈ [0, ∞ ) and let e q be an exponentially with mean q −1 distributed random variable (e 0 = ∞ a.s.) independent of X. Finally, let ω : ℝ → [0, ∞ ) be Borel measurable and locally bounded.
$$\tau _c^+ := \inf \{ t \in (0,\infty ):{X_t} > c\} $$ the first hitting time of the set (c, ∞ ) by the process X. Further, let q ∈ [0, ∞ ) and let e q be an exponentially with mean q −1 distributed random variable (e 0 = ∞ a.s.) independent of X. Finally, let ω : ℝ → [0, ∞ ) be Borel measurable and locally bounded.
Then, for real x ≤ c, we will be interested in the quantity
it may be interpreted as the first passage probability of X killed at e q over the level c when started at x under ‘ ω-killing’, i.e. when X is killed (in addition to being killed at the time e q) according to a rate that depends on the position of X and that is given by the function ω. To be precise, if e is a mean-one exponentially distributed random variable independent of (X, e q), then ![]() $${\cal B}_q^{(\omega )}(x,c) = {{\rm{P}}_x}(\tau _c^ + \lt {e_q} \wedge \eta )$$, where
$${\cal B}_q^{(\omega )}(x,c) = {{\rm{P}}_x}(\tau _c^ + \lt {e_q} \wedge \eta )$$, where ![]() $$\eta :=\inf \{ t \in (0,\infty ){\kern 1pt} :{\kern 1pt} \int_0^t \omega ({X_u}){\kern 1pt} {\rm{d}}u > {\rm{e}}\} $$ when ω is a constant r ∈ [0, ∞ ), then η = e/r is exponential of rate r. Another way of viewing
$$\eta :=\inf \{ t \in (0,\infty ){\kern 1pt} :{\kern 1pt} \int_0^t \omega ({X_u}){\kern 1pt} {\rm{d}}u > {\rm{e}}\} $$ when ω is a constant r ∈ [0, ∞ ), then η = e/r is exponential of rate r. Another way of viewing ![]() $${\cal B}_q^{(\omega )}(x,c)$$ is as
$${\cal B}_q^{(\omega )}(x,c)$$ is as ![]() $${{\rm{P}}_x}[{M_{\tau _c^ + }};\tau _c^ + \lt {e_q}]$$, where
$${{\rm{P}}_x}[{M_{\tau _c^ + }};\tau _c^ + \lt {e_q}]$$, where ![]() $$M:=\exp \{ - \int_0^ \cdot \omega ({X_u}){\kern 1pt} {\rm{d}}u\} $$ is a multiplicative functional [Reference Getoor and Blumenthal7, Chapter 3] of X. Also,
$$M:=\exp \{ - \int_0^ \cdot \omega ({X_u}){\kern 1pt} {\rm{d}}u\} $$ is a multiplicative functional [Reference Getoor and Blumenthal7, Chapter 3] of X. Also, ![]() $${\cal B}_q^{(\omega )}(x,c) = {\cal B}_0^{(\omega + q)}(x,c)$$, but it will be convenient to keep the independent exponential killing separate.
$${\cal B}_q^{(\omega )}(x,c) = {\cal B}_0^{(\omega + q)}(x,c)$$, but it will be convenient to keep the independent exponential killing separate.
1.2. Motivation
Assume now that ω is strictly positive everywhere.
Remark 1.1. It would be enough to assume here that ω is strictly positive just Lebesgue-almost everywhere without any of the statements to follow being meaningfully affected. Indeed, for p ∈ (0, ∞ ), the p-potential measure of X is absolutely continuous with respect to Lebesgue measure [Reference Kyprianou11, Corollary 8.9]. Hence, the additive functional ![]() $${(\int _0^t\omega ({X_u}){\kern 1pt} {\rm{d}}u)_{t \in [0,\infty )}}$$ changes only on a negligible set if ω is altered on a Lebesgue-null Borel set. Still, to avoid some extra a.s. qualifications, we assume here simply (and, in view of the preceding, without loss of generality) that ω is strictly positive everywhere.
$${(\int _0^t\omega ({X_u}){\kern 1pt} {\rm{d}}u)_{t \in [0,\infty )}}$$ changes only on a negligible set if ω is altered on a Lebesgue-null Borel set. Still, to avoid some extra a.s. qualifications, we assume here simply (and, in view of the preceding, without loss of generality) that ω is strictly positive everywhere.
Our main motivation for the interest in (1.1) then comes from its involvement in the solution of the first passage problem upwards for the process that we will denote by Y = (Y s)s∈[0,∞) and is defined as follows. Setting![]() $$\zeta \int_0^{{e_q}} \omega ({X_u}){\kern 1pt} {\rm{d}}u$$ (see [Reference Khoshnevisan, Salminen and YOR8, Remark 5] and [Reference DöRing and Kyprianou5, Theorem 1] for deterministic conditions on the finiteness/divergence of this integral in the case q = 0, i.e. e q =∞ a.s.), then
$$\zeta \int_0^{{e_q}} \omega ({X_u}){\kern 1pt} {\rm{d}}u$$ (see [Reference Khoshnevisan, Salminen and YOR8, Remark 5] and [Reference DöRing and Kyprianou5, Theorem 1] for deterministic conditions on the finiteness/divergence of this integral in the case q = 0, i.e. e q =∞ a.s.), then
 $$\matrix{
{} & {\;{\rm{for\,s}} \ge \zeta {\rm{,\,}}{{\rm{Y}}_{\rm{s}}}{\rm{ = }}\partial {\rm{,\,where\,}}\partial {\rm{\,is\,some\,`cemetery'\,state,}}} \hfill \cr
{{\rm{while}}} & {\;{\rm{for\,s}} \in {\rm{[0,\,}}\zeta {\rm{),\,}}{{\rm{Y}}_{\rm{s}}}{\rm{ = }}{{\rm{X}}_{{\rho _{\rm{s}}}}}{\rm{,}}} \hfill \cr
} $$
$$\matrix{
{} & {\;{\rm{for\,s}} \ge \zeta {\rm{,\,}}{{\rm{Y}}_{\rm{s}}}{\rm{ = }}\partial {\rm{,\,where\,}}\partial {\rm{\,is\,some\,`cemetery'\,state,}}} \hfill \cr
{{\rm{while}}} & {\;{\rm{for\,s}} \in {\rm{[0,\,}}\zeta {\rm{),\,}}{{\rm{Y}}_{\rm{s}}}{\rm{ = }}{{\rm{X}}_{{\rho _{\rm{s}}}}}{\rm{,}}} \hfill \cr
} $$
with
Notice that ρ = ( ρ s)s ∈ [0,∞ is continuous (because ω is strictly positive, and hence ![]() $$\int_0^ \cdot \omega ({X_u}){\kern 1pt} {\rm{d}}u$$ is strictly increasing) and it is strictly increasing where it is finite (because ω is locally bounded, and hence
$$\int_0^ \cdot \omega ({X_u}){\kern 1pt} {\rm{d}}u$$ is strictly increasing) and it is strictly increasing where it is finite (because ω is locally bounded, and hence![]() $$\int_0^ \cdot \omega ({X_u}){\kern 1pt} {\rm{d}}u$$ is continuous). Thus, the paths of Y up to ζ are the same as the paths of X up to e q, modulo the random time change ρ. Also, if ℱ = (ℱ t)t∈[0,∞) is any filtration relative to which X is adapted and has independent increments, with e q independent of ℱ ∞, then thanks to the strong Markov property of X and the memoryless property of the exponential distribution, the process Y is Markovian with state space (ℝ, B ℝ) and lifetime ζ under the probabilities (Py)y∈ℝ and in the filtration
$$\int_0^ \cdot \omega ({X_u}){\kern 1pt} {\rm{d}}u$$ is continuous). Thus, the paths of Y up to ζ are the same as the paths of X up to e q, modulo the random time change ρ. Also, if ℱ = (ℱ t)t∈[0,∞) is any filtration relative to which X is adapted and has independent increments, with e q independent of ℱ ∞, then thanks to the strong Markov property of X and the memoryless property of the exponential distribution, the process Y is Markovian with state space (ℝ, B ℝ) and lifetime ζ under the probabilities (Py)y∈ℝ and in the filtration ![]() $${\cal G} = ({{\cal G}_s}{)_{s \in [0,\infty )}}:={({{\cal F}_{{\rho _s}}} \vee \sigma (\{ \{ {\rho _u} \lt {e_q}\} {\kern 1pt} :{\kern 1pt} u \in [0,s]\} ))_{s \in [0,\infty )}}$$, in the precise sense that it is G-adapted and that for any Borel measurable
$${\cal G} = ({{\cal G}_s}{)_{s \in [0,\infty )}}:={({{\cal F}_{{\rho _s}}} \vee \sigma (\{ \{ {\rho _u} \lt {e_q}\} {\kern 1pt} :{\kern 1pt} u \in [0,s]\} ))_{s \in [0,\infty )}}$$, in the precise sense that it is G-adapted and that for any Borel measurable ![]() $$h{\kern 1pt} :{\kern 1pt}{\mathbb R}\to [0,\infty ]$$,
$$h{\kern 1pt} :{\kern 1pt}{\mathbb R}\to [0,\infty ]$$, ![]() $$y \in {\mathbb R},\{ s,t\} \subset [0,\infty )$$ we have, a.s.-Py, Py [ h (Y t+s)1{t+s <}| G t] = PYt [ h (Y s); s < ζ]1{t< ζ}. (Of course, if in addition we have a P∂ such that Y t = ∂ for all t ∈ [0, ∞ ) a.s.-P∂, then as a consequence Y is also simply Markovian with state space (ℝ ∪{∂} ,σ (B ℝ ∪{{∂ }})) and infinite lifetime.)
$$y \in {\mathbb R},\{ s,t\} \subset [0,\infty )$$ we have, a.s.-Py, Py [ h (Y t+s)1{t+s <}| G t] = PYt [ h (Y s); s < ζ]1{t< ζ}. (Of course, if in addition we have a P∂ such that Y t = ∂ for all t ∈ [0, ∞ ) a.s.-P∂, then as a consequence Y is also simply Markovian with state space (ℝ ∪{∂} ,σ (B ℝ ∪{{∂ }})) and infinite lifetime.)
By way of example, when ω = exp and ∂ =−∞, then, under the probabilities (Plog x)x ∈(0, ∞), S ≔ eY is a spectrally negative positive self-similar Markov process (pssMp) absorbed at the origin, with index of self-similarity 1, associated to X via the Lamperti transform for pssMp [Reference Kyprianou11, Theorem 13.1]. And, for c ∈ (0, ∞ ), on ![]() $$\{ \tau _{\log c}^ + \lt {e_q}\} $$,
$$\{ \tau _{\log c}^ + \lt {e_q}\} $$, ![]() $$\int_0^{\tau _{\log c}^ + } {{\rm{e}}^{{X_u}}}{\kern 1pt} {\rm{d}}u$$ is the first time that S hits the set (c, ∞), the latter time being =∞ on the complement of
$$\int_0^{\tau _{\log c}^ + } {{\rm{e}}^{{X_u}}}{\kern 1pt} {\rm{d}}u$$ is the first time that S hits the set (c, ∞), the latter time being =∞ on the complement of ![]() $$\{ \tau _{\log c}^ + \lt {e_q}\} $$. We understand in the preceding, of course, that e −∞ = 0, so that 0 is, as usual, the cemetery state for S; it is known that S hits 0 eventually with positive probability (and then a.s.) if and only if either q > 0 or else X drifts to −∞ [Reference Kyprianou11, Theorem 13.1]. See Example 3.2.
$$\{ \tau _{\log c}^ + \lt {e_q}\} $$. We understand in the preceding, of course, that e −∞ = 0, so that 0 is, as usual, the cemetery state for S; it is known that S hits 0 eventually with positive probability (and then a.s.) if and only if either q > 0 or else X drifts to −∞ [Reference Kyprianou11, Theorem 13.1]. See Example 3.2.
Similarly, for c ∈ (0, ∞ ), with ![]() $$\omega (x) = {1 \over {|x|}}$$ for x ∈ (−∞, − c] and again ∂ = − ∞,
$$\omega (x) = {1 \over {|x|}}$$ for x ∈ (−∞, − c] and again ∂ = − ∞,![]() $$ - {Y^{\tau _{ - c}^ + }}$$ becomes, under the probabilities (P−x)x∈[0, ∞), a continuous state branching process (csbp) B stopped on hitting the set [0, c), where B is the csbp associated to − X under the Lamperti transform for csbp [Reference Kyprianou11, Theorem 12.2]. (We are forced to stop at
$$ - {Y^{\tau _{ - c}^ + }}$$ becomes, under the probabilities (P−x)x∈[0, ∞), a continuous state branching process (csbp) B stopped on hitting the set [0, c), where B is the csbp associated to − X under the Lamperti transform for csbp [Reference Kyprianou11, Theorem 12.2]. (We are forced to stop at ![]() $$\tau _{ - c}^ + $$ in order to remain in the setting of a locally bounded ω, which is an assumption that remains in force throughout this paper.) And, on
$$\tau _{ - c}^ + $$ in order to remain in the setting of a locally bounded ω, which is an assumption that remains in force throughout this paper.) And, on ![]() $$\{ \tau _{ - c}^ + \lt {e_q}\} $$,
$$\{ \tau _{ - c}^ + \lt {e_q}\} $$, ![]() $$\int_0^{\tau _{ - c}^ + } {{{d}}u \over {|x _u|}}$$ is the first time B hits [0, c), the latter time being =∞ on the complement of
$$\int_0^{\tau _{ - c}^ + } {{{d}}u \over {|x _u|}}$$ is the first time B hits [0, c), the latter time being =∞ on the complement of ![]() $$\{ \tau _{ - c}^ + \lt {e_q}\} $$. [Reference Kyprianou11, Theorem 13.1]. See Example 3.3.
$$\{ \tau _{ - c}^ + \lt {e_q}\} $$. [Reference Kyprianou11, Theorem 13.1]. See Example 3.3.
More generally, denote for d ∈ ℝ by ![]() $$T_d^ + :=\inf \{ s \in (0,\infty ){\kern 1pt} :{\kern 1pt} {Y_s} \in (d,\infty )\} $$ the first hitting time of the set (d, ∞ ) by the process Y. Then, for γ ∈ [0, ∞) and real y ≤ d, under Py, the Laplace transform of
$$T_d^ + :=\inf \{ s \in (0,\infty ){\kern 1pt} :{\kern 1pt} {Y_s} \in (d,\infty )\} $$ the first hitting time of the set (d, ∞ ) by the process Y. Then, for γ ∈ [0, ∞) and real y ≤ d, under Py, the Laplace transform of ![]() $$T_d^ + = \int_0^{\tau _d^ + } \omega ({X_u}){\kern 1pt} {\rm{d}}u$$ on
$$T_d^ + = \int_0^{\tau _d^ + } \omega ({X_u}){\kern 1pt} {\rm{d}}u$$ on ![]() $$\{ T_d^ + \lt \zeta \} = \{ \tau _d^ + \lt {e_q}\} $$ at the point γ is given simply by
$$\{ T_d^ + \lt \zeta \} = \{ \tau _d^ + \lt {e_q}\} $$ at the point γ is given simply by
Moreover, knowledge of this expression automatically also furnishes the joint Laplace transform of ![]() $$\tau _d^ + $$ and
$$\tau _d^ + $$ and ![]() $$T_d^ + $$: if, further, p ∈ [0, ∞ ), then
$$T_d^ + $$: if, further, p ∈ [0, ∞ ), then ![]() $${{\rm{P}}_y}[{{\rm{e}}^{ - \gamma T_d^ + - p\tau _d^ + }};{\kern 1pt} T_d^ + \lt \zeta ] = {\cal B}_{q + p}^{(\gamma \omega )}(y,d)$$.
$${{\rm{P}}_y}[{{\rm{e}}^{ - \gamma T_d^ + - p\tau _d^ + }};{\kern 1pt} T_d^ + \lt \zeta ] = {\cal B}_{q + p}^{(\gamma \omega )}(y,d)$$.
1.3. Overview of literature and results
Literature-wise, fluctuation results for the ‘ ω-killed’ SNLP X have been the subject of the substantial recent study in [Reference Li and Palmowski12], to which the reader is referred for a further review of existing and related results as well as extra motivation for considering such processes. Expressions of the form (1.1) or (1.3) are particularly relevant in optimal stopping problems with (generalized) discounting for spectrally negative processes (when the optimal stopping time is a first passage time upwards): here the (generalized) discounting corresponds to the term ‘exp ![]() $$\{ - \int_0^{\tau _c^ + } \omega ({X_u}){\kern 1pt} {\rm{d}}u\} {{\bf{1}}_{\{ \tau _c^ + \lt {e_q}\} }}$$ in (1.1) or to
$$\{ - \int_0^{\tau _c^ + } \omega ({X_u}){\kern 1pt} {\rm{d}}u\} {{\bf{1}}_{\{ \tau _c^ + \lt {e_q}\} }}$$ in (1.1) or to ![]() $${{\rm{e}}^{ - \gamma T_d^ + }}{{\bf{1}}_{\{ T_d^ + \lt \zeta \} }}$$ (1.3), while any ‘reward’ function of a spectrally negative process at a first passage time upwards will simply be constant (on the event that this first passage is finite, owing to the absence of positive jumps). For further deliberations on this we refer the reader to [Reference Cissé, Patie and Tanré3], where such problems were considered for regular linear diffusions and, more generally, spectrally negative Feller processes (see especially [Reference Cissé, Patie and Tanré3, Theorem 4.2]), and to [Reference Long and Zhang13] in the context of Lévy processes (we return to this reference in more detail in Section 4). Outside of optimal stopping, in addition to the cases of pssMp and csbp mentioned above, connections between the values of the additive functional
$${{\rm{e}}^{ - \gamma T_d^ + }}{{\bf{1}}_{\{ T_d^ + \lt \zeta \} }}$$ (1.3), while any ‘reward’ function of a spectrally negative process at a first passage time upwards will simply be constant (on the event that this first passage is finite, owing to the absence of positive jumps). For further deliberations on this we refer the reader to [Reference Cissé, Patie and Tanré3], where such problems were considered for regular linear diffusions and, more generally, spectrally negative Feller processes (see especially [Reference Cissé, Patie and Tanré3, Theorem 4.2]), and to [Reference Long and Zhang13] in the context of Lévy processes (we return to this reference in more detail in Section 4). Outside of optimal stopping, in addition to the cases of pssMp and csbp mentioned above, connections between the values of the additive functional ![]() $$\int_0^ \cdot \omega ({X_u}){\kern 1pt} {\rm{d}}u$$ evaluated at a first passage (hitting) time, on the one hand, and of the first passage (hitting) time of the associated time-changed process, see (1.3), have also been found to be useful in the context of linear diffusions [Reference Khoshnevisan, Salminen and YOR8, Eq. (6)]. Finally, an expression somewhat reminiscent of the one in (1.1) appears in [Reference Pitman, YOR and Williams15, Eq. (1.h)] in the context of Bessel processes.
$$\int_0^ \cdot \omega ({X_u}){\kern 1pt} {\rm{d}}u$$ evaluated at a first passage (hitting) time, on the one hand, and of the first passage (hitting) time of the associated time-changed process, see (1.3), have also been found to be useful in the context of linear diffusions [Reference Khoshnevisan, Salminen and YOR8, Eq. (6)]. Finally, an expression somewhat reminiscent of the one in (1.1) appears in [Reference Pitman, YOR and Williams15, Eq. (1.h)] in the context of Bessel processes.
Our contribution is only a small complement to the findings of [Reference Li and Palmowski12], but still one that seems to deserve recording. To be precise, [Reference Li and Palmowski12] provides information on the one-sided upwards passage problem when ω is constant on (−∞, 0] (see [Reference Li and Palmowski12, Subsection 2.4]); we will extend this to a far more general class of functions ω. In this class, the solution to (1.1) will be given in terms of a function ![]() $${\cal H}_q^{(\omega )}$$ that will be found to solve (uniquely) a natural convolution equation on the real line involving the q -scale function of X (Theorem 3.1). In contrast to the two-sided exit problem, where the pertinent convolution equation is on the non-negative half-line [Reference Li and Palmowski12, Eq. (1.2)], this introduces some extra finiteness issues, making the analysis slightly more delicate. The function
$${\cal H}_q^{(\omega )}$$ that will be found to solve (uniquely) a natural convolution equation on the real line involving the q -scale function of X (Theorem 3.1). In contrast to the two-sided exit problem, where the pertinent convolution equation is on the non-negative half-line [Reference Li and Palmowski12, Eq. (1.2)], this introduces some extra finiteness issues, making the analysis slightly more delicate. The function ![]() $${\cal H}_q^{(\omega )}$$ will also be associated with a family of (local) martingales involving the process Y (Proposition 3.1).
$${\cal H}_q^{(\omega )}$$ will also be associated with a family of (local) martingales involving the process Y (Proposition 3.1).
1.4. Structure of this paper
We turn to the results and their proofs presently, in Section 3, after briefly introducing some necessary further notation and recalling some known facts in Section 2. Section 4 concludes by illustrating the findings in the context of determining the optimal level at which to sell an asset whose price process is given by the exponential of the process Y from (1.2).
2. Further notation and some preliminaries
We denote by ψ the Laplace exponent of X, ψ (z) = log P[ezX1] for z ∈ [0, ∞), and by Ф its right-continuous inverse, Ф(p) ≔ inf{ z ∈ [0, ∞): ψ (z) > p } for p ∈ [0, ∞); ψ is strictly convex and continuous, limz →∞ ψ (z) =∞, and Ф(0) is the largest zero of ψ. For real x ≤ c, recall the classical identity [Reference Kyprianou11, Eq. (3.15)]
Further, for λ ∈ [0, ∞), W (λ) :ℝ → [0, ∞) will be the λ -scale function of X, characterized by being continuous on [0, ∞), vanishing on (−∞, 0), and having Laplace transform
In particular, we set W (0) = : W. The reader is referred to [Reference Kuznetsov, Kyprianou and Rivero10] for further background on scale functions of SNLP; we note explicitly only the asymptotic behavior [Reference Kuznetsov, Kyprianou and Rivero10, Eq. (33), Lemmas 2.3 and 3.3]
that we shall use repeatedly in what follows (here, 1 / 0 :=∞ when λ = Ф(0) = ψ′ (0 +) = 0, and otherwise ψ′(Ф λ) +) ∈ (0, ∞); W Ф(λ) is the scale function of an Esscher transformed process – its precise character is unimportant, what matters is only the monotone convergence).
Convolution on the real line will be denoted by a⋆ : for Borel-measurable f, g : ℝ →; ℝ,
whenever the Lebesgue integral is well defined for all x ∈ ℝ (it is, e.g., when f and g are both non-negative, or both integrable, or when one of f, g is integrable, while the other is bounded).
Finally, it will be convenient to introduce the following concepts.
Definition 2.1. For a function f : ℝ ↦ ℝ, we will (i) say that it has a bounded left tail (resp. left tail that is bounded below away from zero) if f is bounded (resp. bounded below away from zero) on (−∞, x 0] for some x 0 ∈ ℝ; (ii) for further α ∈ [0, ∞), say that it has a left tail that is α -subexponential provided that for some x 0 ∈ ℝ, some γ < ∞, and then all x ∈ (−∞, x 0 ], we have ![]() $$|{\kern 1pt} f(x)| \le \gamma {{\rm{e}}^{\alpha x}}$$; and (iii) say simply that it has a subexponential left tail if, for some α > 0, it has a left tail that is α-subexponential.
$$|{\kern 1pt} f(x)| \le \gamma {{\rm{e}}^{\alpha x}}$$; and (iii) say simply that it has a subexponential left tail if, for some α > 0, it has a left tail that is α-subexponential.
3. Results and their proofs
3.1. Main result
Here is the main result of this note.
Theorem 3.1. There exists a unique function ![]() $${\cal H}_q^{(\omega )}{\kern 1pt} :{\mathbb R}{\kern 1pt} \to (0,\infty )$$ satisfying (the arbitrary normalization condition)
$${\cal H}_q^{(\omega )}{\kern 1pt} :{\mathbb R}{\kern 1pt} \to (0,\infty )$$ satisfying (the arbitrary normalization condition) ![]() $${\cal H}_q^{(\omega )}(0) = 1$$ such that
$${\cal H}_q^{(\omega )}(0) = 1$$ such that
 $${\cal B}_q^{(\omega )}(x,c) = {{{\cal H}_q^{(\omega )}(x)} \over {{\cal H}_q^{(\omega )}(c)}}{\rm{for\,all\,real\,}}x \le c.$$
$${\cal B}_q^{(\omega )}(x,c) = {{{\cal H}_q^{(\omega )}(x)} \over {{\cal H}_q^{(\omega )}(c)}}{\rm{for\,all\,real\,}}x \le c.$$
The function ![]() $${\cal H}_q^{(\omega )}$$
enjoys the following properties.
$${\cal H}_q^{(\omega )}$$
enjoys the following properties.
(I) It is non-decreasing (hence locally bounded), continuous, and it is strictly increasing provided ω> 0.
(II) For each c ∈ R the following holds: ω 1 (⋅ ∧c) = ω 2 (⋅ ∧c) implies
 $${{\cal H}^{({\omega _1})}}( \cdot \wedge {\kern 1pt} c) = \alpha {{\cal H}^{({\omega _2})}}( \cdot \wedge {\kern 1pt} c)$$ for some α ∈ (0, ∞), this α being 1 if c ≥ 0.
$${{\cal H}^{({\omega _1})}}( \cdot \wedge {\kern 1pt} c) = \alpha {{\cal H}^{({\omega _2})}}( \cdot \wedge {\kern 1pt} c)$$ for some α ∈ (0, ∞), this α being 1 if c ≥ 0.(III) If ω 1 ,ω 2 : ℝ → [0, ∞) are both locally bounded and Borel measurable with ω 1 ≤ ω 2 (resp. ω 1 <ω 2 ), then
 $${\cal H}_q^{({\omega _1})} \le {\cal H}_q^{({\omega _2})}$$ (resp.
$${\cal H}_q^{({\omega _1})} \le {\cal H}_q^{({\omega _2})}$$ (resp.  $${\cal H}_q^{({\omega _1})} \lt {\cal H}_q^{({\omega _2})}$$) on (0, ∞) and
$${\cal H}_q^{({\omega _1})} \lt {\cal H}_q^{({\omega _2})}$$) on (0, ∞) and  $${\cal H}_q^{({\omega _1})} \ge {\cal H}_q^{({\omega _2})}$$ (resp.
$${\cal H}_q^{({\omega _1})} \ge {\cal H}_q^{({\omega _2})}$$ (resp.  $${\cal H}_q^{({\omega _1})} > {\cal H}_q^{({\omega _2})}$$) on (−∞, 0) ; of course,
$${\cal H}_q^{({\omega _1})} > {\cal H}_q^{({\omega _2})}$$) on (−∞, 0) ; of course,  $${\cal H}_q^{({\omega _1})}(0) = 1 = {\cal H}_q^{({\omega _2})}(0)$$
$${\cal H}_q^{({\omega _1})}(0) = 1 = {\cal H}_q^{({\omega _2})}(0)$$(IV) For real x ≤ c
 $${\cal H}_q^{(\omega )}(x) \le {\cal H}_q^{(\omega )}(c){{\rm{e}}^{ - \Phi (q)(c - x)}}$$; in particular,
$${\cal H}_q^{(\omega )}(x) \le {\cal H}_q^{(\omega )}(c){{\rm{e}}^{ - \Phi (q)(c - x)}}$$; in particular,  $${\cal H}_q^{(\omega )}(x) \le {{\rm{e}}^{\Phi (q)x}}$$ for all
$${\cal H}_q^{(\omega )}(x) \le {{\rm{e}}^{\Phi (q)x}}$$ for all  $$x \in ( - \infty ,0]$$, so that
$$x \in ( - \infty ,0]$$, so that  $${\cal H}_q^{(\omega )}$$ has a left tail that is Ф(q) -subexponential.
$${\cal H}_q^{(\omega )}$$ has a left tail that is Ф(q) -subexponential.
Furthermore, if (ωeФ(q + p)⋅) ⋆W (q) is finite-valued for all p ∈ (0, ∞) , in particular if ω has a left tail that is bounded, then for some unique ![]() $$L_q^{(\omega )} \in [0,1]$$,
$$L_q^{(\omega )} \in [0,1]$$, ![]() $${\cal H}_q^{(\omega )}$$ satisfies the convolution equation
$${\cal H}_q^{(\omega )}$$ satisfies the convolution equation
More specifically:
(i) If, moreover, ω has a left tail that is bounded and bounded below away from zero, then
 $${\cal H}_q^{(\omega )}$$ satisfies the (homogeneous) convolution equation(3.3)
$${\cal H}_q^{(\omega )}$$ satisfies the (homogeneous) convolution equation(3.3) $${\cal H}_q^{(\omega )} = (\omega {\cal H}_q^{(\omega )}) \star {W^{(q)}}.$$
$${\cal H}_q^{(\omega )} = (\omega {\cal H}_q^{(\omega )}) \star {W^{(q)}}.$$
(ii) If
 $$(\omega {{\rm{e}}^{\Phi (q) \cdot }}) \star {W^{(q)}}$$ is finite-valued, in particular if ω has a subexponential left tail, then
$$(\omega {{\rm{e}}^{\Phi (q) \cdot }}) \star {W^{(q)}}$$ is finite-valued, in particular if ω has a subexponential left tail, then  $${\cal H}_q^{(\omega )}$$is the unique locally bounded Borel measurable function H : ℝ → ℝ admitting a left tail that is Ф(q) -subexponential and satisfying the (inhomogeneous) convolution equation(3.4)
$${\cal H}_q^{(\omega )}$$is the unique locally bounded Borel measurable function H : ℝ → ℝ admitting a left tail that is Ф(q) -subexponential and satisfying the (inhomogeneous) convolution equation(3.4) $$H = L_q^{(\omega )}{{\rm{e}}^{\Phi (q) \cdot }} + (\omega H) \star {W^{(q)}},$$
$$H = L_q^{(\omega )}{{\rm{e}}^{\Phi (q) \cdot }} + (\omega H) \star {W^{(q)}},$$
where
(3.5) $$\matrix{
{L_q^{(\omega )} = \mathop {\lim }\limits_{x \to - \infty } {\cal H}_q^{(\omega )}(x){{\rm{e}}^{ - \Phi (q)x}}\quad } \hfill \cr
{ = \mathop {\lim }\limits_{x \to - \infty } {{\rm{P}}_x}[\exp \{ - \int_0^{\tau _0^ + } \omega ({X_s}){\kern 1pt} {\rm{d}}s\} {\kern 1pt} |{\kern 1pt} \tau _0^ + \lt {e_q}] \in (0,1].} \hfill \cr
} $$
$$\matrix{
{L_q^{(\omega )} = \mathop {\lim }\limits_{x \to - \infty } {\cal H}_q^{(\omega )}(x){{\rm{e}}^{ - \Phi (q)x}}\quad } \hfill \cr
{ = \mathop {\lim }\limits_{x \to - \infty } {{\rm{P}}_x}[\exp \{ - \int_0^{\tau _0^ + } \omega ({X_s}){\kern 1pt} {\rm{d}}s\} {\kern 1pt} |{\kern 1pt} \tau _0^ + \lt {e_q}] \in (0,1].} \hfill \cr
} $$
This function is given as
 $${\cal H}_q^{(\omega )} = \uparrow - \mathop {\lim }\nolimits_{n \to \infty } {H_n}$$, where
$${\cal H}_q^{(\omega )} = \uparrow - \mathop {\lim }\nolimits_{n \to \infty } {H_n}$$, where  $${H_0}L_q^{(\omega )}{{\rm{e}}^{\Phi (q) \cdot }}$$ and recursively
$${H_0}L_q^{(\omega )}{{\rm{e}}^{\Phi (q) \cdot }}$$ and recursively  $${H_{n + 1}}:=L_q^{(\omega )}{{\rm{e}}^{\Phi (q) \cdot }} + (\omega {H_n}) \star {W^{(q)}}$$ for n ∈ ℕ0.
$${H_{n + 1}}:=L_q^{(\omega )}{{\rm{e}}^{\Phi (q) \cdot }} + (\omega {H_n}) \star {W^{(q)}}$$ for n ∈ ℕ0.After some remarks and examples we turn to the proof of this theorem on p. 480.
Remark 3.1. Since ![]() $${\cal H}_q^{(\omega )} = {\cal H}_0^{(\omega + q)}$$ (3.3) may be rewritten as
$${\cal H}_q^{(\omega )} = {\cal H}_0^{(\omega + q)}$$ (3.3) may be rewritten as ![]() $${\cal H}_q^{(\omega )} = ((\omega + q){\cal H}_q^{(\omega )}) \star W$$. For the same reason, when q > 0 then automatically
$${\cal H}_q^{(\omega )} = ((\omega + q){\cal H}_q^{(\omega )}) \star W$$. For the same reason, when q > 0 then automatically ![]() $${\cal H}_q^{(\omega )} = ((\omega + q){\cal H}_q^{(\omega )}) \star W$$.
$${\cal H}_q^{(\omega )} = ((\omega + q){\cal H}_q^{(\omega )}) \star W$$.
Remark 3.2. Because of (2.3), cases (i) and (ii) are seen to be mutually exclusive (but they are not exhaustive). Of course, (ωeФ(q +p)⋅) ⋆ W (q) is finite-valued for all p ∈ (0, ∞) if and only if (ωeα.⋅ eФ(q).) ⋆ W (q) is finite-valued for all α ∈ (0, ∞), in which case, for each α ∈ (0, ∞), ωeα. falls under the provisos of case (ii). For the resulting convolution equation (3.4) we then have suitable uniqueness of the solution as well as an explicit recursion to (at least in principle) produce it. At the same time, by bounded convergence in (3.1) and (1.1), ![]() $${\lim_{\alpha \downarrow 0}}{\cal H}_q^{(\omega {e^{\alpha .}})} = {\cal H}_q^{(\omega )}$$
$${\lim_{\alpha \downarrow 0}}{\cal H}_q^{(\omega {e^{\alpha .}})} = {\cal H}_q^{(\omega )}$$
Example 3.1. When ω is constant and equal to some μ ∈ [0, ∞), then from (2.1), ![]() $${\cal H}_q^{(\omega )} = {\cal H}_q^{(\mu )} = {{\rm{e}}^{\Phi (q + \mu ) \cdot }}$$, and this instance falls under case (i) or (ii) according as μ> 0 or μ = 0.
$${\cal H}_q^{(\omega )} = {\cal H}_q^{(\mu )} = {{\rm{e}}^{\Phi (q + \mu ) \cdot }}$$, and this instance falls under case (i) or (ii) according as μ> 0 or μ = 0.
Example 3.2. When ω = γ eα., with γ ∈ [0, ∞) and α ∈ (0, ∞), a situation that falls under case (ii ), using (2.2) we obtain
 $${\cal H}_q^{(\gamma {{\rm{e}}^{\alpha \cdot }})}(x) = \sum\limits_{k = 0}^\infty {{{\gamma ^k}{{\rm{e}}^{(\Phi (q) + \alpha k)x}}} \over {\prod\nolimits_{l = 1}^k (\psi (\Phi (q) + l\alpha ) - q)}}/\sum\limits_{k = 0}^\infty {{{\gamma ^k}} \over {\prod\nolimits_{l = 1}^k (\psi (\Phi (q) + l\alpha ) - q)}},\quad x \in {\mathbb R},$$
$${\cal H}_q^{(\gamma {{\rm{e}}^{\alpha \cdot }})}(x) = \sum\limits_{k = 0}^\infty {{{\gamma ^k}{{\rm{e}}^{(\Phi (q) + \alpha k)x}}} \over {\prod\nolimits_{l = 1}^k (\psi (\Phi (q) + l\alpha ) - q)}}/\sum\limits_{k = 0}^\infty {{{\gamma ^k}} \over {\prod\nolimits_{l = 1}^k (\psi (\Phi (q) + l\alpha ) - q)}},\quad x \in {\mathbb R},$$
with the series converging to finite values. (As usual the empty product is interpreted as being equal to 1.) Of course, when γ > 0 then, from (3.1), by spatial homogeneity, ![]() $${\cal H}_q^{(\gamma {{\rm{e}}^{\alpha \cdot }})}(x) = {{{\cal H}_q^{({{\rm{e}}^{\alpha \cdot }})}(x + {1 \over \alpha }\log \gamma )} \over {{\cal H}_q^{({{\rm{e}}^{\alpha \cdot }})}({1 \over \alpha }\log \gamma )}},\,x \in {\mathbb R}$$. Note that this reproduces (up to trivial transformations) Patie’s [Reference Patie14] scale functions from the fluctuation theory of spectrally negative pssMp [Reference Kyprianou11, Section 13.7]. We can also identify the limit (3.5) as
$${\cal H}_q^{(\gamma {{\rm{e}}^{\alpha \cdot }})}(x) = {{{\cal H}_q^{({{\rm{e}}^{\alpha \cdot }})}(x + {1 \over \alpha }\log \gamma )} \over {{\cal H}_q^{({{\rm{e}}^{\alpha \cdot }})}({1 \over \alpha }\log \gamma )}},\,x \in {\mathbb R}$$. Note that this reproduces (up to trivial transformations) Patie’s [Reference Patie14] scale functions from the fluctuation theory of spectrally negative pssMp [Reference Kyprianou11, Section 13.7]. We can also identify the limit (3.5) as ![]() $$L_q^{(\gamma {{\rm{e}}^{\alpha \cdot }})} = (\sum\nolimits_{k = 0}^\infty {{{\gamma ^k}} \over {\prod\nolimits_{l = 1}^k (\psi (\Phi (q) + l\alpha ) - q)}}{)^{ - 1}}$$. For the special case when X is Brownian motion and when γ > 0 (γ = 0 being trivial), if q = 0 we have
$$L_q^{(\gamma {{\rm{e}}^{\alpha \cdot }})} = (\sum\nolimits_{k = 0}^\infty {{{\gamma ^k}} \over {\prod\nolimits_{l = 1}^k (\psi (\Phi (q) + l\alpha ) - q)}}{)^{ - 1}}$$. For the special case when X is Brownian motion and when γ > 0 (γ = 0 being trivial), if q = 0 we have ![]() $${\cal H}_q^{(\gamma {{\rm{e}}^{\alpha \cdot }})}(x) = {\cal H}_0^{(\gamma {{\rm{e}}^{\alpha \cdot }})}(x) = {{{I_0}(2{{\rm{e}}^{\alpha x/2}}\sqrt \gamma /\alpha )} \over {{I_0}(2\sqrt \gamma /\alpha )}}$$, x ∈ ℝ, where I 0 is the modified Bessel function of the first kind (of order 0); for q > 0 the function
$${\cal H}_q^{(\gamma {{\rm{e}}^{\alpha \cdot }})}(x) = {\cal H}_0^{(\gamma {{\rm{e}}^{\alpha \cdot }})}(x) = {{{I_0}(2{{\rm{e}}^{\alpha x/2}}\sqrt \gamma /\alpha )} \over {{I_0}(2\sqrt \gamma /\alpha )}}$$, x ∈ ℝ, where I 0 is the modified Bessel function of the first kind (of order 0); for q > 0 the function ![]() $${\cal H}_q^{(\gamma {{\rm{e}}^{\alpha \cdot }})}$$ evaluates in terms of a generalized hypergeometric function.
$${\cal H}_q^{(\gamma {{\rm{e}}^{\alpha \cdot }})}$$ evaluates in terms of a generalized hypergeometric function.
Remark 3.3. Let γ ∈[0,∞] and α∈(0, ∞). Suppose ![]() $$\omega (x) \le\gamma {{\rm{e}}^{\alpha x }}$$ for all x ∈ ℝ. Then, again via (2.2), we get the following a priori bound on the absolute error in case (ii) from computing only finitely many terms of the recursion for
$$\omega (x) \le\gamma {{\rm{e}}^{\alpha x }}$$ for all x ∈ ℝ. Then, again via (2.2), we get the following a priori bound on the absolute error in case (ii) from computing only finitely many terms of the recursion for ![]() $${\cal H}_q^{(\omega )}$$:
$${\cal H}_q^{(\omega )}$$:
 $$\matrix{
{{\cal H}_q^{(\omega )} - {H_n} \le L_q^{(\omega )}\sum\limits_{k = n + 1}^\infty {{{\gamma ^k}} \over {\prod\nolimits_{l = 1}^k (\psi (\Phi (q) + \alpha l) - q)}}{{\rm{e}}^{(\Phi (q) + \alpha k) \cdot }}} \cr
{ \le \sum\limits_{k = n + 1}^\infty {{{\gamma ^k}} \over {\prod\nolimits_{l = 1}^k (\psi (\Phi (q) + \alpha l) - q)}}{{\rm{e}}^{(\Phi (q) + \alpha k) \cdot }}} \cr
} $$
$$\matrix{
{{\cal H}_q^{(\omega )} - {H_n} \le L_q^{(\omega )}\sum\limits_{k = n + 1}^\infty {{{\gamma ^k}} \over {\prod\nolimits_{l = 1}^k (\psi (\Phi (q) + \alpha l) - q)}}{{\rm{e}}^{(\Phi (q) + \alpha k) \cdot }}} \cr
{ \le \sum\limits_{k = n + 1}^\infty {{{\gamma ^k}} \over {\prod\nolimits_{l = 1}^k (\psi (\Phi (q) + \alpha l) - q)}}{{\rm{e}}^{(\Phi (q) + \alpha k) \cdot }}} \cr
} $$
for all n ∈ ℕ0. (In particular, ![]() $${\cal H}_q^{(\omega )} \le L_q^{(\omega )}\sum\nolimits_{k = 0}^\infty {{{\gamma ^k}} \over {\prod\nolimits_{l = 1}^k (\psi (\Phi (q) + \alpha l) - q)}}{{\rm{e}}^{(\Phi (q) + \alpha k) \cdot }} \le $$
$${\cal H}_q^{(\omega )} \le L_q^{(\omega )}\sum\nolimits_{k = 0}^\infty {{{\gamma ^k}} \over {\prod\nolimits_{l = 1}^k (\psi (\Phi (q) + \alpha l) - q)}}{{\rm{e}}^{(\Phi (q) + \alpha k) \cdot }} \le $$ ![]() $$\sum\nolimits_{k = 0}^\infty {{{\gamma ^k}} \over {\prod\nolimits_{l = 1}^k (\psi (\Phi (q) + \alpha l) - q)}}{{\rm{e}}^{(\Phi (q) + \alpha k) \cdot }}$$
$$\sum\nolimits_{k = 0}^\infty {{{\gamma ^k}} \over {\prod\nolimits_{l = 1}^k (\psi (\Phi (q) + \alpha l) - q)}}{{\rm{e}}^{(\Phi (q) + \alpha k) \cdot }}$$
In the following, an expression of the form ![]() $${\cal H}_q^{(\omega )}(x) \propto b(x)$$’ means that there is a C ∈ (0, ∞) such that
$${\cal H}_q^{(\omega )}(x) \propto b(x)$$’ means that there is a C ∈ (0, ∞) such that ![]() $${\cal H}_q^{(\omega )}(x) = Cb(x)$$ for all x in the relevant domain; the constant C depends only on ω, q, and the characteristics of X, not on x (it is ultimately determined by the (arbitrary) normalization condition
$${\cal H}_q^{(\omega )}(x) = Cb(x)$$ for all x in the relevant domain; the constant C depends only on ω, q, and the characteristics of X, not on x (it is ultimately determined by the (arbitrary) normalization condition ![]() $${\cal H}_q^{(\omega )}(0) = 1$$).
$${\cal H}_q^{(\omega )}(0) = 1$$).
Example 3.3. Let c ∈ (0, ∞), γ ∈ (0, ∞), and ![]() $$\omega (x) = {\gamma \over {|x|}}$$ for x ∈ (−∞, −c]. Using the result for csbp of [Reference Duhalde, Foucart and MA6, Theorem 1] we identify
$$\omega (x) = {\gamma \over {|x|}}$$ for x ∈ (−∞, −c]. Using the result for csbp of [Reference Duhalde, Foucart and MA6, Theorem 1] we identify ![]() $${\cal H}_q^{(\omega )}$$ up to a multiplicative constant;
$${\cal H}_q^{(\omega )}$$ up to a multiplicative constant;
 $${\cal H}_q^{(\omega )}(x) \propto \int_{\Phi (q)}^\infty {{{\kern 1pt} {\rm{d}}z} \over {\psi (z) - q}}\exp \,\{ xz + \int_\theta ^z {\gamma \over {\psi (u) - q}}{\kern 1pt} {\rm{d}}u\} ,\quad x \in ( - \infty , - c],$$
$${\cal H}_q^{(\omega )}(x) \propto \int_{\Phi (q)}^\infty {{{\kern 1pt} {\rm{d}}z} \over {\psi (z) - q}}\exp \,\{ xz + \int_\theta ^z {\gamma \over {\psi (u) - q}}{\kern 1pt} {\rm{d}}u\} ,\quad x \in ( - \infty , - c],$$
where θ ∈ (Ф(q), ∞) is arbitrary but fixed. Indeed, [Reference Duhalde, Foucart and MA6, Eq. (11)] identifies (by other means) the expression (1.3), and even the joint Laplace transform ‘![]() $${{\rm{P}}_y}[{{\rm{e}}^{ - \delta T_d^ + - p\tau _d^ + }};{\kern 1pt} T_d^ + \lt \zeta ]$$’, from which the expression for
$${{\rm{P}}_y}[{{\rm{e}}^{ - \delta T_d^ + - p\tau _d^ + }};{\kern 1pt} T_d^ + \lt \zeta ]$$’, from which the expression for ![]() $${\cal H}_q^{(\omega )}$$ can easily be recovered via (3.1). Note that this ω falls under neither case (i) nor case (ii ), but it does fall under (3.2). In fact, while it is not so obvious, an easy computation shows that (3.2) is verified in this case with
$${\cal H}_q^{(\omega )}$$ can easily be recovered via (3.1). Note that this ω falls under neither case (i) nor case (ii ), but it does fall under (3.2). In fact, while it is not so obvious, an easy computation shows that (3.2) is verified in this case with ![]() $$L_q^{(\omega )} = 0$$. For the special case when X is Brownian motion and when γ > 0: if q = 0 we have
$$L_q^{(\omega )} = 0$$. For the special case when X is Brownian motion and when γ > 0: if q = 0 we have ![]() $${\cal H}_q^{(\omega )}(x) \propto 2\sqrt { - 2\gamma x} {K_1}(2\sqrt { - 2\gamma x} )$$,
$${\cal H}_q^{(\omega )}(x) \propto 2\sqrt { - 2\gamma x} {K_1}(2\sqrt { - 2\gamma x} )$$, ![]() $$x \in (\infty , - c]$$, where K 1 is the modified Bessel function of the second kind (of order 1); for q > 0 the function
$$x \in (\infty , - c]$$, where K 1 is the modified Bessel function of the second kind (of order 1); for q > 0 the function ![]() $${\cal H}_q^{(\gamma {{\rm{e}}^{\alpha \cdot }})}$$ does not appear to have a closed-form expression in terms of elementary/special functions.
$${\cal H}_q^{(\gamma {{\rm{e}}^{\alpha \cdot }})}$$ does not appear to have a closed-form expression in terms of elementary/special functions.
Example 3.4. Let n ∈ N≥2, γ ∈ [0, ∞), c ∈ (0, ∞), and ![]() $$\omega (x) = {\gamma \over {|x{|^n}}}$$ for x ∈ (−∞, − c]. Except possibly when q = Ф(0) = ψ′ (0 +) = 0, we then automatically have, because of the asymptotic properties of W (q) (see (2.3)) that (ωe Ф(q).)* W (q) is finite-valued, and in any event we assume now that this is so. Then note, using (2.2), that for x ∈ (−∞, − c], v ∈ [Ф(q), ∞), and for α > 0,
$$\omega (x) = {\gamma \over {|x{|^n}}}$$ for x ∈ (−∞, − c]. Except possibly when q = Ф(0) = ψ′ (0 +) = 0, we then automatically have, because of the asymptotic properties of W (q) (see (2.3)) that (ωe Ф(q).)* W (q) is finite-valued, and in any event we assume now that this is so. Then note, using (2.2), that for x ∈ (−∞, − c], v ∈ [Ф(q), ∞), and for α > 0,![]() $${{{{\rm{d}}^n}} \over {{\rm{d}}{\alpha ^n}}}\int_0^\infty {{{{\rm{e}}^{(v + \alpha )(x - y)}}} \over {{{(x - y)}^n}}}{W^{(q)}}(y){\kern 1pt} {\rm{d}}y = {{{{\rm{e}}^{(v + \alpha )x}}} \over {\psi (v + \alpha ) - q}}$$, which implies that
$${{{{\rm{d}}^n}} \over {{\rm{d}}{\alpha ^n}}}\int_0^\infty {{{{\rm{e}}^{(v + \alpha )(x - y)}}} \over {{{(x - y)}^n}}}{W^{(q)}}(y){\kern 1pt} {\rm{d}}y = {{{{\rm{e}}^{(v + \alpha )x}}} \over {\psi (v + \alpha ) - q}}$$, which implies that
 $$\matrix{
{\int_0^\infty {{{{\rm{e}}^{(v + \alpha )(x - y)}}} \over {|x - y{|^n}}}{W^{(q)}}(y){\kern 1pt} {\rm{d}}y = \int_{v + \alpha }^\infty {\kern 1pt} {\rm{d}}{v_1}\int_{{v_1}}^\infty {\kern 1pt} {\rm{d}}{v_2} \cdots \int_{{v_{n - 1}}}^\infty {\kern 1pt} {\rm{d}}{v_n}{{{{\rm{e}}^{{v_n}x}}} \over {\psi ({v_n}) - q}}} \cr
{ = \int_{v + \alpha }^\infty {\kern 1pt} {\rm{d}}{v_n}{{{{\rm{e}}^{x{v_n}}}} \over {\psi ({v_n}) - q}}\int_{v + \alpha }^{{v_n}} {\kern 1pt} {\rm{d}}{v_{n - 1}} \cdots \int_{v + \alpha }^{{v_2}} {\kern 1pt} {\rm{d}}{v_1} = \int_{v + \alpha }^\infty {\kern 1pt} {\rm{d}}y{{{{\rm{e}}^{xy}}} \over {\psi (y) - q}}{{{{(y - v - \alpha )}^{n - 1}}} \over {(n - 1)!}}.} \cr
} $$
$$\matrix{
{\int_0^\infty {{{{\rm{e}}^{(v + \alpha )(x - y)}}} \over {|x - y{|^n}}}{W^{(q)}}(y){\kern 1pt} {\rm{d}}y = \int_{v + \alpha }^\infty {\kern 1pt} {\rm{d}}{v_1}\int_{{v_1}}^\infty {\kern 1pt} {\rm{d}}{v_2} \cdots \int_{{v_{n - 1}}}^\infty {\kern 1pt} {\rm{d}}{v_n}{{{{\rm{e}}^{{v_n}x}}} \over {\psi ({v_n}) - q}}} \cr
{ = \int_{v + \alpha }^\infty {\kern 1pt} {\rm{d}}{v_n}{{{{\rm{e}}^{x{v_n}}}} \over {\psi ({v_n}) - q}}\int_{v + \alpha }^{{v_n}} {\kern 1pt} {\rm{d}}{v_{n - 1}} \cdots \int_{v + \alpha }^{{v_2}} {\kern 1pt} {\rm{d}}{v_1} = \int_{v + \alpha }^\infty {\kern 1pt} {\rm{d}}y{{{{\rm{e}}^{xy}}} \over {\psi (y) - q}}{{{{(y - v - \alpha )}^{n - 1}}} \over {(n - 1)!}}.} \cr
} $$
Hence, letting α ↓ 0, by monotone convergence,
 $$\matrix{
{((\omega {{\rm{e}}^{v \cdot }}) \star {W^{(q)}})(x) = \gamma \int_0^\infty {{{{\rm{e}}^{v(x - y)}}} \over {|x - y{|^n}}}{W^{(q)}}(y){\kern 1pt} {\rm{d}}y} \cr
{ = \gamma \int_v^\infty {\kern 1pt} {\rm{d}}y{{{{\rm{e}}^{xy}}} \over {\psi (y) - q}}{{{{(y - v)}^{n - 1}}} \over {(n - 1)!}} = \gamma \int_0^\infty {\kern 1pt} {\rm{d}}y{{{{\rm{e}}^{x(v + y)}}} \over {\psi (v + y) - q}}{{{y^{n - 1}}} \over {(n - 1)!}}.} \cr
} $$
$$\matrix{
{((\omega {{\rm{e}}^{v \cdot }}) \star {W^{(q)}})(x) = \gamma \int_0^\infty {{{{\rm{e}}^{v(x - y)}}} \over {|x - y{|^n}}}{W^{(q)}}(y){\kern 1pt} {\rm{d}}y} \cr
{ = \gamma \int_v^\infty {\kern 1pt} {\rm{d}}y{{{{\rm{e}}^{xy}}} \over {\psi (y) - q}}{{{{(y - v)}^{n - 1}}} \over {(n - 1)!}} = \gamma \int_0^\infty {\kern 1pt} {\rm{d}}y{{{{\rm{e}}^{x(v + y)}}} \over {\psi (v + y) - q}}{{{y^{n - 1}}} \over {(n - 1)!}}.} \cr
} $$
Thus, the recursion of case (ii) allows us to identify ![]() $${\cal H}_q^{(\omega )}$$, up to a proportionality constant, in terms of an infinite series of iterated integrals:
$${\cal H}_q^{(\omega )}$$, up to a proportionality constant, in terms of an infinite series of iterated integrals:
 $$\matrix{
{{\cal H}_q^{(\omega )}(x) \propto {{\rm{e}}^{\Phi (q)x}}[1 + \sum\limits_{k = 1}^\infty {{({\gamma \over {(n - 1)!}})}^k}\int_{{{(0,\infty )}^k}} {{{{({x_1} \cdots {x_k})}^{n - 1}}{{\rm{e}}^{x({x_1} + \cdots + {x_k})}}{\kern 1pt} {\rm{d}}{x_1} \cdots {\kern 1pt} {\rm{d}}{x_k}} \over {(\psi (\Phi (q) + {x_1}) - q) \cdots (\psi (\Phi (q) + {x_1} + \cdots + {x_k}) - q)}}]} \cr
{ = {{\rm{e}}^{\Phi (q)x}}[1 + {\gamma \over {(n - 1)!}}\int_0^\infty {\kern 1pt} {\rm{d}}y{{{y^{n - 1}}{{\rm{e}}^{xy}}} \over {\psi (\Phi (q) + y) - q}}} \cr
{ + {\kern 1pt} {{({\gamma \over {(n - 1)!}})}^2}\int_0^\infty {\kern 1pt} {\rm{d}}y{{{y^{n - 1}}{{\rm{e}}^{xy}}} \over {\psi (\Phi (q) + y) - q}}\int_0^\infty {\kern 1pt} {\rm{d}}z{{{z^{n - 1}}{{\rm{e}}^{xz}}} \over {\psi (\Phi (q) + y + z) - q}} + \cdots ],\quad x \in ( - \infty , - c].} \cr
} $$
$$\matrix{
{{\cal H}_q^{(\omega )}(x) \propto {{\rm{e}}^{\Phi (q)x}}[1 + \sum\limits_{k = 1}^\infty {{({\gamma \over {(n - 1)!}})}^k}\int_{{{(0,\infty )}^k}} {{{{({x_1} \cdots {x_k})}^{n - 1}}{{\rm{e}}^{x({x_1} + \cdots + {x_k})}}{\kern 1pt} {\rm{d}}{x_1} \cdots {\kern 1pt} {\rm{d}}{x_k}} \over {(\psi (\Phi (q) + {x_1}) - q) \cdots (\psi (\Phi (q) + {x_1} + \cdots + {x_k}) - q)}}]} \cr
{ = {{\rm{e}}^{\Phi (q)x}}[1 + {\gamma \over {(n - 1)!}}\int_0^\infty {\kern 1pt} {\rm{d}}y{{{y^{n - 1}}{{\rm{e}}^{xy}}} \over {\psi (\Phi (q) + y) - q}}} \cr
{ + {\kern 1pt} {{({\gamma \over {(n - 1)!}})}^2}\int_0^\infty {\kern 1pt} {\rm{d}}y{{{y^{n - 1}}{{\rm{e}}^{xy}}} \over {\psi (\Phi (q) + y) - q}}\int_0^\infty {\kern 1pt} {\rm{d}}z{{{z^{n - 1}}{{\rm{e}}^{xz}}} \over {\psi (\Phi (q) + y + z) - q}} + \cdots ],\quad x \in ( - \infty , - c].} \cr
} $$
For instance, when X is Brownian motion, q = 0, and n = 3, then ![]() $${\cal H}_q^{(\omega )}(x) \propto 1 + {\gamma \over { - x}} + {{{\gamma ^2}} \over {3{x^2}}} + \cdots $$, with the first three terms of the preceding series having been made explicit; already the fourth term does not (appear to) evaluate to any nice expression. It is clear from the representation of the series, however, that in this special case its kth term will be of the form c k / | x | k, for some c k ∈ (0, ∞), so that by adding the successive terms to the series we get an asymptotic expansion of
$${\cal H}_q^{(\omega )}(x) \propto 1 + {\gamma \over { - x}} + {{{\gamma ^2}} \over {3{x^2}}} + \cdots $$, with the first three terms of the preceding series having been made explicit; already the fourth term does not (appear to) evaluate to any nice expression. It is clear from the representation of the series, however, that in this special case its kth term will be of the form c k / | x | k, for some c k ∈ (0, ∞), so that by adding the successive terms to the series we get an asymptotic expansion of ![]() $${\cal H}_q^{(\omega )}$$.
$${\cal H}_q^{(\omega )}$$.
Remark 3.4. In connection with the results of [12]:
(a) Let q = 0. If ω |(−∞,0] = 0, then
 $$L_q^{(\omega )} = 1$$ and (3.4) recovers [Reference Li and Palmowski12, Eq. (2.23) with ϕ = 0]. If
$$L_q^{(\omega )} = 1$$ and (3.4) recovers [Reference Li and Palmowski12, Eq. (2.23) with ϕ = 0]. If  $$\omega {|_{( - \infty ,0]}} = \phi \in (0,\infty )$$ then
$$\omega {|_{( - \infty ,0]}} = \phi \in (0,\infty )$$ then  $${\cal H}_q^{(\omega )}{|_{( - \infty ,0]}} = {{\rm{e}}^{\Phi (\phi ) \cdot }}$$ and (3.3) is seen – via W (ϕ) = W + ϕ W Ф(ϕ) ⋆ W, which may be checked by taking Laplace transforms using (2.2), and via ϕ eФ(ϕ). ⋆ W = eФ(ϕ)., which follows directly from (2.2) – to be a slight rewriting of [Reference Li and Palmowski12, Eq. (2.23) with ϕ> 0].
$${\cal H}_q^{(\omega )}{|_{( - \infty ,0]}} = {{\rm{e}}^{\Phi (\phi ) \cdot }}$$ and (3.3) is seen – via W (ϕ) = W + ϕ W Ф(ϕ) ⋆ W, which may be checked by taking Laplace transforms using (2.2), and via ϕ eФ(ϕ). ⋆ W = eФ(ϕ)., which follows directly from (2.2) – to be a slight rewriting of [Reference Li and Palmowski12, Eq. (2.23) with ϕ> 0].(b) In [Reference Li and Palmowski12, Eq. (2.25)], for real x ≤ c the ‘ ω-resolvent’ identity
 $$\int_0^\infty {{\rm{P}}_x}[\exp \{ - \int_0^t \omega ({X_u}){\kern 1pt} {\rm{d}}u\} ;{\kern 1pt} t \lt \tau _c^ + ,{X_t} \in {\rm{d}}y]{\rm{d}}t$$
$$\int_0^\infty {{\rm{P}}_x}[\exp \{ - \int_0^t \omega ({X_u}){\kern 1pt} {\rm{d}}u\} ;{\kern 1pt} t \lt \tau _c^ + ,{X_t} \in {\rm{d}}y]{\rm{d}}t$$
is formally asserted only for the case when ω |(−∞,0] is constant, but it of course prevails in full generality (with our
 $${\cal H}_0^{(\omega )}$$ replacing the H (ω) there); the proof consists only in using the resolvent identity for the two-sided exit problem [Reference Li and Palmowski12, Eq. (2.15)] and the fact that
$${\cal H}_0^{(\omega )}$$ replacing the H (ω) there); the proof consists only in using the resolvent identity for the two-sided exit problem [Reference Li and Palmowski12, Eq. (2.15)] and the fact that $${{{\cal H}_0^{(\omega )}(x)} \over {{\cal H}_0^{(\omega )}(c)}} = {\cal B}_0^{(\omega )}(x,c) = \mathop {\lim }\limits_{b \to - \infty } {{\rm{P}}_x}[\exp \{ - \int_0^{\tau _c^ + } \omega ({X_u}){\kern 1pt} {\rm{d}}u\} ;\tau _c^ + \lt \tau _b^ - ].$$
$${{{\cal H}_0^{(\omega )}(x)} \over {{\cal H}_0^{(\omega )}(c)}} = {\cal B}_0^{(\omega )}(x,c) = \mathop {\lim }\limits_{b \to - \infty } {{\rm{P}}_x}[\exp \{ - \int_0^{\tau _c^ + } \omega ({X_u}){\kern 1pt} {\rm{d}}u\} ;\tau _c^ + \lt \tau _b^ - ].$$
For this reason we omit reproducing the expression here.
(c) The approach of [Reference Li and Palmowski12] to handle the case when ω is constant on (−∞, 0] is by taking limits in the two-sided exit problem (as indicated in the previous item). We will follow an alternate, more direct, route (also inspired by [12]), which will allow us to prove the result in greater generality.
As previously indicated, we turn now to the proof of our main result. We resume providing further complements to Theorem 3.1 in Proposition 3.1 on p. 485. Below, as usual, the statement ![]() $$\tau _d^ + \downarrow \tau _c^ + as d \downarrow c'$$ means that the map
$$\tau _d^ + \downarrow \tau _c^ + as d \downarrow c'$$ means that the map ![]() $$(c,\infty )d \mapsto \tau _d^ + $$ is non-decreasing and that
$$(c,\infty )d \mapsto \tau _d^ + $$ is non-decreasing and that ![]() $$\mathop {\lim }\nolimits_{d \to c,d > c} \tau _d^ + = \tau _c^ + $$ (all pointwise). Other statements of this form are interpreted in an analogous manner.
$$\mathop {\lim }\nolimits_{d \to c,d > c} \tau _d^ + = \tau _c^ + $$ (all pointwise). Other statements of this form are interpreted in an analogous manner.
Proof of Theorem 3.1. We separate the proof into several parts. The reader who wishes (at first) only to see the main idea without being preoccupied with the technical details may proceed (first) to (•3) below.
(•1) We begin by arguing that there exists a unique function ![]() $${\cal H}_q^{(\omega )}{\kern 1pt} : {\mathbb R}{\kern 1pt} \to (0,\infty )$$ satisfying
$${\cal H}_q^{(\omega )}{\kern 1pt} : {\mathbb R}{\kern 1pt} \to (0,\infty )$$ satisfying ![]() $${\cal H}_q^{(\omega )}(0) = 1$$ and (3.1). This is basically a consequence of the strong Markov property and of the absence of positive jumps of X.
$${\cal H}_q^{(\omega )}(0) = 1$$ and (3.1). This is basically a consequence of the strong Markov property and of the absence of positive jumps of X.
Let x ≤ y ≤ c be real numbers. Since X has no positive jumps, then Px -a.s. ![]() $${X_{\tau _y^ + }} = y$$ on
$${X_{\tau _y^ + }} = y$$ on ![]() $$\{ \tau _y^ + \lt \infty \} $$, and it follows by the strong Markov property of X applied at the time
$$\{ \tau _y^ + \lt \infty \} $$, and it follows by the strong Markov property of X applied at the time ![]() $$\tau _y^ + $$, and by the memoryless property of the exponential distribution, that one has the multiplicative structure
$$\tau _y^ + $$, and by the memoryless property of the exponential distribution, that one has the multiplicative structure
Furthermore, it is clear that ![]() $${\cal B}_q^{(\omega )}(x,c) > 0$$ for all real x ≤ c. As a consequence, we may unambiguously define (with a preemptive choice of notation)
$${\cal B}_q^{(\omega )}(x,c) > 0$$ for all real x ≤ c. As a consequence, we may unambiguously define (with a preemptive choice of notation) ![]() $${\cal H}_q^{(\omega )}(x):={{{\cal B}_q^{(\omega )}(x,c)} \over {{\cal B}_q^{(\omega )}(0,c)}}$$ for real x ≤ c, c ≥ 0. In short, then,
$${\cal H}_q^{(\omega )}(x):={{{\cal B}_q^{(\omega )}(x,c)} \over {{\cal B}_q^{(\omega )}(0,c)}}$$ for real x ≤ c, c ≥ 0. In short, then, ![]() $${\cal H}_q^{(\omega )}{\kern 1pt} : {\mathbb R}{\kern 1pt} \to (0,\infty )$$,
$${\cal H}_q^{(\omega )}{\kern 1pt} : {\mathbb R}{\kern 1pt} \to (0,\infty )$$, ![]() $${\cal H}_q^{(\omega )}(0) = 1$$ and (3.1) holds. It is clear that
$${\cal H}_q^{(\omega )}(0) = 1$$ and (3.1) holds. It is clear that ![]() $${\cal H}_q^{(\omega )}$$ is unique in having the preceding properties.
$${\cal H}_q^{(\omega )}$$ is unique in having the preceding properties.
(•2) We consider statements ( I ), (II ), (III ), and (IV ). Apart from the continuity of ![]() $${\cal H}_q^{(\omega )}$$, (I), ( II ), and (II I) follow immediately from (3.1) and (1.1) and simple comparison arguments. To prove the continuity of
$${\cal H}_q^{(\omega )}$$, (I), ( II ), and (II I) follow immediately from (3.1) and (1.1) and simple comparison arguments. To prove the continuity of ![]() $${\cal H}_q^{(\omega )}$$, note that, for real c,
$${\cal H}_q^{(\omega )}$$, note that, for real c,
(r)![]() $$\tau _d^ + \downarrow \tau _c^ + as d \downarrow c'$$ (this is simply directly from the definition of the first passage times
$$\tau _d^ + \downarrow \tau _c^ + as d \downarrow c'$$ (this is simply directly from the definition of the first passage times ![]() $${(\tau _y^ + )_{y \in {\mathbb R}}}$$ involving the strict inequality >),
$${(\tau _y^ + )_{y \in {\mathbb R}}}$$ involving the strict inequality >),
and further that for x ∈ (−∞, c), by quasi-left-continuity and regularity of 0 for (0, ∞), also
(l) ![]() $$\tau _d^ + \uparrow \tau _c^ + \,{P_x}$$ -a.s. (on
$$\tau _d^ + \uparrow \tau _c^ + \,{P_x}$$ -a.s. (on ![]() $$\{ \mathop {\lim }\nolimits_{d \uparrow c} \tau _d^ + \lt \infty \} $$} and hence everywhere) as d ↑ c.
$$\{ \mathop {\lim }\nolimits_{d \uparrow c} \tau _d^ + \lt \infty \} $$} and hence everywhere) as d ↑ c.
Then item (r), the fact that ω is locally bounded, and bounded convergence in (3.1) and (1.1), immediately yield the right-continuity of ![]() $${\cal H}_q^{(\omega )}$$. Left-continuity follows similarly from item (l) in lieu of (r), except that now one notices in addition that Px -a.s. on
$${\cal H}_q^{(\omega )}$$. Left-continuity follows similarly from item (l) in lieu of (r), except that now one notices in addition that Px -a.s. on ![]() $$\{ \tau _c^ + = \infty \} $$ also
$$\{ \tau _c^ + = \infty \} $$ also ![]() $$\tau _d^ + = \infty $$ for all d < c that are sufficiently close to c (this is needed to ensure, when q = 0, the Px -a.s. convergence
$$\tau _d^ + = \infty $$ for all d < c that are sufficiently close to c (this is needed to ensure, when q = 0, the Px -a.s. convergence ![]() $${{\bf{1}}_{\{ \tau _d^ + \lt {e_q}\} }} \to {{\bf{1}}_{\{ \tau _c^ + \lt {e_q}\} }}$$ as d ↑ c also on the event
$${{\bf{1}}_{\{ \tau _d^ + \lt {e_q}\} }} \to {{\bf{1}}_{\{ \tau _c^ + \lt {e_q}\} }}$$ as d ↑ c also on the event![]() $$\{ \tau _c^ + = \infty \} $$; the issue is moot when q > 0 because then automatically
$$\{ \tau _c^ + = \infty \} $$; the issue is moot when q > 0 because then automatically ![]() $${{\rm{P}}_x}(\tau _c^ + = {e_q}) = 0$$. The latter property in turn is a consequence of the fact that the law of the overall supremum,
$${{\rm{P}}_x}(\tau _c^ + = {e_q}) = 0$$. The latter property in turn is a consequence of the fact that the law of the overall supremum, ![]() $${\overline X _\infty }$$, being exponential (2.1), has no finite atoms.
$${\overline X _\infty }$$, being exponential (2.1), has no finite atoms.
For (IV), notice that by (2.1), for real x ≤ c, ![]() $${\cal H}_q^{(\omega )}(x) \le {\cal H}_q^{(\omega )}(c){{\rm{P}}_x}(\tau _c^ + \lt {e_q}) = {\cal H}_q^{(\omega )}(c){\mathbb P}{_x}[{{\rm{e}}^{ - q\tau _c^ + }};\tau _c^ + \lt \infty ] = {\cal H}_q^{(\omega )}(c){{\rm{e}}^{ - \Phi (q)(c - x)}}$$.
$${\cal H}_q^{(\omega )}(x) \le {\cal H}_q^{(\omega )}(c){{\rm{P}}_x}(\tau _c^ + \lt {e_q}) = {\cal H}_q^{(\omega )}(c){\mathbb P}{_x}[{{\rm{e}}^{ - q\tau _c^ + }};\tau _c^ + \lt \infty ] = {\cal H}_q^{(\omega )}(c){{\rm{e}}^{ - \Phi (q)(c - x)}}$$.
(•3) We now prove (i), exploiting the marked Poisson process technique of [12]. Suppose then that ω has a left tail that is bounded and bounded below away from zero.
As a preliminary observation, note that the homogeneous convolution equation (3.3) may be checked ‘locally’, separately on each (−∞, c] for c ∈ ℝ (this is trivial); then replacing ω with ω(⋅∧c) if necessary, we may assume – by (II), and because W (q) vanishes on (−∞, 0) – without loss of generality that ω is bounded by a λ ∈ (0, ∞). Also, by assumption, there is an x 0 ∈ ℝ such that ω is bounded below away from zero on (−∞, x 0 ] by some a > 0.
Next, again let x ≤ c be real numbers. Recall the expression for the resolvent [Reference Kuznetsov, Kyprianou and Rivero10, Theorem 2.7(ii)],
for y ∈ (−∞, c], and the classical identity (2.1) ![]() $${{\rm{P}}_x}[{{\rm{e}}^{ - \lambda \tau _c^ + }};\tau _c^ + \lt {e_q}] = {{\rm{e}}^{ - \Phi (\lambda + q)(c - x)}}$$. Furthermore, let (T i)i ∈ℕ be the arrival times of a homogeneous Poisson process of intensity λ, marked by an independent sequence (M i)i∈ℕ of independent, identically, uniformly on [0 ,λ], distributed random variables, all independent of X. Then, by properties of marked Poisson processes,
$${{\rm{P}}_x}[{{\rm{e}}^{ - \lambda \tau _c^ + }};\tau _c^ + \lt {e_q}] = {{\rm{e}}^{ - \Phi (\lambda + q)(c - x)}}$$. Furthermore, let (T i)i ∈ℕ be the arrival times of a homogeneous Poisson process of intensity λ, marked by an independent sequence (M i)i∈ℕ of independent, identically, uniformly on [0 ,λ], distributed random variables, all independent of X. Then, by properties of marked Poisson processes,
 $$\matrix{
{{\cal B}_q^{(\omega )}(x,c) = {{\rm{P}}_x}({M_i} > \omega ({X_{{T_i}}}){\rm{for\,all\,i}} \in {\mathbb N}{\rm{such\,that\,}}{T_i} \lt \tau _c^ + ,\tau _c^ + \lt {e_q})} \cr
{ = {{\rm{P}}_x}({T_1} > \tau _c^ + ,\tau _c^ + \lt {e_q}) + {{\rm{P}}_x}[{\cal B}_q^{(\omega )}({X_{{T_1}}},c);{T_1} \lt \tau _c^ + \wedge {e_q},{M_1} > \omega ({X_{{T_1}}})]} \cr
{ = {{\rm{e}}^{ - \Phi (\lambda + q)(c - x)}} + \int_{ - \infty }^c {\cal B}_q^{(\omega )}(y,c)({{\rm{e}}^{ - \Phi (\lambda + q)(c - x)}}{W^{(\lambda + q)}}(c - y) - {W^{(\lambda + q)}}(x - y))(\lambda - \omega (y)){\kern 1pt} {\rm{d}}y.} \cr
} $$
$$\matrix{
{{\cal B}_q^{(\omega )}(x,c) = {{\rm{P}}_x}({M_i} > \omega ({X_{{T_i}}}){\rm{for\,all\,i}} \in {\mathbb N}{\rm{such\,that\,}}{T_i} \lt \tau _c^ + ,\tau _c^ + \lt {e_q})} \cr
{ = {{\rm{P}}_x}({T_1} > \tau _c^ + ,\tau _c^ + \lt {e_q}) + {{\rm{P}}_x}[{\cal B}_q^{(\omega )}({X_{{T_1}}},c);{T_1} \lt \tau _c^ + \wedge {e_q},{M_1} > \omega ({X_{{T_1}}})]} \cr
{ = {{\rm{e}}^{ - \Phi (\lambda + q)(c - x)}} + \int_{ - \infty }^c {\cal B}_q^{(\omega )}(y,c)({{\rm{e}}^{ - \Phi (\lambda + q)(c - x)}}{W^{(\lambda + q)}}(c - y) - {W^{(\lambda + q)}}(x - y))(\lambda - \omega (y)){\kern 1pt} {\rm{d}}y.} \cr
} $$
Further, plugging (3.1) into (3.7), multiplying both sides by ![]() $${\cal H}_q^{(\omega )}(c)$$, and rearranging, we see that
$${\cal H}_q^{(\omega )}(c)$$, and rearranging, we see that
 $$\matrix{
{0 \le {\cal H}_q^{(\omega )}(x) - \int_{ - \infty }^c {\cal H}_q^{(\omega )}(y)({{\rm{e}}^{ - \Phi (\lambda + q)(c - x)}}{W^{(\lambda + q)}}(c - y) - {W^{(\lambda + q)}}(x - y))(\lambda - \omega (y)){\kern 1pt} {\rm{d}}y} \cr
{ = {\cal H}_q^{(\omega )}(c){{\rm{e}}^{ - \Phi (\lambda + q)(c - x)}}.} \cr
} $$
$$\matrix{
{0 \le {\cal H}_q^{(\omega )}(x) - \int_{ - \infty }^c {\cal H}_q^{(\omega )}(y)({{\rm{e}}^{ - \Phi (\lambda + q)(c - x)}}{W^{(\lambda + q)}}(c - y) - {W^{(\lambda + q)}}(x - y))(\lambda - \omega (y)){\kern 1pt} {\rm{d}}y} \cr
{ = {\cal H}_q^{(\omega )}(c){{\rm{e}}^{ - \Phi (\lambda + q)(c - x)}}.} \cr
} $$
Letting c ↑∞ in (3.8), we then obtain, by monotone convergence and using (2.3), that
 $${\cal H}_q^{(\omega )} = {{\rm{e}}^{\Phi (\lambda + q) \cdot }}{h_\lambda } + ((\lambda - \omega ){\cal H}_q^{(\omega )}) \star \left({{{{\rm{e}}^{\Phi (\lambda + q) \cdot }}} \over {\psi '(\Phi (\lambda + q))}} - {W^{(\lambda + q)}}\right),$$
$${\cal H}_q^{(\omega )} = {{\rm{e}}^{\Phi (\lambda + q) \cdot }}{h_\lambda } + ((\lambda - \omega ){\cal H}_q^{(\omega )}) \star \left({{{{\rm{e}}^{\Phi (\lambda + q) \cdot }}} \over {\psi '(\Phi (\lambda + q))}} - {W^{(\lambda + q)}}\right),$$
with ![]() $${h_\lambda }:=\mathop {\lim }\nolimits_{c \to \infty } {\cal H}_q^{(\omega )}(c){{\rm{e}}^{ - \Phi (\lambda + q)c}}$$; a priori this limit must exist in [0, ∞), because the limit of the left-hand side in (3.8) exists in [0, ∞) (by monotone convergence), hence so too must the limit of the right-hand side (so the limit defining h λ is even monotone non-increasing, but we do not need this).
$${h_\lambda }:=\mathop {\lim }\nolimits_{c \to \infty } {\cal H}_q^{(\omega )}(c){{\rm{e}}^{ - \Phi (\lambda + q)c}}$$; a priori this limit must exist in [0, ∞), because the limit of the left-hand side in (3.8) exists in [0, ∞) (by monotone convergence), hence so too must the limit of the right-hand side (so the limit defining h λ is even monotone non-increasing, but we do not need this).
Note now the relations ![]() $${{\rm{e}}^{\Phi (\lambda + q) \cdot }} = \lambda {{\rm{e}}^{\Phi (\lambda + q) \cdot }} \star {W^{(q)}}$$ (which is a direct consequence of (2.2)) and W (λ +q) = W (q) + λ W (λ +q) ⋆ W (q) (which may be checked by taking Laplace transforms and again using (2.2)). They together imply that
$${{\rm{e}}^{\Phi (\lambda + q) \cdot }} = \lambda {{\rm{e}}^{\Phi (\lambda + q) \cdot }} \star {W^{(q)}}$$ (which is a direct consequence of (2.2)) and W (λ +q) = W (q) + λ W (λ +q) ⋆ W (q) (which may be checked by taking Laplace transforms and again using (2.2)). They together imply that
 $$\left({{{{\rm{e}}^{\Phi (\lambda + q) \cdot }}} \over {\psi '(\Phi (\lambda + q))}} - {W^{(\lambda + q)}}\right) \star \lambda {W^{(q)}} = \left({{{{\rm{e}}^{\Phi (\lambda + q) \cdot }}} \over {\psi '(\Phi (\lambda + q))}} - {W^{(\lambda + q)}}\right) + {W^{(q)}}.$$
$$\left({{{{\rm{e}}^{\Phi (\lambda + q) \cdot }}} \over {\psi '(\Phi (\lambda + q))}} - {W^{(\lambda + q)}}\right) \star \lambda {W^{(q)}} = \left({{{{\rm{e}}^{\Phi (\lambda + q) \cdot }}} \over {\psi '(\Phi (\lambda + q))}} - {W^{(\lambda + q)}}\right) + {W^{(q)}}.$$
Using this, we convolute both sides of (3.9) with λ W (q) to obtain
 $$\matrix{
{\lambda {\cal H}_q^{(\omega )} \star {W^{(q)}} = {{\rm{e}}^{\Phi (\lambda + q) \cdot }}{h_\lambda } + ((\lambda - \omega ){\cal H}_q^{(\omega )}) \star \left({{{{\rm{e}}^{\Phi (\lambda ) \cdot }}} \over {\psi '(\Phi (q))}} - {W^{(\lambda + q)}} + {W^{(q)}}\right)} \cr
{ = {\cal H}_q^{(\omega )} + ((\lambda - \omega ){\cal H}_q^{(\omega )}) \star {W^{(q)}}.} \cr
} $$
$$\matrix{
{\lambda {\cal H}_q^{(\omega )} \star {W^{(q)}} = {{\rm{e}}^{\Phi (\lambda + q) \cdot }}{h_\lambda } + ((\lambda - \omega ){\cal H}_q^{(\omega )}) \star \left({{{{\rm{e}}^{\Phi (\lambda ) \cdot }}} \over {\psi '(\Phi (q))}} - {W^{(\lambda + q)}} + {W^{(q)}}\right)} \cr
{ = {\cal H}_q^{(\omega )} + ((\lambda - \omega ){\cal H}_q^{(\omega )}) \star {W^{(q)}}.} \cr
} $$
Then the estimate (IV) ![]() $${{{\cal H}_q^{(\omega )}(x)} \over {{\cal H}_q^{(\omega )}({x_0})}} = {\cal B}_q^{(\omega )}(x,{x_0}) = {\cal B}_{q + a}^{((\omega - a) \vee 0)}(x,{x_0}) \le {{\rm{e}}^{ - \Phi (q + a)({x_0} - x)}}$$ for x ∈ (−∞, x 0] implies (via (2.2) and via the local boundedness of
$${{{\cal H}_q^{(\omega )}(x)} \over {{\cal H}_q^{(\omega )}({x_0})}} = {\cal B}_q^{(\omega )}(x,{x_0}) = {\cal B}_{q + a}^{((\omega - a) \vee 0)}(x,{x_0}) \le {{\rm{e}}^{ - \Phi (q + a)({x_0} - x)}}$$ for x ∈ (−∞, x 0] implies (via (2.2) and via the local boundedness of ![]() $${\cal H}_q^{(\omega )}$$ (see (I)) and of W (q)) that
$${\cal H}_q^{(\omega )}$$ (see (I)) and of W (q)) that ![]() $${\cal H}_q^{(\omega )} \star {W^{(q)}}$$ is finite-valued, and upon subtracting finite quantities we obtain (3.3). This concludes the proof of (i).
$${\cal H}_q^{(\omega )} \star {W^{(q)}}$$ is finite-valued, and upon subtracting finite quantities we obtain (3.3). This concludes the proof of (i).
(•4) We now turn to (3.2). Suppose then that (ωeФ(q +p)⋅) ⋆ W (q) is finite-valued for all p ∈ (0, ∞) (on account of (2.2) and because ω is locally bounded, this condition is satisfied when ω has a bounded left tail). The basic idea here is to reduce this case to (i) via a suitable approximation. As the reader will see, some care is needed to pass to the relevant limits.
Indeed, from (i), for each p ∈ (0, ∞) and n ∈ ℕ, one has, for all x ∈ ℝ,
 $$\matrix{
{{\cal H}_q^{(p + \omega \wedge n)}(x) = [((\omega \wedge n + p){\cal H}_q^{(p + \omega \wedge n)}) \star {W^{(q)}}](x)} \cr
{ = [((\omega \wedge n){\cal H}_q^{(p + \omega \wedge n)}) \star {W^{(q)}}](x) + p[{\cal H}_q^{(p + \omega \wedge n)} \star {W^{(q)}}](x)} \cr
{ = [\int_{ - \infty }^{0 \wedge x} + \int_0^{0 \vee x} ](\omega (y) \wedge n){\cal H}_q^{(p + \omega \wedge n)}(y){W^{(q)}}(x - y){\kern 1pt} {\rm{d}}y} \cr
{\quad + p[\int_{ - \infty }^{0 \wedge x} + \int_0^{x \vee 0} ]{\cal H}_q^{(p + \omega \wedge n)}(y){W^{(q)}}(x - y){\kern 1pt} {\rm{d}}y.} \cr
} $$
$$\matrix{
{{\cal H}_q^{(p + \omega \wedge n)}(x) = [((\omega \wedge n + p){\cal H}_q^{(p + \omega \wedge n)}) \star {W^{(q)}}](x)} \cr
{ = [((\omega \wedge n){\cal H}_q^{(p + \omega \wedge n)}) \star {W^{(q)}}](x) + p[{\cal H}_q^{(p + \omega \wedge n)} \star {W^{(q)}}](x)} \cr
{ = [\int_{ - \infty }^{0 \wedge x} + \int_0^{0 \vee x} ](\omega (y) \wedge n){\cal H}_q^{(p + \omega \wedge n)}(y){W^{(q)}}(x - y){\kern 1pt} {\rm{d}}y} \cr
{\quad + p[\int_{ - \infty }^{0 \wedge x} + \int_0^{x \vee 0} ]{\cal H}_q^{(p + \omega \wedge n)}(y){W^{(q)}}(x - y){\kern 1pt} {\rm{d}}y.} \cr
} $$
We now first pass to the limit n ↦∞ as follows. In (3.1) and (1.1),
monotone (for the integral against the Lebesgue measure)
and
bounded (for the expectation)
convergence yield ![]() $${\cal H}_q^{(p + \omega \wedge n)} \to {\cal H}_q^{(p + \omega )}$$. Then, in (3.10),
$${\cal H}_q^{(p + \omega \wedge n)} \to {\cal H}_q^{(p + \omega )}$$. Then, in (3.10),
monotone (for the integrals on [0, x∨0]; recall (III)) and
dominated (for the integrals on (−∞, 0 ∧ x], using the assumed finiteness condition and the estimate (IV) ![]() $${\cal H}_q^{(p + \omega \wedge n)}(y) \le {{\rm{e}}^{\Phi (q + p)y}}$$ for y ∈ (−∞, 0])
$${\cal H}_q^{(p + \omega \wedge n)}(y) \le {{\rm{e}}^{\Phi (q + p)y}}$$ for y ∈ (−∞, 0])
convergence produce
 $$\matrix{
{{\cal H}_q^{(p + \omega )}(x) = [(\omega {\cal H}_q^{(p + \omega )}) \star {W^{(q)}}](x) + p[{\cal H}_q^{(p + \omega )} \star {W^{(q)}}](x)} \cr
{ = [\int_{ - \infty }^{0 \wedge x} + \int_0^{0 \vee x} ]\omega (y){\cal H}_q^{(p + \omega )}(y){W^{(q)}}(x - y){\kern 1pt} {\rm{d}}y + p\int_{ - \infty }^x {\cal H}_q^{(p + \omega )}(y){W^{(q)}}(x - y){\kern 1pt} {\rm{d}}y.} \cr
} $$
$$\matrix{
{{\cal H}_q^{(p + \omega )}(x) = [(\omega {\cal H}_q^{(p + \omega )}) \star {W^{(q)}}](x) + p[{\cal H}_q^{(p + \omega )} \star {W^{(q)}}](x)} \cr
{ = [\int_{ - \infty }^{0 \wedge x} + \int_0^{0 \vee x} ]\omega (y){\cal H}_q^{(p + \omega )}(y){W^{(q)}}(x - y){\kern 1pt} {\rm{d}}y + p\int_{ - \infty }^x {\cal H}_q^{(p + \omega )}(y){W^{(q)}}(x - y){\kern 1pt} {\rm{d}}y.} \cr
} $$
Let us next write, for the purposes of the remainder of this proof only, ![]() $${\cal H}_q^{(p + \omega )} = :{\kern 1pt} {H_p}$$ and
$${\cal H}_q^{(p + \omega )} = :{\kern 1pt} {H_p}$$ and ![]() $${\cal H}_q^{(\omega )} = :{\kern 1pt} H$$ for short. We proceed to pass to the limit p ↓ 0.
$${\cal H}_q^{(\omega )} = :{\kern 1pt} H$$ for short. We proceed to pass to the limit p ↓ 0.
In (3.1) and (1.1), as before, by
bounded (for the integral against the Lebesgue measure; recall that ω is locally bounded)
and
monotone (for the expectation)
convergence, we obtain that H p ↦ H as p ↓ 0.
Then, in (3.11), [(ω H p) W (q) ](x) ↦ [(ω H) ⋆ W (q) ](x) as p ↓ 0, by
monotone (for the integral on (−∞, 0 ∧ x] ; recall (III))
and
bounded (for the integral on [0, x∨0]; use the facts that H p is non-decreasing (see (I)), that H p (c) is bounded in bounded p given a fixed c ∈ [0, ∞) (see (III)), and that W (q) and ω are locally bounded)
convergence.
Finally, we consider
a priori this limit must exist in [0, ∞), because the limits of ![]() $${\cal H}_q^{(p + \omega )}(x)$$ and
$${\cal H}_q^{(p + \omega )}(x)$$ and ![]() $$[(\omega {\cal H}_q^{(p + \omega )}) \star {W^{(q)}}](x)$$ in (3.11) have already been found to exist (and are finite, because the limit of
$$[(\omega {\cal H}_q^{(p + \omega )}) \star {W^{(q)}}](x)$$ in (3.11) have already been found to exist (and are finite, because the limit of ![]() $${\cal H}_q^{(p + \omega )}(x)$$, being
$${\cal H}_q^{(p + \omega )}(x)$$, being ![]() $${\cal H}_q^{(\omega )}(x)$$, is finite). We show that L x does not depend on x, thus demonstrating that (3.2) is indeed satisfied for some, necessarily unique,
$${\cal H}_q^{(\omega )}(x)$$, is finite). We show that L x does not depend on x, thus demonstrating that (3.2) is indeed satisfied for some, necessarily unique, ![]() $$L_q^{(\omega )} \in [0,1]$$.
$$L_q^{(\omega )} \in [0,1]$$.
Now, since W (q) is locally bounded, since H p is non-decreasing for each p ∈ (0, ∞), and since H p (c) is bounded in bounded p given a fixed real c, it is clear that for any choice of a ∈ (−∞, x],
Suppose first that ψ′ (Ф(q) +) > 0. Then, given any ∈ > 0 we may (2.3) choose this a to be (for simplicity) ≤ 0 and such as to render |W (q) (x − y)e −Ф (q)(x −y) − 1 /ψ′ (Ф(q) +) | ≤ ∈ for all y ≤ a. Consequently, since (using the estimate H p (y) ≤ eФ(q +p)y for y ≤ 0, p ∈ (0, ∞))
 $$\mathop {\limsup }\limits_{p \downarrow 0} p\int_{ - \infty }^0 {H_p}(y){{\rm{e}}^{ - \Phi (q)y}}{\kern 1pt} {\rm{d}}y \le \mathop {\lim }\limits_{p \downarrow 0} {p \over {\Phi (q + p) - \Phi (q)}} = \psi '(\Phi (q) + ) \lt \infty ,$$
$$\mathop {\limsup }\limits_{p \downarrow 0} p\int_{ - \infty }^0 {H_p}(y){{\rm{e}}^{ - \Phi (q)y}}{\kern 1pt} {\rm{d}}y \le \mathop {\lim }\limits_{p \downarrow 0} {p \over {\Phi (q + p) - \Phi (q)}} = \psi '(\Phi (q) + ) \lt \infty ,$$
we conclude that L x in fact does not depend on x.
For the case when ψ′ (Ф(q) +) = 0, i.e. the case q = Ф(q) = ψ′ (0 +) = 0, we have that ![]() $${L_x} = \mathop {\lim }\nolimits_{p \downarrow 0} p\int_{ - \infty }^a {H_p}(y)W(x - y){\kern 1pt} {\rm{d}}y$$ for any a ∈ (−∞, x]. We argue that
$${L_x} = \mathop {\lim }\nolimits_{p \downarrow 0} p\int_{ - \infty }^a {H_p}(y)W(x - y){\kern 1pt} {\rm{d}}y$$ for any a ∈ (−∞, x]. We argue that
 $$Q\mathop {\limsup }\limits_{p \downarrow 0} p\int_{ - \infty }^a {H_p}(y)(W(x - y) - W(a - y)){\kern 1pt} {\rm{d}}y = 0$$
$$Q\mathop {\limsup }\limits_{p \downarrow 0} p\int_{ - \infty }^a {H_p}(y)(W(x - y) - W(a - y)){\kern 1pt} {\rm{d}}y = 0$$
for a that are (again for simplicity) ≤ 0 ∧ x, which will complete the verification that L x does not depend on x. Indeed, since ![]() $${H_p}(y) \le {H_p}(a){{\rm{e}}^{ - \Phi (p)(a - y)}} \le {{\rm{e}}^{ - \Phi (p)(a - y)}}$$ for real y ≤ a ≤ 0 and p > 0, we have that
$${H_p}(y) \le {H_p}(a){{\rm{e}}^{ - \Phi (p)(a - y)}} \le {{\rm{e}}^{ - \Phi (p)(a - y)}}$$ for real y ≤ a ≤ 0 and p > 0, we have that
 $$\matrix{
{Q \le \mathop {\lim }\limits_{p \downarrow 0} p\int_{ - a}^\infty {{\rm{e}}^{ - \Phi (p)(y + a)}}(W(x + y) - W(a + y)){\kern 1pt} {\rm{d}}y} \cr
{ = \mathop {\lim }\limits_{p \downarrow 0} p\left[{{\rm{e}}^{\Phi (p)(x - a)}}\left({p^{ - 1}} - \int_0^{x - a} {{\rm{e}}^{ - \Phi (p)z}}W(z){\kern 1pt} {\rm{d}}z\right) - {p^{ - 1}}\right] = 0.} \cr
} $$
$$\matrix{
{Q \le \mathop {\lim }\limits_{p \downarrow 0} p\int_{ - a}^\infty {{\rm{e}}^{ - \Phi (p)(y + a)}}(W(x + y) - W(a + y)){\kern 1pt} {\rm{d}}y} \cr
{ = \mathop {\lim }\limits_{p \downarrow 0} p\left[{{\rm{e}}^{\Phi (p)(x - a)}}\left({p^{ - 1}} - \int_0^{x - a} {{\rm{e}}^{ - \Phi (p)z}}W(z){\kern 1pt} {\rm{d}}z\right) - {p^{ - 1}}\right] = 0.} \cr
} $$
(•5) The claims of (ii) follow at once from the above (in particular from (IV)) and from Lemma 3.1 below.
Regarding the uniqueness of the solutions to (3.4), we have the following lemma.
Lemma 3.1. Suppose (ωeФ(q)⋅) ⋆ W (q) is finite-valued (which occurs if ω has a subexponential left tail). Let G : ℝ ↦ ℝ be Borel measurable and locally bounded with a left tail that is Ф(q)- subexponential. Then:
(i)
 $$\mathop {\lim }\nolimits_{x \to - \infty } {{\rm{e}}^{ - \Phi (q)x}}((\omega G) \star {W^{(q)}})(x) = 0$$.
$$\mathop {\lim }\nolimits_{x \to - \infty } {{\rm{e}}^{ - \Phi (q)x}}((\omega G) \star {W^{(q)}})(x) = 0$$.(ii)
 $$G = (G\omega ) \star {W^{(q)}}$$ implies G = 0.
$$G = (G\omega ) \star {W^{(q)}}$$ implies G = 0.(iii) Further, now let g: ℝ →[0,∞] be locally bounded, Borel measurable, and with a left tail that is Ф(q)-subexponential. Suppose G ≥ 0 and G = g +(ωG) ⋆ W (q). Then G ∞:= ↑ −limn →∞ G n, where the G n are given recursively: G 0 := g and G n + 1 := g + (ωG n) ⋆ W (q) for n ∈ ℕ0.
The proof of the lemma is technical; the reader may safely skip it without it affecting their understanding of the remainder of the text.
Proof. (i). We have ![]() $$|{{\rm{e}}^{ - \Phi (q)x}}((\omega G) \star {W^{(q)}})(x)| \le \int_{ - \infty }^\infty \omega (y)|G(y)|{{\rm{e}}^{ - \Phi (q)y}}{W^{(q)}}(x - y){{\rm{e}}^{ - \Phi (q)(x - y)}}{\kern 1pt} {\rm{d}}y$$ for all x ∈ ℝ. Since G has a left tail that is Ф (q)-subexponential and since it is locally bounded, it follows that there is a γ < ∞ such that | G (y) | e− Ф(q)y ≤ γ for all y ∈ (−∞, 0] (say). Therefore, for x ∈ (−∞, 0],
$$|{{\rm{e}}^{ - \Phi (q)x}}((\omega G) \star {W^{(q)}})(x)| \le \int_{ - \infty }^\infty \omega (y)|G(y)|{{\rm{e}}^{ - \Phi (q)y}}{W^{(q)}}(x - y){{\rm{e}}^{ - \Phi (q)(x - y)}}{\kern 1pt} {\rm{d}}y$$ for all x ∈ ℝ. Since G has a left tail that is Ф (q)-subexponential and since it is locally bounded, it follows that there is a γ < ∞ such that | G (y) | e− Ф(q)y ≤ γ for all y ∈ (−∞, 0] (say). Therefore, for x ∈ (−∞, 0],
which is < ∞ by assumption. Now, by (2.3), W (q) (x − y)e −Ф(q)(x −y) is non-increasing to 0 as x ↓−∞. Thus the conclusion follows by dominated convergence.
(ii). Denote, for x ∈ ℝ, ||G||x ≔ supy∈(−∞, x] |G (y) |e−Ф(q)y. Note that this quantity is finite because G has a tail that is Ф(q)-subexponential and because it is locally bounded. Then G = (G ω) ⋆ W (q) implies that for all x ∈ ℝ we have
By (i), (ω ⋆ (e−Ф(q)⋅ W (q)))(x) = e −Ф(q)x ((ωe(q)⋅) ⋆ W (q))(x) → 0 as x ↓−∞, so there is an x 0 ∈ ℝ such that ![]() $$(\omega \star ({{\rm{e}}^{ - \Phi (q) \cdot }}{W^{(q)}}))(x) \le {I_{{x_0}}}:=(\omega \star ({{\rm{e}}^{ - \Phi (q) \cdot }}{W^{(q)}}))({x_0}) \lt 1$$ for all x ∈ (−∞, x 0]. At the same time, the above estimate implies
$$(\omega \star ({{\rm{e}}^{ - \Phi (q) \cdot }}{W^{(q)}}))(x) \le {I_{{x_0}}}:=(\omega \star ({{\rm{e}}^{ - \Phi (q) \cdot }}{W^{(q)}}))({x_0}) \lt 1$$ for all x ∈ (−∞, x 0]. At the same time, the above estimate implies ![]() $$\parallel G{\parallel _{{x_0}}} \le {I_{{x_0}}}\parallel G{\parallel _{{x_0}}}$$, hence
$$\parallel G{\parallel _{{x_0}}} \le {I_{{x_0}}}\parallel G{\parallel _{{x_0}}}$$, hence ![]() $$\parallel G{\parallel _{{x_0}}} = 0$$, which forces G to vanish on (−∞, x 0].
$$\parallel G{\parallel _{{x_0}}} = 0$$, which forces G to vanish on (−∞, x 0].
Let us now shift all the functions by x 0 for (notational) convenience; to wit, F : = G (x 0 +⋅) and θ : = ω(x 0 +⋅) are Borel measurable and locally bounded, and F = (F ⋆ θ) W (q). From this we obtain finally that F = 0 by the following argument.
Fix y 0 ∈ [0, ∞) and let θ 0 be an upper bound for θ on [0, y 0]. We may choose s 0 ∈ (0, ∞) such that ψ (s 0) − q >θ 0. Denote ||F||≔ supy∈[0, y 0] |F (y) | e −s 0y. Then, for each y ∈ [0, y 0], F = (F θ) ⋆ W (q) and (2.2) imply that
Again this renders ||F|| = 0, and completes the proof of (ii).
(iii). By induction we can prove that G n ≤ G for all n ∈ ℕ0. To see that the sequence (G n)n ∈ℕ0 is pointwise non-decreasing, define the operator ![]() $$\cal L$$, acting on Borel measurable functions h : ℝ → [0, ∞], by ℒ h: = (ω h) ⋆ W (q), and argue by induction that, for n ∈ ℕ0,
$$\cal L$$, acting on Borel measurable functions h : ℝ → [0, ∞], by ℒ h: = (ω h) ⋆ W (q), and argue by induction that, for n ∈ ℕ0, ![]() $${G_n} = \sum\nolimits_{k = 0}^n {{\cal L}^k}g$$, where for k ∈ℕ0,
$${G_n} = \sum\nolimits_{k = 0}^n {{\cal L}^k}g$$, where for k ∈ℕ0, 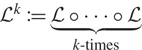 $${{\cal L}^k}:=\underbrace {{\cal L} \circ \cdots \circ {\cal L}}_{k - {\rm{times}}}$$ is the k-fold composition of the operator
$${{\cal L}^k}:=\underbrace {{\cal L} \circ \cdots \circ {\cal L}}_{k - {\rm{times}}}$$ is the k-fold composition of the operator ![]() $$\cal L$$ with itself (of course,
$$\cal L$$ with itself (of course, ![]() $$\cal L ^0$$ is just the identity operator). Then, passing to the limit in the recursion via monotone convergence, we find that G ∞ = g + (ω G ∞) ⋆ W (q). It follows that G − G ∞ has a Ф(q)-subexponential left tail, is locally bounded, Borel measurable, and satisfies G − G ∞ = ((G − G ∞) ω) ⋆ W (q). By (ii), this means that G = G ∞.
$$\cal L ^0$$ is just the identity operator). Then, passing to the limit in the recursion via monotone convergence, we find that G ∞ = g + (ω G ∞) ⋆ W (q). It follows that G − G ∞ has a Ф(q)-subexponential left tail, is locally bounded, Borel measurable, and satisfies G − G ∞ = ((G − G ∞) ω) ⋆ W (q). By (ii), this means that G = G ∞.
3.2. Further complements
As is to be expected, the solution to (1.1) is associated with a family of (local) martingales. Recall the process Y from (1.2).
Proposition 3.1. Let c ∈ℝ, γ ∈ (0, ∞). Define the processes Z = (Z t)t∈[0,∞) and V = (V s)s∈[0,∞) as follows:
 $${Z_t}:=\exp \left\{ - \int_0^t \omega ({X_u}){\kern 1pt} {\rm{d}}u - qt\right\} {\cal H}_q^{(\omega )}({X_t}),\quad t \in [0,\infty ),$$
$${Z_t}:=\exp \left\{ - \int_0^t \omega ({X_u}){\kern 1pt} {\rm{d}}u - qt\right\} {\cal H}_q^{(\omega )}({X_t}),\quad t \in [0,\infty ),$$
and
Further, let ![]() $$\cal F = {({\cal F_t})_{t \in [0,\infty )}}$$ be any right-continuous filtration relative to which X is adapted and has independent increments. Then:
$$\cal F = {({\cal F_t})_{t \in [0,\infty )}}$$ be any right-continuous filtration relative to which X is adapted and has independent increments. Then:
(i) The stopped process
 $${Z^{\tau _c^ + }}$$ is a bounded cádlág martingale in the filtration
$${Z^{\tau _c^ + }}$$ is a bounded cádlág martingale in the filtration  $$\cal F$$ under Px for each x ∈ ∝; for real x ≤ c the Px -terminal value of this martingale is
$$\cal F$$ under Px for each x ∈ ∝; for real x ≤ c the Px -terminal value of this martingale is  $${\cal H}_q^{(\omega )}(c)\exp \left\{ - \int_0^{\tau _c^ + } \omega ({X_s}){\kern 1pt} {\rm{d}}s - q\tau _c^ + \right\} {{\bf{1}}_{\{ \tau _c^ + \lt \infty \} }}$$
$${\cal H}_q^{(\omega )}(c)\exp \left\{ - \int_0^{\tau _c^ + } \omega ({X_s}){\kern 1pt} {\rm{d}}s - q\tau _c^ + \right\} {{\bf{1}}_{\{ \tau _c^ + \lt \infty \} }}$$(ii) Assume ω is strictly positive and e q is independent of
 $$\cal F _\infty$$. Then the stopped process
$$\cal F _\infty$$. Then the stopped process  $${V^{T_c^ + }}$$
is a cádlág bounded martingale in the filtration
$${V^{T_c^ + }}$$
is a cádlág bounded martingale in the filtration  $${\cal G} = ({{\cal G}_s}{)_{s \in [0,\infty )}}:={({{\cal F}_{{\rho _s}}} \vee \sigma (\{ \{ {\rho _u} \lt {e_q}\} :u \in [0,s]\} ))_{s \in [0,\infty )}}$$ under Px for each x ∈ ℝ.
$${\cal G} = ({{\cal G}_s}{)_{s \in [0,\infty )}}:={({{\cal F}_{{\rho _s}}} \vee \sigma (\{ \{ {\rho _u} \lt {e_q}\} :u \in [0,s]\} ))_{s \in [0,\infty )}}$$ under Px for each x ∈ ℝ.
Remark 3.5. As a check, since ![]() $${V^{T_c^ + }}$$ has a constant expectation, we recover (1.3) in the limit as time goes to infinity.
$${V^{T_c^ + }}$$ has a constant expectation, we recover (1.3) in the limit as time goes to infinity.
Proof of Proposition 3.1. We may assume x ≤ c.
(i). Let t ∈ [0, ∞). Then in Markov process theory parlance, with (for the purposes of this proof, and for notational simplicity only) (θ u)u∈[0,∞) being the shift operators, we have ![]() $$\tau _c^ + \wedge t + \tau _c^ + ^\circ {\theta _{\tau _c^ + \wedge t}} = \tau _c^ + \,and\,{P_x} - as $$,
$$\tau _c^ + \wedge t + \tau _c^ + ^\circ {\theta _{\tau _c^ + \wedge t}} = \tau _c^ + \,and\,{P_x} - as $$,
 $$\matrix{
{{Z_{t \wedge \tau _c^ + }} = {\cal H}_q^{(\omega )}(c){{\rm{e}}^{ - \int_0^{t \wedge \tau _c^ + } \omega ({X_u}){\kern 1pt} {\rm{d}}u - q(t \wedge \tau _c^ + )}}{{\rm{P}}_{{X_{t \wedge \tau _c^ + }}}}[\exp \{ - \int_0^{\tau _c^ + } \omega ({X_u}){\kern 1pt} {\rm{d}}u - q\tau _c^ + \} ;\tau _c^ + \lt \infty ]} \cr
{ = {\cal H}_q^{(\omega )}(c){{\rm{P}}_x}[{{\rm{e}}^{ - \int_0^{t \wedge \tau _c^ + } \omega ({X_u}){\kern 1pt} {\rm{d}}u - q(t \wedge \tau _c^ + )}}(\exp \{ - \int_0^{\tau _c^ + } \omega ({X_u}){\kern 1pt} {\rm{d}}u - q\tau _c^ + \} {{\bf{1}}_{\{ \tau _c^ + \lt \infty \} }}) \circ {\theta _{\tau _c^ + \wedge t}}{\kern 1pt} |{\kern 1pt} {{\cal F}_{t \wedge \tau _c^ + }}]} \cr
{ = {\cal H}_q^{(\omega )}(c){{\rm{P}}_x}[\exp \{ - \int_0^{\tau _c^ + } \omega ({X_u}){\kern 1pt} {\rm{d}}u - q\tau _c^ + \} {{\bf{1}}_{\{ \tau _c^ + \lt \infty \} }}{\kern 1pt} |{\kern 1pt} {{\cal F}_{t \wedge \tau _c^ + }}]} \cr
{ = {\cal H}_q^{(\omega )}(c){{\rm{P}}_x}[\exp \{ - \int_0^{\tau _c^ + } \omega ({X_u}){\kern 1pt} {\rm{d}}u - q\tau _c^ + \} {{\bf{1}}_{\{ \tau _c^ + \lt \infty \} }}{\kern 1pt} |{\kern 1pt} {{\cal F}_t}],} \cr
} $$
$$\matrix{
{{Z_{t \wedge \tau _c^ + }} = {\cal H}_q^{(\omega )}(c){{\rm{e}}^{ - \int_0^{t \wedge \tau _c^ + } \omega ({X_u}){\kern 1pt} {\rm{d}}u - q(t \wedge \tau _c^ + )}}{{\rm{P}}_{{X_{t \wedge \tau _c^ + }}}}[\exp \{ - \int_0^{\tau _c^ + } \omega ({X_u}){\kern 1pt} {\rm{d}}u - q\tau _c^ + \} ;\tau _c^ + \lt \infty ]} \cr
{ = {\cal H}_q^{(\omega )}(c){{\rm{P}}_x}[{{\rm{e}}^{ - \int_0^{t \wedge \tau _c^ + } \omega ({X_u}){\kern 1pt} {\rm{d}}u - q(t \wedge \tau _c^ + )}}(\exp \{ - \int_0^{\tau _c^ + } \omega ({X_u}){\kern 1pt} {\rm{d}}u - q\tau _c^ + \} {{\bf{1}}_{\{ \tau _c^ + \lt \infty \} }}) \circ {\theta _{\tau _c^ + \wedge t}}{\kern 1pt} |{\kern 1pt} {{\cal F}_{t \wedge \tau _c^ + }}]} \cr
{ = {\cal H}_q^{(\omega )}(c){{\rm{P}}_x}[\exp \{ - \int_0^{\tau _c^ + } \omega ({X_u}){\kern 1pt} {\rm{d}}u - q\tau _c^ + \} {{\bf{1}}_{\{ \tau _c^ + \lt \infty \} }}{\kern 1pt} |{\kern 1pt} {{\cal F}_{t \wedge \tau _c^ + }}]} \cr
{ = {\cal H}_q^{(\omega )}(c){{\rm{P}}_x}[\exp \{ - \int_0^{\tau _c^ + } \omega ({X_u}){\kern 1pt} {\rm{d}}u - q\tau _c^ + \} {{\bf{1}}_{\{ \tau _c^ + \lt \infty \} }}{\kern 1pt} |{\kern 1pt} {{\cal F}_t}],} \cr
} $$
which establishes the first claim.
(ii). For all real 0 ≤ s ≤ t, ![]() $$A\in \cal F _\rho s$$, applying the optional sampling theorem to the process
$$A\in \cal F _\rho s$$, applying the optional sampling theorem to the process ![]() $$Z ^{{\tau {{_c^ +}}}}$$ at the times ρ s and ρ t, we obtain
$$Z ^{{\tau {{_c^ +}}}}$$ at the times ρ s and ρ t, we obtain
 $$\matrix{
{{{\rm{P}}_x}[\exp \{ - \int_0^{{\rho _t} \wedge \tau _c^ + } \omega ({X_u}){\kern 1pt} {\rm{d}}u - q({\rho _t} \wedge \tau _c^ + )\} {\cal H}_q^{(\omega )}({X_{{\rho _t} \wedge \tau _c^ + }});{\kern 1pt} A \cap \{ {\rho _t} \wedge \tau _c^ + \lt \infty \} ]} \cr
{ = {{\rm{P}}_x}[\exp \{ - \int_0^{{\rho _s} \wedge \tau _c^ + } \omega ({X_u}){\kern 1pt} {\rm{d}}u - q({\rho _s} \wedge \tau _c^ + )\} {\cal H}_q^{(\omega )}({X_{{\rho _s} \wedge \tau _c^ + }});{\kern 1pt} A \cap \{ {\rho _s} \wedge \tau _c^ + \lt \infty \} ];} \cr
} $$
$$\matrix{
{{{\rm{P}}_x}[\exp \{ - \int_0^{{\rho _t} \wedge \tau _c^ + } \omega ({X_u}){\kern 1pt} {\rm{d}}u - q({\rho _t} \wedge \tau _c^ + )\} {\cal H}_q^{(\omega )}({X_{{\rho _t} \wedge \tau _c^ + }});{\kern 1pt} A \cap \{ {\rho _t} \wedge \tau _c^ + \lt \infty \} ]} \cr
{ = {{\rm{P}}_x}[\exp \{ - \int_0^{{\rho _s} \wedge \tau _c^ + } \omega ({X_u}){\kern 1pt} {\rm{d}}u - q({\rho _s} \wedge \tau _c^ + )\} {\cal H}_q^{(\omega )}({X_{{\rho _s} \wedge \tau _c^ + }});{\kern 1pt} A \cap \{ {\rho _s} \wedge \tau _c^ + \lt \infty \} ];} \cr
} $$
that is because ![]() $${\rho _t} \wedge \tau _c^ + = {\rho _t} \wedge {\rho _{T_c^ + }} = {\rho _{t \wedge T_c^ + }}$$ on
$${\rho _t} \wedge \tau _c^ + = {\rho _t} \wedge {\rho _{T_c^ + }} = {\rho _{t \wedge T_c^ + }}$$ on ![]() $$\{ {\rho _t} \wedge \tau _c^ + \lt {e_q}\} = \{ t \wedge T_c^ + \lt \zeta \} $$ since ρ is the inverse of
$$\{ {\rho _t} \wedge \tau _c^ + \lt {e_q}\} = \{ t \wedge T_c^ + \lt \zeta \} $$ since ρ is the inverse of ![]() $$\int_0^ \cdot \omega ({X_u}){\kern 1pt} {\rm{d}}u$$, and by the independence of e q from
$$\int_0^ \cdot \omega ({X_u}){\kern 1pt} {\rm{d}}u$$, and by the independence of e q from ![]() $$\cal F _\infty$$,
$$\cal F _\infty$$,
 $$\matrix{
{{{\rm{P}}_x}[\exp \{ - t \wedge T_c^ + \} {\cal H}_q^{(\omega )}({Y_{t \wedge T_c^ + }});{\kern 1pt} A \cap \{ t \wedge T_c^ + \lt \zeta \} ]} \cr
{ = {{\rm{P}}_x}[\exp \{ - s \wedge T_c^ + \} {\cal H}_q^{(\omega )}({Y_{s \wedge T_c^ + }});{\kern 1pt} A \cap \{ s \wedge T_c^ + \lt \zeta \} ].} \cr
} $$
$$\matrix{
{{{\rm{P}}_x}[\exp \{ - t \wedge T_c^ + \} {\cal H}_q^{(\omega )}({Y_{t \wedge T_c^ + }});{\kern 1pt} A \cap \{ t \wedge T_c^ + \lt \zeta \} ]} \cr
{ = {{\rm{P}}_x}[\exp \{ - s \wedge T_c^ + \} {\cal H}_q^{(\omega )}({Y_{s \wedge T_c^ + }});{\kern 1pt} A \cap \{ s \wedge T_c^ + \lt \zeta \} ].} \cr
} $$
This implies that ![]() $${({{\rm{e}}^{ - s}}{\cal H}_q^{(\omega )}({Y_s}){{\bf{1}}_{\{ s \lt \zeta \} }})_{s \in [0,\infty )}}$$
stopped at
$${({{\rm{e}}^{ - s}}{\cal H}_q^{(\omega )}({Y_s}){{\bf{1}}_{\{ s \lt \zeta \} }})_{s \in [0,\infty )}}$$
stopped at ![]() $$T_c^ + $$ is a martingale in the filtration
$$T_c^ + $$ is a martingale in the filtration ![]() $${\cal G}$$ under Px, because this process is constant on [ζ ∞), and since for s ∈ [0, ∞), { s < ζ}= {ρ s < e q } with the equality of the trace σ fields
$${\cal G}$$ under Px, because this process is constant on [ζ ∞), and since for s ∈ [0, ∞), { s < ζ}= {ρ s < e q } with the equality of the trace σ fields ![]() $${{\cal G}_s}{|_{\{ {\rho _s} \lt {e_q}\} }} = {{\cal F}_{{\rho _s}}}{|_{\{ {\rho _s} \lt {e_q}\} }}$$ holding true. Replacing ω with γω shows that the same is true of the process
$${{\cal G}_s}{|_{\{ {\rho _s} \lt {e_q}\} }} = {{\cal F}_{{\rho _s}}}{|_{\{ {\rho _s} \lt {e_q}\} }}$$ holding true. Replacing ω with γω shows that the same is true of the process ![]() $${({{\rm{e}}^{ - \gamma s}}{\cal H}_q^{(\gamma \omega )}({Y_s}){{\bf{1}}_{\{ s \lt \zeta \} }})_{s \in [0,\infty )}}$$ stopped at
$${({{\rm{e}}^{ - \gamma s}}{\cal H}_q^{(\gamma \omega )}({Y_s}){{\bf{1}}_{\{ s \lt \zeta \} }})_{s \in [0,\infty )}}$$ stopped at ![]() $$T_c^ + $$.
$$T_c^ + $$.
Apart from the solutions presented in Examples 3.1–3.4, it seems difficult to come up with ‘nice’ ω for which ![]() $${\cal H}_q^{(\omega )}$$ is given explicitly (in terms of ψ and Ф, say), at least for a general W (q). However, based on Example 3.2, we can ‘reverse engineer’ a class of ω for which
$${\cal H}_q^{(\omega )}$$ is given explicitly (in terms of ψ and Ф, say), at least for a general W (q). However, based on Example 3.2, we can ‘reverse engineer’ a class of ω for which ![]() $${\cal H}_q^{(\omega )}$$ is (semi-)explicit, in the precise sense of the following proposition.
$${\cal H}_q^{(\omega )}$$ is (semi-)explicit, in the precise sense of the following proposition.
Proposition 3.2. Let ν be a probability measure on the Borel sets of (0, ∞) , whose support is compactly contained in (0, ∞) ;q ∈ [0, ∞) is still fixed. Set
 $$w(x):={{\int {\cal H}_q^{({{\rm{e}}^{\alpha \cdot }})}(x){{\rm{e}}^{\alpha x}}\nu ({\rm{d}}\alpha )} \over {\int {\cal H}_q^{({{\rm{e}}^{\alpha \cdot }})}(x)\nu ({\rm{d}}\alpha )}},\quad x \in {\mathbb R}$$
$$w(x):={{\int {\cal H}_q^{({{\rm{e}}^{\alpha \cdot }})}(x){{\rm{e}}^{\alpha x}}\nu ({\rm{d}}\alpha )} \over {\int {\cal H}_q^{({{\rm{e}}^{\alpha \cdot }})}(x)\nu ({\rm{d}}\alpha )}},\quad x \in {\mathbb R}$$
(see Example 3.2 for an explicit expression for ![]() $${\cal H}_q^{({{\rm{e}}^{\alpha \cdot }})}$$. Then w : ℝ → ℝ is well defined, Borel measurable, and locally bounded,
$${\cal H}_q^{({{\rm{e}}^{\alpha \cdot }})}$$. Then w : ℝ → ℝ is well defined, Borel measurable, and locally bounded, ![]() $$L_q^{(w)} = \int L_q^{({{\rm{e}}^{\alpha \cdot }})}\nu ({\rm{d}}\alpha )$$, and, for x ∈ Ф
$$L_q^{(w)} = \int L_q^{({{\rm{e}}^{\alpha \cdot }})}\nu ({\rm{d}}\alpha )$$, and, for x ∈ Ф![]() $${\cal H}_q^{(w)}(x) = \int {\cal H}_q^{({{\rm{e}}^{\alpha \cdot }})}(x)\nu ({\rm{d}}\alpha )$$.
$${\cal H}_q^{(w)}(x) = \int {\cal H}_q^{({{\rm{e}}^{\alpha \cdot }})}(x)\nu ({\rm{d}}\alpha )$$.
Remark 3.6. Even though the functions ![]() $${\cal H}_q^{({{\rm{e}}^{\alpha \cdot }})}$$ are given explicitly by (3.6), because of the intricate involvement of α in
$${\cal H}_q^{({{\rm{e}}^{\alpha \cdot }})}$$ are given explicitly by (3.6), because of the intricate involvement of α in ![]() $${\cal H}_q^{({{\rm{e}}^{\alpha \cdot }})}$$ it seems impossible to actually carry out the above integrals against ν (dα) analytically (unless of course ν is finitely supported, in which case the integrals turn into sums).
$${\cal H}_q^{({{\rm{e}}^{\alpha \cdot }})}$$ it seems impossible to actually carry out the above integrals against ν (dα) analytically (unless of course ν is finitely supported, in which case the integrals turn into sums).
Proof of Proposition 3.2. To ease the notation, set: for α ∈ (0, ∞), ![]() $${\cal H}_q^\alpha :={\cal H}_q^{({{\rm{e}}^{\alpha \cdot }})}$$ and
$${\cal H}_q^\alpha :={\cal H}_q^{({{\rm{e}}^{\alpha \cdot }})}$$ and ![]() $$L_q^\alpha :=L_q^{({{\rm{e}}^{\alpha \cdot }})}$$;
$$L_q^\alpha :=L_q^{({{\rm{e}}^{\alpha \cdot }})}$$; ![]() $$L:=\int L_q^\alpha \nu ({\rm{d}}\alpha )$$ and for x ∈ ℝ,
$$L:=\int L_q^\alpha \nu ({\rm{d}}\alpha )$$ and for x ∈ ℝ, ![]() $$H(x):=\int {\cal H}_q^\alpha (x)\nu ({\rm{d}}\alpha )$$. From the explicit form of
$$H(x):=\int {\cal H}_q^\alpha (x)\nu ({\rm{d}}\alpha )$$. From the explicit form of ![]() $${\cal H}_q^\alpha $$ given in Example 3.2 we see that H : ℝ → (0, ∞] is well defined and Borel measurable. Also, the fact that ν has a support bounded from above ensures, via Theorem 3.1, items (I) and (II I), that H is locally bounded, and in particular it is finite; then, w : ℝ → (0, ∞) is well defined, Borel measurable, and locally bounded (the latter again because the support of ν is bounded from above).
$${\cal H}_q^\alpha $$ given in Example 3.2 we see that H : ℝ → (0, ∞] is well defined and Borel measurable. Also, the fact that ν has a support bounded from above ensures, via Theorem 3.1, items (I) and (II I), that H is locally bounded, and in particular it is finite; then, w : ℝ → (0, ∞) is well defined, Borel measurable, and locally bounded (the latter again because the support of ν is bounded from above).
Further, we know that ![]() $${\cal H}_q^\alpha = L_q^\alpha {{\rm{e}}^{\Phi (q) \cdot }} + ({{\rm{e}}^{\alpha \cdot }}{\cal H}_q^\alpha ) \star {W^{(q)}}$$ for each α ∈ (0, ∞). Integrating both sides against ν (dα) we obtain, via Tonelli’s theorem,
$${\cal H}_q^\alpha = L_q^\alpha {{\rm{e}}^{\Phi (q) \cdot }} + ({{\rm{e}}^{\alpha \cdot }}{\cal H}_q^\alpha ) \star {W^{(q)}}$$ for each α ∈ (0, ∞). Integrating both sides against ν (dα) we obtain, via Tonelli’s theorem, ![]() $$H = L{{\rm{e}}^{\Phi (q) \cdot }} + (Hw) \star {W^{(q)}}$$. At the same time, for x ∈(−∞, 0]
$$H = L{{\rm{e}}^{\Phi (q) \cdot }} + (Hw) \star {W^{(q)}}$$. At the same time, for x ∈(−∞, 0] ![]() $${{\rm{e}}^{ - \Phi (q)x}}H(x) = \int {\cal H}_q^\alpha (x){{\rm{e}}^{ - \Phi (q)x}}\nu ({\rm{d}}\alpha ) \le 1$$, so H has a left tail that is Ф(q)-subexponential. Next, because the support of ν is bounded from below away from zero, w has a subexponential left tail. By Lemma 3.1, we obtain
$${{\rm{e}}^{ - \Phi (q)x}}H(x) = \int {\cal H}_q^\alpha (x){{\rm{e}}^{ - \Phi (q)x}}\nu ({\rm{d}}\alpha ) \le 1$$, so H has a left tail that is Ф(q)-subexponential. Next, because the support of ν is bounded from below away from zero, w has a subexponential left tail. By Lemma 3.1, we obtain ![]() $$H = {L \over {L_q^{(w)}}}{\cal H}_q^{(w)}$$. But we also have
$$H = {L \over {L_q^{(w)}}}{\cal H}_q^{(w)}$$. But we also have ![]() $$H(1) = 1 = {\cal H}_q^{(w)}(1)$$, hence
$$H(1) = 1 = {\cal H}_q^{(w)}(1)$$, hence ![]() $$L = L_q^{(w)}$$, and the proof is complete.
$$L = L_q^{(w)}$$, and the proof is complete.
Another fairly general class of ω that can be handled with some success is considered in the following remark.
Remark 3.7. Let P be a real polynomial, α ∈ (0, ∞), and c ∈ ℝ. Suppose that ω(x) = P (x)eα x for all x ∈ (−∞, c]. Then the recursion of Theorem 3.1 (ii) can, on (−∞, c], be successively computed in essentially closed form; we obtain algebraic expressions involving only ψ and its higher-order derivatives. This is because, together with the Laplace transform of W (q) (2.2) that is given in terms of ψ, we can also obtain via successive differentiation expressions for its higher-order derivatives. In a similar vein, if c < 0 and ω(x) = P (1 / x)e α x for x ∈ (−∞, c], then we get iterated integrals involving ψ (cf. Example 3.4).
Finally, when given a concrete W (q), it may of course very well happen that for a specific form of ω, the convolution equation of Theorem 3.1 (ii) admits an explicit solution (even as it fails to do so for a general W (q)). A flavor of this is given in the next section.
4. Application to a model for the price of a financial asset
4.1. The model
Assume ω> 0. We consider the process S defined by
as a model for the price of a (speculative) financial asset (here, Y is the process from (1.2)). When ω = 1 then ζ = e q, Y = X on [0, e q), and S is nothing but the classical exponential Lévy model for the price of a risky asset (defaulted at ζ); see [Reference Tankov19] for a recent review. The idea in allowing a more general ω is that the asset price may ‘move faster or slower along its trajectory’, depending on the price level, destroying the stationary independent increments property of the log-returns but preserving their Markovian character. Using time-changed Lévy processes to model financial assets is not new, of course – see, e.g., [Reference Carr and WU2, Reference Klingler, Kim, Rachev and Fabozzi9]. We set Qz ≔ Plog z, z ∈ (0, ∞), for convenience.
4.2. The optimization problem
Suppose in the above setting that we are interested in the simple problem of the determination of the optimal level b at which to sell the asset, having bought it at the level z ∈ (0, ∞), under an inflation/impatience rate γ ∈ (0, ∞). In other words, if we let, for b ∈ (0, ∞), ![]() $$R_b^ + :=\inf \{ s \in (0,\infty ){\kern 1pt} :{\kern 1pt} {S_s} > b\} $$ denote the first hitting time of the set (b, ∞) by the process S, then we would like a solution to the problem
$$R_b^ + :=\inf \{ s \in (0,\infty ){\kern 1pt} :{\kern 1pt} {S_s} > b\} $$ denote the first hitting time of the set (b, ∞) by the process S, then we would like a solution to the problem
(More generally, we may simply be interested in ![]() $$\cal A{(b)}$$ itself if we are predetermined to sell at the level b ∈ [ z, ∞).)
$$\cal A{(b)}$$ itself if we are predetermined to sell at the level b ∈ [ z, ∞).)
Remark 4.1. Because of the regularity of 0 for (0, ∞), on account of the quasi-left-continuity, and by the strong Markov property (all for the process X), for each c ∈ ℝ, a.s. ![]() $$\tau _c^ + = \inf \{ t \in [0,\infty ){\kern 1pt} :{\kern 1pt} {X_t} > c\} = \inf \{ t \in [0,\infty ){\kern 1pt} :{\kern 1pt} {X_t} \ge c\} = \inf \{ t \in [0,\infty ){\kern 1pt} :{\kern 1pt} {X_{t - }} \vee {X_t} \ge c\} $$ (where, as usual, X 0− = X 0). This implies analogous a.s. equalities for the times
$$\tau _c^ + = \inf \{ t \in [0,\infty ){\kern 1pt} :{\kern 1pt} {X_t} > c\} = \inf \{ t \in [0,\infty ){\kern 1pt} :{\kern 1pt} {X_t} \ge c\} = \inf \{ t \in [0,\infty ){\kern 1pt} :{\kern 1pt} {X_{t - }} \vee {X_t} \ge c\} $$ (where, as usual, X 0− = X 0). This implies analogous a.s. equalities for the times ![]() $$R_b^ + $$, b ∈ (0, α) , and the process S.
$$R_b^ + $$, b ∈ (0, α) , and the process S.
But, for b ∈ [ z, ∞), since ![]() $${S_{R_b^ + }} = b$$ on
$${S_{R_b^ + }} = b$$ on ![]() $$\{ R_b^ + \lt \infty \} $$,
$$\{ R_b^ + \lt \infty \} $$,
 $$ = b{\cal B}_q^{(\gamma \omega )}(\log z,\log b) = b{{{\cal H}_q^{(\gamma \omega )}(\log z)} \over {{\cal H}_q^{(\gamma \omega )}(\log b)}}.$$
$$ = b{\cal B}_q^{(\gamma \omega )}(\log z,\log b) = b{{{\cal H}_q^{(\gamma \omega )}(\log z)} \over {{\cal H}_q^{(\gamma \omega )}(\log b)}}.$$
Hence, (4.1) is intimately related to the determination of the quantity (1.1).
Remark 4.2. More difficult is the optimal stopping problem
where T ranges over all stopping times (of the completed natural filtration) of S, i.e. we maximize the optimal selling time over all stopping rules of S, not just the first upcrossing times ![]() $${(R_b^ + )_{b \in [z,\infty )}}$$ as in (4.1). On the level of the process X it corresponds to
$${(R_b^ + )_{b \in [z,\infty )}}$$ as in (4.1). On the level of the process X it corresponds to
where τ ranges over all stopping times (of the completed natural filtration) of X (progressively enlarged by e q).
Now, for the case q = 0 (without loss of generality), such problems have recently been studied (in even greater generality: allowing an additive functional A of X in place of ![]() $$\int_0^ \cdot \gamma \omega ({X_u}){\kern 1pt} {\rm{d}}u$$; a general Lévy process for X; f (X τ) in place of eX τ for a lower semi-continuous map f) in [13]. In the latter paper, sufficient conditions for the optimality of a first upcrossing time were provided [Reference Long and Zhang13, Theorem 2.1], these being further strengthened in the spectrally negative case [Reference Long and Zhang13, Theorem 2.2]. In our present case, [Reference Long and Zhang13, Assumption 2.1] requires that
$$\int_0^ \cdot \gamma \omega ({X_u}){\kern 1pt} {\rm{d}}u$$; a general Lévy process for X; f (X τ) in place of eX τ for a lower semi-continuous map f) in [13]. In the latter paper, sufficient conditions for the optimality of a first upcrossing time were provided [Reference Long and Zhang13, Theorem 2.1], these being further strengthened in the spectrally negative case [Reference Long and Zhang13, Theorem 2.2]. In our present case, [Reference Long and Zhang13, Assumption 2.1] requires that
(C 1): either X drifts to −∞, or else ![]() $${{\rm{P}}_x}(\int_0^\infty \omega ({X_u}){\kern 1pt} {\rm{d}}u = \infty ) = 1$$ for all x ∈ R (in the case when X drifts to ∞ the latter is equivalent to
$${{\rm{P}}_x}(\int_0^\infty \omega ({X_u}){\kern 1pt} {\rm{d}}u = \infty ) = 1$$ for all x ∈ R (in the case when X drifts to ∞ the latter is equivalent to ![]() $$\int^\infty \omega (y){\kern 1pt} {\rm{d}}y = \infty $$ [Reference DöRing and Kyprianou5, Theorem 1]).
$$\int^\infty \omega (y){\kern 1pt} {\rm{d}}y = \infty $$ [Reference DöRing and Kyprianou5, Theorem 1]).
When this is so, [Reference Long and Zhang13, Theorem 2.2] provides relatively explicit sufficient conditions under which a first upcrossing time from the family ![]() $${(\tau _c^ + )_{c \in {\mathbb R}}}$$ is optimal in (**). Indeed, let e be an exponential random time of mean 1, independent of X, and set
$${(\tau _c^ + )_{c \in {\mathbb R}}}$$ is optimal in (**). Indeed, let e be an exponential random time of mean 1, independent of X, and set ![]() $$\tilde \eta :={\rho _{{\rm{e}}/\gamma }}$$. We then have, for real x < z,
$$\tilde \eta :={\rho _{{\rm{e}}/\gamma }}$$. We then have, for real x < z,
 $$\matrix{
{{{\rm{P}}_x}({{\overline X }_{\tilde \eta }} > z) = {{\rm{P}}_x}({{\overline X }_{{\rho _{{\rm{e/}}\gamma }}}} > z) = {{\rm{P}}_x}(\tau _z^ + \lt {\rho _{{\rm{e/}}\gamma }}) = {{\rm{P}}_x}(\int_0^{\tau _z^ + } \gamma \omega ({X_u}){\kern 1pt} {\rm{d}}u \lt {\rm{e}},\tau _z^ + \lt \infty )} \cr
{ = {{\rm{P}}_x}[\exp \{ - \int_0^{\tau _z^ + } \gamma \omega ({X_u}){\kern 1pt} {\rm{d}}u\} ;{\kern 1pt} \tau _z^ + \lt \infty ] = {\cal B}_0^{(\gamma \omega )}(x,z) = {{{\cal H}_0^{(\gamma \omega )}(x)} \over {{\cal H}_0^{(\gamma \omega )}(z)}}} \cr
} $$
$$\matrix{
{{{\rm{P}}_x}({{\overline X }_{\tilde \eta }} > z) = {{\rm{P}}_x}({{\overline X }_{{\rho _{{\rm{e/}}\gamma }}}} > z) = {{\rm{P}}_x}(\tau _z^ + \lt {\rho _{{\rm{e/}}\gamma }}) = {{\rm{P}}_x}(\int_0^{\tau _z^ + } \gamma \omega ({X_u}){\kern 1pt} {\rm{d}}u \lt {\rm{e}},\tau _z^ + \lt \infty )} \cr
{ = {{\rm{P}}_x}[\exp \{ - \int_0^{\tau _z^ + } \gamma \omega ({X_u}){\kern 1pt} {\rm{d}}u\} ;{\kern 1pt} \tau _z^ + \lt \infty ] = {\cal B}_0^{(\gamma \omega )}(x,z) = {{{\cal H}_0^{(\gamma \omega )}(x)} \over {{\cal H}_0^{(\gamma \omega )}(z)}}} \cr
} $$
(here, ![]() $$\overline X $$ is the running supremum process of X), i.e. the ‘hazard rate’ of
$$\overline X $$ is the running supremum process of X), i.e. the ‘hazard rate’ of ![]() $${\overline X _{\tilde \eta }}$$ is equal to (cf. [Reference Long and Zhang13, Assumption 2.2])
$${\overline X _{\tilde \eta }}$$ is equal to (cf. [Reference Long and Zhang13, Assumption 2.2])
 $${\Lambda ^{(\gamma \omega )}}(z) :=- {{\rm{d}} \over {{\rm{d}}z}}\log {{\rm{P}}_x}({\overline X _{\tilde \eta }} > z) = {{\rm{d}} \over {{\rm{d}}z}}\log ({\cal H}_0^{(\gamma \omega )}(z)) = {{{\cal H}_0^{(\gamma \omega )'}(z)} \over {{\cal H}_0^{(\gamma \omega )}(z)}},\quad z \in {\mathbb R},$$
$${\Lambda ^{(\gamma \omega )}}(z) :=- {{\rm{d}} \over {{\rm{d}}z}}\log {{\rm{P}}_x}({\overline X _{\tilde \eta }} > z) = {{\rm{d}} \over {{\rm{d}}z}}\log ({\cal H}_0^{(\gamma \omega )}(z)) = {{{\cal H}_0^{(\gamma \omega )'}(z)} \over {{\cal H}_0^{(\gamma \omega )}(z)}},\quad z \in {\mathbb R},$$
when the derivative of ![]() $${\cal H}_0^{(\gamma \omega )}$$ exists, which we now assume it does. If, further,
$${\cal H}_0^{(\gamma \omega )}$$ exists, which we now assume it does. If, further, ![]() $${\cal H}_0^{(\gamma \omega )}$$ is absolutely continuous, which occurs if
$${\cal H}_0^{(\gamma \omega )}$$ is absolutely continuous, which occurs if ![]() $${\cal H}_0^{(\gamma \omega )'}$$ is locally bounded or even continuous [Reference Yeh21, Theorem 13.18], then it follows by the fundamental theorem of calculus that
$${\cal H}_0^{(\gamma \omega )'}$$ is locally bounded or even continuous [Reference Yeh21, Theorem 13.18], then it follows by the fundamental theorem of calculus that ![]() $${\Lambda ^{(\gamma \omega )}} \in L_{{\rm{loc}}}^1({\mathbb R})$$, while
$${\Lambda ^{(\gamma \omega )}} \in L_{{\rm{loc}}}^1({\mathbb R})$$, while ![]() $$\int^\infty {\Lambda ^{(\gamma \omega )}} = \infty $$ (recall (C 1)). Suppose for simplicity (for absolutely minimal conditions that apply in the context of [Reference Long and Zhang13] the reader is asked to consult the latter reference directly) that
$$\int^\infty {\Lambda ^{(\gamma \omega )}} = \infty $$ (recall (C 1)). Suppose for simplicity (for absolutely minimal conditions that apply in the context of [Reference Long and Zhang13] the reader is asked to consult the latter reference directly) that
![]() $$({C_2}):{\cal H}_0^{(\gamma \omega )}$$ is continuously differentiable with a derivative that has no zeros.
$$({C_2}):{\cal H}_0^{(\gamma \omega )}$$ is continuously differentiable with a derivative that has no zeros.
Set ![]() $${{\cal K}^{(\gamma \omega )}}(x):={{\rm{e}}^x}(1 - {{{\cal H}_0^{(\gamma \omega )}(x)} \over {{\cal H}_0^{(\gamma \omega )'}(x)}})$$ for x ∈ ℝ. Then, according to [Reference Long and Zhang13, Theorem 2.2, Assumption 2.3, Lemma 2.2], if
$${{\cal K}^{(\gamma \omega )}}(x):={{\rm{e}}^x}(1 - {{{\cal H}_0^{(\gamma \omega )}(x)} \over {{\cal H}_0^{(\gamma \omega )'}(x)}})$$ for x ∈ ℝ. Then, according to [Reference Long and Zhang13, Theorem 2.2, Assumption 2.3, Lemma 2.2], if
(C 3): there exists a (necessarily unique) x * ∈ [−∞, ∞ ] such that the function ![]() $${{\cal K}^{(\gamma \omega )}}{\kern 1pt} : {\mathbb R}{\kern 1pt} \to {\mathbb R}$$ is > 0 and non-decreasing on (x *, ∞), and is ≤ 0 on (−∞, x *),
$${{\cal K}^{(\gamma \omega )}}{\kern 1pt} : {\mathbb R}{\kern 1pt} \to {\mathbb R}$$ is > 0 and non-decreasing on (x *, ∞), and is ≤ 0 on (−∞, x *),
then 0 is optimal, ![]() $$\tau _{{x^*}}^ + $$ is optimal, or
$$\tau _{{x^*}}^ + $$ is optimal, or ![]() $${(\tau _n^ + )_{n \in {\mathbb N}}}$$ is an optimizing sequence in (**) according as x * = −∞, x * ∈ ℝ, or x * = ∞.
$${(\tau _n^ + )_{n \in {\mathbb N}}}$$ is an optimizing sequence in (**) according as x * = −∞, x * ∈ ℝ, or x * = ∞.
Generally speaking, it appears to be a non-trivial matter to ascertain whether and when the conditions (C 1), (C 2), and (C 3) are met. We leave investigating this for future research. In particular, without further qualifications, we make no claim that an optimizer in (4.1) is also a general optimal selling rule (it is merely optimal in the class of first upcrossing passage times). We can, however, make the following immediate observations concerning (C 2) and (C 3) (leaving aside (C 1), whose validity or non-validity is not difficult to check, except possibly when X oscillates).
Let γ = 1 without loss of generality. By standard excursion-theoretic arguments (see, e.g., [Reference Vidmar20, p. 13, proof of Lemma 3.6] and [Reference Kuznetsov, Kyprianou and Rivero10, Section 2.3]) we obtain the following representation of the quantity ![]() $${\cal B}_0^{(\omega )}(x,c)$$ for real x ≤ c (incidentally, it is true even if ω is not strictly positive):
$${\cal B}_0^{(\omega )}(x,c)$$ for real x ≤ c (incidentally, it is true even if ω is not strictly positive):
 $${{{\cal H}_0^{(\omega )}(x)} \over {{\cal H}_0^{(\omega )}(c)}} = {\cal B}_0^{(\omega )}(x,c) = {{\rm{e}}^{ - \int_x^c \omega (y){\kern 1pt} {\rm{d}}y/\delta }}\exp \{ - \int_x^c {\rm{n}}[1 - {{\rm{e}}^{ - \int_0^\chi \omega (g + {\xi _u}){\kern 1pt} {\rm{d}}u}}{{\bf{1}}_{\{ \chi \lt \infty \} }}]{\kern 1pt} {\rm{d}}g\} ,$$
$${{{\cal H}_0^{(\omega )}(x)} \over {{\cal H}_0^{(\omega )}(c)}} = {\cal B}_0^{(\omega )}(x,c) = {{\rm{e}}^{ - \int_x^c \omega (y){\kern 1pt} {\rm{d}}y/\delta }}\exp \{ - \int_x^c {\rm{n}}[1 - {{\rm{e}}^{ - \int_0^\chi \omega (g + {\xi _u}){\kern 1pt} {\rm{d}}u}}{{\bf{1}}_{\{ \chi \lt \infty \} }}]{\kern 1pt} {\rm{d}}g\} ,$$
where the first factor appears only when X has paths of finite variation, in which case δ is the drift of X, and where n is the (suitably normalized) excursion measure for excursions away from the maximum of X, ξ is the canonical process, and χ ≔ inf{ u ∈ (0, ∞): ξ u ≥ 0 } is the lifetime of the excursions. Now, if ω is continuous and has a bounded left tail then, by dominated convergence, the map ![]() $${\mathbb R} \ni g \mapsto {\rm{n}}[1 - {{\rm{e}}^{ - \int_0^\chi \omega (g + {\xi _u}){\kern 1pt} {\rm{d}}u}}{{\bf{1}}_{\{ \chi \lt \infty \} }}]$$ is continuous so that (4.3) implies, via the fundamental theorem of calculus, that
$${\mathbb R} \ni g \mapsto {\rm{n}}[1 - {{\rm{e}}^{ - \int_0^\chi \omega (g + {\xi _u}){\kern 1pt} {\rm{d}}u}}{{\bf{1}}_{\{ \chi \lt \infty \} }}]$$ is continuous so that (4.3) implies, via the fundamental theorem of calculus, that
 $${{{\cal H}_0^{(\omega )'}(x)} \over {{\cal H}_0^{(\omega )}(x)}} = {{\omega (x)} \over \delta } + {\rm{n}}[1 - {{\rm{e}}^{ - \int_0^\chi \omega (x + {\xi _u}){\kern 1pt} {\rm{d}}u}}{{\bf{1}}_{\{ \chi \lt \infty \} }}],\quad x \in {\mathbb R},$$
$${{{\cal H}_0^{(\omega )'}(x)} \over {{\cal H}_0^{(\omega )}(x)}} = {{\omega (x)} \over \delta } + {\rm{n}}[1 - {{\rm{e}}^{ - \int_0^\chi \omega (x + {\xi _u}){\kern 1pt} {\rm{d}}u}}{{\bf{1}}_{\{ \chi \lt \infty \} }}],\quad x \in {\mathbb R},$$
(again, the first term appears only when X has paths of finite variation); ![]() $${\cal H}_0^{(\omega )'}$$ therefore exists, is continuous, and has no zeros (the latter because ω> 0), i.e. (C 2) obtains. Besides, if in addition ω is non-decreasing (resp. non-increasing, strictly increasing on a neighborhood of −∞ and non-decreasing, strictly decreasing on a neighborhood of −∞ and non-increasing), then
$${\cal H}_0^{(\omega )'}$$ therefore exists, is continuous, and has no zeros (the latter because ω> 0), i.e. (C 2) obtains. Besides, if in addition ω is non-decreasing (resp. non-increasing, strictly increasing on a neighborhood of −∞ and non-decreasing, strictly decreasing on a neighborhood of −∞ and non-increasing), then ![]() $${\mathbb R} \ni x \mapsto 1 - {{{\cal H}_0^{(\omega )}(x)} \over {{\cal H}_0^{(\omega )'}(x)}}$$ is non-decreasing (resp. non-increasing, strictly increasing, strictly decreasing). Hence, if ω is strictly increasing and bounded on a neighborhood of −∞, continuous, and non-decreasing, then there exists a (necessarily unique) x * ∈ [−∞, ∞ ] such that the function
$${\mathbb R} \ni x \mapsto 1 - {{{\cal H}_0^{(\omega )}(x)} \over {{\cal H}_0^{(\omega )'}(x)}}$$ is non-decreasing (resp. non-increasing, strictly increasing, strictly decreasing). Hence, if ω is strictly increasing and bounded on a neighborhood of −∞, continuous, and non-decreasing, then there exists a (necessarily unique) x * ∈ [−∞, ∞ ] such that the function ![]() $${\mathbb R} \ni x \mapsto 1 - {{{\cal H}_0^{(\omega )}(x)} \over {{\cal H}_0^{(\omega )'}(x)}}$$ is > 0 on (x *, ∞) and is < 0 on (−∞, x *); with this x *, condition (C 3) is met.
$${\mathbb R} \ni x \mapsto 1 - {{{\cal H}_0^{(\omega )}(x)} \over {{\cal H}_0^{(\omega )'}(x)}}$$ is > 0 on (x *, ∞) and is < 0 on (−∞, x *); with this x *, condition (C 3) is met.
Remark 4.3. For another similar optimal stopping problem see [17]; the first upcrossing times were found therein to be not always optimal.
4.3. Analysis in some special cases
If ω = 1 then, because of the martingale property of (exp{X t − Ψ (1) t})t∈[0, ∞) and on account of the optional sampling theorem, ![]() $${\cal A} (b) $$ is monotone in b ∈ [ z, ∞) and the problem (4.1) is trivial. However, for a general ω this is no longer true, as we will see in an example shortly. To this end we specialize now to the case when
$${\cal A} (b) $$ is monotone in b ∈ [ z, ∞) and the problem (4.1) is trivial. However, for a general ω this is no longer true, as we will see in an example shortly. To this end we specialize now to the case when
As a possible rationale for such a choice we can imagine that the asset moves faster along its trajectory at smaller price levels, reflecting that the investors are then more jittery, increasing the velocity of the trades.
Remark 4.4. With the ω of (4.4), condition (C 1) of Remark 4.2 is always met; it is only not clear when X oscillates, and in that case we see that ![]() $$\int_0^\infty \omega ({X_u}){\kern 1pt} {\rm{d}}u = \infty $$ a.s., because a.s. X will spend an infinite Lebesgue amount of time in [0, ∞) (in turn, we can convince ourselves of the latter as follows: every time the process X goes above the level 1, it will take it a strictly positive amount of time to pass below 0; because X oscillates it will do this infinitely often, and by the strong Markov property and the absence of positive jumps for X, these successive sojourn times of X – between hitting the level 1 and then going below 0 – will be independent and identically distributed and now the claim follows by the strong law of large numbers). In addition, by the discussion at the end of Remark 4.2, conditions (C 2) and (C 3) for an as yet unknown x * also obtain.
$$\int_0^\infty \omega ({X_u}){\kern 1pt} {\rm{d}}u = \infty $$ a.s., because a.s. X will spend an infinite Lebesgue amount of time in [0, ∞) (in turn, we can convince ourselves of the latter as follows: every time the process X goes above the level 1, it will take it a strictly positive amount of time to pass below 0; because X oscillates it will do this infinitely often, and by the strong Markov property and the absence of positive jumps for X, these successive sojourn times of X – between hitting the level 1 and then going below 0 – will be independent and identically distributed and now the claim follows by the strong law of large numbers). In addition, by the discussion at the end of Remark 4.2, conditions (C 2) and (C 3) for an as yet unknown x * also obtain.
We have chosen the ω of (4.4) because as a consequence we can now be quite explicit about the nature of ![]() $${\cal H}_q^{(\gamma \omega )} = :{\kern 1pt} H$$. Denote
$${\cal H}_q^{(\gamma \omega )} = :{\kern 1pt} H$$. Denote ![]() $$L : = L_q^{(\gamma \omega )}$$, and by P the Patie scale function (3.6) of Example 3.2, so that
$$L : = L_q^{(\gamma \omega )}$$, and by P the Patie scale function (3.6) of Example 3.2, so that ![]() $$L = (\sum\nolimits_{k = 0}^\infty {a_k}{\gamma ^k}{)^{ - 1}}$$ and
$$L = (\sum\nolimits_{k = 0}^\infty {a_k}{\gamma ^k}{)^{ - 1}}$$ and
 $$P(x) = L{{\rm{e}}^{\Phi (q)x}}\sum\limits_{k = 0}^\infty {a_k}{(\gamma {{\rm{e}}^{\alpha x}})^k},\quad x \in {\mathbb R}, $$
$$P(x) = L{{\rm{e}}^{\Phi (q)x}}\sum\limits_{k = 0}^\infty {a_k}{(\gamma {{\rm{e}}^{\alpha x}})^k},\quad x \in {\mathbb R}, $$
where we have set ![]() $${a_k} : = {(\prod\nolimits_{l = 1}^k (\psi (\Phi (q) + l\alpha ) - q))^{ - 1}}$$ for k ∈ ℕ0. Then, by Theorem 3.1(II), H = P on (−∞, 0], while by Theorem 3.1(ii), for x∈[0,∞),
$${a_k} : = {(\prod\nolimits_{l = 1}^k (\psi (\Phi (q) + l\alpha ) - q))^{ - 1}}$$ for k ∈ ℕ0. Then, by Theorem 3.1(II), H = P on (−∞, 0], while by Theorem 3.1(ii), for x∈[0,∞),
where
 $$h(x) := L{{\rm{e}}^{\Phi (q)x}} + \gamma \int_{ - \infty }^0 {{\rm{e}}^{\alpha y}}P(y){W^{(q)}}(x - y){\kern 1pt} {\rm{d}}y,\quad x \in [0,\infty ).$$
$$h(x) := L{{\rm{e}}^{\Phi (q)x}} + \gamma \int_{ - \infty }^0 {{\rm{e}}^{\alpha y}}P(y){W^{(q)}}(x - y){\kern 1pt} {\rm{d}}y,\quad x \in [0,\infty ).$$
As in the proof of Lemma 3.1 we see that, on [0,∞), H = ↑− limn →∞ H n where H 0 := h, and then recursively H n+1 = h + γ H n ⋆ W (q) for n ∈ ℕ0, the latter convolution being now on [0, ∞). Taking Laplace transforms on [0, ∞) in (4.6) (denoting them by a hat) and using (2.2), it is also true that ![]() $$\hat H(s) = \hat h(s) + \gamma \hat H(s)/(\psi (s) - q)$$, and hence
$$\hat H(s) = \hat h(s) + \gamma \hat H(s)/(\psi (s) - q)$$, and hence
(using Theorem 3.1(III) and the known solution for ω =1, it is easily checked that ![]() $$\hat H(s) \lt \infty $$ for S ∈(Ф(q + γ), ∞)).
$$\hat H(s) \lt \infty $$ for S ∈(Ф(q + γ), ∞)).
Now, if q + γ <ψ (1) then a comparison argument (with ω = 1) shows that ![]() $${\cal A} (b) \to \infty $$ as b → ∞. However, it does not in general seem obvious how to analytically determine an optimal b in (4.1) (or, which amounts to the same thing, the x * of (C 3) of Remark 4.2), nor is it our intent to pursue this further here. We content ourselves with demonstrating (numerically, on a concrete example) how 𝒜(b) may fail to be monotone in b, and how a non-trivial b may be optimal, i.e. how the x * from (C 3) of Remark 4.2 can fall into (z, ∞).
$${\cal A} (b) \to \infty $$ as b → ∞. However, it does not in general seem obvious how to analytically determine an optimal b in (4.1) (or, which amounts to the same thing, the x * of (C 3) of Remark 4.2), nor is it our intent to pursue this further here. We content ourselves with demonstrating (numerically, on a concrete example) how 𝒜(b) may fail to be monotone in b, and how a non-trivial b may be optimal, i.e. how the x * from (C 3) of Remark 4.2 can fall into (z, ∞).
In fact, this transpires already in the (presumably simplest) case when
1. ψ (s) = s 2, s ∈ [0, ∞), corresponding to X − X 0 being a multiple (by the factor
 $$\sqrt 2 $$) of Brownian motion, and
$$\sqrt 2 $$) of Brownian motion, and2. q = 0, α = 1,
to which we specialize all discussion henceforth.
Remark 4.5. In still more explicit terms, we now have, a.s., ![]() $$S = {{\rm{e}}^{{X_0} + \sqrt 2 {B_\rho }}}$$, where
$$S = {{\rm{e}}^{{X_0} + \sqrt 2 {B_\rho }}}$$, where ![]() $$B(X - {X_0})/\sqrt 2 $$ is a standard linear Brownian motion and
$$B(X - {X_0})/\sqrt 2 $$ is a standard linear Brownian motion and ![]() $${\rho _s} = \inf \{ t \in [0,\infty ){\kern 1pt} :\int_0^t {{\rm{e}}^{{X_0} + \sqrt 2 {B_u}}} \wedge 1{\kern 1pt} {\rm{d}}u > s\} $$ for s ∈ [0, ∞). Furthermore, setting
$${\rho _s} = \inf \{ t \in [0,\infty ){\kern 1pt} :\int_0^t {{\rm{e}}^{{X_0} + \sqrt 2 {B_u}}} \wedge 1{\kern 1pt} {\rm{d}}u > s\} $$ for s ∈ [0, ∞). Furthermore, setting ![]() $$Z := ({{\rm{e}}^{({X_0} + \sqrt 2 B)/2}} \wedge 1) \cdot B$$ (where⋅ denotes stochastic integration [16]), it follows by the usual stochastic calculus techniques that W : = Z ρ is a standard linear Brownian motion and that
$$Z := ({{\rm{e}}^{({X_0} + \sqrt 2 B)/2}} \wedge 1) \cdot B$$ (where⋅ denotes stochastic integration [16]), it follows by the usual stochastic calculus techniques that W : = Z ρ is a standard linear Brownian motion and that ![]() $$U := {{{X_0}} \over {\sqrt 2 }} + {B_\rho }$$ satisfies the stochastic differental equation (SDE)
$$U := {{{X_0}} \over {\sqrt 2 }} + {B_\rho }$$ satisfies the stochastic differental equation (SDE) ![]() $$U - {U_0} = ({{\rm{e}}^{ - U/\sqrt 2 }} \vee 1) \cdot W$$. This provides a description of the dynamics of
$$U - {U_0} = ({{\rm{e}}^{ - U/\sqrt 2 }} \vee 1) \cdot W$$. This provides a description of the dynamics of ![]() $$\log S = \sqrt 2 U$$, and hence, by Itô’s fromula, of S, from the SDE point of view.
$$\log S = \sqrt 2 U$$, and hence, by Itô’s fromula, of S, from the SDE point of view.
Continuing with our analysis, under the above specifications Φ(0) = 0 and ψ(1) = 1, while W (x) = x and (via (4.7)) h (x) = 1 + b γx, x ∈ [0, ∞), where
 $${b_\gamma } := \gamma \sum\limits_{k = 0}^\infty {{{\gamma ^k}} \over {k{!^2}(k + 1)}}/\sum\limits_{k = 0}^\infty {{{\gamma ^k}} \over {k{!^2}}}.$$
$${b_\gamma } := \gamma \sum\limits_{k = 0}^\infty {{{\gamma ^k}} \over {k{!^2}(k + 1)}}/\sum\limits_{k = 0}^\infty {{{\gamma ^k}} \over {k{!^2}}}.$$
Furthermore, inverting the Laplace transform (4.8) for H we obtain
 $$H(x) = {{\sqrt \gamma - {b_\gamma }} \over {2\sqrt \gamma }}{{\rm{e}}^{ - \sqrt \gamma x}} + {{\sqrt \gamma + {b_\gamma }} \over {2\sqrt \gamma }}{{\rm{e}}^{\sqrt \gamma x}},\quad x \in [0,\infty )$$
$$H(x) = {{\sqrt \gamma - {b_\gamma }} \over {2\sqrt \gamma }}{{\rm{e}}^{ - \sqrt \gamma x}} + {{\sqrt \gamma + {b_\gamma }} \over {2\sqrt \gamma }}{{\rm{e}}^{\sqrt \gamma x}},\quad x \in [0,\infty )$$
(H |[0,∞) is uniquely determined by its Laplace transform, because by Theorem 3.1 (I) this function is continuous).
With (4.9) having been established, Figure 1 depicts the case z = 1of (4.1) for three different values of γ (0.9, 1, and 1.1) corresponding to three fundamentally different behaviors of the objective function ![]() $${\cal A} $$. When γ = 1.1 (still z = 1), then numerically the optimal b in (4.1) is approximately b * ≔ 2.533 42. We reinforce this using Remark 4.2. Indeed, we have already observed that conditions (C 1), (C 2), and (C 3), for a suitable x *, of Remark 4.2 hold in this case. Let us further set
$${\cal A} $$. When γ = 1.1 (still z = 1), then numerically the optimal b in (4.1) is approximately b * ≔ 2.533 42. We reinforce this using Remark 4.2. Indeed, we have already observed that conditions (C 1), (C 2), and (C 3), for a suitable x *, of Remark 4.2 hold in this case. Let us further set ![]() $${K_\gamma }\,: = \,{{\cal K}^{(\gamma \omega)}} $$ for short. Then we can compute
$${K_\gamma }\,: = \,{{\cal K}^{(\gamma \omega)}} $$ for short. Then we can compute

Figure 1: The function A of (4.1)and (4.2) on the interval [Reference Bertoin1, 30] in the case when q = 0, α = z = 1, and ψ(s) = s 2, s ∈ [0, ∞), for three values of the inflation/impatience parameter γ – from top to bottom, γ = 0.9 (blue, dotted), γ = 1 (red, dashed), and γ = 1.1 (black, full). The case γ = 1.1 exhibits nontrivial behavior. Unlike when ω = 1, for which the optimal b would be 1, now the optimal b is strictly greater than 1. Intuitively this is due to the fact that the clock ‘runs faster’ when the price level is small, thus ‘buying’ us some time in terms of the inflation depreciation as we wait for a higher price level.
 $${K_\gamma }(x) = \left( {\matrix{{{{\rm{e}}^x}\left( {\matrix{{1 - {1 \over {\sqrt \gamma }}{{1 + {{1 - {{{b_\gamma }} \over {\sqrt \gamma }}} \over {1 + {{{b_\gamma }} \over {\sqrt \gamma }}}}{{\rm{e}}^{ - 2\sqrt \gamma x}}} \over {1 - {{1 - {{{b_\gamma }} \over {\sqrt \gamma }}} \over {1 + {{{b_\gamma }} \over {\sqrt \gamma }}}}{{\rm{e}}^{ - 2\sqrt \gamma x}}}}} \cr} } \right)} \:{{\rm{for}}\,x \in {\rm{[0,}}\infty {\rm{),while}}} \cr {{{\rm{e}}^x}\left( {\matrix{{1 - {{\sum\nolimits_{k = 0}^\infty {{{{(\gamma {{\rm{e}}^x})}^k}} \over {k{!^2}}}} \over {\gamma {{\rm{e}}^x}\sum\nolimits_{k = 0}^\infty {{{{(\gamma {{\rm{e}}^x})}^k}} \over {k{!^2}(k + 1)}}}}} \cr} } \right)}\:\: {{\rm{for}}\,x \in {\rm{(}} - \infty {\rm{,0)}}{\rm{.}}} \cr} } \right.$$
$${K_\gamma }(x) = \left( {\matrix{{{{\rm{e}}^x}\left( {\matrix{{1 - {1 \over {\sqrt \gamma }}{{1 + {{1 - {{{b_\gamma }} \over {\sqrt \gamma }}} \over {1 + {{{b_\gamma }} \over {\sqrt \gamma }}}}{{\rm{e}}^{ - 2\sqrt \gamma x}}} \over {1 - {{1 - {{{b_\gamma }} \over {\sqrt \gamma }}} \over {1 + {{{b_\gamma }} \over {\sqrt \gamma }}}}{{\rm{e}}^{ - 2\sqrt \gamma x}}}}} \cr} } \right)} \:{{\rm{for}}\,x \in {\rm{[0,}}\infty {\rm{),while}}} \cr {{{\rm{e}}^x}\left( {\matrix{{1 - {{\sum\nolimits_{k = 0}^\infty {{{{(\gamma {{\rm{e}}^x})}^k}} \over {k{!^2}}}} \over {\gamma {{\rm{e}}^x}\sum\nolimits_{k = 0}^\infty {{{{(\gamma {{\rm{e}}^x})}^k}} \over {k{!^2}(k + 1)}}}}} \cr} } \right)}\:\: {{\rm{for}}\,x \in {\rm{(}} - \infty {\rm{,0)}}{\rm{.}}} \cr} } \right.$$This function is seen numerically, when γ = 1.1, to satisfy condition (C 3) of Remark 4.2 with (to within numerical precision) x * ≔ log (b *) – see Figure 2. On the other hand, when, ceteris paribus, γ is 0.9 or 1, then numerical experiments also show (or at least suggest) that K γ is bounded away from zero (resp. is tending to 0 at ∞) and that it is strictly negative when γ = 0.9 (resp. γ = 1). (Of course, given the explicit nature of the above expressions one could in principle also verify all the preceding numerical claims analytically, but it would be an extremely tedious exercise with little apparent gain, so we refrain from doing so.)

Figure 2: Plot of K γ from (4.10) on the interval [− 2, 3] with γ = 1.1.
Finally, let us introduce the value function V :(0, ∞) → (0, ∞ ](cf.( 4.1) and (4.2)):
It then follows analytically from the explicit form (4.9) of H obtained above that V ≡ ∞ when γ = 0.9, while ![]() $$V(z) = z + {{1 - {b_1}} \over {1 + {b_1}}}{z^{ - 1}} \in (z,\infty )$$ for z ∈ [1, ∞) when γ = 1; for the latter case we focus (for simplicity) only on the interval [1, ∞), so that the relevant values of H are all given by (4.9) rather than being a mixture of these and the values of P from (4.5) (recall that H |(−∞,0] = P |(−∞,0]). The case γ = 1.1 is handled numerically and reported in Figure 3.
$$V(z) = z + {{1 - {b_1}} \over {1 + {b_1}}}{z^{ - 1}} \in (z,\infty )$$ for z ∈ [1, ∞) when γ = 1; for the latter case we focus (for simplicity) only on the interval [1, ∞), so that the relevant values of H are all given by (4.9) rather than being a mixture of these and the values of P from (4.5) (recall that H |(−∞,0] = P |(−∞,0]). The case γ = 1.1 is handled numerically and reported in Figure 3.

Figure 3: Plot of V from (4.11) on the interval [Reference Bertoin1, Reference Carr and WU2] with γ = 1.1 (top, black, full) together with the identity function (bottom, red, dashed) that corresponds to immediate selling (and must therefore everywhere minorize the value function).
Acknowledgements
Financial support from the Slovenian Research Agency is acknowledged (research core fundings Nos. P1-0222 and P1-0402). The author is indebted to two anonymous referees whose comments and suggestions have helped to significantly improve the presentation as well as the content of this paper.