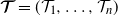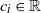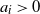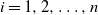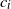1. Introduction
Let X(t),
![]() $t\ge0$
, be an almost surely (a.s.) continuous centered Gaussian process with stationary increments and
$t\ge0$
, be an almost surely (a.s.) continuous centered Gaussian process with stationary increments and
![]() $X(0)=0$
. Motivated by its applications to the hybrid fluid and ruin models, the seminal paper [Reference DĘbicki, Zwart and Borst18] derived the exact tail asymptotics of
$X(0)=0$
. Motivated by its applications to the hybrid fluid and ruin models, the seminal paper [Reference DĘbicki, Zwart and Borst18] derived the exact tail asymptotics of
with
![]() $\mathcal T$
being a regularly varying random variable independent of the Gaussian process X. Since then, the study of the tail asymptotics of supremum on random interval has attracted substantial interest in the literature. We refer to [Reference Arendarczyk1], [Reference Arendarczyk and DĘbicki2], [Reference Arendarczyk and DĘbicki3], [Reference DĘbicki and Peng10], [Reference DĘbicki, Hashorva and Ji11], and [Reference Tan and Hashorva36] for various extensions to general (non-centered) Gaussian or Gaussian-related processes. In these contributions, various different tail distributions for
$\mathcal T$
being a regularly varying random variable independent of the Gaussian process X. Since then, the study of the tail asymptotics of supremum on random interval has attracted substantial interest in the literature. We refer to [Reference Arendarczyk1], [Reference Arendarczyk and DĘbicki2], [Reference Arendarczyk and DĘbicki3], [Reference DĘbicki and Peng10], [Reference DĘbicki, Hashorva and Ji11], and [Reference Tan and Hashorva36] for various extensions to general (non-centered) Gaussian or Gaussian-related processes. In these contributions, various different tail distributions for
![]() $\mathcal T$
have been discussed, and it has been shown that the variability of
$\mathcal T$
have been discussed, and it has been shown that the variability of
![]() $\mathcal T$
influences the form of the asymptotics of (1.1), leading to qualitatively different structures.
$\mathcal T$
influences the form of the asymptotics of (1.1), leading to qualitatively different structures.
The primary aim of this paper is to analyse the asymptotics of a multi-dimensional counterpart of (1.1). More precisely, consider a multi-dimensional centered Gaussian process
with independent coordinates, each
![]() $X_i(t)$
,
$X_i(t)$
,
![]() $t\ge0$
, has stationary increments, a.s. continuous sample paths and
$t\ge0$
, has stationary increments, a.s. continuous sample paths and
![]() $X_i(0)=0$
, and let
$X_i(0)=0$
, and let
![]() $\boldsymbol{\mathcal{T}}=(\mathcal{T}_1, \ldots, \mathcal{T}_n)$
be a regularly varying random vector with positive components, which is independent of the multi-dimensional Gaussian process
$\boldsymbol{\mathcal{T}}=(\mathcal{T}_1, \ldots, \mathcal{T}_n)$
be a regularly varying random vector with positive components, which is independent of the multi-dimensional Gaussian process
![]() $\boldsymbol{X}$
in (1.2) (we use
$\boldsymbol{X}$
in (1.2) (we use
![]() $\boldsymbol{X}$
for short). We are interested in the exact asymptotics of
$\boldsymbol{X}$
for short). We are interested in the exact asymptotics of
where
![]() $c_i\in \mathbb{R}$
,
$c_i\in \mathbb{R}$
,
![]() $a_i>0$
,
$a_i>0$
,
![]() $i=1,2,\ldots,n$
.
$i=1,2,\ldots,n$
.
Extremal analysis of multi-dimensional Gaussian processes has been an active research area in recent years; see [Reference Azais and Pham5], [Reference DĘbicki, Hashorva, Ji and TabiŚ12], [Reference DĘbicki, Hashorva and Kriukov13], [Reference DĘbicki, Hashorva and Wang15], [Reference DĘbicki, Kosiński, Mandjes and Rolski17], and [Reference Pham29], and references therein. Most of these contributions discuss the asymptotic behaviour of the probability that
![]() $\boldsymbol{X}$
(possibly with trend) enters an upper orthant over a finite-time or infinite-time interval; this problem is also connected with the conjunction problem for Gaussian processes first studied by Worsley and Friston [Reference Worsley and Friston38]. Investigations of the joint tail asymptotics of multiple extrema as defined in (1.3) are known to be more challenging. The current literature has only focused on the case with deterministic times
$\boldsymbol{X}$
(possibly with trend) enters an upper orthant over a finite-time or infinite-time interval; this problem is also connected with the conjunction problem for Gaussian processes first studied by Worsley and Friston [Reference Worsley and Friston38]. Investigations of the joint tail asymptotics of multiple extrema as defined in (1.3) are known to be more challenging. The current literature has only focused on the case with deterministic times
![]() $\mathcal{T}_1=\cdots=\mathcal{T}_n$
and some additional assumptions on the correlation structure of the
$\mathcal{T}_1=\cdots=\mathcal{T}_n$
and some additional assumptions on the correlation structure of the
![]() $X_i$
. In [Reference DĘbicki, Kosiński, Mandjes and Rolski17] and [Reference Piterbarg and Stamatovich31] large deviation type results are obtained, and more recently in [Reference DĘbicki, Hashorva and Krystecki14] and [Reference DĘbicki, Ji and Rolski16] exact asymptotics are obtained for correlated two-dimensional Brownian motion. It is worth mentioning that a large deviation result for the multivariate maxima of a discrete Gaussian model has been discussed recently in [Reference van der Hofstad and Honnappa37].
$X_i$
. In [Reference DĘbicki, Kosiński, Mandjes and Rolski17] and [Reference Piterbarg and Stamatovich31] large deviation type results are obtained, and more recently in [Reference DĘbicki, Hashorva and Krystecki14] and [Reference DĘbicki, Ji and Rolski16] exact asymptotics are obtained for correlated two-dimensional Brownian motion. It is worth mentioning that a large deviation result for the multivariate maxima of a discrete Gaussian model has been discussed recently in [Reference van der Hofstad and Honnappa37].
In order to avoid more technical difficulties, the coordinates of the multi-dimensional Gaussian process
![]() $\boldsymbol{X}$
in (1.2) are assumed to be independent. The dependence among the extrema in (1.3) is driven by the structure of the multivariate regularly varying
$\boldsymbol{X}$
in (1.2) are assumed to be independent. The dependence among the extrema in (1.3) is driven by the structure of the multivariate regularly varying
![]() $\boldsymbol{\mathcal{T}}$
. Interestingly, we observe in Theorem 3.1 that the form of the asymptotics of (1.3) is determined by the signs of the drifts
$\boldsymbol{\mathcal{T}}$
. Interestingly, we observe in Theorem 3.1 that the form of the asymptotics of (1.3) is determined by the signs of the drifts
![]() $c_i$
.
$c_i$
.
Apart from its theoretical interest, the motivation to analyse the asymptotic properties of P(u) is related to numerous applications in modern multi-dimensional risk theory, financial mathematics, or fluid queueing networks. For example, we consider an insurance company that runs n lines of business. The surplus process of the ith business line can be modelled by a time-changed Gaussian process
where
![]() $a_i u>0$
is the initial capital (considered as a proportion of u allocated to the ith business line, with
$a_i u>0$
is the initial capital (considered as a proportion of u allocated to the ith business line, with
![]() $\sum_{i=1}^n a_i=1$
),
$\sum_{i=1}^n a_i=1$
),
![]() $c_i>0$
is the net premium rate,
$c_i>0$
is the net premium rate,
![]() $X_i(t)$
,
$X_i(t)$
,
![]() $t\ge0$
, is the net loss process, and
$t\ge0$
, is the net loss process, and
![]() $Y_i(t)$
,
$Y_i(t)$
,
![]() $t\ge 0$
, is a positive increasing function modelling the so-called ‘operational time’ for the ith business line. We refer to [Reference Asmussen and Albrecher4, Reference Ji and Robert23] and [Reference DĘbicki, Hashorva and Ji11], respectively, for detailed discussions of multi-dimensional risk models and time-changed risk models. Of interest in risk theory is the study of the probability of ruin of all the business lines within some finite (deterministic) time
$t\ge 0$
, is a positive increasing function modelling the so-called ‘operational time’ for the ith business line. We refer to [Reference Asmussen and Albrecher4, Reference Ji and Robert23] and [Reference DĘbicki, Hashorva and Ji11], respectively, for detailed discussions of multi-dimensional risk models and time-changed risk models. Of interest in risk theory is the study of the probability of ruin of all the business lines within some finite (deterministic) time
![]() $T>0$
, defined by
$T>0$
, defined by
If additionally all the operational time processes
![]() $Y_i(t)$
,
$Y_i(t)$
,
![]() $t\ge0$
, have a.s. continuous sample paths, then we have
$t\ge0$
, have a.s. continuous sample paths, then we have
![]() $\varphi(u) = P(u)$
with
$\varphi(u) = P(u)$
with
![]() $\boldsymbol{\mathcal{T}}=\boldsymbol{Y}(T)$
, and thus the derived result can be used to estimate this ruin probability. Note that the dependence among different business lines is introduced by the dependence among the operational time processes
$\boldsymbol{\mathcal{T}}=\boldsymbol{Y}(T)$
, and thus the derived result can be used to estimate this ruin probability. Note that the dependence among different business lines is introduced by the dependence among the operational time processes
![]() $Y_i$
. As a simple example we can consider
$Y_i$
. As a simple example we can consider
![]() $Y_i(t)= \Theta_i t$
,
$Y_i(t)= \Theta_i t$
,
![]() $ t\ge 0$
, with
$ t\ge 0$
, with
![]() $\boldsymbol{\Theta}= (\Theta_1,\ldots, \Theta_n)$
being a multivariate regularly varying random vector. Additionally, multi-dimensional time-changed (or subordinate) Gaussian processes have recently been proved to be good candidates for modelling the log-return processes of multiple assets; see e.g. [Reference Barndorff-Nielsen, Pedersen and Sato6], [Reference Kim25], and [Reference Luciano and Semeraro26]. As the joint distribution of extrema of asset returns is important in finance problems (e.g. [Reference He, Keirstead and Rebholz20]), we expect the results obtained for (1.3) might also be interesting in financial mathematics.
$\boldsymbol{\Theta}= (\Theta_1,\ldots, \Theta_n)$
being a multivariate regularly varying random vector. Additionally, multi-dimensional time-changed (or subordinate) Gaussian processes have recently been proved to be good candidates for modelling the log-return processes of multiple assets; see e.g. [Reference Barndorff-Nielsen, Pedersen and Sato6], [Reference Kim25], and [Reference Luciano and Semeraro26]. As the joint distribution of extrema of asset returns is important in finance problems (e.g. [Reference He, Keirstead and Rebholz20]), we expect the results obtained for (1.3) might also be interesting in financial mathematics.
As a relevant application, we shall discuss a multi-dimensional regenerative model, which is motivated by its relevance to risk models and fluid queueing models. Essentially, the multi-dimensional regenerative process is a process with a random alternating environment, where an independent multi-dimensional fractional Brownian motion (fBm) with trend is assigned at each environment alternating time. We refer to Section 4 for more details. By analysing a related multi-dimensional perturbed random walk, we obtain in Theorem 4.1 the ruin probability of the multi-dimensional regenerative model. This generalizes some of the results in [Reference Palmowski and Zwart28] and [Reference Zwart, Borst and DDĘbicki40] to the multi-dimensional setting. Note in passing that some related stochastic models with random sampling or resetting have been discussed in the recent literature; see e.g. [Reference Constantinescu, Delsing, Mandjes and Rojas Nandayapa9], [Reference Kella and Whitt24], and [Reference Ratanov32].
Organization of the rest of the paper. In Section 2 we introduce some notation, recall the definition of multivariate regular variation, and present some preliminary results on the extremes of one-dimensional Gaussian processes. The result for (1.3) is displayed in Section 3, and the ruin probability of the multi-dimensional regenerative model is discussed in Section 4. The proofs are relegated to Sections 5 and 6. Some useful results on multivariate regular variation are discussed in the Appendix.
2. Notation and preliminaries
We shall use some standard notation that is common when dealing with vectors. All the operations on vectors are meant componentwise. For instance, for any given
![]() $ \boldsymbol{x} = (x_1,\ldots,x_n)\in \mathbb{R} ^n$
and
$ \boldsymbol{x} = (x_1,\ldots,x_n)\in \mathbb{R} ^n$
and
![]() $\boldsymbol{y} = (y_1,\ldots,y_n) \in \mathbb{R} ^n $
, we write
$\boldsymbol{y} = (y_1,\ldots,y_n) \in \mathbb{R} ^n $
, we write
![]() $\boldsymbol{x} \boldsymbol{y} = (x_1y_1, \ldots, x_ny_n)$
, and write
$\boldsymbol{x} \boldsymbol{y} = (x_1y_1, \ldots, x_ny_n)$
, and write
![]() $ \boldsymbol{x} > \boldsymbol{y} $
if and only if
$ \boldsymbol{x} > \boldsymbol{y} $
if and only if
![]() $ x_i > y_i $
for all
$ x_i > y_i $
for all
![]() $ 1 \leq i \leq n $
. Furthermore, for two positive functions f, h and some
$ 1 \leq i \leq n $
. Furthermore, for two positive functions f, h and some
![]() $u_0\in[\!-\!\infty , \infty ]$
, write
$u_0\in[\!-\!\infty , \infty ]$
, write
![]() $ f(u) \lesssim h(u)$
or
$ f(u) \lesssim h(u)$
or
![]() $h(u)\gtrsim f(u)$
if
$h(u)\gtrsim f(u)$
if
![]() $ \limsup_{u \rightarrow u_0} f(u) /h(u) \le 1 $
, write
$ \limsup_{u \rightarrow u_0} f(u) /h(u) \le 1 $
, write
![]() $h(u)\sim f(u)$
if
$h(u)\sim f(u)$
if
![]() $ \lim_{u \rightarrow u_0} f(u) /h(u) = 1 $
, write
$ \lim_{u \rightarrow u_0} f(u) /h(u) = 1 $
, write
![]() $ f(u) = {\textrm{o}}(h(u)) $
if
$ f(u) = {\textrm{o}}(h(u)) $
if
![]() $ \lim_{u \rightarrow u_0} {f(u)}/{h(u)} = 0$
, and write
$ \lim_{u \rightarrow u_0} {f(u)}/{h(u)} = 0$
, and write
![]() $ f(u) \asymp h(u) $
if
$ f(u) \asymp h(u) $
if
![]() $ f(u)/h(u)$
is bounded from both below and above for all sufficiently large u. Moreover,
$ f(u)/h(u)$
is bounded from both below and above for all sufficiently large u. Moreover,
![]() $\boldsymbol{Z}_{1} \overset D= \boldsymbol{Z}_{2}$
means that
$\boldsymbol{Z}_{1} \overset D= \boldsymbol{Z}_{2}$
means that
![]() $\boldsymbol{Z}_{1}$
and
$\boldsymbol{Z}_{1}$
and
![]() $\boldsymbol{Z}_{2}$
have the same distribution.
$\boldsymbol{Z}_{2}$
have the same distribution.
Next, let us recall the definition and some implications of multivariate regular variation. We refer to [Reference Hult, Lindskog, Mikosch and Samorodnitsky21], [Reference Jessen and Mikosch22], and [Reference Resnick34] for more detailed discussions. Let
![]() $\overline{\mathbb{R}}_0^n=\overline{\mathbb{R}}^n \setminus \{\textbf{0}\}$
with
$\overline{\mathbb{R}}_0^n=\overline{\mathbb{R}}^n \setminus \{\textbf{0}\}$
with
![]() $\overline{\mathbb{R}}=\mathbb{R}\cup\{-\infty , \infty \}$
. An
$\overline{\mathbb{R}}=\mathbb{R}\cup\{-\infty , \infty \}$
. An
![]() $\mathbb{R}^n$
-valued random vector
$\mathbb{R}^n$
-valued random vector
![]() $\boldsymbol{X}$
is said to be regularly varying if there exists a non-null Radon measure
$\boldsymbol{X}$
is said to be regularly varying if there exists a non-null Radon measure
![]() $\nu$
on the Borel
$\nu$
on the Borel
![]() $\sigma$
-field
$\sigma$
-field
![]() $\mathcal B(\overline{\mathbb{R}}_0^n)$
with
$\mathcal B(\overline{\mathbb{R}}_0^n)$
with
![]() $\nu(\overline{\mathbb{R}}^n \setminus \mathbb{R}^n)=0$
such that
$\nu(\overline{\mathbb{R}}^n \setminus \mathbb{R}^n)=0$
such that
Here
![]() $\vert { \cdot } \vert$
is any norm in
$\vert { \cdot } \vert$
is any norm in
![]() $\mathbb{R}^n$
and
$\mathbb{R}^n$
and
![]() $\overset{v}\rightarrow$
refers to vague convergence on
$\overset{v}\rightarrow$
refers to vague convergence on
![]() $\mathcal B(\overline{\mathbb{R}}_0^n)$
. It is known that
$\mathcal B(\overline{\mathbb{R}}_0^n)$
. It is known that
![]() $\nu$
necessarily satisfies the homogeneity property
$\nu$
necessarily satisfies the homogeneity property
![]() $\nu(s K) =s^{-\alpha} \nu (K)$
,
$\nu(s K) =s^{-\alpha} \nu (K)$
,
![]() $s>0$
, for some
$s>0$
, for some
![]() $\alpha>0$
and any Borel set K in
$\alpha>0$
and any Borel set K in
![]() $\mathcal B(\overline{\mathbb{R}}_0^n)$
. In what follows, we say that such a defined
$\mathcal B(\overline{\mathbb{R}}_0^n)$
. In what follows, we say that such a defined
![]() $\boldsymbol{X}$
is regularly varying with index
$\boldsymbol{X}$
is regularly varying with index
![]() $\alpha$
and limiting measure
$\alpha$
and limiting measure
![]() $\nu$
. An implication of the homogeneity property of
$\nu$
. An implication of the homogeneity property of
![]() $\nu$
is that all the rectangle sets of the form
$\nu$
is that all the rectangle sets of the form
![]() $[\boldsymbol{a}, \boldsymbol{b}]=\{\boldsymbol{x} \colon \boldsymbol{a} \le \boldsymbol{x}\le \boldsymbol{b}\}$
in
$[\boldsymbol{a}, \boldsymbol{b}]=\{\boldsymbol{x} \colon \boldsymbol{a} \le \boldsymbol{x}\le \boldsymbol{b}\}$
in
![]() $\overline{\mathbb{R}}_0^n$
are
$\overline{\mathbb{R}}_0^n$
are
![]() $\nu$
-continuity sets. Furthermore, we find that
$\nu$
-continuity sets. Furthermore, we find that
![]() $\vert {\boldsymbol{X}} \vert$
is regularly varying at infinity with index
$\vert {\boldsymbol{X}} \vert$
is regularly varying at infinity with index
![]() $\alpha$
, i.e.
$\alpha$
, i.e.
![]() $\mathbb{P} \{ {\vert {\boldsymbol{X}} \vert>x} \} \sim x^{-\alpha} L(x)$
,
$\mathbb{P} \{ {\vert {\boldsymbol{X}} \vert>x} \} \sim x^{-\alpha} L(x)$
,
![]() $x\rightarrow\infty $
, with some slowly varying function L(x). Some useful results on multivariate regular variation are discussed in the Appendix.
$x\rightarrow\infty $
, with some slowly varying function L(x). Some useful results on multivariate regular variation are discussed in the Appendix.
In what follows, we review some results on the extremes of one-dimensional Gaussian process with negative drift derived in [Reference Dieker19]. Let X(t),
![]() $t\ge0 $
, be an a.s. continuous centered Gaussian process with stationary increments and
$t\ge0 $
, be an a.s. continuous centered Gaussian process with stationary increments and
![]() $X(0)=0$
, and let
$X(0)=0$
, and let
![]() $c>0$
be some constant. We shall present the exact asymptotics of
$c>0$
be some constant. We shall present the exact asymptotics of
Below are some assumptions that the variance function
![]() $\sigma^2(t)=\operatorname{Var}(X(t))$
might satisfy:
$\sigma^2(t)=\operatorname{Var}(X(t))$
might satisfy:
-
C1
 $\sigma$
is continuous on
$\sigma$
is continuous on
 $[0,\infty )$
and ultimately strictly increasing;
$[0,\infty )$
and ultimately strictly increasing; -
C2
 $\sigma$
is regularly varying at infinity with index H for some
$\sigma$
is regularly varying at infinity with index H for some
 $H\in(0,1)$
;
$H\in(0,1)$
; -
C3
 $\sigma$
is regularly varying at 0 with index
$\sigma$
is regularly varying at 0 with index
 $\lambda$
for some
$\lambda$
for some
 $\lambda\in(0,1)$
;
$\lambda\in(0,1)$
; -
C4
 $\sigma^2$
is ultimately twice continuously differentiable and its first derivative
$\sigma^2$
is ultimately twice continuously differentiable and its first derivative
 $\dot{\sigma}^2$
and second derivative
$\dot{\sigma}^2$
and second derivative
 $\ddot{ \sigma}^2$
are both ultimately monotone.
$\ddot{ \sigma}^2$
are both ultimately monotone.
Note that in the above
![]() $\dot{\sigma}^2$
and
$\dot{\sigma}^2$
and
![]() $\ddot{ \sigma}^2$
denote the first and second derivative of
$\ddot{ \sigma}^2$
denote the first and second derivative of
![]() $\sigma^2$
, not the square of the derivatives of
$\sigma^2$
, not the square of the derivatives of
![]() $\sigma$
. Henceforth, provided it exists, we let
$\sigma$
. Henceforth, provided it exists, we let
![]() $\overleftarrow{\sigma}$
denote an asymptotic inverse near infinity or zero of
$\overleftarrow{\sigma}$
denote an asymptotic inverse near infinity or zero of
![]() $\sigma$
; recall that it is (asymptotically uniquely) defined by
$\sigma$
; recall that it is (asymptotically uniquely) defined by
![]() $\overleftarrow{\sigma}(\sigma(t))\sim \sigma(\overleftarrow{\sigma}(t))\sim t.$
It depends on the context whether
$\overleftarrow{\sigma}(\sigma(t))\sim \sigma(\overleftarrow{\sigma}(t))\sim t.$
It depends on the context whether
![]() $\overleftarrow{\sigma}$
is an asymptotic inverse near zero or infinity.
$\overleftarrow{\sigma}$
is an asymptotic inverse near zero or infinity.
One known example that satisfies the assumptions C1–C4 is the fBm
![]() $\{B_H(t),\, t\ge 0\}$
with Hurst index
$\{B_H(t),\, t\ge 0\}$
with Hurst index
![]() $H\in(0,1)$
, i.e. an H-self-similar centered Gaussian process with stationary increments and covariance function given by
$H\in(0,1)$
, i.e. an H-self-similar centered Gaussian process with stationary increments and covariance function given by
We introduce the following notation:
For an a.s. continuous centered Gaussian process Z(t),
![]() $t\ge 0$
, with stationary increments and variance function
$t\ge 0$
, with stationary increments and variance function
![]() $\sigma_Z^2$
, we define the generalized Pickands constant
$\sigma_Z^2$
, we define the generalized Pickands constant
provided both the expectation and the limit exist. When
![]() $Z=B_H$
, the constant
$Z=B_H$
, the constant
![]() $\mathcal{H}_{B_H}$
is the well-known Pickands constant; see [Reference Piterbarg30]. For convenience, sometimes we also write
$\mathcal{H}_{B_H}$
is the well-known Pickands constant; see [Reference Piterbarg30]. For convenience, sometimes we also write
![]() $\mathcal{H}_{\sigma_Z^2}$
for
$\mathcal{H}_{\sigma_Z^2}$
for
![]() $\mathcal{H}_Z$
. In the following we let
$\mathcal{H}_Z$
. In the following we let
![]() $\Psi(\cdot)$
denote the survival function of the N(0,1) distribution. It is known that
$\Psi(\cdot)$
denote the survival function of the N(0,1) distribution. It is known that
The following result is derived in Proposition 2 of [Reference Dieker19] (here we consider a particular trend function
![]() $\phi(t)= ct$
,
$\phi(t)= ct$
,
![]() $t\ge 0$
).
$t\ge 0$
).
Proposition 2.1. Let X(t),
![]() $t\ge0$
, be an a.s. continuous centered Gaussian process with stationary increments and
$t\ge0$
, be an a.s. continuous centered Gaussian process with stationary increments and
![]() $X(0)=0$
. Suppose that C1–C4 hold. We have the following, as
$X(0)=0$
. Suppose that C1–C4 hold. We have the following, as
![]() $u\rightarrow\infty $
.
$u\rightarrow\infty $
.
-
(i) If
 $\sigma^2(u)/u\rightarrow \infty $
, then
$\sigma^2(u)/u\rightarrow \infty $
, then  \begin{equation*}\psi(u) \sim \mathcal{H}_{B_H} C_{H,1,H} \biggl(\dfrac{1-H}{H}\biggr)\dfrac{c^{1-H}\sigma(u) }{{\overleftarrow{\sigma}}(\sigma^2(u)/u)}\Psi\biggl(\inf_{t\ge0}\dfrac{u(1+t)}{\sigma(ut/c)}\biggr).\end{equation*}
\begin{equation*}\psi(u) \sim \mathcal{H}_{B_H} C_{H,1,H} \biggl(\dfrac{1-H}{H}\biggr)\dfrac{c^{1-H}\sigma(u) }{{\overleftarrow{\sigma}}(\sigma^2(u)/u)}\Psi\biggl(\inf_{t\ge0}\dfrac{u(1+t)}{\sigma(ut/c)}\biggr).\end{equation*}
-
(ii) If
 $\sigma^2(u)/u\rightarrow \mathcal{G} \in(0,\infty )$
, then
$\sigma^2(u)/u\rightarrow \mathcal{G} \in(0,\infty )$
, then  \begin{equation*}\psi(u) \sim \mathcal{H}_{(2c^2/\mathcal{G}^2 )\sigma^2} \biggl(\dfrac{\sqrt{2/\pi}}{c^{1+H}H}\biggr) \sigma(u)\Psi\biggl(\inf_{t\ge0}\dfrac{u(1+t)}{\sigma(ut/c)}\biggr).\end{equation*}
\begin{equation*}\psi(u) \sim \mathcal{H}_{(2c^2/\mathcal{G}^2 )\sigma^2} \biggl(\dfrac{\sqrt{2/\pi}}{c^{1+H}H}\biggr) \sigma(u)\Psi\biggl(\inf_{t\ge0}\dfrac{u(1+t)}{\sigma(ut/c)}\biggr).\end{equation*}
-
(iii) If
 $\sigma^2(u)/u\rightarrow 0$
, then (here we need regularity of
$\sigma^2(u)/u\rightarrow 0$
, then (here we need regularity of
 $\sigma$
and its inverse at 0)
$\sigma$
and its inverse at 0)  \begin{equation*}\psi(u) \sim \mathcal{H}_{B_\lambda} C_{H,1,\lambda} \biggl(\dfrac{1-H}{H}\biggr)^{H/\lambda}\dfrac{c^{{-1-H+2H/\lambda}}\sigma(u) }{{\overleftarrow{\sigma}}(\sigma^2(u)/u)}\Psi\biggl(\inf_{t\ge0}\dfrac{u(1+t)}{\sigma(ut/c)}\biggr).\end{equation*}
\begin{equation*}\psi(u) \sim \mathcal{H}_{B_\lambda} C_{H,1,\lambda} \biggl(\dfrac{1-H}{H}\biggr)^{H/\lambda}\dfrac{c^{{-1-H+2H/\lambda}}\sigma(u) }{{\overleftarrow{\sigma}}(\sigma^2(u)/u)}\Psi\biggl(\inf_{t\ge0}\dfrac{u(1+t)}{\sigma(ut/c)}\biggr).\end{equation*}
As a special case of the Proposition 2.1 we have the following result (see [Reference Dieker19, Corollary 1] or [Reference Ji and Robert23]). This will be useful in the proofs below.
Corollary 2.1. If
![]() $X(t)=B_H(t)$
,
$X(t)=B_H(t)$
,
![]() $t\ge 0$
, the fBm with index
$t\ge 0$
, the fBm with index
![]() $H\in(0,1)$
, then as
$H\in(0,1)$
, then as
![]() $u\rightarrow\infty $
$u\rightarrow\infty $
with constant
3. Main results
Without loss of generality, we assume that in (1.3) there are
![]() $n_-$
coordinates with negative drift,
$n_-$
coordinates with negative drift,
![]() $n_0$
coordinates without drift, and
$n_0$
coordinates without drift, and
![]() $n_+$
coordinates with positive drift, that is,
$n_+$
coordinates with positive drift, that is,
 \begin{align*} c_i&<0, \quad i=1,\ldots, n_-, \\ c_i&=0, \quad i=n_-+1,\ldots, n_-+n_0,\\ c_i&>0, \quad i=n_-+n_0+1,\ldots, n,\end{align*}
\begin{align*} c_i&<0, \quad i=1,\ldots, n_-, \\ c_i&=0, \quad i=n_-+1,\ldots, n_-+n_0,\\ c_i&>0, \quad i=n_-+n_0+1,\ldots, n,\end{align*}
where
![]() $0\le n_-,n_0,n_+\le n$
such that
$0\le n_-,n_0,n_+\le n$
such that
![]() $n_-+n_0+n_+=n$
. We impose the following assumptions on the standard deviation functions
$n_-+n_0+n_+=n$
. We impose the following assumptions on the standard deviation functions
![]() $\sigma_i(t)=\sqrt{\textrm{Var}(X_i(t))}$
of the Gaussian processes
$\sigma_i(t)=\sqrt{\textrm{Var}(X_i(t))}$
of the Gaussian processes
![]() $X_i(t),$
$X_i(t),$
![]() $i=1,\ldots,n$
.
$i=1,\ldots,n$
.
Assumption I. For
![]() $i=1,\ldots, n_-$
,
$i=1,\ldots, n_-$
,
![]() $\sigma_i(t)$
satisfies the assumptions C1–C4 with the parameters involved indexed by i. For
$\sigma_i(t)$
satisfies the assumptions C1–C4 with the parameters involved indexed by i. For
![]() $i=n_{-}+1,\ldots, n_{-}+n_0$
,
$i=n_{-}+1,\ldots, n_{-}+n_0$
,
![]() $\sigma_i(t)$
satisfies the assumptions C1– C3 with the parameters involved indexed by i. For
$\sigma_i(t)$
satisfies the assumptions C1– C3 with the parameters involved indexed by i. For
![]() $i=n_{-}+n_0+1,\ldots, n$
,
$i=n_{-}+n_0+1,\ldots, n$
,
![]() $\sigma_i(t)$
satisfies the assumptions C1– C2 with the parameters involved indexed by i.
$\sigma_i(t)$
satisfies the assumptions C1– C2 with the parameters involved indexed by i.
Denote
Given a Radon measure
![]() $\nu$
, define
$\nu$
, define
where
Further, note that for
![]() $i=1,\ldots, n_-$
(where
$i=1,\ldots, n_-$
(where
![]() $c_i<0$
), the asymptotic formula, as
$c_i<0$
), the asymptotic formula, as
![]() $u\rightarrow\infty $
, of
$u\rightarrow\infty $
, of
is available from Proposition 2.1 under Assumption I.
Below is the principal result of this paper.
Theorem 3.1. Suppose that
![]() $\boldsymbol{X}(t)$
,
$\boldsymbol{X}(t)$
,
![]() $t\ge 0$
, satisfies Assumption I, and
$t\ge 0$
, satisfies Assumption I, and
![]() $\boldsymbol{\mathcal{T}}$
is a regularly varying random vector with index
$\boldsymbol{\mathcal{T}}$
is a regularly varying random vector with index
![]() $\alpha$
and limiting measure
$\alpha$
and limiting measure
![]() $\nu$
, and is independent of
$\nu$
, and is independent of
![]() $\boldsymbol{X}$
. Further assume, without loss of generality, that there are
$\boldsymbol{X}$
. Further assume, without loss of generality, that there are
![]() $m(\leq n_0)$
positive constants
$m(\leq n_0)$
positive constants
![]() $k_i$
such that
$k_i$
such that
![]() $\overleftarrow{\sigma_i}(u) \sim k_i \overleftarrow{\sigma}_{n_-+1}(u) $
for
$\overleftarrow{\sigma_i}(u) \sim k_i \overleftarrow{\sigma}_{n_-+1}(u) $
for
![]() $i=n_-+1,\ldots, n_-+m$
and
$i=n_-+1,\ldots, n_-+m$
and
![]() $\overleftarrow{\sigma_i}(u) ={\textrm{o}}({\overleftarrow{\sigma}_{n_-+1}}(u))$
for
$\overleftarrow{\sigma_i}(u) ={\textrm{o}}({\overleftarrow{\sigma}_{n_-+1}}(u))$
for
![]() $i=n_-+m+1,\ldots, n_-+n_0$
. With the convention
$i=n_-+m+1,\ldots, n_-+n_0$
. With the convention
![]() $\prod_{i=1}^{0}=1$
, we have the following.
$\prod_{i=1}^{0}=1$
, we have the following.
-
(i) If
 $ n_0>0$
, then, as
$ n_0>0$
, then, as
 $u\rightarrow\infty $
, where
$u\rightarrow\infty $
, where \begin{equation*}P(u)\sim \widetilde{\nu}\bigl(\bigl( \boldsymbol{k}\boldsymbol{a}_{0}^{1/{H_{n_-+1}}},\boldsymbol{\infty} \bigr]\bigr) \, \mathbb{P} \{ {\vert {\boldsymbol{\mathcal T}} \vert > \overleftarrow{\sigma}_{n_-+1}(u)} \} \ \prod_{i=1}^{n_-} \psi_i(a_i u),\end{equation*}
\begin{equation*}P(u)\sim \widetilde{\nu}\bigl(\bigl( \boldsymbol{k}\boldsymbol{a}_{0}^{1/{H_{n_-+1}}},\boldsymbol{\infty} \bigr]\bigr) \, \mathbb{P} \{ {\vert {\boldsymbol{\mathcal T}} \vert > \overleftarrow{\sigma}_{n_-+1}(u)} \} \ \prod_{i=1}^{n_-} \psi_i(a_i u),\end{equation*}
 $\widetilde{\nu}$
and
$\widetilde{\nu}$
and
 $\psi_i$
are defined in (3.2) and (3.3), respectively, and
$\psi_i$
are defined in (3.2) and (3.3), respectively, and  \begin{equation*}\boldsymbol{k}\boldsymbol{a}_{0}^{1/{H_{n_-+1}}}=(0,\ldots, 0, k_{n_-+1}a_{n_-+1}^{1/H_{n_-+1}}, \ldots, k_{n_-+m}a_{n_-+m}^{1/H_{n_-+1}}, 0,\ldots, 0).\end{equation*}
\begin{equation*}\boldsymbol{k}\boldsymbol{a}_{0}^{1/{H_{n_-+1}}}=(0,\ldots, 0, k_{n_-+1}a_{n_-+1}^{1/H_{n_-+1}}, \ldots, k_{n_-+m}a_{n_-+m}^{1/H_{n_-+1}}, 0,\ldots, 0).\end{equation*}
-
(ii) If
 $n_0=0$
, then, as
$n_0=0$
, then, as
 $u\rightarrow\infty $
, where
$u\rightarrow\infty $
, where \begin{equation*}P(u)\sim \nu((\boldsymbol{a}_{1}, \boldsymbol{\infty} ])\, \mathbb{P} \{ {\vert {\boldsymbol{\mathcal T}} \vert>u} \} \ \prod_{i=1}^{n_-} \psi_i(a_i u),\end{equation*}
\begin{equation*}P(u)\sim \nu((\boldsymbol{a}_{1}, \boldsymbol{\infty} ])\, \mathbb{P} \{ {\vert {\boldsymbol{\mathcal T}} \vert>u} \} \ \prod_{i=1}^{n_-} \psi_i(a_i u),\end{equation*}
 $\boldsymbol{a}_{1} =( t^*_1/\vert {c_1} \vert\ldots, t^*_{n_-}/\vert {c_{n_-}} \vert , a_{n_-+1}/{ c_{n_-+1}}, \ldots, a_n/c_n).$
$\boldsymbol{a}_{1} =( t^*_1/\vert {c_1} \vert\ldots, t^*_{n_-}/\vert {c_{n_-}} \vert , a_{n_-+1}/{ c_{n_-+1}}, \ldots, a_n/c_n).$
Remark 3.1. As a special case, we can obtain from Theorem 3.1 some results for the one-dimensional model. Specifically, let
![]() $c>0$
be some constant; then, as
$c>0$
be some constant; then, as
![]() $u\rightarrow\infty $
,
$u\rightarrow\infty $
,
Note that (3.4) is derived in Theorem 2.1 of [Reference DĘbicki, Zwart and Borst18], (3.5) is discussed in [Reference DĘbicki, Hashorva and Ji11] only for the fBm case. The result in (3.6) seems to be new.
We conclude this section with an interesting example of multi-dimensional subordinate Brownian motion; see e.g. [Reference Luciano and Semeraro26].
Example 3.1. For each
![]() $i=0,1,\ldots, n$
, let
$i=0,1,\ldots, n$
, let
![]() $\{S_i(t),\, t\ge0\}$
be an independent
$\{S_i(t),\, t\ge0\}$
be an independent
![]() $\alpha_i$
-stable subordinator with
$\alpha_i$
-stable subordinator with
![]() $\alpha_i\in(0,1)$
, i.e.
$\alpha_i\in(0,1)$
, i.e.
![]() $S_i(t)\overset{D}=\mathcal S_{\alpha_i}(t^{1/\alpha_i}, 1,0)$
, where
$S_i(t)\overset{D}=\mathcal S_{\alpha_i}(t^{1/\alpha_i}, 1,0)$
, where
![]() $\mathcal S_\alpha(\sigma, \beta, d)$
denotes a stable random variable with stability index
$\mathcal S_\alpha(\sigma, \beta, d)$
denotes a stable random variable with stability index
![]() $\alpha$
, scale parameter
$\alpha$
, scale parameter
![]() $\sigma$
, skewness parameter
$\sigma$
, skewness parameter
![]() $\beta$
, and drift parameter d. It is known (e.g. [Reference Samorodnitsky and Taqq35, Property 1.2.15]) that for any fixed constant
$\beta$
, and drift parameter d. It is known (e.g. [Reference Samorodnitsky and Taqq35, Property 1.2.15]) that for any fixed constant
![]() $T>0$
,
$T>0$
,
with
Assume
![]() $\alpha_0<\alpha_i$
, for all
$\alpha_0<\alpha_i$
, for all
![]() $i=1,2,\ldots, n.$
Define an n-dimensional subordinator as
$i=1,2,\ldots, n.$
Define an n-dimensional subordinator as
We consider an n-dimensional subordinate Brownian motion with drift defined as
where
![]() $ B_i(t)$
,
$ B_i(t)$
,
![]() $t\ge0$
,
$t\ge0$
,
![]() $i=1,\ldots, n$
, are independent standard Brownian motions that are independent of
$i=1,\ldots, n$
, are independent standard Brownian motions that are independent of
![]() $\boldsymbol{Y}$
and
$\boldsymbol{Y}$
and
![]() $c_i\in \mathbb{R}$
. For any
$c_i\in \mathbb{R}$
. For any
![]() $a_i>0, i=1,2,\ldots, n$
,
$a_i>0, i=1,2,\ldots, n$
,
![]() $T>0$
and
$T>0$
and
![]() $u>0$
, define
$u>0$
, define
For illustrative purposes and to avoid further technicalities, we only consider the case where all
![]() $c_i$
in the above have the same sign. As an application of Theorem 3.1, we obtain the asymptotic behaviour of
$c_i$
in the above have the same sign. As an application of Theorem 3.1, we obtain the asymptotic behaviour of
![]() $P_B(u), u\rightarrow\infty $
, as follows.
$P_B(u), u\rightarrow\infty $
, as follows.
-
(i) If
 $c_i>0$
for all
$c_i>0$
for all
 $i=1,\ldots, n$
, then
$i=1,\ldots, n$
, then
 $ P_B(u) \sim C_{\alpha_0,T} (\max_{i=1}^n (a_i/c_i) u) ^{-\alpha_0} .$
$ P_B(u) \sim C_{\alpha_0,T} (\max_{i=1}^n (a_i/c_i) u) ^{-\alpha_0} .$
-
(ii) If
 $c_i=0$
for all
$c_i=0$
for all
 $i=1,\ldots, n$
, then
$i=1,\ldots, n$
, then
 $ P_B(u) \asymp u^{-2\alpha_0}.$
$ P_B(u) \asymp u^{-2\alpha_0}.$
-
(iii) If
 $c_i<0$
and the density function of
$c_i<0$
and the density function of
 $S_i(T)$
is ultimately monotone for all
$S_i(T)$
is ultimately monotone for all
 $i=0, 1,\ldots, n$
, then
$i=0, 1,\ldots, n$
, then
 $\ln P_B(u) \sim 2 \sum_{i=1}^n (a_i c_i) u.$
$\ln P_B(u) \sim 2 \sum_{i=1}^n (a_i c_i) u.$
The proof of the above is displayed in Section 5.
4. Ruin probability of a multi-dimensional regenerative model
As it is known in the literature that the maximum of random processes over a random interval is relevant to the regenerated models (e.g. [Reference Palmowski and Zwart28], [Reference Zwart, Borst and DDĘbicki40]), this section is focused on a multi-dimensional regenerative model that is motivated by its applications in queueing theory and ruin theory. More precisely, there are four elements in this model: two sequences of strictly positive random variables,
![]() $\{T_i \colon i\ge 1\}$
and
$\{T_i \colon i\ge 1\}$
and
![]() $\{S_i \colon i\ge 1\}$
, and two sequences of n-dimensional processes,
$\{S_i \colon i\ge 1\}$
, and two sequences of n-dimensional processes,
![]() $\{\{\boldsymbol{X}^{(i)}(t),\, t\ge 0\} \colon i\ge 1\}$
and
$\{\{\boldsymbol{X}^{(i)}(t),\, t\ge 0\} \colon i\ge 1\}$
and
![]() $\{\{\boldsymbol{Y}^{(i)}(t),\, t\ge 0\} \colon i\ge 1\}$
, where
$\{\{\boldsymbol{Y}^{(i)}(t),\, t\ge 0\} \colon i\ge 1\}$
, where
![]() $\boldsymbol{X}^{(i)}(t)=(X_1^{(i)}(t),\ldots, X_n^{(i)}(t))$
and
$\boldsymbol{X}^{(i)}(t)=(X_1^{(i)}(t),\ldots, X_n^{(i)}(t))$
and
![]() $\boldsymbol{Y}^{(i)}(t)=(Y_1^{(i)}(t),\ldots, Y_n^{(i)}(t))$
. We assume that the above four elements are mutually independent. Here
$\boldsymbol{Y}^{(i)}(t)=(Y_1^{(i)}(t),\ldots, Y_n^{(i)}(t))$
. We assume that the above four elements are mutually independent. Here
![]() $T_i, S_i$
are two successive times representing the random length of the alternating environment (called T-stage and S-stage), and we assume a T-stage starts at time 0. The model grows according to
$T_i, S_i$
are two successive times representing the random length of the alternating environment (called T-stage and S-stage), and we assume a T-stage starts at time 0. The model grows according to
![]() $\{\boldsymbol{X}^{(i)}(t),\, t\ge 0\}$
during the ith T-stage and according to
$\{\boldsymbol{X}^{(i)}(t),\, t\ge 0\}$
during the ith T-stage and according to
![]() $\{\boldsymbol{Y}^{(i)}(t), t\ge 0\}$
during the ith S-stage.
$\{\boldsymbol{Y}^{(i)}(t), t\ge 0\}$
during the ith S-stage.
Based on the above, we define an alternating renewal process with renewal epochs
with
![]() $V_i=(T_1+S_1)+\cdots +(T_i+S_i)$
, which is the ith environment cycle time. Then the resulting n-dimensional process
$V_i=(T_1+S_1)+\cdots +(T_i+S_i)$
, which is the ith environment cycle time. Then the resulting n-dimensional process
![]() $\boldsymbol{Z}(t)=(Z_1(t),\ldots, Z_n(t))$
is defined as
$\boldsymbol{Z}(t)=(Z_1(t),\ldots, Z_n(t))$
is defined as
 \begin{equation*}\boldsymbol{Z}(t)\;:\!=\; \begin{cases} \boldsymbol{Z}(V_i)+\boldsymbol{X}^{(i+1)}(t-V_i) & \text{if $V_i < t\le V_i+T_{i+1}$,} \\\boldsymbol{Z}(V_i)+ \boldsymbol{X}^{(i+1)}(T_{i+1})+\boldsymbol{Y}^{(i+1)}(t-V_i-T_{i+1}) & \text{if $ V_i+T_{i+1} < t \le V_{i+1}$}. \end{cases}\end{equation*}
\begin{equation*}\boldsymbol{Z}(t)\;:\!=\; \begin{cases} \boldsymbol{Z}(V_i)+\boldsymbol{X}^{(i+1)}(t-V_i) & \text{if $V_i < t\le V_i+T_{i+1}$,} \\\boldsymbol{Z}(V_i)+ \boldsymbol{X}^{(i+1)}(T_{i+1})+\boldsymbol{Y}^{(i+1)}(t-V_i-T_{i+1}) & \text{if $ V_i+T_{i+1} < t \le V_{i+1}$}. \end{cases}\end{equation*}
Note that this is a multi-dimensional regenerative process with regeneration epochs
![]() $V_i, i\ge1$
. This is a generalization of the one-dimensional model discussed in [Reference Kella and Whitt24].
$V_i, i\ge1$
. This is a generalization of the one-dimensional model discussed in [Reference Kella and Whitt24].
We assume that
![]() $\{\{\boldsymbol{X}^{(i)}(t),\, t\ge 0\} \colon i\ge 1\}$
and
$\{\{\boldsymbol{X}^{(i)}(t),\, t\ge 0\} \colon i\ge 1\}$
and
![]() $\{\{\boldsymbol{Y}^{(i)}(t),\, t\ge 0\} \colon i\ge 1\}$
are independent samples of
$\{\{\boldsymbol{Y}^{(i)}(t),\, t\ge 0\} \colon i\ge 1\}$
are independent samples of
![]() $\{\boldsymbol{X}(t),\, t\ge 0\}$
and
$\{\boldsymbol{X}(t),\, t\ge 0\}$
and
![]() $\{\boldsymbol{Y}(t),\, t\ge 0\}$
, respectively, where
$\{\boldsymbol{Y}(t),\, t\ge 0\}$
, respectively, where
with all the fBms
![]() $B_{H_j}, \widetilde B_{\widetilde H_j}$
being mutually independent and
$B_{H_j}, \widetilde B_{\widetilde H_j}$
being mutually independent and
![]() $p_j, q_j>0$
,
$p_j, q_j>0$
,
![]() $1\le j\le n$
. Suppose that
$1\le j\le n$
. Suppose that
![]() $(T_i,S_i), i\ge 1$
are independent samples of (T, S) and T is regularly varying with index
$(T_i,S_i), i\ge 1$
are independent samples of (T, S) and T is regularly varying with index
![]() $\lambda>1$
. We further assume that
$\lambda>1$
. We further assume that
For notational simplicity we shall restrict ourselves to the two-dimensional case. The general n-dimensional problem can be analysed similarly. Thus, for the rest of this section and related proofs in Section 6, all vectors (or multi-dimensional processes) are considered to be two-dimensional ones.
We are interested in the asymptotics of the following tail probability:
with
![]() $a_1, a_2>0$
. In the fluid queueing context, Q(u) can be interpreted as the probability that both buffers overflow in some environment cycle. In the insurance context, Q(u) can be interpreted as the probability that in some business cycle the two lines of business of the insurer are both ruined (not necessarily at the same time). Similar one-dimensional models have been discussed in the literature; see e.g. [Reference Asmussen and Albrecher4], [Reference Palmowski and Zwart28], and [Reference Zwart, Borst and DDĘbicki40].
$a_1, a_2>0$
. In the fluid queueing context, Q(u) can be interpreted as the probability that both buffers overflow in some environment cycle. In the insurance context, Q(u) can be interpreted as the probability that in some business cycle the two lines of business of the insurer are both ruined (not necessarily at the same time). Similar one-dimensional models have been discussed in the literature; see e.g. [Reference Asmussen and Albrecher4], [Reference Palmowski and Zwart28], and [Reference Zwart, Borst and DDĘbicki40].
We introduce the following notation:
Then we have
Note that
![]() $\boldsymbol{U}^{(n)}$
,
$\boldsymbol{U}^{(n)}$
,
![]() $n\ge 1$
and
$n\ge 1$
and
![]() $\boldsymbol{M}^{(n)}$
,
$\boldsymbol{M}^{(n)}$
,
![]() $n\ge 1$
are both (independent and identically distributed) sequences. By the second assumption in (4.1) we have
$n\ge 1$
are both (independent and identically distributed) sequences. By the second assumption in (4.1) we have
which ensures that the event in the above probability is a rare event for large u, i.e.
![]() $Q(u)\rightarrow 0$
, as
$Q(u)\rightarrow 0$
, as
![]() $u\rightarrow\infty $
.
$u\rightarrow\infty $
.
It is noted that our question now becomes an exit problem of a two-dimensional perturbed random walk. The exit problems of a multi-dimensional random walk have been discussed in many papers, e.g. [Reference Hult, Lindskog, Mikosch and Samorodnitsky21]. However, as far as we know, the multi-dimensional perturbed random walk has not been discussed in the existing literature.
Since T is regularly varying with index
![]() $\lambda>1$
, we have that
$\lambda>1$
, we have that
is regularly varying with index
![]() $\lambda$
and some limiting measure
$\lambda$
and some limiting measure
![]() $\mu$
(whose form depends on the norm
$\mu$
(whose form depends on the norm
![]() $| \cdot |$
that is chosen). We now present the main result of this section, leaving its proof to Section 6.
$| \cdot |$
that is chosen). We now present the main result of this section, leaving its proof to Section 6.
Theorem 4.1. Under the above assumptions on regenerative model
![]() ${\boldsymbol{Z}}(t)$
,
${\boldsymbol{Z}}(t)$
,
![]() $t\ge0$
, we have that, as
$t\ge0$
, we have that, as
![]() $u\rightarrow\infty $
,
$u\rightarrow\infty $
,
where
![]() $\boldsymbol{c}$
and
$\boldsymbol{c}$
and
![]() $\widetilde {\boldsymbol{T}}$
are given by (4.4) and (4.5), respectively.
$\widetilde {\boldsymbol{T}}$
are given by (4.4) and (4.5), respectively.
Remark 4.1. Consider
![]() $\vert {\cdot } \vert$
to be the
$\vert {\cdot } \vert$
to be the
![]() $L^1$
-norm in Theorem 4.1. We have
$L^1$
-norm in Theorem 4.1. We have
and thus, as
![]() $u\rightarrow\infty $
,
$u\rightarrow\infty $
,
5. Proof of main results
This section is devoted to the proof of Theorem 3.1, followed by a proof of Example 3.1.
First we give a result in line with Proposition 2.1. Note that in the proof of the main results in [Reference Dieker19], the minimum point
![]() $t_u^*$
of the function
$t_u^*$
of the function
plays an important role. It has been discussed therein that
![]() $t_u^*$
converges, as
$t_u^*$
converges, as
![]() $u\rightarrow\infty $
, to
$u\rightarrow\infty $
, to
![]() $t^*\;:\!=\; H/(1-H)$
, which is the unique minimum point of
$t^*\;:\!=\; H/(1-H)$
, which is the unique minimum point of
![]() $\lim_{u\rightarrow\infty } f_u(t) \sigma(u)/u= (1+t)/ (t/c)^H$
,
$\lim_{u\rightarrow\infty } f_u(t) \sigma(u)/u= (1+t)/ (t/c)^H$
,
![]() $t\ge 0$
. In this sense,
$t\ge 0$
. In this sense,
![]() $t_u^*$
is asymptotically unique. We have the following corollary of [Reference Dieker19], which is useful for the proofs below.
$t_u^*$
is asymptotically unique. We have the following corollary of [Reference Dieker19], which is useful for the proofs below.
Lemma 5.1. Let X(t),
![]() $t\ge0$
, be an a.s. continuous centered Gaussian process with stationary increments and
$t\ge0$
, be an a.s. continuous centered Gaussian process with stationary increments and
![]() $X(0)=0$
. Suppose that C1–C4 hold. For any fixed
$X(0)=0$
. Suppose that C1–C4 hold. For any fixed
![]() $0<\varepsilon<t^*/c$
, we have, as
$0<\varepsilon<t^*/c$
, we have, as
![]() $u\rightarrow\infty $
,
$u\rightarrow\infty $
,
with
![]() $\psi(u)$
the same as in Proposition 2.1. Furthermore, for any
$\psi(u)$
the same as in Proposition 2.1. Furthermore, for any
![]() $\gamma>0$
we have
$\gamma>0$
we have
Proof. Note that
The first claim follows from [Reference Dieker19], as the main interval that determines the asymptotics is in
![]() $[0, (t^* + c\varepsilon)]$
(see Lemma 7 and the comments in Section 2.1 therein). Similarly, we have
$[0, (t^* + c\varepsilon)]$
(see Lemma 7 and the comments in Section 2.1 therein). Similarly, we have
Since
![]() $t^*_u$
is asymptotically unique and
$t^*_u$
is asymptotically unique and
![]() $\lim_{u\rightarrow\infty }t^*_u=t^*$
, we can show that, for all u large,
$\lim_{u\rightarrow\infty }t^*_u=t^*$
, we can show that, for all u large,
for some
![]() $\rho>1$
. Thus, by arguments similar to those in the proof of Lemma 7 of [Reference Dieker19] using the Borel inequality, we conclude the second claim.
$\rho>1$
. Thus, by arguments similar to those in the proof of Lemma 7 of [Reference Dieker19] using the Borel inequality, we conclude the second claim.
The following lemma is crucial for the proof of Theorem 3.1.
Lemma 5.2. Let
![]() $X_i(t)$
,
$X_i(t)$
,
![]() $t\ge 0$
,
$t\ge 0$
,
![]() $i=1,2,\ldots, n_0 (< n)$
be independent centered Gaussian processes with stationary increments, and let
$i=1,2,\ldots, n_0 (< n)$
be independent centered Gaussian processes with stationary increments, and let
![]() $\boldsymbol{\mathcal{T}}$
be an independent regularly varying random vector with index
$\boldsymbol{\mathcal{T}}$
be an independent regularly varying random vector with index
![]() $\alpha$
and limiting measure
$\alpha$
and limiting measure
![]() $\nu$
. Suppose that all of
$\nu$
. Suppose that all of
![]() $\sigma_i(t), i=1,2,\ldots, n_0$
satisfy the assumptions C1–C3 with the parameters involved indexed by i, which further satisfy that
$\sigma_i(t), i=1,2,\ldots, n_0$
satisfy the assumptions C1–C3 with the parameters involved indexed by i, which further satisfy that
![]() $\overleftarrow{\sigma_i}(u)\sim k_i \overleftarrow{\sigma_1}(u) $
for some positive constants
$\overleftarrow{\sigma_i}(u)\sim k_i \overleftarrow{\sigma_1}(u) $
for some positive constants
![]() $k_i,i=1,2,\ldots,m\leq n_0$
and
$k_i,i=1,2,\ldots,m\leq n_0$
and
![]() $\overleftarrow{\sigma_{j} }(u)={\textrm{o}}(\overleftarrow{\sigma_1 }(u))$
for all
$\overleftarrow{\sigma_{j} }(u)={\textrm{o}}(\overleftarrow{\sigma_1 }(u))$
for all
![]() $j=m+1,\ldots, n_0$
. Then, for any increasing to infinity functions
$j=m+1,\ldots, n_0$
. Then, for any increasing to infinity functions
![]() $h_i(u), n_0+1\le i\le n$
such that
$h_i(u), n_0+1\le i\le n$
such that
![]() $h_i(u)={\textrm{o}}(\overleftarrow{\sigma_1}(u)), n_0+1\le i\le n$
, and any
$h_i(u)={\textrm{o}}(\overleftarrow{\sigma_1}(u)), n_0+1\le i\le n$
, and any
![]() $a_i>0$
,
$a_i>0$
,
where
![]() $\widetilde{\nu}$
is defined in (3.2) and
$\widetilde{\nu}$
is defined in (3.2) and
![]() $\boldsymbol{k}\boldsymbol{a}_{m,0}^{1/{\boldsymbol{H}}}=(k_1a_1^{1/H_1}, \ldots, k_ma_m^{1/H_m}, 0\ldots, 0)$
with
$\boldsymbol{k}\boldsymbol{a}_{m,0}^{1/{\boldsymbol{H}}}=(k_1a_1^{1/H_1}, \ldots, k_ma_m^{1/H_m}, 0\ldots, 0)$
with
![]() $H_1=H_2=\cdots=H_m$
.
$H_1=H_2=\cdots=H_m$
.
Proof. We use an argument similar to that in the proof of Theorem 2.1 of [Reference DĘbicki, Zwart and Borst18] to verify our conclusion. For notational convenience, denote
We first give an asymptotically lower bound for H(u). Let
![]() $G(\boldsymbol{x})= \mathbb{P} \{ {\boldsymbol{\mathcal{T}} \le \boldsymbol{x}} \} $
be the distribution function of
$G(\boldsymbol{x})= \mathbb{P} \{ {\boldsymbol{\mathcal{T}} \le \boldsymbol{x}} \} $
be the distribution function of
![]() $\boldsymbol{\mathcal{T}}$
. Note that, for any constants r and R such that
$\boldsymbol{\mathcal{T}}$
. Note that, for any constants r and R such that
![]() $0<r<R$
,
$0<r<R$
,
 \begin{align*} H(u)&\geq \mathbb{P}\biggl\{{ \cap_{i=1}^{n_0} \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t)>a_i u \biggr), \cap_{i=1}^m (r\overleftarrow{\sigma_1}(u) \le \mathcal{T}_i\le R\overleftarrow{\sigma_1}(u)),\cap_{i=m+1}^n (\mathcal{T}_i>r\overleftarrow{\sigma_1}(u))} \biggr\}\\&= \oint_{[r,R]^{m}\times (r,\infty)^{n-m}} \mathbb{P}\biggl\{{\cap_{i=1}^{n_0} \biggl(\sup_{t\in[0, \overleftarrow{\sigma_1}(u)t_i]} X_{i}(t)>a_i u\biggr)} \biggr\} \,{\textrm{d}} G(\overleftarrow{\sigma_1}(u) t_1,\ldots, \overleftarrow{\sigma_{1}}(u) t_{n})\\ &= \oint_{[r,R]^{m}\times (r,\infty)^{n-m}}\prod_{i=1}^{n_0} \mathbb{P}\biggl\{{ \sup_{s\in[0,1]} X_{i}^{u,t_i}(s)>a_i u_i(t_i)} \biggr\} \,{\textrm{d}} G(\overleftarrow{\sigma_1}(u) t_1,\ldots, \overleftarrow{\sigma_{1}}(u) t_{n})\end{align*}
\begin{align*} H(u)&\geq \mathbb{P}\biggl\{{ \cap_{i=1}^{n_0} \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t)>a_i u \biggr), \cap_{i=1}^m (r\overleftarrow{\sigma_1}(u) \le \mathcal{T}_i\le R\overleftarrow{\sigma_1}(u)),\cap_{i=m+1}^n (\mathcal{T}_i>r\overleftarrow{\sigma_1}(u))} \biggr\}\\&= \oint_{[r,R]^{m}\times (r,\infty)^{n-m}} \mathbb{P}\biggl\{{\cap_{i=1}^{n_0} \biggl(\sup_{t\in[0, \overleftarrow{\sigma_1}(u)t_i]} X_{i}(t)>a_i u\biggr)} \biggr\} \,{\textrm{d}} G(\overleftarrow{\sigma_1}(u) t_1,\ldots, \overleftarrow{\sigma_{1}}(u) t_{n})\\ &= \oint_{[r,R]^{m}\times (r,\infty)^{n-m}}\prod_{i=1}^{n_0} \mathbb{P}\biggl\{{ \sup_{s\in[0,1]} X_{i}^{u,t_i}(s)>a_i u_i(t_i)} \biggr\} \,{\textrm{d}} G(\overleftarrow{\sigma_1}(u) t_1,\ldots, \overleftarrow{\sigma_{1}}(u) t_{n})\end{align*}
holds for sufficiently large u, where
 \begin{align*} & X_{i}^{u,t_{i}}(s) \;=\!:\; \dfrac{X_i(\overleftarrow{\sigma_1}(u) t_i s)}{\sigma_i(\overleftarrow{\sigma_1}(u) t_i)},\quad u_i(t_i)\;=\!:\; \dfrac{u}{\sigma_i(\overleftarrow{\sigma_1}(u) t_i)},\\ & s\in[0,1],(t_1,t_2,\ldots,t_{n_0})\in [r,R]^{m}\times(r,\infty)^{n_0-m}. \end{align*}
\begin{align*} & X_{i}^{u,t_{i}}(s) \;=\!:\; \dfrac{X_i(\overleftarrow{\sigma_1}(u) t_i s)}{\sigma_i(\overleftarrow{\sigma_1}(u) t_i)},\quad u_i(t_i)\;=\!:\; \dfrac{u}{\sigma_i(\overleftarrow{\sigma_1}(u) t_i)},\\ & s\in[0,1],(t_1,t_2,\ldots,t_{n_0})\in [r,R]^{m}\times(r,\infty)^{n_0-m}. \end{align*}
By Lemma 5.2 of [Reference DĘbicki, Zwart and Borst18], we know that, as
![]() $u\rightarrow\infty$
, the processes
$u\rightarrow\infty$
, the processes
![]() $X_{i}^{u,t_i}(s)$
converge weakly in C([0,Reference Arendarczyk1]) to
$X_{i}^{u,t_i}(s)$
converge weakly in C([0,Reference Arendarczyk1]) to
![]() $B_{H_i}(s)$
, uniformly in
$B_{H_i}(s)$
, uniformly in
![]() $t_i\in(r,\infty)$
, for
$t_i\in(r,\infty)$
, for
![]() $i=1,2,\ldots,n_0$
. Further, according to the assumptions on
$i=1,2,\ldots,n_0$
. Further, according to the assumptions on
![]() $\sigma_i(t)$
, Theorems 1.5.2 and 1.5.6 of [Reference Bingham, Goldie and Teugels8], we find that as
$\sigma_i(t)$
, Theorems 1.5.2 and 1.5.6 of [Reference Bingham, Goldie and Teugels8], we find that as
![]() $u\rightarrow\infty$
,
$u\rightarrow\infty$
,
![]() $u_i(t_i)$
converges to
$u_i(t_i)$
converges to
![]() $k_i ^{H_i}t_i^{-H_i}$
uniformly in
$k_i ^{H_i}t_i^{-H_i}$
uniformly in
![]() $t_i\in[r,R]$
, for
$t_i\in[r,R]$
, for
![]() $i=1,2,\ldots,m$
, and
$i=1,2,\ldots,m$
, and
![]() $u_i(t_i)$
converges to 0 uniformly in
$u_i(t_i)$
converges to 0 uniformly in
![]() $t_i\in[r,\infty )$
, for
$t_i\in[r,\infty )$
, for
![]() $i=m+1,\ldots,n_0$
. Then, by the continuous mapping theorem and recalling that
$i=m+1,\ldots,n_0$
. Then, by the continuous mapping theorem and recalling that
![]() $\xi_i$
defined in (3.1) is a continuous random variable (e.g. [Reference Zaïdi and Nualart39]), we get
$\xi_i$
defined in (3.1) is a continuous random variable (e.g. [Reference Zaïdi and Nualart39]), we get
where
 \begin{align*}J_1(u)&\;=\!:\; \mathbb{P}\bigl\{\cap_{i=1}^m\bigl(\xi_i^{{1}/{H_i}}\mathcal{T}_i>k_ia_i^{{1}/{H_i}}\overleftarrow{\sigma_1}(u)\bigr), \cap_{i=m+1}^n (\mathcal{T}_i>r\overleftarrow{\sigma_1}(u))\bigr\},\\J_2(u)&\;=\!:\; \mathbb{P} \bigl\{\cap_{i=1}^m\bigl(\xi_i^{{1}/{H_i}}\mathcal{T}_i>k_ia_i^{{1}/{H_i}}\overleftarrow{\sigma_1}(u)\bigr),\\&\quad\,\ \cap_{i=m+1}^n (\mathcal{T}_i>r\overleftarrow{\sigma_1}(u)),\cup_{i=1}^{m} ( (\mathcal{T}_i< r\overleftarrow{\sigma_1}(u)) \cup (\mathcal{T}_i>R\overleftarrow{\sigma_1}(u) ))\bigr\}.\end{align*}
\begin{align*}J_1(u)&\;=\!:\; \mathbb{P}\bigl\{\cap_{i=1}^m\bigl(\xi_i^{{1}/{H_i}}\mathcal{T}_i>k_ia_i^{{1}/{H_i}}\overleftarrow{\sigma_1}(u)\bigr), \cap_{i=m+1}^n (\mathcal{T}_i>r\overleftarrow{\sigma_1}(u))\bigr\},\\J_2(u)&\;=\!:\; \mathbb{P} \bigl\{\cap_{i=1}^m\bigl(\xi_i^{{1}/{H_i}}\mathcal{T}_i>k_ia_i^{{1}/{H_i}}\overleftarrow{\sigma_1}(u)\bigr),\\&\quad\,\ \cap_{i=m+1}^n (\mathcal{T}_i>r\overleftarrow{\sigma_1}(u)),\cup_{i=1}^{m} ( (\mathcal{T}_i< r\overleftarrow{\sigma_1}(u)) \cup (\mathcal{T}_i>R\overleftarrow{\sigma_1}(u) ))\bigr\}.\end{align*}
Putting
![]() ${\boldsymbol{\eta}}=(\xi_1^{1/H_1},\ldots,\xi_m^{1/H_m},1,\ldots,1)$
, then by Lemma A.2 and the continuity of the limiting measure
${\boldsymbol{\eta}}=(\xi_1^{1/H_1},\ldots,\xi_m^{1/H_m},1,\ldots,1)$
, then by Lemma A.2 and the continuity of the limiting measure
![]() $\widehat\nu$
defined therein, we have
$\widehat\nu$
defined therein, we have
Furthermore,
Then, by the fact that
![]() $\vert {\boldsymbol{\mathcal{T}}} \vert$
is regularly varying with index
$\vert {\boldsymbol{\mathcal{T}}} \vert$
is regularly varying with index
![]() $\alpha$
, and using the same arguments as in the proof of Theorem 2.1 of [Reference DĘbicki, Zwart and Borst18] (see the asymptotic for integral
$\alpha$
, and using the same arguments as in the proof of Theorem 2.1 of [Reference DĘbicki, Zwart and Borst18] (see the asymptotic for integral
![]() $I_4$
and (5.14) therein), we conclude that
$I_4$
and (5.14) therein), we conclude that
which combined with (5.1) and (5.2) yields
Next we give an asymptotic upper bound for H(u). Note that
 \begin{align*}H(u)&\le\mathbb{P}\biggl\{{ \cap_{i=1}^{m} \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t)>a_i u \biggr) } \biggr\} \\&= \mathbb{P}\biggl\{{ \cap_{i=1}^{m} \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t)>a_i u \biggr), \cap_{i=1}^m (r\overleftarrow{\sigma_1}(u) \le \mathcal{T}_i\le R\overleftarrow{\sigma_1}(u))} \biggr\}\\& \quad\, + \mathbb{P}\biggl\{{ \cap_{i=1}^{m} \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t)>a_i u \biggr), \cup_{i=1}^{m} ( (\mathcal{T}_i< r\overleftarrow{\sigma_1}(u)) \cup (\mathcal{T}_i>R\overleftarrow{\sigma_1}(u) ))} \biggr\}\\&\;=\!:\; J_3(u)+J_4(u).\end{align*}
\begin{align*}H(u)&\le\mathbb{P}\biggl\{{ \cap_{i=1}^{m} \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t)>a_i u \biggr) } \biggr\} \\&= \mathbb{P}\biggl\{{ \cap_{i=1}^{m} \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t)>a_i u \biggr), \cap_{i=1}^m (r\overleftarrow{\sigma_1}(u) \le \mathcal{T}_i\le R\overleftarrow{\sigma_1}(u))} \biggr\}\\& \quad\, + \mathbb{P}\biggl\{{ \cap_{i=1}^{m} \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t)>a_i u \biggr), \cup_{i=1}^{m} ( (\mathcal{T}_i< r\overleftarrow{\sigma_1}(u)) \cup (\mathcal{T}_i>R\overleftarrow{\sigma_1}(u) ))} \biggr\}\\&\;=\!:\; J_3(u)+J_4(u).\end{align*}
By the same reasoning as that used in the deduction for (5.2), we can show that
Moreover,
Thus, by the same arguments as in the proof of Theorem 2.1 of [Reference DĘbicki, Zwart and Borst18] (see the asymptotics for integrals
![]() $I_1, I_2, I_4$
therein), we conclude that
$I_1, I_2, I_4$
therein), we conclude that
which together with (5.4) implies that
Notice that by the assumptions on
![]() $\{\overleftarrow{\sigma_i}(u)\}_{i=1}^{m}$
, we in fact have
$\{\overleftarrow{\sigma_i}(u)\}_{i=1}^{m}$
, we in fact have
![]() $H_1=H_2=\cdots=H_m$
. Consequently, combining (5.3) and (5.5) we complete the proof.
$H_1=H_2=\cdots=H_m$
. Consequently, combining (5.3) and (5.5) we complete the proof.
Proof of Theorem 3.1. In the following we use the convention that
![]() $\cap_{i=1}^0=\Omega$
, the sample space. We first verify the claim for case (i),
$\cap_{i=1}^0=\Omega$
, the sample space. We first verify the claim for case (i),
![]() $n_0>0$
. For arbitrarily small
$n_0>0$
. For arbitrarily small
![]() $\varepsilon>0$
, we have
$\varepsilon>0$
, we have
 \begin{align*}P(u)&\ge \mathbb{P}\biggl\{\cap_{i=1}^{n_-} \biggl(\sup_{t\in[0,\mathcal{T}_i]} (X_{i}(t) +c_i t) >a_i u,\mathcal{T}_i>(t^*_i/\vert {c_i} \vert+\varepsilon) u \biggr), \cap_{i=n_-+1}^{n_-+n_0} \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t) >a_i u \biggr), \\& \quad\, \cap_{i=n_-+n_0+1}^{n} \biggl(\sup_{t\in[0,\mathcal{T}_i]} (X_{i}(t) +c_i t) >a_i u,\mathcal{T}_i>\dfrac{a_i+\varepsilon}{c_i}u \biggr)\biggr\}\\&\geq \mathbb{P}\biggl\{\cap_{i=1}^{n_-} \biggl(\sup_{t\in[0, (t^*_i/\vert {c_i} \vert+\varepsilon) u ]} (X_{i}(t) +c_i t) >a_i u,\mathcal{T}_i>(t^*_i/\vert {c_i} \vert+\varepsilon) u \biggr), \\& \quad\, \cap_{i=n_-+1}^{n_-+n_0} \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t) >a_i u \biggr), \cap_{i=n_-+n_0+1}^{n} \biggl( X_{i}\biggl(\dfrac{a_i+\varepsilon}{c_i}u\biggr) >-\varepsilon u,\mathcal{T}_i>\dfrac{a_i+\varepsilon}{c_i}u \biggr)\biggr\}\\&= Q_1(u)\times Q_2(u)\times Q_3(u),\end{align*}
\begin{align*}P(u)&\ge \mathbb{P}\biggl\{\cap_{i=1}^{n_-} \biggl(\sup_{t\in[0,\mathcal{T}_i]} (X_{i}(t) +c_i t) >a_i u,\mathcal{T}_i>(t^*_i/\vert {c_i} \vert+\varepsilon) u \biggr), \cap_{i=n_-+1}^{n_-+n_0} \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t) >a_i u \biggr), \\& \quad\, \cap_{i=n_-+n_0+1}^{n} \biggl(\sup_{t\in[0,\mathcal{T}_i]} (X_{i}(t) +c_i t) >a_i u,\mathcal{T}_i>\dfrac{a_i+\varepsilon}{c_i}u \biggr)\biggr\}\\&\geq \mathbb{P}\biggl\{\cap_{i=1}^{n_-} \biggl(\sup_{t\in[0, (t^*_i/\vert {c_i} \vert+\varepsilon) u ]} (X_{i}(t) +c_i t) >a_i u,\mathcal{T}_i>(t^*_i/\vert {c_i} \vert+\varepsilon) u \biggr), \\& \quad\, \cap_{i=n_-+1}^{n_-+n_0} \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t) >a_i u \biggr), \cap_{i=n_-+n_0+1}^{n} \biggl( X_{i}\biggl(\dfrac{a_i+\varepsilon}{c_i}u\biggr) >-\varepsilon u,\mathcal{T}_i>\dfrac{a_i+\varepsilon}{c_i}u \biggr)\biggr\}\\&= Q_1(u)\times Q_2(u)\times Q_3(u),\end{align*}
where
 \begin{align*}Q_{1} (u) & \;:\!=\; \mathbb{P} \biggl\{\cap_{i=1}^{n_-} \biggl(\sup_{t\in[0, (t^{\ast}_{i}/\vert {c_{i}} \vert+\varepsilon) u ]} X_{i}(t) +c_{i} t > a_{i} u \biggr) \biggr\}\\ Q_{2}(u)&\;:\!=\; \mathbb{P}\biggl\{\cap_{i=1}^{n_-} ( \mathcal{T}_i>(t^{\ast}_{i} /\vert {c_i} \vert+\varepsilon) u ),\\ &\quad\, \cap_{i=n_-+1}^{n_-+n_0} \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t)>a_i u \biggr), \cap_{i=n_-+n_0+1}^n \biggl( \mathcal{T}_i>\dfrac{a_i+\varepsilon}{c_i}u \biggr) \biggr\},\\ Q_3(u)&\;:\!=\; \prod_{i=n_-+n_0+1}^n \mathbb{P}\biggl\{{N_i> \dfrac{-\varepsilon u}{ \sigma_i(\frac{a_i+\varepsilon}{c_i}u)} } \biggr\}\rightarrow1,\quad u\rightarrow\infty , \end{align*}
\begin{align*}Q_{1} (u) & \;:\!=\; \mathbb{P} \biggl\{\cap_{i=1}^{n_-} \biggl(\sup_{t\in[0, (t^{\ast}_{i}/\vert {c_{i}} \vert+\varepsilon) u ]} X_{i}(t) +c_{i} t > a_{i} u \biggr) \biggr\}\\ Q_{2}(u)&\;:\!=\; \mathbb{P}\biggl\{\cap_{i=1}^{n_-} ( \mathcal{T}_i>(t^{\ast}_{i} /\vert {c_i} \vert+\varepsilon) u ),\\ &\quad\, \cap_{i=n_-+1}^{n_-+n_0} \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t)>a_i u \biggr), \cap_{i=n_-+n_0+1}^n \biggl( \mathcal{T}_i>\dfrac{a_i+\varepsilon}{c_i}u \biggr) \biggr\},\\ Q_3(u)&\;:\!=\; \prod_{i=n_-+n_0+1}^n \mathbb{P}\biggl\{{N_i> \dfrac{-\varepsilon u}{ \sigma_i(\frac{a_i+\varepsilon}{c_i}u)} } \biggr\}\rightarrow1,\quad u\rightarrow\infty , \end{align*}
with
![]() $N_i,i=n_-+n_0+1,\ldots,n$
being standard normally distributed random variables. By Lemma 5.1, we know, as
$N_i,i=n_-+n_0+1,\ldots,n$
being standard normally distributed random variables. By Lemma 5.1, we know, as
![]() $u\rightarrow\infty $
, that
$u\rightarrow\infty $
, that
Further, according to the assumptions on
![]() $\sigma_i$
and Lemma 5.2, we get
$\sigma_i$
and Lemma 5.2, we get
and thus
Similarly, we can show that
 \begin{align*}P(u)&\le \mathbb{P}\biggl\{{\cap_{i=1}^{n_-} \biggl(\sup_{t\in[0,\infty )} X_{i}(t) +c_i t >a_i u \biggr), \cap_{i=n_-+1}^{n_-+n_0} \biggl(\sup_{t\in[0,\mathcal{T}_i]} X_{i}(t)>a_i u \biggr)} \biggr\} \\& \sim\ \widetilde{\nu}\bigl(\bigl(\boldsymbol{k}\boldsymbol{a}_0^{1/{H_{n_-+1}}},\boldsymbol{\infty} \bigr]\bigr) \, \mathbb{P} \{ {\vert {\boldsymbol{\mathcal{T}}} \vert>\overleftarrow{\sigma}_{n_-+1}(u)} \} \prod_{i=1}^{n_-}\psi_i(a_i u),\quad u\rightarrow\infty .\end{align*}
\begin{align*}P(u)&\le \mathbb{P}\biggl\{{\cap_{i=1}^{n_-} \biggl(\sup_{t\in[0,\infty )} X_{i}(t) +c_i t >a_i u \biggr), \cap_{i=n_-+1}^{n_-+n_0} \biggl(\sup_{t\in[0,\mathcal{T}_i]} X_{i}(t)>a_i u \biggr)} \biggr\} \\& \sim\ \widetilde{\nu}\bigl(\bigl(\boldsymbol{k}\boldsymbol{a}_0^{1/{H_{n_-+1}}},\boldsymbol{\infty} \bigr]\bigr) \, \mathbb{P} \{ {\vert {\boldsymbol{\mathcal{T}}} \vert>\overleftarrow{\sigma}_{n_-+1}(u)} \} \prod_{i=1}^{n_-}\psi_i(a_i u),\quad u\rightarrow\infty .\end{align*}
This completes the proof of case (i).
Next we consider case (ii),
![]() $n_0=0$
. Similarly to case (i) we have, for any small
$n_0=0$
. Similarly to case (i) we have, for any small
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
 \begin{align*}P(u)&\geq \mathbb{P}\biggl\{\cap_{i=1}^{n_-} \biggl(\sup_{t\in[0, (t^*_i/\vert {c_i} \vert+\varepsilon) u ]} (X_{i}(t) +c_i t) >a_i u,\mathcal{T}_i>(t^*_i/\vert {c_i} \vert+\varepsilon) u \biggr), \\& \quad\, \cap_{i=n_-+1}^{n} \biggl( X_{i}\biggl(\dfrac{a_i+\varepsilon}{c_i}u\biggr) >-\varepsilon u,\mathcal{T}_i>\dfrac{a_i+\varepsilon}{c_i}u \biggr)\biggr\}\\&= Q_1(u)\times Q_3(u)\times Q_4(u),\end{align*}
\begin{align*}P(u)&\geq \mathbb{P}\biggl\{\cap_{i=1}^{n_-} \biggl(\sup_{t\in[0, (t^*_i/\vert {c_i} \vert+\varepsilon) u ]} (X_{i}(t) +c_i t) >a_i u,\mathcal{T}_i>(t^*_i/\vert {c_i} \vert+\varepsilon) u \biggr), \\& \quad\, \cap_{i=n_-+1}^{n} \biggl( X_{i}\biggl(\dfrac{a_i+\varepsilon}{c_i}u\biggr) >-\varepsilon u,\mathcal{T}_i>\dfrac{a_i+\varepsilon}{c_i}u \biggr)\biggr\}\\&= Q_1(u)\times Q_3(u)\times Q_4(u),\end{align*}
where
By Lemma A.1, we know that
and thus
For the upper bound, we have for any small
![]() $\varepsilon>0$
$\varepsilon>0$
with
 \begin{align*} I_1(u)&\;:\!=\; \mathbb{P}\biggl\{\cap_{i=1}^{n_-} \biggl(\sup_{t\in[0,\mathcal{T}_i]} X_{i}(t) +c_i t >a_i u \biggr),\\ &\quad\, \cap_{i=1}^{n_-} ( \mathcal{T}_i>(t^*_i/\vert {c_i} \vert-\varepsilon) u ), \cap_{i=n_-+1}^n \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t) +c_i \mathcal{T}_i>a_i u \biggr)\biggr\},\\ I_2(u)&\;:\!=\; \mathbb{P}\biggl\{\cap_{i=1}^{n_-} \biggl(\sup_{t\in[0,\mathcal{T}_i]} X_{i}(t) +c_i t >a_i u \biggr), \\ &\quad\, \cup_{i=1}^{n_-} ( \mathcal{T}_i\le(t^*_i/\vert {c_i} \vert-\varepsilon) u ), \cap_{i=n_-+1}^n \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t)+c_i \mathcal{T}_i>a_i u \biggr)\biggr\}.\end{align*}
\begin{align*} I_1(u)&\;:\!=\; \mathbb{P}\biggl\{\cap_{i=1}^{n_-} \biggl(\sup_{t\in[0,\mathcal{T}_i]} X_{i}(t) +c_i t >a_i u \biggr),\\ &\quad\, \cap_{i=1}^{n_-} ( \mathcal{T}_i>(t^*_i/\vert {c_i} \vert-\varepsilon) u ), \cap_{i=n_-+1}^n \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t) +c_i \mathcal{T}_i>a_i u \biggr)\biggr\},\\ I_2(u)&\;:\!=\; \mathbb{P}\biggl\{\cap_{i=1}^{n_-} \biggl(\sup_{t\in[0,\mathcal{T}_i]} X_{i}(t) +c_i t >a_i u \biggr), \\ &\quad\, \cup_{i=1}^{n_-} ( \mathcal{T}_i\le(t^*_i/\vert {c_i} \vert-\varepsilon) u ), \cap_{i=n_-+1}^n \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t)+c_i \mathcal{T}_i>a_i u \biggr)\biggr\}.\end{align*}
It follows that
 \begin{align*} I_1(u)&\le \mathbb{P}\biggl\{\cap_{i=1}^{n_-} \biggl(\sup_{t\in[0,\infty )} X_{i}(t) +c_i t >a_i u \biggr), \\ &\quad\, \cap_{i=1}^{n_-} ( \mathcal{T}_i>(t^*_i/\vert {c_i} \vert-\varepsilon) u ), \cap_{i=n_-+1}^n \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t)+c_i \mathcal{T}_i>a_i u \biggr)\biggr\}\\&= \prod_{i=1}^{n_-} \psi_i(a_iu) \, \mathbb{P}\biggl\{{\cap_{i=1}^{n_-} ( \mathcal{T}_i>(t^*_i/\vert {c_i} \vert-\varepsilon) u ), \cap_{i=n_-+1}^n \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t)+c_i \mathcal{T}_i>a_i u \biggr)} \biggr\}.\end{align*}
\begin{align*} I_1(u)&\le \mathbb{P}\biggl\{\cap_{i=1}^{n_-} \biggl(\sup_{t\in[0,\infty )} X_{i}(t) +c_i t >a_i u \biggr), \\ &\quad\, \cap_{i=1}^{n_-} ( \mathcal{T}_i>(t^*_i/\vert {c_i} \vert-\varepsilon) u ), \cap_{i=n_-+1}^n \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t)+c_i \mathcal{T}_i>a_i u \biggr)\biggr\}\\&= \prod_{i=1}^{n_-} \psi_i(a_iu) \, \mathbb{P}\biggl\{{\cap_{i=1}^{n_-} ( \mathcal{T}_i>(t^*_i/\vert {c_i} \vert-\varepsilon) u ), \cap_{i=n_-+1}^n \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t)+c_i \mathcal{T}_i>a_i u \biggr)} \biggr\}.\end{align*}
Next, for the small chosen
![]() $\varepsilon>0$
we have
$\varepsilon>0$
we have
 \begin{align*}& \mathbb{P}\biggl\{{\cap_{i=1}^{n_-} ( \mathcal{T}_i>(t^*_i/\vert {c_i} \vert-\varepsilon) u ), \cap_{i=n_-+1}^n \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t) +c_i \mathcal{T}_i>a_i u \biggr)} \biggr\}\\& \quad = \mathbb{P}\biggl\{{\cap_{i=1}^{n_-} ( \mathcal{T}_i>(t^*_i/\vert {c_i} \vert-\varepsilon) u ), \cap_{i=n_-+1}^n \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t) +c_i \mathcal{T}_i>a_i u, \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t) \le \varepsilon u\biggr)} \biggr\}\\ & \quad\quad +\mathbb{P}\biggl\{\cap_{i=1}^{n_-} ( \mathcal{T}_i>(t^*_i/\vert {c_i} \vert-\varepsilon) u ),\\ &\quad\quad\quad\, \cap_{i=n_-+1}^n \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t)+c_i \mathcal{T}_i>a_i u\biggr), \cup_{i=n_-+1}^n \biggl(\sup_{t\in[0,\mathcal{T}_i]} X_{i}(t) > \varepsilon u\biggr) \biggr\}\\& \quad \le \mathbb{P} \{ {\cap_{i=1}^{n_-} ( \mathcal{T}_i>(t^*_i/\vert {c_i} \vert-\varepsilon) u ), \cap_{i=n_-+1}^n ( c_i \mathcal{T}_i>(a_i-\varepsilon) u )} \} +\sum_{i=n_-+1}^n \, \mathbb{P}\biggl\{{ \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t)> \varepsilon u } \biggr\}.\end{align*}
\begin{align*}& \mathbb{P}\biggl\{{\cap_{i=1}^{n_-} ( \mathcal{T}_i>(t^*_i/\vert {c_i} \vert-\varepsilon) u ), \cap_{i=n_-+1}^n \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t) +c_i \mathcal{T}_i>a_i u \biggr)} \biggr\}\\& \quad = \mathbb{P}\biggl\{{\cap_{i=1}^{n_-} ( \mathcal{T}_i>(t^*_i/\vert {c_i} \vert-\varepsilon) u ), \cap_{i=n_-+1}^n \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t) +c_i \mathcal{T}_i>a_i u, \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t) \le \varepsilon u\biggr)} \biggr\}\\ & \quad\quad +\mathbb{P}\biggl\{\cap_{i=1}^{n_-} ( \mathcal{T}_i>(t^*_i/\vert {c_i} \vert-\varepsilon) u ),\\ &\quad\quad\quad\, \cap_{i=n_-+1}^n \biggl( \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t)+c_i \mathcal{T}_i>a_i u\biggr), \cup_{i=n_-+1}^n \biggl(\sup_{t\in[0,\mathcal{T}_i]} X_{i}(t) > \varepsilon u\biggr) \biggr\}\\& \quad \le \mathbb{P} \{ {\cap_{i=1}^{n_-} ( \mathcal{T}_i>(t^*_i/\vert {c_i} \vert-\varepsilon) u ), \cap_{i=n_-+1}^n ( c_i \mathcal{T}_i>(a_i-\varepsilon) u )} \} +\sum_{i=n_-+1}^n \, \mathbb{P}\biggl\{{ \sup_{t\in[0,\mathcal{T}_i]} X_{i}(t)> \varepsilon u } \biggr\}.\end{align*}
Furthermore, it follows from Theorem 2.1 of [Reference DĘbicki, Zwart and Borst18] that, for any
![]() $i=n_-+1,\ldots, n$
,
$i=n_-+1,\ldots, n$
,
with some constant
![]() $C_i(\varepsilon)>0$
. This implies that
$C_i(\varepsilon)>0$
. This implies that
Consequently, applying Lemma A.1 and letting
![]() $\varepsilon \rightarrow 0$
, we can obtain the required asymptotic upper bound if we can further show that
$\varepsilon \rightarrow 0$
, we can obtain the required asymptotic upper bound if we can further show that
Indeed, we have
 \begin{align}I_2(u)&\le \sum_{i=1}^{n_-} \mathbb{P}\biggl\{\cap_{j=1}^{n_-} \biggl(\sup_{t\in[0,\mathcal{T}_j]} X_{j}(t) +c_j t >a_j u \biggr), \mathcal{T}_i\le(t^*_i/\vert {c_i} \vert-\varepsilon) u \biggr\}\notag \\&\le \sum_{i=1}^{n_-} \underset{j\neq i}{\prod_{j=1}^{n_-}} \psi_j(a_ju) \, \mathbb{P}\biggl\{{ \sup_{t\in[0,(t^*_i/\vert {c_i} \vert-\varepsilon) u ]} X_{i}(t) +c_i t >a_i u } \biggr\}.\end{align}
\begin{align}I_2(u)&\le \sum_{i=1}^{n_-} \mathbb{P}\biggl\{\cap_{j=1}^{n_-} \biggl(\sup_{t\in[0,\mathcal{T}_j]} X_{j}(t) +c_j t >a_j u \biggr), \mathcal{T}_i\le(t^*_i/\vert {c_i} \vert-\varepsilon) u \biggr\}\notag \\&\le \sum_{i=1}^{n_-} \underset{j\neq i}{\prod_{j=1}^{n_-}} \psi_j(a_ju) \, \mathbb{P}\biggl\{{ \sup_{t\in[0,(t^*_i/\vert {c_i} \vert-\varepsilon) u ]} X_{i}(t) +c_i t >a_i u } \biggr\}.\end{align}
Furthermore, by Lemma 5.1 we have that for any
![]() $\gamma>0$
$\gamma>0$
which together with (5.7) implies (5.6). This completes the proof.
Proof of Example 3.1. The proof is based on the following obvious bounds:
 \begin{align*} P_L(u)&\;:\!=\; \mathbb{P} \{ {\cap_{i=1}^n ( ( B_{i}(Y_i(T)) +c_i Y_i(T) )> a_iu )} \} \\ &\le P_B(u)\notag \\ & \le \mathbb{P}\biggl\{{\cap_{i=1}^n \biggl(\sup_{t\in[0, Y_i(T)]} ( B_{i}(t) +c_i t ) > a_i u \biggr)} \biggr\}\\ &\;=\!:\; P_U(u). \end{align*}
\begin{align*} P_L(u)&\;:\!=\; \mathbb{P} \{ {\cap_{i=1}^n ( ( B_{i}(Y_i(T)) +c_i Y_i(T) )> a_iu )} \} \\ &\le P_B(u)\notag \\ & \le \mathbb{P}\biggl\{{\cap_{i=1}^n \biggl(\sup_{t\in[0, Y_i(T)]} ( B_{i}(t) +c_i t ) > a_i u \biggr)} \biggr\}\\ &\;=\!:\; P_U(u). \end{align*}
Since
![]() $\alpha_0<\min_{i=1}^n \alpha_i$
, by Lemma A.3 we have that
$\alpha_0<\min_{i=1}^n \alpha_i$
, by Lemma A.3 we have that
![]() $\boldsymbol{Y}(T)$
is a multivariate regularly varying random vector with index
$\boldsymbol{Y}(T)$
is a multivariate regularly varying random vector with index
![]() $\alpha_0$
and the same limiting measure
$\alpha_0$
and the same limiting measure
![]() $\nu$
as that of
$\nu$
as that of
![]() $\boldsymbol{S}_{0}(T)\;:\!=\; (S_0(T), \ldots, S_0(T))\in \mathbb{R}^n$
, and further
$\boldsymbol{S}_{0}(T)\;:\!=\; (S_0(T), \ldots, S_0(T))\in \mathbb{R}^n$
, and further
The asymptotics of
![]() $P_U(u)$
can be obtained by applying Theorem 3.1. Below we focus on
$P_U(u)$
can be obtained by applying Theorem 3.1. Below we focus on
![]() $P_L(u)$
.
$P_L(u)$
.
First, consider case (i), where
![]() $c_i>0$
for all
$c_i>0$
for all
![]() $i=1,\ldots,n$
. We have
$i=1,\ldots,n$
. We have
Thus, by Lemma A.3 we obtain
which is the same as the asymptotic upper bound obtained by using Theorem 3.1(ii).
Next, consider case (ii), where
![]() $c_i=0$
for all
$c_i=0$
for all
![]() $i=1,\ldots,n$
. We have
$i=1,\ldots,n$
. We have
Thus, by Lemma A.2, we obtain
which is the same as the asymptotic upper bound obtained by using Theorem 3.1(i).
Finally, consider case (iii), where
![]() $c_i<0$
for all
$c_i<0$
for all
![]() $i=1,\ldots,n$
. We have
$i=1,\ldots,n$
. We have
 \begin{align*} P_L(u) & \ge \mathbb{P} \{ {\cap_{i=1}^n ( B_{i}(Y_i(T)) +c_i Y_i(T)> a_iu, Y_i(T)\in [a_iu/\vert {c_i} \vert -\sqrt u, a_iu/\vert {c_i} \vert +\sqrt u]) } \} \\ & \ge \prod_{i=1}^n \biggl(\min_{t\in [a_iu/\vert {c_i} \vert-\sqrt u, a_iu/\vert {c_i} \vert+\sqrt u]} \, \mathbb{P} \{ { B_{1}(t) +c_i t > a_i u } \} \biggr) \\ &\quad\, \times \mathbb{P} \{ {\cap_{i= 1}^n ( Y_i(T)\in [a_iu/\vert {c_i} \vert -\sqrt u, a_iu/\vert {c_i} \vert +\sqrt u] ) } \} . \end{align*}
\begin{align*} P_L(u) & \ge \mathbb{P} \{ {\cap_{i=1}^n ( B_{i}(Y_i(T)) +c_i Y_i(T)> a_iu, Y_i(T)\in [a_iu/\vert {c_i} \vert -\sqrt u, a_iu/\vert {c_i} \vert +\sqrt u]) } \} \\ & \ge \prod_{i=1}^n \biggl(\min_{t\in [a_iu/\vert {c_i} \vert-\sqrt u, a_iu/\vert {c_i} \vert+\sqrt u]} \, \mathbb{P} \{ { B_{1}(t) +c_i t > a_i u } \} \biggr) \\ &\quad\, \times \mathbb{P} \{ {\cap_{i= 1}^n ( Y_i(T)\in [a_iu/\vert {c_i} \vert -\sqrt u, a_iu/\vert {c_i} \vert +\sqrt u] ) } \} . \end{align*}
Recalling (2.1), we derive that
 \begin{align*} &\min_{t\in [a_iu/\vert {c_i} \vert-\sqrt u, a_iu/\vert {c_i} \vert+\sqrt u]} \, \mathbb{P} \{ { B_{1}(t) +c_i t > a_i u } \} \\ &\quad = \min_{t\in [a_i /\vert {c_i} \vert-1/\sqrt u, a_i /\vert {c_i} \vert+1/\sqrt u]} \, \mathbb{P} \{ { B_{1}(1) > (a_i-c_it)\sqrt u/\sqrt{t}} \} \\& \quad \gtrsim \textrm{Constant} \cdot \dfrac{1}{\sqrt u} {\textrm{e}}^{2a_ic_i u+{\textrm{o}}(u)},\quad u\rightarrow\infty .\end{align*}
\begin{align*} &\min_{t\in [a_iu/\vert {c_i} \vert-\sqrt u, a_iu/\vert {c_i} \vert+\sqrt u]} \, \mathbb{P} \{ { B_{1}(t) +c_i t > a_i u } \} \\ &\quad = \min_{t\in [a_i /\vert {c_i} \vert-1/\sqrt u, a_i /\vert {c_i} \vert+1/\sqrt u]} \, \mathbb{P} \{ { B_{1}(1) > (a_i-c_it)\sqrt u/\sqrt{t}} \} \\& \quad \gtrsim \textrm{Constant} \cdot \dfrac{1}{\sqrt u} {\textrm{e}}^{2a_ic_i u+{\textrm{o}}(u)},\quad u\rightarrow\infty .\end{align*}
Furthermore,
 \begin{align}\notag& \mathbb{P} \{ {\cap_{i= 1}^n \bigl( Y_i(T)\in [a_iu/\vert {c_i} \vert -\sqrt u, a_iu/\vert {c_i} \vert +\sqrt u] \bigr) } \} \\ & \quad \ge\prod_{i= 0}^n \, \mathbb{P} \{ { S_i(T)\in [a_iu/\vert {2c_i} \vert -\sqrt u/2, a_iu/\vert {2c_i} \vert +\sqrt u/2] } \} .\end{align}
\begin{align}\notag& \mathbb{P} \{ {\cap_{i= 1}^n \bigl( Y_i(T)\in [a_iu/\vert {c_i} \vert -\sqrt u, a_iu/\vert {c_i} \vert +\sqrt u] \bigr) } \} \\ & \quad \ge\prod_{i= 0}^n \, \mathbb{P} \{ { S_i(T)\in [a_iu/\vert {2c_i} \vert -\sqrt u/2, a_iu/\vert {2c_i} \vert +\sqrt u/2] } \} .\end{align}
Due to the assumptions on the density functions of
![]() $S_i(T),i=0,1,\ldots,n$
, by the Monotone Density Theorem (see e.g. [Reference Mikosch27]), we know that (5.8) is asymptotically larger than
$S_i(T),i=0,1,\ldots,n$
, by the Monotone Density Theorem (see e.g. [Reference Mikosch27]), we know that (5.8) is asymptotically larger than
![]() $C u^{-\beta}$
for some constants
$C u^{-\beta}$
for some constants
![]() $C, \beta>0$
. Therefore
$C, \beta>0$
. Therefore
The same asymptotic upper bound can be obtained by the fact that
This completes the proof.
6. Proof of Theorem 4.1
We first show one lemma that is crucial for the proof of Theorem 4.1.
Lemma 6.1. Let
![]() $\boldsymbol{U}^{(1)}$
,
$\boldsymbol{U}^{(1)}$
,
![]() $\boldsymbol{M}^{(1)}$
, and
$\boldsymbol{M}^{(1)}$
, and
![]() $\widetilde {\boldsymbol{T}}$
be given by (4.2), (4.3), and (4.5) respectively. Then
$\widetilde {\boldsymbol{T}}$
be given by (4.2), (4.3), and (4.5) respectively. Then
![]() $\boldsymbol{U}^{(1)}$
and
$\boldsymbol{U}^{(1)}$
and
![]() $\boldsymbol{M}^{(1)}$
are both regularly varying with the same index
$\boldsymbol{M}^{(1)}$
are both regularly varying with the same index
![]() $\lambda$
and limiting measure
$\lambda$
and limiting measure
![]() $\mu$
as that of
$\mu$
as that of
![]() $\widetilde {\boldsymbol{T}}$
. Moreover,
$\widetilde {\boldsymbol{T}}$
. Moreover,
Proof. First note that, by self-similarity of fBms,
where
Since every two norms on
![]() $R^d$
are equivalent, then by the fact that
$R^d$
are equivalent, then by the fact that
![]() $H_i, \widetilde H_i<1$
for
$H_i, \widetilde H_i<1$
for
![]() $i=1,2$
and (4.1), we have
$i=1,2$
and (4.1), we have
Thus the claim for
![]() $\boldsymbol{U}^{(1)}$
follows directly by Lemma A.3.
$\boldsymbol{U}^{(1)}$
follows directly by Lemma A.3.
Next, note that
 \begin{align*}\boldsymbol{M}^{(1)}&\overset{D}= \biggl(\sup_{0\le t\le T+S} (X_1(t) I_{(0\le t<T)} + (X_1(T) +Y_1(t-T) ) I_{(T\le t<T+S)}),\\& \quad \quad \sup_{0\le t\le T+S} (X_2(t) I_{(0\le t<T)} + (X_2(T) +Y_2(t-T) ) I_{(T\le t<T+S)} ) \biggr) \;=\!:\; \boldsymbol{M},\end{align*}
\begin{align*}\boldsymbol{M}^{(1)}&\overset{D}= \biggl(\sup_{0\le t\le T+S} (X_1(t) I_{(0\le t<T)} + (X_1(T) +Y_1(t-T) ) I_{(T\le t<T+S)}),\\& \quad \quad \sup_{0\le t\le T+S} (X_2(t) I_{(0\le t<T)} + (X_2(T) +Y_2(t-T) ) I_{(T\le t<T+S)} ) \biggr) \;=\!:\; \boldsymbol{M},\end{align*}
then
and
 \begin{align*}\boldsymbol{M}&\leq \biggl(\sup_{0\leq t\leq T}B_{H_1}(t)+p_1T+\sup_{t\geq0}Y_1(t),\sup_{0\leq t\leq T}B_{H_2}(t)+ {p_2}T+\sup_{t\geq0}Y_2(t)\biggr)\\&\overset{D}=\biggl(\xi_1 T^{H_1} + \sup_{t\ge 0} Y_1(t),\xi_2 T^{H_2} +\sup_{t\ge 0} Y_2(t)\biggr)+\widetilde {\boldsymbol{T}},\end{align*}
\begin{align*}\boldsymbol{M}&\leq \biggl(\sup_{0\leq t\leq T}B_{H_1}(t)+p_1T+\sup_{t\geq0}Y_1(t),\sup_{0\leq t\leq T}B_{H_2}(t)+ {p_2}T+\sup_{t\geq0}Y_2(t)\biggr)\\&\overset{D}=\biggl(\xi_1 T^{H_1} + \sup_{t\ge 0} Y_1(t),\xi_2 T^{H_2} +\sup_{t\ge 0} Y_2(t)\biggr)+\widetilde {\boldsymbol{T}},\end{align*}
with
![]() $\xi_i$
defined in (3.1). By Corollary 2.1 we know that
$\xi_i$
defined in (3.1). By Corollary 2.1 we know that
![]() $\mathbb{P} \{ { \sup_{t\ge 0} Y_i(t)>x} \} ={\textrm{o}}(\mathbb{P} \{ {T>x} \} )$
as
$\mathbb{P} \{ { \sup_{t\ge 0} Y_i(t)>x} \} ={\textrm{o}}(\mathbb{P} \{ {T>x} \} )$
as
![]() $x\rightarrow\infty $
. Therefore the claim for
$x\rightarrow\infty $
. Therefore the claim for
![]() $\boldsymbol{M}^{(1)}$
is a direct consequence of Lemmas A.3 and A.4. This completes the proof.
$\boldsymbol{M}^{(1)}$
is a direct consequence of Lemmas A.3 and A.4. This completes the proof.
Proof of Theorem 4.1. First, note that, for any
![]() $\boldsymbol{a}, \boldsymbol{c}>\textbf{0}$
, by the homogeneity property of
$\boldsymbol{a}, \boldsymbol{c}>\textbf{0}$
, by the homogeneity property of
![]() $\mu$
,
$\mu$
,
 \begin{align}& \int_0^\infty \mu( (v\boldsymbol{c}+\boldsymbol{a}, \boldsymbol{\infty} ]) \,{\textrm{d}} v\leq \mu( (\boldsymbol{a}, \boldsymbol{\infty} ]) \notag \\ &\quad +\int_1^\infty v^{-\lambda}\mu( (\boldsymbol{c}+\boldsymbol{a}/v, \boldsymbol{\infty} ]) \,{\textrm{d}} v\leq \mu( (\boldsymbol{a}, \boldsymbol{\infty} ]) + \dfrac{1}{\lambda-1}\mu( (\boldsymbol{c}, \boldsymbol{\infty} ]).\end{align}
\begin{align}& \int_0^\infty \mu( (v\boldsymbol{c}+\boldsymbol{a}, \boldsymbol{\infty} ]) \,{\textrm{d}} v\leq \mu( (\boldsymbol{a}, \boldsymbol{\infty} ]) \notag \\ &\quad +\int_1^\infty v^{-\lambda}\mu( (\boldsymbol{c}+\boldsymbol{a}/v, \boldsymbol{\infty} ]) \,{\textrm{d}} v\leq \mu( (\boldsymbol{a}, \boldsymbol{\infty} ]) + \dfrac{1}{\lambda-1}\mu( (\boldsymbol{c}, \boldsymbol{\infty} ]).\end{align}
For simplicity we denote
![]() $\boldsymbol{W}^{(n)}\;:\!=\; \sum_{i=1}^n \boldsymbol{U}^{(i)}.$
We consider the lower bound, for which we adopt a standard technique of ‘one big jump’ (see [Reference Palmowski and Zwart28]). Informally speaking, we choose an event on which
$\boldsymbol{W}^{(n)}\;:\!=\; \sum_{i=1}^n \boldsymbol{U}^{(i)}.$
We consider the lower bound, for which we adopt a standard technique of ‘one big jump’ (see [Reference Palmowski and Zwart28]). Informally speaking, we choose an event on which
![]() $ \boldsymbol{W}^{(n-1)}+ \boldsymbol{M}^{(n)}$
,
$ \boldsymbol{W}^{(n-1)}+ \boldsymbol{M}^{(n)}$
,
![]() $n\ge 1$
, behaves in a typical way up to some time k for which
$n\ge 1$
, behaves in a typical way up to some time k for which
![]() $\boldsymbol{M}^{(k+1)}$
is large. Let
$\boldsymbol{M}^{(k+1)}$
is large. Let
![]() $\delta, \varepsilon$
be small positive numbers. By the Weak Law of Large Numbers, we can choose large
$\delta, \varepsilon$
be small positive numbers. By the Weak Law of Large Numbers, we can choose large
![]() $K=K_{\varepsilon,\delta}$
so that
$K=K_{\varepsilon,\delta}$
so that
For any
![]() $u>0$
, we have
$u>0$
, we have
 \begin{align*}Q(u)&= \mathbb{P} \{ \exists n\ge 1\colon \boldsymbol{W}^{(n-1)} + \boldsymbol{M}^{(n)} >\boldsymbol{a} u \} \\ &= \mathbb{P} \{ \boldsymbol{M}^{(1)} >\boldsymbol{a} u \} +\sum_{k\ge 1}\, \mathbb{P} \{ {\cap_{n=1}^k (\boldsymbol{W}^{(n-1)} + \boldsymbol{M}^{(n)} \not> \boldsymbol{a} u), \boldsymbol{W}^{(k)} + \boldsymbol{M}^{(k+1)} >\boldsymbol{a} u} \} \\&\ge \mathbb{P} \{ \boldsymbol{M}^{(1)} >\boldsymbol{a} u \} +\sum_{k\ge 1}\mathbb P\left\{ \cap_{n=1}^k (\boldsymbol{W}^{(n-1)} + \boldsymbol{M}^{(n)} \not> \boldsymbol{a} u), \boldsymbol{W}^{(k)}>-k(1+\varepsilon )\boldsymbol{c}-K\textbf{1}, \right. \\& \qquad\qquad\qquad\qquad\qquad\; \left. \boldsymbol{M}^{(k+1)} >\boldsymbol{a} u +k(1+\varepsilon )\boldsymbol{c}+K\textbf{1}\right\}\\&\ge \mathbb{P} \{ {\boldsymbol{M}^{(1)}} >\boldsymbol{a} \textbf{u} \} \\&\quad\, +\sum_{k\ge 1} (1-\delta-\mathbb{P} \{ {\cup_{n=1}^k (\boldsymbol{W}^{(n-1)} + \boldsymbol{M}^{(n)} > \boldsymbol{a} u)} \} ) \, \mathbb{P} \{ {\boldsymbol{M}^{(k+1)} >\boldsymbol{a} u +k(1+\varepsilon)\boldsymbol{c}+K\textbf{1}} \} \\&\ge (1-\delta-Q(u)) \sum_{k\ge 0}\, \mathbb{P} \{ {\boldsymbol{M}^{(1)} >\boldsymbol{a} u +k(1+\varepsilon )\boldsymbol{c}+K\textbf{1}} \} \\&\ge \dfrac{(1-\delta-Q(u)) }{1+\varepsilon} \int_0^\infty \, \mathbb{P} \{ {{\boldsymbol{M}^{(1)}} >\boldsymbol{a} u + v\boldsymbol{c}+K\textbf{1}} \} \,{\textrm{d}} v.\end{align*}
\begin{align*}Q(u)&= \mathbb{P} \{ \exists n\ge 1\colon \boldsymbol{W}^{(n-1)} + \boldsymbol{M}^{(n)} >\boldsymbol{a} u \} \\ &= \mathbb{P} \{ \boldsymbol{M}^{(1)} >\boldsymbol{a} u \} +\sum_{k\ge 1}\, \mathbb{P} \{ {\cap_{n=1}^k (\boldsymbol{W}^{(n-1)} + \boldsymbol{M}^{(n)} \not> \boldsymbol{a} u), \boldsymbol{W}^{(k)} + \boldsymbol{M}^{(k+1)} >\boldsymbol{a} u} \} \\&\ge \mathbb{P} \{ \boldsymbol{M}^{(1)} >\boldsymbol{a} u \} +\sum_{k\ge 1}\mathbb P\left\{ \cap_{n=1}^k (\boldsymbol{W}^{(n-1)} + \boldsymbol{M}^{(n)} \not> \boldsymbol{a} u), \boldsymbol{W}^{(k)}>-k(1+\varepsilon )\boldsymbol{c}-K\textbf{1}, \right. \\& \qquad\qquad\qquad\qquad\qquad\; \left. \boldsymbol{M}^{(k+1)} >\boldsymbol{a} u +k(1+\varepsilon )\boldsymbol{c}+K\textbf{1}\right\}\\&\ge \mathbb{P} \{ {\boldsymbol{M}^{(1)}} >\boldsymbol{a} \textbf{u} \} \\&\quad\, +\sum_{k\ge 1} (1-\delta-\mathbb{P} \{ {\cup_{n=1}^k (\boldsymbol{W}^{(n-1)} + \boldsymbol{M}^{(n)} > \boldsymbol{a} u)} \} ) \, \mathbb{P} \{ {\boldsymbol{M}^{(k+1)} >\boldsymbol{a} u +k(1+\varepsilon)\boldsymbol{c}+K\textbf{1}} \} \\&\ge (1-\delta-Q(u)) \sum_{k\ge 0}\, \mathbb{P} \{ {\boldsymbol{M}^{(1)} >\boldsymbol{a} u +k(1+\varepsilon )\boldsymbol{c}+K\textbf{1}} \} \\&\ge \dfrac{(1-\delta-Q(u)) }{1+\varepsilon} \int_0^\infty \, \mathbb{P} \{ {{\boldsymbol{M}^{(1)}} >\boldsymbol{a} u + v\boldsymbol{c}+K\textbf{1}} \} \,{\textrm{d}} v.\end{align*}
For u sufficiently large that
![]() $\varepsilon u>K$
, we have
$\varepsilon u>K$
, we have
Rearranging the above inequality and using a change of variable, we obtain
and thus by Lemma 6.1 and Fatou’s lemma,
Since
![]() $\varepsilon$
and
$\varepsilon$
and
![]() $\delta$
are arbitrary, and by (6.1) the integration on the right-hand side is finite, taking
$\delta$
are arbitrary, and by (6.1) the integration on the right-hand side is finite, taking
![]() $\varepsilon\rightarrow0$
,
$\varepsilon\rightarrow0$
,
![]() $\delta\rightarrow0$
and applying the dominated convergence theorem yields
$\delta\rightarrow0$
and applying the dominated convergence theorem yields
Next we consider the asymptotic upper bound. Let
![]() $y_1, y_2>0$
be given. We shall construct an auxiliary random walk
$y_1, y_2>0$
be given. We shall construct an auxiliary random walk
![]() $\widetilde{\boldsymbol{W}}^{(n)}$
,
$\widetilde{\boldsymbol{W}}^{(n)}$
,
![]() $n\ge 0$
, with
$n\ge 0$
, with
![]() $\widetilde{\boldsymbol{W}}^{(0)}=0$
and
$\widetilde{\boldsymbol{W}}^{(0)}=0$
and
![]() $\widetilde{\boldsymbol{W}}^{(n)}=\sum_{i=1}^n \widetilde{\boldsymbol{U}}^{(i)}$
,
$\widetilde{\boldsymbol{W}}^{(n)}=\sum_{i=1}^n \widetilde{\boldsymbol{U}}^{(i)}$
,
![]() $n\ge 1$
, where
$n\ge 1$
, where
![]() $\widetilde{\boldsymbol{U}}^{(n)} =(\widetilde{U}_1^{(n)}, \widetilde{U}_2^{(n)})$
is given by
$\widetilde{\boldsymbol{U}}^{(n)} =(\widetilde{U}_1^{(n)}, \widetilde{U}_2^{(n)})$
is given by
 \begin{align*}\widetilde{U}_i^{(n)}= \begin{cases} M^{(n)}_i & \text{if $M^{(n)}_i> y_1$,} \\ U^{(n)}_i & \text{if $-y_2< U^{(n)}_i\le M^{(n)}_i\le y_1$,} \\ -y_2 & \text{if $M^{(n)}_i\le y_1, U^{(n)}_i\le -y_2 $,} \end{cases}\quad i=1,2.\end{align*}
\begin{align*}\widetilde{U}_i^{(n)}= \begin{cases} M^{(n)}_i & \text{if $M^{(n)}_i> y_1$,} \\ U^{(n)}_i & \text{if $-y_2< U^{(n)}_i\le M^{(n)}_i\le y_1$,} \\ -y_2 & \text{if $M^{(n)}_i\le y_1, U^{(n)}_i\le -y_2 $,} \end{cases}\quad i=1,2.\end{align*}
Obviously,
![]() ${\boldsymbol{W}^{(n)}}\le \widetilde{\boldsymbol{W}}^{(n)}$
for any
${\boldsymbol{W}^{(n)}}\le \widetilde{\boldsymbol{W}}^{(n)}$
for any
![]() $n\ge 1.$
Furthermore, one can show that
$n\ge 1.$
Furthermore, one can show that
Then
Thus, for any
![]() $\varepsilon>0$
and sufficiently large u,
$\varepsilon>0$
and sufficiently large u,
 \begin{align*}Q(u)&\le \mathbb{P} \{ {\exists n\ge 1\colon \widetilde{\boldsymbol{W}}^{(n)} >\boldsymbol{a} u - (y_1+y_2) \textbf{1}} \} \\&\le \mathbb{P} \{ {\exists n\ge 1 \colon \widetilde{\boldsymbol{W}}^{(n)} >(\boldsymbol{a} -\varepsilon \textbf{1}) u } \} .\end{align*}
\begin{align*}Q(u)&\le \mathbb{P} \{ {\exists n\ge 1\colon \widetilde{\boldsymbol{W}}^{(n)} >\boldsymbol{a} u - (y_1+y_2) \textbf{1}} \} \\&\le \mathbb{P} \{ {\exists n\ge 1 \colon \widetilde{\boldsymbol{W}}^{(n)} >(\boldsymbol{a} -\varepsilon \textbf{1}) u } \} .\end{align*}
Define
![]() $c_{y_1,y_2}=-\mathbb{E}\{{\widetilde{\boldsymbol{U}}^{(1)}}\}$
. Since
$c_{y_1,y_2}=-\mathbb{E}\{{\widetilde{\boldsymbol{U}}^{(1)}}\}$
. Since
![]() $\lim_{y_1, y_2\rightarrow\infty } \boldsymbol{c}_{y_1,y_2}=\boldsymbol{c}$
, we have that for any
$\lim_{y_1, y_2\rightarrow\infty } \boldsymbol{c}_{y_1,y_2}=\boldsymbol{c}$
, we have that for any
![]() $y_1,y_2$
large enough
$y_1,y_2$
large enough
![]() $\boldsymbol{c}_{y_1,y_2} >\textbf{0} $
. It follows from Lemmas 6.1 and A.4 that for any
$\boldsymbol{c}_{y_1,y_2} >\textbf{0} $
. It follows from Lemmas 6.1 and A.4 that for any
![]() $y_1, y_2>0$
,
$y_1, y_2>0$
,
![]() $\widetilde{\boldsymbol{U}}^{(1)}$
is regularly varying with index
$\widetilde{\boldsymbol{U}}^{(1)}$
is regularly varying with index
![]() $\lambda$
and limiting measure
$\lambda$
and limiting measure
![]() $\mu$
, and
$\mu$
, and
![]() $\mathbb{P} \{ { \vert {\widetilde{\boldsymbol{U}}^{(1)} } \vert>u} \} \sim\mathbb{P} \{ {\vert {\widetilde {\boldsymbol{T}}} \vert>u} \} $
as
$\mathbb{P} \{ { \vert {\widetilde{\boldsymbol{U}}^{(1)} } \vert>u} \} \sim\mathbb{P} \{ {\vert {\widetilde {\boldsymbol{T}}} \vert>u} \} $
as
![]() $u\rightarrow\infty$
. Then, applying Theorem 3.1 and Remark 3.2 of [Reference Hult, Lindskog, Mikosch and Samorodnitsky21], we obtain that
$u\rightarrow\infty$
. Then, applying Theorem 3.1 and Remark 3.2 of [Reference Hult, Lindskog, Mikosch and Samorodnitsky21], we obtain that
 \begin{align*}\mathbb{P} \{ {\exists n\ge 1 \colon {\widetilde{\boldsymbol{W}}^{(n)}} >(\boldsymbol{a} -\varepsilon \textbf{1}) u} \}&\sim u\mathbb{P} \{ { \vert {\widetilde{\boldsymbol{U}}^{(1)} } \vert>u} \} \int_0^\infty \mu ((\boldsymbol{c}_{y_1,y_2} v+\boldsymbol{a}-\varepsilon \textbf{1}, \boldsymbol{\infty} ]) \,{\textrm{d}} v\\&\sim u \mathbb{P} \{ {\vert {\widetilde {\boldsymbol{T}}} \vert>u} \} \int_0^\infty \mu ((\boldsymbol{c}_{y_1,y_2} v+\boldsymbol{a}-\varepsilon \textbf{1}, \boldsymbol{\infty} ]) \,{\textrm{d}} v.\end{align*}
\begin{align*}\mathbb{P} \{ {\exists n\ge 1 \colon {\widetilde{\boldsymbol{W}}^{(n)}} >(\boldsymbol{a} -\varepsilon \textbf{1}) u} \}&\sim u\mathbb{P} \{ { \vert {\widetilde{\boldsymbol{U}}^{(1)} } \vert>u} \} \int_0^\infty \mu ((\boldsymbol{c}_{y_1,y_2} v+\boldsymbol{a}-\varepsilon \textbf{1}, \boldsymbol{\infty} ]) \,{\textrm{d}} v\\&\sim u \mathbb{P} \{ {\vert {\widetilde {\boldsymbol{T}}} \vert>u} \} \int_0^\infty \mu ((\boldsymbol{c}_{y_1,y_2} v+\boldsymbol{a}-\varepsilon \textbf{1}, \boldsymbol{\infty} ]) \,{\textrm{d}} v.\end{align*}
Consequently, the claimed asymptotic upper bound is obtained by letting
![]() $\varepsilon\rightarrow0$
,
$\varepsilon\rightarrow0$
,
![]() $y_1, y_2\rightarrow\infty $
. The proof is complete.
$y_1, y_2\rightarrow\infty $
. The proof is complete.
Appendix A. Auxiliary results
This section includes some results on the regularly varying random vectors.
Lemma A.1. Let
![]() $\boldsymbol{\mathcal{T}}>\textbf{0}$
be a regularly varying random vector with index
$\boldsymbol{\mathcal{T}}>\textbf{0}$
be a regularly varying random vector with index
![]() $\alpha$
and limiting measure
$\alpha$
and limiting measure
![]() $\nu$
, and let
$\nu$
, and let
![]() $x_i(u), 1\le i\le n$
be increasing (to infinity) functions such that for some
$x_i(u), 1\le i\le n$
be increasing (to infinity) functions such that for some
![]() $1\le m \le n$
,
$1\le m \le n$
,
![]() $x_1(u) \sim \cdots \sim x_m(u)$
, and
$x_1(u) \sim \cdots \sim x_m(u)$
, and
![]() $x_j(u)={\textrm{o}}(x_{1}(u))$
for all
$x_j(u)={\textrm{o}}(x_{1}(u))$
for all
![]() $j=m+1,\ldots, n$
. Then, for any
$j=m+1,\ldots, n$
. Then, for any
![]() $\boldsymbol{a}>\textbf{0}$
,
$\boldsymbol{a}>\textbf{0}$
,
holds as
![]() $u\rightarrow \infty $
, with
$u\rightarrow \infty $
, with
![]() $\boldsymbol{a}_{m,0}=(a_1,\ldots, a_m, 0, \ldots, 0)$
.
$\boldsymbol{a}_{m,0}=(a_1,\ldots, a_m, 0, \ldots, 0)$
.
Proof. Obviously, for any small enough
![]() $\varepsilon>0$
we find that when u is sufficiently large
$\varepsilon>0$
we find that when u is sufficiently large
where
![]() $\boldsymbol{a}_{-\varepsilon}=(a_1-\varepsilon,\ldots, a_m-\varepsilon, 0, \ldots, 0)$
, and
$\boldsymbol{a}_{-\varepsilon}=(a_1-\varepsilon,\ldots, a_m-\varepsilon, 0, \ldots, 0)$
, and
with
![]() $\boldsymbol{a}_{\varepsilon+}=(a_1+\varepsilon,\ldots, a_m+\varepsilon, a_{m+1} \varepsilon, \ldots, a_{n}\varepsilon)$
. Letting
$\boldsymbol{a}_{\varepsilon+}=(a_1+\varepsilon,\ldots, a_m+\varepsilon, a_{m+1} \varepsilon, \ldots, a_{n}\varepsilon)$
. Letting
![]() $\varepsilon \rightarrow 0$
, the claim follows by the continuity of
$\varepsilon \rightarrow 0$
, the claim follows by the continuity of
![]() $\nu([\boldsymbol{a}_{\varepsilon\pm}, \boldsymbol{\infty} ])$
in
$\nu([\boldsymbol{a}_{\varepsilon\pm}, \boldsymbol{\infty} ])$
in
![]() $\varepsilon$
. The proof is complete.
$\varepsilon$
. The proof is complete.
Lemma A.2. Let
![]() $\boldsymbol{\mathcal{T}}$
,
$\boldsymbol{\mathcal{T}}$
,
![]() $a_i$
,
$a_i$
,
![]() $x_i(u)$
, and
$x_i(u)$
, and
![]() $\boldsymbol{a}_{m,0}$
be the same as in Lemma A.1. Further, consider
$\boldsymbol{a}_{m,0}$
be the same as in Lemma A.1. Further, consider
![]() ${\boldsymbol{\eta}}=(\eta_1, \ldots, \eta_n)$
to be a non-negative random vector independent of
${\boldsymbol{\eta}}=(\eta_1, \ldots, \eta_n)$
to be a non-negative random vector independent of
![]() $\boldsymbol{\mathcal{T}}$
such that
$\boldsymbol{\mathcal{T}}$
such that
![]() $\max_{1\le i\le n}\mathbb{E}\{{\eta_i^{\alpha+\delta}}\}<\infty $
for some
$\max_{1\le i\le n}\mathbb{E}\{{\eta_i^{\alpha+\delta}}\}<\infty $
for some
![]() $\delta>0$
. Then
$\delta>0$
. Then
holds as
![]() $u\rightarrow \infty $
, where
$u\rightarrow \infty $
, where
![]() $\widehat{\nu}(K)=\mathbb{E}\{{\nu(\boldsymbol{\eta}^{-1} K)}\}$
, with
$\widehat{\nu}(K)=\mathbb{E}\{{\nu(\boldsymbol{\eta}^{-1} K)}\}$
, with
![]() $\boldsymbol{\eta}^{-1} K=\{(\eta_1^{-1}b_1,\ldots, \eta_n^{-1}b_n),$
$\boldsymbol{\eta}^{-1} K=\{(\eta_1^{-1}b_1,\ldots, \eta_n^{-1}b_n),$
![]() $ (b_1,\ldots,b_n)\in K\}$
for any
$ (b_1,\ldots,b_n)\in K\}$
for any
![]() $K\in \mathcal{B}([0,\infty ]^n \setminus \{\textbf{0}\})$
.
$K\in \mathcal{B}([0,\infty ]^n \setminus \{\textbf{0}\})$
.
Proof. It follows directly from Lemma 4.6 of [Reference Jessen and Mikosch22] (see also Proposition A.1 of [Reference Basrak, Davis and Mikosch7]) that the second asymptotic equivalence holds. The first claim follows from the same arguments as in Lemma A.1.
Lemma A.3. Assume
![]() $\boldsymbol{X}\in \mathbb{R}^n$
is regularly varying with index
$\boldsymbol{X}\in \mathbb{R}^n$
is regularly varying with index
![]() $\alpha$
and limiting measure
$\alpha$
and limiting measure
![]() $\mu$
, and
$\mu$
, and
![]() $\boldsymbol{A}$
is a random
$\boldsymbol{A}$
is a random
![]() $n\times d$
matrix independent of random vector
$n\times d$
matrix independent of random vector
![]() $\boldsymbol{Y}\in \mathbb{R}^d$
. If
$\boldsymbol{Y}\in \mathbb{R}^d$
. If
![]() $0<\mathbb{E}\{{\lVert {\boldsymbol{A}} \rVert^{\alpha+\delta}}\}<\infty$
for some
$0<\mathbb{E}\{{\lVert {\boldsymbol{A}} \rVert^{\alpha+\delta}}\}<\infty$
for some
![]() $\delta>0$
, with
$\delta>0$
, with
![]() $\lVert {\cdot} \rVert$
some matrix norm and
$\lVert {\cdot} \rVert$
some matrix norm and
then
![]() $\boldsymbol{X}+\boldsymbol{A} \boldsymbol{Y}$
is regularly varying with index
$\boldsymbol{X}+\boldsymbol{A} \boldsymbol{Y}$
is regularly varying with index
![]() $\alpha$
and limiting measure
$\alpha$
and limiting measure
![]() $\mu$
, and
$\mu$
, and
Proof. By Lemma 3.12 of [Reference Jessen and Mikosch22], it suffices to show that
Defining
![]() $g(x)=x^{{(\alpha+\delta/2)}/{(\alpha+\delta})}$
,
$g(x)=x^{{(\alpha+\delta/2)}/{(\alpha+\delta})}$
,
![]() $x\ge 0$
, we have
$x\ge 0$
, we have
Due to (A.1), for arbitrary
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
holds for large enough x. Furthermore, by Potter’s theorem (see e.g. Theorem 1.5.6 of [Reference Bingham, Goldie and Teugels8]), we have
for sufficiently large x, and thus, by the dominated convergence theorem,
 \begin{align}&\lim_{x\rightarrow\infty } \int_0^{g(x)} \dfrac{\mathbb{P} \{ {\vert {\boldsymbol{Y}} \vert>x/t} \} }{ \mathbb{P} \{ {\vert {\boldsymbol{X}} \vert>x} \} } \, \mathbb{P} \{ {\lVert {\boldsymbol{A}} \rVert \in {\textrm{d}} t} \} \notag \\&\quad \le \lim_{x\rightarrow\infty } \int_0^{g(x)} \dfrac{\varepsilon\mathbb{P} \{ {\vert {\boldsymbol{X}} \vert>x/t} \} }{ \mathbb{P} \{ {\vert {\boldsymbol{X}} \vert>x} \} } \, \mathbb{P} \{ {\lVert {\boldsymbol{A}} \rVert \in {\textrm{d}} t} \}= \varepsilon \mathbb{E}\{{\lVert {\boldsymbol{A}} \rVert^{\alpha}}\}.\end{align}
\begin{align}&\lim_{x\rightarrow\infty } \int_0^{g(x)} \dfrac{\mathbb{P} \{ {\vert {\boldsymbol{Y}} \vert>x/t} \} }{ \mathbb{P} \{ {\vert {\boldsymbol{X}} \vert>x} \} } \, \mathbb{P} \{ {\lVert {\boldsymbol{A}} \rVert \in {\textrm{d}} t} \} \notag \\&\quad \le \lim_{x\rightarrow\infty } \int_0^{g(x)} \dfrac{\varepsilon\mathbb{P} \{ {\vert {\boldsymbol{X}} \vert>x/t} \} }{ \mathbb{P} \{ {\vert {\boldsymbol{X}} \vert>x} \} } \, \mathbb{P} \{ {\lVert {\boldsymbol{A}} \rVert \in {\textrm{d}} t} \}= \varepsilon \mathbb{E}\{{\lVert {\boldsymbol{A}} \rVert^{\alpha}}\}.\end{align}
Moreover, Markov’s inequality implies that
Therefore claim (A.2) follows from (A.3)–(A.5) and the arbitrariness of
![]() $\varepsilon$
. This completes the proof.
$\varepsilon$
. This completes the proof.
Lemma A.4. Assume
![]() $\boldsymbol{X} , \boldsymbol{Y} \in \mathbb{R}^n$
are regularly varying with the same index
$\boldsymbol{X} , \boldsymbol{Y} \in \mathbb{R}^n$
are regularly varying with the same index
![]() $\alpha$
and the same limiting measure
$\alpha$
and the same limiting measure
![]() $\mu$
. Moreover, if
$\mu$
. Moreover, if
![]() $\boldsymbol{X} \geq \boldsymbol{Y}$
and
$\boldsymbol{X} \geq \boldsymbol{Y}$
and
![]() $\mathbb{P} \{ {\vert {\boldsymbol{X}} \vert>x} \} \sim \mathbb{P} \{{\vert {\boldsymbol{Y}} \vert>x} \} $
as
$\mathbb{P} \{ {\vert {\boldsymbol{X}} \vert>x} \} \sim \mathbb{P} \{{\vert {\boldsymbol{Y}} \vert>x} \} $
as
![]() $x\rightarrow\infty $
, then for any random vector
$x\rightarrow\infty $
, then for any random vector
![]() $\boldsymbol{Z}$
satisfying
$\boldsymbol{Z}$
satisfying
![]() $\boldsymbol{X} \geq \boldsymbol{Z} \geq \boldsymbol{Y}$
,
$\boldsymbol{X} \geq \boldsymbol{Z} \geq \boldsymbol{Y}$
,
![]() $\boldsymbol{Z}$
is regularly varying with index
$\boldsymbol{Z}$
is regularly varying with index
![]() $\alpha$
and limiting measure
$\alpha$
and limiting measure
![]() $\mu$
, and
$\mu$
, and
![]() $\mathbb{P} \{ {\vert {\boldsymbol{Z}} \vert>x} \} \sim \mathbb{P} \{ {\vert {\boldsymbol{X}} \vert>x} \} $
as
$\mathbb{P} \{ {\vert {\boldsymbol{Z}} \vert>x} \} \sim \mathbb{P} \{ {\vert {\boldsymbol{X}} \vert>x} \} $
as
![]() $x\rightarrow\infty $
.
$x\rightarrow\infty $
.
Proof. We only prove the claim for
![]() $n=2$
; a similar argument can be used to verify the claim for
$n=2$
; a similar argument can be used to verify the claim for
![]() $n\geq3$
. For any
$n\geq3$
. For any
![]() $x>0$
, define a measure
$x>0$
, define a measure
![]() $\mu_x$
as
$\mu_x$
as
We shall show that
Given that the above is established, by letting
![]() $A=\{\boldsymbol{x} \colon |\boldsymbol{x}|>1\}$
(which is relatively compact and satisfies
$A=\{\boldsymbol{x} \colon |\boldsymbol{x}|>1\}$
(which is relatively compact and satisfies
![]() $\mu(\partial A)=0$
), we have
$\mu(\partial A)=0$
), we have
![]() $\mu_x(A)\rightarrow\mu(A)=1$
as
$\mu_x(A)\rightarrow\mu(A)=1$
as
![]() $x\rightarrow\infty$
and thus
$x\rightarrow\infty$
and thus
![]() $\mathbb{P} \{ {|\boldsymbol{Z}|>x} \} \sim\mathbb{P} \{ {|\boldsymbol{X}|>x} \} $
. Furthermore, by replacing the denominator in the definition of
$\mathbb{P} \{ {|\boldsymbol{Z}|>x} \} \sim\mathbb{P} \{ {|\boldsymbol{X}|>x} \} $
. Furthermore, by replacing the denominator in the definition of
![]() $\mu_x$
with
$\mu_x$
with
![]() $\mathbb{P} \{ {|\boldsymbol{Z}|>x} \} $
, we conclude that
$\mathbb{P} \{ {|\boldsymbol{Z}|>x} \} $
, we conclude that
showing that
![]() $\boldsymbol{Z}$
is regularly varying with index
$\boldsymbol{Z}$
is regularly varying with index
![]() $\alpha$
and limiting measure
$\alpha$
and limiting measure
![]() $\mu$
.
$\mu$
.
Now it remains to prove (A.6). To this end, we define a set
![]() $\mathcal D$
consisting of all sets in
$\mathcal D$
consisting of all sets in
![]() $ \overline{\mathbb{R}}_0^2$
that are of the following form:
$ \overline{\mathbb{R}}_0^2$
that are of the following form:
 \begin{alignat*}{5}& \textrm{(a)}\quad && (a_1,\infty ]\times [a_2,\infty ],\quad && a_1>0, a_2\in \mathbb{R},\\& \textrm{(b)}\quad && [\!-\!\infty , a_1]\times (a_2,\infty ],\quad && a_1\in \mathbb{R}, a_2>0,\\& \textrm{(c)}\quad && [\!-\!\infty , a_1)\times [\!-\!\infty , a_2],\quad && a_1<0, a_2\in \mathbb{R},\\& \textrm{(d)}\quad && [a_1,\infty ]\times [\!-\!\infty , a_2),\quad && a_1\in \mathbb{R}, a_2<0.\end{alignat*}
\begin{alignat*}{5}& \textrm{(a)}\quad && (a_1,\infty ]\times [a_2,\infty ],\quad && a_1>0, a_2\in \mathbb{R},\\& \textrm{(b)}\quad && [\!-\!\infty , a_1]\times (a_2,\infty ],\quad && a_1\in \mathbb{R}, a_2>0,\\& \textrm{(c)}\quad && [\!-\!\infty , a_1)\times [\!-\!\infty , a_2],\quad && a_1<0, a_2\in \mathbb{R},\\& \textrm{(d)}\quad && [a_1,\infty ]\times [\!-\!\infty , a_2),\quad && a_1\in \mathbb{R}, a_2<0.\end{alignat*}
Note that every
![]() $A\in\mathcal D$
is relatively compact and satisfies
$A\in\mathcal D$
is relatively compact and satisfies
![]() $\mu(\partial A)=0$
. We first show that
$\mu(\partial A)=0$
. We first show that
If
![]() $A=(a_1,\infty ]\times (a_2,\infty ]$
or
$A=(a_1,\infty ]\times (a_2,\infty ]$
or
![]() $A=(a_1,\infty ]\times [a_2,\infty ]$
with
$A=(a_1,\infty ]\times [a_2,\infty ]$
with
![]() $a_i\in \mathbb{R}$
and at least one
$a_i\in \mathbb{R}$
and at least one
![]() $a_i>0, i=1,2$
, or
$a_i>0, i=1,2$
, or
![]() $A=\overline{\mathbb{R}}\times (a_2,\infty ]$
with some
$A=\overline{\mathbb{R}}\times (a_2,\infty ]$
with some
![]() $a_2>0$
, by the order relations of
$a_2>0$
, by the order relations of
![]() $\boldsymbol{X},\boldsymbol{Y},\boldsymbol{Z}$
, we have, for any
$\boldsymbol{X},\boldsymbol{Y},\boldsymbol{Z}$
, we have, for any
![]() $x>0$
,
$x>0$
,
Letting
![]() $x\rightarrow\infty$
, using the regularity properties as supposed for
$x\rightarrow\infty$
, using the regularity properties as supposed for
![]() $\boldsymbol{X}$
and
$\boldsymbol{X}$
and
![]() $\boldsymbol{Y}$
, and then appealing to Proposition 3.12(ii) of [Reference Resnick33], we verify (A.7) for case (a). If
$\boldsymbol{Y}$
, and then appealing to Proposition 3.12(ii) of [Reference Resnick33], we verify (A.7) for case (a). If
![]() $A=[\!-\!\infty , a_1]\times (a_2,\infty ]$
with some
$A=[\!-\!\infty , a_1]\times (a_2,\infty ]$
with some
![]() $a_1\in \mathbb{R}, a_2>0$
, then we have
$a_1\in \mathbb{R}, a_2>0$
, then we have
and thus, by the convergence in case (a),
this validates (A.7) for case (b). If
![]() $A= [\!-\!\infty , a_1)\times [\!-\!\infty , a_2]$
or
$A= [\!-\!\infty , a_1)\times [\!-\!\infty , a_2]$
or
![]() $A= [\!-\!\infty , a_1)\times [\!-\!\infty , a_2)$
with
$A= [\!-\!\infty , a_1)\times [\!-\!\infty , a_2)$
with
![]() $a_i\in \mathbb{R}$
and at least one
$a_i\in \mathbb{R}$
and at least one
![]() $a_i<0, i=1,2$
, or
$a_i<0, i=1,2$
, or
![]() $A= \overline{\mathbb{R}}\times [\!-\!\infty , a_2)$
with some
$A= \overline{\mathbb{R}}\times [\!-\!\infty , a_2)$
with some
![]() $a_2<0$
, then we get a similar formula to (A.8) with the reverse inequalities. If
$a_2<0$
, then we get a similar formula to (A.8) with the reverse inequalities. If
![]() $A=[a_1,\infty ]\times [\!-\!\infty , a_2)$
with some
$A=[a_1,\infty ]\times [\!-\!\infty , a_2)$
with some
![]() $a_1\in \mathbb{R}, a_2<0$
, then
$a_1\in \mathbb{R}, a_2<0$
, then
Therefore, similarly to the proof for cases (a) and (b), one can establish (A.7) for cases (c) and (d).
Next, let f defined on
![]() $ \overline{\mathbb{R}}_0^2$
be any positive, continuous function with compact support. We see that the support of f is contained in
$ \overline{\mathbb{R}}_0^2$
be any positive, continuous function with compact support. We see that the support of f is contained in
![]() $[\boldsymbol{a},\boldsymbol{b}]^c$
for some
$[\boldsymbol{a},\boldsymbol{b}]^c$
for some
![]() $\boldsymbol{a}<\textbf{0}<\boldsymbol{b}$
. Note that
$\boldsymbol{a}<\textbf{0}<\boldsymbol{b}$
. Note that
 \begin{align*}[\boldsymbol{a},\boldsymbol{b}]^c &=(b_1,\infty]\times[a_2,\infty]\cup[\!-\!\infty,b_1]\times(b_2,\infty]\cup[\!-\!\infty,a_1)\times[\!-\!\infty,b_2]\cup[a_1,\infty] \\ & \quad \times[\!-\!\infty,a_2)\\ &\;=\!:\; \bigcup_{i=1}^4A_i,\end{align*}
\begin{align*}[\boldsymbol{a},\boldsymbol{b}]^c &=(b_1,\infty]\times[a_2,\infty]\cup[\!-\!\infty,b_1]\times(b_2,\infty]\cup[\!-\!\infty,a_1)\times[\!-\!\infty,b_2]\cup[a_1,\infty] \\ & \quad \times[\!-\!\infty,a_2)\\ &\;=\!:\; \bigcup_{i=1}^4A_i,\end{align*}
where the
![]() $A_i$
are sets of the form (a)–(d) respectively, and thus (A.7) holds for these
$A_i$
are sets of the form (a)–(d) respectively, and thus (A.7) holds for these
![]() $A_i$
. Therefore
$A_i$
. Therefore
 \begin{equation*}\sup_{x>0}\mu_x(f)\leq \sup_{\boldsymbol{z}\in\overline{\mathbb{R}}_0^2}f(\boldsymbol{z}) \cdot \sup_{x>0}\mu_x([\boldsymbol{a},\boldsymbol{b}]^c)\leq \sup_{\boldsymbol{z}\in\overline{\mathbb{R}}_0^2}f(\boldsymbol{z}) \cdot \sum_{i=1}^4\sup_{x>0}\mu_x(A_i)<\infty,\end{equation*}
\begin{equation*}\sup_{x>0}\mu_x(f)\leq \sup_{\boldsymbol{z}\in\overline{\mathbb{R}}_0^2}f(\boldsymbol{z}) \cdot \sup_{x>0}\mu_x([\boldsymbol{a},\boldsymbol{b}]^c)\leq \sup_{\boldsymbol{z}\in\overline{\mathbb{R}}_0^2}f(\boldsymbol{z}) \cdot \sum_{i=1}^4\sup_{x>0}\mu_x(A_i)<\infty,\end{equation*}
which by Proposition 3.16 of [Reference Resnick33] implies that
![]() $\{\mu_x\}_{x>0}$
is a vaguely relatively compact subset of the metric space consisting of all the non-negative Radon measures on
$\{\mu_x\}_{x>0}$
is a vaguely relatively compact subset of the metric space consisting of all the non-negative Radon measures on
![]() $(\overline{\mathbb{R}}_0^2, \mathcal B(\overline{\mathbb{R}}_0^2))$
. If
$(\overline{\mathbb{R}}_0^2, \mathcal B(\overline{\mathbb{R}}_0^2))$
. If
![]() $\mu_0$
and
$\mu_0$
and
![]() $\mu_0'$
are two subsequential vague limits of
$\mu_0'$
are two subsequential vague limits of
![]() $\{\mu_x\}_{x>0}$
as
$\{\mu_x\}_{x>0}$
as
![]() $x\rightarrow\infty$
, then by (A.7) we have
$x\rightarrow\infty$
, then by (A.7) we have
![]() $\mu_0(A)=\mu_0'(A)$
for any
$\mu_0(A)=\mu_0'(A)$
for any
![]() $A\in \mathcal D$
. Since any rectangle in
$A\in \mathcal D$
. Since any rectangle in
![]() $\overline{\mathbb{R}}_0^2$
can be obtained from a finite number of sets in
$\overline{\mathbb{R}}_0^2$
can be obtained from a finite number of sets in
![]() $\mathcal D$
by operating union, intersection, difference, or complementary, and these rectangles constitute a
$\mathcal D$
by operating union, intersection, difference, or complementary, and these rectangles constitute a
![]() $\pi$
-system and generate the
$\pi$
-system and generate the
![]() $\sigma$
-field
$\sigma$
-field
![]() $\mathcal B(\overline{\mathbb{R}}_0^2)$
, we get
$\mathcal B(\overline{\mathbb{R}}_0^2)$
, we get
![]() $\mu_0=\mu_0'$
on
$\mu_0=\mu_0'$
on
![]() $ \mathcal{B}(\overline{\mathbb{R}}_0^2)$
. Consequently (A.6) is valid and thus the proof is complete.
$ \mathcal{B}(\overline{\mathbb{R}}_0^2)$
. Consequently (A.6) is valid and thus the proof is complete.
Acknowledgements
We are grateful to the editor and the referees for their constructive suggestions, which have led to a significant improvement of the manuscript.
Funding information
The research of Xiaofan Peng is partially supported by the National Natural Science Foundation of China (11701070, 71871046).
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.