1. Introduction
As part of fluctuation theory, exit problems for spectrally negative Lévy processes and the associated reflected processes have been studied extensively over the past ten years. Such problems often concern the joint distributions of the process when it first leaves either a finite or a semi-finite interval, or when its draw-down (from the running maximum) or its draw-up (from the running minimum) first exceeds a fixed level. These results are often expressed in terms of the scale functions. We refer to [Reference Kyprianou8] and references therein for a collection of such results; see also [Reference Avram, Kyprianou and Pistorius1], [Reference Landriault, Li and Zhang10], [Reference Pistorius13], and [Reference Zhou16] for research on the draw-down times and draw-up times for spectrally negative Lévy processes reflected at the running maximum and running minimum processes, respectively. We refer to [Reference Zhang15] for recent work on draw-down(up) times of regular diffusions.
Exit problems involving more general first passage times had been considered earlier for time homogeneous diffusions. In [Reference Lehoczky11] an exit problem with exit level depending on the running maximum of the diffusion was studied and a joint Laplace transform was found for such a general draw-down time. The general draw-down times find interesting applications in [Reference Azéma and Yor3], defining the Azéma–Yor martingales to solve the Skorokhod embedding problem. The draw- down problem for renewal processes was studied in [Reference Landriault, Li and Li9]. More recent work on applications of draw-down times can be found in [Reference Carraro, Karoui and ObłόJ5], [Reference Landriault, Li and Li9], and references therein.
Pistorius [Reference Pistorius14] studied the general draw-down times of spectrally negative Lévy processes with an excursion theory approach, to obtain the Skorokhod embedding for the spectrally negative Lévy process and for the associated reflected process from its maximum. Following a similar approach, Mijatović and Pistorius [Reference Mijatović and Pistorius12] then considered a sextuple law related to the draw-down time. In [Reference Avram, Vu and Zhou2] we considered a perturbed spectrally negative Lévy risk process, the so-called Lévy tax process, with a draw-down exit level that is a linear function of the running maximum process, and found expressions on the expected present values of amount of tax for this process. To this end, we applied both the excursion theory and an approximation approach using solutions to the exit problems with fixed boundaries.
In this paper we continue to investigate the exit problems for a spectrally negative Lévy process with a dynamic draw-down exit level that depends on the running maximum in a general way. Applying the excursion theory, which comes in handy for analysing the draw- down fluctuation behaviours for the spectrally negative Lévy processes, we first find the expressions for a joint Laplace transform of the process at the draw-down time. We also find the Laplace transforms for the hitting time and creeping time of the draw-down level, respectively. In addition, we obtain an expression for a potential measure associated with the draw-down time.
This paper is structured as follows. After the Introduction, in Section 2 we review basic facts on spectrally negative Lévy processes to prepare for the main proofs. The main results are presented in Section 3. Section 4 focuses on results with linear draw-down functions for which the expressions can be simplified and some previous results can be easily recovered. Proofs of the main results are deferred to Section 5.
2. Spectrally negative Lévy processes
Throughout this paper, let X = {Xt, t ≥ 0} be a spectrally negative Lévy process (SNLP for short), i.e. a one-dimensional stochastic process with stationary independent increments and with no positive jumps, defined on a filtered probability space (Ω, ℱ, (ℱt)t≥0, ℙ). We also assume that X is not the negative of a subordinator. Denote by ℙx the probability law of X given X 0 = x, and the corresponding expectation by 𝔼x. Write ℙ and 𝔼 when x = 0. Its Laplace transform always exists, with the Laplace exponent given by
$$\psi (\lambda ){\kern 1pt} : = {\kern 1pt} {1 \over t}\log {\mathbb{E}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{\lambda {X_t}}})\quad {\rm{for}} \ \lambda \ge 0$$
where
$$\psi (\lambda ) = \mu \lambda + {1 \over 2}{\sigma ^2}{\lambda ^2} + \int_{( - \infty ,0)} ({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{\lambda x}} - 1 - \lambda x{{\bf{1}}_{\{ x \gt - 1\} }})\Pi ({\kern 1pt} \;{\rm{d}}{\kern 1pt} x)$$
for μ ∈ ℝ, σ ≥ 0 and the σ-finite Lévy measure Π on (−∞, 0) satisfying
$$\int_{( - \infty ,0)} (1 \wedge {x^2})\Pi ({\kern 1pt} \;{\rm{d}}{\kern 1pt} x) \lt \infty .$$
Further, there exists a function Φ :[0, ∞) → [0, ∞) defined by
$$\Phi (q){\kern 1pt} : = {\kern 1pt} \sup \{ \lambda \ge 0:\psi (\lambda ) = q\} \quad {\rm{for}} \ q \ge 0.$$
Scale functions play a central role in the fluctuation theory for SNLPs. For q ≥ 0, the q-scale function W (q) for process X is defined as a continuous function on [0, ∞) satisfying
$$\int_0^\infty {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - \lambda y}}{W^{(q)}}(y){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y = {1 \over {\psi (\lambda ) - q}}\quad {\rm{for}} \ \lambda \gt \Phi (q).$$
For convenience, we extend the domain of W (q) to the whole real line by setting W (q)(x) = 0 for all x < 0. Given W (q), the second scale function is defined by
$${Z^{(q)}}(x){\kern 1pt} : = {\kern 1pt} 1 + q\int_0^x {W^{(q)}}(y){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y.$$
Write W = W (0) and Z = Z (0) whenever q = 0.
It is well known that W (q)(x) is strictly increasing on ℝ+. W (q)(0) = W(0) > 0 if and only if the process X has paths of bounded variation, and if and only if σ = 0 and 
$$\int _{ - 1}^0|x|\Pi ({\kern 1pt} \;{\rm{d}}{\kern 1pt} x) \lt \infty $$. The scale function W (q) is continuously differentiable on (0, ∞) if the process X has paths of unbounded variation (and, in particular, if it has a nontrivial Gaussian component) or if the process X has paths of bounded variation and the Lévy measure has no atoms. Moreover, if σ > 0, W (q) has a continuous derivative of order two on (0, ∞) and W ′ (0 + ) = 2/σ 2. We refer the readers to [Reference Chan, Kyprianou and Savov6] for more detailed discussions on the smoothness of scale functions.
For c ≥ 0, process 
$$\{ {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{c{X_t} - \psi (c)t}},{\kern 1pt} t \ge 0\} $$ is a martingale under ℙ. Introduce a new probability measure satisfying
$${{{\kern 1pt} \;{\rm{d}}{\mathbb{P}}{\kern 1pt} {^{(c)}}} \over {{\kern 1pt} \;{\rm{d}}{\mathbb{P}}{\kern 1pt} }}{|_{{{\cal F}_t}}} = {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{c{X_t} - \psi (c)t}}\quad {\rm{for \ every}} \ t \ge {\rm{0}}.$$
It is well known that X is still an SNLP under ℙ(c). Denoting the associated Laplace exponent and scale functions with a subscript c under ℙ(c), a straightforward calculation shows that, for c ≥ 0, q + ψ(c) ≥ 0,
$${\psi _c}(s) = \psi (c + s) - \psi (c)\quad {\rm{and}}\quad {\Phi _c}(s) = \Phi (s + \psi (c)) - c\quad {\rm{for}} \ s \ge 0;$$
in addition,
$$W_c^{(q)}(x) = {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - cx}}{W^{(q + \psi (c))}}(x)\quad {\rm{and}}\quad Z_c^{(q)}(x) = 1 + q\int_0^x W_c^{(q)}(y){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y.$$
Note that, for x ≥ 0, W (q)(x) and Z (q)(x) are analytically extendable to all q ∈ ℂ ([Reference Kyprianou8, Lemma 8.3, Corollary 8.5]), and identity (2.2) in Lemma 2.1 below holds for all u, v ≥ 0.
For any c, b ∈ ℝ, defining the first passage times
$$\tau _b^ + {\kern 1pt} : = {\kern 1pt} \inf \{ t \ge 0:{X_t} \gt b\} \quad {\rm{and}}\quad \tau _c^ - {\kern 1pt} : = {\kern 1pt} \inf \{ t \ge 0:{X_t} \lt c\} $$
with the convention that inf Ø = ∞, we have the following result.
Lemma 2.1. For c ≤ x ≤ b, q, u, v ≥ 0 and for p ≔ u − ψ(v), we have
$${{\mathbb{E}}_x}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\tau _b^ + }}:\tau _b^ + \lt \tau _c^ - ) = {{{W^{(q)}}(x - c)} \over {{W^{(q)}}(b - c)}},$$
$$\eqalign{
& {{\mathbb{E}}_x}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - u\tau _c^ - + vX(\tau _c^ - )}}:\tau _c^ - \lt \tau _b^ + ) = {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{vx}}(Z_v^{(p)}(x - c) - {{W_v^{(p)}(x - c)} \over {W_v^{(p)}(b - c)}}Z_v^{(p)}(b - c)), \cr
& \cr} $$
and, for x ∈ (c, b),
$${{\mathbb{E}}_x}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\tau _c^ - }}:X(\tau _c^ - ) = c,\tau _c^ - \lt \tau _b^ + ) = {{{\sigma ^2}} \over 2}({W^{(q)'}}(x - c) - {W^{(q)}}(x - c){{{W^{(q)'}}(b - c)} \over {{W^{(q)}}(b - c)}}).$$
In addition, the resolvent of process X killed at the first exit time of interval [c, b] is specified by
$$\int_0^\infty {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - qt}}{{\mathbb{E}}_x}(f({X_t}),t \lt \tau _b^ + \wedge \tau _c^ - ){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} t = \int_c^b f(y)({{{W^{(q)}}(x - c)} \over {{W^{(q)}}(b - c)}}{W^{(q)}}(b - y) - {W^{(q)}}(x - y)){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y.$$
Identity (2.1) can be found in [Reference Kyprianou8, Theorem 8.1]. To obtain the joint Laplace transform in (2.2), we apply [Reference Kyprianou8, Theorem 8.1] under the new measure 
$${\mathbb{P}}_x^{(v)}$$. Identity (2.3) can be found in [Reference Mijatović and Pistorius12, equation (2.6)], and 
$$\{ X(\tau _c^ - ) = c\} $$ is known as the creeping event, which happens for an SNLP when the first downward passage over a level occurs by hitting the level with a positive probability. The result shows that an SNLP creeps downwards if and only if it has a Gaussian component.
Let τ {a} ≔ inf{t > 0, Xt = a} be the first hitting time of level a. We could not find the following result in the literature, and provide a proof for the readers’ convenience.
Lemma 2.2. For x, a ∈ (c, b), we have
$${{\mathbb{E}}_x}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q{\tau ^{\{ a\} }}}}:{\tau ^{\{ a\} }} \lt \tau _b^ + \wedge \tau _c^ - ) = {{{W^{(q)}}(x - c)} \over {{W^{(q)}}(a - c)}} - {{{W^{(q)}}(x - a){W^{(q)}}(b - c)} \over {{W^{(q)}}(b - a){W^{(q)}}(a - c)}}.$$
Proof of Lemma 2.2. As observed in [Reference Ivanovs and Palmowski7, Lemma 11] that 
$$\{ \tau _b^ + \lt {\tau ^{\{ a\} }}\} = \{ \tau _b^ + \lt \tau _a^ - \} $$ for a < b, applying the strong Markov property of X at τ {a}, we have
$$\matrix{
{{{\mathbb{E}}_x}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\tau _b^ + }}:\tau _b^ + \lt \tau _c^ - )} \hfill \cr
{\quad \quad = {{\mathbb{E}}_x}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\tau _b^ + }}:{\tau ^{\{ a\} }} \lt \tau _b^ + \lt \tau _c^ - ) + {{\mathbb{E}}_x}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\tau _b^ + }}:\tau _b^ + \lt \tau _c^ - \wedge {\tau ^{\{ a\} }})} \hfill \cr
{\quad \quad = {{\mathbb{E}}_x}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q{\tau ^{\{ a\} }}}}:{\tau ^{\{ a\} }} \lt \tau _b^ + \wedge \tau _c^ - ){{\mathbb{E}}_a}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\tau _b^ + }}:\tau _b^ + \lt \tau _c^ - ) + {{\mathbb{E}}_x}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\tau _b^ + }}:\tau _b^ + \lt \tau _a^ - ).} \hfill \cr
} $$
The Laplace transform (2.4) for the hitting time follows by applying (2.1).
3. Main results
Write 
$${\bar X_t}{\kern 1pt} : = {\kern 1pt} \mathop {\sup }\nolimits_{0 \le s \le t} {X_s}$$ for the running maximum process for X. The process X reflected at its running maximum is defined by 
$${Y_t}{\kern 1pt} : = {\kern 1pt} {\bar X_t} - {X_t}$$. Let ξ(·) be a measurable function on ℝ. Define the draw-down time for X with respect to the draw-down function ξ as
$${\tau _\xi }{\kern 1pt} : = {\kern 1pt} \inf \{ t \gt 0,{X_t} \lt \xi ({\bar X_t})\} = \inf \{ t \gt 0,{Y_t} \gt \bar \xi ({\bar X_t})\} ,$$
where 
$$\bar \xi (z){\kern 1pt} : = {\kern 1pt} z - \xi (z)$$ and 
$$\{ \xi ({\bar X_t}),t \ge 0\} $$ is the associated draw-down level process. For the case of constant function 
$$\bar \xi $$, a sextuple law was found in [Reference Mijatović and Pistorius12], where the concerned quantities include the time of reaching the last maximum and minimum value of X before τξ together with the undershoot at τξ. The process Y is referred to as the draw-down process in [Reference Mijatović and Pistorius12]. In this paper, we focus on an arbitrary measurable and strictly positive function 
$$\bar \xi $$ on ℝ and we assume that W (q)′ (x) exists on (0, ∞) for simplicity.
In this section we first present expressions for the solutions to the two-sided exit problems involving τξ.
Proposition 3.1. For any q > 0 and x < b, we have
$${{\mathbb{E}}_x}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\tau _b^ + }}:\tau _b^ + \lt {\tau _\xi }) = \exp ( - \int_x^b {{{W^{(q)'}}(\bar \xi (y))} \over {{W^{(q)}}(\bar \xi (y))}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y).$$
For any u, v > 0, k ∈ ℝ and x < b, with p ≔ u − ψ(v), we have
$$\matrix{
{{{\mathbb{E}}_x}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - u{\tau _\xi } + vX({\tau _\xi }) + k\bar X({\tau _\xi })}}:{\tau _\xi } \lt \tau _b^ + )} \hfill \cr
{\quad \quad = {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{vx}}\int_x^b {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ky - \int_x^y {{W_v^{(p)'}(\bar \xi (z))} \over {W_v^{(p)}(\bar \xi (z))}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} z}}({{W_v^{(p)'}(\bar \xi (y))} \over {W_v^{(p)}(\bar \xi (y))}}Z_v^{(p)}(\bar \xi (y)) - pW_v^{(p)}(\bar \xi (y))){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y.} \hfill \cr
} $$
Remark 3.1. The assumption 
$$\bar \xi \gt 0$$ 0 on [x, b] is necessary. In fact, if 
$$\bar \xi (a) = 0$$ for some a ∈ (x, b), one can find that 
$${\tau _\xi } \le \tau _a^ + $$ ℙx-a.s. by definition, and then (3.1) and (3.2) fail to hold. It is often the case that the process X is bounded from above by a constant b for the event of interest. When this happens, under ℙx the effective domain of 
$$\bar \xi $$ is [x, b] instead of ℝ, that is, only the values of 
$$\bar \xi (y)$$ for y ∈ [x, b] really matter, and the conditions on 
$$\bar \xi (y)$$ only need to be imposed for y ∈ [x, b].
For the potential measure up to time 
$$\tau _b^ + \wedge {\tau _\xi }$$, we also have the next result.
Proposition 3.2. For any x < b, we have
$$\matrix{
{\int_0^\infty {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - qt}}{{\mathbb{P}}_x}({X_t} \in {\kern 1pt} \;{\rm{d}}{\kern 1pt} y:t \lt \tau _b^ + \wedge {\tau _\xi }){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} t} \hfill \cr
{\quad \quad = (\int_x^b {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - \int_x^z {{{W^{(q)'}}(\bar \xi (s))} \over {{W^{(q)}}(\bar \xi (s))}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} s}}({W^{(q)'}}(z - y) - {{{W^{(q)'}}(\bar \xi (z))} \over {{W^{(q)}}(\bar \xi (z))}}{W^{(q)}}(z - y)){{\bf{1}}_{\{ y \in (\xi (z),z)\} }}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} z){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y} \hfill \cr
{\quad \quad \quad {\kern 1pt} + W(0)({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - \int_x^y {{{W^{(q)'}}(\bar \xi (z))} \over {{W^{(q)}}(\bar \xi (z))}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} z}}{{\bf{1}}_{\{ y \in (x,b)\} }}){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y.} \hfill \cr
} $$
Remark 3.2. The resolvent density in (3.3) consists of two parts, where the second term degenerates if process X has sample paths of unbounded variation. By further analysis, one can find that it is contributed by the total amount of time in
$${\cal L}{\kern 1pt} : = {\kern 1pt} \{ t \gt 0:{X_t} = {\bar X_t}\} $$
until time 
$$\tau _b^ + \wedge {\tau _\xi }$$, that is,
$$\int_0^\infty {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - qt}}{{\bf{1}}_{\{ t \in {\cal L}\} }}{{\bf{1}}_{\{ t \lt \tau _b^ + \wedge {\tau _\xi }\} }}{{\bf{1}}_{\{ {X_t} \in {\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y\} }}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} t;$$
and for the case of W(0) = 0, we see that ℒ is a Lebesgue null set ℙx-a.s.
Remark 3.3. If ξ ≡ c for some c < x, then Proposition 3.2 implies that the support of the resolvent is [c, b]. For any y ∈ (c, b), since y > ξ(z) = c in the following integral, we have
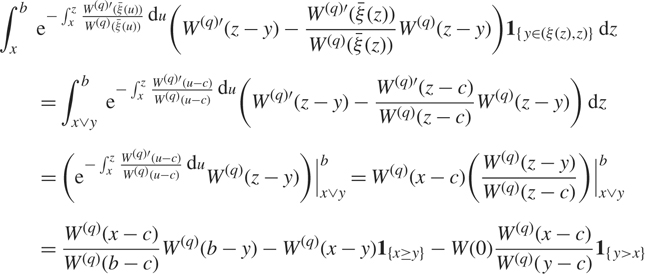$$\matrix{
{\int_x^b {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - \int_x^z {{{W^{(q)'}}(\bar \xi (u))} \over {{W^{(q)}}(\bar \xi (u))}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} u}}({W^{(q)'}}(z - y) - {{{W^{(q)'}}(\bar \xi (z))} \over {{W^{(q)}}(\bar \xi (z))}}{W^{(q)}}(z - y)){{\bf{1}}_{\{ y \in (\xi (z),z)\} }}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} z} \hfill \cr
{\quad \quad = \int_{x \vee y}^b {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - \int_x^z {{{W^{(q)'}}(u - c)} \over {{W^{(q)}}(u - c)}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} u}}({W^{(q)'}}(z - y) - {{{W^{(q)'}}(z - c)} \over {{W^{(q)}}(z - c)}}{W^{(q)}}(z - y)){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} z} \hfill \cr
{\quad \quad = ({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - \int_x^z {{{W^{(q)'}}(u - c)} \over {{W^{(q)}}(u - c)}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} u}}{W^{(q)}}(z - y))|_{x \vee y}^b = {W^{(q)}}(x - c)({{{W^{(q)}}(z - y)} \over {{W^{(q)}}(z - c)}})|_{x \vee y}^b} \hfill \cr
{\quad \quad = {{{W^{(q)}}(x - c)} \over {{W^{(q)}}(b - c)}}{W^{(q)}}(b - y) - {W^{(q)}}(x - y){{\bf{1}}_{\{ x \ge y\} }} - W(0){{{W^{(q)}}(x - c)} \over {{W^{(q)}}(y - c)}}{{\bf{1}}_{\{ y \gt x\} }}} \hfill \cr
} $$
and
$$W(0){\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - \int_x^y {{{W^{(q)'}}(\bar \xi (z))} \over {{W^{(q)}}(\bar \xi (z))}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} z}}{{\bf{1}}_{\{ y \gt x\} }} = W(0){\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - \int_x^y {{{W^{(q)'}}(z - c)} \over {{W^{(q)}}(z - c)}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} z}}{{\bf{1}}_{\{ y \gt x\} }} = W(0){{{W^{(q)}}(x - c)} \over {{W^{(q)}}(y - c)}}{{\bf{1}}_{\{ y \gt x\} }}.$$
Making use of the fact that W (q)(z) = 0for z < 0 again, we recover the expression of the classical potential density.
Notice that 
$${\tau _\xi } \wedge \tau _c^ - = {\tau _{\xi \vee c}}$$ for any c < x and initial value x. Applying Proposition 3.2,in the next result we can also obtain a joint distribution involving the running minimum and maximum before τξ together with 
$${X_{{\tau _\xi } - }}$$ and 
$${X_{{\tau _\xi }}}$$ when there is an overshoot at the draw-down time τξ.
Let 
$${\underline X _t}{\kern 1pt} : = {\kern 1pt} \mathop {\inf }\nolimits_{s \in [0,t]} {X_s}$$ be the running minimum process of X.
Corollary 3.1. For any nonnegative measurable function f on ℝ2 satisfying f (z, z) = 0 for all z ∈ ℝ and for any c < x < b, we have
$$\matrix{
{{{\mathbb{E}}_x}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q{\tau _\xi }}}f({X_{{\tau _\xi } - }},{X_{{\tau _\xi }}}):{{\underline X }_{{\tau _\xi } - }} \gt c,{{\bar X}_{{\tau _\xi }}} \le b)} \hfill \cr
{\quad \quad = W(0)\int_c^b ({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - \int_x^z {{{W^{(q)'}}(\overline {\xi \vee c} (s))} \over {{W^{(q)}}(\overline {\xi \vee c} (s))}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} s}}){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} z\int_{ - \infty }^{ - \bar \xi (z)} f(z,z + u)\Pi ({\kern 1pt} \;{\rm{d}}{\kern 1pt} u)} \hfill \cr
{\quad \quad \quad {\kern 1pt} + \int_c^b {\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} z\int_{\xi (z) \vee c}^z {\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y\int_{ - \infty }^{\xi (z) - y} f(y,y + u)\Pi ({\kern 1pt} \;{\rm{d}}{\kern 1pt} u)} \hfill \cr
{\quad \quad \quad {\kern 1pt} \times ({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - \int_x^z {{{W^{(q)'}}(\overline {\xi \vee c} (s))} \over {{W^{(q)}}(\overline {\xi \vee c} (s))}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} s}}{W^{(q)'}}(z - y) - {{{W^{(q)'}}(\overline {\xi \vee c} (z))} \over {{W^{(q)}}(\overline {\xi \vee c} (z))}}{W^{(q)}}(z - y)).} \hfill \cr
} $$
We now consider the hitting problem of a draw-down level. Let
$${\tau ^{\{ \xi \} }}{\kern 1pt} : = {\kern 1pt} \inf \{ t \gt 0,{X_t} = \xi ({\bar X_t})\} = \inf \{ t \gt 0,{Y_t} = \bar \xi ({\bar X_t})\} $$
denote the first time for X to hit the draw-down level 
$$\xi (\bar X)$$. A particularly interesting case of hitting is the event of creeping, 
$$\{ {\tau ^{\{ \xi \} }} = {\tau _\xi }\} $$, which happens for an SNLP when the first downward passage over a level occurs by hitting the level with a positive probability. It is well known that the classical creeping of a fixed level happens only if σ > 0, i.e. only if process X has a nontrivial Brownian motion component. If the downward passage time is replaced with a draw-down time, observe that within the duration of each downward sample path of excursion away from the running maximum, the draw-down level 
$$\xi (\bar X)$$ remains constant. Therefore, one would expect that the draw-down creeping occurs if and only if process X has a nontrivial Brownian motion component.
In the following proposition, another draw-down level with draw-down function θ(z) is introduced with 
$$\bar \theta (z) = z - \theta (z) \gt 0$$ for all z ∈ ℝ.
Proposition 3.3. For any x < b and I ≔{z ∈ ℝ: θ(z) < ξ(z)}, we have
$$\matrix{
{{{\mathbb{E}}_x}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q{\tau _\xi }}}:{\tau ^{\{ \xi \} }} = {\tau _\xi } \lt \tau _b^ + \wedge {\tau _\theta })} \hfill \cr
{\quad \quad = {{{\sigma ^2}} \over 2}\int_{[x,b] \cap I} {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - \int_x^y {{{W^{(q)'}}(\overline {\xi \vee \theta } (z))} \over {{W^{(q)}}(\overline {\xi \vee \theta } (z))}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} z}}({{{{({W^{(q)'}}(\bar \xi (y)))}^2}} \over {{W^{(q)}}(\bar \xi (y))}} - {W^{(q)''}}(\bar \xi (y))){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y.} \hfill \cr
} $$
Moreover, for any x < b we have
$$\matrix{
{{{\mathbb{E}}_x}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q{\tau ^{\{ \xi \} }}}}:{\tau ^{\{ \xi \} }} \lt \tau _b^ + \wedge {\tau _\theta })} \hfill \cr
{\quad \quad = \int_{[x,b] \cap I} {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - \int_x^y {{{W^{(q)'}}(\overline {\xi \vee \theta } (z))} \over {{W^{(q)}}(\overline {\xi \vee \theta } (z))}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} z}}{{{W^{(q)}}(\bar \theta (y))} \over {{W^{(q)}}(\bar \theta (y) - \bar \xi (y))}}({{{W^{(q)'}}(\bar \xi (y))} \over {{W^{(q)}}(\bar \xi (y))}} - {{{W^{(q)'}}(\bar \theta (y))} \over {{W^{(q)}}(\bar \theta (y))}}){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y.} \hfill \cr
} $$
Remark 3.4. If θ < ξ = c for some c < x < b, Proposition 3.3 reduces to the classical result (2.3). In this case, I = ℝ and 
$$\overline {\xi \vee \theta } (y) = y - c = \bar \xi (y)$$. As in Remark 3.3, we have
$$\int_x^y {{{W^{(q)'}}(\overline {\xi \vee \theta } (z))} \over {{W^{(q)}}(\overline {\xi \vee \theta } (z))}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} z = \int_x^y {{{W^{(q)'}}(z - c)} \over {{W^{(q)}}(z - c)}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} z = \log ({{{W^{(q)}}(y - c)} \over {{W^{(q)}}(x - c)}})\quad {\rm{fory}} \in {\rm{(x,b)}}.$$
Then the right-hand side of (3.4) is equal to
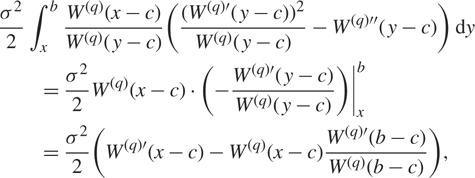$$\matrix{
{{{{\sigma ^2}} \over 2}\int_x^b {{{W^{(q)}}(x - c)} \over {{W^{(q)}}(y - c)}}({{{{({W^{(q)'}}(y - c))}^2}} \over {{W^{(q)}}(y - c)}} - {W^{(q)''}}(y - c)){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y} \hfill \cr
{\quad \quad = {{{\sigma ^2}} \over 2}{W^{(q)}}(x - c) \cdot ( - {{{W^{(q)'}}(y - c)} \over {{W^{(q)}}(y - c)}})|_x^b} \hfill \cr
{\quad \quad = {{{\sigma ^2}} \over 2}({W^{(q)'}}(x - c) - {W^{(q)}}(x - c){{{W^{(q)'}}(b - c)} \over {{W^{(q)}}(b - c)}}),} \hfill \cr
} $$
which recovers (2.3).
Similarly, one can recover Lemma 2.2 from (3.5) by taking ξ = a, θ = c with c < a < b and x ∈ (c, b).
It is also interesting to study similar problems associated with the draw-up times (from the running minimum) with a general draw-up function for a spectrally negative Lévy process. However, it seems challenging to express the desired results in terms of the scale functions.
4. Applications
In this section we present two applications of the results from Section 3.
4.1. Selling a stock at a draw-down time
Example 4.1. The decision to sell a stock is a combination of art and science. In general, it is ideal to sell a stock at a price as high as possible or just before it starts to decline. However, very few investors can buy at the absolute bottom and sell at the absolute high. If one does not sell at the right time, the profit disappears. There are a number of considerations to determine the best time. In this example, we assume that the price process of an underlying security is given by 
$$S = \{ {S_t} = {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{{X_t}}},t \ge 0\} $$. The investor sells a stock either when it hits a price target in order to lock in gains or before the ratio 
$$S/\overline S $$ leaves too far below 1 to stop the loss, where 
$$\overline S $$ is the historical high process for S. Using the Cobb–Douglas function, the investor sells out of a stock when the utility process
$$\{ ({S_t}/{S_0}{)^\gamma }{({S_t}/{\overline S _t})^{1 - \gamma }},{\kern 1pt} {\kern 1pt} t \ge 0\} $$
leaves a predetermined interval [a, b]for some λ, a ∈ (0, 1) and b > 1. It can be checked directly that 
$${T_{a,b}} = T_{a,b}^ + \wedge T_{a,b}^ - $$, where
$$T_{a,b}^ + {\kern 1pt} : = {\kern 1pt} \inf \{ t \gt 0:{S_t} \gt {b^{1/\gamma }}{S_0}\} \quad {\rm{and}}\quad T_{a,b}^ - {\kern 1pt} : = {\kern 1pt} \inf \{ t \gt 0:{S_t}/{S_0} \lt a \cdot {({\overline S _t}/{S_0})^{1 - \gamma }}\} .$$
Without loss of generality, we take S 0 = 1 and then X 0 = 0. Formulated in terms of the first passage time for X under ℙ, we have 
$$T_{a,b}^ + = \tau _{(\log b)/\gamma }^ + $$ and 
$$T_{a,b}^ - = {\tau _\xi }$$ for ξ(z) = (1 − λ )z + log a. Let q > 0 be the risk-free interest rate and p = q − ψ(1). Then we have
$${{\mathbb{E}}_1}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q{T_{a,b}}}}{S_{{T_{a,b}}}}:{T_{a,b}} = T_{a,b}^ + ) = {b^{1/\gamma }}{({{{W^{(q)}}(\log 1/a)} \over {{W^{(q)}}(\log b/a)}})^{1/\gamma }}$$
and
$$\matrix{
{{{\mathbb{E}}_1}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q{T_{a,b}}}}{S_{{T_{a,b}}}}:{T_{a,b}} = T_{a,b}^ - ) = Z_1^{(p)}(\log 1/a) - Z_1^{(p)}(\log b/a)({{W_1^{(p)}(\log 1/a)} \over {W_1^{(p)}(\log b/a)}}{)^{1/\gamma }}} \hfill \cr
{\quad {\kern 1pt} - p{{1 - \gamma } \over \gamma }\int_{\log 1/a}^{\log b/a} {{(W_1^{(p)}(\log 1/a))}^{1/\gamma }}{{(W_1^{(p)}(y))}^{(\gamma - 1)/\gamma }}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y.} \hfill \cr
} $$
Proof of (4.1) and (4.2). In this case, for z ∈ [0, (log b)/λ], 
$$\bar \xi (z) = \gamma z - \log a \gt 0$$ by definition. Then 
$$\bar \xi '(z) = \gamma $$ and, for x ∈ [0, (log b)/γ ], we have
$$\int_0^x {{{W^{(q)'}}(\bar \xi (y))} \over {{W^{(q)}}(\bar \xi (y))}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y = {1 \over \gamma }(\log ({W^{(q)}}(\bar \xi (y))))|_0^x = {1 \over \gamma }\log ({{{W^{(q)}}(\bar \xi (x))} \over {{W^{(q)}}(\bar \xi (0))}}).$$
Applying the formula (3.1) and the fact that 
$${S_{T_{a,b}^ + }} = {b^{1/\gamma }}$$ on the event 
$$\{ T_{a,b}^ + \lt \infty \} $$ gives (4.1).
Similarly, we have
$$\matrix{
{\int_0^{(\log b)/\gamma } \exp ( - \int_0^y {{W_1^{(p)'}(\bar \xi (z))} \over {W_1^{(p)}(\bar \xi (z))}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} z)({{W_1^{(p)'}(\bar \xi (y))} \over {W_1^{(p)}(\bar \xi (y))}}Z_1^{(p)}(\bar \xi (y)) - p\gamma W_1^{(p)}(\bar \xi (y))){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y} \hfill \cr
{\quad \quad = ( - Z_1^{(p)}(\bar \xi (y)){\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - \int_0^y {{W_1^{(p)'}(\bar \xi (z))} \over {W_1^{(p)}(\bar \xi (z))}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} z}})|_0^{(\log b)/\gamma }} \hfill \cr
{\quad \quad = Z_1^{(p)}(\log {1 \over a}) - Z_1^{(p)}(\log {b \over a})({{W_1^{(p)}(\log 1/a)} \over {W_1^{(p)}(\log b/a)}}{)^{1/\gamma }}.} \hfill \cr
} $$
The identity (4.2) can be proved by applying (3.2) and a change of variable argument.
4.2. First passage times of the reflected SNLP
Example 4.2. For function ξ(z) = z − d for some d > 0, the draw-down time τξ reduces to the first passage time of SNLP reflected at its running maximum, which was investigated in [Reference Avram, Kyprianou and Pistorius1] and [Reference Pistorius13], that is, 
$${\tau _\xi } = \kappa _d^ + $$ for
$$\kappa _d^ + {\kern 1pt} : = {\kern 1pt} \inf \{ t \gt 0,{Y_t} \gt d\} .$$
For b, q, u, v > 0 and k ∈ ℝ, we have
$${\mathbb{E}}({\rm{e}}{{\kern 1pt} ^{ - q\tau _b^ + }}:\tau _b^ + \lt \kappa _d^ + ) = \exp ( - {{{W^{(q)'}}(d)} \over {{W^{(q)}}(d)}}b),$$
$$\matrix{
{{\mathbb{E}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - u\kappa _d^ + + vX(\kappa _d^ + ) + k\bar X(\kappa _d^ + )}}:\kappa _d^ + \lt \tau _b^ + ) = ({{W_v^{(p)'}(d)} \over {W_v^{(p)}(d)}}Z_v^{(p)}(d) - pW_v^{(p)}(d))} \hfill \cr
{\quad {\kern 1pt} \times (1 - {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{(k - {{W_v^{(p)'}(d)} \over {W_v^{(p)}(d)}})b}})/({{W_v^{(p)'}(d)} \over {W_v^{(p)}(d)}} - k),} \hfill \cr
} $$
and
$${\mathbb{E}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\kappa _d^ + }}:Y(\kappa _d^ + ) = d,\kappa _d^ + \lt \tau _b^ + ) = {{{\sigma ^2}} \over 2}({W^{(q)'}}(d) - {{{W^{(q)}}(d){W^{(q)''}}(d)} \over {{W^{(q)'}}(d)}})(1 - {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - {{{W^{(q)'}}(d)} \over {{W^{(q)}}(d)}}b}}),$$
where p = u − ψ(v). In addition, for y ∈ (−d, b) we have
$$\int_0^\infty {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - qt}}{\mathbb{P}}({X_t} \in {\kern 1pt} \;{\rm{d}}{\kern 1pt} y,t \lt \kappa _d^ + \wedge \tau _b^ + ){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} t = ({W^{(q)}}(d \wedge (b - y)){\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - {{{W^{(q)'}}(d)} \over {{W^{(q)}}(d)}}(y + d) \wedge b}} - {W^{(q)}}( - y)){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y.$$
Note that 
$$\bar \xi (t) \equiv d$$ in this case, so the above results follow directly from Propositions 3.1, 3.3, and 3.2, respectively, where an argument similar to Remark 3.3 is applied in obtaining (4.6).
Remark 4.1. Denote by eq an exponential random variable with parameter q and independent of X. Since
$${\mathbb{E}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\tau _b^ + }}:\tau _b^ + \lt \kappa _d^ + ) = {\mathbb{P}}(\tau _b^ + \lt {e_q} \wedge \kappa _d^ + ) = {\mathbb{P}}({\bar X_{{e_q} \wedge \kappa _d^ + }} \gt b),$$
it follows from (4.3) that 
$${\bar X_{{e_q} \wedge \kappa _d^ + }}$$ is exponentially distributed with parameter W (q)′ (d)/W (q)(d). Taking k = −v < 0 in (4.4) and letting b →∞, we have
$${\mathbb{E}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - u\kappa _d^ + - vY(\kappa _d^ + )}}:\kappa _d^ + \lt \infty ) = Z_v^{(p)}(d) - W_v^{(p)}(d){{pW_v^{(p)}(d) + vZ_v^{(p)}(d)} \over {W_v^{(p)'}(d) + vW_v^{(p)}(d)}},$$
which coincides with [Reference Avram, Kyprianou and Pistorius1, Theorem 1].
Remark 4.2. For 0 < b − y < d and b > 0, identity (4.6) can be rewritten as
$${\mathbb{P}}({X_{{e_q}}} \in {\kern 1pt} \;{\rm{d}}{\kern 1pt} y,{e_q} \lt \kappa _d^ + ,{\bar X_{{e_q}}} \lt b) = q({W^{(q)}}(b - y){\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - {{{W^{(q)'}}(d)} \over {{W^{(q)}}(d)}}b}} - {W^{(q)}}( - y)){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y.$$
Then
$${\mathbb{P}}({X_{{e_q}}} \in {\kern 1pt} \;{\rm{d}}{\kern 1pt} y,{e_q} \lt \kappa _d^ + ,{\bar X_{{e_q}}} \in {\kern 1pt} \;{\rm{d}}{\kern 1pt} b) = q({W^{(q)'}}(b - y) - {{{W^{(q)'}}(d)} \over {{W^{(q)}}(d)}}{W^{(q)}}(b - y)){\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - {{{W^{(q)'}}(d)} \over {{W^{(q)}}(d)}}b}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} b.$$
Therefore, for z ∈ (0, d) we have
$$\matrix{
{{\mathbb{P}}({Y_{{e_q}}} \in {\kern 1pt} \;{\rm{d}}{\kern 1pt} z,{e_q} \lt \kappa _d^ + )} \hfill & = \hfill & {q({W^{(q)'}}(z) - {{{W^{(q)'}}(d)} \over {{W^{(q)}}(d)}}{W^{(q)}}(z))\int_0^\infty {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - {{{W^{(q)'}}(d)} \over {{W^{(q)}}(d)}}b}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} b} \hfill \cr
{} \hfill & = \hfill & {q({W^{(q)}}(d){{{W^{(q)'}}(z)} \over {{W^{(q)'}}(d)}} - {W^{(q)}}(z)){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} z,} \hfill \cr
} $$
which coincides with the resolvent given in [Reference Pistorius13, Theorem 1(ii)].
By Remark 3.2, for the case W(0) > 0, we have for y ∈ (0, b)
$${\mathbb{P}}({e_q} \lt \kappa _d^ + \wedge \tau _b^ + ,\bar X({e_q}) \in {\kern 1pt} \;{\rm{d}}{\kern 1pt} y,Y({e_q}) = 0) = qW(0){\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - {{{W^{(q)'}}(d)} \over {{W^{(q)}}(d)}}y}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y.$$
Therefore,
$${\mathbb{P}}({e_q} \lt \kappa _d^ + \wedge \tau _b^ + ,Y({e_q}) = 0) = q{{W(0){W^{(q)}}(d)} \over {{W^{(q)'}}(d)}}(1 - {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - {{{W^{(q)'}}(d)} \over {{W^{(q)}}(d)}}b}}).$$
It follows that
$${\mathbb{P}}(Y({e_q}) = 0,{e_q} \lt \kappa _d^ + ) = qW(0){{{W^{(q)}}(d)} \over {{W^{(q)'}}(d)}},$$
which gives the time Y spent at 0 before 
$$\kappa _d^ + $$ and coincides with [Reference Pistorius13, Theorem 1(ii)].
5. Proofs of the main results
This section is dedicated to the proofs for our main results, where we make use of the excursion theory for Markov processes, and appeal to the compensation formula and the exponential formula for Poisson point processes; see for example [4, O.5]. To this end, we first restate the formula concerned in terms of excursions, and then apply the compensation formula. For this we use the following notations from [Reference Avram, Kyprianou and Pistorius1], [Reference Bertoin4, IV], and [Reference Pistorius14], and refer the readers to the book for a detailed discussion of the related excursion theory. Moreover, by the spatial homogeneity of X, we mainly focus on the cases under ℙ. More general results for ℙx can be derived by a shifting argument, as shown in the proof of Proposition 3.1.
Recall that 
$$\bar X$$ is the running maximum process of X and let 
$$Y{\kern 1pt} : = {\kern 1pt} \bar X - X$$ be the reflected process. It is known that Y is a ‘nice’ Markov process with 0 being instantaneous whenever W(0) = 0. Let ℒ ≔ {t > 0, Yt = 0} be the zero set of Y and let 
$$\overline {\cal L} $$ be its closure. A local time process L of Y at 0 is a continuous process that increases only on 
$$\overline {\cal L} $$ and is unique up to a multiplicative factor. Thus, there exists ν ≥ 0 such that
$$\int_0^t {{\bf{1}}_{\{ s \in {\cal L}\} }}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} s = \nu L(t)\quad {\rm{for \ all}} \ t \ge 0$$
(see [Reference Bertoin4, Corollary IV.6]). The right inverse of L is defined by
$$L_t^{ - 1}{\kern 1pt} : = {\kern 1pt} \inf \{ s \gt 0:L(s) \gt t\} ,\quad \quad t \ge 0.$$
Under the new time scale, the excursion process of Y away from zero, associated with L and denoted by ϵ ≡ {ϵ r, r ≥ 0}, takes values in the so-called excursion space of paths away from 0 with an additional isolated point λ, ℰ ∪ {λ }, and is defined by
$${\epsilon_r}{\kern 1pt} : = {\kern 1pt} \{ {Y_t},L_{r - }^{ - 1} \le t \lt L_r^{ - 1}\} \quad {\rm{if }}L_{r - }^{ - 1} \lt L_r^{ - 1},$$
and ϵr ≔ λ otherwise. The excursion process ϵ is a Poisson point process, possibly stopped at time L(∞) with an excursion of infinite lifetime, characterized by a σ-finite measure n(·) on ℰ. Set 
$${(\overline {\cal L} )^c}$$ consists of countable excursion intervals, and ℒ differs from 
$$\overline {\cal L} $$ by at most countable points. In particular,
$$\int_0^{L_r^{ - 1}} {{\bf{1}}_{\{ s \in \overline {\cal L} \} }}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} s = \nu r$$
on 
$$\{ L_r^{ - 1} \lt \infty \} $$ under ℙ (see [Reference Bertoin4, Lemma VI.8]). For a Borel function f ≥ 0 on ℰ {γ } with f (γ ) = 0, we write
$$n(f){\kern 1pt} : = {\kern 1pt} \int_{\cal E} f({\cal E} )n({\kern 1pt} \;{\rm{d}}{\kern 1pt} {\cal E} ).$$
For any c ≥ 0, n (c) denotes the associated excursion measure for X under ℙ(c).
For an SNLP X under ℙ, its running maximum process 
$$\bar X$$ fulfils the condition of a local time and is chosen to be the local time of Y at 0 (see [Reference Bertoin4, VII]). For this choice of local time L,
$$L(t) = \mathop {\sup }\limits_{s \in [0,t]} {X_s},$$
and 
$$L_s^{ - 1} = \tau _s^ + $$ is a subordinator with Laplace exponent Φ. Since ν is the drift parameter of L −1 (see [Reference Bertoin4, Theorem IV.8]), we have
$$\nu = \mathop {\lim }\limits_{s \to \infty } {{\Phi (s)} \over s} = \mathop {\lim }\limits_{s \to \infty } {s \over {\psi (s)}} = W(0).$$
For an excursion ɛ ∈ ℰ, its lifetime is denoted by ζ and its excursion height is denoted by 
$$\overline \varepsilon $$. The first passage and the first hitting time of ε are defined by
$$\rho _c^ + {\kern 1pt} : = {\kern 1pt} \inf \{ s \in (0,\zeta ):\varepsilon (s) \gt c\} \quad {\rm{and}}\quad {\rho ^{\{ c\} }}{\kern 1pt} : = {\kern 1pt} \inf \{ s \in (0,\zeta ):\varepsilon (s) = c\} $$
respectively, with the convention that inf Ø = ∞. We write 
$$\rho _c^ + (r)$$, ρ {c}(r) and ζ (r) for the first passage time, the first hitting time and the lifetime, respectively, of the excursion at local time r, that is, ϵr = ε ∈ ℰ. As before, we let eq denote an exponential variable with parameter q > 0 and independent of X.
Proof of Proposition 3.1. Observe from their definitions that under ℙ,
on the event
$$\{ \tau _b^ + \lt \infty \} $$,
$$\tau _b^ + = L_b^{ - 1} = \int_0^{L_b^{ - 1}} {{\bf{1}}_{\{ t \in \overline {\cal L} \} }}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} t + \int_0^{L_b^{ - 1}} {{\bf{1}}_{\{ t \notin \overline {\cal L} \} }}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} t = \nu b + \sum\limits_{r \in [0,b]} \zeta (r);$$
on the event {τζ < ∞},
$${\tau _\xi } = L_{r - }^{ - 1} + \rho _{\bar \xi (r)}^ + (r)$$ and $$\bar X({\tau _\xi }) = r$$ for r = L(τξ );on the event {τ {ξ} < ∞},
$${\tau ^{\{ \xi \} }} = L_{r - }^{ - 1} + {\rho ^{\{ \bar \xi (r)\} }}(r)$$ and $$\bar X({\tau _\xi }) = r$$ for r = L(τ {ξ}).
From the idea in the proof of [Reference Bertoin4, Theorem VII.8], it holds that
$$\{ \tau _b^ + \lt {\tau _\xi }\} = \{ {\bar \epsilon _r} \le \bar \xi (r)\;{\rm{for}}\,{\rm{all}}\,r \in [0,b]\} .$$
Therefore, using the exponential compensation formula (see [Reference Bertoin4, O.5]), we obtain
$$\matrix{
{{\mathbb{E}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\tau _b^ + }}:\tau _b^ + \lt {\tau _\xi })} \hfill & = \hfill & {{\rm{e}}{{\kern 1pt} ^{ - q\nu b}} \times {\mathbb{E}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\sum\limits_{r \in [0,b]} \zeta (r)}}\prod\limits_{r \in [0,b]} {{\bf{1}}_{\{ {{\bar \epsilon }_r} \le \bar \xi (r)\} }})} \hfill \cr
{} \hfill & = \hfill & {{\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\nu b}} \times {\mathbb{E}}(\exp ( - \sum\limits_{r \in [0,b]} (q\zeta (r) + \infty \cdot {{\bf{1}}_{\{ {{\bar \epsilon }_r} \gt \bar \xi (r)\} }})))} \hfill \cr
{} \hfill & = \hfill & {\exp ( - \int_0^b (q\nu + \int_{\cal E} (1 - {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\zeta }}{{\bf{1}}_{\{ \overline \epsilon \le \bar \xi (r)\} }})n({\kern 1pt} \;{\rm{d}}{\kern 1pt} \varepsilon )){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} r),} \hfill \cr
} $$
with the understanding that e−∞ = 0 and ∞ × 0 = 0. To solve the problem, we recall the classical case of constant ξ ≡ c < 0 in Lemma 2.1:
$$\matrix{
{{{{W^{(q)}}( - c)} \over {{W^{(q)}}(b - c)}}} \hfill & = \hfill & {{\mathbb{E}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\tau _b^ + }}:\tau _b^ + \lt \tau _c^ - )} \hfill \cr
{} \hfill & = \hfill & {\exp ( - \int_0^b (q\nu + \int_{\cal E} (1 - {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\zeta }}{{\bf{1}}_{\{ \overline \varepsilon \le (r - c)\} }})n({\kern 1pt} \;{\rm{d}}{\kern 1pt} \varepsilon )){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} r).} \hfill \cr
} $$
Differentiating in b on both sides of the equation above gives
$$q\nu + \int_{\cal E} (1 - {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\zeta }}{{\bf{1}}_{\{ \overline \varepsilon \le z\} }})n({\kern 1pt} \;{\rm{d}}{\kern 1pt} \varepsilon ) = {{{W^{(q)'}}(z)} \over {{W^{(q)}}(z)}}\quad {\rm{for}} \, z \gt 0.$$
Applying the formula (5.3) to the previous equation (5.2) gives identity (3.1) under ℙ.
For the event 
$$\{ {\tau _\xi } \lt \tau _b^ + \} $$ and for p = u − ψ(v) > 0, taking a change of measure we have
$$\matrix{
{{\mathbb{E}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - u{\tau _\xi } + vX({\tau _\xi }) + k\bar X({\tau _\xi })}}:{\tau _\xi } \lt \tau _b^ + )} \hfill \cr
{\quad \quad = {{\mathbb{E}}^{(v)}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - p{\tau _\xi } + k\bar X({\tau _\xi })}}:{\tau _\xi } \lt \tau _b^ + )} \hfill \cr
{\quad \quad = {{\mathbb{E}}^{(v)}}(\sum\limits_{r \in [0,b]} ({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{kr - pL_{r - }^{ - 1}}}\prod\limits_{s \lt r} {{\bf{1}}_{\{ {{\overline \epsilon }_s} \le \bar \xi (s)\} }}) \times {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - p\rho _{\bar \xi (r)}^ + (r)}}{{\bf{1}}_{\{ {{\bar \epsilon }_r} \gt \bar \xi (r)\} }})} \hfill \cr
{\quad \quad = \int_0^b {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{kr}}{{\mathbb{E}}^{(v)}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - pL_{r - }^{ - 1}}}\prod\limits_{s \lt r} {{\bf{1}}_{\{ {{\overline \epsilon }_s} \le \bar \xi (s)\} }}) \times {n^{(v)}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - p\rho _{\bar \xi (r)}^ + }}:\overline \varepsilon \gt \bar \xi (r)){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} r} \hfill \cr
{\quad \quad = \int_0^b {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{kr}}{{\mathbb{E}}^{(v)}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - pL_r^{ - 1}}}:L_r^{ - 1} \lt {\tau _\xi }) \times {n^{(v)}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - p\rho _{\bar \xi (r)}^ + }}:\overline \varepsilon \gt \bar \xi (r)){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} r,} \hfill \cr
} $$
where a compensation formula is applied for the third equality (see e.g. [Reference Bertoin4, O.5]) and where we used the fact that 
$$L_t^{ - 1} \ne L_{t - }^{ - 1}$$ for at most countably many values of t.
Considering now the case where ξ ≡ c < 0, u = q > 0 and v = k = 0, we have
$$\matrix{
{{Z^{(q)}}( - c) - {{{W^{(q)}}( - c)} \over {{W^{(q)}}(b - c)}}{Z^{(q)}}(b - c)} \hfill \cr
{\quad \quad = {\mathbb{E}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\tau _c^ - }}:\tau _c^ - \lt \tau _b^ + )} \hfill \cr
{\quad \quad = \int_0^b {\mathbb{E}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\tau _r^ + }}:\tau _r^ + \lt \tau _c^ - ) \times n({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\rho _{r - c}^ + }}:\overline \varepsilon \gt (r - c)){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} r} \hfill \cr
{\quad \quad = \int_0^b {{{W^{(q)}}( - c)} \over {{W^{(q)}}(r - c)}} \times n({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\rho _{r - c}^ + }}:\overline \varepsilon \gt (r - c)){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} r.} \hfill \cr
} $$
Differentiating in b on both sides of the above equation gives
$$n({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\rho _z^ + }}:\overline \varepsilon \gt z) = {{{W^{(q)'}}(z)} \over {{W^{(q)}}(z)}}{Z^{(q)}}(z) - q{W^{(q)}}(z)\quad {\rm{for}} \ z \gt 0.$$
Plugging (3.1) and (5.4) into the equation gives the formula (3.2) under ℙ. The general result for u, v > 0 and k ∈ ℝ follows by an analytic extension.
To consider the general case of X(0) = x with x < b, we introduce a function ζ(y)≔ ξ(y + x) − x. Then
$$\bar \varsigma (y) = y + x - \xi (y + x) = \bar \xi (y + x).$$
Since X is spatially homogeneous, we have
$$(X,\bar X,{\tau _\xi }{)|_{\mathbb{P}_x}} = (x + X,x + \bar X,{\tau _\varsigma }{)|_{\mathbb{P}}}.$$
Therefore,
$$\matrix{
{{{\mathbb{E}}_x}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\tau _b^ + }}:\tau _b^ + \lt {\tau _\xi })} \hfill & = \hfill & {{\mathbb{E}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\tau _{b - x}^ + }}:\tau _{b - x}^ + \lt {\tau _\varsigma })} \hfill \cr
{} \hfill & = \hfill & {\exp ( - \int_0^{b - x} {{{W^{(q)'}}(\bar \varsigma (y))} \over {{W^{(q)}}(\bar \varsigma (y))}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y)} \hfill \cr
{} \hfill & = \hfill & {\exp ( - \int_x^b {{{W^{(q)'}}(\bar \xi (y))} \over {{W^{(q)}}(\bar \xi (y))}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y),} \hfill \cr
} $$
which gives (3.1). Similarly, we have from the spatial homogeneity of X that
$$\matrix{
{{{\mathbb{E}}_x}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - u{\tau _\xi } + vX({\tau _\xi }) + k\bar X({\tau _\xi })}}:{\tau _\xi } \lt \tau _b^ + )} \hfill \cr
{\quad \quad = {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{vx + kx}}{\mathbb{E}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - u{\tau _\varsigma } + vX({\tau _\varsigma }) + k\bar X({\tau _\varsigma })}}:{\tau _\varsigma } \lt \tau _{b - x}^ + )} \hfill \cr
{\quad \quad = {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{vx + kx}}\int_0^{b - x} {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ky - \int_0^y {{W_v^{(p)'}(\bar \varsigma (z))} \over {W_v^{(p)}(\bar \varsigma (z))}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} z}}({{W_v^{(p)'}(\bar \varsigma (y))} \over {W_v^{(p)}(\bar \varsigma (y))}}Z_v^{(p)}(\bar \varsigma (y)) - pW_v^{(p)}(\bar \varsigma (y))){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y} \hfill \cr
{\quad \quad = {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{vx}}\int_x^b {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ky - \int_x^y {{W_v^{(p)'}(\bar \xi (z))} \over {W_v^{(p)}(\bar \xi (z))}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} z}}({{W_v^{(p)'}(\bar \xi (y))} \over {W_v^{(p)}(\bar \xi (y))}}Z_v^{(p)}(\bar \xi (y)) - pW_v^{(p)}(\bar \xi (y))){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y.} \hfill \cr
} $$
This concludes the proof of Proposition 3.1.☐
In the following proofs, we use an idea from [Reference Bertoin4, Lemma VI.8] and the compensation formula, and we only focus on the case under ℙ and for b > 0.
Proof of Proposition 3.2. Let f ≥ 0 be a bounded and continuous function on ℝ. For the resolvent of X killed at 
$$\tau _b^ + \wedge {\tau _\xi }$$, which is defined in (3.3), we have
$$\matrix{
{\int_0^\infty {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - qt}}{\mathbb{E}}(f({X_t}):t \lt \tau _b^ + \wedge {\tau _\xi }){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} t} \hfill \cr
{\quad \quad = \int_0^\infty {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - qt}}{\mathbb{E}}(f({X_t}),t \in \overline {\cal L} ,t \lt \tau _b^ + \wedge {\tau _\xi }){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} t + \int_0^\infty {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - qt}}{\mathbb{E}}(f({X_t}),t \notin \overline {\cal L} ,t \lt \tau _b^ + \wedge {\tau _\xi }){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} t} \hfill \cr
{\quad \quad = :{I_1} + {I_2}.} \hfill \cr
} $$
Recalling equation (5.1), applying Fubini’s theorem and a change of variable, we have
$$\matrix{
{{I_1}} \hfill & = \hfill & {\nu {\mathbb{E}}(\int_0^\infty {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - qt}}f({X_t}){{\bf{1}}_{\{ t \lt \tau _b^ + \wedge {\tau _\xi }\} }}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} {L_t})} \hfill \cr
{} \hfill & = \hfill & {\nu {\mathbb{E}}(\int_0^\infty {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - qL_r^{ - 1}}}f(X(L_r^{ - 1})){{\bf{1}}_{\{ L_r^{ - 1} \lt \tau _b^ + \wedge {\tau _\xi }\} }}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} r)} \hfill \cr
{} \hfill & = \hfill & {\nu \int_0^b f(r){\mathbb{E}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - qL_r^{ - 1}}}:L_r^{ - 1} \lt {\tau _\xi }){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} r,} \hfill \cr
} $$
where 
$$L_r^{ - 1} = \tau _r^ + $$ and 
$$X(L_r^{ - 1}) = r$$ on event 
$$\{ L_r^{ - 1} \lt \infty \} $$. On the other hand, we have
$$\matrix{
{q{I_2}} \hfill & = \hfill & {{\mathbb{E}}(f({X_{{e_q}}}):{e_q} \notin \overline {\cal L} ,{e_q} \lt \tau _b^ + \wedge {\tau _\xi })} \hfill \cr
{} \hfill & = \hfill & {{\mathbb{E}}(\sum\limits_{r \in [0,b]} f(r - {\epsilon _r}({e_q} - L_{r - }^{ - 1})) \times \prod\limits_{s \lt r} {{\bf{1}}_{\{ {{\overline \epsilon }_s} \le \bar \xi (s)\} }}{{\bf{1}}_{\{ {e_q} \lt L_{r - }^{ - 1} + \rho _{\bar \xi (r)}^ + (r)\} }}:L_{r - }^{ - 1} \lt {e_q} \lt L_r^{ - 1}),} \hfill \cr
} $$
where 
$${\bar X_{{e_q}}} = L({e_q}) = r$$ on the event 
$$\{ L_{r - }^{ - 1} \lt {e_q} \lt L_r^{ - 1}\} $$. By the memoryless property of eq and the compensation formula, we further have
$$\matrix{
{q{I_2}} \hfill & = \hfill & {{\mathbb{E}}(\sum\limits_{r \in [0,b]} {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - qL_{r - }^{ - 1}}}\prod\limits_{s \lt r} {{\bf{1}}_{\{ {{\overline \epsilon }_s} \le \bar \xi (s)\} }} \times f(r - {\epsilon _r}({e_q})){{\bf{1}}_{\{ {e_q} \lt \rho _{\bar \xi (r)}^ + (r) \wedge \zeta (r)\} }})} \hfill \cr
{} \hfill & = \hfill & {\int_0^b {\mathbb{E}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - qL_r^{ - 1}}}:L_r^{ - 1} \lt {\tau _\xi }) \times q\int_0^\infty n({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - qs}}f(r - \varepsilon (s)):s \lt \rho _{\bar \xi (r)}^ + \wedge \zeta ){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} s{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} r.} \hfill \cr
} $$
Putting these together gives
$$\matrix{
{\int_0^\infty {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - qt}}{\mathbb{E}}(f({X_t}):t \lt \tau _b^ + \wedge {\tau _\xi }){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} t} \hfill \cr
{\quad \quad = \int_0^b {\mathbb{E}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\tau _r^ + }}:\tau _r^ + \lt {\tau _\xi }) \times (\nu f(r) + \int_0^\infty {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - qs}}n(f(r - \varepsilon (s)):s \lt \rho _{\bar \xi (r)}^ + \wedge \zeta ){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} s){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} r.} \hfill \cr
} $$
For the case of ξ ≡ c < 0, we have
$$\matrix{
{\int_0^\infty {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - qt}}{\mathbb{E}}(f({X_t}):t \lt \tau _b^ + \wedge \tau _c^ - ){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} t} \hfill \cr
{\quad \quad = \int_0^b {{{W^{(q)}}( - c)} \over {{W^{(q)}}(r - c)}}(\nu f(r) + \int_0^\infty {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - qs}}n(f(r - \varepsilon (s)):s \lt \rho _{r - c}^ + \wedge \zeta ){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} s){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} r} \hfill \cr
{\quad \quad = \int_c^b f(y)({{{W^{(q)}}( - c)} \over {{W^{(q)}}(b - c)}}{W^{(q)}}(b - y) - {W^{(q)}}( - y)){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y.} \hfill \cr
} $$
Further differentiating in b on the above equation, we eventually have
$$\matrix{
{\nu f(b) + \int_0^\infty {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - qs}}n(f(b - \varepsilon (s)):s \lt \rho _{b - c}^ + \wedge \zeta ){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} s} \hfill \cr
{\quad \quad = W(0)f(b) + \int_c^b f(y)({W^{(q)'}}(b - y) - {{{W^{(q)'}}(b - c)} \over {{W^{(q)}}(b - c)}}{W^{(q)}}(b - y)){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y.} \hfill \cr
} $$
Since ν = W(0), formula (3.3) is thus proved for x = 0.☐
Proof of Proposition 3.3. As in the proofs of Propositions 3.1 and 3.2, for the event of creeping 
$$\{ {\tau ^{\{ \xi \} }} = {\tau _\xi } \lt \tau _b^ + \wedge {\tau _\theta }\} $$, i.e. the event that the draw-down event happens before X leaves interval 
$$[\theta (\bar X),b]$$ by hitting the draw-down level 
$$\xi (\bar X)$$, we have
$$\matrix{
{{\mathbb{E}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q{\tau _\xi }}}:{\tau ^{\{ \xi \} }} = {\tau _\xi } \lt \tau _b^ + \wedge {\tau _\theta })} \hfill \cr
{\quad \quad = {\mathbb{E}}(\sum\limits_{r \in [0,b]} ({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - qL_{r - }^{ - 1}}}\prod\limits_{s \lt r} {{\bf{1}}_{\{ {{\overline \epsilon }_s} \le \bar \theta (s)\} }}{{\bf{1}}_{\{ {{\overline \epsilon }_s} \le \bar \xi (s)\} }}) \times ({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\rho _{\bar \xi (r)}^ + (r)}}{{\bf{1}}_{\{ {\epsilon _r}(\rho _{\bar \xi (r)}^ + ) = \bar \xi (r)\} }}{{\bf{1}}_{\{ \bar \xi (r) \lt \bar \theta (r)\} }}))} \hfill \cr
{\quad \quad = \int_0^b {\mathbb{E}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - qL_r^{ - 1}}}:L_r^{ - 1} \lt {\tau _{\xi \vee \theta }}) \times n({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\rho _{\bar \xi (r)}^ + }}:\varepsilon (\rho _{\bar \xi (r)}^ + ) = \bar \xi (r)) \times {{\bf{1}}_{\{ r \in I\} }}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} r.} \hfill \cr
} $$
For the case of ξ(z) = θ(z) + 1 ≡ c, we have I = ℝ and 
$$\{ {\tau _\xi } \le \tau _b^ + \wedge {\tau _\theta }\} = \{ \tau _c^ - \le \tau _b^ + \} $$. Since
$$\matrix{
{{\mathbb{E}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\tau _c^ - }}:X(\tau _c^ - ) = c,\tau _c^ - \lt \tau _b^ + )} \hfill & = \hfill & {{{{\sigma ^2}} \over 2}({W^{(q)'}}( - c) - {W^{(q)}}( - c){{{W^{(q)'}}(b - c)} \over {{W^{(q)}}(b - c)}})} \hfill \cr
{} \hfill & = \hfill & {\int_0^b {{{W^{(q)}}( - c)} \over {{W^{(q)}}(r - c)}} \times n({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\rho _{r - c}^ + }}:\varepsilon (\rho _{r - c}^ + ) = r - c){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} r,} \hfill \cr
} $$
differentiating on both sides of the equation above, we have
$$n({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\rho _z^ + }}:\varepsilon (\rho _z^ + ) = z) = {{{\sigma ^2}} \over 2}({{{{({W^{(q)'}}(z))}^2}} \over {{W^{(q)}}(z)}} - {W^{(q)''}}(z))\quad {\rm{for}} \ z \gt 0.$$
Identity (3.4) is thus proved by applying (3.1) for x = 0.
The hitting of a maximum dependent level cannot be derived by applying the strong Markov property of X as in the classical case in Lemma 2.2. However, due to the absence of positive jumps, a similar observation is that
$$\{ L_s^{ - 1} \lt {\tau ^{\{ \xi \} }} \wedge {\tau _\theta }\} = \{ L_s^{ - 1} \lt {\tau _\xi } \wedge {\tau _\theta }\} \quad {\rm{on \ the \ event}} \{L_s^-1 \lt \infty \} ,$$
that is, every excursion at time 
$$s \lt r = L({\tau ^{\{ \xi \} }})$$ fails to go above level 
$$\overline {\xi \vee \theta } (s)$$. Therefore,
$$\matrix{
{{\mathbb{E}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q{\tau ^{\{ \xi \} }}}}:{\tau ^{\{ \xi \} }} \lt \tau _b^ + \wedge {\tau _\theta })} \hfill \cr
{\quad \quad = {\mathbb{E}}(\sum\limits_{r \in [0,b]} ({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - qL_{r - }^{ - 1}}}\prod\limits_{s \lt r} {{\bf{1}}_{\{ {{\overline \epsilon }_s} \le \bar \xi (s)\} }}{{\bf{1}}_{\{ {{\overline \epsilon }_s} \le \bar \theta (s)\} }}) \times ({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q{\rho ^{\{ \bar \xi (r)\} }}(r)}}{{\bf{1}}_{\{ {\rho ^{\{ \bar \xi (r)\} }}(r) \lt \rho _{\bar \theta (r)}^ + (r)\} }}))} \hfill \cr
{\quad \quad = \int_0^b {\mathbb{E}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - qL_r^{ - 1}}}:L_r^{ - 1} \le {\tau _{\xi \vee \theta }}) \times n({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q{\rho ^{\{ \bar \xi (r)\} }}}}:{\rho ^{\{ \bar \xi (r)\} }} \lt \rho _{\bar \theta (r)}^ + ){{\bf{1}}_{\{ \bar \xi (r) \lt \bar \theta (r)\} }}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} r.} \hfill \cr
} $$
For the case of ξ ≡ a and θ ≡ c with c < a < 0 < b, we have
$$\matrix{
{{{{W^{(q)}}( - c)} \over {{W^{(q)}}(a - c)}} - {{{W^{(q)}}( - a){W^{(q)}}(b - c)} \over {{W^{(q)}}(b - a){W^{(q)}}(a - c)}}} \hfill \cr
{\quad \quad = {\mathbb{E}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q{\tau ^{\{ a\} }}}}:{\tau ^{\{ a\} }} \lt \tau _b^ + \wedge \tau _c^ - )} \hfill \cr
{\quad \quad = \int_0^b {\mathbb{E}}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q\tau _r^ + }}:\tau _r^ + \lt \tau _a^ - ) \times n({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q{\rho ^{\{ r - a\} }}}}:{\rho ^{\{ r - a\} }} \lt \rho _{r - c}^ + ){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} r.} \hfill \cr
} $$
Differentiating in b on both sides of the above equation gives, for b > a > c,
$$n({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q{\rho ^{\{ b - a\} }}}}:{\rho ^{\{ b - a\} }} \lt \rho _{b - c}^ + ) = {{{W^{(q)}}(b - c)} \over {{W^{(q)}}(a - c)}}({{{W^{(q)'}}(b - a)} \over {{W^{(q)}}(b - a)}} - {{{W^{(q)'}}(b - c)} \over {{W^{(q)}}(b - c)}}),$$
which leads to identity (3.5).☐
Remark 5.1. We remark that the excursion theory for a (reflected) SNLP has been employed to solve several similar problems. The formulas (5.4), (5.5), (5.6), (5.3)for q = 0 and (5.7) for b − c = ∞ have also been found as well; see [Reference Pistorius14] for a collection of such results.
Proof of Corollary 3.1. Since 
$$\{ t \lt \tau _b^ + \} = \{ {\bar X_t} \lt b\} $$ and 
$$\{ t \lt \tau _c^ - \} = \{ {\underline X _t} \gt c\} $$ for every t > 0, we have by Proposition 3.2 that, for z > x ≥ c and ξ(z) ∨ c < y ≤ z,
$$\matrix{
{\int_0^\infty {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - qt}}{{\mathbb{P}}_x}({X_t} \in {\kern 1pt} \;{\rm{d}}{\kern 1pt} y,{{\bar X}_t} \in {\kern 1pt} \;{\rm{d}}{\kern 1pt} z,t \lt {\tau _\xi },{{\underline X }_t} \ge c){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} t} \hfill \cr
{\quad \quad = \int_0^\infty {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - qt}}{{\mathbb{P}}_x}({X_t} \in {\kern 1pt} \;{\rm{d}}{\kern 1pt} y,{{\bar X}_t} \in {\kern 1pt} \;{\rm{d}}{\kern 1pt} z,t \lt {\tau _{\xi \vee c}}){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} t} \hfill \cr
{\quad \quad = ({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - \int_x^z {{{W^{(q)'}}(\overline {\xi \vee c} (s))} \over {{W^{(q)}}(\overline {\xi \vee c} (s))}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} s}}{W^{(q)'}}(z - y) - {{{W^{(q)'}}(\overline {\xi \vee c} (z))} \over {{W^{(q)}}(\overline {\xi \vee c} (z))}}{W^{(q)}}(z - y)){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} z{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} y} \hfill \cr
{\quad \quad \quad {\kern 1pt} + W(0)({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - \int_x^z {{{W^{(q)'}}(\overline {\xi \vee c} (s))} \over {{W^{(q)}}(\overline {\xi \vee c} (s))}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} s}}){\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} z \cdot {\delta _z}({\kern 1pt} \;{\rm{d}}{\kern 1pt} y),} \hfill \cr
} $$
where δz denotes the Dirac measure concentrated at z. Note that τξ ∈{t > 0, Xt − ≠ Xt} on the event 
$$\{ {X_{{\tau _\xi }}} \ne {X_{{\tau _\xi } - }}\} \cap \{ {\tau _\xi } \lt \infty \} $$, and process {(Xt − X t−), t ≥ 0} can be identified as a Poisson point process with characteristic measure Π (·). Therefore, for f ≥ 0 satisfying f (z, z) = 0, we have by Fubini’s theorem
$$\matrix{
{{{\mathbb{E}}_x}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q{\tau _\xi }}}f({X_{{\tau _\xi } - }},{X_{{\tau _\xi }}}):{{\underline X }_{{\tau _\xi } - }} \ge c,{{\bar X}_{{\tau _\xi }}} \le b)} \hfill \cr
{\quad \quad = {{\mathbb{E}}_x}({\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - q{\tau _\xi }}}f({X_{{\tau _\xi } - }},{X_{{\tau _\xi }}}):{X_{{\tau _\xi }}} \ne {X_{{\tau _\xi } - }},{{\underline X }_{{\tau _\xi } - }} \ge c,{{\bar X}_{{\tau _\xi }}} \le b)} \hfill \cr
{\quad \quad = {{\mathbb{E}}_x}(\sum\limits_{\{ t:{X_{t - }} \ne {X_t}\} } {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - qt}}f({X_{t - }},{X_{t - }} + \Delta {X_t}){\bf{1}}({{\underline X }_{t - }} \ge c){\bf{1}}({{\bar X}_t} \le b)} \hfill \cr
{\quad \quad \quad \times {\bf{1}}(t \le {\tau _\xi }){\bf{1}}({X_{t - }} + \Delta {X_t} \lt \xi ({{\bar X}_t})))} \hfill \cr
{\quad \quad = \int_0^\infty {\kern 1pt} {\kern 1pt} \;{\rm{e}}{{\kern 1pt} ^{ - qt}}{\kern 1pt} {\kern 1pt} \;{\rm{d}}{\kern 1pt} t\int_x^b \int_c^z {{\mathbb{P}}_x}({X_{t - }} \in {\kern 1pt} \;{\rm{d}}{\kern 1pt} y,{{\bar X}_{t - }} \in {\kern 1pt} \;{\rm{d}}{\kern 1pt} z,t \lt {\tau _\xi },{{\underline X }_{t - }} \ge c)} \hfill \cr
{\quad \quad \quad {\kern 1pt} \times \int_{ - \infty }^{\xi (z) - y} f(y,y + u)\Pi ({\kern 1pt} \;{\rm{d}}{\kern 1pt} u),} \hfill \cr
} $$
where the compensation formula is applied for the last equation. The desired result then follows from the quasi-left-continuity for process X.
Acknowledgements
The authors are thankful to anonymous referees for careful reading and helpful comments and suggestions. Bo Li is supported by National Natural Science Foundation of China (no. 11601243). Bo Li, Nhat Linh Vu, and Xiaowen Zhou are supported by a National Sciences and Engineering Research Council of Canada grant (no. RGPIN-2016-06704). Xiaowen Zhou is supported by Natural Science Foundation of Hunan Province (no. 2017JJ2274)
