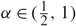1. Introduction
Consider a random walk 
$S_{n}=\sum_{i=1}^{n}X_{i}$ for n ≥ 1 and S 0 = 0, where {Xi : i ≥ 1} is a sequence of independent and identically distributed random variables with 
$\mathbb {E}[X_{1}]=0$ and var (X 1) < ∞. Without loss of generality, we shall also assume that var (X 1) = 1. Moreover, we shall impose the following light-tailed assumption on the distribution of the Xi.
Assumption 1. There exists δ > 0, such that 
$\mathbb {E}[\!\exp(\theta X_{1})]<\infty$ for all θ ∈ (−δ, δ).
In this paper we develop the first algorithm that generates perfect samples (i.e. samples without any bias) from the random variable
\begin{align*}
{M_\alpha } = \mathop {\max }\limits_{n \ge 0} \{ {S_n} - {n^\alpha }\},
\end{align*}
where 
$\alpha\in(\tfrac12,1)$. Moreover, we will show that our algorithm has finite expected running time.
There has been a substantial amount of work on exact sampling (i.e. sampling without any bias) from the distribution of the maximum of a negative drifted random walk, e.g. M 1 in our setting. Ensor and Glynn [Reference Ensor and Glynn6] proposed an algorithm to sample the maximum when the increments of the random walk are light tailed (i.e. Assumption 1 holds). Blanchet et al. [Reference Blanchet and Chen2] proposed an algorithm to simulate a multidimensional version of M 1 driven by Markov random walks. Blanchet and Wallwater [Reference Blanchet and Wallwater4] developed an algorithm to sample M 1 for the heavy-tailed case, which requires only that 
$\mathbb {E}[\vert X_{1}\vert ^{2+\varepsilon}]<\infty$ for some ε > 0 to guarantee finite expected termination time.
Some of this work was motivated by the fact that M 1 plays an important role in ruin theory and queueing models. For example, the steady-state waiting time of a GI/GI/1 queue has the same distribution as M 1, where Xi corresponds to the (centred) difference between the ith service time and the ith interarrival time (see [Reference Asmussen1]). Moreover, applying coupling from the past (CFTP) (see, for example, [Reference Propp and Wilson9] and [Reference Kendall8]), the techniques to sample M 1 jointly with the random walk {Sn : n ≥ 0} have been used to obtain perfect sampling algorithms for more general queueing systems, including multi-server queues [Reference Blanchet, Dong and Pei5], infinite-server queues, and loss networks [Reference Blanchet and Dong3], and multidimensional reflected Brownian motion with oblique reflection [Reference Blanchet and Chen2].
The fact that Mα stochastically dominates M 1 makes the development of a perfect sampler for Mα more difficult. For example, the direct use of exponential tilting techniques as in [Reference Ensor and Glynn6] is not applicable. However, similar to some of the previous work, the algorithmic development uses the idea of record-breakers (see, e.g. [Reference Blanchet and Dong3]) and randomization procedures similar to the heavy-tailed context studied in [Reference Blanchet and Wallwater4].
The techniques that we study here can be easily extended, using the techniques studied in [Reference Blanchet and Chen2], to obtain exact samplers of a multidimensional analogue of Mα driven by Markov random walks (as done in [Reference Blanchet and Chen2] for the case α = 1). Moreover, using the domination technique introduced in Section 5 of [Reference Blanchet, Dong and Pei5], the algorithms that we present here can be applied to the case in which the term nα is replaced by g(n) as long as there exists n 0 > 0 such that g(n) ≥ nα for all n ≥ n 0.
We mentioned earlier that algorithms which simulate M 1 jointly with {Sn : n ≥ 0} have been used in applications of CFTP. Since the random variable Mα dominates M 1, and we also simulate Mα jointly with {Sn : n ≥ 0}, we expect our results here to be applicable to perfect sampling (using CFTP) for a wide range of processes. In this paper, we will show how to use the ability to simulate Mα jointly with {Sn : n ≥ 0} to obtain the first algorithm which samples from the steady-state departure process of an infinite-server queue in which the job requirements have infinite mean; the case of finite mean service/job requirements is treated in [Reference Blanchet and Dong3].
The rest of the paper is organized as follows. In Section 2 we discuss our sampling strategy. Then we provide a detailed running time analysis in Section 3. Finally, the application to exact simulation of the steady-state departure process of an infinite-server queue with infinite mean service time is given in Section 4.
2. Sampling strategy and main algorithmic development
Our goal is to simulate Mα using a finite but random number of Xi. To achieve this goal, we introduce the idea of record breakers.
Let 
$\psi(\theta)\,:\!=\log \mathbb {E}[\!\exp(\theta X_{i})]$. As 
$\psi(\theta)=\frac{1}{2}\theta^{2}+ o(\theta^{2})$ by Taylor’s expansion, there exists δ′ < δ such that ψ(θ) ≤ θ 2 for θ ∈ (−δ′, δ′). Let
\begin{align}
a \in \Big(0 , \min\Big\{ 4\delta^{\prime},\frac{1}{2}\Big\} \Big)
\quad \mbox{and} \quad b=\frac{4}{a}\log\bigg(4\bigg( \sum_{n=0}^{\infty}2^{n}
\exp({-}a^{2} 2^{2n\alpha-n-4}\bigg) \bigg).
\end{align}
These choices of a and b will become clear in the proof of Lemma 1. We define a sequence of record-breaking times as T 0 := 0. For k = 1, 2, …, if Tk −1 < ∞,
\begin{align*}
{T_k}{\kern 1pt} : = \inf \{ n > {T_{k - 1}}:{S_n} > {S_{{T_{k - 1}}}} + a{(n - {T_{k - 1}})^\alpha } + b{(n - {T_{k - 1}})^{1 - \alpha }}\} ;
\end{align*}
otherwise if Tk −1 = ∞ then Tk = ∞. We also define
\begin{align*}
\kappa\,:\!=\inf\{k>0\colon T_{k}=\infty\}.
\end{align*}
Because the random walk has independent increments, ℙ(Ti = ∞ | Ti −1 < ∞) = ℙ(T 1 = ∞). Thus, κ is a geometric random variable with probability of success
\begin{align*}
\mathbb {P}(T_{1}=\infty).
\end{align*}
We first show that κ is well defined.
Lemma 1. For a and b satisfying (1),
\begin{align*}
\mathbb {P}(T_{1}=\infty) \geq\tfrac{3}{4}.
\end{align*}
Proof. We first note that
\begin{align*}
{\mathbb{P}}({T_1} < \infty ) = \sum\limits_{n = 0}^\infty {\mathbb{P}}(T \in {2^n}{,2^{n + 1}})) \le \sum\limits_{n = 0}^\infty \sum\limits_{k \in {2^n}{{,2}^{n + 1}})} {\mathbb{P}}({S_k} > a{k^\alpha } + b{k^{1 - \alpha }}).
\end{align*}
For any k ∈ [2n, 2n+1),
\begin{align*}
{\mathbb{P}}({S_k} > a{k^\alpha } + b{k^{1 - \alpha }}) \le \exp (k\psi (\theta ) - \theta (a{k^\alpha } + b{k^{1 - \alpha }}))\\
\le \exp {(2^{n + 1}}\psi (\theta ) - \theta a{2^{\alpha n}} - \theta b{2^{(1 - \alpha )n}})
\end{align*}
for any θ ∈ (−δ, δ). We define θn = a2(α−1)n−2. Since a < 4δ′, we have θn < δ′. Then
\begin{align*}
kP({S_k} > a{k^\alpha } + b{k^{1 - \alpha }}) \le \exp \,({2^{n + 1}}\theta _n^2 - {\theta _n}a{2^{\alpha n}} - {\theta _n}b{2^{(1 - \alpha )n}})\\
= \exp ( - {a^2}{2^{2n\alpha - n - 3}} - \frac{{ab}}{4}).
\end{align*}
Therefore,
\begin{align*}
\mathbb {P}(T_{1}<\infty)\leq\bigg(\sum_{n=0}^{\infty}2^{n}\exp({-}a^{2}\\
{}&2^{2n\alpha-n-3})\bigg) \exp\Big( -\frac{ab}{4}\Big) \leq\\[4pt]
{}&\frac{1}{4},\\[4pt]
\end{align*}
where the last inequality follows from our choice of b.
Let
\begin{align}
\label{eq:xi}\xi\,:\!= \max_{n \ge 0}\Big\{(an^{\alpha}+bn^{1-\alpha})
-\frac{1}{2}n^{\alpha} \Big\}.
\end{align}
As 
$a<\tfrac12$, ξ < ∞. Conditional on the value of κ and the values of {Xicolon1 ≤ i ≤ Tκ −1}, we define
\begin{align}
\label{eq:Gamma}
\Gamma(\kappa) \,:\!= \lceil (2S_{T_{\kappa-1}}+2\xi)^{1/\alpha} \rceil.
\end{align}
The choice of ξ will become clear in the proof of Lemma 2. We will next establish that
\begin{align*}
{M_\alpha } = \mathop {\max }\limits_{0 \le n \le {T_{\kappa - 1}} + \Gamma (\kappa )} \{ {S_n} - {n^\alpha }\}.
\end{align*}
Lemma 2. For n ≥ Tκ −1 + Г(κ),
\begin{align*}
S_{n} \leq n^{\alpha}.
\end{align*}
Proof. For ξ defined in (2), we have, for any n ≥ 0,
\begin{align*}
an^{\alpha}+bn^{1-\alpha}\leq\frac{1}{2}n^{\alpha}+\xi.
\end{align*}
Since Tκ = ∞, for n ≥ Г(κ),
\begin{align*}
{S_{{T_{\kappa - 1}} + n}} \le a{n^\alpha } + b{n^{1 - \alpha }} + {S_{{T_{\kappa - 1}}}} \le {1 \over 2}{n^\alpha } + \xi + {1 \over 2}\Gamma {(\kappa )^\alpha } - \xi \le {n^\alpha } \le {({T_{\kappa - 1}} + n)^\alpha }.
\end{align*}
Figure 1 demonstrates the basic idea of our algorithmic development. (Note that the figure is rescaled for illustrative purposes. In actual simulation, the record-breaking events happen with a very small probability.) The solid line is nα. The first dotted line from the left (lowest dashed curve) is the record-breaking boundary that we start with, anα + bn 1−α. T 1 is the first record-breaking time. Based on the value of S T 1, we construct a new record-breaking boundary, S T 1 + a(n − T 1)α + b(n − T 1)1−α (the second dashed line from the left). At time T 2, we have another record breaker. Based on the value of S T 2, we construct again a new record-breaking boundary, S T 2 + a(n − T 2)α + b(n − T 2)1−α (the third dashed line from the left). If, from T 2 on, we never break the record again (T 3 = ∞), then we know that, for large enough n (say, n > 100 in the figure), Sn will never pass the solid boundary again. Note that here we will need a < 1, which is guaranteed by (1), but a tighter constraint is imposed on a in (1) for algorithmic development and technical reasons related to Lemma 1 and 2.
Figure 1: Bounds for record breakers.
The actual simulation strategy goes as follows.
Algorithm 1. Sampling Г(κ) together with (Xi : 1 ≤ i ≤ Tκ −1 + Г(κ)).
(i) Initialize T 0 = 0, k = 1.
(ii) For Tk −1 < ∞, sample J ~ Bernoulli(ℙ(Tk = ∞ | Tk −1)).
(iii) If J = 0, sample (Xi : i = Tk −1 + 1, …, Tk) conditional on Tk < ∞. Set k = k + 1 and go back to step (ii); otherwise (J = 1), set κ = k and go to step (iv).
(iv) Calculate Г(κ), sample (Xi : i = Tk −1 + 1, …, Tk −1 + Г(κ)) conditional on Tk = ∞.
Remark 1. In general, any 
$a<\min\Big\{ 4\delta^{\prime},\dfrac{1}{2}\Big\}$, and
\begin{align*}
b\geq\frac{4}{a}\log\bigg(4\bigg(\sum_{n=0}^{\infty}2^{n}\exp({-}a^{2}
2^{2n\alpha-n-4})\bigg) \bigg)
\end{align*}
would work. However, there is a trade-off. The larger the values of a and b, the smaller the value of κ, but the value of Г(κ) would be larger. We conduct a numerical study on the choice of these parameters in Section 3.1.
In what follows, we shall elaborate on how to carry out steps (ii), (iii) and (iv) of Algorithm 1. In particular, steps (ii) and (iii) are outlined in Procedure A below. Step (iv) is outlined in Procedure B below.
2.1. Steps (ii) and (iii) in Algorithm 1
It turns out steps (ii) and (iii) can be carried out simultaneously using exponential tilting based on the results and proof of Lemma 1.
We start by explaining how to sample the first record-breaking time T 1. We introduce an auxiliary random variable N with probability mass function (PMF)
\begin{align}
p(n) = {\mathbb{P}}(N = n) = {{{2^n}\exp ( - {a^2}{2^{2n\alpha - n - 3}})} \over {\sum {_{m = 0}^\infty } {2^m}\exp ( - {a^2}{2^{2m\alpha - m - 3}})}}\quad {\kern 1pt} {\rm{for}}\;n \ge 1{\kern 1pt}.
\end{align}
We can then apply exponential tilting to sample the path (X 1, X 2 …, X T 1) conditional on T 1 < ∞.
When sampling the random walk, we use ℙ(·) to represent the measure induced by the original distribution of the random walk, which we refer to as the nominal distribution. We also denote ℙθ( ·) as the measure induced by the exponential tilting with tilting parameter θ. The actual sampling algorithm goes as follows.
Procedure A. Sampling a Bernoulli J with probability of success ℙ(J = 1) = ℙ(T 1 = ∞). If J = 0, output (X 1, …, X T 1).
(i) Sample a random time N with PMF (4).
(ii) Let θN = a2N(α−1)−2. Generate X 1, X 2, …, X 2N+1−1 under exponential tilting with tilting parameter θN, i.e.
\begin{align*}
{{{\rm d{\mathbb{P}}_{{\theta _N}}}} \over \rm d{\mathbb{P}}}1\{ {X_i} \in A\} = \exp ({\theta _N}{X_i} - \psi ({\theta _N}))1\{ {X_i} \in A\}.
\end{align*}
Let T 1 = inf{n ≥ 1: Sn > anα + bn 1−α} ^ 2N+1.
(iii) Sample U ~Uniform[0, 1]. If
\begin{align*}
U\leq\frac{\exp({-}\theta_{N} S_{T_{1}} + T_{1}\psi(\theta_{N}))}{p(N)}{\bf 1}\{
T_{1}\in[ 2^{N}, 2^{N+1}) \},
\end{align*}
then set J = 0 and output (X 1, X 2, …, X T 1); otherwise, set J = 1.
We next show that Procedure A works.
Theorem 1. In Procedure A, J is a Bernoulli random variable with probability of success ℙ(T 1 = ∞). If J = 0, the output (X 1, X 2, …, XT 1) follows the distribution of (X 1, X 2, …, XT 1) conditional on T 1 < ∞.
Proof. We first show that the likelihood ratio in step (iii) is less than 1 almost surely. Based on this, we will then prove that ℙ(J = 0) = ℙ(T 1 < ∞). That is,
\begin{align*}
\frac{\exp({-}\theta_{n} S_{T_{1}} + T_{1} \psi(\theta_{n}))}{\mathbb {P}(
N=n) } {\bf 1}\big\{T_{1}\in[2^{n}, 2^{n+1} )\big\}
\le \frac{\exp({-}\theta_{n} (a 2^{\alpha n}+b 2^{(1-\alpha)n})+ 2^{n+1}
\theta_{n}^{2}))}{\mathbb {P}(N=n)}
\\
= \frac{\exp({-}a^{2} 2^{2n\alpha-n -3}-ab/4 ) }{\mathbb {P}(N=n)}
\\
= 2^{-n} \exp\!\Big({-}\frac{ab}{4}\Big)\! \sum_{m=0}^{\infty}2^{m} \exp({-}a^{2}
2^{2m\alpha-m -3})
\\
\le \frac{1}{4},
\end{align*}
where the last inequality follows from our choice of b as in the proof of Lemma 1. We next prove that ℙ(J = 0) = ℙ(T 1 < ∞):
\begin{align*}
\mathbb {E}[{\bf 1}\{J=0\}|N=n] =\mathbb {E}_{\theta_{n}}\Big[ {\bf 1}\Big\{ U\leq\frac{\exp
({-}\theta_{n} S_{T_{1}} + T_{1}\psi(\theta_{n}))}{p(n)}\Big\} {\bf 1}\{T_{1}
\in[2^{n}, 2^{n-1})\}\Big]\\
= \mathbb {E}_{\theta_{n}}\Big[ \frac{\exp({-}\theta_{n} S_{T_{1}} + T_{1}\psi
(\theta_{n}))}{p(n)}{\bf 1}\{T_{1}\in[2^{n}, 2^{n+1})\}\Big] \\
=\frac{\mathbb {P}(T_{1}\in[2^{n}, 2^{n+1}))}{p(n)},
\end{align*}
where the second equation uses the result that the likelihood ratio is less than 1; the last equation follows from the observation that
\begin{align*}
\frac{\rm d \mathbb {P}}{\rm d \mathbb {P}_{\theta_n}}({\bf 1}\{T_{1}\in[2^{n}, 2^{n+1})\}) = \exp({-}\theta_{n} S_{T_{1}} + T_{1}\psi
(\theta_{n})){\bf 1}\{T_{1}\in[2^{n}, 2^{n+1})\}.
\end{align*}
Then we have
\begin{align*}
\mathbb {E}[{\bf 1}\{J=0\}] =\sum_{n=0}^{\infty}\mathbb {E}[{\bf 1}\{J=0\}\mid N=n]p(n)
= \sum_{n=0}^{\infty}\mathbb {P}(T_{1}\in[2^{n}, 2^{n+1}))=\mathbb {P}(T_{1}<\infty).
\end{align*}
Let ℙ*(·) denote the measure induced by Procedure A. We next show that ℙ*(X 1 ∈ A 1, …, Xt ∈ At | J = 0) = ℙ(X 1 ∈ A 1, …, Xt ∈ At|T 1 < ∞), where t is a positive integer, and Ai ⊂ ℝ, i = 1, 2, …, t, is a sequence of Borel measurable sets satisfying Ai ⊂ {x ∈ ℝ: x ≤ aiα + bi 1−α} for i < t and At ⊂ {x ∈ ℝ: x > atα + bt 1−α}. Let nt := ⌊log2⌋ t. Then
\begin{align*}
\mathbb {P}^{*}(X_{1} \in A_{1}, \ldots, X_{t} \in A_{t} \mid J=0 )\\
\qquad = \frac{\mathbb {P}^{*}(X_{1} \in A_{1}, \ldots, X_{t} \in A_{t} , J=0 )}{\mathbb {P}(J=0)}\\
\qquad = \frac{\mathbb {P}(N=n_{t})}{\mathbb {P}(T_{1}<\infty)}E_{\theta_{n_{t}}} \Big[ {\bf 1} \{
X_{1} \in A_{1}, \ldots, X_{t} \in A_{t} \} {\bf 1} \Big\{ U \leq\frac
{\exp({-}\theta_{n_{t}} S_{t}+t \psi(\theta_{n_{t}}))}{p(n_{t})} \Big\}
\Big] \\
\qquad = \frac{p(n_{t})}{\mathbb {P}(T_{1}<\infty)} \mathbb {E}_{\theta_{n_{t}}}\Big[{\bf 1} \{
X_{1} \in A_{1}, \ldots, X_{t} \in A_{t} \} \frac{\exp({-}\theta_{n_{t}}
S_{t}+t \psi(\theta_{n_{t}}))}{p(n_{t})} \Big] \\
\qquad = \frac{\mathbb {E}[ {\bf 1} \{ X_{1} \in A_{1}, \ldots, X_{t} \in A_{t}
\} ] }{\mathbb {P}(T_{1}<\infty)}\\
\qquad = \mathbb {P}(X_{1}\in A_{1}, \ldots, X_{t} \in A_{t} \mid T_{1}<\infty).\\
\end{align*}
The extension from T 1 to Tk is straightforward: for Tk −1 < ∞, given the value of Tk −1 and S T k−1, we essentially start the random walk afresh from S T k−1 for each Tk −1. Thus, to execute steps (ii) and (iii) of Algorithm 1, given Tk −1 < ∞, we can apply Procedure A. If J = 0, we denote (X̃ 1, X̃ 2, …, X̃T) as the output from Procedure A, and set (X T k−1+1, …, X T k−1+T) = (X̃ 1, …, X̃T) and Tk = Tk −1 + T; otherwise, set κ = k.
2.2. Step (iv) in Algorithm 1
Sampling (X 1, …, X T k−1) is realized by iteratively applying Procedure A until it outputs J = 1. Once we have found κ, we achieve sampling (X T k−1+1, …, X T k−1+Г(κ)) by developing a procedure that could sample (X T k−1+1, …, X T k−1+n) with any given n > 0, conditioning on the fact that the trajectory of the random walk never passes the nonlinear upper bound, S T k−1 + a(n − Tκ −1)α + b(n − Tκ −1)1−α. To be more precise, given κ = k, for any n > 0 (including n = Г(κ)), we would like to sample (X T k−1+1, …, X T k−1+n) from 
$\mathbb {P}({\cdot}\!\mid \mathcal{F}_{k-1}, T_{k}=\infty)$, where 
$\{\mathcal{F}_{k}\colon k \geq0\}$ denote the filtration generated by the random walk. We can achieve this conditional sampling using the acceptance–rejection technique.
We first introduce a method to simulate a Bernoulli random variable with probability of success ℙ(T 1 = ∞ | T 1 > t, St), which follows a similar exponential tilting idea as that used in Section 2.1. In analogy to Section 2.1, we introduce a record-breaking time with a temporal– spatial shift, and an auxiliary random variable leading to the definition of the tilting parameter.
Let
\begin{align*}
{\tilde T_{t,s}}{\kern 1pt} : = \inf \{ n \ge 0:s + {S_n} > a{(n + t)^\alpha } + b{(n + t)^{1 - \alpha }}\}.
\end{align*}
Given t, we introduce an auxiliary random variable Ñ(t) with PMF
\begin{align}
{p_t}(n) = {\mathbb{P}}(2\tilde N(t) = n) = {{{2^n}\exp ( - {2^{ - n - 4}}{a^2}{{{{(2}^n} + t)}^{2\alpha }})} \over {\sum {_{m = 0}^\infty } {2^m}\exp ( - {2^{ - m - 4}}{a^2}{{{{(2}^m} + t)}^{2\alpha }})}}\quad {\kern 1pt} \rm for\;n \ge 1{\kern 1pt}.
\end{align}
Given Ñ(t) = n, we apply exponential tilting to sample (X̃ 1, X̃ 2, …, X̃ 2n+1−1), with tilting parameter
\begin{align*}
{\tilde \theta _n}(t{) = 2^{ - n - 2}}a{{(2^n} + t)^\alpha },
\end{align*}
i.e.
\begin{align*}
{{{\rm{d}}{{\mathbb{P}}_{{{\tilde \theta }_n}(t)}}} \over {{{\rm {d}\mathbb P}}}}{\bf {1}}\{ {X_i} \in A\} = \exp ({\tilde \theta _n}(t){X_i} - \psi (2{\tilde \theta _n}(t))){\bf {1}}\{ {X_i} \in A\}.
\end{align*}
We also define S̃k := X̃ 1 + · · · + X̃k for k ≥ 1, and
\begin{align*}
\tilde T = \inf \{ n \ge 0:s + {\tilde S_n} > a{(n + t)^\alpha } + b{(n + t)^{1 - \alpha }}\} \wedge {2^{n + 1}}.
\end{align*}
Let
\begin{align}
\tilde J = 1 - {\bf {1}}\{ U \le {{\exp ( - {{\tilde \theta }_n}{{\tilde S}_{2\tilde T}} + \tilde T\psi ({{\tilde \theta }_n}))} \over {{p_t}(n)}}{\bf {1}}\{ \tilde T \in {[2^n}{,2^{n + 1}})\} \},
\end{align}
where U ~Uniform[0, 1].
Lemma 3. For J̃ defined in (6), when s < atα/4, we have
\begin{align*}
{\mathbb{P}}(4\tilde J = 1) = {\mathbb{P}}(2{\tilde T_{t,s}} = \infty ).
\end{align*}
Proof. We first note that
\begin{align*}
\\{{\exp ( - {{\tilde \theta }_n}{S_{2\tilde T}} + \tilde T\psi ({{\tilde \theta }_n}))} \over {{p_t}(n)}}I\{\tilde T \in {[2^n}{,2^{n + 1}})\}
\\\quad \quad \le {1 \over {{p_t}(n)}}\exp ( - {\tilde \theta _n}(a{{(2^n} + t)^\alpha } + b{{(2^n} + t)^{1 - \alpha }} - {a \over 4}{t^\alpha }) + {2^{n + 1}}\tilde \theta _n^2)
\\\quad \quad \le {1 \over {{p_t}(n)}}\exp ( - {2^{ - n - 3}}{a^2}{{(2^n} + t)^{2\alpha }} + {2^{ - n - 4}}{a^2}{{(2^n} + t)^{2\alpha }} - {{ab} \over 4})
\\\quad \quad = {1 \over {{p_t}(n)}}\exp ( - {2^{ - n - 4}}{a^2}{{(2^n} + t)^{2\alpha }} - {{ab} \over 4})
\\\quad \quad \le (\sum\limits_{m = 0}^\infty {2^m}\exp ( - {2^{ - m - 4}}{a^2}{{(2^m} + t)^{2\alpha }}))\exp ( - {{ab} \over 4})
\\\quad \quad \le (\sum\limits_{m = 0}^\infty {2^m}\exp ( - {a^2}{2^{2m\alpha - m - 4}}))\exp ( - {{ab} \over 4})
\\\quad \quad \le {1 \over 4},
\end{align*}
where the last inequality follows from our choice of a and b. The rest of the proof follows exactly the same steps as the proof of Theorem 1. We shall omit it here.
Let
\begin{align*}
L(n) = \inf \{ k \ge n:{S_k} > a{k^\alpha } + b{k^{1 - \alpha }}{\kern 1pt} \;{\rm or}\;{\kern 1pt} {S_k} < {a \over 4}{k^\alpha }\}.
\end{align*}
The sampling algorithm goes as follows.
Procedure B. Sampling (X 1, …, Xn) conditional on T 1 = ∞.
(i) Sample (X 1, …, Xn) under the nominal distribution ℙ(·).
(ii) If max1≤k≤n{Sk − akα − bk 1−α} > 0, go back to step (i); otherwise, go to step (iii).
(iii) Sample L(n) and (Xn +1, Xn +2, …, XL (n)) under the nominal distribution ℙ(·). If SL (n) > aL(n)α + bL(n)1−α, go back to step (i); otherwise, go to step (iv).
(iv) Sample Ñ with probability mass function pL (n) defined in (5). Generate
\begin{align*}
\big(\tilde X_{1}, \tilde X_{2}, \ldots, \tilde
X_{2^{\tilde N+1}-1}\big)
\end{align*}
under exponential tilting with tilting parameter θ̃Ñ = 2Ñ-2a(2Ñ-2 + L(n))α. Let
\begin{align*}
\tilde T=\inf\{k\geq1\colon S_{L(n)}+\tilde S_{k}
>a(k+L(n))^{\alpha}+b(k+L(n))^{1-\alpha}\} \wedge2^{\tilde N+1}.
\end{align*}
(v) Sample U ~Uniform[0, 1]. If
\begin{align*}
U\leq\frac{\exp({-}\tilde\theta_{\tilde N} S_{\tilde T} + \tilde
T\psi(\tilde\theta_{\tilde N})) }{p_{t}(\tilde N)}{\bf 1} \big\{ \tilde
T\in \big[ 2^{\tilde N}, 2^{\tilde N+1}\big) \big\},
\end{align*}
set J̃ = 0 and go back to step (i); otherwise, set J̃ = 1 and output (X 1, …, Xn).
We next show that Procedure B works.
Theorem 2. The output of Procedure B follows the distribution of (X 1, …, Xn) conditional on T 1 = ∞.
Proof. Let ℙ′(·) =ℙ( · | T 1 = ∞). We first notice that
\begin{align*}
{{{\rm{d\mathbb P'}}} \over {{\rm{d}{\mathbb P}}}}({X_1}, \ldots ,{X_n}) = {{1\{ {T_1} > n\} {{\mathbb P}}({T_1} = \infty {\kern 1pt} {\kern 1pt} |{\kern 1pt} {\kern 1pt} {S_n},{T_1} > n)} \over {{{\mathbb P}}({T_1} = \infty )}} \le {1 \over {{{\mathbb P}}({T_1} = \infty )}}.
\end{align*}
Let ℙ″(·) denote the measure induced by Procedure B. Then we have, for any sequence of Borel measurable sets Ai ⊂ ℝ, i = 1, 2, …, n,
\begin{align*}
{{\mathbb{P}}^{\prime \prime }}({X_1} \in {A_1}, \ldots ,{X_n} \in {A_n}) = {\mathbb{P}}({X_1} \in {A_1}, \ldots ,{X_n} \in {A_n}\mid {T_1} > L(n),\tilde J = 1)\\
= {\mathbb{P}}({X_1} \in {A_1}, \ldots ,{X_n} \in {A_n}\mid {T_1} > L(n),{{\tilde T}_{L(n),{S_{L(n)}}}} = \infty )\\
= {\mathbb{P}}({X_1} \in {A_1}, \ldots ,{X_n} \in {A_n}\mid {T_1} = \infty ),
\end{align*}
where the second equality follows from Lemma 3, and the third equality follows from the fact that
\begin{align*}
\mathbb {P}(T_{1}=\infty\mid S_{t}, T_{1}>t)=\mathbb {P}( \tilde T_{t, S_{t}}=\infty).
\end{align*}
To execute step (iv) of Algorithm 1, we apply Procedure B with n = Г(κ).
3. Running time analysis
In this section we provide a detailed running time analysis of Algorithm 1.
Theorem 3. Algorithm 1 has finite expected running time.
We divide the analysis into the following steps.
(a) From Lemma 1, the number of iterations between steps (ii) and (iii) follows a geometric distribution with probability of success ℝ(T 1 = ∞) ≥ 3/4.
(b) In each iteration (when applying Procedure A), we will show that the length of the path needed to sample J has finite moments of all orders (Lemma 4).
(c) For step (iv), we will show that Г(κ) has finite moments of all orders (Lemma 5).
(d) When applying Procedure B for step (iv), we will show that the total length of the paths needed in Procedure B has finite moments of every order (Lemma 6).
Lemma 4. The length of the path needed to sample the Bernoulli J in Procedure A has finite moments of every order.
Proof. The length of the path generated in Procedure A is bounded by 2N+1, where the distribution of N is defined in (4). Therefore, for all r > 0,
\begin{align*}
{\mathbb{E}}[{2^{(N + 1)r}}] = \frac{{\sum {_{m = 0}^\infty } {2^{(m + 1)}}{2^m}\exp ( - {a^2}{2^{2m\alpha - m - 3}})}}{{\sum {_{m = 0}^\infty } {2^m}\exp ( - {a^2}{2^{2m\alpha - m - 3}})}}\\
= \frac{{\sum {_{m = 0}^\infty } \exp \,( - {a^2}{2^{2m\alpha - m - 3}} + (mr + r + m)\log 2)}}{{\sum {_{m = 0}^\infty } {2^m}\exp ( - {a^2}{2^{2m\alpha - m - 3}})}}.
\end{align*}
Since, for sufficiently large m,
\begin{align*}
\exp({-}a^{2} 2^{2m\alpha-m -3} +(mr+r+m)\log2 ) \le\exp({-}a^{2} 2^{2m\alpha-m -4});
\end{align*}
for fixed r > 0, there exists C > 0 such that
\begin{align*}
{{\sum {_{m = 0}^\infty } \exp ( - {a^2}{2^{2m\alpha - m - 3}} + (mr + r + m)\log 2)} \over {\sum {_{m = 0}^\infty } {2^m}\exp ( - {a^2}{2^{2m\alpha - m - 3}})}} \le C{{\sum {_{m = 0}^\infty } \exp ( - {a^2}{2^{2m\alpha - m - 4}})} \over {\sum {_{m = 0}^\infty } {2^m}\exp ( - {a^2}{2^{2m\alpha - m - 3}})}} < \infty.
\end{align*}
Note that this also implies that
\begin{align*}
\mathbb {E}[T_1^{r} {\bf 1}(T_1 < \infty)] \le \mathbb {E}[2^{(N+1)r}{\bf 1} (J = 0)] \le
\mathbb {E}[2^{(N+1)r}] < \infty.
\end{align*}
Lemma 5. Г(κ) and L(Г(κ)) have finite moments of any order.
Proof. We start with Г(κ). Let Rn := Sn − anα − bn 1−α. For Ti < ∞, we also define
\begin{align*}
\mathcal{R}_{i}\,:\!=S_{T_{i}}-S_{T_{i-1}}-a(T_{i}-T_{i-1})^{\alpha}-b
(T_{i}-T_{i-1})^{1-\alpha}.
\end{align*}
Then we have
\begin{align*}
\Gamma(\kappa) =\big\lceil (2S_{T_{\kappa-1}} + 2\xi)^{1/\alpha}\big\rceil\\
=\bigg\lceil \bigg(2\sum_{i=1}^{\kappa-1}(S_{T_{i}}-S_{T_{i-1}}) + 2\xi\bigg)^{1/\alpha}\bigg\rceil\\
=\bigg\lceil \bigg(2\sum_{i=1}^{\kappa-1}\mathcal{R}_{i}\\
+2\sum_{i=1}^{\kappa-1}\big(a(T_{i}-T_{i-1})^{\alpha}+b(T_{i}-T_{i-1})^{1-\alpha}\big)\\
+2\xi\bigg)^{1/\alpha}\bigg\rceil\\
\leq\bigg\lceil \bigg(2\sum_{i=1}^{\kappa-1}\mathcal{R}_{i}\\
+2\kappa\xi +\sum_{i=1}^{\kappa-1}(T_{i}-T_{i-1})^{\alpha}\bigg) ^{1/\alpha}\bigg\rceil,
\end{align*}
where the last inequality follows from the definition of ξ in (2).
In what follows, we first prove that, conditioning on T 1 < ∞, R T 1 has finite moments of every order. That is,
\begin{align*}
{}&{\mathbb{E}}{[^{\gamma {R_{{T_1}}}}}1({T_1} < \infty )]\\
{}&= \sum\limits_{n = 0}^\infty {[^{\gamma {R_n}}}1({T_1} = n)]\\
{}&= \sum\limits_{n = 0}^\infty {\mathbb{E}}{[^{\gamma ({X_n} + {S_{n - 1}} - a{n^\alpha } - b{n^{1 - \alpha }})}}1({T_1} = n)]\\
{}&\le \sum\limits_{n = 0}^\infty {\mathbb{E}}{[^{\gamma {X_n}}}1({T_1} = n)]\\
{}&\le \sum\limits_{n = 0}^\infty {\mathbb{E}}{{[^{p\gamma {X_n}}}]^{1/p}}{\mathbb{E}}{[1({T_1} = n)]^{1/q}}\quad ({\kern 1pt} {\rm{for}}\;{\kern 1pt} p,q > 1,{1 \over p} + {1 \over q} = 1{\kern 1pt} \;{\rm{by}}\;{\rm{H\ddot older's}}\;{\rm{inequality}}{\kern 1pt} )\\
{}&= {\mathbb{E}}{{[^{p\gamma {X_1}}}]^{1/p}}\sum\limits_{n = 0}^\infty {\mathbb{P}}{({T_1} = n)^{1/q}}.
\end{align*}
Because X 1 has moment generating function within a neighbourhood of 0, we can choose p > 0 and γ > 0 such that 
${\mathbb{E}}{{[^{p\gamma {X_1}}}]^{1/p}} < \infty$. In the proof of Lemma 4 we showed that, for all r > 0, 
${\mathbb{E}}[T_1^r1({T_1} < \infty )] < \infty $, which implies that ℝ(T 1 = n) = O(1/nr). As r can be any positive value, 
$\mathbb {E}[T_{1}^{r} {\bf 1}(T_{1}<\infty)]<\infty$.
We next show that Г(κ) has finite moments of all orders. By Jensen’s inequality, for any fixed r ≥ 1,
\begin{align}
\label{eq:bound}
\mathbb {E}[\Gamma(\kappa)^r] &\leq \mathbb {E}\bigg[ \bigg( \sum_{i=1}^{\kappa-1}(T_{i}
-T_{i-1})^{\alpha}+2\kappa\xi+2\sum_{i=1}^{\kappa-1}\mathcal{R} _{i}\bigg)
^{r/\alpha} \bigg]\\
& \le3^{{r}/{\alpha}-1}\mathbb {E}\bigg[ \bigg( \sum_{i=1}^{\kappa-1}
(T_{i}-T_{i-1})^{\alpha}\bigg) ^{r/\alpha} + ( 2 \kappa\xi)
^{r/\alpha}+ \bigg( 2\sum_{i=1}^{\kappa-1}\mathcal{R} _{i} \bigg)
^{r/\alpha} \bigg].
\end{align}
We shall analyse each of the three parts on the right-hand side of (7). As κ is a geometric random variable, 
$\mathbb {E}[( 2 \kappa\xi) ^{r/\alpha}] < \infty$. Hence,
\begin{align*}
{{\mathbb{E}}[{{(\sum\limits_{i = 1}^{\kappa - 1} {{{({T_i} - {T_{i - 1}})}^\alpha }} )}^{r/\alpha }}]}&{ = {\mathbb{E}}[{\mathbb{E}}[{{(\sum\limits_{i = 1}^{\kappa - 1} {{{({T_i} - {T_{i - 1}})}^\alpha }} )}^{r/\alpha }}|\kappa ]]}\\
{}&{ \le {\mathbb{E}}[{\kappa ^{r/\alpha - 1}}{\mathbb{E}}[\sum\limits_{i = 1}^{\kappa - 1} {{{({T_i} - {T_{i - 1}})}^r}} |\kappa ]]}\\
{}&{ \le {\mathbb{E}}[{\kappa ^{r/\alpha }}{\mathbb{E}}[T_1^r\mid {T_1} < \infty ]]}\\
{}&= {\mathbb{E}}[{\kappa ^{r/\alpha }}]{\mathbb{E}}[T_1^r\mid {T_1} < \infty ]\\
{}&< \infty .
\end{align*}
Similarly, we have
\begin{align*}
\mathbb {E}\bigg[ \bigg( 2\sum_{i=1}^{\kappa-1}\mathcal{R} _{i} \bigg) ^{r/\alpha}
\bigg] \le \mathbb {E} [ (2\kappa)^{r/\alpha} ] \mathbb {E} [ R_{T_{1}
}^{r/\alpha}\mid T_{1}<\infty] < \infty.
\end{align*}
Therefore, we have
\begin{align*}
\mathbb {E}[\Gamma(\kappa)^r ]<\infty.
\end{align*}
As for L(Г(κ)), we first note that
\begin{align*}
L(\Gamma(\kappa))-\Gamma(\kappa) \le\inf\Big\{ n \ge0\colon S_{n+\Gamma(\kappa)}
<\frac{a}{4} (n+\Gamma(\kappa))^{\alpha}\Big\}.
\end{align*}
Given Г(κ) = n* and S Г(κ) = s*, since 
$s_{*}<a n_{*}^{\alpha}+b n_{*}^{1-\alpha}$,
\begin{align*}
& \mathbb {P}(L(\Gamma(\kappa))-\Gamma(\kappa) > n|\Gamma(\kappa)=n_{*}, S_{\Gamma
(\kappa)}=s_{*})\\
& \quad \le \mathbb {P}\Big( {S}_{n} \ge\frac{a}{4}(n+n_{\ast})^{\alpha}-s_{*}\Big) \\
& \quad \le \mathbb {P}\Big( {S}_{n} \ge\frac{a}{4}(n+n_{\ast})^{\alpha}
-a n_{\ast}^{\alpha}-b n_{\ast}^{1-\alpha}\Big) \\
& \quad \le \mathbb {P}\Big( {S}_{n} \ge\frac{a}{4}(n+n_{\ast})^{\alpha}-\frac{1}{2}
n_{\ast}^{\alpha}-\xi\Big) \\
& \quad \le \exp\Big( n \theta^{2}-\theta\Big( \frac{a}{4}(n+n_{\ast})^{\alpha
}-\frac{1}{2} n_{\ast}^{\alpha}-\xi\Big) \Big)
\quad \text{for $0<\theta<\delta^{\prime}$}.
\end{align*}
Let 
$w_{n}={a}(n+n_{\ast})^{\alpha}/{4}-n_{\ast}^{\alpha}/{2}-\xi$. If we pick θ = ∊n|wn/n|, where ∊n is chosen such that θ < δ′, then
\begin{align*}
\exp( n \theta^{2}-\theta w_{n}) \leq\exp\Big(\!-\frac{w_{n}^{2}}{n}\epsilon_{n}(1-\epsilon_{n})\Big) \leq\exp\Big(\!-\frac{w_{n}^{2}
}{4n}\Big).
\end{align*}
We note that, for large enough n,
\begin{align*}
w_{n}\leq\frac{a}{5}(n+n_{*})^{\alpha}.
\end{align*}
Thus, there exists C > 0, such that
\begin{align*}
\mathbb {P}(L(\Gamma(\kappa))-\Gamma(\kappa) > n\mid \Gamma(\kappa)=n_{*}, S_{\Gamma
(\kappa)}=s_{*}) & \leq C\exp\Big( -\frac{a^{2}}{100}\frac{(n+n_{*}
)^{2\alpha}}{n}\Big) \\
& \leq C\exp\Big( -\frac{a^{2}}{100} n^{2\alpha-1}\Big).
\end{align*}
This implies that, given Г(κ) and S Г(κ), L(Г(κ)) − Г(κ) has finite moments of all orders.
Lemma 6. The total length of the paths needed to sample the Bernoulli J̃ in Procedure B has finite moments of every order.
Proof. To sample the trajectory, using the notations defined in Procedure B, the length of each path generated, steps (i)–(iv), either accepted or rejected, satisfies
\begin{align*}
&n+(L(n)-n){\bf 1}\{\tilde{S}_k \le a k^\alpha+b k^{1-\alpha}, 1\le k\le
n\}+2^{\tilde{N}+1}{\bf 1}\{\tilde{S}_k \le a k^\alpha+b k^{1-\alpha}, 1\le k \le
L(n) \} \\ & \qquad \le L(n)+2^{\tilde{N}+1},
\end{align*}
where Ñ is sampled in step (iv) according to (5).
We start by establishing a bound for E[2rÑ] for any fixed r > 0. We have proved in Lemma 5 that, for all n, L(n) has finite moments of all orders. Moreover, for any r > 0, t > 0, Ñ(t) generated from pt(·) (defined in (5)) satisfies
\begin{align}\label{eq:Nt_main}
{\mathbb{E}}{[2^{2\tilde N(t)r}}] = {{\sum {_{m = 0}^\infty } {2^{(r + 1)m}}\exp ( - {2^{ - m - 4}}{a^2}{{{{(2}^m} + t)}^{2\alpha }})} \over {\sum {_{m = 0}^\infty } {2^m}\exp ( - {2^{ - m - 4}}{a^2}{{{{(2}^m} + t)}^{2\alpha }})}}.
\end{align}
We next prove that 
$\mathbb {E}[2^{\tilde{N}(t)r}]=O(t^r)$, which leads to the desired bound for 
$\mathbb {E}[2^{r\tilde{N}}]$. This is achieved in two steps. In the first step we show that, for large enough m, the summand in the numerator of (8) decays exponentially fast.
Let η 1 := (22α − 2)/2. For large enough m, we have
\begin{align} \label{eq:m_bd}
&2^m \ge \frac{(2+\eta_1)^{1/(2\alpha)}-1}{2-(2+\eta_1)^{1/(2\alpha)}}t\\
\Longleftrightarrow\quad & \ 2^m (2-(2+\eta_1)^{1/(2\alpha)})\ge (2+\eta_1)^{1/(2\alpha)}t-t \nonumber\\
\Longleftrightarrow\quad & \ 2^{m+1}+t \ge (2^m+t)(2+\eta_1)^{1/(2\alpha)} \nonumber\\
\Longleftrightarrow\quad & \ (2^{m+1}+t )^{2\alpha}\ge (2+\eta_1) (2^m+t)^{2\alpha}. \nonumber
\end{align}
Then we have
\begin{align} \label{eq:grow_bd}
&\frac{ 2^{(1+r)(m+1)}\exp ({-}2^{-(m+1)-4}a^2 (2^{m+1}+t)^{2\alpha} )}{ 2^{(1+r)m} \exp ({-}2^{-m-4}a^2 (2^m+t)^{2\alpha} )} \nonumber\\
& \qquad = \exp ({-}2^{-(m+1)-4}a^2 (2^{m+1}+t)^{2\alpha} +2^{-m-4}a^2 (2^m+t)^{2\alpha} +(1+r)\log 2 )\nonumber\\
& \qquad = \exp ({-}2^{-m-5}a^2 ( (2^{m+1}+t)^{2\alpha} - 2 (2^m+t)^{2\alpha} )+(1+r)\log 2 )\nonumber\\
& \qquad \le \exp ({-}2^{-m-5}a^2 \eta_1 (2^m+t)^{2\alpha} +(1+r)\log 2 )\nonumber\\
& \qquad \le \exp ({-}2^{-5}a^2 \eta_1 2^{(2\alpha-1)m} +(1+r)\log 2 ).
\end{align}
Note that (10) can be made arbitrarily small by having sufficiently large m. Thus, there exists m(r) large enough such that, for m ≥ m(r),
\begin{align*}
2^{(1+r)(m+1)}\exp({-}2^{-(m+1)-4}a^2 (2^{m+1}+t)^{2\alpha})
\leq \frac{1}{2} 2^{(1+r)m(r)} \exp ({-}2^{-m-4}a^2 (2^{m}+t)^{2\alpha}).
\end{align*}
We now carry out the second step. Based on (9), let
\begin{align*}
\eta_2\,:\!=\frac{(2+\eta_1)^{1/(2\alpha)}-1}{2-(2+\eta_1)^{1/(2\alpha)}}.
\end{align*}
Then, for large enough t, we have
\begin{align*}
& \sum_{m= \lceil \log (\eta_2 t) \rceil +1}^\infty 2^{(1+r)m} \exp ({-}2^{-m-4}a^2 (2^m+t)^{2\alpha} )\\
& \qquad \le 2^{(1+r) \lceil \log (\eta_2 t) \rceil } \exp ({-}2^{- \lceil \log (\eta_2 t) \rceil -4}a^2 (2^ {\lceil \log (\eta_2 t) \rceil} +t)^{2\alpha} ) \sum_{k=1}^\infty \frac{1}{2^k}\\
& \qquad \le 2^{(1+r) \lceil \log (\eta_2 t) \rceil } \exp ({-}2^{- \lceil \log (\eta_2 t) \rceil -4}a^2 (2^ {\lceil \log (\eta_2 t) \rceil }+t)^{2\alpha} ).
\end{align*}
Thus,
\begin{align*}
& \mathbb {E}[2^{\tilde{N}(t)r}]
\\[4pt]
&\quad =
\mbox{$
\frac{\sum_{m=0}^{ \lceil \log (\eta_2 t) \rceil} 2^{(1+r)m} \exp (
-2^{-m-4}a^2 (2^m+t)^{2\alpha})+ \sum_{m=\lceil \log (\eta_2 t)
\rceil+1}^{\infty} 2^{(1+r)m} \exp ( -2^{-m-4}a^2 (2^m+t)^{2\alpha})
}{\sum_{m=0}^{\infty }2^m \exp ( -2^{-m-4}a^2 (2^m+t)^{2\alpha})}
$}
\\[4pt]
&\quad \le
\mbox{$
\frac{\sum_{m=0}^{ \lceil \log (\eta_2 t) \rceil} 2^{(1+r)m} \exp (
-2^{-m-4}a^2 (2^m+t)^{2\alpha} )+ 2^{(1+r) \lceil \log (\eta_2 t) \rceil }
\exp ( -2^{- \lceil \log (\eta_2 t) \rceil -4}a^2 (2^ {\lceil \log (\eta_2
t) \rceil }+t)^{2\alpha} ) }{\sum_{m=0}^{\infty }2^m \exp ( -2^{-m-4}a^2
(2^m+t)^{2\alpha} )}
$}
\\[4pt]
&\quad \le
\mbox{$
\frac{2^{r \lceil \log (\eta_2 t) \rceil } \sum_{m=0}^{ \lceil \log
(\eta_2 t) \rceil} 2^{m} \exp ( -2^{-m-4}a^2 (2^m+t)^{2\alpha})+ 2^{(1+r)
\lceil \log (\eta_2 t) \rceil } \exp ( -2^{- \lceil \log (\eta_2 t) \rceil
-4}a^2 (2^ {\lceil \log (\eta_2 t) \rceil }+t)^{2\alpha} ) }
{\sum_{m=0}^{\lceil \log (\eta_2 t) \rceil}2^m \exp ( -2^{-m-4}a^2
(2^m+t)^{2\alpha} )}
$}\\
&\quad \le 2^{r \lceil \log (\eta_2 t) \rceil +1}\\
&\quad \le 3 \eta_2^r t^r.
\end{align*}
We are now ready to establish the bound for 
$\mathbb {E}[(L(n)+2^{\tilde{N}+1})^r]$ for any fixed r ≥ 1. Hence,
\begin{align*}
\mathbb{E} [(L(n)+2^{\tilde{N}+1})^r ] &\le \mathbb{E} [2^{r-1}(L(n)^r+2^{(\tilde{N}+1)r})]\\[4pt]
& \le 2^{r-1} \mathbb{E}[L(n)^r ] +2^{2r-1} \mathbb{E}[2^{\tilde{N}r}]
\quad \text{(by Jensen's inequality)}\\[4pt]
&\le 2^{r-1} \mathbb{E}[L(n)^r ] +2^{2r-1}3\eta_2^r \mathbb{E}[L(n)^r]\\[4pt]
&<\infty.
\end{align*}
We have thus shown that each path has finite moments of all orders.
As for the acceptance probability in steps (ii), (iii) and (v), we note that
\begin{align*}
&\mathbb {P} (\{S_k \le ak^\alpha+b k^{1-\alpha}, 1\le k \le L(n)\} \cap \{\tilde{J} =1\} )\\[4pt]
& \quad = \mathbb {P}(T_1 > L(n),\tilde T_{L(n), S_{L(n)}}=\infty)\\[4pt]
& \quad = \mathbb {P}(T_1 = \infty) \quad \text{(as
$\mathbb {P}(T_{1}=\infty\mid S_{t}, T_{1}>t)=\mathbb {P}( \tilde T_{t, S_{t}}=\infty)$)}\\[4pt]
& \quad \ge \frac{3}{4} \quad \text{(by Lemma 1).}
\end{align*}
Then the number of times a path is rejected is stochastically bounded by a geometric random variable with probability of success 
$\tfrac34$. Therefore, the total length of paths generated in Procedure B has finite moments of all orders.
3.1. Numerical experiments
In this section we conduct numerical experiments to analyse the performance of Algorithm 1 for different values of the parameter a. In Remark 1, we briefly discussed how the parameters a and b would affect the performance of Algorithm 1. We shall fix the value of b upon our choice of a as in (1), as we want to guarantee that the probability of record-breaking is small enough, while keeping Г(κ) as small as possible.
For the computational cost, we first note that the choices of a and b will affect the distribution of N, which is the length of trajectory generated in Procedure A. In Procedure B, the values of Г(κ), L(Г(κ)) and the distribution of Ñ also depends on the values of a and b.
Let 
${X_i}\mathop = \limits^{\rm{D}} X - 1$, where X is a unit-rate exponential random variable. Then ψ(θ) = −θ −log (1 − θ) for θ < 1. Let g(θ) := ψ(θ) − θ 2. As g′(0) = 0, g″(θ) = 1/(1 − θ)2 − 2, we have
\begin{align*}
g(\theta ) < 0\quad {\rm{for}}\,{\rm{all}} \theta \in ( - 1,1 - {{\sqrt 2 } \over 2}).
\end{align*}
Therefore, we can set 
$\delta^{\prime}=1-{\sqrt{2}}/{2}$, and when θ ∈ (-δ′, δ′), ψ(θ) = −θ 2. According to (1) 
$a<\min(\tfrac{1}{2}, 4\delta^{\prime})=\tfrac{1}{2}$. We ran Algorithm 1 with different values of a and α. Table 1 summarizes the running time of the algorithm in different settings.
TABLE 1: Running time of Algorithm 1 (in seconds).
We observe that when a is relatively far away from the upper bound 
$\tfrac{1}{2}$ (e.g. a ≤ 0.45), the running time decreases as a increases. However, as a approaches 
$\tfrac{1}{2}$, increasing in a. This is because ξ → ∞ as 
$a \to \tfrac{1}{2}$ (see (2)). We also observe that the changing rate of running time regarding a is larger for smaller values of α, which in general implies greater curvature of the nonlinear boundary.
4. Departure process of an infinite-server queue
We finish the paper with an application of the algorithm developed in Section 2 to sample the steady-state departure process of an infinite-server queue with general interarrival time and service time distributions. We assume the interarrival times are independent and identically distributed (i.i.d.). Independent of the arrival process, the service times are also i.i.d. and may have infinite mean.
Suppose that the system starts operating from the infinite past. Then it would be at stationarity at time 0. We want to sample all the departures in the interval [0, h].
We start by introducing a point process representation of an infinite-server queue to facilitate the explanation of the simulation strategy. We mark each arriving customer as a point in a two-dimensional space, where the x-coordinate records its arrival time and the y-coordinate records its service time (service requirement). Figure 2 provides an illustration with two points representing two arriving customers. Customer 1 arrives at −A 1 and has a service requirement of V 1. Note that, as there are infinitely many servers, this customer will enter service immediately upon arrival and will leave the system at time −A 1 + V 1. If we draw a minus 45-degree line from (−A 1, V 1), the intersection of this line with the x-axis represents customer 1’s departure time. Likewise, we can also denote the departure time of customer 2 by the intersect of the minus 45-degree line staring from (−A 2, V 2) with the x-axis. We observe that in this particular example, customer 1 would leave the system in the interval [0, h], while customer 2 would leave the system before time 0. Based on this observation, we can draw a shaded region in Figure 2, which has the property that all the points (customers) that fall into this region will leave the system during [0, h]. Therefore, to sample the departure process on [0, h], we essentially would like to sample all the points (customers) that fall into the shaded area.
Figure 2: Point process representation of an infinite-server queue.
We further divide the shaded area into two parts, namely H and G. Points in the shaded area G are customers that arrive after time 0 and depart before time h, while points in area H are customers who arrive before time 0 and depart between times 0 and h. Sampling the points that fall into G is easy. As G is a bounded area, we can simply sample all the arrivals between 0 and h, and decide, using their service time information, whether they fall into region G or not. The challenge lies in sampling the points in H, as it is an unbounded region.
For the rest of this section, we explain how to sample all the points (customers) that fall into region H. We mark the points sequentially (according to their arrival times) backwards in time from time 0 as (−A 1, V 1), (−A 2, V 2), …, where −An is the arrival time of the nth arrival counting backwards in time and Vn is its service time. Let A 0 := 0. We then denote Xn := An − An −1 as the interarrival time between the nth arrival and the (n − 1)th arrival. Let 
$\mu\,:\!=\mathbb {E}[X]$ denote the mean interarrival time and σ 2 : = var (X) denote its variance. For simplicity of notation, we write
\begin{align*}
\mathcal{H}\,:\!=\{({-}A_{n}, V_{n})\colon A_{n}<V_{n}<A_{n}+h\}.
\end{align*}
It is the collection of points that fall into region H.
The following observation builds the foundation of our simulation strategy. Suppose that we can find a random number Ξ such that
\begin{align*}
V_{n} < A_{n} \quad\mbox{or}\quad V_{n} < A_{n}+h
\end{align*}
for n ≥ Ξ. Then we can sample the point process up to Ξ, i.e. {(−Ai, Vi), 1 ≤ i ≤ Ξ}, and find 
$\mathcal{H}$. Built on this observation, we further introduce an idea to separate the simulation of the arrival process and the service time process. It requires us to find a sequence of {∊n : n ≥ 1}, satisfying the following two properties.
(P1) There exists a well-defined random number Ξ1 such that
\begin{align*}
n\mu-\epsilon_{n}<A_{n}<n\mu+\epsilon_{n} \quad \mbox{for all } n \geq\Xi_{1}.
\end{align*}
(P2) There exists a well-defined random number Ξ2 such that
\begin{align*}
V_{n} < n\mu-\epsilon_{n} \mbox{ or } V_{n} > n\mu+\epsilon_{n}+h
\quad \mbox{for all } n \geq\Xi_{2}.
\end{align*}
Now, set Ξ = max{Ξ1,Ξ2}. Then we have Vn < An or Vn > An + h for n ≥ Ξ. Note that, based on the introduction of the ∊n, we can find Ξ1 and Ξ2 separately.
To guarantee that Ξ1 and Ξ2 are well defined, i.e. finite, we need to choose ∊n that satisfy the following two conditions:
\begin{align*}
\eqalign{
& \matrix{
{\left( {{\rm{C1}}} \right)\,} & {\sum\nolimits_{n = 1}^\infty {\rm{P}}(|{A_n} - n\mu | > {\varepsilon _n}) < \infty } \cr}\cr
& \matrix{
{\left( {{\rm{C2}}} \right)} & {\sum\nolimits_{n = 1}^\infty {\rm{P}}({V_n} \in (n\mu - {\varepsilon _n},n\mu + {\varepsilon _n} + h)) < \infty } \cr
} \cr}
\end{align*}
Under (C1) and (C2), the Borel–Cantelli lemma guarantees that Ξ1 and Ξ2 are finite almost surely.
We next introduce a specific choice of ∊n when the service times follow a Pareto distribution with shape parameter 
$\beta\in (\tfrac12,1)$. We denote the PDF of Vi as f (·), which takes the form
\begin{align}
f(v) = \beta {v^{ - (\beta + 1)}}1\{ v \ge 1\}.
\end{align}
We also write F̄(·) as the tail distribution of Vi. We assume the interarrival time has a finite moment generating function in a neighbourhood of the origin. This is without loss of generality. If the interarrival time is heavy tailed, we can simulate a coupled infinite-server queue with truncated interarrival times, 
$X_{i}^{C}=\min\{X_{i}, C\}$. This coupled infinite-server queue would serve as an upper bound (in terms of the number of departures) of the original infinite-server queue in a path-by-path sense.
Set ∊n = nα for 
${\textstyle{1 \over 2}} < \alpha < \beta $. In what follows, we shall show that our choice of ∊n satisfies (C1) and (C2), respectively. We shall also explain how to find (simulate) Ξ1 and Ξ2.
4.1. Sampling of the arrival process and Ξ1
The following lemma verifies (C1).
Lemma 7. If ∊n = nα for 
$\alpha>\dfrac{1}{2}$,
\begin{align*}
\sum_{n=1}^{\infty} \mathbb {P}( \vert A_{n}- n\mu\vert > \epsilon
_{n}) <\infty.
\end{align*}
Proof. We note that 
$A_{n}=\sum_{i=1}^{n}X_{i}$ is a random walk with Xi being i.i.d. interarrival times with mean μ, except the first one. X 1 follows the backward recurrent time distribution of the interarrival time distribution. By the moderate deviation principle [Reference Ganesh, O’Connell and Wischik7], we have
\begin{align*}
\frac{1}{n^{2\alpha-1}} \log \mathbb {P}(\vert A_{n}-n\mu\vert > n^{\alpha
})\rightarrow-\frac{1}{2\sigma^{2}}.
\end{align*}
As 2α − 1 > 0, 
$\sum_{n=1}^{\infty}\mathbb {P}( \vert A_{n}-n\mu \vert > n^{\alpha}) <\infty$.
Let Sn = An − nμ. We note that both Sn and −Sn are mean zero random walks:
\begin{align*}
\mathbb {P}(|S_{n}|>n^{\alpha})\leq \mathbb {P}(S_{n}>n^{\alpha})+\mathbb {P}({-}S_{n}>n^{\alpha}).
\end{align*}
Thus, we can apply a modified version of Algorithm 1 to find Ξ1. In particular, we define a modified sequence of record-breaking times as follows. Let 
$T_{0}^{\prime}\,:\!=0$. For k ≥ 1, if 
$T_{k-1}^{\prime}<\infty$,
\begin{align*}
T_{k}^{\prime} & \,:\!=\inf\big\{ n>T_{k-1}^{\prime}\colon S_{n}
>S_{T_{k-1}^{\prime}}+a(n-T_{k-1}^{\prime})^{\alpha}+b(n- T_{k-1}^{\prime})^{1-\alpha
} \\
& \qquad\quad \mbox{ or } S_{n}<S_{T_{k-1}^{\prime}}-a(n-T_{k-1}^{\prime
})^{\alpha}-b(n- T_{k-1}^{\prime})^{1-\alpha}\big\};
\end{align*}
otherwise, 
$T_{k}^{\prime} =\infty$. Then the modified version of Algorithm 1 goes as follows.
Algorithm 1′. Sampling Ξ together with (Xi : 1 ≤ i ≤ Ξ).
(i) Initialize
$T'_{0}=0$, k = 1.(ii) For
$T'_{k-1}<\infty$, sample J̃ ~ Bernoulli $(\mathbb {P}(T'_{k}=\infty\mid T'_{k-1}))$.(iii) If J′ = 0, sample
$(X_{i}\colon i=T'_{k-1}+1, \ldots, T'_{k})$ conditional on $T'_{k}<\infty$ (see Procedure A′ below). Set k = k + 1 and go back to step (ii); otherwise (J′ = 1), set $\Xi_1=T'_{k-1}$ and go to step (iv).(iv) Apply Procedure C (detailed in Section 4.2) iteratively to sample Ξ2.
(v) Set Ξ = max{Ξ1,Ξ2}. If Ξ > Ξ1, sample
$(X_{i}\colon i=T'_{k-1}+1, \ldots, \Xi )$ conditional on $T'_{k}=\infty$ (see Procedure B′ below).
We also modify Procedure A and Procedure B as follows.
Procedure A′. Sampling J′with 
$\mathbb {P}(J^{\prime}=1)=\mathbb {P}(T_{1}^{\prime}=\infty)$. If J′ = 0, output 
$(X_{1}, \ldots, X_{T_{1}^{\prime}})$}.
(i) Sample a random time N with PMF (4). Let θN = a2N(α−1)−2. Sample U 1 ~ Uniform[0, 1]. If
$U_{1}\leq\tfrac12$, go to step (ii(a)); otherwise, go to step (ii(b)).(ii)
(a) Generate X 1, …, X 2N+1−1 under exponential tilting with tilting parameter θN Let
\begin{align*}
T_{1}^{\prime} =\inf\{n\geq1\colon \vert S_{n} \vert > an^{\alpha
}+bn^{1-\alpha} \} \wedge2^{N}.
\end{align*}
(b) Generate X 1, …, X 2N+1−1 under exponential tilting with tilting parameter −θN. Let
\begin{align*}
T_1^{'} = \inf \{ n \ge 1:|{S_n}| > a{n^\alpha } + b{n^{1 - \alpha }}\} \wedge {2^N}.
\end{align*}
(iii) Generate U 2 ~ Uniform[0, 1]. If
\begin{align*}
{U_2} \le {{{{(\exp ({\theta _N}{S_{T_1^{'}}} - \psi ({\theta _N})T_1^{'})/2 + \exp ( - {\theta _N}{S_{T_1^{'}}} - \psi ( - {\theta _N})T_1^{'})/2)}^{ - 1}}} \over {p(N)}}\\
\quad {\kern 1pt} \times 1\{ T_1^{'} \in {[2^N}{,2^{N + 1}})\},
\end{align*}
then set J′ = 0 and output
$((X_{1}, X_{2}, \ldots, X_{T_{1}^{\prime}}))$; otherwise, set J′ = 1.
Propsition 1. In Procedure A′, J′ is a Bernoulli random variable with probability of success 
$\mathbb {P}(T_{1}^{\prime}=\infty)$. If J = 0, the output 
$((X_{1}, X_{2}, \ldots, X_{T_{1}^{\prime}}))$ follows the distribution of 
$((X_{1}, X_{2}, \ldots, X_{T_{1}^{\prime}}))$ conditional on 
$T_{1}^{\prime}<\infty$.
The proof of Proposition 1 follows exactly the same line of analysis as the proof of Theorem 1. We shall omit it here.
Let
\begin{align*}
{L^{'}}(n) = \inf \{ k > n:{S_k} \in ( - {a \over 4}{k^\alpha },{a \over 4}{k^\alpha }){\kern 1pt} \;{\rm{or}}\;{S_k} > a{k^\alpha } + b{k^{1 - \alpha }}{\kern 1pt} \;{\rm{or}}\;{\kern 1pt} {S_k} < - a{k^\alpha } - b{k^{1 - \alpha }}\} .
\end{align*}
Procedure B′. Sampling (X 1, …, Xn) conditional on 
$T_{1}=\infty$.
(i) Sample (X 1, …, Xn) under the nominal distribution ℙ(·).
(ii) If max1≤k≤n{Sk − akα − bk 1−α} > 0 or min1≤k≤n{Sk + akα + bk 1−α} < 0, go back to step (i); otherwise, go to step (iii).
(iii) Sample L′(n) and (Xn +1, …, XL ′(n)) under the nominal distribution ℙ(·). If |SL ′(n)| > aL′(n)α + bL′(n)1−α, go back to step (i); otherwise, go to step (iv).
(iv) Sample Ñ with PMF pL (n) defined in (5). Set θ̃Ñ = 2Ñ−2a(2Ñ + L(n))α. Sample U 1 ~ Uniform[0, 1]. If
$S_{L(n)}> aL(n)^{\alpha}+bL(n)^{1-\alpha }$, go to step (v(a)); otherwise, go to step (v(b)).(v)
(a) Generate X̃ 1, X̃ 2, …, X̃ 2Ñ+1−1 under exponential tilting with tilting parameter θ̃Ñ. Let
\begin{align*}
{\tilde T^{'}} = \inf \{ n \ge 1:|{S_{{L^{'}}(n)}} + 2{\tilde S_k}| > a{(k + {L^{'}}(n))^\alpha } + b{(k + {L^{'}}(n))^{1 - \alpha }}\} \wedge {2^{2\tilde N + 1}}.
\end{align*}
(b) Generate X̃ 1, X̃ 2, …, X̃ 2Ñ+1−1 under exponential tilting with tilting parameter − θ̃Ñ. Let
\begin{align*}
{\tilde T^{'}} = \inf \{ n \ge 1:|{S_{{L^{'}}(n)}} + {\tilde S_k}| > a{(k + {L^{'}}(n))^\alpha } + b{(k + {L^{'}}(n))^{1 - \alpha }}\} \wedge {2^{2\tilde N + 1}}.
\end{align*}
(vi) Sample U 2 ~ Uniform[0, 1]. If
\begin{align*}
U_{2}&\leq\frac{(\exp(\tilde\theta_{\tilde
N}\tilde S_{\tilde T^{\prime}}-\tilde\psi(\tilde\theta_{\tilde N}))/2 +
\exp( -\tilde\theta_{\tilde N}\tilde S_{\tilde T^{\prime}} - \tilde
\psi({-}\tilde\theta_{\tilde N}))/2) ^{-1}}{p_{t}(\tilde N)}\\
&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad
\times{\bf 1}\{ \tilde T^{\prime}\in[ 2^{\tilde N}, 2^{\tilde N+1})
\},
\end{align*}
set J̃′ = 0 and go back to step (i); otherwise, set J̃′ = 1 and output (X 1, …, Xn).
4.2. Sampling of the service time process and Ξ2
We start by verifying (C2).
Lemma 8. If 
$\tfrac12<\alpha<\beta$,
\begin{align*}
\sum_{n=1}^{\infty} \mathbb {P}(V_{n}\in(n\mu-\epsilon_{n}, n\mu+\epsilon_{n}
+h))<\infty.
\end{align*}
Proof. We have
\begin{align*}
\mathbb {P}(V_{n}\in(n\mu-\epsilon_{n}, n\mu+\epsilon_{n}+h)) =\bar F(n\mu
-\epsilon_{n})-\bar F(n\mu+\epsilon_{n}+h)\\[4pt]
\leq\frac{\beta}{(n\mu- n^{\alpha})^{(\beta+1)}} (2 n^{\alpha}+h)\\[4pt]
=\frac{\beta(2+hn^{-\alpha})}{n^{\beta+1-\alpha}(\mu-n^{-(\beta-\alpha
)})^{\beta+1}}.
\end{align*}
As β + 1 − α > 1,
\begin{align*}
\sum_{n=1}^{\infty} \frac{\beta(2+hn^{-\alpha})}{n^{\beta+1-\alpha}
(\mu-n^{\alpha-\beta})^{\beta+1}}<\infty.\\[-48pt]
\end{align*}
To find Ξ2, we use a similar record-breaker idea. In particular, we say that Vn is a record breaker if
\begin{align*}
V_{n} \in(n\mu- \epsilon_n, n\mu+\epsilon_{n}+h).
\end{align*}
The idea is to find the record breakers sequentially until there are no more record breakers. Specifically, let K 0 := 0. If Ki −1 < ∞,
\begin{align*}
K_{i}=\inf\{n>K_{i-1}\colon V_{n} \in(n\mu- \epsilon_n, n\mu+\epsilon_{n}+h)\};
\end{align*}
if Ki −1 = ∞, Ki = ∞. Let τ = min{i > 0: Ki = ∞}. Then we can set Ξ2 = Kτ −1.
The task now is to find the Ki one by one. We achieve this by finding a proper sequence of upper and lower bounds for ℙ(Ki = ∞). We start with K 1. Note that
\begin{align*}
\mathbb {P}(K_{1}=\infty)=\prod_{n=1}^{\infty}( 1-\mathbb {P}(V_{n}\in(n\mu-\epsilon_{n},
n\mu+\epsilon_{n}+h))).
\end{align*}
Let
\begin{align*}
u(k)=\prod_{n=1}^{k}( 1-\mathbb {P}(V_{n}\in(n\mu-\epsilon_{n}, n\mu+\epsilon
_{n}+h))).
\end{align*}
Then we have ℙ(K 1 = ∞) < u(k + 1) < u(k) for any k ≥ 1, and limk→∞ u(k) = ℙ(K 1 = ∞). We also note that u(k) − u(k − 1) = ℙ(K 1 = k).
From the proof of Lemma 8, we have, for n > (2/μ)1/(β−α),
\begin{align*}
\mathbb {P}(V_{n}\in(n\mu-\epsilon_{n}, n\mu+\epsilon_{n}+h))<\frac{2(2+h)\beta}{\mu
}\frac{1}{n^{\beta+1-\alpha}}.
\end{align*}
Then for large enough k* such that k* > (2/μ)1/(β−α) and
\begin{align*}
{{2(2 + h)\beta } \over \mu }{1 \over {{k^{*,\beta + 1 - \alpha }}}} < 1,
\end{align*}
we have, for k > k*,
\begin{align*}
\prod_{n=k+1}^{\infty}( 1-\mathbb {P}(V_{n}\in(n\mu-\epsilon_{n}, n\mu
+\epsilon_{n}+h)))
& \geq\prod_{n=k+1}^{\infty}\Big( 1-\frac{2(2+h)\beta}{\mu}\frac
{1}{n^{\beta+1-\alpha}}\Big) \\[4pt]
& \geq\exp\bigg( -\frac{(2+h)\beta}{\mu}\sum_{n=k+1}^{\infty}\frac
{1}{n^{\beta+1-\alpha}}\bigg) \\[4pt]
& \geq\exp\Big( -\frac{(2+h)\beta}{\mu} (k+1)^{-(\beta-\alpha)}\Big).
\end{align*}
Let l(k) = 0 for k < k*, and
\begin{align*}
l(k)=u(k)\exp\Big( -\frac{2(2+h)\beta}{\mu} (k+1)^{-(\beta-\alpha)}\Big)
\end{align*}
for k > k*. Then we have l(k) ≤ l(k + 1) < ℙ(K 1 = ∞) and limk→∞ l(k) = ℙ(K 1 = ∞).
Similarly, given Ki −1 = m < ∞, we can construct the sequences of upper and lower bounds for ℙ(Ki = ∞ | Ki −1 = m) as
\begin{align*}
u_{m}(k)=\prod_{n=m+1}^{k}( 1-\mathbb {P}(V_{n}\in(n\mu-\epsilon_{n},
n\mu+\epsilon_{n}+h)))
\end{align*}
for k > m, and
\begin{align*}
l_{m}(k)=u_{m}(k)\exp\Big( -\frac{(2+h)\beta}{\mu} (k+1)^{-(\beta-\alpha
)}\Big).
\end{align*}
Based on the sequence of lower and upper bounds, given Ki −1 = m, we can sample Ki using the following iterative procedure.
Procedure C. Sample Ki conditional on Ki −1 = m.
(i) Generate U ~ Uniform[0, 1]. Set k = m + 1. Calculate um(k) and lm(k).
(ii) While lm(k) < U < um(k)
Set k = k + 1. Update um (k) and lm(k).
end while.
(iii) If U < lm(k), output Ki = ∞; otherwise, output Ki = k.
Once we find the values of the Ki, sampling the Vn conditional on the information of the Ki is straightforward. We summarize the simulation of the service time process together with Ξ in Algorithm 2.
Algorithm 2. Sampling Ξ together with (Vi : 1 ≤ i ≤ Ξ).
(i) Initialize K 0 = 0, i = 1.
(ii) Given the value of Ki −1 < ∞, sample Ki using Procedure C.
(iii) If Ki < ∞, set i = i + 1 and go back to step (ii); otherwise, set Ξ2 = Ki −1 and go to step (iv).
(iv) Apply Algorithm 1′ to find Ξ.
(v) Sample (Vi : i = 1, 2, … ,Ξ) conditional on (K 1, K 2, …, Ki −1) using the acceptance– rejection method with the nominal distribution of the service times as the proposal distribution.
We next provide some comments about the running time of Procedure C. Let Φi denote the number of iterations in Procedure C to generate Ki. We shall show that, while ℙ(Φi < ∞) = 1, 
$\mathbb {E}[\Phi_i] =\infty$. Taking Φ1 as an example,
\begin{align*}
&{\mathbb{P}}({\Phi _1} > n) = {\mathbb{P}}({K_1} > n)\\
&= {\rm{P}}({l_1}(n) < U < {u_1}(n))\\
&\ge {u_1}(n)(1 - \exp ( - {{2(2 + h)\beta } \over \mu }{(n + 1)^{ - (\beta - \alpha )}})),
\end{align*}
with
\begin{align*}
1- \exp\Big(\Big({-}\frac{2(2+h)\beta}{\mu} (n+1)^{-(\beta-\alpha)}\Big)\Big)=O(n^{-(\beta-\alpha)}),
\end{align*}
and u 1(n) ≥ ℙ(K 1 = ∞) for any n ≥ 1. As 1 < β − α < 1, we have ℙ(K 1 < ∞) = 1, but 
$\sum\nolimits_{n = 1}^\infty {\mathbb{P}}({K_1} > n) = \infty $. Thus, ℙ(Φ1 < ∞) = 1, but 
$\mathbb {E}[\Phi_1]=\infty$.
The fact that the Procedure C has infinite expected termination time may be unavoidable in the following sense. In the absence of additional assumptions on the traffic feeding into the infinite-server queue, any algorithm which simulates stationary departures during, say, time interval [0, 1], must be able to directly simulate the earliest arrival, from the infinite past, which departs in [0, 1]. If the arrivals are simulated sequentially backwards in time, we now argue that the expected time to detect such an arrival must be infinite. Assuming, for simplicity, deterministic interarrival times equal to 1, and letting −T < 0 be the time at which such earliest arrival occurs, then we have
\begin{align*}
&{\mathbb{P}}(T > n) \ge {\rm{P}}\left( {\bigcup\limits_{k = n + 1}^\infty \{ {V_k} \in [k,k + 1]\} } \right)\\
&\ge (1 - {\mathbb{P}}(V > n))\sum\limits_{k = n + 1}^\infty {\mathbb{P}}({V_k} \in [k,k + 1])\\
&= (1 - {\mathbb{P}}(V > n)){\mathbb{P}}(V > n + 1).
\end{align*}
As 
$\sum_{n=0}^\infty \mathbb {P}(V>n) =\infty$, we must have 
$\mathbb {E}[T]=\infty$.
Remark 2. Based on our analysis above, in general, the choice of ∊n imposes a trade-off between Ξ1 and Ξ2. The smaller ∊n is, the larger the value of Ξ1 and the smaller the value of Ξ2.
4.3. Numerical experiment on the departure process of an M/G/∞ queue
In this section we apply Algorithms 1′ and 2 to simulate the steady-state departure process of an infinite-server queue whose service times have infinite mean.
We consider an infinite-server queue having Poisson arrival process with rate 1, and Pareto service time distributions with probability density function
\begin{align*}
f(v)=\beta v^{-(\beta+1)}{\bf 1}\{v\geq1\},
\end{align*}
for 
$\beta\in(\tfrac12,1)$. Note that we already know that the departure process of this M/G/∞ queue should also be Poisson process with rate 1. Therefore, this numerical experiment would help us verify the correctness of our algorithm.
We truncate the length of path at 106 steps. We tried different pairs of parameters α and β, and executed 1000 trials for each pair of α and β. We count the number of departures between times 0 and 1 for each run and construct the corresponding relative frequency bar plot in Figure 3. We observe that the distribution of simulated departures between times 0 and 1 indeed follows a Poisson distribution with rate 1. In particular, the distribution is independent of the values of α and β, which is consistent with what we expected. We also conduct the χ 2 test as goodness of fit tests with the four groups of sampled data against the Poisson distribution. The corresponding p-values are 0.2404, 0.2589, 0.4835, and 0.1137, respectively. Therefore, the tests fail to reject that the generated samples are Poisson distributed.
Figure 3: Histograms comparison for sampled departure.
