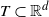1. Introduction
Let T be a compact set in
![]() $\mathbb{R}^{d}$
, and consider a continuous Gaussian random field
$\mathbb{R}^{d}$
, and consider a continuous Gaussian random field
![]() $f=\left\{ f(t)\,:\,t\in T\right\} $
with zero mean and unit variance. For each
$f=\left\{ f(t)\,:\,t\in T\right\} $
with zero mean and unit variance. For each
![]() $s,t\in T$
, we denote its covariance function by
$s,t\in T$
, we denote its covariance function by
![]() $C\left( s,t\right) = \text{Cov}\left( f(s),f(t)\right) $
. Let
$C\left( s,t\right) = \text{Cov}\left( f(s),f(t)\right) $
. Let
![]() $\mu \left( \cdot\right) $
and
$\mu \left( \cdot\right) $
and
![]() $\sigma \left( \cdot \right) $
be two deterministic functions, where
$\sigma \left( \cdot \right) $
be two deterministic functions, where
![]() $\sigma \left( \cdot \right) $
is assumed to be strictly positive. Define
$\sigma \left( \cdot \right) $
is assumed to be strictly positive. Define
where
![]() $g(t)=\mu (t)+\sigma (t)f(t)$
. We are interested in designing an efficient Monte Carlo estimator for computing the tail probabilities
$g(t)=\mu (t)+\sigma (t)f(t)$
. We are interested in designing an efficient Monte Carlo estimator for computing the tail probabilities
![]() $w(u)=\mathbb{P}\left( \mathcal{I}\left( T\right) >u\right)$
as
$w(u)=\mathbb{P}\left( \mathcal{I}\left( T\right) >u\right)$
as
![]() $u\rightarrow \infty $
.
$u\rightarrow \infty $
.
1.1. Motivation and literature
The exponential integral of a Gaussian random field appears in several applied probability models. Liu [Reference Liu4] presented some examples where
![]() $\mathcal{I}\left( T\right) $
plays a key role in spatial point processes, portfolio risk analysis, and asset pricing. The tail event of
$\mathcal{I}\left( T\right) $
plays a key role in spatial point processes, portfolio risk analysis, and asset pricing. The tail event of
![]() $\mathcal{I}\left( T\right) $
is an important topic for risk management.
$\mathcal{I}\left( T\right) $
is an important topic for risk management.
Tail approximations of
![]() $\mathcal{I}\left( T\right) $
have received little attention. Liu [Reference Liu4] provided for the first time analytic approximations of w(u) when f is a homogeneous Gaussian random field,
$\mathcal{I}\left( T\right) $
have received little attention. Liu [Reference Liu4] provided for the first time analytic approximations of w(u) when f is a homogeneous Gaussian random field,
![]() $\mu =0$
,
$\mu =0$
,
![]() $\sigma =1$
, and under smoothness conditions; in particular, f was assumed to be almost surely at least three times continuously differentiable with respect to t. Liu [Reference Liu4] proved that the extremal behavior of
$\sigma =1$
, and under smoothness conditions; in particular, f was assumed to be almost surely at least three times continuously differentiable with respect to t. Liu [Reference Liu4] proved that the extremal behavior of
![]() $\mathcal{I}\left(T\right) $
connects very closely to that of
$\mathcal{I}\left(T\right) $
connects very closely to that of
![]() $\sup_{t\in T}f(t)$
. Liu and Xu [Reference Liu and Xu6] further extended this result to the case where the mean function
$\sup_{t\in T}f(t)$
. Liu and Xu [Reference Liu and Xu6] further extended this result to the case where the mean function
![]() $\mu$
is a smooth function.
$\mu$
is a smooth function.
The tail asymptotics of
![]() $\mathcal{I}\left( T\right) $
are actually difficult to develop when f is non-differentiable. Therefore, rare-event simulation appears as an appealing alternative since the design and analysis of specific estimators do not in general require very sharp approximations of
$\mathcal{I}\left( T\right) $
are actually difficult to develop when f is non-differentiable. Therefore, rare-event simulation appears as an appealing alternative since the design and analysis of specific estimators do not in general require very sharp approximations of
![]() $w(u)$
. Liu and Xu [Reference Liu and Xu5] introduced and studied an importance sampling algorithm whose efficiency only requires that f is uniformly Hölder continuous over the compact set T. Therefore, their results are applicable to a large number of families of Gaussian processes. To the best of our knowledge, this article is the first to develop a provably efficient rare-event simulation algorithm to compute w(u) for a general class of non-differentiable and differentiable fields.
$w(u)$
. Liu and Xu [Reference Liu and Xu5] introduced and studied an importance sampling algorithm whose efficiency only requires that f is uniformly Hölder continuous over the compact set T. Therefore, their results are applicable to a large number of families of Gaussian processes. To the best of our knowledge, this article is the first to develop a provably efficient rare-event simulation algorithm to compute w(u) for a general class of non-differentiable and differentiable fields.
The integral in
![]() $\left( 1\right) $
can be viewed as the limit of a weighted sum of correlated lognormal random variables. There exists a small rare-event simulation literature for the sum of a finite number of dependent lognormal random variables. Asmussen et al. [Reference Asmussen, Blanchet, Juneja and Rojas-Nandayapa1] proposed several efficient importance sampling estimators for the sum of a finite number of correlated lognormal random variables. The authors first used cross-entropy methods for finding the best tuning for the importance distribution, but they also observed that the largest of the increments dominates the large-deviations behavior of the sums of the correlated lognormals. Therefore, they decomposed the tail event of interest into two contributions, a dominant component corresponding to the tail of the maximum, and the remaining contribution. Motivated by [Reference Asmussen, Blanchet, Juneja and Rojas-Nandayapa1], Kortschak and Hashorva [Reference Kortschak and Hashorva3] introduced an Asmussen–Kroese conditional Monte Carlo type estimator for sums of log-elliptical risks. The conditional Monte Carlo type approach replaces a naive estimate Z of a number z by its conditional expectation given a suitable piece of information to drastically reduce its variance.
$\left( 1\right) $
can be viewed as the limit of a weighted sum of correlated lognormal random variables. There exists a small rare-event simulation literature for the sum of a finite number of dependent lognormal random variables. Asmussen et al. [Reference Asmussen, Blanchet, Juneja and Rojas-Nandayapa1] proposed several efficient importance sampling estimators for the sum of a finite number of correlated lognormal random variables. The authors first used cross-entropy methods for finding the best tuning for the importance distribution, but they also observed that the largest of the increments dominates the large-deviations behavior of the sums of the correlated lognormals. Therefore, they decomposed the tail event of interest into two contributions, a dominant component corresponding to the tail of the maximum, and the remaining contribution. Motivated by [Reference Asmussen, Blanchet, Juneja and Rojas-Nandayapa1], Kortschak and Hashorva [Reference Kortschak and Hashorva3] introduced an Asmussen–Kroese conditional Monte Carlo type estimator for sums of log-elliptical risks. The conditional Monte Carlo type approach replaces a naive estimate Z of a number z by its conditional expectation given a suitable piece of information to drastically reduce its variance.
Using the fact that the rare event,
![]() $\{\mathcal{I}\left( T\right) >u\}$
, is generally caused by the abnormal behavior of the random field at one location, we decide to propose a modified Asmussen–Kroese conditional Monte Carlo type estimator for estimating w(u).
$\{\mathcal{I}\left( T\right) >u\}$
, is generally caused by the abnormal behavior of the random field at one location, we decide to propose a modified Asmussen–Kroese conditional Monte Carlo type estimator for estimating w(u).
1.2. Assumptions
In this paper we will mainly consider two sets of assumptions for the Gaussian random field g. These two sets were introduced in [Reference Liu and Xu5] and [Reference Liu4] respectively.
Assumptions 1. The functions
![]() $\mu \left( \cdot \right) $
,
$\mu \left( \cdot \right) $
,
![]() $\sigma \left( \cdot \right) $
, and
$\sigma \left( \cdot \right) $
, and
![]() $C\left( \cdot ,\cdot \right) $
satisfy the following conditions. There exist
$C\left( \cdot ,\cdot \right) $
satisfy the following conditions. There exist
![]() $\delta $
,
$\delta $
,
![]() $\kappa >0$
, and
$\kappa >0$
, and
![]() $\beta \in (0,1]$
such that, for all
$\beta \in (0,1]$
such that, for all
![]() $\left\Vert s-t\right\Vert <\delta $
, the mean and variance functions satisfy
$\left\Vert s-t\right\Vert <\delta $
, the mean and variance functions satisfy
![]() $\left\vert \mu \left( s\right) -\mu \left( t\right) \right\vert +\left\vert \sigma \left( s\right) -\sigma \left( t\right) \right\vert \leq \kappa\left\Vert s-t\right\Vert ^{\beta }$
, where
$\left\vert \mu \left( s\right) -\mu \left( t\right) \right\vert +\left\vert \sigma \left( s\right) -\sigma \left( t\right) \right\vert \leq \kappa\left\Vert s-t\right\Vert ^{\beta }$
, where
![]() $\left\Vert t\right\Vert $
is the Euclidean norm of
$\left\Vert t\right\Vert $
is the Euclidean norm of
![]() $t\in \mathbb{R}^{d}$
. For all
$t\in \mathbb{R}^{d}$
. For all
![]() $\left\Vert s-s^{\prime }\right\Vert <\delta $
and
$\left\Vert s-s^{\prime }\right\Vert <\delta $
and
![]() $\left\Vert t-t^{\prime }\right\Vert <\delta $
, the covariance function satisfies
$\left\Vert t-t^{\prime }\right\Vert <\delta $
, the covariance function satisfies
![]() $\left\vert C\left( t,s\right) -C\left( t^{\prime },s^{\prime }\right)\right\vert \leq \kappa \big( \left\Vert s-s^{\prime }\right\Vert ^{2\beta}+\left\Vert t-t^{\prime }\right\Vert ^{2\beta }\big) $
.
$\left\vert C\left( t,s\right) -C\left( t^{\prime },s^{\prime }\right)\right\vert \leq \kappa \big( \left\Vert s-s^{\prime }\right\Vert ^{2\beta}+\left\Vert t-t^{\prime }\right\Vert ^{2\beta }\big) $
.
Assumptions 2. The random field f is a homogeneous Gaussian random field that is almost surely at least three times continuously differentiable with respect to t. We denote its covariance function by
![]() $C(t-s)=\text{Cov}(f(s),f(t))$
. The Hessian matrix of C(t) at the origin is
$C(t-s)=\text{Cov}(f(s),f(t))$
. The Hessian matrix of C(t) at the origin is
![]() $-I$
, where I is a
$-I$
, where I is a
![]() $d\times d$
identity matrix. It is also assumed that
$d\times d$
identity matrix. It is also assumed that
![]() $\mu \left( t\right) =0$
and
$\mu \left( t\right) =0$
and
![]() $\sigma \left(t\right) =\sigma >0$
for all
$\sigma \left(t\right) =\sigma >0$
for all
![]() $t\in T$
. Finally, T is a d-dimensional Jordan-measurable compact subset of
$t\in T$
. Finally, T is a d-dimensional Jordan-measurable compact subset of
![]() $\mathbb{R}^{d}$
.
$\mathbb{R}^{d}$
.
1.3. Tail approximations and importance sampling estimators
For Assumptions 1, no asymptotic equivalent form of w(u) is known. Only bounds were provided in [Reference Liu and Xu5]: there exist constants
![]() $c_{0}$
,
$c_{0}$
,
![]() $c_{1}$
,
$c_{1}$
,
![]() $c_{2}$
, such that, for large u,
$c_{2}$
, such that, for large u,
 \begin{equation*}\exp \left( -\frac{\left( \log u\right) ^{2}+c_{1}\log u\log \left( \log u\right) +c_{0}}{2\sigma _{\ast }}\right) \leq w(u)\leq \exp \left( -\frac{\left( \log u\right) ^{2}}{2\sigma _{\ast }}+c_{2}\log u\right) ,\end{equation*}
\begin{equation*}\exp \left( -\frac{\left( \log u\right) ^{2}+c_{1}\log u\log \left( \log u\right) +c_{0}}{2\sigma _{\ast }}\right) \leq w(u)\leq \exp \left( -\frac{\left( \log u\right) ^{2}}{2\sigma _{\ast }}+c_{2}\log u\right) ,\end{equation*}
where
![]() $\sigma _{\ast }=\sup_{t\in T}\sigma (t)$
. In [Reference Liu and Xu5], the authors introduced an importance sampling estimator and proved that it is logarithmically efficient. Central to their method analysis is a change of measure that mimics the conditional distribution of g given the occurrence of the rare event
$\sigma _{\ast }=\sup_{t\in T}\sigma (t)$
. In [Reference Liu and Xu5], the authors introduced an importance sampling estimator and proved that it is logarithmically efficient. Central to their method analysis is a change of measure that mimics the conditional distribution of g given the occurrence of the rare event
![]() $\{\mathcal{I}\left( T\right) >u\}$
. An appealing feature of their change of measure is that it does not rely much on the specific mean, variance, and covariance structure of the random field g. Their approach consists first in approximating the integral by a discrete sum and controlling the bias caused by the discretization, and second in bounding the second moment of the (discrete) importance sampling estimator.
$\{\mathcal{I}\left( T\right) >u\}$
. An appealing feature of their change of measure is that it does not rely much on the specific mean, variance, and covariance structure of the random field g. Their approach consists first in approximating the integral by a discrete sum and controlling the bias caused by the discretization, and second in bounding the second moment of the (discrete) importance sampling estimator.
For Assumptions 2, [Reference Liu4] provided an exact asymptotic approximation of w(u). For u large enough, let v be the unique solution to
![]() $(2\pi /\sigma )^{d/2}v^{-d/2}\text{e}^{\sigma v}=u$
. For some positive constant H, [Reference Liu4] showed that
$(2\pi /\sigma )^{d/2}v^{-d/2}\text{e}^{\sigma v}=u$
. For some positive constant H, [Reference Liu4] showed that
![]() $w(u)\sim H\text{mes}\left( T\right) v^{d-1}\exp \left( -v^{2}/2\right)$
as
$w(u)\sim H\text{mes}\left( T\right) v^{d-1}\exp \left( -v^{2}/2\right)$
as
![]() $u\rightarrow \infty $
, where
$u\rightarrow \infty $
, where
![]() $\text{mes}\left( T\right) $
is the Lebesgue measure of T. Liu and Xu [Reference Liu and Xu6] studied another importance sampling estimator of w(u) that runs in polynomial time with respect to
$\text{mes}\left( T\right) $
is the Lebesgue measure of T. Liu and Xu [Reference Liu and Xu6] studied another importance sampling estimator of w(u) that runs in polynomial time with respect to
![]() $\log u$
, and proved that it is asymptotically strongly efficient (i.e. it has an asymptotically vanishing error). The authors used the same strategy as in [Reference Liu and Xu5], which consists of approximating the integral by a discrete sum. However, the change of measure that approximates the conditional distribution of f given
$\log u$
, and proved that it is asymptotically strongly efficient (i.e. it has an asymptotically vanishing error). The authors used the same strategy as in [Reference Liu and Xu5], which consists of approximating the integral by a discrete sum. However, the change of measure that approximates the conditional distribution of f given
![]() $\{\mathcal{I}\left( T\right) >u\}$
now exploits the knowledge of the joint distribution of the two first derivatives of the random field f.
$\{\mathcal{I}\left( T\right) >u\}$
now exploits the knowledge of the joint distribution of the two first derivatives of the random field f.
Our main contributions can be summarized as follows. First, we introduce a modified Kortschak–Hashorva conditional Monte Carlo type estimator by splitting the probability that we want to estimate into two parts, of which one part can be computed without simulation. This increases the accuracy of our estimator. Second, we provide theoretical arguments that show that our estimator is logarithmically efficient or polynomially efficient according to the sets of assumptions. Third, we present a numerical study which shows that, with the same computational time budget, our estimator is more efficient than the estimator in [Reference Liu and Xu5] (at least for the examples considered in this paper).
The paper is organized as follows. Section 2 provides the construction of our conditional Monte Carlo algorithm and presents the main results. Section 3 includes simulation experiments. Proofs of our main theorems are given in Section 4.
2. Main results
We assume without loss of generality that 0 belongs to the interior of T and that
![]() $\sigma (0)=\sigma _{\ast }=\sup_{t\in T}\sigma (t)$
. As in [Reference Liu and Xu5, Reference Liu and Xu6], we introduce a discretization scheme on T. For any positive
$\sigma (0)=\sigma _{\ast }=\sup_{t\in T}\sigma (t)$
. As in [Reference Liu and Xu5, Reference Liu and Xu6], we introduce a discretization scheme on T. For any positive
![]() $S_{u}$
, let
$S_{u}$
, let
![]() $G_{S_{u}}$
be a subset of
$G_{S_{u}}$
be a subset of
![]() $\mathbb{R}^{d}$
defined by
$\mathbb{R}^{d}$
defined by
where
![]() $\mathbb{Z}$
is the set of integers, i.e.
$\mathbb{Z}$
is the set of integers, i.e.
![]() $G_{S_{u}}$
is a regular lattice on
$G_{S_{u}}$
is a regular lattice on
![]() $\mathbb{R}^{d}$
. For each
$\mathbb{R}^{d}$
. For each
![]() $t=(t_{1},\ldots,t_{d})\in G_{s_{u}}$
, define
$t=(t_{1},\ldots,t_{d})\in G_{s_{u}}$
, define
![]() $T_{S_{u}}\left( t\right) = \{ (u_{1},\ldots,u_{d})\in T\,:\,u_{j}\in(t_{j}-1/(2S_{u});\ t_{j}+1/(2S_{u})]$
for
$T_{S_{u}}\left( t\right) = \{ (u_{1},\ldots,u_{d})\in T\,:\,u_{j}\in(t_{j}-1/(2S_{u});\ t_{j}+1/(2S_{u})]$
for
![]() $j=1,\ldots,d\}$
, i.e. the intersection of T and the
$j=1,\ldots,d\}$
, i.e. the intersection of T and the
![]() $(1/S_{u})$
-cube centered at t. Furthermore, let
$(1/S_{u})$
-cube centered at t. Furthermore, let
![]() $T_{S_{u}}=\left\{ t\in G_{S_{u}}\,:\, \text{mes}\left( T_{S_{u}}\left( t\right) \right)>0\right\}.$
Since T is compact,
$T_{S_{u}}=\left\{ t\in G_{S_{u}}\,:\, \text{mes}\left( T_{S_{u}}\left( t\right) \right)>0\right\}.$
Since T is compact,
![]() $T_{S_{u}}$
is a finite set. We enumerate the elements in
$T_{S_{u}}$
is a finite set. We enumerate the elements in
![]() $T_{S_{u}}=\left\{ t_{0},t_{1},\ldots,t_{M_{u}}\right\} $
, where
$T_{S_{u}}=\left\{ t_{0},t_{1},\ldots,t_{M_{u}}\right\} $
, where
![]() $t_{0}=0$
and
$t_{0}=0$
and
![]() $M_{u}= \# T_{S_{u}}-1$
. Note that
$M_{u}= \# T_{S_{u}}-1$
. Note that
![]() $M_{u}\sim \text{mes}(T)S_{u}^{d}$
as
$M_{u}\sim \text{mes}(T)S_{u}^{d}$
as
![]() $u\rightarrow \infty $
.
$u\rightarrow \infty $
.
The approximation of
![]() $\mathcal{I}\left( T\right) $
by a discrete sum is given by
$\mathcal{I}\left( T\right) $
by a discrete sum is given by
 \begin{equation*}\mathcal{I}_{M_{u}}\left( T\right) =\sum_{i=0}^{M_{u}}m_{i,u}\text{e}^{\mu(t_{i})+\sigma (t_{i})f(t_{i})} , \end{equation*}
\begin{equation*}\mathcal{I}_{M_{u}}\left( T\right) =\sum_{i=0}^{M_{u}}m_{i,u}\text{e}^{\mu(t_{i})+\sigma (t_{i})f(t_{i})} , \end{equation*}
where
![]() $m_{i,u} = \text{mes}\left( T_{S_{u}}\left( t_{i}\right) \right) $
and we let
$m_{i,u} = \text{mes}\left( T_{S_{u}}\left( t_{i}\right) \right) $
and we let
![]() $w_{M_{u}}(u)=\mathbb{P}\left( \mathcal{I}_{M_{u}}\left( T\right) >u\right)$
.
$w_{M_{u}}(u)=\mathbb{P}\left( \mathcal{I}_{M_{u}}\left( T\right) >u\right)$
.
The following proposition helps us to understand how to control the difference between
![]() $w_{M_{u}}(u)$
and w(u), and therefore how to control the bias for an estimator of w(u). It gathers two results from [Reference Liu and Xu5, Reference Liu and Xu6].
$w_{M_{u}}(u)$
and w(u), and therefore how to control the bias for an estimator of w(u). It gathers two results from [Reference Liu and Xu5, Reference Liu and Xu6].
Proposition 1. Under Assumptions 1, for any
![]() $0<\varepsilon <1/2$
there exists a constant
$0<\varepsilon <1/2$
there exists a constant
![]() $\kappa _{0}$
such that, for any
$\kappa _{0}$
such that, for any
![]() $\eta >0$
,
$\eta >0$
,
![]() $u>\text{e}$
, and lattice size
$u>\text{e}$
, and lattice size
![]() $S_{u}=\kappa _{0}^{1/\beta } \left\vert \log \eta \right\vert ^{1/\beta }\eta ^{-1/\beta }\left( \log u\right)^{2(1+\varepsilon )/\beta }$
, we have
$S_{u}=\kappa _{0}^{1/\beta } \left\vert \log \eta \right\vert ^{1/\beta }\eta ^{-1/\beta }\left( \log u\right)^{2(1+\varepsilon )/\beta }$
, we have
Under Assumptions 2, for any
![]() $\varepsilon >0$
there exists a constant
$\varepsilon >0$
there exists a constant
![]() $\kappa _{0}$
such that, for any
$\kappa _{0}$
such that, for any
![]() $\eta \in (0,1)$
,
$\eta \in (0,1)$
,
![]() $u>2$
, and lattice size
$u>2$
, and lattice size
![]() $S_{u}=\kappa _{0}\eta ^{-(1+\varepsilon )}\left( \log u\right)^{2+\varepsilon }$
, we have
$S_{u}=\kappa _{0}\eta ^{-(1+\varepsilon )}\left( \log u\right)^{2+\varepsilon }$
, we have
For the proof under Assumptions 1, see [Reference Liu and Xu5, Theorem 2.4]; under Assumptions 2, see [Reference Liu and Xu6, Theorem 10].
We now explain how we construct our conditional Monte Carlo type estimator of
![]() $w_{M_{u}}(u)$
. We mainly modify the Asmussen–Kroese estimator introduced in [Reference Kortschak and Hashorva3] in the following way. Let
$w_{M_{u}}(u)$
. We mainly modify the Asmussen–Kroese estimator introduced in [Reference Kortschak and Hashorva3] in the following way. Let
![]() $\omega_{i,u}=m_{i,u}\text{e}^{\mu (t_{i})}$
and
$\omega_{i,u}=m_{i,u}\text{e}^{\mu (t_{i})}$
and
![]() $X_{i,u}=\text{e}^{\sigma (t_{i})f(t_{i})}$
for
$X_{i,u}=\text{e}^{\sigma (t_{i})f(t_{i})}$
for
![]() $i=0,\ldots,M_{u}$
. We have
$i=0,\ldots,M_{u}$
. We have
![]() $\mathcal{I}_{M_{u}}\left( T\right) =$
$\mathcal{I}_{M_{u}}\left( T\right) =$
![]() $\sum_{i=0}^{M_{u}}m_{i,u}\text{e}^{\mu(t_{i})}X_{i,u}=\sum_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}$
. Let
$\sum_{i=0}^{M_{u}}m_{i,u}\text{e}^{\mu(t_{i})}X_{i,u}=\sum_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}$
. Let
![]() $\bar{\omega}_{u}=\sum_{i=0}^{M_{u}}\omega _{i,u}$
and define
$\bar{\omega}_{u}=\sum_{i=0}^{M_{u}}\omega _{i,u}$
and define
![]() $v_{1,M_{u}}(u) = \mathbb{P}\big( \bar{\omega}_{u}\exp$
$v_{1,M_{u}}(u) = \mathbb{P}\big( \bar{\omega}_{u}\exp$
![]() $\big(\sum_{i=0}^{M_{u}}\omega _{i,u}\log X_{i,u}/\bar{\omega}_{u}\big)>u\big)$
,
$\big(\sum_{i=0}^{M_{u}}\omega _{i,u}\log X_{i,u}/\bar{\omega}_{u}\big)>u\big)$
,
![]() $v_{2,M_{u}}(u) = \sum_{j=0}^{M_{u}}\Psi _{j}\left( u\right)$
, where
$v_{2,M_{u}}(u) = \sum_{j=0}^{M_{u}}\Psi _{j}\left( u\right)$
, where
 \begin{align*} \Psi_{j}\left( u\right) & = \mathbb{P}\Bigg( \sum_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}>u,\ \bar{\omega}_{u}\exp \left( \sum_{i=0}^{M_{u}}\omega_{i,u}\log X_{i,u}/\bar{ \omega}_{u}\right) \leq u, \bigvee_{i=0}^{M_{u}}\omega_{i,u}X_{i,u}=\omega_{j,u}X_{j,u}\Bigg).\end{align*}
\begin{align*} \Psi_{j}\left( u\right) & = \mathbb{P}\Bigg( \sum_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}>u,\ \bar{\omega}_{u}\exp \left( \sum_{i=0}^{M_{u}}\omega_{i,u}\log X_{i,u}/\bar{ \omega}_{u}\right) \leq u, \bigvee_{i=0}^{M_{u}}\omega_{i,u}X_{i,u}=\omega_{j,u}X_{j,u}\Bigg).\end{align*}
Since, by Jensen’s inequality, we have
 \begin{equation*}\exp \left( \sum_{i=0}^{M_{u}}\omega _{i,u}\log X_{i,u}/\bar{\omega}_{u}\right) \leq \frac{1}{\bar{\omega}_{u}}\sum_{i=0}^{M_{u}}\omega_{i,u}X_{i,u},\end{equation*}
\begin{equation*}\exp \left( \sum_{i=0}^{M_{u}}\omega _{i,u}\log X_{i,u}/\bar{\omega}_{u}\right) \leq \frac{1}{\bar{\omega}_{u}}\sum_{i=0}^{M_{u}}\omega_{i,u}X_{i,u},\end{equation*}
we deduce that
 \begin{equation*}\mathbb{P}( \mathcal{I}_{M_{u}}( T) >u) =v_{1,M_{u}}(u)+\mathbb{P}\Bigg(\sum_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}>u,\bar{\omega}_{u}\exp \left(\sum_{i=0}^{M_{u}}\omega _{i,u}\log X_{i,u}/\bar{\omega}_{u}\right) \leq u\Bigg) ,\end{equation*}
\begin{equation*}\mathbb{P}( \mathcal{I}_{M_{u}}( T) >u) =v_{1,M_{u}}(u)+\mathbb{P}\Bigg(\sum_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}>u,\bar{\omega}_{u}\exp \left(\sum_{i=0}^{M_{u}}\omega _{i,u}\log X_{i,u}/\bar{\omega}_{u}\right) \leq u\Bigg) ,\end{equation*}
and we finally get the following decomposition of
![]() $w_{M_{u}}(u)$
:
$w_{M_{u}}(u)$
:
Such a decomposition is interesting for several reasons. First, note that
![]() $v_{1,M_{u}}(u)$
may be numerically computed since the random variable
$v_{1,M_{u}}(u)$
may be numerically computed since the random variable
![]() $\sum_{i=0}^{M_{u}}\omega _{i,u}\log X_{i,u}$
has a Gaussian distribution. Second, we have noted in experiments that the variance of the estimator from [Reference Kortschak and Hashorva3] may be large when the Gaussian random variables are highly correlated and when
$\sum_{i=0}^{M_{u}}\omega _{i,u}\log X_{i,u}$
has a Gaussian distribution. Second, we have noted in experiments that the variance of the estimator from [Reference Kortschak and Hashorva3] may be large when the Gaussian random variables are highly correlated and when
![]() $\bar{\omega}_{u}\exp \big( \sum_{i=0}^{M_{u}}\omega_{i,u}\log X_{i,u}/\bar{\omega}_{u}\big) >u$
. Consequently, it is more efficient to replace the probability of such an event by its value.
$\bar{\omega}_{u}\exp \big( \sum_{i=0}^{M_{u}}\omega_{i,u}\log X_{i,u}/\bar{\omega}_{u}\big) >u$
. Consequently, it is more efficient to replace the probability of such an event by its value.
For
![]() $j=0,1,\ldots,M_{u}$
, let
$j=0,1,\ldots,M_{u}$
, let
![]() $N_{j,u}$
be a vector of
$N_{j,u}$
be a vector of
![]() $M_{u}+1$
independent standard Gaussian random variables, and
$M_{u}+1$
independent standard Gaussian random variables, and
![]() $A_{j,u}$
be a lower non-singular triangular matrix of size
$A_{j,u}$
be a lower non-singular triangular matrix of size
![]() $M_{u}+1$
such that
$M_{u}+1$
such that
 \begin{equation*}\Bigg(\,\begin{array}{c} f(t_{j}) \\[5pt]f(t_{(-j)}) \end{array}\Bigg) =A_{j,u}N_{j,u},\end{equation*}
\begin{equation*}\Bigg(\,\begin{array}{c} f(t_{j}) \\[5pt]f(t_{(-j)}) \end{array}\Bigg) =A_{j,u}N_{j,u},\end{equation*}
with
![]() $f(t_{(-j)})=\left( f(t_{i})\right) _{i\neq j}$
. We introduce the following unbiased estimator of
$f(t_{(-j)})=\left( f(t_{i})\right) _{i\neq j}$
. We introduce the following unbiased estimator of
![]() $\Psi _{j}\left( u\right) $
:
$\Psi _{j}\left( u\right) $
:
 \begin{align*}Z_{j}\left( u\right) & = \mathbb{P}\Bigg( \sum_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}>u,\ \bar{\omega}_{u}\exp \left( \sum_{i=0}^{M_{u}}\omega _{i,u}\log X_{i,u}/\bar{\omega}_{u}\right) \leq u, \\ & \qquad \quad \bigvee_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}=\omega_{j,u}X_{j,u} \, \Big \vert \, N_{j,u}^{(-1)}\Bigg) ,\end{align*}
\begin{align*}Z_{j}\left( u\right) & = \mathbb{P}\Bigg( \sum_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}>u,\ \bar{\omega}_{u}\exp \left( \sum_{i=0}^{M_{u}}\omega _{i,u}\log X_{i,u}/\bar{\omega}_{u}\right) \leq u, \\ & \qquad \quad \bigvee_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}=\omega_{j,u}X_{j,u} \, \Big \vert \, N_{j,u}^{(-1)}\Bigg) ,\end{align*}
where
![]() $N_{j,u}^{(-1)}=\left( N_{j,u,2},\ldots,N_{j,u,M_{u}+1}\right) ^{\prime }$
. We have
$N_{j,u}^{(-1)}=\left( N_{j,u,2},\ldots,N_{j,u,M_{u}+1}\right) ^{\prime }$
. We have
 \begin{align*}&\left\{ \sum_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}>u,\bar{\omega}_{u}\exp\left( \sum_{i=0}^{M_{u}}\omega _{i,u}\log X_{i,u}/\bar{\omega}_{u}\right)\leq u,\bigvee_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}=\omega_{j,u}X_{j,u}\right\} \\[5pt]&\quad =\left\{ \sum_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}>u\right\} \bigcap \left\{\bar{\omega}_{u}\exp \left( \sum_{i=0}^{M_{u}}\omega _{i,u}\log X_{i,u}/\bar{\omega}_{u}\right) \leq u\right\} \\[5pt] & \qquad \bigcap_{i\neq j}\left\{ \omega_{i,u}X_{i,u}\leq \omega _{j,u}X_{j,u}\right\} .\end{align*}
\begin{align*}&\left\{ \sum_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}>u,\bar{\omega}_{u}\exp\left( \sum_{i=0}^{M_{u}}\omega _{i,u}\log X_{i,u}/\bar{\omega}_{u}\right)\leq u,\bigvee_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}=\omega_{j,u}X_{j,u}\right\} \\[5pt]&\quad =\left\{ \sum_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}>u\right\} \bigcap \left\{\bar{\omega}_{u}\exp \left( \sum_{i=0}^{M_{u}}\omega _{i,u}\log X_{i,u}/\bar{\omega}_{u}\right) \leq u\right\} \\[5pt] & \qquad \bigcap_{i\neq j}\left\{ \omega_{i,u}X_{i,u}\leq \omega _{j,u}X_{j,u}\right\} .\end{align*}
It is noteworthy that all the events in the previous intersection may be written as an event that
![]() $N_{j,u,1}$
is smaller or greater than a threshold that only depends on
$N_{j,u,1}$
is smaller or greater than a threshold that only depends on
![]() $N_{j,u}^{(-1)}$
,
$N_{j,u}^{(-1)}$
,
![]() $A_{j,u}$
,
$A_{j,u}$
,
![]() $\left( \omega_{i,u}\right) _{i}$
, and
$\left( \omega_{i,u}\right) _{i}$
, and
![]() $\left( \sigma (t_{i})\right) _{i}$
. The threshold for the event
$\left( \sigma (t_{i})\right) _{i}$
. The threshold for the event
![]() $\big\{\sum_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}>u\big\}$
has to be computed numerically, while the others have analytical expressions. The computational cost for
$\big\{\sum_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}>u\big\}$
has to be computed numerically, while the others have analytical expressions. The computational cost for
![]() $Z_{j}\left( u\right) $
is mainly due to the cost of computing the matrix
$Z_{j}\left( u\right) $
is mainly due to the cost of computing the matrix
![]() $A_{j,u}$
through a Cholesky decomposition: the serial version of the Cholesky algorithm is of cubic complexity, i.e. the cost of decomposition of the
$A_{j,u}$
through a Cholesky decomposition: the serial version of the Cholesky algorithm is of cubic complexity, i.e. the cost of decomposition of the
![]() $(M_{u}+1)\times (M_{u}+1)$
matrix is of order
$(M_{u}+1)\times (M_{u}+1)$
matrix is of order
![]() $O\left(M_{u}^{3}\right) $
.
$O\left(M_{u}^{3}\right) $
.
Let
![]() $\mathcal{J}_{u}$
be a random variable independent of
$\mathcal{J}_{u}$
be a random variable independent of
![]() $\left(N_{j,u}\right) _{j=0,\ldots,M_{u}}$
, such that
$\left(N_{j,u}\right) _{j=0,\ldots,M_{u}}$
, such that
Our unbiased estimator of
![]() $w_{M_{u}}(u)$
is finally given by
$w_{M_{u}}(u)$
is finally given by
 \begin{equation*}Z_{M_{u}}\left( u\right) =v_{1,M_{u}}(u)+\left( \sum_{i=0}^{M_{u}}\mathbb{P}\left(X_{i,u}>u\right) \right) \sum_{j=0}^{M_{u}}\textbf{1}_{\{\mathcal{J}_{u}=j\}}\frac{Z_{j}\left( u\right) }{\mathbb{P}\left( X_{j,u}>u\right) }. \end{equation*}
\begin{equation*}Z_{M_{u}}\left( u\right) =v_{1,M_{u}}(u)+\left( \sum_{i=0}^{M_{u}}\mathbb{P}\left(X_{i,u}>u\right) \right) \sum_{j=0}^{M_{u}}\textbf{1}_{\{\mathcal{J}_{u}=j\}}\frac{Z_{j}\left( u\right) }{\mathbb{P}\left( X_{j,u}>u\right) }. \end{equation*}
Compared to [Reference Kortschak and Hashorva3], we split
![]() $w_{M_{u}}(u)$
into two parts, of which one part (
$w_{M_{u}}(u)$
into two parts, of which one part (
![]() $v_{1,M_{u}}(u)$
) can be computed without simulation, which will increase the accuracy of our estimator.
$v_{1,M_{u}}(u)$
) can be computed without simulation, which will increase the accuracy of our estimator.
2.1. Assumptions 1
Given that the tail probability w(u) converges to zero, it is usually meaningful to consider the relative error of a Monte Carlo estimator Z(u) with respect to w(u). A well-accepted efficiency concept is so-called weak efficiency, also known as logarithmic efficiency [Reference Asmussen and Glynn2, Chapter VI].
An unbiased estimator Z(u) of w(u) is said to be logarithmically efficient if
The following proposition establishes that the unbiased estimator
![]() $Z_{M_{u}}(u)$
of
$Z_{M_{u}}(u)$
of
![]() $w_{M_{u}}(u)$
is an asymptotically logarithmic efficient estimator, and that the relative bias to estimate w(u) is well controlled with an appropriate choice of
$w_{M_{u}}(u)$
is an asymptotically logarithmic efficient estimator, and that the relative bias to estimate w(u) is well controlled with an appropriate choice of
![]() $S_{u}$
.
$S_{u}$
.
Proposition 2. Assume that Assumptions 1 are satisfied. Let
![]() $\left( \eta _{u}\right) $
be a sequence of positive constants such that
$\left( \eta _{u}\right) $
be a sequence of positive constants such that
![]() $\lim_{u\rightarrow \infty }\eta _{u}=0$
and
$\lim_{u\rightarrow \infty }\eta _{u}=0$
and
![]() $\lim_{u\rightarrow \infty }\log \eta _{u}/\log (w(u))=0$
. If
$\lim_{u\rightarrow \infty }\log \eta _{u}/\log (w(u))=0$
. If
![]() $S_{u}$
is chosen such that
$S_{u}$
is chosen such that
![]() $S_{u}=O\big( \left\vert \log \eta _{u}\right\vert ^{1/\beta }\eta_{u}^{-1/\beta }\left( \log u\right) ^{2(1+\varepsilon )/\beta }\big)$
for some
$S_{u}=O\big( \left\vert \log \eta _{u}\right\vert ^{1/\beta }\eta_{u}^{-1/\beta }\left( \log u\right) ^{2(1+\varepsilon )/\beta }\big)$
for some
![]() $0<\varepsilon <1/2$
, then
$0<\varepsilon <1/2$
, then
It is shown in [Reference Liu and Xu5] that the importance sampling estimator introduced in this paper also satisfies
![]() $\left( 3\right) $
.
$\left( 3\right) $
.
2.2. Assumptions 2
A slightly stronger efficiency concept is polynomial efficiency. An unbiased estimator Z(u) of w(u) is said to be polynomially efficient of order q if
When
![]() $q=0$
, Z(u) is also said to be strongly efficient.
$q=0$
, Z(u) is also said to be strongly efficient.
Proposition 3. Assume that Assumptions 2 are satisfied. Let
![]() $\left( \eta _{u}\right) $
be a sequence of positive constants such that
$\left( \eta _{u}\right) $
be a sequence of positive constants such that
![]() $\lim_{u\rightarrow \infty }\eta _{u}=0$
and
$\lim_{u\rightarrow \infty }\eta _{u}=0$
and
![]() $\lim \inf_{u\rightarrow \infty}\eta _{u}\left( \log u\right) ^{\nu }>0$
for some positive constant
$\lim \inf_{u\rightarrow \infty}\eta _{u}\left( \log u\right) ^{\nu }>0$
for some positive constant
![]() $\nu $
. If
$\nu $
. If
![]() $S_{u}$
is chosen such that
$S_{u}$
is chosen such that
![]() $S_{u}=O\big( \eta _{u}^{-(1+\varepsilon )}\left( \log u\right) ^{2+\varepsilon }\big)$
for some
$S_{u}=O\big( \eta _{u}^{-(1+\varepsilon )}\left( \log u\right) ^{2+\varepsilon }\big)$
for some
![]() $\varepsilon >0$
, then
$\varepsilon >0$
, then
It is shown in [Reference Liu and Xu6] that the importance sampling estimator introduced in this paper is strongly efficient, which is slightly better than our estimator (from a theoretical point of view at least).
We should point out that, contrary to [Reference Kortschak and Hashorva3], our estimator has a number of terms (
![]() $M_{u}$
) in its construction that depend on the threshold u (due to the discrete approximation of the integral). Since
$M_{u}$
) in its construction that depend on the threshold u (due to the discrete approximation of the integral). Since
![]() $M_{u}$
tends to infinity as u tends to infinity, this adds several technical issues and leads to a slower rate of convergence than in [Reference Kortschak and Hashorva3].
$M_{u}$
tends to infinity as u tends to infinity, this adds several technical issues and leads to a slower rate of convergence than in [Reference Kortschak and Hashorva3].
3. Simulation
In this section we present numerical examples to study the performance of our estimator (denoted here by
![]() $Z_{\text{NR}}$
) compared to the importance sampling estimator of [Reference Liu and Xu5] (denoted by
$Z_{\text{NR}}$
) compared to the importance sampling estimator of [Reference Liu and Xu5] (denoted by
![]() $Z_{\text{LX}}$
). We only consider the importance sampling estimator of [Reference Liu and Xu5] and not [Reference Liu and Xu6] because we do not necessarily want to assume that f is a differentiable Gaussian random field. To understand the advantage of splitting the probability
$Z_{\text{LX}}$
). We only consider the importance sampling estimator of [Reference Liu and Xu5] and not [Reference Liu and Xu6] because we do not necessarily want to assume that f is a differentiable Gaussian random field. To understand the advantage of splitting the probability
![]() $w_{M_{u}}(u)$
into two parts in the construction of our estimator, we also decided to include the estimator of [Reference Kortschak and Hashorva3], denoted by
$w_{M_{u}}(u)$
into two parts in the construction of our estimator, we also decided to include the estimator of [Reference Kortschak and Hashorva3], denoted by
![]() $Z_{\text{AK}}$
. All the results are based on
$Z_{\text{AK}}$
. All the results are based on
![]() $N=10^{4}$
independent simulations for
$N=10^{4}$
independent simulations for
![]() $Z_{\text{NR}}$
and
$Z_{\text{NR}}$
and
![]() $Z_{\text{LX}}$
. The CPU time to generate
$Z_{\text{LX}}$
. The CPU time to generate
![]() $10^{4}$
samples is less than one second for the LX estimator, but more than ten seconds for both our estimator and the AK estimator.
$10^{4}$
samples is less than one second for the LX estimator, but more than ten seconds for both our estimator and the AK estimator.
As in [Reference Liu and Xu5], we assume in this section that f is a zero-mean homogeneous Gaussian random field with covariance function
![]() $C(s,t)=\text{e}^{-|t-s|^{\alpha }}$
. When
$C(s,t)=\text{e}^{-|t-s|^{\alpha }}$
. When
![]() $\alpha =2$
, f is infinitely differentiable, whereas when
$\alpha =2$
, f is infinitely differentiable, whereas when
![]() $\alpha =1$
, f is non-differentiable. We take
$\alpha =1$
, f is non-differentiable. We take
![]() $T=[-1/2,1/2]$
and discretize it with discretization size
$T=[-1/2,1/2]$
and discretize it with discretization size
![]() $S_{u}=100$
following the procedure given in the previous section. The detailed simulation is described in the following steps.
$S_{u}=100$
following the procedure given in the previous section. The detailed simulation is described in the following steps.
-
i. Generate a random variable
 $\mathcal{J}_{u}$
according to the distribution
$\mathcal{J}_{u}$
according to the distribution
 $\left(2\right)$
. For
$\left(2\right)$
. For
 $j=\mathcal{J}_{u}$
,
$j=\mathcal{J}_{u}$
, -
ii. Generate a vector
 $N_{j,u}$
of
$N_{j,u}$
of
 $M_{u}+1$
independent standard Gaussian random variables; compute the matrix
$M_{u}+1$
independent standard Gaussian random variables; compute the matrix
 $A_{j,u}$
and the vector
$A_{j,u}$
and the vector
 $A_{j,u}N_{j,u}$
.
$A_{j,u}N_{j,u}$
. -
iii. Compute the probability
 \begin{align*} & \mathbb{P}\Bigg( \sum_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}>u,\bar{\omega}_{u}\exp\left( \sum_{i=0}^{M_{u}}\omega _{i,u}\log X_{i,u}/\bar{\omega}_{u}\right)\leq u, \nonumber\\& \qquad\bigvee_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}=w_{j,u}X_{j,u} \, \Big\vert \,N_{j,u}^{(-1)}\Bigg). \end{align*}
\begin{align*} & \mathbb{P}\Bigg( \sum_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}>u,\bar{\omega}_{u}\exp\left( \sum_{i=0}^{M_{u}}\omega _{i,u}\log X_{i,u}/\bar{\omega}_{u}\right)\leq u, \nonumber\\& \qquad\bigvee_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}=w_{j,u}X_{j,u} \, \Big\vert \,N_{j,u}^{(-1)}\Bigg). \end{align*}
-
iv. Compute
 \begin{equation*}Z_{M_{u}}\left( u\right) =v_{1,M_{u}}(u)+\left( \sum_{i=0}^{M_{u}}P\left(X_{i,u}>u\right) \right) \frac{Z_{j}\left( u\right) }{\mathbb{P}\left(X_{j,u}>u\right) }.\end{equation*}
\begin{equation*}Z_{M_{u}}\left( u\right) =v_{1,M_{u}}(u)+\left( \sum_{i=0}^{M_{u}}P\left(X_{i,u}>u\right) \right) \frac{Z_{j}\left( u\right) }{\mathbb{P}\left(X_{j,u}>u\right) }.\end{equation*}
The computational complexity for generating an estimate of
![]() $w_{M_{u}}(u)$
with our approach is the number of simulations multiplied by the cost for generating one copy of
$w_{M_{u}}(u)$
with our approach is the number of simulations multiplied by the cost for generating one copy of
![]() $Z_{M_{u}}\left( u\right) $
, which is mainly the cost of computing the matrix
$Z_{M_{u}}\left( u\right) $
, which is mainly the cost of computing the matrix
![]() $A_{j,u}$
, i.e. of order
$A_{j,u}$
, i.e. of order
![]() $O\left( S_{u}^{3d}\right) $
. The overall computational cost is also a polynomial in
$O\left( S_{u}^{3d}\right) $
. The overall computational cost is also a polynomial in
![]() $\eta ^{-1}$
and
$\eta ^{-1}$
and
![]() $\log \left( u\right)$
.
$\log \left( u\right)$
.
First, we consider the case where
![]() $\mu (t)=0$
and
$\mu (t)=0$
and
![]() $\sigma (t)=1$
as in [Reference Liu and Xu5]. To validate the simulation results, [Reference Liu and Xu5] computed crude Monte Carlo estimators:
$\sigma (t)=1$
as in [Reference Liu and Xu5]. To validate the simulation results, [Reference Liu and Xu5] computed crude Monte Carlo estimators:
Based on
![]() $10^{6}$
independent simulations, for
$10^{6}$
independent simulations, for
![]() $b=3$
, the estimated tail probabilities were 4.7e–4 (Std. 2e–5) and 8.2e–4 (Std. 3e–5) when
$b=3$
, the estimated tail probabilities were 4.7e–4 (Std. 2e–5) and 8.2e–4 (Std. 3e–5) when
![]() $\alpha =1$
and 2, respectively; based on
$\alpha =1$
and 2, respectively; based on
![]() $10^{9}$
independent simulations, for
$10^{9}$
independent simulations, for
![]() $b=5$
, the estimated tail probabilities are 1.2e–8 (Std. 3e–9) and 7.7e–8 (Std. 9e–9) when
$b=5$
, the estimated tail probabilities are 1.2e–8 (Std. 3e–9) and 7.7e–8 (Std. 9e–9) when
![]() $\alpha =1$
and 2, respectively.
$\alpha =1$
and 2, respectively.
The estimated tail probabilities of w(u) are shown in Table 1 (
![]() $u=\text{e}^{b}$
). To compare the performance of the estimators, we provide their estimated coefficient of variation (CV, the ratio of the standard deviation over the mean) as well as the ratio of their variance per unit computer time over the variance per unit computer time of
$u=\text{e}^{b}$
). To compare the performance of the estimators, we provide their estimated coefficient of variation (CV, the ratio of the standard deviation over the mean) as well as the ratio of their variance per unit computer time over the variance per unit computer time of
![]() $Z_{\text{LX}}$
(RVCT). The variance per unit computer time for a given estimator Z equals
$Z_{\text{LX}}$
(RVCT). The variance per unit computer time for a given estimator Z equals
![]() $\tau (Z)\text{Var}(Z)$
, where
$\tau (Z)\text{Var}(Z)$
, where
![]() $\tau(Z)$
is the expected time to generate Z.
$\tau(Z)$
is the expected time to generate Z.
Table 1. Estimates of w(u) on
![]() $T=[-1/2,1/2]$
,
$T=[-1/2,1/2]$
,
![]() $\mu (t)=0$
, and
$\mu (t)=0$
, and
![]() $\sigma(t)=1 $
for
$\sigma(t)=1 $
for
![]() $u=\text{e}^{b}$
. The results for
$u=\text{e}^{b}$
. The results for
![]() $Z_{\text{LX}}$
are from [Reference Liu and Xu5].
$Z_{\text{LX}}$
are from [Reference Liu and Xu5].

Comparing the simulation results for
![]() $\alpha =1,2$
and
$\alpha =1,2$
and
![]() $b=3,5,7$
, we can see that the conditional Monte Carlo estimators have better performance for both measures (CV and RVCT) than the estimator of [Reference Liu and Xu5]. Our estimator is also the better of the two conditional Monte Carlo estimators. which proves that the split of the probability into two parts is very useful.
$b=3,5,7$
, we can see that the conditional Monte Carlo estimators have better performance for both measures (CV and RVCT) than the estimator of [Reference Liu and Xu5]. Our estimator is also the better of the two conditional Monte Carlo estimators. which proves that the split of the probability into two parts is very useful.
Next, we consider the case with
![]() $\mu (t)=2|t|$
and
$\mu (t)=2|t|$
and
![]() $\sigma (t)=1-t^{2}$
. To validate the simulation results, [Reference Liu and Xu5] computed crude Monte Carlo estimators:
$\sigma (t)=1-t^{2}$
. To validate the simulation results, [Reference Liu and Xu5] computed crude Monte Carlo estimators:
For
![]() $b=3$
, the crude Monte Carlo estimator based on
$b=3$
, the crude Monte Carlo estimator based on
![]() $10^{6} $
independent simulations gives the estimated tail probabilities 1.4e–3 (Std. 4e–5) and 2.3e–3 (Std. 5e–5) when
$10^{6} $
independent simulations gives the estimated tail probabilities 1.4e–3 (Std. 4e–5) and 2.3e–3 (Std. 5e–5) when
![]() $\alpha =1$
and
$\alpha =1$
and
![]() $\alpha =2$
, respectively; for
$\alpha =2$
, respectively; for
![]() $b=5$
, the crude Monte Carlo estimator based on
$b=5$
, the crude Monte Carlo estimator based on
![]() $10^{9}$
independent simulations gives the estimated tail probabilities 1.8e–8 (Std. 4e–9) and 1.4e–7 (Std. 1e–8) when
$10^{9}$
independent simulations gives the estimated tail probabilities 1.8e–8 (Std. 4e–9) and 1.4e–7 (Std. 1e–8) when
![]() $\alpha =1$
and
$\alpha =1$
and
![]() $\alpha =2$
, respectively.
$\alpha =2$
, respectively.
The estimated tail probabilities of w(u) with their estimated coefficient of variation (CV) and their ratio of the variances per unit computer times (RVCT) are shown in Table 2 (
![]() $u=\text{e}^{b}$
).
$u=\text{e}^{b}$
).
As in [Reference Liu and Xu5], the simulation results show that the coefficients of variation increase as the tail probabilities become smaller. The coefficients of variation and the ratios of the variance per unit computer times of the conditional Monte Carlo estimators are also much smaller in this case than the LX estimator. Moreover, the continuity of the process affects the empirical performance of the three estimators: they admit smaller coefficients of variation when the process is more continuous (corresponding to a larger value of
![]() $\alpha $
).
$\alpha $
).
Table 2. Estimates of w(u) on
![]() $T=[-1/2,1/2]$
,
$T=[-1/2,1/2]$
,
![]() $\mu (t)=2|t|$
, and
$\mu (t)=2|t|$
, and
![]() $\sigma(t)=1-t^{2}$
for
$\sigma(t)=1-t^{2}$
for
![]() $u=\text{e}^{b}$
. The results for
$u=\text{e}^{b}$
. The results for
![]() $Z_{\text{LX}}$
are from [Reference Liu and Xu5].
$Z_{\text{LX}}$
are from [Reference Liu and Xu5].

4. Proofs of the main results
4.1 Proofs under Assumptions 1
Lemma 1. As
![]() $u\rightarrow \infty $
, for some positive constants
$u\rightarrow \infty $
, for some positive constants
![]() $\tilde{c}_{1}$
and
$\tilde{c}_{1}$
and
![]() $\tilde{c}_{2}$
we have
$\tilde{c}_{2}$
we have
 \begin{align*} w_{M_{u}}(u) & \geq \exp \left( -\frac{(\log u)^{2}+\tilde{c}_{1}\log u\log S_{u}}{2\sigma _{\ast }^{2}}\right) , \\ w_{M_{u}}(u) & \leq \exp \left( -\frac{(\log u)^{2}-\tilde{c}_{2}(\log u)}{ 2\sigma _{\ast }^{2}}\right). \end{align*}
\begin{align*} w_{M_{u}}(u) & \geq \exp \left( -\frac{(\log u)^{2}+\tilde{c}_{1}\log u\log S_{u}}{2\sigma _{\ast }^{2}}\right) , \\ w_{M_{u}}(u) & \leq \exp \left( -\frac{(\log u)^{2}-\tilde{c}_{2}(\log u)}{ 2\sigma _{\ast }^{2}}\right). \end{align*}
Proof. For the lower bound, we have
 \begin{align*}w_{M_{u}}(u) &\geq P\left( w_{0,u}X_{0,u}>u\right) \\&= P\left( S_{u}^{-d}\text{e}^{\mu (0)+\sigma _{\ast }f(0)}>u\right) \\&= P\left( \sigma _{\ast }f(0)>\log u+d\log S_{u}-\mu (0)\right) \\&\geq \exp \left( -\frac{(\log u)^{2}+\tilde{c}_{1}\log u\log S_{u}}{2\sigma _{\ast }^{2}}\right)\end{align*}
\begin{align*}w_{M_{u}}(u) &\geq P\left( w_{0,u}X_{0,u}>u\right) \\&= P\left( S_{u}^{-d}\text{e}^{\mu (0)+\sigma _{\ast }f(0)}>u\right) \\&= P\left( \sigma _{\ast }f(0)>\log u+d\log S_{u}-\mu (0)\right) \\&\geq \exp \left( -\frac{(\log u)^{2}+\tilde{c}_{1}\log u\log S_{u}}{2\sigma _{\ast }^{2}}\right)\end{align*}
for some positive constant
![]() $\tilde{c}_{1}$
.
$\tilde{c}_{1}$
.
For the upper bound, we have
 \begin{align*}w_{M_{u}}(u) &\leq P\left( \left( M_{u}+1\right)\bigvee_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}>u\right) \\&\leq P\left( \max_{t\in T}\text{e}^{\mu (t)+\sigma (t)f(t)}>\frac{u}{\text{mes}\left(T\right) }\right) \\&\leq P\left( \max_{t\in T}\sigma (t)f(t)>\log u-\log \left( \text{mes}\left(T\right) \right) -\max_{t\in T}\mu (t)\right) .\end{align*}
\begin{align*}w_{M_{u}}(u) &\leq P\left( \left( M_{u}+1\right)\bigvee_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}>u\right) \\&\leq P\left( \max_{t\in T}\text{e}^{\mu (t)+\sigma (t)f(t)}>\frac{u}{\text{mes}\left(T\right) }\right) \\&\leq P\left( \max_{t\in T}\sigma (t)f(t)>\log u-\log \left( \text{mes}\left(T\right) \right) -\max_{t\in T}\mu (t)\right) .\end{align*}
By the Borel–TIS lemma and for sufficiently large u, we deduce that
 \begin{align*}w_{M_{u}}(u) &\leq \exp \left( -\frac{\left( \log u-\log \left( \text{mes}\left(T\right) \right) -\max_{t\in T}\mu (t)\right) ^{2}}{2\sigma _{\ast }^{2}}\right) \\&\leq \exp \left( -\frac{(\log u)^{2}-\tilde{c}_{2}(\log u)}{2\sigma_{\ast }^{2}}\right)\end{align*}
\begin{align*}w_{M_{u}}(u) &\leq \exp \left( -\frac{\left( \log u-\log \left( \text{mes}\left(T\right) \right) -\max_{t\in T}\mu (t)\right) ^{2}}{2\sigma _{\ast }^{2}}\right) \\&\leq \exp \left( -\frac{(\log u)^{2}-\tilde{c}_{2}(\log u)}{2\sigma_{\ast }^{2}}\right)\end{align*}
for some positive constant
![]() $\tilde{c}_{2}$
.
$\tilde{c}_{2}$
.
Lemma 2. Let
and
![]() $\epsilon >0$
be such that
$\epsilon >0$
be such that
![]() $\sigma _{A}^{2}\left( 1+\epsilon \right)<\sigma _{\ast }^{2}$
. We have, as
$\sigma _{A}^{2}\left( 1+\epsilon \right)<\sigma _{\ast }^{2}$
. We have, as
![]() $u\rightarrow \infty $
,
$u\rightarrow \infty $
,
 \begin{equation*}v_{1,M_{u}}(u)\leq \exp \left( -\frac{\left( \log u-\log \left(\int_{T}\text{e}^{\mu (t)} \, \text{d} t\right) \right) ^{2}}{2\sigma _{A}^{2}\left( 1+\epsilon\right) }\right)\end{equation*}
\begin{equation*}v_{1,M_{u}}(u)\leq \exp \left( -\frac{\left( \log u-\log \left(\int_{T}\text{e}^{\mu (t)} \, \text{d} t\right) \right) ^{2}}{2\sigma _{A}^{2}\left( 1+\epsilon\right) }\right)\end{equation*}
and, for some positive constant
![]() $\tilde{c}_{1}$
,
$\tilde{c}_{1}$
,
Therefore, we have
Proof. We have
 \begin{equation*}v_{1,M_{u}}(u)=P\left( \bar{\omega}_{u}\exp \left( \sum_{i=0}^{M_{u}}\omega_{i,u}\log X_{i,u}/\bar{\omega}_{u}\right) >u\right) .\end{equation*}
\begin{equation*}v_{1,M_{u}}(u)=P\left( \bar{\omega}_{u}\exp \left( \sum_{i=0}^{M_{u}}\omega_{i,u}\log X_{i,u}/\bar{\omega}_{u}\right) >u\right) .\end{equation*}
By Riemann integrability, we know that
![]() $\lim_{u\rightarrow \infty }\bar{\omega}_{u}=\int_{T}\text{e}^{\mu (t)} \, \text{d} t$
. Moreover, the random variable
$\lim_{u\rightarrow \infty }\bar{\omega}_{u}=\int_{T}\text{e}^{\mu (t)} \, \text{d} t$
. Moreover, the random variable
![]() $\frac{1}{\bar{\omega}_{u}}\sum_{i=0}^{M_{u}}\omega _{i,u}\log X_{i,u}=\frac{1}{\bar{\omega}_{u}}\sum_{i=0}^{M_{u}}\omega _{i,u}\sigma (t_{i})f(t_{i})$
is a centered Gaussian random variable with variance
$\frac{1}{\bar{\omega}_{u}}\sum_{i=0}^{M_{u}}\omega _{i,u}\log X_{i,u}=\frac{1}{\bar{\omega}_{u}}\sum_{i=0}^{M_{u}}\omega _{i,u}\sigma (t_{i})f(t_{i})$
is a centered Gaussian random variable with variance
 \begin{equation*}\frac{1}{\bar{\omega}_{u}^{2}}\sum_{i=0}^{M_{u}}\sum_{j=0}^{M_{u}}\text{mes}\left(T_{S_{u}}\left( t_{i}\right) \right) \text{e}^{\mu (t_{i})}\sigma (t_{i})\text{mes}\left(T_{S_{u}}\left( t_{j}\right) \right) \text{e}^{\mu (t_{j})}\sigma (t_{j})C\left(t_{i},t_{j}\right)\end{equation*}
\begin{equation*}\frac{1}{\bar{\omega}_{u}^{2}}\sum_{i=0}^{M_{u}}\sum_{j=0}^{M_{u}}\text{mes}\left(T_{S_{u}}\left( t_{i}\right) \right) \text{e}^{\mu (t_{i})}\sigma (t_{i})\text{mes}\left(T_{S_{u}}\left( t_{j}\right) \right) \text{e}^{\mu (t_{j})}\sigma (t_{j})C\left(t_{i},t_{j}\right)\end{equation*}
converging to
Therefore, for large u,
 \begin{equation*}v_{1,M_{u}}(u)\leq \exp \left( -\frac{\left( \log u-\log \left(\int_{T}\text{e}^{\mu (t)} \, \text{d} t\right) \right) ^{2}}{2\sigma _{A}^{2}\left( 1+\epsilon\right) }\right) .\end{equation*}
\begin{equation*}v_{1,M_{u}}(u)\leq \exp \left( -\frac{\left( \log u-\log \left(\int_{T}\text{e}^{\mu (t)} \, \text{d} t\right) \right) ^{2}}{2\sigma _{A}^{2}\left( 1+\epsilon\right) }\right) .\end{equation*}
Now,
 \begin{align*}v_{2,M_{u}}(u) &= P\left( \sum_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}>u,\bar{\omega}_{u}\exp \left( \sum_{i=0}^{M_{u}}\omega _{i,u}\log X_{i,u}/\bar{\omega}_{u}\right) \leq u\right) \\&= P\left( \sum_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}>u\right) -v_{1,M_{u}}(u) \\&\geq P\left( w_{0,u}X_{0,u}>u\right) -v_{1,M_{u}}(u).\end{align*}
\begin{align*}v_{2,M_{u}}(u) &= P\left( \sum_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}>u,\bar{\omega}_{u}\exp \left( \sum_{i=0}^{M_{u}}\omega _{i,u}\log X_{i,u}/\bar{\omega}_{u}\right) \leq u\right) \\&= P\left( \sum_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}>u\right) -v_{1,M_{u}}(u) \\&\geq P\left( w_{0,u}X_{0,u}>u\right) -v_{1,M_{u}}(u).\end{align*}
Moreover, in the same way as in Lemma 1,
for some positive constant
![]() $\tilde{c}_{1}$
. It follows that, for large u,
$\tilde{c}_{1}$
. It follows that, for large u,
 \begin{align*}P( w_{0,u} & X_{0,u}>u) -v_{1,M_{u}}(u) \\& \geq \exp \left( -\frac{(\log u)^{2}+\tilde{c}_{1}\log u\log S_{u}}{2\sigma _{\ast }^{2}}\right) -\exp \left( -\frac{\left( \log u-\log \left(\int_{T}\text{e}^{\mu (t)} \, \text{d} t\right) \right) ^{2}}{2\sigma _{A}^{2}\left(1+\epsilon \right) }\right) \\&\geq \frac{1}{2}\exp \left( -\frac{(\log u)^{2}+\tilde{c}_{1}\log u\log S_{u}}{2\sigma _{\ast }^{2}}\right)\end{align*}
\begin{align*}P( w_{0,u} & X_{0,u}>u) -v_{1,M_{u}}(u) \\& \geq \exp \left( -\frac{(\log u)^{2}+\tilde{c}_{1}\log u\log S_{u}}{2\sigma _{\ast }^{2}}\right) -\exp \left( -\frac{\left( \log u-\log \left(\int_{T}\text{e}^{\mu (t)} \, \text{d} t\right) \right) ^{2}}{2\sigma _{A}^{2}\left(1+\epsilon \right) }\right) \\&\geq \frac{1}{2}\exp \left( -\frac{(\log u)^{2}+\tilde{c}_{1}\log u\log S_{u}}{2\sigma _{\ast }^{2}}\right)\end{align*}
and
Lemma 3.
 \begin{equation*}\mathbb{E}\left\{ \left( Z_{M_{u}}(u)-v_{1,M_{u}}(u)\right) ^{2}\right\}=\sum_{j=0}^{M_{u}}\frac{\mathbb{E}\left\{ Z_{j}\left( u\right) ^{2}\right\}}{P\left( \mathcal{J}_{u}=j\right) }.\end{equation*}
\begin{equation*}\mathbb{E}\left\{ \left( Z_{M_{u}}(u)-v_{1,M_{u}}(u)\right) ^{2}\right\}=\sum_{j=0}^{M_{u}}\frac{\mathbb{E}\left\{ Z_{j}\left( u\right) ^{2}\right\}}{P\left( \mathcal{J}_{u}=j\right) }.\end{equation*}
Proof. As in [Reference Liu and Xu5, Lemma A.3], the proof follows by straightforward calculations.
Proof of Proposition 2. It is easily seen that
By Lemma 2, we have, for large u,
 \begin{equation*}v_{1,M_{u}}(u)\leq \exp \left( -\frac{\left( \log u-\log \left(\int_{T}\text{e}^{\mu (t)} \, \text{d} t\right) \right) ^{2}}{2\sigma _{A}^{2}\left( 1+\epsilon\right) }\right) ,\end{equation*}
\begin{equation*}v_{1,M_{u}}(u)\leq \exp \left( -\frac{\left( \log u-\log \left(\int_{T}\text{e}^{\mu (t)} \, \text{d} t\right) \right) ^{2}}{2\sigma _{A}^{2}\left( 1+\epsilon\right) }\right) ,\end{equation*}
and, by Lemma 1,
Moreover, we have
 \begin{align*}\mathbb{E}\{ (Z_{M_{u}}(u)-w(u))^{2}\} &= \mathbb{E}\{(Z_{M_{u}}(u))^{2}\} -w_{M_{u}}^{2}(u)+(w_{M_{u}}(u)-w(u))^{2} \\&= \mathbb{E}\{ \left( Z_{M_{u}}(u)-v_{1,M_{u}}(u)\right) ^{2}\}+v_{1,M_{u}}(u)\left( v_{1,M_{u}}(u)+2v_{2,M_{u}}(u)\right) \\& \quad -w_{M_{u}}^{2}(u)+(w_{M_{u}}(u)-w(u))^{2}\end{align*}
\begin{align*}\mathbb{E}\{ (Z_{M_{u}}(u)-w(u))^{2}\} &= \mathbb{E}\{(Z_{M_{u}}(u))^{2}\} -w_{M_{u}}^{2}(u)+(w_{M_{u}}(u)-w(u))^{2} \\&= \mathbb{E}\{ \left( Z_{M_{u}}(u)-v_{1,M_{u}}(u)\right) ^{2}\}+v_{1,M_{u}}(u)\left( v_{1,M_{u}}(u)+2v_{2,M_{u}}(u)\right) \\& \quad -w_{M_{u}}^{2}(u)+(w_{M_{u}}(u)-w(u))^{2}\end{align*}
and, for large u,
by Proposition 1.
By Lemma 3, we deduce that
 \begin{equation*}\mathbb{E}\left\{ \left( Z_{M_{u}}(u)-v_{1,M_{u}}(u)\right) ^{2}\right\}=\sum_{j=0}^{M_{u}}\frac{\mathbb{E}\left\{ Z_{j}\left( u\right) ^{2}\right\}}{P\left( \mathcal{J}_{u}=j\right) }=\sum_{j=0}^{M_{u}}P\left( \mathcal{J}_{u}=j\right) \frac{\mathbb{E}\left\{ Z_{j}\left( u\right) ^{2}\right\} }{P\left( \mathcal{J}_{u}=j\right) ^{2}}.\end{equation*}
\begin{equation*}\mathbb{E}\left\{ \left( Z_{M_{u}}(u)-v_{1,M_{u}}(u)\right) ^{2}\right\}=\sum_{j=0}^{M_{u}}\frac{\mathbb{E}\left\{ Z_{j}\left( u\right) ^{2}\right\}}{P\left( \mathcal{J}_{u}=j\right) }=\sum_{j=0}^{M_{u}}P\left( \mathcal{J}_{u}=j\right) \frac{\mathbb{E}\left\{ Z_{j}\left( u\right) ^{2}\right\} }{P\left( \mathcal{J}_{u}=j\right) ^{2}}.\end{equation*}
It is important to note that
![]() $Z_{j}\left( u\right) $
is bounded in the following way:
$Z_{j}\left( u\right) $
is bounded in the following way:
Since
it follows that, for large u,
 \begin{align*}\frac{\mathbb{E}\left\{ Z_{j}\left( u\right) ^{2}\right\} }{P\left( \mathcal{J}_{u}=j\right) ^{2}} &\leq \frac{P\left( X_{j,u}>\frac{u}{\text{e}^{\mu(t_{j})}\text{mes}\left( T\right) }\right) ^{2}}{P\left( X_{j,u}>u\right) ^{2}}\left( \sum_{i=0}^{M_{u}}P\left( X_{i,u}>u\right) \right) ^{2} \\&\leq \frac{(\log u)^{2}}{\sigma ^{2}(t_{j})}\exp \left( -\frac{(\log u-\mu(t_{j})-\log \left( \text{mes}\left( T\right) \right) )^{2}}{\sigma ^{2}(t_{j})}+\frac{(\log u)^{2}}{\sigma ^{2}(t_{j})}\right) \\ & \quad \times \left(\sum_{i=0}^{M_{u}}P\left( X_{i,u}>u\right) \right) ^{2} \\&\leq C(\log u)^{2}\exp \left( 2\frac{\mu (t_{j})+\log \left( \text{mes}\left(T\right) \right) }{\sigma ^{2}(t_{j})}\log u\right) \left(\sum_{i=0}^{M_{u}}P\left( X_{i,u}>u\right) \right) ^{2} \\& = C(\log u)^{2}u^{2(\mu (t_{j})+\log \left( \text{mes}\left( T\right) \right)/\sigma ^{2}(t_{j})}\left( \sum_{i=0}^{M_{u}}P\left( X_{i,u}>u\right)\right) ^{2}\end{align*}
\begin{align*}\frac{\mathbb{E}\left\{ Z_{j}\left( u\right) ^{2}\right\} }{P\left( \mathcal{J}_{u}=j\right) ^{2}} &\leq \frac{P\left( X_{j,u}>\frac{u}{\text{e}^{\mu(t_{j})}\text{mes}\left( T\right) }\right) ^{2}}{P\left( X_{j,u}>u\right) ^{2}}\left( \sum_{i=0}^{M_{u}}P\left( X_{i,u}>u\right) \right) ^{2} \\&\leq \frac{(\log u)^{2}}{\sigma ^{2}(t_{j})}\exp \left( -\frac{(\log u-\mu(t_{j})-\log \left( \text{mes}\left( T\right) \right) )^{2}}{\sigma ^{2}(t_{j})}+\frac{(\log u)^{2}}{\sigma ^{2}(t_{j})}\right) \\ & \quad \times \left(\sum_{i=0}^{M_{u}}P\left( X_{i,u}>u\right) \right) ^{2} \\&\leq C(\log u)^{2}\exp \left( 2\frac{\mu (t_{j})+\log \left( \text{mes}\left(T\right) \right) }{\sigma ^{2}(t_{j})}\log u\right) \left(\sum_{i=0}^{M_{u}}P\left( X_{i,u}>u\right) \right) ^{2} \\& = C(\log u)^{2}u^{2(\mu (t_{j})+\log \left( \text{mes}\left( T\right) \right)/\sigma ^{2}(t_{j})}\left( \sum_{i=0}^{M_{u}}P\left( X_{i,u}>u\right)\right) ^{2}\end{align*}
for some positive constant C. Then we have
 \begin{align*}\sum_{j=0}^{M_{u}}\frac{\mathbb{E}\left\{ Z_{j}\left( u\right) ^{2}\right\}}{P\left( \mathcal{J}_{u}=j\right) } & = \sum_{j=0}^{M_{u}}P\left( \mathcal{J}_{u}=j\right) \frac{\mathbb{E}\left\{ Z_{j}\left( u\right) ^{2}\right\} }{P\left( \mathcal{J}_{u}=j\right) ^{2}} \\&\leq C(\log u)^{2}\sum_{j=0}^{M_{u}}P\left( \mathcal{J}_{u}=j\right)u^{2\left( \max_{T}\mu (t)+\log \left( \text{mes}\left( T\right) \right) \right)/\min_{T}\sigma ^{2}(t)} \\ & \quad \times \left( \sum_{i=0}^{M_{u}}P\left( X_{i,u}>u\right)\right) ^{2} \\&\leq C(\log u)^{2}u^{2\left( \max_{T}\mu (t)+\log \left( \text{mes}\left(T\right) \right) \right) /\min_{T}\sigma ^{2}(t)}\left(\sum_{i=0}^{M_{u}}P\left( X_{i,u}>u\right) \right) ^{2}.\end{align*}
\begin{align*}\sum_{j=0}^{M_{u}}\frac{\mathbb{E}\left\{ Z_{j}\left( u\right) ^{2}\right\}}{P\left( \mathcal{J}_{u}=j\right) } & = \sum_{j=0}^{M_{u}}P\left( \mathcal{J}_{u}=j\right) \frac{\mathbb{E}\left\{ Z_{j}\left( u\right) ^{2}\right\} }{P\left( \mathcal{J}_{u}=j\right) ^{2}} \\&\leq C(\log u)^{2}\sum_{j=0}^{M_{u}}P\left( \mathcal{J}_{u}=j\right)u^{2\left( \max_{T}\mu (t)+\log \left( \text{mes}\left( T\right) \right) \right)/\min_{T}\sigma ^{2}(t)} \\ & \quad \times \left( \sum_{i=0}^{M_{u}}P\left( X_{i,u}>u\right)\right) ^{2} \\&\leq C(\log u)^{2}u^{2\left( \max_{T}\mu (t)+\log \left( \text{mes}\left(T\right) \right) \right) /\min_{T}\sigma ^{2}(t)}\left(\sum_{i=0}^{M_{u}}P\left( X_{i,u}>u\right) \right) ^{2}.\end{align*}
Moreover, we have
 \begin{equation*}\sum_{i=0}^{M_{u}}P\left( X_{i,u}>u\right) \leq (1+M_{u})P\left(\bigvee_{i=0}^{M_{u}}X_{i,u}>u\right)\leq (1+M_{u})P\left( \text{e}^{\max_{t\in T}\sigma (t)f(t)}>u\right) ,\end{equation*}
\begin{equation*}\sum_{i=0}^{M_{u}}P\left( X_{i,u}>u\right) \leq (1+M_{u})P\left(\bigvee_{i=0}^{M_{u}}X_{i,u}>u\right)\leq (1+M_{u})P\left( \text{e}^{\max_{t\in T}\sigma (t)f(t)}>u\right) ,\end{equation*}
where
![]() $P\left( \exp\left\{\max_{t\in T}\sigma (t)f(t)\right\}>u\right) =P\left( \max_{t\in T}\sigma (t)f(t)>\log u\right)$
. By the Borel–TIS lemma, we also have
$P\left( \exp\left\{\max_{t\in T}\sigma (t)f(t)\right\}>u\right) =P\left( \max_{t\in T}\sigma (t)f(t)>\log u\right)$
. By the Borel–TIS lemma, we also have
It follows that
 \begin{multline*}\mathbb{E}\left\{ \left( Z_{M_{u}}(u)-v_{1,M_{u}}(u)\right) ^{2}\right\}\leq \\C(\log u)^{2}u^{2\left( \max_{T}\mu (t)+\log \left( \text{mes}\left( T\right)\right) \right) /\min_{T}\sigma ^{2}(t)}(1+M_{u})^{2}\exp \left( -\frac{(\log u)^{2}}{\sigma _{\ast }^{2}}\right) .\end{multline*}
\begin{multline*}\mathbb{E}\left\{ \left( Z_{M_{u}}(u)-v_{1,M_{u}}(u)\right) ^{2}\right\}\leq \\C(\log u)^{2}u^{2\left( \max_{T}\mu (t)+\log \left( \text{mes}\left( T\right)\right) \right) /\min_{T}\sigma ^{2}(t)}(1+M_{u})^{2}\exp \left( -\frac{(\log u)^{2}}{\sigma _{\ast }^{2}}\right) .\end{multline*}
We know from [Reference Liu and Xu5, Lemma 4.3] that there exist constants
![]() $c_{0}$
,
$c_{0}$
,
![]() $c_{1}$
,
$c_{1}$
,
![]() $c_{2}$
such that
$c_{2}$
such that
We therefore deduce from (4) that
4.2. Proofs under Assumptions 2
Lemma 4. Let
and
![]() $\epsilon >0$
be such that
$\epsilon >0$
be such that
![]() $\sigma _{A}^{2}\left( 1+\epsilon \right)<\sigma _{\ast }^{2}$
. We have, as
$\sigma _{A}^{2}\left( 1+\epsilon \right)<\sigma _{\ast }^{2}$
. We have, as
![]() $u\rightarrow \infty $
,
$u\rightarrow \infty $
,
 \begin{equation*}v_{1,M_{u}}(u)\leq \exp \left( -\frac{\left( \log u-\log \left(\int_{T}\text{e}^{\mu (t)} \, \text{d} t\right) \right) ^{2}}{2\sigma _{A}^{2}\left( 1+\epsilon\right) }\right)\end{equation*}
\begin{equation*}v_{1,M_{u}}(u)\leq \exp \left( -\frac{\left( \log u-\log \left(\int_{T}\text{e}^{\mu (t)} \, \text{d} t\right) \right) ^{2}}{2\sigma _{A}^{2}\left( 1+\epsilon\right) }\right)\end{equation*}
and, for some positive constant
![]() $\tilde{c}_{1}$
,
$\tilde{c}_{1}$
,
Therefore, we have
Proof. The proof proceeds in the same way as for Lemma 2.
Lemma 5. For some positive constant C, we have, for large u,
![]() $\mathbb{E}\{ Z_{0}\left( u\right) ^{2}\} \leq Cw^{2}\left(u\right)$
.
$\mathbb{E}\{ Z_{0}\left( u\right) ^{2}\} \leq Cw^{2}\left(u\right)$
.
Proof. Let
![]() $c_{u}$
be defined as
$c_{u}$
be defined as
with
![]() $\varepsilon >0$
.
$\varepsilon >0$
.
Note that there exist standard Gaussian random variables
![]() $\tilde{N}_{j}$
for
$\tilde{N}_{j}$
for
![]() $j\neq 0$
(independent of f(0), i.e.
$j\neq 0$
(independent of f(0), i.e.
![]() $N_{0,u,1}$
) such that
$N_{0,u,1}$
) such that
![]() $f(t_{j})=\rho _{j}\,f(0)+\sqrt{1-\rho _{j}^{2}}\tilde{N}_{j}$
,
$f(t_{j})=\rho _{j}\,f(0)+\sqrt{1-\rho _{j}^{2}}\tilde{N}_{j}$
,
![]() $j\neq 0$
, where
$j\neq 0$
, where
![]() $\rho _{j}=C(t_{j})$
.
$\rho _{j}=C(t_{j})$
.
We have
Let us consider the first component of the previous sum. We have
 \begin{align*}\mathbb{E}\left\{ Z_{0}\left( u\right) ^{2}\textbf{1}_{\left\{\bigvee_{i=1}^{M_{u}}\left\vert \tilde{N}_{i}\right\vert >c_{u}\sqrt{\log (u)}\right\} }\right\} &\leq \sum_{i=1}^{M_{u}}\mathbb{E}\left\{Z_{0}\left( u\right) ^{2}\textbf{1}_{\left\{ \left\vert \tilde{N}_{i}\right\vert >c_{u}\sqrt{\log (u)}\right\} }\right\} \\&\leq M_{u}P^{2}\bigg( \text{e}^{\sigma f(t_{0})}>\frac{u}{\text{mes}\left( T\right) }\bigg) P\big( |\tilde{N}_{i}|>c_{u}\sqrt{\log (u)}\big) .\end{align*}
\begin{align*}\mathbb{E}\left\{ Z_{0}\left( u\right) ^{2}\textbf{1}_{\left\{\bigvee_{i=1}^{M_{u}}\left\vert \tilde{N}_{i}\right\vert >c_{u}\sqrt{\log (u)}\right\} }\right\} &\leq \sum_{i=1}^{M_{u}}\mathbb{E}\left\{Z_{0}\left( u\right) ^{2}\textbf{1}_{\left\{ \left\vert \tilde{N}_{i}\right\vert >c_{u}\sqrt{\log (u)}\right\} }\right\} \\&\leq M_{u}P^{2}\bigg( \text{e}^{\sigma f(t_{0})}>\frac{u}{\text{mes}\left( T\right) }\bigg) P\big( |\tilde{N}_{i}|>c_{u}\sqrt{\log (u)}\big) .\end{align*}
Moreover, for large u, we have
and
 \begin{align*}P^{2}\bigg( \text{e}^{\sigma f(0)}>\frac{u}{\text{mes}\left( T\right) }\bigg)&= P^{2}\left( f(0)>\log u/\sigma \right) \\&\sim \frac{\sigma ^{2}}{\left( \log u-\log \left( \text{mes}\left( T\right)\right) \right)^{2}}\exp \left( -\frac{\left( \log u-\log \left( \text{mes}\left(T\right) \right) \right) ^{2}}{\sigma ^{2}}\right) .\end{align*}
\begin{align*}P^{2}\bigg( \text{e}^{\sigma f(0)}>\frac{u}{\text{mes}\left( T\right) }\bigg)&= P^{2}\left( f(0)>\log u/\sigma \right) \\&\sim \frac{\sigma ^{2}}{\left( \log u-\log \left( \text{mes}\left( T\right)\right) \right)^{2}}\exp \left( -\frac{\left( \log u-\log \left( \text{mes}\left(T\right) \right) \right) ^{2}}{\sigma ^{2}}\right) .\end{align*}
Therefore, using the definition of
![]() $c_{u}$
, there exists a positive constant
$c_{u}$
, there exists a positive constant
![]() $\alpha $
such that, for large u,
$\alpha $
such that, for large u,
 \begin{multline*}\mathbb{E}\left\{ Z_{0}\left( u\right) ^{2}\textbf{1}_{\left\{\bigvee_{i=1}^{M_{u}}\left\vert \tilde{N}_{i}\right\vert >c_{u}\sqrt{\log (u)}\right\} }\right\} \leq \\CS_{u}^{d}\frac{1}{c_{u}( \log (u))^{3/2}}\exp \bigg( {-}\frac{(\log u)^{2}+2\log ( 1+M_{u}) \log (u)}{\sigma ^{2}}-\alpha\log ( 1+M_{u}) \log (u)\bigg) .\end{multline*}
\begin{multline*}\mathbb{E}\left\{ Z_{0}\left( u\right) ^{2}\textbf{1}_{\left\{\bigvee_{i=1}^{M_{u}}\left\vert \tilde{N}_{i}\right\vert >c_{u}\sqrt{\log (u)}\right\} }\right\} \leq \\CS_{u}^{d}\frac{1}{c_{u}( \log (u))^{3/2}}\exp \bigg( {-}\frac{(\log u)^{2}+2\log ( 1+M_{u}) \log (u)}{\sigma ^{2}}-\alpha\log ( 1+M_{u}) \log (u)\bigg) .\end{multline*}
Note that, for some positive constant C,
 \begin{align*}P\left( \omega _{0,u}X_{0,u}>u\right) ^{2} & \sim P\left( f(0)>\left( \log u+\log M_{u}+\log \text{mes}(T)\right) /\sigma \right) ^{2} \\&\sim C\frac{1}{(\log u)^{2}}\exp \left( -\frac{(\log u)^{2}+2\log \left(M_{u}\right) \log (u)}{\sigma ^{2}}\right) .\end{align*}
\begin{align*}P\left( \omega _{0,u}X_{0,u}>u\right) ^{2} & \sim P\left( f(0)>\left( \log u+\log M_{u}+\log \text{mes}(T)\right) /\sigma \right) ^{2} \\&\sim C\frac{1}{(\log u)^{2}}\exp \left( -\frac{(\log u)^{2}+2\log \left(M_{u}\right) \log (u)}{\sigma ^{2}}\right) .\end{align*}
It follows that
and also
since
![]() $w_{0,u}X_{0,u}\leq \mathcal{I}\left( T\right) $
.
$w_{0,u}X_{0,u}\leq \mathcal{I}\left( T\right) $
.
Let us now consider the second component. Let
 \begin{equation*}\Omega _{u}=\Bigg\{\! \sum_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}>u,\bar{\omega}_{u}\exp \! \Bigg(\! \sum_{i=0}^{M_{u}}\omega _{i,u}\log X_{i,u}/\bar{\omega}_{u}\Bigg)\! \leq u,\bigvee_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}=\omega_{0,u}X_{0,u}\Bigg\} .\end{equation*}
\begin{equation*}\Omega _{u}=\Bigg\{\! \sum_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}>u,\bar{\omega}_{u}\exp \! \Bigg(\! \sum_{i=0}^{M_{u}}\omega _{i,u}\log X_{i,u}/\bar{\omega}_{u}\Bigg)\! \leq u,\bigvee_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}=\omega_{0,u}X_{0,u}\Bigg\} .\end{equation*}
We have
 \begin{align*}& \mathbb{E}\left\{ Z_{0}\left( u\right) ^{2}\textbf{1}_{\left\{\bigvee_{i=1}^{M_{u}}\left\vert \tilde{N}_{i}\right\vert \leq c_{u}\sqrt{\log (u)}\right\} }\right\} \\[3pt]& = \mathbb{E}\left\{ \left( P\left( \left. \Omega _{u}\right\vert N_{0,u}^{(-1)}\right) \textbf{1}_{\left\{ \bigvee_{i=1}^{M_{u}}\left\vert \tilde{N}_{i}\right\vert \leq c_{u}\sqrt{\log (u)}\right\} }\right)^{2}\right\} \\[3pt]& = \mathbb{E}\left\{ P\left( \Omega_{u},\bigvee_{i=1}^{M_{u}}\left\vert \tilde{N}_{i}\right\vert \leq c_{u}\sqrt{\log (u)} \, \Big\vert \, N_{0,u}^{(-1)}\right) ^{2}\right\} \\[3pt]& \leq \mathbb{E}\Bigg\{ P\Bigg( \sum_{i=0}^{M_{u}}\omega_{i,u}X_{i,u}>u,\bigvee_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}=\omega_{0,u}X_{0,u}, \bigvee_{i=1}^{M_{u}}\left\vert \tilde{N}_{i}\right\vert \leq c_{u}\sqrt{\log (u)} \, \Big\vert \, N_{0,u}^{(-1)}\Bigg) ^{2}\Bigg\} \\[3pt]& \leq \mathbb{E}\Bigg\{ P\Bigg(w_{0,u}X_{0,u}+\sum_{i=1}^{M_{u}}\omega _{i,u}X_{i,u}>u, \omega _{0,u}X_{0,u}>\frac{u}{1+M_{u}}, \bigvee_{i=1}^{M_{u}}\left\vert \tilde{N}_{i}\right\vert \leq c_{u}\sqrt{\log (u)} \, \Big\vert \, N_{0,u}^{(-1)}\Bigg) ^{2}\Bigg\} .\end{align*}
\begin{align*}& \mathbb{E}\left\{ Z_{0}\left( u\right) ^{2}\textbf{1}_{\left\{\bigvee_{i=1}^{M_{u}}\left\vert \tilde{N}_{i}\right\vert \leq c_{u}\sqrt{\log (u)}\right\} }\right\} \\[3pt]& = \mathbb{E}\left\{ \left( P\left( \left. \Omega _{u}\right\vert N_{0,u}^{(-1)}\right) \textbf{1}_{\left\{ \bigvee_{i=1}^{M_{u}}\left\vert \tilde{N}_{i}\right\vert \leq c_{u}\sqrt{\log (u)}\right\} }\right)^{2}\right\} \\[3pt]& = \mathbb{E}\left\{ P\left( \Omega_{u},\bigvee_{i=1}^{M_{u}}\left\vert \tilde{N}_{i}\right\vert \leq c_{u}\sqrt{\log (u)} \, \Big\vert \, N_{0,u}^{(-1)}\right) ^{2}\right\} \\[3pt]& \leq \mathbb{E}\Bigg\{ P\Bigg( \sum_{i=0}^{M_{u}}\omega_{i,u}X_{i,u}>u,\bigvee_{i=0}^{M_{u}}\omega _{i,u}X_{i,u}=\omega_{0,u}X_{0,u}, \bigvee_{i=1}^{M_{u}}\left\vert \tilde{N}_{i}\right\vert \leq c_{u}\sqrt{\log (u)} \, \Big\vert \, N_{0,u}^{(-1)}\Bigg) ^{2}\Bigg\} \\[3pt]& \leq \mathbb{E}\Bigg\{ P\Bigg(w_{0,u}X_{0,u}+\sum_{i=1}^{M_{u}}\omega _{i,u}X_{i,u}>u, \omega _{0,u}X_{0,u}>\frac{u}{1+M_{u}}, \bigvee_{i=1}^{M_{u}}\left\vert \tilde{N}_{i}\right\vert \leq c_{u}\sqrt{\log (u)} \, \Big\vert \, N_{0,u}^{(-1)}\Bigg) ^{2}\Bigg\} .\end{align*}
Moreover, we have
![]() $\sum_{i=1}^{M_{u}}\omega _{i,u}X_{i,u}=\sum_{i=1}^{M_{u}}\omega_{i,u}\exp\big\{\sigma (t_{i})\big( \rho _{i}f(0)+\sqrt{1-\rho _{i}^{2}}\tilde{N}_{i}\big) \big\}$
and, if
$\sum_{i=1}^{M_{u}}\omega _{i,u}X_{i,u}=\sum_{i=1}^{M_{u}}\omega_{i,u}\exp\big\{\sigma (t_{i})\big( \rho _{i}f(0)+\sqrt{1-\rho _{i}^{2}}\tilde{N}_{i}\big) \big\}$
and, if
![]() $\bigvee_{i=1}^{M_{u}}\big\vert \tilde{N}_{i}\big\vert \leq c_{u}\sqrt{\log (u)}$
, we deduce that
$\bigvee_{i=1}^{M_{u}}\big\vert \tilde{N}_{i}\big\vert \leq c_{u}\sqrt{\log (u)}$
, we deduce that
 \begin{align*}\sum_{i=1}^{M_{u}}\omega _{i,u}X_{i,u} &\leq \sum_{i=1}^{M_{u}}\omega_{i,u}\exp\left\{\sigma (t_{i})\left( \rho _{i}f(0)+\sqrt{1-\rho _{i}^{2}}c_{u}\sqrt{\log (u)}\right) \right\} \\&=\sum_{i=1}^{M_{u}}\omega _{i,u}\exp\left\{\sigma (t_{i})f(0)\left( \rho _{i}+\sqrt{1-\rho _{i}^{2}}c_{u}\sqrt{\log (u)/f(0)^{2}}\right) \right\}.\end{align*}
\begin{align*}\sum_{i=1}^{M_{u}}\omega _{i,u}X_{i,u} &\leq \sum_{i=1}^{M_{u}}\omega_{i,u}\exp\left\{\sigma (t_{i})\left( \rho _{i}f(0)+\sqrt{1-\rho _{i}^{2}}c_{u}\sqrt{\log (u)}\right) \right\} \\&=\sum_{i=1}^{M_{u}}\omega _{i,u}\exp\left\{\sigma (t_{i})f(0)\left( \rho _{i}+\sqrt{1-\rho _{i}^{2}}c_{u}\sqrt{\log (u)/f(0)^{2}}\right) \right\}.\end{align*}
If we also assume that
![]() $w_{0,u}X_{0,u}>u/(1+M_{u})$
, or equivalently
$w_{0,u}X_{0,u}>u/(1+M_{u})$
, or equivalently
![]() $f(0)>(\log u-\log \left( \text{mes}(T)\right) )/\sigma $
, we get, for large u,
$f(0)>(\log u-\log \left( \text{mes}(T)\right) )/\sigma $
, we get, for large u,
 \begin{align*}c_{u}\sqrt{\log (u)/f(0)^{2}} &= \left( 1+\varepsilon \right) \sqrt{4\frac{\log \left( 1+M_{u}\right) }{\sigma ^{2}}}\sqrt{\frac{\log (u)}{(\log u-\log \left( \text{mes}(T)\right) )^{2}/\sigma ^{2}}} \\&\sim \left( 1+\varepsilon \right) \sqrt{4\frac{\log \left( 1+M_{u}\right)}{\log (u)}}.\end{align*}
\begin{align*}c_{u}\sqrt{\log (u)/f(0)^{2}} &= \left( 1+\varepsilon \right) \sqrt{4\frac{\log \left( 1+M_{u}\right) }{\sigma ^{2}}}\sqrt{\frac{\log (u)}{(\log u-\log \left( \text{mes}(T)\right) )^{2}/\sigma ^{2}}} \\&\sim \left( 1+\varepsilon \right) \sqrt{4\frac{\log \left( 1+M_{u}\right)}{\log (u)}}.\end{align*}
Then we have, for some positive constant c and for large u,
 \begin{equation*}\sum_{i=1}^{M_{u}}\omega _{i,u}X_{i,u}\leq \sum_{i=1}^{M_{u}}\omega_{i,u}\exp\left\{\sigma (t_{i})f(0)\left( \rho _{i}+\sqrt{1-\rho _{i}^{2}}c\sqrt{\log \left( 1+M_{u}\right) /\log (u)}\right) \right\}.\end{equation*}
\begin{equation*}\sum_{i=1}^{M_{u}}\omega _{i,u}X_{i,u}\leq \sum_{i=1}^{M_{u}}\omega_{i,u}\exp\left\{\sigma (t_{i})f(0)\left( \rho _{i}+\sqrt{1-\rho _{i}^{2}}c\sqrt{\log \left( 1+M_{u}\right) /\log (u)}\right) \right\}.\end{equation*}
It follows that
 \begin{multline*}\left\{ \omega _{0,u}X_{0,u}+\sum_{i=1}^{M_{u}}\omega_{i,u}X_{i,u}>u,w_{0,u}X_{0,u}>\frac{u}{1+M_{u}},\bigvee_{i=1}^{M_{u}}\left\vert \tilde{N}_{i}\right\vert \leq c_{u}\sqrt{\log (u)}\right\} \\\subset \left\{ \omega _{0,u}X_{0,u}+\sum_{i=1}^{M_{u}}\omega_{i,u}\exp\left\{\sigma f(0)\left( \rho _{i}+\sqrt{1-\rho _{i}^{2}}c\sqrt{\log \left( 1+M_{u}\right) /\log (u)}\right) \right\}\right\} .\end{multline*}
\begin{multline*}\left\{ \omega _{0,u}X_{0,u}+\sum_{i=1}^{M_{u}}\omega_{i,u}X_{i,u}>u,w_{0,u}X_{0,u}>\frac{u}{1+M_{u}},\bigvee_{i=1}^{M_{u}}\left\vert \tilde{N}_{i}\right\vert \leq c_{u}\sqrt{\log (u)}\right\} \\\subset \left\{ \omega _{0,u}X_{0,u}+\sum_{i=1}^{M_{u}}\omega_{i,u}\exp\left\{\sigma f(0)\left( \rho _{i}+\sqrt{1-\rho _{i}^{2}}c\sqrt{\log \left( 1+M_{u}\right) /\log (u)}\right) \right\}\right\} .\end{multline*}
Since
![]() $M_{u}\sim \text{mes}(T)S_{u}^{d}$
, we have
$M_{u}\sim \text{mes}(T)S_{u}^{d}$
, we have
 \begin{equation*}\lim_{u\rightarrow \infty }\left( \sup_{i=1,\ldots,M_{u}}\sqrt{1-\rho _{i}^{2}}\right) \sqrt{\log \left( 1+M_{u}\right) /\log (u)}=0\end{equation*}
\begin{equation*}\lim_{u\rightarrow \infty }\left( \sup_{i=1,\ldots,M_{u}}\sqrt{1-\rho _{i}^{2}}\right) \sqrt{\log \left( 1+M_{u}\right) /\log (u)}=0\end{equation*}
and
 \begin{align*}\omega _{0,u}X_{0,u}+\sum_{i=1}^{M_{u}}\omega _{i,u}\exp\left\{\sigma f(0)\left(\rho _{i}+\sqrt{1-\rho _{i}^{2}}c\sqrt{\log \left( 1+M_{u}\right) /\log (u)}\right) \right\} \sim \int_{T}\text{e}^{\sigma f(0)C(t)} \, \text{d} t.\end{align*}
\begin{align*}\omega _{0,u}X_{0,u}+\sum_{i=1}^{M_{u}}\omega _{i,u}\exp\left\{\sigma f(0)\left(\rho _{i}+\sqrt{1-\rho _{i}^{2}}c\sqrt{\log \left( 1+M_{u}\right) /\log (u)}\right) \right\} \sim \int_{T}\text{e}^{\sigma f(0)C(t)} \, \text{d} t.\end{align*}
Now, by the method of steepest descent we know that, for large v,
and then, for large u,
![]() $P\left( \int_{T}\text{e}^{\sigma f(0)C(t)} \, \text{d} t>u\right) \sim P\left( f(0)>v\right)$
, where v is the unique solution to
$P\left( \int_{T}\text{e}^{\sigma f(0)C(t)} \, \text{d} t>u\right) \sim P\left( f(0)>v\right)$
, where v is the unique solution to
![]() $(2\pi /\sigma )^{d/2}v^{-d/2}\text{e}^{\sigma v}=u$
. Since
$(2\pi /\sigma )^{d/2}v^{-d/2}\text{e}^{\sigma v}=u$
. Since
we deduce that, for some positive constant C,
and the result follows.
Proof of Proposition 3. Recall that
![]() $S_{u}$
is chosen as
$S_{u}$
is chosen as
![]() $S_{u}=\kappa _{0}\eta _{u}^{-(1+\varepsilon )}\left( \log u\right)^{2+\varepsilon }$
for some
$S_{u}=\kappa _{0}\eta _{u}^{-(1+\varepsilon )}\left( \log u\right)^{2+\varepsilon }$
for some
![]() $\varepsilon >0$
, where
$\varepsilon >0$
, where
![]() $\left( \eta _{u}\right) $
is a sequence such that lim
$\left( \eta _{u}\right) $
is a sequence such that lim
![]() $_{u\rightarrow \infty }\eta _{u}=0$
, and that we have
$_{u\rightarrow \infty }\eta _{u}=0$
, and that we have
Due to homogeneity, we have, for large u,
![]() $P\left( \mathcal{J}_{u}=j\right) \sim 1/M_{u}$
and, by Lemma 5,
$P\left( \mathcal{J}_{u}=j\right) \sim 1/M_{u}$
and, by Lemma 5,
![]() $\mathbb{E}\{Z_{j}\left( u\right) ^{2}\}\leq Cw(u)^{2}$
.
$\mathbb{E}\{Z_{j}\left( u\right) ^{2}\}\leq Cw(u)^{2}$
.
We have
By Lemma 3,
 \begin{equation*}\mathbb{E}\left\{ \left( Z_{M_{u}}(u)-v_{1,M_{u}}(u)\right) ^{2}\right\}=\sum_{j=0}^{M_{u}}\frac{\mathbb{E}\left\{ Z_{j}\left( u\right) ^{2}\right\}}{P\left( \mathcal{J}_{u}=j\right) }=\sum_{j=0}^{M_{u}}P\left( \mathcal{J}_{u}=j\right) \frac{\mathbb{E}\left\{ Z_{j}\left( u\right) ^{2}\right\} }{P\left( \mathcal{J}_{u}=j\right) ^{2}}.\end{equation*}
\begin{equation*}\mathbb{E}\left\{ \left( Z_{M_{u}}(u)-v_{1,M_{u}}(u)\right) ^{2}\right\}=\sum_{j=0}^{M_{u}}\frac{\mathbb{E}\left\{ Z_{j}\left( u\right) ^{2}\right\}}{P\left( \mathcal{J}_{u}=j\right) }=\sum_{j=0}^{M_{u}}P\left( \mathcal{J}_{u}=j\right) \frac{\mathbb{E}\left\{ Z_{j}\left( u\right) ^{2}\right\} }{P\left( \mathcal{J}_{u}=j\right) ^{2}}.\end{equation*}
By Lemma 4,
 \begin{equation*}v_{1,M_{u}}(u)\leq C\exp \left( -\frac{\left( \log u-\log \left(\int_{T}\text{e}^{\mu (t)} \, \text{d} t\right) \right) ^{2}}{2\sigma _{A}^{2}\left( 1+\epsilon\right) }\right) ,\end{equation*}
\begin{equation*}v_{1,M_{u}}(u)\leq C\exp \left( -\frac{\left( \log u-\log \left(\int_{T}\text{e}^{\mu (t)} \, \text{d} t\right) \right) ^{2}}{2\sigma _{A}^{2}\left( 1+\epsilon\right) }\right) ,\end{equation*}
and
as in Lemma 1. Moreover, we have
 \begin{align*}\mathbb{E}\left\{ (Z_{M_{u}}(u)-w(u))^{2}\right\} &= \mathbb{E}\left\{(Z_{M_{u}}(u))^{2}\right\} -w_{M_{u}}^{2}(u)+(w_{M_{u}}(u)-w(u))^{2} \\&= \mathbb{E}\big\{ ( Z_{M_{u}}(u)-v_{1,M_{u}}(u)) ^{2}\big\}+v_{1,M_{u}}(u)( v_{1,M_{u}}(u)+2v_{2,M_{u}}(u)) \\& \quad -w_{M_{u}}^{2}(u)+(w_{M_{u}}(u)-w(u))^{2}\end{align*}
\begin{align*}\mathbb{E}\left\{ (Z_{M_{u}}(u)-w(u))^{2}\right\} &= \mathbb{E}\left\{(Z_{M_{u}}(u))^{2}\right\} -w_{M_{u}}^{2}(u)+(w_{M_{u}}(u)-w(u))^{2} \\&= \mathbb{E}\big\{ ( Z_{M_{u}}(u)-v_{1,M_{u}}(u)) ^{2}\big\}+v_{1,M_{u}}(u)( v_{1,M_{u}}(u)+2v_{2,M_{u}}(u)) \\& \quad -w_{M_{u}}^{2}(u)+(w_{M_{u}}(u)-w(u))^{2}\end{align*}
and, for large u,
![]() $\mathbb{E}\left\{ (Z_{M_{u}}(u)-w(u))^{2}\right\} \leq \mathbb{E}\big\{\left( Z_{M_{u}}(u)-v_{1,M_{u}}(u)\right) ^{2}\big\}+3v_{1,M_{u}}(u)w(u)+\eta _{u}^{2}w(u)^{2}$
by Proposition 1.
$\mathbb{E}\left\{ (Z_{M_{u}}(u)-w(u))^{2}\right\} \leq \mathbb{E}\big\{\left( Z_{M_{u}}(u)-v_{1,M_{u}}(u)\right) ^{2}\big\}+3v_{1,M_{u}}(u)w(u)+\eta _{u}^{2}w(u)^{2}$
by Proposition 1.
Now,
 \begin{equation*}\frac{\mathbb{E}\left\{ \left( Z_{M_{u}}(u)-v_{1,M_{u}}(u)\right)^{2}\right\} }{w_{M_{u}}(u)^{2}} \leq \left( \frac{w(u)^{2}}{w_{M_{u}}(u)^{2}}\right) \sum_{j=0}^{M_{u}}\frac{1}{P\left( \mathcal{J}_{u}=j\right) }\frac{\mathbb{E}\left\{ Z_{j}\left( u\right) ^{2}\right\} }{w(u)^{2}}\leq C\left( M_{u}\right) ^{2}\end{equation*}
\begin{equation*}\frac{\mathbb{E}\left\{ \left( Z_{M_{u}}(u)-v_{1,M_{u}}(u)\right)^{2}\right\} }{w_{M_{u}}(u)^{2}} \leq \left( \frac{w(u)^{2}}{w_{M_{u}}(u)^{2}}\right) \sum_{j=0}^{M_{u}}\frac{1}{P\left( \mathcal{J}_{u}=j\right) }\frac{\mathbb{E}\left\{ Z_{j}\left( u\right) ^{2}\right\} }{w(u)^{2}}\leq C\left( M_{u}\right) ^{2}\end{equation*}
as
![]() $u\rightarrow \infty $
. We deduce that, for large u,
$u\rightarrow \infty $
. We deduce that, for large u,
Finally,
![]() $M_{u}\sim \text{mes}(T)S_{u}^{d}\sim \text{mes}(T)\eta _{u}^{-(1+\varepsilon )d}\left(\log u\right) ^{(2+\varepsilon )d}$
, and, for large u and some positive constants
$M_{u}\sim \text{mes}(T)S_{u}^{d}\sim \text{mes}(T)\eta _{u}^{-(1+\varepsilon )d}\left(\log u\right) ^{(2+\varepsilon )d}$
, and, for large u and some positive constants
![]() $c_{1}^{\prime }$
and
$c_{1}^{\prime }$
and
![]() $c_{2}^{\prime }$
, we have
$c_{2}^{\prime }$
, we have
![]() $c_{1}^{\prime }|\log w(u)|\leq \left( \log u\right) ^{2}\leq c_{2}^{\prime}|\log w(u)|$
. It follows that
$c_{1}^{\prime }|\log w(u)|\leq \left( \log u\right) ^{2}\leq c_{2}^{\prime}|\log w(u)|$
. It follows that
Funding Information
There are no funding bodies to thank relating to this creation of this article.
Competing Interests
There were no competing interests to declare which arose during the preparation or publication process of this article.