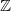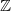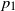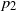1. Introduction and main result
Frog models are growth models that have been studied in various guises for about two decades. They are also related to activated random walks (see, e.g., [Reference Rolla7]) with sleep rate 0. The name has been attributed to R. Durrett, but the first occurrence of this class of models in print seems to be [Reference Telcs and Wormald9]. In such models, on a graph
![]() $G=(V,E)$
, at each site
$G=(V,E)$
, at each site
![]() $v\in V$
there are
$v\in V$
there are
![]() $\eta(v)$
dormant frogs, where
$\eta(v)$
dormant frogs, where
![]() $(\eta(v))_{v \in V}$
are independent and identically distributed (i.i.d.)
$(\eta(v))_{v \in V}$
are independent and identically distributed (i.i.d.)
![]() ${\mathbb{Z}}_+=\{0,1,\dots\}$
-valued random variables with law
${\mathbb{Z}}_+=\{0,1,\dots\}$
-valued random variables with law
![]() $\nu$
. Let
$\nu$
. Let
![]() $\mu={\mathbb{E}}[\eta(x)]$
denote the mean of
$\mu={\mathbb{E}}[\eta(x)]$
denote the mean of
![]() $\nu$
. Some chosen finite collection of sites (often just the origin), and all dormant frogs located at them, are activated at time 0. Each active frog moves independently of all others according to a simple (symmetric) random walk, and remains active thereafter. On the first visit of any (active) frog to a site
$\nu$
. Some chosen finite collection of sites (often just the origin), and all dormant frogs located at them, are activated at time 0. Each active frog moves independently of all others according to a simple (symmetric) random walk, and remains active thereafter. On the first visit of any (active) frog to a site
![]() $v\in V$
, that site, and all dormant frogs there, are instantly activated.
$v\in V$
, that site, and all dormant frogs there, are instantly activated.
In this paper time is discrete, and an active frog can only move at times
![]() $n \in {\mathbb{N}}=\{1,2,\dots\}$
after being activated. In the lazy frog model, each active frog moves according to a lazy (symmetric) simple random walk, i.e. it moves with probability
$n \in {\mathbb{N}}=\{1,2,\dots\}$
after being activated. In the lazy frog model, each active frog moves according to a lazy (symmetric) simple random walk, i.e. it moves with probability
![]() $p\in (0,1]$
on any given step (independent of previous steps and other frogs). The reader will hopefully excuse the awkward terminology here—that active frogs are lazy walkers! By applying the subadditive ergodic theorem, shape theorems are known for such models (see, e.g., [Reference Alves, Machado and Popov1] when there is exactly one frog per site, and [Reference Alves, Machado, Popov and Ravishankar2] more generally). In general dimensions the shape theorem describes the set of sites
$p\in (0,1]$
on any given step (independent of previous steps and other frogs). The reader will hopefully excuse the awkward terminology here—that active frogs are lazy walkers! By applying the subadditive ergodic theorem, shape theorems are known for such models (see, e.g., [Reference Alves, Machado and Popov1] when there is exactly one frog per site, and [Reference Alves, Machado, Popov and Ravishankar2] more generally). In general dimensions the shape theorem describes the set of sites
![]() $\xi_n$
that have been visited by time n, and takes the following form: there exists a non-empty convex set
$\xi_n$
that have been visited by time n, and takes the following form: there exists a non-empty convex set
![]() $A\subset \mathbb{R}^d$
such that, for any
$A\subset \mathbb{R}^d$
such that, for any
![]() $\varepsilon>0$
, we almost surely (a.s.) have that
$\varepsilon>0$
, we almost surely (a.s.) have that
![]() $(1-\varepsilon)A\subset n^{-1}\xi_n \subset (1+\varepsilon)A$
for all n sufficiently large.
$(1-\varepsilon)A\subset n^{-1}\xi_n \subset (1+\varepsilon)A$
for all n sufficiently large.
We assume throughout this paper that
![]() $G={\mathbb{Z}}$
(with nearest-neighbour edges) and that
$G={\mathbb{Z}}$
(with nearest-neighbour edges) and that
![]() $\mu\in (0,\infty)$
. In this setting
$\mu\in (0,\infty)$
. In this setting
![]() $\xi_n\subset {\mathbb{Z}}$
and the shape theorem takes a simpler form. Let
$\xi_n\subset {\mathbb{Z}}$
and the shape theorem takes a simpler form. Let
![]() $R_n=\max \xi_n$
denote the rightmost point visited by time n, and
$R_n=\max \xi_n$
denote the rightmost point visited by time n, and
![]() $L_n=\min\xi_n$
denote the leftmost point. As stated in [Reference Deijfen, Hirscher and Lopes4, Theorem 1.2], for
$L_n=\min\xi_n$
denote the leftmost point. As stated in [Reference Deijfen, Hirscher and Lopes4, Theorem 1.2], for
![]() $p>0$
there exists a constant
$p>0$
there exists a constant
![]() $A=A(\nu,p)>0$
such that
$A=A(\nu,p)>0$
such that
As the authors point out in [Reference Deijfen, Hirscher and Lopes4], the proof of this result (where for
![]() $p<1$
the frogs are lazy) requires only minor modifications of the case
$p<1$
the frogs are lazy) requires only minor modifications of the case
![]() $p=1$
handled in [Reference Alves, Machado and Popov1, Reference Alves, Machado, Popov and Ravishankar2].
$p=1$
handled in [Reference Alves, Machado and Popov1, Reference Alves, Machado, Popov and Ravishankar2].
Deijfen, Hirscher, and Lopes [Reference Deijfen, Hirscher and Lopes4] introduced a model with two types of (lazy) frogs. Active frogs of type i have probability
![]() $p_i\in (0,1]$
of moving on any given step, independent of all other frogs, but again an active frog never becomes dormant. When a frog of type
$p_i\in (0,1]$
of moving on any given step, independent of all other frogs, but again an active frog never becomes dormant. When a frog of type
![]() $i\in \{1,2\}$
visits a site containing dormant frogs (i.e. a site previously unvisited by active frogs), all of the dormant frogs at that site become active frogs of type i. Since the model is defined in discrete time, it is possible that a site y containing dormant frogs is simultaneously visited by active frogs of two different types, in which case a tiebreaker rule is specified to decide which active frog is the one that activates the dormant frogs at y. Although it does not affect the validity of our main results, for definiteness we will assume that ‘the’ activator is chosen uniformly at random (and independent of the past) from among those frogs that are first to arrive at a site. The locations of the active frogs at time 0 will also be largely unimportant for us, but elements of our proof require that there is a finite number of active frogs of each type initially. To fix ideas, we will assume that at time 0 there are
$i\in \{1,2\}$
visits a site containing dormant frogs (i.e. a site previously unvisited by active frogs), all of the dormant frogs at that site become active frogs of type i. Since the model is defined in discrete time, it is possible that a site y containing dormant frogs is simultaneously visited by active frogs of two different types, in which case a tiebreaker rule is specified to decide which active frog is the one that activates the dormant frogs at y. Although it does not affect the validity of our main results, for definiteness we will assume that ‘the’ activator is chosen uniformly at random (and independent of the past) from among those frogs that are first to arrive at a site. The locations of the active frogs at time 0 will also be largely unimportant for us, but elements of our proof require that there is a finite number of active frogs of each type initially. To fix ideas, we will assume that at time 0 there are
![]() $\eta(x)$
dormant frogs at each
$\eta(x)$
dormant frogs at each
![]() $x\ne 0$
and
$x\ne 0$
and
![]() $\eta_i(0)$
active frogs of type
$\eta_i(0)$
active frogs of type
![]() $i \in \{1,2\}$
at the origin, and we will condition on
$i \in \{1,2\}$
at the origin, and we will condition on
![]() $\eta_1(0)\wedge \eta_2(0)>0$
(see Fig. 1). However, as a tool for proving our main result, we will compare the evolution of the model with this initial distribution of active and dormant frogs with 1-type or 2-type frog models with different initial distributions.
$\eta_1(0)\wedge \eta_2(0)>0$
(see Fig. 1). However, as a tool for proving our main result, we will compare the evolution of the model with this initial distribution of active and dormant frogs with 1-type or 2-type frog models with different initial distributions.

Figure 1. Our default initial configuration. Frogs at the origin are activated at time 0 (at least one of each type), and all other frogs are dormant.
Let
![]() $N_n(i)$
denote the number of (active) frogs of type i at time n. Let
$N_n(i)$
denote the number of (active) frogs of type i at time n. Let
![]() $G_i=\{N_n(i)\to \infty\}$
. We say that there is coexistence of frogs of types 1 and 2 if
$G_i=\{N_n(i)\to \infty\}$
. We say that there is coexistence of frogs of types 1 and 2 if
![]() $G_1\cap G_2$
occurs. Deijfen et al. [Reference Deijfen, Hirscher and Lopes4] showed that if
$G_1\cap G_2$
occurs. Deijfen et al. [Reference Deijfen, Hirscher and Lopes4] showed that if
![]() $p_1=p_2>0$
then there is coexistence on
$p_1=p_2>0$
then there is coexistence on
![]() ${\mathbb{Z}}^d$
with positive probability. They asked [Reference Deijfen, Hirscher and Lopes4, Section 1.3] what happens when
${\mathbb{Z}}^d$
with positive probability. They asked [Reference Deijfen, Hirscher and Lopes4, Section 1.3] what happens when
![]() $p_1\ne p_2$
, and surmised that if
$p_1\ne p_2$
, and surmised that if
![]() $\mu<\infty$
then there is coexistence with positive probability if and only if
$\mu<\infty$
then there is coexistence with positive probability if and only if
![]() $A(p_1)=A(p_2)$
(where A(p) denotes the linear growth rate of the rightmost visited point of a one-type lazy frog model with parameter p). In [Reference Deijfen and Rosengren5], it is shown that the initial configuration of active frogs (as long as it is finite) does not affect whether there is coexistence with positive probability. Our main result is the following theorem.
$A(p_1)=A(p_2)$
(where A(p) denotes the linear growth rate of the rightmost visited point of a one-type lazy frog model with parameter p). In [Reference Deijfen and Rosengren5], it is shown that the initial configuration of active frogs (as long as it is finite) does not affect whether there is coexistence with positive probability. Our main result is the following theorem.
Theorem 1. Let
![]() $G={\mathbb{Z}}$
and
$G={\mathbb{Z}}$
and
![]() $\mu\in (0,\infty)$
. For any
$\mu\in (0,\infty)$
. For any
![]() $p_1,p_2\in (0,1]$
,
$p_1,p_2\in (0,1]$
,
![]() ${\mathbb{P}}(G_1\cap G_2)>0$
, i.e. with positive probability there will be infinitely many frogs of each kind.
${\mathbb{P}}(G_1\cap G_2)>0$
, i.e. with positive probability there will be infinitely many frogs of each kind.
This resolves the open problem of [Reference Deijfen, Hirscher and Lopes4] on
![]() ${\mathbb{Z}}$
(we do not know what happens in more than one dimension), except that it is a priori possible that A(p) does not depend on p. Thus, to ensure that our theorem has new content, we should provide examples where
${\mathbb{Z}}$
(we do not know what happens in more than one dimension), except that it is a priori possible that A(p) does not depend on p. Thus, to ensure that our theorem has new content, we should provide examples where
![]() $A(p)\ne A(p')$
if
$A(p)\ne A(p')$
if
![]() $p\ne p'$
. Trivially,
$p\ne p'$
. Trivially,
![]() $A(p)\le 1$
for all p. A simple coupling argument (see, e.g., Lemma 1) shows that
$A(p)\le 1$
for all p. A simple coupling argument (see, e.g., Lemma 1) shows that
![]() $A(p)\le A(p')$
when
$A(p)\le A(p')$
when
![]() $p<p'$
. We expect that the inequality is strict if
$p<p'$
. We expect that the inequality is strict if
![]() $A(p')<1$
. We do not prove this here, but instead show that arbitrarily small growth rates are possible by taking p close to 0. This then gives us the aforementioned examples (for any
$A(p')<1$
. We do not prove this here, but instead show that arbitrarily small growth rates are possible by taking p close to 0. This then gives us the aforementioned examples (for any
![]() $p'>0$
one can find
$p'>0$
one can find
![]() $p<p'$
such that
$p<p'$
such that
![]() $A(p)<A(p')$
).
$A(p)<A(p')$
).
Proposition 1. If
![]() $\mu \in (0,\infty)$
then
$\mu \in (0,\infty)$
then
![]() $A(p)\downarrow 0$
as
$A(p)\downarrow 0$
as
![]() $p\downarrow 0$
.
$p\downarrow 0$
.
Proposition 1 follows from an elementary relation between the frog model and a particular branching random walk, together with standard bounds on the expected speed of the maximum of a branching random walk (see Section 5). As indicated above, from Theorem 1 and Proposition 1 we have the following corollary.
Corollary 1. For any
![]() $\nu$
such that
$\nu$
such that
![]() $\mu\in (0,\infty)$
and any
$\mu\in (0,\infty)$
and any
![]() $p>0$
, there exists
$p>0$
, there exists
![]() $p'\in (0,p)$
with
$p'\in (0,p)$
with
![]() $0<A(p')<A(p)$
such that there is coexistence for the corresponding 2-type frog model on
$0<A(p')<A(p)$
such that there is coexistence for the corresponding 2-type frog model on
![]() ${\mathbb{Z}}$
with positive probability.
${\mathbb{Z}}$
with positive probability.
Concepts of coexistence (or lack thereof) of two or more types of interacting particles have been considered in various other settings as well, including the setting of first passage percolation; see, e.g., the survey [Reference Deijfen and Häggström3] and more recently [Reference Finn and Stauffer6]. Our results give a small and relatively simple contribution to the literature in this general area.
To prove Theorem 1, we will consider the one-sided one-type model with
![]() $\eta(x)$
dormant frogs at
$\eta(x)$
dormant frogs at
![]() $x> 0$
and 0 frogs at
$x> 0$
and 0 frogs at
![]() $y<0$
(and, e.g.,
$y<0$
(and, e.g.,
![]() $\eta(0)$
active frogs at 0 at time 0). Let
$\eta(0)$
active frogs at 0 at time 0). Let
![]() $A_+(p)=\liminf_{n \to \infty}n^{-1}R_n\ge 0$
denote the
$A_+(p)=\liminf_{n \to \infty}n^{-1}R_n\ge 0$
denote the
![]() $\liminf$
linear growth rate of the rightmost activated site, and
$\liminf$
linear growth rate of the rightmost activated site, and
![]() $A_-(p)=\liminf_{n \to \infty}n^{-1}L_n\le 0$
the
$A_-(p)=\liminf_{n \to \infty}n^{-1}L_n\le 0$
the
![]() $\liminf$
linear growth rate of the leftmost. A simple coupling argument (see Lemma 1) shows that the
$\liminf$
linear growth rate of the leftmost. A simple coupling argument (see Lemma 1) shows that the
![]() $\limsup$
linear growth rate
$\limsup$
linear growth rate
![]() $\limsup_{n \to \infty}n^{-1}R_n$
is at most A(p). Note that
$\limsup_{n \to \infty}n^{-1}R_n$
is at most A(p). Note that
![]() $A_+(p)$
and
$A_+(p)$
and
![]() $A_-(p)$
are a priori random, whereas A(p) has been proved to be deterministic. We will prove that, almost surely,
$A_-(p)$
are a priori random, whereas A(p) has been proved to be deterministic. We will prove that, almost surely,
![]() $A_+(p)=A(p)$
and
$A_+(p)=A(p)$
and
![]() $A_-(p)=0$
. Assuming that this is true, it is fairly easy to see how to proceed; one then shows that, with positive probability, both of the following happen:
$A_-(p)=0$
. Assuming that this is true, it is fairly easy to see how to proceed; one then shows that, with positive probability, both of the following happen:
-
type 1 frogs only ever activate frogs to the right of 0, with the rightmost (resp. leftmost) site visited by type 1 frogs up to time n being roughly
 $nA(p_1)$
(resp. not growing linearly with time);
$nA(p_1)$
(resp. not growing linearly with time); -
type 2 frogs only ever activate frogs to the left of 0, with the leftmost (resp. rightmost) site visited by type 2 frogs up to time n being roughly
 $-nA(p_2)$
(resp. not growing linearly with time).
$-nA(p_2)$
(resp. not growing linearly with time).
This then proves Theorem 1. Of course, one needs to start with an active frog at time 0 to ensure that
![]() $A(p)>0$
, so we will always (implicitly or explicitly) condition on having at least one active frog at 0 at time 0.
$A(p)>0$
, so we will always (implicitly or explicitly) condition on having at least one active frog at 0 at time 0.
In Section 2 we state and prove a simple monotonicity result (for one-type frog models) that will be used in other parts of the proof. In Section 3 we prove that
![]() $A_+(p)=A(p)$
and
$A_+(p)=A(p)$
and
![]() $A_-(p)=0$
. Proposition 1 is proved in Section 5. Two-type frog models appear only in Section 4, where Theorem 1 is proved.
$A_-(p)=0$
. Proposition 1 is proved in Section 5. Two-type frog models appear only in Section 4, where Theorem 1 is proved.
2. Frog domination
We use the notation (x, l) to denote the lth frog at location x at time zero, where
![]() $l\le \eta(x)$
.
$l\le \eta(x)$
.
For
![]() $p \in (0,1]$
,
$p \in (0,1]$
,
![]() $\boldsymbol{\eta}=(\eta(x))_{x \in {\mathbb{Z}}}\in {\mathbb{Z}}^{{\mathbb{Z}}_+}$
, and (finite or infinite)
$\boldsymbol{\eta}=(\eta(x))_{x \in {\mathbb{Z}}}\in {\mathbb{Z}}^{{\mathbb{Z}}_+}$
, and (finite or infinite)
![]() $S\subset {\mathbb{Z}}$
, we will denote by
$S\subset {\mathbb{Z}}$
, we will denote by
![]() $X(p,\boldsymbol{\eta},S)$
a (one-type) frog process on
$X(p,\boldsymbol{\eta},S)$
a (one-type) frog process on
![]() ${\mathbb{Z}}$
with initial configuration
${\mathbb{Z}}$
with initial configuration
![]() $\boldsymbol{\eta}$
and initial activated set of sites S.
$\boldsymbol{\eta}$
and initial activated set of sites S.
For
![]() $\boldsymbol{\eta},\boldsymbol{\eta'}\in {\mathbb{Z}}^{{\mathbb{Z}}_+}$
, we write
$\boldsymbol{\eta},\boldsymbol{\eta'}\in {\mathbb{Z}}^{{\mathbb{Z}}_+}$
, we write
![]() $\boldsymbol{\eta}\le \boldsymbol{\eta'}$
if
$\boldsymbol{\eta}\le \boldsymbol{\eta'}$
if
![]() $\eta(x)\le \eta'(x)$
for every
$\eta(x)\le \eta'(x)$
for every
![]() $x \in {\mathbb{Z}}$
. We have the following straightforward monotonicity result. Although this result is undoubtedly well known, we will apply it often so we include a proof for completeness.
$x \in {\mathbb{Z}}$
. We have the following straightforward monotonicity result. Although this result is undoubtedly well known, we will apply it often so we include a proof for completeness.
Lemma 1. For any
![]() $\boldsymbol{\eta}$
,
$\boldsymbol{\eta}$
,
![]() $\boldsymbol{\eta'}$
such that
$\boldsymbol{\eta'}$
such that
![]() $\boldsymbol{\eta}\le \boldsymbol{\eta'}$
, and any S, S
$\boldsymbol{\eta}\le \boldsymbol{\eta'}$
, and any S, S
![]() $^{\prime}$
such that
$^{\prime}$
such that
![]() $S\subset S'$
, there exists a probability space
$S\subset S'$
, there exists a probability space
![]() $(\Omega, \mathcal{F},{\mathbb{P}})$
on which, for every
$(\Omega, \mathcal{F},{\mathbb{P}})$
on which, for every
![]() $0<p\le p'\le 1$
, we can define frog processes
$0<p\le p'\le 1$
, we can define frog processes
![]() $X(p,\boldsymbol{\eta},S)$
and
$X(p,\boldsymbol{\eta},S)$
and
![]() $X'(p',\boldsymbol{\eta'},S')$
such that
$X'(p',\boldsymbol{\eta'},S')$
such that
![]() $\xi_n\subset \xi'_n$
for every
$\xi_n\subset \xi'_n$
for every
![]() $n \in {\mathbb{Z}}_+$
,
$n \in {\mathbb{Z}}_+$
,
![]() ${\mathbb{P}}$
-almost surely.
${\mathbb{P}}$
-almost surely.
Proof. Let
![]() $(\Omega, \mathcal{F}, {\mathbb{P}})$
be a probability space on which
$(\Omega, \mathcal{F}, {\mathbb{P}})$
be a probability space on which
![]() $\boldsymbol{\Delta}=(\Delta_{x,l,j})_{x \in {\mathbb{Z}}, l,j \in {\mathbb{N}}}$
is a collection of i.i.d. random variables satisfying
$\boldsymbol{\Delta}=(\Delta_{x,l,j})_{x \in {\mathbb{Z}}, l,j \in {\mathbb{N}}}$
is a collection of i.i.d. random variables satisfying
![]() ${\mathbb{P}}(\Delta_{x,l,j}=1)={\mathbb{P}}(\Delta_{x,l,j}=-1)=1/2$
, and
${\mathbb{P}}(\Delta_{x,l,j}=1)={\mathbb{P}}(\Delta_{x,l,j}=-1)=1/2$
, and
![]() $(U_{x,l,k})_{x \in {\mathbb{Z}}, l,k \in {\mathbb{Z}}_+}$
be independent uniform random variables on [0, 1], independent of
$(U_{x,l,k})_{x \in {\mathbb{Z}}, l,k \in {\mathbb{Z}}_+}$
be independent uniform random variables on [0, 1], independent of
![]() $\boldsymbol{\Delta}$
. Given
$\boldsymbol{\Delta}$
. Given
![]() $0<p\le p'\le 1$
,
$0<p\le p'\le 1$
,
![]() $\boldsymbol{\eta}\in {\mathbb{Z}}^{{\mathbb{Z}}_+}$
, and
$\boldsymbol{\eta}\in {\mathbb{Z}}^{{\mathbb{Z}}_+}$
, and
![]() $S\subset {\mathbb{Z}}$
, let
$S\subset {\mathbb{Z}}$
, let
![]() $X(p,\boldsymbol{\eta},S)$
denote the frog process with
$X(p,\boldsymbol{\eta},S)$
denote the frog process with
![]() $\eta(x)$
frogs starting at x, with sites in S activated at time 0, and such that, once activated, the frog (x, l) with
$\eta(x)$
frogs starting at x, with sites in S activated at time 0, and such that, once activated, the frog (x, l) with
![]() $1\le l\le \eta(x)$
conducts a lazy walk, stepping k time units after it was activated (
$1\le l\le \eta(x)$
conducts a lazy walk, stepping k time units after it was activated (
![]() $k\ge 1$
) if
$k\ge 1$
) if
![]() $U_{x,l,k}\le p$
. Its jth step is given by
$U_{x,l,k}\le p$
. Its jth step is given by
![]() $\Delta_{x,l,j}$
. Also let
$\Delta_{x,l,j}$
. Also let
![]() $X'(p',\boldsymbol{\eta'},S')$
denote the frog process with
$X'(p',\boldsymbol{\eta'},S')$
denote the frog process with
![]() $\eta'(x)$
frogs starting at x, with sites in S
$\eta'(x)$
frogs starting at x, with sites in S
![]() $^{\prime}$
activated at time 0, and such that, once activated, the frog (x, l) with
$^{\prime}$
activated at time 0, and such that, once activated, the frog (x, l) with
![]() $l\le \eta'(x)$
conducts a lazy walk, stepping k time units after it was activated (
$l\le \eta'(x)$
conducts a lazy walk, stepping k time units after it was activated (
![]() $k\ge 1$
) if
$k\ge 1$
) if
![]() $U_{x,l,k}\le p'$
. Its jth step is given by
$U_{x,l,k}\le p'$
. Its jth step is given by
![]() $\Delta_{x,l,j}$
.
$\Delta_{x,l,j}$
.
By the construction on this space we have the following trivial facts:
-
For fixed p, the range (set of vertices visited) of any particle/frog
 $\beta=(x,l)$
at time n is increasing in its time since activation.
$\beta=(x,l)$
at time n is increasing in its time since activation. -
Each frog (x, l) has the same sequence of moves in the X process and the X
 $^{\prime}$
process (given by the
$^{\prime}$
process (given by the
 $\Delta_{x,l,j}$
variables).
$\Delta_{x,l,j}$
variables). -
If
 $U_{x,l,k}\le p$
then
$U_{x,l,k}\le p$
then
 $U_{x,l,k}\le p'$
, so the range of a single p frog is dominated by that of the corresponding p
$U_{x,l,k}\le p'$
, so the range of a single p frog is dominated by that of the corresponding p
 $^{\prime}$
frog, relative to their times of activation.
$^{\prime}$
frog, relative to their times of activation.
We can thus conclude that all frogs in the X process are activated no earlier than in the X
![]() $^{\prime}$
process, and their ranges trail those in X
$^{\prime}$
process, and their ranges trail those in X
![]() $^{\prime}$
from that time forward.
$^{\prime}$
from that time forward.
3. One-sided frogs
Let
![]() $\mathbb{P}^+$
denote the law of the one-sided frog model with
$\mathbb{P}^+$
denote the law of the one-sided frog model with
![]() $(\eta(x))_{x\in {\mathbb{Z}}_+}$
i.i.d. each with law
$(\eta(x))_{x\in {\mathbb{Z}}_+}$
i.i.d. each with law
![]() $\nu$
, conditional on
$\nu$
, conditional on
![]() $\eta(0)\ge 1$
, and where only the origin is activated at time 0. When proving our main result we will force the frogs to take a prescribed sequence of steps initially, and the evolution of each type of frog thereafter will be stochastically dominated by a frog model with a different law
$\eta(0)\ge 1$
, and where only the origin is activated at time 0. When proving our main result we will force the frogs to take a prescribed sequence of steps initially, and the evolution of each type of frog thereafter will be stochastically dominated by a frog model with a different law
![]() ${\mathbb{P}}^*$
which we now define.
${\mathbb{P}}^*$
which we now define.
Let
![]() ${\mathbb{P}}^*$
denote the law of the one-sided frog model with
${\mathbb{P}}^*$
denote the law of the one-sided frog model with
![]() $\eta'(x)=\eta(x)+\eta(x+1)+\eta(0)$
frogs at
$\eta'(x)=\eta(x)+\eta(x+1)+\eta(0)$
frogs at
![]() $x\ge 0$
at time 0 (where
$x\ge 0$
at time 0 (where
![]() $\eta(x)$
are
$\eta(x)$
are
![]() $\mathrm{i.i.d.} \sim \mu$
except that
$\mathrm{i.i.d.} \sim \mu$
except that
![]() $\eta(0)$
is conditioned to be strictly positive), all of which are activated (so
$\eta(0)$
is conditioned to be strictly positive), all of which are activated (so
![]() $S={\mathbb{Z}}_+$
is infinite), and no other frogs. Let
$S={\mathbb{Z}}_+$
is infinite), and no other frogs. Let
![]() ${\mathbb{P}}^{*-}$
be defined in the same way, but the frogs are only at negative sites
${\mathbb{P}}^{*-}$
be defined in the same way, but the frogs are only at negative sites
![]() $x\le 0$
. By Lemma 1 the range of the frog model under
$x\le 0$
. By Lemma 1 the range of the frog model under
![]() ${\mathbb{P}}^*$
dominates that under
${\mathbb{P}}^*$
dominates that under
![]() ${\mathbb{P}}^+$
.
${\mathbb{P}}^+$
.
Let P(x) denote the original location of the frog that first reaches x (if there are ties, choose one from those that reach x first, uniformly at random).
Lemma 2. We have
![]() ${\mathbb{P}}^*(A_-(p)=0)=1$
for every
${\mathbb{P}}^*(A_-(p)=0)=1$
for every
![]() $p\in (0,1]$
. Moreover, for all
$p\in (0,1]$
. Moreover, for all
![]() $\delta,\varepsilon>0$
there exists
$\delta,\varepsilon>0$
there exists
![]() $m_0(\varepsilon,\delta)<\infty$
such that, for all
$m_0(\varepsilon,\delta)<\infty$
such that, for all
![]() $m\ge m_0$
and all
$m\ge m_0$
and all
![]() $p\in (0,1]$
,
$p\in (0,1]$
,
Proof. By Lemma 1 it suffices to prove the result in the case
![]() $p=1$
, since the range is stochastically increasing in p.
$p=1$
, since the range is stochastically increasing in p.
Let
![]() $T_x$
denote the first time that an active frog reaches x. We use a (non-lazy) simple symmetric random walk
$T_x$
denote the first time that an active frog reaches x. We use a (non-lazy) simple symmetric random walk
![]() $(S_k)_{k \ge 0}$
defined under a measure
$(S_k)_{k \ge 0}$
defined under a measure
![]() ${\mathbb{P}}'$
. Then, for
${\mathbb{P}}'$
. Then, for
![]() $n \in {\mathbb{N}}$
the following holds:
$n \in {\mathbb{N}}$
the following holds:
 \begin{align*}&{\mathbb{P}}^*\Big( T_{-n}\le n^{3/2}\Big)\\&= \sum_{y=0}^\infty \sum_{\ell=0}^\infty\sum_{k=0}^\infty\sum_{j=1}^{\infty}{\mathbb{P}}^*\big(T_{-n}\le n^{3/2},P(\!-n)=y,\eta(y)=\ell,\eta(y+1)=k,\eta(0)=j\big)\\&\le \sum_{y=0}^\infty \sum_{\ell\ge 0}\sum_{k\ge 0}\sum_{j\ge 1} \nu(\{\ell\})\nu(\{k\}){\mathbb{P}}^*(\eta(0)=j)\cdot(\ell+k+j) \cdot{\mathbb{P}}'\Big(\max_{1\le k\le n^{3/2}}S_k\ge n+y\Big)\\&\le \frac{3\mu}{(1-\nu(\{0\}))}\sum_{y=0}^\infty {\mathbb{P}}'\Big(\max_{1\le k\le n^{3/2}}S_k\ge n+y\Big),\end{align*}
\begin{align*}&{\mathbb{P}}^*\Big( T_{-n}\le n^{3/2}\Big)\\&= \sum_{y=0}^\infty \sum_{\ell=0}^\infty\sum_{k=0}^\infty\sum_{j=1}^{\infty}{\mathbb{P}}^*\big(T_{-n}\le n^{3/2},P(\!-n)=y,\eta(y)=\ell,\eta(y+1)=k,\eta(0)=j\big)\\&\le \sum_{y=0}^\infty \sum_{\ell\ge 0}\sum_{k\ge 0}\sum_{j\ge 1} \nu(\{\ell\})\nu(\{k\}){\mathbb{P}}^*(\eta(0)=j)\cdot(\ell+k+j) \cdot{\mathbb{P}}'\Big(\max_{1\le k\le n^{3/2}}S_k\ge n+y\Big)\\&\le \frac{3\mu}{(1-\nu(\{0\}))}\sum_{y=0}^\infty {\mathbb{P}}'\Big(\max_{1\le k\le n^{3/2}}S_k\ge n+y\Big),\end{align*}
where the first inequality is obtained by conditioning and using a union bound. Using a union bound, Chernoff’s bound, and
![]() $\cosh\!(t)\le \mathrm{e}^{t^2/2}$
yields, for any
$\cosh\!(t)\le \mathrm{e}^{t^2/2}$
yields, for any
![]() $t>0$
,
$t>0$
,
 \begin{align*}{\mathbb{P}}^*\!\Big( T_{-n}\le n^{3/2}\Big)&\le\frac{3\mu}{(1-\nu(\{0\}))}\sum_{y=0}^\infty \sum_{k\le n^{3/2}} \frac{(\!\cosh\!(t))^k}{\mathrm{e}^{t(n+y)}}\le \frac{3\mu}{(1-\nu(\{0\}))}n^{3/2}\sum_{y=0}^\infty \frac{\mathrm{e}^{\frac12 t^2n^{3/2}}}{\mathrm{e}^{t(n+y)}}.\end{align*}
\begin{align*}{\mathbb{P}}^*\!\Big( T_{-n}\le n^{3/2}\Big)&\le\frac{3\mu}{(1-\nu(\{0\}))}\sum_{y=0}^\infty \sum_{k\le n^{3/2}} \frac{(\!\cosh\!(t))^k}{\mathrm{e}^{t(n+y)}}\le \frac{3\mu}{(1-\nu(\{0\}))}n^{3/2}\sum_{y=0}^\infty \frac{\mathrm{e}^{\frac12 t^2n^{3/2}}}{\mathrm{e}^{t(n+y)}}.\end{align*}
Now take
![]() $t=(n+y)n^{-3/2}$
and
$t=(n+y)n^{-3/2}$
and
![]() $c=3\mu (1-\nu(\{0\}))^{-1}$
to see that
$c=3\mu (1-\nu(\{0\}))^{-1}$
to see that
 \begin{align*}{\mathbb{P}}^*\!\Big( T_{-n}\le n^{3/2}\Big)\le c\cdot n^{3/2}\cdot \sum_{y=0}^\infty\exp\!\bigg\{{-}\dfrac{(n+y)^2}{2n^{3/2}}\bigg\}.\end{align*}
\begin{align*}{\mathbb{P}}^*\!\Big( T_{-n}\le n^{3/2}\Big)\le c\cdot n^{3/2}\cdot \sum_{y=0}^\infty\exp\!\bigg\{{-}\dfrac{(n+y)^2}{2n^{3/2}}\bigg\}.\end{align*}
By comparing the sum to an integral and using standard Gaussian tail bounds, we obtain
 \begin{align}{\mathbb{P}}^*\!\Big( T_{-n}\le n^{3/2}\Big)&\le c n^{3/2}\left(\exp\!\bigg\{{-}\dfrac{n^2}{2n^{3/2}}\bigg\}+\int_0^\infty\exp\!\bigg\{{-}\dfrac{(n+y)^2}{2n^{3/2}}\bigg\}\mathrm{d}y\right)\nonumber\\&=cn^{3/2}\!\left(\exp\!\big\{{-}\sqrt{n}/2\big\}+\int_n^\infty\exp\!\bigg\{{-}\dfrac{y^2}{2n^{3/2}}\bigg\}\mathrm{d}y\right)\nonumber\\&\le cn^{3/2}\!\left( \exp\!\big\{{-}\sqrt{n}/2\big\}+\int_n^\infty\frac{y}{n}\exp\!\bigg\{{-}\dfrac{y^2}{2n^{3/2}}\bigg\}\mathrm{d}y\right)\nonumber\\&=cn^{3/2}\!\left(\exp\!\big\{{-}\sqrt{n}/2\big\}+\sqrt{n}\exp\!\big\{{-}n^2/(2n^{3/2})\big\}\right) \nonumber\\&\le 2cn^2\exp\!\big\{{-}\sqrt{n}/2\big\}.\nonumber\end{align}
\begin{align}{\mathbb{P}}^*\!\Big( T_{-n}\le n^{3/2}\Big)&\le c n^{3/2}\left(\exp\!\bigg\{{-}\dfrac{n^2}{2n^{3/2}}\bigg\}+\int_0^\infty\exp\!\bigg\{{-}\dfrac{(n+y)^2}{2n^{3/2}}\bigg\}\mathrm{d}y\right)\nonumber\\&=cn^{3/2}\!\left(\exp\!\big\{{-}\sqrt{n}/2\big\}+\int_n^\infty\exp\!\bigg\{{-}\dfrac{y^2}{2n^{3/2}}\bigg\}\mathrm{d}y\right)\nonumber\\&\le cn^{3/2}\!\left( \exp\!\big\{{-}\sqrt{n}/2\big\}+\int_n^\infty\frac{y}{n}\exp\!\bigg\{{-}\dfrac{y^2}{2n^{3/2}}\bigg\}\mathrm{d}y\right)\nonumber\\&=cn^{3/2}\!\left(\exp\!\big\{{-}\sqrt{n}/2\big\}+\sqrt{n}\exp\!\big\{{-}n^2/(2n^{3/2})\big\}\right) \nonumber\\&\le 2cn^2\exp\!\big\{{-}\sqrt{n}/2\big\}.\nonumber\end{align}
By the Borel–Cantelli lemma,
![]() $T_{-n}>n^{3/2}$
for all but finitely many n,
$T_{-n}>n^{3/2}$
for all but finitely many n,
![]() ${\mathbb{P}}^+$
-a.s., which implies that
${\mathbb{P}}^+$
-a.s., which implies that
![]() $n/T_{-n}$
converges to 0
$n/T_{-n}$
converges to 0
![]() ${\mathbb{P}}^+$
-almost surely, which implies that
${\mathbb{P}}^+$
-almost surely, which implies that
![]() ${\mathbb{P}}^+(A_-(p)=0)=1$
for every p.
${\mathbb{P}}^+(A_-(p)=0)=1$
for every p.
Let us prove the second statement. Since
![]() $\liminf_{n\to \infty}n^{-1}L_n=0$
, for any
$\liminf_{n\to \infty}n^{-1}L_n=0$
, for any
![]() $\delta,\varepsilon>0$
there exists
$\delta,\varepsilon>0$
there exists
![]() $m_0\in {\mathbb{N}}$
such that, for all
$m_0\in {\mathbb{N}}$
such that, for all
![]() $m\ge m_0$
,
$m\ge m_0$
,
As we work in discrete time, for all
![]() $0\le n\le m$
,
$0\le n\le m$
,
![]() $L_n+m\ge0$
almost surely, which proves the second statement.
$L_n+m\ge0$
almost surely, which proves the second statement.
Corollary 2. For every
![]() $\delta>0$
there exists
$\delta>0$
there exists
![]() $k_\delta\in{\mathbb{N}}$
such that
$k_\delta\in{\mathbb{N}}$
such that
![]() ${\mathbb{P}}(P(x)\ge 0\ {\ for\ all\ } x\ge k_\delta)\ge 1-\delta$
.
${\mathbb{P}}(P(x)\ge 0\ {\ for\ all\ } x\ge k_\delta)\ge 1-\delta$
.
Proof. Let
![]() $\bar{A}_+(p)=\limsup_{n \to \infty}n^{-1}R_n(p)$
denote the
$\bar{A}_+(p)=\limsup_{n \to \infty}n^{-1}R_n(p)$
denote the
![]() $\limsup$
of the rightmost visited site up to time n. By Lemma 2 and the definition of
$\limsup$
of the rightmost visited site up to time n. By Lemma 2 and the definition of
![]() ${\mathbb{P}}^{*-}$
we have
${\mathbb{P}}^{*-}$
we have
![]() ${\mathbb{P}}^{*-}(\bar{A}_+(p)=0)=1$
. By Lemma 1 this implies that for the one-sided model with
${\mathbb{P}}^{*-}(\bar{A}_+(p)=0)=1$
. By Lemma 1 this implies that for the one-sided model with
![]() $\eta(x)$
frogs per site (
$\eta(x)$
frogs per site (
![]() $x\le 0$
) and with all frogs activated at time zero, also
$x\le 0$
) and with all frogs activated at time zero, also
![]() $\bar{A}_+(p)=0$
a.s.
$\bar{A}_+(p)=0$
a.s.
Now let
![]() $R^{(\!-)}_n$
denote the rightmost point reached by frogs originating from sites
$R^{(\!-)}_n$
denote the rightmost point reached by frogs originating from sites
![]() $x<0$
up to time n. For the two-sided model under
$x<0$
up to time n. For the two-sided model under
![]() ${\mathbb{P}}$
, this quantity is stochastically dominated by the same quantity when all such frogs are activated at time 0. But the latter grows sublinearly as above (
${\mathbb{P}}$
, this quantity is stochastically dominated by the same quantity when all such frogs are activated at time 0. But the latter grows sublinearly as above (
![]() $\bar{A}_+(p)=0$
a.s.). Since
$\bar{A}_+(p)=0$
a.s.). Since
![]() ${\mathbb{P}}(A_+(p)=A(p))=1$
and
${\mathbb{P}}(A_+(p)=A(p))=1$
and
![]() $A(p)>0$
, this shows that there exists an a.s. finite random variable K such that
$A(p)>0$
, this shows that there exists an a.s. finite random variable K such that
![]() ${\mathbb{P}}(P(x)\ge 0 \mathrm{\ for\ all\ } x\ge K)=1$
. The claim now follows since
${\mathbb{P}}(P(x)\ge 0 \mathrm{\ for\ all\ } x\ge K)=1$
. The claim now follows since
![]() ${\mathbb{P}}(K>k_\delta)<\delta$
for
${\mathbb{P}}(K>k_\delta)<\delta$
for
![]() $k_\delta$
sufficiently large.
$k_\delta$
sufficiently large.
Since the two-sided model under
![]() ${\mathbb{P}}$
dominates the one-sided model under
${\mathbb{P}}$
dominates the one-sided model under
![]() ${\mathbb{P}}^+$
, the following implies that both models have the same linear growth rate for the rightmost visited site.
${\mathbb{P}}^+$
, the following implies that both models have the same linear growth rate for the rightmost visited site.
Lemma 3. For any
![]() $p\in (0,1]$
,
$p\in (0,1]$
,
![]() $\mathbb{P}^+(A_+(p)=A(p))=1$
.
$\mathbb{P}^+(A_+(p)=A(p))=1$
.
Proof. Let
![]() $\delta>0$
. From Corollary 2 there exists
$\delta>0$
. From Corollary 2 there exists
![]() $k_{\delta} \in {\mathbb{N}}$
such that
$k_{\delta} \in {\mathbb{N}}$
such that
![]() ${\mathbb{P}}(P(x)\ge 0 \mathrm{\ for\ all\ } x\ge k_{\delta})\ge 1-\delta$
. Since the activation time
${\mathbb{P}}(P(x)\ge 0 \mathrm{\ for\ all\ } x\ge k_{\delta})\ge 1-\delta$
. Since the activation time
![]() $T^+_{k_{\delta}}$
of
$T^+_{k_{\delta}}$
of
![]() $k_{\delta}$
in the one-sided model is a.s. finite, there exists
$k_{\delta}$
in the one-sided model is a.s. finite, there exists
![]() $t_{\delta}>0$
such that
$t_{\delta}>0$
such that
![]() ${\mathbb{P}}^+(T^+_{k_{\delta}}\le t_\delta)\ge 1-\delta$
. Both of these statements are conditional on
${\mathbb{P}}^+(T^+_{k_{\delta}}\le t_\delta)\ge 1-\delta$
. Both of these statements are conditional on
![]() $\eta(0)\ge 1$
, with (only) the origin activated at time 0.
$\eta(0)\ge 1$
, with (only) the origin activated at time 0.
A natural coupling
![]() $\overline{{\mathbb{P}}}$
of these two processes is as follows. Under
$\overline{{\mathbb{P}}}$
of these two processes is as follows. Under
![]() $\overline{\mathbb{P}}$
, the initial configuration for X is
$\overline{\mathbb{P}}$
, the initial configuration for X is
![]() $(\eta(x))_{ x\in\mathbb{Z}}$
which are
$(\eta(x))_{ x\in\mathbb{Z}}$
which are
![]() $\mathrm{i.i.d.} \sim \nu$
, with
$\mathrm{i.i.d.} \sim \nu$
, with
![]() $\eta(0)$
conditioned to be strictly positive. The initial configuration
$\eta(0)$
conditioned to be strictly positive. The initial configuration
![]() $(\eta^+(x))_{x\in\mathbb{Z}}$
for the one-sided process is defined as
$(\eta^+(x))_{x\in\mathbb{Z}}$
for the one-sided process is defined as
![]() $\eta^+(x)=0$
if
$\eta^+(x)=0$
if
![]() $x<0$
and
$x<0$
and
![]() $\eta^+(x)=\eta(x)$
otherwise. On top of this structure define two frog processes X and
$\eta^+(x)=\eta(x)$
otherwise. On top of this structure define two frog processes X and
![]() $X^+$
from an i.i.d. collection of steps
$X^+$
from an i.i.d. collection of steps
![]() $\boldsymbol{\Delta}$
as in Lemma 1, with
$\boldsymbol{\Delta}$
as in Lemma 1, with
![]() $S=S^+=\{0\}$
, so that X dominates
$S=S^+=\{0\}$
, so that X dominates
![]() $X^+$
. On this space we therefore have
$X^+$
. On this space we therefore have
 \begin{equation}\overline{\mathbb{P}}\Bigg(\bigcap_{x\ge k_{\delta}}\{P(x)\ge 0\}, \, T^+_{k_{\delta}}\le t_\delta\Bigg)\ge 1-2\delta.\end{equation}
\begin{equation}\overline{\mathbb{P}}\Bigg(\bigcap_{x\ge k_{\delta}}\{P(x)\ge 0\}, \, T^+_{k_{\delta}}\le t_\delta\Bigg)\ge 1-2\delta.\end{equation}
Now note that
![]() $\bigcap_{x\ge k_{\delta}}\{P(x)\ge 0\}\cap\Big\{ T^+_{k_{\delta}}\le t_\delta\Big\}\subset \bigcap_{x\ge k_{\delta}}\{T_x\le T^+_x\le T_x+t_{\delta}\}$
, where
$\bigcap_{x\ge k_{\delta}}\{P(x)\ge 0\}\cap\Big\{ T^+_{k_{\delta}}\le t_\delta\Big\}\subset \bigcap_{x\ge k_{\delta}}\{T_x\le T^+_x\le T_x+t_{\delta}\}$
, where
![]() $T_x$
denotes the activation time of x by the two-sided process. Since
$T_x$
denotes the activation time of x by the two-sided process. Since
![]() $R_{T_n}/T_n=n/T_n\to A(p)$
a.s., this shows that
$R_{T_n}/T_n=n/T_n\to A(p)$
a.s., this shows that
![]() $T^+_n/n\to A(p)^{-1}$
a.s. on the event in (1), and therefore also
$T^+_n/n\to A(p)^{-1}$
a.s. on the event in (1), and therefore also
![]() $R_m^+/m \to A(p)$
a.s. on this event (consider
$R_m^+/m \to A(p)$
a.s. on this event (consider
![]() $m\in [T^+_n,T^+_{n+1})$
). This shows that
$m\in [T^+_n,T^+_{n+1})$
). This shows that
![]() ${\mathbb{P}}^+(A^+(p)=A(p))=\overline{\mathbb{P}}(A^+(p)=A(p))\ge 1-2\delta$
. Since
${\mathbb{P}}^+(A^+(p)=A(p))=\overline{\mathbb{P}}(A^+(p)=A(p))\ge 1-2\delta$
. Since
![]() $\delta$
was arbitrary, this completes the proof.
$\delta$
was arbitrary, this completes the proof.
Corollary 3. For any
![]() $\delta>0$
and
$\delta>0$
and
![]() $p\in (0,1]$
there exists
$p\in (0,1]$
there exists
![]() $m_{{1}}(p,\delta)\in {\mathbb{N}}$
such that, for all
$m_{{1}}(p,\delta)\in {\mathbb{N}}$
such that, for all
![]() $m\ge m_{{1}}$
,
$m\ge m_{{1}}$
,
Proof. On the almost sure (by Lemma 3) event
![]() $\{A_+(p)=A(p)\}$
,
$\{A_+(p)=A(p)\}$
,
![]() $\inf_{n\ge m}R_n/n\to A(p)$
almost surely as m goes to infinity. Thus, there exists
$\inf_{n\ge m}R_n/n\to A(p)$
almost surely as m goes to infinity. Thus, there exists
![]() $m_1<\infty$
such that, for all
$m_1<\infty$
such that, for all
![]() $m\ge m_1$
,
$m\ge m_1$
,
Now, for all
![]() $0\le n\le m$
,
$0\le n\le m$
,
![]() $(R_n+m)/n\ge m/n\ge1$
, which gives the conclusion.
$(R_n+m)/n\ge m/n\ge1$
, which gives the conclusion.
Remark 1. Corollary 3 implies that, for any
![]() $k\ge 1$
such that
$k\ge 1$
such that
![]() $\mathbb{P}^+\left(\eta(0)=k\right)>0$
, we have
$\mathbb{P}^+\left(\eta(0)=k\right)>0$
, we have
for all
![]() $m\ge m_{{1}}(p,\delta \mathbb{P}^+\left(\eta(0)=k\right))\in {\mathbb{N}}$
. This is because (letting
$m\ge m_{{1}}(p,\delta \mathbb{P}^+\left(\eta(0)=k\right))\in {\mathbb{N}}$
. This is because (letting
![]() $G_m$
denote the event being measured, and
$G_m$
denote the event being measured, and
![]() $Q_k$
the event being conditioned on) we have for such m that
$Q_k$
the event being conditioned on) we have for such m that
4. The two-type frog model
Let
![]() ${\mathbb{P}}^+_p$
denote the law of the one-sided frog process, conditional on
${\mathbb{P}}^+_p$
denote the law of the one-sided frog process, conditional on
![]() $\eta(0)>0$
, where now the laziness parameter p of the walkers appears explicitly as the subscript of the probability measure. We will denote by
$\eta(0)>0$
, where now the laziness parameter p of the walkers appears explicitly as the subscript of the probability measure. We will denote by
![]() ${\mathbb{P}}_{p_1,p_2}$
the law of a two-type frog model with
${\mathbb{P}}_{p_1,p_2}$
the law of a two-type frog model with
![]() $\eta(x)\sim \nu$
dormant frogs at
$\eta(x)\sim \nu$
dormant frogs at
![]() $x\in {\mathbb{Z}}$
at time 0, and with
$x\in {\mathbb{Z}}$
at time 0, and with
![]() $\eta_i(0)\sim \nu$
active frogs of type
$\eta_i(0)\sim \nu$
active frogs of type
![]() $i \in \{1,2\}$
at 0 at time 0 (with all frog counts independent of each other), conditional on
$i \in \{1,2\}$
at 0 at time 0 (with all frog counts independent of each other), conditional on
![]() $\eta_1(0)>0$
and
$\eta_1(0)>0$
and
![]() $\eta_2(0)>0$
. Type i frogs have laziness parameter
$\eta_2(0)>0$
. Type i frogs have laziness parameter
![]() $p_i\in (0,1]$
. Similarly, we will use the notation
$p_i\in (0,1]$
. Similarly, we will use the notation
![]() $\mathbb{P}^*_p$
when we want to make the parameter p more explicit.
$\mathbb{P}^*_p$
when we want to make the parameter p more explicit.
Proof of Theorem 1. We choose to provide a detailed proof of our main theorem, but the idea is fairly simple and easily obtained from Lemma 2, Corollary 3 and Remark 1.
Let
![]() $p_1,p_2>0$
be given. Under the measure
$p_1,p_2>0$
be given. Under the measure
![]() ${\mathbb{P}}_{p_1,p_2}$
, let the following collection of random variables all be mutually independent:
${\mathbb{P}}_{p_1,p_2}$
, let the following collection of random variables all be mutually independent:
-
 $(\eta(x))_{x\in {\mathbb{Z}}\setminus \{0\}}$
, all
$(\eta(x))_{x\in {\mathbb{Z}}\setminus \{0\}}$
, all
 $\sim \nu$
and with
$\sim \nu$
and with
 $\eta_1\!(0)$
,
$\eta_1\!(0)$
,
 $\eta_2(0)$
having distribution
$\eta_2(0)$
having distribution
 $\nu$
conditional on being strictly positive;
$\nu$
conditional on being strictly positive; -
 $\boldsymbol{\Delta}=(\Delta_{x,l,j})_{x \in {\mathbb{Z}}, l,j \in {\mathbb{N}}}$
satisfying
$\boldsymbol{\Delta}=(\Delta_{x,l,j})_{x \in {\mathbb{Z}}, l,j \in {\mathbb{N}}}$
satisfying
 ${\mathbb{P}}_{p_1,p_2}(\Delta_{x,l,j}=1)={\mathbb{P}}_{p_1,p_2}(\Delta_{x,l,j}=-1)=1/2$
;
${\mathbb{P}}_{p_1,p_2}(\Delta_{x,l,j}=1)={\mathbb{P}}_{p_1,p_2}(\Delta_{x,l,j}=-1)=1/2$
; -
 $(U_{x,l,k})_{x \in {\mathbb{Z}}, l,k \in {\mathbb{Z}}_+}$
are independent standard uniform random variables.
$(U_{x,l,k})_{x \in {\mathbb{Z}}, l,k \in {\mathbb{Z}}_+}$
are independent standard uniform random variables.
Define
 \[\eta_1(x)=\begin{cases}\eta(x) & \text{ if }x>0 , \\ \\[-8pt] 0 & \text{ if }x<0,\end{cases}\qquad \eta_2(x)=\begin{cases}0 & \text{ if }x>0 , \\ \\[-8pt] \eta(x) & \text{ if }x<0.\end{cases}\]
\[\eta_1(x)=\begin{cases}\eta(x) & \text{ if }x>0 , \\ \\[-8pt] 0 & \text{ if }x<0,\end{cases}\qquad \eta_2(x)=\begin{cases}0 & \text{ if }x>0 , \\ \\[-8pt] \eta(x) & \text{ if }x<0.\end{cases}\]
We will define three processes on this space:
-
 $X^1$
denotes a one-sided one-type frog process with initial configuration
$X^1$
denotes a one-sided one-type frog process with initial configuration
 $\boldsymbol{\eta_1}$
(with only the frogs at 0 activated at time 0) such that, once activated, the frog (x, l) with
$\boldsymbol{\eta_1}$
(with only the frogs at 0 activated at time 0) such that, once activated, the frog (x, l) with
 $1\le l\le \eta_1(x)$
conducts a lazy walk, stepping on the kth attempt (
$1\le l\le \eta_1(x)$
conducts a lazy walk, stepping on the kth attempt (
 $k\ge 1$
) if
$k\ge 1$
) if
 $U_{x,l,k}\le p_1$
. Its jth step is given by
$U_{x,l,k}\le p_1$
. Its jth step is given by
 $\Delta_{x,l,j}$
.
$\Delta_{x,l,j}$
. -
 $X^2$
denotes a one-sided one-type frog process with initial configuration
$X^2$
denotes a one-sided one-type frog process with initial configuration
 $\boldsymbol{\eta_2}$
(with only the frogs at 0 activated at time 0, and where the
$\boldsymbol{\eta_2}$
(with only the frogs at 0 activated at time 0, and where the
 $\eta_2(0)$
frogs started at 0 are labelled
$\eta_2(0)$
frogs started at 0 are labelled
 $(0,\eta_1(0)+1), \dots ,(0,\eta_1(0)+\eta_2(0)$
), such that, once activated, the frog (x, l) (with
$(0,\eta_1(0)+1), \dots ,(0,\eta_1(0)+\eta_2(0)$
), such that, once activated, the frog (x, l) (with
 $x\ne 0$
and
$x\ne 0$
and
 $1\le l\le \eta_1(x)$
, or with
$1\le l\le \eta_1(x)$
, or with
 $x=0$
and
$x=0$
and
 $l=\eta_1(0)+1,\dots, \eta_1(0)+\eta_2(0)$
) conducts a lazy walk, stepping on the kth attempt (
$l=\eta_1(0)+1,\dots, \eta_1(0)+\eta_2(0)$
) conducts a lazy walk, stepping on the kth attempt (
 $k\ge 1$
) if
$k\ge 1$
) if
 $U_{x,l,k}\le p_2$
. Its jth step is given by
$U_{x,l,k}\le p_2$
. Its jth step is given by
 $\Delta_{x,l,j}$
.
$\Delta_{x,l,j}$
. -
X denotes a two-sided two-type frog process with initial configuration
 $\boldsymbol{\eta}$
(with only the frogs at 0 activated at time 0), where the frogs labelled
$\boldsymbol{\eta}$
(with only the frogs at 0 activated at time 0), where the frogs labelled
 $(0,1),\dots, (0,\eta_1(0))$
are type 1, and those labelled
$(0,1),\dots, (0,\eta_1(0))$
are type 1, and those labelled
 $(0,\eta_1(0)+1),\dots, (0,\eta_1(0)+\eta_2(0))$
are type 2. Once activated, if activated by a frog of type
$(0,\eta_1(0)+1),\dots, (0,\eta_1(0)+\eta_2(0))$
are type 2. Once activated, if activated by a frog of type
 $i\in \{1,2\}$
, the frog (x, l)
$i\in \{1,2\}$
, the frog (x, l)
 $1\le l\le \eta(x)$
conducts a lazy walk, stepping on the kth attempt (
$1\le l\le \eta(x)$
conducts a lazy walk, stepping on the kth attempt (
 $k\ge 1$
) if
$k\ge 1$
) if
 $U_{x,l,k}\le p_i$
. If
$U_{x,l,k}\le p_i$
. If
 $k_i$
frogs of type i land on a previously unvisited site y at the same time, we use the random variable
$k_i$
frogs of type i land on a previously unvisited site y at the same time, we use the random variable
 $U_{y,0,0}$
to choose the activator—all dormant frogs at y become type 2 if
$U_{y,0,0}$
to choose the activator—all dormant frogs at y become type 2 if
 $U_{y,0,0}\le k_2/(k_1+k_2)$
, and otherwise they all become type 1.
$U_{y,0,0}\le k_2/(k_1+k_2)$
, and otherwise they all become type 1.
Let
![]() $\tau$
be the first time (possibly infinite) that in the process X a frog of type 2 activates a site in
$\tau$
be the first time (possibly infinite) that in the process X a frog of type 2 activates a site in
![]() ${\mathbb{N}}$
(i.e. a type 2 frog arrives at a positive site before any type 1 frog has), or a frog of type 1 activates a site in
${\mathbb{N}}$
(i.e. a type 2 frog arrives at a positive site before any type 1 frog has), or a frog of type 1 activates a site in
![]() $-{\mathbb{N}}$
. On the event
$-{\mathbb{N}}$
. On the event
![]() $\{\tau=\infty\}$
for each
$\{\tau=\infty\}$
for each
![]() $i \in \{1,2\}$
we have that the moves of all the frogs in the frog process
$i \in \{1,2\}$
we have that the moves of all the frogs in the frog process
![]() $X^i$
follow exactly those of the frogs of type i in the frog process X.
$X^i$
follow exactly those of the frogs of type i in the frog process X.
Let
![]() $R^{i}_n$
and
$R^{i}_n$
and
![]() $L^{i}_n$
be the rightmost and leftmost positions visited by active frogs of type
$L^{i}_n$
be the rightmost and leftmost positions visited by active frogs of type
![]() $i\in \{1,2\}$
up to time n for the
$i\in \{1,2\}$
up to time n for the
![]() $X^i$
process. We will show that
$X^i$
process. We will show that
On the event in (2) we have coexistence because type 1 frogs activate every positive site, and frogs of type 2 every negative site. Clearly the first event in (2) has probability 1 since simple random walk has infinite range almost surely (as a Markov chain on an infinite irreducible class,
![]() $\mathbb{Z}$
), so we need only show that
$\mathbb{Z}$
), so we need only show that
![]() ${\mathbb{P}}_{p_1,p_2}(\tau=\infty)>0$
.
${\mathbb{P}}_{p_1,p_2}(\tau=\infty)>0$
.
Let
![]() $\ell_{\min}=\min\{\ell\ge0 \colon \nu(\{\ell\})>0\}$
and
$\ell_{\min}=\min\{\ell\ge0 \colon \nu(\{\ell\})>0\}$
and
![]() $\ell^+_{\min}=\min\{\ell>0 \colon \nu(\{\ell\})>0\}$
. Define
$\ell^+_{\min}=\min\{\ell>0 \colon \nu(\{\ell\})>0\}$
. Define
![]() $\varepsilon=\min\{A(p_1), A(p_2)\}/4$
and let us fix
$\varepsilon=\min\{A(p_1), A(p_2)\}/4$
and let us fix
![]() $m\in{\mathbb{N}}$
so that
$m\in{\mathbb{N}}$
so that
![]() $m= m_0(\varepsilon,1/5)+m_1(p_1,\nu(\{\ell^+_{\min}\})/5)+m_1(p_2,\nu(\{\ell^+_{\min}\})/5)$
, where
$m= m_0(\varepsilon,1/5)+m_1(p_1,\nu(\{\ell^+_{\min}\})/5)+m_1(p_2,\nu(\{\ell^+_{\min}\})/5)$
, where
![]() $m_0$
and
$m_0$
and
![]() $m_1$
are given by Lemma 2 and Corollary 3.
$m_1$
are given by Lemma 2 and Corollary 3.
Now let
![]() $A^1_{m}$
be the event that
$A^1_{m}$
be the event that
![]() $\eta_1(0)=\ell^+_{\min}$
,
$\eta_1(0)=\ell^+_{\min}$
,
![]() $\eta(x)=\ell_{\min}$
for all
$\eta(x)=\ell_{\min}$
for all
![]() $1\le x< 2m$
, and, in the first 2m time units for the process X, the frogs of type 1 at the origin all take 2m steps to the right while all the activated frogs from the region
$1\le x< 2m$
, and, in the first 2m time units for the process X, the frogs of type 1 at the origin all take 2m steps to the right while all the activated frogs from the region
![]() $[1,2m-1]$
take alternate steps left and right (in that order). Let
$[1,2m-1]$
take alternate steps left and right (in that order). Let
![]() $A^2_{m}$
be the event that
$A^2_{m}$
be the event that
![]() $\eta_2(0)=\ell^+_{\min}$
,
$\eta_2(0)=\ell^+_{\min}$
,
![]() $\eta(x)=\ell_{\min}$
for all
$\eta(x)=\ell_{\min}$
for all
![]() $-2m< x\le -1$
, and, in the first 2m time units, the frogs of type 2 at the origin all take 2m steps to the left while all the activated frogs from the region
$-2m< x\le -1$
, and, in the first 2m time units, the frogs of type 2 at the origin all take 2m steps to the left while all the activated frogs from the region
![]() $[\!-(2m-1),-1]$
alternate stepping right and left (in that order). Let
$[\!-(2m-1),-1]$
alternate stepping right and left (in that order). Let
![]() $A_{m}=A^1_{m}\cap A^2_{m}$
(see Fig. 2).
$A_{m}=A^1_{m}\cap A^2_{m}$
(see Fig. 2).

Figure 2. A depiction of the event
![]() $A_{{m}}$
when
$A_{{m}}$
when
![]() $m=2$
and
$m=2$
and
![]() $\ell_{\min}=1$
. The first (resp. second) diagram shows an example of an initial configuration
$\ell_{\min}=1$
. The first (resp. second) diagram shows an example of an initial configuration
![]() $\boldsymbol{\eta}_1$
(resp.
$\boldsymbol{\eta}_1$
(resp.
![]() $\boldsymbol{\eta}_2$
) on the event
$\boldsymbol{\eta}_2$
) on the event
![]() $A_{{m}}$
. The third diagram shows the corresponding configuration of frogs at time
$A_{{m}}$
. The third diagram shows the corresponding configuration of frogs at time
![]() $2m=4$
, in particular, the original type 1 (resp. type 2) frog at the origin at time 0 is now at 2m (resp.
$2m=4$
, in particular, the original type 1 (resp. type 2) frog at the origin at time 0 is now at 2m (resp.
![]() $-2m$
).
$-2m$
).
Recall that
![]() $\varepsilon=\min\{A(p_1), A(p_2)\}/4$
, and define
$\varepsilon=\min\{A(p_1), A(p_2)\}/4$
, and define
 \begin{alignat*}{2} B_m^{1,\mathrm{l}} & = \left\{\inf_{n\ge0}{\frac{L_{n+2m}^{1}+m}{n}}\ge-\varepsilon\right\} , & B_m^{1,\mathrm{r}} & = \left\{ \inf_{n\ge0} \frac{R_{n+2m}^{1}-m}{n}>\frac{A(p_1)}{2}\right\} , \\ B_m^{2,\mathrm{l}} & = \left\{ \sup_{n\ge0} \frac{L_{n+2m}^{2}+m}{n}<-\frac{A(p_2)}{2}\right\} , \qquad & B_m^{2,\mathrm{r}} & = \left\{\sup_{n\ge0}{\frac{R_{n+2m}^{2}-m}{n}}\le\varepsilon\right\}.\end{alignat*}
\begin{alignat*}{2} B_m^{1,\mathrm{l}} & = \left\{\inf_{n\ge0}{\frac{L_{n+2m}^{1}+m}{n}}\ge-\varepsilon\right\} , & B_m^{1,\mathrm{r}} & = \left\{ \inf_{n\ge0} \frac{R_{n+2m}^{1}-m}{n}>\frac{A(p_1)}{2}\right\} , \\ B_m^{2,\mathrm{l}} & = \left\{ \sup_{n\ge0} \frac{L_{n+2m}^{2}+m}{n}<-\frac{A(p_2)}{2}\right\} , \qquad & B_m^{2,\mathrm{r}} & = \left\{\sup_{n\ge0}{\frac{R_{n+2m}^{2}-m}{n}}\le\varepsilon\right\}.\end{alignat*}
Also define
![]() $B_m^i=B_m^{i,\mathrm{l}}\cap B_m^{i,\mathrm{r}}$
and
$B_m^i=B_m^{i,\mathrm{l}}\cap B_m^{i,\mathrm{r}}$
and
![]() $B_m=B_m^1\cap B_m^2$
. Note that
$B_m=B_m^1\cap B_m^2$
. Note that
![]() $A_m\subset \{\tau>2m\}$
, while on
$A_m\subset \{\tau>2m\}$
, while on
![]() $B_m$
we have, for any
$B_m$
we have, for any
![]() $n\ge 0$
,
$n\ge 0$
,
![]() $L_{n+2m}^{1}\ge -n\varepsilon-m> -nA(p_2)/2-m\ge L_{n+2m}^{2}$
and similarly
$L_{n+2m}^{1}\ge -n\varepsilon-m> -nA(p_2)/2-m\ge L_{n+2m}^{2}$
and similarly
![]() $R_{n+2m}^{1}> R_{n+2m}^{2}$
, so
$R_{n+2m}^{1}> R_{n+2m}^{2}$
, so
![]() $\tau\ne n+2m$
for any n on
$\tau\ne n+2m$
for any n on
![]() $B_m$
. This shows that
$B_m$
. This shows that
![]() $A_m\cap B_m\subset \{\tau=\infty\}$
.
$A_m\cap B_m\subset \{\tau=\infty\}$
.
It therefore remains to show that
![]() ${\mathbb{P}}_{p_1,p_2}(A_m\cap B_m)>0$
. The event
${\mathbb{P}}_{p_1,p_2}(A_m\cap B_m)>0$
. The event
![]() $A_m$
does not depend on
$A_m$
does not depend on
![]() $\eta(x)=\eta_i(x)$
for
$\eta(x)=\eta_i(x)$
for
![]() $|x|\ge 2m$
. On the other hand, we have that
$|x|\ge 2m$
. On the other hand, we have that
![]() ${\mathbb{P}}_{p_1,p_2}(A_m)>0$
for all
${\mathbb{P}}_{p_1,p_2}(A_m)>0$
for all
![]() $m\ge1$
, since
$m\ge1$
, since
![]() $A_m$
only prescribes the value of the environment in a finite box and requires a bounded number of frogs to perform a fixed finite set of moves. We say that a
$A_m$
only prescribes the value of the environment in a finite box and requires a bounded number of frogs to perform a fixed finite set of moves. We say that a
![]() ${\mathbb{Z}}$
-valued process
${\mathbb{Z}}$
-valued process
![]() $\boldsymbol{W}=(W_n)_{n \ge 0}$
stochastically dominates
$\boldsymbol{W}=(W_n)_{n \ge 0}$
stochastically dominates
![]() $\boldsymbol{Y}=(Y_n)_{n \ge 0}$
if there exists a probability space with processes
$\boldsymbol{Y}=(Y_n)_{n \ge 0}$
if there exists a probability space with processes
![]() $\boldsymbol{W}'\sim \boldsymbol{W}$
and
$\boldsymbol{W}'\sim \boldsymbol{W}$
and
![]() $\boldsymbol{W}'\sim \boldsymbol{Y}$
on which
$\boldsymbol{W}'\sim \boldsymbol{Y}$
on which
![]() $W'_n\ge Y'_n$
for every n a.s. Let us briefly justify that, conditional on
$W'_n\ge Y'_n$
for every n a.s. Let us briefly justify that, conditional on
![]() $A_m$
, the following dominations hold:
$A_m$
, the following dominations hold:
-
 $\left(R^{1}_{n+2m}-2m\right)_{n\ge0}$
stochastically dominates the rightmost position of a one-sided frog process
$\left(R^{1}_{n+2m}-2m\right)_{n\ge0}$
stochastically dominates the rightmost position of a one-sided frog process
 $\left(R_{n}\right)_{n\ge0}$
under
$\left(R_{n}\right)_{n\ge0}$
under
 $\mathbb{P}^+_{p_1}$
, conditioned on
$\mathbb{P}^+_{p_1}$
, conditioned on
 $\Big\{\eta(0)=\ell^+_{\min}\Big\}$
.
$\Big\{\eta(0)=\ell^+_{\min}\Big\}$
. -
 $\left(L^{1}_{n+2m}\right)_{n\ge 0}$
stochastically dominates
$\left(L^{1}_{n+2m}\right)_{n\ge 0}$
stochastically dominates
 $\left(L_{n}\right)_{n\ge0}$
under
$\left(L_{n}\right)_{n\ge0}$
under
 $\mathbb{P}^*_{p_1}$
.
$\mathbb{P}^*_{p_1}$
. -
 $\left(\!-L^{2}_{n+2m}-2m\right)_{n\ge0}$
stochastically dominates the rightmost position of a one-sided frog process
$\left(\!-L^{2}_{n+2m}-2m\right)_{n\ge0}$
stochastically dominates the rightmost position of a one-sided frog process
 $\left(R_{n}\right)_{n\ge0}$
under
$\left(R_{n}\right)_{n\ge0}$
under
 $\mathbb{P}^+_{p_2}$
, conditioned on
$\mathbb{P}^+_{p_2}$
, conditioned on
 $\{\eta(0)=\ell^+_{\min}\}$
.
$\{\eta(0)=\ell^+_{\min}\}$
. -
 $\left(\!-R^{2}_{n+2m}\right)_{n\ge0}$
stochastically dominates the leftmost position of a one-sided frog process
$\left(\!-R^{2}_{n+2m}\right)_{n\ge0}$
stochastically dominates the leftmost position of a one-sided frog process
 $\left(L_{n}\right)_{n\ge0}$
under
$\left(L_{n}\right)_{n\ge0}$
under
 $\mathbb{P}^*_{p_2}$
.
$\mathbb{P}^*_{p_2}$
.
We will prove the first two items, as the other two follow by symmetry. For this purpose, let us denote by
![]() $N_1(x)$
the number of active frogs on site x for the
$N_1(x)$
the number of active frogs on site x for the
![]() $X^1$
process at time 2m; see Fig. 2.
$X^1$
process at time 2m; see Fig. 2.
Note that, on
![]() $A_m$
, at time 2m,
$A_m$
, at time 2m,
![]() $N_1(x)=0$
for
$N_1(x)=0$
for
![]() $x\le-1$
and x odd,
$x\le-1$
and x odd,
![]() $N_1(0)=\ell_{\min}$
,
$N_1(0)=\ell_{\min}$
,
![]() $N_1(x)=2\ell_{\min}$
for all even
$N_1(x)=2\ell_{\min}$
for all even
![]() $x\in [1,2m-1]$
, and finally
$x\in [1,2m-1]$
, and finally
![]() $N_1(2m)=\eta_1(2m)+\ell_{\min}^+$
. On all
$N_1(2m)=\eta_1(2m)+\ell_{\min}^+$
. On all
![]() $x\ge 2m+1$
, there are
$x\ge 2m+1$
, there are
![]() $\eta_1(x)$
dormant frogs.
$\eta_1(x)$
dormant frogs.
The first item follows by the monotonicity provided by Lemma 1 and using that
![]() $\eta_1(x)$
has the same law as
$\eta_1(x)$
has the same law as
![]() $\eta_1(x-2m)$
for all
$\eta_1(x-2m)$
for all
![]() $x>2m$
, as there are at least
$x>2m$
, as there are at least
![]() $\ell^+_{\min}$
active frogs on 2m. To prove the second item, note that, for every
$\ell^+_{\min}$
active frogs on 2m. To prove the second item, note that, for every
![]() $x\ge 0$
,
$x\ge 0$
,
![]() $N_1(x)\le \eta_1(0)+\eta_1(x)+\eta_1(x+1)$
, and use the definition of
$N_1(x)\le \eta_1(0)+\eta_1(x)+\eta_1(x+1)$
, and use the definition of
![]() $\ell^+_{\min}$
together with Lemma 1.
$\ell^+_{\min}$
together with Lemma 1.
Thus, by our choice of
![]() $\varepsilon$
and m, using Lemma 2 we obtain
$\varepsilon$
and m, using Lemma 2 we obtain
Similarly, by Corollary 3 together with Remark 1, we obtain
 \begin{align*}{\mathbb{P}}_{p_1,p_2}\big(\big(B^{1,\mathrm{r}}_m\big)^\mathrm{c} \mid A_m\big) & = {\mathbb{P}}_{p_1,p_2}\bigg(\inf_{n\ge 0}\frac{R^{+1}_{n+2m}-2m+m}{n}\le \frac{A(p_1)}{2} \, \Big| \, A_m\bigg) \\&\le {\mathbb{P}}^+_{p_1}\bigg(\inf_{n\ge 0}\frac{R_n+m}{n}\le \frac{A(p_1)}{2} \, \Big| \, \eta(0)=\ell^+_{\min}\bigg)\le \frac15.\end{align*}
\begin{align*}{\mathbb{P}}_{p_1,p_2}\big(\big(B^{1,\mathrm{r}}_m\big)^\mathrm{c} \mid A_m\big) & = {\mathbb{P}}_{p_1,p_2}\bigg(\inf_{n\ge 0}\frac{R^{+1}_{n+2m}-2m+m}{n}\le \frac{A(p_1)}{2} \, \Big| \, A_m\bigg) \\&\le {\mathbb{P}}^+_{p_1}\bigg(\inf_{n\ge 0}\frac{R_n+m}{n}\le \frac{A(p_1)}{2} \, \Big| \, \eta(0)=\ell^+_{\min}\bigg)\le \frac15.\end{align*}
Similarly,
![]() ${\mathbb{P}}_{p_1,p_2}\big(\big(B^{2,\mathrm{r}}_m\big)^\mathrm{c}\mid A_m\big) \le 1/5$
and
${\mathbb{P}}_{p_1,p_2}\big(\big(B^{2,\mathrm{r}}_m\big)^\mathrm{c}\mid A_m\big) \le 1/5$
and
![]() ${\mathbb{P}}_{p_1,p_2}\big(\big(B^{2,\mathrm{l}}_m\big)^\mathrm{c}\mid A_m\big)\le 1/5$
, and thus
${\mathbb{P}}_{p_1,p_2}\big(\big(B^{2,\mathrm{l}}_m\big)^\mathrm{c}\mid A_m\big)\le 1/5$
, and thus
![]() ${\mathbb{P}}_{p_1,p_2}(B_m \mid A_m)\ge1/5$
. This proves that
${\mathbb{P}}_{p_1,p_2}(B_m \mid A_m)\ge1/5$
. This proves that
![]() ${\mathbb{P}}_{p_1,p_2}\left(A_m\cap B_m\right)>0$
as claimed.
${\mathbb{P}}_{p_1,p_2}\left(A_m\cap B_m\right)>0$
as claimed.
5. Extremely lazy frogs
In this section we return to studying the one-type frog model.
Proof of Proposition 1. Recall that
![]() $\nu$
is the probability measure on
$\nu$
is the probability measure on
![]() ${\mathbb{Z}}_+$
that is the law of
${\mathbb{Z}}_+$
that is the law of
![]() $\eta(x)$
. Let
$\eta(x)$
. Let
![]() $\mu={\mathbb{E}}[\eta(x)]<\infty$
.
$\mu={\mathbb{E}}[\eta(x)]<\infty$
.
Consider a branching random walk where each individual (independently of other particles) has:
-
(i) exactly one offspring, with displacement 0, with probability
 $1-p$
;
$1-p$
; -
(ii) exactly
 $1+k$
offspring, all at displacement
$1+k$
offspring, all at displacement
 $+1$
, with probability
$+1$
, with probability
 $\nu(\{k\}){p}/{2}$
;
$\nu(\{k\}){p}/{2}$
; -
(iii) exactly
 $1+k$
offspring at displacement
$1+k$
offspring at displacement
 ${-}1$
, with probability
${-}1$
, with probability
 $\nu(\{k\}){p}/{2}$
,
$\nu(\{k\}){p}/{2}$
,
and then the parent particle dies immediately. The number of offspring is always at least 1, with mean
![]() $1+p\mu$
. It is easy to couple this branching random walk (BRW) with our lazy frog model such that the set of visited points in the BRW contains that of the frog model. To see this, note that in the lazy frog model an active frog at x either doesn’t move (with probability
$1+p\mu$
. It is easy to couple this branching random walk (BRW) with our lazy frog model such that the set of visited points in the BRW contains that of the frog model. To see this, note that in the lazy frog model an active frog at x either doesn’t move (with probability
![]() $1-p$
), and then it doesn’t activate any new frogs, or it moves left or right with probability
$1-p$
), and then it doesn’t activate any new frogs, or it moves left or right with probability
![]() $p/2$
each, and then it activates at most
$p/2$
each, and then it activates at most
![]() $\eta(x+1)$
or
$\eta(x+1)$
or
![]() $\eta(x-1)$
new frogs.
$\eta(x-1)$
new frogs.
It is therefore sufficient to show that the speed of the front (the maximal site visited) for the BRW model goes to zero as
![]() $p\downarrow 0$
. We will verify this by applying small modifications to standard results (in particular [Reference Shi8, Lemma 1.5]) that are typically stated for the position of the rightmost particle at time n (so this differs slightly from the quantity we are after).
$p\downarrow 0$
. We will verify this by applying small modifications to standard results (in particular [Reference Shi8, Lemma 1.5]) that are typically stated for the position of the rightmost particle at time n (so this differs slightly from the quantity we are after).
First, note that since
![]() $R_n/n$
converges almost surely and is bounded above by 1 for every n, we have, by dominated convergence, that the limiting speed A(p) for the lazy frog model with parameter p is equal to
$R_n/n$
converges almost surely and is bounded above by 1 for every n, we have, by dominated convergence, that the limiting speed A(p) for the lazy frog model with parameter p is equal to
![]() $\limsup_{n \to \infty}{\mathbb{E}}_p[n^{-1}R_n]$
. By the above coupling it is therefore enough for us to show that
$\limsup_{n \to \infty}{\mathbb{E}}_p[n^{-1}R_n]$
. By the above coupling it is therefore enough for us to show that
![]() $\limsup_{n \to \infty}{\mathbb{E}}_p[n^{-1}M^*_n]\to 0$
as
$\limsup_{n \to \infty}{\mathbb{E}}_p[n^{-1}M^*_n]\to 0$
as
![]() $p \to 0$
, where
$p \to 0$
, where
![]() $M^*_n$
is the largest site visited by the BRW up to (and including) time n. Let
$M^*_n$
is the largest site visited by the BRW up to (and including) time n. Let
![]() $|x|$
denote the generation of a particle x in the BRW, and V(x) denote the location of x. Then
$|x|$
denote the generation of a particle x in the BRW, and V(x) denote the location of x. Then
 \begin{align*} \frac{1}{n}{\mathbb{E}}_p[M^*_n] & = \frac{1}{n}{\mathbb{E}}_p\Big[\max_{x:|x|\le n} V(x)\Big]\le \frac{1}{n}\log\!\Big({\mathbb{E}}_p\Big[\mathrm{e}^{\max_{x:|x|\le n} V(x)}\Big]\Big) \\&\le \frac{1}{n}\log\!\Bigg({\mathbb{E}}_p\Bigg[\sum_{x:|x|\le n} \mathrm{e}^{V(x)}\Bigg]\Bigg) = \frac{1}{n}\log\!\Bigg(\sum_{k=0}^n {\mathbb{E}}_p\Bigg[\sum_{x:|x|=k} \mathrm{e}^{V(x)}\Bigg]\Bigg).\end{align*}
\begin{align*} \frac{1}{n}{\mathbb{E}}_p[M^*_n] & = \frac{1}{n}{\mathbb{E}}_p\Big[\max_{x:|x|\le n} V(x)\Big]\le \frac{1}{n}\log\!\Big({\mathbb{E}}_p\Big[\mathrm{e}^{\max_{x:|x|\le n} V(x)}\Big]\Big) \\&\le \frac{1}{n}\log\!\Bigg({\mathbb{E}}_p\Bigg[\sum_{x:|x|\le n} \mathrm{e}^{V(x)}\Bigg]\Bigg) = \frac{1}{n}\log\!\Bigg(\sum_{k=0}^n {\mathbb{E}}_p\Bigg[\sum_{x:|x|=k} \mathrm{e}^{V(x)}\Bigg]\Bigg).\end{align*}
By conditioning on generation
![]() $k-1$
of the branching process we have
$k-1$
of the branching process we have
 \begin{equation*}{\mathbb{E}}_p\Bigg[\sum_{x:|x|=k} \mathrm{e}^{V(x)}\Bigg] = {\mathbb{E}}_p\Bigg[\sum_{x:|x|=k-1} \mathrm{e}^{V(x)}\Bigg] \mathrm{e}^{\psi_p(1)},\end{equation*}
\begin{equation*}{\mathbb{E}}_p\Bigg[\sum_{x:|x|=k} \mathrm{e}^{V(x)}\Bigg] = {\mathbb{E}}_p\Bigg[\sum_{x:|x|=k-1} \mathrm{e}^{V(x)}\Bigg] \mathrm{e}^{\psi_p(1)},\end{equation*}
where, for
![]() $t>0$
,
$t>0$
,
 \begin{equation*}\psi_p(t)=\log {\mathbb{E}}_p\Bigg[\sum_{x:|x|=1} \mathrm{e}^{V(x)}\Bigg] = \log\!\left( (1-p) +\frac{p}{2}\sum_{k=0}^\infty \nu(\{k\})(k+1)(\mathrm{e}^{-t} + \mathrm{e}^{t})\right).\end{equation*}
\begin{equation*}\psi_p(t)=\log {\mathbb{E}}_p\Bigg[\sum_{x:|x|=1} \mathrm{e}^{V(x)}\Bigg] = \log\!\left( (1-p) +\frac{p}{2}\sum_{k=0}^\infty \nu(\{k\})(k+1)(\mathrm{e}^{-t} + \mathrm{e}^{t})\right).\end{equation*}
Thus, by induction, we obtain
![]() ${\mathbb{E}}_p\big[\sum_{x:|x|=k} \mathrm{e}^{V(x)}\big]=\mathrm{e}^{k \psi_p(1)}$
. Alternatively, we could have applied the many-to-one lemma (see [Reference Shi8, Theorem 1.1]).
${\mathbb{E}}_p\big[\sum_{x:|x|=k} \mathrm{e}^{V(x)}\big]=\mathrm{e}^{k \psi_p(1)}$
. Alternatively, we could have applied the many-to-one lemma (see [Reference Shi8, Theorem 1.1]).
Thus, we have
![]() $\frac{1}{n}{\mathbb{E}}_p[M^*_n] \le \frac{1}{n}\log\!\big(\sum_{k=0}^n \mathrm{e}^{k\psi_p(1)}\big)$
, where
$\frac{1}{n}{\mathbb{E}}_p[M^*_n] \le \frac{1}{n}\log\!\big(\sum_{k=0}^n \mathrm{e}^{k\psi_p(1)}\big)$
, where
Thus,
Since
![]() $\log\!(1+x)\le x$
, we see that
$\log\!(1+x)\le x$
, we see that
![]() $\psi_p(1)$
can be made arbitrarily small by making p arbitrarily small, which completes the proof.
$\psi_p(1)$
can be made arbitrarily small by making p arbitrarily small, which completes the proof.
Acknowledgements
The authors thank Delta Holmes and Alma Kious for drawing the frogs.
The authors also thank an anonymous referee for various helpful suggestions, including simplifying the proof of Lemma 3.
Funding information
The work of Holmes is supported by Future Fellowship FT160100166 from the Australian Research Council.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.