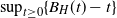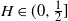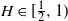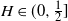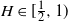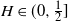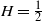1. Introduction
Due to its ability to model a wide variety of correlation structures, fractional Brownian motion (fBm) is a frequently used Gaussian process. Indeed, whereas for classical Brownian motion the increments are independent, depending on the value of the Hurst parameter
$H\in(0,1)$
, fBm covers the cases of both negatively (
$H<\frac{1}{2}$
) and positively (
$H>\frac{1}{2}$
) correlated increments. Owing to its broad applicability, fBm has become an intensively studied object across a broad range of scientific disciplines, such as physics [Reference Regnerand, Vucinić, Domnisoru, Bartol, Hetzer, Tartakovsky and Sejnowski30, Reference Sagi, Brook, Almog and Davidson31], biology [Reference Caspi, Granek and Elbaum7], hydrology [Reference Montanari, Doukhan, Oppenheim and Taqqu26], mathematical finance [Reference Baillie4, Reference Cont, LÉvy-VÉhel and Lutton8], insurance and risk [Reference Asmussen and Albrecher3, Chapter VIII], and operations research [Reference Taqqu, Willinger and Sherman33].
This paper considers the all-time supremum attained by an fBm with negative drift. This supremum is clearly a key quantity in the application areas mentioned; for example, think of ruin probabilities in the insurance context. Importantly, such suprema are also of great importance in queueing theory, due to the fact that the stationary workload has the same distribution as the supremum of (the time-reversed version of) the queue’s net input process [Reference Mandjes19, Theorem 5.1.1]. The main objective of our work is to analyze the expected value of the supremum attained by fBm with negative drift as a function of the Hurst parameter H. As exact analysis has been beyond reach so far (apart from the Brownian case of
$H=\frac{1}{2}$
), we focus on identifying upper and lower bounds on its expected value.
Throughout this paper
$B_H(\!\cdot\!)$
denotes a zero-mean, variance-normalized version of fBm with
$H\in(0,1)$
. More specifically,
$B_H(\!\cdot\!)$
is a Gaussian process with stationary increments such that
${\mathbb E}\,B_H(t)=0$
for all
$t\in{\mathbb R}$
, and
\begin{equation*}\mathrm{Var}(B_H(t)-B_H(s)) = |t-s|^{2H}\end{equation*}
for all
$s,t\in{\mathbb R}.$
As mentioned, the primary focus of this paper is on deriving upper and lower bounds on the mean of the all-time supremum of fBm with negative drift. In other words, we wish to analyze, for some
$c>0$
,
\begin{equation*}\mathscr{M}(H,c)\,{:}\,{\raise-1.5pt{=}}\, {\mathbb E}\biggl[\sup_{t\geq0} \{B_H(t) - ct\}\biggr].\end{equation*}
Interestingly, exploiting fBm’s self-similarity, for any
$c>0$
we can express
$\mathscr{M}(H,c)$
directly in terms of
$\mathscr{M}(H)\,{:}\,{\raise-1.5pt{=}}\, \mathscr{M}(H,1)$
. This can be seen as follows. Renormalizing time yields, with
$\gamma\,{:}\,{\raise-1.5pt{=}}\, (2H-2)^{-1}$
,
\begin{equation} \sup_{t\geq0} \{B_H(t) - ct\}= \sup_{t\geq 0} \big\{B_H({c^{2\gamma }t})-c\cdot c^{2\gamma }t\big\} = \sup_{t\geq 0} \big\{B_H\big({c^{2\gamma }t}\big)-c^{2H\gamma}t\big\}.\end{equation}
As a consequence of the self-similarity of fBm,
$B_H(x t)$
is distributed as
$x^{H} B_H(t)$
, and therefore
$B_H({c^{2\gamma }t})$
is distributed as
$c^{2H\gamma}B_H(t)$
. Hence the random variable (1) is, in the distributional sense, equal to
\begin{equation*} \sup_{t\geq 0} \big\{B_H\big({c^{2\gamma }t}\big)-c^{2H\gamma}t\big\}= c^{2H\gamma}\sup_{t\geq 0}\{B_H(t) - t\}.\end{equation*}
In other words, in order to analyze the behavior of
$\mathscr{M}(H,c)$
for any
$c>0$
, it suffices to consider its unit-drift counterpart
$\mathscr{M}(H)$
. Only in the Brownian case is the value of this function known: for
$H=\frac{1}{2}$
,
$\sup_{t\geq 0}\{B_{{1}/{2}}(t) - t\}$
is exponentially distributed with parameter 2, so that
$\mathscr{M}(\frac{1}{2})=\frac{1}{2}$
.
A substantial body of literature has focused on characterizing the distribution of the supremum of fBm, either over a finite time interval (often assuming that the drift equals 0), or over an infinite time interval (in which a negative drift ensures a finite supremum). In general terms, one could say that the vast majority of the results obtained are of an asymptotic nature. For instance, in [Reference Hüsler and Piterbarg16], [Reference Massoulié and Simonian23], and [Reference Narayan27] a function f(u) is found such that, as
$u\to\infty$
,
\begin{equation}f(u)\cdot {\mathbb P}\bigg(\sup_{t\geq 0}\{B_H(t) - t\}>u\bigg)\to 1;\end{equation}
for the precise statement see [Reference Mandjes19, Proposition 5.6.2]. We also refer to [Reference Dębicki9], [Reference Dieker14], and [Reference Hüsler and Piterbarg17] for extensions of (2) to a broader class of Gaussian processes with stationary increments and to [Reference Duffield and O’Connell15] for a seminal paper on the corresponding logarithmic asymptotics. Similar large-deviations results in another asymptotic regime can be found in [Reference Dębicki and Mandjes11], namely a setting in which the Gaussian process is interpreted as the superposition of many i.i.d. Gaussian processes. Other asymptotic results relate to higher-dimensional systems, such as tandem queues; see e.g. [Reference Dębicki, Kosiński, Mandjes and Rolski12] and [Reference Mandjes and van Uitert20]. The logarithmic asymptotics of long busy periods in fBm-driven queues have been identified in [Reference Mandjes, Mannersalo, Norros and van Uitert21], where it is noted that a similar approach could be relied upon to characterize the speed of convergence of fractional Brownian storage to its stationary limit [Reference Mandjes, Norros and Glynn22].
While computing bounds pertaining to the extreme values attained by Gaussian processes is a large and mature research area (see e.g. [Reference Adler1], [Reference Piterbarg29], and [Reference Talagrand32]), there are only a limited number of results that provide computable upper and lower bounds on the expected supremum. A notable exception concerns the recent results by Borovkov et al. [Reference Borovkov, Mishura, Novikov and Zhitlukhin5, Reference Borovkov, Mishura, Novikov and Zhitlukhin6], presenting (non-asymptotic) bounds on the expected supremum of a driftless fBm over a finite time interval (as functions of the Hurst parameter H, that is). The same setting is considered in [Reference Malsagov and Mandjes18], but a more pragmatic approach has been followed: the objective is to accurately fit a curve to estimated values of the expected supremum. In addition, we would like to stress that an intrinsic drawback of asymptotics is that, in the absence of error bounds, one does not know whether such asymptotic results provide any accurate approximations for instances in a pre-limit setting. The above considerations motivate the objective of our work: identifying computable bounds on the expected supremum of fBm with drift. We note that the identification of such bounds is clearly relevant in its own right, but in addition they play a pivotal role when one aims to apply Borell-type inequalities [Reference Adler1] so as to obtain uniform estimates for the tail distribution of suprema.
We proceed by stating some of our results. With
$\mathscr{N}$
denoting a standard normal random variable, we define, for
$H\in(0,1)$
,
\begin{equation*}{\kappa(H)\,{:}\,{\raise-1.5pt{=}}\, {\mathbb E}\bigl[| \mathscr{N} |^{{{1}/{(1-H)}}}\bigr],}\end{equation*}
which can be given explicitly in terms of the gamma function (see Lemma 1). The first main result concerns the behavior of
$\mathscr{M}(H)$
for
$H\downarrow 0$
and
$H\uparrow 1$
, respectively.
Theorem 1. We have
\begin{equation}0.2055 \approx \dfrac{1}{2\sqrt{\pi e \log 2}} \leq \liminf_{H\downarrow 0} \dfrac{\mathscr{M}(H)}{\sqrt{H}} \leq \limsup_{H\downarrow 0} \dfrac{\mathscr{M}(H)}{\sqrt{H}} \leq 1.695,\end{equation}
and
\begin{equation}\liminf_{H\uparrow 1} \dfrac{\mathscr{M}(H)}{(1-H)\,\kappa({H})}\geq\dfrac{1}{2e},\quad \limsup_{H\uparrow 1} \dfrac{\mathscr{M}(H)}{\kappa({H})}\leq \dfrac{1}{2}.\end{equation}
The asymptotic inequalities (4), in combination with the exact value of
$\kappa({H})$
derived in Lemma 1 in Section 2, straightforwardly imply that
$\mathscr{M}(H)$
and
$\kappa(H)$
‘logarithmically match’ as
$H\uparrow 1$
, in the sense that
\begin{equation*}\lim_{H\uparrow 1}\dfrac{\log \mathscr{M}(H)}{\log \kappa({H})}=1.\end{equation*}
The second main result concerns bounds for
$H\in(0,1)$
. These differ by at most a multiplicative constant that is uniformly bounded over
$H\in(0,\frac{1}{2}]$
, whereas they differ by at most a factor
$e/(1-H)$
for
$H\in[\frac{1}{2},1).$
We define
\begin{align*}\mathscr{U}(H) \,{:}\,{\raise-1.5pt{=}}\, \begin{cases}\mathscr{U}_2^{\circ}(H) & H\in(0,\frac{1}{2}], \\[3pt] \mathscr{U}_1(H) & H\in[\frac{1}{2},1),\end{cases}\quad\mathscr{L}(H) \,{:}\,{\raise-1.5pt{=}}\, \begin{cases}\max\ \{\mathscr{L}_2(H), \mathscr{L}_3(H)\} & H\in(0,\frac{1}{2}], \\[3pt] \mathscr{L}_1(H) & H\in[\frac{1}{2},1),\end{cases}\end{align*}
with functions
$\mathscr{U}_1(\!\cdot\!), \mathscr{L}_1(\!\cdot\!), \mathscr{L}_2(\!\cdot\!), \mathscr{L}_3(\!\cdot\!)$
that are defined in Propositions 1–4, and a function
$\mathscr{U}_2^{\circ}(\!\cdot\!)$
that is defined in Corollary 2 and that uses the function
$\mathscr{U}_2(\!\cdot\!)$
from Proposition 5. As such,
$\mathscr{U}(H)$
and
$\mathscr{L}(H)$
are the best upper and lower bound for
$\mathscr{M}(H)$
that we were able to find. It is noted that all these functions can be computed through elementary numerical procedures.
Theorem 2. We have
$\mathscr{L}(H)$
and
$\mathscr{U}(H)$
satisfying
\begin{equation*}\mathscr{L}(H)\leq \mathscr{M}(H) \leq \mathscr{U}(H),\end{equation*}
such that
\begin{equation*}\sup_{H\in(0,{{1}/{2}}]}\dfrac{\mathscr{U}(H)}{\mathscr{L}(H)} \leq 18.063,\end{equation*}
whereas for
$H\in[\frac{1}{2},1)$
it holds that
$2/(1-H) \leq \mathscr{U}(H)/\mathscr{L}(H) \leq e/(1-H).$
The proofs of Theorems 1 and 2 will be given later in the paper, as well as the procedure to compute
$\mathscr{L}(H)$
and
$\mathscr{U}(H)$
in Theorem 2. The bounds
$\mathscr{U}_1(\!\cdot\!)$
, and
$\mathscr{L}_1(\!\cdot\!), \mathscr{L}_2(\!\cdot\!), \mathscr{L}_3(\!\cdot\!)$
are explicit functions of H, whereas the tightest upper bound
$\mathscr{U}_2^{\circ}(\!\cdot\!)$
follows by performing a numerical procedure on the (semi-) closed-form upper bound
$\mathscr{U}_2(\!\cdot\!)$
. The resulting bounds are summarized in Figure 1. We note that the bounds are tight in
$H=\frac{1}{2}.$
Notably, as a by-product of the proof for the upper bound
$\mathscr{U}_2^{\,\circ}(\!\cdot\!)$
, we present in Corollary 1 a new upper bound on the mean of
$\sup_{t\in[0,1]} B_H(t)$
for the regime
$H\in(0,\frac{1}{2}]$
. Further, this bound is tight at
$H=\frac{1}{2}$
, and improves the upper bound that was established in [Reference Borovkov, Mishura, Novikov and Zhitlukhin5].
Figure 1: All upper and lower bounds for
$\mathscr{M}(H)$
derived in this work.
This paper is organized as follows. As it turns out, we have to consider the cases
$H\in(0,\frac{1}{2}]$
and
$H\in[\frac{1}{2},1)$
separately. As in the former case
$\mathrm{Var}\, B_H(t)$
grows slower than linearly, in the physics literature [Reference Meroz and Sokolov24, Reference Metzler, Jeon, Cherstvya and Barkaid25] this regime is sometimes referred to as subdiffusive. Analogously, in the latter case
$\mathrm{Var}\, B_H(t)$
is superlinear in t, explaining why this regime is called superdiffusive. Section 2, dealing with the superdiffusive case, presents an upper and lower bound that have a strongly similar shape. Then, in Section 3, we focus on the subdiffusive regime, with an upper bound and two lower bounds (one of them being tighter for small
$H\in(0,\frac{1}{2}]$
, the other one being tighter for larger H). This section also presents additional bounds and a procedure to numerically improve the upper bound. Section 4 covers the proofs of Theorems 1 and 2. The paper is concluded in Section 5.
2. Superdiffusive regime
In this section we consider the case
$H\in[\frac{1}{2},1)$
. We start our exposition with a useful auxiliary result; see also [Reference Winkelbauer34].
Lemma 1. For
$H\in(0,1)$
,
\begin{equation*}\kappa(H) =\sqrt{\dfrac{1}{\pi}}\big(\sqrt{2}\big)^{{{1}/{(1-H)}}} \Gamma\biggl(\dfrac{2-H}{2-2H}\biggr).\end{equation*}
Proof. Observe that, performing the change-of-variable
$x^2=2y$
,
\begin{equation*}\kappa(H) = \sqrt{\dfrac{2}{\pi}} \int_0^{\infty} \,\mathrm{e}^{-x^2/2} x^{{{1}/{(1-H)}}}\,\mathrm{d}x=\sqrt{\dfrac{1}{\pi}}\big(\sqrt{2}\big)^{{{1}/{(1-H)}}} \int_0^{\infty} \,\mathrm{e}^{-y} y^{{{H}/{(2(1-H))}}}\,\mathrm{d}y,\end{equation*}
which, after interpreting the integral in terms of the gamma function, proves the claim.
With this lemma at our disposal, we can present our lower bound. It relies on the ‘principle of the largest term’: the probability of a union of events is bounded from below by the probability of the most likely of these events. The following quantity will feature regularly from now on:
\begin{equation*}\nu(H)\,{:}\,{\raise-1.5pt{=}}\, H^H(1-H)^{1-H}.\end{equation*}
Proposition 1. For
$H\in[\frac{1}{2},1)$
we have
$\mathscr{M}(H)\geq \mathscr{L}_1(H)$
, where
\begin{equation}\mathscr{L}_1(H) \,{:}\,{\raise-1.5pt{=}}\, \dfrac{1}{2}\nu(H)^{{{1}/{(1-H)}}} \cdot \kappa(H).\end{equation}
As noted from the proof, the lower bound
$\mathscr{L}_1(H)$
holds in the entire domain, i.e. for any
$H\in(0,1)$
.
Proof. This proof is due to [Reference Norros28]. Let
$t_u$
be the maximizer, for a given
$u>0$
, of the mapping
\begin{equation*}t\mapsto\mathbb{P}(B_H(t)-t > u)=1-\Phi\biggl(\dfrac{u+t}{t^{H}}\biggr),\end{equation*}
with
$\Phi(\!\cdot\!)$
the cumulative distribution function of a standard normal random variable. As
$\Phi(\!\cdot\!)$
is increasing,
$t_u$
is the minimizer of
$$({\rm{u + t}}){\rm{/}}{{\rm{t}}^H}$$
, that is,
\begin{equation*}t_u = u\,\dfrac{H}{1-H}.\end{equation*}
This means that we have the lower bound
\begin{align*} \mathscr{M}(H)&=\int_0^{\infty} \mathbb{P}\biggl(\sup_{t\geq 0}\{B_H(t) - t\} > u\biggr)\,\mathrm{d} u \\[3pt] &\geq \int_0^{\infty} \mathbb{P}(B_H(t_u) - t_u > u)\,\mathrm{d} u\\[3pt] &=\int_0^{\infty} \biggl(1-\Phi\biggl(\dfrac{u+t_u}{t_u^{H}}\biggr)\biggr)\,\mathrm{d}u\\[3pt] &=\int_0^{\infty} \biggl(1-\Phi\biggl(\dfrac{u^{1-H}}{\nu(H)}\biggr)\biggr)\,\mathrm{d}u\\[3pt]&=H^{{{H}/{(1-H)}}}\int_0^{\infty} v^{{{H}/{(1-H)}}}(1-\Phi(v))\,\mathrm{d}v.\end{align*}
By an elementary application of integration by parts, we obtain that the integral in the last expression can be written as
\begin{equation*}\int_0^{\infty} (1-\Phi(v)) \,\mathrm{d} ((1-H) v^{{{1}/{(1-H)}}}) =(1-H) \int_0^{\infty} v^{{{1}/{(1-H)}}} \Phi'(v)\,\mathrm{d}v=\dfrac{1}{2}(1-H)\,\kappa(H),\end{equation*}
from which (5) follows.
We proceed by deriving an upper bound. It will make use of the following results, which were proved in Dębicki et al. [Reference Dębicki10, Reference Dębicki, Michna and Rolski13]. We define
\begin{equation*}\lambda(u,H)\,{:}\,{\raise-1.5pt{=}}\, \biggl(\int_0^{\infty} \big(2\pi t^{2H}\big)^{-1/2}\exp\big(\!-(t+u)^2/\big(2t^{2H}\big)\big)\,\mathrm{d} t\biggr)^{-1}.\end{equation*}
Lemma 2. Let
$B(\!\cdot\!)\equiv B_{{{1}/{2}}}(\!\cdot\!)$
denote a standard Brownian motion. Then, for any
$H\in(0,1)$
, we have
\begin{equation}2-2H \leq \lambda(u,H)\cdot\mathbb{P}\biggl(\sup_{t\geq 0} \big\{B \big(t^{2H}\big) - t\big\} > u\biggr) \leq 2.\end{equation}
For
$H\geq \frac{1}{2}$
, a tighter upper bound holds:
\begin{equation} \lambda(u,H)\cdot\mathbb{P}\biggl(\sup_{t\geq 0} \big\{B\big(t^{2H}\big) - t \big\}> u\biggr) \leq 1.\end{equation}
Proof. See [Reference Dębicki10] for the proof of (6) and [Reference Dębicki, Michna and Rolski13] for the proof of (7).
Proposition 2. For
$H\in[\frac{1}{2},1)$
we have
$\mathscr{M}(H)\leq \mathscr{U}_1(H)$
, where
\begin{equation*}\mathscr{U}_1(H)= \dfrac{1}{2}\cdot \kappa(H).\end{equation*}
Proof. Informally, Slepian’s lemma compares the tail probabilities pertaining to the suprema of two Gaussian processes when the corresponding variance and mean functions are equal and the variograms are ordered; for the precise statement see e.g. [Reference Adler1]. In the case of
$H\in[ \frac{1}{2},1)$
, applying Slepian’s lemma yields that
\begin{equation*} \mathbb{P}\biggl(\sup_{t\geq0} \{B_H(t) - t \}> u\biggr)\leq\mathbb{P}\biggl(\sup_{t\geq 0} \big\{B\big(t^{2H}\big) - t \big\}> u\biggr),\end{equation*}
for all
$u\in \mathbb{R}$
.
Using this bound in the first inequality, and equation (7) from Lemma 2 in the second inequality, we obtain
\begin{align*}\mathscr{M}(H)& = \int_0^{\infty} \mathbb{P}\biggl(\sup_{t\geq0} \{B_H(t) - t \}> u\biggr)\,\mathrm{d} u \\[4pt]
&\leq\int_0^{\infty} \mathbb{P}\biggl(\sup_{t\geq 0} \big\{B\big(t^{2H}\big) - t \big\}> u\biggr)\,\mathrm{d} u \\[4pt]
& \leq \int_0^{\infty}\int_0^{\infty} \dfrac{1}{\sqrt{2\pi t^{2H}}}\exp\biggl(\!-\dfrac{(t+u)^2}{2t^{2H}}\biggr)\,\mathrm{d} u\, \mathrm{d} t \\[4pt]
&= \int_0^{\infty} \mathbb{P}\big(B\big(t^{2H}\big) > t\big)\,\mathrm{d} t \\[4pt]
&= \dfrac{1}{2}\int_0^{\infty} \mathbb{P}\big(|\mathscr{N}| > t^{1-H}\big)\,\mathrm{d} t\\[3pt]
&= \dfrac{1}{2}\int_0^{\infty} \mathbb{P}\big(|\mathscr{N}|^{{{1}/{(1-H)}}} > t\big)\,\mathrm{d} t,\end{align*}
which equals
$\frac{1}{2}\cdot \kappa(H).$
3. Subdiffusive regime
This section covers the case
$H\in(0,\frac{1}{2}]$
. Section 3.1 provides various bounds that allow (semi-) closed-form expressions. Then in Section 3.2 we develop a numerical procedure that improves the upper bound, and in addition we present bounds on various quantities featuring in Section 3.1.
3.1. Closed-form bounds
We start with a theorem that is the immediate counterpart of Proposition 2. Due to the nature of Slepian’s inequality, however, for
$H\in(0,\frac{1}{2}]$
it constitutes a lower bound. As its proof is essentially analogous to that of Proposition 2, we only provide the main steps.
Proposition 3. For
$H\in(0,\frac{1}{2})$
we have
$\mathscr{M}(H)\geq \mathscr{L}_2(H)$
, where
$\begin{equation*}\mathscr{L}_2(H) \,{:}\,{\raise-1.5pt{=}}\, (1-H)\cdot \kappa(H).\end{equation*}$
Proof. For
$H\geq \frac{1}{2}$
, Slepian’s lemma yields
\begin{equation*}\int_0^{\infty} \mathbb{P}\biggl(\sup_{t\geq0} \{B_H(t) - t \}> u\biggr)\,\mathrm{d} u \geq \int_0^{\infty} \mathbb{P}\biggl(\sup_{t\geq 0} \big\{B\big(t^{2H}\big) - t \big\}> u\biggr)\,\mathrm{d} u,\end{equation*}
which majorizes, by the lower bound in (6),
\begin{equation*}(2-2H)\int_0^{\infty}\int_0^{\infty} \dfrac{1}{\sqrt{2\pi t^{2H}}}\exp\biggl(\!-\dfrac{(t+u)^2}{2t^{2H}}\biggr)\,\mathrm{d} u\, \mathrm{d} t,\end{equation*}
equalling
$(1-H)\cdot \kappa(H).$
We now present a second lower bound,
$\mathscr{L}_3(H)$
. It is noted that this
$\mathscr{L}_3(H)$
provides a lower bound on
$\mathscr{M}(H)$
for all
$H\in(0,1)$
, but for
$H\in(\frac{1}{2},1)$
it performs worse than the bound
$\mathscr{L}_1(H)$
from Proposition 3. In this lower bound the object
\begin{equation} \mu(H)\,{:}\,{\raise-1.5pt{=}}\, \mathbb{E}\biggl[\biggl(\sup_{t\in[0,1]} B_H(t)\biggr)^{{{1}/{(1-H)}}}\biggr]\end{equation}
plays a key role. This quantity will be analyzed in greater detail in Section 3.2: while we lack a closed-form expression for
$\mu(H)$
, we derive upper and lower bounds. From Lemma 4 and Corollary 1, which will be stated and proved in Section 3.2, we conclude that
\begin{equation*}\underline\mu(H) \leq \mu(H) \leq \overline\mu(H),\end{equation*}
with
\begin{equation}\underline\mu(H) \,{:}\,{\raise-1.5pt{=}}\, \biggl(\dfrac{C^-}{\sqrt{ H}}\biggr)^{{{1}/{(1-H)}}}, \quad \overline\mu(H) \,{:}\,{\raise-1.5pt{=}}\, (\overline\mu^{\circ}(H,1))^{{{1}/{(1-H)}}} + \dfrac{\sqrt{\pi/2}}{1-H}\big((\overline\mu^{\circ}(H,1))^{\varsigma(H)}+ \mathbb{E}|\mathscr{N}|^{\varsigma(H)}\big),\end{equation}
where
$\mathscr{N}$
denotes a standard normal random variable,
$\varsigma(H)\,{:}\,{\raise-1.5pt{=}}\, H/(1-H)$
, and
$C^-$
and
$\overline\mu^{\circ}(\cdot\,, 1)$
are introduced in Lemma 4 and Corollary 1. It is noted that
$\mathbb{E}|\mathscr{N}|^{\varsigma(H)}$
can be expressed in terms of the gamma function, similarly to how this was done in Lemma 1.
Proposition 4. For
$H\in(0,\frac{1}{2}]$
we have
$\mathscr{M}(H)\geq \mathscr{L}_3(H)$
, where
\begin{equation} \mathscr{L}_3(H) \,{:}\,{\raise-1.5pt{=}}\, \nu(H)^{{{1}/{(1-H)}}} \cdot \underline\mu(H).\end{equation}
Proof. Using the time-scaling property of fBm we obtain that
$\mathscr{M}(H)$
equals
\begin{align*}\int_0^{\infty} \mathbb{P}\biggl(\sup_{t\geq 0}\{B_H(t) - t\} > u\biggr)\,\mathrm{d} u & = \int_0^{\infty} \mathbb{P}\biggl(\sup_{t\geq0}\dfrac{B_H(t)}{1+t} > u^{1-H}\biggr)\,\mathrm{d} u \\& = \mathbb{E} \Biggl[\biggl(\sup_{t\geq 0}\dfrac{B_H(t)}{1+t}\biggr)^{{{1}/{(1-H)}}}\Biggr].\end{align*}
The last expression in the previous display obviously majorizes, for any
$T>0$
,
\begin{equation*}\mathbb{E}\Biggl[ \biggl(\sup_{t\in[0,T]}\dfrac{B_H(t)}{1+t}\biggr)^{{{1}/{(1-H)}}}\Biggr].\end{equation*}
Again using the time-scaling property of fBm, we see that
\begin{equation*}\mathbb{E}\Biggl[\biggl( \sup_{t\in[0,T]}\dfrac{B_H(t)}{1+t}\biggr)^{{{1}/{(1-H)}}}\Biggr] \geq \biggl(\dfrac{T^H}{1+T}\biggr)^{{{1}/{(1-H)}}} \cdot\mathbb{E}\Biggl[\biggl( \sup_{t\in[0,1]}B_H(t)\biggr)^{{{1}/{(1-H)}}}\Biggr].\end{equation*}
For a given H, the maximum of a function
$T\mapsto T^H/(1+T)$
is attained at
$T = H/(1-H)$
and equals
$\nu(H)$
, which in combination with (9) yields the bound in (10).
Numerical experiments show that
$\mathscr{L}_3(H)$
is the tightest of the two lower bounds for H close to 0, whereas
$\mathscr{L}_2(H)$
is the tightest for larger values of H.
The next objective is to derive an upper bound. In this result we make extensive use of the quantity
\begin{equation*}\psi(T,H)\,{:}\,{\raise-1.5pt{=}}\, \min\bigg\{T\cdot \dfrac{1-2H}{2H}, 1\bigg\},\end{equation*}
which is non-negative for
$H\in(0,\frac{1}{2}]$
. After the proof of the following proposition, we will comment on the computation of the quantity
$\omega(H)$
that features in this upper bound. We recall that
$\overline\mu(H)$
was defined in (9).
Proposition 5. For
$H\in(0,\frac{1}{2}]$
we have
$\mathscr{M}(H)\leq \mathscr{U}_2(H)$
, where
\begin{equation}\mathscr{U}_2(H) \,{:}\,{\raise-1.5pt{=}}\, \omega(H) \cdot \overline\mu(H),\end{equation}
and
\begin{equation}\omega(H) \,{:}\,{\raise-1.5pt{=}}\, \inf_{T>0} \biggl\{T^{{{H}/{(1-H)}}} + \biggl(\dfrac{\psi(T,H)^{1-2H}\, T^H}{\psi(T,H)+T} \biggr)^{{{1}/{(1-H)}}} \biggr\}.\end{equation}
In addition,
$\omega(H) \leq \min\{\omega_1(H), \omega_2(H)\}$
, where
\begin{equation}\omega_1(H) \,{:}\,{\raise-1.5pt{=}}\, 2\cdot (2H)^{{{H}/{(1-H)}}}(1-2H)^{{{(1-2H)}/{(2-2H)}}}, \quad \omega_2(H) \,{:}\,{\raise-1.5pt{=}}\, \dfrac{1}{\nu(H)}.\end{equation}
Proof. Our starting point is again
\begin{equation*}\mathscr{M}(H) = \int_0^{\infty} \mathbb{P}\biggl(\sup_{t\geq0}\dfrac{B_H(t)}{1+t} > u^{1-H}\biggr)\,\mathrm{d} u.\end{equation*}
The idea is now to split the interval
$[0,\infty)$
into [0,T) and
$[T,\infty)$
, in the sense that the expression in the previous display is majorized by
\begin{align*} \int_0^{\infty} &\mathbb{P}\biggl(\sup_{t\in[0,T]}\dfrac{B_H(t)}{1+t} > u^{1-H}\biggr)\,\mathrm{d} u + \int_0^{\infty} \mathbb{P}\biggl(\sup_{t\in[T,\infty)}\dfrac{B_H(t)}{1+t} > u^{1-H}\biggr)\,\mathrm{d} u \\[3pt]
& = \mathbb{E} \Biggl[\biggl(\sup_{t\in[0,T]}\dfrac{B_H(t)}{1+t}\biggr)^{{{1}/{(1-H)}}}\Biggr] + \mathbb{E} \Biggl[\biggl(\sup_{t\in[T,\infty)}\dfrac{B_H(t)}{1+t}\biggr)^{{{1}/{(1-H)}}}\Biggr].\end{align*}
The next step is to consider these two terms separately. We deal with the second term using self-similarity and the fact that
\begin{equation*}{\big\{B_H(t)\big\}_{t\in\mathbb{R}_+} \stackrel{\mathrm{d}}{=} \big\{t^{2H}B_H(1/t)\big\}_{t\in\mathbb{R}_+},}\end{equation*}
with the objective of arriving at an expression similar to the first term. Concentrating on this second term, we thus obtain
\begin{align*} \sup_{t\in[T,\infty)}\dfrac{B_H(t)}{1+t} & = \sup_{t\in(0,1/T]}\dfrac{B_H(1/t)}{1+1/t} \\[3pt] &\stackrel{\mathrm{d}}{=} \sup_{t\in(0,1/T]}\dfrac{t^{-2H}B_H(t)}{1+1/t} \\[3pt] &= \sup_{t\in(0,1]}\dfrac{(t/T)^{-2H}B_H(t/T)}{1+T/t} \\[3pt] & \stackrel{\mathrm{d}}{=} \sup_{t\in(0,1]}\dfrac{t^{-2H}T^H}{1+T/t} \cdot B_H(t)\\[3pt] &= \sup_{t\in(0,1]}\dfrac{t^{1-2H}T^H}{t+T} \cdot B_H(t).\end{align*}
Upon combining the above,
\begin{align*}& \mathbb{E}\Biggl[ \biggl(\sup_{t\in[0,T]}\dfrac{B_H(t)}{1+t}\biggr)^{{{1}/{(1-H)}}}\Biggr] + \mathbb{E}\Biggl[ \biggl(\sup_{t\in[T,\infty)}\dfrac{B_H(t)}{1+t}\biggr)^{{{1}/{(1-H)}}}\Biggr] \notag \\[3pt]
& \quad = \mathbb{E} \Biggl[\biggl( \sup_{t\in[0,1]} \dfrac{T^H}{1+tT} \cdot B_H(t) \biggr)^{{{1}/{(1-H)}}}\Biggr]+ \mathbb{E} \Biggl[\biggl( \sup_{t\in[0,1]} \dfrac{t^{1-2H}T^H}{t+T} \cdot B_H(t) \biggr)^{{{1}/{(1-H)}}}\Biggr] \notag \\[3pt]
&\quad \leq \Biggl( T^{{{H}/{(1-H)}}} + \biggl(\sup_{t\in[0,1]} \dfrac{t^{1-2H} T^H}{t+T} \biggr)^{{{1}/{(1-H)}}} \Biggr) \cdot \mathbb{E}\Biggl[ \biggl( \sup_{t\in[0,1]} B_H(t) \biggr)^{{{1}/{(1-H)}}}\Biggr].\end{align*}
It takes some elementary calculus to verify that, for given values of T and H, the supremum of the function
$t\mapsto {t^{1-2H}}/({t+T})$
over [0,1] is attained at
$\psi(T,H)$
. This, combined with (9), proves that, indeed, (11) holds with
$\omega(H)$
as defined in (12).
It is left to show that
$\omega(H) \leq \min\{\omega_1(H), \omega_2(H)\}$
. The bound
$\omega(H) \leq \omega_1(H)$
results from taking the infimum in
$\omega(H)$
in (12), but over a subinterval of
$(0,\infty)$
. More concretely, we consider the interval
$(0,\tau(H))$
with
$\tau(H)\,{:}\,{\raise-1.5pt{=}}\, 2H/(1-2H)$
, in which we can replace
$\psi(T,H)$
with
$T(1-2H)/(2H)$
. We obtain
\begin{align} \omega(H)& \leq\omega_1(H)\notag \\[3pt] &= \inf_{T \in(0,\tau(H))}\biggl\{T^{{{H}/{(1-H)}}} + \biggl(\dfrac{\psi(T,H)^{1-2H} T^H}{\psi(T,H)+T} \biggr)^{{{1}/{(1-H)}}} \biggr\} \notag \\[3pt] &= \inf_{T \in(0,\tau(H))}\bigl(T^{{{H}/{(1-H)}}}+ T^{-{{H}/{(1-H)}}}(1-2H)^{{{(1-2H)}/{(1-H)}}}(2H)^{{{2H}/{(1-H)}}}\bigr).\end{align}
Computing the derivative with respect to T and solving the first-order condition yields that the infimum above is attained at
\begin{equation*}T = 2H(1-2H)^{{{(1-2H)}/{2H}}}.\end{equation*}
It is directly seen that this minimizer does not exceed
${2H}/({1-2H})$
, and hence it is also the minimizer of (14). Further standard algebraic manipulations yield the expression in (13).
Further, the bound
$\omega(H) \leq \omega_2(H)$
results from realizing that
$\psi(T,H)\leq 1$
:
\begin{equation*}\omega(H) \leq \omega_2(H) = \inf_{T > 0}\biggl\{T^{{{H}/{(1-H)}}} + \biggl(\dfrac{T^H}{T} \biggr)^{{{1}/{(1-H)}}} \biggr\}.\end{equation*}
The infimum above is attained at
\begin{equation*}T = \biggl(\dfrac{1-H}{H}\biggr)^{1-H} \end{equation*}
and again simple algebra then directly leads to the expression
$1/\nu(H)$
in (13).
Although we have the two upper bounds from (13), it is worthwhile exploring whether we can analyze
$\omega(H)$
in a more precise fashion. The next lemma deals with this issue. Here
$H_0 \approx 0.1541$
is the unique solution to the equation
\begin{equation} \dfrac{H}{1-H} = \Big(\dfrac{2-H}{1-H}\Big)^{-{{(2-H)}/{(1-H)}}},\end{equation}
and
$\tau^{\circ}(H)$
is the unique solution to the equation, for
$\tau\geq (1-H)^{-1}$
,
\begin{equation}\dfrac{H}{1-H} + \Big({\dfrac{H}{1-H}-\tau}\Big){(1+\tau)^{-{{(2-H)}/{(1-H)}}}} = 0.\end{equation}
Lemma 3. The function
$\omega(H)$
, as defined in (12), with
$H\in(0,\frac{1}{2}]$
, satisfies
\begin{align*}\omega(H) = \begin{cases}\min\{\omega_0(H), \omega_1(H)\} & H\leq H_0 ,\\[3pt] \omega_1(H) & H > H_0,\end{cases}\end{align*}
where
\begin{equation*} \omega_0(H) = \tau^{\circ}(H)^{{{H}/{(1-H)}}} \bigg(1+ \dfrac{1}{{(1+\tau^{\circ}(H))^{{{1}/{(1-H)}}}}}\bigg).\end{equation*}
Proof. Above we already considered the infimum in (12), but with the minimization performed only over
$T<\tau(H)\,{:}\,{\raise-1.5pt{=}}\, 2H/(1-2H).$
This resulted in the expression for
$\omega_1(H)$
as given in (13).
We continue by considering the infimum in (12), but now with the minimization performed only over
$T\geq \tau(H).$
To this end, we define the functions
\begin{equation*}F(T) \,{:}\,{\raise-1.5pt{=}}\, T^{\alpha}\biggl(1 + \dfrac{1}{(1+T)^{\alpha+1}}\biggr),\quad f(T) \,{:}\,{\raise-1.5pt{=}}\, \alpha + \dfrac{\alpha-T}{(1+T)^{\alpha+2}}.\end{equation*}
Hence, for a given value of
$H\in(0,\frac{1}{2}]$
, the infimum we are looking for is
$\inf_T F(T)$
, with
$T>\tau(H)$
and
$\alpha=H(1-H)^{-1}$
. It is directly seen that
$F'(T) = T^{\alpha-1} f(T)$
, so that the first-order condition reduces to
$f(T)=0.$
We also have that
$f(0) = 2\alpha$
,
$\lim_{T\to\infty}f(T) = \alpha$
, and
\begin{equation*}f'(T) = \dfrac{1+\alpha}{(1+T)^{3+\alpha}} \cdot (T - (1+\alpha)).\end{equation*}
This means that the function
$f(\!\cdot\!)$
is strictly decreasing on
$T\in[0,1+\alpha)$
and strictly increasing on
$(1+\alpha,\infty)$
, that is, it attains its minimum at
$T = 1+\alpha$
. As a consequence, the function
$f(\!\cdot\!)$
has at most two zeros. We distinguish between three cases.
-
(1) Suppose
$f(1+\alpha) > 0$
. In this case the equation
$f(T) = 0$
does not have any positive solutions and thus
$F'(T) > 0$
for all T, meaning that the infimum of function
$F(\!\cdot\!)$
over
$T>\tau(H)$
is attained at
$T=\tau(H)$
. -
(2) Suppose
$f(1+\alpha) = 0$
. Then the equation
$f(T)=0$
has exactly one solution, namely
$T = 1+\alpha = ({1-H})^{-1}$
. This means that the infimum of
$F(\!\cdot\!)$
over
$T>\tau(H)$
is attained at
$\max\{\tau(H), ({1-H})^{-1}\}$
. -
(3) Suppose
$f(1+\alpha) < 0$
. Then the equation
$f(T)=0$
has at most two solutions, say
$T_1(H)$
and
$T_2(H)$
, where
$T_1(H) < 1+\alpha < T_2(H)$
. The infimum of
$F(\!\cdot\!)$
over
$T>\tau(H)$
is then attained at
$\max\{\tau(H), T_2(H)\}$
. Finally, since
$\tau(H) \leq 1+\alpha$
for
$H\in(0,1-\frac{1}{2}\sqrt{2}]$
, we remark that the maximum is attained at
$T_2(H)$
as long as H belongs to that interval. Observe that
$T_2(H)$
solves (16), so that we can identify it with
$\tau^{\circ}(H)$
.
Now that we have analyzed the minimum over
$T<\tau(H)$
and
$T\geq \tau(H)$
, we have to pick the smallest of these numbers. Across all
$H\in(0,\frac{1}{2}]$
we have that
$F(\tau(H)) \geq \omega_1(H)$
, because
\begin{equation*}\dfrac{F(\tau(H))}{\omega_1(H)} = \dfrac{1}{2} \cdot \Big(\beta + \dfrac{1}{\beta}\Big),\end{equation*}
where
$\beta = (1-2H)^{1/(2-2H)}$
, in combination with the known equality
$\beta + \beta^{-1} \geq 2$
, for any
$\beta>0.$
It thus suffices to compare
$\omega_1(H)$
with the value of function
$F(\!\cdot\!)$
at
$\tau^{\circ}(H)$
. Observing that
$f(1+\alpha)=0$
coincides with (15), we obtain the desired result.
3.2. Numerical techniques for improved bounds
We start by stating and proving an upper and lower bound on the function
$\mu(\!\cdot\!)$
. These are the functions
$\overline\mu(\!\cdot\!)$
and
$\underline\mu(\!\cdot\!)$
, which were given in (9) and appeared in Propositions 4 and 5. Then we focus on developing numerical procedures to find a tighter upper bound on
$\mathscr{M}(H).$
We do so by studying the object
\begin{equation*}\mu(H,\alpha)\,{:}\,{\raise-1.5pt{=}}\, \mathbb{E}\biggl[\biggl(\sup_{t\in[0,1]} B_H(t)\biggr)^{\alpha}\,\biggr],\end{equation*}
where we note that
$\mu(H, (1-H)^{-1})=\mu(H)$
, with
$\mu(\!\cdot\!)$
as defined in (8).
The next lemma presents (i) bounds on
$\mu(H,\alpha)$
in terms of
$\mu(H,1)$
, and (ii) explicit bounds on
$\mu(H,1)$
. With
$\lceil x\rceil$
denoting the smallest integer larger than or equal to x, we note that
$2/\log_2 \lceil 2^{2/H}\rceil = H$
when
$2^{2/H}$
is an integer.
Lemma 4. For any
$H\in(0,1)$
and
$\alpha>1$
,
\begin{equation}(\mu(H,1))^{\alpha} \leq \mu(H,\alpha) \leq (\mu(H,1))^{\alpha} + \max\{1,2^{\alpha-2}\}\alpha\sqrt{\dfrac{\pi}{2}}\bigl((\mu(H,1))^{\alpha-1} + \mathbb{E}|\mathscr{N}|^{\alpha-1}\bigr).\end{equation}
For
$H \in(0,\frac{1}{2}]$
,
\begin{equation}\dfrac{C^-}{\sqrt{ H}} \leq \mu(H,1) \leq \overline\mu(H,1) \,{:}\,{\raise-1.5pt{=}}\, \dfrac{C^+}{\sqrt{2/\log_2 \lceil 2^{2/H}\rceil}},\end{equation}
where
$C^-\,{:}\,{\raise-1.5pt{=}}\, ({2\sqrt{\pi e \log 2}})^{-1} \approx 0.2055$
and
$C^+\,{:}\,{\raise-1.5pt{=}}\, 1.695$
.
Proof. The inequalities (18) are due to work by Borovkov et al.: for the lower bound consult [Reference Borovkov, Mishura, Novikov and Zhitlukhin6, Theorem 1(i)] and for the upper bound consult [Reference Borovkov, Mishura, Novikov and Zhitlukhin5, Corollary 2].
Hence the inequalities (17) are left to be proved. The lower bound is an immediate consequence of Jensen’s inequality. For the upper bound we rely on the Borell–TIS inequality [Reference Adler and Taylor2, Theorem 2.1.1]: locally abbreviating
$\mu\,{:}\,{\raise-1.5pt{=}}\, \mu(H,1)$
,
\begin{align*} \mu(H,\alpha) & = \int_0^{\infty} \mathbb{P}\biggl(\sup_{t\in[0,1]} B_H(t) > u^{1/\alpha}\biggr)\,\mathrm{d} u \\[3pt]
&\leq \int_0^{\mu^{\alpha}}1\,\mathrm{d} u+ \int_{\mu^{\alpha}}^{\infty} \exp\biggl(\!-\dfrac{1}{2}(u^{1/\alpha} - \mu)^2\biggr)\,\mathrm{d} u \\[3pt]
& = \int_0^{\mu^{\alpha}}1\,\mathrm{d} u + \alpha\int_0^{\infty} (\mu+y)^{\alpha-1} \exp\big(\!-y^2/2\big)\,\mathrm{d} y \\[3pt]
& \leq \mu^{\alpha} + \max\big\{1,2^{\alpha-2}\big\}\,\alpha\int_{0}^{\infty} \big(\mu^{\alpha-1} + y^{\alpha-1}\big) \exp\big(\!-y^2/2\big)\,\mathrm{d} y \\[3pt]
& = \mu^{\alpha} + \max\big\{1,2^{\alpha-2}\big\}\,\alpha\sqrt{\dfrac{\pi}{2}}\big(\mu^{\alpha-1} + \mathbb{E}|\mathscr{N}|^{\alpha-1}\big),\end{align*}
where in the fourth line we used the inequality
$(x+y)^p\leq \max\{1, 2^{p-1}\}\cdot(x^p + y^p)$
, which holds for any
$x,y,p>0$
.
We further improve the upper bound in (18) with the following result. For
$H^{\circ}\in(0,\frac{1}{2})$
, define
\begin{equation}A(H \mid H^{\circ}) \,{:}\,{\raise-1.5pt{=}}\, \dfrac{2(H-H^{\circ})}{1-2H^{\circ}}.\end{equation}
Lemma 5. For any
$H\in[H^{\circ},\frac{1}{2}]$
,
\begin{equation*}\mu(H,1) \leq \sqrt{A(H \mid H^{\circ})}\,\mu\biggl(\dfrac{1}{2},1\biggr) + \sqrt{1-A(H \mid H^{\circ})} \,\mu(H^{\circ},1),\end{equation*}
where
$\mu(\frac{1}{2},1)=\sqrt{\pi/2}$
.
We remark that
$A(H \mid H^{\circ})\to1$
as
$H\uparrow\frac{1}{2}$
, so this upper bound is tight at
$H=\frac{1}{2}$
.
Proof. Consider a new process
$X(\!\cdot\!)$
, defined by
\begin{equation}X(t) \,{:}\,{\raise-1.5pt{=}}\, \sqrt{A(H \mid H^{\circ})}\,B(t) + \sqrt{1-A(H \mid H^{\circ})}\,B_{{H^{\circ}}}(t),\end{equation}
with processes
$B(\!\cdot\!)\equiv B_{{{1}/{2}}}(\!\cdot\!)$
and
$B_{{H^{\circ}}}(\!\cdot\!)$
being independent. We will write
$A\,{:}\,{\raise-1.5pt{=}}\, A(H \mid H^{\circ})$
for brevity. Then
\begin{equation*}\mathrm{Var}\, X(t) - \mathrm{Var} \,B_H(t) = At + (1-A)t^{2{H^{\circ}}} - t^{2H} = t\big(A + (1-A)t^{2{H^{\circ}}-1}-t^{2H-1}\big).\end{equation*}
The function
$t\mapsto A + (1-A)t^{2{H^{\circ}}-1}-t^{2H-1}$
attains its global minimum at
$t = 1$
, which implies that
$\mathrm{Var} \,X(t) \geq \mathrm{Var}\, B_H(t)$
for all
$t\geq 0$
. This means that we are in a position to apply Sudakov’s inequality; see e.g. [Reference Adler and Taylor2, Theorem 2.6.5] or [Reference Borovkov, Mishura, Novikov and Zhitlukhin6, Proposition 1]. For all
$s,t\in [0,1]$
we have
$\mathbb{E}[B_H(t)]=\mathbb{E}[X(t)]=0$
and (due to the stationarity of the increments of
$B_H(\!\cdot\!)$
and
$X(\!\cdot\!)$
)
\begin{align*}\mathbb{E}\bigl[ ( B_H(t)-B_H(s) )^2 \bigr]&=\mathbb{E}\bigl[ ( B_H(|t-s|) )^2 \bigr]\\[3pt]&\leq\mathbb{E}\bigl[ ( X(|t-s|) )^2 \bigr]\\[3pt]&=\mathbb{E}\bigl[ ( X(t)-X(s) )^2 \bigr].\end{align*}
This gives us
\begin{align*} \mu(H,1)& = \mathbb{E}\biggl[\sup_{t\in[0,1]} B_H(t)\biggr]\\[3pt] &\leq \mathbb{E}\biggl[\sup_{t\in[0,1]} X(t)\biggr]\\[3pt] &= \mathbb{E}\biggl[\sup_{t\in[0,1]}\big\{\sqrt{A}\,B(t) + \sqrt{1-A}\,B_{{H^{\circ}}}(t)\big\}\biggr]\\[3pt] &\leq \sqrt{A}\cdot\mathbb{E}\biggl[\sup_{t\in[0,1]}B(t)\biggr] + \sqrt{1-A}\cdot\mathbb{E}\biggl[\sup_{t\in[0,1]}B_{{H^{\circ}}}(t)\biggr],\end{align*}
which completes the proof.
Lemma 5 can be used to improve the upper bound for
$\mu(H,1)$
that was presented in Lemma 4. The following corollary provides this sharper upper bound.
Corollary 1. For any
$H\in(0,\frac{1}{2}]$
,
\begin{equation*}\mu(H, 1) \leq \overline\mu^{\circ}(H, 1) \,{:}\,{\raise-1.5pt{=}}\, \min\{\overline\mu(H,1), \overline\mu'(H,1)\},\end{equation*}
where
\begin{equation*}\overline\mu'(H, 1) \,{:}\,{\raise-1.5pt{=}}\, \inf_{H^{\circ}\in(0,H)}\bigl\{ \sqrt{A(H \mid H^{\circ})\cdot \pi/2} + \sqrt{1-A(H \mid H^{\circ})} \, \overline\mu(H,1)\bigr\},\end{equation*}
with
$\overline\mu(H,1)$
defined in (18).
Notably, in the neighborhood for
$H=\frac{1}{2}$
the upper bound in Corollary 1 improves the upper bound that was found in [Reference Borovkov, Mishura, Novikov and Zhitlukhin5]; see Figure 2. More precisely, the figure shows that the above upper bound improves the previous bound
$\overline\mu(H,1)$
for
$H\in[0.412, 0.5]$
. The discontinuities are due to the upper bound in (18) being piecewise constant.
Relying on similar ideas, we can improve the upper bound
$\mathscr{U}_2(\!\cdot\!)$
found in Proposition 5. Recall that
$\mathscr{U}_2(\!\cdot\!)$
has the undesirable property that it has a jump at
$H=\frac{1}{2}$
, where the exact value of
$\mathscr{M}(H)$
is known (
$\mathscr{M}(\frac{1}{2}) = \frac{1}{2}$
). For
${H^{\circ}}\in(0,\frac{1}{2})$
, define
\begin{equation*}\gamma(H \mid H^{\circ}) \,{:}\,{\raise-1.5pt{=}}\, \biggl(\dfrac{1-2H}{1-2{H^{\circ}}}\biggr)^{{{(1-2{H^{\circ}})}/{(2(1-{H^{\circ}}))}}}.\end{equation*}
We remark that
$\gamma(H \mid H^{\circ})\to0$
as
$H\uparrow\frac{1}{2}$
, so the upper bound in the following lemma is tight at
$H=\frac{1}{2}$
.
Lemma 6. For any
$H\in[{H^{\circ}},\frac{1}{2}]$
,
\begin{equation*}\mathscr{M}(H) \leq \mathscr{M}\biggl({\dfrac{1}{2}}\biggr) +\gamma(H \mid H^{\circ}) \mathscr{M}({{H^{\circ}}}).\end{equation*}
Proof. Analogously to the proof of Lemma 5, the application of Sudakov’s inequality, with A defined as in (19) and process X(t) defined in (20), for any fixed
$c\in(0,1)$
, yields
\begin{align*} \mathscr{M}(H)& = \mathbb{E}\biggl[\sup_{t\geq 0} \{B_H(t)-t\} \biggr]\\[3pt] &\leq \mathbb{E}\biggl[\sup_{t\geq 0} \{X(t)-t \}\biggr]\\[3pt] &= \mathbb{E}\biggl[\sup_{t\geq 0} \{\sqrt{A}\,B(t) + \sqrt{1-A}\,B_{{H^{\circ}}}(t) - t \}\biggr]\\[3pt] & = \mathbb{E}\biggl[\sup_{t\geq 0} \bigl\{\bigl(\sqrt{A}\,B(t)-ct\bigr) + \bigl(\sqrt{1-A}\,B_{{H^{\circ}}} (t)- (1-c)t\bigr)\bigr\}\biggr] \\[3pt] & \leq \mathbb{E}\biggl[\sup_{t\geq 0}\bigl\{\sqrt{A}\,B(t)-ct\bigr\}\biggr] + \mathbb{E}\biggl[\sup_{t\geq 0} \bigl\{\sqrt{1-A}\,B_{{H^{\circ}}}(t) - (1-c)t\bigr\}\biggr].\end{align*}
Finally, an application of the self-similarity property with
$c=A$
yields, after some straightforward computations, the desired upper bound.
We remark that Lemma 6 can be further improved by optimizing over all constants A (or equivalently
$H^{\circ}$
) and c in the proof; the resulting optimized bound is not explicit (but can be obtained numerically using standard software).
In the following corollary, the upper bound of Lemma 6 is combined with Proposition 5, and in addition optimized over
$H^{\circ}\in(0,H]$
.
Corollary 2. For any
$H\in(0,\frac{1}{2}]$
,
\begin{equation*}\mathscr{M}(H) \leq \mathscr{U}_2^{\circ}(H) = \min\ \{\mathscr{U}_2(H), \mathscr{U}^{\prime}_2(H)\},\end{equation*}
where
\begin{equation*}\mathscr{U}_2^{\prime}(H) \,{:}\,{\raise-1.5pt{=}}\, \dfrac{1}{2} + \inf_{H^{\circ}\in(0,H)} \gamma(H \mid H^{\circ})\,\mathscr{U}_2(H^{\circ})\end{equation*}
and
$\mathscr{U}_2(\!\cdot\!)$
is defined in Proposition 5.
4. Proofs of Theorems 1–2
In this section we use the results from the previous sections to establish Theorems 1–2, using the bounds developed in the previous sections.
Proof of Theorem 1. The result concerning
$H\uparrow 1$
, in (4), is an immediate consequence of the results presented in Propositions 1 and 2, in combination with the observation that
\begin{equation*}\lim_{H\uparrow 1} H^{{{H}/{(1-H)}}} = \dfrac{1}{e}.\end{equation*}
We continue by showing the result concerning
$H\downarrow 0$
, i.e. (3). From the proofs of Propositions 4 and 5,
$\mu(H)$
and
$\omega_2(\!\cdot\!)$
defined as in Proposition 5, we have
\begin{equation*}(1-H)H^{{{H}/{(1-H)}}} \leq \dfrac{\mathscr{M}(H)}{\mu(H)} \leq \omega_2(H) = H^{-H}(1-H)^{-(1-H)},\end{equation*}
which implies that
$\lim_{H\downarrow 0} \mathscr{M}(H)/\mu(H) = 1$
. From the first part of Lemma 4, locally using the short notation
$\mu\,{:}\,{\raise-1.5pt{=}}\, \mu(H,1)$
, and with
$\alpha=({1-H})^{-1}$
and
$H<1/2$
,
\begin{equation*}\mu^{\alpha-1} \leq \dfrac{\mu(H)}{\mu} \leq \mu^{\alpha-1} +\dfrac{\alpha\sqrt{{{\pi}/{2}}} (\mu^{\alpha-1} + \mathbb{E}|\mathscr{N}|^{\alpha-1})}{\mu}.\end{equation*}
Now, due to the second part of Lemma 4, we know that
$C^- H^{-1/2}\leq\mu\leq \bar C^+ H^{-1/2}$
, where
$C^-=0.2$
, and
$\bar C^+$
is some constant larger than the
$C^+=1.695$
. This shows that
\begin{equation*}\dfrac{\mu^{\alpha-1} + \mathbb{E}|\mathscr{N}|^{\alpha-1}}{\mu}=\dfrac{1}{\mu^{2-\alpha}} + \dfrac{\mathbb{E}|\mathscr{N}|^{\alpha-1}}{\mu}\end{equation*}
tends to 0, as
$H\downarrow 0$
. What is more,
\begin{equation*}(C^-)^{{{H}/{(1-H)}}} \cdot H^{-{{H}/{(2(1-H))}}} \leq \mu^{\alpha-1} \leq (C^+)^{{{H}/{(1-H)}}} \cdot H^{-{{H}/{(2(1-H))}}},\end{equation*}
which shows that
$\mu^{\alpha-1}\to1$
as
$H\downarrow0$
. We thus conclude that
$\lim_{H\downarrow 0} \mathscr{M}(H)/\mu = 1$
, and hence (3) holds.
Proof of Theorem 2. The first part follows directly from the numerical computations underlying Figure 3. The second part follows from Propositions 1 and 2 by observing that, on the interval
$H\in[\frac{1}{2},1)$
,
$H\mapsto H^{{H}/({H-1})}$
monotonically increases from 2 to e.
Figure 3:
The ratio between the upper and lower bounds for
$\mathscr{M}(H)$
for
$H\in[0,\frac{1}{2}]$
.
5. Discussion and conclusions
In this paper we have developed upper and lower bounds on the expected supremum of fBm with drift. Some of these bounds are in closed form, whereas we also include numerical procedures to improve on such bounds. Future work could aim at further shrinking the gap between the upper and lower bounds. In addition, one could pursue developing similar bounds for higher moments of the supremum, or alternatively the variance. Regarding the variance, various complications are foreseen, most notably the magnitude of the best lower bound on the second moment potentially exceeding the square of the best upper bound on the first moment, rendering the resulting lower bound on the variance useless. Another branch of research could concentrate on finding bounds on the expected supremum for non-fBm Gaussian processes.
Acknowledgements
We are grateful to the referee and Associate Editor for their careful reading of the manuscript and the constructive reports.
K. Bisewski’s research is funded by the Swiss National Science Foundation grant 200021-175752/1. Part of this work was done while KB was visiting the Mathematical Institute, Wrocław University, Poland.
K. Dębicki’s research is partly funded by NCN grant 2018/31/B/ST1/00370.
M. Mandjes is also with Eurandom, Eindhoven University of Technology, The Netherlands, and Amsterdam Business School, Faculty of Economics and Business, University of Amsterdam, The Netherlands. His research is partly funded by the NWO Gravitation project Networks, grant 024.002.003.
