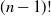1. Introduction
A uniform recursive tree (URT) on n vertices is a rooted random recursive tree where each possible ![]() $(n-1)!$
distinct tree has the same probability of appearing. Another way of looking at uniform recursive trees is that one starts constructing the tree with only the root (node 1) and node 2 attached to the root. At each subsequent step,
$(n-1)!$
distinct tree has the same probability of appearing. Another way of looking at uniform recursive trees is that one starts constructing the tree with only the root (node 1) and node 2 attached to the root. At each subsequent step, ![]() $k = 3,\ldots,n$
, node k connects to one of the prior nodes with equal probability
$k = 3,\ldots,n$
, node k connects to one of the prior nodes with equal probability ![]() $1 / (k-1)$
. A detailed survey on URTs can be found in [Reference Smythe and Mahmoud11], and a book length treatment of random trees can be found in [Reference Drmota5].
$1 / (k-1)$
. A detailed survey on URTs can be found in [Reference Smythe and Mahmoud11], and a book length treatment of random trees can be found in [Reference Drmota5].
URTs have been used in various applications. These include, but are not restricted to, the spread of epidemics [Reference Feng, Su and Hu6], determining the genealogy of ancient and medieval texts [Reference Najock and Heyde13], analysing pyramid schemes [Reference Gastwirth8], and the spread of a fire in a tree [Reference Marzouk12]. Though these investigations use uniformity in their models, having different distributions would provide more flexibility to the researcher. Using URTs implies that in the model all nodes are assumed to be identical in a certain sense. In the spread of epidemics, this means, for instance, that every infected person is equally likely to infect the next one. Similarly, it means that in the study of medieval texts every book is equally likely to be copied. This is obviously not the case in real-world applications.
Parallel to the development of the theory of uniform recursive trees, various other recursive tree structures have already been studied. Among the most well known are binary recursive trees, which are described in [Reference Bergeron, Flajolet and Salvy3]. Other non-uniform recursive tree models include plane-oriented recursive trees [Reference Szymanski, Barlotti, Biliotti, Cossu, Korchmaros and Tallini16], scaled attachment random recursive trees [Reference Devroye, Fawzi and Fraiman4], and biased recursive trees [Reference Altok and Işlak1].
Our interest here is on another natural generalization, Hoppe trees, as recently considered in [Reference Leckey and Neininger10]. There, the root is assigned a weight ![]() $\theta$
; all other nodes get weight 1. Node i then attaches to the root with probability
$\theta$
; all other nodes get weight 1. Node i then attaches to the root with probability ![]() $\frac{\theta}{\theta+i-2}$
and to any other node with probability
$\frac{\theta}{\theta+i-2}$
and to any other node with probability ![]() $\frac{1}{\theta+i-2}$
. This model is associated with Hoppe’s urn, which has an application in modelling the alleles of a gene with mutation rate
$\frac{1}{\theta+i-2}$
. This model is associated with Hoppe’s urn, which has an application in modelling the alleles of a gene with mutation rate ![]() $\theta>0$
. Concerning many properties like the number of leaves, the height, and the depth of node n, Hoppe trees behave similarly to uniform recursive trees in an asymptotic sense.
$\theta>0$
. Concerning many properties like the number of leaves, the height, and the depth of node n, Hoppe trees behave similarly to uniform recursive trees in an asymptotic sense.
The model in this paper generalizes the idea of Hoppe trees: we assign every node a weight ![]() $w_i$
. Node j then attaches to node
$w_i$
. Node j then attaches to node ![]() $1 \leq i<j$
with probability
$1 \leq i<j$
with probability ![]() $\frac{w_i}{w_1 + \cdots + w_{j-1}}$
. We call the resulting tree construction a weighted recursive tree (WRT).
$\frac{w_i}{w_1 + \cdots + w_{j-1}}$
. We call the resulting tree construction a weighted recursive tree (WRT).
Using weights is interesting from the point of view of applications since it allows one to introduce diversity among the nodes. In the other non-uniform models discussed above, all nodes have the same behaviour, or in other words they attract nodes according to the same rule. When a recursive process does not satisfy such conditions, weighted recursive trees can be used to model it more precisely. Moreover, the properties of weighted recursive trees and how much they differ from the uniform model can be interpreted as an indicator for the stability of a process. In various applications it is reasonable to assume that it is more probable for some nodes to get children than others. For example, some persons might be more likely to infect others, some copies of ancient texts are more likely to have been copied again, and some people might be more likely to recruit new individuals. Thus it is interesting to see how much fluctuation in the attachment probabilities can be tolerated when using the uniform model.
The rest of the paper is organized as follows. The next section introduces a coupling used to construct a specific WRT from a Hoppe tree. Section 3 applies the coupling construction for an analysis of the number of leaves and the height of the resulting random tree. In Section 4 we relate Hoppe trees to Hoppe permutations, and use the coupling construction of Section 2 to study the size of the largest branch. In Sections 5 and 6 we study the depth and the number of branches of a general WRT.
2. A useful coupling construction
2.1. Constructing WRTs from URTs
We will first introduce a coupling allowing us to construct a special kind of WRT from a URT. We will not use this coupling in the analysis of random tree statistics because the second coupling construction introduced below can be applied to a more general class of WRTs. We still wanted to discuss this version because it has URTs rather than Hoppe trees as a starting point, and URTs are a much better studied structure.
We will call trees that have a weight sequence such that the first k nodes have a constant weight equal to ![]() $\theta$
and all other nodes have weight 1,
$\theta$
and all other nodes have weight 1, ![]() $\theta^k$
-RTs. It is possible to construct a
$\theta^k$
-RTs. It is possible to construct a ![]() $\theta^k$
-RT from a URT by a coupling construction when
$\theta^k$
-RT from a URT by a coupling construction when ![]() $\theta \in \mathbb{N}^+$
. To emphasize this assumption we will use m instead of
$\theta \in \mathbb{N}^+$
. To emphasize this assumption we will use m instead of ![]() $\theta$
in this part. In particular, we can construct Hoppe trees for which the weight of the root is a natural number by this coupling. To avoid confusion let us denote the nodes in the URT by i and the nodes in the
$\theta$
in this part. In particular, we can construct Hoppe trees for which the weight of the root is a natural number by this coupling. To avoid confusion let us denote the nodes in the URT by i and the nodes in the ![]() $m^k$
-RT obtained by the coupling by
$m^k$
-RT obtained by the coupling by ![]() $i^*$
.
$i^*$
.
The coupling construction in that case goes as follows: First construct a URT with ![]() $mk + n-k$
nodes. We write
$mk + n-k$
nodes. We write ![]() $\mathcal{T}_{mk+n-k}$
for this URT and
$\mathcal{T}_{mk+n-k}$
for this URT and ![]() $\mathcal{T}_n^{m^k}$
for the tree that we obtain at the end of the coupling. Since we want the weight of the first k nodes to be m, we need to join several nodes into one. More precisely, we combine m nodes of the URT to get each of the first k nodes of the
$\mathcal{T}_n^{m^k}$
for the tree that we obtain at the end of the coupling. Since we want the weight of the first k nodes to be m, we need to join several nodes into one. More precisely, we combine m nodes of the URT to get each of the first k nodes of the ![]() $m^k$
-RT in the following way:
$m^k$
-RT in the following way:
• Nodes
 $1, \dots, m$
become node
$1, \dots, m$
become node  $1^*$
;
$1^*$
;•
 $m+1, \dots, 2m$
become node
$m+1, \dots, 2m$
become node  $2^*$
;
$2^*$
;•
 $(k-1)m +1, \dots, km$
become node
$(k-1)m +1, \dots, km$
become node  $k^*$
.
$k^*$
.
All nodes after km in ![]() $\mathcal{T}_{mk+n-k}$
correspond only to a single node in
$\mathcal{T}_{mk+n-k}$
correspond only to a single node in ![]() $\mathcal{T}_n^{m^k}$
; we just need to ‘translate’ the names of the nodes to take into account that we used mk nodes instead of k for the first k nodes in the reconstructed tree. More precisely, for
$\mathcal{T}_n^{m^k}$
; we just need to ‘translate’ the names of the nodes to take into account that we used mk nodes instead of k for the first k nodes in the reconstructed tree. More precisely, for ![]() $j>km$
, node j in the URT becomes node
$j>km$
, node j in the URT becomes node ![]() $(\,j-k(m-1))^*$
in the WRT.
$(\,j-k(m-1))^*$
in the WRT.
The parent–child relations in the WRT follow from those in the URT as follows: If, for ![]() $j>km$
and
$j>km$
and ![]() $i \leq k $
, j is a child of one of the nodes
$i \leq k $
, j is a child of one of the nodes ![]() $(i-1)m+1, \dots, im$
in the URT,
$(i-1)m+1, \dots, im$
in the URT, ![]() $(\,j-k(m-1))^*$
becomes a child of
$(\,j-k(m-1))^*$
becomes a child of ![]() $i^*$
in the WRT. If, for
$i^*$
in the WRT. If, for ![]() $j>km$
, the parent of node j is h with
$j>km$
, the parent of node j is h with ![]() $h>km$
, the parent of node
$h>km$
, the parent of node ![]() $(\,j-k(m-1))^*$
is node
$(\,j-k(m-1))^*$
is node ![]() $(h-k(m-1))^*$
.
$(h-k(m-1))^*$
.
For the nodes before or equal to km, we need to be more careful, since we joined several nodes into one and the nodes ![]() $(\,j-1)m +1, \dots, jm$
might have different parents in the URT. To settle this ambiguity, for
$(\,j-1)m +1, \dots, jm$
might have different parents in the URT. To settle this ambiguity, for ![]() $1<j\leq k$
we set the parent of
$1<j\leq k$
we set the parent of ![]() $j^*$
as the parent of
$j^*$
as the parent of ![]() $(\,j-1)m+1$
, i.e. of the node with the smallest label among those that become
$(\,j-1)m+1$
, i.e. of the node with the smallest label among those that become ![]() $j^*$
. Thus, if in the URT the parent of
$j^*$
. Thus, if in the URT the parent of ![]() $(\,j-1)m+1$
is any of the nodes
$(\,j-1)m+1$
is any of the nodes ![]() $(i-1)m+1, \dots, im$
, the parent of
$(i-1)m+1, \dots, im$
, the parent of ![]() $j^*$
is
$j^*$
is ![]() $i^*$
. It can be easily verified that the attachment probabilities obtained correspond to those of an
$i^*$
. It can be easily verified that the attachment probabilities obtained correspond to those of an ![]() $m^k$
-tree; for details, see [Reference Hiesmayr9].
$m^k$
-tree; for details, see [Reference Hiesmayr9].
In Figure 1 we present a small example of the coupling construction. In the example, nodes 1 and 2 combine to form node ![]() $1^*$
, and nodes 3 and 4 become node
$1^*$
, and nodes 3 and 4 become node ![]() $2^*$
. Then nodes 5 and 6 become node
$2^*$
. Then nodes 5 and 6 become node ![]() $3^*$
, and
$3^*$
, and ![]() $3^*$
is a child of
$3^*$
is a child of ![]() $2^*$
, since node 5 is a child of node 4 in the URT. Nodes 7 and 8 become node
$2^*$
, since node 5 is a child of node 4 in the URT. Nodes 7 and 8 become node ![]() $4^*$
, and
$4^*$
, and ![]() $4^*$
is a child of
$4^*$
is a child of ![]() $1^*$
since node 7 is a child of node 1 in the URT. Finally, node 9 becomes node
$1^*$
since node 7 is a child of node 1 in the URT. Finally, node 9 becomes node ![]() $5^*$
, and
$5^*$
, and ![]() $5^*$
is a child of
$5^*$
is a child of ![]() $4^*$
since node 9 is a child of node 7 in the URT.
$4^*$
since node 9 is a child of node 7 in the URT.

Figure 1: A WRT ![]() $\mathcal{T}_5^{2^4}$
is constructed from a URT
$\mathcal{T}_5^{2^4}$
is constructed from a URT ![]() $\mathcal{T}_9$
.
$\mathcal{T}_9$
.
We now show, as an example, how the coupling can be used to study the number of leaves, i.e. the number of nodes without children, of an ![]() $m^k$
-RT. Let
$m^k$
-RT. Let ![]() $\mathcal{L}_{mk+n-k}$
denote the number of leaves of
$\mathcal{L}_{mk+n-k}$
denote the number of leaves of ![]() $\mathcal{T}_{mk+n-k}$
, and
$\mathcal{T}_{mk+n-k}$
, and ![]() $\mathcal{L}_n^{m^k}$
denote the number of leaves of
$\mathcal{L}_n^{m^k}$
denote the number of leaves of ![]() $\mathcal{T}_{n}^{m^k}$
. Then
$\mathcal{T}_{n}^{m^k}$
. Then ![]() $\mathcal{L}_{mk+n-k}$
can be used to bound
$\mathcal{L}_{mk+n-k}$
can be used to bound ![]() $\mathcal{L}_n^{m^k}$
. First, if node
$\mathcal{L}_n^{m^k}$
. First, if node ![]() $i > km $
is a leaf in
$i > km $
is a leaf in ![]() $\mathcal{T}_{mk+n-k}$
, the corresponding node in
$\mathcal{T}_{mk+n-k}$
, the corresponding node in ![]() $\mathcal{T}_n^{m^k}$
, which is
$\mathcal{T}_n^{m^k}$
, which is ![]() ${(i-k(m-1))}^*$
, is also a leaf. The reconstruction process thus only affects the children of the nodes
${(i-k(m-1))}^*$
, is also a leaf. The reconstruction process thus only affects the children of the nodes ![]() $i^*$
with
$i^*$
with ![]() $1 \leq i \leq k$
, and the root cannot be a leaf, so we can have at most
$1 \leq i \leq k$
, and the root cannot be a leaf, so we can have at most ![]() $k-1$
additional leaves. Moreover, for each
$k-1$
additional leaves. Moreover, for each ![]() $1 \leq i \leq k$
we can ‘lose’ at most
$1 \leq i \leq k$
we can ‘lose’ at most ![]() $m-1$
leaves since if all of
$m-1$
leaves since if all of ![]() $(i\,{-}\,1)m+1, \dots, im$
are leaves in
$(i\,{-}\,1)m+1, \dots, im$
are leaves in ![]() $\mathcal{T}_{mk+n-k}$
,
$\mathcal{T}_{mk+n-k}$
, ![]() $i^*$
will be a leaf in
$i^*$
will be a leaf in ![]() $\mathcal{T}_n^{m^k}$
too. Hence, we can conclude that
$\mathcal{T}_n^{m^k}$
too. Hence, we can conclude that
Together with results about the expected number of leaves of URTs, this implies, after some simple manipulations, that
where ![]() $\mathcal{L}_n$
denotes the number of leaves in a URT on n nodes. It is possible to derive other results from this coupling, but since the coupling we present below is more general, we will not go further into it here.
$\mathcal{L}_n$
denotes the number of leaves in a URT on n nodes. It is possible to derive other results from this coupling, but since the coupling we present below is more general, we will not go further into it here.
2.2. Constructing WRTs from Hoppe trees
We will now introduce a coupling construction for WRTs whose nodes have constant weight after a certain index, a class similar to, but more general, than ![]() $\theta^k$
-RTs. Let
$\theta^k$
-RTs. Let ![]() $\mathcal{T}_n^w$
be a WRT, and
$\mathcal{T}_n^w$
be a WRT, and ![]() $(w_i)_{i \in \mathbb{N}}$
, the weight sequence of
$(w_i)_{i \in \mathbb{N}}$
, the weight sequence of ![]() $\mathcal{T}_n^w$
, be such that there is a
$\mathcal{T}_n^w$
, be such that there is a ![]() $k \in \mathbb{N}$
such that
$k \in \mathbb{N}$
such that ![]() $w_i=1$
for all
$w_i=1$
for all ![]() $i>k$
. Then we can construct
$i>k$
. Then we can construct ![]() $\mathcal{T}_n^w$
from a Hoppe tree with root weight
$\mathcal{T}_n^w$
from a Hoppe tree with root weight ![]() $\theta=\sum_{i=1}^{k} w_i$
by a coupling construction, more precisely by splitting the root into k nodes. To avoid confusion we will write i for node i in the Hoppe tree and
$\theta=\sum_{i=1}^{k} w_i$
by a coupling construction, more precisely by splitting the root into k nodes. To avoid confusion we will write i for node i in the Hoppe tree and ![]() $i^*$
for node i in the reconstructed tree.
$i^*$
for node i in the reconstructed tree.
We now describe the coupling construction: First construct a Hoppe tree on ![]() $n-k+1$
nodes and with
$n-k+1$
nodes and with ![]() $\theta$
, the weight of the root, equal to
$\theta$
, the weight of the root, equal to ![]() $\sum_{i=1}^{k} w_i$
. Then construct a WRT of size k corresponding to
$\sum_{i=1}^{k} w_i$
. Then construct a WRT of size k corresponding to ![]() $(w_i)_{i \in \{1,\dots,k\}}$
. Now we replace the root of the Hoppe tree by this weighted recursive tree of size k in the following way: nodes
$(w_i)_{i \in \{1,\dots,k\}}$
. Now we replace the root of the Hoppe tree by this weighted recursive tree of size k in the following way: nodes ![]() $1^*$
,
$1^*$
, ![]() $2^*$
, …,
$2^*$
, …, ![]() $k^*$
are the nodes of the WRT of size k we just constructed. For
$k^*$
are the nodes of the WRT of size k we just constructed. For ![]() $i \geq 2$
, node i in the Hoppe tree becomes node
$i \geq 2$
, node i in the Hoppe tree becomes node ![]() $(i+k-1)^*$
in the reconstructed tree, so we shift the names of the rest of the nodes by
$(i+k-1)^*$
in the reconstructed tree, so we shift the names of the rest of the nodes by ![]() $k-1$
. Then, for all
$k-1$
. Then, for all ![]() $i \geq 2$
, if i is a child of node 1 in the Hoppe tree,
$i \geq 2$
, if i is a child of node 1 in the Hoppe tree, ![]() $(i+k-1)^*$
becomes a child of one of the nodes
$(i+k-1)^*$
becomes a child of one of the nodes ![]() $1^*, \dots, k^*$
in the reconstructed tree, proportionally to their weights. This means that if i is a child of node 1 in the Hoppe tree, for
$1^*, \dots, k^*$
in the reconstructed tree, proportionally to their weights. This means that if i is a child of node 1 in the Hoppe tree, for ![]() $1\leq j^* \leq k$
, node
$1\leq j^* \leq k$
, node ![]() $(i+k-1)^*$
will become a child of a node
$(i+k-1)^*$
will become a child of a node ![]() $j^*$
in the reconstructed tree with probability
$j^*$
in the reconstructed tree with probability ![]() $\frac{w_{j}}{\sum_{\ell=1}^{k} w_{\ell}}$
.
$\frac{w_{j}}{\sum_{\ell=1}^{k} w_{\ell}}$
.
Let us check that this gives the attachment probabilities corresponding to the WRT we aim to construct.
For ![]() $1\leq i^* \leq k<j^*$
,
$1\leq i^* \leq k<j^*$
,
 \begin{equation*}\begin{split}\mathrm{P} & (\,j^* \text{ is child of } i^*) = \mathrm{P}(\,j-k+1 \text{ is child of } 1, \, i^*\text{ is chosen as the parent of } j^*) \\&= \frac{\sum_{\ell=1}^{k} w_{\ell}}{j-k+1 -2 +\sum_{\ell=1}^{k} w_{\ell}} \frac{w_i}{\sum_{\ell=1}^{k} w_{\ell}} = \frac{w_i}{j-1 -k+\sum_{\ell=1}^{k} w_{\ell} }. \\\end{split}\end{equation*}
\begin{equation*}\begin{split}\mathrm{P} & (\,j^* \text{ is child of } i^*) = \mathrm{P}(\,j-k+1 \text{ is child of } 1, \, i^*\text{ is chosen as the parent of } j^*) \\&= \frac{\sum_{\ell=1}^{k} w_{\ell}}{j-k+1 -2 +\sum_{\ell=1}^{k} w_{\ell}} \frac{w_i}{\sum_{\ell=1}^{k} w_{\ell}} = \frac{w_i}{j-1 -k+\sum_{\ell=1}^{k} w_{\ell} }. \\\end{split}\end{equation*}
For ![]() $k<i^*<j^*$
,
$k<i^*<j^*$
,
 \begin{equation*}\begin{split}\mathrm{P} & (\,j^* \text{ is child of } i^*)= \mathrm{P}(\,j-k+1 \text{ is child of } i-k+1)\\&= \frac{1}{j-k+1 -2 +\sum_{\ell=1}^{k} w_{\ell}} = \frac{1}{j-1-k+\sum_{\ell=1}^{k} w_{\ell}}. \\\end{split}\end{equation*}
\begin{equation*}\begin{split}\mathrm{P} & (\,j^* \text{ is child of } i^*)= \mathrm{P}(\,j-k+1 \text{ is child of } i-k+1)\\&= \frac{1}{j-k+1 -2 +\sum_{\ell=1}^{k} w_{\ell}} = \frac{1}{j-1-k+\sum_{\ell=1}^{k} w_{\ell}}. \\\end{split}\end{equation*}
The following two sections will be using the coupling construction just described.
3. Use of the coupling in WRT statistics
In this section we apply the coupling construction of the previous section to study the number of leaves in a WRT and the height of a Hoppe tree. Later, in Section 4, the coupling construction will also be used in order to understand the size of the largest branch in a WRT.
3.1. Number of leaves
A node in a tree with degree one is said to be a leaf. Focusing on the number of leaves, the reconstruction process in our coupling construction implies that all the leaves of the Hoppe tree are still leaves in the reconstructed tree, since we do not change any relation among the nodes ![]() $2, \dots, n-k+1$
of the Hoppe tree or, respectively, nodes
$2, \dots, n-k+1$
of the Hoppe tree or, respectively, nodes ![]() $(k+1)^*, \dots, n^*$
of the reconstructed tree. There can be at most
$(k+1)^*, \dots, n^*$
of the reconstructed tree. There can be at most ![]() $k-1$
additional leaves among the first k nodes. Thus, we can bound the number of leaves
$k-1$
additional leaves among the first k nodes. Thus, we can bound the number of leaves ![]() $ \mathcal{L}_n^{w} $
of
$ \mathcal{L}_n^{w} $
of ![]() $\mathcal{T}^w$
by the number of leaves
$\mathcal{T}^w$
by the number of leaves ![]() $\mathcal{L}_{n}^{\theta}$
of
$\mathcal{L}_{n}^{\theta}$
of ![]() $\mathcal{T}^\theta$
:
$\mathcal{T}^\theta$
:
In [Reference Leckey and Neininger10] the following results about the leaves of Hoppe trees are given. In this theorem and below, ![]() $\mathcal{G}$
denotes a standard normal random variable.
$\mathcal{G}$
denotes a standard normal random variable.
Theorem 1. ([Reference Leckey and Neininger10].) Let ![]() $\mathcal{L}_n^{\theta}$
denote the number of leaves of a Hoppe tree with
$\mathcal{L}_n^{\theta}$
denote the number of leaves of a Hoppe tree with ![]() $n \geq 2 $
nodes. Then
$n \geq 2 $
nodes. Then
 \begin{equation*}\begin{split}&\mathrm{E} [\mathcal{L}_n^{\theta}] = \frac{n}{2} + \frac{\theta -1}{2} + \mathcal{O}\bigg(\frac{1}{n} \bigg), \\[2pt]&\mathrm{Var} (\mathcal{L}_n^{\theta}) = \frac{n}{12} + \frac{\theta -1}{12} + \mathcal{O}\bigg(\frac{1}{n} \bigg), \\[2pt]& \mathrm{P}(|\mathcal{L}_n^{\theta} - \mathrm{E}[\mathcal{L}_n^{\theta}] | \geq t) \leq 2 \exp\bigg\{-\frac{6t^2}{n+\theta+1}\bigg\} \quad \text{ for all } t>0, \text{ and } \\[2pt]&\frac{\mathcal{L}_n^{\theta} - \mathrm{E}[\mathcal{L}_n^{\theta}]}{\sqrt{\mathrm{Var}\left (\mathcal{L}_n^{\theta}\right)}} \longrightarrow_{\rm d} \mathcal{G} \text{ as } n \to \infty.\end{split}\end{equation*}
\begin{equation*}\begin{split}&\mathrm{E} [\mathcal{L}_n^{\theta}] = \frac{n}{2} + \frac{\theta -1}{2} + \mathcal{O}\bigg(\frac{1}{n} \bigg), \\[2pt]&\mathrm{Var} (\mathcal{L}_n^{\theta}) = \frac{n}{12} + \frac{\theta -1}{12} + \mathcal{O}\bigg(\frac{1}{n} \bigg), \\[2pt]& \mathrm{P}(|\mathcal{L}_n^{\theta} - \mathrm{E}[\mathcal{L}_n^{\theta}] | \geq t) \leq 2 \exp\bigg\{-\frac{6t^2}{n+\theta+1}\bigg\} \quad \text{ for all } t>0, \text{ and } \\[2pt]&\frac{\mathcal{L}_n^{\theta} - \mathrm{E}[\mathcal{L}_n^{\theta}]}{\sqrt{\mathrm{Var}\left (\mathcal{L}_n^{\theta}\right)}} \longrightarrow_{\rm d} \mathcal{G} \text{ as } n \to \infty.\end{split}\end{equation*}
Using the above theorem we can derive results on the number of leaves in WRTs whose nodes have constant weight after a certain index.
Theorem 2. Let ![]() $\mathcal{L}^{w}_{n}$
denote the number of leaves of a WRT of size n with weight sequence
$\mathcal{L}^{w}_{n}$
denote the number of leaves of a WRT of size n with weight sequence ![]() $(w_i)_{i \in \mathbb{N}}$
such that there is a
$(w_i)_{i \in \mathbb{N}}$
such that there is a ![]() $k \in \mathbb{N}$
such that for all
$k \in \mathbb{N}$
such that for all ![]() $i>k$
we have
$i>k$
we have ![]() $w_i = 1$
. Then
$w_i = 1$
. Then
 \begin{equation*}\begin{split}&\mathrm{E} [\mathcal{L}_n^{w}] = \frac{n}{2} + C + \mathcal{O} \left ( \frac{1}{n} \right ) \text{ with } |C| \leq \frac{\sum_{i=1}^{k} w_i +k}{2},\\[2pt] &\mathrm{Var}(\mathcal{L}_n^{w}) = \frac{n}{12} + \mathcal{O} (\sqrt{n}), \\[2pt] & \mathrm{P} (|\mathcal{L}_n^{w} - \mathrm{E}[\mathcal{L}_n^{w}] | \geq t) \leq 2 \exp\Bigg\{- \frac{6(t-2k+2)^2}{n-k+2+ \sum_{i=1}^k w_i}\Bigg\} \quad \text{ for all } t>2k-2, \text{ and } \\[2pt] & \frac{\mathcal{L}^{w}_{n} - \mathrm{E}[\mathcal{L}^{w}_{n}]}{\sqrt{\mathrm{Var}\left (\mathcal{L}_n^{w}\right)}} \longrightarrow_{\rm d} \mathcal{G} \text{ as } n \to \infty.\end{split}\end{equation*}
\begin{equation*}\begin{split}&\mathrm{E} [\mathcal{L}_n^{w}] = \frac{n}{2} + C + \mathcal{O} \left ( \frac{1}{n} \right ) \text{ with } |C| \leq \frac{\sum_{i=1}^{k} w_i +k}{2},\\[2pt] &\mathrm{Var}(\mathcal{L}_n^{w}) = \frac{n}{12} + \mathcal{O} (\sqrt{n}), \\[2pt] & \mathrm{P} (|\mathcal{L}_n^{w} - \mathrm{E}[\mathcal{L}_n^{w}] | \geq t) \leq 2 \exp\Bigg\{- \frac{6(t-2k+2)^2}{n-k+2+ \sum_{i=1}^k w_i}\Bigg\} \quad \text{ for all } t>2k-2, \text{ and } \\[2pt] & \frac{\mathcal{L}^{w}_{n} - \mathrm{E}[\mathcal{L}^{w}_{n}]}{\sqrt{\mathrm{Var}\left (\mathcal{L}_n^{w}\right)}} \longrightarrow_{\rm d} \mathcal{G} \text{ as } n \to \infty.\end{split}\end{equation*}
Proof. First, for the expected value we get, from Theorem 1 and (1),
 \begin{align*}&\mathcal{L}_{n-k+1}^{\theta} \leq \mathcal{L}_n^{w} \leq \mathcal{L}_{n-k+1}^{\theta} +k-1 \\[2pt]&\quad \Rightarrow \frac{n-k+1}{2} + \frac{\sum_{i=1}^{k} w_i-1}{2} + \mathcal{O}\left ( \frac{1}{n} \right ) \leq \mathrm{E}\left [\mathcal{L}_n^{w}\right ] \\[2pt]&\qquad \leq \frac{n-k+1}{2} + \frac{\sum_{i=1}^{k} w_i-1}{2} + k -1 + \mathcal{O}\left ( \frac{1}{n} \right ) \\[2pt]&\quad \Rightarrow \frac{n}{2} + \frac{\sum_{i=1}^{k} w_i-k}{2} + \mathcal{O}\left ( \frac{1}{n} \right ) \leq \mathrm{E} \left [\mathcal{L}_n^{w}\right ] \leq \frac{n}{2} + \frac{\sum_{i=1}^{k} w_i+k-2}{2} + \mathcal{O}\left ( \frac{1}{n} \right ) \\[2pt]&\quad \Rightarrow \mathrm{E}\left [\mathcal{L}_n^{w}\right ] = \frac{n}{2} + C + \mathcal{O}\left ( \frac{1}{n} \right ),\end{align*}
\begin{align*}&\mathcal{L}_{n-k+1}^{\theta} \leq \mathcal{L}_n^{w} \leq \mathcal{L}_{n-k+1}^{\theta} +k-1 \\[2pt]&\quad \Rightarrow \frac{n-k+1}{2} + \frac{\sum_{i=1}^{k} w_i-1}{2} + \mathcal{O}\left ( \frac{1}{n} \right ) \leq \mathrm{E}\left [\mathcal{L}_n^{w}\right ] \\[2pt]&\qquad \leq \frac{n-k+1}{2} + \frac{\sum_{i=1}^{k} w_i-1}{2} + k -1 + \mathcal{O}\left ( \frac{1}{n} \right ) \\[2pt]&\quad \Rightarrow \frac{n}{2} + \frac{\sum_{i=1}^{k} w_i-k}{2} + \mathcal{O}\left ( \frac{1}{n} \right ) \leq \mathrm{E} \left [\mathcal{L}_n^{w}\right ] \leq \frac{n}{2} + \frac{\sum_{i=1}^{k} w_i+k-2}{2} + \mathcal{O}\left ( \frac{1}{n} \right ) \\[2pt]&\quad \Rightarrow \mathrm{E}\left [\mathcal{L}_n^{w}\right ] = \frac{n}{2} + C + \mathcal{O}\left ( \frac{1}{n} \right ),\end{align*}
where C depends on k and ![]() $w_1, \dots, w_k$
, and we have
$w_1, \dots, w_k$
, and we have ![]() $|C| \leq \frac{\sum_{i=1}^{k} w_i +k}{2}$
.
$|C| \leq \frac{\sum_{i=1}^{k} w_i +k}{2}$
.
Equation (1) also directly gives a concentration inequality. We have that
 \begin{equation*}\begin{split}\mathrm{P} & (|\mathcal{L}_n^{w} - \mathrm{E}[\mathcal{L}_n^{w}]|\geq t) \\[2pt] & \leq \mathrm{P}( |\mathcal{L}_n^{w} - \mathcal{L}_{n-k+1}^{\theta} | + |\mathcal{L}_{n-k+1}^{\theta} - \mathrm{E} [\mathcal{L}_{n-k+1}^{\theta} ] | + | \mathrm{E} [\mathcal{L}_{n-k+1}^{\theta} ] - \mathrm{E} [\mathcal{L}_n^{w} ] |\geq t) \\[2pt] & \leq \mathrm{P}(|\mathcal{L}_{n-k+1}^{\theta} - \mathrm{E} [\mathcal{L}_{n-k+1}^{\theta} ] | \geq t-2k+2) \\[2pt] & \leq 2 \exp\Bigg\{- \frac{6(t-2k+2)^2}{n-k+2+ \sum_{i=1}^k w_i}\Bigg\}.\end{split}\end{equation*}
\begin{equation*}\begin{split}\mathrm{P} & (|\mathcal{L}_n^{w} - \mathrm{E}[\mathcal{L}_n^{w}]|\geq t) \\[2pt] & \leq \mathrm{P}( |\mathcal{L}_n^{w} - \mathcal{L}_{n-k+1}^{\theta} | + |\mathcal{L}_{n-k+1}^{\theta} - \mathrm{E} [\mathcal{L}_{n-k+1}^{\theta} ] | + | \mathrm{E} [\mathcal{L}_{n-k+1}^{\theta} ] - \mathrm{E} [\mathcal{L}_n^{w} ] |\geq t) \\[2pt] & \leq \mathrm{P}(|\mathcal{L}_{n-k+1}^{\theta} - \mathrm{E} [\mathcal{L}_{n-k+1}^{\theta} ] | \geq t-2k+2) \\[2pt] & \leq 2 \exp\Bigg\{- \frac{6(t-2k+2)^2}{n-k+2+ \sum_{i=1}^k w_i}\Bigg\}.\end{split}\end{equation*}
The coupling also gives us an approximation for the variance. Let Y denote the number of additional leaves among the first k nodes in the reconstructed tree. Then ![]() $\mathrm{Var}(Y) = { \mathcal{O}(k^2)}$
since
$\mathrm{Var}(Y) = { \mathcal{O}(k^2)}$
since ![]() $Y \leq k$
. Since
$Y \leq k$
. Since ![]() $\mathrm{Var}(\mathcal{L}_n^{w}) = \mathrm{Var}(\mathcal{L}_{n-k+1}^{\theta} +Y ) = \mathrm{Var}(\mathcal{L}_{n-k+1}^{\theta}) + \mathrm{Var}(Y) + { 2 \mathrm{Cov}(\mathcal{L}_{n-k+1}^{\theta} ,Y)}$
, we get, by the Cauchy–Schwarz inequality,
$\mathrm{Var}(\mathcal{L}_n^{w}) = \mathrm{Var}(\mathcal{L}_{n-k+1}^{\theta} +Y ) = \mathrm{Var}(\mathcal{L}_{n-k+1}^{\theta}) + \mathrm{Var}(Y) + { 2 \mathrm{Cov}(\mathcal{L}_{n-k+1}^{\theta} ,Y)}$
, we get, by the Cauchy–Schwarz inequality,
In a similar way, one can make conclusions about the asymptotic distribution. For this we will need Slutsky’s theorem: Let ![]() $X_n$
and
$X_n$
and ![]() $Y_n$
be sequences of random variables such that
$Y_n$
be sequences of random variables such that ![]() $X_n \to_{\rm d} X$
and
$X_n \to_{\rm d} X$
and ![]() $Y_n \to c$
in probability for
$Y_n \to c$
in probability for ![]() $c \in \mathbb{R}$
. Then
$c \in \mathbb{R}$
. Then
In order to derive a central limit theorem for ![]() $\mathcal{L}^{w}_{n}$
, we write
$\mathcal{L}^{w}_{n}$
, we write
 \begin{align*}\frac{\mathcal{L}^{w}_{n}- \mathrm{E}[\mathcal{L}_{n}^w]}{\sqrt{\mathrm{Var}(\mathcal{L}_{n}^w)}}&= \frac{\mathcal{L}^{w}_{n}- \mathcal{L}_{n-k+1}^\theta}{\sqrt{\mathrm{Var}(\mathcal{L}_{n}^w)}}+ \frac{\mathcal{L}^{\theta}_{n-k+1}- \mathrm{E}[\mathcal{L}_{n-k+1}^\theta]}{\sqrt{\mathrm{Var}(\mathcal{L}_{n}^w)}} \\[2pt]&\quad + \frac{\mathrm{E}[\mathcal{L}^{\theta}_{n-k+1}]- \mathrm{E}[\mathcal{L}_{n}^w]}{\sqrt{\mathrm{Var}(\mathcal{L}_{n}^w)}}.\end{align*}
\begin{align*}\frac{\mathcal{L}^{w}_{n}- \mathrm{E}[\mathcal{L}_{n}^w]}{\sqrt{\mathrm{Var}(\mathcal{L}_{n}^w)}}&= \frac{\mathcal{L}^{w}_{n}- \mathcal{L}_{n-k+1}^\theta}{\sqrt{\mathrm{Var}(\mathcal{L}_{n}^w)}}+ \frac{\mathcal{L}^{\theta}_{n-k+1}- \mathrm{E}[\mathcal{L}_{n-k+1}^\theta]}{\sqrt{\mathrm{Var}(\mathcal{L}_{n}^w)}} \\[2pt]&\quad + \frac{\mathrm{E}[\mathcal{L}^{\theta}_{n-k+1}]- \mathrm{E}[\mathcal{L}_{n}^w]}{\sqrt{\mathrm{Var}(\mathcal{L}_{n}^w)}}.\end{align*}
Now, by Theorem 1 and our previous result on ![]() $\mathrm{Var}(\mathcal{L}_n^w)$
we have
$\mathrm{Var}(\mathcal{L}_n^w)$
we have
 \begin{equation*}\frac{\mathcal{L}^{\theta}_{n-k+1}- \mathrm{E}[\mathcal{L}_{n-k+1}^\theta]}{\sqrt{\mathrm{Var}(\mathcal{L}_{n-k+1}^\theta)}} \sqrt{\frac{\mathrm{Var}(\mathcal{L}_{n-k+1}^\theta)}{\mathrm{Var}(\mathcal{L}_{n}^w)}} \longrightarrow_{\rm d}\mathcal{G} \quad \text{as } {n \to \infty} ,\end{equation*}
\begin{equation*}\frac{\mathcal{L}^{\theta}_{n-k+1}- \mathrm{E}[\mathcal{L}_{n-k+1}^\theta]}{\sqrt{\mathrm{Var}(\mathcal{L}_{n-k+1}^\theta)}} \sqrt{\frac{\mathrm{Var}(\mathcal{L}_{n-k+1}^\theta)}{\mathrm{Var}(\mathcal{L}_{n}^w)}} \longrightarrow_{\rm d}\mathcal{G} \quad \text{as } {n \to \infty} ,\end{equation*}
and since ![]() $\mathrm{Var}(\mathcal{L}_{n}^w) \longrightarrow \infty$
as
$\mathrm{Var}(\mathcal{L}_{n}^w) \longrightarrow \infty$
as ![]() $n \to \infty$
we have, by (1), that
$n \to \infty$
we have, by (1), that
 \begin{equation*}\left | \frac{\mathcal{L}^{w}_{n}- \mathcal{L}_{n-k+1}^\theta}{\sqrt{\mathrm{Var}(\mathcal{L}_{n}^w)}} + \frac{\mathrm{E}[\mathcal{L}^{\theta}_{n-k+1}]- \mathrm{E}[\mathcal{L}_{n}^w]}{\sqrt{\mathrm{Var}(\mathcal{L}_{n}^w)}} \right | \leq \frac{2k}{\sqrt{\mathrm{Var}(\mathcal{L}_{n}^w)}} \rightarrow 0 \text{ almost surely}.\end{equation*}
\begin{equation*}\left | \frac{\mathcal{L}^{w}_{n}- \mathcal{L}_{n-k+1}^\theta}{\sqrt{\mathrm{Var}(\mathcal{L}_{n}^w)}} + \frac{\mathrm{E}[\mathcal{L}^{\theta}_{n-k+1}]- \mathrm{E}[\mathcal{L}_{n}^w]}{\sqrt{\mathrm{Var}(\mathcal{L}_{n}^w)}} \right | \leq \frac{2k}{\sqrt{\mathrm{Var}(\mathcal{L}_{n}^w)}} \rightarrow 0 \text{ almost surely}.\end{equation*}
Now we can apply Slutsky’s theorem and conclude that
□
Remark 1. It might be possible to get results on the number of leaves of a general WRT ![]() $\mathcal{T}_n^w$
by writing
$\mathcal{T}_n^w$
by writing ![]() $\mathcal{L}_{n}^{w}$
as the sum of
$\mathcal{L}_{n}^{w}$
as the sum of ![]() $\textbf{1}(\ell_i^{w})$
, where
$\textbf{1}(\ell_i^{w})$
, where ![]() $\ell_i^{w}$
denotes the event that node i is a leaf in
$\ell_i^{w}$
denotes the event that node i is a leaf in ![]() $\mathcal{T}_n^w$
. It follows from the construction principle that
$\mathcal{T}_n^w$
. It follows from the construction principle that
 \begin{equation*}\mathrm{P} \left (\ell_i^{w}\right ) = \prod_{j=i+1}^{n} \left ( 1- \frac{w_i}{w_1 + \dots + w_{j-1}} \right ).\end{equation*}
\begin{equation*}\mathrm{P} \left (\ell_i^{w}\right ) = \prod_{j=i+1}^{n} \left ( 1- \frac{w_i}{w_1 + \dots + w_{j-1}} \right ).\end{equation*}
After some manipulation this expression becomes
 \begin{equation*}\mathrm{P} \left (\ell_i^{w}\right ) = \frac{ w_1 + \dots + w_{i-1}}{w_1 + \dots + w_{n-1}} \prod_{j=i+1}^{n-1} \left ( 1 + \frac{w_{j} - w_{i}}{w_1 + \dots + w_{j-1}} \right ).\end{equation*}
\begin{equation*}\mathrm{P} \left (\ell_i^{w}\right ) = \frac{ w_1 + \dots + w_{i-1}}{w_1 + \dots + w_{n-1}} \prod_{j=i+1}^{n-1} \left ( 1 + \frac{w_{j} - w_{i}}{w_1 + \dots + w_{j-1}} \right ).\end{equation*}
An exact expression for the expectation of the number of leaves of a ![]() $\theta^k$
-RT can be obtained by writing
$\theta^k$
-RT can be obtained by writing
and using the expression above. After some computations we get
 \begin{equation*}\mathrm{E}\left [\mathcal{L}_n^{\theta^k} \right ] = \frac{n}{2} + \frac{k(\theta-1)}{2} + \frac{k \theta(1-k\theta)}{2(k (\theta-1) + n-1)}+ \frac{k-1}{2} \prod_{i=1}^{n-1-k} \frac{\theta (k-1)+i}{\theta k +i}.\end{equation*}
\begin{equation*}\mathrm{E}\left [\mathcal{L}_n^{\theta^k} \right ] = \frac{n}{2} + \frac{k(\theta-1)}{2} + \frac{k \theta(1-k\theta)}{2(k (\theta-1) + n-1)}+ \frac{k-1}{2} \prod_{i=1}^{n-1-k} \frac{\theta (k-1)+i}{\theta k +i}.\end{equation*}
Remark 2. For ![]() $\theta^k$
-RTs it is also possible to obtain results about the expectation, variance, and concentration rate of the number of leaves by using a martingale argument similar to the one in [Reference Leckey and Neininger10]; for details, see [Reference Hiesmayr9].
$\theta^k$
-RTs it is also possible to obtain results about the expectation, variance, and concentration rate of the number of leaves by using a martingale argument similar to the one in [Reference Leckey and Neininger10]; for details, see [Reference Hiesmayr9].
3.2. Height
As a second example we discuss the height of a WRT, which is defined as the length of the longest path from the root to a leaf. Let ![]() $\mathcal{H}_n^w$
denote the height of a WRT with weight sequence
$\mathcal{H}_n^w$
denote the height of a WRT with weight sequence ![]() $(w_i)_{i \in \mathbb{N}}$
such that
$(w_i)_{i \in \mathbb{N}}$
such that ![]() $w_i =1$
for
$w_i =1$
for ![]() $i>k$
. Let, moreover,
$i>k$
. Let, moreover, ![]() $\mathcal{D}_{1,i}^w$
and
$\mathcal{D}_{1,i}^w$
and ![]() $\mathcal{D}_{1,i}^\theta$
denote the distance between the root and node i in the reconstructed weighted tree and the original Hoppe tree respectively. For
$\mathcal{D}_{1,i}^\theta$
denote the distance between the root and node i in the reconstructed weighted tree and the original Hoppe tree respectively. For ![]() $i \leq k$
,
$i \leq k$
, ![]() $\mathcal{D}_{1,i}^w$
is at most
$\mathcal{D}_{1,i}^w$
is at most ![]() $k-1$
. Also, for any
$k-1$
. Also, for any ![]() $i>k$
, the path from the root to
$i>k$
, the path from the root to ![]() $i^*$
corresponds to the path from the root to the corresponding node in the original Hoppe tree, i.e. the distance from the root to
$i^*$
corresponds to the path from the root to the corresponding node in the original Hoppe tree, i.e. the distance from the root to ![]() $i-k+1$
, except that we might have an additional path among the first k nodes instead of the first edge. Thus,
$i-k+1$
, except that we might have an additional path among the first k nodes instead of the first edge. Thus, ![]() $\mathcal{D}^w_{1,i}$
is at least as big as
$\mathcal{D}^w_{1,i}$
is at least as big as ![]() $\mathcal{D}_{i-k+1}^\theta$
.
$\mathcal{D}_{i-k+1}^\theta$
.
Also, ![]() $\mathcal{D}^w_{1,i}$
is at most
$\mathcal{D}^w_{1,i}$
is at most ![]() $k-1$
bigger than the distance between the root and the corresponding node in the original tree. Let
$k-1$
bigger than the distance between the root and the corresponding node in the original tree. Let ![]() $j-k+1$
be the first node on the path from node 1 to
$j-k+1$
be the first node on the path from node 1 to ![]() $i-k+1$
in the original tree. Then, in the reconstructed tree
$i-k+1$
in the original tree. Then, in the reconstructed tree ![]() $j^*$
will be attached to some
$j^*$
will be attached to some ![]() $h^*$
, where
$h^*$
, where ![]() $1\leq h \leq k$
. Thus, when we consider the path consisting of the path from the root to
$1\leq h \leq k$
. Thus, when we consider the path consisting of the path from the root to ![]() $h^*$
in the reconstructed tree, the edge from
$h^*$
in the reconstructed tree, the edge from ![]() $h^*$
to
$h^*$
to ![]() $j^*$
and the path from
$j^*$
and the path from ![]() $j-k+1$
to
$j-k+1$
to ![]() $i-k+1$
in the Hoppe tree, we get a path from
$i-k+1$
in the Hoppe tree, we get a path from ![]() $1^*$
to
$1^*$
to ![]() $i^*$
in the reconstructed tree. Thus, for all
$i^*$
in the reconstructed tree. Thus, for all ![]() $k+1 \leq i \leq n$
, there is some
$k+1 \leq i \leq n$
, there is some ![]() $h \leq k$
such that
$h \leq k$
such that
Also, ![]() $\mathcal{D}_{1,h}^w \leq k-1$
, so we have
$\mathcal{D}_{1,h}^w \leq k-1$
, so we have
which implies that
Thus, from the definition of the height as ![]() $\mathcal{H}_n = \max_{i =1, \dots, n} \{\mathcal{D}_{1,i}\},$
we have
$\mathcal{H}_n = \max_{i =1, \dots, n} \{\mathcal{D}_{1,i}\},$
we have
We have the following result about the height of Hoppe trees.
Theorem 3. ([Reference Leckey and Neininger10].) Let ![]() $\mathcal{H}_n^{\theta}$
denote the height of a Hoppe tree with n nodes. Then
$\mathcal{H}_n^{\theta}$
denote the height of a Hoppe tree with n nodes. Then
 \begin{align*}\mathrm{E} [\mathcal{H}_n^{\theta}] &= {\rm e}\ln(n) - \frac{3}{2}\ln \ln n + \mathcal{O}(1) , \\[3pt] \mathrm{Var}(\mathcal{H}_n^{\theta}) &= \mathcal{O}(1).\end{align*}
\begin{align*}\mathrm{E} [\mathcal{H}_n^{\theta}] &= {\rm e}\ln(n) - \frac{3}{2}\ln \ln n + \mathcal{O}(1) , \\[3pt] \mathrm{Var}(\mathcal{H}_n^{\theta}) &= \mathcal{O}(1).\end{align*}
Together with the coupling, this allows us to derive the following theorem.
Theorem 4. Let ![]() $\mathcal{H}^{w}_{n}$
denote the height of a WRT of size n with weight sequence
$\mathcal{H}^{w}_{n}$
denote the height of a WRT of size n with weight sequence ![]() $(w_i)_{i \in \mathbb{N}}$
such that there is a
$(w_i)_{i \in \mathbb{N}}$
such that there is a ![]() $k \in \mathbb{N}$
such that, for all
$k \in \mathbb{N}$
such that, for all ![]() $i>k$
, we have
$i>k$
, we have ![]() $w_i = 1$
. Then
$w_i = 1$
. Then
 \begin{align*}\mathrm{E}\left [\mathcal{H}_n^{w} \right ] &= {\rm e} \ln(n) - \frac{3}{2} \ln \ln (n) + \mathcal{O}(1) , \\[3pt] \mathrm{Var}(\mathcal{H}_n^{w}) &= \mathcal{O}(1).\end{align*}
\begin{align*}\mathrm{E}\left [\mathcal{H}_n^{w} \right ] &= {\rm e} \ln(n) - \frac{3}{2} \ln \ln (n) + \mathcal{O}(1) , \\[3pt] \mathrm{Var}(\mathcal{H}_n^{w}) &= \mathcal{O}(1).\end{align*}
Proof. According to Theorem 3 we have ![]() $\mathrm{E}[\mathcal{H}_{n-k+1}^{\theta}] = {\rm e}\ln(n-k+1) - \frac{3}{2}\ln \ln (n-k\,{+}\,1) + \mathcal{O}(1)$
. Note that
$\mathrm{E}[\mathcal{H}_{n-k+1}^{\theta}] = {\rm e}\ln(n-k+1) - \frac{3}{2}\ln \ln (n-k\,{+}\,1) + \mathcal{O}(1)$
. Note that
 \begin{align*} {\rm e}\ln(n-k+1) - \frac{3}{2}\ln \ln (n-k+1) & = {\rm e}\Big( \ln(n) + \ln\Big(1-\frac{k-1}{n} \Big) \Big) \\& \quad - \frac{3}{2} \bigg( \ln \ln(n) + \ln \Big( 1+ \frac{\ln\big(1-\frac{k-1}{n} \big)}{\ln(n)} \Big) \bigg) \\& = {\rm e} \ln(n) - \frac{3}{2} \ln \ln (n) + o(1).\end{align*}
\begin{align*} {\rm e}\ln(n-k+1) - \frac{3}{2}\ln \ln (n-k+1) & = {\rm e}\Big( \ln(n) + \ln\Big(1-\frac{k-1}{n} \Big) \Big) \\& \quad - \frac{3}{2} \bigg( \ln \ln(n) + \ln \Big( 1+ \frac{\ln\big(1-\frac{k-1}{n} \big)}{\ln(n)} \Big) \bigg) \\& = {\rm e} \ln(n) - \frac{3}{2} \ln \ln (n) + o(1).\end{align*}
Thus, we get, by (2) for ![]() $n>k$
,
$n>k$
,
which implies
As before, we might define ![]() $Y\coloneqq \mathcal{H}_n^{w} - \mathcal{H}_{n-k+1}^\theta$
. Then, by (2), we have
$Y\coloneqq \mathcal{H}_n^{w} - \mathcal{H}_{n-k+1}^\theta$
. Then, by (2), we have ![]() $Y<k$
, so
$Y<k$
, so
 \begin{align*}\mathrm{Var}(\mathcal{H}_n^{w}) &= \mathrm{Var}(\mathcal{H}_{n-k+1}^\theta+Y) \\[3pt] &= \mathrm{Var}(\mathcal{H}_{n-k+1}^\theta) + \mathrm{Var}(Y) + { 2 \mathrm{Cov}(\mathcal{H}_{n-k+1}^\theta, Y) } \\[3pt] &= \mathcal{O}(1).\\[-30pt] \end{align*}
\begin{align*}\mathrm{Var}(\mathcal{H}_n^{w}) &= \mathrm{Var}(\mathcal{H}_{n-k+1}^\theta+Y) \\[3pt] &= \mathrm{Var}(\mathcal{H}_{n-k+1}^\theta) + \mathrm{Var}(Y) + { 2 \mathrm{Cov}(\mathcal{H}_{n-k+1}^\theta, Y) } \\[3pt] &= \mathcal{O}(1).\\[-30pt] \end{align*}
□
4. Largest branch
4.1. Permutations view
In this section we focus on standard Hoppe trees and study the size of the largest branch in this tree model. The results will sharpen the corresponding observations of [Reference Feng, Su and Hu6] for URTs. Before moving on to largest branches, we need to discuss constructions of Hoppe trees via random permutations, in particular permutations that are generated via the Ewens sampling formula.
For each n, the Ewens distribution gives a family of distributions over the vectors
with ![]() $\sum_{i=1}^n i C_i^{(n)} = n$
. In particular, for given
$\sum_{i=1}^n i C_i^{(n)} = n$
. In particular, for given ![]() $\theta > 0$
, the Ewens distribution
$\theta > 0$
, the Ewens distribution ![]() ${\rm EW}(\theta)$
is defined with the probabilities
${\rm EW}(\theta)$
is defined with the probabilities
 \begin{equation*}\mathrm{P}_{\theta} (C^{(n)} = (c_1,\ldots,c_n))= \textbf{1}\left(\sum_{j=1}^n j c_j = n \right) \frac{n!}{\theta_{(n)}} \prod_{j=1}^n \left( \frac{\theta}{j} \right)^{c_j} \frac{1}{c_j!}, \qquad c_1,\ldots,c_n \in \mathbb{N},\end{equation*}
\begin{equation*}\mathrm{P}_{\theta} (C^{(n)} = (c_1,\ldots,c_n))= \textbf{1}\left(\sum_{j=1}^n j c_j = n \right) \frac{n!}{\theta_{(n)}} \prod_{j=1}^n \left( \frac{\theta}{j} \right)^{c_j} \frac{1}{c_j!}, \qquad c_1,\ldots,c_n \in \mathbb{N},\end{equation*}
where ![]() $\theta_{(n)} = \theta(\theta + 1) \cdots (\theta + n - 1)$
.
$\theta_{(n)} = \theta(\theta + 1) \cdots (\theta + n - 1)$
.
Below we call a permutation whose cycle structure results from ![]() ${\rm EW}(\theta)$
a Hoppe permutation. In this setting,
${\rm EW}(\theta)$
a Hoppe permutation. In this setting, ![]() $c_i$
stands for the number of cycles in the permutation of size i. In order to relate the topic to Hoppe trees, we need to discuss a recursive construction of Hoppe permutations. The discussion here is similar to the one in [Reference Altok and Işlak1]. For convenience, the permutation will be constructed on the label set
$c_i$
stands for the number of cycles in the permutation of size i. In order to relate the topic to Hoppe trees, we need to discuss a recursive construction of Hoppe permutations. The discussion here is similar to the one in [Reference Altok and Işlak1]. For convenience, the permutation will be constructed on the label set ![]() $\{2,3,\ldots,n\}$
. We first begin with the permutation (2) with only one cycle. Then 3 either joins the first cycle to the right of 2 with probability
$\{2,3,\ldots,n\}$
. We first begin with the permutation (2) with only one cycle. Then 3 either joins the first cycle to the right of 2 with probability ![]() $\frac{1}{\theta + 1}$
, or starts the second cycle with probability
$\frac{1}{\theta + 1}$
, or starts the second cycle with probability ![]() $\frac{\theta}{\theta + 1}$
. Once we have constructed a permutation on
$\frac{\theta}{\theta + 1}$
. Once we have constructed a permutation on ![]() $\{2,3,\ldots,k-1\}$
, k either starts a new cycle with probability
$\{2,3,\ldots,k-1\}$
, k either starts a new cycle with probability ![]() $\frac{\theta}{\theta +k - 2}$
, or is inserted to the right of a randomly chosen integer already assigned to a cycle. The resulting permutation then has the cycle structure from the distribution
$\frac{\theta}{\theta +k - 2}$
, or is inserted to the right of a randomly chosen integer already assigned to a cycle. The resulting permutation then has the cycle structure from the distribution ![]() ${\rm EW}(\theta)$
[Reference Arratia, Barbour and Tavaré2].
${\rm EW}(\theta)$
[Reference Arratia, Barbour and Tavaré2].
Next, we construct a Hoppe tree based on the permutation construction of the previous paragraph. Begin with node 1 as the root and node 2 attached to it. Then, if node 3 begins a new cycle in the corresponding Hoppe permutation, attach it to node 1, and otherwise attach it to node 2. Then, for node ![]() $k \geq 4$
, if k starts a new cycle in the Hoppe permutation, attach node k to node 1, and otherwise attach it to node j where k was inserted to the right of j in the corresponding permutation.
$k \geq 4$
, if k starts a new cycle in the Hoppe permutation, attach node k to node 1, and otherwise attach it to node j where k was inserted to the right of j in the corresponding permutation.
It is then clear that this gives a bijection between Hoppe permutations and Hoppe trees. In particular, the cycles in a Hoppe permutation are in a one-to-one relation with the branches in the corresponding tree. This reduces the study of the size of the largest branch in a Hoppe tree to the study of the largest cycle in its permutation correspondence.
4.2. Size of the largest branch
For a given tree ![]() $\mathcal{T}$
on n vertices, the number of branches is the number of children of the root, i.e. all nodes that are attached to the root. If a node i is attached to the root, then node i with its descendants is said to form a branch of the tree. Let
$\mathcal{T}$
on n vertices, the number of branches is the number of children of the root, i.e. all nodes that are attached to the root. If a node i is attached to the root, then node i with its descendants is said to form a branch of the tree. Let ![]() $\mathcal{B}_{n,i}(\mathcal{T})$
be the number of branches of size i in
$\mathcal{B}_{n,i}(\mathcal{T})$
be the number of branches of size i in ![]() $\mathcal{T}$
. Also define
$\mathcal{T}$
. Also define
to be the number of nodes in the largest branch of a given tree, ![]() $\mathcal{T}$
. In [Reference Feng, Su and Hu6], it was shown that
$\mathcal{T}$
. In [Reference Feng, Su and Hu6], it was shown that
when ![]() $\mathcal{T}_n$
is a URT on n vertices. The first purpose of this section and the next theorem is to extend the result of [Reference Feng, Su and Hu6] to Hoppe trees, and to provide more details about the asymptotic distribution, via exploiting the relation between Hoppe trees and Hoppe permutations. Further, the result in (3) is now extended to an explicit expression for
$\mathcal{T}_n$
is a URT on n vertices. The first purpose of this section and the next theorem is to extend the result of [Reference Feng, Su and Hu6] to Hoppe trees, and to provide more details about the asymptotic distribution, via exploiting the relation between Hoppe trees and Hoppe permutations. Further, the result in (3) is now extended to an explicit expression for ![]() $\lim_{n \rightarrow \infty} \mathrm{P} \left(\nu_n(\mathcal{T}_n) \geq cn \right)$
for
$\lim_{n \rightarrow \infty} \mathrm{P} \left(\nu_n(\mathcal{T}_n) \geq cn \right)$
for ![]() $c \in [1/2,1]$
. Once we have the results for the Hoppe tree case, the coupling construction of Section 2 will also generalize these results to WRTs.
$c \in [1/2,1]$
. Once we have the results for the Hoppe tree case, the coupling construction of Section 2 will also generalize these results to WRTs.
(i) Let
 $\mathcal{T}_n^{\theta}$
be a Hoppe tree. Then
$\mathcal{T}_n^{\theta}$
be a Hoppe tree. Then  $\frac{\nu_n (\mathcal{T}_n^{\theta})}{n}$
converges weakly to a random variable
$\frac{\nu_n (\mathcal{T}_n^{\theta})}{n}$
converges weakly to a random variable  $\nu$
with Poisson–Dirichlet distribution, whose cumulative distribution function is given by
where
$\nu$
with Poisson–Dirichlet distribution, whose cumulative distribution function is given by
where \begin{equation*}F_{\theta}(x) = 1 + \sum_{k=1}^{\infty} \frac{(- \theta)^k}{k!} \int \cdots \int_{\mathcal{S}_k(x)} \frac{\left(1 - \sum_{j=1}^k y_j \right)^{\theta - 1}}{y_1 \cdots y_k} \, {\rm d} y_1 \cdots {\rm d} y_k, \quad x > 0,\end{equation*}
\begin{equation*}F_{\theta}(x) = 1 + \sum_{k=1}^{\infty} \frac{(- \theta)^k}{k!} \int \cdots \int_{\mathcal{S}_k(x)} \frac{\left(1 - \sum_{j=1}^k y_j \right)^{\theta - 1}}{y_1 \cdots y_k} \, {\rm d} y_1 \cdots {\rm d} y_k, \quad x > 0,\end{equation*}
 $\gamma$
is Euler’s constant [Reference Finch7] and
$\gamma$
is Euler’s constant [Reference Finch7] and
 \begin{equation*}\mathcal{S}_k(x)= \bigg\{y_1 >x, \ldots, y_k > x , \sum_{j=1}^k y_j
< 1\bigg\}.\end{equation*}
\begin{equation*}\mathcal{S}_k(x)= \bigg\{y_1 >x, \ldots, y_k > x , \sum_{j=1}^k y_j
< 1\bigg\}.\end{equation*}
(ii) When
 $\theta = 1$
, for any
$\theta = 1$
, for any  $c \ in [\frac{1}{2}, 1]$
we have
In particular,
$c \ in [\frac{1}{2}, 1]$
we have
In particular, \begin{equation*}\lim_{n \rightarrow \infty} \mathrm{P}(\nu_n(\mathcal{T}_n) \leq c n) = 1 - \ln (c^{-1}).\end{equation*}
\begin{equation*}\lim_{n \rightarrow \infty} \mathrm{P}(\nu_n(\mathcal{T}_n) \leq c n) = 1 - \ln (c^{-1}).\end{equation*}
 \begin{equation*}\mathrm{E}[\nu] \geq \frac{1}{2}.\end{equation*}
\begin{equation*}\mathrm{E}[\nu] \geq \frac{1}{2}.\end{equation*}
Proof.
(i) First, we translate the problem into the random permutation setting. We have
where \begin{equation*}\nu_n(\mathcal{T}_n^{\theta}) =_{\rm d} \max\{i \in [n-1] \,{:}\, C_{n-1,i}(\theta) \geq 1\}\eqqcolon \alpha_n(\theta),\end{equation*}
\begin{equation*}\nu_n(\mathcal{T}_n^{\theta}) =_{\rm d} \max\{i \in [n-1] \,{:}\, C_{n-1,i}(\theta) \geq 1\}\eqqcolon \alpha_n(\theta),\end{equation*}
 $C_{n-1,i}(\theta)$
is the number of cycles of length i in a
$C_{n-1,i}(\theta)$
is the number of cycles of length i in a  $\theta$
-biased Hoppe permutation. In this setting, Lemma 5.7 in [Reference Arratia, Barbour and Tavaré2] shows that
$\theta$
-biased Hoppe permutation. In this setting, Lemma 5.7 in [Reference Arratia, Barbour and Tavaré2] shows that  $\frac{\alpha_n(\theta)}{n}$
converges in distribution to a random variable
$\frac{\alpha_n(\theta)}{n}$
converges in distribution to a random variable  $\alpha$
with cumulative distribution function
where
$\alpha$
with cumulative distribution function
where \begin{equation*}F_{\theta}(x) = 1 + \sum_{k=1}^{\infty} \frac{(- \theta)^k}{k!} \int \cdots \int_{\mathcal{S}_k(x)} \frac{\left(1 - \sum_{j=1}^k y_j \right)^{\theta - 1}}{y_1 \cdots y_k} \, {\rm d} y_1 \cdots {\rm d} y_k, \quad x > 0,\end{equation*}
\begin{equation*}F_{\theta}(x) = 1 + \sum_{k=1}^{\infty} \frac{(- \theta)^k}{k!} \int \cdots \int_{\mathcal{S}_k(x)} \frac{\left(1 - \sum_{j=1}^k y_j \right)^{\theta - 1}}{y_1 \cdots y_k} \, {\rm d} y_1 \cdots {\rm d} y_k, \quad x > 0,\end{equation*}
 $\gamma$
is Euler’s constant [Reference Finch7] and
This proves the first part.
$\gamma$
is Euler’s constant [Reference Finch7] and
This proves the first part. \begin{equation*}\mathcal{S}_k(x)= \bigg\{y_1 >x, \ldots, y_k > x , \sum_{j=1}^k y_j
< 1\bigg\}.\end{equation*}
\begin{equation*}\mathcal{S}_k(x)= \bigg\{y_1 >x, \ldots, y_k > x , \sum_{j=1}^k y_j
< 1\bigg\}.\end{equation*}
(ii) Setting
 $\theta =1$
in the argument of (i), and recalling that the random permutation in this case reduces to a uniformly random permutation, yields that
$\theta =1$
in the argument of (i), and recalling that the random permutation in this case reduces to a uniformly random permutation, yields that  $\frac{\nu_n(\mathcal{T}_n)}{n}$
converges weakly to a random variable
$\frac{\nu_n(\mathcal{T}_n)}{n}$
converges weakly to a random variable  $\nu$
whose cumulative distribution function is given by
where
$\nu$
whose cumulative distribution function is given by
where \begin{equation*}F_1(x) =\begin{cases}0, & \text{if } x<0 , \\[3pt]1 + \sum_{k=1}^{\infty} \frac{(-1)^k}{k!} \int \cdots \int_{\mathcal{S}_k(x)} \frac{{\rm d} y_1\ldots {\rm d} y_k}{y_1\ldots y_k}, & \text{if } x \in [0,1] , \\[3pt]1, & \text{if } x >1,\end{cases}\end{equation*}
\begin{equation*}F_1(x) =\begin{cases}0, & \text{if } x<0 , \\[3pt]1 + \sum_{k=1}^{\infty} \frac{(-1)^k}{k!} \int \cdots \int_{\mathcal{S}_k(x)} \frac{{\rm d} y_1\ldots {\rm d} y_k}{y_1\ldots y_k}, & \text{if } x \in [0,1] , \\[3pt]1, & \text{if } x >1,\end{cases}\end{equation*}
 $\mathcal{S}_k(x)$
is as before.
$\mathcal{S}_k(x)$
is as before.
Note that if ![]() $x \geq \frac{1}{2}$
,
$x \geq \frac{1}{2}$
, ![]() $\mathcal{S}_k(x)= \emptyset$
for any
$\mathcal{S}_k(x)= \emptyset$
for any ![]() $k \geq 2$
. Thus the expression simplifies for
$k \geq 2$
. Thus the expression simplifies for ![]() $\frac{1}{2} \leq x \leq 1$
to
$\frac{1}{2} \leq x \leq 1$
to
This in particular implies that the derivative of ![]() $F_1(x)$
over
$F_1(x)$
over ![]() $[1/2, 1]$
simplifies to
$[1/2, 1]$
simplifies to
Hence, for any ![]() $c \in [\frac{1}{2}, 1]$
,
$c \in [\frac{1}{2}, 1]$
,
Finally, we have
Remark 3. The value ![]() $\lim_{n \rightarrow \infty} \mathrm{E}\left[\frac{\nu_n(\mathcal{T}_n)}{n}\right]$
when
$\lim_{n \rightarrow \infty} \mathrm{E}\left[\frac{\nu_n(\mathcal{T}_n)}{n}\right]$
when ![]() $\mathcal{T}_n$
is a URT is known to be the Golomb–Dickman constant in the literature. Its exact value is known to be
$\mathcal{T}_n$
is a URT is known to be the Golomb–Dickman constant in the literature. Its exact value is known to be ![]() $0.62432998854\ldots$
$0.62432998854\ldots$
Now, let ![]() $\mathcal{T}_n^{w}$
be a WRT of size n with weight sequence
$\mathcal{T}_n^{w}$
be a WRT of size n with weight sequence ![]() $(w_i)_{i \in \mathbb{N}}$
such that there is a
$(w_i)_{i \in \mathbb{N}}$
such that there is a ![]() $k \in \mathbb{N}$
such that, for all
$k \in \mathbb{N}$
such that, for all ![]() $i>k$
, we have
$i>k$
, we have ![]() $w_i = 1$
. Since we can find a coupling of a Hoppe tree to a WRT in which the number of nodes in the largest branch differs at most by k, the following now follows immediately.
$w_i = 1$
. Since we can find a coupling of a Hoppe tree to a WRT in which the number of nodes in the largest branch differs at most by k, the following now follows immediately.
Theorem 6. Let ![]() $\mathcal{T}^{w}_{n}$
be a WRT of size n with weight sequence
$\mathcal{T}^{w}_{n}$
be a WRT of size n with weight sequence ![]() $(w_i)_{i \in \mathbb{N}}$
such that there is a
$(w_i)_{i \in \mathbb{N}}$
such that there is a ![]() $k \in \mathbb{N}$
such that, for all
$k \in \mathbb{N}$
such that, for all ![]() $i>k$
, we have
$i>k$
, we have ![]() $w_i = 1$
. Then, for any
$w_i = 1$
. Then, for any ![]() $c \ in \big[\frac{1}{2}, 1\big]$
, we have
$c \ in \big[\frac{1}{2}, 1\big]$
, we have
5. Depth of node n
The depth of node n is defined as the length of the path from the root to n. We call all the nodes on the single path from the root to n ancestors of n, so the depth of n is also equal to the number of ancestors of n. Note that in this and the next section we have no restrictions on the weight sequence ![]() $(w_i)_{i\in \mathbb{N}}$
.
$(w_i)_{i\in \mathbb{N}}$
.
Theorem 7. Let ![]() $\mathcal{D}_n^{w}$
denote the depth of node n in a WRT
$\mathcal{D}_n^{w}$
denote the depth of node n in a WRT ![]() $\mathcal{T}_n^{w}$
, and let
$\mathcal{T}_n^{w}$
, and let ![]() $Z_n^w$
denote the set of ancestors of n. Define
$Z_n^w$
denote the set of ancestors of n. Define ![]() $A_{i,n}^w \coloneqq \textbf{1}(i \in Z_n^w)$
. Then
$A_{i,n}^w \coloneqq \textbf{1}(i \in Z_n^w)$
. Then
 \begin{equation*}\mathcal{D}_n^w = 1 + \sum_{i=2}^{n-1} A_{i,n}^w.\end{equation*}
\begin{equation*}\mathcal{D}_n^w = 1 + \sum_{i=2}^{n-1} A_{i,n}^w.\end{equation*}
The ![]() $A_{i,n}^w$
are mutually independent Bernoulli random variables with
$A_{i,n}^w$
are mutually independent Bernoulli random variables with
This directly yields the expectation and the variance:
 \begin{align*}\mathrm{E}[\mathcal{D}_n^w] & = \sum_{i=1}^{n-1} \frac{w_i}{\sum_{j=1}^{i}w_j} , \\[3pt]\mathrm{Var}(\mathcal{D}_n^w) & = \sum_{i=2}^{n-1} \frac{w_i}{\sum_{j=1}^{i}w_j} \left (1 - \frac {w_i}{\sum_{j=1}^{i}w_j} \right ).\end{align*}
\begin{align*}\mathrm{E}[\mathcal{D}_n^w] & = \sum_{i=1}^{n-1} \frac{w_i}{\sum_{j=1}^{i}w_j} , \\[3pt]\mathrm{Var}(\mathcal{D}_n^w) & = \sum_{i=2}^{n-1} \frac{w_i}{\sum_{j=1}^{i}w_j} \left (1 - \frac {w_i}{\sum_{j=1}^{i}w_j} \right ).\end{align*}
Proof. Each claim will follow easily once we show that ![]() $\mathcal{D}_n^w$
can be written as a sum of independent Bernoulli random variables. For this purpose, we first observe that in a given rooted tree the depth of a node is equal to its number of ancestors, since these determine the path from the root to the node. Using that node 1 is definitely an ancestor of n, in the notation of the theorem we thus get
$\mathcal{D}_n^w$
can be written as a sum of independent Bernoulli random variables. For this purpose, we first observe that in a given rooted tree the depth of a node is equal to its number of ancestors, since these determine the path from the root to the node. Using that node 1 is definitely an ancestor of n, in the notation of the theorem we thus get
 \begin{equation*}\mathcal{D}_n^w = 1 + \sum_{i=2}^{n-1} A_{i,n}^w.\end{equation*}
\begin{equation*}\mathcal{D}_n^w = 1 + \sum_{i=2}^{n-1} A_{i,n}^w.\end{equation*}
We will first find the distribution law of the ![]() $A_{i,n}^w$
and then show mutual independence. For the distribution law we will use the method used in [Reference Feng, Su and Hu6]: we first find the values for
$A_{i,n}^w$
and then show mutual independence. For the distribution law we will use the method used in [Reference Feng, Su and Hu6]: we first find the values for ![]() $n-1$
and
$n-1$
and ![]() $n-2$
and then proceed by induction.
$n-2$
and then proceed by induction.
Node ![]() $n-1$
can only be an ancestor of n if it is the parent of n, so we get
$n-1$
can only be an ancestor of n if it is the parent of n, so we get
Similarly, ![]() $n-2$
can only be an ancestor of n if it is the parent of n or it is the grandparent of n, in which case
$n-2$
can only be an ancestor of n if it is the parent of n or it is the grandparent of n, in which case ![]() $n-2$
needs to be the parent of
$n-2$
needs to be the parent of ![]() $n-1$
, which needs to be the parent of n. This gives
$n-1$
, which needs to be the parent of n. This gives
 \begin{equation*}\begin{split}\mathrm{P}({ A_{n-2,n}^w = 1}) = \underbrace{\frac{w_{n-2}}{\sum_{i=1}^{n-1} w_i}}_{n-2 \text{ is parent of } n} + \underbrace{\frac{w_{n-2}}{\sum_{i=1}^{n-2} w_i}\frac{w_{n-1}}{\sum_{i=1}^{n-1} w_i}}_{n-2 \text{ is grandparent of } n}= \frac{w_{n-2}}{\sum_{i=1}^{n-2} w_i}.\end{split}\end{equation*}
\begin{equation*}\begin{split}\mathrm{P}({ A_{n-2,n}^w = 1}) = \underbrace{\frac{w_{n-2}}{\sum_{i=1}^{n-1} w_i}}_{n-2 \text{ is parent of } n} + \underbrace{\frac{w_{n-2}}{\sum_{i=1}^{n-2} w_i}\frac{w_{n-1}}{\sum_{i=1}^{n-1} w_i}}_{n-2 \text{ is grandparent of } n}= \frac{w_{n-2}}{\sum_{i=1}^{n-2} w_i}.\end{split}\end{equation*}
We will now show by induction that, for all ![]() $j = 2, \dots, n-1$
,
$j = 2, \dots, n-1$
,
Let the above be true for all ![]() $j \geq i+1$
, and let
$j \geq i+1$
, and let ![]() $C_{i,j}^w$
denote the event that j is a child of i. Then
$C_{i,j}^w$
denote the event that j is a child of i. Then
 \begin{equation*}\mathrm{P}( { A_{i,n}^w = 1}) = \sum_{j = i+1}^{n-1} { \mathrm{P}(A_{j,n}^w = 1}, C_{i,j}^w) + \mathrm{P}(C_{i,n}^w).\end{equation*}
\begin{equation*}\mathrm{P}( { A_{i,n}^w = 1}) = \sum_{j = i+1}^{n-1} { \mathrm{P}(A_{j,n}^w = 1}, C_{i,j}^w) + \mathrm{P}(C_{i,n}^w).\end{equation*}
Since ![]() $C_{i,j}^w$
only relates to the jth step of the construction process and
$C_{i,j}^w$
only relates to the jth step of the construction process and ![]() $A_{j,n}^w$
only depends on the (
$A_{j,n}^w$
only depends on the (![]() $j+1$
)th,…, nth steps, these two events are independent. Thus,
$j+1$
)th,…, nth steps, these two events are independent. Thus,
 \begin{align*}\mathrm{P}({ A_{i,n}^w=1}) &= \sum_{j = i+1}^{n-1} \mathrm{P}( { A_{j,n}^w=1})\mathrm{P}(C_{i,j}^w)+\mathrm{P}(C_{i,n}^w) \\[3pt] &= \sum_{j = i+1}^{n-1} \left (\frac{w_j}{\sum_{k=1}^{j}w_k} \frac{w_i}{\sum_{k=1}^{j-1}w_k} \right )+ \frac{w_i}{\sum_{j=1}^{n-1}w_{j}}.\end{align*}
\begin{align*}\mathrm{P}({ A_{i,n}^w=1}) &= \sum_{j = i+1}^{n-1} \mathrm{P}( { A_{j,n}^w=1})\mathrm{P}(C_{i,j}^w)+\mathrm{P}(C_{i,n}^w) \\[3pt] &= \sum_{j = i+1}^{n-1} \left (\frac{w_j}{\sum_{k=1}^{j}w_k} \frac{w_i}{\sum_{k=1}^{j-1}w_k} \right )+ \frac{w_i}{\sum_{j=1}^{n-1}w_{j}}.\end{align*}
To simplify this expression we first note that we can factor out ![]() $w_i$
and, by some elementary operations, get:
$w_i$
and, by some elementary operations, get:
In general, the following holds for ![]() $l \in \mathbb{N}$
:
$l \in \mathbb{N}$
:
By using this equality ![]() $n-i-2$
times, we thus get
$n-i-2$
times, we thus get
 \begin{equation*}\begin{split}\mathrm{P}( { A_{i,n}^w = 1}) &= w_i \left ( \frac{w_{i+1} + \cdots + w_{n-1}}{\sum_{k=1}^{i}w_k \sum_{k=1}^{n-1}w_k} + \frac{1}{\sum_{k=1}^{n-1}w_k} \right ) = \frac{w_i}{\sum_{k=1}^{i} w_k}.\end{split}\end{equation*}
\begin{equation*}\begin{split}\mathrm{P}( { A_{i,n}^w = 1}) &= w_i \left ( \frac{w_{i+1} + \cdots + w_{n-1}}{\sum_{k=1}^{i}w_k \sum_{k=1}^{n-1}w_k} + \frac{1}{\sum_{k=1}^{n-1}w_k} \right ) = \frac{w_i}{\sum_{k=1}^{i} w_k}.\end{split}\end{equation*}
Now we will show that the random variables ![]() $A_{i,n}^w$
are mutually independent for
$A_{i,n}^w$
are mutually independent for ![]() $j = 2, \dots,\break n-1$
. For this we will use the method used in [Reference Leckey and Neininger10]: for any
$j = 2, \dots,\break n-1$
. For this we will use the method used in [Reference Leckey and Neininger10]: for any ![]() $2 \leq k \leq n-2$
and
$2 \leq k \leq n-2$
and ![]() $2 \leq j_k < \dots < j_2 < j_1 \leq n-1$
, consider the event that all the
$2 \leq j_k < \dots < j_2 < j_1 \leq n-1$
, consider the event that all the ![]() $j_i$
and only the
$j_i$
and only the ![]() $j_i$
are ancestors of n. We will denote this event by E. Then
$j_i$
are ancestors of n. We will denote this event by E. Then
By the structure of the recursive tree, to realize this event, n must be a child of ![]() $j_1$
,
$j_1$
, ![]() $j_1$
a child of
$j_1$
a child of ![]() $j_2$
,…,
$j_2$
,…,![]() $\,j_{k-1}$
a child of
$\,j_{k-1}$
a child of ![]() $j_k$
, and
$j_k$
, and ![]() $j_k$
a child of 1. In general, for
$j_k$
a child of 1. In general, for ![]() $i=1, \dots, k-1$
,
$i=1, \dots, k-1$
, ![]() $j_i$
must be a child of
$j_i$
must be a child of ![]() $j_{i+1}$
. It does not matter to which nodes
$j_{i+1}$
. It does not matter to which nodes ![]() $j \neq j_i$
attach. Hence, by the attachment probabilities we get
$j \neq j_i$
attach. Hence, by the attachment probabilities we get
 \begin{align*}\mathrm{P}(E) & = \mathrm{P}({ A_{j_i,n}^w=1}, { A_{j,n}^w=0}, \text{ for } j \neq j_i, i=1, \dots, k) \\[2pt] &= \underbrace{\frac{w_{j_1}}{\sum_{\ell=1}^{n-1} w_{\ell}}}_{n \text{ child of } j_1} \prod_{i=1}^{k-1} \underbrace{\frac{w_{j_{i+1}}}{\sum_{\ell=1}^{j_i-1}w_{\ell}}}_{j_i \text{ child of } j_{i+1}} \underbrace{\frac{w_1}{\sum_{\ell=1}^{j_k-1}w_{\ell}}}_{j_k \text{ child of } 1} \\[2pt] &= w_1 w_{j_1} \cdots w_{j_k} \prod_{i=1}^{n-1} \frac{1}{\sum_{\ell=1}^{i}w_{\ell}} \prod_{\substack{1<j<n \\[2pt] j \neq j_i, i=1, \dots, k}} \bigg(\sum_{\ell=1}^{j-1}w_{\ell} \bigg ) \\[2pt] & = \prod_{i=1}^{k}\frac{w_{j_i}}{\sum_{\ell=1}^{j_i}w_{\ell}} \prod_{\substack{1<j<n \\[2pt] j \neq j_i, i=1, \dots, k}} \bigg( \frac{\sum_{\ell=1}^{j-1}w_{\ell}}{\sum_{\ell=1}^{j}w_{\ell}}\bigg) \frac{w_1}{\sum_{\ell=1}^{1}{w_{\ell}}} \\[2pt] &= \prod_{i=1}^{k}\frac{w_{j_i}}{\sum_{\ell=1}^{j_i}w_{\ell}} \prod_{\substack{1<j<n \\[2pt] j \neq j_i, i=1, \dots, k}} \bigg( 1 - \frac{w_j}{\sum_{\ell=1}^{j}w_{\ell}}\bigg) \\[2pt] &= \prod_{i=1}^{k} \mathrm{P}({ A_{j_i,n}^w = 1}) \prod_{\substack{1<j<n \\[2pt] j \neq j_i, i=1, \dots, k}} \mathrm{P}({ A_{j,n}^w=0}).\end{align*}
\begin{align*}\mathrm{P}(E) & = \mathrm{P}({ A_{j_i,n}^w=1}, { A_{j,n}^w=0}, \text{ for } j \neq j_i, i=1, \dots, k) \\[2pt] &= \underbrace{\frac{w_{j_1}}{\sum_{\ell=1}^{n-1} w_{\ell}}}_{n \text{ child of } j_1} \prod_{i=1}^{k-1} \underbrace{\frac{w_{j_{i+1}}}{\sum_{\ell=1}^{j_i-1}w_{\ell}}}_{j_i \text{ child of } j_{i+1}} \underbrace{\frac{w_1}{\sum_{\ell=1}^{j_k-1}w_{\ell}}}_{j_k \text{ child of } 1} \\[2pt] &= w_1 w_{j_1} \cdots w_{j_k} \prod_{i=1}^{n-1} \frac{1}{\sum_{\ell=1}^{i}w_{\ell}} \prod_{\substack{1<j<n \\[2pt] j \neq j_i, i=1, \dots, k}} \bigg(\sum_{\ell=1}^{j-1}w_{\ell} \bigg ) \\[2pt] & = \prod_{i=1}^{k}\frac{w_{j_i}}{\sum_{\ell=1}^{j_i}w_{\ell}} \prod_{\substack{1<j<n \\[2pt] j \neq j_i, i=1, \dots, k}} \bigg( \frac{\sum_{\ell=1}^{j-1}w_{\ell}}{\sum_{\ell=1}^{j}w_{\ell}}\bigg) \frac{w_1}{\sum_{\ell=1}^{1}{w_{\ell}}} \\[2pt] &= \prod_{i=1}^{k}\frac{w_{j_i}}{\sum_{\ell=1}^{j_i}w_{\ell}} \prod_{\substack{1<j<n \\[2pt] j \neq j_i, i=1, \dots, k}} \bigg( 1 - \frac{w_j}{\sum_{\ell=1}^{j}w_{\ell}}\bigg) \\[2pt] &= \prod_{i=1}^{k} \mathrm{P}({ A_{j_i,n}^w = 1}) \prod_{\substack{1<j<n \\[2pt] j \neq j_i, i=1, \dots, k}} \mathrm{P}({ A_{j,n}^w=0}).\end{align*}
This implies that the random variables ![]() $A_{i,n}^w$
are mutually independent Bernoulli random variables. Expectation and variance formulas for
$A_{i,n}^w$
are mutually independent Bernoulli random variables. Expectation and variance formulas for ![]() $\mathcal{D}_{n}^w$
follow from this observation right away. □
$\mathcal{D}_{n}^w$
follow from this observation right away. □
The following central limit theorem now follows.
Theorem 8. If ![]() $\mathrm{E}[\mathcal{D}_n^w ] \rightarrow \infty$
and
$\mathrm{E}[\mathcal{D}_n^w ] \rightarrow \infty$
and ![]() $\limsup_{n \to \infty} \frac{w_n}{\sum_{i=1}^{n} w_i} < 1$
, then we have
$\limsup_{n \to \infty} \frac{w_n}{\sum_{i=1}^{n} w_i} < 1$
, then we have
Proof. By Lyapunov’s central limit theorem for sums of independent Bernoulli random variables, if ![]() $\mathrm{Var}({D}_n^w) \to \infty$
then we have
$\mathrm{Var}({D}_n^w) \to \infty$
then we have ![]() $\frac{\mathcal{D}_n^w - \mathrm{E}[\mathcal{D}_n^w ]}{\sqrt{\mathrm{Var}(\mathcal{D}_n^w )}} \longrightarrow_{\rm d} \mathcal{G}$
as
$\frac{\mathcal{D}_n^w - \mathrm{E}[\mathcal{D}_n^w ]}{\sqrt{\mathrm{Var}(\mathcal{D}_n^w )}} \longrightarrow_{\rm d} \mathcal{G}$
as ![]() $n \rightarrow \infty$
. Now let
$n \rightarrow \infty$
. Now let ![]() $p_n = \frac{w_n}{\sum_{j=1}^{n} w_j}$
. Since
$p_n = \frac{w_n}{\sum_{j=1}^{n} w_j}$
. Since ![]() $\limsup_{n \to \infty} p_n <1$
, there is a
$\limsup_{n \to \infty} p_n <1$
, there is a ![]() $0<\varepsilon<1$
and an
$0<\varepsilon<1$
and an ![]() $N \in \mathbb{N}$
such that, for all
$N \in \mathbb{N}$
such that, for all ![]() $n >N$
,
$n >N$
, ![]() $ 1- p_n > \varepsilon$
. Then,
$ 1- p_n > \varepsilon$
. Then,
 \begin{equation*}\mathrm{Var}({D}_n^w) = \sum_{i=1}^{n} p_i(1-p_i) = \sum_{i=1}^{N} p_i(1-p_i) + \sum_{i=N+1}^{n} p_i(1-p_i) > \varepsilon \sum_{i=N+1}^{n} p_i. \end{equation*}
\begin{equation*}\mathrm{Var}({D}_n^w) = \sum_{i=1}^{n} p_i(1-p_i) = \sum_{i=1}^{N} p_i(1-p_i) + \sum_{i=N+1}^{n} p_i(1-p_i) > \varepsilon \sum_{i=N+1}^{n} p_i. \end{equation*}
Since we know that ![]() $\mathrm{E}[\mathcal{D}_n^w ] = \sum_{i=1}^{n} p_i \rightarrow \infty$
as
$\mathrm{E}[\mathcal{D}_n^w ] = \sum_{i=1}^{n} p_i \rightarrow \infty$
as ![]() $n \to \infty$
, this implies that
$n \to \infty$
, this implies that ![]() $\mathrm{Var}(\mathcal{D}_n^w) \to \infty$
as
$\mathrm{Var}(\mathcal{D}_n^w) \to \infty$
as ![]() $n \to \infty$
.□
$n \to \infty$
.□
(i) If the weights are limited from below and above, the expectation and variance of the depth of node n will still be equal to
 $\mathcal{O}(\ln(n))$
asymptotically.
$\mathcal{O}(\ln(n))$
asymptotically.(ii) For the Hoppe tree, we write
 $\mathcal{D}_n^\theta$
for the depth of node n and have
Notice that the depth in a URT and a Hoppe tree are asymptotically equivalent. The same conclusion also holds for a wide range of statistics whose dependence on the root is small and vanishes asymptotically. This makes the asymptotic study of Hoppe trees slightly uninteresting. Another such example is the number of leaves in a Hoppe tree, which was studied earlier.
$\mathcal{D}_n^\theta$
for the depth of node n and have
Notice that the depth in a URT and a Hoppe tree are asymptotically equivalent. The same conclusion also holds for a wide range of statistics whose dependence on the root is small and vanishes asymptotically. This makes the asymptotic study of Hoppe trees slightly uninteresting. Another such example is the number of leaves in a Hoppe tree, which was studied earlier. \begin{align*}\mathrm{E}[\mathcal{D}_n^\theta] & = 1+ \sum_{i=1}^{n-2} \frac{1}{{ \theta+i}} = \log(n) + \mathcal{O}(1) , \\[3pt] \mathrm{Var} \left (\mathcal{D}_n^\theta \right ) & = \sum_{i=1}^{n-2} \frac{\theta+i-1}{(\theta+i)^2} = \log(n) + \mathcal{O}(1).\end{align*}
\begin{align*}\mathrm{E}[\mathcal{D}_n^\theta] & = 1+ \sum_{i=1}^{n-2} \frac{1}{{ \theta+i}} = \log(n) + \mathcal{O}(1) , \\[3pt] \mathrm{Var} \left (\mathcal{D}_n^\theta \right ) & = \sum_{i=1}^{n-2} \frac{\theta+i-1}{(\theta+i)^2} = \log(n) + \mathcal{O}(1).\end{align*}
(iii) There are weight sequences for which the behaviour of the depth of the WRT is totally different from the URT case. Let
 $(w_i)_{i\in \mathbb{N}} = \left (\frac{1}{i^2} \right )_{i \in \mathbb{N}}$
. Then
and since for all
$(w_i)_{i\in \mathbb{N}} = \left (\frac{1}{i^2} \right )_{i \in \mathbb{N}}$
. Then
and since for all \begin{equation*}\mathrm{E}[\mathcal{D}_n^w] = \sum_{i=1}^{n-1} \frac{\frac{1}{i^2}}{\sum_{j=1}^{i}\frac{1}{j^2}},\end{equation*}
\begin{equation*}\mathrm{E}[\mathcal{D}_n^w] = \sum_{i=1}^{n-1} \frac{\frac{1}{i^2}}{\sum_{j=1}^{i}\frac{1}{j^2}},\end{equation*}
 $i \in \mathbb{N}$
we have
$i \in \mathbb{N}$
we have  $1<\sum_{j=1}^{i}\frac{1}{j^2}<\frac{\pi^2}{6}$
, we get, for
$1<\sum_{j=1}^{i}\frac{1}{j^2}<\frac{\pi^2}{6}$
, we get, for  $n \geq 2$
,
Also, since
$n \geq 2$
,
Also, since \begin{equation*}\begin{split}{ 1} \leq \mathrm{E}[\mathcal{D}_n^w] \leq \sum_{i=1}^{n-1} \frac{1}{i^2}\Longrightarrow { 1 } \leq \mathrm{E}[\mathcal{D}_n^w] \leq \frac{\pi^2}{6}.\end{split}\end{equation*}
and, for all
\begin{equation*}\begin{split}{ 1} \leq \mathrm{E}[\mathcal{D}_n^w] \leq \sum_{i=1}^{n-1} \frac{1}{i^2}\Longrightarrow { 1 } \leq \mathrm{E}[\mathcal{D}_n^w] \leq \frac{\pi^2}{6}.\end{split}\end{equation*}
and, for all \begin{equation*}\mathrm{Var}(\mathcal{D}_n^w) = \sum_{i=2}^{n-1} \frac{\frac{1}{i^2} \sum_{j=1}^{i-1} \frac{1}{j^2}}{\left (\sum_{j=1}^{i}\frac{1}{j^2}\right )^2},\end{equation*}
\begin{equation*}\mathrm{Var}(\mathcal{D}_n^w) = \sum_{i=2}^{n-1} \frac{\frac{1}{i^2} \sum_{j=1}^{i-1} \frac{1}{j^2}}{\left (\sum_{j=1}^{i}\frac{1}{j^2}\right )^2},\end{equation*}
 $i\geq 2$
,
we get
$i\geq 2$
,
we get \begin{equation*}\frac{4^2}{5^2} \leq \frac{\sum_{j=1}^{i-1} \frac{1}{j^2}}{\left (\sum_{j=1}^{i}\frac{1}{j^2}\right )^2}\leq 1,\end{equation*}
\begin{equation*}\frac{4^2}{5^2} \leq \frac{\sum_{j=1}^{i-1} \frac{1}{j^2}}{\left (\sum_{j=1}^{i}\frac{1}{j^2}\right )^2}\leq 1,\end{equation*}
 \begin{equation*}\begin{split}\frac{4^2}{5^2} \sum_{i=2}^{n-1} \frac{1}{i^2} \leq \mathrm{Var}(\mathcal{D}_n^w) \leq \sum_{i=2}^{n-1} \frac{1}{i^2}\Longrightarrow \frac{4}{5^2} \leq \mathrm{Var}(\mathcal{D}_n^w) \leq \frac{\pi^2}{6} -1.\end{split}\end{equation*}
\begin{equation*}\begin{split}\frac{4^2}{5^2} \sum_{i=2}^{n-1} \frac{1}{i^2} \leq \mathrm{Var}(\mathcal{D}_n^w) \leq \sum_{i=2}^{n-1} \frac{1}{i^2}\Longrightarrow \frac{4}{5^2} \leq \mathrm{Var}(\mathcal{D}_n^w) \leq \frac{\pi^2}{6} -1.\end{split}\end{equation*}
6. Number of branches
Finally, we study the number of branches in a WRT. Recall that the number of branches of a tree is equal to the number of children of the root. Our results are summarized in the following theorem.
Theorem 9. Let ![]() $(w_i)_{i \in \mathbb{N}}$
be a sequence of positive weights. Denote the number of branches in
$(w_i)_{i \in \mathbb{N}}$
be a sequence of positive weights. Denote the number of branches in ![]() $\mathcal{T}_n^w$
by
$\mathcal{T}_n^w$
by ![]() $\mathcal{B}_n^w$
.
$\mathcal{B}_n^w$
.
(i) We have
 \begin{equation*} \mathrm{E}[\mathcal{B}_n^w] = \sum_{i=2}^{n} \frac{w_1}{\sum_{k=1}^{i-1} w_k} , \qquad \mathrm{Var}(\mathcal{B}_n^w) = \sum_{i=2}^{n} \frac{w_1}{\sum_{k=1}^{i-1} w_k} \left ( 1-\frac{w_1}{ \sum_{k=1}^{i-1} w_k }\right ).\end{equation*}
\begin{equation*} \mathrm{E}[\mathcal{B}_n^w] = \sum_{i=2}^{n} \frac{w_1}{\sum_{k=1}^{i-1} w_k} , \qquad \mathrm{Var}(\mathcal{B}_n^w) = \sum_{i=2}^{n} \frac{w_1}{\sum_{k=1}^{i-1} w_k} \left ( 1-\frac{w_1}{ \sum_{k=1}^{i-1} w_k }\right ).\end{equation*}
(ii) If
 $\mathrm{E} [\mathcal{B}_n^w]$
diverges then a central limit theorem results:
$\mathrm{E} [\mathcal{B}_n^w]$
diverges then a central limit theorem results:
 \begin{equation*}\frac{\mathcal{B}_n^w - \mathrm{E}[\mathcal{B}_n^w]}{\sqrt{\mathrm{Var}(\mathcal{B}_n^w)}} \longrightarrow_{\rm d} \mathcal{G} \qquad \text{as } n \rightarrow \infty.\end{equation*}
\begin{equation*}\frac{\mathcal{B}_n^w - \mathrm{E}[\mathcal{B}_n^w]}{\sqrt{\mathrm{Var}(\mathcal{B}_n^w)}} \longrightarrow_{\rm d} \mathcal{G} \qquad \text{as } n \rightarrow \infty.\end{equation*}
(iii) Further, one has
where, for any two probability measures, the Wasserstein metric \begin{equation*}d_{\rm W} \left(\frac{\mathcal{B}_n^w - \mathrm{E}[\mathcal{B}_n^w]}{\sqrt{\mathrm{Var}(\mathcal{B}_n^w)}}, \mathcal{G} \right) \leq \frac{1}{\sqrt{\mathrm{Var}(\mathcal{B}_n^w)}\,} \frac{\sqrt{28} + \sqrt{\pi}}{\sqrt{\pi}},\end{equation*}
\begin{equation*}d_{\rm W} \left(\frac{\mathcal{B}_n^w - \mathrm{E}[\mathcal{B}_n^w]}{\sqrt{\mathrm{Var}(\mathcal{B}_n^w)}}, \mathcal{G} \right) \leq \frac{1}{\sqrt{\mathrm{Var}(\mathcal{B}_n^w)}\,} \frac{\sqrt{28} + \sqrt{\pi}}{\sqrt{\pi}},\end{equation*}
 $d_{\rm W}(\mu,\nu)$
is defined as
$d_{\rm W}(\mu,\nu)$
is defined as  $\sup_{h \in \mathcal{H}} \left | \int h(x) \, {\rm d} \mu (x) - \int h(x) \, {\rm d} \nu (x)\right |$
, where
$\sup_{h \in \mathcal{H}} \left | \int h(x) \, {\rm d} \mu (x) - \int h(x) \, {\rm d} \nu (x)\right |$
, where  $\mathcal{H}=\{h\,{:}\, \mathbb{R} \to \mathbb{R}\,{:}\, |h(x)-h(y)| \leq |x-y|\}$
.
$\mathcal{H}=\{h\,{:}\, \mathbb{R} \to \mathbb{R}\,{:}\, |h(x)-h(y)| \leq |x-y|\}$
.
Proof. Letting ![]() $b_i = \textbf{1}(\text{node \textit{i} attaches to node 1})$
, observe that
$b_i = \textbf{1}(\text{node \textit{i} attaches to node 1})$
, observe that ![]() $B_n^w = \sum_{i=2}^{n} b_i$
and the
$B_n^w = \sum_{i=2}^{n} b_i$
and the ![]() $b_i$
are independent with
$b_i$
are independent with
The formulas for ![]() $\mathrm{E}[\mathcal{B}_n^w] = \sum_{i=2}^{n} \mathrm{E}[b_i]$
and
$\mathrm{E}[\mathcal{B}_n^w] = \sum_{i=2}^{n} \mathrm{E}[b_i]$
and ![]() $\mathrm{Var}(\mathcal{B}_n^w)= \sum_{i=2}^{n} \mathrm{Var}(b_i)$
are then clear.
$\mathrm{Var}(\mathcal{B}_n^w)= \sum_{i=2}^{n} \mathrm{Var}(b_i)$
are then clear.
The central limit theorem follows from Lyapunov’s central limit theorem. If ![]() $\mathrm{E}[\mathcal{B}_n^w] \to \infty$
, we show that this implies that
$\mathrm{E}[\mathcal{B}_n^w] \to \infty$
, we show that this implies that ![]() $\mathrm{Var}(\mathcal{B}_n^w) \to \infty$
too. Notice that, for all
$\mathrm{Var}(\mathcal{B}_n^w) \to \infty$
too. Notice that, for all ![]() $i \geq 2$
,
$i \geq 2$
,
Hence, one obtains
The convergence rates can be obtained by using Theorem 3.6 in [Reference Ross15] for independent random variables: Let ![]() $Y_1, Y_2, \dots, Y_n$
be independent random variables for which
$Y_1, Y_2, \dots, Y_n$
be independent random variables for which ![]() $\mathrm{E}[Y_i^4] < \infty$
and
$\mathrm{E}[Y_i^4] < \infty$
and ![]() $\mathrm{E}[Y_i]=0$
holds. Set
$\mathrm{E}[Y_i]=0$
holds. Set ![]() $\sigma^2 = \mathrm{Var}\big ( \sum_{i=1}^n Y_i\big )$
and define
$\sigma^2 = \mathrm{Var}\big ( \sum_{i=1}^n Y_i\big )$
and define ![]() $W\coloneqq \sum_{i=1}^n \frac{Y_i}{\sigma}$
. Then
$W\coloneqq \sum_{i=1}^n \frac{Y_i}{\sigma}$
. Then
 \begin{equation*}d_{\rm W}(W,\mathcal{G}) \leq \frac{1}{\sigma^3} \sum_{i=1}^{n} \mathrm{E}[|Y_i|^3] + \frac{\sqrt{28}}{\sqrt{\pi}\sigma^2} \sqrt{\sum_{i=1}^n \mathrm{E}[Y_i^4]}.\end{equation*}
\begin{equation*}d_{\rm W}(W,\mathcal{G}) \leq \frac{1}{\sigma^3} \sum_{i=1}^{n} \mathrm{E}[|Y_i|^3] + \frac{\sqrt{28}}{\sqrt{\pi}\sigma^2} \sqrt{\sum_{i=1}^n \mathrm{E}[Y_i^4]}.\end{equation*}
Defining ![]() $Y_i = b_{i+1}^w - \mathrm{E}[b_{i+1}^w]$
, simple manipulations give
$Y_i = b_{i+1}^w - \mathrm{E}[b_{i+1}^w]$
, simple manipulations give ![]() $\mathrm{E}[|Y_i|^3] < \mathrm{Var}(b_{i+1}^w)$
and
$\mathrm{E}[|Y_i|^3] < \mathrm{Var}(b_{i+1}^w)$
and ![]() $\mathrm{E}[Y_i^4] < \mathrm{Var}(b_{i+1}^w)$
; for details, see [Reference Hiesmayr9]. Plugging these results into the expression of the theorem, we get the bound. □
$\mathrm{E}[Y_i^4] < \mathrm{Var}(b_{i+1}^w)$
; for details, see [Reference Hiesmayr9]. Plugging these results into the expression of the theorem, we get the bound. □
(i) When
 $w_1 = \theta > 0$
, and
$w_1 = \theta > 0$
, and  $w_i = 1$
for
$w_i = 1$
for  $i =2,3,\dots$
, we obtain
In particular, when
$i =2,3,\dots$
, we obtain
In particular, when \begin{equation*}\frac{\mathcal{B}_n - \theta \ln n}{\sqrt{\theta \ln n}} \longrightarrow_{\rm d} \mathcal{G} \qquad \text{as } n \rightarrow \infty.\end{equation*}
\begin{equation*}\frac{\mathcal{B}_n - \theta \ln n}{\sqrt{\theta \ln n}} \longrightarrow_{\rm d} \mathcal{G} \qquad \text{as } n \rightarrow \infty.\end{equation*}
 $\theta = 1$
as well, one recovers the central limit theorem for the URT case.
$\theta = 1$
as well, one recovers the central limit theorem for the URT case.(ii) When there exist
 $\alpha_1, \alpha_2$
such that
$\alpha_1, \alpha_2$
such that  $0 < \alpha_1 \leq \sup_i w_i \leq \alpha_2 < \infty$
, it can be shown that both the expectation and the variance are still of order
$0 < \alpha_1 \leq \sup_i w_i \leq \alpha_2 < \infty$
, it can be shown that both the expectation and the variance are still of order  $\ln n$
and a central limit theorem holds.
$\ln n$
and a central limit theorem holds.(iii) When the
 $w_i$
are not bounded, there can be big differences compared to the case of URTs. One such extreme case is when
$w_i$
are not bounded, there can be big differences compared to the case of URTs. One such extreme case is when  $w_i =i$
, where
$w_i =i$
, where  $\mathrm{E}[\mathcal{B}_n^w] \sim 2$
and
$\mathrm{E}[\mathcal{B}_n^w] \sim 2$
and  $\mathrm{Var}(\mathcal{B}_n^w) \sim 14 - \frac{4 \pi^2}{3}$
. Another one is when
$\mathrm{Var}(\mathcal{B}_n^w) \sim 14 - \frac{4 \pi^2}{3}$
. Another one is when  $w_i = 1 / i$
, in which case
$w_i = 1 / i$
, in which case
 \begin{equation*}\frac{6}{\pi^2} (n - 1) \leq \mathrm{E}[\mathcal{B}_n^w] \leq n -1, \qquad \frac{6}{5\pi^2} (n - 2) \leq \mathrm{Var}(\mathcal{B}_n^w) \leq \frac{1}{4} (n-2).\end{equation*}
\begin{equation*}\frac{6}{\pi^2} (n - 1) \leq \mathrm{E}[\mathcal{B}_n^w] \leq n -1, \qquad \frac{6}{5\pi^2} (n - 2) \leq \mathrm{Var}(\mathcal{B}_n^w) \leq \frac{1}{4} (n-2).\end{equation*}
(iv) It is well known that the number of branches and the depth of node n have the same distribution in a URT. This is not the case when the tree is non-uniform. Indeed, this is intuitively clear since having more branches increases the chance that node n attaches to a node at a lower level.