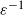1. Introduction
Let
$\mathcal M$
be a d-dimensional compact
$\mathcal C^\infty$
manifold. Markov-modulated ODEs on
$\mathcal M$
are dynamical systems
$(x(t))_{t\geqslant 0}$
that are solutions to
\begin{equation} x^\prime(t) = F_{\sigma(t)} \left( x(t) \right),\end{equation}
where
$(\sigma(t))_{t\geqslant 0}$
is a Markov process on some space
$\mathcal S$
and, for all
$s\in\mathcal S$
,
$F_s$
is a vector field on
$\mathcal M$
.
We are interested in the high-frequency regime, namely when
$\sigma(t)$
is replaced in (1.1) by
$\sigma(t/\varepsilon)$
for some small
$\varepsilon$
. Provided
$\sigma$
is ergodic with respect to some probability measure
$\pi$
, the modulated process x(t) is known to converge, as
$\varepsilon$
vanishes, to the solution of the averaged ODE
\begin{equation} x'(t) = \bar F(x(t)) , \qquad\text{where}\ \bar F(x) = \int_{\mathcal S} F_s(x)\,\pi({\text{d}} s).\end{equation}
In the case where this averaged ODE has a unique global attractor
$\bar x$
, we expect the solution of (1.1) to be close to
$\bar x$
for t large and
$\varepsilon$
small. In other words, the invariant measure of the Markov process
$(x(t),\sigma(t/\varepsilon))_{t\geqslant 0}$
converges, as
$\varepsilon$
vanishes, to
$\delta_{\bar x} \otimes \pi$
. The goal of the present work is to provide an infinitesimal expansion in terms of
$\varepsilon$
for this invariant measure. This is obtained by combining a similar expansion for the law of the process for a fixed
$t>0$
(following [Reference Pakdaman, Thieullen and Wainrib24]) with a long-time convergence result for the limit process. The structure of the proof follows [Reference Talay and Tubaro25], which established a similar expansion for the invariant measure of Euler–Maruyam schemes for diffusion processes (the averaging estimates for a fixed
$t>0$
being in that case replaced by finite-time discretization error expansions).
One of our main motivations is to get the first-order term in the expansion of the top Lyapunov exponent of systems of switched linear ODEs [Reference Benaïm, Le Borgne, Malrieu and Zitt5, Reference Chitour, Mazanti, Monmarché and Sigalotti9, Reference Gurvits, Shorten and Mason17], as detailed in Section 3.1. Our result also has applications, for instance, in some population models [Reference Benaïm4, Reference Benaïm and Lobry6, Reference Malrieu and Zitt22] or random splitting numerical schemes [Reference Agazzi, Mattingly and Melikechi1], cf. Section 3. More generally, Markov-modulated ODEs form a flexible class of Markov processes which appear in a variety of models, often to describe systems evolving in a randomly fluctuating environment, as in finance [Reference Elliott and Siu13], biology [Reference Hatzikirou, Kavallaris and Leocata18] or reliability [Reference Kharoufeh and Cox20]. It is related to random ODEs; see, e.g., [Reference Arnold, Crauel and Eckmann2, Reference Chueshov10] and references within.
In the specific context of piecewise-deterministic Markov processes (namely, when
$\sigma$
is a Markov chain on a finite set), the question of fast averaging has been addressed in [Reference Faggionato, Gabrielli and Ribezzi Crivellari14], where a large-deviation principle is proved; in [Reference Pakdaman, Thieullen and Wainrib24], where the expansion of the law of the process at fixed time t is given; or in [Reference Benaïm and Strickler8], where the convergence of the invariant measure of the Markov process
$(x(t), \sigma(t/\varepsilon))_{t \geqslant 0}$
is proved. In the recent paper [Reference Goddard, Ottobre, Painter and Souttar16], the authors deal with the case where
$\sigma$
is not ergodic.
The convergence of the invariant measure of the process in the fast-switching regime has been studied in some situations where the limit flow has a unique attractive point or cycle and possibly several unstable equilibria; see, for instance, in [Reference Benaïm, Le Borgne, Malrieu and Zitt5, Reference Chitour, Mazanti, Monmarché and Sigalotti9, Reference Du, Hening, Nguyen and Yin12]. The analysis is then much more intricate than in our case (simply to get a convergence, without any asymptotic expansion) as the convergence toward the stable element cannot be uniform over the space. Some controllability conditions in the vicinity of unstable points are then necessary to ensure switching Markov process does not get stuck there, leading to some estimates on the exit times from small balls around these points or to the construction of suitable Lyapunov functions. Refining these arguments to get an asymptotic expansion in such more general situations is outside the scope of the present work.
The paper is organized as follows. In the remainder of this introduction we introduce our general notation and assumptions. Our main result, Theorem 2.1, is stated and proved in Section 2. Section 3 is devoted to examples of applications. Finally, an appendix gathers the proofs of some intermediate results.
1.1. Notation and assumptions
To conclude this section, let us clarify our setup. Denote by
$(\mathcal Q_t)_{t\geqslant 0}$
the semigroup associated with
$(\sigma_t)_{t\geqslant 0}$
, namely
$\mathcal Q_t f(\sigma) = \mathbb E_{\sigma}\!\left( \,f(\sigma_t)\right)$
, and by Q its infinitesimal generator.
Denote by
$\mathcal A$
the set of bounded measurable functions from
$\mathcal M\times\mathcal S$
to
${\mathbb R}$
which are
$\mathcal C^\infty$
in their first variable x and such that all their derivatives in x are bounded over
$\mathcal M\times\mathcal S$
, and which, moreover, are such that, for all
$x\in \mathcal M$
and all multi-index
$\alpha$
,
$s\mapsto \partial_x^\alpha f(x,s)$
is in the domain of Q. We consider on
$\mathcal A$
the norms
$\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert\,{f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j} = \sum_{|\alpha|\leqslant j} \| \partial^\alpha_x f \|_{\infty}$
.
Assumption 1.1.
-
(i) Almost surely, the ODE (1.1) is well-defined for all times, with values in
$\mathcal M$
. Moreover, the coordinates of
$(x,s) \mapsto F_s(x) $
are in
$\mathcal A$
. -
(ii) The semigroup
$(\mathcal Q_t)_{t\geqslant 0}$
admits a unique invariant probability measure
$\pi$
. Moreover, there exist
$C,\gamma > 0$
such that (1.3)for all bounded measurable f on
\begin{equation} \|\mathcal Q_t\, f- \pi f \|_{\infty} \leqslant C {\mathrm{e}}^{-\gamma t} \|\,f\|_{\infty } \end{equation}
$\mathcal S$
and all
$t\geqslant 0$
.
The uniform exponential ergodicity (1.3) implies that the operator
$Q^{-1}$
given by
\begin{equation} Q^{-1} f :\!= \int_0^\infty \mathcal Q_t\left( \pi f - f\right)\, {\text{d}} t\end{equation}
is well-defined for all
$f\in\mathcal A$
, with
$Q^{-1} f\in \mathcal A$
and
$\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{Q^{-1} f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_j \leqslant C /\gamma \lvert\kern-1.1pt\lvert\kern-1.1pt\lvert\,{f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j }$
for all
$j\in{\mathbb{N}}$
. Moreover, using that
$\partial_t \mathcal Q_t f = Q \mathcal Q_t f = \mathcal Q_t Q f $
for all
$t\geqslant 0$
, we get that
$QQ^{-1} f = Q^{-1}Q f = f - \pi f$
for
$f\in\mathcal A$
, i.e.
$Q^{-1}$
is the pseudo-inverse of Q.
Example 1.1. A case of interest is given by
$Qf = \pi f - f$
, which corresponds to
$\sigma(t) = Y_{N_t}$
where
$(N_t)_{t\geqslant 0}$
is a standard Poisson process with intensity 1,
$Y_0=\sigma(0)$
, and
$(Y_k)_{k\geqslant 1}$
is an indpendent and identically distributed sequence of random variables distributed according to
$\pi$
. It is readily checked that, in that case,
$\mathcal Q_t f = {\mathrm{e}}^{-t} f + (1-{\mathrm{e}}^{-t}) \pi f$
, and then
$Q^{-1} = Q$
.
Example 1.2. We will be particularly concerned with the case when
$\mathcal{S}$
is a finite state space and
$(\sigma_t)_{t \geqslant 0}$
is an irreducible continuous-time Markov chain on
$\mathcal{S}$
, with transition rate matrix Q. In that case,
$Q^{-1}$
is the group inverse of Q, defined as the unique matrix solution X to
\begin{equation} QXQ= Q, \qquad XQX=X, \qquad XQ = QX. \end{equation}
[Such a matrix exists and is unique since Q has index 1, meaning that
$ Q^2$
and Q have the same rank, because 0 is a simple eigenvalue of Q; see [Reference Ben-Israel and Greville3, Chapter 4] for more details.] In the particular case when the cardinality of
$\mathcal{S}$
is two, Q can be written as
\begin{align*} Q = \left(\begin{array} {c@{\quad}c} -p & p \\ q & -q \end{array} \right) \end{align*}
for some
$p, q > 0$
. Moreover, we can easily check, using
$Q^2 = - (p+q) Q$
, that
$X = ({1}/{(p+q)^2})Q$
satisfies (1.5), and therefore
$Q^{-1} = ({1}/{(p+q)^2})Q$
.
2. High-frequency expansion
The process
$(X(t),\sigma(t/\varepsilon))_{t\geqslant 0}$
is a Markov process on
$\mathcal M\times\mathcal S$
with generator
$L = L_c + (1/\varepsilon)Q$
, where Q is seen as an operator on functions on
$\mathcal M\times \mathcal S$
acting only on the second variable, and
$L_c f(x,s) = F_s(x) \cdot {\nabla}_x f(x,s)$
for all
$f\in\mathcal A$
. For
$t\geqslant 0$
, denote by
$P_t^\varepsilon$
the associated Markov semigroup, namely
$P_t^\varepsilon f(x,s) = \mathbb E_{x,s} \left( f(X(t),\sigma(t/\varepsilon))\right)$
.
We start by stating an expansion in
$\varepsilon$
of
$P_t^\varepsilon$
for a fixed t (the proof is postponed to the Appendix). This is essentially the result (and proof) of [Reference Pakdaman, Thieullen and Wainrib24] but written in a dual form and with more explicit functional settings. Moreover, [Reference Pakdaman, Thieullen and Wainrib24] only considers the case where
$\mathcal S$
is a finite set, but it allows the jump rates of
$\sigma$
to depend on x.
Proposition 2.1.
There exist two families of operators
$P_t^{(k)},S_t^{(k)}$
indexed by
$t\geqslant 0,k\in{\mathbb{N}}$
and acting on
$\mathcal A$
, with the following properties:
-
• For all
$k,j \in {\mathbb{N}}$
and
$T>0$
, there exists
$C>0$
such that, for all
$f\in\mathcal A$
, (2.1)
\begin{equation} \sup_{t\in[0,T]}\left\vert\kern-1.5pt\left\vert\kern-1.5pt\left\vert{ P_{t}^{(k)} f}\right\vert\kern-1.5pt\right\vert\kern-1.5pt\right\vert_{j } \leqslant C \lvert\kern-1.1pt\lvert\kern-1.1pt\lvert\,{f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+2k }. \end{equation}
-
• For all
$k,j \in {\mathbb{N}}$
, there exist
$C,\gamma>0$
such that, for all
$t\geqslant 0$
and all
$f\in\mathcal A$
, (2.2)
\begin{equation} \left\vert\kern-1.5pt\left\vert\kern-1.5pt\left\vert{ S_{t}^{(k)} f}\right\vert\kern-1.5pt\right\vert\kern-1.5pt\right\vert_{j } \leqslant C {\mathrm{e}}^{- \gamma t}\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert\,{f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+2k }. \end{equation}
-
• For all
$n\in{\mathbb{N}}$
,
$T\geqslant 0$
, and
$j\in{\mathbb{N}}$
, there exists
$C>0$
such that, for all
$\varepsilon >0$
and
$f\in\mathcal A$
, the remainder
$R_{n,t}^\varepsilon f$
defined by (2.3)satisfies
\begin{equation} R_{n,t}^\varepsilon f = P_t^{\varepsilon}f - \sum_{k=0}^n\varepsilon^k P_t^{(k)}f - \sum_{k=0}^n\varepsilon^k S_{{t}/{\varepsilon}}^{(k)} \,f \end{equation}
(2.4)
\begin{equation} \lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{ R_{n,t}^{\varepsilon}\,f }\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_j \leqslant C \varepsilon^{n+1}\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert\,{f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+3+2n}. \end{equation}
-
• The first operators are given by
(2.5)where
\begin{align} P_t^{(0)} f(x,s) & = \pi f(\bar{\varphi}_t(x)), \\ S_{t}^{(0)}f(x,s) & = \mathcal Q_t f(x,s) - \pi f(x), \nonumber \\ P_t^{(1)}f(x,s) & = {\mathbf{b}}_1(t,x,s) + \int_0^{+\infty}\pi(L_c S_r^{(0)}f)(x)\,{\text{d}} r + \int_0^t\pi(L_c{\mathbf{b}}_1)(r,\bar{\varphi}_{t-r}(x))\,{\text{d}} r, \nonumber \end{align}
(2.6)
\begin{equation} {\mathbf{b}}_1 (t, x,s) = Q^{-1} ( \partial_t P_t^{(0)}f - L_c P_t^{(0)}f) (x,s). \end{equation}
Next, to address the question of the long-time behaviour of the process, we work under the following condition.
Assumption 2.1.
There is a globally attractive
$\bar x\in\mathcal M$
for the averaged flow
$\bar F$
given in (1.2) and, for all
$j\in{\mathbb{N}}$
, there exist
$C,a>0$
such that, for all
$t\geqslant 0$
and
$f\in\mathcal C^\infty(\mathcal M)$
,
\begin{align*} \lvert\kern-1.1pt\lvert\kern-1.1pt\lvert {\, f \circ \varphi_t - f\!\left( \bar x\right) }\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_j \leqslant C {\mathrm{e}}^{-at}\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert\,{f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+1},\end{align*}
where
$\varphi$
is the flow associated with
$\bar F$
.
Under Assumption 2.1,
$\mu_0=\delta_{\bar x}\otimes\pi$
is the unique invariant measure of
$P_t^{(0)}$
given in (2.5). Our main result is the following expansion in terms of
$\varepsilon$
of any invariant measure of the process
$(P_t^\varepsilon)_{t\geqslant 0}$
, in the spirit of Talay–Tubaro expansions in terms of the step size for discretization schemes [Reference Talay and Tubaro25].
Theorem 2.1.
Under Assumptions 1.1 and 2.1, for all
$f\in\mathcal A$
there exist real sequences
$(c_k)_{k\geqslant 1} $
and
$(M_k)_{k\geqslant 1}$
such that, for all
$n\in{\mathbb{N}}$
and any invariant measure
$\mu_\varepsilon$
of
$(P_t^\varepsilon)_{t\geqslant 0}$
,
\begin{equation} \Bigg|\mu_\varepsilon f - \mu_0 f - \sum_{k=1}^n c_k\varepsilon^k\Bigg| \leqslant M_n \varepsilon^{n+1}. \end{equation}
Moreover,
\begin{equation} c_1 = \pi L_c Q^{-1} \left( L_c h - f \right) (\bar x) \end{equation}
where, for
$(x,s)\in\mathcal M\times \mathcal S$
,
\begin{equation} h(x,s) = \int_0^\infty \pi\! \left(\, f(\bar x) - f\!\left( \varphi_r(x)\right)\right) \,{\text{d}} r. \end{equation}
Remark 2.1. In dimension 1, it is possible to get an alternative expression for the function h appearing in (2.8). Indeed, for fixed
$x \in \mathbb{R}$
, with the change of variables
$y = \varphi_r(x)$
we obtain, since
${{\text{d}}\varphi_r(x)}/{{\text{d}} r} = \bar F ( \varphi_r(x))$
,
\begin{align*} h(x,s) = \int_0^{+ \infty} \left( \pi f(\bar x) - \pi f(\varphi_r(x)) \right)\,{\text{d}} r = \int_{\bar x}^x \frac{\pi f(y) - \pi f(\bar x)}{\bar F(y)}\,{\text{d}} y. \end{align*}
We will use this expression in Section 3.3.
Proof of Theorem
2.1. The proof is divided into two parts. In the first one we prove (2.7), and we give an expression for
$c_1$
which depends on an arbitrary time
$t>0$
. In the second part, we obtain the stated expression for
$c_1$
by letting t vanish in this first expression.
Step 1. Fix
$t>0$
,
$f \in\mathcal A$
, and let
$\mu_\varepsilon$
be an invariant measure of
$(P_s^\varepsilon)_{s\geqslant 0}$
. By definition of the flow
$\varphi_t$
,
\begin{align*}(P_t^{(0)})^n f(x,i) = \pi f \left( \varphi_t^{\circ n}(x) \right) = \pi f \left( \varphi_{tn}(x) \right). \end{align*}
Hence,
$\left\vert\kern-1.5pt\left\vert\kern-1.5pt\left\vert{\big(P_t^{(0)}\big)^n(\mu_0 \,f - f)}\right\vert\kern-1.5pt\right\vert\kern-1.5pt\right\vert_j = \lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\pi f(\bar x) - \pi(f \circ \varphi_{tn})}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_j \leqslant C{\mathrm{e}}^{-at n}\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert\,{f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+1}$
. As a consequence, the function
$\Psi_t$
given by
$\Psi_t = \sum_{n=0}^{\infty} \big(P_t^{(0)}\big)^n (\mu_0 f - f)$
is well-defined in
$\mathcal A$
and such that, for all
$j\geqslant 0$
,
$\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\Psi_t}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_j \leq C_j\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert\,{f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+1}$
for some
$C_j>0$
independent of f. Moreover,
\begin{align*} \big(P_t^{(0)} - {\mathrm{Id}}\big)\Psi_t = \sum_{n=1}^{\infty}\big(P_t^{(0)}\big)^n(\mu_0 \,f - f) - \sum_{n=0}^{\infty}\big(P_t^{(0)}\big)^n(\mu_0 \,f - f) = f - \mu_0\, f. \end{align*}
Then, using this Poisson equation and that
$\mu_\varepsilon$
is invariant for
$P_t^\varepsilon$
,
\begin{align*} \mu_\varepsilon \,f - \mu_0 \,f = \mu_\varepsilon\big(P_t^{(0)} - {\mathrm{Id}}\big)\Psi_t = \mu_\varepsilon\big(P_t^{(0)} - P_t^\varepsilon\big)\Psi_t. \end{align*}
To get the convergence of
$\mu_\varepsilon f$
to
$\mu_0 f$
at zeroth order, we simply bound, thanks to Proposition 2.1,
\begin{align*} |\mu_\varepsilon \,f - \mu_0 \,f| \leqslant \big\|\big(P_t^{(0)} - P_t^\varepsilon\big)\Psi_t\big\|_\infty \leqslant C\varepsilon\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\Psi_t}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_3 . \end{align*}
To get the higher-order expansion, write
\begin{equation} \mu_\varepsilon \,f - \mu_0 \,f = \mu_\varepsilon \big(P_t^{(0)} - P_t^{\varepsilon}\big) \Psi_t = -\mu_\varepsilon \left( \sum_{k=1}^n \varepsilon^k P_t^{(k)} + \sum_{k=0}^n \varepsilon^k S_{{t}/{\varepsilon}}^{(k)} + R_{n,t}^{\varepsilon}\right) \Psi_t. \end{equation}
From Proposition 2.1 and the bounds on
$\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\Psi_t}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_j$
for all
$j\in{\mathbb{N}}$
,
\begin{align*}\Bigg|\mu_\varepsilon\left(\sum_{k=0}^n\varepsilon^k S_{{t}/{\varepsilon}}^{(k)} + R_{n,t}^{\varepsilon}\right) \Psi_t\Bigg| \leqslant C_n\varepsilon^{n+1} \end{align*}
for some
$C_n$
. Using that, from the convergence at order 0,
$\big|\mu_\varepsilon P_t^{(k)}\Psi_t - \mu_0 P_t^{(k)}\Psi_t\big| \leqslant C_{0,k}\varepsilon$
for all
$k\in{\mathbb{N}}$
for some
$C_{0,k}>0$
, we get first with (2.10) at order
$n=1$
that
\begin{equation} \big|\mu_\varepsilon \,f - \mu_0 \,f + \varepsilon\mu_0 P_t^{(1)}\Psi_t\big| \leqslant C_{1,0}\varepsilon^2 \end{equation}
for some
$C_{1,0}>0$
. We can thus apply this first-order expansion with f replaced by
$P_t^{(k)} \Psi_t$
to get
$\big|\mu_\varepsilon P_t^{(k)}\Psi_t - c_{0,k} - c_{1,k}\varepsilon\big| \leqslant C_{1,k}\varepsilon^2$
for some
$c_{0,k},c_{1,k},C_{1,k}$
. Hence, considering the expansion (2.10) at order
$n=2$
, we get
\begin{align*}|\mu_\varepsilon \,f - \mu_0 \,f - \varepsilon c_{0,1} - \varepsilon^2 c_{1,1} - \varepsilon^2 c_{0,2}| \leqslant C_{2,0} \varepsilon^{3} \end{align*}
for some
$C_{2,0}>0$
. Again, this can be used with f replaced by
$P_t^{(k)}\Psi_t$
, and a straightforward induction on n concludes the proof of (2.7). In particular, from (2.11), we see that, for all
$t>0$
,
$c_1$
can be written as
$c_1 = -\mu_0 P_t^{(1)} \Psi_t$
.
Step 2. The goal is now to let t vanish in this last expression. For a fixed
$t>0$
, denote by
${\mathbf{b}}_1^\Psi$
the function given by (2.6) but with f replaced by
$\Psi_t$
. Then
\begin{align*}P_t^{(1)}\Psi_t(x,s) = {\mathbf{b}}_1^\Psi(t,x,s) + \alpha(x) + \beta(t,x), \end{align*}
with
\begin{align*}\alpha(x) = \int_0^{+\infty}\pi\big(L_c S_r^{(0)}\Psi_t\big)(x)\,{\text{d}} r, \qquad \beta(t,x) = \int_0^t\pi\big(L_c{\mathbf{b}}_1^\Psi\big)(r,\bar\varphi_{t-r}(x))\,{\text{d}} r. \end{align*}
First, by definition of
$Q^{-1}$
, the average of
${\mathbf{b}}_1^\Psi$
with respect to
$\pi$
, hence with respect to
$\mu_0$
, is zero. At this stage, we have obtained that
$c_1=-\mu_0\alpha-\mu_0 \beta$
. Recalling that
$S_r^{(0)} f = \mathcal Q_r(\,f-\pi f)$
, from
\begin{align*}\Psi_t(x,s) = \pi f(\bar x) - f(x,s) + \sum_{n=1}^\infty\pi\!\left( \,f(\bar x) - f(\varphi_{tn}(x))\right), \end{align*}
integrating with respect to
$\pi$
, we get
\begin{align*}{\nabla}_x S_r^{(0)}\Psi_t(\bar x,s) = {\nabla}_x\mathcal Q_r\left(\Psi_t - \pi\Psi_t\right)(\bar x,s) = {\nabla}_x\mathcal Q_r\!\left(\pi f - f\right)(\bar x,s). \end{align*}
As a consequence,
\begin{align*} \mu_0(\alpha) = \alpha(\bar x) = \int_0^\infty\pi L_c S_r^{(0)}\Psi_t(\bar x)\,{\text{d}} r & = \int_{\mathcal{S}}F_s(\bar x) \cdot \left[\int_0^\infty{\nabla}_x Q_r\!\left(\pi f - f\right)\,{\text{d}} r\right] (\bar x, s)\,\pi({\text{d}}s) \\ & = \int_{\mathcal S}F_s(\bar x) \cdot {\nabla}_x Q^{-1} f(\bar x,s)\,\pi({\text{d}} s) \\ & = \pi L_c Q^{-1} f(\bar x). \end{align*}
Also,
\begin{align*} \mu_0(\beta) = \int_0^t\pi L_c{\mathbf{b}}_1^\Psi(r,\bar x)\,{\text{d}} r & = \pi\left[ L_c\int_0^t{\mathbf{b}}_1^\Psi(r,\cdot)\,{\text{d}} r\right](\bar x) \\ & = \pi\left[ L_c\int_0^t Q^{-1}\left(\partial_r P_r^{(0)}\Psi_t - L_c P_r^{(0)}\Psi_t\right)\,{\text{d}} r\right] (\bar x) \\ & = -\pi\left[ L_c Q^{-1}\int_0^t L_c P_r^{(0)}\Psi_t\,{\text{d}} r\right](\bar x), \end{align*}
where we used that
$\partial_r P_r^{(0)} \Psi_t$
does not depend on s and is thus in the kernel of
$Q^{-1}$
. Hence,
\begin{equation*} \int_0^t\pi L_c{\mathbf{b}}_1^\Psi(s,\bar x)\,{\text{d}} s = -\pi\left[ L_c Q^{-1}\frac1t\int_0^t L_c P_r^{(0)}(t\Psi_t)\,{\text{d}} r\right](\bar x) \underset{t\rightarrow 0}\longrightarrow -\pi\left[ L_c Q^{-1} L_c(\pi h)\right](\bar x), \end{equation*}
where we used that
$P_0^{(0)} f= \pi f$
and that
$t\Psi_t \rightarrow h$
. Indeed, thanks to Assumption 2.1,
\begin{align*} t\Psi_t(x) & = t\pi f(\bar x) - tf(x,s) + t\sum_{n=1}^\infty\pi\left( \,f(\bar x) - f(\varphi_{tn}(x))\right) \\ & \underset{t\rightarrow0}\longrightarrow \int_0^\infty\pi\left(\, f(\bar x) - f\left(\varphi_r(x)\right)\right)\,{\text{d}} r = h(x), \end{align*}
and the convergence
$t\Psi \rightarrow h$
holds in all norms
$\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\cdot}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_j$
. The proof of (2.8) is concluded by letting t vanish in the equality
$c_1 = -\mu_0\alpha - \mu_0\beta$
(since
$c_1$
is independent of t).
3. Applications
3.1. Top Lyapunov exponent for cooperative linear Markov-modulated ODEs
In this section, we consider linear Markov-modulated ODEs on
${\mathbb R}^d$
of the form
\begin{equation} z'(t) = A\left( \sigma(t/\varepsilon )\right) z(t)\end{equation}
where, for all
$\sigma \in\mathcal S$
,
$A\!\left( \sigma\right)$
is a
$d\times d$
matrix. We work under Assumption 1.1 and write
$\bar A = \int_{\mathcal S} A(s)\,\pi({\text{d}} s)$
. Moreover, we focus on the setup of [Reference Benaïm, Lobry, Sari and Strickler7], given as the following assumptions.
Assumption 3.1
-
(i) The Markov process
$(\sigma(t))_{t\geqslant 0}$
is Feller. -
(ii) For all
$s\in\mathcal S$
, A(s) is a cooperative matrix, in the sense that its off-diagonal coefficients are non-negative.
-
(iii) The averaged matrix
$\bar A$
is irreducible in the sense that, for all
$i,j\in{[\![} 1,d{]\!]}$
there exists a path
$i=i_0,\dots,i_q=j$
with
$\bar A_{i_{k-1},i_{k}} >0$
for all
$k \in {[\![} 1,q {]\!]}$
.
The fact that the matrices are cooperative implies that
${\mathbb R}_+^d$
is fixed by (3.1) for
$t\geqslant 0$
and that Assumption 2.1 holds. We decompose solutions of (3.1) on
${\mathbb R}_+^d$
as
$z(t) = \rho(t)\theta(t)$
, where
$\rho(t) = {\unicode{x1D7D9}}\cdot z(t)>0$
with
${\unicode{x1D7D9}}=(1,\dots,1) \in {\mathbb R}^d$
and
$\theta(t) = z(t)/\rho(t) \in \Delta = \{x\in{\mathbb R}_+^d, x_1+\dots+x_d=1\}$
. The ODE (3.1) is then equivalent to
\begin{align*} \rho'(t) = ({\unicode{x1D7D9}}\cdot A\left( \sigma(t/\varepsilon)\right)\theta(t))\rho(t), \quad \theta'(t) = F_{\sigma(t/\varepsilon)}(\theta(t)), \quad \text{with}\ F_s(\theta) = A(s)\theta - ({\unicode{x1D7D9}}\cdot A(s)\theta)\theta. \end{align*}
It is proved in [Reference Benaïm, Lobry, Sari and Strickler7] that, under Assumption 3.1, the Markov process
$(\theta(t),\sigma(t/\varepsilon))_{t\geqslant 0}$
admits a unique invariant measure
$\mu_\varepsilon$
on
$\Delta \times \mathcal S$
and that, for all initial conditions
$z\in {\mathbb R}_+^d\setminus\{0\}$
, almost surely,
$\lim_{t \to \infty}{\rho(t)}/{t} = \Lambda_\varepsilon$
, where
$\Lambda_\varepsilon :\!= \int_{\Delta\times\mathcal S}{\unicode{x1D7D9}}\cdot A(s)\theta\,\mu_\varepsilon({\text{d}}\theta,{\text{d}} s)$
is called the top Lyapunov exponent of the process. Denoting by
$\lambda_{\max}(\bar A)$
the principal eigenvalue of
$\bar A$
(i.e. with maximal real part), [Reference Benaïm, Lobry, Sari and Strickler7, Proposition 4] entails that
$\lim_{ \varepsilon \to 0} \Lambda_ \varepsilon = \lambda_{\max}( \bar A)$
. From Theorem 2.1 applied to the function
$f\colon(\theta,s) \mapsto {\unicode{x1D7D9}} \cdot A(s) \theta $
, we get an expansion of
$\Lambda_\varepsilon$
for small
$\varepsilon$
.
Proposition 3.1.
Under Assumptions 1.1 and 3.1, there exists a sequence
$(c_k)_{k\geqslant 1}$
of real numbers such that, for all
$n\geqslant 1$
,
\begin{align*} \Lambda_\varepsilon = \lambda_{\max}(\bar A) + \sum_{k=1}^n c_k\varepsilon^k + \underset{\varepsilon\rightarrow 0}o(\varepsilon^n). \end{align*}
Moreover, denoting by
$\bar x$
and
$\bar y$
, respectively, the right and left eigenvectors of
$\bar A$
associated with
$\lambda_{\max}(\bar A)$
and such that
$\bar x\in\Delta$
and
$\bar x \cdot \bar y = 1$
,
\begin{align*} c_1 = \int_{\mathcal{S}}\bar y^{\top}Q^{-1}(A)(s)\left(\bar x\bar y^{\top} - I\right) A(s)\bar x\,\pi({\text{d}} s). \end{align*}
Proof. First, considering h given by (2.9), we claim that, for all
$(x, s) \in \Delta \times \mathcal{S}$
,
\begin{equation} h(x,s) = - \ln( \bar y \cdot x). \end{equation}
Indeed, note that, for all
$x \in \mathcal{M}$
,
\begin{equation*} \pi f\left(\varphi_r(x)\right) = \frac{{\unicode{x1D7D9}}\cdot\bar A{\mathrm{e}}^{r\bar A}x}{{\unicode{x1D7D9}}_d\cdot{\mathrm{e}}^{r\bar A}x} = \frac{{\text{d}}}{{\text{d}} r}\ln\big({\unicode{x1D7D9}}\cdot{\mathrm{e}}^{r\bar A}x\big). \end{equation*}
Therefore, using that
$\bar x = \varphi_r(\bar x)$
,
\begin{align*} \int_0^\infty\left(\pi f\left(\bar x\right) - \pi f\left(\varphi_r(x)\right)\right)\,{\text{d}} r & = \int_0^\infty\frac{{\text{d}}}{{\text{d}} r}\left(\ln\left( \frac{{\unicode{x1D7D9}}\cdot{\mathrm{e}}^{r\bar A}\bar x}{{\unicode{x1D7D9}}\cdot{\mathrm{e}}^{r\bar A}x}\right)\right)\,{\text{d}} r \\ & = \lim_{r\to\infty}\ln\left(\frac{{\unicode{x1D7D9}}\cdot{\mathrm{e}}^{r\bar A}\bar x}{{\unicode{x1D7D9}}\cdot{\mathrm{e}}^{r\bar A}x}\right) = -\ln(\bar y \cdot x), \end{align*}
where we have used the Perron–Frobenius theorem. From (3.2), we deduce that
$L_c h(x,s) = -F_s(x)\cdot({\bar y}/({\bar y\cdot x}))$
. Now, since
$F_s(x) = A(s) x - f_s(x) x$
, we get
\begin{align*} L_c h(x,s) - f(x,s) = - \frac{A(s) x \cdot \bar y}{\bar y \cdot x}, \end{align*}
and then
\begin{align*} Q^{-1}(L_c h-f)(x,s) =- \frac{Q^{-1}(A)(s) x \cdot \bar y}{\bar y \cdot x}, \end{align*}
from which we deduce that
\begin{align*} {\nabla}_x Q^{-1}(L_c h-f)(\bar x,s) & = \frac{Q^{-1}(A)(s) \bar x \cdot \bar y}{(\bar y \cdot \bar x)^2 }\bar y - \frac{[Q^{-1}(A)(s)]^{\top}\bar y}{\bar y \cdot \bar x} \\ & = (Q^{-1}(A)(s) \bar x \cdot \bar y )\bar y - [Q^{-1}(A)(s)]^{\top}\bar y, \end{align*}
where we have used that
$\bar x \cdot \bar y = 1$
. As a consequence,
\begin{align*} F_s(\bar x) & \cdot {\nabla}_x Q^{-1}(L_c h-f)(\bar x,s) \\ & = \left( A(s)\bar x - ({\unicode{x1D7D9}}\cdot A(s)\bar x)\bar x\right)\cdot \left((Q^{-1}(A)(s)\bar x\cdot\bar y )\bar y - [Q^{-1}(A)(s)]^{\top}\bar y\right) \\ & = (Q^{-1}(A)(s)\bar x\cdot\bar y)A(s)\bar x\cdot\bar y - A(s)\bar x\cdot[Q^{-1}(A)(s)]^{\top}\bar y \\ & \quad - ({\unicode{x1D7D9}}\cdot A(s)\bar x)(Q^{-1}(A)(s)\bar x\cdot\bar y)\bar x\cdot\bar y + ({\unicode{x1D7D9}}\cdot A(s)\bar x)\bar x\cdot[Q^{-1}(A)(s)]^{\top}\bar y. \end{align*}
Since
$\bar x \cdot \bar y =1$
, we see that the last line is equal to
\begin{align*}-({\unicode{x1D7D9}}\cdot A(s)\bar x)Q^{-1}(A)(s)\bar x\cdot\bar y + ({\unicode{x1D7D9}}\cdot A(s)\bar x)Q^{-1}(A)(s)\bar x\cdot\bar y = 0. \end{align*}
We end up with
\begin{align*} F_s(\bar x) \cdot {\nabla}_x Q^{-1}(L_c h-f)(\bar x,s) & = (Q^{-1}(A)(s)\bar x\cdot\bar y)A(s)\bar x\cdot\bar y - Q^{-1}(A)(s)A(s)\bar x\cdot\bar y \\ & = \bar y^{\top}Q^{-1}(A)(s)\left[\bar x\bar y^{\top} - I\right] A(s)\bar x. \end{align*}
Integrating with respect to
$\pi$
leads to
\begin{equation*} c_1 = \int_{\mathcal{S}}\bar y^{\top}Q^{-1}(A)(s)\left(\bar x\bar y^{\top} - I\right) A(s)\bar x\,\pi({\text{d}} s). \end{equation*}
Example 3.1. If
$\sigma$
is a Markov chain on
$\mathcal{S}=\{0,1\}$
with matrix rates given by
\begin{equation} Q =\left( \begin{array} {c@{\quad}c} - p & p \\ 1 -p & -(1 - p) \end{array}\right), \end{equation}
we get the following simple expression for
$c_1$
:
\begin{equation} c_1 = p(1-p)\big[\bar y^{\top}(A_0 - A_1)^2\bar x - (\bar y^{\top}(A_0 - A_1)\bar x)^2\big]. \end{equation}
Indeed, recalling that
$Q^{-1} = Q$
(see Example 1.2) and using that
$\pi_s Q_{s,s^{\prime}}= p(1-p)$
if
$s\neq s'$
and
$-p(1-p)$
if
$s=s'$
, we get
$c_1 = \bar y^{\top}(A_0PA_0 + A_1PA_1 - A_0PA_1 - A_1PA_0)\bar x$
, where
$P = I - \bar x\bar y^{\top}$
. Now,
\begin{equation*} \bar y^{\top}A_0\bar x\bar y^{\top}A_1\bar x + \bar y^{\top}A_1\bar x\bar y^{\top}A_0\bar x - \bar y^{\top}A_0\bar x\bar y^{\top}A_0\bar x - \bar y^{\top}A_1\bar x\bar y^{\top}A_1\bar x = -(\bar y^{\top}(A_0 - A_1)\bar x)^2 \end{equation*}
and
$\bar y^{\top}A_0A_1\bar x + \bar y^{\top}A_1A_0\bar x - \bar y^{\top}A_0A_0\bar x - \bar y^{\top}A_1A_1\bar x = -\bar y^{\top}(A_0 - A_1)^2\bar x$
, which induces (3.4).
When considering the switching between matrices
$(A_i)_{i \in \mathcal{S}}$
, the following natural question arises: if all the matrices are stable (i.e.
$\lambda_{\max}(A_i) < 0$
for all
$i \in \mathcal{S}$
), is the switched system (3.1) stable, in the sense that
$\Lambda_{\varepsilon} < 0$
? It is now known that this is not true. In the case of random switching between two
$2 \times 2$
matrices, examples of stable matrices giving an unstable system can be founded in [Reference Benaïm, Le Borgne, Malrieu and Zitt5] and [Reference Lawley, Mattingly and Reed21]. In the first reference, for
$p=\frac12$
,
$\lambda_{\max}(\bar A) < 0$
so that fast switching leads to an unstable system. In the second reference it is a bit more complicated, since
$\lambda_{\max}(\bar A) > 0$
for all
$p \in (0,1)$
, meaning that both slow and fast switching lead to a stable system. However, [Reference Lawley, Mattingly and Reed21] showed that if switching neither too fast nor too slowly, the system is unstable. Yet, in [Reference Lawley, Mattingly and Reed21], the matrices are not cooperative in the sense of Assumption 3.1. This is not surprising, since it is proved in [Reference Gurvits, Shorten and Mason17] that switching between cooperative matrices of size
$2 \times 2$
such that every matrix in the convex hull of the given matrices is stable, will always lead to a stable system. However, it is also shown in [Reference Gurvits, Shorten and Mason17] that it is possible in some higher dimensions to construct an example where all the matrices in the convex hull are stable, and for which there exists a periodic switching such that the linear system explodes. Later, an explicit example in dimension 3 was given in [Reference Fainshil, Margaliot and Chigansky15]. Precisely, consider the matrices
\begin{equation} A_0 = \left(\begin{array}{c@{\quad}c@{\quad}c} -1 & 0 & 0 \\ 10 & -1 & 0 \\ 0 & 0 & -10 \end{array}\right), \qquad A_1 = \left(\begin{array} {c@{\quad}c@{\quad}c} -10 & 0 & 10 \\ 0 & -10 & 0 \\ 0 & 10 & -1 \end{array}\right).\end{equation}
It is shown in [Reference Fainshil, Margaliot and Chigansky15] that every convex combination of
$A_0$
and
$A_1$
is stable, and yet a switch of period 1 between
$A_0$
and
$A_1$
yields an explosion. In [Reference Benaïm and Strickler8], the authors asked the question whether the same system but with Markovian switching can lead to explosion. Using numerical simulations, they suggest that this is true and the Lyapunov exponent is positive for neither too fast nor too slow switching. Now, using (3.4), we rigorously prove the following assertion.
Proposition 3.2.
There exist two cooperative matrices
$B_0$
and
$B_1$
such that:
Proof. To emphasize the dependency on p, we write
$\bar A(p)$
,
$\Lambda_{\varepsilon}(p)$
, and
$c_1(p)$
for the mean matrix, the top Lyapunov exponent, and the first-order derivative, respectively, when the switching rates are given by the matrix Q in (3.3), and the matrices are (3.5). We also write
$\lambda_{\max}(p)$
for
$\lambda_{\max}(\bar A (p))$
. Figure 1(a) shows
$p \mapsto \lambda_{\max}(p)$
, and we can see that the maximal value of this function is attained at some
$p^* \in [0.3, 0.5]$
and is worth
$\lambda_{\max}^* \in [-\!0.5, -0.45]$
. We can see from Figure 1(b), which shows
$p \mapsto c_1(p)$
, that on the interval
$[0.3, 0.5]$
we have
$c_1(p) \geqslant 15$
, so that, in particular,
$c_1(p^*) \geqslant 15 > 0$
.
Figure 1. Plots of p from the proof of Proposition 3.2.
Let
$\delta > 0$
and
$A_i^{\delta} = A_i + \delta I$
. Replacing
$A_i$
by
$A_i^{\delta}$
in (3.1), we can easily check that the Lyapunov exponent of the system is
$\Lambda_{\varepsilon}^{\delta}(p) = \Lambda_{\varepsilon}(p) + \delta$
. Moreover,
$f_i^{\delta}(x) = {\unicode{x1D7D9}} \cdot (A_i + \delta I)x$
, so that
$F_i^{\delta} = F_i$
, and the dynamic of the angular part of (3.1) is independent of
$\delta$
. Hence, Proposition 3.1 entails that
$\Lambda_{\varepsilon}^{\delta}(p) \geqslant \lambda_{\max}(p) + \delta + c_1(p)\varepsilon - M(p)\varepsilon^2$
for some constant M(p) depending on p. Choosing
$p=p^*$
and
$\varepsilon = {c_1(p^*)}/{2M(p^*)} > 0$
yields
\begin{align*} \Lambda_{\varepsilon}^{\delta}(p^*) \geqslant \lambda_{\max}(p^*) + \delta + \frac{c_1(p^*)^2}{4M(p^*)}. \end{align*}
Letting
$\delta = -({c_1(p^*)^2}/{8M(p^*)}) - \lambda_{\max}(p^*)$
concludes the proof, since
-
•
$\Lambda_{\varepsilon}^{\delta}(p^*) \geqslant {c_1^2(p^*)}/{8M(p^*)} > 0$
; -
• for all
$p \in [0,1]$
,
$\lambda_{\max}(A_p^{\delta}) \leq \lambda_{\max}(A_{p^*}^{\delta}) = \lambda_{\max}(p^*) + \delta = -{c_1^2(p^*)}/{8M(p^*)} < 0$
.
Example 3.2. Assume as in Example 1.1 that
$Qf = Q^{-1}f = \pi f - f$
. Then we have
$Q^{-1}(A)(s) = \bar A - A(s)$
. Using
$\bar y^{\top}\bar A = \lambda(\bar A)\bar y^{\top}$
and
$\bar y^{\top}\bar x = 1$
, we get
$\bar y^{\top}\bar A(\bar x\bar y^{\top} - I) = 0$
, which yields
$c_1 = \int_{\mathcal{S}}\bar y^{\top}A^2(s)\bar x - (\bar y^\top A(s)\bar x)^2\,\pi({\text{d}} s)$
. Notice that, from Jensen’s inequality,
\begin{align*} \int_{\mathcal{S}}(\bar y^\top A(s)\bar x)^2\,\pi({\text{d}} s) \geqslant \bigg(\int_{\mathcal{S}}\bar y^\top A(s)\bar x\,\pi({\text{d}} s)\bigg)^2 = \lambda_{\max}(\bar A)^2, \end{align*}
so that
\begin{align*} c_1 \leqslant \int_{\mathcal{S}}\bar y^{\top}A^2(s)\bar x\,\pi({\text{d}} s) - \lambda_{\max}(\bar A)^2 = \bar y^{\top}\overline{A^2}\bar x - \lambda_{\max}(\overline{A}^2) = \bar y^{\top}\big(\overline{A^2} - \overline{A}^2\big)\bar x. \end{align*}
For further considerations and examples on the monotonicity of Lyapunov exponents in terms of the switching rate, we refer the interested reader to the follow-up work [Reference Monmarché, Schreiber and Strickler23].
3.2. Richardson extrapolation for randomized splitting schemes
In [Reference Agazzi, Mattingly and Melikechi1], in order to approximate the solution of an ODE of the form
\begin{equation} \dot y(t) = \bar F(y(t)),\end{equation}
the vector field
$\bar F$
is split into
$\bar F(x) = \sum_{k=1}^N F_k(x)$
, where each flow
$\dot x=F_k(x)$
can be solved exactly. More precisely, the two main examples of interest in [Reference Agazzi, Mattingly and Melikechi1] (to which we refer for details and motivation) are the so-called Lorenz-96 model and a finite-dimensional Galerkin projection of the vorticity formulation of two-dimensional Navier–Stokes. The trajectory y is then approximated by a discrete-time scheme of the form
\begin{align*}x^\varepsilon_{n+1} = \Phi^1_{\tau_1/\varepsilon}\circ \dots \circ \Phi^N_{\tau_N/\varepsilon} (x^\varepsilon_n), \end{align*}
where
$\Phi^i_t$
is the flow associated to
$F_i$
at time t and
$\tau_1,\dots,\tau_N$
are independent random variables distributed according to the standard exponential law. More precisely, for a fixed
$t>0$
, y(t) is approximated by
$x_n^\varepsilon$
with
$n\varepsilon =t$
, for a small
$\varepsilon$
. Notice that this does not enter directly our framework. However, consider the Markov-modulated ODE
$\dot x_\varepsilon(t) = F_{\sigma(N t/\varepsilon)} (x_\varepsilon(t))$
, where
$\sigma$
is a cyclic chain on
${[\![} 1,N{]\!]}$
with rate 1 (i.e. it is a standard Poisson process modulo N). We can take the times
$\tau_i$
to define the jump times of
$\sigma$
, and thus
$x_{n}^\varepsilon$
is exactly
$x_\varepsilon(\varepsilon S_n/N)$
, where
$S_n$
is the (nN)th jump time of
$\sigma$
. In particular, if
$n\varepsilon = t$
, assuming that the vector fields
$F_k$
are bounded,
\begin{align*} |x_\varepsilon(t) - x_n^\varepsilon| & = |x_\varepsilon(t) - x_\varepsilon\!\left( \varepsilon S_n /N \right) | \leqslant \max_{k\in{[\![} 1,N{]\!]}}\|F_k\|_\infty |\varepsilon S_n/N-t|, \\ \mathbb E|({\varepsilon S_n}/N)-t|^2 & = {n\varepsilon^2}/{N} = {t\varepsilon}/{N}.\end{align*}
In other words,
$(x_\varepsilon(t))_{t\geqslant 0}$
(which can be sampled exactly if
$(x_n^\varepsilon)_{n\in{\mathbb{N}}} $
can) can be seen as an alternative variation of the scheme of [Reference Agazzi, Mattingly and Melikechi1].
The convergence of
$x_n^\varepsilon$
to y(t) as
$\varepsilon \rightarrow 0$
for a fixed
$t=n\varepsilon$
, or more precisely of the corresponding Markov transition operators, is stated in [Reference Agazzi, Mattingly and Melikechi1, Theorem 4.1], which is thus similar to our Proposition 2.1 at order
$n=0$
. Notice that, a priori, the ODE (3.6) is in
${\mathbb R}^d$
but [Reference Agazzi, Mattingly and Melikechi1, Theorem 4.1] is proved by restricting the study on the orbit of the process, which is assumed to be bounded (this is [Reference Agazzi, Mattingly and Melikechi1, Assumption 1]), so that our results apply in this context.
The higher-order expansion in Proposition 2.1 enables the use of a Richardson extrapolation to get better convergence rates.
Indeed, we get that, for any fixed
$x_0\in{\mathbb R}^d$
,
$t>0$
and
$f\in\mathcal A$
, setting
$c_t = P_t^{(1)}f(x_0)$
, there exists
$C>0$
such that, for all
$\varepsilon\in(0,1]$
,
$|\mathbb E\left( \,f\left(\varphi_t(x_0)\right) - f(x_{\varepsilon}(t))\right) - c_t\varepsilon| \leqslant C\varepsilon^2$
. As a consequence, for any
$r>1$
, taking
$\theta=r/(r-1)$
so that
$\theta + (1-\theta)r = 0$
, we get
\begin{align*}\big|f\!\left(\varphi_t(x_0)\right) - \left[\theta\mathbb E\left( f(x_{\varepsilon}(t))\right) + (1-\theta)\mathbb E\left( f(x_{\varepsilon r}(t))\right) \right]\big| \leqslant \left( 2\theta-1\right) C\|f\|_3\varepsilon^2, \end{align*}
providing an approximation of
$f\!\left( \varphi_t(x_0)\right) $
with a second-order weak error in terms of
$\varepsilon$
, at a numerical cost less than twice the simulation of
$x_{\varepsilon}(t)$
(since
$r>1$
, there are on average fewer jumps for
$x_{\varepsilon r}(t)$
).
As a simple illustration, we consider the conservative Lorenz-96 model from [Reference Agazzi, Mattingly and Melikechi1], which is (3.6) with, denoting by
$e_k$
the kth vector of the canonical basis of
${\mathbb R}^d$
,
\begin{align*}F_k(x) = (x_{k+1} e_k - x_k e_{k+1}) x_{k-1}, \end{align*}
where the indexes are periodized in the sense that
$x_{n+1}=x_1$
,
$x_n=x_0$
, and
$x_{-1}=x_{n-1}$
. Along the flow
$\dot x = F_k(x)$
, all coordinates but
$x_k$
and
$x_{k+1}$
are preserved, and
\begin{align*}\left(\begin{array}{c}x_k(t) \\ x_{k+1}(t)\end{array}\right) =\left( \begin{array}{c@{\quad}c}\cos\!(x_{k-1}(0) t) & \sin\!(x_{k-1}(0) t) \\-\sin\!(x_{k-1}(0) t) & \cos\!(x_{k-1}(0) t)\end{array}\right) \left(\begin{array}{c}x_k(0) \\ x_{k+1}(0)\end{array}\right). \end{align*}
We run a trajectory up to time
$t=10$
starting from
$x(0)=(1,\dots,1)$
, which is a fixed point of
$\bar F$
but not of any
$F_k$
. We compute
$\hat x_\varepsilon(t)$
, the average of
$x_\varepsilon(t)$
over
$m=10^5$
independent experiments for each value of
$\varepsilon \in \big\{\big(\frac34\big)^k,\ k\in{[\![} 0,20{]\!]}\big\}$
. Taking
$r=\big(\frac43\big)^5 \simeq 4.21$
and
$\theta=r/(r-1)$
we define the extrapolation
$\hat y_\varepsilon(t) = \theta \hat x_{\varepsilon}(t)+(1-\theta)\hat x_{r\varepsilon}(t)$
for
$\varepsilon \in \big\{\big(\frac34\big)^k,\ k\in{[\![} 5,20{]\!]}\big\}$
. The errors
$|\hat x(t)-x(0)|$
and
$|\hat y(t)-x(0)|$
in terms of
$\varepsilon$
are plotted (in log–log scale) in Figure 2, where the speed-up of the extrapolation is clear.
Figure 2. Weak error for the conservative Lorenz-96 model for the basic estimator
$\hat x_\varepsilon(t)$
and the extrapolation
$\hat y_\varepsilon(t)$
.
3.3. Species invasion rate in a two-species Lotka–Volterra model in a random environment
We consider a model of two species in interaction, in a random environment, described by the following system of Lotka–Volterra equations:
\begin{equation} \begin{cases} \dfrac{{\text{d}} X(t)}{{\text{d}} t} = X(t)\big(a_{10}^{\sigma(t)} - a_{11}^{\sigma(t)}X(t) + a_{12}^{\sigma(t)}Y(t)\big), \\[8pt] \dfrac{{\text{d}} Y(t)}{{\text{d}} t} = Y(t)\big(a_{20}^{\sigma(t)} + a_{21}^{\sigma(t)}X(t) - a_{22}^{\sigma(t)}Y(t)\big). \end{cases}\end{equation}
We assume that
$a^s_{11}, a^s_{22} > 0$
(intraspecific competition); the other parameters can be positive or negative. The coefficients
$a_{10}^s$
and
$a_{20}^s$
represent the growth rates of species 1 and 2 respectively, while the coefficients
$a_{12}^s$
and
$a_{21}^s$
model the interaction between the two species. If, for example,
$a_{10}^s, a_{21}^s >0$
while
$a_{20}^s, a_{12}^s < 0$
, we get a prey–predator system (species 1 being the prey, and species 2 the predator). Assumption 1.1 is also enforced in this whole section.
In the absence of species 2 and after accelerating the dynamics of
$\sigma$
by a factor
$1/\varepsilon$
, species 1 evolves according to a logistic equation in a random environment:
\begin{equation} \frac{{\text{d}} X(t)}{{\text{d}} t} = X(t)\big(a_{10}^{\sigma(t/\varepsilon)} - a_{11}^{\sigma(t/\varepsilon)}X(t)\big).\end{equation}
We prove the following result in the Appendix.
Lemma 3.1.
Assume that
$p_0 :\!= \inf_{s\in\mathcal{S}}{a_{10}^s}/{a_{11}^s} > 0$
,
$p_1 :\!= \sup_{s\in\mathcal{S}}{a_{10}^s}/{a_{11}^s} < +\infty$
, and
$\inf_{s\in\mathcal{S}}a_s^{11} > 0$
. Then the process
$(X(t), \sigma(t/\varepsilon))_{t\geqslant 0}$
with X given by (3.8) and
$X(0) \neq 0$
will ultimately lie in
$E :\!= [p_0, p_1] \times \mathcal{S}$
and admits a unique stationary distribution
$\mu_{\varepsilon}$
on E. Moreover,
$(X(t), \sigma(t/ \varepsilon))$
converges in law to
$\mu_{\varepsilon}$
when t goes to infinity.
The stationary distribution
$\mu_{\varepsilon}$
represents the population of species 1 at equilibrium in the absence of species 2. The invasion growth rate of species 2 when species 1 is at equilibrium is then given by
$\Lambda_y(\varepsilon) = \int_{\mathcal{M}\times\mathcal{S}}(a_{20}^s + a_{21}^s x)\,\mu_{\varepsilon}({\text{d}} x,{\text{d}} s)$
. Intuitively, we are interested in the sign of this quantity, since when the abundance of the second species is close to 0 we have, roughly,
\begin{align*} \frac{1}{t}\ln(Y(t)) \simeq \frac{1}{t}\int_0^t\big[ a^{\sigma(u/\varepsilon)}_{20} + a^{\sigma(u/\varepsilon)}_{21}X(u)\big]\,{\text{d}} u, \end{align*}
where X solves (3.8) and the right-hand side converges to
$\Lambda_y(\varepsilon)$
when t goes to infinity, thanks to Lemma 3.1 and the ergodic theorem. It is made rigorous in [Reference Benaïm4] that, indeed, the sign of
$\Lambda_y(\varepsilon)$
gives information on the local behaviour of (3.7) near the boundary
$\{y = 0\}$
. We illustrate this in Figure 3, considering two cases with two environments (i.e.
$\sigma\in\{1,2\}$
), with the parameters detailed in Table 1. These parameters are chosen so that
$\Lambda_y$
is increasing in Case 1 and decreasing in Case 2, and changes sign at some point in both cases.
Figure 3. Simulation of Lotka–Volterra models with the parameters of Table 1.
In Figure 3(a),
$\Lambda_y(\varepsilon)$
is estimated by Monte Carlo with a long simulation of (3.8). We see that the Lyapunov exponent decreases (resp. increases) when the switching rate
$\varepsilon^{-1}$
increases in Case 1 (resp. Case 2). In Figure 3(b), (c), and (d), (3.7) is simulated with initial condition
$(X_0,Y_0)=(1,10^{-2})$
. In Case 1 in Figure 3(b), the second species is persistent (i.e. invasion occurs) for
$\varepsilon=1$
(where
$\Lambda_y(\varepsilon)>0$
), but as the switching rate increases, extinction occurs (for
$\varepsilon=10^{-3}$
, the trajectory is close to the deterministic averaged flow, for which
$y_t$
vanishes exponentially fast). Conversely, in Figure 3(c) and (d) with the parameters of Case 2, slow switching (
$\varepsilon\in\{1,10\}$
) gives
$\Lambda_y(\varepsilon)<0$
and extinction, while fast switching leads to persistence/invasion (as in the deterministic averaged flow, close to the
$\varepsilon=10^{-3}$
case).
Denoting by
$\bar\alpha = \int_{\mathcal S}\alpha^s\,\pi({\text{d}} s)$
the mean with respect to
$\pi$
of a function
$\alpha$
defined on
$\mathcal{S}$
, it is proved in [Reference Benaïm and Lobry6], in the specific case when
$\sigma$
is a two-state Markov chain, that
$\Lambda_y(\varepsilon)$
converges as
$\varepsilon$
goes to 0 to
$\bar a_{20} + \bar a_{21} \bar x$
. The following proposition extends this result to the general case of a process
$\sigma$
satisfying Assumption 1.1 and with a first-order expansion.
Proposition 3.3.
Assume that
$\inf_{s\in\mathcal{S}}a_{10}^s > 0$
and
$\sup_{s\in\mathcal{S}}a_{11}^s < + \infty$
. Then, for any invariant probability measure
$\mu_{\varepsilon}$
of
$(X_t,\sigma(t/\varepsilon))_{t \geq 0}$
,
\begin{align*} \Lambda_y(\varepsilon) = \bar{a}_{20} + \bar{a}_{21}\bar x + \varepsilon\frac{\bar{a}_{21}\bar{a}_{10}^2}{\bar{a}_{11}} \int_{\mathcal{S}}\left(\frac{a_{10}^s}{\bar{a}_{10}} - \frac{a_{11}^s}{\bar{a}_{11}}\right)Q^{-1} \left(\frac{a_{11}}{\bar{a}_{11}} - \frac{a_{21}}{\bar{a}_{21}}\right)(s)\,\pi({\text{d}} s) + \underset{\varepsilon\rightarrow 0}{o}(\varepsilon). \end{align*}
Proof. First, note that the unique equilibrium of
$\bar F(x) = x(\bar{a}_{10} - \bar{a}_{11} x)$
is
$\bar x :\!= \bar{a}_{10}/\bar{a}_{11}$
, and Assumption 2.1 holds (since, thanks to Lemma 3.1, it is sufficient to consider initial conditions in the compact set
$ [p_0, p_1]$
). By Theorem 2.1, and since the marginal of
$\mu_\varepsilon$
in s is independent of
$\varepsilon$
(so that
$\mu_\varepsilon(a_{20}) = \bar{a}_{20}$
), we have
\begin{equation*} \Lambda_y(\varepsilon) = \bar{a}_{20} + \bar{a}_{21}\bar{x} + \varepsilon c_1 + \underset{\varepsilon\rightarrow 0}{o}(\varepsilon), \end{equation*}
with
$c_1 = \pi L_c Q^{-1} \left( L_c h - f \right) (\bar x)$
for
$f(x,s) = a^s_{21} x$
. Using the formula for h derived in Remark 2.1, we have
\begin{equation*} h(x,s) = \int_{\bar x}^x\frac{\bar f(y) - \bar f(\bar x)}{\bar F(y)}\,{\text{d}} y = \int_{\bar x}^x\bar{a}_{21}\frac{y-\bar x}{y(\bar{a}_{10} - \bar{a}_{11}y)}\,{\text{d}} y = \frac{\bar{a}_{21}}{\bar{a}_{11}}\ln\left(\frac{\bar x}{x}\right), \end{equation*}
which yields
$L_c h(x,s) = -(a_{10}^s - a_{11}^s x){\bar{a}_{21}}/{\bar{a}_{11}}$
. Then,
${\nabla}_x(L_c h - f) = a_{11} \bar a_{21}/\bar a_{11} - a_{21} $
, so that
\begin{equation*} L_c Q^{-1}\left( L_c h - f\right)(\bar x,s) = \bar x(a_{10}^s - a_{11}^s\bar x)Q^{-1} \left(\frac{\bar{a}_{21}}{\bar{a}_{11}}a_{11} - a_{21}\right)(s), \end{equation*}
and finally, integrating this with respect to
$\pi$
and using that
$\bar x = \bar{a}_{10}/\bar{a}_{11}$
,
\begin{equation} c_1 = \frac{\bar{a}_{21}\bar{a}_{10}^2}{\bar{a}_{11}}\int_{\mathcal S} \left(\frac{a_{10}^s}{\bar{a}_{10}} - \frac{a^s_{11}}{\bar{a}_{11}}\right) Q^{-1} \left(\frac{a_{11}}{\bar{a}_{11}} - \frac{a_{21}}{\bar{a}_{21}}\right)(s)\,\pi({\text{d}} s), \end{equation}
which concludes the proof.
Let us discuss the sign of the expression (3.9) in some particular cases.
-
• If
$a_{11}^s = \bar{a}_{11}$
and
$a_{10}^s = \bar{a}_{10}$
for all s, then
$\Lambda_{y}^{\prime}(0) =0$
. This is expected, since in that case, the process X that is the solution to (3.8) is deterministic and does not depend on
$\varepsilon$
, and
$\mu_{\varepsilon} = \delta_{{\bar{a}_{10}}/{\bar{a}_{11}}} \otimes \pi$
for all
$\varepsilon$
. More interestingly, if
$a_{11}^s = \bar{a}_{11}$
and
$a_{21}^s = \bar{a}_{21}$
but
$a_{10}$
is varying, we still have
$\Lambda_y^{\prime}(0) = 0$
. -
• If
$a_{10}^s = \bar{a}_{10}$
and
$a_{21}^s = \bar{a}_{21}$
for all s, using that
$\pi Q^{-1} = Q^{-1} 1 = 0$
, we get This is always non-negative, as it can be interpreted as an asymptotic variance. Indeed, considering
\begin{align*} c_1 & = -\frac{\bar{a}_{21}\bar{a}_{10}^2}{\bar{a}_{11}}\int_{\mathcal S}\frac{a_{11}^s}{\bar{a}_{11}}Q^{-1} \left(\frac{a_{11}}{\bar{a}_{11}}\right)(s)\,\pi({\text{d}} s) \\ & = -\frac{\bar{a}_{21}\bar{a}_{10}^2}{\bar{a}_{11}^3}\int_{\mathcal S}(a_{11}^s - \bar{a}_{11})Q^{-1} \left( a_{11} - \bar{a}_{11}\right)(s)\,\pi({\text{d}} s). \end{align*}
$g\in\mathcal A$
with
$\pi g=0$
, for
$t\geqslant 0$
, where we used that
\begin{align*} t\mathbb E_{\pi}\bigg|\frac1t\int_0^t g(\sigma(s))\,{\text{d}} s\bigg|^2 & = \frac2t\mathbb E_{\pi}\int_0^t\int_s^t g(\sigma(u))g(\sigma(s))\,{\text{d}} s\,{\text{d}} u \\ & = \frac2t\int_0^t\int_s^t\pi\!\left( g\mathcal Q_{u-s}g\right)\,{\text{d}} s\,{\text{d}} u \\ & = \frac2t\int_0^t\int_0^t{\unicode{x1D7D9}}_{v \lt t-s}\pi\left( g\mathcal Q_{v}g\right)\,{\text{d}} s\,{\text{d}} v \\ & = \frac2t\int_0^t(t-v)\pi\left( g\mathcal Q_{v}g\right)\,{\text{d}} v \underset{t\rightarrow \infty}\longrightarrow -2\pi\left( gQ^{-1}g\right), \end{align*}
$\int_0^t\mathcal Q_v g$
converges to
$-Q^{-1}g$
, and
\begin{align*} \bigg|\int_0^t v\pi\left( g\mathcal Q_{v}g\right)\,{\text{d}} v\bigg| \leqslant \int_0^{\infty}Cv{\mathrm{e}}^{-\gamma v}\|g\|_\infty^2\,{\text{d}} v. \end{align*}
Example 3.3. We consider the case described in Example 1.1, where
$Qf = Q^{-1}f = \pi f - f$
. In that case, we get
\begin{align*} Q^{-1}\bigg(\frac{a_{11}}{\bar{a}_{11}} - \frac{a_{21}}{\bar{a}_{21}}\bigg)(s) = \frac{a^s_{21}}{\bar{a}_{21}} - \frac{a^s_{11}}{\bar{a}_{11}}, \end{align*}
which entails
\begin{align*} c_1 = \frac{\overline{a_{10}a_{21}}}{\bar{a}_{10}\bar{a}_{21}} + \frac{\overline{a_{11}^2}}{(\bar{a}_{11})^2} - \frac{\overline{a_{10}a_{11}}}{\bar{a}_{10}\bar{a}_{11}} - \frac{\overline{a_{11}a_{21}}}{\bar{a}_{11}\bar{a}_{21}}. \end{align*}
Example 3.4. We now consider the two-state case, i.e.
$\sigma$
is a Markov chain on
$\mathcal{S} = \{0,1\}$
, with matrix rates given by
\begin{align*} Q = \left(\begin{array} {c@{\quad}c} - p & p \\ 1 -p & -(1 - p) \end{array} \right) \end{align*}
for some
$p \in (0,1)$
. The behaviour of the solutions to (3.7) was studied in [Reference Benaïm and Lobry6] through the signs of the invasion growth rates of species 1 and 2 in the competitive case (i.e. when
$a_{21}^s$
and
$a_{12}^s$
are negative). That study was complemented by [Reference Malrieu and Zitt22], which proposed an alternative formula for the invasion growth rate that made it possible for them to understand the monotonicity of
$\varepsilon \mapsto \Lambda_y(\varepsilon)$
. In particular, it is a consequence of the proof of [Reference Malrieu and Zitt22, Lemma 4.1] that
$\varepsilon \mapsto \Lambda_y(\varepsilon)$
is increasing if
$A_2 > 0$
while it is decreasing if
$A_2 < 0$
, where
$A_2$
is the coefficient of the second-order term of the polynomial
\begin{align*} P(x) = \bigg[\frac{a_{20}^1}{a_{10}^1}\bigg(1 + \frac{a_{21}^1}{a_{20}^1}x\bigg) \bigg(1 - \frac{a_{11}^0}{a_{10}^0}x\bigg) - \frac{a_{20}^0}{a_{10}^0}\bigg(1 + \frac{a_{21}^0}{a_{20}^0}x\bigg) \bigg(1 - \frac{a_{11}^1}{a_{10}^1}x\bigg)\bigg] \frac{{a_{11}^1}/{a_{10}^1} - {a_{11}^0}/{a_{10}^0}}{|{a_{11}^1}/{a_{10}^1} - {a_{11}^0}/{a_{10}^0}|}, \end{align*}
that is,
$A_2 = (a_{11}^1a_{21}^0 - a_{11}^0a_{21}^1)/(a_{10}^0a_{10}^1)$
, if we assume without loss of generality that
${a_{11}^1}{a_{10}^1} \geqslant {a_{11}^0}{a_{10}^0}$
. Let us prove that our results are in accordance with the results of [Reference Malrieu and Zitt22] by studying the sign of the first-order term of the expansion of
$\varepsilon \mapsto \Lambda_y(\varepsilon)$
when
$ \varepsilon \to 0$
. Using Example 1.2, we have
$\pi=(1-p,p)$
,
$Q^{-1}= Q$
, and
$\pi_s Q_{s,s'}= p(1-p)$
if
$s\neq s'$
and
$-p(1-p)$
if
$s=s'$
, from which we compute
\begin{align*} c_1 & = \frac{\bar{a}_{21}\bar{a}_{10}^2}{\bar{a}_{11}}\sum_{s,s'\in{0,1}}\pi_sQ_{s,s'} \left(\frac{a_{10}^s}{\bar{a}_{10}} - \frac{a_{11}^s}{\bar{a}_{11}}\right) \left(\frac{a_{11}^{s'}}{\bar{a}_{11}} - \frac{a_{21}^{s'}}{\bar{a}_{21}}\right) \\ & = \frac{\bar{a}_{21}\bar{a}_{10}^2}{\bar{a}_{11}}p(1-p)\bigg[ \left(\frac{a_{10}^0}{\bar{a}_{10}} - \frac{a_{11}^0}{\bar{a}_{11}}\right) \left(\frac{a_{11}^1}{\bar{a}_{11}} - \frac{a_{21}^1}{\bar{a}_{21}}\right) + \left(\frac{a_{10}^1}{\bar{a}_{10}} - \frac{a_{11}^1}{\bar{a}_{11}}\right) \left(\frac{a_{11}^{0}}{\bar{a}_{11}} - \frac{a_{21}^{0}}{\bar{a}_{21}}\right) \\ & \qquad\qquad\qquad\qquad -\left(\frac{a_{10}^0}{\bar{a}_{10}} - \frac{a_{11}^0}{\bar{a}_{11}}\right) \left(\frac{a_{11}^{0}}{\bar{a}_{11}} - \frac{a_{21}^{0}}{\bar{a}_{21}}\right) - \left(\frac{a_{10}^1}{\bar{a}_{10}} - \frac{a_{11}^1}{\bar{a}_{11}}\right) \left(\frac{a_{11}^{1}}{\bar{a}_{11}} - \frac{a_{21}^{1}}{\bar{a}_{21}}\right)\bigg] \\ & = \frac{\bar{a}_{21}\bar{a}_{10}^2}{\bar{a}_{11}}p(1-p)\bigg[ \frac{a_{10}^0}{\bar{a}_{10}} - \frac{a_{11}^0}{\bar{a}_{11}} - \left(\frac{a_{10}^1}{\bar{a}_{10}} - \frac{a_{11}^1}{\bar{a}_{11}}\right)\bigg]\bigg[ \frac{a_{11}^{1}}{\bar{a}_{11}} - \frac{a_{21}^{1}}{\bar{a}_{21}} - \left(\frac{a_{11}^{0}}{\bar{a}_{11}} - \frac{a_{21}^{0}}{\bar{a}_{21}}\right)\bigg] \\ & = \frac{\bar{a}_{21}\bar{a}_{10}^2}{\bar{a}_{11}}p(1-p) \left(\frac{a_{10}^0-a_{10}^1}{\bar{a}_{10}} - \frac{a_{11}^0-a_{11}^1}{\bar{a}_{11}}\right) \left(\frac{a_{11}^1-a_{11}^0}{\bar{a}_{11}} - \frac{a_{21}^1-a_{21}^0}{\bar{a}_{21}}\right) \\ & = \frac{p(1-p)a_{10}^0a_{10}^1\bar{a}_{10}}{(\bar{a}_{11})^3} \bigg(\frac{a_{11}^1}{a_{10}^1} - \frac{a_{11}^0}{a_{10}^0}\bigg) \big(a_{11}^1a_{21}^0 - a_{11}^0a_{21}^1\big). \end{align*}
Since we have assumed that
${a_{11}^1}/{a_{10}^1} \geqslant {a_{11}^0}/{a_{10}^0}$
, the sign of
$\Lambda_y^{\prime}(0)$
is indeed the same as that of
$a_{11}^1 a_{21}^0 - a_{11}^0 a_{21}^1$
.
In Example 3.4 we see that the sign of
$c_1$
only depends on the coefficients of the vector fields, through the sign of
$a_{11}^1 a_{21}^0 - a_{11}^0 a_{21}^1$
. The proof in [Reference Malrieu and Zitt22] of the monotonicity of
$\varepsilon \mapsto \Lambda_y(\varepsilon)$
relies on an explicit formula for
$\mu_{\varepsilon}$
. Such an explicit formula is, however, in general only computable in the case of two environments. In contrast, our formula can provide some insights on the local behaviour of
$\varepsilon \mapsto \Lambda_y(\varepsilon)$
near 0 for any number of environmental states. We now give an example where, contrary to the previous situation, the sign of
$c_1$
depends also on the switching rates of
$\sigma$
.
Example 3.5. Let
$\sigma$
be an irreducible Markov chain on
$\mathcal{S} = \{ 1, 2, 3 \}$
. We consider two different rate matrices for
$\sigma$
:
\begin{align*} Q = \left(\begin{array} {c@{\quad}c@{\quad}c} - (\frac{1}{2} + \delta) & \frac{1}{2} & \delta \\[5pt] \frac{1}{2} & - (\frac{1}{2} + \delta) & \delta \\[5pt] \frac{1}{2} & \frac{1}{2} & -1 \end{array}\right), \qquad Q' = \left(\begin{array} {c@{\quad}c@{\quad}c} - 1 & \frac{1}{2} & \frac{1}{2} \\[5pt] \delta & - (\frac{1}{2} + \delta) & \frac{1}{2} \\[5pt] \delta & \frac{1}{2} & -( \frac{1}{2} + \delta) \end{array} \right) \end{align*}
for some small
$\delta > 0$
. Intuitively, if the rates matrix is Q, then
$\sigma$
will spend most of the time in states 1 and 2, while if the rates matrix is Q
′, then
$\sigma$
will spend most of the time in states 2 and 3. Hence, we can expect that in the first case, for small
$\delta$
,
$c_1$
will be close to
$c_1(1,2)$
, given by
\begin{align*} c_1(1,2) = \frac{a_{10}^1a_{10}^2\bar{a}_{10}}{4(\bar{a}_{11})^3} \bigg(\frac{a_{11}^2}{a_{10}^2} - \frac{a_{11}^1}{a_{10}^1}\bigg)\big(a_{11}^2 a_{21}^1 - a_{11}^1 a_{21}^2\big), \end{align*}
which is the expression derived in Example 3.4 when
$\sigma$
is a Markov chain on
$\{1,2\}$
with
$p=\frac{1}{2}$
. In the second case,
$c_1$
should be close to
\begin{align*} c_1(2,3) = \frac{a_{10}^2a_{10}^3\bar{a}_{10}}{4(\bar{a}_{11})^3} \bigg(\frac{a_{11}^3}{a_{10}^3} - \frac{a_{11}^2}{a_{10}^2}\bigg)\big(a_{11}^3 a_{21}^2 - a_{11}^2 a_{21}^3\big), \end{align*}
the expression when
$\sigma$
is a Markov chain on
$\{2,3\}$
with
$p=\frac{1}{2}$
. In particular, we can choose the coefficients
$(a_{jk}^s)_{j,k,s}$
in such a way that
$c_1(1,2) < 0$
and
$c_1(2,3) > 0$
, meaning that, with the same environmental states, different switching mechanisms can lead to opposite signs for the derivative at 0 of the growth rate. In other words, it can be as beneficial as it is detrimental for species y to increase the switching rates, depending on the switching structure.
Using (3.9) with
$a_{11}^s = 1$
for all s and
$a_{10}^1 = 3$
,
$a_{10}^2 = 2$
,
$a_{10}^3 = 1$
,
$a_{21}^1= 2$
,
$a_{21}^2=5$
,
$a_{21}^3 = 3$
, and
$\delta = 0.0005$
, we compute in the first case
$c_1 \simeq -1.871\,628\,9 < 0$
and in the second case
$c_1 \simeq 0.747\,377\,2 > 0$
. As expected, these two values are respectively close to
$c_1(1,2) \simeq - 1.874\,437\,8$
and
$c_1(2,3) \simeq 0.750\,374\,8$
.
Notice that, for the two-environment processes, these parameters are those used in Table 1, and thus we get that the sign of
$c_1$
in each case is consistent with the monotonicity displayed in Figure 3(a).
Appendix A. Proof of Proposition 2.1
Proof. This is essentially the proof from [24], in dual form since we work with
$P_t f$
rather than the law of the process. It is organized in three steps. First, assuming formally that (2.3) gives an expansion in
$\varepsilon$
of
$P_t^\varepsilon$
, we deduce the expressions for
$P_t^{(k)}$
and
$S_t^{(k)}$
. With these definitions, in the second step we establish the bounds in (2.1) and (2.2) on
$P_t^{(k)}$
and
$S_t^{(k)}$
. Finally, from this, we obtain the bound in (2.4) on
$R_{n,t}^\varepsilon$
.
Step 1. Fix
$f \in \mathcal{C}^{\infty}(\mathcal M\times \mathcal S)$
. For all
$t \geqslant 0$
,
\begin{equation} \partial_t P_t^{\varepsilon} f = L^{\varepsilon} P_t^{\varepsilon} f. \end{equation}
Bearing in mind the ansatz that (2.3) gives an expansion in
$\varepsilon$
of
$P_t^\varepsilon f$
, developing each side of the above equality in
$\varepsilon$
, and equating terms of the same order (treating the terms
$P_t^{(k)}f$
and
$S_t^{(k)}f$
separately), we end up with the following equations for all
$k \geqslant 0$
:
\begin{align} QP_t^{(0)}f & = 0 , \end{align}
\begin{align} \partial_t P_t^{(k)}f & = L_c \big(P_t^{(k)}f\big) + QP_t^{(k+1)}f, \end{align}
\begin{align} \partial_t S_t^{(0)} f & = Q S_t^{(0)}f, \end{align}
\begin{align} \partial_t S_t^{(k)} f & = Q S_t^{(k)} f + L_c(S_t^{(k-1)}f). \end{align}
To shorten the notation, for
$k \in {\mathbb{N}}$
we write
$u_k(t,x,s)=P_t^{(k)}f(x,s)$
. Moreover, for a function g(t, x, s) we use the notation
$\pi g(t,x) = \int_{\mathcal S} g(t,x,s)\,\pi({\text{d}} s)$
. Equation (A.2) is equivalent to say that there exists
$\theta_{0}(t,x)$
such that, for all
$s\in\mathcal S$
,
$u_0(t,x,s) = \theta_{0}(t,x)$
. Now, if we want (A.3) for
$k = 0$
to have a solution
$u_1$
, this will induce a constraint, fixing the value of
$\theta_{0}$
. Indeed, this equation can be rewritten as
$Qu_{1} = \partial_t u_{0} - L_c u_{0}$
. The left-hand side averages to 0 with respect to
$\pi$
(for all fixed
$x\in\mathcal M t\geqslant 0$
), and thus we have to impose that
$\pi(\partial_t u_{0} - L_c u_{0}) = 0$
. This is equivalent to
\begin{equation} \partial_t \theta_{0}(t,x) - \bar F(x) \cdot{\nabla} \theta_{0}(t,x) = 0, \end{equation}
which is a transport equation with solution given by
$\theta_{0}(t,x) = \theta_{0}(0,\varphi_t(x))$
. In order to identify a suitable initial condition
$\theta_{0}(0,x)= \pi u_0(0,x)$
, we formally let
$\varepsilon$
and then t go to 0 in
\begin{align*} \pi P_t^\varepsilon f(x) = \pi f(x) + \int_0^t \pi L_c P_r^\varepsilon f( x)\,{\text{d}} r, \end{align*}
which is obtained by integrating (A.1) and using that
$\pi Q = 0$
. This yields
$\theta_0(0,x) = \pi f(x)$
and, as stated,
\begin{equation} P_t^{(0)}f(x,s) = u_{0}(t,x,s) = \pi f( \varphi_t(x)). \end{equation}
Now, reasoning by induction, we assume that for some
$k \geqslant 1$
we have constructed
$u_{k-1}$
satisfying
$\pi(\partial_t u_{k-1} - L_c u_{k-1}) = 0$
, from which we want to define
$u_k$
. Recalling the definition in (1.4) of the pseudo-inverse
$Q^{-1}$
, (A.3) is then equivalent to the existence of a function
$\theta_{k} \colon {\mathbb R}_+ \times {\mathbb R}^d \to {\mathbb R}$
such that
\begin{equation} u_{k}(t,x,s) = Q^{-1}(\partial_t u_{k-1} - L_c u_{k-1})(t,x,s) + \theta_{k}(t,x). \end{equation}
Once again, to find a suitable
$\theta_{k}$
we use (A.3) at order
$k+1$
, which we rewrite as
$Q u_{k+1} = \partial_t u_k - L_c u_k$
. As before, for fixed (t, x), since the left-hand side averages to 0 with respect to
$\pi$
, we impose
\begin{equation} \pi(\partial_t u_k - L_c u_k)(t,x) = 0. \end{equation}
Notice that
$\pi Q^{-1} = 0$
, so that, averaging (A.8) with respect to
$\pi$
and differentiating with respect to time,
\begin{equation} \pi \partial_t u_k = \partial_t \theta_{k}. \end{equation}
Injecting (A.10) and (A.8) into (A.9) yields
\begin{equation} \partial_t \theta_{k}(t,x) - \bar F(x) \cdot \nabla \theta_{k}(t,x) = \pi L_c {\mathbf{b}}_k(t,x), \end{equation}
where we set
${\mathbf{b}}_k = Q^{-1} ( \partial_t u_{k-1} - L_c u_{k-1})$
. This is again a transport equation, similar to (A.6), but with a source term. The solution is given by
\begin{equation} \theta_k(t,x) = \theta_k(0,\varphi_t(x)) + \int_0^t\pi L_c{\mathbf{b}}_k(r,\varphi_{t-r}(x))\,{\text{d}} r. \end{equation}
For now, by construction, for any choice of the function
$\theta_k(0,\cdot)$
, the function
$u_k$
defined by (A.8) where
$\theta_k$
is given by (A.12) satisfies (A.3) and (A.9). It remains to specify a suitable initial condition
$\theta_k(0,x)$
. To do so, we need to first look at the so-called boundary layer correction terms
$S^{(j)}$
.
Set
$v_k(t,x,s)=S_t^{(k)}f(x,s)$
. Then, (A.4) and (A.5) read
\begin{align} \partial_t v_0 & = Q v_0, \end{align}
\begin{align} \partial_t v_k & = Q v_k + L_c v_{k-1}. \end{align}
Equation (A.13) is simply solved as
$v_0(t,x,s) = \mathcal Q_t v_0(0,x,s)$
. Moreover, taking
$t = 0$
and letting
$\varepsilon \to 0$
in (2.3) yields
$v_0(0,x,s) + u_0(0,x,s) = f(x,s)$
, and hence we set
\begin{equation} v_0(t,x,s) = \mathcal Q_t f(x,s) - \pi f(x) , \end{equation}
which indeed solves (A.13). Next, assuming by induction that
$v_{k-1}$
has been defined for some
$k \geqslant 1$
, we can solve (A.14) to find
\begin{align*} v_k(t,x,s) = \mathcal Q_t v_k(0,x,s) + \int_0^t \mathcal Q_{t-r} L_c v_{k-1}(r,x,s)\,{\text{d}} r. \end{align*}
It remains to choose a suitable initial condition
$v_k(0,x)$
, which will be determined by the requirement of the long-time decay (2.2). Indeed, since
$\lim_{t\to\infty}\mathcal Q_t = \pi$
, (2.2) can only hold if
\begin{align*} 0 = \pi\bigg(v_k(0,x) + \int_0^{\infty}\mathcal Q_r L_c v_{k-1}(r,x)\,{\text{d}} r\bigg), \end{align*}
and therefore
\begin{equation} \pi v_k(0,x) = -\int_0^{\infty}\pi\mathcal Q_r L_c v_{k-1}(r,x)\,{\text{d}} r = -\int_0^{\infty}\pi L_c v_{k-1}(r,x)\,{\text{d}} r. \end{equation}
Also, from (2.3) applied with
$t=0$
, we get that
$v_k(0,x,s) + u_k(0,x,s)=0$
for all
$k\geqslant 1$
and, integrating (A.8) at
$t=0$
with respect to
$\pi$
,
$\theta_k(0,x) = \pi u_{k}(0,x)$
. Hence, the only choice of
$\theta_k(0,\cdot)$
that is compatible with (2.2) is
\begin{align*} \theta_k(0,x) = \int_0^{\infty}pi L_c v_{k-1}(r,x)\,{\text{d}} r. \end{align*}
Finally,
$v_k(0,x,s) = - u_k(0,x,s)$
is determined, again using (A.8) at
$t=0$
. At this point, we have completely determined a definition of
$P_t^{(k)}$
and
$S_t^{(k)}$
, which is the one that we use in the rest of the proof. It is such that (A.2), (A.3), (A.4), and (A.5) hold.
Step 2. We prove that the bounds (2.1) and (2.2) on
$P_t^{(k)}$
and
$S_t^{(k)}$
hold. We work by induction on k, starting with
$k=0$
. By compactness, recalling the definition of
$u_0$
in (A.7), it is straightforward that for all
$T > 0$
there exists
$C_0(T,j ,p)$
such that, for all
$j \geqslant 0$
and all
$f \in \mathcal{C}^{\infty}(\mathcal M\times\mathcal S)$
,
\begin{align*} \sup_{t \in [0,T]}\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{ \partial_t^p u_0}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j} \leq C_0(T,j ,p) \lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{f }\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+p }. \end{align*}
Let
$j \geqslant 0$
,
$\alpha \in {[\![} 1, N {]\!]}^j$
, and
$p \in {\mathbb{N}}$
. Then, by (A.15),
$\partial^{\alpha}_xv_0 = \mathcal Q_t(\partial^{\alpha}_xf - \pi(\partial^{\alpha}_xf))$
. Using the ergodicity condition in (1.3), we get, for all
$f \in \mathcal{C}^{\infty}$
,
$t \geqslant 0$
, and
$j\in{\mathbb{N}}$
,
$\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{v_0(t,\cdot)}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j} \leq C{\mathrm{e}}^{-\gamma t}\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert\,{f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j}$
.
For
$k\geqslant 1$
, reasoning by induction, we assume that there exist constants
$C_{k-1}(T,j ,p)$
and
$C_{k-1}(j)$
such that
\begin{align*} \sup_{t \in [0,T]} \lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{ \partial_t^p u_{k-1}(t,\cdot) }\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j } \leq C_{k-1}(T,j ,p) \lvert\kern-1.1pt\lvert\kern-1.1pt\lvert\,{f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+p+2(k-1) } \end{align*}
and, for all
$t \geqslant 0$
,
\begin{align*} \lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{v_{k-1}(t,\cdot)}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j} \leqslant C_{k-1}(j){\mathrm{e}}^{-\gamma t}(1 + t^{k-1})\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert\,{f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+2(k-1)} . \end{align*}
Since
$s,x\mapsto F_{s}(x)$
and its derivatives in x are uniformly bounded over
$\mathcal M\times\mathcal S$
, it is straightforward to check that that, for any
$j,p \in {\mathbb{N}}$
and
$T > 0$
, there exist C(j) and C(T, j, p) such that, for any
$g \in \mathcal{C}^{\infty}(\mathcal M)$
,
\begin{equation*} \lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{L_c g}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j} \leqslant C(j) \lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{g}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+1}, \qquad \sup_{t \in [0,T]}\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\partial_t^p(g\circ\varphi_t)}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j} \leqslant C(T,j,p)\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{g}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+p}, \end{equation*}
which we use extensively in the rest of this step. In the following, T, p, j, k are fixed, and we denote by C a constant which may change from line to line and depends only on T, p, j, k. First, for all
$t \leq T$
,
\begin{align*} \lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\partial_t^p(\theta_k(0,\cdot)\circ\varphi_t)}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j} & \leqslant C\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\theta_k(0,\cdot)}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+p} \\ & \leqslant C\int_0^{\infty}\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{L_c v_{k-1}(r,\cdot)}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+p}\,{\text{d}} r \\ & \leqslant C\int_0^{\infty}\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{v_{k-1}(r,\cdot)}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+p+1}\,{\text{d}} r \leq C\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert\,{f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+p+1+2(k-1)} \end{align*}
by induction. Next, using that
$\partial_t^p{\mathbf{b}}_k = Q^{-1}(\partial_t^{p+1}u_{k-1} - L_c(\partial_t^pu_{k-1}))$
, we get that, for all
$t \leq T$
,
\begin{align*} \lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\partial_t^p{\mathbf{b}}_k}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j} & \leqslant C\big(\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\partial_t^{p+1}u_{k-1}}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j} + \lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{L_c(\partial_t^p u_{k-1})}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j}\big) \\ & \leqslant C\big(\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\partial_t^{p+1}u_{k-1}}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j} + \lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\partial_t^p u_{k-1}}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+1}\big) \leq C\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert\,{f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+p+1+2(k-1)} \end{align*}
by induction. Now, from (A.12), for all
$t\leq T$
,
\begin{align*} \lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\theta_k(t,\cdot)}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j} & \leqslant \lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\theta_k(0,\cdot)\circ\varphi_t}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j} + \int_0^t\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{L_c{\mathbf{b}}_k(s,\cdot)\circ\varphi_{t-s}}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j}\,{\text{d}} s \\ & \leqslant C\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\theta_k(0,\cdot)}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j} + C\int_0^t\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{{\mathbf{b}}_k(s,\cdot)}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+1}\,{\text{d}} s \leq C\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert\,{f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+2+2(k-1)}. \end{align*}
To bound the derivatives in the time of
$ \theta_k$
, instead of using (A.12) it is simpler to work with (A.11), which gives, for
$p\geqslant 1$
,
\begin{align*} \lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\partial_t^{p}\theta_k(t,\cdot)}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j} & \leqslant \lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\pi L_c\partial_t^{p-1}\theta_k(t,\cdot)}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j} + \lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\pi L_c\partial_t^{p-1}{\mathbf{b}}_k(t,\cdot)}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j} \\ & \leqslant C\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\partial_t^{p-1}\theta_k(t,\cdot)}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+1} + C\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\partial_t^{p-1}{\mathbf{b}}_k(t,\cdot)}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+1} \\ & \leqslant C\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\partial_t^{p-1}\theta_k(t,\cdot)}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+1} + C\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert\,{f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+p+1+2(k-1)}. \end{align*}
Reasoning by induction on p yields
$\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\partial_t^{p}\theta_k(t,\cdot)}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j} \leq C\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert\,{f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+p+2+2(k-1)}$
. Gathering the previous bounds in (A.8) yields
\begin{align*} \lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\partial_t^pu_k(t,\cdot)}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j} \leqslant \lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\partial_t^{p}\theta_k(t,\cdot)}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j,0} + \lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\partial_t^p{\mathbf{b}}_k(t,\cdot)}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j} \leq C\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert\,{f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+p+2k}. \end{align*}
This concludes the study of
$u_k$
by induction. We now turn to the study of
$v_k$
. Using (A.16) and omitting the dependency on x, s to alleviate the notation, we decompose
$v_k$
as
\begin{align*} v_k(t) & = \mathcal Q_tv_k(0) + \int_0^t\mathcal Q_{t-r}L_cv_{k-1}(r)\,{\text{d}} r \\ & = \mathcal Q_t(v_k(0) - \pi v_k(0)) + \int_0^t\mathcal Q_{t-r}(L_cv_{k-1}(r) - \pi L_cv_{k-1}(r))\,{\text{d}} r - \int_t^{\infty}\pi L_cv_{k-1}(r)\,{\text{d}} r. \end{align*}
We have
$ \lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\mathcal Q_t(v_k(0) - \pi v_k(0))}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j} \leq C{\mathrm{e}}^{-\gamma t}\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{v_k(0)}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j} \leq C{\mathrm{e}}^{-\gamma t}\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert\,{f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+2k}, $
where we used that
$v_k(0) = - u_k(0)$
and the previous bound on
$u_k(0)$
. Similarly,
\begin{align*} \left\vert\kern-1.5pt\left\vert\kern-1.5pt\left\vert{\int_0^t\mathcal Q_{t-r}(L_cv_{k-1}(r) - \pi L_cv_{k-1}(r))\,{\text{d}} r}\right\vert\kern-1.5pt\right\vert\kern-1.5pt\right\vert _{j} & \leqslant C\int_0^t{\mathrm{e}}^{-\gamma(t-r)}\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{L_cv_{k-1}(r)}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j}\,{\text{d}} r \\ & \leqslant C\int_0^t{\mathrm{e}}^{-\gamma(t-r)}\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{v_{k-1}(r)}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+1}\,{\text{d}} r \\ & \leqslant C{\mathrm{e}}^{-\gamma t}(1+t^k)\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert\,{f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+1+2(k-1)}, \end{align*}
where we have used the induction hypothesis on
$v_{k-1}$
. Finally,
\begin{align*} \int_t^{\infty}\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{L_cv_{k-1}(r)}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j}\,{\text{d}} r & \leq C\int_t^{\infty}\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{v_{k-1}(r)}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+1}\,{\text{d}} r \\ & \leq C\int_t^{\infty}(1 + r^{k-1}){\mathrm{e}}^{-\gamma r}\,{\text{d}} r\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert\,{f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+1+2(k-1)} \\ & \leq C(1 + t^{k-1}){\mathrm{e}}^{-\gamma t}\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert\,{f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+1+2(k-1)}. \end{align*}
This proves the desired bounds on
$v_k$
. In particular, at this stage we have proved (2.1) and (2.2).
Step 3. We now bound the remainder
$R_{n,t}^{\varepsilon}$
given by (2.3) for a given
$n\geqslant 1$
. Introducing
$\eta_t = (\partial_t - L_\varepsilon)R_{n,t}^\varepsilon f$
for a given
$f\in\mathcal C^\infty$
, we see that, thanks to (A.2), (A.3), (A.4), and (A.5), all the low-order terms in
$\varepsilon$
vanish (as designed) so that
\begin{equation*} \eta_t = (\partial_t - L_\varepsilon)\left( P_t^{\varepsilon}f - \sum_{k=0}^n\varepsilon^kP_t^{(k)}f + \sum_{k=0}^n\varepsilon^kS_{{t}/{\varepsilon}}^{(k)}\,f\right) = \varepsilon^n\big( L_cP_t^{(n)}f - \partial_tP_t^{(n)}f + L_cS_{t/\varepsilon}^{(n)}f\big). \end{equation*}
The bounds obtained in the previous step yield
$\sup_{t\in[0,T]}\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\eta_t}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j} \leq C\varepsilon^n\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert\,{f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+1+2n}$
for some C depending only on T, j, n. Interpreting
$R_{n,t}^\varepsilon \,f$
as the solution of the equation
$\partial_tR_{n,t}^\varepsilon f = L_\varepsilon R_{n,t}^\varepsilon f + \eta_t$
with
$R_{n,0}^\varepsilon \,f=0$
yields the Feynman–Kac representation
\begin{align*}R_{n,t}f(x,s) = \mathbb E_{x,s}\bigg(\int_0^t\eta_r(X(r),\sigma(r))\,{\text{d}} r\bigg), \end{align*}
see [Reference Davis11, Theorem 6.3]. The bounds on
$\eta_t$
immediately yield
\begin{align*}\sup_{t\in[0,T]}\|R_{n,t}^\varepsilon f\|_\infty \leq C\varepsilon^n\|f\|_{1+2n} \end{align*}
for some C depending only on T, n.
Now, to get similar bounds for the derivatives in space of
$R_{n,t}^\varepsilon f$
, we work by induction on j, assuming that we have already obtained that
\begin{equation} \sup_{t\in[0,T]}\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{R_{n,t}^\varepsilon f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j'} \leq C\varepsilon^n\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert\,{f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j'+1+2n} \end{equation}
for all
$j'<j$
for some
$j\geqslant 1$
and some
$C>0$
. Indeed, then, considering a multi-index
$\alpha \in {[\![} 1,d{]\!]}^j$
, differentiating the equation
$\partial_tR_{n,t}^\varepsilon = L_\varepsilon R_{n,t}^\varepsilon f + \eta_t$
yields
\begin{equation} \partial_t\partial_x^\alpha R_{n,t}^\varepsilon f = L_\varepsilon\partial_x^\alpha R_{n,t}^\varepsilon f + \partial_x^\alpha\eta_t + \sum_{|\alpha'|\leq j}B_{\alpha'}\partial_x^{\alpha'}R_{n,t}^\varepsilon f , \end{equation}
where, for all multi-index
$\alpha'$
,
$B_{\alpha'}(x,s)$
is a matrix whose coefficients are some derivatives in x of
$F_s$
. In other words, considering a vector
$G_t$
whose coefficients are all the partial derivatives in x of
$R_{n,t}^\varepsilon f$
of order j, then
$G_t$
solves an equation of the form
\begin{equation} \partial_t G_t = L_\varepsilon G_t + B'G_t + \eta_t^{\prime}, \end{equation}
where
$L_\varepsilon$
acts coefficient-wise on
$G_t$
, the coefficients of the matrix B
′(x, s) are derivatives in x of
$F_s$
, and
$\eta_t^{\prime}$
gathers
$\partial_x^\alpha\eta_t$
and all the terms in (A.18) involving derivatives of
$R_{n,t}^\varepsilon f$
of order
$|\alpha'| \lt j$
. In particular, thanks to the bounds in (2.1) and (2.2) established in Step 2 and to the induction assumption, we have
$\sup_{t\in[0,T]}\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{\eta_t^{\prime}}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{\infty} \leq C\varepsilon^n\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert\,{f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+1+2n}$
for some
$C>0$
depending on T, n, j. We again use the Feynman–Kac formula for
$G_t$
based on (A.19), which reads
\begin{align*}G_t(x,s) = \mathbb E_{x,s}\bigg(\int_0^tE_r{\eta_{t-r}^{\prime}}(X(r),\sigma(r))\,{\text{d}} r\bigg), \end{align*}
where
$(E_t)_{t\geqslant 0}$
is the solution of the matrix-valued ODE
$\partial_t E_t = E_tB'(X(t),\sigma(t))$
(for completeness, we provide a proof of this formula in Appendix B). Since B
′ is uniformly bounded, so is
$E_r$
over
$r\in[0,T]$
, and thus
$\sup_{t\in[0,T]}\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{G_t}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{\infty} \leq C\varepsilon^n\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert\,{f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+1+2n}$
for some
$C>0$
depending on T, n, j. Since this holds for all
$\alpha \in{[\![} 1,d{]\!]}^{j}$
, this concludes the proof by induction of (A.17) for all j
′. To conclude, using that
\begin{align*}R_{n,t}^\varepsilon \,f = R_{n+1,t}^\varepsilon f + \varepsilon^{n+1}P_t^{(n+1)}f + \varepsilon^{n+1}S_{t/\varepsilon}^{(n+1)}f, \end{align*}
we get that, for all
$j\geqslant 0$
,
\begin{equation*} \lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{R_{n,t}^\varepsilon \,f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_j \leq \lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{R_{n+1,t}^\varepsilon \,f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_j + \varepsilon^{n+1}\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{P_t^{(n+1)}\,f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_j + \varepsilon^{n+1}\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert{S_{t/\varepsilon}^{(n+1)}\,f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_j \leq C\varepsilon^{n+1}\lvert\kern-1.1pt\lvert\kern-1.1pt\lvert\,{\,f}\rvert\kern-1.1pt\rvert\kern-1.1pt\rvert_{j+3+2n}, \end{equation*}
where we used (2.1), (2.2), and (A.17) (for
$n+1$
). This concludes the proof of (2.4), and thus the proof of Proposition 2.1.
Appendix B. Feynman–Kac formula
Lemma B.1.
Let L be a Markov generator on a set
$\mathcal S'$
. For
$n\geqslant 1$
, consider
$f_t(z) = (f_{1,t}(z),\dots,f_{n,t}(z)) \in {\mathbb R}^n$
for
$z\in\mathcal S'$
,
$t\geqslant 0$
, a solution of
\begin{equation*} \partial_tf_t(z) = Lf_t(z) + A_t(z)f_t(z) + c_t(z), \quad z\in\mathcal S',\, t\geqslant 0, \end{equation*}
where
$(t,z)\mapsto A$
is a bounded
$n\times n$
matrix field,
$(t,z)\mapsto c$
is a bounded vector field, and
$Lf_t$
is to be understood component-wise. Then, for all
$t\geqslant 0$
and
$z\in\mathcal S'$
,
\begin{align*}f_t(z) = \mathbb E\!\left( E_tf_{0}(Z_t)\right) + \int_0^t\mathbb E\!\left( E_rc_{t-r}(Z_r)\right)\,{\text{d}} r, \end{align*}
where
$(Z_t)_{t\geqslant 0}$
is a Markov process associated to L with
$Z_0=z$
, and
$(E_r)_{r\in[0,t]}$
is the solution of the
$n\times n$
matrix-valued random ODE
$\partial_r E_r = E_r A_{t-r}(Z_r) $
with
$E_0=I_n$
, provided this is well-defined almost surely.
Proof. Fix
$t>0$
,
$z\in\mathcal S'$
. Then
$(Z_r,E_r)_{r\geqslant0}$
given in the statement of the lemma is a time-inhomogeneous Markov process with generator
\begin{align*}\mathcal L_r g(z,e) = e A_{t-r}(z)\cdot {\nabla}_e g(z,e) + L g(z,e), \end{align*}
and thus, considering the vector-valued function
$h(r,z,e)=e f_{t-r}(z)$
, we end up with
\begin{align*} \partial_r\mathbb E\!\left( E_rf_{t-r}(Z_r)\right) & = \partial_r\mathbb E\!\left( h(r,Z_r,E_r)\right) \\ & = \mathbb E\!\left(\left(\partial_r + \mathcal L_r\right) h(r,Z_r,E_r)\right) \\ & = \mathbb E\!\left( E_s\!\left( - \partial_r + A_{t-r} + L\right) f_{t-r}(Z_r)\right) \\ & = -\mathbb E\!\left( E_rc_{t-r}(Z_r)\right) . \end{align*}
Using that
$E_0=I$
, the conclusion follows from
\begin{equation*} f_t(z) = \mathbb E\left( E_0f_t(Z_0)\right) = \mathbb E\left( E_tf_0(Z_t)\right) - \int_0^t\partial_r\mathbb E\left( E_rf_{t-r}(Z_r)\right)\,{\text{d}} r. \end{equation*}
Appendix C. Proof of Lemma 3.1
Proof. We can write
$\sigma^\varepsilon(t) = \sigma(t/\varepsilon)$
, and then drop the superscript
$\varepsilon$
to alleviate the notation; in other words, without loss of generality it is sufficient to treat the case
$\varepsilon=1$
(up to replacing
$\gamma$
by
$\gamma/\varepsilon$
in Assumption 1.1).
For
$s \in \mathcal{S}$
, let
$F_s(x) = x\!\left(a_{10}^s - a_{11}^s x\right)$
. By the definition of
$p_0$
and
$p_1$
we have that, for all
$s\in \mathcal{S}$
,
$F_s(x) > 0$
for
$x \in (0,p_0)$
and
$F_s(x) < 0$
for
$x > p_1$
, which implies that for all
$X_0 \neq 0$
there exists a time
$T_0$
such that, for all
$t \geqslant T_0$
,
$X_t \in [p_0, p_1]$
. Now, on the state space
$E= [p_0, p_1] \times \mathcal{S}$
, we introduce the metric
\begin{align*} d((x,s),(y,s')) = 1_{ s \neq s'} + 1_{s = s'} \frac{| x - y|}{p_1 -p_0}, \end{align*}
and we consider on the space of probability measures on E the associated Wasserstein distance defined for all
$\mu, \nu$
by
\begin{align*} \mathcal{W}_d ( \mu, \nu) = \inf_{\Gamma} \int d((x,s), (y,s')) \,{\text{d}}\Gamma( (x,s), (x,s')), \end{align*}
where the infimum runs over all the coupling measures of
$\mu$
and
$\nu$
. We will show that there exist
$C,\delta > 0$
such that, for all
$(x,s), (y,s') \in E$
and all
$t \geqslant 0$
,
\begin{equation} \mathcal{W}_d ( \delta_{(x,s)} P_t, \delta_{(y,s^{\prime})} P_t ) \leq C {\mathrm{e}}^{ - \delta t} d( (x,s), (y,s^{\prime})), \end{equation}
where
$P_t$
stands for
$P_t^{1}$
, the semigroup of
$(X, \sigma)$
at time t. The above inequality implies Lemma 3.1 by classical arguments, since the space of probability measures on E endowed with the Wasserstein metric
$\mathcal{W}_d$
is complete.
We first prove (C.1) for points (x, s) and (y, s
′) such that
$s'=s$
. In that case, a coupling of
$\delta_{(x,s)} P_t$
and
$\delta_{(y,s)} P_t$
is given by the random variables
$((X_t^{x,s}, \sigma^s_t),(X_t^{y,s}, \sigma^s_t))$
where, for all
$T \geqslant 0$
,
\begin{align*} X_T^{x,s} = x + \int_0^T F_{\sigma^s(u)}(X_u^{x,s})\,{\text{d}} u, \qquad X_T^{x,s} = y + \int_0^T F_{\sigma^s(u)}(X_u^{y,s})\,{\text{d}} u. \end{align*}
In other words,
$X_t^{x,s}$
and
$X_t^{y,s}$
denote the solution to (3.8) with respective initial conditions x and y and constructed with the same realisation of the process
$(\sigma(u)_{u \geqslant 0}$
starting from s.
Lemma C.1.
Almost surely, for all
$x,y \in [p_0, p_1]$
,
$s \in \mathcal{S}$
, and
$t\geqslant 0$
,
\begin{equation} | X_t^{x,s} - X_t^{y,s} | \leq \frac{p_1}{p_0}{\mathrm{e}}^{ - \eta t} | x - y|, \end{equation}
where
$\eta = p_0\inf_{s \in \mathcal{S}}a_{11}^s > 0$
. This immediately yields
\begin{align*} \mathcal{W}_d(\delta_{(x,s)}P_t^{\varepsilon},\delta_{(y,s)}P_t^{\varepsilon}) \leq \frac{p_1}{p_0}{\mathrm{e}}^{-\eta t}d((x,s),(y,s)). \end{align*}
Proof. Let
$s \in \mathcal{S}$
and write
$\alpha_t = a^{\sigma^s(t)}_{10}$
,
$\beta_t = a^{\sigma^s(t)}_{11}$
. Let
$\varphi_t(z)$
be the solution of the differential equation
\begin{equation} \dot z_t = \alpha_t - \beta_t{\mathrm{e}}^{z_t}, \quad z_0=z. \end{equation}
Then, for all
$z,z^{\prime} \geqslant \ln(p_0)$
, and all
$t \geqslant 0$
, we have
\begin{equation} |\varphi_t(z) - \varphi_t(z^{\prime})|\leq \exp\bigg\{{-}p_0\int_0^t\beta_u\,{\text{d}} u\bigg\}|z - z^{\prime} |. \end{equation}
Indeed, the associated variational equation is
\begin{align*} \frac{{\text{d}}}{{\text{d}} t}(\partial_z\varphi_t(z)) = -\beta_u(\partial_z\varphi_t(z)){\mathrm{e}}^{\varphi_t(z)}, \end{align*}
and thus
\begin{equation*} \partial_z\varphi_t(z) = \exp\bigg({-}\int_0^t\beta_u{\mathrm{e}}^{\varphi_u(z)}\,{\text{d}} u\bigg) \leq \exp\bigg({-}p_0\int_0^t\beta_u\,{\text{d}} u\bigg), \end{equation*}
where the inequality comes from the fact that
$z \geqslant\ln(p_0)$
implies
$\varphi_t(z) \geqslant\ln(p_0)$
for all
$t \geqslant 0$
.
Now, consider the differential equation
\begin{equation} \dot x_t = x_t ( \alpha_t - \beta_t x_t), \quad x_0 = x, \end{equation}
and set
$z_t = \ln(x_t)$
. Then,
$z_t$
solves (C.3) with initial condition
$\ln\!(x)$
. Denoting by
$\psi_t(x)$
the solution to (C.5), using (C.4), we have, for all
$x,y \in [p_0, p_1]$
and all
$t \geqslant 0$
,
\begin{align*} | \psi_t(x) - \psi_t(y) | = | {\mathrm{e}}^{\varphi_t(\ln(x))} - {\mathrm{e}}^{\varphi_t(\ln(y))}| & \leq p_1 |\varphi_t(x) - \varphi_t(y)| \\ & \leq p_1 \exp\bigg\{{-}p_0\int_0^t\beta_u\,{\text{d}} u\bigg\}| \ln\!(x) - \ln\!(y) | \\ & \leq \frac{p_1}{p_0}\exp\bigg\{{-}p_0\int_0^t\beta_u\,{\text{d}} u\bigg\}|x - y|. \end{align*}
This entails the result since
$X_t^{x,s}$
and
$X_t^{y,s}$
solve (C.5) with the respective initial conditions x and y.
We now tackle the case where the initial conditions of
$\sigma$
in the two chains are distinct:
$s\neq s' \in\mathcal S$
. Let
$t>0$
. Thanks to Assumption 1.1, there exists a coupling
$\big(\sigma_{t/2}^s,\sigma_{t/2}^{s'}\big)$
of
$\delta_{s}\mathcal Q_{t/2}$
and
$\delta_{s'}\mathcal Q_{t/2}$
with
$\mathbb P\big(\sigma_{t/2}^{s} \neq \sigma_{t/2}^{s'}\big) \leqslant C{\mathrm{e}}^{-\gamma t}$
. Fix
$x,y\in [p_0,p_1]$
, and let
$X_{t/2}^{x,s}$
be such that
$\big(\sigma_{t/2}^s,X_{t/2}^{x,s}\big)$
is distributed according to
$\delta_{x,s}P_{t/2}^{\varepsilon}$
(which is possible since the regular version of the conditional laws exists in Polish spaces; see, e.g., [Reference Kallenberg19, Theorem 5.3]), and similarly for
$X_{t/2}^{y,s'}$
. Then, we define
$\big(\sigma_r^s,X_r^{x,s},\sigma_r^{s'},X_r^{y,s^{\prime}}\big)_{r\geqslant t/2}$
as follows: under the event
$\big\{\sigma_{t/2}^s = \sigma_{t/2}^{s^{\prime}}\big\}$
, we let
$(\sigma_{r}^s)_{r\geqslant t/2}$
be a Markov process associated to
$(\mathcal Q_r)_{r\geqslant 0}$
with initial condition
$\sigma_{t/2}^{s}$
, and we set
$\sigma_{r}^{s^{\prime}}=\sigma_r^{s}$
for all
$r\geqslant t/2$
; otherwise, we define these processes as two independent processes associated to
$(\mathcal Q_r)_{r\geqslant 0}$
with respective initial conditions
$\sigma_{t/2}^s$
and
$\sigma_{t/2}^{s^{\prime}}$
. In both cases, we define
$\big(X_r^{x,s},X_r^{y,s^{\prime}}\big)_{r\geqslant t/2}$
as solutions to
\begin{align*} X_r^{x,s} = X_{t/2}^{x,s} + \int_{t/2}^r F_{\sigma^s(u)}\big(X_u^{x,s}\big)\,{\text{d}} u, \qquad X_r^{y,s^{\prime}} = X_{t/2}^{y,s^{\prime}} + \int_{t/2}^r F_{\sigma^{s^{\prime}}(u)}\big(X_u^{y,s^{\prime}}\big)\,{\text{d}} u. \end{align*}
Then
$\big(\sigma_t^s,X_t^{x,s},\sigma_t^{s^{\prime}},X_t^{y,s^{\prime}}\big)$
is a coupling of
$\delta_{(x,s)}P_t^{\varepsilon}$
and
$\delta_{(y,s)}P_t^{\varepsilon}$
with, using (C.2) and that
$\big|X_{t/2}^{x,s} - X_{t/2}^{x,s}\big| \leqslant p_1-p_0 $
almost surely,
\begin{align*} \mathbb{E}\big(d\big(\big(X_t^{x,s},\sigma_t^s\big), (X_t^{y,s^{\prime}},\sigma_t^{s^{\prime}})\big)\big) & = \mathbb P\big(\sigma_{t/2}^{s} \neq \sigma_{t/2}^{s^{\prime}}\big) + \mathbb{E}\bigg(\frac{|X_t^{x,s} - X_t^{y,s^{\prime}}|}{p_1-p_0}1_{\sigma_{t/2}^{s} = \sigma_{t/2}^{s^{\prime}}}\bigg) \\ & \leq C{\mathrm{e}}^{-\gamma t/2} + \frac{p_1}{p_0}{\mathrm{e}}^{-\eta t/2} \\ & \leq \bigg( C + \frac{p_1}{p_0}\bigg){\mathrm{e}}^{-(\gamma \wedge \eta) t/2}d\left((x,s),(y,s^{\prime})\right). \end{align*}
As a conclusion, we have obtained that (C.1) holds for all
$(x,s),(y,s^{\prime}) \in [p_0,p_1]\times \mathcal S$
for some constants
$C,\delta>0$
, which completes the proof.
Acknowledgements
We wish to thank two anonymous referees for their useful comments.
Funding information
The research of P. Monmarché is supported by the French ANR grant SWIDIMS (ANR-20-CE40-0022).
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.
