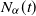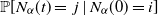1. Introduction
The birth and death processes have been extensively studied in various areas of both probability theory and its applications in population models, epidemiology, queuing theory, and engineering, to name just a few. Two fundamental aspects related to its analysis are the representation of the transition probabilities that model the evolution of the system and the asymptotic behavior after a long time.
Since many processes exhibit the phenomenon of long memory, a Markov process does not seem at all appropriate, so that fractional models appear to be more precise. Time-fractional models in the context of anomalous diffusion were studied by Orsingher in [Reference Orsingher and Beghin21] and [Reference Orsingher and Beghin22], where he analyzed the time-fractional telegraph equation and a fractional diffusion equation, respectively. Previous results for fractional birth and death processes can be found in the articles of Orsingher [Reference Orsingher and Polito23] for the linear case, Meerschaert [Reference Meerschaert, Nane and Vellaisamy20] for the fractional Poisson process, and Jumarie [Reference Jumarie13] for a pure birth and death process with multiple births. Surprisingly, none of them provide representations for an arbitrary time-fractional birth and death process, and consequently results concerning the asymptotic behavior for this class of process are not available in the literature.
For Markov processes, the study of the number of survivors after a long time started with the early work of Kolmogorov in 1938. Later in 1947, Yaglom [Reference Yaglom25] showed that the limit behavior of sub-critical branching processes conditioned to survival was given by a proper distribution. In 1965, Darroch and Seneta [Reference Darroch and Seneta7] began the study of quasi-stationary distributions (QSDs) on finite-state irreducible Markov chains, and Seneta and Vere-Jones [Reference Seneta and Vere-Jones24] in 1966 did it for Markov chains with countable states. A very important publication is that of Van Doorn in 1991 [Reference van Doorn8], which states a criterion to determine the existence and uniqueness of QSDs for birth and death chains. More recent results about the existence and uniqueness of QSDs can be found in [Reference van Doorn9] and [Reference van Doorn and Pollett10].
For diffusion processes on the half-line, the first work is due to Mandl [Reference Mandl15], who studied the existence of a QSD on the half-line for
![]() $+\infty$
being a natural boundary according to Feller’s classification. Subsequently many results on the existence of QSDs and limit laws for one-dimensional diffusions killed at 0 were provided by Ferrari [Reference Ferrari, Kesten, Martínez and Picco11], Collet, Martínez, and San Martín [Reference Collet, Martínez and San Martín5], and Martínez and San Martín [Reference Martínez and San Martín16, Reference Martínez, Picco and San Martín17].
$+\infty$
being a natural boundary according to Feller’s classification. Subsequently many results on the existence of QSDs and limit laws for one-dimensional diffusions killed at 0 were provided by Ferrari [Reference Ferrari, Kesten, Martínez and Picco11], Collet, Martínez, and San Martín [Reference Collet, Martínez and San Martín5], and Martínez and San Martín [Reference Martínez and San Martín16, Reference Martínez, Picco and San Martín17].
Most of these works are based on studying the spectral decomposition of the infinitesimal operator associated with the process. Applying similar ideas, we can study the asymptotic behavior of time-fractional models, which is precisely one of the main objectives of this article.
This article is organized as follows. In Section 2 we present the model description. More specifically, we introduce the system of time-fractional equations that governs the transition probabilities. In Section 3 two equivalent characterizations are shown: the first one is a time-changed birth and death process, whereas the second one is a Markov renewal process. In Section 4 we follow a different approach based on a spectral representation of the transition probabilities to study the quasi-limiting behavior of the process conditioned not to be killed. In Section 5.1 we study the concept of quasi-stationary distributions, proving that the quasi-limiting distribution and quasi-stationary distribution are not the same. Finally, in Section 6, we apply our main theorems to the linear model.
2. Model formulation
We let
![]() $N_{\alpha}(t)$
,
$N_{\alpha}(t)$
,
![]() $t \geq 0$
denote the fractional birth and death process killed at zero. The transition probabilities denoted by
$t \geq 0$
denote the fractional birth and death process killed at zero. The transition probabilities denoted by
are governed by the time-fractional system of differential equations (coprovidedonly called the system of backward equations)
 \begin{equation} \begin{aligned}\mathbb{D}^\alpha p_{i,j,\alpha}(t)&= \mu_ip_{i-1,j,\alpha}(t)-(\lambda_i+\mu_i)p_{i,j,\alpha}(t)+\lambda_i p_{i+1,j,\alpha}(t),\quad j \geq 0, i \geq 1,\\[5pt]p_{0,j,\alpha}(t)&= 0, \quad j \geq 1.\end{aligned}\end{equation}
\begin{equation} \begin{aligned}\mathbb{D}^\alpha p_{i,j,\alpha}(t)&= \mu_ip_{i-1,j,\alpha}(t)-(\lambda_i+\mu_i)p_{i,j,\alpha}(t)+\lambda_i p_{i+1,j,\alpha}(t),\quad j \geq 0, i \geq 1,\\[5pt]p_{0,j,\alpha}(t)&= 0, \quad j \geq 1.\end{aligned}\end{equation}
As usual, the values
![]() $\lambda_i>0, \mu_i>0$
(with the convention
$\lambda_i>0, \mu_i>0$
(with the convention
![]() $\mu_0=\lambda_0=0$
) are the birth rates and death rates respectively, whereas the parameter
$\mu_0=\lambda_0=0$
) are the birth rates and death rates respectively, whereas the parameter
![]() $\alpha \in (0,1]$
determines the order of the Caputo fractional operator
$\alpha \in (0,1]$
determines the order of the Caputo fractional operator
![]() $\mathbb{D}^\alpha (\!\cdot\!)$
, defined as
$\mathbb{D}^\alpha (\!\cdot\!)$
, defined as
 \begin{align*}\mathbb{D}^{\alpha} f(t)&= \dfrac{1}{\Gamma(1-{\alpha})}\int_0^t \dfrac{f^{\prime}(u)}{(t-u)^{\alpha}}\,{\textrm{d}} u,\quad \alpha \in (0,1),\\[5pt]\mathbb{D}^{1} f(t)&= f^{\prime}(t), \quad \alpha =1.\end{align*}
\begin{align*}\mathbb{D}^{\alpha} f(t)&= \dfrac{1}{\Gamma(1-{\alpha})}\int_0^t \dfrac{f^{\prime}(u)}{(t-u)^{\alpha}}\,{\textrm{d}} u,\quad \alpha \in (0,1),\\[5pt]\mathbb{D}^{1} f(t)&= f^{\prime}(t), \quad \alpha =1.\end{align*}
In particular, when
![]() $\alpha=1$
the operator is just the derivative and
$\alpha=1$
the operator is just the derivative and
![]() $N_1(t)$
is the classical birth and death process. The matrix formulation for the system of equations (2.1) is
$N_1(t)$
is the classical birth and death process. The matrix formulation for the system of equations (2.1) is
where P(t) is the matrix with coefficients
![]() $p_{i,j,\alpha}(t)$
,
$p_{i,j,\alpha}(t)$
,
![]() $i \geq 1$
,
$i \geq 1$
,
![]() $j \geq 1$
. The components
$j \geq 1$
. The components
![]() $q_{i,j}$
,
$q_{i,j}$
,
![]() $i \geq 1$
,
$i \geq 1$
,
![]() $j \geq 1$
of the matrix
$j \geq 1$
of the matrix
![]() $Q^{(a)}$
are
$Q^{(a)}$
are
 \begin{align}q_{i,j}= \begin{cases}-(\lambda_i+\mu_i) & \text{if $ i=\,j$,} \\[5pt]\mu_i & \text{if $i=\,j+1$,} \\[5pt] \lambda_i & \text{if $ i=\,j-1 $.}\end{cases}\end{align}
\begin{align}q_{i,j}= \begin{cases}-(\lambda_i+\mu_i) & \text{if $ i=\,j$,} \\[5pt]\mu_i & \text{if $i=\,j+1$,} \\[5pt] \lambda_i & \text{if $ i=\,j-1 $.}\end{cases}\end{align}
We recall that
![]() $p_{0,j,\alpha}(t)=0$
for all
$p_{0,j,\alpha}(t)=0$
for all
![]() $j \geq 1$
. This fact makes the matrix formulation consistent with the system of fractional differential equations (2.1). The initial condition is the Kronecker delta
$j \geq 1$
. This fact makes the matrix formulation consistent with the system of fractional differential equations (2.1). The initial condition is the Kronecker delta
![]() $p_{i,j,\alpha}(0)=\delta_{i,j}$
.
$p_{i,j,\alpha}(0)=\delta_{i,j}$
.
3. Two equivalent characterizations
In this section we introduce the representation of the process
![]() $N_\alpha (t)$
as a standard birth and death chain changed in time, i.e.
$N_\alpha (t)$
as a standard birth and death chain changed in time, i.e.
![]() $N_\alpha (t)=N_1(L^{(\alpha)}({t}))$
, where
$N_\alpha (t)=N_1(L^{(\alpha)}({t}))$
, where
![]() $L^{(\alpha)}({t})$
is the inverse of a stable subordinator. Also, we get a representation as a Markov renewal process in the general case. To make this work self-contained, we first introduce a brief summary of the stable subordinators and its inverse.
$L^{(\alpha)}({t})$
is the inverse of a stable subordinator. Also, we get a representation as a Markov renewal process in the general case. To make this work self-contained, we first introduce a brief summary of the stable subordinators and its inverse.
3.1. The stable subordinator and its inverse
A subordinator
![]() $D^{(\alpha)}(t)$
,
$D^{(\alpha)}(t)$
,
![]() $t \geq 0$
is a one-dimensional Levy process such that its trajectories are non-decreasing with probability 1. We say that a subordinator is stable when the Laplace transform of
$t \geq 0$
is a one-dimensional Levy process such that its trajectories are non-decreasing with probability 1. We say that a subordinator is stable when the Laplace transform of
![]() $D^{(\alpha)}(t)$
satisfies
$D^{(\alpha)}(t)$
satisfies
Associated to a subordinator
![]() $D^{(\alpha)}(t)$
, we define the inverse process
$D^{(\alpha)}(t)$
, we define the inverse process
![]() $L^{(\alpha)}({t})$
,
$L^{(\alpha)}({t})$
,
![]() $t \geq 0$
as follows:
$t \geq 0$
as follows:
The process
![]() $L^{(\alpha)}({t})$
denotes the first time that
$L^{(\alpha)}({t})$
denotes the first time that
![]() $D^{(\alpha)}(\!\cdot\!)$
exceeds a level
$D^{(\alpha)}(\!\cdot\!)$
exceeds a level
![]() $t>0$
. It is clear that the trajectories of the process
$t>0$
. It is clear that the trajectories of the process
![]() $L^{(\alpha)}({t})$
are non-decreasing and moreover they are continuous (see Theorem 2 on page 642 of [Reference Bertoin2] for a technical proof concerning the modulus of continuity of
$L^{(\alpha)}({t})$
are non-decreasing and moreover they are continuous (see Theorem 2 on page 642 of [Reference Bertoin2] for a technical proof concerning the modulus of continuity of
![]() $L^{(\alpha)}({\cdot})$
). From (3.2) we can deduce that the finite-dimensional distributions of
$L^{(\alpha)}({\cdot})$
). From (3.2) we can deduce that the finite-dimensional distributions of
![]() $D^{(\alpha)}(t)$
and
$D^{(\alpha)}(t)$
and
![]() $L^{(\alpha)}({t})$
satisfy the identity
$L^{(\alpha)}({t})$
satisfy the identity
Equation (3.1) directly implies that the process
![]() $D^{(\alpha)}(t)$
is self-similar of index
$D^{(\alpha)}(t)$
is self-similar of index
![]() $1/\alpha$
, that is,
$1/\alpha$
, that is,
Moreover, from (3.3) and (3.4) we have that the process
![]() $L^{(\alpha)}({t})$
is self-similar of index
$L^{(\alpha)}({t})$
is self-similar of index
![]() $\alpha$
:
$\alpha$
:
For all
![]() $t>0$
, the distribution of
$t>0$
, the distribution of
![]() $D^{(\alpha)}(t)$
has only a density component, here denoted by
$D^{(\alpha)}(t)$
has only a density component, here denoted by
![]() $g_\alpha(\cdot,t)$
. In the same way, the inverse
$g_\alpha(\cdot,t)$
. In the same way, the inverse
![]() $L^{(\alpha)}({t})$
has only a density component
$L^{(\alpha)}({t})$
has only a density component
![]() $h_\alpha(\cdot,t)$
satisfying
$h_\alpha(\cdot,t)$
satisfying
Concerning the Laplace transform of
![]() $h_\alpha(u,t)$
we have the identities
$h_\alpha(u,t)$
we have the identities
 \begin{equation} \begin{aligned}\int_{0}^{\infty} \,{\textrm{e}}^{-s t} h_\alpha(u,t) \,{\textrm{d}} t&= s^{\alpha-1}\,{\textrm{e}}^{-us^\alpha},\\[5pt]\int_{0}^{\infty} \,{\textrm{e}}^{-su} h_\alpha(u,t) \,{\textrm{d}} u&= \mathcal{E}_{\alpha,1}(\!-\!st^\alpha),\end{aligned}\end{equation}
\begin{equation} \begin{aligned}\int_{0}^{\infty} \,{\textrm{e}}^{-s t} h_\alpha(u,t) \,{\textrm{d}} t&= s^{\alpha-1}\,{\textrm{e}}^{-us^\alpha},\\[5pt]\int_{0}^{\infty} \,{\textrm{e}}^{-su} h_\alpha(u,t) \,{\textrm{d}} u&= \mathcal{E}_{\alpha,1}(\!-\!st^\alpha),\end{aligned}\end{equation}
where
![]() $\mathcal{E}_{\alpha,1}(\!\cdot\!)$
is the Mittag–Leffler function formally defined as
$\mathcal{E}_{\alpha,1}(\!\cdot\!)$
is the Mittag–Leffler function formally defined as
 \begin{equation*}\mathcal{E}_{\alpha,1}(z)=\sum_{k \geq 0}\dfrac{z^k}{\Gamma(\alpha k+1)},\quad z \in \mathbb{C}.\end{equation*}
\begin{equation*}\mathcal{E}_{\alpha,1}(z)=\sum_{k \geq 0}\dfrac{z^k}{\Gamma(\alpha k+1)},\quad z \in \mathbb{C}.\end{equation*}
Finally, we emphasize that the increments of the process
![]() $L^{(\alpha)}({t})$
are dependent and non-stationary (see [Reference Meerschaert and Scheffler18, Corollaries 3.3 and 3.4] for more details).
$L^{(\alpha)}({t})$
are dependent and non-stationary (see [Reference Meerschaert and Scheffler18, Corollaries 3.3 and 3.4] for more details).
3.2. The time-changed process
The following theorem is a generalization from the previous ones given by Orsingher and Polito [Reference Orsingher and Polito23] for fractional linear birth and death process, and by Meerschaert [Reference Meerschaert and Straka19, Reference Meerschaert, Nane and Vellaisamy20] in the context of the time-fractional Brownian motion and the fractional Poisson processes, respectively. The arguments given below do not differ too much in comparison with the aforementioned references. However, we consider it important to write a detailed formal proof for the general case in order to introduce some techniques that will be used in the forthcoming sections.
Theorem 3.1. For all
![]() $\alpha \in (0,1)$
, the stochastic process
$\alpha \in (0,1)$
, the stochastic process
![]() $N_\alpha(t)$
,
$N_\alpha(t)$
,
![]() $t \geq 0$
admits a representation (in the sense ot the finite-dimensional distributions) of the form
$t \geq 0$
admits a representation (in the sense ot the finite-dimensional distributions) of the form
where
![]() $N_1(t)$
is a standard birth and death process and
$N_1(t)$
is a standard birth and death process and
![]() $L^{(\alpha)}({t})$
is the inverse of a stable subordinator independent of
$L^{(\alpha)}({t})$
is the inverse of a stable subordinator independent of
![]() $N_1(t)$
.
$N_1(t)$
.
Proof. Given fixed
![]() $i > 1$
and
$i > 1$
and
![]() $j \geq 0$
, for all
$j \geq 0$
, for all
![]() $t>0$
we have
$t>0$
we have
We will show that
![]() $\mathbb{P}_{}[N_1(L^{(\alpha)}({t}))=\,j\mid N_1(0)=i]$
defined above is the solution to the system of fractional differential equations (2.1) through its Laplace transform. We notice first that
$\mathbb{P}_{}[N_1(L^{(\alpha)}({t}))=\,j\mid N_1(0)=i]$
defined above is the solution to the system of fractional differential equations (2.1) through its Laplace transform. We notice first that
satisfies the identity
where
is the Laplace transform of
![]() $p_{i,j,1}(t)$
. This follows from the simple computation
$p_{i,j,1}(t)$
. This follows from the simple computation
 \begin{align} \Psi_{i,j}(s)&= \int_{0}^{\infty}\,{\textrm{e}}^{-s t}\biggl( \int_{0}^{\infty} p_{i,j,1}(u) h_\alpha(u,t) \,{\textrm{d}} u\biggr) \,{\textrm{d}} t\nonumber\\[5pt] &= \int_{0}^{\infty}p_{i,j,1}(u) \biggl( \int_{0}^{\infty} \,{\textrm{e}}^{-s t} h_\alpha(u,t) \,{\textrm{d}} t \biggr) \,{\textrm{d}} u\nonumber\\[5pt] &= s^{\alpha-1}\int_{0}^{\infty}p_{i,j,1}(u) \,{\textrm{e}}^{-s^\alpha u} \,{\textrm{d}} u\nonumber\\[5pt] &= s^{\alpha-1}\Phi_{i,j}(s^\alpha). \end{align}
\begin{align} \Psi_{i,j}(s)&= \int_{0}^{\infty}\,{\textrm{e}}^{-s t}\biggl( \int_{0}^{\infty} p_{i,j,1}(u) h_\alpha(u,t) \,{\textrm{d}} u\biggr) \,{\textrm{d}} t\nonumber\\[5pt] &= \int_{0}^{\infty}p_{i,j,1}(u) \biggl( \int_{0}^{\infty} \,{\textrm{e}}^{-s t} h_\alpha(u,t) \,{\textrm{d}} t \biggr) \,{\textrm{d}} u\nonumber\\[5pt] &= s^{\alpha-1}\int_{0}^{\infty}p_{i,j,1}(u) \,{\textrm{e}}^{-s^\alpha u} \,{\textrm{d}} u\nonumber\\[5pt] &= s^{\alpha-1}\Phi_{i,j}(s^\alpha). \end{align}
By keeping
![]() $j \geq 0$
fixed, it is not difficult to check that the sequence
$j \geq 0$
fixed, it is not difficult to check that the sequence
![]() $\Phi_{i,j}(s^\alpha)$
defined above satisfies the recurrence relation
$\Phi_{i,j}(s^\alpha)$
defined above satisfies the recurrence relation
By combining (3.6) and (3.7) we get
Since
![]() $\mathbb{P}_{}[N_1(L^{(\alpha)}({0}))=\,j\mid N_1(0)=i]=\delta_{i,j}$
, from (A.3) we have the identities
$\mathbb{P}_{}[N_1(L^{(\alpha)}({0}))=\,j\mid N_1(0)=i]=\delta_{i,j}$
, from (A.3) we have the identities
 \begin{align*} \dfrac{s \Psi_{i,j}(s)-\delta_{i,j}}{s^{1-\alpha}}&= s^\alpha \Psi_{i,j}(s)-s^{\alpha-1}\mathbb{P}_{}[N_1(L^{(\alpha)}({0}))=\,j\mid N_1(0)=i]\\[5pt]&= \int_{0}^{\infty} \,{\textrm{e}}^{-s t}\mathbb{D}^\alpha (\mathbb{P}_{}[N_1(L^{(\alpha)}({t}))=\,j\mid N_1(0)=i])\,{\textrm{d}} t.\end{align*}
\begin{align*} \dfrac{s \Psi_{i,j}(s)-\delta_{i,j}}{s^{1-\alpha}}&= s^\alpha \Psi_{i,j}(s)-s^{\alpha-1}\mathbb{P}_{}[N_1(L^{(\alpha)}({0}))=\,j\mid N_1(0)=i]\\[5pt]&= \int_{0}^{\infty} \,{\textrm{e}}^{-s t}\mathbb{D}^\alpha (\mathbb{P}_{}[N_1(L^{(\alpha)}({t}))=\,j\mid N_1(0)=i])\,{\textrm{d}} t.\end{align*}
By taking the inverse of the Laplace transform in (3.8), we conclude that
![]() $\mathbb{P}_{}[N_1(L^{(\alpha)}({t}))=\,j \mid N_1(0)=i]$
is the solution to (2.1), finishing the proof.
$\mathbb{P}_{}[N_1(L^{(\alpha)}({t}))=\,j \mid N_1(0)=i]$
is the solution to (2.1), finishing the proof.
Remark 3.1. The trajectories of the process
![]() $L^{(\alpha)}({t})$
,
$L^{(\alpha)}({t})$
,
![]() $t \geq 0$
are non-decreasing, so that Theorem 3.1 can be used to obtain the finite-dimensional distributions of
$t \geq 0$
are non-decreasing, so that Theorem 3.1 can be used to obtain the finite-dimensional distributions of
![]() $N_\alpha(t)$
,
$N_\alpha(t)$
,
 \begin{align*} & \mathbb{P}[N_\alpha(t_\ell)=\,j_\ell;\; 1 \leq \ell \leq n\mid N_\alpha(0)=i]\\[5pt] &\quad = \mathbb{P}[N_1(L^{(\alpha)}({t_\ell}))=\,j_\ell;\; 1 \leq \ell \leq n\mid N_\alpha(0)=i]\\[5pt] &\quad = \prod_{\ell=0}^{n-1}\mathbb{P}_{}[N_1(L^{(\alpha)}({t_{\ell+1}})-L^{(\alpha)}({t_\ell}))=\,j_{\ell+1}\mid N_\alpha(t_\ell)=\,j_\ell], \end{align*}
\begin{align*} & \mathbb{P}[N_\alpha(t_\ell)=\,j_\ell;\; 1 \leq \ell \leq n\mid N_\alpha(0)=i]\\[5pt] &\quad = \mathbb{P}[N_1(L^{(\alpha)}({t_\ell}))=\,j_\ell;\; 1 \leq \ell \leq n\mid N_\alpha(0)=i]\\[5pt] &\quad = \prod_{\ell=0}^{n-1}\mathbb{P}_{}[N_1(L^{(\alpha)}({t_{\ell+1}})-L^{(\alpha)}({t_\ell}))=\,j_{\ell+1}\mid N_\alpha(t_\ell)=\,j_\ell], \end{align*}
with the convention
![]() $j_0=i$
,
$j_0=i$
,
![]() $t_0=0$
.
$t_0=0$
.
3.3. Markov renewal process
Definition 3.1. Let
![]() $(X_n)_{n \in \mathbb{N}_0}$
be a Markov chain with states in
$(X_n)_{n \in \mathbb{N}_0}$
be a Markov chain with states in
![]() $\mathbb{N}_0$
and let
$\mathbb{N}_0$
and let
![]() $(\mathcal{S}_n)_{n \in \mathbb{N}_0}$
be a sequence of random times satisfying
$(\mathcal{S}_n)_{n \in \mathbb{N}_0}$
be a sequence of random times satisfying
![]() $\mathcal{S}_0=0$
,
$\mathcal{S}_0=0$
,
![]() $\mathcal{S}_n < \mathcal{S}_{n+1}$
for all
$\mathcal{S}_n < \mathcal{S}_{n+1}$
for all
![]() $n \geq 0$
. The stochastic process
$n \geq 0$
. The stochastic process
![]() $(X_n,\mathcal{S}_n)_{n \in \mathbb{N}_0}$
is called a Markov renewal process with state space
$(X_n,\mathcal{S}_n)_{n \in \mathbb{N}_0}$
is called a Markov renewal process with state space
![]() $\mathbb{N}_0=\{0,1,2,3,\ldots\}$
if the identity
$\mathbb{N}_0=\{0,1,2,3,\ldots\}$
if the identity
holds for all
![]() $j \in \mathbb{N}_0$
,
$j \in \mathbb{N}_0$
,
![]() $n \in \mathbb{N}_0$
, and
$n \in \mathbb{N}_0$
, and
![]() $t \geq 0$
. Here
$t \geq 0$
. Here
![]() $\mathcal{T}_{n+1}=\mathcal{S}_{n+1}-\mathcal{S}_n$
,
$\mathcal{T}_{n+1}=\mathcal{S}_{n+1}-\mathcal{S}_n$
,
![]() $n \geq 0$
are called the inter-arrival times. The stochastic process
$n \geq 0$
are called the inter-arrival times. The stochastic process
![]() $(Y(t))_{t \geq 0}$
defined as
$(Y(t))_{t \geq 0}$
defined as
![]() $ Y(t)=\sum_{n \geq 0} X_n \unicode{x1d7d9}_{\mathcal{S}_{n} \leq t<\mathcal{S}_{n+1}}$
is called the minimal semi-Markov process associated with
$ Y(t)=\sum_{n \geq 0} X_n \unicode{x1d7d9}_{\mathcal{S}_{n} \leq t<\mathcal{S}_{n+1}}$
is called the minimal semi-Markov process associated with
![]() $(X_n,\mathcal{S}_n)_{n \in \mathbb{N}_0}$
.
$(X_n,\mathcal{S}_n)_{n \in \mathbb{N}_0}$
.
Connected to a Markov renewal process, we consider the transition probabilities
and the kernel
The transition probabilities are recovered in the limit
![]() $t \rightarrow \infty$
,
$t \rightarrow \infty$
,
By introducing the notation
from a direct computation we get
and more generally, for all finite collections of times
![]() $0<t_1<t_2<\cdots <t_n$
,
$0<t_1<t_2<\cdots <t_n$
,
Equation (3.10) implies that the inter-arrival times
![]() $(\mathcal{T}_\ell)_{\ell \in \mathbb{N}_0}$
are conditionally independent given the Markov chain
$(\mathcal{T}_\ell)_{\ell \in \mathbb{N}_0}$
are conditionally independent given the Markov chain
![]() $(X_n)_{n \in \mathbb{N}_0}$
with a distribution
$(X_n)_{n \in \mathbb{N}_0}$
with a distribution
![]() $G_{X_\ell,X_{\ell+1}}(\!\cdot\!)$
depending only on
$G_{X_\ell,X_{\ell+1}}(\!\cdot\!)$
depending only on
![]() $X_\ell$
and
$X_\ell$
and
![]() $X_{\ell+1}$
. It is well known that a Markov renewal process is characterized by
$X_{\ell+1}$
. It is well known that a Markov renewal process is characterized by
![]() $G_{X_\ell,X_{\ell+1}}(t)$
and the transition probabilities
$G_{X_\ell,X_{\ell+1}}(t)$
and the transition probabilities
![]() $p_{i,j}$
. In addition, this is a Markov process if and only if
$p_{i,j}$
. In addition, this is a Markov process if and only if
![]() $G_{X_\ell,X_{\ell+1}}(t)=1-{\textrm{e}}^{-r(X_\ell,X_{\ell+1})t}$
, for some positive rate
$G_{X_\ell,X_{\ell+1}}(t)=1-{\textrm{e}}^{-r(X_\ell,X_{\ell+1})t}$
, for some positive rate
![]() $r(X_\ell,X_{\ell+1})$
. A more detailed review of Markov renewal processes can be found in [Reference Çinlar4, Chapter 8]. In the following theorem we provide a characterization for the sample paths of the process
$r(X_\ell,X_{\ell+1})$
. A more detailed review of Markov renewal processes can be found in [Reference Çinlar4, Chapter 8]. In the following theorem we provide a characterization for the sample paths of the process
![]() $(N_\alpha(t))_{t \geq 0}$
.
$(N_\alpha(t))_{t \geq 0}$
.
Theorem 3.2. For all
![]() $\alpha \in (0,1)$
the process
$\alpha \in (0,1)$
the process
![]() $(N_\alpha(t))_{t \geq 0}$
admits a representation of the form
$(N_\alpha(t))_{t \geq 0}$
admits a representation of the form
where
![]() $(X_n,\mathcal{S}_{n,\alpha})_{n \geq 0}$
is a Markov renewal process. The transition probabilities are
$(X_n,\mathcal{S}_{n,\alpha})_{n \geq 0}$
is a Markov renewal process. The transition probabilities are
and
![]() $\mathbb{P}[X_{n+1}=\,j\mid X_n=0]=\delta_{0,j}$
,
$\mathbb{P}[X_{n+1}=\,j\mid X_n=0]=\delta_{0,j}$
,
![]() $j \geq 0$
. Before
$j \geq 0$
. Before
![]() $L_0=\inf \{n>0\colon X_n=0 \}$
, the distributions of the inter-arrival times
$L_0=\inf \{n>0\colon X_n=0 \}$
, the distributions of the inter-arrival times
conditioned on
![]() $(X_\ell)_{0 \leq \ell \leq n}$
,
$(X_\ell)_{0 \leq \ell \leq n}$
,
![]() $1 \leq n \leq L_0-1$
, are independent and they follow a Mittag–Leffler distribution with parameter
$1 \leq n \leq L_0-1$
, are independent and they follow a Mittag–Leffler distribution with parameter
![]() $\lambda_{X_n}+\mu_{X_n}$
, that is,
$\lambda_{X_n}+\mu_{X_n}$
, that is,
Proof. We first construct the process associated with
![]() $\alpha=1$
. Let
$\alpha=1$
. Let
![]() $(X_n)_{n \in \mathbb{N}_0}$
be a Markov chain with transition probabilities given by (3.11) and the killing condition
$(X_n)_{n \in \mathbb{N}_0}$
be a Markov chain with transition probabilities given by (3.11) and the killing condition
![]() $\mathbb{P}[X_{n+1}=\,j\mid X_n=0]=\delta_{0,j}$
,
$\mathbb{P}[X_{n+1}=\,j\mid X_n=0]=\delta_{0,j}$
,
![]() $j \geq 1$
. Let
$j \geq 1$
. Let
![]() $(\mathcal{S}_{n,1})_{n \in \mathbb{N}_0}$
be an increasing sequence of random variables defined recursively as
$(\mathcal{S}_{n,1})_{n \in \mathbb{N}_0}$
be an increasing sequence of random variables defined recursively as
![]() $\mathcal{S}_{0,1}=0$
,
$\mathcal{S}_{0,1}=0$
,
![]() $\mathcal{S}_{n,1}=\sum_{\ell=1}^{n}\mathcal{T}_{\ell,1}$
,
$\mathcal{S}_{n,1}=\sum_{\ell=1}^{n}\mathcal{T}_{\ell,1}$
,
![]() $n \geq 1$
. Here the sequence of random variables
$n \geq 1$
. Here the sequence of random variables
![]() $\mathcal{T}_{n+1,1}=\mathcal{S}_{n+1,1}-\mathcal{S}_{n,1}$
satisfies
$\mathcal{T}_{n+1,1}=\mathcal{S}_{n+1,1}-\mathcal{S}_{n,1}$
satisfies
for all
![]() $t \geq 0$
,
$t \geq 0$
,
![]() $n \in \mathbb{N}_0$
and they are conditionally independent of
$n \in \mathbb{N}_0$
and they are conditionally independent of
![]() $(X_n)_{n \in \mathbb{N}_0}$
. Let us recall the definition
$(X_n)_{n \in \mathbb{N}_0}$
. Let us recall the definition
![]() $L_0=\inf \{n>0\colon X_n=0 \}$
. For
$L_0=\inf \{n>0\colon X_n=0 \}$
. For
![]() $0 \leq n \leq L_0-1$
, the distribution of
$0 \leq n \leq L_0-1$
, the distribution of
![]() $\mathcal{T}_{n+1,1}$
conditioned on
$\mathcal{T}_{n+1,1}$
conditioned on
![]() $(X_n,X_{n+1})$
is
$(X_n,X_{n+1})$
is
Note that the origin is an absorbing state, so we automatically have
![]() $X_\ell=0$
for all
$X_\ell=0$
for all
![]() $\ell \geq L_0$
and consequently
$\ell \geq L_0$
and consequently
![]() $N_1(t)=0$
for all
$N_1(t)=0$
for all
![]() $t \geq S_{L_0,1}$
. This implies that the sequence of random variables
$t \geq S_{L_0,1}$
. This implies that the sequence of random variables
![]() $(\mathcal{T}_{\ell,1})_{\ell \geq L_0+1}$
has no influence on the evolution of
$(\mathcal{T}_{\ell,1})_{\ell \geq L_0+1}$
has no influence on the evolution of
![]() $(N_1(t))_{t \geq S_{L_0,1}}$
. The process
$(N_1(t))_{t \geq S_{L_0,1}}$
. The process
![]() $(N_1(t))_{t \geq 0}$
is defined by
$(N_1(t))_{t \geq 0}$
is defined by
where
![]() $n \wedge L_0=\min\{n,L_0\}$
is a Markov process (see [Reference Çinlar4, Chapter 8, Section 3] for more details). Now, from Theorem 3.1, we know that
$n \wedge L_0=\min\{n,L_0\}$
is a Markov process (see [Reference Çinlar4, Chapter 8, Section 3] for more details). Now, from Theorem 3.1, we know that
![]() $(N_\alpha(t))_{t \geq 0}=(N_1(L^{(\alpha)}({t})))_{t \geq 0}$
is a time-changed version of
$(N_\alpha(t))_{t \geq 0}=(N_1(L^{(\alpha)}({t})))_{t \geq 0}$
is a time-changed version of
![]() $N_1(t)$
, so
$N_1(t)$
, so
where
![]() $L^{(\alpha)}({t})$
is the inverse of a stable subordinator
$L^{(\alpha)}({t})$
is the inverse of a stable subordinator
![]() $(D^{(\alpha)}(t))_{t \geq 0}$
independent of
$(D^{(\alpha)}(t))_{t \geq 0}$
independent of
![]() $(X_n,\mathcal{S}_{n,1})_{n \in \mathbb{N}_0}$
. The sequence
$(X_n,\mathcal{S}_{n,1})_{n \in \mathbb{N}_0}$
. The sequence
![]() $(\mathcal{S}_{n,\alpha})_{n \in \mathbb{N}_0}$
is defined via the equivalence
$(\mathcal{S}_{n,\alpha})_{n \in \mathbb{N}_0}$
is defined via the equivalence
Once the process
![]() $N_\alpha(t)$
is properly defined, the next step is to prove that the pairs
$N_\alpha(t)$
is properly defined, the next step is to prove that the pairs
![]() $(X_n,\mathcal{S}_{n,\alpha})_{ n \in \mathbb{N}_0}$
defined above form a Markov renewal process with the specified properties. To prove the condition (3.9), we first note that
$(X_n,\mathcal{S}_{n,\alpha})_{ n \in \mathbb{N}_0}$
defined above form a Markov renewal process with the specified properties. To prove the condition (3.9), we first note that
for any collection
![]() $0=t_0<t_1<\cdots t_n$
. From the definition of an inverse subordinator we have
$0=t_0<t_1<\cdots t_n$
. From the definition of an inverse subordinator we have
![]() $\mathcal{S}_{n,1} \leq L^{(\alpha)}({t}) \iff D^{(\alpha)}(\mathcal{S}_{n,1}) \leq t$
for all
$\mathcal{S}_{n,1} \leq L^{(\alpha)}({t}) \iff D^{(\alpha)}(\mathcal{S}_{n,1}) \leq t$
for all
![]() $t \geq 0$
, so that
$t \geq 0$
, so that
![]() $\mathcal{S}_{n,\alpha} = D^{(\alpha)}(\mathcal{S}_{n,1})$
in the finite distributional sense. This implies that for all
$\mathcal{S}_{n,\alpha} = D^{(\alpha)}(\mathcal{S}_{n,1})$
in the finite distributional sense. This implies that for all
![]() $n \geq 0$
$n \geq 0$
 \begin{align}\mathcal{S}_{n+1,\alpha}-\mathcal{S}_{n,\alpha}&= D^{(\alpha)}(\mathcal{S}_{n+1,1})-D^{(\alpha)}(\mathcal{S}_{n,1}) \notag \\[5pt]&= D^{(\alpha)}(\mathcal{T}_{n+1,1}+\mathcal{S}_{n,1})-D^{(\alpha)}(\mathcal{S}_{n,1}).\end{align}
\begin{align}\mathcal{S}_{n+1,\alpha}-\mathcal{S}_{n,\alpha}&= D^{(\alpha)}(\mathcal{S}_{n+1,1})-D^{(\alpha)}(\mathcal{S}_{n,1}) \notag \\[5pt]&= D^{(\alpha)}(\mathcal{T}_{n+1,1}+\mathcal{S}_{n,1})-D^{(\alpha)}(\mathcal{S}_{n,1}).\end{align}
Since
![]() $D^{(\alpha)}(\!\cdot\!)$
is a stable subordinator, (3.12) implies that
$D^{(\alpha)}(\!\cdot\!)$
is a stable subordinator, (3.12) implies that
![]() $\mathcal{T}_{n+1,\alpha}=\mathcal{S}_{n+1,\alpha}-\mathcal{S}_{n,\alpha}$
is independent of
$\mathcal{T}_{n+1,\alpha}=\mathcal{S}_{n+1,\alpha}-\mathcal{S}_{n,\alpha}$
is independent of
![]() $\mathcal{S}_{\ell,\alpha}=D^{(\alpha)}(\mathcal{S}_{\ell,1})$
,
$\mathcal{S}_{\ell,\alpha}=D^{(\alpha)}(\mathcal{S}_{\ell,1})$
,
![]() ${1 \leq \ell \leq n}$
and has the same distribution as
${1 \leq \ell \leq n}$
and has the same distribution as
![]() $D^{(\alpha)}(\mathcal{T}_{n+1,1})$
. But
$D^{(\alpha)}(\mathcal{T}_{n+1,1})$
. But
![]() $D^{(\alpha)}(\mathcal{T}_{n+1,1}) \leq t$
is equivalent to
$D^{(\alpha)}(\mathcal{T}_{n+1,1}) \leq t$
is equivalent to
![]() $\mathcal{T}_{n+1,1} \leq L^{(\alpha)}({t})$
. Consequently it follows that
$\mathcal{T}_{n+1,1} \leq L^{(\alpha)}({t})$
. Consequently it follows that
 \begin{align*} & \mathbb{P}[X_{n+1}=\,j,\mathcal{T}_{n+1,\alpha} \leq t\mid (X_\ell=i_\ell,\mathcal{S}_{\ell,\alpha}\leq t_\ell)_{1 \leq \ell \leq n}]\\[5pt] &\quad = \mathbb{P}[X_{n+1}=\,j,\mathcal{T}_{n+1,1} \leq L^{(\alpha)}({t})\mid (X_\ell=i_\ell,\mathcal{S}_{\ell,1}\leq L^{(\alpha)}({t_\ell}))_{0 \leq \ell \leq n}]\\[5pt]&\quad = \mathbb{P}[X_{n+1}=\,j,\mathcal{T}_{n+1,1} \leq L^{(\alpha)}({t})\mid X_n=i_n]\\[5pt]&\quad = \mathbb{P}[X_{n+1}=\,j,\mathcal{T}_{n+1,\alpha} \leq t\mid X_n=i_n]. \end{align*}
\begin{align*} & \mathbb{P}[X_{n+1}=\,j,\mathcal{T}_{n+1,\alpha} \leq t\mid (X_\ell=i_\ell,\mathcal{S}_{\ell,\alpha}\leq t_\ell)_{1 \leq \ell \leq n}]\\[5pt] &\quad = \mathbb{P}[X_{n+1}=\,j,\mathcal{T}_{n+1,1} \leq L^{(\alpha)}({t})\mid (X_\ell=i_\ell,\mathcal{S}_{\ell,1}\leq L^{(\alpha)}({t_\ell}))_{0 \leq \ell \leq n}]\\[5pt]&\quad = \mathbb{P}[X_{n+1}=\,j,\mathcal{T}_{n+1,1} \leq L^{(\alpha)}({t})\mid X_n=i_n]\\[5pt]&\quad = \mathbb{P}[X_{n+1}=\,j,\mathcal{T}_{n+1,\alpha} \leq t\mid X_n=i_n]. \end{align*}
We will now show that
![]() $N_\alpha(t)$
preserves the transition probabilities of the original process
$N_\alpha(t)$
preserves the transition probabilities of the original process
![]() $N_1(t)$
. Since
$N_1(t)$
. Since
![]() $\lim_{t \rightarrow \infty}L^{(\alpha)}({t})=\infty$
with probability 1, we get for all
$\lim_{t \rightarrow \infty}L^{(\alpha)}({t})=\infty$
with probability 1, we get for all
![]() $j \geq 0$
,
$j \geq 0$
,
![]() $i \geq 0$
$i \geq 0$
 \begin{align*}p_{i,j}^\alpha&= \lim_{t \rightarrow \infty } \mathbb{P}[X_{n+1}=\,j,\mathcal{T}_{n+1,\alpha} \leq t\mid X_n=i]\\[5pt]&= \lim_{t \rightarrow \infty } \mathbb{P}[X_{n+1}=\,j,\mathcal{T}_{n+1,1} \leq L^{(\alpha)}({t})\mid X_n=i]\\[5pt]&= \lim_{u \rightarrow \infty } \mathbb{P}[X_{n+1}=\,j,\mathcal{T}_{n+1,1} \leq u\mid X_n=i]\\[5pt]&= p_{i,j}. \end{align*}
\begin{align*}p_{i,j}^\alpha&= \lim_{t \rightarrow \infty } \mathbb{P}[X_{n+1}=\,j,\mathcal{T}_{n+1,\alpha} \leq t\mid X_n=i]\\[5pt]&= \lim_{t \rightarrow \infty } \mathbb{P}[X_{n+1}=\,j,\mathcal{T}_{n+1,1} \leq L^{(\alpha)}({t})\mid X_n=i]\\[5pt]&= \lim_{u \rightarrow \infty } \mathbb{P}[X_{n+1}=\,j,\mathcal{T}_{n+1,1} \leq u\mid X_n=i]\\[5pt]&= p_{i,j}. \end{align*}
The next step is to prove that the random variables
![]() $\mathcal{T}_{n+1,\alpha}$
, conditioned on
$\mathcal{T}_{n+1,\alpha}$
, conditioned on
![]() $(X_n,X_{n+1})$
,
$(X_n,X_{n+1})$
,
![]() $1 \leq n \leq L_0-1$
, follow a Mittag–Leffler distribution. For
$1 \leq n \leq L_0-1$
, follow a Mittag–Leffler distribution. For
![]() $i \geq 1$
we have
$i \geq 1$
we have
 \begin{align*} \mathbb{P}[\mathcal{T}_{n+1,\alpha}>t\mid X_{n+1}=\,j,X_n=i]&= \mathbb{P}[\mathcal{T}_{n+1,1}>L^{(\alpha)}({t})\mid X_{n+1}=\,j,X_n=i]\\[5pt] &= \int_{0}^{\infty}\mathbb{P}[\mathcal{T}_{n+1,1}>u\mid X_{n+1}=\,j,X_n=i]h_\alpha(u,t) \,{\textrm{d}} u\\[5pt] &= \int_{0}^{\infty}\,{\textrm{e}}^{-(\lambda_{i}+\mu_{i}) u }h_\alpha(u,t) \,{\textrm{d}} u\\[5pt] &= \mathbb{E}[{\textrm{e}}^{-(\lambda_{i}+\mu_{i}) L^{(\alpha)}({t}) }]\\[5pt] &= \mathcal{E}_{\alpha,1}(\!-\!(\lambda_{i}+\mu_{i}) t^\alpha). \end{align*}
\begin{align*} \mathbb{P}[\mathcal{T}_{n+1,\alpha}>t\mid X_{n+1}=\,j,X_n=i]&= \mathbb{P}[\mathcal{T}_{n+1,1}>L^{(\alpha)}({t})\mid X_{n+1}=\,j,X_n=i]\\[5pt] &= \int_{0}^{\infty}\mathbb{P}[\mathcal{T}_{n+1,1}>u\mid X_{n+1}=\,j,X_n=i]h_\alpha(u,t) \,{\textrm{d}} u\\[5pt] &= \int_{0}^{\infty}\,{\textrm{e}}^{-(\lambda_{i}+\mu_{i}) u }h_\alpha(u,t) \,{\textrm{d}} u\\[5pt] &= \mathbb{E}[{\textrm{e}}^{-(\lambda_{i}+\mu_{i}) L^{(\alpha)}({t}) }]\\[5pt] &= \mathcal{E}_{\alpha,1}(\!-\!(\lambda_{i}+\mu_{i}) t^\alpha). \end{align*}
The independence of
![]() $(\mathcal{T}_{\ell,\alpha})_{1 \leq \ell \leq n}$
conditioned on
$(\mathcal{T}_{\ell,\alpha})_{1 \leq \ell \leq n}$
conditioned on
![]() $(X_\ell)_{0 \leq \ell \leq n}$
, is more delicate. We first notice that from (A.4), for all
$(X_\ell)_{0 \leq \ell \leq n}$
, is more delicate. We first notice that from (A.4), for all
![]() $s > 0$
and
$s > 0$
and
![]() $i \geq 1$
, we have
$i \geq 1$
, we have
 \begin{align} \int_{0}^{\infty}\,{\textrm{e}}^{-st}\mathbb{P}[\mathcal{T}_{n+1,\alpha}\leq t\mid X_{n+1}=\,j,X_n=i]\,{\textrm{d}} t & =\int_{0}^{\infty}\,{\textrm{e}}^{-st} (1-\mathcal{E}_{\alpha,1}(\!-\!(\lambda_{i}+\mu_{i}) t^\alpha)) \,{\textrm{d}} t \notag \\[5pt] & =\dfrac{1}{s}\dfrac{\lambda_{i}+\mu_{i}}{s^\alpha+\lambda_{i}+\mu_{i}}.\end{align}
\begin{align} \int_{0}^{\infty}\,{\textrm{e}}^{-st}\mathbb{P}[\mathcal{T}_{n+1,\alpha}\leq t\mid X_{n+1}=\,j,X_n=i]\,{\textrm{d}} t & =\int_{0}^{\infty}\,{\textrm{e}}^{-st} (1-\mathcal{E}_{\alpha,1}(\!-\!(\lambda_{i}+\mu_{i}) t^\alpha)) \,{\textrm{d}} t \notag \\[5pt] & =\dfrac{1}{s}\dfrac{\lambda_{i}+\mu_{i}}{s^\alpha+\lambda_{i}+\mu_{i}}.\end{align}
By integrating by parts, we can deduce that the identity (3.13) is the same as
Now we set
Similarly to (3.14), from the construction of
![]() $\varphi_{n,\alpha}(s)$
we can see that
$\varphi_{n,\alpha}(s)$
we can see that
 \begin{equation}\varphi_{n,\alpha}(s)=\dfrac{1}{s}\mathbb{E}[{\textrm{e}}^{-s \mathcal{S}_{n,\alpha}}\mid (X_\ell)_{0 \leq \ell \leq n}]=\dfrac{1}{s}\mathbb{E}\Biggl[\prod_{m=1}^{n}\,{\textrm{e}}^{-s\mathcal{T}_{m,\alpha}}\mid (X_\ell)_{0 \leq \ell \leq n}\Biggr]. \end{equation}
\begin{equation}\varphi_{n,\alpha}(s)=\dfrac{1}{s}\mathbb{E}[{\textrm{e}}^{-s \mathcal{S}_{n,\alpha}}\mid (X_\ell)_{0 \leq \ell \leq n}]=\dfrac{1}{s}\mathbb{E}\Biggl[\prod_{m=1}^{n}\,{\textrm{e}}^{-s\mathcal{T}_{m,\alpha}}\mid (X_\ell)_{0 \leq \ell \leq n}\Biggr]. \end{equation}
We need to compute
![]() $\varphi_{n,\alpha}(s)$
more explicitly. Since
$\varphi_{n,\alpha}(s)$
more explicitly. Since
![]() $N_\alpha(t)$
is a time-changed process, we have
$N_\alpha(t)$
is a time-changed process, we have
 \begin{align*} \varphi_{n,\alpha}(s) &= \int_{0}^{\infty} \,{\textrm{e}}^{-st}\mathbb{P}[\mathcal{S}_{n,1}\leq L^{(\alpha)}({t})\mid (X_\ell)_{0 \leq \ell \leq n}] \,{\textrm{d}} t\\[5pt] &= \int_{0}^{\infty} \,{\textrm{e}}^{-st}\biggl(\int_{0}^{\infty}\mathbb{P}[\mathcal{S}_{n,1}\leq u\mid (X_\ell)_{0 \leq \ell \leq n}]h_\alpha(u,t) \,{\textrm{d}} u \biggr) \,{\textrm{d}} t, \end{align*}
\begin{align*} \varphi_{n,\alpha}(s) &= \int_{0}^{\infty} \,{\textrm{e}}^{-st}\mathbb{P}[\mathcal{S}_{n,1}\leq L^{(\alpha)}({t})\mid (X_\ell)_{0 \leq \ell \leq n}] \,{\textrm{d}} t\\[5pt] &= \int_{0}^{\infty} \,{\textrm{e}}^{-st}\biggl(\int_{0}^{\infty}\mathbb{P}[\mathcal{S}_{n,1}\leq u\mid (X_\ell)_{0 \leq \ell \leq n}]h_\alpha(u,t) \,{\textrm{d}} u \biggr) \,{\textrm{d}} t, \end{align*}
by using Fubini’s theorem and recalling the identity
Thus we obtain
 \begin{align*} \varphi_{n,\alpha}(s) &= \int_{0}^{\infty} \,{\textrm{e}}^{-st}\biggl(\int_{0}^{\infty}\mathbb{P}[\mathcal{S}_{n,1}\leq u\mid (X_\ell)_{0 \leq \ell \leq n}]h_\alpha(u,t) \,{\textrm{d}} u\biggr) \,{\textrm{d}} t\\[5pt] &= \int_{0}^{\infty}\mathbb{P}[\mathcal{S}_{n,1}\leq u\mid (X_\ell)_{0 \leq \ell \leq n}] \biggl(\int_{0}^{\infty}\,{\textrm{e}}^{-st} h_\alpha(u,t) \,{\textrm{d}} t \biggr) \,{\textrm{d}} u\\[5pt] &= \int_{0}^{\infty}\mathbb{P}[\mathcal{S}_{n,1}\leq u\mid (X_\ell)_{0 \leq \ell \leq n}] s^{\alpha-1}\,{\textrm{e}}^{- s^\alpha u}\,{\textrm{d}} u \\[5pt] &= s^{\alpha-1} \varphi_{n,1}(s^\alpha). \end{align*}
\begin{align*} \varphi_{n,\alpha}(s) &= \int_{0}^{\infty} \,{\textrm{e}}^{-st}\biggl(\int_{0}^{\infty}\mathbb{P}[\mathcal{S}_{n,1}\leq u\mid (X_\ell)_{0 \leq \ell \leq n}]h_\alpha(u,t) \,{\textrm{d}} u\biggr) \,{\textrm{d}} t\\[5pt] &= \int_{0}^{\infty}\mathbb{P}[\mathcal{S}_{n,1}\leq u\mid (X_\ell)_{0 \leq \ell \leq n}] \biggl(\int_{0}^{\infty}\,{\textrm{e}}^{-st} h_\alpha(u,t) \,{\textrm{d}} t \biggr) \,{\textrm{d}} u\\[5pt] &= \int_{0}^{\infty}\mathbb{P}[\mathcal{S}_{n,1}\leq u\mid (X_\ell)_{0 \leq \ell \leq n}] s^{\alpha-1}\,{\textrm{e}}^{- s^\alpha u}\,{\textrm{d}} u \\[5pt] &= s^{\alpha-1} \varphi_{n,1}(s^\alpha). \end{align*}
For
![]() $\alpha=1$
, conditioned on
$\alpha=1$
, conditioned on
![]() $(X_\ell)_{0 \leq \ell \leq n}$
, the inter-arrival times are independent and exponentially distributed, so
$(X_\ell)_{0 \leq \ell \leq n}$
, the inter-arrival times are independent and exponentially distributed, so
 \begin{equation*} \varphi_{n,1}(s^\alpha)=\dfrac{1}{s^\alpha}\prod_{\ell=0}^{n-1}\dfrac{\lambda_{X_\ell}+\mu_{X_\ell}}{s^ \alpha+\lambda_{X_\ell}+\mu_{X_\ell}} , \end{equation*}
\begin{equation*} \varphi_{n,1}(s^\alpha)=\dfrac{1}{s^\alpha}\prod_{\ell=0}^{n-1}\dfrac{\lambda_{X_\ell}+\mu_{X_\ell}}{s^ \alpha+\lambda_{X_\ell}+\mu_{X_\ell}} , \end{equation*}
leading to the formula
 \begin{equation} \varphi_{n,\alpha}(s)=\dfrac{1}{s}\prod_{\ell=0}^{n-1}\dfrac{\lambda_{X_\ell}+\mu_{X_\ell}}{s^ \alpha+\lambda_{X_\ell}+\mu_{X_\ell}}. \end{equation}
\begin{equation} \varphi_{n,\alpha}(s)=\dfrac{1}{s}\prod_{\ell=0}^{n-1}\dfrac{\lambda_{X_\ell}+\mu_{X_\ell}}{s^ \alpha+\lambda_{X_\ell}+\mu_{X_\ell}}. \end{equation}
By combining (3.14), (3.15), and (3.16), we now get
 \begin{equation}s \varphi_{n,\alpha}(s)=\mathbb{E}\Biggl[\prod_{m=1}^{n}\,{\textrm{e}}^{-s\mathcal{T}_{m,\alpha}}\mid (X_\ell)_{0 \leq \ell \leq n}\Biggr]=\prod_{m=1}^{n}\mathbb{E}[{\textrm{e}}^{-s\mathcal{T}_{m,\alpha}}\mid (X_{m},X_{m-1})].\end{equation}
\begin{equation}s \varphi_{n,\alpha}(s)=\mathbb{E}\Biggl[\prod_{m=1}^{n}\,{\textrm{e}}^{-s\mathcal{T}_{m,\alpha}}\mid (X_\ell)_{0 \leq \ell \leq n}\Biggr]=\prod_{m=1}^{n}\mathbb{E}[{\textrm{e}}^{-s\mathcal{T}_{m,\alpha}}\mid (X_{m},X_{m-1})].\end{equation}
Equation (3.17) directly implies that for all
![]() $1 \leq n \leq L_0-1$
, conditioned on
$1 \leq n \leq L_0-1$
, conditioned on
![]() $(X_\ell)_{0\leq \ell \leq n}$
, the inter-arrival times
$(X_\ell)_{0\leq \ell \leq n}$
, the inter-arrival times
![]() $\mathcal{T}_{\ell+1,\alpha}=\mathcal{S}_{\ell+1,\alpha}-\mathcal{S}_{\ell,\alpha}$
,
$\mathcal{T}_{\ell+1,\alpha}=\mathcal{S}_{\ell+1,\alpha}-\mathcal{S}_{\ell,\alpha}$
,
![]() $0 \leq \ell \leq n$
are independent, concluding the proof.
$0 \leq \ell \leq n$
are independent, concluding the proof.
4. The spectral representation of the transition probabilities
4.1. Preliminaries
For all
![]() $i \geq 0$
fixed, we let
$i \geq 0$
fixed, we let
denote the first time the process
![]() $N_{\alpha}(t)$
attains the state i. In particular, for
$N_{\alpha}(t)$
attains the state i. In particular, for
![]() $i=0$
, we say that
$i=0$
, we say that
![]() $T_{0,\alpha}$
is the absorption time or the extinction time of the process. For the sake of convenience, for
$T_{0,\alpha}$
is the absorption time or the extinction time of the process. For the sake of convenience, for
![]() $\alpha=1$
we write
$\alpha=1$
we write
![]() $T_0$
instead of
$T_0$
instead of
![]() $T_{0,1}$
. In the following we will use the notation
$T_{0,1}$
. In the following we will use the notation
![]() $\mathbb{P}_{i}[\!\cdot\!]$
for
$\mathbb{P}_{i}[\!\cdot\!]$
for
![]() $\mathbb{P}[\cdot \mid N_{\alpha}(0)=i]$
and
$\mathbb{P}[\cdot \mid N_{\alpha}(0)=i]$
and
![]() $\mathbb{E}_{i}[\!\cdot\!]$
for
$\mathbb{E}_{i}[\!\cdot\!]$
for
![]() $\mathbb{E}[\cdot \mid N_{\alpha}(0)=i]$
to denote the dependence on the initial condition
$\mathbb{E}[\cdot \mid N_{\alpha}(0)=i]$
to denote the dependence on the initial condition
![]() $N_{\alpha}(0)$
. For
$N_{\alpha}(0)$
. For
![]() $n \geq 1$
we define the coefficients
$n \geq 1$
we define the coefficients
 \begin{align*} \pi_1&= 1,\\[5pt]\pi_n&= \prod_{i=1}^{n-1}\dfrac{\lambda_i}{\mu_{i+1}}, \quad n \geq 2.\end{align*}
\begin{align*} \pi_1&= 1,\\[5pt]\pi_n&= \prod_{i=1}^{n-1}\dfrac{\lambda_i}{\mu_{i+1}}, \quad n \geq 2.\end{align*}
Note that these coefficients satisfy the identity
![]() $\pi_{n+1}/\pi_{n}=\lambda_{n}/\mu_{n+1}$
. This implies that
$\pi_{n+1}/\pi_{n}=\lambda_{n}/\mu_{n+1}$
. This implies that
![]() $Q^{(a)}$
is reversible with respect to the measure
$Q^{(a)}$
is reversible with respect to the measure
![]() $\pi$
, that is,
$\pi$
, that is,
The following series are essential to describe some properties of the process:
 \begin{equation*} A= \sum_{i\geq 1}(\lambda_{i}\pi_{i})^{-1}, \quad B= \sum_{i\geq 1}\pi_{i},\quad D= \sum_{j \geq 1}\pi_j\sum_{k=1}^{j-1}\dfrac{1}{\lambda_k \pi_k}.\end{equation*}
\begin{equation*} A= \sum_{i\geq 1}(\lambda_{i}\pi_{i})^{-1}, \quad B= \sum_{i\geq 1}\pi_{i},\quad D= \sum_{j \geq 1}\pi_j\sum_{k=1}^{j-1}\dfrac{1}{\lambda_k \pi_k}.\end{equation*}
For
![]() $\alpha=1$
, some well-known results are as follows (see e.g. [Reference Collet, Martínez and San Martín6, Chapter 5]).
$\alpha=1$
, some well-known results are as follows (see e.g. [Reference Collet, Martínez and San Martín6, Chapter 5]).
-
(1). The process is almost surely absorbed at zero, i.e.
 $\mathbb{P}_i[T_0< \infty] =1$
, if and only if
$\mathbb{P}_i[T_0< \infty] =1$
, if and only if
 $A=\infty$
.
$A=\infty$
. -
(2). The absorption time has a finite mean, i.e.
 $\mathbb{E}_i[T_0]<\infty$
, if and only if
$\mathbb{E}_i[T_0]<\infty$
, if and only if
 $B<\infty$
.
$B<\infty$
. -
(3). The process comes from infinity, i.e.
 $\sup_{i \geq 1}\mathbb{E}_i[T_0]<\infty$
, if and only if
$\sup_{i \geq 1}\mathbb{E}_i[T_0]<\infty$
, if and only if
 $D<\infty$
.
$D<\infty$
.
4.2. Main results
Here we present the approach of Karlin and McGregor’s polynomials originally introduced in [Reference Karlin and McGregor14] ([Reference Collet, Martínez and San Martín6, Section 5.2] is also recommended for a detailed discussion). Given a fixed
![]() $\theta > 0$
, we define recursively the sequence of polynomials
$\theta > 0$
, we define recursively the sequence of polynomials
These polynomials satisfy the orthogonality condition
where
![]() $\Gamma$
is a probability measure supported in
$\Gamma$
is a probability measure supported in
![]() $[\theta^\star,\infty)$
, for some
$[\theta^\star,\infty)$
, for some
![]() $\theta^\star \geq 0$
, and
$\theta^\star \geq 0$
, and
![]() $\delta_{j,k}$
is the Kronecker delta.
$\delta_{j,k}$
is the Kronecker delta.
Based on these polynomials, it can be shown that when
![]() $\alpha=1$
, the spectral representation of the transition probabilities is
$\alpha=1$
, the spectral representation of the transition probabilities is
The following theorem generalizes the representation (4.3) to the complete case
![]() $\alpha \in (0,1]$
.
$\alpha \in (0,1]$
.
Theorem 4.1. The solution to the system of equations (2.1) can be written as
where
![]() $\mathcal{E}_{\alpha,1}(\!\cdot\!)$
is the Mittag–Leffler function with parameter
$\mathcal{E}_{\alpha,1}(\!\cdot\!)$
is the Mittag–Leffler function with parameter
![]() $\alpha$
.
$\alpha$
.
Proof. By combining Theorem 3.1 and equation (4.3), we have for
![]() $j \geq 1$
,
$j \geq 1$
,
![]() $i \geq 1$
$i \geq 1$
 \begin{align}p_{i,j,\alpha}(t)&= \mathbb{P}_i[N_1(L^{(\alpha)}({t}))=\,j] \notag \\[5pt]&= \int_{0}^{\infty}\mathbb{P}_i[N_1(u) =\,j]h_\alpha(u,t) \,{\textrm{d}} u \notag \\[5pt]&= \pi_j \int_{0}^{\infty} \biggl(\int_{ \theta^\star}^{\infty} \,{\textrm{e}}^{-\theta u}\psi_{i}(\theta)\psi_{j}(\theta)\,{\textrm{d}} \Gamma(\theta)\biggr)h_\alpha(u,t) \,{\textrm{d}} u.\end{align}
\begin{align}p_{i,j,\alpha}(t)&= \mathbb{P}_i[N_1(L^{(\alpha)}({t}))=\,j] \notag \\[5pt]&= \int_{0}^{\infty}\mathbb{P}_i[N_1(u) =\,j]h_\alpha(u,t) \,{\textrm{d}} u \notag \\[5pt]&= \pi_j \int_{0}^{\infty} \biggl(\int_{ \theta^\star}^{\infty} \,{\textrm{e}}^{-\theta u}\psi_{i}(\theta)\psi_{j}(\theta)\,{\textrm{d}} \Gamma(\theta)\biggr)h_\alpha(u,t) \,{\textrm{d}} u.\end{align}
We now define the integrals
Recalling that
![]() $\Gamma$
is a probability measure, it is clear that
$\Gamma$
is a probability measure, it is clear that
![]() $I_{j,j}(t)\leq I_{j,j}(0)$
for all
$I_{j,j}(t)\leq I_{j,j}(0)$
for all
![]() $t \geq 0$
,
$t \geq 0$
,
![]() $j \geq 1$
. In addition, from the Cauchy–Schwarz inequality and (4.2) we get
$j \geq 1$
. In addition, from the Cauchy–Schwarz inequality and (4.2) we get
For each
![]() $t \geq 0$
fixed,
$t \geq 0$
fixed,
![]() $h_\alpha(u,t)$
is a probability density function supported on
$h_\alpha(u,t)$
is a probability density function supported on
![]() $\mathbb{R}^+_0$
. By applying Fubini’s theorem in (4.5) we get
$\mathbb{R}^+_0$
. By applying Fubini’s theorem in (4.5) we get
and recalling the identity
we deduce (4.4), concluding the proof.
The following theorem provides an explicit form for the distribution of the absorption time.
Theorem 4.2. Assume
![]() $A=\infty$
. For all
$A=\infty$
. For all
![]() $i \geq 1$
, the probability of non-extinction before the instant
$i \geq 1$
, the probability of non-extinction before the instant
![]() $t\geq 0$
is
$t\geq 0$
is
Proof. If
![]() $A=\infty$
, it is well known that the probability measure
$A=\infty$
, it is well known that the probability measure
![]() $\Gamma$
satisfies
$\Gamma$
satisfies
![]() $\Gamma(\{0\})=0$
, and moreover
$\Gamma(\{0\})=0$
, and moreover
![]() ${\textrm{d}} \Gamma^d(\theta)=\mu_1 {\theta}^{-1}\,{\textrm{d}} \Gamma(\theta)$
is a probability measure with no atoms at zero (see formula (2.20) from [Reference van Doorn8]). In this case we have for
${\textrm{d}} \Gamma^d(\theta)=\mu_1 {\theta}^{-1}\,{\textrm{d}} \Gamma(\theta)$
is a probability measure with no atoms at zero (see formula (2.20) from [Reference van Doorn8]). In this case we have for
![]() $\alpha=1$
$\alpha=1$
We first check that
For any
![]() $\delta>0$
we have
$\delta>0$
we have
For the first term on the right-hand side of (4.7), we have that
![]() $\psi_{i}(\theta)$
is a polynomial of degree
$\psi_{i}(\theta)$
is a polynomial of degree
![]() $i-1$
, so it is bounded on any closed interval. Since
$i-1$
, so it is bounded on any closed interval. Since
![]() ${\textrm{d}} \Gamma^d$
is a probability measure, we have
${\textrm{d}} \Gamma^d$
is a probability measure, we have
By choosing
![]() $j=1$
in (4.6) we get
$j=1$
in (4.6) we get
The proof finishes by following the same approach as Theorem 4.1.
Remark 4.1. The transition probabilities
![]() $p_{i,j,\alpha}(t)$
are also the solution to the forward system of equations
$p_{i,j,\alpha}(t)$
are also the solution to the forward system of equations
with the convention
![]() $\lambda_0=\mu_0=0$
. In fact, by combining (2.1), (4.1), and (4.4), for
$\lambda_0=\mu_0=0$
. In fact, by combining (2.1), (4.1), and (4.4), for
![]() $i \geq 1$
,
$i \geq 1$
,
![]() $j \geq 1$
we have
$j \geq 1$
we have
 \begin{align*}\mathbb{D}^\alpha p_{i,j,\alpha}(t)&= \mu_ip_{i-1,j,\alpha}(t)-(\lambda_i+\mu_i)p_{i,j,\alpha}(t)+\lambda_i p_{i+1,j,\alpha}(t)\\[5pt]&= \pi_j \int_{\theta^\star}^{\infty}\mathcal{E}_{\alpha,1}(\!-\!\theta t^\alpha)(\mu_i \psi_{i-1}(\theta)-(\lambda_i+\mu_i)\psi_{i}(\theta)+\lambda_i \psi_{i+1}(\theta))\psi_{j}(\theta)\,{\textrm{d}} \Gamma(\theta)\\[5pt]&= \pi_j \int_{\theta^\star}^{\infty}\mathcal{E}_{\alpha,1}(\!-\!\theta t^\alpha)(\!-\!\theta\psi_{i}(\theta))\psi_{j}(\theta)\,{\textrm{d}} \Gamma(\theta).\end{align*}
\begin{align*}\mathbb{D}^\alpha p_{i,j,\alpha}(t)&= \mu_ip_{i-1,j,\alpha}(t)-(\lambda_i+\mu_i)p_{i,j,\alpha}(t)+\lambda_i p_{i+1,j,\alpha}(t)\\[5pt]&= \pi_j \int_{\theta^\star}^{\infty}\mathcal{E}_{\alpha,1}(\!-\!\theta t^\alpha)(\mu_i \psi_{i-1}(\theta)-(\lambda_i+\mu_i)\psi_{i}(\theta)+\lambda_i \psi_{i+1}(\theta))\psi_{j}(\theta)\,{\textrm{d}} \Gamma(\theta)\\[5pt]&= \pi_j \int_{\theta^\star}^{\infty}\mathcal{E}_{\alpha,1}(\!-\!\theta t^\alpha)(\!-\!\theta\psi_{i}(\theta))\psi_{j}(\theta)\,{\textrm{d}} \Gamma(\theta).\end{align*}
We now apply the recursive formula (4.1) to
![]() $-\theta \psi_{j}(\theta)$
,
$-\theta \psi_{j}(\theta)$
,
and we use (4.4) to obtain
This is equivalent to (4.8), since
![]() $\pi_j\mu_j={\pi_{j-1}\lambda_{j-1}}$
and
$\pi_j\mu_j={\pi_{j-1}\lambda_{j-1}}$
and
![]() $\pi_j\lambda_j={\pi_{j+1}\mu_{j+1}}$
. For
$\pi_j\lambda_j={\pi_{j+1}\mu_{j+1}}$
. For
![]() $j=0$
, (4.9) can be deduced in a similar way. From Theorem 4.2 we get for all
$j=0$
, (4.9) can be deduced in a similar way. From Theorem 4.2 we get for all
![]() $i \geq 1$
$i \geq 1$
By replacing (4.10) in the backward equation (2.1) for
![]() $j=0$
,
$j=0$
,
![]() $i \geq 1$
,
$i \geq 1$
,
 \begin{align*}\mathbb{D}^\alpha p_{i,0,\alpha}(t)&= \mu_ip_{i-1,0,\alpha}(t)-(\lambda_i+\mu_i)p_{i,0,\alpha}(t)+\lambda_i p_{i+1,0,\alpha}(t)\\[5pt]&= -\mu_1\int_{ \theta^\star}^\infty \mathcal{E}_{\alpha,1}(\!-\!\theta t^\alpha)\dfrac{\mu_i \psi_{i-1}(\theta)-(\lambda_i+\mu_i)\psi_{i}(\theta)+\lambda_i \psi_{i+1}(\theta)}{\theta}\,{\textrm{d}} \Gamma(\theta),\end{align*}
\begin{align*}\mathbb{D}^\alpha p_{i,0,\alpha}(t)&= \mu_ip_{i-1,0,\alpha}(t)-(\lambda_i+\mu_i)p_{i,0,\alpha}(t)+\lambda_i p_{i+1,0,\alpha}(t)\\[5pt]&= -\mu_1\int_{ \theta^\star}^\infty \mathcal{E}_{\alpha,1}(\!-\!\theta t^\alpha)\dfrac{\mu_i \psi_{i-1}(\theta)-(\lambda_i+\mu_i)\psi_{i}(\theta)+\lambda_i \psi_{i+1}(\theta)}{\theta}\,{\textrm{d}} \Gamma(\theta),\end{align*}
and from the recurrence relation (4.1),
5. Asymptotic behavior and quasi-limiting distributions
Theorem 4.2 allows us to deduce some new results related to the quasi-limiting behavior. We start by defining the integrals
When
![]() $\theta^\star>0$
, the coefficients
$\theta^\star>0$
, the coefficients
![]() $C_{i,j,k}$
are finite. In fact
$C_{i,j,k}$
are finite. In fact
From a probabilistic point of view, the parameter
![]() $\theta^\star$
can be identified as
$\theta^\star$
can be identified as
We remark that the definition of
![]() $\theta^\star$
does not depend on i. In particular, the condition
$\theta^\star$
does not depend on i. In particular, the condition
![]() $\theta^\star>0$
implies that the absorption time
$\theta^\star>0$
implies that the absorption time
![]() $T_{0}$
has finite exponential moments for all
$T_{0}$
has finite exponential moments for all
![]() $\theta \in (0,\theta^\star)$
(see [Reference Collet, Martínez and San Martín6, Lemma 4.1]). In the following proposition, we establish the asymptotic behavior of both the transition probabilities and the distribution of the absorption time
$\theta \in (0,\theta^\star)$
(see [Reference Collet, Martínez and San Martín6, Lemma 4.1]). In the following proposition, we establish the asymptotic behavior of both the transition probabilities and the distribution of the absorption time
![]() $T_{0,\alpha}$
.
$T_{0,\alpha}$
.
Proposition 5.1. Assume
![]() $\theta^\star>0$
. For all
$\theta^\star>0$
. For all
![]() $0<\alpha<1$
the following limits are fulfilled:
$0<\alpha<1$
the following limits are fulfilled:
Proof. For all
![]() $\theta>0$
the following limit applies (see (A.8) from the Appendix):
$\theta>0$
the following limit applies (see (A.8) from the Appendix):
In addition, we know that
Given
![]() $\epsilon>0$
, the limit (5.3) in particular implies that
$\epsilon>0$
, the limit (5.3) in particular implies that
for
![]() $t>t_\epsilon$
large enough. This means that the limit (5.1) follows from the dominated convergence theorem
$t>t_\epsilon$
large enough. This means that the limit (5.1) follows from the dominated convergence theorem
 \begin{align*} \lim_{t \rightarrow \infty} t^\alpha \mathbb{P}_i[T_{0,\alpha}>t]&= \mu_1 \int_{ \theta^\star}^\infty\Bigl(\lim_{t \rightarrow \infty} t^\alpha \mathcal{E}_{\alpha,1}(\!-\!\theta t^\alpha)\Bigr)\dfrac{\psi_{i}(\theta)}{\theta}\,{\textrm{d}} \Gamma(\theta)\\[5pt] &= \dfrac{\mu_1}{\Gamma(1-\alpha)}\int_{ \theta^\star}^\infty \dfrac{\psi_{i}(\theta)}{\theta^2}\,{\textrm{d}} \Gamma(\theta). \end{align*}
\begin{align*} \lim_{t \rightarrow \infty} t^\alpha \mathbb{P}_i[T_{0,\alpha}>t]&= \mu_1 \int_{ \theta^\star}^\infty\Bigl(\lim_{t \rightarrow \infty} t^\alpha \mathcal{E}_{\alpha,1}(\!-\!\theta t^\alpha)\Bigr)\dfrac{\psi_{i}(\theta)}{\theta}\,{\textrm{d}} \Gamma(\theta)\\[5pt] &= \dfrac{\mu_1}{\Gamma(1-\alpha)}\int_{ \theta^\star}^\infty \dfrac{\psi_{i}(\theta)}{\theta^2}\,{\textrm{d}} \Gamma(\theta). \end{align*}
The limit (5.2) is proved by using the same argument.
Proposition 5.1 leads us to the following theorem, interpreted as a Yaglom limit for the fractional case.
Theorem 5.1. Assume
![]() $\theta^\star>0$
. For all
$\theta^\star>0$
. For all
![]() $0<\alpha<1$
we have
$0<\alpha<1$
we have
where
 \begin{align}P_{i,j}&= \pi_j\Biggl(P_{i,1}+\sum_{k=1}^{\min\{i-1,j-1\}}\dfrac{1}{\lambda_k \pi_k}\Biggr), \quad j\geq 2,\end{align}
\begin{align}P_{i,j}&= \pi_j\Biggl(P_{i,1}+\sum_{k=1}^{\min\{i-1,j-1\}}\dfrac{1}{\lambda_k \pi_k}\Biggr), \quad j\geq 2,\end{align}
Remark 5.1. Before proving Theorem 5.1, let us make some comments.
-
1. The limit (5.4) is the same for the complete interval
 $\alpha \in (0,1)$
and strongly depends on the initial condition
$\alpha \in (0,1)$
and strongly depends on the initial condition
 $i \geq 1$
. This behavior is completely different to the non-fractional case
$i \geq 1$
. This behavior is completely different to the non-fractional case
 $\alpha=1$
,because the limit
$\alpha=1$
,because the limit \begin{equation*}\lim_{t \rightarrow \infty}{\mathbb{P}_i[N_1(t)=\,j\mid T_{0}>t]}=\nu_j(\theta^\star), \end{equation*}
\begin{equation*}\lim_{t \rightarrow \infty}{\mathbb{P}_i[N_1(t)=\,j\mid T_{0}>t]}=\nu_j(\theta^\star), \end{equation*}
 $\nu_j(\theta^\star)$
is independent of the initial condition
$\nu_j(\theta^\star)$
is independent of the initial condition
 $i \geq 1$
. Here
$i \geq 1$
. Here
 $\nu_j(\theta^\star)$
is a probability measure, also called the quasi-stationary distribution or quasi-limiting distribution.
$\nu_j(\theta^\star)$
is a probability measure, also called the quasi-stationary distribution or quasi-limiting distribution.
-
2. We analyze in more detail the two extreme cases for the limit (5.4).
-
For
 $i=1$
, the second term in (5.5) vanishes, so
$i=1$
, the second term in (5.5) vanishes, so \begin{equation*} \lim_{t \rightarrow \infty}{\mathbb{P}_i[N_\alpha(t)=\,j\mid T_{0,\alpha}>t]}=\dfrac{\pi_j}{\sum_{j \geq 1} \pi_j}. \end{equation*}
\begin{equation*} \lim_{t \rightarrow \infty}{\mathbb{P}_i[N_\alpha(t)=\,j\mid T_{0,\alpha}>t]}=\dfrac{\pi_j}{\sum_{j \geq 1} \pi_j}. \end{equation*}
-
For
 $i \rightarrow \infty$
(assuming that the limit exists) we get
$i \rightarrow \infty$
(assuming that the limit exists) we get \begin{equation*} \lim_{i \rightarrow \infty}\lim_{t \rightarrow \infty}{\mathbb{P}_i[N_\alpha(t)=\,j\mid T_{0,\alpha}>t]}=\dfrac{\pi_j\bigl(\frac{1}{\mu_1}+\sum_{k=1}^{j-1}\frac{1}{\lambda_k \pi_k}\bigr)}{\sum_{j \geq 1}\pi_j\bigl(\frac{1}{\mu_1}+\sum_{k=1}^{j-1}\frac{1}{\lambda_k \pi_k}\bigr)}. \end{equation*}
\begin{equation*} \lim_{i \rightarrow \infty}\lim_{t \rightarrow \infty}{\mathbb{P}_i[N_\alpha(t)=\,j\mid T_{0,\alpha}>t]}=\dfrac{\pi_j\bigl(\frac{1}{\mu_1}+\sum_{k=1}^{j-1}\frac{1}{\lambda_k \pi_k}\bigr)}{\sum_{j \geq 1}\pi_j\bigl(\frac{1}{\mu_1}+\sum_{k=1}^{j-1}\frac{1}{\lambda_k \pi_k}\bigr)}. \end{equation*}
The condition
![]() $\sum_{j \geq 1}\pi_j <\infty$
is equivalent to the positive recurrence of the process, i.e.
$\sum_{j \geq 1}\pi_j <\infty$
is equivalent to the positive recurrence of the process, i.e.
![]() $\mathbb{E}_i[T_0]<\infty$
for all
$\mathbb{E}_i[T_0]<\infty$
for all
![]() $i \geq 1$
. On the other hand, the series
$i \geq 1$
. On the other hand, the series
 \begin{equation*}\sum_{j \geq 1}\pi_j\sum_{k=1}^{j-1}\frac{1}{\lambda_k \pi_k}= \sum_{k\geq 1}\frac{1}{\lambda_{k}\pi_{k}}\sum_{j\geq k+1}\pi_{j}\end{equation*}
\begin{equation*}\sum_{j \geq 1}\pi_j\sum_{k=1}^{j-1}\frac{1}{\lambda_k \pi_k}= \sum_{k\geq 1}\frac{1}{\lambda_{k}\pi_{k}}\sum_{j\geq k+1}\pi_{j}\end{equation*}
converges if and only if the process comes down from infinity, i.e.
![]() $\sup_{j \geq 1} \mathbb{E}_j[{\textrm{e}}^{\theta T_{0,1}}]<\infty$
for all
$\sup_{j \geq 1} \mathbb{E}_j[{\textrm{e}}^{\theta T_{0,1}}]<\infty$
for all
![]() $\theta \in (0,\theta^\star)$
. According to Theorem 3.2 of [Reference van Doorn8], this is equivalent to the existence of a unique quasi-stationary distribution, which is associated with
$\theta \in (0,\theta^\star)$
. According to Theorem 3.2 of [Reference van Doorn8], this is equivalent to the existence of a unique quasi-stationary distribution, which is associated with
![]() $\theta^\star$
. As we mention below, in the fractional model (i.e.
$\theta^\star$
. As we mention below, in the fractional model (i.e.
![]() $\alpha \in (0,1)$
) the quasi-limiting behavior strongly depends on the initial condition, so its behavior changes drastically compared to the Markovian case. This fact is not at all intuitive, and constitutes an interesting result on asymptotic behavior associated with a long memory process.
$\alpha \in (0,1)$
) the quasi-limiting behavior strongly depends on the initial condition, so its behavior changes drastically compared to the Markovian case. This fact is not at all intuitive, and constitutes an interesting result on asymptotic behavior associated with a long memory process.
Proof of Theorem 5.1. As a direct consequence of Proposition 5.1, we have
Since
![]() $p_{i,j,1}(t)=\mathbb{P}_{i}[N_1(t)=\,j,T_0>t]$
, we get from (4.3)
$p_{i,j,1}(t)=\mathbb{P}_{i}[N_1(t)=\,j,T_0>t]$
, we get from (4.3)
By taking the integral over
![]() $t \geq 0$
, Fubini’s theorem yields
$t \geq 0$
, Fubini’s theorem yields
 \begin{align}\int_{0 }^{\infty}\mathbb{P}_{i}[N_1(t)=\,j,T_0>t]\,{\textrm{d}} t&= \pi_j \int_{ 0}^{\infty}\int_{\theta^\star}^{\infty}\,{\textrm{e}}^{-t \theta}\psi_{i}(\theta)\psi_{j}(\theta)\,{\textrm{d}} \Gamma(\theta) \,{\textrm{d}} t \notag \\[5pt]&= \pi_j \int_{\theta^\star}^{\infty}\dfrac{\psi_{i}(\theta)\psi_{j}(\theta)}{\theta}\,{\textrm{d}} \Gamma(\theta), \end{align}
\begin{align}\int_{0 }^{\infty}\mathbb{P}_{i}[N_1(t)=\,j,T_0>t]\,{\textrm{d}} t&= \pi_j \int_{ 0}^{\infty}\int_{\theta^\star}^{\infty}\,{\textrm{e}}^{-t \theta}\psi_{i}(\theta)\psi_{j}(\theta)\,{\textrm{d}} \Gamma(\theta) \,{\textrm{d}} t \notag \\[5pt]&= \pi_j \int_{\theta^\star}^{\infty}\dfrac{\psi_{i}(\theta)\psi_{j}(\theta)}{\theta}\,{\textrm{d}} \Gamma(\theta), \end{align}
and analogously
so the limit (5.6) is equivalent to
We recall the system of equations (4.8) for
![]() $\alpha=1$
$\alpha=1$
By taking the integral over
![]() $t \geq 0$
, from the right-hand side of (5.9), we obtain for
$t \geq 0$
, from the right-hand side of (5.9), we obtain for
![]() $j \geq 1$
$j \geq 1$
When
![]() $j=0$
, from (4.9) we get for
$j=0$
, from (4.9) we get for
![]() $\alpha=1$
that
$\alpha=1$
that
![]() $p_{i,0,1}^\prime(t)=\mu_1 p_{i,1,\alpha}(t)$
, and consequently
$p_{i,0,1}^\prime(t)=\mu_1 p_{i,1,\alpha}(t)$
, and consequently
By introducing the notation
with the convention
![]() $P_{i,0}=0$
we get the recurrence formula
$P_{i,0}=0$
we get the recurrence formula
whose solution can be computed explicitly. Let us rearrange some terms,
by taking the sum over
![]() $1 \leq k \leq j$
:
$1 \leq k \leq j$
:
 \begin{equation*} -\sum_{k=1}^j \delta_{i,k} = \lambda_0 P_{i,0}-\lambda_j P_{i,j}+\mu_{j+1}P_{i,j+1}-\mu_1P_{i,1},\quad j \geq 1.\end{equation*}
\begin{equation*} -\sum_{k=1}^j \delta_{i,k} = \lambda_0 P_{i,0}-\lambda_j P_{i,j}+\mu_{j+1}P_{i,j+1}-\mu_1P_{i,1},\quad j \geq 1.\end{equation*}
Since
![]() $P_{i,0}=0$
and
$P_{i,0}=0$
and
![]() $P_{i,1}={{1}/{\mu_1}}$
, we get
$P_{i,1}={{1}/{\mu_1}}$
, we get
 \begin{align}1-\sum_{k=1}^j \delta_{i,k} = -\lambda_j P_{i,j}+\mu_{j+1}P_{i,j+1}.\end{align}
\begin{align}1-\sum_{k=1}^j \delta_{i,k} = -\lambda_j P_{i,j}+\mu_{j+1}P_{i,j+1}.\end{align}
We notice that
 \begin{equation*}1-\sum_{k=1}^j \delta_{i,k}=\begin{cases}0& \text{if $j \geq i$,}\\[5pt]1 &\text{if $j< i$,}\end{cases}\end{equation*}
\begin{equation*}1-\sum_{k=1}^j \delta_{i,k}=\begin{cases}0& \text{if $j \geq i$,}\\[5pt]1 &\text{if $j< i$,}\end{cases}\end{equation*}
equation (5.10) becomes
Recalling the identity
we now get
whose solution is
 \begin{align*}P_{i,j}&= \pi_j\Biggl(P_{i,1}+\sum_{k=1}^{j-1}\dfrac{\unicode{x1d7d9}_{k<i}}{\lambda_k \pi_k}\Biggr), \quad j\geq 2,\\[5pt]P_{i,1}&= \dfrac{1}{\mu_1}.\end{align*}
\begin{align*}P_{i,j}&= \pi_j\Biggl(P_{i,1}+\sum_{k=1}^{j-1}\dfrac{\unicode{x1d7d9}_{k<i}}{\lambda_k \pi_k}\Biggr), \quad j\geq 2,\\[5pt]P_{i,1}&= \dfrac{1}{\mu_1}.\end{align*}
For
![]() $j \geq 2$
this is the same as
$j \geq 2$
this is the same as
 \begin{align}P_{i,j} = \pi_j\Biggl(\dfrac{1}{\mu_1}+\sum_{k=1}^{\min\{i-1,j-1\}}\dfrac{1}{\lambda_k \pi_k}\Biggr),\end{align}
\begin{align}P_{i,j} = \pi_j\Biggl(\dfrac{1}{\mu_1}+\sum_{k=1}^{\min\{i-1,j-1\}}\dfrac{1}{\lambda_k \pi_k}\Biggr),\end{align}
so the limit is
concluding the proof.
The following theorem provides the convergence rate of the limit obtained in (5.6).
Theorem 5.2. For all
![]() $0 < \alpha <1$
,
$0 < \alpha <1$
,
![]() $\alpha \neq 1/2$
, we have
$\alpha \neq 1/2$
, we have
and similarly for
![]() $\alpha=1/2$
,
$\alpha=1/2$
,
Proof. For
![]() $\alpha\neq 1/2$
we recall the asymptotic expansion of the Mittag–Leffler function for t large enough (see (A.5) from the Appendix):
$\alpha\neq 1/2$
we recall the asymptotic expansion of the Mittag–Leffler function for t large enough (see (A.5) from the Appendix):
The constants
![]() $C_{i,j,k}$
are finite, so the following asymptotic expansions are valid,
$C_{i,j,k}$
are finite, so the following asymptotic expansions are valid,
 \begin{align*} p_{i,j,\alpha}(t)&= \pi_j \biggl( \dfrac{C_{i,j,1}}{\Gamma(1-\alpha)}\dfrac{1}{t^\alpha}-\dfrac{C_{i,j,2}}{\Gamma(1-2\alpha)}\dfrac{1}{t^{2\alpha}}+{\textrm{o}}(t^{-2\alpha})\biggr),\\[5pt] \mathbb{P}_i[T_{0,\alpha}>t]&= \mu_1 \biggl( \dfrac{C_{i,1,2}}{\Gamma(1-\alpha)}\dfrac{1}{t^\alpha}-\dfrac{C_{i,1,3}}{\Gamma(1-2\alpha)}\dfrac{1}{t^{2\alpha}}+{\textrm{o}}(t^{-2\alpha})\biggr), \end{align*}
\begin{align*} p_{i,j,\alpha}(t)&= \pi_j \biggl( \dfrac{C_{i,j,1}}{\Gamma(1-\alpha)}\dfrac{1}{t^\alpha}-\dfrac{C_{i,j,2}}{\Gamma(1-2\alpha)}\dfrac{1}{t^{2\alpha}}+{\textrm{o}}(t^{-2\alpha})\biggr),\\[5pt] \mathbb{P}_i[T_{0,\alpha}>t]&= \mu_1 \biggl( \dfrac{C_{i,1,2}}{\Gamma(1-\alpha)}\dfrac{1}{t^\alpha}-\dfrac{C_{i,1,3}}{\Gamma(1-2\alpha)}\dfrac{1}{t^{2\alpha}}+{\textrm{o}}(t^{-2\alpha})\biggr), \end{align*}
and after some algebraic manipulations,
 \begin{equation*} \dfrac{p_{i,j,\alpha}(t)}{\mathbb{P}_i[T_{0,\alpha}>t]} = \dfrac{\pi_j}{\mu_1}\dfrac{C_{i,j,1}}{C_{i,1,2}}\Biggl( \dfrac{1-\frac{C_{i,j,2}}{C_{i,j,1}}\frac{\Gamma(1-\alpha)}{\Gamma(1-2\alpha)}\frac{1}{t^\alpha}+{\textrm{o}}(t^{-\alpha})}{1-\frac{C_{i,1,3}}{C_{i,1,2}}\frac{\Gamma(1-\alpha)}{\Gamma(1-2\alpha)}\frac{1}{t^\alpha}+{\textrm{o}}(t^{-\alpha})}\Biggr). \end{equation*}
\begin{equation*} \dfrac{p_{i,j,\alpha}(t)}{\mathbb{P}_i[T_{0,\alpha}>t]} = \dfrac{\pi_j}{\mu_1}\dfrac{C_{i,j,1}}{C_{i,1,2}}\Biggl( \dfrac{1-\frac{C_{i,j,2}}{C_{i,j,1}}\frac{\Gamma(1-\alpha)}{\Gamma(1-2\alpha)}\frac{1}{t^\alpha}+{\textrm{o}}(t^{-\alpha})}{1-\frac{C_{i,1,3}}{C_{i,1,2}}\frac{\Gamma(1-\alpha)}{\Gamma(1-2\alpha)}\frac{1}{t^\alpha}+{\textrm{o}}(t^{-\alpha})}\Biggr). \end{equation*}
For
![]() $|z|$
small enough, we know that
$|z|$
small enough, we know that
![]() $(1-z)^{-1}=1+z+{\textrm{o}}(z)$
, so
$(1-z)^{-1}=1+z+{\textrm{o}}(z)$
, so
and consequently
The limit is obtained by letting
![]() $t \rightarrow \infty$
and recalling the identity
$t \rightarrow \infty$
and recalling the identity
For
![]() $\alpha=1/2$
we now have to consider the asymptotic expansion (A.7),
$\alpha=1/2$
we now have to consider the asymptotic expansion (A.7),
Following the same approach we now obtain
Since
the proof concludes by using the same argument as the case
![]() $\alpha \neq 1/2$
.
$\alpha \neq 1/2$
.
5.1. Quasi-stationary distributions
In this section we suppose that the initial state
![]() $N_\alpha(0)$
is random, with a distribution
$N_\alpha(0)$
is random, with a distribution
![]() $\nu$
supported on
$\nu$
supported on
![]() $\mathbb{N}^+=\{1,2,3,\ldots\}$
. In this case we set
$\mathbb{N}^+=\{1,2,3,\ldots\}$
. In this case we set
 \begin{align*} \mathbb{P}_{\nu}[N_\alpha(t)=\,j]&\;:\!=\; \sum_{i \geq 1} \mathbb{P}[N_\alpha(0)=i]\mathbb{P}[N_\alpha(t)=\,j\mid N_\alpha(0)=i]\\[5pt]&= \sum_{i \geq 1} \nu_ip_{i,j,\alpha}(t),\end{align*}
\begin{align*} \mathbb{P}_{\nu}[N_\alpha(t)=\,j]&\;:\!=\; \sum_{i \geq 1} \mathbb{P}[N_\alpha(0)=i]\mathbb{P}[N_\alpha(t)=\,j\mid N_\alpha(0)=i]\\[5pt]&= \sum_{i \geq 1} \nu_ip_{i,j,\alpha}(t),\end{align*}
where
![]() $p_{i,j,\alpha}(t)$
are the transition probabilities defined in the previous sections. More generally, given
$p_{i,j,\alpha}(t)$
are the transition probabilities defined in the previous sections. More generally, given
![]() $A \subseteq \mathbb{N}^+$
we write
$A \subseteq \mathbb{N}^+$
we write
It can be shown that
is the unique ‘honest’ solution, that is, it is a non-negative solution to the system of equations
satisfying
![]() $\sum_{j \geq 0} p_{j,\alpha}(t)=1$
and
$\sum_{j \geq 0} p_{j,\alpha}(t)=1$
and
![]() $p_{j,\alpha}(0)=\nu_j$
, for all
$p_{j,\alpha}(0)=\nu_j$
, for all
![]() $t \geq 0$
,
$t \geq 0$
,
![]() $j\geq 1$
. In fact, for
$j\geq 1$
. In fact, for
![]() $\alpha \in (0,1)$
we know from Theorem 3.1 that
$\alpha \in (0,1)$
we know from Theorem 3.1 that
This implies
Since
![]() $p_{j,1}(t)=\sum_{i \geq 1} \nu_i p_{i,j,1}(t)$
is the unique honest solution for
$p_{j,1}(t)=\sum_{i \geq 1} \nu_i p_{i,j,1}(t)$
is the unique honest solution for
![]() $\alpha=1$
(see [Reference van Doorn8, pages 685–686] for more details on the non-fractional case), necessarily
$\alpha=1$
(see [Reference van Doorn8, pages 685–686] for more details on the non-fractional case), necessarily
![]() $p_{j,\alpha}(t)$
defined above is the unique solution for
$p_{j,\alpha}(t)$
defined above is the unique solution for
![]() $\alpha \in (0,1)$
.
$\alpha \in (0,1)$
.
Definition 5.1. We say that a probability measure
![]() $\nu$
is a quasi-stationary distribution (QSD) if, for all
$\nu$
is a quasi-stationary distribution (QSD) if, for all
![]() $A \subseteq \mathbb{N}^+$
and
$A \subseteq \mathbb{N}^+$
and
![]() $t \geq 0$
, we have the identity
$t \geq 0$
, we have the identity
When
![]() $\alpha=1$
, a probability measure
$\alpha=1$
, a probability measure
![]() $\nu$
is a QSD if and only if it is a solution to the system
$\nu$
is a QSD if and only if it is a solution to the system
![]() $\nu^t Q^{(a)}=-\theta \nu$
for some
$\nu^t Q^{(a)}=-\theta \nu$
for some
![]() $\theta \in (0, \theta^*]$
, where
$\theta \in (0, \theta^*]$
, where
![]() $Q^{(a)}$
is the matrix defined in (2.2). Moreover,
$Q^{(a)}$
is the matrix defined in (2.2). Moreover,
Similar properties appear in the fractional case. They are enunciated in the following results.
Proposition 5.2. Let
![]() $\nu$
be a QSD for
$\nu$
be a QSD for
![]() $(N_1(t))_{t \geq 0}$
. Then, for all
$(N_1(t))_{t \geq 0}$
. Then, for all
![]() $\alpha \in (0,1)$
, the following identities are satisfied:
$\alpha \in (0,1)$
, the following identities are satisfied:
for some
![]() $\theta \in (0,\theta^\star]$
. Consequently,
$\theta \in (0,\theta^\star]$
. Consequently,
![]() $\nu$
is a QSD for
$\nu$
is a QSD for
![]() $(N_\alpha(t))_{t \geq 0}$
,
$(N_\alpha(t))_{t \geq 0}$
,
![]() $\alpha \in (0,1)$
.
$\alpha \in (0,1)$
.
Proof. If
![]() $\nu$
is a QSD for
$\nu$
is a QSD for
![]() $(N_1(t))_{t \geq 0}$
, then (5.16) and (5.17) hold for some
$(N_1(t))_{t \geq 0}$
, then (5.16) and (5.17) hold for some
![]() $\theta \in (0,\theta^\star]$
. To prove (5.18), from Theorem 3.1 we have
$\theta \in (0,\theta^\star]$
. To prove (5.18), from Theorem 3.1 we have
 \begin{align*} \mathbb{P}_{\nu}[T_{0,\alpha}>t]&= \int_{0}^{\infty}\mathbb{P}_{\nu}[T_{0}>u]h_\alpha(u,t) \,{\textrm{d}} u\\[5pt] &= \int_{0}^{\infty}\,{\textrm{e}}^{-\theta u}h_\alpha(u,t) \,{\textrm{d}} u\\[5pt] &= \mathcal{E}_{\alpha,1}(\!-\!\theta t^\alpha) \end{align*}
\begin{align*} \mathbb{P}_{\nu}[T_{0,\alpha}>t]&= \int_{0}^{\infty}\mathbb{P}_{\nu}[T_{0}>u]h_\alpha(u,t) \,{\textrm{d}} u\\[5pt] &= \int_{0}^{\infty}\,{\textrm{e}}^{-\theta u}h_\alpha(u,t) \,{\textrm{d}} u\\[5pt] &= \mathcal{E}_{\alpha,1}(\!-\!\theta t^\alpha) \end{align*}
for all
![]() $t \geq 0$
and
$t \geq 0$
and
![]() $\alpha \in (0,1)$
fixed. Equation (5.19) is obtained from (5.17) by using the same argument. The proof concludes by noticing that (5.15) can be directly deduced from (5.18) and (5.19).
$\alpha \in (0,1)$
fixed. Equation (5.19) is obtained from (5.17) by using the same argument. The proof concludes by noticing that (5.15) can be directly deduced from (5.18) and (5.19).
Proposition 5.2 asserts that if the initial distribution coincides with some QSD of
![]() $(N_1(t))_{t \geq 0}$
, then the distribution of the absorption time follows a Mittag–Leffler distribution. The following theorem establishes that the family of quasi-stationary distributions for
$(N_1(t))_{t \geq 0}$
, then the distribution of the absorption time follows a Mittag–Leffler distribution. The following theorem establishes that the family of quasi-stationary distributions for
![]() $(N_\alpha(t))_{t \geq 0}$
coincides for all
$(N_\alpha(t))_{t \geq 0}$
coincides for all
![]() $\alpha \in (0,1]$
.
$\alpha \in (0,1]$
.
Theorem 5.3. A probability measure
![]() $\nu$
is a QSD for
$\nu$
is a QSD for
![]() $(N_\alpha(t))_{t \geq 0}$
if and only if it solves the system of equations
$(N_\alpha(t))_{t \geq 0}$
if and only if it solves the system of equations
where
![]() $\theta=\mu_1 \nu_1$
. Consequently
$\theta=\mu_1 \nu_1$
. Consequently
![]() $\nu$
is a QSD for
$\nu$
is a QSD for
![]() $(N_\alpha(t))_{t \geq 0}$
if and only if
$(N_\alpha(t))_{t \geq 0}$
if and only if
![]() $\nu$
is a QSD for
$\nu$
is a QSD for
![]() $(N_1(t))_{t \geq 0}$
.
$(N_1(t))_{t \geq 0}$
.
Proof. From Proposition 5.2 we know that any QSD associated with
![]() $N_1(t)$
is necessarily a QSD for
$N_1(t)$
is necessarily a QSD for
![]() $N_\alpha(t)$
,
$N_\alpha(t)$
,
![]() $\alpha \in (0,1]$
, so the system of equations (5.20), (5.21) is a sufficient condition to be a QSD for
$\alpha \in (0,1]$
, so the system of equations (5.20), (5.21) is a sufficient condition to be a QSD for
![]() $(N_\alpha(t))_{t \geq 0}$
.
$(N_\alpha(t))_{t \geq 0}$
.
To prove the converse, we first notice that if
![]() $\nu$
is a QSD, then for all
$\nu$
is a QSD, then for all
![]() $j \geq 1$
$j \geq 1$
By taking the operator
![]() $\mathbb{D}^\alpha $
on both sides we now get
$\mathbb{D}^\alpha $
on both sides we now get
Since
![]() $p_{ j,\alpha}(t)$
is a solution to (5.12) satisfying
$p_{ j,\alpha}(t)$
is a solution to (5.12) satisfying
![]() $p_{j,\alpha}(0)=\nu_j$
,
$p_{j,\alpha}(0)=\nu_j$
,
![]() $j \geq 1$
, we get for all
$j \geq 1$
, we get for all
![]() $t>0$
$t>0$
The existence of the limit
![]() $\nu_1 \mu_1=\lim_{t \rightarrow 0^+}\mathbb{D}^\alpha ( \mathbb{P}_{\nu}[T_{0,\alpha} >t])$
can be deduced by noticing first that
$\nu_1 \mu_1=\lim_{t \rightarrow 0^+}\mathbb{D}^\alpha ( \mathbb{P}_{\nu}[T_{0,\alpha} >t])$
can be deduced by noticing first that
By letting
![]() $t \to 0^+$
in the equation
$t \to 0^+$
in the equation
![]() $\mathbb{D}^\alpha p_{0,\alpha}(t)=\mu_1p_{1,\alpha}(t)$
, we get
$\mathbb{D}^\alpha p_{0,\alpha}(t)=\mu_1p_{1,\alpha}(t)$
, we get
Finally, we take the limit
![]() $t \rightarrow 0^+$
in (5.22), (5.23) to conclude that any QSD
$t \rightarrow 0^+$
in (5.22), (5.23) to conclude that any QSD
![]() $\nu$
is a solution to (5.20), (5.21) for
$\nu$
is a solution to (5.20), (5.21) for
![]() $\theta=\nu_1 \mu_1$
.
$\theta=\nu_1 \mu_1$
.
Since the family of quasi-stationary distributions is the same for the complete interval
![]() $\alpha \in (0,1]$
, its characterization coincides with the one originally presented by Van Doorn, enunciated below.
$\alpha \in (0,1]$
, its characterization coincides with the one originally presented by Van Doorn, enunciated below.
Theorem 5.4. (Van Doorn [Reference van Doorn8].) If the series
 \begin{equation*} \sum_{j \geq 1}\pi_j\sum_{k=1}^{j-1}\frac{1}{\lambda_k \pi_k}= \sum_{k\geq 1}\frac{1}{\lambda_{k}\pi_{k}}\sum_{j\geq k+1}\pi_{j} \end{equation*}
\begin{equation*} \sum_{j \geq 1}\pi_j\sum_{k=1}^{j-1}\frac{1}{\lambda_k \pi_k}= \sum_{k\geq 1}\frac{1}{\lambda_{k}\pi_{k}}\sum_{j\geq k+1}\pi_{j} \end{equation*}
diverges, then either
![]() $\theta^\star=0$
and there is no QSD distribution, or
$\theta^\star=0$
and there is no QSD distribution, or
![]() $\theta^\star>0$
, in which case there is a family of QSD distributions indexed by
$\theta^\star>0$
, in which case there is a family of QSD distributions indexed by
![]() $\nu_\theta$
,
$\nu_\theta$
,
![]() $\theta\in (0,\theta^\star]$
. If the D series converges, then there is a unique distribution QSD indexed by
$\theta\in (0,\theta^\star]$
. If the D series converges, then there is a unique distribution QSD indexed by
![]() $\theta^\star$
.
$\theta^\star$
.
6. The linear process
We revisit the linear model, previously studied by Orsingher and Polito [Reference Orsingher and Polito23]. The birth rates and death rates are
![]() $\lambda_{i}=i \lambda $
and
$\lambda_{i}=i \lambda $
and
![]() $\mu_{i}=i \mu$
respectively. To make our analysis simpler, we assume first that the initial condition is
$\mu_{i}=i \mu$
respectively. To make our analysis simpler, we assume first that the initial condition is
![]() $N_\alpha(0)=1$
. It is well known that in the case
$N_\alpha(0)=1$
. It is well known that in the case
![]() $\alpha=1$
, the transition probabilities are
$\alpha=1$
, the transition probabilities are
 \begin{equation*} p_{1,j,1}(t)= \begin{cases} \dfrac{(\lambda t)^{j-1}}{(1+\lambda t)^{j+1}}, & {\lambda=\mu} ,\\[12pt] \dfrac{(\lambda(1-{\textrm{e}}^{-(\lambda-\mu) t}))^{j-1}}{(\lambda-\mu \,{\textrm{e}}^{-(\lambda-\mu) t})^{j+1}} (\lambda-\mu)^{2} \,{\textrm{e}}^{-(\lambda-\mu) t} , & {\lambda \neq \mu}. \end{cases}\end{equation*}
\begin{equation*} p_{1,j,1}(t)= \begin{cases} \dfrac{(\lambda t)^{j-1}}{(1+\lambda t)^{j+1}}, & {\lambda=\mu} ,\\[12pt] \dfrac{(\lambda(1-{\textrm{e}}^{-(\lambda-\mu) t}))^{j-1}}{(\lambda-\mu \,{\textrm{e}}^{-(\lambda-\mu) t})^{j+1}} (\lambda-\mu)^{2} \,{\textrm{e}}^{-(\lambda-\mu) t} , & {\lambda \neq \mu}. \end{cases}\end{equation*}
Similarly, the probabilities of non-extinction are
 \begin{equation*} \mathbb{P}_1[T_{0}>t]=\begin{cases}\displaystyle \dfrac{\lambda-\mu}{\lambda}\Biggl(1- \sum_{m \geq 1}\biggl(\dfrac{\mu}{\lambda}\biggr)^{m} \,{\textrm{e}}^{-(\lambda-\mu) m t }\Biggr) ,& {\lambda>\mu}, \\[16pt] \displaystyle \dfrac{\mu-\lambda}{\lambda} \sum_{m \geq 1}\biggl(\dfrac{\lambda}{\mu}\biggr)^{m} \,{\textrm{e}}^{-(\mu-\lambda) m t }, & {\lambda<\mu}, \\[16pt] \dfrac{1}{1+\lambda t}, & {\lambda=\mu} \end{cases}\end{equation*}
\begin{equation*} \mathbb{P}_1[T_{0}>t]=\begin{cases}\displaystyle \dfrac{\lambda-\mu}{\lambda}\Biggl(1- \sum_{m \geq 1}\biggl(\dfrac{\mu}{\lambda}\biggr)^{m} \,{\textrm{e}}^{-(\lambda-\mu) m t }\Biggr) ,& {\lambda>\mu}, \\[16pt] \displaystyle \dfrac{\mu-\lambda}{\lambda} \sum_{m \geq 1}\biggl(\dfrac{\lambda}{\mu}\biggr)^{m} \,{\textrm{e}}^{-(\mu-\lambda) m t }, & {\lambda<\mu}, \\[16pt] \dfrac{1}{1+\lambda t}, & {\lambda=\mu} \end{cases}\end{equation*}
(see Section 8.6 of [Reference Bailey1]). A widely known fact is that the asymptotic behavior depends on the ratio
![]() $\lambda/\mu$
. In the fractional case the same occurs, so we study the three cases separately.
$\lambda/\mu$
. In the fractional case the same occurs, so we study the three cases separately.
The case
![]() $\lambda<\mu$
. As mentioned above, we first study the asymptotic behavior of the process with initial state
$\lambda<\mu$
. As mentioned above, we first study the asymptotic behavior of the process with initial state
![]() $N_\alpha(0)=1$
. When
$N_\alpha(0)=1$
. When
![]() $\alpha \in (0,1)$
, the probability of non-extinction is
$\alpha \in (0,1)$
, the probability of non-extinction is
(see formula (2.20) from [Reference Orsingher and Polito23]). We recall that from (A.8) we have for all
![]() $m\geq 1$
$m\geq 1$
From (6.1) and the dominated convergence theorem, we obtain
 \begin{align*} \lim_{t \rightarrow \infty } t^\alpha \mathbb{P}_1[T_{0,\alpha}>t]&= \biggl( \dfrac{\mu-\lambda}{\lambda}\biggr) \lim_{t \rightarrow \infty } t^\alpha \sum_{m \geq 1}({\lambda}/{\mu})^m \mathcal{E}_{\alpha,1}(\!-\!(\mu-\lambda)mt^\alpha)\\[5pt]&= \biggl( \dfrac{\mu-\lambda}{\lambda}\biggr) \sum_{m \geq 1}({\lambda}/{\mu})^m \lim_{t \rightarrow \infty } t^\alpha \mathcal{E}_{\alpha,1}(\!-\!(\mu-\lambda)mt^\alpha)\\[5pt]&= \dfrac{1}{\Gamma(1-\alpha)}\dfrac{1}{ \lambda }\sum_{m \geq 1}\dfrac{(\lambda/\mu)^m}{m}\\[5pt]&= -\dfrac{1}{\Gamma(1-\alpha)}\dfrac{1}{\lambda}\ln \biggl( 1-\dfrac{\lambda}{\mu}\biggr).\end{align*}
\begin{align*} \lim_{t \rightarrow \infty } t^\alpha \mathbb{P}_1[T_{0,\alpha}>t]&= \biggl( \dfrac{\mu-\lambda}{\lambda}\biggr) \lim_{t \rightarrow \infty } t^\alpha \sum_{m \geq 1}({\lambda}/{\mu})^m \mathcal{E}_{\alpha,1}(\!-\!(\mu-\lambda)mt^\alpha)\\[5pt]&= \biggl( \dfrac{\mu-\lambda}{\lambda}\biggr) \sum_{m \geq 1}({\lambda}/{\mu})^m \lim_{t \rightarrow \infty } t^\alpha \mathcal{E}_{\alpha,1}(\!-\!(\mu-\lambda)mt^\alpha)\\[5pt]&= \dfrac{1}{\Gamma(1-\alpha)}\dfrac{1}{ \lambda }\sum_{m \geq 1}\dfrac{(\lambda/\mu)^m}{m}\\[5pt]&= -\dfrac{1}{\Gamma(1-\alpha)}\dfrac{1}{\lambda}\ln \biggl( 1-\dfrac{\lambda}{\mu}\biggr).\end{align*}
The limit can be deduced in an alternative way. We now consider the representation
Equations (5.1) and (5.8) jointly imply
By using this equivalence we get for
![]() $i =1$
$i =1$
 \begin{align}\lim_{t \rightarrow \infty } t^{\alpha}\mathbb{P}_1[T_{0,\alpha}>t]&= \dfrac{1}{\Gamma(1-\alpha)}\int_{0}^{\infty}\dfrac{\mu-\lambda}{\lambda}\dfrac{(\lambda/\mu)\,{\textrm{e}}^{-(\mu-\lambda)u}}{1-\dfrac{\lambda}{\mu}\,{\textrm{e}}^{-(\mu-\lambda)u}}\,{\textrm{d}} u \notag \\[5pt]&= \dfrac{1}{\Gamma(1-\alpha)}\dfrac{1}{\lambda} \ln \biggl( 1-\dfrac{\lambda}{\mu}\,{\textrm{e}}^{-(\mu-\lambda)u}\biggr)\biggr|_{0}^{\infty} \notag \\[5pt]&= -\dfrac{1}{\Gamma(1-\alpha)}\dfrac{1}{\lambda}\ln \biggl( 1-\dfrac{\lambda}{\mu}\biggr).\end{align}
\begin{align}\lim_{t \rightarrow \infty } t^{\alpha}\mathbb{P}_1[T_{0,\alpha}>t]&= \dfrac{1}{\Gamma(1-\alpha)}\int_{0}^{\infty}\dfrac{\mu-\lambda}{\lambda}\dfrac{(\lambda/\mu)\,{\textrm{e}}^{-(\mu-\lambda)u}}{1-\dfrac{\lambda}{\mu}\,{\textrm{e}}^{-(\mu-\lambda)u}}\,{\textrm{d}} u \notag \\[5pt]&= \dfrac{1}{\Gamma(1-\alpha)}\dfrac{1}{\lambda} \ln \biggl( 1-\dfrac{\lambda}{\mu}\,{\textrm{e}}^{-(\mu-\lambda)u}\biggr)\biggr|_{0}^{\infty} \notag \\[5pt]&= -\dfrac{1}{\Gamma(1-\alpha)}\dfrac{1}{\lambda}\ln \biggl( 1-\dfrac{\lambda}{\mu}\biggr).\end{align}
Similarly, from (5.2) and (5.7) we have for all
![]() $j \geq 1$
$j \geq 1$
We obtain in the linear case
 \begin{align*}\int_{0 }^{\infty}\mathbb{P}_{1}[N_1(u)=\,j,T_0>u]\,{\textrm{d}} u&= (\lambda-\mu)^{2} \int_{0}^{\infty} \dfrac{(\lambda(1-{\textrm{e}}^{-(\lambda-\mu) u}))^{j-1}}{(\lambda-\mu {\textrm{e}}^{-(\lambda-\mu) u})^{j+1}} \,{\textrm{e}}^{-(\lambda-\mu) u}\,{\textrm{d}} u\\[7pt]&= (\lambda-\mu)^{2} \int_{0}^{\infty} \dfrac{(\lambda({\textrm{e}}^{(\lambda-\mu) u}-1))^{j-1}}{(\lambda \,{\textrm{e}}^{(\lambda-\mu) u}-\mu)^{j+1}} \,{\textrm{e}}^{(\lambda-\mu) u}\,{\textrm{d}} u.\end{align*}
\begin{align*}\int_{0 }^{\infty}\mathbb{P}_{1}[N_1(u)=\,j,T_0>u]\,{\textrm{d}} u&= (\lambda-\mu)^{2} \int_{0}^{\infty} \dfrac{(\lambda(1-{\textrm{e}}^{-(\lambda-\mu) u}))^{j-1}}{(\lambda-\mu {\textrm{e}}^{-(\lambda-\mu) u})^{j+1}} \,{\textrm{e}}^{-(\lambda-\mu) u}\,{\textrm{d}} u\\[7pt]&= (\lambda-\mu)^{2} \int_{0}^{\infty} \dfrac{(\lambda({\textrm{e}}^{(\lambda-\mu) u}-1))^{j-1}}{(\lambda \,{\textrm{e}}^{(\lambda-\mu) u}-\mu)^{j+1}} \,{\textrm{e}}^{(\lambda-\mu) u}\,{\textrm{d}} u.\end{align*}
By taking the change of variable
![]() $z={\textrm{e}}^{(\lambda-\mu) u}$
, after some manipulation we find
$z={\textrm{e}}^{(\lambda-\mu) u}$
, after some manipulation we find
For
![]() $z \in [0,1]$
, it is certain that
$z \in [0,1]$
, it is certain that
so the expansion series
holds, and by applying Tonelli’s theorem we get
 \begin{align*}(\mu-\lambda)\dfrac{\lambda^{j-1}}{\mu^{j+1}}\int_{0}^{1} \frac{(1-z)^{j-1}}{(1-{{\lambda z}/{\mu}})^{j+1}} \,{\textrm{d}} z &= (\mu-\lambda)\dfrac{\lambda^{j-1}}{\mu^{j+1}}\int_0^1 (1-z)^{j-1}\sum_{\ell \geq 0} \left(\substack{\ell +j \\[5pt] \ell}\right) ({\lambda z}/{\mu})^{\ell} \,{\textrm{d}} z \\[5pt]&= (\mu-\lambda)\dfrac{\lambda^{j-1}}{\mu^{j+1}} \sum_{\ell \geq 0} (\lambda/\mu)^{\ell} \left(\substack{\ell +j \\[5pt] \ell}\right) \int_0^1 (1-z)^{j-1}z^\ell \,{\textrm{d}} z \\[5pt]&= (\mu-\lambda)\dfrac{\lambda^{j-1}}{\mu^{j+1}} \sum_{\ell \geq 0} (\lambda/\mu)^{\ell} \left(\substack{\ell +j \\[5pt] \ell}\right) \dfrac{\Gamma(j)\Gamma(\ell+1)}{\Gamma(\ell+j+1)}.\end{align*}
\begin{align*}(\mu-\lambda)\dfrac{\lambda^{j-1}}{\mu^{j+1}}\int_{0}^{1} \frac{(1-z)^{j-1}}{(1-{{\lambda z}/{\mu}})^{j+1}} \,{\textrm{d}} z &= (\mu-\lambda)\dfrac{\lambda^{j-1}}{\mu^{j+1}}\int_0^1 (1-z)^{j-1}\sum_{\ell \geq 0} \left(\substack{\ell +j \\[5pt] \ell}\right) ({\lambda z}/{\mu})^{\ell} \,{\textrm{d}} z \\[5pt]&= (\mu-\lambda)\dfrac{\lambda^{j-1}}{\mu^{j+1}} \sum_{\ell \geq 0} (\lambda/\mu)^{\ell} \left(\substack{\ell +j \\[5pt] \ell}\right) \int_0^1 (1-z)^{j-1}z^\ell \,{\textrm{d}} z \\[5pt]&= (\mu-\lambda)\dfrac{\lambda^{j-1}}{\mu^{j+1}} \sum_{\ell \geq 0} (\lambda/\mu)^{\ell} \left(\substack{\ell +j \\[5pt] \ell}\right) \dfrac{\Gamma(j)\Gamma(\ell+1)}{\Gamma(\ell+j+1)}.\end{align*}
Since
we can simplify some terms in the series, obtaining
 \begin{equation*}(\mu-\lambda)\dfrac{\lambda^{j-1}}{\mu^{j+1}} \sum_{\ell \geq 0} (\lambda/\mu)^{\ell} \left(\substack{\ell +j \\[5pt] \ell}\right) \dfrac{\Gamma(j)\Gamma(\ell+1)}{\Gamma(\ell+j+1)}=\dfrac{1}{j} (\mu-\lambda)\dfrac{\lambda^{j-1}}{\mu^{j+1}} \sum_{\ell \geq 0} (\lambda/\mu)^{\ell}=\dfrac{1}{j \lambda}(\lambda/\mu)^{j}.\end{equation*}
\begin{equation*}(\mu-\lambda)\dfrac{\lambda^{j-1}}{\mu^{j+1}} \sum_{\ell \geq 0} (\lambda/\mu)^{\ell} \left(\substack{\ell +j \\[5pt] \ell}\right) \dfrac{\Gamma(j)\Gamma(\ell+1)}{\Gamma(\ell+j+1)}=\dfrac{1}{j} (\mu-\lambda)\dfrac{\lambda^{j-1}}{\mu^{j+1}} \sum_{\ell \geq 0} (\lambda/\mu)^{\ell}=\dfrac{1}{j \lambda}(\lambda/\mu)^{j}.\end{equation*}
For
![]() $j \geq 1$
, from a direct computation we have shown the limit
$j \geq 1$
, from a direct computation we have shown the limit
For
![]() $N_\alpha(0)=1$
, the quasi-limiting distribution can be deduced from (6.2) and (6.3), by noticing that
$N_\alpha(0)=1$
, the quasi-limiting distribution can be deduced from (6.2) and (6.3), by noticing that
 \begin{equation*}-\ln \biggl( 1-\frac{\lambda}{\mu}\biggr)=\sum_{j \geq 1} \frac{(\lambda/\mu)^j}{j},\end{equation*}
\begin{equation*}-\ln \biggl( 1-\frac{\lambda}{\mu}\biggr)=\sum_{j \geq 1} \frac{(\lambda/\mu)^j}{j},\end{equation*}
so that
Since
![]() $P_{1,j}={{(\lambda/\mu)^{j-1}}/{j}}$
, the limit (6.4) can also be written in the form
$P_{1,j}={{(\lambda/\mu)^{j-1}}/{j}}$
, the limit (6.4) can also be written in the form
which is consistent with our theorems. Now, the quasi-limiting behavior when the initial condition is
![]() $N_\alpha(0) > 1$
can be obtained directly from (5.4). We recall the expressions
$N_\alpha(0) > 1$
can be obtained directly from (5.4). We recall the expressions
![]() $\pi_j={{(\lambda/\mu)^{j-1}}/{j}}$
and
$\pi_j={{(\lambda/\mu)^{j-1}}/{j}}$
and
![]() $\lambda_j=\,j\lambda$
, so
$\lambda_j=\,j\lambda$
, so
![]() $\lambda_j \pi_j=\mu (\lambda/\mu)^j$
and (5.11) becomes
$\lambda_j \pi_j=\mu (\lambda/\mu)^j$
and (5.11) becomes
 \begin{align}P_{i,j}&= \dfrac{(\lambda/\mu)^{j-1}}{j}\Biggl[ \dfrac{1}{\mu}+\sum_{k=1}^{\min\{ i-1,j-1\}}\dfrac{1}{\mu (\lambda/\mu)^k}\Biggr] \notag \\[12pt]&= \dfrac{(\lambda/\mu)^{j}}{\lambda j} \sum_{k=0}^{\min\{ i-1,j-1\}}\dfrac{1}{ (\lambda/\mu)^k}\notag \\[5pt]&= {\dfrac{(\lambda/\mu)^{j}}{\lambda j} \dfrac{(\lambda/\mu)^{-\min\{ i,j\}}-1}{(\lambda/\mu)^{-1}-1}.}\end{align}
\begin{align}P_{i,j}&= \dfrac{(\lambda/\mu)^{j-1}}{j}\Biggl[ \dfrac{1}{\mu}+\sum_{k=1}^{\min\{ i-1,j-1\}}\dfrac{1}{\mu (\lambda/\mu)^k}\Biggr] \notag \\[12pt]&= \dfrac{(\lambda/\mu)^{j}}{\lambda j} \sum_{k=0}^{\min\{ i-1,j-1\}}\dfrac{1}{ (\lambda/\mu)^k}\notag \\[5pt]&= {\dfrac{(\lambda/\mu)^{j}}{\lambda j} \dfrac{(\lambda/\mu)^{-\min\{ i,j\}}-1}{(\lambda/\mu)^{-1}-1}.}\end{align}
Equation (6.5) is the same as
 \begin{equation*}P_{i,j}= \begin{cases}\dfrac{1}{\lambda j} \dfrac{1-(\lambda/\mu)^{j}}{(\lambda/\mu)^{-1}-1}, & j \leq i ,\\[12pt] \dfrac{1}{\lambda j} \dfrac{(\lambda/\mu)^{j-i}-(\lambda/\mu)^{j}}{(\lambda/\mu)^{-1}-1}, & j \geq i+1.\end{cases}\end{equation*}
\begin{equation*}P_{i,j}= \begin{cases}\dfrac{1}{\lambda j} \dfrac{1-(\lambda/\mu)^{j}}{(\lambda/\mu)^{-1}-1}, & j \leq i ,\\[12pt] \dfrac{1}{\lambda j} \dfrac{(\lambda/\mu)^{j-i}-(\lambda/\mu)^{j}}{(\lambda/\mu)^{-1}-1}, & j \geq i+1.\end{cases}\end{equation*}
The quasi-limiting distribution is
We notice that in the limit case
![]() $i \rightarrow \infty$
we have
$i \rightarrow \infty$
we have
which is not a finite measure since
![]() $\sum_{j \geq 1}{j}^{-1}=\infty$
.
$\sum_{j \geq 1}{j}^{-1}=\infty$
.
The case
![]() $\lambda \geq \mu$
. We first study the case
$\lambda \geq \mu$
. We first study the case
![]() $\lambda =\mu$
. The probability of non-extinction is
$\lambda =\mu$
. The probability of non-extinction is
(see [Reference Orsingher and Polito23, formula (2.26)]). Alternatively, for
![]() $\alpha=1$
we have the identity
$\alpha=1$
we have the identity
![]() $\mathbb{P}_1[T_{0}>t]={{1}/{(1+\lambda t)}}$
. From Theorem 3.1 we get the formula
$\mathbb{P}_1[T_{0}>t]={{1}/{(1+\lambda t)}}$
. From Theorem 3.1 we get the formula
In order to study the asymptotic behavior, we introduce the function
It is well known that (see [Reference Bertoin3, equation 4.2, page 31])
with probability 1, for some positive constant
![]() $C_\alpha$
depending only on
$C_\alpha$
depending only on
![]() $\alpha$
. By taking the limit
$\alpha$
. By taking the limit
![]() $t \rightarrow \infty$
, we now get
$t \rightarrow \infty$
, we now get
 \begin{align*} \liminf_{t \rightarrow \infty} f(t) \mathbb{P}_1[T_{0,\alpha}>t] &= \liminf_{t \rightarrow \infty} \mathbb{E}\biggl[\dfrac{f(t)}{1+\lambda L^{(\alpha)}({t}) }\biggr]\\[5pt] &\geq \mathbb{E}\biggl[\liminf_{t \rightarrow \infty} \dfrac{f(t)}{1+\lambda L^{(\alpha)}({t}) }\biggr]\\[5pt] &\geq \mathbb{E}\Biggl[ \dfrac{1}{\limsup_{t \rightarrow \infty} \frac{1}{f(t)}+\lambda \frac{ L^{(\alpha)}({t})}{f(t)} }\Biggr]. \end{align*}
\begin{align*} \liminf_{t \rightarrow \infty} f(t) \mathbb{P}_1[T_{0,\alpha}>t] &= \liminf_{t \rightarrow \infty} \mathbb{E}\biggl[\dfrac{f(t)}{1+\lambda L^{(\alpha)}({t}) }\biggr]\\[5pt] &\geq \mathbb{E}\biggl[\liminf_{t \rightarrow \infty} \dfrac{f(t)}{1+\lambda L^{(\alpha)}({t}) }\biggr]\\[5pt] &\geq \mathbb{E}\Biggl[ \dfrac{1}{\limsup_{t \rightarrow \infty} \frac{1}{f(t)}+\lambda \frac{ L^{(\alpha)}({t})}{f(t)} }\Biggr]. \end{align*}
From (6.6) and noticing that
![]() $\lim_{t \rightarrow \infty} f(t)=\infty$
, we conclude
$\lim_{t \rightarrow \infty} f(t)=\infty$
, we conclude
Similarly, we compute
 \begin{align*}\limsup_{t \rightarrow \infty } \dfrac{p_{1,j,\alpha}(t)}{ \mathbb{P}_1[T_{0,\alpha}>t]}&= \limsup_{t \rightarrow \infty } \dfrac{f(t)p_{1,j,\alpha}(t)}{ f(t)\mathbb{P}_1[T_{0,\alpha}>t]}\\[5pt]&\leq \dfrac{ \limsup_{t \rightarrow \infty }f(t)p_{1,j,\alpha}(t)}{ \liminf_{t \rightarrow \infty }f(t)\mathbb{P}_1[T_{0,\alpha}>t]}\\[5pt]&\leq \lambda C_\alpha \limsup_{t \rightarrow \infty }f(t)p_{1,j,\alpha}(t).\end{align*}
\begin{align*}\limsup_{t \rightarrow \infty } \dfrac{p_{1,j,\alpha}(t)}{ \mathbb{P}_1[T_{0,\alpha}>t]}&= \limsup_{t \rightarrow \infty } \dfrac{f(t)p_{1,j,\alpha}(t)}{ f(t)\mathbb{P}_1[T_{0,\alpha}>t]}\\[5pt]&\leq \dfrac{ \limsup_{t \rightarrow \infty }f(t)p_{1,j,\alpha}(t)}{ \liminf_{t \rightarrow \infty }f(t)\mathbb{P}_1[T_{0,\alpha}>t]}\\[5pt]&\leq \lambda C_\alpha \limsup_{t \rightarrow \infty }f(t)p_{1,j,\alpha}(t).\end{align*}
The identity
allows us to compute the limit
 \begin{align*}\limsup_{t \rightarrow \infty } f^2(t)p_{1,j,\alpha}(t) &= \limsup_{t \rightarrow \infty }f^{2}(t)\mathbb{E}\biggl[ \dfrac{(\lambda L^{(\alpha)}({t}))^{j-1}}{(1+\lambda L^{(\alpha)}({t}))^{j+1}}\biggr]\\[5pt]&\leq \mathbb{E}\biggl[ \limsup_{t \rightarrow \infty } f^{2}(t)\dfrac{(\lambda L^{(\alpha)}({t}))^{j-1}}{(1+\lambda L^{(\alpha)}({t}))^{j+1}}\biggr]\\[5pt]&\leq \dfrac{1}{\lambda^2}\mathbb{E}\biggl[ \limsup_{t \rightarrow \infty }\dfrac{1}{(L^{(\alpha)}({t})/f(t))^2}\biggr]\\[5pt]&= \dfrac{1}{(\lambda C_\alpha)^2}.\end{align*}
\begin{align*}\limsup_{t \rightarrow \infty } f^2(t)p_{1,j,\alpha}(t) &= \limsup_{t \rightarrow \infty }f^{2}(t)\mathbb{E}\biggl[ \dfrac{(\lambda L^{(\alpha)}({t}))^{j-1}}{(1+\lambda L^{(\alpha)}({t}))^{j+1}}\biggr]\\[5pt]&\leq \mathbb{E}\biggl[ \limsup_{t \rightarrow \infty } f^{2}(t)\dfrac{(\lambda L^{(\alpha)}({t}))^{j-1}}{(1+\lambda L^{(\alpha)}({t}))^{j+1}}\biggr]\\[5pt]&\leq \dfrac{1}{\lambda^2}\mathbb{E}\biggl[ \limsup_{t \rightarrow \infty }\dfrac{1}{(L^{(\alpha)}({t})/f(t))^2}\biggr]\\[5pt]&= \dfrac{1}{(\lambda C_\alpha)^2}.\end{align*}
In conclusion,
Consequently there is no quasi-limiting distribution as expected. Finally, when
![]() $\lambda>\mu$
the probability of non-extinction is
$\lambda>\mu$
the probability of non-extinction is
which is a strictly positive value (see [Reference Orsingher and Polito23, formula (2.13)]), so there is no quasi-limiting distribution. By following an argument similar to the previous case, we get the limit
Appendix A. The Mittag–Leffler function
We present a summary concerning the basic properties of the Mittag–Leffler function.
Definition A.1. The complex-valued Mittag–Leffler function with parameter
![]() $\alpha \in (0,1]$
is defined as
$\alpha \in (0,1]$
is defined as
 \begin{equation*} \mathcal{E}_{\alpha,1}(z)=\sum_{k \geq 0}\dfrac{z^k}{\Gamma(\alpha k+1)},\quad z \in \mathbb{C}. \end{equation*}
\begin{equation*} \mathcal{E}_{\alpha,1}(z)=\sum_{k \geq 0}\dfrac{z^k}{\Gamma(\alpha k+1)},\quad z \in \mathbb{C}. \end{equation*}
In particular, when
![]() $\alpha=1$
we have that
$\alpha=1$
we have that
![]() $\mathcal{E}_{1,1}(z)={\textrm{e}}^z$
is the exponential function.
$\mathcal{E}_{1,1}(z)={\textrm{e}}^z$
is the exponential function.
In the real-valued case it is well known (see [Reference Gorenflo, Kilbas, Mainardi and Rogosin12, Proposition 3.23]) that the Mittag–Leffler function with negative argument
![]() $\mathcal{E}_{\alpha,1}(\!-\!x)$
,
$\mathcal{E}_{\alpha,1}(\!-\!x)$
,
![]() $x>0$
is completely monotonic for all
$x>0$
is completely monotonic for all
![]() $0 \leq \alpha \leq 1$
, that is,
$0 \leq \alpha \leq 1$
, that is,
This is equivalent to the existence of a representation of
![]() $\mathcal{E}_{\alpha,1}(\!-\!x)$
in the form of a Laplace–Stieltjes integral with non-decreasing density and non-negative measure
$\mathcal{E}_{\alpha,1}(\!-\!x)$
in the form of a Laplace–Stieltjes integral with non-decreasing density and non-negative measure
![]() ${\textrm{d}} \mu$
:
${\textrm{d}} \mu$
:
Since
![]() $\mathcal{E}_{\alpha,1}(0)=1$
we have from the dominated convergence theorem that
$\mathcal{E}_{\alpha,1}(0)=1$
we have from the dominated convergence theorem that
![]() $\mu$
is a probability measure. In fact we know from (3.5), for
$\mu$
is a probability measure. In fact we know from (3.5), for
![]() $s=x$
and
$s=x$
and
![]() $t=1$
, that
$t=1$
, that
and consequently the measure is
![]() ${\textrm{d}} \mu(u)=h_\alpha(u,1) \,{\textrm{d}} u$
. The density
${\textrm{d}} \mu(u)=h_\alpha(u,1) \,{\textrm{d}} u$
. The density
![]() $h_\alpha(u,1)$
is known as the Lamperti distribution obtained as the law of the ratio of two independent subordinators of order
$h_\alpha(u,1)$
is known as the Lamperti distribution obtained as the law of the ratio of two independent subordinators of order
![]() $\alpha$
. In particular, the integral representation (A.1) implies that the function
$\alpha$
. In particular, the integral representation (A.1) implies that the function
![]() $\mathcal{E}_{\alpha,1}(x)$
is strictly positive for
$\mathcal{E}_{\alpha,1}(x)$
is strictly positive for
![]() $x \geq 0$
.
$x \geq 0$
.
Proposition A.1. For all
![]() $\lambda>0$
,
$\lambda>0$
,
![]() $f(x)=\mathcal{E}_{\alpha,1}(\!-\!\lambda x^\alpha)$
is the unique solution to the equation
$f(x)=\mathcal{E}_{\alpha,1}(\!-\!\lambda x^\alpha)$
is the unique solution to the equation
Proof. It proceeds by direct computation by taking the Laplace transform
on both sides of (A.2). On the right-hand side we just have
![]() $\mathcal{L}[\!-\!\lambda f](s)=-\lambda\mathcal{L}[f](s)$
, whereas on the left-hand side we have
$\mathcal{L}[\!-\!\lambda f](s)=-\lambda\mathcal{L}[f](s)$
, whereas on the left-hand side we have
 \begin{align} \mathcal{L}[\mathbb{D}^{\alpha}f](s)&= \dfrac{1}{\Gamma(1-\alpha)}\mathcal{L}\biggl[\int_0^x\dfrac{f^\prime(u) }{(x-u)^{\alpha}}\,{\textrm{d}} u\biggr](s) \notag \\[5pt] &= \mathcal{L}[f^\prime](s)\mathcal{L}\biggl[\dfrac{t^{-\alpha}}{\Gamma(1-\alpha)}\biggr](s) \notag \\[5pt] &= ( s\mathcal{L}[f](s)-f(0))s^{\alpha-1}. \end{align}
\begin{align} \mathcal{L}[\mathbb{D}^{\alpha}f](s)&= \dfrac{1}{\Gamma(1-\alpha)}\mathcal{L}\biggl[\int_0^x\dfrac{f^\prime(u) }{(x-u)^{\alpha}}\,{\textrm{d}} u\biggr](s) \notag \\[5pt] &= \mathcal{L}[f^\prime](s)\mathcal{L}\biggl[\dfrac{t^{-\alpha}}{\Gamma(1-\alpha)}\biggr](s) \notag \\[5pt] &= ( s\mathcal{L}[f](s)-f(0))s^{\alpha-1}. \end{align}
This implies
By taking the inverse
 \begin{equation*}f(x)=\sum_{k \geq 0}\dfrac{(\!-\!\lambda x^\alpha)^k}{\Gamma(\alpha k+1)},\end{equation*}
\begin{equation*}f(x)=\sum_{k \geq 0}\dfrac{(\!-\!\lambda x^\alpha)^k}{\Gamma(\alpha k+1)},\end{equation*}
we conclude
![]() $f(x)=\mathcal{E}_{\alpha,1}(\!-\!\lambda x^\alpha)$
.
$f(x)=\mathcal{E}_{\alpha,1}(\!-\!\lambda x^\alpha)$
.
Concerning the asymptotic behavior of the complex-valued Mittag–Leffler function, we take formulas 4.7.4 and 4.7.5 from page 75 of [Reference Gorenflo, Kilbas, Mainardi and Rogosin12]. Let
![]() $\alpha \in (0,2)$
and let
$\alpha \in (0,2)$
and let
![]() ${{\pi \alpha}/{2}}<\theta<\min\{\pi,\alpha \pi\}$
, where
${{\pi \alpha}/{2}}<\theta<\min\{\pi,\alpha \pi\}$
, where
![]() $\theta=\arg\!(z)$
. For all
$\theta=\arg\!(z)$
. For all
![]() $|z|$
large enough we have
$|z|$
large enough we have
 \begin{align*} \mathcal{E}_{\alpha,1}(z)&= \dfrac{1}{\alpha}{{\textrm{e}}^{z^{1/\alpha}}}-\sum_{m=1}^{N-1}\dfrac{z^{-m}}{\Gamma(1-m\alpha)}+{\textrm{O}}\left(|z|^{-N}\right),\quad |\arg\!(z)|\leq \theta, \\[5pt] \mathcal{E}_{\alpha,1}(z)&= -\sum_{m=1}^{N-1}\dfrac{z^{-m}}{\Gamma(1-m\alpha)}+{\textrm{O}}\left(|z|^{-N}\right),\quad \theta \leq |\arg\!(z)|\leq \pi. \end{align*}
\begin{align*} \mathcal{E}_{\alpha,1}(z)&= \dfrac{1}{\alpha}{{\textrm{e}}^{z^{1/\alpha}}}-\sum_{m=1}^{N-1}\dfrac{z^{-m}}{\Gamma(1-m\alpha)}+{\textrm{O}}\left(|z|^{-N}\right),\quad |\arg\!(z)|\leq \theta, \\[5pt] \mathcal{E}_{\alpha,1}(z)&= -\sum_{m=1}^{N-1}\dfrac{z^{-m}}{\Gamma(1-m\alpha)}+{\textrm{O}}\left(|z|^{-N}\right),\quad \theta \leq |\arg\!(z)|\leq \pi. \end{align*}
In particular, when
![]() $\arg\!(z)=0$
and
$\arg\!(z)=0$
and
![]() $\arg\!(z)=\pi$
, we recover the asymptotic expansion for the real-valued case. In fact when
$\arg\!(z)=\pi$
, we recover the asymptotic expansion for the real-valued case. In fact when
![]() $|x|$
is large enough we get the following approximations:
$|x|$
is large enough we get the following approximations:
 \begin{equation} \begin{aligned}\mathcal{E}_{\alpha,1}(x)&= \dfrac{1}{\alpha}{{\textrm{e}}^{x^{1/\alpha}}}-\dfrac{1}{x}\dfrac{1}{\Gamma(1-\alpha)}-\dfrac{1}{x^2}\dfrac{1}{\Gamma(1-2\alpha)}+{\textrm{O}}(x^{-3}), \\[5pt]\mathcal{E}_{\alpha,1}(\!-\!x)&= \dfrac{1}{x}\dfrac{1}{\Gamma(1-\alpha)}-\dfrac{1}{x^2}\dfrac{1}{\Gamma(1-2\alpha)}+{\textrm{O}}(x^{-3}). \end{aligned} \end{equation}
\begin{equation} \begin{aligned}\mathcal{E}_{\alpha,1}(x)&= \dfrac{1}{\alpha}{{\textrm{e}}^{x^{1/\alpha}}}-\dfrac{1}{x}\dfrac{1}{\Gamma(1-\alpha)}-\dfrac{1}{x^2}\dfrac{1}{\Gamma(1-2\alpha)}+{\textrm{O}}(x^{-3}), \\[5pt]\mathcal{E}_{\alpha,1}(\!-\!x)&= \dfrac{1}{x}\dfrac{1}{\Gamma(1-\alpha)}-\dfrac{1}{x^2}\dfrac{1}{\Gamma(1-2\alpha)}+{\textrm{O}}(x^{-3}). \end{aligned} \end{equation}
The variable x can be replaced by
![]() $\pm \lambda t^{\alpha}$
, so that for
$\pm \lambda t^{\alpha}$
, so that for
![]() $\alpha \neq 1/2$
,
$\alpha \neq 1/2$
,
![]() $\lambda>0$
fixed and
$\lambda>0$
fixed and
![]() $t>0$
large enough, we obtain the following asymptotic formulas:
$t>0$
large enough, we obtain the following asymptotic formulas:
 \begin{equation} \begin{aligned}\mathcal{E}_{\alpha,1}(\lambda t^\alpha)&= \dfrac{1}{\alpha}{{\textrm{e}}^{\lambda ^{1/\alpha}t}}-\dfrac{1}{\lambda t^\alpha }\dfrac{1}{\Gamma(1-\alpha)}-\dfrac{1}{\lambda^2 t^{2 \alpha}}\dfrac{1}{\Gamma(1-2\alpha)}+{\textrm{O}}(t^{-3\alpha }), \\[5pt]\mathcal{E}_{\alpha,1}(\!-\!\lambda t^\alpha)&= \dfrac{1}{\lambda t^\alpha }\dfrac{1}{\Gamma(1-\alpha)}-\dfrac{1}{\lambda^2t^{2 \alpha}}\dfrac{1}{\Gamma(1-2\alpha)}+{\textrm{O}}(t^{-3\alpha }). \end{aligned} \end{equation}
\begin{equation} \begin{aligned}\mathcal{E}_{\alpha,1}(\lambda t^\alpha)&= \dfrac{1}{\alpha}{{\textrm{e}}^{\lambda ^{1/\alpha}t}}-\dfrac{1}{\lambda t^\alpha }\dfrac{1}{\Gamma(1-\alpha)}-\dfrac{1}{\lambda^2 t^{2 \alpha}}\dfrac{1}{\Gamma(1-2\alpha)}+{\textrm{O}}(t^{-3\alpha }), \\[5pt]\mathcal{E}_{\alpha,1}(\!-\!\lambda t^\alpha)&= \dfrac{1}{\lambda t^\alpha }\dfrac{1}{\Gamma(1-\alpha)}-\dfrac{1}{\lambda^2t^{2 \alpha}}\dfrac{1}{\Gamma(1-2\alpha)}+{\textrm{O}}(t^{-3\alpha }). \end{aligned} \end{equation}
For
![]() $\alpha=1/2$
, the second term in (A.6) vanishes, yielding
$\alpha=1/2$
, the second term in (A.6) vanishes, yielding
Moreover, the following limits are valid for all
![]() $\lambda>0$
:
$\lambda>0$
:
 \begin{equation} \begin{aligned}\lim_{t \rightarrow \infty} t^\alpha{\mathcal{E}_{\alpha,1}(\!-\!\lambda t^\alpha)}&= \dfrac{1}{\lambda}\dfrac{1}{\Gamma(1-\alpha)},\\[5pt]\lim_{t \rightarrow \infty} {{\textrm{e}}^{-\lambda^{1/\alpha} t}}\mathcal{E}_{\alpha,1}(\lambda t^\alpha)&= \dfrac{1}{\alpha}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned}\lim_{t \rightarrow \infty} t^\alpha{\mathcal{E}_{\alpha,1}(\!-\!\lambda t^\alpha)}&= \dfrac{1}{\lambda}\dfrac{1}{\Gamma(1-\alpha)},\\[5pt]\lim_{t \rightarrow \infty} {{\textrm{e}}^{-\lambda^{1/\alpha} t}}\mathcal{E}_{\alpha,1}(\lambda t^\alpha)&= \dfrac{1}{\alpha}. \end{aligned} \end{equation}
Acknowledgements
The author acknowledges the following mathematical institutes, where part of this work was done: Universidad Católica del Norte (Antofagasta, Chile) and Instituto Potosino de Investigación Científica y Tecnológica (San Luis Potosí, México). Finally, the author acknowledges the anonymous referees for their useful suggestions which substantially helped to improve the quality of this work.
Funding information
The author acknowledges the financial support of the grant program FONDECYT de Iniciación en Investigación, project no. 11140479.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.