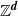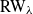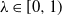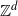1. Introduction
The biased random walk 
${\text{RW}}_\lambda$
with parameter 
$\lambda\in [0, \infty)$
was introduced to design a Monte Carlo algorithm for the self-avoiding walk by Berretti and Sokal [Reference Berretti and Sokal5]. The idea was refined and developed in [Reference Lawler and Sokal12, Reference Randall20, Reference Sinclair and Jerrum22]. In the 1990s, Lyons [Reference Lyons13, Reference Lyons14, Reference Lyons15] and Lyons et al. [Reference Lyons, Pemantle and Peres16, Reference Lyons, Pemantle and Peres17] made fundamental advances in the study of biased random walks on Cayley graphs and trees. In particular, they proved remarkable results on transience/recurrence phase transition for 
${\text{RW}}_{\lambda}$
when 
$\lambda$
changes. The critical value 
$\lambda_{\text{c}}$
is equal to the exponential growth rate of a Cayley graph or the branching number of a tree. The phase transition and speed for 
${\text{RW}}_{\lambda}$
were also obtained on Galton–Watson trees in [Reference Lyons, Pemantle and Peres16]. In recent years, problems of 
${\text{RW}}_\lambda$
on Galton–Watson trees continue to attract much interest, where some variants of the biased random walk are possibly modified (see, for example, [Reference Aϊdékon1, Reference Arous and Fribergh2, Reference Arous, Fribergh, Gantert and Hammond3, Reference Arous, Hu, Olla and Zeitouni4, Reference Hu and Shi10]). For the invariance principle of 
${\text{RW}}_{\lambda}$
, Bowditch [Reference Bowditch6] proved a quenched invariance principle for 
${\text{RW}}_{\lambda}$
on a supercritical Galton–Watson tree where the corresponding scaling limit is a one-dimensional Brownian motion. On a typical Cayley graph, Euclidean lattice 
${\mathbb{Z}}^d$
, the speed and spectral radius for 
${\text{RW}}_{\lambda}$
were studied in [Reference Shi, Sidoravicius, Song, Wang and Xiang21]. To understand the limit behavior of 
${\text{RW}}_{\lambda}$
on 
${\mathbb{Z}}^d$
is one of the motivations of this paper.
We first introduce the notion of a biased random walk. Let 
$\textbf{0}=(0,\ldots,0)\in \mathbb{Z}^d$
and 
$|x| = \sum_{i=1}^d |x_i|$
denote the graph distance between 
$x = (x_1,\ldots,x_d) \in {\mathbb{Z}}^d$
and 
${\textbf{0}}$
. Write 
$\mathbb{N}$
for the set of natural numbers, and let 
$\mathbb{Z}_{+}=\mathbb{N}\cup\{0\}$
. For any 
$n\in\mathbb{Z}_{+}$
, define
\begin{equation*}B(n)=\{x\in \mathbb{Z}^d\,:\, \vert x\vert\leq n\},\qquad \partial B(n)=\{x\in \mathbb{Z}^d\,:\, \vert x\vert=n\}.\end{equation*}
Let 
$\lambda \in [0, \infty)$
. If an edge 
$e = \{x, y\}$
is at distance n from 
$\textbf{0}$
, i.e. 
$\min(|x|, |y|) = n$
, its conductance is defined as 
$c(e) =c(x, y) = \lambda^{-n}$
. Denote by 
${\text{RW}}_\lambda$
the random walk associated with such conductances, and call it the biased random walk with parameter 
$\lambda$
. In other words, 
${\text{RW}}_{\lambda}$
is the Markov chain on 
${\mathbb{Z}}^d$
with the following transition probabilities: for 
$v, u \in {\mathbb{Z}}^d$
with 
$|v-u| = 1$
,
\begin{equation} p(v,u) = \frac{c(v, u)}{\sum_{w: |w-v| = 1} c(v, w)}=\begin{cases}\frac{1}{d_{v}} &\text{if}\ v=\textbf{0},\\[4pt] \frac{\lambda}{d_v+(\lambda-1)d_v^-} & \text{if}\ u\in \partial B(|v|-1)\ \text{and}\ v\neq \textbf{0},\\[4pt] \frac{1}{d_v+(\lambda-1)d_v^-} &\text{otherwise}. \end{cases}\end{equation}
Here, 
$d_v=2d$
is the degree of the vertex v, and 
$d_v^-$
(resp. 
$d_v^+$
) is the number of edges connecting v to 
$\partial B(|v|-1)$
(resp. 
$\partial B(|v|+1)$
). When 
$\lambda = 1$
, 
${\text{RW}}_{\lambda}$
is the usual simple random walk (SRW).
Let 
${(X_n)_{n = 0}^{\infty} = (X_n^1, \ldots, X_n^d)_{n = 0}^{\infty}}$
be 
${\text{RW}}_{\lambda}$
on 
${\mathbb{Z}}^d$
. It is known that 
${(X_n)_{n = 0}^{\infty}}$
is transient for 
$0\leq \lambda<1$
and positive recurrent for 
$\lambda>1$
(see [Reference Lyons15] and [Reference Lyons and Peres18, Theorem 3.10]). In the latter case, the related central limit theorem and invariance principle can be derived from [Reference Jones11] and [Reference Merlevède, Peligrad and Utev19] straightforwardly. In this paper we will focus on the case 
$0\leq \lambda < 1$
.
Note that we have, for 
$v=(v_1,\ldots,v_d)\in\mathbb{Z}^d$
,
\begin{eqnarray*} d_v^+=d+\kappa (v),\qquad d_v^-=d-\kappa (v),\end{eqnarray*}
where 
$\kappa(v)$
is the number of 
$1 \leq i \leq d$
such that 
$v_i = 0$
. It is easy to see from (1) that 
${(X_n)_{n = 0}^{\infty}}$
is closely related to a drifted random walk on 
${\mathbb{Z}}^d$
. More precisely, before leaving the first open orthant, 
${(X_n)_{n = 0}^{\infty}}$
has the same transition probabilities as those of the drifted random walk on 
${\mathbb{Z}}^d$
with step distribution 
$\nu$
given by
\begin{equation} \nu(e_1) = \cdots = \nu(e_d) = \frac{1}{d(1+\lambda)} \quad \text{and} \quad \nu({-}e_1) = \cdots = \nu({-}e_d) = \frac{\lambda}{d(1+\lambda)}, \end{equation}
where 
$\{e_1, \ldots, e_d \}$
is the standard basis in 
${\mathbb{Z}}^d$
. See Figure 1 for an illustration of transition probabilities for biased and drifted random walks on 
${\mathbb{Z}}^2$
.
Figure 1: Illustration of transition probabilities for biased and drifted random walks at 
$\textbf{0}$
, on axis, and in the first open quadrant. Left: biased random walk. Right: drifted random walk.
Using this connection to the drifted random walk, it is proved in [Reference Shi, Sidoravicius, Song, Wang and Xiang21] that, for 
$\lambda \in (0, 1)$
, 
${(X_n)_{n=0}^{\infty}}$
almost surely (a.s.) visits the union of axial hyperplanes
\begin{equation} {\mathcal{X}} = \{ x=(x_1,\ldots,x_d) \in {\mathbb{Z}}^d\,:\, x_i = 0 \text{ for some } 1 \leq i \leq d \} \end{equation}
only finitely many times, and the following strong law of large numbers holds:
\begin{equation} \lim_{n \to \infty} \frac{1}{n} (|X_n^1|, \ldots, |X_n^d|) \rightarrow \frac{1- \lambda}{1+ \lambda} \Big(\frac{1}{d},\ldots,\frac{1}{d}\Big) \quad \text{a.s.} \end{equation}
In this paper we prove the invariance principle (IP) and central limit theorem (CLT) for the reflected 
${\text{RW}}_\lambda$
$\{( | X_n^1 |, \, \ldots,\, | X_n^d | )\}_{n=0}^{\infty}$
in Section 2, and the large deviation principle (LDP) for the scaled reflected 
${\text{RW}}_\lambda$
$\{\frac{1}{n}(\vert X_n^1\vert,\ldots,\vert X_n^d\vert)\}_{n=0}^{\infty}$
in Section 3. The aforementioned connection between biased and drifted random walks will also play an important role in the proofs of our main results. We will see in the proof that the scaling limit in the IP of the reflected 
${\text{RW}}_\lambda$
is the same as that of the drifted random walk, and hence is not a d-dimensional Brownian motion. However, their rate functions in the LDP are quite different from each other. Here, we can only calculate the rate function 
$\Lambda^\ast$
when 
$d\in\{1,2\}$
and 
$\lambda\in (0,1)$
as well as 
$d\geq 2$
and 
$\lambda=0$
. To obtain an explicit rate function when 
$d\geq 3$
and 
$\lambda\in (0,1)$
remains an open problem.
2. CLT and IP for reflected 
${\text{RW}}_\lambda$
with
$\lambda\in [0,1)$
In this section we use the martingale CLT for 
$\mathbb{R}^d$
-valued martingales [Reference Ethier and Kurtz9, Chapter 7, Theorem 1.4] and the martingale characterization of Markov chains to prove the IP for the reflected 
${\text{RW}}_\lambda$
$\{(|X_n^1|, |X_n^2|,\ldots, |X_n^d|)\}$
(Theorem 2.1). The CLT for the reflected 
${\text{RW}}_\lambda$
is a consequence of the corresponding IP.
To describe our main result we need to introduce some notation. For any nonnegative definite symmetric 
$d\times d$
matrix A, let 
$\mathcal{N}(\textbf{0},A)$
be the normal distribution with mean 
$\textbf{0}$
and covariance matrix A. Define the following positive definite symmetric 
$d\times d$
matrix 
$\Sigma=(\Sigma_{ij})_{1\leq i,j\leq d}$
:
\begin{equation*}\Sigma_{ii}=\frac{1}{d}-\frac{(1-\lambda)^2}{d^2(1+\lambda)^2},\qquad \Sigma_{ij}=-\frac{(1-\lambda)^2}{d^2(1+\lambda)^2},\qquad 1\leq i\not=j\leq d.\end{equation*}
For a random sequence 
${(Y_n)_{n=0}^{\infty}}$
and a random variable X in the Skorokhod space 
$D([0,\infty), \mathbb{R}^d)$
, 
$Y_n\rightarrow X$
means that as 
$n\rightarrow\infty$
, 
$Y_n$
converges in distribution to X in 
$D([0,\infty),\mathbb{R}^d)$
. For any 
$a\in\mathbb{R},$
let 
$\lfloor a\rfloor$
be the integer part of a. Put
\begin{equation*}v=\bigg(\frac{1-\lambda}{d(1+\lambda)},\ldots,\frac{1-\lambda}{d(1+\lambda)}\bigg)\in\mathbb{R}^d.\end{equation*}
Theorem 2.1. (IP and CLT.) Let 
$0 \leq \lambda < 1$
, and 
${(X_m)_{m=0}^{\infty}}$
be 
${\text{RW}}_{\lambda}$
on 
$\mathbb{Z}^d$
starting at 
$x\in \mathbb{Z}^d$
. Then, on 
$D([0,\infty),\mathbb{R}^d)$
,
\begin{equation} \bigg(\frac{(|X_{\lfloor nt\rfloor}^1|,\ldots, |X_{\lfloor nt\rfloor}^d|)-nvt}{\sqrt{n}}\bigg)_{t\geq 0} \end{equation}
converges in distribution to 
$\frac{1}{\sqrt{d}\,}[I- \frac{1-\rho_\lambda}{d}E]W_t$
as 
$n\rightarrow\infty$
, where 
${(W_t)_{t\geq 0}}$
is the d-dimensional Brownian motion starting at 
${\bf 0}$
, I is the identity matrix, and E denotes the 
$d\times d$
matrix whose entries are all equal to 1. Here, 
$\rho_\lambda = 2 \sqrt{\lambda}/(1+\lambda)$
is the spectral radius of 
${(X_n)_{n\geq 1}}$
(see [Reference Shi, Sidoravicius, Song, Wang and Xiang21, Theorem 1.1]).
In particular, we have
\begin{eqnarray*}\frac{(|X_n^1|,\ldots,|X_n^d|)-nv}{\sqrt{n}}\rightarrow \mathcal{N}({\bf 0},\Sigma)\end{eqnarray*}
in distribution as 
$n \to \infty$
.
Remark 2.1. (i) Note that 
$\Sigma=0$
when 
$d=1$
and 
$\lambda=0$
. Hence, for 
$d=1$
and 
$\lambda=0$
, both
\begin{equation*}\frac{|X_n|-nv}{\sqrt{n}}=\frac{\vert X_0\vert+n-nv}{\sqrt{n}}\rightarrow \mathcal{N}(\textbf{0},\Sigma)\end{equation*}
and
\begin{equation*}\bigg(\frac{|X_{\lfloor nt\rfloor}|-nvt}{\sqrt{n}}\bigg)_{t\geq 0}\end{equation*}
converging in distribution to 
$Y=(Y_t)_{t\geq 0}$
are not interesting.
From Theorem 2.1, the following holds: For 
${\text{RW}}_{\lambda}$
${(X_m)_{m=0}^{\infty}}$
with 
$\lambda<1$
on 
$\mathbb{Z}^d$
which starts at any fixed vertex, as 
$n\rightarrow\infty,$
\begin{equation*}\bigg(\frac{|X_{\lfloor nt\rfloor}|-n\frac{1-\lambda}{1+\lambda}t}{\sqrt{n}}\bigg)_{t\geq 0}\end{equation*}
converges in distribution to 
${(\rho_{\lambda} B_t)_{t\geq 0}}$
on 
$D([0,\infty),\mathbb{R})$
and 
${(B_t)_{t\geq 0}}$
is the 1-dimensional Brownian motion starting at 0.
(ii) The limit process is not a d-dimensional Brownian motion since the cross-variation process of 
$M^{n, i}$
and 
$M^{n, j}$
(as below) doesn’t converge to 
${\textbf{0}}$
as 
$n\rightarrow \infty$
, 
$1\leq i\neq j\leq d$
. Note that by the martingale CLT, the drifted random walk defined in (2) has the same limit process in IP, which is not a d-dimensional Brownian motion.
Proof of Theorem 2.1. We only prove IP for
\begin{equation*}\bigg(\frac{(|X_{\lfloor nt\rfloor}^1|,\ldots, |X_{\lfloor nt\rfloor}^d|)-nvt}{\sqrt{n}}\bigg)_{t\geq 0}.\end{equation*}
Let 
$\mathcal{F}_k=\sigma(X_0,X_1,\ldots,X_k)$
, 
$k\in\mathbb{Z}_{+}$
. For 
$1 \leq i \leq d$
, define functions 
$f_i$
: 
${\mathbb{Z}}^d \to {\mathbb{R}}$
by
\begin{equation*} f_i(x) = \begin{cases} \frac{2}{d+\kappa(x)+\lambda (d- \kappa(x))} & \text{if } x_i= 0,\\[4pt] \frac{1- \lambda}{d+\kappa(x)+\lambda (d-\kappa(x))} & \text{if } x_i\neq 0. \end{cases} \end{equation*}
Note that, given 
${\mathcal{F}}_{k-1}$
, the conditional distribution of 
$X_k$
is 
$p(X_{k-1}, \cdot)$
, where p(v, u) is the transition probability of 
${(X_n)_{n = 0}^{\infty}}$
defined in (1). By a direct calculation, we have, for 
$k \in \mathbb{N}$
,
\begin{equation*} f_i(X_{k-1}) = \text{E} ( |X_k^i| - |X_{k-1}^i| \mid {\mathcal{F}}_{k-1} ). \end{equation*}
Therefore, 
$\{|X_k^i|-|X_{k-1}^i|-f_i(X_{k-1})\}_{k\geq 1}$
is an 
$\mathcal{F}_k$
-adapted martingale-difference sequence, and so is
\begin{eqnarray}\bigg\{\xi_{n, k}^i\,:\!= \frac{1}{\sqrt{n}\,}(|X_k^i|-|X_{k-1}^i|-f_i(X_{k-1}))\bigg\}_{k\geq 1}\end{eqnarray}
for any 
$n\in\mathbb{N}$
. Define 
$M^n=(M^n_t)_{t\geq 0}$
and 
$A_n=(A_n(t))_{t\geq 0}$
as follows:
\begin{align}M_t^n&=(M_t^{n,1},\ldots,M_t^{n,d})=\sum\limits_{k= 1}^{\lfloor nt\rfloor} \xi_{n,k}, \nonumber \\ A_n(t)&=(A_n^{i,j}(t))_{1\leq i,j\leq d}=\sum\limits_{k= 1}^{\lfloor nt\rfloor}(\xi_{n,k}^i\xi_{n,k}^{\kern1ptj})_{1\leq i,j\leq d},\quad t\geq 0.\end{align}
Then each 
${(M_t^{n,i})_{t\geq 0}}$
is an 
$\mathcal{F}_{\lfloor nt\rfloor}$
-martingale with 
$M^{n,i}_0=0$
, and, further, each 
$M^n$
is an 
$\mathbb{R}^d$
-valued 
$\mathcal{F}_{\lfloor nt\rfloor}$
-martingale with 
$M_0=\textbf{0}$
.
Note that, for any 
$t>0$
,
\begin{equation*}\vert M_t^n-M^n_{t-}\vert\leq \vert \xi_{n,\lfloor nt\rfloor}\vert =\sum\limits_{i=1}^d\vert\xi_{n,\lfloor nt\rfloor}^i\vert\leq \frac{2d}{\sqrt{n}\,},\end{equation*}
and for any 
$T\in (0,\infty)$
,
\begin{eqnarray}\lim\limits_{n\rightarrow\infty}\text{E}\Big[\sup_{t\leq T}|M^n_t-M^n_{t-}|\Big]\leq\lim\limits_{n \rightarrow \infty} \frac{2d}{\sqrt{n}\,} = 0.\end{eqnarray}
By [Reference Ethier and Kurtz9, Chapter 7, Theorem 1.4], to show the convergence of (5) it suffices to prove that
\begin{equation} A_n^{i,j}(t)= [M^{n, i}_{\cdot}, M^{n, j}_{\cdot}]_{t} \end{equation}
and
\begin{equation} \lim_{n\rightarrow \infty}A_n(t)=t\Sigma, \end{equation}
where 
$[M^{n, i}_{\cdot}, M^{n, j}_{\cdot}]$
is the cross-variation process of 
$M^{n, i}_{\cdot}$
and 
$M^{n, j}_{\cdot}$
.
We first prove (9). Fix any 
$1\leq i,j\leq d$
and 
$0\leq s<t<\infty$
. By the martingale property,
\begin{eqnarray*}\text{E}[ M_s^{n,j}(M_t^{n,i}-M_s^{n,i}) \mid \mathcal{F}_{\lfloor ns\rfloor}]=M_s^{n,j} \text{E}[ M_t^{n,i}-M_s^{n,i} \mid \mathcal{F}_{\lfloor ns\rfloor}]=0,\end{eqnarray*}
and similarly 
$\text{E}[ M_s^{n,i}(M_t^{n,j}-M_s^{n,j}) \mid \mathcal{F}_{\lfloor ns\rfloor}]=0$
. Additionally,
\begin{align*}\text{E}&[ (M_t^{n,i}-M_s^{n,i})(M_t^{n,j}-M_s^{n,j}) \mid \mathcal{F}_{\lfloor ns\rfloor}]\\&=\text{E}\left[ \sum\limits_{k=\lfloor ns\rfloor+1}^{\lfloor nt\rfloor}\xi_{n,k}^i\xi_{n,k}^{\kern1ptj} \ \Big|\ \mathcal{F}_{\lfloor ns\rfloor}\right]+ \text{E}\left[ \sum\limits_{\lfloor ns\rfloor+1\leq r<k\leq \lfloor nt\rfloor}\xi_{n,k}^i\xi_{n,r}^{\kern1ptj} \ \Big|\ \mathcal{F}_{\lfloor ns\rfloor}\right]\\&\quad + \text{E}\left[ \sum\limits_{\lfloor ns\rfloor+1\leq r<k\leq \lfloor nt\rfloor}\xi_{n,k}^{\kern1ptj}\xi_{n,r}^i \ \Big|\ \mathcal{F}_{\lfloor ns\rfloor}\right]\\&=\text{E}\left[ \sum\limits_{k=\lfloor ns\rfloor+1}^{\lfloor nt\rfloor}\xi_{n,k}^i\xi_{n,k}^{\kern1ptj} \ \Big|\ \mathcal{F}_{\lfloor ns\rfloor}\right]+ \sum\limits_{\lfloor ns\rfloor+1\leq r<k\leq \lfloor nt\rfloor}\text{E}[ \text{E}[ \xi_{n,k}^i\xi_{n,r}^{\kern1ptj} \mid \mathcal{F}_r] \mid \mathcal{F}_{\lfloor ns\rfloor}]\\&\quad + \sum\limits_{\lfloor ns\rfloor+1\leq r<k\leq \lfloor nt\rfloor}\text{E}[ \text{E}[ \xi_{n,k}^{\kern1ptj}\xi_{n,r}^i \mid \mathcal{F}_r] \mid \mathcal{F}_{\lfloor ns\rfloor}]\\&=\text{E}\left[ \sum\limits_{k=\lfloor ns\rfloor+1}^{\lfloor nt\rfloor}\xi_{n,k}^i\xi_{n,k}^{\kern1ptj} \ \Big|\ \mathcal{F}_{\lfloor ns\rfloor}\right]\\&=\text{E}[ A_n^{i,j}(t)-A_n^{i,j}(s) \mid \mathcal{F}_{\lfloor ns\rfloor}].\end{align*}
Since
\begin{multline*}M_t^{n,i}M_t^{n,j}-A_n^{i,j}(t) \\=M_s^{n,i}M_s^{n,j}-A_n^{i,j}(s)+M_s^{n,i}(M_t^{n,j}-M_s^{n,j})+M_s^{n,j}(M_t^{n,i}-M_s^{n,i})\\ +(M_t^{n,i}-M_s^{n,i})(M_t^{n,j}-M_s^{n,j})-(A_n^{i,j}(t)-A_n^{i,j}(s)),\end{multline*}
we see that
\begin{equation*} \text{E}[M_t^{n,i}M_t^{n,j}-A_n^{i,j}(t) \mid \mathcal{F}_{\lfloor ns\rfloor}]=M_s^{n,i}M_s^{n,j}-A_n^{i,j}(s),\end{equation*}
which implies (9).
It remains to prove (10). Recall from the introduction that 
${(X_n)_{n=0}^{\infty}}$
visits the union of axial hyperplanes 
${\mathcal{X}}$
defined by (3) finitely many times. Thus, for large enough k, 
$X_{k-1}$
belongs to one of the 
$2^d$
open orthants, and hence, for any 
$1 \leq i \not= j \leq d$
, 
$f_i(X_{k-1})=f_j(X_{k-1})=\frac{1-\lambda}{d(1+\lambda)}$
. As a consequence, we have
\begin{equation*}\frac{1}{n} \sum\limits_{k=1}^{\lfloor nt \rfloor}(|X_{k}^{\kern1ptj}|-|X_{k-1}^{\kern1ptj}|)=\frac{1}{n}(|X_{\lfloor nt \rfloor}^{\kern1ptj}|-|X_{0}^{\kern1ptj}|)\rightarrow \frac{(1-\lambda)t}{d(1+\lambda)} , \end{equation*}
which also holds with j replaced by i. Recall the definition of 
$\xi_{n,k}^i$
from (6). We have that
\begin{align}\nonumber\sum_{k=1}^{\lfloor nt \rfloor} \xi_{n,k}^{i}\xi_{n, k}^{\kern1ptj} & = \sum_{k=1}^{\lfloor nt \rfloor} \frac{(|X_{k}^i|-|X_{k-1}^i|-f_{i}(X_{k-1}))}{\sqrt{n}} \frac{(|X_{k}^{\kern1ptj}|-|X_{k-1}^{\kern1ptj}|-f_{j}(X_{k-1}))}{\sqrt{n}} \\\nonumber & =\frac{1}{n} \sum\limits_{k=1}^{\lfloor nt \rfloor} \{(|X_{k}^i|-|X_{k-1}^i|)(|X_{k}^{\kern1ptj}|-|X_{k-1}^{\kern1ptj}|)- (|X_{k}^i|-|X_{k-1}^i|)\, f_j(X_{k-1})\\\nonumber & \qquad\qquad \ - (|X_{k}^{\kern1ptj}|-|X_{k-1}^{\kern1ptj}|)\, f_i(X_{k-1})+ f_i(X_{k-1})\, f_j(X_{k-1})\}\\\nonumber & = \frac{1}{n} \sum\limits_{k=1}^{\lfloor nt \rfloor} \{-(|X_{k}^i|-|X_{k-1}^i|)\, f_j(X_{k-1})-(|X_{k}^{\kern1ptj}|-|X_{k-1}^{\kern1ptj}|)\, f_i(X_{k-1}) \\\nonumber & \qquad\qquad \ + f_i(X_{k-1})\, f_j(X_{k-1})\}\\& \rightarrow -\frac{(1-\lambda)^2}{d^2 (1+\lambda)^2}t.\end{align}
In the second equality, we used the fact that 
$X^i$
and 
$X^{\kern1ptj}$
with 
$i \neq j$
cannot jump together to ensure that 
${(|X_{k}^i|-|X_{k-1}^i|)(|X_{k}^{\kern1ptj}|-|X_{k-1}^{\kern1ptj}|)=0}$
.
On the other hand, for any fixed 
$1\leq i\leq d$
, construct the following martingale-difference sequence 
${(\zeta_{n, k}^i)_{k\geq 1}}$
:
\begin{equation*}\zeta_{n, k}^i=(\sqrt{n}\xi_{n, k}^i)^2- \text{E}[(\sqrt{n} \xi_{n, k}^i)^2 \mid \mathcal{F}_{k-1}],\qquad k\in\mathbb{N}.\end{equation*}
Then, for any 
$1\leq k<\ell<\infty$
, 
$\text{E}[\zeta_{n,k}^i]=\text{E}[\zeta_{n,\ell}^i]=0$
and
\begin{equation*}\text{E}[\zeta_{n, k}^i\zeta_{n, \ell}^i]=\text{E}[\zeta_{n,k}^i\text{E}[ \zeta_{n, \ell}^i \mid \mathcal{F}_{\ell-1}]]=0,\end{equation*}
which implies that 
${(\zeta_{n, k}^i)_k}$
is a sequence of uncorrelated random variables. Notice that, for any 
$k\in\mathbb{N}$
, 
$\vert \zeta_{n,k}^i\vert\leq 4\ \mbox{and hence}\ \text{Var}(\zeta_{n,k}^i)\leq 16$
. By the strong law of large numbers for uncorrelated random variables ([Reference Lyons and Peres18, Theorem 13.1]), we have that almost surely, as 
$n\rightarrow\infty$
,
\begin{eqnarray}\frac{1}{n}\sum\limits_{k=1}^{\lfloor nt\rfloor}\zeta^i_{n,k}=\sum\limits_{k=1}^{\lfloor nt\rfloor}\{ (\xi_{n, k}^i)^2- \text{E}[ (\xi_{n,k}^i)^2 \mid \mathcal{F}_{k-1}]\}\rightarrow 0.\end{eqnarray}
Due to (4) and (6), almost surely, as 
$n\rightarrow\infty$
,
\begin{align*}\sum\limits_{k=1}^{\lfloor nt \rfloor}\text{E}[ (\xi_{n, k}^i)^2 \mid \mathcal{F}_{k-1}] & = \sum\limits_{k=1}^{\lfloor nt \rfloor} \text{E}\bigg[ \bigg(\frac{|X_{k}^i|-|X_{k-1}^i|- f_{i}(X_{k-1})}{\sqrt{n}}\bigg)^2 \ \Big|\ \mathcal{F}_{k-1}\bigg] \\& = \frac{1}{n}\sum\limits_{k=1}^{\lfloor nt \rfloor}\{\text{E}[ (|X_{k}^i|-|X_{k-1}^i|)^2 \mid \mathcal{F}_{k-1}] \\ & \qquad\qquad\ -\ 2\text{E}[ (|X_{k}^i|-|X_{k-1}^i|)\,f_i(X_{k-1}^i) \mid \mathcal{F}_{k-1}]\\& \qquad\qquad \ +\ \text{E}[ ({\kern1pt}f_i(X_{k-1}^i))^2 \mid \mathcal{F}_{k-1}]\}\\& = \frac{1}{n} \sum\limits_{k=1}^{\lfloor nt \rfloor}\{\text{E}[ (|X_{k}^i|-|X_{k-1}^i|)^2 \mid \mathcal{F}_{k-1}]-({\kern1pt}f_i(X_{k-1}^i))^2\}\\& \rightarrow t \frac{1}{d }-t \frac{(1-\lambda)^2}{d^2 (1+\lambda)^2}.\end{align*}
Together with (12), we have
\begin{equation} \sum\limits_{k=1}^{\lfloor nt\rfloor} (\xi_{n, k}^i)^2 \rightarrow t \frac{1}{d }-t \frac{(1-\lambda)^2}{d^2 (1+\lambda)^2}.\end{equation}
By the definition of 
$A_n$
in (7), (11), and (13), we complete the proof of (10).
In view of (8), (9), and (10), we have from [Reference Ethier and Kurtz9, Chapter 7, Theorem 1.4] that, on 
$D([0,\infty),\mathbb{R}^d)$
, as 
$n\rightarrow\infty$
, 
$M^n$
converges in distribution to an 
$\mathbb{R}^d$
-valued process 
$Y \,:\,Y_t=\frac{1}{\sqrt{d}\,}[I- \frac{1-\rho_\lambda}{d}E]W_t$
with independent Gaussian increments such that 
$Y_0=\textbf{0}$
and 
$Y_{t+s}-Y_s$
has the law 
$\mathcal{N}(\textbf{0},t\Sigma)$
for any 
$0\leq s, t<\infty$
. Then it is easy to verify that on 
$D([0,\infty),\mathbb{R}^d)$
,
\begin{equation*}\left(\frac{(|X_{\lfloor nt\rfloor}^1|,\ldots, |X_{\lfloor nt\rfloor}^d|)-nvt}{\sqrt{n}}\right)_{t\geq 0}\end{equation*}
converges in distribution to Y, which completes the proof. □
3. LDP for scaled reflected
$\text{RW}_\lambda$
with
$\lambda\in [0,1)$
In this section we prove the LDP for the sequence 
$\{\frac{1}{n}(|X_n^1|, \ldots ,|X_n^d|)\}_{n=0}^{\infty}$
. Before stating our main result in this section, we recall the definition of LDP from [Reference Dembo and Zeitouni7, Chapter 1].
For 
$n \geq 1$
, let 
$W_n$
be a random variable in 
${\mathbb{R}}^d$
, with distribution 
$\mu_n$
. We say that the sequence 
$\{ W_n \}_{n=0}^{\infty}$
satisfies the LDP with a good rate function I if the following inequalities hold:
(i) For any closed set
$F \subseteq {\mathbb{R}}^d$
,
\begin{equation*} \limsup_{n \to \infty} \frac{1}{n} \ln \mu_n(F) \leq - \inf_{x \in F} I(x). \end{equation*}
(ii) For any open set
$G \subseteq {\mathbb{R}}^d$
,
\begin{equation*} \liminf_{n \to \infty} \frac{1}{n} \ln \mu_n(G) \geq - \inf_{x \in G} I(x). \end{equation*}
Here, a function 
$I\,:\, {\mathbb{R}}^d \to [0, \infty]$
is said to be a good rate function if it is lower semicontinuous and if all the level sets 
$\{x\in {\mathbb{R}}^d\,:\, I(x)\leq \alpha\}$
for 
$\alpha\in [0, \infty)$
are compact.
Recall from [Reference Shi, Sidoravicius, Song, Wang and Xiang21] that 
$\rho_{\lambda} = 2 \sqrt{\lambda} / (1 + \lambda)$
is the spectral radius of 
${(X_n)_{n=0}^{\infty}}$
. Let 
$s_0 \,:\!= s_0(\lambda) = \frac{1}{2} \ln \lambda$
. For 
$s= (s_1, \ldots, s_d)$
and 
$x = (x_1, \ldots, x_d) \in\mathbb{R}^d$
, define 
${(s, x) = \sum_{i=1}^d s_i x_i}$
and
\begin{equation} \psi(s)=N(s)\frac{\rho _\lambda}{d}+\frac{1}{d(1+ \lambda)}\sum\limits_{i=1}^d\{\lambda {\text{e}}^{-s_i}+ {\text{e}}^{s_i}\}\,I_{\{s_i\geq s_0\}}, \quad \text{where } N(s)=\sum\limits_{i=1}^dI_{\{s_i<s_0\}}.\end{equation}
Our main result in this section is as follows.
Theorem 3.1. (LDP.) Let 
$\{ X_n \}_{n=0}^{\infty}$
be a biased random walk on 
${\mathbb{Z}}^d$
with parameter 
$\lambda \in [0, 1)$
. We assume further that 
$\lambda > 0$
when 
$d = 1$
. Then 
$\{\frac{1}{n}(|X_n^1|, \ldots ,|X_n^d|)\}_{n=0}^{\infty}$
satisfies the LDP with the good rate function given by
\begin{eqnarray*}\Lambda^{\ast}(x)= \sup_{s\in \mathbb{R}^d}\{(s,x)-\ln\psi (s)\},\qquad x\in\mathbb{R}^d.\end{eqnarray*}
Our proof of Theorem 3.1 is based on the Gärtner–Ellis theorem (cf. [Reference Dembo and Zeitouni7, Theorem 2.3.6]), which will be recalled in Subsection 3.1. Then, in Subsection 3.2 we consider the limit for the logarithmic moment generating functions of 
$\frac{1}{n}( |X_n^1|, \ldots, |X_n^d| )$
, and we prove Theorem 3.1 in Subsection 3.3.
Remark 3.1. (i) The effective domain of the rate function 
$\Lambda^{*}$
will be described in Lemmas 3.7 and 3.8. We shall see in (22) that, for any 
$x=(x_1,\ldots,x_d)\in\mathbb{R}_+^d$
,
\begin{equation*}\Lambda^*(x)=\frac{1}{2}\sum\limits_{i=1}^dx_i\ln\lambda-\ln\rho_\lambda+\overline{\Lambda^*}(x),\end{equation*}
where
\begin{equation*}\overline{\Lambda^*}(x)=\sup\limits_{y\in\mathbb{R}^d}\ln\left\{\frac{\exp[\sum_{i=1}^dy_ix_i]}{\frac{1}{2d}\sum_{i=1}^d({\text{e}}^{-y_i}+{\text{e}}^{y_i})}\right\},\qquad x\in\mathbb{R}^d,\end{equation*}
is the SRW rate function from the Cramér theorem. Therefore, the rate function 
$\Lambda^{*}$
can be calculated explicitly when 
$d = 1$
, 2, and 
$\lambda \in (0,\, 1)$
. More precisely, we have for 
$d = 1$
that
\begin{align*} \Lambda^*(x) = \begin{cases} \frac{x}{2}\ln\lambda - \ln \rho_\lambda+ (1+x)\ln \sqrt{1+ x}+ (1-x)\ln\sqrt{1-x} & x \in [0,\, 1], \\ \infty & \text{otherwise}, \end{cases} \end{align*}
and for 
$d = 2$
that
\begin{align*} \Lambda^*(x) = \begin{cases} \frac{1}{2}(x_1+x_2)\ln\lambda-\ln\rho_\lambda +\overline{\Lambda^*}(x) & (x_1, x_2)\in\mathcal{D}_{\Lambda^*}, \\ \infty & \text{otherwise}, \end{cases} \end{align*}
where 
$\mathcal{D}_{\Lambda^*} = \{ x = (x_1, \, x_2) \in {\mathbb{R}}^2_+\,:\, x_1 + x_2 \leq 1 \}$
and, for 
$x \in \mathcal{D}_{\Lambda^*}$
,
\begin{align*} \overline{\Lambda^*}(x) & = x_1\ln \left[\frac{2x_1+\sqrt{x_1^2-x_2^2+1}}{\sqrt{(x_1^2-x_2^2)^2+1-2(x_1^2+x_2^2)}\,}\right] \\ & \quad + x_2\ln \left[\frac{2x_2+\sqrt{x_2^2-x_1^2+1}}{\sqrt{(x_1^2-x_2^2)^2+1-2(x_1^2+x_2^2)}\,}\right]\\ & \quad - \ln \left[\frac{\sqrt{x_1^2-x_2^2+1}+\sqrt{x_2^2-x_1^2+1}}{\sqrt{(x_1^2-x_2^2)^2+1-2(x_1^2+x_2^2)}\,}\right]+\ln 2. \end{align*}
When 
$d\geq 3$
and 
$\lambda\in (0,1)$
we cannot calculate 
$\Lambda^\ast$
to get an explicit expression; this remains an open problem.
(ii) Assume 
$\lambda\in [0,1)$
if 
$d\geq 2$
and 
$\lambda\in (0,1)$
if 
$d=1$
. The following sample path large deviation principle (Mogulskii type theorem) holds for the reflected 
${\text{RW}}_\lambda$
starting at 
$\textbf{0}$
. In fact, for any 
$0\leq t\leq 1$
, let
\begin{align*}&Y_n(t)=\frac{1}{n}(\vert X_{\lfloor nt\rfloor}^1\vert,\ldots,\vert X_{\lfloor nt\rfloor}^d\vert),\\&\widetilde{Y}_n(t)=Y_n(t)+\bigg(t-\frac{\lfloor nt\rfloor}{n}\bigg)[(\vert X_{\lfloor nt\rfloor+1}^1\vert,\ldots,\vert X_{\lfloor nt\rfloor+1}^d\vert)-(\vert X_{\lfloor nt\rfloor}^1\vert,\ldots,\vert X_{\lfloor nt\rfloor}^d\vert)].\end{align*}
Write 
$L_{\infty}([0,1])$
for the 
$\mathbb{R}^d$
-valued 
$L_{\infty}$
space on interval [0, 1], and 
$\mu_n$
(resp. 
$\widetilde{\mu}_n$
) for the law of 
$Y_n(\!\cdot\!)$
(resp. 
$\widetilde{Y}_n(\!\cdot\!)$
) in 
$L_{\infty}([0,1])$
. From [Reference Dembo and Zeitouni7, Lemma 5.1.4], 
$\mu_n$
and 
$\tilde{\mu}_n$
are exponentially equivalent. Denote by 
$\mathcal{AC}'$
the space of nonnegative absolutely continuous 
$\mathbb{R}^d$
-valued functions 
$\phi$
on [0, 1] such that
\begin{equation*}||\phi||\leq 1,\qquad \phi(0)=\textbf{0},\end{equation*}
where 
$||\cdot||$
is the supremum norm. Let
\begin{equation*}C_{\textbf{0}}([0,1])=\{\,f\,:\, [0,1]\rightarrow\mathbb{R}^d \mid f\ \mbox{is continuous},\ f(0)=\textbf{0}\},\end{equation*}
and
\begin{equation*}\mathcal{K}=\Big\{\,f\in C_{\textbf{0}}([0,1]) \ |\ \sup\limits_{0\leq s<t\leq 1}\frac{\vert f(t)-f(s)\vert}{t-s}\leq 1,\ \sup\limits_{0\leq t\leq 1}\vert f(t)\vert\leq 1 \Big\}.\end{equation*}
By the Arzelà–Ascoli theorem, 
$\mathcal{K}$
is compact in 
${(C_{\textbf{0}}([0,1]),\Vert\cdot\Vert)}$
. Note that each 
$\widetilde{\mu}_n$
concentrates on 
$\mathcal{K}$
, which implies exponential tightness in 
$C_0[0, 1]$
equipped with supremum topology. Define 
$p_j\,:\, L^{\infty}[0, 1]\rightarrow ({\mathbb{R}}^{d})^{|j|}$
for any 
$j\in J$
, where J denotes all ordered finite sets with each element taking a value in (0, 1], as follows:
\begin{equation*}p_j({\kern1pt}f)= ({\kern1pt}f(t_1), f(t_2), \ldots, f(t_{|j|})) ,\end{equation*}
where 
$j=(t_1, t_2, \ldots, t_{|j|})$
and 
$0< t_1< t_2< \cdots<t_{|j|}\leq 1$
. Given that the finite-dimensional LDPs for 
$\{\mu_n\circ p_j^{-1}\}$
in 
${({\mathbb{R}}^d)^{|j|}}$
follow from Theorem 3.1, 
$\{\mu_n\circ p_j^{-1}\}$
and 
$\{\tilde{\mu}_n\circ p_j^{-1}\}$
are exponentially equivalent, and the 
$\{\tilde{\mu}_n\}$
satisfy the LDP in 
$L_{\infty}[0,1]$
with pointwise convergence topology by the Dawson–Gärtner theorem [Reference Dembo and Zeitouni7]. Together with exponential tightness in 
$C_0[0, 1]$
, we can lift the LDP of 
$\{\tilde{\mu}_n\}$
to 
$L_{\infty}[0,1]$
with supremum topology with the good rate function
\begin{equation*}I(\phi)=\begin{cases} \int_0^1\Lambda^*(\dot{\phi}(t))\, \text{d}t & \text{if}\ \phi\in\mathcal{AC}',\\ \infty & \text{otherwise}.\end{cases}\end{equation*}
The same holds for 
$\{\mu_n\}$
due to exponential equivalence. The proof of the above sample path LDP is similar to that of [Reference Dembo and Zeitouni7, Theorem 5.1.2].
3.1. Gärtner–Ellis theorem
Consider a sequence of probability measures 
$\{ \mu_n \}_{n=0}^{\infty}$
on 
${\mathbb{R}}^d$
. Let 
$\Lambda_n(s)$
be the logarithmic moment generating function of 
$\mu_n$
, that is,
\begin{equation*} \Lambda_n(s) = \ln \int_{{\mathbb{R}}^d} {\text{e}}^{( s, \, x )} \mu_n({\text{d}} x), \qquad s = (s_1, \ldots, s_d) \in {\mathbb{R}}^d. \end{equation*}
Assume that, for each 
$s \in {\mathbb{R}}^d$
, the limit
\begin{equation} \Lambda(s) = \lim_{n \to \infty} \frac{1}{n} \Lambda_n(ns) \end{equation}
exists as a number in 
$\mathbb{R} \cup \{ \infty \}$
. Let 
${\mathcal{D}}_{\Lambda} = \{ s \in {\mathbb{R}}^d\,:\, \Lambda(s) < \infty \}$
. The Fenchel–Legendre transform 
$\Lambda^{*}$
of 
$\Lambda$
is defined by
\begin{equation*} \Lambda^{\ast}(x)= \sup\limits_{s\in \mathbb{R}^d}\{(s,x)- \Lambda(s)\},\qquad x\in\mathbb{R}^d, \end{equation*}
with domain 
${\mathcal{D}}_{\Lambda^{*}} = \{ x \in {\mathbb{R}}^d \,:\, \Lambda^{*}(x) < \infty \}$
. We say 
$y \in {\mathbb{R}}^d$
is an exposed point of 
$\Lambda^{*}$
if, for some 
$s \in {\mathbb{R}}^d$
and all 
$x \neq y$
,
\begin{equation} ({\kern1pt}y,s)-\Lambda^\ast({\kern1pt}y)>(x,s)-\Lambda^\ast(x). \end{equation}
An s satisfying (16) is called an exposing hyperplane. We recall the Gärtner–Ellis theorem from [Reference Dembo and Zeitouni7, Theorem 2.3.6].
Theorem 3.2. (Gärtner–Ellis theorem.) Suppose that the function 
$\Lambda$
in (15) is well defined, and that 
${\textbf{0}} \in {\mathcal{D}}_{\Lambda}^o$
, the interior of 
${\mathcal{D}}_{\Lambda}$
.
(a) For any closed set
$F \subseteq {\mathbb{R}}^d$
,
\begin{equation*} \limsup_{n \to \infty} \frac{1}{n} \ln \mu_n(F) \leq - \inf_{x \in F} \Lambda^{*}(x). \end{equation*}
(b) For any open set
$G \subseteq {\mathbb{R}}^d$
,
where
\begin{equation*} \liminf_{n \to \infty} \frac{1}{n} \ln \mu_n(G) \geq - \inf_{x \in G \cap \mathbb{F}} \Lambda^{*}(x), \end{equation*}
$\mathbb{F}$
is the set of exposed points of
$\Lambda^{*}$
whose exposing hyperplane belongs to
${\mathcal{D}}_{\Lambda}^o$
.
3.2. Logarithmic moment generating function
To apply the Gärtner–Ellis theorem, we need to prove the convergence of the rescaled logarithmic moment generating functions defined as
\begin{equation*} \Lambda_n (s,x)= \ln\text{E}_x\left[\!\exp\left\{\left(n s, \left(\frac{|X^1_n|}{n},\ldots,\frac{\vert X^d_n\vert}{n}\right)\right)\right\}\right] =\ln\text{E}_x\left[\!\exp\left\{\sum\limits_{i=1}^d s_i|X_n^i|\right\} \right]. \end{equation*}
Proposition 3.1. For every 
$s \in {\mathbb{R}}^d$
and 
$x \in {\mathbb{Z}}^d$
, we have
\begin{equation} \lim_{n \to \infty} \frac{1}{n} \Lambda_n(s,\, x) = \ln \psi(s), \end{equation}
where 
$\psi$
is defined in (14).
The rest of this subsection is devoted to the proof of Proposition 3.1. Note that, for 
$s \in {\mathbb{R}}^d$
with 
$s_i \geq s_0$
for 
$1 \leq i \leq d$
, 
$\psi(s)$
coincides with the logarithmic moment generating function of the drifted random walk with step distribution given by (2). The main idea to prove Proposition 3.1 is to compare the transition probabilities of the biased random walk 
$\{ X_n \}_{n=0}^{\infty}$
with those of the drifted random walk 
$\{ Z_n \}_{n=0}^{\infty}$
; see Lemmas 3.2 and 3.3. As a consequence, 
$\Lambda_n(s, x)$
is bounded above and below by the logarithmic moment generating function of 
$Z_n$
for 
$s\in {\mathbb{R}}^d$
with 
$s_i \geq s_0$
for 
$1 \leq i \leq d$
, and the convergence follows. However, for s in other regions we need more precise estimates for the lower bound of 
$\Lambda_n(s, x)$
; see Lemmas 3.4 and 3.6.
We start the proof of Proposition 3.1 with the following lemma, which shows that the limit (17) is independent of the starting point x of the biased random walk.
Lemma 3.1. For each 
$s \in {\mathbb{R}}^d$
and 
$x \in {\mathbb{Z}}^d$
, there exists a constant 
$C > 0$
such that
\begin{equation} \Lambda_{n-|x|}(s,\, x) - C \leq \Lambda_n(s,\, {{\bf 0}}) \leq \Lambda_{n+|x|}(s,\, x) + C, \qquad n > |x|. \end{equation}
Proof. By the Markov property, we have
\begin{align*} {\text{E}}_{\textbf{0}} \bigg[\!\exp\bigg\{\sum_{i=1}^d s_i |X_n^i|\bigg\} \bigg] & \geq {\text{E}}_0 \bigg[ I_{\{X_{|x|}=x\}} \exp\bigg\{\sum_{i=1}^d s_i |X_n^i|\bigg\} \bigg] \\ & \geq {\text{P}}_{0} ( X_{|x|} = x )\, {\text{E}}_x \bigg[\!\exp\bigg\{\sum_{i=1}^d s_i |X_{n-|x|}^i|\bigg\} \bigg],\end{align*}
and the first inequality in (18) follows. The second inequality is proved similarly. □
Recall the definition of the drifted random walk 
$\{Z_n=(Z_n^1,\ldots,Z_n^d)\}_{n=0}^{\infty}$
on 
${\mathbb{Z}}^d$
by (2).
Lemma 3.2. We have that, for 
$k \in {\mathbb{Z}}_+^d$
,
\begin{equation*} {\text{P}}_{{\bf 0}} ( X_n = k ) \leq {\text{P}} ( Z_n = k \,|\, Z_0 = {{\bf 0}} ), \qquad n \geq 0. \end{equation*}
Proof. For 
$x, k \in {\mathbb{Z}}^d$
and 
$n \in {\mathbb{N}}$
, let 
$\Gamma_n(x,\, k)$
be the set of all nearest-neighbor paths in 
${\mathbb{Z}}^d$
from x to k with length n. For a path 
$\gamma = \gamma_0\gamma_1\cdots\gamma_n \in \Gamma_n(x,\, k)$
, let
\begin{equation*} p(\gamma) = p(x,\, \gamma_1) p(\gamma_1,\, \gamma_2) \cdots p(\gamma_{n-1},\, k). \end{equation*}
Consider the first n steps of 
${\text{RW}}_{\lambda}$
along the path 
$\gamma \in \Gamma_n(0,\, k)$
. Note that for each 
$0 \leq i\leq n-1$
, 
$p(\gamma_i,\, \gamma_{i+1})$
is either 
$\frac{1}{d+m + (d-m) \lambda}$
or 
$\frac{\lambda}{d+m + (d-m) \lambda}$
, with 
$m = \kappa(\gamma_i)$
. The total number of terms of the forms 
$\frac{1}{d + m + (d-m)\lambda\vphantom{\frac{a}{b}}}$
(resp. 
$\frac{\lambda}{d + m + (d-m)\lambda}$
) is exactly 
$\frac{n + |k|}{2}$
(resp. 
$\frac{n - |k|}{2}$
). Note that 
$d+m + (d-m)\lambda \geq d(1+\lambda)$
. Therefore, we have, for 
$\gamma \in \Gamma_n({\textbf{0}},\, k)$
,
\begin{equation*} p(\gamma) \leq \left( \frac{1}{d(1+\lambda)} \right)^{\frac{n+|k|}{2}} \left( \frac{\lambda}{d(1+\lambda)} \right)^{\frac{n-|k|}{2}}. \end{equation*}
As a consequence,
\begin{align*} {\text{P}}_{{\textbf{0}}}(X_n = k) & = \sum_{\gamma \in \Gamma_n({\textbf{0}},\, k)} p(\gamma) \leq \sum_{\gamma \in \Gamma_n({\textbf{0}},\, k)} \left( \frac{1}{d(1+\lambda)} \right)^{\frac{n+|k|}{2}} \left( \frac{\lambda}{d(1+\lambda)} \right)^{\frac{n-|k|}{2}} \\ & = {\text{P}} ( Z_n = k \, |\, Z_0 = {\textbf{0}} ). \nonumber\end{align*}
□
Lemma 3.3. For every 
$k \in {\mathbb{Z}}_+^d$
and 
$z \in {\mathbb{Z}}_+^d \setminus \mathcal{X}$
, we have that
\begin{equation*} {\text{P}}_z ( X_n = k ) \geq n^{-d} {\text{P}} ( Z_n = k \mid Z_0 = z ). \end{equation*}
Proof. Recall that 
$\mathcal{X}$
denotes the union of all axial hyperplanes of 
${\mathbb{Z}}^d$
. Define
\begin{equation*} \sigma = \inf \{ n\,:\, X_n \in \mathcal{X} \}, \qquad \tau = \inf \left\{ n\,:\, Z_n \in \mathcal{X} \right\}. \end{equation*}
Starting at 
$z \in {\mathbb{Z}}_+^d \setminus \mathcal{X}$
, the process 
$\left( X_n \right)_{0 \leq n \leq \sigma}$
has the same distribution as the drifted random walk 
${(Z_n)_{0 \leq n \leq \tau}}$
. Then we have, for 
$k \in {\mathbb{Z}}_+^d$
,
\begin{equation} {\text{P}}_z ( X_n = k ) \geq {\text{P}} ( Z_n = k,\, n \leq \tau \mid Z_0 = z ). \end{equation}
For 
$\alpha, \beta \in {\mathbb{Z}}$
and 
$n \in {\mathbb{N}}$
, denote by 
$P_{n,\, \beta}(\alpha)$
the number of paths 
$\gamma = \gamma_0 \gamma_1 \cdots \gamma_n$
in 
${\mathbb{Z}}$
with 
$\gamma_0 = \alpha$
and 
$\gamma_n = \beta$
, and by 
$Q_{n,\, \beta}(\alpha)$
the number of those paths with the additional property that 
$\gamma_i\geq \alpha \wedge \beta$
for 
$0 \leq i \leq n$
if 
$\alpha= \beta$
and 
$\gamma_i> \alpha \wedge \beta$
for 
$1 \leq i \leq n-1$
if 
$\alpha \neq \beta$
. Assume 
$P_{0,\alpha}(\alpha) = Q_{0,\alpha}(\alpha) = 1$
for convenience in this lemma and next lemma. By the Ballot theorem ([Reference Durrett8, Theorem 4.3.2]) and the property of the Catalan number, we have, for 
$n > 0$
,
\begin{equation} Q_{n,\, \beta}(\alpha) \geq \frac{|\alpha-\beta| \vee 1}{n} P_{n,\, \beta}(\alpha). \end{equation}
For 
$k = (k_1, \ldots, k_d) \in {\mathbb{Z}}_+^d$
and 
$z = (z_1, \ldots, z_d) \in {\mathbb{Z}}_+^d \setminus {\mathcal{X}}$
, write 
$a = \frac{n + |k| - |z|}{2}$
and 
$b = \frac{n - |k| + |z|}{2}$
. By (20), we obtain that
\begin{align*} {\text{P}} ( Z_n &= k, n \leq \tau \mid Z_{0}= z) \\ &\quad \geq \sum_{m} \binom{n}{m_1, \ldots, m_d} d^{-n} \left( \frac{\lambda}{1+\lambda} \right)^b \left( \frac{1}{1+\lambda} \right)^a \prod_{j=1}^d Q_{m_j,\, k_j}(z_j) \\ &\quad \geq \sum_{m} \binom{n}{m_1, \ldots, m_d} d^{-n} \left( \frac{\lambda}{1+\lambda} \right)^b \left( \frac{1}{1+\lambda} \right)^a \prod_{j=1}^d \frac{|k_j-z_j|\vee 1}{m_j} P_{m_j,\, k_j}(z_j) \\ &\quad \geq n^{-d} \sum_{m} \binom{n}{m_1, \ldots, m_d} d^{-n} \left( \frac{\lambda}{1+\lambda} \right)^b \left( \frac{1}{1+\lambda} \right)^a \prod_{j=1}^d P_{m_j,\, k_j}(z_j) \\ & = n^{-d} {\text{P}} ( Z_n = k \mid Z_{0} = z ), \end{align*}
where the sum is over all tuples 
$m = (m_1, \ldots, m_d) \in {\mathbb{Z}}^d$
such that 
$|m| = n$
and 
$m_j \geq |k_j - z_j|$
for 
$1 \leq j \leq d$
. In the second inequality we should replace 
${( |k_j - z_j| \vee 1 ) / m_j}$
by 1 when 
$m_j = 0$
. Together with (19), this completes the proof. □
Recall that 
$s_0 = \frac{1}{2} \ln \lambda$
. For fixed 
$s \in {\mathbb{R}}^d$
, let 
$I_1 = \{ 1 \leq i \leq d\,:\, s_i < s_0 \}$
and 
$I_2 = \{ 1, \ldots, d \} \setminus I_1$
. Then 
$N(s)= |I_{1}|$
from (14). Define 
$s^{I_1} =( s_i )_{i \in I_1}$
; 
$s^{I_2}$
, 
$Z_n^{I_1}$
, and 
$Z_n^{I_2}$
are defined similarly.
Lemma 3.4. Let 
$y_0 = {\textbf{0}}^{I_1}$
if n is even and 
$y_0 = (1, 0, \ldots, 0) \in {\mathbb{R}}^{N(s)}$
otherwise. For any 
$z \in {\mathbb{Z}}^d$
and 
$s \in {\mathbb{R}}^d$
, we have that
\begin{multline*} {\text{E}} \bigg[\!\exp\bigg\{\sum_{i=1}^d s_i Z_n^i\bigg\} \prod_{i=1}^d I_{\{Z_n^i \geq z_i\}} \,|\, Z_0 = z \bigg] \\ \geq 2^{-|I_2|} ( {\text{e}}^{s_1} \wedge 1 ) {\text{E}} \bigg[\!\exp\bigg\{\sum_{i\in I_2} s_i Z_n^i\bigg\} I_{\{Z_n^{I_1} = z^{I_1} + y_0\}} \,|\, Z_0 = z \bigg]. \end{multline*}
Proof. Without loss of generality, we assume that 
$z = {\textbf{0}}$
. As in the proof of Lemma 3.3, for 
$\alpha, \beta \in {\mathbb{Z}}$
we denote by 
$P_{n,\,\beta}(\alpha)$
the number of nearest-neighbor paths in 
${\mathbb{Z}}$
from 
$\alpha$
to 
$\beta$
. Then we have, for 
$k \in {\mathbb{Z}}^d$
,
\begin{align} \nonumber {\text{P}} & ( Z_n = k \,|\, Z_0 = {\textbf{0}} ) \\ & = \nonumber \sum_m \binom{n}{m_1, \ldots, m_d} d^{-n} \left( \frac{\lambda}{1+\lambda} \right)^{\sum_{i=1}^d \frac{m_i-k_i}{2}} \left( \frac{1}{1+\lambda} \right)^{\sum_{i=1}^d \frac{m_i + k_i}{2}} \prod_{j=1}^{d} P_{m_j,\, k_j}(0) \\ & = \lambda^{\frac{n - \sum_{i=1}^d k_i}{2}} \sum_m \binom{n}{m_1, \ldots, m_d} \left(\frac{1}{d(1+\lambda)}\right)^n \prod_{j= 1}^{d} P_{m_j,\, k_j}(0), \end{align}
where the sum is over all tuples 
$m = (m_1, \ldots, m_d) \in {\mathbb{Z}}^d$
such that 
$|m| = n$
and 
$m_j \geq |k_j|$
for 
$1 \leq j \leq d$
. Note that
\begin{multline*} {\text{E}} \bigg[\!\exp\bigg\{\sum_{i=1}^d s_i Z_n^i\bigg\} I_{\{Z_n \in {\mathbb{Z}}_+^d\}} \,|\, Z_0 = {\textbf{0}} \bigg] \\ \geq ( {\text{e}}^{s_1} \wedge 1 ) {\text{E}} \bigg[\!\exp\bigg\{\sum_{i \in I_2} s_i Z_n^i\bigg\} I_{\{ Z_n^{I_1} = y_0,\, Z_n^{I_2} \in {\mathbb{Z}}_+^{I_2} \}} \,|\, Z_0 = {\textbf{0}} \bigg].\end{multline*}
For 
$\varepsilon = ( \varepsilon_i )_{i \in I_2} \in \{ -1,\, 1 \}^{I_2}$
, let
\begin{equation*} {\mathcal{O}}_{\varepsilon} = \{ y = ( y_i )_{i \in I_2} \in {\mathbb{Z}}^{I_2} \,:\, \varepsilon_i y_i \geq 0,\ i \in I_2 \}. \end{equation*}
Note that for every 
$k \in {\mathbb{Z}}^d$
, 
$P_{m_j,\, k_j}(0) = P_{m_j,\, \varepsilon_j k_j}(0)$
. Therefore, by (21),
\begin{equation*} {\text{P}} ( Z_n = k \,|\, Z_0 = {\textbf{0}} ) = \lambda^{\sum_{i=1}^d \frac{1}{2} ( \varepsilon_i - 1 ) k_i} {\text{P}} ( Z_n = ( \varepsilon_1 k_1, \ldots, \varepsilon_d k_d ) \,|\, Z_0 = 0 ).\end{equation*}
Applying the fact that 
${\text{e}}^{s_i} \lambda^{-1/2} \geq 1$
for 
$i \in I_2$
, we obtain that, for every 
$\varepsilon \in \{ -1,\, 1 \}^{I_2}$
,
\begin{align*} {\text{E}} & \bigg[\!\exp\bigg\{\sum_{i \in I_2} s_i Z_n^i\bigg\} I_{\{ Z_n^{I_1} = y_0,\, Z_n^{I_2} \in {\mathbb{Z}}_+^{I_2} \}} \,|\, Z_0 = {\textbf{0}} \bigg] \\ & \geq \sum_{k \in {\mathbb{Z}}_+^{I_2}} ( {\text{e}}^{s_i} \lambda^{-1/2} )^{\sum_{i \in I_2} ( 1 - \varepsilon_i ) k_i} \\ & \qquad\qquad \times \exp\bigg\{\sum_{i\in I_2} s_i \varepsilon_i k_i\bigg\} {\text{P}} ( Z_n^{I_1} = y_0,\, Z_n^{I_2} = ( \varepsilon_i k_i)_{i\in I_2} \,|\, Z_0 = {\textbf{0}} ) \\ & \geq {\text{E}} \bigg[\!\exp\bigg\{\sum_{i\in I_2} s_i Z_n^i\bigg\} I_{\{ Z_n^{I_1} = y_0, Z_n^{I_2} \in {\mathcal{O}}_{\varepsilon}\}} \,|\, Z_0 = {\textbf{0}} \bigg].\end{align*}
By taking sum over all 
$\varepsilon \in \{-1,\, 1\}^{I_2}$
, we complete the proof of this lemma. □
Recall the definition of 
$\psi$
from (14).
Lemma 3.5. For every 
$s \in {\mathbb{R}}^d$
and 
$x \in {\mathbb{Z}}^d$
we have that
\begin{equation*} \limsup_{n \to \infty} \frac{1}{n} \Lambda_n(s,\, x) \leq \ln \psi(s). \end{equation*}
Proof. By Lemma 3.1, we only need to consider the case 
$x = {\textbf{0}}$
. Recall that 
$s_0\,:\!= \frac{1}{2} \ln \lambda$
. For 
$s \in {\mathbb{R}}^d$
, define 
$\tilde{s} \,:\!= ( s_1\vee s_0, \ldots, s_d \vee s_0 )$
, which leads to 
$\psi(s)= \psi(\tilde{s})$
. Since 
$\Lambda_n(s,\, 0)$
is increasing in each coordinate 
$s_i$
, we have that 
$\Lambda_n(s,\, 0) \leq \Lambda_n(\tilde{s},\, 0)$
. Then, by Lemma 3.2,
\begin{align*} {\text{E}}_{{\textbf{0}}} \bigg[\!\exp\bigg\{\sum_{i=1}^d \tilde{s}_i |X_n^i|\bigg\} \bigg] & \leq 2^d \sum_{k \in {\mathbb{Z}}_+^d} \exp\bigg\{\sum_{i=1}^d \tilde{s}_i k_i\bigg\} {\text{P}} ( Z_n = k \,|\, Z_0 = {\textbf{0}} ) \\ & \leq 2^d {\text{E}} \bigg[ \exp\bigg\{\sum_{i=1}^d \tilde{s}_i Z_n^i\bigg\} \,|\, Z_0 = {\textbf{0}} \bigg] \\ & = 2^d \prod_{m=1}^{n}{\text{E}} \bigg[ \exp\bigg\{\sum_{i=1}^d \tilde{s}_i (Z_m^i- Z_{m-1}^i)\bigg\} \,|\, Z_0 = {\textbf{0}} \bigg] \\ & = 2^d \bigg( \sum_{i=1}^d \frac{\lambda {\text{e}}^{-\tilde{s}_i} + {\text{e}}^{\tilde{s}_i}}{d(1+\lambda)} \bigg)^n = 2^d ( \psi(s) )^n, \end{align*}
where we have used the fact that 
$\{Z_n- Z_{n-1}\}_{n\in {\mathbb{N}}}$
are mutually independent and identically distributed. Then the lemma follows immediately. □
Lemma 3.6. For every 
$s \in {\mathbb{R}}^d$
and 
$x \in {\mathbb{Z}}^d$
, we have that
\begin{equation*} \liminf_{n \to \infty} \frac{1}{n} \Lambda_n(s,\, x) \geq \ln \psi(s). \end{equation*}
Proof. It suffices to prove only for n even. We use the same notation as before Lemma 3.4. Fix 
$x \in {\mathbb{Z}}_+^d \setminus {\mathcal{X}}$
. By Lemmas 3.3 and 3.4, we have
\begin{align*} {\text{E}}_x \bigg[\!\exp\bigg\{\sum_{i=1}^d s_i |X_{2n}^i|\bigg\} \bigg] & \geq n^{-d} \sum_{k \in {\mathbb{Z}}_+^d} \exp\bigg\{\sum_{i=1}^d s_i k_i\bigg\} {\text{P}} ( Z_{2n} = k \,|\, Z_0 = x ) \\ & = n^{-d} {\text{E}} \bigg[\!\exp\bigg\{\sum_{i=1}^d s_i Z_{2n}^i\bigg\} I_{\{Z_{2n} \in {\mathbb{Z}}_+^d\}} \,|\, Z_0 =x \bigg] \\ & \geq c n^{-d} {\text{E}} \bigg[\!\exp\bigg\{\sum_{i \in I_2} s_i Z_{2n}^i\bigg\} I_{\{Z_{2n}^{I_1} = x^{I_1} \}} \,|\, Z_0 = x \bigg] \end{align*}
for some constant 
$c > 0$
. Let 
$\Gamma_1(2n)$
be the number of nearest-neighbor paths of length 2n in 
${\mathbb{Z}}^{I_1}$
from 
${\textbf{0}}^{I_1}$
to 
${\textbf{0}}^{I_1}$
. Similarly, for 
$k \in {\mathbb{Z}}^{I_2}$
, let 
$\Gamma_2(2n,\, k)$
be the number of paths of length 2n in 
${\mathbb{Z}}^{I_2}$
from 
${\textbf{0}}^{I_2}$
to k. Then we have, for 
$k \in {\mathbb{Z}}^{I_2}$
,
\begin{equation*} {\text{P}} ( Z_{2n}^{I_1} = x^{I_1}, \, Z_{2n}^{I_2} = x^{I_2} + k \,|\, Z_0 = x ) = \sum_{m=0}^{n} \binom{2n}{2m} \frac{\lambda^{n - \sum_{i \in I_2} k_i}}{[ d ( 1+\lambda ) ]^{2n}} \Gamma_1(2m) \Gamma_2(2n-2m,\, k). \end{equation*}
Recall that 
$N(s) = |I_1|$
. Let 
${(W_n)}$
be the drifted random walk in 
${\mathbb{Z}}^{I_2}$
starting at 
${\textbf{0}}$
, i.e. the step distribution is defined similarly to (2) with d replaced by 
$d - N(s)$
. Since 
$\Gamma_1(2m) \geq c m^{-N(s)/2} ( 2 N(s) )^{2m}$
, we obtain that
\begin{multline*} {\text{P}} ( Z_{2n}^{I_1} = x^{I_1}, \, Z_{2n}^{I_2} = x^{I_2} + k \,|\, Z_0 = x ) \\ \geq c n^{-N(s)/2} d^{-2n} \sum_{m=0}^{n} \binom{2n}{2m} ( N(s) \rho_{\lambda} )^{2m} ( d - N(s) )^{2n-2m} {\text{P}} ( W_{2n-2m} = k ). \end{multline*}
Therefore,
\begin{align*} {\text{E}}_x & \bigg[\!\exp\bigg\{\sum_{i=1}^d s_i |X_{2n}^i|\bigg\} \bigg] \\ & \geq c n^{-3d/2} d^{-2n}\sum_{m=0}^n \sum_{k \in {\mathbb{Z}}^{I_2}} \exp\bigg\{\sum_{i \in I_2} s_i (k_i+ x_i)\bigg\} \binom{2n}{2m} ( N(s) \rho_{\lambda} )^{2m} \\ & \qquad\qquad\qquad\qquad\qquad\qquad \times( d-N(s) )^{2n-2m} {\text{P}} ( W_{2n-2m} = k ) \\ & = c n^{-3d/2} d^{-2n}\sum_{m=0}^n \binom{2n}{2m} ( N(s) \rho_{\lambda} )^{2m} ( d-N(s) )^{2n-2m} {\text{E}} \bigg[\!\exp\bigg\{\sum_{i \in I_2} s_i W_{2n-2m}^i\bigg\} \bigg] \\ & = c n^{-3d/2} d^{-2n} \sum_{m=0}^n \binom{2n}{2m} ( N(s) \rho_{\lambda} )^{2m} ( d-N(s) )^{2n-2m} \bigg( \frac{\sum_{i \in I_2} ( \lambda {\text{e}}^{-s_i} + {\text{e}}^{s_i} )}{(d-N(s)) (1+\lambda)} \bigg)^{2n-2m} \\ & \geq \frac{c}{3} n^{-3d/2} ( \psi(s) )^{2n}. \end{align*}
The last inequality holds since, for any positive real number a, b,
\begin{equation*}\frac{\sum_{m=0}^{n} \binom{2n}{2m} a^{2n-2m} b^{2m}}{(a+ b)^{2n}}\rightarrow \frac{1}{2}, \qquad n\rightarrow \infty. \end{equation*}
The proof is complete. □
Now we are ready to complete the proof of Proposition 3.1.
Proof of Proposition 3.1. The upper bound for the limit in Equation (17) is proved in Lemma 3.5, and the lower bound is proved in Lemma 3.6.□
3.3. Proof of Theorem 3.1
For 
$s \in {\mathbb{R}}^d$
, define 
$\Lambda(s) = \ln \psi(s)$
where 
$\psi$
is given by (14). Let 
$\Lambda^{*}$
be the Fenchel–Legendre transform of 
$\Lambda$
. By the Gärtner–Ellis theorem and Proposition 3.1, to complete the proof of Theorem 3.1 it remains to study the effective domain and the set of exposed points of 
$\Lambda^{*}$
.
Lemma 3.7. For any 
$d\geq 1$
and 
$\lambda\in (0,1)$
, the effective domain of 
$\Lambda^{\ast}(\!\cdot\!)$
is
\begin{align*} \mathcal{D}_{\Lambda^{\ast}}(\lambda) & \,:\!= \{x\in\mathbb{R}^d\,:\, \Lambda^\ast(x)<\infty\} \\ & = \Big\{x=(x_1,\ldots,x_d)\in\mathbb{R}^d\,:\, \sum\limits_{i=1}^dx_i\leq 1,\ 0\leq x_i\leq 1,\ 1\leq i\leq d\Big\}.\end{align*}
Furthermore, 
$\Lambda^{\ast}(\!\cdot\!)$
is strictly convex in 
$x=(x_1,\ldots,x_d)\in \mathcal{D}_{\Lambda^{\ast}}(\lambda)$
with 
$\sum_{i=1}^dx_i<1,$
and 
$\Lambda^{\ast}(x) = 0$
if and only if 
$x =\left(\frac{1-\lambda}{d(1+\lambda)},\ldots,\frac{1-\lambda}{d(1+\lambda)}\right)$
.
Proof. Note that 
$s_0=\frac{1}{2}\ln\lambda$
. First, let
\begin{equation*}\mathcal{D}=\Big\{x=(x_1,\ldots,x_d)\in\mathbb{R}^d_{+}\,:\, \sum\limits_{j=1}^{d}x_j\leq 1\Big\}.\end{equation*}
Then, for any 
$x\in \mathcal{D}$
, we have
\begin{align}\nonumber \Lambda^*(x)&=\sup\limits_{s_i\geq s_0,1\leq i\leq d}\ln\left\{\frac{1}{2}(1+\lambda)\frac{\exp\{\sum_{i=1}^ds_ix_i\}}{\frac{1}{2d}\sum_{i=1}^d(\lambda {\text{e}}^{-s_i}+{\text{e}}^{s_i})}\right\}\\ \nonumber&=\sup\limits_{y_i\geq 0,1\leq i\leq d}\ln\left\{\frac{1}{2}(1+\lambda)\lambda^{-\frac{1}{2}+\frac{1}{2}\sum_{i=1}^dx_i}\frac{\exp\{\sum_{i=1}^dy_ix_i\}}{\frac{1}{2d}\sum_{i=1}^d({\text{e}}^{-y_i}+{\text{e}}^{y_i})}\right\}\\ &=\frac{1}{2}\sum\limits_{i=1}^d x_i \ln (\lambda)- \ln(\rho_{\lambda})+ \sup\limits_{y_i\geq 0,1\leq i\leq d}\ln\left\{\frac{\exp\{\sum_{i=1}^dy_ix_i\}}{\frac{1}{2d}\sum_{i=1}^d({\text{e}}^{-y_i}+{\text{e}}^{y_i})}\right\}
< \infty. \end{align}
Here, 
$y_i= s_i- s_{0}$
, 
$1\leq i\leq d$
. The first equality holds since 
$\sum_{i=1}^d s_ix_i$
is increasing in s and 
$\psi(s)=\psi(\tilde{s})$
(cf. Lemma 3.5). For 
$x \in \mathcal{D}^c$
, it is easy to verify that 
$\Lambda^*(x)= \infty$
.
By [Reference Dembo and Zeitouni7, Lemma 2.3.9], 
$\Lambda^*$
is a good convex rate function. On
\begin{equation*}\bigg\{x=(x_1,\ldots,x_d)\in\mathbb{R}_+^d\,:\, \sum\limits_{i=1}^{d} x_i
< 1\bigg\},\end{equation*}
it is obvious that the Hessian matrix of 
$\Lambda(s)$
is positive definite, which implies strict concavity of 
$s\cdot x- \Lambda(s)$
; thus the local maximum of 
$s\cdot x- \Lambda(s)$
exists uniquely and is attained at a finite solution 
$s=s(x)$
, i.e. 
$\Lambda^{\ast}(x)=s(x)\cdot x- \Lambda(s(x))$
. Applying the implicit function theorem, we see that 
$\Lambda^*$
is strictly convex. By (22), for any 
$x=(x_1,\ldots,x_d)\in\mathbb{R}_+^d$
with 
$\sum_{i=1}^dx_i=1$
,
\begin{equation}\Lambda^*(x)\geq\limsup\limits_{n\rightarrow\infty}\Lambda^*\left[x-\frac{1}{n}\left(x-\left(\frac{1-\lambda}{d(1+\lambda)},\ldots, \frac{1-\lambda}{d(1+\lambda)}\right)\right)\right].\end{equation}
By (23), we can verify that 
${(\frac{1-\lambda}{d(1+\lambda)},\ldots,\frac{1-\lambda}{d(1+\lambda)})}$
is the unique solution of 
$\Lambda^{*}(x)= 0$
. □
For 
$\lambda=0$
, we have the following explicit expression.
Lemma 3.8. For any 
$d\geq 2$
and 
$\lambda=0$
,
\begin{gather*} \mathcal{D}_{\Lambda^{\ast}}(0)\,:\!=\{x\in\mathbb{R}^d\,:\, \Lambda^\ast(x)<\infty\}=\bigg\{x=(x_1,\ldots,x_d)\in\mathbb{R}^d_+\,:\, \sum\limits_{i=1}^dx_i=1\bigg\},\\ \Lambda^\ast (x)= \begin{cases} \ln d+\sum\limits_{i=1}^dx_i\ln x_i &x\in\mathcal{D}_{\Lambda^\ast}(0),\\ +\infty & \text{otherwise}, \end{cases} \\ \{x\in\mathbb{R}^d\,:\, \Lambda^\ast(x)=0\}=\left\{\left(\frac{1}{d},\ldots,\frac{1}{d}\right)\right\}. \end{gather*}
Proof. When 
$\lambda= 0$
, we have 
$\Lambda^{\ast}(x)= \sup\limits_{s\in {\mathbb{R}}^d} \{(s, x)-\ln(\frac{1}{d}\sum_{i=1}^d {\text{e}}^{s_i})\}$
. Consider the supremum over the line 
$s_1 = s_2 = \cdots = s_d$
in 
${\mathbb{R}}^d$
. We have that
\begin{equation*} \Lambda^*(x) \geq \sup_{s_1 \in {\mathbb{R}}} s_1 ( x_1 + \cdots + x_d - 1 ) \geq + \infty, \end{equation*}
provided 
$x_1 + \cdots + x_d \neq 1$
. Therefore,
\begin{equation*}\mathcal{D}_{\Lambda^{\ast}}(0)\subseteq \bigg\{x=(x_1,\ldots,x_d)\in\mathbb{R}^d_+\,:\, \sum\limits_{i=1}^dx_i=1\bigg\}.\end{equation*}
Assume first that 
$x_i> 0$
, 
$1\leq i\leq d$
. Let 
$y_i={\text{e}}^{s_i}$
, 
$1\leq i\leq d$
; then, by the Jensen inequality,
\begin{align*}(s, x)-\ln\bigg(\frac{1}{d}\sum\limits_{i=1}^d{\text{e}}^{s_i}\bigg) & = \sum\limits_{i=1}^dx_i\ln\frac{y_i}{x_i}-\ln\bigg(\sum\limits_{i=1}^dy_i\bigg)+ \sum\limits_{i=1}^dx_i\ln x_i+\ln d \\& \leq \ln\bigg(\sum\limits_{i=1}^d x_i\frac{y_i}{x_i}\bigg)-\ln\bigg(\sum\limits_{i=1}^dy_i\bigg)+\sum\limits_{i=1}^dx_i\ln x_i+\ln d\\& = \sum\limits_{i=1}^dx_i\ln x_i+\ln d,\end{align*}
and the inequality in the second line becomes equality only if each 
$s_i=\ln x_i$
.
If there exists some i such that 
$x_i=0$
, we still have that
\begin{eqnarray*}(s, x)-\ln\bigg(\frac{1}{d}\sum\limits_{i=1}^d{\text{e}}^{s_i}\bigg)\leq \sum\limits_{i=1}^dx_i\ln x_i+\ln d ; \end{eqnarray*}
then 
$\sup\limits_{s\in {\mathbb{R}}^{d}}\{(s, x)-\ln(\frac{1}{d}\sum_{i=1}^d{\text{e}}^{s_i})\}=\sum_{i=1}^dx_i\ln x_i+\ln d$
by the lower semicontinuity of 
$\Lambda^*(\!\cdot\!)$
. Hence the conclusions follow from direct computation. □
Note that 
$\mathcal{D}_{\Lambda}^{o}= {\mathbb{R}}^d$
by the definition of 
$\mathcal{D}_{\Lambda}^{o}$
in Subsection 3.1. Let 
$\mathbb{F}$
be the set of exposed points of 
$\Lambda^{*}$
. Then we have the following result.
Lemma 3.9. For any open set G of 
$\mathbb{R}^d$
,
\begin{equation*}\inf_{x\in G\cap{\mathbb{F}}} \Lambda^{\ast}(x)=\inf_{x\in G} \Lambda^{\ast}(x).\end{equation*}
Proof. Assume 
$\lambda\in (0,1)$
and 
$d\geq 1.$
By the duality lemma [Reference Dembo and Zeitouni7, Lemma 4.5.8], we have that
\begin{equation*}\bigg\{x=(x_1,\ldots,x_d)\in\mathbb{R}_+^d\,:\, \sum\limits_{i=1}^d x_i
< 1\bigg\}\subseteq \mathbb{F}.\end{equation*}
By the strict convexity of 
$\Lambda^*(\!\cdot\!)$
and (23), we have that, for any open set G,
\begin{equation*}\inf_{x\in G\cap \mathbb{F}} \Lambda^{\ast}(x)=\inf_{x\in G} \Lambda^{\ast}(x).\end{equation*}
Assume 
$\lambda=0$
and 
$d\geq 2$
. We have that
\begin{equation*}\mathbb{F}= \bigg\{x=(x_1,\ldots,x_d)\in\mathbb{R}_+^d\,:\, \sum\limits_{i=1}^d x_i = 1,\mbox{ and } x_i >0,\ 1\leq i\leq d\bigg\}.\end{equation*}
Then, by Lemma 3.8, for any open set G,
\begin{equation*}\inf_{x\in G\cap \mathbb{F}} \Lambda^{\ast}(x)=\inf_{x\in G} \Lambda^{\ast}(x).\end{equation*}
□
Proof of Theorem 3.1. Let 
$\mu_n$
be the law of 
$\Big(\frac{\vert X_n^1\vert}{n},\ldots,\frac{\vert X_n^d\vert}{n}\Big)$
for any 
$n\in\mathbb{N}$
. From Proposition 3.1 and Lemmas 3.7 and 3.8, the logarithmic moment generating function exists with 
$\Lambda(s)= \ln \psi(s)$
and
\begin{equation*}\textbf{0}\in \mathcal{D}_\Lambda^o=\mathbb{R}^d.\end{equation*}
By (a) and (b) of the Gärtner–Ellis theorem (Theorem 3.2) and Lemma 3.9, we have that, for any closed set 
$F\subseteq\mathbb{R}^d$
,
\begin{equation*}\limsup\limits_{n \rightarrow \infty} \frac{1}{n} \ln\mu_n(F)\leq-\inf\limits_{x\in F}\Lambda^{\ast}(x),\end{equation*}
and, for any open set G of 
$\mathbb{R}^d$
,
\begin{equation*}\liminf\limits_{n \rightarrow \infty} \frac{1}{n} \ln \mu_n(G)\geq-\inf\limits_{x\in G} \Lambda^{\ast}(x).\end{equation*}
The proof is complete. □
Acknowledgements
The authors would like to thank the referee for helpful comments. The project is supported partially by the National Natural Science Foundation of China (No. 11671216) and by Hu Xiang Gao Ceng Ci Ren Cai Ju Jiao Gong Cheng-Chuang Xin Ren Cai (No. 2019RS1057). Y. Liu, L. Wang, and K. Xiang thank NYU Shanghai – ECNU Mathematical Institute for hospitality and financial support. V. Sidoravicius thanks the Chern Institute of Mathematics for hospitality and financial support.
