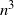1. Introduction
The standard Kingman coalescent [Reference Kingman16] is often used in evolutionary biology and population genetics to model the ancestry of n molecular sequences, such as DNA from a single segment (locus). This ancestry is represented by a genealogy, a timed and rooted binary tree [Reference Wakeley33]. In the neutral coalescent, the tree topology and the coalescent times, i.e. the times when two branches merge into a single node, are independent, and the density of the coalescent times is usually parameterized in terms of parameters of interest, such as the effective population size. The central idea of coalescent modeling in population genetics is that the observed molecular sequences at the tips are the result of a process of mutations superimposed on the genealogy. Therefore the more similar sequences are, the more recent their common ancestors (short coalescent times) are in the genealogy.
Bayesian inference methods under this model usually approximate the posterior distribution of model parameters via Markov chain Monte Carlo (MCMC) methods [Reference Drummond, Suchard, Xie and Rambaut10]. Therefore it is important to understand the mixing of Markov chains on the space of genealogies. In particular, we are interested in understanding the mixing of Markov chains on discrete tree topologies only: labeled and unlabeled ranked tree shapes. We will therefore assume a unit interval length between consecutive coalescing (branching) events.
A labeled ranked tree shape
$T^{L} \in \mathcal{T}^{L}_{n}$
with n leaves is a rooted labeled and ranked binary tree. The leaves are labeled by the set
$\{\ell_{1},\ell_{2},\ldots,\ell_{n}\}$
and internal nodes are labeled
$1,\ldots,n-1$
in increasing order, with label
$n-1$
at the root (Figure 1(b)). The cardinality of
$\mathcal{T}^{L}_n$
is given by
\begin{equation*}|\mathcal{T}^{L}_{n}|=\dfrac{n!(n-1)!}{2^{n-1}}.\end{equation*}
This equation can be derived by imagining building the tree from leaves to root: Initially there are n leaves and n lineages, and at successive steps two lineages are chosen to merge. It takes
$n-1$
merges to get to a single lineage and at merge
$k+1$
there are
$\binom{n -k}{2}$
choices. The total number of trees is
\begin{equation*}\prod_{k = 0}^{n-2} \binom{n - k}{2} = \prod_{j = 2}^n j(j - 1)/2.\end{equation*}
Figure 1. Examples of coalescent tree topologies: (a) ranked and unlabeled; (b) ranked and labeled. A ranked and unlabeled tree shape T has internal nodes labeled by their ranking from leaves to root and unlabeled leaves. Tree (a) has ordered matched pairs:
$(0,0)^{1},(0,0)^{2},(0,1)^{3},(0,3)^{4},(2,4)^{5},(0,5)^{6}$
. A ranked and labeled tree
$T^{L}$
has unique leaf and internal node labels. Tree (b) has ordered matched pairs:
$(\ell_{3},\ell_{4})^{1},(\ell_{1},\ell_{2})^{2},(\ell_{5},1)^{3},(\ell_{6},3)^{4},(2,4)^{5},(\ell_{7},5)^{6}$
.
Figure 2. Example of an adjacent-swap move on ranked tree shapes. The pair
$k=6$
is selected uniformly at random among pairs
$1,\ldots,6$
. We then select uniformly at random one element from pair 6 and one element from pair 7. The only allowable swaps are 5 and 0 or 3 and 0. The new state (right tree) is obtained by swapping 5 and 0 from pairs 6 and 7 respectively in the left tree.
In many applications, the quantity of interest is the overall shape of the tree [Reference Frost and Volz14, Reference Kirkpatrick and Slatkin17, Reference Maliet, Gascuel and Lambert22]; the specific labels of the samples are unimportant. In fact, a key feature of simple coalescent models, such as the Kingman coalescent, is the assumption that the leaves are exchangeable. Recently, Palacios et al. [Reference Palacios, Véber, Cappello, Wang, Wakeley and Ramachandran25] proposed a new Bayesian approach from binary molecular data in which the Kingman coalescent model on genealogies is replaced by the Tajima coalescent. The Tajima coalescent is a lumping of the Kingman coalescent that ignores leaf labels. The premise in [Reference Palacios, Véber, Cappello, Wang, Wakeley and Ramachandran25] is that the new target Tajima posterior distribution is more evenly spread among several tree topologies than the Kingman posterior distribution, and hence Markov chain exploration of the whole state space is more efficient [Reference Cappello, Veber and Palacios4]. This motivates the study of unlabeled ranked tree shapes with n leaves
$\mathcal{T}_n$
(Figure 1(a)). The cardinality of
$\mathcal{T}_{n}$
is given by the (
$n-1$
)th Euler zig-zag number
$E_{n-1}$
[Reference Kuznetsov, Pak and Postnikov18] and
$E_{n-1} \ll |T^{L}_{n}|$
. While one appealing feature of modeling unlabeled ranked tree shapes (Tajima coalescent) is the reduction in the cardinality of the state space, when compared to the cardinality of the state space under Kingman coalescent [Reference Cappello and Palacios3], the mixing of the chains can still be of the same order. Although the initial motivation is to compare the mixing of Markov chains on labeled and unlabeled ranked tree shape posterior distributions, we center our work on the Markov chains whose stationary distributions are uniform (or coalescent) distributions on the corresponding spaces (ignoring the data). This study should provide a first step towards a better understanding of coalescent chains in more general settings.
Related work in the context of evolutionary models includes the analysis of Markov chains on cladograms (or phylogenies). Cladograms are rooted or unrooted binary trees with labeled leaves and no ranking of internal nodes. In [Reference Diaconis and Holmes5], the space of cladograms with l leaves is shown to be in bijection with the space of perfect matchings of 2n labels, with
$n = l - 1$
. The bijection with perfect matchings is used to define a Markov chain on the space of cladograms. Using the perfect matching perspective, the chain is analogous to a random transpositions chain on the space
$S_{2n}$
of permutations of 2n elements. This representation allows the use of known results for the random transposition chain to be applied to the chain on trees to determine sharp bounds on rates of convergence [Reference Diaconis and Holmes6]. Motivated by this result, we propose a new representation of labeled and unlabeled ranked tree shapes as a type of matching. We use this representation to define an adjacent-swap chain on the spaces of labeled and unlabeled ranked tree shapes, and to study their mixing time. It is important to study the mixing time for chains on ranked trees because these results have implications for the design of MCMC algorithms used to infer evolutionary parameters from molecular data in a Bayesian setting [Reference Dinh, Darling and Matsen8, Reference Drummond, Suchard, Xie and Rambaut10]. Another use for Markov chains on the space of ranked tree shapes is combinatorial optimization, either for finding the maximum likelihood tree topology [Reference Friedman, Ninio, Pe’er and Pupko13] or for summarizing samples from the output of a Bayesian algorithm via finding the Fréchet mean ranked tree shape [Reference Rajanala and Palacios26]. These models are routinely used for analyzing molecular sequences of pathogens and tracking epidemics [Reference Volz, Koelle and Bedford32], and for understanding past population dynamics from present day and ancient DNA samples [Reference Liu, Westbury, Dussex, Mitchell, Sinding, Heintzman, Duchêne, Kapp, von Seth and Heiniger21].
In the rest of this section we define a bijective representation of ranked trees as constrained ordered matchings and define the adjacent-swap chain. We then state our main results concerning mixing times and discuss related work. In Section 2, we state known results on Markov chains that will be used in the following sections. In Section 3 we state important properties of the proposed adjacent-swap chain. The lower bound for the mixing time of the adjacent-swap chains is proved in Section 4 and it is obtained by finding a specific function that gives a lower bound for the relaxation time of the chains. In Section 5 we prove the upper bounds on the mixing time of the adjacent-swap chains via a coupling argument. In the discussion in Section 6 we mention future directions and other related chains on labeled and unlabeled coalescent trees which could be defined using the matching representations, and discuss implications for MCMC methods applied in practice.
1.1. Matching representations
We first establish some definitions. Let m be an integer and S a multiset of size 2m. A matching of S objects is a partition of the elements into m disjoint subsets of size two. An ordered matching is a matching with a linear ordering (ranking) of the m pairs.
Definition 1. The space
$\mathrm{COM}_m(S)$
(constrained ordered matchings) is the set of all ordered matchings of S with pairs labeled
$\textbf{p}_{1}, \textbf{p}_2, \ldots, \textbf{p}_{m}$
, which satisfy, for
$k = 1, \ldots, m$
and
$a \in S$
,
\begin{equation} a \in \textbf{p}_k \implies \begin{cases} a \in \mathbb{Z} \ \text{and} \ a < k , \quad \text{or } \\ \\[-9pt] a \in \{\ell_{1},\ldots,\ell_{n}\}.\end{cases}\end{equation}
To represent a labeled ranked tree shape as a constrained ordered matching, we take S to be the set of leaf and internal node labels, and each pair in the matching represents a coalescence in the tree, with
$\textbf{p}_{k}$
representing the kth coalescence event. The condition (2) then simply ensures that no interior node can be merged before it has been introduced. A leaf can merge at any point and thus there is no constraint on a leaf’s position in the matching.
Lemma 1. With
$S = \{\ell_{1},\ell_{2}, \ldots, \ell_{n}, 1, 2, \ldots, n - 2 \}$
, the space
$\mathrm{COM}_{n-1}(S)$
is in bijection with
$\mathcal{T}_n^L$
. With multiset
$S = \{0, 0, \ldots, 0, 1, 2, \ldots, n - 2\}$
, with 0 repeated n times, the space
$\mathrm{COM}_{n-1}(S)$
is in bijection with
$\mathcal{T}_n$
.
Proof. First assume that
$S = \{\ell_{1},\ell_{2}, \ldots, \ell_{n}, 1, 2, \ldots, n - 2 \}$
. The first matched pair can be formed by any two leaves in
$\binom{n}{2}$
possible ways. The second pair can be formed by any of the
$n-2$
remaining leaves or 1, the label of the first matched pair, in
$\binom{n-1}{2}$
ways; in general, the kth matched pair can be formed in
$\binom{n-k+1}{2}$
ways, because there are
$n - k + 1$
unique labels that could be matched at that time. Thus
\begin{equation*} |\mathrm{COM}_{n-1}(S)|=\prod^{n}_{i=2}\binom{i}{2}=|\mathcal{T}^{L}_{n}| \end{equation*}
and for every element
$T^{L} \in\mathcal{T}^{L}_{n}$
there is a one-to-one mapping between every coalescence event in
$T^{L}$
and every matched pair in one element of
$\mathrm{COM}_{n-1}(S)$
. These two facts imply there is a one-to-one mapping between
$\mathcal{T}^{L}_{n}$
and
$\mathrm{COM}_{n-1}(S)$
.
With the leaf labels
$\ell_1, \ldots, \ell_n$
replaced by the repeated element 0, the space of matchings is in bijection with
$\mathcal{T}_n$
due to the fact that the space of
$\mathcal{T}_n$
is equivalent to the space of
$\mathcal{T}_n^L$
with the leaf labels removed. That is, there is a surjection
$\mathcal{T}_n^L \to \mathcal{T}_n$
equivalent to the surjection
$\mathrm{COM}_{n-1}(S_1) \to \mathrm{COM}_{n-1}(S_2)$
, with
$S_1 = \{\ell_{1},\ell_{2}, \ldots, \ell_{n}, 1, 2, \ldots, n - 2 \}$
and
$S_2 = \{0, 0, \ldots, 0, 1, 2, \ldots, n - 2 \}$
. The bijective matching representations of the ranked trees
$\mathcal{T}_n$
and
$\mathcal{T}_n^L$
of Figure 1 are shown in the legend.
1.2. Markov chain and main results
Definition 2. The adjacent-swap Markov chain on the space
$\mathrm{COM}_{n-1}(S)$
is defined by the following update move.
-
1. Pick an index
$k \in \{1, \ldots, n-2 \}$
uniformly at random. -
2. Pick labels
$a_1$
and
$a_2$
uniformly from the pairs
$\textbf{p}_{k}$
and
$\textbf{p}_{k+1}$
respectively.-
(a) If swapping the positions of
$a_1, a_2$
does not violate constraint (1), make the swap. -
(b) Otherwise, remain in the current state.
-
For the sets S which give the bijections with
$\mathcal{T}_n$
and
$\mathcal{T}_n^L$
, this Markov chain is connected and reversible. In the case of
$\mathcal{T}_n^L$
it is also symmetric and hence it has a uniform stationary distribution. For
$\mathcal{T}_n$
, the chain is not symmetric; the stationary distribution is the Tajima distribution on the space of ranked unlabeled trees. These facts, as well as the relationship between the two chains, will be proved in a later section.
We are interested in the convergence rates of this Markov chain and how this rate compares depending on the space
$\mathcal{T}_n$
or
$\mathcal{T}_n^L$
. The measure that we study for convergence rate is the mixing time. That is, for a Markov chain on a space
$\Omega$
with transition probability P and stationary distribution
$\pi$
, the mixing time is defined as
\begin{equation*}t_{\mathrm{mix}} = \sup_{x_0 \in \Omega} \inf \{ t > 0 \colon \| P^t(x_0, \cdot) - \pi(\cdot) \|_{TV} < 1/4 \}.\end{equation*}
To state the result, let
$t_n$
and
$t_n^L$
be the mixing times for the chains on
$\mathcal{T}_n$
and
$\mathcal{T}_n^L$
respectively. Our main result is as follows.
Theorem 1. There exist constants
$C_1, C_2, C_3$
such that
\begin{equation*}C_1 \cdot n^3 \le t_n \le C_2 \cdot n^4\end{equation*}
and
\begin{equation*}C_1 \cdot n^3 \le t_n^L \le C_3 \cdot n^4.\end{equation*}
The lower bound of
$n^3$
comes from the relaxation time, and involves a standard trick of finding a specific function for which the variance under the stationary distribution can be bounded. The chain on
$\mathcal{T}_n$
is a certain type of ‘lumping’ of the chain on
$\mathcal{T}_n^L$
, and so the same lower bound applies to both spaces. The upper bounds are obtained using a coupling argument. We conjecture that the mixing time
$t_n$
is indeed smaller than the time
$t_n^L$
, though it is not evident whether this is by a significant order, or just a constant factor.
1.3. Related work
Mixing of chains on other tree spaces have been previously studied, in particular, the mixing of Markov chains on the space of cladograms. An n-leaf cladogram is a rooted or unrooted tree with n labeled leaves and unlabeled internal nodes of degree 3. The main difference between cladograms and the tree topologies studied in this manuscript is that cladograms do not rank internal branching events. The cardinality of the space of cladograms of n leaves is
$(2(n-1))!/2^{n-1}(n-1)!$
, smaller than the cardinality of the space of ranked and labeled trees but larger than the cardinality of the space of ranked unlabeled trees. Cladograms are fundamental objects in phylogenetics to model ancestral relationships at the species level, while ranked tree shapes are fundamental objects in population genetics and phylodynamics of infectious diseases. Ranked tree shapes are used to model ancestral relationships of a sample of individuals from a single population of the same species [Reference Felsenstein12].
Markov chains on cladograms. Aldous [Reference Aldous2] studied a chain on unrooted cladograms that removes a leaf chosen uniformly at random from the current cladogram and reattaches it to a random edge. Using coupling methods, Aldous [Reference Aldous2] showed that the relaxation time for this chain is
$\tau_{\mathrm{rel}} \leq c_{2}n^{3}$
. The same chain was later analyzed by Schweinsberg [Reference Schweinsberg28], who showed that
$\tau_{\mathrm{rel}} = {\mathrm{O}}(n^{2})$
using a modified method of distinguished paths. In [Reference Diaconis and Holmes5], Diaconis and Holmes show that the space of rooted cladograms with n leaves is in bijection with the space of perfect matchings in the complete graph on
$2(n-1)$
vertices. This bijection was later used by Diaconis and Holmes [Reference Diaconis and Holmes6] to define a Markov chain by randomly choosing two pairs and transposing two randomly selected entries of each pair. They showed that this random transposition chain mixed after
$\frac{1}{2}n \log n$
steps. In [Reference Spade, Herbei and Kubatko29], Spade, Herbei, and Kubatko study the nearest neighbor interchange (NNI) chain and a subtree prune and regraft (SPR) chain on the space of rooted cladograms. They showed that the upper bounds on the relaxation time of the SPR and the NNI chains are
${\mathrm{O}}(n^{5/2})$
and
${\mathrm{O}}(n^{4})$
respectively.
Other related work includes the study of mixing times of chains whose stationary distribution is the posterior distribution over cladograms [Reference Mossel and Vigoda24, Reference Štefankovič and Vigoda31]. In [Reference Mossel and Vigoda24], Mossel and Vigoda show exponential mixing times under a misspecified model in which data is generated from a mixture of cladograms.
Markov chains on related spaces. The adjacent-swap Markov chain on the space of ranked trees studied in this manuscript is closely related to the adjacent transposition chain on the space
$S_n$
of permutations. As is often done, one can think of an element
$\sigma \in S_n$
as an ordering of a deck of cards with unique labels
$1, \ldots, n$
. In [Reference Aldous1, Example 4.10], the chain is defined by picking at random two adjacent cards from the deck; with probability 1/2, the cards are swapped and with probability 1/2 nothing happens. The chain is symmetric with uniform stationary distribution. Aldous [Reference Aldous1] showed that the mixing time of this chain has a lower bound of
$c_{1}n^{3}$
and an upper bound of
$c_{2}n^3 \log(n)$
. In [Reference Wilson34], the now-famous ‘Wilson’s method’ was introduced and applied to the adjacent transposition chain as an example to improve the lower bound to order
$n^3 \log(n)$
with the explicit constant
$(1/\pi^2) n^3 \log(n)$
, as well as an upper bound of
$(2/\pi^2) n^3 \log(n)$
. Finally, in [Reference Lacoin19], the upper bound was improved to
$(1/\pi^2) n^3 \log(n)$
, so that the upper and lower bounds matched; in addition, the chain was proved to follow the cut-off phenomenon. Durrett generalized the adjacent transposition chain to the L-reversal chain, introduced as a model for the evolution of DNA in a chromosome [Reference Durrett11].
As noted in [Reference Misra, Blelloch, Ravi and Schwartz23], to the best of our knowledge, bounds on the mixing time of chains on ranked tree shapes have not been studied before.
2. Preliminaries
In this section we review some results of Markov chain theory that will be used to bound the mixing time of the adjacent-swap chains on
$\mathcal{T}^{L}_{n}$
and
$\mathcal{T}_{n}$
. We use the coupling method to find the upper bounds. A coupling of Markov chains with transition matrix P is a process
$(X_t, Y_t)_{t \ge 0}$
such that both
$(X_t)$
and
$(Y_t)$
are marginally Markov chains with transition matrix P. The goal is to define a coupling of two chains from different starting distributions such that the two chains will quickly reach the same state, and once this occurs the two chains stay matched forever. This coupling time gives an upper bound on the mixing time; see Chapter 5 from [Reference Levin and Peres20] for more details.
Theorem 2. (Theorem 5.4 [Reference Levin and Peres20].) Suppose that for each pair of states
$x,y \in \mathcal{X}$
there is a coupling
$(X_{t},Y_{t})$
with
$X_{0}=x$
and
$Y_{0}=y$
. For each such coupling, let
$\tau_{\mathrm{couple}}$
be the coalescence time of the chains, that is,
\begin{equation*} \tau_{\mathrm{couple}}\,{:\!=}\, \min \{t\colon X_{s}=Y_{s} {\ for\ all\ } s \geq t\}.\end{equation*}
Then
\begin{equation*}t_{\mathrm{mix}} \leq 4 \max_{x,y}E_{x,y}(\tau_{\mathrm{couple}}). \end{equation*}
To find a lower bound on the mixing time, we bound the relaxation time and use the following result.
Theorem 3. (Theorem 12.5 [Reference Levin and Peres20].) Suppose P is the transition matrix of an irreducible, aperiodic, and reversible Markov chain. Then
\begin{equation}t_{\mathrm{mix}} \geq (\tau_{n}-1)\log(2).\end{equation}
The relaxation time is defined as the inverse of the absolute spectral gap,
$\tau_{n} = 1/\gamma^*$
, where
$\gamma^* = 1-|\lambda_{n,2}|$
, one minus the absolute value of the eigenvalue of the transition matrix of the chain that has second-largest magnitude. The spectral gap
$\gamma$
is one minus the second-largest eigenvalue. If the Markov chain is lazy, then
$\gamma = \gamma^*$
, since all eigenvalues are positive. As we defined it, the adjacent-swap chain is not lazy, so we have
$\gamma^* \le \gamma$
. We will get a lower bound on
$\tau_n$
by finding an upper bound on
$\gamma$
using the following variational characterization.
Theorem 4. (Lemma 13.7 [Reference Levin and Peres20].) Let P be the transition matrix for a reversible Markov chain. The spectral gap
$\gamma$
satisfies
\begin{equation*}\gamma = \min _{f\colon \mathcal{X} \rightarrow \mathbb{R}, \mathrm{Var}_{\pi}(f) \neq 0} \dfrac{\mathcal{E}(f)}{\mathrm{Var}_{\pi}(f)},\end{equation*}
where
\begin{equation*}\mathcal{E}(f)\,{:\!=}\, \dfrac{1}{2}\sum_{x,y \in \mathcal{X}}[f(x)-f(y)]^{2}\pi(x)P(x,y).\end{equation*}
3. The adjacent-swap chain on ranked tree shapes
Lemma 2. The adjacent-swap Markov chain on
$\mathcal{T}_n^L$
is irreducible, aperiodic, and reversible with respect to the uniform stationary distribution
$\pi^L(x) \,{:\!=}\, 1/|\mathcal{T}_n^L|$
.
Proof. This can be seen by noting the transition matrix is symmetric. Let
$P^{L}$
be the transition matrix for the adjacent-swap chain on
$\mathcal{T}_n^L$
. That is, for
$x, y \in \mathcal{T}_n^L$
,
\begin{equation*}P^L(x, y) = \dfrac{1}{n-2} \cdot \dfrac{1}{4},\end{equation*}
where y is a tree that can be obtained by swapping two elements from two adjacent pairs in x, e.g. consider the following states at pairs k and
$k + 1$
:
\begin{align*}&x\colon (a, b)^k, (c, d)^{k + 1}, \\[3pt] &y\colon (a, c)^k, (b, d)^{k + 1}.\end{align*}
In a labeled ranked tree shape
$T^{L}_{n}$
, all pairs are formed by distinct elements, so a, b, c, d are all unique and the only way to transition from x to y is to swap the labels b and c, which happens with probability
$1/4(n - 2)$
if
$c<k$
or
$c \in \{\ell_{1},\ldots,\ell_{n}\}$
.
To see that the chain is irreducible, we note that any label can be moved to any pair to the right, one pair (or step) at a time with positive probability, and that any label can be moved to a pair with index k to the left (one pair at a time) as long as the label corresponds to a leaf or an internal node smaller than k, satisfying constraint (1). To see that the chain is aperiodic, we note that
$P^{L}(x,x)>0$
, for all
$x\in \mathcal{T}^{L}_{n}$
. Independent of the current state, we can pick pair
$k=n-2$
and attempt to swap any element of the
$n-2$
pair with label
$n-2$
from the
$n-1$
pair with probability
$1/2(n-2)$
. Since this move violates constraint (1), the move is rejected and the chain remains in the current state.
We note that the transition matrix P of the adjacent-swap chain on unlabeled ranked tree shapes is not symmetric. For example, consider the transition x to y of the type
\begin{equation} (0, a)^k, (0, b)^{k+1} \to (0, 0)^k, (a, b)^{k+1}\end{equation}
for labels
$a, b \neq 0$
(recall the 0s represent leaf labels). The probability of this transition is
$P(x,y)=1/(n-2) \cdot 1/4$
, since once pairs k and
$k + 1$
are chosen, there is a
$1/4$
chance of choosing label a from pair k and label 0 from pair
$k+1$
. However, the reverse transition,
\begin{equation*}(0, 0)^k, (a, b)^{k+1} \to (0, a)^k, (0, b)^{k+1},\end{equation*}
has probability
$1/(n-2) \cdot 1/2$
. It turns out that the stationary distribution
$\pi$
for the chain is the Tajima coalescent distribution [Reference Sainudiin, Stadler and Véber27] (also known as the Yule distribution). For
$T \in \mathcal{T}_n$
,
\begin{equation*}\pi(T) = \dfrac{2^{n - c(T) - 1}}{(n-1)!},\end{equation*}
where c(T) is the number of cherries of T, i.e. the number of pairs of the type (0,0) in the
$\mathrm{COM}_{n-1}(S)$
representation. Indeed, for transitions x to y of the type of (3), y has one more cherry than x and
$\pi(x)P(x,y)=\pi(y)P(y,x)$
; for other types of transitions
$P(x,y)>0$
that do not affect the number of cherries,
$P(x,y)=P(y,x)$
,
$\pi(x)=\pi(y)$
and the detailed balance equation is satisfied.
Another way of proving that the Tajima coalescent distribution is the stationary distribution on unlabeled ranked tree shapes is to view the chain as a lumping of the chain on
$\mathcal{T}^{L}_{n}$
. This perspective also gives us an initial comparison of the relaxation times of the chains. The space
$\mathcal{T}_n$
of unlabeled ranked tree shapes can be considered as a set of equivalency classes of the trees
$\mathcal{T}_n^L$
. That is, for trees
$x, y \in \mathcal{T}_n^L$
, define the equivalence relation
$x \sim y$
if the trees have the same ranked tree shape. From the
$\mathrm{COM}_{n-1}(S)$
perspective with
$S = \{\ell_1, \ldots, \ell_n, 1, 2, \ldots, n - 2\}$
, two matchings are equivalent if all internal node labels
$1,\ldots,n-2$
occur in the same pairs.
This equivalence relation induces a partition of
$\mathcal{T}_n^L$
using equivalence classes. That is, we can write
$\mathcal{T}_n^L$
as the disjoint union of sets
$\Omega_1, \ldots, \Omega_M$
, where
$M = |\mathcal{T}_n|$
, and all trees in
$\Omega_i$
have the same ranked tree shape.
Lemma 3. For any
$x, x' \in \mathcal{T}_n^L$
, equivalence class
$\Omega_i$
, and
$x \sim x'$
, the following relation holds:
\begin{equation*}P^L(x, \Omega_i) \,{:\!=}\, \sum_{y \in \Omega_i} P^L(x, y) = P^L(x', \Omega_i).\end{equation*}
Proof. If
$x\in \Omega_{i}$
, then the transition from x to
$y\in \Omega_{i}$
is of the type
\begin{equation*}(a, b)^k, (c, d)^{k+1} \to (c, b)^k, (a, d)^{k+1},\end{equation*}
where
$a, c \in \{\ell_1, \ell_2, \ldots, \ell_{n} \}$
correspond to leaf labels. Since x and x
$^{\prime}$
differ only at leaf labels, the transition probability of swapping two leaf labels is the same and
$P^{L}(x,\Omega_{i})=P^{L}(x',\Omega_{i})$
. If
$x \not\in \Omega_{i}$
, and therefore
$x' \not\in \Omega_{i}$
, then the transition from x to y is of the type
\begin{equation*}(a, b)^k, (c, d)^{k+1} \to (c, b)^k, (a, d)^{k+1},\end{equation*}
where a and c are not both in
$\{\ell_1, \ell_2, \ldots, \ell_{n} \}$
. Since x and x
$^{\prime}$
differ only at leaf labels, again
$P^{L}(x,\Omega_{i})=P^{L}(x',\Omega_{i})$
.
In words, Lemma 3 says that the probability of transitioning to a different ranked tree shape is independent of the leaf configuration of the current tree. A well-known result (e.g. Lemma 2.5 in [Reference Levin and Peres20]) is that the induced chain on the space of equivalence classes defined by
$\tilde{P}([x], [y]) \,{:\!=}\, P(x, [y])$
is a Markov chain; then observe that the induced chain
$\tilde{P}$
is equivalent to adjacent-swap Markov chain P on the space
$\mathcal{T}_n$
. This allows a comparison of the spectral gaps of the two chains. Lemma 12.9 in [Reference Levin and Peres20] states that the eigenvalues of the transition matrix of the lumped chain are eigenvalues of the transition matrix of the full chain, hence we have the following lemma.
Lemma 4. Let
$\gamma, \gamma^L$
be the spectral gaps of the chains
$P, P^L$
respectively. Then
$\gamma^L \leq \gamma$
.
From Lemma 3 we can immediately see that the stationary distribution for P is indeed the Tajima coalescent distribution. Suppose
$T \in \mathcal{T}_n$
corresponds to the equivalence class
$\Omega_i \subset \mathcal{T}_n^L$
. Then
\begin{equation*}\pi(T) = \sum_{y \in \Omega_i} \pi^L(y) = \dfrac{|\Omega_i|}{|\mathcal{T}_n^L|}.\end{equation*}
A uniformly sampled labeled ranked tree shape with the leaf labels erased gives an unlabeled ranked tree shape according to the Tajima distribution [Reference Sainudiin, Stadler and Véber27]. This implies that
$|\Omega_i|/|\mathcal{T}_n^L|$
is equal to the probability under the Tajima distribution for the ranked tree shape corresponding to
$\Omega_i$
.
4. Lower bound
To prove the lower bounds in Theorem 1, we use the variational characterization of the relaxation time from Theorem 4:
\begin{equation} \tau_{n} = \sup_{f\colon \Omega \to \mathbb{R}} \dfrac{\mathrm{Var}_\pi(f)}{\mathcal{E}(f)}.\end{equation}
The variational characterization can be used to obtain a lower bound on the relaxation time using a specific function f. To achieve a tight lower bound, a common strategy is to find a function f which has a large variance but can only be changed by a constant amount by one step of the Markov chain. That is, for
$x, y \in \Omega$
such that
$P(x, y) > 0$
, we have
$(f(x) - f(y))^2 \le C$
.
We will use the internal tree length as a function
$\varphi(x)\colon \mathcal{T}_{n} \rightarrow \mathbb{R}$
to find a lower bound for
$\tau_n$
. Since the internal tree length is independent of the leaf labels, we get the same lower mixing time bound for the adjacent-swap chains on
$\mathcal{T}_{n}$
and
$\mathcal{T}^{L}_{n}$
. For ease of exposition we will focus the following discussion on
$\mathcal{T}_{n}$
.
We will define the internal tree length function on the space
$\mathcal{T}_n$
using the correspondence with
$\mathrm{COM}_{n-1}(S)$
and assuming unit length between consecutive coalescence events. For a label
$j \in \{1, \ldots, n - 2 \}$
, let
$I_{x}(j)$
denote the pair index k such that
$j \in \textbf{p}_k$
. In the example of Figure 3,
$I_{x}(2) = 5$
. Note that from the constraints (equation (1)), we have
\begin{equation*}I_{x}(j) \in \{j+1, \ldots, n - 1 \}.\end{equation*}
We now define the internal tree length function on
$\mathcal{T}_n$
as follows:
\begin{equation*}\varphi(x) = \sum_{j = 1}^{n-2} (I_{x}(j) - j).\end{equation*}
Figure 3. Example of internal tree length calculation. A ranked tree shape T with ordered matched pairs:
$x=(0,0)^{1},(0,0)^{2},(0,1)^{3},(0,3)^{4},(2,4)^{5},(0,5)^{6}$
. The corresponding total internal tree length is the sum of the lengths of the internal branches:
$\varphi(x)=(3-1)+(5-2)+(4-3)+(5-4)+(6-5)=8$
.
As an example consider the ranked unlabeled tree shape with
$n = 7$
depicted in Figure 3. Note that the function is minimized for the ‘caterpillar tree’,
$(0,0)^{1},(0,1)^{2},(0,2)^{3},\ldots,(0,n-2)^{n-1}$
, where
$I_{x}(j) = j + 1$
for all j, giving
$\varphi(x) = n - 2$
.
This function
$\varphi$
is useful in bounding the relaxation time because it is ‘local’ with respect to the Markov chain. That is, suppose
$P(x, y) > 0$
and
$x \neq y$
. The change from x to y could have moved an interior node label to the left, in which case
$\varphi(y) = \varphi(x) - 1$
. If it moved an interior node label to the right, then
$\varphi(y) = \varphi(x) + 1$
. If two interior node labels were swapped, then
$\varphi(y) = \varphi(x)$
. Thus
$(\varphi(x) - \varphi(y))^2 \le 1$
. The denominator of equation (4) can then be upper-bounded by
$1/2$
.
To find the variance of the internal tree length, we note that
$\mathrm{Var}_{\pi}[\varphi(X)]=\mathrm{Var}_{\pi^{L}}[\varphi(X)]$
since the internal tree length is independent of the leaf labels. We now restate the standard coalescent of labeled ranked tree shapes as an urn process.
Consider an urn containing n balls labeled
$\ell_{1},\ldots,\ell_{n}$
. At step k, draw two balls without replacement from the urn. Let
$a_1, a_2$
be the labels of the balls drawn, then set
$\textbf{p}_k = (a_1, a_2)^{k}$
. Add in a new ball with label k. Repeat this process for
$k = 1, \ldots, n - 1$
until only a single ball labeled
$(n-1)$
remains in the urn. The resulting sequence of pairs
$\textbf{p} = (\textbf{p}_1, \ldots, \textbf{p}_{n-1})$
corresponds to a labeled ranked tree shape
$T \in \mathcal{T}^{L}_{n}$
drawn from the standard coalescent, i.e.
$\textbf{p} \sim \pi^{L}$
.
We can now simplify the urn process as follows. Start with n white balls in the urn. At each step, draw two balls and add back in a single red ball (representing an interior node of the tree). Let
$R_0 = 0$
and
$R_k$
be the number of red balls in the urn after k coalescence events. Note that after k mergers (coalescence events), there are
$n - k$
total balls left and
$R_{n - 1} = 1$
.
The simplified urn process is useful because the internal tree length can be computed by counting the number of red balls at each step and adding them all together (Figure 3), that is,
\begin{equation*}\varphi(\textbf{p}) = \sum_{k = 1}^{n-2} R_k.\end{equation*}
The quantities
$\{R_k \}_{k = 1}^{n-2}$
are fairly easy to analyze and have been studied before in various contexts. In [Reference Janson and Kersting15], the values are used to study the asymptotic behavior of the external tree length of the Kingman coalescent and it is shown that
\begin{align*} \mathbb{E}[R_k] &= \dfrac{k(n - k)}{n-1}, \\ \mathrm{Cov}(R_k \cdot R_l) &= \dfrac{k(k - 1)(n - l)(n - l -1)}{(n - 1)^2 (n - 2)}, \,\,\quad k \le l.\end{align*}
Using this, we get
\begin{equation*}\mathbb{E}_\pi[\varphi(\textbf{p})] = \sum_{k = 1}^{n-2} \dfrac{k(n - k)}{n-1} = \dfrac{1}{6}(n^2 + n - 6).\end{equation*}
Then we calculate
\begin{align}\!\!\!\!\!\sum_{k = 1}^{n - 2} \mathbb{E}[R_k^2] &= \dfrac{1}{30}(n^3 + 3n^2 + 2n - 30), \end{align}
\begin{align}2 \cdot \sum_{k = 1}^{n-3} \sum_{l = k + 1}^{n - 2} \mathbb{E}[R_k R_l] &= \dfrac{1}{180}(n - 3)(5n^3 + 21 n^2 - 14n - 120). \end{align}
The second moment
$\mathbb{E}_\pi[\varphi(\textbf{p})^2]$
is the sum of these two lines (5) and (6), which gives
\begin{equation*}\mathrm{Var}_\pi(\varphi(\textbf{p})) = \mathbb{E}_\pi[\varphi(\textbf{p})^2] - \mathbb{E}_\pi[\varphi(\textbf{p})]^2 = \dfrac{1}{90}n (n + 1)(n - 3).\end{equation*}
Theorem 5. Let
$\tau_{n}, \tau_n^L$
be the relaxation time of the adjacent-swap chains on
$\mathcal{T}_n$
and
$\mathcal{T}^{L}_{n}$
, respectively. Then
\begin{equation*}\tau^{L}_{n} \ge \tau_n \ge \dfrac{\mathrm{Var}_\pi(\varphi)}{\mathcal{E}(\varphi)} \ge \dfrac{2}{90} n (n + 1)(n - 3).\end{equation*}
The lower bound on the relaxation time is applicable to labeled and unlabeled ranked tree shapes, but Lemma 4 further allows us to state the first inequality on the left-hand side of Theorem 5.
5. Upper bound
In this section we prove the upper bounds in Theorem 1 using a coupling argument. The coupling is similar to the one used by Aldous for analyzing the adjacent transposition chain on
$S_n$
[Reference Aldous1]. The main difference from our approach is that in order to preserve the constraints of the ranked tree shapes, the coupling matches the labels in a specific order. This results in the pairs matching, starting at the root and becoming matched successively from right to left, ending with the first cherry.
We analyze a lazy version of the chain to make the coupling. That is, at each step, we generate a random coin flip
$\theta \sim \text{Bernoulli}(1/2)$
. If
$\theta = 1$
, attempt a move of the chain, and if
$\theta = 0$
then make no change. Let
$X_t = (\textbf{p}_1, \ldots, \textbf{p}_{n-1})$
and
$Y_t = (\textbf{q}_1, \ldots, \textbf{q}_{n-1})$
be the two copies of the chain at time t, one started from x and the other from y. We will first describe the coupling for the chain on
$\mathcal{T}_n$
.
Coupling of unlabeled ranked tree shapes. We will define a coupling that jointly matches the internal node labels of the two copies in the order
$n-2$
,
$n-3$
,
$n -4, \ldots, 1$
. Note that label
$n -2$
is already jointly matched in the
$n-1$
pairs because it can only occur in the final pair. Let
$N_{t} \in \{1,2,\ldots,n-2\}$
be the minimum label that is jointly matched, i.e.
$N_t - 1$
is the maximum element that occurs in different pairs in
$X_{t}$
and
$Y_{t}$
. Let
$X_t(a)$
denote the index of the air in the matching
$X_{t}$
that contains a, i.e.
$X_t(a) = i$
if
$a \in \textbf{p}_i$
at time t. Then, at time t, the elements
$\geq N_{t}$
match in both
$X_{t}$
and
$Y_{t}$
, i.e. for every
$a \geq N_{t}$
there is
$X_{t}(a)=Y_{t}(a)$
.
For any label
$a \in \{1, 2, \ldots, n - 2 \}$
, the coupling will have two properties.
Property 1. If
$a \ge N_t$
, then
$X_s(a) = Y_s(a)$
for all
$s \ge t$
.
Property 2. If
$a = N_t - 1$
and
$X_t(a) < Y_t(a)$
then
$X_{t+1}(a) \le Y_{t+1}(a)$
, and if
$X_t(a) > Y_t(a)$
then
$X_{t+1}(a) \ge Y_{t+1}(a)$
. This condition will ensure that the label `a' will eventually get matched in the two copies.
Define the following quantities.
-
• Let
$M_{t}$
be the set of all indices
$2 \le i \le n -2$
that contain labels
$\geq N_{t}$
jointly matched. That is, there is a label
$a \geq N_{t}$
such that
$X_{t}(a)=Y_{t}(a)=i$
. Note that it is possible to have other matches for labels
$< N_t$
, but we do not keep track of those matches and breaking those matches does not violate the two properties of the coupling. -
• Let
$AM_t = i$
if label
$N_t - 1$
is in pairs
$\textbf{p}_i$
and
$\textbf{q}_{i+1}$
, or if it is in pairs
$\textbf{p}_{i+1}$
and
$\textbf{q}_{i}$
. Otherwise, set
$AM_t = 0$
.
At each step, pick an index
$1 \le i \le n - 2$
uniformly at random and consider the following cases.
-
1.
$i, i+1 \notin M_t$
and
$i \neq AM_t$
. There are no joint matchings of labels
$\geq N_{t}$
in pairs i and
$i+1$
and swapping two elements in both copies will not match label
$N_{t}-1$
. In this case, propose independent swaps in
$X_{t}$
and
$Y_{t}$
according to their (lazy) marginal dynamics. -
2.
$i \in M_{t}$
and/or
$i+1 \in M_t$
, and
$i \neq AM_t$
. There is at least one joint matching of labels
$\geq N_{t}$
in pairs i or
$i+1$
and swapping two elements in both copies will not create a new joint matching of
$N_{t}-1$
. To preserve Property 1 it is necessary to perform the same move (or no move at all) on both chains. Toss a single coin
$\theta \sim \text{Bernoulli}(1/2)$
to determine whether a move will be proposed on both copies or not.-
(a) Suppose
$\theta=1$
and the pairs at i and
$i + 1$
are of the type with the possibility of
\begin{align*}&X\colon (a, b)^i, (c, d)^{i+1}, \\ &Y\colon (a, e)^i, (f, g)^{i+1},\end{align*}
$b=e$
, and
$\{c, d \} \cap \{f, g \} = \emptyset$
. The concern here comes since the probability that a specific label in pair i moves to the right depends on whether or not label i occurs in pair
$i + 1$
. That is, for X, if
$c, d \neq i$
then the probability of moving a, given that index i has been chosen, is
$1/2$
. If
$c = i$
or
$d = i$
then the probability of moving a is
$1/4$
.
The coupling procedure, however, ensures that none of c, d, f, g are equal to i: because label a occurs in pair i, it must either represent a leaf or have value less than i; and
$a \geq N_{t}$
since it is a label that was jointly matched before. Then c, d, f or g cannot be label i since i is already a match. This implies that the labels c, d, f, g can all occur in either pair i or
$i+1$
, thus there are no constraints on possible swap moves, and the marginal probability of swapping a would be the same in each chain. -
(b) Suppose
$\theta=1$
and the pairs at i and
$i + 1$
are of the type with the possibility of
\begin{align*}&X\colon (a, b)^i, (c, d)^{i+1}, \\ &Y\colon (e, f)^i, (g, d)^{i+1},\end{align*}
$d=i$
, or and allowing the possibility
\begin{align*}&X\colon (a, b)^i, (i, d)^{i+1}, \\ &Y\colon (e, f)^i, (i, d)^{i+1},\end{align*}
$i \in M_t$
in both cases. Then, if a matched label, e.g. d, is chosen to be swapped in chain X, it must also be swapped in Y.
-
-
3.
$i,i+1 \notin M_t$
and
$i = AM_t$
. There are no joint matchings of labels
$\geq N_{t}$
in pairs i and
$i+1$
, and label
$N_{t}-1$
is either in
$\textbf{p}_{i}$
and
$\textbf{q}_{i+1}$
or in
$\textbf{p}_{i+1}$
and
$\textbf{q}_{i}$
. In order to preserve Property 2, simply set
$\theta_Y = 1 - \theta_X$
. This ensures that label
$a = N_t - 1$
will only possibly move in one of the chains. -
4.
$i \in M_t$
and/or
$i+1 \in M_{t}$
, and
$i = AM_t$
. There is one joint matching in pair i and/or
$i+1$
, and label
$N_{t}-1$
is either in
$\textbf{p}_{i}$
and
$\textbf{q}_{i+1}$
or in
$\textbf{p}_{i+1}$
and
$\textbf{q}_{i}$
. To preserve Properties 1 and 2 while keeping the correct marginal transition probabilities for each chain we define the joint transitions as follows.-
(a) Suppose
$c = N_t - 1$
and the pairs at indices
$i, i + 1$
are of the type with
\begin{align*}&X\colon (a, b)^i, (c, d)^{i+1}, \\ &Y\colon (e, c)^i, (f, g)^{i+1},\end{align*}
$a = e$
and/or
$d = g$
. By the same argument as for case 2,
$c,d, g,f \neq i$
. Table 1 defines the joint proposal probabilities that preserve Properties 1 and 2 with the correct marginal transition probabilities.
Note that this would preserve the matches if
$a = e$
and/or
$d = g$
.Table 1. Coupling transition probabilities in case 4(a).
-
(b) Suppose now that
$c=N_{t}-1$
and that pairs at indices i and
$i+1$
are of the type with possibly
\begin{align*}&X\colon (a, b)^i, (c, i)^{i+1}, \\ &Y\colon (e, c)^i, (f, i)^{i+1},\end{align*}
$a = e$
. Table 2 defines the joint proposal probabilities that preserve Properties 1 and 2 with correct marginal transition probabilities.Table 2. Coupling transition probabilities in case 4(b).
-
Coupling of labeled ranked tree shapes. The coupling for
$\mathcal{T}_n^L$
can proceed exactly as the coupling for
$\mathcal{T}_n$
until every interior node label is matched, say at time T. After that point, the leaf labels can be matched in any order. We extend the set
$M_t$
to contain the indices
$1 \le i \le n -2$
of any label
$a \in \{\ell_{1},\ldots,\ell_{n}\}$
such that
$X_t(a) = Y_t(a)$
and
$AM_t$
to be the set of indices i such that any label
$a\in \{\ell_{1},\ldots,\ell_{n}\}$
is in pair
$\textbf{p}_i$
and
$\textbf{q}_{i+1}$
or
$\textbf{p}_{i+1}$
and
$\textbf{q}_i$
.
The transition probabilities defined in cases 1–4 above work with these sets
$M_t$
,
$AM_t$
and have the following properties, for
$t \ge T$
and label a.
-
1. Property 1. If
$X_t(a) = Y_t(a)$
, then
$X_s(a) = Y_s(a)$
for all
$s \ge t$
. -
2. Property 2. If
$X_t(a) < Y_t(a)$
, then
$X_s(a) \le Y_s(a)$
for all
$s \ge t$
. If
$X_t(a) > Y_t(a)$
, then
$X_s(a) \ge Y_s(a)$
for all
$s \ge t$
.
Note that now in case 4(a) we have the possibility
$b = f$
, and the transition probabilities defined in Table 1 will work to preserve Property 2.
5.1. Coupling time
For the chain on unlabeled ranked tree shapes
$\mathcal{T}_n$
, the time to couple is
$T = T_{n-3} + T_{n-4} + \cdots + T_1$
, where
$T_a$
is the time it takes to match interior node label a, after the labels
$a +1, \ldots, n - 2$
are already matched. Property 2 is crucial to study
$T_{a}$
. Suppose that at time
$t = T_{n-3} + \cdots + T_{a + 1}$
, when label
$a + 1$
is matched we have
$X_t(a) < Y_t(a)$
. Let
$S_a$
be the time it takes for
$Y_t$
to hit the left boundary of its range, i.e.
$Y_t(a) = a + 1$
. Then necessarily at this time, by Property 2,
$X_t(a) = Y_t(a)$
.
Note that
$X_t(a) \in \{a+1, \ldots, n - 2\}$
. If a is not at the left boundary, the probability of moving a to the left is
\begin{equation*}\mathbb{P}(X_{t+1}(a) = X_t(a) - 1 \mid X_t \neq a + 1 ) = \dfrac{1}{n - 2} \cdot \dfrac{1}{2} \cdot \dfrac{1}{2} = \dfrac{1}{4(n-2)}.\end{equation*}
The probability that a moves to the right will depend on the exact configuration and whether or not there is a constraint, e.g. in the situation
\begin{align*}& (a, b)^i, (c, i)^{i+1},\end{align*}
in which the probability a moves to the right is
$1/8(n - 2)$
. Thus we can bound
\begin{equation*}\dfrac{1}{8(n - 2)} \le \mathbb{P}(X_{t+1}(a) = X_t(a) + 1 \mid X_t \neq n - 2 ) \le \dfrac{1}{4(n-2)}.\end{equation*}
The following is an easy result about the hitting time of a symmetric random walk on a line.
Lemma 5. Let
$(Z_t)_{t \ge 0}$
be a random walk on the line
$\{1, 2, 3, \ldots, m\}$
with the transitions
\begin{align*}P(i, i+1) &= p, \quad i \neq m, \\ P(i, i-1) &= p, \quad i \neq 1, \\P(i, i) &= 1 - 2p, \quad i \neq 1, m ,\\P(m, m) &= 1 - p,\\ P(1, 1) &= 1,\end{align*}
for some
$0 < p \le 1/2$
. Suppose
$Z_0 = m$
and let
$T_m = \inf \{t > 0\colon Z_t =1 \}$
. Then
$\mathbb{E}[T_m] = (1/2p)\cdot m(m - 1)$
.
Proof. We can prove the result for
$p = 1/2$
, then scale. Let
$a_x$
be the expected first time of hitting 1 if
$Z_0 = x$
. Note that the following identities are satisfied:
\begin{align*}a_1 &= 0 , \\ a_x &= 1 + \dfrac{1}{2}(a_{x + 1} + a_{x - 1}),\quad x \in \{2, 3, \ldots, m - 1 \} , \\ a_m &= 1 + \dfrac{1}{2} a_{m-1} + \dfrac{1}{2} a_m.\end{align*}
This is a second-order recursion, with solution
$a_x = x(2m - x + 1) - 2m$
. So this means
$a_m = m(m - 1)$
. When
$p < 1/2$
the probability of moving is
$2p < 1$
, so the expected time to hit 1 started from m is
$(1/2p)m(m - 1)$
.
Let
$Z_t$
be a random walk on the line
$a+1, \ldots, n - 2$
with
$p = 1/4(n-2)$
, defined as in Lemma 5. We can couple
$Z_t$
with
$Y_t(a)$
so that
$Y_t(a) \le Z_t$
almost surely for all
$t \ge 0$
, because
$Z_t$
is moving to the right with probability larger than the probability that Y(t) moves to the right. In conclusion,
\begin{equation*}\mathbb{E}[T_a] \le 2(n-2) (n - 2 - a)^2\end{equation*}
and thus the total coupling time is
\begin{equation*}\mathbb{E}[\tau_{\mathrm{couple}}] \le \sum_{a = 1}^{n - 3} \mathbb{E}[T_a] \le \sum_{a = 1}^{n - 3} 2(n-2) (n - 2 - a)^2 = \dfrac{1}{3}(n - 2)^2(n-3) (2n-5) \leq \dfrac{2}{3} n^4.\end{equation*}
This together with Theorem 2 gives the upper bound in Theorem 1 for
$\mathcal{T}_n$
:
\begin{equation*}t_n \le 4 \cdot \mathbb{E}[\tau_{\mathrm{couple}}] \leq \dfrac{8}{3}n^4.\end{equation*}
Leaf-labeled trees. The coupling time for leaf-labeled trees can be written
$\tau_{\mathrm{couple}}^L = T + T^{\mathrm{leaves}}$
, where T is the time from the previous section for the interior labels to match. For the time
$T^{\mathrm{leaves}}$
for the leaves to match, note that time is saved because the leaves are allowed to match in any order. Moreover, leaf labels can be moved without constraints. In analogy with the result from Example 4.10 in [Reference Aldous1] for adjacent transpositions on
$S_n$
, this would take time of order
$n^3 \log(n)$
. Therefore
\begin{equation*}\mathbb{E}\bigl[\tau_{\mathrm{couple}}^{L}\bigr]\leq \dfrac{2}{3} n^4 + C_{4}n^{3}\log(n).\end{equation*}
6. Discussion
The representation of ranked tree shapes as ordered matchings can be used to define many other Markov chains in analogy to well-studied chains on
$S_n$
. For example, in addition to the adjacent-swap chain, another natural chain would be a random-swap Markov chain: pick two pairs uniformly at random, within each pair pick a label, and swap the two elements if it is allowed. The internal tree length function defined in Section 4 gives a lower bound of n for this chain, because a single move could change the function by at most n, and thus the Dirichlet form can be bounded by
$n^2$
. A naive coupling argument would give an upper bound of order
$n^3$
. The focus of this paper was on the adjacent-swap chain because it is a local-move chain which could be more useful for Metropolis algorithms in applications.
The upper bound on the mixing time relies on a coupling that matches one label at a time in a specific order giving a sub-optimal upper bound. We conjecture that the mixing time of the adjacent-swap chain on unlabeled ranked tree shapes is of the order of
$n^{3}\log(n)$
, as it is in the case of adjacent transpositions on
$S_{n}$
. Figure 4 shows the total variation distance between the adjacent-swap chain on unlabeled ranked tree shapes and the Tajima stationary distribution for trees with
$n<10$
leaves. Due to the large size of the state space, this calculation could not be extended for larger trees in order to inform about the presence of a cut-off phenomenon.
Figure 4. Total variation distance for adjacent-swap chain on unlabeled ranked tree shapes. Each curve depicts the total variation distance between the probability of the chain at time t and the Tajima stationary distribution for trees with
$n=6$
, 7, 8, and 9 leaves.
We also note another connection between trees and permutations: Unlabeled ranked tree shapes are in bijection with alternating permutations [Reference Donaghey9, Reference Stanley30] and hence some results concerning Markov chains on alternating permutations could be used to analyze the mixing of Markov chains on unlabeled ranked trees and vice versa. However, we are not aware of mixing time results of Markov chains on the space of alternating permutations [Reference Diaconis and Wood7].
Finally, in this work we analyzed Markov chains on trees whose stationary distributions are coalescent distributions. These coalescent distributions are used as prior distributions over the set of ancestral relationships of samples of DNA [Reference Palacios, Véber, Cappello, Wang, Wakeley and Ramachandran25]. In practice, these Markov chains are used to approximate the posterior distribution, and hence the state space is more restricted in the sense that some trees will not have positive likelihood under some mutation models. Future research is needed to investigate the adjacent-swap Markov chain and its convergence times on these restricted state spaces.
Acknowledgement
We wish to thank the two anonymous referees for helpful comments.
Funding information
MS is supported by a National Defense Science & Engineering Graduate fellowship. JAP is supported by National Institutes of Health Grant R01-GM-131404 and the Alfred P. Sloan Foundation.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.
