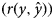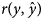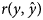Introduction
Live body weight at different ages has decisive effects on the profitability of breeding enterprises. Therefore, these traits may be considered as selection criteria for developing efficient breeding programmes (Tosh and Kemp Reference Tosh and Kemp1994). Selection of the best animals for body weight recorded at different ages to be parents of the next generation is a possible way for increasing meat production (Boujenane and Kansari Reference Boujenane and Kansari2002).
Rosa et al. (Reference Rosa, Valente, de los Campos, Wu, Gianola and Silva2011) have pointed out that in any breeding programme dealing with multiple traits, genetic evaluation has great importance for studying potential causal relationships among the traits. In the classical breeding programmes, breeding values of the selected candidates are predicted using standard mixed models [standard multivariate models (SMMs)], in which the existed potential causal relationships among the traits are ignored (Valente et al. Reference Valente, Rosa, Gianola, Wu and Weigel2013). Gianola and Sorensen (Reference Gianola and Sorensen2004) developed the theory of quantitative genetics to become suitable for situations in which causal relationships exist between the phenotypes in a multivariate system.
Structural equation models (SEMs) enable fitting and studying cause-and-effect relationships between the traits (Wright, Reference Wright1934) and were first introduced in genetics by Wright (Reference Wright1921) but have been ignored in quantitative genetics for many years. The work of Gianola and Sorensen (Reference Gianola and Sorensen2004) stimulated the application of SEMs in animal breeding and genetics (Lopez de Maturana et al. Reference Lopez de Maturana, de los Campos, Wu, Gianola, Weigel and Rosa2010; Valente et al. Reference Valente, Rosa, de los Campos, Gianola and Silva2010; Inoue et al. Reference Inoue, Valente, Shoji, Honda, Oyama and Rosa2016; Mokhtari et al. Reference Mokhtari, Moghbeli Damaneh and Abdollahi Arpanahi2018). Genetic parameters pertaining to SEMs can be useful for modelling biological relationships among the phenotypes (Valente et al. Reference Valente, Rosa, de los Campos, Gianola and Silva2010). Furthermore, considering the high computational demands, fitting SEMs in the model is more parsimonious than SMMs, due to assumed uncorrelated residual effects. A number of studies have applied mixed-effects SEMs in the animal breeding context (Lopez de Maturana et al. Reference Lopez de Maturana, de los Campos, Wu, Gianola, Weigel and Rosa2010; Mokhtari et al. Reference Mokhtari, Moghbeli Damaneh and Abdollahi Arpanahi2018; Amou Posht-e Masari et al. Reference Amou Posht-e Masari, Hafezian, Abdollahi-Arpanahi, Mokhtari MS and Taheri Yeganeh2019).
Despite the advances in agricultural methods in developing countries, the number of goats has increased worldwide during the last few decades (Abadi et al. Reference Abadi, Askari, Baghizadeh and Esmailizadeh2011; Shamsalddini et al. Reference Shamsalddini, Mohammadabadi and Esmailizadeh2016). About 96% of goat's meat and milk are produced in developing countries, whereas only 4% are found in developed countries (Esmaeili et al. Reference Esmaeili, Esmaeilizadeh Koshkooieh, Aytolahi, Mohammadabadi, Babenko, Bushtruk, Tkachenko, Stavetska and Klopenko2019). Goat production is one of the major sources of income for farmers in the arid and semi-arid regions of the world (Barazandeh et al. Reference Barazandeh, Moghbeli, Vatankhah and Mohammadabadi2012). Increasing meat, milk and fibre production of goats is not out of reach for farmers by using accurate and precise selection programmes (Moghbeli et al. Reference Moghbeli, Barazandeh, Vatankhah and Mohammadabadi2013). Markhoz goat is one of the most important indigenous goat breeds in Iran. The breed is mainly kept by local flock holders in a wide range of forest mountain habitats in the region of Kurdistan, north-west of Iran. Markhoz goats are small-sized with a wide range in coat colour, varying from white to black (Rashidi et al. Reference Rashidi, Mokhtari and Gutierrez2015). Many researchers have undertaken several studies on genetic evaluation of growth traits in Markhoz goat (Rashidi et al. Reference Rashidi, Sheikhahmadi, Rostamzadeh and Shrestha2008, Reference Rashidi, Bishop and Matika2011) and other goat breeds (Maghsoudi et al. Reference Maghsoudi, Vaez Torshizi and Safi Jahanshahi2009; Gholizadeh et al. Reference Gholizadeh, Rahimi Mianji, Hashemi and Hafezian2010; Mohammadi et al. Reference Mohammadi, Moradi Shahrebabak and Moradi Shahrebabak2012); however, these studies have not considered possible causal relationships.
To the best of our knowledge, there is only one report on genetic evaluation of growth traits in breeds of goat considering possible causal relationships among them. Mokhtari et al. (Reference Mokhtari, Moghbeli Damaneh and Abdollahi Arpanahi2018) compared the SMM, which ignores the possible causal effects among the traits, with the recursive multivariate model (RMM), a type of SEM, which handles the existence of causal relationships among the traits, in terms of the predictive ability of models and the estimates of genetic parameters of growth traits in Raeini Cashmere goat. They concluded that RMM was more plausible for the genetic evaluation of growth traits in Raeini Cashmere goat in terms of better predictive ability over SMM. The importance of considering causal relationships among the traits for the accurate ranking of animals was documented (Amou Posht-e Masari et al. Reference Amou Posht-e Masari, Hafezian, Abdollahi-Arpanahi, Mokhtari MS and Taheri Yeganeh2019).
Therefore, the objectives of the present research were to compare SMM and fully recursive multivariate model (FRM) in terms of their predictive ability. Furthermore, the effect of different mathematical models on the ranking of the animals based on their predicted breeding values was also examined.
Materials and methods
Flock management and the studied traits
The data set and pedigree information used in the present study were collected from 1993 to 2016 in Markhoz goat Breeding Station located in Sanandaj, Kurdistan province, north-western part of Iran. The herd was reared under a semi-intensive production system, in which goats were grazed on natural pastures in spring and were fed by a standard ration in other seasons of the year. The period of mating started in October and lasted until November, and the kidding season was from February to March. Does were first exposed to the bucks approximately at 18 months of age. Annually, 20–30 bucks were randomly allocated to mate with about 10 or 15 does each, with sire identification recorded. Some of the sires were used for two or three mating seasons. New-born kids were weighed and ear-tagged after birth time and allowed to remain with their dam for a week. One week after birth, the kids were separated from their dams and suckled twice a day until 3–4 months of age. All kids weaned on the same day (Rashidi et al. Reference Rashidi, Bishop and Matika2011).
The studied characteristics were body weight traits including birth weight (BW), weaning weight (WW), six months weight (6MW), nine months weight (9MW) and yearling weight (YW). Animals with body weights outside of the range of mean ± 3 × sd have been excluded from the data set. The structure and summary of the data set used are presented in Table 1.
Table 1. Descriptive statistics for the studied traits
BW, birth weight; WW, weaning weight; 6MW, six months weight; 9MW, nine months weight; YW, yearling weight.
Statistical analyses
Investigating the importance of maternal effects on the studied traits
In mammalian species, growth traits especially in early life are determined not only by the animal's own additive genetic merit but also by maternal effects. The maternal effects mainly denote those related to the milk production of dam and its mothering ability (Roy et al. Reference Roy, Mandal and Notter2008). Previous studies confirmed the importance of including maternal effects in genetic evaluation of growth traits in several goat breeds (Roy et al. Reference Roy, Mandal and Notter2008; Rashidi et al. Reference Rashidi, Bishop and Matika2011). Therefore, for studying the role of maternal effects on the genetic evaluation of the studied traits a restricted maximum likelihood procedure under average information algorithm, applying DMU programme (Madsen et al. Reference Madsen, Jensen, Labouriau, Christensen and Sahana2014), was used and nine models including different combinations of direct additive effects, maternal additive genetic, maternal permanent environmental and maternal temporary environmental, were tested. The considered models (in matrix notation) are as below:
where y is a vector of records for the studied traits; b, a, m, pe, l and e are vectors of fixed, direct genetic, maternal genetic, maternal permanent environmental, maternal temporary environmental (common litter effects) and the residual effects, respectively. The matrices of X, Z a, Z m, Z pe, and Z l are design ones associating corresponding effects to a vector of y. Also, A is the numerator relationship matrix and σ am denotes covariance between additive and maternal effects. Common fixed effects included in the models for the studied traits were the sex of kids in 2 classes (male and female), dam age at lambing in 6 classes (2–7 years old), birth year in 23 classes (1993–2016) and birth type in 3 classes (single, twin and triplet). Interactions among fixed effects were also fitted. Age of kids at weaning, at six months, at nine months, and at yearling body weight weighing (in days) was considered as a linear covariate for WW, 6MW, 9MW, and YW, respectively. Significance testing of fixed effects and least square analyses were carried out using the general linear model procedure of the SAS software (SAS 2004). The interactions between considered fixed effects were not significant and therefore dropped out.
The Akaike's information criterion (AIC) was applied for determining the most appropriate model among tested models (Akaike Reference Akaike1974):
where log L i is the maximized log-likelihood and P i is the number of parameters fitted for model i. In each case, the model with the lowest AIC was considered as the best model. The AIC values under the considered animal models are given in Table 2, with the most appropriate model in boldface for each trait.
Table 2. AIC values from univariate analysis for the studied traits with the best model in bold
BW, birth weight; WW, weaning weight; 6MW, six months weight; 9MW, nine months weight; YW, yearling weight.
a Model 1 included direct additive and residual effects; Model 2 included direct additive, maternal permanent environmental and residual effects; Model 3 included direct additive, maternal additive and residual effects; Model 4 is similar to Model 3, but a covariance between direct and maternal additive effects was assumed; Model 5 included direct additive, maternal additive, maternal permanent environmental and residual effects; Model 6 is similar to Model 5, but a covariance between direct and maternal additive effects was assumed; Model 7 included direct additive, maternal permanent environmental, maternal temporary environmental and residual effects; Model 8 included direct additive, maternal additive, maternal permanent environmental, maternal temporary environmental and residual effects; Model 9 is similar to Model 8, but a covariance between direct and maternal additive effects was assumed. The best model is shown in bold.
Statistical inference
After the selection of the most suitable model of genetic analysis for the studied traits, Bayesian Markov Chain Monte Carlo (MCMC) implementation was carried out applying the GIBBS2F90 programme of Misztal et al. (Reference Misztal, Tsuruta, Strabel, Auvray, Druet and Lee2002), which implements Gibbs sampling to evaluate the posterior density of the parameter estimates. The length of the chain and the burn-in period were examined by visual inspection of the trace plots of posterior samples of the parameters in several preliminary analyses. For each model, 100 000 iterations were run and posterior samples from each chain were thinned considering thinning intervals of 10 iterations after discarding the first 10 000 iterations as burn-in. Hence, 9000 samples were considered for computing features of the posterior distribution. Posterior analyses for calculating posterior means and posterior standard deviations (PSDs) were carried out applying the POSTGIBBSF90 programme of Misztal et al. (Reference Misztal, Tsuruta, Strabel, Auvray, Druet and Lee2002).
It was assumed that the direct additive and maternal additive genetic effects followed a multivariate normal distribution, a priori, with a null mean vector and a (co)variance matrix G⊗A, where G and A are the genetic (co)variance matrix and numerator relationship matrix among animals, respectively. Furthermore, it was assumed that the vector of residual effects followed a multivariate normal distribution with a null mean vector and (co)variance matrix R⊗In, where In is an identity matrix and R is the residual (co)variance matrix; ⊗ shows the Kronecker product. Multivariate normal distribution was also assumed for maternal permanent environmental and maternal temporary environmental effects so that their fully conditional distributions were also multivariate normal. The prior distribution of the genetic (G), maternal permanent environmental (Pe) and maternal temporary environmental (L) (co)variance matrices were follow inverted Wishart distribution so that their fully conditional posterior distributions were also inverted Wishart (Sorensen and Gianola Reference Sorensen and Gianola2002). The SEMs are not identifiable at the likelihood level due to the presence of extra parameters, including structural coefficients. For achieving identification, it was assumed that residual correlations in the system were uncorrelated. In other words, in SEMs, R was assumed to be a diagonal matrix for the identification purposes.
Lopez de Maturana et al. (Reference Lopez de Maturana, Legarra, Varona and Ugarte2007) pointed out that the method described by Gianola and Sorensen (Reference Gianola and Sorensen2004) for incorporating causal effects in quantitative genetics is not straightforward enough to perform in a general manner and showed that recursive models could be handled by fitting parent trait as a covariate for other trait(s) while genetic correlations between traits are considered in multivariate analyses. In this case, the parent trait denotes trait which causally influences other trait(s). Therefore, this methodology was applied in the present study. Detailed information and the theoretical background about the methodology used in the present study for fitting recursive models are given by Lopez de Maturana et al. (Reference Lopez de Maturana, Legarra, Varona and Ugarte2007).
Model comparisons
The SMM and FRM were compared by applying deviance information criterion (DIC), predictive ability measures, and Spearman's rank correlations between posterior means of genetic effects under SMM and FRM. The DIC takes the trade-off between model goodness-of-fit and the corresponding complexity of model into account (Bouwman et al. Reference Bouwman, Valente, Janss, Bovenhuis and Rosa2014). A model with smaller DIC values is better supported by the data.
For assessing the predictive ability of the tested models (SMM and FRM), the dataset was randomly partitioned five times into two sets including the training set (50% of data set) and testing set (retained 50% data set). Then, solutions for all fixed and random effects of the training set were estimated and used to predict body weight records in the testing set. The predictive ability of the models was assessed by PREDICTF90 programme of Misztal et al. (Reference Misztal, Tsuruta, Strabel, Auvray, Druet and Lee2002) and compared applying two measures. The first measure was the mean square of error (MSE) as follow:
where, $y_i\,\,{\rm and}\,\,\hat{y}_i$
represent the ith observed and predicted record for each trait in the testing data set, respectively, and n is the number of records. The second measure was the Pearson correlation between observed and predicted values $\lpar r\lpar y\comma \;\hat{y}\rpar \rpar$
in the testing data set. The MSE and $r\lpar y\comma \;\hat{y}\rpar$
values were calculated five times, and the average of obtained results was used as the final value. The lower MSE and higher $r\lpar y\comma \;\hat{y}\rpar$
indicate the superiority of the model.
The SMM and FRM were also compared using Spearman's rank correlations between the posterior means of genetic effects for all, 50% top-ranked, 10% top-ranked and 1% top-ranked animals. For this purpose, breeding values (equivalent to the SMM) were estimated as (Konig et al. Reference Konig, Wu, Gianola, Heringstad and Simianer2008):
where BV is a vector of breeding values estimated under FRM. The matrix Λ is the structural coefficients matrix, in which diagonal elements are filled with 1 and the off-diagonal elements are determined based on the causal relationships between the traits. Structural coefficients are in fact a kind of regression coefficient, which are estimated by fitting SEMs (Gianola and Sorensen Reference Gianola and Sorensen2004). The matrix of structural coefficients with five traits under a FRM, which is used in the present study, is as follows:
where the first trait affects second, third, fourth, and fifth traits, the second trait affects the third, fourth, and fifth traits, the third trait affects fourth and fifth traits, and eventually, the fourth trait has a causal effect on the fifth trait.
Results
Direct additive genetic and maternal additive genetic effects, without considering covariance between them, and maternal permanent environmental effects (Model 5) were random sources of variation for BW. Model 2, in which direct additive genetic effects and maternal permanent environmental effects were significant random effects, determined as the best one for WW, 6MW and 9MW traits. Maternal effects had no influencing effects on YW.
The outcome of comparisons between SMM and FRM based on DIC is presented in Table 3. The lower DIC was obtained under FRM than SMM. The SMM and FRM were also compared in terms of the predictive ability of models based on the average MSE and average Pearson's correlation coefficient between observed and predicted records $\lpar r\lpar y\comma \;\hat{y}\rpar \rpar$
of the traits under these models (Table 4). For all the studied traits, the lowest MSE and the highest $r\lpar y\comma \;\hat{y}\rpar$
values were obtained under FRM, which was more pronounced for 6MW, 9MW and YW than BW and WW.
Table 3. DIC values from the different multivariate studied models
SMM, standard multivariate model; FRM, fully recursive multivariate model.
Table 4. Predictive ability for the studied traits under the different multivariate studied models
BW, birth weight; WW, weaning weight; 6MW, six months weight; 9MW, nine months weight; YW, yearling weight; SMM, standard multivariate model, FRM, fully recursive multivariate model; MSE, mean square of error, $r\lpar y\comma \;\hat{y}\rpar =$
Pearson correlation between observed and predicted values.
Applying FRM features of posterior means and PSDs for structural coefficients among the studied body weight traits of Markhoz goat are presented in Table 5. All the estimated structural coefficients were positive and highly significant, except for that of 6MW on YW. Considering the causal structure considered under FRM (Fig. 1) among the studied body weight traits of Markhoz goat, BW had direct causal effects on all other studied traits the estimated direct causal effects of BW on WW, 6MW, 9MW and YW were 1.24, 0.79, 0.87 and 0.50, respectively. In other words, each 1 kg increase in BW of Markhoz kids will increase WW, 6MW, MW and YW as 1.24, 0.79, 0.87 and 0.50 kg, respectively. Direct causal effects of WW on 6MW, 9MW and YW were 0.65, 0.22 and 0.16, respectively.
Table 5. Posterior means ± PSD for the structural coefficients under the fully recursive multivariate (FRM) model
BW, birth weight; WW, weaning weight; 6MW, six months weight; 9MW, nine months weight; YW, yearling weight; PSD, posterior standard deviation.
a 99% HPD intervals did not include zero.
Fig. 1. Multivariate fully recursive model considered among the studied growth traits in Markhoz goat (BW, birth weight; WW, weaning weight; 6MW, six months weight; 9MW, nine months weight; YW, yearling weight).
Spearman's rank correlations between posterior means of direct genetic effects within the studied traits applying SMM and FRM for the whole animals, 50, 10 and 1% of top-ranked animals are shown in Table 6. The highest Spearman's rank correlation (1.00) between posterior means of direct genetic effects was obtained for BW. Rankings of the ten top-ranked animals for the trait studied based on the posterior direct genetic effects under SMM and FRM are shown in Table 7. Substantial changes were observed in the rank of the ten top-rank animals especially for 6MW, 9MW and YW. For example, for YW, the best animal when applying SMM was ranked as the rank of 231 under FRM.
Table 6. Spearman's rank correlations of posterior means of direct genetic effects for studied growth traits in Markhoz goat under the standard multivariate (SMM) and fully recursive multivariate (FRM) models
BW, birth weight; WW, weaning weight; 6MW, six months weight; 9MW, nine months weight; YW, yearling weight.
**P-value <0.01, ns, P-value <0.05.
Table 7. Rank comparison of ten top-ranked animals based on posterior means of genetic effects under the standard multivariate (SMM) and fully recursive multivariate (FRM) models
BW, birth weight; WW, weaning weight; 6MW, six months weight; 9MW, nine months weight; YW, yearling weight.
Discussion
Statistical comparisons between SMM and FRM
Mokhtari et al. (Reference Mokhtari, Moghbeli Damaneh and Abdollahi Arpanahi2018) compared RMM and SMM for genetic evaluation of early growth traits in Raeini Cashmere goat including BW, WW and 6MW in terms of DIC, MSE and $r\lpar y\comma \;\hat{y}\rpar$
and found lower DIC, lower MSE and higher $r\lpar y\comma \;\hat{y}\rpar$
(for WW and 6MW) under RMM than the SMM one. They concluded that considering causal relationships among the studied growth traits in Raeini goat may provide a better explanation for biological relationships among the studied traits. Amou Posht-e Masari et al. (Reference Amou Posht-e Masari, Hafezian, Abdollahi-Arpanahi, Mokhtari MS and Taheri Yeganeh2019) compared three multivariate models including SMM, temporal RMM and FRM for genetic evaluation of growth traits in Lori-Bakhtiari sheep breed, temporal RMM favoured over other models in terms of lower DIC.
In a previous study, Lopez de Maturana et al. (Reference Lopez de Maturana, de los Campos, Wu, Gianola, Weigel and Rosa2010) considered causal relationships among calving traits including gestation length (as parent trait), calving difficulty and stillbirth in first-parity US Holsteins under three RMMs and compared them with the SMM in terms of mean square error and Pearson's correlation coefficient between predicted and observed records. They generally concluded that models included causal relationships performed better than SMM by lower mean square error and higher Pearson correlation coefficient between predicted and observed records.
Structural coefficients
In the present study, any improvement in BW had positive causal effects on the other body weight traits in Markhoz goat. Mokhtari et al. (Reference Mokhtari, Moghbeli Damaneh and Abdollahi Arpanahi2018) reported direct causal effects of BW on WW and on 6MW of Raeini Cashmere kids as 1.94 and 2.48 kg, respectively, which were higher than the corresponding values estimated in the present study. Mioc et al. (Reference Mioc, Susic, Antunovic, Prpic, Vnucec and Kasap2011) studied the BW and WW of Croatian multicoloured goat kids and reported that kids with higher BW have higher WW, also. Valente et al. (Reference Valente, Rosa, Gianola, Wu and Weigel2013) pointed out that the genetic effects from SMM and SEM have different meanings, while the SMM represent overall genetic effects that included all direct and indirect (which mediating by other traits) effects on each trait and SEM represent only direct effects (which not mediating by other traits in the causal network). Overall effects may be partitioned into direct and indirect ones by applying SEM (Valente et al. Reference Valente, Rosa, Gianola, Wu and Weigel2013). As shown in Fig. 1, BW had indirect causal effects on 6MW (mediated via WW), on 9MW (mediated via WW and 6MW) and YW (mediated via WW, 6MW and 9MW). The indirect causal effect of BW on 6MW was calculated as the product direct causal effects of BW on WW (1.24), WW on 6MW (0.65) which was 0.806. The overall causal effects of BW on 6MW are the summation of direct (0.79) and indirect (0.806) causal effects, which is equal to 1.596. In general, each 1 kg increase in BW of Markhoz kids will increase 6MW as 1.1596 kg. The overall causal effect (direct and indirect) of BW on 6MW of Raeini Cashmere goat was obtained as 4.48 kg by Mokhtari et al. (Reference Mokhtari, Moghbeli Damaneh and Abdollahi Arpanahi2018) which was higher than the corresponding value obtained in the present study. Considering the same manner, the overall effects of BW on 9MW and YW were calculated as 1.337 and 0.832 kg, respectively.
It may be concluded that any increase in WW of Markhoz kids significantly will increase 6MW, 9MW and YW. Mokhtari et al. (Reference Mokhtari, Moghbeli Damaneh and Abdollahi Arpanahi2018) studied causal relationships among early growth traits in Raeini Cashmere goat by fitting a FRM. They estimated direct causal recursive effects of WW on 6MW as 1.03 kg which was higher than the corresponding value obtained in the present study. WW had indirect causal effects on 9MW (mediated via 6MW) and on YW (mediated via 6MW and 9MW), which were calculated as 0.38 and 0.27 kg, respectively. Overall causal effects of WW on 9MW and YW were obtained as 0.60 and 0.43 kg, respectively. Direct causal effects of 0.58 and 0.71 kg were obtained from 6MW on 9MW and from 9MW on YW, respectively. The indirect causal effect of 6MW on YW (mediated via 9MW) was calculated as 0.411. No significant direct causal effect was observed from 6MW on YW.
Ranking of animals under SMM and FRM
Considering causal relationships among the studied growth traits of Markhoz goat had no impact on posterior means of direct genetic effects of BW. In the fully recursive model considered among growth traits of Markhoz goat (Fig. 1) BW is considered as a parent trait, which influenced all other traits but not influenced by the others. The obtained Spearman's rank correlation between posterior means of direct genetic effects of BW may be explained partly by such a causal structure. When 50% and 10% of top-ranked animals were considered, the lowest Spearman's rank correlations were obtained for YW (Table 6). There were substantial changes for rank correlations between posterior means of genetic effects under SMM and FRM for 1% top-ranked animals, except for BW. Spearman's rank correlations between posterior means of direct genetic effects for 9MW and YW were not statistically significant (P > 0.05); implied substantial re-ranking of animals under SMM and FRM. Therefore, this underlies the importance of model choice in breeding value estimation and it may be concluded that accounting for causal relationships among the studied growth traits in Markhoz goat may has beneficial effects for accurate predicting of breeding values and correspondingly accurate ranking of top-ranked animals. Konig et al. (Reference Konig, Wu, Gianola, Heringstad and Simianer2008) studied causal relationships between claw disorders and milk yield in Holstein cows via recursive models and reported changes in the ranking of top-ranked sires under SMM and TRM. Amou Posht-e Masari et al. (Reference Amou Posht-e Masari, Hafezian, Abdollahi-Arpanahi, Mokhtari MS and Taheri Yeganeh2019) reported re-ranking of the top-ranked animal for 6MW of Lori-Bakhtiari lambs under SMM and temporal recursive model.
In conclusion, inferring relationships among the studied growth traits in Markhoz could help to identify the development of the growth process from birth to yearling age. Furthermore, FRM showed more superiority over SMM in terms of lower MSE and higher Pearson's correlation coefficient between observed and predicted records of the studied growth traits. Furthermore, for fitting FRM, the residual correlations among the traits studied were set zero, which reduced the number of parameters to be estimated (15 residual correlations were not estimated under FRM). On the other hand, FRM included extra parameters over SMM as structural coefficients (10 structural coefficients were estimated in the present study). It may be concluded that the FRM is a more parsimonious model than the corresponding SMM which reduces computational demands in a multivariate genetic evaluation context. Comparisons of rank correlations between posterior means of direct genetic effects for the studied growth traits under SMM and FRM revealed that taking the causal relationships among the studied growth traits of Markhoz goat into account may cause considerable re-ranking for the animals, especially top-ranked ones, in terms of the estimated breeding values.
In conclusion, the present study revealed that causal effects had more statistical advantages than ignoring them for accurate genetic evaluation of the studied growth traits in Markhoz goat in terms of predictive ability of models and ranking of animals.
Financial support
This research received no specific grant from any funding agency, commercial or not-for-profit sectors.
Conflicts of interest
The authors certify that there are no conflicts of interest among authors and between authors and other people and organizations.
Ethical standards
All applicable international, national, and/or institutional guidelines for the care and use of animals were followed.
