I. INTRODUCTION
Nowadays, Mode-S multilateration (MLAT) systems are a feasible option to be used in the air traffic control (ATC) technological infrastructures, so much that the European Organization for the Safety or Air Navigation (EUROCONTROL) published in its report “The ATM Surveillance Strategy for ECAC” [1] that these systems will be one of three pillars of the ground-based surveillance infrastructure for 2020. These systems exploit the transmitted signals from the on-board transponder of the secondary surveillance radar in the selective and conventional mode, i.e. SSR Mode-S (and Mode A/C), in order to calculate the position of aircraft and vehicles in the coverage area. As a matter of fact, each mobile (aircraft, vehicle) to be detected and localized has an SSR Mode-S transponder on board, emitting standard signals at regular, but unknown, time intervals. A number of receiving and measurement stations in the surveillance area generate a set of time of arrival measurements, from which the localization is performed by solving a system of hyperbolic equations based on the Time Difference of Arrival (TDOA) technique; the pertaining algorithms run at real time in a CPS (Central Processor System) [2]. This is sketched in Fig. 1, which, for the sake of simplicity, refers to the two-dimensional case.
Fig. 1. A pictorial view (2D) of TDOA localization.
In some scenarios, it is common to find a numerical problem when solving the system of hyperbolic equations, i.e., the coefficient matrix has a very large condition number [Reference Golub and Loan3]. This problem is defined in the literature as an ill-conditioned problem and the consequence of this is that, when the system of equations is solved, the solution is not correct or it has a big error. The mathematical interpretation of this problem goes back to the three conditions of Jacques Hadamard [Reference Hadamard4], namely, the solution exists, the solution is unique, and the solution depends continuously on the data. If at least one of these conditions is not satisfied the problem becomes ill-conditioned. On the other hand, the effects of this problem in the multilateration systems accuracy have been highlighted in [Reference Leonardi, Mathias and Galati5, Reference Galati, Leonardi and Tosti6].
Some ill-conditioned problems can also be found in other fields as image processing [Reference Bertero, Boccacci, Brakenhoff, Malfanti and Voort7], electromagnetic scattering [Reference Harrington8], or geophysics [Reference Menke9]. In these fields, this problem has been solved by applying a group of methods called regularization methods. These methods basically convert the ill-conditioned problem in a well-conditioned problem where the three Hadamard's conditions are satisfied. In this paper, we study and apply one of these methods to solve the ill-conditioned problem in multilateration systems.
This paper is organized as follows: in Section II, the general aspects and the classical solution for the location problem, in MLAT, are shown. Then, in Section III the location strategy as proposed in this work, is fully described whereas, in Section IV some simulations and results are shown for two different scenarios. Finally, Section V gives the main conclusions.
II. LOCATION PROBLEM IN MLAT
In MLAT systems, a number of ground stations (at least three for 2D or four for 3D localization) are placed in some strategic locations around the airport or the area to be covered. The system uses the Mode-S transmission and asynchronous transponder (Mode-S) replies as well as the responses to interrogations elicited by the MLAT system. Then, the received signal is sent to a CPS (Central Processor System) where the transponder position is calculated. This calculation is based on the TDOA method, where the intersections of multiple hyperboloids, which have been created with the relative time differences, are computed. Each of these hyperboloids follows the expression:
where c is the speed of light, (x,y,z) the unknown target position (aircraft position), and (x i,y i,z i) is the known position of the ith station (i = 1 denotes the reference station). Linearizing (1) by Taylor series expansion [Reference Foy10, Reference Torrieri11] is the most accepted strategy to solve these hyperbolic equations, for estimating the target position. In the current literature, the solution of this inverse problem has been presented as an iterative procedure in the sense of the least-squares [Reference Foy10, Reference Torrieri11]. Denoting the unknown target position as θ = [x, y, z]T and comprising the system measurements (for a number of N s ground stations) in a N s−1 vector ![$\hat{\bi m}=\left[{TDOA_{i\comma \, 1}\comma \; {\ldots }\,\comma \; TDOA_{N_s\comma \, 1} } \right]^T $](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151130141029191-0042:S1759078712000104_inline6.gif?pub-status=live){kind=small}
, the final formulation can be summarized as follows:
where k = 1, … ,K; G is the (N s − 1) × 3 Jacobian matrix of the N s − 1 hyperbolic equations (1), 
is the starting point required for this method, 
, and 
is a (N s − 1 )× 1 vector comprising the TDOA (see (1)) quantities evaluated at the partial solution 
. Finally, because this method is based on an iterative procedure, K is the number of refinement iterations, in practice set by the maximum acceptable residual error.
The solution provided by (2) is the minimum residual norm solution and the matrices product (GTG)−1GT is known as the pseudoinverse matrix G† [3]. For some scenarios, due to the system geometry, to the measurements noise and to the starting point quality, this inverse problem is ill-conditioned and therefore the solution obtained by (2) is not correct or it diverges with very large errors.
Nowadays, the problem of ill-conditioning is solved by applying different hardware and software solutions. Regarding the hardware-based solutions, one of these is by adding more stations, i.e. usually the problem of ill-conditioning is found for situations with a number of stations smaller than seven or eight. Another one is by adding new measurement capabilities to the system, such as the angle of arrival [Reference Galati, Leonardi and Tosti6] or the round-trip-delay [Reference Galati, Leonardi and Tosti6, Reference Perl and Gerry12], i.e., in a numerical sense, adding new measurements means to change the ill-conditioned Jacobian matrix into a well-conditioned Jacobian matrix. However all these solutions, although are efficient options, require in much cases significant economic investments.
On the other hand, regarding the software-based solutions, two possible options can be implemented. One is by using a horizontal (2D) projected version of the Taylor-series expansion method and solving the resulting system of equations with the pseudoinverse matrix. This option, although the corresponding coefficient matrix is initially well-conditioned, has the disadvantage that it adds a spatial bias due to the projection from 3D to 2D in the coefficient matrix but of course not in the measurements. The second option is by implementing a family of location algorithms called closed-form algorithms [Reference Leonardi, Mathias and Galati5, Reference Schau and Robinson13, Reference Ho and Chan14]. These algorithms have the advantage of not needing a starting point but on the contrary, they introduce quadratic and cubic relations between the solution (target position) and the measurement noise as well as the necessity to choose one of the two possible solutions. Horizontal projection for this kind of algorithms is also possible but the problem of bias is equally present. Finally, as it will be shown in the results section, these algorithms, in some cases, are also affected by the ill-conditioning problem.
In this paper we propose an efficient software-based strategy, based on the use of the Tikhonov [Reference Tikhonov15] regularization method, to solve the iterative procedure of Taylor-series expansion and to avoid those errors due to the ill-conditioned problem but also bridging those disadvantages of hardware and software-based solutions as mentioned above.
III. SOLUTION OF LOCATION PROBLEM IN MLAT BY TIKHONOV REGULARIZATION
This method was originally and independently derived by Tikhonov [Reference Tikhonov15] and Phillips [Reference Phillips16]; it has been used to solve the ill-conditioned problems in an important number of applications to engineering and science. The main idea of this method is to incorporate a priori information about the size and smoothness of the final solution. This a priori information is in the form of a semi-norm. Generally, the Tikhonov regularization leads to minimize a function that takes the following form:
where θ is the unknown vector, A is the coefficient matrix for the inverse problem, 
is the estimated measurement vector, λ is called regularization parameter, and L is called regularization matrix. The regularization parameter λ controls the importance given to the regularization term ||L θ||2. We have denoted the Euclidean norm by ||·||2.
Using the Tikhonov regularization concept, the likelihood function [Reference Torrieri11] for the Mode-S location problem can be expressed as follows:
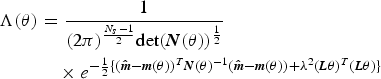
where N(θ) is the covariance matrix of the TDOA measurements noise and det denotes the determinant operator. The maximum likelihood solution of (4) is that 
which minimizes the following function:
Solving (5) by Taylor-series expansion, the estimation for the unknown target position in the Tikhonov sense takes the following form:
where A−1λ is known in the literature as the regularized inverse matrix of Tikhonov [Reference Tikhonov15] and it is defined as follows:
It is worth to say that, due to the fact that the covariance matrix N(θ), for real applications, is often not known because it depends on the true target position, in practice it is common to remove it from (7), assuming an identity matrix.
The choice of the regularization parameter λ and of the regularization matrix L is the most critical aspect to make a correct use of the procedure described above. Firstly, the choice of the regularization matrix is directly connected with the statistics of the target position vector θ. If the components of θ are assumed to be non-random and uncorrelated, a standard choice of the regularization matrix is L = I3, where I3 is a 3 × 3 identity matrix.
On the other hand, the choice of the regularization parameter value is not as straightforward as the choice of regularization matrix. In the literature there exist a considerable number of methods and procedures to calculate/estimate an approximated regularization parameter value. These methods provide regularization parameter values which allow finding accurate numerical solutions for a variety of applications (e.g. image processing, biologic computation, remote sensing, electromagnetic scattering, etc.) and they are basically based on the solution of an optimization problem, i.e. to find a parameter that satisfies some equalities [Reference Morozov17] or find a parameter that minimizes some special functions [Reference Gfrerer18–Reference Golub, Heath and Wahba20]. However, it is worth to say that, due to their nature, these methods introduce a significant computational load and therefore the computation time required might be not suitable for real-time location in MLAT.
In this work, we evaluate the problem for several regularization parameter values (no more than three) and then we choose as true solution the one that corresponds to the minimum residual error. This option is feasible for the considered application because the typical size of the coefficients matrices (Jacobian matrix) is normally smaller than 10 × 3.
In general, the residual error for an inverse problem is given by:
Remembering that for Taylor-series expansion method, the matrix G is an approximation of an exact coefficient matrix, then (8) could not be a correct value for the residual error regarding to the true target position θ. Therefore, in this work, we propose to calculate the residual error by replacing the regularized solution 
in the non-linear TDOA function (1), instead in the matrix G, as follows:
where the vector 
is given by
![{\bi h}_{\lambda _j } =\left[{\matrix{ {TDOA_{i\comma 1} \left({\hat{\bi \theta}_{\lambda _j } } \right)} \cr \vdots \cr {TDOA_{N_s\comma 1} \left({\hat{\bi \theta}_{\lambda _j } } \right)} \cr } } \right]_{\left({N_s - 1} \right)\times 1}\comma \; \quad i=2\comma \;...\comma \; N_s .\eqno\lpar 10\rpar](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151130141029191-0042:S1759078712000104_eqn10.gif?pub-status=live)
IV. RESULTS
Preliminary results are shown to validate the improvement of the system accuracy and its convergence by applying the Tikhonov method in the iterative procedure of Taylor-series expansion. Two scenarios have been simulated; the first one is the operating system of Linate Airport (Milan, Italy) and the second one is a multilateration system which is well described and studied by Cramér–Rao Lower Bound – CRLB – analysis in [Reference Galati, Leonardi and Tosti6].
For each scenario, the horizontal (2D) r.m.s. error (obtained via Monte-Carlo simulation with 100 trials), the theoretical accuracy provided by the CRLB [Reference Galati, Leonardi and Tosti6], the bias of the estimator, and the spatial convergence are calculated. Moreover, a probability of location is defined and calculated for both scenarios.
Let Δij be the spatial error between the exact target position θi =[ x i, y i, z i]T, for the ith simulated point, and the estimated solution ![$\hat{\bi \theta}_i^j =\left[{\hat x_i^j\comma \; \hat y_i^j\comma \; \hat z_i^j } \right]^T $](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151130141029191-0042:S1759078712000104_inline15.gif?pub-status=live){kind=small}
, for the jth Monte-Carlo trial at the same ith point, which can be calculated as follows:
Then, the probability of location PoL is defined as the probability of calculate a target position with an error Δij smaller than a threshold δ and it can be expressed, for any location method, as follows:
where L S is the total number of simulated points and L M is the total number of Monte-Carlo trials.
A) Linate airport system
The Linate airport system is composed of eight ground stations. For this scenario we have simulated a path of surface movement around the airport. The system layout and simulated path are shown in Fig. 2.
Fig. 2. Linate airport system layout.
For this scenario, the starting point for the Taylor-series expansion method has been assumed to be a fixed point over the airport and it is shown as the star in Fig. 2. For this scenario it has been found that using only one regularization parameter value (
) is sufficient to obtain satisfactory results.
Figure 3 shows the horizontal r.m.s. error for the horizontal projection of Taylor-series expansion method and for the non-projected (3D) version solved by the pseudoinverse matrix. It also shows the non-projected (full version) Taylor-series expansion method solved by Tikhonov regularization and the corresponding CRLB analysis.
Fig. 3. Horizontal accuracy for Linate airport. Each abscissa point corresponds to a point in the simulated path.
Initially, the CRLB analysis predicts a good accuracy over the entire path, presenting only a few peaks around the points 40 and 50, where the horizontal accuracy is slightly larger than 7 m. However, for the non-projected Taylor (circles), it can be seen how the ill-conditioned problem avoids the convergence of the method solved by the pseudoinverse matrix, i.e., the r.m.s. error tends to infinity in the most of points. On the other hand, the horizontal projected version obtains acceptable accuracy levels but the effect of the spatial bias is present, for this scenario, in the most of points (more for those points within the N°. 30 and the N°. 120). Finally, it is clear how the solution obtained by applying Tikhonov regularization improves both the ill-conditioned problem, which is directly related with the system accuracy and convergence, and the spatial bias added by the projected version.
Figure 4 shows the bias of the estimator for the projected version of Taylor as solved by the pseudoinverse and that one corresponding to the full version of Taylor as solved by the Tikhonov regularization. In this figure, it can be noted the improvement, regarding to the spatial bias of the horizontal projection of Taylor-series method, added by using the Tikhonov regularization. This aspect is very important when using tracking algorithms (which are present in all the ATC systems) because they can improve the r.m.s. error of the location algorithm but not the bias. In this way, it is clear to see how Tikhonov method also helps to the tracking algorithms to reach more accurate tracks.
Fig. 4. Horizontal bias of the estimator for Linate airport. Each abscissa point corresponds to a point in the simulated path.
Figure 5 shows the spatial convergence for a specific Monte-Carlo trial. In this figure it can be observed how the solution by Tikhonov regularization allows the Taylor-series expansion to ensure the convergence to the true point.
Fig. 5. Spatial convergence for one trial.
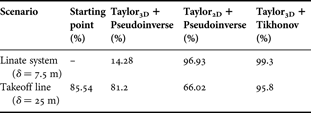
Finally, the probability of location, for this simulation, is shown in the first row of Table 1. Because the Linate system is intended only for surface surveillance, we have set the threshold in (12) to 
= 7.5 m [2]. From this table, we can observe the location strategy proposed herein provides the highest probability of location with a value of 99.3%. The classical solution (Taylor3D + Pseudoinverse) practically does not allow any location (PoL = 14.28%) whereas the projection version of this provides a high probably of location but, due to the bias problem, it is not better than that of the strategy proposed herein.
Table 1. Probability of Location resulting from the simulations.
B) MLAT system for a takeoff line
This system is composed of four stations and it is well analyzed in [Reference Galati, Leonardi and Tosti6]. The layout of the simulated scenario is shown in Fig. 6.
Fig. 6. Layout of the MLAT system for a takeoff line.
For this scenario, the starting point for the Taylor-series expansion method has been obtained by means of the closed-form algorithm described in [Reference Schau and Robinson13]. This algorithm is based on spherical intersections and it does not need for a starting point but, as it is shown in the results, it is also affected by the ill-conditioning of the problem due to the system geometry. The horizontal coordinates of the starting point (x,y) are taken from the closed-form algorithm and the vertical coordinate (z) is simulated as the barometric altitude, i.e., with a bias of 40 m regarding the real target height. Also for this scenario it has been found that only using one regularization parameter value (
) is sufficient to obtain satisfactory results.
The amount of ill-conditioning of this scenario is significantly greater than that of the first scenario. It is because the number of stations here (four) is much smaller than the first one (eight). This effect can be noted in the CRLB analysis shown in Fig. 7 since the theoretical accuracy diverges for points within 0 and 5 km and for those around 20 km. On the other hand, due to the fact that for this scenario, the target height is increasing with the distance, the vertical separation of this with the plane of the ground stations considerably affects the accuracy provided by the horizontal projection of Taylor-series method (crosses), and the spatial bias added by this is considerably larger for points beyond 15 km.
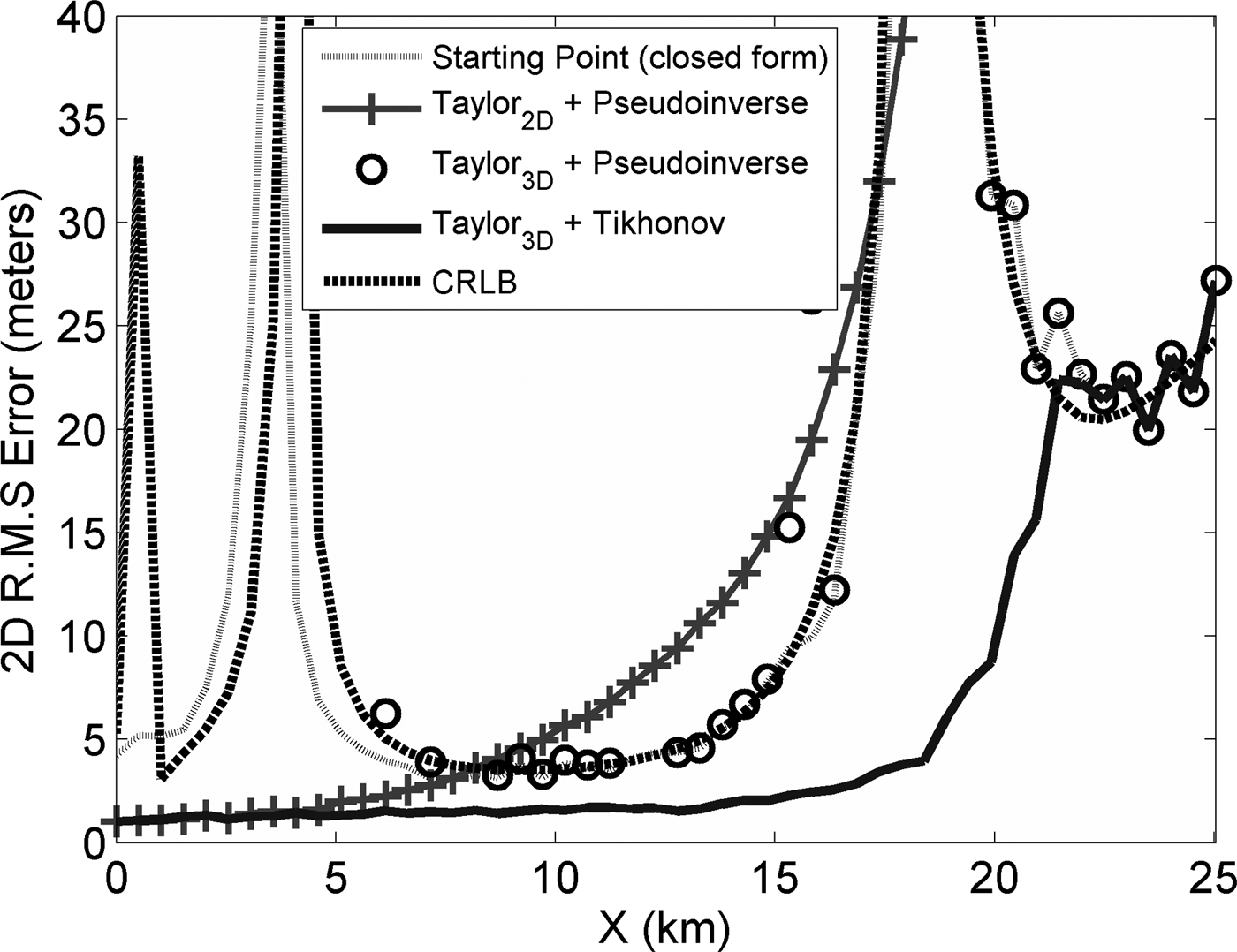
Fig. 7. Horizontal accuracy over the takeoff line.
Owing to the ill-conditioning, it can be observed that, for this scenario, the accuracy levels provided by the full version of Taylor, using the pseudoinverse matrix, diverge far from the theoretical accuracy values (CRLB) for points within 0–5 and 15–20 km. On the contrary, the closed-form algorithm presents a more stable accuracy, but it is also affected by system geometry (dilution of precision). Finally, it is evident that the significant improvement, of the system accuracy, is obtained by applying Tikhonov regularization. The accuracy for this option is stable for the whole of takeoff line and it is not larger than 25 m. It is worth to say that this solution is below the CRLB values because the CRLB is also affected by the ill-conditioning of the problem, specifically that part due to the system geometry.
Figure 8 shows the bias for the solutions obtained by the closed-form algorithm and by the full version of Taylor series using both pseudoinverse matrix and Tikhonov regularization. Firstly, it can be noted that for a few points close to 10 and 15 km, the bias of the solution obtained by pseudoinverse is smaller (no more than 1 m) than that of the Tikhonov method. It can be explained because in the case of well-conditioned problems the pseudoinverse matrix is the solution with minimum norm [Reference Golub and Loan3] and in contrast Tikhonov always adds certain amount of bias [Reference Tikhonov15]. The important aspect is that, if the correct regularization parameter value is chosen, this amount of bias can be neglected regarding the rest of the options to improve the problem (i.e. the horizontal projection of Taylor-series method). Moreover, due to the ill-conditioned problem, for the rest of the points, the bias added by pseudoinverse matrix solution is infinity and for most of points the bias added by the closed-form algorithm has been found greater than that of Tikhonov regularization.
Fig. 8. Horizontal bias of the estimator over the takeoff line.
Figure 9 shows the spatial convergence for a specific Monte-Carlo trial; in this figure, it can be noted how the regularization of the location problem ensures the convergence also for this scenario.
Fig. 9. Spatial convergence for one trial over the takeoff line.
Finally, the probability of location, for this simulation, is shown in the second row of Table 1. Because this system is intended for surface surveillance in a takeoff line (more than 5 Nm from the runway), we have set the threshold in (12) as 
= 25 m [2]. From this table, we can observe the location strategy proposed herein provides the highest probability of location with a value of 95.8%, which is significantly much greater than those of the remaining strategies. This parameter also evidence the bias problem of the projected version of Taylor, i.e., only PoL = 66.02%. On the other hand, the starting point, obtained by the closed-form algorithm [Reference Schau and Robinson13], provides a PoL = 85.54%, value that is not significantly improved by the application of the classical strategy (PoL = 81.2%).
V. CONCLUSION
The implementation of Tikhonov regularization to solve the inverse problem of Taylor-series expansion method, for location in multilateration systems, has been described and evaluated. The theoretical aspects of the method with a practical strategy to calculate the regularization parameter have been described.
For the scenarios simulated herein, significant improvements, for the system accuracy and convergence, have been found with the implementation of Tikhonov regularization. For both scenarios, it was found that the regularization of the location problem significantly mitigates the ill-conditioning due to the system geometry, i.e., those points where the CRLB analysis predicts poor accuracy levels; to the measurements noise, i.e., those points where the CRLB predicts good accuracy levels but the solution obtained by the pseudoinverse matrix diverges; and also due to the quality of the starting point for Taylor-series expansion method. Moreover, these improvements are also evidenced by the increment of the probability of location for all the cases evaluated in this work, which, in other words, means to meet the accuracy values from the regulatory bodies (e.g. those in [2]).
Another important advantage of the strategy proposed herein is that, it does not require significant economic investments such as the hardware-based solutions and, at the same time, it does not introduce the bias problem due to the implementation of projected versions of the location algorithms.
For both scenarios it was found that a regularization parameter value of 
was sufficient to obtain satisfactory results but, it is worth to say that in the situations where the problem is better conditioned, it is necessary to use, at least, one or two more values smaller than 
, i.e., the smaller the amount of ill-conditioning the smaller should be 
.
The regularization of the location problem is most useful for those situations where the vertical separation between the ground stations and the target is quite small or for those situations with a small number of stations.
ACKNOWLEDGEMENTS
Mr. Ivan A. Mantilla-Gaviria has been supported by a FPU scholarship (AP2008-03300) from the Spanish Ministry of Education. Moreover, the authors are grateful to Thales Italia S.p.A. (Dr. Ing. R. Scaroni) who supplied the geometry of the Multilateration system in Linate (Milan, Italy) airport.
Ivan A. Mantilla-Gaviria was born in Bucaramanga, Colombia in 1985. He received the degree in Telecommunications Engineer (Cum Laude) from Saint Thomas University, Bucaramanga, Colombia, in 2006 and the Master of Science degree in Technologies, System and Communications Network from Polytechnic University of Valencia (UPV), Valencia, Spain, in 2007. In December 2006 he joined the ITACA (Institute for the Application of Advanced Information and Communication Technologies) research institute as Ph.D. student in the Electromagnetism Applied Group, where he has collaborated in several R&D projects with companies and public administrations in radar applications and, design, and quality control of software. In 2009 he joined Communication Department at UPV as a researcher with FPU scholarship from Spanish Ministry of Education, where currently he also teaches navigation systems laboratory. His main research interests are radar topics and optimization methods.
Mauro Leonardi was born in 1974, in Rome, Laurea cum laude in Electronic Engineering (May 2000) at Tor Vergata University in Rome. Ph.D. in October 2003, focusing his work on target tracking, air traffic control, and navigation. From January 2004 he is Assistant Professor at Tor Vergata University in Rome where he teaches “Detection and Navigation Systems” and “Radar Systems,” his main research activities are focused on air traffic control and advanced surface movement guidance and control system (A-SMGCS); satellite navigation, integrity, and signal analysis. He is author/co-author of over 25 papers, two patents and many technical reports.
Gaspare Galati from 1970 till 1986 was with the company Selenia where he was involved in radar systems analysis and design. From March, 1986 he is Associate Professor (Full Professor from November 1994) of Radar Theory and Techniques at the Tor Vergata University of Rome, where he also teaches probability, statistics, and random processes. He is senior member of the IEEE, member of the IEE, and of the Associazione Elettrotecnica ed Elettronica Italiana, AEI. Within the AEI he is the chairman of the Remote Sensing, Navigation and Surveillance Group.
Juan V. Balbastre-Tejedor was born in Mislata, Spain, in August 1969. He received the Engineering and Ph.D. degrees from the Polytechnic University of Valencia, Valencia, Spain, in 1993 and 1996, respectively. Since 1993, he has been a member of the research and teaching staff in the Department of Communications at the Polytechnic University of Valencia. In 2001, he joined the research staff of the ITACA Research Institute, Polytechnic University of Valencia. From 1998 to 2006, he was the Academic Vice-Dean at E.T.S.I. Telecomunicación of Valencia, Valencia. His current research interests include electromagnetic theory and computational electromagnetic applied to industrial microwave systems, electromagnetic compatibility, and radar. Currently, he is the Director of the E.T.S.I. Telecomunicación of Valencia, Valencia.
Elías de los Reyes Davó was born in Albatera, Spain, in 1950. He received the Engineering degree from the Polytechnic University of Madrid (UPM), Madrid, Spain, in 1974 and the Ph.D. degree from Polytechnic University of Catalunya (UPC), Barcelona, Spain, in 1978. From 1974 to 1988 he was with the E.T.S.I.T. of the UPC, Barcelona, Spain, as a Full Professor. Since 1988 he is a Full Professor in the Communication Department at the Polytechnic University of Valencia (UPV), Valencia, Spain, where he has taught electromagnetic fields and radar. Currently, he is the Director of the Applied Electromagnetism Group at the ITACA research institute in UPV. He has published several books on electromagnetism and numerous (more than 100) national and international papers, having received the favorable assessment of his research by the ANECA (National Quality Assessment Agency) in several 6-year assessment exercise periods. His current research interests include electromagnetic theory, microwave heating, and radar applications.
