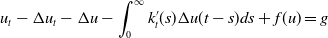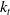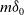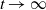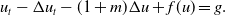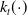1. Introduction
In this study, we consider the following semilinear nonclassical diffusion equation with time-dependent memory
 \begin{equation}\begin{aligned}\begin{cases}\partial_t u -\partial_t \Delta u - \Delta u - \int_0^\infty k^{\prime}_t (s) \Delta u(t-s)ds+ f(u) = g, & x\in \Omega, t>\tau ,\\ \\[-9pt] u(x,t)=0, & x\in \partial \Omega,t>\tau,\\ \\[-9pt] u(x,\tau) = u_{\tau }(x),& x\in \Omega, \\ \\[-9pt] u(x, \tau -s)=\phi_\tau(x,s), &x\in \Omega, s> 0,\end{cases} \end{aligned}\end{equation}
\begin{equation}\begin{aligned}\begin{cases}\partial_t u -\partial_t \Delta u - \Delta u - \int_0^\infty k^{\prime}_t (s) \Delta u(t-s)ds+ f(u) = g, & x\in \Omega, t>\tau ,\\ \\[-9pt] u(x,t)=0, & x\in \partial \Omega,t>\tau,\\ \\[-9pt] u(x,\tau) = u_{\tau }(x),& x\in \Omega, \\ \\[-9pt] u(x, \tau -s)=\phi_\tau(x,s), &x\in \Omega, s> 0,\end{cases} \end{aligned}\end{equation}
where
![]() $\Omega$
is a bounded domain in
$\Omega$
is a bounded domain in
![]() $\mathbb{R}^N$
with smooth boundary
$\mathbb{R}^N$
with smooth boundary
![]() $\partial \Omega$
. The first equation in (1.1) arises in the classical diffusion theory when assuming that the diffusing species behaves as a linear viscous fluid, which leads to include its velocity gradient in the constitutive laws [Reference Aifantis1, Reference Peter and Gurtin22, Reference Truesdell and Noll27]). In the past years, the existence and long-time behavior of solutions to nonclassical diffusion equations have been studied extensively, in both autonomous case [Reference Liu and Ma20, Reference Sun, Wang and Zhong24, Reference Sun and Yang25, Reference Wang, Li and Zhong28, Reference Xiao31, Reference Xie, Li and Zhu32] and non-autonomous case [Reference Anh and Bao2–Reference Anh and Toan4, Reference Sun and Yang25, Reference Toan26, Reference Zhang and Liu33]. The time-dependent global attractor for the nonclassical diffusion equations was studied in [Reference Liu19, Reference Ma, Wang and Xu21].
$\partial \Omega$
. The first equation in (1.1) arises in the classical diffusion theory when assuming that the diffusing species behaves as a linear viscous fluid, which leads to include its velocity gradient in the constitutive laws [Reference Aifantis1, Reference Peter and Gurtin22, Reference Truesdell and Noll27]). In the past years, the existence and long-time behavior of solutions to nonclassical diffusion equations have been studied extensively, in both autonomous case [Reference Liu and Ma20, Reference Sun, Wang and Zhong24, Reference Sun and Yang25, Reference Wang, Li and Zhong28, Reference Xiao31, Reference Xie, Li and Zhu32] and non-autonomous case [Reference Anh and Bao2–Reference Anh and Toan4, Reference Sun and Yang25, Reference Toan26, Reference Zhang and Liu33]. The time-dependent global attractor for the nonclassical diffusion equations was studied in [Reference Liu19, Reference Ma, Wang and Xu21].
The convolution term takes into account the influence of the past history of u on its future evolution, providing a more accurate description of the diffusive process in certain materials, such as high-viscosity liquids at low temperatures and polymers (see e.g. [Reference Jäkle16]). In the past years, the existence and long-time behavior of solutions to nonclassical diffusion equations with memory have been explored in the case of the memory kernel independent on the time [Reference Anh, Thanh and Toan5, Reference Anh, Thanh and Toan6, Reference Conti, Marchini and Pata9]. In particular, the existence of global attractors of weak solutions to a class of nonclassical diffusion equations with hereditary memory and nonlinear terms of exponential type has been studied in [Reference Anh, Thanh and Toan5].
To the best of our knowledge, although there are several results on attractors for evolution equations with constant-in-time memory kernels, only M. Conti has studied time-dependent memory kernels [Reference Conti, Danese and Pata7]. In this study, we therefore build on the M. Conti’s results by removing the technical conditions imposed on the memory kernels. We will prove the existence of weak solutions and existence of a time-dependent global attractor under a weak assumption on the time-dependent memory kernel
![]() $k_t(s)$
and a very large class of nonlinearities that particularly covers both above classes and even exponential nonlinearities.
$k_t(s)$
and a very large class of nonlinearities that particularly covers both above classes and even exponential nonlinearities.
When
![]() $k_t$
approaches a multiple
$k_t$
approaches a multiple
![]() $m\delta_0$
of the Dirac mass at zero as
$m\delta_0$
of the Dirac mass at zero as
![]() $t\to \infty$
, we prove that the asymptotic dynamics of our problem is close to the one of its formal limit
$t\to \infty$
, we prove that the asymptotic dynamics of our problem is close to the one of its formal limit
This is the main novelty of our paper.
To study problem (1.1), we assume that the initial datum
![]() $u_\tau \in H_0^1(\Omega)$
is given, and that the nonlinearity f and the external force g satisfy the following conditions:
$u_\tau \in H_0^1(\Omega)$
is given, and that the nonlinearity f and the external force g satisfy the following conditions:
-
(H1)
 $f\,{:}\, \mathbb{R}\to \mathbb{R}$
is a continuously differentiable function satisfying (1.2)
$f\,{:}\, \mathbb{R}\to \mathbb{R}$
is a continuously differentiable function satisfying (1.2) \begin{equation}f^{\prime} ( u) \geq -\ell,\end{equation}
(1.3)
\begin{equation}f^{\prime} ( u) \geq -\ell,\end{equation}
(1.3) \begin{equation}f( u) u \geq -\beta u^2-C_0 , \text{ for all } u \in \mathbb{R},\end{equation}
\begin{equation}f( u) u \geq -\beta u^2-C_0 , \text{ for all } u \in \mathbb{R},\end{equation}
where
 $\ell, \beta, C_0$
are positive constants,
$\ell, \beta, C_0$
are positive constants,
 $0< \beta<\lambda_1$
with
$0< \beta<\lambda_1$
with
 $\lambda_1>0$
is the first eigenvalue of the operator
$\lambda_1>0$
is the first eigenvalue of the operator
 $-\Delta$
in
$-\Delta$
in
 $\Omega$
with the homogeneous Dirichlet condition,
$\Omega$
with the homogeneous Dirichlet condition,It follows from (1.2) that
 $0\leq \int_0^u (f^{\prime}(s)s+\ell s)ds$
, and therefore by integrating by parts, we obtain (1.4)where
$0\leq \int_0^u (f^{\prime}(s)s+\ell s)ds$
, and therefore by integrating by parts, we obtain (1.4)where \begin{equation}F(u) \leq\, f(u)u+ \frac{\ell u^2}{2}, \text{ for all } u \in \mathbb{R},\end{equation}
\begin{equation}F(u) \leq\, f(u)u+ \frac{\ell u^2}{2}, \text{ for all } u \in \mathbb{R},\end{equation}
 $F(u) = \int_{0}^{u}f(s)ds$
is a primitive of f.
$F(u) = \int_{0}^{u}f(s)ds$
is a primitive of f.
-
(H2) The external force
 $g \in H^{-1}(\Omega )$
.
$g \in H^{-1}(\Omega )$
. -
(H3) The convolution (or memory) kernel
 $k_t$
is a nonnegative summable function having the explicit form (1.5)where
$k_t$
is a nonnegative summable function having the explicit form (1.5)where \begin{equation}k_t (s)= \int_s^{\infty} \mu_t(r)dr,\end{equation}
\begin{equation}k_t (s)= \int_s^{\infty} \mu_t(r)dr,\end{equation}
 $ (t,s) \mapsto \mu_t(s)\,{:}\, \mathbb R \times \mathbb R^+ \to \mathbb R^+$
is allowed to exhibit (infinitely many) jumps. Moreover, we require that
$ (t,s) \mapsto \mu_t(s)\,{:}\, \mathbb R \times \mathbb R^+ \to \mathbb R^+$
is allowed to exhibit (infinitely many) jumps. Moreover, we require that
-
(M1) For every fixed
 $ t \in \mathbb R$
, the map
$ t \in \mathbb R$
, the map
 $ s \mapsto \mu_t(s)$
is nonincreasing, absolutely continuous and summable.
$ s \mapsto \mu_t(s)$
is nonincreasing, absolutely continuous and summable.We denote the total mass of
 $\mu_t$
by
$\mu_t$
by  \begin{equation*}\kappa(t) = \int_0^\infty \mu_t(s) ds.\end{equation*}
\begin{equation*}\kappa(t) = \int_0^\infty \mu_t(s) ds.\end{equation*}
-
(M2) There exists
 $\delta > 0$
such that for every
$\delta > 0$
such that for every \begin{equation*}\partial_t \mu_t (s) + \partial_s \mu_t(s) + \delta \kappa (t) \mu_t(s) \leq 0\end{equation*}
\begin{equation*}\partial_t \mu_t (s) + \partial_s \mu_t(s) + \delta \kappa (t) \mu_t(s) \leq 0\end{equation*}
 $t \in \mathbb R$
and almost every
$t \in \mathbb R$
and almost every
 $s >0$
.
$s >0$
.
-
(M3) The function
 $t \mapsto \kappa (t)$
fulfills
$t \mapsto \kappa (t)$
fulfills  \begin{equation*}\inf\limits_{t \in \mathbb R} \kappa (t) >0.\end{equation*}
\begin{equation*}\inf\limits_{t \in \mathbb R} \kappa (t) >0.\end{equation*}
Remark 1.1. We recall the example of time-dependent memory kernels arising in the physical applications, already introduced in [Reference Conti, Danese and Pata7, Reference Conti, Danese, Giorgi and Pata8].
Let
![]() $ \mu \in \mathcal{C}^1(\mathbb{R}) \cap L^1(\mathbb{R^+}) $
be a (nonnull and nonnegative) nonincreasing function with
$ \mu \in \mathcal{C}^1(\mathbb{R}) \cap L^1(\mathbb{R^+}) $
be a (nonnull and nonnegative) nonincreasing function with
![]() $\mu(0)< \infty$
. Given a bounded positive function
$\mu(0)< \infty$
. Given a bounded positive function
![]() $\varepsilon \in \mathcal{C}^1(\mathbb{R})$
satisfying
$\varepsilon \in \mathcal{C}^1(\mathbb{R})$
satisfying
we define the time-dependent rescaled kernel
According to (1.5), the corresponding integrated memory kernel reads
Especially, assuming k summable with total mass
![]() $m > 0$
, the most interesting situation is when
$m > 0$
, the most interesting situation is when
![]() $\varepsilon(t) \to 0$
as
$\varepsilon(t) \to 0$
as
![]() $t \to \infty$
. In this case, we recover the distributional convergence
$t \to \infty$
. In this case, we recover the distributional convergence
![]() $k_t \to m\delta_0$
to (a multiple of) the Dirac mass at zero. As shown in [Reference Conti, Danese and Pata7, Reference Conti, Danese, Giorgi and Pata8], this
$k_t \to m\delta_0$
to (a multiple of) the Dirac mass at zero. As shown in [Reference Conti, Danese and Pata7, Reference Conti, Danese, Giorgi and Pata8], this
![]() $\mu_t$
complies with (M1)–(M3). Here, we make two further assumptions: there exists
$\mu_t$
complies with (M1)–(M3). Here, we make two further assumptions: there exists
![]() $\sigma $
such that
$\sigma $
such that
Example For instance, a possible choice is the exponential kernel
![]() $\mu(s)=e^{-s}$
and
$\mu(s)=e^{-s}$
and
The study is organized as follows. In Section 3, we prove the existence and uniqueness of weak solutions to problem (1.1) by utilizing the compactness method and weak convergence techniques in Orlicz spaces [Reference Geredeli and Khanmamedov15]. In Section 4, the existence of a time-dependent global attractor for the process associated to the problem is studied. In the final section, we show the asymptotic closeness to the nonclassical diffusion equation (without memory term) when the kernel approaches the Dirac mass.
2. Notations and preliminaries
In this section, we review some notations about function spaces and preliminary results.
As in [Reference Dafermos12], a new variable which reflects the history of (1.1) is introduced, that is
then we can check that
Since
![]() $\mu_t(s)=- k_t^{\prime}(s)$
, problem (1.1) can be transformed into the following system
$\mu_t(s)=- k_t^{\prime}(s)$
, problem (1.1) can be transformed into the following system
 \begin{equation}\begin{aligned}\begin{cases}\partial_t u -\partial_t \Delta u - \Delta u - \int_0^\infty \mu_t(s) \Delta \eta^t(s)ds+ f(u) = g(x), &x\in \Omega, t > \tau,\\\partial_t \eta^t (x,s) = - \partial_s \eta^t (x,s)+ u(x,t), &x\in \Omega, t > \tau, s\geq 0,\\u(x,t) = 0, &x\in \partial \Omega, t > \tau,\\\eta^t(x,s)=0, &(x,s )\in \partial \Omega \times \mathbb R^+, t > \tau,\\u(x, \tau ) = u_{\tau }(x),& x\in \Omega,\\\eta^\tau (x,s)=\eta_\tau (x,s)\,{:\!=}\, \int_\tau^s g_0 (x,r)dr,& (x,s )\in \Omega \times \mathbb R^+.\end{cases} \end{aligned}\end{equation}
\begin{equation}\begin{aligned}\begin{cases}\partial_t u -\partial_t \Delta u - \Delta u - \int_0^\infty \mu_t(s) \Delta \eta^t(s)ds+ f(u) = g(x), &x\in \Omega, t > \tau,\\\partial_t \eta^t (x,s) = - \partial_s \eta^t (x,s)+ u(x,t), &x\in \Omega, t > \tau, s\geq 0,\\u(x,t) = 0, &x\in \partial \Omega, t > \tau,\\\eta^t(x,s)=0, &(x,s )\in \partial \Omega \times \mathbb R^+, t > \tau,\\u(x, \tau ) = u_{\tau }(x),& x\in \Omega,\\\eta^\tau (x,s)=\eta_\tau (x,s)\,{:\!=}\, \int_\tau^s g_0 (x,r)dr,& (x,s )\in \Omega \times \mathbb R^+.\end{cases} \end{aligned}\end{equation}
Now, let
Unless otherwise specified, it is understood that we consider spaces of functions which are defined on the domain
![]() $\Omega$
. Let
$\Omega$
. Let
![]() $\left\langle{\cdot,\cdot}\right\rangle$
and
$\left\langle{\cdot,\cdot}\right\rangle$
and
![]() $\|\cdot\|$
denote the
$\|\cdot\|$
denote the
![]() $L^2(\Omega)$
-inner product and
$L^2(\Omega)$
-inner product and
![]() $L^2(\Omega)$
-norm, respectively.
$L^2(\Omega)$
-norm, respectively.
Let
![]() $L^2_{\mu_t}(\mathbb{R}^+,L^2(\Omega))$
be the Hilbert space of functions
$L^2_{\mu_t}(\mathbb{R}^+,L^2(\Omega))$
be the Hilbert space of functions
![]() $\varphi\colon\mathbb{R}^+\rightarrow L^2(\Omega)$
endowed with the inner product
$\varphi\colon\mathbb{R}^+\rightarrow L^2(\Omega)$
endowed with the inner product
and let
![]() $\|\varphi\|_{\mu_t}$
be the corresponding norm. In a similar manner, we introduce the inner products
$\|\varphi\|_{\mu_t}$
be the corresponding norm. In a similar manner, we introduce the inner products
![]() $\left\langle{\cdot,\cdot}\right\rangle_{1,\mu_t}, \left\langle{\cdot,\cdot}\right\rangle_{2,\mu_t}$
on
$\left\langle{\cdot,\cdot}\right\rangle_{1,\mu_t}, \left\langle{\cdot,\cdot}\right\rangle_{2,\mu_t}$
on
![]() $L^2_{\mu_t}(\mathbb{R}^+, H_0^1(\Omega))$
and
$L^2_{\mu_t}(\mathbb{R}^+, H_0^1(\Omega))$
and
![]() $L^2_{\mu_t}(\mathbb{R}^+, H^2(\Omega) \cap H_0^1(\Omega) )$
by
$L^2_{\mu_t}(\mathbb{R}^+, H^2(\Omega) \cap H_0^1(\Omega) )$
by
and the corresponding norms are denoted by
![]() $\|\cdot\|_{1,\mu_t}, \|\cdot\|_{2,\mu_t}$
.
$\|\cdot\|_{1,\mu_t}, \|\cdot\|_{2,\mu_t}$
.
We now introduce the following Hilbert spaces
 \begin{equation*}\begin{split}\mathcal{V}_t&=H_0^1(\Omega)\times L^2_{\mu_t}(\mathbb{R}^+, H_0^1(\Omega)),\\[3pt] \mathcal{W}_t&=\left (H^2(\Omega) \cap H_0^1(\Omega)\right)\times L^2_{\mu_t}(\mathbb{R}^+, H^2(\Omega) \cap H_0^1(\Omega)), \end{split} \end{equation*}
\begin{equation*}\begin{split}\mathcal{V}_t&=H_0^1(\Omega)\times L^2_{\mu_t}(\mathbb{R}^+, H_0^1(\Omega)),\\[3pt] \mathcal{W}_t&=\left (H^2(\Omega) \cap H_0^1(\Omega)\right)\times L^2_{\mu_t}(\mathbb{R}^+, H^2(\Omega) \cap H_0^1(\Omega)), \end{split} \end{equation*}
which are, respectively, endowed with the inner products
where
![]() $w_i=(\psi_i, \varphi_i)\in \mathcal V_t, \mathcal W_t, \,\, i=1,2$
.
$w_i=(\psi_i, \varphi_i)\in \mathcal V_t, \mathcal W_t, \,\, i=1,2$
.
The norms induced on
![]() $\mathcal V_t, \mathcal W_t$
, are
$\mathcal V_t, \mathcal W_t$
, are
 \begin{align*}\|(\psi,\varphi)\|_{\mathcal V_t}^2&=\|\nabla \psi\|^2 +\int_{0}^{\infty}\mu_t(s)\|\nabla\varphi(s)\|^2ds,\\\|(\psi,\varphi)\|_{\mathcal W_t}^2&= \|\Delta\psi\|^2 +\int_{0}^{\infty}\mu_t(s)\|\Delta\varphi(s)\|^2ds.\end{align*}
\begin{align*}\|(\psi,\varphi)\|_{\mathcal V_t}^2&=\|\nabla \psi\|^2 +\int_{0}^{\infty}\mu_t(s)\|\nabla\varphi(s)\|^2ds,\\\|(\psi,\varphi)\|_{\mathcal W_t}^2&= \|\Delta\psi\|^2 +\int_{0}^{\infty}\mu_t(s)\|\Delta\varphi(s)\|^2ds.\end{align*}
The following results will be used to prove the existence of time-dependent global attractors.
For
![]() $t \in R$
, let
$t \in R$
, let
![]() $X_t$
be a family of normed spaces, the two-parameter family of operators
$X_t$
be a family of normed spaces, the two-parameter family of operators
is called a process on time-dependent spaces (see [Reference Conti, Pata and Temam10, Reference Di Plinio, Duane and Temam13]), characterized by the two properties:
-
(i)
 $U(\tau,\tau)$
is the identity map on
$U(\tau,\tau)$
is the identity map on
 $X_\tau$
for every
$X_\tau$
for every
 $\tau$
;
$\tau$
; -
(ii)
 $U(t,\tau)U(\tau,s)=U(t,s)$
for every
$U(t,\tau)U(\tau,s)=U(t,s)$
for every
 $t\ge \tau\ge s$
.
$t\ge \tau\ge s$
.
As introduced in [Reference Conti, Pata and Temam10], we consider the following definitions and theorem.
Definition 2.1. A time-dependent absorbing set for the process
![]() $U(t, \tau)$
is a uniformly bounded family
$U(t, \tau)$
is a uniformly bounded family
![]() $\mathcal{B} = \{B_t\}_{t\in \mathbb{R}}$
with the following property: for every
$\mathcal{B} = \{B_t\}_{t\in \mathbb{R}}$
with the following property: for every
![]() $R \ge 0$
there exists
$R \ge 0$
there exists
![]() $\theta_e=\theta_e(R) \ge 0$
such that
$\theta_e=\theta_e(R) \ge 0$
such that
Definition 2.2. Let
![]() $\mathbb K = \{ \mathcal K=\{K_t\}_{t \in \mathbb R}\,{:}\, K_t \subset X_t \text{ compact, }\mathcal K \text{ pullback attracting} \}$
. The family
$\mathbb K = \{ \mathcal K=\{K_t\}_{t \in \mathbb R}\,{:}\, K_t \subset X_t \text{ compact, }\mathcal K \text{ pullback attracting} \}$
. The family
![]() $\mathcal A= \{A_t\}_{t\in \mathbb R} \in \mathbb K$
is said to be a time-dependent global attractors if
$\mathcal A= \{A_t\}_{t\in \mathbb R} \in \mathbb K$
is said to be a time-dependent global attractors if
![]() $ \mathcal A$
is the smallest element of
$ \mathcal A$
is the smallest element of
![]() $\mathbb K$
such that
$\mathbb K$
such that
for any element
![]() $\mathcal K=\{K_t\}_{t \in \mathbb R} \in \mathbb K$
.
$\mathcal K=\{K_t\}_{t \in \mathbb R} \in \mathbb K$
.
We know that the minimal element of
![]() $\mathbb K$
exists (and it is unique) if and only if
$\mathbb K$
exists (and it is unique) if and only if
![]() $\mathbb K$
is not empty.
$\mathbb K$
is not empty.
Theorem 2.1. If
![]() $U(t,\tau)$
is asymptotic compact, that is,
$U(t,\tau)$
is asymptotic compact, that is,
then
![]() $\{ U(t,\tau)\}$
has a unique time-dependent global attractors
$\{ U(t,\tau)\}$
has a unique time-dependent global attractors
![]() $\mathcal A= \{A_t\}_{t\in \mathbb R}$
and
$\mathcal A= \{A_t\}_{t\in \mathbb R}$
and
Moreover, if
![]() $U(t,\tau)$
is a continuous (or norm-to-weak continuous) map for all
$U(t,\tau)$
is a continuous (or norm-to-weak continuous) map for all
![]() $t \ge \tau$
, then
$t \ge \tau$
, then
![]() $\mathcal A$
is invariant.
$\mathcal A$
is invariant.
3. Existence and uniqueness of weak solutions
Definition 3.1. A function
![]() $z=(u, \eta^t)$
is called a weak solution of problem (2.1) on the interval
$z=(u, \eta^t)$
is called a weak solution of problem (2.1) on the interval
![]() $(\tau, T)$
with the initial datum
$(\tau, T)$
with the initial datum
![]() $z(\tau)=z_\tau \in \mathcal {V_\tau}$
if
$z(\tau)=z_\tau \in \mathcal {V_\tau}$
if
 \begin{equation*}\begin{aligned}&u\in C([\tau ,T];\ H^{1}_0 (\Omega) ), f(u) \in L^1(Q_T),\\[3pt] & \partial_tu \in L^2(\tau ,T;H_0^1(\Omega) ),\eta^t \in C([\tau ,T];L^2_{\mu_t} (\mathbb R^+, H^{1}_0(\Omega) )),\end{aligned}\end{equation*}
\begin{equation*}\begin{aligned}&u\in C([\tau ,T];\ H^{1}_0 (\Omega) ), f(u) \in L^1(Q_T),\\[3pt] & \partial_tu \in L^2(\tau ,T;H_0^1(\Omega) ),\eta^t \in C([\tau ,T];L^2_{\mu_t} (\mathbb R^+, H^{1}_0(\Omega) )),\end{aligned}\end{equation*}
and
 \begin{equation*}\begin{aligned}&\langle\partial_t u ,\varphi\rangle +\langle\partial_t \nabla u ,\nabla \varphi \rangle +\langle \nabla u ,\nabla \varphi \rangle +\langle \eta^t, \varphi \rangle_{1,\mu_t } +\langle f(u),\varphi \rangle_{L^1, L^\infty} =\langle g,\varphi \rangle_{H^{-1}, H^1_0}, \\[3pt] &\langle \partial_t \eta^t + \partial_s \eta^t ,\xi \rangle_{1,\mu_t } = \langle u ,\xi \rangle_{1,\mu_t } ,\end{aligned}\end{equation*}
\begin{equation*}\begin{aligned}&\langle\partial_t u ,\varphi\rangle +\langle\partial_t \nabla u ,\nabla \varphi \rangle +\langle \nabla u ,\nabla \varphi \rangle +\langle \eta^t, \varphi \rangle_{1,\mu_t } +\langle f(u),\varphi \rangle_{L^1, L^\infty} =\langle g,\varphi \rangle_{H^{-1}, H^1_0}, \\[3pt] &\langle \partial_t \eta^t + \partial_s \eta^t ,\xi \rangle_{1,\mu_t } = \langle u ,\xi \rangle_{1,\mu_t } ,\end{aligned}\end{equation*}
for all test functions
![]() $\varphi \in W = H_0^1(\Omega)\cap L^\infty (\Omega), \xi \in L^2_{\mu_t}(\mathbb R^+, H_0^1(\Omega))$
, and for a.e.
$\varphi \in W = H_0^1(\Omega)\cap L^\infty (\Omega), \xi \in L^2_{\mu_t}(\mathbb R^+, H_0^1(\Omega))$
, and for a.e.
![]() $t\in [\tau , T]$
.
$t\in [\tau , T]$
.
We are now ready to state the existence and uniqueness result for problem (2.1).
Theorem 3.1. Assume that hypotheses (H1)–(H3) hold. Then for any
![]() $ z_\tau =(u_\tau ,\eta_\tau )\in \mathcal{V}_\tau$
and
$ z_\tau =(u_\tau ,\eta_\tau )\in \mathcal{V}_\tau$
and
![]() $T>\tau$
given, problem (2.1) has a unique weak solution
$T>\tau$
given, problem (2.1) has a unique weak solution
![]() $z=(u,\eta^t)$
on the interval
$z=(u,\eta^t)$
on the interval
![]() $(\tau ,T)$
satisfying
$(\tau ,T)$
satisfying
Moreover, the weak solutions depend continuously on the initial data.
Proof. We use the Faedo–Galerkin method. As argued in [Reference Anh, Thanh and Toan5], because of the separability of
![]() $H_0^1(\Omega)$
, one can choose a sequence
$H_0^1(\Omega)$
, one can choose a sequence
![]() $\{\omega_j\}_{j=1}^{\infty}$
which forms a smooth orthonormal basis in both
$\{\omega_j\}_{j=1}^{\infty}$
which forms a smooth orthonormal basis in both
![]() $L^2(\Omega)$
and
$L^2(\Omega)$
and
![]() $H_0^1(\Omega)$
spaces. For instance, one can take a complete set of normalized eigenfunctions for
$H_0^1(\Omega)$
spaces. For instance, one can take a complete set of normalized eigenfunctions for
![]() $-\Delta$
in
$-\Delta$
in
![]() $H_0^1(\Omega)$
, such that
$H_0^1(\Omega)$
, such that
![]() $-\Delta\omega_j=\nu_j\omega_j$
, where
$-\Delta\omega_j=\nu_j\omega_j$
, where
![]() $\nu_j$
is the eigenvalue corresponding to
$\nu_j$
is the eigenvalue corresponding to
![]() $\omega_j$
. Next, we want to choose an orthonormal basis
$\omega_j$
. Next, we want to choose an orthonormal basis
![]() $\{\zeta_j\}_{j=1}^{\infty}$
of
$\{\zeta_j\}_{j=1}^{\infty}$
of
![]() $L^2_{\mu_t}(\mathbb{R}^+, H_0^1(\Omega))$
which also belong to
$L^2_{\mu_t}(\mathbb{R}^+, H_0^1(\Omega))$
which also belong to
![]() $\mathcal{D}(\mathbb{R}^+, H_0^1(\Omega))$
, where
$\mathcal{D}(\mathbb{R}^+, H_0^1(\Omega))$
, where
![]() $\mathcal{D}(I, X)$
is the space of infinitely differentiable X-valued functions with compact support in
$\mathcal{D}(I, X)$
is the space of infinitely differentiable X-valued functions with compact support in
![]() $I\subset\mathbb{R}$
. For this purpose, we select vectors of the form
$I\subset\mathbb{R}$
. For this purpose, we select vectors of the form
![]() $l_k\omega_j$
(
$l_k\omega_j$
(
![]() $k,j=1,\ldots,\infty$
), where
$k,j=1,\ldots,\infty$
), where
![]() $\{l_j\}_{j=1}^{\infty}$
is an orthonormal basis in both
$\{l_j\}_{j=1}^{\infty}$
is an orthonormal basis in both
![]() $L_{\mu_t}^2(\mathbb{R}^+)$
and
$L_{\mu_t}^2(\mathbb{R}^+)$
and
![]() $\mathcal{D}(\mathbb{R}^+)$
spaces.
$\mathcal{D}(\mathbb{R}^+)$
spaces.
-
(i) Existence. Given an integer n, denote by
 $P_n$
and
$P_n$
and
 $Q_n$
the projections on the subspaces respectively. We look for a function
$Q_n$
the projections on the subspaces respectively. We look for a function \begin{equation*}\mathrm{span}(\omega_1,\ldots,\omega_n)\in H_0^1(\Omega)\quad\text{ and }\quad\mathrm{span}(\zeta_1,\ldots,\zeta_n)\in L_{\mu_t}^2(\mathbb{R}^+,H_0^1(\Omega)),\end{equation*}
\begin{equation*}\mathrm{span}(\omega_1,\ldots,\omega_n)\in H_0^1(\Omega)\quad\text{ and }\quad\mathrm{span}(\zeta_1,\ldots,\zeta_n)\in L_{\mu_t}^2(\mathbb{R}^+,H_0^1(\Omega)),\end{equation*}
 $z_n=(u_n,\eta^t_n)$
of the form satisfying
$z_n=(u_n,\eta^t_n)$
of the form satisfying \begin{equation*}u_n(t)=\sum_{j=1}^{n}a_j(t)\omega_j\quad\text{ and }\quad\eta^t_{n} (s)=\sum_{j=1}^{n}b_j(t)\zeta_j(s)\end{equation*}
(3.1)for a.e.
\begin{equation*}u_n(t)=\sum_{j=1}^{n}a_j(t)\omega_j\quad\text{ and }\quad\eta^t_{n} (s)=\sum_{j=1}^{n}b_j(t)\zeta_j(s)\end{equation*}
(3.1)for a.e. \begin{equation}\begin{split}&\left\langle{(\partial_t u_n - \Delta \partial_t u_n , \partial_t \eta^t_n ),(\omega_k,\zeta_j)}\right\rangle_{\mathcal V_t}\\ &\qquad = \left\langle{( \Delta u_n + \int_0^\infty \mu_t(s) \Delta \eta^t_n(s)ds +g - f(u_n) , u_n - \partial_s \eta^t_n),(\omega_k,\zeta_j)}\right\rangle_{\mathcal V_t}\\&u_n(\tau)= P_n u_\tau \to u_\tau = \sum_{j=1}^{\infty}\alpha_j \omega_j \quad \text{ in } H_0^1(\Omega), \text{ as } n \to \infty,\\&\eta^t_n(\tau) = Q_n\eta_\tau \to \eta_\tau =\sum_{j=1}^{\infty}\beta_j\zeta_j(s) \quad\text{ in } L_{\mu_t}^2(\mathbb{R}^+,H_0^1(\Omega)), \text{ as } n \to \infty,\end{split}\end{equation}
\begin{equation}\begin{split}&\left\langle{(\partial_t u_n - \Delta \partial_t u_n , \partial_t \eta^t_n ),(\omega_k,\zeta_j)}\right\rangle_{\mathcal V_t}\\ &\qquad = \left\langle{( \Delta u_n + \int_0^\infty \mu_t(s) \Delta \eta^t_n(s)ds +g - f(u_n) , u_n - \partial_s \eta^t_n),(\omega_k,\zeta_j)}\right\rangle_{\mathcal V_t}\\&u_n(\tau)= P_n u_\tau \to u_\tau = \sum_{j=1}^{\infty}\alpha_j \omega_j \quad \text{ in } H_0^1(\Omega), \text{ as } n \to \infty,\\&\eta^t_n(\tau) = Q_n\eta_\tau \to \eta_\tau =\sum_{j=1}^{\infty}\beta_j\zeta_j(s) \quad\text{ in } L_{\mu_t}^2(\mathbb{R}^+,H_0^1(\Omega)), \text{ as } n \to \infty,\end{split}\end{equation}
 $\tau \leq t\leq T$
, for every
$\tau \leq t\leq T$
, for every
 $k,j=0,\ldots,n$
, where
$k,j=0,\ldots,n$
, where
 $\omega_0$
and
$\omega_0$
and
 $\zeta_0$
are the zero vectors in the respective spaces. Taking
$\zeta_0$
are the zero vectors in the respective spaces. Taking
 $(\omega_k,\zeta_0)$
and
$(\omega_k,\zeta_0)$
and
 $(\omega_0,\zeta_k)$
in (3.1), and applying the divergence theorem to the term we get a system of Ordinary Differential Equation (ODE) in the variables
$(\omega_0,\zeta_k)$
in (3.1), and applying the divergence theorem to the term we get a system of Ordinary Differential Equation (ODE) in the variables \begin{equation*}\left\langle{\int_{0}^{\infty}\mu_t(s)\Delta\eta^t_n(s)ds,\omega_k}\right\rangle,\end{equation*}
\begin{equation*}\left\langle{\int_{0}^{\infty}\mu_t(s)\Delta\eta^t_n(s)ds,\omega_k}\right\rangle,\end{equation*}
 $a_k(t)$
and
$a_k(t)$
and
 $b_k(t)$
of the form (3.2)subject to the initial conditions
$b_k(t)$
of the form (3.2)subject to the initial conditions \begin{equation}\begin{split}&\frac{d}{dt}\bigg( (1+\nu_k) a_k \bigg) =-\nu_k a_k - \sum_{j=1}^{n}b_j\left\langle{\zeta_j,\omega_k}\right\rangle_{1,\mu_t}+\left\langle{g,\omega_k}\right\rangle - \left\langle{f(u_n),\omega_k}\right\rangle,\\[3pt] &\frac{d}{dt}b_k=\sum_{j=1}^{n}a_j\left\langle{\omega_j,\zeta_k}\right\rangle_{1,\mu_t}- \sum_{j=1}^{n}b_j\left\langle{\zeta^{\prime}_j,\zeta_k}\right\rangle_{1,\mu_t},\end{split}\end{equation}
(3.3)According to standard existence theory for ODEs, there exists a continuous solution
\begin{equation}\begin{split}&\frac{d}{dt}\bigg( (1+\nu_k) a_k \bigg) =-\nu_k a_k - \sum_{j=1}^{n}b_j\left\langle{\zeta_j,\omega_k}\right\rangle_{1,\mu_t}+\left\langle{g,\omega_k}\right\rangle - \left\langle{f(u_n),\omega_k}\right\rangle,\\[3pt] &\frac{d}{dt}b_k=\sum_{j=1}^{n}a_j\left\langle{\omega_j,\zeta_k}\right\rangle_{1,\mu_t}- \sum_{j=1}^{n}b_j\left\langle{\zeta^{\prime}_j,\zeta_k}\right\rangle_{1,\mu_t},\end{split}\end{equation}
(3.3)According to standard existence theory for ODEs, there exists a continuous solution \begin{equation}\begin{split}&a_k(\tau )=\left\langle{u_\tau ,\omega_k}\right\rangle_{H_0^1(\Omega)},\\[3pt] &b_k(\tau )=\left\langle{\eta_\tau ,\zeta_k}\right\rangle_{1,\mu_\tau}.\end{split}\end{equation}
\begin{equation}\begin{split}&a_k(\tau )=\left\langle{u_\tau ,\omega_k}\right\rangle_{H_0^1(\Omega)},\\[3pt] &b_k(\tau )=\left\langle{\eta_\tau ,\zeta_k}\right\rangle_{1,\mu_\tau}.\end{split}\end{equation}
 $(a_k, b_k)$
of (3.2)–(3.3) on some interval
$(a_k, b_k)$
of (3.2)–(3.3) on some interval
 $(\tau ,T_n)$
for each n. The a priori estimates below imply that in fact
$(\tau ,T_n)$
for each n. The a priori estimates below imply that in fact
 $T_n=+\infty$
.
$T_n=+\infty$
.
Multiplying the first equation of (3.2) by
 $a_k$
and the second by
$a_k$
and the second by
 $b_k$
, then summing over k and adding the results, we get (3.4)Using (1.3) and the Cauchy inequality, we have
$b_k$
, then summing over k and adding the results, we get (3.4)Using (1.3) and the Cauchy inequality, we have \begin{equation}\begin{aligned}\frac{1}{2}\frac{d}{dt}\|z_n\|^2_{\mathcal{V}_t}= - \|\nabla u_n\|^2-&\left\langle{\partial_s\eta^t_n,\eta^t_n}\right\rangle_{1,\mu_t} + \left\langle{g,u_n}\right\rangle_{H^{-1}, H^1_0}\\&-\left\langle f(u_n),u_n\right\rangle + \int_{0}^{\infty}\partial_t \mu_t(s)\|\nabla\eta^t_n(s)\|^2ds. \end{aligned}\end{equation}
(3.5)where
\begin{equation}\begin{aligned}\frac{1}{2}\frac{d}{dt}\|z_n\|^2_{\mathcal{V}_t}= - \|\nabla u_n\|^2-&\left\langle{\partial_s\eta^t_n,\eta^t_n}\right\rangle_{1,\mu_t} + \left\langle{g,u_n}\right\rangle_{H^{-1}, H^1_0}\\&-\left\langle f(u_n),u_n\right\rangle + \int_{0}^{\infty}\partial_t \mu_t(s)\|\nabla\eta^t_n(s)\|^2ds. \end{aligned}\end{equation}
(3.5)where \begin{equation} \left\langle{g,u_n}\right\rangle_{H^{-1}, H^1_0}-\left\langle f(u_n),u_n\right\rangle \leq \varepsilon \| \nabla u_n\|^2+\frac{1}{4\varepsilon}\|g\|^2_{H^{-1}(\Omega)}+ \beta \|u_n\|^{2}+C_0|\Omega|,\end{equation}
\begin{equation} \left\langle{g,u_n}\right\rangle_{H^{-1}, H^1_0}-\left\langle f(u_n),u_n\right\rangle \leq \varepsilon \| \nabla u_n\|^2+\frac{1}{4\varepsilon}\|g\|^2_{H^{-1}(\Omega)}+ \beta \|u_n\|^{2}+C_0|\Omega|,\end{equation}
 $\varepsilon >0$
will be chosen later. From (3.4) and (3.5) we have Integrating by parts and using (M2), we get
$\varepsilon >0$
will be chosen later. From (3.4) and (3.5) we have Integrating by parts and using (M2), we get \begin{equation*}\begin{aligned}&\frac{d}{dt}\|z_n\|_{\mathcal{V}_t}^2+2\left\langle{\partial_s\eta^t_n,\eta^t_n}\right\rangle_{1,\mu_t} - 2\int_{0}^{\infty}\partial_t \mu_t(s)\|\nabla\eta^t_n(s)\|^2ds+ 2\!\left(1- \frac{\beta }{\lambda_1}-\varepsilon \right)\|\nabla u_n\|^{2}\\\leq & \, \, \frac{1}{2\varepsilon}\|g\|^2_{H^{-1}(\Omega)} + 2C_0|\Omega| .\end{aligned}\end{equation*}
(3.6)Thus,
\begin{equation*}\begin{aligned}&\frac{d}{dt}\|z_n\|_{\mathcal{V}_t}^2+2\left\langle{\partial_s\eta^t_n,\eta^t_n}\right\rangle_{1,\mu_t} - 2\int_{0}^{\infty}\partial_t \mu_t(s)\|\nabla\eta^t_n(s)\|^2ds+ 2\!\left(1- \frac{\beta }{\lambda_1}-\varepsilon \right)\|\nabla u_n\|^{2}\\\leq & \, \, \frac{1}{2\varepsilon}\|g\|^2_{H^{-1}(\Omega)} + 2C_0|\Omega| .\end{aligned}\end{equation*}
(3.6)Thus, \begin{equation}\begin{aligned}&2\left\langle{\partial_s\eta^t_n,\eta^t_n}\right\rangle_{1,\mu_t} - 2\int_{0}^{\infty}\partial_t \mu_t(s)\|\nabla\eta^t_n(s)\|^2ds \\=& \,\,-2\int_{0}^{\infty}(\partial_s \mu_t(s) +\partial_t\mu_t(s) ) \|\nabla\eta^t_n(s)\|^2ds\geq 0.\end{aligned}\end{equation}
Choosing
\begin{equation}\begin{aligned}&2\left\langle{\partial_s\eta^t_n,\eta^t_n}\right\rangle_{1,\mu_t} - 2\int_{0}^{\infty}\partial_t \mu_t(s)\|\nabla\eta^t_n(s)\|^2ds \\=& \,\,-2\int_{0}^{\infty}(\partial_s \mu_t(s) +\partial_t\mu_t(s) ) \|\nabla\eta^t_n(s)\|^2ds\geq 0.\end{aligned}\end{equation}
Choosing \begin{equation*}\frac{d}{dt}\|z_n\|_{\mathcal{V}_t}^2 + 2(1- \frac{\beta }{\lambda_1}-\varepsilon )\|\nabla u_n\|^{2}\leq C( \|g\|^2_{H^{-1}(\Omega)} +1).\end{equation*}
\begin{equation*}\frac{d}{dt}\|z_n\|_{\mathcal{V}_t}^2 + 2(1- \frac{\beta }{\lambda_1}-\varepsilon )\|\nabla u_n\|^{2}\leq C( \|g\|^2_{H^{-1}(\Omega)} +1).\end{equation*}
 $\varepsilon >0$
small enough so that
$\varepsilon >0$
small enough so that
 $1- \dfrac{\beta }{\lambda_1}-\varepsilon >0$
and integrating on
$1- \dfrac{\beta }{\lambda_1}-\varepsilon >0$
and integrating on
 $(\tau ,t)$
,
$(\tau ,t)$
,
 $t\in(\tau ,T)$
, lead to the following estimate Hence, in particular, we see that
$t\in(\tau ,T)$
, lead to the following estimate Hence, in particular, we see that \begin{equation*}\|z_n(t)\|_{\mathcal{V}_t}^2+2\!\left(1- \frac{\beta }{\lambda_1}-\varepsilon \right)\int_{\tau }^{t}\|\nabla u_n(r)\|^{2} dr \leq \|z_n(\tau) \|_{\mathcal{V}_\tau}^2+ CT( \|g\|^2_{H^{-1}(\Omega)} +1).\end{equation*}
(3.7)Therefore, by the Banach–Alaoglu theorem, there exists a function
\begin{equation*}\|z_n(t)\|_{\mathcal{V}_t}^2+2\!\left(1- \frac{\beta }{\lambda_1}-\varepsilon \right)\int_{\tau }^{t}\|\nabla u_n(r)\|^{2} dr \leq \|z_n(\tau) \|_{\mathcal{V}_\tau}^2+ CT( \|g\|^2_{H^{-1}(\Omega)} +1).\end{equation*}
(3.7)Therefore, by the Banach–Alaoglu theorem, there exists a function \begin{equation}\begin{aligned}&\{u_n\} \quad\text{ is bounded in }\quad L^{\infty}( \tau ,T;\ H_0^1(\Omega)),\\[3pt]&\{\eta^t_n\} \quad\text{ is bounded in }\quad L^{\infty}( \tau ,T;\ L^2_{\mu_t}(\mathbb{R}^+,H_0^1(\Omega))).\end{aligned}\end{equation}
\begin{equation}\begin{aligned}&\{u_n\} \quad\text{ is bounded in }\quad L^{\infty}( \tau ,T;\ H_0^1(\Omega)),\\[3pt]&\{\eta^t_n\} \quad\text{ is bounded in }\quad L^{\infty}( \tau ,T;\ L^2_{\mu_t}(\mathbb{R}^+,H_0^1(\Omega))).\end{aligned}\end{equation}
 $z=(u,\eta^t)$
such that (3.8)and
$z=(u,\eta^t)$
such that (3.8)and \begin{align}&u_n\rightharpoonup u\quad\text{ weakly star in }\quad L^{\infty}(\tau ,T;\ H_0^1(\Omega)),\nonumber\\[3pt]&\eta^t_n\rightharpoonup \eta^t\quad\text{ weakly star in }\quad L^{\infty}(\tau ,T;\ L_{\mu_t}^{2}(\mathbb{R}^+,H_0^1(\Omega))),\end{align}
(3.9)up to a subsequence. Now, we estimate
\begin{align}&u_n\rightharpoonup u\quad\text{ weakly star in }\quad L^{\infty}(\tau ,T;\ H_0^1(\Omega)),\nonumber\\[3pt]&\eta^t_n\rightharpoonup \eta^t\quad\text{ weakly star in }\quad L^{\infty}(\tau ,T;\ L_{\mu_t}^{2}(\mathbb{R}^+,H_0^1(\Omega))),\end{align}
(3.9)up to a subsequence. Now, we estimate \begin{align}&\Delta u_n\rightharpoonup \Delta u\quad\text{ weakly in }\quad L^{2}( \tau ,T;\ H^{-1}(\Omega)),\nonumber\\[3pt]& \Delta \eta^t_n\rightharpoonup \Delta \eta^t\quad\text{ weakly in }\quad L^{2}( \tau ,T;\ L_{\mu_t}^{2}(\mathbb{R}^+,H^{-1}(\Omega))),\end{align}
\begin{align}&\Delta u_n\rightharpoonup \Delta u\quad\text{ weakly in }\quad L^{2}( \tau ,T;\ H^{-1}(\Omega)),\nonumber\\[3pt]& \Delta \eta^t_n\rightharpoonup \Delta \eta^t\quad\text{ weakly in }\quad L^{2}( \tau ,T;\ L_{\mu_t}^{2}(\mathbb{R}^+,H^{-1}(\Omega))),\end{align}
 $\partial_t z_n$
. From (3.4) and (3.6), we get (3.10)Integrating (3.10) from
$\partial_t z_n$
. From (3.4) and (3.6), we get (3.10)Integrating (3.10) from \begin{equation}\frac{d}{dt}\|z_n\|_{\mathcal{V}_t}^2 + \|\nabla u_n\|^{2}+ 2\int_\Omega f(u_n)u_ndx \leq \|g\|^2_{H^{-1}(\Omega)}.\end{equation}
\begin{equation}\frac{d}{dt}\|z_n\|_{\mathcal{V}_t}^2 + \|\nabla u_n\|^{2}+ 2\int_\Omega f(u_n)u_ndx \leq \|g\|^2_{H^{-1}(\Omega)}.\end{equation}
 $\tau $
to T, we obtain In particular,
$\tau $
to T, we obtain In particular, \begin{equation*} \|z_n(T) \|_{\mathcal{V}_T}^2 + \int_\tau ^T \|\nabla u_n(t)\|^{2}dt+ 2\int_{Q_T} f(u_n)u_ndxdt \leq \|z_\tau \|_{\mathcal{V}_n(\tau)}^2 + T\|g\|^2_{H^{-1}(\Omega)}.\end{equation*}
(3.11)Multiplying the first equation of (3.2) by
\begin{equation*} \|z_n(T) \|_{\mathcal{V}_T}^2 + \int_\tau ^T \|\nabla u_n(t)\|^{2}dt+ 2\int_{Q_T} f(u_n)u_ndxdt \leq \|z_\tau \|_{\mathcal{V}_n(\tau)}^2 + T\|g\|^2_{H^{-1}(\Omega)}.\end{equation*}
(3.11)Multiplying the first equation of (3.2) by \begin{equation}\int_{Q_T}f(u_n)u_ndxdt \leq C.\end{equation}
\begin{equation}\int_{Q_T}f(u_n)u_ndxdt \leq C.\end{equation}
 $a_k+ \varepsilon a^{\prime}_k$
and the second by
$a_k+ \varepsilon a^{\prime}_k$
and the second by
 $b_k$
, then summing over k and adding the results, we get (3.12)Using Young inequality and
$b_k$
, then summing over k and adding the results, we get (3.12)Using Young inequality and \begin{equation}\begin{aligned}\frac{1}{2}\frac{d}{dt}&\left( \|u_n\|^2+(1+\varepsilon)\|\nabla u_n\|^2 + \int_0^\infty \mu_t(s)\|\eta_n^t\|^2ds+ 2\varepsilon \langle F(u_n),1\rangle \right) + \|\nabla u_n\|^2 \\[3pt] &+\varepsilon \left(\|\partial_t u_n\|^2+\|\nabla \partial_t u_n\|^2\right) +\langle f(u_n),u_n \rangle - \int_{0}^{\infty}(\partial_s \mu_t(s) +\partial_t\mu_t(s) ) \|\nabla\eta^t_n(s)\|^2ds\\[3pt] &= - \int_{0}^{\infty} \mu_t(s)\langle \nabla\eta^t_n(s), \nabla \partial_tu_n \rangle ds+ \left\langle{g,u_n + \varepsilon \partial_t u_n}\right\rangle_{H^{-1}, H^1_0}. \end{aligned}\end{equation}
\begin{equation}\begin{aligned}\frac{1}{2}\frac{d}{dt}&\left( \|u_n\|^2+(1+\varepsilon)\|\nabla u_n\|^2 + \int_0^\infty \mu_t(s)\|\eta_n^t\|^2ds+ 2\varepsilon \langle F(u_n),1\rangle \right) + \|\nabla u_n\|^2 \\[3pt] &+\varepsilon \left(\|\partial_t u_n\|^2+\|\nabla \partial_t u_n\|^2\right) +\langle f(u_n),u_n \rangle - \int_{0}^{\infty}(\partial_s \mu_t(s) +\partial_t\mu_t(s) ) \|\nabla\eta^t_n(s)\|^2ds\\[3pt] &= - \int_{0}^{\infty} \mu_t(s)\langle \nabla\eta^t_n(s), \nabla \partial_tu_n \rangle ds+ \left\langle{g,u_n + \varepsilon \partial_t u_n}\right\rangle_{H^{-1}, H^1_0}. \end{aligned}\end{equation}
 $\kappa(t)= \int_{0}^{\infty} \mu_t(s)ds$
, we have and
$\kappa(t)= \int_{0}^{\infty} \mu_t(s)ds$
, we have and \begin{equation*} \begin{aligned} - \int_{0}^{\infty} \mu_t(s)\langle \nabla\eta^t_n(s), \nabla \partial_tu_n \rangle ds& \leq \int_{0}^{\infty} \mu_t(s) \| \nabla\eta^t_n(s)\| \| \nabla \partial_tu_n \| ds\\[3pt]& \leq \sqrt{\varepsilon} \delta \kappa(t) \int_{0}^{\infty} \mu_t(s) \| \nabla\eta^t_n(s)\|^2 ds + \frac{\varepsilon \sqrt{\varepsilon} }{\delta} \| \nabla \partial_tu_n \|^2,\end{aligned}\end{equation*}
(3.13)Combining (3.12)–(3.13), and owing to (M2) and (1.4), we get
\begin{equation*} \begin{aligned} - \int_{0}^{\infty} \mu_t(s)\langle \nabla\eta^t_n(s), \nabla \partial_tu_n \rangle ds& \leq \int_{0}^{\infty} \mu_t(s) \| \nabla\eta^t_n(s)\| \| \nabla \partial_tu_n \| ds\\[3pt]& \leq \sqrt{\varepsilon} \delta \kappa(t) \int_{0}^{\infty} \mu_t(s) \| \nabla\eta^t_n(s)\|^2 ds + \frac{\varepsilon \sqrt{\varepsilon} }{\delta} \| \nabla \partial_tu_n \|^2,\end{aligned}\end{equation*}
(3.13)Combining (3.12)–(3.13), and owing to (M2) and (1.4), we get \begin{equation} \left\langle{g,u_n + \varepsilon \partial_t u_n}\right\rangle_{H^{-1}, H^1_0} \leq \frac{1}{2} \| \nabla u_n \|^2+ \frac{\varepsilon}{2} \|\partial_t \nabla u_n \|^2+ C(\varepsilon) \|g\|^2_{H^{-1}(\Omega)}.\end{equation}
(3.14)Integrating (3.14) from
\begin{equation} \left\langle{g,u_n + \varepsilon \partial_t u_n}\right\rangle_{H^{-1}, H^1_0} \leq \frac{1}{2} \| \nabla u_n \|^2+ \frac{\varepsilon}{2} \|\partial_t \nabla u_n \|^2+ C(\varepsilon) \|g\|^2_{H^{-1}(\Omega)}.\end{equation}
(3.14)Integrating (3.14) from \begin{equation}\begin{aligned} \frac{d}{dt}&\left( \|u_n\|^2+(1+\varepsilon)\|\nabla u_n\|^2 + \int_0^\infty \mu_t(s)\|\eta_n^t\|^2ds+ 2\varepsilon \langle F(u_n),1\rangle \right) + \|\nabla u_n\|^2 \\[3pt]&+2\left(\varepsilon - \frac{\varepsilon \sqrt{\varepsilon} }{\delta} \right) \left( \|\partial_t u_n\|^2+\|\nabla \partial_t u_n\|^2 \right) +2\langle f(u_n),u_n \rangle\\[3pt]&+ 2(1-\sqrt{\varepsilon}) \delta \kappa(t) \int_{0}^{\infty} \mu_t(s) \|\nabla\eta^t_n(s)\|^2ds \leq C(\varepsilon) \|g\|^2_{H^{-1}(\Omega)}. \end{aligned}\end{equation}
\begin{equation}\begin{aligned} \frac{d}{dt}&\left( \|u_n\|^2+(1+\varepsilon)\|\nabla u_n\|^2 + \int_0^\infty \mu_t(s)\|\eta_n^t\|^2ds+ 2\varepsilon \langle F(u_n),1\rangle \right) + \|\nabla u_n\|^2 \\[3pt]&+2\left(\varepsilon - \frac{\varepsilon \sqrt{\varepsilon} }{\delta} \right) \left( \|\partial_t u_n\|^2+\|\nabla \partial_t u_n\|^2 \right) +2\langle f(u_n),u_n \rangle\\[3pt]&+ 2(1-\sqrt{\varepsilon}) \delta \kappa(t) \int_{0}^{\infty} \mu_t(s) \|\nabla\eta^t_n(s)\|^2ds \leq C(\varepsilon) \|g\|^2_{H^{-1}(\Omega)}. \end{aligned}\end{equation}
 $\tau $
to t and using (1.4), (3.11) and (3.7), we can deduce that so, up to a subsequence,
$\tau $
to t and using (1.4), (3.11) and (3.7), we can deduce that so, up to a subsequence, \begin{align*}\{\partial_t u_n\} \quad\text{ is bounded in }\quad L^{2}( \tau ,T;\ H_0^1(\Omega)) ,\end{align*}
(3.15)We now prove that
\begin{align*}\{\partial_t u_n\} \quad\text{ is bounded in }\quad L^{2}( \tau ,T;\ H_0^1(\Omega)) ,\end{align*}
(3.15)We now prove that \begin{align} \begin{split}&\partial_t u_n \rightharpoonup \partial_tu \quad \text{ weakly in }\quad L^{2}( \tau ,T;\ H_0^1(\Omega)),\\[3pt]& \partial_t \Delta u_n \rightharpoonup \partial_t\Delta u \quad \text{ weakly in }\quad L^{2}( \tau ,T;\ H^{-1}(\Omega)).\end{split}\end{align}
\begin{align} \begin{split}&\partial_t u_n \rightharpoonup \partial_tu \quad \text{ weakly in }\quad L^{2}( \tau ,T;\ H_0^1(\Omega)),\\[3pt]& \partial_t \Delta u_n \rightharpoonup \partial_t\Delta u \quad \text{ weakly in }\quad L^{2}( \tau ,T;\ H^{-1}(\Omega)).\end{split}\end{align}
 $\{f(u_n)\}$
is bounded in
$\{f(u_n)\}$
is bounded in
 $L^1(Q_T)$
where
$L^1(Q_T)$
where
 $Q_T=\Omega \times (\tau, T)$
. Putting
$Q_T=\Omega \times (\tau, T)$
. Putting
 $h(s) = f(s)-f(0) + \gamma s$
, where
$h(s) = f(s)-f(0) + \gamma s$
, where
 $\gamma > \ell$
. Note that
$\gamma > \ell$
. Note that
 $h(s)s=(f(s)-f(0))s+\gamma s^2 =f^{\prime}(c) s^2+\gamma s^2\geq (\gamma -\ell)s^2 \ge 0$
for all
$h(s)s=(f(s)-f(0))s+\gamma s^2 =f^{\prime}(c) s^2+\gamma s^2\geq (\gamma -\ell)s^2 \ge 0$
for all
 $s\in \mathbb R$
, we have where we have used (3.7), (3.11) and the boundedness of
$s\in \mathbb R$
, we have where we have used (3.7), (3.11) and the boundedness of \begin{align*}\int\limits_{Q_T} \left| h(u_n) \right|dxdt &\le \int\limits_{Q_T \cap \{ \left| u_n \right| > 1\} } \left| h(u_n)u_n \right|dxdt + \int\limits_{Q_T \cap \{ \left| u_n\right| \le 1\}} \left| h(u_n)\right|dxdt\\[3pt] &\le \int\limits_{Q_T} h({u_n}){u_n}dxdt + \mathop {\sup }\limits_{\left| s \right| \le 1} \left| h(s) \right|\left| Q_T\right|\\[3pt]& \le \int\limits_{Q_T} f({u_n}){u_n}dxdt + |f(0)|\|u_n\|_{L^1(Q_T)}+\gamma \|u_n\|^2_{L^2(Q_T)}\\[3pt]&\;\;\;+ \mathop {\sup }\limits_{\left| s \right| \le 1} \left| h(s) \right|\left| Q_T\right|\\[3pt]&\le C, \end{align*}
\begin{align*}\int\limits_{Q_T} \left| h(u_n) \right|dxdt &\le \int\limits_{Q_T \cap \{ \left| u_n \right| > 1\} } \left| h(u_n)u_n \right|dxdt + \int\limits_{Q_T \cap \{ \left| u_n\right| \le 1\}} \left| h(u_n)\right|dxdt\\[3pt] &\le \int\limits_{Q_T} h({u_n}){u_n}dxdt + \mathop {\sup }\limits_{\left| s \right| \le 1} \left| h(s) \right|\left| Q_T\right|\\[3pt]& \le \int\limits_{Q_T} f({u_n}){u_n}dxdt + |f(0)|\|u_n\|_{L^1(Q_T)}+\gamma \|u_n\|^2_{L^2(Q_T)}\\[3pt]&\;\;\;+ \mathop {\sup }\limits_{\left| s \right| \le 1} \left| h(s) \right|\left| Q_T\right|\\[3pt]&\le C, \end{align*}
 $\{u_n\}$
in
$\{u_n\}$
in
 $L^\infty (\tau,T;\ H^1_0(\Omega ))$
. Hence it implies that
$L^\infty (\tau,T;\ H^1_0(\Omega ))$
. Hence it implies that
 $\{h(u_n)\}$
, and therefore
$\{h(u_n)\}$
, and therefore
 $\{f(u_n)\}$
is bounded in
$\{f(u_n)\}$
is bounded in
 $L^1(Q_T)$
.
$L^1(Q_T)$
.
Using the Aubin–Lions lemma in [Reference Lions18], we can suppose that
 $u_n \to u$
strongly in
$u_n \to u$
strongly in
 $L^2(\tau ,T;\ L^2(\Omega))$
. Hence
$L^2(\tau ,T;\ L^2(\Omega))$
. Hence
 $u_n \to u$
a.e. in
$u_n \to u$
a.e. in
 $Q_T$
, up to a subsequence. Besides, using the definition of h(s) and (3.10), (3.7), we have Therefore, by Lemma 6.1 in [Reference Geredeli14], we obtain that
$Q_T$
, up to a subsequence. Besides, using the definition of h(s) and (3.10), (3.7), we have Therefore, by Lemma 6.1 in [Reference Geredeli14], we obtain that \begin{equation*}\int_{Q_T}h(u_n)u_ndxdt \leq C.\end{equation*}
\begin{equation*}\int_{Q_T}h(u_n)u_ndxdt \leq C.\end{equation*}
 $h(u) \in L^{1}(Q_T ) $
and for all test functions
$h(u) \in L^{1}(Q_T ) $
and for all test functions
 $\varphi \in C_0^\infty ([\tau,T];\ H_0^1(\Omega) \cap L^\infty (\Omega)), $
Hence,
$\varphi \in C_0^\infty ([\tau,T];\ H_0^1(\Omega) \cap L^\infty (\Omega)), $
Hence, \begin{equation*}\int_{Q_T} h(u_n) \varphi dxdt \to \int_{Q_T} h(u) \varphi dxdt.\end{equation*}
\begin{equation*}\int_{Q_T} h(u_n) \varphi dxdt \to \int_{Q_T} h(u) \varphi dxdt.\end{equation*}
 $f(u)\in L^1(Q_T)$
and (3.16)
$f(u)\in L^1(Q_T)$
and (3.16) \begin{equation}\int_{Q_T} f(u_n) \varphi dxdt \to \int_{Q_T} f(u) \varphi dxdt, \text{ for all }\varphi \in C_0^\infty ([\tau,T];\ H_0^1(\Omega) \cap L^\infty (\Omega)).\end{equation}
\begin{equation}\int_{Q_T} f(u_n) \varphi dxdt \to \int_{Q_T} f(u) \varphi dxdt, \text{ for all }\varphi \in C_0^\infty ([\tau,T];\ H_0^1(\Omega) \cap L^\infty (\Omega)).\end{equation}
We are now ready to show that the limit
 $z=(u, \eta^t)$
is a weak solution of (2.1). Choose an arbitrary test function of the form
$z=(u, \eta^t)$
is a weak solution of (2.1). Choose an arbitrary test function of the form \begin{equation*} \phi=(\varphi, \xi) \in \mathcal D ( [\tau ,T], H_0^1(\Omega)\cap L^\infty(\Omega)) \times \mathcal D ( [\tau ,T], \mathcal D(\mathbb R^+, H_0^1(\Omega)) )\end{equation*}
where m is a fixed integer,
\begin{equation*} \phi=(\varphi, \xi) \in \mathcal D ( [\tau ,T], H_0^1(\Omega)\cap L^\infty(\Omega)) \times \mathcal D ( [\tau ,T], \mathcal D(\mathbb R^+, H_0^1(\Omega)) )\end{equation*}
where m is a fixed integer, \begin{equation*} \varphi(t)= \sum\limits_{j=1}^{m} a_j(t)\omega_j \quad \text{ and }\quad \xi(t)=\sum\limits_{j=1}^{m} b_j(t)\zeta_j,\end{equation*}
\begin{equation*} \varphi(t)= \sum\limits_{j=1}^{m} a_j(t)\omega_j \quad \text{ and }\quad \xi(t)=\sum\limits_{j=1}^{m} b_j(t)\zeta_j,\end{equation*}
 $\{a_j\}_{j=1}^m$
and
$\{a_j\}_{j=1}^m$
and
 $\{b_j\}_{j=1}^m$
are given functions in
$\{b_j\}_{j=1}^m$
are given functions in
 $\mathcal D( (\tau ,T))$
. Then (3.1) holds with
$\mathcal D( (\tau ,T))$
. Then (3.1) holds with
 $(v(t), \xi(t))$
in place of
$(v(t), \xi(t))$
in place of
 $(\omega_k, \zeta_j)$
. Integrating the resulting equation over
$(\omega_k, \zeta_j)$
. Integrating the resulting equation over
 $(\tau , T)$
and passing to the limits, in view of (3.8), (3.9), (3.15) and (3.16), we get Using a density argument, we conclude that
$(\tau , T)$
and passing to the limits, in view of (3.8), (3.9), (3.15) and (3.16), we get Using a density argument, we conclude that \begin{equation*}\begin{aligned}\int_\tau ^T \bigg[\langle \partial_tu , \varphi\rangle +\langle\partial_t \nabla u ,\nabla \varphi\rangle +&\langle \partial_t\eta^t , \xi \rangle_{1,\mu_t}\bigg] dt \\[3pt]=& -\int_\tau ^T \bigg[ \langle \nabla u, \nabla \varphi \rangle + \langle \eta^t, \varphi \rangle_{1,\mu_t}\bigg]dt \\[3pt]&-\int_\tau ^T\bigg[\int_\Omega f(u )\varphi dx- \langle g, \varphi \rangle_{H^{-1}, H^1_0}\bigg] dt \\[3pt]&+\int_\tau ^T\bigg[ - \langle \partial_s\eta^t, \xi \rangle_{1,\mu_t} + \langle u, \xi \rangle_{1,\mu_t}\bigg]dt.\end{aligned}\end{equation*}
\begin{equation*}\begin{aligned}\int_\tau ^T \bigg[\langle \partial_tu , \varphi\rangle +\langle\partial_t \nabla u ,\nabla \varphi\rangle +&\langle \partial_t\eta^t , \xi \rangle_{1,\mu_t}\bigg] dt \\[3pt]=& -\int_\tau ^T \bigg[ \langle \nabla u, \nabla \varphi \rangle + \langle \eta^t, \varphi \rangle_{1,\mu_t}\bigg]dt \\[3pt]&-\int_\tau ^T\bigg[\int_\Omega f(u )\varphi dx- \langle g, \varphi \rangle_{H^{-1}, H^1_0}\bigg] dt \\[3pt]&+\int_\tau ^T\bigg[ - \langle \partial_s\eta^t, \xi \rangle_{1,\mu_t} + \langle u, \xi \rangle_{1,\mu_t}\bigg]dt.\end{aligned}\end{equation*}
 $z=(u,\eta^t)$
satisfies the equation in the weak sense. By standard arguments, we can check that z satisfies the initial condition
$z=(u,\eta^t)$
satisfies the equation in the weak sense. By standard arguments, we can check that z satisfies the initial condition
 $z(\tau ) =z_{\tau}$
. This implies that
$z(\tau ) =z_{\tau}$
. This implies that
 $z(\!\cdot\!)$
is a weak solution of problem (2.1).
$z(\!\cdot\!)$
is a weak solution of problem (2.1).
-
(ii) Uniqueness and continuous dependence on the initial data. We assume that
 $z_1=(u_1, \eta^t_1)$
and
$z_1=(u_1, \eta^t_1)$
and
 $z_2=(u_2, \eta^t_2)$
are two solutions of (2.1) with initial data
$z_2=(u_2, \eta^t_2)$
are two solutions of (2.1) with initial data
 $z_{1\tau }$
and
$z_{1\tau }$
and
 $z_{2\tau }$
, respectively. Denote
$z_{2\tau }$
, respectively. Denote
 $w = z_1 -z_2 = (u_3, \eta^t_3)$
, then (3.17)where
$w = z_1 -z_2 = (u_3, \eta^t_3)$
, then (3.17)where \begin{equation} \partial_t u_3 - \partial_t \Delta u_3 -\Delta u_3 - \int_0^{\infty} \mu_t(s) \Delta \eta^t_3(x,s)ds + (\hat{f}(u_1(t) -\hat{f}(u_2)) - \ell u_3 =0, \text{ for all } t >0,\end{equation}
\begin{equation} \partial_t u_3 - \partial_t \Delta u_3 -\Delta u_3 - \int_0^{\infty} \mu_t(s) \Delta \eta^t_3(x,s)ds + (\hat{f}(u_1(t) -\hat{f}(u_2)) - \ell u_3 =0, \text{ for all } t >0,\end{equation}
 $\hat{f}(s) = f(s) +\ell s$
. Here, because
$\hat{f}(s) = f(s) +\ell s$
. Here, because
 $u_3(t)$
does not belong to
$u_3(t)$
does not belong to
 $W=H_0^1(\Omega)\cap L^\infty(\Omega)$
, we cannot choose
$W=H_0^1(\Omega)\cap L^\infty(\Omega)$
, we cannot choose
 $u_3(t)$
as a test function. Consequently, the proof will be more involved than that in [Reference Conti, Marchini and Pata9, Reference Wang, Yang and Zhong29, Reference Wang and Zhong30].
$u_3(t)$
as a test function. Consequently, the proof will be more involved than that in [Reference Conti, Marchini and Pata9, Reference Wang, Yang and Zhong29, Reference Wang and Zhong30].
We use some ideas in [Reference Geredeli and Khanmamedov15]. Let
Consider the corresponding Nemytskii mapping \begin{equation*}B_k(s) =\begin{cases}k & \text{ if } s>k,\\[3pt]s & \text{ if } |s| \leq k,\\[3pt]-k & \text{ if } s< -k.\end{cases}\end{equation*}
\begin{equation*}B_k(s) =\begin{cases}k & \text{ if } s>k,\\[3pt]s & \text{ if } |s| \leq k,\\[3pt]-k & \text{ if } s< -k.\end{cases}\end{equation*}
 $\hat{B}_k\,{:}\, W \to W$
defined as follows By Theorem 4.7 in [Reference Krasnoselskii, Zabreiko, Pustylnik and Sobolevskii17] (see also Lemma 2.3 in [Reference Geredeli and Khanmamedov15]), we have that
$\hat{B}_k\,{:}\, W \to W$
defined as follows By Theorem 4.7 in [Reference Krasnoselskii, Zabreiko, Pustylnik and Sobolevskii17] (see also Lemma 2.3 in [Reference Geredeli and Khanmamedov15]), we have that \begin{equation*}\hat{B}_k(u_3)(x)=B_k(u_3(x)), \text{ for all } x \in \Omega.\end{equation*}
\begin{equation*}\hat{B}_k(u_3)(x)=B_k(u_3(x)), \text{ for all } x \in \Omega.\end{equation*}
 $\|\hat{B}_k(u_3) - u_3\|_W\to 0$
as
$\|\hat{B}_k(u_3) - u_3\|_W\to 0$
as
 $k \to \infty$
. Now multiplying (3.17) by
$k \to \infty$
. Now multiplying (3.17) by
 $\hat{B}_k(u_3)$
, then integrating over
$\hat{B}_k(u_3)$
, then integrating over
 $\Omega $
we get Thus,
$\Omega $
we get Thus, \begin{equation*} \begin{aligned} \frac{d}{dt}& \bigg( \int_\Omega u_3 \hat{B}_k(u_3)dx + \int_\Omega \nabla u_3 \nabla \hat{B}_k(u_3)dx - \frac{1}{2}\bigl(\|\hat{B}_k(u_3)\|^2 + \|\nabla\hat{B}_k(u_3)\|^2\bigr) \bigg)\\[3pt]& + \int_\Omega \nabla u_3 \nabla\hat{B}_k(u_3)dx + \int_0^\infty \mu_t(s) \int_\Omega \nabla \eta^t_3 \nabla \hat{B}_k(u_3)dxds \\[3pt]&+ \int_\Omega (\hat{f}(u_1) - \hat{f}(u_2)) \hat{B}_k(u_3)dx - \ell \int_\Omega u_3 \hat{B}_k(u_3) dx=0.\end{aligned}\end{equation*}
(3.18)Note that
\begin{equation*} \begin{aligned} \frac{d}{dt}& \bigg( \int_\Omega u_3 \hat{B}_k(u_3)dx + \int_\Omega \nabla u_3 \nabla \hat{B}_k(u_3)dx - \frac{1}{2}\bigl(\|\hat{B}_k(u_3)\|^2 + \|\nabla\hat{B}_k(u_3)\|^2\bigr) \bigg)\\[3pt]& + \int_\Omega \nabla u_3 \nabla\hat{B}_k(u_3)dx + \int_0^\infty \mu_t(s) \int_\Omega \nabla \eta^t_3 \nabla \hat{B}_k(u_3)dxds \\[3pt]&+ \int_\Omega (\hat{f}(u_1) - \hat{f}(u_2)) \hat{B}_k(u_3)dx - \ell \int_\Omega u_3 \hat{B}_k(u_3) dx=0.\end{aligned}\end{equation*}
(3.18)Note that \begin{equation} \begin{aligned}\frac{d}{dt}& \bigg( \int_\Omega u_3 \hat{B}_k(u_3)dx + \int_\Omega \nabla u_3 \nabla \hat{B}_k(u_3)dx - \frac{1}{2}\bigl(\|\hat{B}_k(u_3)\|^2 + \|\nabla\hat{B}_k(u_3)\|^2\bigr) \bigg)\\[3pt]& + \int_{ \{x \in \Omega\,{:}\, |u_3(x,t)| \leq k \}} | \nabla u_3 |^2 dx + \int_0^\infty \mu_t(s) \int_{ \{x \in \Omega\,{:}\, |u_3(x,t)| \leq k \}}\nabla \eta^t_3 \nabla u_3 dxds \\[3pt] &+ \int_\Omega \hat{f}^{\prime} (\xi) u_3\hat{B}_k(u_3) dx = \ell \int_\Omega u_3 \hat{B}_k(u_3) dx.\end{aligned} \end{equation}
\begin{equation} \begin{aligned}\frac{d}{dt}& \bigg( \int_\Omega u_3 \hat{B}_k(u_3)dx + \int_\Omega \nabla u_3 \nabla \hat{B}_k(u_3)dx - \frac{1}{2}\bigl(\|\hat{B}_k(u_3)\|^2 + \|\nabla\hat{B}_k(u_3)\|^2\bigr) \bigg)\\[3pt]& + \int_{ \{x \in \Omega\,{:}\, |u_3(x,t)| \leq k \}} | \nabla u_3 |^2 dx + \int_0^\infty \mu_t(s) \int_{ \{x \in \Omega\,{:}\, |u_3(x,t)| \leq k \}}\nabla \eta^t_3 \nabla u_3 dxds \\[3pt] &+ \int_\Omega \hat{f}^{\prime} (\xi) u_3\hat{B}_k(u_3) dx = \ell \int_\Omega u_3 \hat{B}_k(u_3) dx.\end{aligned} \end{equation}
 $\hat{f}^{\prime}(s) \geq 0$
and
$\hat{f}^{\prime}(s) \geq 0$
and
 $sB_k(s) \geq 0$
for all
$sB_k(s) \geq 0$
for all
 $s \in \mathbb{R}$
, we have Moreover,
$s \in \mathbb{R}$
, we have Moreover, \begin{equation*}\int_\Omega \hat{f}^{\prime} (\xi) u_3\hat{B}_k(u_3) dx \geq 0.\end{equation*}
and
\begin{equation*}\int_\Omega \hat{f}^{\prime} (\xi) u_3\hat{B}_k(u_3) dx \geq 0.\end{equation*}
and \begin{equation*}\int_{ \{x \in \Omega\,{:}\, |u_3(x,t)| \leq k \}} | \nabla u_3 |^2 dx \geq 0,\end{equation*}
From the above inequalities we deduce from (3.18) that
\begin{equation*}\int_{ \{x \in \Omega\,{:}\, |u_3(x,t)| \leq k \}} | \nabla u_3 |^2 dx \geq 0,\end{equation*}
From the above inequalities we deduce from (3.18) that \begin{align*} \int_0^\infty \mu_t(s) &\int_{ \{x \in \Omega\,{:}\, |u_3(x,t)| \leq k \}} \nabla \eta^t_3 \nabla u_3 dxds \\[3pt]= & \int_0^\infty \mu_t(s) \int_{ \{x \in \Omega\,{:}\, |u_3(x,t)| \leq k \}}\nabla \eta^t_3 \partial_t \nabla \eta^t_3 dxds \\[3pt]&\qquad + \int_0^\infty \mu_t(s) \int_{ \{x \in \Omega\,{:}\, |u_3(x,t)| \leq k \}}\nabla \eta^t_3 \partial_s\nabla \eta^t_3 dxds \\[3pt] = & \int_0^\infty \mu_t(s) \int_{ \{x \in \Omega\,{:}\, |u_3(x,t)| \leq k \}} \nabla \eta^t_3 \partial_t \nabla \eta^t_3 dxds\\[3pt]&\qquad - \frac{1}{2}\int_0^\infty \partial_s \mu_t(s) \int_{ \{x \in \Omega\,{:}\, |u_3(x,t)| \leq k \}}| \nabla \eta^t_3 |^2 dxds.\end{align*}
Integrating from
\begin{align*} \int_0^\infty \mu_t(s) &\int_{ \{x \in \Omega\,{:}\, |u_3(x,t)| \leq k \}} \nabla \eta^t_3 \nabla u_3 dxds \\[3pt]= & \int_0^\infty \mu_t(s) \int_{ \{x \in \Omega\,{:}\, |u_3(x,t)| \leq k \}}\nabla \eta^t_3 \partial_t \nabla \eta^t_3 dxds \\[3pt]&\qquad + \int_0^\infty \mu_t(s) \int_{ \{x \in \Omega\,{:}\, |u_3(x,t)| \leq k \}}\nabla \eta^t_3 \partial_s\nabla \eta^t_3 dxds \\[3pt] = & \int_0^\infty \mu_t(s) \int_{ \{x \in \Omega\,{:}\, |u_3(x,t)| \leq k \}} \nabla \eta^t_3 \partial_t \nabla \eta^t_3 dxds\\[3pt]&\qquad - \frac{1}{2}\int_0^\infty \partial_s \mu_t(s) \int_{ \{x \in \Omega\,{:}\, |u_3(x,t)| \leq k \}}| \nabla \eta^t_3 |^2 dxds.\end{align*}
Integrating from \begin{equation*} \begin{aligned}\frac{d}{dt}& \bigg( \int_\Omega u_3 \hat{B}_k(u_3)dx + \int_\Omega \nabla u_3 \nabla \hat{B}_k(u_3)dx - \frac{1}{2}\bigl(\|\hat{B}_k(u_3)\|^2 + \|\nabla\hat{B}_k(u_3)\|^2\bigr) \bigg)\\[3pt]& + \frac{1}{2} \int_0^\infty \mu_t(s) \int_{ \{x \in \Omega\,{:}\, |u_3(x,t)| \leq k \}} \frac{d}{dt} | \nabla \eta^t_3|^2 dxds \\[3pt] & \leq \ell \int_\Omega u_3 \hat{B}_k(u_3) dx + \frac{1}{2}\int_0^\infty \partial_s \mu_t(s) \int_{ \{x \in \Omega\,{:}\, |u_3(x,t)| \leq k \}}| \nabla \eta^t_3 |^2 dxds.\end{aligned}\end{equation*}
\begin{equation*} \begin{aligned}\frac{d}{dt}& \bigg( \int_\Omega u_3 \hat{B}_k(u_3)dx + \int_\Omega \nabla u_3 \nabla \hat{B}_k(u_3)dx - \frac{1}{2}\bigl(\|\hat{B}_k(u_3)\|^2 + \|\nabla\hat{B}_k(u_3)\|^2\bigr) \bigg)\\[3pt]& + \frac{1}{2} \int_0^\infty \mu_t(s) \int_{ \{x \in \Omega\,{:}\, |u_3(x,t)| \leq k \}} \frac{d}{dt} | \nabla \eta^t_3|^2 dxds \\[3pt] & \leq \ell \int_\Omega u_3 \hat{B}_k(u_3) dx + \frac{1}{2}\int_0^\infty \partial_s \mu_t(s) \int_{ \{x \in \Omega\,{:}\, |u_3(x,t)| \leq k \}}| \nabla \eta^t_3 |^2 dxds.\end{aligned}\end{equation*}
 $\tau$
to t, where
$\tau$
to t, where
 $t \in (\tau,T)$
, then letting
$t \in (\tau,T)$
, then letting
 $ k \to \infty$
, we obtain By the Gronwall inequality of integral form, we get
$ k \to \infty$
, we obtain By the Gronwall inequality of integral form, we get \begin{align*}&\| u_3(t) \|^2 + \| \nabla u_3(t) \|^2 + \| \eta_3^t \|^2_{1, \mu_t } \\[3pt] \leq & \quad \| u_3(\tau) \|^2 + \| \nabla u_3(\tau) \|^2+ \| \eta_3^\tau \|^2_{1, \mu_\tau} + 2 \ell \int_\tau^t \| u_3 (s) \|^2 ds \\[3pt]& \; + \int_\tau^t \biggl( \int_0^\infty ( \partial_s \mu_r(s) + \partial_r \mu_r(s))\| \nabla \eta^t_3 \|^2 ds \biggr)dr \\[3pt] \leq & \quad \| u_3(\tau) \|^2 + \| \nabla u_3(\tau) \|^2 + \| \eta_3^\tau \|^2_{1, \mu_\tau} + 2 \ell \int_\tau^t ( \| u_3 (s) \|^2 + \| \nabla u_3 (s) \|^2 + \| \eta_3^s \|^2_{1, \mu_s}) ds.\end{align*}
Hence we get the continuous dependence on the initial data of the solutions, and in particular, the uniqueness when
\begin{align*}&\| u_3(t) \|^2 + \| \nabla u_3(t) \|^2 + \| \eta_3^t \|^2_{1, \mu_t } \\[3pt] \leq & \quad \| u_3(\tau) \|^2 + \| \nabla u_3(\tau) \|^2+ \| \eta_3^\tau \|^2_{1, \mu_\tau} + 2 \ell \int_\tau^t \| u_3 (s) \|^2 ds \\[3pt]& \; + \int_\tau^t \biggl( \int_0^\infty ( \partial_s \mu_r(s) + \partial_r \mu_r(s))\| \nabla \eta^t_3 \|^2 ds \biggr)dr \\[3pt] \leq & \quad \| u_3(\tau) \|^2 + \| \nabla u_3(\tau) \|^2 + \| \eta_3^\tau \|^2_{1, \mu_\tau} + 2 \ell \int_\tau^t ( \| u_3 (s) \|^2 + \| \nabla u_3 (s) \|^2 + \| \eta_3^s \|^2_{1, \mu_s}) ds.\end{align*}
Hence we get the continuous dependence on the initial data of the solutions, and in particular, the uniqueness when \begin{equation*}\| w(t) \|^2_{\mathcal V_t } \leq \| w(\tau) \|^2_{\mathcal V _\tau } e^{2 \ell (t - \tau)} \leq \| w(\tau) \|^2_{\mathcal V_\tau } e^{2 \ell (T-\tau)}, \text { for all } t \in [\tau,T].\end{equation*}
\begin{equation*}\| w(t) \|^2_{\mathcal V_t } \leq \| w(\tau) \|^2_{\mathcal V _\tau } e^{2 \ell (t - \tau)} \leq \| w(\tau) \|^2_{\mathcal V_\tau } e^{2 \ell (T-\tau)}, \text { for all } t \in [\tau,T].\end{equation*}
 $ w(\tau) = 0$
.
$ w(\tau) = 0$
.
4. Existence of a time-dependent global attractor
Theorem 3.1 allows us to define a process on time-dependent spaces
![]() $U(t, \tau): \mathcal V_\tau \to \mathcal V_t $
associated to problem (2.1) by the formula
$U(t, \tau): \mathcal V_\tau \to \mathcal V_t $
associated to problem (2.1) by the formula
where
![]() $z(\!\cdot\!) $
is the unique global weak solution of (2.1) with the initial datum
$z(\!\cdot\!) $
is the unique global weak solution of (2.1) with the initial datum
![]() $z_\tau \in \mathcal V_\tau$
.
$z_\tau \in \mathcal V_\tau$
.
4.1. Existence of a time-dependent absorbing set
Lemma 4.1. Under assumptions (H1)–(H3), there exists a time-dependent absorbing set in
![]() $\mathcal V_t $
for the process
$\mathcal V_t $
for the process
![]() $U(t, \tau)$
.
$U(t, \tau)$
.
Proof. Multiplying the first equation of (2.1) by u(t) and integrating over
![]() $\Omega$
, we obtain
$\Omega$
, we obtain
 \begin{equation}\begin{aligned}\frac{1}{2}\frac{d}{dt} \left(\|u\|^2+ \|\nabla u\|^2 \right) +\|\nabla u\|^2 +\int_\Omega f(u)u dx+ \int_0^\infty &\mu_t(s) \langle \nabla \eta^t(s), \nabla u \rangle ds \\& = \langle g, u \rangle_{H^{-1}(\Omega), H^1_0(\Omega)}. \end{aligned}\end{equation}
\begin{equation}\begin{aligned}\frac{1}{2}\frac{d}{dt} \left(\|u\|^2+ \|\nabla u\|^2 \right) +\|\nabla u\|^2 +\int_\Omega f(u)u dx+ \int_0^\infty &\mu_t(s) \langle \nabla \eta^t(s), \nabla u \rangle ds \\& = \langle g, u \rangle_{H^{-1}(\Omega), H^1_0(\Omega)}. \end{aligned}\end{equation}
Using the hypothesis (1.3) and the Cauchy inequality, we have
 \begin{equation} \begin{aligned} \int_\Omega f(u)u dx &\geq -\beta\|u\|^2-C_0|\Omega|,\\ \langle g, u \rangle_{H^{-1}(\Omega), H^1_0(\Omega)}& \leq \varepsilon_0 \| \nabla u \|^2 + \dfrac{1}{4\varepsilon_0} \|g\|^2_{H^{-1}(\Omega)}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \int_\Omega f(u)u dx &\geq -\beta\|u\|^2-C_0|\Omega|,\\ \langle g, u \rangle_{H^{-1}(\Omega), H^1_0(\Omega)}& \leq \varepsilon_0 \| \nabla u \|^2 + \dfrac{1}{4\varepsilon_0} \|g\|^2_{H^{-1}(\Omega)}. \end{aligned} \end{equation}
Recalling that
![]() $ u(t) =\partial_t\eta^t(s) + \partial_s \eta^t(s)$
, we have
$ u(t) =\partial_t\eta^t(s) + \partial_s \eta^t(s)$
, we have
 \begin{equation} \begin{aligned} &\int_0^\infty \mu_t(s) \langle \nabla \eta^t(s), \nabla u \rangle ds \\[2pt]=& \int_0^\infty \mu_t(s) \langle \nabla \eta^t(s), \nabla \partial_s \eta^t(s) \rangle ds +\int_0^\infty \mu_t(s) \langle \nabla \eta^t(s), \nabla \partial_t\eta^t(s) \rangle ds \\[2pt]=& -\dfrac{1}{2}\int_0^\infty \partial_s \mu_t(s) \|\eta^t(s)\|^2ds +\dfrac{1}{2}\dfrac{d}{dt} \|\eta^t(s)\|^2-\dfrac{1}{2}\int_0^\infty \partial_t \mu_t(s) \|\eta^t(s)\|^2ds \\[2pt] =& -\dfrac{1}{2}\int_0^\infty \left( \partial_s \mu_t(s)+\partial_t \mu_t(s)\right) \|\eta^t(s)\|^2ds +\dfrac{1}{2}\dfrac{d}{dt} \|\eta^t \|^2_{1,\mu_t}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} &\int_0^\infty \mu_t(s) \langle \nabla \eta^t(s), \nabla u \rangle ds \\[2pt]=& \int_0^\infty \mu_t(s) \langle \nabla \eta^t(s), \nabla \partial_s \eta^t(s) \rangle ds +\int_0^\infty \mu_t(s) \langle \nabla \eta^t(s), \nabla \partial_t\eta^t(s) \rangle ds \\[2pt]=& -\dfrac{1}{2}\int_0^\infty \partial_s \mu_t(s) \|\eta^t(s)\|^2ds +\dfrac{1}{2}\dfrac{d}{dt} \|\eta^t(s)\|^2-\dfrac{1}{2}\int_0^\infty \partial_t \mu_t(s) \|\eta^t(s)\|^2ds \\[2pt] =& -\dfrac{1}{2}\int_0^\infty \left( \partial_s \mu_t(s)+\partial_t \mu_t(s)\right) \|\eta^t(s)\|^2ds +\dfrac{1}{2}\dfrac{d}{dt} \|\eta^t \|^2_{1,\mu_t}. \end{aligned} \end{equation}
From (4.3) and (M2), we get
Combining (4.2), (4.4) and (4.1), we get
 \begin{equation*}\begin{aligned}\frac{d}{dt} \left(\|u\|^2+ \|\nabla u\|^2+ \|\eta^t\|^2_{1,\mu_t} \right) + 2 \left(1- \dfrac {\beta}{\lambda_1}-\varepsilon_0 \right) & \| \nabla u \|^2 + \delta \kappa(t) \|\eta^t(s)\|^2_{1,\mu_t}\\[2pt]&\leq \dfrac{1}{2\varepsilon} \|g\|^2_{H^{-1}(\Omega)} +2C_0|\Omega|. \end{aligned}\end{equation*}
\begin{equation*}\begin{aligned}\frac{d}{dt} \left(\|u\|^2+ \|\nabla u\|^2+ \|\eta^t\|^2_{1,\mu_t} \right) + 2 \left(1- \dfrac {\beta}{\lambda_1}-\varepsilon_0 \right) & \| \nabla u \|^2 + \delta \kappa(t) \|\eta^t(s)\|^2_{1,\mu_t}\\[2pt]&\leq \dfrac{1}{2\varepsilon} \|g\|^2_{H^{-1}(\Omega)} +2C_0|\Omega|. \end{aligned}\end{equation*}
Using hypothesis (M3), we deduce
![]() $ \exists \delta_0 >0$
, so that
$ \exists \delta_0 >0$
, so that
![]() $ \kappa(t) \ge \delta_0 >0 \,\, \forall t \in \mathbb{R}$
. Therefore
$ \kappa(t) \ge \delta_0 >0 \,\, \forall t \in \mathbb{R}$
. Therefore
 \begin{equation*}\begin{aligned}\frac{d}{dt} \left(\|u\|^2+ \|\nabla u\|^2+ \|\eta^t\|^2_{1,\mu_t} \right) + \gamma&\left(\|u\|^2+ \|\nabla u\|^2+ \|\eta^t\|^2_{1,\mu_t} \right) \\&\leq C \left( \|g\|^2_{H^{-1}(\Omega)} +1\right). \end{aligned}\end{equation*}
\begin{equation*}\begin{aligned}\frac{d}{dt} \left(\|u\|^2+ \|\nabla u\|^2+ \|\eta^t\|^2_{1,\mu_t} \right) + \gamma&\left(\|u\|^2+ \|\nabla u\|^2+ \|\eta^t\|^2_{1,\mu_t} \right) \\&\leq C \left( \|g\|^2_{H^{-1}(\Omega)} +1\right). \end{aligned}\end{equation*}
By the Gronwall inequality, we get
where
Hence, there exists
![]() $\rho_{0}>0$
such that
$\rho_{0}>0$
such that
for all
![]() $z_\tau \in B$
and
$z_\tau \in B$
and
![]() $t\geq t_\tau=t_\tau(B)$
, where B is an arbitrary bounded subset of
$t\geq t_\tau=t_\tau(B)$
, where B is an arbitrary bounded subset of
![]() $\mathcal{V}_t$
. This completes the proof.
$\mathcal{V}_t$
. This completes the proof.
4.2 Asymptotic compactness
Recall that in this paper we only assume the external force
![]() $g \in H^{-1}(\Omega)$
. However, we know that for any
$g \in H^{-1}(\Omega)$
. However, we know that for any
![]() $g\in H^{-1}(\Omega)$
and
$g\in H^{-1}(\Omega)$
and
![]() $\varepsilon >0$
given, there is a
$\varepsilon >0$
given, there is a
![]() $g^\varepsilon \in L^2(\Omega)$
, which depends on g and
$g^\varepsilon \in L^2(\Omega)$
, which depends on g and
![]() $\varepsilon$
, such that
$\varepsilon$
, such that
Now, in order to show that the process is asymptotically compact, we shall exhibit a pullback attracting family of compact sets. To this aim, the strategy classically consists in finding a suitable decomposition of the process in the sum of a decaying part and of a compact one.
4.2.1 Decomposition of the equation
Since
![]() $\mathcal{B}=\{\mathbb{B}_t(R)\}_{t \in\mathbb{R}}$
is a time-dependent absorbing set for
$\mathcal{B}=\{\mathbb{B}_t(R)\}_{t \in\mathbb{R}}$
is a time-dependent absorbing set for
![]() $U(t, \tau)z_\tau$
, then for each initial data
$U(t, \tau)z_\tau$
, then for each initial data
![]() $z_\tau \in \mathbb{B}_t(R)$
, we decompose
$z_\tau \in \mathbb{B}_t(R)$
, we decompose
![]() $U(t, \tau)z_\tau$
as follows
$U(t, \tau)z_\tau$
as follows
where
![]() $U_1(t,\tau) z_\tau=z_1(t)$
and
$U_1(t,\tau) z_\tau=z_1(t)$
and
![]() $U_2(t,\tau) z_\tau=z_2(t)$
, that is,
$U_2(t,\tau) z_\tau=z_2(t)$
, that is,
![]() $z= (u,\eta^t)=z_1+z_2$
, the decomposition is of the following form
$z= (u,\eta^t)=z_1+z_2$
, the decomposition is of the following form
where
![]() $z_1(t)$
is the unique solution of the following problem
$z_1(t)$
is the unique solution of the following problem
 \begin{equation}\begin{aligned}\begin{cases}&\partial_t v^\varepsilon -\partial_t \Delta v^\varepsilon - \Delta v^\varepsilon + f(u)-f(w^\varepsilon) - \int_0^\infty \mu_t(s)\Delta \zeta^{t\varepsilon}(s)ds + \lambda v^\varepsilon = g- g^\varepsilon, \; \lambda > \ell,\\ \\[-8pt]&\partial_t \zeta^{t\varepsilon} = - \partial_s \zeta^{t\varepsilon} +v^\varepsilon,\\ \\[-8pt] &v^\varepsilon(x,t)|_{\partial \Omega} = 0, \; v^\varepsilon(x,t)|_{t = \tau}=u_\tau(x),\\ \\[-8pt]&\zeta^{t\varepsilon}(x,s)|_{\partial \Omega} = 0, \; \zeta^\tau(x,s)=\zeta_\tau(x,s)\,{:\!=}\,\int\limits_\tau^sg_0(x, r)dr,\end{cases}\end{aligned} \end{equation}
\begin{equation}\begin{aligned}\begin{cases}&\partial_t v^\varepsilon -\partial_t \Delta v^\varepsilon - \Delta v^\varepsilon + f(u)-f(w^\varepsilon) - \int_0^\infty \mu_t(s)\Delta \zeta^{t\varepsilon}(s)ds + \lambda v^\varepsilon = g- g^\varepsilon, \; \lambda > \ell,\\ \\[-8pt]&\partial_t \zeta^{t\varepsilon} = - \partial_s \zeta^{t\varepsilon} +v^\varepsilon,\\ \\[-8pt] &v^\varepsilon(x,t)|_{\partial \Omega} = 0, \; v^\varepsilon(x,t)|_{t = \tau}=u_\tau(x),\\ \\[-8pt]&\zeta^{t\varepsilon}(x,s)|_{\partial \Omega} = 0, \; \zeta^\tau(x,s)=\zeta_\tau(x,s)\,{:\!=}\,\int\limits_\tau^sg_0(x, r)dr,\end{cases}\end{aligned} \end{equation}
and
![]() $z_2(t)$
is the unique solution of the following problem
$z_2(t)$
is the unique solution of the following problem
 \begin{equation}\begin{aligned}\begin{cases} \partial_tw^\varepsilon - \partial_t\Delta w^\varepsilon - \Delta w^\varepsilon + f(w^\varepsilon) - \int_0^\infty \mu_t(s)\Delta \xi^{t\varepsilon}(s)ds - \lambda ( u - w^\varepsilon ) = g^\varepsilon, \; \lambda > \ell, \\ \\[-8pt] \partial_t \xi^{t\varepsilon} = - \partial_s \xi^{t\varepsilon} +w^\varepsilon,\\ \\[-8pt] w^\varepsilon(x,t)|_{\partial \Omega} = 0, \; w^\varepsilon(x,t)|_{t =\tau}=0,\\ \\[-8pt] \xi^{t\varepsilon}(x,s)|_{\partial \Omega} = 0, \; \xi^\tau(x,s)=\xi_\tau(x,s)=0.\end{cases}\end{aligned}\end{equation}
\begin{equation}\begin{aligned}\begin{cases} \partial_tw^\varepsilon - \partial_t\Delta w^\varepsilon - \Delta w^\varepsilon + f(w^\varepsilon) - \int_0^\infty \mu_t(s)\Delta \xi^{t\varepsilon}(s)ds - \lambda ( u - w^\varepsilon ) = g^\varepsilon, \; \lambda > \ell, \\ \\[-8pt] \partial_t \xi^{t\varepsilon} = - \partial_s \xi^{t\varepsilon} +w^\varepsilon,\\ \\[-8pt] w^\varepsilon(x,t)|_{\partial \Omega} = 0, \; w^\varepsilon(x,t)|_{t =\tau}=0,\\ \\[-8pt] \xi^{t\varepsilon}(x,s)|_{\partial \Omega} = 0, \; \xi^\tau(x,s)=\xi_\tau(x,s)=0.\end{cases}\end{aligned}\end{equation}
By using similar arguments as in the proof of Theorem 3.1, one can prove the existence and uniqueness of solutions to problems (4.7) and (4.8). Moreover, for problem (4.8), because the external force
![]() $g^{\varepsilon}\in L^2(\Omega)$
and the initial data are zero (so it belong to
$g^{\varepsilon}\in L^2(\Omega)$
and the initial data are zero (so it belong to
![]() $\mathcal{W}_t\,{:\!=}\,\left (H^2(\Omega) \cap H_0^1(\Omega)\right)\times L^2_{\mu_t}(\mathbb{R}^+, H^2(\Omega) \cap H_0^1(\Omega))$
), we can show that the solution
$\mathcal{W}_t\,{:\!=}\,\left (H^2(\Omega) \cap H_0^1(\Omega)\right)\times L^2_{\mu_t}(\mathbb{R}^+, H^2(\Omega) \cap H_0^1(\Omega))$
), we can show that the solution
![]() $(w^\varepsilon, \xi^{t\varepsilon})$
is in fact a strong solution. In particular, we will have
$(w^\varepsilon, \xi^{t\varepsilon})$
is in fact a strong solution. In particular, we will have
![]() $w^{\varepsilon}\in C([0,T];\ H^2(\Omega)\cap H^1_0(\Omega))$
for any
$w^{\varepsilon}\in C([0,T];\ H^2(\Omega)\cap H^1_0(\Omega))$
for any
![]() $T>0$
. This will be used in the proof of Lemma 4.3 below.
$T>0$
. This will be used in the proof of Lemma 4.3 below.
We begin with the decay estimate for solutions of (4.7).
Lemma 4.2. For any
![]() $\varepsilon >0$
, the solutions of equation (4.7) satisfy the following estimates: there is a constant
$\varepsilon >0$
, the solutions of equation (4.7) satisfy the following estimates: there is a constant
![]() $d_0$
which depends on
$d_0$
which depends on
![]() $\lambda_1, \ell$
, such that for every
$\lambda_1, \ell$
, such that for every
![]() $t \ge 0 $
,
$t \ge 0 $
,
Proof. Multiplying the first equation of (4.7) by
![]() $v^\varepsilon$
we get
$v^\varepsilon$
we get
 \begin{equation*} \begin{aligned} \frac{1}{2}\frac{d}{dt} \bigl(\|v^\varepsilon\|^2 + \|\nabla v^\varepsilon\|^2\bigr) + \lambda \|v^\varepsilon\|^2 + \|\nabla v^\varepsilon\|^2+ \int_0^\infty \mu_t(s) \int_\Omega \nabla \zeta^{t\varepsilon} \nabla v^\varepsilon dxds \\+ \langle f(u) - f(w^\varepsilon), v^\varepsilon \rangle = \langle g- g^\varepsilon , v^\varepsilon \rangle_{H^{-1}, H^1_0}.\end{aligned}\end{equation*}
\begin{equation*} \begin{aligned} \frac{1}{2}\frac{d}{dt} \bigl(\|v^\varepsilon\|^2 + \|\nabla v^\varepsilon\|^2\bigr) + \lambda \|v^\varepsilon\|^2 + \|\nabla v^\varepsilon\|^2+ \int_0^\infty \mu_t(s) \int_\Omega \nabla \zeta^{t\varepsilon} \nabla v^\varepsilon dxds \\+ \langle f(u) - f(w^\varepsilon), v^\varepsilon \rangle = \langle g- g^\varepsilon , v^\varepsilon \rangle_{H^{-1}, H^1_0}.\end{aligned}\end{equation*}
Applying Cauchy inequality, we get
Noting that
![]() $\partial_t\zeta^{t\varepsilon}=-\partial_s\zeta ^{t\varepsilon}+v^{\varepsilon}$
and reasoning exactly as in (4.3), (4.4), we obtain
$\partial_t\zeta^{t\varepsilon}=-\partial_s\zeta ^{t\varepsilon}+v^{\varepsilon}$
and reasoning exactly as in (4.3), (4.4), we obtain
Therefore, because
![]() $f^{\prime}(\xi) \geq -\ell$
, we have
$f^{\prime}(\xi) \geq -\ell$
, we have
 \begin{equation*} \begin{aligned} &\frac{d}{dt}\bigg( \|v^\varepsilon\|^2 + \|\nabla v^\varepsilon\|^2 +\|\zeta^{t\varepsilon}\|^2_{1,\mu_t}\bigg) + \| \nabla v^\varepsilon\|^2+2(\lambda - \ell) \|v^\varepsilon\|^2+ \delta \kappa(t) \|\zeta^{t\varepsilon}(s)\|^2_{1,\mu_t} \\ \leq &\,\, \|g- g^\varepsilon \|^2_{H^{-1}(\Omega)}.\end{aligned}\end{equation*}
\begin{equation*} \begin{aligned} &\frac{d}{dt}\bigg( \|v^\varepsilon\|^2 + \|\nabla v^\varepsilon\|^2 +\|\zeta^{t\varepsilon}\|^2_{1,\mu_t}\bigg) + \| \nabla v^\varepsilon\|^2+2(\lambda - \ell) \|v^\varepsilon\|^2+ \delta \kappa(t) \|\zeta^{t\varepsilon}(s)\|^2_{1,\mu_t} \\ \leq &\,\, \|g- g^\varepsilon \|^2_{H^{-1}(\Omega)}.\end{aligned}\end{equation*}
Using hypothesis (M3), we deduce
![]() $ \exists \delta_0 >0$
, so that
$ \exists \delta_0 >0$
, so that
![]() $ \kappa(t) \ge \delta_0 >0 \,\, \forall t \in \mathbb{R}$
.
$ \kappa(t) \ge \delta_0 >0 \,\, \forall t \in \mathbb{R}$
.
Thus, similarly to the proof of Lemma 4.1, we obtain for some
![]() $d_0>0$
,
$d_0>0$
,
Taking
![]() $\varepsilon^2 \leq C \varepsilon$
in (4.6) we have
$\varepsilon^2 \leq C \varepsilon$
in (4.6) we have
About the solution
![]() $z_2(t)$
of (4.8), we have the following lemma.
$z_2(t)$
of (4.8), we have the following lemma.
Lemma 4.3. For any
![]() $\varepsilon >0$
, there is
$\varepsilon >0$
, there is
![]() $M>0$
such that for any
$M>0$
such that for any
![]() $z_\tau \in \mathcal W_t$
, there exists
$z_\tau \in \mathcal W_t$
, there exists
![]() $T>0$
large enough, which depends on
$T>0$
large enough, which depends on
![]() $\|g \|^2_{H^{-1}(\Omega)}$
,
$\|g \|^2_{H^{-1}(\Omega)}$
,
![]() $\varepsilon$
, such that
$\varepsilon$
, such that
Proof. Multiplying the first equation of (4.8) by
![]() $- \Delta w^\varepsilon$
, then using (1.2), (M2) and the Cauchy inequality, we have
$- \Delta w^\varepsilon$
, then using (1.2), (M2) and the Cauchy inequality, we have
 \begin{equation*} \begin{aligned} \dfrac{d}{dt}\bigg( \|\nabla w^\varepsilon\|^2 &+ \|\Delta w^\varepsilon\|^2 +\|\xi^{t\varepsilon}\|^2_{2,\mu_t}\bigg) + \| \Delta w^\varepsilon\|^2+ 2 (\lambda - \ell) \|\nabla w^\varepsilon\|^2\\& + \delta \kappa(t) \|\xi^{t\varepsilon}(s)\|^2_{1,\mu_t} \leq \dfrac{1}{2} \left(\|g^\varepsilon\|^2_{H^{-1}(\Omega)}+ \| u\|_{H_0^1(\Omega)}^2 \right)\leq C( \|g^\varepsilon\|^2_{H^{-1}(\Omega)}+ \rho_0)\end{aligned}\end{equation*}
\begin{equation*} \begin{aligned} \dfrac{d}{dt}\bigg( \|\nabla w^\varepsilon\|^2 &+ \|\Delta w^\varepsilon\|^2 +\|\xi^{t\varepsilon}\|^2_{2,\mu_t}\bigg) + \| \Delta w^\varepsilon\|^2+ 2 (\lambda - \ell) \|\nabla w^\varepsilon\|^2\\& + \delta \kappa(t) \|\xi^{t\varepsilon}(s)\|^2_{1,\mu_t} \leq \dfrac{1}{2} \left(\|g^\varepsilon\|^2_{H^{-1}(\Omega)}+ \| u\|_{H_0^1(\Omega)}^2 \right)\leq C( \|g^\varepsilon\|^2_{H^{-1}(\Omega)}+ \rho_0)\end{aligned}\end{equation*}
when
![]() $t \ge t_0(B)$
. Note that we used the estimate (4.5) for this expression.
$t \ge t_0(B)$
. Note that we used the estimate (4.5) for this expression.
Hence, similarly to the proof of Lemma 4.1, we obtain a number
![]() $T>0$
large enough such that
$T>0$
large enough such that
The proof is complete.
Remark 4.1. From Lemma 4.3, we immediately have the following regularity result:
![]() $\mathcal A_t$
is bounded in
$\mathcal A_t$
is bounded in
![]() $\mathcal W_t$
(with a bound independent of t).
$\mathcal W_t$
(with a bound independent of t).
Since
![]() $\mathcal{B}=\{B_t\}_{t\in \mathbb{R}}$
is a time-dependent absorbing set, collecting Lemmas 4.2 and 4.3 we infer that the family of
$\mathcal{B}=\{B_t\}_{t\in \mathbb{R}}$
is a time-dependent absorbing set, collecting Lemmas 4.2 and 4.3 we infer that the family of
![]() $\mathcal W_t$
-ball
$\mathcal W_t$
-ball
![]() $\mathcal K = \{K_t(r)\}_{t\in \mathbb{R}}$
is pullback attracting provided that
$\mathcal K = \{K_t(r)\}_{t\in \mathbb{R}}$
is pullback attracting provided that
![]() $r > 0$
is sufficiently large, for
$r > 0$
is sufficiently large, for
Unfortunately, there are not enough conditions to conclude the existence of the unique time-dependent global attractor. Indeed, although closed balls of
![]() $\mathcal{W}_t$
are uniformly bounded by the embedding constant of
$\mathcal{W}_t$
are uniformly bounded by the embedding constant of
![]() $ \mathcal{W}_t \hookrightarrow \mathcal V_t$
is independent of t, they fail to be compact in
$ \mathcal{W}_t \hookrightarrow \mathcal V_t$
is independent of t, they fail to be compact in
![]() $\mathcal V_t$
due to the lack of compactness of the embedding
$\mathcal V_t$
due to the lack of compactness of the embedding
![]() $L^2_{\mu_t}(\mathbb{R}^+, H_0^1(\Omega)) \hookrightarrow L^2_{\mu_t}(\mathbb{R}^+, H^2(\Omega) \cap H_0^1(\Omega)) $
. The argument as in the proof of [Reference Wang and Zhong30, Theorem 3.13], where the same model is considered for a constant-in-time memory kernel, we get that the process
$L^2_{\mu_t}(\mathbb{R}^+, H_0^1(\Omega)) \hookrightarrow L^2_{\mu_t}(\mathbb{R}^+, H^2(\Omega) \cap H_0^1(\Omega)) $
. The argument as in the proof of [Reference Wang and Zhong30, Theorem 3.13], where the same model is considered for a constant-in-time memory kernel, we get that the process
![]() $U(t, \tau)$
is asymptotically compact, which proves the existence of the unique time-dependent global attractor in below.
$U(t, \tau)$
is asymptotically compact, which proves the existence of the unique time-dependent global attractor in below.
Theorem 4.4. Assume that (H1)–(H3) hold. Then the process
![]() $\{U(t,\tau )\}_{t \ge \tau }$
generated by problem (2.1) admits an invariant time-dependent global attractor
$\{U(t,\tau )\}_{t \ge \tau }$
generated by problem (2.1) admits an invariant time-dependent global attractor
![]() $\mathcal A = \{ A_t \}_{t \in \mathbb R}$
.
$\mathcal A = \{ A_t \}_{t \in \mathbb R}$
.
5. Recovering nonclassical diffusion equation
In the last section, using the idea of Conti et al. in [Reference Conti, Danese and Pata7], we discuss the case when
![]() $k_t \to m\delta_0$
for some
$k_t \to m\delta_0$
for some
![]() $m >0$
, that is,
$m >0$
, that is,
 \begin{equation} \begin{aligned} \lim_{t\to \infty} \int_\varepsilon^\infty k_t(s) ds = \begin{cases} m \quad \text{ if } \varepsilon = 0,\\ 0 \quad \text{ if } \varepsilon > 0. \end{cases} \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \lim_{t\to \infty} \int_\varepsilon^\infty k_t(s) ds = \begin{cases} m \quad \text{ if } \varepsilon = 0,\\ 0 \quad \text{ if } \varepsilon > 0. \end{cases} \end{aligned} \end{equation}
Then, for long times our problem becomes the nonclassical diffusion equation (without memory kernel)
Equation (5.2) generates a
![]() $\mathcal{C}_0$
-semigroup of solutions
$\mathcal{C}_0$
-semigroup of solutions
possessing the global attractor
![]() $\hat{A}$
in the classical sense. Besides,
$\hat{A}$
in the classical sense. Besides,
![]() $\hat{A}$
is a bounded subset of
$\hat{A}$
is a bounded subset of
![]() $H^2(\Omega)\cap H_0^1(\Omega) $
, and coincides with the sections at (any) time
$H^2(\Omega)\cap H_0^1(\Omega) $
, and coincides with the sections at (any) time
![]() $t_0 \in \mathbb{R}$
of the set of all complete bounded trajectories (CBT) of S(t) (see, [Reference Wang, Li and Zhong28]). Namely, for any fixed
$t_0 \in \mathbb{R}$
of the set of all complete bounded trajectories (CBT) of S(t) (see, [Reference Wang, Li and Zhong28]). Namely, for any fixed
![]() $t_0 \in \mathbb{R}$
,
$t_0 \in \mathbb{R}$
,
where a CBT the semigroup S(t) is a map
satisfying
On the other hand, according to Theorem 4.4 and [Reference Conti and Pata11, Theorem 3.2], the invariant time-dependent global attractor is characterized as the set of all CBT of the process, that is,
where a CBT of
![]() $U(t,\tau)$
is a map
$U(t,\tau)$
is a map
satisfying
Using ideas as in [Reference Conti, Danese and Pata7], we have the following theorem which establishes the closeness of the long-term dynamics of (1.1) to the one of the “limit problem” (5.2) when
![]() $k_t \to m\delta_0$
.
$k_t \to m\delta_0$
.
Theorem 5.1. Assume that (5.1) hold. Then, for any sequence
![]() $(u_n, \eta^t_n)$
of CBT of
$(u_n, \eta^t_n)$
of CBT of
![]() $U(t,\tau)$
and any
$U(t,\tau)$
and any
![]() $t_n \to \infty$
, there exists a CBT
$t_n \to \infty$
, there exists a CBT
![]() $ \hat u $
of S(t) such that the convergence
$ \hat u $
of S(t) such that the convergence
holds up to a subsequence as
![]() $n \to \infty$
for every
$n \to \infty$
for every
![]() $T > 0$
.
$T > 0$
.
Defining the canonical projection
![]() $\mathbb{P}_t\,{:}\, \mathcal V_t \to H_0^1(\Omega)$
by
$\mathbb{P}_t\,{:}\, \mathcal V_t \to H_0^1(\Omega)$
by
![]() $\mathbb P_t(u, \eta) = u$
, and denoting the Hausdorff semidistance of two (nonempty) sets
$\mathbb P_t(u, \eta) = u$
, and denoting the Hausdorff semidistance of two (nonempty) sets
![]() $B, C \subset X$
by
$B, C \subset X$
by
then we have an immediate corollary.
Corollary 5.1. Assume that (5.1) hold. Then, we have the convergence
Indeed, from (5.3), we deduce that for every
![]() $t_n \to \infty$
the convergence
$t_n \to \infty$
the convergence
holds (up to a sequence) as
![]() $n \to \infty$
. This is clearly enough to draw the desired conclusion.
$n \to \infty$
. This is clearly enough to draw the desired conclusion.
Proof of Theorem 5.1.Let
![]() $w_n(\!\cdot\!)= u_n(\cdot+t_n)$
, for every n. Then the function
$w_n(\!\cdot\!)= u_n(\cdot+t_n)$
, for every n. Then the function
![]() $w_n$
fulfills the equation
$w_n$
fulfills the equation
From the estimates of Lemmas 4.2 and 4.3, we get that
Then, there exists
![]() $\hat u \in L^\infty(\mathbb{R};\ H^2(\Omega)\cap H_0^1(\Omega))$
such that, up to a subsequence,
$\hat u \in L^\infty(\mathbb{R};\ H^2(\Omega)\cap H_0^1(\Omega))$
such that, up to a subsequence,
Since
![]() $\lim_{n\to\infty} k_{t+t_n} = m \delta_0$
in the sense of (5.1), we can see that, for every
$\lim_{n\to\infty} k_{t+t_n} = m \delta_0$
in the sense of (5.1), we can see that, for every
![]() $T>0$
,
$T>0$
,
for every n sufficiently large (depending on T).
Multiplying equation (5.4) by
![]() $w_n+ \partial_t w_n$
then integrating from
$w_n+ \partial_t w_n$
then integrating from
![]() $-T $
to T we conclude that
$-T $
to T we conclude that
From (5.5) and (5.6) and applying the classical Simon-Aubin Theorem [Reference Simon23], the strong convergence
holds (up to a subsequence), implying in particular (5.3).
Now, we are left to prove that
![]() $ \hat u $
solves the nonclassical diffusion equation, namely
$ \hat u $
solves the nonclassical diffusion equation, namely
Indeed, we will prove that the equality above is recovered when passing to the limit as
![]() $ n \to \infty$
in (5.4), the only nonstandard convergence being
$ n \to \infty$
in (5.4), the only nonstandard convergence being
Let
![]() $\phi$
be fixed, and
$\phi$
be fixed, and
Then, we decompose the function
![]() $\Lambda_n(t)$
into the sum
$\Lambda_n(t)$
into the sum
where
 \begin{align*}&\Lambda^1_n(t) = \int_0^1 k_{t+t_n} (s) \langle \hat u(t-s), -\Delta \phi\rangle ds,\\ &\Lambda_n^2(t)= \int_0^1 k_{t+t_n} (s) \langle w_n(t-s)- \hat u(t-s), -\Delta \phi\rangle ds,\\ &\Lambda_n^3(t)= \int_1^\infty k_{t+t_n} (s) \langle w_n(t-s), -\Delta \phi\rangle ds.\end{align*}
\begin{align*}&\Lambda^1_n(t) = \int_0^1 k_{t+t_n} (s) \langle \hat u(t-s), -\Delta \phi\rangle ds,\\ &\Lambda_n^2(t)= \int_0^1 k_{t+t_n} (s) \langle w_n(t-s)- \hat u(t-s), -\Delta \phi\rangle ds,\\ &\Lambda_n^3(t)= \int_1^\infty k_{t+t_n} (s) \langle w_n(t-s), -\Delta \phi\rangle ds.\end{align*}
Since
![]() $\langle w_n, -\Delta \phi\rangle \in L^\infty (\mathbb{R})$
uniformly with respect to n, and
$\langle w_n, -\Delta \phi\rangle \in L^\infty (\mathbb{R})$
uniformly with respect to n, and
![]() $\langle w_n, -\Delta \phi\rangle \to \langle \hat u, -\Delta \phi\rangle $
in C(I) for every closed interval I, and using (5.1) once again
$\langle w_n, -\Delta \phi\rangle \to \langle \hat u, -\Delta \phi\rangle $
in C(I) for every closed interval I, and using (5.1) once again
 \begin{align*}|\Lambda_n^2(t)+\Lambda_n^3(t)| \leq &\,\|\langle w_n - \hat u, -\Delta\phi\rangle \|_{\mathcal{C}([t-1,t])}\int_0^1 k_{t+t_n} (s) ds\\&+ \|\langle w_n, -\Delta \phi\rangle \|_{L^\infty(\mathbb{R})}\int_1^\infty k_{t+t_n} (s) ds \to 0,\end{align*}
\begin{align*}|\Lambda_n^2(t)+\Lambda_n^3(t)| \leq &\,\|\langle w_n - \hat u, -\Delta\phi\rangle \|_{\mathcal{C}([t-1,t])}\int_0^1 k_{t+t_n} (s) ds\\&+ \|\langle w_n, -\Delta \phi\rangle \|_{L^\infty(\mathbb{R})}\int_1^\infty k_{t+t_n} (s) ds \to 0,\end{align*}
while
Therefore, we conclude that
for any sufficiently regular
![]() $\phi$
. Thus
$\phi$
. Thus
This completes the proof.
Acknowledgements
The authors would like to thank the reviewers for the helpful comments and suggestions which improved the presentation of the paper.