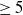1. Introduction
Throughout the paper, we work out over the complex number field
$\mathbb{C}$
. It is an important problem whether a log terminal Fano variety
$X$
is K-polystable. In order to interpret the criterion for the K-(poly)stability of
$X$
, the delta invariant
$\delta (X)$
is introduced in [Reference Blum and Jonsson3, Reference Fujita and Odaka10]. In fact, it is known by [Reference Blum and Jonsson3, Reference Blum and Xu4, Reference Fujita and Odaka10, Reference Fujita11, Reference Li12, Reference Liu, Xu and Zhuang13] that
\begin{equation*} \delta (X) \gt 1 \iff X \text { is K-stable } \iff X \text { is K-polystable and }\sharp \mathrm {Aut}(X)\lt \infty . \end{equation*}
The delta invariants of smooth del Pezzo surfaces are known in [Reference Araujo, Castravet and Cheltsov2, §2]. On the other hand, it is hard to estimate the delta invariant for higher dimensional Fano varieties. In order to estimate the delta invariant, Abban and Zhuang introduced the local delta invariant instead of the delta invariant in [Reference Abban and Zhuang1]. They gave an important idea for reducing the estimation of local delta invariants to that of lower dimensional cases.
We recall the definition of the local delta invariant. Let
$X$
be a
$n$
-dimensional weak Fano variety with at worst log terminal singularities and let
$p \in X$
be a closed point. Take a projective birational morphism
$\sigma\ :\ Y \to X$
with smooth variety
$Y$
and a prime divisor
$E$
on
$Y$
. We call
$E$
a divisor over
$X$
. Let
\begin{equation*} A_{X}(E)\,:\!=\,1+ \mathrm {ord}_{E}(K_{Y}-\sigma ^{\ast }K_{X}), \end{equation*}
and we let
\begin{equation*} S(E)\,:\!=\,\frac {1}{({-}K_{X})^{n}}\int _{0}^{\tau }\mathrm {vol}(\sigma ^{\ast }({-}K_{X})-uE)du, \end{equation*}
where
$\tau$
is the pseudo effective threshold of
$E$
with respect to
$-K_{X}$
, that is,
\begin{equation*} \tau \,:\!=\, \mathrm {sup} \{ u \in \mathbb {Q}_{\geq 0}\mid \sigma ^{\ast }({-}K_{X})-uE \text { is big } \}. \end{equation*}
The local delta invariant
$\delta _{p}(X)$
of
$X$
at
$p \in X$
is defined as follows:
\begin{equation*} \delta _{p}(X)\,:\!=\,\mathrm {inf}\left \{\frac {A_{X}(E)}{S(E)}\mid \text {$E$ is a prime divisor over $X$ with $p \in C_{X}(E)$} \right \}. \end{equation*}
Moreover, the delta invariant
$\delta (X)$
of
$X$
is given by
\begin{equation*} \delta (X)\,:\!=\,\inf _{p \in X}\delta _{p}(X). \end{equation*}
In this paper, for every weak del Pezzo surface
$S$
with the anti-canonical degree
$\geq 5$
, we compute the local delta invariant at each
$p \in S$
. These results are important in the following aspects:
-
(1) As a directed corollary, we compute the delta invariant for a du Val del Pezzo surface
$\overline{S}$
with the anti-canonical degree
$\geq 5$
. Indeed, let
$\sigma\,:\,S \to \overline{S}$
be its minimal resolution, then for each
$\overline{p} \in \overline{S}$
, we can immediately giveTherefore, we get
\begin{equation*}\delta _{\overline {p}}(\overline {S})= \inf _{\substack {p \in S\\ \sigma (p)=\overline {p}}} \delta _{p}(S).\end{equation*}
$\delta (\overline{S})=\delta (S)$
for any du Val del Pezzo surface
$\overline{S}$
with the anti-canonical degree
$\geq 5$
.
-
(2) The estimation of the local delta invariant of weak del Pezzo surfaces is useful for the K-stability of higher dimensional Fano varieties. In fact, the estimation of the local delta invariant of the quintic del Pezzo surfaces plays a crucial role in determining the K-stability of certain Fano
$3$
-folds in [Reference Cheltsov, Fujita, Kishimoto and Okada5, Lemma 24, 25]. Our results are useful for determining the K-stability of other higher dimensional Fano varieties.
The (global) delta invariants of del Pezzo surfaces (the case
$-K_{S}$
is ample) are exhibited in the book [Reference Araujo, Castravet and Cheltsov2, Table 2.1]. Denisova [Reference Denisova8] has also independently computed (global) delta invariants of all Du Val del Pezzo surfaces of anti-canonical degree
$\geq 4$
.
Now, the main results can be stated as follows. Let
$S$
be a weak del Pezzo surface with the anti-canonical degree
$\geq 5$
, let
$E_1, \dots, E_k$
be
$({-}1)$
-curves in
$S$
, let
$F_1, \dots, F_r$
be
$({-}2)$
-curves in
$S$
. We present the local delta invariants of weak del Pezzo surfaces with the anti-canonical degree
$\geq 5$
. We note that each surface is uniquely determined by the configuration of
$({-}1)$
and
$({-}2)$
curves (see [Reference Dolgachev9, §8]). We refer to some papers [Reference Cheltsov and Prokhorov6, Reference Coray and Tsfasman7, Reference Dolgachev9] for the basic properties of these surfaces.
At first, we present the local delta invariants of weak del Pezzo surfaces of degree
$5$
. It is known that there exist
$7$
types of the configuration of negative curves.
Theorem 1.1.
The local delta invariant
$\delta _{p}(S)$
of
$S$
at
$p \in S$
is as follows.
-
(1) If the configuration of negative curves on
$S$
is
then the local delta invariant
$\delta _{p}(S)$
of
$S$
at
$p \in S$
is as follows.
-
(2) If the configuration of negative curves on
$S$
is
then the local delta invariant
$\delta _{p}(S)$
of
$S$
at
$p \in S$
is as follows.
-
(3) If the configuration of negative curves on
$S$
is
then the local delta invariant
$\delta _{p}(S)$
of
$S$
at
$p \in S$
is as follows.
-
(4) If the configuration of negative curves on
$S$
is
then the local delta invariant
$\delta _{p}(S)$
of
$S$
at
$p \in S$
is as follows.
-
(5) If the configuration of negative curves on
$S$
is
then the local delta invariant
$\delta _{p}(S)$
of
$S$
at
$p \in S$
is as follows.
-
(6) If the configuration of negative curves on
$S$
is
then the local delta invariant
$\delta _{p}(S)$
of
$S$
at
$p \in S$
is as follows.
-
(7) If
$S$
is a del Pezzo surface with the anti-canonical degree
$5$
, then the local delta invariants
$\delta _{p}(S)$
of
$S$
at
$p \in S$
is as follows.
We present the local delta invariants of weak del Pezzo surfaces with the anti-canonical degree
$6$
. It is known that there exist
$6$
types of the configuration of negative curves ([Reference Coray and Tsfasman7]).
Theorem 1.2.
The local delta invariant at
$p \in S$
is as follows.
-
(1) If the configuration of negative curves on
$S$
is
then the local delta invariant
$\delta _{p}(S)$
of
$S$
at
$p \in S$
is as follows.
-
(2) If the configuration of negative curves on
$S$
is
then the local delta invariant
$\delta _{p}(S)$
of
$S$
at
$p \in S$
is as follows.
-
(3) If the configuration of negative curves on
$S$
is
then the local delta invariant
$\delta _{p}(S)$
of
$S$
at
$p \in S$
is as follows.
-
(4) If the configuration of negative curves on
$S$
is
then the local delta invariant
$\delta _{p}(S)$
of
$S$
at
$p \in S$
is as follows.
-
(5) If the configuration of negative curves on
$S$
is
then the local delta invariant
$\delta _{p}(S)$
of
$S$
at
$p \in S$
is as follows.
-
(6) If
$S$
is a del Pezzo surface with the anti-canonical degree
$6$
, then the local delta invariant
$\delta _{p}(S)$
of
$S$
at
$p \in S$
is as follows.
We present the local delta invariants of weak del Pezzo surfaces with the anti-canonical degree
$7$
. It is known that there exist
$2$
types of the configuration of negative curves ([Reference Coray and Tsfasman7], [Reference Dolgachev9, §8.4]).
Theorem 1.3.
The local delta invariant at
$p \in S$
is as follows.
-
(1) If the configuration of negative curves on
$S$
is
then the local delta invariant
$\delta _{p}(S)$
of
$S$
at
$p \in S$
is as follows.
-
(2) Let
$S$
be a del Pezzo surface with the anti-canonical degree
$7$
. If the configuration of negative curves on
$S$
is
then the local delta invariant
$\delta _{p}(S)$
of
$S$
at
$p \in S$
is as follows.
We present the local delta invariants for weak del Pezzo surfaces of the anti-canonical degree
$8$
. Denote by
$\pi\,:\,\Sigma _n \to \mathbb{P}^1$
the
$n$
-th Hirzebruch surface. Let
$C_0$
be the section of
$\pi$
with
$C_0^2=-n$
and
$\Gamma$
the fiber of
$\pi$
. It is known that a weak del Pezzo surface of the anti-canonical degree
$8$
is either
$\Sigma _0$
,
$\Sigma _1$
or
$\Sigma _2$
( [Reference Coray and Tsfasman7], [Reference Dolgachev9, §8.4]).
Theorem 1.4.
Let
$S$
be a weak del Pezzo surface of the anti-canonical degree
$8$
.
-
(1) If
$S = \Sigma _2$
, then for any point
$p \in S$
, it holds that
\begin{equation*} \delta _{p}(S)=\frac{3}{4}. \end{equation*}
-
(2) If
$S = \Sigma _1$
, then for any point
$p \in S$
, it holds that
\begin{equation*} \delta _{p}(S)= \begin{cases} \frac{6}{7} & \text{if $p \in C_0$,} \\ \frac{12}{13} & \text{if $p \in S \setminus C_0 . $} \end{cases} \end{equation*}
-
(3) If
$S = \Sigma _0=\mathbb{P}^1 \times \mathbb{P}^1$
, then for any point
$p \in S$
, it holds that
\begin{equation*} \delta _{p}(S)=1. \end{equation*}
Notation
In this paper, we tacitly use the following notations.
-
• The symbol
$\sim$
means the linearly equivalence between Cartier divisors. -
• We denote by
$H$
a general hyperplane of
$\mathbb{P}^2$
. -
• We denote by
$\overline{pq}$
the line on
$\mathbb{P}^2$
passing through two distinct points
$p,q \in \mathbb{P}^2$
. -
• We denote by
$\mathrm{Bl}_{\{q_1, \cdots, q_k\}}\mathbb{P}^2$
the surface obtained by the composition of the blowing-ups at
$k$
distinct points
$ q_1, \cdots, q_k \in \mathbb{P}^2$
. -
• Let
$ \sigma\,:\,Y \to X$
be a birational morphism between projective varieties. For a Cartier divisor
$D$
on
$X$
, we denote by
$\sigma _{\ast }^{-1}D$
the proper transform of it.
2. Scheme of the proof
We fix the notations for this section. Let
$S$
be a weak del Pezzo surface with the anti-canonical degree
$\geq 5$
, let
$E_1, \dots, E_k$
be
$({-}1)$
-curves in
$S$
, let
$F_1, \dots, F_r$
be
$({-}2)$
-curves in
$S$
and let
$p$
be a point in
$S$
.
We explain how to estimate
$\delta _{p}(S)$
. Fix a smooth curve
$C$
on
$S$
that passes through
$p$
. Let
$ \tau \,:\!=\, \mathrm{sup} \{ u \in \mathbb{Q}_{\geq 0}\mid -K_{S}-uC \text{ is big } \}$
, let
$P(u)+N(u)$
be the Zariski decomposition of
$-K_{S}-uC$
. By the definition of
$\delta _{p}(S)$
, we note that
$\delta _{p}(S) \leq 1/S(C)$
. So we explain how to estimate
$\delta _{p}(S)$
from the below using these data and Abban-Zhuang Theory. Set
\begin{equation*} S(W_{\bullet, \bullet }^{C},p)\,:\!=\, \frac {2}{({-}K_{S})^2} \int _{0}^{\tau }(P(u)\cdot C)\cdot \mathrm {ord}_{p}N(u)|_{C}\; du + \frac {1}{({-}K_{S})^2} \int _{0}^{\tau } (P(u)\cdot C)^2 du. \end{equation*}
Then it follows from [Reference Araujo, Castravet and Cheltsov2, Theorem 1.106],
\begin{align} \delta _{p}(S) \geq \mathrm{min}\left \{\frac{1}{S(C)},\frac{1}{S(W_{\bullet, \bullet }^{C},p)} \right \}. \end{align}
If
$p$
is contained in a
$({-}1)$
-curve or
$({-}2)$
-curve, we always choose
$C$
to be one of these curves. In many cases, these estimates actually compute
$\delta _{p}(S)$
. If
$p$
is not contained in any
$({-}1)$
-curve and any
$({-}2)$
-curve, then we have to consider the (ordinary) blowing up
$\sigma\,:\,\widetilde{S} \to S$
at the point
$p \in S$
. Let
$Z$
be a exceptional curve over
$p$
, let
$\widetilde{\tau } \,:\!=\, \mathrm{sup} \{ u \in \mathbb{Q}_{\geq 0}\mid \sigma ^{\ast }({-}K_{S})-uZ \text{ is big } \}$
and let
$\widetilde{P}(u)+\widetilde{N}(u)$
be the Zariski decomposition of
$\sigma ^{\ast }({-}K_{S})-uZ$
. By the definition of
$\delta _{p}(S)$
, we note that
$\delta _{p}(S) \leq 2/S(Z)$
. For
$q \in Z$
, set
\begin{equation*} S(W_{\bullet, \bullet }^{Z},q)\,:\!=\, \frac {2}{({-}K_{S})^2} \int _{0}^{\widetilde {\tau }}(\widetilde {P}(u)\cdot Z)\cdot \mathrm {ord}_{q}\widetilde {N}(u)|_{Z}\; du + \frac {1}{({-}K_{S})^2} \int _{0}^{\widetilde {\tau }} (\widetilde {P}(u)\cdot Z)^2 du. \end{equation*}
Then it follows from [Reference Araujo, Castravet and Cheltsov2, Theorem 1.106],
\begin{align} \delta _{p}(S) \geq \mathrm{min}\left \{\frac{2}{S(E)},\underset{q \in Z}{\mathrm{inf}}\frac{1}{S(W_{\bullet, \bullet }^{Z},q)} \right \}. \end{align}
These estimates compute
$\delta _{p}(S)$
in every case except for one special case. In this special case, we use a
$(0)$
-curve
$C$
in
$S$
that passes through
$p$
to compute
$\delta _{p}(S)$
. Combining with what we already have, we get equality for
$\delta _{p}(S)$
.
So from now on, we just need to compute
$\tau, P(u), N(u)$
and
$S(W_{\bullet, \bullet }^{C},p)$
for
$C$
being
$({-}1)$
-curves or
$({-}2)$
-curves passing through
$p$
. If
$p$
is not contained in any of these curves, we have to compute either
$\widetilde{\tau }, \widetilde{P}(u), \widetilde{N}(u)$
and
$S(W_{\bullet, \bullet }^{Z},q)$
for exceptional curve
$Z$
or
$\tau, P(u), N(u)$
and
$S(W_{\bullet, \bullet }^{C},p)$
for a
$(0)$
-curve
$C$
that passes through
$p$
. This will be done in the next sections.
In what follows, we will write every
$\mathbb{R}$
-divisor
\begin{equation*} D \sim _{\mathbb {R}} \sum _{i=1}^{k}a_{i}E_{i}+ \sum _{j=1}^{r}b_{j}F_{j} \end{equation*}
as
$(a_1, \dots, a_k, b_1, \dots, b_r)$
. To ease notation, we rewrite
$(\overbrace{a,\cdots, a}^{l \text{ times}}, \overbrace{b,\cdots, b}^{m \text{ times}},\overbrace{c,\cdots, c}^{n \text{ times}})$
as
$(\overset{l}{a},\overset{m}{b}, \overset{n}{c})$
. Denote by
$A$
the intersection matrix of
$E_1, \cdots, E_k, F_1, \cdots, F_r$
:
\begin{equation*}A\,:\!=\, \left ( \begin {array}{ccc|ccc} E_{1}^2 & & E_k E_1 & F_1 E_1 & & F_r E_1 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ E_1 E_k & & E_{k}^2 & F_1 E_k & & F_r E_k \\ \hline E_1 F_1 & & E_k F_1 & F_{1}^2 & & F_r F_1 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ E_1 F_r & & E_k F_r & F_1 F_r & & F_r F_r \end {array} \right ). \end{equation*}
We mention that for a curve
$C$
being one of the curves
$E_1, \cdots E_k, F_1, \cdots F_r$
, we can immediately compute
$\tau$
,
$P(u)$
, and
$N(u)$
using
$(a_1, \dots, a_k, b_1, \dots, b_r)$
and the matrix
$A$
, since
$({-}1)$
-curves and
$({-}2)$
curves generate the Kleiman–Mori cone if
$K_{S}^2 \neq 8$
.
3. The case of the anti-canonical degree
$5$
Let us use the assumptions and notations of Section 2. Suppose
$K^2=5$
Proposition 3.1.
Suppose that the dual graph of the
$({-}1)$
-curves and
$({-}2)$
-curves on
$S$
is same as in Theorem 1.1 (1). Then the local delta invariant
$\delta _{p}(S)$
is as follows.
Proof. We recall the construction of
$S$
. Take non-colinear three points
$q_{0}, q_{1}, q_{3} \in \mathbb{P}^{2}$
and
$q_{2} \in \overline{q_{1}q_{3}}\setminus \{q_1,q_3\}$
. Then
$S$
is obtained by
$\rho : S = \mathrm{Bl}_{\{q_{1}, q_{2}, q_{3}, q_{4}\}}\mathbb{P}^{2} \to \mathbb{P}^2$
. Moreover, we have
$F=\rho ^{-1}_{\ast }\overline{q_1 q_3}$
,
$E_1 = \rho ^{-1}(q_1)$
,
$E_2 = \rho ^{-1}(q_2)$
,
$E_3 = \rho ^{-1}(q_3)$
,
$E_4 = \rho ^{-1}_{\ast }(\overline{q_0 q_1})$
,
$E_5 = \rho ^{-1}_{\ast }(\overline{q_0 q_2})$
,
$E_6 = \rho ^{-1}_{\ast }(\overline{q_0 q_3})$
and
$E_7 = \rho ^{-1}(q_0)$
. We denote a divisor by
$D=(a_1,a_2,a_3,a_4,a_5,a_6,a_7,b)$
. The intersection matrix of
$\{E_1, E_2, E_3, E_4, E_5, E_6, E_7, F \}$
is
\begin{equation*}A\,:\!=\, \left ( \begin {array}{ccccccc|c} -1 & 0 & 0 & 1 & 0 & 0 & 0 & 1 \\ 0 & -1 & 0 & 0 & 1 & 0 & 0 & 1 \\ 0 & 0 & -1 & 0 & 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & -1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & -1 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & -1 & 1 & 0 \\ 0 & 0 & 0 & 1 & 1 & 1 & -1 & 0 \\ \hline 1 & 1 & 1 & 0 & 0 & 0 & 0 & -2 \end {array} \right ). \end{equation*}
We note that
$-K_{S}\sim (0,0,0,1,1,1,2,0)=(\overset{3}{0},\overset{3}{1},2,0)$
.
(1) The case
$p \in F$
. Set
$C=F$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Hence we get
\begin{align*} S(F)=\frac{17}{15}, \quad S(W_{\bullet, \bullet }^{F},p) &=\begin{cases} \frac{11}{15} & \text{if $p \in E_{i}\cap F $ for $i=1,2,3$},\\ & \\ \frac{7}{15} & \text{if $p \in F \setminus \bigcup _{i=1}^{3} E_{i}$}. \\ \end{cases} \end{align*}
Therefore, we have
\begin{align*} \frac{A_{S}(F)}{S(F)}=\frac{15}{17} \geq \delta _{p}(S) \geq \mathrm{min}\left \{ \frac{1}{S(F)}, \frac{1}{S(W_{\bullet, \bullet }^{F},p)} \right \} = \frac{15}{17} \end{align*}
from (1). Thus, we have
$\delta _{p}(S)= 15/17$
in this case.
(2) The case
$p \in E_{i} \setminus (F \cup E_{i+3})$
for
$i=1,2,3$
. Set
$C=E_1$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following table:
Hence we get
$S(E_1)=1$
and
$S(W_{\bullet, \bullet }^{E_{1}},p) = 19/30$
. Therefore, we have
\begin{align*} 1 \geq \delta _{p}(S) \geq \mathrm{min}\left \{ \frac{1}{S(E_1)}, \frac{1}{S(W_{\bullet, \bullet }^{E_1},p)} \right \} = 1. \end{align*}
We can show
$\delta _{p}(S)= 1$
for
$p \in E_{i} \setminus (F \cup E_{i+3}) (i=2,3)$
by the same calculation.
(3) The case
$p \in E_{i}\setminus E_7$
$(i=4,5,6)$
. Set
$C=E_4$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Hence we get
\begin{align*} S(E_4)=\frac{13}{15}, \quad S(W_{\bullet, \bullet }^{E_{4}},p) &= \begin{cases} 1 & \text{if $p \in (E_{1} \cap E_{4})$},\\ & \\ \frac{11}{15} & \text{if $p \in E_{4}\setminus (E_1 \cup E_{7}) $}. \\ \end{cases} \end{align*}
Therefore, we have
$\delta _{p}(S)= 15/13$
for
$p \in E_{4}\setminus (E_1 \cup E_{7})$
. If
$\{p\}=E_{1} \cap E_{4}$
, we have
$1=S(E_1) \geq \delta _{p}(S)$
by the calculation in (2). Thus, we have
\begin{align*} \delta _{p}(S)= \begin{cases} 1 & \text{if $p \in (E_{1} \cap E_{4})$},\\ & \\ \frac{15}{13} & \text{if $p \in E_{4}\setminus (E_1 \cup E_{7}) $}. \\ \end{cases} \end{align*}
We can show
\begin{align*} \delta _{p}(S)= \begin{cases} 1 & \text{if $p \in (E_{i-3} \cap E_{i})$},\\ & \\ \frac{15}{13} & \text{if $p \in E_{i}\setminus (E_{i-3} \cup E_{7}) $}, \\ \end{cases} \end{align*}
for
$i=5,6$
by the same calculation.
(4) The case
$p \in E_{7}$
. Set
$C=E_7$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Hence we get
\begin{align*} S(E_7)=\frac{13}{15}, \quad S(W_{\bullet, \bullet }^{E_{7}},p) &= \begin{cases} \frac{13}{15} & \text{if $p \in E_{i}\cap E_{7} $ for $i=4,5,6$},\\ & \\ \frac{11}{15} & \text{if $p \in E_{7} \setminus \bigcup _{i=4}^{6} E_{i}$}. \\ \end{cases} \end{align*}
Therefore, we have
\begin{align*} \frac{15}{13} \geq \delta _{p}(S) \geq \mathrm{min}\left \{ \frac{1}{S(E_7)}, \frac{1}{S(W_{\bullet, \bullet }^{E_7},p)} \right \} = \frac{15}{13}. \end{align*}
from (1). Thus, we have
$\delta _{p}(S)= 15/13$
in this case.
(5) The case
$p \in S \setminus \left (F \cup \bigcup _{i=1}^{7} E_{i} \right )$
. Consider a blowing up
$\sigma :\widetilde{S} \to S$
at
$p$
. Let
$\widetilde{F}$
and
$\widetilde{E}_{i}$
be the proper transform of
$F$
and
$E_{i}$
, respectively. Put
$G_{i}\,:\!=\,(\rho \sigma )_{\ast }^{-1}\overline{\rho (p)q_i}$
for
$i=0,1,2,3$
. Then we have
$\sigma ^{\ast }({-}K_{S})-uZ \sim G_0 + G_2 + \widetilde{F} + \widetilde{E}_2 + (2-u)Z$
and
$\widetilde{\tau } = 5/2$
. The values
$\widetilde{P}(u)$
,
$\widetilde{N}(u)$
,
$\widetilde{P}(u)^2$
,
$\widetilde{P}(u)\cdot Z$
and
$\mathrm{ord}_{q}(\widetilde{N}(u)|_{Z})$
are given by the following tables:
Therefore, we get
\begin{align*} S(Z) =\frac{3}{2}, \quad S(W_{\bullet, \bullet }^{Z},q) &= \begin{cases} \frac{11}{15} & \text{if $q \in Z \cap G_0 $},\\ & \\ \frac{7}{10} & \text{if $q \in Z\cap G_i$ for $i=1,2,3$}, \\ & \\ \frac{2}{3} & \text{if $q \in Z \setminus \bigcup _{i=0}^{3} G_{i}$}. \\ \end{cases} \end{align*}
Hence, we have
\begin{align*} \frac{4}{3} \geq \delta _{p}(S) \geq \mathrm{min}\left \{ \frac{2}{S(Z)}, \underset{q \in Z}{\mathrm{inf}}\frac{1}{S(W_{\bullet, \bullet }^{Z},q)} \right \} = \frac{4}{3} \end{align*}
from (2). Thus, we have
$\delta _{p}(S)= 4/3$
in this case.
Proposition 3.2.
Suppose that the dual graph of the
$({-}1)$
-curves and
$({-}2)$
-curves on
$S$
is same as in Theorem 1.1 (2). Then the local delta invariant
$\delta _{p}(S)$
is as follows.
Proof. We can assume that we get
$S$
from
$\mathbb{P}^2$
as follows.
-
(1) Let
$\rho _{1}:S_{1}=\mathrm{Bl}_{\{q_{1}, q_{2}, q_{3}\}}\mathbb{P}^{2} \to \mathbb{P}^2$
be a blowing-up at non-colinear points
$q_1$
,
$q_2$
,
$q_3$
. -
(2) Let
$q_4$
be a point at which
$\rho _{1}^{-1}(q_4)$
and
$(\rho _{1})_{\ast }^{-1}\overline{q_1 q_2}$
meet. Take a blowing-up
$\rho _{2}: S_2 \to S_1$
at
$q_4$
. Then
$S=S_{2}$
. Put
$\rho =\rho _{1} \rho _{2}: S \to \mathbb{P}^2$
.
Moreover, we have
$E_{1}= \rho _{2}^{-1}(q_4)$
,
$E_2 = \rho ^{-1}(q_2)$
,
$E_{3}=\rho ^{-1}_{\ast }(\overline{q_2 q_3})$
,
$E_4=\rho ^{-1}(q_3)$
,
$E_5 = \rho ^{-1}_{\ast }(\overline{q_3 q_1})$
,
$F_1= \rho ^{-1}_{\ast }(\overline{q_1 q_2})$
and
$F_2 = (\rho _{2})^{-1}_{\ast }(\rho _{1}^{-1}(q_1))$
. We denote a divisor
$D=\sum _{i=1}^{5}a_{i} E_{i} + \sum _{j=1}^{2}b_{j}F_{j} \in \mathrm{Div}(S)$
(
$a_i, b \in \mathbb{Z}$
) by
$D=(a_1,a_2,a_3,a_4,a_5,b_1, b_2)$
. The intersection matrix of
$\{E_1, E_2, E_3, E_4, E_5, F_1, F_2 \}$
is
\begin{equation*}A\,:\!=\, \left ( \begin {array}{ccccc|cc} -1 & 0 & 0 & 0 & 0 & 1 & 1 \\ 0 & -1 & 1 & 0 & 0 & 1 & 0 \\ 0 & 1 & -1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & -1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & -1 & 0 & 1 \\ \hline 1 & 1 & 0 & 0 & 0 & -2 & 0 \\ 1 & 0 & 0 & 0 & 1 & 0 & -2 \\ \end {array} \right ). \end{equation*}
We note that
$-K_{S} \sim \sum _{i=1}^{5}E_{i} + \sum _{i=j}^{2}F_{j}=(1,1,1,1,1,1,1)=(\overset{7}{1})$
.
(1) The case
$p \in E_1$
. Set
$C=E_1$
, then we get
$\tau =3$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Therefore, we get
\begin{align*} S(E_1)=\frac{19}{15}, \quad S(W_{\bullet, \bullet }^{E_{1}},p) &= \begin{cases} \frac{17}{15} & \text{if $p \in E_{1}\cap F_{j} $ for $j=1,2$},\\ & \\ \frac{7}{15} & \text{if $p \in E_{1} \setminus \bigcup _{j=1}^{2} F_{j}$}. \\ \end{cases} \end{align*}
Hence we have
\begin{align*} \frac{15}{19} \geq \delta _{p}(S) \geq \mathrm{min}\left \{ \frac{1}{S(E_1)}, \frac{1}{S(W_{\bullet, \bullet }^{E_1},p)} \right \} = \frac{15}{19} \end{align*}
from (1). Thus, we have
$\delta _{p}(S)= 15/19$
in this case.
(2) The case
$p \in F_1\setminus E_1$
. Set
$C=F_1$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Therefore, we get
\begin{align*} S(F_1)=\frac{17}{15}, \quad S(W_{\bullet, \bullet }^{F_{1}},p) &= \begin{cases} 1 & \text{if $p \in F_{1}\cap E_{2} $},\\ & \\ \frac{11}{15} & \text{if $p \in F_{1} \setminus (E_1 \cup E_{2}) $}. \\ \end{cases} \end{align*}
Hence we have
\begin{align*} \frac{15}{17} \geq \delta _{p}(S) \geq \mathrm{min}\left \{ \frac{1}{S(F_1)}, \frac{1}{S(W_{\bullet, \bullet }^{F_1},p)} \right \} = \frac{15}{17} \end{align*}
from (1). Thus, we have
$\delta _{p}(S)= 15/17$
in this case.
(3) The case
$p \in E_2 \setminus F_1$
. Set
$C=E_2$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Therefore, we get
\begin{align*} S(E_2)=1, \quad S(W_{\bullet, \bullet }^{E_{2}},p) &= \begin{cases} \frac{13}{15} & \text{if $p \in E_{2}\cap E_{3} $},\\ & \\ \frac{19}{30} & \text{if $p \in E_{2} \setminus (F_1 \cup E_{3}) $}. \\ \end{cases} \end{align*}
Hence we have
\begin{align*} 1 \geq \delta _{p}(S) \geq \mathrm{min}\left \{ \frac{1}{S(E_2)}, \frac{1}{S(W_{\bullet, \bullet }^{E_2},p)} \right \} = 1 \end{align*}
from (1). Thus, we have
$\delta _{p}(S)= 1$
in this case.
(4) The case
$p \in E_3 \setminus E_2$
. Set
$C=E_3$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Therefore, we get
\begin{align*} S(E_3)=\frac{13}{15}, \quad S(W_{\bullet, \bullet }^{E_{3}},p) &= \begin{cases} \frac{13}{15} & \text{if $p \in E_{3}\cap E_{4} $},\\ & \\ \frac{11}{15} & \text{if $p \in E_{3} \setminus (E_{2} \cup E_{4}) $}. \\ \end{cases} \end{align*}
Hence we have
\begin{align*} \frac{15}{13} \geq \delta _{p}(S) \geq \mathrm{min}\left \{ \frac{1}{S(E_3)}, \frac{1}{S(W_{\bullet, \bullet }^{E_3},p)} \right \} = \frac{15}{13} \end{align*}
from (1). Thus, we have
$\delta _{p}(S)= 15/13$
in this case.
(5) The case
$p \in S \setminus \left ( \bigcup _{i,j}( E_{i} \cup F_{j})\right )$
. Consider a blowing up
$\sigma :\widetilde{S} \to S$
at
$p$
. Let
$\widetilde{E}_{i}$
and
$\widetilde{F}_{j}$
be the proper transform of
$E_{i}$
and
$F_{j}$
, respectively. Put
$G_{i}\,:\!=\,(\rho \sigma )_{\ast }^{-1}\overline{\rho (p)q_i}$
for
$i=1,2,3$
. Then we have
$\sigma ^{\ast }({-}K_{S})-uZ \sim \widetilde{F}_1 + \widetilde{E}_2 + G_2 + G_3+ (2-u)Z$
and
$\widetilde{\tau }=5/2$
. The values
$\widetilde{P}(u)$
,
$\widetilde{N}(u)$
,
$\widetilde{P}(u)^2$
,
$\widetilde{P}(u)\cdot Z$
and
$\mathrm{ord}_{q}(\widetilde{N}(u)|_{Z})$
are given by the following tables:
Therefore, we get
\begin{align*} S(Z)=\frac{3}{2}, \quad S(W_{\bullet, \bullet }^{Z},p) &= \begin{cases} \frac{11}{15} & \text{if $q \in Z \cap G_1 $},\\ & \\ \frac{7}{10} & \text{if $q \in Z\cap \left ( G_2 \cup G_3 \right )$}, \\ & \\ \frac{2}{3} & \text{if $q \in Z \setminus \left (G_1 \cup G_2 \cup G_3\right )$}. \\ \end{cases} \end{align*}
Hence we have
\begin{align*} \frac{4}{3} \geq \delta _{p}(S) \geq \mathrm{min}\left \{ \frac{2}{S(Z)}, \underset{q \in Z}{\mathrm{inf}}\frac{1}{S(W_{\bullet, \bullet }^{Z},q)} \right \} = \frac{4}{3} \end{align*}
from (2). Thus, we have
$\delta _{p}(S)= 4/3$
in this case.
Proposition 3.3.
Suppose that the dual graph of the
$({-}1)$
-curves and
$({-}2)$
-curves on
$S$
is same as in Theorem 1.1 (3). Then the local delta invariant
$\delta _{p}(S)$
is as follows.
Proof. We can assume that we get
$S$
from
$\mathbb{P}^2$
as follows.
-
(1) Take two distinct points
$q_1,q_4 \in \mathbb{P}^2$
and a line
$l (\neq \overline{q_1 q_4})$
passing through
$q_1$
. Let
$\rho _{1}:S_{1}=\mathrm{Bl}_{\{q_{1}, q_{4}\}}\mathbb{P}^{2} \to \mathbb{P}^2$
be a blowing-up at points
$q_1$
,
$q_4$
, let
$l_1 = (\rho _1)^{-1}_{\ast }l$
and let
$q_2$
be a point at which
$l_1$
and
$\rho _{1}^{-1}(q_1)$
meet. -
(2) Let
$\rho _{2}: S_2 \to S_1$
be a blowing-up at
$q_2$
, let
$l_2 = (\rho _2)_{\ast }^{-1}l_1$
and let
$q_3$
be a point at which
$l_2$
and
$\rho _{2}^{-1}(q_2)$
meet. -
(3) Let
$\rho _{3}: S_3 \to S_2$
be a blowing-up at
$q_3$
. Then
$S=S_3$
. Put
$\rho =\rho _1 \rho _2 \rho _3$
.
Moreover, we have
$E_{1}=\rho ^{-1}(q_4)$
,
$E_2 = \rho ^{-1}_{\ast }(\overline{q_1 q_4})$
,
$F_{1}=(\rho _2 \rho _3)^{-1}_{\ast }(\rho _1^{-1}(q_1))$
,
$F_2= (\rho _3)^{-1}_{\ast }(\rho ^{-1}(q_2))$
,
$E_3 =\rho _{3}^{-1}(q_3)$
,
$F_3 = \rho ^{-1}_{\ast }l$
. We denote
$D=\sum _{i=1}^{3}a_{i} E_{i} + \sum _{j=1}^{3}b_{j}F_{j} \in \mathrm{Div}(S)$
(
$a_i, b \in \mathbb{Z}$
) by
$D=(a_1,a_2,a_3, b_1, b_2, b_3)$
. The intersection matrix of
$\{E_1, E_2, E_3, F_1, F_2, F_3 \}$
is
\begin{equation*}A\,:\!=\, \left ( \begin {array}{ccc|ccc} -1 & 1 & 0 & 0 & 0 & 0 \\ 1 & -1 & 0 & 1 & 0 & 0 \\ 0 & 0 & -1 & 0 & 1 & 1 \\ \hline 0 & 1 & 0 & -2 & 1 & 0 \\ 0 & 0 & 1 & 1 & -2 & 0 \\ 0 & 0 & 1 & 0 & 0 & -2 \\ \end {array} \right ). \end{equation*}
We note that
$-K_{S} \sim 2E_1+ 3E_2 + 2F_1 + F_2 = (2,3,0,2,1,0)$
.
(1) The case
$p \in E_1 \setminus E_2$
. Set
$C=E_1$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following table:
So we get
$S(E_1)=13/15$
and
$S(W_{\bullet, \bullet }^{E_{1}},p) = 11/15$
. Thus,
$\delta _{p}(S)= 15/13$
from (1).
(2) The case
$p \in E_2 \setminus F_1$
. Set
$C=E_2$
, then we get
$\tau =3$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Therefore, we get
\begin{align*} S(E_2)=\frac{17}{15}, \quad S(W_{\bullet, \bullet }^{E_{2}},p) &= \begin{cases} \frac{13}{15} & \text{if $p \in E_{2}\cap E_{1}$},\\ & \\ \frac{23}{45} & \text{if $p \in E_{2} \setminus (E_1 \cup F_1) $}. \\ \end{cases} \end{align*}
Thus, we have
$\delta _{p}(S)= 15/17$
from (1).
(3) The case
$p \in F_1 \setminus F_2$
. Set
$C=F_1$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following table:
Therefore, we get
\begin{align*} S(F_1)=\frac{19}{15}, \quad S(W_{\bullet, \bullet }^{F_{1}},p) &= \begin{cases} \frac{17}{15} & \text{if $p \in F_{1}\cap E_{2}$},\\ & \\ \frac{23}{30} & \text{if $p \in F_{1} \setminus (E_2 \cup F_2) $}. \\ \end{cases} \end{align*}
Thus, we have
$\delta _{p}(S)= 15/19$
from (1).
(4) The case
$p \in F_2 \setminus E_3$
. Set
$C=F_2$
, then we get
$\tau =3$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Therefore, we get
\begin{align*} S(F_2)=\frac{7}{5}, \quad S(W_{\bullet, \bullet }^{F_{2}},p) &= \begin{cases} \frac{23}{30} & \text{if $p \in F_{2}\cap F_{1}$},\\ & \\ \frac{8}{15} & \text{if $p \in F_{2} \setminus (E_3 \cup F_1) $}. \\ \end{cases} \end{align*}
Thus, we have
$\delta _{p}(S)= 5/7$
from (1).
(5) The case
$p \in E_3$
. Set
$C=E_3$
, then we get
$\tau =4$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Therefore, we get
\begin{align*} S(E_3)=\frac{23}{15}, \quad S(W_{\bullet, \bullet }^{E_{3}},p) &= \begin{cases} \frac{7}{5} & \text{if $p \in E_{3}\cap F_{2}$},\\ & \\ \frac{17}{15} & \text{if $p \in E_{3}\cap F_{3}$},\\ & \\ \frac{11}{30} & \text{if $p \in E_{3} \setminus (F_2 \cup F_3) $}. \end{cases} \end{align*}
Thus, we have
$\delta _{p}(S)= 15/23$
from (1).
(6) The case
$p \in F_3 \setminus E_3$
. Set
$C=F_3$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
and
$P(u)\cdot C$
are given by the following table:
Moreover,
$\mathrm{ord}_{p}(N(u)|_{C})=0$
. Therefore, we get
$S(F_3)=17/15$
and
$S(W_{\bullet, \bullet }^{F_{3}},p)=17/15$
. Thus, we have
$\delta _{p}(S)= 15/17$
from (1).
(7) The case
$p \in S \setminus \left ( \bigcup _{i,j}( E_{i} \cup F_{j})\right )$
. Consider a blowing up
$\sigma :\widetilde{S} \to S$
at
$p$
. Let
$\widetilde{E}_{i}$
and
$\widetilde{F}_{j}$
be the proper transform of
$E_{i}$
and
$F_{j}$
, respectively. Take two
$({-}1)$
-curves
$G_1 \,:\!=\, (\rho \sigma )_{\ast }^{-1}(\overline{\rho \sigma (p)q_4})$
and
$G_2 \,:\!=\, (\rho \sigma )_{\ast }^{-1}(\overline{\rho \sigma (p)q_1})$
on
$\widetilde{S}$
. Since
$\overline{\rho \sigma (p)q_4}+\overline{\rho \sigma (p)q_1}+l \in |-K_{\mathbb{P}^2}|$
, we have
$\sigma ^{\ast }({-}K_{S})-uE \sim \widetilde{E}_3 + \widetilde{F}_1 + \widetilde{F}_2 + \widetilde{F}_3 + G_1 + G_2 + (2-u)Z$
and
$\widetilde{\tau }=5/2$
. The values
$\widetilde{P}(u)$
,
$\widetilde{N}(u)$
,
$\widetilde{P}(u)^2$
,
$\widetilde{P}(u)\cdot Z$
and
$\mathrm{ord}_{q}(\widetilde{N}(u)|_{Z})$
are given by the following tables:
Therefore, we get
\begin{align*} S(Z)=\frac{3}{2}, \quad S(W_{\bullet, \bullet }^{Z},p) &= \begin{cases} \frac{11}{15} & \text{if $q \in Z \cap G_1 $},\\ & \\ \frac{23}{30} & \text{if $q \in Z\cap G_2 $}, \\ & \\ \frac{2}{3} & \text{if $q \in Z \setminus \left (G_1 \cup G_2 \right )$}. \\ \end{cases} \end{align*}
Hence we have
\begin{align*} \frac{4}{3} \geq \delta _{p}(S) \geq \mathrm{min}\left \{ \frac{2}{S(E)}, \frac{1}{S(W_{\bullet, \bullet }^{E},p)} \right \} = \frac{30}{23}. \end{align*}
We also calculate
$S(G_2)$
. Take
$u \in \mathbb{R}_{\geq 0}$
. Let
$\widetilde{P}(u)+\widetilde{N}(u)$
be the Zariski decomposition of
$\sigma ^{\ast }({-}K_{S})-uG_2$
. The values
$\widetilde{P}(u)$
,
$\widetilde{N}(u)$
and
$\widetilde{P}(u)^2$
are given by the following tables:
Therefore, we get
$S(G_2)=23/30$
by the definition of
$S(G_2)$
. Hence we have
$30/23 \geq \delta _{p}(S)$
. Therefore, we get
$ \delta _{p}(S) = 30/23.$
Proposition 3.4.
Suppose that the dual graph of the
$({-}1)$
-curves and
$({-}2)$
-curves on
$S$
is same as in Theorem 1.1 (4). Then the local delta invariant
$\delta _{p}(S)$
is as follows.
Proof. We can assume that we get
$S$
from
$\mathbb{P}^2$
as follows.
-
(1) Take three distinct co-linear points
$q_1, q_3, q_4 \in \mathbb{P}^2$
and a line
$l (\neq \overline{q_1q_3})$
passing through
$q_1$
. Let
$\rho _{1}:S_{1}=\mathrm{Bl}_{\{q_{1}, q_3, q_{4}\}}\mathbb{P}^{2} \to \mathbb{P}^2$
be a blowing-up at points
$q_1$
,
$q_3$
,
$q_4$
, and let
$q_2 \in S_1$
be a point at which of
$(\rho _{1})^{-1}_{\ast }l$
and
$\rho _{1}^{-1}(q_1)$
meet. -
(2) Let
$\rho _{2}: S_2 \to S_1$
be a blowing-up at
$q_2$
. Then
$S=S_2$
. Put
$\rho =\rho _1 \rho _2$
.
Moreover, we have
$E_{1}=\rho _{\ast }^{-1}l$
,
$E_2 = \rho _{2}^{-1}(q_2)$
,
$F_{1}=(\rho _2)^{-1}_{\ast }(\rho _1^{-1}(q_1))$
,
$F_2= (\rho )^{-1}_{\ast }(\overline{q_1 q_3})$
,
$E_3 =\rho ^{-1}(q_3)$
,
$E_4 =\rho ^{-1}(q_4)$
. We denote
$D=\sum _{i=1}^{4}a_{i} E_{i} + \sum _{j=1}^{2}b_{j}F_{j} \in \mathrm{Div}(S)$
(
$a_i, b \in \mathbb{Z}$
) by
$D=(a_1,a_2,a_3,a_4, b_1, b_2)$
. The intersection matrix of
$\{E_1, E_2, E_3, E_4, F_1, F_2 \}$
is
\begin{equation*}A\,:\!=\, \left ( \begin {array}{cccc|cc} -1 & 1 & 0 & 0 & 0 & 0 \\ 1 & -1 & 0 & 0 & 1 & 0 \\ 0 & 0 & -1 & 0 & 0 & 1 \\ 0 & 0 & 0 & -1 & 0 & 1 \\ \hline 0 & 1 & 0 & 0 & -2 & 1 \\ 0 & 0 & 1 & 1 & 1 & -2 \\ \end {array} \right ). \end{equation*}
We note that
\begin{equation*} -K_{S} \sim 2E_1+ 3E_2 + 2F_1 + F_2 = \left (2, 3, \overset {2}{0}, 2, 1\right ). \end{equation*}
(1) The case
$p \in E_1 \setminus E_2$
. Set
$C=E_1$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
and
$P(u)\cdot C$
is given by the following table:
So we get
$S(E_1)=13/15$
and
$S(W_{\bullet, \bullet }^{E_{1}},p)=11/15$
. Thus,
$\delta _{p}(S)= 15/13$
from (1).
(2) The case
$p \in E_2 \setminus F_1$
. Set
$C=E_2$
, then we get
$\tau =3$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Therefore, we get
\begin{align*} S(E_2)=\frac{17}{15}, \quad S(W_{\bullet, \bullet }^{E_{2}},p) &= \begin{cases} \frac{13}{15} & \text{if $p \in E_{2}\cap E_{1}$},\\ & \\ \frac{23}{45} & \text{if $p \in E_{2} \setminus (E_1 \cup F_1) $}. \\ \end{cases} \end{align*}
Thus, we have
$\delta _{p}(S)= 15/17$
from (1).
(3) The case
$p \in F_1 \setminus F_2$
. Set
$C=F_1$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Therefore, we get
\begin{align*} S(F_1)=\frac{19}{15}, \quad S(W_{\bullet, \bullet }^{F_{1}},p) &= \begin{cases} \frac{17}{15} & \text{if $p \in F_{1}\cap E_{2}$},\\ & \\ \frac{23}{30} & \text{if $p \in F_{1} \setminus (E_2 \cup F_2) $}. \\ \end{cases} \end{align*}
Thus, we have
$\delta _{p}(S)= 15/19$
from (1).
(4) The case
$p \in F_2$
. Set
$C=F_2$
, then we get
$\tau =3$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Therefore, we get
\begin{align*} S(F_2)=\frac{7}{5}, \quad S(W_{\bullet, \bullet }^{F_{2}},p)= \begin{cases} \frac{19}{15} & \text{if $p \in (F_{1}\cap F_2) $ },\\ & \\ \frac{31}{30} & \text{if $p \in F_{2} \cap E_i (i =3, 4) $}, \\ & \\ \frac{8}{15} &\text{if $p \in F_{2} \setminus (F_1 \cup E_3 \cup E_4) $}.\\ \end{cases} \end{align*}
Thus, we have
$\delta _{p}(S)= 5/7$
from (1).
(5) The case
$p \in E_3 \setminus F_2$
. Set
$C=E_3$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
and
$P(u)\cdot C$
is given by the following table:
Moreover,
$\mathrm{ord}_{p}(N(u)|_{C})=0$
. Therefore, we get
$S(E_3)=31/30$
and
$S(W_{\bullet, \bullet }^{E_{3}},p) = 19/30$
. Thus, we have
$\delta _{p}(S)= 30/31$
from (1).
(6) The case
$p \in S \setminus \left ( \bigcup _{i,j}( E_{i} \cup F_{j})\right )$
. Set
$C= \rho ^{-1}_{\ast }\overline{\rho (p)q_1}$
. We note that
$C \in |\rho ^{\ast }H-E_{2} -F_{1}|$
and
$C \sim E_1 + E_2$
. Hence we have
$-K_{S}-uC \sim (2-u)E_{1} + (3-u)E_{2} + 2 F_1 + F_2=\left (2-u, 3-u, \overset{2}{0}, 2, 1\right )$
and
$\widetilde{\tau } = 2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
and
$P(u)\cdot C$
is given by the following table:
Moreover,
$\mathrm{ord}_{p}(N(u)|_{C})=0$
. Therefore, we get
$S(C)=23/30$
and
$S(W_{\bullet, \bullet }^{C},p)=22/30$
. Thus, we have
$\delta _{p}(S)= 30/23$
from (1).
Proposition 3.5.
Suppose that the dual graph of the
$({-}1)$
-curves and
$({-}2)$
-curves on
$S$
is same as in Theorem 1.1 (5). Then the local delta invariant
$\delta _{p}(S)$
is as follows.
Proof. We can assume that we get
$S$
from
$\mathbb{P}^2$
as follows.
-
(1) Take two distinct points
$q_1, q_4 \in \mathbb{P}^2$
. Let
$\rho _{1}:S_{1}=\mathrm{Bl}_{\{q_{1}, q_{4}\}}\mathbb{P}^{2} \to \mathbb{P}^2$
be the composition of blowing-ups at points
$q_1$
,
$q_4$
and let
$q_2 \in S_1$
be the point at which
$(\rho _1)^{-1}_{\ast }(\overline{q_1 q_4})$
and
$\rho _{1}^{-1}(q_1)$
meet. -
(2) Let
$\rho _{2}: S_2 \to S_1$
be a blowing-up at
$q_2$
. Take a point
\begin{equation*} q_3 \in \rho _{2}^{-1}(q_2) \setminus \left ((\rho _1 \rho _2)^{-1}_{\ast }(\overline {q_1 q_4}) \cup (\rho _2)^{-1}_{\ast }\left (\rho _{1}^{-1}(q_1)\right ) \right ). \end{equation*}
-
(3) Let
$\rho _{3}: S_3 \to S_2$
be a blowing-up at
$q_3$
. Then
$S=S_3$
. Put
$\rho =\rho _1 \rho _2 \rho _3$
.
Moreover, we have
$E_{1}=(\rho _2 \rho _3)^{-1}_{\ast }(\rho _1^{-1}(q_4))$
,
$F_1 = \rho ^{-1}_{\ast }(\overline{q_1 q_4})$
,
$F_2= (\rho _3)^{-1}_{\ast }(\rho _2^{-1}(q_2))$
,
$F_3 =(\rho _2 \rho _3)^{-1}_{\ast }(\rho _1^{-1}(q_1))$
,
$E_2 =\rho _{3}^{-1}(q_3)$
. by
$D=(a_1,a_2, b_1, b_2, b_3)$
. The intersection matrix of
$\{E_1, E_2, F_1, F_2, F_3 \}$
is
\begin{equation*}A\,:\!=\, \left ( \begin {array}{cc|ccc} -1 & 0 & 1 & 0 & 0 \\ 0 & -1 & 0 & 1 & 0 \\ \hline 1 & 0 & -2 & 1 & 0 \\ 0 & 1 & 1 & -2 & 1 \\ 0 & 0 & 0 & 1 & -2 \\ \end {array} \right ). \end{equation*}
We note that
$ -K_{S} \sim 2E_1+ 3E_2 + 3F_1 + 4F_2 + 2F_3 = (2,3,3,4,2).$
(1) The case
$p \in E_1 \setminus F_1$
. Set
$C=E_1$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Therefore, we get
$S(E_1)=16/15$
and
$S(W_{\bullet, \bullet }^{E_{1}},p)=4/5$
. Thus, we have
$\delta _{p}(S)= 15/16$
.
(2) The case
$p \in F_1 \setminus F_2$
. Set
$C=F_1$
, then we get
$\tau =3$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Therefore, we get
\begin{align*} S(F_1)=\frac{43}{30}, \quad S(W_{\bullet, \bullet }^{F_{1}},p) =\begin{cases} \frac{16}{15} & \text{if $p \in (F_{1}\cap E_1)$},\\ & \\ \frac{49}{90} &\text{if $p \in F_{1} \setminus (E_1\cup F_2) $}.\\ \end{cases} \end{align*}
Thus, we have
$\delta _{p}(S)= 30/43$
.
(3) The case
$p \in F_2$
. Set
$C=F_2$
, then we get
$\tau =3$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Therefore, we get
\begin{align*} S(F_2)=\frac{9}{5}, \quad S(W_{\bullet, \bullet }^{F_{2}},p) = \begin{cases} \frac{13}{10} & \text{if $p \in (F_{2}\cap F_3)$},\\ & \\ \frac{43}{30} & \text{if $p \in (F_{2} \cap F_1)$}, \\ & \\ \frac{19}{15} & \text{if $p \in (F_{2} \cap E_2)$}, \\ & \\ \frac{2}{5} &\text{if $p \in F_{2} \setminus ( E_2 \cup F_1\cup F_3) $}.\\ \end{cases} \end{align*}
Thus, we have
$\delta _{p}(S)= 5/9$
.
(4) The case
$p \in E_2 \setminus F_2$
. Set
$C=E_2$
, then we get
$\tau =3$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
and
$P(u)\cdot C$
are given by the following table:
Moreover,
$\mathrm{ord}_{p}(N(u)|_{C})=0$
. Therefore, we get
$S(E_2)=19/15$
and
$S(W_{\bullet, \bullet }^{E_{2}},p)= 7/15$
. Thus, we have
$\delta _{p}(S)= 15/19$
from (1).
(5) The case
$p \in F_3 \setminus F_2$
. Set
$C=F_3$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
and
$P(u)\cdot C$
are given by the following table:
Moreover,
$\mathrm{ord}_{p}(N(u)|_{C})=0$
. Therefore, we get
$S(F_3)=13/10$
and
$S(W_{\bullet, \bullet }^{F_{3}},p) = 4/5$
. Thus, we have
$\delta _{p}(S)= 10/13$
from (1).
(6) The case
$p \in S \setminus \left ( \bigcup _{i,j}( E_{i} \cup F_{j})\right )$
. Let
$C\,:\!=\, \rho _{\ast }^{-1} \overline{\rho (p)q_1}$
. We note that
$C \in |\rho ^{\ast }H-E_{2} -F_{2} - F_{3}|$
and
$C \sim E_1 + E_2 + F_1 + F_2$
. Hence we have
$-K_{S}-uC \sim (2-u)E_{1} + (3-u)E_{2} + (3-u) F_1 + (4-u) F_2 + 2F_3$
and
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following table:
Therefore, we get
$S(C)=4/5$
and
$S(W_{\bullet, \bullet }^{C},p)= 7/10$
. We have
$\delta _{p}(S)= 5/4$
.
Proposition 3.6.
Suppose that the dual graph of the
$({-}1)$
-curves and
$({-}2)$
-curves on
$S$
is same as in Theorem 1.1 (6). Then the local delta invariant
$\delta _{p}(S)$
is as follows.
Proof. We can assume that we get
$S$
from
$\mathbb{P}^2$
as follows.
-
(1) Take a point
$q_1 \in \mathbb{P}^2$
and a line
$l$
passing through
$q_1$
. Let
$\rho _{1}:S_{1}=\mathrm{Bl}_{\{q_{1}\}}\mathbb{P}^{2} \to \mathbb{P}^2$
be the blowing-up at point
$q_1$
, and let
$q_2 \in S_1$
be the point at which
$(\rho _1)^{-1}_{\ast }l$
and
$\rho _{1}^{-1}(q_1)$
meet. -
(2) Let
$\rho _{2}: S_2 \to S_1$
be a blowing-up at
$q_2$
and let
$q_3 \in S_2$
be the point at which
$(\rho _1 \rho _2)^{-1}_{\ast }l$
and
$\rho _{2}^{-1}(q_2)$
meet. -
(3) Let
$\rho _{3}: S_3 \to S_2$
be a blowing-up at
$q_3$
. Take a point
\begin{equation*} q_4 \in \rho _{3}^{-1}(q_3) \setminus \left ((\rho _1 \rho _2 \rho _3)^{-1}_{\ast }l \cup (\rho _3)^{-1}_{\ast }\left (\rho _{2}^{-1}(q_2)\right ) \right ). \end{equation*}
-
(4) Let
$\rho _{4}: S_4 \to S_3$
be the blowing-up at
$q_4$
. Then
$S=S_4$
. Put
$\rho =\rho _1 \rho _2 \rho _3 \rho _4$
.
Moreover, we have
$E_{1}=\rho _{4}^{-1}(q_4)$
,
$F_{1}=(\rho _2 \rho _3 \rho _4)^{-1}_{\ast }(\rho _1^{-1}(q_1))$
,
$F_2= (\rho _3 \rho _4)^{-1}_{\ast }(\rho _2^{-1}(q_2))$
,
$F_3 =(\rho _4)^{-1}_{\ast }(\rho _3^{-1}(q_3))$
,
$F_4 =\rho ^{-1}_{\ast }l$
. We denote
$D=a_{1} E_{1} + \sum _{j=1}^{4}b_{j}F_{j} \in \mathrm{Div}(S)$
(
$a_i, b \in \mathbb{Z}$
) by
$D=(a_1, b_1, b_2, b_3, b_4)$
. The intersection matrix of
$\{E_1, F_1, F_2, F_3, F_4 \}$
is
\begin{equation*}A\,:\!=\, \left ( \begin {array}{c|cccc} -1 & 0 & 0 & 1 & 0 \\ \hline 0 & -2 & 1 & 0 & 0 \\ 0 & 1 & -2 & 1 & 0 \\ 1 & 0 & 1 & -2 & 1 \\ 0 & 0 & 0 & 1 & -2 \\ \end {array} \right ). \end{equation*}
We note that
$ -K_{S} \sim 5E_1 + 2F_1 + 4F_2 + 6F_3 + 3F_4 = (5,2,4,6,3).$
(1) The case
$p \in F_1 \setminus F_2$
. Set
$C=F_1$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
and
$P(u)\cdot C$
are given by the following table:
Therefore, we get
$S(F_1)=4/3$
and
$S(W_{\bullet, \bullet }^{F_{1}},p)=11/6$
. Thus, we have
$\delta _{p}(S)= 3/4$
.
(2) The case
$p \in F_2 \setminus F_3$
. Set
$C=F_2$
, then we get
$\tau =4$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Therefore, we get
\begin{align*} S(F_2)=\frac{11}{6}, \quad S(W_{\bullet, \bullet }^{F_{2}},p) = \begin{cases} \frac{4}{3} & \text{if $p \in (F_{2}\cap F_1)$},\\ & \\ \frac{5}{12} &\text{if $p \in F_{2} \setminus (F_1\cup F_3) $}.\\ \end{cases} \end{align*}
Thus, we have
$\delta _{p}(S)= 6/11$
.
(3) The case
$p \in F_3$
. Set
$C=F_3$
, then we get
$\tau =6$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Therefore, we get
\begin{align*} S(F_3)=\frac{7}{3}, \quad S(W_{\bullet, \bullet }^{F_{3}},p) = \begin{cases} \frac{11}{6} & \text{if $p \in (F_{3}\cap F_2)$},\\ & \\ \frac{13}{9} & \text{if $p \in (F_{3} \cap F_4)$}, \\ & \\ \frac{5}{3} & \text{if $p \in (F_{3} \cap E_1)$}, \\ & \\ \frac{5}{18} &\text{if $p \in F_{3} \setminus ( F_2 \cup F_4\cup E_1) $}.\\ \end{cases} \end{align*}
Thus, we have
$\delta _{p}(S)= 3/7$
.
(4) The case
$p \in F_4 \setminus F_3$
. Set
$C=F_4$
, then we get
$\tau =3$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following table:
Moreover, we have
$\mathrm{ord}_{p}(N(u)|_{C})=0$
. Therefore, we get
$S(F_4)=13/9$
and
$S(W_{\bullet, \bullet }^{F_4},p) = 5/9$
. Thus, we have
$\delta _{p}(S)= 9/13$
.
(5) The case
$p \in E_1 \setminus F_3$
. Set
$C=E_1$
, then we get
$\tau =5$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following table:
Therefore, we get
$S(E_1)=5/3$
and
$S(W_{\bullet, \bullet }^{E_1},p) = 1/3$
. Thus, we have
$\delta _{p}(S)= 3/5$
.
(6) The case
$p \in S \setminus \left ( E_1 \bigcup _{j} F_{j}\right )$
.
Let
$C\,:\!=\, \rho ^{-1}_{\ast }\overline{\rho (p)q_1}$
. We note that
$C \sim 2E_1 + F_2 + 2F_3 + F_4$
. Hence we have
$-K_{S}-uC \sim (5-2u)E_{1} + 2F_1 + (4-u) F_2 + (6-2u)F_3 + (3-u)F_4 = (5-2u, 2, 4-u, 6-2u, 3-u)$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following table:
Therefore, we get
$S(C)=5/6$
and
$S(W_{\bullet, \bullet }^{C},p)= 1/6$
. Thus, we have
$\delta _{p}(S)= 6/5$
.
At the end of this section, we introduce the local delta invariants of del Pezzo surface of degree
$5$
. Since the computation of local delta invariants of the surface is essentially done in [Reference Araujo, Castravet and Cheltsov2, Lemma 2.11], we omit the proof.
Proposition 3.7.
Let
$S$
be the del Pezzo surface with the anti-canonical degree
$5$
. Then, for a point
$p \in S$
, it holds that
\begin{equation*} \delta _{p}(S)= \begin{cases} \frac{15}{13} & \text{if $p$ lies on a $({-}1)$-curve,} \\ \frac{4}{3} & \text{if $p$ does not lies on all $({-}1)$-curves.} \\ \end{cases} \end{equation*}
4. The case of the anti-canonical degree
$6$
Let us use the assumptions and notations of Section 2. Suppose
$K^2=6$
.
Proposition 4.1.
Suppose that the dual graph of the
$({-}1)$
-curves and
$({-}2)$
-curves on
$S$
is same as in Theorem 1.2 (1). Then the local delta invariant
$\delta _{p}(S)$
is as follows.
Proof. We can assume that we get
$S$
from
$\mathbb{P}^2$
as follows. Take three colinear points
$q_1, q_2, q_3 \in \mathbb{P}^2$
and the line
$l$
passing through these points. Then we have
$\rho :S=\mathrm{Bl}_{\{q_1, q_2, q_3\}}\mathbb{P}^{2} \to \mathbb{P}^2$
. Moreover, we have
$E_i \,:\!=\, \rho ^{-1}(q_i)$
(
$i=1,2,3$
) and
$F=\rho ^{-1}_{\ast }l$
. We denote
$D=\sum _{i=1}^{3}a_i E_{i} + bF \in \mathrm{Div}(S)$
(
$a_i, b \in \mathbb{Z}$
) by
$D=(a_1, a_2, a_3, b)$
. The intersection matrix of
$\{E_1, E_2, E_3, F \}$
is
\begin{equation*}A\,:\!=\, \left ( \begin {array}{ccc|c} -1 & 0 & 0 & 1 \\ 0 & -1 & 1 & 1 \\ 0 & 1 & -1 & 1 \\ \hline 1 & 1 & 1 & -2 \\ \end {array} \right ). \end{equation*}
We note that
$ -K_{S} \sim 2E_1 + 2E_2 + 2E_3 + 3F = (2,2,2,3).$
(1) The case
$p \in E_1$
. Set
$C=E_1$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Therefore, we get
\begin{align*} S(E_1)=\frac{10}{9}, \quad S(W_{\bullet, \bullet }^{E_{1}},p) &=\begin{cases} \frac{7}{9} & \text{if $p \in E_{1} \setminus F $},\\ & \\ \frac{4}{3} & \text{if $p \in E_{1} \cap F $}. \\ \end{cases} \end{align*}
Thus, we have
\begin{align*} \delta _{p}(S) & \begin{cases} =\frac{9}{10} & \text{if $p \in E_{1} \setminus F $},\\ & \\ \geq \frac{3}{4} & \text{if $p \in E_{1} \cap F $}. \\ \end{cases} \end{align*}
For
$i=2,3$
, one can show
\begin{align*} \delta _{p}(S) & \begin{cases} =\frac{9}{10} & \text{if $p \in E_{i} \setminus F $},\\ & \\ \geq \frac{3}{4} & \text{if $p \in E_{i} \cap F $}, \\ \end{cases} \end{align*}
by the same calculation.
(2) The case
$p \in F$
. Set
$C=F$
, then we get
$\tau =3$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Therefore, we get
$ S(F)=4/3$
by the definition of
$S(F)$
. Hence we get
$3/4 \geq \delta _{p}(S)$
for any
$p \in F$
. If
$p \in F \cap \bigcup _{i=1,2,3} E_i$
, then we have
$\delta _{p}(S) \geq 3/4$
by (1). Hence we get
$\delta _{p}(S) = 3/4$
at
$p \in F \cap \bigcup _{i=1,2,3} E_i$
. If
$p \in F \setminus \bigcup _{i=1,2,3} E_i$
, then we have
$S(W_{\bullet, \bullet }^{F},p) =10/9.$
Hence, we have
\begin{align*} \frac{3}{4} \geq \delta _{p}(S) \geq \mathrm{min}\left \{ \frac{1}{S(F)}, \frac{1}{S(W_{\bullet, \bullet }^{F},p)} \right \} = \frac{3}{4} \end{align*}
at a point
$p \in F \setminus \bigcup _{i=1,2,3} E_i$
. Thus, we have
$\delta _{p}(S)= 3/4$
for any
$p \in F$
.
(3) The case
$p \in S \setminus \left ( \bigcup _{i} E_{i} \cup F\right )$
. Consider a blowing up
$\sigma :\widetilde{S} \to S$
at
$p$
. Let
$\widetilde{E}_{i}$
and
$\widetilde{F}$
be the proper transform of
$E_{i}$
and
$F$
, respectively. Take three
$({-}1)$
-curves
$G_i \,:\!=\, (\rho \sigma )_{\ast }^{-1}(\overline{\rho \sigma (p)q_i})$
for
$i=1,2,3$
. We note that
$\sigma ^{\ast }({-}K_{S})\sim G_1 + G_2 +G_3 +3Z$
. Hence, we have
$\sigma ^{\ast }({-}K_{S})-uZ \sim G_1 + G_2 +G_3 +(3-u)Z$
and
$\widetilde{\tau } =3$
. The values
$\widetilde{P}(u)$
,
$\widetilde{N}(u)$
,
$\widetilde{P}(u)^2$
,
$\widetilde{P}(u)\cdot Z$
and
$\mathrm{ord}_{q}(\widetilde{N}(u)|_{Z})$
are given by the following tables:
Therefore, we get
\begin{align*} S(Z)=\frac{5}{3}, \quad S(W_{\bullet, \bullet }^{Z},q) &= \begin{cases} \frac{7}{9} & \text{if $q \in Z \cap G_i $},\\ \\ \frac{2}{3} & \text{if $q \in Z \setminus \left (G_1 \cup G_2 \cup G_3\right )$}. \\ \end{cases} \end{align*}
Thus, we have
$\delta _{p}(S)= 6/5$
from Corollary 1.
Proposition 4.2.
Suppose that the dual graph of the
$({-}1)$
-curves and
$({-}2)$
-curves on
$S$
is same as in Theorem 1.2 (2). Then the local delta invariant
$\delta _{p}(S)$
is as follows.
Proof. We denote
$D=\sum _{i=1}^{4} a_i E_{i} + bF \in \mathrm{Div}(S)$
(
$a_i, b \in \mathbb{Z}$
) by
$D=(a_1, a_2, a_3, a_4, b)$
. The intersection matrix of
$\{E_1, E_2, E_3, E_4, F \}$
is
\begin{equation*}A\,:\!=\, \left ( \begin {array}{cccc|c} -1 & 1 & 0 & 0 & 0 \\ 1 & -1 & 0 & 0 & 1 \\ 0 & 0 & -1 & 1 & 1 \\ 0 & 0 & 1 & -1 & 0 \\ \hline 0 & 1 & 1 & 0 & -2 \\ \end {array} \right ). \end{equation*}
We note that
$ -K_{S} \sim 2E_1 + 3E_2 + E_3 + 2F = (2,3,1,0,2).$
(1) The case
$p \in E_1 \setminus E_2$
. Set
$C=E_1$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following table:
Therefore, we get
$S(E_1)=10/9$
and
$S(W_{\bullet, \bullet }^{E_{1}},p)=7/9$
. Hence we have
$\delta _{p}(S)= 9/10$
. We can check
$\delta _{p}(S)= 9/10$
for
$p \in E_4 \setminus E_3$
by the same calculation.
(2) The case
$p \in E_2$
. Set
$C=E_2$
, then we get
$\tau =3$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Therefore, we get
\begin{align*} S(E_2)=\frac{11}{9}, \quad S(W_{\bullet, \bullet }^{E_{2}},p) &=\begin{cases} 1 & \text{if $p \in E_{2}\cap E_1 $},\\ & \\ \frac{11}{9} & \text{if $p \in E_{2} \cap F $}, \\ & \\ \frac{7}{12} & \text{if $p \in E_{2} \setminus (E_1 \cup F ) $}. \\ \end{cases} \end{align*}
Thus, we have
$\delta _{p}(S)= 9/11$
. We can check
$\delta _{p}(S)= 9/11$
for
$p \in E_3$
by the same calculation.
(3) The case
$p \in F \setminus (E_2 \cup E_3)$
. Set
$C=F$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following table:
Therefore, we get
$S(F)=11/9$
and
$S(W_{\bullet, \bullet }^{F},p)=8/9$
. Thus, we have
$\delta _{p}(S)= 9/11$
.
(4) The case
$p \in S \setminus \left ( \bigcup _{i}E_{i} \cup F)\right )$
. Let
$L \in |E_1+E_2|$
be a smooth irreducible curve. Set
$C=L$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following table:
Therefore, we get
$S(L)=8/9$
and
$S(W_{\bullet, \bullet }^{L},p)=7/9$
. Thus, we have
$\delta _{p}(S)= 9/8$
.
Proposition 4.3.
Suppose that the dual graph of the
$({-}1)$
-curves and
$({-}2)$
-curves on
$S$
is same as in Theorem 1.2 (3). Then the local delta invariant
$\delta _{p}(S)$
is as follows.
Proof. We denote
$D=\sum _{i=1,2} a_{i}E_{i} + \sum _{j=1,2}b_jF_{j} \in \mathrm{Div}(S)$
(
$a_i, b_j \in \mathbb{Z}$
) by
$D=(a_1, a_2, b_1,b_2)$
. The intersection matrix of
$\{E_1, E_2, F_1,F_2 \}$
is
\begin{equation*}A\,:\!=\, \left ( \begin {array}{cc|cc} -1 & 0 & 1 & 1 \\ 0 & -1 & 0 & 1 \\ \hline 1 & 0 & -2 & 0 \\ 1 & 1 & 0 & -2 \\ \end {array} \right ). \end{equation*}
We note that
$ -K_{S} \sim 4E_1 + 2E_2 + 2F_1 + 3F_2 = (4,2,2,3).$
(1) The case
$p \in F_1 \setminus E_1$
. Set
$C=F_1$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following table:
Therefore, we get
$S(F_1)=11/9$
and
$S(W_{\bullet, \bullet }^{F_{1}},p)=8/9$
. Thus, we have
$\delta _{p}(S)= 9/11$
.
(2) The case
$p \in E_1$
. Set
$C=E_1$
, then we get
$\tau =4$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Therefore, we get
\begin{align*} S(E_1)=\frac{14}{9}, \quad S(W_{\bullet, \bullet }^{E_{1}},p) = \begin{cases} 1 & \text{if $p \in E_1 \cap F_1 $},\\ & \\ \frac{10}{9} & \text{if $p \in E_1 \cap F_2 $},\\ & \\ \frac{4}{9} & \text{if $p \in E_{1} \setminus \bigcup _{j=1}^{2} F_{j}$}. \\ \end{cases} \end{align*}
Thus, we have
$\delta _{p}(S)= 9/14$
.
(3) The case
$p \in F_2 \setminus E_1$
. Set
$C=F_2$
, then we get
$\tau =3$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Therefore, we get
\begin{align*} S(F_2)=\frac{4}{3}, \quad S(W_{\bullet, \bullet }^{F_{2}},p) = \begin{cases} \frac{16}{9} & \text{if $p \in F_2 \cap E_2 $},\\ & \\ \frac{4}{3} & \text{if $p \in F_{2} \setminus (E_1 \cup E_{2})$}. \\ \end{cases} \end{align*}
Thus, we have
\begin{align*} \delta _{p}(S) \begin{cases} = \frac{3}{4} & \text{if $p \in F_{2} \setminus (E_1 \cup E_2)$},\\ & \\ \leq \frac{3}{4} & \text{if $\{p\} = F_{2}\cap E_{2}$}. \\ \end{cases} \end{align*}
(4) The case
$p \in E_2$
. Set
$C=E_2$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Therefore, we get
\begin{align*} S(E_2)=\frac{10}{9}, \quad S(W_{\bullet, \bullet }^{E_{2}},p) = \begin{cases} \frac{4}{3} & \text{if $p \in E_2 \cap F_2 $},\\ & \\ \frac{7}{9} & \text{if $p \in E_{2} \setminus F_2$}. \\ \end{cases} \end{align*}
Thus, we have
\begin{align*} \delta _{p}(S) \begin{cases} \geq \frac{3}{4} & \text{if $\{p\} = F_{2}\cap E_{2}$}, \\ & \\ = \frac{9}{10} & \text{if $p \in E_{2} \setminus F_2$}. \\ \end{cases} \end{align*}
By (3), we have
$ 3/4 \geq \delta _{p}(S)$
for
$\{p\} = F_{2}\cap E_{2}$
. Therefore, we get
$\delta _{p}(S) = 3/4$
for
$\{p\} = F_{2}\cap E_{2}$
.
(5) The case
$p \in S \setminus \left ( E_1\cup E_2 \cup F_1 \cup F_2\right )$
. Let
$L \in |E_1+E_2+F_2|$
be a smooth irreducible curve. Set
$C=L$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following table:
Therefore, we get
$S(L)=8/9$
and
$S(W_{\bullet, \bullet }^{L},p)=7/9$
. Thus, we have
$\delta _{p}(S)= 9/8$
.
Proposition 4.4.
Suppose that the dual graph of the
$({-}1)$
-curves and
$({-}2)$
-curves on
$S$
is same as in Theorem 1.2 (4). Then the local delta invariant
$\delta _{p}(S)$
is as follows.
Proof. We denote
$D=\sum _{i=1,2} a_{i}E_{i} + \sum _{j=1,2}b_jF_{j} \in \mathrm{Div}(S)$
(
$a_i, b_j \in \mathbb{Z}$
) by
$D=(a_1, a_2, b_1,b_2)$
. The intersection matrix of
$\{E_1, E_2, F_1,F_2 \}$
is
\begin{equation*}A\,:\!=\, \left ( \begin {array}{cc|cc} -1 & 0 & 0 & 1 \\ 0 & -1 & 0 & 1 \\ \hline 0 & 0 & -2 & 1 \\ 1 & 1 & 1 & -2 \\ \end {array} \right ). \end{equation*}
We note that
$ -K_{S} \sim 3E_1 + 3E_2 + 2F_1 + 4F_2 = (3,3,2,4).$
(1) The case
$p \in F_1 \setminus F_2$
. Set
$C=F_1$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following table:
Therefore, we get
$S(F_1)=4/3$
and
$S(W_{\bullet, \bullet }^{F_{1}},p)=1$
. Thus, we have
$\delta _{p}(S)= 3/4$
.
(2) The case
$p \in F_2$
. Set
$C=F_2$
, then we get
$\tau =4$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Therefore, we get
\begin{align*} S(F_2)=\frac{5}{3}, \quad S(W_{\bullet, \bullet }^{F_{2}},p) &= \begin{cases} \frac{4}{3} & \text{if $p \in F_{2}\cap F_{1} $},\\ & \\ \frac{5}{4} & \text{if $p \in F_{2} \cap ( E_1 \cup E_2)$}, \\ & \\ \frac{1}{2} & \text{if $p \in F_{2} \setminus (F_{1}\cup E_1 \cup E_2)$}. \\ \end{cases} \end{align*}
Thus, we have
$\delta _{p}(S)= 3/5$
in this case.
(3) The case
$p \in E_1 \setminus F_2$
. Set
$C=E_1$
, then we get
$\tau =3$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following table:
Therefore, we get
$S(E_1)=5/4$
and
$S(W_{\bullet, \bullet }^{E_1},p)=7/12$
. Thus, we have
$\delta _{p}(S)= 4/5$
.
(4) The case
$p \in S \setminus \left ( E_1\cup E_2 \cup F_1 \cup F_2\right )$
. Let
$L \in |E_1+E_2+F_2|$
be a smooth irreducible curve. Set
$C=L$
, then we get
$\tau =3$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following table:
Therefore, we get
$S(L)=1$
and
$S(W_{\bullet, \bullet }^{L},p)=2/3$
. Thus, we have
$\delta _{p}(S)= 1$
.
Proposition 4.5.
Suppose that the dual graph of the
$({-}1)$
-curves and
$({-}2)$
-curves on
$S$
is same as in Theorem 1.2 (5). Then the local delta invariant
$\delta _{p}(S)$
is as follows.
Proof. We denote
$D= a E + \sum _{j=1,2,3}b_jF_{j} \in \mathrm{Div}(S)$
(
$a, b_j \in \mathbb{Z}$
) by
$D=(a, b_1,b_2, b_3)$
. The intersection matrix of
$\{E, F_1,F_2, F_3 \}$
is
\begin{equation*}A\,:\!=\, \left ( \begin {array}{c|ccc} -1 & 0 & 1 & 1 \\ \hline 0 & -2 & 1 & 0 \\ 1 & 1 & -2 & 0 \\ 1 & 0 & 0 & -2 \\ \end {array} \right ). \end{equation*}
We note that
$ -K_{S} \sim 6E + 2F_1 + 4F_2 + 3F_3 = (6,2,4,3).$
(1) The case
$p \in F_1 \setminus F_2$
. Set
$C=F_1$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following table:
Therefore, we get
$S(F_1) =4/3$
and
$S(W_{\bullet, \bullet }^{F_{1}},p) =1$
. Thus, we have
$\delta _{p}(S)= 3/4$
.
(2) The case
$p \in F_2 \setminus E$
. Set
$C=F_2$
, then we get
$\tau =4$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following table:
Therefore, we get
\begin{align*} S(F_2)=\frac{5}{3}, \quad S(W_{\bullet, \bullet }^{F_{2}},p) &= \begin{cases} \frac{4}{3} & \text{if $p \in F_{2}\cap F_{1} $},\\ & \\ \frac{1}{2} & \text{if $p \in F_{2} \setminus (F_{1}\cup E)$}. \\ \end{cases} \end{align*}
Thus, we have
$\delta _{p}(S)= 3/5$
.
(3) The case
$p \in E$
. Set
$C=E$
, then we get
$\tau =6$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Therefore, we get
\begin{align*} S(E)=2, \quad S(W_{\bullet, \bullet }^{E},p) &= \begin{cases} \frac{5}{3} & \text{if $p \in E \cap F_{2}$},\\ & \\ \frac{4}{3} & \text{if $p \in E \cap F_{3} $},\\ & \\ \frac{1}{3} & \text{if $p \in E \setminus (F_2 \cup F_3)$}. \\ \end{cases} \end{align*}
Thus, we have
$\delta _{p}(S)= 1/2$
in this case.
(4) The case
$p \in F_3 \setminus E$
. Set
$C=F_3$
, then we get
$\tau =3$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following table:
Therefore, we get
$S(F_3)=4/3$
and
$S(W_{\bullet, \bullet }^{F_{3}},p) =2/3$
. Thus, we have
$\delta _{p}(S)= 3/4$
.
(5) The case
$p \in S \setminus \left ( E \cup F_1 \cup F_2 \cup F_3\right )$
. Let
$L \in |2E+F_2+F_3|$
be a smooth irreducible curve. Set
$C=L$
, then we get
$\tau =3$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following table:
Therefore, we get
$S(L)=1$
and
$S(W_{\bullet, \bullet }^{L},p)=2/3$
. Thus, we have
$\delta _{p}(S)= 1$
.
At the end of this section, we introduce the local delta invariants of del Pezzo surface of degree
$6$
. We omit the proof.
Proposition 4.6.
Let
$S$
be the del Pezzo surface with the anti-canonical degree
$6$
. The local delta invariant
$\delta _{p}(S)$
of
$S$
at
$p \in S$
is as follows.
5. The case of the anti-canonical degree
$7$
Let us use the assumptions and notations of Section 2. Suppose
$K^2=7$
.
Proposition 5.1.
Suppose that the dual graph of the
$({-}1)$
-curves and
$({-}2)$
-curves on
$S$
is same as in Theorem 1.3 (1). Then the local delta invariant
$\delta _{p}(S)$
is as follows.
Proof. We denote
$D= \sum _{i=1,2} a_i E_i + F \in \mathrm{Div}(S)$
(
$a_i, b \in \mathbb{Z}$
) by
$D=(a_1, a_2, b)$
. The intersection matrix of
$\{E_1, E_2, F \}$
is
\begin{equation*}A\,:\!=\, \left ( \begin {array}{cc|c} -1 & 1 & 0 \\ 1 & -2 & 1 \\ \hline 0 & 1 & -2 \\ \end {array} \right ). \end{equation*}
We note that
$ -K_{S} \sim 3E_1 + 4E_2 + 2F = (3,4,2).$
(1) The case
$p \in E_1 \setminus E_2$
. Set
$C=E_1$
, then we get
$\tau =3$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following table:
Therefore,
$S(E_1)=25/21$
and
$S(W_{\bullet, \bullet }^{E_1},p)=15/21$
. Thus, we have
$\delta _{p}(S)= 21/25$
.
(2) The case
$p \in E_2$
. Set
$C=E_2$
, then we get
$\tau =4$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following tables:
Therefore, we get
\begin{align*} S(E_2)=\frac{31}{21}, \quad S(W_{\bullet, \bullet }^{E_{2}},p) = \begin{cases} \frac{25}{21} & \text{if $p \in E_2 \cap E_1 $},\\ & \\ \frac{9}{7} & \text{if $p \in E_2 \cap F$},\\ & \\ \frac{23}{42} & \text{if $p \in E_{2} \setminus (F \cup E_1)$}. \\ \end{cases} \end{align*}
Thus, we have
$\delta _{p}(S)= 21/31$
for
$p \in E_{2}$
.
(3) The case
$p \in F \setminus E_2$
. Set
$C=F$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following table:
Therefore, we get
$S(F)=9/7$
and
$S(W_{\bullet, \bullet }^{F},p)=23/21$
. Thus, we have
$\delta _{p}(S)= 7/9$
.
(4) The case
$p \in S \setminus \left ( E_1 \cup E_2 \cup F \right )$
. Let
$L \in |E_1+E_2|$
be a smooth irreducible curve.
Set
$C=L$
, then we get
$\tau =3$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following table:
Since we get
$S(L)=23/21$
and
$S(W_{\bullet, \bullet }^{L},p)=15/21$
, we have
$\delta _{p}(S)= 21/23$
.
At the end of this section, we introduce the local delta invariants of del Pezzo surface of degree
$7$
. We omit the proof.
Proposition 5.2.
Suppose that the dual graph of the
$({-}1)$
-curves on
$S$
is same as in Theorem 1.3 (2). Then the local delta invariant
$\delta _{p}(S)$
is as follows.
6. The case of the anti-canonical degree
$8$
Let us use assumptions and notations of Section 2. Suppose
$K^2=8$
.
Proposition 6.1.
If
$S = \Sigma _2$
, then for any point
$p \in S$
, it holds that
\begin{equation*} \delta _{p}(S)=\frac{3}{4}. \end{equation*}
Proof. We denote
$D= aC_0 + b\Gamma \in \mathrm{Div}(S)$
(
$a, b \in \mathbb{Z}$
) by
$D=(a, b)$
. The intersection matrix of
$\{C_0, \Gamma \}$
is
\begin{equation*}A\,:\!=\, \left ( \begin {array}{cc} -2 & 1 \\ 1 & 0 \\ \end {array} \right ). \end{equation*}
We note that
$ -K_{S} \sim 2C_0 + 4\Gamma = (2,4).$
(1) The case
$p \in C_0$
. Set
$C=C_0$
, then we get
$\tau =2$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following table:
Therefore, we get
$S(C_0)=4/3$
and
$S(W_{\bullet, \bullet }^{C_0},p)=4/3$
. Thus, we have
$\delta _{p}(S)= 3/4$
.
(2) The case
$p \in S\setminus C_0$
. Let
$\Gamma$
be the fiber of
$\pi$
passing through
$p$
. Set
$C=\Gamma$
, then we get
$\tau =4$
. The values
$P(u)$
,
$N(u)$
,
$P(u)^2$
,
$P(u)\cdot C$
and
$\mathrm{ord}_{p}(N(u)|_{C})$
are given by the following table:
Therefore, we get
$S(\Gamma ) = 4/3$
and
$S(W_{\bullet, \bullet }^{\Gamma },p) = 2/3$
. Thus, we have
$\delta _{p}(S)= 3/4$
.
At the end of this section, we introduce the local delta invariants of del Pezzo surface of degree
$8$
. We omit the proof.
Proposition 6.2.
If
$S = \Sigma _1$
, then for any point
$p \in S$
, it holds that
\begin{equation*} \delta _{p}(S)= \begin{cases} \frac{6}{7} & \text{if $p \in C_0$,} \\ \frac{12}{13} & \text{if $p \in S \setminus C_0 $.} \end{cases} \end{equation*}
If
$S = \Sigma _0=\mathbb{P}^1 \times \mathbb{P}^1$
, then for any point
$p \in S$
, it holds that
$\delta _{p}(S)=1$
.
Acknowledgements
The author is deeply grateful to Professor Kento Fujita for his valuable advice and support. The research is supported by JSPS KAKENHI No. 20J20055.
