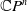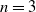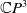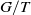1. Introduction
A fundamental problem on H-spaces is to find whether or not a given H-space is homotopy commutative. This was intensely studied for finite H-spaces, and a complete answer was given by Hubbuck [Reference Hubbuck15] such that if a connected finite H-space is homotopy commutative, then it is homotopy equivalent to a torus. As for infinite H-spaces, the problem should be studied by fixing a class of infinite H-spaces because there are too many classes of infinite H-spaces, each of which has its own special features.
In [Reference Ganea8], Ganea studied the homotopy nilpotency of the loop spaces of complex projective spaces, and in particular, he proved that the loop space of the complex projective space
$\mathbb{C} P^n$
is homotopy commutative if and only if
$n=3$
. Then, we continue this work to study the homotopy commutativity of the loop spaces of homogeneous spaces. Recently, Golasiński [Reference Golasiński9] showed that the loop spaces of some homogeneous spaces such as complex Grassmannians are homotopy nilpotent. However, their homotopy nilpotency class is not computed: it is not even proved that they are homotopy commutative or not. In this paper, we study the homotopy commutativity of the loop spaces of Hermitian symmetric spaces, which generalizes Ganea’s result and makes Golasiński’s result more concrete. Hermitian symmetric spaces were first studied by Cartan [Reference Cartan5], who classified them by means of his classification [Reference Cartan4] of Riemannian symmetric spaces. The work of Borel and de Siebethal on subgroups of maximal rank in compact Lie groups [Reference Borel and de Siebenthal2] gives a simpler proof of Cartan’s classification result. It states that every Hermitian symmetric space is a product of irreducible ones in the following table.
Then, we only need to consider the loop spaces of irreducible Hermitian symmetric spaces. Now, we state the main theorem.
Theorem 1.1 The loop spaces of all irreducible Hermitian symmetric spaces but
$\mathbb{C} P^3$
are not homotopy commutative.
Theorem 1.1 will be proved by a case-by-case analysis of irreducible Hermitian symmetric spaces. Our main tools for the analysis are rational homotopy theory (Section 2) and Steenrod operations (Section 3). The rational homotopy technique also applies to flag manifolds, so that we can prove the following, where the definition of the homotopy nilpotency will be given in Section 2.
Theorem 1.2 Let G be a compact connected non-trivial Lie group with maximal torus T. Then, the loop space of the flag manifold
$G/T$
is homotopy nilpotent of class 2.
2. Rational homotopy
In this section, we apply rational homotopy theory to prove that the loop spaces of irreducible Hermitian symmetric spaces of type CI, DIII, and EVII are not homotopy commutative. We also consider the homotopy nilpotency of the loop spaces of flag manifolds. By [Reference Félix, Halperin and Thomas7, Proposition 13.16] and the adjointness of Whitehead products and Samelson products, we have the following criterion for a loop space not being homotopy commutative.
Lemma 2.1. Let
$(\Lambda V,d)$
be the minimal Sullivan model of a simply connected CW complex of finite type X. If there is
$x\in V$
such that
\begin{equation*} dx\not\equiv 0\mod\Lambda^3V, \end{equation*}
then
$\Omega X$
is not homotopy commutative.
In order to apply Lemma 2.1, we will use the following lemma.
Lemma 2.2. Let X,Y be simply connected spaces such that
\begin{equation*} H^*(X;\mathbb{Q})=\mathbb{Q}[x_1,\ldots,x_m]\quad\text{and}\quad H^*(Y;\mathbb{Q})=\mathbb{Q}[y_1,\ldots,y_n]. \end{equation*}
If a map
$f\colon X\to Y$
is injective in rational cohomology, then there is a Sullivan model of the homotopy fiber of f such that
\begin{equation*} (\Lambda(x_1,\ldots,x_m,z_1,\ldots,z_n),d),\quad dx_i=0,\quad dz_i=f^*(y_i). \end{equation*}
Proof. By the Borel transgression theorem,
$H^*(\Omega Y;\mathbb{Q})=E(z_1,\ldots,z_n)$
such that
$\tau(z_i)=y_i$
, where
$E(z_1,\ldots,z_n)$
denotes the exterior algebra generated by
$z_1,\ldots,z_n$
and
$\tau$
denotes the transgression. Let F denote the homotopy fiber of the map f. Then, the sequence
\begin{equation*} (\Lambda(x_1,\ldots,x_m),0)\xrightarrow{\rm incl}(\Lambda(x_1,\ldots,x_m,z_1,\ldots,z_n),d)\xrightarrow{\rm proj}(\Lambda(z_1,\ldots,z_n),0) \end{equation*}
is a model of the principal fibration
$\Omega Y\to F\to X$
, where
$dx_i=0$
and
$dz_i=f^*(y_i)$
. Thus, the statement is proved.
Proposition 2.3. The loop spaces of
$Sp(n)/U(n)$
and
$SO(2n)/U(n)$
are not homotopy commutative.
Proof. First, we consider
$Sp(n)/U(n)$
. Recall that the cohomology of BU(n) and BSp(n) are given by
\begin{equation*} H^*(BU(n);\mathbb{Z})=\mathbb{Z}[c_1,\ldots,c_n]\quad\text{and}\quad H^*(BSp(n);\mathbb{Z})=\mathbb{Z}[q_1,\ldots,q_n], \end{equation*}
where
$c_i$
and
$q_i$
are the Chern classes and the symplectic Pontrjagin classes. Then as in [Reference Mimura and Toda22, Chapter III, Theorem 5.8], the natural map
$q\colon BU(n)\to BSp(n)$
satisfies
\begin{equation*} q^*(q_i)=\sum_{k+l=2i}(-1)^{i+k}c_kc_l, \end{equation*}
where
$c_0=1$
and
$c_i=0$
for
$i>n$
. Then by Lemma 2.2, there is a Sullivan model of
$Sp(n)/U(n)$
such that
\begin{equation*} (\Lambda(c_1,\ldots,c_n,r_{1},\ldots r_n),d),\quad dc_i=0,\quad dr_i=\sum_{k+l=2i}(-1)^{i+k}c_kc_l, \end{equation*}
where
$c_0=1$
and
$c_i=0$
for
$i>n$
. Hence, the minimal model of
$Sp(n)/U(n)$
is given by
\begin{gather*} (\Lambda(c_1,c_3,\ldots,c_{2n-2[n/2]-1},r_{[n/2]+1},\ldots r_n),d)\\ dc_i=0,\quad dr_i\equiv\sum_{k+l=i-1}(-1)^{i+1}c_{2k+1}c_{2l+1}\mod(c_1,c_3,\ldots,c_{2n-2[n/2]-1})^4, \end{gather*}
where
$c_0=1$
,
$c_i=0$
for
$i>n$
. Thus, modulo
$(c_1,c_3,\ldots,c_{2n-2[n/2]-1})^4$
,
\begin{equation*} dr_{n-1}\equiv c_{n-1}^2\quad(n\text{ is even}),\quad dr_n\equiv c_n^2\quad(n\text{ is odd}). \end{equation*}
Therefore, by Lemma 2.1,
$\Omega(Sp(n)/U(n))$
is not homotopy commutative.
Next, we consider
$SO(2n)/U(n)$
. The rational cohomology of BSO(2n) is given by
\begin{equation*} H^*(BSO(2n);\mathbb{Q})=\mathbb{Q}[p_1,\ldots,p_{n-1},e], \end{equation*}
where
$p_i$
is the i-the Pontrjagin classes and e is the Euler class. By [Reference Mimura and Toda22, Chapter III, Lemma 5.15 and Theorem 5.17]. Then, the natural map
$r\colon BU(n)\to BSO(2n)$
satisfies
\begin{equation*} r^*(p_i)=\sum_{k+l=2i}(-1)^kc_kc_l\quad\text{and}\quad r^*(e)=c_n, \end{equation*}
where
$c_0=1$
and
$c_i=0$
for
$i>n$
. Thus arguing as above, we can see that the minimal model of
$SO(2n)/U(n)$
coincides with that of
$Sp(n-1)/U(n-1)$
, implying that
$\Omega(SO(2n)/U(n))$
is not homotopy commutative.
Proposition 2.4. The loop space of
$E_7/E_6\cdot T^1$
is not homotopy commutative.
Proof. As in the proof of [Reference Watanabe27, Lemma 2.1], we have
\begin{align*} H^*(BE_7;\mathbb{Q})&=\mathbb{Q}[x_4,x_{12},x_{16},x_{20},x_{24},x_{28},x_{36}]\\[3pt] H^*(B(E_6\cdot T^1);\mathbb{Q})&=\mathbb{Q}[u,v,w,x_4,x_{12},x_{16},x_{24}], \end{align*}
where
$|x_i|=i$
,
$|u|=2$
,
$|v|=10$
and
$|w|=18$
. Moreover, the natural map
$j\colon B(E_6\cdot T^1)\to BE_7$
satisfies
$j^*(x_i)=x_i$
for
$i=4,12,16,24$
and
$j^*(x_i)\equiv z_i\mod(x_4,x_{12},x_{16},x_{24})$
for
$i=20,28,36$
, where
\begin{alignat*}{2} z_{20}&=v^2-2uv&z_{28}&=-2vw+18u^5w-6u^6v+u^{14}\\[3pt] z_{36}&=w^2+20u^4vw-18u^9w+2u^{13}v.\quad \end{alignat*}
Then by Lemma 2.2, there is a Sullivan model of
$E_7/E_6\cdot T^1$
such that
\begin{equation*} (\Lambda(u,v,w,x_4,x_{12},x_{16},x_{24},y_3,y_{11},y_{15},y_{19},y_{23},y_{27},y_{36}),d), \end{equation*}
where
$du=dv=dw=0$
and
$dy_i=x_{i+1}$
for
$i=3,11,15,23$
and
$dy_i\equiv z_{i+1}\mod(x_4,x_{12},x_{16},x_{24})$
. Thus, we can easily see that the minimal model of
$E_7/E_6\cdot T^1$
is given by
$(\Lambda(u,v,w,y_{19},y_{27},y_{36}),d)$
such that
$du=dv=dw=0$
and
$dy_i=z_{i+1}$
for
$i=19,27,36$
. Therefore by Lemma 2.1,
$\Omega(E_7/E_6\cdot T^1)$
is not homotopy commutative as stated.
We consider the homotopy nilpotency of flag manifolds. Let X be an H-group. Let
$\gamma\colon X\wedge X\to X$
denote the reduced commutator map, and let
$\gamma_n=\gamma\circ(\gamma_{n-1}\wedge 1_X)$
for
$n\ge 2$
and
$\gamma_1=1_X$
. Recall from [Reference Zabrodsky28, Definition 2.6.2] that X is called homotopy nilpotent of class
$<n$
if
$\gamma_n\simeq*$
. Let
$\operatorname{honil}(X)$
denote the homotopy nilpotency class of X. Then, X is homotopy commutative if and only if
$\operatorname{honil}(X)\le 1$
.
Proposition 2.5. Let G be a Lie group, and let K be a subgroup of G. Then
\begin{equation*} \operatorname{honil}(\Omega(G/K))\le\operatorname{honil}(K)+1. \end{equation*}
Proof. There is a homotopy fibration
$G/K\to BK\to BG$
, and so the result follows from [Reference Berstein and Ganea1, Theorem 3.3].
Hopkins [Reference Hopkins14, Corollary 2.2] proved that a connected finite H-space is homotopy nilpotent whenever it is torsion free in homology. Then for a compact connected Lie group G and its closed subgroup K, it follows from Corollary 2.5 that
$\Omega(G/K)$
is homotopy nilpotent whenever K is torsion free in homology (cf. [Reference Golasiński9, Proposition 2.2]). In particular, we obtain that the loop space of the flag manifold
$G/T$
is homotopy nilpotent, where T is a maximal torus of G. Now we are ready to prove Theorem 1.2.
Proof of Theorem 1.2. Clearly, we may assume G is simply connected. Since T is homotopy commutative and non-contractible, we have
$\operatorname{honil}(T)=1$
. Then by Corollary 2.5,
$\operatorname{honil}(\Omega(G/T))\le 2$
, and so it remains to show that
$\Omega(G/T)$
is not homotopy commutative. It is well known that the natural map
$H^*(BG;\mathbb{Q})\to H^*(BT;\mathbb{Q})^W$
is an isomorphism and
\begin{equation*} H^*(BT;\mathbb{Q})^W=\mathbb{Q}[x_1,\ldots,x_n], \end{equation*}
where W is the Weyl group of G. Since G is simply connected,
$H^*(BG;\mathbb{Q})=0$
for
$*\le 3$
and
$H^4(BG;\mathbb{Q})\ne 0$
. Then, we may assume
$|x_1|=4$
. By Lemma 2.2, there is a Sullivan model of
$G/T$
such that
\begin{equation*} (\Lambda(t_1,\ldots,t_n,y_1,\ldots,y_n),d),\quad dt_i=0,\quad dy_i=x_i, \end{equation*}
where
$t_1,\ldots,t_n$
are generators of
$H^*(BT;\mathbb{Q})$
which are of degree 2. Since all
$x_i$
are decomposable by degree reasons, this is the minimal model of
$G/T$
. Moreover,
$x_1$
is a quadratic polynomial in
$t_1,\ldots,t_n$
. Then by Lemma 2.1,
$G/T$
has non-trivial Whitehead product, implying that
$\Omega(G/T)$
is not homotopy commutative.
3. Steenrod operation
In this section, we prove that the loop spaces of the irreducible Hermitian symmetric spaces of type AIII, BDI, EIII are not homotopy commutative by applying the following lemma. The lemma was proved by Kono and Ōshima [Reference Kono and Ōshima21] when A and B are spheres and p is odd, and its variants are used in [Reference Hamanaka and Kono10, Reference Hamanaka and Kono11, Reference Hasui, Kishimoto, Miyauchi and Ohsita12, Reference Hasui, Kishimoto and Ohsita13, Reference Kaji and Kishimoto17, Reference Kishimoto and Miyauchi18, Reference Kishimoto, Ohsita and Takeda19, Reference Kishimoto and Tsutaya20, Reference Tsutaya26]. For an augmented graded algebra A, let
$QA^n$
denote the module of indecomposables of dimension n.
Lemma 3.1. Let X be a path-connected space X, let
$\alpha\colon\Sigma A\to X,\,\beta\colon\Sigma B\to X$
be maps, and let p be a prime. Suppose the following conditions hold:
-
(1) there are
$a,b\in H^*(X;\mathbb{Z}/p)$
such that
$\alpha^*(a)\ne 0$
,
$\beta^*(b)\ne 0$
, and
-
(a)
$\alpha^*(b)=0$
or
$\beta^*(a)=0$
for
$p=2$
, -
(b)
$A=B$
,
$\alpha=\beta$
and
$a=b$
for
$|a|=|b|$
and p odd;
-
-
(2) there are
$x\in H^*(X;\mathbb{Z}/p)$
and a Steenrod operation
$\theta$
such that
$\theta(x)$
is decomposable and includes the term
$ab\ne 0$
; -
(3)
$\dim QH^{*}(X;\mathbb{Z}/p)=1$
for
$*=|a|,|b|$
; -
(4)
$\theta$
acts trivially on
$H^*(\Sigma A\times\Sigma B;\mathbb{Z}/p)$
.
Then, the Whitehead product
$[\alpha,\beta]$
in X is non-trivial.
Proof. Suppose
$[\alpha,\beta]=0$
. Then, there is a homotopy commutative diagram
By the conditions (1), (2), and (3), the
$H^{|a|}(\Sigma A;\mathbb{Z}/p)\otimes H^{|b|}(\Sigma B;\mathbb{Z}/p)$
-part of
$\mu^*(\theta(x))$
is
\begin{align*} \mu^*(ab)&=(\alpha^*(a)\times 1+1\times\beta^*(a))(\alpha^*(b)\times 1+1\times\beta^*(b))\\[3pt] &= \begin{cases} 2\alpha^*(a)\times\beta^*(b)&|a|=|b|\text{ and }p\text{ odd}\\[3pt] \alpha^*(a)\times\beta^*(b)&\text{otherwise}, \end{cases} \end{align*}
implying
$\mu^*(\theta(x))\ne 0$
. By the condition (4), we have
$\mu^*(\theta(x))=\theta(\mu^*(x))=0$
. Then, we obtain a contradiction, implying
$[\alpha,\beta]\ne 0$
, as stated.
Let
$G_{m,n}=U(m+n)/U(m)\times U(n)$
. Since
$G_{m,n}\cong G_{n,m}$
, we may assume
$m\le n$
. Let
$j\colon G_{m,n}\to BU(m)$
denote the natural map. Then since
$m\le n$
, the map j is a
$(2m+1)$
-equivalence. Let
$g_i\colon S^{2i}\to BU(m)$
denote a generator of
$\pi_{2i}(BU(m))\cong\mathbb{Z}$
for
$i=1,\ldots,m$
. Then, since j is a
$(2m+1)$
-equivalence, there is a map
$\bar{g}_i\colon S^{2i}\to G_{m,n}$
such that
$j\circ\bar{g}_i=g_i$
for each
$i\le m$
. Thus
\begin{equation*} j\circ[\bar{g}_k,\bar{g}_l]=[j\circ\bar{g}_k,j\circ\bar{g}_l]=[g_k,g_l].\end{equation*}
So if
$[g_k,g_l]\ne 0$
, then
$[\bar{g}_k,\bar{g}_l]\ne 0$
, implying that
$\Omega G_{m,n}$
is not homotopy commutative. We can find a non-trivial Whitehead product
$[g_k,g_l]$
by using the result of Bott [Reference Bott3], but here we use Lemma 3.1 instead.
Recall from [Reference Mimura and Toda22, Chapter III, Theorem 6.9] that the cohomology of
$G_{m,n}$
is given by
\begin{equation*} H^*(G_{m,n};\mathbb{Z})=\mathbb{Z}[c_1,\ldots,c_m,\bar{c}_1,\ldots,\bar{c}_n]/\left(\sum_{i+j=k}c_i\bar{c}_j\mid k\ge 1\right)\end{equation*}
such that
$j^*(c_i)=c_i$
for each i, where
$c_0=\bar{c}_0=1$
,
$c_i=0$
for
$i>m$
,
$\bar{c}_j=0$
for
$j>n$
and the cohomology of BU(m) is as in the proof of Proposition 2.3. We say that a cohomology class
$x\in H^k(X;\mathbb{Z}/p)$
is mod p spherical if there is a map
$\alpha\colon S^k\to X$
such that
$\alpha^*(x)\ne 0$
. We denote the mod p reduction of an integral cohomology class by the same symbol x.
Lemma 3.2. If p is a prime, then
$c_i$
is mod p spherical for
$i\le p$
.
Proof. By [Reference Mimura and Toda22, Chapter IV, Lemma 5.8],
$g_i^*(c_i)=\pm(i-1)!u_{2i}$
, where
$u_{2i}$
is a generator of
$H^{2i}(S^{2i};\mathbb{Z})\cong\mathbb{Z}$
. Then the proof is done.
Proposition 3.3. The loop space of
$G_{m,n}$
for
$m,n\ge 2$
is not homotopy commutative.
Proof. As observed above, it suffices to show
$[g_k,g_l]\ne 0$
for some k,l. First, we consider the
$m=2$
case. By Lemma 3.2,
$c_1,c_2\in H^*(G_{2,n};\mathbb{Z}/2)$
are mod 2 spherical. By the Wu formula,
$\mathrm{Sq}^2c_2=c_1c_2\ne 0$
in
$H^*(BU(2);\mathbb{Z}/2)$
. Then by Lemmas 3.1 and 3.2,
$[g_1,g_2]\ne 0$
.
Next, we consider the
$m>2$
case. Take any odd prime p with
$m/2<p\le m$
, where such an odd prime exists by Bertrand’s postulate. Let
$k=m/2$
for m even and
$k=(m+1)/2$
for m odd. By Lemma 3.2,
$c_k$
and
$c_{m-k+1}$
are mod p spherical. By the mod p Wu formula proved by Shay [Reference Shay24],
$\mathcal{P}^1c_{m-p+2}$
is decomposable and includes the term
\begin{equation*} -(m+1)c_kc_{m-k+1} \end{equation*}
in
$H^*(BU(m);\mathbb{Z}/p)$
. So if
$m+1\not\equiv 0\mod p$
, then
$[g_k,g_{m-k+1}]\ne 0$
. Now we suppose
$m+1\equiv 0\mod p$
. Then, we must have
$m=2p-1$
. So if there is another prime q in
$(m/2,m]$
, then
$m+1\not\equiv 0\mod q$
. So the above argument for the
$m+1\not\equiv 0\mod p$
case works, and thus,
$[g_k,g_{m-k+1}]\ne 0$
. Hence, we aim to show that there are two primes in
$(m/2,m]$
. Recall from [Reference Sondow25] that the Ramanujan prime
$R_n$
is the least integer k such that for each
$x\ge k$
, there are at least n primes in the interval
$(x/2,x]$
. It is proved in [Reference Sondow25] that
$R_n$
exists for each n and
$R_2=11$
. Then, it remains the cases
$m=2\cdot 3-1=5$
and
$m=2\cdot 5-1=9$
, and we have
$5/2<3,5\le 5$
and
$9/2<5,7\le 9$
. Thus, there are at least two primes in
$(m/2,m]$
, completing the proof.
Let
$Q_n=SO(n+2)/SO(2)\times SO(n)$
.
Proposition 3.4. The loop space of
$Q_n$
for
$n\ge 2$
is not homotopy commutative.
Proof. There is a homotopy fibration
\begin{equation} S^1=SO(2)\to SO(n+2)/SO(n)\xrightarrow{q}Q_n. \end{equation}
Then the projection
$q\colon SO(n+2)/SO(n)\to Q_n$
is injective in
$\pi_*$
for
$*\ge 2$
, and so by the naturality of Whitehead products, it is sufficient to show that there is a non-trivial Whitehead products in
$\pi_*(SO(n+2)/SO(n))$
for some
$*\ge 2$
. Let
$\iota\colon S^n=SO(n+1)/SO(n)\to SO(n+2)/SO(n)$
denote the inclusion. Then, Ōshima [Reference Ōshima23] proved that the Whitehead product
$[\iota,\iota]\in\pi_{2n-1}(SO(n+2)/SO(n))$
is non-trivial whenever
$n+1$
is not the power of 2. Thus, we obtain that
$\Omega Q_n$
is not homotopy commutative if
$n+1$
is not the power of 2.
Suppose
$n=2m-1$
. Then as in [Reference Ishitoya16], the cohomology of
$Q_n$
is given by
\begin{equation*} H^*(Q_n;\mathbb{Z})=\mathbb{Z}[t,e]/(t^{m}-2e,e^2),\quad\mathrm{Sq}^2e=te, \end{equation*}
where
$|t|=2$
and
$|e|=2m$
. Since
$Q_n$
is simply connected, the Hurewicz theorem implies that t is mod 2 spherical. Let
$B=S^{n-1}\cup_2e^n$
. Then,
$SO(n+2)/SO(n)=\Sigma B\cup e^{2n+1}$
, so that
\begin{equation*} H^*(SO(n+2)/SO(n);\mathbb{Z}/2)=E(x_n,x_{n+1}),\quad|x_i|=i. \end{equation*}
Let
$j\colon\Sigma B\to Q_n$
denote the composition of the inclusion
$\Sigma B\to SO(n+2)/SO(n)$
and the projection
$q\colon SO(n+2)/SO(n)\to Q_n$
. Then by the Gysin sequence for the fibration (3.1), we get
$j^*(e)=x_{n+1}$
. Thus by Lemma 3.1, we obtain that
$Q_n$
has non-trivial Whitehead product, implying
$\Omega Q_n$
is not homotopy commutative.
Proposition 3.5. The loop space of
$E_6/Spin(10)\cdot T^1$
is not homotopy commutative.
Proof. As in [Reference Ishitoya16], the mod 2 cohomology of
$E_6/Spin(10)\cdot T^1$
is given by
\begin{equation*} H^*(E_6/Spin(10)\cdot T^1;\mathbb{Z}/2)=\mathbb{Z}/2[t,w']/(tw'^2,t^{12}+w'^3),\quad \mathrm{Sq}^2w'=tw', \end{equation*}
where
$|t|=2$
and
$|w'|=8$
. Since
$E_6/Spin(10)\cdot T^1$
is simply connected, the Hurewicz theorem implies that t is mod 2 spherical. We can deduce from Conlon’s result [Reference Conlon6] that
$\pi_*(E_6/Spin(10),F_4/Spin(9))=0$
for
$*\le 31$
. In particular,
\begin{equation*} H^*(E_6/Spin(10);\mathbb{Z}/2)\cong H^*(F_4/Spin(9);\mathbb{Z}/2)\quad(*\le 30). \end{equation*}
Note that
$F_4/Spin(9)$
is the Cayley plane
$\mathbb{O}P^2$
. Then since
$\mathbb{O}P^2=S^8\cup e^{16}$
, a generator
$u\in H^8(F_4/Spin(9);\mathbb{Z}/2)\cong\mathbb{Z}/2$
is mod 2 spherical, and so a generator
$v\in H^8(E_6/Spin(10))\cong\mathbb{Z}/2$
is mod 2 spherical too. By the Gysin sequence associated with the fibration
$S^1\to E_6/Spin(10)\xrightarrow{q}E_6/Spin(10)\cdot T^1$
, we can see that
$q^*(w')=v$
, implying w
$^{\prime}$
is mod 2 spherical. Thus by Lemma 3.1, we obtain that
$E_6/Spin(10)\cdot T^1$
has a non-trivial Whitehead product, and so
$\Omega(E_6/Spin(10)\cdot T^1)$
is not homotopy commutative.
Now we are ready to prove Theorem 1.1.
Proof of Theorem 1.1. Combine Propositions 2.3, 2.4, 3.3, 3.4, 3.5 and the result of Ganea [Reference Ganea8] on the homotopy commutativity of the loop space of
$\mathbb{C} P^n$
mentioned in Section 1.
Acknowledgement
The authors are grateful to Toshiyuki Miyauchi for informing them the result of Ōshima [Reference Ōshima23]. They are also grateful to the referee for improving the presentation of the paper. The authors were partially supported by JSPS KAKENHI Grant Number JP17K05248 and JP19K03473 (Kishimoto), JSPS KAKENHI Grant Number JP21J10117 (Takeda), and JST SPRING Grant Number JPMJSP2110 (Tong).
