Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-11T11:56:46.321Z Has data issue: false hasContentIssue false
  • English
  • Français

HERMITIANS IN MATRIX ALGEBRAS WITH OPERATOR NORM

Part of: General theory of linear operators Basic linear algebra

Published online by Cambridge University Press:  27 April 2020

MICHAEL J. CRABB ,
JOHN DUNCAN  and
COLIN M. McGREGOR
MICHAEL J. CRABB
Affiliation:
School of Mathematics and Statistics, University of Glasgow, GlasgowG12 8QW, Scotland, UK
JOHN DUNCAN
Affiliation:
Department of Mathematical Sciences, University of Arkansas, Fayetteville, AR72701, USA, e-mail: jduncan@uark.edu
COLIN M. McGREGOR
Affiliation:
School of Mathematics and Statistics, University of Glasgow, GlasgowG12 8QW, Scotland, UK, e-mail: Colin.McGregor@glasgow.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate the real space H of Hermitian matrices in 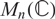$M_n(\mathbb{C})$ with respect to norms on $\mathbb{C}^n$ . For absolute norms, the general form of Hermitian matrices was essentially established by Schneider and Turner [Schneider and Turner, Linear and Multilinear Algebra (1973), 9–31]. Here, we offer a much shorter proof. For non-absolute norms, we begin an investigation of H by means of a series of examples, with particular reference to dimension and commutativity.

MSC classification

Primary: 15A60: Norms of matrices, numerical range, applications of functional analysis to matrix theory
Secondary: 47A12: Numerical range, numerical radius
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 63 , Issue 2 , May 2021 , pp. 280 - 290
Copyright
© The Author(s) 2020. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Footnotes

To the memory of Michael J. Crabb

References

REFERENCES

Bauer, F. L., Theory of norms, infolab.stanford.edu/pub/cstr/reports/cs/tr/67/75/CS-TR-67-75.pdf (Stanford University, 1967).Google Scholar
Bonsall, F. F. and Duncan, J., Numerical ranges of operators on normed spaces and of elements of normed algebras, LMS Lecture Note Series, vol. 2 (Cambridge University Press, New York, 1971).CrossRefGoogle Scholar
Bonsall, F. F. and Duncan, J., Numerical ranges II, LMS Lecture Note Series, vol. 10 (Cambridge University Press, New York, 1973).CrossRefGoogle Scholar
Crabb, M. J., Duncan, J., McGregor, C. M. and Ransford, T. J., Hermitian powers: a Müntz theorem and extremal algebras, Studia Math. 146(1) (2001), 83–97.CrossRefGoogle Scholar
Kleinecke, D. C., On operator commutators, Proc. Amer. Math. Soc. 8 (1957), 535–536.Google Scholar
Prasolov, V. V., Problems and theorems in linear algebra, Mathematical Monographs, 134 (American Mathematical Society, 1996).Google Scholar
Schneider, H. and Turner, R. E., Matrices Hermitian for an absolute norm, Linear Multilinear Algebra (1973), 9–31.CrossRefGoogle Scholar
Sinclair, A. M., The norm of a Hermitian element in a Banach algebra, Proc. Amer. Math. Soc. 1 (1971), 446–450.CrossRefGoogle Scholar
Širokov, F. V., Proof of a conjecture of Kaplansky, Uspehi Mat. Nauk 11 (1956), 167–168.Google Scholar