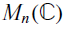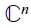Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Duncan, John
and
McGregor, Colin M.
2024.
Hermitians in matrix algebras with operator norm and associated Lie algebras.
Linear Algebra and its Applications,
Vol. 682,
Issue. ,
p.
238.