Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-06T09:56:56.977Z Has data issue: false hasContentIssue false
  • English
  • Français

ANNIHILATOR-STABILITY AND TWO QUESTIONS OF NICHOLSON

Part of: Conditions on elements Grothendieck groups and $K_0$ Homological methods

Published online by Cambridge University Press:  07 April 2020

GUOLI XIA  and
YIQIANG ZHOU
GUOLI XIA
Affiliation:
Department of Mathematics and Statistics, Memorial University of Newfoundland, St.John’s, NLA1C 5S7, Canada e-mails: xglxia@mun.ca; zhou@mun.ca
YIQIANG ZHOU
Affiliation:
Department of Mathematics and Statistics, Memorial University of Newfoundland, St.John’s, NLA1C 5S7, Canada e-mails: xglxia@mun.ca; zhou@mun.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An element a in a ring R is left annihilator-stable (or left AS) if, whenever 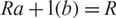$Ra+{\rm l}(b)=R$ with 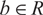$b\in R$ , 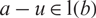$a-u\in {\rm l}(b)$ for a unit u in R, and the ring R is a left AS ring if each of its elements is left AS. In this paper, we show that the left AS elements in a ring form a multiplicatively closed set, giving an affirmative answer to a question of Nicholson [J. Pure Appl. Alg.221 (2017), 2557–2572.]. This result is used to obtain a necessary and sufficient condition for a formal triangular matrix ring to be left AS. As an application, we provide examples of left AS rings R over which the triangular matrix rings 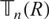${\mathbb T}_n(R)$ are not left AS for all 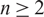$n\ge 2$ . These examples give a negative answer to another question of Nicholson [J. Pure Appl. Alg.221 (2017), 2557–2572.] whether R/J(R) being left AS implies that R is left AS.

MSC classification

Primary: 16U60: Units, groups of units 16E50: von Neumann regular rings and generalizations 19A13: Stability for projective modules
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 63 , Issue 2 , May 2021 , pp. 258 - 265
Copyright
© The Author(s) 2020. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

References

Anderson, D. D., Axtell, M., Forman, S. J. and Stickles, J., When are associates unit multiples? Rocky Mountain J. Math. 34(3) (2004), 811–828.CrossRefGoogle Scholar
Anderson, D. D. and Valdes-Leon, S., Factorization in commutative rings with zero divisors, Rocky Mountain J. Math. 26 (1996), 439–480.CrossRefGoogle Scholar
Azarpanah, F., Farokhpay, F. and Ghashghaei, E., Annihilator-stability and unique generation in C(X), J. Alg. Appl. 18(7) (2019), 1950122 (16 pages).CrossRefGoogle Scholar
Canfell, M. J., Completion of diagrams by automorphisms and Bass’ first stable range condition, J. Algebra 176 (1995), 480–503.CrossRefGoogle Scholar
Chen, H. and Nicholson, W. K., Stable modules and a theorem of Camillo and Yu, J. Pure Appl. Alg. 218 (2014), 1431–1442.CrossRefGoogle Scholar
Ghanem, M., Some properties of associate and presimplifiable rings, Turkish J. Math. 35(2) (2011), 333–340.Google Scholar
Hartwig, R. and Luh, J., A note on the group structure of unit regular ring elements, Pacific J. Math. 71 (1977), 449–461.CrossRefGoogle Scholar
Horoub, A., $\mathcal L$ -stability in rings and left Quasi-duo rings, PhD Thesis (The University of Calgary, Canada, 2018).Google Scholar
Kaplansky, I., Elementary divisors and modules, Trans. AMS. 66 (1949), 464–491.CrossRefGoogle Scholar
Khurana, D. and Lam, T. Y., Rings with internal cancellation, J. Algebra 284 (2005), 203–235.CrossRefGoogle Scholar
Marks, G. A., A criterion for unit-regularity, Acta Math. Hung. 111(4) (2006), 311–312.CrossRefGoogle Scholar
Nicholson, W. K., Lifting idempotents and exchange rings, Trans. AMS. 229 (1977), 269–278.CrossRefGoogle Scholar
Nicholson, W. K., Annihilator-stability and unique generation, J. Pure Appl. Alg. 221 (2017), 2557–2572.CrossRefGoogle Scholar
Nicholson, W. K., Corrigendum to “Annihilator-stability and unique generation” [J. Pure Appl. Algebra 221 (2017) 2557–2572], J. Pure Appl. Alg. 222 (2018), 3334–3335.Google Scholar
Spellman, D., Benkart, G. M., Gaglione, A. M., Joyner, W. D., Kidwell, M. E., Meyerson, M. D. and Wardlaw, W. P., Principal ideals and associate rings, JP J. Algebra Number Theory Appl. 2(2) (2002), 181–193.Google Scholar