We propose a notion of multi-scale stability conditions with the goal of providing a smooth compactification of the quotient of the space of projectivized Bridgeland stability conditions by the group of autoequivalence. For the case of the 3CY category associated with the $A_n$-quiver, this goal is achieved by defining a topology and complex structure that relies on a plumbing construction.

We compare this compactification to the multi-scale compactification of quadratic differentials and briefly indicate why even for the Kronecker quiver, this notion needs refinement to provide a full compactification.

For any prime p and S a p-group isomorphic to a Sylow p-subgroup of a rank $2$ simple group of Lie type in characteristic p, we determine all saturated fusion systems supported on S up to isomorphism.

We compute the integral Chow ring of the moduli stack of smooth elliptic curves with n marked points for $3\leq n\leq 10$.

For positive integers k and n, the shuffle group $G_{k,kn}$ is generated by the $k!$ permutations of a deck of $kn$ cards performed by cutting the deck into k piles with n cards in each pile, and then perfectly interleaving these cards following a certain permutation of the k piles. For $k=2$, the shuffle group $G_{2,2n}$ was determined by Diaconis, Graham and Kantor in 1983. The Shuffle Group Conjecture states that, for general k, the shuffle group $G_{k,kn}$ contains $\mathrm {A}_{kn}$ whenever $k\notin \{2,4\}$ and n is not a power of k. In particular, the conjecture in the case $k=3$ was posed by Medvedoff and Morrison in 1987. The only values of k for which the Shuffle Group Conjecture has been confirmed so far are powers of $2$, due to recent work of Amarra, Morgan and Praeger based on Classification of Finite Simple Groups. In this paper, we confirm the Shuffle Group Conjecture for all cases using results on $2$-transitive groups and elements of large fixed point ratio in primitive groups.

Let $P_1, \ldots , P_m \in \mathbb {K}[\mathrm {y}]$ be polynomials with distinct degrees, no constant terms and coefficients in a general local field $\mathbb {K}$. We give a quantitative count of the number of polynomial progressions $x, x+P_1(y), \ldots , x + P_m(y)$ lying in a set $S\subseteq \mathbb {K}$ of positive density. The proof relies on a general $L^{\infty }$ inverse theorem which is of independent interest. This inverse theorem implies a Sobolev improving estimate for multilinear polynomial averaging operators which in turn implies our quantitative estimate for polynomial progressions. This general Sobolev inequality has the potential to be applied in a number of problems in real, complex and p-adic analysis.

In this paper, we develop two new homological invariants called relative dominant dimension with respect to a module and relative codominant dimension with respect to a module. Among the applications are precise connections between Ringel duality, split quasi-hereditary covers and double centralizer properties, constructions of split quasi-hereditary covers of quotients of Iwahori-Hecke algebras using Ringel duality of q-Schur algebras and a new proof for Ringel self-duality of the blocks of the Bernstein-Gelfand-Gelfand category $\mathcal {O}$. These homological invariants are studied over Noetherian algebras which are finitely generated and projective as a module over the ground ring. They are shown to behave nicely under change of rings techniques.

In this article, we investigate the topological structure of large-scale interacting systems on infinite graphs, by constructing a suitable cohomology which we call the uniform cohomology. The central idea for the construction is the introduction of a class of functions called uniform functions. Uniform cohomology provides a new perspective for the identification of macroscopic observables from the microscopic system. As a straightforward application of our theory when the underlying graph has a free action of a group, we prove a certain decomposition theorem for shift-invariant closed uniform forms. This result is a uniform version in a very general setting of the decomposition result for shift-invariant closed $L^2$-forms originally proposed by Varadhan, which has repeatedly played a key role in the proof of the hydrodynamic limits of nongradient large-scale interacting systems. In a subsequent article, we use this result as a key to prove Varadhan’s decomposition theorem for a general class of large-scale interacting systems.

In this paper, the authors introduce a new notion called the quantum wreath product, which is the algebra $B \wr _Q \mathcal {H}(d)$ produced from a given algebra B, a positive integer d and a choice $Q=(R,S,\rho ,\sigma )$ of parameters. Important examples that arise from our construction include many variants of the Hecke algebras, such as the Ariki–Koike algebras, the affine Hecke algebras and their degenerate version, Wan–Wang’s wreath Hecke algebras, Rosso–Savage’s (affine) Frobenius Hecke algebras, Kleshchev–Muth’s affine zigzag algebras and the Hu algebra that quantizes the wreath product $\Sigma _m \wr \Sigma _2$ between symmetric groups.

In the first part of the paper, the authors develop a structure theory for the quantum wreath products. Necessary and sufficient conditions for these algebras to afford a basis of suitable size are obtained. Furthermore, a Schur–Weyl duality is established via a splitting lemma and mild assumptions on the base algebra B. Our uniform approach encompasses many known results which were proved in a case by case manner. The second part of the paper involves the problem of constructing natural subalgebras of Hecke algebras that arise from wreath products. Moreover, a bar-invariant basis of the Hu algebra via an explicit formula for its extra generator is also described.

In this paper, we study the universal lifting spaces of local Galois representations valued in arbitrary reductive group schemes when $\ell \neq p$. In particular, under certain technical conditions applicable to any root datum, we construct a canonical smooth component in such spaces, generalizing the minimally ramified deformation condition previously studied for classical groups. Our methods involve extending the notion of isotypic decomposition for a $\operatorname {\mathrm {GL}}_n$-valued representation to general reductive group schemes. To deal with certain scheme-theoretic issues coming from this notion, we are led to a detailed study of certain families of disconnected reductive groups, which we call weakly reductive group schemes. Our work can be used to produce geometric lifts for global Galois representations, and we illustrate this for $\mathrm {G}_2$-valued representations.

Assuming Stanley’s P-partitions conjecture holds, the regular Schur labeled skew shape posets are precisely the finite posets P with underlying set $\{1, 2, \ldots , |P|\}$ such that the P-partition generating function is symmetric and the set of linear extensions of P, denoted $\Sigma _L(P)$, is a left weak Bruhat interval in the symmetric group $\mathfrak {S}_{|P|}$. We describe the permutations in $\Sigma _L(P)$ in terms of reading words of standard Young tableaux when P is a regular Schur labeled skew shape poset, and classify $\Sigma _L(P)$’s up to descent-preserving isomorphism as P ranges over regular Schur labeled skew shape posets. The results obtained are then applied to classify the $0$-Hecke modules $\mathsf {M}_P$ associated with regular Schur labeled skew shape posets P up to isomorphism. Then we characterize regular Schur labeled skew shape posets as the finite posets P whose linear extensions form a dual plactic-closed subset of $\mathfrak {S}_{|P|}$. Using this characterization, we construct distinguished filtrations of $\mathsf {M}_P$ with respect to the Schur basis when P is a regular Schur labeled skew shape poset. Further issues concerned with the classification and decomposition of the $0$-Hecke modules $\mathsf {M}_P$ are also discussed.

We prove that the period mapping is dominant for elliptic surfaces over an elliptic curve with $12$ nodal fibers, and that its degree is larger than $1$. This settles the final case of infinitesimal Torelli for a generic elliptic surface.

We study the enumerativity of Gromov–Witten invariants where the domain curve is fixed in moduli and required to pass through the maximum possible number of points. We say a Fano manifold satisfies asymptotic enumerativity if such invariants are enumerative whenever the degree of the curve is sufficiently large. Lian and Pandharipande speculate that every Fano manifold satisfies asymptotic enumerativity. We give the first counterexamples, as well as some new examples where asymptotic enumerativity holds. The negative examples include special hypersurfaces of low Fano index and certain projective bundles, and the new positive examples include many Fano threefolds and all smooth hypersurfaces of degree $d \leq (n+3)/3$ in ${\mathbb P}^n$.

Chow rings of flag varieties have bases of Schubert cycles $\sigma _u $, indexed by permutations. A major problem of algebraic combinatorics is to give a positive combinatorial formula for the structure constants of this basis. The celebrated Littlewood–Richardson rules solve this problem for special products $\sigma _u \cdot \sigma _v$, where u and v are p-Grassmannian permutations.

Building on work of Wyser, we introduce backstable clans to prove such a rule for the problem of computing the product $\sigma _u \cdot \sigma _v$ when u is p-inverse Grassmannian and v is q-inverse Grassmannian. By establishing several new families of linear relations among structure constants, we further extend this result to obtain a positive combinatorial rule for $\sigma _u \cdot \sigma _v$ in the case that u is covered in weak Bruhat order by a p-inverse Grassmannian permutation and v is a q-inverse Grassmannian permutation.

We enrich the class of power-constructible functions, introduced in [CCRS23], to a class $\mathcal {C}^{\mathcal {M,F}}$ of algebras of functions which contains all complex powers of subanalytic functions and their parametric Mellin and Fourier transforms, and which is stable under parametric integration. By describing a set of generators of a special prepared form, we deduce information on the asymptotics and on the loci of integrability of the functions of $\mathcal {C}^{\mathcal {M,F}}$. We furthermore identify a subclass $\mathcal {C}^{\mathbb {C},\mathcal {F}}$ of $\mathcal {C}^{\mathcal {M,F}}$, which is the smallest class containing all power-constructible functions and stable under parametric Fourier transforms and right-composition with subanalytic maps. This class is also stable under parametric integration, under taking pointwise and $\text {L}^p$-limits and under parametric Fourier-Plancherel transforms. Finally, we give a full asymptotic expansion in the power-logarithmic scale, uniformly in the parameters, for functions in $\mathcal {C}^{\mathbb {C},\mathcal {F}}$.

Let $\mathrm {R}$ be a real closed field. Given a closed and bounded semialgebraic set 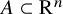$A \subset \mathrm {R}^n$ and semialgebraic continuous functions 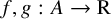$f,g:A \rightarrow \mathrm {R}$ such that 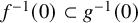$f^{-1}(0) \subset g^{-1}(0)$, there exist an integer 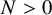$N> 0$ and 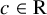$c \in \mathrm {R}$ such that the inequality (Łojasiewicz inequality) 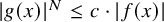$|g(x)|^N \le c \cdot |f(x)|$ holds for all 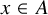$x \in A$. In this paper, we consider the case when A is defined by a quantifier-free formula with atoms of the form 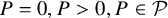$P = 0, P>0, P \in \mathcal {P}$ for some finite subset of polynomials $\mathcal {P} \subset \mathrm {R}[X_1,\ldots ,X_n]_{\leq d}$, and the graphs of $f,g$ are also defined by quantifier-free formulas with atoms of the form $Q = 0, Q>0, Q \in \mathcal {Q}$, for some finite set $\mathcal {Q} \subset \mathrm {R}[X_1,\ldots ,X_n,Y]_{\leq d}$. We prove that the Łojasiewicz exponent in this case is bounded by 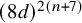$(8 d)^{2(n+7)}$. Our bound depends on d and n but is independent of the combinatorial parameters, namely the cardinalities of 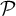$\mathcal {P}$ and $\mathcal {Q}$. The previous best-known upper bound in this generality appeared in P. Solernó, Effective Łojasiewicz Inequalities in Semi-Algebraic Geometry, Applicable Algebra in Engineering, Communication and Computing (1991) and depended on the sum of degrees of the polynomials defining 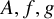$A,f,g$ and thus implicitly on the cardinalities of 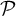$\mathcal {P}$ and $\mathcal {Q}$. As a consequence, we improve the current best error bounds for polynomial systems under some conditions. Finally, we prove a version of Łojasiewicz inequality in polynomially bounded o-minimal structures. We prove the existence of a common upper bound on the Łojasiewicz exponent for certain combinatorially defined infinite (but not necessarily definable) families of pairs of functions. This improves a prior result of Chris Miller (C. Miller, Expansions of the real field with power functions, Ann. Pure Appl. Logic (1994)).

We establish a McKay correspondence for finite and linearly reductive subgroup schemes of ${\mathbf {SL}}_2$ in positive characteristic. As an application, we obtain a McKay correspondence for all rational double point singularities in characteristic $p\geq 7$. We discuss linearly reductive quotient singularities and canonical lifts over the ring of Witt vectors. In dimension 2, we establish simultaneous resolutions of singularities of these canonical lifts via G-Hilbert schemes. In the appendix, we discuss several approaches towards the notion of conjugacy classes for finite group schemes: This is an ingredient in McKay correspondences, but also of independent interest.

The Eichler–Selberg trace formula expresses the trace of Hecke operators on spaces of cusp forms as weighted sums of Hurwitz–Kronecker class numbers. We extend this formula to a natural class of relations for traces of singular moduli, where one views class numbers as traces of the constant function $j_0(\tau )=1$. More generally, we consider the singular moduli for the Hecke system of modular functions

For each $\nu \geq 0$ and $m\geq 1$, we obtain an Eichler–Selberg relation. For $\nu =0$ and $m\in \{1, 2\},$ these relations are Kaneko’s celebrated singular moduli formulas for the coefficients of $j(\tau ).$ For each $\nu \geq 1$ and $m\geq 1,$ we obtain a new Eichler–Selberg trace formula for the Hecke action on the space of weight $2 \nu +2$ cusp forms, where the traces of $j_m(\tau )$ singular moduli replace Hurwitz–Kronecker class numbers. These formulas involve a new term that is assembled from values of symmetrized shifted convolution L-functions.

A classical problem, due to Gerencsér and Gyárfás from 1967, asks how large a monochromatic connected component can we guarantee in any r-edge colouring of $K_n$? We consider how big a connected component we can guarantee in any r-edge colouring of $K_n$ if we allow ourselves to use up to s colours. This is actually an instance of a more general question of Bollobás from about 20 years ago which asks for a k-connected subgraph in the same setting. We complete the picture in terms of the approximate behaviour of the answer by determining it up to a logarithmic term, provided n is large enough. We obtain more precise results for certain regimes which solve a problem of Liu, Morris and Prince from 2007, as well as disprove a conjecture they pose in a strong form.

We also consider a generalisation in a similar direction of a question first considered by Erdős and Rényi in 1956, who considered given n and m, what is the smallest number of m-cliques which can cover all edges of $K_n$? This problem is essentially equivalent to the question of what is the minimum number of vertices that are certain to be incident to at least one edge of some colour in any r-edge colouring of $K_n$. We consider what happens if we allow ourselves to use up to s colours. We obtain a more complete understanding of the answer to this question for large n, in particular, determining it up to a constant factor for all $1\le s \le r$, as well as obtaining much more precise results for various ranges including the correct asymptotics for essentially the whole range.

We give a mathematically precise statement of the SYZ conjecture between mirror space pairs and prove it for any toric Calabi-Yau manifold with the Gross Lagrangian fibration. To date, it is the first time we realize the SYZ proposal with singular fibers beyond the topological level. The dual singular fibration is explicitly written and proved to be compatible with the family Floer mirror construction. Moreover, we discover that the Maurer-Cartan set of a singular Lagrangian is only a strict subset of the corresponding dual singular fiber. This responds negatively to the previous expectation and leads to new perspectives of SYZ singularities. As extra evidence, we also check some computations for a well-known folklore conjecture for the Landau-Ginzburg model.

The box-ball systems are integrable cellular automata whose long-time behavior is characterized by soliton solutions, with rich connections to other integrable systems such as the Korteweg-de Vries equation. In this paper, we consider a multicolor box-ball system with two types of random initial configurations and obtain sharp scaling limits of the soliton lengths as the system size tends to infinity. We obtain a sharp scaling limit of soliton lengths that turns out to be more delicate than that in the single color case established in [LLP20]. A large part of our analysis is devoted to studying the associated carrier process, which is a multidimensional Markov chain on the orthant, whose excursions and running maxima are closely related to soliton lengths. We establish the sharp scaling of its ruin probabilities, Skorokhod decomposition, strong law of large numbers and weak diffusive scaling limit to a semimartingale reflecting Brownian motion with explicit parameters. We also establish and utilize complementary descriptions of the soliton lengths and numbers in terms of modified Greene-Kleitman invariants for the box-ball systems and associated circular exclusion processes.