Let $U$ be a unipotent group which is graded in the sense that it has an extension $H$ by the multiplicative group of the complex numbers such that all the weights of the adjoint action on the Lie algebra of $U$ are strictly positive. We study embeddings of $H$ in a general linear group $G$ which possess Grosshans-like properties. More precisely, suppose $H$ acts on a projective variety $X$ and its action extends to an action of $G$ which is linear with respect to an ample line bundle on $X$. Then, provided that we are willing to twist the linearization of the action of $H$ by a suitable (rational) character of $H$, we find that the $H$-invariants form a finitely generated algebra and hence define a projective variety $X/\!/H$; moreover, the natural morphism from the semistable locus in $X$ to $X/\!/H$ is surjective, and semistable points in $X$ are identified in $X/\!/H$ if and only if the closures of their $H$-orbits meet in the semistable locus. A similar result applies when we replace $X$ by its product with the projective line; this gives us a projective completion of a geometric quotient of a $U$-invariant open subset of $X$ by the action of the unipotent group $U$.

We study uniform and coarse embeddings between Banach spaces and topological groups. A particular focus is put on equivariant embeddings, that is, continuous cocycles associated to continuous affine isometric actions of topological groups on separable Banach spaces with varying geometry.

We prove that Boolean functions on $S_{n}$, whose Fourier transform is highly concentrated on irreducible representations indexed by partitions of $n$ whose largest part has size at least $n-t$, are close to being unions of cosets of stabilizers of $t$-tuples. We also obtain an edge-isoperimetric inequality for the transposition graph on $S_{n}$ which is asymptotically sharp for subsets of $S_{n}$ of size $n!/\text{poly}(n)$, using eigenvalue techniques. We then combine these two results to obtain a sharp edge-isoperimetric inequality for subsets of $S_{n}$ of size $(n-t)!$, where $n$ is large compared to $t$, confirming a conjecture of Ben Efraim in these cases.

Given a finite group $G$, the generating graph $\unicode[STIX]{x1D6E4}(G)$ of $G$ has as vertices the (nontrivial) elements of $G$ and two vertices are adjacent if and only if they are distinct and generate $G$ as group elements. In this paper we investigate properties about the degrees of the vertices of $\unicode[STIX]{x1D6E4}(G)$ when $G$ is an alternating group or a symmetric group of degree $n$. In particular, we determine the vertices of $\unicode[STIX]{x1D6E4}(G)$ having even degree and show that $\unicode[STIX]{x1D6E4}(G)$ is Eulerian if and only if $n\geqslant 3$ and $n$ and $n-1$ are not equal to a prime number congruent to 3 modulo 4.

Let $G$ be a finite almost simple group. It is well known that $G$ can be generated by three elements, and in previous work we showed that 6 generators suffice for all maximal subgroups of $G$. In this paper, we consider subgroups at the next level of the subgroup lattice—the so-called second maximal subgroups. We prove that with the possible exception of some families of rank 1 groups of Lie type, the number of generators of every second maximal subgroup of $G$ is bounded by an absolute constant. We also show that such a bound holds without any exceptions if and only if there are only finitely many primes $r$ for which there is a prime power $q$ such that $(q^{r}-1)/(q-1)$ is prime. The latter statement is a formidable open problem in Number Theory. Applications to random generation and polynomial growth are also given.

Let $Y$ be a principal homogeneous space of an abelian surface, or a K3 surface, over a finitely generated extension of $\mathbb{Q}$. In 2008, Skorobogatov and Zarhin showed that the Brauer group modulo algebraic classes $\text{Br}\,Y/\text{Br}_{1}\,Y$ is finite. We study this quotient for the family of surfaces that are geometrically isomorphic to a product of isogenous non-CM elliptic curves, as well as the related family of geometrically Kummer surfaces; both families can be characterized by their geometric Néron–Severi lattices. Over a field of characteristic $0$, we prove that the existence of a strong uniform bound on the size of the odd torsion of $\text{Br}Y/\text{Br}_{1}Y$ is equivalent to the existence of a strong uniform bound on integers $n$ for which there exist non-CM elliptic curves with abelian $n$-division fields. Using the same methods we show that, for a fixed prime $\ell$, a number field $k$ of fixed degree $r$, and a fixed discriminant of the geometric Néron–Severi lattice, $\#(\text{Br}Y/\text{Br}_{1}Y)[\ell ^{\infty }]$ is bounded by a constant that depends only on $\ell$, $r$, and the discriminant.

We prove a conjecture of Rouquier relating the decomposition numbers in category ${\mathcal{O}}$ for a cyclotomic rational Cherednik algebra to Uglov’s canonical basis of a higher level Fock space. Independent proofs of this conjecture have also recently been given by Rouquier, Shan, Varagnolo and Vasserot and by Losev, using different methods. Our approach is to develop two diagrammatic models for this category ${\mathcal{O}}$; while inspired by geometry, these are purely diagrammatic algebras, which we believe are of some intrinsic interest. In particular, we can quite explicitly describe the representations of the Hecke algebra that are hit by projectives under the $\mathsf{KZ}$-functor from the Cherednik category ${\mathcal{O}}$ in this case, with an explicit basis. This algebra has a number of beautiful structures including categorifications of many aspects of Fock space. It can be understood quite explicitly using a homogeneous cellular basis which generalizes such a basis given by Hu and Mathas for cyclotomic KLR algebras. Thus, we can transfer results proven in this diagrammatic formalism to category ${\mathcal{O}}$ for a cyclotomic rational Cherednik algebra, including the connection of decomposition numbers to canonical bases mentioned above, and an action of the affine braid group by derived equivalences between different blocks.

A celebrated result of Rödl and Ruciński states that for every graph 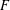$F$, which is not a forest of stars and paths of length 3, and fixed number of colours $r\geqslant 2$ there exist positive constants 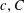$c,C$ such that for 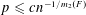$p\leqslant cn^{-1/m_{2}(F)}$ the probability that every colouring of the edges of the random graph 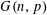$G(n,p)$ contains a monochromatic copy of 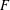$F$ is $o(1)$ (the ‘0-statement’), while for 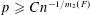$p\geqslant Cn^{-1/m_{2}(F)}$ it is 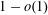$1-o(1)$ (the ‘1-statement’). Here $m_{2}(F)$ denotes the 2-density of $F$. On the other hand, the case where $F$ is a forest of stars has a coarse threshold which is determined by the appearance of a certain small subgraph in 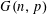$G(n,p)$. Recently, the natural extension of the 1-statement of this theorem to $k$-uniform hypergraphs was proved by Conlon and Gowers and, independently, by Friedgut, Rödl and Schacht. In particular, they showed an upper bound of order 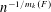$n^{-1/m_{k}(F)}$ for the 1-statement, where $m_{k}(F)$ denotes the $k$-density of $F$. Similarly as in the graph case, it is known that the threshold for star-like hypergraphs is given by the appearance of small subgraphs. In this paper we show that another type of threshold exists if $k\geqslant 4$: there are $k$-uniform hypergraphs for which the threshold is determined by the asymmetric Ramsey problem in which a different hypergraph has to be avoided in each colour class. Along the way we obtain a general bound on the 1-statement for asymmetric Ramsey properties in random hypergraphs. This extends the work of Kohayakawa and Kreuter, and of Kohayakawa, Schacht and Spöhel who showed a similar result in the graph case. We prove the corresponding 0-statement for hypergraphs satisfying certain balancedness conditions.

Let $p$ be a prime number and $F$ a totally real number field. For each prime $\mathfrak{p}$ of $F$ above $p$ we construct a Hecke operator $T_{\mathfrak{p}}$ acting on $(\text{mod}\,p^{m})$ Katz Hilbert modular classes which agrees with the classical Hecke operator at $\mathfrak{p}$ for global sections that lift to characteristic zero. Using these operators and the techniques of patching complexes of Calegari and Geraghty we prove that the Galois representations arising from torsion Hilbert modular classes of parallel weight $\mathbf{1}$ are unramified at $p$ when $[F:\mathbb{Q}]=2$. Some partial and some conjectural results are obtained when $[F:\mathbb{Q}]>2$.

The ‘square peg problem’ or ‘inscribed square problem’ of Toeplitz asks if every simple closed curve in the plane inscribes a (nondegenerate) square, in the sense that all four vertices of that square lie on the curve. By a variety of arguments of a ‘homological’ nature, it is known that the answer to this question is positive if the curve is sufficiently regular. The regularity hypotheses are needed to rule out the possibility of arbitrarily small squares that are inscribed or almost inscribed on the curve; because of this, these arguments do not appear to be robust enough to handle arbitrarily rough curves. In this paper, we augment the homological approach by introducing certain integrals associated to the curve. This approach is able to give positive answers to the square peg problem in some new cases, for instance if the curve is the union of two Lipschitz graphs $f$, $g:[t_{0},t_{1}]\rightarrow \mathbb{R}$ that agree at the endpoints, and whose Lipschitz constants are strictly less than one. We also present some simpler variants of the square problem which seem particularly amenable to this integration approach, including a periodic version of the problem that is not subject to the problem of arbitrarily small squares (and remains open even for regular curves), as well as an almost purely combinatorial conjecture regarding the sign patterns of sums $y_{1}+y_{2}+y_{3}$ for $y_{1},y_{2},y_{3}$ ranging in finite sets of real numbers.

We use concepts of continuous higher randomness, developed in Bienvenu et al. [‘Continuous higher randomness’, J. Math. Log. 17(1) (2017).], to investigate $\unicode[STIX]{x1D6F1}_{1}^{1}$-randomness. We discuss lowness for $\unicode[STIX]{x1D6F1}_{1}^{1}$-randomness, cupping with $\unicode[STIX]{x1D6F1}_{1}^{1}$-random sequences, and an analogue of the Hirschfeldt–Miller characterization of weak 2-randomness. We also consider analogous questions for Cohen forcing, concentrating on the class of $\unicode[STIX]{x1D6F4}_{1}^{1}$-generic reals.

We establish the compactness of the moduli space of noncollapsed Calabi–Yau spaces with mild singularities. Based on this compactness result, we develop a new approach to study the weak compactness of Riemannian manifolds.