Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-02-06T14:14:30.711Z Has data issue: false hasContentIssue false
  • English
  • Français

Sharp condition for blow-up and global existence in a two species chemotactic Keller–Segel system in 2

Published online by Cambridge University Press:  07 December 2012

ELIO ESPEJO ,
KARINA VILCHES  and
CARLOS CONCA
ELIO ESPEJO
Affiliation:
Department of Mathematics, Technion, 32000 Haifa, Israel email: eespejo@techunix.technion.ac.il
KARINA VILCHES
Affiliation:
Departamento de Ingeniería Matemática (DIM) and Centro de Modelamiento Matemático (CMM), Universidad de Chile (UMI CNRS 2807), Casilla 170-3, Correo 3, Santiago, Chile email: kvilches@dim.uchile.cl
CARLOS CONCA
Affiliation:
Departamento de Ingeniería Matemática (DIM) and Centro de Modelamiento Matemático (CMM), Universidad de Chile (UMI CNRS 2807), Casilla 170-3, Correo 3, Santiago, Chile email: kvilches@dim.uchile.cl Institute for Cell Dynamics and Biotechnology: A Centre for Systems Biology, University of Chile, Santiago, Chile email: cconca@dim.uchile.cl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

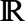
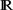For the parabolic–elliptic Keller–Segel system in 2 it has been proved that if the initial mass is less than 8π/χ, a global solution exists, and in case the initial mass is larger than 8π/χ, blow-up happens. The case of several chemotactic species introduces an additional question: What is the analog for the critical mass obtained for the single species system? We find a threshold curve in the two species case that allows us to determine if the system is a blow-up or a global in time solution. No radial symmetry is assumed.

Keywords

chemotaxismulticomponent Keller–Segel modelsharp conditions
Type
Papers
Information
European Journal of Applied Mathematics , Volume 24 , Issue 2 , April 2013 , pp. 297 - 313
Copyright
Copyright © Cambridge University Press 2012

References

[1]Attouch, H., Buttazzo, G. & Michaille, G. (2006) Variational Analysis in Sobolev and BV Spaces: Applications to PDEs and Optimization. MPS-SIAM Series on Optimization, SIAM Philadelphia.Google Scholar
[2]Biler, P. (1998) Local and global solvability of some parabolic systems modelling chemotaxis. Adv. Math. Sci. Appl. 8, 715–743.Google Scholar
[3]Blanchet, A., Carrillo, J. & Masmoudi, N. (2008) Infinite Time Aggregation for the Critical Patlak–Keller–Segel Model in 2. Commun. Pure Appl. Math. LXI, 1449–1481.Google Scholar
[4]Blanchet, A., Dolbeault, J. & Perthame, B. (2006) Two-dimensional Keller–Segel model: Optimal critical mass and qualitative properties of the solutions. Electron. J. Differ. Equ. 44, 1–32.Google Scholar
[5]Childress, S. & Percus, J. K. (1984) Chemotactic Collapse in Two Dimensions, Lecture Notes in Biomathematics, Vol. 56, Springer, Berlim, Germany, pp. 217–237.Google Scholar
[6]Conca, C., Espejo, E. & Vilches, K. (2011) Remarks on the blowup and global existence for a two species chemotactic Keller–Segel system in 2. Eur. J. Appl. Math. 22, 553–580 doi:10.1017/S0956792511000258.Google Scholar
[7]Espejo, E., Stevens, A. & Velázquez, J. J. L. (2009) Simultaneous finite time blow-up in a two-species model for chemotaxis, Analysis 29, 317–338.Google Scholar
[8]Fonseca, I. & Leoni, G. (2007) Modern Methods in the Calculus of Variations: Lp Spaces, Springer Monographs in Mathematics, Springer, Berlin, Germany.Google Scholar
[9]Horstmann, D. (2003) From 1970 until present: The Keller–Segel model in chemotaxis and its consequences I. Jahresber. Dutsch. Math. Ver. 105, 103–165.Google Scholar
[10]Horstmann, D. (2004) From 1970 until present: The Keller–Segel model in chemotaxis and its consequences II. Jahresber. Dutsch. Math. Ver. 106, 51–69.Google Scholar
[11]Jäger, W. & Luckhaus, S. (1992) On explosions of solutions to a system of partial differential equations modelling chemotaxis. Trans. Amer. Math. Soc. 329, 819–824.Google Scholar
[12]Keller, E. F. & Segel, L. A. (1971) Traveling bands of chemotactic bacteria. J. Theor. Biol. 30, 235–248.Google Scholar
[13]Nagai, T. (1995) Blow-up of radially symmetric solutions to a chemotaxis system. Adv. Math. Sci. Appl. 5, 581–601.Google Scholar
[14]Shafrir, I., & Wolansky, G. (2005) Moser-Trudinger and logarithmic HLS inequalities for systems. J. Eur. Math. Soc. 4, 413–448.Google Scholar
[15]VelÁzquez, J. J. L. (2004) Point dynamics in a singular limit of the Keller–Segel model II. Formation of the concentration regions. SIAM J. Appl. Math. 64, 1224–1248 (electronic).Google Scholar
[16]Wolansky, G. (2002) Multi-components chemotactic system in the absence of conflicts. European J. Appl. Math. 13, 641–661.Google Scholar