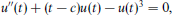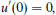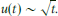Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bolley, C.
and
Helffer, B.
2002.
Nonlinear PDE’s in Condensed Matter and Reactive Flows.
p.
355.
Castillo, Pierre Del
2002.
Expansion for the superheating field in a semi-infinite film in the weak-κlimit.
ESAIM: Mathematical Modelling and Numerical Analysis,
Vol. 36,
Issue. 6,
p.
971.
Clarkson, Peter A
2003.
Painlevé equations—nonlinear special functions.
Journal of Computational and Applied Mathematics,
Vol. 153,
Issue. 1-2,
p.
127.
Palamides, P.K.
2003.
Generalized painlevé equation and superconductivity. asymptotic behavior of unbounded solutions.
Mathematical and Computer Modelling,
Vol. 38,
Issue. 1-2,
p.
177.
Palamides, P.K.
and
Galanis, G.N.
2004.
Positive, unbounded and monotone solutions of the singular second Painlevé equation on the half-line.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 57,
Issue. 3,
p.
401.
Amster, Pablo
Vicchi, Leonardo
and
Rogers, Colin
2009.
Boundary value problems on the half-line for a generalised Painlevé II equation.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 71,
Issue. 1-2,
p.
149.
Del Castillo, P.
and
Mefire, S. M.
2011.
Numerical study of the stability of solutions for the half-space Ginzburg–Landau model.
Journal of Engineering Mathematics,
Vol. 69,
Issue. 4,
p.
327.
Karali, Georgia
and
Sourdis, Christos
2015.
The Ground State of a Gross–Pitaevskii Energy with General Potential in the Thomas–Fermi Limit.
Archive for Rational Mechanics and Analysis,
Vol. 217,
Issue. 2,
p.
439.
Amster, Pablo
and
Rogers, Colin
2015.
On a Ermakov-Painlevé II reduction in three-ion electrodiffusion. A Dirichlet boundary value problem.
Discrete & Continuous Dynamical Systems - A,
Vol. 35,
Issue. 8,
p.
3277.
Clerc, Marcel G.
Dávila, Juan Diego
Kowalczyk, Michał
Smyrnelis, Panayotis
and
Vidal-Henriquez, Estefania
2017.
Theory of light-matter interaction in nematic liquid crystals and the second Painlevé equation.
Calculus of Variations and Partial Differential Equations,
Vol. 56,
Issue. 4,
Agarwal, Ravi P.
Hodis, Simona
and
O’Regan, Donal
2019.
500 Examples and Problems of Applied Differential Equations.
p.
293.
Smyrnelis, Panayotis
2021.
Vortex-filament solutions in the Ginzburg-Landau-Painlevé theory of phase transition.
Journal de Mathématiques Pures et Appliquées,
Vol. 156,
Issue. ,
p.
328.