Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-06T13:52:53.072Z Has data issue: false hasContentIssue false
  • English
  • Français

The large-time asymptotic solution of the mKdV equation

Published online by Cambridge University Press:  04 June 2015

J. A. LEACH  and
ANDREW P. BASSOM
J. A. LEACH
Affiliation:
School of Mathematics, University of Birmingham, Edgbaston, Birmingham, B15 2TT, UK email: j.a.leach@bham.ac.uk
ANDREW P. BASSOM
Affiliation:
School of Mathematics & Statistics, The University of Western Australia, Crawley WA 6009, Australia email: andrew.bassom@uwa.edu.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, an initial-value problem for the modified Korteweg-de Vries (mKdV) equation is addressed. Previous numerical simulations of the solution of

\[u_{t} - 6u^{2} u_{x}+u_{xxx}=0, \quad -\infty<x<\infty, \quad t>0,\]
where x and t represent dimensionless distance and time respectively, have considered the evolution when the initial data is given by
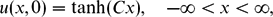\[u(x,0)=\tanh ( Cx ), \quad -\infty<x<\infty,\]
for C constant. These computations suggest that kink and soliton structures develop from this initial profile and here the method of matched asymptotic coordinate expansions is used to obtain the complete large-time structure of the solution in the particular case C = 1/3. The technique is able to confirm some of the numerical predictions, but also forms a basis that could be easily extended to account for other initial conditions and other physically significant equations. Not only can the details of the relevant long-time structure be determined but rates of convergence of the solution of the initial-value problem be predicted.

Keywords

Asymptotic methodslarge time solutionsolitons and kinks
Type
Papers
Information
European Journal of Applied Mathematics , Volume 26 , Issue 6 , December 2015 , pp. 931 - 943
Copyright
Copyright © Cambridge University Press 2015 

References

[1]Chanteur, G. & Raadu, M. (1987) Formation of shocklike modified Korteweg-de Vries solitions: Application to double layers. Phys. Fluids 30, 2708–2719.CrossRefGoogle Scholar
[2]Gardner, L. R. T., Gardner, G. A. & Geyikli, T. (1995) Solitary wave solutions of the MKdV− equation. Comput. Methods Appl. Mech. Engrg. 124, 321–333.CrossRefGoogle Scholar
[3]Kamchatnov, A. M., Kuo, Y.-H., Lin, T.-C., Horng, T.-L., Gou, S.-C., Clift, R., El, G. A. & Grimshaw, R. H. J. (2012) Undular bore theory for the Gardner equation. Phys. Rev. E 86, 036605-1-23.Google Scholar
[4]Kotlyarov, V. & Minakov, A. (2010) Riemann-Hilbert problem to the modified Korteveg-de Vries equation: Long-time dynamics of the steplike initial data. J. Math. Phys. 51, 093506-1-31.CrossRefGoogle Scholar
[5]Kruskal, M. D. (1962) Asymptotology in Mathematical Models in Physical Sciences, S. Drobot and P. A. Viebrock (editors), Proceedings of the Conference at the University of Notre Dame, Prentice-Hall, Englewood Cliffs, NJ, 1963, pp. 17–48.Google Scholar
[6]Leach, J. A. & Needham, D. J. (2003) The large-time development of the solution to an initial-value problem for the Korteweg-de Vries equation. I. Initial data has a discontinuous expansive step. Nonlinearity 21, 2391–2408.CrossRefGoogle Scholar
[7]Leach, J. A. & Needham, D. J. (2003) Matched Asymptotic Expansions in Reaction-Diffusion Theory, London, Springer Monographs in Mathematics.Google Scholar
[8]Leach, J. A. & Needham, D. J. (2009) The evolution of travelling wave-fronts in a hyperbolic Fisher model. III. The initial-value problem when the initial data has exponential decay rates. IMA J. Appl. Math. 74, 870–903.CrossRefGoogle Scholar
[9]Marchant, T. R. (2008) Undular bores and the initial-boundary value problem for the modified Korteweg-de Vries equation. Wave Motion 45, 540–555.CrossRefGoogle Scholar