In this article, we derive a complete mathematical analysis of acoupled 1D-2D model for 2D wave propagation in media including thin slots. Our error estimates are illustrated by numerical results.

The reduced basis element method is a new approach for approximating the solution of problems described by partial differential equations. The method takes its roots in domain decomposition methods and reduced basis discretizations. The basic idea is to first decomposethe computational domain into a series of subdomains that are deformationsof a few reference domains (or generic computational parts). Associated with each reference domain are precomputed solutions corresponding to the same governing partial differential equation,but solved for different choices of deformations of the referencesubdomains and mapped onto the reference shape.The approximation corresponding to a new shape is then taken to be a linear combination of the precomputed solutions, mappedfrom the generic computational part to the actual computational part.We extend earlier work in this direction to solve incompressible fluid flow problems governed by the steady Stokes equations. Particular focus is given to satisfying the inf-sup condition,to a posteriori error estimation, and to “gluing” the local solutions together in the multidomain case.

In this paper, we study the dynamic frictional contact of a viscoelastic beam with a deformableobstacle. The beam is assumed to be situated horizontally and to move, in both horizontal andtangential directions, by the effect of applied forces. The left end of the beam is clampedand the right one is free. Its horizontal displacement is constrained because of the presenceof a deformable obstacle, the so-called foundation, which is modelled by a normal compliance contact condition.The effect of the friction is included in the vertical motion ofthe free end, by using Tresca's law or Coulomb's law. In both cases, the variationalformulation leads to a nonlinear variational equation for the horizontal displacement coupledwith a nonlinear variational inequality for the vertical displacement. We recall an existenceand uniqueness result. Then, by using the finite element method to approximate the spatial variableand an Euler scheme to discretize the time derivatives, a numerical scheme is proposed. Error estimates on the approximative solutions are derived. Numerical results demonstrate the application of the proposed algorithm.

We consider the Stokes problem provided with non standard boundary conditions which involve the normal component of the velocity and the tangential components of the vorticity. We write a variational formulation of this problem with three independent unknowns: the vorticity, the velocity and the pressure. Next we propose a discretization by spectral element methods which relies on this formulation. A detailed numerical analysis leads to optimal error estimates for the three unknowns and numerical experiments confirm the interest of the discretization.

We construct a Roe-type numerical scheme for approximating the solutionsof a drift-flux two-phase flow model. The model incorporates a set ofhighly complex closure laws, and the fluxes are generally not algebraic functions of the conserved variables. Hence, the classical approach of constructing a Roe solver by means of parameter vectors is unfeasible.Alternative approaches for analytically constructing the Roe solver are discussed, and a formulation of the Roe solver valid for general closure laws is derived. In particular, a fully analytical Roe matrix is obtained for the special case of the Zuber–Findlay law describing bubbly flows.First and second-order accurate versions of the scheme are demonstrated bynumerical examples.


In recent years several papers have been devoted to stabilityand smoothing properties in maximum-norm offinite element discretizations of parabolic problems.Using the theory of analytic semigroups it has been possibleto rephrase such properties as bounds for the resolventof the associated discrete elliptic operator. In all thesecases the triangulations of the spatial domain has beenassumed to be quasiuniform. In the present paper weshow a resolvent estimate, in one and two space dimensions,under weaker conditions on the triangulations than quasiuniformity.In the two-dimensional case, the bound for the resolvent containsa logarithmic factor.


We consider the use of finite volume methods for the approximation of aparabolic variational inequality arising in financial mathematics.We show, under some regularityconditions, the convergence of the upwind implicit finite volume schemeto a weak solution of the variational inequality in a bounded domain.Some results, obtained in comparison with other methodson two dimensional cases, show that finite volume schemes can be accurate and efficient.

We construct finite volume schemes, on unstructured and irregular grids andin any space dimension, for non-linear elliptic equations of the p-Laplacian kind: -div(|∇u|p-2 ∇u) = ƒ(with 1 < p < ∞). We prove the existence and uniqueness of the approximate solutions,as well as their strong convergence towards the solution of the PDE.The outcome of some numerical tests are also provided.

In this paper, we present extensive numerical tests showing the performanceand robustness of a Balancing Neumann-Neumann method for the solution of algebraic linear systems arising from hp finite element approximations of scalar ellipticproblems on geometrically refined boundary layer meshes inthree dimensions. The numerical results are in good agreement with the theoretical bound for the condition number of the preconditioned operator derived in [Toselli and Vasseur, IMA J. Numer. Anal.24 (2004) 123–156]. They confirm that the condition numbers are independent of theaspect ratio of the mesh and of potentially large jumps of thecoefficients. Good results are also obtained for certain singularly perturbed problems. The condition numbers only grow polylogarithmically with thepolynomial degree, as in the case of p approximations on shape-regular meshes [Pavarino, RAIRO: Modél. Math. Anal. Numér.31 (1997) 471–493]. This paper follows [Toselli and Vasseur, Comput. Methods Appl. Mech. Engrg.192 (2003) 4551–4579] on two dimensional problems.

We consider a quasistatic system involving a Volterra kernel modellingan hereditarily-elastic aging body. We are concerned with the behavior of displacement and stress fields in the neighborhood of cracks. In this paper, we investigate the case of a straight crack in a two-dimensional domain with a possiblyanisotropic material law.We study the asymptotics of the time dependent solution near the crack tips. We prove that, depending on the regularity of the materiallaw and the Volterra kernel, these asymptotics contain singular functions which are simple homogeneousfunctions of degree $\frac12$ or have a more complicated dependence onthe distance variable r to the crack tips. In the latter situation,we observe a novel behavior of the singular functions, incompatible withthe usual fracture criteria, involving super polynomial functions of ln r growing in time.

In this paper we introduce and analyze new mixed finite volume methods for second order elliptic problemswhich are based on H(div)-conforming approximations for the vector variable anddiscontinuous approximations for the scalar variable.The discretization is fulfilled by combining the ideas of the traditional finite volume box method andthe local discontinuous Galerkin method.We propose two different types of methods, called Methods I and II, and show that they have distinct advantagesover the mixed methods used previously.In particular, a clever elimination of the vector variable leads to a primal formulation for the scalar variablewhich closely resembles discontinuous finite element methods.We establish error estimates for these methods that are optimal for the scalar variable in both methodsand for the vector variable in Method II.

An algorithm for approximation of an unsteady fluid-structure interaction problem isproposed. The fluid is governed by the Navier-Stokes equations with boundary conditionson pressure, while for the structure a particular plate model is used. The algorithm is based on the modal decomposition and the Newmark Method for the structure and on the Arbitrary Lagrangian Eulerian coordinates and the Finite Element Method for the fluid.In this paper, the continuity of the stresses at the interface was treated by theLeast Squares Method. At each time step we have to solve an optimization problemwhich permits us to use moderate time step. This is the main advantage of this approach. In order to solve the optimization problem, we have employed the Broyden, Fletcher, Goldforb, Shano Method wherethe gradient of the cost function was approached by the Finite Difference Method.Numerical results are presented.

We consider the following reaction-diffusion equation:

$$ {\rm (KS)}\left\{\begin{array}{llll}u_t=\nabla \cdot \Big( \nabla u^m - u^{q-1} \nabla v \Big),& x \in \mathbb{R}^N, \ 0<t<\infty, \nonumber0 = \Delta v - v + u, & x \in \mathbb{R}^N, \ 0<t<\infty, \nonumberu(x,0) = u_0(x), & x \in \mathbb{R}^N,\end{array}\right.$$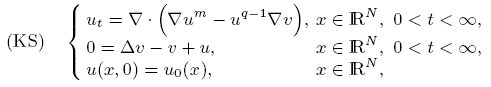

where $N \ge 1, \ m > 1, \ q \ge \max\{m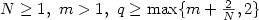+\frac{2}{N},2\}$ .
In [Sugiyama, Nonlinear Anal.63 (2005) 1051–1062; Submitted; J. Differential Equations (in press)]it was shown that in the case of $q \ge \max\{m+\frac{2}{N},2\}$ 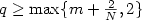, the above problem (KS) is solvable globally in time for “small $L^{\frac{N(q-m)}{2}}$ 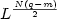data”.Moreover, the decay of the solution (u,v) in $L^p(\mathbb{R}^N)$ 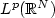was proved.In this paper, we consider the case of “ $q \ge \max\{m+\frac{2}{N},2\}$ 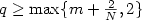and small $L^{\ell}$ 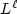data” with any fixed $\ell \ge \frac{N(q-m)}{2}$ 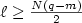and show that (i) there exists a time global solution (u,v) of (KS) andit decays to 0 as t tends to ∞ and(ii) a solution u of the first equation in (KS)behaveslike the Barenblatt solution asymptotically as t tends to ∞,where the Barenblatt solution is the exact solution (with self-similarity) of the porous medium equation $u_t = \Delta u^m$ 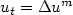with m>1.

We consider models based on conservation laws. For the optimizationof such systems, a sensitivity analysis is essential to determinehow changes in the decision variables influence the objectivefunction. Here we study the sensitivity with respect to the initialdata of objective functions that depend upon the solution of Riemannproblems with piecewise linear flux functions. We presentrepresentations for the one–sided directional derivatives of theobjective functions. The results can be used in the numerical methodcalled Front-Tracking.

This work deals with the study of some stratigraphic models for the formation of geological basins under a maximal erosion rate constrain. It leads to introduce differentialinclusions of degenerated hyperbolic-parabolic type $0\in \partial _{t}u-div\{H(\partial _{t}u+E)\nabla u\}$ , where H is the maximal monotonous graph of the Heaviside function and E is a given non-negative function. Firstly, we present the new and realistic models and an original mathematical formulation, taking into account the weather-limited rate constraint in the conservation law, with a unilateral constraint on the outflow boundary. Then, we give a study of the 1-D case with numerical illustrations.

In this work, we propose a general framework for the construction of pressure law for phase transition. These equations of state are particularly suitable for a use in a relaxation finite volume scheme. The approach is based on a constrained convex optimizationproblem on the mixture entropy. It is valid for both miscible and immiscible mixtures. We also propose a rough pressure law for modelling a super-critical fluid.

A simplified stochastic Hookean dumbbells model arising from viscoelastic flows is considered, the convective terms being disregarded. A finite element discretization in space is proposed. Existence of the numerical solution is proved for small data, so as a priori error estimates,using an implicit function theorem and regularity results obtained in [Bonito et al., J. Evol. Equ.6 (2006) 381–398] for the solution of the continuous problem. A posteriori error estimates are also derived.Numerical results with small time steps and a large number of realizations confirm theconvergence rate with respect to the mesh size.

Many inverse problems for differential equationscan be formulated as optimal control problems.It is well known that inverse problems often need tobe regularized to obtain good approximations.This work presents a systematic method to regularizeand to establish error estimates for approximations tosome control problems in high dimension, based on symplectic approximationof the Hamiltonian system for the control problem. In particularthe work derives error estimatesand constructs regularizations for numerical approximations tooptimally controlled ordinary differential equations in ${\mathbb R}^d$ ,with non smooth control.Though optimal controls in general becomenon smooth,viscosity solutions to the corresponding Hamilton-Jacobi-Bellmanequation provide good theoretical foundation, but poor computational efficiencyin high dimensions.The computational method here uses the adjoint variable and worksefficiently also for high dimensional problems with d >> 1.Controls can be discontinuous due to a lack of regularityin the Hamiltonian or due to colliding backward paths, i.e. shocks.The error analysis, for both these cases, is based on consistency with theHamilton-Jacobi-Bellman equation, in the viscosity solution sense,and a discrete Pontryagin principle:the bi-characteristic Hamiltonian ODE system is solvedwith a C 2 approximate Hamiltonian.
The error analysis leads to estimatesuseful also in high dimensions since the bounds depend on the Lipschitznorms of the Hamiltonian and the gradient of the value functionbut not on d explicitly.Applications to inverse implied volatility estimation, in mathematical finance,and to a topology optimization problem are presented.An advantage with the Pontryagin based method is that the Newton method can be applied to efficientlysolve the discrete nonlinear Hamiltonian system,with a sparse Jacobian that can be calculated explicitly.

In this work, the quasistatic thermoviscoelastic thermistor problem isconsidered. The thermistor model describes the combination of the effects due tothe heat, electrical current conduction and Joule's heat generation. The variationalformulation leads to a coupled system of nonlinear variational equations for whichthe existence of a weak solution is recalled.Then, a fully discrete algorithm is introduced based on the finite elementmethod to approximate the spatial variable and an Euler scheme to discretizethe time derivatives. Error estimates are derived and, under suitableregularity assumptions, the linear convergence of the scheme is deduced.Finally, some numerical simulations are performed in order to show the behaviourof the algorithm.

We consider a degenerate parabolic system which modelsthe evolution of nematic liquid crystal with variable degree of orientation.The systemis a slight modificationto that proposed in [Calderer et al., SIAM J. Math. Anal.33 (2002) 1033–1047], which is a special case of Ericksen's general continuum model in [Ericksen, Arch. Ration. Mech. Anal.113 (1991) 97–120]. We prove the global existence of weak solutions by passing to the limit in a regularized system. Moreover, we propose a practical fully discrete finite element method for this regularized system, and we establish the (subsequence) convergence of this finite element approximation to the solution of the regularized system as the mesh parameters tend to zero; andto a solution of the original degenerate parabolic system when the the mesh and regularization parameters all approach zero. Finally, numerical experiments are included which show the formation, annihilation and evolution of line singularities/defects in such models.