Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-12T05:49:31.273Z Has data issue: false hasContentIssue false
  • English
  • Français

Zero-dimensional isomorphic dynamical models

Part of: Topological dynamics

Published online by Cambridge University Press:  11 December 2018

TOMASZ DOWNAROWICZ Open the ORCID record for TOMASZ DOWNAROWICZ [Opens in a new window] ,
LEI JIN ,
WOLFGANG LUSKY  and
YIXIAO QIAO
TOMASZ DOWNAROWICZ
Affiliation:
Faculty of Mathematics and Faculty of Fundamental Problems of Technology, Wrocław University of Technology, Wybrzeże Wyspiańskiego 27, 50-370 Wrocław, Poland email Tomasz.Downarowicz@pwr.edu.pl
LEI JIN
Affiliation:
Institute of Mathematics, Polish Academy of Sciences, ul. Śniadeckich 8, 00-656 Warszawa, Poland email jinleim@mail.ustc.edu.cn
WOLFGANG LUSKY
Affiliation:
Institut für Mathematik, Universität Paderborn, Warburger Strasse 100, 33098 Paderborn, Germany email lusky@math.uni-paderborn.de
YIXIAO QIAO
Affiliation:
School of Mathematical Sciences, South China Normal University, Guangzhou, Guangdong 510631, China email yxqiao@mail.ustc.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

By an assignment we mean a mapping from a Choquet simplex 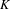$K$ to probability measure-preserving systems obeying some natural restrictions. We prove that if 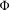$\unicode[STIX]{x1D6F7}$ is an aperiodic assignment on a Choquet simplex $K$ such that the set of extreme points 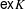$\mathsf{ex}K$ is a countable union $\bigcup _{n}E_{n}$, where each set 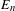$E_{n}$ is compact, zero-dimensional and the restriction of 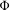$\unicode[STIX]{x1D6F7}$ to the Bauer simplex 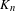$K_{n}$ spanned by 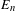$E_{n}$ can be ‘embedded’ in some topological dynamical system, then 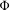$\unicode[STIX]{x1D6F7}$ can be ‘realized’ in a zero-dimensional system.

Keywords

assignmentzero-dimensional systemisomorphic modelmeasure-theoretic isomorphism

MSC classification

Primary: 37B10: Symbolic dynamics 37B40: Topological entropy
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 8 , August 2020 , pp. 2116 - 2130
Check for updates
Copyright
© Cambridge University Press, 2018

References

Boyle, M. and Downarowicz, T.. The entropy theory of symbolic extensions. Invent. Math. 156 (2004), 119–161.10.1007/s00222-003-0335-2CrossRefGoogle Scholar
Boyle, M.. Lower entropy factors of sofic systems. Ergod. Th. & Dynam. Sys. 3 (1983), 541–557.10.1017/S0143385700002133CrossRefGoogle Scholar
Downarowicz, T. and Karpel, O.. Dynamics in dimension zero: a survey. Discrete Cont. Dynam. Syst. A 38(3) (2018), 1033–1062.10.3934/dcds.2018044CrossRefGoogle Scholar
Downarowicz, T.. Survey of odometers and Toeplitz flows. Contemp. Math. 385 (2005), 7–38.10.1090/conm/385/07188CrossRefGoogle Scholar
Downarowicz, T.. Minimal models for noninvertible and not uniquely ergodic systems. Israel J. Math. 156 (2006), 93–124.10.1007/BF02773826CrossRefGoogle Scholar
Downarowicz, T.. Faces of simplexes of invariant measures. Israel J. Math. 165(1) (2008), 189–210.10.1007/s11856-008-1009-yCrossRefGoogle Scholar
Downarowicz, T.. Entropy in Dynamical Systems. Cambridge University Press, Cambridge, 2011.10.1017/CBO9780511976155CrossRefGoogle Scholar
Downarowicz, T.. The Choquet simplex of invariant measures for minimal flows. Israel J. Math. 74 (1991), 241–256.10.1007/BF02775789CrossRefGoogle Scholar
Downarowicz, T. and Serafin, J.. Possible entropy functions. Israel J. Math. 135 (2003), 221–250.10.1007/BF02776059CrossRefGoogle Scholar
Fonf, V. P., Lindenstrauss, J. and Phelps, R. R.. Infinite Dimensional Convexity (Handbook of the Geometry of Banach Spaces, 1). North-Holland, Amsterdam, 2001, pp. 599–670.Google Scholar
Kornfeld, I. and Ormes, N.. Topological realizations of families of ergodic automorphisms, multitowers and orbit equivalence. Israel J. Math. 155 (2006), 335–357.10.1007/BF02773959CrossRefGoogle Scholar
Lazar, A. J.. Spaces of affine continuous functions on simplices. Trans. Amer. Math. Soc. 134 (1968), 503–525.10.1090/S0002-9947-1968-0233188-2CrossRefGoogle Scholar
Lindenstrauss, E.. Mean dimension, small entropy factors and an embedding theorem. Publ. Math. Inst. Hautes Études Sci. 89 (1999), 227–262.10.1007/BF02698858CrossRefGoogle Scholar
Lindenstrauss, J., Olsen, G. and Sternfeld, Y.. The Poulsen simplex. Ann. Inst. Fourier (Grenoble) 28 (1978), 91–114.10.5802/aif.682CrossRefGoogle Scholar
Phelps, R. R.. Lectures on Choquet’s Theorem (Lecture Notes in Mathematics, 1757). Springer, Berlin, 2001.10.1007/b76887CrossRefGoogle Scholar