Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-02-11T10:12:38.215Z Has data issue: false hasContentIssue false
  • English
  • Français

Unique equilibrium states, large deviations and Lyapunov spectra for the Katok map

Part of: Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  20 March 2020

TIANYU WANG
TIANYU WANG*
Affiliation:
Department of Mathematics, The Ohio State University, Columbus, OH43210, USA email wang.7828@buckeyemail.osu.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the thermodynamic formalism of a 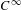$C^{\infty }$ non-uniformly hyperbolic diffeomorphism on the 2-torus, known as the Katok map. We prove for a Hölder continuous potential with one additional condition, or geometric $t$-potential 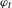$\unicode[STIX]{x1D711}_{t}$ with 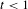$t<1$, the equilibrium state exists and is unique. We derive the level-2 large deviation principle for the equilibrium state of 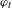$\unicode[STIX]{x1D711}_{t}$. We study the multifractal spectra of the Katok map for the entropy and dimension of level sets of Lyapunov exponents.

Keywords

thermodynamical formalismlarge deviation principlemultifractal analysis

MSC classification

Primary: 37D35: Thermodynamic formalism, variational principles, equilibrium states
Secondary: 37D25: Nonuniformly hyperbolic systems (Lyapunov exponents, Pesin theory, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 7 , July 2021 , pp. 2182 - 2219
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

References

Bowen, R.. Topological entropy for noncompact sets. Trans. Amer. Math. Soc. 184 (1973), 125–136.CrossRefGoogle Scholar
Bowen, R.. Some systems with unique equilibrium states. Math. Syst. Theory 8(3) (1974/75), 193–202.CrossRefGoogle Scholar
Burns, K., Climenhaga, V., Fisher, T. and Thompson, D.. Unique equilibrium states for geodesic flows in nonpositive curvature. Geom. Funct. Anal. 28 (2018), 1209–1259.CrossRefGoogle Scholar
Burns, K. and Gelfert, K.. Lyapunov spectrum for geodesic flows of rank 1 surfaces. Discrete Contin. Dyn. Syst. Ser. A 34(5) 1841–1872.CrossRefGoogle Scholar
Climenhaga, V.. Thermodynamic formalism and multifractal analysis for general topological dynamical systems. Doctoral Thesis, Pennsylvania State University.Google Scholar
Climenhaga, V., Fisher, T. and Thompson, D.. Unique equilibrium states for Bonatti–Viana diffeomorphisms. Nonlinearity 31(6) (2018), 2532–2570.10.1088/1361-6544/aab1cdCrossRefGoogle Scholar
Climenhaga, V., Fisher, T. and Thompson, D.. Unique equilibrium states for Mañé Diffeomorphisms. Ergod. Th. & Dynam. Sys. 39(9) (2019), 2433–2455.10.1017/etds.2017.125CrossRefGoogle Scholar
Climenhaga, V. and Thompson, D.. Unique Equilibrium states for flows and homeomorphisms with non-uniform structure. Adv. Math. 303 (2016), 745–799.CrossRefGoogle Scholar
Fisher, T.. Hyperbolic sets that are not locally maximal. Ergod. Th. & Dynam. Sys. 26(5) (2006), 1491–1509.CrossRefGoogle Scholar
Gorodetski, A. and Pesin, Y.. Path connectness and entropy density of the space of hyperbolic ergodic measures. Modern Theory of Dynamical Systems: A Tribute to Dmitry Victorovich Anosov (Contemporary Mathematics, 692) . American Mathematical Society, Providence, RI, 2017, pp. 111–121.CrossRefGoogle Scholar
Katok, A.. Bernoulli diffeomorphisms on surfaces. Ann. of Math. (2) 110(3) (1979), 529–547.10.2307/1971237CrossRefGoogle Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems (Encyclopedia of Mathematics and Its Applications, 54) . Cambrige University Press, Cambrige, 1995.CrossRefGoogle Scholar
Ledrappier, F. and Young, L. S.. The metric entropy of diffeomorphisms. I. Characterization of measures satisfying Pesin’s entropy formula. Ann. of Math. (2) 122(3) (1985), 509–539.CrossRefGoogle Scholar
Parry, W. and Pollicott, M.. Zeta Functions and the Periodic Orbit Structure of Hyperbolic Dynamics. Société Mathématique de France, Montrouge, 1990.Google Scholar
Pesin, Y.. Lectures on Partial Hyperbolicity and Stable Ergodicity (Zurich Lectures in Advanced Mathematics) . European Mathematician Society, Zurich, 2004.10.4171/003CrossRefGoogle Scholar
Pesin, Y., Senti, S. and Zhang, K.. Thermodynamics of towers of hyperbolic type. Trans. Amer. Math. Soc. 368(12) (2016), 8519–8552.CrossRefGoogle Scholar
Pesin, Y., Senti, S. and Zhang, K.. Thermodynamics of the Katok map. Ergod. Th. & Dynam. Sys. 39(3) (2019), 764–794.CrossRefGoogle Scholar
Pfister, C.-E. and Sullivan, W. G.. Large deviations estimates for dynamical systems without the specification property. Application to the 𝛽-shifts. Nonlinearity 18 (2005), 237–261.CrossRefGoogle Scholar
Ruelle, D.. Statistical Mechanics: Rigorous Results. W. A. Benjamin, Inc., New York, Amsterdam, 1969.Google Scholar
Senti, S. and Takahashi, H.. Equilibrium measures for the Hénon map at the first bifurcation: uniqueness and geometric/statistical properties. Ergod. Th. & Dynam. Sys. 36 (2016), 215–255.CrossRefGoogle Scholar
Shahidi, F. and Zelerowicz, A.. Thermodynamics via inducing. J. Stat. Phys. 175 (2019), 351–383.10.1007/s10955-019-02256-wCrossRefGoogle Scholar
Takens, F. and Verbitskiy, E.. On the variational principle for the topological entropy of certain non-compact sets. Ergod. Th. & Dynam. Sys. 23 (2003), 317–348.CrossRefGoogle Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79) . Springer, New York, 1982.CrossRefGoogle Scholar
Young, L. S.. Dimension, entropy, and Lyapunov exponents. Ergod. Th. & Dynam. Sys. 2 (1982), 109–124.CrossRefGoogle Scholar
Young, L. S.. Some large deviation results for dynamical systems. Trans. Amer. Math. Soc. 318(2) (1990), 525–543.Google Scholar