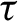1 Introduction
The first result on solutions of the cohomological equation for a parabolic non-homogeneous (but ‘locally homogeneous’) smooth flow was given by the author in [Reference ForniF97] in the case of translation flows (and their smooth time-changes) on higher-genus translation surfaces, by methods of harmonic analysis based on the theory of boundary behavior of holomorphic functions.
Since then refined versions of that result have been proved by (dynamical) renormalization methods based on ‘spectral gap’ (and hyperbolicity) properties of the Rauzy–Veech–Zorich cocycle [Reference Marmi, Moussa and YoccozMMY05, Reference Marmi and YoccozMY16], of the Kontsevich–Zorich cocycle over the Teichmüller flow [Reference ForniF07] and, more recently, of the transfer operator of a pseudo-Anosov map on appropriate anisotropic Banach spaces of currents [Reference Faure, Gouëzel and LanneauFGL]. The renormalization approach has the immediate advantage of a refined control on the regularity loss and of more explicit conditions of Diophantine type on the dynamics, and in particular applies to self-similar translation flows or interval exchange transformations. It also gives a direct approach to results for almost all translation surfaces, while an extension to almost all directions for any given translation surface had to wait for the work of Chaika and Eskin [Reference Chaika and EskinCE] based on the breakthroughs of Eskin and Mirzakhani [Reference Eskin and MirzakhaniEM], Eskin, Mirzakhani and Mohammadi [Reference Eskin, Mirzakhani and MohammadiEMM] and Filip [Reference FilipFi].
In this paper we apply a twisted version of the arguments of [Reference ForniF97] to the solution of the twisted cohomological equation for translation flows and derive results on the cohomological equation for three-dimensional ‘translation flows’ on products of a higher-genus translation surface with a circle. For these problems no renormalization approach is available at the moment, although steps in that direction have been taken in the work of Bufetov and Solomyak [Reference Bufetov and SolomyakBS14, Reference Bufetov and SolomyakBS18a, Reference Bufetov and SolomyakBS18b, Reference Bufetov and SolomyakBS18c, Reference Bufetov and SolomyakBS19] and of the author [Reference ForniF19], who have introduced twisted versions of the Rauzy–Veech–Zorich and Kontsevich–Zorich cocycles respectively, and proved ‘spectral gap’ results for them.
The study of solutions of the twisted cohomological equation is therefore motivated in part by its connection to the question of asymptotics of twisted integrals, investigated in the above-mentioned papers. In fact, twisted integrals of twisted coboundaries with bounded transfer function are bounded for all times. However, there are other more direct motivations, related to the theory of cohomological equations. From results on the twisted cohomological equation (Theorem 1.1 below) we derive results on the (untwisted) cohomological equation for translation flows on the three-dimensional product of a higher-genus surface with a circle (Theorem 1.4) and results on the cohomological equation for time-
$\tau $
maps of translation flows (Corollary 1.5). These are the first results of this kind for non-homogeneous ‘parabolic flows’ beyond the case of (translation) flows on higher-genus surfaces.
For any translation surface
$(M,h)$
(a pair of a Riemann surface M and an abelian differential h on M) let
$H^s_h(M)$
denote the scale of (weighted) Sobolev spaces (introduced in [Reference ForniF97], and recalled below in §2), based on the Hilbert space
$H^0_h(M):=L^2(M, \omega _h)$
of square-integrable functions with respect to the area form
$\omega _h$
of the abelian differential, and defined by the Lie derivative operators given by translation vector fields on the translation surface
$(M,h)$
.
For the horizontal translation flow
$\phi _{\mathbb R}^h$
on M (of generator the horizontal vector field S) and for any
$\sigma \in {\mathbb R}$
, let
$\mathcal I^s_{h, \sigma } \subset H^{-s}_h(M)$
denote the space of
$(S+ \imath \sigma )$
-invariant distributions, that is, the subspace
$$ \begin{align*}\mathcal I^s_{h, \sigma}:=\{ D\in H^{-s}_h(M) \mid (S+ \imath \sigma) D=0 \in H^{-(s+1)}_h(M)\}. \end{align*} $$
For all
$\theta \in { \mathbb T}$
, let
$h_\theta := e^{-\imath \theta } h$
denote the rotated abelian differential and let
$S_\theta $
denote the generator of the horizontal translation flow on
$(M, h_\theta )$
.
We prove the following results.
Theorem 1.1 For any translation surface
$(M,h)$
, for almost all
$\theta \in { \mathbb T}$
and for almost all
$\sigma \in {\mathbb R}$
(with respect to the Lebesgue measure), the following statement holds. For all
$s>0$
the space
$\mathcal I^s_{h_\theta , \sigma } \subset H^{-s}_h (M)$
of
$(S_\theta + \imath \sigma )$
-invariant distributions has finite dimension (bounded above and below by linear functions of the regularity
$s>0$
). For all
$f \in H^s_h(M)$
with
$s>3$
, satisfying the distributional conditions
$D(f)=0$
for all
$(S_\theta + \imath \sigma )$
-invariant distributions
$D \in \mathcal I^s_{h_\theta , \sigma }$
, the twisted cohomological equation
$(S_\theta + \imath \sigma ) u =f$
has a solution
$u\in H^r_h(M)$
for all
$r< s-3$
, and there exists a constant
$C_{r,s} (\theta , \sigma )>0$
such that
$$ \begin{align*}\vert u \vert_r \leq C_{r,s} (\theta, \sigma) \vert f \vert_s. \end{align*} $$
In other words, the theory of the twisted cohomological equation of translation flows is analogous, for Lebesgue almost all twisting parameters, to the untwisted theory of the cohomological equation for translation flows.
Remark 1.2 In the untwisted case the optimal loss of regularity of solutions of the cohomological equation is known to be
$1+$
for
$L^2$
Sobolev norms, for almost all translation flows with respect to any
$SL(2,{\mathbb R})$
invariant measure under the hypothesis of hyperbolicity of the Kontsevich–Zorich cocycle [Reference ForniF07]. Marmi and Yoccoz [Reference Marmi and YoccozMY16] proved a similar, but slightly weaker, statement for Hölder norms. For self-similar translation flows, the loss of
$1+$
derivatives for Hölder norms should follow from the recent work of Faure, Gouëzel and Lanneau [Reference Faure, Gouëzel and LanneauFGL], although spaces with fractional exponents are not explicitly considered in their paper.
It is natural to conjecture that the optimal loss of derivatives is
$1+$
also in the twisted case, and it seems plausible that the whole argument of [Reference ForniF07] would carry over under the (equivalent?) hypotheses of hyperbolicity of the twisted cocycles introduced in [Reference Bufetov and SolomyakBS18c, Reference ForniF19]. At the moment the only known results on such twisted exponents are upper bounds (in particular, that the top exponent is less than
$1$
) [Reference Bufetov and SolomyakBS18c, Reference Bufetov and SolomyakBS19, Reference ForniF19] but no lower bounds are known.
Remark 1.3 The problem of solution of the cohomological equation
$(S + \unicode{x3bb} ) u=f$
is interesting only in the case, considered in Theorem 1.1, of
$\unicode{x3bb} \in \imath {\mathbb R}$
. In fact, the Lie derivative operator with respect to a translation flow S on a higher-genus translation surface
$(M, h)$
is essentially skew-adjoint (see [Reference NelsonNe59, Lemma 3.10]), hence its spectrum is contained in
$\imath {\mathbb R}$
. For
$\unicode{x3bb} \not \in \imath {\mathbb R}$
, that is, for
$\unicode{x3bb} $
in the resolvent set of the operator, we have the standard
$L^2$
a priori estimate
$$ \begin{align*}{ \operatorname{Re} } (\unicode{x3bb})^2 \vert u \vert^2_0 \leq { \operatorname{Re} } (\unicode{x3bb})^2 \vert u \vert^2_0 + \vert (S+ \imath { \operatorname{Im} }(\unicode{x3bb}) ) u \vert^2_0 = \vert (S+ \unicode{x3bb} ) u \vert^2_0. \end{align*} $$
From the above a priori estimate, it is possible to derive, for all
$\unicode{x3bb} \not \in \imath {\mathbb R}$
, the existence of (unique) solutions
$u\in L^2(M, \omega _h)$
of the cohomological equation
$(S + \unicode{x3bb} ) u=f$
, for all data
$f \in H^0_h(M)$
, and by regularization, the existence of regular solutions
$u \in H^s_h(M)$
for all regular data
$f \in H^s_h(M)$
(in the appropriate weighted Sobolev spaces), with no loss of derivatives.
A result on the existence of solutions of the cohomological equation for twisted horocycle flows was recently proved by Flaminio, Forni and Tanis [Reference Flaminio, Forni and TanisFFT16], who were motivated by applications to the cohomological equation for horocycle time-
$\tau $
maps (see also [Reference TanisTa12]) and to deviation of ergodic averages for twisted horocycle integrals and horocycle time-
$\tau $
maps. Twisted nilflows are still nilflows, hence the theory of twisted cohomological equations in the nilpotent case is covered by the general results of Flaminio and Forni [Reference Flaminio and ForniFlaFo07]. As for results on deviation of ergodic averages for nilflows, they are related to bounds on Weyl sums for polynomials. The Heisenberg, and the general step-2, case are better understood by renormalization methods (see, for instance, [Reference Flaminio and ForniFlaFo06]), while the higher-step case is not renormalizable, hence harder (see, for instance, [Reference Green and TaoGT12, Reference Flaminio and ForniFlaFo14]). Results on twisted ergodic integrals of translation flows and applications to effective weak mixing were recently proved by the author [Reference ForniF19].
For all
$(s, \nu ) \in { \mathbb N}\times { \mathbb N}$
, let
$H^{s, \nu }_h(M\times { \mathbb T})$
denote the
$L^2$
Sobolev space on
$M\times { \mathbb T}$
with respect to the invariant volume form
$\omega _h \wedge d\phi $
and the vector fields S, T, and
$\partial /\partial \phi $
: for all
$(s, \nu ) \in { \mathbb N}\times { \mathbb N}$
, we define
$$ \begin{align*}H^{s,\nu}_h (M\times{ \mathbb T}):= \bigg\{ f \in L^2(M\times { \mathbb T}, d \text{vol})\ \Big| \sum_{i+j\leq s}\sum_{\ell \leq \nu} \bigg\Vert S^i T^j \frac{\partial^\ell f}{\partial \phi^\ell} \bigg\Vert_0 < +\infty\bigg\}; \end{align*} $$
the space
$H^{s,\nu }_h (M\times { \mathbb T})$
can be defined for all
$(s, \nu )\in {\mathbb R}^+ \times {\mathbb R}^+$
by interpolation [Reference Lions and MagenesLM] and the space
$H^{-s, -\nu }_h(M\times { \mathbb T})$
is defined as the dual of the space
$H^{s,\nu }_h(M\times { \mathbb T})$
.
The space
$L^2(M\times { \mathbb T}, d \text {vol})$
of the product manifold with respect to the invariant volume form
$\omega _h \wedge d\phi $
decomposes as a direct sum of the eigenspaces
$\{H^0_n \mid n\in { \mathbb Z}\}$
of the circle action:
$$ \begin{align*}L^2(M\times { \mathbb T}, d \text{vol}) = \bigoplus_{n\in { \mathbb Z}} H^0_n. \end{align*} $$
Let now
$X_{\theta , c}= S_\theta + c ({\partial }/{\partial \phi })$
denote a translation vector field on the translation manifold
$M \times { \mathbb T}$
, and let
$\mathcal I^{s,\nu }_{h_\theta , c} \subset H^{-s, -\nu }_h(M\times { \mathbb T})$
denote the space of
$X_{\theta , c}$
-invariant distributions. The subspace of
$X_{\theta , c}$
-invariant distributions in
$\mathcal I^{s,\nu }_{h_\theta , c}$
supported on the Sobolev subspace of
$H_n^s \subset H_n^0$
has finite and non-zero dimension, uniformly bounded with respect to
$n\in { \mathbb N}$
. It follows that the space
$\mathcal I^{s,\nu }_{h_\theta , c}$
has countable dimension.
Theorem 1.4 For any translation surface
$(M,h)$
, for almost all
$\theta \in { \mathbb T}$
and for almost all
$c \in {\mathbb R}$
(with respect to the Lebesgue measure), the following statement holds.
For all
$s>3$
and
$\nu>2$
, the space
$\mathcal I^{s,\nu }_{h_\theta ,c} \subset H^{-s,-\nu }_h(M\times { \mathbb T})$
of
$X_{\theta ,c}$
-invariant distributions has infinite (countable) dimension, and for all
$f \in H^{s,\nu }_h(M \times { \mathbb T})$
such that
$D(f)=0$
for all
$D \in \mathcal I^{s,\nu }_{h_\theta ,c}$
, the cohomological equation
$X_{\theta ,c} u =f$
has a solution
$u\in H^{r, \mu }_h(M \times { \mathbb T})$
for all
$r< s-3$
and
$\mu <\nu -2$
. In addition, there exists a constant
$C^{(\mu , \nu )}_{r,s} (\theta , c)>0$
such that
$$ \begin{align*}\Vert u \Vert_{r, \mu} \leq C^{(\mu, \nu)}_{r,s} (\theta, c) \Vert f \Vert_{s, \nu}. \end{align*} $$
Following Katok (see [Reference KatokKa01, §3.1] or [Reference KatokKa03, §11.1]) a smooth flow on a smooth compact, connected manifold
$\mathcal M$
is called
$C^\infty $
-stable if the range of the Lie derivative operator on
$C^\infty (\mathcal M)$
is closed in
$C^\infty (\mathcal M)$
(see also [Reference Forni, Burns, Dolgopyat and PesinF08]). In this terminology, Theorem 1.4 implies that for almost all
$(\theta , c)\in { \mathbb T} \times {\mathbb R}$
, the flow of the vector field
$X_{\theta ,c}$
on
$M\times { \mathbb T}$
is
$C^\infty $
-stable. Indeed, the closed-range property is an immediate consequence of the (Sobolev) estimates on the solutions of the cohomological equation. Our theorem implies more generally stability in weighted Sobolev spaces of finitely differentiable functions.
In fact, ours is the first example of a
$C^\infty $
-stable non-homogeneous (although locally homogeneous), non-hyperbolic (partially hyperbolic) hyperbolic flow on a manifold of dimension at least
$3$
. Indeed, we recall that the only known examples of stable (and renormalizable) three-dimensional parabolic flows are (up to smooth conjugacies and time-changes) homogeneous flows: horocycle flows of hyperbolic surfaces [Reference Flaminio and ForniFlaFo03] and Heisenberg nilflows [Reference Flaminio and ForniFlaFo06]. However, there has been recent progress (although conditional) on ‘Ruelle asymptotics’ and deviation of ergodic averages for horocycle flows for negatively curved metrics on surfaces [Reference Adam and BaladiAB] (see also [Reference Faure and GuillarmouFG18]), hence a proof of smooth stability (at least in low regularity) for such flows seems within reach of current methods for the analysis for the transfer operator of hyperbolic flows, along the lines of the work of Giulietti and Liverani [Reference Giulietti and LiveraniGL] for Anosov maps of tori.
We recall, again following A. Katok’s terminology, that a stable flow on a smooth, compact, connected manifold
$\mathcal M$
such that the range of the Lie derivative operator has codimension one in
$C^\infty (\mathcal M)$
is called rigid or cohomology free. The Katok–Hurder conjecture (known for flows only up to dimension
$3$
; see [Reference Forni, Burns, Dolgopyat and PesinF08] and references therein) states that all smooth rigid flows are smoothly conjugate to linear Diophantine flows on tori. It is therefore expected that all non-toral uniquely ergodic stable flows have invariant distributions which are not signed measures, a property which is confirmed by our result, since the range of the Lie derivative has higher codimension. In fact, in all known examples of
$C^\infty $
-stable flows, the space of invariant distributions is infinite-dimensional, with the only partial exception of typical translation flows on compact orientable surfaces, which have finite codimension in finite differentiability [Reference ForniF97]. Our result confirms once more the expectation that, in dimension greater than
$2$
, the space of invariant distributions of a generic smooth non-toral stable flow has infinite dimension even in finite differentiability.
Finally, from Theorem 1.4 on the cohomological equation for the product of translation flows on higher-genus surfaces with translation flows on the circle we derive, by a general argument, a result on the cohomological equation for the time-
$\tau $
maps of translation flows on higher-genus surfaces.
Let
$\Phi ^\tau _\theta $
denote the time-
$\tau $
map of the horizontal translation flow of the abelian differential
$h_\theta $
on M. For all
$s\geq 0$
, let
$\mathcal I^{s}_{h_\theta , \tau } \subset H^{-s}_h(M)$
denote the space of
$\Phi ^\tau _\theta $
-invariant distributions, that is, the space of all distributions in
$H^{-s}_h(M)$
which vanish on the subspace
$$ \begin{align*}\overline{ \{ u \circ \Phi^\tau_\theta - u \mid u\in H^\infty_h(M)\} \cap H^s_h(M)} \subset H^s_h(M). \end{align*} $$
We have the following result.
Corollary 1.5 For any translation surface
$(M,h)$
, for almost all
$\theta \in { \mathbb T}$
and for almost all
$T \in {\mathbb R}$
(with respect to the Lebesgue measure), the following statement holds. For all
$f \in H^{s}_h(M)$
with
$s>3$
, satisfying the distributional conditions
$D(f)=0$
for all
$\Phi ^\tau _\theta $
-invariant distributions
$D \in \mathcal I^{s}_{h_\theta , \tau } \subset H^{-s}_h(M)$
, the cohomological equation
$ u\circ \Phi ^\tau _\theta -u =f$
has a solution
$u\in H^{r}_h(M)$
, for all
$r< s-3$
, and there exists a constant
$C_{r,s} (\theta , \tau )>0$
such that
$$ \begin{align*}\vert u \vert_r \leq C_{r,s} (\theta, \tau) \vert f \vert_s. \end{align*} $$
The paper is organized as follows. In §2 we recall basic facts of analysis on translation surfaces as developed by the author in [Reference ForniF07, Reference ForniF97]. In §3 we introduce a twisted version of the Beurling-type isometry of the
$L^2$
space of a translation surface defined in [Reference ForniF97] (see also [Reference ForniF02]). Section 4 recalls results from the theory of boundary behavior of Cauchy integrals of finite measures on the circle and applications to the spectral theory of general unitary operators on Hilbert spaces, following [Reference ForniF97]. In §5 we prove the core result about the existence of solutions of the cohomological equation, by the following the presentation given in [Reference ForniF07] of the original argument of [Reference ForniF97], generalized to the twisted case. Section 5.1 is devoted to the core result about existence of distributional solutions, §5.2 to finiteness results for the spaces of twisted invariant distributions, and §5.3 to the proof of the main results on existence of smooth solutions for the twisted cohomological equations, product flows and time-
$\tau $
maps.
Note. Although the paper is mostly self-contained, it is largely based on ideas and techniques from [Reference ForniF97], already revisited and streamlined in [Reference ForniF07, §§2 and 3]. A familiarity with these earlier works will therefore greatly facilitate the reading of the present work.
2 Analysis on translation surfaces
This section gathers basic results on the flat Laplacian of a translation surface, following [Reference ForniF97, §§2 and 3] and [Reference ForniF07, §2].
Let
$\Sigma _{h}:=\{p_{1},\ldots ,p_{\sigma }\}\subset M_h$
be the set of zeros of the holomorphic abelian differential h on a Riemann surface M, of orders
$(k_{1},\ldots ,k_{\sigma })$
respectively with
$k_{1} + \cdots + k_{\sigma }=2g-2$
. Let
$R_{h}:=\vert h\vert $
be the flat metric with cone singularities at
$\Sigma _{h}$
induced by the abelian differential h on M and let
$\omega _h$
denote its area form. With respect to a holomorphic local coordinate
$z=x+\imath y$
at a regular point, the abelian differential h has the form
$h=\phi (z)dz$
, where
$\phi $
is a locally defined holomorphic function, and, consequently,
$$ \begin{align} R_h= |\phi(z)| (dx^2 +dy^2)^{1/2},\quad \omega_h=|\phi(z)|^2\,dx\wedge dy. \end{align} $$
The metric
$R_{h}$
is flat, degenerate at the finite set
$\Sigma _{h}$
of zeros of h and has trivial holonomy, hence h induces a translation surface structure on M.
The weighted
$L^{2}$
space is the standard space
$L^{2}_{h}(M):= L^{2}(M,\omega _{h})$
with respect to the area element
$\omega _{h}$
of the metric
$R_{h}$
. Hence the weighted
$L^{2}$
norm
$\vert \cdot \vert _{0}$
is induced by the hermitian product
${\langle }\cdot , \cdot {\rangle }_{h}$
defined as follows: for all functions u,
$v\in L^{2}_{h}(M)$
,
$$ \begin{align} {\langle} u ,v{\rangle}_{h} := \int _{M} u\,\bar v \, \omega_{h}. \end{align} $$
Let
$\mathcal F_{{ \operatorname {Im} } (h)}$
be the horizontal foliation,
$\mathcal F_{{ \operatorname {Re} }(h)}$
be the vertical foliation for the holomorphic abelian differential h on M. The foliations
$\mathcal F_{{ \operatorname {Im} }(h)}$
and
$\mathcal F_{{ \operatorname {Re} }(h)}$
are measured foliations (in the sense of Thurston):
$\mathcal F_{{ \operatorname {Im} } (h)}$
is the foliation given by the equation
${ \operatorname {Im} } h=0$
endowed with the invariant transverse measure
$\vert { \operatorname {Im} }\ h \vert $
,
$\mathcal F_{{ \operatorname {Re} }(h)}$
the foliation given by the equation
${ \operatorname {Re} } h=0$
endowed with the invariant transverse measure
$\vert { \operatorname {Re} }\ h \vert $
. Since the metric
$R_h$
is flat with trivial holonomy, there exist commuting vector fields
$S_h$
and
$T_h$
on
$M\setminus \Sigma _{h}$
such that:
-
(1) the frame
$\{S_h,T_h\}$
is a parallel orthonormal frame with respect to the metric
$R_{h}$
for the restriction of the tangent bundle
$TM$
to the complement
$M\setminus \Sigma _{h}$
of the set of cone points; -
(2) the vector field
$S_{h}$
is tangent to the horizontal foliation
$\mathcal F_{{ \operatorname {Im} }(h)}$
, and the vector field
$T_{h}$
is tangent to the vertical foliation
$\mathcal F_{{ \operatorname {Re} }(h)}$
on
$M\setminus \Sigma _{h}$
[Reference ForniF07, Reference ForniF97].
In the following we will often drop the dependence of the vector fields
$S_{h}$
,
$T_{h}$
on the abelian differential in order to simplify the notation. The symbols
$\mathcal L _{S}$
,
$\mathcal L _{T}$
denote the Lie derivatives, and
$\imath _S$
,
$\imath _T$
the contraction operators with respect to the vector field S, T on
$M\setminus \Sigma _h$
. We have:
-
(1)
$\mathcal L _{S} \omega _{h} = \mathcal L_{T}\omega _{h} =0$
on
$M\setminus \Sigma _{h}$
, that is, the area form
$\omega _{h}$
is invariant with respect to the flows generated by S and T; -
(2)
$\imath _{S} \omega _{h}= { \operatorname {Re} } h$
and
$\imath _{T} \omega _{h}= { \operatorname {Im} } h$
, hence the 1-forms
$\eta _{S} :=\imath _{S} \omega _{h}$
,
$\eta _{T} :=-\imath _{T} \omega _{h}$
are smooth and closed on M and
$\omega _{h}= \eta _{T}\wedge \eta _{S}$
.
Let
$C_0^\infty (M\setminus \Sigma _{h})$
denote the space of complex-valued smooth functions with compact support in
$M\setminus \Sigma _h$
. It follows from the area-preserving property
$(1)$
that the vector fields S, T are anti-symmetric as densely defined operators on
$L^{2}_{h}(M)$
, that is, for all functions u,
$v \in C_0^{\infty } (M\setminus \Sigma _h)$
(see [Reference ForniF97, formula (2.5)]),
$$ \begin{align} {\langle} Su ,v{\rangle}_{h} = -{\langle} u ,Sv{\rangle}_{h}, \quad {\langle} Tu ,v{\rangle}_{h} =-{\langle} u ,Tv{\rangle}_{h}, \end{align} $$
respectively. In fact, by Nelson’s criterion [Reference NelsonNe59, Lemma 3.10], the anti-symmetric operators S, T are essentially skew-adjoint on the Hilbert space
$L^{2}_{h}(M)$
.
The weighted Sobolev space
$H^{k}_h(M)$
, with integer exponent
$k\in { \mathbb Z}$
, introduced in [Reference ForniF97], is defined for
$k>0$
as the common domain
$$ \begin{align*}H^{k}_h(M):= \bigcap_{ i+j \leq k} D( \bar S^i \bar T^j) \cap D( \bar T^i \bar S^j) \end{align*} $$
of the products of non-negative powers of the closures
$\bar S$
,
$\bar T$
of the essentially skew-adjoint operators S, T on
$L^2_h(M)$
up to order
$k\in { \mathbb N}$
. It is endowed with the weighted Sobolev norms
$\vert \cdot \vert _{k}$
, with integer exponent
$k>0$
, which are the euclidean norms induced by the following hermitian product: for all functions u,
$v\in H^k_{h}(M)$
,
$$ \begin{align} {\langle} u,v {\rangle}_{k} := \frac{1}{2}\sum_{i+j\leq k}{\langle}S^{i}T^{j}u, S^{i}T^{j}v{\rangle}_{h} + {\langle}T^{i}S^{j}u, T^{i}S^{j}v{\rangle}_{h}. \end{align} $$
The weighted Sobolev spaces with integer exponent
$-k<0$
are defined to be the dual Hilbert spaces, endowed with the dual norms.
The weighted Sobolev space
$H^{k}_h(M)$
, with integer exponent
$k\in { \mathbb Z}$
, coincides with the Hilbert space obtained as the completion with respect to the norm
$\vert \cdot \vert _{k}$
of the maximal common invariant domain
$$ \begin{align} H^{\infty}_h(M):= \bigcap_{i,j\in { \mathbb N}} D( \bar S^i \bar T^j) \cap D( \bar T^i \bar S^j) \end{align} $$
of the closures
$\bar S$
,
$\bar T$
of the essentially skew-adjoint operators S, T on
$L^2_h(M)$
.
Since the vector fields S, T commute as operators on
$C_0^\infty (M\setminus \Sigma _{h})$
, the following weak commutation identity holds on M.
Lemma 2.1 [Reference ForniF97, Lemma 3.1]
For all functions u,
$v \in H^{1}_{h}(M)$
,
$$ \begin{align} {\langle}Su,Tv{\rangle}_{h} = {\langle}Tu,Sv{\rangle}_{h}. \end{align} $$
By the anti-symmetry property (3) and the commutativity property (6), the frame
$\{S,T\}$
yields an essentially skew-adjoint action of the Lie algebra
${\mathbb R}^{2}$
on the Hilbert space
$L^{2}_{h}(M)$
with common domain
$H^{1}_{h}(M)$
.
If
$\Sigma _{h}\not =\emptyset $
, the (flat) Riemannian manifold
$(M\setminus \Sigma _{h}, R_{h})$
is not complete, hence its Laplacian
$\Delta _h$
is not essentially self-adjoint on
$C_{0}^{\infty }(M \setminus \Sigma _{h})$
. By a theorem of Nelson [Reference NelsonNe59, §9], this is equivalent to the non-integrability of the action of
${\mathbb R}^{2}$
as a Lie algebra (to an action of
${\mathbb R}^{2}$
as a Lie group).
Following [Reference ForniF97], the Fourier analysis on the flat surface
$(M,h)$
will be based on a canonical self-adjoint extension
$\Delta _h^F$
of the Laplacian
$\Delta _h$
, called the Friedrichs extension, which is uniquely determined by the Dirichlet hermitian form
${\mathcal Q:H^{1}_{h}(M)\times H^{1}_{h}(M) \to {\mathbb C}}$
. We recall that, for all u,
$v \in H^{1}_{h}(M)$
,
$$ \begin{align} \mathcal Q(u,v) := {\langle}Su,Sv{\rangle}_{h} \,+\, {\langle}Tu,Tv{\rangle}_{h}. \end{align} $$
Theorem 2.2 [Reference ForniF97, Theorem 2.3]
The hermitian form
$\mathcal Q$
on
$L^{2}_{h}(M)$
has the following spectral properties.
-
(1)
$\mathcal Q$
is positive semi-definite and the set
$\textrm {EV}(\mathcal Q)$
of its eigenvalues is a discrete subset of
$[0,+\infty )$
. -
(2) Each eigenvalue has finite multiplicity. In particular,
$0\in \textrm {EV}(\mathcal Q)$
is simple and the kernel of
$\mathcal Q$
consists only of constant functions. -
(3) The space
$L^{2}_{h}(M)$
splits as the orthogonal sum of the eigenspaces. In addition, all eigenfunctions are
$C^{\infty }$
(real analytic) on M.
The Weyl asymptotics holds for the eigenvalue spectrum of the Dirichlet form. For any
$\Lambda>0$
, let
$N_{h}(\Lambda ):=\textrm {card} \{ \unicode{x3bb} \in \textrm {EV}(\mathcal Q)\,/\, \unicode{x3bb} \leq \Lambda \}$
, where each eigenvalue
$\unicode{x3bb} \in \textrm {EV}(\mathcal Q)$
is counted according to its multiplicity.
Theorem 2.3 [Reference ForniF97, Theorem 2.5]
There exists a constant
$C>0$
such that
$$ \begin{align} \lim_{\Lambda\to + \infty} \,\frac {N_{h}(\Lambda)}{\Lambda} \,\, = \,\, \mathrm{vol}(M,R_{h}). \end{align} $$
Let
$\partial ^{\pm }_{h}:=S_{h}\pm \imath \, T_{h}$
(with
$\imath =\sqrt {-1}$
) be the Cauchy–Riemann operatorsinduced by the holomorphic abelian differential h on M, introduced in [Reference ForniF97, §3]. Let
$\mathcal M^{\pm }_{h}\subset L^{2}_{h}(M)$
be the subspaces of meromorphic (respectively, anti-meromorphic) functions (with poles at
$\Sigma _{h}$
). By the Riemann–Roch theorem, the subspaces
$\mathcal M^{\pm }_{h}$
have the same complex dimension equal to the genus
$g\geq 1$
of the Riemann surface M. In addition,
${\mathcal M^{+}_{h}\cap \mathcal M^{-}_{h}={\mathbb C}}$
, hence
$$ \begin{align} H_{h}:= (\mathcal M^{+}_{h})^{\perp} \oplus (\mathcal M^{-}_{h})^{\perp} = \left\{ u\in L^{2}_{h}(M) \ \bigg|\ \int_{M} u\, \omega_{h} \,=\,0\,\right\}. \end{align} $$
Let
$H^{1}_{h}: = H_{h} \cap H^{1}_{h}(M)$
. By Theorem 2.2, the restriction of the hermitian form to
$H^{1}_{h}$
is positive definite, hence it induces a norm. By the Poincaré inequality (see [Reference ForniF97, Lemma 2.2] or [Reference ForniF02, Lemma 6.9]), the Hilbert space
$(H^{1}_{h}, \mathcal Q)$
is isomorphic to the Hilbert space
$(H^{1}_{h}, {\langle }\cdot ,\cdot {\rangle }_{1})$
.
Proposition 2.4 [Reference ForniF97, Proposition 3.2]
The Cauchy–Riemann operators
$\partial ^{\pm }_{h}$
are closable operators on the common domain
$C^{\infty }_{0}(M\setminus \Sigma _{h}) \subset L^{2}_{h}(M)$
and their closures (denoted by the same symbols) have the following properties:
-
(1) the domains
$D(\partial ^{\pm }_{h}) = H^{1}_{h}(M)$
and the kernels
$N(\partial ^{\pm }_{h}) = {\mathbb C}$
; -
(2) the ranges
$R_h^{\pm } :=\textrm {Ran}(\partial ^{\pm }_{h}) = (\mathcal M^{\mp }_{h})^{\perp } $
are closed in
$L^{2}_{h}(M)$
; -
(3) the operators
$\partial ^{\pm }_{h}: (H^{1}_{h}, \mathcal Q) \to (R^{\pm }, {\langle }\cdot ,\cdot {\rangle }_{h})$
are isometric.
Let
$\mathcal E= \{ e_{n} \,\vert \, n\in { \mathbb N} \}\subset H^{1}_{h}(M)\cap C^{\infty }(M)$
be an orthonormal basis of the Hilbert space
$L^{2}_{h}(M)$
of eigenfunctions of the Dirichlet form (7) and let
$\unicode{x3bb} :{ \mathbb N}\to {\mathbb R}^{+}\cup \{0\}$
be the corresponding sequence of eigenvalues:
The sequence
$\{\unicode{x3bb} _n \mid n\in { \mathbb N}\}$
can be equivalently defined as the sequence of eigenvalues of the non-negative Friedrichs extension
$-\Delta ^F_h$
of the flat Laplacian
$\Delta _h$
on M.
We then recall the definition of the Friedrichs (fractional) weighted Sobolev norms and spaces introduced in [Reference ForniF07, §2.2].
Definition 2.5
-
(i) The Friedrichs (fractional) weighted Sobolev norm
$\Vert \cdot \Vert _{s}$
of order
$s\geq 0$
is the norm induced by the hermitian product defined as follows: for all u,
$v\in L^{2}_{h}(M)$
, (11) -
(ii) The Friedrichs weighted Sobolev space
$\bar H_{h}^{s} (M)$
of order
$s\geq 0$
is the Hilbert space (12)endowed with the hermitian product given by (11). -
(iii) The Friedrichs weighted Sobolev space
$\bar H_{h}^{-s} (M)$
of order
$-s<0$
is the dual space of the Hilbert space
$\bar H_{h}^{s} (M)$
.
As stated in [Reference ForniF07, Lemma 2.6], the family of Friedrichs (fractional) weighted Sobolev spaces is a holomorphic interpolation family in the Lions–Magenes sense [Reference Lions and MagenesLM, Ch. 1], endowed with the canonical interpolation norm.
The family
$\{H^s_h(M)\}_{s\in {\mathbb R}}$
of fractional weighted Sobolev spaces will be defined as follows. Let
$[s]\in { \mathbb N}$
denote the integer part and
$\{s\} \in [0,1)$
the fractional part of any real number
$s\geq 0$
.
Definition 2.6 [Reference ForniF07, Definition 2.7]
-
(i) The fractional weighted Sobolev norm
$\vert \cdot \vert _{s}$
of order
$s\geq 0$
is the euclidean norm induced by the hermitian product defined as follows: for all functions u,
$v\in H^{\infty }_{h}(M)$
, (13)
$$ \begin{align} {\langle} u,v {\rangle}_{s} := \frac{1}{2}\sum_{i+j\leq [s]} (S^{i}T^{j}u, S^{i}T^{j}v)_{\{s\}} + (T^{i}S^{j}u, T^{i}S^{j}v)_{\{s\}}. \end{align} $$
-
(ii) The fractional weighted Sobolev norm
$\vert \cdot \vert _{-s}$
of order
$-s<0$
is defined as the dual norm of the weighted Sobolev norm
$\vert \cdot \vert _{s}$
. -
(iii) The fractional weighted Sobolev space
$H^{s}_h(M)$
of order
$s\in {\mathbb R}$
is defined as the completion with respect to the norm
$\vert \cdot \vert _{s}$
of the maximal common invariant domain
$H^{\infty }_h(M)$
.
It can be proved that the weighted Sobolev space
$H^{-s}_h(M)$
is isomorphic to the dual space of the Hilbert space
$H^{s}_h(M)$
, for all
$s\in {\mathbb R}$
.
The definition of the fractional weighted Sobolev norms is motivated by the following basic result.
Lemma 2.7 [Reference ForniF07, Lemma 2.9]
For all
$s\geq 0$
, the restrictions of the Cauchy–Riemann operators
$\partial ^{\pm }_{h}:H^1_h(M) \to L^2_h(M)$
to the subspaces
$H^{s+1}_h(M)\subset H^1_h(M)$
yield bounded operators
$$ \begin{align*}\partial^{\pm}_{s}:H_{h}^{s+1} (M) \to H_{h}^{s} (M) \end{align*} $$
(which do not extend to operators
$\bar H_{h}^{s+1} (M) \to \bar H_{h}^{s} (M)$
unless M is the torus). On the other hand, the Laplace operator
$$ \begin{align} \Delta_{h} =\partial^{+}_{h} \partial^{-}_{h} =\partial^{-}_{h} \partial^{+}_{h}: H^{2}_{h}(M) \to L^{2}_{h}(M) \end{align} $$
yields a bounded operator
$\bar \Delta _{s} :\bar H_{h}^{s+2} (M) \to \bar H_{h}^{s} (M)$
, defined as the restriction of the Friedrichs extension
$\Delta _h^F: \bar H_{h}^{2} (M) \to L^2_h(M)$
.
We do not know whether the fractional weighted Sobolev spaces form a holomorphic interpolation family. However, the fractional weighted Sobolev norms do satisfy interpolation inequalities (see [Reference ForniF07, Lemma 2.10 and Corollary 2.26]).
A detailed comparison between Friedrichs weighted Sobolev norms and weighted Sobolev norms and the corresponding weighted Sobolev spaces is carried out in [Reference ForniF07, §2]. In particular, we have the following result.
Let
$H^{s}(M)$
,
$s\in {\mathbb R}$
, denote a family of standard Sobolev spaces on the compact manifold M (defined with respect to a Riemannian metric).
Lemma 2.8 [Reference ForniF07, Lemma 2.11]
The following continuous embedding and isomorphisms of Banach spaces hold:
-
(1)
$H^{s}(M)\subset H_{h}^{s}(M) \equiv \bar H_{h}^{s}(M) \text { for } 0\leq s<1$
; -
(2)
$H^{s}(M) \equiv H_{h}^{s}(M) \equiv \bar H_{h}^{s}(M) \text { for } s=1$
; -
(3)
$H_{h}^{s}(M) \subset \bar H_{h}^{s}(M) \subset H^{s}(M) \text { for } s>1$
.
For
$s \in [0,1]$
, the space
$H^{s}(M)$
is dense in
$H_{h}^{s}(M)$
and, for
$s>1$
, the closure of
$H_{h}^{s}(M)$
in
$\bar H_{h}^{s}(M)$
or
$H^s(M)$
has finite codimension.
We also have the following sharp version of [Reference ForniF97].
Theorem 2.9 [Reference ForniF07, Lemma 2.5 and Corollary 2.25]
For each
$k\in { \mathbb Z}^{+}$
there exists a constant
$C_{k}>1$
such that, for any holomorphic abelian differential h on M and for all
$u\in H^{k}_{h}(M)$
,
$$ \begin{align} C_{k}^{-1}\, \vert u \vert_{k} \leq \Vert u \Vert_{k} \leq C_{k} \, \vert u \vert_{k}. \end{align} $$
For any
$0<r<s$
there exists constants
$C_r>0$
and
$C_{r,s}>0$
such that, for all
$u\in H^s_h(M)$
, the following inequalities hold:
$$ \begin{align} C_r^{-1} \Vert u \Vert_r \leq \vert u\vert_r \leq C_{r,s} \, \Vert u \Vert_s. \end{align} $$
3 The twisted Beurling transform
For every
$\sigma \in {\mathbb R}$
and for every abelian differential h, we introduce a family of partial isometries
$U_{h,\sigma }$
(of Beurling transform type), defined on a finite-codimensional subspace of
$L^2_h(M):=L^2(M,\omega _h)$
, which generalized the partial isometry
$U_q=U_{h,0}$
(for
$q=h^2$
) first introduced in [Reference ForniF97, §3], in the study of the cohomological equation for translation flows.
The partial isometry
$U_{h,\sigma }$
is extended in an arbitrary way to a unitary operator
$U_{J,\sigma }$
on the whole space
$L^2_h(M)$
. Resolvent estimates for
$U_{J,\sigma }$
will appear to be related with a priori estimates for the twisted cohomological equations for translation flows on
$(M, h)$
. Consequently, we derive our results on twisted cohomological equations from basic estimates on the limiting behavior as
$z\to \partial D$
of the resolvent
${\mathcal R}_U(z):=(U-zI)^{-1}$
, defined on the unit disk
$D \subset {\mathbb C}$
, of a unitary operator U on a general Hilbert space. Such estimates, established in [Reference ForniF97], are based on fundamental facts of classical harmonic analysis, in particular on Fatou’s theory on the boundary behavior of holomorphic functions. The results obtained are then specialized to the case of the unitary operator
$U:=U_{J,\sigma }$
.
Let h be a holomorphic abelian differential on a Riemann surface M of genus
$g\geq 2$
. Let
$\{S,T\}$
be the orthonormal frame for
$TM$
on
$M\setminus \Sigma $
introduced in §2. We recall that the 1-forms
$\eta _S=\imath _S\omega _h$
and
$\eta _T=-\imath _T\omega _h$
are closed and describe the horizontal (respectively, vertical) foliation of
$\omega $
on M. It is possible to associate to h a one-parameter family of measured foliations parametrized by
$\theta \in { \mathbb T} := {\mathbb R}/ 2\pi { \mathbb Z}$
in the following way. Let
$h_{\theta }:=e^{-\imath \theta } \,h$
and let
${\mathcal F}_{\theta }$
be the horizontal foliation of the abelian differential
$h_{\theta }$
, that is, the foliation defined by the closed 1-form
$$ \begin{align*}{ \operatorname{Im} }\ h_{\theta} =\{e^{-\imath\theta}(\eta_T+\imath\eta_S)- e^{\imath\theta}(\eta_T-\imath\eta_S)\}/2\imath.\end{align*} $$
The foliation
${\mathcal F}_{\theta }$
can also be obtained by integrating the dual vector field
$$ \begin{align} S_{\theta}:= (\cos \theta) S + (\sin\theta) T =\{e^{-\imath\theta}(S+\imath\,T)+e^{\imath\theta}(S-\imath\,T)\}/2, \end{align} $$
which corresponds to the rotation of the vector field S by an angle
$\theta \in { \mathbb T}$
in the positive direction.
In the following we will denote by
$\partial ^{\pm }_h$
the Cauchy–Riemannoperators
$S\pm \imath \,T$
, respectively. The twisted Cauchy–Riemannoperators
$$ \begin{align} \partial^{\pm}_{h, \sigma} := (S+ \imath\sigma) \pm \imath T = \partial^{\pm}_h + \imath\sigma \end{align} $$
will play a crucial role. For all
$\theta \in { \mathbb T}$
, let
$\sigma _\theta := \sigma \cos \theta $
. We remark that, for every
$\theta \in { \mathbb T}$
, we have
$$ \begin{align*}S_{\theta} + \imath\sigma_\theta:=\{e^{-\imath\theta} \partial^{+}_{h, \sigma} +e^{\imath\theta}\partial^{-}_{h, \sigma}\}/2, \end{align*} $$
hence we have the formal factorization
$$ \begin{align} S_{\theta} + \imath\sigma_\theta &={ \frac{e^{-\imath\theta}}{2}}\, (((\partial^+_{h, \sigma}) (\partial^-_{h, \sigma})^{-1}+e^{2\imath\theta} )) \,\partial^{-}_{h, \sigma} \nonumber\\ &={\frac{e^{\imath\theta}}{2}}\, (((\partial^-_{h, \sigma}) (\partial^+_{h, \sigma})^{-1}+e^{-2\imath\theta} )) \,\partial^{+}_{h, \sigma}. \end{align} $$
Let
$Q_{h, \sigma }$
denote the bilinear form defined, for all
$u, v\in H^1_h(M)$
, as follows:
$$ \begin{align*}Q_{h, \sigma} (u,v) := {\langle}(S+ \imath\sigma) u, (S+ \imath\sigma)v{\rangle}_h + {\langle}Tu, Tv{\rangle}_h. \end{align*} $$
Let
$K_{h, \sigma }\subset H^1_h(M) \cap C^\infty (M\setminus \Sigma )$
denote the finite-dimensional subspace
$$ \begin{align} K_{h, \sigma} := \{ u \in H^1_h(M) \cap C^\infty(M\setminus \Sigma)\vert (S+\imath \sigma)u= Tu=0\}. \end{align} $$
Lemma 3.1 The twisted bilinear form
$Q_{h, \sigma }$
induces a norm on
$K^\perp _{h, \sigma } \cap H^1_h(M)$
. In fact, for all
$\sigma \in {\mathbb R}$
, there exists a constant
$C_{h}>1$
such that, for all
$u\in K^\perp _{h, \sigma } \cap H^1_h(M)$
,
$$ \begin{align*}C_{h}^{-1} Q_{h,0} (u,u) \leq Q_{h, \sigma} (u,u) \leq C_{h} (1+\sigma^2) \bigg ( Q_{h,0} (u,u) +\bigg\vert \int_M u \omega_h \bigg\vert \bigg ). \end{align*} $$
Proof. Since translation flows are area-preserving, hence symmetric on their common domain, we have, for all
$u\in H^1_h(M)$
,
$$ \begin{align} Q_{h, \sigma} (u,u) :&= {\langle}(S+ \imath\sigma) u, (S+ \imath\sigma)u{\rangle}_h + \Vert Tu \Vert^2_{L^2_h(M)} \nonumber\\ &= \Vert Su \Vert^2_{L^2_h(M)} + 2 \imath\sigma {\langle}u,Su{\rangle}_h + \sigma^2 \Vert u\Vert^2_{L^2_h(M)} + \Vert Tu \Vert^2_{L^2_h(M)}. \end{align} $$
By the Cauchy–Schwarz inequality, we have
$$ \begin{align*}\vert {\langle}u,Su{\rangle}_h \vert \leq \Vert u\Vert_{L^2_h(M)} \Vert Su\Vert_{L^2_h(M)} \leq \frac{ \Vert Su\Vert^2_{L^2_h(M)} + \Vert u\Vert^2_{L^2_h(M)}}{2}. \end{align*} $$
It follows that
$$ \begin{align*}\Vert Su \Vert^2_{L^2_h(M)} + 2 \imath\sigma {\langle}u,Su{\rangle}_h \leq (1+ \vert \sigma\vert) \Vert Su \Vert^2_{L^2_h(M)} + \vert \sigma\vert \Vert u \Vert^2_{L^2_h(M)}, \end{align*} $$
hence we derive that
$$ \begin{align*}Q_{h, \sigma} (u,u) \leq (1+ \vert \sigma\vert) Q_{h,0} (u,u) + (\sigma^2 + \vert \sigma\vert) \Vert u \Vert^2_{L^2_h(M)}. \end{align*} $$
By the Poincaré inequality there exists a constant
$C_h>0$
such that, for all
$u\in H^1_h(M)$
, we have
$$ \begin{align*}\begin{aligned} Q_{h, \sigma} (u,u) &\leq (1+ \vert \sigma\vert) Q_{h, 0} (u,u) + (\sigma^2 + \vert \sigma\vert) \Vert u \Vert^2_{L^2_h(M)} \\ &\leq [(1+ \vert \sigma\vert) + C (\sigma^2 + \vert \sigma\vert)]Q_{h, 0} (u,u) + (\sigma^2 + \vert \sigma\vert) \bigg\vert \int_M u \omega_h\bigg\vert. \end{aligned} \end{align*} $$
The upper bound in the statement is therefore proved.
To prove the lower bound, we proceed as follows. By the definition of
$Q_{h,\sigma }$
, for the splitting
$u = v + \bar u \in {\mathbb C}^\perp \oplus ^\perp {\mathbb C} \subset H^1_h(M)$
we have
$$ \begin{align} Q_{h, \sigma} (u,u) = Q_{h, \sigma} (v,v) + \sigma^2 \bar u^2; \end{align} $$
hence without loss of generality we can reduce the argument to functions
$u\in H^1_h(M)$
of zero average. By the compact embedding
$H^1_h(M) \to L^2(M)$
we derive that there exists a constant
$c_h>0$
such that, for all
$u\in H^1_h(M)$
, we have
$$ \begin{align*}\Vert u \Vert^2_{L^2_h(M)} \geq c^2_h Q_{h,0} (u,u) \geq c^2_h \Vert Su \Vert^2_{L^2_h(M)}. \end{align*} $$
It follows then by formula (21) that, for
$\vert \sigma \vert \geq 2 c_h^{-1}$
, we have
$$ \begin{align*}Q_{h, \sigma} (u,u) \geq Q_{h, 0} (u,u) + \vert \sigma\vert \Vert u \Vert_{L^2_h(M)} ( \vert \sigma\vert \Vert u \Vert_{L^2_h(M)} - 2 \Vert Su \Vert_{L^2_h(M)} ) \geq Q_{h, 0} (u,u). \end{align*} $$
It remains to prove the bound for
$\vert \sigma \vert \leq 2 c_h^{-1}$
. Let us then assume by contradiction that for all
$n\in { \mathbb N}$
there exist a bounded sequence
$(\sigma _n)$
and a sequence
$u_n\in K_{h, \sigma _n}^\perp \subset H^1_h(M)$
of zero average such that
$$ \begin{align*}Q_{h, 0} (u_n,u_n) \geq n Q_{h, \sigma_n} (u_n,u_n).\end{align*} $$
After normalizing, it is not restrictive to assume that
$Q_{h, 0} (u_n,u_n)=1$
, for all
$n\in { \mathbb N}$
, hence
$Q_{h, \sigma _n} (u_n,u_n)\to 0$
. By the Poincaré inequality, it follows that after passing to a subsequence we can assume that
$u_n \to u$
in
$L^2(M)$
and u has zero average, as well as that
$\sigma _n \to \sigma \in {\mathbb R}$
. Let
$\Phi _S^{\mathbb R}$
and
$\Phi _T^{\mathbb R}$
denote the horizontal and the vertical flow, respectively. By assumption, since
$$ \begin{align*}\begin{aligned} \Vert e^{\imath \sigma_n t} u_n\circ \Phi_S^t - u_n \Vert_{L^2_h(M)} &= \bigg\Vert \int_0^t (S+ \imath \sigma_n) u_n\circ \Phi_S^s \,ds\bigg\Vert_{L^2_h(M)} \\& \leq \int_0^t \Vert (S+ \imath \sigma_n)u_n\circ \Phi_S^s \Vert_{L^2_h(M)} \,ds \leq t Q^{1/2}_{h, \sigma_n}(u_n,u_n) \to 0, \\ \Vert u_n\circ \Phi_T^t - u_n \Vert_{L^2_h(M)} &= \bigg\Vert \int_0^t Tu_n\circ \Phi_T^s \,ds \bigg\Vert_{L^2_h(M)} \\ &\leq \int_0^t \Vert Tu_n\circ \Phi_T^s \Vert_{L^2_h(M)} \,ds \leq t Q^{1/2}_{h, \sigma_n}(u_n,u_n) \to 0, \end{aligned} \end{align*} $$
it follows that the limit function
$u\in K_{h, \sigma }^\perp \subset L^2_h(M)$
is a zero-average eigenfunction of eigenvalue
$- \imath \sigma $
for the flow
$\Phi _S^{\mathbb R}$
and it is invariant for the flow
$\Phi _T^{\mathbb R}$
. It follows, in particular, that
$u\in C^\infty (M\setminus \Sigma )\cap H^1_h(M)$
, which implies that u is constant on all minimal components of the flow
$\Phi _T^{\mathbb R}$
and
$\Phi _T^{\mathbb R}$
-invariant on the cylindrical component. In particular,
$u\in K_{h, \sigma }$
, hence
$u=0$
. However, from
$u_n\to 0$
in
$L^2_h(M)$
and
$\sigma _n \to \sigma $
, from the identity in formula (21) we then derive
$$ \begin{align*}0= \lim_{n\to \infty} Q_{h, \sigma_n} (u_n,u_n) = \lim_{n\to \infty} Q_{h, 0}(u_n,u_n) =1, \end{align*} $$
a contradiction. We have thus proved that there exists
$C_{h}>1$
such that, for all
$u\in K_{h, \sigma }^\perp \cap H^1_h(M)$
,
$$ \begin{align*}C_h^{-1} Q_{h, 0}(u,u) \leq Q_{h, \sigma} (u,u).\\[-36pt] \end{align*} $$
The twisted Cauchy–Riemann operators appear in the Hodge decomposition of the twisted exterior differential, which we now introduce (see [Reference VoisinV02] or [Reference DemaillyDe96] for a general introduction to Hodge theory). For all
$\sigma \in {\mathbb R}$
, the twisted exterior differential
$d_{h, \sigma }$
is defined on the space
$\Omega ^\ast (M)$
of complex-valued smooth forms on the surface M by the formula
$$ \begin{align*}d_{h,\sigma} \alpha :=d\alpha + \imath \sigma { \operatorname{Re} } (h) \wedge \alpha \quad \text{for all } \alpha \in \Omega^\ast(M). \end{align*} $$
Since
$d^2_{h,\sigma }=0$
(as is readily verified), the cohomology
$H^\ast _{h,\sigma }(M, {\mathbb C})$
of the complex
$(\Omega ^\ast (M), d_{h,\sigma })$
is well defined and will be called the twisted cohomology of the translation surface
$(M,h)$
. We have the following more general definition.
Definition 3.2 Let
$\Omega ^*(M)$
denote the space of all smooth differential forms on M. Let
$\eta $
be a real closed smooth 1-form on D and let
$d_\eta $
denote the twisted exterior derivative defined as
$$ \begin{align*}d_\eta \alpha = d\alpha + \imath \eta \wedge \alpha \quad \text{for all } \alpha \in \Omega^*(D). \end{align*} $$
The twisted cohomology (with complex coefficients)
$H^\ast _\eta (M, {\mathbb C})$
is the cohomology of the differential complex
$(\Omega ^*(M), d_\eta )$
.
Let
$\Omega ^*(M, \Sigma _h)$
denote the space of all smooth differential forms on M vanishing at
$\Sigma _h$
. The relative twisted cohomology (with complex coefficients)
$H^\ast _\eta (M, \Sigma _h,{\mathbb C})$
is the cohomology of the differential complex
$(\Omega ^*(M, \Sigma _h), d_\eta )$
.
By definition we have
$H^\ast _{h,\sigma }(M, {\mathbb C}):= H^\ast _{\sigma { \operatorname {Re} }(h)}(M, {\mathbb C})$
. A twisted cohomology cocycle on a twisted cohomology bundle over the Teichmüller flow is introduced in [Reference ForniF19] in the study of twisted ergodic integral and effective weak mixing.
The twisted cohomology has a Hodge decomposition with respect to the Hodge operator
$\ast _h$
associated to the flat metric on the translation surface
$(M, h)$
, which by definition satisfies the identities
$$ \begin{align*}\ast_h ({ \operatorname{Re} } (h)) = { \operatorname{Im} }(h) \quad \text{and} \quad \ast_h ({ \operatorname{Im} } (h)) = -{ \operatorname{Re} }(h). \end{align*} $$
By the Hodge decomposition of the space of 1-forms into a holomorphic and an anti-holomorphic part (respectively, the eigenspaces of eigenvalues
$\mp \imath $
of the Hodge operator), there exist twisted Cauchy–Riemann differentials
$d^\pm _\eta $
on forms such that
$$ \begin{align*}d_\eta = \frac{ d^+_\eta + d^-_\eta }{2} \end{align*} $$
(here
$d^+_\eta $
denotes the projection onto the anti-holomorphic part, and
$d^-_\eta $
the projection onto the holomorphic part). As a consequence, the twisted cohomology
$H^1_\eta (M, {\mathbb C})$
splits a direct (Hodge orthogonal) sum of the holomorphic part
$H^{1,+}_\eta (M, {\mathbb C})$
and the anti-holomorphic part
$H^{1,-}_\eta (M, {\mathbb C})$
:
$$ \begin{align*}H^1_\eta(M, {\mathbb C}) = H^{1,+}_\eta(M, {\mathbb C}) \oplus H^{1,-}_\eta(M, {\mathbb C}). \end{align*} $$
The twisted Cauchy–Riemann differentials
$d^\pm _\eta $
on functions can be written in terms of twisted Cauchy–Riemann operators
$\partial ^\pm _\eta $
as follows: for all
$f \in H^1_h(M)$
,
$$ \begin{align*}d^+_\eta f = (\partial ^+_\eta f) \bar{h} \quad \text{and} \quad d^-_\eta f = (\partial ^-_\eta f) h. \end{align*} $$
The twisted Cauchy–Riemann operators
$\partial ^\pm _{h, \sigma }$
introduced in formula (18) correspond to the special case of
$\eta = \sigma { \operatorname {Re} }(h)$
:
$$ \begin{align*}\partial ^\pm_{h, \sigma} = \partial^\pm_h + \imath \sigma = \partial ^\pm_{\sigma{ \operatorname{Re} }(h)}. \end{align*} $$
The dimension of the twisted cohomology can be exactly computed. In fact we have the following results.
Lemma 3.3 For all closed real smooth 1-form
$\eta \in \Omega ^1(M)$
, the following dimension identity holds:
$$ \begin{align*}\mathrm{dim}_{\mathbb C} \,H^0_\eta (M, {\mathbb C}) = \begin{cases} 1 \quad& \text{if }\,\, [\eta] \in H^1(M, { \mathbb Z}) , \\ 0 \quad& \text{otherwise}. \end{cases} \end{align*} $$
Proof. We repeat here for the convenience of the reader the argument given in [Reference ForniF19, Lemma 4.1]. Let
$Z^0_\eta (M, {\mathbb C})$
denote the space of functions
$f \in C^\infty (M)$
such that
$$ \begin{align*}d_\eta f= df + 2\pi \imath \eta f =0. \end{align*} $$
It follows from the above equation that the function f is constant along each leaf of the measured foliation
$\mathcal F_\eta = \{ \eta =0\}$
, hence all the leaves of
$\mathcal F_\eta $
are compact. In addition, we have
$$ \begin{align*}d (f \bar f) = (df) {\bar f} + (\overline {df}) f = - 2\pi \imath \eta f \bar f + 2\pi \imath \eta f \bar f =0, \end{align*} $$
hence either
$f \equiv 0$
or there exists
$c_f\in {\mathbb C}\setminus \{0\}$
such that
$f/c_f: M \to U(1)= \{z \in {\mathbb C} \mid \vert z\vert =1\}$
and there exists a real-valued function
$\theta : M\to {\mathbb R}/{ \mathbb Z}$
such that
$$ \begin{align*}f(x) = \exp (-2\pi \imath \theta(x)) \quad \text{for all } x\in M. \end{align*} $$
By definition we have
$df = -2\pi \imath f d\theta $
, and since by assumption
$f\in Z^0_\eta (M, {\mathbb C})$
, the space of
$d_\eta $
-closed
$0$
-forms, that is, complex-valued functions, and
$f(x) \not =0$
for all
$x\in M$
, it follows that
$d\theta = \eta $
. Since
$\theta : M\to {\mathbb R}/{ \mathbb Z}$
, we conclude that
$\eta \in H^1(M, { \mathbb Z})$
.
Conversely, let us assume that
$[\eta ]\in H^1(M, { \mathbb Z})$
. Given any point
$p\in M$
, the function
$$ \begin{align*}f_p (x) = \exp \bigg(-2\pi \imath \int_p^x \eta\bigg) \quad \text{for all } x\in M, \end{align*} $$
is a well-defined, non-zero element of
$Z^0_\eta (M, {\mathbb C})$
since
$$ \begin{align*}df_p = -2\pi \imath f_p \eta. \end{align*} $$
In addition, given any
$g \in Z^0_\eta (M, {\mathbb C})$
we have
$$ \begin{align*}d (\bar {f_p} g) = (\overline{ df_p}) g + \bar{ f_p } (dg) = 2\pi \imath {\bar {f_p}} g \eta - 2\pi \imath \bar {f_p} g \eta =0, \end{align*} $$
hence
$\bar {f_p} g$
is a constant, which implies that
$H^0_\eta (M, {\mathbb C})$
has dimension equal to
$1$
.
Lemma 3.4 For all closed real smooth 1-forms
$\eta \in \Omega ^1(M)$
, the following dimension identities hold:
$$ \begin{align*}\begin{aligned} \mathrm{dim}_{\mathbb C} \,H^1_\eta (M, {\mathbb C}) &= 2 \,\mathrm{dim}_{\mathbb C} \, H^0_\eta (M, {\mathbb C}) + 2g -2, \\ \mathrm{dim}_{\mathbb C} \,H^1_\eta (M, \Sigma_h, {\mathbb C}) & = \# (\Sigma_h)+ \,\mathrm{dim}_{\mathbb C} \, H^0_\eta (M, {\mathbb C}) + 2g -2. \end{aligned} \end{align*} $$
Proof. The proof of the above dimension relation is given in greater generality by Goldman in [Reference GoldmanGo84, §1.5], and also explained in our context in [Reference ForniF19, Lemma 4.3]. We outline the argument for the convenience of the reader.
Let
$\mathcal L_\eta $
denote the local system on M defined as the subbundle of the space
$\Omega ^*(\hat M)$
of complex-valued forms
$\hat \alpha $
on the universal cover
$\hat M$
such that
$$ \begin{align*}\gamma^* (\hat \alpha) = \exp \bigg(\imath \int_\gamma \eta \bigg) \hat \alpha \quad \text{for all } \gamma \in \pi_1 (M, \ast). \end{align*} $$
The twisted cohomology
$H^*_\eta (M, {\mathbb C})$
, defined as the cohomology of the complex of the twisted differential
$d_\eta $
on complex-valued forms
$\Omega ^*(M)$
, is isomorphic to the cohomology
$H^*(M, {\mathcal L}_\eta )$
, defined as the cohomology of the complex of the exterior differential d on
$\mathcal L_\eta $
-valued forms
$\Omega ^*(M, \mathcal L_\eta )$
.
The cohomology
$H^1(M, \mathcal L_\eta )$
, defined as the de Rham cohomology of the corresponding local system
$\mathcal L_\eta $
, can be identified with other cohomologies such as the singular, Čech, or simplicial cohomologies with local coefficients in
$\mathcal L_\eta $
. In simplicial cohomology, we have that the (finite-dimensional) cochain complex is independent of the flat connection which defines the local system, so its Euler characteristic equals
$2-2g$
, since the local system
$\mathcal L_\eta $
has rank equal to
$1$
. Now the Euler characteristic is invariant under taking the cohomology of the complex, so the Euler characteristic of the graded cohomology space also equals
$2-2g$
. Finally, since M is a closed orientable surface, by the Poincaré duality
$H^2 (M, \mathcal L_\eta ) \equiv H^0 (M, \mathcal L_\eta )$
. By definition of Euler characteristic of a complex, we have
$$ \begin{align*}\mathrm{dim}_{\mathbb C}\, H^0 (M,\mathcal L_\eta) - \mathrm{dim}_{\mathbb C}\, H^1 (M,\mathcal L_\eta) + \mathrm{dim}_{\mathbb C}\, H^2 (M,\mathcal L_\eta) = 2- 2g,\end{align*} $$
so that
$\textrm {dim}_{\mathbb C} \,H^1 (M,\mathcal L_\eta ) = 2\,\textrm {dim}_{\mathbb C}\, H^0(M,\mathcal L_\eta ) + 2g-2$
, as stated.
It remains to prove the dimension formula for the relative cohomology. Since
$\Omega ^1(M, \Sigma _h) \subset \Omega ^1(M)$
and any twisted cohomology class in
$H^1(M, {\mathbb C})$
can be represented by a twisted closed 1-form with compact support in
$M\setminus \Sigma _h$
there exists a natural surjective map
$H^1(M, \Sigma _h, {\mathbb C}) \to H^1(M, {\mathbb C})$
. It remains to compute the kernel of such a map. An element of its kernel can be represented by a 1-form
$\alpha $
with compact support in
$M\setminus \Sigma _h$
such that there exists a function
$f \in C^\infty (M)$
with
$\alpha = d_\eta f$
. The function f is uniquely determined up to kernel of the twisted differential, that is, up to cohomology classes in
$H^0 (M, {\mathbb C})$
. By a local calculation, since the form
$\alpha =d_\eta f$
vanishes near
$\Sigma _h$
, it has vanishing cohomology class in
$H^1(M, \Sigma _h, {\mathbb C})$
if and only if the function f vanishes at
$\Sigma _h$
. It follows that the kernel of the map has dimension
$\#(\Sigma _h) - \textrm {dim}_{\mathbb C} \,H^0 (M,\mathcal L_\eta )$
, and the dimension formula for the relative homology follows from that for the absolute homology.
The twisted Cauchy–Riemann operators
$\partial ^{\pm }_{h, \sigma }$
on the Hilbert space
$L^2_h(M)$
are described in the following proposition.
Proposition 3.5 The Cauchy–Riemann operators
$\partial ^{\pm }_{h, \sigma }$
are closable operators on
$C^{\infty }_0(M\setminus \Sigma )\subset L^2_h(M)$
and their closures (denoted by the same symbols) have the following properties.
-
(i)
$D(\partial ^{\pm }_{h, \sigma })=H^1_h(M)$
and
$N(\partial ^{\pm }_{h, \sigma })=K_{h, \sigma }\subset H^1_h(M)$
. -
(ii) The kernels
${\mathcal M}^\pm _{\Sigma }(\sigma ) \subset L^2_h(M)$
of the adjoint operators
$(\partial ^{\mp }_{h, \sigma })^*$
have finite dimensions
$d^\pm (\sigma )$
such that
$$ \begin{align*}d^+ (\sigma) = d^- (-\sigma) = g-1 + \mathrm{dim}_{\mathbb C} (K_{h, \sigma}) \quad \text{for all } \sigma \in {\mathbb R}. \end{align*} $$
-
(iii) The adjoints
$(\partial ^\pm _{h, \sigma })^*$
of
$\partial ^\pm _{h, \sigma }$
are extensions of
$-\partial ^\mp _{h, \sigma }$
, and we have closed ranges
$$ \begin{align*}R^{\pm}_{h, \sigma}:=\text{Ran}\,(\partial^\pm_{h, \sigma})=[{\mathcal M}^\mp_{\Sigma}(\sigma)] ^{\perp}.\end{align*} $$
-
(iv) The operators
$\partial ^{\pm }_{h, \sigma } :(K^\perp _{h, \sigma } \cap H^1_h(M), Q_{h, \sigma })\to (R^{\pm }_{h, \sigma },(\,\cdot ,\,\cdot \,)_h)$
are isometric.
Proof. If u,
$v\in H^1_h(M)$
, Lemma 2.1 implies the following identity:
$$ \begin{align} {\langle}\partial^{\pm}_{h, \sigma} u,\partial^{\pm}_{h, \sigma} v{\rangle}_h\,{=}\, &{\langle}(S+\imath \sigma )u, (S+\imath \sigma )v{\rangle}_h+ {\langle}Tu,Tv{\rangle}_h \nonumber\\ &\pm \imath ({\langle}Tu,(S+\imath \sigma )v{\rangle}_h-{\langle}(S+\imath \sigma )u,Tv{\rangle}_h)= Q_{h, \sigma} (u,v). \end{align} $$
It follows immediately that the operators
$\partial ^{\pm }_{h, \sigma }$
are closed with domain
$D(\partial ^{\pm }_{h, \sigma })=H^1_h(M)$
and that their kernels are both equal to
$K_{h, \sigma } \subset H^1_h(M)$
.
Since, for all
$u,v\in H^1_h(M)$
, we have
$$ \begin{align*}\begin{aligned} {\langle}\partial^\pm_{h, \sigma} u, v{\rangle}_h&= {\langle}[(S+\imath \sigma) \pm \imath T] u, v{\rangle}_h \\ &= -{\langle} u, [(S+\imath \sigma) \mp \imath T] v{\rangle}_h = -{\langle} u, \partial^\mp_{h, \sigma} v{\rangle}_h, \end{aligned} \end{align*} $$
and the adjoint
$(\partial ^\pm _{h, \sigma })^*$
of
$\partial ^\pm _{h, \sigma }$
is an extension of
$-\partial ^\mp _{h, \sigma }$
.
The dimension of the kernels
${\mathcal M}^\pm _{\Sigma }(\sigma )$
of the Cauchy–Riemann operators
$\partial ^\mp _{h, \sigma }$
in
$L^2_h(M)$
follows from the fact that the quotients
${\mathcal M}^\pm _{\Sigma }(\sigma )/K_{h, \sigma }$
are, respectively, isomorphic to the anti-holomorphic and holomorphic twisted cohomology spaces
$H^{1,\pm }_{h, \sigma }(M, {\mathbb C})$
, which have half the dimension of the twisted cohomology
$H^{1}_{h, \sigma }(M, {\mathbb C})$
. We describe the isomorphism below. The maps
$j^\pm _{h} : {\mathcal M}^+_{\Sigma }(\sigma )\to H^{1,\pm }_{h, \sigma }(M, {\mathbb C})$
defined as
$$ \begin{align*}j^+_{h} (m^+) = [m^+ h] \quad \text{and} \quad j^-_{h} (m^-) = [m^- \bar{h}] \quad \text{for all } m^\pm \in {\mathcal M}^\pm_{\Sigma}(\sigma), \end{align*} $$
are isomorphisms. In, fact the maps
$j^\pm _h$
are onto since by definition any cohomology class
$c^\pm \in H^{1,\pm }_{h, \sigma }(M, {\mathbb C})$
is represented by a twisted holomorphic section
$m^+ h$
(respectively, by a twisted anti-holomorphic section
$m^- \bar {h}$
), hence we have, in the weak sense,
$$ \begin{align*}0=d^+_{h,\sigma} ( m^+ h )= (\partial^+_{h, \sigma} m^+) (\bar h \wedge h) \quad \text{and} \quad 0=d^-_{h,\sigma} ( m^- \bar {h} )= (\partial^-_{h, \sigma} m^-) (h \wedge \bar h) \end{align*} $$
which implies that
$\partial ^\pm _{h, \sigma } m^\pm =0$
, hence
$m^\pm \in {\mathcal M}^\pm _{\Sigma }(\sigma )$
. We the prove that the maps
$j^\pm $
are injective. The kernels of the maps
$j^\pm _h$
can be described as follows. By definition, we have that
$j^\pm (m^\pm )=0$
if and only if there exists
$f^\pm \in H^1_h(M)$
such that
$d_{h, \sigma } f^+ = m^+h$
and
$d_{h, \sigma } f^- = m^- \bar {h}$
, respectively. The latter identities imply that
$$ \begin{align*}\partial^\pm_{h, \sigma} f^\pm =0 \quad \text{and} \quad \frac{\partial^\mp_{h, \sigma} f^\pm }{2} = m^\pm. \end{align*} $$
Since the condition
$\partial ^\pm _{h, \sigma } f^\pm =0$
for functions
$f^\pm \in H^1_h(M)$
implies that
$f^\pm \in K_{h, \sigma }$
, by definition it follows that
$(S+ \imath \sigma ) f^\pm = Tf^\pm =0$
, hence
$m^\pm = \partial ^\mp _{h, \sigma } f^\pm / 2=0$
. We have thus proved that the spaces
${\mathcal M}^\pm _{\Sigma }(\sigma )$
are isomorphic to the spaces
$H^{1,\pm }_{h, \sigma }(M, {\mathbb C})$
, respectively, hence they have the same dimensions. Finally, by definition, the cohomology
$H^0_{h, \sigma } (M, {\mathbb C})$
coincides with the subspace
$K_{h, \sigma }$
, hence by Lemma 3.4 we derive
$$ \begin{align*}\begin{aligned} \mathrm{dim}_{\mathbb C} ({\mathcal M}^\pm_{\Sigma}(\sigma)) &= \mathrm{dim}_{\mathbb C} (H^{1,\pm}_{h, \sigma}(M, {\mathbb C})) =\tfrac{1}{2} \mathrm{dim}_{\mathbb C} (H^{1}_{h, \sigma}(M, {\mathbb C})) \\ &= g-1 + \mathrm{dim}_{\mathbb C} (H^{0}_{h, \sigma}(M, {\mathbb C}))= g-1 + \mathrm{dim}_{\mathbb C} (K_{h, \sigma}). \end{aligned} \end{align*} $$
The formula for the range
$R^\pm _{h, \sigma }$
follows from a general fact of Hilbert space theory, as soon as we have proved that the range is closed. It follows from Lemma 3.1 that
$R^\pm _{h, \sigma }$
are closed. In fact, the subspaces
$R^\pm _{h, \sigma }$
coincide with the range of restrictions of the operators
$\partial ^\pm _{h, \sigma }$
to the subspace
$K_{h, \sigma }^\perp \cap H^1_h(M)$
. By Lemma 3.1 these restrictions have closed range.
Finally, (iv) is a direct consequence of the identity in formula (23).
The results just proved in Proposition 3.5, in particular (iv), allow us to give a precise meaning to the formal factorization (19), by introducing a family of unitary operators on
$L^2_h(M)$
, which, as will be seen, contains a great deal of information about the properties of the differential operator
$S_{\theta } + \imath \sigma $
(
$\theta \in { \mathbb T}$
) defined in formula (17). Let
$U_{h, \sigma } :R^-_{h, \sigma } \to R^+_{h, \sigma }$
be defined as
$$ \begin{align} U_{h,\sigma}:=(\partial^+_{h, \sigma})(\partial^-_{h, \sigma})^{-1}. \end{align} $$
It is an immediate consequence of assertion (iv) of Proposition 3.5 that
$U_{h,\sigma }$
is a partial isometry. Thus, we extend in the natural way the domain of definition of
$U_{h,\sigma }$
as follows. Let
$$ \begin{align} J:{\mathcal M}^+_{\Sigma}(\sigma) \to {\mathcal M}^-_{\Sigma} (\sigma) \end{align} $$
be an isometric operator, with respect to the euclidean structures induced on
${\mathcal M}^+_{\Sigma }(\sigma )$
and
$ {\mathcal M}^-_{\Sigma }(\sigma )$
by the Hilbert space
$L^2_h(M)$
. The existence of J is a consequence of the fact that the deficiency subspaces
${\mathcal M}^+_{\Sigma }(\sigma )$
and
${\mathcal M}^-_{\Sigma }(\sigma )$
are isomorphic finite-dimensional vector spaces of the same complex dimension (equal to the genus g of the surface M). In fact, there exists a whole family of operators J as required, parametrized by the Lie group
$U(g,{\mathbb C})$
. Let
$\pi ^{\pm }_{h, \sigma }:L^2_h(M) \to R^{\pm }_{h, \sigma }$
be the orthogonal projections. We recall that
$R^\pm _{h, \sigma }$
are the orthogonal complements of
${\mathcal M}^\mp _{\Sigma }(\sigma )$
, respectively (Proposition 3.5). Once an isometric operator J as in formula (25) is fixed, the partial isometry
$U_{h,\sigma }$
, associated with the holomorphic abelian differential h on M and
$\sigma \in {\mathbb R}$
as in formula (24), will be extended to a unitary operator
$U_{J,\sigma }$
on the whole
$L^2_h(M)$
by the formula
$$ \begin{align*}U_{J,\sigma} (u):=U_{h,\sigma} \pi^-_{h, \sigma}(u) +J(I-\pi^-_{h, \sigma})(u) \quad \text{for all }\,u\in L_h^2(M) \end{align*} $$
(the dependence of the unitary operator
$U_{J, \sigma }$
on the abelian differential is omitted in the notation for convenience).
The following version of the formal identities (19) holds on
$H^1_h(M)$
:
$$ \begin{align} S_{\theta} +\imath \sigma_\theta ={\frac{e^{-\imath\theta}}{2}}\, ((U_{J, \sigma}+e^{2\imath\theta} )) \,\partial^-_{h,\sigma}={\frac{e^{\imath\theta}}{2}}\, ((U_{J, \sigma} ^{-1}+e^{-2\imath\theta} )) \,\partial^+_{h, \sigma}. \end{align} $$
A priori estimates for
$S_{\theta }$
are related by formula (26) to estimates for the resolvent
${\mathcal R}_{J, \sigma }(z):=(U_{J, \sigma }-zI)^{-1}$
of any of the operators
$U_{J, \sigma }$
, as
$z\to { \mathbb T}$
non-tangentially. Since these are unitary operators, their spectrum is contained in the unit circle
$\{z\in {\mathbb C} \mid \vert z\vert =1\}$
. As a consequence, the resolvent
${\mathcal R}_{J, \sigma }(z)$
is a well-defined operator-valued holomorphicfunction on the unit disk
$D:=\{z\in {{\mathbb C}}\,|\,|z|<1\}$
. In addition, by the spectral theoremfor unitary operators, it is given by a Cauchy integralon
$\partial D$
of the spectral measure associated with
$U_{J, \sigma }$
.
4 Spectral theory of unitary operators
Let
$U:{\mathcal H}\to {\mathcal H}$
be anyunitary operator on a (separable) Hilbert space
$\mathcal H$
. By the spectral theorem [Reference YosidaYo, XI.4], its resolvent
${\mathcal R}_U(z):=(U-zI)^{-1}$
can be represented as a Cauchy integral of the spectral family as follows. For any u,
$v\in {\mathcal H}$
,
$$ \begin{align*}({\mathcal R}_U(z)u,v)_{\mathcal H}=\int_0^{2\pi} (z-e^{i t})^{-1}\,d(E_U(t)u,v)_{\mathcal H} \quad \text{for all } z\in D,\end{align*} $$
where
$(\,\cdot ,\,\cdot \,)_{\mathcal H}$
denotes the inner product in
${\mathcal H}$
and
$\{E_U(t)\}_{0\leq t\leq 2\pi }$
denotes the spectral family associated with the unitary operator U on
$\mathcal H$
. Our approach from [Reference ForniF97] is based on the fundamental property of holomorphic functions on D, which can be represented as Cauchy integrals on
$\partial D$
of complex measures, of having non-tangential boundary values almost everywhere.
We recall below general results on the boundary behavior of Cauchy integrals of complex measures. The modern theory of these singular integrals, based on the Lebesgue integral, was initiated by Fatou in his thesis [Reference FatouFt]. The results gathered below were originally obtained by Riesz [Reference RieszRz], Smirnov [Reference SmirnovSm], Hardy and Littlewood [Reference Hardy and LittlewoodHL]. The arguments, given in [Reference ForniF97, §3], follow the approach of Zygmund [Reference ZygmundZy, VII.9], based on real variables methods, and are taken from the books by Rudin [Reference RudinRd] and Stein and Weiss [Reference Stein and WeissSW].
Let
$\mu $
be a complex Borel measure (of finite total mass) on
$\partial D$
. The Cauchy integral of
$\mu $
is the holomorphic function
$I_{\mu }$
on D defined as
$$ \begin{align} I_{\mu}(z):=\int_0^{2\pi}(z-e^{i t})^{-1}\,d\mu (t) \quad \text{for all }z\in D. \end{align} $$
Lemma 4.1 [Reference ForniF97, Lemma 3.3A]
The non-tangential limit
$$ \begin{align*}I_{\mu}(z)\to I_{\mu}^{\ast}(\theta) \quad \text{as } z\to e^{\imath\theta},\end{align*} $$
exists almost everywhere with respect to the (normalized) Lebesgue measure
$\mathcal L$
on the circle
${ \mathbb T}$
. In addition, there exists a constant
$C>0$
such that the following weak type estimate holds:
$$ \begin{align*}{\mathcal L}\{\theta\in { \mathbb T}\,|\,\,|I_{\mu}^{\ast}(\theta)|> t \}\leq { \frac{C}{t}}\,|\mu| \quad \text{for all } t>0,\end{align*} $$
where
$|\mu |$
denotes the total mass of the measure
$\mu $
.
Lemma 4.1 is not enough for our purposes, since it gives no information concerning the behavior of Cauchy integrals (27) as the convergence to the limiting boundary values takes place. The necessary estimates are given below, following [Reference ForniF97], in terms of non-tangential maximal functions, the definition of which we recall below following [Reference RudinRd, §11.18].
For
$0<\alpha <1$
, we define the non-tangential approach region
$\Omega _{\alpha }$
to be the cone over
$D(0,\alpha )$
of vertex
$z=1$
, that is, the union of the disk
$D(0,\alpha )$
and the line segments from the point
$z=1$
to the points of
$D(0,\alpha )$
. Rotated copies of
$\Omega _{\alpha }$
, having vertex at
$e^{\imath \theta }$
, will be denoted by
$\Omega _{\alpha }(\theta )$
.
For any complex function
$\Phi $
on the unit disk D and
$0<\alpha <1$
, its non-tangential maximal function
$N_{\alpha }(\Phi )$
is defined on
${ \mathbb T}$
as
$$ \begin{align} N_{\alpha}(\Phi)(\theta):=\sup\{|\Phi(z)|\,|\,z\in \Omega_{\alpha} (\theta)\}. \end{align} $$
We would like to complete Lemma 4.1 with estimates on the non-tangential maximal function
$N_{\alpha }(I_{\mu })$
of the Cauchy integral in formula (27). This can be accomplished by a standard argument of basic Hardy space theory.
For the convenience of the reader, we will recall the definition of Hardy spaces
$H^p(D)$
on the unit disk D [Reference RudinRd, §§7 and 17.6]. Let
$\Phi $
be a complex function on D. For
$0<r<1$
, we define the functions
$\Phi _r$
on
${ \mathbb T}$
by the formula
$$ \begin{align*}\Phi_r(\theta):=\Phi(re^{\imath\theta}) \quad \text{for all } \theta \in { \mathbb T},\end{align*} $$
and, for
$0<p\leq \infty $
, we define
$$ \begin{align*}|\Phi|_p=\sup \{|\Phi_r|_p \mid 0\leq r<1\},\end{align*} $$
where
$|\cdot |_p$
denotes the
$L^p$
norm on
${ \mathbb T}$
with respect to the Lebesgue measure. The Hardy space
$H^p(D)$
is defined to be the space of holomorphic functions
$\Phi $
on the unit disk D such that
$|\Phi |_p<\infty $
.
Lemma 4.2 [Reference ForniF97, Lemma 3.3B]
The holomorphic function
$I_\mu $
, given as a Cauchy integral (see formula (27)) of a Borel complex measure
$\mu $
on
$\partial D$
, belongs to the Hardy spaces
$H^p(D)$
, for any
$0<p<1$
. (Consequently, it admits a non-tangential limit almost everywhere on
$\partial D$
.) In addition, its non-tangential maximal function
$N_{\alpha }(I_{\mu })$
belongs to
$L^p({ \mathbb T},{\mathcal L})$
, for any
$0<p<1$
and for all
$\alpha <1$
, and there exist constants
$A_{\alpha }$
,
$A_{\alpha ,p}>0$
, with
$A_{\alpha ,p}\to \infty $
as
$p\to 1$
, such that the following estimates hold:
$$ \begin{align*}\vert N_{\alpha}(I_{\mu}) \vert_p\leq A_{\alpha}|I_{\mu}|_p\leq A_{\alpha,p} |\mu|,\end{align*} $$
where
$|\mu |$
denotes the total mass of the measure
$\mu $
.
The general harmonic analysis lemmas (Lemmas 4.1 and 4.2) are then applied via the spectral theorem to the resolvent of an arbitrary unitary operator on a Hilbert space. The abstract Hilbert space result which we obtain in this way will then be applied to the unitary operators
$U_{J, \sigma } $
,
$U_{J, \sigma } ^{-1}$
introduced in §3.
Corollary 4.3 [Reference ForniF97, Corollary 3.4]
Let
${\mathcal R}_U(z):{\mathcal H}\to {\mathcal H}$
,
$z\in D$
, denote the resolvent of a unitary operator
$U:{\mathcal H}\to {\mathcal H}$
on a Hilbert space
$\mathcal H$
. Then, for any u,
$v\in {\mathcal H}$
, the holomorphic functions
$\Phi (u,v)(\cdot ):= ({\mathcal R}(\cdot )u,v)_{\mathcal H}$
belong to the Hardy spaces
$H^p(D)$
, for any
$0<p<1$
. Consequently, they admit a non-tangential limit almost everywhere on
$\partial D$
. Furthermore, their non-tangential maximal functions
$N_{\alpha }(u,v)$
belong to
$L^p( { \mathbb T},{\mathcal L})$
, for any
$0<p<1$
and for all
$\alpha <1$
, and there exist constants
$A_{\alpha }$
,
$A_{\alpha ,p}>0$
, with
$A_{\alpha ,p}\to \infty $
as
$p\to 1$
, such that the following estimates hold:
$$ \begin{align*}|N_{\alpha}(u,v)|_p\leq A_{\alpha}|\Phi(u,v)|_p\leq A_{\alpha,p} |u|_{\mathcal H}\,|v|_{\mathcal H},\end{align*} $$
where
$|\cdot |_{\mathcal H}$
denotes the Hilbert space norm.
5 Solutions of the twisted cohomological equation
In this section we adapt to the twisted cohomological equation the streamlined version [Reference ForniF07] of the main argument of [Reference ForniF97, Theorem 4.1] given with the goal of establishing the sharpest bound on the loss of Sobolev regularity within the reach of the methods of [Reference ForniF97].
We prove in §5.1 a priori Sobolev bounds for distributional solutions of the cohomological equation with respect to the Friedrichs weighted Sobolev norms, then in §5.3 for smooth solutions with respect to fractional weighted Sobolev norms.
In §5.2 we prove results on the structure of the space of twisted invariant distributions, which give obstructions to the existence of solutions of the cohomological equations.
5.1 Distributional solutions
We derive results on distributional solutions of the twisted cohomological equation from the harmonic analysis results of §4 about the boundary behavior of the resolvent of a unitary operator.
We recall the definition of the Friedrichs weighted Sobolev spaces and norms, given in Definition 2.5. The Friedrichs weighted Sobolev space
$\bar H^s_h(M)$
can be defined, for all
$s\in {\mathbb R}$
, as the maximal domain of the (fractional) power
$(-\Delta ^F_h)^{s/2}$
of the Friedrichs extension
$-\Delta ^F_h$
of the non-negative flat Laplacian, endowed with the following norms. Let
$\{\unicode{x3bb} _k \mid k\in { \mathbb N}\}$
denote the sequence of eigenvalues (repeated according to their multiplicities) of the non-negative Friedrichs Laplacian
$-\Delta ^F_h$
relative to a orthonormal basis
$\mathcal E= \{e_k \mid k\in { \mathbb N}\}$
of eigenfunctions. The Friedrichs weighted Sobolev norms are given, for all
$s\in {\mathbb R}$
, as
Definition 5.1 Let h be an abelian differential and let
$\sigma \in {\mathbb R}$
. A distribution
$u\in \bar H^{-r}_h(M)$
will be called a (distributional) solution of the cohomological equation
$(S + \imath \sigma ) u =f$
for a given function
$f\in \bar H^{-s}_h(M)$
if
$$ \begin{align*}{\langle}u, (S + \imath\sigma) v{\rangle} = - {\langle} f, v{\rangle}\quad \text{for all } v\in H^{r+1}_h(M) \cap \bar H^{s}_h(M). \end{align*} $$
Let
$h_\theta = e^{-\imath \theta } h$
be its rotation and let
$\sigma _\theta := \sigma \cos \theta $
. Let
$\{S_\theta \}$
denote the one-parameter family of rotated vector fields introduced in formula (17):
$$ \begin{align*}S_{\theta}:=\{e^{-\imath\theta}(S+\imath\,T)+e^{\imath\theta}(S-\imath\,T)\}/2. \end{align*} $$
For all
$s\in {\mathbb R}$
, let
$\mathcal H ^s_h (M) \subset H^s_{h} (M)$
and
$\bar {\mathcal H} ^s_h (M) \subset \bar H^s_{h} (M)$
the subspaces of distributions vanishing on constant functions. By Lemma 2.8, for all
$s \in [-1, 1]$
, we have
$\bar H^s_{h} (M)\equiv H^s_{h} (M)$
, hence
$\bar {\mathcal H}^s_{h} (M)\equiv {\mathcal H}^s_{h} (M)$
.
Theorem 5.2 Let h be an abelian differential on M with minimal vertical foliation. Let
$r>2$
and
$p\in (0,1)$
be such that
$rp>2$
. For any
$\sigma \in {\mathbb R}$
, there exists a bounded linear operator
$$ \begin{align*}\mathcal U_\sigma: \mathcal H^{-1}_{h}(M) \to L^p( { \mathbb T}, {\bar H}^{-r}_h(M)) \end{align*} $$
such that the following statement holds. For any
$\sigma \in {\mathbb R}$
and any
$f\in H^{-1}(M)$
there exists a full measure subset
${\mathcal F}_r(\sigma ,f)\subset { \mathbb T}$
such that
$u:=\mathcal U_\sigma (f)(\theta )\in {\bar H}^{-r}_h(M)$
is a distributional solution of the cohomological equation
$(S_{\theta } + \imath \sigma _\theta ) u= f$
, for all
$\theta \in {\mathcal F}_r(f,\sigma )$
. In addition, there exists a constant
$B_h:=B_h(p,r)>0$
such that, for all
$f\in \mathcal H_h^{-1}(M)$
, vanishing on constant functions,
$$ \begin{align*}\vert \mathcal U_\sigma(f) \vert_{p}:= \bigg(\int_{ { \mathbb T}} \Vert \mathcal U_\sigma(f)(\theta) \Vert_{-r}^p \,d\theta \bigg)^{1/p} \,\, \leq \,\, B_{h} \, \Vert f \Vert_{-1}. \end{align*} $$
The above theorem is a consequence of the following estimate.
Lemma 5.3 Let h be an abelian differential on M with minimal vertical foliation. Let
$r>2$
and
$p\in (0,1)$
be such that
$rp>2$
. For any
$\sigma \in {\mathbb R}$
and any
$f\in \mathcal H_{h}^{-1}(M)$
, vanishing on constant functions, there exists a measurable function
$A_{h,\sigma }(f):=A_{h,\sigma } (f, p,r) \in L^p( { \mathbb T}, {\mathcal L})$
such that, for all
$v\in H_h^{r+1}(M)$
, we have
$$ \begin{align} \vert {\langle}f,v{\rangle} \vert \leq A_{h,\sigma}(f, \theta) \,\Vert (S_{\theta}+ \imath\sigma_\theta) v \Vert_r. \end{align} $$
In addition, the following bound for the
$L^p$
norm of the function
$A_{h,\sigma }(f)$
holds. There exists a constant
$B_h:=B_{h}(p,r)>0$
such that, for every
$\sigma \in {\mathbb R}$
and for every
$f\in H^{-1}_h(M)$
, vanishing on constant functions, we have
$$ \begin{align} \vert A_{h,\sigma}(f) \vert_p \leq B_{h} \, \Vert f \Vert_{-1}. \end{align} $$
Proof. We recall formulas (26):
$$ \begin{align} S_{\theta} +\imath \sigma_\theta ={\frac{e^{-\imath\theta}} {2}}\, ((U_{J, \sigma}+e^{2\imath\theta} )) \,\partial^-_{h, \sigma}={\frac{e^{\imath\theta}}{2}}\, ((U_{J, \sigma} ^{-1}+e^{-2\imath\theta} )) \,\partial^+_{h, \sigma}. \end{align} $$
It appears from the above formulas that, since the twisted Cauchy–Riemann operators, which are elliptic partial differential operators, have finite-dimensional kernel and cokernel, a formal solution of the cohomological equation
$(S_{\theta } +\imath \sigma _\theta ) u=f$
(up to a finite-dimensional cokernel) can be written in terms of the inverses of the operator
$U_{J, \sigma }+e^{2\imath \theta }I$
or
$U_{J, \sigma } ^{-1}+e^{-2\imath \theta }I$
. However, since
$U_J$
and
$U_J^{-1}$
are unitary operators, their spectrum in contained in the unit circle, hence the inverses of the operators
$U_{J, \sigma }+e^{2\imath \theta }I$
or
$U_{J, \sigma } ^{-1}+e^{-2\imath \theta }I$
are a priori unbounded on
$L^2_h(M)$
. (It can in fact be proved that the spectra of
$U_J$
and
$U_J^{-1}$
coincide with the full unit circle.) The key idea of the argument is to construct inverses in the distributional (weak) sense by taking non-tangential boundary limits of the resolvents
$(U_{J, \sigma }+zI)^{-1}$
or
$(U_{J, \sigma }^{-1}+z I)^{-1}$
, which are well-defined bounded operators on the Hilbert space
$L^2_h(M)$
as long as the spectral parameter
$z\in {\mathbb C}$
belongs to the interior of the unit disk.
Thus, our proof of estimate (29) is based on properties of the resolvent of the operators
$U_{J,\sigma }$
,
$U_{J,\sigma }^{-1}$
. In fact, it is based on the general results, summarized below in §4, concerning the non-tangential boundary behavior of the resolvent of a unitary operator on a Hilbert space, applied to the operators
$U_{J, \sigma }$
,
$U_{J, \sigma }^{-1}$
on
$L^2_h(M)$
. The Fourier analysis of [Reference ForniF97, §2], also plays a relevant role through Lemma 2.9 and the Weyl’s asymptotic formula (Theorem 2.3).
Since the vertical foliation of h is minimal, it follows that all T-invariant functions in the space
$H^1_h(M)$
are constant, hence the common kernel of the twisted Cauchy–Riemann operators
$K_{h,\sigma } \subset H^1_h(M)$
coincides with the subspace of constant functions.
Following [Reference ForniF97, Proposition 4.6A] or [Reference ForniF02, Lemma 7.3], we prove that there exists a constant
$C_{h}>0$
such that the following statement holds. For any
$\sigma \in {\mathbb R}$
and for any distribution
$f\in H^{-1}_h(M)$
there exist (weak) solutions
$F^{\pm }_\sigma \in L^2_h(M)$
of the equations
$\partial _{h,\sigma } ^{\pm } F^{\pm }_\sigma =f$
such that
$$ \begin{align} \vert F^{\pm}_\sigma\vert_0 \leq C_{h} \, \Vert f \Vert_{-1}. \end{align} $$
In fact, the maps given by
$$ \begin{align} \partial^{\pm}_{h,\sigma} v \to - {\langle}f,v{\rangle} \quad \mbox{for all }v\in H^1_h(M), \end{align} $$
are bounded linear functionals on the (closed) ranges
$R^{\pm }_{h,\sigma }\subset L^2_h(M)$
of the twisted Cauchy–Riemann operator
$\partial ^{\pm }_{h, \sigma } :H^1_h(M)\to L^2_h(M)$
. In fact, the functionals are well defined since by assumption
$K_{h, \sigma }={\mathbb C}$
and f vanishes on constant functions, and they are bounded since, by Lemma 3.1 and Proposition 3.5, there exists a constant
$C_{h}>0$
such that, for any
$\sigma \in {\mathbb R}$
and for any
$v\in H^1_h(M)$
of zero average,
$$ \begin{align} \begin{aligned} \vert {\langle}f,v{\rangle} \vert \,&\leq\, \Vert f\Vert_{-1} \vert v \vert_1 \leq C'_h \Vert f\Vert_{-1} Q_{h,0}(v) \\ & \leq \, C_h \Vert f\Vert_{-1} Q_{h,\sigma}(v)\, = \, C_{h} \, \Vert f\Vert_{-1} \, \vert \partial^{\pm}_{h,\sigma} v \vert_0. \end{aligned} \end{align} $$
Let
$\Phi ^{\pm }_\sigma $
be the unique linear extension of the linear map (33) to
$L^2_h(M)$
which vanishes on the orthogonal complement of
$R^{\pm }_{h,\sigma }$
in
$L^2_h(M)$
. By (34), the functionals
$\Phi ^{\pm }_\sigma $
are bounded on
$L^2_h(M)$
with norm
$$ \begin{align*}\Vert \Phi^{\pm}_\sigma \Vert \leq C_{h} \, \Vert f\Vert_{-1}. \end{align*} $$
By the Riesz representation theorem, there exist two (unique) functions
$F^{\pm }_\sigma \in L^2_h(M)$
such that
$$ \begin{align*}{\langle}v, F^{\pm}_\sigma{\rangle}_h \,=\, \Phi^{\pm}_\sigma (v) \quad \text{for all } v\in L^2_h(M). \end{align*} $$
The functions
$F^{\pm }_\sigma $
are by construction (weak) solutions of the twisted Cauchy–Riemann equations
$\partial _{h,\sigma }^{\pm } F^{\pm }_\sigma =f$
satisfying the required bound (32).
The identities (31) immediately imply that
$$ \begin{align} {\langle}{\partial}^{\pm}_{h,\sigma} v,F^{\pm}_\sigma{\rangle}_h&=2 e^{\mp i \theta}\, {\langle}{\mathcal R}^{\pm}_{J,\sigma}(z)(S_{\theta}+ \imath\sigma_\theta) v,F^{\pm}_\sigma{\rangle}_h \nonumber\\ &\quad-(z+e^{\mp2 \imath\theta}){\langle}{\mathcal R}^{\pm}_{J,\sigma}(z){\partial}^{\pm}_h v,F^{\pm}_\sigma{\rangle}_h, \end{align} $$
where
${\mathcal R}^{+}_{J,\sigma }(z)$
and
${\mathcal R}^{-}_{J,\sigma }(z)$
denote the resolvents of the unitary operators
$U_{J,\sigma }$
and
$U_{J,\sigma }^{-1}$
respectively, which yield holomorphic families of bounded operators on the unit disk
${D\subset {\mathbb C}}$
.
Let
$r>2$
and let
$p\in (0,1)$
be such that
$pr>2$
. Let
$\mathcal E=\{e_k\}_{k\in {{ \mathbb N}}}$
denote the orthonormal Fourier basis of the Hilbert space
$L^2_h(M)$
of eigenfunctions of the Friedrichs Laplacian, described in §2. By Corollary 4.3 all holomorphic functions
$$ \begin{align} {\mathcal R}^{\pm}_{h,\sigma,k}(z):={\langle}{\mathcal R}^{\pm}_{J,\sigma}(z) e_k,F^{\pm}_\sigma{\rangle}_h,\quad k \in {{ \mathbb N}}, \end{align} $$
belong to the Hardy space
$H^p(D)$
, for any
$0<p<1$
. The corresponding non-tangential maximal functions
$N_k^{\pm }$
(over cones of arbitrary fixed aperture
$0<\alpha <1$
) belong to the space
$L^p( { \mathbb T},{\mathcal L})$
and for all
$0<p<1$
there exists a constant
$A_{\alpha ,p}>0$
such that, for any abelian differential h on M, for every
$\sigma \in {\mathbb R}$
and
$k\in { \mathbb N}$
, the following inequalities hold:
$$ \begin{align} \vert N_{h,\sigma,k}^{\pm} \vert_p\leq A_{\alpha,p} \vert e_k \vert_0\, \vert F^{\pm} _\sigma\vert_0= A_{\alpha,p} \, \vert F^{\pm} _\sigma\vert_0 \leq A_{\alpha,p}\, C_{h} \, \vert f\vert _{-1}. \end{align} $$
Let
$\{\unicode{x3bb} _k\}_{k\in {{ \mathbb N}}}$
be the sequence of the eigenvalues of the Dirichlet form
$\mathcal Q:= \mathcal Q_{h,0}$
introduced in §2. Let
$w\in \bar H^r_h(M)$
. We have
$$ \begin{align} {\langle}{\mathcal R}^{\pm}_{J,\sigma}(z)w,F^{\pm}_\sigma{\rangle}_h = \sum_{k=0}^{\infty}{\langle}w,e_k{\rangle}_h\,\,{\mathcal R}^{\pm}_{h,\sigma,k}(z), \end{align} $$
hence, by the Cauchy–Schwarz inequality,
Let
$N^{\pm }_{h,\sigma }(\theta )$
be the functions defined as
Let
$N^{\pm }_{h, \sigma }(w)$
denote the non-tangential maximal function for the holomorphic function
${\langle }{\mathcal R}^{\pm }_{J,\sigma }(z)w,F^{\pm }_\sigma {\rangle }_h$
. By formulas (39) and (40), it follows that, for all
$\theta \in { \mathbb T}$
and all functions
$w \in {\bar H}^r_h(M)$
, we have
$$ \begin{align} N^{\pm}_{h,\sigma}(w)(\theta) \leq N^{\pm}_{h,\sigma}(\theta) \, \Vert w\Vert_r. \end{align} $$
The functions
$N^{\pm }_{h,\sigma } \in L^p( { \mathbb T},{\mathcal L})$
for any
$0<p<1$
. In fact, by formula (37) and (following a suggestion of Stephen Semmes) by the ‘triangular inequality’ for the space
$L^{p/2}$
with
$0<p<1$
, we have
The series in formula (42) is convergent by the Weyl asymptotics (Theorem 2.3) since
$pr/2>1$
. Let then
By taking the non-tangential limit as
$z\to -e^{\mp 2 \imath \theta } $
in identity (35), formula (41) implies that, for all
$\theta \in { \mathbb T}$
such that
$N^{\pm }_{h,\sigma } (\pi \mp 2\theta )<+\infty $
,
$$ \begin{align*}\vert {\langle}{\partial}^{\pm}_{h,\sigma} v,F^{\pm}_\sigma{\rangle}_h \vert \leq N^{\pm}_{h,\sigma} (\pi\mp 2\theta) \, \Vert (S_{\theta} + \imath \sigma_\theta) v \Vert_r, \end{align*} $$
hence the required estimates (29) and (30) are proved with the choice of the function
$A_{h,\sigma } (f,\theta ):= N^+_{h,\sigma } (\pi -2\theta )$
or
$A_{h,\sigma } (f,\theta ):= N^- _{h,\sigma } (\pi +2\theta )$
, for all
$\theta \in { \mathbb T}$
.
Proof Proof of Theorem 5.2
By the estimate (29) of Lemma 5.3, the linear map given by
$$ \begin{align} (S_{\theta} + \imath \sigma_\theta) v\to -{\langle}f,v{\rangle} \quad \mbox{for all } v\in H_h^{r+1}(M), \end{align} $$
is well defined and extends by continuity to the closure of the range
${\bar R}^r_\sigma (\theta )$
of the linear operator
$S_{\theta }+ \imath \sigma _\theta $
in
${\bar H}^r_h(M)$
. Let
$\mathcal U_\sigma (f)(\theta )$
be the extension uniquely defined by the condition that
$\mathcal U_\sigma (f)(\theta )$
vanishes on the orthogonal complement of
${\bar R}^r_\sigma (\theta )$
in
${\bar H}^r_h(M)$
. By construction, for almost all
$\theta \in { \mathbb T}$
the linear functional
$u:=\mathcal U_\sigma (f)(\theta )\in {\bar H}^{-r}_h(M)$
yields a distributional solution of the cohomological equation
$(S_{\theta }+ \imath \sigma _\theta ) u=f$
whose norm satisfies the bound
$$ \begin{align*}\Vert \mathcal U_\sigma(f)(\theta) \Vert_{-r} \leq A_{h,\sigma}(f,\theta). \end{align*} $$
By (30) the
$L^p$
norm of the measurable function
$\mathcal U_\sigma (f): { \mathbb T} \to {\bar H}^{-r}_h(M)$
satisfies the required estimate
$$ \begin{align*}\vert \mathcal U_\sigma(f) \vert_{p}:= \bigg(\int_{ { \mathbb T}} \Vert \mathcal U_\sigma(f)(\theta) \Vert_{-r}^p \,d\theta \bigg)^{1/p} \,\, \leq \,\, B_{h} \, \Vert f \Vert_{-1}.\\[-42pt] \end{align*} $$
Theorem 5.4 Let h be an abelian differential with minimal vertical foliation. For any
$r>2$
and
$p\in (0,1)$
such that
$pr>2$
, there exists a constant
$C_{h,p,r}>0$
such that, for all zero-average functions
$f\in {\bar H}^{r-1}_h(M)$
, for all
$\sigma \in {\mathbb R}$
and for Lebesgue almost all
$\theta \in { \mathbb T}$
, the twisted cohomological equation
$(S_{\theta } + \imath \sigma _\theta ) u=f$
has a distributional solution
$u_\theta \in {\bar H}^{-r}_h(M)$
satisfying the following estimate:
$$ \begin{align} \bigg(\int_{ \mathbb T} \Vert u_\theta \Vert_{-r}^p\, d\theta \bigg)^{1/p} \leq C_{h,p,r}\, \Vert f \Vert_{r-1}. \end{align} $$
Proof. Let
$\{\unicode{x3bb} _k \vert k\in { \mathbb N}\}$
denote the sequence of eigenvalues of the Friedrichs Laplacian relative to the orthonormal Fourier basis
$\mathcal E=\{e_k\}_{k\in {{ \mathbb N}}}$
of eigenfunctions of the Hilbert space
$L^2_h(M)$
, described in §2. Let
$r>2$
and
$p\in (0,1)$
be such that
$pr>2$
.
By Theorem 5.2, for any
$k\in { \mathbb N}\setminus \{0\}$
there exists a function with distributional values
$u_k := \mathcal U_\sigma (e_k)\in L^p( { \mathbb T}, {\bar H}^{-r}_h(M))$
such that the following statement holds. There exists a constant
$C_{h,r}:=C_h(p,r)>0$
such that
In addition, for any
$k\in { \mathbb N}\setminus \{0\}$
, there exists a full measure set
$\mathcal F_k(\sigma )\subset { \mathbb T}$
such that, for all
$\theta \in {\mathcal F}_k(\sigma )$
, the distribution
$u:=u_k(\theta ) \in {\bar H}^{-r}_h(M)$
is a (distributional) solution of the cohomological equation
$(S_{\theta } + \imath \sigma _\theta ) u = e_k$
.
Any function
$f\in {\bar H}^{r-1}_h(M)$
of zero average has a Fourier decomposition in
$L^2_h(M)$
:
$$ \begin{align*}f = \sum_{k\in{ \mathbb N}\setminus\{0\}} {\langle}f,e_k{\rangle}_h \, e_k. \end{align*} $$
A (formal) solution of the cohomological equation
$(S_{\theta } + \imath \sigma _\theta ) u =f$
is therefore given by the series
$$ \begin{align} u_{\theta}:= \sum_{k\in{ \mathbb N}\setminus\{0\}} {\langle}f,e_k{\rangle}_h\, u_k(\theta). \end{align} $$
By the triangular inequality in
${\bar H}^{-r}_h(M)$
and by the Hölder inequality, we have
hence by the ‘triangular inequality’ for
$L^p$
spaces (with
$0<p<1$
) and by estimate (45),
Since
$pr/2>1$
the series in (47) is convergent, hence
$u_{\theta }\in {\bar H}^{-r}_h(M)$
is a solution of the equation
$(S_{\theta }+ \imath \sigma _\theta ) u=f$
which satisfies the required bound (44).
5.2 Twisted invariant distributions and basic currents
In this section we describe the structure of the space of obstructions to the existence of solutions of the twisted cohomological equation
$(S + \imath \sigma )u =f$
.
Definition 5.5 For all
$r>0$
, let
$\mathcal I^r_{h,\sigma } \subset H^{-r}_h(M)$
denote the space of distributions invariant for the twisted Lie derivative operator
$S + \imath \sigma $
, that is, the space
$$ \begin{align*}\mathcal I^r_{h,\sigma} :=\{ D \in H^{-r}_h(M) \vert (S + \imath \sigma ) D =0 \}. \end{align*} $$
Twisted invariant distributions are in one-to-one correspondence with twisted basic currents. We introduce Sobolev space of 1-forms and of one-dimensional currents.
Definition 5.6 Let
$\mathcal S(M, T^\ast M)$
denote the space of all Borel measurable sections of the cotangent bundle
$T^\ast M$
. For all
$r>0$
, the weighted Sobolev space of 1-forms
$W^r_h(M)$
is defined as follows:
$$ \begin{align} W^r_h(M):= \{ \alpha \in \mathcal S(M, T^\ast M) \,\vert \, (\imath_S\alpha, \imath_T\alpha) \in H_h^r(M) \times H_h^r(M) \}. \end{align} $$
The weighted Sobolev space of
$1$
-currents
$W^{-r}_h(M)$
is defined as the dual space of the weighted Sobolev space of 1-forms
$W^{r}_h(M)$
.
Twisted basic currents are defined as follows.
Definition 5.7 For all
$r>0$
, let
$\mathcal B^r_{h,\sigma }\subset H^{-r}_h(M)$
denote the space of twisted basic currents, that is, the space
$$ \begin{align*}\mathcal B^r_{h,\sigma}:=\{ C \in W^{-r}_h(M) \mid (\mathcal L_{S} + \imath \sigma ) C = \imath_{S} C=0 \}. \end{align*} $$
(Here
$\mathcal L_{S}$
denotes the Lie derivative operator on currents in the direction of the vector field S on
$M\setminus \Sigma _h$
.)
The notions of twisted invariant distributions and twisted basic currents are related (for the untwisted case see [Reference ForniF02, Lemmas 6.5 and 6.6] or [Reference ForniF07, Lemma 3.14]):
Lemma 5.8 A one-dimensional current
$C\in {\mathcal B}^r_{h, \sigma }$
if and only if the distribution
$C\wedge { \operatorname {Re} } (h) \in {\mathcal I}^r_{h,\sigma }$
. In addition, the map
$$ \begin{align} \mathcal D_h: C \to - C\wedge{ \operatorname{Re} }(h) \end{align} $$
is a bijection from the space
${\mathcal B}^r_{h,\sigma }$
onto the space
${\mathcal I}^r_{\sigma , h}$
.
Proof. The map
$\mathcal D_h$
is well defined since for any
$C\in {\mathcal B}^r_{h, \sigma }$
we have
$$ \begin{align*}(\mathcal L_S + \imath \sigma)[ C\wedge { \operatorname{Re} } (h) ]= [(\mathcal L_S + \imath \sigma) C] \wedge { \operatorname{Re} }(h) =0. \end{align*} $$
The inverse map is the map
$\mathcal B_h: {\mathcal I}^r_{\sigma , h} \to {\mathcal B}^r_{h,\sigma }$
defined as
$$ \begin{align*}\mathcal B_h (D) = \imath_S D \quad \text{for all } D \in {\mathcal I}^r_{\sigma, h}. \end{align*} $$
(Here
$\imath _S$
denotes the contraction operator with respect the vector field S on
$M\setminus \Sigma _h$
, which maps distributions, as currents of degree
$2$
, to currents of degree
$1$
.)
The map
$\mathcal B_h$
is well defined since
$\imath _S \circ \imath _S =0$
, and
$$ \begin{align*}(\mathcal L_S + \imath \sigma) \circ \imath_S = \imath_S \circ (\mathcal L_S + \imath \sigma). \end{align*} $$
It follows that if
$D \in {\mathcal I}^r_{h, \sigma }$
then
$C=\imath _S D \in {\mathcal B}^r_{h, \sigma }$
since
$$ \begin{align*}(\mathcal L_S + \imath \sigma) C =\imath_S \circ (\mathcal L_S + \imath \sigma)D =0 \quad \text{and} \quad \imath_S C= \imath_S (\imath_S D) =0. \end{align*} $$
Finally, the map
$\mathcal B_h$
is the inverse of the map
$\mathcal D_h$
. In fact, since
$\imath _S C=0$
(as C is basic) and
$D \wedge { \operatorname {Re} }(h)=0$
(as a current of degree
$3$
), and
$\imath _S { \operatorname {Re} } (h)=1$
, we have
$$ \begin{align*}\begin{aligned} (\mathcal B_h \circ \mathcal D_h) (C)& = -\imath_S(C \wedge { \operatorname{Re} } (h) ) = -\imath_S C \wedge { \operatorname{Re} } (h) + C \wedge \imath_S { \operatorname{Re} } h = C, \\ (\mathcal D_h \circ \mathcal B_h) (D) &= -( \imath_S D \wedge { \operatorname{Re} }(h)) = -\imath_S (D \wedge { \operatorname{Re} }(h)) + (D \wedge\imath_S { \operatorname{Re} }(h)) = D. \end{aligned} \end{align*} $$
The argument is complete.
We recall the definition of the twisted exterior differential
$d_{h,\sigma }$
:
$$ \begin{align*}d_{h,\sigma} \alpha :=d\alpha + \imath \sigma { \operatorname{Re} } (h) \wedge \alpha \quad \text{for all } \alpha \in W^{s}_h(M). \end{align*} $$
The twisted exterior differential extends to currents by duality.
Definition 5.9 A current
$C\in W^{-s}_h(M)$
is
$d_{h,\sigma }$
-closed if
$$ \begin{align*}d_{h,\sigma} C = dC +\imath \sigma ({ \operatorname{Re} } (h) \wedge C )=0. \end{align*} $$
Lemma 5.10 A current
$C \in \mathcal B_{h, \sigma }^r$
if and only if
$\imath _S C=0$
and C is
$d_{h,\sigma }$
-closed.
Proof. If
$C\in \mathcal B_{h, \sigma } ^r$
, then
$\imath _SC=0$
by definition, and
$$ \begin{align*}\imath_S d_{h,\sigma} C = \imath_S [dC +\imath \sigma ({ \operatorname{Re} }(h) \wedge C )] = \mathcal L_S C +\imath \sigma C =0, \end{align*} $$
so that
$\imath _S d_{h,\sigma } C=0$
, which implies
$d_{h,\sigma } C=0$
, as
$d_{h,\sigma } C$
is a current of degree
$2$
(and dimension
$0$
) and the contraction operator
$\imath _S$
is surjective onto
$2$
-forms.
Conversely, if
$\imath _S C=0$
and
$d_{h,\sigma } C=0$
, then by the above formula
$\mathcal L_S C +\imath \sigma C =0$
, hence
$C \in \mathcal B_{h, \sigma } ^r$
, thereby completing the argument.
By the de Rham theorem for twisted cohomology, it is possible to attach a twisted cohomology class to any
$d_{h,\sigma }$
-closed current.
For any real closed 1-form
$\eta $
on M, let
$H^1_\eta (M, \Sigma _h, {\mathbb C})$
denote the relative twisted cohomology introduced in Definition 3.2. For every abelian differential h on M and
$\sigma \in {\mathbb R}$
, let us adopt the notation
$$ \begin{align*}H^1_{h,\sigma} (M, \Sigma_h, {\mathbb C}) := H^1_{\sigma{ \operatorname{Re} } (h)} (M, \Sigma_h,{\mathbb C}). \end{align*} $$
Lemma 5.11 For every
$r\geq 0$
, the cohomology map
$ j_r : \mathcal B_{h, \sigma }^r \to H^1_{h, \sigma }(M, \Sigma _h, {\mathbb C})$
such that
$j_r(C)$
is the twisted cohomology class of the twisted basic current
$C \in \mathcal B_{h, \sigma }^r$
is a well-defined linear map.
Proof. A current
$C\in W^{-r}_h(M)$
does not in general extend to a linear functional on
$C^\infty (M)$
, hence is not a current on the compact surface M. However, since the space
$\Omega ^1_c(M\setminus \Sigma _h)$
of smooth 1-forms with compact support in
$M\setminus \Sigma _h$
is a subspace of the Sobolev space of 1-forms
$W^r_h(M)$
, for all
$r>0$
, it follows from the de Rham theorem for the twisted cohomology that the current
$C \in W^{-r}_h(M)$
such that
$d_{h, \sigma } C=0$
in
$W^{-(r+1)}_h(M)$
has a well-defined twisted cohomology class
$[C] \in H^1_{h, \sigma } (M, \Sigma _h, {\mathbb C})$
. In fact, C defines a linear functional on the twisted cohomology with compact support
$H^1_{h, \sigma ,c} (M\setminus \Sigma _h, {\mathbb C})$
, which is dual to the relative cohomology
$H^1_{h, \sigma } (M, \Sigma _h, {\mathbb C})$
by the intersection pairing on 1-forms given by integration.
The structure of the space of basic currents with vanishing cohomology class, with respect to the filtration induced by weighted Sobolev spaces with integer exponent, was described in [Reference ForniF02, §7] (see also [Reference ForniF07, §3.3], with respect to the filtration induced by weighted Sobolev spaces with general real exponent). We extend these results below to the space of twisted basic currents.
Let
$\delta _r: \mathcal B^{r-1}_{h,\sigma } \to \mathcal B^r_{h,\sigma }$
be the linear maps defined as follows (see [Reference ForniF02, formula (7.18′)] and [Reference ForniF07, formulas (3.61) and (3.62)] for the untwisted case):
$$ \begin{align} \delta_{r}(C) := (d_{h,\sigma} \circ \imath_T)( C )= -\,d_{h,\sigma} \bigg(\frac{C\wedge { \operatorname{Re} }(h)}{\omega_h} \bigg) \quad \text{for }C\in \,\mathcal B^r_{h, \sigma}. \end{align} $$
Indeed, it can be proved by Lemma 5.8 and by the definition of the weighted Sobolev spaces
$H^r_h(M)$
and
$W^r_h(M)$
that formula (50) defines, for all
$r>0$
, bounded linear maps
$\delta _{r}: \mathcal B^{r-1}_{h,\sigma } \to \mathcal B^r_{h,\sigma }$
.
Let
$\mathcal K^{r}_{h, \sigma } \subset \mathcal I^{r}_{h, \sigma } \subset H^{-r}_h(M)$
denote the subspace of distributions which are twisted S-invariant and T-invariant, that is,
$$ \begin{align*}\mathcal K^{r}_{h, \sigma}:= \{ D \in H^{-r}_h(M) \mid (S+\imath \sigma) D = TD =0 \}. \end{align*} $$
Let
$i_r: \mathcal K^{r}_{h, \sigma } \to \mathcal B^r_{h,\sigma }$
denote the restriction to
$\mathcal K^{r}_{h, \sigma }$
of the inverse of the map
$\mathcal D^h:\mathcal I^{r}_{h, \sigma }\to \mathcal B^r_{h,\sigma }$
(see Lemma 5.8), that is, the map defined as
$$ \begin{align*}i_r (D) := \imath_S D \quad \text{for all } D\in \mathcal K^{r}_{h, \sigma}. \end{align*} $$
Theorem 5.12 For all
$r>0$
there exist exact sequences
$$ \begin{align} 0\to \mathcal K^{r-1}_{h, \sigma} {{}^{\underrightarrow{\,\,\,\,i_{r-1}\,\,\,\,}} } {\mathcal B}_{h, \sigma}^{r-1} {{}^{\underrightarrow{\,\,\,\,\delta_{r}\,\,\,\,}} } {\mathcal B}_{h,\sigma}^r {{}^{\underrightarrow{\,\,\,\,j_{r}\,\,\,\,}}} H^1_{h, \sigma} (M, \Sigma_h,{{\mathbb C}}). \end{align} $$
Proof. The map
$i_{r-1}: \mathcal K^{r-1}_{h, \sigma } \to {\mathcal B}_{h, \sigma }^{r-1}$
is by definition injective, since the contraction operator is surjective onto the space of functions (
$0$
-forms).
The identity
$\text {Im}(i_{r-1})= \text {ker} (\delta _r)$
holds since by Lemma 5.8 a current
$C \in {\mathcal B}_{h, \sigma }^{r-1}$
if and only if
$C= \imath _S D$
with
$D\in {\mathcal I}_{h, \sigma }^{r-1}$
and in addition
$$ \begin{align*}\delta_r (\imath_S D)= d_{h,\sigma} (\imath_T \imath_S D)= \imath_T (S+ \imath \sigma)D - \imath_S (T D) = - \imath_S (T D), \end{align*} $$
hence
$ \delta _r (\imath _S D)=0$
if and only if
$TD=0$
(since
$TD$
has degree
$2$
and the contraction is surjective onto the space of functions (
$0$
-forms).
The identity
$\text {Im}(\delta _r)= \text {ker} (j_r)$
holds by the following argument. Let
$C' \in \mathcal B^r_{h,\sigma }$
be a current such that
$[C']=0 \in H^1_{h,\sigma }(M, \Sigma _h, {\mathbb C})$
, hence there exists a current U of degree
$0$
(and dimension
$2$
) such that
$C'= d_{h,\sigma } U$
. Let
$C= U \wedge { \operatorname {Im} }(h)$
. By definition we have
$C'= \delta _r (C)$
. We claim that
$C= U \wedge { \operatorname {Im} }(h) \in \mathcal B^{r-1}_{h,\sigma }$
. In fact, by definition
$\imath _S (U \wedge { \operatorname {Im} }(h))=0$
, and since
$\imath _S C'=0$
, we have
$$ \begin{align*}\begin{aligned} (\mathcal L_S + \imath \sigma) (U \wedge { \operatorname{Im} }(h)) &= (\mathcal L_S + \imath \sigma) (U) \wedge { \operatorname{Im} }(h) \\ &= \imath_S d_{h, \sigma} U \wedge { \operatorname{Im} }(h) = \imath_S C' \wedge { \operatorname{Im} }(h) =0. \end{aligned} \end{align*} $$
The argument is thus complete.
The above theorem and Lemma 5.8 imply the following finiteness result.
Corollary 5.13 For any abelian differential h on M, for all
$\sigma \in {\mathbb R}$
and for all
$s\geq 0$
, the spaces
$\mathcal I^s_{h, \sigma }$
of twisted invariant distributions for the operator
$S+ \imath \sigma $
and the corresponding space of
$\mathcal B^s_{h, \sigma }$
of twisted basic currents have finite dimension.
We conclude this subsection by proving a lower bound on the dimensions of the spaces of twisted invariant distributions.
Corollary 5.14 Let h be an abelian differential with minimal vertical foliation. For all
$\theta \in { \mathbb T}$
, let
$h_\theta := e^{-\imath \theta }h$
be the rotated abelian differential and let
$\sigma _\theta := \sigma \cos \theta $
. For any
$r>2$
and for almost all
$\theta \in { \mathbb T}$
, the subspace
$j_r (\mathcal B^r_{h_\theta , \sigma _\theta }) \cap H^1_{h_\theta ,\sigma _\theta }(M, {\mathbb C})$
has codimension at most equal to
$1$
in
$H^1_{h_\theta ,\sigma _\theta }(M, {\mathbb C})$
.
Proof. Let
$\alpha $
be any twisted closed 1-form, that is, a 1-form such that
$$ \begin{align*}d_{h_\theta, \sigma_\theta} \alpha:=d\alpha + \imath \sigma_\theta { \operatorname{Re} }(h_\theta)\wedge \alpha =0.\end{align*} $$
Let
$\alpha := f { \operatorname {Re} }(h_\theta ) + g { \operatorname {Im} }(h_\theta )$
and assume that
$f\in \bar H^{r-1}_h(M)$
with
$r>2$
and that f is orthogonal to constant functions. Then by Theorem 5.4 it follows that the cohomological equation
$$ \begin{align*}(S_\theta + \imath \sigma_\theta) u = f \end{align*} $$
has a distributional solution
$u\in \bar H^{-r}_h(M)$
for almost all
$\theta \in { \mathbb T}$
. Let C denote the current of degree
$1$
(and dimension
$1$
) uniquely determined by the formula
$$ \begin{align*}d_{h_\theta, \sigma_\theta} u:= (d + \imath \sigma_\theta { \operatorname{Re} } (h_\theta)) u= \alpha + C. \end{align*} $$
It is clear from the definition that C is closed with respect to the twisted differential
$d_{h_\theta , \sigma _\theta }$
, that is,
$d_{h_\theta , \sigma _\theta } C=0$
, and in addition
$\imath _{S_\theta } C=0$
, hence, by Lemma 5.10, the current C is a twisted basic current
$d_{h_\theta , \sigma _\theta }$
-cohomologous to the 1-form
$\alpha $
.
Finally, it can be proved that for all
$\sigma \in {\mathbb R}$
all cohomology classes in
$H^1_{h,\sigma }(M, {\mathbb C})$
can be represented by
$d_{h, \sigma }$
-closed 1-forms
$\alpha \in W^r_h(M)$
with
$r>1$
.
5.3 Smooth solutions
In this section we prove our main result on the existence of smooth solutions of the twisted cohomological equation for translation flows, which holds for any abelian differential in almost all directions, and derive as a corollary our result on cohomological equations for product translation flows.
Lemma 5.15 Let h be an abelian differential with minimal vertical foliation. For every
$s>r \geq 0$
such that
$s-r>3$
there exists
$p\in (0,1)$
such that for every
$\sigma \in {\mathbb R}$
there exists a function
$A_{h, \sigma }:= A_{h,\sigma } (p,r,s)\in L^p({ \mathbb T}, {\mathcal L})$
such that the following statement holds. For almost all
$\theta \in { \mathbb T}$
and for all zero-average functions
$v\in H^{s+1}_h(M)$
, we have
$$ \begin{align} \vert v \vert_r \leq A_{h,\sigma} (\theta) \, \vert (S_\theta + \imath \sigma_\theta) v \vert_{s}, \end{align} $$
and there exists a constant
$B_h:= B_h (p,r,s)>0$
such that, for all
$\sigma \in {\mathbb R}$
, we have
$$ \begin{align*}\vert A_{h,\sigma} \vert_p \leq B_h. \end{align*} $$
Proof. Let
$\{\unicode{x3bb} _k \mid k\in { \mathbb N}\}$
denote the sequence of eigenvalues of the Friedrichs extension
$-\Delta ^F_h$
of the non-negative flat Laplacian, relative to the orthonormal Fourier basis
$\mathcal E=\{e_k \mid k\in { \mathbb N}\}$
of eigenfunctions of the Hilbert space
$L^2_h(M)$
, described in §2. We recall that the Friedrichs weighted Sobolev norms are given, for all
$s>0$
, as follows (see Definition 2.5):
Let
$\alpha>2$
and let
$p\in (0,1)$
be such that
$\alpha p>2$
. By Lemma 5.3, for all
$k\in { \mathbb N}\setminus \{0\}$
there exists a function
$A^{(k)}_{h,\sigma }:= A^{(k)}_{h,\sigma }(p,\alpha ) \in L^p({ \mathbb T}, {\mathcal L})$
such that, for all
$v\in H^{\alpha +1}_h(M)$
of zero average, we have
$$ \begin{align*}\vert {\langle}v,e_k{\rangle}\vert \leq A^{(k)}_{h,\sigma}(\theta) \Vert (S_\theta + \imath \sigma_\theta)v \Vert_\alpha. \end{align*} $$
In addition, there exists a constant
$B_h:= B_h(p,\alpha )$
such that
Let
$\beta>1$
such that
$(\beta +1)p>2$
. It follows that, for any
$v \in H^{\alpha +1}_h(M)$
of zero average, we have
Let then
$A_{h,\sigma }:= A_{h, \sigma }(p,\alpha , \beta )$
denote the function defined, for
$\theta \in { \mathbb T}$
, as follows:
By the triangular inequality for the space
$L^{p/2}$
(with
$p/2<1$
) we have
By the Weyl asymptotics, the series on the right-hand side of the above formula is convergent as soon as
$(\beta +1)p> 2$
. Let then
$v\in H^{\alpha +3}_h(M)$
so that
$\Delta _h v \in H^\alpha _h(M)$
and we have
$$ \begin{align*}\begin{aligned} \Vert v \Vert_{-\beta+2} &= \Vert (I-\Delta^F_h) v \Vert_{-\beta} \leq A_{h,\sigma}(\theta) \Vert (S_\theta + \imath \sigma_\theta) (I-\Delta^F_h) v \Vert_\alpha \\ & = A_{h,\sigma}(\theta) \Vert (I-\Delta_h) (S_\theta + \imath \sigma_\theta) v \Vert_\alpha=A_{h,\sigma}(\theta) \Vert (S_\theta + \imath \sigma_\theta) v \Vert_{\alpha+2}. \end{aligned} \end{align*} $$
By the interpolation inequality for the Friedrichs norms and by Lemma 2.8, for every
$ \rho \in [0, 1)$
, whenever
$\alpha p>2$
,
$(\beta +1)p>2$
and
$\rho + \beta \leq 2$
, we have
$$ \begin{align*}\vert v \vert_{\rho} = \Vert v \Vert_\rho\leq A_{h, \sigma}(\theta) \Vert (S_\theta + \imath \sigma_\theta) v \Vert_{\alpha+\beta+\rho} \leq A_{h, \sigma}(\theta) \vert (S_\theta + \imath \sigma_\theta) v \vert_{\alpha+\beta+\rho}. \end{align*} $$
Finally, for all
$r\geq 0$
, by applying the above bound to all functions
$S^i T^j v$
and
$T^iS^j$
, for all
$i,j \leq [r]$
, we finally have that there exists a constant
$C_r>0$
such that
$$ \begin{align} \vert v \vert_r \leq C_r A_{h, \sigma} (\theta) \vert (S_\theta + \imath \sigma_\theta) v \vert_{\alpha +\beta +r}. \end{align} $$
Since, given
$s>r\geq 0$
with
$s-r>3$
, it is always possible to find
$\alpha>2$
,
$\beta>1$
and
$p\in (0, 1)$
such that
$$ \begin{align*}s= \alpha+ \beta, \quad \alpha p>2, \quad (\beta+1)p >1 \quad \text{and} \quad \{r\} + \beta \leq 2, \end{align*} $$
the bound in formula (52) follows immediately from that in the above formula (53), hence the argument is complete.
Theorem 5.16 Let h be an abelian differential with minimal vertical foliation. For any
$s>r\geq 0$
such that
$s-r>3$
, there exist
$p\in (0, 1)$
and a constant
$C_{r,s}>0$
such that the following statement holds. For any
$\sigma \in {\mathbb R}$
and for almost all
$\theta \in { \mathbb T}$
, for any
$f\in H^{s}_h(M)$
of zero average such that
$\mathcal D(f)=0$
for all twisted invariant distributions
$\mathcal D \in \mathcal I^s_{h_\theta , \sigma _\theta }$
, the cohomological equation
$(S_{\theta } +\imath \sigma _\theta ) u=f$
has a zero-average solution
$\mathcal U_\theta (f) \in H^{r}_h(M)$
satisfying the following estimate:
$$ \begin{align} \left(\int_{ \mathbb T} \vert \mathcal U_\theta (f) \vert_{r}^p \, d\theta \right)^{1/p} \leq C_{r,s} \, \vert f \vert_{s}. \end{align} $$
Proof. It follows from the a priori bound of Lemma 5.15 that, for all
$\sigma \in {\mathbb R}$
and for almost all
$\theta \in { \mathbb T}$
, the subspace
$$ \begin{align*}\{ f\in \mathcal H^s_h(M) \mid f \in (S_\theta + \imath \sigma_\theta) [ {\mathcal H}^r_h(M)] \} \end{align*} $$
is closed in
$\mathcal H^s_h(M)$
, hence it coincides with the kernel of the subspace
$\mathcal I^{-s}_{h_\theta , \sigma _\theta } \cap \mathcal H^{-s}(M)$
of all twisted invariant distributions vanishing on constant functions. In addition, it follows by continuity that there exist
$p\in (0, 1)$
and a function
$A_{h,\sigma } \in L^p({ \mathbb T},{\mathcal L})$
such that, for all
$f\in \mathcal H^s_h(M) \cap \text {Ker} ( \mathcal I^{-s}_{h_\theta , \sigma _\theta } )$
, the unique zero-average solution
$\mathcal U_\theta (f) \in H^r_h(M)$
of the cohomological equation
$(S_\theta + \imath \sigma _\theta ) u =f$
satisfies the bound
$$ \begin{align*}\vert \mathcal U_\theta(f) \vert_r \leq A_{h, \sigma} (\theta) \vert f \vert_s. \end{align*} $$
From the above inequality and the bounds on the
$L^p$
norm of the function
$A_{h, \sigma }$
established in Lemma 5.15, it follows immediately that
$$ \begin{align*}\left( \int_{ \mathbb T} \vert \mathcal U_\theta(f) \vert_r^p\, d\theta \right)^{1/p} \leq \vert A_{h, \sigma}\vert_p \, \vert f \vert_s \leq B_h\, \vert f \vert_s. \end{align*} $$
The proof of the theorem is therefore complete.
Proof Proof of Theorem 1.1
The condition that h has a minimal vertical foliation it is not restrictive since the statement is rotation-invariant, and any abelian differential has a minimal direction [Reference MaierMa, Reference Aranson and GrinesAG].
The finiteness of the dimension of the space
$\mathcal I^{s}_{h, \sigma } \subset H^{-s}_h(M)$
of
$(S +\imath \sigma )$
-invariant distributions has been proved in Corollary 5.13 (for all
$\sigma \in {\mathbb R}$
and all
$\theta \in { \mathbb T}$
). A linear upper bound on the dimension of the space
$\mathcal I^{s}_{h, \sigma }$
follows from Theorem 5.12, and a linear lower bound on the dimension of the space
$\mathcal I^{s}_{h_\theta , \sigma _\theta }$
, for all
$\sigma \in {\mathbb R}$
and for almost all
$\theta \in { \mathbb T}$
, follows from Theorem 5.12 and Corollary 5.14.
If the function
$f \in H^s_h(M)$
is constant, then for
$\sigma \not =0$
the constant function
$u=-\imath f/\sigma $
is a solution (which is unique in
$L^2_h(M)$
) for almost all
$\theta \in { \mathbb T}$
. For
$\sigma =0$
, there is no solution unless
$f=0$
, in which case the solution is the zero constant. The argument is therefore reduced to the case of functions of zero average.
By Theorem 5.16, for any abelian differential h with minimal vertical foliation, the twisted cohomological equation
$(S_\theta + \imath \sigma \cos \theta ) u=f$
can be solved with Sobolev bounds for all
$f \in H^s_h(M)$
of zero average in the kernel of all twisted invariant distributions, for all
$\sigma \in {\mathbb R}$
and for almost all
$\theta \in { \mathbb T}$
. Let then
$\mathcal F \subset { \mathbb T}\times {\mathbb R}$
be the set of
$(\theta , \sigma ) \in { \mathbb T} \times {\mathbb R}$
such that the twisted cohomological equation
$(S_\theta + \imath \sigma ) u=f$
can be solved with Sobolev bounds for all
$f \in H^s_h(M)$
of zero average in the kernel of all twisted invariant distributions. Since the map
$(\theta , \sigma ) \to (\theta , \sigma \cos \theta )$
from
${ \mathbb T} \times {\mathbb R}$
into itself is absolutely continuous, it follows from Theorem 5.16 that the set
$\mathcal F$
has full Lebesgue measure. Finally, the statement of the theorem follows by Fubini’s theorem.
For all
$s, \nu \in { \mathbb N}$
, let
$H^{s, \nu }_h (M\times { \mathbb T})$
denote the
$L^2$
Sobolev space on
$M\times { \mathbb T}$
with respect to the invariant volume form
$\omega _h \wedge d\phi $
and the vector fields S, T, and
$\partial /\partial \phi $
:
$$ \begin{align*}H^{s,\nu} _h(M\times{ \mathbb T}):= \bigg\{ f \in L^2(M\times { \mathbb T}, d \text{vol})\ \Big| \ \sum_{i+j\leq s}\sum_{\ell \leq \nu} \bigg\Vert S^i T^j \frac{\partial^\ell f}{\partial \phi^\ell} \bigg\Vert_0 < +\infty\bigg\}; \end{align*} $$
the space
$H^{s,\nu }_h (M\times { \mathbb T})$
can be defined for all
$(s, \nu )\in {\mathbb R}^+ \times {\mathbb R}^+$
by interpolation [Reference Lions and MagenesLM] and the space
$H^{-s, -\nu }_h(M\times { \mathbb T})$
is defined as the dual of the space
$H^{s,\nu }_h(M\times { \mathbb T})$
.
Now let
$V_{\theta , c}= S_\theta + c\cos \theta ({\partial }/{\partial \phi })$
denote a translation vector field on
$M \times { \mathbb T}$
, and let
$\mathcal I^{s,\nu }_{h_\theta , c}$
denote the space of
$V_{\theta , c}$
invariant distributions.
The space
$L^2(M\times { \mathbb T}, d \text {vol})$
of the product manifold with respect to the invariant volume form
$\omega _h \wedge d\phi $
decomposes as a direct sum of the eigenspaces
$\{H^0_n \vert n\in { \mathbb Z}\}$
of the circle action:
$$ \begin{align*}L^2(M\times { \mathbb T}, d \text{vol}) = \bigoplus_{n\in { \mathbb Z}} H^0_n. \end{align*} $$
Corollary 5.17 Let h be an abelian differential with minimal vertical foliation. Let
$s>r \geq 0$
be such that
$s-r>3$
and let
$\nu>2$
and
$\mu <\nu -2$
. For all
$c\in {\mathbb R}$
and for almost all
$\theta \in { \mathbb T}$
there exists a constant
$C^{(\mu ,\nu )}_{r,s} (\theta ,c)>0$
such that the following statement holds. For any
$f \in H^{s,\nu }_h(M\times { \mathbb T})$
such that
$D(f) =0$
for all
$V_{\theta ,c}$
-invariant distributions
$D \in \mathcal I^{s,\nu }_{h_\theta ,c} \subset H^{-s,-\nu }_h(M\times { \mathbb T})$
, the cohomological equation
$V_{\theta ,c} u=f$
has a solution
$u:=\mathcal U_\theta (f) \in H^{r, \mu }_h(M)$
satisfying the following estimate:
$$ \begin{align} \vert \mathcal U_\theta (f) \vert_{r,\mu}\leq C^{(\mu,\nu)}_{r,s}(\theta,c)\, \vert f \vert_{s,\nu}. \end{align} $$
Proof. By the Fourier decomposition with respect to the circle action, the argument is reduced to proving the existence of solutions for the cohomological equations
$$ \begin{align} (S_\theta + 2\pi \imath c n \cos\theta ) u_n =f_n. \end{align} $$
For
$n=0$
the above equation reduces to the cohomological equation for the translation flow on M, so that the result already follows from [Reference ForniF07]. For every
$n\in { \mathbb N}\setminus \{0\}$
, let
$\sigma ^{c,n}:= 2\pi c n\in {\mathbb R}$
. The (finite-dimensional) space
$\mathcal I^s_{h_\theta , \sigma ^{c,n}_{\theta }} \subset H^{-s}_h(M)$
of twisted
$(S_\theta + \imath \sigma ^{c,n}_\theta )$
-invariant distributions embeds as a subspace of the space
$\mathcal I^{s, \nu }_{h_\theta ,c} \subset H^{-s, -\nu }_h(M\times { \mathbb T})$
of
$V_{\theta ,c}$
-invariant distributions, for all
$\nu \in { \mathbb N}$
, by the formula
$$ \begin{align*}D \bigg ( \sum_{n\in { \mathbb Z}} f_n e^{2\pi \imath \phi} \bigg) = D(f_n). \end{align*} $$
By Theorem 5.16 there exist constants
$C_{r,s}>0$
and
$p\in (0,1)$
and, for every
$\epsilon>0$
, there exists a full measure set
$\mathcal F_{c,n}(\epsilon ) \subset { \mathbb T}$
of measure at least
$1 -\epsilon /n^2$
, such that for all
$\theta \in \mathcal F_{c,n}(\epsilon )$
, for every
$f_n \in \mathcal I^s _{h_\theta , \sigma ^{c,n}_\theta }$
there exists a solution
$u_n\in H^r_h(M) \cap H^0_n$
of the cohomological equation (56) which satisfies the Sobolev estimate
$$ \begin{align*}\vert u_n \vert _r \leq C_{r,s} \epsilon ^{-1/p} n^{2/p} \vert f_n \vert_s. \end{align*} $$
In fact, the above claim follows immediately from Theorem 5.16.
From the claim it follows that for all functions
$f \in H^{s,\nu }_h(M\times { \mathbb T})$
with
$\nu>2/p$
, such that
$f_n \in \mathcal I^{s,\nu } _{h_\theta , \sigma ^{c,n}_\theta }$
for all
$n\not =0$
, for all
$\theta \in \mathcal F_{c}(\epsilon ):= \bigcap _{n\not =0} \mathcal F_{c,n}(\epsilon )$
the function
$u = \sum _{n\not =0} u_n \in H^{r, \nu - 2/p }(M)$
is a solution of the cohomological equation
$V_{\theta , c} u =f$
. Since, for any
$\epsilon>0$
, the set
$\mathcal F_{c}(\epsilon )$
has Lebesgue measure at least
$1- C \epsilon $
with
$C=\sum _{n\not =0} 1/n^2$
, the argument is complete.
Proof Proof of Theorem 1.4
The space
$\mathcal I^{s,\nu }_{h_\theta ,c}$
of
$V_{\theta , c}$
-invariant distributions is generated by the union of subspaces
$\mathcal I^s _{h_\theta , \sigma ^{c,n}_\theta }$
over all
$n\in { \mathbb Z}$
. The statement of the theorem then follows from Corollary 5.17 by Fubini’s theorem.
Proof Proof of Corollary 1.5
For any
$\phi _0\in { \mathbb T}$
, let
$M_{\phi _0} = M \times \{\phi _0\} \subset M\times { \mathbb T}$
. The return map of the flow of the vector field
$X_{\theta ,c}$
to the transverse surface
$M_{\phi _0}\equiv M$
is smoothly conjugate to the time-
$1/c$
map
$\Phi _{\theta ,c}^{1/c}$
of the translation flow generated by the horizontal vector field
$S_\theta $
on M. Since the return time function is constant (equal to
$1$
), it is possible to derive results on the cohomological equation for the return (Poincaré) map (the time-
$1/c$
map) from results on the cohomological equation for the flow. In fact, the procedure is as follows. Let
$\Phi _{\theta , c}^{\mathbb R}$
denote the flow of the vector field
$X_{\theta , c}$
on
$M\times { \mathbb T}$
. Let
$ \chi \in C^\infty ({ \mathbb T})$
be a smooth function with integral equal to
$1$
supported on a closed interval
$I \subset { \mathbb T}\setminus \{\phi _0\}$
. Let
$F(f)\in H^{s, \infty }_h(M\times { \mathbb T})$
be the function defined as follows:
$$ \begin{align*}F(f) \circ \Phi_{\theta, c}^t (x, \phi_0) = \begin{cases} f(x) \chi (t) \quad &\text{for } t \in I, \\ 0 \quad &\text{for } t \not \in I. \end{cases} \end{align*} $$
Let
$f\in H^s_h(M)$
and let us assume that the cohomological equation
$ X_{\theta , c} U = F(f)$
has a solution
$U\in H^{r, \mu }_h(M\times { \mathbb T})$
. Then the restriction
$u = U\vert M_{\phi _0}$
is a solution of the cohomological equation
$u \circ \Phi ^{1/c}_{\theta ,c} -u =f$
for the time-
$1/c$
map. In fact, for all
$x\in M$
, we have
$$ \begin{align*}u \circ \Phi^{1/c}_{\theta,c} -u = \int_0^{1/c} X_{\theta, c} U \circ \Phi_{\theta, c}^t\, dt = \int_0^{1/c} f \chi (\phi_0 + c t)\, dt = f(x) \end{align*} $$
By the Sobolev trace theorem, for any
$\mu> 1/2$
, the restriction
$U\vert M_{\phi _0}$
of a function
$U\in H^{r, \mu }_h (M\times { \mathbb T})$
is a function
$u\in H^r_h(M)$
, and there exists
$C_\mu>0$
such that
$$ \begin{align*}\vert u \vert_r \leq C_\mu \Vert U \Vert_{ H^{r,\mu}_h(M\times { \mathbb T})}. \end{align*} $$
The result then follows from Theorem 1.4. In fact, for every
$X_{\theta ,c}$
-invariant distribution
$D \in \mathcal I^{s, \nu }_{h_\theta ,c} \subset H^{-s,-\nu }_h(M\times { \mathbb T})$
, we define the distribution
$D_M \in H^{-s}_h(M)$
as
$$ \begin{align*}D_M(f) := D (F(f) ). \end{align*} $$
By Theorem 1.4 it follows that, for
$D_M(f)=0$
for all
$D \in \mathcal I^{s, \nu }_{h_\theta ,c}$
, there exists a solution
$U\in H^{r, \mu }_h(M\times { \mathbb T})$
of the cohomological equation
$X_{\theta ,c} U=F(f)$
, hence a solution
$u=U\vert M \in H^r_h(M)$
of the equation
$u\circ \Phi ^{1/c} _\theta -u = f$
. Finally, for all
$u\in H^{\infty }_h(M)$
such that
$u\circ \Phi ^{1/c} _\theta -u \in H^s_h(M)$
, we have
$$ \begin{align*}D_M (u\circ \Phi^{1/c} _{\theta,c} -u )= D (F(u\circ \Phi^{1/c} _{\theta,c} -u)) =D( F(u) \circ \Phi_{\theta, c}^{1/c} - F(u) ) =0, \end{align*} $$
since
$D \in \mathcal I^{s, \nu }_{h_\theta ,c}$
is by assumption
$X_{\theta , c}$
-invariant.
Acknowledgements
We wish to thank Pascal Hubert and Carlos Matheus for their interest in this work and their encouragement. This research was supported by the NSF grant DMS 1600687 and by a Research Chair of the Fondation Sciences Mathématiques de Paris. The author is grateful to the Institut de Mathématiques de Jussieu for its hospitality.
