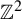1 Introduction
Starting with the seminal work of Katok and Spatzier on Anosov actions [Reference Katok and Spatzier11], smooth local classification of abelian actions with hyperbolic features has deserved a lot of attention. Hyperbolicity implies existence of invariant geometric structures whose properties were exploited in obtaining very strong local classification results [Reference Damjanović and Katok6, Reference Vinhage and Wang17]. The main goal of local classification is completely understanding the dynamics of smooth actions, which are small perturbations of the given action.
For actions with no hyperbolicity, such as parabolic and elliptic actions, there are no convenient invariant geometric structures and the methods from the hyperbolic theory are not applicable [Reference Damjanović and Katok5]. Also, for parabolic and elliptic actions the local classification results are weaker than for hyperbolic actions and the methods used are more analytical. For elliptic abelian actions the main feature allowing local classification has been the Diophantine property [Reference Moser12, Reference Petkovic13] for torus translations, while the main strategy for proving local classification results has been the method of successive iterations labeled in the 1960s by the KAM method after Kolmogorov, Arnold and Moser, who devised it for the purpose of showing persistence of Diophantine tori in Hamiltonian dynamics. The method has been more recently adapted to certain kinds of parabolic continuous-time actions in [Reference Damjanović and Katok7] and later used in [Reference Damjanović3, Reference Wang18]. This adapted method is described for general Lie group actions in [Reference Damjanović2].
In this paper we apply this adapted KAM method of successive iterations to a class of discrete-time abelian actions that are parabolic, meaning that the derivative of the action has polynomial growth. We describe a class of discrete abelian actions on a
![]() $(2n+1)$
-dimensional Heisenberg nilmanifold, which on the induced torus have certain Diophantine properties. For the purpose of this introduction we call these actions ‘Diophantine’. We show that these Diophantine actions belong to a finite-dimensional
$(2n+1)$
-dimensional Heisenberg nilmanifold, which on the induced torus have certain Diophantine properties. For the purpose of this introduction we call these actions ‘Diophantine’. We show that these Diophantine actions belong to a finite-dimensional
![]() $(4g-1)$
-dimensional family of algebraic actions for which we prove a local classification result. Namely we show that a small perturbation of the family around the Diophantine member contains a smooth conjugate of that Diophantine action. This implies that every perturbed family contains an element which is dynamically the same as the Diophantine action. This phenomenon has been previously labeled transversal local rigidity and has been studied for classes of continuous-time actions [Reference Damjanović3, Reference Damjanović and Katok7]. For discrete abelian actions, we are not aware of any results in the literature where transversal local rigidity is proved and where it does not follow from a stronger local (or global) rigidity result for actions of
$(4g-1)$
-dimensional family of algebraic actions for which we prove a local classification result. Namely we show that a small perturbation of the family around the Diophantine member contains a smooth conjugate of that Diophantine action. This implies that every perturbed family contains an element which is dynamically the same as the Diophantine action. This phenomenon has been previously labeled transversal local rigidity and has been studied for classes of continuous-time actions [Reference Damjanović3, Reference Damjanović and Katok7]. For discrete abelian actions, we are not aware of any results in the literature where transversal local rigidity is proved and where it does not follow from a stronger local (or global) rigidity result for actions of
![]() $\mathbb Z$
or
$\mathbb Z$
or
![]() $\mathbb R$
.
$\mathbb R$
.
The analytic method of obtaining local classification results interprets the local conjugation problem as a nonlinear operator, which after linearization describes the cohomology over the unperturbed actions. The linearized version of the local classification problem is precisely the first cohomology group with coefficients in smooth vector fields. If the first cohomology is finite dimensional and both first and second coboundary operators have inverses with sufficiently nice tame norm estimates, then one can reasonably hope to employ the KAM iterative method. Tameness means that the
![]() $C^r$
norm of the solution can be bounded by the
$C^r$
norm of the solution can be bounded by the
![]() $C^{r+\sigma }$
norm of the given data, where r is arbitrarily large while
$C^{r+\sigma }$
norm of the given data, where r is arbitrarily large while
![]() $\sigma $
is a constant. In short, the analytic method has two major ingredients: a detailed analysis of the first cohomology and coboundary operators, and an application of the KAM iteration. Such detailed analysis of cohomology is usually hard to perform, and usually needs to use the full machinery of the representation theory, which is why results are often restricted to actions on manifolds of smaller dimension and simpler structure of representation spaces. This is the main reason that there is a lack of local rigidity results for parabolic actions on higher step nilmanifolds.
$\sigma $
is a constant. In short, the analytic method has two major ingredients: a detailed analysis of the first cohomology and coboundary operators, and an application of the KAM iteration. Such detailed analysis of cohomology is usually hard to perform, and usually needs to use the full machinery of the representation theory, which is why results are often restricted to actions on manifolds of smaller dimension and simpler structure of representation spaces. This is the main reason that there is a lack of local rigidity results for parabolic actions on higher step nilmanifolds.
We remark that even when careful analysis of first cohomology is possible, the inverses of coboundary operators may lack tameness, in which case the KAM method may not work. Namely, in [Reference Damjanović and Tanis8], we carried out analysis of the first cohomology for the discrete parabolic homogeneous action on
![]() $SL(2, \mathbb R)\times SL(2, \mathbb R)/\Gamma $
. However, the inverse of the second coboundary operator turned out not to be tame; in fact, Tanis and Wang [Reference Tanis and Wang14] proved that there can be no tame inverse (see also [Reference Tanis and Wang15, Theorem 2.2]). No local classification results have been obtained for this example.
$SL(2, \mathbb R)\times SL(2, \mathbb R)/\Gamma $
. However, the inverse of the second coboundary operator turned out not to be tame; in fact, Tanis and Wang [Reference Tanis and Wang14] proved that there can be no tame inverse (see also [Reference Tanis and Wang15, Theorem 2.2]). No local classification results have been obtained for this example.
In this paper we perform detailed analysis of cohomology for a class of discrete-time actions with Diophantine properties on
![]() $(2n+1)$
-dimensional Heisenberg nilmanifolds. It turns out that their cohomology is finite dimensional and we can obtain tame estimates for solutions of coboundary operators. Once we get complete cohomological information, we use the KAM method to prove transversal local rigidity. This is similar to the proof of the main results in [Reference Damjanović2, Reference Damjanović and Katok7], except that in the case of discrete actions we have somewhat more complicated (linear and nonlinear) operators to work with. As far as we know this is the first example of a discrete parabolic (but not elliptic) abelian action for which some kind of local rigidity property holds.
$(2n+1)$
-dimensional Heisenberg nilmanifolds. It turns out that their cohomology is finite dimensional and we can obtain tame estimates for solutions of coboundary operators. Once we get complete cohomological information, we use the KAM method to prove transversal local rigidity. This is similar to the proof of the main results in [Reference Damjanović2, Reference Damjanović and Katok7], except that in the case of discrete actions we have somewhat more complicated (linear and nonlinear) operators to work with. As far as we know this is the first example of a discrete parabolic (but not elliptic) abelian action for which some kind of local rigidity property holds.
The analysis of first cohomology for the corresponding continuous-time group actions on Heisenberg nilmanifolds has been carried out in [Reference Cosentino and Flaminio1]. In the continuation of the work presented in this paper, we intend to address local classification of the
![]() $\mathbb R^k$
actions described in [Reference Cosentino and Flaminio1] as well as their discrete subactions.
$\mathbb R^k$
actions described in [Reference Cosentino and Flaminio1] as well as their discrete subactions.
1.1 Setting
Let
![]() $n\ge 2$
be an integer. The Heisenberg group over
$n\ge 2$
be an integer. The Heisenberg group over
![]() ${ \mathbb R}^n$
is the set
${ \mathbb R}^n$
is the set
![]() $\mathsf H := \mathsf H(n) = { \mathbb R}^n \times { \mathbb R}^n \times { \mathbb R}$
, and it is equipped with the group multiplication
$\mathsf H := \mathsf H(n) = { \mathbb R}^n \times { \mathbb R}^n \times { \mathbb R}$
, and it is equipped with the group multiplication
The Lie algebra of
![]() $\mathsf H$
is the vector space
$\mathsf H$
is the vector space
![]() ${ \mathbb R}^n \times { \mathbb R}^n \times { \mathbb R}$
, which is generated by the vector fields
${ \mathbb R}^n \times { \mathbb R}^n \times { \mathbb R}$
, which is generated by the vector fields
that satisfy the commutation relations
The set
![]() $\Gamma := { \mathbb Z}^{n} \times { \mathbb Z}^{n} \times \tfrac {1}{2} { \mathbb Z} \subset \mathsf H$
is the standard lattice of
$\Gamma := { \mathbb Z}^{n} \times { \mathbb Z}^{n} \times \tfrac {1}{2} { \mathbb Z} \subset \mathsf H$
is the standard lattice of
![]() $\mathsf H$
. The lattice is cocompact and the compact quotient manifold
$\mathsf H$
. The lattice is cocompact and the compact quotient manifold
![]() $M := \Gamma \backslash \mathsf H$
is called the standard Heisenberg nilmanifold.
$M := \Gamma \backslash \mathsf H$
is called the standard Heisenberg nilmanifold.
Even though our proofs are written for the case of the standard lattice
![]() $\Gamma $
, this not a restriction; the results in fact automatically hold for general lattices of
$\Gamma $
, this not a restriction; the results in fact automatically hold for general lattices of
![]() ${\mathsf H}$
due to the complete description of all lattices in
${\mathsf H}$
due to the complete description of all lattices in
![]() $\mathsf H$
and the corresponding representation of
$\mathsf H$
and the corresponding representation of
![]() $\Gamma \backslash {\mathsf H}$
by Tolimieri in [Reference Tolimieri16].
$\Gamma \backslash {\mathsf H}$
by Tolimieri in [Reference Tolimieri16].
Let
![]() $L^2(M)$
be the space of complex-valued square-integrable functions on M. As in [Reference Cosentino and Flaminio1], we define the Laplacian on
$L^2(M)$
be the space of complex-valued square-integrable functions on M. As in [Reference Cosentino and Flaminio1], we define the Laplacian on
![]() $L^2(M)$
by
$L^2(M)$
by
 $$ \begin{align} \triangle := - Z^2 - \sum_{i = 1}^n X_i^2 + \Lambda_i^2. \end{align} $$
$$ \begin{align} \triangle := - Z^2 - \sum_{i = 1}^n X_i^2 + \Lambda_i^2. \end{align} $$
Then
![]() $\triangle $
is an essentially self-adjoint, non-negative operator, and
$\triangle $
is an essentially self-adjoint, non-negative operator, and
![]() $(I + \triangle )^s$
is defined by the spectral theorem for all
$(I + \triangle )^s$
is defined by the spectral theorem for all
![]() $s> 0$
. The space
$s> 0$
. The space
![]() $W^s(M)$
is the Sobolev space of s-differentiable functions defined to be the maximal domain of
$W^s(M)$
is the Sobolev space of s-differentiable functions defined to be the maximal domain of
![]() $(I + \triangle )^s$
, and it is equipped with the inner product
$(I + \triangle )^s$
, and it is equipped with the inner product
The norm of a function
![]() $f \in W^s(M)$
is denoted
$f \in W^s(M)$
is denoted
![]() $\Vert f \Vert _s$
. Because M is compact, we have
$\Vert f \Vert _s$
. Because M is compact, we have
For
![]() $\mathbf {m} \in { \mathbb Z}^{2n}$
, let
$\mathbf {m} \in { \mathbb Z}^{2n}$
, let
Then let
be Diophantine over
![]() ${ \mathbb Z}^{n}$
in
${ \mathbb Z}^{n}$
in
![]() ${ \mathbb R}^n$
and satisfy
${ \mathbb R}^n$
and satisfy
 $$ \begin{align} \sum_{j = 1}^n \tau_j \eta_j = 0. \end{align} $$
$$ \begin{align} \sum_{j = 1}^n \tau_j \eta_j = 0. \end{align} $$
By Diophantine, we mean that there are constants
![]() $c := c_{\boldsymbol {\tau }, \boldsymbol {\eta }}> 0$
and
$c := c_{\boldsymbol {\tau }, \boldsymbol {\eta }}> 0$
and
![]() $\gamma := \gamma _{\boldsymbol {\tau }, \boldsymbol {\eta }}> 0$
such that for any
$\gamma := \gamma _{\boldsymbol {\tau }, \boldsymbol {\eta }}> 0$
such that for any
![]() $\mathbf {m} \in { \mathbb Z}^{2n}$
and
$\mathbf {m} \in { \mathbb Z}^{2n}$
and
![]() $p \in { \mathbb Z}$
, we have
$p \in { \mathbb Z}$
, we have
The above condition is saying that the vectors of the form
![]() $\boldsymbol {\tau } $
and
$\boldsymbol {\tau } $
and
![]() $\boldsymbol {\eta }$
are simultaneously Diophantine, which is the natural condition that has appeared in previous works on classification of perturbations of actions by translations on the torus (for example in [Reference Wilkinson and Xue19] or [Reference Petkovic13]).
$\boldsymbol {\eta }$
are simultaneously Diophantine, which is the natural condition that has appeared in previous works on classification of perturbations of actions by translations on the torus (for example in [Reference Wilkinson and Xue19] or [Reference Petkovic13]).
Next let
 $$ \begin{align*} Y_{\boldsymbol{\tau}} := \sum_{i = 1}^n \tau_i X_{i} , \quad Y_{\boldsymbol{\eta}} := \sum_{i = 1}^n \eta_i \Lambda_i \end{align*} $$
$$ \begin{align*} Y_{\boldsymbol{\tau}} := \sum_{i = 1}^n \tau_i X_{i} , \quad Y_{\boldsymbol{\eta}} := \sum_{i = 1}^n \eta_i \Lambda_i \end{align*} $$
and notice that these vector fields commute because
is equivalent to (4).
We consider the
![]() ${ \mathbb Z}^2$
right action on M given by
${ \mathbb Z}^2$
right action on M given by
The action
![]() $\rho $
induces a
$\rho $
induces a
![]() ${ \mathbb Z}^2$
action on
${ \mathbb Z}^2$
action on
![]() $L^2(M)$
(which we also denote by
$L^2(M)$
(which we also denote by
![]() $\rho $
), defined by
$\rho $
), defined by
1.2 Results on cohomological rigidity
Let
![]() $\rho :{ \mathbb Z}^k\rightarrow \textrm{ Diff}^{\infty }{(M)}$
be a smooth
$\rho :{ \mathbb Z}^k\rightarrow \textrm{ Diff}^{\infty }{(M)}$
be a smooth
![]() ${ \mathbb Z}^k$
action on a compact manifold M. Let V be a
${ \mathbb Z}^k$
action on a compact manifold M. Let V be a
![]() $\rho $
-module, by which we mean that there is a
$\rho $
-module, by which we mean that there is a
![]() ${ \mathbb Z}^k$
action on V, which we label by
${ \mathbb Z}^k$
action on V, which we label by
![]() $\rho _*$
. Let
$\rho _*$
. Let
![]() $C^l({ \mathbb Z}^k,V)$
denote the space of multilinear maps from
$C^l({ \mathbb Z}^k,V)$
denote the space of multilinear maps from
![]() ${ \mathbb Z}^k\times \cdots \times { \mathbb Z}^k$
to V.
${ \mathbb Z}^k\times \cdots \times { \mathbb Z}^k$
to V.
Then we have the cohomology sequence
where the operators
![]() ${\mathbf {d}}_1$
and
${\mathbf {d}}_1$
and
![]() ${\mathbf {d}}_2$
are defined as follows. For
${\mathbf {d}}_2$
are defined as follows. For
![]() $H \in C({ \mathbb Z}^k,V)=V$
and
$H \in C({ \mathbb Z}^k,V)=V$
and
![]() $\beta \in C^1({ \mathbb Z}^k,V)$
, define
$\beta \in C^1({ \mathbb Z}^k,V)$
, define
 $$ \begin{align} {\mathbf{d}}_1H(g) &= \rho_*(g)H-H, \nonumber\\ ({\mathbf{d}}_2\beta)(g_1,g_2) &= (\rho_*(g_2)\beta(g_1)-\beta(g_1)) - (\rho_*(g_1)\beta(g_2)-\beta(g_2)). \end{align} $$
$$ \begin{align} {\mathbf{d}}_1H(g) &= \rho_*(g)H-H, \nonumber\\ ({\mathbf{d}}_2\beta)(g_1,g_2) &= (\rho_*(g_2)\beta(g_1)-\beta(g_1)) - (\rho_*(g_1)\beta(g_2)-\beta(g_2)). \end{align} $$
The first cohomology
![]() $H_{\rho }^1(V)$
over the action
$H_{\rho }^1(V)$
over the action
![]() $\rho $
with coefficients in the module V is defined to be
$\rho $
with coefficients in the module V is defined to be
![]() $\rm Ker ({\mathbf {d}}_2)/\rm Im ({\mathbf {d}}_1)$
. Elements of
$\rm Ker ({\mathbf {d}}_2)/\rm Im ({\mathbf {d}}_1)$
. Elements of
![]() $\rm Ker ({\mathbf {d}}_2)$
are called cocycles over
$\rm Ker ({\mathbf {d}}_2)$
are called cocycles over
![]() $\rho $
with coefficients in V, and elements of
$\rho $
with coefficients in V, and elements of
![]() $\rm Im ({\mathbf {d}}_1)$
are called coboundaries over
$\rm Im ({\mathbf {d}}_1)$
are called coboundaries over
![]() $\rho $
with coefficients in V.
$\rho $
with coefficients in V.
We consider here two situations:
-
(1)
 $V=C^{\infty }(M)$
and
$V=C^{\infty }(M)$
and
 $\rho _*(g) f= f\circ \rho (g)$
for any
$\rho _*(g) f= f\circ \rho (g)$
for any
 $g\in \mathbb Z^k$
and any
$g\in \mathbb Z^k$
and any
 $f\in C^{\infty }(M)$
; and
$f\in C^{\infty }(M)$
; and -
(2)
 $V=\textrm{ Vect}^{\infty }{M}$
and
$V=\textrm{ Vect}^{\infty }{M}$
and
 $\rho _*(g)X= D\rho (g)X\circ \rho (g)^{-1}$
for any
$\rho _*(g)X= D\rho (g)X\circ \rho (g)^{-1}$
for any
 $g\in \mathbb Z^k$
and any
$g\in \mathbb Z^k$
and any
 $X\in \textrm{ Vect}^{\infty }{M}.$
$X\in \textrm{ Vect}^{\infty }{M}.$
We say that
![]() $H_{\rho }^1(C^{\infty }(M))$
is constant if up to a modification by a constant cocycle, every cocycle is a coboundary. This means that
$H_{\rho }^1(C^{\infty }(M))$
is constant if up to a modification by a constant cocycle, every cocycle is a coboundary. This means that
![]() $H_{\rho }^1(C^{\infty }(M))$
is isomorphic to
$H_{\rho }^1(C^{\infty }(M))$
is isomorphic to
![]() $\mathbb R^k$
.
$\mathbb R^k$
.
Now let M be the homogeneous space
![]() $\Gamma \setminus G$
, where G is a Lie group with Lie algebra
$\Gamma \setminus G$
, where G is a Lie group with Lie algebra
![]() $\frak g$
and
$\frak g$
and
![]() $\Gamma $
is a lattice in G. Let
$\Gamma $
is a lattice in G. Let
![]() $\rho $
be a
$\rho $
be a
![]() $\mathbb Z^k$
action on M by right multiplication. Then
$\mathbb Z^k$
action on M by right multiplication. Then
![]() $\rho $
induces an action
$\rho $
induces an action
![]() $\rho _*$
on
$\rho _*$
on
![]() $\frak g$
via the adjoint operator
$\frak g$
via the adjoint operator
![]() $\rm ad$
. This action makes
$\rm ad$
. This action makes
![]() $\frak g$
into a module, so one can consider the cohomology
$\frak g$
into a module, so one can consider the cohomology
![]() $H_{\rho }^1( \frak g)$
, which is of course finite dimensional. If
$H_{\rho }^1( \frak g)$
, which is of course finite dimensional. If
![]() $H_{\rho }^1( \textrm{ Vect}^{\infty }{M})= H_{\rho }^1( \frak g)$
, that is, if the cohomology with coefficients in vector fields is the same as the cohomology over
$H_{\rho }^1( \textrm{ Vect}^{\infty }{M})= H_{\rho }^1( \frak g)$
, that is, if the cohomology with coefficients in vector fields is the same as the cohomology over
![]() $\rho $
with coefficients in constant vector fields, then we say that
$\rho $
with coefficients in constant vector fields, then we say that
![]() $H_{\rho }^1( \textrm{ Vect}^{\infty }{M})$
is constant. In particular, the constant
$H_{\rho }^1( \textrm{ Vect}^{\infty }{M})$
is constant. In particular, the constant
![]() $H_{\rho }^1( \textrm{ Vect}^{\infty }{M})$
is exceptionally small: it is finite dimensional.
$H_{\rho }^1( \textrm{ Vect}^{\infty }{M})$
is exceptionally small: it is finite dimensional.
Theorem 1.1. For the action
![]() $\rho $
defined in §1.1, both
$\rho $
defined in §1.1, both
![]() $H_{\rho }^1(C^{\infty }(M))$
and
$H_{\rho }^1(C^{\infty }(M))$
and
![]() $H_{\rho }^1( \textrm{ Vect}^{\infty }{M})$
are constant. Moreover, in both cases, the operators
$H_{\rho }^1( \textrm{ Vect}^{\infty }{M})$
are constant. Moreover, in both cases, the operators
![]() ${\mathbf {d}}_1$
and
${\mathbf {d}}_1$
and
![]() ${\mathbf {d}}_2$
have tame inverses. Namely, there exist positive constants
${\mathbf {d}}_2$
have tame inverses. Namely, there exist positive constants
![]() $\sigma $
and
$\sigma $
and
![]() $s_0$
, and there exists a left inverse
$s_0$
, and there exists a left inverse
![]() ${\mathbf {d}}^*_i$
of
${\mathbf {d}}^*_i$
of
![]() ${\mathbf {d}}^*_i$
, for
${\mathbf {d}}^*_i$
, for
![]() $i=1,2$
, such that for all
$i=1,2$
, such that for all
![]() $s\ge s_0$
there is a constant
$s\ge s_0$
there is a constant
![]() $C_s> 0$
such that
$C_s> 0$
such that
![]() $\|{\mathbf {d}}^*_i \gamma _i\|_{s}\le C_s \|\gamma _i\|_{s+\sigma }$
, where
$\|{\mathbf {d}}^*_i \gamma _i\|_{s}\le C_s \|\gamma _i\|_{s+\sigma }$
, where
![]() $\gamma _i$
is a cochain in
$\gamma _i$
is a cochain in
![]() $\rm Im ({\mathbf {d}}_i)$
.
$\rm Im ({\mathbf {d}}_i)$
.
The above theorem for
![]() $H_{\rho }^1(C^{\infty }(M))$
is a direct consequence of the following two results which contain precise information on estimates for the norms of solutions to cohomological equations, which is essential for application of the KAM method. The precise formulation of Theorem 1.1 for
$H_{\rho }^1(C^{\infty }(M))$
is a direct consequence of the following two results which contain precise information on estimates for the norms of solutions to cohomological equations, which is essential for application of the KAM method. The precise formulation of Theorem 1.1 for
![]() $H_{\rho }^1( \textrm{ Vect}^{\infty }{M})$
, with concrete estimates, is Proposition 3.7 in §3.5. The property of a cohomology group described in Theorem 1.1 is usually in the literature referred to as tame splitting in cohomology. For more details on cohomology operators and splitting in cohomology, we refer to [Reference Damjanović3], [Reference Damjanović and Tanis8] or [Reference Petkovic13].
$H_{\rho }^1( \textrm{ Vect}^{\infty }{M})$
, with concrete estimates, is Proposition 3.7 in §3.5. The property of a cohomology group described in Theorem 1.1 is usually in the literature referred to as tame splitting in cohomology. For more details on cohomology operators and splitting in cohomology, we refer to [Reference Damjanović3], [Reference Damjanović and Tanis8] or [Reference Petkovic13].
We define the first coboundary operators associated to the generators of
![]() $\rho $
. These are operators
$\rho $
. These are operators
![]() $L_{\boldsymbol {\tau }}$
and
$L_{\boldsymbol {\tau }}$
and
![]() $L_{\boldsymbol {\eta }}$
on
$L_{\boldsymbol {\eta }}$
on
![]() $L^2(M)$
given by
$L^2(M)$
given by
Theorem 1.2. For any
![]() $s \geq 0$
and for any
$s \geq 0$
and for any
![]() $\epsilon> 0$
, there is a constant
$\epsilon> 0$
, there is a constant
![]() $C_{s, \epsilon } := C_{s, \epsilon , \boldsymbol {\tau }, \boldsymbol {\eta }}> 0$
such that for any
$C_{s, \epsilon } := C_{s, \epsilon , \boldsymbol {\tau }, \boldsymbol {\eta }}> 0$
such that for any
![]() $f, g \in C^{\infty }(M)$
of zero average with respect to the Haar measure, and that satisfy
$f, g \in C^{\infty }(M)$
of zero average with respect to the Haar measure, and that satisfy
![]() $L_{\boldsymbol {\tau }} g = L_{\boldsymbol {\eta }} f$
, there is a solution
$L_{\boldsymbol {\tau }} g = L_{\boldsymbol {\eta }} f$
, there is a solution
![]() $P \in C^{\infty }(M)$
such that
$P \in C^{\infty }(M)$
such that
and
where
![]() $\gamma $
is the Diophantine exponent in (5).
$\gamma $
is the Diophantine exponent in (5).
Theorem 1.3. For any
![]() $s \geq 0$
and for any
$s \geq 0$
and for any
![]() $\epsilon> 0$
, there is a constant
$\epsilon> 0$
, there is a constant
![]() $C_{s, \epsilon }:= C_{s, \epsilon , \boldsymbol {\tau }, \boldsymbol {\eta }}> 0$
such that for any
$C_{s, \epsilon }:= C_{s, \epsilon , \boldsymbol {\tau }, \boldsymbol {\eta }}> 0$
such that for any
![]() $f, g, \phi \in C^{\infty }(M)$
of zero average, and that satisfy
$f, g, \phi \in C^{\infty }(M)$
of zero average, and that satisfy
![]() $L_{\boldsymbol {\eta }} f - L_{\boldsymbol {\tau }} g = \phi $
, there exists a non-constant function
$L_{\boldsymbol {\eta }} f - L_{\boldsymbol {\tau }} g = \phi $
, there exists a non-constant function
![]() $P \in C^{\infty }(M)$
such that
$P \in C^{\infty }(M)$
such that
 $$ \begin{align*} \begin{array}{l} \|g - L_{\boldsymbol{\eta}} P\|_s \leq C_{s, \epsilon}\| \phi\|_{s+ \sigma(n, \gamma, \epsilon)}, \\ \|f - L_{\boldsymbol{\tau}} P\|_s \leq C_{s, \epsilon} \| \phi\|_{s+\sigma(n, \gamma, \epsilon)} , \\ \| P \|_s \leq C_{s, \epsilon} (\| f\|_{s+\sigma(n, \gamma, \epsilon)} + \Vert g \Vert_{s + \sigma(n, \gamma, \epsilon)}), \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l} \|g - L_{\boldsymbol{\eta}} P\|_s \leq C_{s, \epsilon}\| \phi\|_{s+ \sigma(n, \gamma, \epsilon)}, \\ \|f - L_{\boldsymbol{\tau}} P\|_s \leq C_{s, \epsilon} \| \phi\|_{s+\sigma(n, \gamma, \epsilon)} , \\ \| P \|_s \leq C_{s, \epsilon} (\| f\|_{s+\sigma(n, \gamma, \epsilon)} + \Vert g \Vert_{s + \sigma(n, \gamma, \epsilon)}), \end{array} \end{align*} $$
where
![]() $\sigma (n, \gamma , \epsilon ) := \max \{2\gamma , 3n + 1 +\epsilon \}$
.
$\sigma (n, \gamma , \epsilon ) := \max \{2\gamma , 3n + 1 +\epsilon \}$
.
Remark 1.4. Results of this section can be viewed as the first step of obtaining discrete counterparts of the results of Cosentino and Flaminio on Lie group actions on Heisenberg nilmanifolds [Reference Cosentino and Flaminio1]. An additional difficulty in the discrete case is that the space of obstructions to solutions of the cohomological equation is infinite dimensional in each irreducible, infinite-dimensional representation. We trust that the following general result holds: for actions of Lie groups P considered in [Reference Cosentino and Flaminio1], every non-degenerate lattice subaction of P satisfies the statement of Theorem 1.1.
Remark 1.5. The Diophantine constants in (5) could have different values for
![]() $\boldsymbol {\tau }$
and for
$\boldsymbol {\tau }$
and for
![]() $ \boldsymbol {\eta }$
. It would not affect results, only the values of the constants in the estimates. For simplicity we used the same
$ \boldsymbol {\eta }$
. It would not affect results, only the values of the constants in the estimates. For simplicity we used the same
![]() $\gamma $
throughout.
$\gamma $
throughout.
Remark 1.6. We note that for a typical element of the action
![]() $\rho $
, the first cohomology is infinite dimensional as a consequence of the results of Flaminio and Forni in [Reference Flaminio and Forni9]. The results in [Reference Flaminio and Forni9] hold for nilmanifolds of any step, and it is an interesting open problem to construct
$\rho $
, the first cohomology is infinite dimensional as a consequence of the results of Flaminio and Forni in [Reference Flaminio and Forni9]. The results in [Reference Flaminio and Forni9] hold for nilmanifolds of any step, and it is an interesting open problem to construct
![]() ${ \mathbb R}^k$
and
${ \mathbb R}^k$
and
![]() ${ \mathbb Z}^k$
homogeneous actions satisfying Theorem 1.1 on nilmanifolds of step greater than two.
${ \mathbb Z}^k$
homogeneous actions satisfying Theorem 1.1 on nilmanifolds of step greater than two.
1.3 Transversal local rigidity result
Let
![]() $\rho $
be a smooth action of a discrete group G by diffeomorphisms of a smooth compact manifold M. Suppose that there exists a finite-dimensional family
$\rho $
be a smooth action of a discrete group G by diffeomorphisms of a smooth compact manifold M. Suppose that there exists a finite-dimensional family
![]() $\{\rho ^{\unicode{x3bb} }\}_{{\unicode{x3bb} }\in \mathbb R^d}$
of smooth G actions on M such that
$\{\rho ^{\unicode{x3bb} }\}_{{\unicode{x3bb} }\in \mathbb R^d}$
of smooth G actions on M such that
![]() $\rho ^0=\rho $
, and the family is
$\rho ^0=\rho $
, and the family is
![]() $C^1$
transversally, that is, it is
$C^1$
transversally, that is, it is
![]() $C^1$
in the parameter
$C^1$
in the parameter
![]() ${\unicode{x3bb} }$
.
${\unicode{x3bb} }$
.
The action
![]() $\rho $
is transversally locally rigid with respect to the family
$\rho $
is transversally locally rigid with respect to the family
![]() $\{\rho ^{\unicode{x3bb} }\}$
if every sufficiently small perturbation of the family
$\{\rho ^{\unicode{x3bb} }\}$
if every sufficiently small perturbation of the family
![]() $\rho ^{\unicode{x3bb} }$
in a neighborhood of
$\rho ^{\unicode{x3bb} }$
in a neighborhood of
![]() ${\unicode{x3bb} }=0$
intersects the smooth conjugacy class of
${\unicode{x3bb} }=0$
intersects the smooth conjugacy class of
![]() $\rho $
, where the smooth conjugacy class of
$\rho $
, where the smooth conjugacy class of
![]() $\rho $
consists of all actions
$\rho $
consists of all actions
![]() $\{h\circ \rho \circ h^{-1}:\, h\in \textrm{ Diff}^{\infty }{(M)}\}$
. By sufficiently small we mean that the perturbed family consists of sufficiently small perturbations of the elements in the initial family, in a fixed
$\{h\circ \rho \circ h^{-1}:\, h\in \textrm{ Diff}^{\infty }{(M)}\}$
. By sufficiently small we mean that the perturbed family consists of sufficiently small perturbations of the elements in the initial family, in a fixed
![]() $C^l$
norm determined by the given initial family data, and that transversally in the direction of the parameter
$C^l$
norm determined by the given initial family data, and that transversally in the direction of the parameter
![]() $\lambda $
the perturbed family is close to the initial one in the
$\lambda $
the perturbed family is close to the initial one in the
![]() $C^1$
topology. The precise smallness conditions we need are given in Theorem 3.10, which is the more precise formulation of our main local rigidity result.
$C^1$
topology. The precise smallness conditions we need are given in Theorem 3.10, which is the more precise formulation of our main local rigidity result.
Theorem 1.7. Let
![]() $\rho $
be the
$\rho $
be the
![]() $\mathbb Z^2$
action defined in (
7
), where
$\mathbb Z^2$
action defined in (
7
), where
![]() $\boldsymbol {\tau }$
and
$\boldsymbol {\tau }$
and
![]() $\boldsymbol {\eta }$
are Diophantine as in (
5
). Then
$\boldsymbol {\eta }$
are Diophantine as in (
5
). Then
![]() $\rho $
is transversally locally rigid with respect to an explicit
$\rho $
is transversally locally rigid with respect to an explicit
![]() $(4n-1)$
-dimensional family of homogeneous
$(4n-1)$
-dimensional family of homogeneous
![]() $\mathbb Z^2$
actions.
$\mathbb Z^2$
actions.
The explicit family of actions is defined in §3.1.
1.4 Structure of the paper
The paper has two parts with analysis of different flavor. In §2 we prove the cohomological results in Theorems 1.2 and 1.3. These results are further used in §3.5 to prove Proposition 3.7. All these results together imply directly Theorem 1.1. The main analytic tool for the proof of cohomological results is representation theory on the Heisenberg nilmanifold. The calculation in finite-dimensional representation is significantly simpler and is written in the appendix. The main calculation in infinite-dimensional representation is done in §2.3. In the second part of the paper we apply cohomological results to prove Theorem 1.7. We describe the finite-dimensional family relative to which transversal rigidity holds in §3.2 and we prove the main iterative step needed for Theorem 1.7 in §3.6.
2 Proofs of Theorems 1.2 and 1.3
2.1 Representation spaces
Let
![]() $L^2(M)$
be the Hilbert space of complex-valued square-integrable functions with respect to the
$L^2(M)$
be the Hilbert space of complex-valued square-integrable functions with respect to the
![]() $\mathsf H$
-invariant volume form for M. By the Stone–von Neumann theorem, the space
$\mathsf H$
-invariant volume form for M. By the Stone–von Neumann theorem, the space
![]() $L^2(M)$
decomposes into an orthogonal sum of irreducible, unitary representations that are unitarily equivalent to certain one-dimensional or infinite-dimensional models that we describe at the top of §§2.2 and 2.3. Moreover, by irreducibility, Sobolev spaces
$L^2(M)$
decomposes into an orthogonal sum of irreducible, unitary representations that are unitarily equivalent to certain one-dimensional or infinite-dimensional models that we describe at the top of §§2.2 and 2.3. Moreover, by irreducibility, Sobolev spaces
![]() $W^s(M)$
are also decomposable in the above sense, because vector fields in
$W^s(M)$
are also decomposable in the above sense, because vector fields in
![]() $\operatorname {\mathfrak h}$
split into irreducible, unitary representation spaces, and the infinitesimal representations of
$\operatorname {\mathfrak h}$
split into irreducible, unitary representation spaces, and the infinitesimal representations of
![]() $\operatorname {\mathfrak h}$
extend to representations of the enveloping algebra. For this reason, we may prove our Sobolev estimates concerning coboundary operators (Theorems 1.2 and 1.3) in simpler, orthogonal components of
$\operatorname {\mathfrak h}$
extend to representations of the enveloping algebra. For this reason, we may prove our Sobolev estimates concerning coboundary operators (Theorems 1.2 and 1.3) in simpler, orthogonal components of
![]() $W^s(M)$
, and then we glue the estimates together at the end (see (50)).
$W^s(M)$
, and then we glue the estimates together at the end (see (50)).
2.2 Finite-dimensional representations
The one-dimensional representations are unitarily equivalent to characters
![]() $\rho _{\mathbf {m}}$
of
$\rho _{\mathbf {m}}$
of
![]() ${ \mathbb R}^{2n}$
in
${ \mathbb R}^{2n}$
in
![]() $L^2({ \mathbb T}^{2n})$
, for
$L^2({ \mathbb T}^{2n})$
, for
![]() $\mathbf {m} \in { \mathbb Z}^{2n}$
, and are given by
$\mathbf {m} \in { \mathbb Z}^{2n}$
, and are given by
For each integer
![]() $1 \leq j \leq n$
, the derived representations of
$1 \leq j \leq n$
, the derived representations of
![]() $\rho _{\mathbf {m}}$
are
$\rho _{\mathbf {m}}$
are
Write
So, given
![]() $f \in L^2({ \mathbb T}^{2n})$
, we have the orthogonal decomposition
$f \in L^2({ \mathbb T}^{2n})$
, we have the orthogonal decomposition
where
![]() $\triangle $
acts on irreducible, unitary representations of
$\triangle $
acts on irreducible, unitary representations of
![]() $L^2({ \mathbb T}^{2n})$
by
$L^2({ \mathbb T}^{2n})$
by
For
![]() $s> 0$
, the subspace of s-differentiable functions is
$s> 0$
, the subspace of s-differentiable functions is
![]() $W^s({ \mathbb T}^{2n}) \subset L^2({ \mathbb T}^{2n})$
, defined to be the maximal domain of the operator
$W^s({ \mathbb T}^{2n}) \subset L^2({ \mathbb T}^{2n})$
, defined to be the maximal domain of the operator
![]() $(I + \rho (\triangle ))^{s/2}$
on
$(I + \rho (\triangle ))^{s/2}$
on
![]() $L^2({ \mathbb T}^{2n})$
with inner product and norm given by (2). In particular,
$L^2({ \mathbb T}^{2n})$
with inner product and norm given by (2). In particular,
We denote the space of smooth functions in
![]() $L^2({ \mathbb T}^{2n})$
by
$L^2({ \mathbb T}^{2n})$
by
Furthermore, for every s, we have
![]() $W^s({ \mathbb T}^{2n}) = \mathbb C \langle 1 \rangle \oplus W_0^s({ \mathbb T}^{2n})$
, where
$W^s({ \mathbb T}^{2n}) = \mathbb C \langle 1 \rangle \oplus W_0^s({ \mathbb T}^{2n})$
, where
![]() $W_0^s({ \mathbb T}^{2n})$
is the Sobolev space of s-differentiable, zero-average functions on
$W_0^s({ \mathbb T}^{2n})$
is the Sobolev space of s-differentiable, zero-average functions on
![]() ${ \mathbb T}^{2n}$
. So, it follows that
${ \mathbb T}^{2n}$
. So, it follows that
where
![]() $W_0^{\infty }({ \mathbb T}^{2n}) = \bigcap _{s \geq 0} W_0^s({ \mathbb T}^{2n})$
.
$W_0^{\infty }({ \mathbb T}^{2n}) = \bigcap _{s \geq 0} W_0^s({ \mathbb T}^{2n})$
.
The two propositions below establish Theorems 1.2 and 1.3 in the case of finite-dimensional representations. The proofs are straightforward and deferred to the appendix.
Proposition 2.1. There is a constant
![]() $C_{\boldsymbol {\tau }, \boldsymbol {\eta }}> 0$
such that for any zero-average
$C_{\boldsymbol {\tau }, \boldsymbol {\eta }}> 0$
such that for any zero-average
![]() $f, g \in W_0^{\infty }({ \mathbb T}^{2n})$
that satisfy
$f, g \in W_0^{\infty }({ \mathbb T}^{2n})$
that satisfy
![]() $L_{\boldsymbol {\tau }} g = L_{\boldsymbol {\eta }} f$
, there is a solution
$L_{\boldsymbol {\tau }} g = L_{\boldsymbol {\eta }} f$
, there is a solution
![]() $P \in W^{\infty }({ \mathbb T}^{2n})$
such that
$P \in W^{\infty }({ \mathbb T}^{2n})$
such that
and, for any
![]() $s \geq 0$
,
$s \geq 0$
,
Proposition 2.2. There is a constant
![]() $C_{\boldsymbol \tau , \boldsymbol \eta }> 0$
such that for any
$C_{\boldsymbol \tau , \boldsymbol \eta }> 0$
such that for any
![]() $\phi \in W^{\infty }({ \mathbb T}^{2n})$
and any non-constant zero-average functions
$\phi \in W^{\infty }({ \mathbb T}^{2n})$
and any non-constant zero-average functions
![]() $f, g\in W_0^{\infty }({ \mathbb T}^{2n})$
that satisfy
$f, g\in W_0^{\infty }({ \mathbb T}^{2n})$
that satisfy
![]() $L_{\boldsymbol {\eta }} f - L_{\boldsymbol {\tau }} g = \phi $
, there is a non-constant function
$L_{\boldsymbol {\eta }} f - L_{\boldsymbol {\tau }} g = \phi $
, there is a non-constant function
![]() $P \in W^{\infty }({ \mathbb T}^{2n})$
such that for any
$P \in W^{\infty }({ \mathbb T}^{2n})$
such that for any
![]() $s \geq 0$
,
$s \geq 0$
,
 $$ \begin{align*} \begin{array}{l} \|g - L_{\boldsymbol{\eta}} P\|_s \leq C_{\boldsymbol \tau, \boldsymbol \eta} \|\phi \|_{s+2\gamma} , \\ \|f - L_{\boldsymbol{\tau}} P\|_s \leq C_{\boldsymbol \tau, \boldsymbol \eta} \|\phi \|_{s+2\gamma} , \\ \| P \|_s \leq C_{\boldsymbol \tau, \boldsymbol \eta} (\Vert f \Vert_{s + 2\gamma} + \| g \|_{s+2\gamma}). \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l} \|g - L_{\boldsymbol{\eta}} P\|_s \leq C_{\boldsymbol \tau, \boldsymbol \eta} \|\phi \|_{s+2\gamma} , \\ \|f - L_{\boldsymbol{\tau}} P\|_s \leq C_{\boldsymbol \tau, \boldsymbol \eta} \|\phi \|_{s+2\gamma} , \\ \| P \|_s \leq C_{\boldsymbol \tau, \boldsymbol \eta} (\Vert f \Vert_{s + 2\gamma} + \| g \|_{s+2\gamma}). \end{array} \end{align*} $$
2.3 Schrödinger representations
Next we consider the irreducible, infinite-dimensional representations. By the Stone–von Neumann theorem, any infinite-dimensional representation is unitarily equivalent to a Schrödinger representation of
![]() $\mathsf H$
on
$\mathsf H$
on
![]() $L^2({ \mathbb R}^n)$
with a parameter
$L^2({ \mathbb R}^n)$
with a parameter
![]() $h \neq 0$
. When acting on the right, this is
$h \neq 0$
. When acting on the right, this is
where
![]() $\epsilon = \text {sign}(h) = \pm 1.$
For integers
$\epsilon = \text {sign}(h) = \pm 1.$
For integers
![]() $1 \leq j \leq n$
, we have
$1 \leq j \leq n$
, we have
 $$ \begin{align*} \mu_h(X_j) = -\vert h \vert^{1/2} \frac{\partial}{\partial y_j}, \ \ \ \mu_h(\Lambda_j) = i \epsilon \vert h \vert^{1/2} y_j, \ \ \ \mu_h(Z) = -i h. \end{align*} $$
$$ \begin{align*} \mu_h(X_j) = -\vert h \vert^{1/2} \frac{\partial}{\partial y_j}, \ \ \ \mu_h(\Lambda_j) = i \epsilon \vert h \vert^{1/2} y_j, \ \ \ \mu_h(Z) = -i h. \end{align*} $$
The derived representation extends to the enveloping algebra of the Lie algebra of
![]() $\mathsf H$
.
$\mathsf H$
.
In §1.1, we noted that we will work with the standard lattice and, in this case, the Schr
![]() $\ddot {\textrm {o}}$
dinger representations are parameterized by
$\ddot {\textrm {o}}$
dinger representations are parameterized by
![]() $h \in 2\pi { \mathbb Z}\setminus \{0\}$
(see [Reference Cosentino and Flaminio1, §3.2]). Then observe that
$h \in 2\pi { \mathbb Z}\setminus \{0\}$
(see [Reference Cosentino and Flaminio1, §3.2]). Then observe that
and define the operator
![]() $\Box $
in the model
$\Box $
in the model
![]() $\mu _h$
to be
$\mu _h$
to be
 $$ \begin{align*} \mu_h(\Box) & := \frac{1}{2\pi}\bigg( \vert \mu_h(Z) \vert -\sum_{i = 1}^n \mu_h(X_i^2) + \mu_h(\Lambda_i^2) \bigg)\\ & = \frac{\vert h \vert}{2\pi} \bigg(1 + \sum_{i = 1}^n y_i^2 -\frac{\partial^2}{\partial y_i^2}\bigg), \end{align*} $$
$$ \begin{align*} \mu_h(\Box) & := \frac{1}{2\pi}\bigg( \vert \mu_h(Z) \vert -\sum_{i = 1}^n \mu_h(X_i^2) + \mu_h(\Lambda_i^2) \bigg)\\ & = \frac{\vert h \vert}{2\pi} \bigg(1 + \sum_{i = 1}^n y_i^2 -\frac{\partial^2}{\partial y_i^2}\bigg), \end{align*} $$
which is homogeneous in
![]() $\vert h \vert $
. The operator
$\vert h \vert $
. The operator
![]() $\mu _h(\Box )$
is related to
$\mu _h(\Box )$
is related to
![]() $\mu _h(\triangle )$
by
$\mu _h(\triangle )$
by
Define
![]() $W^s(\mu _h, { \mathbb R}^n) \subset L^2({ \mathbb R}^n)$
to be Hilbert Sobolev space of s-differentiable functions, that is, the maximal domain of the operator
$W^s(\mu _h, { \mathbb R}^n) \subset L^2({ \mathbb R}^n)$
to be Hilbert Sobolev space of s-differentiable functions, that is, the maximal domain of the operator
![]() $\mu _h(\Box )^s$
on
$\mu _h(\Box )^s$
on
![]() $L^2({ \mathbb R}^n)$
with inner product
$L^2({ \mathbb R}^n)$
with inner product
 $$ \begin{align*} \langle \mu_h(\Box)^s f, g \rangle_{L^2({ \mathbb R}^n)} = \bigg(\frac{\vert h \vert}{2\pi}\bigg)^s \bigg\langle \bigg(I + \sum_{i = 1}^n y_i^2 -\frac{\partial^2}{\partial y_i^2}\bigg)^s f, g\bigg\rangle_{L^2({ \mathbb R}^n)}. \end{align*} $$
$$ \begin{align*} \langle \mu_h(\Box)^s f, g \rangle_{L^2({ \mathbb R}^n)} = \bigg(\frac{\vert h \vert}{2\pi}\bigg)^s \bigg\langle \bigg(I + \sum_{i = 1}^n y_i^2 -\frac{\partial^2}{\partial y_i^2}\bigg)^s f, g\bigg\rangle_{L^2({ \mathbb R}^n)}. \end{align*} $$
Denote the Sobolev norm of this operator by
Clearly, the space of smooth functions in
![]() $L^2({ \mathbb R}^n)$
with respect to
$L^2({ \mathbb R}^n)$
with respect to
![]() $\mu _h(\Box )$
is the Schwartz space
$\mu _h(\Box )$
is the Schwartz space
Following [Reference Cosentino and Flaminio1], estimates of linear operators with respect to the Laplacian (1) are a consequence of such estimates in the homogeneous norm. This estimate differs from Lemma 3.15 of [Reference Cosentino and Flaminio1] in that our homogeneous operator
![]() $\mu _h(\Box )$
includes the term
$\mu _h(\Box )$
includes the term
![]() $\vert \mu _h(Z)\vert $
, whereas that operator in [Reference Cosentino and Flaminio1] does not. The argument below is the same as in [Reference Cosentino and Flaminio1, Lemma 3.15].
$\vert \mu _h(Z)\vert $
, whereas that operator in [Reference Cosentino and Flaminio1] does not. The argument below is the same as in [Reference Cosentino and Flaminio1, Lemma 3.15].
Lemma 2.3. Let
![]() $T: \mathscr {S}({ \mathbb R}^n) \to \mathscr {S}({ \mathbb R}^n)$
be a linear map for the representation
$T: \mathscr {S}({ \mathbb R}^n) \to \mathscr {S}({ \mathbb R}^n)$
be a linear map for the representation
![]() $\mu _h$
such that for every
$\mu _h$
such that for every
![]() $s \geq 0$
, there are a constant
$s \geq 0$
, there are a constant
![]() $C_s> 0$
and some
$C_s> 0$
and some
![]() $t \geq 0$
satisfying
$t \geq 0$
satisfying
Then, for every
![]() $s \geq 0$
, there is a constant
$s \geq 0$
, there is a constant
![]() $C_{s, t} = 2^{(s + t)/2} \max _{0 \leq k \leq s} \{C_k\}> 0$
such that
$C_{s, t} = 2^{(s + t)/2} \max _{0 \leq k \leq s} \{C_k\}> 0$
such that
Proof First let
![]() $s \geq 0$
be an integer. Then
$s \geq 0$
be an integer. Then
 $$ \begin{align} \Vert T f \Vert_s^2 & = \bigg\langle \bigg(I -\mu_h(Z)^2 -\sum_{i = 1}^n \mu_h(X_i)^2 + \mu_h(\Lambda_i)^2\bigg)^s T f, T f\bigg\rangle \notag \\ & \leq \sum_{k = 0}^s {s \choose k} (1 + h^2)^{s - k} \langle \mu_h(\Box)^k T f, T f\rangle. \end{align} $$
$$ \begin{align} \Vert T f \Vert_s^2 & = \bigg\langle \bigg(I -\mu_h(Z)^2 -\sum_{i = 1}^n \mu_h(X_i)^2 + \mu_h(\Lambda_i)^2\bigg)^s T f, T f\bigg\rangle \notag \\ & \leq \sum_{k = 0}^s {s \choose k} (1 + h^2)^{s - k} \langle \mu_h(\Box)^k T f, T f\rangle. \end{align} $$
By the definition of
![]() $|\mkern -1.5mu|\mkern -1.5mu|T f |\mkern -1.5mu|\mkern -1.5mu|_k$
, by (14) and because all terms are positive, we have
$|\mkern -1.5mu|\mkern -1.5mu|T f |\mkern -1.5mu|\mkern -1.5mu|_k$
, by (14) and because all terms are positive, we have
 $$ \begin{align} (16) & \leq \sum_{k = 0}^s {s \choose k} (1 + h^2)^{s - k} C_k^2 \langle \mu_h(\Box)^{k + t} f, f\rangle \notag \\ & = \max_{0 \leq k \leq s} \{C_k^2\} \langle (I - \mu_h(Z)^2 + \mu_h(\Box))^{s} \mu_h(\Box)^{t/2} f , \mu_h(\Box)^{t/2} f\rangle. \end{align} $$
$$ \begin{align} (16) & \leq \sum_{k = 0}^s {s \choose k} (1 + h^2)^{s - k} C_k^2 \langle \mu_h(\Box)^{k + t} f, f\rangle \notag \\ & = \max_{0 \leq k \leq s} \{C_k^2\} \langle (I - \mu_h(Z)^2 + \mu_h(\Box))^{s} \mu_h(\Box)^{t/2} f , \mu_h(\Box)^{t/2} f\rangle. \end{align} $$
Because
![]() $\mu _h(Z)^2$
is a constant,
$\mu _h(Z)^2$
is a constant,
![]() $(I - \mu _h(Z)^2 + \mu _h(\Box ))$
and
$(I - \mu _h(Z)^2 + \mu _h(\Box ))$
and
![]() $\mu _h(\Box )$
commute. Then, using that
$\mu _h(\Box )$
commute. Then, using that
![]() $- \mu _h(Z)^2$
is positive again, we have
$- \mu _h(Z)^2$
is positive again, we have
 $$ \begin{align*} (17) & \leq \max_{0 \leq k \leq s} \{C_k^2\} \langle (I - \mu_h(Z)^2 + 2\pi \mu_h(\Box))^{s + t} f , f\rangle \\ & = \max_{0 \leq k \leq s} \{C_k^2\} \langle (I + \mu_h(\triangle) + 2\pi \vert\mu_h(Z)\vert )^{s + t} f , f\rangle \\ & \leq 2^{s + t} \max_{0 \leq k \leq s} \{C_k^2\} \Vert f \Vert_{s + t}^2. \end{align*} $$
$$ \begin{align*} (17) & \leq \max_{0 \leq k \leq s} \{C_k^2\} \langle (I - \mu_h(Z)^2 + 2\pi \mu_h(\Box))^{s + t} f , f\rangle \\ & = \max_{0 \leq k \leq s} \{C_k^2\} \langle (I + \mu_h(\triangle) + 2\pi \vert\mu_h(Z)\vert )^{s + t} f , f\rangle \\ & \leq 2^{s + t} \max_{0 \leq k \leq s} \{C_k^2\} \Vert f \Vert_{s + t}^2. \end{align*} $$
The estimate for
![]() $s \geq 0$
follows by interpolation.
$s \geq 0$
follows by interpolation.
We will use the above lemma to reduce our estimates to the case
![]() $h = 1$
. Because the norm (15) is homogeneous in h, by rescaling by the factor
$h = 1$
. Because the norm (15) is homogeneous in h, by rescaling by the factor
![]() $\vert h \vert ^{s/2}$
from
$\vert h \vert ^{s/2}$
from
![]() $|\mkern -1.5mu|\mkern -1.5mu|f|\mkern -1.5mu|\mkern -1.5mu|_{s}$
, we can restrict ourselves to the case
$|\mkern -1.5mu|\mkern -1.5mu|f|\mkern -1.5mu|\mkern -1.5mu|_{s}$
, we can restrict ourselves to the case
![]() $ \vert h \vert = 2\pi $
, as in [Reference Cosentino and Flaminio1]. In what follows, we set
$ \vert h \vert = 2\pi $
, as in [Reference Cosentino and Flaminio1]. In what follows, we set
![]() $h = 2\pi $
, as the argument for
$h = 2\pi $
, as the argument for
![]() $h = -2\pi $
is analogous.
$h = -2\pi $
is analogous.
Then, to simplify notation, we write
 $$ \begin{align*} X_j = -\frac{\partial}{\partial y_j}, \quad \Lambda_j = i y_j , \quad Z = -i \end{align*} $$
$$ \begin{align*} X_j = -\frac{\partial}{\partial y_j}, \quad \Lambda_j = i y_j , \quad Z = -i \end{align*} $$
and we refer to the Schrödinger representation on
![]() $L^2({ \mathbb R}^n)$
as
$L^2({ \mathbb R}^n)$
as
For
![]() $s> 0$
, we denote
$s> 0$
, we denote
![]() $W^s({ \mathbb R}^n) := W^s(\mu , { \mathbb R}^n)$
.
$W^s({ \mathbb R}^n) := W^s(\mu , { \mathbb R}^n)$
.
It will be convenient to define the Sobolev space
![]() $W^s({ \mathbb R}^{n-1})$
that is the maximal domain of the operator
$W^s({ \mathbb R}^{n-1})$
that is the maximal domain of the operator
![]() $I + \sum _{i = 2}^{n} y_i^2 - ({\partial ^2}/{\partial y_i^2})$
on
$I + \sum _{i = 2}^{n} y_i^2 - ({\partial ^2}/{\partial y_i^2})$
on
![]() $L^2({ \mathbb R}^{n-1})$
. We use the same notation for the inner product, where in this setting
$L^2({ \mathbb R}^{n-1})$
. We use the same notation for the inner product, where in this setting
 $$ \begin{align*} \langle f, g \rangle_s := \bigg\langle \bigg(I + \sum_{i = 2}^{n} y_i^2 - \frac{\partial^2}{\partial y_i^2}\bigg)^{s} f, g\bigg\rangle_{L^2({ \mathbb R}^{n-1})}. \end{align*} $$
$$ \begin{align*} \langle f, g \rangle_s := \bigg\langle \bigg(I + \sum_{i = 2}^{n} y_i^2 - \frac{\partial^2}{\partial y_i^2}\bigg)^{s} f, g\bigg\rangle_{L^2({ \mathbb R}^{n-1})}. \end{align*} $$
Definition 2.4. Denote the norm of
![]() $W^s({ \mathbb R}^{n-1})$
by
$W^s({ \mathbb R}^{n-1})$
by
![]() $\vert f \vert _s.$
$\vert f \vert _s.$
2.3.1 Change of variable
Define
 $$ \begin{align*} \tau = \sqrt{\sum_{j = 1}^{n} \tau_j^2}. \end{align*} $$
$$ \begin{align*} \tau = \sqrt{\sum_{j = 1}^{n} \tau_j^2}. \end{align*} $$
Let
![]() $A = [\mathbf a_1, \mathbf a_2, \ldots , \mathbf a_n] \in O(n)$
be an
$A = [\mathbf a_1, \mathbf a_2, \ldots , \mathbf a_n] \in O(n)$
be an
![]() $n\times n$
matrix with orthonormal rows
$n\times n$
matrix with orthonormal rows
![]() $\mathbf a_i$
such that
$\mathbf a_i$
such that
Observe that
![]() $(\tau _j)$
and
$(\tau _j)$
and
![]() $(\eta _j)$
span a two-dimensional subspace of
$(\eta _j)$
span a two-dimensional subspace of
![]() ${ \mathbb R}^n$
, so we can choose
${ \mathbb R}^n$
, so we can choose
![]() $\mathbf a_2$
to be such that
$\mathbf a_2$
to be such that
Further, choose the signs of the vectors
![]() $\mathbf a_j$
, for
$\mathbf a_j$
, for
![]() $2 \leq j \leq n$
, so that
$2 \leq j \leq n$
, so that
![]() $A \in \operatorname {SO}(n)$
. Then A is the determinant one rotation of
$A \in \operatorname {SO}(n)$
. Then A is the determinant one rotation of
![]() ${ \mathbb R}^n$
such that
${ \mathbb R}^n$
such that
for some
![]() $(\nu _1, \nu _2) \in { \mathbb R}^2$
.
$(\nu _1, \nu _2) \in { \mathbb R}^2$
.
For
![]() $y = (y_1, y_2, \ldots , y_n)$
, define
$y = (y_1, y_2, \ldots , y_n)$
, define
![]() $z = (z_1, z_2, \ldots , z_n)$
via matrix–vector multiplication by
$z = (z_1, z_2, \ldots , z_n)$
via matrix–vector multiplication by
Therefore,
Clearly, because A is an orthogonal matrix, the operator
![]() $U_A: L^2({ \mathbb R}^n, dy) \to L^2({ \mathbb R}^n, dz)$
given by
$U_A: L^2({ \mathbb R}^n, dy) \to L^2({ \mathbb R}^n, dz)$
given by
is unitary. Let
![]() $\tilde {\mu }$
be the representation on
$\tilde {\mu }$
be the representation on
![]() $\mathsf H$
such that for any
$\mathsf H$
such that for any
![]() $g \in \mathsf H$
,
$g \in \mathsf H$
,
![]() $\tilde {\mu }(g): L^2({ \mathbb R}^n, dz) \to L^2({ \mathbb R}^n, dz)$
is given by
$\tilde {\mu }(g): L^2({ \mathbb R}^n, dz) \to L^2({ \mathbb R}^n, dz)$
is given by
So,
![]() $\tilde {\mu }$
is unitarily equivalent to
$\tilde {\mu }$
is unitarily equivalent to
![]() $\mu $
.
$\mu $
.
Now we compute a basis for
![]() $\operatorname {\mathfrak h}$
in terms of the derived representations of
$\operatorname {\mathfrak h}$
in terms of the derived representations of
![]() $\tilde {\mu }$
. For each
$\tilde {\mu }$
. For each
![]() $j \in \{1, 2, \ldots , n\}$
, let
$j \in \{1, 2, \ldots , n\}$
, let
![]() $(x_{j, t}, \lambda _{j, t}, z_{j, t})_{t\in [-1,1]}$
be smooth curves in
$(x_{j, t}, \lambda _{j, t}, z_{j, t})_{t\in [-1,1]}$
be smooth curves in
![]() $\mathsf H$
such that
$\mathsf H$
such that
Then set
Let
![]() $A^{-1}$
be the matrix
$A^{-1}$
be the matrix
for some coefficients
![]() $b_{i j}$
. A calculation shows that for
$b_{i j}$
. A calculation shows that for
![]() $j \in \{1, 2, \ldots , n\}$
,
$j \in \{1, 2, \ldots , n\}$
,
 $$ \begin{align*} \tilde{X}_j = -\sum_{k = 1}^n b_{j k} \frac{\partial}{\partial z_k} , \quad \tilde{\Lambda}_j = i \sum_{j = k}^{n} b_{j k} z_k , \quad \tilde{Z} = -i. \end{align*} $$
$$ \begin{align*} \tilde{X}_j = -\sum_{k = 1}^n b_{j k} \frac{\partial}{\partial z_k} , \quad \tilde{\Lambda}_j = i \sum_{j = k}^{n} b_{j k} z_k , \quad \tilde{Z} = -i. \end{align*} $$
One can check that these operators satisfy the commutation relations
for
![]() $i, j \in \{1, 2, \ldots , n\}$
.
$i, j \in \{1, 2, \ldots , n\}$
.
Lemma 2.5. We have
 $$ \begin{align*} \tilde{\mu}(\Box) = I + \sum_{i = 1}^n z_i^2 - \frac{\partial^2}{\partial z_i^2}. \end{align*} $$
$$ \begin{align*} \tilde{\mu}(\Box) = I + \sum_{i = 1}^n z_i^2 - \frac{\partial^2}{\partial z_i^2}. \end{align*} $$
Proof By definition,
 $$ \begin{align} \tilde{\mu}(\Box) = I + \sum_{i = 1}^n -\tilde{X}_i^2 - \tilde{\Lambda}_i^2. \end{align} $$
$$ \begin{align} \tilde{\mu}(\Box) = I + \sum_{i = 1}^n -\tilde{X}_i^2 - \tilde{\Lambda}_i^2. \end{align} $$
Notice that
 $$ \begin{align*} \tilde{X}_i^2 & = \bigg(-\sum_{j = 1}^n b_{i j} \frac{\partial}{\partial z_j}\bigg)^2 \\[4pt] & = \sum_{j, m = 1}^n b_{i j} b_{i m} \frac{\partial^2}{\partial z_j \partial z_m}. \end{align*} $$
$$ \begin{align*} \tilde{X}_i^2 & = \bigg(-\sum_{j = 1}^n b_{i j} \frac{\partial}{\partial z_j}\bigg)^2 \\[4pt] & = \sum_{j, m = 1}^n b_{i j} b_{i m} \frac{\partial^2}{\partial z_j \partial z_m}. \end{align*} $$
Because the columns of
![]() $A^{-1}$
are orthonormal, we get
$A^{-1}$
are orthonormal, we get
 $$ \begin{align*} \sum_{i = 1}^n \tilde{X}_i^2 & = \sum_{i = 1}^n \sum_{j, m = 1}^n b_{i j} b_{i m} \frac{\partial^2}{\partial z_j \partial z_m} \\ & = \sum_{j, m = 1}^n \sum_{i = 1}^n b_{i j} b_{i m} \frac{\partial^2}{\partial z_j \partial z_m} \\ & = \sum_{1 \leq j \neq m \leq n} \frac{\partial}{\partial z_j \partial z_m} \sum_{i = 1}^n b_{i j} b_{i m} + \sum_{j = 1}^n \frac{\partial^2}{\partial z_j^2} \sum_{i = 1}^n b_{i j}^2 \\ & = \sum_{j = 1}^n \frac{\partial^2}{\partial z_j^2}. \end{align*} $$
$$ \begin{align*} \sum_{i = 1}^n \tilde{X}_i^2 & = \sum_{i = 1}^n \sum_{j, m = 1}^n b_{i j} b_{i m} \frac{\partial^2}{\partial z_j \partial z_m} \\ & = \sum_{j, m = 1}^n \sum_{i = 1}^n b_{i j} b_{i m} \frac{\partial^2}{\partial z_j \partial z_m} \\ & = \sum_{1 \leq j \neq m \leq n} \frac{\partial}{\partial z_j \partial z_m} \sum_{i = 1}^n b_{i j} b_{i m} + \sum_{j = 1}^n \frac{\partial^2}{\partial z_j^2} \sum_{i = 1}^n b_{i j}^2 \\ & = \sum_{j = 1}^n \frac{\partial^2}{\partial z_j^2}. \end{align*} $$
Similarly,
 $$ \begin{align*} \sum_{i = 1}^n \tilde{\Lambda}_i^2 & = - \sum_{j, m = 1}^n \sum_{i = 1}^n b_{i j} b_{i m} z_j z_m \\ & = -\sum_{1 \leq j \neq m \leq n} z_j z_m \sum_{i = 1}^n b_{i j} b_{i m} - \sum_{j = 1}^n z_j^2 \sum_{i = 1}^n b_{i j}^2 \\ & = - \sum_{j = 1}^n z_j^2. \end{align*} $$
$$ \begin{align*} \sum_{i = 1}^n \tilde{\Lambda}_i^2 & = - \sum_{j, m = 1}^n \sum_{i = 1}^n b_{i j} b_{i m} z_j z_m \\ & = -\sum_{1 \leq j \neq m \leq n} z_j z_m \sum_{i = 1}^n b_{i j} b_{i m} - \sum_{j = 1}^n z_j^2 \sum_{i = 1}^n b_{i j}^2 \\ & = - \sum_{j = 1}^n z_j^2. \end{align*} $$
Hence,
 $$ \begin{align*} (20) = I + \sum_{i = 1}^n z_i^2 - \frac{\partial^2}{\partial z_i^2}.\\ \end{align*} $$
$$ \begin{align*} (20) = I + \sum_{i = 1}^n z_i^2 - \frac{\partial^2}{\partial z_i^2}.\\ \end{align*} $$
Finally, we compute the operator
![]() $\tilde \mu (\textrm{ exp}(Y_{\boldsymbol {\kappa }}))$
for
$\tilde \mu (\textrm{ exp}(Y_{\boldsymbol {\kappa }}))$
for
![]() $\boldsymbol \kappa \in \{\boldsymbol {\tau }, \boldsymbol \eta \}$
.
$\boldsymbol \kappa \in \{\boldsymbol {\tau }, \boldsymbol \eta \}$
.
Lemma 2.6. For any
![]() $f \in L^2({ \mathbb R}^n)$
and
$f \in L^2({ \mathbb R}^n)$
and
![]() $z \in { \mathbb R}^n$
, we have
$z \in { \mathbb R}^n$
, we have
 $$ \begin{align*} &\tilde\mu(\textrm{ exp}(Y_{\boldsymbol{\tau}})) f(z) = f(z - (\tau, 0, \ldots, 0)), \\ &\tilde\mu(\textrm{ exp}(Y_{\boldsymbol{\eta}})) f(z) = \textrm{ exp}(i\nu_2 z_2) f(z) \end{align*} $$
$$ \begin{align*} &\tilde\mu(\textrm{ exp}(Y_{\boldsymbol{\tau}})) f(z) = f(z - (\tau, 0, \ldots, 0)), \\ &\tilde\mu(\textrm{ exp}(Y_{\boldsymbol{\eta}})) f(z) = \textrm{ exp}(i\nu_2 z_2) f(z) \end{align*} $$
for some
![]() $\nu _2 \in { \mathbb R}^*$
.
$\nu _2 \in { \mathbb R}^*$
.
Proof To help keep track of which coordinate system we are working in, note that
![]() $U_A f = f\circ A^{-1}$
, where
$U_A f = f\circ A^{-1}$
, where
![]() $z = A y$
. So,
$z = A y$
. So,
and of course the Schrödinger representation
![]() $\mu $
satisfies
$\mu $
satisfies
for any
![]() $g \in \mathsf H$
. Then
$g \in \mathsf H$
. Then
 $$ \begin{align*} \tilde{\mu}(\textrm{ exp}(Y_{\boldsymbol \tau})) f(z) &:= U_A \mu(\textrm{ exp}(Y_{\boldsymbol \tau})) U_A^{-1} f(z) \notag \\[3pt] & = \mu(\textrm{ exp}(Y_{\boldsymbol \tau}))U_A^{-1} f(A^{-1} z) \notag \\[3pt] & = \mu(\textrm{ exp}(Y_{\boldsymbol \tau})) U_A^{-1} f(y) \notag \\[3pt] & = U_A^{-1} f(y_1 - \tau_1, \ldots , y_n - \tau_n) \notag \\[3pt] & = f(A(y_1 - \tau_1, \ldots , y_n - \tau_n)) \notag \\[3pt] & = f(Ay - A(\tau_1, \ldots , \tau_n)) \notag \\[3pt] & = f(z - (\tau, 0, \ldots, 0)). \notag \end{align*} $$
$$ \begin{align*} \tilde{\mu}(\textrm{ exp}(Y_{\boldsymbol \tau})) f(z) &:= U_A \mu(\textrm{ exp}(Y_{\boldsymbol \tau})) U_A^{-1} f(z) \notag \\[3pt] & = \mu(\textrm{ exp}(Y_{\boldsymbol \tau}))U_A^{-1} f(A^{-1} z) \notag \\[3pt] & = \mu(\textrm{ exp}(Y_{\boldsymbol \tau})) U_A^{-1} f(y) \notag \\[3pt] & = U_A^{-1} f(y_1 - \tau_1, \ldots , y_n - \tau_n) \notag \\[3pt] & = f(A(y_1 - \tau_1, \ldots , y_n - \tau_n)) \notag \\[3pt] & = f(Ay - A(\tau_1, \ldots , \tau_n)) \notag \\[3pt] & = f(z - (\tau, 0, \ldots, 0)). \notag \end{align*} $$
Next, recall that
![]() $\boldsymbol \eta = (\mathbf 0, \eta _1, \eta _2, \ldots , \eta _n) \in { \mathbb R}^{2n}$
and define
$\boldsymbol \eta = (\mathbf 0, \eta _1, \eta _2, \ldots , \eta _n) \in { \mathbb R}^{2n}$
and define
![]() $\underline {\boldsymbol \eta } := (\eta _1, \eta _2, \ldots , \eta _n)$
. Then
$\underline {\boldsymbol \eta } := (\eta _1, \eta _2, \ldots , \eta _n)$
. Then
![]() $\mu (\textrm{ exp}(Y_{\boldsymbol {\eta }}))$
is the multiplication operator
$\mu (\textrm{ exp}(Y_{\boldsymbol {\eta }}))$
is the multiplication operator
So,
 $$ \begin{align} \tilde{\mu}(Y_{\boldsymbol{\eta}}) f (z) &:= U_A \mu(\textrm{ exp}(Y_{\boldsymbol{\eta}})) U_A^{-1} f(z) \notag \\[3pt] & = \mu(\textrm{ exp}(Y_{\boldsymbol{\eta}})) U_A^{-1} f (A^{-1} z) \notag \\[3pt] & = \mu(\textrm{ exp}(Y_{\boldsymbol{\eta}})) U_A^{-1} f (y) \notag \\[3pt] & = e^{i \underline{\boldsymbol{\eta}} \cdot y} U_A^{-1} f(y) \notag \\[3pt] & = e^{i \underline{\boldsymbol{\eta}} \cdot y} f(Ay) \notag \\[3pt] & = e^{i \underline{\boldsymbol{\eta}} \cdot A^{-1} z} f(z) \notag \\[3pt] & = e^{i A \underline{\boldsymbol{\eta}} \cdot z} f(z). \end{align} $$
$$ \begin{align} \tilde{\mu}(Y_{\boldsymbol{\eta}}) f (z) &:= U_A \mu(\textrm{ exp}(Y_{\boldsymbol{\eta}})) U_A^{-1} f(z) \notag \\[3pt] & = \mu(\textrm{ exp}(Y_{\boldsymbol{\eta}})) U_A^{-1} f (A^{-1} z) \notag \\[3pt] & = \mu(\textrm{ exp}(Y_{\boldsymbol{\eta}})) U_A^{-1} f (y) \notag \\[3pt] & = e^{i \underline{\boldsymbol{\eta}} \cdot y} U_A^{-1} f(y) \notag \\[3pt] & = e^{i \underline{\boldsymbol{\eta}} \cdot y} f(Ay) \notag \\[3pt] & = e^{i \underline{\boldsymbol{\eta}} \cdot A^{-1} z} f(z) \notag \\[3pt] & = e^{i A \underline{\boldsymbol{\eta}} \cdot z} f(z). \end{align} $$
Now recall from (18) that
![]() $A\underline {\boldsymbol {\eta }} = (\nu _1, \nu _2, 0, \ldots , 0)$
for some
$A\underline {\boldsymbol {\eta }} = (\nu _1, \nu _2, 0, \ldots , 0)$
for some
![]() $(\nu _1, \nu _2) \in { \mathbb R}^2$
, so
$(\nu _1, \nu _2) \in { \mathbb R}^2$
, so
Furthermore, observe that the assumption
![]() $[Y_{\boldsymbol {\tau }}, Y_{\boldsymbol {\eta }}] = 0$
from (6) is equivalent to the condition
$[Y_{\boldsymbol {\tau }}, Y_{\boldsymbol {\eta }}] = 0$
from (6) is equivalent to the condition
 $$ \begin{align*} \sum_{j = 1}^n \tau_j \eta_j = 0. \end{align*} $$
$$ \begin{align*} \sum_{j = 1}^n \tau_j \eta_j = 0. \end{align*} $$
We also have
![]() $A^{-1} (\tau , 0, \ldots , 0) = (\tau _j)$
, where
$A^{-1} (\tau , 0, \ldots , 0) = (\tau _j)$
, where
![]() $A^{-1} = (b_{i j})$
. Then, for all
$A^{-1} = (b_{i j})$
. Then, for all
![]() $1 \leq j \leq n$
,
$1 \leq j \leq n$
,
Because
![]() $A \in \operatorname {SO}(n)$
, we have
$A \in \operatorname {SO}(n)$
, we have
Hence,
 $$ \begin{align} \nu_1 & = (A \boldsymbol \eta)_1 = \sum_{j = 1}^n a_{1 j} \eta_j = \frac{1}{\tau}\sum_{j = 1}^n \tau_j \eta_j = 0. \end{align} $$
$$ \begin{align} \nu_1 & = (A \boldsymbol \eta)_1 = \sum_{j = 1}^n a_{1 j} \eta_j = \frac{1}{\tau}\sum_{j = 1}^n \tau_j \eta_j = 0. \end{align} $$
Because A is a rotation and
![]() $\nu _1 = 0$
, we get that
$\nu _1 = 0$
, we get that
![]() $\vert \nu _2\vert = \vert \boldsymbol \eta \vert> 0$
. Finally, because A is a real matrix and
$\vert \nu _2\vert = \vert \boldsymbol \eta \vert> 0$
. Finally, because A is a real matrix and
![]() $\boldsymbol \eta \in { \mathbb R}^n$
, it follows that
$\boldsymbol \eta \in { \mathbb R}^n$
, it follows that
![]() $\nu _2 \in { \mathbb R}^*$
. The lemma now follows from (22) and (23).
$\nu _2 \in { \mathbb R}^*$
. The lemma now follows from (22) and (23).
For
![]() $\boldsymbol \kappa \in \{\boldsymbol {\tau }, \boldsymbol \eta \}$
, the operator
$\boldsymbol \kappa \in \{\boldsymbol {\tau }, \boldsymbol \eta \}$
, the operator
![]() $L_{\boldsymbol {\kappa }}$
is defined on functions of the
$L_{\boldsymbol {\kappa }}$
is defined on functions of the
![]() $\mathbf z$
-variable by
$\mathbf z$
-variable by
so, by the above lemma,
 $$ \begin{align} L_{\boldsymbol{\kappa}} f(z) = \begin{cases} f(z - (\tau, 0, \ldots, 0)) - f(z) & \text{ if } \boldsymbol\kappa = \boldsymbol{\tau}, \\ [\textrm{ exp}(i \nu_2 z_2 ) - 1] f(z) & \text{ if } \boldsymbol\kappa = \boldsymbol\eta. \ \end{cases} \end{align} $$
$$ \begin{align} L_{\boldsymbol{\kappa}} f(z) = \begin{cases} f(z - (\tau, 0, \ldots, 0)) - f(z) & \text{ if } \boldsymbol\kappa = \boldsymbol{\tau}, \\ [\textrm{ exp}(i \nu_2 z_2 ) - 1] f(z) & \text{ if } \boldsymbol\kappa = \boldsymbol\eta. \ \end{cases} \end{align} $$
The coordinates
![]() $(z_3, z_4, \ldots , z_n)$
will not play a central role, so for any
$(z_3, z_4, \ldots , z_n)$
will not play a central role, so for any
![]() $f \in L^2({ \mathbb R}^n)$
and for any
$f \in L^2({ \mathbb R}^n)$
and for any
![]() $z \in { \mathbb R}^n$
, define
$z \in { \mathbb R}^n$
, define
 $$ \begin{align*} &\mathbf z_3 := (z_3, z_4, \ldots, z_n) \in { \mathbb R}^{n-2}, \\ &f_{\mathbf z_3}(z_1, z_2) := f(z). \end{align*} $$
$$ \begin{align*} &\mathbf z_3 := (z_3, z_4, \ldots, z_n) \in { \mathbb R}^{n-2}, \\ &f_{\mathbf z_3}(z_1, z_2) := f(z). \end{align*} $$
For
![]() $j = 1, 2$
, let
$j = 1, 2$
, let
![]() $\mathcal F_j$
be the Fourier transform in the
$\mathcal F_j$
be the Fourier transform in the
![]() $z_j$
-variable, so
$z_j$
-variable, so
 $$ \begin{align*} &\mathcal F_1 f_{\mathbf z_3}(\omega_1, z_2) := \int_{ \mathbb R} f_{\mathbf z_3}(z_1, z_2) e^{-2\pi i \omega_1 z_1}\,dz_1, \\ &\mathcal F_2 f_{\mathbf z_3}(z_1, \omega_2) := \int_{ \mathbb R} f_{\mathbf z_3}(z_1, z_2) e^{-2\pi i \omega_2 z_2}\,dz_2. \end{align*} $$
$$ \begin{align*} &\mathcal F_1 f_{\mathbf z_3}(\omega_1, z_2) := \int_{ \mathbb R} f_{\mathbf z_3}(z_1, z_2) e^{-2\pi i \omega_1 z_1}\,dz_1, \\ &\mathcal F_2 f_{\mathbf z_3}(z_1, \omega_2) := \int_{ \mathbb R} f_{\mathbf z_3}(z_1, z_2) e^{-2\pi i \omega_2 z_2}\,dz_2. \end{align*} $$
We begin with a short lemma.
Lemma 2.7. For any
![]() $s \geq 0$
and for any
$s \geq 0$
and for any
![]() $\epsilon \in (0, 1)$
, there is a constant
$\epsilon \in (0, 1)$
, there is a constant
![]() $C_{\epsilon }> 0$
such that for any
$C_{\epsilon }> 0$
such that for any
![]() $\mathbf z \in { \mathbb R}^n$
and for any
$\mathbf z \in { \mathbb R}^n$
and for any
![]() $f \in W^{s+n/2+\epsilon }({ \mathbb R}^n)$
, the functions f,
$f \in W^{s+n/2+\epsilon }({ \mathbb R}^n)$
, the functions f,
![]() $\mathcal F_1 f$
and
$\mathcal F_1 f$
and
![]() $\mathcal F_2 f$
are continuous on
$\mathcal F_2 f$
are continuous on
![]() ${ \mathbb R}^n$
, and
${ \mathbb R}^n$
, and
 $$ \begin{align} & \vert f_{\mathbf z_3}(z_1, z_2) \vert \leq\dfrac {C_{\epsilon}}{\big(1 + \displaystyle\sum\nolimits_{i=1}^n z_i^2\big)^{s/2}} |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_{s + n/2 + \epsilon}, \end{align} $$
$$ \begin{align} & \vert f_{\mathbf z_3}(z_1, z_2) \vert \leq\dfrac {C_{\epsilon}}{\big(1 + \displaystyle\sum\nolimits_{i=1}^n z_i^2\big)^{s/2}} |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_{s + n/2 + \epsilon}, \end{align} $$
 $$ \begin{align} & \vert \mathcal F_2 f_{\mathbf z_3}(z_1, \omega_2) \vert \leq \dfrac{C_{\epsilon}}{\big(1 + \omega_2^2 + \displaystyle\sum\nolimits_{\substack{1 \leq i \leq n \\ i \neq 2}} z_i^2\big)^{s/2}} |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_{s + n/2 + \epsilon}. \end{align} $$
$$ \begin{align} & \vert \mathcal F_2 f_{\mathbf z_3}(z_1, \omega_2) \vert \leq \dfrac{C_{\epsilon}}{\big(1 + \omega_2^2 + \displaystyle\sum\nolimits_{\substack{1 \leq i \leq n \\ i \neq 2}} z_i^2\big)^{s/2}} |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_{s + n/2 + \epsilon}. \end{align} $$
Similarly, for any
![]() $(\omega , z_2) \in { \mathbb R}^2$
, for any
$(\omega , z_2) \in { \mathbb R}^2$
, for any
![]() $r \geq 0$
and for any
$r \geq 0$
and for any
![]() $f \in W^{s+r+ n/2+\epsilon }({ \mathbb R}^n)$
,
$f \in W^{s+r+ n/2+\epsilon }({ \mathbb R}^n)$
,
 $$ \begin{align} & \vert f_{\mathbf z_3}(z_1, z_2) \vert \leq\frac {C_\epsilon}{(1 + z_1^2)^{r/2}\big(1 + \displaystyle\sum\nolimits_{i = 2}^n z_i^2\big)^{s/2} } |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_{s +r+ n/2 + \epsilon}, \end{align} $$
$$ \begin{align} & \vert f_{\mathbf z_3}(z_1, z_2) \vert \leq\frac {C_\epsilon}{(1 + z_1^2)^{r/2}\big(1 + \displaystyle\sum\nolimits_{i = 2}^n z_i^2\big)^{s/2} } |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_{s +r+ n/2 + \epsilon}, \end{align} $$
 $$ \begin{align} & \vert \mathcal F_1 f_{\mathbf z_3} (\omega_1, z_2) \vert \leq \frac{C_\epsilon}{(1 + \omega_1^2)^{r/2}\big(1 + \displaystyle\sum\nolimits_{i = 2}^n z_i^2\big)^{s/2} } |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_{r+s + n/2+\epsilon}. \end{align} $$
$$ \begin{align} & \vert \mathcal F_1 f_{\mathbf z_3} (\omega_1, z_2) \vert \leq \frac{C_\epsilon}{(1 + \omega_1^2)^{r/2}\big(1 + \displaystyle\sum\nolimits_{i = 2}^n z_i^2\big)^{s/2} } |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_{r+s + n/2+\epsilon}. \end{align} $$
Proof The Sobolev embedding theorem implies that there is a constant
![]() $C_\epsilon> 0$
such that
$C_\epsilon> 0$
such that

This implies the first inequality and that f is continuous. The inequality (26) follows in the same way by applying the inverse Fourier transform
![]() $\mathcal F_2^{-1}$
. Then
$\mathcal F_2^{-1}$
. Then
![]() $\mathcal F_2 f$
is also continuous.
$\mathcal F_2 f$
is also continuous.
For (28), the Sobolev embedding theorem again gives a constant
![]() $C_\epsilon> 0$
such that
$C_\epsilon> 0$
such that
 $$ \begin{align*} &\bigg\Vert (I + \omega_1^2)^{r/2} \bigg(I + \sum_{i = 2}^n z_i^2\bigg)^{s/2} \mathcal F_1 f\bigg\Vert_{ C^{0, \epsilon} ({ \mathbb R}^n)} \\ &\quad \leq C_\epsilon \bigg\Vert \bigg(I - \frac{\partial^2}{\partial \omega_1^2} - \sum_{i = 2}^n\frac{\partial^2}{\partial z_i^2}\bigg)^{(n/2 + \epsilon)/2} (I + \omega_1^2)^{r/2} \bigg(I+\sum_{i = 2}^n z_i^2\bigg)^{s/2} \mathcal F_1 f \bigg\Vert_{L^2({ \mathbb R}^n)}\\ &\quad \leq C_\epsilon \bigg\Vert \bigg(I + z_1^2 - \sum_{i = 2}^n\frac{\partial^2}{\partial z_i^2}\bigg)^{(n/2 + \epsilon)/2} \bigg(I - \frac{\partial^2}{\partial z_1^2}\bigg)^{r/2}\bigg(I + \sum_{i = 2}^n z_i^2\bigg)^{s/2} f \bigg\Vert_{L^2({ \mathbb R}^n)} \\ &\quad \leq C_\epsilon |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_{r + s + n/2 + \epsilon}. \end{align*} $$
$$ \begin{align*} &\bigg\Vert (I + \omega_1^2)^{r/2} \bigg(I + \sum_{i = 2}^n z_i^2\bigg)^{s/2} \mathcal F_1 f\bigg\Vert_{ C^{0, \epsilon} ({ \mathbb R}^n)} \\ &\quad \leq C_\epsilon \bigg\Vert \bigg(I - \frac{\partial^2}{\partial \omega_1^2} - \sum_{i = 2}^n\frac{\partial^2}{\partial z_i^2}\bigg)^{(n/2 + \epsilon)/2} (I + \omega_1^2)^{r/2} \bigg(I+\sum_{i = 2}^n z_i^2\bigg)^{s/2} \mathcal F_1 f \bigg\Vert_{L^2({ \mathbb R}^n)}\\ &\quad \leq C_\epsilon \bigg\Vert \bigg(I + z_1^2 - \sum_{i = 2}^n\frac{\partial^2}{\partial z_i^2}\bigg)^{(n/2 + \epsilon)/2} \bigg(I - \frac{\partial^2}{\partial z_1^2}\bigg)^{r/2}\bigg(I + \sum_{i = 2}^n z_i^2\bigg)^{s/2} f \bigg\Vert_{L^2({ \mathbb R}^n)} \\ &\quad \leq C_\epsilon |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_{r + s + n/2 + \epsilon}. \end{align*} $$
The estimate of (27) follows as above.
2.3.2 Invariant operators and cohomological equations
For any
![]() $m \in { \mathbb Z}$
, let
$m \in { \mathbb Z}$
, let
![]() $\pi _{m, \boldsymbol {\tau }}$
be the formal operator
$\pi _{m, \boldsymbol {\tau }}$
be the formal operator
 $$ \begin{align} \pi_{m, \boldsymbol{\tau}} f(z) := \mathcal F_1 f\bigg(\frac{m}{\tau}, z_2, \ldots, z_n\bigg). \end{align} $$
$$ \begin{align} \pi_{m, \boldsymbol{\tau}} f(z) := \mathcal F_1 f\bigg(\frac{m}{\tau}, z_2, \ldots, z_n\bigg). \end{align} $$
Now we record a decay estimate of
![]() $\vert \pi _{m, \boldsymbol {\tau }}(f) \vert _s$
with respect to m, which will be used later in the splitting result, Theorem 1.3. Recall Definition 2.4 for the meaning of
$\vert \pi _{m, \boldsymbol {\tau }}(f) \vert _s$
with respect to m, which will be used later in the splitting result, Theorem 1.3. Recall Definition 2.4 for the meaning of
![]() $\vert f \vert _s$
.
$\vert f \vert _s$
.
Corollary 2.8. For any
![]() $\epsilon> 0$
, there is a constant
$\epsilon> 0$
, there is a constant
![]() $C_\epsilon> 0$
such that for any
$C_\epsilon> 0$
such that for any
![]() ${s, r \geq 0}$
and for any
${s, r \geq 0}$
and for any
![]() $m \in { \mathbb Z}$
, the operator
$m \in { \mathbb Z}$
, the operator
![]() $\pi _{m, \boldsymbol {\tau }}$
satisfies the following estimate. For any
$\pi _{m, \boldsymbol {\tau }}$
satisfies the following estimate. For any
![]() $f \in W^{r+s+3n/2-1+\epsilon }({ \mathbb R}^n)$
, we have
$f \in W^{r+s+3n/2-1+\epsilon }({ \mathbb R}^n)$
, we have
 $$ \begin{align*} \vert \pi_{m, \boldsymbol{\tau}}(f) \vert_s \leq C_\epsilon \bigg(1 + \bigg\vert \frac{m}{\tau}\bigg\vert \bigg)^{-r} |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_{r+s+3n/2-1+\epsilon}. \end{align*} $$
$$ \begin{align*} \vert \pi_{m, \boldsymbol{\tau}}(f) \vert_s \leq C_\epsilon \bigg(1 + \bigg\vert \frac{m}{\tau}\bigg\vert \bigg)^{-r} |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_{r+s+3n/2-1+\epsilon}. \end{align*} $$
Proof First let
![]() $f \in \mathscr {S}({ \mathbb R}^n)$
. Because
$f \in \mathscr {S}({ \mathbb R}^n)$
. Because
![]() $\mathcal F_1$
commutes with
$\mathcal F_1$
commutes with
![]() $(I - \sum _{i = 2}^n ({\partial ^2}/{\partial z_i^2}) + z_i^2)^{s/2}$
, for any
$(I - \sum _{i = 2}^n ({\partial ^2}/{\partial z_i^2}) + z_i^2)^{s/2}$
, for any
![]() $m \in { \mathbb Z}$
, we have
$m \in { \mathbb Z}$
, we have
 $$ \begin{align} \vert \pi_{m, \boldsymbol{\tau}}(f) \vert_s & = \bigg\Vert \bigg(I - \sum_{i = 2}^n \frac{\partial^2}{\partial z_i^2} + z_i^2\bigg)^{s/2} \mathcal F_1 f_{\mathbf z_3}\bigg(\frac{m}{\tau}, z_2\bigg)\bigg\Vert_{L^2({ \mathbb R}^{n-1})} \notag \\ & = \bigg\Vert \mathcal F_1\bigg(\bigg(I - \sum_{i = 2}^n \frac{\partial^2}{\partial z_i^2} + z_i^2\bigg)^{s/2} f_{\mathbf z_3}\bigg)\bigg(\frac{m}{\tau}, z_2\bigg) \bigg\Vert_{L^2({ \mathbb R}^{n-1})}. \end{align} $$
$$ \begin{align} \vert \pi_{m, \boldsymbol{\tau}}(f) \vert_s & = \bigg\Vert \bigg(I - \sum_{i = 2}^n \frac{\partial^2}{\partial z_i^2} + z_i^2\bigg)^{s/2} \mathcal F_1 f_{\mathbf z_3}\bigg(\frac{m}{\tau}, z_2\bigg)\bigg\Vert_{L^2({ \mathbb R}^{n-1})} \notag \\ & = \bigg\Vert \mathcal F_1\bigg(\bigg(I - \sum_{i = 2}^n \frac{\partial^2}{\partial z_i^2} + z_i^2\bigg)^{s/2} f_{\mathbf z_3}\bigg)\bigg(\frac{m}{\tau}, z_2\bigg) \bigg\Vert_{L^2({ \mathbb R}^{n-1})}. \end{align} $$
Then (28) gives

so
 $$ \begin{align*} (30) & \leq C_\epsilon \bigg(1 + \bigg\vert \frac{m}{\tau}\bigg\vert \bigg)^{-r} |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_{r+s+3n/2-1+2\epsilon} \notag.\\ \end{align*} $$
$$ \begin{align*} (30) & \leq C_\epsilon \bigg(1 + \bigg\vert \frac{m}{\tau}\bigg\vert \bigg)^{-r} |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_{r+s+3n/2-1+2\epsilon} \notag.\\ \end{align*} $$
The next lemma shows that for any
![]() $m \in { \mathbb Z}$
,
$m \in { \mathbb Z}$
,
![]() $\pi _{m, \boldsymbol {\tau }}$
are invariant operators for
$\pi _{m, \boldsymbol {\tau }}$
are invariant operators for
![]() $\tilde {\mu }(\textrm{ exp}(Y_{\boldsymbol {\tau }}))$
on sufficiently regular functions.
$\tilde {\mu }(\textrm{ exp}(Y_{\boldsymbol {\tau }}))$
on sufficiently regular functions.
Lemma 2.9. For any
![]() $m \in { \mathbb Z}$
and for any
$m \in { \mathbb Z}$
and for any
![]() $\epsilon> 0$
,
$\epsilon> 0$
,
holds on
![]() $W^{n/2 + \epsilon }({ \mathbb R}^n)$
.
$W^{n/2 + \epsilon }({ \mathbb R}^n)$
.
Proof Lemma 2.7 shows that for any
![]() $m \in { \mathbb Z}$
and any
$m \in { \mathbb Z}$
and any
![]() $f \in W^{n/2+\epsilon }({ \mathbb R}^n)$
,
$f \in W^{n/2+\epsilon }({ \mathbb R}^n)$
,
![]() $\pi _{m, \boldsymbol {\tau }} f$
is continuous on
$\pi _{m, \boldsymbol {\tau }} f$
is continuous on
![]() ${ \mathbb R}^{n-1}$
. Moreover,
${ \mathbb R}^{n-1}$
. Moreover,
 $$ \begin{align*} \pi_{m, \boldsymbol{\tau}}\tilde{\mu}(\textrm{ exp}(Y_{\boldsymbol{\tau}}))f(z)& = \pi_{m, \boldsymbol{\tau}} f(z - (\tau, 0, \ldots, 0))\\ & = \pi_{m, \boldsymbol{\tau}}f(z).\\ \end{align*} $$
$$ \begin{align*} \pi_{m, \boldsymbol{\tau}}\tilde{\mu}(\textrm{ exp}(Y_{\boldsymbol{\tau}}))f(z)& = \pi_{m, \boldsymbol{\tau}} f(z - (\tau, 0, \ldots, 0))\\ & = \pi_{m, \boldsymbol{\tau}}f(z).\\ \end{align*} $$
For any
![]() $s> 2$
, define
$s> 2$
, define
Proposition 2.10. For any
![]() $f \in \textrm{ Ann}_{\boldsymbol {\tau }}$
, the cohomological equation
$f \in \textrm{ Ann}_{\boldsymbol {\tau }}$
, the cohomological equation
has a unique solution P in
![]() $L^2({ \mathbb R}^n)$
and, moreover, for any
$L^2({ \mathbb R}^n)$
and, moreover, for any
![]() $\epsilon> 0$
, there is a constant
$\epsilon> 0$
, there is a constant
![]() $C_{\epsilon }> 0$
such that for any
$C_{\epsilon }> 0$
such that for any
![]() $s \geq 0$
,
$s \geq 0$
,
Proof Let
![]() $s \geq 0$
,
$s \geq 0$
,
![]() $f \in \mathscr {S}({ \mathbb R}^n)$
and
$f \in \mathscr {S}({ \mathbb R}^n)$
and
![]() $T: \mathscr {S}({ \mathbb R}^n) \to \mathscr {S}({ \mathbb R}^n)$
be the linear map
$T: \mathscr {S}({ \mathbb R}^n) \to \mathscr {S}({ \mathbb R}^n)$
be the linear map
 $$ \begin{align} T f(z) = \sum_{m = 1}^{\infty} f(z_1 + m \tau, z_2, \ldots, z_n), \end{align} $$
$$ \begin{align} T f(z) = \sum_{m = 1}^{\infty} f(z_1 + m \tau, z_2, \ldots, z_n), \end{align} $$
which converges absolutely and uniformly on compact sets.
By (24), the cohomological equation (31) is
Clearly, there is at most one
![]() $L^2({ \mathbb R}^n)$
solution P to the above equation. Because
$L^2({ \mathbb R}^n)$
solution P to the above equation. Because
![]() $T f$
is a solution,
$T f$
is a solution,
on
![]() ${ \mathbb R}^n$
.
${ \mathbb R}^n$
.
Because
![]() $f \in \textrm{ Ann}_{\boldsymbol {\tau }}$
, the Poisson summation formula gives that for any
$f \in \textrm{ Ann}_{\boldsymbol {\tau }}$
, the Poisson summation formula gives that for any
![]() $z \in { \mathbb R}^n$
,
$z \in { \mathbb R}^n$
,
By combining the above equality with (32), we get that
 $$ \begin{align} T f(z) = \sum_{m = 0}^{\infty} f(z_1 - m\tau, z_2, \ldots, z_n), \end{align} $$
$$ \begin{align} T f(z) = \sum_{m = 0}^{\infty} f(z_1 - m\tau, z_2, \ldots, z_n), \end{align} $$
which is again convergent.
Now we estimate the homogeneous norm
![]() $ |\mkern -1.5mu|\mkern -1.5mu| T f |\mkern -1.5mu|\mkern -1.5mu|_s$
. By (25) and formula (32), we get that for all
$ |\mkern -1.5mu|\mkern -1.5mu| T f |\mkern -1.5mu|\mkern -1.5mu|_s$
. By (25) and formula (32), we get that for all
![]() $z\in ({ \mathbb R}^+\cup \{0\}) \times { \mathbb R}^{n-1}$
,
$z\in ({ \mathbb R}^+\cup \{0\}) \times { \mathbb R}^{n-1}$
,
 $$ \begin{align} &\kern-15pt\bigg\vert \bigg(I + \sum_{i= 1}^n z_i^2-\frac{\partial}{\partial z_i^2}\bigg)^{s/2} T f (z) \bigg\vert\qquad\qquad\qquad\qquad\qquad\qquad\qquad \end{align} $$
$$ \begin{align} &\kern-15pt\bigg\vert \bigg(I + \sum_{i= 1}^n z_i^2-\frac{\partial}{\partial z_i^2}\bigg)^{s/2} T f (z) \bigg\vert\qquad\qquad\qquad\qquad\qquad\qquad\qquad \end{align} $$
 $$ \begin{align} & \leq \sum_{m = 0}^{\infty} \bigg\vert \bigg(I + \sum_{i= 1}^n z_i^2-\frac{\partial}{\partial z_i^2}\bigg)^{s/2} f(z_1+m\tau, z_2, \ldots, z_n) \bigg\vert \notag \\ & \leq \sum_{m = 0}^{\infty} \bigg|\bigg(I - \frac{\partial^2}{\partial (z_1+m\tau)^2} +(z_1+m\tau)^2+ \sum_{i=2}^n z_i^2 - \frac{\partial^2}{\partial z_i^2}\bigg)^{s/2} \notag \\ & \qquad\qquad\times f(z_1+m\tau, z_2, \ldots, z_n)\bigg\vert. \end{align} $$
$$ \begin{align} & \leq \sum_{m = 0}^{\infty} \bigg\vert \bigg(I + \sum_{i= 1}^n z_i^2-\frac{\partial}{\partial z_i^2}\bigg)^{s/2} f(z_1+m\tau, z_2, \ldots, z_n) \bigg\vert \notag \\ & \leq \sum_{m = 0}^{\infty} \bigg|\bigg(I - \frac{\partial^2}{\partial (z_1+m\tau)^2} +(z_1+m\tau)^2+ \sum_{i=2}^n z_i^2 - \frac{\partial^2}{\partial z_i^2}\bigg)^{s/2} \notag \\ & \qquad\qquad\times f(z_1+m\tau, z_2, \ldots, z_n)\bigg\vert. \end{align} $$
Let
![]() $r = n + 1 + 2\epsilon $
, so equation (25) gives
$r = n + 1 + 2\epsilon $
, so equation (25) gives

Using (33), we get by a completely analogous argument that for all
![]() $z \in { \mathbb R}^- \times { \mathbb R}^{n-1}$
,
$z \in { \mathbb R}^- \times { \mathbb R}^{n-1}$
,
 $$ \begin{align*} \bigg\vert \bigg(I + \sum_{i= 1}^n z_i^2 - \frac{\partial}{\partial z_i^2}\bigg)^{s/2} T f (z) \bigg\vert\leq \frac{C_{\epsilon}}{\tau} \bigg(1 + \sum_{i = 1}^n z_i^2\bigg)^{-(n + \epsilon)/2} |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_{s + 3n/2 +1+ 3\epsilon}. \end{align*} $$
$$ \begin{align*} \bigg\vert \bigg(I + \sum_{i= 1}^n z_i^2 - \frac{\partial}{\partial z_i^2}\bigg)^{s/2} T f (z) \bigg\vert\leq \frac{C_{\epsilon}}{\tau} \bigg(1 + \sum_{i = 1}^n z_i^2\bigg)^{-(n + \epsilon)/2} |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_{s + 3n/2 +1+ 3\epsilon}. \end{align*} $$
It follows that
Because
![]() $s \geq 0$
was arbitrary, we have shown that the above estimate in terms of the norm that is homogeneous in h holds for any
$s \geq 0$
was arbitrary, we have shown that the above estimate in terms of the norm that is homogeneous in h holds for any
![]() $s \geq 0$
. Then we apply Lemma 2.3 to get the estimate with respect to the Laplacian. So,
$s \geq 0$
. Then we apply Lemma 2.3 to get the estimate with respect to the Laplacian. So,
The lemma is now proved with
![]() $P = T f$
.
$P = T f$
.
Now we find a solution with Sobolev estimates to the equation
![]() $L_{\boldsymbol \eta } P = f. $
For any
$L_{\boldsymbol \eta } P = f. $
For any
![]() $m \in { \mathbb Z}$
, define
$m \in { \mathbb Z}$
, define
![]() $\pi _{m, \boldsymbol \eta }$
to be the formal operator
$\pi _{m, \boldsymbol \eta }$
to be the formal operator
 $$ \begin{align*} \pi_{m, \boldsymbol\eta} f(z_1, z_3, \ldots, z_n) := f\bigg(z_1, \frac{2\pi m}{\nu_2}, z_3, \ldots, z_n\bigg). \end{align*} $$
$$ \begin{align*} \pi_{m, \boldsymbol\eta} f(z_1, z_3, \ldots, z_n) := f\bigg(z_1, \frac{2\pi m}{\nu_2}, z_3, \ldots, z_n\bigg). \end{align*} $$
We get as in Corollary 2.8 that for any
![]() $s \geq 0$
and
$s \geq 0$
and
![]() $\epsilon> 0$
,
$\epsilon> 0$
,
![]() $\pi _{m, \boldsymbol \eta } : W^{s+3n/2-1+\epsilon }({ \mathbb R}^n) \to W^{s}({ \mathbb R}^{n-1})$
and, by Lemma 2.7 that for any
$\pi _{m, \boldsymbol \eta } : W^{s+3n/2-1+\epsilon }({ \mathbb R}^n) \to W^{s}({ \mathbb R}^{n-1})$
and, by Lemma 2.7 that for any
![]() $f \in W^{n/2 + \epsilon }({ \mathbb R}^n)$
,
$f \in W^{n/2 + \epsilon }({ \mathbb R}^n)$
,
![]() $\pi _{m, \boldsymbol \eta } f$
is continuous on
$\pi _{m, \boldsymbol \eta } f$
is continuous on
![]() ${ \mathbb R}^{n-1}$
.
${ \mathbb R}^{n-1}$
.
As in Lemma 2.9, it can be immediately verified that for any
![]() $m \in { \mathbb Z}$
,
$m \in { \mathbb Z}$
,
![]() $\pi _{m, \boldsymbol \eta }$
is invariant for the operator
$\pi _{m, \boldsymbol \eta }$
is invariant for the operator
![]() $\tilde {\mu }(\textrm{ exp}(Y_{\boldsymbol \eta }))$
. Define
$\tilde {\mu }(\textrm{ exp}(Y_{\boldsymbol \eta }))$
. Define
We have a corresponding estimate for the cohomological equation
![]() $L_{\boldsymbol {\eta }} P = f$
.
$L_{\boldsymbol {\eta }} P = f$
.
Corollary 2.11. For any
![]() $f \in \textrm{ Ann}_{\boldsymbol {\eta }}$
, the equation
$f \in \textrm{ Ann}_{\boldsymbol {\eta }}$
, the equation
has a unique solution P in
![]() $L^2({ \mathbb R}^n)$
and, moreover, for any
$L^2({ \mathbb R}^n)$
and, moreover, for any
![]() $\epsilon> 0$
, there is a constant
$\epsilon> 0$
, there is a constant
![]() $C_{\epsilon }> 0$
such that for any
$C_{\epsilon }> 0$
such that for any
![]() $s \geq 0$
,
$s \geq 0$
,
Proof Writing (24) as a Fourier transform, we get
 $$ \begin{align} \mathcal F_2 L_{\boldsymbol{\eta}} f_{\mathbf z_3}(z_1, \omega_2) = \mathcal F_2 f_{\mathbf z_3}\bigg(z_1, \omega_2 - \frac{\nu_2}{2\pi}\bigg) - \mathcal F_2 f_{\mathbf z_3}(z_1, \omega_2). \end{align} $$
$$ \begin{align} \mathcal F_2 L_{\boldsymbol{\eta}} f_{\mathbf z_3}(z_1, \omega_2) = \mathcal F_2 f_{\mathbf z_3}\bigg(z_1, \omega_2 - \frac{\nu_2}{2\pi}\bigg) - \mathcal F_2 f_{\mathbf z_3}(z_1, \omega_2). \end{align} $$
Then, setting
![]() $\tau = ({\nu _2}/{2\pi })$
, the corollary follows in the same way as Proposition 2.10, using the decay estimate (26) in place of (25).
$\tau = ({\nu _2}/{2\pi })$
, the corollary follows in the same way as Proposition 2.10, using the decay estimate (26) in place of (25).
Next, we prove Theorem 1.2 for Schrödinger representations.
Theorem 2.12. For any
![]() $f, g \in \mathscr {S}({ \mathbb R}^n)$
that satisfy
$f, g \in \mathscr {S}({ \mathbb R}^n)$
that satisfy
![]() $L_{\boldsymbol {\tau }} g = L_{\boldsymbol {\eta }} f$
, there is a solution
$L_{\boldsymbol {\tau }} g = L_{\boldsymbol {\eta }} f$
, there is a solution
![]() $P \in \mathscr {S}({ \mathbb R}^n)$
such that
$P \in \mathscr {S}({ \mathbb R}^n)$
such that
Moreover, for any
![]() $\epsilon> 0$
, there is a constant
$\epsilon> 0$
, there is a constant
![]() $C_{\epsilon }> 0$
such that for any
$C_{\epsilon }> 0$
such that for any
![]() $s \geq 0$
,
$s \geq 0$
,
Proof Let
![]() $m \in { \mathbb Z}$
. Because
$m \in { \mathbb Z}$
. Because
![]() $\pi _{m, \boldsymbol {\tau }}$
is invariant for
$\pi _{m, \boldsymbol {\tau }}$
is invariant for
![]() $\tilde {\mu }(\textrm{ exp}(Y_{\boldsymbol {\tau }}))$
, we have that
$\tilde {\mu }(\textrm{ exp}(Y_{\boldsymbol {\tau }}))$
, we have that
From the formulas for
![]() $\pi _{m, \boldsymbol {\tau }}$
and
$\pi _{m, \boldsymbol {\tau }}$
and
![]() $L_{\boldsymbol \eta }$
, see (29) and (24), respectively, we get
$L_{\boldsymbol \eta }$
, see (29) and (24), respectively, we get
Moreover, for any
![]() $(z_2, \ldots , z_n) \in { \mathbb R}^{n-1}$
,
$(z_2, \ldots , z_n) \in { \mathbb R}^{n-1}$
,
 $$ \begin{align*} 0 = L_{\boldsymbol{\eta}} \pi_{m, \boldsymbol{\tau}}f (z_2, \ldots, z_n) = [\textrm{ exp}( i \nu_2 z_2) - 1] \mathcal F_1f\bigg(\frac{m}{\tau}, z_2, \ldots, z_n\bigg). \end{align*} $$
$$ \begin{align*} 0 = L_{\boldsymbol{\eta}} \pi_{m, \boldsymbol{\tau}}f (z_2, \ldots, z_n) = [\textrm{ exp}( i \nu_2 z_2) - 1] \mathcal F_1f\bigg(\frac{m}{\tau}, z_2, \ldots, z_n\bigg). \end{align*} $$
So, we get that off a countable set of
![]() $z_2 \in { \mathbb R}$
,
$z_2 \in { \mathbb R}$
,
 $$ \begin{align*} \mathcal F_1f\bigg(\frac{m}{\tau}, z_2, \ldots, z_n\bigg) = 0. \end{align*} $$
$$ \begin{align*} \mathcal F_1f\bigg(\frac{m}{\tau}, z_2, \ldots, z_n\bigg) = 0. \end{align*} $$
Lemma 2.7 shows that
![]() $\mathcal F_1f$
is continuous, which implies that
$\mathcal F_1f$
is continuous, which implies that
![]() $\pi _{m, \boldsymbol {\tau }} f \equiv 0$
. Because
$\pi _{m, \boldsymbol {\tau }} f \equiv 0$
. Because
![]() $m \in { \mathbb Z}$
was arbitrary, we conclude that
$m \in { \mathbb Z}$
was arbitrary, we conclude that
![]() $f \in \textrm{ Ann}_{\boldsymbol {\tau }}$
.
$f \in \textrm{ Ann}_{\boldsymbol {\tau }}$
.
Proposition 2.10 now implies that there is a unique function P in
![]() $L^2({ \mathbb R}^n)$
that is a solution to
$L^2({ \mathbb R}^n)$
that is a solution to
and, for any
![]() $\epsilon> 0$
, there is a constant
$\epsilon> 0$
, there is a constant
![]() $C_\epsilon> 0$
such that
$C_\epsilon> 0$
such that
Finally, because
![]() $[Y_{\boldsymbol \eta }, Y_{\boldsymbol {\tau }}] = 0$
, we use
$[Y_{\boldsymbol \eta }, Y_{\boldsymbol {\tau }}] = 0$
, we use
![]() $L_{\boldsymbol {\tau }} g = L_{\boldsymbol {\eta }} f$
and get
$L_{\boldsymbol {\tau }} g = L_{\boldsymbol {\eta }} f$
and get
So,
![]() $L_{\boldsymbol {\tau }}(g- L_{\boldsymbol {\eta }} P) = 0$
and, because
$L_{\boldsymbol {\tau }}(g- L_{\boldsymbol {\eta }} P) = 0$
and, because
![]() $g - L_{\boldsymbol {\eta }}P \in L^2({ \mathbb R}^n)$
, it follows that
$g - L_{\boldsymbol {\eta }}P \in L^2({ \mathbb R}^n)$
, it follows that
in
![]() $L^2({ \mathbb R}^n)$
.
$L^2({ \mathbb R}^n)$
.
Now we will prove Theorem 1.3 in the case of Schrödinger representations. Recall from Lemma 2.6 that
![]() $\nu _2 \neq 0$
.
$\nu _2 \neq 0$
.
Theorem 2.13. For any
![]() $f, g, \phi \in \mathscr {S}({ \mathbb R}^n)$
that satisfy
$f, g, \phi \in \mathscr {S}({ \mathbb R}^n)$
that satisfy
![]() $L_{\boldsymbol {\eta }} f - L_{\boldsymbol {\tau }} g = \phi $
, there exists a non-constant function
$L_{\boldsymbol {\eta }} f - L_{\boldsymbol {\tau }} g = \phi $
, there exists a non-constant function
![]() $P \in \mathscr {S}({ \mathbb R}^n)$
such that the following holds. For any
$P \in \mathscr {S}({ \mathbb R}^n)$
such that the following holds. For any
![]() $s \geq 0$
and for any
$s \geq 0$
and for any
![]() $\epsilon> 0$
, there is a constant
$\epsilon> 0$
, there is a constant
![]() $C_{s, \epsilon }> 0$
such that
$C_{s, \epsilon }> 0$
such that
 $$\begin{gather*} \|g - L_{\boldsymbol{\eta}} P\|_s \leq C_{s, \epsilon} (\tau^{-1} + \tau^{\epsilon}) \| \phi\|_{s + 3n + 1 + 2\epsilon}, \\ \|f - L_{\boldsymbol{\tau}} P\|_s \leq \frac{C_{s, \epsilon}}{\nu_2} (1 + \tau^{1+\epsilon}) \| \phi\|_{s + 3n + 1 + 2\epsilon} , \\ \| P \|_s \leq C_{s, \epsilon} (\tau^{-1} + \tau^{\epsilon}) (\| f\|_{s + 3n + 1 + \epsilon} + \| g\|_{s + 3n + 1 + 2\epsilon}). \end{gather*}$$
$$\begin{gather*} \|g - L_{\boldsymbol{\eta}} P\|_s \leq C_{s, \epsilon} (\tau^{-1} + \tau^{\epsilon}) \| \phi\|_{s + 3n + 1 + 2\epsilon}, \\ \|f - L_{\boldsymbol{\tau}} P\|_s \leq \frac{C_{s, \epsilon}}{\nu_2} (1 + \tau^{1+\epsilon}) \| \phi\|_{s + 3n + 1 + 2\epsilon} , \\ \| P \|_s \leq C_{s, \epsilon} (\tau^{-1} + \tau^{\epsilon}) (\| f\|_{s + 3n + 1 + \epsilon} + \| g\|_{s + 3n + 1 + 2\epsilon}). \end{gather*}$$
Proof Notice that if
![]() $f = g = 0$
, then
$f = g = 0$
, then
![]() $\phi = 0$
and the above statement holds trivially. Without loss of generality, we assume that
$\phi = 0$
and the above statement holds trivially. Without loss of generality, we assume that
![]() $f \neq 0$
.
$f \neq 0$
.
Let
![]() $\psi \in \mathscr {S}({ \mathbb R})$
, whose Fourier transform is compactly supported on
$\psi \in \mathscr {S}({ \mathbb R})$
, whose Fourier transform is compactly supported on
![]() $[-({1}/{2\tau }), ({1}/{2 \tau })]$
and satisfies
$[-({1}/{2\tau }), ({1}/{2 \tau })]$
and satisfies
![]() $\mathcal F\psi (0) = 1$
. For each
$\mathcal F\psi (0) = 1$
. For each
![]() $m \in { \mathbb Z}$
, define the functional
$m \in { \mathbb Z}$
, define the functional
![]() $\Pi _{m, \boldsymbol {\tau }}$
on
$\Pi _{m, \boldsymbol {\tau }}$
on
![]() $L^2({ \mathbb R}^{n-1})$
by
$L^2({ \mathbb R}^{n-1})$
by
Below,
![]() $\Pi _{m, \boldsymbol {\tau }}$
will be a component of an operator that maps sufficiently regular functions to coboundaries. See (39) and Lemma 2.16 for details. For now, we have the following estimate.
$\Pi _{m, \boldsymbol {\tau }}$
will be a component of an operator that maps sufficiently regular functions to coboundaries. See (39) and Lemma 2.16 for details. For now, we have the following estimate.
Lemma 2.14. For any
![]() $s \in 2 { \mathbb N}$
, for any
$s \in 2 { \mathbb N}$
, for any
![]() $m \in { \mathbb Z}$
and for any
$m \in { \mathbb Z}$
and for any
![]() $F \in W^s({ \mathbb R}^{n-1})$
, there is a constant
$F \in W^s({ \mathbb R}^{n-1})$
, there is a constant
![]() $C_s> 0$
such that
$C_s> 0$
such that
 $$ \begin{align*} \kern-25pt|\mkern-1.5mu|\mkern-1.5mu| \Pi_{m, \boldsymbol{\tau}} F |\mkern-1.5mu|\mkern-1.5mu|_s \leq C_s \Vert \bigg(I + z_1^2- \frac{\partial^2}{\partial z_1^2}\bigg)^{s/2} \psi \Vert_{L^{\infty}({ \mathbb R})} \sum_{k = 0}^{s/2} \bigg(1+\bigg\vert\frac{m}{\tau}\bigg\vert\bigg)^{2k} \vert F \vert_{s-2k}.\\ \end{align*} $$
$$ \begin{align*} \kern-25pt|\mkern-1.5mu|\mkern-1.5mu| \Pi_{m, \boldsymbol{\tau}} F |\mkern-1.5mu|\mkern-1.5mu|_s \leq C_s \Vert \bigg(I + z_1^2- \frac{\partial^2}{\partial z_1^2}\bigg)^{s/2} \psi \Vert_{L^{\infty}({ \mathbb R})} \sum_{k = 0}^{s/2} \bigg(1+\bigg\vert\frac{m}{\tau}\bigg\vert\bigg)^{2k} \vert F \vert_{s-2k}.\\ \end{align*} $$
Proof Because
![]() $\psi $
is supported on
$\psi $
is supported on
![]() $[-1/2, 1/2]$
, we have
$[-1/2, 1/2]$
, we have
 $$ \begin{align} |\mkern-1.5mu|\mkern-1.5mu| \Pi_{m, \tau} F |\mkern-1.5mu|\mkern-1.5mu|_s & = \bigg\Vert \bigg(\bigg(z_1^2 - \frac{\partial^2}{\partial z_1^2}\bigg)+\bigg(I +\sum_{i = 2}^n z_i^2-\frac{\partial^2}{\partial z_i^2}\bigg)\bigg)^{s/2} (e^{- 2\pi i z_1 m/\tau} \psi F)\bigg\Vert_{L^2({ \mathbb R}^n)}. \end{align} $$
$$ \begin{align} |\mkern-1.5mu|\mkern-1.5mu| \Pi_{m, \tau} F |\mkern-1.5mu|\mkern-1.5mu|_s & = \bigg\Vert \bigg(\bigg(z_1^2 - \frac{\partial^2}{\partial z_1^2}\bigg)+\bigg(I +\sum_{i = 2}^n z_i^2-\frac{\partial^2}{\partial z_i^2}\bigg)\bigg)^{s/2} (e^{- 2\pi i z_1 m/\tau} \psi F)\bigg\Vert_{L^2({ \mathbb R}^n)}. \end{align} $$
Then, because
![]() $z_1^2 - ({\partial ^2}/{\partial z_1^2})$
and
$z_1^2 - ({\partial ^2}/{\partial z_1^2})$
and
![]() $(I +\sum _{i = 2}^n z_i^2-({\partial ^2}/{\partial z_i^2}))$
commute, the triangle inequality gives
$(I +\sum _{i = 2}^n z_i^2-({\partial ^2}/{\partial z_i^2}))$
commute, the triangle inequality gives
 $$ \begin{align*} (38) &\leq C_s \sum_{k = 0}^{s/2} \bigg\Vert \bigg(z_1^2 - \frac{\partial^2}{\partial z_1^2}\bigg)^k \bigg(I +\sum_{i = 2}^n z_i^2-\frac{\partial^2}{\partial z_i^2}\bigg)^{s/2-k} (e^{- 2\pi i z_1 m/\tau} \psi F) \bigg\Vert_{L^2({ \mathbb R}^n)} \notag \\ & \leq C_s \sum_{k = 0}^{s/2} \bigg\Vert \bigg(z_1^2 - \frac{\partial^2}{\partial z_1^2}\bigg)^k e^{- 2\pi i z_1m/\tau} \psi \bigg\Vert_{L^{\infty}({ \mathbb R})} \bigg\Vert \bigg(I +\sum_{i = 2}^n z_i^2-\frac{\partial^2}{\partial z_i^2}\bigg)^{s/2-k} F \bigg\Vert_{L^2({ \mathbb R}^{n-1})}. \notag\\ \end{align*} $$
$$ \begin{align*} (38) &\leq C_s \sum_{k = 0}^{s/2} \bigg\Vert \bigg(z_1^2 - \frac{\partial^2}{\partial z_1^2}\bigg)^k \bigg(I +\sum_{i = 2}^n z_i^2-\frac{\partial^2}{\partial z_i^2}\bigg)^{s/2-k} (e^{- 2\pi i z_1 m/\tau} \psi F) \bigg\Vert_{L^2({ \mathbb R}^n)} \notag \\ & \leq C_s \sum_{k = 0}^{s/2} \bigg\Vert \bigg(z_1^2 - \frac{\partial^2}{\partial z_1^2}\bigg)^k e^{- 2\pi i z_1m/\tau} \psi \bigg\Vert_{L^{\infty}({ \mathbb R})} \bigg\Vert \bigg(I +\sum_{i = 2}^n z_i^2-\frac{\partial^2}{\partial z_i^2}\bigg)^{s/2-k} F \bigg\Vert_{L^2({ \mathbb R}^{n-1})}. \notag\\ \end{align*} $$
Note that
![]() $\Pi _{m, \boldsymbol {\tau }}$
depends on
$\Pi _{m, \boldsymbol {\tau }}$
depends on
![]() $\psi $
. Then we formally define the operator
$\psi $
. Then we formally define the operator
![]() $R_\psi $
on
$R_\psi $
on
![]() $L^2({ \mathbb R}^n)$
by
$L^2({ \mathbb R}^n)$
by
Over the next two lemmas, we describe properties of
![]() $R_\psi $
.
$R_\psi $
.
Lemma 2.15. For any
![]() $s \geq 0$
and for any
$s \geq 0$
and for any
![]() $\epsilon> 0$
, there is a constant
$\epsilon> 0$
, there is a constant
![]() $C_{s, \epsilon }> 0$
such that for any non-zero
$C_{s, \epsilon }> 0$
such that for any non-zero
![]() $f \in W^{s+n/2+\epsilon }({ \mathbb R}^n)$
, we can choose
$f \in W^{s+n/2+\epsilon }({ \mathbb R}^n)$
, we can choose
![]() $\psi $
such that
$\psi $
such that
![]() $R_\psi f \neq 0$
and
$R_\psi f \neq 0$
and
Proof We first claim that we can choose
![]() $\psi $
such that
$\psi $
such that
![]() $R_{\psi } f \neq 0$
and, for some universal constant
$R_{\psi } f \neq 0$
and, for some universal constant
![]() $C_s^{(0)}> 0$
,
$C_s^{(0)}> 0$
,
 $$ \begin{align*} \bigg\Vert \bigg(I + z_1^2- \frac{\partial^2}{\partial z_1^2}\bigg)^{s/2} \psi \bigg\Vert_{L^{\infty}({ \mathbb R})} \leq C_s^{(0)} (1 + \tau^s). \end{align*} $$
$$ \begin{align*} \bigg\Vert \bigg(I + z_1^2- \frac{\partial^2}{\partial z_1^2}\bigg)^{s/2} \psi \bigg\Vert_{L^{\infty}({ \mathbb R})} \leq C_s^{(0)} (1 + \tau^s). \end{align*} $$
Fix
![]() $\psi $
. So, for some
$\psi $
. So, for some
![]() $C_s^{(0)}> 0$
, the above estimate holds. If
$C_s^{(0)}> 0$
, the above estimate holds. If
![]() $R_\psi f \neq 0$
, then the claim is holds, so suppose that
$R_\psi f \neq 0$
, then the claim is holds, so suppose that
![]() $R_\psi f = 0$
. Hence,
$R_\psi f = 0$
. Hence,
 $$ \begin{align*} f(z) = \psi(z_1) \sum_{m \in { \mathbb Z}}\textrm{ exp}(2\pi i z_1 m/\tau) \mathcal F_1 f\bigg(\frac{m}{\tau}, z_2, \ldots, z_n\bigg). \end{align*} $$
$$ \begin{align*} f(z) = \psi(z_1) \sum_{m \in { \mathbb Z}}\textrm{ exp}(2\pi i z_1 m/\tau) \mathcal F_1 f\bigg(\frac{m}{\tau}, z_2, \ldots, z_n\bigg). \end{align*} $$
So, we can perturb
![]() $\psi $
to a smooth function compactly supported in
$\psi $
to a smooth function compactly supported in
![]() $[-({1}/{2\tau }), ({1}/{2\tau })]$
satisfying
$[-({1}/{2\tau }), ({1}/{2\tau })]$
satisfying
![]() $\mathcal F\psi _0(0) = 1, \psi _0 \neq \psi $
and
$\mathcal F\psi _0(0) = 1, \psi _0 \neq \psi $
and
![]() $R_\psi f \neq 0$
, where also
$R_\psi f \neq 0$
, where also
 $$ \begin{align} \bigg\Vert \bigg(I + z_1^2 - \frac{\partial^2}{\partial z_1^2}\bigg)^{s/2} \psi_0 \bigg\Vert_{L^{\infty}({ \mathbb R})} \leq (C_s^{(0)} + 1) (1 + \tau^s). \end{align} $$
$$ \begin{align} \bigg\Vert \bigg(I + z_1^2 - \frac{\partial^2}{\partial z_1^2}\bigg)^{s/2} \psi_0 \bigg\Vert_{L^{\infty}({ \mathbb R})} \leq (C_s^{(0)} + 1) (1 + \tau^s). \end{align} $$
This proves the claim.
Now we say that
![]() $s \in { \mathbb N}$
is even and let
$s \in { \mathbb N}$
is even and let
![]() $R_\psi f \neq 0$
, where
$R_\psi f \neq 0$
, where
![]() $\psi $
satisfies (40). By the triangle inequality and Lemma 2.14, we get a constant
$\psi $
satisfies (40). By the triangle inequality and Lemma 2.14, we get a constant
![]() $C_s^{(1)}> C_s^{(0)} + 1$
such that
$C_s^{(1)}> C_s^{(0)} + 1$
such that
 $$ \begin{align} |\mkern-1.5mu|\mkern-1.5mu| R_\psi f |\mkern-1.5mu|\mkern-1.5mu|_s & \leq |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_s + \sum_{m \in { \mathbb Z}} |\mkern-1.5mu|\mkern-1.5mu| \Pi_{m, \tau} \pi_{m, \tau} f |\mkern-1.5mu|\mkern-1.5mu|_s \notag \\ & \leq |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_s + C_s^{(1)} (1 + \tau^s) \sum_{m \in { \mathbb Z}} \sum_{k = 0}^{s/2} \bigg(1+\bigg\vert\frac{m}{\tau}\bigg\vert\bigg)^{2k} \vert \pi_{m, \tau} f \vert_{s-2k}. \end{align} $$
$$ \begin{align} |\mkern-1.5mu|\mkern-1.5mu| R_\psi f |\mkern-1.5mu|\mkern-1.5mu|_s & \leq |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_s + \sum_{m \in { \mathbb Z}} |\mkern-1.5mu|\mkern-1.5mu| \Pi_{m, \tau} \pi_{m, \tau} f |\mkern-1.5mu|\mkern-1.5mu|_s \notag \\ & \leq |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_s + C_s^{(1)} (1 + \tau^s) \sum_{m \in { \mathbb Z}} \sum_{k = 0}^{s/2} \bigg(1+\bigg\vert\frac{m}{\tau}\bigg\vert\bigg)^{2k} \vert \pi_{m, \tau} f \vert_{s-2k}. \end{align} $$
By Corollary 2.8, there is a constant
![]() $C_\epsilon> 0$
such that for any
$C_\epsilon> 0$
such that for any
![]() $m \in { \mathbb Z}$
,
$m \in { \mathbb Z}$
,
 $$ \begin{align*} \bigg(1+\bigg\vert\frac{m}{\tau}\bigg\vert\bigg)^{2k} \vert \pi_{m, \tau} f \vert_{s-2k} & \leq C_{\epsilon} \bigg(1+\bigg\vert\frac{m}{\tau}\bigg\vert\bigg)^{2k} \bigg(1+\bigg\vert\frac{m}{\tau}\bigg\vert\bigg)^{-(2k + 1 + \epsilon)} |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_{s + 3n/2 + \epsilon} \notag \\ & \leq C_\epsilon (1 + \tau)^{s+ 1 + \epsilon} (1 + \vert m\vert)^{-(1 + \epsilon)} |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_{s + 3n/2 + \epsilon}. \notag \end{align*} $$
$$ \begin{align*} \bigg(1+\bigg\vert\frac{m}{\tau}\bigg\vert\bigg)^{2k} \vert \pi_{m, \tau} f \vert_{s-2k} & \leq C_{\epsilon} \bigg(1+\bigg\vert\frac{m}{\tau}\bigg\vert\bigg)^{2k} \bigg(1+\bigg\vert\frac{m}{\tau}\bigg\vert\bigg)^{-(2k + 1 + \epsilon)} |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_{s + 3n/2 + \epsilon} \notag \\ & \leq C_\epsilon (1 + \tau)^{s+ 1 + \epsilon} (1 + \vert m\vert)^{-(1 + \epsilon)} |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_{s + 3n/2 + \epsilon}. \notag \end{align*} $$
Hence, there is a constant
![]() $C_{s, \epsilon }> 0$
such that
$C_{s, \epsilon }> 0$
such that
 $$ \begin{align*} \begin{array}{l@{\,}l} (41) & \leq |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_s + C_{s, \epsilon}(1 + \tau)^{s+ 1 + \epsilon} \displaystyle\sum\limits_{m \in { \mathbb Z}} (1 + m^2)^{-(1+\epsilon)/2} |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_{s+3n/2+\epsilon} \\ & \leq C_{s, \epsilon} (1 + \tau)^{s + 1 + \epsilon} |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_{s+3n/2+\epsilon}. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l@{\,}l} (41) & \leq |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_s + C_{s, \epsilon}(1 + \tau)^{s+ 1 + \epsilon} \displaystyle\sum\limits_{m \in { \mathbb Z}} (1 + m^2)^{-(1+\epsilon)/2} |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_{s+3n/2+\epsilon} \\ & \leq C_{s, \epsilon} (1 + \tau)^{s + 1 + \epsilon} |\mkern-1.5mu|\mkern-1.5mu| f |\mkern-1.5mu|\mkern-1.5mu|_{s+3n/2+\epsilon}. \end{array} \end{align*} $$
By interpolation, the above estimate holds for all
![]() $s \geq 0$
. Because
$s \geq 0$
. Because
![]() $R_\psi $
is a linear operator and the estimate holds for all s, Lemma 2.3 gives the estimate for
$R_\psi $
is a linear operator and the estimate holds for all s, Lemma 2.3 gives the estimate for
![]() $s \geq 0$
.
$s \geq 0$
.
Next we show that the operator
![]() $R_\psi $
is a projection into
$R_\psi $
is a projection into
![]() $\textrm{ Ann}_{\boldsymbol {\tau }}$
and it commutes with
$\textrm{ Ann}_{\boldsymbol {\tau }}$
and it commutes with
![]() $L_{\boldsymbol {\eta }}$
.
$L_{\boldsymbol {\eta }}$
.
Lemma 2.16. Let
![]() $\psi $
be as in the previous lemma. Then
$\psi $
be as in the previous lemma. Then
and
on
![]() $\mathscr {S}({ \mathbb R}^n)$
.
$\mathscr {S}({ \mathbb R}^n)$
.
Proof Let
![]() $f \in \mathscr {S}({ \mathbb R}^n)$
. By the previous lemma,
$f \in \mathscr {S}({ \mathbb R}^n)$
. By the previous lemma,
![]() $R_{\psi } f \in \mathscr {S}({ \mathbb R}^n)$
, so we need to show that
$R_{\psi } f \in \mathscr {S}({ \mathbb R}^n)$
, so we need to show that
![]() $R_{\psi } f$
is in the kernel of every
$R_{\psi } f$
is in the kernel of every
![]() $\pi _{m, \boldsymbol {\tau }}$
. Using the property that
$\pi _{m, \boldsymbol {\tau }}$
. Using the property that
![]() $\mathcal F\psi $
is supported on the interval
$\mathcal F\psi $
is supported on the interval
![]() $[-({1}/{2\tau }), ({1}/{2\tau })]$
and
$[-({1}/{2\tau }), ({1}/{2\tau })]$
and
![]() $\mathcal F\psi (0) = 1$
, we get that for any
$\mathcal F\psi (0) = 1$
, we get that for any
![]() $m \in { \mathbb Z}$
,
$m \in { \mathbb Z}$
,
 $$ \begin{align} \pi_{m, \tau} R_\psi f & = \pi_{m, \tau}f - \sum_{k \in { \mathbb Z}} \pi_{m, \tau} \Pi_{k, \tau} \pi_{k, \tau}f \notag \\ & = \pi_{m, \tau}f - \pi_{m, \tau} \Pi_{m, \tau} \pi_{m, \tau}f \notag \\ & = \pi_{m, \tau}f - \pi_{m, \tau}f \notag \\ & = 0. \end{align} $$
$$ \begin{align} \pi_{m, \tau} R_\psi f & = \pi_{m, \tau}f - \sum_{k \in { \mathbb Z}} \pi_{m, \tau} \Pi_{k, \tau} \pi_{k, \tau}f \notag \\ & = \pi_{m, \tau}f - \pi_{m, \tau} \Pi_{m, \tau} \pi_{m, \tau}f \notag \\ & = \pi_{m, \tau}f - \pi_{m, \tau}f \notag \\ & = 0. \end{align} $$
This implies that
![]() $R_{\psi } :\mathscr {S}({ \mathbb R}^n) \to \textrm{ Ann}_{\boldsymbol {\tau }}$
.
$R_{\psi } :\mathscr {S}({ \mathbb R}^n) \to \textrm{ Ann}_{\boldsymbol {\tau }}$
.
By Lemma 2.9, for any
![]() $m \in { \mathbb Z}$
,
$m \in { \mathbb Z}$
,
![]() $\pi _{m, \boldsymbol {\tau }} L_{\boldsymbol {\tau }} = 0$
. We have
$\pi _{m, \boldsymbol {\tau }} L_{\boldsymbol {\tau }} = 0$
. We have
 $$ \begin{align*} R_\psi L_{\boldsymbol{\tau}} & = \bigg(I - \sum_{m \in { \mathbb Z}} \Pi_{m, \tau} \pi_{m, \tau}\bigg) L_{\boldsymbol{\tau}} \\ & = L_{\boldsymbol{\tau}}. \end{align*} $$
$$ \begin{align*} R_\psi L_{\boldsymbol{\tau}} & = \bigg(I - \sum_{m \in { \mathbb Z}} \Pi_{m, \tau} \pi_{m, \tau}\bigg) L_{\boldsymbol{\tau}} \\ & = L_{\boldsymbol{\tau}}. \end{align*} $$
Finally, we prove that
![]() $[L_{\boldsymbol {\eta }}, R_\psi ] = 0$
. We have
$[L_{\boldsymbol {\eta }}, R_\psi ] = 0$
. We have
 $$ \begin{align*} \Pi_{m, \boldsymbol{\tau}} \pi_{m, \boldsymbol{\tau}} L_{\boldsymbol{\eta}} f(z) & = \textrm{ exp}(2\pi i z_1 m/\tau)\, \psi(z_1) [\pi_{m, \boldsymbol{\tau}} L_{\boldsymbol{\eta}} f](z_2, \ldots, z_n) \\ & = \textrm{ exp}(2\pi i z_1 m/\tau)\, \psi(z_1) \mathcal F_1[L_{\boldsymbol{\eta}} f]\bigg(\frac{m}{\tau}, z_2, \ldots, z_n\bigg) \\ & = (\textrm{ exp}(i \nu_2 z_2) - 1) \,\textrm{ exp}(2\pi i z_1 m/\tau)\, \psi(z_1) \mathcal F_1f\bigg(\frac{m}{\tau}, z_2, \ldots, z_n\bigg) \\ & = L_{\boldsymbol{\eta}} \,\textrm{ exp}(2\pi i z_1 m/\tau)\, \psi(z_1) \mathcal F_1 f\bigg(\frac{m}{\tau}, z_2, \ldots, z_n\bigg) \\ & = L_{\boldsymbol{\eta}} \Pi_{m, \boldsymbol{\tau}} \mathcal F_1 f\bigg(\frac{m}{\tau}, z_2, \ldots, z_n\bigg) \\ & = L_{\boldsymbol{\eta}} \Pi_{m, \boldsymbol{\tau}} \pi_{m, \boldsymbol{\tau}} f. \end{align*} $$
$$ \begin{align*} \Pi_{m, \boldsymbol{\tau}} \pi_{m, \boldsymbol{\tau}} L_{\boldsymbol{\eta}} f(z) & = \textrm{ exp}(2\pi i z_1 m/\tau)\, \psi(z_1) [\pi_{m, \boldsymbol{\tau}} L_{\boldsymbol{\eta}} f](z_2, \ldots, z_n) \\ & = \textrm{ exp}(2\pi i z_1 m/\tau)\, \psi(z_1) \mathcal F_1[L_{\boldsymbol{\eta}} f]\bigg(\frac{m}{\tau}, z_2, \ldots, z_n\bigg) \\ & = (\textrm{ exp}(i \nu_2 z_2) - 1) \,\textrm{ exp}(2\pi i z_1 m/\tau)\, \psi(z_1) \mathcal F_1f\bigg(\frac{m}{\tau}, z_2, \ldots, z_n\bigg) \\ & = L_{\boldsymbol{\eta}} \,\textrm{ exp}(2\pi i z_1 m/\tau)\, \psi(z_1) \mathcal F_1 f\bigg(\frac{m}{\tau}, z_2, \ldots, z_n\bigg) \\ & = L_{\boldsymbol{\eta}} \Pi_{m, \boldsymbol{\tau}} \mathcal F_1 f\bigg(\frac{m}{\tau}, z_2, \ldots, z_n\bigg) \\ & = L_{\boldsymbol{\eta}} \Pi_{m, \boldsymbol{\tau}} \pi_{m, \boldsymbol{\tau}} f. \end{align*} $$
This proves that
![]() $[L_{\boldsymbol {\eta }}, R_\psi ] = 0$
and finishes the proof of the lemma.
$[L_{\boldsymbol {\eta }}, R_\psi ] = 0$
and finishes the proof of the lemma.
Now we prove Theorem 2.13. Let
be as in the theorem and recall from the beginning of its proof that we take
![]() $f \neq 0$
. By Lemmas 2.15 and 2.16, we can choose
$f \neq 0$
. By Lemmas 2.15 and 2.16, we can choose
![]() $\psi $
such that there is a non-constant function P that is a solution to
$\psi $
such that there is a non-constant function P that is a solution to
![]() $R_\psi f = L_{\boldsymbol {\tau }} P$
and, for a fixed constant
$R_\psi f = L_{\boldsymbol {\tau }} P$
and, for a fixed constant
![]() $C_s^{(1)}> 0$
,
$C_s^{(1)}> 0$
,
 $$ \begin{align*} \bigg\Vert \bigg(I - \frac{\partial^2}{\partial z_1^2}\bigg)^{s/2} \psi \bigg\Vert_{L^{\infty}({ \mathbb R})} \leq C_s^{(1)}. \end{align*} $$
$$ \begin{align*} \bigg\Vert \bigg(I - \frac{\partial^2}{\partial z_1^2}\bigg)^{s/2} \psi \bigg\Vert_{L^{\infty}({ \mathbb R})} \leq C_s^{(1)}. \end{align*} $$
In particular, Lemma 2.16 implies that
 $$ \begin{align} R_\psi \phi & = R_\psi L_{\boldsymbol{\eta}} f - R_\psi L_{\boldsymbol{\tau}} g \nonumber\\ & = L_{\boldsymbol{\eta}} R_\psi f - L_{\boldsymbol{\tau}} g \nonumber\\ & = L_{\boldsymbol{\eta}} L_{\boldsymbol{\tau}} P - L_{\boldsymbol{\tau}} g\nonumber\\ & = L_{\boldsymbol{\tau}} (L_{\boldsymbol{\eta}} P - g). \end{align} $$
$$ \begin{align} R_\psi \phi & = R_\psi L_{\boldsymbol{\eta}} f - R_\psi L_{\boldsymbol{\tau}} g \nonumber\\ & = L_{\boldsymbol{\eta}} R_\psi f - L_{\boldsymbol{\tau}} g \nonumber\\ & = L_{\boldsymbol{\eta}} L_{\boldsymbol{\tau}} P - L_{\boldsymbol{\tau}} g\nonumber\\ & = L_{\boldsymbol{\tau}} (L_{\boldsymbol{\eta}} P - g). \end{align} $$
Then, by Proposition 2.10 and by Lemmas 2.15 and 2.5, we get that for any
![]() $s \geq 0$
and for any
$s \geq 0$
and for any
![]() $\epsilon> 0$
, there is a constant
$\epsilon> 0$
, there is a constant
![]() $C_{s, \epsilon }> 0$
such that
$C_{s, \epsilon }> 0$
such that
 $$ \begin{align} & \kern129pt\leq \frac{C_{s, \epsilon}}{\tau} \Vert R_\psi \phi \Vert_{s + 3n/2 + 1 + \epsilon} \notag \\ & \kern129pt\leq C_{s, \epsilon} (\tau^{-1} + \tau^{s+\epsilon}) \Vert \phi \Vert_{s + 3n + 1 + 2\epsilon}. \end{align} $$
$$ \begin{align} & \kern129pt\leq \frac{C_{s, \epsilon}}{\tau} \Vert R_\psi \phi \Vert_{s + 3n/2 + 1 + \epsilon} \notag \\ & \kern129pt\leq C_{s, \epsilon} (\tau^{-1} + \tau^{s+\epsilon}) \Vert \phi \Vert_{s + 3n + 1 + 2\epsilon}. \end{align} $$
To estimate
![]() $\Vert L_{\boldsymbol {\tau }} P - f \Vert _s$
, because
$\Vert L_{\boldsymbol {\tau }} P - f \Vert _s$
, because
![]() $R_\psi f = L_{\boldsymbol {\tau }} P$
and by Lemma 2.5,
$R_\psi f = L_{\boldsymbol {\tau }} P$
and by Lemma 2.5,
 $$ \begin{align} \Vert L_{\boldsymbol{\tau}} P - f \Vert_s & = \Vert L_{\boldsymbol{\tau}} P - f \Vert_s \notag \\ & = \Vert L_{\boldsymbol{\tau}} P - R_\psi f + R_\psi f - f\Vert_s \notag \\ & = \Vert (R_\psi -I) f\Vert_s. \end{align} $$
$$ \begin{align} \Vert L_{\boldsymbol{\tau}} P - f \Vert_s & = \Vert L_{\boldsymbol{\tau}} P - f \Vert_s \notag \\ & = \Vert L_{\boldsymbol{\tau}} P - R_\psi f + R_\psi f - f\Vert_s \notag \\ & = \Vert (R_\psi -I) f\Vert_s. \end{align} $$
Notice that by Lemma 2.16,
Then, using
![]() $L_{\boldsymbol {\eta }} f - L_{\boldsymbol {\tau }} g = \phi $
, we get
$L_{\boldsymbol {\eta }} f - L_{\boldsymbol {\tau }} g = \phi $
, we get
 $$ \begin{align} (R_\psi - I) L_{\boldsymbol{\eta}} f & = (R_\psi - I) \phi + (R_\psi - I) L_{\boldsymbol{\tau}} g \nonumber\\ & = (R_\psi - I) \phi. \end{align} $$
$$ \begin{align} (R_\psi - I) L_{\boldsymbol{\eta}} f & = (R_\psi - I) \phi + (R_\psi - I) L_{\boldsymbol{\tau}} g \nonumber\\ & = (R_\psi - I) \phi. \end{align} $$
Then, by Lemma 2.16 again, we get
We conclude by Corollary 2.11 and Lemmas 2.15 and 2.5 that
 $$ \begin{align} (46) & \leq \frac{C_{s, \epsilon}}{\nu_2} \Vert (R_\psi - I) \phi \Vert_{s + 3n/2 + 1 + \epsilon} \notag \\ & \leq \frac{C_{s, \epsilon}}{\nu_2} (1 + \tau^{s + 1+\epsilon}) \Vert \phi \Vert_{s + 3n + 1 + 2\epsilon}. \end{align} $$
$$ \begin{align} (46) & \leq \frac{C_{s, \epsilon}}{\nu_2} \Vert (R_\psi - I) \phi \Vert_{s + 3n/2 + 1 + \epsilon} \notag \\ & \leq \frac{C_{s, \epsilon}}{\nu_2} (1 + \tau^{s + 1+\epsilon}) \Vert \phi \Vert_{s + 3n + 1 + 2\epsilon}. \end{align} $$
Finally, because
![]() $L_{\boldsymbol {\tau }} P = R_\psi f$
, Proposition 2.10 and Lemma 2.15 give
$L_{\boldsymbol {\tau }} P = R_\psi f$
, Proposition 2.10 and Lemma 2.15 give
 $$ \begin{align*} \Vert P \Vert_s & \leq \frac{C_{s, \epsilon}}{\tau} \Vert R_\psi f \Vert_{s + 3n/2 + 1 + \epsilon} \notag \\ & \leq C_{s, \epsilon} (\tau^{-1} + \tau^{s + \epsilon}) \Vert f \Vert_{s + 3n + 1 + 2\epsilon} \notag. \notag \end{align*} $$
$$ \begin{align*} \Vert P \Vert_s & \leq \frac{C_{s, \epsilon}}{\tau} \Vert R_\psi f \Vert_{s + 3n/2 + 1 + \epsilon} \notag \\ & \leq C_{s, \epsilon} (\tau^{-1} + \tau^{s + \epsilon}) \Vert f \Vert_{s + 3n + 1 + 2\epsilon} \notag. \notag \end{align*} $$
At the start of the proof of Theorem 2.13, we assumed that
![]() $f \neq 0$
. If we instead choose
$f \neq 0$
. If we instead choose
![]() $g \neq 0$
, then by first applying the Fourier transform, the same argument proves the above estimates in terms of
$g \neq 0$
, then by first applying the Fourier transform, the same argument proves the above estimates in terms of
![]() $\Vert \phi \Vert _{ s + 3n + 1 + \epsilon }$
and
$\Vert \phi \Vert _{ s + 3n + 1 + \epsilon }$
and
This completes the proof of Theorem 2.13.
Proof Proof of Theorem 1.2
The regular representation of
![]() $\mathsf H$
on
$\mathsf H$
on
![]() $L^2(M)$
decomposes as
$L^2(M)$
decomposes as
 $$ \begin{align*} L^2(M) = \mathbb C \langle 1 \rangle \oplus \bigoplus_{\mathbf{m} \in { \mathbb Z}^{2n} \setminus\{0\}} \mathcal P_{\mathbf{m}} \oplus \bigoplus_{h \in { \mathbb Z}} \mathcal P_h, \end{align*} $$
$$ \begin{align*} L^2(M) = \mathbb C \langle 1 \rangle \oplus \bigoplus_{\mathbf{m} \in { \mathbb Z}^{2n} \setminus\{0\}} \mathcal P_{\mathbf{m}} \oplus \bigoplus_{h \in { \mathbb Z}} \mathcal P_h, \end{align*} $$
where each
![]() $\mathcal P_{\mathbf {m}}$
is an abelian representation of
$\mathcal P_{\mathbf {m}}$
is an abelian representation of
![]() ${ \mathbb R}^{2n}$
equivalent to a character given by (11), and each
${ \mathbb R}^{2n}$
equivalent to a character given by (11), and each
![]() $\mathcal P_h$
is equivalent to a countable collection of Schrödinger representations
$\mathcal P_h$
is equivalent to a countable collection of Schrödinger representations
![]() $\mu _h$
of
$\mu _h$
of
![]() $\mathsf H$
on
$\mathsf H$
on
![]() $L^2({ \mathbb R}^n)$
given by (13). The subspace of zero-average functions in
$L^2({ \mathbb R}^n)$
given by (13). The subspace of zero-average functions in
![]() $L^2(M)$
is denoted
$L^2(M)$
is denoted
![]() $L_0^2(M)$
, which therefore decomposes as
$L_0^2(M)$
, which therefore decomposes as
 $$ \begin{align*} L_0^2(M) & = \bigoplus_{\mathbf{m} \in { \mathbb Z}^{2n} \setminus\{0\}} \mathcal P_{\mathbf{m}} \oplus \bigoplus_{h \in { \mathbb Z}} \mathcal P_h \\ & = L_0^2({ \mathbb T}^{2n}) \oplus \bigoplus_{h \in { \mathbb Z}} \mathcal P_h. \end{align*} $$
$$ \begin{align*} L_0^2(M) & = \bigoplus_{\mathbf{m} \in { \mathbb Z}^{2n} \setminus\{0\}} \mathcal P_{\mathbf{m}} \oplus \bigoplus_{h \in { \mathbb Z}} \mathcal P_h \\ & = L_0^2({ \mathbb T}^{2n}) \oplus \bigoplus_{h \in { \mathbb Z}} \mathcal P_h. \end{align*} $$
As indicated in §2.1, vector fields in
![]() $\operatorname {\mathfrak h}$
split into the unitary components in the above Hilbert space. Then the decomposition of the Sobolev space of s-differentiable, zero-average functions is
$\operatorname {\mathfrak h}$
split into the unitary components in the above Hilbert space. Then the decomposition of the Sobolev space of s-differentiable, zero-average functions is
where
![]() $W_0^s({ \mathbb T}^{2n})$
and
$W_0^s({ \mathbb T}^{2n})$
and
![]() $W^s(\mathcal P_h)$
are s-order Sobolev spaces on the torus
$W^s(\mathcal P_h)$
are s-order Sobolev spaces on the torus
![]() ${ \mathbb T}^{2n}$
and of the representation
${ \mathbb T}^{2n}$
and of the representation
![]() $\mathcal P_h$
, respectively.
$\mathcal P_h$
, respectively.
Now, in Theorem 1.2, we are given zero-average functions
![]() $f, g \in C^{\infty }(M)$
that satisfy
$f, g \in C^{\infty }(M)$
that satisfy
![]() $L_{\boldsymbol \tau } g = L_{\boldsymbol \eta } f$
and we aim to find a solution
$L_{\boldsymbol \tau } g = L_{\boldsymbol \eta } f$
and we aim to find a solution
![]() $P \in C^{\infty }(M)$
such that
$P \in C^{\infty }(M)$
such that
Write
where
![]() $f_t, g_t \in W_0^{\infty }({ \mathbb T}^{2n})$
and, for each
$f_t, g_t \in W_0^{\infty }({ \mathbb T}^{2n})$
and, for each
![]() $h \in { \mathbb Z}$
,
$h \in { \mathbb Z}$
,
![]() $f_h, g_h \in \mathcal P_h$
. Proposition 2.1 and Theorem 2.12 give smooth solutions
$f_h, g_h \in \mathcal P_h$
. Proposition 2.1 and Theorem 2.12 give smooth solutions
![]() $P_t \in W_0^{\infty }({ \mathbb T}^{2n})$
and
$P_t \in W_0^{\infty }({ \mathbb T}^{2n})$
and
![]() $\{P_h\}_{h \in { \mathbb Z}} \subset W^{\infty }(\mathcal P_h)$
satisfying the estimate of Theorem 1.2 in the finite- and infinite-dimensional representations, respectively. Define
$\{P_h\}_{h \in { \mathbb Z}} \subset W^{\infty }(\mathcal P_h)$
satisfying the estimate of Theorem 1.2 in the finite- and infinite-dimensional representations, respectively. Define
![]() $P \in C^{\infty }(M)$
by
$P \in C^{\infty }(M)$
by
So, there exists a constant
![]() $C_{s, \epsilon }:= C_{s, \epsilon , \boldsymbol {\tau }, \boldsymbol {\eta }}> 0$
such that
$C_{s, \epsilon }:= C_{s, \epsilon , \boldsymbol {\tau }, \boldsymbol {\eta }}> 0$
such that
 $$ \begin{align} \Vert P \Vert_{W^s(M)}^2 & = \Vert P_t \Vert_{s}^2 + \sum_{h \in { \mathbb Z}} \Vert P_h \Vert_{s}^2 \nonumber\\ & \leq C_{s, \epsilon} (\Vert f_t \Vert_{s + 2\gamma} + \Vert g_t \Vert_{s + 2 \gamma})^2 + C_{s, \epsilon} \sum_{h \in { \mathbb Z}} \Vert f_h \Vert_{s + 3n/2 + 1 + \epsilon}^2 \nonumber\\ & \leq C_{s, \epsilon} (\Vert f \Vert_{s + \max\{2\gamma, \ 3n/2 + 1 + \epsilon\}} + \Vert g \Vert_{s + 2 \gamma})^2.\nonumber\\ \end{align} $$
$$ \begin{align} \Vert P \Vert_{W^s(M)}^2 & = \Vert P_t \Vert_{s}^2 + \sum_{h \in { \mathbb Z}} \Vert P_h \Vert_{s}^2 \nonumber\\ & \leq C_{s, \epsilon} (\Vert f_t \Vert_{s + 2\gamma} + \Vert g_t \Vert_{s + 2 \gamma})^2 + C_{s, \epsilon} \sum_{h \in { \mathbb Z}} \Vert f_h \Vert_{s + 3n/2 + 1 + \epsilon}^2 \nonumber\\ & \leq C_{s, \epsilon} (\Vert f \Vert_{s + \max\{2\gamma, \ 3n/2 + 1 + \epsilon\}} + \Vert g \Vert_{s + 2 \gamma})^2.\nonumber\\ \end{align} $$
3 Proof of Theorem 1.7
We fix now
![]() $Y_{\boldsymbol \tau }$
and
$Y_{\boldsymbol \tau }$
and
![]() $Y_{\boldsymbol \eta }$
with
$Y_{\boldsymbol \eta }$
with
![]() ${\boldsymbol \tau }\cdot {\boldsymbol \eta }=0$
and
${\boldsymbol \tau }\cdot {\boldsymbol \eta }=0$
and
![]() ${\boldsymbol \tau }$
and
${\boldsymbol \tau }$
and
![]() ${\boldsymbol \eta }$
Diophantine, as in the main setting. We denote by
${\boldsymbol \eta }$
Diophantine, as in the main setting. We denote by
![]() $\rho $
the
$\rho $
the
![]() $\mathbb Z^2$
action generated by
$\mathbb Z^2$
action generated by
![]() $Y_{\boldsymbol \tau }$
and
$Y_{\boldsymbol \tau }$
and
![]() $Y_{\boldsymbol \eta }$
as described in (7) in §1.1.
$Y_{\boldsymbol \eta }$
as described in (7) in §1.1.
In this section we prove Theorem 1.7. We will apply here a similar method which was applied in [Reference Damjanović and Katok7]. The method consists in taking successive iterations and adjustment of the parameter
![]() $\lambda $
at each step. The procedure is outlined in a general theorem which was proved in [Reference Damjanović2]. There, a set of conditions in cohomology is given, which imply transversal local rigidity of a finite-dimensional family of Lie group actions. This general theorem was then used in [Reference Damjanović3] to obtain transversal local rigidity of certain
$\lambda $
at each step. The procedure is outlined in a general theorem which was proved in [Reference Damjanović2]. There, a set of conditions in cohomology is given, which imply transversal local rigidity of a finite-dimensional family of Lie group actions. This general theorem was then used in [Reference Damjanović3] to obtain transversal local rigidity of certain
![]() $\mathbb R^2$
actions on two-step nilmanifolds. Even though we have a similar situation here, we cannot unfortunately use the general theorem from [Reference Damjanović2] because that theorem is for Lie group actions, and here we have a discrete group action. This is the only difference though; the method of successive iterations is completely parallel to that used in the above-mentioned papers.
$\mathbb R^2$
actions on two-step nilmanifolds. Even though we have a similar situation here, we cannot unfortunately use the general theorem from [Reference Damjanović2] because that theorem is for Lie group actions, and here we have a discrete group action. This is the only difference though; the method of successive iterations is completely parallel to that used in the above-mentioned papers.
We write the proof of Theorem 1.7 here in the case where the manifold is the five-dimensional Heisenberg nilmanifold, that is, in the case
![]() $n=2$
. This is the lowest dimensional case in which our result holds. We chose to present the proof for concrete n for the benefit of the reader because computations are more clear and notation is simpler. Otherwise, the proof is clearly completely parallel for any
$n=2$
. This is the lowest dimensional case in which our result holds. We chose to present the proof for concrete n for the benefit of the reader because computations are more clear and notation is simpler. Otherwise, the proof is clearly completely parallel for any
![]() $n\ge 2$
. We stress the points in computation of cohomology where dimension matters, and how it affects the computation.
$n\ge 2$
. We stress the points in computation of cohomology where dimension matters, and how it affects the computation.
We will first compute in §3.1 the cohomology with coefficients in constant vector fields (that is, in the Lie algebra
![]() $\frak h$
) for the action
$\frak h$
) for the action
![]() $\rho $
. Then we describe in §3.2 the finite-dimensional family
$\rho $
. Then we describe in §3.2 the finite-dimensional family
![]() $\rho ^{{\unicode{x3bb} }}$
of algebraic actions to which this action belongs, where
$\rho ^{{\unicode{x3bb} }}$
of algebraic actions to which this action belongs, where
![]() $\rho ^0= \rho $
. This family is completely determined by the cocycles (with values in
$\rho ^0= \rho $
. This family is completely determined by the cocycles (with values in
![]() $\frak h$
) over
$\frak h$
) over
![]() $\rho $
. Then we move on to analyze the conjugacy operator and the commutator operator in §§3.3 and 3.4 and their linearized operators. The linearizations of these two operators are corresponding to the first and the second coboundary operators for the cohomology over
$\rho $
. Then we move on to analyze the conjugacy operator and the commutator operator in §§3.3 and 3.4 and their linearized operators. The linearizations of these two operators are corresponding to the first and the second coboundary operators for the cohomology over
![]() $\rho $
with coefficients in smooth vector fields
$\rho $
with coefficients in smooth vector fields
![]() $\textrm{ Vect}^{\infty }{M}$
. Using the results from the previous part of the paper (specifically Theorem 1.3), we show in §3.5 that this cohomology sequence splits and that the first cohomology with coefficients in
$\textrm{ Vect}^{\infty }{M}$
. Using the results from the previous part of the paper (specifically Theorem 1.3), we show in §3.5 that this cohomology sequence splits and that the first cohomology with coefficients in
![]() $\textrm{ Vect}^{\infty }{M}$
is the same as the cohomology with coefficients in
$\textrm{ Vect}^{\infty }{M}$
is the same as the cohomology with coefficients in
![]() $\frak h$
. This allows us to prove Theorem 1.7 by showing convergence of successive iterations in §3.6.
$\frak h$
. This allows us to prove Theorem 1.7 by showing convergence of successive iterations in §3.6.
For a vector field
![]() $H\in \textrm{ Vect}^{\infty }{M}$
, we denote by
$H\in \textrm{ Vect}^{\infty }{M}$
, we denote by
![]() $H_c$
its component in the center direction and by
$H_c$
its component in the center direction and by
![]() $H_T$
the remainder, that is, the component of H in the off-center directions. We denote by
$H_T$
the remainder, that is, the component of H in the off-center directions. We denote by
![]() $\textrm{ Ave}(H)$
the constant vector field (that is, an element in
$\textrm{ Ave}(H)$
the constant vector field (that is, an element in
![]() $\frak h$
) which is obtained by taking the average of H with respect to the Haar measure.
$\frak h$
) which is obtained by taking the average of H with respect to the Haar measure.
For two vector fields
![]() $F, G\in \textrm{ Vect}^{\infty }{M}$
, we use the notation
$F, G\in \textrm{ Vect}^{\infty }{M}$
, we use the notation
![]() $\|F, G\|_r:= \max \{\|F\|_r, \|G\|_r\}$
, where
$\|F, G\|_r:= \max \{\|F\|_r, \|G\|_r\}$
, where
![]() $\|\cdot \|_r$
denotes the
$\|\cdot \|_r$
denotes the
![]() $C^r$
norm.
$C^r$
norm.
3.1 Constant cohomology for the discrete-time action
We have
Furthermore,
 $$ \begin{align*} e^{Y_{\boldsymbol \tau}} e^{t \Lambda_1} & = (e^{Y_{\boldsymbol \tau}} e^{t \Lambda_1} e^{-Y_{\boldsymbol \tau}}) e^{Y_{\boldsymbol \tau}} \\ & = \textrm{ exp}(e^{\text{ad}_{Y_{\boldsymbol \tau}}} t \Lambda_1) e^{Y_{\boldsymbol \tau}} = \textrm{ exp}(t \Lambda_1 + t [Y_{\boldsymbol \tau}, \Lambda_1]) e^{Y_{\boldsymbol \tau}}\\ & = \textrm{ exp}(t (\Lambda_1 + \tau_1Z)) e^{Y_{\boldsymbol \tau}}. \end{align*} $$
$$ \begin{align*} e^{Y_{\boldsymbol \tau}} e^{t \Lambda_1} & = (e^{Y_{\boldsymbol \tau}} e^{t \Lambda_1} e^{-Y_{\boldsymbol \tau}}) e^{Y_{\boldsymbol \tau}} \\ & = \textrm{ exp}(e^{\text{ad}_{Y_{\boldsymbol \tau}}} t \Lambda_1) e^{Y_{\boldsymbol \tau}} = \textrm{ exp}(t \Lambda_1 + t [Y_{\boldsymbol \tau}, \Lambda_1]) e^{Y_{\boldsymbol \tau}}\\ & = \textrm{ exp}(t (\Lambda_1 + \tau_1Z)) e^{Y_{\boldsymbol \tau}}. \end{align*} $$
Therefore, for a constant vector field
where
![]() $h_i$
are constants, we have
$h_i$
are constants, we have
Another way to write this is
A similar computation can be done for
![]() $D e^{Y_{\boldsymbol \eta }}$
. In the matrix form, we have
$D e^{Y_{\boldsymbol \eta }}$
. In the matrix form, we have
 $$ \begin{align*} D e^{Y_{\boldsymbol \tau}} = \begin{pmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & \tau_1 & \tau_2 & 1 \\ \end{pmatrix}, \quad D e^{Y_{\boldsymbol \eta}} = \begin{pmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ -\eta_1 & -\eta_2 & 0 &0 & 1 \\ \end{pmatrix}. \end{align*} $$
$$ \begin{align*} D e^{Y_{\boldsymbol \tau}} = \begin{pmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & \tau_1 & \tau_2 & 1 \\ \end{pmatrix}, \quad D e^{Y_{\boldsymbol \eta}} = \begin{pmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ -\eta_1 & -\eta_2 & 0 &0 & 1 \\ \end{pmatrix}. \end{align*} $$
A pair of constant vector fields
![]() $(F, G)\in \frak h\times \frak h$
is a cocycle over the
$(F, G)\in \frak h\times \frak h$
is a cocycle over the
![]() ${ \mathbb Z}^2$
action generated by
${ \mathbb Z}^2$
action generated by
![]() $Y_{\boldsymbol \tau }$
and
$Y_{\boldsymbol \tau }$
and
![]() $Y_{\boldsymbol \eta }$
if
$Y_{\boldsymbol \eta }$
if
which implies that
Because H is two-step nilpotent, this condition is only on the off-center coordinates of F and G. More precisely, if
![]() $F= f_1X_1+ f_2X_2+ f_3{\Lambda }_1+ f_4{\Lambda }_2+ f_5Z$
and
$F= f_1X_1+ f_2X_2+ f_3{\Lambda }_1+ f_4{\Lambda }_2+ f_5Z$
and
![]() $G=g_1X_1+ g_2X_2+ g_3{\Lambda }_1+ g_4{\Lambda }_2+ g_5Z$
, then (51) implies that
$G=g_1X_1+ g_2X_2+ g_3{\Lambda }_1+ g_4{\Lambda }_2+ g_5Z$
, then (51) implies that
![]() $g_i$
and
$g_i$
and
![]() $f_i$
for
$f_i$
for
![]() $i=1,2,3,4$
satisfy the relation
$i=1,2,3,4$
satisfy the relation
Since the constants
![]() $f_5$
and
$f_5$
and
![]() $g_5$
are arbitrary, the space of constant cocycles has dimension nine.
$g_5$
are arbitrary, the space of constant cocycles has dimension nine.
A pair of constant vector fields
![]() $(F, G)$
is a coboundary if
$(F, G)$
is a coboundary if
that is, if
This implies that off-center coordinates of both F and G must be zero, and the center ones must satisfy certain relations. More precisely, if
![]() $H= h_1X_1+ h_2X_2+ h_3{\Lambda }_1+ h_4{\Lambda }_2+ h_5Z$
, the equations (53) imply that
$H= h_1X_1+ h_2X_2+ h_3{\Lambda }_1+ h_4{\Lambda }_2+ h_5Z$
, the equations (53) imply that
and these equations always have solutions for coefficients of H.
This implies that the first cohomology is seven dimensional, and each cohomology class is represented by cocycles
![]() $(F, G)$
of the following form:
$(F, G)$
of the following form:
![]() $F= f_1X_1+ f_2X_2+ f_3{\Lambda }_1+ f_4{\Lambda }_2$
and
$F= f_1X_1+ f_2X_2+ f_3{\Lambda }_1+ f_4{\Lambda }_2$
and
![]() $G=g_1X_1+ g_2X_2+ g_3{\Lambda }_1+ g_4{\Lambda }_2$
, where the coefficients
$G=g_1X_1+ g_2X_2+ g_3{\Lambda }_1+ g_4{\Lambda }_2$
, where the coefficients
![]() $g_i$
and
$g_i$
and
![]() $f_i$
for
$f_i$
for
![]() $i=1,2,3,4$
satisfy the relation (52).
$i=1,2,3,4$
satisfy the relation (52).
It is clear from the above computation that the dimension of the constant cohomology over the action generated by
![]() $Y_{\boldsymbol \tau }$
and
$Y_{\boldsymbol \tau }$
and
![]() $Y_{\boldsymbol \eta }$
in the case where the manifold is a
$Y_{\boldsymbol \eta }$
in the case where the manifold is a
![]() $(2n+1)$
-dimensional Heisenberg nilmanifold is parallel to what we wrote above in the case
$(2n+1)$
-dimensional Heisenberg nilmanifold is parallel to what we wrote above in the case
![]() $n=2$
and that the resulting cohomology has dimension
$n=2$
and that the resulting cohomology has dimension
![]() $4n-1$
.
$4n-1$
.
3.2 The finite-dimensional family of
 $\mathbb Z^2$
algebraic actions
$\mathbb Z^2$
algebraic actions
For easier notation, in the rest of the paper we let
![]() $Y_1=Y_{\boldsymbol \tau }$
and
$Y_1=Y_{\boldsymbol \tau }$
and
![]() $Y_2=Y_{\boldsymbol \eta }$
. In what follows we will use the fact that in
$Y_2=Y_{\boldsymbol \eta }$
. In what follows we will use the fact that in
![]() $\frak h$
we have
$\frak h$
we have
![]() $\textrm{ exp}(X+Y+ {\tfrac {1}{2}}[X, Y])= \textrm{ exp}(X)\textrm{ exp}(Y)$
. In the remainder of the paper the brackets
$\textrm{ exp}(X+Y+ {\tfrac {1}{2}}[X, Y])= \textrm{ exp}(X)\textrm{ exp}(Y)$
. In the remainder of the paper the brackets
![]() $[\cdot , \cdot ]$
denote the bracket in the Lie algebra
$[\cdot , \cdot ]$
denote the bracket in the Lie algebra
![]() $\frak h$
, so each bracket which appears as a result has a vector field in the Z-direction only.
$\frak h$
, so each bracket which appears as a result has a vector field in the Z-direction only.
We define now a nine-dimensional family of
![]() $\mathbb Z^2$
actions
$\mathbb Z^2$
actions
![]() $\rho ^{\unicode{x3bb} }$
on
$\rho ^{\unicode{x3bb} }$
on
![]() $M=\Gamma \setminus H$
generated by the following maps:
$M=\Gamma \setminus H$
generated by the following maps:
for
![]() $i=1,2$
, subject to the commutativity relation
$i=1,2$
, subject to the commutativity relation
![]() $y_1^{\unicode{x3bb} }\circ y_2^{\unicode{x3bb} }=y_2^{\unicode{x3bb} }\circ y_1^{\unicode{x3bb} }$
, where
$y_1^{\unicode{x3bb} }\circ y_2^{\unicode{x3bb} }=y_2^{\unicode{x3bb} }\circ y_1^{\unicode{x3bb} }$
, where
![]() $F_i^{\unicode{x3bb} }\in \frak h$
. In particular, at the parameter
$F_i^{\unicode{x3bb} }\in \frak h$
. In particular, at the parameter
![]() ${\unicode{x3bb} }$
equal to 0,
${\unicode{x3bb} }$
equal to 0,
![]() $F_i^0=0$
and
$F_i^0=0$
and
![]() $y_i^0=y_i$
, where
$y_i^0=y_i$
, where
![]() $y_1=\textrm{ exp}\, Y_1$
and
$y_1=\textrm{ exp}\, Y_1$
and
![]() $y_2=\textrm{ exp}\, Y_2$
are generators of our original action
$y_2=\textrm{ exp}\, Y_2$
are generators of our original action
![]() $\rho $
.
$\rho $
.
The following lemma is a simple computation.
Lemma 3.1. The two maps
![]() $y_1^{\unicode{x3bb} }$
and
$y_1^{\unicode{x3bb} }$
and
![]() $y_2^{\unicode{x3bb} }$
commute if and only if one of the following equivalent conditions hold.
$y_2^{\unicode{x3bb} }$
commute if and only if one of the following equivalent conditions hold.
-
(1)
 $[Y_1 +F^{\unicode{x3bb} }_1, Y_2+ F^{\unicode{x3bb} }_2]=0$
.
$[Y_1 +F^{\unicode{x3bb} }_1, Y_2+ F^{\unicode{x3bb} }_2]=0$
. -
(2)
 $[Y_1, F^{\unicode{x3bb} }_2]-[Y_2, F^{\unicode{x3bb} }_1]+ [F^{\unicode{x3bb} }_1, F^{\unicode{x3bb} }_2]=0.$
$[Y_1, F^{\unicode{x3bb} }_2]-[Y_2, F^{\unicode{x3bb} }_1]+ [F^{\unicode{x3bb} }_1, F^{\unicode{x3bb} }_2]=0.$
If
![]() $F_i^{\unicode{x3bb} }= f_i^1X_1+ f_i^2X_2+ f_i^3{\Lambda }_1+ f_i^4{\Lambda }_2+f_i^5Z$
, the coefficients
$F_i^{\unicode{x3bb} }= f_i^1X_1+ f_i^2X_2+ f_i^3{\Lambda }_1+ f_i^4{\Lambda }_2+f_i^5Z$
, the coefficients
![]() $f_i^k\in \mathbb R$
for
$f_i^k\in \mathbb R$
for
![]() $i=1,2$
and
$i=1,2$
and
![]() $k= 1,2,3,4, 5$
, commutativity implies that the coefficients are subject to the relation
$k= 1,2,3,4, 5$
, commutativity implies that the coefficients are subject to the relation
Therefore, the parameter
![]() ${\unicode{x3bb} }$
is understood here as a vector in the nine-dimensional space:
${\unicode{x3bb} }$
is understood here as a vector in the nine-dimensional space:
Within this nine-dimensional family of actions we impose identifications via conjugacies obtained by constant vector fields. More precisely, if
and, for some
![]() $H\in \frak h$
and
$H\in \frak h$
and
![]() $h(x):=x\cdot \textrm{ exp}\, H$
, we have
$h(x):=x\cdot \textrm{ exp}\, H$
, we have
then
This implies that
Thus,
This implies that in the off-center direction the components of
![]() $F_i^{\unicode{x3bb} }$
are trivial and, for the center direction, we have
$F_i^{\unicode{x3bb} }$
are trivial and, for the center direction, we have
In particular, this defines a coordinate change H which produces conjugate algebraic actions in the family, and each conjugacy class is two dimensional, determined only by the values
![]() $(F_i^{\unicode{x3bb} })_c$
(
$(F_i^{\unicode{x3bb} })_c$
(
![]() $i=1,2$
).
$i=1,2$
).
So, the nine-dimensional family of algebraic actions modulo the algebraic conjugacy classes gives a seven-dimensional family of non-conjugate algebraic actions. This is the family
![]() $\rho ^{\unicode{x3bb} }$
in Theorem 1.7.
$\rho ^{\unicode{x3bb} }$
in Theorem 1.7.
In the case where the manifold is a
![]() $(2n+1)$
-dimensional Heisenberg nilmanifold, the dimension of the family of non-conjugate algebraic actions in Theorem 1.7 is
$(2n+1)$
-dimensional Heisenberg nilmanifold, the dimension of the family of non-conjugate algebraic actions in Theorem 1.7 is
![]() $4n-1$
and the family is described as in (55).
$4n-1$
and the family is described as in (55).
3.3 The commutator operator
Now we analyze the commutator operator for non-algebraic perturbations of translations which generate
![]() $\rho $
. Recall that
$\rho $
. Recall that
![]() $\rho $
is the
$\rho $
is the
![]() $\mathbb Z^2$
action generated by the translation maps
$\mathbb Z^2$
action generated by the translation maps
![]() $y_i$
,
$y_i$
,
![]() $i=1,2$
, where
$i=1,2$
, where
![]() $y_i(x)=x\cdot \textrm{ exp}(Y_i)$
and
$y_i(x)=x\cdot \textrm{ exp}(Y_i)$
and
![]() $Y_i$
are the two commuting elements in
$Y_i$
are the two commuting elements in
![]() $\frak H$
.
$\frak H$
.
Lemma 3.2. Let
![]() $F, G\in \textrm{ Vect}^{\infty }{M}$
be two sufficiently small vector fields so that the maps
$F, G\in \textrm{ Vect}^{\infty }{M}$
be two sufficiently small vector fields so that the maps
![]() $f(x)= x\cdot \textrm{ exp}(Y_1+F(x))$
and
$f(x)= x\cdot \textrm{ exp}(Y_1+F(x))$
and
![]() $g(x)= x\cdot \textrm{ exp}(Y_2+G(x))$
are in
$g(x)= x\cdot \textrm{ exp}(Y_2+G(x))$
are in
![]() $\textrm{ Diff}^{\infty }{M}$
. If f and g commute, then the vector fields F and G satisfy the following nonlinear equation:
$\textrm{ Diff}^{\infty }{M}$
. If f and g commute, then the vector fields F and G satisfy the following nonlinear equation:
where
 $$ \begin{align} E(F, G)&= (F\circ g-F\circ y_2)- (G\circ f-G\circ y_1)\nonumber \\ &\quad+ {\tfrac{1}{2}} [Y_2, F\circ g-F\circ y_2]- {\tfrac{1}{2}}[Y_1, G\circ f-G\circ y_1]\nonumber\\ &\quad+ {\tfrac{1}{2}} [G, F\circ g]-{\tfrac{1}{2}} [F, G\circ f]. \end{align} $$
$$ \begin{align} E(F, G)&= (F\circ g-F\circ y_2)- (G\circ f-G\circ y_1)\nonumber \\ &\quad+ {\tfrac{1}{2}} [Y_2, F\circ g-F\circ y_2]- {\tfrac{1}{2}}[Y_1, G\circ f-G\circ y_1]\nonumber\\ &\quad+ {\tfrac{1}{2}} [G, F\circ g]-{\tfrac{1}{2}} [F, G\circ f]. \end{align} $$
Proof The commutation
![]() $f\circ g= g\circ f$
implies that
$f\circ g= g\circ f$
implies that
Hence,
 $$ \begin{align*} x \cdot &\textrm{ exp}(Y_1+ Y_2+ G+ F\circ g+ {\tfrac{1}{2}} [Y_2, F\circ g]- {\tfrac{1}{2}} [Y_1, G]+ {\tfrac{1}{2}} [G, F\circ g])\\ &= x\cdot\textrm{ exp}(Y_1+ Y_2+ F+ G\circ f+ {\tfrac{1}{2}} [Y_1, G\circ f]- {\tfrac{1}{2}} [Y_2, F]+ {\tfrac{1}{2}} [F, G\circ f]). \end{align*} $$
$$ \begin{align*} x \cdot &\textrm{ exp}(Y_1+ Y_2+ G+ F\circ g+ {\tfrac{1}{2}} [Y_2, F\circ g]- {\tfrac{1}{2}} [Y_1, G]+ {\tfrac{1}{2}} [G, F\circ g])\\ &= x\cdot\textrm{ exp}(Y_1+ Y_2+ F+ G\circ f+ {\tfrac{1}{2}} [Y_1, G\circ f]- {\tfrac{1}{2}} [Y_2, F]+ {\tfrac{1}{2}} [F, G\circ f]). \end{align*} $$
The above implies the nonlinear equation directly due to the following very simple fact:
![]() $x \cdot \textrm{ exp}(Y+ F)= x \cdot \textrm{ exp}(Y+G)$
with
$x \cdot \textrm{ exp}(Y+ F)= x \cdot \textrm{ exp}(Y+G)$
with
![]() $Y\in \frak h$
and
$Y\in \frak h$
and
![]() $F, G\in \textrm{ Vect}^{\infty }{M}$
if and only if
$F, G\in \textrm{ Vect}^{\infty }{M}$
if and only if
![]() $F=G$
.
$F=G$
.
The following immediate consequence of the lemma above will be used later.
Corollary 3.3. In the setting of Lemma 3.2,
![]() $|\textrm{ Ave}[Y_2, F]-\textrm{ Ave}[Y_1, G]|\le C\|F\|_1\|G\|_1$
.
$|\textrm{ Ave}[Y_2, F]-\textrm{ Ave}[Y_1, G]|\le C\|F\|_1\|G\|_1$
.
3.4 The conjugation operator
Here we analyze the conjugation operator for conjugacies close to the identity, we derive the linear part of the conjugacy operator and estimate the error.
Lemma 3.4. Let
![]() $f(x)=x\cdot \textrm{ exp}(Y +F(x))$
be a diffeomorphism of M, where
$f(x)=x\cdot \textrm{ exp}(Y +F(x))$
be a diffeomorphism of M, where
![]() $Y\in {\frak h}$
and
$Y\in {\frak h}$
and
![]() $F\in \textrm{ Vect}^{\infty }{M}$
is a smooth vector field. Let
$F\in \textrm{ Vect}^{\infty }{M}$
is a smooth vector field. Let
![]() $h\in \textrm{ Diff}^{\infty }{M}$
be a diffeomorphism close to the identity given by a small vector field
$h\in \textrm{ Diff}^{\infty }{M}$
be a diffeomorphism close to the identity given by a small vector field
![]() $H\in \textrm{ Vect}^{\infty }{M}$
via
$H\in \textrm{ Vect}^{\infty }{M}$
via
![]() $h(x)=x\cdot \textrm{ exp}\, H(x)$
. Then
$h(x)=x\cdot \textrm{ exp}\, H(x)$
. Then
![]() $g:=h^{-1}\circ f\circ h$
is a diffeomorphism close to f given by
$g:=h^{-1}\circ f\circ h$
is a diffeomorphism close to f given by
![]() $G\in \textrm{ Vect}^{\infty }{M}$
via
$G\in \textrm{ Vect}^{\infty }{M}$
via
![]() $g(x)=x\cdot \textrm{ exp}(Y +G(x))$
and
$g(x)=x\cdot \textrm{ exp}(Y +G(x))$
and
Proof We have
 $$ \begin{align*} h^{-1}\circ & f\circ h(x) =x\cdot \textrm{ exp}\, H(x)\,\textrm{ exp}(Y+F\circ h(x))\,\textrm{ exp}(-H\circ h^{-1}\circ f\circ h(x)) \\ & =x\cdot \textrm{ exp}(H+Y+F\circ h+{\tfrac{1}{2}}[H, Y]+[H, F\circ h])(x)\,\textrm{ exp}(-H\circ g)(x) \\ & =x\cdot \textrm{ exp}(H+Y-H\circ g+F\circ h+ {\tfrac{1}{2}}[H, Y]+ [H, F\circ h] \\ & \quad-{\tfrac{1}{2}} [H, -H\circ g]-{\tfrac{1}{2}}[Y, H\circ g]-{\tfrac{1}{2}} [F\circ h, H\circ g])(x). \end{align*} $$
$$ \begin{align*} h^{-1}\circ & f\circ h(x) =x\cdot \textrm{ exp}\, H(x)\,\textrm{ exp}(Y+F\circ h(x))\,\textrm{ exp}(-H\circ h^{-1}\circ f\circ h(x)) \\ & =x\cdot \textrm{ exp}(H+Y+F\circ h+{\tfrac{1}{2}}[H, Y]+[H, F\circ h])(x)\,\textrm{ exp}(-H\circ g)(x) \\ & =x\cdot \textrm{ exp}(H+Y-H\circ g+F\circ h+ {\tfrac{1}{2}}[H, Y]+ [H, F\circ h] \\ & \quad-{\tfrac{1}{2}} [H, -H\circ g]-{\tfrac{1}{2}}[Y, H\circ g]-{\tfrac{1}{2}} [F\circ h, H\circ g])(x). \end{align*} $$
This implies the equality claimed for G.
3.5 Linearizations of the conjugacy and the commutator operators: first and second coboundary operators on vector fields, splitting
The linear part of the nonlinear equation (57) defines the second coboundary operator on vector fields over the action
![]() $\rho $
generated by
$\rho $
generated by
![]() $y_1$
and
$y_1$
and
![]() $y_2$
.
$y_2$
.
Definition 3.5. Let
![]() ${\mathbf {d}}_2: \textrm{ Vect}^{\infty }{M}\times \textrm{ Vect}^{\infty }{M} \to \textrm{ Vect}^{\infty }{M}$
be the linear operator defined by
${\mathbf {d}}_2: \textrm{ Vect}^{\infty }{M}\times \textrm{ Vect}^{\infty }{M} \to \textrm{ Vect}^{\infty }{M}$
be the linear operator defined by
We say that a pair of smooth vector fields
![]() $(F, G)$
generates a cocycle over the action
$(F, G)$
generates a cocycle over the action
![]() $\rho $
if
$\rho $
if
![]() $(F, G)\in \text {Ker}\, {\mathbf {d}}_2$
.
$(F, G)\in \text {Ker}\, {\mathbf {d}}_2$
.
The first coboundary operator on vector fields over the action
![]() $\rho $
is given by the following definition.
$\rho $
is given by the following definition.
Definition 3.6. Let
![]() $H\in \textrm{ Vect}^{\infty }{M}.$
Then we define
$H\in \textrm{ Vect}^{\infty }{M}.$
Then we define
![]() ${\mathbf {d}}_1:\textrm{ Vect}^{\infty }{M}\to \text { Vect}^{\infty }{M} \times \textrm{ Vect}^{\infty }{M}$
by
${\mathbf {d}}_1:\textrm{ Vect}^{\infty }{M}\to \text { Vect}^{\infty }{M} \times \textrm{ Vect}^{\infty }{M}$
by
It is an easy exercise to check that
![]() $\rm {Im}\, {\mathbf {d}}_1\subset \text {Ker}\, {\mathbf {d}}_2$
. The first cohomology over
$\rm {Im}\, {\mathbf {d}}_1\subset \text {Ker}\, {\mathbf {d}}_2$
. The first cohomology over
![]() $\rho $
with coefficients in vector fields is the quotient space
$\rho $
with coefficients in vector fields is the quotient space
![]() $H^1_{\rho }(\textrm{ Vect}^{\infty }{M}):= \rm Ker\, {\mathbf {d}}_2/\rm Im\, {\mathbf {d}}_1$
. Notice that for constant vector fields
$H^1_{\rho }(\textrm{ Vect}^{\infty }{M}):= \rm Ker\, {\mathbf {d}}_2/\rm Im\, {\mathbf {d}}_1$
. Notice that for constant vector fields
![]() $H\in \frak h$
cocycles and coboundaries defined here coincide with those defined in §3.1. The subsequent proposition has as a corollary that for our fixed action
$H\in \frak h$
cocycles and coboundaries defined here coincide with those defined in §3.1. The subsequent proposition has as a corollary that for our fixed action
![]() $\rho $
the cohomology
$\rho $
the cohomology
![]() $H^1_{\rho }(\textrm{ Vect}^{\infty }{M})$
is the same as the cohomology
$H^1_{\rho }(\textrm{ Vect}^{\infty }{M})$
is the same as the cohomology
![]() $H^1_{\rho }(\frak h)$
with coefficients in the constant vector fields
$H^1_{\rho }(\frak h)$
with coefficients in the constant vector fields
![]() $\frak h$
which was computed in §3.1.
$\frak h$
which was computed in §3.1.
Proposition 3.7. If the two vector fields
![]() $F, G\in \textrm{ Vect}^{\infty }{M}$
satisfy
$F, G\in \textrm{ Vect}^{\infty }{M}$
satisfy
![]() ${\mathbf {d}}_2(F, G)=\Phi $
and
${\mathbf {d}}_2(F, G)=\Phi $
and
![]() $(\textrm{ Ave}\, F, \textrm{ Ave}\, G) $
is in the trivial cohomology class in
$(\textrm{ Ave}\, F, \textrm{ Ave}\, G) $
is in the trivial cohomology class in
![]() $H_{\rho }^1(\frak n)$
, then there exist
$H_{\rho }^1(\frak n)$
, then there exist
![]() $H, \tilde {F}, \tilde {G}\in \textrm{ Vect}^{\infty }{M}$
such that
$H, \tilde {F}, \tilde {G}\in \textrm{ Vect}^{\infty }{M}$
such that
![]() $(F, G)= {\mathbf {d}}_1H+ (\tilde {F}, \tilde {G})$
and the following estimates hold:
$(F, G)= {\mathbf {d}}_1H+ (\tilde {F}, \tilde {G})$
and the following estimates hold:
 $$ \begin{align} \|\tilde{F}\|_s &\leq C_{s} \| \Phi\|_{s+\sigma}, \notag\\ \|\tilde{G}\|_s &\leq C_{s}\| \Phi\|_{s+\sigma}, \notag\\ \| H \|_s &\leq C_{s, r, S, T, \Gamma}\| F\|_{s+\sigma}. \end{align} $$
$$ \begin{align} \|\tilde{F}\|_s &\leq C_{s} \| \Phi\|_{s+\sigma}, \notag\\ \|\tilde{G}\|_s &\leq C_{s}\| \Phi\|_{s+\sigma}, \notag\\ \| H \|_s &\leq C_{s, r, S, T, \Gamma}\| F\|_{s+\sigma}. \end{align} $$
Proof Recall that we disintegrate an arbitrary vector field
![]() $H\in \textrm{ Vect}^{\infty }{M}$
into
$H\in \textrm{ Vect}^{\infty }{M}$
into
![]() $H= H_c+ H_T$
, where
$H= H_c+ H_T$
, where
![]() $ H_c$
is the component of H in the direction of Z and
$ H_c$
is the component of H in the direction of Z and
![]() $H_T$
is the component of H in all the directions other than Z. So, one can view
$H_T$
is the component of H in all the directions other than Z. So, one can view
![]() $H_T$
as
$H_T$
as
![]() $H_T=\sum h_t^ iX_i+\bar h_t^i\Lambda _i$
, where
$H_T=\sum h_t^ iX_i+\bar h_t^i\Lambda _i$
, where
![]() $h_t^ i, \bar h_t^i$
are smooth functions.
$h_t^ i, \bar h_t^i$
are smooth functions.
The equation
![]() ${\mathbf {d}}_2(F_T, G_T)=\Phi $
(since
${\mathbf {d}}_2(F_T, G_T)=\Phi $
(since
![]() ${\mathbf {d}}_2$
is a linear operator) splits then in the off-center directions into finitely many functional equations each of which has a form
${\mathbf {d}}_2$
is a linear operator) splits then in the off-center directions into finitely many functional equations each of which has a form
Since by assumption
![]() $(\textrm{ Ave}\, F, \textrm{ Ave}\, G) $
is assumed to be in the trivial constant cohomology class, it implies in particular that all the off-center components are 0 (see §3.1).
$(\textrm{ Ave}\, F, \textrm{ Ave}\, G) $
is assumed to be in the trivial constant cohomology class, it implies in particular that all the off-center components are 0 (see §3.1).
Now we may apply Theorem 1.3, which for each of these finitely many equations gives as an output smooth functions
![]() $\tilde {f}, \tilde {g}, h$
such that
$\tilde {f}, \tilde {g}, h$
such that
such that the corresponding estimates hold. Putting these coordinate functions all together gives functions
![]() $\tilde {F}_T, \tilde {G}_T, H_t$
such that
$\tilde {F}_T, \tilde {G}_T, H_t$
such that
![]() $({\mathbf {d}}_2(\tilde {F}_T, \tilde {G}_T))_T=\Phi _T$
,
$({\mathbf {d}}_2(\tilde {F}_T, \tilde {G}_T))_T=\Phi _T$
,
![]() $(F_T, G_T)=({\mathbf {d}}_1H_T)_T + (\tilde {F}_T, \tilde {G}_T)$
and
$(F_T, G_T)=({\mathbf {d}}_1H_T)_T + (\tilde {F}_T, \tilde {G}_T)$
and
![]() $\tilde {F}_T, \tilde {G}_T, H_T$
satisfy the estimates (59).
$\tilde {F}_T, \tilde {G}_T, H_T$
satisfy the estimates (59).
Now let
![]() $ F_c, G_c$
be the components of F and G in the center direction. Then, because the Z components within the brackets do not contribute, we have
$ F_c, G_c$
be the components of F and G in the center direction. Then, because the Z components within the brackets do not contribute, we have
 $$ \begin{align*} {\mathbf{d}}_2(F_c, G_c)& = F_c\circ y_2-F_c + \tfrac{1}{2}[Y_2, F_T\circ y_2+F_T] \\ & \quad-\big(G_c\circ y_1-G_c + \tfrac{1}{2}[Y_1, G_T\circ y_1+G_T]\big)= \Phi_c. \end{align*} $$
$$ \begin{align*} {\mathbf{d}}_2(F_c, G_c)& = F_c\circ y_2-F_c + \tfrac{1}{2}[Y_2, F_T\circ y_2+F_T] \\ & \quad-\big(G_c\circ y_1-G_c + \tfrac{1}{2}[Y_1, G_T\circ y_1+G_T]\big)= \Phi_c. \end{align*} $$
Since we already have
![]() $(F_T, G_T)=({\mathbf {d}}_1H_T)_T + (\tilde {F}_T, \tilde {G}_T)$
, we can substitute this in the above expression to obtain
$(F_T, G_T)=({\mathbf {d}}_1H_T)_T + (\tilde {F}_T, \tilde {G}_T)$
, we can substitute this in the above expression to obtain
 $$ \begin{align} &\big(F_c-{\tfrac{1}{2}}[Y_1, H_T\circ y_1+H_T]\big)\circ y_2 -\big(F_c-{\tfrac{1}{2}}[Y_1, H_T\circ y_1+H_T]\big) \nonumber\\ &\quad-\big(\big(G_c-{\tfrac{1}{2}}[Y_2, H_T\circ y_2+H_T]\big)\circ y_1 -\big(G_c-{\tfrac{1}{2}}[Y_2, H_T\circ y_2+H_T]\big)\big)=\Phi^{\prime}_c, \end{align} $$
$$ \begin{align} &\big(F_c-{\tfrac{1}{2}}[Y_1, H_T\circ y_1+H_T]\big)\circ y_2 -\big(F_c-{\tfrac{1}{2}}[Y_1, H_T\circ y_1+H_T]\big) \nonumber\\ &\quad-\big(\big(G_c-{\tfrac{1}{2}}[Y_2, H_T\circ y_2+H_T]\big)\circ y_1 -\big(G_c-{\tfrac{1}{2}}[Y_2, H_T\circ y_2+H_T]\big)\big)=\Phi^{\prime}_c, \end{align} $$
where
Clearly, since for any s we have
![]() $\|\tilde {F}_T\|_s,\|\tilde {G}_T\|_s\le \|\tilde {\Phi }_T\|_{s+\sigma }$
, it follows that
$\|\tilde {F}_T\|_s,\|\tilde {G}_T\|_s\le \|\tilde {\Phi }_T\|_{s+\sigma }$
, it follows that
![]() $\| \Phi ^{\prime }_c\|_s\le \|\tilde {\Phi }\|_{s+\sigma }$
, where
$\| \Phi ^{\prime }_c\|_s\le \|\tilde {\Phi }\|_{s+\sigma }$
, where
![]() $\sigma $
is re-defined to be
$\sigma $
is re-defined to be
![]() $\sigma + 1$
.
$\sigma + 1$
.
The vector field
![]() $H_T$
is determined only up to a constant vector field, so we may choose
$H_T$
is determined only up to a constant vector field, so we may choose
![]() $H_T$
so that
$H_T$
so that
![]() $\textrm{ Ave}\, F_c= \textrm{ Ave}[Y_1, H_T]$
. This forces
$\textrm{ Ave}\, F_c= \textrm{ Ave}[Y_1, H_T]$
. This forces
![]() $F_c-{\tfrac {1}{2}}[Y_1, H_T\circ y_1+H_T]$
to have the average 0. Moreover, because of the assumption that
$F_c-{\tfrac {1}{2}}[Y_1, H_T\circ y_1+H_T]$
to have the average 0. Moreover, because of the assumption that
![]() $(\textrm{ Ave}\, F, \textrm{ Ave}\, G) $
is in the trivial cohomology class, we also have that
$(\textrm{ Ave}\, F, \textrm{ Ave}\, G) $
is in the trivial cohomology class, we also have that
![]() $\textrm{ Ave}\, F_c= \textrm{ Ave}\, G_c$
.
$\textrm{ Ave}\, F_c= \textrm{ Ave}\, G_c$
.
So, the equation (60) is again the same type of equation as in Theorem 1.3. By applying the theorem, we get
![]() $\tilde {F}_c, \tilde {G}_c, H_c$
such that
$\tilde {F}_c, \tilde {G}_c, H_c$
such that
 $$ \begin{align*} & F_c-{\tfrac{1}{2}}[Y_1, H_T\circ y_1+H_T]= H_c\circ y_1-H_c + \tilde{F}_c, \\ & G_c-{\tfrac{1}{2}}[Y_2, H_T\circ y_2+H_T]= H_c\circ y_2-H_c + \tilde{G}_c. \end{align*} $$
$$ \begin{align*} & F_c-{\tfrac{1}{2}}[Y_1, H_T\circ y_1+H_T]= H_c\circ y_1-H_c + \tilde{F}_c, \\ & G_c-{\tfrac{1}{2}}[Y_2, H_T\circ y_2+H_T]= H_c\circ y_2-H_c + \tilde{G}_c. \end{align*} $$
This clearly implies that
Putting the c- and T-components together gives the solution. Estimates (59) are direct consequences of coordinate-wise estimates which are obtained already in Theorem 1.3.
3.6 Set-up of the perturbative problem and the iterative scheme
We will frequently refer here to [Reference Damjanović and Katok7], so we recommend that the reader has that paper at hand.
We consider here a family of perturbations
![]() $\tilde {\rho }^{\unicode{x3bb} }$
of
$\tilde {\rho }^{\unicode{x3bb} }$
of
![]() $\rho ^{\unicode{x3bb} }$
, which are generated by commuting maps
$\rho ^{\unicode{x3bb} }$
, which are generated by commuting maps
![]() $\tilde {y}_1^{\unicode{x3bb} }$
and
$\tilde {y}_1^{\unicode{x3bb} }$
and
![]() $\tilde {y}_2^{\unicode{x3bb} }$
, where, for
$\tilde {y}_2^{\unicode{x3bb} }$
, where, for
![]() $i=1,2$
,
$i=1,2$
,
Here
![]() $\tilde {F}_i^{\unicode{x3bb} }$
are small vector fields such that
$\tilde {F}_i^{\unicode{x3bb} }$
are small vector fields such that
![]() $\tilde {y}_1^{\unicode{x3bb} }$
and
$\tilde {y}_1^{\unicode{x3bb} }$
and
![]() $\tilde {y}_2^{\unicode{x3bb} }$
commute.
$\tilde {y}_2^{\unicode{x3bb} }$
commute.
Now let h be a diffeomorphism of the manifold, close to the identity, defined via the smooth vector field H as follows:
The iterative step consists of the following: given the perturbation
![]() $\tilde {\rho }^{\unicode{x3bb} }$
of
$\tilde {\rho }^{\unicode{x3bb} }$
of
![]() $\rho ^{\unicode{x3bb} }$
, define a new perturbation
$\rho ^{\unicode{x3bb} }$
, define a new perturbation
![]() $\bar \rho ^{\unicode{x3bb} }$
which is a conjugation of
$\bar \rho ^{\unicode{x3bb} }$
which is a conjugation of
![]() $\tilde {\rho }^{\unicode{x3bb} }$
via h, so
$\tilde {\rho }^{\unicode{x3bb} }$
via h, so
![]() $\bar \rho ^{\unicode{x3bb} }$
is generated by two diffeomorphisms
$\bar \rho ^{\unicode{x3bb} }$
is generated by two diffeomorphisms
![]() $\bar y_i^{\unicode{x3bb} }$
,
$\bar y_i^{\unicode{x3bb} }$
,
![]() $i\in \{1,2\}$
, defined by
$i\in \{1,2\}$
, defined by
In each iterative step this is done for the
![]() $\lambda $
parameter in some ball, and it is shown that in that ball there is a parameter for which the new family of perturbations is much (quadratically) closer to
$\lambda $
parameter in some ball, and it is shown that in that ball there is a parameter for which the new family of perturbations is much (quadratically) closer to
![]() $\rho $
for parameters in some smaller ball. The next proposition shows that that this process is controlled in the sequence of
$\rho $
for parameters in some smaller ball. The next proposition shows that that this process is controlled in the sequence of
![]() $C^r$
norms.
$C^r$
norms.
We will need to control derivatives of each perturbed family
![]() $\tilde {\rho }^{\unicode{x3bb} }$
in the direction of the parameter
$\tilde {\rho }^{\unicode{x3bb} }$
in the direction of the parameter
![]() $\lambda $
as well, so we will use the following norms for a family of vector fields
$\lambda $
as well, so we will use the following norms for a family of vector fields
![]() $\tilde {F}_i^{\unicode{x3bb} }$
:
$\tilde {F}_i^{\unicode{x3bb} }$
:
![]() $\|\tilde {F}_i^{\unicode{x3bb} }\|_{0, k}$
stands for the supremum of the
$\|\tilde {F}_i^{\unicode{x3bb} }\|_{0, k}$
stands for the supremum of the
![]() $C^k$
norms of
$C^k$
norms of
![]() $\tilde {F}_i^{\unicode{x3bb} }$
in the
$\tilde {F}_i^{\unicode{x3bb} }$
in the
![]() ${\unicode{x3bb} }$
variable.
${\unicode{x3bb} }$
variable.
![]() $\|\tilde {F}_i^{\unicode{x3bb} }\|_{r, k}$
is the same only taken over all the derivatives of
$\|\tilde {F}_i^{\unicode{x3bb} }\|_{r, k}$
is the same only taken over all the derivatives of
![]() $\tilde {F}_i^{\unicode{x3bb} }$
in the manifold direction. As before, we reserve the notation
$\tilde {F}_i^{\unicode{x3bb} }$
in the manifold direction. As before, we reserve the notation
![]() $\|\tilde {F}_i^{\unicode{x3bb} }\|_{r}$
for the usual
$\|\tilde {F}_i^{\unicode{x3bb} }\|_{r}$
for the usual
![]() $C^r$
norm on M of the vector field
$C^r$
norm on M of the vector field
![]() $ \tilde {F}_i^{\unicode{x3bb} }\in \textrm{ Vect}^{\infty }{M}$
for a fixed parameter
$ \tilde {F}_i^{\unicode{x3bb} }\in \textrm{ Vect}^{\infty }{M}$
for a fixed parameter
![]() ${\unicode{x3bb} }$
.
${\unicode{x3bb} }$
.
The following is an immediate corollary of the classical implicit function theorem and we will use it for the maps which compute averages of vector fields for actions in the perturbed family.
Lemma 3.8. There exists an open ball
![]() $\mathcal O=\mathcal O(\mathrm{Id}, R)$
in
$\mathcal O=\mathcal O(\mathrm{Id}, R)$
in
![]() $C^1(\mathbb R^d, \mathbb R^d)$
, there exist a neighborhood
$C^1(\mathbb R^d, \mathbb R^d)$
, there exist a neighborhood
![]() $\mathcal U$
of
$\mathcal U$
of
![]() $0\in \mathbb R^d$
and a
$0\in \mathbb R^d$
and a
![]() $C^1$
map
$C^1$
map
![]() $\Psi : \mathcal O\to \mathcal U$
such that for every
$\Psi : \mathcal O\to \mathcal U$
such that for every
![]() $G\in \mathcal O$
,
$G\in \mathcal O$
,
![]() $G(\Psi (G))=0$
.
$G(\Psi (G))=0$
.
Now we state the main iterative step proposition where we show that one can obtain indeed estimates which are needed for the convergence of the process to a smooth conjugation map.
Proposition 3.9. There exist constants
![]() $\bar C$
and
$\bar C$
and
![]() $r_0$
such that the following holds.
$r_0$
such that the following holds.
Given the family
![]() $\tilde {\rho }_n^{\unicode{x3bb} }$
of perturbations of
$\tilde {\rho }_n^{\unicode{x3bb} }$
of perturbations of
![]() $\rho ^0$
generated by
$\rho ^0$
generated by
![]() $\tilde {y}_{i, n}^{\unicode{x3bb} }$
(
$\tilde {y}_{i, n}^{\unicode{x3bb} }$
(
![]() $i=1,2$
), assume that for all
$i=1,2$
), assume that for all
![]() ${\unicode{x3bb} }$
in a ball B centered at 0, for
${\unicode{x3bb} }$
in a ball B centered at 0, for
![]() $r\in \mathbb N$
and
$r\in \mathbb N$
and
![]() $t>0$
:
$t>0$
:
-
(1)
 $\| \tilde {F}_{i, n}^{\unicode{x3bb} }\|_0\le {\varepsilon }_n<1$
;
$\| \tilde {F}_{i, n}^{\unicode{x3bb} }\|_0\le {\varepsilon }_n<1$
; -
(2) the map
 ${\unicode{x3bb} }\mapsto \tilde {F}_{i, n}^{\unicode{x3bb} }$
is
${\unicode{x3bb} }\mapsto \tilde {F}_{i, n}^{\unicode{x3bb} }$
is
 $C^2$
in
$C^2$
in
 ${\unicode{x3bb} }$
,
${\unicode{x3bb} }$
,
 $\|\tilde {F}_{i, n}^{\unicode{x3bb} }\|_{0, 1}\le {\varepsilon }_n$
and
$\|\tilde {F}_{i, n}^{\unicode{x3bb} }\|_{0, 1}\le {\varepsilon }_n$
and
 $\|\tilde {F}_{i, n}^{\unicode{x3bb} }\|_{0, 2}\le K_n$
;
$\|\tilde {F}_{i, n}^{\unicode{x3bb} }\|_{0, 2}\le K_n$
; -
(3) the map
 $\Phi ^n : {\unicode{x3bb} }\mapsto \textrm{ Ave}(\tilde {F}_{i, n}^{\unicode{x3bb} })$
is in
$\Phi ^n : {\unicode{x3bb} }\mapsto \textrm{ Ave}(\tilde {F}_{i, n}^{\unicode{x3bb} })$
is in
 $\mathcal O$
and has a zero at
$\mathcal O$
and has a zero at
 ${\unicode{x3bb} }_n$
;
${\unicode{x3bb} }_n$
; -
(4)
 $\| \tilde {F}_{i, n}^{\unicode{x3bb} }\|_{r_0+r}\le \delta _{r, n}$
;
$\| \tilde {F}_{i, n}^{\unicode{x3bb} }\|_{r_0+r}\le \delta _{r, n}$
; -
(5)
 $t^{r_0}{\varepsilon } _n^{1-({1}/({r+r_0}))}\delta _{r}^{({1}/({r+r_0}))}<\bar C$
.
$t^{r_0}{\varepsilon } _n^{1-({1}/({r+r_0}))}\delta _{r}^{({1}/({r+r_0}))}<\bar C$
.
There exists a
![]() $H_n\in \textrm{ Vect}^{\infty }{M}$
such that
$H_n\in \textrm{ Vect}^{\infty }{M}$
such that
![]() $h_n$
defined by
$h_n$
defined by
![]() $ h(x)= x\cdot \textrm{ exp}\, H_n(x) $
is such that the newly formed family of perturbations
$ h(x)= x\cdot \textrm{ exp}\, H_n(x) $
is such that the newly formed family of perturbations
![]() $\tilde {\rho }_{n+1}^{\unicode{x3bb} }$
of
$\tilde {\rho }_{n+1}^{\unicode{x3bb} }$
of
![]() $\rho $
, generated by
$\rho $
, generated by
![]() $\tilde {y}_{i, n+1}^{\unicode{x3bb} }= h^{-1}\circ \tilde {y}_{i, n}^{\unicode{x3bb} }\circ h$
, with
$\tilde {y}_{i, n+1}^{\unicode{x3bb} }= h^{-1}\circ \tilde {y}_{i, n}^{\unicode{x3bb} }\circ h$
, with
![]() $\tilde {y}_{i, n+1}^{\unicode{x3bb} }(x)= x\,\textrm{ exp}(Y_i+ \tilde {F}_{i, n+1}^{\unicode{x3bb} }(x))$
, satisfies the following:
$\tilde {y}_{i, n+1}^{\unicode{x3bb} }(x)= x\,\textrm{ exp}(Y_i+ \tilde {F}_{i, n+1}^{\unicode{x3bb} }(x))$
, satisfies the following:
-
(a)
 $\|H_n\|_r\le C_rt^{2r_0}\|\tilde {F}_i^{{\unicode{x3bb} }_n}\|_r$
;
$\|H_n\|_r\le C_rt^{2r_0}\|\tilde {F}_i^{{\unicode{x3bb} }_n}\|_r$
; -
(b)
 $ \|\tilde {F}_{i, n+1}^{{\unicode{x3bb} }}\|_0\le K_n\|{\unicode{x3bb} }-{\unicode{x3bb} }_n\|+ {\rm Err}(t, r)$
, where
$ \|\tilde {F}_{i, n+1}^{{\unicode{x3bb} }}\|_0\le K_n\|{\unicode{x3bb} }-{\unicode{x3bb} }_n\|+ {\rm Err}(t, r)$
, where  $$ \begin{align*}\textrm{ Err}_{n+1}(t,r)&:=C {\varepsilon }_n^2 +C\delta_{r, n}^{{(r_0+1)}/({r_0+r})}{\varepsilon }_n^{2-(({r_0+1})/({r_0+r}))}+C_{r}t^{-r}\delta_{r,n}\\&\quad+C_{r_0}t^{2r_0}{\varepsilon }_n^{2-({1}/({r_0+r}))}\delta_{r,n}^{{1}/({r_0+r})}+C_{r_0}t^{2r_0}{\varepsilon }_n^{3-({1}/({r_0+r}))}\delta_{r,n}^{{2}/({r_0+r})}; \end{align*} $$
$$ \begin{align*}\textrm{ Err}_{n+1}(t,r)&:=C {\varepsilon }_n^2 +C\delta_{r, n}^{{(r_0+1)}/({r_0+r})}{\varepsilon }_n^{2-(({r_0+1})/({r_0+r}))}+C_{r}t^{-r}\delta_{r,n}\\&\quad+C_{r_0}t^{2r_0}{\varepsilon }_n^{2-({1}/({r_0+r}))}\delta_{r,n}^{{1}/({r_0+r})}+C_{r_0}t^{2r_0}{\varepsilon }_n^{3-({1}/({r_0+r}))}\delta_{r,n}^{{2}/({r_0+r})}; \end{align*} $$
-
(c)
 $\| \tilde {F}_{i, n+1}^{\unicode{x3bb} }\|_{r_0+r}\le C_rt^{2r_0}\delta _{r, n}:=\delta _{r, n+1} $
;
$\| \tilde {F}_{i, n+1}^{\unicode{x3bb} }\|_{r_0+r}\le C_rt^{2r_0}\delta _{r, n}:=\delta _{r, n+1} $
; -
(d) the map
 $\Phi ^{n+1}:={\unicode{x3bb} }\mapsto \textrm{ Ave}(\tilde {F}_{i, n+1}^{\unicode{x3bb} })$
satisfies
$\Phi ^{n+1}:={\unicode{x3bb} }\mapsto \textrm{ Ave}(\tilde {F}_{i, n+1}^{\unicode{x3bb} })$
satisfies
 $$ \begin{align*} \|\Phi^{n+1}-\Phi^n\|_{(0)}&\le \textrm{ Err}_{n+1}(t,r),\\ \|\Phi^{n+1}-\Phi^n\|_{(1)}&\le K_nt^{r_0}{\varepsilon }_n+\textrm{ Err}_{n+1}(t,r). \end{align*} $$
$$ \begin{align*} \|\Phi^{n+1}-\Phi^n\|_{(0)}&\le \textrm{ Err}_{n+1}(t,r),\\ \|\Phi^{n+1}-\Phi^n\|_{(1)}&\le K_nt^{r_0}{\varepsilon }_n+\textrm{ Err}_{n+1}(t,r). \end{align*} $$
If
![]() $\Phi ^{n+1}$
is in
$\Phi ^{n+1}$
is in
![]() $\mathcal O$
, then it has a zero at
$\mathcal O$
, then it has a zero at
![]() ${\unicode{x3bb} }_{n+1}\in B$
which satisfies
${\unicode{x3bb} }_{n+1}\in B$
which satisfies
-
(e)
 $\tilde {F}_{i, n+1}^{\unicode{x3bb} }$
is
$\tilde {F}_{i, n+1}^{\unicode{x3bb} }$
is
 $C^2$
in
$C^2$
in
 ${\unicode{x3bb} }$
and
${\unicode{x3bb} }$
and  $$ \begin{align*}\| \tilde{F}_{i, n+1}^{\unicode{x3bb}}\|_{0, 2}\le (1+Ct^{r_0}{\varepsilon }_n^{1-({1}/({r+r_0}))}\delta_{r,n}^{{1}/({r+r_0})})K_n=:K_{n+1}(t,r).\end{align*} $$
$$ \begin{align*}\| \tilde{F}_{i, n+1}^{\unicode{x3bb}}\|_{0, 2}\le (1+Ct^{r_0}{\varepsilon }_n^{1-({1}/({r+r_0}))}\delta_{r,n}^{{1}/({r+r_0})})K_n=:K_{n+1}(t,r).\end{align*} $$
Proof As was mentioned in [Reference Damjanović and Katok7, Remark 6.3], the proof of the iterative step is universal given tame splitting for vector fields (Proposition 3.7). We repeat the main points here for the sake of completeness with fewer details than in the proof of the corresponding proposition in [Reference Damjanović and Katok7, Proposition 6.2].
In this proof, as is customary whenever there is a loss of regularity for solutions of linearized equations, we will use the smoothing operators. For the construction of smoothing operators on
![]() $C^{\infty }(M)$
, see the following in [Reference Hamilton10]: Example 1.1.2(2), Definition 1.3.2, Theorem 1.3.6 and Corollary 1.4.2. There exists a collection of smoothing operators
$C^{\infty }(M)$
, see the following in [Reference Hamilton10]: Example 1.1.2(2), Definition 1.3.2, Theorem 1.3.6 and Corollary 1.4.2. There exists a collection of smoothing operators
![]() $S_t:C^{\infty }(M)\to C^{\infty }(M)$
,
$S_t:C^{\infty }(M)\to C^{\infty }(M)$
,
![]() $t>0$
, such that the following holds:
$t>0$
, such that the following holds:
 $$ \begin{align} \|S_tF\|_{s+s'}&\le C_{s,s'}t^{s'}\|F\|_s,\nonumber\\ \|(I-S_t)F\|_{s-s'}&\le C_{s,s'}t^{-s'}\|F\|_s. \end{align} $$
$$ \begin{align} \|S_tF\|_{s+s'}&\le C_{s,s'}t^{s'}\|F\|_s,\nonumber\\ \|(I-S_t)F\|_{s-s'}&\le C_{s,s'}t^{-s'}\|F\|_s. \end{align} $$
Smoothing operators on
![]() $C^{\infty }(M)$
clearly induce smoothing operators on
$C^{\infty }(M)$
clearly induce smoothing operators on
![]() $\textrm{ Vect}^{\infty }{M}$
via smoothing operators applied to coordinate maps.
$\textrm{ Vect}^{\infty }{M}$
via smoothing operators applied to coordinate maps.
It is easy to see that averages of F with respect to the Haar measure on M, in various directions in the tangent space, do not affect the properties of smoothing operators listed above, so without loss of generality we may assume that
![]() $S_t$
are such that averages of
$S_t$
are such that averages of
![]() $S_tF$
are the same as those of F.
$S_tF$
are the same as those of F.
Given
![]() ${ \tilde {F}_{i, n}^{\unicode{x3bb} }}$
, we first apply the smoothing operators to it and write
${ \tilde {F}_{i, n}^{\unicode{x3bb} }}$
, we first apply the smoothing operators to it and write
![]() ${ \tilde {F}_{i, n}^{\unicode{x3bb} }}= S_t{ \tilde {F}_{i, n}^{\unicode{x3bb} }}+ (I-S_t) { \tilde {F}_{i, n}^{\unicode{x3bb} }}$
. Now
${ \tilde {F}_{i, n}^{\unicode{x3bb} }}= S_t{ \tilde {F}_{i, n}^{\unicode{x3bb} }}+ (I-S_t) { \tilde {F}_{i, n}^{\unicode{x3bb} }}$
. Now
![]() $\textrm{ Ave}({ \tilde {F}_{i, n}^{\unicode{x3bb} }})= \textrm{ Ave}(S_t{ \tilde {F}_{i, n}^{\unicode{x3bb} }})$
. From the commutativity of
$\textrm{ Ave}({ \tilde {F}_{i, n}^{\unicode{x3bb} }})= \textrm{ Ave}(S_t{ \tilde {F}_{i, n}^{\unicode{x3bb} }})$
. From the commutativity of
![]() ${ \tilde {F}_{i, n}^{\unicode{x3bb} }}$
for
${ \tilde {F}_{i, n}^{\unicode{x3bb} }}$
for
![]() $i=1$
and
$i=1$
and
![]() $i=2$
(see Corollary 3.3), it follows that
$i=2$
(see Corollary 3.3), it follows that
![]() $|\textrm{ Ave}[Y_2, \tilde {F}_{1, n}]-\textrm{ Ave}[Y_1, \tilde {F}_{2, n}]|\le C\|\tilde {F}_{1, n}\|_1\|\tilde {F}_{2, n}\|_1\le C{\varepsilon }_n^2$
and clearly the same holds after application of the corresponding smoothing operators. Now we can apply Proposition 3.7 to
$|\textrm{ Ave}[Y_2, \tilde {F}_{1, n}]-\textrm{ Ave}[Y_1, \tilde {F}_{2, n}]|\le C\|\tilde {F}_{1, n}\|_1\|\tilde {F}_{2, n}\|_1\le C{\varepsilon }_n^2$
and clearly the same holds after application of the corresponding smoothing operators. Now we can apply Proposition 3.7 to
![]() $S_t{ \tilde {F}_{i, n}^{\unicode{x3bb} }}- \textrm{ Ave}({ \tilde {F}_{i, n}^{\unicode{x3bb} }})_T$
,
$S_t{ \tilde {F}_{i, n}^{\unicode{x3bb} }}- \textrm{ Ave}({ \tilde {F}_{i, n}^{\unicode{x3bb} }})_T$
,
![]() $i=1, 2$
(recall that
$i=1, 2$
(recall that
![]() $\textrm{ Ave}({ \tilde {F}_{i, n}^{\unicode{x3bb} }})_T$
are averages in the off-center directions). Proposition 3.7 gives existence of
$\textrm{ Ave}({ \tilde {F}_{i, n}^{\unicode{x3bb} }})_T$
are averages in the off-center directions). Proposition 3.7 gives existence of
![]() $H_n$
such that
$H_n$
such that
where (see (58))
From the expression for E in (58), we have the following estimate for
![]() $\Phi $
:
$\Phi $
:
where we use short notation
![]() $ \|{ \tilde {F}_{i, n}^{\unicode{x3bb} }}\|_r$
for the maximum of the norms for
$ \|{ \tilde {F}_{i, n}^{\unicode{x3bb} }}\|_r$
for the maximum of the norms for
![]() $i=1$
and
$i=1$
and
![]() $i=2$
. Also, from Proposition 3.7, we have
$i=2$
. Also, from Proposition 3.7, we have
From Lemma 3.4, it follows that if we define
![]() $h_n$
by
$h_n$
by
![]() $h_n(x) = x\cdot \textrm{ exp}\, H_n(x)$
, and
$h_n(x) = x\cdot \textrm{ exp}\, H_n(x)$
, and
![]() $\tilde {y}_{i, n+1}^{\unicode{x3bb} }= h^{-1}\circ \tilde {y}_{i, n}^{\unicode{x3bb} }\circ h$
, with
$\tilde {y}_{i, n+1}^{\unicode{x3bb} }= h^{-1}\circ \tilde {y}_{i, n}^{\unicode{x3bb} }\circ h$
, with
![]() $\tilde {y}_{i, n+1}^{\unicode{x3bb} }(x)= x\cdot \textrm{ exp}(Y_i+ \tilde {F}_{i, n+1}^{\unicode{x3bb} }(x))$
, then
$\tilde {y}_{i, n+1}^{\unicode{x3bb} }(x)= x\cdot \textrm{ exp}(Y_i+ \tilde {F}_{i, n+1}^{\unicode{x3bb} }(x))$
, then
![]() $ \tilde {F}_{i, n+1}^{\unicode{x3bb} }$
satisfy the following, after applying the interpolation estimates and the smoothing estimates and assumptions (2) and (3) (compare to [Reference Damjanović and Katok7, (6.7)]):
$ \tilde {F}_{i, n+1}^{\unicode{x3bb} }$
satisfy the following, after applying the interpolation estimates and the smoothing estimates and assumptions (2) and (3) (compare to [Reference Damjanović and Katok7, (6.7)]):
 $$ \begin{align} \|\tilde{F}_{i, n+1}^{\unicode{x3bb}}\|_0&\le K_n\|{\unicode{x3bb}}-{\unicode{x3bb}}_n\| + C {\varepsilon }_n^2+C\delta_{r, n}^{({r_0+1})/({r_0+r})}{\varepsilon }_n^{2-(({r_0+1})/({r_0+r}))}\nonumber\\ &+C_{r}t^{-r}\delta_{r,n}+C_{r_0}t^{2r_0}{\varepsilon }_n^{2-({1}/({r_0+r}))}\delta_{r,n}^{{1}/({r_0+r})}+C_{r_0}t^{2r_0}{\varepsilon }_n^{3-({1}/({r_0+r}))}\delta_{r,n}^{{2}/({r_0+r})}. \end{align} $$
$$ \begin{align} \|\tilde{F}_{i, n+1}^{\unicode{x3bb}}\|_0&\le K_n\|{\unicode{x3bb}}-{\unicode{x3bb}}_n\| + C {\varepsilon }_n^2+C\delta_{r, n}^{({r_0+1})/({r_0+r})}{\varepsilon }_n^{2-(({r_0+1})/({r_0+r}))}\nonumber\\ &+C_{r}t^{-r}\delta_{r,n}+C_{r_0}t^{2r_0}{\varepsilon }_n^{2-({1}/({r_0+r}))}\delta_{r,n}^{{1}/({r_0+r})}+C_{r_0}t^{2r_0}{\varepsilon }_n^{3-({1}/({r_0+r}))}\delta_{r,n}^{{2}/({r_0+r})}. \end{align} $$
For the
![]() $C^{r_0+r}$
norm of the new error
$C^{r_0+r}$
norm of the new error
![]() $\tilde {F}_{i, n+1}^{\unicode{x3bb} }$
, as usual in this type of proofs, we only need a ‘linear’ bound with respect to the corresponding norm of the old error. This follows easily from the conjugacy relation and we obtain for any
$\tilde {F}_{i, n+1}^{\unicode{x3bb} }$
, as usual in this type of proofs, we only need a ‘linear’ bound with respect to the corresponding norm of the old error. This follows easily from the conjugacy relation and we obtain for any
![]() $s\ge 0$
:
$s\ge 0$
:
which, as in [Reference Damjanović and Katok7], implies that
The remaining two statements (e) and (d) follow exactly in the same way as in the proof of [Reference Damjanović and Katok7, Proposition 6.2].
Given Proposition 3.9 (compare to [Reference Damjanović and Katok7, Proposition 6.2]), we can now apply the convergence of the successive iterative scheme proved in [Reference Damjanović and Katok7, §7]. Consequently, we obtain the following theorem, which is a more precise statement of our main transversal local rigidity result in Theorem 1.7.
Theorem 3.10. There exist
![]() $l>0$
,
$l>0$
,
![]() $\epsilon>0$
,
$\epsilon>0$
,
![]() $R>0$
such that if a family
$R>0$
such that if a family
![]() $\tilde {\rho }^{\unicode{x3bb} }$
of perturbations of
$\tilde {\rho }^{\unicode{x3bb} }$
of perturbations of
![]() $\rho $
generated by
$\rho $
generated by
![]() $\tilde {y}_i^{\unicode{x3bb} }$
is
$\tilde {y}_i^{\unicode{x3bb} }$
is
![]() $\epsilon $
close to
$\epsilon $
close to
![]() $\rho $
in the
$\rho $
in the
![]() $C^l$
norm for parameters
$C^l$
norm for parameters
![]() $\lambda $
in an R-ball around 0, and in the
$\lambda $
in an R-ball around 0, and in the
![]() $C^1$
norm in the parameter
$C^1$
norm in the parameter
![]() $\lambda $
direction, then there exists a small parameter
$\lambda $
direction, then there exists a small parameter
![]() $\bar \lambda $
such that the action
$\bar \lambda $
such that the action
![]() $\tilde {\rho }^{\bar {\unicode{x3bb} }}$
is conjugate to
$\tilde {\rho }^{\bar {\unicode{x3bb} }}$
is conjugate to
![]() $\rho $
via h, that is, for
$\rho $
via h, that is, for
![]() $i=1, 2$
, we have
$i=1, 2$
, we have
where h is a smooth diffeomorphism order of
![]() $\epsilon $
close to the identity in the
$\epsilon $
close to the identity in the
![]() $C^1$
norm.
$C^1$
norm.
Acknowledgements
Based on research supported by the Swedish Research Council grant 2015-04644. Approved for public release; distribution unlimited. Case number 18-2318. The second author’s affiliation with The MITRE Corporation is provided for identification purposes only, and is not intended to convey or imply MITRE’s concurrence with, or support for, the positions, opinions or viewpoints expressed by the authors.
A Appendix. Proof of Propositions 2.1 and 2.2
The classical Diophantine condition (5) stated in §1.1 is clearly equivalent to the following condition: there are constants
![]() $c := c_{\boldsymbol {\tau }, \boldsymbol {\eta }}> 0$
and
$c := c_{\boldsymbol {\tau }, \boldsymbol {\eta }}> 0$
and
![]() $\gamma := \gamma _{\boldsymbol {\tau }, \boldsymbol {\eta }}> 0$
such that for any
$\gamma := \gamma _{\boldsymbol {\tau }, \boldsymbol {\eta }}> 0$
such that for any
![]() $\mathbf {m} \in { \mathbb Z}^{2n}$
and
$\mathbf {m} \in { \mathbb Z}^{2n}$
and
![]() $p \in { \mathbb Z}$
, we have
$p \in { \mathbb Z}$
, we have
 $$ \begin{align} & \vert \boldsymbol{\tau} \cdot \mathbf{m} - p \vert> c \vert \mathbf{m} \cdot \mathbf{m} \vert^{-\gamma} \quad\text{ if } \mathbf{m}_1 \neq 0, \nonumber\\ & \vert \boldsymbol{\eta} \cdot \mathbf{m} - p \vert > c \vert \mathbf{m} \cdot \mathbf{m} \vert^{-\gamma} \quad\text{ if } \mathbf{m}_2 \neq 0. \end{align} $$
$$ \begin{align} & \vert \boldsymbol{\tau} \cdot \mathbf{m} - p \vert> c \vert \mathbf{m} \cdot \mathbf{m} \vert^{-\gamma} \quad\text{ if } \mathbf{m}_1 \neq 0, \nonumber\\ & \vert \boldsymbol{\eta} \cdot \mathbf{m} - p \vert > c \vert \mathbf{m} \cdot \mathbf{m} \vert^{-\gamma} \quad\text{ if } \mathbf{m}_2 \neq 0. \end{align} $$
We will use the above version of the Diophantine condition to prove the splitting results for finite-dimensional representations in this section. The same splitting results were needed and used in three other works so far: [Reference Damjanović and Fayad4, Reference Petkovic13, Reference Wilkinson and Xue19] and they follow closely Moser’s splitting construction on the circle in [Reference Moser12]. Our presentation here is somewhat different in that it follows a general splitting construction which applies to abelian actions where cohomological equations in irreducible representations have a finite-dimensional space of obstructions (as in [Reference Damjanović and Tanis8], for example).
For any
![]() $\mathbf {m} \in { \mathbb Z}^{2n}$
and for any
$\mathbf {m} \in { \mathbb Z}^{2n}$
and for any
![]() $\boldsymbol \kappa \in \{\boldsymbol \tau , \boldsymbol \eta \}$
, define the constant
$\boldsymbol \kappa \in \{\boldsymbol \tau , \boldsymbol \eta \}$
, define the constant
![]() $\zeta (\mathbf {m}, \boldsymbol \kappa )$
by
$\zeta (\mathbf {m}, \boldsymbol \kappa )$
by
The next lemma describes the operator
![]() $L_{\boldsymbol {\kappa }}$
on smooth functions in
$L_{\boldsymbol {\kappa }}$
on smooth functions in
![]() $L^2({ \mathbb T}^{2n})$
. Its proof is straightforward and follows from the Diophantine condition (A.1).
$L^2({ \mathbb T}^{2n})$
. Its proof is straightforward and follows from the Diophantine condition (A.1).
Lemma A.1. Let
![]() $h = \sum _{\mathbf {m} \in { \mathbb Z}^{2n}} h_{\mathbf {m}}\,\textrm{ exp}(2\pi i \mathbf {m} \cdot (\mathbf {x}, \boldsymbol \xi ))\in W_0^{\infty }({ \mathbb T}^{2n})$
be a smooth, zero- average function with coefficients (
$h = \sum _{\mathbf {m} \in { \mathbb Z}^{2n}} h_{\mathbf {m}}\,\textrm{ exp}(2\pi i \mathbf {m} \cdot (\mathbf {x}, \boldsymbol \xi ))\in W_0^{\infty }({ \mathbb T}^{2n})$
be a smooth, zero- average function with coefficients (
![]() $h_{\mathbf {m}})$
. Then, for
$h_{\mathbf {m}})$
. Then, for
![]() $\boldsymbol \kappa \in \{\boldsymbol {\tau }, \boldsymbol \eta \}$
,
$\boldsymbol \kappa \in \{\boldsymbol {\tau }, \boldsymbol \eta \}$
,
 $$ \begin{align*} L_{\boldsymbol{\kappa}} h(\mathbf{x}, \boldsymbol \xi) = \sum_{\mathbf{m} \in { \mathbb Z}^{2n}\setminus\{0\}} h_{\mathbf{m}} \zeta(\mathbf{m}, \boldsymbol\kappa)\,\textrm{ exp}(2\pi i \mathbf{m} \cdot (\mathbf{x}, \boldsymbol \xi)). \end{align*} $$
$$ \begin{align*} L_{\boldsymbol{\kappa}} h(\mathbf{x}, \boldsymbol \xi) = \sum_{\mathbf{m} \in { \mathbb Z}^{2n}\setminus\{0\}} h_{\mathbf{m}} \zeta(\mathbf{m}, \boldsymbol\kappa)\,\textrm{ exp}(2\pi i \mathbf{m} \cdot (\mathbf{x}, \boldsymbol \xi)). \end{align*} $$
Moreover, there is a constant
![]() $C_{\boldsymbol {\tau }, \boldsymbol \eta }> 0$
such that for any
$C_{\boldsymbol {\tau }, \boldsymbol \eta }> 0$
such that for any
![]() $\mathbf {m} \in { \mathbb Z}^{2n} \setminus \{0\}$
,
$\mathbf {m} \in { \mathbb Z}^{2n} \setminus \{0\}$
,
 $$ \begin{align*} & \vert\zeta(\mathbf{m}, \boldsymbol{\tau})\vert^{-1} \leq C_{\boldsymbol{\tau}, \boldsymbol{\eta}}\vert \mathbf{m} \cdot \mathbf{m}\vert^{\gamma} \quad \text{ if } \mathbf{m}_1 \neq 0, \\ & \vert\zeta(\mathbf{m}, \boldsymbol\eta)\vert^{-1} \leq C_{\boldsymbol{\tau}, \boldsymbol{\eta}} \vert \mathbf{m} \cdot \mathbf{m}\vert^{\gamma} \quad \text{ otherwise}, \end{align*} $$
$$ \begin{align*} & \vert\zeta(\mathbf{m}, \boldsymbol{\tau})\vert^{-1} \leq C_{\boldsymbol{\tau}, \boldsymbol{\eta}}\vert \mathbf{m} \cdot \mathbf{m}\vert^{\gamma} \quad \text{ if } \mathbf{m}_1 \neq 0, \\ & \vert\zeta(\mathbf{m}, \boldsymbol\eta)\vert^{-1} \leq C_{\boldsymbol{\tau}, \boldsymbol{\eta}} \vert \mathbf{m} \cdot \mathbf{m}\vert^{\gamma} \quad \text{ otherwise}, \end{align*} $$
where, for
![]() $j = 1, 2$
,
$j = 1, 2$
,
![]() $\mathbf {m}_j$
is defined in (3) and
$\mathbf {m}_j$
is defined in (3) and
![]() $\gamma $
is the exponent in the Diophantine condition for
$\gamma $
is the exponent in the Diophantine condition for
![]() $\boldsymbol {\tau }, \boldsymbol {\eta }$
; see (A.1).
$\boldsymbol {\tau }, \boldsymbol {\eta }$
; see (A.1).
We now prove the estimates from Theorems 1.2 and 1.3 in the context of finite-dimensional representations.
Proof Proof of Proposition 2.1
Because
![]() $f, g \in W^{\infty }({ \mathbb T}^{2n})$
are zero-average functions, there are coefficients
$f, g \in W^{\infty }({ \mathbb T}^{2n})$
are zero-average functions, there are coefficients
![]() $(g_{\mathbf {m}}) , (f_{\mathbf {m}}) \in \ell ^2({ \mathbb Z}^{2n})$
, with
$(g_{\mathbf {m}}) , (f_{\mathbf {m}}) \in \ell ^2({ \mathbb Z}^{2n})$
, with
![]() $f_{\mathbf 0} = g_{\mathbf 0} = 0$
, such that
$f_{\mathbf 0} = g_{\mathbf 0} = 0$
, such that
 $$ \begin{align} g = \sum_{\mathbf{m} \in { \mathbb Z}^{2n}\setminus\{0\}} g_{\mathbf{m}}\,\textrm{ exp}(2\pi i \mathbf{m} \cdot (\mathbf{x}, \boldsymbol \xi)), \nonumber\\ f = \sum_{\mathbf{m} \in { \mathbb Z}^{2n}\setminus\{0\}} f_{\mathbf{m}}\,\textrm{ exp}(2\pi i \mathbf{m} \cdot (\mathbf{x}, \boldsymbol \xi)). \end{align} $$
$$ \begin{align} g = \sum_{\mathbf{m} \in { \mathbb Z}^{2n}\setminus\{0\}} g_{\mathbf{m}}\,\textrm{ exp}(2\pi i \mathbf{m} \cdot (\mathbf{x}, \boldsymbol \xi)), \nonumber\\ f = \sum_{\mathbf{m} \in { \mathbb Z}^{2n}\setminus\{0\}} f_{\mathbf{m}}\,\textrm{ exp}(2\pi i \mathbf{m} \cdot (\mathbf{x}, \boldsymbol \xi)). \end{align} $$
By Lemma A.1, we get
 $$ \begin{align*} &L_{\boldsymbol{\tau}} g(\mathbf{x}, \boldsymbol \xi) = \sum_{\mathbf{m} \in { \mathbb Z}^{2n}\setminus\{0\}} g_{\mathbf{m}} \zeta(\mathbf{m}, \boldsymbol{\tau})\,\textrm{ exp}(2\pi i \mathbf{m} \cdot (\mathbf{x}, \boldsymbol \xi)), \\ &L_{\boldsymbol{\eta}} f(\mathbf{x}, \boldsymbol \xi) = \sum_{\mathbf{m} \in { \mathbb Z}^{2n}\setminus\{0\}} f_{\mathbf{m}} \zeta(\mathbf{m}, \boldsymbol\eta)\,\textrm{ exp}(2\pi i \mathbf{m} \cdot (\mathbf{x}, \boldsymbol \xi)). \end{align*} $$
$$ \begin{align*} &L_{\boldsymbol{\tau}} g(\mathbf{x}, \boldsymbol \xi) = \sum_{\mathbf{m} \in { \mathbb Z}^{2n}\setminus\{0\}} g_{\mathbf{m}} \zeta(\mathbf{m}, \boldsymbol{\tau})\,\textrm{ exp}(2\pi i \mathbf{m} \cdot (\mathbf{x}, \boldsymbol \xi)), \\ &L_{\boldsymbol{\eta}} f(\mathbf{x}, \boldsymbol \xi) = \sum_{\mathbf{m} \in { \mathbb Z}^{2n}\setminus\{0\}} f_{\mathbf{m}} \zeta(\mathbf{m}, \boldsymbol\eta)\,\textrm{ exp}(2\pi i \mathbf{m} \cdot (\mathbf{x}, \boldsymbol \xi)). \end{align*} $$
Then, because (
![]() $\textrm{ exp}(2\pi i \mathbf {m}\cdot (\mathbf {x}, \boldsymbol \xi )))_{\mathbf {m} \in { \mathbb Z}^{2n}}$
is an orthogonal basis for
$\textrm{ exp}(2\pi i \mathbf {m}\cdot (\mathbf {x}, \boldsymbol \xi )))_{\mathbf {m} \in { \mathbb Z}^{2n}}$
is an orthogonal basis for
![]() $L^2({ \mathbb T}^{2n})$
,
$L^2({ \mathbb T}^{2n})$
,
![]() $L_{\boldsymbol {\tau }} g = L_{\boldsymbol {\eta }} f$
implies that for any
$L_{\boldsymbol {\tau }} g = L_{\boldsymbol {\eta }} f$
implies that for any
![]() $\mathbf {m} \in { \mathbb Z}^{2n}\setminus \{0\}$
,
$\mathbf {m} \in { \mathbb Z}^{2n}\setminus \{0\}$
,
From the definition of
![]() $\zeta $
and the Diophantine property for
$\zeta $
and the Diophantine property for
![]() $\boldsymbol \tau $
and
$\boldsymbol \tau $
and
![]() $\boldsymbol \eta $
(see (A.1)), we get that for any
$\boldsymbol \eta $
(see (A.1)), we get that for any
![]() $\mathbf {m} \in { \mathbb Z}^{2n} \setminus \{0\}$
,
$\mathbf {m} \in { \mathbb Z}^{2n} \setminus \{0\}$
,
 $$ \begin{align} \begin{cases} \zeta(\mathbf{m}, \boldsymbol{\tau}) \neq 0 & \text{ if } \mathbf{m}_1 \neq 0, \\ \zeta(\mathbf{m}, \boldsymbol{\tau}) = 0 & \text{ if } \mathbf{m}_1 = 0, \\ \zeta(\mathbf{m}, \boldsymbol\eta) \neq 0 & \text{ if } \mathbf{m}_1 = 0. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \zeta(\mathbf{m}, \boldsymbol{\tau}) \neq 0 & \text{ if } \mathbf{m}_1 \neq 0, \\ \zeta(\mathbf{m}, \boldsymbol{\tau}) = 0 & \text{ if } \mathbf{m}_1 = 0, \\ \zeta(\mathbf{m}, \boldsymbol\eta) \neq 0 & \text{ if } \mathbf{m}_1 = 0. \end{cases} \end{align} $$
Hence,
 $$ \begin{align} \begin{aligned} & g_{\mathbf{m}} = f_{\mathbf{m}} \frac{\zeta(\mathbf{m}, \boldsymbol\eta)}{\zeta(\mathbf{m}, \boldsymbol{\tau})} & \text{ if } \mathbf{m}_1 \neq 0, \\ & f_{\mathbf{n}} = 0, & \text{otherwise}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & g_{\mathbf{m}} = f_{\mathbf{m}} \frac{\zeta(\mathbf{m}, \boldsymbol\eta)}{\zeta(\mathbf{m}, \boldsymbol{\tau})} & \text{ if } \mathbf{m}_1 \neq 0, \\ & f_{\mathbf{n}} = 0, & \text{otherwise}. \end{aligned} \end{align} $$
Now define the sequence (
![]() $P_{\mathbf {m}})_{\mathbf {m} \in { \mathbb Z}^{2n}}$
by
$P_{\mathbf {m}})_{\mathbf {m} \in { \mathbb Z}^{2n}}$
by
![]() $P_{\mathbf {0}} = 0$
and, for any non-zero
$P_{\mathbf {0}} = 0$
and, for any non-zero
![]() $\mathbf {m}$
, set
$\mathbf {m}$
, set
 $$ \begin{align} P_{\mathbf{m}} := \begin{cases} \displaystyle\frac{f_{\mathbf{m}}}{\zeta(\mathbf{m}, \boldsymbol{\tau})} & \text{ if } \mathbf{m}_1 \neq 0, \\ \displaystyle\frac{g_{\mathbf{n}}}{\zeta(\mathbf{m}, \boldsymbol\eta)} & \text{ otherwise}. \end{cases} \end{align} $$
$$ \begin{align} P_{\mathbf{m}} := \begin{cases} \displaystyle\frac{f_{\mathbf{m}}}{\zeta(\mathbf{m}, \boldsymbol{\tau})} & \text{ if } \mathbf{m}_1 \neq 0, \\ \displaystyle\frac{g_{\mathbf{n}}}{\zeta(\mathbf{m}, \boldsymbol\eta)} & \text{ otherwise}. \end{cases} \end{align} $$
Let
Then a calculation formally gives
![]() $ L_{\boldsymbol {\tau }} P = f,\, L_{\boldsymbol {\eta }} P = g,$
where the first equation follows from the second equalities in (A.3) and (A.4), and the second equation follows from the first equality in (A.4) and equation (A.5).
$ L_{\boldsymbol {\tau }} P = f,\, L_{\boldsymbol {\eta }} P = g,$
where the first equation follows from the second equalities in (A.3) and (A.4), and the second equation follows from the first equality in (A.4) and equation (A.5).
Now we estimate the Sobolev norm of P. Recall from (12) that for any
![]() $f \in W^{\infty }({ \mathbb T}^{2n})$
and for any
$f \in W^{\infty }({ \mathbb T}^{2n})$
and for any
![]() $s \in { \mathbb N}$
,
$s \in { \mathbb N}$
,
Set
![]() $s \in { \mathbb N}$
. By Lemma A.1 and formula (A.5), for any
$s \in { \mathbb N}$
. By Lemma A.1 and formula (A.5), for any
![]() $\mathbf {m} \in { \mathbb Z}^{2n}\setminus \{0\}$
such that
$\mathbf {m} \in { \mathbb Z}^{2n}\setminus \{0\}$
such that
![]() $\mathbf {m}_1 \neq 0$
, we have
$\mathbf {m}_1 \neq 0$
, we have
On the other hand, when
![]() $\mathbf {m}_1 = 0$
, we have
$\mathbf {m}_1 = 0$
, we have
Then, for any
![]() $s \in { \mathbb N}$
, there is a constant
$s \in { \mathbb N}$
, there is a constant
![]() $C_{\boldsymbol {\tau }, \boldsymbol {\eta }}> 0$
such that
$C_{\boldsymbol {\tau }, \boldsymbol {\eta }}> 0$
such that
 $$ \begin{align} \Vert P \Vert_{s}^2 & = \sum_{\substack{\mathbf{m} \in { \mathbb Z}^{2n}\setminus\{0\} \\ \mathbf{m}_1 \neq 0}} (1 + 4\pi^2 \mathbf{m} \cdot \mathbf{m})^{s} \vert P_{\mathbf{m}}\vert^2 + \sum_{\substack{\mathbf{m} \in { \mathbb Z}^{2n}\setminus\{0\} \\ \mathbf{m}_1 = 0}} (1 + 4\pi^2 \mathbf{m} \cdot \mathbf{m})^{s} \vert P_{\mathbf{m}}\vert^2 \notag \\ & \leq C_{\boldsymbol \tau, \boldsymbol \eta} \sum_{\mathbf{m} \in { \mathbb Z}^{2n}\setminus\{0\}} (1 + 4\pi^2 \mathbf{m} \cdot \mathbf{m})^{s+2\gamma} (\vert f_{\mathbf{m}}\vert^2 + \vert g_{\mathbf{m}}\vert^2). \end{align} $$
$$ \begin{align} \Vert P \Vert_{s}^2 & = \sum_{\substack{\mathbf{m} \in { \mathbb Z}^{2n}\setminus\{0\} \\ \mathbf{m}_1 \neq 0}} (1 + 4\pi^2 \mathbf{m} \cdot \mathbf{m})^{s} \vert P_{\mathbf{m}}\vert^2 + \sum_{\substack{\mathbf{m} \in { \mathbb Z}^{2n}\setminus\{0\} \\ \mathbf{m}_1 = 0}} (1 + 4\pi^2 \mathbf{m} \cdot \mathbf{m})^{s} \vert P_{\mathbf{m}}\vert^2 \notag \\ & \leq C_{\boldsymbol \tau, \boldsymbol \eta} \sum_{\mathbf{m} \in { \mathbb Z}^{2n}\setminus\{0\}} (1 + 4\pi^2 \mathbf{m} \cdot \mathbf{m})^{s+2\gamma} (\vert f_{\mathbf{m}}\vert^2 + \vert g_{\mathbf{m}}\vert^2). \end{align} $$
By interpolation, the above estimate holds for any
![]() $s \geq 0$
. Hence, for any
$s \geq 0$
. Hence, for any
![]() $s \geq 0$
,
$s \geq 0$
,
We conclude that
Proof Proof of Proposition 2.2
Let
![]() $s \in { \mathbb N}$
. Let
$s \in { \mathbb N}$
. Let
![]() $f, g$
be given by (A.2) and write
$f, g$
be given by (A.2) and write
![]() $\phi $
as
$\phi $
as
where
![]() $(\phi _{\mathbf {m}}) \in \ell ^2({ \mathbb Z}^{2n})$
. Because
$(\phi _{\mathbf {m}}) \in \ell ^2({ \mathbb Z}^{2n})$
. Because
![]() $\phi = L_{\boldsymbol {\eta }} f - L_{\boldsymbol {\tau }} g$
, we get
$\phi = L_{\boldsymbol {\eta }} f - L_{\boldsymbol {\tau }} g$
, we get
By assumption, f and g also have zero average, so
Define P by the sequence
![]() $(P_{\mathbf {m}})_{\mathbf {m} \in { \mathbb Z}}$
given in (A.5), where
$(P_{\mathbf {m}})_{\mathbf {m} \in { \mathbb Z}}$
given in (A.5), where
![]() $P_{\mathbf 0} = 0$
.
$P_{\mathbf 0} = 0$
.
Let R be the orthogonal projection in
![]() $L^2({ \mathbb T}^{2n})$
onto the space generated by
$L^2({ \mathbb T}^{2n})$
onto the space generated by
 $$ \begin{align*} \bigcup_{\substack{\mathbf{m} \in { \mathbb Z}^{2n} \\ \mathbf{m}_1 \neq 0 }} \{\textrm{ exp}(2\pi i \mathbf{m} \cdot (\mathbf{x}, \boldsymbol \xi))\}. \end{align*} $$
$$ \begin{align*} \bigcup_{\substack{\mathbf{m} \in { \mathbb Z}^{2n} \\ \mathbf{m}_1 \neq 0 }} \{\textrm{ exp}(2\pi i \mathbf{m} \cdot (\mathbf{x}, \boldsymbol \xi))\}. \end{align*} $$
That is, for any
![]() $h = \sum _{\mathbf {m} \in { \mathbb Z}^{2n}} h_{\mathbf {m}}\,\textrm{ exp}(2\pi i (\mathbf {m} \cdot (\mathbf {x}, \boldsymbol \xi )))$
in
$h = \sum _{\mathbf {m} \in { \mathbb Z}^{2n}} h_{\mathbf {m}}\,\textrm{ exp}(2\pi i (\mathbf {m} \cdot (\mathbf {x}, \boldsymbol \xi )))$
in
![]() $L^2({ \mathbb T}^{2n})$
,
$L^2({ \mathbb T}^{2n})$
,
 $$ \begin{align} \begin{aligned} R h(\mathbf{x}, \boldsymbol \xi) & = \sum_{\substack{\mathbf{m} \in { \mathbb Z}^{2n} \\ \mathbf{m}_1 \neq 0}} h_{\mathbf{m}}\,\textrm{ exp}(2\pi i (\mathbf{m} \cdot (\mathbf{x}, \boldsymbol \xi))). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} R h(\mathbf{x}, \boldsymbol \xi) & = \sum_{\substack{\mathbf{m} \in { \mathbb Z}^{2n} \\ \mathbf{m}_1 \neq 0}} h_{\mathbf{m}}\,\textrm{ exp}(2\pi i (\mathbf{m} \cdot (\mathbf{x}, \boldsymbol \xi))). \end{aligned} \end{align} $$
A direct calculation gives the next lemma.
Lemma A.2. The following equalities hold on
![]() $L^2({ \mathbb T}^{2n})$
:
$L^2({ \mathbb T}^{2n})$
:
Now let P be defined by (A.5). Then
 $$ \begin{align*} L_{\boldsymbol{\tau}} P & = \sum_{\substack{\mathbf{m} \in { \mathbb Z}^{2n} \\ \mathbf{m}_1 \neq 0}} f_{\mathbf{m}}\,\textrm{ exp}(2\pi i \mathbf{m} \cdot (\mathbf{x}, \boldsymbol \xi)) = R f. \end{align*} $$
$$ \begin{align*} L_{\boldsymbol{\tau}} P & = \sum_{\substack{\mathbf{m} \in { \mathbb Z}^{2n} \\ \mathbf{m}_1 \neq 0}} f_{\mathbf{m}}\,\textrm{ exp}(2\pi i \mathbf{m} \cdot (\mathbf{x}, \boldsymbol \xi)) = R f. \end{align*} $$
By the above equality and Lemma A.2, we get as in (43):
![]() $R\phi = L_{\boldsymbol {\tau }} (L_{\boldsymbol {\eta }} P - g).$
From (A.7), it follows that for any
$R\phi = L_{\boldsymbol {\tau }} (L_{\boldsymbol {\eta }} P - g).$
From (A.7), it follows that for any
![]() $\mathbf {m} \in { \mathbb Z}^{2n}$
such that
$\mathbf {m} \in { \mathbb Z}^{2n}$
such that
![]() $\mathbf {m}_1 = 0$
,
$\mathbf {m}_1 = 0$
,
![]() $(R \phi )_{\mathbf {m}} = 0.$
Moreover, for any
$(R \phi )_{\mathbf {m}} = 0.$
Moreover, for any
![]() $h \in L^2({ \mathbb T}^{2n}),$
we get from the definition of
$h \in L^2({ \mathbb T}^{2n}),$
we get from the definition of
![]() $L_{\boldsymbol {\tau }}$
that for such
$L_{\boldsymbol {\tau }}$
that for such
![]() $\mathbf {m}$
,
$\mathbf {m}$
,
This means that
 $$ \begin{align*} \sum_{\substack{\mathbf{m} \in { \mathbb Z}^{2n}\\ \mathbf{m}_1 \neq 0}} & (R \phi)_{\mathbf{m}}\,\textrm{ exp}(2\pi i \mathbf{m} \cdot (\mathbf{x}, \boldsymbol \xi)) = R \phi(\mathbf{x}, \boldsymbol \xi) = L_{\boldsymbol{\tau}} (L_{\boldsymbol{\eta}} P - g) (\mathbf{x}, \boldsymbol \xi) \\ & = \sum_{\substack{\mathbf{m} \in { \mathbb Z}^{2n} \\ \mathbf{m}_1 \neq 0}} (L_{\boldsymbol{\eta}}P - g)_{\mathbf{m}} \zeta(\mathbf{m}, \boldsymbol{\tau})\,\textrm{ exp}(2\pi i \mathbf{m} \cdot (\mathbf{x}, \boldsymbol \xi)). \end{align*} $$
$$ \begin{align*} \sum_{\substack{\mathbf{m} \in { \mathbb Z}^{2n}\\ \mathbf{m}_1 \neq 0}} & (R \phi)_{\mathbf{m}}\,\textrm{ exp}(2\pi i \mathbf{m} \cdot (\mathbf{x}, \boldsymbol \xi)) = R \phi(\mathbf{x}, \boldsymbol \xi) = L_{\boldsymbol{\tau}} (L_{\boldsymbol{\eta}} P - g) (\mathbf{x}, \boldsymbol \xi) \\ & = \sum_{\substack{\mathbf{m} \in { \mathbb Z}^{2n} \\ \mathbf{m}_1 \neq 0}} (L_{\boldsymbol{\eta}}P - g)_{\mathbf{m}} \zeta(\mathbf{m}, \boldsymbol{\tau})\,\textrm{ exp}(2\pi i \mathbf{m} \cdot (\mathbf{x}, \boldsymbol \xi)). \end{align*} $$
By orthogonality, it follows that for all
![]() $\mathbf {m} \in { \mathbb Z}^{2n} \setminus \{0\}$
with
$\mathbf {m} \in { \mathbb Z}^{2n} \setminus \{0\}$
with
![]() $\mathbf {m}_1 \neq 0$
,
$\mathbf {m}_1 \neq 0$
,
Note that the definition of
![]() $P_{\mathbf {m}}$
gives
$P_{\mathbf {m}}$
gives
So, by the above equality, formula (A.8) and Lemma A.1, we get that for any
![]() $\mathbf {m} \in { \mathbb Z}^{2n}$
,
$\mathbf {m} \in { \mathbb Z}^{2n}$
,
Hence,
 $$ \begin{align*} \Vert L_{\boldsymbol{\eta}} P - g\Vert_s^2 & = \sum_{\substack{\mathbf{m} \in { \mathbb Z}^{2n} \\ \mathbf{m}_1 \neq 0}} (1 + 4\pi^2 \mathbf{m} \cdot \mathbf{m})^s \vert (L_{\boldsymbol{\eta}} P - g)_{\mathbf{m}} \vert^2 \\ & \leq C_{\boldsymbol \tau, \boldsymbol \eta} \sum_{\substack{\mathbf{m} \in { \mathbb Z}^{2n} \\ \mathbf{m}_1 \neq 0}} (1 + 4\pi^2 \mathbf{m} \cdot \mathbf{m})^{s + 2\gamma} \vert (R \phi)_{\mathbf{m}} \vert^2 \\ & = C_{\boldsymbol \tau, \boldsymbol \eta} \Vert R \phi \Vert_{s + 2\gamma}^2 \leq C_{\boldsymbol \tau, \boldsymbol \eta} \Vert \phi \Vert_{s + 2\gamma}^2. \end{align*} $$
$$ \begin{align*} \Vert L_{\boldsymbol{\eta}} P - g\Vert_s^2 & = \sum_{\substack{\mathbf{m} \in { \mathbb Z}^{2n} \\ \mathbf{m}_1 \neq 0}} (1 + 4\pi^2 \mathbf{m} \cdot \mathbf{m})^s \vert (L_{\boldsymbol{\eta}} P - g)_{\mathbf{m}} \vert^2 \\ & \leq C_{\boldsymbol \tau, \boldsymbol \eta} \sum_{\substack{\mathbf{m} \in { \mathbb Z}^{2n} \\ \mathbf{m}_1 \neq 0}} (1 + 4\pi^2 \mathbf{m} \cdot \mathbf{m})^{s + 2\gamma} \vert (R \phi)_{\mathbf{m}} \vert^2 \\ & = C_{\boldsymbol \tau, \boldsymbol \eta} \Vert R \phi \Vert_{s + 2\gamma}^2 \leq C_{\boldsymbol \tau, \boldsymbol \eta} \Vert \phi \Vert_{s + 2\gamma}^2. \end{align*} $$
Next, as in (46), we get
By Lemma A.2, it follows as in (47) that
Next, a calculation proves that for any
![]() $\mathbf {m} \in { \mathbb Z}^{2n} \setminus \{0\}$
such that
$\mathbf {m} \in { \mathbb Z}^{2n} \setminus \{0\}$
such that
![]() $\mathbf {m}_1 = 0$
,
$\mathbf {m}_1 = 0$
,
Then, using Lemma A.1, we conclude that
The third inequality in Proposition 2.2 holds because P is the same function from Proposition 2.1, which gives
Now, if P is non-constant, then we are done. So, suppose that P is constant and therefore zero. Notice that by the above estimate,
![]() $\phi = 0$
implies that
$\phi = 0$
implies that
![]() $f = 0$
, which contradicts the assumption that
$f = 0$
, which contradicts the assumption that
![]() $f \neq 0$
. So, we conclude that there is some
$f \neq 0$
. So, we conclude that there is some
![]() $\mathbf {m}_0 \in { \mathbb Z}^{2n}$
such that
$\mathbf {m}_0 \in { \mathbb Z}^{2n}$
such that
Then define
By the orthogonal decomposition of
![]() $\phi $
, we have
$\phi $
, we have
![]() $ \Vert \widetilde P \Vert _s \leq \Vert \phi \Vert _s.$
So, the above estimates of
$ \Vert \widetilde P \Vert _s \leq \Vert \phi \Vert _s.$
So, the above estimates of
![]() $\Vert L_{\boldsymbol {\eta }} P - g\Vert _s$
and
$\Vert L_{\boldsymbol {\eta }} P - g\Vert _s$
and
![]() $\Vert L_{\boldsymbol {\tau }} P - f \Vert _s$
imply that
$\Vert L_{\boldsymbol {\tau }} P - f \Vert _s$
imply that
 $$ \begin{align*} \|L_{\boldsymbol{\eta}} \widetilde P-g\|_s & = \Vert (L_{\boldsymbol{\eta}} P-g) + L_{\boldsymbol{\eta}} \widetilde P\Vert_s \\ & \leq \Vert L_{\boldsymbol{\eta}} P-g\Vert_s + \Vert L_{\boldsymbol{\eta}} \widetilde P\Vert_s \\ & \leq (C_{\boldsymbol \tau, \boldsymbol \eta} +1)\|\phi \|_{s+2\gamma} \end{align*} $$
$$ \begin{align*} \|L_{\boldsymbol{\eta}} \widetilde P-g\|_s & = \Vert (L_{\boldsymbol{\eta}} P-g) + L_{\boldsymbol{\eta}} \widetilde P\Vert_s \\ & \leq \Vert L_{\boldsymbol{\eta}} P-g\Vert_s + \Vert L_{\boldsymbol{\eta}} \widetilde P\Vert_s \\ & \leq (C_{\boldsymbol \tau, \boldsymbol \eta} +1)\|\phi \|_{s+2\gamma} \end{align*} $$
and, analogously,
![]() $\Vert L_{\boldsymbol {\tau }} \widetilde P-f \Vert _s \leq (C_{\boldsymbol \tau , \boldsymbol \eta } +1)\|\phi \|_{s+2\gamma }.$
$\Vert L_{\boldsymbol {\tau }} \widetilde P-f \Vert _s \leq (C_{\boldsymbol \tau , \boldsymbol \eta } +1)\|\phi \|_{s+2\gamma }.$
This concludes the proof of Proposition 2.2.