Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
ZEGOWITZ, STEFANIE
2017.
Closed orbits in quotient systems.
Ergodic Theory and Dynamical Systems,
Vol. 37,
Issue. 7,
p.
2337.
Carnevale, Angela
and
Voll, Christopher
2018.
Orbit Dirichlet series and multiset permutations.
Monatshefte für Mathematik,
Vol. 186,
Issue. 2,
p.
215.
Ward, Tom
2018.
Integer sequences and dynamics.
Electronic Notes in Discrete Mathematics,
Vol. 70,
Issue. ,
p.
83.
Jaidee, Sawian
Moss, Patrick
and
Ward, Tom
2019.
Time-changes preserving zeta functions.
Proceedings of the American Mathematical Society,
Vol. 147,
Issue. 10,
p.
4425.
Byszewski, Jakub
Graff, Grzegorz
and
Ward, Thomas
2021.
Dold sequences, periodic points, and dynamics.
Bulletin of the London Mathematical Society,
Vol. 53,
Issue. 5,
p.
1263.
Moss, Patrick
and
Ward, Tom
2022.
Fibonacci Along Even Powers Is (Almost) Realizable.
The Fibonacci Quarterly,
Vol. 60,
Issue. 1,
p.
40.
Ward, Thomas
2023.
People, Places, and Mathematics.
p.
141.


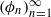 is said to be
is said to be 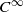 diffeomorphism of
diffeomorphism of 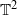 .
.