Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-06T06:22:08.288Z Has data issue: false hasContentIssue false
  • English
  • Français

Reducibility of a class of nonlinear quasi-periodic systems with Liouvillean basic frequencies

Part of: Qualitative theory Finite-dimensional Hamiltonian, Lagrangian, contact, and nonholonomic systems

Published online by Cambridge University Press:  09 March 2020

DONGFENG ZHANG Open the ORCID record for DONGFENG ZHANG [Opens in a new window]  and
JUNXIANG XU
DONGFENG ZHANG
Affiliation:
School of Mathematics, Southeast University, Nanjing 210096, PR China email zhdf@seu.edu.cn, xujun@seu.edu.cn
JUNXIANG XU
Affiliation:
School of Mathematics, Southeast University, Nanjing 210096, PR China email zhdf@seu.edu.cn, xujun@seu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we consider the following nonlinear quasi-periodic system: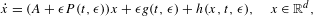

$$\begin{eqnarray}{\dot{x}}=(A+\unicode[STIX]{x1D716}P(t,\unicode[STIX]{x1D716}))x+\unicode[STIX]{x1D716}g(t,\unicode[STIX]{x1D716})+h(x,t,\unicode[STIX]{x1D716}),\quad x\in \mathbb{R}^{d},\end{eqnarray}$$
where $A$ is a 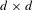$d\times d$ constant matrix of elliptic type, 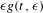$\unicode[STIX]{x1D716}g(t,\unicode[STIX]{x1D716})$ is a small perturbation with $\unicode[STIX]{x1D716}$ as a small parameter, 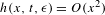$h(x,t,\unicode[STIX]{x1D716})=O(x^{2})$ as $x\rightarrow 0$, and $P,g$ and 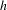$h$ are all analytic quasi-periodic in $t$ with basic frequencies 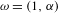$\unicode[STIX]{x1D714}=(1,\unicode[STIX]{x1D6FC})$, where $\unicode[STIX]{x1D6FC}$ is irrational. It is proved that for most sufficiently small $\unicode[STIX]{x1D716}$, the system is reducible to the following form: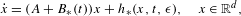
$$\begin{eqnarray}{\dot{x}}=(A+B_{\ast }(t))x+h_{\ast }(x,t,\unicode[STIX]{x1D716}),\quad x\in \mathbb{R}^{d},\end{eqnarray}$$
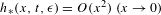 where $h_{\ast }(x,t,\unicode[STIX]{x1D716})=O(x^{2})~(x\rightarrow 0)$ is a high-order term. Therefore, the system has a quasi-periodic solution with basic frequencies $\unicode[STIX]{x1D714}=(1,\unicode[STIX]{x1D6FC})$, such that it goes to zero when $\unicode[STIX]{x1D716}$ does.

Keywords

reducibilityquasi-periodicKAM iterationLiouvillean frequencies

MSC classification

Primary: 37J40: Perturbations, normal forms, small divisors, KAM theory, Arnol'd diffusion
Secondary: 34C27: Almost and pseudo-almost periodic solutions
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 6 , June 2021 , pp. 1883 - 1920
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

References

Avila, A., Fayad, B. and Krikorian, R.. A KAM scheme for SL(2, R) cocycles with Liouvillean frequencies. Geom. Funct. Anal. 21 (2011), 1001–1019.CrossRefGoogle Scholar
Bambusi, D.. Reducibility of 1-d Schrödinger equation with time quasiperiodic unbounded perturbations, II. Comm. Math. Phys. 353(1) (2017), 353–378.CrossRefGoogle Scholar
Bambusi, D.. Reducibility of 1-d Schrödinger equation with time quasiperiodic unbounded perturbations, I. Trans. Amer. Math. Soc. 370(3) (2018), 1823–1865.CrossRefGoogle Scholar
Chavaudret, C.. Strong almost reducibility for analytic and Gevrey quasi-periodic cocycles. Bull. Soc. Math. France 141 (2013), 47–106.CrossRefGoogle Scholar
Chavaudret, C. and Marmi, S.. Reducibility of quasiperiodic cocycles under a Brjuno–Rüssmann arithmetical condition. J. Mod. Dyn. 6(1) (2012), 59–78.CrossRefGoogle Scholar
Chavaudret, C. and Stolovitch, L.. Analytic reducibility of resonant cocycles to a normal form. J. Inst. Math. Jussieu 15(1) (2016), 203–223.CrossRefGoogle Scholar
Dinaburg, E. I. and Sinai, Y. G.. The one dimensional Schrödinger equation with quasi-perioidc potential. Funct. Anal. Appl. 9 (1975), 8–21.Google Scholar
Eliasson, L. H.. Floquet solutions for the 1-dimensional quasi-periodic Schrödinger equation. Comm. Math. Phys. 146 (1992), 447–482.CrossRefGoogle Scholar
Eliasson, L. H.. Almost reducibility of linear quasi-periodic systems. Smooth Ergodic Theory and its Applications (Seattle, WA, 1999) (Proceedings of Symposia in Pure Mathematics, 69) . American Mathematical Society, Providence, RI, 2001, pp. 679–705.CrossRefGoogle Scholar
Eliasson, L. H. and Kuksin, S. B.. On reducibility of Schrödinger equations with quasi-periodic in time potentials. Comm. Math. Phys. 286 (2009), 125–135.CrossRefGoogle Scholar
Fayad, B. and Krikorian, R.. Herman’s last geometric theorem. Ann. Sci. Éc. Norm. Supér. (4) 42 (2009), 193–219.CrossRefGoogle Scholar
Fayad, B. and Krikorian, R.. Rigidity results for quasiperiodic SL(2, R)-cocycles. J. Mod. Dyn. 3(4) (2009), 497–510.Google Scholar
Her, H. and You, J.. Full measure reducibility for generic one-parameter family of quasi-periodic linear systems. J. Dynam. Differential Equations 20 (2008), 831–866.CrossRefGoogle Scholar
Hou, X. and You, J.. Almost reducibility and non-perturbative reducibility of quasi-periodic linear systems. Invent. Math. 190 (2012), 209–260.CrossRefGoogle Scholar
Johnson, R. A. and Sell, G. R.. Smoothness of spectral subbundles and reducibility of quasi-periodic linear differential systems. J. Differential Equations 41 (1981), 262–288.CrossRefGoogle Scholar
Jorba, À. and Simó, C.. On the reducibility of linear differential equation with quasi-perioidc coefficients. J. Differential Equations 98(1) (1992), 111–124.CrossRefGoogle Scholar
Jorba, À. and Simó, C.. On quasi-periodic perturbations of elliptic equilibrium points. SIAM J. Math. Anal. 27(6) (1996), 1704–1737.CrossRefGoogle Scholar
Krikorian, R.. Global density of reducible quasi-periodic cocycles on T 1 × SU(2). Ann. of Math. (2) 154 (2001), 269–326.CrossRefGoogle Scholar
Liang, J. and Xu, J.. A note on the extension of Dinaburg–Sinai theorem to higher dimension. Ergod. Th. & Dynam. Sys. 25 (2005), 1539–1549.Google Scholar
Liu, B.. Boundedness for solutions of nonlinear Hill’s equations with periodic forcing terms via Moser’s twist theorem. J. Differential Equations 79 (1989), 304–315.Google Scholar
Lopes Dias, J.. A normal form theorem for Brjuno skew systems through renormalization. J. Differential Equations 230(1) (2006), 1–23.CrossRefGoogle Scholar
Lopes Dias, J.. Brjuno condition and renormalization for Poincaré flows. Discrete Contin. Dyn. Syst. 15(2) (2006), 641–656.CrossRefGoogle Scholar
Moser, J.. Combination tones for Duffing’s equation. Comm. Pure Appl. Math. 18 (1965), 167–181.CrossRefGoogle Scholar
Pöschel, J.. KAM à la R. Regul. Chaotic Dyn. 16 (2011), 17–23.CrossRefGoogle Scholar
Rüssmann, H.. On the one dimensional Schrödinger equation with a quasi-periodic potential. Ann. N. Y. Acad. Sci. 357 (1980), 90–107.CrossRefGoogle Scholar
Rüssmann, H.. Convergent transformations into a normal form in analytic Hamiltonian systems with two degrees of freedom on the zero energy surface near degenerate elliptic singularities. Ergod. Th. & Dynam. Sys. 24 (2004), 1787–1832.CrossRefGoogle Scholar
Stoker, J. J.. Nonlinear Vibrations. Interscience, New York, 1950, esp. pp. 235–239.Google Scholar
Wang, X. and Xu, J.. On the reducibility of a class of nonlinear quasi-periodic system with small perturbation parameter near zero equilibrium point. Nonlinear Anal. 69 (2008), 2318–2329.CrossRefGoogle Scholar
Wang, X., Xu, J. and Zhang, D.. On the persistence of degenerate lower-dimensional tori in reversible systems. Ergod. Th. & Dynam. Sys. 35 (2015), 2311–2333.CrossRefGoogle Scholar
Wang, J., You, J. and Zhou, Q.. Response solutions for quasi-periodically forced harmonic oscillators. Trans. Amer. Math. Soc. 369 (2017), 4251–4274.CrossRefGoogle Scholar
Xu, J.. On the reducibility of a class of linear differential equation with quasi-periodic coefficients. Mathematika 46 (1999), 443–451.Google Scholar
Xu, J. and Lu, X.. On the reducibility of two-dimensional linear quasi-periodic systems with small parameter. Ergod. Th. & Dynam. Sys. 35 (2015), 2334–2352.CrossRefGoogle Scholar
Xu, J. and Zheng, Q.. On the reducibility of linear differential equations with quasiperiodic coefficients which are degenerate. Proc. Amer. Math. Soc. 126 (1998), 1445–1451.Google Scholar
Zhang, D. and Liang, J.. On high dimensional Schrödinger equation with quasi-periodic potentials. J. Dyn. Control Syst. 23 (2017), 655–666.CrossRefGoogle Scholar
Zhang, D. and Xu, J.. Invariant curves of analytic reversible mappings under Brjuno–Rüssmann’s non-resonant condition. J. Dynam. Differential Equations 26 (2014), 989–1005.CrossRefGoogle Scholar
Zhang, D. and Xu, J.. On invariant tori of vector field under weaker non-degeneracy condition. NoDEA Nonlinear Differential Equations Appl. 22 (2015), 1381–1394.CrossRefGoogle Scholar
Zhang, D., Xu, J. and Wu, H.. On invariant tori with prescribed frequency in Hamiltonian systems. Adv. Nonlinear Stud. 16(4) (2016), 719–737.CrossRefGoogle Scholar
Zhang, D., Xu, J. and Xu, X.. Reducibility of three dimensional skew symmetric system with Liouvillean basic frequencies. Discrete Contin. Dyn. Syst. 38(6) (2018), 2851–2877.CrossRefGoogle Scholar
Zhao, H.. A note on quasi-periodic perturbations of elliptic equilibrium points. Bull. Korean Math. Soc. 49(6) (2012), 1223–1240.CrossRefGoogle Scholar
Zhou, Q. and Wang, J.. Reducibility results for quasiperiodic cocycles with Liouvillean frequency. J. Dynam. Differential Equations 24 (2012), 61–83.CrossRefGoogle Scholar