Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-11T21:12:02.125Z Has data issue: false hasContentIssue false
  • English
  • Français

Proper minimal sets on compact connected 2-manifolds are nowhere dense

Published online by Cambridge University Press:  01 June 2008

SERGII˘ KOLYADA ,
L’UBOMÍR SNOHA  and
SERGEI˘ TROFIMCHUK
SERGII˘ KOLYADA
Affiliation:
Institute of Mathematics, NASU, Tereshchenkivs’ka 3, 01601 Kiev, Ukraine (email: skolyada@imath.kiev.ua)
L’UBOMÍR SNOHA
Affiliation:
Department of Mathematics, Faculty of Natural Sciences, Matej Bel University, Tajovského 40, 974 01 Banská Bystrica, Slovakia (email: snoha@fpv.umb.sk)
SERGEI˘ TROFIMCHUK
Affiliation:
Instituto de Matemática y Física, Universidad de Talca, Casilla 747, Talca, Chile (email: trofimch@inst-mat.utalca.cl)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

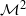Let be a compact connected two-dimensional manifold, with or without boundary, and let 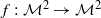be a continuous map. We prove that if 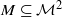is a minimal set of the dynamical system 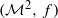then either or M is a nowhere dense subset of . Moreover, we add a shorter proof of the recent result of Blokh, Oversteegen and Tymchatyn, that in the former case is a torus or a Klein bottle.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 28 , Issue 3 , June 2008 , pp. 863 - 876
Copyright
Copyright © Cambridge University Press 2008

References

[1]Balibrea, F., Downarowicz, T., Hric, R., Snoha, L’. and Špitalský, V.. Almost totally disconnected minimal systems. Submitted.Google Scholar
[2]Balibrea, F., Hric, R. and Snoha, L’.. Minimal sets on graphs and dendrites (Dynamical systems and functional equations, Murcia, 2000). Internat. J. Bifur. Chaos Appl. Sci. Engrg. 13(7) (2003), 1721–1725.Google Scholar
[3]Blokh, A., Oversteegen, L. and Tymchatyn, E.. On minimal maps of 2-manifolds. Ergod. Th. & Dynam. Sys. 25 (2005), 41–57.CrossRefGoogle Scholar
[4]Blokh, A., Oversteegen, L. and Tymchatyn, E.. On almost one-to-one maps. Trans. Amer. Math. Soc. 358(11) (2006), 5003–5014 (electronic).CrossRefGoogle Scholar
[5]Bruin, H., Kolyada, S. and Snoha, L’.. Minimal nonhomogeneous continua. Colloq. Math. 95(1) (2003), 123–132.CrossRefGoogle Scholar
[6]Daverman, R. J.. Decompositions of Manifolds (Pure and Applied Mathematics, 124). Academic Press, Orlando, FL, 1986.Google Scholar
[7]Dowker, Y. N.. On minimal sets in dynamical systems. Quart. J. Math. Oxford Ser. (2) 7 (1956), 5–16.CrossRefGoogle Scholar
[8]Ellis, R.. The construction of minimal discrete flows. Amer. J. Math. 87 (1965), 564–574.CrossRefGoogle Scholar
[9] K. P. Hart, J.-I. Nagata and J. E. Vaughan (eds.). Encyclopedia of General Topology. Elsevier, Amsterdam, 2004.Google Scholar
[10]Engelking, R. and Sieklucki, K.. Topology: A Geometric Approach (Sigma Series in Pure Mathematics, 4). Heldermann, Berlin, 1992.Google Scholar
[11]Fathi, A. and Herman, M.. Existence de difféomorphismes minimaux. Asterisque 49 (1977), 37–59.Google Scholar
[12]Fuller, F. B.. The existence of periodic points. Ann. of Math. (2) 57 (1953), 229–230.CrossRefGoogle Scholar
[13]Gottschalk, W. H.. Orbit-closure decompositions and almost periodic properties. Bull. Amer. Math. Soc. 50 (1944), 915–919.CrossRefGoogle Scholar
[14]Halpern, B.. Fixed points for iterates. Pacific J. Math. 25 (1968), 255–275.CrossRefGoogle Scholar
[15]Kolyada, S., Snoha, L’. and Trofimchuk, S.. Noninvertible minimal maps. Fund. Math. 168 (2001), 141–163.CrossRefGoogle Scholar
[16]Kuratowski, K.. Topology II. Academic Press, New York, 1968.Google Scholar
[17]Le Calvez, P. and Yoccoz, J.. Un théorème d’indice pour homeomorphismes du plan au voisinage d’un point fixe. Ann. Math. 146 (1997), 241–293.CrossRefGoogle Scholar
[18]Mai, J.-H.. Pointwise-recurrent graph maps. Ergod. Th. & Dynam. Sys. 25(2) (2005), 629–637.Google Scholar
[19]Moore, R. L.. Concerning upper semi-continuous collections. Monatsh. Math. Phys. 36(1) (1929), 81–88.CrossRefGoogle Scholar
[20]Nadler, S. B. Jr. Continuum Theory: An Introduction (Monographs and Textbooks in Pure and Applied Mathematics, 158). Marcel Dekker, New York, 1992.Google Scholar
[21]Parry, W.. A note on cocycles in ergodic theory. Compositio Math. 28 (1974), 343–350.Google Scholar
[22]Rees, M.. A point distal transformation of the torus. Israel J. Math. 32 (1979), 201–208.CrossRefGoogle Scholar
[23]Roberts, J. H. and Steenrod, N. E.. Monotone transformations of two-dimensional manifolds. Ann. of Math. 39 (1938), 851–862.CrossRefGoogle Scholar
[24]Whyburn, G. T.. Analytic Topology, Vol. 28. American Mathematical Society, Providence, RI, 1942.Google Scholar
[25]Ye, X.. D-function of a minimal set and an extension of Sharkovskii’s theorem to minimal sets. Ergod. Th. & Dynam. Sys. 12 (1992), 365–376.CrossRefGoogle Scholar