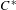Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-02-06T09:12:28.107Z Has data issue: false hasContentIssue false
  • English
  • Français

On simplicity of intermediate $C^{\ast }$-algebras

Part of: Ergodic theory Selfadjoint operator algebras

Published online by Cambridge University Press:  06 June 2019

TATTWAMASI AMRUTAM  and
MEHRDAD KALANTAR
TATTWAMASI AMRUTAM
Affiliation:
Department of Mathematics, 3551 Cullen Blvd, Room 641, Philip Guthrie Hoffman Hall, Houston, TX77204, USA email tamrutam@math.uh.edu, kalantar@math.uh.edu
MEHRDAD KALANTAR
Affiliation:
Department of Mathematics, 3551 Cullen Blvd, Room 641, Philip Guthrie Hoffman Hall, Houston, TX77204, USA email tamrutam@math.uh.edu, kalantar@math.uh.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove simplicity of all intermediate 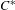$C^{\ast }$-algebras 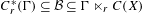$C_{r}^{\ast }(\unicode[STIX]{x1D6E4})\subseteq {\mathcal{B}}\subseteq \unicode[STIX]{x1D6E4}\ltimes _{r}C(X)$ in the case of minimal actions of 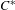$C^{\ast }$-simple groups $\unicode[STIX]{x1D6E4}$ on compact spaces 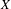$X$. For this, we use the notion of stationary states, recently introduced by Hartman and Kalantar [Stationary 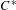$C^{\ast }$-dynamical systems. Preprint, 2017, arXiv:1712.10133]. We show that the Powers’ averaging property holds for the reduced crossed product 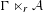$\unicode[STIX]{x1D6E4}\ltimes _{r}{\mathcal{A}}$ for any action 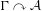$\unicode[STIX]{x1D6E4}\curvearrowright {\mathcal{A}}$ of a 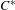$C^{\ast }$-simple group $\unicode[STIX]{x1D6E4}$ on a unital $C^{\ast }$-algebra ${\mathcal{A}}$, and use it to prove a one-to-one correspondence between stationary states on 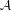${\mathcal{A}}$ and those on 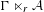$\unicode[STIX]{x1D6E4}\ltimes _{r}{\mathcal{A}}$.

Keywords

group actionsoperator algebrascrossed product C∗ -algebrasstationary group actionsC∗ -simplicity

MSC classification

Primary: 46L10: General theory of von Neumann algebras 46L55: Noncommutative dynamical systems
Secondary: 37A55: Relations with the theory of $C^*$-algebras 46L89: Other “noncommutative” mathematics based on $C^*$-algebra theory
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 12 , December 2020 , pp. 3181 - 3187
Check for updates
Copyright
© Cambridge University Press, 2019

References

Archbold, R. J. and Spielberg, J. S.. Topologically free actions and ideals in discrete C ∗ -dynamical systems. Proc. Edinb. Math. Soc. (2) 37 (1994), 119–124.Google Scholar
Bédos, E.. Discrete groups and simple C ∗ -algebras. Math. Proc. Cambridge Philos. Soc. 109(3) (1991), 521–537.Google Scholar
Breuillard, E., Kalantar, M., Kennedy, M. and Ozawa, N.. C ∗ -simplicity and the unique trace property for discrete groups. Publ. Math. Inst. Hautes Études Sci. 126 (2017), 35–71.Google Scholar
Brown, N. and Ozawa, N.. C ∗ -Algebras and Finite-dimensional Approximations (Graduate Studies in Mathematics, 88). American Mathematical Society, Providence, RI, 2008.Google Scholar
Bryder, R. S. and Kennedy, M.. Reduced twisted crossed products over C ∗ -simple groups. Int. Math. Res. Not. IMRN 6 (2018), 1638–1655.Google Scholar
de la Harpe, P. and Skandalis, G.. Powers’ property and simple C ∗ -algebras. Math. Ann. 273 (1986), 241–250.Google Scholar
Elliott, G. A.. Some simple C ∗ -algebras constructed as crossed products with discrete outer automorphism groups. Publ. Res. Inst. Math. Sci. 16(1) (1980), 299–311.Google Scholar
Haagerup, U.. A new look at C ∗ -simplicity and the unique trace property of a group. Operator Algebras and Applications (The Abel Symposium 2015) (Abel Sympia, 12). Springer, Cham, 2017, pp. 167–176.Google Scholar
Hartman, Y. and Kalantar, M.. Stationary $C^{\ast }$-dynamical systems. Preprint, 2017, arXiv:1712.10133.Google Scholar
Jang, S. Y. and Lee, S. G.. Simplicity of crossed products of C ∗ -algebras. Proc. Amer. Math. Soc. 118(3) (1993), 823–826.Google Scholar
Kalantar, M. and Kennedy, M.. Boundaries of reduced C ∗ -algebras of discrete groups. J. Reine Angew. Math. 727 (2017), 247–267.Google Scholar
Kawamura, S. and Tomiyama, J.. Properties of topological dynamical systems and corresponding C ∗ -algebras. Tokyo J. Math. 13 (1990), 251–257.Google Scholar
Kennedy, M.. An intrinsic characterization of $C^{\ast }$-simplicity. Ann. Sci. Éc. Norm. Supér., accepted. Preprint, 2015, arXiv:1509.01870.Google Scholar
Sierakowski, A.. The ideal structure of reduced crossed products. Münster J. Math. 3 (2010), 237–261.Google Scholar
Suzuki, Y.. Minimal ambient nuclear C∗ -algebras. Adv. Math. 304 (2017), 421–433.Google Scholar
Suzuki, Y.. Complete descriptions of intermediate operator algebras by intermediate extensions of dynamical systems. Commun. Math. Phys., accepted. Preprint, 2018, arXiv:1805.02077.Google Scholar
Takesaki, M.. On the cross-norm of the direct product of C ∗ -algebras. Tôhoku Math. J. (2) 16 (1964), 111–122.Google Scholar