Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-11T01:41:26.779Z Has data issue: false hasContentIssue false
  • English
  • Français

On Khintchine exponents and Lyapunov exponents of continued fractions

Published online by Cambridge University Press:  01 February 2009

AI-HUA FAN ,
LING-MIN LIAO ,
BAO-WEI WANG  and
JUN WU
AI-HUA FAN
Affiliation:
Department of Mathematics, Wuhan University, Wuhan, 430072, PR China CNRS UMR 6140-LAMFA, Université de Picardie, 80039 Amiens, France (email: ai-hua.fan@u-picaride.fr, lingmin.liao@u-picardie.fr)
LING-MIN LIAO
Affiliation:
Department of Mathematics, Wuhan University, Wuhan, 430072, PR China CNRS UMR 6140-LAMFA, Université de Picardie, 80039 Amiens, France (email: ai-hua.fan@u-picaride.fr, lingmin.liao@u-picardie.fr)
BAO-WEI WANG
Affiliation:
Department of Mathematics, Huazhong University of Science and Technology, Wuhan, 430074, PR China (email: bwei_wang@yahoo.com.cn, wujunyu@public.wh.hb.cn)
JUN WU
Affiliation:
Department of Mathematics, Huazhong University of Science and Technology, Wuhan, 430074, PR China (email: bwei_wang@yahoo.com.cn, wujunyu@public.wh.hb.cn)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Assume that x∈[0,1) admits its continued fraction expansion x=[a1(x),a2(x),…]. The Khintchine exponent γ(x) of x is defined by when the limit exists. The Khintchine spectrum dim Eξ is studied in detail, where Eξ:={x∈[0,1):γ(x)=ξ}(ξ≥0) and dim denotes the Hausdorff dimension. In particular, we prove the remarkable fact that the Khintchine spectrum dim Eξ, as a function of , is neither concave nor convex. This is a new phenomenon from the usual point of view of multifractal analysis. Fast Khintchine exponents defined by 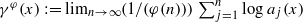are also studied, where φ(n) tends to infinity faster than n does. Under some regular conditions on φ, it is proved that the fast Khintchine spectrum dim ({x∈[0,1]:γφ(x)=ξ}) is a constant function. Our method also works for other spectra such as the Lyapunov spectrum and the fast Lyapunov spectrum.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 29 , Issue 1 , February 2009 , pp. 73 - 109
Copyright
Copyright © 2008 Cambridge University Press

References

[1]Barreira, L., Saussol, B. and Schmeling, J.. Higher-dimensional multifractal analysis. J. Math. Pures Appl. 81 (2002), 67–91.CrossRefGoogle Scholar
[2]Bernstein, F.. Über eine Anwendung der Mengenlehre auf ein der Theorie der säkularen Störungen herrührendes Problem. Math. Ann. 71 (1912), 417–439.CrossRefGoogle Scholar
[3]Billingsley, P.. Ergodic Theory and Information. John Wiley & Sons, New York, 1965.Google Scholar
[4]Borel, E.. Les probabilités dénombrables et leurs applications arithmétiques. Rend. Circ. Mat. Palermo 27 (1909), 247–271.CrossRefGoogle Scholar
[5]Borel, E.. Sur un problème de probabilités relatif aux fractions continues. Math. Ann. 72 (1912), 578–584.CrossRefGoogle Scholar
[6]Bosma, W., Dajani, K. and Kraaikamp, C.. Entropy and counting correct digits. Report No. 9925, University of Nijmegen, 1999. http://www-math.sci.kun.nl/math/onderzoek/reports/reports1999.html.Google Scholar
[7]Brin, M. and Katok, A.. On local entropy. Geometric Dynamics (Lecture Notes in Mathematics, 1007). Springer, Berlin, 1983, pp. 30–38.CrossRefGoogle Scholar
[8]Bumby, R. T.. Hausdorff dimension of sets arising in number theory. Number Theory, New York, 1983–84 (Lecture Notes in Mathematics, 1135). Springer, Berlin, 1985, pp. 1–8.Google Scholar
[9]Cassels, J.. An Introduction to Diophantine Approximation. Cambridge University Press, New York, 1957.Google Scholar
[10]Cornfeld, I., Fomin, S. and Sinai, Ya.. Ergodic Theory. Springer, New York, 1982.CrossRefGoogle Scholar
[11]Falconer, K. J.. Fractal Geometry, Mathematical Foundations and Application. John Wiley & Sons, Chichester, 1990.CrossRefGoogle Scholar
[12]Fan, A. H.. Sur les dimensions de mesures. Studia Math. 111 (1994), 1–17.CrossRefGoogle Scholar
[13]Fan, A. H. and Feng, D. J.. On the distribution of long-term average on the symbolic space. J. Stat. Phys. 99(3) (2000), 813–856.CrossRefGoogle Scholar
[14]Fan, A. H., Feng, D. J. and Wu, J.. Recurrence, dimension and entropy. J. London Math. Soc. 64(2) (2001), 229–244.CrossRefGoogle Scholar
[15]Good, I. J.. The fractional dimensional theory of continued fractions. Proc. Camb. Philos. Soc. 37 (1941), 199–228.CrossRefGoogle Scholar
[16]Hanus, P., Mauldin, R. D. and Urbański, M.. Thermodynamic formalism and multifractal analysis of conformal infinite iterated function systems. Acta. Math. Hungar. 96(1–2) (2002), 27–98.CrossRefGoogle Scholar
[17]Hardy, G. and Wright, E.. An Introduction to the Theory of Numbers, 5th edn. Oxford University Press, New York, 1979.Google Scholar
[18]Hensley, D.. The Hausdorff dimensions of some continued fraction Cantor sets. J. Number Theory 33(2) (1989), 182–198.CrossRefGoogle Scholar
[19]Hensley, D.. A polynomial time algorithm for the Hausdorff dimension of continued fraction Cantor sets. J. Number Theory 58(1) (1996), 9–45.CrossRefGoogle Scholar
[20]Jarnik, I.. Zur metrischen Theorie der diophantischen Approximationen. Proc. Mat. Fyz. 36 (1928), 91–106.Google Scholar
[21]Jenkinson, O. and Pollicott, M.. Computing the dimension of dynamically defined sets: E 2 and bounded continued fractions. Ergod. Th. & Dynam. Sys. 21(5) (2001), 1429–1445.CrossRefGoogle Scholar
[22]Jenkinson, O.. On the density of Hausdorff dimensions of bounded type continued fraction sets: the Texan conjecture. Stoch. Dyn. 4(1) (2004), 63–76.CrossRefGoogle Scholar
[23]Jenkinson, O.. Geometric barycentres of invariant measures for circle maps. Ergod. Th. & Dynam. Sys. 21(2) (2001), 511–532.CrossRefGoogle Scholar
[24]Kesseböhmer, M. and Stratmann, B.. A multifractal analysis for Stern–Brocot intervals, continued fractions and Diophantine growth rates. J. Reine Angew. Math. 605 (2007), 133–163.Google Scholar
[25]Khintchine, A. Ya.. Continued Fractions. University of Chicago Press, Chicago, London, 1964.Google Scholar
[26]Iosifescu, M. and Kraaikamp, C.. The Metrical Theory on Continued Fractions (Mathematics and its Applications, 547). Kluwer Academic, Dordrecht, 2002.CrossRefGoogle Scholar
[27]Mauldin, R. D. and Urbański, M.. Dimensions and measures in infinite iterated fuction systems. Proc. London Math. Soc. (3) 73(1) (1996), 105–154.CrossRefGoogle Scholar
[28]Mauldin, R. D. and Urbański, M.. Conformal iterated function systems with applications to the geometry of continued fractions. Trans. Amer. Math. Soc. 351(12) (1999), 4995–5025.CrossRefGoogle Scholar
[29]Mauldin, R. D. and Urbański, M.. Graph Directed Markov Systems – Geometry and Dynamics of Limit Sets Series (Cambridge Tracts in Mathematics, 148). Cambridge University Press, Cambridge, 2003.CrossRefGoogle Scholar
[30]Mayer, D.. A zeta function related to the continued fraction transformation. Bull. Soc. Math. France 104 (1976), 195–203.CrossRefGoogle Scholar
[31]Mayer, D.. Continued fractions and related transformations. Ergodic Theory, Symbolic Dynamics, and Hyperbolic Spaces (Trieste, 1989). Oxford Science Publications, Oxford University Press, New York, 1991, pp. 175–222.Google Scholar
[32]Mayer, D.. On the thermodynamics formalism for the Gauss map. Comm. Math. Phys. 130 (1990), 311–333.CrossRefGoogle Scholar
[33]Pesin, Y. B.. Dimension Theory in Dynamical Systems: Contemporary Views and Applications (Chicago Lectures in Mathematics). University of Chicago Press, Chicago, 1998.Google Scholar
[34]Pollicott, M. and Weiss, H.. Multifractal analysis of Lyapunov exponent for continued fraction and Manneville–Pomeau transformations and applications to Diophantine approximation. Comm. Math. Phys. 207(1) (1999), 145–171.CrossRefGoogle Scholar
[35]Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79). Springer, Berlin, 1982.CrossRefGoogle Scholar
[36]Walters, P.. Invariant measures and equilibrium states for some mappings which expand distances. Trans. Amer. Math. Soc. 236 (1978), 121–153.CrossRefGoogle Scholar
[37]Walters, P.. Convergence of the Ruelle operator for a function satisfying Bowen’s condition. Trans. Amer. Math. Soc. 353(1) (2001), 327–347.CrossRefGoogle Scholar
[38]Walters, P.. A variational principle for the pressure of continuous transformations. Amer. J. Math. 97(4) (1975), 937–971.CrossRefGoogle Scholar
[39]Wu, J.. A remark on the growth of the denominators of convergents. Monatsh. Math. 147(3) (2006), 259–264.CrossRefGoogle Scholar