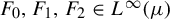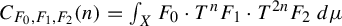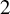1 Introduction
Let
![]() $(X,\mathscr {B}, \mu , T)$
be a measure-preserving system and let
$(X,\mathscr {B}, \mu , T)$
be a measure-preserving system and let
![]() $F_0, F_1,\ldots , F_k \in L^{\infty }(\mu )$
. Motivated in large part by applications in combinatorics and, in particular, to questions about arithmetic progressions, there has been much interest in multiple correlation sequences
$F_0, F_1,\ldots , F_k \in L^{\infty }(\mu )$
. Motivated in large part by applications in combinatorics and, in particular, to questions about arithmetic progressions, there has been much interest in multiple correlation sequences
In fact, much more general types of correlation sequences in which the powers
![]() $T, T^2,\ldots , T^k$
appearing here are replaced by measure-preserving maps
$T, T^2,\ldots , T^k$
appearing here are replaced by measure-preserving maps
![]() $T_1,\ldots , T_k$
have been studied, but here we restrict attention to this special form.
$T_1,\ldots , T_k$
have been studied, but here we restrict attention to this special form.
In the case
![]() $k = 1$
, there is a very satisfactory spectral theory of such sequences and indeed one has
$k = 1$
, there is a very satisfactory spectral theory of such sequences and indeed one has
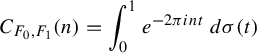 $$ \begin{align} C_{F_0, F_1}(n) = \int^1_0 e^{-2\pi i n t} \, d\sigma(t)\end{align} $$
$$ \begin{align} C_{F_0, F_1}(n) = \int^1_0 e^{-2\pi i n t} \, d\sigma(t)\end{align} $$
for some complex Borel measure
![]() $\sigma $
of bounded total variation. This follows from the Herglotz theorem on positive-definite sequences (which applies directly in the case
$\sigma $
of bounded total variation. This follows from the Herglotz theorem on positive-definite sequences (which applies directly in the case
![]() $F_0 = \overline {F_1}$
) and a depolarization identity.
$F_0 = \overline {F_1}$
) and a depolarization identity.
It is natural to ask to what extent this generalizes to
![]() $k \geqslant 2$
. In the words of Frantzikinakis [Reference Frantzikinakis7]:
$k \geqslant 2$
. In the words of Frantzikinakis [Reference Frantzikinakis7]:
‘Finding a formula analogous to (1.1), with the multiple correlation sequences in place of the single correlation sequences, is a problem of fundamental importance which has been in the mind of experts for several years. A satisfactory solution is going to give us new insights and significantly improve our ability to deal with multiple ergodic averages.’
A result of Bergelson et al [Reference Bergelson, Host and Kra2] describes the structure of multiple correlation sequences up to an error in
![]() $\ell ^1$
or
$\ell ^1$
or
![]() $\ell ^2$
. To state their result, we need to recall the notion of a nilsequence.
$\ell ^2$
. To state their result, we need to recall the notion of a nilsequence.
Definition 1.1. (Nilsequence)
Let
![]() $k \geqslant 1$
be an integer. A k-step nilsequence is a sequence
$k \geqslant 1$
be an integer. A k-step nilsequence is a sequence
![]() $(\phi (g^n x_0))_{n \in \mathbb {Z}}$
. Here,
$(\phi (g^n x_0))_{n \in \mathbb {Z}}$
. Here,
![]() $\phi : G \rightarrow \mathbb {C}$
is a continuous function satisfying the automorphy (essentially equivalently,
$\phi : G \rightarrow \mathbb {C}$
is a continuous function satisfying the automorphy (essentially equivalently,
![]() $\phi $
is a function on the nilmanifold
$\phi $
is a function on the nilmanifold
![]() $G/\Gamma $
) condition
$G/\Gamma $
) condition
![]() $\phi (x\gamma ) = \phi (x)$
for all
$\phi (x\gamma ) = \phi (x)$
for all
![]() $x \in G$
and all
$x \in G$
and all
![]() $\gamma \in \Gamma $
, where G is a simply connected k-step nilpotent Lie group with discrete and cocompact subgroup
$\gamma \in \Gamma $
, where G is a simply connected k-step nilpotent Lie group with discrete and cocompact subgroup
![]() $\Gamma $
, and
$\Gamma $
, and
![]() $g,x_0$
are fixed elements of G.
$g,x_0$
are fixed elements of G.
A careful discussion of this notion may be found in many places, for instance [Reference Bergelson, Host and Kra2]. The following result is [Reference Bergelson, Host and Kra2, Theorem 1.9].
Theorem 1.2. Suppose that
![]() $(X,\mathscr {B}, \mu , T)$
is a measure-preserving system and that
$(X,\mathscr {B}, \mu , T)$
is a measure-preserving system and that
![]() $F_0, F_1,\ldots , F_k \in L^{\infty }(\mu )$
. Suppose that
$F_0, F_1,\ldots , F_k \in L^{\infty }(\mu )$
. Suppose that
![]() $\Vert F_i \Vert _{\infty } \leqslant 1$
. Then we have a decomposition
$\Vert F_i \Vert _{\infty } \leqslant 1$
. Then we have a decomposition
where
![]() $a(n)$
is a uniform limit of k-step nilsequences with
$a(n)$
is a uniform limit of k-step nilsequences with
![]() $\Vert a \Vert _{\infty } \leqslant 1$
, and b is small in the sense that
$\Vert a \Vert _{\infty } \leqslant 1$
, and b is small in the sense that
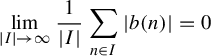 $$ \begin{align*} \lim_{|I| \rightarrow \infty} \frac{1}{|I|}\sum_{n \in I} |b(n)| = 0\end{align*} $$
$$ \begin{align*} \lim_{|I| \rightarrow \infty} \frac{1}{|I|}\sum_{n \in I} |b(n)| = 0\end{align*} $$
as I ranges over all subintervals of
![]() $\mathbb {N}$
.
$\mathbb {N}$
.
For applications involving the behaviour of correlation sequences at a sparse sequence of n, the error term here is too big. Frantzikinakis [Reference Frantzikinakis7, Problem 1] has suggested, in the context of seeking a generalization of (1.1), that a variant of Theorem 1.1 should hold with an
![]() $\ell ^{\infty }$
error term. Note that in (1.1), we have not just one nilsequence
$\ell ^{\infty }$
error term. Note that in (1.1), we have not just one nilsequence
![]() $(e^{2\pi i n t})_{n \in \mathbb {N}}$
, but an integral combination of (1-step) nilsequences. Frantzikinakis’s formulation generalizes this concept to higher-step nilsequences.
$(e^{2\pi i n t})_{n \in \mathbb {N}}$
, but an integral combination of (1-step) nilsequences. Frantzikinakis’s formulation generalizes this concept to higher-step nilsequences.
Definition 1.3. An integral combination of k-step nilsequences is a sequence of the form
Here, M is a compact metric space,
![]() $\sigma $
is a complex Borel measure of bounded variation and the
$\sigma $
is a complex Borel measure of bounded variation and the
![]() $a_m$
are k-step nilsequences, where the map
$a_m$
are k-step nilsequences, where the map
![]() $m \mapsto a_m(n)$
is measurable for each n.
$m \mapsto a_m(n)$
is measurable for each n.
Our main theorem states that, even in the case
![]() $k = 2$
, one cannot hope for a version of Theorem 1.1 in which the error b is small in
$k = 2$
, one cannot hope for a version of Theorem 1.1 in which the error b is small in
![]() $\ell ^{\infty }$
, even if one allows a to be an integral combination of nilsequences.
$\ell ^{\infty }$
, even if one allows a to be an integral combination of nilsequences.
Theorem 1.4. There is a measure-preserving system
![]() $(X,\mathscr {B}, \mu , T)$
, functions
$(X,\mathscr {B}, \mu , T)$
, functions
![]() $F_0, F_1, F_2 \in L^{\infty }(\mu )$
and an
$F_0, F_1, F_2 \in L^{\infty }(\mu )$
and an
![]() $\varepsilon> 0$
such that the correlation sequence
$\varepsilon> 0$
such that the correlation sequence
cannot be written as
![]() $a(n) + b(n)$
, where
$a(n) + b(n)$
, where
![]() $\Vert b \Vert _{\infty } \leqslant \varepsilon $
and a is an integral combination of
$\Vert b \Vert _{\infty } \leqslant \varepsilon $
and a is an integral combination of
![]() $2$
-step nilsequences.
$2$
-step nilsequences.
This theorem casts some serious doubt on the existence of a formula generalizing (1.1).
Theorem 1.2 does not provide a negative answer to [Reference Frantzikinakis7, Problem 1], because Frantzikinakis allows the automorphic functions
![]() $\phi $
in the definition of a nilsequence to be merely Riemann-integrable, rather than continuous. He calls these generalized nilsequences. An explanation of why our construction does not allow one to establish an analogue of Theorem 1.2 for generalized nilsequences is given in Appendix A. Note, however, that the Riemann-integrable functions
$\phi $
in the definition of a nilsequence to be merely Riemann-integrable, rather than continuous. He calls these generalized nilsequences. An explanation of why our construction does not allow one to establish an analogue of Theorem 1.2 for generalized nilsequences is given in Appendix A. Note, however, that the Riemann-integrable functions
![]() $\phi $
appearing in Appendix A are very singular and we certainly do not expect that the corresponding generalized nilsequences have any important role to play in the theory.
$\phi $
appearing in Appendix A are very singular and we certainly do not expect that the corresponding generalized nilsequences have any important role to play in the theory.
One reason for considering Riemann-integrable functions rather than just continuous ones is that there is a somewhat natural and well-studied class of nilsequences in which
![]() $\phi $
is not continuous, namely the bracket polynomial phases [Reference Bergelson and Leibman3]. In this case, the corresponding
$\phi $
is not continuous, namely the bracket polynomial phases [Reference Bergelson and Leibman3]. In this case, the corresponding
![]() $\phi $
have only mild discontinuities, and our argument adapts easily to show that Theorem 1.2 remains true even if one allows a to be an integral combination of this more general class of nilsequences. We sketch the argument at the end of §3.
$\phi $
have only mild discontinuities, and our argument adapts easily to show that Theorem 1.2 remains true even if one allows a to be an integral combination of this more general class of nilsequences. We sketch the argument at the end of §3.
A key motivation for Frantzikinakis in formulating [Reference Frantzikinakis7, Problem 1] was that it provides a potential route to understanding Szemerédi’s theorem with common difference in a sparse random set, a problem for which our current understanding is extremely incomplete for progressions of length 3 or longer (see [Reference Briët and Gopi4] for recent progress). Whilst Theorem 1.2 seems to rule this out as a viable strategy, our example unfortunately does not give any new information about Szemerédi’s theorem with common differences from a random set, which remains a tantalizing open problem.
Notation. Our notation is standard. We occasionally write
![]() $\mathbb {E}_{x \in A}$
for
$\mathbb {E}_{x \in A}$
for
![]() ${1}/{|A|}\sum _{x \in A}$
, where A is a finite set. We write
${1}/{|A|}\sum _{x \in A}$
, where A is a finite set. We write
![]() $[N] = \{1,2,\ldots , N\}$
as usual, and sometimes we write
$[N] = \{1,2,\ldots , N\}$
as usual, and sometimes we write
![]() $[0,N-1] = \{0,1,2,\ldots , N-1\}$
. For real t, we write
$[0,N-1] = \{0,1,2,\ldots , N-1\}$
. For real t, we write
![]() $e(t) = e^{2\pi i t}$
.
$e(t) = e^{2\pi i t}$
.
2 Outline of the argument
Our argument is part deterministic and part random. It is random in the sense that we do not explicitly construct a system
![]() $(X,\mathscr {B}, \mu , T)$
and functions
$(X,\mathscr {B}, \mu , T)$
and functions
![]() $F_0, F_1, F_2$
for which the correlation sequence
$F_0, F_1, F_2$
for which the correlation sequence
![]() $C_{F_0, F_1, F_2}(n)$
is not approximable by an integral combination of nilsequences, but rather we show there are too many possibilities for the correlation functions
$C_{F_0, F_1, F_2}(n)$
is not approximable by an integral combination of nilsequences, but rather we show there are too many possibilities for the correlation functions
![]() $C_{F_0, F_1, F_2}(n)$
for this to be so.
$C_{F_0, F_1, F_2}(n)$
for this to be so.
To do this, we first explicitly construct a certain infinite sequence
![]() $\mathscr {S} \subset \mathbb {N}$
whose growth is slower than exponential in the sense that
$\mathscr {S} \subset \mathbb {N}$
whose growth is slower than exponential in the sense that
where
![]() $\mathscr {S}[N] := \# \{n \in \mathscr {S} : n \leqslant N\}$
.
$\mathscr {S}[N] := \# \{n \in \mathscr {S} : n \leqslant N\}$
.
We show that for any choice of function
![]() $\eta : \mathscr {S} \rightarrow \{1, -\tfrac {1}{3}\}$
there is a system
$\eta : \mathscr {S} \rightarrow \{1, -\tfrac {1}{3}\}$
there is a system
![]() $(X,\mathscr {B}, \mu , T)$
and functions
$(X,\mathscr {B}, \mu , T)$
and functions
![]() $F_0, F_1, F_2$
such that
$F_0, F_1, F_2$
such that
![]() $C_{F_0 ,F_1, F_2}(n) = \eta (n)$
for
$C_{F_0 ,F_1, F_2}(n) = \eta (n)$
for
![]() $n \in \mathscr {S}$
.
$n \in \mathscr {S}$
.
For a random choice of
![]() $\eta $
, such a function will almost surely not be approximable by an integral combination of nilsequences. We give the details of this deduction, which uses nothing about
$\eta $
, such a function will almost surely not be approximable by an integral combination of nilsequences. We give the details of this deduction, which uses nothing about
![]() $\mathscr {S}$
other than the growth property (2.1), in Proposition 3.1.
$\mathscr {S}$
other than the growth property (2.1), in Proposition 3.1.
The heart of the argument, then, is the construction of the system
![]() $(X,\mathscr {B}, \mu , T)$
and the functions
$(X,\mathscr {B}, \mu , T)$
and the functions
![]() $F_0, F_1, F_2$
, given
$F_0, F_1, F_2$
, given
![]() $\eta : \mathscr {S} \rightarrow \{1, -\tfrac {1}{3}\}$
. This is assembled from a sequence of finitary examples, via a (well-known) variant of Furstenberg’s correspondence principle, and here the specific nature of
$\eta : \mathscr {S} \rightarrow \{1, -\tfrac {1}{3}\}$
. This is assembled from a sequence of finitary examples, via a (well-known) variant of Furstenberg’s correspondence principle, and here the specific nature of
![]() $\mathscr {S}$
is critical.
$\mathscr {S}$
is critical.
The idea behind the construction of these finitary examples ultimately comes from coding theory, and in particular a construction of Yekhanin [Reference Yekhanin9]. We will only need the most basic form of these ideas; for instance, we can replace all the finite-field theory in Yekhanin’s work with the simple observation that the function
![]() $\psi : \mathbb {Z} \rightarrow \{-1,1\}$
defined by
$\psi : \mathbb {Z} \rightarrow \{-1,1\}$
defined by
![]() $\psi (0) = 1$
,
$\psi (0) = 1$
,
![]() $\psi (1) = \psi (2) = -1$
, and periodic mod
$\psi (1) = \psi (2) = -1$
, and periodic mod
![]() $3$
has the property that
$3$
has the property that
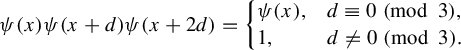 $$ \begin{align*} \psi(x) \psi(x+d)\psi(x+2d) = \left\{\begin{array}{@{}ll} \psi(x), & d \equiv 0\; (\operatorname{mod}\, 3), \\ 1, & d \neq 0\; (\operatorname{mod}\, 3) .\end{array} \right.\end{align*} $$
$$ \begin{align*} \psi(x) \psi(x+d)\psi(x+2d) = \left\{\begin{array}{@{}ll} \psi(x), & d \equiv 0\; (\operatorname{mod}\, 3), \\ 1, & d \neq 0\; (\operatorname{mod}\, 3) .\end{array} \right.\end{align*} $$
The idea of using Yekhanin’s construction to give interesting examples in the additive combinatorics of higher-order correlations first arose in the finite field setting, in a joint work of the first author and Labib [Reference Briët and Labib5]. Those ideas have inspired the present work.
Remark. The sequence
![]() $\mathscr {S}$
we construct has
$\mathscr {S}$
we construct has
![]() $|\mathscr {S}[N]| \gg _{\varepsilon } (\log N)^{2 - \varepsilon }$
; we do not know or have any reasonable guess as to what might be the best possible growth rate for sequences with the desired properties.
$|\mathscr {S}[N]| \gg _{\varepsilon } (\log N)^{2 - \varepsilon }$
; we do not know or have any reasonable guess as to what might be the best possible growth rate for sequences with the desired properties.
3 Entropy and nilsequences
Proposition 3.1. Let
![]() $\mathscr {S}$
be an increasing sequence of natural numbers such that
$\mathscr {S}$
be an increasing sequence of natural numbers such that
Then there is a function
![]() $\eta : \mathscr {S} \rightarrow \{1, -\tfrac {1}{3}\}$
such that
$\eta : \mathscr {S} \rightarrow \{1, -\tfrac {1}{3}\}$
such that
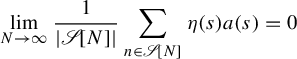 $$ \begin{align} \lim_{N \rightarrow \infty} \frac{1}{|\mathscr{S}[N]|}\sum_{n \in \mathscr{S}[N]} \eta(s) a(s) = 0\end{align} $$
$$ \begin{align} \lim_{N \rightarrow \infty} \frac{1}{|\mathscr{S}[N]|}\sum_{n \in \mathscr{S}[N]} \eta(s) a(s) = 0\end{align} $$
for all nilsequences a.
Proof The space of
![]() $C^{\infty }$
-functions on
$C^{\infty }$
-functions on
![]() $G/\Gamma $
is dense in the space of continuous functions; to approximate a continuous function by a smooth function, average with respect to a smooth kernel supported near the identity on G. It therefore suffices to verify (3.2) for
$G/\Gamma $
is dense in the space of continuous functions; to approximate a continuous function by a smooth function, average with respect to a smooth kernel supported near the identity on G. It therefore suffices to verify (3.2) for
![]() $a(n) = \phi (g^n x)$
with
$a(n) = \phi (g^n x)$
with
![]() $\phi \in C^{\infty }(G/\Gamma )$
. Now we use the fact that there is a map
$\phi \in C^{\infty }(G/\Gamma )$
. Now we use the fact that there is a map
and a function
![]() $M : (0,\infty ) \times (0,1) \rightarrow (0,\infty )$
such that the set
$M : (0,\infty ) \times (0,1) \rightarrow (0,\infty )$
such that the set
can be covered by
![]() $N^{M(C,\varepsilon )}$
balls of radius
$N^{M(C,\varepsilon )}$
balls of radius
![]() $\varepsilon $
in
$\varepsilon $
in
![]() $\ell ^{\infty }[N]$
.
$\ell ^{\infty }[N]$
.
Results of this type were first observed by Frantzikinakis [Reference Frantzikinakis6, Proposition 6.2], and in fact Proposition 3.1 and its proof are very closely related to [Reference Frantzikinakis6, Theorem 1.4]. A discussion which gives what we need here is in the appendix of Altman [Reference Altman1] (note that
![]() $(g^n x_0)_{n \in \mathbb {Z}}$
is a particular example of a polynomial sequence as considered by Altman).
$(g^n x_0)_{n \in \mathbb {Z}}$
is a particular example of a polynomial sequence as considered by Altman).
We pick the values of
![]() $\eta (n)$
at random, choosing
$\eta (n)$
at random, choosing
![]() $\eta (n) = -\tfrac {1}{3}$
with probability
$\eta (n) = -\tfrac {1}{3}$
with probability
![]() $\tfrac {3}{4}$
and
$\tfrac {3}{4}$
and
![]() $\eta (n) = 1$
with probability
$\eta (n) = 1$
with probability
![]() $\tfrac {1}{4}$
, these choices being independent for different values of
$\tfrac {1}{4}$
, these choices being independent for different values of
![]() $n \in \mathscr {S}$
. Then
$n \in \mathscr {S}$
. Then
![]() $\mathbb {E} \eta (n) = 0$
. By well-known large deviation estimates (Hoeffding’s inequality), for any fixed
$\mathbb {E} \eta (n) = 0$
. By well-known large deviation estimates (Hoeffding’s inequality), for any fixed
![]() $1$
-bounded function b and for any distinct
$1$
-bounded function b and for any distinct
![]() $n_1,\ldots , n_m$
,
$n_1,\ldots , n_m$
,
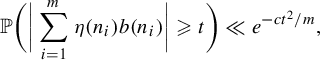 $$ \begin{align} \mathbb{P}\bigg( \bigg|\sum_{i = 1}^m \eta(n_i) b(n_i)\bigg| \geqslant t \bigg) \ll e^{-ct^2/m}, \end{align} $$
$$ \begin{align} \mathbb{P}\bigg( \bigg|\sum_{i = 1}^m \eta(n_i) b(n_i)\bigg| \geqslant t \bigg) \ll e^{-ct^2/m}, \end{align} $$
where
![]() $c> 0$
is absolute.
$c> 0$
is absolute.
Let
![]() $\omega : \mathbb {N} \rightarrow (0,\infty )$
be some function tending to infinity, to be specified later.
$\omega : \mathbb {N} \rightarrow (0,\infty )$
be some function tending to infinity, to be specified later.
For each N, let
![]() $E_N$
be the following event: for all
$E_N$
be the following event: for all
![]() $1$
-bounded nilsequences a of complexity
$1$
-bounded nilsequences a of complexity
![]() $\leqslant \omega (N)$
,
$\leqslant \omega (N)$
,
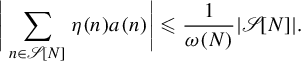 $$ \begin{align} \bigg|\sum_{n \in \mathscr{S}[N] } \eta(n) a(n)\bigg| \leqslant \frac{1}{\omega(N)} | \mathscr{S}[N] |.\end{align} $$
$$ \begin{align} \bigg|\sum_{n \in \mathscr{S}[N] } \eta(n) a(n)\bigg| \leqslant \frac{1}{\omega(N)} | \mathscr{S}[N] |.\end{align} $$
We estimate
![]() $\mathbb {P}(E_N)$
as follows. Pick some collection
$\mathbb {P}(E_N)$
as follows. Pick some collection
![]() $\{ a_1,\ldots , a_J\}$
,
$\{ a_1,\ldots , a_J\}$
,
![]() $J \leqslant N^{M(\omega (N),1/2\omega (N))}$
of functions such that, for every
$J \leqslant N^{M(\omega (N),1/2\omega (N))}$
of functions such that, for every
![]() $1$
-bounded nilsequence a of complexity at most
$1$
-bounded nilsequence a of complexity at most
![]() $\omega (N)$
, there is some
$\omega (N)$
, there is some
![]() $a_i$
with
$a_i$
with
![]() $\Vert a - a_i \Vert _{\ell ^{\infty }[N]} \leqslant 1/2\omega (N)$
. Note that we do not need to assume that the
$\Vert a - a_i \Vert _{\ell ^{\infty }[N]} \leqslant 1/2\omega (N)$
. Note that we do not need to assume that the
![]() $a_i$
are nilsequences (though this could be arranged if desired) and they are automatically
$a_i$
are nilsequences (though this could be arranged if desired) and they are automatically
![]() $2$
-bounded.
$2$
-bounded.
If we are not in
![]() $E_N$
, there is some
$E_N$
, there is some
![]() $a_i$
such that
$a_i$
such that
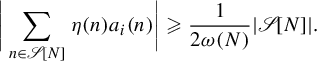 $$ \begin{align} \bigg|\sum_{n \in \mathscr{S}[N] } \eta(n) a_i(n)\bigg| \geqslant \frac{1}{2 \omega(N)} | \mathscr{S}[N] |.\end{align} $$
$$ \begin{align} \bigg|\sum_{n \in \mathscr{S}[N] } \eta(n) a_i(n)\bigg| \geqslant \frac{1}{2 \omega(N)} | \mathscr{S}[N] |.\end{align} $$
By (3.3), the probability of (3.5) happening, for some fixed i, is bounded above by
![]() $e^{-c' |\mathscr {S}[N]|/\omega (N)^2}$
for some
$e^{-c' |\mathscr {S}[N]|/\omega (N)^2}$
for some
![]() $c'> 0$
. Summing over i, it follows that
$c'> 0$
. Summing over i, it follows that
Choose
![]() $\omega $
(with
$\omega $
(with
![]() $\omega (N) \rightarrow \infty )$
so that
$\omega (N) \rightarrow \infty )$
so that
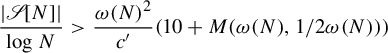 $$ \begin{align*} \frac{|\mathscr{S}[N]|}{\log N}> \frac{\omega(N)^2}{c'} ( 10 + M(\omega(N), 1/2\omega(N)))\end{align*} $$
$$ \begin{align*} \frac{|\mathscr{S}[N]|}{\log N}> \frac{\omega(N)^2}{c'} ( 10 + M(\omega(N), 1/2\omega(N)))\end{align*} $$
for N sufficiently large. (Here, of course, we have used the assumption on
![]() $\mathscr {S}$
.) This then means that
$\mathscr {S}$
.) This then means that
for large N. In particular,
![]() $\sum _N \mathbb {P}(\neg E_N) < \infty $
which, by Borel–Cantelli, implies that almost surely only finitely many of the
$\sum _N \mathbb {P}(\neg E_N) < \infty $
which, by Borel–Cantelli, implies that almost surely only finitely many of the
![]() $\neg E_N$
occur. In particular, there is some particular choice of
$\neg E_N$
occur. In particular, there is some particular choice of
![]() $\eta $
such that (3.4) holds for all sufficiently large N. Because every nilsequence has finite complexity, this implies the result.
$\eta $
such that (3.4) holds for all sufficiently large N. Because every nilsequence has finite complexity, this implies the result.
Remark. There is, of course, nothing special about
![]() $\{1, -\tfrac {1}{3}\}$
; any set containing both positive and negative numbers would do.
$\{1, -\tfrac {1}{3}\}$
; any set containing both positive and negative numbers would do.
To conclude this section, let us quickly sketch how one could extend Proposition 3.1 to include the case where
![]() $a()$
is a bracket polynomial or a product of such (and hence not a nilsequence with a continuous automorphic function
$a()$
is a bracket polynomial or a product of such (and hence not a nilsequence with a continuous automorphic function
![]() $\phi $
). Write
$\phi $
). Write
![]() $\chi _{\alpha , \beta }(n) := e(\alpha n\lfloor \beta n\rfloor )$
. The key point is that the set of functions
$\chi _{\alpha , \beta }(n) := e(\alpha n\lfloor \beta n\rfloor )$
. The key point is that the set of functions
![]() $\chi _{\alpha , \beta }(n)$
, like the set of nilsequences of fixed complexity, has polynomially bounded covering numbers in
$\chi _{\alpha , \beta }(n)$
, like the set of nilsequences of fixed complexity, has polynomially bounded covering numbers in
![]() $\ell ^{\infty }[N]$
.
$\ell ^{\infty }[N]$
.
To see why this is so, first note that
![]() $\chi _{\alpha , \beta }$
depends only on
$\chi _{\alpha , \beta }$
depends only on
![]() $\alpha (\operatorname {mod}\, 1)$
, so we may assume
$\alpha (\operatorname {mod}\, 1)$
, so we may assume
![]() $0 \leqslant \alpha < 1$
. Next, replacing
$0 \leqslant \alpha < 1$
. Next, replacing
![]() $\beta $
by
$\beta $
by
![]() $\beta +k$
for
$\beta +k$
for
![]() $k \in \mathbb {Z}$
has the effect of multiplying by a quadratic phase
$k \in \mathbb {Z}$
has the effect of multiplying by a quadratic phase
![]() $e(\gamma n^2)$
(where
$e(\gamma n^2)$
(where
![]() $\gamma = \alpha k$
). However, the set of all quadratic phases
$\gamma = \alpha k$
). However, the set of all quadratic phases
![]() $e(\gamma n^2)$
is covered by
$e(\gamma n^2)$
is covered by
![]() $\ll _{\varepsilon } N^2$
balls of radius
$\ll _{\varepsilon } N^2$
balls of radius
![]() $\varepsilon $
in
$\varepsilon $
in
![]() $\ell ^{\infty }[N]$
, because we may assume
$\ell ^{\infty }[N]$
, because we may assume
![]() $0 \leqslant \gamma < 1$
and changing
$0 \leqslant \gamma < 1$
and changing
![]() $\gamma $
by
$\gamma $
by
![]() ${\varepsilon }/{N^2}$
only changes
${\varepsilon }/{N^2}$
only changes
![]() $e(\gamma n^2)$
by
$e(\gamma n^2)$
by
![]() $O(\varepsilon )$
, uniformly for
$O(\varepsilon )$
, uniformly for
![]() $n \leqslant N$
.
$n \leqslant N$
.
It therefore suffices to show that the covering numbers of the set
![]() $\Xi := \{ \chi _{\alpha , \beta } : 0 \leqslant \alpha , \beta < 1\}$
are polynomially bounded in
$\Xi := \{ \chi _{\alpha , \beta } : 0 \leqslant \alpha , \beta < 1\}$
are polynomially bounded in
![]() $\ell ^{\infty }[N]$
. Now, restricted to
$\ell ^{\infty }[N]$
. Now, restricted to
![]() $n \leqslant N$
, there are only polynomially many functions
$n \leqslant N$
, there are only polynomially many functions
![]() $\lfloor \beta n\rfloor $
as
$\lfloor \beta n\rfloor $
as
![]() $\beta $
ranges in
$\beta $
ranges in
![]() $[0, 1)$
. Indeed, the map
$[0, 1)$
. Indeed, the map
![]() $\beta \mapsto (\lfloor \beta n\rfloor )_{n \leqslant N}$
is only discontinuous at the points where
$\beta \mapsto (\lfloor \beta n\rfloor )_{n \leqslant N}$
is only discontinuous at the points where
![]() $\beta n \in \mathbb {Z}$
for some
$\beta n \in \mathbb {Z}$
for some
![]() $n \leqslant N$
, of which there are no more than
$n \leqslant N$
, of which there are no more than
![]() $N^2$
with
$N^2$
with
![]() $0 \leqslant \beta < 1$
. Thus,
$0 \leqslant \beta < 1$
. Thus,
![]() $\chi _{\alpha , \beta } = \chi _{\alpha , \beta '}$
, with
$\chi _{\alpha , \beta } = \chi _{\alpha , \beta '}$
, with
![]() $\beta '$
varying in a set of size
$\beta '$
varying in a set of size
![]() $N^2$
. Changing
$N^2$
. Changing
![]() $\alpha $
by
$\alpha $
by
![]() ${\varepsilon }/{N^2}$
only changes
${\varepsilon }/{N^2}$
only changes
![]() $\chi _{\alpha , \beta }(n)$
by
$\chi _{\alpha , \beta }(n)$
by
![]() $O(\varepsilon )$
, uniformly for
$O(\varepsilon )$
, uniformly for
![]() $n \leqslant N$
. Therefore, the covering number of
$n \leqslant N$
. Therefore, the covering number of
![]() $\Xi $
in
$\Xi $
in
![]() $\ell ^{\infty }[N]$
is
$\ell ^{\infty }[N]$
is
![]() $\ll _{\varepsilon } N^4$
.
$\ll _{\varepsilon } N^4$
.
It follows immediately that, for fixed C, the set of functions of type
![]() $e(\sum _{i = 1}^k \alpha _i n [\beta _i n])$
, where
$e(\sum _{i = 1}^k \alpha _i n [\beta _i n])$
, where
![]() $k \leqslant C$
, is covered by
$k \leqslant C$
, is covered by
![]() $N^{M(C,\varepsilon )}$
balls of radius
$N^{M(C,\varepsilon )}$
balls of radius
![]() $\varepsilon $
in
$\varepsilon $
in
![]() $\ell ^{\infty }[N]$
. One could include various types of 1-step nilsequence or bracket polynomial and obtain a similar result.
$\ell ^{\infty }[N]$
. One could include various types of 1-step nilsequence or bracket polynomial and obtain a similar result.
Bounds on covering numbers were all we needed to know about nilsequences, and the rest of the argument goes over verbatim.
4 The heart of the construction
Define
![]() $\psi : \mathbb {Z} \rightarrow \{-1,1\}$
to be the function with
$\psi : \mathbb {Z} \rightarrow \{-1,1\}$
to be the function with
![]() $\psi (0) = 1$
,
$\psi (0) = 1$
,
![]() $\psi (1) = \psi (2) = -1$
, and periodic mod
$\psi (1) = \psi (2) = -1$
, and periodic mod
![]() $3$
. The crucial property of this function we use is the following, which is easily checked:
$3$
. The crucial property of this function we use is the following, which is easily checked:
if
![]() $d \equiv 0\; (\operatorname {mod}\, 3)$
, and
$d \equiv 0\; (\operatorname {mod}\, 3)$
, and
![]() $1$
if
$1$
if
![]() $d \neq 0\; (\operatorname {mod}\, 3)$
.
$d \neq 0\; (\operatorname {mod}\, 3)$
.
Fix, once and for all, a sequence
![]() $M_1 < M_2 < \cdots $
of positive integers such that:
$M_1 < M_2 < \cdots $
of positive integers such that:
-
(1) each
 $M_i$
is a multiple of
$M_i$
is a multiple of
 $3$
;
$3$
; -
(2)
 $\lim _{k \rightarrow \infty } k^{-2} \sum _{i=1}^k \log M_i = 0$
;
$\lim _{k \rightarrow \infty } k^{-2} \sum _{i=1}^k \log M_i = 0$
; -
(3)
 $\prod _{i=1}^{\infty } (1 - ({3}/{M_i})) = \gamma> 0$
.
$\prod _{i=1}^{\infty } (1 - ({3}/{M_i})) = \gamma> 0$
.
For instance, one could take
![]() $M_i = 3i^2$
.
$M_i = 3i^2$
.
Define
Later on we will need the technical variant
Define also
![]() $\Sigma _k$
to consist of all sequences
$\Sigma _k$
to consist of all sequences
![]() $(x_1,x_2,\ldots )$
with precisely two non-zero entries
$(x_1,x_2,\ldots )$
with precisely two non-zero entries
![]() $x_a, x_b$
, both of which equal 1, and with
$x_a, x_b$
, both of which equal 1, and with
![]() $x_{k+1} = x_{k+2} = \cdots = 0$
. Write
$x_{k+1} = x_{k+2} = \cdots = 0$
. Write
We have a bijective map
defined by
Let
![]() $\mathscr {S} = \beta (\Sigma )$
. Thus,
$\mathscr {S} = \beta (\Sigma )$
. Thus,
![]() $\mathscr {S}$
consists of the sums of two distinct elements of the sequence
$\mathscr {S}$
consists of the sums of two distinct elements of the sequence
![]() $\{1, M_1, M_1M_2, M_1M_2M_3,\ldots \}$
. We claim that
$\{1, M_1, M_1M_2, M_1M_2M_3,\ldots \}$
. We claim that
![]() $\mathscr {S}$
satisfies the hypothesis (3.1) of Lemma 3.1, that is,
$\mathscr {S}$
satisfies the hypothesis (3.1) of Lemma 3.1, that is,
![]() $\lim _{N \rightarrow \infty } {|\mathscr {S}[N]|}/{\log N} = \infty $
.
$\lim _{N \rightarrow \infty } {|\mathscr {S}[N]|}/{\log N} = \infty $
.
To see this, let k be maximal so that
![]() $M_1 \cdots M_k \leqslant N/2$
. Then
$M_1 \cdots M_k \leqslant N/2$
. Then
![]() $|\mathscr {S}[N]| \geqslant \binom {k}{2}$
, whilst
$|\mathscr {S}[N]| \geqslant \binom {k}{2}$
, whilst
![]() $\log (N/2) \leqslant \sum _{i=1}^{k+1} \log M_i$
. Therefore, it is enough that
$\log (N/2) \leqslant \sum _{i=1}^{k+1} \log M_i$
. Therefore, it is enough that
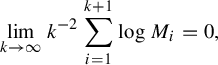 $$ \begin{align*} \lim_{k \rightarrow \infty} k^{-2}\sum_{i=1}^{k+1} \log M_i = 0,\end{align*} $$
$$ \begin{align*} \lim_{k \rightarrow \infty} k^{-2}\sum_{i=1}^{k+1} \log M_i = 0,\end{align*} $$
which follows immediately from assumption 2 above.
We now apply Proposition 3.1 to get a function
![]() $\eta : \mathscr {S} \rightarrow \{1, -\tfrac {1}{3}\}$
satisfying (3.2). Define
$\eta : \mathscr {S} \rightarrow \{1, -\tfrac {1}{3}\}$
satisfying (3.2). Define
Thus,
![]() $\Sigma _k = \Sigma ^-_k\cup \Sigma ^+_k$
.
$\Sigma _k = \Sigma ^-_k\cup \Sigma ^+_k$
.
We introduce one more piece of notation. If
![]() $z \in \Sigma _k$
and if
$z \in \Sigma _k$
and if
![]() $x \in \Omega _{k}$
, then we write
$x \in \Omega _{k}$
, then we write
 $$ \begin{align*} \sigma_z(x ) := \sum_{i \in [k] : z_i = 0} x_i.\end{align*} $$
$$ \begin{align*} \sigma_z(x ) := \sum_{i \in [k] : z_i = 0} x_i.\end{align*} $$
Now we come to the crucial definition. Let
![]() $k \in \mathbb {N}$
. For
$k \in \mathbb {N}$
. For
![]() $x \in \Omega _{k}$
define
$x \in \Omega _{k}$
define
 $$ \begin{align} f_k(\beta(x)) = \prod_{z \in \Sigma^k_-} \psi(\sigma_z(x)).\end{align} $$
$$ \begin{align} f_k(\beta(x)) = \prod_{z \in \Sigma^k_-} \psi(\sigma_z(x)).\end{align} $$
Note that
![]() $\beta (\Omega _{k}) = [0,N_k-1]$
, where
$\beta (\Omega _{k}) = [0,N_k-1]$
, where
and so
![]() $f_k$
is a well-defined function on
$f_k$
is a well-defined function on
![]() $[0, N_k-1]$
, taking values in
$[0, N_k-1]$
, taking values in
![]() $\{-1,1\}$
.
$\{-1,1\}$
.
Remark. As mentioned previously, the idea of making this definition ultimately comes from coding theory (see [Reference Briët and Labib5] for further discussion). The important feature is that averages of
![]() $f_k(n) f_k(n+d)f_k(n + 2d)$
over n simplify substantially by using (4.1); we give the details of this in (4.5).
$f_k(n) f_k(n+d)f_k(n + 2d)$
over n simplify substantially by using (4.1); we give the details of this in (4.5).
Define also the technical variant
Thus,
![]() $\tilde f_k$
is defined on
$\tilde f_k$
is defined on
![]() $[0,N_k - 1]$
and takes values in
$[0,N_k - 1]$
and takes values in
![]() $\{-1,0,1\}$
. Extend both
$\{-1,0,1\}$
. Extend both
![]() $f_k$
and
$f_k$
and
![]() $\tilde f_k$
to functions on all of
$\tilde f_k$
to functions on all of
![]() $\mathbb {Z}_{\geqslant 0}$
by defining
$\mathbb {Z}_{\geqslant 0}$
by defining
![]() $f_k(n) = \tilde f_k(n) = 0$
for
$f_k(n) = \tilde f_k(n) = 0$
for
![]() $n \geqslant N_k$
.
$n \geqslant N_k$
.
The following lemma is the heart of the argument. Here, recall that
![]() $\gamma> 0$
is just a positive constant (appearing in point 3 of the list of properties satisfied by the
$\gamma> 0$
is just a positive constant (appearing in point 3 of the list of properties satisfied by the
![]() $M_i$
).
$M_i$
).
Lemma 4.1. For
![]() $d \in \mathbb {Z}_{\geqslant 0}$
, write
$d \in \mathbb {Z}_{\geqslant 0}$
, write
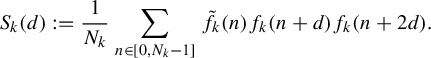 $$ \begin{align*} S_k(d) := \frac{1}{N_k} \sum_{n \in [0,N_k-1]} \tilde f_k(n) f_k(n + d) f_k(n + 2d).\end{align*} $$
$$ \begin{align*} S_k(d) := \frac{1}{N_k} \sum_{n \in [0,N_k-1]} \tilde f_k(n) f_k(n + d) f_k(n + 2d).\end{align*} $$
Then for
![]() $d \in \mathscr {S}$
we have
$d \in \mathscr {S}$
we have
![]() $\lim _{k \rightarrow \infty } S_k(d) = \gamma \eta (d)$
.
$\lim _{k \rightarrow \infty } S_k(d) = \gamma \eta (d)$
.
Proof Let
![]() $d \in \mathscr {S} = \beta (\Sigma )$
. For k large enough,
$d \in \mathscr {S} = \beta (\Sigma )$
. For k large enough,
![]() $d \in \beta (\Sigma _k)$
, and we assume this is so in what follows.
$d \in \beta (\Sigma _k)$
, and we assume this is so in what follows.
From the definition of
![]() $\tilde f_k$
, we see that the sum over n ranges over
$\tilde f_k$
, we see that the sum over n ranges over
![]() $n = \beta (x)$
,
$n = \beta (x)$
,
![]() $x \in \tilde \Omega _{k}$
. Now for n of this form and for
$x \in \tilde \Omega _{k}$
. Now for n of this form and for
![]() $d = \beta (y)$
,
$d = \beta (y)$
,
![]() $y \in \Sigma _k$
, we have
$y \in \Sigma _k$
, we have
![]() $x+y, x+ 2y \in \Omega _{k}$
and, moreover,
$x+y, x+ 2y \in \Omega _{k}$
and, moreover,
Note that this ‘lack of carries’ was precisely the reason for defining the set
![]() $\tilde \Omega _{k}$
. It follows that
$\tilde \Omega _{k}$
. It follows that
for
![]() $d = \beta (y)$
,
$d = \beta (y)$
,
![]() $y \in \Sigma _k$
. Substituting the definitions (4.2), (4.4) of
$y \in \Sigma _k$
. Substituting the definitions (4.2), (4.4) of
![]() $f_k, \tilde f_k$
(and noting that
$f_k, \tilde f_k$
(and noting that
![]() $\sigma _z$
is linear), we see that
$\sigma _z$
is linear), we see that
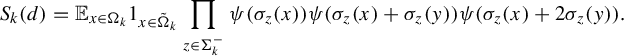 $$ \begin{align*} S_k(d) = \mathbb{E}_{x \in \Omega_{k}} 1_{x \in \tilde \Omega_k} \prod_{z \in \Sigma^-_k} \psi(\sigma_z(x))\psi(\sigma_z(x) + \sigma_z(y))\psi(\sigma_z(x)+ 2\sigma_z(y)).\end{align*} $$
$$ \begin{align*} S_k(d) = \mathbb{E}_{x \in \Omega_{k}} 1_{x \in \tilde \Omega_k} \prod_{z \in \Sigma^-_k} \psi(\sigma_z(x))\psi(\sigma_z(x) + \sigma_z(y))\psi(\sigma_z(x)+ 2\sigma_z(y)).\end{align*} $$
From (4.1) it follows that
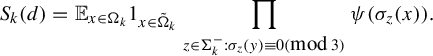 $$ \begin{align*} S_k(d) = \mathbb{E}_{x \in \Omega_{k}} 1_{x \in \tilde \Omega_k} \prod_{z \in \Sigma^-_k: \sigma_z(y) \equiv 0 (\mbox{mod}\, 3)} \psi(\sigma_z(x)).\end{align*} $$
$$ \begin{align*} S_k(d) = \mathbb{E}_{x \in \Omega_{k}} 1_{x \in \tilde \Omega_k} \prod_{z \in \Sigma^-_k: \sigma_z(y) \equiv 0 (\mbox{mod}\, 3)} \psi(\sigma_z(x)).\end{align*} $$
Now both y and z here are vectors with only two non-zero entries and so
![]() $\sigma _z(y)$
takes only the values
$\sigma _z(y)$
takes only the values
![]() $0,1,2$
with
$0,1,2$
with
![]() $\sigma _z(y) = 0$
if and only if
$\sigma _z(y) = 0$
if and only if
![]() $y = z$
. Therefore,
$y = z$
. Therefore,
 $$ \begin{align} S_k(d) = \bigg\{ \begin{array}{@{}ll} \mathbb{E}_{x \in \Omega_{k}} 1_{x \in \tilde\Omega_k} \psi(\sigma_y(x)) & \text{if } y \in \Sigma^-_k,\\ \mathbb{E}_{x \in \Omega_{k}} 1_{x \in \tilde\Omega_{k}} & \text{if }y \in \Sigma^+_k.\end{array} \end{align} $$
$$ \begin{align} S_k(d) = \bigg\{ \begin{array}{@{}ll} \mathbb{E}_{x \in \Omega_{k}} 1_{x \in \tilde\Omega_k} \psi(\sigma_y(x)) & \text{if } y \in \Sigma^-_k,\\ \mathbb{E}_{x \in \Omega_{k}} 1_{x \in \tilde\Omega_{k}} & \text{if }y \in \Sigma^+_k.\end{array} \end{align} $$
The second expression is
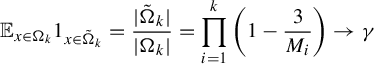 $$ \begin{align*} \mathbb{E}_{x \in \Omega_{k}} 1_{x \in \tilde\Omega_{k}} = \frac{|\tilde \Omega_k|}{|\Omega_k|} = \prod_{i=1}^k \bigg(1 - \frac{3}{M_i}\bigg) \rightarrow \gamma\end{align*} $$
$$ \begin{align*} \mathbb{E}_{x \in \Omega_{k}} 1_{x \in \tilde\Omega_{k}} = \frac{|\tilde \Omega_k|}{|\Omega_k|} = \prod_{i=1}^k \bigg(1 - \frac{3}{M_i}\bigg) \rightarrow \gamma\end{align*} $$
as
![]() $k \rightarrow \infty $
. The first expression in (4.5) may be written explicitly as
$k \rightarrow \infty $
. The first expression in (4.5) may be written explicitly as
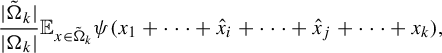 $$ \begin{align} \frac{|\tilde \Omega_k|}{|\Omega_k|}\mathbb{E}_{x \in \tilde\Omega_k} \psi(x_1 + \cdots + \hat{x}_i + \cdots + \hat{x}_j + \cdots + x_k),\end{align} $$
$$ \begin{align} \frac{|\tilde \Omega_k|}{|\Omega_k|}\mathbb{E}_{x \in \tilde\Omega_k} \psi(x_1 + \cdots + \hat{x}_i + \cdots + \hat{x}_j + \cdots + x_k),\end{align} $$
where y has non-zero coordinates at
![]() $i,j$
and the hat means that
$i,j$
and the hat means that
![]() $\hat {x}_i$
does not appear in the sum. Note, however, that
$\hat {x}_i$
does not appear in the sum. Note, however, that
![]() $\tilde \Omega _k$
is a box with sidelengths
$\tilde \Omega _k$
is a box with sidelengths
![]() $M_i - 3$
, each of which is a multiple of
$M_i - 3$
, each of which is a multiple of
![]() $3$
. Therefore
$3$
. Therefore
![]() $x_1 + \cdots + \hat {x}_i + \cdots + \hat {x}_j + \cdots + x_k$
is uniformly distributed mod
$x_1 + \cdots + \hat {x}_i + \cdots + \hat {x}_j + \cdots + x_k$
is uniformly distributed mod
![]() $3$
, as x ranges uniformly over
$3$
, as x ranges uniformly over
![]() $\tilde \Omega _k$
, and the average in (4.6) is
$\tilde \Omega _k$
, and the average in (4.6) is
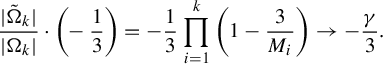 $$ \begin{align*} \frac{|\tilde \Omega_k|}{|\Omega_k|} \cdot \bigg(\!-\frac{1}{3}\bigg) = -\frac{1}{3} \prod_{i=1}^k \bigg(1 - \frac{3}{M_i}\bigg) \rightarrow -\frac{\gamma}{3}.\end{align*} $$
$$ \begin{align*} \frac{|\tilde \Omega_k|}{|\Omega_k|} \cdot \bigg(\!-\frac{1}{3}\bigg) = -\frac{1}{3} \prod_{i=1}^k \bigg(1 - \frac{3}{M_i}\bigg) \rightarrow -\frac{\gamma}{3}.\end{align*} $$
This completes the proof.
5 Putting everything together
Our final task is to build a measure-preserving system from the functions constructed in the last section. For this we need a slight variant of the usual Furstenberg correspondence principle, proven in a very similar way. An essentially equivalent statement may be found, for instance, in [Reference Frantzikinakis8, Proposition 3.3].
Proposition 5.1. Let
![]() $A \subset \mathbb {R}$
be a finite set. Suppose that for each
$A \subset \mathbb {R}$
be a finite set. Suppose that for each
![]() $k \in \mathbb {N}$
we have functions
$k \in \mathbb {N}$
we have functions
![]() $f_{0,k}, \cdots , f_{r,k} : \mathbb {Z}_{\geqslant 0} \rightarrow A$
, and that
$f_{0,k}, \cdots , f_{r,k} : \mathbb {Z}_{\geqslant 0} \rightarrow A$
, and that
![]() $(N_k)_{k=1}^{\infty }$
is an increasing sequence of positive integers. Then there is a measure-preserving system
$(N_k)_{k=1}^{\infty }$
is an increasing sequence of positive integers. Then there is a measure-preserving system
![]() $(X, \mathscr {B}, \mu , T)$
and functions
$(X, \mathscr {B}, \mu , T)$
and functions
![]() $F_0,F_1,\ldots , F_r \in L^{\infty }(\mu )$
such that the following is true: if
$F_0,F_1,\ldots , F_r \in L^{\infty }(\mu )$
such that the following is true: if
![]() $(d_1,\ldots , d_r)$
is a tuple of distinct positive integers such that
$(d_1,\ldots , d_r)$
is a tuple of distinct positive integers such that
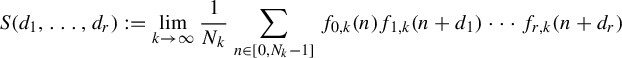 $$ \begin{align*} S(d_1,\ldots, d_r) := \lim_{k \rightarrow \infty} \frac{1}{N_k} \sum_{n \in [0,N_k-1]} f_{0,k}(n) f_{1,k}(n + d_1)\cdots f_{r,k}(n + d_r)\end{align*} $$
$$ \begin{align*} S(d_1,\ldots, d_r) := \lim_{k \rightarrow \infty} \frac{1}{N_k} \sum_{n \in [0,N_k-1]} f_{0,k}(n) f_{1,k}(n + d_1)\cdots f_{r,k}(n + d_r)\end{align*} $$
exists, then
We apply this with the functions constructed in the last section, taking
![]() $r = 2$
,
$r = 2$
,
![]() $f_{0,k} := \tilde f_k$
,
$f_{0,k} := \tilde f_k$
,
![]() $f_{1,k} = f_{2,k} = f_k$
and
$f_{1,k} = f_{2,k} = f_k$
and
![]() $N_k = M_1 \cdots M_k$
as before.
$N_k = M_1 \cdots M_k$
as before.
By Proposition 5.1 and Lemma 4.1, there is a measure-preserving system
![]() $(X,\mathscr {B}, \mu , T)$
together with functions
$(X,\mathscr {B}, \mu , T)$
together with functions
![]() $F_0, F_1, F_2 \in L^{\infty }(\mu )$
such that, writing
$F_0, F_1, F_2 \in L^{\infty }(\mu )$
such that, writing
![]() $C_{F_0, F_1, F_2}(d) := \int _X F_0 \cdot T^d F_1 \cdot T^{2d} F_2\,d\mu $
, we have
$C_{F_0, F_1, F_2}(d) := \int _X F_0 \cdot T^d F_1 \cdot T^{2d} F_2\,d\mu $
, we have
(Note it is clearly possible to scale the
![]() $F_i$
to remove
$F_i$
to remove
![]() $\gamma $
factor appearing in Lemma 4.1.) We claim that it is impossible to write
$\gamma $
factor appearing in Lemma 4.1.) We claim that it is impossible to write
with a an integral combination of
![]() $2$
-step nilsequences and
$2$
-step nilsequences and
![]() $\Vert b \Vert _{\infty } \leqslant {1}/{100}$
. Suppose that this were possible. Then, from (5.1) and the fact that
$\Vert b \Vert _{\infty } \leqslant {1}/{100}$
. Suppose that this were possible. Then, from (5.1) and the fact that
![]() $\eta $
takes values in
$\eta $
takes values in
![]() $\{1, -\tfrac {1}{3}\}$
, we would have
$\{1, -\tfrac {1}{3}\}$
, we would have
![]() $(a(d) + b(d)) \eta (d) \in \{\tfrac {1}{9}, 1\}$
for all
$(a(d) + b(d)) \eta (d) \in \{\tfrac {1}{9}, 1\}$
for all
![]() $d \in \mathscr {S}$
. However,
$d \in \mathscr {S}$
. However,
![]() $|b(d) \eta (d)| \leqslant {1}/{100}$
and, therefore,
$|b(d) \eta (d)| \leqslant {1}/{100}$
and, therefore,
for all
![]() $d \in \mathscr {S}$
.
$d \in \mathscr {S}$
.
Suppose that
Here, M is a compact metric space,
![]() $\sigma $
is a complex Borel measure of bounded variation and the
$\sigma $
is a complex Borel measure of bounded variation and the
![]() $a_m$
are nilsequences, with the map
$a_m$
are nilsequences, with the map
![]() $m \mapsto a_m(n)$
being in
$m \mapsto a_m(n)$
being in
![]() $L^{\infty }(\sigma )$
.
$L^{\infty }(\sigma )$
.
Then (5.2) implies that
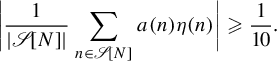 $$ \begin{align*} \bigg| \frac{1}{|\mathscr{S}[N]|} \sum_{n \in \mathscr{S}[N]} a(n) \eta(n) \bigg| \geqslant \frac{1}{10}.\end{align*} $$
$$ \begin{align*} \bigg| \frac{1}{|\mathscr{S}[N]|} \sum_{n \in \mathscr{S}[N]} a(n) \eta(n) \bigg| \geqslant \frac{1}{10}.\end{align*} $$
On the other hand, we have
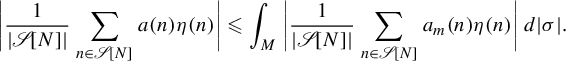 $$ \begin{align*} \bigg| \frac{1}{|\mathscr{S}[N]|} \sum_{n \in \mathscr{S}[N]} a(n) \eta(n) \bigg| \leqslant \int_M \bigg| \frac{1}{|\mathscr{S}[N]|} \sum_{n \in \mathscr{S}[N]} a_m(n) \eta(n) \bigg| \, d|\sigma|. \end{align*} $$
$$ \begin{align*} \bigg| \frac{1}{|\mathscr{S}[N]|} \sum_{n \in \mathscr{S}[N]} a(n) \eta(n) \bigg| \leqslant \int_M \bigg| \frac{1}{|\mathscr{S}[N]|} \sum_{n \in \mathscr{S}[N]} a_m(n) \eta(n) \bigg| \, d|\sigma|. \end{align*} $$
However, by the choice of
![]() $\eta $
(Lemma 3.1) we have
$\eta $
(Lemma 3.1) we have
 $$ \begin{align*} \lim_{N \rightarrow \infty} \frac{1}{|\mathscr{S}[N]|} \sum_{n \in \mathscr{S}[N]} a_m(n) \eta(n) = 0\end{align*} $$
$$ \begin{align*} \lim_{N \rightarrow \infty} \frac{1}{|\mathscr{S}[N]|} \sum_{n \in \mathscr{S}[N]} a_m(n) \eta(n) = 0\end{align*} $$
for all m. Therefore, by the dominated convergence theorem,
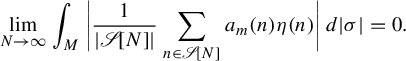 $$ \begin{align*} \lim_{N \rightarrow \infty} \int_M \bigg| \frac{1}{|\mathscr{S}[N]|} \sum_{n \in \mathscr{S}[N]} a_m(n) \eta(n) \bigg| \, d|\sigma| = 0.\end{align*} $$
$$ \begin{align*} \lim_{N \rightarrow \infty} \int_M \bigg| \frac{1}{|\mathscr{S}[N]|} \sum_{n \in \mathscr{S}[N]} a_m(n) \eta(n) \bigg| \, d|\sigma| = 0.\end{align*} $$
Putting these statements together gives a contradiction, and this completes the proof of Theorem 1.2.
Acknowledgements
JB would like to thank Xuancheng Shao for helpful discussions and pointers to the literature. The authors would like to thank Bryna Kra for pointing them to a reference for Proposition 5.1, and Nikos Frantzikinakis for helpful comments on the first draft of the paper. The first author is supported by the Gravitation grant NETWORKS-024.002.003 from the Dutch Research Council (NWO). The second author is supported by a Simons Investigator Award and is grateful to the Simons Foundation for their support.
A Appendix. Generalized nilsequences
In this appendix, we explain why our example does not seem to give a negative solution to [Reference Frantzikinakis7, Problem 1]. That is, we explain why our example (or similar ones) do not seem to be able to rule out the possibility that
![]() $C_{F_0, F_1, F_2}(n)$
is an approximate integral combination of generalized
$C_{F_0, F_1, F_2}(n)$
is an approximate integral combination of generalized
![]() $2$
-step nilsequences, in which the automorphic function
$2$
-step nilsequences, in which the automorphic function
![]() $\phi $
is allowed to be merely Riemann-integrable. In fact, our examples agree with
$\phi $
is allowed to be merely Riemann-integrable. In fact, our examples agree with
![]() $1$
-step generalized nilsequences on the crucial set
$1$
-step generalized nilsequences on the crucial set
![]() $\mathscr {S}$
.
$\mathscr {S}$
.
Recall that
![]() $\mathscr {S} = \mathscr {A} \hat {+} \mathscr {A}$
, where
$\mathscr {S} = \mathscr {A} \hat {+} \mathscr {A}$
, where
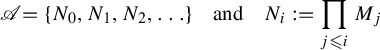 $$ \begin{align*} \mathscr{A} = \{ N_0, N_1, N_2,\ldots\} \quad \text{and} \quad N_i := \prod_{j \leqslant i} M_j\end{align*} $$
$$ \begin{align*} \mathscr{A} = \{ N_0, N_1, N_2,\ldots\} \quad \text{and} \quad N_i := \prod_{j \leqslant i} M_j\end{align*} $$
(thus,
![]() $N_0 = 1$
,
$N_0 = 1$
,
![]() $N_1 = M_1$
,
$N_1 = M_1$
,
![]() $N_2 = M_1M_2$
and so on). Here,
$N_2 = M_1M_2$
and so on). Here,
![]() $\mathscr {A} \hat {+} \mathscr {A}$
means the restricted sumset of
$\mathscr {A} \hat {+} \mathscr {A}$
means the restricted sumset of
![]() $\mathscr {A}$
with itself, that is, the set of sums of two distinct elements of
$\mathscr {A}$
with itself, that is, the set of sums of two distinct elements of
![]() $\mathscr {A}$
.
$\mathscr {A}$
.
Proposition A.1. There is
![]() $\theta \in \mathbb {R}/\mathbb {Z}$
such that the following is true. Let
$\theta \in \mathbb {R}/\mathbb {Z}$
such that the following is true. Let
![]() $\eta : \mathscr {S} \rightarrow [-1,1]$
be any function. Then there is a Riemann-integrable function
$\eta : \mathscr {S} \rightarrow [-1,1]$
be any function. Then there is a Riemann-integrable function
![]() $\phi : \mathbb {R}/\mathbb {Z} \rightarrow [-1,1]$
such that
$\phi : \mathbb {R}/\mathbb {Z} \rightarrow [-1,1]$
such that
![]() $\phi (\theta n) = \eta (n)$
for all
$\phi (\theta n) = \eta (n)$
for all
![]() $n \in \mathscr {S}$
.
$n \in \mathscr {S}$
.
Proof Set
![]() $\theta := \sum _{i=1}^{\infty } {1}/{N_i}$
. Because
$\theta := \sum _{i=1}^{\infty } {1}/{N_i}$
. Because
![]() $M_1 < M_2 < \cdots $
, we certainly have
$M_1 < M_2 < \cdots $
, we certainly have
![]() $M_j \geqslant j$
. As a consequence, the usual proof that e is irrational may be adapted easily to show that
$M_j \geqslant j$
. As a consequence, the usual proof that e is irrational may be adapted easily to show that
![]() $\theta $
is irrational: if
$\theta $
is irrational: if
![]() $\theta = {p}/{q}$
, then
$\theta = {p}/{q}$
, then
![]() $\alpha := ({M_1 \cdots M_q p})/{q} \in ({1}/{q})\mathbb {Z}$
, but, on the other hand, the fractional part of
$\alpha := ({M_1 \cdots M_q p})/{q} \in ({1}/{q})\mathbb {Z}$
, but, on the other hand, the fractional part of
![]() $\alpha $
satisfies
$\alpha $
satisfies
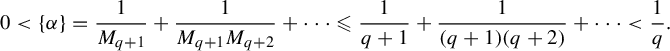 $$ \begin{align*} 0 < \{\alpha\} = \frac{1}{M_{q+1}} + \frac{1}{M_{q+1}M_{q+2}} + \cdots \leqslant \frac{1}{q+1} + \frac{1}{(q+1)(q+2)} + \cdots < \frac{1}{q}.\end{align*} $$
$$ \begin{align*} 0 < \{\alpha\} = \frac{1}{M_{q+1}} + \frac{1}{M_{q+1}M_{q+2}} + \cdots \leqslant \frac{1}{q+1} + \frac{1}{(q+1)(q+2)} + \cdots < \frac{1}{q}.\end{align*} $$
Now define
![]() $\phi : \mathbb {R}/\mathbb {Z}\to [-1,1]$
as follows:
$\phi : \mathbb {R}/\mathbb {Z}\to [-1,1]$
as follows:
![]() $\phi (\theta n) = \eta (n)$
for all
$\phi (\theta n) = \eta (n)$
for all
![]() $n \in \mathscr {S}$
, and
$n \in \mathscr {S}$
, and
![]() $\phi (x) = 0$
if
$\phi (x) = 0$
if
![]() $x \notin \theta \mathscr {S}$
. Because
$x \notin \theta \mathscr {S}$
. Because
![]() $\theta $
is irrational, this is a well-defined function.
$\theta $
is irrational, this is a well-defined function.
We claim that it is Riemann-integrable, with integral zero. It is enough to show that for every
![]() $\varepsilon> 0$
, there is some finite collection of intervals, of total length
$\varepsilon> 0$
, there is some finite collection of intervals, of total length
![]() $< \varepsilon $
, whose union covers
$< \varepsilon $
, whose union covers
![]() $\theta \mathscr {S}$
.
$\theta \mathscr {S}$
.
Note that for every j we have
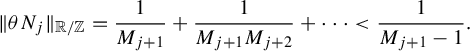 $$ \begin{align} \Vert \theta N_j \Vert_{\mathbb{R}/\mathbb{Z}} = \frac{1}{M_{j+1}} + \frac{1}{M_{j+1}M_{j+2}} + \cdots < \frac{1}{M_{j+1} - 1}.\end{align} $$
$$ \begin{align} \Vert \theta N_j \Vert_{\mathbb{R}/\mathbb{Z}} = \frac{1}{M_{j+1}} + \frac{1}{M_{j+1}M_{j+2}} + \cdots < \frac{1}{M_{j+1} - 1}.\end{align} $$
Moreover, condition 3 in the definition of the
![]() $M_j$
implies that
$M_j$
implies that
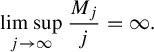 $$ \begin{align} \limsup_{j \rightarrow \infty} \frac{M_j}{j} = \infty.\end{align} $$
$$ \begin{align} \limsup_{j \rightarrow \infty} \frac{M_j}{j} = \infty.\end{align} $$
In particular, we may choose k so that
![]() ${1}/({M_{k+1} - 1}) < {\varepsilon }/{10k}$
, and by (A.1) it follows that
${1}/({M_{k+1} - 1}) < {\varepsilon }/{10k}$
, and by (A.1) it follows that
It follows that
where
![]() $I = (-\varepsilon /10k, \varepsilon /10k) \subseteq \mathbb {R}/\mathbb {Z}$
. Therefore,
$I = (-\varepsilon /10k, \varepsilon /10k) \subseteq \mathbb {R}/\mathbb {Z}$
. Therefore,
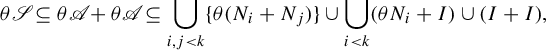 $$ \begin{align*} \theta \mathscr{S} \subseteq \theta \mathscr{A} + \theta \mathscr{A} \subseteq \bigcup_{i,j < k} \{ \theta(N_i + N_j) \} \cup \bigcup_{i < k}( \theta N_i + I) \cup (I + I),\end{align*} $$
$$ \begin{align*} \theta \mathscr{S} \subseteq \theta \mathscr{A} + \theta \mathscr{A} \subseteq \bigcup_{i,j < k} \{ \theta(N_i + N_j) \} \cup \bigcup_{i < k}( \theta N_i + I) \cup (I + I),\end{align*} $$
which makes it clear that
![]() $\theta \mathscr {S}$
is contained in a finite union of intervals of length less than
$\theta \mathscr {S}$
is contained in a finite union of intervals of length less than
![]() $\varepsilon $
.
$\varepsilon $
.