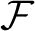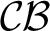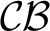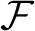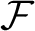1. Introduction
An important development in ergodic theory that began in the late 1990s is the emergence of anti-classification results for measure-preserving transformations (MPTs) up to isomorphism. Here, an MPT is a measure-preserving automorphism of a standard non-atomic probability space, and two such MPTs, T and
![]() $S,$
are said to be isomorphic if there is a measure-preserving isomorphism between the underlying probability spaces that intertwines the actions of T and
$S,$
are said to be isomorphic if there is a measure-preserving isomorphism between the underlying probability spaces that intertwines the actions of T and
![]() $S.$
We denote by X the set of MPTs on a fixed standard non-atomic probability space
$S.$
We denote by X the set of MPTs on a fixed standard non-atomic probability space
![]() $(\Omega ,\mathcal {M},\mu )$
, and let the equivalence relation
$(\Omega ,\mathcal {M},\mu )$
, and let the equivalence relation
![]() $\mathcal {R}\subset X\times X$
be defined by
$\mathcal {R}\subset X\times X$
be defined by
![]() $\mathcal {R}:=\{(T,S):T\text { and }S\text { are isomorphic}\}.$
We endow X with the weak topology. (Recall that
$\mathcal {R}:=\{(T,S):T\text { and }S\text { are isomorphic}\}.$
We endow X with the weak topology. (Recall that
![]() $T_{n}\rightarrow T$
in the weak topology if and only if
$T_{n}\rightarrow T$
in the weak topology if and only if
![]() $\mu (T_{n}(A)\triangle T(A))\to 0$
for every
$\mu (T_{n}(A)\triangle T(A))\to 0$
for every
![]() $A\in \mathcal {M}$
.) The first anti-classification theorem in ergodic theory is due to Beleznay and Foreman [Reference Beleznay and ForemanBF96], who showed that a certain natural class of measure-distal transformations is not a Borel set in X. In the present context of isomorphism of MPTs, the first result is due to Hjorth [Reference HjorthHj01], who proved that
$A\in \mathcal {M}$
.) The first anti-classification theorem in ergodic theory is due to Beleznay and Foreman [Reference Beleznay and ForemanBF96], who showed that a certain natural class of measure-distal transformations is not a Borel set in X. In the present context of isomorphism of MPTs, the first result is due to Hjorth [Reference HjorthHj01], who proved that
![]() $\mathcal {R}$
is not a Borel subset of
$\mathcal {R}$
is not a Borel subset of
![]() $X\times X.$
However, this left open the question of what happens if we replace X by the subset
$X\times X.$
However, this left open the question of what happens if we replace X by the subset
![]() $\widetilde {X}$
consisting of ergodic MPTs, with the relative topology. Foreman, Rudolph, and Weiss [Reference Foreman, Rudolph and WeissFRW11] proved that the equivalence relation
$\widetilde {X}$
consisting of ergodic MPTs, with the relative topology. Foreman, Rudolph, and Weiss [Reference Foreman, Rudolph and WeissFRW11] proved that the equivalence relation
![]() $\widetilde {R}:=\mathcal {R}\cap (\widetilde {X}\times \widetilde {X})$
is also not a Borel set. These results show that the problem of classifying MPTs (or ergodic MPTs) up to isomorphism, which goes back to von Neumann’s 1932 paper [Reference von NeumannNe32], is inaccessible to countable methods that use countable amounts of information. (See [Reference Foreman and WeissFW1, Reference Foreman and WeissFW2, Reference Foreman and WeissFW3] for further discussion of this interpretation of these anti-classification results.)
$\widetilde {R}:=\mathcal {R}\cap (\widetilde {X}\times \widetilde {X})$
is also not a Borel set. These results show that the problem of classifying MPTs (or ergodic MPTs) up to isomorphism, which goes back to von Neumann’s 1932 paper [Reference von NeumannNe32], is inaccessible to countable methods that use countable amounts of information. (See [Reference Foreman and WeissFW1, Reference Foreman and WeissFW2, Reference Foreman and WeissFW3] for further discussion of this interpretation of these anti-classification results.)
The most important positive results consist of Halmos and von Neumann’s classification of ergodic MPTs with pure point spectrum [Reference Halmos and von NeumannHN42] and the classification of Bernoulli shifts by their (metric) entropy due to Kolmogorov [Reference Katok and HasselblattKH95, §4.3], Sinai [Reference SinaiSi62], and Ornstein [Reference OrnsteinOr70]. Yet many open questions remain. For example, the rank-one transformations, which have been studied extensively, form a dense
![]() $G_{\delta }$
subset of X, and the restriction of the equivalence relation
$G_{\delta }$
subset of X, and the restriction of the equivalence relation
![]() $\mathcal {R}$
to rank-one transformations is Borel [Reference Foreman, Rudolph and WeissFRW11]. However, there is still no known classification of rank-one transformations up to isomorphism.
$\mathcal {R}$
to rank-one transformations is Borel [Reference Foreman, Rudolph and WeissFRW11]. However, there is still no known classification of rank-one transformations up to isomorphism.
In view of the anti-classification results mentioned above and, in general, the difficulty of classifying ergodic MPTs, other versions of the classification problem have been considered. One possibility is to restrict the attempted classification to smooth ergodic diffeomorphisms of a compact manifold M with respect to a smooth measure
![]() $\mu .$
Except in dimensions one and two, there are no known obstructions to realizing an arbitrary ergodic MPT as a diffeomorphism of a compact manifold except the requirement, proved by Kushnirenko [Reference KushnirenkoKu65], that the ergodic MPT have finite entropy. Thus, it is not clear that this restricted classification problem is any easier. Indeed, in this context there is also an anti-classification result due to Foreman and Weiss [Reference Foreman and WeissFW3]. They showed that if X is replaced by the collection
$\mu .$
Except in dimensions one and two, there are no known obstructions to realizing an arbitrary ergodic MPT as a diffeomorphism of a compact manifold except the requirement, proved by Kushnirenko [Reference KushnirenkoKu65], that the ergodic MPT have finite entropy. Thus, it is not clear that this restricted classification problem is any easier. Indeed, in this context there is also an anti-classification result due to Foreman and Weiss [Reference Foreman and WeissFW3]. They showed that if X is replaced by the collection
![]() $\widehat {X}$
of smooth Lebesgue-measure-preserving diffeomorphisms of the two-dimensional torus and
$\widehat {X}$
of smooth Lebesgue-measure-preserving diffeomorphisms of the two-dimensional torus and
![]() $\widehat {X}$
is given the
$\widehat {X}$
is given the
![]() $C^{\infty }$
topology, then the equivalence relation
$C^{\infty }$
topology, then the equivalence relation
![]() $\widehat {R}$
consisting of pairs of isomorphic elements of
$\widehat {R}$
consisting of pairs of isomorphic elements of
![]() $\widehat {X}$
still fails to be a Borel set.
$\widehat {X}$
still fails to be a Borel set.
Another modification of the classification problem is to consider Kakutani equivalence instead of isomorphism. Two ergodic MPTs are said to be Kakutani equivalent if they are isomorphic to measurable cross-sections of the same ergodic flow. It follows from Abramov’s formula that two Kakutani-equivalent MPTs have the same entropy type: zero entropy, finite entropy, or infinite entropy. Until the work of Katok [Reference KatokKa75, Reference KatokKa77] in the case of zero entropy, and Feldman [Reference FeldmanFe76] in the general case, no other restrictions were known for achieving Kakutani equivalence. Ornstein, Rudolph, and Weiss [Reference Ornstein, Rudolph and WeissORW82] showed, by building on the work of Feldman, that there are uncountably many non-Kakutani equivalent ergodic MPTs of each entropy type. Thus there is a rich variety of Kakutani equivalence classes, and classification of ergodic MPTs up to Kakutani equivalence also remains an open problem. It is not known whether anti-classification results analogous to those in [Reference Foreman, Rudolph and WeissFRW11, Reference Foreman and WeissFW3] can be obtained for Kakutani equivalence, either in the original setting of ergodic MPTs or in the setting of smooth diffeomorphisms preserving a smooth measure.
In transferring the results of [Reference Foreman, Rudolph and WeissFRW11] to the smooth setting, Foreman and Weiss [Reference Foreman and WeissFW2] introduced a continuous functor
![]() $\mathcal {F}$
that maps odometer-based systems to circular systems. (See §3 for definitions of these terms.) According to an announcement in [Reference Foreman and WeissFW2], any finite-entropy system that has an odometer factor can be represented as an odometer-based system. It is a difficult open question whether any transformation with a non-trivial odometer factor can be realized as a smooth diffeomorphism on a compact manifold. Foreman and Weiss [Reference Foreman and WeissFW2] were able to circumvent this difficulty by using the functor
$\mathcal {F}$
that maps odometer-based systems to circular systems. (See §3 for definitions of these terms.) According to an announcement in [Reference Foreman and WeissFW2], any finite-entropy system that has an odometer factor can be represented as an odometer-based system. It is a difficult open question whether any transformation with a non-trivial odometer factor can be realized as a smooth diffeomorphism on a compact manifold. Foreman and Weiss [Reference Foreman and WeissFW2] were able to circumvent this difficulty by using the functor
![]() $\mathcal {F}$
to transfer the classification problem for odometer-based systems to circular systems. Under mild growth conditions on the parameters, circular systems can be realized as smooth diffeomorphisms of the two-dimensional torus using the Anosov–Katok method [Reference Anosov and KatokAK70]. The functor
$\mathcal {F}$
to transfer the classification problem for odometer-based systems to circular systems. Under mild growth conditions on the parameters, circular systems can be realized as smooth diffeomorphisms of the two-dimensional torus using the Anosov–Katok method [Reference Anosov and KatokAK70]. The functor
![]() $\mathcal {F}$
preserves weakly mixing extensions, compact extensions, factor maps, the rank-one property, and certain types of isomorphisms, as well as numerous other properties (see [Reference Foreman and WeissFW2]). While all circular systems have zero entropy, there exist positive-entropy odometer-based systems, and thus
$\mathcal {F}$
preserves weakly mixing extensions, compact extensions, factor maps, the rank-one property, and certain types of isomorphisms, as well as numerous other properties (see [Reference Foreman and WeissFW2]). While all circular systems have zero entropy, there exist positive-entropy odometer-based systems, and thus
![]() $\mathcal {F}$
does not preserve the entropy type. In connection with a possible Kakutani-equivalence version of the results in [Reference Foreman and WeissFW3], a natural question is whether
$\mathcal {F}$
does not preserve the entropy type. In connection with a possible Kakutani-equivalence version of the results in [Reference Foreman and WeissFW3], a natural question is whether
![]() $\mathcal {F}$
preserves Kakutani equivalence (at least for zero-entropy odometer-based systems). In particular, J.-P. Thouvenot asked whether
$\mathcal {F}$
preserves Kakutani equivalence (at least for zero-entropy odometer-based systems). In particular, J.-P. Thouvenot asked whether
![]() $\mathcal {F}$
maps loosely Bernoulli automorphisms (those Kakutani-equivalent to an irrational rotation of the circle in case of zero entropy, or those Kakutani-equivalent to a Bernoulli shift in case of positive entropy) to loosely Bernoulli automorphisms. We provide examples to show that the answer to both of these questions is ‘no’. We also obtain an example which shows that
$\mathcal {F}$
maps loosely Bernoulli automorphisms (those Kakutani-equivalent to an irrational rotation of the circle in case of zero entropy, or those Kakutani-equivalent to a Bernoulli shift in case of positive entropy) to loosely Bernoulli automorphisms. We provide examples to show that the answer to both of these questions is ‘no’. We also obtain an example which shows that
![]() $\mathcal {F}^{-1}$
fails to preserve the loosely Bernoulli property. Our examples suggest that a different approach may be needed for Kakutani-equivalence versions of anti-classification results in the diffeomorphism setting.
$\mathcal {F}^{-1}$
fails to preserve the loosely Bernoulli property. Our examples suggest that a different approach may be needed for Kakutani-equivalence versions of anti-classification results in the diffeomorphism setting.
In §§4.1 and 4.2 we give an example of a positive-entropy odometer-based system
![]() $\mathbb {E}$
that is loosely Bernoulli, but the circular system
$\mathbb {E}$
that is loosely Bernoulli, but the circular system
![]() $\mathcal {F}(\mathbb {E})$
is not loosely Bernoulli. In this example,
$\mathcal {F}(\mathbb {E})$
is not loosely Bernoulli. In this example,
![]() $(n+1)$
-blocks of the odometer-based system are constructed mostly by independent concatenation of n-blocks. Because of this,
$(n+1)$
-blocks of the odometer-based system are constructed mostly by independent concatenation of n-blocks. Because of this,
![]() $\mathbb {E}$
satisfies the positive-entropy version of the loosely Bernoulli property. However, using techniques of Rothstein [Reference RothsteinRo80], we show that this independent concatenation, when transferred to
$\mathbb {E}$
satisfies the positive-entropy version of the loosely Bernoulli property. However, using techniques of Rothstein [Reference RothsteinRo80], we show that this independent concatenation, when transferred to
![]() $\mathcal {F}(\mathbb {E}),$
causes the zero-entropy version of the loosely Bernoulli property to fail.
$\mathcal {F}(\mathbb {E}),$
causes the zero-entropy version of the loosely Bernoulli property to fail.
The zero-entropy odometer-based system
![]() $\mathbb {K}$
constructed in §§5.1–5.4, is of greater interest in connection with [Reference Foreman and WeissFW2, Reference Foreman and WeissFW3], because the anti-classification results of Foreman and Weiss can be obtained by considering only zero-entropy odometer-based systems. Our zero-entropy example is more difficult to construct than our positive-entropy example, and it uses some delicate refinements of the methods in [Reference Ornstein, Rudolph and WeissORW82]. However, the heuristics of the construction can be described fairly easily, as illustrated in Figure 2. This example is loosely Bernoulli, but its image under
$\mathbb {K}$
constructed in §§5.1–5.4, is of greater interest in connection with [Reference Foreman and WeissFW2, Reference Foreman and WeissFW3], because the anti-classification results of Foreman and Weiss can be obtained by considering only zero-entropy odometer-based systems. Our zero-entropy example is more difficult to construct than our positive-entropy example, and it uses some delicate refinements of the methods in [Reference Ornstein, Rudolph and WeissORW82]. However, the heuristics of the construction can be described fairly easily, as illustrated in Figure 2. This example is loosely Bernoulli, but its image under
![]() $\mathcal {F}$
is not loosely Bernoulli. There is also a simple example (see Example 3.12) of a zero-entropy odometer-based system that is loosely Bernoulli and whose image under
$\mathcal {F}$
is not loosely Bernoulli. There is also a simple example (see Example 3.12) of a zero-entropy odometer-based system that is loosely Bernoulli and whose image under
![]() $\mathcal {F}$
is again loosely Bernoulli. This example, together with our example
$\mathcal {F}$
is again loosely Bernoulli. This example, together with our example
![]() $\mathbb {K},$
shows that
$\mathbb {K},$
shows that
![]() $\mathcal {F}$
does not preserve Kakutani equivalence.
$\mathcal {F}$
does not preserve Kakutani equivalence.
Finally, in §§6.1–6.4, we give an example
![]() $\mathbb {M}$
of a zero-entropy non-loosely Bernoulli odometer-based system whose corresponding circular system is loosely Bernoulli. Figure 3 shows the idea for this construction. Our §§5.1–6.4 with the zero-entropy odometer-based systems can be read independently of §§4.1 and 4.2.
$\mathbb {M}$
of a zero-entropy non-loosely Bernoulli odometer-based system whose corresponding circular system is loosely Bernoulli. Figure 3 shows the idea for this construction. Our §§5.1–6.4 with the zero-entropy odometer-based systems can be read independently of §§4.1 and 4.2.
Our results may also be of interest as another way that non-loosely Bernoulli transformations arise naturally from loosely Bernoulli transformations. Previous examples in this spirit include non-loosely Bernoulli Cartesian products in which the factors are loosely Bernoulli [Reference Kanigowski and De La RueKR, Reference Kanigowski and WeiKW19, Reference Ornstein, Rudolph and WeissORW82, Reference RatnerRa78, Reference RatnerRa79]. The functor
![]() $\mathcal {F}$
in [Reference Foreman and WeissFW2] changes the way
$\mathcal {F}$
in [Reference Foreman and WeissFW2] changes the way
![]() $(n+1)$
-blocks are built out of n-blocks according to a scheme that seems, upon first consideration, likely to preserve the loosely Bernoulli property. In this sense, our zero-entropy examples
$(n+1)$
-blocks are built out of n-blocks according to a scheme that seems, upon first consideration, likely to preserve the loosely Bernoulli property. In this sense, our zero-entropy examples
![]() $\mathbb {K}$
and
$\mathbb {K}$
and
![]() $\mathbb {M}$
were unexpected.
$\mathbb {M}$
were unexpected.
2. The
 $\overline {f}$
metric and the loosely Bernoulli property
$\overline {f}$
metric and the loosely Bernoulli property
Feldman [Reference FeldmanFe76] introduced a notion of distance, now called
![]() $\overline {f}$
, between strings of symbols. He replaced the Hamming metric in Ornstein’s very weak Bernoulli property [Reference OrnsteinOr] to define loosely Bernoulli transformations (see Definitions 2.2 and 2.3 below). A zero-entropy version of this property was introduced independently by Katok [Reference KatokKa77].
$\overline {f}$
, between strings of symbols. He replaced the Hamming metric in Ornstein’s very weak Bernoulli property [Reference OrnsteinOr] to define loosely Bernoulli transformations (see Definitions 2.2 and 2.3 below). A zero-entropy version of this property was introduced independently by Katok [Reference KatokKa77].
Definition 2.1. A match between two strings of symbols
![]() $a_{1}a_{2}\ldots a_{n}$
and
$a_{1}a_{2}\ldots a_{n}$
and
![]() $b_{1}b_{2}\ldots b_{m}$
, from a given alphabet
$b_{1}b_{2}\ldots b_{m}$
, from a given alphabet
![]() $\Sigma ,$
is a collection I of pairs of indices
$\Sigma ,$
is a collection I of pairs of indices
![]() $(i_s,j_s)$
,
$(i_s,j_s)$
,
![]() $s=1,\ldots ,r$
, such that
$s=1,\ldots ,r$
, such that
![]() $1\le i_1 <i_2<\cdots <i_r\le n$
,
$1\le i_1 <i_2<\cdots <i_r\le n$
,
![]() $1\le j_1 <j_2 <\cdots <j_r\le m$
and
$1\le j_1 <j_2 <\cdots <j_r\le m$
and
![]() $a_{i_s}=b_{j_s}$
for
$a_{i_s}=b_{j_s}$
for
![]() $s=1,2,\ldots ,r.$
Then
$s=1,2,\ldots ,r.$
Then
 $$ \begin{align} \begin{array}{ll} &\overline{f}(a_{1}a_{2}\ldots a_{n},b_{1}b_{2}\ldots b_{m})\hfill \\[6pt] & \quad = \displaystyle{1-\frac{2\sup\{|I|:I\text{ is a match between }a_{1}a_{2}\ldots a_{n}\text{ and }b_{1}b_{2}\ldots b_{m}\}}{n+m}.} \end{array} \end{align} $$
$$ \begin{align} \begin{array}{ll} &\overline{f}(a_{1}a_{2}\ldots a_{n},b_{1}b_{2}\ldots b_{m})\hfill \\[6pt] & \quad = \displaystyle{1-\frac{2\sup\{|I|:I\text{ is a match between }a_{1}a_{2}\ldots a_{n}\text{ and }b_{1}b_{2}\ldots b_{m}\}}{n+m}.} \end{array} \end{align} $$
We will refer to
![]() $\overline {f}(a_{1}a_{2}\ldots a_{n},b_{1}b_{2}\ldots b_{m})$
as the ‘
$\overline {f}(a_{1}a_{2}\ldots a_{n},b_{1}b_{2}\ldots b_{m})$
as the ‘
![]() $\overline {f}$
-distance’ between
$\overline {f}$
-distance’ between
![]() $a_{1}a_{2}\ldots a_{n}$
and
$a_{1}a_{2}\ldots a_{n}$
and
![]() $b_{1}b_{2}\ldots b_{m},$
even though
$b_{1}b_{2}\ldots b_{m},$
even though
![]() $\overline {f}$
does not satisfy the triangle inequality unless the strings are all of the same length. A match I is called a best possible match if it realizes the supremum in the definition of
$\overline {f}$
does not satisfy the triangle inequality unless the strings are all of the same length. A match I is called a best possible match if it realizes the supremum in the definition of
![]() $\overline {f}$
.
$\overline {f}$
.
Suppose
![]() $(T,\mathcal {P})$
is a process, that is, T is a measurable automorphism of a measurable space
$(T,\mathcal {P})$
is a process, that is, T is a measurable automorphism of a measurable space
![]() $(\Omega ,\mathcal {M})$
and
$(\Omega ,\mathcal {M})$
and
![]() $\mathcal {P}=\{P_{\sigma }:\sigma \in \Sigma \}$
is a finite measurable partition of
$\mathcal {P}=\{P_{\sigma }:\sigma \in \Sigma \}$
is a finite measurable partition of
![]() $\Omega .$
For
$\Omega .$
For
![]() $x,y\in \Omega $
with
$x,y\in \Omega $
with
![]() $T^i(x)\in P_{a_i}$
and
$T^i(x)\in P_{a_i}$
and
![]() $T^i(y)\in P_{b_i}$
for
$T^i(y)\in P_{b_i}$
for
![]() $i=1,\ldots ,K$
, we define
$i=1,\ldots ,K$
, we define
![]() $\overline {f}_{K}(x,y):= \overline {f}(a_{1}a_{2}\ldots a_{K},b_{1}b_{2}\ldots b_{K}).$
If
$\overline {f}_{K}(x,y):= \overline {f}(a_{1}a_{2}\ldots a_{K},b_{1}b_{2}\ldots b_{K}).$
If
![]() $\nu $
and
$\nu $
and
![]() $\omega $
are probability measures on
$\omega $
are probability measures on
![]() $(\Omega ,\mathcal {M})$
then we say
$(\Omega ,\mathcal {M})$
then we say
![]() $\overline {f}_{K}(\nu ,\omega )<\epsilon $
if there is a measure-preserving invertible map
$\overline {f}_{K}(\nu ,\omega )<\epsilon $
if there is a measure-preserving invertible map
![]() $\phi :(\Omega ,\mathcal {M},\nu )\to (\Omega ,\mathcal {M},\omega )$
such that there exists a set
$\phi :(\Omega ,\mathcal {M},\nu )\to (\Omega ,\mathcal {M},\omega )$
such that there exists a set
![]() $G\subset \Omega $
with
$G\subset \Omega $
with
![]() $\nu (G)>1-\varepsilon $
and
$\nu (G)>1-\varepsilon $
and
![]() $\overline {f}_{K}(x,\phi (x))<\varepsilon $
for all
$\overline {f}_{K}(x,\phi (x))<\varepsilon $
for all
![]() $x\in G.$
$x\in G.$
We now define loosely Bernoulli in the general case (no assumptions on the entropy of the process).
Definition 2.2. (Loosely Bernoulli in the general case)
A measure-preserving process
![]() $(T,\mathcal {P},\nu )$
is loosely Bernoulli if for every
$(T,\mathcal {P},\nu )$
is loosely Bernoulli if for every
![]() $\varepsilon>0,$
there exists a positive integer
$\varepsilon>0,$
there exists a positive integer
![]() $K=K(\varepsilon )$
such that for every positive integer M the following holds: there exists a collection
$K=K(\varepsilon )$
such that for every positive integer M the following holds: there exists a collection
![]() $\mathcal {G}$
of ‘good’ atoms of
$\mathcal {G}$
of ‘good’ atoms of
 $\lor _{-M}^{0}T^{-i}\mathcal {P}$
whose union has measure greater than
$\lor _{-M}^{0}T^{-i}\mathcal {P}$
whose union has measure greater than
![]() $1-\varepsilon ,$
so that for each pair
$1-\varepsilon ,$
so that for each pair
![]() $A,B$
of atoms in
$A,B$
of atoms in
![]() $\mathcal {G}$
of positive
$\mathcal {G}$
of positive
![]() $\nu $
-measure, the measures
$\nu $
-measure, the measures
![]() $\nu _{A}$
and
$\nu _{A}$
and
![]() $\nu _{B}$
satisfy
$\nu _{B}$
satisfy
![]() $\overline {f}_{K}(\nu _{A},\nu _{B})<\varepsilon .$
Here
$\overline {f}_{K}(\nu _{A},\nu _{B})<\varepsilon .$
Here
![]() $\nu _{A}$
and
$\nu _{A}$
and
![]() $\nu _{B}$
denote the conditional measures on
$\nu _{B}$
denote the conditional measures on
![]() $\Omega $
defined by
$\Omega $
defined by
![]() $\nu _{A}(C)=\nu (C|A)=\nu (C\cap A)/\nu (A),$
and similarly for
$\nu _{A}(C)=\nu (C|A)=\nu (C\cap A)/\nu (A),$
and similarly for
![]() $\nu _{B}.$
$\nu _{B}.$
An ergodic measure-preserving transformation
![]() $(T,\nu )$
is loosely Bernoulli if
$(T,\nu )$
is loosely Bernoulli if
![]() $(T,\mathcal {P},\nu )$
is a loosely Bernoulli process for every partition
$(T,\mathcal {P},\nu )$
is a loosely Bernoulli process for every partition
![]() $\mathcal {P}.$
In fact, it suffices for
$\mathcal {P}.$
In fact, it suffices for
![]() $(T,\mathcal {P},\nu )$
to be loosely Bernoulli for a generating partition
$(T,\mathcal {P},\nu )$
to be loosely Bernoulli for a generating partition
![]() $\mathcal {P}$
. (By Krieger’s generator theorem [Reference KriegerKr70] every ergodic measure-preserving transformation of finite entropy has a finite generator.)
$\mathcal {P}$
. (By Krieger’s generator theorem [Reference KriegerKr70] every ergodic measure-preserving transformation of finite entropy has a finite generator.)
As was pointed out in [Reference FeldmanFe76], Definition 2.2 is equivalent to the definition obtained by replacing ‘there exists a positive integer
![]() $K=K(\varepsilon )$
’ by ‘for any sufficiently large positive integer K (how large depends on
$K=K(\varepsilon )$
’ by ‘for any sufficiently large positive integer K (how large depends on
![]() $\varepsilon )$
’. Moreover, according to [Reference FeldmanFe76, Corollary 2], ‘every positive integer M’ can be replaced by ‘for every sufficiently large positive integer M’. In fact, our Lemma 4.5 implies [Reference FeldmanFe76, Corollary 2], and the proof is similar.
$\varepsilon )$
’. Moreover, according to [Reference FeldmanFe76, Corollary 2], ‘every positive integer M’ can be replaced by ‘for every sufficiently large positive integer M’. In fact, our Lemma 4.5 implies [Reference FeldmanFe76, Corollary 2], and the proof is similar.
In the case of zero entropy, no conditioning on the past is needed, and there is a simpler definition of loosely Bernoulli. That is, the definition reduces to the following version.
Definition 2.3. (Loosely Bernoulli in the case of zero entropy)
A measure-preserving process
![]() $(T,\mathcal {P},\nu )$
is zero-entropy loosely Bernoulli if for every
$(T,\mathcal {P},\nu )$
is zero-entropy loosely Bernoulli if for every
![]() $\varepsilon>0,$
there exist a positive integer
$\varepsilon>0,$
there exist a positive integer
![]() $K=K(\varepsilon )$
and a collection
$K=K(\varepsilon )$
and a collection
![]() $\mathcal {G}$
of ‘good’ atoms of
$\mathcal {G}$
of ‘good’ atoms of
 $\lor _{1}^{K}T^{-i}\mathcal {P}$
with total measure greater than
$\lor _{1}^{K}T^{-i}\mathcal {P}$
with total measure greater than
![]() $1-\varepsilon $
such that for each pair
$1-\varepsilon $
such that for each pair
![]() $A,B$
of atoms in
$A,B$
of atoms in
![]() $\mathcal {G}, \overline {f}_{K}(x,y)<\varepsilon $
for
$\mathcal {G}, \overline {f}_{K}(x,y)<\varepsilon $
for
![]() $x\in A, y\in B.$
$x\in A, y\in B.$
If this condition is satisfied, then routine estimates show that the
![]() $(T,\mathcal {P},\nu )$
process indeed has zero entropy.
$(T,\mathcal {P},\nu )$
process indeed has zero entropy.
Remark 2.4. For infinite strings of symbols
![]() $a_{0}a_{1}\ldots , b_{0}b_{1}\ldots ,$
we can define
$a_{0}a_{1}\ldots , b_{0}b_{1}\ldots ,$
we can define
 $$ \begin{align*} \overline{f}(a_{0}a_{1}\ldots,b_{0}b_{1}\ldots)=\limsup_{n\to\infty}\overline{f}(a_{0}a_{1}\ldots a_{n},b_{0}b_{1}\ldots b_{n}). \end{align*} $$
$$ \begin{align*} \overline{f}(a_{0}a_{1}\ldots,b_{0}b_{1}\ldots)=\limsup_{n\to\infty}\overline{f}(a_{0}a_{1}\ldots a_{n},b_{0}b_{1}\ldots b_{n}). \end{align*} $$
There is an alternate definition of zero-entropy loosely Bernoulli (which we do not make use of) that can be formulated as follows. The process
![]() $(T,\mathcal {P},\nu )$
is zero-entropy loosely Bernoulli if there is a
$(T,\mathcal {P},\nu )$
is zero-entropy loosely Bernoulli if there is a
 $G\in \lor _{0}^{\infty }T^{-i}\mathcal {P}$
with
$G\in \lor _{0}^{\infty }T^{-i}\mathcal {P}$
with
![]() $\nu (G)=1$
such that for
$\nu (G)=1$
such that for
![]() $x,y\in G$
, and for
$x,y\in G$
, and for
![]() $T^{i}x\in P_{a_{i}},T^{i}y\in P_{b_{i}}$
for
$T^{i}x\in P_{a_{i}},T^{i}y\in P_{b_{i}}$
for
![]() $i=0,1,2,\ldots ,$
we have
$i=0,1,2,\ldots ,$
we have
![]() $\overline {f}(a_{0}a_{1}\ldots , b_{0}b_{1}\ldots )=0.$
$\overline {f}(a_{0}a_{1}\ldots , b_{0}b_{1}\ldots )=0.$
The following simple properties of
![]() $\overline {f}$
, which were already used in [Reference FeldmanFe76, Reference Ornstein, Rudolph and WeissORW82], will appear frequently in our arguments. These properties can be proved easily by considering the fit,
$\overline {f}$
, which were already used in [Reference FeldmanFe76, Reference Ornstein, Rudolph and WeissORW82], will appear frequently in our arguments. These properties can be proved easily by considering the fit,
![]() $1-\overline {f}(a,b),$
between two strings a and b.
$1-\overline {f}(a,b),$
between two strings a and b.
Property 2.5. Suppose a and b are strings of symbols of length n and
![]() $m,$
respectively, from an alphabet
$m,$
respectively, from an alphabet
![]() $\Sigma $
. If
$\Sigma $
. If
![]() $\tilde {a}$
and
$\tilde {a}$
and
![]() $\tilde {b}$
are strings of symbols obtained by deleting at most
$\tilde {b}$
are strings of symbols obtained by deleting at most
![]() $\lfloor \gamma (n+m)\rfloor $
terms from a and b altogether, where
$\lfloor \gamma (n+m)\rfloor $
terms from a and b altogether, where
![]() $0<\gamma <1$
, then
$0<\gamma <1$
, then
Moreover, if there exists a best possible match between a and b such that no term that is deleted from a and b to form
![]() $\tilde {a}$
and
$\tilde {a}$
and
![]() $\tilde {b}$
is matched with a non-deleted term, then
$\tilde {b}$
is matched with a non-deleted term, then
Likewise, if
![]() $\tilde {a}$
and
$\tilde {a}$
and
![]() $\tilde {b}$
are obtained by adding at most
$\tilde {b}$
are obtained by adding at most
![]() $\lfloor \gamma (n+m)\rfloor $
symbols to a and b, then (2.3) holds.
$\lfloor \gamma (n+m)\rfloor $
symbols to a and b, then (2.3) holds.
Property 2.6. Suppose
![]() $x=x_{1}x_{2}\ldots x_{n}$
and
$x=x_{1}x_{2}\ldots x_{n}$
and
![]() $y=y_{1}y_{2}\ldots y_{n}$
are decompositions of the strings of symbols x and y into substrings such that there exists a best possible match between x and y where terms in
$y=y_{1}y_{2}\ldots y_{n}$
are decompositions of the strings of symbols x and y into substrings such that there exists a best possible match between x and y where terms in
![]() $x_i$
are only matched with terms in
$x_i$
are only matched with terms in
![]() $y_i$
(if they are matched with any term in y). Then
$y_i$
(if they are matched with any term in y). Then
 $$ \begin{align*} \overline{f}(x,y)=\sum_{i=1}^{n}\overline{f}(x_{i},y_{i})v_{i}, \end{align*} $$
$$ \begin{align*} \overline{f}(x,y)=\sum_{i=1}^{n}\overline{f}(x_{i},y_{i})v_{i}, \end{align*} $$
where
 $$ \begin{align} v_{i}=\frac{|x_{i}|+|y_{i}|}{|x|+|y|}. \end{align} $$
$$ \begin{align} v_{i}=\frac{|x_{i}|+|y_{i}|}{|x|+|y|}. \end{align} $$
Property 2.7. If x and y are strings of symbols such that
![]() $\overline {f}(x,y)\le \gamma ,$
for some
$\overline {f}(x,y)\le \gamma ,$
for some
![]() $0\le \gamma <1,$
then
$0\le \gamma <1,$
then
 $$ \begin{align} \bigg(\frac{1-\gamma}{1+\gamma}\bigg)|x|\leq|y|\le\bigg(\frac{1+\gamma}{1-\gamma}\bigg)|x|. \end{align} $$
$$ \begin{align} \bigg(\frac{1-\gamma}{1+\gamma}\bigg)|x|\leq|y|\le\bigg(\frac{1+\gamma}{1-\gamma}\bigg)|x|. \end{align} $$
We often use this property with
![]() $\gamma =1/7,$
in which case the conclusion can be formulated as
$\gamma =1/7,$
in which case the conclusion can be formulated as
 $$ \begin{align} \frac{3|x|}{4}\le|y|\le\frac{4|x|}{3}. \end{align} $$
$$ \begin{align} \frac{3|x|}{4}\le|y|\le\frac{4|x|}{3}. \end{align} $$
3. Odometer-based and circular symbolic systems
In this section we review the notation and definitions for odometer-based and circular symbolic systems. We also present the functor
![]() $\mathcal {F}$
of [Reference Foreman and WeissFW2] between these two systems.
$\mathcal {F}$
of [Reference Foreman and WeissFW2] between these two systems.
3.1. Symbolic systems
An alphabet is a countable or finite collection of symbols. In the following, let
![]() $\Sigma $
be a finite alphabet endowed with the discrete topology. Then
$\Sigma $
be a finite alphabet endowed with the discrete topology. Then
![]() $\Sigma ^{\mathbb {Z}}$
with the product topology is a separable, totally disconnected and compact space. The shift
$\Sigma ^{\mathbb {Z}}$
with the product topology is a separable, totally disconnected and compact space. The shift
is a homeomorphism. If
![]() $\mu $
is a shift-invariant Borel measure, then the measure-preserving dynamical system
$\mu $
is a shift-invariant Borel measure, then the measure-preserving dynamical system
![]() $(\Sigma ^{\mathbb {Z}},\mathcal {B},\mu ,sh)$
is called a symbolic system. The closed support of
$(\Sigma ^{\mathbb {Z}},\mathcal {B},\mu ,sh)$
is called a symbolic system. The closed support of
![]() $\mu $
is a shift-invariant subset of
$\mu $
is a shift-invariant subset of
![]() $\Sigma ^{\mathbb {Z}}$
called a symbolic shift or subshift.
$\Sigma ^{\mathbb {Z}}$
called a symbolic shift or subshift.
Symbolic shifts are often described by giving a collection of words that constitute a basis for the support of an invariant measure. A word w in
![]() $\Sigma $
is a finite sequence of elements of
$\Sigma $
is a finite sequence of elements of
![]() $\Sigma $
, and we denote its length by
$\Sigma $
, and we denote its length by
![]() $\lvert w\rvert $
. A language (over
$\lvert w\rvert $
. A language (over
![]() $\Sigma $
) is a subset of the set of all words.
$\Sigma $
) is a subset of the set of all words.
Definition 3.1. A sequence of collection of words
![]() $(W_{n})_{n\in \mathbb {N}}$
, where
$(W_{n})_{n\in \mathbb {N}}$
, where
![]() $\mathbb {N}=\{ 0,1,2,\ldots \} $
, satisfying the following properties is called a construction sequence.
$\mathbb {N}=\{ 0,1,2,\ldots \} $
, satisfying the following properties is called a construction sequence.
-
(1) For every
 $n\in \mathbb {N}$
all words in
$n\in \mathbb {N}$
all words in
 $W_{n}$
have the same length
$W_{n}$
have the same length
 $h_{n}$
.
$h_{n}$
. -
(2) Each
 $w\in W_{n}$
occurs at least once as a subword of each
$w\in W_{n}$
occurs at least once as a subword of each
 $w^{\prime }\in W_{n+1}$
.
$w^{\prime }\in W_{n+1}$
. -
(3) There is a summable sequence
 $(\varepsilon _{n})_{n\in \mathbb {N}}$
of positive numbers such that for every
$(\varepsilon _{n})_{n\in \mathbb {N}}$
of positive numbers such that for every
 $n\in \mathbb {N}$
, every word
$n\in \mathbb {N}$
, every word
 $w\in W_{n+1}$
can be uniquely parsed into segments
$w\in W_{n+1}$
can be uniquely parsed into segments
 $u_{0}w_{1}u_{1}w_{1}\ldots w_{l}u_{l+1}$
such that each
$u_{0}w_{1}u_{1}w_{1}\ldots w_{l}u_{l+1}$
such that each
 $w_{i}\in W_{n}$
, each
$w_{i}\in W_{n}$
, each
 $u_{i}$
(called spacer or boundary) is a word in
$u_{i}$
(called spacer or boundary) is a word in
 $\Sigma $
of finite length, and for this parsing
$\Sigma $
of finite length, and for this parsing  $$ \begin{align*} \frac{\sum_{i=0}^{l+1}\lvert u_{i}\rvert}{h_{n+1}}<\varepsilon_{n+1}. \end{align*} $$
$$ \begin{align*} \frac{\sum_{i=0}^{l+1}\lvert u_{i}\rvert}{h_{n+1}}<\varepsilon_{n+1}. \end{align*} $$
We will often call words in
![]() $W_{n}\, n$
-words or n-blocks, while a general concatenation of symbols from
$W_{n}\, n$
-words or n-blocks, while a general concatenation of symbols from
![]() $\Sigma $
is called a string. We also associate a symbolic shift with a construction sequence. Let
$\Sigma $
is called a string. We also associate a symbolic shift with a construction sequence. Let
![]() $\mathbb {K}$
be the collection of
$\mathbb {K}$
be the collection of
![]() $x\in \Sigma ^{\mathbb {Z}}$
such that every finite contiguous substring of x occurs inside some
$x\in \Sigma ^{\mathbb {Z}}$
such that every finite contiguous substring of x occurs inside some
![]() $w\in W_{n}$
. Then
$w\in W_{n}$
. Then
![]() $\mathbb {K}$
is a closed shift-invariant subset of
$\mathbb {K}$
is a closed shift-invariant subset of
![]() $\Sigma ^{\mathbb {Z}}$
that is compact if
$\Sigma ^{\mathbb {Z}}$
that is compact if
![]() $\Sigma $
is finite. In order to be able to unambiguously parse elements of
$\Sigma $
is finite. In order to be able to unambiguously parse elements of
![]() $\mathbb {K}$
we will use construction sequences consisting of uniquely readable words.
$\mathbb {K}$
we will use construction sequences consisting of uniquely readable words.
Definition 3.2. Let
![]() $\Sigma $
be a language and W be a collection of finite words in
$\Sigma $
be a language and W be a collection of finite words in
![]() $\Sigma $
. Then W is uniquely readable if and only if whenever
$\Sigma $
. Then W is uniquely readable if and only if whenever
![]() $u,v,w\in W$
and
$u,v,w\in W$
and
![]() $uv=pws$
with p and s strings of symbols in
$uv=pws$
with p and s strings of symbols in
![]() $\Sigma $
, then either p or s is the empty word.
$\Sigma $
, then either p or s is the empty word.
Moreover, our
![]() $(n+1)$
-words will be uniform in the n-words as defined below.
$(n+1)$
-words will be uniform in the n-words as defined below.
Definition 3.3. We call a construction sequence
![]() $(W_{n})_{n\in \mathbb {N}}$
uniform if for each
$(W_{n})_{n\in \mathbb {N}}$
uniform if for each
![]() $n\in \mathbb {N}$
there is a constant
$n\in \mathbb {N}$
there is a constant
![]() $c>0$
such that for all words
$c>0$
such that for all words
![]() $w^{\prime }\in W_{n+1}$
and
$w^{\prime }\in W_{n+1}$
and
![]() $w\in W_{n}$
the number of occurrences of w in
$w\in W_{n}$
the number of occurrences of w in
![]() $w^{\prime }$
is equal to c.
$w^{\prime }$
is equal to c.
Remark 3.4. In [Reference Foreman and WeissFW2] such construction sequences are called ‘strongly uniform’. Since we will only deal with this strong notion of uniformity in this paper, we abbreviate that terminology.
To check the zero-entropy loosely Bernoulli property for our symbolic systems we will use the following criterion, which follows from Rothstein’s Lemma 2.6 in [Reference RothsteinRo80] and the fact that the given condition in terms of n-blocks implies entropy zero. (See p. 18 of [Reference Ornstein, Rudolph and WeissORW82] for the type of estimate that is needed.)
Lemma 3.5. Suppose
![]() $\mathbb {K}$
is a symbolic system with uniform and uniquely readable construction sequence. Then
$\mathbb {K}$
is a symbolic system with uniform and uniquely readable construction sequence. Then
![]() $\mathbb {K}$
is zero-entropy loosely Bernoulli if and only if for every
$\mathbb {K}$
is zero-entropy loosely Bernoulli if and only if for every
![]() $\varepsilon>0$
there exists N such that for
$\varepsilon>0$
there exists N such that for
![]() $n\ge N,$
there is a set of n-blocks
$n\ge N,$
there is a set of n-blocks
![]() $\mathcal {G}_{n}$
with cardinality
$\mathcal {G}_{n}$
with cardinality
![]() $\lvert \mathcal {G}_n \rvert> (1-\varepsilon )\lvert W_n \rvert $
such that for
$\lvert \mathcal {G}_n \rvert> (1-\varepsilon )\lvert W_n \rvert $
such that for
![]() $A,B\in \mathcal {G}_{n}, \overline {f}(A,B)<\varepsilon .$
$A,B\in \mathcal {G}_{n}, \overline {f}(A,B)<\varepsilon .$
3.2. Odometer-based systems
Let
![]() $(k_{n})_{n\in \mathbb {N}}$
be a sequence of natural numbers
$(k_{n})_{n\in \mathbb {N}}$
be a sequence of natural numbers
![]() $k_{n}\geq 2$
and
$k_{n}\geq 2$
and
 $$ \begin{align*} O=\prod_{n\in\mathbb{N}}(\mathbb{Z}/k_{n}\mathbb{Z}) \end{align*} $$
$$ \begin{align*} O=\prod_{n\in\mathbb{N}}(\mathbb{Z}/k_{n}\mathbb{Z}) \end{align*} $$
be the
![]() $(k_{n})_{n\in \mathbb {N}}$
-adic integers. Then O has a compact abelian group structure and hence carries a Haar measure
$(k_{n})_{n\in \mathbb {N}}$
-adic integers. Then O has a compact abelian group structure and hence carries a Haar measure
![]() $\unicode{x3bb} $
. We define a transformation
$\unicode{x3bb} $
. We define a transformation
![]() $T:O\to O$
to be addition by
$T:O\to O$
to be addition by
![]() $1$
in the
$1$
in the
![]() $(k_{n})_{n\in \mathbb {N}}$
-adic integers (that is, the map that adds one in
$(k_{n})_{n\in \mathbb {N}}$
-adic integers (that is, the map that adds one in
![]() $\mathbb {Z}/k_{0}\mathbb {Z}$
and carries right). Then T is a
$\mathbb {Z}/k_{0}\mathbb {Z}$
and carries right). Then T is a
![]() $\unicode{x3bb} $
-preserving invertible transformation called odometer transformation which is ergodic and has discrete spectrum.
$\unicode{x3bb} $
-preserving invertible transformation called odometer transformation which is ergodic and has discrete spectrum.
We now define the collection of symbolic systems that have odometer systems as their timing mechanism to parse typical elements of the system.
Definition 3.6. Let
![]() $(\mathtt {W}_{n})_{n\in \mathbb {N}}$
be a uniquely readable construction sequence with
$(\mathtt {W}_{n})_{n\in \mathbb {N}}$
be a uniquely readable construction sequence with
![]() $\mathtt {W}_{0}=\Sigma $
and
$\mathtt {W}_{0}=\Sigma $
and
![]() $\mathtt {W}_{n+1}\subseteq (\mathtt {W}_{n})^{k_{n}}$
for every
$\mathtt {W}_{n+1}\subseteq (\mathtt {W}_{n})^{k_{n}}$
for every
![]() $n\in \mathbb {N}$
. The associated symbolic shift will be called an odometer-based system.
$n\in \mathbb {N}$
. The associated symbolic shift will be called an odometer-based system.
Thus, odometer-based systems are those built from construction sequences
![]() $(\mathtt {W}_{n})_{n\in \mathbb {N}}$
such that the words in
$(\mathtt {W}_{n})_{n\in \mathbb {N}}$
such that the words in
![]() $\mathtt {W}_{n+1}$
are concatenations of a fixed number
$\mathtt {W}_{n+1}$
are concatenations of a fixed number
![]() $k_{n}$
of words in
$k_{n}$
of words in
![]() $\mathtt {W}_{n}$
. Hence, the words in
$\mathtt {W}_{n}$
. Hence, the words in
![]() $\mathtt {W}_{n}$
have length
$\mathtt {W}_{n}$
have length
![]() $\mathtt {h}_{n}$
, where
$\mathtt {h}_{n}$
, where
 $$ \begin{align*} \mathtt{h}_{n}=\prod_{i=0}^{n-1}k_{i} \end{align*} $$
$$ \begin{align*} \mathtt{h}_{n}=\prod_{i=0}^{n-1}k_{i} \end{align*} $$
if
![]() $n>0$
, and
$n>0$
, and
![]() $\mathtt {h}_{0}=1$
. Moreover, the spacers in part (3) of Definition 3.1 are all the empty words (that is, an odometer-based transformation can be built by a cut-and-stack construction using no spacers).
$\mathtt {h}_{0}=1$
. Moreover, the spacers in part (3) of Definition 3.1 are all the empty words (that is, an odometer-based transformation can be built by a cut-and-stack construction using no spacers).
3.3. Circular systems
A circular coefficient sequenceis a sequence of pairs of integers
![]() $(k_{n},l_{n})_{n\in \mathbb {N}}$
such that
$(k_{n},l_{n})_{n\in \mathbb {N}}$
such that
![]() $k_{n}\geq 2$
and
$k_{n}\geq 2$
and
![]() $\sum _{n\in \mathbb {N}}({1}/{l_{n}})<\infty .$
From these numbers we inductively define numbers
$\sum _{n\in \mathbb {N}}({1}/{l_{n}})<\infty .$
From these numbers we inductively define numbers
 $$ \begin{align*} q_{n+1}=k_{n}l_{n}q_{n}^{2} \end{align*} $$
$$ \begin{align*} q_{n+1}=k_{n}l_{n}q_{n}^{2} \end{align*} $$
and
where we set
![]() $p_{0}=0$
and
$p_{0}=0$
and
![]() $q_{0}=1$
. Obviously,
$q_{0}=1$
. Obviously,
![]() $p_{n+1}$
and
$p_{n+1}$
and
![]() $q_{n+1}$
are relatively prime. Moreover, let
$q_{n+1}$
are relatively prime. Moreover, let
![]() $\Sigma $
be a non-empty finite alphabet and
$\Sigma $
be a non-empty finite alphabet and
![]() $b,e$
be two additional symbols (called spacers). Then, given a circular coefficient sequence
$b,e$
be two additional symbols (called spacers). Then, given a circular coefficient sequence
![]() $(k_{n},l_{n})_{n\in \mathbb {N}}$
, we build collections of words
$(k_{n},l_{n})_{n\in \mathbb {N}}$
, we build collections of words
![]() $\mathcal {W}_{n}$
in the alphabet
$\mathcal {W}_{n}$
in the alphabet
![]() $\Sigma \cup \{b,e\}$
by induction as follows.
$\Sigma \cup \{b,e\}$
by induction as follows.
-
• Set
 $\mathcal {W}_{0}=\Sigma $
.
$\mathcal {W}_{0}=\Sigma $
. -
• Having built
 $\mathcal {W}_{n}$
, choose a set
$\mathcal {W}_{n}$
, choose a set
 $P_{n+1}\subseteq (\mathcal {W}_{n})^{k_{n}}$
of so-called prewords and form
$P_{n+1}\subseteq (\mathcal {W}_{n})^{k_{n}}$
of so-called prewords and form
 $\mathcal {W}_{n+1}$
by taking all words of the form with
$\mathcal {W}_{n+1}$
by taking all words of the form with $$ \begin{align*} \mathcal{C}_{n}(w_{0},w_{1},\ldots,w_{k_{n}-1})=\prod_{i=0}^{q_{n}-1}\prod_{j=0}^{k_{n}-1}(b^{q_{n}-j_{i}}w_{j}^{l_{n}-1}e^{j_{i}}) \end{align*} $$
$$ \begin{align*} \mathcal{C}_{n}(w_{0},w_{1},\ldots,w_{k_{n}-1})=\prod_{i=0}^{q_{n}-1}\prod_{j=0}^{k_{n}-1}(b^{q_{n}-j_{i}}w_{j}^{l_{n}-1}e^{j_{i}}) \end{align*} $$
 $w_{0}\ldots w_{k_{n}-1}\in P_{n+1}$
. If
$w_{0}\ldots w_{k_{n}-1}\in P_{n+1}$
. If
 $n=0$
take
$n=0$
take
 $j_0=0$
, and for
$j_0=0$
, and for
 $n>0$
let
$n>0$
let
 $j_i\in \{0,\ldots , q_n-1\}$
be such that We note that each word in
$j_i\in \{0,\ldots , q_n-1\}$
be such that We note that each word in $$ \begin{align*} j_{i}\equiv(p_{n})^{-1}i \mod q_{n}. \end{align*} $$
$$ \begin{align*} j_{i}\equiv(p_{n})^{-1}i \mod q_{n}. \end{align*} $$
 $\mathcal {W}_{n+1}$
has length
$\mathcal {W}_{n+1}$
has length
 $k_{n}l_{n}q_{n}^{2}=q_{n+1}$
.
$k_{n}l_{n}q_{n}^{2}=q_{n+1}$
.
Definition 3.7. A construction sequence
![]() $(\mathcal {W}_{n})_{n\in \mathbb {N}}$
will be called circular if it is built in this manner using the
$(\mathcal {W}_{n})_{n\in \mathbb {N}}$
will be called circular if it is built in this manner using the
![]() $\mathcal {C}$
-operators and a circular coefficient sequence, and each
$\mathcal {C}$
-operators and a circular coefficient sequence, and each
![]() $P_{n+1}$
is uniquely readable in the alphabet with the words from
$P_{n+1}$
is uniquely readable in the alphabet with the words from
![]() $\mathcal {W}_{n}$
as letters (this last property is called the strong readability assumption).
$\mathcal {W}_{n}$
as letters (this last property is called the strong readability assumption).
Remark 3.8. By [Reference Foreman and WeissFW2, Lemma 45] each
![]() $\mathcal {W}_{n}$
in a circular construction sequence is uniquely readable even if the prewords are not uniquely readable. However, the definition of a circular construction sequence requires this stronger readability assumption.
$\mathcal {W}_{n}$
in a circular construction sequence is uniquely readable even if the prewords are not uniquely readable. However, the definition of a circular construction sequence requires this stronger readability assumption.
The definition of a circular construction sequence stems from a symbolic representation for untwisted Anosov–Katok diffeomorphisms on
![]() $\mathbb {T}^2$
(and similarly on
$\mathbb {T}^2$
(and similarly on
![]() $\mathbb {D}^2$
and
$\mathbb {D}^2$
and
![]() $\mathbb {S}^1\times [0,1]$
) described in [Reference Foreman and WeissFW1]. Such a diffeomorphism is constructed inductively as the limit of a sequence
$\mathbb {S}^1\times [0,1]$
) described in [Reference Foreman and WeissFW1]. Such a diffeomorphism is constructed inductively as the limit of a sequence
 $T_{n+1}=H_{n+1} \circ R_{\alpha _{n+1}} \circ H^{-1}_{n+1}$
, where
$T_{n+1}=H_{n+1} \circ R_{\alpha _{n+1}} \circ H^{-1}_{n+1}$
, where
![]() $R_{\alpha _{n+1}}(x,y)=(x+\alpha _{n+1},y)$
is the rotation by
$R_{\alpha _{n+1}}(x,y)=(x+\alpha _{n+1},y)$
is the rotation by
![]() $\alpha _{n+1}=({p_{n+1}}/{q_{n+1}})$
with the numbers
$\alpha _{n+1}=({p_{n+1}}/{q_{n+1}})$
with the numbers
![]() $p_{n+1},q_{n+1}$
from above, and
$p_{n+1},q_{n+1}$
from above, and
![]() $H_{n+1}=H_{n}\circ h_{n+1}$
with area-preserving diffeomorphisms
$H_{n+1}=H_{n}\circ h_{n+1}$
with area-preserving diffeomorphisms
![]() $h_{n+1}$
satisfying
$h_{n+1}$
satisfying
![]() $h_{n+1} \circ R_{1/q_{n}} = R_{1/q_{n}} \circ h_{n+1}$
. In the untwisted version of the Anosov–Katok method the fundamental domain
$h_{n+1} \circ R_{1/q_{n}} = R_{1/q_{n}} \circ h_{n+1}$
. In the untwisted version of the Anosov–Katok method the fundamental domain
![]() $[0,1/q_n] \times [0,1]$
is required to map to itself under
$[0,1/q_n] \times [0,1]$
is required to map to itself under
![]() $h_{n+1}$
. The conjugation map
$h_{n+1}$
. The conjugation map
![]() $h_{n+1}$
approximately permutes sets of the form
$h_{n+1}$
approximately permutes sets of the form
![]() $[i/(k_nq_n),(i+1)/(k_nq_n))\times [s/s_{n+1}, (s+1)/s_{n+1})$
, where
$[i/(k_nq_n),(i+1)/(k_nq_n))\times [s/s_{n+1}, (s+1)/s_{n+1})$
, where
![]() $s_{n+1}\geq 2$
is the number of
$s_{n+1}\geq 2$
is the number of
![]() $(n+1)$
-words. The combinatorics of
$(n+1)$
-words. The combinatorics of
![]() $h_{n+1}$
on the fundamental domain is determined by
$h_{n+1}$
on the fundamental domain is determined by
![]() $s_{n+1}$
different concatenations
$s_{n+1}$
different concatenations
![]() $w_0\ldots w_{k_n-1}$
of n-words, and each n-word codes a
$w_0\ldots w_{k_n-1}$
of n-words, and each n-word codes a
![]() $T_n$
trajectory of length
$T_n$
trajectory of length
![]() $q_n$
. Since
$q_n$
. Since
![]() $k_nl_nq_n \alpha _{n+1}=1/q_n\ \mathrm {mod}\ 1$
and
$k_nl_nq_n \alpha _{n+1}=1/q_n\ \mathrm {mod}\ 1$
and
![]() $h_{n+1}$
commutes with
$h_{n+1}$
commutes with
![]() $R_{1/q_n}$
, the code repeats but starting at a different position within the n-words. Thus one uses the spacer symbols b and e to label the incomplete beginning and end segments of words. We refer to [Reference Foreman and WeissFW1, §7.5] for a detailed exposition. The newly introduced spacers
$R_{1/q_n}$
, the code repeats but starting at a different position within the n-words. Thus one uses the spacer symbols b and e to label the incomplete beginning and end segments of words. We refer to [Reference Foreman and WeissFW1, §7.5] for a detailed exposition. The newly introduced spacers
![]() $b,e$
will not matter for our arguments since they occupy a small proportion of the
$b,e$
will not matter for our arguments since they occupy a small proportion of the
![]() $(n+1)$
-words and we will often neglect them in our estimates with the aid of Property 2.5.
$(n+1)$
-words and we will often neglect them in our estimates with the aid of Property 2.5.
Definition 3.9. A symbolic shift
![]() $\mathbb {K}$
built from a circular construction sequence is called a circular system. For emphasis we will often denote it by
$\mathbb {K}$
built from a circular construction sequence is called a circular system. For emphasis we will often denote it by
![]() $\mathbb {K}^{c}$
.
$\mathbb {K}^{c}$
.
For a word
![]() $w\in \mathcal {W}_{n+1}$
we introduce the following subscales as in [Reference Foreman and WeissFW2, §3.3].
$w\in \mathcal {W}_{n+1}$
we introduce the following subscales as in [Reference Foreman and WeissFW2, §3.3].
-
• Subscale
 $0$
is the scale of the individual powers of
$0$
is the scale of the individual powers of
 $w_{j}\in \mathcal {W}_{n}$
of the form
$w_{j}\in \mathcal {W}_{n}$
of the form
 $w_{j}^{l-1}$
, and each such occurrence of a
$w_{j}^{l-1}$
, and each such occurrence of a
 $w_{j}^{l-1}$
is called a
$w_{j}^{l-1}$
is called a
 $0$
-subsubsection.
$0$
-subsubsection. -
• Subscale
 $1$
is the scale of each term in the product
$1$
is the scale of each term in the product
 $\prod _{j=0}^{k_{n}-1}(b^{q_{n}-j_{i}}w_{j}^{l_{n}-1}e^{j_{i}})$
that has the form
$\prod _{j=0}^{k_{n}-1}(b^{q_{n}-j_{i}}w_{j}^{l_{n}-1}e^{j_{i}})$
that has the form
 $(b^{q_{n}-j_{i}}w_{j}^{l_{n}-1}e^{j_{i}})$
and these terms are called
$(b^{q_{n}-j_{i}}w_{j}^{l_{n}-1}e^{j_{i}})$
and these terms are called
 $1$
-subsections.
$1$
-subsections. -
• Subscale
 $2$
is the scale of each term of
$2$
is the scale of each term of
 $\prod _{i=0}^{q_{n}-1}\prod _{j=0}^{k_{n}-1}(b^{q_{n}-j_{i}}w_{j}^{l_{n}-1}e^{j_{i}})$
that has the form
$\prod _{i=0}^{q_{n}-1}\prod _{j=0}^{k_{n}-1}(b^{q_{n}-j_{i}}w_{j}^{l_{n}-1}e^{j_{i}})$
that has the form
 $\prod _{j=0}^{k_{n}-1}(b^{q_{n}-j_{i}}w_{j}^{l_{n}-1}e^{j_{i}})$
, and these terms are called
$\prod _{j=0}^{k_{n}-1}(b^{q_{n}-j_{i}}w_{j}^{l_{n}-1}e^{j_{i}})$
, and these terms are called
 $2$
-subsections.
$2$
-subsections.
3.4. The functor
 $\mathcal {F}$
$\mathcal {F}$
For a fixed circular coefficient sequence
![]() $(k_{n},l_{n})_{n\in \mathbb {N}}$
we consider two categories
$(k_{n},l_{n})_{n\in \mathbb {N}}$
we consider two categories
![]() $\mathcal {OB}$
and
$\mathcal {OB}$
and
![]() $\mathcal {CB}$
whose objects are odometer-based and circular systems, respectively. The morphisms in these categories are (synchronous and anti-synchronous) graph joinings. In [Reference Foreman and WeissFW2] Foreman and Weiss define a functor taking odometer-based systems to circular systems that preserve the factor and conjugacy structure. In this subsubsection we review the definition of the functor from the odometer-based symbolic systems to the circular symbolic systems.
$\mathcal {CB}$
whose objects are odometer-based and circular systems, respectively. The morphisms in these categories are (synchronous and anti-synchronous) graph joinings. In [Reference Foreman and WeissFW2] Foreman and Weiss define a functor taking odometer-based systems to circular systems that preserve the factor and conjugacy structure. In this subsubsection we review the definition of the functor from the odometer-based symbolic systems to the circular symbolic systems.
For this purpose, we fix a circular coefficient sequence
![]() $(k_{n},l_{n})_{n\in \mathbb {N}}$
. Let
$(k_{n},l_{n})_{n\in \mathbb {N}}$
. Let
![]() $\Sigma $
be an alphabet and
$\Sigma $
be an alphabet and
![]() $(\mathtt {W}_{n})_{n\in \mathbb {N}}$
be a construction sequence for an odometer-based system with coefficients
$(\mathtt {W}_{n})_{n\in \mathbb {N}}$
be a construction sequence for an odometer-based system with coefficients
![]() $(k_{n})_{n\in \mathbb {N}}$
. Then we define a circular construction sequence
$(k_{n})_{n\in \mathbb {N}}$
. Then we define a circular construction sequence
![]() $(\mathcal {W}_{n})_{n\in \mathbb {N}}$
and bijections
$(\mathcal {W}_{n})_{n\in \mathbb {N}}$
and bijections
![]() $c_{n}:\mathtt {W}_{n}\to \mathcal {W}_{n}$
by induction.
$c_{n}:\mathtt {W}_{n}\to \mathcal {W}_{n}$
by induction.
-
• Let
 $\mathcal {W}_{0}=\Sigma $
and
$\mathcal {W}_{0}=\Sigma $
and
 $c_{0}$
be the identity map.
$c_{0}$
be the identity map. -
• Suppose that
 $\mathtt {W}_{n}$
,
$\mathtt {W}_{n}$
,
 $\mathcal {W}_{n}$
and
$\mathcal {W}_{n}$
and
 $c_{n}$
have already been defined. Then we define and the map
$c_{n}$
have already been defined. Then we define and the map $$ \begin{align*} \mathcal{W}_{n+1}=\{ \mathcal{C}_{n}(c_{n}(\mathtt{w}_{0}),c_{n}(\mathtt{w}_{1}),\ldots,c_{n}(\mathtt{w}_{k_{n}-1}))\::\:\mathtt{w}_{0}\mathtt{w}_{1}\ldots\mathtt{w}_{k_{n}-1}\in\mathtt{W}_{n+1}\} \end{align*} $$
$$ \begin{align*} \mathcal{W}_{n+1}=\{ \mathcal{C}_{n}(c_{n}(\mathtt{w}_{0}),c_{n}(\mathtt{w}_{1}),\ldots,c_{n}(\mathtt{w}_{k_{n}-1}))\::\:\mathtt{w}_{0}\mathtt{w}_{1}\ldots\mathtt{w}_{k_{n}-1}\in\mathtt{W}_{n+1}\} \end{align*} $$
 $c_{n+1}$
by setting In particular, the prewords are
$c_{n+1}$
by setting In particular, the prewords are $$ \begin{align*} c_{n+1}(\mathtt{w}_{0}\mathtt{w}_{1}\ldots\mathtt{w}_{k_{n}-1})=\mathcal{C}_{n}(c_{n}(\mathtt{w}_{0}),c_{n}(\mathtt{w}_{1}),\ldots,c_{n}(\mathtt{w}_{k_{n}-1})). \end{align*} $$
$$ \begin{align*} c_{n+1}(\mathtt{w}_{0}\mathtt{w}_{1}\ldots\mathtt{w}_{k_{n}-1})=\mathcal{C}_{n}(c_{n}(\mathtt{w}_{0}),c_{n}(\mathtt{w}_{1}),\ldots,c_{n}(\mathtt{w}_{k_{n}-1})). \end{align*} $$
 $$ \begin{align*} P_{n+1}=\{ c_{n}(\mathtt{w}_{0})c_{n}(\mathtt{w}_{1})\ldots c_{n}(\mathtt{w}_{k_{n}-1})\::\:\mathtt{w}_{0}\mathtt{w}_{1}\ldots\mathtt{w}_{k_{n}-1}\in\mathtt{W}_{n+1}\}. \end{align*} $$
$$ \begin{align*} P_{n+1}=\{ c_{n}(\mathtt{w}_{0})c_{n}(\mathtt{w}_{1})\ldots c_{n}(\mathtt{w}_{k_{n}-1})\::\:\mathtt{w}_{0}\mathtt{w}_{1}\ldots\mathtt{w}_{k_{n}-1}\in\mathtt{W}_{n+1}\}. \end{align*} $$
Definition 3.10. Suppose that
![]() $\mathbb {K}$
is built from a construction sequence
$\mathbb {K}$
is built from a construction sequence
![]() $(\mathtt {W}_{n})_{n\in \mathbb {N}}$
and
$(\mathtt {W}_{n})_{n\in \mathbb {N}}$
and
![]() $\mathbb {K}^{c}$
has the circular construction sequence
$\mathbb {K}^{c}$
has the circular construction sequence
![]() $(\mathcal {W}_{n})_{n\in \mathbb {N}}$
as constructed above. Then we define a map
$(\mathcal {W}_{n})_{n\in \mathbb {N}}$
as constructed above. Then we define a map
![]() $\mathcal {F}$
from the set of odometer-based systems (viewed as subshifts) to circular systems (viewed as subshifts) by
$\mathcal {F}$
from the set of odometer-based systems (viewed as subshifts) to circular systems (viewed as subshifts) by
Remark 3.11. The map
![]() $\mathcal {F}$
is a bijection between odometer-based symbolic systems with coefficients
$\mathcal {F}$
is a bijection between odometer-based symbolic systems with coefficients
![]() $(k_{n})_{n\in \mathbb {N}}$
and circular symbolic systems with coefficients
$(k_{n})_{n\in \mathbb {N}}$
and circular symbolic systems with coefficients
![]() $(k_{n},l_{n})_{n\in \mathbb {N}}$
that preserves uniformity. Since the construction sequences for our odometer-based systems will be uniquely readable, the corresponding circular construction sequences will automatically satisfy the strong readability assumption.
$(k_{n},l_{n})_{n\in \mathbb {N}}$
that preserves uniformity. Since the construction sequences for our odometer-based systems will be uniquely readable, the corresponding circular construction sequences will automatically satisfy the strong readability assumption.
In the following we will denote blocks in the odometer-based system by letters in typewriter font (for example,
![]() $\mathtt {A}$
). For the corresponding block in the circular system we will use calligraphic letters (for example,
$\mathtt {A}$
). For the corresponding block in the circular system we will use calligraphic letters (for example,
![]() $\mathcal {A}$
). As already noted, the length of a n-block
$\mathcal {A}$
). As already noted, the length of a n-block
![]() $\mathtt {w}$
in the odometer-based system is
$\mathtt {w}$
in the odometer-based system is
 $\mathtt {h}_{n}=\prod _{i=0}^{n-1}k_{i}$
if
$\mathtt {h}_{n}=\prod _{i=0}^{n-1}k_{i}$
if
![]() $n>0$
, and
$n>0$
, and
![]() $\mathtt {h}_{0}=1$
, while the length of a n-block in the circular system is
$\mathtt {h}_{0}=1$
, while the length of a n-block in the circular system is
![]() $q_{n}$
, that is,
$q_{n}$
, that is,
![]() $\lvert c_{n}(\mathtt {w})\rvert =q_{n}$
. Moreover, we will use the following map from substrings of the underlying odometer-based system to the circular system:
$\lvert c_{n}(\mathtt {w})\rvert =q_{n}$
. Moreover, we will use the following map from substrings of the underlying odometer-based system to the circular system:
 $$ \begin{align*} \mathcal{C}_{n,i}(\mathtt{w}_{s}\mathtt{w_{s+1}}\ldots\mathtt{w}_{t})=\prod_{j=s}^{t}(b^{q_{n}-j_{i}}(c_{n}(\mathtt{w}_{j}))^{l_{n}-1}e^{j_{i}}) \end{align*} $$
$$ \begin{align*} \mathcal{C}_{n,i}(\mathtt{w}_{s}\mathtt{w_{s+1}}\ldots\mathtt{w}_{t})=\prod_{j=s}^{t}(b^{q_{n}-j_{i}}(c_{n}(\mathtt{w}_{j}))^{l_{n}-1}e^{j_{i}}) \end{align*} $$
for any
![]() $0\leq i\leq q_{n}-1$
and
$0\leq i\leq q_{n}-1$
and
![]() $0\leq s\leq t\leq k_{n}-1$
.
$0\leq s\leq t\leq k_{n}-1$
.
Example 3.12. We give an example of a loosely Bernoulli odometer-based system
![]() $\mathbb {K}$
of zero measure-theoretic entropy with uniform and uniquely readable construction sequence such that
$\mathbb {K}$
of zero measure-theoretic entropy with uniform and uniquely readable construction sequence such that
![]() $\mathcal {F}(\mathbb {K})$
is also loosely Bernoulli. For this purpose, let
$\mathcal {F}(\mathbb {K})$
is also loosely Bernoulli. For this purpose, let
![]() $\Sigma $
be an alphabet with two symbols and
$\Sigma $
be an alphabet with two symbols and
![]() $\varepsilon _{n}\searrow 0$
. Assume that we have two n-blocks
$\varepsilon _{n}\searrow 0$
. Assume that we have two n-blocks
![]() $\mathtt {w}_{0}$
and
$\mathtt {w}_{0}$
and
![]() $\mathtt {w}_{1}$
in the odometer-based system. Then we define two
$\mathtt {w}_{1}$
in the odometer-based system. Then we define two
![]() $(n+1)$
-blocks by the following rule:
$(n+1)$
-blocks by the following rule:
 $$ \begin{align*} \mathtt{B}_{0}^{(n+1)}&= \mathtt{w}_{1}\mathtt{w}_{1}\underbrace{\mathtt{w}_{0}\mathtt{w}_{1}\mathtt{w}_{0}\mathtt{w}_{1}\ldots\mathtt{w}_{0}\mathtt{w}_{1}}_{2s_{n} \text{ blocks}}\mathtt{w}_{0}\mathtt{w}_{0},\\ \mathtt{B}_{1}^{(n+1)}&= \mathtt{w}_{1}\mathtt{w}_{1}\mathtt{w}_{1}\underbrace{\mathtt{w}_{0}\mathtt{w}_{1}\ldots\mathtt{w}_{0}\mathtt{w}_{1}}_{2s_{n}-2 \text{ blocks}}\mathtt{w}_{0}\mathtt{w}_{0}\mathtt{w}_{0}, \end{align*} $$
$$ \begin{align*} \mathtt{B}_{0}^{(n+1)}&= \mathtt{w}_{1}\mathtt{w}_{1}\underbrace{\mathtt{w}_{0}\mathtt{w}_{1}\mathtt{w}_{0}\mathtt{w}_{1}\ldots\mathtt{w}_{0}\mathtt{w}_{1}}_{2s_{n} \text{ blocks}}\mathtt{w}_{0}\mathtt{w}_{0},\\ \mathtt{B}_{1}^{(n+1)}&= \mathtt{w}_{1}\mathtt{w}_{1}\mathtt{w}_{1}\underbrace{\mathtt{w}_{0}\mathtt{w}_{1}\ldots\mathtt{w}_{0}\mathtt{w}_{1}}_{2s_{n}-2 \text{ blocks}}\mathtt{w}_{0}\mathtt{w}_{0}\mathtt{w}_{0}, \end{align*} $$
where we choose the integer
![]() $s_{n}$
sufficiently large to guarantee that
$s_{n}$
sufficiently large to guarantee that
 $\mathtt {B}_{0}^{(n+1)}$
and
$\mathtt {B}_{0}^{(n+1)}$
and
 $\mathtt {B}_{1}^{(n+1)}$
are
$\mathtt {B}_{1}^{(n+1)}$
are
![]() $\varepsilon _{n}$
-close to each other in
$\varepsilon _{n}$
-close to each other in
![]() $\overline {f}$
. Clearly, the construction sequence defined like this is uniform and uniquely readable. Moreover, the corresponding
$\overline {f}$
. Clearly, the construction sequence defined like this is uniform and uniquely readable. Moreover, the corresponding
![]() $(n+1)$
-blocks
$(n+1)$
-blocks
 $\mathcal {B}_{0}^{(n+1)}$
and
$\mathcal {B}_{0}^{(n+1)}$
and
 $\mathcal {B}_{1}^{(n+1)}$
in the circular system are also
$\mathcal {B}_{1}^{(n+1)}$
in the circular system are also
![]() $\varepsilon _{n}$
-close to each other in
$\varepsilon _{n}$
-close to each other in
![]() $\overline {f}$
. Hence,
$\overline {f}$
. Hence,
![]() $\mathbb {K}$
and
$\mathbb {K}$
and
![]() $\mathcal {F}(\mathbb {K})$
are loosely Bernoulli by Lemma 3.5.
$\mathcal {F}(\mathbb {K})$
are loosely Bernoulli by Lemma 3.5.
4. Positive-entropy example
4.1. Positive-entropy loosely Bernoulli odometer-based system
In this section we construct a uniquely readable uniform odometer-based system
![]() $\mathbb {E}$
of positive entropy that is loosely Bernoulli. In the next section we will prove that
$\mathbb {E}$
of positive entropy that is loosely Bernoulli. In the next section we will prove that
![]() $\mathcal {F}(\mathbb {E})$
is not loosely Bernoulli. The main idea in the construction of
$\mathcal {F}(\mathbb {E})$
is not loosely Bernoulli. The main idea in the construction of
![]() $\mathbb {E}$
is to concatenate n-blocks independently in long initial segments of
$\mathbb {E}$
is to concatenate n-blocks independently in long initial segments of
![]() $(n+1)$
-blocks, and use a relatively small final segment of the
$(n+1)$
-blocks, and use a relatively small final segment of the
![]() $(n+1)$
-block to achieve uniformity and unique readability. If we used only the independent concatenation, then
$(n+1)$
-block to achieve uniformity and unique readability. If we used only the independent concatenation, then
![]() $\mathbb {E}$
would be Bernoulli (and hence loosely Bernoulli), and
$\mathbb {E}$
would be Bernoulli (and hence loosely Bernoulli), and
![]() $\mathcal {F}(\mathbb {E})$
would still be non-loosely Bernoulli. In this case the proof given in the next section that
$\mathcal {F}(\mathbb {E})$
would still be non-loosely Bernoulli. In this case the proof given in the next section that
![]() $\mathcal {F}(\mathbb {E})$
is not loosely Bernoulli could be simplified, but we want to achieve uniformity and unique readability to make our example fit the framework of the odometer-based constructions in [Reference Foreman and WeissFW2, Reference Foreman and WeissFW3].
$\mathcal {F}(\mathbb {E})$
is not loosely Bernoulli could be simplified, but we want to achieve uniformity and unique readability to make our example fit the framework of the odometer-based constructions in [Reference Foreman and WeissFW2, Reference Foreman and WeissFW3].
Our approach takes advantage of the fact that in the case of positive entropy, in particular for the system
![]() $\mathbb {E}$
, there will be many n-blocks that are bounded apart in
$\mathbb {E}$
, there will be many n-blocks that are bounded apart in
![]() $\overline {f}$
-distance and the loosely Bernoulli property can still be satisfied. However, all circular systems, as described in §2, and in particular
$\overline {f}$
-distance and the loosely Bernoulli property can still be satisfied. However, all circular systems, as described in §2, and in particular
![]() $\mathcal {F}(\mathbb {E}),$
have entropy zero. In this case the loosely Bernoulli property fails to hold if most of the n-blocks are bounded apart in the
$\mathcal {F}(\mathbb {E}),$
have entropy zero. In this case the loosely Bernoulli property fails to hold if most of the n-blocks are bounded apart in the
![]() $\overline {f}$
metric. In the next section we will use the approach of Rothstein [Reference RothsteinRo80] to prove that the independent concatenation of n-blocks that are mostly bounded apart in
$\overline {f}$
metric. In the next section we will use the approach of Rothstein [Reference RothsteinRo80] to prove that the independent concatenation of n-blocks that are mostly bounded apart in
![]() $\overline {f}$
distance leads to
$\overline {f}$
distance leads to
![]() $(n+1)$
-blocks that are also mostly bounded apart in
$(n+1)$
-blocks that are also mostly bounded apart in
![]() $\overline {f}$
distance, and the lower bound on the
$\overline {f}$
distance, and the lower bound on the
![]() $\overline {f}$
distance decreases only slightly in going from n-blocks to
$\overline {f}$
distance decreases only slightly in going from n-blocks to
![]() $(n+1)$
-blocks.
$(n+1)$
-blocks.
We begin by describing some of the conditions on the parameters involved in the construction of
![]() $\mathbb {E}.$
Further requirements on the lower bound on the
$\mathbb {E}.$
Further requirements on the lower bound on the
![]() $k_{n}$
will be imposed in the next section and after the first lemma in the present section. First we choose positive rational numbers
$k_{n}$
will be imposed in the next section and after the first lemma in the present section. First we choose positive rational numbers
![]() $\varepsilon _{n}$
such that
$\varepsilon _{n}$
such that
![]() $\varepsilon _{n}<2^{-(n+12)}.$
Then we choose
$\varepsilon _{n}<2^{-(n+12)}.$
Then we choose
![]() $k_{n}$
(depending on
$k_{n}$
(depending on
![]() $\ell _{n},N(n),\varepsilon _{n})$
so that
$\ell _{n},N(n),\varepsilon _{n})$
so that
 $\sum _{n=1}^{\infty }N(n)^{2}/(\varepsilon _{n}^{2}k_{n})<1/8.$
Furthermore, we require that
$\sum _{n=1}^{\infty }N(n)^{2}/(\varepsilon _{n}^{2}k_{n})<1/8.$
Furthermore, we require that
![]() $\varepsilon _{n}N(n)>2$
,
$\varepsilon _{n}N(n)>2$
,
![]() $\varepsilon _{n}k_{n}$
is an integer, and
$\varepsilon _{n}k_{n}$
is an integer, and
![]() $k_{n}$
is a multiple of
$k_{n}$
is a multiple of
![]() $N(n).$
Let
$N(n).$
Let
![]() $k_{n}'=(1-\varepsilon _{n})k_{n}.$
$k_{n}'=(1-\varepsilon _{n})k_{n}.$
We now describe the construction sequence
![]() $(\mathtt {W}_{n})_{n\in \mathbb {N}}$
for
$(\mathtt {W}_{n})_{n\in \mathbb {N}}$
for
![]() $\mathbb {E}.$
Recall that
$\mathbb {E}.$
Recall that
![]() $\mathtt {W}_{0}=\Sigma .$
Suppose there are
$\mathtt {W}_{0}=\Sigma .$
Suppose there are
![]() $N(n)$
distinct n-blocks of length
$N(n)$
distinct n-blocks of length
![]() $\mathtt {h}_{n}$
in
$\mathtt {h}_{n}$
in
![]() $\mathtt {W}_{n},$
say
$\mathtt {W}_{n},$
say
![]() $\mathtt {W}_{n}=\{\mathtt {y}_{1},\ldots ,\mathtt {y}_{N(n)}\}.$
Then
$\mathtt {W}_{n}=\{\mathtt {y}_{1},\ldots ,\mathtt {y}_{N(n)}\}.$
Then
![]() $\mathtt {W}_{n+1}$
consists of all words of the form
$\mathtt {W}_{n+1}$
consists of all words of the form
![]() $\mathtt {w}_{1}\mathtt {w}_{2}\ldots \mathtt {w}_{k_{n}},$
where each
$\mathtt {w}_{1}\mathtt {w}_{2}\ldots \mathtt {w}_{k_{n}},$
where each
![]() $\mathtt {w}_{j}=\mathtt {y}_{i(j)}$
for some
$\mathtt {w}_{j}=\mathtt {y}_{i(j)}$
for some
![]() $i(j)\in \{1,\ldots ,N_{n}(n)\},$
subject to the following conditions.
$i(j)\in \{1,\ldots ,N_{n}(n)\},$
subject to the following conditions.
-
(1) For each
 $i\in \{1,2,\ldots ,N(n)-1\},$
card
$i\in \{1,2,\ldots ,N(n)-1\},$
card
 $\{j\in \{1,2,\ldots ,k_{n}'\}:\mathtt {w}_{j}=\mathtt {y}_{i}\}\le {k_{n}}/{N(n)},$
and
$\{j\in \{1,2,\ldots ,k_{n}'\}:\mathtt {w}_{j}=\mathtt {y}_{i}\}\le {k_{n}}/{N(n)},$
and
 $\mathtt {w}_{j}\ne \mathtt {y}_{N(n)}$
for
$\mathtt {w}_{j}\ne \mathtt {y}_{N(n)}$
for
 $j\in \{1,2,\ldots ,k_{n}'$
}.
$j\in \{1,2,\ldots ,k_{n}'$
}. -
(2) For
 $j\in \{k_{n}-(k_{n}/N(n)),k_{n}-(k_{n}/N(n))+1,\ldots ,k_{n}-1\}, \mathtt {w}_{j}=\mathtt {y}_{N(n)}.$
$j\in \{k_{n}-(k_{n}/N(n)),k_{n}-(k_{n}/N(n))+1,\ldots ,k_{n}-1\}, \mathtt {w}_{j}=\mathtt {y}_{N(n)}.$
-
(3) The substring
 $\mathtt {w}_{(1-\varepsilon _{n})k_{n}}\ldots \mathtt {w}_{k_{n}-(k_{n}/N(n))-1}$
consists of a finite string of
$\mathtt {w}_{(1-\varepsilon _{n})k_{n}}\ldots \mathtt {w}_{k_{n}-(k_{n}/N(n))-1}$
consists of a finite string of
 $\mathtt {y}_{1}$
's, followed by a finite string of
$\mathtt {y}_{1}$
's, followed by a finite string of
 $\mathtt {y}_{2}$
's, etc. ending with a finite string of
$\mathtt {y}_{2}$
's, etc. ending with a finite string of
 $\mathtt {y}_{N(n)-1}$
's such that card
$\mathtt {y}_{N(n)-1}$
's such that card
 $\{j\in \{1,2,\ldots k_{n}\}:\mathtt {w}_{j}=\mathtt {y}_{i}\}=k_{n}/{N(n)}$
for every
$\{j\in \{1,2,\ldots k_{n}\}:\mathtt {w}_{j}=\mathtt {y}_{i}\}=k_{n}/{N(n)}$
for every
 $i\in \{1,2,\ldots ,N(n)\}.$
$i\in \{1,2,\ldots ,N(n)\}.$
Whenever condition (1) on the first
![]() $k_{n}'\ n$
-blocks is satisfied, there is a unique way of completing the
$k_{n}'\ n$
-blocks is satisfied, there is a unique way of completing the
![]() $(n+1)$
-block so that conditions (2) and (3) are satisfied. Condition (2) implies unique readability, and condition (3) implies uniformity. Our block construction and Lemma 4.1 below are essentially a special case of the techniques in the substitution lemma in [Reference Foreman, Rudolph and WeissFRW11].
$(n+1)$
-block so that conditions (2) and (3) are satisfied. Condition (2) implies unique readability, and condition (3) implies uniformity. Our block construction and Lemma 4.1 below are essentially a special case of the techniques in the substitution lemma in [Reference Foreman, Rudolph and WeissFRW11].
Lemma 4.1. (Chebyshev application)
Suppose
![]() $k_{n}'=(1-\varepsilon _n)k_n$
symbols are chosen independently from
$k_{n}'=(1-\varepsilon _n)k_n$
symbols are chosen independently from
![]() $\{1,2,\ldots ,N(n)-1\},$
where each symbol is equally likely to be chosen. Then the probability
$\{1,2,\ldots ,N(n)-1\},$
where each symbol is equally likely to be chosen. Then the probability
![]() $\tau _{n}$
that there exists a symbol that is chosen more than
$\tau _{n}$
that there exists a symbol that is chosen more than
![]() $k_{n}/{N(n)}$
times satisfies
$k_{n}/{N(n)}$
times satisfies
![]() $\tau _{n}<4N(n)^{2}/(\varepsilon _{n}^{2}k_{n}).$
$\tau _{n}<4N(n)^{2}/(\varepsilon _{n}^{2}k_{n}).$
Proof. For a fixed
![]() $i_{0}\in \{1,\ldots ,N(n)-1\},$
let
$i_{0}\in \{1,\ldots ,N(n)-1\},$
let
![]() $S=S_{k_{n}'}$
be the number of times
$S=S_{k_{n}'}$
be the number of times
![]() $i_{0}$
is chosen in
$i_{0}$
is chosen in
![]() $k_{n}'$
Bernoulli trials, where the probability of
$k_{n}'$
Bernoulli trials, where the probability of
![]() $i_{0}$
being chosen in any one trial is
$i_{0}$
being chosen in any one trial is
![]() $1/({N(n)-1}).$
Then the expected value of S is
$1/({N(n)-1}).$
Then the expected value of S is
![]() $E(S)=k_{n}'/(N(n)-1)$
and the standard deviation of S is
$E(S)=k_{n}'/(N(n)-1)$
and the standard deviation of S is
 $\sigma =\sqrt {k_{n}'(N(n)-2)}/({N(n)-1}).$
Note that the condition
$\sigma =\sqrt {k_{n}'(N(n)-2)}/({N(n)-1}).$
Note that the condition
![]() $\varepsilon _{n}N(n)>2$
implies that
$\varepsilon _{n}N(n)>2$
implies that
![]() $1/{N(n)}>(1-(\varepsilon _{n}/2))/({N(n)-1}).$
We have the following estimates on the probabilities, where we apply Chebyshev’s inequality in the last step:
$1/{N(n)}>(1-(\varepsilon _{n}/2))/({N(n)-1}).$
We have the following estimates on the probabilities, where we apply Chebyshev’s inequality in the last step:
 $$ \begin{align*} \text{Pr}(S>k_{n}/{N(n)})& \le\text{Pr}\bigg(|S-E(S)|>\dfrac{k_{n}}{N(n)}-\dfrac{(1-\varepsilon_{n})k_{n}}{N(n)-1}\bigg)\\ & \le\text{Pr}\bigg(|S-E(S)|>\dfrac{(1-(\varepsilon_{n}/2))k_{n}}{N(n)-1}-\dfrac{(1-\varepsilon_{n})k_{n}}{N(n)-1}\bigg)\\ & =\text{Pr}\bigg(|S-E(S)|>\dfrac{(\varepsilon_{n}/2)k_{n}}{N(n)-1}\bigg)\\ & =\text{Pr}(|S-E(S)|>\alpha\sigma)\\ & <1/\alpha^{2}, \end{align*} $$
$$ \begin{align*} \text{Pr}(S>k_{n}/{N(n)})& \le\text{Pr}\bigg(|S-E(S)|>\dfrac{k_{n}}{N(n)}-\dfrac{(1-\varepsilon_{n})k_{n}}{N(n)-1}\bigg)\\ & \le\text{Pr}\bigg(|S-E(S)|>\dfrac{(1-(\varepsilon_{n}/2))k_{n}}{N(n)-1}-\dfrac{(1-\varepsilon_{n})k_{n}}{N(n)-1}\bigg)\\ & =\text{Pr}\bigg(|S-E(S)|>\dfrac{(\varepsilon_{n}/2)k_{n}}{N(n)-1}\bigg)\\ & =\text{Pr}(|S-E(S)|>\alpha\sigma)\\ & <1/\alpha^{2}, \end{align*} $$
where
 $\alpha =\varepsilon _{n}k_{n}/(2{\sqrt {k_{n}'(N(n)-2)}}).$
Thus
$\alpha =\varepsilon _{n}k_{n}/(2{\sqrt {k_{n}'(N(n)-2)}}).$
Thus
![]() $\text {Pr}(S>k_n/{N(n)})<4N(n)/(\varepsilon _{n}^{2}k_{n}).$
Since
$\text {Pr}(S>k_n/{N(n)})<4N(n)/(\varepsilon _{n}^{2}k_{n}).$
Since
![]() $i_{0}$
was only one of
$i_{0}$
was only one of
![]() $N(n)-1$
possible symbols, the upper bound in the statement of the lemma is obtained by multiplying the upper bound on
$N(n)-1$
possible symbols, the upper bound in the statement of the lemma is obtained by multiplying the upper bound on
![]() $\text {Pr}(S>k_{n}/N(n))$
by
$\text {Pr}(S>k_{n}/N(n))$
by
![]() $N(n).$
$N(n).$
We require the
![]() $k_{n}$
's to be sufficiently large so that
$k_{n}$
's to be sufficiently large so that
 $\sum _{n=1}^{\infty }\tau _{n}^{(2^{-n})}<\infty .$
From Lemma 4.1, this is possible because
$\sum _{n=1}^{\infty }\tau _{n}^{(2^{-n})}<\infty .$
From Lemma 4.1, this is possible because
![]() $k_{n}$
is chosen after
$k_{n}$
is chosen after
![]() $\varepsilon _{n}$
and
$\varepsilon _{n}$
and
![]() $N(n)$
are determined.
$N(n)$
are determined.
We apply Lemma 4.1 to the independent choice of
![]() $k_{n}'\, n$
-blocks from the first
$k_{n}'\, n$
-blocks from the first
![]() $N(n)-1 n$
-blocks. Suppose E is a string of
$N(n)-1 n$
-blocks. Suppose E is a string of
![]() $k_{n}'\, n$
-blocks chosen from the first
$k_{n}'\, n$
-blocks chosen from the first
![]() $N(n)-1\, n$
-blocks. If this string of
$N(n)-1\, n$
-blocks. If this string of
![]() $k_{n}'\, n$
-blocks satisfies condition (1) above, then E is a possible initial string of
$k_{n}'\, n$
-blocks satisfies condition (1) above, then E is a possible initial string of
![]() $k_{n}'\, n$
-blocks in an
$k_{n}'\, n$
-blocks in an
![]() $(n+1)$
-block. If
$(n+1)$
-block. If
![]() $\text {Pr}_{n}(E)$
is the probability of E in the process
$\text {Pr}_{n}(E)$
is the probability of E in the process
![]() $\mathbb {E},$
and
$\mathbb {E},$
and
![]() $\widetilde {\text {Pr}}_{n}(E)$
is the probability of E in the process that consists of concatenating
$\widetilde {\text {Pr}}_{n}(E)$
is the probability of E in the process that consists of concatenating
![]() $k_{n}'\, n$
-blocks chosen independently from the first
$k_{n}'\, n$
-blocks chosen independently from the first
![]() $N(n)-1\, n$
-blocks, then
$N(n)-1\, n$
-blocks, then
 $$ \begin{align} \text{Pr}_{n}(E)=\bigg(\frac{1}{1-\tau_{n}}\bigg)\widetilde{\text{Pr}}_{n}(E) \end{align} $$
$$ \begin{align} \text{Pr}_{n}(E)=\bigg(\frac{1}{1-\tau_{n}}\bigg)\widetilde{\text{Pr}}_{n}(E) \end{align} $$
if E is a possible initial string, and
![]() $\text {Pr}{}_{n}(E)=0$
if E is not a possible initial string. Note that if we compare the probability distributions
$\text {Pr}{}_{n}(E)=0$
if E is not a possible initial string. Note that if we compare the probability distributions
![]() $\text {Pr}_{n}$
and
$\text {Pr}_{n}$
and
![]() $\widetilde {\text {Pr}}_{n}$
on the collection
$\widetilde {\text {Pr}}_{n}$
on the collection
![]() $\mathcal {A}$
of all strings of
$\mathcal {A}$
of all strings of
![]() $k_{n}'\, n$
-blocks, and the collection
$k_{n}'\, n$
-blocks, and the collection
![]() $\mathcal {A}'$
of possible initial strings of
$\mathcal {A}'$
of possible initial strings of
![]() $k_{n}'\, n$
-blocks chosen from the first
$k_{n}'\, n$
-blocks chosen from the first
![]() $N(n)-1\, n$
-blocks, we obtain
$N(n)-1\, n$
-blocks, we obtain
 $$ \begin{align} \sum_{E\in\mathcal{A}}|\text{Pr}_{n}(E)-\widetilde{\text{Pr}}_{n}(E)|& =\tau_{n}+\sum_{E\in\mathcal{A}'}|\text{Pr}_{n}(E)-\widetilde{\text{Pr}}_{n}(E)| \nonumber\\ & =\tau_{n}+\bigg(\frac{1}{1-\tau_{n}}-1\bigg)(1-\tau_{n})=2\tau_{n}. \end{align} $$
$$ \begin{align} \sum_{E\in\mathcal{A}}|\text{Pr}_{n}(E)-\widetilde{\text{Pr}}_{n}(E)|& =\tau_{n}+\sum_{E\in\mathcal{A}'}|\text{Pr}_{n}(E)-\widetilde{\text{Pr}}_{n}(E)| \nonumber\\ & =\tau_{n}+\bigg(\frac{1}{1-\tau_{n}}-1\bigg)(1-\tau_{n})=2\tau_{n}. \end{align} $$
For
![]() $i=1,2,\ldots ,|\Sigma |,$
let
$i=1,2,\ldots ,|\Sigma |,$
let
![]() $P_{i}$
be the set of points in
$P_{i}$
be the set of points in
![]() $\Sigma ^{\mathbb {Z}}$
with the symbol i in position
$\Sigma ^{\mathbb {Z}}$
with the symbol i in position
![]() $0.$
Then
$0.$
Then
![]() $\mathcal {P}:=\{P_{1},P_{2},\ldots ,P_{|\Sigma |}\}$
is a generating partition for the odometer system. For integers a and b with
$\mathcal {P}:=\{P_{1},P_{2},\ldots ,P_{|\Sigma |}\}$
is a generating partition for the odometer system. For integers a and b with
![]() $a\le b,$
let
$a\le b,$
let
![]() $\mathcal {P}_{a}^{b}$
denote the partition of
$\mathcal {P}_{a}^{b}$
denote the partition of
![]() $\Sigma ^{\mathbb {Z}}$
into sets with the same
$\Sigma ^{\mathbb {Z}}$
into sets with the same
![]() $\mathcal {P}$
-name from time a to time
$\mathcal {P}$
-name from time a to time
![]() $b.$
As before, we let
$b.$
As before, we let
![]() $\mu $
denote the invariant measure on
$\mu $
denote the invariant measure on
![]() $\Sigma ^{\mathbb {Z}}$
corresponding to the process
$\Sigma ^{\mathbb {Z}}$
corresponding to the process
![]() $\mathbb {E}.$
We let
$\mathbb {E}.$
We let
![]() $H=H$
(sh,
$H=H$
(sh,
![]() $\mathcal {P})$
denote the measure entropy of the left shift on
$\mathcal {P})$
denote the measure entropy of the left shift on
![]() $\Sigma ^{\mathbb {Z}}$
with respect to
$\Sigma ^{\mathbb {Z}}$
with respect to
![]() $\mathcal {P},$
and we let
$\mathcal {P},$
and we let
![]() $H_{{\textrm {top}}}({\textrm {sh}},\mathcal {P})$
denote the topological entropy. Note that uniformity and unique readability imply that sh
$H_{{\textrm {top}}}({\textrm {sh}},\mathcal {P})$
denote the topological entropy. Note that uniformity and unique readability imply that sh
![]() $:\Sigma ^{\mathbb {Z}}\to \Sigma ^{\mathbb {\mathbb {Z}}}$
is uniquely ergodic. Therefore, by the variational principle [Reference Katok and HasselblattKH95, Theorem 4.5.3],
$:\Sigma ^{\mathbb {Z}}\to \Sigma ^{\mathbb {\mathbb {Z}}}$
is uniquely ergodic. Therefore, by the variational principle [Reference Katok and HasselblattKH95, Theorem 4.5.3],
![]() $H=H_{{\textrm {top}}}({\textrm {sh}},\mathcal {P}).$
$H=H_{{\textrm {top}}}({\textrm {sh}},\mathcal {P}).$
Lemma 4.2. If
![]() $\mathbb {E}$
is the odometer-based system constructed above, then the entropy of
$\mathbb {E}$
is the odometer-based system constructed above, then the entropy of
![]() $\mathbb {E}$
is positive.
$\mathbb {E}$
is positive.
Proof. The number of elements in
 $\mathcal {P}_{1}^{\mathtt {h}_{n}}$
is at least
$\mathcal {P}_{1}^{\mathtt {h}_{n}}$
is at least
![]() $N(n),$
while the number of elements in
$N(n),$
while the number of elements in
 $\mathcal {P}_{1}^{k\mathtt {h}_{n}}$
is at most
$\mathcal {P}_{1}^{k\mathtt {h}_{n}}$
is at most
![]() $\mathtt {h}_{n}N(n)^{k+1}$
. These estimates show that
$\mathtt {h}_{n}N(n)^{k+1}$
. These estimates show that
 $$ \begin{align*} H=\lim_{n\to\infty}\frac{\log N(n)}{\mathtt{h}_{n}}. \end{align*} $$
$$ \begin{align*} H=\lim_{n\to\infty}\frac{\log N(n)}{\mathtt{h}_{n}}. \end{align*} $$
Here
 $\mathtt {h}_{n}=\prod _{i=0}^{n-1}k_{i}$
and
$\mathtt {h}_{n}=\prod _{i=0}^{n-1}k_{i}$
and
![]() $N(n+1)=N(n)^{k_{n}'}(1-\tau _{n})>N(n)^{k_{n}'-1}.$
Thus
$N(n+1)=N(n)^{k_{n}'}(1-\tau _{n})>N(n)^{k_{n}'-1}.$
Thus
 $$ \begin{align*} \frac{\log N(n+1)}{\mathtt{h}_{n+1}}\ge\frac{(k_{n}'-1)\log N(n)}{k_{n}\mathtt{h}_{n}}\ge\frac{(1-2\varepsilon_{n})\log N(n)}{\mathtt{h}_{n}}. \end{align*} $$
$$ \begin{align*} \frac{\log N(n+1)}{\mathtt{h}_{n+1}}\ge\frac{(k_{n}'-1)\log N(n)}{k_{n}\mathtt{h}_{n}}\ge\frac{(1-2\varepsilon_{n})\log N(n)}{\mathtt{h}_{n}}. \end{align*} $$
Therefore
 $$ \begin{align*} \frac{\log N(n)}{\mathtt{h}_{n}}\ge(\log|\Sigma|)\prod_{i=0}^{n-1}(1-2\varepsilon_{i}). \end{align*} $$
$$ \begin{align*} \frac{\log N(n)}{\mathtt{h}_{n}}\ge(\log|\Sigma|)\prod_{i=0}^{n-1}(1-2\varepsilon_{i}). \end{align*} $$
Since
![]() $\prod _{i=0}^{\infty }(1-2\varepsilon _{i})$
converges to a positive value, it follows that
$\prod _{i=0}^{\infty }(1-2\varepsilon _{i})$
converges to a positive value, it follows that
![]() $H>0.$
$H>0.$
Lemma 4.3. (Conditioning lemma)
Suppose
![]() $\mathrm{Pr}$
and
$\mathrm{Pr}$
and
![]() $\mathrm{Pr}'$
are two probability distributions defined on the join
$\mathrm{Pr}'$
are two probability distributions defined on the join
![]() $\mathcal {Q}\lor \mathcal {R}$
of two partitions
$\mathcal {Q}\lor \mathcal {R}$
of two partitions
![]() $\mathcal {Q}$
and
$\mathcal {Q}$
and
![]() $\mathcal {R}$
of the same space. Suppose that for some
$\mathcal {R}$
of the same space. Suppose that for some
![]() $0<\varepsilon <1,$
$0<\varepsilon <1,$
 $$ \begin{align} \sum_{Q\in\mathcal{Q},R\in\mathcal{R}}|\mathrm{Pr}(Q\cap R)-\mathrm{Pr}'(Q\cap R)|<\varepsilon. \end{align} $$
$$ \begin{align} \sum_{Q\in\mathcal{Q},R\in\mathcal{R}}|\mathrm{Pr}(Q\cap R)-\mathrm{Pr}'(Q\cap R)|<\varepsilon. \end{align} $$
Also assume that
![]() $\mathrm{Pr}'(Q)>0$
whenever
$\mathrm{Pr}'(Q)>0$
whenever
![]() $\mathrm{Pr}(Q)>0$
. Then for all but
$\mathrm{Pr}(Q)>0$
. Then for all but
![]() $\mathrm{Pr}$
at most
$\mathrm{Pr}$
at most
![]() $\sqrt {\varepsilon }$
of the Qs in
$\sqrt {\varepsilon }$
of the Qs in
![]() $\mathcal {Q},$
the conditional probabilities corresponding to
$\mathcal {Q},$
the conditional probabilities corresponding to
![]() $\mathrm{Pr}$
and
$\mathrm{Pr}$
and
![]() $\mathrm{Pr}'$
satisfy
$\mathrm{Pr}'$
satisfy
 $$ \begin{align*} \sum_{R\in\mathcal{R}}|\mathrm{Pr}(R|Q)-\mathrm{Pr}'(R|Q)|<2\sqrt{\varepsilon}. \end{align*} $$
$$ \begin{align*} \sum_{R\in\mathcal{R}}|\mathrm{Pr}(R|Q)-\mathrm{Pr}'(R|Q)|<2\sqrt{\varepsilon}. \end{align*} $$
Proof. It follows from (4.3) that for all but
![]() $\text {Pr }$
at most
$\text {Pr }$
at most
![]() $\sqrt {\varepsilon }$
of the Qs in
$\sqrt {\varepsilon }$
of the Qs in
![]() $\mathcal {Q},$
$\mathcal {Q},$
 $$ \begin{align} \sum_{R\in\mathcal{R}}|\text{Pr}(Q\cap R)-\text{Pr}'(Q\cap R)|<\sqrt{\varepsilon}\text{Pr}(Q). \end{align} $$
$$ \begin{align} \sum_{R\in\mathcal{R}}|\text{Pr}(Q\cap R)-\text{Pr}'(Q\cap R)|<\sqrt{\varepsilon}\text{Pr}(Q). \end{align} $$
Suppose
![]() $Q\in \mathcal {Q}$
is chosen so that (4.4) holds. Then
$Q\in \mathcal {Q}$
is chosen so that (4.4) holds. Then
 $$ \begin{align*} |\text{Pr}(Q)-\text{Pr}'(Q)|=\bigg|\sum_{R\in\mathcal{R}}[\text{Pr}(Q\cap R)-\text{Pr}'(Q\cap R)]\bigg\rvert <\sqrt{\varepsilon}\text{Pr}(Q). \end{align*} $$
$$ \begin{align*} |\text{Pr}(Q)-\text{Pr}'(Q)|=\bigg|\sum_{R\in\mathcal{R}}[\text{Pr}(Q\cap R)-\text{Pr}'(Q\cap R)]\bigg\rvert <\sqrt{\varepsilon}\text{Pr}(Q). \end{align*} $$
If we divide (4.4) by
![]() $\text {Pr}(Q)$
, we obtain
$\text {Pr}(Q)$
, we obtain
 $$ \begin{align} \sum_{R\in\mathcal{R}}\bigg|\frac{\text{Pr}(Q\cap R)}{\text{Pr}(Q)}-\frac{\text{Pr}'(Q\cap R)}{\text{Pr}(Q)}\bigg|<\sqrt{\varepsilon}. \end{align} $$
$$ \begin{align} \sum_{R\in\mathcal{R}}\bigg|\frac{\text{Pr}(Q\cap R)}{\text{Pr}(Q)}-\frac{\text{Pr}'(Q\cap R)}{\text{Pr}(Q)}\bigg|<\sqrt{\varepsilon}. \end{align} $$
We also have
 $$ \begin{align} \displaystyle{\sum_{R\in\mathcal{R}}\bigg|\frac{\text{Pr}'(Q\cap R)}{\text{Pr}(Q)}-\frac{\text{Pr}'(Q\cap R)}{\text{Pr}'(Q)}\bigg|} & = \displaystyle{\sum_{R\in\mathcal{R}}\text{Pr}'(Q\cap R)\bigg|\frac{1}{\text{Pr}(Q)}-\frac{1}{\text{Pr}'(Q)}\bigg|}\nonumber\\ & = \displaystyle{\text{Pr}'(Q)\frac{|\text{Pr}(Q)-\text{Pr}'(Q)|}{\text{Pr}(Q)\text{Pr}'(Q)}<\sqrt{\varepsilon}.} \end{align} $$
$$ \begin{align} \displaystyle{\sum_{R\in\mathcal{R}}\bigg|\frac{\text{Pr}'(Q\cap R)}{\text{Pr}(Q)}-\frac{\text{Pr}'(Q\cap R)}{\text{Pr}'(Q)}\bigg|} & = \displaystyle{\sum_{R\in\mathcal{R}}\text{Pr}'(Q\cap R)\bigg|\frac{1}{\text{Pr}(Q)}-\frac{1}{\text{Pr}'(Q)}\bigg|}\nonumber\\ & = \displaystyle{\text{Pr}'(Q)\frac{|\text{Pr}(Q)-\text{Pr}'(Q)|}{\text{Pr}(Q)\text{Pr}'(Q)}<\sqrt{\varepsilon}.} \end{align} $$
Remark 4.4. The above proof also holds in case
![]() $\text {Pr}'$
is a probability distribution on a larger space that contains
$\text {Pr}'$
is a probability distribution on a larger space that contains
![]() $\cup _{Q\in \mathcal {Q},R\in \mathcal {R}}$
. That is,
$\cup _{Q\in \mathcal {Q},R\in \mathcal {R}}$
. That is,
 $\sum _{Q\in \mathcal {Q},R\in \mathcal {R}}{\text {Pr}'(Q\cap R)}$
can be less than
$\sum _{Q\in \mathcal {Q},R\in \mathcal {R}}{\text {Pr}'(Q\cap R)}$
can be less than
![]() $1$
.
$1$
.
Lemma 4.5. (Finer partitioning lemma)
Let
![]() $0<\varepsilon <1.$
Suppose
$0<\varepsilon <1.$
Suppose
![]() $\mathcal {Q}$
is a refinement of
$\mathcal {Q}$
is a refinement of
 $\mathcal {P}_{-M}^{0}$
and there is a probability measure
$\mathcal {P}_{-M}^{0}$
and there is a probability measure
![]() $\omega $
on
$\omega $
on
![]() $\Sigma ^{\mathbb {Z}}$
such that there is a collection
$\Sigma ^{\mathbb {Z}}$
such that there is a collection
![]() $\tilde {\mathcal {G}}$
of ‘good atoms’ in
$\tilde {\mathcal {G}}$
of ‘good atoms’ in
![]() $\mathcal {Q}$
with total
$\mathcal {Q}$
with total
![]() $\mu $
-measure greater than
$\mu $
-measure greater than
![]() $1-\varepsilon ^{2}/16$
such that for
$1-\varepsilon ^{2}/16$
such that for
![]() $\tilde {Q}\in \tilde {\mathcal {G}}$
we have
$\tilde {Q}\in \tilde {\mathcal {G}}$
we have
Then there is a collection
![]() $\mathcal {G}$
of ‘good atoms’ in
$\mathcal {G}$
of ‘good atoms’ in
 $\mathcal {P}_{-M}^{0}$
with total
$\mathcal {P}_{-M}^{0}$
with total
![]() $\mu $
-measure greater than
$\mu $
-measure greater than
![]() $1-\varepsilon /4$
such that for
$1-\varepsilon /4$
such that for
![]() $Q\in \mathcal {G}$
we have
$Q\in \mathcal {G}$
we have
Consequently,
for
![]() $Q,R \in \mathcal {G}.$
$Q,R \in \mathcal {G}.$
Proof. We let
![]() $\mathcal {G}$
consist of those atoms Q in
$\mathcal {G}$
consist of those atoms Q in
 $\mathcal {P}_{-M}^{0}$
such that a subset of Q of measure greater than
$\mathcal {P}_{-M}^{0}$
such that a subset of Q of measure greater than
![]() $(1-\varepsilon /4)\mu (Q)$
is a union of atoms in
$(1-\varepsilon /4)\mu (Q)$
is a union of atoms in
![]() $\tilde {\mathcal {G}}.$
$\tilde {\mathcal {G}}.$
The following definition is due to Ornstein [Reference OrnsteinOr70].
Definition 4.6. A partition
![]() $\mathcal {R}$
is said to be
$\mathcal {R}$
is said to be
![]() $\varepsilon $
-independent of a partition
$\varepsilon $
-independent of a partition
![]() $\mathcal {Q}$
(with respect to a given measure
$\mathcal {Q}$
(with respect to a given measure
![]() $\nu $
) if for a collection of atoms
$\nu $
) if for a collection of atoms
![]() $Q\in \mathcal {Q}$
of total
$Q\in \mathcal {Q}$
of total
![]() $\nu $
-measure at least
$\nu $
-measure at least
![]() $1-\varepsilon ,$
$1-\varepsilon ,$
 $$ \begin{align*} \sum_{R\in\mathcal{R}}|\nu(R|Q)-\nu(R)|\le\varepsilon. \end{align*} $$
$$ \begin{align*} \sum_{R\in\mathcal{R}}|\nu(R|Q)-\nu(R)|\le\varepsilon. \end{align*} $$
In this case we write
![]() $\mathcal {R}\perp _{\nu }^{\varepsilon }\mathcal {Q}.$
If the measure
$\mathcal {R}\perp _{\nu }^{\varepsilon }\mathcal {Q}.$
If the measure
![]() $\nu $
is understood, we may omit the subscript
$\nu $
is understood, we may omit the subscript
![]() $\nu .$
$\nu .$
Remark 4.7. If
![]() $\mathcal {Q},\mathcal {R},$
and
$\mathcal {Q},\mathcal {R},$
and
![]() $\mathcal {S}$
are partitions such that
$\mathcal {S}$
are partitions such that
![]() $\mathcal {R}$
refines
$\mathcal {R}$
refines
![]() $\mathcal {S}$
and
$\mathcal {S}$
and
![]() $\mathcal {R}\perp _{\nu }^{\varepsilon }\mathcal {Q}$
, then by the triangle inequality,
$\mathcal {R}\perp _{\nu }^{\varepsilon }\mathcal {Q}$
, then by the triangle inequality,
![]() $\mathcal {S}\perp _{\nu }^{\varepsilon }\mathcal {Q}.$
$\mathcal {S}\perp _{\nu }^{\varepsilon }\mathcal {Q}.$
Remark 4.8. The definition of
![]() $\varepsilon $
-independence is not symmetric in
$\varepsilon $
-independence is not symmetric in
![]() $\mathcal {Q}$
and
$\mathcal {Q}$
and
![]() $\mathcal {R},$
but
$\mathcal {R},$
but
![]() $\mathcal {R}\perp _{\nu }^{\varepsilon }\mathcal {Q}$
implies
$\mathcal {R}\perp _{\nu }^{\varepsilon }\mathcal {Q}$
implies
 $\mathcal {Q}\perp _{\nu }^{\sqrt {3\varepsilon }}\mathcal {R}.$
(See [Reference SmorodinskySm71].)
$\mathcal {Q}\perp _{\nu }^{\sqrt {3\varepsilon }}\mathcal {R}.$
(See [Reference SmorodinskySm71].)
Lemma 4.9. (Epsilon independence lemma)
Let
![]() $\tau _{n}$
be as in the Chebyshev application, and let Pr
$\tau _{n}$
be as in the Chebyshev application, and let Pr
![]() $_{n}$
be the probability distribution on possible initial strings of
$_{n}$
be the probability distribution on possible initial strings of
![]() $k_{n}'\, n$
-blocks within
$k_{n}'\, n$
-blocks within
![]() $(n+1)$
-blocks. Let
$(n+1)$
-blocks. Let
![]() $\mathcal {Q}$
and
$\mathcal {Q}$
and
![]() $\mathcal {R}$
be partitions of the union of all
$\mathcal {R}$
be partitions of the union of all
![]() $(n+1)$
-blocks such that
$(n+1)$
-blocks such that
![]() $\mathcal {Q}$
is the partition into sets that have the same
$\mathcal {Q}$
is the partition into sets that have the same
![]() $a_{n}$
initial n-blocks and
$a_{n}$
initial n-blocks and
![]() $\mathcal {R}$
is the partition into sets that have the same
$\mathcal {R}$
is the partition into sets that have the same
![]() $b_{n}\, n$
-blocks appearing as the
$b_{n}\, n$
-blocks appearing as the
![]() $(a_{n}+1)$
th through
$(a_{n}+1)$
th through
![]() $(a_{n}+b_{n})$
th n-blocks of an
$(a_{n}+b_{n})$
th n-blocks of an
![]() $(n+1)$
-block. Assume that
$(n+1)$
-block. Assume that
![]() $a_{n}+b_{n}\le k_{n}'.$
Then
$a_{n}+b_{n}\le k_{n}'.$
Then
 $\mathcal {R}\perp _{\mathrm{Pr}_{n}}^{3\sqrt {\tau _{n}}}\mathcal {Q}.$
$\mathcal {R}\perp _{\mathrm{Pr}_{n}}^{3\sqrt {\tau _{n}}}\mathcal {Q}.$
Proof. Let
![]() $\widetilde {\text {Pr}}_{n}$
be the probability distribution for
$\widetilde {\text {Pr}}_{n}$
be the probability distribution for
![]() $k_{n}'\, n$
-blocks chosen independently from the first
$k_{n}'\, n$
-blocks chosen independently from the first
![]() $N(n)-1\, n$
-blocks, with each of these n-blocks equally likely. Then by equation (4.2),
$N(n)-1\, n$
-blocks, with each of these n-blocks equally likely. Then by equation (4.2),
 $$ \begin{align*} \sum_{Q\cap R\in\mathcal{Q}\lor\mathcal{R}}|\text{Pr}_{n}(Q\cap R)-\widetilde{\text{Pr}}_{n}(Q\cap R)|\le\tau_{n}. \end{align*} $$
$$ \begin{align*} \sum_{Q\cap R\in\mathcal{Q}\lor\mathcal{R}}|\text{Pr}_{n}(Q\cap R)-\widetilde{\text{Pr}}_{n}(Q\cap R)|\le\tau_{n}. \end{align*} $$
Note that we are only summing over those
![]() $Q\cap R$
that actually occur as initial strings of some
$Q\cap R$
that actually occur as initial strings of some
![]() $(n+1)$
-block(s). Therefore by Lemma 4.3 and Remark 4.4, for a collection
$(n+1)$
-block(s). Therefore by Lemma 4.3 and Remark 4.4, for a collection
![]() $\mathcal {G}$
of
$\mathcal {G}$
of
![]() $Q\in \mathcal {Q}$
of total
$Q\in \mathcal {Q}$
of total
![]() $\text {Pr}_{n}$
measure at least
$\text {Pr}_{n}$
measure at least
![]() $1-\sqrt {\tau _{n}},$
$1-\sqrt {\tau _{n}},$
 $$ \begin{align*} \sum_{R\in\mathcal{R}}|\text{Pr}_{n}(R|Q)-\widetilde{\text{Pr}}_{n}(R|Q)|\le2\sqrt{\tau_{n}}. \end{align*} $$
$$ \begin{align*} \sum_{R\in\mathcal{R}}|\text{Pr}_{n}(R|Q)-\widetilde{\text{Pr}}_{n}(R|Q)|\le2\sqrt{\tau_{n}}. \end{align*} $$
But
![]() $\widetilde {\text {Pr}}_{n}(R|Q)=\widetilde {\text {Pr}}_{n}(R),$
and
$\widetilde {\text {Pr}}_{n}(R|Q)=\widetilde {\text {Pr}}_{n}(R),$
and
 $\sum _{R\in \mathcal {R}}|\text {Pr}_{n}(R)-\widetilde {\text {Pr}}_{n}(R)|\le \tau _{n}.$
Therefore for
$\sum _{R\in \mathcal {R}}|\text {Pr}_{n}(R)-\widetilde {\text {Pr}}_{n}(R)|\le \tau _{n}.$
Therefore for
![]() $Q\in \mathcal {G},$
$Q\in \mathcal {G},$
 $$ \begin{align*} \sum_{R\in\mathcal{R}}|\text{Pr}_{n}(R|Q)-\text{Pr}_{n}(R)|\le2\sqrt{\tau_{n}}+\tau_{n}<3\sqrt{\tau_{n}}.\\[-3.8pc] \end{align*} $$
$$ \begin{align*} \sum_{R\in\mathcal{R}}|\text{Pr}_{n}(R|Q)-\text{Pr}_{n}(R)|\le2\sqrt{\tau_{n}}+\tau_{n}<3\sqrt{\tau_{n}}.\\[-3.8pc] \end{align*} $$
Remark 4.10. If
![]() $b_{n}=1,$
then
$b_{n}=1,$
then
![]() $\text {Pr}_{n}(R)=\widetilde {\text {Pr}}_{n}(R)$
and
$\text {Pr}_{n}(R)=\widetilde {\text {Pr}}_{n}(R)$
and
 $\mathcal {R}\perp _{\text {Pr}_{n}}^{2\sqrt {\tau _{n}}}\mathcal {Q}.$
$\mathcal {R}\perp _{\text {Pr}_{n}}^{2\sqrt {\tau _{n}}}\mathcal {Q}.$
The following lemma will be used in the inductive step of the proof that the odometer-based system
![]() $\mathbb {E}$
is loosely Bernoulli.
$\mathbb {E}$
is loosely Bernoulli.
Lemma 4.11. (Inductive step)
Suppose
![]() $\nu $
is a probability measure, and
$\nu $
is a probability measure, and
![]() $\mathcal {R}_{1}$
,
$\mathcal {R}_{1}$
,
![]() $\mathcal {R}_{2}$
,
$\mathcal {R}_{2}$
,
![]() $\mathcal {Q}_{1}$
,
$\mathcal {Q}_{1}$
,
![]() $\mathcal {Q}_{2}$
are measurable partitions. If
$\mathcal {Q}_{2}$
are measurable partitions. If
![]() $\mathcal {R}_{1}\perp _{\nu }^{\varepsilon _{1}}\mathcal {Q}_{1}$
and
$\mathcal {R}_{1}\perp _{\nu }^{\varepsilon _{1}}\mathcal {Q}_{1}$
and
![]() $\mathcal {R}_{1}=\mathcal {Q}_{2}\lor \mathcal {R}_{2},$
where
$\mathcal {R}_{1}=\mathcal {Q}_{2}\lor \mathcal {R}_{2},$
where
![]() $\mathcal {R}_{2}\perp _{\nu }^{\varepsilon _{2}}\mathcal {Q}_{2}$
and
$\mathcal {R}_{2}\perp _{\nu }^{\varepsilon _{2}}\mathcal {Q}_{2}$
and
![]() $0<\varepsilon _1,\varepsilon _2<1$
, then
$0<\varepsilon _1,\varepsilon _2<1$
, then
 $\mathcal {R}_{2}\perp _{\nu }^{2\sqrt {\varepsilon _{1}}+2\sqrt {\varepsilon _{2}}}\mathcal {Q}_{1}\lor \mathcal {Q}_{2}.$
$\mathcal {R}_{2}\perp _{\nu }^{2\sqrt {\varepsilon _{1}}+2\sqrt {\varepsilon _{2}}}\mathcal {Q}_{1}\lor \mathcal {Q}_{2}.$
Proof. Since
![]() $\mathcal {R}_{2}\perp _{\nu }^{\varepsilon _{2}}\mathcal {Q}_{2},$
for a collection
$\mathcal {R}_{2}\perp _{\nu }^{\varepsilon _{2}}\mathcal {Q}_{2},$
for a collection
![]() $\mathcal {G}_{2}$
of atoms
$\mathcal {G}_{2}$
of atoms
![]() $Q_{2}$
of
$Q_{2}$
of
![]() $\mathcal {Q}_{2}$
with
$\mathcal {Q}_{2}$
with
![]() $\nu (\cup _{Q_{2}\in \mathcal {G}_{2}}Q_{2})\ge 1-\varepsilon _{2},$
$\nu (\cup _{Q_{2}\in \mathcal {G}_{2}}Q_{2})\ge 1-\varepsilon _{2},$
 $$ \begin{align} \sum_{R_{2}\in\mathcal{R}_{2}}|\nu(R_{2}|Q_{2})-\nu(R_{2})|\le\varepsilon_{2}. \end{align} $$
$$ \begin{align} \sum_{R_{2}\in\mathcal{R}_{2}}|\nu(R_{2}|Q_{2})-\nu(R_{2})|\le\varepsilon_{2}. \end{align} $$
For at least total
![]() $\nu $
-measure
$\nu $
-measure
![]() $1-\sqrt {\varepsilon _{2}}$
of the
$1-\sqrt {\varepsilon _{2}}$
of the
![]() $Q_{1}$
in
$Q_{1}$
in
![]() $\mathcal {Q}_{1},$
$\mathcal {Q}_{1},$
That is,
![]() $\mathcal {G}_{2}$
has total
$\mathcal {G}_{2}$
has total
![]() $\nu (\cdot |Q_{1})$
measure at least
$\nu (\cdot |Q_{1})$
measure at least
![]() $1-\sqrt {\varepsilon _{2}}.$
Since
$1-\sqrt {\varepsilon _{2}}.$
Since
![]() $\mathcal {R}_{1}=\mathcal {Q}_{2}\lor \mathcal {R}_{2}$
and
$\mathcal {R}_{1}=\mathcal {Q}_{2}\lor \mathcal {R}_{2}$
and
![]() $\mathcal {R}_{1}\perp _{\nu }^{\varepsilon _{1}}\mathcal {Q}_{1}$
, for a collection of atoms
$\mathcal {R}_{1}\perp _{\nu }^{\varepsilon _{1}}\mathcal {Q}_{1}$
, for a collection of atoms
![]() $Q_{1}\in \mathcal {Q}_{1}$
of total
$Q_{1}\in \mathcal {Q}_{1}$
of total
![]() $\nu $
-measure at least
$\nu $
-measure at least
![]() $1-\varepsilon _{1},$
$1-\varepsilon _{1},$
 $$ \begin{align} \sum_{Q_{2}\cap R_{2}\in\mathcal{Q}_{2}\lor\mathcal{R}_{2}}|\nu(Q_{2}\cap R_{2}|Q_{1})-\nu(Q_{2}\cap R_{2})|\le\varepsilon_{1}. \end{align} $$
$$ \begin{align} \sum_{Q_{2}\cap R_{2}\in\mathcal{Q}_{2}\lor\mathcal{R}_{2}}|\nu(Q_{2}\cap R_{2}|Q_{1})-\nu(Q_{2}\cap R_{2})|\le\varepsilon_{1}. \end{align} $$
Let
![]() $\mathcal {G}_{1}$
be the collection of
$\mathcal {G}_{1}$
be the collection of
![]() $Q_{1}\in \mathcal {Q}_{1}$
such that (4.8) and (4.9) hold. Then we have
$Q_{1}\in \mathcal {Q}_{1}$
such that (4.8) and (4.9) hold. Then we have
![]() $\nu (\cup _{Q_{1}\in \mathcal {G}_{1}}Q_{1})\ge 1-\varepsilon _{1}-\sqrt {\varepsilon _{2}}.$
Fix a choice of
$\nu (\cup _{Q_{1}\in \mathcal {G}_{1}}Q_{1})\ge 1-\varepsilon _{1}-\sqrt {\varepsilon _{2}}.$
Fix a choice of
![]() $Q_{1}\in \mathcal {G}_{1}.$
By Lemma 4.3 applied to
$Q_{1}\in \mathcal {G}_{1}.$
By Lemma 4.3 applied to
![]() $\text {Pr}=\nu (\cdot |Q_{1})$
and
$\text {Pr}=\nu (\cdot |Q_{1})$
and
![]() $\text {Pr}'=\nu ,$
it follows from (4.9) that for a collection
$\text {Pr}'=\nu ,$
it follows from (4.9) that for a collection
![]() $\mathcal {G}_{3}=\mathcal {G}_{3}(Q_{1})$
of atoms
$\mathcal {G}_{3}=\mathcal {G}_{3}(Q_{1})$
of atoms
![]() $Q_{2}\in \mathcal {Q}_{2}$
with total
$Q_{2}\in \mathcal {Q}_{2}$
with total
![]() $\nu (\cdot |Q_{1})$
measure at least
$\nu (\cdot |Q_{1})$
measure at least
![]() $1-\sqrt {\varepsilon _{1}},$
$1-\sqrt {\varepsilon _{1}},$
 $$ \begin{align} \sum_{R_{2}\in\mathcal{R}_{2}}|\nu(R_{2}|Q_{1}\cap Q_{2})-\nu(R_{2}|Q_{2})|\le2\sqrt{\varepsilon_{1}}. \end{align} $$
$$ \begin{align} \sum_{R_{2}\in\mathcal{R}_{2}}|\nu(R_{2}|Q_{1}\cap Q_{2})-\nu(R_{2}|Q_{2})|\le2\sqrt{\varepsilon_{1}}. \end{align} $$
Then
![]() $\nu (\cup _{Q_{2}\in \mathcal {G}_{2}\cap \mathcal {G}_{3}}Q_{2}|Q_{1})\ge 1-\sqrt {\varepsilon _{1}}-\sqrt {\varepsilon _{2}},$
and for
$\nu (\cup _{Q_{2}\in \mathcal {G}_{2}\cap \mathcal {G}_{3}}Q_{2}|Q_{1})\ge 1-\sqrt {\varepsilon _{1}}-\sqrt {\varepsilon _{2}},$
and for
![]() $Q_{2}\in \mathcal {G}_{2}\cap \mathcal {G}_{3},$
it follows from (4.7) and (4.10) that
$Q_{2}\in \mathcal {G}_{2}\cap \mathcal {G}_{3},$
it follows from (4.7) and (4.10) that
 $$ \begin{align} \sum_{R_{2}\in\mathcal{R}_{2}}|\nu(R_{2}|Q_{1}\cap Q_{2})-\nu(R_{2})|\le2\sqrt{\varepsilon_{1}}+\varepsilon_{2}. \end{align} $$
$$ \begin{align} \sum_{R_{2}\in\mathcal{R}_{2}}|\nu(R_{2}|Q_{1}\cap Q_{2})-\nu(R_{2})|\le2\sqrt{\varepsilon_{1}}+\varepsilon_{2}. \end{align} $$
Since
![]() $\nu (\cup _{Q_{1}\in \mathcal {G}_{1}}Q_{1})\ge 1-\varepsilon _{1}-\sqrt {\varepsilon _{2}}$
and for any
$\nu (\cup _{Q_{1}\in \mathcal {G}_{1}}Q_{1})\ge 1-\varepsilon _{1}-\sqrt {\varepsilon _{2}}$
and for any
![]() $Q_{1}\in \mathcal {G}_{1}, \nu (\cup _{Q_{2}\in \mathcal {G}_{2}\cap \mathcal {G}_{3}}Q_{2}|Q_{1})\ge 1-\sqrt {\varepsilon _{1}}-\sqrt {\varepsilon _{2}},$
the collection
$Q_{1}\in \mathcal {G}_{1}, \nu (\cup _{Q_{2}\in \mathcal {G}_{2}\cap \mathcal {G}_{3}}Q_{2}|Q_{1})\ge 1-\sqrt {\varepsilon _{1}}-\sqrt {\varepsilon _{2}},$
the collection
![]() $\mathcal {G}$
of
$\mathcal {G}$
of
![]() $Q_{1}\cap Q_{2}\in \mathcal {Q}_{1}\lor \mathcal {Q}_{2}$
such that (4.11) holds has total
$Q_{1}\cap Q_{2}\in \mathcal {Q}_{1}\lor \mathcal {Q}_{2}$
such that (4.11) holds has total
![]() $\nu $
-measure at least
$\nu $
-measure at least
![]() $(1-\varepsilon _{1}-\sqrt {\varepsilon _{2}})(1-\sqrt {\varepsilon _{1}}-\sqrt {\varepsilon _{2}})>1-2\sqrt {\varepsilon _{1}}-2\sqrt {\varepsilon _{2}}.$
Therefore
$(1-\varepsilon _{1}-\sqrt {\varepsilon _{2}})(1-\sqrt {\varepsilon _{1}}-\sqrt {\varepsilon _{2}})>1-2\sqrt {\varepsilon _{1}}-2\sqrt {\varepsilon _{2}}.$
Therefore
 $\mathcal {R}_{2}\perp _{\nu }^{2\sqrt {\varepsilon _{1}}+2\sqrt {\varepsilon _{2}}}\mathcal {Q}_{1}\lor \mathcal {Q}_{2}.$
$\mathcal {R}_{2}\perp _{\nu }^{2\sqrt {\varepsilon _{1}}+2\sqrt {\varepsilon _{2}}}\mathcal {Q}_{1}\lor \mathcal {Q}_{2}.$
Theorem 4.12. The odometer-based system
![]() $\mathbb {E}$
constructed in this section is loosely Bernoulli.
$\mathbb {E}$
constructed in this section is loosely Bernoulli.
Proof. Let
![]() $0<\varepsilon <1.$
Fix a choice of
$0<\varepsilon <1.$
Fix a choice of
![]() $n\ge 2$
sufficiently large so that
$n\ge 2$
sufficiently large so that
 $\sum _{j\ge n}\varepsilon _{j}<\varepsilon ^{2}/100$
,
$\sum _{j\ge n}\varepsilon _{j}<\varepsilon ^{2}/100$
,
 $\sum _{j\ge n}\tau _j^{(2^{-j})}<\varepsilon ^{2}/100$
, and
$\sum _{j\ge n}\tau _j^{(2^{-j})}<\varepsilon ^{2}/100$
, and
![]() $(\varepsilon _{n}k_{n})^{-1}<\varepsilon ^{2}/16.$
Let
$(\varepsilon _{n}k_{n})^{-1}<\varepsilon ^{2}/16.$
Let
![]() $K=(\varepsilon _{n}k_{n}+1)h_{n}$
and
$K=(\varepsilon _{n}k_{n}+1)h_{n}$
and
![]() $M\ge h_{n+1}.$
We will show that the conclusion of Definition 2.2 holds for these choices of K and
$M\ge h_{n+1}.$
We will show that the conclusion of Definition 2.2 holds for these choices of K and
![]() $M.$
Let
$M.$
Let
![]() $\omega $
be any probability measure on
$\omega $
be any probability measure on
![]() $\Sigma ^{\mathbb {Z}}$
such that
$\Sigma ^{\mathbb {Z}}$
such that
which is the probability that the string
![]() $c_{1}c_{2}\cdots c_{\varepsilon _{n}k_{n}h_{n}}$
comprises the
$c_{1}c_{2}\cdots c_{\varepsilon _{n}k_{n}h_{n}}$
comprises the
![]() $\varepsilon _{n}k_{n}$
initial n-blocks in an
$\varepsilon _{n}k_{n}$
initial n-blocks in an
![]() $(n+1)$
-block. By Lemma 4.5, it suffices to show that for some refinement
$(n+1)$
-block. By Lemma 4.5, it suffices to show that for some refinement
![]() $\mathcal {Q}$
of
$\mathcal {Q}$
of
 $\mathcal {P}_{-M}^{0},$
there is a collection
$\mathcal {P}_{-M}^{0},$
there is a collection
![]() $\mathcal {G}$
of good atoms of
$\mathcal {G}$
of good atoms of
![]() $\mathcal {Q}$
of total measure at least
$\mathcal {Q}$
of total measure at least
![]() $1-\varepsilon ^{2}/16$
such that for
$1-\varepsilon ^{2}/16$
such that for
![]() $Q\in \mathcal {G},$
$Q\in \mathcal {G},$
Fix a choice of m such that
![]() $h_{n+m-1}\ge M.$
Let
$h_{n+m-1}\ge M.$
Let
![]() $\mathcal {S}$
be the partition of the space
$\mathcal {S}$
be the partition of the space
![]() $\Sigma ^{\mathbb {Z}}$
into sets that have the same
$\Sigma ^{\mathbb {Z}}$
into sets that have the same
![]() $(n+m)$
-block structure, that is, time
$(n+m)$
-block structure, that is, time
![]() $0$
is in the same position within the
$0$
is in the same position within the
![]() $(n+m)$
-block.
$(n+m)$
-block.
We now describe the collection
![]() $\tilde {\mathcal {G}}$
of good atoms in
$\tilde {\mathcal {G}}$
of good atoms in
![]() $\mathcal {S}.$
First we eliminate those atoms in
$\mathcal {S}.$
First we eliminate those atoms in
![]() $\mathcal {S}$
such that for any
$\mathcal {S}$
such that for any
![]() $j=2,\ldots ,m$
, the deterministic part of the
$j=2,\ldots ,m$
, the deterministic part of the
![]() $(n+j)$
-block containing time
$(n+j)$
-block containing time
![]() $0$
overlaps with the time interval
$0$
overlaps with the time interval
![]() $[1,K].$
(The deterministic part of an
$[1,K].$
(The deterministic part of an
![]() $(n+j)$
-block consists of the last
$(n+j)$
-block consists of the last
![]() $\varepsilon _{n+j-1}k_{n+j-1}\, (n+j-1)$
-blocks within the
$\varepsilon _{n+j-1}k_{n+j-1}\, (n+j-1)$
-blocks within the
![]() $(n+j)$
-block.) We also eliminate those atoms in
$(n+j)$
-block.) We also eliminate those atoms in
![]() $\mathcal {S}$
such that time
$\mathcal {S}$
such that time
![]() $0$
lies in the first
$0$
lies in the first
![]() $(n+m-1)$
-block within the
$(n+m-1)$
-block within the
![]() $(n+m)$
-block containing time
$(n+m)$
-block containing time
![]() $0.$
Moreover, we eliminate those atoms in
$0.$
Moreover, we eliminate those atoms in
![]() $\mathcal {S}$
such that time
$\mathcal {S}$
such that time
![]() $0$
occurs in any of the last
$0$
occurs in any of the last
![]() $2\varepsilon _{n}k_{n}\, n$
-blocks within an
$2\varepsilon _{n}k_{n}\, n$
-blocks within an
![]() $(n+1)$
-block. The total measure of the sets eliminated is less than
$(n+1)$
-block. The total measure of the sets eliminated is less than
![]() $2(\varepsilon _{n}+\cdots +\varepsilon _{n+m-1})<\varepsilon ^{2}/50.$
Let
$2(\varepsilon _{n}+\cdots +\varepsilon _{n+m-1})<\varepsilon ^{2}/50.$
Let
![]() $\tilde {\mathcal {G}}$
be the collection of atoms in
$\tilde {\mathcal {G}}$
be the collection of atoms in
![]() $\mathcal {S}$
that remain, and fix a choice
$\mathcal {S}$
that remain, and fix a choice
![]() $S\in \tilde {\mathcal {G}}.$
For this S and
$S\in \tilde {\mathcal {G}}.$
For this S and
![]() $j=0,\ldots ,m-1,$
let
$j=0,\ldots ,m-1,$
let
![]() $a_{n+j}$
be the number of
$a_{n+j}$
be the number of
![]() $(n+j)$
-blocks preceding the
$(n+j)$
-blocks preceding the
![]() $(n+j)$
-block containing time
$(n+j)$
-block containing time
![]() $0$
within the
$0$
within the
![]() $(n+j+1)$
-block containing time
$(n+j+1)$
-block containing time
![]() $0.$
Since
$0.$
Since
![]() $a_{n+m-1}\ge 1$
and
$a_{n+m-1}\ge 1$
and
![]() $h_{n+m-1}\ge M,$
the beginning of the
$h_{n+m-1}\ge M,$
the beginning of the
![]() $(n+m)$
-block containing time
$(n+m)$
-block containing time
![]() $0$
occurs at or before time
$0$
occurs at or before time
![]() $-M.$
Let
$-M.$
Let
![]() $\nu =\nu _{S}$
be the normalized restriction of
$\nu =\nu _{S}$
be the normalized restriction of
![]() $\mu $
to
$\mu $
to
![]() $S.$
$S.$
Let
![]() $\mathcal {Q}_{n}$
be the partition of S into sets with the same collection of n-blocks appearing in positions
$\mathcal {Q}_{n}$
be the partition of S into sets with the same collection of n-blocks appearing in positions
![]() $1$
to
$1$
to
![]() $a_{n}+1$
at the beginning of the
$a_{n}+1$
at the beginning of the
![]() $(n+1)$
-block containing time
$(n+1)$
-block containing time
![]() $0,$
and let
$0,$
and let
![]() $\mathcal {R}_{n}$
be the partition of S into sets with the same collection of n-blocks appearing in the
$\mathcal {R}_{n}$
be the partition of S into sets with the same collection of n-blocks appearing in the
![]() $\varepsilon _{n}k_{n}\, n$
-blocks that follow the n-block containing time
$\varepsilon _{n}k_{n}\, n$
-blocks that follow the n-block containing time
![]() $0.$
For
$0.$
For
![]() $k=1,2,\ldots ,m-1,$
let
$k=1,2,\ldots ,m-1,$
let
![]() $\mathcal {Q}_{n+m-k}$
be the partition of S into sets with the same collection of
$\mathcal {Q}_{n+m-k}$
be the partition of S into sets with the same collection of
![]() $(n+m-k)$
-blocks comprising the
$(n+m-k)$
-blocks comprising the
![]() $a_{n+m-k}\, (n+m-k)$
-blocks that precede the
$a_{n+m-k}\, (n+m-k)$
-blocks that precede the
![]() $(n+m-k)$
-block that contains time
$(n+m-k)$
-block that contains time
![]() $0,$
and let
$0,$
and let
![]() $\mathcal {R}_{n+m-k}$
be the partition of S into sets with
$\mathcal {R}_{n+m-k}$
be the partition of S into sets with
![]() $(n+m-k)$
-blocks containing time
$(n+m-k)$
-blocks containing time
![]() $0$
agreeing up to the position of the last symbol in the
$0$
agreeing up to the position of the last symbol in the
![]() $\varepsilon _nk_n\, n$
-blocks that follow the n-block containing time
$\varepsilon _nk_n\, n$
-blocks that follow the n-block containing time
![]() $0$
(see Figure 1).
$0$
(see Figure 1).

Figure 1 For
![]() $j=n,n+1,n+2$
, the
$j=n,n+1,n+2$
, the
![]() $\mathcal {Q}_j$
and
$\mathcal {Q}_j$
and
![]() $\mathcal {R}_j$
are partitions into sets according to the
$\mathcal {R}_j$
are partitions into sets according to the
![]() $\mathcal {P}$
-names that appear in the indicated j-blocks. The actual numbers of j-blocks are much larger than can be depicted in the figure.
$\mathcal {P}$
-names that appear in the indicated j-blocks. The actual numbers of j-blocks are much larger than can be depicted in the figure.
Claim. Let
 $\eta _{n+m-k}=4(\tau _{n+m-1}^{2^{-(k+1)}}+\tau _{n+m-2}^{2^{-k}}+\cdots +\tau _{n+m-(k-1)}^{2^{-3}}+\tau _{n+m-k}^{2^{-2}})$
for
$\eta _{n+m-k}=4(\tau _{n+m-1}^{2^{-(k+1)}}+\tau _{n+m-2}^{2^{-k}}+\cdots +\tau _{n+m-(k-1)}^{2^{-3}}+\tau _{n+m-k}^{2^{-2}})$
for
![]() $k=1, 2,\ldots ,m.$
Then
$k=1, 2,\ldots ,m.$
Then
![]() $\mathcal {R}_{n+m-k}\perp _{\nu }^{\eta _{n+m-k}}(\mathcal {Q}_{n+m-1}\lor \mathcal {Q}_{n+m-2}\lor \cdots \lor \mathcal {Q}_{n+m-k}),$
for
$\mathcal {R}_{n+m-k}\perp _{\nu }^{\eta _{n+m-k}}(\mathcal {Q}_{n+m-1}\lor \mathcal {Q}_{n+m-2}\lor \cdots \lor \mathcal {Q}_{n+m-k}),$
for
![]() $k=1, 2,\ldots ,m.$
$k=1, 2,\ldots ,m.$
Proof. According to Lemma 4.9 and Remark 4.7,
 $\mathcal {R}_{n+m-1}\perp _{\nu }^{3\sqrt {\tau _{n+m-1}}}\mathcal {Q}_{n+m-1}.$
Since
$\mathcal {R}_{n+m-1}\perp _{\nu }^{3\sqrt {\tau _{n+m-1}}}\mathcal {Q}_{n+m-1}.$
Since
 $3\sqrt {\tau _{n+m-1}}<4\tau _{n+m-1}^{2^{-2}}=\eta _{n+m-1},$
the claim holds for
$3\sqrt {\tau _{n+m-1}}<4\tau _{n+m-1}^{2^{-2}}=\eta _{n+m-1},$
the claim holds for
![]() $k=1.$
Now suppose the claim holds for some
$k=1.$
Now suppose the claim holds for some
![]() $k=1,2,\ldots ,m-1,$
that is,
$k=1,2,\ldots ,m-1,$
that is,
![]() $\mathcal {R}_{n+m-k}\perp _{\nu }^{\eta _{n+m-k}}(\mathcal {Q}_{n+m-1}\lor \mathcal {Q}_{n+m-2}\lor \cdots \lor \mathcal {Q}_{n+m-k}).$
We have
$\mathcal {R}_{n+m-k}\perp _{\nu }^{\eta _{n+m-k}}(\mathcal {Q}_{n+m-1}\lor \mathcal {Q}_{n+m-2}\lor \cdots \lor \mathcal {Q}_{n+m-k}).$
We have
![]() $\mathcal {R}_{n+m-k}=\mathcal {Q}_{n+m-(k+1)}\lor \mathcal {R}_{n+m-(k+1)},$
and by Lemma 4.9 and Remark 4.7,
$\mathcal {R}_{n+m-k}=\mathcal {Q}_{n+m-(k+1)}\lor \mathcal {R}_{n+m-(k+1)},$
and by Lemma 4.9 and Remark 4.7,
 $\mathcal {R}_{n+m-(k+1)}\perp _{\nu }^{3\sqrt {\tau _{n+m-(k+1)}}}\mathcal {Q}_{n+m-(k+1)}.$
Therefore, by Lemma 4.11,
$\mathcal {R}_{n+m-(k+1)}\perp _{\nu }^{3\sqrt {\tau _{n+m-(k+1)}}}\mathcal {Q}_{n+m-(k+1)}.$
Therefore, by Lemma 4.11,
![]() $\mathcal {R}_{n+m-(k+1)}\perp _{\nu }^{\eta }(\mathcal {Q}_{n+m-1}\lor \mathcal {Q}_{n+m-2}\lor \cdots \lor \mathcal {Q}_{n+m-(k+1)}),$
where
$\mathcal {R}_{n+m-(k+1)}\perp _{\nu }^{\eta }(\mathcal {Q}_{n+m-1}\lor \mathcal {Q}_{n+m-2}\lor \cdots \lor \mathcal {Q}_{n+m-(k+1)}),$
where
 $$ \begin{align*} \eta & =2\sqrt{\eta_{n+m-k}}+2\sqrt{3}\tau_{n+m-(k+1)}^{2^{-2}}\\ & =4[\tau_{n+m-1}^{2^{-(k+1)}}+\tau_{n+m-2}^{2^{-k}}+\cdots+\tau_{n+m-(k+1)}^{2^{-3}}+\tau_{n+m-k}^{2^{-2}}]^{1/2}+2\sqrt{3}\tau_{n+m-(k+1)}^{2^{-2}}\\ & \le4[\tau_{n+m-1}^{2^{-(k+2)}}+\tau_{n+m-2}^{2^{-(k+1)}}+\cdots+\tau_{n+m-(k+1)}^{2^{-4}}+\tau_{n+m-k}^{2^{-3}}+\tau_{n+m-(k+1)}^{2^{-2}}]\\ & =\eta_{n+m-(k+1).} \end{align*} $$
$$ \begin{align*} \eta & =2\sqrt{\eta_{n+m-k}}+2\sqrt{3}\tau_{n+m-(k+1)}^{2^{-2}}\\ & =4[\tau_{n+m-1}^{2^{-(k+1)}}+\tau_{n+m-2}^{2^{-k}}+\cdots+\tau_{n+m-(k+1)}^{2^{-3}}+\tau_{n+m-k}^{2^{-2}}]^{1/2}+2\sqrt{3}\tau_{n+m-(k+1)}^{2^{-2}}\\ & \le4[\tau_{n+m-1}^{2^{-(k+2)}}+\tau_{n+m-2}^{2^{-(k+1)}}+\cdots+\tau_{n+m-(k+1)}^{2^{-4}}+\tau_{n+m-k}^{2^{-3}}+\tau_{n+m-(k+1)}^{2^{-2}}]\\ & =\eta_{n+m-(k+1).} \end{align*} $$
This completes the inductive step. Therefore the claim holds.
Applying the claim with
![]() $k=m,$
we obtain
$k=m,$
we obtain
![]() $\mathcal {R}_{n}\perp _{\nu }^{\eta _{n}}(\mathcal {Q}_{n+m-1}\lor \cdots \lor \mathcal {Q}_{n}).$
Note that
$\mathcal {R}_{n}\perp _{\nu }^{\eta _{n}}(\mathcal {Q}_{n+m-1}\lor \cdots \lor \mathcal {Q}_{n}).$
Note that
![]() $\mathcal {Q}_{n+m-1}\lor \cdots \lor \mathcal {Q}_{n}$
is a refinement of
$\mathcal {Q}_{n+m-1}\lor \cdots \lor \mathcal {Q}_{n}$
is a refinement of
 $S\cap \mathcal {P}_{-M}^{0}$
and
$S\cap \mathcal {P}_{-M}^{0}$
and
![]() $\mathcal {R}_{n}$
is the partition into the possible
$\mathcal {R}_{n}$
is the partition into the possible
![]() $\varepsilon _{n}k_{n}\, n$
-blocks comprising a fraction
$\varepsilon _{n}k_{n}\, n$
-blocks comprising a fraction
![]() $\varepsilon _{n}k_{n}h_{n}/K=\varepsilon _{n}k_{n}/(\varepsilon _{n}k_{n}+1)>1-\varepsilon ^{2}/16$
of the
$\varepsilon _{n}k_{n}h_{n}/K=\varepsilon _{n}k_{n}/(\varepsilon _{n}k_{n}+1)>1-\varepsilon ^{2}/16$
of the
 $\mathcal {P}_{1}^{K}$
names. Since
$\mathcal {P}_{1}^{K}$
names. Since
![]() $\mathcal {R}_{n}\perp _{\nu }^{\eta _{n}}(\mathcal {Q}_{n+m-1}\lor \cdots \lor \mathcal {Q}_{n}),$
for a set
$\mathcal {R}_{n}\perp _{\nu }^{\eta _{n}}(\mathcal {Q}_{n+m-1}\lor \cdots \lor \mathcal {Q}_{n}),$
for a set
![]() $\mathcal {G}_{S}$
of atoms
$\mathcal {G}_{S}$
of atoms
![]() $Q\in \mathcal {Q}_{n+m-1}\lor \cdots \lor \mathcal {Q}_{n}$
of
$Q\in \mathcal {Q}_{n+m-1}\lor \cdots \lor \mathcal {Q}_{n}$
of
![]() $\nu $
-measure at least
$\nu $
-measure at least
![]() $1-\eta _{n},$
there is a measure-preserving map
$1-\eta _{n},$
there is a measure-preserving map
![]() $\phi _{S}:(S,\nu )\to (S\cap Q,\nu (\cdot |Q))$
such that on a set of
$\phi _{S}:(S,\nu )\to (S\cap Q,\nu (\cdot |Q))$
such that on a set of
![]() $\nu $
-measure at least
$\nu $
-measure at least
![]() $1-\eta _{n}, \phi _{S}(x)$
is contained in the intersection with Q of that atom of
$1-\eta _{n}, \phi _{S}(x)$
is contained in the intersection with Q of that atom of
![]() $\mathcal {R}_{n}$
that contains
$\mathcal {R}_{n}$
that contains
![]() $x,$
and the
$x,$
and the
![]() $\mathcal {R}_{n}$
part of the
$\mathcal {R}_{n}$
part of the
 $\mathcal {P}_{1}^{K}$
name of x is the same as that of
$\mathcal {P}_{1}^{K}$
name of x is the same as that of
![]() $\phi _{S}(x).$
Thus,
$\phi _{S}(x).$
Thus,
![]() $\overline {f}_{K}(\nu (\cdot |Q),\omega )<\varepsilon /4$
for
$\overline {f}_{K}(\nu (\cdot |Q),\omega )<\varepsilon /4$
for
![]() $Q\in \mathcal {G}_{S}.$
Finally, we let
$Q\in \mathcal {G}_{S}.$
Finally, we let
 $\mathcal {G}=\cup _{S\in \tilde{\mathcal {G}}}\mathcal {G}_{S}.$
Then the total
$\mathcal {G}=\cup _{S\in \tilde{\mathcal {G}}}\mathcal {G}_{S}.$
Then the total
![]() $\mu $
-measure of atoms in
$\mu $
-measure of atoms in
![]() $\mathcal {G}$
is greater than
$\mathcal {G}$
is greater than
![]() $1-\varepsilon ^{2}/50-\eta _{n}>1-\varepsilon ^{2}/16.$
Note that for
$1-\varepsilon ^{2}/50-\eta _{n}>1-\varepsilon ^{2}/16.$
Note that for
![]() $Q\in \mathcal {G}_{S}, \nu _{S}(\cdot |Q)$
is the same as
$Q\in \mathcal {G}_{S}, \nu _{S}(\cdot |Q)$
is the same as
![]() $\mu (\cdot |Q).$
Therefore, for
$\mu (\cdot |Q).$
Therefore, for
![]() $Q\in \mathcal {G}_{S}, \overline {f}_{K}(\mu (\cdot |Q),\omega )<\varepsilon /4.$
Then Lemma 4.5 implies that Definition 2.2 is satisfied.□
$Q\in \mathcal {G}_{S}, \overline {f}_{K}(\mu (\cdot |Q),\omega )<\varepsilon /4.$
Then Lemma 4.5 implies that Definition 2.2 is satisfied.□
4.2. Non-loosely Bernoulli circular system arising from positive-entropy loosely Bernoulli odometer-based system
Theorem 4.13. If
![]() $\mathbb {E}$
is the positive-entropy loosely Bernoulli odometer-based system constructed in the previous section, and
$\mathbb {E}$
is the positive-entropy loosely Bernoulli odometer-based system constructed in the previous section, and
![]() $\mathcal {F}$
is the map from odometer-based systems to circular systems defined in §3, then
$\mathcal {F}$
is the map from odometer-based systems to circular systems defined in §3, then
![]() $\mathcal {F}(\mathbb {E})$
is non-loosely Bernoulli.
$\mathcal {F}(\mathbb {E})$
is non-loosely Bernoulli.
We will prove
![]() $\mathcal {F}(\mathbb {E})$
is not loosely Bernoulli by proving that the condition in Lemma 3.5 does not hold.
$\mathcal {F}(\mathbb {E})$
is not loosely Bernoulli by proving that the condition in Lemma 3.5 does not hold.
In the construction of
![]() $\mathcal {W}_{n+1}$
words in the circular system, we have many repetitions of
$\mathcal {W}_{n+1}$
words in the circular system, we have many repetitions of
![]() $\mathcal {W}_{n}\text { words.}$
To get lower bounds on the
$\mathcal {W}_{n}\text { words.}$
To get lower bounds on the
![]() $\overline {f}$
distance between
$\overline {f}$
distance between
![]() $\mathcal {W}_{n+1}$
words, we will make use of Definition 4.14 and Lemma 4.15 below.
$\mathcal {W}_{n+1}$
words, we will make use of Definition 4.14 and Lemma 4.15 below.
Definition 4.14. If
![]() $b_{1}b_{2}\ldots b_{s}$
is any string of s symbols, let
$b_{1}b_{2}\ldots b_{s}$
is any string of s symbols, let
![]() $\mathcal {T}(b_{1}b_{2}\ldots b_{s})$
denote the collection of all finite consecutive substrings of
$\mathcal {T}(b_{1}b_{2}\ldots b_{s})$
denote the collection of all finite consecutive substrings of
![]() $(b_{1}b_{2}\ldots b_{s})^{t}$
for any
$(b_{1}b_{2}\ldots b_{s})^{t}$
for any
![]() $t\ge 1.$
$t\ge 1.$
Lemma 4.15. (Repeated substring matching lemma)
Suppose
![]() $a_{1}\ldots a_{r}$
and
$a_{1}\ldots a_{r}$
and
![]() $b_{1}\ldots b_{s}$
are strings of symbols. Then for any
$b_{1}\ldots b_{s}$
are strings of symbols. Then for any
![]() $\ell ,\tilde {\ell }\ge 1$
,
$\ell ,\tilde {\ell }\ge 1$
,
 $$ \begin{align*} \overline{f}((a_{1}\ldots a_{r})^{\ell},(b_{1}\ldots b_{s})^{\tilde{\ell}})\ge\overline{f}(a_{1}\ldots a_{r},\mathcal{T}(b_{1}\ldots b_{s})), \end{align*} $$
$$ \begin{align*} \overline{f}((a_{1}\ldots a_{r})^{\ell},(b_{1}\ldots b_{s})^{\tilde{\ell}})\ge\overline{f}(a_{1}\ldots a_{r},\mathcal{T}(b_{1}\ldots b_{s})), \end{align*} $$
where the right-hand side denotes the infimum of the
![]() $\overline {f}$
distance from
$\overline {f}$
distance from
![]() $a_{1}\ldots a_{r}$
to any element of
$a_{1}\ldots a_{r}$
to any element of
![]() $\mathcal {T}(b_{1}\ldots b_{s}).$
$\mathcal {T}(b_{1}\ldots b_{s}).$
Proof. Apply Property 2.6 with
![]() $x_{1}=x_{2}=\cdots =x_{\ell }=a_{1}a_{2}\ldots a_{r}.$
$x_{1}=x_{2}=\cdots =x_{\ell }=a_{1}a_{2}\ldots a_{r}.$
The estimate below is proved in [Reference RothsteinRo80] by a simple argument using just the binomial theorem. A similar estimate can be obtained from Stirling’s formula.
Lemma 4.16. If m is a positive integer and
![]() $0<\sigma <1,$
then we have the following inequality for the binomial coefficient:
$0<\sigma <1,$
then we have the following inequality for the binomial coefficient:
 $$ \begin{align*} \left(\begin{array}{@{}c@{}} m\\ \lfloor\sigma m\rfloor \end{array}\right)<2^{3m\sqrt{\sigma}}. \end{align*} $$
$$ \begin{align*} \left(\begin{array}{@{}c@{}} m\\ \lfloor\sigma m\rfloor \end{array}\right)<2^{3m\sqrt{\sigma}}. \end{align*} $$
We make the following choices of parameters (in addition to those already described in the previous section). Let
![]() $b_{n}=2^{-(n+10)}, \ell _{n}>2^{n+10}$
. Recall that
$b_{n}=2^{-(n+10)}, \ell _{n}>2^{n+10}$
. Recall that
![]() $\varepsilon _{n}<2^{-(n+12)}$
.
$\varepsilon _{n}<2^{-(n+12)}$
.
Lemma 4.17. (Inductive step in Rothstein’s argument to obtain a lower bound on the
 $\overline {f}$
distance)
$\overline {f}$
distance)
For
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $0<\delta _{n}<1$
define
$0<\delta _{n}<1$
define
 $$ \begin{align} \xi_{n}=\xi_{n}(\delta_{n}):=2^{8}(3\delta_{n})^{((b_{n}/2)-\varepsilon_{n})(1-\varepsilon_{n})}2^{3(1-\varepsilon_{n})\sqrt{(b_{n}/2)}}. \end{align} $$
$$ \begin{align} \xi_{n}=\xi_{n}(\delta_{n}):=2^{8}(3\delta_{n})^{((b_{n}/2)-\varepsilon_{n})(1-\varepsilon_{n})}2^{3(1-\varepsilon_{n})\sqrt{(b_{n}/2)}}. \end{align} $$
Fix a particular
![]() $n\in \mathbb {N}$
and suppose
$n\in \mathbb {N}$
and suppose
![]() $\delta _{n}$
is sufficiently small that
$\delta _{n}$
is sufficiently small that
![]() $\xi _{n}<1.$
Assume that for at least
$\xi _{n}<1.$
Assume that for at least
![]() $(1-\delta _{n})$
of the n-blocks in
$(1-\delta _{n})$
of the n-blocks in
![]() $\mathcal {W}_{n}$
the
$\mathcal {W}_{n}$
the
![]() $\overline {f}$
distance from the n-block to any specific n-block or substrings of its extensions (as in Definition 4.14) is greater than
$\overline {f}$
distance from the n-block to any specific n-block or substrings of its extensions (as in Definition 4.14) is greater than
![]() $a_{n}$
, where
$a_{n}$
, where
![]() $0<a_{n}<1/3.$
Then for
$0<a_{n}<1/3.$
Then for
![]() $k_{n}$
sufficiently large, depending only on parameters with subscript
$k_{n}$
sufficiently large, depending only on parameters with subscript
![]() $n,$
there exists
$n,$
there exists
![]() $\delta _{n+1}$
such that
$\delta _{n+1}$
such that
![]() $\xi _{n+1}=\xi _{n+1}(\delta _{n+1})<1,$
and for at least
$\xi _{n+1}=\xi _{n+1}(\delta _{n+1})<1,$
and for at least
![]() $(1-\delta _{n+1})$
of the
$(1-\delta _{n+1})$
of the
![]() $(n+1)$
-blocks in
$(n+1)$
-blocks in
![]() $\mathcal {W}_{n+1}$
the
$\mathcal {W}_{n+1}$
the
![]() $\overline {f}$
distance from the
$\overline {f}$
distance from the
![]() $(n+1)$
-block to any specific
$(n+1)$
-block to any specific
![]() $(n+1)$
-block or substrings of its extensions is greater than
$(n+1)$
-block or substrings of its extensions is greater than
![]() $a_{n+1}:=a_{n}(1-b_{n})-15\ell _{n}^{-1}.$
$a_{n+1}:=a_{n}(1-b_{n})-15\ell _{n}^{-1}.$
Proof. Fix a particular choice
 $$ \begin{align*} \prod_{i=0}^{q_{n}-1}\prod_{j=0}^{k_{n}-1}(b^{q_{n}-j_{i}}\mathcal{B}_{j}^{\ell_{n}-1}e^{j_{i}}) \end{align*} $$
$$ \begin{align*} \prod_{i=0}^{q_{n}-1}\prod_{j=0}^{k_{n}-1}(b^{q_{n}-j_{i}}\mathcal{B}_{j}^{\ell_{n}-1}e^{j_{i}}) \end{align*} $$
of
![]() $(n+1)$
-block in
$(n+1)$
-block in
![]() $\mathcal {W}_{n+1}$
, where
$\mathcal {W}_{n+1}$
, where
![]() $\mathcal {B}_{0},\mathcal {B}_{1},\ldots ,\mathcal {B}_{k_{n-1}}$
are n-blocks in
$\mathcal {B}_{0},\mathcal {B}_{1},\ldots ,\mathcal {B}_{k_{n-1}}$
are n-blocks in
![]() $\mathcal {W}_{n}$
. Let
$\mathcal {W}_{n}$
. Let
 $\mathcal {T}_0:= \mathcal {T}(\prod _{i=0}^{q_{n}-1}\prod _{j=0}^{k_{n}-1}(b^{q_{n}-j_{i}}\mathcal {B}_{j}^{\ell _{n}-1}e^{j_{i}}))$
. We will prove that the inequality
$\mathcal {T}_0:= \mathcal {T}(\prod _{i=0}^{q_{n}-1}\prod _{j=0}^{k_{n}-1}(b^{q_{n}-j_{i}}\mathcal {B}_{j}^{\ell _{n}-1}e^{j_{i}}))$
. We will prove that the inequality
 $$ \begin{align} \overline{f}\bigg(\prod_{i=0}^{q_{n}-1}\prod_{j=0}^{k_{n}-1}(b^{q_{n}-j_{i}}\mathcal{A}_{j}^{\ell_{n}-1}e^{j_{i}}),\mathcal{T}_0\bigg)> a_{n}(1-b_{n})-15\ell_{n}^{-1} \end{align} $$
$$ \begin{align} \overline{f}\bigg(\prod_{i=0}^{q_{n}-1}\prod_{j=0}^{k_{n}-1}(b^{q_{n}-j_{i}}\mathcal{A}_{j}^{\ell_{n}-1}e^{j_{i}}),\mathcal{T}_0\bigg)> a_{n}(1-b_{n})-15\ell_{n}^{-1} \end{align} $$
holds for at least
![]() $(1-\delta _{n+1})$
of the
$(1-\delta _{n+1})$
of the
![]() $(n+1)$
-blocks
$(n+1)$
-blocks
 $\prod _{i=0}^{q_{n}-1}\prod _{j=0}^{k_{n}-1}(b^{q_{n}-j_{i}}\mathcal {A}_{j}^{\ell _{n}-1}e^{j_{i}})$
in
$\prod _{i=0}^{q_{n}-1}\prod _{j=0}^{k_{n}-1}(b^{q_{n}-j_{i}}\mathcal {A}_{j}^{\ell _{n}-1}e^{j_{i}})$
in
![]() $\mathcal {W}_{n+1},$
where
$\mathcal {W}_{n+1},$
where
![]() $\delta _{n+1}$
will be specified later in the proof. The b's and e's that are newly added in constructing
$\delta _{n+1}$
will be specified later in the proof. The b's and e's that are newly added in constructing
![]() $(n+1$
)-blocks from n-blocks in the circular system make up a fraction
$(n+1$
)-blocks from n-blocks in the circular system make up a fraction
![]() $\ell _{n}^{-1}$
of the symbols in any
$\ell _{n}^{-1}$
of the symbols in any
![]() $(n+1)$
-block. We may assume that the smallest
$(n+1)$
-block. We may assume that the smallest
![]() $\overline {f}$
distance between
$\overline {f}$
distance between
 $\prod _{i=0}^{q_{n}-1}\prod _{j=0}^{k_{n}-1}(b^{q_{n}-j_{i}}\mathcal {A}_{j}^{\ell _{n}-1}e^{j_{i}})$
and any element of
$\prod _{i=0}^{q_{n}-1}\prod _{j=0}^{k_{n}-1}(b^{q_{n}-j_{i}}\mathcal {A}_{j}^{\ell _{n}-1}e^{j_{i}})$
and any element of
![]() $\mathcal {T}_0 $
occurs for an element of
$\mathcal {T}_0 $
occurs for an element of
![]() $\mathcal {T}_0$
of length at least
$\mathcal {T}_0$
of length at least
![]() $q^2_{n}k_{n}\ell _{n}/2,$
because otherwise it follows from (2.5) that the
$q^2_{n}k_{n}\ell _{n}/2,$
because otherwise it follows from (2.5) that the
![]() $\overline {f}$
distance in (4.14) is greater than
$\overline {f}$
distance in (4.14) is greater than
![]() $1/3.$
For such an element of
$1/3.$
For such an element of
![]() $\mathcal {T}_0,$
the number of newly added b's and e's is a fraction less than
$\mathcal {T}_0,$
the number of newly added b's and e's is a fraction less than
![]() $2\ell _{n}^{-1}$
of the length of that element. Therefore by Property 2.5 and Lemma 4.15, to obtain (4.14) it suffices to show that
$2\ell _{n}^{-1}$
of the length of that element. Therefore by Property 2.5 and Lemma 4.15, to obtain (4.14) it suffices to show that
 $$ \begin{align} \overline{f}(\mathcal{A}_{1}^{\ell_{n}-1}\mathcal{A}_{2}^{\ell_{n}-1}\ldots \mathcal{A}_{k_{n}}^{\ell_{n}-1},\mathcal{T}(\mathcal{B}_{1}^{\ell_{n}-1}\mathcal{B}_{2}^{\ell_{n}-1}\ldots \mathcal{B}_{k_{n}}^{\ell_{n}-1}))>a_{n}(1-b_{n})-9\ell_{n}^{-1}, \end{align} $$
$$ \begin{align} \overline{f}(\mathcal{A}_{1}^{\ell_{n}-1}\mathcal{A}_{2}^{\ell_{n}-1}\ldots \mathcal{A}_{k_{n}}^{\ell_{n}-1},\mathcal{T}(\mathcal{B}_{1}^{\ell_{n}-1}\mathcal{B}_{2}^{\ell_{n}-1}\ldots \mathcal{B}_{k_{n}}^{\ell_{n}-1}))>a_{n}(1-b_{n})-9\ell_{n}^{-1}, \end{align} $$
without repeating the strings
![]() $q_{n}$
times. Suppose to the contrary of (4.15) that
$q_{n}$
times. Suppose to the contrary of (4.15) that
 $$ \begin{align} &\overline{f}(\mathcal{A}_{1}^{\ell_{n}-1}\mathcal{A}_{2}^{\ell_{n}-1}\ldots \mathcal{A}_{k_{n}}^{\ell_{n}-1},\mathcal{T}(\mathcal{B}_{1}^{\ell_{n}-1}\mathcal{B}_{2}^{\ell_{n}-1}\ldots \mathcal{B}_{k_{n}}^{\ell_{n}-1})) \nonumber\\ &\quad\le a_{n}(1-b_{n})-9\ell_{n}^{-1} <(a_{n}-9\ell_{n}^{-1})(1-b_{n})<1/3, \end{align} $$
$$ \begin{align} &\overline{f}(\mathcal{A}_{1}^{\ell_{n}-1}\mathcal{A}_{2}^{\ell_{n}-1}\ldots \mathcal{A}_{k_{n}}^{\ell_{n}-1},\mathcal{T}(\mathcal{B}_{1}^{\ell_{n}-1}\mathcal{B}_{2}^{\ell_{n}-1}\ldots \mathcal{B}_{k_{n}}^{\ell_{n}-1})) \nonumber\\ &\quad\le a_{n}(1-b_{n})-9\ell_{n}^{-1} <(a_{n}-9\ell_{n}^{-1})(1-b_{n})<1/3, \end{align} $$
for some
![]() $k_{n}\, n$
-blocks
$k_{n}\, n$
-blocks
![]() $\mathcal {A}_{1},\mathcal {A}_{2},\ldots ,\mathcal {A}_{k_{n}}.$
We will show that this happens for at most
$\mathcal {A}_{1},\mathcal {A}_{2},\ldots ,\mathcal {A}_{k_{n}}.$
We will show that this happens for at most
![]() $\delta _{n+1}$
of the
$\delta _{n+1}$
of the
![]() $(n+1)$
-blocks in
$(n+1)$
-blocks in
![]() $\mathcal {W}_{n+1}.$
Choose a match between the
$\mathcal {W}_{n+1}.$
Choose a match between the
![]() $\mathcal {A}$
-string and a
$\mathcal {A}$
-string and a
![]() $\mathcal {B}$
-string that realizes the
$\mathcal {B}$
-string that realizes the
![]() $\overline {f}$
distance in (4.16). For each substring
$\overline {f}$
distance in (4.16). For each substring
 $\mathcal {A}_{i}^{\ell _{n}-1}$
of the
$\mathcal {A}_{i}^{\ell _{n}-1}$
of the
![]() $\mathcal {A}$
-string, let
$\mathcal {A}$
-string, let
![]() $f_{i}$
be the
$f_{i}$
be the
![]() $\overline {f}$
distance between
$\overline {f}$
distance between
 $\mathcal {A}_{i}^{\ell _{n}-1}$
and the corresponding part of the
$\mathcal {A}_{i}^{\ell _{n}-1}$
and the corresponding part of the
![]() $\mathcal {B}$
-string. Let
$\mathcal {B}$
-string. Let
![]() $v_{i}$
be the ratio of the number of symbols in
$v_{i}$
be the ratio of the number of symbols in
 $\mathcal {A}_{i}^{\ell _{n}-1}$
plus the number of symbols in the corresponding part of the
$\mathcal {A}_{i}^{\ell _{n}-1}$
plus the number of symbols in the corresponding part of the
![]() $\mathcal {B}$
-string to the total length of the
$\mathcal {B}$
-string to the total length of the
![]() $\mathcal {A}$
- and
$\mathcal {A}$
- and
![]() $\mathcal {B}$
-strings. Then by Property 2.6, the
$\mathcal {B}$
-strings. Then by Property 2.6, the
![]() $\overline {f}$
distance for the entire strings is
$\overline {f}$
distance for the entire strings is
 $\sum _{i=1}^{k_{n}}f_{i}v_{i},$
that is, a weighted average of the
$\sum _{i=1}^{k_{n}}f_{i}v_{i},$
that is, a weighted average of the
![]() $f_{i}$
with weights
$f_{i}$
with weights
![]() $v_{i}.$
Since this weighted average is less than
$v_{i}.$
Since this weighted average is less than
![]() $(a_{n}-9\ell _{n}^{-1})(1-b_{n})$
, the weights
$(a_{n}-9\ell _{n}^{-1})(1-b_{n})$
, the weights
![]() $v_{i}$
for those
$v_{i}$
for those
![]() $f_{i}$
with
$f_{i}$
with
![]() $f_{i}<a_{n}-9\ell _{n}^{-1}<1/3$
must have sum at least
$f_{i}<a_{n}-9\ell _{n}^{-1}<1/3$
must have sum at least
![]() $b_{n}.$
For these weights
$b_{n}.$
For these weights
![]() $v_{i},$
Property 2.7 and the assumptions that the
$v_{i},$
Property 2.7 and the assumptions that the
![]() $\overline {f}$
distance in (4.16) and
$\overline {f}$
distance in (4.16) and
![]() $f_{i}$
are both less than
$f_{i}$
are both less than
![]() $1/3$
imply that
$1/3$
imply that
![]() $v_{i}<2k_{n}^{-1}.$
Thus there must be at least
$v_{i}<2k_{n}^{-1}.$
Thus there must be at least
![]() $(b_{n}/2)k_{n}$
indices i such that
$(b_{n}/2)k_{n}$
indices i such that
![]() $f_{i}<a_{n}-9\ell _{n}^{-1}.$
Then for at least a fraction
$f_{i}<a_{n}-9\ell _{n}^{-1}.$
Then for at least a fraction
![]() $(b_{n}/2)-\varepsilon _{n}$
of the indices
$(b_{n}/2)-\varepsilon _{n}$
of the indices
![]() $i\in \{1,2,\ldots ,k_{n}'\}$
the
$i\in \{1,2,\ldots ,k_{n}'\}$
the
![]() $\overline {f}$
distance between
$\overline {f}$
distance between
 $\mathcal {A}_{i}^{\ell _{n}-1}$
and the corresponding part of the
$\mathcal {A}_{i}^{\ell _{n}-1}$
and the corresponding part of the
![]() $\mathcal {B}$
-block is less than
$\mathcal {B}$
-block is less than
![]() $a_{n}-9\ell _{n}^{-1}.$
For each such i, let
$a_{n}-9\ell _{n}^{-1}.$
For each such i, let
![]() $\sigma (i)$
be the first index such that the part of the
$\sigma (i)$
be the first index such that the part of the
![]() $\mathcal {B}$
-block corresponding to
$\mathcal {B}$
-block corresponding to
 $\mathcal {A}_{i}^{\ell _{n}-1}$
starts with a substring of a
$\mathcal {A}_{i}^{\ell _{n}-1}$
starts with a substring of a
 $\mathcal {B}_{\sigma (i)}^{\ell _{n}-1}.$
Then
$\mathcal {B}_{\sigma (i)}^{\ell _{n}-1}.$
Then
 $\mathcal {A}_{i}^{\ell _{n}-1}$
may correspond just to a substring of
$\mathcal {A}_{i}^{\ell _{n}-1}$
may correspond just to a substring of
 $\mathcal {B}_{\sigma (i)}^{\ell _{n}-1}$
or to a substring of
$\mathcal {B}_{\sigma (i)}^{\ell _{n}-1}$
or to a substring of
 $\mathcal {B}_{\sigma (i)}^{\ell _{n}-1}\mathcal {B}_{\sigma (i)+1}^{\ell _{n}-1}$
or to a substring of
$\mathcal {B}_{\sigma (i)}^{\ell _{n}-1}\mathcal {B}_{\sigma (i)+1}^{\ell _{n}-1}$
or to a substring of
 $\mathcal {B}_{\sigma (i)}^{\ell _{n}-1}\mathcal {B}_{\sigma (i)+1}^{\ell _{n}-1}\mathcal {B}_{\sigma (i)+2}^{\ell _{n}-1}.$
Here the addition in the subscripts is modulo
$\mathcal {B}_{\sigma (i)}^{\ell _{n}-1}\mathcal {B}_{\sigma (i)+1}^{\ell _{n}-1}\mathcal {B}_{\sigma (i)+2}^{\ell _{n}-1}.$
Here the addition in the subscripts is modulo
![]() $k_{n}.$
Any correspondence between
$k_{n}.$
Any correspondence between
 $\mathcal {A}_{i}^{\ell _{n}-1}$
and strings of four or more
$\mathcal {A}_{i}^{\ell _{n}-1}$
and strings of four or more
 $\mathcal {B}_{j}^{\ell _{n}-1}$
would lead to the
$\mathcal {B}_{j}^{\ell _{n}-1}$
would lead to the
![]() $\overline {f}$
distance between
$\overline {f}$
distance between
 $\mathcal {A}_{i}^{\ell _{n}-1}$
and the corresponding part of the
$\mathcal {A}_{i}^{\ell _{n}-1}$
and the corresponding part of the
![]() $\mathcal {B}$
-string being greater than
$\mathcal {B}$
-string being greater than
![]() $1/3,$
and therefore we may disregard this possibility. The number of ways of choosing the
$1/3,$
and therefore we may disregard this possibility. The number of ways of choosing the
![]() $\sigma (i)$
's and deciding whether to use just
$\sigma (i)$
's and deciding whether to use just
![]() $\sigma (i)$
or to continue with just
$\sigma (i)$
or to continue with just
![]() $\sigma (i)+1$
or to continue with both
$\sigma (i)+1$
or to continue with both
![]() $\sigma (i)+1$
and
$\sigma (i)+1$
and
![]() $\sigma (i)+2$
is at most
$\sigma (i)+2$
is at most
 $k_{n}\Big (\!\begin {smallmatrix} 7k_{n}\\ k_{n} \end {smallmatrix}\!\Big )$
. Here we estimate
$k_{n}\Big (\!\begin {smallmatrix} 7k_{n}\\ k_{n} \end {smallmatrix}\!\Big )$
. Here we estimate
![]() $7k_{n}>3(2k_{n}+1),$
which is an upper bound on the number of possible
$7k_{n}>3(2k_{n}+1),$
which is an upper bound on the number of possible
![]() $\sigma (i)$
combinations corresponding to
$\sigma (i)$
combinations corresponding to
 $\mathcal {A}_{i}^{\ell _{n}-1}$
strings, allowing for the
$\mathcal {A}_{i}^{\ell _{n}-1}$
strings, allowing for the
![]() $\mathcal {B}$
-string to be up to twice the length of the
$\mathcal {B}$
-string to be up to twice the length of the
![]() $\mathcal {A}$
-string (and thus contained in at most
$\mathcal {A}$
-string (and thus contained in at most
![]() $2k_n+1$
consecutive
$2k_n+1$
consecutive
 $\mathcal {B}_j^{l_n-1}$
strings) and allowing for the three choices: just
$\mathcal {B}_j^{l_n-1}$
strings) and allowing for the three choices: just
![]() $\sigma (i),$
just
$\sigma (i),$
just
![]() $\sigma (i)$
and
$\sigma (i)$
and
![]() $\sigma (i)+1,$
and all of
$\sigma (i)+1,$
and all of
![]() $\sigma (i)$
,
$\sigma (i)$
,
![]() $\sigma (i)$
+1, and
$\sigma (i)$
+1, and
![]() $\sigma (i)+2.$
The additional factor of
$\sigma (i)+2.$
The additional factor of
![]() $k_{n}$
in front is due to being able to start the
$k_{n}$
in front is due to being able to start the
![]() $\mathcal {B}$
-string with
$\mathcal {B}$
-string with
![]() $\sigma (1)$
being any of
$\sigma (1)$
being any of
![]() $1,2,\ldots ,k_{n}.$
According to the estimate on binomial coefficients given in Lemma 4.16,
$1,2,\ldots ,k_{n}.$
According to the estimate on binomial coefficients given in Lemma 4.16,
 $\Big (\!\begin {smallmatrix} 7k_{n}\\ k_{n} \end {smallmatrix}\!\Big )\le 2^{21k_{n}\sqrt {1/7}}\le 2^{8k_{n}}.$
When we match
$\Big (\!\begin {smallmatrix} 7k_{n}\\ k_{n} \end {smallmatrix}\!\Big )\le 2^{21k_{n}\sqrt {1/7}}\le 2^{8k_{n}}.$
When we match
 $\mathcal {A}_{i}^{l_{n}-1}$
with a substring of
$\mathcal {A}_{i}^{l_{n}-1}$
with a substring of
 $\mathcal {B}_{\sigma (i)}^{\ell _{n}-1}\mathcal {B}_{\sigma (i)+1}^{\ell _{n}-1}\mathcal {B}_{\sigma (i)+2}^{\ell _{n}-1},$
we divide
$\mathcal {B}_{\sigma (i)}^{\ell _{n}-1}\mathcal {B}_{\sigma (i)+1}^{\ell _{n}-1}\mathcal {B}_{\sigma (i)+2}^{\ell _{n}-1},$
we divide
 $\mathcal {A}_{i}^{\ell _{n}-1}$
into as many as three substrings according to which part corresponds to each of
$\mathcal {A}_{i}^{\ell _{n}-1}$
into as many as three substrings according to which part corresponds to each of
 $\mathcal {B}_{\sigma (i)}^{\ell _{n}-1}, B_{\sigma (i)+1}^{\ell _{n}-1},$
or
$\mathcal {B}_{\sigma (i)}^{\ell _{n}-1}, B_{\sigma (i)+1}^{\ell _{n}-1},$
or
 $\mathcal {B}_{\sigma (i)+2}^{\ell _{n}-1}.$
By removing at most a fraction
$\mathcal {B}_{\sigma (i)+2}^{\ell _{n}-1}.$
By removing at most a fraction
![]() $4(\ell _{n}-1)^{-1}$
of the symbols in each
$4(\ell _{n}-1)^{-1}$
of the symbols in each
 $\mathcal {A}_{i}^{\ell _{n}-1}$
string, we may assume that full
$\mathcal {A}_{i}^{\ell _{n}-1}$
string, we may assume that full
![]() $\mathcal {A}_{i}$
strings correspond to each corresponding substring of
$\mathcal {A}_{i}$
strings correspond to each corresponding substring of
 $\mathcal {B}_{\sigma (i)}^{\ell _{n}-1}, \mathcal {B}_{\sigma (i)+1}^{\ell _{n}-1},$
and
$\mathcal {B}_{\sigma (i)}^{\ell _{n}-1}, \mathcal {B}_{\sigma (i)+1}^{\ell _{n}-1},$
and
 $\mathcal {B}_{\sigma (i)+2}^{\ell _{n}-1}.$
By Property 2.5 this removal will increase the
$\mathcal {B}_{\sigma (i)+2}^{\ell _{n}-1}.$
By Property 2.5 this removal will increase the
![]() $\overline {f}$
distance from
$\overline {f}$
distance from
 $\mathcal {A}_{i}^{\ell _{n}-1}$
to the corresponding part of the
$\mathcal {A}_{i}^{\ell _{n}-1}$
to the corresponding part of the
![]() $\mathcal {B}$
-string by at most
$\mathcal {B}$
-string by at most
![]() $9\ell _{n}^{-1}.$
Thus by Lemma 4.15, for a fraction of at least
$9\ell _{n}^{-1}.$
Thus by Lemma 4.15, for a fraction of at least
![]() $(b_{n}/2)-\varepsilon _{n}$
of the indices in
$(b_{n}/2)-\varepsilon _{n}$
of the indices in
![]() $\{1,2,\ldots ,k_{n}'\},$
at least one of the three
$\{1,2,\ldots ,k_{n}'\},$
at least one of the three
![]() $\overline {f}$
distances from
$\overline {f}$
distances from
![]() $\mathcal {A}_{i}$
to a string in
$\mathcal {A}_{i}$
to a string in
![]() $\mathcal {T}(\mathcal {B}_{\sigma (i)})$
or from
$\mathcal {T}(\mathcal {B}_{\sigma (i)})$
or from
![]() $\mathcal {A}_{i}$
to a string in
$\mathcal {A}_{i}$
to a string in
![]() $\mathcal {T}(\mathcal {B}_{\sigma (i)+1})$
or from
$\mathcal {T}(\mathcal {B}_{\sigma (i)+1})$
or from
![]() $\mathcal {A}_{i}$
to a string in
$\mathcal {A}_{i}$
to a string in
![]() $\mathcal {T}(\mathcal {B}_{\sigma (i)+2})$
must be less than
$\mathcal {T}(\mathcal {B}_{\sigma (i)+2})$
must be less than
![]() $a_{n}.$
By assumption, the probability that the n-block
$a_{n}.$
By assumption, the probability that the n-block
![]() $\mathcal {A}_{i}$
satisfies at least one of these three conditions is less than
$\mathcal {A}_{i}$
satisfies at least one of these three conditions is less than
![]() $3\delta _{n}.$
Thus if the first
$3\delta _{n}.$
Thus if the first
![]() $k_{n}'\, n$
-blocks in the odometer
$k_{n}'\, n$
-blocks in the odometer
![]() $(n+1)$
-block corresponding to the
$(n+1)$
-block corresponding to the
![]() $\mathcal {A}$
-string were selected independently, then the probability
$\mathcal {A}$
-string were selected independently, then the probability
![]() $\delta _{n+1}$
that
$\delta _{n+1}$
that
 $$ \begin{align*} \overline{f}(\mathcal{A}_{1}^{\ell_{n}-1}\mathcal{A}_{2}^{\ell_{n}-1}\ldots \mathcal{A}_{k_{n}}^{\ell_{n}-1},\mathcal{T}(\mathcal{B}_{1}^{\ell_{n}-1}\mathcal{B}_{2}^{\ell_{n}-1}\ldots \mathcal{B}_{k_{n}}^{\ell_{n}-1}))<a_{n}-9\ell_{n}^{-1} \end{align*} $$
$$ \begin{align*} \overline{f}(\mathcal{A}_{1}^{\ell_{n}-1}\mathcal{A}_{2}^{\ell_{n}-1}\ldots \mathcal{A}_{k_{n}}^{\ell_{n}-1},\mathcal{T}(\mathcal{B}_{1}^{\ell_{n}-1}\mathcal{B}_{2}^{\ell_{n}-1}\ldots \mathcal{B}_{k_{n}}^{\ell_{n}-1}))<a_{n}-9\ell_{n}^{-1} \end{align*} $$
would be less than
 $k_{n}2^{8k_{n}}(3\delta _{n})^{((b_{n}/2)-\varepsilon _{n})k_{n}'}\Big (\!\begin {smallmatrix} k_{n}'\\ (b_{n}/2)k_{n}' \end {smallmatrix}\!\Big ).$
Since the selection of the
$k_{n}2^{8k_{n}}(3\delta _{n})^{((b_{n}/2)-\varepsilon _{n})k_{n}'}\Big (\!\begin {smallmatrix} k_{n}'\\ (b_{n}/2)k_{n}' \end {smallmatrix}\!\Big ).$
Since the selection of the
![]() $k_{n}'\, n$
-blocks is not quite independent, we apply (4.1), and multiply our bound on the probability by
$k_{n}'\, n$
-blocks is not quite independent, we apply (4.1), and multiply our bound on the probability by
![]() $(1-\tau _{n})^{-1}.$
Therefore from Lemma 4.16, we obtain
$(1-\tau _{n})^{-1}.$
Therefore from Lemma 4.16, we obtain
 $\delta _{n+1}<k_{n}(1-\tau _{n})^{-1}\xi _{n}^{k_{n}}$
. By assumption
$\delta _{n+1}<k_{n}(1-\tau _{n})^{-1}\xi _{n}^{k_{n}}$
. By assumption
![]() $\xi _{n}<1.$
Thus we can choose
$\xi _{n}<1.$
Thus we can choose
![]() $k_{n}$
sufficiently large so that
$k_{n}$
sufficiently large so that
![]() $\delta _{n+1}$
is sufficiently small to imply
$\delta _{n+1}$
is sufficiently small to imply
![]() $\xi _{n+1}<1.$
For at least
$\xi _{n+1}<1.$
For at least
![]() $1-\delta _{n+1}$
of the
$1-\delta _{n+1}$
of the
![]() $(n+1)$
-blocks in
$(n+1)$
-blocks in
![]() $\mathcal {W}_{n+1}$
the
$\mathcal {W}_{n+1}$
the
![]() $\overline {f}$
distance from the
$\overline {f}$
distance from the
![]() $(n+1)$
-block to any specific
$(n+1)$
-block to any specific
![]() $(n+1)$
-block or substrings of its extensions is greater than
$(n+1)$
-block or substrings of its extensions is greater than
![]() $a_{n+1}:=a_{n}(1-b_{n})-15\ell _{n}^{-1}.$
$a_{n+1}:=a_{n}(1-b_{n})-15\ell _{n}^{-1}.$
Proof Proof of Theorem 4.13
The inductive step is contained in Lemma 4.17. For the base case, we recall that
![]() $0$
-blocks are single symbols
$0$
-blocks are single symbols
![]() $1,2,\ldots ,|\Sigma |.$
Choose
$1,2,\ldots ,|\Sigma |.$
Choose
![]() $0<\delta _{0}<1$
so that
$0<\delta _{0}<1$
so that
![]() $\xi _{0}(\delta _{0})<1.$
Then require
$\xi _{0}(\delta _{0})<1.$
Then require
![]() $|\Sigma |$
to be sufficiently large that
$|\Sigma |$
to be sufficiently large that
![]() $\delta _{0}>|\Sigma |^{-1}.$
We let
$\delta _{0}>|\Sigma |^{-1}.$
We let
![]() $a_{1}=1/4.$
According to the recursive formula for
$a_{1}=1/4.$
According to the recursive formula for
![]() $a_{n},$
we have
$a_{n},$
we have
![]() $a_{n}>1/8$
for all
$a_{n}>1/8$
for all
![]() $n.$
Thus, if
$n.$
Thus, if
![]() $\varepsilon =1/8$
, the condition in Lemma 3.5 is not satisfied. Therefore
$\varepsilon =1/8$
, the condition in Lemma 3.5 is not satisfied. Therefore
![]() $\mathcal {F}(\mathbb {E})$
is not loosely Bernoulli.
$\mathcal {F}(\mathbb {E})$
is not loosely Bernoulli.
5. Zero-entropy example
In this section we prove the following theorem, which gives a zero-entropy version of the example constructed in §§4.1 and 4.2.
Theorem 5.1. There exist circular coefficients
![]() $(l_{n})$
and a loosely Bernoulli odometer- based system
$(l_{n})$
and a loosely Bernoulli odometer- based system
![]() $\mathbb {K}$
of zero measure-theoretic entropy with uniform and uniquely readable construction sequence such that
$\mathbb {K}$
of zero measure-theoretic entropy with uniform and uniquely readable construction sequence such that
![]() $\mathcal {F}(\mathbb {K})$
is not loosely Bernoulli.
$\mathcal {F}(\mathbb {K})$
is not loosely Bernoulli.
Outline of the proof of Theorem 5.1. In §5.4 we give a precise description of the inductive building process of the uniform and uniquely readable construction sequence for the odometer-based system
![]() $\mathbb {K}$
such that
$\mathbb {K}$
such that
![]() $\mathbb {K}$
will be loosely Bernoulli but
$\mathbb {K}$
will be loosely Bernoulli but
![]() $\mathcal {F}(\mathbb {K})$
will not be loosely Bernoulli. The creation of this sequence relies on two mechanisms. On the one hand, we will use what we will call the Feldman mechanism presented in §5.2. This will allow us to produce an arbitrarily large number of blocks that in the circular system remain almost as far apart in
$\mathcal {F}(\mathbb {K})$
will not be loosely Bernoulli. The creation of this sequence relies on two mechanisms. On the one hand, we will use what we will call the Feldman mechanism presented in §5.2. This will allow us to produce an arbitrarily large number of blocks that in the circular system remain almost as far apart in
![]() $\overline {f}$
as the building blocks. In particular, we can produce sufficiently many blocks to apply the second mechanism, the so-called shifting mechanism introduced in §5.3 (see Figure 2 for a sketch of its idea). This mechanism requires not only sufficiently many n-words to start with but also a sufficiently large number of stages p. Then we can produce
$\overline {f}$
as the building blocks. In particular, we can produce sufficiently many blocks to apply the second mechanism, the so-called shifting mechanism introduced in §5.3 (see Figure 2 for a sketch of its idea). This mechanism requires not only sufficiently many n-words to start with but also a sufficiently large number of stages p. Then we can produce
![]() $(n+p)$
-words in our construction sequence in such a way that these are close to each other in the
$(n+p)$
-words in our construction sequence in such a way that these are close to each other in the
![]() $\overline {f}$
metric and that the corresponding blocks in the circular construction sequence stay apart from each other in the
$\overline {f}$
metric and that the corresponding blocks in the circular construction sequence stay apart from each other in the
![]() $\overline {f}$
metric. Both mechanisms will make use of Feldman patterns for which we prove a general statement in §5.1.□
$\overline {f}$
metric. Both mechanisms will make use of Feldman patterns for which we prove a general statement in §5.1.□

Figure 2 Heuristic representation of two stages of the shifting mechanism. Parts of three
![]() $(n+2)$
-blocks
$(n+2)$
-blocks
![]() $\mathtt {B}_1, \mathtt {B}_2, \mathtt {B}_3$
in the odometer-based system and parts of their images
$\mathtt {B}_1, \mathtt {B}_2, \mathtt {B}_3$
in the odometer-based system and parts of their images
![]() $\mathcal {B}_1, \mathcal {B}_2, \mathcal {B}_3$
under the circular operator are represented. The marked letters indicate a best possible
$\mathcal {B}_1, \mathcal {B}_2, \mathcal {B}_3$
under the circular operator are represented. The marked letters indicate a best possible
![]() $\overline {f}$
match between
$\overline {f}$
match between
![]() $\mathcal {B}_1$
and
$\mathcal {B}_1$
and
![]() $\mathcal {B}_2$
with a fit of approximately
$\mathcal {B}_2$
with a fit of approximately
 $\big(1-\tfrac 13\big)^2$
(ignoring spacers and boundary effects) while the blocks
$\big(1-\tfrac 13\big)^2$
(ignoring spacers and boundary effects) while the blocks
![]() $\mathtt {B}_1$
and
$\mathtt {B}_1$
and
![]() $\mathtt {B}_2$
have a very good fit in the odometer-based system.
$\mathtt {B}_2$
have a very good fit in the odometer-based system.
5.1. Feldman patterns for blocks
In [Reference FeldmanFe76] Feldman constructed the first example of an ergodic zero-entropy automorphism that is not loosely Bernoulli. The construction is based on the observation that no pair of the strings
 $$ \begin{align*} abababab\\ aabbaabb\\ aaaabbbb \end{align*} $$
$$ \begin{align*} abababab\\ aabbaabb\\ aaaabbbb \end{align*} $$
can be matched very well. We use his construction of blocks (which we call Feldman patterns) frequently in our two mechanisms in §§5.2 and 5.3. The basic Feldman patterns are displayed in Lemma 5.8. In applying these patterns, we substitute blocks of symbols for the individual symbols to produce a large number of strings that are almost as far apart in
![]() $\overline {f}$
as their building blocks.
$\overline {f}$
as their building blocks.
Our presentation of the Feldman patterns is similar to the one in [Reference Ornstein, Rudolph and WeissORW82], but we apply the patterns in the odometer system and then examine the
![]() $\overline {f}$
distance between strings in the corresponding circular system. We also allow the consideration of different families of strings and a preliminary concatenation of blocks (which will prove useful when dealing with grouped blocks in §5.3). While we make a statement about substrings of different Feldman patterns from either the same or different families in Proposition 5.10, we focus on the situation of the same Feldman pattern but different families in Lemma 5.11.
$\overline {f}$
distance between strings in the corresponding circular system. We also allow the consideration of different families of strings and a preliminary concatenation of blocks (which will prove useful when dealing with grouped blocks in §5.3). While we make a statement about substrings of different Feldman patterns from either the same or different families in Proposition 5.10, we focus on the situation of the same Feldman pattern but different families in Lemma 5.11.
In order to obtain lower bounds on the
![]() $\overline {f}$
distance between strings that are built from blocks of symbols (as in Proposition 5.4 and Corollary 5.5), it is convenient to introduce a notion of approximate
$\overline {f}$
distance between strings that are built from blocks of symbols (as in Proposition 5.4 and Corollary 5.5), it is convenient to introduce a notion of approximate
![]() $\overline {f}$
distance that we call
$\overline {f}$
distance that we call
![]() $\tilde {f}$
.
$\tilde {f}$
.
Definition 5.2. If
![]() $(i,j)$
and
$(i,j)$
and
![]() $(i',j')\in \mathbb {N}\times \mathbb {N}$
, then we define
$(i',j')\in \mathbb {N}\times \mathbb {N}$
, then we define
![]() $(i,j)\preceq (i',j')$
if
$(i,j)\preceq (i',j')$
if
![]() $i\le i'$
and
$i\le i'$
and
![]() $j\le j'$
. If
$j\le j'$
. If
![]() $(i,j)\preceq (i',j')$
and
$(i,j)\preceq (i',j')$
and
![]() $(i,j)\ne (i',j'),$
then we say
$(i,j)\ne (i',j'),$
then we say
![]() $(i,j)\prec (i',j').$
An approximate match between two strings of symbols
$(i,j)\prec (i',j').$
An approximate match between two strings of symbols
![]() $a_{1}a_{2}\ldots a_{n}$
and
$a_{1}a_{2}\ldots a_{n}$
and
![]() $b_{1}b_{2}\ldots b_{m}$
from a given alphabet
$b_{1}b_{2}\ldots b_{m}$
from a given alphabet
![]() $\Sigma $
is a collection
$\Sigma $
is a collection
![]() $\tilde {I}$
of pairs of indices
$\tilde {I}$
of pairs of indices
![]() $(i_{s},j_{s}),s=1,\ldots ,r,$
such that the following conditions hold.
$(i_{s},j_{s}),s=1,\ldots ,r,$
such that the following conditions hold.
-
•
 $(1,1)\preceq (i_{1},j_{1})\prec (i_{2},j_{2})\prec \cdots \prec (i_{r},j_{r})\preceq (n,m).$
$(1,1)\preceq (i_{1},j_{1})\prec (i_{2},j_{2})\prec \cdots \prec (i_{r},j_{r})\preceq (n,m).$
-
•
 $a_{i_{s}}=b_{j_{s}}$
for
$a_{i_{s}}=b_{j_{s}}$
for
 $s=1,2,\ldots ,r.$
$s=1,2,\ldots ,r.$
-
• If
 $(i,j)\in \tilde {I}$
, then there exist
$(i,j)\in \tilde {I}$
, then there exist
 $s,t\in \{1,\ldots ,r-2\}$
such that
$s,t\in \{1,\ldots ,r-2\}$
such that
 $\{s':(i,s')\in \tilde {I}\}\subset \{s,s+1,s+2\}$
and
$\{s':(i,s')\in \tilde {I}\}\subset \{s,s+1,s+2\}$
and
 $\{t':(t',j)\in \tilde {I}\}\subset \{t,t+1,t+2\}$
.
$\{t':(t',j)\in \tilde {I}\}\subset \{t,t+1,t+2\}$
.
Then
 $$ \begin{align*} \kern-6pt\begin{array}{ll} \tilde{f}(a_{1}a_{2}\ldots a_{n},b_{1}b_{2}\ldots b_{m})\\ =\displaystyle{\max\bigg(0,1-\frac{2\sup\{|\tilde{I}|:\tilde{I}\text{ is an approx. match between }a_{1}a_{2}\ldots a_{n}\text{ and }b_{1}b_{2}\ldots b_{m}\}}{n+m}\bigg).} \end{array} \end{align*} $$
$$ \begin{align*} \kern-6pt\begin{array}{ll} \tilde{f}(a_{1}a_{2}\ldots a_{n},b_{1}b_{2}\ldots b_{m})\\ =\displaystyle{\max\bigg(0,1-\frac{2\sup\{|\tilde{I}|:\tilde{I}\text{ is an approx. match between }a_{1}a_{2}\ldots a_{n}\text{ and }b_{1}b_{2}\ldots b_{m}\}}{n+m}\bigg).} \end{array} \end{align*} $$
Clearly
![]() $\overline {f}(a_{1}a_{2}\ldots a_{n},b_{1},b_{2}\ldots b_{m})\ge \tilde {f}(a_{1}a_{2}\ldots a_{n},b_{1},b_{2}\ldots b_{m}).$
Moreover, if every three consecutive symbols
$\overline {f}(a_{1}a_{2}\ldots a_{n},b_{1},b_{2}\ldots b_{m})\ge \tilde {f}(a_{1}a_{2}\ldots a_{n},b_{1},b_{2}\ldots b_{m}).$
Moreover, if every three consecutive symbols
![]() $a_{s},a_{s+1},a_{s+2}$
are distinct and every three consecutive symbols
$a_{s},a_{s+1},a_{s+2}$
are distinct and every three consecutive symbols
![]() $b_{s},b_{s+1},b_{s+2}$
are distinct, then
$b_{s},b_{s+1},b_{s+2}$
are distinct, then
![]() $\overline {f}(a_{1}a_{2}\ldots a_{n},b_{1},b_{2}\ldots b_{m})= \tilde {f}(a_{1}a_{2}\ldots a_{n},b_{1},b_{2}\ldots b_{m}).$
Note that it is possible for
$\overline {f}(a_{1}a_{2}\ldots a_{n},b_{1},b_{2}\ldots b_{m})= \tilde {f}(a_{1}a_{2}\ldots a_{n},b_{1},b_{2}\ldots b_{m}).$
Note that it is possible for
![]() $\tilde {f}(a_1a_2\ldots a_n,b_1b_2\ldots b_m)$
to be zero, even for
$\tilde {f}(a_1a_2\ldots a_n,b_1b_2\ldots b_m)$
to be zero, even for
![]() $a_1a_2\ldots a_n\ne b_1b_2\ldots b_m$
; for example,
$a_1a_2\ldots a_n\ne b_1b_2\ldots b_m$
; for example,
![]() $\tilde {f}(11000,11100)=0.$
$\tilde {f}(11000,11100)=0.$
Lemma 5.3. Suppose
![]() $\overline {f}(a_{1}a_{2}\ldots a_{n},b_{1}b_{2}\ldots b_{m})=1-\varepsilon $
, where
$\overline {f}(a_{1}a_{2}\ldots a_{n},b_{1}b_{2}\ldots b_{m})=1-\varepsilon $
, where
 $0\le \varepsilon < \tfrac 13.$
Then
$0\le \varepsilon < \tfrac 13.$
Then
![]() $\tilde {f}(a_{1}a_{2}\ldots a_{n},b_{1}b_{2},\ldots b_{m})\ge 1-3\varepsilon .$
$\tilde {f}(a_{1}a_{2}\ldots a_{n},b_{1}b_{2},\ldots b_{m})\ge 1-3\varepsilon .$
Proof. Suppose
![]() $\tilde {I}=\{(i_1,j_1),\ldots ,(i_r,j_r)\}$
is an approximate match between
$\tilde {I}=\{(i_1,j_1),\ldots ,(i_r,j_r)\}$
is an approximate match between
![]() $a_{1}a_{2}\ldots a_{n}$
and
$a_{1}a_{2}\ldots a_{n}$
and
![]() $b_{1}b_{2}\ldots b_{m}$
, as in Definition 5.2. We construct a match I with
$b_{1}b_{2}\ldots b_{m}$
, as in Definition 5.2. We construct a match I with
![]() $|I|\ge |\tilde {I}|/3.$
Select the first element
$|I|\ge |\tilde {I}|/3.$
Select the first element
![]() $(i_1,j_1)$
in
$(i_1,j_1)$
in
![]() $\tilde {I}$
as an element of I and discard those at most two other elements of
$\tilde {I}$
as an element of I and discard those at most two other elements of
![]() $\tilde {I}$
that have the same first coordinate or the same second coordinate as
$\tilde {I}$
that have the same first coordinate or the same second coordinate as
![]() $(i_{1},j_{1}).$
Then select the next element
$(i_{1},j_{1}).$
Then select the next element
![]() $(i_{s},j_{s})$
in
$(i_{s},j_{s})$
in
![]() $\tilde {I}$
that has not already been selected for I or discarded. We again retain this
$\tilde {I}$
that has not already been selected for I or discarded. We again retain this
![]() $(i_{s},j_{s})$
for I and discard those at most two other elements of
$(i_{s},j_{s})$
for I and discard those at most two other elements of
![]() $\tilde {I}$
that have not been discarded previously and that have the same first coordinate or the same second coordinate as
$\tilde {I}$
that have not been discarded previously and that have the same first coordinate or the same second coordinate as
![]() $(i_{s},j_{s}).$
Continue in this way until all elements of
$(i_{s},j_{s}).$
Continue in this way until all elements of
![]() $\tilde {I}$
have either been discarded or retained for
$\tilde {I}$
have either been discarded or retained for
![]() $I.$
Then
$I.$
Then
![]() $|\tilde {I}|\le 3|I|.$
$|\tilde {I}|\le 3|I|.$
Proposition 5.4. (Symbol by block replacement)
Suppose
![]() $A_{a_{1}},A_{a_{2}},\ldots ,A_{a_{n}}$
and
$A_{a_{1}},A_{a_{2}},\ldots ,A_{a_{n}}$
and
![]() $B_{b_{1}},B_{b_{2}},\ldots ,B_{b_{m}}$
are blocks of symbols, with each block of length
$B_{b_{1}},B_{b_{2}},\ldots ,B_{b_{m}}$
are blocks of symbols, with each block of length
![]() $L.$
Assume that
$L.$
Assume that
 $\alpha \in \big(0,\tfrac 17\big)$
,
$\alpha \in \big(0,\tfrac 17\big)$
,
 $\beta \in \big[0,\tfrac 17\big)$
,
$\beta \in \big[0,\tfrac 17\big)$
,
![]() $\alpha \ge \beta $
,
$\alpha \ge \beta $
,
![]() $R\geq 1$
, and for all substrings C and D consisting of consecutive symbols from
$R\geq 1$
, and for all substrings C and D consisting of consecutive symbols from
![]() $A_{a_{i}}$
and
$A_{a_{i}}$
and
![]() $B_{b_{j}}$
, respectively, with
$B_{b_{j}}$
, respectively, with
![]() $|C|,|D|\ge {L}/{R}$
we have
$|C|,|D|\ge {L}/{R}$
we have
 $$ \begin{align*} \overline{f}(C,D)\ge\alpha\quad\text{if }a_{i}\ne b_{j} \end{align*} $$
$$ \begin{align*} \overline{f}(C,D)\ge\alpha\quad\text{if }a_{i}\ne b_{j} \end{align*} $$
and
 $$ \begin{align*} \overline{f}(C,D)\ge\beta\quad\text{if }a_{i}=b_{j}. \end{align*} $$
$$ \begin{align*} \overline{f}(C,D)\ge\beta\quad\text{if }a_{i}=b_{j}. \end{align*} $$
Let
![]() $\tilde {f}=\tilde {f}(a_{1}a_{2}\ldots a_{n},b_{1}b_{2}\ldots b_{m}).$
Then
$\tilde {f}=\tilde {f}(a_{1}a_{2}\ldots a_{n},b_{1}b_{2}\ldots b_{m}).$
Then
 $$ \begin{align*} \overline{f}(A_{a_{1}}A_{a_{2}}\ldots A_{a_{n}},B_{b_{1}}B_{b_{2}}\ldots B_{b_{m}})& \ge\alpha \left(\tilde{f}-\frac{3}{R}\right)+\beta(1-\tilde{f)}>\alpha\tilde{f}+\beta(1-\tilde{f})-\frac{1}{R} \\ & >\alpha-(1-\tilde{f})+\beta(1-\tilde{f})-\frac{1}{R}. \end{align*} $$
$$ \begin{align*} \overline{f}(A_{a_{1}}A_{a_{2}}\ldots A_{a_{n}},B_{b_{1}}B_{b_{2}}\ldots B_{b_{m}})& \ge\alpha \left(\tilde{f}-\frac{3}{R}\right)+\beta(1-\tilde{f)}>\alpha\tilde{f}+\beta(1-\tilde{f})-\frac{1}{R} \\ & >\alpha-(1-\tilde{f})+\beta(1-\tilde{f})-\frac{1}{R}. \end{align*} $$
Proof. We may assume
![]() $R\geq 3$
; otherwise the conclusion holds trivially. We may also assume that
$R\geq 3$
; otherwise the conclusion holds trivially. We may also assume that
![]() $n\le m.$
We decompose
$n\le m.$
We decompose
![]() $A_{a_1}A_{a_2}\ldots A_{a_n}$
into the substrings
$A_{a_1}A_{a_2}\ldots A_{a_n}$
into the substrings
![]() $A_{a_{1}},A_{a_{2}},\ldots ,A_{a_{n}}$
and decompose
$A_{a_{1}},A_{a_{2}},\ldots ,A_{a_{n}}$
and decompose
![]() $B_{b_1}B_{b_2}\ldots B_{b_m}$
into corresponding substrings
$B_{b_1}B_{b_2}\ldots B_{b_m}$
into corresponding substrings
![]() $\tilde {B}_{1},\tilde {B}_{2},\ldots ,\tilde {B}_{n}$
according to a best possible match between the two strings. Then we decompose each
$\tilde {B}_{1},\tilde {B}_{2},\ldots ,\tilde {B}_{n}$
according to a best possible match between the two strings. Then we decompose each
![]() $A_{a_{i}}$
into at most three further substrings
$A_{a_{i}}$
into at most three further substrings
![]() $A_{a_{i},0},A_{a_{i},1},A_{a_{i},2}$
corresponding to substrings
$A_{a_{i},0},A_{a_{i},1},A_{a_{i},2}$
corresponding to substrings
![]() $B_{i,b_{j_{i}}},B_{i,b_{j_{i}+1}},B_{i,b_{j_{i}+2}}$
of
$B_{i,b_{j_{i}}},B_{i,b_{j_{i}+1}},B_{i,b_{j_{i}+2}}$
of
![]() $\tilde {B}_{i}$
that lie entirely in
$\tilde {B}_{i}$
that lie entirely in
![]() $B_{b_{j_{i}}},B_{b_{j_{i}+1}},B_{b_{j_{i}+2}}$
respectively, to obtain a best possible match between
$B_{b_{j_{i}}},B_{b_{j_{i}+1}},B_{b_{j_{i}+2}}$
respectively, to obtain a best possible match between
![]() $A_{a_i}$
and
$A_{a_i}$
and
![]() $\tilde {B}_i$
. We will apply Property 2.6 to this decomposition. We may ignore any
$\tilde {B}_i$
. We will apply Property 2.6 to this decomposition. We may ignore any
![]() $A_{a_{i}}$
and corresponding
$A_{a_{i}}$
and corresponding
![]() $\tilde {B}_{i}$
for which
$\tilde {B}_{i}$
for which
![]() $\tilde {B}_{i}$
fails to lie in three consecutive blocks
$\tilde {B}_{i}$
fails to lie in three consecutive blocks
![]() $B_{b_{j_{i}}},B_{b_{j_{i}+1}},B_{b_{j_{i}+2}},$
because in this case it follows from equation (2.6) in Property 2.7, that
$B_{b_{j_{i}}},B_{b_{j_{i}+1}},B_{b_{j_{i}+2}},$
because in this case it follows from equation (2.6) in Property 2.7, that
 $\overline {f}(A_{a_{i}},\tilde {B}_{i})>\tfrac 17>\alpha .$
For the same reason we may also ignore any
$\overline {f}(A_{a_{i}},\tilde {B}_{i})>\tfrac 17>\alpha .$
For the same reason we may also ignore any
![]() $B_{b_{j}}$
whose corresponding substring in
$B_{b_{j}}$
whose corresponding substring in
![]() $A_{a_{1}}A_{a_{2}}\ldots A_{a_{n}}$
fails to lie in three consecutive blocks
$A_{a_{1}}A_{a_{2}}\ldots A_{a_{n}}$
fails to lie in three consecutive blocks
![]() $A_{a_{i}},A_{a_{i+1}},A_{a_{i+2}}.$
We let
$A_{a_{i}},A_{a_{i+1}},A_{a_{i+2}}.$
We let
![]() $\tilde {I}$
consist of those remaining pairs
$\tilde {I}$
consist of those remaining pairs
![]() $(i',j')\in \cup _{i=1}^{n}\{(i,j_{i}),(i,j_{i}+1),(i,j_{i}+2)\}$
such that
$(i',j')\in \cup _{i=1}^{n}\{(i,j_{i}),(i,j_{i}+1),(i,j_{i}+2)\}$
such that
![]() $a_{i'}=b_{j'}.$
Then
$a_{i'}=b_{j'}.$
Then
![]() $\tilde {I}$
gives an approximate match between
$\tilde {I}$
gives an approximate match between
![]() $a_{1}a_{2}\ldots a_{n}$
and
$a_{1}a_{2}\ldots a_{n}$
and
![]() $b_{1}b_{2}\ldots b_{m}.$
The symbols in all
$b_{1}b_{2}\ldots b_{m}.$
The symbols in all
 $A_{a_{i'}}\cup B_{b_{j'}}$
for all
$A_{a_{i'}}\cup B_{b_{j'}}$
for all
![]() $(i',j')\in \tilde {I}$
form a fraction of at most
$(i',j')\in \tilde {I}$
form a fraction of at most
![]() $\min (1,({2|\tilde {I}|}/({n+m})))\le 1-\tilde {f}$
of the total number of symbols in
$\min (1,({2|\tilde {I}|}/({n+m})))\le 1-\tilde {f}$
of the total number of symbols in
![]() $A_{a_{1}}A_{a_{2}}\ldots A_{a_{n}}$
and
$A_{a_{1}}A_{a_{2}}\ldots A_{a_{n}}$
and
![]() $B_{b_{1}}B_{b_{2}}\ldots B_{b_{m}}.$
$B_{b_{1}}B_{b_{2}}\ldots B_{b_{m}}.$
For any substring
![]() $A_{a_{i},s}$
corresponding to a substring
$A_{a_{i},s}$
corresponding to a substring
![]() $B_{i,b_{j_{i}+s}}$
such that the length of at least one of these two substrings is less than
$B_{i,b_{j_{i}+s}}$
such that the length of at least one of these two substrings is less than
![]() ${L}/{R},$
the other substring has length less than
${L}/{R},$
the other substring has length less than
![]() ${4L}/{3R}$
(unless
${4L}/{3R}$
(unless
 $\overline {f}(A_{a_{i},s},B_{i,b_{j_{i}+s}})>\alpha ,$
a case that we again ignore). Moreover, if
$\overline {f}(A_{a_{i},s},B_{i,b_{j_{i}+s}})>\alpha ,$
a case that we again ignore). Moreover, if
![]() $A_{a_{i},0}$
and
$A_{a_{i},0}$
and
![]() $A_{a_{i},2}$
are both non-empty, then
$A_{a_{i},2}$
are both non-empty, then
![]() $B_{i,b_{j_{i}+1}}=B_{j_{i}}$
and
$B_{i,b_{j_{i}+1}}=B_{j_{i}}$
and
![]() $|A_{a_{i},1}|\ge (3/4)L\ge L/R$
(unless
$|A_{a_{i},1}|\ge (3/4)L\ge L/R$
(unless
![]() $\overline {f}(A_{a_{i},1},B_{j_{i}})>\alpha ).$
Hence if we eliminate substrings
$\overline {f}(A_{a_{i},1},B_{j_{i}})>\alpha ).$
Hence if we eliminate substrings
![]() $A_{a_{i},s}$
and
$A_{a_{i},s}$
and
![]() $B_{i,b_{j_{i}+s}}$
such that the length of at least one of the two substrings is less than
$B_{i,b_{j_{i}+s}}$
such that the length of at least one of the two substrings is less than
![]() ${L}/{R},$
we eliminate at most
${L}/{R},$
we eliminate at most
![]() ${14Ln}/{3R}$
symbols from the two strings
${14Ln}/{3R}$
symbols from the two strings
![]() $A_{a_{1}}A_{a_{2}}\ldots A_{a_{n}}$
and
$A_{a_{1}}A_{a_{2}}\ldots A_{a_{n}}$
and
![]() $B_{b_{1}}B_{b_{2}}\ldots B_{b_{m}}$
whose total combined length is
$B_{b_{1}}B_{b_{2}}\ldots B_{b_{m}}$
whose total combined length is
![]() $L(n+m)\ge 2Ln.$
Thus the fraction of symbols that are eliminated due to such short substrings is at most
$L(n+m)\ge 2Ln.$
Thus the fraction of symbols that are eliminated due to such short substrings is at most
![]() ${7}/{3R}<{3}/{R}$
. For those pairs
${7}/{3R}<{3}/{R}$
. For those pairs
![]() $(i,j_{i}+s), s\in \{0,1,2\},$
such that neither of the strings
$(i,j_{i}+s), s\in \{0,1,2\},$
such that neither of the strings
![]() $A_{a_{i},s}$
and
$A_{a_{i},s}$
and
![]() $B_{b_{j_{i}+s}}$
has length less than
$B_{b_{j_{i}+s}}$
has length less than
![]() ${L}/{R},$
it follows from the hypothesis that
${L}/{R},$
it follows from the hypothesis that
 $$ \begin{align*} \overline{f}(A_{a_{i},s},B_{b_{j_{i}+s}})\ge\alpha \quad \text{ if }(i,j_{i}+s)\notin\tilde{I}, \end{align*} $$
$$ \begin{align*} \overline{f}(A_{a_{i},s},B_{b_{j_{i}+s}})\ge\alpha \quad \text{ if }(i,j_{i}+s)\notin\tilde{I}, \end{align*} $$
and
 $$ \begin{align*} \overline{f}(A_{a_{i},s},B_{b_{j_{i}+s}})\ge\beta \quad \text{ if }(i,j_{i}+s)\in\tilde{I}. \end{align*} $$
$$ \begin{align*} \overline{f}(A_{a_{i},s},B_{b_{j_{i}+s}})\ge\beta \quad \text{ if }(i,j_{i}+s)\in\tilde{I}. \end{align*} $$
Therefore by Property 2.6, we obtain
 $$ \begin{align*} \overline{f}(A_{a_{1}}A_{a_{2}}\ldots A_{a_{n}},B_{b_{1}}B_{b_{2}}\ldots B_{b_{m}}) & \geq \alpha \bigg(1-(1-\tilde{f})-\frac{3}{R}\bigg)+\beta(1-\tilde{f}) \\ &>\alpha\tilde{f}+\beta(1-\tilde{f})-\frac{1}{R} \\ & \ge\alpha-(1-\tilde{f})+\beta(1-\tilde{f})-\frac{1}{R}.\\[-3.5pc] \end{align*} $$
$$ \begin{align*} \overline{f}(A_{a_{1}}A_{a_{2}}\ldots A_{a_{n}},B_{b_{1}}B_{b_{2}}\ldots B_{b_{m}}) & \geq \alpha \bigg(1-(1-\tilde{f})-\frac{3}{R}\bigg)+\beta(1-\tilde{f}) \\ &>\alpha\tilde{f}+\beta(1-\tilde{f})-\frac{1}{R} \\ & \ge\alpha-(1-\tilde{f})+\beta(1-\tilde{f})-\frac{1}{R}.\\[-3.5pc] \end{align*} $$
Corollary 5.5 Suppose
![]() $A_{a_{1}},A_{a_{2}},\ldots ,A_{a_{n}}$
and
$A_{a_{1}},A_{a_{2}},\ldots ,A_{a_{n}}$
and
![]() $A_{b_{1}},A_{b_{2}},\ldots ,A_{b_{m}}$
are blocks of symbols with each block of length
$A_{b_{1}},A_{b_{2}},\ldots ,A_{b_{m}}$
are blocks of symbols with each block of length
![]() $L.$
Assume that
$L.$
Assume that
 $\alpha \in \big(0,\tfrac 17\big)$
,
$\alpha \in \big(0,\tfrac 17\big)$
,
![]() $R\geq 1$
, and
$R\geq 1$
, and
for all substrings C and D consisting of consecutive symbols from
![]() $A_{a_{i}}$
and
$A_{a_{i}}$
and
![]() $A_{b_{j}}$
respectively, where
$A_{b_{j}}$
respectively, where
![]() $a_{i}\ne b_{j},$
and
$a_{i}\ne b_{j},$
and
![]() $|C|,|D|\ge {L}/{R}.$
Then for
$|C|,|D|\ge {L}/{R}.$
Then for
![]() $\tilde {f}=\tilde {f}(a_{1}a_{2}\ldots a_{n},b_{1}b_{2}\ldots b_{m}),$
we have
$\tilde {f}=\tilde {f}(a_{1}a_{2}\ldots a_{n},b_{1}b_{2}\ldots b_{m}),$
we have
 $$ \begin{align*} \overline{f}(A_{a_{1}}A_{a_{2}}\ldots A_{a_{n}},A_{b_{1}}A_{b_{2}}\ldots A_{b_{m}})>\alpha\tilde{f}-\frac{1}{R}\ge\alpha-(1-\tilde{f})-\frac{1}{R}. \end{align*} $$
$$ \begin{align*} \overline{f}(A_{a_{1}}A_{a_{2}}\ldots A_{a_{n}},A_{b_{1}}A_{b_{2}}\ldots A_{b_{m}})>\alpha\tilde{f}-\frac{1}{R}\ge\alpha-(1-\tilde{f})-\frac{1}{R}. \end{align*} $$
Proof. Let
![]() $B_{b_{j}}=A_{b_{j}}$
for
$B_{b_{j}}=A_{b_{j}}$
for
![]() $j=1,2,\ldots ,m,$
and
$j=1,2,\ldots ,m,$
and
![]() $\beta =0$
in Proposition 5.4.
$\beta =0$
in Proposition 5.4.
Remark 5.6. In fact, Corollary 5.5 and the case
![]() $\beta =0$
of Proposition 5.4 hold with
$\beta =0$
of Proposition 5.4 hold with
![]() $\tilde {f}$
replaced by
$\tilde {f}$
replaced by
![]() $\overline {f}(a_1a_2\ldots a_n,b_1b_2\ldots b_m)$
. We omit the proof because these versions are not needed for our results.
$\overline {f}(a_1a_2\ldots a_n,b_1b_2\ldots b_m)$
. We omit the proof because these versions are not needed for our results.
Remark 5.7. The following lemma is essentially the same as [Reference FeldmanFe76, Theorem 4] and [Reference Ornstein, Rudolph and WeissORW82, Proposition 1.1 in Ch. 10]. The proof is also essentially the same, but the estimates are more suited to our applications.
Lemma 5.8. Suppose
![]() $a_{1},a_{2},\ldots ,a_{N}$
are distinct symbols in
$a_{1},a_{2},\ldots ,a_{N}$
are distinct symbols in
![]() $\Sigma .$
Let
$\Sigma .$
Let
 $$ \begin{align*} {B}_{1}&= (a_{1}^{N^{2}}a_{2}^{N^{2}}\ldots a_{N}^{N^{2}})^{N^{2M}},\\ {B}_{2}&= (a_{1}^{N^{4}}a_{2}^{N^{4}}\ldots a_{N}^{N^{4}})^{N^{2M-2}},\\ \vdots\;\; & \;\;\vdots\\ {B}_{M}&= (a_{1}^{N^{2M}}a_{2}^{N^{2M}}\ldots a_{N}^{N^{2M}})^{N^{2}}. \end{align*} $$
$$ \begin{align*} {B}_{1}&= (a_{1}^{N^{2}}a_{2}^{N^{2}}\ldots a_{N}^{N^{2}})^{N^{2M}},\\ {B}_{2}&= (a_{1}^{N^{4}}a_{2}^{N^{4}}\ldots a_{N}^{N^{4}})^{N^{2M-2}},\\ \vdots\;\; & \;\;\vdots\\ {B}_{M}&= (a_{1}^{N^{2M}}a_{2}^{N^{2M}}\ldots a_{N}^{N^{2M}})^{N^{2}}. \end{align*} $$
Suppose B and
![]() $\overline {B}$
are strings of consecutive symbols in
$\overline {B}$
are strings of consecutive symbols in
![]() $B_{j}$
and
$B_{j}$
and
![]() $B_{k}$
respectively, where
$B_{k}$
respectively, where
![]() $|B|\ge N^{2M+2}$
,
$|B|\ge N^{2M+2}$
,
![]() $|\overline {B}|\ge N^{2M+2}$
, and
$|\overline {B}|\ge N^{2M+2}$
, and
![]() $j\ne k$
. Assume that
$j\ne k$
. Assume that
![]() $N\ge 20$
and
$N\ge 20$
and
![]() $M\ge 2$
. Then
$M\ge 2$
. Then
 $$ \begin{align*} \overline{f}(B,\overline{B})>1-\frac{4}{\sqrt{N}}\quad\text{and}\quad\tilde{f}(B,\overline{B})>1-\frac{12}{\sqrt{N}}. \end{align*} $$
$$ \begin{align*} \overline{f}(B,\overline{B})>1-\frac{4}{\sqrt{N}}\quad\text{and}\quad\tilde{f}(B,\overline{B})>1-\frac{12}{\sqrt{N}}. \end{align*} $$
Proof. We may assume that
![]() $j>k.$
By removing fewer than
$j>k.$
By removing fewer than
![]() $2N^{2j}$
symbols from the beginning and end of
$2N^{2j}$
symbols from the beginning and end of
![]() $B,$
we can decompose the remaining part of B into strings
$B,$
we can decompose the remaining part of B into strings
![]() $C_{1},C_{2},\ldots ,C_{r}$
each of the form
$C_{1},C_{2},\ldots ,C_{r}$
each of the form
 $a_{i}^{N^{2j}}.$
Since
$a_{i}^{N^{2j}}.$
Since
![]() $2N^{2j}\le ({|B|+|\overline {B}|})/{N^{2}},$
it follows from Property 2.5 that removing these symbols increases the
$2N^{2j}\le ({|B|+|\overline {B}|})/{N^{2}},$
it follows from Property 2.5 that removing these symbols increases the
![]() $\overline {f}$
distance between B and
$\overline {f}$
distance between B and
![]() $\overline {B}$
by less than
$\overline {B}$
by less than
![]() ${2}/{N^{2}}.$
Let
${2}/{N^{2}}.$
Let
![]() $\overline {C}_{1},\overline {C}_{2},\ldots ,\overline {C}_{r}$
be the decomposition of
$\overline {C}_{1},\overline {C}_{2},\ldots ,\overline {C}_{r}$
be the decomposition of
![]() $\overline {B}$
into substrings corresponding to
$\overline {B}$
into substrings corresponding to
![]() $C_{1},C_{2},\ldots ,C_{r}$
under a best possible match between
$C_{1},C_{2},\ldots ,C_{r}$
under a best possible match between
![]() $C_{1}C_{2}\ldots C_{r}$
and
$C_{1}C_{2}\ldots C_{r}$
and
![]() $\overline {B}.$
$\overline {B}.$
Let
![]() $i\in \{1,2,\ldots ,r\}.$
$i\in \{1,2,\ldots ,r\}.$
Case 1.
![]() $|\overline {C}_{i}|<({3}/{2\sqrt {N}})|C_{i}|$
. Then by Property 2.7,
$|\overline {C}_{i}|<({3}/{2\sqrt {N}})|C_{i}|$
. Then by Property 2.7,
![]() $\overline {f}(C_{i},\overline {C}_{i})>1-({3}/{\sqrt {N}})$
.
$\overline {f}(C_{i},\overline {C}_{i})>1-({3}/{\sqrt {N}})$
.
Case 2.
![]() $|\overline {C}_{i}|\ge ({3}/{2\sqrt {N}})|C_{i}|=(3/2)N^{2j-(1/2)}$
. A cycle
$|\overline {C}_{i}|\ge ({3}/{2\sqrt {N}})|C_{i}|=(3/2)N^{2j-(1/2)}$
. A cycle
 $a_1^{N^{2k}}a_2^{N^{2k}}\dots a_N{N^{2k}}$
in
$a_1^{N^{2k}}a_2^{N^{2k}}\dots a_N{N^{2k}}$
in
![]() $B_{k}$
has length at most
$B_{k}$
has length at most
![]() $N^{2j-1}$
. Therefore
$N^{2j-1}$
. Therefore
![]() $\overline {C}_{i}$
contains at least
$\overline {C}_{i}$
contains at least
![]() $\lfloor {3\sqrt {N}}/{2}\rfloor -1>\sqrt {N}$
complete cycles. Thus deleting any partial cycles at the beginning and end of
$\lfloor {3\sqrt {N}}/{2}\rfloor -1>\sqrt {N}$
complete cycles. Thus deleting any partial cycles at the beginning and end of
![]() $\overline {C}_{i}$
would increase the
$\overline {C}_{i}$
would increase the
![]() $\overline {f}$
distance between
$\overline {f}$
distance between
![]() $C_{i}$
and
$C_{i}$
and
![]() $\overline {C}_{i}$
by less than
$\overline {C}_{i}$
by less than
![]() ${2}/{\sqrt {N}}.$
On the rest of
${2}/{\sqrt {N}}.$
On the rest of
![]() $\overline {C}_{i}$
, only
$\overline {C}_{i}$
, only
![]() ${1}/{N}$
of the symbols in
${1}/{N}$
of the symbols in
![]() $\overline {C}_{i}$
can match the symbol in
$\overline {C}_{i}$
can match the symbol in
![]() $C_{i}.$
Thus
$C_{i}.$
Thus
![]() $\overline {f}(C_{i},\overline {C}_{i})>1-({2}/{\sqrt {N}})-({4}/{N})>1-({3}/{\sqrt {N}}).$
$\overline {f}(C_{i},\overline {C}_{i})>1-({2}/{\sqrt {N}})-({4}/{N})>1-({3}/{\sqrt {N}}).$
Therefore, by Property 2.6,
![]() $\overline {f}(C_{1}C_{2}\ldots C_{r},\overline {C}_{1},\overline {C}_{2}\ldots ,\overline {C}_r)> 1-({3}/{\sqrt {N}}). $
By Lemma 5.3 the claimed
$\overline {f}(C_{1}C_{2}\ldots C_{r},\overline {C}_{1},\overline {C}_{2}\ldots ,\overline {C}_r)> 1-({3}/{\sqrt {N}}). $
By Lemma 5.3 the claimed
![]() $\tilde {f}$
inequality holds as well.
$\tilde {f}$
inequality holds as well.
Remark 5.9. If we replace each symbol
![]() $a_i$
by a constant number of repetitions
$a_i$
by a constant number of repetitions
![]() $a_i^l$
, then the same conclusion still holds for substrings of length at least
$a_i^l$
, then the same conclusion still holds for substrings of length at least
![]() $lN^{2M+2}$
.
$lN^{2M+2}$
.
Proposition 5.10. Let
 $\alpha \in \big(0,\tfrac 17\big)$
,
$\alpha \in \big(0,\tfrac 17\big)$
,
![]() $n \in \mathbb {N}$
, and
$n \in \mathbb {N}$
, and
![]() $K,R,S,N,M\in \mathbb {N}\setminus \{ 0\} $
with
$K,R,S,N,M\in \mathbb {N}\setminus \{ 0\} $
with
![]() $N\geq 20$
and
$N\geq 20$
and
![]() $M\geq 2$
. For
$M\geq 2$
. For
![]() $1\leq s\leq S$
, let
$1\leq s\leq S$
, let
 $\mathtt {A}_{1}^{(s)},\ldots ,\mathtt {A}_{N}^{(s)}$
be a family of strings, where each
$\mathtt {A}_{1}^{(s)},\ldots ,\mathtt {A}_{N}^{(s)}$
be a family of strings, where each
 $\mathtt {A}_{j}^{(s)}$
is a concatenation of
$\mathtt {A}_{j}^{(s)}$
is a concatenation of
![]() $K\, n$
-blocks. Assume that for all
$K\, n$
-blocks. Assume that for all
![]() $0\leq i_{1},i_{2}<q_{n}$
, all
$0\leq i_{1},i_{2}<q_{n}$
, all
![]() $1\leq s_{1},s_{2}\leq S$
and all
$1\leq s_{1},s_{2}\leq S$
and all
![]() $j_{1},j_{2}\in \{ 1,\ldots ,N\} $
,
$j_{1},j_{2}\in \{ 1,\ldots ,N\} $
,
![]() $j_{1}\neq j_{2}$
, we have
$j_{1}\neq j_{2}$
, we have
![]() $\overline {f}(\mathcal {A},\overline {\mathcal {A}})>\alpha $
for all sequences
$\overline {f}(\mathcal {A},\overline {\mathcal {A}})>\alpha $
for all sequences
![]() $\mathcal {A},\overline {\mathcal {A}}$
each consisting of at least
$\mathcal {A},\overline {\mathcal {A}}$
each consisting of at least
![]() $K l_{n} q_{n}/R$
consecutive symbols from
$K l_{n} q_{n}/R$
consecutive symbols from
 $\mathcal {C}_{n,i_{1}}(\mathtt {A}_{j_{1}}^{(s_{1})})$
and
$\mathcal {C}_{n,i_{1}}(\mathtt {A}_{j_{1}}^{(s_{1})})$
and
 $\mathcal {C}_{n,i_{2}}(\mathtt {A}_{j_{2}}^{(s_{2})})$
, respectively.
$\mathcal {C}_{n,i_{2}}(\mathtt {A}_{j_{2}}^{(s_{2})})$
, respectively.
Then for
![]() $1\leq s\leq S$
, we can construct a family of strings
$1\leq s\leq S$
, we can construct a family of strings
 $\mathtt {B}_{1}^{(s)},\ldots ,\mathtt {B}_{M}^{(s)}$
(of equal length
$\mathtt {B}_{1}^{(s)},\ldots ,\mathtt {B}_{M}^{(s)}$
(of equal length
![]() $N^{2M+3} K \mathtt {h}_{n}$
and containing each block
$N^{2M+3} K \mathtt {h}_{n}$
and containing each block
 $\mathtt {A}_{1}^{(s)},\ldots ,\mathtt {A}_{N}^{(s)}$
exactly
$\mathtt {A}_{1}^{(s)},\ldots ,\mathtt {A}_{N}^{(s)}$
exactly
![]() $N^{2M+2}$
times) such that for all
$N^{2M+2}$
times) such that for all
![]() $0\leq i_{1},i_{2}<q_{n}$
, all
$0\leq i_{1},i_{2}<q_{n}$
, all
![]() $1\leq s_{1},s_{2}\leq S$
, all
$1\leq s_{1},s_{2}\leq S$
, all
![]() $j,k\in \{ 1,\ldots ,M\} $
,
$j,k\in \{ 1,\ldots ,M\} $
,
![]() $j\neq k,$
and all sequences
$j\neq k,$
and all sequences
![]() $\mathcal {B}$
,
$\mathcal {B}$
,
![]() $\overline {\mathcal {B}}$
of at least
$\overline {\mathcal {B}}$
of at least
![]() $N^{2M+2} l_{n} K q_{n}$
consecutive symbols from
$N^{2M+2} l_{n} K q_{n}$
consecutive symbols from
 $\mathcal {C}_{n,i_{1}}(\mathtt {B}_{j}^{(s_{1})})$
and
$\mathcal {C}_{n,i_{1}}(\mathtt {B}_{j}^{(s_{1})})$
and
 $\mathcal {C}_{n,i_{2}}(\mathtt {B}_{k}^{(s_{2})})$
we have
$\mathcal {C}_{n,i_{2}}(\mathtt {B}_{k}^{(s_{2})})$
we have
 $$ \begin{align*} \overline{f}(\mathcal{B},\overline{\mathcal{B}})>\alpha-\frac{13}{\sqrt{N}}-\frac{1}{R}. \end{align*} $$
$$ \begin{align*} \overline{f}(\mathcal{B},\overline{\mathcal{B}})>\alpha-\frac{13}{\sqrt{N}}-\frac{1}{R}. \end{align*} $$
Proof. For every
![]() $1\leq s\leq S$
we define
$1\leq s\leq S$
we define
 $$ \begin{align*} \mathtt{B}_{1}^{(s)}&= \Big((\mathtt{A}_{1}^{(s)})^{N^{2}}(\mathtt{A}_{2}^{(s)})^{N^{2}}\ldots(\mathtt{A}_{N}^{(s)})^{N^{2}}\Big)^{N^{2M}},\\ \mathtt{B}_{2}^{(s)}&= \Big((\mathtt{A}_{1}^{(s)})^{N^{4}}(\mathtt{A}_{2}^{(s)})^{N^{4}}\ldots(\mathtt{A}_{N}^{(s)})^{N^{4}}\Big)^{N^{2M-2}},\\ \vdots\;\; & \;\;\vdots\\ \mathtt{B}_{M}^{(s)}&= \Big((\mathtt{A}_{1}^{(s)})^{N^{2M}}(\mathtt{A}_{2}^{(s)})^{N^{2M}}\ldots(\mathtt{A}_{N}^{(s)})^{N^{2M}}\Big)^{N^{2}}. \end{align*} $$
$$ \begin{align*} \mathtt{B}_{1}^{(s)}&= \Big((\mathtt{A}_{1}^{(s)})^{N^{2}}(\mathtt{A}_{2}^{(s)})^{N^{2}}\ldots(\mathtt{A}_{N}^{(s)})^{N^{2}}\Big)^{N^{2M}},\\ \mathtt{B}_{2}^{(s)}&= \Big((\mathtt{A}_{1}^{(s)})^{N^{4}}(\mathtt{A}_{2}^{(s)})^{N^{4}}\ldots(\mathtt{A}_{N}^{(s)})^{N^{4}}\Big)^{N^{2M-2}},\\ \vdots\;\; & \;\;\vdots\\ \mathtt{B}_{M}^{(s)}&= \Big((\mathtt{A}_{1}^{(s)})^{N^{2M}}(\mathtt{A}_{2}^{(s)})^{N^{2M}}\ldots(\mathtt{A}_{N}^{(s)})^{N^{2M}}\Big)^{N^{2}}. \end{align*} $$
Let
 $\mathcal {B}_{j,i_{1}}^{(s_{1})}=\mathcal {C}_{n,i_{1}}(\mathtt {B}_{j}^{(s_{1})}), \mathcal {B}_{j,i_{2}}^{(s_{2})}=\mathcal {C}_{n,i_{2}}(\mathtt {B}_{j}^{(s_{1})})$
,
$\mathcal {B}_{j,i_{1}}^{(s_{1})}=\mathcal {C}_{n,i_{1}}(\mathtt {B}_{j}^{(s_{1})}), \mathcal {B}_{j,i_{2}}^{(s_{2})}=\mathcal {C}_{n,i_{2}}(\mathtt {B}_{j}^{(s_{1})})$
,
 $\mathcal {A}_{j,i_{1}}^{(s_{1})}=\mathcal {C}_{n,i_{1}}(\mathtt {A}_{j}^{(s_{1})}),$
and
$\mathcal {A}_{j,i_{1}}^{(s_{1})}=\mathcal {C}_{n,i_{1}}(\mathtt {A}_{j}^{(s_{1})}),$
and
 $\mathcal {A}_{j,i_{2}}^{(s_{2})}=\mathcal {C}_{n,i_{2}}(\mathtt {A}_{j}^{(s_{2})}).$
Then the formulas for the
$\mathcal {A}_{j,i_{2}}^{(s_{2})}=\mathcal {C}_{n,i_{2}}(\mathtt {A}_{j}^{(s_{2})}).$
Then the formulas for the
 $\mathcal {B}_{j,i_{1}}^{(s_{1})},j=1,\ldots ,M,$
in terms of the
$\mathcal {B}_{j,i_{1}}^{(s_{1})},j=1,\ldots ,M,$
in terms of the
 $\mathcal {A}_{1,i_{1}}^{(s_{1})},\ldots $
,
$\mathcal {A}_{1,i_{1}}^{(s_{1})},\ldots $
,
 $\mathcal {A}_{N,i_{1}}^{(s_{1})}$
can be obtained from the formulas for the
$\mathcal {A}_{N,i_{1}}^{(s_{1})}$
can be obtained from the formulas for the
 $\mathtt {B}_{j}^{(s_{1})}$
in terms of the
$\mathtt {B}_{j}^{(s_{1})}$
in terms of the
 $\mathtt {A}_{1}^{(s_{1})},\ldots ,\mathtt {A}_{N}^{(s_{1})}$
by replacing each typewriter font
$\mathtt {A}_{1}^{(s_{1})},\ldots ,\mathtt {A}_{N}^{(s_{1})}$
by replacing each typewriter font
![]() $\mathtt {A,B}$
by the calligraphic
$\mathtt {A,B}$
by the calligraphic
![]() $\mathcal {A},\mathcal {B}$
with the corresponding sub- and superscripts, and the analogous statement is true for the
$\mathcal {A},\mathcal {B}$
with the corresponding sub- and superscripts, and the analogous statement is true for the
 $\mathcal {B}_{j,i_{2}}^{(s_{2})},j=1,\ldots ,M.$
$\mathcal {B}_{j,i_{2}}^{(s_{2})},j=1,\ldots ,M.$
By adding fewer than
![]() $2l_{n}Kq_{n}$
symbols to each of
$2l_{n}Kq_{n}$
symbols to each of
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\overline {\mathcal {B}}$
we can complete any partial
$\overline {\mathcal {B}}$
we can complete any partial
 $\mathcal {A}_{j,i_{1}}^{(s_{1})}$
at the beginning and end of
$\mathcal {A}_{j,i_{1}}^{(s_{1})}$
at the beginning and end of
![]() $\mathcal {B}$
and any partial
$\mathcal {B}$
and any partial
 $\mathcal {A}_{j,i_{2}}^{(s_{2})}$
at the beginning and end of
$\mathcal {A}_{j,i_{2}}^{(s_{2})}$
at the beginning and end of
![]() $\overline {\mathcal {B}}.$
Let
$\overline {\mathcal {B}}.$
Let
![]() $\mathcal {B}_{\text {aug}}$
and
$\mathcal {B}_{\text {aug}}$
and
 $\overline {\mathcal {B}}_{\text {aug}}$
be the augmented
$\overline {\mathcal {B}}_{\text {aug}}$
be the augmented
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\overline {\mathcal {B}}$
strings obtained in this way. By Property 2.5,
$\overline {\mathcal {B}}$
strings obtained in this way. By Property 2.5,
 $\overline {f}(\mathcal {B},\overline {\mathcal {B}})> \overline {f}(\mathcal {B}_{\text {aug}},\overline {\mathcal {B}}_{\text {aug}})- (4l_{n}Kq_{n})/(2N^{2M+2}l_{n}Kq_{n})=\overline {f}(\mathcal {B}_{\text {aug}},\overline {\mathcal {B}}_{\text {aug}})-2/{N^{2M+2}}.$
Then we are comparing two different Feldman patterns of blocks, and by Lemma 5.8 and Corollary 5.5 with
$\overline {f}(\mathcal {B},\overline {\mathcal {B}})> \overline {f}(\mathcal {B}_{\text {aug}},\overline {\mathcal {B}}_{\text {aug}})- (4l_{n}Kq_{n})/(2N^{2M+2}l_{n}Kq_{n})=\overline {f}(\mathcal {B}_{\text {aug}},\overline {\mathcal {B}}_{\text {aug}})-2/{N^{2M+2}}.$
Then we are comparing two different Feldman patterns of blocks, and by Lemma 5.8 and Corollary 5.5 with
![]() $\tilde {f}>1-({12}/{\sqrt {N}})$
, we have
$\tilde {f}>1-({12}/{\sqrt {N}})$
, we have
 $$ \begin{align*} \overline{f}(\mathcal{B}_{\text{aug}},\overline{\mathcal{B}}_{\text{aug}})>\alpha-\frac{12}{\sqrt{N}}-\frac{1}{R}. \end{align*} $$
$$ \begin{align*} \overline{f}(\mathcal{B}_{\text{aug}},\overline{\mathcal{B}}_{\text{aug}})>\alpha-\frac{12}{\sqrt{N}}-\frac{1}{R}. \end{align*} $$
Therefore
 $$ \begin{align*} \overline{f}(\mathcal{B},\overline{\mathcal{B}})>\alpha-\frac{12}{\sqrt{N}}-\frac{1}{R}-\frac{2}{N^{2M+2}}>\alpha-\frac{13}{\sqrt{N}}-\frac{1}{R}.\\[-3.7pc] \end{align*} $$
$$ \begin{align*} \overline{f}(\mathcal{B},\overline{\mathcal{B}})>\alpha-\frac{12}{\sqrt{N}}-\frac{1}{R}-\frac{2}{N^{2M+2}}>\alpha-\frac{13}{\sqrt{N}}-\frac{1}{R}.\\[-3.7pc] \end{align*} $$
For an application in §5.3 we will need the following result on the
![]() $\overline {f}$
distance between strings that can be built as the same or different Feldman patterns but with building blocks from different families.
$\overline {f}$
distance between strings that can be built as the same or different Feldman patterns but with building blocks from different families.
Lemma 5.11. Let
 $\alpha \in \big(0,\tfrac 17\big)$
,
$\alpha \in \big(0,\tfrac 17\big)$
,
![]() $n\in \mathbb {N}$
, and
$n\in \mathbb {N}$
, and
![]() $K,R,S,N,M\in \mathbb {N}\setminus \{0\}$
with
$K,R,S,N,M\in \mathbb {N}\setminus \{0\}$
with
![]() $N\geq 20$
, and
$N\geq 20$
, and
![]() $M,S$
at least
$M,S$
at least
![]() $2$
. For
$2$
. For
![]() $1\leq s\leq S$
, let
$1\leq s\leq S$
, let
 $\mathtt {A}_{1}^{(s)},\ldots ,\mathtt {A}_{N}^{(s)}$
be a family of strings, where each
$\mathtt {A}_{1}^{(s)},\ldots ,\mathtt {A}_{N}^{(s)}$
be a family of strings, where each
 $\mathtt {A}_{j}^{(s)}$
is a concatenation of
$\mathtt {A}_{j}^{(s)}$
is a concatenation of
![]() $K\, n$
-blocks. Assume that for all
$K\, n$
-blocks. Assume that for all
![]() $0\leq i_{1},i_{2}<q_{n}$
, all
$0\leq i_{1},i_{2}<q_{n}$
, all
![]() $s_{1}\neq s_{2}$
, and all
$s_{1}\neq s_{2}$
, and all
![]() $j_{1},j_{2}\in \{ 1,\ldots ,N\} $
we have
$j_{1},j_{2}\in \{ 1,\ldots ,N\} $
we have
![]() $\overline {f}(\mathcal {A},\overline {\mathcal {A}})>\alpha $
for all strings
$\overline {f}(\mathcal {A},\overline {\mathcal {A}})>\alpha $
for all strings
![]() $\mathcal {A},\overline {\mathcal {A}}$
of at least
$\mathcal {A},\overline {\mathcal {A}}$
of at least
![]() $K l_{n} q_{n}/R$
consecutive symbols from
$K l_{n} q_{n}/R$
consecutive symbols from
 $\mathcal {C}_{n,i_{1}}(\mathtt {A}_{j_{1}}^{(s_{1})})$
and
$\mathcal {C}_{n,i_{1}}(\mathtt {A}_{j_{1}}^{(s_{1})})$
and
 $\mathcal {C}_{n,i_{2}}(\mathtt {A}_{j_{2}}^{(s_{2})})$
respectively.
$\mathcal {C}_{n,i_{2}}(\mathtt {A}_{j_{2}}^{(s_{2})})$
respectively.
Then for
![]() $1\leq s\leq S$
we can construct a family of strings
$1\leq s\leq S$
we can construct a family of strings
 $\mathtt {B}_{1}^{(s)},\ldots \mathtt {B}_{M}^{(s)}$
, as in Proposition 5.10, and obtain that for all
$\mathtt {B}_{1}^{(s)},\ldots \mathtt {B}_{M}^{(s)}$
, as in Proposition 5.10, and obtain that for all
![]() $0\leq i_{1},i_{2}<q_{n}$
, all
$0\leq i_{1},i_{2}<q_{n}$
, all
![]() $j_{1},j_{2}\in \{ 1,\ldots ,M\} $
, and all sequences
$j_{1},j_{2}\in \{ 1,\ldots ,M\} $
, and all sequences
![]() $\mathcal {B}$
,
$\mathcal {B}$
,
![]() $\overline {\mathcal {B}}$
of at least
$\overline {\mathcal {B}}$
of at least
![]() $N^{2M+2} l_{n} K q_{n}$
consecutive symbols from
$N^{2M+2} l_{n} K q_{n}$
consecutive symbols from
 $\mathcal {C}_{n,i_{1}}(\mathtt {B}_{j_{1}}^{(s_{1})})$
and
$\mathcal {C}_{n,i_{1}}(\mathtt {B}_{j_{1}}^{(s_{1})})$
and
 $\mathcal {C}_{n,i_{2}}(\mathtt {B}_{j_{2}}^{(s_{2})})$
,
$\mathcal {C}_{n,i_{2}}(\mathtt {B}_{j_{2}}^{(s_{2})})$
,
![]() $s_{1}\neq s_{2}$
, we have
$s_{1}\neq s_{2}$
, we have
 $$ \begin{align} \overline{f}(\mathcal{B},\overline{\mathcal{B}})>\alpha-\frac{2}{N^{2M+2}}-\frac{1}{R}. \end{align} $$
$$ \begin{align} \overline{f}(\mathcal{B},\overline{\mathcal{B}})>\alpha-\frac{2}{N^{2M+2}}-\frac{1}{R}. \end{align} $$
5.2. Feldman mechanism to produce sufficiently many blocks
Recall that the images of odometer n-blocks under
![]() $\mathcal {C}_{n,i}$
are part of the circular
$\mathcal {C}_{n,i}$
are part of the circular
![]() $(n+1)$
-block. The following statement allows us to obtain lower bounds on the
$(n+1)$
-block. The following statement allows us to obtain lower bounds on the
![]() $\overline {f}$
distance between substrings of images of odometer n-blocks under
$\overline {f}$
distance between substrings of images of odometer n-blocks under
![]() $\mathcal {C}_{n,i}$
, given a lower bound on the
$\mathcal {C}_{n,i}$
, given a lower bound on the
![]() $\overline {f}$
distance between substrings of the circular n-blocks. Since we will apply this result several times in the proofs of Propositions 5.13 and 5.15, we state it as a separate lemma.
$\overline {f}$
distance between substrings of the circular n-blocks. Since we will apply this result several times in the proofs of Propositions 5.13 and 5.15, we state it as a separate lemma.
Lemma 5.12. Let
 $\alpha \in \big(0,\tfrac 17\big)$
and
$\alpha \in \big(0,\tfrac 17\big)$
and
![]() $n,N,R\in \mathbb {N}\setminus \{0\}$
. Moreover, let N odometer n-blocks
$n,N,R\in \mathbb {N}\setminus \{0\}$
. Moreover, let N odometer n-blocks
 $\mathtt {B}_{1}^{(n)},\ldots ,\mathtt {B}_{N}^{(n)}$
be given such that for all
$\mathtt {B}_{1}^{(n)},\ldots ,\mathtt {B}_{N}^{(n)}$
be given such that for all
![]() $j,k\in \{ 1,\ldots ,N\} $
,
$j,k\in \{ 1,\ldots ,N\} $
,
![]() $j\neq k$
, we have
$j\neq k$
, we have
![]() $\overline {f}(\mathcal {A},\overline {\mathcal {A}})>\alpha $
for any sequences
$\overline {f}(\mathcal {A},\overline {\mathcal {A}})>\alpha $
for any sequences
![]() $\mathcal {A},\overline {\mathcal {A}}$
of at least
$\mathcal {A},\overline {\mathcal {A}}$
of at least
![]() $q_{n}/R$
consecutive symbols from the circular n-blocks
$q_{n}/R$
consecutive symbols from the circular n-blocks
 $\mathcal {B}_{j}^{(n)}$
and
$\mathcal {B}_{j}^{(n)}$
and
 $\mathcal {B}_{k}^{(n)}$
respectively. Then for all
$\mathcal {B}_{k}^{(n)}$
respectively. Then for all
![]() $j,k\in \{ 1,\ldots ,N\} $
,
$j,k\in \{ 1,\ldots ,N\} $
,
![]() $j\neq k$
, any
$j\neq k$
, any
![]() $0\leq i_{1},i_{2}<q_{n}$
, and any sequences
$0\leq i_{1},i_{2}<q_{n}$
, and any sequences
![]() $\mathcal {D},\overline {\mathcal {D}}$
of at least
$\mathcal {D},\overline {\mathcal {D}}$
of at least
![]() $q_{n}l_{n}/R$
consecutive symbols from
$q_{n}l_{n}/R$
consecutive symbols from
 $\mathcal {C}_{n,i_{1}}(\mathtt {B}_{j}^{(n)})$
and
$\mathcal {C}_{n,i_{1}}(\mathtt {B}_{j}^{(n)})$
and
 $\mathcal {C}_{n,i_{2}}(\mathtt {B}_{k}^{(n)})$
respectively, we have
$\mathcal {C}_{n,i_{2}}(\mathtt {B}_{k}^{(n)})$
respectively, we have
 $$ \begin{align*} \overline{f}(\mathcal{D},\overline{\mathcal{D}})>\alpha-\frac{1}{R}-\frac{4R}{l_{n}}. \end{align*} $$
$$ \begin{align*} \overline{f}(\mathcal{D},\overline{\mathcal{D}})>\alpha-\frac{1}{R}-\frac{4R}{l_{n}}. \end{align*} $$
Proof. Let
![]() $\mathcal {D},\overline {\mathcal {D}}$
be arbitrary sequences of at least
$\mathcal {D},\overline {\mathcal {D}}$
be arbitrary sequences of at least
![]() $q_{n}l_{n}/R$
consecutive symbols from
$q_{n}l_{n}/R$
consecutive symbols from
 $\mathcal {C}_{n,i_{1}}(\mathtt {B}_{j}^{(n)})=b^{q_n-j_{i_1}}(\mathcal {B}_j^{(n)})^{l_n-1}e^{j_{i_1}}$
and from
$\mathcal {C}_{n,i_{1}}(\mathtt {B}_{j}^{(n)})=b^{q_n-j_{i_1}}(\mathcal {B}_j^{(n)})^{l_n-1}e^{j_{i_1}}$
and from
 $\mathcal {C}_{n,i_{2}}(\mathtt {B}_{k}^{(n)}) = b^{q_n-j_{i_2}} (\mathcal {B}_j^{(n)})^{l_n-1}e^{j_{i_2}}$
, respectively, for any
$\mathcal {C}_{n,i_{2}}(\mathtt {B}_{k}^{(n)}) = b^{q_n-j_{i_2}} (\mathcal {B}_j^{(n)})^{l_n-1}e^{j_{i_2}}$
, respectively, for any
![]() $j\neq k$
and any
$j\neq k$
and any
![]() $0\leq i_{1},i_{2}<q_{n}$
. We modify
$0\leq i_{1},i_{2}<q_{n}$
. We modify
![]() $\mathcal {D}$
and
$\mathcal {D}$
and
![]() $\overline {\mathcal {D}}$
by first completing any partial blocks
$\overline {\mathcal {D}}$
by first completing any partial blocks
 $\mathcal {B}_j^{(n)}$
and
$\mathcal {B}_j^{(n)}$
and
 $\mathcal {B}_k^{(n)}$
, which can be accomplished by adding fewer than
$\mathcal {B}_k^{(n)}$
, which can be accomplished by adding fewer than
![]() $2q_n$
symbols to each of
$2q_n$
symbols to each of
![]() $\mathcal {D}$
and
$\mathcal {D}$
and
![]() $\overline {\mathcal {D}}$
. Then we remove any of the b's preceding the
$\overline {\mathcal {D}}$
. Then we remove any of the b's preceding the
 $\mathcal {B}_j^{(n)}$
s and any of the e's following the
$\mathcal {B}_j^{(n)}$
s and any of the e's following the
 $\mathcal {B}_j^{(n)}$
s that are included in
$\mathcal {B}_j^{(n)}$
s that are included in
![]() $\mathcal {D}$
s, and similarly for such b's and e's in
$\mathcal {D}$
s, and similarly for such b's and e's in
![]() $\overline {\mathcal {D}}$
. At most
$\overline {\mathcal {D}}$
. At most
![]() $q_n$
symbols are removed from each of
$q_n$
symbols are removed from each of
![]() $\mathcal {D}$
and
$\mathcal {D}$
and
![]() $\overline {\mathcal {D}}$
. Let
$\overline {\mathcal {D}}$
. Let
![]() $\mathcal {D}_{\text {mod}}$
and
$\mathcal {D}_{\text {mod}}$
and
![]() $\overline {\mathcal {D}}_{\text {mod}}$
be these modified versions of
$\overline {\mathcal {D}}_{\text {mod}}$
be these modified versions of
![]() $\mathcal {D}$
and
$\mathcal {D}$
and
![]() $\overline {\mathcal {D}}.$
Then by Property 2.5,
$\overline {\mathcal {D}}.$
Then by Property 2.5,
 $$ \begin{align*} \overline{f}(\mathcal{D},\overline{\mathcal{D}})>\overline{f}(\mathcal{D}_{\text{mod}},\overline{\mathcal{D}}_{\text{mod}})-\frac{2R}{l_n}-\frac{2R}{l_n}. \end{align*} $$
$$ \begin{align*} \overline{f}(\mathcal{D},\overline{\mathcal{D}})>\overline{f}(\mathcal{D}_{\text{mod}},\overline{\mathcal{D}}_{\text{mod}})-\frac{2R}{l_n}-\frac{2R}{l_n}. \end{align*} $$
We have
 $\mathcal {D}_{\text {mod}}=(\mathcal {B}^{(n)}_j)^l$
and
$\mathcal {D}_{\text {mod}}=(\mathcal {B}^{(n)}_j)^l$
and
 $\overline {\mathcal {D}}_{\text {mod}}=(\mathcal {B}^{(n)}_k)^{\overline {l}}$
, for some positive integers l and
$\overline {\mathcal {D}}_{\text {mod}}=(\mathcal {B}^{(n)}_k)^{\overline {l}}$
, for some positive integers l and
![]() $\overline {l}$
. We are given that
$\overline {l}$
. We are given that
![]() $\overline {f}(\mathcal {A},\overline {\mathcal {A}})>\alpha $
for any strings of at least
$\overline {f}(\mathcal {A},\overline {\mathcal {A}})>\alpha $
for any strings of at least
![]() $q_n/R$
consecutive symbols from
$q_n/R$
consecutive symbols from
 $\mathcal {B}_j^{(n)}$
and
$\mathcal {B}_j^{(n)}$
and
 $\mathcal {B}_k^{(n)}$
, respectively. Thus it follows from Corollary 5.5 with
$\mathcal {B}_k^{(n)}$
, respectively. Thus it follows from Corollary 5.5 with
![]() $\tilde {f}=1$
that
$\tilde {f}=1$
that
 $$ \begin{align*} \overline{f}(\mathcal{D}_{\text{mod}},\overline{\mathcal{D}}_{\text{mod}})>\alpha-\frac{1}{R}.\\[-3.4pc] \end{align*} $$
$$ \begin{align*} \overline{f}(\mathcal{D}_{\text{mod}},\overline{\mathcal{D}}_{\text{mod}})>\alpha-\frac{1}{R}.\\[-3.4pc] \end{align*} $$
In the proofs of both Propositions 5.13 and 5.15 we will also use the sequence
![]() $(R_{n})^{\infty }_{n=1}$
, where
$(R_{n})^{\infty }_{n=1}$
, where
![]() $R_1=N(0)$
(with
$R_1=N(0)$
(with
![]() $N(0)+1$
the number of symbols in our alphabet) and
$N(0)+1$
the number of symbols in our alphabet) and
 $R_{n}=k_{n-2}\cdot q_{n-2}^{2}$
for
$R_{n}=k_{n-2}\cdot q_{n-2}^{2}$
for
![]() $n\geq 2$
. We note that for
$n\geq 2$
. We note that for
![]() $n\geq 2$
,
$n\geq 2$
,
 $$ \begin{align} \frac{q_{n}}{R_{n}}=\frac{k_{n-1}\cdot l_{n-1}\cdot(k_{n-2}\cdot l_{n-2}\cdot q_{n-2}^{2})\cdot q_{n-1}}{k_{n-2}\cdot q_{n-2}^{2}}=l_{n-2}\cdot k_{n-1}\cdot l_{n-1}\cdot q_{n-1}. \end{align} $$
$$ \begin{align} \frac{q_{n}}{R_{n}}=\frac{k_{n-1}\cdot l_{n-1}\cdot(k_{n-2}\cdot l_{n-2}\cdot q_{n-2}^{2})\cdot q_{n-1}}{k_{n-2}\cdot q_{n-2}^{2}}=l_{n-2}\cdot k_{n-1}\cdot l_{n-1}\cdot q_{n-1}. \end{align} $$
Hence, for
![]() $n\geq 2$
a substring of at least
$n\geq 2$
a substring of at least
![]() $q_{n}/R_{n}$
consecutive symbols in a circular n-block contains at least
$q_{n}/R_{n}$
consecutive symbols in a circular n-block contains at least
![]() $l_{n-2}-1$
complete
$l_{n-2}-1$
complete
![]() $2$
-subsections which have length
$2$
-subsections which have length
![]() $k_{n-1}l_{n-1}q_{n-1}$
(recall the notion of a
$k_{n-1}l_{n-1}q_{n-1}$
(recall the notion of a
![]() $2$
-subsubsection from the end of §3.3). This will allow us to ignore incomplete
$2$
-subsubsection from the end of §3.3). This will allow us to ignore incomplete
![]() $2$
-subsections at the ends of the substring.
$2$
-subsections at the ends of the substring.
Proposition 5.13. Let
 $\alpha \in \big(0,\tfrac 17\big)$
and
$\alpha \in \big(0,\tfrac 17\big)$
and
![]() $n,N,M\in \mathbb {N}$
with
$n,N,M\in \mathbb {N}$
with
![]() $N\geq 100$
and
$N\geq 100$
and
![]() $M\geq 2$
. Suppose
$M\geq 2$
. Suppose
![]() $\mathtt {A}_{0},\ldots ,\mathtt {A}_{N}$
is the collection of n-blocks, which have equal length
$\mathtt {A}_{0},\ldots ,\mathtt {A}_{N}$
is the collection of n-blocks, which have equal length
![]() $\mathtt {h_{n}}$
and satisfy the unique readability property. Furthermore, if
$\mathtt {h_{n}}$
and satisfy the unique readability property. Furthermore, if
![]() $n>0$
assume that for all
$n>0$
assume that for all
![]() $j_{1},j_{2}\in \{ 0,\ldots ,N\} $
,
$j_{1},j_{2}\in \{ 0,\ldots ,N\} $
,
![]() $j_{1}\neq j_{2}$
, we have
$j_{1}\neq j_{2}$
, we have
![]() $\overline {f}(\mathcal {A},\overline {\mathcal {A}})>\alpha $
for any sequences
$\overline {f}(\mathcal {A},\overline {\mathcal {A}})>\alpha $
for any sequences
![]() $\mathcal {A},\overline {\mathcal {A}}$
of at least
$\mathcal {A},\overline {\mathcal {A}}$
of at least
![]() $q_{n}/R_{n}$
consecutive symbols from
$q_{n}/R_{n}$
consecutive symbols from
![]() $\mathcal {A}_{j_{1}}$
and
$\mathcal {A}_{j_{1}}$
and
![]() $\mathcal {A}_{j_{2}}$
, respectively. Then we can construct
$\mathcal {A}_{j_{2}}$
, respectively. Then we can construct
![]() $M\, (n+1)$
-blocks
$M\, (n+1)$
-blocks
![]() $\mathtt {B}_{1},\ldots ,\mathtt {B}_{M}$
of equal length
$\mathtt {B}_{1},\ldots ,\mathtt {B}_{M}$
of equal length
![]() $\mathtt {h}_{n+1}$
(which are uniform in the n-blocks and satisfy the unique readability property) such that for all
$\mathtt {h}_{n+1}$
(which are uniform in the n-blocks and satisfy the unique readability property) such that for all
![]() $j,k\in \{ 1,\ldots ,M\} $
,
$j,k\in \{ 1,\ldots ,M\} $
,
![]() $j\neq k$
, and any sequences
$j\neq k$
, and any sequences
![]() $\mathcal {B}$
,
$\mathcal {B}$
,
![]() $\overline {\mathcal {B}}$
of at least
$\overline {\mathcal {B}}$
of at least
![]() $q_{n+1}/R_{n+1}$
consecutive symbols from
$q_{n+1}/R_{n+1}$
consecutive symbols from
![]() $\mathcal {B}_{j}$
and
$\mathcal {B}_{j}$
and
![]() $\mathcal {B}_{k}$
we have
$\mathcal {B}_{k}$
we have
 $$ \begin{align*} \overline{f}(\mathcal{B},\overline{\mathcal{B}})> \begin{cases} \alpha-\bigg(\dfrac{4}{R_n}+\dfrac{4R_n}{l_n}+\dfrac{14}{\sqrt{N}}+\dfrac{2}{l_{n-1}}\bigg) & \text{ if } n>0, \\ 1-\dfrac{5}{\sqrt{N}}-\dfrac{2}{l_0} & \text{ if } n=0. \end{cases} \end{align*} $$
$$ \begin{align*} \overline{f}(\mathcal{B},\overline{\mathcal{B}})> \begin{cases} \alpha-\bigg(\dfrac{4}{R_n}+\dfrac{4R_n}{l_n}+\dfrac{14}{\sqrt{N}}+\dfrac{2}{l_{n-1}}\bigg) & \text{ if } n>0, \\ 1-\dfrac{5}{\sqrt{N}}-\dfrac{2}{l_0} & \text{ if } n=0. \end{cases} \end{align*} $$
Proof. We choose the block
![]() $\mathtt {A}_{0}$
as a ‘marker’, that is, an n-block whose appearances can be used to identify the end of an
$\mathtt {A}_{0}$
as a ‘marker’, that is, an n-block whose appearances can be used to identify the end of an
![]() $(n+1)$
-block. We distribute the marker blocks over the new words and modify the classical Feldman patterns on the building blocks
$(n+1)$
-block. We distribute the marker blocks over the new words and modify the classical Feldman patterns on the building blocks
![]() $\mathtt {A}_{1},\ldots ,\mathtt {A}_{N}$
in the following way to define the
$\mathtt {A}_{1},\ldots ,\mathtt {A}_{N}$
in the following way to define the
![]() $(n+1)$
-blocks:
$(n+1)$
-blocks:
 $$ \begin{align*} \mathtt{B}_{1}&= \Big(\Big((\mathtt{A}_{1})^{N^{2}}(\mathtt{A}_{2})^{N^{2}}\ldots(\mathtt{A}_{N})^{N^{2}}\Big)^{N^{2M-1}}(\mathtt{A}_{0})^{N^{2M+1}-1}\Big)^N(\mathtt{A}_{0})^{N},\\ \mathtt{B}_{2}&= \Big(\Big((\mathtt{A}_{1})^{N^{4}}(\mathtt{A}_{2})^{N^{4}}\ldots(\mathtt{A}_{N})^{N^{4}}\Big)^{N^{2M-3}}(\mathtt{A}_{0})^{N^{2M+1}-1}\Big)^N(\mathtt{A}_{0})^{N},\\ \vdots\;\; & \;\;\vdots\\ \mathtt{B}_{M}&= \Big(\Big((\mathtt{A}_{1})^{N^{2M}}(\mathtt{A}_{2})^{N^{2M}}\ldots(\mathtt{A}_{N})^{N^{2M}}\Big)^{N}(\mathtt{A}_{0})^{N^{2M+1}-1}\Big)^N(\mathtt{A}_{0})^{N}. \end{align*} $$
$$ \begin{align*} \mathtt{B}_{1}&= \Big(\Big((\mathtt{A}_{1})^{N^{2}}(\mathtt{A}_{2})^{N^{2}}\ldots(\mathtt{A}_{N})^{N^{2}}\Big)^{N^{2M-1}}(\mathtt{A}_{0})^{N^{2M+1}-1}\Big)^N(\mathtt{A}_{0})^{N},\\ \mathtt{B}_{2}&= \Big(\Big((\mathtt{A}_{1})^{N^{4}}(\mathtt{A}_{2})^{N^{4}}\ldots(\mathtt{A}_{N})^{N^{4}}\Big)^{N^{2M-3}}(\mathtt{A}_{0})^{N^{2M+1}-1}\Big)^N(\mathtt{A}_{0})^{N},\\ \vdots\;\; & \;\;\vdots\\ \mathtt{B}_{M}&= \Big(\Big((\mathtt{A}_{1})^{N^{2M}}(\mathtt{A}_{2})^{N^{2M}}\ldots(\mathtt{A}_{N})^{N^{2M}}\Big)^{N}(\mathtt{A}_{0})^{N^{2M+1}-1}\Big)^N(\mathtt{A}_{0})^{N}. \end{align*} $$
We note that every
![]() $(n+1)$
-block
$(n+1)$
-block
![]() $\mathtt {B}_{k}$
contains each n-block
$\mathtt {B}_{k}$
contains each n-block
![]() $\mathtt {A}_{l}$
exactly
$\mathtt {A}_{l}$
exactly
![]() $N^{2M+2}$
times and has length
$N^{2M+2}$
times and has length
![]() $(N+1)\cdot N^{2M+2}\cdot \mathtt {h}_{n}$
. Moreover, the new blocks are uniquely readable because the string
$(N+1)\cdot N^{2M+2}\cdot \mathtt {h}_{n}$
. Moreover, the new blocks are uniquely readable because the string
 $(\mathtt {A}_{0})^{N^{2M+1}+N-1}$
only occurs at the end of an
$(\mathtt {A}_{0})^{N^{2M+1}+N-1}$
only occurs at the end of an
![]() $(n+1)$
-block. We also observe that
$(n+1)$
-block. We also observe that
![]() $\mathtt {B}_{k}$
is built with
$\mathtt {B}_{k}$
is built with
![]() $N^{2\cdot (M-k+1)}$
cycles
$N^{2\cdot (M-k+1)}$
cycles
 $$ \begin{align*} \mathtt{F}_k := (\mathtt{A}_{1})^{N^{2k}}(\mathtt{A}_{2})^{N^{2k}}\ldots(\mathtt{A}_{N})^{N^{2k}}. \end{align*} $$
$$ \begin{align*} \mathtt{F}_k := (\mathtt{A}_{1})^{N^{2k}}(\mathtt{A}_{2})^{N^{2k}}\ldots(\mathtt{A}_{N})^{N^{2k}}. \end{align*} $$
Let
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\overline {\mathcal {B}}$
be sequences of at least
$\overline {\mathcal {B}}$
be sequences of at least
![]() $q_{n+1}/R_{n+1}$
consecutive symbols from
$q_{n+1}/R_{n+1}$
consecutive symbols from
![]() $\mathcal {B}_{j}$
and
$\mathcal {B}_{j}$
and
![]() $\mathcal {B}_{k}, j\ne k$
. In the case
$\mathcal {B}_{k}, j\ne k$
. In the case
![]() $n>0$
we note that
$n>0$
we note that
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\overline {\mathcal {B}}$
have at least the length of
$\overline {\mathcal {B}}$
have at least the length of
![]() $l_{n-1}$
complete
$l_{n-1}$
complete
![]() $2$
-subsections by equation (5.2). By adding fewer than
$2$
-subsections by equation (5.2). By adding fewer than
![]() $2l_nk_nq_n$
symbols to each of
$2l_nk_nq_n$
symbols to each of
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\overline {\mathcal {B}}$
, we can complete any partial
$\overline {\mathcal {B}}$
, we can complete any partial
![]() $2$
-subsections at the beginning and end of
$2$
-subsections at the beginning and end of
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\overline {\mathcal {B}}$
. This change can increase the
$\overline {\mathcal {B}}$
. This change can increase the
![]() $\overline {f}$
distance between
$\overline {f}$
distance between
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\overline {\mathcal {B}}$
, but by less than
$\overline {\mathcal {B}}$
, but by less than
![]() $2/l_{n-1}$
. In addition, we remove the marker blocks, possibly increasing
$2/l_{n-1}$
. In addition, we remove the marker blocks, possibly increasing
![]() $\overline {f}$
by at most
$\overline {f}$
by at most
![]() ${2}/({N+1})$
. The modified strings
${2}/({N+1})$
. The modified strings
![]() $\mathcal {B}_{\text {mod}}$
and
$\mathcal {B}_{\text {mod}}$
and
![]() $\overline {\mathcal {B}}_{\text {mod}}$
obtained satisfy
$\overline {\mathcal {B}}_{\text {mod}}$
obtained satisfy
![]() $\overline {f}(\mathcal {B},\overline {\mathcal {B}})>\overline {f}(\mathcal {B}_{\text {mod}},\overline {\mathcal {B}}_{\text {mod}})-({2}/{l_{n-1}})-({2}/({N+1})).$
$\overline {f}(\mathcal {B},\overline {\mathcal {B}})>\overline {f}(\mathcal {B}_{\text {mod}},\overline {\mathcal {B}}_{\text {mod}})-({2}/{l_{n-1}})-({2}/({N+1})).$
By Lemma 5.12,
![]() $\overline {f}(\mathcal {D},\overline {\mathcal {D}})>\alpha -({2}/{R_n})-({4R_n}/{l_n})$
for any substrings
$\overline {f}(\mathcal {D},\overline {\mathcal {D}})>\alpha -({2}/{R_n})-({4R_n}/{l_n})$
for any substrings
![]() $\mathcal {D}$
,
$\mathcal {D}$
,
![]() $\overline {\mathcal {D}}$
of at least
$\overline {\mathcal {D}}$
of at least
![]() $q_nl_n/R_n$
consecutive symbols from
$q_nl_n/R_n$
consecutive symbols from
![]() $\mathcal {C}_{n,i_1}(\mathtt {A}_{j_1})$
and
$\mathcal {C}_{n,i_1}(\mathtt {A}_{j_1})$
and
![]() $\mathcal {C}_{n,i_2}(\mathtt {A}_{j_2})$
with
$\mathcal {C}_{n,i_2}(\mathtt {A}_{j_2})$
with
![]() $j_1\ne j_2$
. If we let
$j_1\ne j_2$
. If we let
![]() $\Phi _{j,i_1}$
and
$\Phi _{j,i_1}$
and
![]() $\Phi _{k,i_2}$
be the jth and kth Feldman patterns built from
$\Phi _{k,i_2}$
be the jth and kth Feldman patterns built from
![]() $\mathcal {C}_{n,i_1}(\mathtt {A}_1),\mathcal {C}_{n,i_1}(\mathtt {A}_2),\ldots , \mathcal {C}_{n,i_1}(\mathtt {A}_{N})$
and
$\mathcal {C}_{n,i_1}(\mathtt {A}_1),\mathcal {C}_{n,i_1}(\mathtt {A}_2),\ldots , \mathcal {C}_{n,i_1}(\mathtt {A}_{N})$
and
![]() $\mathcal {C}_{n,i_2}(\mathtt {A}_1),\mathcal {C}_{n,i_2}(\mathtt {A}_2),\ldots ,\mathcal {C}_{n,i_2}(\mathtt {A}_{N})$
respectively, then the same argument as in Proposition 5.10 shows that for any substrings
$\mathcal {C}_{n,i_2}(\mathtt {A}_1),\mathcal {C}_{n,i_2}(\mathtt {A}_2),\ldots ,\mathcal {C}_{n,i_2}(\mathtt {A}_{N})$
respectively, then the same argument as in Proposition 5.10 shows that for any substrings
![]() $\mathcal {E}$
,
$\mathcal {E}$
,
![]() $\overline {\mathcal {E}}$
consisting of at least
$\overline {\mathcal {E}}$
consisting of at least
![]() ${|\Phi _{j,i_1}|}/{N}={|\Phi _{k,i_1}|}/{N}$
consecutive symbols from
${|\Phi _{j,i_1}|}/{N}={|\Phi _{k,i_1}|}/{N}$
consecutive symbols from
![]() $\Phi _{j,i_2}$
and
$\Phi _{j,i_2}$
and
![]() $\Phi _{k,i_2}$
, we have
$\Phi _{k,i_2}$
, we have
![]() $\overline {f}(\mathcal {E},\overline {\mathcal {E}})>\alpha -({4}/{R_n})-({4R_n}/{l_n})-({13}/{\sqrt {N}})$
.
$\overline {f}(\mathcal {E},\overline {\mathcal {E}})>\alpha -({4}/{R_n})-({4R_n}/{l_n})-({13}/{\sqrt {N}})$
.
Note that
![]() $\mathcal {B}_{\text {mod}}$
and
$\mathcal {B}_{\text {mod}}$
and
![]() $\overline {\mathcal {B}}_{\text {mod}}$
consist respectively of a string of
$\overline {\mathcal {B}}_{\text {mod}}$
consist respectively of a string of
![]() $\Phi _{j,i}$
s and a string of
$\Phi _{j,i}$
s and a string of
![]() $\Phi _{k,i}$
s (j and k fixed, i varying). Therefore, by Corollary 5.5 with
$\Phi _{k,i}$
s (j and k fixed, i varying). Therefore, by Corollary 5.5 with
![]() $\tilde {f}=1$
,
$\tilde {f}=1$
,
![]() $\overline {f}(\mathcal {B}_{\text {mod}},\overline {\mathcal {B}}_{\text {mod}})>\alpha -({4}/{R_n})-({4R_n}/{l_n})-({13}/{\sqrt {N}})-({2}/{N})$
. Thus in the case
$\overline {f}(\mathcal {B}_{\text {mod}},\overline {\mathcal {B}}_{\text {mod}})>\alpha -({4}/{R_n})-({4R_n}/{l_n})-({13}/{\sqrt {N}})-({2}/{N})$
. Thus in the case
![]() $n>0$
we obtain
$n>0$
we obtain
 $$ \begin{align*} \overline {f}(\mathcal {B},\overline {\mathcal {B}}) &> \alpha -({4}/{R_n})\,-\,({4R_n}/{l_n})\,-\,({13}/{\sqrt {N}})\,-\,({2}/{N})\,-\,({2}/{l_{n-1}})-({2}/{N})\\ &>\alpha -({4}/{R_n})-({4R_n}/{l_n})-({14}/{\sqrt {N}})-({2}/{l_{n-1}}). \end{align*} $$
$$ \begin{align*} \overline {f}(\mathcal {B},\overline {\mathcal {B}}) &> \alpha -({4}/{R_n})\,-\,({4R_n}/{l_n})\,-\,({13}/{\sqrt {N}})\,-\,({2}/{N})\,-\,({2}/{l_{n-1}})-({2}/{N})\\ &>\alpha -({4}/{R_n})-({4R_n}/{l_n})-({14}/{\sqrt {N}})-({2}/{l_{n-1}}). \end{align*} $$
In the case
![]() $n=0$
we complete strings
$n=0$
we complete strings
![]() $\mathcal {C}_{0,0}(\mathtt {F}_{j})$
and
$\mathcal {C}_{0,0}(\mathtt {F}_{j})$
and
![]() $\mathcal {C}_{0,0}(\mathtt {F}_{k})$
at the beginning and end of
$\mathcal {C}_{0,0}(\mathtt {F}_{k})$
at the beginning and end of
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\overline {\mathcal {B}}$
respectively by adding fewer than
$\overline {\mathcal {B}}$
respectively by adding fewer than
![]() $2l_0N^{2M+1}$
symbols to each of
$2l_0N^{2M+1}$
symbols to each of
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\overline {\mathcal {B}}$
. This corresponds to a fraction of at most
$\overline {\mathcal {B}}$
. This corresponds to a fraction of at most
![]() $2/(N+1)$
of the total length. In the next step we remove the marker blocks and spacers b, possibly increasing
$2/(N+1)$
of the total length. In the next step we remove the marker blocks and spacers b, possibly increasing
![]() $\overline {f}$
by at most
$\overline {f}$
by at most
![]() $({6}/{N})+({2}/{l_0})$
. On the remaining strings we apply Remark 5.9 (note that we have enough symbols by our completion above) to obtain the claim for
$({6}/{N})+({2}/{l_0})$
. On the remaining strings we apply Remark 5.9 (note that we have enough symbols by our completion above) to obtain the claim for
![]() $n=0$
.
$n=0$
.
Remark 5.14. In the proof above we cannot put all markers at the end of the new
![]() $(n+1)$
-block since these markers would cover a fraction
$(n+1)$
-block since these markers would cover a fraction
![]() ${\mathtt {h}_{n+1}}/({N+1})$
of that block due to uniformity. Thus, the conclusion would not hold true for
${\mathtt {h}_{n+1}}/({N+1})$
of that block due to uniformity. Thus, the conclusion would not hold true for
![]() $n=0$
. We will also need the chosen form of the
$n=0$
. We will also need the chosen form of the
![]() $(n+1)$
-blocks in an analogous statement for the odometer-based system in Proposition 6.2.
$(n+1)$
-blocks in an analogous statement for the odometer-based system in Proposition 6.2.
5.3. Mechanism to produce closeness in odometer-based system and separation in corresponding circular system
We impose the following conditions on the circular coefficients
![]() $(l_n)_{n\in \mathbb {N}}$
:
$(l_n)_{n\in \mathbb {N}}$
:
 $$ \begin{align} l_{n+1} \geq l^2_n \text{ and } l_{n} \geq 4R_{n+1}\quad \text{for every } n \in \mathbb{N}. \end{align} $$
$$ \begin{align} l_{n+1} \geq l^2_n \text{ and } l_{n} \geq 4R_{n+1}\quad \text{for every } n \in \mathbb{N}. \end{align} $$
Proposition 5.15. Let
![]() $K\geq 2$
,
$K\geq 2$
,
![]() $0<\varepsilon <\alpha $
,
$0<\varepsilon <\alpha $
,
![]() $\delta>0$
, and
$\delta>0$
, and
 $\alpha \in \big(0,\tfrac 17\big)$
. Then there are numbers
$\alpha \in \big(0,\tfrac 17\big)$
. Then there are numbers
![]() $N,p\in \mathbb {N}$
such that for
$N,p\in \mathbb {N}$
such that for
![]() $N+1$
uniquely readable n-blocks
$N+1$
uniquely readable n-blocks
 $\mathtt {B}^{(n)}_{0},\mathtt {B}^{(n)}_{1},\ldots ,\mathtt {B}^{(n)}_{N}$
with
$\mathtt {B}^{(n)}_{0},\mathtt {B}^{(n)}_{1},\ldots ,\mathtt {B}^{(n)}_{N}$
with
![]() $\overline {f}(\mathcal {A},\overline {\mathcal {A}})>\alpha $
for all sequences
$\overline {f}(\mathcal {A},\overline {\mathcal {A}})>\alpha $
for all sequences
![]() $\mathcal {A},\overline {\mathcal {A}}$
of at least
$\mathcal {A},\overline {\mathcal {A}}$
of at least
![]() $q_{n}/R_{n}$
consecutive symbols from
$q_{n}/R_{n}$
consecutive symbols from
 $\mathcal {B}^{(n)}_{i}$
and
$\mathcal {B}^{(n)}_{i}$
and
 $\mathcal {B}^{(n)}_{j}$
,
$\mathcal {B}^{(n)}_{j}$
,
![]() $i>j$
, we can build
$i>j$
, we can build
![]() $K\, (n+p)$
-blocks
$K\, (n+p)$
-blocks
 $\mathtt {B}^{(n+p)}_{1},\ldots ,\mathtt {B}^{(n+p)}_{K}$
of equal length
$\mathtt {B}^{(n+p)}_{1},\ldots ,\mathtt {B}^{(n+p)}_{K}$
of equal length
![]() $\mathtt {h}_{n+p}$
(satisfying the unique readability property and uniformity in all blocks from stage n through
$\mathtt {h}_{n+p}$
(satisfying the unique readability property and uniformity in all blocks from stage n through
![]() $n+p$
) with the following properties:
$n+p$
) with the following properties:
-
(1)
 $\overline {f}(\mathtt {B}^{(n+p)}_{i},\mathtt {B}^{(n+p)}_{j})<\delta $
for all
$\overline {f}(\mathtt {B}^{(n+p)}_{i},\mathtt {B}^{(n+p)}_{j})<\delta $
for all
 $i,j$
;
$i,j$
; -
(2)
 $\overline {f}(\mathcal {B},\overline {\mathcal {B}})>\alpha -\varepsilon - \sum ^{p-1}_{s=0} ({6}/{R_{n+s}})$
for all sequences
$\overline {f}(\mathcal {B},\overline {\mathcal {B}})>\alpha -\varepsilon - \sum ^{p-1}_{s=0} ({6}/{R_{n+s}})$
for all sequences
 $\mathcal {B}$
,
$\mathcal {B}$
,
 $\overline {\mathcal {B}}$
of at least
$\overline {\mathcal {B}}$
of at least
 $q_{n+p}/R_{n+p}$
consecutive symbols from
$q_{n+p}/R_{n+p}$
consecutive symbols from
 $\mathcal {B}^{(n+p)}_{i}$
and
$\mathcal {B}^{(n+p)}_{i}$
and
 $\mathcal {B}^{(n+p)}_{j}$
,
$\mathcal {B}^{(n+p)}_{j}$
,
 $i>j$
.
$i>j$
.
The number of stages p will be the least integer such that
 $$ \begin{align*} \bigg(1-\frac{1}{K}\bigg)^{p} < \frac{\varepsilon}{2}. \end{align*} $$
$$ \begin{align*} \bigg(1-\frac{1}{K}\bigg)^{p} < \frac{\varepsilon}{2}. \end{align*} $$
The proof is based upon an inductive construction (called a shifting mechanism; see Figure 2 for a sketch of its idea) and a final step to align blocks in the odometer-based system. For this construction process and the given
![]() $n\in \mathbb {N}$
, let
$n\in \mathbb {N}$
, let
![]() $(u_{n+m})_{m\in \mathbb {N}}$
and
$(u_{n+m})_{m\in \mathbb {N}}$
and
![]() $(e_{n+m})_{m\in \mathbb {N}}$
be increasing sequences of natural numbers such that
$(e_{n+m})_{m\in \mathbb {N}}$
be increasing sequences of natural numbers such that
 $$ \begin{align} \sum_{m\in\mathbb{N}}\frac{1}{u_{n+m}^{2}}<\frac{\delta}{4} \end{align} $$
$$ \begin{align} \sum_{m\in\mathbb{N}}\frac{1}{u_{n+m}^{2}}<\frac{\delta}{4} \end{align} $$
and
 $$ \begin{align} \sum_{m\in\mathbb{N}}\bigg(\frac{8}{u_{n+m}}+\frac{17}{\sqrt{e_{n+m}}}\bigg)<\frac{\varepsilon}{8}. \end{align} $$
$$ \begin{align} \sum_{m\in\mathbb{N}}\bigg(\frac{8}{u_{n+m}}+\frac{17}{\sqrt{e_{n+m}}}\bigg)<\frac{\varepsilon}{8}. \end{align} $$
Moreover, we will use the sequence
![]() $(d_{n+m})_{m\in \mathbb {N}}$
, where
$(d_{n+m})_{m\in \mathbb {N}}$
, where
 $$ \begin{align} d_{n+m}=u_{n+m}^{2}. \end{align} $$
$$ \begin{align} d_{n+m}=u_{n+m}^{2}. \end{align} $$
In the following, we will also use the notation
and
![]() $N(n+m)+1=K\unicode{x3bb} _{n+m}+1$
will be the number of
$N(n+m)+1=K\unicode{x3bb} _{n+m}+1$
will be the number of
![]() $(n+m)$
-blocks. In particular, we start with
$(n+m)$
-blocks. In particular, we start with
![]() $N(n)+1=N+1\, n$
-blocks and we require N to satisfy
$N(n)+1=N+1\, n$
-blocks and we require N to satisfy
5.3.1. Initial stage of the shifting mechanism: construction of
 $(n+1)$
-blocks
$(n+1)$
-blocks
First of all, we choose one n-block
 $\mathtt {B}^{(n)}_{0}$
as a marker. Then we apply Proposition 5.10 on the remaining n-blocks
$\mathtt {B}^{(n)}_{0}$
as a marker. Then we apply Proposition 5.10 on the remaining n-blocks
 $\mathtt {B}^{(n)}_{1},\ldots ,\mathtt {B}^{(n)}_{N}$
to build
$\mathtt {B}^{(n)}_{1},\ldots ,\mathtt {B}^{(n)}_{N}$
to build
![]() $\tilde {N}(n+1):= 2K\unicode{x3bb} _{n+1}$
pre-
$\tilde {N}(n+1):= 2K\unicode{x3bb} _{n+1}$
pre-
![]() $(n+1)$
-blocks denoted by
$(n+1)$
-blocks denoted by
![]() $\mathtt {A}_{i,j}$
,
$\mathtt {A}_{i,j}$
,
![]() $i=1,\ldots ,K$
,
$i=1,\ldots ,K$
,
![]() $j=1,\ldots ,2\unicode{x3bb} _{n+1}$
. In particular, these have length
$j=1,\ldots ,2\unicode{x3bb} _{n+1}$
. In particular, these have length
 $\tilde {\mathtt {h}}_{n+1}=N^{2\cdot \tilde {N}(n+1)+3}\cdot \mathtt {h}_{n}$
and are uniform in the n-blocks
$\tilde {\mathtt {h}}_{n+1}=N^{2\cdot \tilde {N}(n+1)+3}\cdot \mathtt {h}_{n}$
and are uniform in the n-blocks
 $\mathtt {B}^{(n)}_{1},\ldots ,\mathtt {B}^{(n)}_{N}$
by construction. More precisely, every pre-
$\mathtt {B}^{(n)}_{1},\ldots ,\mathtt {B}^{(n)}_{N}$
by construction. More precisely, every pre-
![]() $(n+1)$
-block contains each n-block
$(n+1)$
-block contains each n-block
 $\mathtt {B}^{(n)}_{j}$
,
$\mathtt {B}^{(n)}_{j}$
,
![]() $1\leq j\leq N$
, exactly
$1\leq j\leq N$
, exactly
![]() $N^{2\cdot \tilde {N}(n+1)+2}$
times, and pre-
$N^{2\cdot \tilde {N}(n+1)+2}$
times, and pre-
![]() $(n+1)$
-blocks
$(n+1)$
-blocks
![]() $\mathcal {A}_{i,j}$
in the circular system (that is, images of
$\mathcal {A}_{i,j}$
in the circular system (that is, images of
![]() $\mathtt {A}_{i,j}$
under the operator
$\mathtt {A}_{i,j}$
under the operator
![]() $\mathcal {C}_{n,k}$
for some
$\mathcal {C}_{n,k}$
for some
![]() $k\in \{ 1,\ldots ,q_{n}\} $
, where the value of k does not matter for the following investigation) have length
$k\in \{ 1,\ldots ,q_{n}\} $
, where the value of k does not matter for the following investigation) have length
 $\tilde {q}_{n+1}=N^{2\cdot \tilde {N}(n+1)+3}\cdot l_{n}\cdot q_{n}$
. Moreover, with the aid of Lemma 5.12, Proposition 5.10 also implies that different pre-
$\tilde {q}_{n+1}=N^{2\cdot \tilde {N}(n+1)+3}\cdot l_{n}\cdot q_{n}$
. Moreover, with the aid of Lemma 5.12, Proposition 5.10 also implies that different pre-
![]() $(n+1)$
-blocks in the circular system are at least
$(n+1)$
-blocks in the circular system are at least
 $$ \begin{align} \alpha-\beta_{n+1} \ \text{ where } \beta_{n+1}:= \frac{4}{R_{n}}+\frac{13}{\sqrt{N}}+\frac{4R_{n}}{l_{n}}, \end{align} $$
$$ \begin{align} \alpha-\beta_{n+1} \ \text{ where } \beta_{n+1}:= \frac{4}{R_{n}}+\frac{13}{\sqrt{N}}+\frac{4R_{n}}{l_{n}}, \end{align} $$
![]() $\overline {f}$
apart on substantial substrings of length at least
$\overline {f}$
apart on substantial substrings of length at least
 $N^{2\cdot \tilde {N}(n+1)+2}\cdot l_{n}\cdot q_{n}={\tilde {q}_{n+1}}/{N}$
. Finally, we introduce the abbreviation
$N^{2\cdot \tilde {N}(n+1)+2}\cdot l_{n}\cdot q_{n}={\tilde {q}_{n+1}}/{N}$
. Finally, we introduce the abbreviation
 $$ \begin{align*} \mathtt{a}_{n}=(\mathtt{B}^{(n)}_{0})^{K\cdot N^{2\tilde{N}(n+1)+2}}. \end{align*} $$
$$ \begin{align*} \mathtt{a}_{n}=(\mathtt{B}^{(n)}_{0})^{K\cdot N^{2\tilde{N}(n+1)+2}}. \end{align*} $$
We use these pre-
![]() $(n+1)$
-blocks to construct
$(n+1)$
-blocks to construct
![]() $(n+1)$
-blocks
$(n+1)$
-blocks
 $\mathtt {B}_{i,j}^{(n+1)}$
of K different types (the index i indicates the type, and
$\mathtt {B}_{i,j}^{(n+1)}$
of K different types (the index i indicates the type, and
![]() $j=1,\ldots ,\unicode{x3bb} _{n+1}=d_{n+1}e_{n+1}$
numbers the
$j=1,\ldots ,\unicode{x3bb} _{n+1}=d_{n+1}e_{n+1}$
numbers the
![]() $(n+1)$
-blocks of that type consecutively):
$(n+1)$
-blocks of that type consecutively):

Moreover, we define an additional
![]() $(n+1)$
-block
$(n+1)$
-block
 $\mathtt {B}_{0}^{(n+1)}$
which will play the role of a marker:
$\mathtt {B}_{0}^{(n+1)}$
which will play the role of a marker:

where the pre-
![]() $(n+1)$
-blocks
$(n+1)$
-blocks
![]() $\mathtt {A}_{i,\unicode{x3bb} _{n+1}+2}$
,
$\mathtt {A}_{i,\unicode{x3bb} _{n+1}+2}$
,
![]() $i=1,\ldots , K$
, are not used in any other
$i=1,\ldots , K$
, are not used in any other
![]() $(n+1)$
-block. In total, there are
$(n+1)$
-block. In total, there are
![]() $Kd_{n+1}e_{n+1}+1\, (n+1)$
-blocks. Since each of the pre-
$Kd_{n+1}e_{n+1}+1\, (n+1)$
-blocks. Since each of the pre-
![]() $(n+1)$
-blocks contains each n-block
$(n+1)$
-blocks contains each n-block
 $\mathtt {B}^{(n)}_{i}$
,
$\mathtt {B}^{(n)}_{i}$
,
![]() $1\leq i\leq N$
, exactly
$1\leq i\leq N$
, exactly
![]() $N^{2\tilde {N}(n+1)+2}$
times, and each
$N^{2\tilde {N}(n+1)+2}$
times, and each
![]() $(n+1)$
-block contains
$(n+1)$
-block contains
 $\mathtt {B}^{(n)}_0$
exactly
$\mathtt {B}^{(n)}_0$
exactly
![]() $KN^{2\tilde {N}(n+1)+2}$
times, every
$KN^{2\tilde {N}(n+1)+2}$
times, every
![]() $(n+1)$
-block is uniform in the n-blocks.
$(n+1)$
-block is uniform in the n-blocks.
Lemma 5.16. (Distance between
 $(n+1)$
-blocks in the odometer-based system)
$(n+1)$
-blocks in the odometer-based system)
For every
![]() $i_{1},i_{2}\in \{1,\ldots ,K\}$
and every
$i_{1},i_{2}\in \{1,\ldots ,K\}$
and every
![]() $j\in \{1,\ldots ,d_{n+1} e_{n+1}\}$
we have
$j\in \{1,\ldots ,d_{n+1} e_{n+1}\}$
we have
 $$ \begin{align} \overline{f}(\mathtt{B}_{i_{1},j}^{(n+1)},\mathtt{B}_{i_{2},j}^{(n+1)})\leq\bigg(\frac{N}{N+1}\bigg)\cdot\frac{\lvert i_{2}-i_{1}\rvert}{K}. \end{align} $$
$$ \begin{align} \overline{f}(\mathtt{B}_{i_{1},j}^{(n+1)},\mathtt{B}_{i_{2},j}^{(n+1)})\leq\bigg(\frac{N}{N+1}\bigg)\cdot\frac{\lvert i_{2}-i_{1}\rvert}{K}. \end{align} $$
Proof. Observe that
 $$ \begin{align*} \lvert\mathtt{a}_{n}\rvert=\frac{\mathtt{h}_{n+1}}{N+1}, \end{align*} $$
$$ \begin{align*} \lvert\mathtt{a}_{n}\rvert=\frac{\mathtt{h}_{n+1}}{N+1}, \end{align*} $$
due to the uniformity of n-blocks within the
![]() $(n+1)$
-blocks. Thus the pre-
$(n+1)$
-blocks. Thus the pre-
![]() $(n+1)$
-block part of each
$(n+1)$
-block part of each
 $\mathtt {B}_{i,j}^{(n+1)}$
, that is, the part before
$\mathtt {B}_{i,j}^{(n+1)}$
, that is, the part before
![]() $\mathtt {a}_n$
, forms a fraction
$\mathtt {a}_n$
, forms a fraction
![]() ${N}/({N+1})$
of
${N}/({N+1})$
of
 $\mathtt {B}_{i,j}^{(n+1)}$
. Without loss of generality, let
$\mathtt {B}_{i,j}^{(n+1)}$
. Without loss of generality, let
![]() $i_{2}>i_{1}$
. We note that
$i_{2}>i_{1}$
. We note that
 $\mathtt {B}_{i_1,j}^{(n+1)}$
and
$\mathtt {B}_{i_1,j}^{(n+1)}$
and
 $\mathtt {B}_{i_2,j}^{(n+1)}$
have
$\mathtt {B}_{i_2,j}^{(n+1)}$
have
as a common substring of their pre-
![]() $(n+1)$
-block parts. This substring forms a fraction
$(n+1)$
-block parts. This substring forms a fraction
![]() $({K-(i_2-i_1)})/{K}$
of the pre-
$({K-(i_2-i_1)})/{K}$
of the pre-
![]() $(n+1)$
-block part of each of
$(n+1)$
-block part of each of
 $\mathtt {B}_{i_1,j}^{(n+1)}$
and
$\mathtt {B}_{i_1,j}^{(n+1)}$
and
 $\mathtt {B}_{i_2,j}^{(n+1)}$
. Therefore (5.9) holds.
$\mathtt {B}_{i_2,j}^{(n+1)}$
. Therefore (5.9) holds.
Lemma 5.17. (Distance between
 $(n+1)$
-blocks in the circular system)
$(n+1)$
-blocks in the circular system)
Let
 $\mathtt {B}_{1}^{(n+1)}$
and
$\mathtt {B}_{1}^{(n+1)}$
and
 $\mathtt {B}_{2}^{(n+1)}$
be
$\mathtt {B}_{2}^{(n+1)}$
be
![]() $(n+1)$
-blocks and J be the number of pre-
$(n+1)$
-blocks and J be the number of pre-
![]() $(n+1)$
-blocks both have in common. Then for any sequences
$(n+1)$
-blocks both have in common. Then for any sequences
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\overline {\mathcal {B}}$
of at least
$\overline {\mathcal {B}}$
of at least
![]() $q_{n+1}/R_{n+1}$
consecutive symbols in
$q_{n+1}/R_{n+1}$
consecutive symbols in
 $\mathcal {B}_{1}^{(n+1)}$
and
$\mathcal {B}_{1}^{(n+1)}$
and
 $\mathcal {B}_{2}^{(n+1)}$
we have
$\mathcal {B}_{2}^{(n+1)}$
we have
 $$ \begin{align*} \overline{f}(\mathcal{B},\overline{\mathcal{B}})\geq\bigg(1-\frac{J}{K}\bigg)\alpha-E_{n+1}, \ \text{ where } E_{n+1} := \beta_{n+1}+ \frac{4}{N}+\frac{4}{l_{n-1}} \end{align*} $$
$$ \begin{align*} \overline{f}(\mathcal{B},\overline{\mathcal{B}})\geq\bigg(1-\frac{J}{K}\bigg)\alpha-E_{n+1}, \ \text{ where } E_{n+1} := \beta_{n+1}+ \frac{4}{N}+\frac{4}{l_{n-1}} \end{align*} $$
with
![]() $\beta _{n+1}$
as in equation (5.8).
$\beta _{n+1}$
as in equation (5.8).
Proof. In order to get the estimate in the circular system we recall that under the circular operator
![]() $\mathcal {C}_{n}$
the whole
$\mathcal {C}_{n}$
the whole
![]() $(n+1)$
-word consists of
$(n+1)$
-word consists of
![]() $q_{n} \text{ many } 2$
-subsections which differ from each other just in the exponents of the newly introduced spacers b and e. Then we consider
$q_{n} \text{ many } 2$
-subsections which differ from each other just in the exponents of the newly introduced spacers b and e. Then we consider
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\overline {\mathcal {B}}$
to be a concatenation of complete
$\overline {\mathcal {B}}$
to be a concatenation of complete
![]() $2$
-subsections ignoring incomplete ones at the ends which constitute a fraction of at most
$2$
-subsections ignoring incomplete ones at the ends which constitute a fraction of at most
![]() $2/l_{n-1}$
of the total length of
$2/l_{n-1}$
of the total length of
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\overline {\mathcal {B}}$
by equation (5.2). In the following consideration we ignore the marker segments which amount to a fraction
$\overline {\mathcal {B}}$
by equation (5.2). In the following consideration we ignore the marker segments which amount to a fraction
![]() ${1}/({N+1})$
of the total length. Accordingly, we consider
${1}/({N+1})$
of the total length. Accordingly, we consider
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\overline {\mathcal {B}}$
to be a concatenation of complete pre-
$\overline {\mathcal {B}}$
to be a concatenation of complete pre-
![]() $(n+1)$
-blocks
$(n+1)$
-blocks
![]() $\mathcal {A}_{h}$
. Using the estimate from equation (5.8) we apply Corollary 5.5 with
$\mathcal {A}_{h}$
. Using the estimate from equation (5.8) we apply Corollary 5.5 with
![]() $\tilde {f} \geq 1-({J}/{K})$
and obtain
$\tilde {f} \geq 1-({J}/{K})$
and obtain
 $$ \begin{align*} \overline{f}(\mathcal{B},\overline{\mathcal{B}})\geq\bigg(1-\frac{J}{K}\bigg)\cdot(\alpha- \beta_{n+1}) - \frac{2}{N}-\frac{4}{l_{n-1}}-\frac{2}{N+1}, \end{align*} $$
$$ \begin{align*} \overline{f}(\mathcal{B},\overline{\mathcal{B}})\geq\bigg(1-\frac{J}{K}\bigg)\cdot(\alpha- \beta_{n+1}) - \frac{2}{N}-\frac{4}{l_{n-1}}-\frac{2}{N+1}, \end{align*} $$
which yields the claim.
5.3.2. Induction step: construction of
 $(n+m)$
-blocks
$(n+m)$
-blocks
We will follow the inductive scheme for the construction of
![]() $(n+m)$
-blocks described here for
$(n+m)$
-blocks described here for
![]() $2\leq m < p$
, where
$2\leq m < p$
, where
![]() $p>2$
is the smallest number such that
$p>2$
is the smallest number such that
 $$ \begin{align} \bigg(1-\frac{1}{K}\bigg)^{p}<\frac{\varepsilon}{2}. \end{align} $$
$$ \begin{align} \bigg(1-\frac{1}{K}\bigg)^{p}<\frac{\varepsilon}{2}. \end{align} $$
Assume that in our inductive construction we have constructed
![]() $K\unicode{x3bb} _{n+m-1}\,(n+m-1)$
-blocks
$K\unicode{x3bb} _{n+m-1}\,(n+m-1)$
-blocks
 $\mathtt {B}_{i,j}^{(n+m-1)}$
of K different types (once again, the index
$\mathtt {B}_{i,j}^{(n+m-1)}$
of K different types (once again, the index
![]() $1\leq i\leq K$
indicates the type, and
$1\leq i\leq K$
indicates the type, and
![]() $1\leq j\leq \unicode{x3bb} _{n+m-1}$
numbers the
$1\leq j\leq \unicode{x3bb} _{n+m-1}$
numbers the
![]() $(n+m-1)$
-blocks of that type consecutively), where for
$(n+m-1)$
-blocks of that type consecutively), where for
![]() $m=2$
the
$m=2$
the
![]() $(n+1)$
-blocks are the ones constructed in §5.3.1 and for
$(n+1)$
-blocks are the ones constructed in §5.3.1 and for
![]() $m>2$
the
$m>2$
the
![]() $(n+m-1)$
-blocks are constructed according to the following formula (with
$(n+m-1)$
-blocks are constructed according to the following formula (with
![]() $\unicode{x3bb} =\unicode{x3bb} _{n+m-1}$
)
$\unicode{x3bb} =\unicode{x3bb} _{n+m-1}$
)
 $$ \begin{align*} &(n+m-1)\text{-blocks of type }1\text{:}\\ & \mathtt{B}_{1,1}^{(n+m-1)}=\mathtt{A}_{1,1}^{(n+m-1)}\mathtt{A}_{2,2}^{(n+m-1)}\ldots\mathtt{A}_{K,K}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \mathtt{B}_{1,2}^{(n+m-1)}=\mathtt{A}_{1,K+1}^{(n+m-1)}\mathtt{A}_{2,K+2}^{(n+m-1)}\ldots\mathtt{A}_{K,2K}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \;\vdots\\ & \mathtt{B}_{1,\unicode{x3bb}}^{(n+m-1)}=\mathtt{A}_{1,(\unicode{x3bb}-1)K+1}^{(n+m-1)}\mathtt{A}_{2,(\unicode{x3bb}-1)K+2}^{(n+m-1)}\ldots\mathtt{A}_{K,\unicode{x3bb} K}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & (n+m-1)\text{-blocks of type }2\text{:} \\ & \mathtt{B}_{2,1}^{(n+m-1)}=\mathtt{A}_{1,2}^{(n+m-1)}\mathtt{A}_{2,3}^{(n+m-1)}\ldots\mathtt{A}_{K,K+1}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \mathtt{B}_{2,2}^{(n+m-1)}=\mathtt{A}_{1,K+2}^{(n+m-1)}\mathtt{A}_{2,K+3}^{(n+m-1)}\ldots\mathtt{A}_{K,2K+1}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \;\vdots\\ & \mathtt{B}_{2,\unicode{x3bb}}^{(n+m-1)}=\mathtt{A}_{1,(\unicode{x3bb}-1)K+2}^{(n+m-1)}\mathtt{A}_{2,(\unicode{x3bb}-1)K+3}^{(n+m-1)}\ldots\mathtt{A}_{K,\unicode{x3bb} K+1}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \;\vdots\\ & (n+m-1)\text{-blocks of type }K\text{:} \\ & \mathtt{B}_{K,1}^{(n+m-1)}=\mathtt{A}_{1,K}^{(n+m-1)}\mathtt{A}_{2,K+1}^{(n+m-1)}\ldots\mathtt{A}_{K,2K-1}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \mathtt{B}_{K,2}^{(n+m-1)}=\mathtt{A}_{1,2K}^{(n+m-1)}\mathtt{A}_{2,2K+1}^{(n+m-1)}\ldots\mathtt{A}_{K,3K-1}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \;\vdots \\ & \mathtt{B}_{K,\unicode{x3bb}}^{(n+m-1)}=\mathtt{A}_{1,\unicode{x3bb} K}^{(n+m-1)}\mathtt{A}_{2,\unicode{x3bb} K+1}^{(n+m-1)}\ldots\mathtt{A}_{K,(\unicode{x3bb} +1)K-1}^{(n+m-1)}\mathtt{a}_{n+m-2}, \end{align*} $$
$$ \begin{align*} &(n+m-1)\text{-blocks of type }1\text{:}\\ & \mathtt{B}_{1,1}^{(n+m-1)}=\mathtt{A}_{1,1}^{(n+m-1)}\mathtt{A}_{2,2}^{(n+m-1)}\ldots\mathtt{A}_{K,K}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \mathtt{B}_{1,2}^{(n+m-1)}=\mathtt{A}_{1,K+1}^{(n+m-1)}\mathtt{A}_{2,K+2}^{(n+m-1)}\ldots\mathtt{A}_{K,2K}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \;\vdots\\ & \mathtt{B}_{1,\unicode{x3bb}}^{(n+m-1)}=\mathtt{A}_{1,(\unicode{x3bb}-1)K+1}^{(n+m-1)}\mathtt{A}_{2,(\unicode{x3bb}-1)K+2}^{(n+m-1)}\ldots\mathtt{A}_{K,\unicode{x3bb} K}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & (n+m-1)\text{-blocks of type }2\text{:} \\ & \mathtt{B}_{2,1}^{(n+m-1)}=\mathtt{A}_{1,2}^{(n+m-1)}\mathtt{A}_{2,3}^{(n+m-1)}\ldots\mathtt{A}_{K,K+1}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \mathtt{B}_{2,2}^{(n+m-1)}=\mathtt{A}_{1,K+2}^{(n+m-1)}\mathtt{A}_{2,K+3}^{(n+m-1)}\ldots\mathtt{A}_{K,2K+1}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \;\vdots\\ & \mathtt{B}_{2,\unicode{x3bb}}^{(n+m-1)}=\mathtt{A}_{1,(\unicode{x3bb}-1)K+2}^{(n+m-1)}\mathtt{A}_{2,(\unicode{x3bb}-1)K+3}^{(n+m-1)}\ldots\mathtt{A}_{K,\unicode{x3bb} K+1}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \;\vdots\\ & (n+m-1)\text{-blocks of type }K\text{:} \\ & \mathtt{B}_{K,1}^{(n+m-1)}=\mathtt{A}_{1,K}^{(n+m-1)}\mathtt{A}_{2,K+1}^{(n+m-1)}\ldots\mathtt{A}_{K,2K-1}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \mathtt{B}_{K,2}^{(n+m-1)}=\mathtt{A}_{1,2K}^{(n+m-1)}\mathtt{A}_{2,2K+1}^{(n+m-1)}\ldots\mathtt{A}_{K,3K-1}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \;\vdots \\ & \mathtt{B}_{K,\unicode{x3bb}}^{(n+m-1)}=\mathtt{A}_{1,\unicode{x3bb} K}^{(n+m-1)}\mathtt{A}_{2,\unicode{x3bb} K+1}^{(n+m-1)}\ldots\mathtt{A}_{K,(\unicode{x3bb} +1)K-1}^{(n+m-1)}\mathtt{a}_{n+m-2}, \end{align*} $$
with marker segment
 $\mathtt {a}_{n+m-2} = (\mathtt {B}_{0}^{(n+m-2)})^{\bar {N}(n+m-1)}$
, where
$\mathtt {a}_{n+m-2} = (\mathtt {B}_{0}^{(n+m-2)})^{\bar {N}(n+m-1)}$
, where
![]() $\bar {N}(n+m-1)$
is chosen according to (5.16) to guarantee uniformity of
$\bar {N}(n+m-1)$
is chosen according to (5.16) to guarantee uniformity of
![]() $(n+m-2)$
-blocks in the
$(n+m-2)$
-blocks in the
![]() $(n+m-1)$
-blocks. Moreover, we have an additional marker block,
$(n+m-1)$
-blocks. Moreover, we have an additional marker block,

These blocks are defined using pre-
![]() $(n+m-1)$
-blocks
$(n+m-1)$
-blocks
 $\mathtt {A}_{i,j}^{(n+m-1)}$
with
$\mathtt {A}_{i,j}^{(n+m-1)}$
with
 $$ \begin{align} \overline{f}(\mathtt{A}_{i_{1},j}^{(n+m-1)},\mathtt{A}_{i_{2},j}^{(n+m-1)})\leq\sum_{u=1}^{m-2}\bigg(\frac{1}{N(n+u-1)+1}+\frac{1}{d_{n+u}}\bigg) \end{align} $$
$$ \begin{align} \overline{f}(\mathtt{A}_{i_{1},j}^{(n+m-1)},\mathtt{A}_{i_{2},j}^{(n+m-1)})\leq\sum_{u=1}^{m-2}\bigg(\frac{1}{N(n+u-1)+1}+\frac{1}{d_{n+u}}\bigg) \end{align} $$
if
![]() $m>2$
(note that the assumption is vacuous if
$m>2$
(note that the assumption is vacuous if
![]() $m=2$
). Moreover, for any sequences
$m=2$
). Moreover, for any sequences
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\overline {\mathcal {B}}$
of at least
$\overline {\mathcal {B}}$
of at least
![]() ${q_{n+m-1}}/{R_{n+m-1}}$
consecutive symbols in
${q_{n+m-1}}/{R_{n+m-1}}$
consecutive symbols in
 $\mathcal {B}_{i_{1},j_{1}}^{(n+m-1)}$
and
$\mathcal {B}_{i_{1},j_{1}}^{(n+m-1)}$
and
 $\mathcal {B}_{i_{2},j_{2}}^{(n+m-1)}$
for some
$\mathcal {B}_{i_{2},j_{2}}^{(n+m-1)}$
for some
![]() $i_{1},i_{2}\in \{ 0,1,\ldots ,K\} $
,
$i_{1},i_{2}\in \{ 0,1,\ldots ,K\} $
,
![]() $i_1 \leq i_2$
, and
$i_1 \leq i_2$
, and
![]() $j_{1},j_{2}\in \{ 1,\ldots ,\unicode{x3bb} _{n+m-1}\} $
, we assume
$j_{1},j_{2}\in \{ 1,\ldots ,\unicode{x3bb} _{n+m-1}\} $
, we assume
 $$ \begin{align} \overline{f}(\mathcal{B},\overline{\mathcal{B}})\geq\bigg(1-\bigg(1-\frac{1}{K}\bigg)^{m-1}\bigg)\alpha-E_{n+m-1}\quad\text{for }i_{1}<i_{2}\text{ and }j_{1}=j_{2}\text{ or }j_{1}=j_{2}+1, \end{align} $$
$$ \begin{align} \overline{f}(\mathcal{B},\overline{\mathcal{B}})\geq\bigg(1-\bigg(1-\frac{1}{K}\bigg)^{m-1}\bigg)\alpha-E_{n+m-1}\quad\text{for }i_{1}<i_{2}\text{ and }j_{1}=j_{2}\text{ or }j_{1}=j_{2}+1, \end{align} $$
where
 $$ \begin{align} E_{n+m-1}=E_{n+1}+\sum_{i=1}^{m-2}\bigg(\frac{6}{R_{n+i}}+\frac{8}{u_{n+i}}+\frac{17}{\sqrt{e_{n+i}}}\bigg). \end{align} $$
$$ \begin{align} E_{n+m-1}=E_{n+1}+\sum_{i=1}^{m-2}\bigg(\frac{6}{R_{n+i}}+\frac{8}{u_{n+i}}+\frac{17}{\sqrt{e_{n+i}}}\bigg). \end{align} $$
We point out that assumptions (5.12)-(5.15) hold for
![]() $m=2$
by Lemma 5.17.
$m=2$
by Lemma 5.17.
In order to continue the inductive construction we define grouped
![]() $(n+m-1)$
-blocks of type i by concatenating
$(n+m-1)$
-blocks of type i by concatenating
![]() $d_{n+m-1}\, (n+m-1)$
-blocks of type i:
$d_{n+m-1}\, (n+m-1)$
-blocks of type i:
 $$ \begin{align*} \mathtt{G}_{i,s}^{(n+m-1)}=\mathtt{B}_{i,s\cdot d_{n+m-1}+1}^{(n+m-1)}\mathtt{B}_{i,s\cdot d_{n+m-1}+2}^{(n+m-1)}\ldots\mathtt{B}_{i,(s+1)\cdot d_{n+m-1}}^{(n+m-1)},\quad\text{for}\;s=0,\ldots,e_{n+m-1}-1. \end{align*} $$
$$ \begin{align*} \mathtt{G}_{i,s}^{(n+m-1)}=\mathtt{B}_{i,s\cdot d_{n+m-1}+1}^{(n+m-1)}\mathtt{B}_{i,s\cdot d_{n+m-1}+2}^{(n+m-1)}\ldots\mathtt{B}_{i,(s+1)\cdot d_{n+m-1}}^{(n+m-1)},\quad\text{for}\;s=0,\ldots,e_{n+m-1}-1. \end{align*} $$
Lemma 5.18. (Distance between grouped
 $(n+m-1)$
-blocks in the circular system)
$(n+m-1)$
-blocks in the circular system)
Let
![]() $\mathcal {G}$
and
$\mathcal {G}$
and
![]() $\overline {\mathcal {G}}$
be sequences of at least
$\overline {\mathcal {G}}$
be sequences of at least
![]() $u_{n+m-1}l_{n+m-1}q_{n+m-1}$
consecutive symbols in
$u_{n+m-1}l_{n+m-1}q_{n+m-1}$
consecutive symbols in
 $\mathcal {G}_{i_{1},s_{1}}^{(n+m-1)}$
and
$\mathcal {G}_{i_{1},s_{1}}^{(n+m-1)}$
and
 $\mathcal {G}_{i_{2},s_{2}}^{(n+m-1)}$
for some
$\mathcal {G}_{i_{2},s_{2}}^{(n+m-1)}$
for some
![]() $i_{1},i_{2}\in \{ 1,\ldots ,K\} $
and
$i_{1},i_{2}\in \{ 1,\ldots ,K\} $
and
![]() $s_{1},s_{2}\in \{ 0,\ldots ,e_{n+m-1}-1\} $
.
$s_{1},s_{2}\in \{ 0,\ldots ,e_{n+m-1}-1\} $
.
-
(1) For
 $i_{1}=i_{2}$
and
$i_{1}=i_{2}$
and
 $s_{1}\neq s_{2}$
we have
$s_{1}\neq s_{2}$
we have  $$ \begin{align*} \overline{f}(\mathcal{G},\overline{\mathcal{G}})\geq \alpha-E_{n+m-1}-\frac{4}{R_{n+m-1}}-\frac{4R_{n+m-1}}{l_{n+m-1}}-\frac{4}{u_{n+m-1}}. \end{align*} $$
$$ \begin{align*} \overline{f}(\mathcal{G},\overline{\mathcal{G}})\geq \alpha-E_{n+m-1}-\frac{4}{R_{n+m-1}}-\frac{4R_{n+m-1}}{l_{n+m-1}}-\frac{4}{u_{n+m-1}}. \end{align*} $$
-
(2) For
 $i_{1}\neq i_{2}$
and
$i_{1}\neq i_{2}$
and
 $s_{1}=s_{2}$
we have
$s_{1}=s_{2}$
we have  $$ \begin{align*} \overline{f}(\mathcal{G},\overline{\mathcal{G}})\geq\bigg(\!1-\bigg(\!1-\frac{1}{K}\!\bigg)^{m-1}\bigg)\cdot\alpha-E_{n+m-1}-\frac{4}{R_{n+m-1}}-\frac{4R_{n+m-1}}{l_{n+m-1}}-\frac{4}{u_{n+m-1}}. \end{align*} $$
$$ \begin{align*} \overline{f}(\mathcal{G},\overline{\mathcal{G}})\geq\bigg(\!1-\bigg(\!1-\frac{1}{K}\!\bigg)^{m-1}\bigg)\cdot\alpha-E_{n+m-1}-\frac{4}{R_{n+m-1}}-\frac{4R_{n+m-1}}{l_{n+m-1}}-\frac{4}{u_{n+m-1}}. \end{align*} $$
-
(3) For
 $i_{1}\neq i_{2}$
and
$i_{1}\neq i_{2}$
and
 $s_{1}\neq s_{2}$
we have
$s_{1}\neq s_{2}$
we have  $$ \begin{align*} \overline{f}(\mathcal{G},\overline{\mathcal{G}})\geq\alpha-E_{n+m-1}-\frac{4}{R_{n+m-1}}-\frac{4R_{n+m-1}}{l_{n+m-1}}-\frac{6}{u_{n+m-1}}. \end{align*} $$
$$ \begin{align*} \overline{f}(\mathcal{G},\overline{\mathcal{G}})\geq\alpha-E_{n+m-1}-\frac{4}{R_{n+m-1}}-\frac{4R_{n+m-1}}{l_{n+m-1}}-\frac{6}{u_{n+m-1}}. \end{align*} $$
Proof. We factor
![]() $\mathcal {G}$
and
$\mathcal {G}$
and
![]() $\overline {\mathcal {G}}$
into 2-subsections
$\overline {\mathcal {G}}$
into 2-subsections
 $\mathcal {C}_{n,j_1}(\mathtt {B}_{i_{1},t}^{(n+m-1)})$
and
$\mathcal {C}_{n,j_1}(\mathtt {B}_{i_{1},t}^{(n+m-1)})$
and
 $\mathcal {C}_{n,j_2}(\mathtt {B}_{i_{2},u}^{(n+m-1)})$
for some
$\mathcal {C}_{n,j_2}(\mathtt {B}_{i_{2},u}^{(n+m-1)})$
for some
![]() $j_1,j_2 \in \{0,1,\ldots ,q_n-1\}$
, omitting partial blocks at the ends which constitute a portion of at most
$j_1,j_2 \in \{0,1,\ldots ,q_n-1\}$
, omitting partial blocks at the ends which constitute a portion of at most
![]() $2/u_{n+m-1}$
of the total length of
$2/u_{n+m-1}$
of the total length of
![]() $\mathcal {G}$
and
$\mathcal {G}$
and
![]() $\overline {\mathcal {G}}$
. With the aid of Lemma 5.12 we can transfer the estimates in equations (5.12)–(5.14) to estimates on the
$\overline {\mathcal {G}}$
. With the aid of Lemma 5.12 we can transfer the estimates in equations (5.12)–(5.14) to estimates on the
![]() $\overline {f}$
distance of substrings of at least
$\overline {f}$
distance of substrings of at least
![]() $q_{n+m-1}l_{n+m-1}/R_{n+m-1}$
consecutive symbols in these strings of the form
$q_{n+m-1}l_{n+m-1}/R_{n+m-1}$
consecutive symbols in these strings of the form
 $\mathcal {C}_{n,j_1}(\mathtt {B}_{i_{1},t}^{(n+m-1)})$
and
$\mathcal {C}_{n,j_1}(\mathtt {B}_{i_{1},t}^{(n+m-1)})$
and
 $\mathcal {C}_{n,j_2}(\mathtt {B}_{i_{2},u}^{(n+m-1)})$
, respectively.
$\mathcal {C}_{n,j_2}(\mathtt {B}_{i_{2},u}^{(n+m-1)})$
, respectively.
We now examine the particular situation of each part of the lemma.
(1) Since the
![]() $(n+m-1)$
-blocks in
$(n+m-1)$
-blocks in
 $\mathcal {G}_{i_{1},s_{1}}^{(n+m-1)}$
and
$\mathcal {G}_{i_{1},s_{1}}^{(n+m-1)}$
and
 $\mathcal {G}_{i_{1},s_{2}}^{(n+m-1)}$
are of same type but different pattern, Corollary 5.5 (with
$\mathcal {G}_{i_{1},s_{2}}^{(n+m-1)}$
are of same type but different pattern, Corollary 5.5 (with
![]() $\tilde {f}=1$
) and the modified version of equation (5.12) yield
$\tilde {f}=1$
) and the modified version of equation (5.12) yield
 $$ \begin{align*} \overline{f}(\mathcal{G},\overline{\mathcal{G}})\geq \alpha-E_{n+m-1}-\frac{2}{R_{n+m-1}}-\frac{4R_{n+m-1}}{l_{n+m-1}}-\frac{2}{R_{n+m-1}}-\frac{4}{u_{n+m-1}}. \end{align*} $$
$$ \begin{align*} \overline{f}(\mathcal{G},\overline{\mathcal{G}})\geq \alpha-E_{n+m-1}-\frac{2}{R_{n+m-1}}-\frac{4R_{n+m-1}}{l_{n+m-1}}-\frac{2}{R_{n+m-1}}-\frac{4}{u_{n+m-1}}. \end{align*} $$
(2) For
![]() $m=2$
we note that
$m=2$
we note that
 $\mathtt {B}_{i_{1},t}^{(n+1)}$
and
$\mathtt {B}_{i_{1},t}^{(n+1)}$
and
 $\mathtt {B}_{i_{2},u}^{(n+1)}$
in
$\mathtt {B}_{i_{2},u}^{(n+1)}$
in
 $\mathtt {G}_{i_{1},s_{1}}^{(n+1)}$
and
$\mathtt {G}_{i_{1},s_{1}}^{(n+1)}$
and
 $\mathtt {G}_{i_{2},s_{1}}^{(n+1)}$
respectively have at most
$\mathtt {G}_{i_{2},s_{1}}^{(n+1)}$
respectively have at most
![]() $J=\max (\lvert i_{2}-i_{1}\rvert ,\:K-\lvert i_{2}-i_{1}\rvert )$
pre-
$J=\max (\lvert i_{2}-i_{1}\rvert ,\:K-\lvert i_{2}-i_{1}\rvert )$
pre-
![]() $(n+1)$
-blocks in common. Then we apply Lemma 5.17, Lemma 5.12, and Corollary 5.5 (with
$(n+1)$
-blocks in common. Then we apply Lemma 5.17, Lemma 5.12, and Corollary 5.5 (with
![]() $\tilde {f}=1$
) to conclude the inequality.
$\tilde {f}=1$
) to conclude the inequality.
In order to obtain a lower bound on the
![]() $\overline {f}$
distance for
$\overline {f}$
distance for
![]() $m>2$
we note that
$m>2$
we note that
 $\mathtt {B}_{i_{1},t}^{(n+m-1)}$
and
$\mathtt {B}_{i_{1},t}^{(n+m-1)}$
and
 $\mathtt {B}_{i_{2},u}^{(n+m-1)}$
in
$\mathtt {B}_{i_{2},u}^{(n+m-1)}$
in
 $\mathtt {G}_{i_{1},s_{1}}^{(n+m-1)}$
and
$\mathtt {G}_{i_{1},s_{1}}^{(n+m-1)}$
and
 $\mathtt {G}_{i_{2},s_{1}}^{(n+m-1)}$
could fall under the situation of the worst possible estimate in equation (5.13). By another application of Lemma 5.12 and Corollary 5.5 (with
$\mathtt {G}_{i_{2},s_{1}}^{(n+m-1)}$
could fall under the situation of the worst possible estimate in equation (5.13). By another application of Lemma 5.12 and Corollary 5.5 (with
![]() $\tilde {f}=1$
) we get the claim.
$\tilde {f}=1$
) we get the claim.
(3) Without loss of generality let
![]() $i_2>i_1$
. Once again, we start with the proof for
$i_2>i_1$
. Once again, we start with the proof for
![]() $m=2$
. There is at most one pair of
$m=2$
. There is at most one pair of
![]() $(n+1)$
-blocks in
$(n+1)$
-blocks in
 $\mathtt {G}_{i_{1},s_{1}}^{(n+1)}$
and
$\mathtt {G}_{i_{1},s_{1}}^{(n+1)}$
and
 $\mathtt {G}_{i_{2},s_{2}}^{(n+1)}$
respectively that have
$\mathtt {G}_{i_{2},s_{2}}^{(n+1)}$
respectively that have
![]() $i_{2}-i_{1}$
pre-
$i_{2}-i_{1}$
pre-
![]() $(n+1)$
-blocks in common while all other pairs have no pair in common. This corresponds to a proportion of at most
$(n+1)$
-blocks in common while all other pairs have no pair in common. This corresponds to a proportion of at most
![]() $2/u_{n+1}$
. Then we use Lemma 5.17, Lemma 5.12, and Proposition 5.4 (with
$2/u_{n+1}$
. Then we use Lemma 5.17, Lemma 5.12, and Proposition 5.4 (with
![]() $\tilde {f}\geq 1-({2}/{u_{n+1}})$
) to obtain
$\tilde {f}\geq 1-({2}/{u_{n+1}})$
) to obtain
 $$ \begin{align*} \overline{f}(\mathcal{G},\overline{\mathcal{G}}) & \geq\bigg(1-\frac{2}{u_{n+1}}+\frac{2}{u_{n+1}}\bigg(1-\frac{i_{2}-i_{1}}{K}\bigg)\bigg)\alpha-E_{n+1}-\frac{4}{R_{n+1}}-\frac{4R_{n+1}}{l_{n+1}}-\frac{4}{u_{n+1}}\\ & \geq \alpha-E_{n+1}-\frac{4}{R_{n+1}}-\frac{4R_{n+1}}{l_{n+1}}-\frac{6}{u_{n+1}}. \end{align*} $$
$$ \begin{align*} \overline{f}(\mathcal{G},\overline{\mathcal{G}}) & \geq\bigg(1-\frac{2}{u_{n+1}}+\frac{2}{u_{n+1}}\bigg(1-\frac{i_{2}-i_{1}}{K}\bigg)\bigg)\alpha-E_{n+1}-\frac{4}{R_{n+1}}-\frac{4R_{n+1}}{l_{n+1}}-\frac{4}{u_{n+1}}\\ & \geq \alpha-E_{n+1}-\frac{4}{R_{n+1}}-\frac{4R_{n+1}}{l_{n+1}}-\frac{6}{u_{n+1}}. \end{align*} $$
We proceed with the case of
![]() $m>2$
. There is at most one pair of n-blocks
$m>2$
. There is at most one pair of n-blocks
 $\mathtt {B}_{i_{1},j_{1}}^{(n+m-1)}$
and
$\mathtt {B}_{i_{1},j_{1}}^{(n+m-1)}$
and
 $\mathtt {B}_{i_{2},j_{2}}^{(n+m-1)}$
in
$\mathtt {B}_{i_{2},j_{2}}^{(n+m-1)}$
in
 $\mathtt {G}_{i_{1},s_{1}}^{(n+m-1)}$
and
$\mathtt {G}_{i_{1},s_{1}}^{(n+m-1)}$
and
 $\mathtt {G}_{i_{2},s_{2}}^{(n+m-1)}$
respectively with
$\mathtt {G}_{i_{2},s_{2}}^{(n+m-1)}$
respectively with
![]() $j_{1}=j_{2}+1$
, while for all other pairs
$j_{1}=j_{2}+1$
, while for all other pairs
![]() $j_{1}\neq j_{2}$
and
$j_{1}\neq j_{2}$
and
![]() $j_{1}\neq j_{2}+1$
. Since this corresponds to a proportion of at most
$j_{1}\neq j_{2}+1$
. Since this corresponds to a proportion of at most
![]() $2/u_{n+m-1}$
, we use the modified versions of equations (5.13) and (5.14) and Proposition 5.4 (with
$2/u_{n+m-1}$
, we use the modified versions of equations (5.13) and (5.14) and Proposition 5.4 (with
![]() $\tilde {f}\geq 1-({2}/{u_{n+m-1}})$
) to obtain the estimate on
$\tilde {f}\geq 1-({2}/{u_{n+m-1}})$
) to obtain the estimate on
![]() $\overline {f}(\mathcal {G},\overline {\mathcal {G}})$
by the same calculation as above, replacing the subscripts
$\overline {f}(\mathcal {G},\overline {\mathcal {G}})$
by the same calculation as above, replacing the subscripts
![]() $n+1$
by
$n+1$
by
![]() $n+m-1$
and the term
$n+m-1$
and the term
![]() $1-({i_{2}-i_{1}}/{K})$
by
$1-({i_{2}-i_{1}}/{K})$
by
![]() $1-(1-({1}/{K}))^{m-1}$
.
$1-(1-({1}/{K}))^{m-1}$
.
In all other cases
![]() $s_{1}\neq s_{2}$
all pairs of n-blocks
$s_{1}\neq s_{2}$
all pairs of n-blocks
 $\mathtt {B}_{i_{1},j_{1}}^{(n+m-1)}$
and
$\mathtt {B}_{i_{1},j_{1}}^{(n+m-1)}$
and
 $\mathtt {B}_{i_{2},j_{2}}^{(n+m-1)}$
in
$\mathtt {B}_{i_{2},j_{2}}^{(n+m-1)}$
in
 $\mathtt {G}_{i_{1},s_{1}}^{(n+m-1)}$
and
$\mathtt {G}_{i_{1},s_{1}}^{(n+m-1)}$
and
 $\mathtt {G}_{i_{2},s_{2}}^{(n+m-1)}$
respectively have
$\mathtt {G}_{i_{2},s_{2}}^{(n+m-1)}$
respectively have
![]() $j_{1}\neq j_{2}$
and
$j_{1}\neq j_{2}$
and
![]() $j_{1}\neq j_{2}+1$
. Then we use the same estimate as in part (1).
$j_{1}\neq j_{2}+1$
. Then we use the same estimate as in part (1).
Let us introduce the notation
 $$ \begin{align*} \gamma_{n+m-1}:= E_{n+m-1}+\frac{4}{R_{n+m-1}}+\frac{4R_{n+m-1}}{l_{n+m-1}}+\frac{6}{u_{n+m-1}}. \end{align*} $$
$$ \begin{align*} \gamma_{n+m-1}:= E_{n+m-1}+\frac{4}{R_{n+m-1}}+\frac{4R_{n+m-1}}{l_{n+m-1}}+\frac{6}{u_{n+m-1}}. \end{align*} $$
We continue the inductive construction by building
![]() $2K^2\unicode{x3bb} _{n+m}=2K^2d_{n+m}e_{n+m}$
pre-
$2K^2\unicode{x3bb} _{n+m}=2K^2d_{n+m}e_{n+m}$
pre-
![]() $(n+m)$
-blocks
$(n+m)$
-blocks
 $\mathtt {A}_{i,j}^{(n+m)}$
, where
$\mathtt {A}_{i,j}^{(n+m)}$
, where
![]() $j\in \{ 1,\ldots ,2\unicode{x3bb} _{n+m}K \}$
stands for the jth Feldman pattern and
$j\in \{ 1,\ldots ,2\unicode{x3bb} _{n+m}K \}$
stands for the jth Feldman pattern and
![]() $i\in \{ 1,\ldots ,K\} $
indicates the type of
$i\in \{ 1,\ldots ,K\} $
indicates the type of
![]() $(n+m-1)$
-blocks used. We let
$(n+m-1)$
-blocks used. We let
 $\mathtt {A}_{i,j}^{(n+m)}$
be the jth Feldman pattern built of the grouped
$\mathtt {A}_{i,j}^{(n+m)}$
be the jth Feldman pattern built of the grouped
![]() $(n+m-1)$
-blocks of type i. We point out that
$(n+m-1)$
-blocks of type i. We point out that
 $\mathtt {A}_{i,j}^{(n+m)}$
contains each
$\mathtt {A}_{i,j}^{(n+m)}$
contains each
![]() $(n+m-1)$
-block of type i
$(n+m-1)$
-block of type i
times because it is uniform in the building blocks
 $\mathtt {G}_{i,s}^{(n+m-1)}$
by construction of the Feldman patterns in Proposition 5.10 and each
$\mathtt {G}_{i,s}^{(n+m-1)}$
by construction of the Feldman patterns in Proposition 5.10 and each
![]() $(n+m-1)$
-block of type i is contained in exactly one grouped
$(n+m-1)$
-block of type i is contained in exactly one grouped
![]() $(n+m-1)$
-block. Moreover, this number of occurrences is the same for every chosen Feldman pattern j. We will denote the length of the circular image
$(n+m-1)$
-block. Moreover, this number of occurrences is the same for every chosen Feldman pattern j. We will denote the length of the circular image
 $\mathcal {A}_{i,j}^{(n+m)}=\mathcal {C}_{n+m-1,k}(\mathtt {A}^{(n+m)}_{i,j})$
,
$\mathcal {A}_{i,j}^{(n+m)}=\mathcal {C}_{n+m-1,k}(\mathtt {A}^{(n+m)}_{i,j})$
,
![]() $k\in \{0,\ldots ,q_{n+m-1}-1\}$
, by
$k\in \{0,\ldots ,q_{n+m-1}-1\}$
, by
![]() $\tilde {q}_{n+m}$
.
$\tilde {q}_{n+m}$
.
Lemma 5.19. (Closeness and separation of pre-
 $(n+m)$
-blocks of same Feldman pattern)
$(n+m)$
-blocks of same Feldman pattern)
For every
![]() $j\in \{ 1,\ldots ,2K d_{n+m} e_{n+m}\} $
and
$j\in \{ 1,\ldots ,2K d_{n+m} e_{n+m}\} $
and
![]() $i_{1},i_{2}\in \{ 1,\ldots ,K\} $
we have
$i_{1},i_{2}\in \{ 1,\ldots ,K\} $
we have
 $$ \begin{align*} \overline{f}(\mathtt{A}_{i_{1},j}^{(n+m)},\mathtt{A}_{i_{2},j}^{(n+m)})\leq\sum_{u=1}^{m-1}\bigg(\frac{1}{N(n+u-1)+1}+\frac{1}{d_{n+u}}\bigg) \end{align*} $$
$$ \begin{align*} \overline{f}(\mathtt{A}_{i_{1},j}^{(n+m)},\mathtt{A}_{i_{2},j}^{(n+m)})\leq\sum_{u=1}^{m-1}\bigg(\frac{1}{N(n+u-1)+1}+\frac{1}{d_{n+u}}\bigg) \end{align*} $$
in the odometer-based system. In the circular system we have for
![]() $i_{1}\neq i_{2}$
and for any sequences
$i_{1}\neq i_{2}$
and for any sequences
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\overline {\mathcal {A}}$
of at least
$\overline {\mathcal {A}}$
of at least
![]() $\tilde {q}_{n+m}/e_{n+m-1}$
consecutive symbols in
$\tilde {q}_{n+m}/e_{n+m-1}$
consecutive symbols in
 $\mathcal {A}_{i_{1},j}^{(n+m)}$
and
$\mathcal {A}_{i_{1},j}^{(n+m)}$
and
 $\mathcal {A}_{i_{2},j}^{(n+m)}$
respectively that
$\mathcal {A}_{i_{2},j}^{(n+m)}$
respectively that
 $$ \begin{align*} \overline{f}(\mathcal{A},\overline{\mathcal{A}}) \geq \bigg(1-\bigg(1-\frac{1}{K}\bigg)^{m-1}\bigg)\alpha-\gamma_{n+m-1}-\frac{2}{e_{n+m-1}} -\frac{2}{u_{n+m-1}}. \end{align*} $$
$$ \begin{align*} \overline{f}(\mathcal{A},\overline{\mathcal{A}}) \geq \bigg(1-\bigg(1-\frac{1}{K}\bigg)^{m-1}\bigg)\alpha-\gamma_{n+m-1}-\frac{2}{e_{n+m-1}} -\frac{2}{u_{n+m-1}}. \end{align*} $$
Proof. Without loss of generality, let
![]() $i_{2}>i_{1}$
.
$i_{2}>i_{1}$
.
We start with the proof of the first statement for
![]() $m=2$
. Ignoring the marker segment
$m=2$
. Ignoring the marker segment
![]() $\mathtt {a}_{n}$
, we note that for every
$\mathtt {a}_{n}$
, we note that for every
![]() $s=0,\ldots ,e_{n+1}-1$
the grouped n-block
$s=0,\ldots ,e_{n+1}-1$
the grouped n-block
 $\mathtt {G}_{i_{2},s}^{(n+1)}$
is obtained from
$\mathtt {G}_{i_{2},s}^{(n+1)}$
is obtained from
 $\mathtt {G}_{i_{1},s}^{(n+1)}$
by a shift of
$\mathtt {G}_{i_{1},s}^{(n+1)}$
by a shift of
![]() $i_{2}-i_{1}$
pre-
$i_{2}-i_{1}$
pre-
![]() $(n+1)$
-blocks. Since a grouped
$(n+1)$
-blocks. Since a grouped
![]() $(n+1)$
-block consists of
$(n+1)$
-block consists of
![]() $Kd_{n+1}$
pre-
$Kd_{n+1}$
pre-
![]() $(n+1)$
-blocks, the grouped
$(n+1)$
-blocks, the grouped
![]() $(n+1)$
-blocks
$(n+1)$
-blocks
 $\mathtt {G}_{i_{1},s}^{(n+1)},\mathtt {G}_{i_{2},s}^{(n+1)}$
can be matched on a portion of at least
$\mathtt {G}_{i_{1},s}^{(n+1)},\mathtt {G}_{i_{2},s}^{(n+1)}$
can be matched on a portion of at least
![]() $1-(({i_{2}-i_{1}})/{K d_{n+1}})$
of the part of pre-
$1-(({i_{2}-i_{1}})/{K d_{n+1}})$
of the part of pre-
![]() $(n+1)$
-blocks. Thus, we have
$(n+1)$
-blocks. Thus, we have
 $$ \begin{align*} \overline{f}(\mathtt{G}_{i_{1},s}^{(n+1)},\mathtt{G}_{i_{2},s}^{(n+1)})\leq\frac{1}{N+1}+\frac{N}{N+1}\cdot\frac{i_{2}-i_{1}}{K d_{n+1}}, \end{align*} $$
$$ \begin{align*} \overline{f}(\mathtt{G}_{i_{1},s}^{(n+1)},\mathtt{G}_{i_{2},s}^{(n+1)})\leq\frac{1}{N+1}+\frac{N}{N+1}\cdot\frac{i_{2}-i_{1}}{K d_{n+1}}, \end{align*} $$
which yields the claim because
 $\mathtt {A}_{i_{1},j}^{(n+2)}$
and
$\mathtt {A}_{i_{1},j}^{(n+2)}$
and
 $\mathtt {A}_{i_{2},j}^{(n+2)}$
are constructed as the same Feldman pattern with these grouped
$\mathtt {A}_{i_{2},j}^{(n+2)}$
are constructed as the same Feldman pattern with these grouped
![]() $(n+1)$
-blocks of different types as building blocks.
$(n+1)$
-blocks of different types as building blocks.
Turning to the proof of the first statement for
![]() $m>2$
, we ignore the marker blocks which occupy a fraction
$m>2$
, we ignore the marker blocks which occupy a fraction

of each
![]() $(n+m-1)$
-block (since there are
$(n+m-1)$
-block (since there are
![]() $1+K\unicode{x3bb} _{n+m-2}\, (n+m-2)$
-blocks, it follows from the uniformity of
$1+K\unicode{x3bb} _{n+m-2}\, (n+m-2)$
-blocks, it follows from the uniformity of
![]() $(n+m-2)$
-blocks within each
$(n+m-2)$
-blocks within each
![]() $(n+m-1)$
-block that the marker segment occupies a fraction
$(n+m-1)$
-block that the marker segment occupies a fraction
![]() $1/(1+K\unicode{x3bb} _{n+m-2})$
of the
$1/(1+K\unicode{x3bb} _{n+m-2})$
of the
![]() $(n+m-1)$
-block). Let M denote the right-hand side from inequality (5.11), that is, an upper bound for the
$(n+m-1)$
-block). Let M denote the right-hand side from inequality (5.11), that is, an upper bound for the
![]() $\overline {f}$
distance between pre-
$\overline {f}$
distance between pre-
![]() $(n+m-1)$
-blocks of type
$(n+m-1)$
-blocks of type
![]() $i_{1}$
and
$i_{1}$
and
![]() $i_{2}$
and the same Feldman pattern. Since in the definition of
$i_{2}$
and the same Feldman pattern. Since in the definition of
![]() $(n+m-1)$
-blocks of types
$(n+m-1)$
-blocks of types
![]() $i_1$
and
$i_1$
and
![]() $i_2$
the Feldman patterns used are shifted by
$i_2$
the Feldman patterns used are shifted by
![]() $i_2-i_1$
, we obtain, for every
$i_2-i_1$
, we obtain, for every
 $s\in \{0,\ldots ,e_{n+m-1}-1\} \mathtt {G}_{i_{1},s}^{(n+m-1)}$
and
$s\in \{0,\ldots ,e_{n+m-1}-1\} \mathtt {G}_{i_{1},s}^{(n+m-1)}$
and
 $\mathtt {G}_{i_{2},s}^{(n+m-1)}$
,
$\mathtt {G}_{i_{2},s}^{(n+m-1)}$
,
 $$ \begin{align*} \overline{f}(\mathtt{G}_{i_{1},s}^{(n+m-1)},\mathtt{G}_{i_{2},s}^{(n+m-1)}) &\leq \frac{1}{N(n+m-2)+1}+\frac{(Kd_{n+m-1}-\lvert i_{1}-i_{2}\rvert)}{Kd_{n+m-1}}\cdot M+\frac{\lvert i_{1}-i_{2}\rvert}{Kd_{n+m-1}}\\ &\leq \sum_{u=1}^{m-1}\bigg(\frac{1}{N(n+u-1)+1}+\frac{1}{d_{n+u}}\bigg) \end{align*} $$
$$ \begin{align*} \overline{f}(\mathtt{G}_{i_{1},s}^{(n+m-1)},\mathtt{G}_{i_{2},s}^{(n+m-1)}) &\leq \frac{1}{N(n+m-2)+1}+\frac{(Kd_{n+m-1}-\lvert i_{1}-i_{2}\rvert)}{Kd_{n+m-1}}\cdot M+\frac{\lvert i_{1}-i_{2}\rvert}{Kd_{n+m-1}}\\ &\leq \sum_{u=1}^{m-1}\bigg(\frac{1}{N(n+u-1)+1}+\frac{1}{d_{n+u}}\bigg) \end{align*} $$
using equation (5.11). This yields the claim because
 $\mathtt {A}_{i_{1},j}^{(n+m)}$
and
$\mathtt {A}_{i_{1},j}^{(n+m)}$
and
 $\mathtt {A}_{i_{2},j}^{(n+m)}$
are constructed as the same Feldman pattern with these grouped
$\mathtt {A}_{i_{2},j}^{(n+m)}$
are constructed as the same Feldman pattern with these grouped
![]() $(n+m-1)$
-blocks of different type as building blocks.
$(n+m-1)$
-blocks of different type as building blocks.
We will need a statement on the
![]() $\overline {f}$
distance of different Feldman patterns in the circular system only, but not in the odometer-based system.
$\overline {f}$
distance of different Feldman patterns in the circular system only, but not in the odometer-based system.
Lemma 5.20. (Separation of pre-
 $(n+m)$
-blocks of different Feldman patterns)
$(n+m)$
-blocks of different Feldman patterns)
For any sequences
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\overline {\mathcal {A}}$
of at least
$\overline {\mathcal {A}}$
of at least
![]() $\tilde {q}_{n+m}/e_{n+m-1}$
consecutive symbols in
$\tilde {q}_{n+m}/e_{n+m-1}$
consecutive symbols in
 $\mathcal {A}_{i_{1},j_{1}}^{(n+m)}$
and
$\mathcal {A}_{i_{1},j_{1}}^{(n+m)}$
and
 $\mathcal {A}_{i_{2},j_{2}}^{(n+m)}$
for some
$\mathcal {A}_{i_{2},j_{2}}^{(n+m)}$
for some
![]() $i_{1},i_{2}\in \{ 1,\ldots ,K\} $
and
$i_{1},i_{2}\in \{ 1,\ldots ,K\} $
and
![]() $j_{1},j_{2}\in \{ 1,\ldots ,2Kd_{n+m}e_{n+m}\} $
,
$j_{1},j_{2}\in \{ 1,\ldots ,2Kd_{n+m}e_{n+m}\} $
,
![]() $j_{1}\neq j_{2}$
, we have
$j_{1}\neq j_{2}$
, we have
 $$ \begin{align*} \overline{f}(\mathcal{A},\overline{\mathcal{A}})\geq \alpha-\gamma_{n+m-1}-\frac{13}{\sqrt{e_{n+m-1}}}-\frac{2}{u_{n+m-1}}. \end{align*} $$
$$ \begin{align*} \overline{f}(\mathcal{A},\overline{\mathcal{A}})\geq \alpha-\gamma_{n+m-1}-\frac{13}{\sqrt{e_{n+m-1}}}-\frac{2}{u_{n+m-1}}. \end{align*} $$
Then we set
 $$ \begin{align*} \beta_{n+m}:= \gamma_{n+m-1}+\frac{13}{\sqrt{e_{n+m-1}}}+\frac{2}{u_{n+m-1}}. \end{align*} $$
$$ \begin{align*} \beta_{n+m}:= \gamma_{n+m-1}+\frac{13}{\sqrt{e_{n+m-1}}}+\frac{2}{u_{n+m-1}}. \end{align*} $$
We continue our construction process by building
![]() $(n+m)$
-blocks
$(n+m)$
-blocks
 $\mathtt {B}_{i,j}^{(n+m)}$
of K different types (once again, the index
$\mathtt {B}_{i,j}^{(n+m)}$
of K different types (once again, the index
![]() $1\leq i \leq K$
indicates the type, and
$1\leq i \leq K$
indicates the type, and
![]() $1 \leq j \leq \unicode{x3bb} =\unicode{x3bb} _{n+m}$
numbers the
$1 \leq j \leq \unicode{x3bb} =\unicode{x3bb} _{n+m}$
numbers the
![]() $(n+m)$
-blocks of that type consecutively) using the formula from the beginning of §5.3.2 (with
$(n+m)$
-blocks of that type consecutively) using the formula from the beginning of §5.3.2 (with
![]() $n+m-1$
replaced by
$n+m-1$
replaced by
![]() $n+m$
). Moreover, we define an additional
$n+m$
). Moreover, we define an additional
![]() $(n+m)$
-block
$(n+m)$
-block
 $\mathtt {B}_{0}^{(n+m)}$
which will play the role of a marker again:
$\mathtt {B}_{0}^{(n+m)}$
which will play the role of a marker again:

where the pre-
![]() $(n+m)$
-blocks
$(n+m)$
-blocks
 $\mathtt {A}_{i,(\unicode{x3bb} _{n+m}+1)K}^{(n+m)}$
are not used in any other
$\mathtt {A}_{i,(\unicode{x3bb} _{n+m}+1)K}^{(n+m)}$
are not used in any other
![]() $(n+m)$
-block. Hence, there are
$(n+m)$
-block. Hence, there are
![]() $K\unicode{x3bb} _{n+m}+1\, (n+m)$
-blocks in total. We also note that each
$K\unicode{x3bb} _{n+m}+1\, (n+m)$
-blocks in total. We also note that each
![]() $(n+m)$
-block
$(n+m)$
-block
 $\mathtt {B}_{i,s}^{(n+m)}$
contains exactly one pre-
$\mathtt {B}_{i,s}^{(n+m)}$
contains exactly one pre-
![]() $(n+m)$
-block of each type. Thus the
$(n+m)$
-block of each type. Thus the
![]() $(n+m)$
-blocks are uniform in the
$(n+m)$
-blocks are uniform in the
![]() $(n+m-1)$
-blocks by our observation above.
$(n+m-1)$
-blocks by our observation above.
Lemma 5.21. (Distance between
 $(n+m)$
-blocks in the circular system)
$(n+m)$
-blocks in the circular system)
Let
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\overline {\mathcal {B}}$
be sequences of at least
$\overline {\mathcal {B}}$
be sequences of at least
![]() $q_{n+m}/R_{n+m}$
consecutive symbols in
$q_{n+m}/R_{n+m}$
consecutive symbols in
 $\mathcal {B}_{i_{1},j_{1}}^{(n+m)}$
and
$\mathcal {B}_{i_{1},j_{1}}^{(n+m)}$
and
 $\mathcal {B}_{i_{2},j_{2}}^{(n+m)}$
for some
$\mathcal {B}_{i_{2},j_{2}}^{(n+m)}$
for some
![]() $i_{1},i_{2}\in \{ 0,1,\ldots ,K\} $
and
$i_{1},i_{2}\in \{ 0,1,\ldots ,K\} $
and
![]() $j_{1},j_{2}\in \{ 1,\ldots ,\unicode{x3bb} _{n+m}\} $
.
$j_{1},j_{2}\in \{ 1,\ldots ,\unicode{x3bb} _{n+m}\} $
.
-
(1) For blocks of same type, for
 $i_{1}=i_{2}$
and
$i_{1}=i_{2}$
and
 $j_{1}\neq j_{2}$
we have
$j_{1}\neq j_{2}$
we have  $$ \begin{align*} \overline{f}(\mathcal{B},\overline{\mathcal{B}})\geq \alpha-\beta_{n+m}-\frac{4}{e_{n+m-1}}-\frac{4}{l_{n+m-2}}. \end{align*} $$
$$ \begin{align*} \overline{f}(\mathcal{B},\overline{\mathcal{B}})\geq \alpha-\beta_{n+m}-\frac{4}{e_{n+m-1}}-\frac{4}{l_{n+m-2}}. \end{align*} $$
-
(2) For blocks of different type, for
 $i_{1}<i_{2}$
we have
$i_{1}<i_{2}$
we have  $$ \begin{align*} \overline{f}(\mathcal{B},\overline{\mathcal{B}})\geq\bigg(1-\bigg(1-\frac{1}{K}\bigg)^{m}\bigg)\cdot \alpha- \beta_{n+m}-\frac{4}{e_{n+m-1}}-\frac{4}{l_{n+m-2}} \end{align*} $$
$$ \begin{align*} \overline{f}(\mathcal{B},\overline{\mathcal{B}})\geq\bigg(1-\bigg(1-\frac{1}{K}\bigg)^{m}\bigg)\cdot \alpha- \beta_{n+m}-\frac{4}{e_{n+m-1}}-\frac{4}{l_{n+m-2}} \end{align*} $$
if
 $j_{1}=j_{2}$
or
$j_{1}=j_{2}$
or
 $j_{1}=j_{2}+1$
. For all other cases of
$j_{1}=j_{2}+1$
. For all other cases of
 $j_{1}\neq j_{2}$
we have
$j_{1}\neq j_{2}$
we have  $$ \begin{align*} \overline{f}(\mathcal{B},\overline{\mathcal{B}})\geq \alpha-\beta_{n+m}-\frac{4}{e_{n+m-1}}-\frac{4}{l_{n+m-2}}. \end{align*} $$
$$ \begin{align*} \overline{f}(\mathcal{B},\overline{\mathcal{B}})\geq \alpha-\beta_{n+m}-\frac{4}{e_{n+m-1}}-\frac{4}{l_{n+m-2}}. \end{align*} $$
Proof. As in the proof of Lemma 5.17 we consider
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\overline {\mathcal {B}}$
to be a concatenation of complete
$\overline {\mathcal {B}}$
to be a concatenation of complete
![]() $2$
-subsections. ignoring incomplete ones at the beginnings and ends which constitute a fraction of at most
$2$
-subsections. ignoring incomplete ones at the beginnings and ends which constitute a fraction of at most
![]() $2/l_{n+m-2}$
of the total length of
$2/l_{n+m-2}$
of the total length of
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\overline {\mathcal {B}}$
by equation (5.2). In the following consideration we ignore the marker segments
$\overline {\mathcal {B}}$
by equation (5.2). In the following consideration we ignore the marker segments
![]() $\mathtt {a}_{n+m-1}$
which amount to a fraction
$\mathtt {a}_{n+m-1}$
which amount to a fraction
![]() ${1}/({1+K\unicode{x3bb} _{n+m-1}})<({1}/{e_{n+m-1}})$
of the total length due to uniformity. Accordingly, we consider
${1}/({1+K\unicode{x3bb} _{n+m-1}})<({1}/{e_{n+m-1}})$
of the total length due to uniformity. Accordingly, we consider
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\overline {\mathcal {B}}$
to be a concatenation of complete pre-
$\overline {\mathcal {B}}$
to be a concatenation of complete pre-
![]() $(n+m)$
-blocks
$(n+m)$
-blocks
 $\mathcal {A}^{(n+m)}_{i_1,h_1}$
and
$\mathcal {A}^{(n+m)}_{i_1,h_1}$
and
 $\mathcal {A}^{(n+m)}_{i_2,h_2}$
, respectively. Finally, we examine the particular situation of each case of this lemma:
$\mathcal {A}^{(n+m)}_{i_2,h_2}$
, respectively. Finally, we examine the particular situation of each case of this lemma:
(1) We note that all Feldman patterns for pre-
![]() $(n+m)$
-blocks used in
$(n+m)$
-blocks used in
 $\mathtt {B}_{i_{1},j_{1}}^{(n+m)}$
and
$\mathtt {B}_{i_{1},j_{1}}^{(n+m)}$
and
 $\mathtt {B}_{i_{1},j_{2}}^{(n+m)}$
are different from each other. Accordingly, we apply Lemma 5.20 and Corollary 5.5 (with
$\mathtt {B}_{i_{1},j_{2}}^{(n+m)}$
are different from each other. Accordingly, we apply Lemma 5.20 and Corollary 5.5 (with
![]() $\tilde {f}=1$
).
$\tilde {f}=1$
).
(2) For
![]() $i_{1}< i_{2}$
the blocks
$i_{1}< i_{2}$
the blocks
 $\mathtt {B}_{i_{1},j_{2}}^{(n+m)}$
and
$\mathtt {B}_{i_{1},j_{2}}^{(n+m)}$
and
 $\mathtt {B}_{i_{2},j_{2}}^{(n+m)}$
have
$\mathtt {B}_{i_{2},j_{2}}^{(n+m)}$
have
![]() $K-( i_{2}-i_{1})$
Feldman patterns in common. Then we use the second statement of Lemma 5.19 to estimate their
$K-( i_{2}-i_{1})$
Feldman patterns in common. Then we use the second statement of Lemma 5.19 to estimate their
![]() $\overline {f}$
distance, while we use Lemma 5.20 for the
$\overline {f}$
distance, while we use Lemma 5.20 for the
![]() $ i_{2}-i_{1}$
differing Feldman patterns. Altogether we conclude with the aid of Proposition 5.4 that
$ i_{2}-i_{1}$
differing Feldman patterns. Altogether we conclude with the aid of Proposition 5.4 that
![]() $\overline {f}(\mathcal {B},\overline {\mathcal {B}})$
is at least
$\overline {f}(\mathcal {B},\overline {\mathcal {B}})$
is at least
 $$ \begin{align*} & \bigg(\frac{ i_{2}-i_{1}}{K}+\bigg( 1-\bigg(1-\frac{1}{K}\bigg)^{m-1}\bigg)\frac{K-( i_{2}-i_{1})}{K}\bigg)\alpha-\beta_{n+m}-\frac{4}{e_{n+m-1}}-\frac{4}{l_{n+m-2}}\\ &\quad\geq \bigg(1-\bigg(1-\frac{1}{K}\bigg)^{m}\bigg) \alpha-\beta_{n+m}-\frac{4}{e_{n+m-1}}-\frac{4}{l_{n+m-2}}. \end{align*} $$
$$ \begin{align*} & \bigg(\frac{ i_{2}-i_{1}}{K}+\bigg( 1-\bigg(1-\frac{1}{K}\bigg)^{m-1}\bigg)\frac{K-( i_{2}-i_{1})}{K}\bigg)\alpha-\beta_{n+m}-\frac{4}{e_{n+m-1}}-\frac{4}{l_{n+m-2}}\\ &\quad\geq \bigg(1-\bigg(1-\frac{1}{K}\bigg)^{m}\bigg) \alpha-\beta_{n+m}-\frac{4}{e_{n+m-1}}-\frac{4}{l_{n+m-2}}. \end{align*} $$
In our case of
![]() $i_{1}<i_{2}$
the blocks
$i_{1}<i_{2}$
the blocks
 $\mathtt {B}_{i_{1},j_{2}+1}^{(n+m)}$
and
$\mathtt {B}_{i_{1},j_{2}+1}^{(n+m)}$
and
 $\mathtt {B}_{i_{2},j_{2}}^{(n+m)}$
have
$\mathtt {B}_{i_{2},j_{2}}^{(n+m)}$
have
![]() $ i_{2}-i_{1}$
Feldman patterns in common. With the aid of the second part of Lemma 5.19, Lemma 5.20, and Proposition 5.4 again we obtain that
$ i_{2}-i_{1}$
Feldman patterns in common. With the aid of the second part of Lemma 5.19, Lemma 5.20, and Proposition 5.4 again we obtain that
![]() $\overline {f}(\mathcal {B},\overline {\mathcal {B}})$
is at least
$\overline {f}(\mathcal {B},\overline {\mathcal {B}})$
is at least
 $$ \begin{align*} & \bigg(\frac{i_{2}-i_{1}}{K}\bigg(1-\bigg(1-\frac{1}{K}\bigg)^{m-1}\bigg)+1-\frac{ i_{2}-i_{1}}{K}\bigg)\alpha-\beta_{n+m}-\frac{4}{e_{n+m-1}}-\frac{4}{l_{n+m-2}}\\ &\quad\geq \bigg(1-\bigg(1-\frac{1}{K}\bigg)^{m}\bigg)\alpha-\beta_{n+m}-\frac{4}{e_{n+m-1}}-\frac{4}{l_{n+m-2}}. \end{align*} $$
$$ \begin{align*} & \bigg(\frac{i_{2}-i_{1}}{K}\bigg(1-\bigg(1-\frac{1}{K}\bigg)^{m-1}\bigg)+1-\frac{ i_{2}-i_{1}}{K}\bigg)\alpha-\beta_{n+m}-\frac{4}{e_{n+m-1}}-\frac{4}{l_{n+m-2}}\\ &\quad\geq \bigg(1-\bigg(1-\frac{1}{K}\bigg)^{m}\bigg)\alpha-\beta_{n+m}-\frac{4}{e_{n+m-1}}-\frac{4}{l_{n+m-2}}. \end{align*} $$
In all other cases of
![]() $j_{1}\neq j_{2}$
,
$j_{1}\neq j_{2}$
,
 $\mathtt {B}_{i_{1},j_{1}}^{(n+m)}$
and
$\mathtt {B}_{i_{1},j_{1}}^{(n+m)}$
and
 $\mathtt {B}_{i_{2},j_{2}}^{(n+m)}$
do not have any Feldman pattern in common. Hence, we use the same estimate as for the statement in part (1).
$\mathtt {B}_{i_{2},j_{2}}^{(n+m)}$
do not have any Feldman pattern in common. Hence, we use the same estimate as for the statement in part (1).
By the conditions on the sequence
![]() $(l_n)_{n\in \mathbb {N}}$
from equation (5.3) we have
$(l_n)_{n\in \mathbb {N}}$
from equation (5.3) we have
 $$ \begin{align*} & \beta_{n+m}+\frac{4}{e_{n+m-1}}+\frac{4}{l_{n+m-2}} \\ &\quad= E_{n+m-1}+\frac{4}{R_{n+m-1}}+\frac{8}{u_{n+m-1}}+\frac{13}{\sqrt{e_{n+m-1}}}+\frac{4}{e_{n+m-1}}+\frac{4}{l_{n+m-2}}+\frac{4R_{n+m-1}}{l_{n+m-1}}\\ &\quad\leq E_{n+m-1}+\frac{6}{R_{n+m-1}}+\frac{8}{u_{n+m-1}}+\frac{17}{\sqrt{e_{n+m-1}}}. \end{align*} $$
$$ \begin{align*} & \beta_{n+m}+\frac{4}{e_{n+m-1}}+\frac{4}{l_{n+m-2}} \\ &\quad= E_{n+m-1}+\frac{4}{R_{n+m-1}}+\frac{8}{u_{n+m-1}}+\frac{13}{\sqrt{e_{n+m-1}}}+\frac{4}{e_{n+m-1}}+\frac{4}{l_{n+m-2}}+\frac{4R_{n+m-1}}{l_{n+m-1}}\\ &\quad\leq E_{n+m-1}+\frac{6}{R_{n+m-1}}+\frac{8}{u_{n+m-1}}+\frac{17}{\sqrt{e_{n+m-1}}}. \end{align*} $$
Accordingly, we set
 $$ \begin{align*} E_{n+m} & := E_{n+m-1}+\frac{6}{R_{n+m-1}}+\frac{8}{u_{n+m-1}}+\frac{17}{\sqrt{e_{n+m-1}}}\\ & =E_{n+1}+\sum_{i=1}^{m-1}\bigg(\frac{6}{R_{n+i}}+\frac{8}{u_{n+i}}+\frac{17}{\sqrt{e_{n+i}}}\bigg). \end{align*} $$
$$ \begin{align*} E_{n+m} & := E_{n+m-1}+\frac{6}{R_{n+m-1}}+\frac{8}{u_{n+m-1}}+\frac{17}{\sqrt{e_{n+m-1}}}\\ & =E_{n+1}+\sum_{i=1}^{m-1}\bigg(\frac{6}{R_{n+i}}+\frac{8}{u_{n+i}}+\frac{17}{\sqrt{e_{n+i}}}\bigg). \end{align*} $$
5.3.3. Final step: construction of
 $(n+p)$
-blocks
$(n+p)$
-blocks
Recall that we follow the inductive scheme described in the previous subsubsection until
 $$ \begin{align*} \bigg(1-\frac{1}{K}\bigg)^{p}<\frac{\varepsilon}{2}, \end{align*} $$
$$ \begin{align*} \bigg(1-\frac{1}{K}\bigg)^{p}<\frac{\varepsilon}{2}, \end{align*} $$
and we have constructed pre-
![]() $(n+p)$
-blocks
$(n+p)$
-blocks
 $\mathtt {A}_{i,j}^{(n+p)}$
(of type i and Feldman pattern j) with the following properties:
$\mathtt {A}_{i,j}^{(n+p)}$
(of type i and Feldman pattern j) with the following properties:
 $$ \begin{align} \overline{f}(\mathtt{A}_{i_{1},j}^{(n+p)},\mathtt{A}_{i_{2},j}^{(n+p)})\leq\sum_{u=1}^{p-1}\bigg(\frac{1}{N(n+u-1)+1}+\frac{1}{d_{n+u}}\bigg); \end{align} $$
$$ \begin{align} \overline{f}(\mathtt{A}_{i_{1},j}^{(n+p)},\mathtt{A}_{i_{2},j}^{(n+p)})\leq\sum_{u=1}^{p-1}\bigg(\frac{1}{N(n+u-1)+1}+\frac{1}{d_{n+u}}\bigg); \end{align} $$
for any sequences
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\overline {\mathcal {A}}$
of at least
$\overline {\mathcal {A}}$
of at least
![]() $\tilde {q}_{n+p}/e_{n+p-1}$
consecutive symbols in
$\tilde {q}_{n+p}/e_{n+p-1}$
consecutive symbols in
 $\mathcal {A}_{i_{1},j_{1}}^{(n+p)}$
and
$\mathcal {A}_{i_{1},j_{1}}^{(n+p)}$
and
 $\mathcal {A}_{i_{2},j_{2}}^{(n+p)}$
respectively, for some
$\mathcal {A}_{i_{2},j_{2}}^{(n+p)}$
respectively, for some
![]() $i_{1},i_{2}\in \{ 1,\ldots ,K\} $
and
$i_{1},i_{2}\in \{ 1,\ldots ,K\} $
and
![]() $j_{1},j_{2}\in \{ 1,\ldots ,2K\unicode{x3bb} _{n+p}\} $
, we have
$j_{1},j_{2}\in \{ 1,\ldots ,2K\unicode{x3bb} _{n+p}\} $
, we have
 $$ \begin{align} \overline{f}(\mathcal{A},\overline{\mathcal{A}})\geq \begin{cases} \bigg(1-\frac{\varepsilon}{2}\bigg)\cdot\alpha -\beta_{n+p} & \text{ for all }i_{1}\neq i_{2} \text{ and } j_1=j_2, \\ \alpha-\beta_{n+p} & \text{ for all }i_{1},i_{2}\text{ and }j_{1}\neq j_{2}, \end{cases} \end{align} $$
$$ \begin{align} \overline{f}(\mathcal{A},\overline{\mathcal{A}})\geq \begin{cases} \bigg(1-\frac{\varepsilon}{2}\bigg)\cdot\alpha -\beta_{n+p} & \text{ for all }i_{1}\neq i_{2} \text{ and } j_1=j_2, \\ \alpha-\beta_{n+p} & \text{ for all }i_{1},i_{2}\text{ and }j_{1}\neq j_{2}, \end{cases} \end{align} $$
where
 $$ \begin{align} \beta_{n+p}=E_{n+p-1}+\frac{4}{R_{n+p-1}}+\frac{8}{u_{n+p-1}}+\frac{13}{\sqrt{e_{n+p-1}}}+\frac{4R_{n+p-1}}{l_{n+p-1}} \end{align} $$
$$ \begin{align} \beta_{n+p}=E_{n+p-1}+\frac{4}{R_{n+p-1}}+\frac{8}{u_{n+p-1}}+\frac{13}{\sqrt{e_{n+p-1}}}+\frac{4R_{n+p-1}}{l_{n+p-1}} \end{align} $$
and
 $$ \begin{align} E_{n+p-1}=E_{n+1}+\sum_{i=1}^{p-2}\bigg(\frac{6}{R_{n+i}}+\frac{8}{u_{n+i}}+\frac{17}{\sqrt{e_{n+i}}}\bigg). \end{align} $$
$$ \begin{align} E_{n+p-1}=E_{n+1}+\sum_{i=1}^{p-2}\bigg(\frac{6}{R_{n+i}}+\frac{8}{u_{n+i}}+\frac{17}{\sqrt{e_{n+i}}}\bigg). \end{align} $$
By construction every pre-
![]() $(n+p)$
-block
$(n+p)$
-block
 $\mathtt {A}_{i,j}^{(n+p)}$
contains each
$\mathtt {A}_{i,j}^{(n+p)}$
contains each
![]() $(n+p-1)$
-block of type i exactly
$(n+p-1)$
-block of type i exactly
![]() $\bar {N}(n+p)$
times and this number of occurrences is the same for every chosen Feldman pattern j.
$\bar {N}(n+p)$
times and this number of occurrences is the same for every chosen Feldman pattern j.
Then we construct
![]() $K (n+p)$
-blocks as follows:
$K (n+p)$
-blocks as follows:
 $$ \begin{align*} (n+p)\text{-block of type }1\text{:} & \;\;\mathtt{B}_{1}^{(n+p)}=\mathtt{A}_{1,1}^{(n+p)}\mathtt{A}_{2,2}^{(n+p)}\ldots\mathtt{A}_{K,K}^{(n+p)}(\mathtt{B}_{0}^{(n+p-1)})^{\bar{N}(n+p)},\\ (n+p)\text{-block of type }2\text{:} & \;\;\mathtt{B}_{2}^{(n+p)}=\mathtt{A}_{2,1}^{(n+p)}\mathtt{A}_{3,2}^{(n+p)}\ldots\mathtt{A}_{1,K}^{(n+p)}(\mathtt{B}_{0}^{(n+p-1)})^{\bar{N}(n+p)},\\ (n+p)\text{-block of type }3\text{:} & \;\;\mathtt{B}_{3}^{(n+p)}=\mathtt{A}_{3,1}^{(n+p)}\mathtt{A}_{4,2}^{(n+p)}\ldots\mathtt{A}_{2,K}^{(n+p)}(\mathtt{B}_{0}^{(n+p-1)})^{\bar{N}(n+p)},\\ \vdots & \;\;\vdots\\ (n+p)\text{-block of type }K\text{:} & \;\;\mathtt{B}_{K}^{(n+p)}=\mathtt{A}_{K,1}^{(n+p)}\mathtt{A}_{1,2}^{(n+p)}\ldots\mathtt{A}_{K-1,K}^{(n+p)}(\mathtt{B}_{0}^{(n+p-1)})^{\bar{N}(n+p)}. \end{align*} $$
$$ \begin{align*} (n+p)\text{-block of type }1\text{:} & \;\;\mathtt{B}_{1}^{(n+p)}=\mathtt{A}_{1,1}^{(n+p)}\mathtt{A}_{2,2}^{(n+p)}\ldots\mathtt{A}_{K,K}^{(n+p)}(\mathtt{B}_{0}^{(n+p-1)})^{\bar{N}(n+p)},\\ (n+p)\text{-block of type }2\text{:} & \;\;\mathtt{B}_{2}^{(n+p)}=\mathtt{A}_{2,1}^{(n+p)}\mathtt{A}_{3,2}^{(n+p)}\ldots\mathtt{A}_{1,K}^{(n+p)}(\mathtt{B}_{0}^{(n+p-1)})^{\bar{N}(n+p)},\\ (n+p)\text{-block of type }3\text{:} & \;\;\mathtt{B}_{3}^{(n+p)}=\mathtt{A}_{3,1}^{(n+p)}\mathtt{A}_{4,2}^{(n+p)}\ldots\mathtt{A}_{2,K}^{(n+p)}(\mathtt{B}_{0}^{(n+p-1)})^{\bar{N}(n+p)},\\ \vdots & \;\;\vdots\\ (n+p)\text{-block of type }K\text{:} & \;\;\mathtt{B}_{K}^{(n+p)}=\mathtt{A}_{K,1}^{(n+p)}\mathtt{A}_{1,2}^{(n+p)}\ldots\mathtt{A}_{K-1,K}^{(n+p)}(\mathtt{B}_{0}^{(n+p-1)})^{\bar{N}(n+p)}. \end{align*} $$
Remark 5.23. We note that every
![]() $(n+p)$
-block contains exactly one pre-
$(n+p)$
-block contains exactly one pre-
![]() $(n+p)$
-block of each type. Hence, it is uniform in the
$(n+p)$
-block of each type. Hence, it is uniform in the
![]() $(n+p-1)$
-blocks by our observation above.
$(n+p-1)$
-blocks by our observation above.
Lemma 5.24. (Closeness of
 $(n+p)$
-blocks in the odometer-based system)
$(n+p)$
-blocks in the odometer-based system)
For every
![]() $i_{1},i_{2}\in \{1,\ldots ,K\}$
we have
$i_{1},i_{2}\in \{1,\ldots ,K\}$
we have
 $$ \begin{align} \overline{f}(\mathtt{B}_{i_{1}}^{(n+p)},\mathtt{B}_{i_{2}}^{(n+p)})\leq\sum_{u=1}^{p-1}\bigg(\frac{1}{N(n+u-1)+1}+\frac{1}{d_{n+u}}\bigg). \end{align} $$
$$ \begin{align} \overline{f}(\mathtt{B}_{i_{1}}^{(n+p)},\mathtt{B}_{i_{2}}^{(n+p)})\leq\sum_{u=1}^{p-1}\bigg(\frac{1}{N(n+u-1)+1}+\frac{1}{d_{n+u}}\bigg). \end{align} $$
Proof. Let M denote the right-hand side of inequality (5.17). We observe that the Feldman patterns of pre-
![]() $(n+p)$
-blocks are aligned in all the
$(n+p)$
-blocks are aligned in all the
![]() $(n+p)$
-blocks by construction. Moreover, the marker segments are aligned as well and these occupy a fraction
$(n+p)$
-blocks by construction. Moreover, the marker segments are aligned as well and these occupy a fraction
![]() ${1}/({N(n+p-1)+1})$
of each
${1}/({N(n+p-1)+1})$
of each
![]() $(n+p)$
-block by uniformity. Hence, by equation (5.17) we have
$(n+p)$
-block by uniformity. Hence, by equation (5.17) we have
 $$ \begin{align*} \overline{f}(\mathtt{B}_{i_{1}}^{(n+p)},\mathtt{B}_{i_{2}}^{(n+p)})\leq\bigg(1-\frac{1}{N(n+p-1)+1}\bigg)\cdot M\leq M. \end{align*} $$
$$ \begin{align*} \overline{f}(\mathtt{B}_{i_{1}}^{(n+p)},\mathtt{B}_{i_{2}}^{(n+p)})\leq\bigg(1-\frac{1}{N(n+p-1)+1}\bigg)\cdot M\leq M. \end{align*} $$
Lemma 5.25. (Distance between
 $(n+p)$
-blocks in the circular system)
$(n+p)$
-blocks in the circular system)
For every
![]() $i_{1},i_{2}\in \{ 1,\ldots ,K\} $
,
$i_{1},i_{2}\in \{ 1,\ldots ,K\} $
,
![]() $i_{1}\neq i_{2}$
, and any sequences
$i_{1}\neq i_{2}$
, and any sequences
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\overline {\mathcal {B}}$
of at least
$\overline {\mathcal {B}}$
of at least
![]() $q_{n+p}/R_{n+p}$
consecutive symbols in
$q_{n+p}/R_{n+p}$
consecutive symbols in
 $\mathcal {B}^{(n+p)}_{i_{1}}$
and
$\mathcal {B}^{(n+p)}_{i_{1}}$
and
 $\mathcal {B}^{(n+p)}_{i_{2}}$
we have
$\mathcal {B}^{(n+p)}_{i_{2}}$
we have
 $$ \begin{align} \overline{f}(\mathcal{B},\overline{\mathcal{B}})\geq\bigg(1-\frac{\varepsilon}{2}\bigg)\cdot\alpha-E_{n+p}. \end{align} $$
$$ \begin{align} \overline{f}(\mathcal{B},\overline{\mathcal{B}})\geq\bigg(1-\frac{\varepsilon}{2}\bigg)\cdot\alpha-E_{n+p}. \end{align} $$
Proof. By the same proof as in Lemma 5.17 (with
![]() $J=0$
), as well as case (1) of Lemma 5.21, and the observation that all pre-
$J=0$
), as well as case (1) of Lemma 5.21, and the observation that all pre-
![]() $(n+p)$
-blocks used in the construction of the
$(n+p)$
-blocks used in the construction of the
![]() $(n+p)$
-blocks are distinct, (5.22) follows from equations (5.18)–(5.20).
$(n+p)$
-blocks are distinct, (5.22) follows from equations (5.18)–(5.20).
Proof Proof of Proposition 5.15
By Lemma 5.24 and equations (5.4), (5.6), and (5.7), we have
 $$ \begin{align*} \overline{f}(\mathtt{B}_{i}^{(n+p)},\mathtt{B}_{j}^{(n+p)}) & \leq\sum_{u=1}^{p-1}\bigg(\frac{1}{N(n+u-1)+1}+\frac{1}{d_{n+u}}\bigg)\\ & <\frac{1}{N+1}+\sum_{u=1}^{p-1}\bigg(\frac{1}{Kd_{n+u}e_{n+u}+1}+\frac{1}{d_{n+u}}\bigg)<\delta, \end{align*} $$
$$ \begin{align*} \overline{f}(\mathtt{B}_{i}^{(n+p)},\mathtt{B}_{j}^{(n+p)}) & \leq\sum_{u=1}^{p-1}\bigg(\frac{1}{N(n+u-1)+1}+\frac{1}{d_{n+u}}\bigg)\\ & <\frac{1}{N+1}+\sum_{u=1}^{p-1}\bigg(\frac{1}{Kd_{n+u}e_{n+u}+1}+\frac{1}{d_{n+u}}\bigg)<\delta, \end{align*} $$
which is the first statement of Proposition 5.15. In order to prove the second statement we note that
 $$ \begin{align*} E_{n+p} & =E_{n+1}+\sum_{i=1}^{p-1}\bigg(\frac{6}{R_{n+i}}+\frac{8}{u_{n+i}}+\frac{17}{\sqrt{e_{n+i}}}\bigg) \\ & \leq \frac{14}{\sqrt{N}}+\sum_{i=1}^{p-1}\bigg(\frac{8}{u_{n+i}}+\frac{17}{\sqrt{e_{n+i}}}\bigg)+\sum^{p-1}_{i=0}\frac{6}{R_{n+i}}\\ & <\frac{\varepsilon}{2}+\sum^{p-1}_{i=0}\frac{6}{R_{n+i}} \end{align*} $$
$$ \begin{align*} E_{n+p} & =E_{n+1}+\sum_{i=1}^{p-1}\bigg(\frac{6}{R_{n+i}}+\frac{8}{u_{n+i}}+\frac{17}{\sqrt{e_{n+i}}}\bigg) \\ & \leq \frac{14}{\sqrt{N}}+\sum_{i=1}^{p-1}\bigg(\frac{8}{u_{n+i}}+\frac{17}{\sqrt{e_{n+i}}}\bigg)+\sum^{p-1}_{i=0}\frac{6}{R_{n+i}}\\ & <\frac{\varepsilon}{2}+\sum^{p-1}_{i=0}\frac{6}{R_{n+i}} \end{align*} $$
by equations (5.5), (5.7), and our assumption on the circular coefficients
![]() $(l_{n})_{n\in \mathbb {N}}$
in (5.3). We conclude for any sequences
$(l_{n})_{n\in \mathbb {N}}$
in (5.3). We conclude for any sequences
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\overline {\mathcal {B}}$
of at least
$\overline {\mathcal {B}}$
of at least
![]() $q_{n+p}/R_{n+p}$
consecutive symbols in
$q_{n+p}/R_{n+p}$
consecutive symbols in
 $\mathcal {B}_{i}^{(n+p)}$
and
$\mathcal {B}_{i}^{(n+p)}$
and
 $\mathcal {B}_{j}^{(n+p)}$
, respectively, that
$\mathcal {B}_{j}^{(n+p)}$
, respectively, that
 $$ \begin{align*} \overline{f}(\mathcal{B},\overline{\mathcal{B}})\geq\bigg(1-\frac{\varepsilon}{2}\bigg)\cdot\alpha-E_{n+p}\geq\alpha-\frac{\varepsilon}{2}-E_{n+p}>\alpha-\varepsilon -\sum^{p -1}_{i=0}\frac{6}{R_{n+i}} \end{align*} $$
$$ \begin{align*} \overline{f}(\mathcal{B},\overline{\mathcal{B}})\geq\bigg(1-\frac{\varepsilon}{2}\bigg)\cdot\alpha-E_{n+p}\geq\alpha-\frac{\varepsilon}{2}-E_{n+p}>\alpha-\varepsilon -\sum^{p -1}_{i=0}\frac{6}{R_{n+i}} \end{align*} $$
with the aid of Lemma 5.25.
5.4. Proof of Theorem 5.1
We define the construction sequence for the odometer-based system inductively. We begin by choosing an integer
![]() $R_1 \geq 400$
, an increasing sequence
$R_1 \geq 400$
, an increasing sequence
![]() $(K_{s})_{s\in \mathbb {N}}$
of positive integers such that
$(K_{s})_{s\in \mathbb {N}}$
of positive integers such that
 $$ \begin{align} \sum_{s\in\mathbb{N}}\frac{14}{\sqrt{K_{s}}}<\frac{1}{32}, \end{align} $$
$$ \begin{align} \sum_{s\in\mathbb{N}}\frac{14}{\sqrt{K_{s}}}<\frac{1}{32}, \end{align} $$
and two decreasing sequences
![]() $(\varepsilon _{s})_{s\in \mathbb {N}}$
and
$(\varepsilon _{s})_{s\in \mathbb {N}}$
and
![]() $(\delta _{s})_{s\in \mathbb {N}}$
of positive real numbers such that
$(\delta _{s})_{s\in \mathbb {N}}$
of positive real numbers such that
![]() $\delta _{s}\searrow 0$
and
$\delta _{s}\searrow 0$
and
 $$ \begin{align} \sum_{s\in\mathbb{N}}\varepsilon_{s}<\frac{1}{64}. \end{align} $$
$$ \begin{align} \sum_{s\in\mathbb{N}}\varepsilon_{s}<\frac{1}{64}. \end{align} $$
In addition to (5.3) we impose the condition
 $$ \begin{align*} \frac{6}{R_1} + \sum_{n\in \mathbb{N}} \frac{6}{k_n} < \frac{1}{32} \end{align*} $$
$$ \begin{align*} \frac{6}{R_1} + \sum_{n\in \mathbb{N}} \frac{6}{k_n} < \frac{1}{32} \end{align*} $$
on the circular coefficients
![]() $(k_n,l_n)_{n\in \mathbb {N}}$
. In particular, this yields
$(k_n,l_n)_{n\in \mathbb {N}}$
. In particular, this yields
 $$ \begin{align} \sum^{\infty}_{n =1} \frac{6}{R_n} < \frac{1}{32} \end{align} $$
$$ \begin{align} \sum^{\infty}_{n =1} \frac{6}{R_n} < \frac{1}{32} \end{align} $$
by
 $R_n = k_{n-2}q^2_{n-2}$
for
$R_n = k_{n-2}q^2_{n-2}$
for
![]() $n\geq 2$
. We start with
$n\geq 2$
. We start with
![]() $R_1+1$
symbols and let
$R_1+1$
symbols and let
 $\alpha _{0}=\tfrac 18$
.
$\alpha _{0}=\tfrac 18$
.
The first application of Proposition 5.15 will be on
![]() $1$
-blocks and we will apply it for
$1$
-blocks and we will apply it for
![]() $\varepsilon =\varepsilon _{1}$
,
$\varepsilon =\varepsilon _{1}$
,
![]() $\delta =\delta _{1}$
, and
$\delta =\delta _{1}$
, and
![]() $K=K_{1}+1$
. In order to apply the proposition we need sufficiently many
$K=K_{1}+1$
. In order to apply the proposition we need sufficiently many
![]() $1$
-blocks. Moreover, we want the
$1$
-blocks. Moreover, we want the
![]() $1$
-blocks in the circular system to be at least
$1$
-blocks in the circular system to be at least
![]() $\alpha _{0}-\varepsilon _{1}$
apart in the
$\alpha _{0}-\varepsilon _{1}$
apart in the
![]() $\overline {f}$
metric on substantial substrings of at least
$\overline {f}$
metric on substantial substrings of at least
![]() ${q_{1}}/{R_{1}}$
consecutive symbols. To produce such a family of
${q_{1}}/{R_{1}}$
consecutive symbols. To produce such a family of
![]() $1$
-blocks we apply Proposition 5.13.
$1$
-blocks we apply Proposition 5.13.
After the application of Proposition 5.15 on the
![]() $1$
-blocks we have
$1$
-blocks we have
![]() $K_{1}+1\ n_{1}$
-blocks (where
$K_{1}+1\ n_{1}$
-blocks (where
![]() $n_{1}=1+p_1$
with
$n_{1}=1+p_1$
with
![]() $p_1$
from Proposition 5.15, that is, the least integer such that
$p_1$
from Proposition 5.15, that is, the least integer such that
![]() $(1-({1}/{K_1+1}))^{p_1}<{\varepsilon _1}/{2}$
) which are
$(1-({1}/{K_1+1}))^{p_1}<{\varepsilon _1}/{2}$
) which are
![]() $\delta _{1}$
-close in the odometer-based system and at least
$\delta _{1}$
-close in the odometer-based system and at least
 $\alpha _{1}:= \alpha _{0}-2\varepsilon _{1}-\sum ^{n_1-1}_{s=1}({6}/{R_{s}})$
apart in the
$\alpha _{1}:= \alpha _{0}-2\varepsilon _{1}-\sum ^{n_1-1}_{s=1}({6}/{R_{s}})$
apart in the
![]() $\overline {f}$
metric on substantial substrings of at least
$\overline {f}$
metric on substantial substrings of at least
![]() $q_{n_{1}}/R_{n_{1}}$
consecutive symbols. The next application of Proposition 5.15 will be on
$q_{n_{1}}/R_{n_{1}}$
consecutive symbols. The next application of Proposition 5.15 will be on
![]() $(n_1+1)$
-blocks and we will apply it for
$(n_1+1)$
-blocks and we will apply it for
![]() $\varepsilon =\varepsilon _{2}$
,
$\varepsilon =\varepsilon _{2}$
,
![]() $\delta =\delta _{2}$
, and
$\delta =\delta _{2}$
, and
![]() $K=K_{2}+1$
. Once again this will require sufficiently many
$K=K_{2}+1$
. Once again this will require sufficiently many
![]() $(n_1+1)$
-blocks, and we apply Proposition 5.13 to produce such a family of
$(n_1+1)$
-blocks, and we apply Proposition 5.13 to produce such a family of
![]() $(n_1+1)$
-blocks that are at least
$(n_1+1)$
-blocks that are at least
![]() $\alpha _{1}-({14}/{\sqrt {K_{1}}})-({4}/{R_{n_1}})-\varepsilon _{2}$
apart on substantial substrings. This imposes the condition
$\alpha _{1}-({14}/{\sqrt {K_{1}}})-({4}/{R_{n_1}})-\varepsilon _{2}$
apart on substantial substrings. This imposes the condition
![]() $({2}/{l_{n_1-1}})+({4R_{n_1}}/{l_{n_1}})<\varepsilon _2$
which by condition (5.3) is fulfilled if
$({2}/{l_{n_1-1}})+({4R_{n_1}}/{l_{n_1}})<\varepsilon _2$
which by condition (5.3) is fulfilled if
![]() $({3}/{l_{n_1-1}})<\varepsilon _2$
, and we choose
$({3}/{l_{n_1-1}})<\varepsilon _2$
, and we choose
![]() $l_{n_1-1}$
sufficiently large to satisfy this requirement.
$l_{n_1-1}$
sufficiently large to satisfy this requirement.
Continuing like this, we use Propositions 5.13 and 5.15 alternately to produce
![]() $K_{s}+1\, n_{s}$
-blocks which are at least
$K_{s}+1\, n_{s}$
-blocks which are at least
 $$ \begin{align} \alpha_{s}=\alpha_{0}-\sum_{i=1}^{s-1}\frac{14}{\sqrt{K_{i}}}-\sum_{i=1}^{s}2\varepsilon_{i} - \sum^{n_s-1}_{i=1}\frac{6}{R_i} \end{align} $$
$$ \begin{align} \alpha_{s}=\alpha_{0}-\sum_{i=1}^{s-1}\frac{14}{\sqrt{K_{i}}}-\sum_{i=1}^{s}2\varepsilon_{i} - \sum^{n_s-1}_{i=1}\frac{6}{R_i} \end{align} $$
apart on substantial substrings of length at least
![]() ${h_{n_s}}/(K_s+1)$
in the circular system and
${h_{n_s}}/(K_s+1)$
in the circular system and
![]() $\delta _{s}$
-close in the odometer-based system. In the next step, we want to apply Proposition 5.15 on
$\delta _{s}$
-close in the odometer-based system. In the next step, we want to apply Proposition 5.15 on
![]() $(n_{s}+1)$
-blocks with
$(n_{s}+1)$
-blocks with
![]() $\varepsilon =\varepsilon _{s+1}$
,
$\varepsilon =\varepsilon _{s+1}$
,
![]() $\delta =\delta _{s+1}$
, and
$\delta =\delta _{s+1}$
, and
![]() $K=K_{s+1}+1$
. In order to have sufficiently many
$K=K_{s+1}+1$
. In order to have sufficiently many
![]() $(n_{s}+1)$
-blocks for this application we make use of Proposition 5.13 (imposing the condition on
$(n_{s}+1)$
-blocks for this application we make use of Proposition 5.13 (imposing the condition on
![]() $l_{n_s-1}$
as described above) and produce the required number of
$l_{n_s-1}$
as described above) and produce the required number of
![]() $(n_{s}+1)$
-blocks which are at least
$(n_{s}+1)$
-blocks which are at least
![]() $\alpha _{s}-({14}/{\sqrt {K_{s}}})-({4}/{R_{n_s}})-\varepsilon _{s+1}$
apart on substantial substrings in the circular system. After the intended application of Proposition 5.15 we have
$\alpha _{s}-({14}/{\sqrt {K_{s}}})-({4}/{R_{n_s}})-\varepsilon _{s+1}$
apart on substantial substrings in the circular system. After the intended application of Proposition 5.15 we have
![]() $K_{s+1}+1\ n_{s+1}$
-blocks (where
$K_{s+1}+1\ n_{s+1}$
-blocks (where
![]() $n_{s+1}=n_s +1 +p_{s+1}$
with
$n_{s+1}=n_s +1 +p_{s+1}$
with
![]() $p_{s+1}$
the least integer such that
$p_{s+1}$
the least integer such that
![]() $(1-({1}/({K_{s+1}+1})))^{p_{s+1}}<({\varepsilon _{s+1}}/{2})$
) which are at least
$(1-({1}/({K_{s+1}+1})))^{p_{s+1}}<({\varepsilon _{s+1}}/{2})$
) which are at least
 $$ \begin{align} \alpha_{s+1}=\alpha_{s}-\frac{14}{\sqrt{K_{s}}}-2\varepsilon_{s+1}- \sum^{n_{s+1}-1}_{i=n_s}\frac{6}{R_i} \end{align} $$
$$ \begin{align} \alpha_{s+1}=\alpha_{s}-\frac{14}{\sqrt{K_{s}}}-2\varepsilon_{s+1}- \sum^{n_{s+1}-1}_{i=n_s}\frac{6}{R_i} \end{align} $$
apart on substantial substrings in the circular system and
![]() $\delta _{s+1}$
-close in the odometer-based system. This completes the inductive step.
$\delta _{s+1}$
-close in the odometer-based system. This completes the inductive step.
By the requirements (5.23)–(5.25) this shows that any two distinct
![]() $n_s$
-blocks in the circular system are at least
$n_s$
-blocks in the circular system are at least
 $$ \begin{align} \alpha_{0}-\sum^{\infty}_{s=1}\bigg(\frac{14}{\sqrt{K_{s}}}+2\varepsilon_{s}+ \frac{6}{R_s}\bigg)>\frac{1}{8}-\frac{1}{32}-\frac{1}{32} - \frac{1}{32}=\frac{1}{32} \end{align} $$
$$ \begin{align} \alpha_{0}-\sum^{\infty}_{s=1}\bigg(\frac{14}{\sqrt{K_{s}}}+2\varepsilon_{s}+ \frac{6}{R_s}\bigg)>\frac{1}{8}-\frac{1}{32}-\frac{1}{32} - \frac{1}{32}=\frac{1}{32} \end{align} $$
apart on substantial substrings. Hence, the circular system cannot be loosely Bernoulli by Lemma 3.5.
On the other hand, the
![]() $\overline {f}$
distance between
$\overline {f}$
distance between
![]() $n_s$
-blocks in the odometer-based system goes to zero because
$n_s$
-blocks in the odometer-based system goes to zero because
![]() $\delta _{s}\searrow 0$
. Thus, the odometer-based system is zero-entropy loosely Bernoulli by Lemma 3.5. Since the blocks constructed by Propositions 5.13 and 5.15 satisfy the properties of uniformity and unique readability, our construction sequence satisfies those as well.
$\delta _{s}\searrow 0$
. Thus, the odometer-based system is zero-entropy loosely Bernoulli by Lemma 3.5. Since the blocks constructed by Propositions 5.13 and 5.15 satisfy the properties of uniformity and unique readability, our construction sequence satisfies those as well.
6. Non-loosely Bernoulli odometer-based system whose corresponding circular system is loosely Bernoulli
In the previous two sections we showed that
![]() $\mathcal {F}$
does not preserve the loosely Bernoulli property. In this section we will show that
$\mathcal {F}$
does not preserve the loosely Bernoulli property. In this section we will show that
![]() $\mathcal {F}^{-1}$
also does not preserve the loosely Bernoulli property.
$\mathcal {F}^{-1}$
also does not preserve the loosely Bernoulli property.
Theorem 6.1. There exist circular coefficients
![]() $(l_{n})_{n\in \mathbb {N}}$
and a non-loosely Bernoulli odometer-based system
$(l_{n})_{n\in \mathbb {N}}$
and a non-loosely Bernoulli odometer-based system
![]() $\mathbb {M}$
of zero measure-theoretic entropy with uniform and uniquely readable construction sequence such that
$\mathbb {M}$
of zero measure-theoretic entropy with uniform and uniquely readable construction sequence such that
![]() $\mathcal {F}(\mathbb {M})$
is loosely Bernoulli.
$\mathcal {F}(\mathbb {M})$
is loosely Bernoulli.
The proof of Theorem 6.1 is based upon two mechanisms. On the one hand, we again use Feldman patterns to produce an arbitrarily large number of new blocks whose substantial substrings are almost as far apart in
![]() $\overline {f}$
as the building blocks. This time we obtain lower bounds on the
$\overline {f}$
as the building blocks. This time we obtain lower bounds on the
![]() $\overline {f}$
-distance between blocks in the odometer-based system. On the other hand, we develop the so-called cycling mechanism in §6.3 to produce an arbitrarily large number of blocks that are still
$\overline {f}$
-distance between blocks in the odometer-based system. On the other hand, we develop the so-called cycling mechanism in §6.3 to produce an arbitrarily large number of blocks that are still
![]() $\overline {f}$
-apart from each other in the odometer-based system but arbitrarily close to each other in the circular system. See Figure 3 for a sketch of this idea.
$\overline {f}$
-apart from each other in the odometer-based system but arbitrarily close to each other in the circular system. See Figure 3 for a sketch of this idea.

Figure 3 Heuristic representation of two stages of the cycling mechanism. Parts of four
![]() $(n+2)$
-blocks
$(n+2)$
-blocks
![]() $\mathtt {B}_i$
,
$\mathtt {B}_i$
,
![]() $i=1,\ldots ,4$
, in the odometer-based system and parts of the images
$i=1,\ldots ,4$
, in the odometer-based system and parts of the images
![]() $\mathcal {B}_1$
and
$\mathcal {B}_1$
and
![]() $\mathcal {B}_2$
under the circular operator (omitting the spacers) are represented. The marked letters indicate a best possible
$\mathcal {B}_2$
under the circular operator (omitting the spacers) are represented. The marked letters indicate a best possible
![]() $\overline {f}$
match between
$\overline {f}$
match between
![]() $\mathtt {B}_1$
and
$\mathtt {B}_1$
and
![]() $\mathtt {B}_2$
with a fit of approximately
$\mathtt {B}_2$
with a fit of approximately
 $\big(1-\tfrac 14\big)^2$
(ignoring boundary effects), while the blocks
$\big(1-\tfrac 14\big)^2$
(ignoring boundary effects), while the blocks
![]() $\mathcal {B}_1$
and
$\mathcal {B}_1$
and
![]() $\mathcal {B}_2$
have a very good fit in the circular system (the lines indicating a best possible
$\mathcal {B}_2$
have a very good fit in the circular system (the lines indicating a best possible
![]() $\overline {f}$
match).
$\overline {f}$
match).
6.1. Feldman patterns revisited
Proposition 6.2. Let
 $\alpha \in \big(0,\tfrac 17\big)$
and
$\alpha \in \big(0,\tfrac 17\big)$
and
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $K,R,S,N,M\in \mathbb {N}\setminus \{0\}$
with
$K,R,S,N,M\in \mathbb {N}\setminus \{0\}$
with
![]() $N\geq 20$
, and
$N\geq 20$
, and
![]() $M\geq 2$
. For
$M\geq 2$
. For
![]() $1\leq s\leq S$
, let
$1\leq s\leq S$
, let
 $\mathtt {A}_{1}^{(s)},\ldots ,\mathtt {A}_{N}^{(s)}$
be a family of strings, where each
$\mathtt {A}_{1}^{(s)},\ldots ,\mathtt {A}_{N}^{(s)}$
be a family of strings, where each
 $\mathtt {A}_{j}^{(s)}$
is a concatenation of
$\mathtt {A}_{j}^{(s)}$
is a concatenation of
![]() $K\, n$
-blocks. Assume that for all
$K\, n$
-blocks. Assume that for all
![]() $1\leq s_{1},s_{2}\leq S$
and all
$1\leq s_{1},s_{2}\leq S$
and all
![]() $j_{1},j_{2}\in \{ 1,\ldots ,N\} $
with
$j_{1},j_{2}\in \{ 1,\ldots ,N\} $
with
![]() $j_{1}\neq j_{2}$
, we have
$j_{1}\neq j_{2}$
, we have
![]() $\overline {f}(\mathtt {A},\overline {\mathtt {A}})>\alpha $
for all strings
$\overline {f}(\mathtt {A},\overline {\mathtt {A}})>\alpha $
for all strings
![]() $\mathtt {A},\overline {\mathtt {A}}$
of at least
$\mathtt {A},\overline {\mathtt {A}}$
of at least
![]() $K\mathtt {h}_n/R$
consecutive symbols from
$K\mathtt {h}_n/R$
consecutive symbols from
 $\mathtt {A}_{j_{1}}^{(s_{1})}$
and
$\mathtt {A}_{j_{1}}^{(s_{1})}$
and
 $\mathtt {A}_{j_{2}}^{(s_{2})},$
respectively.
$\mathtt {A}_{j_{2}}^{(s_{2})},$
respectively.
Then for
![]() $1\leq s\leq S$
, we can construct a family of strings
$1\leq s\leq S$
, we can construct a family of strings
 $\mathtt {B}_{1}^{(s)},\ldots ,\mathtt {B}_{M}^{(s)}$
(of equal length
$\mathtt {B}_{1}^{(s)},\ldots ,\mathtt {B}_{M}^{(s)}$
(of equal length
![]() $N^{2M+3}\cdot K\cdot \mathtt {h}_{n}$
and containing each block
$N^{2M+3}\cdot K\cdot \mathtt {h}_{n}$
and containing each block
 $\mathtt {A}_{1}^{(s)},\ldots ,\mathtt {A}_{N}^{(s)}$
exactly
$\mathtt {A}_{1}^{(s)},\ldots ,\mathtt {A}_{N}^{(s)}$
exactly
![]() $N^{2M+2}$
times) such that for all
$N^{2M+2}$
times) such that for all
![]() $1\leq s_{1},s_{2}\leq S$
, all
$1\leq s_{1},s_{2}\leq S$
, all
![]() $j,k\in \{ 1,\ldots ,M\} $
with
$j,k\in \{ 1,\ldots ,M\} $
with
![]() $j\neq k,$
and all strings
$j\neq k,$
and all strings
![]() $\mathtt {B}$
,
$\mathtt {B}$
,
![]() $\overline {\mathtt {B}}$
of at least
$\overline {\mathtt {B}}$
of at least
![]() $N^{2M+2}\cdot K\cdot \mathtt {h}_{n}$
consecutive symbols from
$N^{2M+2}\cdot K\cdot \mathtt {h}_{n}$
consecutive symbols from
 $\mathtt {B}_{j}^{(s_{1})}$
and
$\mathtt {B}_{j}^{(s_{1})}$
and
 $\mathtt {B}_{k}^{(s_{2})}$
respectively, we have
$\mathtt {B}_{k}^{(s_{2})}$
respectively, we have
 $$ \begin{align*} \overline{f}(\mathtt{B},\overline{\mathtt{B}})>\alpha-\frac{13}{\sqrt{N}}-\frac{1}{R}. \end{align*} $$
$$ \begin{align*} \overline{f}(\mathtt{B},\overline{\mathtt{B}})>\alpha-\frac{13}{\sqrt{N}}-\frac{1}{R}. \end{align*} $$
Proof. The proof follows along the lines of the statement on Feldman patterns for the circular system in Proposition 5.10. (Here
![]() $\mathcal {C}_{n,i_1}$
and
$\mathcal {C}_{n,i_1}$
and
![]() $\mathcal {C}_{n,i_2}$
are not applied since we remain in the odometer-based system.)
$\mathcal {C}_{n,i_2}$
are not applied since we remain in the odometer-based system.)
We will also need a statement on the
![]() $\overline {f}$
distance between the identical Feldman pattern but with building blocks from different families (compare with Lemma 5.11).
$\overline {f}$
distance between the identical Feldman pattern but with building blocks from different families (compare with Lemma 5.11).
Lemma 6.3. Let
 $\alpha \in \big(0,\tfrac 17\big)$
and
$\alpha \in \big(0,\tfrac 17\big)$
and
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $K,R,S,N,M\in \mathbb {N}\setminus \{0\}$
with
$K,R,S,N,M\in \mathbb {N}\setminus \{0\}$
with
![]() $N\geq 20$
, and
$N\geq 20$
, and
![]() $M,S$
at least
$M,S$
at least
![]() $2$
. For
$2$
. For
![]() $1\leq s\leq S$
, let
$1\leq s\leq S$
, let
 $\mathtt {A}_{1}^{(s)},\ldots ,\mathtt {A}_{N}^{(s)}$
be a family of strings, where each
$\mathtt {A}_{1}^{(s)},\ldots ,\mathtt {A}_{N}^{(s)}$
be a family of strings, where each
 $\mathtt {A}_{j}^{(s)}$
is a concatenation of
$\mathtt {A}_{j}^{(s)}$
is a concatenation of
![]() $K\ n$
-blocks. Assume that for all
$K\ n$
-blocks. Assume that for all
![]() $j_{1},j_{2}\in \{ 1,\ldots ,N\} $
and all
$j_{1},j_{2}\in \{ 1,\ldots ,N\} $
and all
![]() $s_{1},s_{2}\in \{ 1,\ldots ,S\} $
with
$s_{1},s_{2}\in \{ 1,\ldots ,S\} $
with
![]() $s_{1}\neq s_{2}$
, we have
$s_{1}\neq s_{2}$
, we have
![]() $\overline {f}(\mathtt {A},\overline {\mathtt {A}})>\alpha $
for all sequences
$\overline {f}(\mathtt {A},\overline {\mathtt {A}})>\alpha $
for all sequences
![]() $\mathtt {A},\overline {\mathtt {A}}$
of at least
$\mathtt {A},\overline {\mathtt {A}}$
of at least
![]() $K\mathtt {h}_{n}/R$
consecutive symbols from
$K\mathtt {h}_{n}/R$
consecutive symbols from
 $\mathtt {A}_{j_{1}}^{(s_{1})}$
and
$\mathtt {A}_{j_{1}}^{(s_{1})}$
and
 $\mathtt {A}_{j_{2}}^{(s_{2})},$
respectively. Then for
$\mathtt {A}_{j_{2}}^{(s_{2})},$
respectively. Then for
![]() $1\leq s\leq S,$
we can construct a family of strings
$1\leq s\leq S,$
we can construct a family of strings
 $\mathtt {B}_{1}^{(s)},\ldots ,\mathtt {B}_{M}^{(s)}$
as in Proposition 6.2 such that for all
$\mathtt {B}_{1}^{(s)},\ldots ,\mathtt {B}_{M}^{(s)}$
as in Proposition 6.2 such that for all
![]() $j,k\in \{ 1,\ldots ,M\} $
, all
$j,k\in \{ 1,\ldots ,M\} $
, all
![]() $s_{1},s_{2}\in \{ 1,\ldots ,S\} $
with
$s_{1},s_{2}\in \{ 1,\ldots ,S\} $
with
![]() $s_{1}\neq s_{2}$
, and all strings
$s_{1}\neq s_{2}$
, and all strings
![]() $\mathtt {B}$
,
$\mathtt {B}$
,
![]() $\overline {\mathtt {B}}$
of at least
$\overline {\mathtt {B}}$
of at least
![]() $N^{2M+2}K\mathtt {h}_{n}$
consecutive symbols from
$N^{2M+2}K\mathtt {h}_{n}$
consecutive symbols from
 $\mathtt {B}_{j}^{(s_{1})}$
and
$\mathtt {B}_{j}^{(s_{1})}$
and
 $\mathtt {B}_{k}^{(s_{2})}$
respectively, we have
$\mathtt {B}_{k}^{(s_{2})}$
respectively, we have
 $$ \begin{align*} \overline{f}(\mathtt{B},\overline{\mathtt{B}})>\alpha-\frac{2}{N^{2M+2}}-\frac{1}{R}. \end{align*} $$
$$ \begin{align*} \overline{f}(\mathtt{B},\overline{\mathtt{B}})>\alpha-\frac{2}{N^{2M+2}}-\frac{1}{R}. \end{align*} $$
6.2. Feldman mechanism in the odometer-based system
Again we use the Feldman mechanism to produce an arbitrarily large number of new blocks whose substantial substrings are almost as far apart in
![]() $\overline {f}$
as the building blocks. In contrast to Proposition 6.2, the constructed words also satisfy the unique readability property.
$\overline {f}$
as the building blocks. In contrast to Proposition 6.2, the constructed words also satisfy the unique readability property.
Proposition 6.4. Let
 $\alpha \in \big(0,\tfrac 17\big)$
and
$\alpha \in \big(0,\tfrac 17\big)$
and
![]() $n ,N,M,R\in \mathbb {N}$
with
$n ,N,M,R\in \mathbb {N}$
with
![]() $R\geq 1$
,
$R\geq 1$
,
![]() $N\geq 100$
, and
$N\geq 100$
, and
![]() $M\geq 2$
. Suppose there are
$M\geq 2$
. Suppose there are
![]() $N+1\, n$
-blocks
$N+1\, n$
-blocks
![]() $\mathtt {A}_{0},\ldots ,\mathtt {A}_{N}$
, which have equal length
$\mathtt {A}_{0},\ldots ,\mathtt {A}_{N}$
, which have equal length
![]() $\mathtt {h_{n}}$
and satisfy the unique readability property. Furthermore, if
$\mathtt {h_{n}}$
and satisfy the unique readability property. Furthermore, if
![]() $n>0$
assume that for all
$n>0$
assume that for all
![]() $j\neq k,$
we have
$j\neq k,$
we have
![]() $\overline {f}(\mathtt {A},\overline {\mathtt {A}})>\alpha $
for all strings
$\overline {f}(\mathtt {A},\overline {\mathtt {A}})>\alpha $
for all strings
![]() $\mathtt {A},\overline {\mathtt {A}}$
of at least
$\mathtt {A},\overline {\mathtt {A}}$
of at least
![]() $\mathtt {h}_{n}/R$
consecutive symbols from
$\mathtt {h}_{n}/R$
consecutive symbols from
![]() $\mathtt {A}_{j}$
and
$\mathtt {A}_{j}$
and
![]() $\mathtt {A}_{k}$
, respectively. Then we can construct
$\mathtt {A}_{k}$
, respectively. Then we can construct
![]() $M\ (n+1)$
-blocks
$M\ (n+1)$
-blocks
![]() $\mathtt {\mathtt {B}_{1}},\ldots ,\mathtt {B}_{M}$
of equal length
$\mathtt {\mathtt {B}_{1}},\ldots ,\mathtt {B}_{M}$
of equal length
![]() $\mathtt {h}_{n+1}$
(which are uniform in the n-blocks and satisfy the unique readability property) such that for all
$\mathtt {h}_{n+1}$
(which are uniform in the n-blocks and satisfy the unique readability property) such that for all
![]() $j \ne k$
and all strings
$j \ne k$
and all strings
![]() $\mathtt {B}$
,
$\mathtt {B}$
,
![]() $\overline {\mathtt {B}}$
of at least
$\overline {\mathtt {B}}$
of at least
![]() $\mathtt {h}_{n+1}/N$
consecutive symbols from
$\mathtt {h}_{n+1}/N$
consecutive symbols from
![]() $\mathtt {B}_{j}$
and
$\mathtt {B}_{j}$
and
![]() $\mathtt {B}_{k}$
respectively, we have
$\mathtt {B}_{k}$
respectively, we have
 $$ \begin{align*} \overline{f}(\mathtt{B},\overline{\mathtt{B}})>\alpha-\frac{12}{\sqrt{ N}}-\frac{1}{R}-\frac{8}{N}\geq \alpha-\frac{13}{\sqrt{ N}}-\frac{1}{R}. \end{align*} $$
$$ \begin{align*} \overline{f}(\mathtt{B},\overline{\mathtt{B}})>\alpha-\frac{12}{\sqrt{ N}}-\frac{1}{R}-\frac{8}{N}\geq \alpha-\frac{13}{\sqrt{ N}}-\frac{1}{R}. \end{align*} $$
Proof. We define the
![]() $(n+1)$
-blocks as in Proposition 5.13. As in its proof for
$(n+1)$
-blocks as in Proposition 5.13. As in its proof for
![]() $n=0$
we complete cycles at the beginning and end of each
$n=0$
we complete cycles at the beginning and end of each
![]() $\mathtt {B}$
and
$\mathtt {B}$
and
![]() $\overline {\mathtt {B}}$
. Once again, we remove the marker blocks and apply Corollary 5.5 and
$\overline {\mathtt {B}}$
. Once again, we remove the marker blocks and apply Corollary 5.5 and
![]() $\tilde {f}>1-({12}/{\sqrt {N}})$
from Lemma 5.8.
$\tilde {f}>1-({12}/{\sqrt {N}})$
from Lemma 5.8.
6.3. Cycling mechanism
Proposition 6.5. If
![]() $n ,K,T\in \mathbb {N}$
,
$n ,K,T\in \mathbb {N}$
,
![]() $K\geq 2$
,
$K\geq 2$
,
![]() $T>0$
,
$T>0$
,
![]() $\alpha \in (4/T,1/7)$
,
$\alpha \in (4/T,1/7)$
,
![]() $\delta>0$
, and
$\delta>0$
, and
![]() $\varepsilon \in (0,\alpha /(4K))$
, then there exist
$\varepsilon \in (0,\alpha /(4K))$
, then there exist
![]() $N,m_n\in \mathbb {N}$
and circular coefficients
$N,m_n\in \mathbb {N}$
and circular coefficients
 $(k_{n+m},\ell _{n+m})_{m=0}^{m_n-1}$
satisfying the following condition. If we are given
$(k_{n+m},\ell _{n+m})_{m=0}^{m_n-1}$
satisfying the following condition. If we are given
![]() $N+1$
uniquely readable n-blocks
$N+1$
uniquely readable n-blocks
 $\mathtt {B}_{0}^{(n)},\mathtt {B}_{1}^{(n)},\ldots ,\mathtt {B}_{N}^{(n)}$
in the odometer-based system such that for all
$\mathtt {B}_{0}^{(n)},\mathtt {B}_{1}^{(n)},\ldots ,\mathtt {B}_{N}^{(n)}$
in the odometer-based system such that for all
![]() $i\ne j$
and all sequences
$i\ne j$
and all sequences
![]() $\mathtt {A}$
and
$\mathtt {A}$
and
![]() $\overline {\mathtt {A}}$
of at least
$\overline {\mathtt {A}}$
of at least
![]() $\mathtt {h}_n/T$
consecutive symbols from
$\mathtt {h}_n/T$
consecutive symbols from
 $\mathtt {B}_{i}^{(n)}$
and
$\mathtt {B}_{i}^{(n)}$
and
 $\mathtt {B}_{j}^{(n)}$
respectively we have
$\mathtt {B}_{j}^{(n)}$
respectively we have
![]() $\overline {f}(\mathtt {A},\overline {\mathtt {A}})\geq \alpha ,$
then we can build
$\overline {f}(\mathtt {A},\overline {\mathtt {A}})\geq \alpha ,$
then we can build
![]() $K\, (n+m_n)$
-blocks
$K\, (n+m_n)$
-blocks
 $\mathtt {B}^{(n+m_n)}_{1},\ldots ,\mathtt {B}^{(n+m_n)}_{K}$
of equal length
$\mathtt {B}^{(n+m_n)}_{1},\ldots ,\mathtt {B}^{(n+m_n)}_{K}$
of equal length
![]() $\mathtt {h}_{n+m_n}$
(with the unique readability property and uniformity in all blocks from stage n through
$\mathtt {h}_{n+m_n}$
(with the unique readability property and uniformity in all blocks from stage n through
![]() $n+m_n$
) satisfying the following properties.
$n+m_n$
) satisfying the following properties.
-
(1) For all
 $i\ne j$
and all sequences
$i\ne j$
and all sequences
 $\mathtt {B}$
and
$\mathtt {B}$
and
 $\overline {\mathtt {B}}$
of at least
$\overline {\mathtt {B}}$
of at least
 $\mathtt {h}_{n+m_n}/K$
consecutive symbols from
$\mathtt {h}_{n+m_n}/K$
consecutive symbols from
 $\mathtt {B}_{i}^{(n+m_n)}$
and
$\mathtt {B}_{i}^{(n+m_n)}$
and
 $\mathtt {B}_{j}^{(n+m_n)}$
respectively, we have
$\mathtt {B}_{j}^{(n+m_n)}$
respectively, we have  $$ \begin{align*} \overline{f}(\mathtt{B},\overline{\mathtt{B}})\geq\alpha-\frac{2}{T}-\varepsilon. \end{align*} $$
$$ \begin{align*} \overline{f}(\mathtt{B},\overline{\mathtt{B}})\geq\alpha-\frac{2}{T}-\varepsilon. \end{align*} $$
-
(2) If
 $\mathcal {B}_1^{(n+m_n)},\ldots ,\mathcal {B}_K^{(n+m_n)}$
are the corresponding circular
$\mathcal {B}_1^{(n+m_n)},\ldots ,\mathcal {B}_K^{(n+m_n)}$
are the corresponding circular
 $(n+m_n)$
-blocks, then for all
$(n+m_n)$
-blocks, then for all
 $1\leq i,j\leq K$
we have
$1\leq i,j\leq K$
we have  $$ \begin{align*} \overline{f}(\mathcal{B}_{i}^{(n+m_n)},\mathcal{B}_{j}^{(n+m_n)})\leq\delta. \end{align*} $$
$$ \begin{align*} \overline{f}(\mathcal{B}_{i}^{(n+m_n)},\mathcal{B}_{j}^{(n+m_n)})\leq\delta. \end{align*} $$
Remark 6.6. Thus we obtain a mechanism to produce an arbitrarily large number of
![]() $(n+m_n)$
-blocks that are still apart from each other in the odometer-based system but arbitrarily close to each other in the circular system. The proof is based on an inductive construction that we call the cycling mechanism (indicated in Figure 3) and a final step to guarantee closeness of blocks in the circular system. In each step of the cycling mechanism the blocks of different types are constructed by cycling the K pre-blocks used. On the one hand, this will yield closeness in the circular system under the repetitions in the circular operator. On the other hand, in a matching in the odometer-based system at least one pair of pre-blocks will have a
$(n+m_n)$
-blocks that are still apart from each other in the odometer-based system but arbitrarily close to each other in the circular system. The proof is based on an inductive construction that we call the cycling mechanism (indicated in Figure 3) and a final step to guarantee closeness of blocks in the circular system. In each step of the cycling mechanism the blocks of different types are constructed by cycling the K pre-blocks used. On the one hand, this will yield closeness in the circular system under the repetitions in the circular operator. On the other hand, in a matching in the odometer-based system at least one pair of pre-blocks will have a
![]() $\overline {f}$
distance close to
$\overline {f}$
distance close to
![]() $\alpha $
and at most
$\alpha $
and at most
![]() $K-1$
pairs will have a smaller
$K-1$
pairs will have a smaller
![]() $\overline {f}$
distance. Over the course of the construction this distance will increase towards
$\overline {f}$
distance. Over the course of the construction this distance will increase towards
![]() $\alpha $
(see equation (6.9)).
$\alpha $
(see equation (6.9)).
For this construction, let
![]() $(u_{n+m})_{m\in \mathbb {N}}$
and
$(u_{n+m})_{m\in \mathbb {N}}$
and
![]() $(e_{n+m})_{m\in \mathbb {N}}$
be increasing sequences of positive integers such that
$(e_{n+m})_{m\in \mathbb {N}}$
be increasing sequences of positive integers such that
 $$ \begin{align} \sum_{m\in\mathbb{N}}\frac{2}{Ku_{n+m}^{2}e_{n+m}}<\frac{\delta}{2} \end{align} $$
$$ \begin{align} \sum_{m\in\mathbb{N}}\frac{2}{Ku_{n+m}^{2}e_{n+m}}<\frac{\delta}{2} \end{align} $$
and
 $$ \begin{align} \sum_{m\in\mathbb{N}}\bigg(\frac{4}{u_{n+m}}+\frac{14}{\sqrt{e_{n+m}}}\bigg)<\frac{\varepsilon}{8}. \end{align} $$
$$ \begin{align} \sum_{m\in\mathbb{N}}\bigg(\frac{4}{u_{n+m}}+\frac{14}{\sqrt{e_{n+m}}}\bigg)<\frac{\varepsilon}{8}. \end{align} $$
Additionally, we define the sequences
![]() $(\unicode{x3bb} _{n+m})_{m\in \mathbb {N}}$
and
$(\unicode{x3bb} _{n+m})_{m\in \mathbb {N}}$
and
![]() $(d_{n+m})_{m\in \mathbb {N}}$
by
$(d_{n+m})_{m\in \mathbb {N}}$
by
 $$ \begin{align} d_{n+m}=u_{n+m}^{2} \end{align} $$
$$ \begin{align} d_{n+m}=u_{n+m}^{2} \end{align} $$
and
Moreover, we choose N sufficiently large such that
 $$ \begin{align} \frac{14}{\sqrt{N}}<\frac{\varepsilon}{8}, \end{align} $$
$$ \begin{align} \frac{14}{\sqrt{N}}<\frac{\varepsilon}{8}, \end{align} $$
and the positive integers
![]() $(l_{n+m})_{m\in \mathbb {N}}$
sufficiently large such that
$(l_{n+m})_{m\in \mathbb {N}}$
sufficiently large such that
 $$ \begin{align} \sum_{m\in\mathbb{N}}\frac{4}{l_{n+m}}<\frac{\delta}{2}. \end{align} $$
$$ \begin{align} \sum_{m\in\mathbb{N}}\frac{4}{l_{n+m}}<\frac{\delta}{2}. \end{align} $$
The terms
![]() $l_n,l_{n+1},\ldots ,l_{n+m_n-1}$
are the coefficients in the circular
$l_n,l_{n+1},\ldots ,l_{n+m_n-1}$
are the coefficients in the circular
![]() $(n+1)$
-,
$(n+1)$
-,
![]() $(n+2)$
-, … ,
$(n+2)$
-, … ,
![]() $(n+m_n)$
-blocks, where
$(n+m_n)$
-blocks, where
![]() $m_n$
is defined below. The proof of Proposition 6.5 utilizes the parameters
$m_n$
is defined below. The proof of Proposition 6.5 utilizes the parameters
![]() $(\alpha _{n+m})^{m=\infty }_{m=2}$
and
$(\alpha _{n+m})^{m=\infty }_{m=2}$
and
![]() $(\beta _{n+m})^{m=\infty }_{m=2}$
defined inductively via
$(\beta _{n+m})^{m=\infty }_{m=2}$
defined inductively via
 $$ \begin{align} \alpha_{n+2}=\alpha-\frac{14}{\sqrt{N}}-\frac{2}{T}-\frac{4}{u_{n+1}}-\frac{13}{\sqrt{e_{n+1}}}, \end{align} $$
$$ \begin{align} \alpha_{n+2}=\alpha-\frac{14}{\sqrt{N}}-\frac{2}{T}-\frac{4}{u_{n+1}}-\frac{13}{\sqrt{e_{n+1}}}, \end{align} $$
 $$ \begin{align} \beta_{n+2}=\frac{1}{K}\alpha -\frac{14}{\sqrt{N}}-\frac{2}{KT}-\frac{4}{u_{n+1}}-\frac{2}{e_{n+1}}, \end{align} $$
$$ \begin{align} \beta_{n+2}=\frac{1}{K}\alpha -\frac{14}{\sqrt{N}}-\frac{2}{KT}-\frac{4}{u_{n+1}}-\frac{2}{e_{n+1}}, \end{align} $$

and

Since
![]() ${1}/{K}(\alpha -({2}/{T}))>{\alpha }/{2K}>2\varepsilon $
, assumptions (6.2) and (6.4) imply that
${1}/{K}(\alpha -({2}/{T}))>{\alpha }/{2K}>2\varepsilon $
, assumptions (6.2) and (6.4) imply that
![]() $\beta _{n+2}>\varepsilon $
. We also note that for every
$\beta _{n+2}>\varepsilon $
. We also note that for every
![]() $m\geq 2$
,
$m\geq 2$
,
 $$ \begin{align*} \alpha_{n+m} \geq\alpha-\frac{14}{\sqrt{N}}-\frac{2}{T}-\sum_{i=1}^{\infty}\bigg(\frac{14}{\sqrt{e_{n+i}}}+\frac{4}{u_{n+i}}\bigg)>\alpha-\frac{2}{T}-\frac{\varepsilon}{8}-\frac{\varepsilon}{8}, \end{align*} $$
$$ \begin{align*} \alpha_{n+m} \geq\alpha-\frac{14}{\sqrt{N}}-\frac{2}{T}-\sum_{i=1}^{\infty}\bigg(\frac{14}{\sqrt{e_{n+i}}}+\frac{4}{u_{n+i}}\bigg)>\alpha-\frac{2}{T}-\frac{\varepsilon}{8}-\frac{\varepsilon}{8}, \end{align*} $$
by equation (6.8) and our assumptions (6.2) and (6.4). Similarly, assumption (6.2) implies that in our
![]() $\beta _{n+m}$
equation (6.9), the terms we subtract from
$\beta _{n+m}$
equation (6.9), the terms we subtract from
![]() $\beta _2$
over the whole course of the construction are bounded by
$\beta _2$
over the whole course of the construction are bounded by
![]() $\varepsilon /8$
. Due to these bounds, we can choose
$\varepsilon /8$
. Due to these bounds, we can choose
![]() $m_n$
as the least integer such that
$m_n$
as the least integer such that
 $$ \begin{align} \beta_{n+m_{n}}>\alpha-\frac{2}{T}-\frac{\varepsilon}{2}, \end{align} $$
$$ \begin{align} \beta_{n+m_{n}}>\alpha-\frac{2}{T}-\frac{\varepsilon}{2}, \end{align} $$
and we will apply our inductive construction until stage
![]() $n+m_n$
.
$n+m_n$
.
6.3.1. Initial step: construction of
 $(n+1)$
-blocks
$(n+1)$
-blocks
First of all, we choose one n-block
 $\mathtt {B}_{0}^{(n)}$
as a marker. Then we apply Proposition 6.2 on the remaining n-blocks
$\mathtt {B}_{0}^{(n)}$
as a marker. Then we apply Proposition 6.2 on the remaining n-blocks
 $\mathtt {B}_{1}^{(n)},\ldots ,\mathtt {B}_{N}^{(n)}$
to build
$\mathtt {B}_{1}^{(n)},\ldots ,\mathtt {B}_{N}^{(n)}$
to build
![]() $\tilde {N}(n+1):= K\cdot (\unicode{x3bb} _{n+1}+1)$
Feldman patterns denoted by
$\tilde {N}(n+1):= K\cdot (\unicode{x3bb} _{n+1}+1)$
Feldman patterns denoted by
![]() $\mathtt {A}_{i,j}$
,
$\mathtt {A}_{i,j}$
,
![]() $i=1,\ldots ,K$
,
$i=1,\ldots ,K$
,
![]() $j=1,\ldots ,\unicode{x3bb} _{n+1}+1$
. We will call them pre-
$j=1,\ldots ,\unicode{x3bb} _{n+1}+1$
. We will call them pre-
![]() $(n+1)$
-blocks. In particular, these have length
$(n+1)$
-blocks. In particular, these have length
 $\tilde {\mathtt {h}}_{n+1}=N^{2\cdot \tilde {N}(n+1)+3}\cdot \mathtt {h}_{n}$
and are uniform in the n-blocks
$\tilde {\mathtt {h}}_{n+1}=N^{2\cdot \tilde {N}(n+1)+3}\cdot \mathtt {h}_{n}$
and are uniform in the n-blocks
 $\mathtt {B}_{1}^{(n)},\ldots ,\mathtt {B}_{N}^{(n)}$
by construction. More precisely, every pre-
$\mathtt {B}_{1}^{(n)},\ldots ,\mathtt {B}_{N}^{(n)}$
by construction. More precisely, every pre-
![]() $(n+1)$
-block contains each n-block
$(n+1)$
-block contains each n-block
 $\mathtt {B}_{i}^{(n)}$
,
$\mathtt {B}_{i}^{(n)}$
,
![]() $1\leq i\leq N$
, exactly
$1\leq i\leq N$
, exactly
 $$ \begin{align} \bar{N}(n):= N^{2\cdot\tilde{N}(n+1)+2} \end{align} $$
$$ \begin{align} \bar{N}(n):= N^{2\cdot\tilde{N}(n+1)+2} \end{align} $$
times and pre-
![]() $(n+1)$
-blocks in the circular system have length
$(n+1)$
-blocks in the circular system have length
 $\tilde {q}_{n+1}=N^{2\cdot \tilde {N}(n+1)+3}\cdot l_{n}\cdot q_{n}$
. In order to obtain uniformity, we will define the marker segment by
$\tilde {q}_{n+1}=N^{2\cdot \tilde {N}(n+1)+3}\cdot l_{n}\cdot q_{n}$
. In order to obtain uniformity, we will define the marker segment by
 $$ \begin{align*} \mathtt{a}_{n}=(\mathtt{B}_{0}^{(n)})^{K\bar{N}(n)}. \end{align*} $$
$$ \begin{align*} \mathtt{a}_{n}=(\mathtt{B}_{0}^{(n)})^{K\bar{N}(n)}. \end{align*} $$
Moreover, we have
 $$ \begin{align} \overline{f}(\mathtt{A},\overline{\mathtt{A}})\geq\alpha-\frac{13}{\sqrt{N}}-\frac{2}{T} \end{align} $$
$$ \begin{align} \overline{f}(\mathtt{A},\overline{\mathtt{A}})\geq\alpha-\frac{13}{\sqrt{N}}-\frac{2}{T} \end{align} $$
for any strings
![]() $\mathtt {A}$
and
$\mathtt {A}$
and
![]() $\overline {\mathtt {A}}$
of at least
$\overline {\mathtt {A}}$
of at least
 $\tilde {\mathtt {h}}_{n+1}/N=N^{2\cdot \tilde {N}(n+1)+2}\cdot \mathtt {h}_{n}$
consecutive symbols in different pre-
$\tilde {\mathtt {h}}_{n+1}/N=N^{2\cdot \tilde {N}(n+1)+2}\cdot \mathtt {h}_{n}$
consecutive symbols in different pre-
![]() $(n+1)$
-blocks by Proposition 6.2.
$(n+1)$
-blocks by Proposition 6.2.
Finally, we define the
![]() $(n+1)$
-blocks:
$(n+1)$
-blocks:

Here, the index
![]() $i\in \{ 1,\ldots ,K\} $
in
$i\in \{ 1,\ldots ,K\} $
in
 $\mathtt {B}_{i,j}^{(n+1)}$
indicates the type and
$\mathtt {B}_{i,j}^{(n+1)}$
indicates the type and
![]() $j=1,\ldots ,\unicode{x3bb} _{n+1}$
numbers the
$j=1,\ldots ,\unicode{x3bb} _{n+1}$
numbers the
![]() $(n+1)$
-blocks of that type consecutively. We note that for j odd the block
$(n+1)$
-blocks of that type consecutively. We note that for j odd the block
 $\mathtt {B}_{i+1,j}^{(n+1)}$
is obtained from
$\mathtt {B}_{i+1,j}^{(n+1)}$
is obtained from
 $\mathtt {B}_{i,j}^{(n+1)}$
by cycling the pre-
$\mathtt {B}_{i,j}^{(n+1)}$
by cycling the pre-
![]() $(n+1)$
-blocks to the left. On the other hand, for j even the block
$(n+1)$
-blocks to the left. On the other hand, for j even the block
 $\mathtt {B}_{i+1,j}^{(n+1)}$
is obtained from
$\mathtt {B}_{i+1,j}^{(n+1)}$
is obtained from
 $\mathtt {B}_{i,j}^{(n+1)}$
by cycling the pre-
$\mathtt {B}_{i,j}^{(n+1)}$
by cycling the pre-
![]() $(n+1)$
-blocks to the right. Additionally, we define the next marker block.
$(n+1)$
-blocks to the right. Additionally, we define the next marker block.

where
 $\mathtt {A}_{i,\unicode{x3bb} _{n+1}+1}^{(n+1)}$
,
$\mathtt {A}_{i,\unicode{x3bb} _{n+1}+1}^{(n+1)}$
,
![]() $i=1,\ldots ,K$
, have not been used in any of the other
$i=1,\ldots ,K$
, have not been used in any of the other
![]() $(n+1)$
-blocks. Hence, there are are
$(n+1)$
-blocks. Hence, there are are
![]() $N(n+1)+1=\unicode{x3bb} _{n+1}K+1 (n+1)$
-blocks in total. We also note that every
$N(n+1)+1=\unicode{x3bb} _{n+1}K+1 (n+1)$
-blocks in total. We also note that every
![]() $(n+1)$
-block is uniform in the n-blocks by equation (6.11).
$(n+1)$
-block is uniform in the n-blocks by equation (6.11).
6.3.2. Inductive step: construction of
 $(n+m)$
-blocks
$(n+m)$
-blocks
In an inductive process we construct
![]() $(n+m)$
-blocks for
$(n+m)$
-blocks for
![]() $m\geq 2$
. Assume that in our inductive construction we have constructed
$m\geq 2$
. Assume that in our inductive construction we have constructed
![]() $K\unicode{x3bb} _{n+m-1}\, (n+m-1)$
-blocks
$K\unicode{x3bb} _{n+m-1}\, (n+m-1)$
-blocks
 $\mathtt {B}_{i,j}^{(n+m-1)}$
of K different types, where for
$\mathtt {B}_{i,j}^{(n+m-1)}$
of K different types, where for
![]() $m=2$
the
$m=2$
the
![]() $(n+1)$
-blocks are the ones constructed in §6.3.1 and for
$(n+1)$
-blocks are the ones constructed in §6.3.1 and for
![]() $m\geq 3$
the
$m\geq 3$
the
![]() $(n+m-1)$
-blocks are constructed according to the following formula (with
$(n+m-1)$
-blocks are constructed according to the following formula (with
![]() $\unicode{x3bb} =\unicode{x3bb} _{n+m-1}$
):
$\unicode{x3bb} =\unicode{x3bb} _{n+m-1}$
):
 $$ \begin{align*} &(n+m-1)\text{-blocks of type 1:} \\ & \mathtt{B}_{1,1}^{(n+m-1)}=\mathtt{A}_{1,1}^{(n+m-1)}\mathtt{A}_{2,2}^{(n+m-1)}\ldots\mathtt{A}_{K,K}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \mathtt{B}_{1,2}^{(n+m-1)}=\mathtt{A}_{1,K+1}^{(n+m-1)}\mathtt{A}_{2,K+2}^{(n+m-1)}\ldots\mathtt{A}_{K,2K}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \mathtt{B}_{1,3}^{(n+m-1)}=\mathtt{A}_{1,2K+1}^{(n+m-1)}\mathtt{A}_{2,2K+2}^{(n+m-1)}\ldots\mathtt{A}_{K,3K}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \mathtt{B}_{1,4}^{(n+m-1)}=\mathtt{A}_{1,3K+1}^{(n+m-1)}\mathtt{A}_{2,3K+2}^{(n+m-1)}\ldots\mathtt{A}_{K,4K}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \;\vdots\\ & \mathtt{B}_{1,\unicode{x3bb}}^{(n+m-1)}=\mathtt{A}_{1,(\unicode{x3bb}-1)K+1}^{(n+m-1)}\mathtt{A}_{2,(\unicode{x3bb}-1)K+2}^{(n+m-1)}\ldots\mathtt{A}_{K,\unicode{x3bb} K}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ &(n+m-1)\text{-blocks of type 2:} \\ & \mathtt{B}_{2,1}^{(n+m-1)}=\mathtt{A}_{1,2}^{(n+m-1)}\mathtt{A}_{2,3}^{(n+m-1)}\ldots\mathtt{A}_{K-1,K}^{(n+m-1)}\mathtt{A}_{K,1}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \mathtt{B}_{2,2}^{(n+m-1)}=\mathtt{A}_{1,2K}^{(n+m-1)}\mathtt{A}_{2,K+1}^{(n+m-1)}\ldots\mathtt{A}_{K,K-1}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \mathtt{B}_{2,3}^{(n+m-1)}=\mathtt{A}_{1,2K+2}^{(n+m-1)}\mathtt{A}_{2,2K+3}^{(n+m-1)}\ldots\mathtt{A}_{K-1,3K}^{(n+m-1)}\mathtt{A}_{K,2K+1}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \mathtt{B}_{2,4}^{(n+m-1)}=\mathtt{A}_{1,4K}^{(n+m-1)}\mathtt{A}_{2,3K+1}^{(n+m-1)}\ldots\mathtt{A}_{K,4K-1}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \;\vdots\\ & \mathtt{B}_{2,\unicode{x3bb}}^{(n+m-1)}=\mathtt{A}_{1,\unicode{x3bb} K}^{(n+m-1)}\mathtt{A}_{2,(\unicode{x3bb}-1)K+1}^{(n+m-1)}\ldots\mathtt{A}_{K,\unicode{x3bb} K-1}^{(n+m-1)}\mathtt{a}_{n+m-2}, \\ & \;\vdots\\ &(n+m-1)\text{-blocks of type K:} \\ & \mathtt{B}_{K,1}^{(n+m-1)}=\mathtt{A}_{1,K}^{(n+m-1)}\mathtt{A}_{2,1}^{(n+m-1)}\ldots\mathtt{A}_{K,K-1}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \mathtt{B}_{K,2}^{(n+m-1)}=\mathtt{A}_{1,K+2}^{(n+m-1)}\mathtt{A}_{2,K+3}^{(n+m-1)}\ldots\mathtt{A}_{K-1,2K}^{(n+m-1)}\mathtt{A}_{K,K+1}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \mathtt{B}_{K,3}^{(n+m-1)}=\mathtt{A}_{1,3K}^{(n+m-1)}\mathtt{A}_{2,2K+1}^{(n+m-1)}\ldots\mathtt{A}_{K,3K-1}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \mathtt{B}_{K,4}^{(n+m-1)}=\mathtt{A}_{1,3K+2}^{(n+m-1)}\mathtt{A}_{2,3K+3}^{(n+m-1)}\ldots\mathtt{A}_{K-1,4K}^{(n+m-1)}\mathtt{A}_{K,3K+1}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \;\vdots \\ & \mathtt{B}_{K,\unicode{x3bb}}^{(n+m-1)}=\mathtt{A}_{1,(\unicode{x3bb}-1)K+2}^{(n+m-1)}\ldots\mathtt{A}_{K-1,\unicode{x3bb} K}^{(n+m-1)}\mathtt{A}_{K,(\unicode{x3bb} -1)K+1}^{(n+m-1)}\mathtt{a}_{n+m-2}, \end{align*} $$
$$ \begin{align*} &(n+m-1)\text{-blocks of type 1:} \\ & \mathtt{B}_{1,1}^{(n+m-1)}=\mathtt{A}_{1,1}^{(n+m-1)}\mathtt{A}_{2,2}^{(n+m-1)}\ldots\mathtt{A}_{K,K}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \mathtt{B}_{1,2}^{(n+m-1)}=\mathtt{A}_{1,K+1}^{(n+m-1)}\mathtt{A}_{2,K+2}^{(n+m-1)}\ldots\mathtt{A}_{K,2K}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \mathtt{B}_{1,3}^{(n+m-1)}=\mathtt{A}_{1,2K+1}^{(n+m-1)}\mathtt{A}_{2,2K+2}^{(n+m-1)}\ldots\mathtt{A}_{K,3K}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \mathtt{B}_{1,4}^{(n+m-1)}=\mathtt{A}_{1,3K+1}^{(n+m-1)}\mathtt{A}_{2,3K+2}^{(n+m-1)}\ldots\mathtt{A}_{K,4K}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \;\vdots\\ & \mathtt{B}_{1,\unicode{x3bb}}^{(n+m-1)}=\mathtt{A}_{1,(\unicode{x3bb}-1)K+1}^{(n+m-1)}\mathtt{A}_{2,(\unicode{x3bb}-1)K+2}^{(n+m-1)}\ldots\mathtt{A}_{K,\unicode{x3bb} K}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ &(n+m-1)\text{-blocks of type 2:} \\ & \mathtt{B}_{2,1}^{(n+m-1)}=\mathtt{A}_{1,2}^{(n+m-1)}\mathtt{A}_{2,3}^{(n+m-1)}\ldots\mathtt{A}_{K-1,K}^{(n+m-1)}\mathtt{A}_{K,1}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \mathtt{B}_{2,2}^{(n+m-1)}=\mathtt{A}_{1,2K}^{(n+m-1)}\mathtt{A}_{2,K+1}^{(n+m-1)}\ldots\mathtt{A}_{K,K-1}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \mathtt{B}_{2,3}^{(n+m-1)}=\mathtt{A}_{1,2K+2}^{(n+m-1)}\mathtt{A}_{2,2K+3}^{(n+m-1)}\ldots\mathtt{A}_{K-1,3K}^{(n+m-1)}\mathtt{A}_{K,2K+1}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \mathtt{B}_{2,4}^{(n+m-1)}=\mathtt{A}_{1,4K}^{(n+m-1)}\mathtt{A}_{2,3K+1}^{(n+m-1)}\ldots\mathtt{A}_{K,4K-1}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \;\vdots\\ & \mathtt{B}_{2,\unicode{x3bb}}^{(n+m-1)}=\mathtt{A}_{1,\unicode{x3bb} K}^{(n+m-1)}\mathtt{A}_{2,(\unicode{x3bb}-1)K+1}^{(n+m-1)}\ldots\mathtt{A}_{K,\unicode{x3bb} K-1}^{(n+m-1)}\mathtt{a}_{n+m-2}, \\ & \;\vdots\\ &(n+m-1)\text{-blocks of type K:} \\ & \mathtt{B}_{K,1}^{(n+m-1)}=\mathtt{A}_{1,K}^{(n+m-1)}\mathtt{A}_{2,1}^{(n+m-1)}\ldots\mathtt{A}_{K,K-1}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \mathtt{B}_{K,2}^{(n+m-1)}=\mathtt{A}_{1,K+2}^{(n+m-1)}\mathtt{A}_{2,K+3}^{(n+m-1)}\ldots\mathtt{A}_{K-1,2K}^{(n+m-1)}\mathtt{A}_{K,K+1}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \mathtt{B}_{K,3}^{(n+m-1)}=\mathtt{A}_{1,3K}^{(n+m-1)}\mathtt{A}_{2,2K+1}^{(n+m-1)}\ldots\mathtt{A}_{K,3K-1}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \mathtt{B}_{K,4}^{(n+m-1)}=\mathtt{A}_{1,3K+2}^{(n+m-1)}\mathtt{A}_{2,3K+3}^{(n+m-1)}\ldots\mathtt{A}_{K-1,4K}^{(n+m-1)}\mathtt{A}_{K,3K+1}^{(n+m-1)}\mathtt{a}_{n+m-2},\\ & \;\vdots \\ & \mathtt{B}_{K,\unicode{x3bb}}^{(n+m-1)}=\mathtt{A}_{1,(\unicode{x3bb}-1)K+2}^{(n+m-1)}\ldots\mathtt{A}_{K-1,\unicode{x3bb} K}^{(n+m-1)}\mathtt{A}_{K,(\unicode{x3bb} -1)K+1}^{(n+m-1)}\mathtt{a}_{n+m-2}, \end{align*} $$
using pre-
![]() $(n+m-1)$
-blocks
$(n+m-1)$
-blocks
 $\mathtt {A}^{(n+m-1)}_{i,j}$
of length
$\mathtt {A}^{(n+m-1)}_{i,j}$
of length
![]() $\tilde {h}_{n+m-1}$
and a marker segment
$\tilde {h}_{n+m-1}$
and a marker segment
 $\mathtt {a}_{n+m-2}=(\mathtt {B}_{0}^{(n+m-2)})^{\bar {N}(n+m-2)}$
with
$\mathtt {a}_{n+m-2}=(\mathtt {B}_{0}^{(n+m-2)})^{\bar {N}(n+m-2)}$
with
![]() $\bar {N}(n+m-2)$
chosen according to equation (6.17) such that the
$\bar {N}(n+m-2)$
chosen according to equation (6.17) such that the
![]() $(n+m-1)$
-blocks are uniform in
$(n+m-1)$
-blocks are uniform in
![]() $(n+m-2)$
-blocks. We note that for j odd the block
$(n+m-2)$
-blocks. We note that for j odd the block
 $\mathtt {B}_{i+1,j}^{(n+m-1)}$
is obtained from
$\mathtt {B}_{i+1,j}^{(n+m-1)}$
is obtained from
 $\mathtt {B}_{i,j}^{(n+m-1)}$
by cycling the second index to the left. On the other hand, for j even the block
$\mathtt {B}_{i,j}^{(n+m-1)}$
by cycling the second index to the left. On the other hand, for j even the block
 $\mathtt {B}_{i+1,j}^{(n+m-1)}$
is obtained from
$\mathtt {B}_{i+1,j}^{(n+m-1)}$
is obtained from
 $\mathtt {B}_{i,j}^{(n+m-1)}$
by cycling the second index to the right. Additionally, we have a marker block
$\mathtt {B}_{i,j}^{(n+m-1)}$
by cycling the second index to the right. Additionally, we have a marker block

where the pre-
![]() $(n+m-1)$
-blocks
$(n+m-1)$
-blocks
 $\mathtt {A}_{i,\unicode{x3bb} _{n+m-1}K+1}^{(n+m-1)}$
have not been used in any other
$\mathtt {A}_{i,\unicode{x3bb} _{n+m-1}K+1}^{(n+m-1)}$
have not been used in any other
![]() $(n+m-1)$
-block. Hence, there are
$(n+m-1)$
-block. Hence, there are
![]() $N(n+m-1)+1=\unicode{x3bb} _{n+m-1}K+1\, (n+m-1)$
-blocks in total.
$N(n+m-1)+1=\unicode{x3bb} _{n+m-1}K+1\, (n+m-1)$
-blocks in total.
In our inductive construction process for
![]() $m\geq 3$
, for any strings
$m\geq 3$
, for any strings
![]() $\mathtt {A},\overline {\mathtt {A}}$
of at least
$\mathtt {A},\overline {\mathtt {A}}$
of at least
![]() $\tilde {h}_{n+m-1}/e_{n+m-2}$
consecutive symbols in
$\tilde {h}_{n+m-1}/e_{n+m-2}$
consecutive symbols in
 $\mathtt {A}_{i_{1},j_{1}}^{(n+m-1)}$
and
$\mathtt {A}_{i_{1},j_{1}}^{(n+m-1)}$
and
 $\mathtt {A}_{i_{2},j_{2}}^{(n+m-1)},$
we assume
$\mathtt {A}_{i_{2},j_{2}}^{(n+m-1)},$
we assume
and
with the numbers
![]() $\alpha _{n+m-1}$
and
$\alpha _{n+m-1}$
and
![]() $\beta _{n+m-1}$
from equations (6.6)–(6.9). In the corresponding circular system we have
$\beta _{n+m-1}$
from equations (6.6)–(6.9). In the corresponding circular system we have
 $$ \begin{align} \overline{f}(\mathcal{A}_{i_{1},j}^{(n+m-1)},\mathcal{A}_{i_{2},j}^{(n+m-1)})\leq\sum_{i=1}^{m-2}\bigg(\frac{4}{l_{n+i}}+\frac{2}{N(n+i-1)+1}\bigg). \end{align} $$
$$ \begin{align} \overline{f}(\mathcal{A}_{i_{1},j}^{(n+m-1)},\mathcal{A}_{i_{2},j}^{(n+m-1)})\leq\sum_{i=1}^{m-2}\bigg(\frac{4}{l_{n+i}}+\frac{2}{N(n+i-1)+1}\bigg). \end{align} $$
Note that this assumption is vacuous if
![]() $m=2$
. In the odometer-based system we will use equation (6.12) for the first inductive step.
$m=2$
. In the odometer-based system we will use equation (6.12) for the first inductive step.
In the inductive step starting with
![]() $m \geq 2$
, we use
$m \geq 2$
, we use
![]() $(n+m-1)$
-blocks to define grouped
$(n+m-1)$
-blocks to define grouped
![]() $(n+m-1)$
-blocks
$(n+m-1)$
-blocks
 $\mathtt {G}_{i,j}^{(n+m-1)}$
(where
$\mathtt {G}_{i,j}^{(n+m-1)}$
(where
![]() $i=1,\ldots ,K$
indicates the type of
$i=1,\ldots ,K$
indicates the type of
![]() $(n+m-1)$
-blocks used and
$(n+m-1)$
-blocks used and
![]() $j=0,\ldots ,e_{n+m-1}-1$
enumerates the grouped
$j=0,\ldots ,e_{n+m-1}-1$
enumerates the grouped
![]() $(n+m-1)$
-blocks of that type) as follows:
$(n+m-1)$
-blocks of that type) as follows:
 $$ \begin{align*} \mathtt{G}_{i,j}^{(n+m-1)}=\mathtt{B}_{i,j\cdot2d_{n+m-1}+1}^{(n+m-1)}\mathtt{B}_{i,j\cdot2d_{n+m-1}+2}^{(n+m-1)}\ldots\mathtt{B}_{i,(j+1)\cdot2d_{n+m-1}}^{(n+m-1)}, \end{align*} $$
$$ \begin{align*} \mathtt{G}_{i,j}^{(n+m-1)}=\mathtt{B}_{i,j\cdot2d_{n+m-1}+1}^{(n+m-1)}\mathtt{B}_{i,j\cdot2d_{n+m-1}+2}^{(n+m-1)}\ldots\mathtt{B}_{i,(j+1)\cdot2d_{n+m-1}}^{(n+m-1)}, \end{align*} $$
that is, it is a concatenation of
![]() $2d_{n+m-1}\, (n+m-1)$
-blocks of the same type. In the following lemmas we see that different grouped blocks are still apart from each other in the odometer-based system but grouped blocks with coinciding index j can be made arbitrarily close to each other in the circular system.
$2d_{n+m-1}\, (n+m-1)$
-blocks of the same type. In the following lemmas we see that different grouped blocks are still apart from each other in the odometer-based system but grouped blocks with coinciding index j can be made arbitrarily close to each other in the circular system.
Lemma 6.7. (Distance between grouped
 $(n+m-1)$
-blocks in the odometer-based system)
$(n+m-1)$
-blocks in the odometer-based system)
Let
![]() $i_{1},i_{2}\in \{ 1,\ldots ,K\} $
,
$i_{1},i_{2}\in \{ 1,\ldots ,K\} $
,
![]() $j_{1},j_{2}\in \{ 0,\ldots ,e_{n+m-1}-1\} $
and
$j_{1},j_{2}\in \{ 0,\ldots ,e_{n+m-1}-1\} $
and
![]() $\mathtt {G},\overline {\mathtt {G}}$
be strings of at least
$\mathtt {G},\overline {\mathtt {G}}$
be strings of at least
![]() $u_{n+m-1}\mathtt {h}_{n+m-1}$
consecutive symbols from grouped
$u_{n+m-1}\mathtt {h}_{n+m-1}$
consecutive symbols from grouped
![]() $(n+m-1)$
-blocks
$(n+m-1)$
-blocks
 $\mathtt {G}_{i_{1},j_{1}}^{(n+m-1)}$
and
$\mathtt {G}_{i_{1},j_{1}}^{(n+m-1)}$
and
 $\mathtt {G}_{i_{2},j_{2}}^{(n+m-1)}$
respectively.
$\mathtt {G}_{i_{2},j_{2}}^{(n+m-1)}$
respectively.
-
(1) For
 $i_{1}\neq i_{2}$
and
$i_{1}\neq i_{2}$
and
 $j_{1}=j_{2}$
we have
$j_{1}=j_{2}$
we have
 $$ \begin{align*} & \overline{f}(\mathtt{G},\overline{\mathtt{G}}) \nonumber\\ & \geq \begin{cases} \dfrac{1}{K}\alpha -\dfrac{14}{\sqrt{N}}-\dfrac{2}{KT}-\dfrac{2}{u_{n+1}} & \text{for } m=2, \\ \beta_{n+m-1}+\dfrac{1}{K}(\alpha_{n+m-1}-\beta_{n+m-1}) -\dfrac{2}{e_{n+m-2}}-\dfrac{2}{u_{n+m-1}}-\dfrac{2}{N(n+m-2)+1} & \text{for } m\geq 3. \end{cases} \end{align*} $$
$$ \begin{align*} & \overline{f}(\mathtt{G},\overline{\mathtt{G}}) \nonumber\\ & \geq \begin{cases} \dfrac{1}{K}\alpha -\dfrac{14}{\sqrt{N}}-\dfrac{2}{KT}-\dfrac{2}{u_{n+1}} & \text{for } m=2, \\ \beta_{n+m-1}+\dfrac{1}{K}(\alpha_{n+m-1}-\beta_{n+m-1}) -\dfrac{2}{e_{n+m-2}}-\dfrac{2}{u_{n+m-1}}-\dfrac{2}{N(n+m-2)+1} & \text{for } m\geq 3. \end{cases} \end{align*} $$
-
(2) For
 $j_{1}\neq j_{2}$
and all
$j_{1}\neq j_{2}$
and all
 $i_{1},i_{2}$
we have
$i_{1},i_{2}$
we have
 $$ \begin{align*} \overline{f}(\mathtt{G},\overline{\mathtt{G}})\geq \begin{cases} \alpha-\dfrac{14}{\sqrt{N}}-\dfrac{2}{T}-\dfrac{2}{u_{n+1}} \quad& \text{for } m=2, \\ \alpha_{n+m-1}-\dfrac{2}{e_{n+m-2}}-\dfrac{2}{u_{n+m-1}}-\dfrac{2}{N(n+m-2)+1} \quad& \text{for } m\geq 3. \end{cases} \end{align*} $$
$$ \begin{align*} \overline{f}(\mathtt{G},\overline{\mathtt{G}})\geq \begin{cases} \alpha-\dfrac{14}{\sqrt{N}}-\dfrac{2}{T}-\dfrac{2}{u_{n+1}} \quad& \text{for } m=2, \\ \alpha_{n+m-1}-\dfrac{2}{e_{n+m-2}}-\dfrac{2}{u_{n+m-1}}-\dfrac{2}{N(n+m-2)+1} \quad& \text{for } m\geq 3. \end{cases} \end{align*} $$
Proof. In the first case we have
![]() $j_{1}=j_{2}$
. We treat
$j_{1}=j_{2}$
. We treat
![]() $\mathtt {G}$
and
$\mathtt {G}$
and
![]() $\overline {\mathtt {G}}$
as strings of complete
$\overline {\mathtt {G}}$
as strings of complete
![]() $(n+m-1)$
-blocks by adding fewer than
$(n+m-1)$
-blocks by adding fewer than
![]() $2h_{n+m-1}$
symbols to complete partial blocks at the beginning and end of
$2h_{n+m-1}$
symbols to complete partial blocks at the beginning and end of
![]() $\mathtt {G}$
and
$\mathtt {G}$
and
![]() $\overline {\mathtt {G}}$
. These constitute a fraction of at most
$\overline {\mathtt {G}}$
. These constitute a fraction of at most
![]() $2/u_{n+m-1}$
of the total length. Additionally, we ignore the marker segments
$2/u_{n+m-1}$
of the total length. Additionally, we ignore the marker segments
![]() $\mathtt {a}_{n+m-2}$
which form a fraction
$\mathtt {a}_{n+m-2}$
which form a fraction
![]() $1/(N(n+m-2)+1)$
of the length of each
$1/(N(n+m-2)+1)$
of the length of each
![]() $(n+m-1)$
-block due to uniformity and so of
$(n+m-1)$
-block due to uniformity and so of
![]() $\mathtt {G}$
as well as
$\mathtt {G}$
as well as
![]() $\overline {\mathtt {G}}$
. On the remaining strings for
$\overline {\mathtt {G}}$
. On the remaining strings for
![]() $m=2$
we apply Corollary 5.5 with
$m=2$
we apply Corollary 5.5 with
![]() $\tilde {f}\geq {1}/{K}$
and equation (6.12) which yields
$\tilde {f}\geq {1}/{K}$
and equation (6.12) which yields
 $$ \begin{align*} \overline{f}(\mathtt{G},\overline{\mathtt{G}})\geq\frac{1}{K} \bigg(\alpha-\frac{13}{\sqrt{N}}-\frac{2}{T}\bigg)-\frac{2}{N}-\frac{2}{N+1}-\frac{2}{u_{n+1}} \geq\frac{1}{K}\alpha -\frac{14}{\sqrt{N}}-\frac{2}{KT}-\frac{2}{u_{n+1}}. \end{align*} $$
$$ \begin{align*} \overline{f}(\mathtt{G},\overline{\mathtt{G}})\geq\frac{1}{K} \bigg(\alpha-\frac{13}{\sqrt{N}}-\frac{2}{T}\bigg)-\frac{2}{N}-\frac{2}{N+1}-\frac{2}{u_{n+1}} \geq\frac{1}{K}\alpha -\frac{14}{\sqrt{N}}-\frac{2}{KT}-\frac{2}{u_{n+1}}. \end{align*} $$
On the remaining strings
![]() $\mathtt {G}_{\text {mod}}$
and
$\mathtt {G}_{\text {mod}}$
and
![]() $\overline {\mathtt {G}}_{\text {mod}}$
for
$\overline {\mathtt {G}}_{\text {mod}}$
for
![]() $m\geq 3$
we use Proposition 5.4 with
$m\geq 3$
we use Proposition 5.4 with
![]() $\tilde {f}\geq {1}/{K}$
and equations (6.13) and (6.14) to obtain
$\tilde {f}\geq {1}/{K}$
and equations (6.13) and (6.14) to obtain
 $$ \begin{align*} \overline{f}(\mathtt{G}_{\text{mod}},\overline{\mathtt{G}}_{\text{mod}})\geq \frac{1}{K} \alpha_{n+m-1} + \bigg(1-\frac{1}{K}\bigg)\beta_{n+m-1}-\frac{2}{e_{n+m-2}}, \end{align*} $$
$$ \begin{align*} \overline{f}(\mathtt{G}_{\text{mod}},\overline{\mathtt{G}}_{\text{mod}})\geq \frac{1}{K} \alpha_{n+m-1} + \bigg(1-\frac{1}{K}\bigg)\beta_{n+m-1}-\frac{2}{e_{n+m-2}}, \end{align*} $$
which implies the claim.
In the second case we observe that
![]() $\mathtt {G}$
and
$\mathtt {G}$
and
![]() $\overline {\mathtt {G}}$
do not have any Feldman pattern of pre-
$\overline {\mathtt {G}}$
do not have any Feldman pattern of pre-
![]() $(n+m-1)$
-blocks in common due to
$(n+m-1)$
-blocks in common due to
![]() $j_{1}\neq j_{2}$
. As before we complete partial blocks at the beginning and end of
$j_{1}\neq j_{2}$
. As before we complete partial blocks at the beginning and end of
![]() $\mathtt {G}$
and
$\mathtt {G}$
and
![]() $\overline {\mathtt {G}}$
and remove the marker segments
$\overline {\mathtt {G}}$
and remove the marker segments
![]() $\mathtt {a}_{n+m-2}$
. On the remaining strings for
$\mathtt {a}_{n+m-2}$
. On the remaining strings for
![]() $m=2$
we apply Corollary 5.5 with
$m=2$
we apply Corollary 5.5 with
![]() $\tilde {f}=1$
and equation (6.12), while for
$\tilde {f}=1$
and equation (6.12), while for
![]() $m\geq 3$
we use Corollary 5.5 with
$m\geq 3$
we use Corollary 5.5 with
![]() $\tilde {f}=1$
and equation (6.14).
$\tilde {f}=1$
and equation (6.14).
Lemma 6.8. (Distance between grouped
 $(n+m-1)$
-blocks in the circular system)
$(n+m-1)$
-blocks in the circular system)
For all
![]() $i_{1},i_{2}\in \{ 1,\ldots ,K\} $
and
$i_{1},i_{2}\in \{ 1,\ldots ,K\} $
and
![]() $j\in \{ 0,\ldots ,e_{n+m-1}-1\},$
we have
$j\in \{ 0,\ldots ,e_{n+m-1}-1\},$
we have
 $$ \begin{align*} \overline{f}(\mathcal{G}_{i_{1},j}^{(n+m-1)},\mathcal{G}_{i_{2},j}^{(n+m-1)})\leq\sum_{i=1}^{m-1}\bigg(\frac{4}{l_{n+i}}+\frac{2}{N(n+i-1)+1}\bigg). \end{align*} $$
$$ \begin{align*} \overline{f}(\mathcal{G}_{i_{1},j}^{(n+m-1)},\mathcal{G}_{i_{2},j}^{(n+m-1)})\leq\sum_{i=1}^{m-1}\bigg(\frac{4}{l_{n+i}}+\frac{2}{N(n+i-1)+1}\bigg). \end{align*} $$
Proof. We recall that the marker segment
![]() $\mathtt {a}_{n+m-2}$
occupies a fraction
$\mathtt {a}_{n+m-2}$
occupies a fraction
![]() $(N(n+m-2)$
$(N(n+m-2)$
![]() $+1)^{-1}$
of the total length of each
$+1)^{-1}$
of the total length of each
![]() $(n+m-1)$
-block. Moreover, for every
$(n+m-1)$
-block. Moreover, for every
![]() $j=1, \ldots ,\unicode{x3bb} _{n+m-1}$
the
$j=1, \ldots ,\unicode{x3bb} _{n+m-1}$
the
![]() $(n+m-1)$
-block
$(n+m-1)$
-block
 $\mathtt {B}_{i_{2},j}^{(n+m-1)}$
is obtained from
$\mathtt {B}_{i_{2},j}^{(n+m-1)}$
is obtained from
 $\mathtt {B}_{i_{1},j}^{(n+m-1)}$
by a cycling permutation of the Feldman patterns used for the pre-
$\mathtt {B}_{i_{1},j}^{(n+m-1)}$
by a cycling permutation of the Feldman patterns used for the pre-
![]() $(n+m-1)$
-blocks. Under the cyclic operator
$(n+m-1)$
-blocks. Under the cyclic operator
![]() $\mathcal {C}_{n+m-1}$
each
$\mathcal {C}_{n+m-1}$
each
![]() $(n+m-1)$
-block is repeated
$(n+m-1)$
-block is repeated
![]() $l_{n+m-1}-1$
times. Hence, the
$l_{n+m-1}-1$
times. Hence, the
![]() $\overline {f}$
distance between
$\overline {f}$
distance between
 $\mathcal {G}_{i_{1},j}^{(n+m-1)}$
and
$\mathcal {G}_{i_{1},j}^{(n+m-1)}$
and
 $\mathcal {G}_{i_{2},j}^{(n+m-1)}$
is at most
$\mathcal {G}_{i_{2},j}^{(n+m-1)}$
is at most
 $$ \begin{align*} M+\frac{4}{l_{n+m-1}}+\frac{2}{N(n+m-2)+1}, \end{align*} $$
$$ \begin{align*} M+\frac{4}{l_{n+m-1}}+\frac{2}{N(n+m-2)+1}, \end{align*} $$
where M is the
![]() $\overline {f}$
distance of pre-
$\overline {f}$
distance of pre-
![]() $(n+m-1)$
-blocks of the same pattern in the circular system. For
$(n+m-1)$
-blocks of the same pattern in the circular system. For
![]() $m=2$
this distance
$m=2$
this distance
![]() $M=0$
, while for
$M=0$
, while for
![]() $m\geq 3$
we obtain the claim with the aid of equation (6.15).
$m\geq 3$
we obtain the claim with the aid of equation (6.15).
For each type
![]() $i\in \{ 1,\ldots ,K\} $
we use the
$i\in \{ 1,\ldots ,K\} $
we use the
![]() $e_{n+m-1}$
grouped
$e_{n+m-1}$
grouped
![]() $(n+m-1)$
-blocks of type i as building blocks for the Feldman patterns
$(n+m-1)$
-blocks of type i as building blocks for the Feldman patterns
 $\mathtt {A}_{i,j}^{(n+m)}$
,
$\mathtt {A}_{i,j}^{(n+m)}$
,
![]() $j=1,\ldots ,(\unicode{x3bb} _{n+m}+1)K$
, which are the pre-
$j=1,\ldots ,(\unicode{x3bb} _{n+m}+1)K$
, which are the pre-
![]() $(n+m)$
-blocks with length
$(n+m)$
-blocks with length
![]() $\tilde {h}_{n+m}$
. Thus there are
$\tilde {h}_{n+m}$
. Thus there are
![]() $\tilde {N}(n+m):= (\unicode{x3bb} _{n+m}+1)K^2$
pre-
$\tilde {N}(n+m):= (\unicode{x3bb} _{n+m}+1)K^2$
pre-
![]() $(n+m)$
-blocks. For every
$(n+m)$
-blocks. For every
![]() $i\in \{ 1,\ldots ,K\} $
each pattern
$i\in \{ 1,\ldots ,K\} $
each pattern
 $\mathtt {A}_{i,j}^{(n+m)}$
,
$\mathtt {A}_{i,j}^{(n+m)}$
,
![]() $j=1,\ldots ,(\unicode{x3bb} _{n+m}+1)K$
, contains each
$j=1,\ldots ,(\unicode{x3bb} _{n+m}+1)K$
, contains each
![]() $(n+m-1)$
-block of type i exactly
$(n+m-1)$
-block of type i exactly
times by the construction in Proposition 6.2.
Lemma 6.9. (Separation and closeness of pre-
 $(n+m)$
-blocks of the same Feldman pattern)
$(n+m)$
-blocks of the same Feldman pattern)
Let
![]() $j\in \{ 1,\ldots ,(\unicode{x3bb} _{n+m}+1)K\} $
and
$j\in \{ 1,\ldots ,(\unicode{x3bb} _{n+m}+1)K\} $
and
![]() $i_{1},i_{2}\in \{ 1,\ldots ,K\} $
,
$i_{1},i_{2}\in \{ 1,\ldots ,K\} $
,
![]() $i_{1}\neq i_{2}$
. For all strings
$i_{1}\neq i_{2}$
. For all strings
![]() $\mathtt {A}$
and
$\mathtt {A}$
and
![]() $\overline {\mathtt {A}}$
of at least
$\overline {\mathtt {A}}$
of at least
![]() $\tilde {h}_{n+m}/e_{n+m-1}$
consecutive symbols in
$\tilde {h}_{n+m}/e_{n+m-1}$
consecutive symbols in
 $\mathtt {A}_{i_{1},j}^{(n+m)}$
and
$\mathtt {A}_{i_{1},j}^{(n+m)}$
and
 $\mathtt {A}_{i_{2},j}^{(n+m)}$
respectively, we have for
$\mathtt {A}_{i_{2},j}^{(n+m)}$
respectively, we have for
![]() $m=2$
,
$m=2$
,
 $$ \begin{align*} \overline{f}(\mathtt{A},\overline{\mathtt{A}})\geq\frac{1}{K}\alpha -\frac{14}{\sqrt{N}}-\frac{2}{TK}-\frac{4}{u_{n+1}}-\frac{2}{e_{n+1}}; \end{align*} $$
$$ \begin{align*} \overline{f}(\mathtt{A},\overline{\mathtt{A}})\geq\frac{1}{K}\alpha -\frac{14}{\sqrt{N}}-\frac{2}{TK}-\frac{4}{u_{n+1}}-\frac{2}{e_{n+1}}; \end{align*} $$
while for
![]() $m\geq 3$
, we have
$m\geq 3$
, we have
![]() $\overline {f}(\mathtt {A},\overline {\mathtt {A}})$
greater than or equal to
$\overline {f}(\mathtt {A},\overline {\mathtt {A}})$
greater than or equal to
 $$ \begin{align*} \beta_{n+m-1}+\frac{1}{K}(\alpha_{n+m-1}-\beta_{n+m-1})-\frac{2}{e_{n+m-2}}-\frac{4}{u_{n+m-1}}-\frac{2}{N(n+m-2)+1}-\frac{2}{e_{n+m-1}}. \end{align*} $$
$$ \begin{align*} \beta_{n+m-1}+\frac{1}{K}(\alpha_{n+m-1}-\beta_{n+m-1})-\frac{2}{e_{n+m-2}}-\frac{4}{u_{n+m-1}}-\frac{2}{N(n+m-2)+1}-\frac{2}{e_{n+m-1}}. \end{align*} $$
For the corresponding strings in the circular system we have
 $$ \begin{align*} \overline{f}(\mathcal{A}_{i_{1},j}^{(n+m)},\mathcal{A}_{i_{2},j}^{(n+m)})\leq\sum_{i=1}^{m-1}\bigg(\frac{4}{l_{n+i}}+\frac{2}{N(n+i-1)+1}\bigg). \end{align*} $$
$$ \begin{align*} \overline{f}(\mathcal{A}_{i_{1},j}^{(n+m)},\mathcal{A}_{i_{2},j}^{(n+m)})\leq\sum_{i=1}^{m-1}\bigg(\frac{4}{l_{n+i}}+\frac{2}{N(n+i-1)+1}\bigg). \end{align*} $$
Proof. The statement in the odometer-based system follows from the first part of Lemma 6.7 and Lemma 6.3 (with
![]() $R=u_{n+m-1}$
) because
$R=u_{n+m-1}$
) because
 $\mathtt {A}_{i_{1},j}^{(n+m)}$
and
$\mathtt {A}_{i_{1},j}^{(n+m)}$
and
 $\mathtt {A}_{i_{2},j}^{(n+m)}$
are constructed as the same Feldman pattern with the grouped
$\mathtt {A}_{i_{2},j}^{(n+m)}$
are constructed as the same Feldman pattern with the grouped
![]() $(n+m-1)$
-blocks of different type but the same pattern as building blocks. This also yields the statement in the circular system as a direct consequence of Lemma 6.8.
$(n+m-1)$
-blocks of different type but the same pattern as building blocks. This also yields the statement in the circular system as a direct consequence of Lemma 6.8.
We will also need a statement on the
![]() $\overline {f}$
distance between different Feldman patterns in the odometer-based system.
$\overline {f}$
distance between different Feldman patterns in the odometer-based system.
Lemma 6.10. (Separation of pre-
 $(n+m)$
-blocks of different Feldman patterns)
$(n+m)$
-blocks of different Feldman patterns)
Let
![]() $j_{1},j_{2}\in \{ 1,\ldots ,(\unicode{x3bb} _{n+m}+1)K\} $
,
$j_{1},j_{2}\in \{ 1,\ldots ,(\unicode{x3bb} _{n+m}+1)K\} $
,
![]() $j_{1}\neq j_{2}$
, and
$j_{1}\neq j_{2}$
, and
![]() $i_{1},i_{2}\in \{ 1,\ldots ,K\} $
. For all strings
$i_{1},i_{2}\in \{ 1,\ldots ,K\} $
. For all strings
![]() $\mathtt {A}$
and
$\mathtt {A}$
and
![]() $\overline {\mathtt {A}}$
of at least
$\overline {\mathtt {A}}$
of at least
![]() $\tilde {h}_{n+m}/{e_{n+m-1}}$
consecutive symbols in
$\tilde {h}_{n+m}/{e_{n+m-1}}$
consecutive symbols in
 $\mathtt {A}_{i_{1},j_1}^{(n+m)}$
and
$\mathtt {A}_{i_{1},j_1}^{(n+m)}$
and
 $\mathtt {A}_{i_{2},j_2}^{(n+m)}$
respectively, we have
$\mathtt {A}_{i_{2},j_2}^{(n+m)}$
respectively, we have
 $$ \begin{align*} &\overline{f}(\mathtt{A},\overline{\mathtt{A}})\\ &\geq \begin{cases} \alpha-\dfrac{14}{\sqrt{N}}-\dfrac{2}{T}-\dfrac{4}{u_{n+1}}-\dfrac{13}{\sqrt{e_{n+1}}} \quad& \text{for } m=2, \\ \alpha_{n+m-1}-\dfrac{2}{e_{n+m-2}}-\dfrac{4}{u_{n+m-1}}-\dfrac{2}{N(n+m-2)+1}-\dfrac{13}{\sqrt{e_{n+m-1}}} \quad& \text{for } m\geq 3. \end{cases} \end{align*} $$
$$ \begin{align*} &\overline{f}(\mathtt{A},\overline{\mathtt{A}})\\ &\geq \begin{cases} \alpha-\dfrac{14}{\sqrt{N}}-\dfrac{2}{T}-\dfrac{4}{u_{n+1}}-\dfrac{13}{\sqrt{e_{n+1}}} \quad& \text{for } m=2, \\ \alpha_{n+m-1}-\dfrac{2}{e_{n+m-2}}-\dfrac{4}{u_{n+m-1}}-\dfrac{2}{N(n+m-2)+1}-\dfrac{13}{\sqrt{e_{n+m-1}}} \quad& \text{for } m\geq 3. \end{cases} \end{align*} $$
Proof. Since we consider different Feldman pattern with the grouped
![]() $(n+m-1)$
-blocks as building blocks, we obtain the result from the second part of Lemma 6.7 and Proposition 6.2 (with
$(n+m-1)$
-blocks as building blocks, we obtain the result from the second part of Lemma 6.7 and Proposition 6.2 (with
![]() $R=u_{n+m-1}$
).
$R=u_{n+m-1}$
).
In the next step, we use these Feldman patterns
 $\mathtt {A}_{i,j}^{(n+m)}$
to define
$\mathtt {A}_{i,j}^{(n+m)}$
to define
![]() $(n+m)$
-blocks for
$(n+m)$
-blocks for
![]() $i=1,\ldots ,K$
and
$i=1,\ldots ,K$
and
![]() $j=1,\ldots ,\unicode{x3bb} _{n+m}$
as in the formula at the beginning of §6.3.2 with
$j=1,\ldots ,\unicode{x3bb} _{n+m}$
as in the formula at the beginning of §6.3.2 with
![]() $n+m-1$
replaced by
$n+m-1$
replaced by
![]() $n+m$
, and an additional marker block
$n+m$
, and an additional marker block
 $\mathtt {B}_{0}^{(n+m)}= \mathtt {A}_{1,\unicode{x3bb} _{n+m}K+1}^{(n+m)}\mathtt {A}_{2,\unicode{x3bb} _{n+m}K+1}^{(n+m)}\ldots \mathtt {A}_{K,\unicode{x3bb} _{n+m}K+1}^{(n+m)}\mathtt {a}_{n+m-1}$
with the marker segment
$\mathtt {B}_{0}^{(n+m)}= \mathtt {A}_{1,\unicode{x3bb} _{n+m}K+1}^{(n+m)}\mathtt {A}_{2,\unicode{x3bb} _{n+m}K+1}^{(n+m)}\ldots \mathtt {A}_{K,\unicode{x3bb} _{n+m}K+1}^{(n+m)}\mathtt {a}_{n+m-1}$
with the marker segment
 $\mathtt {a}_{n+m-1}= (\mathtt {B}_{0}^{(n+m-1)})^{\bar {N}(n+m-1)}$
. We also note that every
$\mathtt {a}_{n+m-1}= (\mathtt {B}_{0}^{(n+m-1)})^{\bar {N}(n+m-1)}$
. We also note that every
![]() $(n+m)$
-block contains exactly one pattern
$(n+m)$
-block contains exactly one pattern
 $\mathtt {A}_{i,j}^{(n+m)}$
of each type
$\mathtt {A}_{i,j}^{(n+m)}$
of each type
![]() $i\in \{ 1,\ldots ,K\} $
and thus it is uniform in the
$i\in \{ 1,\ldots ,K\} $
and thus it is uniform in the
![]() $(n+m-1)$
-blocks. Thus, the inductive step has been accomplished.
$(n+m-1)$
-blocks. Thus, the inductive step has been accomplished.
6.3.3. Final step: construction of
 $(n+m_n)$
-blocks
$(n+m_n)$
-blocks
As foreshadowed in equation (6.10), we follow the inductive construction scheme until
![]() $\beta _{n+m_{n}}>\alpha -({2}/{T})-({\varepsilon }/{2})$
and we have constructed Feldman patterns
$\beta _{n+m_{n}}>\alpha -({2}/{T})-({\varepsilon }/{2})$
and we have constructed Feldman patterns
 $\mathtt {A}_{i,j}^{(n+m_{n})}$
,
$\mathtt {A}_{i,j}^{(n+m_{n})}$
,
![]() $j=1,\ldots ,(\unicode{x3bb} _{n+m_{n}}+1)K$
,
$j=1,\ldots ,(\unicode{x3bb} _{n+m_{n}}+1)K$
,
![]() $i=1,\ldots ,K$
, of length
$i=1,\ldots ,K$
, of length
![]() $\tilde {h}_{n+m_{n}}$
. In particular, we have
$\tilde {h}_{n+m_{n}}$
. In particular, we have
 $$ \begin{align} \overline{f}(\mathtt{A},\overline{\mathtt{A}})\geq\beta_{n+m_{n}}>\alpha-\frac{2}{T}-\frac{\varepsilon}{2} \end{align} $$
$$ \begin{align} \overline{f}(\mathtt{A},\overline{\mathtt{A}})\geq\beta_{n+m_{n}}>\alpha-\frac{2}{T}-\frac{\varepsilon}{2} \end{align} $$
for all strings
![]() $\mathtt {A},\overline {\mathtt {A}}$
of at least
$\mathtt {A},\overline {\mathtt {A}}$
of at least
![]() $\tilde {h}_{n+m_{n}}/e_{n+m_{n}-1}$
consecutive symbols in
$\tilde {h}_{n+m_{n}}/e_{n+m_{n}-1}$
consecutive symbols in
 $\mathtt {A}_{i_{1},j_1}^{(n+m_{n})}$
and
$\mathtt {A}_{i_{1},j_1}^{(n+m_{n})}$
and
 $\mathtt {A}_{i_{2},j_2}^{(n+m_{n})}$
respectively, for
$\mathtt {A}_{i_{2},j_2}^{(n+m_{n})}$
respectively, for
![]() $i_{1}\neq i_{2}$
or
$i_{1}\neq i_{2}$
or
![]() $j_1\neq j_2$
. On the other hand, we have
$j_1\neq j_2$
. On the other hand, we have
 $$ \begin{align} \overline{f}(\mathcal{A}_{i_{1},j}^{(n+m_{n})},\mathcal{A}_{i_{2},j}^{(n+m_{n})})\leq\sum_{i=1}^{m_{n}-1}\bigg(\frac{4}{l_{n+i}}+\frac{2}{N(n+i-1)+1}\bigg) \end{align} $$
$$ \begin{align} \overline{f}(\mathcal{A}_{i_{1},j}^{(n+m_{n})},\mathcal{A}_{i_{2},j}^{(n+m_{n})})\leq\sum_{i=1}^{m_{n}-1}\bigg(\frac{4}{l_{n+i}}+\frac{2}{N(n+i-1)+1}\bigg) \end{align} $$
in the circular system. Moreover, we recall that for every
![]() $i\in \{ 1,\ldots ,K\} $
each pattern
$i\in \{ 1,\ldots ,K\} $
each pattern
 $\mathtt {A}_{i,j}^{(n+m_{n})}$
,
$\mathtt {A}_{i,j}^{(n+m_{n})}$
,
![]() $j=1,\ldots ,(\unicode{x3bb} _{n+m_{n}}+1)K$
, contains each
$j=1,\ldots ,(\unicode{x3bb} _{n+m_{n}}+1)K$
, contains each
![]() $(n+m_{n}-1)$
-block of type i exactly
$(n+m_{n}-1)$
-block of type i exactly

times. In the final step, we define
![]() $K (n+m_{n})$
-blocks as follows (with
$K (n+m_{n})$
-blocks as follows (with
![]() $\unicode{x3bb} =\unicode{x3bb} _{n+m_n}$
):
$\unicode{x3bb} =\unicode{x3bb} _{n+m_n}$
):
 $$ \begin{align*} \mathtt{B}_{1}^{(n+m_{n})}&= \mathtt{A}_{1,1}^{(n+m_{n})}\mathtt{A}_{2,2}^{(n+m_{n})}\ldots\mathtt{A}_{K,K}^{(n+m_{n})}\mathtt{A}_{1,K+1}^{(n+m_{n})}\ldots \mathtt{A}_{K,2K}^{(n+m_{n})}\ldots \mathtt{A}_{K,\unicode{x3bb} K}^{(n+m_{n})}\mathtt{a}_{n+m_n-1},\\ \mathtt{B}_{2}^{(n+m_{n})}&= \mathtt{A}_{2,1}^{(n+m_{n})}\mathtt{A}_{3,2}^{(n+m_{n})}\ldots\mathtt{A}_{1,K}^{(n+m_{n})}\mathtt{A}_{2,K+1}^{(n+m_{n})}\ldots \mathtt{A}_{1,2K}^{(n+m_{n})}\ldots \mathtt{A}_{1,\unicode{x3bb} K}^{(n+m_{n})}\mathtt{a}_{n+m_n-1},\\ \vdots\; & \;\vdots\\ \mathtt{B}_{K}^{(n+m_{n})}&= \mathtt{A}_{K,1}^{(n+m_{n})}\mathtt{A}_{1,2}^{(n+m_{n})}\ldots\mathtt{A}_{K-1,K}^{(n+m_{n})}\mathtt{A}_{K,K+1}^{(n+m_{n})}\ldots \mathtt{A}_{K-1,2K}^{(n+m_{n})}\ldots \mathtt{A}_{K-1,\unicode{x3bb} K}^{(n+m_{n})}\mathtt{a}_{n+m_n-1}, \end{align*} $$
$$ \begin{align*} \mathtt{B}_{1}^{(n+m_{n})}&= \mathtt{A}_{1,1}^{(n+m_{n})}\mathtt{A}_{2,2}^{(n+m_{n})}\ldots\mathtt{A}_{K,K}^{(n+m_{n})}\mathtt{A}_{1,K+1}^{(n+m_{n})}\ldots \mathtt{A}_{K,2K}^{(n+m_{n})}\ldots \mathtt{A}_{K,\unicode{x3bb} K}^{(n+m_{n})}\mathtt{a}_{n+m_n-1},\\ \mathtt{B}_{2}^{(n+m_{n})}&= \mathtt{A}_{2,1}^{(n+m_{n})}\mathtt{A}_{3,2}^{(n+m_{n})}\ldots\mathtt{A}_{1,K}^{(n+m_{n})}\mathtt{A}_{2,K+1}^{(n+m_{n})}\ldots \mathtt{A}_{1,2K}^{(n+m_{n})}\ldots \mathtt{A}_{1,\unicode{x3bb} K}^{(n+m_{n})}\mathtt{a}_{n+m_n-1},\\ \vdots\; & \;\vdots\\ \mathtt{B}_{K}^{(n+m_{n})}&= \mathtt{A}_{K,1}^{(n+m_{n})}\mathtt{A}_{1,2}^{(n+m_{n})}\ldots\mathtt{A}_{K-1,K}^{(n+m_{n})}\mathtt{A}_{K,K+1}^{(n+m_{n})}\ldots \mathtt{A}_{K-1,2K}^{(n+m_{n})}\ldots \mathtt{A}_{K-1,\unicode{x3bb} K}^{(n+m_{n})}\mathtt{a}_{n+m_n-1}, \end{align*} $$
with

We note that each
![]() $(n+m_{n})$
-block contains exactly
$(n+m_{n})$
-block contains exactly
![]() $\unicode{x3bb} _{n+m_n}$
patterns of each type. Hence, it is uniform in the
$\unicode{x3bb} _{n+m_n}$
patterns of each type. Hence, it is uniform in the
![]() $(n+m_{n}-1)$
-blocks. We prove the statement in Proposition 6.5 on the
$(n+m_{n}-1)$
-blocks. We prove the statement in Proposition 6.5 on the
![]() $\overline {f}$
distance in the odometer-based system.
$\overline {f}$
distance in the odometer-based system.
Proof Proof of part (1) of Proposition 6.5
By adding fewer than
![]() $2\tilde {h}_{n+m_n}$
symbols to each
$2\tilde {h}_{n+m_n}$
symbols to each
![]() $\mathtt {B}$
and
$\mathtt {B}$
and
![]() $\overline {\mathtt {B}}$
we can complete any partial pre-
$\overline {\mathtt {B}}$
we can complete any partial pre-
![]() $(n+m_n)$
-blocks at the beginning and end of
$(n+m_n)$
-blocks at the beginning and end of
![]() $\mathtt {B}$
and
$\mathtt {B}$
and
![]() $\overline {\mathtt {B}}$
. This change increases the
$\overline {\mathtt {B}}$
. This change increases the
![]() $\overline {f}$
distance between
$\overline {f}$
distance between
![]() $\mathtt {B}$
and
$\mathtt {B}$
and
![]() $\overline {\mathtt {B}}$
by at most
$\overline {\mathtt {B}}$
by at most

In the next step, we ignore the marker segment
![]() $\mathtt {a}_{n+m_{n}-1}$
which occupies a fraction of
$\mathtt {a}_{n+m_{n}-1}$
which occupies a fraction of
![]() $1/(N(n+m_{n}-1)+1)$
in each
$1/(N(n+m_{n}-1)+1)$
in each
![]() $(n+m_{n})$
-block due to uniformity and so a fraction of at most
$(n+m_{n})$
-block due to uniformity and so a fraction of at most
 $K(N(n+m_{n}-1)+1)^{-1}<e_{n+m_{n}-1}^{-1}$
of the total length of
$K(N(n+m_{n}-1)+1)^{-1}<e_{n+m_{n}-1}^{-1}$
of the total length of
![]() $\mathtt {B}$
and
$\mathtt {B}$
and
![]() $\overline {\mathtt {B}}$
. On the remaining strings all pre-
$\overline {\mathtt {B}}$
. On the remaining strings all pre-
![]() $(n+m_n)$
-blocks are different from each other. Hence, they are at least
$(n+m_n)$
-blocks are different from each other. Hence, they are at least
![]() $\alpha -({2}/{T})-({\varepsilon }/{2})$
apart in
$\alpha -({2}/{T})-({\varepsilon }/{2})$
apart in
![]() $\overline {f}$
on substantial substrings of at least
$\overline {f}$
on substantial substrings of at least
![]() $\tilde {h}_{n+m_{n}}/e_{n+m_{n}-1}$
consecutive symbols by equation (6.18). We apply Corollary 5.5 with
$\tilde {h}_{n+m_{n}}/e_{n+m_{n}-1}$
consecutive symbols by equation (6.18). We apply Corollary 5.5 with
![]() $\tilde {f}=1$
to obtain
$\tilde {f}=1$
to obtain

which yields the claim.
By choosing the circular coefficients
![]() $(l_{n+m})_{m\in \mathbb {N}}$
to grow sufficiently fast as in equation (6.5) we also obtain the second statement in Proposition 6.5.
$(l_{n+m})_{m\in \mathbb {N}}$
to grow sufficiently fast as in equation (6.5) we also obtain the second statement in Proposition 6.5.
Proof Proof of part (2) of Proposition 6.5
Since the marker segments and the used Feldman patterns of the pre-
![]() $(n+m_{n})$
-blocks are aligned and only the used type of blocks differs, we use equation (6.19) to obtain
$(n+m_{n})$
-blocks are aligned and only the used type of blocks differs, we use equation (6.19) to obtain
 $$ \begin{align*} \overline{f}(\mathcal{B}_{i}^{(n+m_{n})},\mathcal{B}_{j}^{(n+m_{n})}) \leq\sum_{i=1}^{m_{n}-1}\frac{4}{l_{n+i}}+\sum_{i=1}^{m_{n}-1}\frac{2}{Ku_{n+i-1}^{2}e_{n+i-1}+1} <\delta \end{align*} $$
$$ \begin{align*} \overline{f}(\mathcal{B}_{i}^{(n+m_{n})},\mathcal{B}_{j}^{(n+m_{n})}) \leq\sum_{i=1}^{m_{n}-1}\frac{4}{l_{n+i}}+\sum_{i=1}^{m_{n}-1}\frac{2}{Ku_{n+i-1}^{2}e_{n+i-1}+1} <\delta \end{align*} $$
with the aid of assumptions (6.1) and (6.5) in the last step.
Hence the proof of Proposition 6.5 has been accomplished.
6.4. Proof of Theorem 6.1
To define the construction sequence for the odometer-based system inductively we choose an increasing sequence
![]() $(K_s)_{s\in \mathbb {N}}$
of positive integers with
$(K_s)_{s\in \mathbb {N}}$
of positive integers with
 $$ \begin{align} \sum_{k\in\mathbb{N}}\frac{15}{\sqrt{K_s}}<\frac{1}{32} \end{align} $$
$$ \begin{align} \sum_{k\in\mathbb{N}}\frac{15}{\sqrt{K_s}}<\frac{1}{32} \end{align} $$
and two decreasing sequences
![]() $(\varepsilon _{s})_{s\in \mathbb {N}}$
and
$(\varepsilon _{s})_{s\in \mathbb {N}}$
and
![]() $(\delta _{s})_{s\in \mathbb {N}}$
of positive real numbers such that
$(\delta _{s})_{s\in \mathbb {N}}$
of positive real numbers such that
![]() $\delta _{s}\searrow 0$
,
$\delta _{s}\searrow 0$
,
![]() $\varepsilon _s <1/(64K_s)$
, and
$\varepsilon _s <1/(64K_s)$
, and
 $$ \begin{align} \sum_{s\in\mathbb{N}}\varepsilon_{s}<\frac{1}{32}. \end{align} $$
$$ \begin{align} \sum_{s\in\mathbb{N}}\varepsilon_{s}<\frac{1}{32}. \end{align} $$
We start by applying Proposition 6.4 on
![]() $K_0+1$
symbols to obtain
$K_0+1$
symbols to obtain
![]() $N(1)+1$
uniform and uniquely readable
$N(1)+1$
uniform and uniquely readable
![]() $1$
-blocks that are
$1$
-blocks that are
 $\alpha _{1}:= \frac 18-13K_0^{-1/2}$
apart in
$\alpha _{1}:= \frac 18-13K_0^{-1/2}$
apart in
![]() $\overline {f}$
on substantial substrings of length at least
$\overline {f}$
on substantial substrings of length at least
![]() $\mathtt {h}_1/K_0$
. Here, the number
$\mathtt {h}_1/K_0$
. Here, the number
![]() $N(1)+1$
is chosen such that it allows the application of the cycling mechanism from Proposition 6.5 to obtain
$N(1)+1$
is chosen such that it allows the application of the cycling mechanism from Proposition 6.5 to obtain
![]() $K_{1}+1\ n_{1}$
-blocks (where
$K_{1}+1\ n_{1}$
-blocks (where
![]() $n_{1}:= 1+m_{1}$
with
$n_{1}:= 1+m_{1}$
with
![]() $m_1$
from Proposition 6.5) that are
$m_1$
from Proposition 6.5) that are
 $\alpha _{2}=\alpha _{1}-2K_0^{-1}-\varepsilon _{0}$
apart on substantial subshifts of length at least
$\alpha _{2}=\alpha _{1}-2K_0^{-1}-\varepsilon _{0}$
apart on substantial subshifts of length at least
![]() $\mathtt {h}_{n_{1}}/(K_{1}+1)$
in the odometer-based system and are
$\mathtt {h}_{n_{1}}/(K_{1}+1)$
in the odometer-based system and are
![]() $\delta _{0}$
-close in the corresponding circular system.
$\delta _{0}$
-close in the corresponding circular system.
We continue by applying Proposition 6.4 on those blocks to obtain sufficiently many
![]() $(n_{1}+1)$
-blocks (which are
$(n_{1}+1)$
-blocks (which are
 $\alpha _{3}=\alpha _{2}-13K_{1}^{-1/2}$
apart on substantial substrings of length at least
$\alpha _{3}=\alpha _{2}-13K_{1}^{-1/2}$
apart on substantial substrings of length at least
![]() $\mathtt {h}_{n_1+1}/K_1$
in the odometer-based system) such that we can apply Proposition 6.5 again to get
$\mathtt {h}_{n_1+1}/K_1$
in the odometer-based system) such that we can apply Proposition 6.5 again to get
![]() $K_{2}+1\ n_{2}$
-blocks (with
$K_{2}+1\ n_{2}$
-blocks (with
![]() $n_{2}:= n_{1}+1+m_{n_{1}+1}$
) that are
$n_{2}:= n_{1}+1+m_{n_{1}+1}$
) that are
 $\alpha _{4}=\alpha _{3}-2K_{1}^{-1}-\varepsilon _{1}$
apart on substantial subshifts of length at least
$\alpha _{4}=\alpha _{3}-2K_{1}^{-1}-\varepsilon _{1}$
apart on substantial subshifts of length at least
![]() $\mathtt {h}_{n_{2}}/(K_{2}+1)$
in the odometer-based system and
$\mathtt {h}_{n_{2}}/(K_{2}+1)$
in the odometer-based system and
![]() $\delta _{1}$
-close in the circular system.
$\delta _{1}$
-close in the circular system.
Continuing like this we produce n-blocks that are at least
 $$ \begin{align*} \frac{1}{8}-\sum_{s\in\mathbb{N}}\bigg(\frac{15}{\sqrt{K_{s}}}+\varepsilon_{s}\bigg)>\frac{1}{16} \end{align*} $$
$$ \begin{align*} \frac{1}{8}-\sum_{s\in\mathbb{N}}\bigg(\frac{15}{\sqrt{K_{s}}}+\varepsilon_{s}\bigg)>\frac{1}{16} \end{align*} $$
apart from each other by the requirements (6.20) and (6.21). Hence, the odometer-based system cannot be loosely Bernoulli by Lemma 3.5, provided that the metric entropy H of the odometer-based system is zero. As in Lemma 4.2, we have the formula
 $$ \begin{align*} H=\lim_{n\to\infty}\frac{N(n)}{\mathtt{h}_{n}}. \end{align*} $$
$$ \begin{align*} H=\lim_{n\to\infty}\frac{N(n)}{\mathtt{h}_{n}}. \end{align*} $$
In our construction of
![]() $(n+1)$
-blocks, we start by producing
$(n+1)$
-blocks, we start by producing
![]() $\tilde {N}(n+1)$
pre-
$\tilde {N}(n+1)$
pre-
![]() $(n+1)$
-blocks of length
$(n+1)$
-blocks of length
 $\tilde {\mathtt {h}}_{n+1}\geq 2^{2\cdot \tilde {N}(n+1)+3}\mathtt {h}_{n}$
. There are fewer
$\tilde {\mathtt {h}}_{n+1}\geq 2^{2\cdot \tilde {N}(n+1)+3}\mathtt {h}_{n}$
. There are fewer
![]() $(n+1)$
-blocks than pre-
$(n+1)$
-blocks than pre-
![]() $(n+1)$
-blocks while the
$(n+1)$
-blocks while the
![]() $\mathtt {h}_{n+1}>\tilde {\mathtt {h}}_{n+1.}$
Therefore
$\mathtt {h}_{n+1}>\tilde {\mathtt {h}}_{n+1.}$
Therefore
 $$ \begin{align*} \frac{\log N(n+1)}{\mathtt{h}_{n+1}}\le\frac{\log\tilde{N}(n+1)}{2^{2\cdot\tilde{N}(n+1)+3}}, \end{align*} $$
$$ \begin{align*} \frac{\log N(n+1)}{\mathtt{h}_{n+1}}\le\frac{\log\tilde{N}(n+1)}{2^{2\cdot\tilde{N}(n+1)+3}}, \end{align*} $$
which converges to zero as n goes to infinity, because
![]() $\lim _{n\to \infty }\tilde {N}(n+1)=\infty .$
Therefore
$\lim _{n\to \infty }\tilde {N}(n+1)=\infty .$
Therefore
![]() $H=0.$
$H=0.$
On the other hand, the
![]() $\overline {f}$
distance between n-blocks in the circular system goes to zero because
$\overline {f}$
distance between n-blocks in the circular system goes to zero because
![]() $\delta _{s}\searrow 0$
. Thus, the odometer-based system is loosely Bernoulli by Lemma 3.5. Since the blocks constructed by Propositions 6.4 and 6.5 satisfy the properties of uniformity and unique readability, our construction sequence satisfies those as well.
$\delta _{s}\searrow 0$
. Thus, the odometer-based system is loosely Bernoulli by Lemma 3.5. Since the blocks constructed by Propositions 6.4 and 6.5 satisfy the properties of uniformity and unique readability, our construction sequence satisfies those as well.
Acknowledgements
We thank M. Foreman and J.-P. Thouvenot for helpful conversations. In particular, we thank Foreman for his patient explanations of his work with B. Weiss during his visit to Indiana University. We are grateful for Thouvenot’s suggestion to use Rothstein’s argument in our positive-entropy example. We thank the referee for helpful comments. P.K. acknowledges financial support from a DFG Forschungsstipendium under grant no. 405305501 and partial support from the visiting research professorship at IU.
Note added in proof: The open questions regarding anti-classification results for Kakutani equivalence mentioned in the introduction were answered recently [Reference Gerber and KundeGK].