No CrossRef data available.
Published online by Cambridge University Press: 18 November 2020
Let
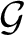 $\mathcal {G}$
be a second countable, Hausdorff topological group. If
$\mathcal {G}$
be a second countable, Hausdorff topological group. If
 $\mathcal {G}$
is locally compact, totally disconnected and T is an expansive automorphism then it is shown that the dynamical system
$\mathcal {G}$
is locally compact, totally disconnected and T is an expansive automorphism then it is shown that the dynamical system
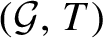 $(\mathcal {G}, T)$
is topologically conjugate to the product of a symbolic full-shift on a finite number of symbols, a totally wandering, countable-state Markov shift and a permutation of a countable coset space of
$(\mathcal {G}, T)$
is topologically conjugate to the product of a symbolic full-shift on a finite number of symbols, a totally wandering, countable-state Markov shift and a permutation of a countable coset space of
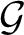 $\mathcal {G}$
that fixes the defining subgroup. In particular if the automorphism is transitive then
$\mathcal {G}$
that fixes the defining subgroup. In particular if the automorphism is transitive then
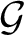 $\mathcal {G}$
is compact and
$\mathcal {G}$
is compact and
 $(\mathcal {G}, T)$
is topologically conjugate to a full-shift on a finite number of symbols.
$(\mathcal {G}, T)$
is topologically conjugate to a full-shift on a finite number of symbols.