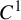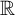1 Introduction
Estimating the Hausdorff dimension of points falling infinitely often in sets
![]() $U_n$
having some algebraic or dynamical meaning is a question which arises naturally in Diophantine approximation as well as in dynamical systems. Given a metric space
$U_n$
having some algebraic or dynamical meaning is a question which arises naturally in Diophantine approximation as well as in dynamical systems. Given a metric space
![]() $(X,d)$
, a measurable mapping
$(X,d)$
, a measurable mapping
![]() $T:X \to X$
, and an ergodic probability measure
$T:X \to X$
, and an ergodic probability measure
![]() $\mu $
, a classical question consists in estimating, for
$\mu $
, a classical question consists in estimating, for
![]() $\mu $
-typical points x, the Hausdorff dimension of points falling infinitely often in balls
$\mu $
-typical points x, the Hausdorff dimension of points falling infinitely often in balls
![]() $B(T^n (x),\phi (n))$
, centered in
$B(T^n (x),\phi (n))$
, centered in
![]() $T^n (x)$
and with radius
$T^n (x)$
and with radius
![]() $\phi (n).$
Such problems have been studied for instance in [Reference Allen and Bárány1, Reference Baker2, Reference Daviaud10, Reference Fan, Schmeling and Troubetzkoy17, Reference Hill and Velani23, Reference Liao and Seuret27, Reference Persson and Rams30] and are called ‘dynamical Diophantine approximation problems’.
$\phi (n).$
Such problems have been studied for instance in [Reference Allen and Bárány1, Reference Baker2, Reference Daviaud10, Reference Fan, Schmeling and Troubetzkoy17, Reference Hill and Velani23, Reference Liao and Seuret27, Reference Persson and Rams30] and are called ‘dynamical Diophantine approximation problems’.
Estimating these dimensions often relies on establishing mass transference principles for the ergodic probability measure
![]() $\mu $
. Given a sequence of balls
$\mu $
. Given a sequence of balls
![]() $(B_n :=B(x_n, r_n))_{n\in \mathbb {N}}$
, these theorems usually aim at giving lower bounds for the dimension of sets of points of the form
$(B_n :=B(x_n, r_n))_{n\in \mathbb {N}}$
, these theorems usually aim at giving lower bounds for the dimension of sets of points of the form
![]() $\limsup _{n\rightarrow +\infty }U_n$
, where
$\limsup _{n\rightarrow +\infty }U_n$
, where
![]() $U_n \subset B_n$
(typically,
$U_n \subset B_n$
(typically,
![]() $U_n =B_n ^{\delta }=B(x_n ,r_n ^{\delta })$
), provided that the sequence of balls
$U_n =B_n ^{\delta }=B(x_n ,r_n ^{\delta })$
), provided that the sequence of balls
![]() $(B_n)_{n\in \mathbb {N}}$
satisfies
$(B_n)_{n\in \mathbb {N}}$
satisfies
![]() $\mu (\limsup _{n\rightarrow +\infty }B_n)=1.$
$\mu (\limsup _{n\rightarrow +\infty }B_n)=1.$
Let
![]() $m\geq 2$
be an integer and
$m\geq 2$
be an integer and
![]() $S=\{f_1 ,\ldots ,f_m\}$
be a weakly conformal family of
$S=\{f_1 ,\ldots ,f_m\}$
be a weakly conformal family of
![]() $m C^{1}$
contracting maps from
$m C^{1}$
contracting maps from
![]() $\mathbb {R}^d \to \mathbb {R}^d$
(see Definition 2.4). Denote by K the attractor of S, that is, the unique non-empty compact set satisfying
$\mathbb {R}^d \to \mathbb {R}^d$
(see Definition 2.4). Denote by K the attractor of S, that is, the unique non-empty compact set satisfying
![]() $K=\bigcup _{i=1}^m f_i (K), \Lambda =\{1,\ldots ,m\}$
,
$K=\bigcup _{i=1}^m f_i (K), \Lambda =\{1,\ldots ,m\}$
,
![]() $\Lambda ^* =\bigcup _{k\geq 0}\Lambda ^k$
, and, for
$\Lambda ^* =\bigcup _{k\geq 0}\Lambda ^k$
, and, for
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
![]() $\underline {i}=(i_1 ,\ldots ,i_k)\in \Lambda ^k$
, write
$\underline {i}=(i_1 ,\ldots ,i_k)\in \Lambda ^k$
, write
![]() $f_{\underline {i}}=f_{i_1}\circ \cdots \circ f_{i_k}.$
$f_{\underline {i}}=f_{i_1}\circ \cdots \circ f_{i_k}.$
In this article, we prove that if
![]() $\dim _H (K)=\dim (S)$
, where
$\dim _H (K)=\dim (S)$
, where
![]() $\dim (S)$
is the conformality dimension, defined by Definition 2.8, then for any
$\dim (S)$
is the conformality dimension, defined by Definition 2.8, then for any
![]() $x_0\in K$
, for any
$x_0\in K$
, for any
![]() $\delta \geq 1$
,
$\delta \geq 1$
,
 $$ \begin{align} \dim_H \Big(\!\limsup_{\underline{i}\in\Lambda^{*}}B(f_{\underline{i}}(x_0),\vert f_{\underline{i}}(K)\vert^ { \delta})\Big)=\frac{\dim_H (K)}{\delta}. \end{align} $$
$$ \begin{align} \dim_H \Big(\!\limsup_{\underline{i}\in\Lambda^{*}}B(f_{\underline{i}}(x_0),\vert f_{\underline{i}}(K)\vert^ { \delta})\Big)=\frac{\dim_H (K)}{\delta}. \end{align} $$
In other words, the set of points x for which the orbit of
![]() $x_0$
,
$x_0$
,
![]() $(f_{\underline {i}}(x_0) )_{\underline {i} \in \Lambda ^*}$
, satisfies infinitely many often that
$(f_{\underline {i}}(x_0) )_{\underline {i} \in \Lambda ^*}$
, satisfies infinitely many often that
![]() $d(x,f_{\underline {i}}(x_0))\leq \vert f_{\underline {i}}(K)\vert ^ { \delta }$
, has dimension
$d(x,f_{\underline {i}}(x_0))\leq \vert f_{\underline {i}}(K)\vert ^ { \delta }$
, has dimension
![]() $ {\dim _H (K)}/{\delta }.$
We mention that this dimension result regarding this dynamical Diophantine approximation problem can be deduced from the mass transference principle [Reference Beresnevitch and Velani7] in the case where the iterated function system (IFS) is conformal and satisfies the open set condition. One emphasizes that the condition
$ {\dim _H (K)}/{\delta }.$
We mention that this dimension result regarding this dynamical Diophantine approximation problem can be deduced from the mass transference principle [Reference Beresnevitch and Velani7] in the case where the iterated function system (IFS) is conformal and satisfies the open set condition. One emphasizes that the condition
![]() $\dim _H (K)=\dim (S)$
is much weaker than the open set condition. For instance, this condition is satisfied for self-similar systems in
$\dim _H (K)=\dim (S)$
is much weaker than the open set condition. For instance, this condition is satisfied for self-similar systems in
![]() $\mathbb {R}$
, as soon as Hochman’s exponential separation condition (given by [Reference Hochman24, Theorem 1.4]) is verified, which provides a large number of examples.
$\mathbb {R}$
, as soon as Hochman’s exponential separation condition (given by [Reference Hochman24, Theorem 1.4]) is verified, which provides a large number of examples.
An other classical problem in Diophantine approximation on fractals is the so-called shrinking target problem, which was originally introduced by Hill and Velani in [Reference Hill and Velani23]. Consider
![]() $S=\{f_1,\ldots ,f_m\}$
as a self-similar IFS satisfying the strong separation condition and let K be its attractor. It is classical that K can be viewed as the attractor of an expending map. This is done by defining
$S=\{f_1,\ldots ,f_m\}$
as a self-similar IFS satisfying the strong separation condition and let K be its attractor. It is classical that K can be viewed as the attractor of an expending map. This is done by defining
![]() $F:K\to K$
by setting
$F:K\to K$
by setting
Let
![]() $\phi :\mathbb {N}\to \mathbb {R}^+$
be a mapping such that
$\phi :\mathbb {N}\to \mathbb {R}^+$
be a mapping such that
![]() $\phi (n)\to 0,$
then the shrinking target set associated with
$\phi (n)\to 0,$
then the shrinking target set associated with
![]() $x_0 \in K, F$
, and
$x_0 \in K, F$
, and
![]() $\phi $
is defined as
$\phi $
is defined as
Writing
![]() $0<c_i<1$
as the contraction ratio of
$0<c_i<1$
as the contraction ratio of
![]() $f_i,$
one can write
$f_i,$
one can write
This naturally leads to further investigate the dimension of limsup sets generated by balls of the form
![]() $B(f_{\underline {i}}(x_0),\vert f_{\underline {i}}(K)\vert \phi (\vert \underline {i}\vert )).$
In the case where the IFS satisfies the open set condition, the dimension of such sets was computed by Hill and Velani in [Reference Hill and Velani23], and the Hausdorff measure by Allen and Barany [Reference Allen and Bárány1]. In this article, we extend the dimension result established in [Reference Hill and Velani23] to a large class of overlapping conformal IFSs.
$B(f_{\underline {i}}(x_0),\vert f_{\underline {i}}(K)\vert \phi (\vert \underline {i}\vert )).$
In the case where the IFS satisfies the open set condition, the dimension of such sets was computed by Hill and Velani in [Reference Hill and Velani23], and the Hausdorff measure by Allen and Barany [Reference Allen and Bárány1]. In this article, we extend the dimension result established in [Reference Hill and Velani23] to a large class of overlapping conformal IFSs.
As an application of our approach, a complement of some results established in [Reference Baker2] are also given (see Theorem 3.3).
An important tool to establish equation (1) is Theorem 5.11, which is a mass transference principle for projection of quasi-Bernoulli measures (without assuming any separation condition on the underlying IFS) and strongly relies on the techniques developed in [Reference Daviaud10].
Before stating our main results, we make some general recalls about contracting iterated function systems. We also recall some known results in the case were the IFS is weakly conformal.
2 Recalls on geometric measure theory and definition of weakly conformal IFSs
Let us start with some notation.
Let
![]() $d \in \mathbb {N}$
. For
$d \in \mathbb {N}$
. For
![]() $x\in \mathbb {R}^{d}$
,
$x\in \mathbb {R}^{d}$
,
![]() $r>0$
,
$r>0$
,
![]() $B(x,r)$
stands for the closed ball of (
$B(x,r)$
stands for the closed ball of (
![]() $\mathbb {R}^{d},\| \ \ \|_{\infty }$
) of center x and radius r. Given a ball B,
$\mathbb {R}^{d},\| \ \ \|_{\infty }$
) of center x and radius r. Given a ball B,
![]() $\vert B\vert $
stands for the diameter of B. For
$\vert B\vert $
stands for the diameter of B. For
![]() $t\geq 0$
,
$t\geq 0$
,
![]() $\delta \in \mathbb {R}$
, and
$\delta \in \mathbb {R}$
, and
![]() $B=B(x,r)$
,
$B=B(x,r)$
,
![]() $t B$
stands for
$t B$
stands for
![]() $B(x,t r)$
, that is, the ball with same center as B and radius multiplied by t, and the
$B(x,t r)$
, that is, the ball with same center as B and radius multiplied by t, and the
![]() $\delta $
-contracted ball
$\delta $
-contracted ball
![]() $B^{\delta }$
is defined by
$B^{\delta }$
is defined by
![]() $B^{\delta }=B(x ,r^{\delta })$
.
$B^{\delta }=B(x ,r^{\delta })$
.
Given a set
![]() $E\subset \mathbb {R}^d$
,
$E\subset \mathbb {R}^d$
, ![]() stands for the interior of the E,
stands for the interior of the E,
![]() $\overline {E}$
its closure, and
$\overline {E}$
its closure, and ![]() its boundary. If E is a Borel subset of
its boundary. If E is a Borel subset of
![]() $\mathbb {R}^d$
, its Borel
$\mathbb {R}^d$
, its Borel
![]() $\sigma $
-algebra is denoted by
$\sigma $
-algebra is denoted by
![]() $\mathcal B(E)$
.
$\mathcal B(E)$
.
Given a topological space X, the Borel
![]() $\sigma $
-algebra of X is denoted
$\sigma $
-algebra of X is denoted
![]() $\mathcal {B}(X)$
and the space of probability measure on
$\mathcal {B}(X)$
and the space of probability measure on
![]() $\mathcal {B}(X)$
is denoted
$\mathcal {B}(X)$
is denoted
![]() $\mathcal {M}(X).$
$\mathcal {M}(X).$
The d-dimensional Lebesgue measure on
![]() $(\mathbb R^d,\mathcal {B}(\mathbb {R}^d))$
is denoted by
$(\mathbb R^d,\mathcal {B}(\mathbb {R}^d))$
is denoted by
![]() $\mathcal {L}^d$
.
$\mathcal {L}^d$
.
For
![]() $\mu \in \mathcal {M}(\mathbb {R}^d)$
,
$\mu \in \mathcal {M}(\mathbb {R}^d)$
,
![]() ${\mathrm {supp}}(\mu )=\{x\in [0,1]: \ \text { for all } r>0, \ \mu (B(x,r))>0\}$
is the topological support of
${\mathrm {supp}}(\mu )=\{x\in [0,1]: \ \text { for all } r>0, \ \mu (B(x,r))>0\}$
is the topological support of
![]() $\mu $
.
$\mu $
.
Given
![]() $E\subset \mathbb {R}^d$
,
$E\subset \mathbb {R}^d$
,
![]() $\dim _{H}(E)$
and
$\dim _{H}(E)$
and
![]() $\dim _{P}(E)$
denote respectively the Hausdorff and the packing dimension of E.
$\dim _{P}(E)$
denote respectively the Hausdorff and the packing dimension of E.
2.1 Dimension of measures and Hausdorff content
Definition 2.1. Let
![]() $\zeta :\mathbb {R}^{+}\mapsto \mathbb {R}^+$
. Suppose that
$\zeta :\mathbb {R}^{+}\mapsto \mathbb {R}^+$
. Suppose that
![]() $\zeta $
is increasing in a neighborhood of
$\zeta $
is increasing in a neighborhood of
![]() $0$
and
$0$
and
![]() $\zeta (0)=0$
. The Hausdorff outer measure at scale
$\zeta (0)=0$
. The Hausdorff outer measure at scale
![]() $t\in (0,+\infty ]$
associated with the gauge
$t\in (0,+\infty ]$
associated with the gauge
![]() $\zeta $
of a set E is defined by
$\zeta $
of a set E is defined by
 $$ \begin{align} \mathcal{H}^{\zeta}_t (E)=\inf \bigg\{\!\sum_{n\in\mathbb{N}}\zeta (\vert B_n\vert) : \, \vert B_n \vert \leq t, \ B_n \text{ closed ball and } E\subset \bigcup_{n\in \mathbb{N}}B_n\bigg\}. \end{align} $$
$$ \begin{align} \mathcal{H}^{\zeta}_t (E)=\inf \bigg\{\!\sum_{n\in\mathbb{N}}\zeta (\vert B_n\vert) : \, \vert B_n \vert \leq t, \ B_n \text{ closed ball and } E\subset \bigcup_{n\in \mathbb{N}}B_n\bigg\}. \end{align} $$
The Hausdorff measure associated with
![]() $\zeta $
of a set E is defined by
$\zeta $
of a set E is defined by
For
![]() $t\in (0,+\infty ]$
,
$t\in (0,+\infty ]$
,
![]() $s\geq 0$
, and
$s\geq 0$
, and
![]() $\zeta :x\mapsto x^s$
, one simply uses the usual notation
$\zeta :x\mapsto x^s$
, one simply uses the usual notation
![]() $\mathcal {H}^{\zeta }_t (E)=\mathcal {H}^{s}_t (E)$
and
$\mathcal {H}^{\zeta }_t (E)=\mathcal {H}^{s}_t (E)$
and
![]() $\mathcal {H}^{\zeta } (E)=\mathcal {H}^{s} (E)$
, and these measures are called s-dimensional Hausdorff outer measure at scale
$\mathcal {H}^{\zeta } (E)=\mathcal {H}^{s} (E)$
, and these measures are called s-dimensional Hausdorff outer measure at scale
![]() $t\in (0,+\infty ]$
and s-dimensional Hausdorff measure, respectively. Thus,
$t\in (0,+\infty ]$
and s-dimensional Hausdorff measure, respectively. Thus,
 $$ \begin{align} \mathcal{H}^{s}_{t}(E)=\inf \bigg\{\!\sum_{n\in\mathbb{N}}\vert B_n\vert^s : \, \vert B_n \vert \leq t, \ B_n \text{ closed ball and } E\subset \bigcup_{n\in \mathbb{N}}B_n\bigg\}. \end{align} $$
$$ \begin{align} \mathcal{H}^{s}_{t}(E)=\inf \bigg\{\!\sum_{n\in\mathbb{N}}\vert B_n\vert^s : \, \vert B_n \vert \leq t, \ B_n \text{ closed ball and } E\subset \bigcup_{n\in \mathbb{N}}B_n\bigg\}. \end{align} $$
The quantity
![]() $\mathcal {H}^{s}_{\infty }(E)$
(obtained for
$\mathcal {H}^{s}_{\infty }(E)$
(obtained for
![]() $t=+\infty $
) is called the s-dimensional Hausdorff content of the set E.
$t=+\infty $
) is called the s-dimensional Hausdorff content of the set E.
Definition 2.2. Let
![]() $\mu \in \mathcal {M}(\mathbb {R}^d)$
. For
$\mu \in \mathcal {M}(\mathbb {R}^d)$
. For
![]() $x\in {\mathrm {supp}}(\mu )$
, the lower and upper local dimensions of
$x\in {\mathrm {supp}}(\mu )$
, the lower and upper local dimensions of
![]() $\mu $
at x are defined as
$\mu $
at x are defined as
Then, the lower and upper Hausdorff dimensions of
![]() $\mu $
are defined by
$\mu $
are defined by
respectively.
It is known (for more details, see [Reference Falconer16]) that
 $$ \begin{align*} \begin{split} \underline{\dim}_H(\mu)&=\inf\{\dim_{H}(E): E\in\mathcal{B}(\mathbb{R}^d),\, \mu(E)>0\}, \\ \overline{\dim}_P (\mu)&=\inf\{\dim_P(E): E\in\mathcal{B}(\mathbb{R}^d),\, \mu(E)=1\}. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \underline{\dim}_H(\mu)&=\inf\{\dim_{H}(E): E\in\mathcal{B}(\mathbb{R}^d),\, \mu(E)>0\}, \\ \overline{\dim}_P (\mu)&=\inf\{\dim_P(E): E\in\mathcal{B}(\mathbb{R}^d),\, \mu(E)=1\}. \end{split} \end{align*} $$
When
![]() $\underline \dim _H(\mu )=\overline \dim _P(\mu )$
, this common value is simply denoted by
$\underline \dim _H(\mu )=\overline \dim _P(\mu )$
, this common value is simply denoted by
![]() $\dim (\mu )$
and
$\dim (\mu )$
and
![]() $\mu $
is said to be exact dimensional.
$\mu $
is said to be exact dimensional.
2.2 Weakly conformal IFS
2.2.1 Generalities about contracting IFS
Let
![]() $m\geq 2$
be an integer. An IFS is a set
$m\geq 2$
be an integer. An IFS is a set
![]() $S=\{f_1,\ldots ,f_m\}$
of mappings
$S=\{f_1,\ldots ,f_m\}$
of mappings
![]() $f_i:X \to X$
, where
$f_i:X \to X$
, where
![]() $X\subset \mathbb {R}^d$
is a closed set. Moreover, one says that f is differentiable on X if there exists an open set
$X\subset \mathbb {R}^d$
is a closed set. Moreover, one says that f is differentiable on X if there exists an open set
![]() $U\supset X$
on which f is differentiable.
$U\supset X$
on which f is differentiable.
Given an open set
![]() $U \subset \mathbb {R}^d$
and
$U \subset \mathbb {R}^d$
and
![]() $f:U\to \mathbb {R}^d$
a differentiable map, for any
$f:U\to \mathbb {R}^d$
a differentiable map, for any
![]() $x\in U$
:
$x\in U$
:
-
•
 $f'(x)$
is the differential of f at x;
$f'(x)$
is the differential of f at x; -
• let
 $k\in \mathbb {N}$
be an integer, we write
$k\in \mathbb {N}$
be an integer, we write
 $\mathcal {L}(\mathbb {R}^k,\mathbb {R}^d)$
the set of linear maps from
$\mathcal {L}(\mathbb {R}^k,\mathbb {R}^d)$
the set of linear maps from
 $\mathbb {R}^k$
to
$\mathbb {R}^k$
to
 $\mathbb {R}^d.$
For
$\mathbb {R}^d.$
For
 $\ell \in \mathcal {L}(\mathbb {R}^k,\mathbb {R}^d)$
, one denotes (6)
$\ell \in \mathcal {L}(\mathbb {R}^k,\mathbb {R}^d)$
, one denotes (6) $$ \begin{align} \| \ell\| =\max_{x\in\mathbb{R}^k \neq 0}\frac{\|\ell(x)\|_{\infty}}{ \| x\|_{\infty}}\quad\text{and}\quad \|{\ell}\| \ =\min_{x\in\mathbb{R}^k \neq 0}\frac{\|\ell(x)\|_{\infty}}{ \| x\|_{\infty}}. \end{align} $$
$$ \begin{align} \| \ell\| =\max_{x\in\mathbb{R}^k \neq 0}\frac{\|\ell(x)\|_{\infty}}{ \| x\|_{\infty}}\quad\text{and}\quad \|{\ell}\| \ =\min_{x\in\mathbb{R}^k \neq 0}\frac{\|\ell(x)\|_{\infty}}{ \| x\|_{\infty}}. \end{align} $$
Let us recall the following result.
Proposition 2.3. (Hutchinson [Reference Hutchinson25])
Let
![]() $m \geq 2$
be an integer,
$m \geq 2$
be an integer,
![]() $X\subset \mathbb {R}^d$
a closed set, and
$X\subset \mathbb {R}^d$
a closed set, and
![]() $S=\{f_1,\ldots ,f_m\}$
a system of
$S=\{f_1,\ldots ,f_m\}$
a system of
![]() $C^1$
maps from X to
$C^1$
maps from X to
![]() $X.$
Assume that S is uniformly contracting, i.e.,
$X.$
Assume that S is uniformly contracting, i.e.,
Then, there exists a unique non-empty compact set K satisfying
Moreover, for any
![]() $(p_1,\ldots ,p_m)\in (0,1)^m$
, there exists a unique measure
$(p_1,\ldots ,p_m)\in (0,1)^m$
, there exists a unique measure
![]() $\mu \in \mathcal {M}(\mathbb {R}^d)$
supported on K satisfying
$\mu \in \mathcal {M}(\mathbb {R}^d)$
supported on K satisfying
From now on, an IFS designates a uniformly contracting system of
![]() $C^1$
maps.
$C^1$
maps.
The following notation is used throughout the manuscript.
-
•
 $\Lambda (S)=\{1,\ldots ,m\}$
and
$\Lambda (S)=\{1,\ldots ,m\}$
and
 $\Lambda (S)^{*}=\bigcup _{k\geq 0}\Lambda (S)^k$
. When there is no ambiguity on the system S involved, one simply writes
$\Lambda (S)^{*}=\bigcup _{k\geq 0}\Lambda (S)^k$
. When there is no ambiguity on the system S involved, one simply writes
 $\Lambda (S)=\Lambda .$
$\Lambda (S)=\Lambda .$
-
•
 $K_{S}$
denotes the attractor of S (or simply K when the context is clear).
$K_{S}$
denotes the attractor of S (or simply K when the context is clear). -
• For
 $\underline {i}=(i_1,\ldots ,i_k)\in \Lambda ^{k}$
, the cylinder
$\underline {i}=(i_1,\ldots ,i_k)\in \Lambda ^{k}$
, the cylinder
 $[\underline {i}]$
is defined by
$[\underline {i}]$
is defined by  $$ \begin{align*}[\underline{i}]=\{(i_1,\ldots,i_k,x_1,x_2,\ldots):(x_1,x_2,\ldots)\in\Lambda^{\mathbb{N}}\}.\end{align*} $$
$$ \begin{align*}[\underline{i}]=\{(i_1,\ldots,i_k,x_1,x_2,\ldots):(x_1,x_2,\ldots)\in\Lambda^{\mathbb{N}}\}.\end{align*} $$
Moreover, if
 $(\alpha _n)_{n\in \mathbb {N}}$
is a sequence of real numbers, one sets and
$(\alpha _n)_{n\in \mathbb {N}}$
is a sequence of real numbers, one sets and $$ \begin{align*}\alpha_{\underline{i}}=\alpha_{i_1}\times \cdots \times \alpha_{i_k}\end{align*} $$
For example, given the probability vector
$$ \begin{align*}\alpha_{\underline{i}}=\alpha_{i_1}\times \cdots \times \alpha_{i_k}\end{align*} $$
For example, given the probability vector $$ \begin{align*}f_{\underline{i}}=f_{i_1}\circ\cdots \circ f_{i_k}.\end{align*} $$
$$ \begin{align*}f_{\underline{i}}=f_{i_1}\circ\cdots \circ f_{i_k}.\end{align*} $$
 $(p_1,\ldots ,p_m), p_{\underline {i}}=p_{i_1}\times \cdots \times p_{i_k}.$
$(p_1,\ldots ,p_m), p_{\underline {i}}=p_{i_1}\times \cdots \times p_{i_k}.$
-
• The set
 $\Lambda ^{\mathbb {N}}$
is endowed with the topology generated by the cylinders. The set of probability measures on the Borel sets with respect to this topology is denoted
$\Lambda ^{\mathbb {N}}$
is endowed with the topology generated by the cylinders. The set of probability measures on the Borel sets with respect to this topology is denoted
 $\mathcal {M}(\Lambda ^{\mathbb {N}})$
.
$\mathcal {M}(\Lambda ^{\mathbb {N}})$
. -
• The shift operator
 $\sigma :\Lambda ^{\mathbb {N}}\to \Lambda ^{\mathbb {N}}$
is defined for any
$\sigma :\Lambda ^{\mathbb {N}}\to \Lambda ^{\mathbb {N}}$
is defined for any
 $(i_1,i_2,\ldots )\in \Lambda ^{\mathbb {N}}$
by (8)
$(i_1,i_2,\ldots )\in \Lambda ^{\mathbb {N}}$
by (8) $$ \begin{align} \sigma((i_1,i_2,\ldots))=(i_2,i_3,\ldots). \end{align} $$
$$ \begin{align} \sigma((i_1,i_2,\ldots))=(i_2,i_3,\ldots). \end{align} $$
-
• The canonical projection of
 $\Lambda ^{\mathbb {N}}$
on K will be denoted
$\Lambda ^{\mathbb {N}}$
on K will be denoted
 $\pi _{ \Lambda }$
(or simply
$\pi _{ \Lambda }$
(or simply
 $\pi $
when there is no ambiguity) and, fixing any
$\pi $
when there is no ambiguity) and, fixing any
 $x\in K,$
is defined, for any
$x\in K,$
is defined, for any
 $(i_1,i_2,\ldots .)\in \Lambda ^{\mathbb {N}}$
, by (9)It is easily verified that
$(i_1,i_2,\ldots .)\in \Lambda ^{\mathbb {N}}$
, by (9)It is easily verified that $$ \begin{align} K\ni\pi((i_1,\ldots))=\lim_{k\rightarrow+\infty}f_{i_1}\circ\cdots \circ f_{i_k}(x). \end{align} $$
$$ \begin{align} K\ni\pi((i_1,\ldots))=\lim_{k\rightarrow+\infty}f_{i_1}\circ\cdots \circ f_{i_k}(x). \end{align} $$
 $\pi $
is independent of the choice of
$\pi $
is independent of the choice of
 $x.$
$x.$
2.2.2 Weakly conformal IFS and pressure function associated with weakly conformal IFSs
Let us recall the definition of a weakly conformal map.
Definition 2.4. [Reference Feng and Hu19]
Let
![]() $m \geq 2$
be an integer,
$m \geq 2$
be an integer,
![]() $U\subset \mathbb {R}^d$
an open set,
$U\subset \mathbb {R}^d$
an open set,
![]() $S=\{f_i\}_{i=1}^m$
, where
$S=\{f_i\}_{i=1}^m$
, where
![]() $f_i:U\to U$
is a
$f_i:U\to U$
is a
![]() $C^{1}$
contraction and K the attractor of S.
$C^{1}$
contraction and K the attractor of S.
One says that S is weakly conformal when, recalling equation (6),
 $$ \begin{align} \lim_{k\rightarrow+\infty}\frac{\sup_{(x_i)_{i\in\mathbb{N}}\in\{1,\ldots,m\}^{\mathbb{N}}}(\log \| f_{(x_1 ,\ldots,x_k)}^{\prime}(\pi (\sigma^k (x)))\|-\log \| f_{(x_1 ,\ldots,x_k)}^{\prime}(\pi (\sigma^k (x)))\| )}{k}=0. \end{align} $$
$$ \begin{align} \lim_{k\rightarrow+\infty}\frac{\sup_{(x_i)_{i\in\mathbb{N}}\in\{1,\ldots,m\}^{\mathbb{N}}}(\log \| f_{(x_1 ,\ldots,x_k)}^{\prime}(\pi (\sigma^k (x)))\|-\log \| f_{(x_1 ,\ldots,x_k)}^{\prime}(\pi (\sigma^k (x)))\| )}{k}=0. \end{align} $$
In this case, a measure defined by equation (7) is called a weakly conformal measure.
Example 2.5.
-
• If the maps
 $f_1 ,\ldots ,f_m$
are affine similarities or conformal maps (i.e., verify
$f_1 ,\ldots ,f_m$
are affine similarities or conformal maps (i.e., verify
 $\| f^{\prime }(x)(y)\|=\| f^{\prime }(x)\| \cdot \| y\|$
for every
$\| f^{\prime }(x)(y)\|=\| f^{\prime }(x)\| \cdot \| y\|$
for every
 $x\in U,y\in \mathbb {R}^d$
), the system
$x\in U,y\in \mathbb {R}^d$
), the system
 $S=\{f_1,\ldots ,f_m\}$
is weakly conformal. In this case, the IFS is called self-similar or self-conformal and the measures satisfying equation (7) are respectively called self-similar and self-conformal measures. Note that this class of IFSs contains, for instance, every system of holomorphic contracting mappings.
$S=\{f_1,\ldots ,f_m\}$
is weakly conformal. In this case, the IFS is called self-similar or self-conformal and the measures satisfying equation (7) are respectively called self-similar and self-conformal measures. Note that this class of IFSs contains, for instance, every system of holomorphic contracting mappings. -
• Assume that for any
 $1\leq i\leq m, f_i: \mathbb {R}^d \to \mathbb {R}^d$
is defined by
$1\leq i\leq m, f_i: \mathbb {R}^d \to \mathbb {R}^d$
is defined by
 $f_i(x)=A_i x +b_i ,$
where for any
$f_i(x)=A_i x +b_i ,$
where for any
 $1\leq i\leq m$
,
$1\leq i\leq m$
,
 $b_i \in \mathbb {R}^d$
and
$b_i \in \mathbb {R}^d$
and
 $A_i \in GL_d (\mathbb {R})$
has its eigenvalues equal in modulus to
$A_i \in GL_d (\mathbb {R})$
has its eigenvalues equal in modulus to
 $0<r_i<1$
, and for any
$0<r_i<1$
, and for any
 $1 \leq i,j \leq m$
,
$1 \leq i,j \leq m$
,
 $A_i A_j=A_j A_i$
. Then,
$A_i A_j=A_j A_i$
. Then,
 $S=\{f_1,\ldots ,f_m\}$
is weakly conformal.
$S=\{f_1,\ldots ,f_m\}$
is weakly conformal.
The pressure function associated with a weakly conformal IFS is naturally related to the dimension of the attractor. It is defined by the following proposition.
Proposition 2.6. Let
![]() $m\geq 2$
be an integer,
$m\geq 2$
be an integer,
![]() $S=\{f_1 ,\ldots ,f_m\}$
be a
$S=\{f_1 ,\ldots ,f_m\}$
be a
![]() $C^{1}$
weakly conformal IFS, and let K be its attractor.
$C^{1}$
weakly conformal IFS, and let K be its attractor.
Let us fix
![]() $s\geq 0$
and
$s\geq 0$
and
![]() $z\in K.$
The following quantity is well defined and independent of the choice of
$z\in K.$
The following quantity is well defined and independent of the choice of
![]() $z:$
$z:$
 $$ \begin{align} P_z(s)=\lim_{k\rightarrow+\infty}\frac{1}{k}\log \sum_{\underline{i}\in \Lambda^k}\| f_{\underline{i}}^{\prime}(z)\|^s. \end{align} $$
$$ \begin{align} P_z(s)=\lim_{k\rightarrow+\infty}\frac{1}{k}\log \sum_{\underline{i}\in \Lambda^k}\| f_{\underline{i}}^{\prime}(z)\|^s. \end{align} $$
Remark 2.7. Let us mention that the proof of Proposition 2.6 is very standard and does not diverge much from the standard proofs made in [Reference Bowen8, Reference Ruelle34], but strictly speaking, due to the weakly conformal settings, unfortunately, one cannot recover the result from these references. So, for the sake of completeness, a proof is given in §4.
Since
![]() $P_z(s) $
does not depend on z, one writes
$P_z(s) $
does not depend on z, one writes
 $$ \begin{align*}P_z (s)=P(s)=\lim_{k\rightarrow+\infty}\frac{1}{k}\log\bigg(\!\sum_{\underline{i}\in\Lambda^k}\vert f_{\underline{i}}(K)\vert ^s\bigg).\end{align*} $$
$$ \begin{align*}P_z (s)=P(s)=\lim_{k\rightarrow+\infty}\frac{1}{k}\log\bigg(\!\sum_{\underline{i}\in\Lambda^k}\vert f_{\underline{i}}(K)\vert ^s\bigg).\end{align*} $$
As said above, the pressure function is naturally connected to the dimension of the attractor K associated with the underlying IFS. More precisely, the following quantity is a natural candidate to be the Hausdorff dimension of K.
Definition 2.8. Let
![]() $m\geq 2$
be an integer. Let
$m\geq 2$
be an integer. Let
![]() $S=\{f_1 ,\ldots ,f_m\}$
be a
$S=\{f_1 ,\ldots ,f_m\}$
be a
![]() $C^{1}$
weakly conformal IFS and K its attractor.
$C^{1}$
weakly conformal IFS and K its attractor.
The unique real number
![]() $\dim (S)$
satisfying
$\dim (S)$
satisfying
![]() $P(\dim (S))=0$
is called the conformality dimension of S.
$P(\dim (S))=0$
is called the conformality dimension of S.
Remark 2.9. If the mappings
![]() $f_1 ,\ldots ,f_m$
are affine similarities, then the conformality dimension is called the similarity dimension. It is the real number solution to
$f_1 ,\ldots ,f_m$
are affine similarities, then the conformality dimension is called the similarity dimension. It is the real number solution to
 $$ \begin{align} \sum_{i=1}^{m}c_i ^s=1, \end{align} $$
$$ \begin{align} \sum_{i=1}^{m}c_i ^s=1, \end{align} $$
where
![]() $c_i$
is the contraction ratio of
$c_i$
is the contraction ratio of
![]() $f_i$
(that is,
$f_i$
(that is,
![]() $c_i=\| f^{\prime }_i \|$
).
$c_i=\| f^{\prime }_i \|$
).
3 Statement of the main results
3.1 Dimension of weakly conformal dynamical Diophantine set
Our main result is the following.
Theorem 3.1. Let
![]() $m\geq 2$
be an integer. Let U be an open set and let
$m\geq 2$
be an integer. Let U be an open set and let
![]() $S=\{f_1:U\to U, \ldots ,f_m:U\to U\}$
be a
$S=\{f_1:U\to U, \ldots ,f_m:U\to U\}$
be a
![]() $C^{1}$
weakly conformal IFS with attractor K. For every
$C^{1}$
weakly conformal IFS with attractor K. For every
![]() $\delta>0,$
set
$\delta>0,$
set
Then, we have the following.
-
(1) For any
 $x_0\in U,$
for any
$x_0\in U,$
for any
 $\delta <1$
,
$\delta <1$
,  $$ \begin{align*}W(x_0,\delta)=K.\end{align*} $$
$$ \begin{align*}W(x_0,\delta)=K.\end{align*} $$
-
(2) Assume in addition that
 $\dim _H (K)=\dim (S)$
, then for any
$\dim _H (K)=\dim (S)$
, then for any
 $x_0\in K$
, for any
$x_0\in K$
, for any
 $\delta \geq 1$
,
$\delta \geq 1$
,  $$ \begin{align*} \dim_H W(x_0,\delta)=\frac{\dim_H (K)}{\delta}. \end{align*} $$
$$ \begin{align*} \dim_H W(x_0,\delta)=\frac{\dim_H (K)}{\delta}. \end{align*} $$
Remark 3.2. In [Reference Daviaud10, Theorem 2.14], the Hausdorff dimension of sets defined as in equation (13) is estimated for a self-similar IFS satisfying the so-called dimension regularity assumption, meaning that the dimension of every self-similar measure does not drop by projecting it on the attractor (see Definition 4.17 below). In the self-similar case, Theorem 3.1 extends this result to any IFS satisfying the weaker assumption that the similarity dimension and the dimension of the attractor agree. We would like to further mention that, even in the self-similar case, Theorem 3.1 currently applies to strictly more cases than the result in [Reference Daviaud10, Theorem 2.14]. Let
![]() $0<\unicode{x3bb} \leq \tfrac 13$
,
$0<\unicode{x3bb} \leq \tfrac 13$
,
![]() $\tau \in \mathbb {R}$
, and set
$\tau \in \mathbb {R}$
, and set
![]() $S=\{g_1,g_2,g_3\}$
, where
$S=\{g_1,g_2,g_3\}$
, where
![]() $g_1(x)=\unicode{x3bb} x, g_2(x)=\unicode{x3bb} x +1$
and
$g_1(x)=\unicode{x3bb} x, g_2(x)=\unicode{x3bb} x +1$
and
![]() $g_3(x)=\unicode{x3bb} x+\tau .$
Due to a result of Rapaport and Varju established in [Reference Rapaport and Varju32], outside a set of parameters
$g_3(x)=\unicode{x3bb} x+\tau .$
Due to a result of Rapaport and Varju established in [Reference Rapaport and Varju32], outside a set of parameters
![]() $(\unicode{x3bb} ,\tau )\in (0,\tfrac 13)\times \mathbb {R}$
of Hausdorff dimension
$(\unicode{x3bb} ,\tau )\in (0,\tfrac 13)\times \mathbb {R}$
of Hausdorff dimension
![]() $0$
, the IFS S satisfies that
$0$
, the IFS S satisfies that
![]() $\dim _H K =\dim (S)$
, so Theorem 3.1 applies to S. Note also that every IFS
$\dim _H K =\dim (S)$
, so Theorem 3.1 applies to S. Note also that every IFS
![]() $S=\{f_1,f_2,f_3\}$
on
$S=\{f_1,f_2,f_3\}$
on
![]() $\mathbb {R}$
is affinely conjugated to the IFS S for some
$\mathbb {R}$
is affinely conjugated to the IFS S for some
![]() $\unicode{x3bb} ,\tau \in (0,1)\times \mathbb {R}.$
It is worth mentioning that for the IFS S corresponding to good parameters, the dimensions of all self-similar measures associated with S are not known, in general. In particular, such cases are not covered by [Reference Daviaud10].
$\unicode{x3bb} ,\tau \in (0,1)\times \mathbb {R}.$
It is worth mentioning that for the IFS S corresponding to good parameters, the dimensions of all self-similar measures associated with S are not known, in general. In particular, such cases are not covered by [Reference Daviaud10].
Let us provide concrete examples of IFSs for which Theorem 3.1 applies and examples of IFS to which the conclusion of Theorem 3.1 does not hold.
-
• Theorem 3.1 applies to any self-similar IFS S on
 $\mathbb {R}$
satisfying the exponential separation condition [Reference Hochman24, Theorem 1.4] or having algebraic contraction ratio and no exact overlaps (i.e., for every
$\mathbb {R}$
satisfying the exponential separation condition [Reference Hochman24, Theorem 1.4] or having algebraic contraction ratio and no exact overlaps (i.e., for every
 $k\in \mathbb {N}$
, every
$k\in \mathbb {N}$
, every
 $\underline {i}\neq \underline {j}\in \Lambda ^k, f_{\underline {i}}\neq f_{\underline {j}}$
) with
$\underline {i}\neq \underline {j}\in \Lambda ^k, f_{\underline {i}}\neq f_{\underline {j}}$
) with
 $\dim (S)\leq 1$
(due to a result of Rapaport [Reference Rapaport31]). For instance, define
$\dim (S)\leq 1$
(due to a result of Rapaport [Reference Rapaport31]). For instance, define
 $g_1,g_2$
, and
$g_1,g_2$
, and
 $g_3$
as three mappings
$g_3$
as three mappings
 $\mathbb {R}\to \mathbb {R}$
by setting for every
$\mathbb {R}\to \mathbb {R}$
by setting for every
 $x\in \mathbb {R}$
,
$x\in \mathbb {R}$
,
 $g_1(x)=\tfrac 14x$
,
$g_1(x)=\tfrac 14x$
,
 $g_2(x)=\tfrac 14(x+1)$
, and
$g_2(x)=\tfrac 14(x+1)$
, and
 $g_3 (x)=\tfrac 14(x+t)$
, where
$g_3 (x)=\tfrac 14(x+t)$
, where
 $t\in \mathbb {R}\setminus \mathbb {Q}.$
Then, Theorem 3.1 applies to
$t\in \mathbb {R}\setminus \mathbb {Q}.$
Then, Theorem 3.1 applies to
 $S=\{g_1,g_2,g_3\}$
.
$S=\{g_1,g_2,g_3\}$
. -
• Let
 $m\geq 2$
be an integer and
$m\geq 2$
be an integer and
 $0<c_1,\ldots ,c_m<1$
be m real numbers satisfying Then (due to a result of Hochman, [Reference Hochman24]), for Lebesgue-almost every choice of
$0<c_1,\ldots ,c_m<1$
be m real numbers satisfying Then (due to a result of Hochman, [Reference Hochman24]), for Lebesgue-almost every choice of $$ \begin{align*}c_1+\cdots +c_m \leq 1.\end{align*} $$
$$ \begin{align*}c_1+\cdots +c_m \leq 1.\end{align*} $$
 $a_1,\ldots ,a_m \in \mathbb {R}$
, Theorem 3.1 applies to the IFS
$a_1,\ldots ,a_m \in \mathbb {R}$
, Theorem 3.1 applies to the IFS
 $S=\{f_1,\ldots ,f_m\}$
where, for every
$S=\{f_1,\ldots ,f_m\}$
where, for every
 $1\leq i\leq m, f_i (x)=c_i x+a_i$
.
$1\leq i\leq m, f_i (x)=c_i x+a_i$
.
-
• It is relatively easy to see that Theorem 3.1 cannot hold when
 $\dim (S)>d.$
One could take, for instance, so many similarities so that for every
$\dim (S)>d.$
One could take, for instance, so many similarities so that for every
 $1\leq \delta \leq 2$
, To be more explicit, fix t a badly approximable (by rationals) number and define
$1\leq \delta \leq 2$
, To be more explicit, fix t a badly approximable (by rationals) number and define $$ \begin{align*}\dim_H \Big(\!\limsup_{\underline{i}\in\Lambda^{*}}B(f_{\underline{i}}(x_0),\vert f_{\underline{i}}(K)\vert^{\delta})\Big)=d .\end{align*} $$
$$ \begin{align*}\dim_H \Big(\!\limsup_{\underline{i}\in\Lambda^{*}}B(f_{\underline{i}}(x_0),\vert f_{\underline{i}}(K)\vert^{\delta})\Big)=d .\end{align*} $$
 $\phi _1 (x)={x}/{2}$
,
$\phi _1 (x)={x}/{2}$
,
 $\phi _2(x)=({x+1})/{2}$
,
$\phi _2(x)=({x+1})/{2}$
,
 $\phi _3 (x)=({x+t})/{2}$
,
$\phi _3 (x)=({x+t})/{2}$
,
 $\phi _4(x)=({x+1+t})/{2}$
, and
$\phi _4(x)=({x+1+t})/{2}$
, and
 $\Lambda =\{1,\ldots ,4\}$
. Then, it is proved in [Reference Baker2, Theorem 2.10] that for every
$\Lambda =\{1,\ldots ,4\}$
. Then, it is proved in [Reference Baker2, Theorem 2.10] that for every
 $x_0\in [0,1+t],$
$x_0\in [0,1+t],$
 $$ \begin{align*}\dim_H\bigg(\limsup_{\underline{i}\in \Lambda^*}B\bigg(\phi_{\underline{i}}(x_0),\frac{1}{4^{\vert \underline{i} \vert}}\bigg)\bigg)=1.\end{align*} $$
$$ \begin{align*}\dim_H\bigg(\limsup_{\underline{i}\in \Lambda^*}B\bigg(\phi_{\underline{i}}(x_0),\frac{1}{4^{\vert \underline{i} \vert}}\bigg)\bigg)=1.\end{align*} $$
In §3.1, we establish that the result applies to a large class of weakly conformal IFSs, namely the weakly conformal IFS satisfying the asymptotically weak separation condition (AWSC).
3.2 An application in the case of homogeneous self-similar IFS
In Theorem 3.1, the choice of the radii of the balls plays an important role on the hypothesis that one needs to assume to be able to estimate
![]() $\dim _H W(x,\delta ).$
In the case of homogeneous IFSs, we will be able to treat the general case where the radii are simply given by a mapping
$\dim _H W(x,\delta ).$
In the case of homogeneous IFSs, we will be able to treat the general case where the radii are simply given by a mapping
![]() $\phi :\mathbb {N}\to \mathbb {R}^+.$
In our settings, we will call a system of affine similarities
$\phi :\mathbb {N}\to \mathbb {R}^+.$
In our settings, we will call a system of affine similarities
![]() $S=\{f_i\}_{1\leq i\leq m}$
homogeneous if for every
$S=\{f_i\}_{1\leq i\leq m}$
homogeneous if for every
![]() $1\leq i,j\leq m,$
$1\leq i,j\leq m,$
Theorem 3.3. Let S be an homogeneous self-similar IFS of common contraction ratio
![]() $0<c<1$
. Let
$0<c<1$
. Let
![]() $\phi :\mathbb {N}\to \mathbb {R}^+$
be such that
$\phi :\mathbb {N}\to \mathbb {R}^+$
be such that
![]() $\lim _{n\rightarrow +\infty }\phi (n)=0$
and set
$\lim _{n\rightarrow +\infty }\phi (n)=0$
and set
 $$ \begin{align} s_{\phi}=\inf\bigg\{s\geq 0 :\sum_{k\geq 0}\sum_{\underline{i}\in\Lambda^k}\phi(k)^{s\dim(S)}<+\infty\bigg\}. \end{align} $$
$$ \begin{align} s_{\phi}=\inf\bigg\{s\geq 0 :\sum_{k\geq 0}\sum_{\underline{i}\in\Lambda^k}\phi(k)^{s\dim(S)}<+\infty\bigg\}. \end{align} $$
Assume that
![]() $\dim _H K=\dim (S)$
. Then,
$\dim _H K=\dim (S)$
. Then,
Remark 3.4. If
![]() $\lim _{n \to +\infty }\phi (n) \neq 0,$
since K is compact,
$\lim _{n \to +\infty }\phi (n) \neq 0,$
since K is compact,
![]() $W(x_0,\phi )$
contains a ball, and hence
$W(x_0,\phi )$
contains a ball, and hence
![]() $\dim _H K=d$
.
$\dim _H K=d$
.
Let us provide a short application to Theorem 3.3. Let
![]() $t\in (0,1)$
be a transcendental number and
$t\in (0,1)$
be a transcendental number and
![]() $\mathcal {A}=\{q_1=0,\ldots ,q_N\}\subset \mathbb {Q},$
where
$\mathcal {A}=\{q_1=0,\ldots ,q_N\}\subset \mathbb {Q},$
where
![]() $N\geq 2$
satisfies
$N\geq 2$
satisfies
![]() $\log N \leq -\log t$
. Define
$\log N \leq -\log t$
. Define
![]() $S=\{f_1(x)=tx+q_1,\ldots ,f_N(x)=tx+q_N\}.$
It is established in [Reference Rapaport and Varju32] that, denoting K as the attractor of S, one has
$S=\{f_1(x)=tx+q_1,\ldots ,f_N(x)=tx+q_N\}.$
It is established in [Reference Rapaport and Varju32] that, denoting K as the attractor of S, one has
In addition, one has
 $$ \begin{align*}\mathcal{P}_{\mathcal{A},t,n}:=\bigg\{P(t)=\sum_{k=0}^n a_i t^i:a_0,\ldots,a_n\in\mathcal{A}\bigg\}=\{f_{\underline{i}}(0),\underline{i}\in\{1,\ldots,m\}^{n+1}\}.\end{align*} $$
$$ \begin{align*}\mathcal{P}_{\mathcal{A},t,n}:=\bigg\{P(t)=\sum_{k=0}^n a_i t^i:a_0,\ldots,a_n\in\mathcal{A}\bigg\}=\{f_{\underline{i}}(0),\underline{i}\in\{1,\ldots,m\}^{n+1}\}.\end{align*} $$
So, given
![]() $\phi :\mathbb {N}\to \mathbb {R}^+,$
writing
$\phi :\mathbb {N}\to \mathbb {R}^+,$
writing
 $$ \begin{align*}W_{\mathcal{A},t}(\phi)=\bigg\{x\in\mathbb{R}^d : \vert x-P(t)\vert\leq \phi(\deg P)\text{ for infinitely many }P\in\bigcup_{n\geq 0}\mathcal{P}_{\mathcal{A},n,t} \bigg\}, \end{align*} $$
$$ \begin{align*}W_{\mathcal{A},t}(\phi)=\bigg\{x\in\mathbb{R}^d : \vert x-P(t)\vert\leq \phi(\deg P)\text{ for infinitely many }P\in\bigcup_{n\geq 0}\mathcal{P}_{\mathcal{A},n,t} \bigg\}, \end{align*} $$
a direct application of Theorem 3.3 yields that
where
![]() $s_{\phi }$
is defined as in equation (14). Finally, we mention that, for the sake of clarity, the present article deals with the case of IFSs without exact overlaps, but one easily could extend the results to the case where the IFS has exact overlaps under suitable assumption (related to the Garcia entropy of the IFS). In particular,
$s_{\phi }$
is defined as in equation (14). Finally, we mention that, for the sake of clarity, the present article deals with the case of IFSs without exact overlaps, but one easily could extend the results to the case where the IFS has exact overlaps under suitable assumption (related to the Garcia entropy of the IFS). In particular,
![]() $\dim _H W_{\mathcal {A},t}(\phi ) $
can also be estimated for t algebraic. The short note [Reference Daviaud11] has been made available to explain how one should proceed in this case.
$\dim _H W_{\mathcal {A},t}(\phi ) $
can also be estimated for t algebraic. The short note [Reference Daviaud11] has been made available to explain how one should proceed in this case.
3.3 The classical shrinking target problem
As mentioned in §1, thanks to the techniques developed in this article, we are able to extend the dimension results established by Hill and Velani in [Reference Hill and Velani23] with a great deal of generality. Let us explain first why one needs a different hypothesis to extend the result of [Reference Hill and Velani23] than in Theorem 3.1. Reading the rest of the article, the reader will find that the proof of Theorem 3.1 is almost completely geometrical (that is, the proof is essentially non-symbolic). The combination of this fact and the fact that establishing dimension results in the context of self-similar IFSs is, in general, difficult and relies on deep ideas (see [Reference Feng and Hu19, Reference Hochman24, Reference Rapaport31, Reference Rapaport and Varju32, Reference Shmerkin36]), which makes it somewhat surprising that Theorem 3.1 holds under the rather weak hypothesis that the similarity dimension and the dimension of the attractor agree. This is completely due to the specific choice of the radii. More precisely, the choice of the necessary hypotheses in Theorem 3.1 are made with regard to the analyzing measures one will need to consider to solve this specific Diophantine problem. In the case of the classical shrinking target problem, these analyzing measures will be Gibbs measures, so the hypothesis one will require to deal with it will be made to ensure that the projections of Gibbs measure have the expected dimension on K. For the sake of simplicity, we will place ourselves in the case where the IFS is conformal and satisfies the so-called bounded distortion property, which we recall.
Definition 3.5. Let
![]() $S=\{f_1,\ldots ,f_m\}$
be a conformal IFS. We say that S satisfies the bounded distortion property if there exists
$S=\{f_1,\ldots ,f_m\}$
be a conformal IFS. We say that S satisfies the bounded distortion property if there exists
![]() $\kappa>0$
such that for every
$\kappa>0$
such that for every
![]() $n\in \mathbb {N},$
for every
$n\in \mathbb {N},$
for every
![]() $\underline {i}\in \{1,\ldots ,m\}^n$
and every
$\underline {i}\in \{1,\ldots ,m\}^n$
and every
![]() $x,y \in K,$
one has
$x,y \in K,$
one has
 $$ \begin{align} \kappa^{-1}\leq\frac{\| f_{\underline{i}}'(x) \|}{\| f_{\underline{i}}'(y) \|} \leq \kappa. \end{align} $$
$$ \begin{align} \kappa^{-1}\leq\frac{\| f_{\underline{i}}'(x) \|}{\| f_{\underline{i}}'(y) \|} \leq \kappa. \end{align} $$
Before stating our main theorem, we recall the following result (see for instance [Reference Allen and Bárány1, equation (2.6), p. 7]).
Theorem 3.6. Let
![]() $s> 0$
be a real number. Assume that
$s> 0$
be a real number. Assume that
![]() $S=\{f_1,\ldots ,f_m\}$
is conformal and satisfies the bounded distortion property, then there exists a unique ergodic measure
$S=\{f_1,\ldots ,f_m\}$
is conformal and satisfies the bounded distortion property, then there exists a unique ergodic measure
![]() $\nu _s \in \mathcal {M}(\Lambda ^{\mathbb {N}})$
satisfying that for every
$\nu _s \in \mathcal {M}(\Lambda ^{\mathbb {N}})$
satisfying that for every
![]() $n\in \mathbb {N}$
and for every
$n\in \mathbb {N}$
and for every
![]() $\underline {i}\in \Lambda ^n,$
one has
$\underline {i}\in \Lambda ^n,$
one has
 $$ \begin{align} C^{-1}\leq\frac{\nu_s ([\underline{i}])}{\vert f_{\underline{i}}(K)\vert^s e^{-nP(s)}}\leq C, \end{align} $$
$$ \begin{align} C^{-1}\leq\frac{\nu_s ([\underline{i}])}{\vert f_{\underline{i}}(K)\vert^s e^{-nP(s)}}\leq C, \end{align} $$
where
![]() $C\geq 1$
is a constant independent of
$C\geq 1$
is a constant independent of
![]() $\underline {i}.$
We will write
$\underline {i}.$
We will write
![]() $\mu _s=\nu _s \circ \pi ^{-1}$
as the projection of
$\mu _s=\nu _s \circ \pi ^{-1}$
as the projection of
![]() $\nu _s$
on the attractor of S.
$\nu _s$
on the attractor of S.
Remark 3.7. By ergodicity, one easily proves that there exists
![]() $h_s\geq 0$
such that for
$h_s\geq 0$
such that for
![]() $\nu _s$
-almost every
$\nu _s$
-almost every
![]() $\underline {i}=(i_n)_{n\in \mathbb {N}}\in \{1,\ldots ,m\}^{\mathbb {N}},$
one has
$\underline {i}=(i_n)_{n\in \mathbb {N}}\in \{1,\ldots ,m\}^{\mathbb {N}},$
one has
Our main result regarding the Hausdorff dimension of shrinking targets set for overlapping conformal IFSs is the following.
Theorem 3.8. Let S be a conformal IFS satisfying the bounded distortion property, given by equation (15), and let
![]() $\phi :\mathbb {N}\to \mathbb {R}^+$
be a mapping satisfying
$\phi :\mathbb {N}\to \mathbb {R}^+$
be a mapping satisfying
![]() $\phi (n)\to 0$
. Set
$\phi (n)\to 0$
. Set
and denote s the solution to
![]() $P(s)={s\alpha }/{\delta }.$
Assume that
$P(s)={s\alpha }/{\delta }.$
Assume that
![]() $\dim _{H}\!y{\mu }_s =h_s$
and
$\dim _{H}\!y{\mu }_s =h_s$
and
![]() $0<\alpha <+\infty $
, then for every
$0<\alpha <+\infty $
, then for every
![]() $\delta \geq 1,$
one has
$\delta \geq 1,$
one has
Remark 3.9.
-
• If
 $\alpha =0,$
then for every
$\alpha =0,$
then for every
 $\varepsilon>0$
, there exists an increasing sequence of integers
$\varepsilon>0$
, there exists an increasing sequence of integers
 $(n_k)_{k\in \mathbb {N}} $
such that for every
$(n_k)_{k\in \mathbb {N}} $
such that for every
 $k\in \mathbb {N},$
for every
$k\in \mathbb {N},$
for every
 $\underline {i}\in \Lambda ^{n_k},$
one has In that case, using the same argument as in the proof of Theorem 3.1, we conclude that
$\underline {i}\in \Lambda ^{n_k},$
one has In that case, using the same argument as in the proof of Theorem 3.1, we conclude that $$ \begin{align*}\vert f_{\underline{i}}(K) \vert^{(1+\varepsilon)\delta}\leq\vert f_{\underline{i}}(K) \vert^\delta\phi(\vert \underline{i}\vert)\leq \vert f_{\underline{i}}(K) \vert^\delta.\end{align*} $$
$$ \begin{align*}\vert f_{\underline{i}}(K) \vert^{(1+\varepsilon)\delta}\leq\vert f_{\underline{i}}(K) \vert^\delta\phi(\vert \underline{i}\vert)\leq \vert f_{\underline{i}}(K) \vert^\delta.\end{align*} $$
 $$ \begin{align*}\dim_H \limsup_{\underline{i}\in\Lambda^*}B(f_{\underline{i}}(x_0),\vert f_{\underline{i}}(K) \vert^\delta\phi(\vert \underline{i}\vert))=\frac{\dim S}{\delta}.\end{align*} $$
$$ \begin{align*}\dim_H \limsup_{\underline{i}\in\Lambda^*}B(f_{\underline{i}}(x_0),\vert f_{\underline{i}}(K) \vert^\delta\phi(\vert \underline{i}\vert))=\frac{\dim S}{\delta}.\end{align*} $$
-
• If
 $\alpha =+\infty ,$
then for every
$\alpha =+\infty ,$
then for every
 $\delta '>0$
, there exists
$\delta '>0$
, there exists
 $N\in \mathbb {N}$
such that for every
$N\in \mathbb {N}$
such that for every
 $n\geq N$
and for every
$n\geq N$
and for every
 $\underline {i}\in \Lambda ^{n}$
, we have and hence,
$\underline {i}\in \Lambda ^{n}$
, we have and hence, $$ \begin{align*} \phi(n)\leq \vert f_{\underline{i}}(K)\vert^{\delta'},\end{align*} $$
$$ \begin{align*} \phi(n)\leq \vert f_{\underline{i}}(K)\vert^{\delta'},\end{align*} $$
 $\vert f_{\underline {i}}(K)\vert ^{\delta }\phi (n)\leq \vert f_{\underline {i}}(K)\vert ^{\delta +\delta '}.$
By Theorem 3.1, this implies that Letting
$\vert f_{\underline {i}}(K)\vert ^{\delta }\phi (n)\leq \vert f_{\underline {i}}(K)\vert ^{\delta +\delta '}.$
By Theorem 3.1, this implies that Letting $$ \begin{align*}\dim_H \limsup_{\underline{i}\in\Lambda^*}B(f_{\underline{i}}(x_0),\vert f_{\underline{i}}(K) \vert^\delta\phi(\vert \underline{i}\vert))\leq \frac{\dim S}{\delta+\delta'}.\end{align*} $$
$$ \begin{align*}\dim_H \limsup_{\underline{i}\in\Lambda^*}B(f_{\underline{i}}(x_0),\vert f_{\underline{i}}(K) \vert^\delta\phi(\vert \underline{i}\vert))\leq \frac{\dim S}{\delta+\delta'}.\end{align*} $$
 $\delta '\to +\infty $
yields
$\delta '\to +\infty $
yields  $$ \begin{align*}\dim_H \limsup_{\underline{i}\in\Lambda^*}B(f_{\underline{i}}(x_0),\vert f_{\underline{i}}(K) \vert^\delta\phi(\vert \underline{i}\vert))=0.\end{align*} $$
$$ \begin{align*}\dim_H \limsup_{\underline{i}\in\Lambda^*}B(f_{\underline{i}}(x_0),\vert f_{\underline{i}}(K) \vert^\delta\phi(\vert \underline{i}\vert))=0.\end{align*} $$
-
• In the case where S is a self-similar IFS on
 $\mathbb {R}$
satisfying the exponential separation condition due to a result established by Jordan and Rapaport in [Reference Rapaport and Jordan33], for every
$\mathbb {R}$
satisfying the exponential separation condition due to a result established by Jordan and Rapaport in [Reference Rapaport and Jordan33], for every
 $s>0,$
one has As a consequence, Theorem 3.8 applies to any
$s>0,$
one has As a consequence, Theorem 3.8 applies to any $$ \begin{align*}\dim_{H}{\mu}_s =\min\{1,h_s\}.\end{align*} $$
$$ \begin{align*}\dim_{H}{\mu}_s =\min\{1,h_s\}.\end{align*} $$
 $\phi $
satisfying that the root s of
$\phi $
satisfying that the root s of
 $P(s)-s({\alpha }/{\delta })$
is such that
$P(s)-s({\alpha }/{\delta })$
is such that
 $h_s \leq 1$
.
$h_s \leq 1$
.
To provide a large class of IFSs to which Theorem 3.8 applies, we start by recalling the definition of the so-called multifractal scaling function of a measure. Let
![]() $\mu \in \mathcal {M}(\mathbb {R}^d)$
and define
$\mu \in \mathcal {M}(\mathbb {R}^d)$
and define
 $$ \begin{align*}\Theta_{\mu}(q,r)= \inf\bigg\{\!\sum_{i\in I} \mu(B(x_i,r))^q\bigg\},\end{align*} $$
$$ \begin{align*}\Theta_{\mu}(q,r)= \inf\bigg\{\!\sum_{i\in I} \mu(B(x_i,r))^q\bigg\},\end{align*} $$
where the infimum is taken over all countable collections of balls
![]() $\{B(x_i,r) \}_{i \in I}$
satisfying the following two properties:
$\{B(x_i,r) \}_{i \in I}$
satisfying the following two properties:
-
(1)
 $x_i \in {\mathrm {supp}}(\mu )$
for every
$x_i \in {\mathrm {supp}}(\mu )$
for every
 $i \in I$
; and
$i \in I$
; and -
(2)
 $B(x_i,r) \cap B(x_j,r) =\emptyset $
for
$B(x_i,r) \cap B(x_j,r) =\emptyset $
for
 $i\neq j.$
$i\neq j.$
Then, the multifractal scaling function of
![]() $\mu $
is defined as
$\mu $
is defined as
Such mappings were first considered in the context of turbulence by Frisch and Parisi in [Reference Frisch, Parisi and Ghil21]. The mapping
![]() $\tau _\mu $
is often connected to the so-called multifractal spectrum of
$\tau _\mu $
is often connected to the so-called multifractal spectrum of
![]() $\mu $
. More precisely, for
$\mu $
. More precisely, for
![]() $h\geq 0,$
denote by
$h\geq 0,$
denote by
![]() $E_{\mu ,h}$
the set of points of lower
$E_{\mu ,h}$
the set of points of lower
![]() $\mu $
-local dimension h, that is,
$\mu $
-local dimension h, that is,
Many natural measures satisfy for every
![]() $h\geq 0$
that
$h\geq 0$
that
where
![]() $\tau _\mu ^*(h)=\inf _{q\in \mathbb {R}}\{qh-\tau _{\mu }(q)\}.$
We refer, for instance, to [Reference Brown, Michon and Peyrière9] for a complete mathematical foundation and to [Reference Feng18, Reference Olsen29, Reference Shmerkin36] for results regarding the multifractal analysis of self-similar measures.
$\tau _\mu ^*(h)=\inf _{q\in \mathbb {R}}\{qh-\tau _{\mu }(q)\}.$
We refer, for instance, to [Reference Brown, Michon and Peyrière9] for a complete mathematical foundation and to [Reference Feng18, Reference Olsen29, Reference Shmerkin36] for results regarding the multifractal analysis of self-similar measures.
When S is conformal and satisfies the bounded distortion property, it is classical (see [Reference Allen and Bárány1] for instance) that there exists a unique ergodic measure
![]() $\nu _0$
on
$\nu _0$
on
![]() $\{1,\ldots ,m\}^{\mathbb {N}}$
such that for every
$\{1,\ldots ,m\}^{\mathbb {N}}$
such that for every
![]() $k\in \mathbb {N},$
for every
$k\in \mathbb {N},$
for every
![]() $\underline {i}\in \{1,\ldots ,m\}^k$
, one has
$\underline {i}\in \{1,\ldots ,m\}^k$
, one has
 $$ \begin{align} C^{-1}\leq\frac{\nu_0([\underline{i}])}{\vert f_{\underline{i}}(K)\vert^{\dim(S)}}\leq C, \end{align} $$
$$ \begin{align} C^{-1}\leq\frac{\nu_0([\underline{i}])}{\vert f_{\underline{i}}(K)\vert^{\dim(S)}}\leq C, \end{align} $$
where
![]() $C>0$
is independent of
$C>0$
is independent of
![]() $\underline {i}.$
In addition, when the IFS is self-similar,
$\underline {i}.$
In addition, when the IFS is self-similar,
![]() $\nu _0$
is simply the self-similar measure corresponding to the similarity dimension (see Remark 2.9). We now introduce the following condition.
$\nu _0$
is simply the self-similar measure corresponding to the similarity dimension (see Remark 2.9). We now introduce the following condition.
Definition 3.10. Let S be a conformal IFS satisfying equation (15), let K be its attractor, let
![]() $\nu _{0}$
be as in equation (18), and set
$\nu _{0}$
be as in equation (18), and set
![]() $\mu _0 =\nu _0 \circ \pi ^{-1},$
where
$\mu _0 =\nu _0 \circ \pi ^{-1},$
where
![]() $\pi $
is the canonical projection from
$\pi $
is the canonical projection from
![]() $\{1,\ldots ,m\}^{\mathbb {N}}$
to K. We say that S satisfies condition
$\{1,\ldots ,m\}^{\mathbb {N}}$
to K. We say that S satisfies condition
![]() $(A)$
if for every
$(A)$
if for every
![]() $q> 1,$
$q> 1,$
We mention that condition
![]() $(A)$
has been proved by Barral and Feng in [Reference Barral and Feng4] to be equivalent to the so-called asymptotically weak separation condition without exact-overlaps mentioned at the end of §3.1 (see Proposition 4.11 thereafter).
$(A)$
has been proved by Barral and Feng in [Reference Barral and Feng4] to be equivalent to the so-called asymptotically weak separation condition without exact-overlaps mentioned at the end of §3.1 (see Proposition 4.11 thereafter).
Thus (due to Remark 4.22 below), the following result holds true.
Lemma 3.11. Assume that S is a conformal IFS satisfying the bounded distortion property and condition
![]() $(A).$
Then, for every
$(A).$
Then, for every
![]() $s>0, \dim _{H}{\mu }_s =h_s.$
In particular, Theorem 3.8 applies to every
$s>0, \dim _{H}{\mu }_s =h_s.$
In particular, Theorem 3.8 applies to every
![]() $\phi :\mathbb {N}\to \mathbb {R}^+.$
$\phi :\mathbb {N}\to \mathbb {R}^+.$
Remark 3.12.
-
• As mentioned above, the advantage of the formulation of condition
 $(A)$
is that the multifractal spectrum of self-similar measures, Gibbs measures, etc. is a topic well studied. For instance, as a consequence of the estimates regarding the
$(A)$
is that the multifractal spectrum of self-similar measures, Gibbs measures, etc. is a topic well studied. For instance, as a consequence of the estimates regarding the
 $L^q$
spectrum of self-similar measures on
$L^q$
spectrum of self-similar measures on
 $\mathbb {R},$
established by Shmerkin in [Reference Shmerkin36], Theorem 3.8 applies to any self-similar IFS satisfying the exponential separation condition on
$\mathbb {R},$
established by Shmerkin in [Reference Shmerkin36], Theorem 3.8 applies to any self-similar IFS satisfying the exponential separation condition on
 $\mathbb {R}$
with similarity dimension smaller than
$\mathbb {R}$
with similarity dimension smaller than
 $1$
(which, for instance, is ensured as soon as the parameters defining the IFS are algebraic and the IFS has no exact-overlaps). In addition, should these estimates have an analog in higher dimension under suitable assumptions, then Theorem 3.8 would apply to IFSs satisfying the same conditions.
$1$
(which, for instance, is ensured as soon as the parameters defining the IFS are algebraic and the IFS has no exact-overlaps). In addition, should these estimates have an analog in higher dimension under suitable assumptions, then Theorem 3.8 would apply to IFSs satisfying the same conditions. -
• We also emphasize that if condition
 $(A)$
is satisfied, every projection of ergodic measure has the dimension one would expect (see Remark 4.22), so, although the class of IFSs satisfying condition
$(A)$
is satisfied, every projection of ergodic measure has the dimension one would expect (see Remark 4.22), so, although the class of IFSs satisfying condition
 $(A)$
is large, condition
$(A)$
is large, condition
 $(A)$
is somewhat an overkill for our problem.
$(A)$
is somewhat an overkill for our problem.
In §4, we recall and establish some geometric properties of a weakly conformal IFS. We also establish Proposition 4.10, which justifies that one can apply Theorem 3.1 to weakly conformal IFS satisfying the AWSC.
The mass transference principle for weakly conformal measures, which is key to prove Theorem 3.1, is established in §5.
4 Geometric properties of weakly conformal IFS
In this section, all the basic geometric properties of a weakly conformal IFS needed in the rest of this article are recalled or established. More precisely, in §4.1, we recall the key Lemma 4.1, which will be used instead of an usual bounded distortion property one often requires when dealing with conformal IFSs. Section 4.2 is dedicated to the proof of Proposition 2.6. In §4.3, we recall the definition of the Lyapunov exponent in the case of a weakly conformal IFS and some basic properties of this exponent. Finally, in §4.4, we recall some facts about the asymptotically weak separation condition.
4.1 Some general estimates
Let
![]() $m \geq 2$
be an integer. One collects some useful geometric results on a
$m \geq 2$
be an integer. One collects some useful geometric results on a
![]() $C^{1}$
weakly conformal IFS.
$C^{1}$
weakly conformal IFS.
Consider a
![]() $C^{1}$
weakly conformal IFS
$C^{1}$
weakly conformal IFS
![]() $S=\{f_1 ,\ldots ,f_m\}$
with attractor K and for every
$S=\{f_1 ,\ldots ,f_m\}$
with attractor K and for every
![]() $x\in K$
,
$x\in K$
,
![]() $k\in \mathbb {N}$
, and
$k\in \mathbb {N}$
, and
![]() $\underline {i}=(i_1,\ldots ,i_k)\in \Lambda ^k$
, write
$\underline {i}=(i_1,\ldots ,i_k)\in \Lambda ^k$
, write
Let us recall the following result established as [Reference Feng and Hu19, Lemma 5.4].
Lemma 4.1. [Reference Feng and Hu19]
For any
![]() $c>1$
, there exists a constant
$c>1$
, there exists a constant
![]() $D(c)>0$
such that, for every
$D(c)>0$
such that, for every
![]() $k\in \mathbb {N}$
, for every
$k\in \mathbb {N}$
, for every
![]() $\underline {i}\in \Lambda ^k$
and every
$\underline {i}\in \Lambda ^k$
and every
![]() $x,y\in K$
,
$x,y\in K$
,
Remark 4.2. Let
![]() $X\subset U$
be a compact set and U as in §2.2.2 (that is, as in the definition of a weakly conformal IFS). It is proved in [Reference Feng and Hu19] that equation (19) actually holds for any
$X\subset U$
be a compact set and U as in §2.2.2 (that is, as in the definition of a weakly conformal IFS). It is proved in [Reference Feng and Hu19] that equation (19) actually holds for any
![]() $(x,y)\in X^2.$
$(x,y)\in X^2.$
Note that for every
![]() $k\in \mathbb {N}$
and every
$k\in \mathbb {N}$
and every
![]() $x\in K,$
one has
$x\in K,$
one has
Moreover, since there exists two constants
![]() $C_1, C_2>0$
such that for every
$C_1, C_2>0$
such that for every
![]() $1\leq i\leq m$
and every
$1\leq i\leq m$
and every
![]() $x\in K$
,
$x\in K$
,
there also exists two constants
![]() $0< t_1 \leq t_2$
such that
$0< t_1 \leq t_2$
such that
 $$ \begin{align*}t_1\leq \frac{k}{\log \| f_{ \underline{i}} ^{\prime}(x)\|}\leq t_2 .\end{align*} $$
$$ \begin{align*}t_1\leq \frac{k}{\log \| f_{ \underline{i}} ^{\prime}(x)\|}\leq t_2 .\end{align*} $$
Combining this fact with Lemma 4.1, for any
![]() $\theta>0$
, there exists
$\theta>0$
, there exists
![]() $\widetilde {C}_{\theta }>0$
such that for every
$\widetilde {C}_{\theta }>0$
such that for every
![]() $k\in \mathbb {N}$
, every
$k\in \mathbb {N}$
, every
![]() $\underline {i}\in \Lambda ^k$
, and every
$\underline {i}\in \Lambda ^k$
, and every
![]() $x,y\in K$
,
$x,y\in K$
,
In particular, there also exists
![]() $\widehat {C}_{\theta }$
such that for every
$\widehat {C}_{\theta }$
such that for every
![]() $\underline {i}\in \Lambda ^{*}$
and every
$\underline {i}\in \Lambda ^{*}$
and every
![]() $x\in K,$
one has
$x\in K,$
one has
Let us remark that equation (22) also implies that there exist
![]() $0<\alpha \leq \beta <1$
as well as
$0<\alpha \leq \beta <1$
as well as
![]() $C_{\alpha },C_{\beta }>0$
such that, for any
$C_{\alpha },C_{\beta }>0$
such that, for any
![]() $k\in \mathbb {N},$
$k\in \mathbb {N},$
4.2 Proof of Proposition 2.6
As mentioned in §2, the proof of Proposition 2.6 is very standard and does not diverge much from the proof in the conformal case. Unfortunately, one cannot derive directly the result from classical cases (see [Reference Bowen8, Reference Ruelle34], for instance) and those computations in the weakly conformal case do not seem to be written explicitly in the literature so for the seek of completeness, it is done below.
Proof. Assume first that the limit exists in
![]() $\mathbb {R}\cup \{-\infty \}$
, and let us show that it is independent of the choice of z and that the limit is
$\mathbb {R}\cup \{-\infty \}$
, and let us show that it is independent of the choice of z and that the limit is
![]() $>-\infty $
. Let
$>-\infty $
. Let
![]() $ c>1$
be a real number. Recalling Lemma 4.1, for any
$ c>1$
be a real number. Recalling Lemma 4.1, for any
![]() $k\in \mathbb {N},$
one has
$k\in \mathbb {N},$
one has
 $$ \begin{align} \log\bigg(\!\sum_{\underline{i}\in\Lambda^k}D(c)^{-s}c^{-sk}\vert f_{\underline{i}}(K)\vert ^s\bigg)&\leq \log\bigg(\!\sum_{\underline{i}\in \Lambda^k}\| f_{\underline{i}}' (z)\|^s\bigg)\nonumber\\ &\leq \log\bigg(\!\sum_{\underline{i}\in\Lambda^k}D(c)^s c^{sk}\vert f_{\underline{i}}(K)\vert^s \bigg). \end{align} $$
$$ \begin{align} \log\bigg(\!\sum_{\underline{i}\in\Lambda^k}D(c)^{-s}c^{-sk}\vert f_{\underline{i}}(K)\vert ^s\bigg)&\leq \log\bigg(\!\sum_{\underline{i}\in \Lambda^k}\| f_{\underline{i}}' (z)\|^s\bigg)\nonumber\\ &\leq \log\bigg(\!\sum_{\underline{i}\in\Lambda^k}D(c)^s c^{sk}\vert f_{\underline{i}}(K)\vert^s \bigg). \end{align} $$
Since equation (24) holds for any
![]() $c>1$
, one gets that
$c>1$
, one gets that
 $$ \begin{align} \lim_{k\rightarrow+\infty}\frac{1}{k}\bigg(\log\bigg( \sum_{\underline{i}\in \Lambda^k}\| f_{\underline{i}}^{\prime}(z)\|^s \bigg)-\log\bigg(\!\sum_{\underline{i}\in\Lambda^k}\vert f_{\underline{i}}(K)\vert ^s\bigg)\bigg)=0, \end{align} $$
$$ \begin{align} \lim_{k\rightarrow+\infty}\frac{1}{k}\bigg(\log\bigg( \sum_{\underline{i}\in \Lambda^k}\| f_{\underline{i}}^{\prime}(z)\|^s \bigg)-\log\bigg(\!\sum_{\underline{i}\in\Lambda^k}\vert f_{\underline{i}}(K)\vert ^s\bigg)\bigg)=0, \end{align} $$
which proves that this quantity does not depend on z. Moreover, there exists
![]() $b>0$
so that for any
$b>0$
so that for any
![]() $k\in \mathbb {N}$
, any
$k\in \mathbb {N}$
, any
![]() $\underline {i}\in \Lambda ^k$
, and any
$\underline {i}\in \Lambda ^k$
, and any
![]() $x\in K$
,
$x\in K$
,
This implies that if
![]() $P_z(s)$
is well defined, then
$P_z(s)$
is well defined, then
![]() $P_z(s)>-\infty .$
$P_z(s)>-\infty .$
Let us now prove that the limit exists. For
![]() $k\in \mathbb {N},$
write
$k\in \mathbb {N},$
write
 $$ \begin{align} g_k =\log\bigg(\!\sum_{\underline{i}\in \Lambda^k}\vert f_{\underline{i}}(K)\vert^s \bigg). \end{align} $$
$$ \begin{align} g_k =\log\bigg(\!\sum_{\underline{i}\in \Lambda^k}\vert f_{\underline{i}}(K)\vert^s \bigg). \end{align} $$
As in the conformal case, the existence of the pressure relies on a sub-additivity argument.
Lemma 4.3. For any
![]() $\varepsilon>0,$
there exists a constant
$\varepsilon>0,$
there exists a constant
![]() $M_{\varepsilon }>0$
such that for any
$M_{\varepsilon }>0$
such that for any
![]() $n,m\in \mathbb {N},$
one has
$n,m\in \mathbb {N},$
one has
Furthermore, any sequence
![]() $(g_n)_{n\in \mathbb {N}}$
verifying equation (27) is such that
$(g_n)_{n\in \mathbb {N}}$
verifying equation (27) is such that
![]() $({g_n}/{n})_{n\in \mathbb {N}}$
converges in
$({g_n}/{n})_{n\in \mathbb {N}}$
converges in
![]() $\mathbb {R}\cup \{-\infty \}$
.
$\mathbb {R}\cup \{-\infty \}$
.
Proof. Let us start by proving the second statement. Let
![]() $(g_n)_{n\in \mathbb {N}}$
be a sequence satisfying equation (27). Fix
$(g_n)_{n\in \mathbb {N}}$
be a sequence satisfying equation (27). Fix
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $M_{\varepsilon }$
satisfying equation (27). For any
$M_{\varepsilon }$
satisfying equation (27). For any
![]() $q\in \mathbb {N}^*, b\in \mathbb {N}^*, 0\leq r< q$
, one has
$q\in \mathbb {N}^*, b\in \mathbb {N}^*, 0\leq r< q$
, one has
 $$ \begin{align*} &g_{bq+r}\leq bg_{q}+g_r +(bq+r) \varepsilon+(b+1)M_{\varepsilon} \\&\quad \Rightarrow \frac{g_{bq+r}}{bq+r}\leq \frac{bq}{bq+r}\cdot \frac{g_q}{q}+\frac{(b+1)M_{\varepsilon}+g_r}{bq+r}+\varepsilon. \end{align*} $$
$$ \begin{align*} &g_{bq+r}\leq bg_{q}+g_r +(bq+r) \varepsilon+(b+1)M_{\varepsilon} \\&\quad \Rightarrow \frac{g_{bq+r}}{bq+r}\leq \frac{bq}{bq+r}\cdot \frac{g_q}{q}+\frac{(b+1)M_{\varepsilon}+g_r}{bq+r}+\varepsilon. \end{align*} $$
Fixing q large enough independently of b so that
![]() $({(b+1)M_{\varepsilon }}/{bq})\leq \varepsilon $
, for any large
$({(b+1)M_{\varepsilon }}/{bq})\leq \varepsilon $
, for any large
![]() $b\in \mathbb {N}^*$
, one has
$b\in \mathbb {N}^*$
, one has
This implies that
Letting
![]() $\varepsilon \to 0$
proves the statement.
$\varepsilon \to 0$
proves the statement.
One now shows that
![]() $g_n$
satisfies equation (27).
$g_n$
satisfies equation (27).
Let
![]() $k\in \mathbb {N}$
and
$k\in \mathbb {N}$
and
![]() $\underline {i}\in \Lambda ^k.$
Let us begin by the following lemma.
$\underline {i}\in \Lambda ^k.$
Let us begin by the following lemma.
Lemma 4.4. Let
![]() $D(c)$
be again defined as in Lemma 4.1, then one has, for any
$D(c)$
be again defined as in Lemma 4.1, then one has, for any
![]() $ \underline {j}\in \Lambda ^{*},$
$ \underline {j}\in \Lambda ^{*},$
Proof. Let us start by establishing the lower bound. Let
![]() $x,y\in K$
be such that
$x,y\in K$
be such that
By Lemma 4.1, one has
and
Combining equations (29), (30), and (31), one obtains
Let us focus now on the upper bound. Let
![]() $x,y\in K$
be such that
$x,y\in K$
be such that
Using again Lemma 4.1, one has
 $$ \begin{align} \| f_{\underline{i}\underline{j}}(x)-f_{\underline{i}\underline{j}}(y)\|&\leq D(c)c^k \| f_{\underline{i}}'(f_{\underline{j}}(x))\| \cdot \| f_{ \underline{j}}(x)-f_{\underline{j}}(y) \|\nonumber\\&\leq D(c)^2 c^{2k}\vert f_{\underline{i}}(K)\vert \cdot \vert f_{\underline{j}}(K)\vert. \end{align} $$
$$ \begin{align} \| f_{\underline{i}\underline{j}}(x)-f_{\underline{i}\underline{j}}(y)\|&\leq D(c)c^k \| f_{\underline{i}}'(f_{\underline{j}}(x))\| \cdot \| f_{ \underline{j}}(x)-f_{\underline{j}}(y) \|\nonumber\\&\leq D(c)^2 c^{2k}\vert f_{\underline{i}}(K)\vert \cdot \vert f_{\underline{j}}(K)\vert. \end{align} $$
The upper bound is obtained by combining equations (32) and (33).
By Lemma 4.4, for any
![]() $c>1$
and any
$c>1$
and any
![]() $n,n^{\prime }\in \mathbb {N},$
one has
$n,n^{\prime }\in \mathbb {N},$
one has
 $$ \begin{align*} g_{n+n'}= &\,\, \log\bigg(\!\sum_{\underline{i}\in\Lambda^{n+n'}}\vert f_{\underline{i}}(K) \vert^s\bigg)=\log\bigg(\!\sum_{\underline{i}\in \Lambda^n,\underline{j}\in\Lambda^{n'}}\vert f_{\underline{i}\underline{j}}(K)\vert^s\bigg)\\ \leq &\,\, \log\bigg(\!\sum_{\underline{i}\in \Lambda^n,\underline{j}\in\Lambda^{n'}}2^s D(c)^{2s}c^{2sn}\vert f_{\underline{i}}(K)\vert^s \vert f_{\underline{j}}(K)\vert^s\bigg)\\ = &\,\, n \cdot 2s\log(c)+\log(2^s D(c)^{2s})+\log\bigg(\bigg(\!\sum_{\underline{i}\in\Lambda^n}\vert f_{\underline{i}}(K)\vert^s\bigg)\times(\sum_{\underline{j}\in\Lambda^{n^{\prime}}}\vert f_{\underline{j}}(K)\vert^s)\bigg)\\ \leq &\,\, 2sn\log(c)+\log(2^s D(c)^{2s})+g_{n}+g_{n'}. \end{align*} $$
$$ \begin{align*} g_{n+n'}= &\,\, \log\bigg(\!\sum_{\underline{i}\in\Lambda^{n+n'}}\vert f_{\underline{i}}(K) \vert^s\bigg)=\log\bigg(\!\sum_{\underline{i}\in \Lambda^n,\underline{j}\in\Lambda^{n'}}\vert f_{\underline{i}\underline{j}}(K)\vert^s\bigg)\\ \leq &\,\, \log\bigg(\!\sum_{\underline{i}\in \Lambda^n,\underline{j}\in\Lambda^{n'}}2^s D(c)^{2s}c^{2sn}\vert f_{\underline{i}}(K)\vert^s \vert f_{\underline{j}}(K)\vert^s\bigg)\\ = &\,\, n \cdot 2s\log(c)+\log(2^s D(c)^{2s})+\log\bigg(\bigg(\!\sum_{\underline{i}\in\Lambda^n}\vert f_{\underline{i}}(K)\vert^s\bigg)\times(\sum_{\underline{j}\in\Lambda^{n^{\prime}}}\vert f_{\underline{j}}(K)\vert^s)\bigg)\\ \leq &\,\, 2sn\log(c)+\log(2^s D(c)^{2s})+g_{n}+g_{n'}. \end{align*} $$
Fixing
![]() $c=e^{{\varepsilon }/{2s}}$
, one has
$c=e^{{\varepsilon }/{2s}}$
, one has
![]() $2s\log (c)=\varepsilon $
and setting
$2s\log (c)=\varepsilon $
and setting
![]() $M_{\varepsilon }=\log (2^s D(c)^{2s})$
shows that
$M_{\varepsilon }=\log (2^s D(c)^{2s})$
shows that
![]() $(g_n)_{n\in \mathbb {N}}$
satisfies the condition of Lemma 4.3.
$(g_n)_{n\in \mathbb {N}}$
satisfies the condition of Lemma 4.3.
Lemma 4.3 together with equation (25) concludes the proof of Proposition 2.6.
4.3 Lyapunov exponent and dimension of weakly conformal measures
Let
![]() $m\geq 2$
and let us fix a
$m\geq 2$
and let us fix a
![]() $C^1$
weakly conformal IFS
$C^1$
weakly conformal IFS
![]() $S=\{f_1,\ldots ,f_m\}$
with attractor K.
$S=\{f_1,\ldots ,f_m\}$
with attractor K.
Given
![]() $x=(x_n)_{n\in \mathbb {N}}\in \Lambda ^{\mathbb {N}},$
the following quantity, called Lyapunov exponent of S at x, defines a logarithmic shrinking rate associated with S at x. See [Reference Feng and Hu19, Proposition 5.6].
$x=(x_n)_{n\in \mathbb {N}}\in \Lambda ^{\mathbb {N}},$
the following quantity, called Lyapunov exponent of S at x, defines a logarithmic shrinking rate associated with S at x. See [Reference Feng and Hu19, Proposition 5.6].
Proposition 4.5. [Reference Feng and Hu19]
For
![]() $x=(x_n)_{n\in \mathbb {N}}\in \Lambda ^{\mathbb {N}},$
the Lyapunov exponent of S at x is defined, when the following limit exists, as
$x=(x_n)_{n\in \mathbb {N}}\in \Lambda ^{\mathbb {N}},$
the Lyapunov exponent of S at x is defined, when the following limit exists, as
Moreover, for every ergodic measure
![]() $\nu \in \mathcal {M}(\Lambda ^{\mathbb {N}})$
(with respect to the shift
$\nu \in \mathcal {M}(\Lambda ^{\mathbb {N}})$
(with respect to the shift
![]() $\sigma $
), there exists
$\sigma $
), there exists
![]() $\unicode{x3bb} _{\nu }\geq 0$
such that for
$\unicode{x3bb} _{\nu }\geq 0$
such that for
![]() $\nu $
-almost any
$\nu $
-almost any
![]() $x=(x_n)_{n \in \mathbb {N}}$
,
$x=(x_n)_{n \in \mathbb {N}}$
,
Remark 4.6.
-
• By equation (23), the Lyapunov exponents are uniformly bounded above and below by some positive constant.
-
• When S is self-similar and
 $0<c_1,\ldots ,c_m<1$
are the contracting ratios associated with the similarities
$0<c_1,\ldots ,c_m<1$
are the contracting ratios associated with the similarities
 $f_1,\ldots ,f_m,$
the Lyapunov exponent of
$f_1,\ldots ,f_m,$
the Lyapunov exponent of
 $\nu $
as in Proposition 4.5 is simply
$\nu $
as in Proposition 4.5 is simply  $$ \begin{align*}\unicode{x3bb}_{\nu}=-\sum_{1 \leq i\leq m}p_i \log c_i.\end{align*} $$
$$ \begin{align*}\unicode{x3bb}_{\nu}=-\sum_{1 \leq i\leq m}p_i \log c_i.\end{align*} $$
The following consequence of Proposition 4.5 will be useful later (see Proposition 6.7).
Corollary 4.7. Let
![]() $((p_1 ^{(k)},\ldots ,p_m ^{(k)}))_{k\in \mathbb {N}}\in ([0,1]^m)^{\mathbb {N}}$
be a sequence of probability vectors such that
$((p_1 ^{(k)},\ldots ,p_m ^{(k)}))_{k\in \mathbb {N}}\in ([0,1]^m)^{\mathbb {N}}$
be a sequence of probability vectors such that
![]() $(p_1^{(k)},\ldots ,p_m^{(k)})\to (p_1,\ldots ,p_m).$
Denote for
$(p_1^{(k)},\ldots ,p_m^{(k)})\to (p_1,\ldots ,p_m).$
Denote for
![]() $k\in \mathbb {N} \nu ,\nu _{k}\in \mathcal {M}(\Lambda ^{\mathbb {N}})$
the measures defined for any cylinder
$k\in \mathbb {N} \nu ,\nu _{k}\in \mathcal {M}(\Lambda ^{\mathbb {N}})$
the measures defined for any cylinder
![]() $[(i_1,\ldots i_n)]$
by
$[(i_1,\ldots i_n)]$
by
Then,
![]() $\nu _k \underset {k\to +\infty }{\rightarrow } \nu $
weakly, so that
$\nu _k \underset {k\to +\infty }{\rightarrow } \nu $
weakly, so that
Let us also recall the following fundamental result established by Feng and Hu [Reference Feng and Hu19, Theorem 2.2].
Theorem 4.8. [Reference Feng and Hu19]
Let
![]() $(p_1,\ldots ,p_m)\in [0,1]^m$
be a probability vector,
$(p_1,\ldots ,p_m)\in [0,1]^m$
be a probability vector,
![]() $\nu \in \mathcal {M}(\Lambda ^{\mathbb {N}})$
defined for any
$\nu \in \mathcal {M}(\Lambda ^{\mathbb {N}})$
defined for any
![]() $\underline {i}\in \Lambda ^*$
by
$\underline {i}\in \Lambda ^*$
by
![]() $\nu ([\underline {i}])=p_{\underline {i}}$
and
$\nu ([\underline {i}])=p_{\underline {i}}$
and
![]() $\mu =\nu \circ \pi ^{-1}.$
$\mu =\nu \circ \pi ^{-1}.$
There is an
![]() $h\geq 0$
such that for
$h\geq 0$
such that for
![]() $\mu $
-almost every
$\mu $
-almost every
![]() $x\in K$
, there exists
$x\in K$
, there exists
![]() $ \mu ^{\pi ^{-1}(\{x\})}\in \mathcal {M}( \Lambda ^{\mathbb {N}})$
such that:
$ \mu ^{\pi ^{-1}(\{x\})}\in \mathcal {M}( \Lambda ^{\mathbb {N}})$
such that:
-
(1)
 $\mu ^{\pi ^{-1}(\{x\})}(\pi ^{-1}(\{x\}))=1;$
$\mu ^{\pi ^{-1}(\{x\})}(\pi ^{-1}(\{x\}))=1;$
-
(2) for
 $\mu ^{\pi ^{-1}(\{x\})}$
-almost
$\mu ^{\pi ^{-1}(\{x\})}$
-almost
 $y=(y_1,\ldots ,y_n,\ldots )$
, (36)
$y=(y_1,\ldots ,y_n,\ldots )$
, (36) $$ \begin{align} \frac{-\log \mu^{\pi^{-1}(\{x\})}([y_1,\ldots,y_n])}{n}\to h; \end{align} $$
$$ \begin{align} \frac{-\log \mu^{\pi^{-1}(\{x\})}([y_1,\ldots,y_n])}{n}\to h; \end{align} $$
-
(3) for every Borel set
 $A\subset \Lambda ^{\mathbb {N}},$
(37)
$A\subset \Lambda ^{\mathbb {N}},$
(37) $$ \begin{align} \nu(A)=\int_{K}\mu^{\pi^{-1}(\{x\})}(A)\ d\mu(x); \end{align} $$
$$ \begin{align} \nu(A)=\int_{K}\mu^{\pi^{-1}(\{x\})}(A)\ d\mu(x); \end{align} $$
-
(4) denoting
 $\unicode{x3bb} $
as the Lyapunov exponent associated with
$\unicode{x3bb} $
as the Lyapunov exponent associated with
 $\nu $
as in equation (35),
$\nu $
as in equation (35),
 $\mu $
is exact-dimensional (Definition 5) and
$\mu $
is exact-dimensional (Definition 5) and  $$ \begin{align*}\dim(\mu)=\frac{-h-\sum_{1\leq i\leq m}p_i\log p_i}{\unicode{x3bb}} .\end{align*} $$
$$ \begin{align*}\dim(\mu)=\frac{-h-\sum_{1\leq i\leq m}p_i\log p_i}{\unicode{x3bb}} .\end{align*} $$
4.4 The AWSC condition
4.4.1 Definition and known results
To provide a larger class of weakly conformal IFSs to which Theorem 3.1 applies, we recall the definition of the AWSC [Reference Feng18]. First, given an IFS
![]() $S=\{f_i\}_{i\in \Lambda },$
let us define
$S=\{f_i\}_{i\in \Lambda },$
let us define
Definition 4.9. One says that
![]() $S=\{f_i\}_{i\in \Lambda }$
satisfies the AWSC [Reference Feng18] when, writing for
$S=\{f_i\}_{i\in \Lambda }$
satisfies the AWSC [Reference Feng18] when, writing for
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
one has
Let us also note here that when the IFS
![]() $S $
has no exact overlaps (i.e., for any
$S $
has no exact overlaps (i.e., for any
![]() $\underline {i}\neq \underline {j}\in \Lambda ^*$
,
$\underline {i}\neq \underline {j}\in \Lambda ^*$
,
![]() $f_{\underline {i}}\neq f_{\underline {j}}$
), one also has
$f_{\underline {i}}\neq f_{\underline {j}}$
), one also has
The introduction of the AWSC condition is motivated by the following result.
Proposition 4.10. Let S be a weakly conformal IFS satisfying the AWSC with no exact overlaps. Then, its attractor K satisfies
As mentioned in §3.3, the advantage of the ASWC is that it can be reformulated in terms of a condition regarding the multifractal spectrum of some natural measures (given by Lemma 4.21) associated with a weakly conformal IFS.
The following proposition was established by Barral and Feng in [Reference Barral and Feng4] in the case of self-similar measures but readily adapts in the case of weakly conformal measures.
Proposition 4.11. [Reference Barral and Feng4]
Let
![]() $S=\{f_1,\ldots ,f_m\}$
be a conformal IFS and let K be its attractor. Assume that there exists a measure
$S=\{f_1,\ldots ,f_m\}$
be a conformal IFS and let K be its attractor. Assume that there exists a measure
![]() $\nu _0 \in \mathcal {M}(\{1,\ldots ,m\}^{\mathbb {N}})$
such that for every
$\nu _0 \in \mathcal {M}(\{1,\ldots ,m\}^{\mathbb {N}})$
such that for every
![]() $\underline {i}\in \{1,\ldots ,m\}^k$
, one has
$\underline {i}\in \{1,\ldots ,m\}^k$
, one has
 $$ \begin{align} C^{-1}\leq\frac{\nu_0([\underline{i}])}{\vert f_{\underline{i}}(K)\vert^{\dim(S)}}\leq C, \end{align} $$
$$ \begin{align} C^{-1}\leq\frac{\nu_0([\underline{i}])}{\vert f_{\underline{i}}(K)\vert^{\dim(S)}}\leq C, \end{align} $$
where
![]() $C>0$
is independent of
$C>0$
is independent of
![]() $\underline {i}.$
Set
$\underline {i}.$
Set
![]() $\mu _0 =\nu _0 \circ \pi ^{-1}$
. If for every
$\mu _0 =\nu _0 \circ \pi ^{-1}$
. If for every
![]() $q\geq 1,$
one has
$q\geq 1,$
one has
where
![]() $\tau _{\mu _0}$
is the scaling function defined by equation (17), then
$\tau _{\mu _0}$
is the scaling function defined by equation (17), then
![]() $\dim _{H}\!y{\mu }_0 =\dim (S), S$
satisfies the AWSC, and S has no exact-overlaps.
$\dim _{H}\!y{\mu }_0 =\dim (S), S$
satisfies the AWSC, and S has no exact-overlaps.
Proposition 4.11 combined with a well-known result established by Shmerkin in [Reference Shmerkin36] regarding the multifractal spectrum of self-similar measures on
![]() $\mathbb {R}$
satisfying the exponential separation yields the following result established as [Reference Barral and Feng4, Theorem 1.3].
$\mathbb {R}$
satisfying the exponential separation yields the following result established as [Reference Barral and Feng4, Theorem 1.3].
Theorem 4.12. [Reference Barral and Feng4]
Let S be a self-similar IFS on
![]() $\mathbb {R}$
satisfying the exponential separation condition [Reference Hochman24, Theorem 1.4]. Then, S satisfies the AWSC if and only if
$\mathbb {R}$
satisfying the exponential separation condition [Reference Hochman24, Theorem 1.4]. Then, S satisfies the AWSC if and only if
![]() $\dim (S)\leq 1$
.
$\dim (S)\leq 1$
.
4.4.2 Some technical results regarding the AWSC
For
![]() $k\in \mathbb {N}$
and
$k\in \mathbb {N}$
and
![]() $x\in \mathbb {R}^d,$
recall equation (38) and define
$x\in \mathbb {R}^d,$
recall equation (38) and define
Moreover, for
![]() $x\in K,$
we set
$x\in K,$
we set
 $$ \begin{align*} T_k(x)&=\{f_{\underline{i}}: \ f_{\underline{i}}(K)\cap B(x,2^{-k})\neq \emptyset , \ \underline{i}\in\widetilde{\Lambda}^{(k)}\}, \\ T^{\prime}_k(x)&=\{f_{\underline{i}}: \ f_{\underline{i}}(K)\cap B(x,2^{-k})\neq \emptyset , \ \underline{i}\in\Lambda^{(k)}\}. \end{align*} $$
$$ \begin{align*} T_k(x)&=\{f_{\underline{i}}: \ f_{\underline{i}}(K)\cap B(x,2^{-k})\neq \emptyset , \ \underline{i}\in\widetilde{\Lambda}^{(k)}\}, \\ T^{\prime}_k(x)&=\{f_{\underline{i}}: \ f_{\underline{i}}(K)\cap B(x,2^{-k})\neq \emptyset , \ \underline{i}\in\Lambda^{(k)}\}. \end{align*} $$
Note that S satisfies AWSC if and only if
![]() $ \lim _{k\rightarrow +\infty }\max _{x\in \mathbb {R}^d}({\log \#T_k(x)}/{k})=0.$
$ \lim _{k\rightarrow +\infty }\max _{x\in \mathbb {R}^d}({\log \#T_k(x)}/{k})=0.$
Proposition 4.13. One has
 $$ \begin{align*}\lim_{k\rightarrow+\infty}\max_{x\in\mathbb{R}^d}\frac{\log\# T_k(x)}{k}=0 \ \Longleftrightarrow \ \lim_{k\rightarrow+\infty}\max_{x\in\mathbb{R}^d}\frac{\log \# T^{\prime}_k(x)}{k}=0.\end{align*} $$
$$ \begin{align*}\lim_{k\rightarrow+\infty}\max_{x\in\mathbb{R}^d}\frac{\log\# T_k(x)}{k}=0 \ \Longleftrightarrow \ \lim_{k\rightarrow+\infty}\max_{x\in\mathbb{R}^d}\frac{\log \# T^{\prime}_k(x)}{k}=0.\end{align*} $$
Proof. By equation (23), there exists
![]() $0<\alpha <\tfrac 12< \beta \leq 1$
such that for every
$0<\alpha <\tfrac 12< \beta \leq 1$
such that for every
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
Remark 4.14.
-
(1) For every
 $k\in \mathbb {N}$
and every
$k\in \mathbb {N}$
and every
 $\underline {i}=(i_1,\ldots ,i_n)\in \Lambda ^{(k)},$
one has
$\underline {i}=(i_1,\ldots ,i_n)\in \Lambda ^{(k)},$
one has  $$ \begin{align*} C(\alpha,\beta)^{-1}k \leq k \frac{-\log 2} {\log \beta}+1\leq n \leq 2 k \frac{-\log 2} {\log \alpha}\leq C(\alpha,\beta) k.\end{align*} $$
$$ \begin{align*} C(\alpha,\beta)^{-1}k \leq k \frac{-\log 2} {\log \beta}+1\leq n \leq 2 k \frac{-\log 2} {\log \alpha}\leq C(\alpha,\beta) k.\end{align*} $$
-
(2) For every
 $c>1$
, by Lemma 4.4, for every
$c>1$
, by Lemma 4.4, for every
 $\underline {i}=(i_1,\ldots ,i_n)\in \widetilde {\Lambda }^{(k)}$
,
$\underline {i}=(i_1,\ldots ,i_n)\in \widetilde {\Lambda }^{(k)}$
,  $$ \begin{align*}D(c)^{-2} \min_{1\leq j\leq m}\vert f_{j}(K)\vert c^{-2 C(\alpha,\beta)k}2^{-k}\leq \vert f_{\underline{i}}(K)\vert \leq 2^{-k}.\end{align*} $$
$$ \begin{align*}D(c)^{-2} \min_{1\leq j\leq m}\vert f_{j}(K)\vert c^{-2 C(\alpha,\beta)k}2^{-k}\leq \vert f_{\underline{i}}(K)\vert \leq 2^{-k}.\end{align*} $$
In particular, for any
 $k\in \mathbb {N}$
large enough, one has (43)
$k\in \mathbb {N}$
large enough, one has (43) $$ \begin{align} c^{-{1}/{2} C(\alpha,\beta)k}2^{-k}\leq \vert f_{\underline{i}}(K)\vert \leq 2^{-k}. \end{align} $$
$$ \begin{align} c^{-{1}/{2} C(\alpha,\beta)k}2^{-k}\leq \vert f_{\underline{i}}(K)\vert \leq 2^{-k}. \end{align} $$
Lemma 4.15. For every
![]() $\varepsilon _0>0$
, there exists
$\varepsilon _0>0$
, there exists
![]() $k_{\varepsilon }\in \mathbb {N}$
such that for every
$k_{\varepsilon }\in \mathbb {N}$
such that for every
![]() $k\geq k_{ \varepsilon _0}$
, for every
$k\geq k_{ \varepsilon _0}$
, for every
![]() $\underline {i}=(i_1,\ldots ,i_{n})\in \Lambda ^{(k)},$
there exists
$\underline {i}=(i_1,\ldots ,i_{n})\in \Lambda ^{(k)},$
there exists
![]() $0\leq p \leq \varepsilon _0 k$
such that
$0\leq p \leq \varepsilon _0 k$
such that
![]() $(i_1,\ldots ,i_{n-p})\in \widetilde {\Lambda }^{(k)}.$
$(i_1,\ldots ,i_{n-p})\in \widetilde {\Lambda }^{(k)}.$
Proof. Fix
![]() $\varepsilon ={\varepsilon _0}/{2C(\alpha ,\beta )}$
and
$\varepsilon ={\varepsilon _0}/{2C(\alpha ,\beta )}$
and
![]() $c>1$
such that
$c>1$
such that
![]() $c^{1-\varepsilon }\beta ^{\varepsilon }<1$
. By Lemma 4.4, for any
$c^{1-\varepsilon }\beta ^{\varepsilon }<1$
. By Lemma 4.4, for any
![]() $(i_1,\ldots ,i_n)\in \Lambda ^*$
and
$(i_1,\ldots ,i_n)\in \Lambda ^*$
and
![]() $0\leq p\leq n,$
$0\leq p\leq n,$
In particular, for
![]() $p\geq n\varepsilon ,$
$p\geq n\varepsilon ,$
 $$ \begin{align*} \vert f_{(i_1,\ldots,i_{n-p})}(K)\vert \geq \frac{D(c)^{-2}c^{-(n-p)}}{\vert f_{(i_{n-p+1},\ldots,i_n)}(K)\vert}2^{-k}\geq 2^{-k}\frac{D(c)^{-2}}{(c^{1-\varepsilon}\beta^{\varepsilon})^n}. \end{align*} $$
$$ \begin{align*} \vert f_{(i_1,\ldots,i_{n-p})}(K)\vert \geq \frac{D(c)^{-2}c^{-(n-p)}}{\vert f_{(i_{n-p+1},\ldots,i_n)}(K)\vert}2^{-k}\geq 2^{-k}\frac{D(c)^{-2}}{(c^{1-\varepsilon}\beta^{\varepsilon})^n}. \end{align*} $$
This yields, for k large enough and
![]() $p_{}=\lfloor \varepsilon C(\alpha ,\beta )k\rfloor +1 \leq 2C( \alpha ,\beta )\varepsilon k$
, that
$p_{}=\lfloor \varepsilon C(\alpha ,\beta )k\rfloor +1 \leq 2C( \alpha ,\beta )\varepsilon k$
, that
As a consequence, there must exist
![]() $p\leq 2C( \alpha ,\beta )\varepsilon k$
such that
$p\leq 2C( \alpha ,\beta )\varepsilon k$
such that
![]() $(i_1,\ldots ,i_{n-p})\in \widetilde {\Lambda }^{(k)}.$
$(i_1,\ldots ,i_{n-p})\in \widetilde {\Lambda }^{(k)}.$
Lemma 4.16. For every
![]() $c>1$
, for every
$c>1$
, for every
![]() $\varepsilon>0,$
for every k large enough (depending on c) and every
$\varepsilon>0,$
for every k large enough (depending on c) and every
![]() $x\in \mathbb {R}^d,$
one has
$x\in \mathbb {R}^d,$
one has
 $$ \begin{align} &\# T_k(x)\nonumber\\&\ \ \leq k\bigg\lfloor \frac{ ({C(\alpha,\beta)}/{2})\log c}{\log 2} \bigg\rfloor C_d c^{kd{(C(\alpha,\beta)}/{2})}\max_{k\leq k" \leq k(1+\lfloor { (({C(\alpha,\beta)}/{2})\log c})/{\log 2} \rfloor)}\max_{y\in\mathbb{R}^d}\# T^{\prime}_{k'}(y) \\&\qquad\qquad\qquad\qquad\qquad\qquad\text{and } \quad \# T^{\prime}_k(x) \leq m^{k\varepsilon}\# T_k(x).\nonumber \end{align} $$
$$ \begin{align} &\# T_k(x)\nonumber\\&\ \ \leq k\bigg\lfloor \frac{ ({C(\alpha,\beta)}/{2})\log c}{\log 2} \bigg\rfloor C_d c^{kd{(C(\alpha,\beta)}/{2})}\max_{k\leq k" \leq k(1+\lfloor { (({C(\alpha,\beta)}/{2})\log c})/{\log 2} \rfloor)}\max_{y\in\mathbb{R}^d}\# T^{\prime}_{k'}(y) \\&\qquad\qquad\qquad\qquad\qquad\qquad\text{and } \quad \# T^{\prime}_k(x) \leq m^{k\varepsilon}\# T_k(x).\nonumber \end{align} $$
Proof. Remark that, for each
![]() $ k' $
such that
$ k' $
such that
there exists a constant
![]() $C_d$
(which depends on
$C_d$
(which depends on
![]() $d,\alpha $
, and
$d,\alpha $
, and
![]() $\beta $
) so that each ball
$\beta $
) so that each ball
![]() $B(x,2^{-k})$
can be covered by less than
$B(x,2^{-k})$
can be covered by less than
balls of radius
![]() $2^{-k'}.$
This implies that
$2^{-k'}.$
This implies that
Since one has
 $$ \begin{align*}\widetilde{\Lambda}^{(k)}\subset \bigcup_{k'=k}^{k(1+\lfloor { (({C(\alpha,\beta)}/{2})\log c})/{\log Z} \rfloor)}\Lambda^{(k')},\end{align*} $$
$$ \begin{align*}\widetilde{\Lambda}^{(k)}\subset \bigcup_{k'=k}^{k(1+\lfloor { (({C(\alpha,\beta)}/{2})\log c})/{\log Z} \rfloor)}\Lambda^{(k')},\end{align*} $$
it holds that
 $$ \begin{align} &\# T_k(x)\nonumber\\ &\ \ \leq k\bigg\lfloor \frac{ ({C(\alpha,\beta)}/{2})\log c}{\log 2} \bigg\rfloor C_d c^{kd({C(\alpha,\beta)}/{2})}\max_{k\leq k" \leq k(1+\lfloor { (({C(\alpha,\beta)}/{2})\log c})/{\log 2} \rfloor)}\max_{y\in\mathbb{R}^d}\# T^{\prime}_{k'}(y). \end{align} $$
$$ \begin{align} &\# T_k(x)\nonumber\\ &\ \ \leq k\bigg\lfloor \frac{ ({C(\alpha,\beta)}/{2})\log c}{\log 2} \bigg\rfloor C_d c^{kd({C(\alpha,\beta)}/{2})}\max_{k\leq k" \leq k(1+\lfloor { (({C(\alpha,\beta)}/{2})\log c})/{\log 2} \rfloor)}\max_{y\in\mathbb{R}^d}\# T^{\prime}_{k'}(y). \end{align} $$
Moreover, by Lemma 4.15, there exists
![]() $\phi _k:T^{\prime }_k (x)\to T_k(x)$
defined by
$\phi _k:T^{\prime }_k (x)\to T_k(x)$
defined by
with
![]() $0\leq p\leq k\varepsilon $
. The mapping
$0\leq p\leq k\varepsilon $
. The mapping
![]() $\phi _k$
verifies that, for every
$\phi _k$
verifies that, for every
![]() $(i_1,\ldots i_{n'})\in T_k(x) $
,
$(i_1,\ldots i_{n'})\in T_k(x) $
,
This implies that
Taking the log of the estimates of Lemma 4.16 and letting k tend to infinity concludes the proof.
4.4.3 AWSC and dimension regularity
The following notion was introduced by Barral and Feng in [Reference Barral and Feng4].
Definition 4.17. [Reference Barral and Feng4]
Let
![]() $S=\{f_1,\ldots ,f_m\}$
be a weakly conformal IFS. For
$S=\{f_1,\ldots ,f_m\}$
be a weakly conformal IFS. For
![]() $P=(p_1,\ldots ,p_m)\in [0,1]^m$
a probability vector, denote again by
$P=(p_1,\ldots ,p_m)\in [0,1]^m$
a probability vector, denote again by
![]() $\nu _P\in \mathcal {M}(\Lambda ^*)$
the measure satisfying for every
$\nu _P\in \mathcal {M}(\Lambda ^*)$
the measure satisfying for every
![]() $(i_1,\ldots ,i_n)\in \Lambda ^*$
,
$(i_1,\ldots ,i_n)\in \Lambda ^*$
,
![]() $\nu _P([i_1,\ldots ,i_n])=p_{i_1}\times \cdots \times p_{i_n}$
and
$\nu _P([i_1,\ldots ,i_n])=p_{i_1}\times \cdots \times p_{i_n}$
and
![]() $\mu _P=\nu _P\circ \pi ^{-1}$
. The IFS S is said to be dimension regular if, for every probability vector P,
$\mu _P=\nu _P\circ \pi ^{-1}$
. The IFS S is said to be dimension regular if, for every probability vector P,
 $$ \begin{align} \dim(\mu_P)=\min\bigg\{\frac{-\sum_{1\leq i\leq m}p_i \log(p_i)}{\unicode{x3bb}_{\nu_P}}, d\bigg\}, \end{align} $$
$$ \begin{align} \dim(\mu_P)=\min\bigg\{\frac{-\sum_{1\leq i\leq m}p_i \log(p_i)}{\unicode{x3bb}_{\nu_P}}, d\bigg\}, \end{align} $$
where
![]() $\unicode{x3bb} _{\nu _P}$
is defined by equation (35).
$\unicode{x3bb} _{\nu _P}$
is defined by equation (35).
Remark 4.18.
-
• When S is self-similar, calling
 $0<c_1,\ldots ,c_m<1$
the contraction ratios of the similarities
$0<c_1,\ldots ,c_m<1$
the contraction ratios of the similarities
 $f_1,\ldots ,f_m$
, for any probability vector
$f_1,\ldots ,f_m$
, for any probability vector
 $(p_1,\ldots ,p_m), \mu $
, and
$(p_1,\ldots ,p_m), \mu $
, and
 $\nu $
as in Definition 4.17, one has (47)
$\nu $
as in Definition 4.17, one has (47) $$ \begin{align} \dim(\mu)=\min\bigg\{\frac{-\!\sum_{1\leq i\leq m}p_i \log(p_i)}{\unicode{x3bb}_{\nu}}, d\bigg\}= \min\bigg\{\frac{\sum_{1\leq i\leq m}p_i \log(p_i)}{\sum_{i=1}^m p_i \log (c_i )}, d\bigg\}. \end{align} $$
$$ \begin{align} \dim(\mu)=\min\bigg\{\frac{-\!\sum_{1\leq i\leq m}p_i \log(p_i)}{\unicode{x3bb}_{\nu}}, d\bigg\}= \min\bigg\{\frac{\sum_{1\leq i\leq m}p_i \log(p_i)}{\sum_{i=1}^m p_i \log (c_i )}, d\bigg\}. \end{align} $$
-
• As proved in [Reference Hochman24], any self-similar IFS on
 $\mathbb {R}$
satisfying the exponential separation condition [Reference Hochman24, Theorem 1.4] is dimension regular.
$\mathbb {R}$
satisfying the exponential separation condition [Reference Hochman24, Theorem 1.4] is dimension regular.
We will prove the following result which implies Proposition 4.10.
Proposition 4.19. Assume that
![]() $S=\{f_1,\ldots ,f_m\}$
satisfies the AWSC without exact overlaps. Then, S is dimension regular and
$S=\{f_1,\ldots ,f_m\}$
satisfies the AWSC without exact overlaps. Then, S is dimension regular and
![]() $\dim (S)=\dim _H(K).$
$\dim (S)=\dim _H(K).$
Had the IFS been conformal and satisfying some bounded distortion properties, the proof of Proposition 4.19 would follow directly from the existence of appropriated Gibbs measures. Unfortunately, such measures do not always exist in the weakly conformal case, but some measures that are close enough from satisfying the desired properties still exist as established by the following lemma.
Lemma 4.20. Let
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $s\geq 0$
be real numbers. There exists
$s\geq 0$
be real numbers. There exists
![]() $k\in \mathbb {N}$
and a probability vector
$k\in \mathbb {N}$
and a probability vector
![]() $(p_{\underline {i}})_{\underline {i}\in \Lambda ^k}$
such that the weakly conformal measure
$(p_{\underline {i}})_{\underline {i}\in \Lambda ^k}$
such that the weakly conformal measure
![]() $\nu $
associated with
$\nu $
associated with
![]() $S'=\{f_{\underline {i}}\}_{\underline {i}\in \Lambda ^k}$
and
$S'=\{f_{\underline {i}}\}_{\underline {i}\in \Lambda ^k}$
and
![]() $(p_{\underline {i}})_{\underline {i}\in \Lambda ^k}$
verifies, for any
$(p_{\underline {i}})_{\underline {i}\in \Lambda ^k}$
verifies, for any
![]() $p\in \mathbb {N}$
and
$p\in \mathbb {N}$
and
![]() $\underline {i}_1 ,\ldots ,\underline {i}_p \in \Lambda ^{k},$
$\underline {i}_1 ,\ldots ,\underline {i}_p \in \Lambda ^{k},$
 $$ \begin{align} e^{-kp\varepsilon}\frac{\vert f_{\underline{i}_1 \cdots \underline{i}_p}(K)\vert^s}{e^{pkP(s)}}\leq \nu([\underline{i}_1 \cdots \underline{i}_p])\leq e^{kp\varepsilon}\frac{\vert f_{\underline{i}_1 \cdots \underline{i}_p}(K)\vert^s}{e^{pkP(s)}}. \end{align} $$
$$ \begin{align} e^{-kp\varepsilon}\frac{\vert f_{\underline{i}_1 \cdots \underline{i}_p}(K)\vert^s}{e^{pkP(s)}}\leq \nu([\underline{i}_1 \cdots \underline{i}_p])\leq e^{kp\varepsilon}\frac{\vert f_{\underline{i}_1 \cdots \underline{i}_p}(K)\vert^s}{e^{pkP(s)}}. \end{align} $$
Proof. Fix
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $c>1$
small enough so that
$c>1$
small enough so that
![]() $8s\log c\leq \varepsilon .$
$8s\log c\leq \varepsilon .$
By Lemma 4.3, there exists
![]() $k\in \mathbb {N}$
so large that the constant named
$k\in \mathbb {N}$
so large that the constant named
![]() $D(c)$
in Lemma 4.1 verifies
$D(c)$
in Lemma 4.1 verifies
![]() $ ({\log D(c)}/{k})\leq \log c $
and
$ ({\log D(c)}/{k})\leq \log c $
and
 $$ \begin{align} \bigg\vert \frac{1}{k}\log \sum_{\underline{i}\in\Lambda^k}\vert f_{\underline{i}}(K)\vert^s -P(s)\bigg\vert\leq \frac{\varepsilon}{2}. \end{align} $$
$$ \begin{align} \bigg\vert \frac{1}{k}\log \sum_{\underline{i}\in\Lambda^k}\vert f_{\underline{i}}(K)\vert^s -P(s)\bigg\vert\leq \frac{\varepsilon}{2}. \end{align} $$
Writing again
![]() $g_k =\log \sum _{\underline {i}\in \Lambda ^k}\vert f_{\underline {i}}(K)\vert ^s,$
let us define the probability vector
$g_k =\log \sum _{\underline {i}\in \Lambda ^k}\vert f_{\underline {i}}(K)\vert ^s,$
let us define the probability vector
![]() $(p_{\underline {i}})_{\underline {i}\in \Lambda ^k}$
by setting
$(p_{\underline {i}})_{\underline {i}\in \Lambda ^k}$
by setting
Let
![]() $\nu $
be the weakly conformal measure associated with
$\nu $
be the weakly conformal measure associated with
![]() $S'=\{f_{\underline {i}}\}_{\underline {i}\in \Lambda ^k}$
and
$S'=\{f_{\underline {i}}\}_{\underline {i}\in \Lambda ^k}$
and
![]() $(p_{\underline {i}})_{\underline {i}\in \Lambda ^k}.$
Applying Lemma 4.4, for any
$(p_{\underline {i}})_{\underline {i}\in \Lambda ^k}.$
Applying Lemma 4.4, for any
![]() $p\in \mathbb {N}, \underline {i}_1,\ldots ,\underline {i}_p\in \Lambda ^k,$
,
$p\in \mathbb {N}, \underline {i}_1,\ldots ,\underline {i}_p\in \Lambda ^k,$
,
 $$ \begin{align} D(c)^{-2p}c^{-2kp}\leq \frac{\vert f_{\underline{i}_1}\circ \cdots \circ f_{\underline{i}_p}(K)\vert}{\prod_{j=1}^p \vert f_{\underline{i}_j}(K)\vert}\leq D(c)^{2p}c^{2kp}. \end{align} $$
$$ \begin{align} D(c)^{-2p}c^{-2kp}\leq \frac{\vert f_{\underline{i}_1}\circ \cdots \circ f_{\underline{i}_p}(K)\vert}{\prod_{j=1}^p \vert f_{\underline{i}_j}(K)\vert}\leq D(c)^{2p}c^{2kp}. \end{align} $$
Also,
As a consequence, for any
![]() $p\in \mathbb {N}$
and any
$p\in \mathbb {N}$
and any
![]() $\underline {i}_1,\ldots ,\underline {i}_p \in \Lambda ^k,$
one has
$\underline {i}_1,\ldots ,\underline {i}_p \in \Lambda ^k,$
one has
 $$ \begin{align*} \nu([\underline{i}_1 \cdots \underline{i}_p])=p_{\underline{i}_1}\cdot \cdots \cdot p_{\underline{i}_p}=\frac{\prod_{j=1}^p \vert f_{\underline{i}_j}(K)\vert^s}{e^{pg_k}}=\frac{\prod_{j=1}^p \vert f_{\underline{i}_j}(K)\vert^s}{e^{kp(({g_k}/{k})-P(s))}e^{pkP(s)}}. \end{align*} $$
$$ \begin{align*} \nu([\underline{i}_1 \cdots \underline{i}_p])=p_{\underline{i}_1}\cdot \cdots \cdot p_{\underline{i}_p}=\frac{\prod_{j=1}^p \vert f_{\underline{i}_j}(K)\vert^s}{e^{pg_k}}=\frac{\prod_{j=1}^p \vert f_{\underline{i}_j}(K)\vert^s}{e^{kp(({g_k}/{k})-P(s))}e^{pkP(s)}}. \end{align*} $$
Remark 4.21. The measure
![]() $\nu $
can be extended over
$\nu $
can be extended over
![]() $\Lambda ^{\mathbb {N}}$
by the usual arguments. Moreover, for any
$\Lambda ^{\mathbb {N}}$
by the usual arguments. Moreover, for any
![]() $\underline {i}=(i_1,\ldots ,i_n)\in \Lambda ^{*},$
write
$\underline {i}=(i_1,\ldots ,i_n)\in \Lambda ^{*},$
write
![]() $n_1=k\lfloor {n}/{k} \rfloor $
and
$n_1=k\lfloor {n}/{k} \rfloor $
and
![]() $n_2=k(\lfloor {n}/{k} \rfloor +1).$
Consider
$n_2=k(\lfloor {n}/{k} \rfloor +1).$
Consider
![]() ${\underline {j}\in \Lambda ^{n_1}}$
such that
${\underline {j}\in \Lambda ^{n_1}}$
such that
![]() $[\underline {i}]\subset [\underline {j}]$
and
$[\underline {i}]\subset [\underline {j}]$
and
![]() $\underline {\ell }=(\ell _1,\ldots ,\ell _{n_2-n})\in \Lambda ^{n_2-n},$
one has
$\underline {\ell }=(\ell _1,\ldots ,\ell _{n_2-n})\in \Lambda ^{n_2-n},$
one has
By Lemma 4.4, there exists a constant
![]() $C>0$
such that, uniformly on
$C>0$
such that, uniformly on
![]() $\underline {i},\underline {j},\underline {i}\underline {\ell },$
one has
$\underline {i},\underline {j},\underline {i}\underline {\ell },$
one has
 $$ \begin{align*} C^{-1}\leq\min\bigg\{\frac{\vert f_{\underline{j}}(K)\vert}{\vert f_{\underline{i}}(K)\vert},\frac{\vert f_{\underline{i}}(K)\vert}{\vert f_{\underline{i}\underline{\ell}}(K)\vert}\bigg\} \leq\max\bigg\{\frac{\vert f_{\underline{j}}(K)\vert}{\vert f_{\underline{i}}(K)\vert},\frac{\vert f_{\underline{i}}(K)\vert}{\vert f_{\underline{i}\underline{\ell}}(K)\vert}\bigg\}\leq C. \end{align*} $$
$$ \begin{align*} C^{-1}\leq\min\bigg\{\frac{\vert f_{\underline{j}}(K)\vert}{\vert f_{\underline{i}}(K)\vert},\frac{\vert f_{\underline{i}}(K)\vert}{\vert f_{\underline{i}\underline{\ell}}(K)\vert}\bigg\} \leq\max\bigg\{\frac{\vert f_{\underline{j}}(K)\vert}{\vert f_{\underline{i}}(K)\vert},\frac{\vert f_{\underline{i}}(K)\vert}{\vert f_{\underline{i}\underline{\ell}}(K)\vert}\bigg\}\leq C. \end{align*} $$
Hence, there exists a constant
![]() $\gamma _{s,\varepsilon }$
such that for any
$\gamma _{s,\varepsilon }$
such that for any
![]() $\underline {i}=(i_1,\ldots ,i_n)\in \Lambda ^{*}$
, one has
$\underline {i}=(i_1,\ldots ,i_n)\in \Lambda ^{*}$
, one has
Let us now prove Proposition 4.19.
Proof. Call K the attractor of S. Let us show first that if any system S satisfying the AWSC also verifies that, for any weakly conformal measure
![]() $\mu \in \mathcal {M}(\mathbb {R}^d)$
associated with a probability vector
$\mu \in \mathcal {M}(\mathbb {R}^d)$
associated with a probability vector
![]() $(p_1,\ldots ,p_m)$
and S,
$(p_1,\ldots ,p_m)$
and S,
 $$ \begin{align} \dim(\mu)=\frac{-\!\sum_{1\leq i\leq m}p_i \log p_i}{\unicode{x3bb}_{\nu}}, \end{align} $$
$$ \begin{align} \dim(\mu)=\frac{-\!\sum_{1\leq i\leq m}p_i \log p_i}{\unicode{x3bb}_{\nu}}, \end{align} $$
where
![]() $\nu $
is the measure associated on
$\nu $
is the measure associated on
![]() $\Lambda ^{\mathbb {N}},$
then
$\Lambda ^{\mathbb {N}},$
then
![]() $\dim (S)=\dim _H (K).$
$\dim (S)=\dim _H (K).$
Fix
![]() $\varepsilon>0$
and consider
$\varepsilon>0$
and consider
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
![]() $S'=\{f_{\underline {i}}\}_{\underline {i}\in \Lambda ^k}$
, and
$S'=\{f_{\underline {i}}\}_{\underline {i}\in \Lambda ^k}$
, and
![]() $\nu $
as in Lemma 4.20 applied with
$\nu $
as in Lemma 4.20 applied with
![]() $s=\dim (S).$
Note that, since S satisfies the AWSC, so does
$s=\dim (S).$
Note that, since S satisfies the AWSC, so does
![]() $S'$
. Then, considering the measure
$S'$
. Then, considering the measure
![]() $\mu =\nu \circ \pi ^{-1}$
, where
$\mu =\nu \circ \pi ^{-1}$
, where
![]() $\pi $
is the canonical projection, one has
$\pi $
is the canonical projection, one has
 $$ \begin{align*} \dim(S)-\varepsilon\leq \dim (\mu)=\frac{-\!\sum_{\underline{i}\in\Lambda^k}p_{\underline{i}}\log p_{\underline{i}}}{\unicode{x3bb}_{\nu}}\leq \dim(S)+\varepsilon. \end{align*} $$
$$ \begin{align*} \dim(S)-\varepsilon\leq \dim (\mu)=\frac{-\!\sum_{\underline{i}\in\Lambda^k}p_{\underline{i}}\log p_{\underline{i}}}{\unicode{x3bb}_{\nu}}\leq \dim(S)+\varepsilon. \end{align*} $$
This proves that
![]() $\dim _H (K)\geq \dim (S)-\varepsilon .$
Since it always holds that
$\dim _H (K)\geq \dim (S)-\varepsilon .$
Since it always holds that
![]() $\dim _H(K)\leq \dim (S)$
(see [Reference Falconer15]) and
$\dim _H(K)\leq \dim (S)$
(see [Reference Falconer15]) and
![]() $\varepsilon $
is arbitrary,
$\varepsilon $
is arbitrary,
Let us show that, for any system satisfying the AWSC, equation (54) holds for every weakly conformal measure
![]() $\mu $
.
$\mu $
.
Let
![]() $\mu \in \mathcal {M}(\mathbb {R}^d)$
be a weakly conformal measure associated with S and a probability vector
$\mu \in \mathcal {M}(\mathbb {R}^d)$
be a weakly conformal measure associated with S and a probability vector
![]() $(p_1,\ldots ,p_m)$
and
$(p_1,\ldots ,p_m)$
and
![]() $\nu \in \mathcal {M}(\Lambda ^{\mathbb {N}})$
such that
$\nu \in \mathcal {M}(\Lambda ^{\mathbb {N}})$
such that
![]() $\mu =\nu \circ \pi ^{-1}.$
$\mu =\nu \circ \pi ^{-1}.$
It comes from the proof of Theorem 4.8 [Reference Feng and Hu19] (applied to
![]() $\mu $
) that for any
$\mu $
) that for any
![]() $\varepsilon>0,$
for
$\varepsilon>0,$
for
![]() $\mu $
-almost any
$\mu $
-almost any
![]() $x\in K$
such that
$x\in K$
such that
![]() $\mu ^{\pi ^{-1}(\{x\})}$
exists and satisfies the two first items of Theorem 4.8, there exists
$\mu ^{\pi ^{-1}(\{x\})}$
exists and satisfies the two first items of Theorem 4.8, there exists
![]() $n_0$
large enough so that, for any
$n_0$
large enough so that, for any
![]() $n\geq n_0$
, there exists
$n\geq n_0$
, there exists
![]() $\underline {i}_1,\ldots ,\underline {i}_{N_n}$
such that:
$\underline {i}_1,\ldots ,\underline {i}_{N_n}$
such that:
-
• for any
 $1\leq j\leq N_n,$
(55)
$1\leq j\leq N_n,$
(55) $$ \begin{align} e^{-n(\unicode{x3bb}+\varepsilon)}\leq\vert f_{\underline{i}_j}(K)\vert\leq e^{-n(\unicode{x3bb}-\varepsilon)}; \end{align} $$
$$ \begin{align} e^{-n(\unicode{x3bb}+\varepsilon)}\leq\vert f_{\underline{i}_j}(K)\vert\leq e^{-n(\unicode{x3bb}-\varepsilon)}; \end{align} $$
-
• one has
(56) $$ \begin{align} \mu^{\pi^{-1}(\{x\})}\bigg(\bigcup_{1\leq j\leq N_n}[\underline{i}_j]\bigg)\geq \frac{1}{2}; \end{align} $$
$$ \begin{align} \mu^{\pi^{-1}(\{x\})}\bigg(\bigcup_{1\leq j\leq N_n}[\underline{i}_j]\bigg)\geq \frac{1}{2}; \end{align} $$
-
• for any
 $1\leq j\leq N_n,$
(57)
$1\leq j\leq N_n,$
(57) $$ \begin{align} e^{-n(h+\varepsilon)}\leq\mu^{\pi^{-1}(\{x\})}([\underline{i}_j])\leq e^{-n(h-\varepsilon)}. \end{align} $$
$$ \begin{align} e^{-n(h+\varepsilon)}\leq\mu^{\pi^{-1}(\{x\})}([\underline{i}_j])\leq e^{-n(h-\varepsilon)}. \end{align} $$
Assume that
![]() $h>0$
and take
$h>0$
and take
![]() $0<\varepsilon <\min \{ {h}/{2},{ \unicode{x3bb} }/{2}\}.$
$0<\varepsilon <\min \{ {h}/{2},{ \unicode{x3bb} }/{2}\}.$
Combining equations (56) and (57), one gets
Note that
![]() $\#\{k:e^{-n(\unicode{x3bb} +\varepsilon )}\leq 2^{-k}\leq e^{-n(\unicode{x3bb} -\varepsilon )}\}\leq ({2n\varepsilon }/{\log 2}).$
As a consequence, there exists
$\#\{k:e^{-n(\unicode{x3bb} +\varepsilon )}\leq 2^{-k}\leq e^{-n(\unicode{x3bb} -\varepsilon )}\}\leq ({2n\varepsilon }/{\log 2}).$
As a consequence, there exists
![]() $k\in [{n(\unicode{x3bb} -\varepsilon )}/{\log 2},{n(\unicode{x3bb} +\varepsilon )}/{\log 2}]$
such that
$k\in [{n(\unicode{x3bb} -\varepsilon )}/{\log 2},{n(\unicode{x3bb} +\varepsilon )}/{\log 2}]$
such that
 $$ \begin{align} \# \Lambda^{(k)}\cap \{[\underline{i}_j]\}_{1\leq j\leq N_n}\geq \frac{N_n}{{2n\varepsilon}/{\log 2}}\geq \frac{({1}/{2})e^{{nh}/{2}}}{{2n\varepsilon}/{\log 2}}. \end{align} $$
$$ \begin{align} \# \Lambda^{(k)}\cap \{[\underline{i}_j]\}_{1\leq j\leq N_n}\geq \frac{N_n}{{2n\varepsilon}/{\log 2}}\geq \frac{({1}/{2})e^{{nh}/{2}}}{{2n\varepsilon}/{\log 2}}. \end{align} $$
Since for any
![]() $\leq j \leq N_n, [ \underline {i}_j]\cap \pi ^{-1}(\{x\})\neq \emptyset ,$
one also has
$\leq j \leq N_n, [ \underline {i}_j]\cap \pi ^{-1}(\{x\})\neq \emptyset ,$
one also has
![]() $f_{\underline {i}_j}(K)\subset B(x,e^{-n(\unicode{x3bb} -\varepsilon )}),$
so that, writing
$f_{\underline {i}_j}(K)\subset B(x,e^{-n(\unicode{x3bb} -\varepsilon )}),$
so that, writing
![]() $n'=\lfloor {n(\unicode{x3bb} -\varepsilon )}/{\log 2} \rfloor $
, one has
$n'=\lfloor {n(\unicode{x3bb} -\varepsilon )}/{\log 2} \rfloor $
, one has
 $$ \begin{align} \#\{\underline{i}\in \Lambda^{(n')}:f_{\underline{i}}(K)\cap B(x,2^{-n'})\}\geq \frac{({1}/{2})e^{{nh}/{2}}}{{2n\varepsilon}/{\log 2}}. \end{align} $$
$$ \begin{align} \#\{\underline{i}\in \Lambda^{(n')}:f_{\underline{i}}(K)\cap B(x,2^{-n'})\}\geq \frac{({1}/{2})e^{{nh}/{2}}}{{2n\varepsilon}/{\log 2}}. \end{align} $$
In particular, recalling equation (40) and Proposition 4.13,
and S does not satisfy the AWSC. As a consequence, S satisfies the AWSC implying
![]() $h=0$
, which, recalling the last item of Theorem 4.8, concludes the proof.
$h=0$
, which, recalling the last item of Theorem 4.8, concludes the proof.
Remark 4.22. For simplicity, we established the result for weakly conformal measures, but Theorem 4.8, that is, [Reference Feng and Hu19, Theorem 2.1], is actually stated for ergodic measures and a careful reader will notice that the same proof combined with [Reference Feng and Hu19, Theorem 2.1] actually shows that if the IFS S satisfies AWSC, for every ergodic measure
![]() $\nu \in \mathcal {M}(\Lambda ^{\mathbb {N}})$
(with respect to the shift
$\nu \in \mathcal {M}(\Lambda ^{\mathbb {N}})$
(with respect to the shift
![]() $\sigma $
), one has
$\sigma $
), one has
where
![]() $\unicode{x3bb} _{\nu }$
is the Lyapunov exponent associated with
$\unicode{x3bb} _{\nu }$
is the Lyapunov exponent associated with
![]() $\nu $
and
$\nu $
and
![]() $h(\nu )$
is defined as the positive number for which, for
$h(\nu )$
is defined as the positive number for which, for
![]() $\nu $
-almost
$\nu $
-almost
![]() $(x_n)_{n\in \mathbb {N}},$
one has
$(x_n)_{n\in \mathbb {N}},$
one has
We also state the following corollary, which will be useful later in the manuscript.
5 Mass transference principle and quasi-Bernoulli measures
The classical mass transference principle of Beresnevitch and Velani [Reference Beresnevitch and Velani7] (and many others [Reference Eriksson-Bique14, Reference Ghosh and Nandi22, Reference Koivusalo and Rams26]) relies on the fact that the ambient measure is Ahlfors-regular. However, to establish Theorem 3.1, one needs a comparable theorem when the measure is inhomogeneous (that is, not Ahlfors-regular).
Such theorems were first established by Barral and Seuret [Reference Barral and Seuret5] and a general version (in terms of the measure involved) was given in [Reference Daviaud10, Theorem 2.2]. The key geometric notion developed in [Reference Daviaud10] to handle inhomogeneous mass transference principles is the following.
Definition 5.1. Let
![]() $\mu \in \mathcal {M}(\mathbb {R}^d)$
and
$\mu \in \mathcal {M}(\mathbb {R}^d)$
and
![]() $s\geq 0$
. The s-dimensional
$s\geq 0$
. The s-dimensional
![]() $\mu $
-essential Hausdorff content of a set
$\mu $
-essential Hausdorff content of a set
![]() $A\subset \mathcal B(\mathbb {R}^d)$
is defined as
$A\subset \mathcal B(\mathbb {R}^d)$
is defined as
As in the self-similar case treated in [Reference Daviaud10, Theorem 2.6], precise estimates of
![]() $ \mathcal {H}^{\mu ,s}_{\infty }(A)$
are established when
$ \mathcal {H}^{\mu ,s}_{\infty }(A)$
are established when
![]() $\mu $
is a
$\mu $
is a
![]() $C^{1}$
weakly conformal measure in Theorem 5.5 below.
$C^{1}$
weakly conformal measure in Theorem 5.5 below.
We will need the following notion of asymptotically covering sequences of balls, developed in [Reference Daviaud13] (and also used in [Reference Daviaud10]), to establish the desired mass transference principle.
Definition 5.2. Let
![]() $\mu \in \mathcal {M}(\mathbb {R}^d)$
. The sequence
$\mu \in \mathcal {M}(\mathbb {R}^d)$
. The sequence
![]() $\mathcal {B}= (B_n)_{n\in \mathbb {N}}$
of closed balls of
$\mathcal {B}= (B_n)_{n\in \mathbb {N}}$
of closed balls of
![]() $\mathbb {R}^d$
satisfying
$\mathbb {R}^d$
satisfying
![]() $\vert B_n \vert \to 0$
is said to be
$\vert B_n \vert \to 0$
is said to be
![]() $\mu $
-asymptotically covering (
$\mu $
-asymptotically covering (
![]() $\mu $
-a.c.) when there exists a constant
$\mu $
-a.c.) when there exists a constant
![]() $C>0$
such that for every open set
$C>0$
such that for every open set
![]() $\Omega \subset \mathbb {R}^d $
and
$\Omega \subset \mathbb {R}^d $
and
![]() $g\in \mathbb {N}$
, there is an integer
$g\in \mathbb {N}$
, there is an integer
![]() $N_\Omega \in \mathbb {N}$
as well as
$N_\Omega \in \mathbb {N}$
as well as
![]() $g\leq n_1 \leq \cdots \leq n_{N_\Omega }$
such that:
$g\leq n_1 \leq \cdots \leq n_{N_\Omega }$
such that:
-
(i)
 $\text {for all } \, 1\leq i\leq N_\Omega $
,
$\text {for all } \, 1\leq i\leq N_\Omega $
,
 $B_{n_i}\subset \Omega $
;
$B_{n_i}\subset \Omega $
; -
(ii)
 $\text {for all } \, 1\leq i\neq j\leq N_\Omega $
,
$\text {for all } \, 1\leq i\neq j\leq N_\Omega $
,
 $B_{n_i}\cap B_{n_j}=\emptyset $
;
$B_{n_i}\cap B_{n_j}=\emptyset $
; -
(iii) also,
(62) $$ \begin{align} \mu\bigg(\bigcup_{i=1}^{N_\Omega}B_{n_i} \bigg )\geq C\mu(\Omega). \end{align} $$
$$ \begin{align} \mu\bigg(\bigcup_{i=1}^{N_\Omega}B_{n_i} \bigg )\geq C\mu(\Omega). \end{align} $$
The following proposition is proved in [Reference Daviaud13], the second item will be used to apply our main theorem to self-conformal measures. For more details about this notion derived from a covering property proved in the KGB lemma in [Reference Beresnevitch and Velani7], one refers to [Reference Daviaud13].
Proposition 5.3. Let
![]() $\mu \in \mathcal {M}(\mathbb {R}^d)$
and
$\mu \in \mathcal {M}(\mathbb {R}^d)$
and
![]() $\mathcal {B} =(B_n :=B(x_n ,r_n))_{n\in \mathbb {N}}$
be a sequence of balls of
$\mathcal {B} =(B_n :=B(x_n ,r_n))_{n\in \mathbb {N}}$
be a sequence of balls of
![]() $\mathbb {R}^d$
with
$\mathbb {R}^d$
with
![]() $\lim _{n\to +\infty } r_{n}= 0$
.
$\lim _{n\to +\infty } r_{n}= 0$
.
-
(1) If
 $\mathcal {B} $
is
$\mathcal {B} $
is
 $\mu $
-a.c., then
$\mu $
-a.c., then
 $\mu (\limsup _{n\rightarrow +\infty }B_n)=1.$
$\mu (\limsup _{n\rightarrow +\infty }B_n)=1.$
-
(2) If there exists
 $v<1$
such that
$v<1$
such that
 $ \mu (\limsup _{n\rightarrow +\infty }(v B_n) )=1$
, then
$ \mu (\limsup _{n\rightarrow +\infty }(v B_n) )=1$
, then
 $\mathcal {B} $
is
$\mathcal {B} $
is
 $\mu $
-a.c.
$\mu $
-a.c. -
(3) If
 $\mu $
is doubling, then
$\mu $
is doubling, then
 $\mathcal {B} $
is
$\mathcal {B} $
is
 $\mu $
-a.c. if and only if there exists
$\mu $
-a.c. if and only if there exists
 $0<v\leq 1$
such that
$0<v\leq 1$
such that
 $ \mu (\limsup _{n\rightarrow +\infty }(v B_n) )=1.$
$ \mu (\limsup _{n\rightarrow +\infty }(v B_n) )=1.$
The mass transference principle associated with these notions is the following [Reference Daviaud10, Theorem 2.2].
Theorem 5.4. [Reference Daviaud10]
Let
![]() $\mu \in \mathcal {M}(\mathbb {R}^d), \mathcal {B} =(B_n)_{n\in \mathbb {N}} $
be a
$\mu \in \mathcal {M}(\mathbb {R}^d), \mathcal {B} =(B_n)_{n\in \mathbb {N}} $
be a
![]() $\mu $
-a.c. sequence of closed balls of
$\mu $
-a.c. sequence of closed balls of
![]() $\mathbb {R}^d$
such that
$\mathbb {R}^d$
such that
![]() $\vert B_n \vert \to 0$
, and
$\vert B_n \vert \to 0$
, and
![]() $\mathcal {U}=(U_n)_{n\in \mathbb {N}}$
a sequence of open sets such that
$\mathcal {U}=(U_n)_{n\in \mathbb {N}}$
a sequence of open sets such that
![]() $U_n \subset B_n$
for all
$U_n \subset B_n$
for all
![]() $n\in \mathbb {N}$
. Let
$n\in \mathbb {N}$
. Let
![]() $0\leq s<\underline {\dim }_H (\mu )$
such that for every n large enough,
$0\leq s<\underline {\dim }_H (\mu )$
such that for every n large enough,
![]() $\mathcal {H}^{\mu ,s}_{\infty }(U_n)\geq \mu (B_n).$
$\mathcal {H}^{\mu ,s}_{\infty }(U_n)\geq \mu (B_n).$
Then,
To apply Theorem 5.4, precise estimates of essential contents of open sets must be achieved. The next subsection is dedicated to this problem when the measure is self-conformal and in the last subsection of §5, the mass transference principle for weakly conformal measures is established.
5.1 Essential content for weakly conformal measures
Estimates on essential contents for weakly conformal measures are now established. These estimates are similar to that established in [Reference Daviaud10, Theorem 2.6] for self-similar measures, but the introduction of the weakly conformal settings brings a number of geometrical difficulties, so for the sake of completeness, we provide all the details regarding these estimates.
Theorem 5.5. Let S be a
![]() $C^{1}$
weakly conformal IFS of
$C^{1}$
weakly conformal IFS of
![]() $\mathbb {R}^d$
.
$\mathbb {R}^d$
.
Let K be the attractor of S and
![]() $\mu $
be a measure on K which satisfies that, for every
$\mu $
be a measure on K which satisfies that, for every
![]() $\underline {i}\in \bigcup _{k\geq 1}\{1,\ldots ,m\}^k$
,
$\underline {i}\in \bigcup _{k\geq 1}\{1,\ldots ,m\}^k$
,
![]() $\mu \circ f_{\underline {i}}^{-1}$
is absolutely continuous with respect to
$\mu \circ f_{\underline {i}}^{-1}$
is absolutely continuous with respect to
![]() $\mu $
. Then, we have the following.
$\mu $
. Then, we have the following.
For any
![]() $0\leq s<\underline {\dim }_H(\mu )$
, for any
$0\leq s<\underline {\dim }_H(\mu )$
, for any
![]() $0<\varepsilon \leq \tfrac 12$
, there exists a constant
$0<\varepsilon \leq \tfrac 12$
, there exists a constant
![]() $c=c(d,\mu ,s,\varepsilon )>0 $
depending on the dimensions d,
$c=c(d,\mu ,s,\varepsilon )>0 $
depending on the dimensions d,
![]() $\mu $
, s, and
$\mu $
, s, and
![]() $\varepsilon $
only, such that for any ball
$\varepsilon $
only, such that for any ball
![]() $B=B(x,r)$
centered on K and
$B=B(x,r)$
centered on K and
![]() $r\leq 1$
, for any open set
$r\leq 1$
, for any open set
![]() $\Omega $
, one has
$\Omega $
, one has

For any
![]() $s>\overline {\dim }_H(\mu )$
,
$s>\overline {\dim }_H(\mu )$
,
![]() $ \mathcal {H}^{\mu ,s}_{\infty }(\Omega )=0.$
$ \mathcal {H}^{\mu ,s}_{\infty }(\Omega )=0.$
-
• The system S is not assumed to verify any separation condition.
-
• When the maps are similarities, one still has, for any
 $s>\overline {\dim }_H(\mu )$
,
$s>\overline {\dim }_H(\mu )$
,
 $ \mathcal {H}^{\mu ,s}_{\infty }(\Omega )=0$
, but for
$ \mathcal {H}^{\mu ,s}_{\infty }(\Omega )=0$
, but for
 $s<\underline {\dim } (\mu )$
, there exists a constant
$s<\underline {\dim } (\mu )$
, there exists a constant
 $c(d,\mu ,s)$
such that the following more precise estimates hold true [Reference Daviaud10, Theorem 2.6]: (65)
$c(d,\mu ,s)$
such that the following more precise estimates hold true [Reference Daviaud10, Theorem 2.6]: (65)
-
• When the measure
 $\mu $
is weakly conformal (Definition 2.3) or the projection of a Gibbs measure,
$\mu $
is weakly conformal (Definition 2.3) or the projection of a Gibbs measure,
 $\mu $
is exact dimensional (see [Reference Feng and Hu19, Theorem 2.1] for instance), which implies that
$\mu $
is exact dimensional (see [Reference Feng and Hu19, Theorem 2.1] for instance), which implies that
 $\underline {\dim }_{H}{\mu } =\overline {\dim }_{H}{\mu }$
. In this case, Theorem 5.5 provides a complete description of the essential Hausdorff content, except at
$\underline {\dim }_{H}{\mu } =\overline {\dim }_{H}{\mu }$
. In this case, Theorem 5.5 provides a complete description of the essential Hausdorff content, except at
 $s=\dim _{H}{\mu }$
(this case must depend in general on the separation property of the IFS).
$s=\dim _{H}{\mu }$
(this case must depend in general on the separation property of the IFS).
Before proving Theorem 5.5, we prove that projections of quasi-Bernoulli measures satisfy the assumptions of Theorem 5.5.
Let
![]() $\nu \in \mathcal {M}(\{1,\ldots ,m\}^{\mathbb {N}})$
be a measure. We call
$\nu \in \mathcal {M}(\{1,\ldots ,m\}^{\mathbb {N}})$
be a measure. We call
![]() $\nu $
a quasi-Bernoulli measure if there exists
$\nu $
a quasi-Bernoulli measure if there exists
![]() $C>0$
such that for every
$C>0$
such that for every
![]() $\underline {i},\underline {j}\in \bigcup _{k\geq 1}\{1,\ldots ,m\}^k,$
one has
$\underline {i},\underline {j}\in \bigcup _{k\geq 1}\{1,\ldots ,m\}^k,$
one has
 $$ \begin{align*}C^{-1}\leq\frac{\nu([\underline{i}\underline{j}])}{\nu([\underline{i}])\times \nu([\underline{j}])}\leq C.\end{align*} $$
$$ \begin{align*}C^{-1}\leq\frac{\nu([\underline{i}\underline{j}])}{\nu([\underline{i}])\times \nu([\underline{j}])}\leq C.\end{align*} $$
Proposition 5.6. Let
![]() $S=\{f_1,\ldots ,f_m\}$
be a weakly conformal IFS, let K be its attractor and
$S=\{f_1,\ldots ,f_m\}$
be a weakly conformal IFS, let K be its attractor and
![]() $\pi $
the canonical projection from
$\pi $
the canonical projection from
![]() $\{1,\ldots ,m\}^{\mathbb {N}}$
to K. Let
$\{1,\ldots ,m\}^{\mathbb {N}}$
to K. Let
![]() $\nu $
be a quasi-Bernoulli measure on
$\nu $
be a quasi-Bernoulli measure on
![]() $\{1,\ldots ,m\}^{\mathbb {N}}$
such that for every
$\{1,\ldots ,m\}^{\mathbb {N}}$
such that for every
![]() $1\leq i\leq m, \nu ([i])\neq 0$
and write
$1\leq i\leq m, \nu ([i])\neq 0$
and write
![]() $\mu =\nu \circ \pi ^{-1}.$
Then, for every
$\mu =\nu \circ \pi ^{-1}.$
Then, for every
![]() $n\in \mathbb {N}$
and every
$n\in \mathbb {N}$
and every
![]() $\underline {i}\in \{1,\ldots ,m\}^n, \mu \circ f_{\underline {i}}^{-1}$
is absolutely continuous with respect to
$\underline {i}\in \{1,\ldots ,m\}^n, \mu \circ f_{\underline {i}}^{-1}$
is absolutely continuous with respect to
![]() $\mu .$
$\mu .$
Proof. Note that since for every
![]() $1\leq i\leq m, \nu ([i])\neq 0,$
one has for every
$1\leq i\leq m, \nu ([i])\neq 0,$
one has for every
![]() $n\in \mathbb {N}$
and every
$n\in \mathbb {N}$
and every
![]() $\underline {i}=(i_1,\ldots ,i_n)\in \{1,\ldots ,m\}^n,$
$\underline {i}=(i_1,\ldots ,i_n)\in \{1,\ldots ,m\}^n,$
 $$ \begin{align*}\nu([\underline{i}])\geq \frac{1}{C^n}\prod_{k=1}^n \nu([i_k])>0.\end{align*} $$
$$ \begin{align*}\nu([\underline{i}])\geq \frac{1}{C^n}\prod_{k=1}^n \nu([i_k])>0.\end{align*} $$
In addition, for every Borel set
![]() $E\subset \mathbb {R}^d$
, one has
$E\subset \mathbb {R}^d$
, one has
 $$ \begin{align*} \nu(\pi^{-1}(E)\cap [\underline{i}])&=\nu\Big\{\underline{i}(x_n)_{n\in\mathbb{N}}:f_{\underline{i}}\Big(\lim_{n\to+\infty}f_{x_1}\circ \cdots \circ f_{x_n}(0)\Big)\in E\Big\}\\ &=\nu\Big\{\underline{i}(x_n)_{n\in\mathbb{N}}:\lim_{n\to+\infty}f_{x_1}\circ \cdots \circ f_{x_n}(0)\in f_{\underline{i}}^{-1}( E)\Big\}\\ &=\nu\{\underline{i}(x_n)_{n\in\mathbb{N}}:(x_n)_{n\in\mathbb{N}}\in \pi^{-1}\circ f_{\underline{i}}^{-1}( E)\}. \end{align*} $$
$$ \begin{align*} \nu(\pi^{-1}(E)\cap [\underline{i}])&=\nu\Big\{\underline{i}(x_n)_{n\in\mathbb{N}}:f_{\underline{i}}\Big(\lim_{n\to+\infty}f_{x_1}\circ \cdots \circ f_{x_n}(0)\Big)\in E\Big\}\\ &=\nu\Big\{\underline{i}(x_n)_{n\in\mathbb{N}}:\lim_{n\to+\infty}f_{x_1}\circ \cdots \circ f_{x_n}(0)\in f_{\underline{i}}^{-1}( E)\Big\}\\ &=\nu\{\underline{i}(x_n)_{n\in\mathbb{N}}:(x_n)_{n\in\mathbb{N}}\in \pi^{-1}\circ f_{\underline{i}}^{-1}( E)\}. \end{align*} $$
This implies that
that is,
Since, for every
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
 $$ \begin{align*} \mu(E)=\nu(\pi^{-1}(E))=\sum_{\underline{j}\in\{1,\ldots,m\}^n}\nu(\pi^{-1}(E)\cap [\underline{j}]),\end{align*} $$
$$ \begin{align*} \mu(E)=\nu(\pi^{-1}(E))=\sum_{\underline{j}\in\{1,\ldots,m\}^n}\nu(\pi^{-1}(E)\cap [\underline{j}]),\end{align*} $$
we have
 $$ \begin{align*} C^{-1} \sum_{\underline{j}\in\{1,\ldots,m\}^n}\nu(\underline{j})\mu(f_{\underline{j}}^{-1}(E))\leq \mu(E)\leq C\sum_{\underline{j}\in\{1,\ldots,m\}^n}\nu(\underline{j})\mu(f_{\underline{j}}^{-1}(E)). \end{align*} $$
$$ \begin{align*} C^{-1} \sum_{\underline{j}\in\{1,\ldots,m\}^n}\nu(\underline{j})\mu(f_{\underline{j}}^{-1}(E))\leq \mu(E)\leq C\sum_{\underline{j}\in\{1,\ldots,m\}^n}\nu(\underline{j})\mu(f_{\underline{j}}^{-1}(E)). \end{align*} $$
So,
which proves that
![]() $\mu \circ f_{\underline {i}}^{-1}$
is absolutely continuous with respect to
$\mu \circ f_{\underline {i}}^{-1}$
is absolutely continuous with respect to
![]() $\mu .$
$\mu .$
Let us now prove Theorem 5.5.
Proof. As mentioned above, the proof of Theorem 5.5 is similar to the proof of (65) from [Reference Daviaud10], only it is made significantly more technical by the assumption that the IFS is weakly conformal.
Let us recall the well-known Besicovitch covering theorem.
Theorem 5.7. [Reference Mattila28]
There exists
![]() $Q_{d} \in \mathbb {N}^{\star }$
, a constant depending only on the dimension d, such that for every
$Q_{d} \in \mathbb {N}^{\star }$
, a constant depending only on the dimension d, such that for every
![]() $E\subset [0,1]^{d}$
, for every set
$E\subset [0,1]^{d}$
, for every set
![]() $\mathcal {F}=\{B(x, r_{(x)} ): x\in E, r_{(x)}>0 \}$
, there exists
$\mathcal {F}=\{B(x, r_{(x)} ): x\in E, r_{(x)}>0 \}$
, there exists
![]() $\mathcal {F}_1,\ldots ,\mathcal {F}_{Q_{d}}$
finite or countable sub-families of
$\mathcal {F}_1,\ldots ,\mathcal {F}_{Q_{d}}$
finite or countable sub-families of
![]() $\mathcal {F}$
such that:
$\mathcal {F}$
such that:
-
•
 $\text { for all } 1\leq i\leq Q_{d}$
,
$\text { for all } 1\leq i\leq Q_{d}$
,
 $\text { for all } L\neq L'\in \mathcal {F}_i$
, one has
$\text { for all } L\neq L'\in \mathcal {F}_i$
, one has
 $L \cap L'=\emptyset .$
$L \cap L'=\emptyset .$
-
• E is covered by the families
 $\mathcal {F}_i$
, that is, (66)
$\mathcal {F}_i$
, that is, (66) $$ \begin{align} E\subset \bigcup_{1\leq i\leq Q_{d}}\bigcup_{L\in \mathcal{F}_i}L. \end{align} $$
$$ \begin{align} E\subset \bigcup_{1\leq i\leq Q_{d}}\bigcup_{L\in \mathcal{F}_i}L. \end{align} $$
The proof of Theorem 5.7 relies on the following geometric lemma, which will also be used.
Lemma 5.8. [Reference Mattila28]
Let
![]() $\mathcal {B} =(B_n )_{n\in \mathbb {N}}$
be a family of balls and B a ball such that:
$\mathcal {B} =(B_n )_{n\in \mathbb {N}}$
be a family of balls and B a ball such that:
-
(i)
 $\text { for all } \ n\geq 1$
,
$\text { for all } \ n\geq 1$
,
 $\vert B_n\vert \geq \tfrac 12\vert B\vert ;$
$\vert B_n\vert \geq \tfrac 12\vert B\vert ;$
-
(ii)
 $\text { for all } \ n_1 \neq n_2 \geq 1 $
, the center of
$\text { for all } \ n_1 \neq n_2 \geq 1 $
, the center of
 $B_{n_1}$
does not belong to
$B_{n_1}$
does not belong to
 $B_{n_2}$
.
$B_{n_2}$
.
Then, B intersects less than
![]() $Q_{d}$
elements of
$Q_{d}$
elements of
![]() $\mathcal {B}$
, where
$\mathcal {B}$
, where
![]() $Q_{d}$
is the same constant as in Theorem 5.7.
$Q_{d}$
is the same constant as in Theorem 5.7.
Let us first prove the above estimates for balls. We fix
![]() $S=\{f_1,\ldots ,f_m\}$
a weakly conformal IFS and we denote by K its attractor.
$S=\{f_1,\ldots ,f_m\}$
a weakly conformal IFS and we denote by K its attractor.
Proposition 5.9. Let
![]() $\mu $
be a measure supported on K satisfying that for every
$\mu $
be a measure supported on K satisfying that for every
![]() $\underline {i}\in \bigcup _{n\geq 1}\{1,\ldots ,m\}^n$
,
$\underline {i}\in \bigcup _{n\geq 1}\{1,\ldots ,m\}^n$
,
![]() $\mu (f_{\underline {i}}^{-1})$
is absolutely continuous with respect to
$\mu (f_{\underline {i}}^{-1})$
is absolutely continuous with respect to
![]() $\mu $
. Then, for any
$\mu $
. Then, for any
![]() $0<\varepsilon \leq \underline {\dim }_H(\mu )$
, any
$0<\varepsilon \leq \underline {\dim }_H(\mu )$
, any
![]() $0\leq \varepsilon ^{\prime }\leq \tfrac 12$
such that
$0\leq \varepsilon ^{\prime }\leq \tfrac 12$
such that
![]() $\underline {\dim }_H (\mu )-\varepsilon +\varepsilon ^{\prime }>0$
, there exists a constant
$\underline {\dim }_H (\mu )-\varepsilon +\varepsilon ^{\prime }>0$
, there exists a constant
![]() $\chi ( d,\mu ,\varepsilon ,\varepsilon ^{\prime })>0 $
such that for any ball
$\chi ( d,\mu ,\varepsilon ,\varepsilon ^{\prime })>0 $
such that for any ball
![]() $B=B(x,r)$
with
$B=B(x,r)$
with
![]() $x\in K$
and
$x\in K$
and
![]() $r\leq 1$
, one has
$r\leq 1$
, one has
In addition, for any
![]() $s>\overline {\dim _H}( \mu )$
,
$s>\overline {\dim _H}( \mu )$
,
![]() $\mathcal {H}^{\mu ,s}_{\infty }(B)=0.$
$\mathcal {H}^{\mu ,s}_{\infty }(B)=0.$
Proof. Note first that, by definition of
![]() $\mathcal {H}^{\mu ,s}_{\infty }$
(Definition 5.1), for any
$\mathcal {H}^{\mu ,s}_{\infty }$
(Definition 5.1), for any
![]() $s>\overline {\dim }_H(\mu )$
,
$s>\overline {\dim }_H(\mu )$
,
![]() $\mathcal {H}^{\mu ,s}_{\infty }(B)=0.$
$\mathcal {H}^{\mu ,s}_{\infty }(B)=0.$
Let us consider
![]() $0\leq s<\underline {\dim }_H (\mu )$
and start by a few remarks.
$0\leq s<\underline {\dim }_H (\mu )$
and start by a few remarks.
Set
![]() $\alpha =\underline {\dim }_H(\mu )$
, and let
$\alpha =\underline {\dim }_H(\mu )$
, and let
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $\rho>0$
be two real numbers. One defines
$\rho>0$
be two real numbers. One defines
By definition of
![]() $\underline {\dim }_{H}{\mu }$
(Definition 2.2), for every
$\underline {\dim }_{H}{\mu }$
(Definition 2.2), for every
![]() $\varepsilon>0,$
$\varepsilon>0,$
 $$ \begin{align*}\mu\bigg(\bigcup_{\rho>0}E_{\mu} ^{\alpha, \rho,\varepsilon}\bigg)=1.\end{align*} $$
$$ \begin{align*}\mu\bigg(\bigcup_{\rho>0}E_{\mu} ^{\alpha, \rho,\varepsilon}\bigg)=1.\end{align*} $$
Let
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $0<\rho _{\varepsilon }\leq 1$
be two real numbers such that
$0<\rho _{\varepsilon }\leq 1$
be two real numbers such that
![]() $\mu (E_{\mu } ^{\alpha , \rho _{\varepsilon },\varepsilon })\geq \tfrac 12$
and write
$\mu (E_{\mu } ^{\alpha , \rho _{\varepsilon },\varepsilon })\geq \tfrac 12$
and write
![]() $E=E_{\mu }^{\alpha ,\rho _{\varepsilon }, \varepsilon }.$
$E=E_{\mu }^{\alpha ,\rho _{\varepsilon }, \varepsilon }.$
Write
![]() $c_{\underline {i}}=\vert f_{\underline {i}}(K)\vert .$
Let us fix
$c_{\underline {i}}=\vert f_{\underline {i}}(K)\vert .$
Let us fix
![]() $\underline {i}=(i_1,\ldots ,i_k)\in \Lambda ^{*}.$
For any
$\underline {i}=(i_1,\ldots ,i_k)\in \Lambda ^{*}.$
For any
![]() $x\in K$
and
$x\in K$
and
![]() $r>0$
, by equations (21) and (22) applied with
$r>0$
, by equations (21) and (22) applied with
![]() $\theta =\varepsilon ^{\prime }$
, one has
$\theta =\varepsilon ^{\prime }$
, one has
 $$ \begin{align*} f_{\underline{i}}(B(x,r))\supset B(f_{\underline{i}}(x_0),\widehat{C}_{\varepsilon'}c_{\underline{i}}(x_0)^{1-\varepsilon'}r)\supset B\bigg(f_{\underline{i}}(x_0),\frac{\widehat{C}_{\varepsilon'}^{-{2}/({1-\varepsilon'})}}{\vert K\vert^{-({1+\varepsilon'})/({1-\varepsilon'})}} c_{\underline{i}} ^{({1+\varepsilon'})/({1-\varepsilon'})}r\bigg). \end{align*} $$
$$ \begin{align*} f_{\underline{i}}(B(x,r))\supset B(f_{\underline{i}}(x_0),\widehat{C}_{\varepsilon'}c_{\underline{i}}(x_0)^{1-\varepsilon'}r)\supset B\bigg(f_{\underline{i}}(x_0),\frac{\widehat{C}_{\varepsilon'}^{-{2}/({1-\varepsilon'})}}{\vert K\vert^{-({1+\varepsilon'})/({1-\varepsilon'})}} c_{\underline{i}} ^{({1+\varepsilon'})/({1-\varepsilon'})}r\bigg). \end{align*} $$
Remember that
![]() $\varepsilon '\leq \tfrac 12.$
Since
$\varepsilon '\leq \tfrac 12.$
Since
![]() $({1+\varepsilon '})/({1-\varepsilon '})\leq 1+4\varepsilon '$
,
$({1+\varepsilon '})/({1-\varepsilon '})\leq 1+4\varepsilon '$
,
Writing
![]() $\mu _{\underline {i}}=\mu (f_{\underline {i}}^{-1})$
, equation (67) yields
$\mu _{\underline {i}}=\mu (f_{\underline {i}}^{-1})$
, equation (67) yields
 $$ \begin{align} \nonumber E_{\underline{i}}&:=f_{\underline{i}}(E)\\\nonumber &=\{f_{\underline{i}}(x)\in K :\text{ for all } \ r\leq \rho_{\varepsilon}, \ \mu(B(x,r))\leq r^{\alpha -\varepsilon}\}\\\nonumber &\subset\bigg\{f_{\underline{i}}(x), x\in K :\text{ for all } \ r \leq \rho_{\varepsilon},\\\nonumber &\quad \mu (f_{\underline{i}} ^{-1}(B(f_{\underline{i}}(x_0),\widehat{C}_{\varepsilon'}^{-{2}/({1-\varepsilon'})}\cdot\vert K\vert^{({1+\varepsilon'})/({1-\varepsilon'})} c_{\underline{i}} ^{1+4\varepsilon'}r) ))\\\nonumber &\leq \bigg(\frac{\widehat{C}_{\varepsilon'}^{-{2}/({1-\varepsilon'})}\cdot\vert K\vert^{({1+\varepsilon'})/({1-\varepsilon'})} c_{\underline{i}} ^{1+4\varepsilon'}r}{\widehat{C}_{\varepsilon'}^{-{2}/({1-\varepsilon'})}\cdot\vert K\vert^{({1+\varepsilon'})/({1-\varepsilon'})} c_{\underline{i}} ^{1+4\varepsilon'}}\bigg)^{\alpha -\varepsilon}\bigg\}\\\nonumber &=\bigg\{y\in f_{\underline{i}}(K) : \text{ for all } \ r'\leq \widehat{C}_{\varepsilon'}^{-{2}/({1-\varepsilon'})}\cdot\vert K\vert^{({1+\varepsilon'})/({1-\varepsilon'})} c_{\underline{i}} ^{1+4\varepsilon'}\rho_{\varepsilon}, \\& \quad \mu_{\underline{i}}(B(y,r'))\leq \bigg(\frac{r'}{\widehat{C}_{\varepsilon'}^{-{2}/({1-\varepsilon'})}\cdot\vert K\vert^{({1+\varepsilon'})/({1-\varepsilon'})} c_{\underline{i}} ^{1+4\varepsilon'}}\bigg)^{\alpha -\varepsilon}\bigg\}. \end{align} $$
$$ \begin{align} \nonumber E_{\underline{i}}&:=f_{\underline{i}}(E)\\\nonumber &=\{f_{\underline{i}}(x)\in K :\text{ for all } \ r\leq \rho_{\varepsilon}, \ \mu(B(x,r))\leq r^{\alpha -\varepsilon}\}\\\nonumber &\subset\bigg\{f_{\underline{i}}(x), x\in K :\text{ for all } \ r \leq \rho_{\varepsilon},\\\nonumber &\quad \mu (f_{\underline{i}} ^{-1}(B(f_{\underline{i}}(x_0),\widehat{C}_{\varepsilon'}^{-{2}/({1-\varepsilon'})}\cdot\vert K\vert^{({1+\varepsilon'})/({1-\varepsilon'})} c_{\underline{i}} ^{1+4\varepsilon'}r) ))\\\nonumber &\leq \bigg(\frac{\widehat{C}_{\varepsilon'}^{-{2}/({1-\varepsilon'})}\cdot\vert K\vert^{({1+\varepsilon'})/({1-\varepsilon'})} c_{\underline{i}} ^{1+4\varepsilon'}r}{\widehat{C}_{\varepsilon'}^{-{2}/({1-\varepsilon'})}\cdot\vert K\vert^{({1+\varepsilon'})/({1-\varepsilon'})} c_{\underline{i}} ^{1+4\varepsilon'}}\bigg)^{\alpha -\varepsilon}\bigg\}\\\nonumber &=\bigg\{y\in f_{\underline{i}}(K) : \text{ for all } \ r'\leq \widehat{C}_{\varepsilon'}^{-{2}/({1-\varepsilon'})}\cdot\vert K\vert^{({1+\varepsilon'})/({1-\varepsilon'})} c_{\underline{i}} ^{1+4\varepsilon'}\rho_{\varepsilon}, \\& \quad \mu_{\underline{i}}(B(y,r'))\leq \bigg(\frac{r'}{\widehat{C}_{\varepsilon'}^{-{2}/({1-\varepsilon'})}\cdot\vert K\vert^{({1+\varepsilon'})/({1-\varepsilon'})} c_{\underline{i}} ^{1+4\varepsilon'}}\bigg)^{\alpha -\varepsilon}\bigg\}. \end{align} $$
Notice also that
We are now ready to estimate the
![]() $\mu $
-essential content of a ball B centered in K.
$\mu $
-essential content of a ball B centered in K.
Let us write
Let
![]() $B=B(x,r)$
with
$B=B(x,r)$
with
![]() $x\in K$
and
$x\in K$
and
![]() $r\leq c_0:=\min _{z\in K}\min _{1\leq i\leq m}\| f_i '(z) \|$
.
$r\leq c_0:=\min _{z\in K}\min _{1\leq i\leq m}\| f_i '(z) \|$
.
Since
![]() $x\in K$
, there exists
$x\in K$
, there exists
![]() $\underline {i }=(i_1,\ldots ,i_k)\in \Lambda ^{*}$
such that:
$\underline {i }=(i_1,\ldots ,i_k)\in \Lambda ^{*}$
such that:
-
•
 $x\in f_{\underline {i}}(K)$
;
$x\in f_{\underline {i}}(K)$
; -
•
 $\vert f_{\underline {i}}(K)\vert \leq \tfrac 13\vert B\vert $
;
$\vert f_{\underline {i}}(K)\vert \leq \tfrac 13\vert B\vert $
; -
•
 $\vert f_{(i_1,\ldots ,i_{k-1})}(K)\vert \geq \tfrac 13\vert B\vert .$
$\vert f_{(i_1,\ldots ,i_{k-1})}(K)\vert \geq \tfrac 13\vert B\vert .$
By equation (22), for any
![]() $y\in K$
, one has
$y\in K$
, one has
and
 $$ \begin{align} \| f_{\underline{i}}(y)\|&=\| f^{\prime}_{(i_1,\ldots,i_{n-1})}(f_n (x))\circ f^{\prime}_{i_n}(x) \|\geq \| f^{\prime}_{(i_1,\ldots,i_{n-1})}(f_n (x))\| c_0 \nonumber\\ &\geq \vert f_{(i_1,\ldots,i_{n-1}}(K) \vert^{{1}/({1-\varepsilon'})}\widehat{C}_{\varepsilon'}^{{-1}/({1-\varepsilon'})}\cdot \vert K\vert^{{-1}/({1-\varepsilon'})}c_0. \end{align} $$
$$ \begin{align} \| f_{\underline{i}}(y)\|&=\| f^{\prime}_{(i_1,\ldots,i_{n-1})}(f_n (x))\circ f^{\prime}_{i_n}(x) \|\geq \| f^{\prime}_{(i_1,\ldots,i_{n-1})}(f_n (x))\| c_0 \nonumber\\ &\geq \vert f_{(i_1,\ldots,i_{n-1}}(K) \vert^{{1}/({1-\varepsilon'})}\widehat{C}_{\varepsilon'}^{{-1}/({1-\varepsilon'})}\cdot \vert K\vert^{{-1}/({1-\varepsilon'})}c_0. \end{align} $$
Combining equations (70) and (71), one obtains
 $$ \begin{align} c_{\underline{i}}=\vert f_{\underline{i}}(K)\vert &\geq \widehat{C}_{\varepsilon'}^{-1-({1+\varepsilon'})/({1-\varepsilon'})}\vert K\vert^{{-2\varepsilon'}/({1-\varepsilon'})}c_0^{1+\varepsilon'}\vert f_{(i_1,\ldots,i_{n-1})}(K)\vert^{({1+\varepsilon'})/({1-\varepsilon'})}\nonumber \\ & \geq \widehat{C}_{\varepsilon'}^{-1-({1+\varepsilon'})/({1-\varepsilon'})}\vert K\vert^{{-2\varepsilon'}/({1-\varepsilon'})}c_0^{1+\varepsilon'}r^{1+4\varepsilon'}. \end{align} $$
$$ \begin{align} c_{\underline{i}}=\vert f_{\underline{i}}(K)\vert &\geq \widehat{C}_{\varepsilon'}^{-1-({1+\varepsilon'})/({1-\varepsilon'})}\vert K\vert^{{-2\varepsilon'}/({1-\varepsilon'})}c_0^{1+\varepsilon'}\vert f_{(i_1,\ldots,i_{n-1})}(K)\vert^{({1+\varepsilon'})/({1-\varepsilon'})}\nonumber \\ & \geq \widehat{C}_{\varepsilon'}^{-1-({1+\varepsilon'})/({1-\varepsilon'})}\vert K\vert^{{-2\varepsilon'}/({1-\varepsilon'})}c_0^{1+\varepsilon'}r^{1+4\varepsilon'}. \end{align} $$
Note that ![]() .
.
Consider a set
![]() $A\subset B$
verifying
$A\subset B$
verifying
![]() $\mu (A)=\mu (B).$
One aims to give a lower bound for the Hausdorff content of A which depends only on B, d,
$\mu (A)=\mu (B).$
One aims to give a lower bound for the Hausdorff content of A which depends only on B, d,
![]() $\varepsilon $
,
$\varepsilon $
,
![]() $\varepsilon ^{\prime }$
, and the measure
$\varepsilon ^{\prime }$
, and the measure
![]() $\mu $
.
$\mu $
.
Consider a sequence of balls
![]() $(L_n=B( x_n,\ell _n))_{n\geq 1}$
covering
$(L_n=B( x_n,\ell _n))_{n\geq 1}$
covering
![]() $A\cap E_{\underline {i}} $
such that
$A\cap E_{\underline {i}} $
such that
![]() $\ell _{n}<\gamma (S,\varepsilon ')\rho _{\varepsilon }c_{ \underline {i}}^{1+4\varepsilon '}$
and
$\ell _{n}<\gamma (S,\varepsilon ')\rho _{\varepsilon }c_{ \underline {i}}^{1+4\varepsilon '}$
and
![]() $ x_n\in A\cap E_{\underline {i}} $
.
$ x_n\in A\cap E_{\underline {i}} $
.
Since
![]() $\mu _{\underline {i}}$
is absolutely continuous with respect to
$\mu _{\underline {i}}$
is absolutely continuous with respect to
![]() $\mu $
, it holds that
$\mu $
, it holds that
![]() $\mu _{\underline {i}}(A)=1.$
$\mu _{\underline {i}}(A)=1.$
By equation (68) applied to each ball
![]() $L_n$
,
$L_n$
,
![]() $n\in \mathbb {N}$
, one has
$n\in \mathbb {N}$
, one has
![]() $({\vert L_n \vert }/{\gamma (S,\varepsilon ' )c_{\underline {i}}^{1+4\varepsilon ^{\prime }}})^{\alpha -\varepsilon }\geq \mu _{\underline {i}}(L_n)$
, so that, recalling equation (72),
$({\vert L_n \vert }/{\gamma (S,\varepsilon ' )c_{\underline {i}}^{1+4\varepsilon ^{\prime }}})^{\alpha -\varepsilon }\geq \mu _{\underline {i}}(L_n)$
, so that, recalling equation (72),
 $$ \begin{align} \sum_{n\in\mathbb{N}}| L_n| ^{\alpha-\varepsilon}\ &\geq \sum_{n\in\mathbb{N}}(\gamma(S,\varepsilon')c_{\underline{i}}^{1+4\varepsilon^{\prime}}) ^{\alpha -\varepsilon}\mu_{\underline{i}}(L _n )\geq (\gamma(S,\varepsilon')c_{\underline{i}}^{1+4\varepsilon^{\prime}}) ^{\alpha -\varepsilon}\mu_{\underline{i}}\bigg(\bigcup_{n\in \mathbb{N} }L_n \bigg)\nonumber\\ &\geq (\gamma(S,\varepsilon')c_{\underline{i}}^{1+4\varepsilon^{\prime}}) ^{\alpha -\varepsilon}\mu_{\underline{i}}(E_{\underline{i}})\geq \tfrac{1}{2}(\gamma(S,\varepsilon')c_{\underline{i}}^{1+4\varepsilon^{\prime}}) ^{\alpha -\varepsilon}\nonumber \\ &\geq \kappa(\mu,\varepsilon^{\prime},\varepsilon)r^{(1+4\varepsilon')^2(\alpha-\varepsilon)}\geq \kappa(\mu,\varepsilon^{\prime},\varepsilon)r^{(1+16\varepsilon')(\alpha-\varepsilon)} , \end{align} $$
$$ \begin{align} \sum_{n\in\mathbb{N}}| L_n| ^{\alpha-\varepsilon}\ &\geq \sum_{n\in\mathbb{N}}(\gamma(S,\varepsilon')c_{\underline{i}}^{1+4\varepsilon^{\prime}}) ^{\alpha -\varepsilon}\mu_{\underline{i}}(L _n )\geq (\gamma(S,\varepsilon')c_{\underline{i}}^{1+4\varepsilon^{\prime}}) ^{\alpha -\varepsilon}\mu_{\underline{i}}\bigg(\bigcup_{n\in \mathbb{N} }L_n \bigg)\nonumber\\ &\geq (\gamma(S,\varepsilon')c_{\underline{i}}^{1+4\varepsilon^{\prime}}) ^{\alpha -\varepsilon}\mu_{\underline{i}}(E_{\underline{i}})\geq \tfrac{1}{2}(\gamma(S,\varepsilon')c_{\underline{i}}^{1+4\varepsilon^{\prime}}) ^{\alpha -\varepsilon}\nonumber \\ &\geq \kappa(\mu,\varepsilon^{\prime},\varepsilon)r^{(1+4\varepsilon')^2(\alpha-\varepsilon)}\geq \kappa(\mu,\varepsilon^{\prime},\varepsilon)r^{(1+16\varepsilon')(\alpha-\varepsilon)} , \end{align} $$
where
![]() $\kappa (\mu ,\varepsilon ^{\prime },\varepsilon )=\tfrac 12\gamma (S,\varepsilon ')^{\alpha -\varepsilon }\cdot (\widehat {C}_{\varepsilon '}^{-1-({1+\varepsilon '})/({1-\varepsilon '})}\vert K\vert ^{{-2\varepsilon '}/({1-\varepsilon '})}c_0^{1+\varepsilon '})^{(1+4\varepsilon ')(\alpha -\varepsilon )}.$
$\kappa (\mu ,\varepsilon ^{\prime },\varepsilon )=\tfrac 12\gamma (S,\varepsilon ')^{\alpha -\varepsilon }\cdot (\widehat {C}_{\varepsilon '}^{-1-({1+\varepsilon '})/({1-\varepsilon '})}\vert K\vert ^{{-2\varepsilon '}/({1-\varepsilon '})}c_0^{1+\varepsilon '})^{(1+4\varepsilon ')(\alpha -\varepsilon )}.$
This series of inequalities holds for any sequence of balls
![]() $(L_n)_{n\in \mathbb {N}}$
with radius less than
$(L_n)_{n\in \mathbb {N}}$
with radius less than
![]() $\gamma (S,\varepsilon ')\rho _{\varepsilon }c_{\underline {i}}^{1+4\varepsilon ^{\prime }} $
centered in
$\gamma (S,\varepsilon ')\rho _{\varepsilon }c_{\underline {i}}^{1+4\varepsilon ^{\prime }} $
centered in
![]() $A\cap E_{\underline {i}}$
. One now proves that one can freely remove those constraints on the center and the radius of the balls used to cover
$A\cap E_{\underline {i}}$
. One now proves that one can freely remove those constraints on the center and the radius of the balls used to cover
![]() $A\cap E_{\underline {i}}$
, up to a multiplicative constant.
$A\cap E_{\underline {i}}$
, up to a multiplicative constant.
Consider balls
![]() $( L_n=B(x_n,\ell _n))_{n\geq 1}$
covering
$( L_n=B(x_n,\ell _n))_{n\geq 1}$
covering
![]() $A\cap E_{\underline {i}} $
such that
$A\cap E_{\underline {i}} $
such that
![]() $\ell _{n}<\gamma (S,\varepsilon ')\rho _{\varepsilon }c_{\underline {i}}^{1+4\varepsilon ^{\prime }} $
but
$\ell _{n}<\gamma (S,\varepsilon ')\rho _{\varepsilon }c_{\underline {i}}^{1+4\varepsilon ^{\prime }} $
but
![]() $x_n$
does not necessarily belongs to
$x_n$
does not necessarily belongs to
![]() $A\cap E_{\underline {i}} $
.
$A\cap E_{\underline {i}} $
.
Let
![]() $n\in \mathbb {N}$
. One constructs recursively a sequence of balls
$n\in \mathbb {N}$
. One constructs recursively a sequence of balls
![]() $(L_{n,j})_{1\leq j\leq J_n}$
such that the following properties hold for any
$(L_{n,j})_{1\leq j\leq J_n}$
such that the following properties hold for any
![]() $1\leq j\leq J_n$
:
$1\leq j\leq J_n$
:
-
•
 $L_{n,j}$
is centered on
$L_{n,j}$
is centered on
 $A\cap E_{\underline {i}}\cap L_n$
;
$A\cap E_{\underline {i}}\cap L_n$
; -
•
 $A\cap E_{\underline {i}}\cap L_n \subset \bigcup _{1\leq j \leq J_n}L_{n,j}$
;
$A\cap E_{\underline {i}}\cap L_n \subset \bigcup _{1\leq j \leq J_n}L_{n,j}$
; -
• for all
 $1\leq j\leq J_n, \vert L_{n,j}\vert = \vert L_n \vert $
;
$1\leq j\leq J_n, \vert L_{n,j}\vert = \vert L_n \vert $
; -
• the center of
 $L_{n,j}$
does not belong to any
$L_{n,j}$
does not belong to any
 $L_{n,j^{\prime }}$
for
$L_{n,j^{\prime }}$
for
 $1\leq j^{\prime }\neq j\leq J_n$
.
$1\leq j^{\prime }\neq j\leq J_n$
.
To achieve this, simply consider
![]() $y_1\in A\cap E_{\underline {i}}\cap L_n$
and set
$y_1\in A\cap E_{\underline {i}}\cap L_n$
and set
![]() $L_{1,n}=B(y_1,\ell _n)$
. If
$L_{1,n}=B(y_1,\ell _n)$
. If
![]() $A\cap E_{\underline {i}}\cap L_n \nsubseteq L_{1,n}$
, consider
$A\cap E_{\underline {i}}\cap L_n \nsubseteq L_{1,n}$
, consider
![]() $y_2 \in A\cap E_{\underline {i}}\cap L_n \setminus L_{1,n}$
and set
$y_2 \in A\cap E_{\underline {i}}\cap L_n \setminus L_{1,n}$
and set
![]() $L_{2,n}=B(y_2 ,\ell _n)$
. If
$L_{2,n}=B(y_2 ,\ell _n)$
. If
![]() $A\cap E_{\underline {i}}\cap L_n \nsubseteq L_{1,n}\cup L_{2,n}$
, consider
$A\cap E_{\underline {i}}\cap L_n \nsubseteq L_{1,n}\cup L_{2,n}$
, consider
![]() $y_3 \in A\cap E_{\underline {i}}\cap L_n \setminus L_{1,n}\cup L_{2,n}$
and set
$y_3 \in A\cap E_{\underline {i}}\cap L_n \setminus L_{1,n}\cup L_{2,n}$
and set
![]() $L_{3,n}=B(y_3 ,\ell _n)$
, and so on.
$L_{3,n}=B(y_3 ,\ell _n)$
, and so on.
Note that for any
![]() $1\leq j\leq J_n$
, any ball
$1\leq j\leq J_n$
, any ball
![]() $L_{j,n}$
has radius
$L_{j,n}$
has radius
![]() $\ell _n$
, intersects
$\ell _n$
, intersects
![]() $L_n$
(which also has radius
$L_n$
(which also has radius
![]() $\ell _n$
), and, because
$\ell _n$
), and, because
![]() $y_j \notin \bigcup _{1 \leq j^{\prime }\neq j\leq J_n}L_{j^{\prime },n}$
, it holds that for any
$y_j \notin \bigcup _{1 \leq j^{\prime }\neq j\leq J_n}L_{j^{\prime },n}$
, it holds that for any
![]() $j\neq j^{\prime }$
,
$j\neq j^{\prime }$
,
![]() $\tfrac 13L_{n,j}\cap \tfrac 13L_{n,j^{\prime }}=\emptyset $
. A volume argument yields that
$\tfrac 13L_{n,j}\cap \tfrac 13L_{n,j^{\prime }}=\emptyset $
. A volume argument yields that
![]() $J_n \leq Q_{d, 1/3},$
where
$J_n \leq Q_{d, 1/3},$
where
![]() $Q_{d, 1/3}$
is constant which only depends on the dimension d and the contraction factor
$Q_{d, 1/3}$
is constant which only depends on the dimension d and the contraction factor
![]() $\tfrac 13.$
$\tfrac 13.$
Hence, denoting by
![]() $(\widetilde L_n)_{n\in \mathbb {N}} $
the collection of the corresponding balls centered on
$(\widetilde L_n)_{n\in \mathbb {N}} $
the collection of the corresponding balls centered on
![]() $A\cap E_{\underline {i}} $
associated with all the balls
$A\cap E_{\underline {i}} $
associated with all the balls
![]() $L_n$
, one has by equation (73) applied to
$L_n$
, one has by equation (73) applied to
![]() $(\widetilde L_n)_{n\in \mathbb N}$
,
$(\widetilde L_n)_{n\in \mathbb N}$
,
 $$ \begin{align*}\sum_{n\in\mathbb{N}}|L_n| ^{\alpha-\varepsilon}\geq \frac{1}{Q_{d,{1}/{3}}} \sum_{n\in\mathbb{N}}|\widetilde L_n| ^{\alpha-\varepsilon} \geq \frac{\kappa (\mu,\varepsilon^{\prime},\varepsilon)}{Q_{d,{1}/{3}}} r ^{(1+4\varepsilon^{\prime})(\alpha -\varepsilon)}.\end{align*} $$
$$ \begin{align*}\sum_{n\in\mathbb{N}}|L_n| ^{\alpha-\varepsilon}\geq \frac{1}{Q_{d,{1}/{3}}} \sum_{n\in\mathbb{N}}|\widetilde L_n| ^{\alpha-\varepsilon} \geq \frac{\kappa (\mu,\varepsilon^{\prime},\varepsilon)}{Q_{d,{1}/{3}}} r ^{(1+4\varepsilon^{\prime})(\alpha -\varepsilon)}.\end{align*} $$
Remark also that any ball of radius smaller than
![]() $c_{\underline {i}}$
can be covered by at most
$c_{\underline {i}}$
can be covered by at most
![]() $({2c_{\underline {i}}^{-4\varepsilon '}}/{\gamma (S,\varepsilon ')\rho _{\varepsilon }})^d$
balls of radius
$({2c_{\underline {i}}^{-4\varepsilon '}}/{\gamma (S,\varepsilon ')\rho _{\varepsilon }})^d$
balls of radius
![]() $\gamma (S,\varepsilon ')\rho _{\varepsilon }c_{\underline {i}}^{1+4\varepsilon ^{\prime }}$
. Moreover, by equation (72),
$\gamma (S,\varepsilon ')\rho _{\varepsilon }c_{\underline {i}}^{1+4\varepsilon ^{\prime }}$
. Moreover, by equation (72),
Setting
 $$ \begin{align*}\widehat{\kappa}(\mu,\varepsilon,\varepsilon^{\prime},d)=\bigg(\frac{2(\widehat{C}_{\varepsilon'}^{-1-({1+\varepsilon'})/({1-\varepsilon'})}\vert K\vert^{{-2\varepsilon'}/({1-\varepsilon'})}c_0^{1+\varepsilon'})^{-4\varepsilon'}}{\gamma(S,\varepsilon')\rho_{\varepsilon}}\bigg)^d ,\end{align*} $$
$$ \begin{align*}\widehat{\kappa}(\mu,\varepsilon,\varepsilon^{\prime},d)=\bigg(\frac{2(\widehat{C}_{\varepsilon'}^{-1-({1+\varepsilon'})/({1-\varepsilon'})}\vert K\vert^{{-2\varepsilon'}/({1-\varepsilon'})}c_0^{1+\varepsilon'})^{-4\varepsilon'}}{\gamma(S,\varepsilon')\rho_{\varepsilon}}\bigg)^d ,\end{align*} $$
any ball of radius less than
![]() $c_{\underline {i}}$
can be covered by less than
$c_{\underline {i}}$
can be covered by less than
![]() $\widehat {\kappa }(\mu ,\varepsilon ,\varepsilon ^{\prime },d)r^{-4d\varepsilon ' \cdot (1+4\varepsilon ')}$
balls of radius less than
$\widehat {\kappa }(\mu ,\varepsilon ,\varepsilon ^{\prime },d)r^{-4d\varepsilon ' \cdot (1+4\varepsilon ')}$
balls of radius less than
![]() $\gamma (S,\varepsilon ')\rho _{\varepsilon }c_{\underline {i}}^{1+4\varepsilon ^{\prime }}$
.
$\gamma (S,\varepsilon ')\rho _{\varepsilon }c_{\underline {i}}^{1+4\varepsilon ^{\prime }}$
.
This proves that for any sequence of balls
![]() $\widehat {L}_n$
with
$\widehat {L}_n$
with
![]() $\vert \widehat {L}_n \vert \leq c_{\underline {i}}$
covering
$\vert \widehat {L}_n \vert \leq c_{\underline {i}}$
covering
![]() $A\cap E_{\underline {i}}$
, recalling equation (73), it holds that
$A\cap E_{\underline {i}}$
, recalling equation (73), it holds that
Recalling that
![]() $\vert E_{\underline {i}}\vert \leq c_{\underline {i}}$
and Definition 4, since equation (74) is valid for any covering
$\vert E_{\underline {i}}\vert \leq c_{\underline {i}}$
and Definition 4, since equation (74) is valid for any covering
![]() $(\widehat {L}_n )_{n\in \mathbb {N}}$
of
$(\widehat {L}_n )_{n\in \mathbb {N}}$
of
![]() $A\cap E_{\underline {i}}$
with
$A\cap E_{\underline {i}}$
with
![]() $\vert L_n \vert \leq c_{\underline {i}}$
, one has
$\vert L_n \vert \leq c_{\underline {i}}$
, one has
 $$ \begin{align} \vert B\vert^{\alpha-\varepsilon}&\geq \mathcal{H}^{\alpha-\varepsilon}_{\infty}(A)\geq \mathcal{H}^{\alpha-\varepsilon}_{\infty}(A \cap E_{\underline{i}})\nonumber\\ &\geq Q_{d,{1}/{3}}^{-1}\widehat{\kappa}(\mu,\varepsilon,\varepsilon^{\prime},d)^{-1}\kappa(\mu,\varepsilon^{\prime},\varepsilon)r^{(1+16\varepsilon')(\alpha-\varepsilon)+4d\varepsilon' \cdot(1+4\varepsilon')}. \end{align} $$
$$ \begin{align} \vert B\vert^{\alpha-\varepsilon}&\geq \mathcal{H}^{\alpha-\varepsilon}_{\infty}(A)\geq \mathcal{H}^{\alpha-\varepsilon}_{\infty}(A \cap E_{\underline{i}})\nonumber\\ &\geq Q_{d,{1}/{3}}^{-1}\widehat{\kappa}(\mu,\varepsilon,\varepsilon^{\prime},d)^{-1}\kappa(\mu,\varepsilon^{\prime},\varepsilon)r^{(1+16\varepsilon')(\alpha-\varepsilon)+4d\varepsilon' \cdot(1+4\varepsilon')}. \end{align} $$
Taking the inf over all the set
![]() $A\subset B$
satisfying
$A\subset B$
satisfying
![]() $\mu (A)=\mu (B)$
, one obtains
$\mu (A)=\mu (B)$
, one obtains
The results stands for balls of diameter less than
![]() $c_0 .$
$c_0 .$
Set
and write
For any ball of radius less than
![]() $1$
centered on K, one has
$1$
centered on K, one has
The estimates of Theorem 5.5 are now established in the case of general open sets.
Recall that by item
![]() $(5)$
of Proposition 5.14, for any
$(5)$
of Proposition 5.14, for any
![]() $s>\dim (\mu )$
and any set E,
$s>\dim (\mu )$
and any set E,
![]() $ \mathcal {H}^{\mu ,s}_{\infty }(E)=0.$
$ \mathcal {H}^{\mu ,s}_{\infty }(E)=0.$
Let us fix
![]() $s<\dim (\mu )$
,
$s<\dim (\mu )$
,
![]() $\varepsilon ^{\prime }>0$
and set
$\varepsilon ^{\prime }>0$
and set
![]() $\varepsilon '=\min \{({\dim (\mu )-s})/{2},\tfrac 12 \}>0.$
$\varepsilon '=\min \{({\dim (\mu )-s})/{2},\tfrac 12 \}>0.$
Since
![]() $K\cap \Omega \subset \Omega $
and
$K\cap \Omega \subset \Omega $
and
![]() $\mu (K\cap \Omega )=\mu (\Omega )$
, it holds that
$\mu (K\cap \Omega )=\mu (\Omega )$
, it holds that
It remains to show that there exists a constant
![]() $c( d,\mu ,s,\varepsilon ^{\prime })$
such that for any open set
$c( d,\mu ,s,\varepsilon ^{\prime })$
such that for any open set
![]() $\Omega $
, the converse inequality
$\Omega $
, the converse inequality
holds.
Let
![]() $E \subset \Omega $
be a Borel set such that
$E \subset \Omega $
be a Borel set such that
![]() $\mu (E)=\mu (\Omega )$
and
$\mu (E)=\mu (\Omega )$
and
Let
![]() $\{L_n \}_{n\in \mathbb {N}}$
be a covering of E by balls verifying
$\{L_n \}_{n\in \mathbb {N}}$
be a covering of E by balls verifying
The covering
![]() $(L_n)_{n\in \mathbb {N}}$
will be modified into a covering
$(L_n)_{n\in \mathbb {N}}$
will be modified into a covering
![]() $(\widetilde {L}_n)_{n\in \mathbb {N}}$
verifying the following properties:
$(\widetilde {L}_n)_{n\in \mathbb {N}}$
verifying the following properties:
-
•
 $K\cap \Omega \subset \bigcup _{n\in \mathbb {N}}\widetilde {L}_n$
;
$K\cap \Omega \subset \bigcup _{n\in \mathbb {N}}\widetilde {L}_n$
; -
•
 $\bigcup _{n\in \mathbb {N}}L_n \subset \bigcup _{n\in \mathbb {N}}\widetilde {L}_n$
;
$\bigcup _{n\in \mathbb {N}}L_n \subset \bigcup _{n\in \mathbb {N}}\widetilde {L}_n$
; -
•
 $$ \begin{align*}\sum_{n\geq 0}\vert \widetilde{L}_n \vert^{s+\varepsilon^{\prime}} \leq 8. 2^{s+\varepsilon^{\prime}}\frac{Q_{d}^2}{\gamma( d,\mu,\varepsilon,\varepsilon^{\prime})}\sum_{n\geq 0}\vert L_n \vert ^s,\end{align*} $$
$$ \begin{align*}\sum_{n\geq 0}\vert \widetilde{L}_n \vert^{s+\varepsilon^{\prime}} \leq 8. 2^{s+\varepsilon^{\prime}}\frac{Q_{d}^2}{\gamma( d,\mu,\varepsilon,\varepsilon^{\prime})}\sum_{n\geq 0}\vert L_n \vert ^s,\end{align*} $$
where
![]() $Q_{d}$
and
$Q_{d}$
and
![]() $\gamma ( d,\mu ,\varepsilon ,\varepsilon ^{\prime })$
are the constants arising from Theorem 5.7 and Proposition 5.9.
$\gamma ( d,\mu ,\varepsilon ,\varepsilon ^{\prime })$
are the constants arising from Theorem 5.7 and Proposition 5.9.
The last item together with equations (77) and (78) then immediately imply that
 $$ \begin{align*}\frac{\gamma( d,\mu,\varepsilon,\varepsilon^{\prime})}{8. 2^{s+\varepsilon^{\prime}} Q_{d}^2}\mathcal{H}^{s+\varepsilon^{\prime}}_{\infty}(K\cap \Omega)\leq \mathcal{H}^{\mu,s}_{\infty}(\Omega).\end{align*} $$
$$ \begin{align*}\frac{\gamma( d,\mu,\varepsilon,\varepsilon^{\prime})}{8. 2^{s+\varepsilon^{\prime}} Q_{d}^2}\mathcal{H}^{s+\varepsilon^{\prime}}_{\infty}(K\cap \Omega)\leq \mathcal{H}^{\mu,s}_{\infty}(\Omega).\end{align*} $$
Setting
![]() $c(d,\mu ,\varepsilon ,\varepsilon ^{\prime })={\gamma ( d,\mu ,\varepsilon ,\varepsilon ^{\prime })}/{8. 2^{s+\varepsilon ^{\prime }} Q_{d}^2} $
will then conclude the proof.
$c(d,\mu ,\varepsilon ,\varepsilon ^{\prime })={\gamma ( d,\mu ,\varepsilon ,\varepsilon ^{\prime })}/{8. 2^{s+\varepsilon ^{\prime }} Q_{d}^2} $
will then conclude the proof.
Let us start the construction of the sequence
![]() $(\widetilde {L}_n )_{n \in \mathbb {N}}.$
$(\widetilde {L}_n )_{n \in \mathbb {N}}.$
Let
![]() $ \Delta =( K \setminus \bigcup _{n\in \mathbb {N}}B_n )\cap \Omega $
. For every
$ \Delta =( K \setminus \bigcup _{n\in \mathbb {N}}B_n )\cap \Omega $
. For every
![]() $x\in \Delta $
, fix
$x\in \Delta $
, fix
![]() $0< r_x \leq 1$
such that
$0< r_x \leq 1$
such that
![]() $B(x,r_x)\subset \Omega .$
One of the following alternatives must occur:
$B(x,r_x)\subset \Omega .$
One of the following alternatives must occur:
-
(1) for any ball
 $L_n$
such that
$L_n$
such that
 $L_n \cap B(x,r_x)\neq \emptyset $
,
$L_n \cap B(x,r_x)\neq \emptyset $
,
 $\vert L_n \vert \leq r_x$
; or
$\vert L_n \vert \leq r_x$
; or -
(2) there exists
 $n_x \in \mathbb {N}$
such that
$n_x \in \mathbb {N}$
such that
 $L_{n_x}\cap B(x,r_x)\neq \emptyset $
and
$L_{n_x}\cap B(x,r_x)\neq \emptyset $
and
 $\vert L_{n_x}\vert \geq r_x$
.
$\vert L_{n_x}\vert \geq r_x$
.
Consider the set
![]() $S_1$
of points of X for which the first alternative holds.
$S_1$
of points of X for which the first alternative holds.
By Theorem 5.7, it is possible to extract from the covering of
![]() $S_1$
,
$S_1$
,
![]() $\{B(x,r_x),x\in S_1\}$
,
$\{B(x,r_x),x\in S_1\}$
,
![]() $Q_{d}$
families of pairwise disjoint balls,
$Q_{d}$
families of pairwise disjoint balls,
![]() $\mathcal {F}_1 ,\ldots ,\mathcal {F}_{Q_{d}}$
such that
$\mathcal {F}_1 ,\ldots ,\mathcal {F}_{Q_{d}}$
such that
 $$ \begin{align*}S_1 \subset \bigcup_{1\leq i\leq Q_{d}}\bigcup_{L\in\mathcal{F}_i}L.\end{align*} $$
$$ \begin{align*}S_1 \subset \bigcup_{1\leq i\leq Q_{d}}\bigcup_{L\in\mathcal{F}_i}L.\end{align*} $$
Now, any ball
![]() $L_n$
intersecting a ball
$L_n$
intersecting a ball
![]() $L\in \bigcup _{1\leq i\leq Q_{d}}\mathcal {F}_i$
must satisfy
$L\in \bigcup _{1\leq i\leq Q_{d}}\mathcal {F}_i$
must satisfy
![]() $\vert L_n \vert \leq L.$
In particular, since for any
$\vert L_n \vert \leq L.$
In particular, since for any
![]() $1\leq i\leq Q_{d}$
, the balls of
$1\leq i\leq Q_{d}$
, the balls of
![]() $\mathcal {F}_i$
are pairwise disjoint, applying Lemma 5.8 to the ball of
$\mathcal {F}_i$
are pairwise disjoint, applying Lemma 5.8 to the ball of
![]() $\mathcal {F}_i$
intersecting L, we get that the ball
$\mathcal {F}_i$
intersecting L, we get that the ball
![]() $L_n$
intersects at most
$L_n$
intersects at most
![]() $Q_{d}$
balls of
$Q_{d}$
balls of
![]() $\mathcal {F}_i$
and hence at most
$\mathcal {F}_i$
and hence at most
![]() $Q_{d}^2$
balls of
$Q_{d}^2$
balls of
![]() $\bigcup _{1\leq i\leq Q_{d}}\mathcal {F}_i .$
$\bigcup _{1\leq i\leq Q_{d}}\mathcal {F}_i .$
Let
![]() $L\in \bigcup _{1\leq i\leq Q_{d}}\mathcal {F}_i .$
One aims at replacing all the balls
$L\in \bigcup _{1\leq i\leq Q_{d}}\mathcal {F}_i .$
One aims at replacing all the balls
![]() $L_n$
intersecting L by the ball
$L_n$
intersecting L by the ball
![]() $2L$
.
$2L$
.
For any
![]() $1\leq i \leq Q_{d}$
and any ball
$1\leq i \leq Q_{d}$
and any ball
![]() $L\in \mathcal {F}_i$
, denote by
$L\in \mathcal {F}_i$
, denote by
![]() $\mathcal {G}_L$
the set of balls
$\mathcal {G}_L$
the set of balls
![]() $L_n$
intersecting L. Since
$L_n$
intersecting L. Since
![]() $E\subset \bigcup _{n\in \mathbb {N}}L_n$
and
$E\subset \bigcup _{n\in \mathbb {N}}L_n$
and
![]() $\mu (E)=\mu (\Omega )$
, one has
$\mu (E)=\mu (\Omega )$
, one has
![]() $E\cap L\subset \bigcup _{B\in \mathcal {G}_L}B$
and
$E\cap L\subset \bigcup _{B\in \mathcal {G}_L}B$
and
![]() $\mu (E\cap L)=\mu (L)$
. By Definition 5.1 and Proposition 5.9, this implies that
$\mu (E\cap L)=\mu (L)$
. By Definition 5.1 and Proposition 5.9, this implies that
 $$ \begin{align} \gamma( d,\mu,\varepsilon,\varepsilon^{\prime})\vert L\vert^{s+\varepsilon^ {\prime}} \leq\mathcal{H}^{\mu,s}_{\infty}(L)\leq \sum_{B\in\mathcal{G}_L}\mathcal{H}^{\mu,s}_{\infty}(B)\leq \sum_{B\in\mathcal{G}_L}\vert B\vert^s. \end{align} $$
$$ \begin{align} \gamma( d,\mu,\varepsilon,\varepsilon^{\prime})\vert L\vert^{s+\varepsilon^ {\prime}} \leq\mathcal{H}^{\mu,s}_{\infty}(L)\leq \sum_{B\in\mathcal{G}_L}\mathcal{H}^{\mu,s}_{\infty}(B)\leq \sum_{B\in\mathcal{G}_L}\vert B\vert^s. \end{align} $$
Replace the balls of
![]() $\mathcal {G}_L$
by the ball
$\mathcal {G}_L$
by the ball
![]() $\widehat {L}=2L$
(recall that
$\widehat {L}=2L$
(recall that
![]() $\bigcup _{B\in \mathcal {G}_{L}}B \subset 2L$
). The new sequence of balls so obtained by the previous construction applied to all the balls
$\bigcup _{B\in \mathcal {G}_{L}}B \subset 2L$
). The new sequence of balls so obtained by the previous construction applied to all the balls
![]() $L\in \bigcup _{\leq i\leq Q_{d}}\mathcal {F}_i$
is denoted by
$L\in \bigcup _{\leq i\leq Q_{d}}\mathcal {F}_i$
is denoted by
![]() $(\widehat {L}_k)_{1\le k \le K}$
, where
$(\widehat {L}_k)_{1\le k \le K}$
, where
![]() $0\le K\le +\infty $
.
$0\le K\le +\infty $
.
It follows from the construction and equation (79) that
![]() $S_1 \subset \bigcup _{1\le k\le K}\widehat {L}_k$
and
$S_1 \subset \bigcup _{1\le k\le K}\widehat {L}_k$
and
 $$ \begin{align} \sum_{1\le k\le K}\bigg (\frac{\vert \widehat{L}_k \vert}{2}\bigg)^{s+\varepsilon^{\prime}} \leq \frac{Q_{d}^2}{\gamma(d,\mu,\varepsilon,\varepsilon^{\prime})}\sum_{n\geq 0}\vert L_n \vert^s. \end{align} $$
$$ \begin{align} \sum_{1\le k\le K}\bigg (\frac{\vert \widehat{L}_k \vert}{2}\bigg)^{s+\varepsilon^{\prime}} \leq \frac{Q_{d}^2}{\gamma(d,\mu,\varepsilon,\varepsilon^{\prime})}\sum_{n\geq 0}\vert L_n \vert^s. \end{align} $$
However, since for any
![]() $x\in S_2 = \Delta \setminus S_1$
, there exists
$x\in S_2 = \Delta \setminus S_1$
, there exists
![]() $n_x\in \mathbb {N}$
such that
$n_x\in \mathbb {N}$
such that
![]() ${L}_{n_x}\cap B(x,r_x)\neq \emptyset $
and
${L}_{n_x}\cap B(x,r_x)\neq \emptyset $
and
![]() $r_x \leq \vert {L}_{n_x}\vert $
, one has
$r_x \leq \vert {L}_{n_x}\vert $
, one has
![]() $S_2\subset \bigcup _{n\in \mathbb {N}}2{L}_n$
, so that
$S_2\subset \bigcup _{n\in \mathbb {N}}2{L}_n$
, so that
 $$ \begin{align*} \bigg (\bigcup_{n\in\mathbb N}L_n\bigg )\cup \bigg(K\cap \Omega \setminus \bigcup_{n\in\mathbb N}L_n\bigg ) \subset \bigg (\bigcup_{1\le k\le K}\widehat L_k\bigg )\cup \bigg ( \bigcup_{n\in\mathbb N}2{L}_n\bigg ). \end{align*} $$
$$ \begin{align*} \bigg (\bigcup_{n\in\mathbb N}L_n\bigg )\cup \bigg(K\cap \Omega \setminus \bigcup_{n\in\mathbb N}L_n\bigg ) \subset \bigg (\bigcup_{1\le k\le K}\widehat L_k\bigg )\cup \bigg ( \bigcup_{n\in\mathbb N}2{L}_n\bigg ). \end{align*} $$
Putting the elements of
![]() $(\widehat {L}_k)_{1\le k \le K}$
and
$(\widehat {L}_k)_{1\le k \le K}$
and
![]() $(2L_n)_{n\ge 0}$
in a single sequence
$(2L_n)_{n\ge 0}$
in a single sequence
![]() $(\widehat { L}_n)_{n\ge 0}$
, writing
$(\widehat { L}_n)_{n\ge 0}$
, writing
![]() $(\widetilde {L}_n :=2\widehat {L}_n)_{n\in \mathbb {N}}$
, by construction,
$(\widetilde {L}_n :=2\widehat {L}_n)_{n\in \mathbb {N}}$
, by construction,
![]() $K\cap \Omega \subset \bigcup _{n\in \mathbb N}\widetilde {L}_n$
and due to equation (80),
$K\cap \Omega \subset \bigcup _{n\in \mathbb N}\widetilde {L}_n$
and due to equation (80),
 $$ \begin{align*} \mathcal{H}^ {s+\varepsilon^{\prime}}_{\infty}(K\cap \Omega)&\leq\sum_{n\geq 0}\vert \widetilde{L}_n \vert^{s+\varepsilon^{\prime}} \leq 2^{s+\varepsilon^{\prime}}\bigg(\frac{Q_{d}^2}{\gamma(d,\mu,\varepsilon,\varepsilon^{\prime})}+1\bigg)\sum_{n\geq 0}\vert L_n \vert^s \\ &\leq 8.2^{s+\varepsilon^{\prime}} \frac{Q_{d}^2}{\gamma( d,\mu,\varepsilon,\varepsilon^{\prime})}\mathcal{H}^{\mu,s}_{\infty}(\Omega). \end{align*} $$
$$ \begin{align*} \mathcal{H}^ {s+\varepsilon^{\prime}}_{\infty}(K\cap \Omega)&\leq\sum_{n\geq 0}\vert \widetilde{L}_n \vert^{s+\varepsilon^{\prime}} \leq 2^{s+\varepsilon^{\prime}}\bigg(\frac{Q_{d}^2}{\gamma(d,\mu,\varepsilon,\varepsilon^{\prime})}+1\bigg)\sum_{n\geq 0}\vert L_n \vert^s \\ &\leq 8.2^{s+\varepsilon^{\prime}} \frac{Q_{d}^2}{\gamma( d,\mu,\varepsilon,\varepsilon^{\prime})}\mathcal{H}^{\mu,s}_{\infty}(\Omega). \end{align*} $$
The proof is concluded now by setting
 $$ \begin{align*}c( d,\mu,s,\varepsilon^{\prime})=\frac{\gamma( d,\mu,\dim(\mu)-s,\varepsilon^{\prime})}{Q_{d}^2 8 .2^{s+\varepsilon^{\prime}}}.\\[-47pt] \end{align*} $$
$$ \begin{align*}c( d,\mu,s,\varepsilon^{\prime})=\frac{\gamma( d,\mu,\dim(\mu)-s,\varepsilon^{\prime})}{Q_{d}^2 8 .2^{s+\varepsilon^{\prime}}}.\\[-47pt] \end{align*} $$
Remark 5.10.
-
(1) The part of the proof of Theorem 5.5 which handles the case of open sets only relies on the fact that there exists
 $\gamma ( d,\mu ,\varepsilon ,\varepsilon ^{\prime })$
such that for any
$\gamma ( d,\mu ,\varepsilon ,\varepsilon ^{\prime })$
such that for any
 $x \in K$
, for any
$x \in K$
, for any
 $\rho>0$
, there exists
$\rho>0$
, there exists
 $0<r_x \leq \rho $
so that, writing
$0<r_x \leq \rho $
so that, writing
 $B=B(x,r_x),$
(81)
$B=B(x,r_x),$
(81)
-
(2) It is easily verified that the estimates of Proposition 5.9 hold in particular if, for
 $s \geq 0,$
there exists a constant
$s \geq 0,$
there exists a constant
 $C>0$
such that for any
$C>0$
such that for any
 $x\in {\mathrm {supp}} (\mu )$
, any
$x\in {\mathrm {supp}} (\mu )$
, any
 $0<r<R$
,
$0<r<R$
,
 $({\mu (B(x,r))}/{\mu (B(x,R))})\leq C.({r}/{R})^s.$
This condition is naturally linked to the lower Assouad dimension
$({\mu (B(x,r))}/{\mu (B(x,R))})\leq C.({r}/{R})^s.$
This condition is naturally linked to the lower Assouad dimension
 $\dim _L (\mu )$
of
$\dim _L (\mu )$
of
 $\mu $
defined as [Reference Fraser and Stuart20] (82)More precisely, the estimates of Proposition 5.9 and Theorem 5.5 hold for any
$\mu $
defined as [Reference Fraser and Stuart20] (82)More precisely, the estimates of Proposition 5.9 and Theorem 5.5 hold for any $$ \begin{align} \dim_L (\mu)=\inf\bigg\{s&\geq 0 : \text{ for all } x\in{\mathrm{supp}} (\mu),\nonumber\\ &\quad\text{for all } 0<r< R, \frac{\mu(B(x,r))}{\mu(B(x,R))}\leq C\bigg(\frac{r}{R}\bigg)^s\bigg\}. \end{align} $$
$$ \begin{align} \dim_L (\mu)=\inf\bigg\{s&\geq 0 : \text{ for all } x\in{\mathrm{supp}} (\mu),\nonumber\\ &\quad\text{for all } 0<r< R, \frac{\mu(B(x,r))}{\mu(B(x,R))}\leq C\bigg(\frac{r}{R}\bigg)^s\bigg\}. \end{align} $$
 $s<\dim _L (\mu )$
.
$s<\dim _L (\mu )$
.
5.2 Mass transference principle in the weakly conformal case
Combining Theorem 5.4 with Theorem 5.5 and Proposition 5.3 yields the following result.
Theorem 5.11. Let
![]() $S=\{f_1,\ldots ,f_m\}$
be a
$S=\{f_1,\ldots ,f_m\}$
be a
![]() $C^{1}$
weakly conformal IFS of a compact X with attractor K and
$C^{1}$
weakly conformal IFS of a compact X with attractor K and
![]() $\mu $
be a measure on K such that for every
$\mu $
be a measure on K such that for every
![]() $\underline {i}\in \bigcup _{k\geq 1}\{1,\ldots ,m\}^k$
,
$\underline {i}\in \bigcup _{k\geq 1}\{1,\ldots ,m\}^k$
,
![]() $\mu \circ f_{\underline {i}}^{-1}$
is absolutely continuous with respect to
$\mu \circ f_{\underline {i}}^{-1}$
is absolutely continuous with respect to
![]() $\mu $
.
$\mu $
.
Let
![]() $(B_{n})_{n\in \mathbb {N}}$
be a sequence of closed balls centered on K with
$(B_{n})_{n\in \mathbb {N}}$
be a sequence of closed balls centered on K with
![]() $\lim _{n\to +\infty } |B_{n}| = 0$
.
$\lim _{n\to +\infty } |B_{n}| = 0$
.
-
(1) Suppose that
 $(B_n)_{n\in \mathbb {N}}$
is
$(B_n)_{n\in \mathbb {N}}$
is
 $\mu $
-a.c. Then, there exists a gauge function
$\mu $
-a.c. Then, there exists a gauge function
 $\zeta $
such that
$\zeta $
such that
 $\lim _{r\to 0^+}({\log (\zeta (r))}/{\log (r)})\ge ({\underline {\dim }_H(\mu )}/{\delta })$
and
$\lim _{r\to 0^+}({\log (\zeta (r))}/{\log (r)})\ge ({\underline {\dim }_H(\mu )}/{\delta })$
and  . In particular, (83)
. In particular, (83)
-
(2) Suppose that
 $\mu (\limsup _{n\rightarrow +\infty }B_n)=1$
. Then, equation (83) still holds but the existence of the gauge function is not ensured. Furthermore, if
$\mu (\limsup _{n\rightarrow +\infty }B_n)=1$
. Then, equation (83) still holds but the existence of the gauge function is not ensured. Furthermore, if
 $\mu $
is doubling, then
$\mu $
is doubling, then
 $(B_n)_{n\in \mathbb {N}}$
is
$(B_n)_{n\in \mathbb {N}}$
is
 $\mu $
-a.c., so that the conclusion of item (1) holds.
$\mu $
-a.c., so that the conclusion of item (1) holds.
Remark 5.12. One emphasizes that, for the purpose of this article, the results are stated for balls but Theorems 5.5 and 5.4 allow to deal with more general open sets. For instance, given
![]() $1\leq \tau _1 \leq \cdots \leq \tau _d$
, if
$1\leq \tau _1 \leq \cdots \leq \tau _d$
, if
![]() $U_n$
is an open rectangle of sidelength
$U_n$
is an open rectangle of sidelength
![]() $\prod _{i=1}^n \vert B_n \vert ^{\tau _i},$
one needs to estimate the (classical) Hausdorff content of the union of the cubes
$\prod _{i=1}^n \vert B_n \vert ^{\tau _i},$
one needs to estimate the (classical) Hausdorff content of the union of the cubes
![]() $C\subset U_n$
of length-side
$C\subset U_n$
of length-side
![]() $\vert B_n \vert ^{\tau _d}$
(the smallest side of
$\vert B_n \vert ^{\tau _d}$
(the smallest side of
![]() $U_n$
) for which
$U_n$
) for which
![]() $C\cap K \neq \emptyset .$
This is achievable as soon as the rectangle has sides in ‘natural directions’ for the IFS we consider (for instance, horizontal rectangles on a self-similar carpet).
$C\cap K \neq \emptyset .$
This is achievable as soon as the rectangle has sides in ‘natural directions’ for the IFS we consider (for instance, horizontal rectangles on a self-similar carpet).
Proof. One proves the first item of Theorem 5.11.
Fix
![]() $\mu \in \mathcal {M}(\mathbb {R}^d)$
supported on K satisfying that for every
$\mu \in \mathcal {M}(\mathbb {R}^d)$
supported on K satisfying that for every
![]() $\underline {i}\in \bigcup _{k\geq 1}\{1,\ldots ,m\}^k, \mu \circ f_{\underline {i}}^{-1}$
is absolutely continuous with respect to
$\underline {i}\in \bigcup _{k\geq 1}\{1,\ldots ,m\}^k, \mu \circ f_{\underline {i}}^{-1}$
is absolutely continuous with respect to
![]() $\mu .$
Let
$\mu .$
Let
![]() $(B_n)_{n\in \mathbb {N}}$
be a
$(B_n)_{n\in \mathbb {N}}$
be a
![]() $\mu $
-a.c. sequence of balls centered on K satisfying
$\mu $
-a.c. sequence of balls centered on K satisfying
![]() $\vert B_n \vert \to 0$
. Let us fix
$\vert B_n \vert \to 0$
. Let us fix
![]() $\varepsilon>0$
.
$\varepsilon>0$
.
Let us start with a lemma whose proof can be found in [Reference Daviaud12, Lemma 4.9].
Lemma 5.13. Let
![]() $\mu \in \mathcal {M}(\mathbb {R}^d)$
. Let
$\mu \in \mathcal {M}(\mathbb {R}^d)$
. Let
![]() $\mathcal {B} =(B_n :=B(x_n ,r_n))_{n\in \mathbb {N}}$
be a
$\mathcal {B} =(B_n :=B(x_n ,r_n))_{n\in \mathbb {N}}$
be a
![]() $\mu $
-a.c. sequence of balls of
$\mu $
-a.c. sequence of balls of
![]() $ \mathbb {R}^d$
. Then, for every
$ \mathbb {R}^d$
. Then, for every
![]() $\varepsilon>0$
, there exists a
$\varepsilon>0$
, there exists a
![]() $\mu $
-a.c. sub-sequence
$\mu $
-a.c. sub-sequence
![]() $(B_{\phi (n)})_{n\in \mathbb {N}}$
of
$(B_{\phi (n)})_{n\in \mathbb {N}}$
of
![]() $\mathcal {B} $
such that for every
$\mathcal {B} $
such that for every
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $\mu (B_{\phi (n)})\leq (r_{\phi (n)})^{\underline {\dim }_H (\mu )-\varepsilon }.$
$\mu (B_{\phi (n)})\leq (r_{\phi (n)})^{\underline {\dim }_H (\mu )-\varepsilon }.$
By Lemma 5.13, up to an extraction, one can assume that
![]() $\mu (B_n)\leq \vert B_n\vert ^{\dim (\mu )-{\varepsilon }/{4}}.$
$\mu (B_n)\leq \vert B_n\vert ^{\dim (\mu )-{\varepsilon }/{4}}.$
The following proposition is proved in [Reference Daviaud10, Proposition 3.12].
Proposition 5.14. Let
![]() $\mu \in \mathcal {M}(\mathbb {R}^d)$
,
$\mu \in \mathcal {M}(\mathbb {R}^d)$
,
![]() $s\geq 0$
, and
$s\geq 0$
, and
![]() $A\subset \mathbb {R}^d $
be a Borel set. The s-dimensional
$A\subset \mathbb {R}^d $
be a Borel set. The s-dimensional
![]() $\mathcal {H}^{\mu ,s}_{\infty }(\cdot )$
outer measure satisfies the following properties.
$\mathcal {H}^{\mu ,s}_{\infty }(\cdot )$
outer measure satisfies the following properties.
-
(1) If
 $\vert A\vert \leq 1$
, the mapping
$\vert A\vert \leq 1$
, the mapping
 $s\geq 0\mapsto \mathcal {H}^{\mu ,s}_{\infty }(A)$
is decreasing from
$s\geq 0\mapsto \mathcal {H}^{\mu ,s}_{\infty }(A)$
is decreasing from
 $\mathcal {H}^{\mu ,0}_{\infty }(A)=1$
to
$\mathcal {H}^{\mu ,0}_{\infty }(A)=1$
to
 $\lim _{t\to +\infty }\mathcal {H}^{\mu ,t}_{\infty }(A)=0$
.
$\lim _{t\to +\infty }\mathcal {H}^{\mu ,t}_{\infty }(A)=0$
. -
(2)
 $0\leq \mathcal {H}^{\mu ,s}_{\infty }(A)\leq \min \{\vert A\vert ^s, \mathcal {H}^{s}_{\infty }(A)\}$
.
$0\leq \mathcal {H}^{\mu ,s}_{\infty }(A)\leq \min \{\vert A\vert ^s, \mathcal {H}^{s}_{\infty }(A)\}$
. -
(3) For every subset
 $ B\subset A$
with
$ B\subset A$
with
 $\mu (A)=\mu (B)$
,
$\mu (A)=\mu (B)$
,
 $\mathcal {H}^{\mu ,s}_{\infty }(A)=\mathcal {H}^{\mu ,s}_{\infty }(B).$
$\mathcal {H}^{\mu ,s}_{\infty }(A)=\mathcal {H}^{\mu ,s}_{\infty }(B).$
-
(4) For every
 $\delta \geq 1$
,
$\delta \geq 1$
,
 $\mathcal {H}^{\mu ,{s}/{\delta }}_{\infty }(A)\geq (\mathcal {H}^{\mu ,s}_{\infty }(A))^{{1}/{\delta }}.$
$\mathcal {H}^{\mu ,{s}/{\delta }}_{\infty }(A)\geq (\mathcal {H}^{\mu ,s}_{\infty }(A))^{{1}/{\delta }}.$
-
(5) For every
 $ s>\overline {\dim }_H (\mu )$
,
$ s>\overline {\dim }_H (\mu )$
,
 $\mathcal {H}^{\mu ,s}_{\infty }(A)=0.$
$\mathcal {H}^{\mu ,s}_{\infty }(A)=0.$
Also, by Theorem 5.5 and item
![]() $(5)$
of Proposition 5.14, there exists a constant
$(5)$
of Proposition 5.14, there exists a constant
![]() $c(d,\mu ,\dim (\mu )-{\varepsilon }/{2},{\varepsilon }/{4})$
such that, for any
$c(d,\mu ,\dim (\mu )-{\varepsilon }/{2},{\varepsilon }/{4})$
such that, for any
![]() $n\in \mathbb {N}$
, for any
$n\in \mathbb {N}$
, for any
![]() $\delta>1$
,
$\delta>1$
,

Taking n large enough so that
![]() $\vert B_n \vert ^{-{\varepsilon }/{4}}\geq c(d,\mu ,\underline {\dim }_H(\mu ))-{\varepsilon }/{2},{\varepsilon }/{4})$
, one gets
$\vert B_n \vert ^{-{\varepsilon }/{4}}\geq c(d,\mu ,\underline {\dim }_H(\mu ))-{\varepsilon }/{2},{\varepsilon }/{4})$
, one gets
Defining ![]() , using equation (84) and Theorem 5.4 with
, using equation (84) and Theorem 5.4 with
![]() $s_{ \varepsilon }{\kern-1pt}={\kern-1pt} ({\underline {\dim }_H(\mu ){\kern-1pt}-{\kern-1pt}\varepsilon }/{\delta })$
and letting
$s_{ \varepsilon }{\kern-1pt}={\kern-1pt} ({\underline {\dim }_H(\mu ){\kern-1pt}-{\kern-1pt}\varepsilon }/{\delta })$
and letting
![]() $\varepsilon \to 0$
finishes the proof of the first item.
$\varepsilon \to 0$
finishes the proof of the first item.
Assume now that the sequence
![]() $(B_n)_{n\in \mathbb {N}}$
satisfies only
$(B_n)_{n\in \mathbb {N}}$
satisfies only
![]() $\mu (\limsup _{n\rightarrow +\infty }B_n).$
Then, by Proposition 5.3,
$\mu (\limsup _{n\rightarrow +\infty }B_n).$
Then, by Proposition 5.3,
![]() $(2B_n)_{n\in \mathbb {N}}$
is
$(2B_n)_{n\in \mathbb {N}}$
is
![]() $\mu $
-a.c.
$\mu $
-a.c.
Since, for any
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
applying the first item of Theorem 5.11 to
![]() $(2B_n )_{n\in \mathbb {N}}$
, one gets
$(2B_n )_{n\in \mathbb {N}}$
, one gets
Since
![]() $\varepsilon $
was arbitrary, the second item is proved.
$\varepsilon $
was arbitrary, the second item is proved.
Remark 5.15. The proof of Theorem 5.11 actually shows more. With the notation of [Reference Daviaud10, Definition 2.5], it is proved that
![]() $s(\mu ,\mathcal {B},\mathcal {U}_{\delta })\geq ({\dim _H (\mu )}/{\delta })$
so that [Reference Daviaud10, Theorem 2.11] holds for self-conformal measures instead of self-similar measures.
$s(\mu ,\mathcal {B},\mathcal {U}_{\delta })\geq ({\dim _H (\mu )}/{\delta })$
so that [Reference Daviaud10, Theorem 2.11] holds for self-conformal measures instead of self-similar measures.
6 Proof of Theorem 3.1
Before starting the proof of Theorem 3.1, we explain why the very natural strategy which consists in approximating the attractor K by the sub-attractor of IFSs satisfying the strong separation condition does not yield any interesting conclusion in most (if not every) cases. Let
![]() $S=\{f_1,\ldots ,f_m\}$
be a self-similar IFS and let K be its attractor. Recall that S is said to satisfy the strong separation condition (SSC) if, for every
$S=\{f_1,\ldots ,f_m\}$
be a self-similar IFS and let K be its attractor. Recall that S is said to satisfy the strong separation condition (SSC) if, for every
![]() $1\leq i\neq j\leq m,$
we have
$1\leq i\neq j\leq m,$
we have
Let us start by proving the following result.
Proposition 6.1. Let
![]() $S=\{f_1,\ldots ,f_m\}$
be a self-similar IFS satisfying the strong separation condition and denote by K its attractor. Then, for every
$S=\{f_1,\ldots ,f_m\}$
be a self-similar IFS satisfying the strong separation condition and denote by K its attractor. Then, for every
 $$ \begin{align*}x_0\notin \bigcup_{\underline{i}\in\Lambda^*}f_{\underline{i}}^{-1}(K),\end{align*} $$
$$ \begin{align*}x_0\notin \bigcup_{\underline{i}\in\Lambda^*}f_{\underline{i}}^{-1}(K),\end{align*} $$
for every
![]() $\delta>1,$
one has
$\delta>1,$
one has
where
![]() $W(x_0,\delta )$
is defined as in Theorem 3.1.
$W(x_0,\delta )$
is defined as in Theorem 3.1.
Proof. Let us write
![]() $c_i$
as the contraction ratio of the map
$c_i$
as the contraction ratio of the map
![]() $f_i.$
$f_i.$
Since S satisfies the strong separation condition, there exists an open set U such that (see [Reference Bandt, Viet Hung and Rao3] for instance):
-
(a)
 $K\subset U;$
$K\subset U;$
-
(b) for every
 $\underline {i}\in \Lambda ^*, f_{\underline {i}}(U)\subset U;$
$\underline {i}\in \Lambda ^*, f_{\underline {i}}(U)\subset U;$
-
(c) for every
 $n\in \mathbb {N},$
for every
$n\in \mathbb {N},$
for every
 $\underline {i}\neq \underline {j}\in \Lambda ^n, f_{\underline {i}}(U)\cap f_{\underline {j}}(U)=\emptyset .$
$\underline {i}\neq \underline {j}\in \Lambda ^n, f_{\underline {i}}(U)\cap f_{\underline {j}}(U)=\emptyset .$
Moreover, there must exist
![]() $N\in \mathbb {N}$
so large that for every
$N\in \mathbb {N}$
so large that for every
![]() $n\geq N,$
for every
$n\geq N,$
for every
![]() $\underline {i}\in \Lambda ^n,$
one has
$\underline {i}\in \Lambda ^n,$
one has
![]() $f_{\underline {i}}(x_0)\in U.$
Now, fix
$f_{\underline {i}}(x_0)\in U.$
Now, fix
![]() $r>0$
small enough so that for every
$r>0$
small enough so that for every
![]() $\underline {i}\in \Lambda ^N,$
one has
$\underline {i}\in \Lambda ^N,$
one has
and set
 $$ \begin{align*}C=\min\bigg\{\frac{r}{c_{\underline{i}}},\underline{i}\in \Lambda^N\bigg\}.\end{align*} $$
$$ \begin{align*}C=\min\bigg\{\frac{r}{c_{\underline{i}}},\underline{i}\in \Lambda^N\bigg\}.\end{align*} $$
Fix
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
![]() $\underline {i},\underline {i}' \in \Lambda ^N$
, and
$\underline {i},\underline {i}' \in \Lambda ^N$
, and
![]() $\underline {j},\underline {j}'\in \Lambda ^k$
. We want to show that there exists a constant
$\underline {j},\underline {j}'\in \Lambda ^k$
. We want to show that there exists a constant
![]() ${C'>0}$
such that, writing
${C'>0}$
such that, writing
![]() $\underline {h}=\underline {j}\underline {i},$
one has
$\underline {h}=\underline {j}\underline {i},$
one has
Assume that
![]() $\underline {j}\neq \underline {j}',$
then by items
$\underline {j}\neq \underline {j}',$
then by items
![]() $(b)$
and
$(b)$
and
![]() $(c),$
one has
$(c),$
one has
which implies that
To deal with the case where
![]() $\underline {j}= \underline {j}'$
, we recall first that, since
$\underline {j}= \underline {j}'$
, we recall first that, since
![]() $x_0\notin \bigcup _{\underline {i}\in \Lambda ^*}f_{\underline {i}}^{-1}(K),$
the following quantity is strictly positive:
$x_0\notin \bigcup _{\underline {i}\in \Lambda ^*}f_{\underline {i}}^{-1}(K),$
the following quantity is strictly positive:
 $$ \begin{align*}\widetilde{C}=\min\bigg\{\frac{d(f_{\underline{i}}(x),f_{\underline{i}'}(K))}{c_{\underline{i}}},\underline{i}, \underline{i}'\in\Lambda^N\bigg\}.\end{align*} $$
$$ \begin{align*}\widetilde{C}=\min\bigg\{\frac{d(f_{\underline{i}}(x),f_{\underline{i}'}(K))}{c_{\underline{i}}},\underline{i}, \underline{i}'\in\Lambda^N\bigg\}.\end{align*} $$
Hence, in this case, we get
In any case, we established that there exists a constant
![]() $C'$
such that for every
$C'$
such that for every
![]() $n\geq N$
and
$n\geq N$
and
![]() $\underline {h},\underline {h}'\in \Lambda ^n,$
we have
$\underline {h},\underline {h}'\in \Lambda ^n,$
we have
This yields
In particular, recalling that
![]() $\delta>1,$
one has
$\delta>1,$
one has
which implies that
We now establish that, in most cases, one cannot handle the case of overlapping self-similar IFSs by approximating the IFS by the sub-attractor of IFSs satisfying the strong separation condition.
Proposition 6.2. Let
![]() $S=\{f_1,\ldots ,f_m\}$
be a self-similar IFS and K its attractor. Assume that S satisfies the following properties:
$S=\{f_1,\ldots ,f_m\}$
be a self-similar IFS and K its attractor. Assume that S satisfies the following properties:
-
•
 $\dim _H K =\dim (S)$
;
$\dim _H K =\dim (S)$
; -
• S does not satisfy the open set condition;
-
• there exists an exact-dimensional measure
 $\mu \in \mathcal {M}(\mathbb {R}^d)$
such that
$\mu \in \mathcal {M}(\mathbb {R}^d)$
such that
 ${\mathrm {supp}}(\mu )=K$
and
${\mathrm {supp}}(\mu )=K$
and
 $\dim _{H}\!y{\mu } =\dim _H K.$
$\dim _{H}\!y{\mu } =\dim _H K.$
Then, there exists a set
![]() $E\subset K$
with
$E\subset K$
with
![]() $\dim _H E =\dim _H K$
such that for every
$\dim _H E =\dim _H K$
such that for every
![]() $x\in E$
, every sub-IFS
$x\in E$
, every sub-IFS
![]() $\widetilde {S}=\{f_{\underline {i}_1},\ldots ,f_{\underline {i}_k}\}$
satisfying the strong separation condition (where
$\widetilde {S}=\{f_{\underline {i}_1},\ldots ,f_{\underline {i}_k}\}$
satisfying the strong separation condition (where
![]() $\underline {i}_1,\ldots ,\underline {i}_k$
are words on
$\underline {i}_1,\ldots ,\underline {i}_k$
are words on
![]() $\{1,\ldots ,m\}$
), one has for every
$\{1,\ldots ,m\}$
), one has for every
![]() $\delta>1$
,
$\delta>1$
,
where
![]() $\widetilde {W}(x,\delta )$
denotes the set
$\widetilde {W}(x,\delta )$
denotes the set
![]() $W(x,\delta )$
defined using the IFS
$W(x,\delta )$
defined using the IFS
![]() $\widetilde {S}.$
$\widetilde {S}.$
Note that the hypotheses of Proposition 6.2 are quite weak. It applies, for instance, to every self-similar IFS on the real line satisfying the exponential separation condition with similarity dimension smaller than
![]() $1$
and not the open set condition. More generally, it also applies to many examples of IFS which do not satisfy the open set condition to which Theorem 3.1 is applied in the present paper.
$1$
and not the open set condition. More generally, it also applies to many examples of IFS which do not satisfy the open set condition to which Theorem 3.1 is applied in the present paper.
Proof. Let us call
 $$ \begin{align*}\mathcal{S}=\bigg\{\widetilde{S}=\{f_{\underline{i}_1},\ldots,f_{\underline{i}_k}\}: \underline{i}_1,\ldots,\underline{i}_k \in \bigcup_{n\geq 0}\{1,\ldots,m\}^n , \widetilde{S}\text{ satisfies SSC}\bigg\}.\end{align*} $$
$$ \begin{align*}\mathcal{S}=\bigg\{\widetilde{S}=\{f_{\underline{i}_1},\ldots,f_{\underline{i}_k}\}: \underline{i}_1,\ldots,\underline{i}_k \in \bigcup_{n\geq 0}\{1,\ldots,m\}^n , \widetilde{S}\text{ satisfies SSC}\bigg\}.\end{align*} $$
Note that
![]() $\mathcal {S}$
is countable and denote by
$\mathcal {S}$
is countable and denote by
![]() $(K_n)_{n\in \mathbb {N}}$
the sequence of attractors associated with the elements of
$(K_n)_{n\in \mathbb {N}}$
the sequence of attractors associated with the elements of
![]() $\mathcal {S}.$
Let us recall that, due to [Reference Schief35], since
$\mathcal {S}.$
Let us recall that, due to [Reference Schief35], since
![]() $\dim _H K = \dim (S)$
and S does not satisfy the open set condition,
$\dim _H K = \dim (S)$
and S does not satisfy the open set condition,
Also, recalling that for every
![]() $n\in \mathbb {N}, K_n \subset K$
satisfies the strong separation condition, one has
$n\in \mathbb {N}, K_n \subset K$
satisfies the strong separation condition, one has
![]() $\mathcal {H}^{\dim _H K_n}(K_n)>0.$
In particular, this implies that
$\mathcal {H}^{\dim _H K_n}(K_n)>0.$
In particular, this implies that
![]() $\dim _H K_n < \dim _H K$
and also that
$\dim _H K_n < \dim _H K$
and also that
 $$ \begin{align*}\dim_H\bigcup_{\underline{i}\in \bigcup_{n\geq 0}\{1,\ldots,m\}^n}f_{\underline{i}}^{-1}(K_n):=\widetilde{K}_n<\dim_H K.\end{align*} $$
$$ \begin{align*}\dim_H\bigcup_{\underline{i}\in \bigcup_{n\geq 0}\{1,\ldots,m\}^n}f_{\underline{i}}^{-1}(K_n):=\widetilde{K}_n<\dim_H K.\end{align*} $$
Let
![]() $\mu $
be a
$\mu $
be a
![]() $\dim _H K$
-exact dimensional measure with
$\dim _H K$
-exact dimensional measure with
![]() ${\mathrm {supp}}(\mu )=K.$
The above argument proves that for every
${\mathrm {supp}}(\mu )=K.$
The above argument proves that for every
![]() $n\in \mathbb {N}, \mu (\widetilde {K}_n)=0,$
so that
$n\in \mathbb {N}, \mu (\widetilde {K}_n)=0,$
so that
 $$ \begin{align*}\mu\bigg(K\setminus \bigcup_{n\geq 0}\widetilde{K}_n\bigg)=1.\end{align*} $$
$$ \begin{align*}\mu\bigg(K\setminus \bigcup_{n\geq 0}\widetilde{K}_n\bigg)=1.\end{align*} $$
In particular, setting
![]() $E=K\setminus \bigcup _{n\geq 0}\widetilde {K}_n$
, one has
$E=K\setminus \bigcup _{n\geq 0}\widetilde {K}_n$
, one has
![]() $\dim _H E =\dim _H K.$
Moreover, for every
$\dim _H E =\dim _H K.$
Moreover, for every
![]() $x\in E$
and every
$x\in E$
and every
![]() $\widetilde {S}\in \mathcal {S},$
by Proposition 6.1, for every
$\widetilde {S}\in \mathcal {S},$
by Proposition 6.1, for every
![]() $\delta>1$
,
$\delta>1$
,
where
![]() $\widetilde {W}(x,\delta )$
is defined as in Theorem 3.1 but using the IFS
$\widetilde {W}(x,\delta )$
is defined as in Theorem 3.1 but using the IFS
![]() $\widetilde {S}.$
$\widetilde {S}.$
Remark 6.3. It would be interesting to extend the above result to a sub-attractor satisfying the open set condition but this question seems related to some open question related to the size of the set of so-called forbidden points in the case of a self-similar IFS. One refers to [Reference Bandt, Viet Hung and Rao3] for more details.
6.1 Proof of item (1) of Theorem 3.1
Write
![]() $s=\dim _H(K)$
. The notation of the proof of Theorem 5.5 is adopted in this section.
$s=\dim _H(K)$
. The notation of the proof of Theorem 5.5 is adopted in this section.
Lemma 6.4. For any
![]() $x_0\in U$
and any
$x_0\in U$
and any
![]() $\delta <1$
,
$\delta <1$
,
Proof. Note first that, since K is the (compact) attractor of S,
We now prove the converse inclusion.
Let
![]() $c>1$
. By Lemma 4.1 and Remark 4.2 applied with
$c>1$
. By Lemma 4.1 and Remark 4.2 applied with
 $$ \begin{align*}X= \bigcup_{\underline{i}\in\Lambda ^*}f_{\underline{i}}(x_0)\cup K,\end{align*} $$
$$ \begin{align*}X= \bigcup_{\underline{i}\in\Lambda ^*}f_{\underline{i}}(x_0)\cup K,\end{align*} $$
there exists
![]() $D(c)>0$
such that for any
$D(c)>0$
such that for any
![]() $y\in K$
and any
$y\in K$
and any
![]() $\underline {i}=(i_1,\ldots ,i_n)\in \Lambda ^*,$
$\underline {i}=(i_1,\ldots ,i_n)\in \Lambda ^*,$
By Lemma 4.1 and equation (20), one has
Combining equations (85) and (86), one gets
Recall that there exist
![]() $0<t_1<t_2$
so that, uniformly on n and
$0<t_1<t_2$
so that, uniformly on n and
![]() $\underline {i}\in \Lambda ^n,$
$\underline {i}\in \Lambda ^n,$
Set
![]() $\varepsilon =\delta -1>0,$
taking
$\varepsilon =\delta -1>0,$
taking
![]() $c=e^{{t_1 \varepsilon }/{4}}$
and writing
$c=e^{{t_1 \varepsilon }/{4}}$
and writing
![]() $\kappa (S,\varepsilon ,x_0)=\max _{z\in K}d(x,z)D(c)^2,$
one gets
$\kappa (S,\varepsilon ,x_0)=\max _{z\in K}d(x,z)D(c)^2,$
one gets
In particular, since
![]() $\vert f_{\underline {i}}(K)\vert \to 0,$
for n large enough, for any
$\vert f_{\underline {i}}(K)\vert \to 0,$
for n large enough, for any
![]() $\underline {i}\in \Lambda ^{n}$
,
$\underline {i}\in \Lambda ^{n}$
,
Recalling that
 $$ \begin{align*}K= \bigcup_{\underline{i}\in\Lambda^n}f_{ \underline{i}}(K), \end{align*} $$
$$ \begin{align*}K= \bigcup_{\underline{i}\in\Lambda^n}f_{ \underline{i}}(K), \end{align*} $$
one concludes that
![]() $K\subset \limsup _{\underline {i}\in \Lambda ^*}B(f_{\underline {i}}(x_0),\vert f_{\underline {i}}(K)\vert ^{1-\varepsilon }).$
$K\subset \limsup _{\underline {i}\in \Lambda ^*}B(f_{\underline {i}}(x_0),\vert f_{\underline {i}}(K)\vert ^{1-\varepsilon }).$
Remark 6.5. In the case where
![]() $S=\{f_1,\ldots ,f_m\}$
is a self-similar system, a more precise statement can be given. Denote by
$S=\{f_1,\ldots ,f_m\}$
is a self-similar system, a more precise statement can be given. Denote by
![]() $0<c_1,\ldots ,c_m <1$
the contracting ratio of respectively
$0<c_1,\ldots ,c_m <1$
the contracting ratio of respectively
![]() $f_1,\ldots ,f_m.$
In the self-similar case, for any
$f_1,\ldots ,f_m.$
In the self-similar case, for any
![]() $z\in K$
and any
$z\in K$
and any
![]() $\underline {i}\in \Lambda ^{*}$
,
$\underline {i}\in \Lambda ^{*}$
,
Writing
![]() $C(x_0,S)=\max _{y\in K}d(y,x)$
, this implies that
$C(x_0,S)=\max _{y\in K}d(y,x)$
, this implies that
![]() $f_{\underline {i}}(K)\subset B(f_{\underline {i}}(x_0),C(x_0,S)c_{\underline {i}})$
and
$f_{\underline {i}}(K)\subset B(f_{\underline {i}}(x_0),C(x_0,S)c_{\underline {i}})$
and
6.2 Proof of item (2) of Theorem 3.1
6.2.1 Variational principle and
 $C^1$
weakly conformal IFS
$C^1$
weakly conformal IFS
A modified version of a proposition of Feng and Hu used in the proof of their variational principle [Reference Feng and Hu19, Theorem 2.13] is needed to prove item (3) of Theorem 3.1. The following subsection is dedicated to this modification.
The result from Feng and Hu we wish to modify as follows.
Proposition 6.6. (Feng and Hu [Reference Feng and Hu19])
Let
![]() $m\geq 2$
be an integer and
$m\geq 2$
be an integer and
![]() $S=\{f_1,\ldots ,f_m \}$
a weakly conformal IFS. For any
$S=\{f_1,\ldots ,f_m \}$
a weakly conformal IFS. For any
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $n_{\varepsilon }\in \mathbb {N}$
as well as words
$n_{\varepsilon }\in \mathbb {N}$
as well as words
![]() $\underline {i}_{1},\ldots ,{\underline {i}_{n_{\varepsilon }}\in \Lambda ^{*}}$
such that:
$\underline {i}_{1},\ldots ,{\underline {i}_{n_{\varepsilon }}\in \Lambda ^{*}}$
such that:
-
• for any
 $1\leq j<j^{\prime }\leq n_{\varepsilon }$
,
$1\leq j<j^{\prime }\leq n_{\varepsilon }$
,
 $f_{\underline {i}_j}(K)\cap f_{\underline {i}_{j^{\prime }}}(K)=\emptyset ;$
$f_{\underline {i}_j}(K)\cap f_{\underline {i}_{j^{\prime }}}(K)=\emptyset ;$
-
• writing
 $S_{\varepsilon }=\{f_{\underline {i}_1},\ldots ,f_{\underline {i}_{n_{\varepsilon }}}\}$
, there exists a probability vector
$S_{\varepsilon }=\{f_{\underline {i}_1},\ldots ,f_{\underline {i}_{n_{\varepsilon }}}\}$
, there exists a probability vector
 $P_{\varepsilon }=(p_1 ,\ldots ,p_{n_{\varepsilon }})$
such that the weakly conformal measure
$P_{\varepsilon }=(p_1 ,\ldots ,p_{n_{\varepsilon }})$
such that the weakly conformal measure
 $\mu _{\varepsilon }$
associated with
$\mu _{\varepsilon }$
associated with
 $P_{\varepsilon }$
and
$P_{\varepsilon }$
and
 $S_{ \varepsilon }$
satisfies
$S_{ \varepsilon }$
satisfies
 $\dim _H (\mu _{ \varepsilon })\geq \dim _H (K)-\varepsilon .$
$\dim _H (\mu _{ \varepsilon })\geq \dim _H (K)-\varepsilon .$
Let us remark that, due to the the first item, the IFS
![]() $S_{\varepsilon }=\{T_ 1,\ldots ,T_{n_{\varepsilon }}\}$
satisfies the SSC and might not have K as attractor. We wish to modify this proposition so that the attractor of the IFS
$S_{\varepsilon }=\{T_ 1,\ldots ,T_{n_{\varepsilon }}\}$
satisfies the SSC and might not have K as attractor. We wish to modify this proposition so that the attractor of the IFS
![]() $S_{\varepsilon }$
can be taken equal to K.
$S_{\varepsilon }$
can be taken equal to K.
Note also that in Proposition 6.6, because
![]() $S_{\varepsilon }$
satisfies the SSC, by Corollary 4.23, the dimension of a weakly conformal measure associated with
$S_{\varepsilon }$
satisfies the SSC, by Corollary 4.23, the dimension of a weakly conformal measure associated with
![]() $S_{\varepsilon }$
depends continuously on the choice of the probability vector. Moreover, writing
$S_{\varepsilon }$
depends continuously on the choice of the probability vector. Moreover, writing
![]() $\nu _{\varepsilon }$
the canonical measure on the coding associated with
$\nu _{\varepsilon }$
the canonical measure on the coding associated with
![]() $\mu _{\varepsilon }$
, then the Lyapunov exponent
$\mu _{\varepsilon }$
, then the Lyapunov exponent
![]() $\unicode{x3bb} _{\nu _{\varepsilon }}>0$
(see Definition 4.5) satisfies for
$\unicode{x3bb} _{\nu _{\varepsilon }}>0$
(see Definition 4.5) satisfies for
![]() $\nu _{\varepsilon }$
-almost every
$\nu _{\varepsilon }$
-almost every
![]() $(x_n)_{n\in \mathbb {N}}$
that
$(x_n)_{n\in \mathbb {N}}$
that
As announced above, one proves the following modified version of Proposition 6.6.
Proposition 6.7. Let
![]() $\varepsilon _0>0$
. There exists an IFS
$\varepsilon _0>0$
. There exists an IFS
![]() $S_{\varepsilon _0}$
and a weakly conformal measure
$S_{\varepsilon _0}$
and a weakly conformal measure
![]() $\mu _{\varepsilon _0}$
(associated with
$\mu _{\varepsilon _0}$
(associated with
![]() $S_{\varepsilon _0}$
) such that
$S_{\varepsilon _0}$
) such that
![]() ${\mathrm {supp}}(\mu _{\varepsilon _0})=K$
and
${\mathrm {supp}}(\mu _{\varepsilon _0})=K$
and
![]() $\dim _H (\mu _{\varepsilon _0})\geq \dim _H K-\varepsilon _0.$
$\dim _H (\mu _{\varepsilon _0})\geq \dim _H K-\varepsilon _0.$
Remark 6.8. Similar to the proof of [Reference Feng and Hu19, Theorem 2.13], Proposition 6.7 yields a measure on
![]() $\Lambda ^{\mathbb {N}}$
and taking weak limits of ergodic averages of this measure gives an ergodic measure fully supported on K with dimension larger
$\Lambda ^{\mathbb {N}}$
and taking weak limits of ergodic averages of this measure gives an ergodic measure fully supported on K with dimension larger
![]() $s-\varepsilon _0.$
$s-\varepsilon _0.$
Proof. Fix
![]() $\varepsilon =({\varepsilon _0}/{2})>0$
. Consider
$\varepsilon =({\varepsilon _0}/{2})>0$
. Consider
![]() $S_{\varepsilon }=\{f_{\underline {i}_1},\ldots ,f_{\underline {i}_{n_{\varepsilon }}}\}$
,
$S_{\varepsilon }=\{f_{\underline {i}_1},\ldots ,f_{\underline {i}_{n_{\varepsilon }}}\}$
,
![]() $P_{\varepsilon }$
,
$P_{\varepsilon }$
,
![]() $\mu _{\varepsilon }$
as in Theorem 6.6 and
$\mu _{\varepsilon }$
as in Theorem 6.6 and
![]() $0<\varepsilon '<({1}/{5n_{\varepsilon }m})\cdot \min _{1\leq i\leq m}p_i$
.
$0<\varepsilon '<({1}/{5n_{\varepsilon }m})\cdot \min _{1\leq i\leq m}p_i$
.
Set
 $$ \begin{align*}\begin{cases}g_{j}=f_j &\text{for }1\leq j\leq m, \\ g_{j}=f_{\underline{i}_{j-m}}&\text{for }m+1\leq j\leq n_{\varepsilon}+m.\end{cases}\end{align*} $$
$$ \begin{align*}\begin{cases}g_{j}=f_j &\text{for }1\leq j\leq m, \\ g_{j}=f_{\underline{i}_{j-m}}&\text{for }m+1\leq j\leq n_{\varepsilon}+m.\end{cases}\end{align*} $$
Also set
![]() $\widetilde {S}_{\varepsilon }=\{g_1 ,\ldots ,g_{m+n_{\varepsilon } } \}$
and note that
$\widetilde {S}_{\varepsilon }=\{g_1 ,\ldots ,g_{m+n_{\varepsilon } } \}$
and note that
![]() $\widetilde {S}_{\varepsilon }$
has attractor K. Denote by
$\widetilde {S}_{\varepsilon }$
has attractor K. Denote by
![]() $\widetilde {P}_{\varepsilon ,\varepsilon ^{\prime }}=(\widetilde {p}_1 ,\ldots ,\widetilde {p}_{m+n_{\varepsilon }})$
the probability vector defined as
$\widetilde {P}_{\varepsilon ,\varepsilon ^{\prime }}=(\widetilde {p}_1 ,\ldots ,\widetilde {p}_{m+n_{\varepsilon }})$
the probability vector defined as
 $$ \begin{align*}\begin{cases}\widetilde{p}_j =\varepsilon^{\prime} & \text{ for }1\leq j \leq m, \\ \widetilde{p}_j =p_{j-m}-\dfrac{m}{n_{\varepsilon}}\varepsilon^{\prime}.& \end{cases}\end{align*} $$
$$ \begin{align*}\begin{cases}\widetilde{p}_j =\varepsilon^{\prime} & \text{ for }1\leq j \leq m, \\ \widetilde{p}_j =p_{j-m}-\dfrac{m}{n_{\varepsilon}}\varepsilon^{\prime}.& \end{cases}\end{align*} $$
Let
![]() $\mu _{\varepsilon ,\varepsilon ^{\prime }}$
be the weakly conformal measure associated with
$\mu _{\varepsilon ,\varepsilon ^{\prime }}$
be the weakly conformal measure associated with
![]() $\widetilde {S}_{\varepsilon }$
and
$\widetilde {S}_{\varepsilon }$
and
![]() $\widetilde {P}_{\varepsilon ,\varepsilon ^{\prime }}.$
Applying Theorem 4.8 to
$\widetilde {P}_{\varepsilon ,\varepsilon ^{\prime }}.$
Applying Theorem 4.8 to
![]() $\mu _{\varepsilon ,\varepsilon ^{\prime }}$
, let us prove that the corresponding h (see second item of Theorem 4.8) tends to 0 as
$\mu _{\varepsilon ,\varepsilon ^{\prime }}$
, let us prove that the corresponding h (see second item of Theorem 4.8) tends to 0 as
![]() $\varepsilon ^{\prime }$
tends to
$\varepsilon ^{\prime }$
tends to
![]() $0$
.
$0$
.
Set
![]() $\Theta =\{1,\ldots ,n_{\varepsilon }+m\}$
and
$\Theta =\{1,\ldots ,n_{\varepsilon }+m\}$
and
![]() $\Theta ^{*}=\bigcup _{k>0}\Theta ^k .$
Let us denote by
$\Theta ^{*}=\bigcup _{k>0}\Theta ^k .$
Let us denote by
![]() $\pi _{\Theta }$
the canonical projection of
$\pi _{\Theta }$
the canonical projection of
![]() $\Theta ^{\mathbb {N}}$
on K. One endows
$\Theta ^{\mathbb {N}}$
on K. One endows
![]() $\Sigma _{\Theta }=\Theta ^{\mathbb {N}}$
with the metric
$\Sigma _{\Theta }=\Theta ^{\mathbb {N}}$
with the metric
![]() $d_{\Theta }$
defined for any
$d_{\Theta }$
defined for any
![]() $x=(x_n),y=(y_n)\in \Sigma _{\Theta }$
by
$x=(x_n),y=(y_n)\in \Sigma _{\Theta }$
by
Let us remark that the metric d allows one to define on
![]() $\Theta ^{\mathbb {N}}$
the Hausdorff dimension and the Packing dimension in a similar way than on
$\Theta ^{\mathbb {N}}$
the Hausdorff dimension and the Packing dimension in a similar way than on
![]() $\mathbb {R}^d.$
$\mathbb {R}^d.$
Let
![]() $\nu _{\varepsilon ,\varepsilon ^{\prime }}\in \mathcal {M}(\Theta ^{\mathbb {N}})$
be the Bernoulli product verifying
$\nu _{\varepsilon ,\varepsilon ^{\prime }}\in \mathcal {M}(\Theta ^{\mathbb {N}})$
be the Bernoulli product verifying
![]() $\nu _{\varepsilon ,\varepsilon ^{\prime }}\circ \pi _{\Theta }^{-1}=\mu _{\varepsilon ,\varepsilon ^{\prime }}.$
$\nu _{\varepsilon ,\varepsilon ^{\prime }}\circ \pi _{\Theta }^{-1}=\mu _{\varepsilon ,\varepsilon ^{\prime }}.$
By the strong law of large numbers, for every
![]() $x=(x_n)_{n\in \mathbb {N}}$
in a set
$x=(x_n)_{n\in \mathbb {N}}$
in a set
![]() $\widetilde {\Sigma }_{\Theta }$
of
$\widetilde {\Sigma }_{\Theta }$
of
![]() $\nu ^{\varepsilon ,\varepsilon ^{\prime }}$
-full measure, there exists
$\nu ^{\varepsilon ,\varepsilon ^{\prime }}$
-full measure, there exists
![]() $N_x \in \mathbb {N}$
such that for any
$N_x \in \mathbb {N}$
such that for any
![]() $n\geq N_x,$
any
$n\geq N_x,$
any
![]() $1\leq i \leq n_{\varepsilon }+m$
,
$1\leq i \leq n_{\varepsilon }+m$
,
 $$ \begin{align} \bigg\vert\frac{\#\{1\leq j\leq n \ : x_j =i\}}{n}-\widetilde{p}_i\bigg\vert\leq\varepsilon^{\prime}. \end{align} $$
$$ \begin{align} \bigg\vert\frac{\#\{1\leq j\leq n \ : x_j =i\}}{n}-\widetilde{p}_i\bigg\vert\leq\varepsilon^{\prime}. \end{align} $$
For
![]() $n\in \mathbb {N}$
, write
$n\in \mathbb {N}$
, write
By Theorem 4.8, there exists N such that, using the notation involved,
 $$ \begin{align*}\mu_{\varepsilon,\varepsilon^{\prime}}(B_N=\bigg\{y: \dim_H(\mu_{\varepsilon,\varepsilon'}^{\pi_{\Theta}^{-1}(\{y\})})=h \text{ and }\mu_{\varepsilon,\varepsilon'}^{\pi_{\Theta}^{-1}(\{y\})} (A_N)\geq \frac{1}{2}\bigg\}\bigg)\geq \frac{1}{2}.\end{align*} $$
$$ \begin{align*}\mu_{\varepsilon,\varepsilon^{\prime}}(B_N=\bigg\{y: \dim_H(\mu_{\varepsilon,\varepsilon'}^{\pi_{\Theta}^{-1}(\{y\})})=h \text{ and }\mu_{\varepsilon,\varepsilon'}^{\pi_{\Theta}^{-1}(\{y\})} (A_N)\geq \frac{1}{2}\bigg\}\bigg)\geq \frac{1}{2}.\end{align*} $$
We fix such an N.
The following lemma is useful to estimate the number of cylinders of generation n which intersects
![]() $A_N$
.
$A_N$
.
Lemma 6.9. Consider
![]() $N\in \mathbb {N}$
,
$N\in \mathbb {N}$
,
![]() $y\in K$
, and
$y\in K$
, and
![]() $x=(x_n)_{n\in \mathbb {N}},\widetilde {x}=(\widetilde { x}_n)_{n\in \mathbb {N}}\in \pi _{\Theta }^{-1}(\{y\}).$
Assume that for every
$x=(x_n)_{n\in \mathbb {N}},\widetilde {x}=(\widetilde { x}_n)_{n\in \mathbb {N}}\in \pi _{\Theta }^{-1}(\{y\}).$
Assume that for every
![]() $1\leq k\leq N$
,
$1\leq k\leq N$
,
Then, for every
![]() $0\leq j\leq N$
such that
$0\leq j\leq N$
such that
![]() $x_j \geq m+1,$
one also has
$x_j \geq m+1,$
one also has
Proof. We proceed by contradiction. Suppose that the claim is not true and let
![]() $x_{j_0} \geq m+1$
be such for any
$x_{j_0} \geq m+1$
be such for any
![]() $1\leq i < j_0$
,
$1\leq i < j_0$
,
![]() $\widetilde {x}_i = x_i$
and
$\widetilde {x}_i = x_i$
and
![]() $\widetilde {x}_{j_0}\neq x_{j_0}.$
Write
$\widetilde {x}_{j_0}\neq x_{j_0}.$
Write
and
Then, recalling that
![]() $x,\widetilde {x}\in \pi _{\Theta }^{-1}(\{y\}),$
$x,\widetilde {x}\in \pi _{\Theta }^{-1}(\{y\}),$
which implies that
Recalling that the system
![]() $\{g_{m+1},\ldots ,g_{m+N_{\varepsilon }}\}$
satisfies the SSC, one also has
$\{g_{m+1},\ldots ,g_{m+N_{\varepsilon }}\}$
satisfies the SSC, one also has
which yields a contradiction.
Continuing the proof of the proposition, we note that, by equation (90), for every
![]() $y\in B_N$
,
$y\in B_N$
,
![]() $x=(x_n)_{n \in \mathbb {N}}\in \pi _{\theta }^{-1}(\{y\})\cap A_N$
, and
$x=(x_n)_{n \in \mathbb {N}}\in \pi _{\theta }^{-1}(\{y\})\cap A_N$
, and
![]() $N'\geq N,$
$N'\geq N,$
Lemma 6.9 together with equation (91) yields for N large enough,
 $$ \begin{align*} \#\{\underline{i}\in\Theta^{N^{\prime}} \ : [\underline{i}]\cap A_{N}\cap \pi_{\Theta}^{-1}(\{y\})\neq \emptyset\}&\leq \sum_{k=0}^{\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+1}\binom{ N^{\prime}} {k}m^{k}. \end{align*} $$
$$ \begin{align*} \#\{\underline{i}\in\Theta^{N^{\prime}} \ : [\underline{i}]\cap A_{N}\cap \pi_{\Theta}^{-1}(\{y\})\neq \emptyset\}&\leq \sum_{k=0}^{\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+1}\binom{ N^{\prime}} {k}m^{k}. \end{align*} $$
Since
![]() $\varepsilon '<({1}/{5m})$
so that
$\varepsilon '<({1}/{5m})$
so that
![]() $2m\varepsilon ' N' <({N'}/{2})$
,
$2m\varepsilon ' N' <({N'}/{2})$
,
 $$ \begin{align*} \#\{\underline{i}\in\Theta^{N^{\prime}} \ : [\underline{i}]\cap A_{N}\cap \pi_{\Theta}^{-1}(\{y\})\neq \emptyset\}\leq (\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+2)\binom{ N^{\prime}} {\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+1}m^{\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+1}. \end{align*} $$
$$ \begin{align*} \#\{\underline{i}\in\Theta^{N^{\prime}} \ : [\underline{i}]\cap A_{N}\cap \pi_{\Theta}^{-1}(\{y\})\neq \emptyset\}\leq (\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+2)\binom{ N^{\prime}} {\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+1}m^{\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+1}. \end{align*} $$
Using the Stierling formula, provided that
![]() $\varepsilon ^{\prime }$
was chosen small enough at the start and N (so
$\varepsilon ^{\prime }$
was chosen small enough at the start and N (so
![]() $N^{\prime }$
too) large enough, there exists a constant
$N^{\prime }$
too) large enough, there exists a constant
![]() $C>0$
such that
$C>0$
such that
 $$ \begin{align} &\#\{\underline{i}\in\Theta^{N^{\prime}} : [\underline{i}]\cap A_{N}\cap \pi_{\Theta}^{-1}(\{y\})\neq \emptyset\} \nonumber\\ &\quad\leq C(\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+2)\frac{(N^{\prime})^{\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+1}\cdot m^{\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+1}}{(({\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+1})/{e})^{\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+1}\sqrt{2\pi(\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+1)}}\nonumber \\ &\quad\leq C(\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+2)\bigg(\frac{m N^{\prime}}{{2m\varepsilon^{\prime}N^{^{\prime}}}/{e}}\bigg)^{\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+1}\frac{1}{\sqrt{2\pi(\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+1)}}\nonumber \\ & \quad\leq C(\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+2)\bigg(\frac{e}{2\varepsilon^{\prime}}\bigg)^{3mN^{\prime}\varepsilon^{\prime}}\nonumber\\ &\quad= C(\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+2)e^{3mN^{\prime}\varepsilon^{\prime}\log ({e}/{2\varepsilon^{\prime}})}\leq e^{\sqrt{\varepsilon^{\prime}}N^{\prime}}. \end{align} $$
$$ \begin{align} &\#\{\underline{i}\in\Theta^{N^{\prime}} : [\underline{i}]\cap A_{N}\cap \pi_{\Theta}^{-1}(\{y\})\neq \emptyset\} \nonumber\\ &\quad\leq C(\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+2)\frac{(N^{\prime})^{\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+1}\cdot m^{\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+1}}{(({\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+1})/{e})^{\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+1}\sqrt{2\pi(\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+1)}}\nonumber \\ &\quad\leq C(\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+2)\bigg(\frac{m N^{\prime}}{{2m\varepsilon^{\prime}N^{^{\prime}}}/{e}}\bigg)^{\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+1}\frac{1}{\sqrt{2\pi(\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+1)}}\nonumber \\ & \quad\leq C(\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+2)\bigg(\frac{e}{2\varepsilon^{\prime}}\bigg)^{3mN^{\prime}\varepsilon^{\prime}}\nonumber\\ &\quad= C(\lfloor 2m\varepsilon^{\prime}N^{\prime}\rfloor+2)e^{3mN^{\prime}\varepsilon^{\prime}\log ({e}/{2\varepsilon^{\prime}})}\leq e^{\sqrt{\varepsilon^{\prime}}N^{\prime}}. \end{align} $$
Since equation (92) holds for any
![]() $N^{\prime }\geq N$
, one obtains that
$N^{\prime }\geq N$
, one obtains that
Recalling that, by definition of
![]() $B_N$
, the measure
$B_N$
, the measure
![]() $\mu ^{\pi _{\theta }^{-1}(\{y\})}$
is h-exact dimensional, that
$\mu ^{\pi _{\theta }^{-1}(\{y\})}$
is h-exact dimensional, that
![]() $\mu ^{\pi _{\theta }^{-1}(\{y\})}(\pi _{\theta }^{-1}(\{y\}))=1 $
, and that
$\mu ^{\pi _{\theta }^{-1}(\{y\})}(\pi _{\theta }^{-1}(\{y\}))=1 $
, and that
![]() $\mu ^{\pi _{\theta }^{-1}(\{y\})}(A_N)\geq \tfrac 12$
, one has
$\mu ^{\pi _{\theta }^{-1}(\{y\})}(A_N)\geq \tfrac 12$
, one has
 $$ \begin{align*} h&=\inf\{\dim_H(A), \text{ A Borel set satisfying }\mu^{\pi_{\theta}^{-1}(\{y\})}(A)>0\}\\ &\leq \dim_P (A_{N}\cap \pi_{\Theta}^{-1}(\{y\}))\leq \sqrt{\varepsilon^{\prime}}. \end{align*} $$
$$ \begin{align*} h&=\inf\{\dim_H(A), \text{ A Borel set satisfying }\mu^{\pi_{\theta}^{-1}(\{y\})}(A)>0\}\\ &\leq \dim_P (A_{N}\cap \pi_{\Theta}^{-1}(\{y\}))\leq \sqrt{\varepsilon^{\prime}}. \end{align*} $$
By Remark 4.6 and the fourth item of Theorem 4.8, there exists a constant
![]() $\widetilde {C}$
depending on the system S such that
$\widetilde {C}$
depending on the system S such that
 $$ \begin{align} \dim_H (\mu_{\varepsilon,\varepsilon^{\prime}})\geq \frac{\dim_H (\nu_{\varepsilon,\varepsilon^{\prime}})}{\unicode{x3bb}_{\nu_{\varepsilon,\varepsilon^{\prime}}}}-\widetilde{C}\sqrt{\varepsilon^{\prime}}, \end{align} $$
$$ \begin{align} \dim_H (\mu_{\varepsilon,\varepsilon^{\prime}})\geq \frac{\dim_H (\nu_{\varepsilon,\varepsilon^{\prime}})}{\unicode{x3bb}_{\nu_{\varepsilon,\varepsilon^{\prime}}}}-\widetilde{C}\sqrt{\varepsilon^{\prime}}, \end{align} $$
where
![]() $\unicode{x3bb} _{\nu _{\varepsilon ,\varepsilon ^{\prime }}}$
is given by Definition 4.5. Also, by Corollary 4.7, for any Bernoulli product
$\unicode{x3bb} _{\nu _{\varepsilon ,\varepsilon ^{\prime }}}$
is given by Definition 4.5. Also, by Corollary 4.7, for any Bernoulli product
![]() $\nu \in \mathcal {M}(\Theta )$
associated with a probability vector
$\nu \in \mathcal {M}(\Theta )$
associated with a probability vector
![]() $\widehat {P}\in (0,1)^{n_{\varepsilon }+m},$
the Lyapunov exponent depends continuously on the vector
$\widehat {P}\in (0,1)^{n_{\varepsilon }+m},$
the Lyapunov exponent depends continuously on the vector
![]() $\widehat {P}.$
Recalling that
$\widehat {P}.$
Recalling that
![]() $\Theta ^{\mathbb {N}}$
is endowed with the metric given by equation (89), it is also classical that
$\Theta ^{\mathbb {N}}$
is endowed with the metric given by equation (89), it is also classical that
![]() $\dim _H(\nu )$
depends continuously on the choice of
$\dim _H(\nu )$
depends continuously on the choice of
![]() $\widehat {P}$
. Since
$\widehat {P}$
. Since
![]() $\lim _{\varepsilon ^{\prime }\to 0}P_{\varepsilon ,\varepsilon ^{\prime }}=\{0\}^m \times P_{\varepsilon }$
,
$\lim _{\varepsilon ^{\prime }\to 0}P_{\varepsilon ,\varepsilon ^{\prime }}=\{0\}^m \times P_{\varepsilon }$
,
 $$ \begin{align} \lim_{\varepsilon'\to 0}\frac{\dim_H (\nu_{\varepsilon,\varepsilon^{\prime}})}{\unicode{x3bb}_{\nu_{\varepsilon,\varepsilon^{\prime}}}} = \frac{\dim_H (\nu_{\varepsilon})}{\unicode{x3bb}_{\nu_{\varepsilon}}}. \end{align} $$
$$ \begin{align} \lim_{\varepsilon'\to 0}\frac{\dim_H (\nu_{\varepsilon,\varepsilon^{\prime}})}{\unicode{x3bb}_{\nu_{\varepsilon,\varepsilon^{\prime}}}} = \frac{\dim_H (\nu_{\varepsilon})}{\unicode{x3bb}_{\nu_{\varepsilon}}}. \end{align} $$
Equation (94) combined with equation (93) proves that for
![]() $\varepsilon ^{\prime }$
small enough, one has
$\varepsilon ^{\prime }$
small enough, one has
 $$ \begin{align*}\dim_H (\mu_{\varepsilon,\varepsilon^{\prime}})\geq \frac{\dim_H (\nu_{\varepsilon})}{\unicode{x3bb}_{\nu_{\varepsilon}}}-2\varepsilon \geq s-2\varepsilon,\end{align*} $$
$$ \begin{align*}\dim_H (\mu_{\varepsilon,\varepsilon^{\prime}})\geq \frac{\dim_H (\nu_{\varepsilon})}{\unicode{x3bb}_{\nu_{\varepsilon}}}-2\varepsilon \geq s-2\varepsilon,\end{align*} $$
which concludes the proof of Proposition 6.7.
We can now finish the proof of item (3) of Theorem 3.1.
6.2.2 Proof of item (2) of Theorem 3.1
Let us recall that, by Proposition 2.6 and Definition 2.8,
![]() $\dim (S)$
verifies, for any
$\dim (S)$
verifies, for any
![]() $z\in K$
,
$z\in K$
,
 $$ \begin{align*}P(\dim(S))=\lim_{k\rightarrow+\infty}\frac{1}{k}\log\sum_{\underline{i}\in \Lambda^k} \vert f_{\underline{i}}(K)\vert^{\dim(S)} =0.\end{align*} $$
$$ \begin{align*}P(\dim(S))=\lim_{k\rightarrow+\infty}\frac{1}{k}\log\sum_{\underline{i}\in \Lambda^k} \vert f_{\underline{i}}(K)\vert^{\dim(S)} =0.\end{align*} $$
Fix
![]() $x_0\in K$
,
$x_0\in K$
,
![]() $\delta \geq 1$
and write
$\delta \geq 1$
and write
Let us first show that
![]() $\dim _H (\mathcal {L}(\delta ))\leq ({\dim (S)}/{\delta }).$
$\dim _H (\mathcal {L}(\delta ))\leq ({\dim (S)}/{\delta }).$
Let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be as in equation (23). If one must change the constants
$\beta $
be as in equation (23). If one must change the constants
![]() $\alpha $
and
$\alpha $
and
![]() $\beta ,$
one can assume that there exists
$\beta ,$
one can assume that there exists
![]() $k_0 \in \mathbb {N}$
such that for every
$k_0 \in \mathbb {N}$
such that for every
![]() $k\geq k_0$
and every
$k\geq k_0$
and every
![]() $\underline {i}\in \Lambda ^k$
,
$\underline {i}\in \Lambda ^k$
,
For every
![]() $k\in \mathbb {N},$
recalling equation (38), for every
$k\in \mathbb {N},$
recalling equation (38), for every
![]() $\underline {i}=(i_1,\ldots ,i_n)\in \Lambda ^{(k)}$
, one has
$\underline {i}=(i_1,\ldots ,i_n)\in \Lambda ^{(k)}$
, one has
In particular, every integer
![]() $p\in \mathbb {N}$
and every
$p\in \mathbb {N}$
and every
![]() $(i_{n+1},\ldots ,i_{n+p})\in \Lambda ^{p}$
such that
$(i_{n+1},\ldots ,i_{n+p})\in \Lambda ^{p}$
such that
![]() $(i_1,\ldots ,i_{n+p})\in \Lambda ^{(k)}$
must satisfy
$(i_1,\ldots ,i_{n+p})\in \Lambda ^{(k)}$
must satisfy
 $$ \begin{align*} \beta^{n+p-1}\geq \alpha^n \Rightarrow p\leq n\times\bigg(\frac{\log \alpha}{\log \beta}-1\bigg)+1\leq 2n\bigg(\frac{\log \alpha}{\log \beta}-1\bigg)\leq k \times C(\alpha,\beta). \end{align*} $$
$$ \begin{align*} \beta^{n+p-1}\geq \alpha^n \Rightarrow p\leq n\times\bigg(\frac{\log \alpha}{\log \beta}-1\bigg)+1\leq 2n\bigg(\frac{\log \alpha}{\log \beta}-1\bigg)\leq k \times C(\alpha,\beta). \end{align*} $$
This implies that, for any
![]() $\nu \in \mathcal {M}(\Lambda ^{\mathbb {N}}),$
$\nu \in \mathcal {M}(\Lambda ^{\mathbb {N}}),$
 $$ \begin{align} \sum_{\underline{i}\in \Lambda^{(k)}}\nu([\underline{i}])\leq kC( \alpha,\beta). \end{align} $$
$$ \begin{align} \sum_{\underline{i}\in \Lambda^{(k)}}\nu([\underline{i}])\leq kC( \alpha,\beta). \end{align} $$
Consider
![]() $\varepsilon>0$
. Let us recall that Lemma 4.20 applied with
$\varepsilon>0$
. Let us recall that Lemma 4.20 applied with
and
![]() $s=\dim (S)$
combined with Remark 4.21 yields a constant
$s=\dim (S)$
combined with Remark 4.21 yields a constant
![]() $\gamma _{\varepsilon '}>0$
and a measure
$\gamma _{\varepsilon '}>0$
and a measure
![]() $\nu _{\varepsilon '}\in \mathcal {M}(\Lambda ^{\mathbb {N}})$
such that for any
$\nu _{\varepsilon '}\in \mathcal {M}(\Lambda ^{\mathbb {N}})$
such that for any
![]() $k\in \mathbb {N}$
and every
$k\in \mathbb {N}$
and every
![]() $\underline {i}=(i_1,\ldots ,i_n)\in \Lambda ^{(k)},$
$\underline {i}=(i_1,\ldots ,i_n)\in \Lambda ^{(k)},$
For any
![]() $\delta \geq 1$
,
$\delta \geq 1$
,
 $$ \begin{align} \sum_{\underline{i}\in\in\bigcup_{k\geq k_0}\Lambda^k}(\vert f_{\underline{i}}(K)\vert^\delta)^{({\dim(S)+\varepsilon})/{\delta}}&=\sum_{\underline{i}=(i_1,\ldots,i_n)\in\bigcup_{k\geq k_0}\Lambda^{(k)}}\vert f_{\underline{i}}(K)\vert^{\dim(S)+\varepsilon}\nonumber\\ &\leq \sum_{k\geq k_0}\sum_{\underline{i}=(i_1,\ldots,i_n)\in\Lambda^{(k)}}2^{-k\varepsilon}\gamma_{\varepsilon'}e^{k({\varepsilon}/{2})\log 2}\nu_{ \varepsilon'}([\underline{i}])\nonumber\\ &\leq \gamma_{\varepsilon'}C(\alpha,\beta)\sum_{k\geq k_0}k2^{-k({\varepsilon}/{2})}<+\infty. \end{align} $$
$$ \begin{align} \sum_{\underline{i}\in\in\bigcup_{k\geq k_0}\Lambda^k}(\vert f_{\underline{i}}(K)\vert^\delta)^{({\dim(S)+\varepsilon})/{\delta}}&=\sum_{\underline{i}=(i_1,\ldots,i_n)\in\bigcup_{k\geq k_0}\Lambda^{(k)}}\vert f_{\underline{i}}(K)\vert^{\dim(S)+\varepsilon}\nonumber\\ &\leq \sum_{k\geq k_0}\sum_{\underline{i}=(i_1,\ldots,i_n)\in\Lambda^{(k)}}2^{-k\varepsilon}\gamma_{\varepsilon'}e^{k({\varepsilon}/{2})\log 2}\nu_{ \varepsilon'}([\underline{i}])\nonumber\\ &\leq \gamma_{\varepsilon'}C(\alpha,\beta)\sum_{k\geq k_0}k2^{-k({\varepsilon}/{2})}<+\infty. \end{align} $$
As a consequence,
 $$ \begin{align*}\dim_H (\limsup_{\underline{i}\in\Lambda^*} B(f_{\underline{i}}(x_0),\vert f_{\underline{i}}(K)\vert^{\delta}))\leq \frac{\dim(S)+\varepsilon}{\delta},\end{align*} $$
$$ \begin{align*}\dim_H (\limsup_{\underline{i}\in\Lambda^*} B(f_{\underline{i}}(x_0),\vert f_{\underline{i}}(K)\vert^{\delta}))\leq \frac{\dim(S)+\varepsilon}{\delta},\end{align*} $$
and letting
![]() $\varepsilon $
tend to
$\varepsilon $
tend to
![]() $0$
establishes the upper bound.
$0$
establishes the upper bound.
Now we prove that
Let
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $\mu _{\varepsilon }$
be a weakly conformal measure as in Proposition 6.7. For any
$\mu _{\varepsilon }$
be a weakly conformal measure as in Proposition 6.7. For any
![]() $k\in \mathbb {N}$
, the balls
$k\in \mathbb {N}$
, the balls
![]() $\{B(f_{\underline {i}}(x_0),\vert f_{\underline {i}}(K)\vert )\}_{\underline {i}\in \Lambda ^{k}}$
are centered on
$\{B(f_{\underline {i}}(x_0),\vert f_{\underline {i}}(K)\vert )\}_{\underline {i}\in \Lambda ^{k}}$
are centered on
![]() $K={\mathrm {supp}} (\mu )$
and their limsup covers K. This implies that
$K={\mathrm {supp}} (\mu )$
and their limsup covers K. This implies that
![]() $ \mu _{\varepsilon }(\limsup _{\underline {i}\in \Lambda ^{*}}B(f_{\underline {i}}(x_0),\vert f_{\underline {i}}(K)\vert ))=1.$
$ \mu _{\varepsilon }(\limsup _{\underline {i}\in \Lambda ^{*}}B(f_{\underline {i}}(x_0),\vert f_{\underline {i}}(K)\vert ))=1.$
Applying Theorem 5.11, one gets
Letting
![]() $\varepsilon \to 0$
finishes the proof.
$\varepsilon \to 0$
finishes the proof.
7 Application to homogeneous self-similar IFS
7.1 Proof of Theorem 3.3
A self-similar IFS
![]() $S=\{f_1,\ldots ,f_m\}$
is said to be c-homogeneous, for
$S=\{f_1,\ldots ,f_m\}$
is said to be c-homogeneous, for
![]() $0<c<1,$
if for every
$0<c<1,$
if for every
![]() $\underline {i}\in \Lambda ^*,$
$\underline {i}\in \Lambda ^*,$
Such overlapping IFSs have been studied recently by various authors. Among the recent results on the topic, a Khintchine-type result is established in [Reference Baker2]. Although it is very tempting to try to combine such a result with Theorem 5.11, it turns out that the study on the Hausdorff dimension of limsup sets obtained via a more general approximation function in the case of homogeneous self-similar IFSs does not require this result and can be achieved only using Theorem 5.11.
Let us fix
![]() $m\geq 2$
an integer,
$m\geq 2$
an integer,
![]() $0<c<1$
, and a c-homogeneous IFS
$0<c<1$
, and a c-homogeneous IFS
![]() $S=\{f_1,\ldots ,f_m\}.$
$S=\{f_1,\ldots ,f_m\}.$
Lemma 7.1. Let
![]() $\psi :\mathbb {N}\to \mathbb {R}^+$
be a mapping such that
$\psi :\mathbb {N}\to \mathbb {R}^+$
be a mapping such that
 $$ \begin{align*}\sum_{n\geq 1}\sum_{\underline{i}\in\Lambda^n}\psi(n)^{\dim(S)} =+\infty,\end{align*} $$
$$ \begin{align*}\sum_{n\geq 1}\sum_{\underline{i}\in\Lambda^n}\psi(n)^{\dim(S)} =+\infty,\end{align*} $$
then, for every
![]() $\varepsilon>0$
, there exists an infinity of integers
$\varepsilon>0$
, there exists an infinity of integers
![]() $(n_k)_{k\in \mathbb {N}}$
such that
$(n_k)_{k\in \mathbb {N}}$
such that
![]() $\psi (n_k)\geq c^{(1+\varepsilon )n_k}.$
$\psi (n_k)\geq c^{(1+\varepsilon )n_k}.$
Proof. Assume that it is not the case: there exists
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $N\in \mathbb {N}$
such that for every
$N\in \mathbb {N}$
such that for every
![]() $n>N, \psi (n)<c^{(1+\varepsilon )n}.$
Let us denote
$n>N, \psi (n)<c^{(1+\varepsilon )n}.$
Let us denote
![]() $v\in \mathcal {M}(\{1,\ldots ,m\}^{\mathbb {N}}),$
the measure defined for every
$v\in \mathcal {M}(\{1,\ldots ,m\}^{\mathbb {N}}),$
the measure defined for every
![]() $\underline {i}=(1,\ldots ,i_n)\in \Lambda ^*$
by
$\underline {i}=(1,\ldots ,i_n)\in \Lambda ^*$
by
In this case, one has
 $$ \begin{align*} \sum_{n\geq N}\sum_{\underline{i}\in\Lambda^n}\psi(n)^{\dim(S)}&\leq \sum_{n\geq N}\sum_{\underline{i}\in\Lambda^n}c^{n(1+\varepsilon)\dim(S)}\\ &=\sum_{n\geq N}\sum_{\underline{i}\in\Lambda^n}c^{n\varepsilon\dim(S)}v([\underline{i}]) \\ &=\sum_{n\geq N}c^{n\varepsilon\dim(S)}v\bigg(\bigcup_{\underline{i}\in\Lambda^n}[\underline{i}]\bigg)=\sum_{n\geq N}c^{n\varepsilon\dim(S)}<+\infty. \end{align*} $$
$$ \begin{align*} \sum_{n\geq N}\sum_{\underline{i}\in\Lambda^n}\psi(n)^{\dim(S)}&\leq \sum_{n\geq N}\sum_{\underline{i}\in\Lambda^n}c^{n(1+\varepsilon)\dim(S)}\\ &=\sum_{n\geq N}\sum_{\underline{i}\in\Lambda^n}c^{n\varepsilon\dim(S)}v([\underline{i}]) \\ &=\sum_{n\geq N}c^{n\varepsilon\dim(S)}v\bigg(\bigcup_{\underline{i}\in\Lambda^n}[\underline{i}]\bigg)=\sum_{n\geq N}c^{n\varepsilon\dim(S)}<+\infty. \end{align*} $$
This is a contradiction.
This lemma implies in particular that for every
![]() $\varepsilon>0,$
there exists an infinity of integers
$\varepsilon>0,$
there exists an infinity of integers
![]() $(n_k)_{k\in \mathbb {N}}$
for every
$(n_k)_{k\in \mathbb {N}}$
for every
![]() $\underline {i}\in \Lambda ^{n_k}$
, writing
$\underline {i}\in \Lambda ^{n_k}$
, writing
![]() $1-\varepsilon ={1}/({1+\varepsilon '}),$
$1-\varepsilon ={1}/({1+\varepsilon '}),$
Since for every
![]() $k\in \mathbb {N}$
and every
$k\in \mathbb {N}$
and every
![]() $x_0 \in K,$
$x_0 \in K,$
 $$ \begin{align*}K\subset\bigcup_{\underline{i}\in\Lambda^{n_k}}B(f_{\underline{i}}(x_0),\vert f_{\underline{i}}(K)\vert),\end{align*} $$
$$ \begin{align*}K\subset\bigcup_{\underline{i}\in\Lambda^{n_k}}B(f_{\underline{i}}(x_0),\vert f_{\underline{i}}(K)\vert),\end{align*} $$
one obtains the following corollary.
Corollary 7.2. Let
![]() $\psi :\mathbb {N}\to \mathbb {R}^+$
be a mapping such that
$\psi :\mathbb {N}\to \mathbb {R}^+$
be a mapping such that
 $$ \begin{align*}\sum_{n\geq 1}\sum_{\underline{i}\in\Lambda^n}\psi(n)^{\dim(S)} =+\infty,\end{align*} $$
$$ \begin{align*}\sum_{n\geq 1}\sum_{\underline{i}\in\Lambda^n}\psi(n)^{\dim(S)} =+\infty,\end{align*} $$
then, for every
![]() $x_0\in K$
and every
$x_0\in K$
and every
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
We now prove Theorem 3.3.
Recall equation (14) and assume first that
![]() $s_{\phi }\geq 1.$
Then by Lemma 7.1, for every
$s_{\phi }\geq 1.$
Then by Lemma 7.1, for every
![]() $\varepsilon>0,$
$\varepsilon>0,$
Let
![]() $\mu \in \mathcal {M}(\mathbb {R}^d)$
be given by Proposition 6.7, one has
$\mu \in \mathcal {M}(\mathbb {R}^d)$
be given by Proposition 6.7, one has
which, by Theorem 5.11, implies that, writing
![]() $\delta _{\varepsilon }={1}/({1-\varepsilon })$
,
$\delta _{\varepsilon }={1}/({1-\varepsilon })$
,
 $$ \begin{align*}\dim_H W(x_0,\phi)\geq \frac{\dim_H K -\varepsilon}{{1}/({1-\varepsilon})}.\end{align*} $$
$$ \begin{align*}\dim_H W(x_0,\phi)\geq \frac{\dim_H K -\varepsilon}{{1}/({1-\varepsilon})}.\end{align*} $$
Since this holds for every
![]() $\varepsilon>0,$
one has
$\varepsilon>0,$
one has
and hence
![]() $\dim _H W(x_0,\phi )= \dim _H K =\min \{1,s_{\phi }\}\dim (S).$
$\dim _H W(x_0,\phi )= \dim _H K =\min \{1,s_{\phi }\}\dim (S).$
We now assume that
![]() $s_{\phi }< 1.$
We first prove that
$s_{\phi }< 1.$
We first prove that
Let
![]() $\varepsilon>0.$
By definition of
$\varepsilon>0.$
By definition of
![]() $s_{\phi }$
(see equation (14)),
$s_{\phi }$
(see equation (14)),
 $$ \begin{align*} \sum_{n\geq 1}\sum_{\underline{i}\in\Lambda^n} \phi(n)^{(s_{\phi}+\varepsilon)\dim(S)}<+\infty, \end{align*} $$
$$ \begin{align*} \sum_{n\geq 1}\sum_{\underline{i}\in\Lambda^n} \phi(n)^{(s_{\phi}+\varepsilon)\dim(S)}<+\infty, \end{align*} $$
which yields
![]() $\mathcal {H}^{(s_{\phi }+\varepsilon )\dim (S)}(W(x_0,\phi ))=0,$
since this holds for every
$\mathcal {H}^{(s_{\phi }+\varepsilon )\dim (S)}(W(x_0,\phi ))=0,$
since this holds for every
![]() $\varepsilon>0,$
$\varepsilon>0,$
Let us show that
Fix again
![]() $\varepsilon>0.$
Since
$\varepsilon>0.$
Since
 $$ \begin{align*} \sum_{n\geq 1}\sum_{\underline{i}\in\Lambda^n} \phi(n)^{(s_{\phi}-\varepsilon)\dim(S)}=+\infty, \end{align*} $$
$$ \begin{align*} \sum_{n\geq 1}\sum_{\underline{i}\in\Lambda^n} \phi(n)^{(s_{\phi}-\varepsilon)\dim(S)}=+\infty, \end{align*} $$
by Lemma 7.1, one has
Let
![]() $\mu \in \mathcal {M}(\mathbb {R}^d)$
be given by Proposition 6.7. One has
$\mu \in \mathcal {M}(\mathbb {R}^d)$
be given by Proposition 6.7. One has
Writing
![]() $\delta _{\varepsilon }={1}/{(s_{\phi }-\varepsilon )(1-\varepsilon )}$
and applying Theorem 5.11, one gets
$\delta _{\varepsilon }={1}/{(s_{\phi }-\varepsilon )(1-\varepsilon )}$
and applying Theorem 5.11, one gets
Letting
![]() $\varepsilon \to 0$
yields
$\varepsilon \to 0$
yields
which concludes the proof.
8 The classical shrinking target problem: proof of Theorem 3.8
Let
![]() $S=\{f_1,\ldots ,f_m\}$
be a conformal IFS satisfying the bounded distortion property (Definition 15) and
$S=\{f_1,\ldots ,f_m\}$
be a conformal IFS satisfying the bounded distortion property (Definition 15) and
![]() $s>0, \nu _s,\mu _s$
, and
$s>0, \nu _s,\mu _s$
, and
![]() $\phi $
as in Theorem 3.8. Write again
$\phi $
as in Theorem 3.8. Write again
![]() $\Lambda =\{1,\ldots ,m\}.$
First, let us recall that
$\Lambda =\{1,\ldots ,m\}.$
First, let us recall that
![]() $\mu _s=\nu _s \circ \pi ^{-1}$
is exact dimensional with
$\mu _s=\nu _s \circ \pi ^{-1}$
is exact dimensional with
where
![]() $\unicode{x3bb} _{\nu _s}$
is the Lyapunov exponent associated with
$\unicode{x3bb} _{\nu _s}$
is the Lyapunov exponent associated with
![]() $\nu _s$
(defined in equation (35)) and
$\nu _s$
(defined in equation (35)) and
![]() $h(\nu _s)\geq 0$
is such that for
$h(\nu _s)\geq 0$
is such that for
![]() $\nu _s$
-almost every
$\nu _s$
-almost every
![]() $(x_n)_{n\in \mathbb {N}}\in \Lambda ^{\mathbb {N}},$
$(x_n)_{n\in \mathbb {N}}\in \Lambda ^{\mathbb {N}},$
Let us collect some remarks.
Remark 8.1. By equations (35) and (16), we have
In particular, we have
and
![]() $s\leq \dim _{H}{\mu }_s.$
$s\leq \dim _{H}{\mu }_s.$
In the rest of the section, given
![]() $\delta \geq 1,$
we write
$\delta \geq 1,$
we write
8.1 Lower bound for
 $\dim _H W_{x_0,\phi ,\delta }$
$\dim _H W_{x_0,\phi ,\delta }$
Proposition 8.2. Let s be the root of
![]() $P(s)={s\alpha }/{\delta }.$
Then, for every
$P(s)={s\alpha }/{\delta }.$
Then, for every
![]() $\varepsilon>0,$
$\varepsilon>0,$
Proof. Fix
![]() $\varepsilon _0>0.$
By definition of the Lyapunov exponent
$\varepsilon _0>0.$
By definition of the Lyapunov exponent
![]() $\unicode{x3bb} _{\nu _s},$
there exists
$\unicode{x3bb} _{\nu _s},$
there exists
![]() $N\in \mathbb {N}$
and a set
$N\in \mathbb {N}$
and a set
![]() $E\subset \Lambda ^{\mathbb {N}} $
such that
$E\subset \Lambda ^{\mathbb {N}} $
such that
![]() $\nu _s(E)\geq 1-\varepsilon _0$
and for every
$\nu _s(E)\geq 1-\varepsilon _0$
and for every
![]() $(x_n)_{n\in \mathbb {N}}\in E$
, for every
$(x_n)_{n\in \mathbb {N}}\in E$
, for every
![]() $n\geq N,$
we have
$n\geq N,$
we have
By definition of
![]() $\alpha ,$
there exists an infinite set of integers
$\alpha ,$
there exists an infinite set of integers
![]() $\mathcal {N}\subset \mathbb {N}$
such that for every
$\mathcal {N}\subset \mathbb {N}$
such that for every
![]() $n\in \mathcal {N},$
we have that
$n\in \mathcal {N},$
we have that
Thus, for every
![]() $(x_n)_{n\in \mathbb {N}}\in E$
, writing
$(x_n)_{n\in \mathbb {N}}\in E$
, writing
![]() $\underline {i}=(x_1,\ldots ,x_n),$
$\underline {i}=(x_1,\ldots ,x_n),$
 $$ \begin{align*} &\vert f_{\underline{i}}(K)\vert^{{s}/{\dim_{H}{\mu}_s}}\phi(\vert \underline{i}\vert)^{{s(1-\varepsilon)}/{\delta\dim_{H}{\mu}_s }}\\&\quad\geq e^{-n(1+\varepsilon_0)({s\unicode{x3bb}_{\nu}}/{\dim_{H}{\mu}_s})}e^{-n(1-\varepsilon)(1+{\varepsilon}/{2})\times ({s\alpha}/{\delta \dim_{H}{\mu}_s})} \end{align*} $$
$$ \begin{align*} &\vert f_{\underline{i}}(K)\vert^{{s}/{\dim_{H}{\mu}_s}}\phi(\vert \underline{i}\vert)^{{s(1-\varepsilon)}/{\delta\dim_{H}{\mu}_s }}\\&\quad\geq e^{-n(1+\varepsilon_0)({s\unicode{x3bb}_{\nu}}/{\dim_{H}{\mu}_s})}e^{-n(1-\varepsilon)(1+{\varepsilon}/{2})\times ({s\alpha}/{\delta \dim_{H}{\mu}_s})} \end{align*} $$
and recalling that
![]() $P(s)={s\alpha }/{\delta },$
one has
$P(s)={s\alpha }/{\delta },$
one has
 $$ \begin{align*} &\vert f_{\underline{i}}(K)\vert^{{s}/{\dim_{H}{\mu}_s}}\phi(\vert \underline{i}\vert)^{{s(1-\varepsilon)}/{\delta\dim_{H}{\mu}_s }}\\&\quad\geq e^{-n(1+\varepsilon_0-(1-\varepsilon)(1+{\varepsilon}/{2}))({s\unicode{x3bb}_{\nu_s}}/{\dim_{H}{\mu}_s})}\times e^{-n(1-\varepsilon)(1+{\varepsilon}/{2})\times (({P(s)+s\unicode{x3bb}_{\nu_s}})/{ \dim_{H}{\mu}_s})}. \end{align*} $$
$$ \begin{align*} &\vert f_{\underline{i}}(K)\vert^{{s}/{\dim_{H}{\mu}_s}}\phi(\vert \underline{i}\vert)^{{s(1-\varepsilon)}/{\delta\dim_{H}{\mu}_s }}\\&\quad\geq e^{-n(1+\varepsilon_0-(1-\varepsilon)(1+{\varepsilon}/{2}))({s\unicode{x3bb}_{\nu_s}}/{\dim_{H}{\mu}_s})}\times e^{-n(1-\varepsilon)(1+{\varepsilon}/{2})\times (({P(s)+s\unicode{x3bb}_{\nu_s}})/{ \dim_{H}{\mu}_s})}. \end{align*} $$
Note also that
 $$ \begin{align*} \bigg(1+\varepsilon_0-(1-\varepsilon)\bigg(1+\frac{\varepsilon}{2}\bigg)\bigg)=\varepsilon_0+\frac{\varepsilon}{2}+\frac{\varepsilon^2}{2}, \end{align*} $$
$$ \begin{align*} \bigg(1+\varepsilon_0-(1-\varepsilon)\bigg(1+\frac{\varepsilon}{2}\bigg)\bigg)=\varepsilon_0+\frac{\varepsilon}{2}+\frac{\varepsilon^2}{2}, \end{align*} $$
so that
 $$ \begin{align*}\bigg(1+\varepsilon_0-(1-\varepsilon)\bigg(1+\frac{\varepsilon}{2}\bigg)\bigg)\frac{s\unicode{x3bb}_{\nu_s}}{\dim_{H}{\mu}_s}\leq C\varepsilon \unicode{x3bb}_{\nu_s}\end{align*} $$
$$ \begin{align*}\bigg(1+\varepsilon_0-(1-\varepsilon)\bigg(1+\frac{\varepsilon}{2}\bigg)\bigg)\frac{s\unicode{x3bb}_{\nu_s}}{\dim_{H}{\mu}_s}\leq C\varepsilon \unicode{x3bb}_{\nu_s}\end{align*} $$
for some
![]() $C>0$
independent of
$C>0$
independent of
![]() $\varepsilon $
provided that
$\varepsilon $
provided that
![]() $\varepsilon _0$
was chosen small enough to begin with. In addition, using Remark 8.1,
$\varepsilon _0$
was chosen small enough to begin with. In addition, using Remark 8.1,
This implies that, for some
![]() $C'>0$
independent of
$C'>0$
independent of
![]() $\varepsilon ,$
provided that
$\varepsilon ,$
provided that
![]() $\varepsilon _0$
was chosen small enough,
$\varepsilon _0$
was chosen small enough,
 $$ \begin{align*} \vert f_{\underline{i}}(K)\vert^{{s}/{\dim_{H}{\mu}_s}}\phi(\vert \underline{i}\vert)^{{s(1-\varepsilon)}/{\delta\dim_{H}{\mu}_s }}&\geq e^{-n(1+\varepsilon_0-(1-\varepsilon)(1+{\varepsilon}/{2}))({s\unicode{x3bb}_{\nu_s}}/{\dim_{H}{\mu}_s})}\\&\quad\times e^{-n(1-\varepsilon)(1+{\varepsilon}/{2})\times ({P(s)+s\unicode{x3bb}_{\nu_s}}/{ \dim_{H}{\mu}_s})}\\ &\geq e^{-n(1-C'\varepsilon)\unicode{x3bb}_{\nu_s}}\geq e^{-n(1-\varepsilon_0)\unicode{x3bb}_{\nu_s}}\geq \vert f_{\underline{i}}(K) \vert. \end{align*} $$
$$ \begin{align*} \vert f_{\underline{i}}(K)\vert^{{s}/{\dim_{H}{\mu}_s}}\phi(\vert \underline{i}\vert)^{{s(1-\varepsilon)}/{\delta\dim_{H}{\mu}_s }}&\geq e^{-n(1+\varepsilon_0-(1-\varepsilon)(1+{\varepsilon}/{2}))({s\unicode{x3bb}_{\nu_s}}/{\dim_{H}{\mu}_s})}\\&\quad\times e^{-n(1-\varepsilon)(1+{\varepsilon}/{2})\times ({P(s)+s\unicode{x3bb}_{\nu_s}}/{ \dim_{H}{\mu}_s})}\\ &\geq e^{-n(1-C'\varepsilon)\unicode{x3bb}_{\nu_s}}\geq e^{-n(1-\varepsilon_0)\unicode{x3bb}_{\nu_s}}\geq \vert f_{\underline{i}}(K) \vert. \end{align*} $$
The last inequality implies that
and hence
![]() $\pi ((x_n)_{n\in \mathbb {N}})\in B(f_{\underline {i}}(x_0),\vert f_{\underline {i}}(K)\vert ^{{s}/{\dim _{H}{\mu }_s}}\phi (\vert \underline {i}\vert )^{{s(1-\varepsilon )}/{\delta \dim _{H}{\mu }_s }}).$
Since this happens for every
$\pi ((x_n)_{n\in \mathbb {N}})\in B(f_{\underline {i}}(x_0),\vert f_{\underline {i}}(K)\vert ^{{s}/{\dim _{H}{\mu }_s}}\phi (\vert \underline {i}\vert )^{{s(1-\varepsilon )}/{\delta \dim _{H}{\mu }_s }}).$
Since this happens for every
![]() $n\in \mathcal {N}$
, we conclude that
$n\in \mathcal {N}$
, we conclude that
This yields
so that
Letting
![]() $\varepsilon _0\to 0$
proves the claim.
$\varepsilon _0\to 0$
proves the claim.
Applying Proposition 5.11 to
![]() $ \limsup _{\underline {i}\in \Lambda ^*}\!B(f_{\underline {i}}(x_0),{\kern-1pt}\vert f_{\underline {i}}(K)\vert ^{{s}/{\dim _{H}{\mu }_s}}\phi (\vert \underline {i}\vert )^{{s(1-\varepsilon )}/ {\delta \dim _{H}{\mu }_s }})$
and
$ \limsup _{\underline {i}\in \Lambda ^*}\!B(f_{\underline {i}}(x_0),{\kern-1pt}\vert f_{\underline {i}}(K)\vert ^{{s}/{\dim _{H}{\mu }_s}}\phi (\vert \underline {i}\vert )^{{s(1-\varepsilon )}/ {\delta \dim _{H}{\mu }_s }})$
and
![]() $\mu _s$
yields the following corollary.
$\mu _s$
yields the following corollary.
Corollary 8.3. Write
![]() $\delta ' = {1}/({{s(1-\varepsilon )}/{\delta \dim _{H}{\mu }_s } }),$
we have
$\delta ' = {1}/({{s(1-\varepsilon )}/{\delta \dim _{H}{\mu }_s } }),$
we have
 $$ \begin{align*}\dim_H \Big(\!\limsup_{\underline{i}\in\Lambda^*}B(f_{\underline{i}}(x_0),\vert f_{\underline{i}}(K)\vert^{{\delta}/({1-\varepsilon})}\phi(\vert \underline{i}\vert))\Big)\geq \frac{\dim_{H}{\mu}_s}{\delta'}=\frac{s(1-\varepsilon)}{\delta}.\end{align*} $$
$$ \begin{align*}\dim_H \Big(\!\limsup_{\underline{i}\in\Lambda^*}B(f_{\underline{i}}(x_0),\vert f_{\underline{i}}(K)\vert^{{\delta}/({1-\varepsilon})}\phi(\vert \underline{i}\vert))\Big)\geq \frac{\dim_{H}{\mu}_s}{\delta'}=\frac{s(1-\varepsilon)}{\delta}.\end{align*} $$
Since this holds for every
![]() $\delta \geq 1$
and
$\delta \geq 1$
and
![]() $\varepsilon>0,$
we conclude that
$\varepsilon>0,$
we conclude that
8.2 Upper bound for
 $\dim _H W_{x_0,\phi ,\delta }$
$\dim _H W_{x_0,\phi ,\delta }$
Fix
![]() $\varepsilon>0.$
By definition of
$\varepsilon>0.$
By definition of
![]() $\alpha ,$
there exists
$\alpha ,$
there exists
![]() $N\in \mathbb {N}$
so large that for every
$N\in \mathbb {N}$
so large that for every
![]() $n\geq N$
, one has
$n\geq N$
, one has
Hence, writing
![]() $0<\varepsilon ' =\min \{\varepsilon ,({1+\varepsilon })/({1+{\varepsilon }/{2}})\}$
and recalling that
$0<\varepsilon ' =\min \{\varepsilon ,({1+\varepsilon })/({1+{\varepsilon }/{2}})\}$
and recalling that
![]() $P(s)={s\alpha }/{\delta },$
we get
$P(s)={s\alpha }/{\delta },$
we get
 $$ \begin{align*} \sum_{n\geq N} \sum_{\underline{i}\in\Lambda^n} (\vert f_{\underline{i}}(K)\vert^{\delta}\phi(n))^{{s(1+\varepsilon)}/{\delta}} &\leq \sum_{n\geq N} \sum_{\underline{i}\in\Lambda^n} \vert f_{\underline{i}}(K)\vert^{s(1+\varepsilon)} e^{-n(({1+\varepsilon})/{1+{\varepsilon}/{2}}){s\alpha}/{\delta}}\\ &\leq \sum_{n\geq N} \sum_{\underline{i}\in\Lambda^n} \vert f_{\underline{i}}(K)\vert^{s(1+\varepsilon)} e^{-n(({1+\varepsilon})/{1+{\varepsilon}/{2}})P(s)}\\ &\leq \sum_{n\geq N} \sum_{\underline{i}\in\Lambda^n} (\vert f_{\underline{i}}(K)\vert^{s} e^{-nP(s)})^{1+\varepsilon'}\\ &= \sum_{n\geq N} \sum_{\underline{i}\in\Lambda^n} \mu_s(\underline{i})^{1+\varepsilon'}. \end{align*} $$
$$ \begin{align*} \sum_{n\geq N} \sum_{\underline{i}\in\Lambda^n} (\vert f_{\underline{i}}(K)\vert^{\delta}\phi(n))^{{s(1+\varepsilon)}/{\delta}} &\leq \sum_{n\geq N} \sum_{\underline{i}\in\Lambda^n} \vert f_{\underline{i}}(K)\vert^{s(1+\varepsilon)} e^{-n(({1+\varepsilon})/{1+{\varepsilon}/{2}}){s\alpha}/{\delta}}\\ &\leq \sum_{n\geq N} \sum_{\underline{i}\in\Lambda^n} \vert f_{\underline{i}}(K)\vert^{s(1+\varepsilon)} e^{-n(({1+\varepsilon})/{1+{\varepsilon}/{2}})P(s)}\\ &\leq \sum_{n\geq N} \sum_{\underline{i}\in\Lambda^n} (\vert f_{\underline{i}}(K)\vert^{s} e^{-nP(s)})^{1+\varepsilon'}\\ &= \sum_{n\geq N} \sum_{\underline{i}\in\Lambda^n} \mu_s(\underline{i})^{1+\varepsilon'}. \end{align*} $$
Using a similar argument as in equation (97), we have
 $$ \begin{align*} \sum_{n\geq N} \sum_{\underline{i}\in\Lambda^n} \mu_s(\underline{i})^{1+\varepsilon'}<+\infty, \end{align*} $$
$$ \begin{align*} \sum_{n\geq N} \sum_{\underline{i}\in\Lambda^n} \mu_s(\underline{i})^{1+\varepsilon'}<+\infty, \end{align*} $$
and hence
 $$ \begin{align*}\sum_{n\geq N} \sum_{\underline{i}\in\Lambda^n} (\vert f_{\underline{i}}(K)\vert^{\delta}\phi(n))^{{s(1+\varepsilon)}/{\delta}} <+\infty, \end{align*} $$
$$ \begin{align*}\sum_{n\geq N} \sum_{\underline{i}\in\Lambda^n} (\vert f_{\underline{i}}(K)\vert^{\delta}\phi(n))^{{s(1+\varepsilon)}/{\delta}} <+\infty, \end{align*} $$
so
Letting
![]() $\varepsilon \to 0$
yields the desired result.
$\varepsilon \to 0$
yields the desired result.