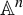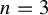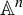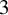1 Introduction
1.1 Dynamical degrees of polynomial endomorphisms
In this text, we work over an arbitrary field
![]() $\mathbf {k}$
. For each
$\mathbf {k}$
. For each
![]() $n\ge 1$
, recall that an endomorphism
$n\ge 1$
, recall that an endomorphism
![]() $f\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
of
$f\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
of
![]() $\mathbb {A}^n=\mathbb {A}^n_{\mathbf {k}}$
is given by
$\mathbb {A}^n=\mathbb {A}^n_{\mathbf {k}}$
is given by
where
![]() $f_1,\ldots ,f_n\in \mathbf {k}[x_1,\ldots ,x_n]$
. To simplify the notation, we often write
$f_1,\ldots ,f_n\in \mathbf {k}[x_1,\ldots ,x_n]$
. To simplify the notation, we often write
![]() $f=(f_1,\ldots ,f_n)$
and thus identify
$f=(f_1,\ldots ,f_n)$
and thus identify
![]() $\operatorname {\mathrm {End}}(\mathbb {A}^n)$
with
$\operatorname {\mathrm {End}}(\mathbb {A}^n)$
with
![]() $(\mathbf {k}[x_1,\ldots ,x_n])^n$
.
$(\mathbf {k}[x_1,\ldots ,x_n])^n$
.
The degree of an endomorphism
![]() $f=(f_1,\ldots ,f_n)$
, denoted by
$f=(f_1,\ldots ,f_n)$
, denoted by
![]() $\deg (f)$
, is defined to be
$\deg (f)$
, is defined to be
![]() $\deg (f)=\max (\deg (f_1),\ldots ,\deg (f_n))$
. The set
$\deg (f)=\max (\deg (f_1),\ldots ,\deg (f_n))$
. The set
![]() $\operatorname {\mathrm {End}}(\mathbb {A}^n)$
of endomorphisms of
$\operatorname {\mathrm {End}}(\mathbb {A}^n)$
of endomorphisms of
![]() $\mathbb {A}^n$
is a monoid, for the composition law, and the subset of invertible elements is the group
$\mathbb {A}^n$
is a monoid, for the composition law, and the subset of invertible elements is the group
![]() $\operatorname {\mathrm {Aut}}(\mathbb {A}^n)$
of automorphisms of
$\operatorname {\mathrm {Aut}}(\mathbb {A}^n)$
of automorphisms of
![]() $\mathbb {A}^n$
.
$\mathbb {A}^n$
.
The dynamics of endomorphisms of
![]() $\mathbb {A}^n$
, specially in the case of the ground field
$\mathbb {A}^n$
, specially in the case of the ground field
![]() $\mathbf {k}=\mathbb {C}$
, was studied intensively in the last decades, see for instance [Reference Fornæss and WuFsW98, Reference SibonySib99, Reference MaegawaMae00, Reference Bonifant and FornæssBFs00, Reference MaegawaMae01a, Reference MaegawaMae01b, Reference GuedjGue02, Reference Guedj and SibonyGS02, Reference GuedjGue04, Reference UedaUed04, Reference Favre and JonssonFJ11, Reference Jonsson and WulcanJW12, Reference XieXie17, Reference Déserti and LeguilDL18]. For each dominant endomorphism
$\mathbf {k}=\mathbb {C}$
, was studied intensively in the last decades, see for instance [Reference Fornæss and WuFsW98, Reference SibonySib99, Reference MaegawaMae00, Reference Bonifant and FornæssBFs00, Reference MaegawaMae01a, Reference MaegawaMae01b, Reference GuedjGue02, Reference Guedj and SibonyGS02, Reference GuedjGue04, Reference UedaUed04, Reference Favre and JonssonFJ11, Reference Jonsson and WulcanJW12, Reference XieXie17, Reference Déserti and LeguilDL18]. For each dominant endomorphism
![]() $f\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
, the (first) dynamical degree is defined as the real number
$f\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
, the (first) dynamical degree is defined as the real number
(the limit exists by Fekete’s subadditivity lemma, see Lemma 2.2.1). If
![]() $f\in \operatorname {\mathrm {End}}(\mathbb {A}^1)$
or
$f\in \operatorname {\mathrm {End}}(\mathbb {A}^1)$
or
![]() $f\in \operatorname {\mathrm {Aut}}(\mathbb {A}^2)$
, then
$f\in \operatorname {\mathrm {Aut}}(\mathbb {A}^2)$
, then
![]() $\unicode{x3bb} (f)$
is an integer, but in higher dimensions, it can be quite complicated to understand the possible dynamical degrees. In [Reference Dang and FavreDF, Corollary 3], the authors conjecture that
$\unicode{x3bb} (f)$
is an integer, but in higher dimensions, it can be quite complicated to understand the possible dynamical degrees. In [Reference Dang and FavreDF, Corollary 3], the authors conjecture that
![]() $\unicode{x3bb} (f)$
is an algebraic integer of degree
$\unicode{x3bb} (f)$
is an algebraic integer of degree
![]() $\le n$
, and of degree
$\le n$
, and of degree
![]() $\le n-1$
if
$\le n-1$
if
![]() $f\in \operatorname {\mathrm {Aut}}(\mathbb {A}^n)$
, a conjecture proven until now only for
$f\in \operatorname {\mathrm {Aut}}(\mathbb {A}^n)$
, a conjecture proven until now only for
![]() $n\le 2$
.
$n\le 2$
.
In this article, we study some particular family of automorphisms of
![]() $\mathbb {A}^n$
that we call affine-triangular. These are compositions consisting of one affine automorphism and one triangular automorphism (see Definition 2.1.1). Our two main results are Theorem 1 and Theorem 2.
$\mathbb {A}^n$
that we call affine-triangular. These are compositions consisting of one affine automorphism and one triangular automorphism (see Definition 2.1.1). Our two main results are Theorem 1 and Theorem 2.
Theorem 1. For each field
![]() $\mathbf {k}$
and each integer
$\mathbf {k}$
and each integer
![]() $d\ge 2$
, the set of dynamical degrees of all affine-triangular automorphisms of
$d\ge 2$
, the set of dynamical degrees of all affine-triangular automorphisms of
![]() $\mathbb {A}^3$
of degree
$\mathbb {A}^3$
of degree
![]() $\le d$
is equal to
$\le d$
is equal to
 $$ \begin{align*} \displaystyle \bigg\{\frac{a+\sqrt{a^2+4bc}}{2}\mid (a,b,c)\in {\mathbb N}^3, a+b\le d, c\le d\bigg\}\setminus \{0\}. \end{align*} $$
$$ \begin{align*} \displaystyle \bigg\{\frac{a+\sqrt{a^2+4bc}}{2}\mid (a,b,c)\in {\mathbb N}^3, a+b\le d, c\le d\bigg\}\setminus \{0\}. \end{align*} $$
Moreover, for
![]() $a,b,c\in {\mathbb N}$
such that
$a,b,c\in {\mathbb N}$
such that
![]() $\unicode{x3bb} =(({a+\sqrt {a^2+4bc}})/{2})\not =0$
, the dynamical degree
$\unicode{x3bb} =(({a+\sqrt {a^2+4bc}})/{2})\not =0$
, the dynamical degree
![]() $\unicode{x3bb} $
is achieved by either of the automorphisms
$\unicode{x3bb} $
is achieved by either of the automorphisms
Using Theorem 1, we prove in [Reference Blanc and van SantenBvS, Theorem 2] that the set of dynamical degrees of all automorphisms of degree
![]() $3$
of
$3$
of
![]() $\mathbb {A}^3$
is equal to
$\mathbb {A}^3$
is equal to
 $$ \begin{align*} \bigg\{1 , \sqrt{2} , \ \frac{1+\sqrt{5}}{2} , \ \sqrt{3} , 2 , \ \frac{1 + \sqrt{13}}{2} , \ 1 + \sqrt{2} , \ \sqrt{6} , \ \frac{1 + \sqrt{17}}{2} , \ \frac{3+\sqrt{5}}{2} , \ 1+ \sqrt{3} , \ 3 \bigg\}. \end{align*} $$
$$ \begin{align*} \bigg\{1 , \sqrt{2} , \ \frac{1+\sqrt{5}}{2} , \ \sqrt{3} , 2 , \ \frac{1 + \sqrt{13}}{2} , \ 1 + \sqrt{2} , \ \sqrt{6} , \ \frac{1 + \sqrt{17}}{2} , \ \frac{3+\sqrt{5}}{2} , \ 1+ \sqrt{3} , \ 3 \bigg\}. \end{align*} $$
Note that
![]() $({3+\sqrt {5}})/{2}$
is the only number that does not belong to the list in Theorem 1 and so it is the dynamical degree of an automorphism of degree
$({3+\sqrt {5}})/{2}$
is the only number that does not belong to the list in Theorem 1 and so it is the dynamical degree of an automorphism of degree
![]() $3$
of
$3$
of
![]() ${\mathbb A}^3$
that is not conjugate to an affine-triangular automorphism of any degree.
${\mathbb A}^3$
that is not conjugate to an affine-triangular automorphism of any degree.
For the next theorem, we recall the definition of (weak) Perron numbers (see Theorem 3.2.4 for some equivalent characterizations).
Definition 1.1.1. A Perron number (respectively weak Perron number) is a real number
![]() $\unicode{x3bb} \geq 1$
that is an algebraic integer such that all other Galois conjugates
$\unicode{x3bb} \geq 1$
that is an algebraic integer such that all other Galois conjugates
![]() $\mu \in {\mathbb C}$
satisfy
$\mu \in {\mathbb C}$
satisfy
![]() $\lvert \mu \rvert <\unicode{x3bb} $
(respectively
$\lvert \mu \rvert <\unicode{x3bb} $
(respectively
![]() $\lvert \mu \rvert \le \unicode{x3bb} $
).
$\lvert \mu \rvert \le \unicode{x3bb} $
).
Theorem 2. Each weak Perron number
![]() $\unicode{x3bb} $
is the dynamical degree of an affine-triangular automorphism of
$\unicode{x3bb} $
is the dynamical degree of an affine-triangular automorphism of
![]() $\mathbb {A}^{n}$
for some integer n. Moreover:
$\mathbb {A}^{n}$
for some integer n. Moreover:
-
(1) if
 $\unicode{x3bb}>1$
is an integer, the least n possible is
$\unicode{x3bb}>1$
is an integer, the least n possible is
 $2$
;
$2$
; -
(2) if
 $\unicode{x3bb} $
is a quadratic integer and its conjugate is negative, the least possible n is
$\unicode{x3bb} $
is a quadratic integer and its conjugate is negative, the least possible n is
 $3$
;
$3$
; -
(3) if
 $\unicode{x3bb} $
is a quadratic integer and its conjugate is positive, the least possible n is
$\unicode{x3bb} $
is a quadratic integer and its conjugate is positive, the least possible n is
 $4$
.
$4$
.
Note that statement (1) in Theorem 2 is well known, as
![]() $\{\unicode{x3bb} (f)\mid f\in \operatorname {\mathrm {Aut}}(\mathbb {A}^2)\}=\mathbb {Z}_{\ge 1}$
. We include it to emphasize the relation between the degree of the weak Perron numbers and the possible n. In view of the above theorems and of the techniques developed in this text, it is natural to ask the following.
$\{\unicode{x3bb} (f)\mid f\in \operatorname {\mathrm {Aut}}(\mathbb {A}^2)\}=\mathbb {Z}_{\ge 1}$
. We include it to emphasize the relation between the degree of the weak Perron numbers and the possible n. In view of the above theorems and of the techniques developed in this text, it is natural to ask the following.
Question 1.1.2. Is every dynamical degree of any element of
![]() $\operatorname {\mathrm {End}}(\mathbb {A}^n)$
(respectively
$\operatorname {\mathrm {End}}(\mathbb {A}^n)$
(respectively
![]() $\operatorname {\mathrm {Aut}}(\mathbb {A}^n)$
) equal to a weak Perron number of degree
$\operatorname {\mathrm {Aut}}(\mathbb {A}^n)$
) equal to a weak Perron number of degree
![]() $\le n$
(respectively of degree
$\le n$
(respectively of degree
![]() $\le n-1$
)?
$\le n-1$
)?
As already mentioned above, a positive answer to this question, where ‘weak Perron number’ is replaced by ‘algebraic integer’, was conjectured in the recent preprint [Reference Dang and FavreDF, Corollary 3] (that appeared after we asked the above question in a first version of this text). In [Reference Dang and FavreDF], it is also proven that the dynamical degree of any element in
![]() $\operatorname {\mathrm {Aut}}({\mathbb A}^3)$
is an algebraic number of degree at most six. More generally, they prove that the dynamical degree of any element of
$\operatorname {\mathrm {Aut}}({\mathbb A}^3)$
is an algebraic number of degree at most six. More generally, they prove that the dynamical degree of any element of
![]() $\operatorname {\mathrm {End}}({\mathbb A}^n)$
is an algebraic number of degree at most n in case the square of the first dynamical degree is bigger than the second dynamical degree of f [Reference Dang and FavreDF, Theorem 2].
$\operatorname {\mathrm {End}}({\mathbb A}^n)$
is an algebraic number of degree at most n in case the square of the first dynamical degree is bigger than the second dynamical degree of f [Reference Dang and FavreDF, Theorem 2].
In particular, Theorem 1 shows that the dynamical degree of every affine-triangular automorphism of
![]() $\mathbb {A}^3$
is equal to the dynamical degree of a shift-like automorphism. However, for each
$\mathbb {A}^3$
is equal to the dynamical degree of a shift-like automorphism. However, for each
![]() $d\ge 3$
, the set of dynamical degrees of all affine-triangular automorphisms of
$d\ge 3$
, the set of dynamical degrees of all affine-triangular automorphisms of
![]() $\mathbb {A}^3$
of degree d strictly contains the set of dynamical degrees of all shift-like automorphisms of
$\mathbb {A}^3$
of degree d strictly contains the set of dynamical degrees of all shift-like automorphisms of
![]() $\mathbb {A}^3$
of degree d. Indeed, the latter set of dynamical degrees consists of the numbers
$\mathbb {A}^3$
of degree d. Indeed, the latter set of dynamical degrees consists of the numbers
![]() $(a + \sqrt {a^2 + 4d-4a})/2$
, where
$(a + \sqrt {a^2 + 4d-4a})/2$
, where
![]() $0 \leq a \leq d$
, and does not contain
$0 \leq a \leq d$
, and does not contain
![]() $(1 + \sqrt {1 + 4d})/2$
, which is the dynamical degree of the affine-triangular automorphism
$(1 + \sqrt {1 + 4d})/2$
, which is the dynamical degree of the affine-triangular automorphism
![]() $(x_3 + x_1 x_2,x_2+x_1^d,x_1)$
, see Corollary 4.3.7.
$(x_3 + x_1 x_2,x_2+x_1^d,x_1)$
, see Corollary 4.3.7.
Table 1 Dynamical degrees of low degree shift-like and affine-triangular automorphisms.

Note that
![]() $2\sqrt {2}$
and
$2\sqrt {2}$
and
![]() $\sqrt {3}$
appear as dynamical degrees of affine-triangular automorphisms in degree
$\sqrt {3}$
appear as dynamical degrees of affine-triangular automorphisms in degree
![]() $4$
and
$4$
and
![]() $3$
, respectively (and not smaller), even if
$3$
, respectively (and not smaller), even if
![]() $2\sqrt {2}<3$
and
$2\sqrt {2}<3$
and
![]() $\sqrt {3} < 2$
. Similarly, for each prime p, the number
$\sqrt {3} < 2$
. Similarly, for each prime p, the number
![]() $\sqrt {p}$
is the dynamical degree of a shift-like automorphism of degree p, but it is not the dynamical degree of an affine-triangular automorphism of degree
$\sqrt {p}$
is the dynamical degree of a shift-like automorphism of degree p, but it is not the dynamical degree of an affine-triangular automorphism of degree
![]() $< p$
.
$< p$
.
1.2 Dynamical degrees of affine-triangular automorphisms in higher dimensions
In dimension
![]() $n\ge 4$
, we are not able to compute all dynamical degrees of all affine-triangular automorphisms, but can get some large families. The case of shift-like automorphisms is covered by our method, and we retrieve a proof of the result of Mattias Jonsson (Proposition 4.2.5), but we can also study wider classes. We give the dynamical degrees of all permutation-elementary automorphisms (a family that strictly includes the shift-like automorphisms) in §4.2 (especially Proposition 4.2.3) and also give the dynamical degrees of other affine-triangular automorphisms. In particular, we show that in any dimension
$n\ge 4$
, we are not able to compute all dynamical degrees of all affine-triangular automorphisms, but can get some large families. The case of shift-like automorphisms is covered by our method, and we retrieve a proof of the result of Mattias Jonsson (Proposition 4.2.5), but we can also study wider classes. We give the dynamical degrees of all permutation-elementary automorphisms (a family that strictly includes the shift-like automorphisms) in §4.2 (especially Proposition 4.2.3) and also give the dynamical degrees of other affine-triangular automorphisms. In particular, we show that in any dimension
![]() $n\ge 4$
, there are affine-triangular automorphisms of
$n\ge 4$
, there are affine-triangular automorphisms of
![]() $\mathbb {A}^n$
whose dynamical degrees are not those of a shift-like automorphism or, more generally, of a permutation-elementary automorphism, contrary to the case of dimension
$\mathbb {A}^n$
whose dynamical degrees are not those of a shift-like automorphism or, more generally, of a permutation-elementary automorphism, contrary to the case of dimension
![]() $n\le 3$
. The reason is that dynamical degrees of shift-like automorphisms are special kinds of weak Perron numbers. Indeed, they are positive real numbers that are roots of a monic integral polynomial where all coefficients (except the first one) are non-positive. These numbers are called Handelman numbers in [Reference BassinoBas97] (see especially [Reference BassinoBas97, Lemma 10]) and they have no other positive real Galois conjugates (Lemma 3.2.7). This implies that Handelman numbers are weak Perron numbers (see Corollary 3.2.8). Theorem 1 implies that the dynamical degree of an affine-triangular automorphism of
$n\le 3$
. The reason is that dynamical degrees of shift-like automorphisms are special kinds of weak Perron numbers. Indeed, they are positive real numbers that are roots of a monic integral polynomial where all coefficients (except the first one) are non-positive. These numbers are called Handelman numbers in [Reference BassinoBas97] (see especially [Reference BassinoBas97, Lemma 10]) and they have no other positive real Galois conjugates (Lemma 3.2.7). This implies that Handelman numbers are weak Perron numbers (see Corollary 3.2.8). Theorem 1 implies that the dynamical degree of an affine-triangular automorphism of
![]() $\mathbb {A}^3$
is a Handelman number (and the same holds for all automorphisms of
$\mathbb {A}^3$
is a Handelman number (and the same holds for all automorphisms of
![]() $\mathbb {A}^1$
and
$\mathbb {A}^1$
and
![]() $\mathbb {A}^2$
), but for any
$\mathbb {A}^2$
), but for any
![]() $n\ge 4$
, there are affine-triangular automorphisms of
$n\ge 4$
, there are affine-triangular automorphisms of
![]() $\mathbb {A}^n$
whose dynamical degrees are not Handelman numbers. This follows in particular from Theorem 2, applied to any weak Perron quadratic integer with a positive conjugate, for instance to
$\mathbb {A}^n$
whose dynamical degrees are not Handelman numbers. This follows in particular from Theorem 2, applied to any weak Perron quadratic integer with a positive conjugate, for instance to
![]() $(3+\sqrt {5})/2$
. We can also apply Theorem 2 to weak Perron numbers of arbitrary large degree.
$(3+\sqrt {5})/2$
. We can also apply Theorem 2 to weak Perron numbers of arbitrary large degree.
1.3 Results in the literature on dynamical degrees of endomorphisms of
 ${\mathbb A}^n$
${\mathbb A}^n$
Let us recall what is known on the dynamical degrees of elements of
![]() $\operatorname {\mathrm {End}}(\mathbb {A}^n)$
.
$\operatorname {\mathrm {End}}(\mathbb {A}^n)$
.
-
(1) The case where
 $n=1$
is obvious: in this case, we have
$n=1$
is obvious: in this case, we have
 $\unicode{x3bb} (f)=\deg (f)$
, so each dynamical degree is an integer, which is moreover equal to
$\unicode{x3bb} (f)=\deg (f)$
, so each dynamical degree is an integer, which is moreover equal to
 $1$
in the case of automorphisms.
$1$
in the case of automorphisms. -
(2) When
 $n=2$
, the case of automorphisms follows from the Jung–van der Kulk theorem [Reference JungJun42, Reference van der KulkvdK53]: every dynamical degree is an integer, as
$n=2$
, the case of automorphisms follows from the Jung–van der Kulk theorem [Reference JungJun42, Reference van der KulkvdK53]: every dynamical degree is an integer, as
 $\deg (f^r)=\deg (f)^r$
for each r, when f is taken to be cyclically reduced (this is explained in Corollary 2.4.3 or in [Reference FurterFur99, Proposition 3]). The set of all dynamical degrees of quadratic endomorphisms of
$\deg (f^r)=\deg (f)^r$
for each r, when f is taken to be cyclically reduced (this is explained in Corollary 2.4.3 or in [Reference FurterFur99, Proposition 3]). The set of all dynamical degrees of quadratic endomorphisms of
 $\mathbb {A}^2_{\mathbb C}$
is equal to
$\mathbb {A}^2_{\mathbb C}$
is equal to
 $\{1,\sqrt {2}, (1+\sqrt {5})/2,2\}$
by [Reference GuedjGue04, Theorem 2.1]. Moreover, the dynamical degree of every element of
$\{1,\sqrt {2}, (1+\sqrt {5})/2,2\}$
by [Reference GuedjGue04, Theorem 2.1]. Moreover, the dynamical degree of every element of
 $\operatorname {\mathrm {End}}(\mathbb {A}^2_{\mathbb {C}})$
is a quadratic integer, by [Reference Favre and JonssonFJ07, Theorem A′].
$\operatorname {\mathrm {End}}(\mathbb {A}^2_{\mathbb {C}})$
is a quadratic integer, by [Reference Favre and JonssonFJ07, Theorem A′]. -
(3) The case of dimension
 $n\ge 3$
is open in general: there is, for the moment, no hope of classifying all dynamical degrees, even when studying only automorphisms.
$n\ge 3$
is open in general: there is, for the moment, no hope of classifying all dynamical degrees, even when studying only automorphisms.The set of dynamical degrees of all automorphisms of
 $\mathbb {A}^3_{\mathbb C}$
of degree
$\mathbb {A}^3_{\mathbb C}$
of degree
 $2$
is equal to
$2$
is equal to
 $\{1,\sqrt {2},(1+\sqrt {5})/2,2\}$
by [Reference MaegawaMae01a, Theorem 3.1] (and the same holds over any field [Reference Blanc and van SantenBvS, Theorem 2]).
$\{1,\sqrt {2},(1+\sqrt {5})/2,2\}$
by [Reference MaegawaMae01a, Theorem 3.1] (and the same holds over any field [Reference Blanc and van SantenBvS, Theorem 2]).
Apart from the above classification results, two natural families are also known: the monomial endomorphisms and the shift-like automorphisms.
-
(A) A monomial endomorphism of
 $\mathbb {A}^n$
is an endomorphism of the form
$\mathbb {A}^n$
is an endomorphism of the form
 $f=(f_1,\ldots ,f_n)$
, where each
$f=(f_1,\ldots ,f_n)$
, where each
 $f_i$
is a monomial. When we write
$f_i$
is a monomial. When we write
 $f_i=\alpha _i x_1^{m_{i,1}}\cdots x_n^{m_{i,n}}$
with
$f_i=\alpha _i x_1^{m_{i,1}}\cdots x_n^{m_{i,n}}$
with
 $\alpha _i\in \mathbf {k}^*$
and
$\alpha _i\in \mathbf {k}^*$
and
 $m_{i,1},\ldots ,m_{i,n}\in {\mathbb N}$
, and assume that f is dominant, then the dynamical degree of f is the spectral radius of the corresponding matrix
$m_{i,1},\ldots ,m_{i,n}\in {\mathbb N}$
, and assume that f is dominant, then the dynamical degree of f is the spectral radius of the corresponding matrix
 $M=(m_{i,j})_{i,j=1}^n\in \mathrm {Mat}_n({\mathbb N})$
. This classical result is proven again in Corollary 3.2.5. The numbers arising this way are the weak Perron numbers (see Theorem 3.2.4).
$M=(m_{i,j})_{i,j=1}^n\in \mathrm {Mat}_n({\mathbb N})$
. This classical result is proven again in Corollary 3.2.5. The numbers arising this way are the weak Perron numbers (see Theorem 3.2.4). -
(B) For each
 $n\ge 1$
, a shift-like automorphism of
$n\ge 1$
, a shift-like automorphism of
 $\mathbb {A}^{n+1}$
is an automorphism of the form
$\mathbb {A}^{n+1}$
is an automorphism of the form
 $(x_{n+1}+p(x_1,\ldots ,x_{n}),x_1,\ldots ,x_{n})$
for some polynomial
$(x_{n+1}+p(x_1,\ldots ,x_{n}),x_1,\ldots ,x_{n})$
for some polynomial
 $p\in \mathbf {k}[x_1,\ldots ,x_n]$
. These are particular examples of affine-triangular automorphisms. The dynamics of such automorphisms have been studied in various texts (see for instance [Reference Bedford and PambuccianBP98, Reference MaegawaMae00, Reference MaegawaMae01b, Reference UedaUed04, Reference Bera and VermaBV18]). The dynamical degrees of shift-like automorphisms are known, by a result of Mattias Jonsson (see Proposition 4.2.5). For a proof of this result, together with a generalization, see §4.2.
$p\in \mathbf {k}[x_1,\ldots ,x_n]$
. These are particular examples of affine-triangular automorphisms. The dynamics of such automorphisms have been studied in various texts (see for instance [Reference Bedford and PambuccianBP98, Reference MaegawaMae00, Reference MaegawaMae01b, Reference UedaUed04, Reference Bera and VermaBV18]). The dynamical degrees of shift-like automorphisms are known, by a result of Mattias Jonsson (see Proposition 4.2.5). For a proof of this result, together with a generalization, see §4.2.
1.4 Description of the techniques associated to degrees
In the rest of this introduction, we describe the main technique that we introduce to compute dynamical degrees of endomorphisms of
![]() ${\mathbb A}^n$
. This is related to degree functions (or monomial valuations) and may be applied to endomorphisms of
${\mathbb A}^n$
. This is related to degree functions (or monomial valuations) and may be applied to endomorphisms of
![]() $\mathbb {A}^n$
, not only affine-triangular automorphisms. We also give an outline of the whole article.
$\mathbb {A}^n$
, not only affine-triangular automorphisms. We also give an outline of the whole article.
Definition 1.4.1. For each
![]() $\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n\setminus \{0\}$
, we define a degree function
$\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n\setminus \{0\}$
, we define a degree function
![]() $\deg _\mu \colon \mathbf {k}[x_1,\ldots ,x_n]\to {\mathbb R}_{\ge 0}\cup \{-\infty \}$
by
$\deg _\mu \colon \mathbf {k}[x_1,\ldots ,x_n]\to {\mathbb R}_{\ge 0}\cup \{-\infty \}$
by
![]() $\deg _\mu (0)=-\infty $
and
$\deg _\mu (0)=-\infty $
and
 $$ \begin{align*}\deg_\mu\bigg(\sum_{(a_1,\ldots,a_n)\in \mathbb{N}^n} \underbrace{c_{(a_1,\ldots,a_n)}}_{\in \mathbf{k}}\cdot x_1^{a_1}x_2^{a_2}\cdots x_n^{a_n}\bigg)=\max\bigg\{\sum\limits_{i=1}^n a_i \mu_i\bigg| c_{(a_1,\ldots,a_n)}\not=0\bigg\}.\end{align*} $$
$$ \begin{align*}\deg_\mu\bigg(\sum_{(a_1,\ldots,a_n)\in \mathbb{N}^n} \underbrace{c_{(a_1,\ldots,a_n)}}_{\in \mathbf{k}}\cdot x_1^{a_1}x_2^{a_2}\cdots x_n^{a_n}\bigg)=\max\bigg\{\sum\limits_{i=1}^n a_i \mu_i\bigg| c_{(a_1,\ldots,a_n)}\not=0\bigg\}.\end{align*} $$
We say that a polynomial
![]() $p\in \mathbf {k}[x_1,\ldots ,x_n]$
is
$p\in \mathbf {k}[x_1,\ldots ,x_n]$
is
![]() $\mu $
-homogeneous of degree
$\mu $
-homogeneous of degree
![]() $\theta \in {\mathbb R}$
if p is a finite sum of monomials
$\theta \in {\mathbb R}$
if p is a finite sum of monomials
![]() $p_i$
with
$p_i$
with
![]() $\deg _\mu (p_i)=\theta $
for each
$\deg _\mu (p_i)=\theta $
for each
![]() $i$
(where the zero polynomial is
$i$
(where the zero polynomial is
![]() $\mu $
-homogeneous of degree
$\mu $
-homogeneous of degree
![]() $\theta $
for each
$\theta $
for each
![]() $\theta$
).
$\theta$
).
We can then write every element
![]() $q\in \mathbf {k}[x_1,\ldots ,x_n]\setminus \{0\}$
uniquely as
$q\in \mathbf {k}[x_1,\ldots ,x_n]\setminus \{0\}$
uniquely as
 $$ \begin{align*} q=\sum\limits_{\theta\in {\mathbb R}_{\ge 0}} q_\theta, \end{align*} $$
$$ \begin{align*} q=\sum\limits_{\theta\in {\mathbb R}_{\ge 0}} q_\theta, \end{align*} $$
where each
![]() $q_\theta \in \mathbf {k}[x_1,\ldots ,x_n]$
is
$q_\theta \in \mathbf {k}[x_1,\ldots ,x_n]$
is
![]() $\mu $
-homogeneous of degree
$\mu $
-homogeneous of degree
![]() $\theta $
(and only finitely many
$\theta $
(and only finitely many
![]() $q_{\theta }$
are non-zero). We then say that
$q_{\theta }$
are non-zero). We then say that
![]() $q_\theta $
is the
$q_\theta $
is the
![]() $\mu $
-homogeneous part of q of degree
$\mu $
-homogeneous part of q of degree
![]() $\theta $
. The
$\theta $
. The
![]() $\mu $
-leading part of q is the
$\mu $
-leading part of q is the
![]() $\mu $
-homogeneous part of q of degree
$\mu $
-homogeneous part of q of degree
![]() $\deg _\mu (q)$
.
$\deg _\mu (q)$
.
Remark 1.4.2. Note that if
![]() $\mu \in ({\mathbb R}_{\geq 0})^n \setminus \{0\}$
, then
$\mu \in ({\mathbb R}_{\geq 0})^n \setminus \{0\}$
, then
is a valuation in the sense of [Reference MatsumuraMat89, p. 75], where
![]() $\mathbf {k}(x_1, \ldots , x_n)$
denotes the field of rational functions in
$\mathbf {k}(x_1, \ldots , x_n)$
denotes the field of rational functions in
![]() $x_1, \ldots , x_n$
over
$x_1, \ldots , x_n$
over
![]() $\mathbf {k}$
. Such valuations are often called ‘monomial valuations’ in the literature.
$\mathbf {k}$
. Such valuations are often called ‘monomial valuations’ in the literature.
Definition 1.4.3. Let
![]() $\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n\setminus \{0\}$
. For each
$\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n\setminus \{0\}$
. For each
![]() $f=(f_1,\ldots ,f_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n) \setminus \{0\}$
, we denote the
$f=(f_1,\ldots ,f_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n) \setminus \{0\}$
, we denote the
![]() $\mu $
-degree of f by
$\mu $
-degree of f by
and we say that
![]() $\deg _\mu (f)=\infty $
if the above set is empty.
$\deg _\mu (f)=\infty $
if the above set is empty.
Moreover, we say that f is
![]() $\mu $
-algebraically stable if
$\mu $
-algebraically stable if
![]() $\deg _\mu (f)<\infty $
and
$\deg _\mu (f)<\infty $
and
![]() $\deg _\mu (f^r)=\deg _\mu (f)^r$
for each
$\deg _\mu (f^r)=\deg _\mu (f)^r$
for each
![]() $r\ge 1$
.
$r\ge 1$
.
Remark 1.4.4. If
![]() $\mu =(1,\ldots ,1)$
, then
$\mu =(1,\ldots ,1)$
, then
![]() $\deg _\mu (f)=\deg (f)$
is the standard degree and the notion of being
$\deg _\mu (f)=\deg (f)$
is the standard degree and the notion of being
![]() $\mu $
-algebraically stable is the standard notion of ‘algebraically stable’, studied for instance in [Reference Guedj and SibonyGS02, Reference BisiBis08, Reference BlancBla16]. The fact of being algebraically stable can be interpreted geometrically by looking at the behaviour of the endomorphism at infinity: [Reference BlancBla16, Corollary 2.16].
$\mu $
-algebraically stable is the standard notion of ‘algebraically stable’, studied for instance in [Reference Guedj and SibonyGS02, Reference BisiBis08, Reference BlancBla16]. The fact of being algebraically stable can be interpreted geometrically by looking at the behaviour of the endomorphism at infinity: [Reference BlancBla16, Corollary 2.16].
To compute the dynamical degree of an endomorphism
![]() $f \in \operatorname {\mathrm {End}}({\mathbb A}^n)$
, the following endomorphism associated to f will be of great importance for us.
$f \in \operatorname {\mathrm {End}}({\mathbb A}^n)$
, the following endomorphism associated to f will be of great importance for us.
Definition 1.4.5. Let
![]() $f=(f_1,\ldots ,f_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
be a dominant endomorphism, let
$f=(f_1,\ldots ,f_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
be a dominant endomorphism, let
![]() $\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n$
be such that
$\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n$
be such that
![]() $\deg _\mu (f)=\theta <\infty $
. We define the
$\deg _\mu (f)=\theta <\infty $
. We define the
![]() $\mu $
-leading part of f to be the endomorphism
$\mu $
-leading part of f to be the endomorphism
![]() $g=(g_1,\ldots ,g_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
, where
$g=(g_1,\ldots ,g_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
, where
![]() $g_j\in \mathbf {k}[x_1,\ldots ,x_n]$
is the
$g_j\in \mathbf {k}[x_1,\ldots ,x_n]$
is the
![]() $\mu $
-homogeneous part of
$\mu $
-homogeneous part of
![]() $f_j$
of degree
$f_j$
of degree
![]() $\theta \mu _j$
for each
$\theta \mu _j$
for each
![]() $j\in \{1,\ldots ,n\}$
.
$j\in \{1,\ldots ,n\}$
.
The degree functions are studied in §2. Basic properties are given in §2.3 and the relation with
![]() $\mu $
-homogeneous endomorphisms is given in §2.5 (we explain in particular when
$\mu $
-homogeneous endomorphisms is given in §2.5 (we explain in particular when
![]() $\deg _\mu (f)=\infty $
in Lemma 2.5.6). In §2.6, we explain how degree functions allow us to give an estimate on the dynamical degrees, and sometimes to compute it exactly. In particular, we prove the following result (at the end of §2.6).
$\deg _\mu (f)=\infty $
in Lemma 2.5.6). In §2.6, we explain how degree functions allow us to give an estimate on the dynamical degrees, and sometimes to compute it exactly. In particular, we prove the following result (at the end of §2.6).
Proposition A. Let
![]() $f=(f_1,\ldots ,f_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
be a dominant endomorphism. For each
$f=(f_1,\ldots ,f_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
be a dominant endomorphism. For each
![]() $\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{> 0})^n$
, the following hold:
$\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{> 0})^n$
, the following hold:
-
(1)
 $\theta : = \deg _\mu (f) < \infty $
;
$\theta : = \deg _\mu (f) < \infty $
; -
(2) the dynamical degree of f satisfies
 $1 \leq \unicode{x3bb} (f)\le \theta $
;
$1 \leq \unicode{x3bb} (f)\le \theta $
; -
(3) let
 $g \in \operatorname {\mathrm {End}}({\mathbb A}^n)$
be the
$g \in \operatorname {\mathrm {End}}({\mathbb A}^n)$
be the
 $\mu $
-leading part of f. If
$\mu $
-leading part of f. If
 $\theta> 1$
, then
$\theta> 1$
, then  $$ \begin{align*} \unicode{x3bb}(f)=\theta \Leftrightarrow f \text{ is}\ \mu\text{-algebraically stable}\Leftrightarrow g^r\not=0 \text{ for each }r\ge 1. \end{align*} $$
$$ \begin{align*} \unicode{x3bb}(f)=\theta \Leftrightarrow f \text{ is}\ \mu\text{-algebraically stable}\Leftrightarrow g^r\not=0 \text{ for each }r\ge 1. \end{align*} $$
Remark 1.4.6. Let
![]() $\mu =(1,\ldots ,1)$
. In this case, the
$\mu =(1,\ldots ,1)$
. In this case, the
![]() $\mu $
-degree is the classical degree and Proposition A(2) is the classical inequality
$\mu $
-degree is the classical degree and Proposition A(2) is the classical inequality
![]() $\unicode{x3bb} (f)\le \deg (f)$
.
$\unicode{x3bb} (f)\le \deg (f)$
.
Remark 1.4.7. Proposition A is false when we apply it to
![]() $\mu \in (\mathbb {R}_{\ge 0})^n\setminus \{0\}$
. For instance, if
$\mu \in (\mathbb {R}_{\ge 0})^n\setminus \{0\}$
. For instance, if
![]() $f=(x_1,x_2^2)$
,
$f=(x_1,x_2^2)$
,
![]() $\mu =(1,0)$
, then
$\mu =(1,0)$
, then
![]() $\deg _\mu (f)=1$
but
$\deg _\mu (f)=1$
but
![]() $1<\unicode{x3bb} (f)=2$
.
$1<\unicode{x3bb} (f)=2$
.
To apply Proposition A to compute the dynamical degree, we need to find some eigenvectors and eigenvalues. This is done here by looking at monomial maps associated to endomorphisms in
![]() $\operatorname {\mathrm {End}}({\mathbb A}^n)$
. These behave quite well with respect to degree functions (see Corollary 3.2.5).
$\operatorname {\mathrm {End}}({\mathbb A}^n)$
. These behave quite well with respect to degree functions (see Corollary 3.2.5).
Definition 1.4.8. Let
![]() $f=(f_1,\ldots ,f_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
be an endomorphism such that
$f=(f_1,\ldots ,f_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
be an endomorphism such that
![]() $f_i\not =0$
for each i. We will say that a square matrix
$f_i\not =0$
for each i. We will say that a square matrix
![]() $M=(m_{i,j})_{i,j=1}^n\in \mathrm {Mat}_n({\mathbb N})$
is contained in f if for each
$M=(m_{i,j})_{i,j=1}^n\in \mathrm {Mat}_n({\mathbb N})$
is contained in f if for each
![]() $i\in \{1,\ldots ,n\}$
, the coefficient of the monomial
$i\in \{1,\ldots ,n\}$
, the coefficient of the monomial
![]() $\prod _{j=1}^n x_j^{m_{i,j}}$
in
$\prod _{j=1}^n x_j^{m_{i,j}}$
in
![]() $f_i$
is non-zero. The set of matrices that are contained in f is then finite and non-empty.
$f_i$
is non-zero. The set of matrices that are contained in f is then finite and non-empty.
The maximal eigenvalue of f is defined to be
An element
![]() $\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n \setminus \{ 0 \}$
is a maximal eigenvector of f if
$\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n \setminus \{ 0 \}$
is a maximal eigenvector of f if
![]() $\deg _\mu (f_i) = \theta \mu _i$
for each
$\deg _\mu (f_i) = \theta \mu _i$
for each
![]() $i\in \{1,\ldots ,n\}$
. In particular, we then get
$i\in \{1,\ldots ,n\}$
. In particular, we then get
![]() $\deg _{\mu }(f) = \theta < \infty $
.
$\deg _{\mu }(f) = \theta < \infty $
.
It often happens that we cannot apply Proposition A to compute the dynamical degree, but that we can do it by allowing
![]() $\mu $
to have some coordinates, but not all, to be equal to zero. In fact, the following generalization of Proposition A is our main tool to compute dynamical degrees.
$\mu $
to have some coordinates, but not all, to be equal to zero. In fact, the following generalization of Proposition A is our main tool to compute dynamical degrees.
Proposition B. Let
![]() $f=(f_1,\ldots ,f_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
be a dominant endomorphism with maximal eigenvalue
$f=(f_1,\ldots ,f_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
be a dominant endomorphism with maximal eigenvalue
![]() $\theta $
. Then the following hold.
$\theta $
. Then the following hold.
-
(1) There exists a maximal eigenvector
 $\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n \setminus \{0\}$
of f.
$\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n \setminus \{0\}$
of f. -
(2) We have
 $1\le \unicode{x3bb} (f)\le \theta \le \deg (f)$
.
$1\le \unicode{x3bb} (f)\le \theta \le \deg (f)$
. -
(3) For each maximal eigenvector
 $\mu $
of f, we have
$\mu $
of f, we have
 $\theta =\deg _\mu (f)$
, and the following hold:
$\theta =\deg _\mu (f)$
, and the following hold:-
(i) if f is
 $\mu $
-algebraically stable, then
$\mu $
-algebraically stable, then
 $\unicode{x3bb} (f)=\theta $
;
$\unicode{x3bb} (f)=\theta $
; -
(ii) if
 $\unicode{x3bb} (f)=\theta $
,
$\unicode{x3bb} (f)=\theta $
,
 $\theta>1$
and
$\theta>1$
and
 $\mu \in ({\mathbb R}_{>0})^n$
, then f is
$\mu \in ({\mathbb R}_{>0})^n$
, then f is
 $\mu $
-algebraically stable;
$\mu $
-algebraically stable; -
(iii) let
 $g \in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
be the
$g \in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
be the
 $\mu $
-leading part of f. If
$\mu $
-leading part of f. If
 $\theta> 1$
, then f is
$\theta> 1$
, then f is
 $\mu $
-algebraically stable if and only if for each
$\mu $
-algebraically stable if and only if for each
 $r \geq 1$
there is
$r \geq 1$
there is
 $i \in \{1, \ldots , n\}$
with
$i \in \{1, \ldots , n\}$
with
 $\mu _i> 0$
such that the ith component of
$\mu _i> 0$
such that the ith component of
 $g^r$
is non-zero.
$g^r$
is non-zero.
-
Remark 1.4.9. In Proposition B(1), there are examples with no possibility for
![]() $\mu $
to be in
$\mu $
to be in
![]() $(\mathbb {R}_{>0})^n$
, as the examples
$(\mathbb {R}_{>0})^n$
, as the examples
![]() $f = (x_1, x_2^2)\in \operatorname {\mathrm {End}}(\mathbb {A}^2)$
or
$f = (x_1, x_2^2)\in \operatorname {\mathrm {End}}(\mathbb {A}^2)$
or
![]() $f=(x_1,x_3,x_2+x_3^2)\in \operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
show. Hence, Proposition A cannot be directly applied to prove Proposition B. However, if some coordinates of
$f=(x_1,x_3,x_2+x_3^2)\in \operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
show. Hence, Proposition A cannot be directly applied to prove Proposition B. However, if some coordinates of
![]() $\mu $
are zero, then a linear projection is preserved (this follows from Lemma 2.5.6, see also Corollary 2.6.2). To prove Proposition B, we will use Lemma 2.6.1, which is a version of Proposition A that also works for
$\mu $
are zero, then a linear projection is preserved (this follows from Lemma 2.5.6, see also Corollary 2.6.2). To prove Proposition B, we will use Lemma 2.6.1, which is a version of Proposition A that also works for
![]() $\mu \in (\mathbb {R}_{\ge 0})^n\setminus \{0\}$
.
$\mu \in (\mathbb {R}_{\ge 0})^n\setminus \{0\}$
.
Remark 1.4.10. The implication of Proposition B(3)(i) is not an equivalence, as we show in Example 3.4.2 below.
The proof of Proposition B is given in §3. For each dominant endomorphism
![]() $f\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
, Proposition B(1) gives the existence of a maximal eigenvector
$f\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
, Proposition B(1) gives the existence of a maximal eigenvector
![]() $\mu $
. Moreover, Proposition B(3) shows that if f is
$\mu $
. Moreover, Proposition B(3) shows that if f is
![]() $\mu $
-algebraically stable, then
$\mu $
-algebraically stable, then
![]() $\unicode{x3bb} (f)$
is equal to the maximal eigenvalue
$\unicode{x3bb} (f)$
is equal to the maximal eigenvalue
![]() $\theta $
of f. We will use this to compute the dynamical degree of many endomorphisms of
$\theta $
of f. We will use this to compute the dynamical degree of many endomorphisms of
![]() $\mathbb {A}^n$
.
$\mathbb {A}^n$
.
The following result allows to compute all dynamical degrees of permutation-elementary endomorphism of
![]() $\mathbb {A}^n$
, and generalizes in particular Proposition 4.2.5. Its proof is given in §4.2.
$\mathbb {A}^n$
, and generalizes in particular Proposition 4.2.5. Its proof is given in §4.2.
Proposition C. Let
![]() $f\in \operatorname {\mathrm {Aut}}(\mathbb {A}^n)$
be a permutation-elementary automorphism. If the maximal eigenvalue
$f\in \operatorname {\mathrm {Aut}}(\mathbb {A}^n)$
be a permutation-elementary automorphism. If the maximal eigenvalue
![]() $\theta $
of f is bigger than
$\theta $
of f is bigger than
![]() $1$
, there exists a maximal eigenvector
$1$
, there exists a maximal eigenvector
![]() $\mu $
of f such that f is
$\mu $
of f such that f is
![]() $\mu $
-algebraically stable. In particular, the dynamical degree
$\mu $
-algebraically stable. In particular, the dynamical degree
![]() $\unicode{x3bb} (f)$
is equal to the maximal eigenvalue
$\unicode{x3bb} (f)$
is equal to the maximal eigenvalue
![]() $\theta $
of f, which is a Handelman number.
$\theta $
of f, which is a Handelman number.
Proposition C is false if we replace ‘permutation-elementary’ by ‘permutation-trian gular’ (see Example 4.3.4 for examples in dimension
![]() $3$
). However, we can obtain the following result, which is proven in §4.3.
$3$
). However, we can obtain the following result, which is proven in §4.3.
Proposition D. Every affine-triangular automorphism
![]() $f\in \operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
is conjugate to a permutation-triangular automorphism
$f\in \operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
is conjugate to a permutation-triangular automorphism
![]() $f'\in \operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
such that
$f'\in \operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
such that
![]() $\deg (f')\le \deg (f)$
and such that
$\deg (f')\le \deg (f)$
and such that
![]() $f'$
has the following property: either the maximal eigenvalue
$f'$
has the following property: either the maximal eigenvalue
![]() $\theta $
of
$\theta $
of
![]() $f'$
is equal to
$f'$
is equal to
![]() $1$
or
$1$
or
![]() $f'$
is
$f'$
is
![]() $\mu $
-algebraically stable for each maximal eigenvector
$\mu $
-algebraically stable for each maximal eigenvector
![]() $\mu $
. In particular, the dynamical degrees
$\mu $
. In particular, the dynamical degrees
![]() $\unicode{x3bb} (f)$
and
$\unicode{x3bb} (f)$
and
![]() $\unicode{x3bb} (f')$
are equal to the maximal eigenvalue
$\unicode{x3bb} (f')$
are equal to the maximal eigenvalue
![]() $\theta $
of
$\theta $
of
![]() $f'$
, which is a Handelman number.
$f'$
, which is a Handelman number.
The proof of Theorem 1 is given at the end of §4.3, directly after proving Proposition D, as it follows almost directly from this result. We use these results in §4.4 to prove Theorem 2.
2 Inequalities associated to degree functions and the proof of Proposition A
2.1 Definitions of elementary, affine and triangular automorphisms
Let us recall the following classical definitions (even if our definition of elementary is slightly more restrictive than what is used in the literature).
Definition 2.1.1. An endomorphism
![]() $f=(f_1,\ldots ,f_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
is said to be:
$f=(f_1,\ldots ,f_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
is said to be:
-
• triangular if
 $f_i\in \mathbf {k}[x_1,\ldots ,x_i]$
for each
$f_i\in \mathbf {k}[x_1,\ldots ,x_i]$
for each
 $i\in \{1,\ldots ,n\}$
;
$i\in \{1,\ldots ,n\}$
; -
• elementary if
 $f_i=x_i$
for for each
$f_i=x_i$
for for each
 $i\in \{1,\ldots ,n-1\}$
;
$i\in \{1,\ldots ,n-1\}$
; -
• an affine automorphism if
 $f\in \operatorname {\mathrm {Aut}}(\mathbb {A}^n)$
and if
$f\in \operatorname {\mathrm {Aut}}(\mathbb {A}^n)$
and if
 $\deg (f)=1$
;
$\deg (f)=1$
; -
• a permutation of the coordinates if
 $\{f_1,\ldots ,f_n\}=\{x_1,\ldots ,x_n\}$
;
$\{f_1,\ldots ,f_n\}=\{x_1,\ldots ,x_n\}$
; -
• affine-triangular if
 $f=\alpha \circ \tau $
, where
$f=\alpha \circ \tau $
, where
 $\alpha $
is an affine automorphism and
$\alpha $
is an affine automorphism and
 $\tau $
is a triangular endomorphism;
$\tau $
is a triangular endomorphism; -
• affine-elementary if
 $f=\alpha \circ e$
, where
$f=\alpha \circ e$
, where
 $\alpha $
is an affine automorphism and e is an elementary endomorphism;
$\alpha $
is an affine automorphism and e is an elementary endomorphism; -
• permutation-triangular if
 $f=\alpha \circ \tau $
, where
$f=\alpha \circ \tau $
, where
 $\alpha $
is a permutation of the coordinates and
$\alpha $
is a permutation of the coordinates and
 $\tau $
is a triangular endomorphism;
$\tau $
is a triangular endomorphism; -
• permutation-elementary if
 $f=\alpha \circ e$
, where
$f=\alpha \circ e$
, where
 $\alpha $
is a permutation of the coordinates and e is an elementary endomorphism.
$\alpha $
is a permutation of the coordinates and e is an elementary endomorphism.
For each
![]() $n\le 4$
, if
$n\le 4$
, if
![]() $\mathrm {char}(\mathbf {k})\not =2$
, every automorphism of
$\mathrm {char}(\mathbf {k})\not =2$
, every automorphism of
![]() $\mathbb {A}^n$
of degree
$\mathbb {A}^n$
of degree
![]() $2$
is conjugate, by an affine automorphism, to an affine-triangular automorphism, see [Reference Meisters and OlechMO91]. This result is false in dimension
$2$
is conjugate, by an affine automorphism, to an affine-triangular automorphism, see [Reference Meisters and OlechMO91]. This result is false in dimension
![]() $n=5$
[Reference SunSun14], as for example
$n=5$
[Reference SunSun14], as for example
shows: the Jacobian of the homogeneous part of degree
![]() $2$
of an affine-triangular automorphism of degree
$2$
of an affine-triangular automorphism of degree
![]() $\leq 2$
contains a zero-column, but the Jacobian of the homogeneous part of degree
$\leq 2$
contains a zero-column, but the Jacobian of the homogeneous part of degree
![]() $2$
of f contains linearly independent columns (see also [Reference SunSun14, Theorem 3.2]).
$2$
of f contains linearly independent columns (see also [Reference SunSun14, Theorem 3.2]).
There are quite a few automorphisms of
![]() $\mathbb {A}^3$
of degree
$\mathbb {A}^3$
of degree
![]() $3$
that are not conjugate, by an affine automorphism, to affine-triangular automorphisms. More precisely, when
$3$
that are not conjugate, by an affine automorphism, to affine-triangular automorphisms. More precisely, when
![]() $\mathbf {k}$
is algebraically closed, then each automorphism of
$\mathbf {k}$
is algebraically closed, then each automorphism of
![]() ${\mathbb A}^3 = \operatorname {\mathrm {Spec}}(\mathbf {k}[x, y, z])$
of degree
${\mathbb A}^3 = \operatorname {\mathrm {Spec}}(\mathbf {k}[x, y, z])$
of degree
![]() $3$
is conjugate, by an affine automorphism, either to an affine-triangular automorphism or to an automorphism of the form
$3$
is conjugate, by an affine automorphism, either to an affine-triangular automorphism or to an automorphism of the form
where
![]() $a \in \mathbf {k}[x, z] \setminus \mathbf {k}[z]$
is homogeneous of degree
$a \in \mathbf {k}[x, z] \setminus \mathbf {k}[z]$
is homogeneous of degree
![]() $2$
,
$2$
,
![]() $r \in \mathbf {k}[z]$
is of degree
$r \in \mathbf {k}[z]$
is of degree
![]() $\leq 3$
and
$\leq 3$
and
![]() $\alpha $
is an affine automorphism, see [Reference Blanc and van SantenBvS, Theorem 3]. In fact, non of the automorphisms in (*) is conjugated, by an affine automorphism, to an affine-triangular automorphism, see [Reference Blanc and van SantenBvS, Proposition 3.9.4].
$\alpha $
is an affine automorphism, see [Reference Blanc and van SantenBvS, Theorem 3]. In fact, non of the automorphisms in (*) is conjugated, by an affine automorphism, to an affine-triangular automorphism, see [Reference Blanc and van SantenBvS, Proposition 3.9.4].
For
![]() $\mathbf {k} = {\mathbb C}$
, various (dynamical) properties of the affine-elementary automorphisms
$\mathbf {k} = {\mathbb C}$
, various (dynamical) properties of the affine-elementary automorphisms
![]() $(x_0+x_1+x_0^q x_2^d, x_0, \alpha x_2) \in \operatorname {\mathrm {Aut}}({\mathbb A}^3)$
with
$(x_0+x_1+x_0^q x_2^d, x_0, \alpha x_2) \in \operatorname {\mathrm {Aut}}({\mathbb A}^3)$
with
![]() $\alpha \in {\mathbb C}$
,
$\alpha \in {\mathbb C}$
,
![]() $0 < |\alpha | \leq 1$
,
$0 < |\alpha | \leq 1$
,
![]() $q \geq 2$
,
$q \geq 2$
,
![]() $d \geq 1$
are studied in [Reference Déserti and LeguilDL18] and, in particular, their dynamical degree is computed, which is equal to the integer q.
$d \geq 1$
are studied in [Reference Déserti and LeguilDL18] and, in particular, their dynamical degree is computed, which is equal to the integer q.
2.2 Existence of dynamical degrees
We recall the following folklore result, which implies that the dynamical degree is well defined.
Lemma 2.2.1. Let
![]() $(a_r)_{r\ge 1}$
be a sequence of real numbers in
$(a_r)_{r\ge 1}$
be a sequence of real numbers in
![]() ${\mathbb R}_{\ge 1}$
such that
${\mathbb R}_{\ge 1}$
such that
![]() $a_{r+s}\le a_{r}\cdot a_s$
for each
$a_{r+s}\le a_{r}\cdot a_s$
for each
![]() $r,s\ge 1$
. Then,
$r,s\ge 1$
. Then,
![]() $((a_r)^{1/r})_{r\ge 1}$
is a sequence that converges towards
$((a_r)^{1/r})_{r\ge 1}$
is a sequence that converges towards
![]() $\inf _{r\geq 1} ((a_r)^{1/r})\in {\mathbb R}_{\ge 1}$
.
$\inf _{r\geq 1} ((a_r)^{1/r})\in {\mathbb R}_{\ge 1}$
.
Proof. As
![]() $(\log (a_r))_{r\ge 1}$
is subadditive,
$(\log (a_r))_{r\ge 1}$
is subadditive,
![]() $({\log (a_r)}/{r})_{r\ge 1}$
converges to
$({\log (a_r)}/{r})_{r\ge 1}$
converges to
![]() $\inf _{r \geq 1}(({\log (a_r)}/{r}) \geq 0$
by Fekete’s subadditivity lemma (see [Reference FeketeFek23, Satz II] or [Reference Michael SteeleSte97, Lemma 1.2.1]).
$\inf _{r \geq 1}(({\log (a_r)}/{r}) \geq 0$
by Fekete’s subadditivity lemma (see [Reference FeketeFek23, Satz II] or [Reference Michael SteeleSte97, Lemma 1.2.1]).
In case
![]() $\mu = (\mu _1, \ldots , \mu _n) \in ({\mathbb R}_{\geq 0})^n \setminus \{0\}$
is of the form
$\mu = (\mu _1, \ldots , \mu _n) \in ({\mathbb R}_{\geq 0})^n \setminus \{0\}$
is of the form
![]() $\mu _1 = \cdots = \mu _m = 0$
and
$\mu _1 = \cdots = \mu _m = 0$
and
![]() $\mu _{m+1} = \cdots = \mu _n = 1$
for some
$\mu _{m+1} = \cdots = \mu _n = 1$
for some
![]() $0 \leq m < n$
, we denote for any polynomial
$0 \leq m < n$
, we denote for any polynomial
![]() $p \in \mathbf {k}[x_1, \ldots , x_n]$
its
$p \in \mathbf {k}[x_1, \ldots , x_n]$
its
![]() $\mu $
-degree
$\mu $
-degree
![]() $\deg _{\mu }(p)$
by
$\deg _{\mu }(p)$
by
![]() $\deg _{x_{m+1}, \ldots , x_{n}}(p)$
. Moreover, we denote for an endomorphism
$\deg _{x_{m+1}, \ldots , x_{n}}(p)$
. Moreover, we denote for an endomorphism
![]() $f = (f_1, \ldots , f_n) \in \operatorname {\mathrm {End}}({\mathbb A}^n)$
by
$f = (f_1, \ldots , f_n) \in \operatorname {\mathrm {End}}({\mathbb A}^n)$
by
If
![]() $m = 0$
, then
$m = 0$
, then
![]() $\deg _{\mu }(f)$
is simply the classical degree that we denote by
$\deg _{\mu }(f)$
is simply the classical degree that we denote by
![]() $\deg (f)$
. If
$\deg (f)$
. If
![]() $m> 0$
, then
$m> 0$
, then
![]() $\deg _{\mu }(f)$
is in general not equal to
$\deg _{\mu }(f)$
is in general not equal to
![]() $\deg _{x_{m+1}, \ldots , x_{n}}(f)$
. In fact,
$\deg _{x_{m+1}, \ldots , x_{n}}(f)$
. In fact,
![]() $\deg _{\mu }(f)$
is equal to
$\deg _{\mu }(f)$
is equal to
![]() $\deg _{x_{m+1}, \ldots , x_{n}}(f)$
in case
$\deg _{x_{m+1}, \ldots , x_{n}}(f)$
in case
![]() $\deg _{x_1, \ldots , x_m}(f_i) = 0$
for all
$\deg _{x_1, \ldots , x_m}(f_i) = 0$
for all
![]() $i \in \{1, \ldots , m\}$
and otherwise it is equal to
$i \in \{1, \ldots , m\}$
and otherwise it is equal to
![]() $\infty $
.
$\infty $
.
Corollary 2.2.2. Let
![]() $f\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
be an endomorphism. For each integer
$f\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
be an endomorphism. For each integer
![]() $m\in \{0,\ldots ,n-1\}$
, the sequence
$m\in \{0,\ldots ,n-1\}$
, the sequence
converges to a real number
![]() $\mu _m\ge 1$
. This gives, in particular, the dynamical degree
$\mu _m\ge 1$
. This gives, in particular, the dynamical degree
![]() $\unicode{x3bb} (f)=\mu _0$
, which satisfies
$\unicode{x3bb} (f)=\mu _0$
, which satisfies
![]() $\unicode{x3bb} (f^d)=\unicode{x3bb} (f)^d$
for each
$\unicode{x3bb} (f^d)=\unicode{x3bb} (f)^d$
for each
![]() $d\ge 1$
.
$d\ge 1$
.
Proof. This follows from Lemma 2.2.1, as
for all
![]() $r,s\ge 1$
.
$r,s\ge 1$
.
2.3 Basic properties of degree functions
Below we list several properties of degree functions (see Definition 1.4.1). Apart from the easy observations
![]() $\deg _\mu |_{\mathbf {k}^*}=0$
,
$\deg _\mu |_{\mathbf {k}^*}=0$
,
![]() $\deg _\mu (f\cdot g)=\deg _\mu (f) + \deg _\mu (g)$
and
$\deg _\mu (f\cdot g)=\deg _\mu (f) + \deg _\mu (g)$
and
![]() $\deg _\mu (f+g)\le \max (\deg _\mu (f),\deg _\mu (g))$
, which correspond to say that
$\deg _\mu (f+g)\le \max (\deg _\mu (f),\deg _\mu (g))$
, which correspond to say that
![]() $-\deg _\mu $
is a valuation (see Remark 1.4.2), we have the following.
$-\deg _\mu $
is a valuation (see Remark 1.4.2), we have the following.
Remark 2.3.1. We fix
![]() $\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n\setminus \{0\}$
and get the following.
$\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n\setminus \{0\}$
and get the following.
-
(1) As explained in Definition 1.4.1, each polynomial
 $p\in \mathbf {k}[x_1,\ldots ,x_n]\setminus \{0\}$
can be written uniquely as a finite sum, where each
$p\in \mathbf {k}[x_1,\ldots ,x_n]\setminus \{0\}$
can be written uniquely as a finite sum, where each $$ \begin{align*} p=\sum\limits_{\theta\in {\mathbb R}_{\ge 0}} p_\theta, \end{align*} $$
$$ \begin{align*} p=\sum\limits_{\theta\in {\mathbb R}_{\ge 0}} p_\theta, \end{align*} $$
 $p_\theta \in \mathbf {k}[x_1,\ldots ,x_n]$
is
$p_\theta \in \mathbf {k}[x_1,\ldots ,x_n]$
is
 $\mu $
-homogeneous of degree
$\mu $
-homogeneous of degree
 $\theta $
. We then obtain
$\theta $
. We then obtain
 $\deg _\mu (p)=\max \{\theta \mid p_\theta \not =0\}$
.
$\deg _\mu (p)=\max \{\theta \mid p_\theta \not =0\}$
.
-
(2) Let
 $m \in \{0, \ldots , n-1 \}$
and assume that
$m \in \{0, \ldots , n-1 \}$
and assume that
 $\mu _i = 0$
for
$\mu _i = 0$
for
 $i \leq m$
, but
$i \leq m$
, but
 $\mu _i> 0$
for
$\mu _i> 0$
for
 $i> m$
. Then we have, for each polynomial
$i> m$
. Then we have, for each polynomial
 $p\in \mathbf {k}[x_1,\ldots ,x_n]\setminus \{0\}$
, where
$p\in \mathbf {k}[x_1,\ldots ,x_n]\setminus \{0\}$
, where $$ \begin{align*} \mu_{\min} \cdot \deg_{x_{m+1}, \ldots, x_n}(p) \leq \deg_{\mu}(p) \leq \mu_{\max} \cdot \deg_{x_{m+1}, \ldots, x_n}(p), \end{align*} $$
$$ \begin{align*} \mu_{\min} \cdot \deg_{x_{m+1}, \ldots, x_n}(p) \leq \deg_{\mu}(p) \leq \mu_{\max} \cdot \deg_{x_{m+1}, \ldots, x_n}(p), \end{align*} $$
 $\mu _{\min } = \min _{m+1 \leq i \leq n} \mu _i$
and
$\mu _{\min } = \min _{m+1 \leq i \leq n} \mu _i$
and
 $\mu _{\max } = \max _{m+1 \leq i \leq n} \mu _i$
. In particular, for each dominant endomorphism
$\mu _{\max } = \max _{m+1 \leq i \leq n} \mu _i$
. In particular, for each dominant endomorphism
 $f \in \operatorname {\mathrm {End}}({\mathbb A}^n)$
, we have where
$f \in \operatorname {\mathrm {End}}({\mathbb A}^n)$
, we have where $$ \begin{align*} \lim_{r \to \infty} \deg_{x_{m+1}, \ldots, x_n}(f^r)^{{1}/{r}} = \lim_{r \to \infty} \max_{i \in \{1, \ldots, n\}}\deg_\mu((f^r)_i)^{{1}/{r}}, \end{align*} $$
$$ \begin{align*} \lim_{r \to \infty} \deg_{x_{m+1}, \ldots, x_n}(f^r)^{{1}/{r}} = \lim_{r \to \infty} \max_{i \in \{1, \ldots, n\}}\deg_\mu((f^r)_i)^{{1}/{r}}, \end{align*} $$
 $(f^r)_i$
denotes the ith coordinate function of
$(f^r)_i$
denotes the ith coordinate function of
 $f^r$
. Note that the left-hand side is the dynamical degree
$f^r$
. Note that the left-hand side is the dynamical degree
 $\unicode{x3bb} (f)$
in case
$\unicode{x3bb} (f)$
in case
 $m = 0$
, that is, when
$m = 0$
, that is, when
 $\mu \in ({\mathbb R}_{>0})^n$
.
$\mu \in ({\mathbb R}_{>0})^n$
.
2.4 Endomorphisms that preserve a linear projection
The following is an algebraic analogue of the application of [Reference Dinh and NguyênDN11, Theorem 1.1] to endomorphisms of
![]() $\mathbb {A}^n$
that preserve a linear projection.
$\mathbb {A}^n$
that preserve a linear projection.
Lemma 2.4.1. Let
![]() $f =(f_1, \ldots , f_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
be a dominant endomorphism. For each
$f =(f_1, \ldots , f_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
be a dominant endomorphism. For each
![]() $r\ge 1$
, we write
$r\ge 1$
, we write
Let
![]() $m\in \{0,\ldots ,n-1\}$
be such that
$m\in \{0,\ldots ,n-1\}$
be such that
![]() $f_1,\ldots ,f_m\in \mathbf {k}[x_1,\ldots ,x_m]$
. Then, the dynamical degree of f is given by
$f_1,\ldots ,f_m\in \mathbf {k}[x_1,\ldots ,x_m]$
. Then, the dynamical degree of f is given by
![]() $\unicode{x3bb} (f)=\max \{\unicode{x3bb} _1,\unicode{x3bb} _2\}$
, where
$\unicode{x3bb} (f)=\max \{\unicode{x3bb} _1,\unicode{x3bb} _2\}$
, where

are two limits which exist. (If
![]() $m = 0$
, by convention we set
$m = 0$
, by convention we set
![]() $\unicode{x3bb} _1 = 1.$
)
$\unicode{x3bb} _1 = 1.$
)
Proof. For each
![]() $r\ge 1$
, we write
$r\ge 1$
, we write
 $$ \begin{align*} a_r&= \max\{\deg((f^r)_1),\ldots, \deg((f^r)_m)\},\\ b_r&= \max\{\deg((f^r)_{m+1}),\ldots, \deg((f^r)_{n})\},\\ c_r&= \max\{\deg_{x_{m+1},\ldots,x_n}((f^r)_{m+1}),\ldots, \deg_{x_{m+1},\ldots,x_n}((f^r)_{n})\} \\ &= \deg_{x_{m+1}, \ldots, x_n}(f^r). \end{align*} $$
$$ \begin{align*} a_r&= \max\{\deg((f^r)_1),\ldots, \deg((f^r)_m)\},\\ b_r&= \max\{\deg((f^r)_{m+1}),\ldots, \deg((f^r)_{n})\},\\ c_r&= \max\{\deg_{x_{m+1},\ldots,x_n}((f^r)_{m+1}),\ldots, \deg_{x_{m+1},\ldots,x_n}((f^r)_{n})\} \\ &= \deg_{x_{m+1}, \ldots, x_n}(f^r). \end{align*} $$
As
![]() $b_r\ge c_r$
, we obtain for each
$b_r\ge c_r$
, we obtain for each
![]() $r \geq 1$
,
$r \geq 1$
,
It follows from Corollary 2.2.2 that the limits
exist (and all belong to
![]() ${\mathbb R}_{\ge 1}$
). We obtain
${\mathbb R}_{\ge 1}$
). We obtain
Thus we may assume that
![]() $\unicode{x3bb} (f)>\unicode{x3bb} _1$
, which implies that
$\unicode{x3bb} (f)>\unicode{x3bb} _1$
, which implies that
![]() $\lim _{r\to \infty } b_r^{1/r}$
exists and is equal to
$\lim _{r\to \infty } b_r^{1/r}$
exists and is equal to
![]() $\unicode{x3bb} (f)$
. It remains to see that, in this case,
$\unicode{x3bb} (f)$
. It remains to see that, in this case,
![]() $\unicode{x3bb} (f)\le \max \{\unicode{x3bb} _1,\unicode{x3bb} _2\}$
.
$\unicode{x3bb} (f)\le \max \{\unicode{x3bb} _1,\unicode{x3bb} _2\}$
.
For all
![]() $r,s \ge 1$
and each
$r,s \ge 1$
and each
![]() $i\in \{m+1,\ldots ,n\}$
, the polynomial
$i\in \{m+1,\ldots ,n\}$
, the polynomial
![]() $(f^{r+s})_i$
is obtained by replacing
$(f^{r+s})_i$
is obtained by replacing
![]() $x_1,\ldots ,x_n$
with
$x_1,\ldots ,x_n$
with
![]() $(f^{r})_1,\ldots ,(f^r)_n$
in
$(f^{r})_1,\ldots ,(f^r)_n$
in
![]() $(f^s)_i$
, so the degree of
$(f^s)_i$
, so the degree of
![]() $(f^{r+s})_i$
is at most
$(f^{r+s})_i$
is at most
 $$ \begin{align*} &\deg_{x_1,\ldots,x_m}((f^s)_i)\cdot \deg((f^r)_1,\ldots,(f^r)_m) \\ &\quad+ \deg_{x_{m+1},\ldots,x_n}((f^s)_i)\cdot \deg((f^r)_{m+1},\ldots,(f^r)_n). \end{align*} $$
$$ \begin{align*} &\deg_{x_1,\ldots,x_m}((f^s)_i)\cdot \deg((f^r)_1,\ldots,(f^r)_m) \\ &\quad+ \deg_{x_{m+1},\ldots,x_n}((f^s)_i)\cdot \deg((f^r)_{m+1},\ldots,(f^r)_n). \end{align*} $$
This gives
![]() $b_{r+s}\le b_s \cdot a_{r}+c_s\cdot b_{r}$
. Then when we choose
$b_{r+s}\le b_s \cdot a_{r}+c_s\cdot b_{r}$
. Then when we choose
![]() $s=r$
, we obtain
$s=r$
, we obtain
As
![]() $\unicode{x3bb} (f)=\lim \nolimits _{r\to \infty } b_{2r}^{1/2r}$
, we have
$\unicode{x3bb} (f)=\lim \nolimits _{r\to \infty } b_{2r}^{1/2r}$
, we have
![]() $\unicode{x3bb} (f)^2=\lim \nolimits _{r\to \infty } b_{2r}^{1/r}$
. The above inequality gives
$\unicode{x3bb} (f)^2=\lim \nolimits _{r\to \infty } b_{2r}^{1/r}$
. The above inequality gives

so
![]() $\unicode{x3bb} (f)\le \max \{\unicode{x3bb} _1,\unicode{x3bb} _2\}$
.
$\unicode{x3bb} (f)\le \max \{\unicode{x3bb} _1,\unicode{x3bb} _2\}$
.
Corollary 2.4.2. Let
![]() $n\ge 2$
and let
$n\ge 2$
and let
![]() $f\in \operatorname {\mathrm {Aut}}(\mathbb {A}^n)$
be an automorphism such that
$f\in \operatorname {\mathrm {Aut}}(\mathbb {A}^n)$
be an automorphism such that
![]() $f_1,\ldots ,f_{n-2}\in \mathbf {k}[x_1,\ldots ,x_{n-2}]$
and such that the dynamical degree of
$f_1,\ldots ,f_{n-2}\in \mathbf {k}[x_1,\ldots ,x_{n-2}]$
and such that the dynamical degree of
![]() $g=(f_1,\ldots ,f_{n-2}) \in \operatorname {\mathrm {Aut}}(\mathbb {A}^{n-2})$
is an integer. Then, the dynamical degree of f is an integer.
$g=(f_1,\ldots ,f_{n-2}) \in \operatorname {\mathrm {Aut}}(\mathbb {A}^{n-2})$
is an integer. Then, the dynamical degree of f is an integer.
Proof. By Lemma 2.4.1, one has
![]() $\unicode{x3bb} (f)=\max \{\unicode{x3bb} (g),\unicode{x3bb} _2\}$
, where
$\unicode{x3bb} (f)=\max \{\unicode{x3bb} (g),\unicode{x3bb} _2\}$
, where
It remains to see that
![]() $\unicode{x3bb} _2$
is an integer. As
$\unicode{x3bb} _2$
is an integer. As
![]() $\mathbf {k}[x_1,\ldots ,x_{n-2},f_{n-1},f_{n}]=\mathbf {k}[x_1,\ldots ,x_{n}]$
, one has
$\mathbf {k}[x_1,\ldots ,x_{n-2},f_{n-1},f_{n}]=\mathbf {k}[x_1,\ldots ,x_{n}]$
, one has
![]() $K[f_{n-1},f_{n}]=K[x_{n-1},x_n]$
, where
$K[f_{n-1},f_{n}]=K[x_{n-1},x_n]$
, where
![]() $K=\mathbf {k}(x_1,\ldots ,x_{n-2})$
. Hence, one can see the automorphism
$K=\mathbf {k}(x_1,\ldots ,x_{n-2})$
. Hence, one can see the automorphism
![]() $(x_1,\ldots ,x_n)\mapsto (x_1,\ldots ,x_{n-1},f_{n-1},f_{n})$
of
$(x_1,\ldots ,x_n)\mapsto (x_1,\ldots ,x_{n-1},f_{n-1},f_{n})$
of
![]() ${\mathbb A}^n$
as an automorphism
${\mathbb A}^n$
as an automorphism
![]() $F\in \operatorname {\mathrm {Aut}}_K(\mathbb {A}^2)$
of
$F\in \operatorname {\mathrm {Aut}}_K(\mathbb {A}^2)$
of
![]() $\mathbb {A}^2$
defined over K. For each
$\mathbb {A}^2$
defined over K. For each
![]() $i \geq 0$
, the automorphism
$i \geq 0$
, the automorphism
![]() $g^{-i} \circ (x_1,\ldots ,x_{n-1},f_{n-1},f_{n}) \circ g^i$
of
$g^{-i} \circ (x_1,\ldots ,x_{n-1},f_{n-1},f_{n}) \circ g^i$
of
![]() ${\mathbb A}^n$
can be seen as an element of
${\mathbb A}^n$
can be seen as an element of
![]() $\operatorname {\mathrm {Aut}}_K({\mathbb A}^2)$
that we denote by
$\operatorname {\mathrm {Aut}}_K({\mathbb A}^2)$
that we denote by
![]() $F^{g^i}$
, where we identify g with the automorphism
$F^{g^i}$
, where we identify g with the automorphism
![]() $(f_1, \ldots , f_{n-2}, x_{n-1}, x_n) \in \operatorname {\mathrm {Aut}}({\mathbb A}^n)$
. This gives
$(f_1, \ldots , f_{n-2}, x_{n-1}, x_n) \in \operatorname {\mathrm {Aut}}({\mathbb A}^n)$
. This gives
where
![]() $G_r=F^{g^{r-1}} \circ \cdots \circ F^{g^2} \circ F^{g} \circ F\in \operatorname {\mathrm {Aut}}_K(\mathbb {A}^2)$
, because
$G_r=F^{g^{r-1}} \circ \cdots \circ F^{g^2} \circ F^{g} \circ F\in \operatorname {\mathrm {Aut}}_K(\mathbb {A}^2)$
, because
![]() $G_r = g^{-r} \circ f^r$
when we consider
$G_r = g^{-r} \circ f^r$
when we consider
![]() $G_r$
, g and f as automorphisms of
$G_r$
, g and f as automorphisms of
![]() ${\mathbb A}^n$
.
${\mathbb A}^n$
.
According to the Jung–van der Kulk theorem [Reference JungJun42, Reference van der KulkvdK53], one can write
![]() $F=F_1\circ \cdots \circ F_s$
, where each
$F=F_1\circ \cdots \circ F_s$
, where each
![]() $F_i\in \operatorname {\mathrm {Aut}}_K(\mathbb {A}^2)$
is either triangular or affine. Moreover, one can assume that two consecutive
$F_i\in \operatorname {\mathrm {Aut}}_K(\mathbb {A}^2)$
is either triangular or affine. Moreover, one can assume that two consecutive
![]() $F_i$
are not both affine or both triangular (as otherwise, one may reduce the description), and get then
$F_i$
are not both affine or both triangular (as otherwise, one may reduce the description), and get then
![]() $\deg (F)=\prod _{i=1}^s \deg (F_i)$
(follows by looking at what happens at infinity or by [Reference van den EssenvdE00, Lemma 5.1.2]). We prove that
$\deg (F)=\prod _{i=1}^s \deg (F_i)$
(follows by looking at what happens at infinity or by [Reference van den EssenvdE00, Lemma 5.1.2]). We prove that
![]() $\unicode{x3bb} _2$
is an integer by induction on s. If
$\unicode{x3bb} _2$
is an integer by induction on s. If
![]() $s=1$
, then F is either affine or triangular; this implies that the set
$s=1$
, then F is either affine or triangular; this implies that the set
![]() $\{\deg (G_r)\mid {r\ge 1}\}$
is bounded, so
$\{\deg (G_r)\mid {r\ge 1}\}$
is bounded, so
![]() $\unicode{x3bb} _2=1$
. If
$\unicode{x3bb} _2=1$
. If
![]() $s>1$
and
$s>1$
and
![]() $F_1$
,
$F_1$
,
![]() $F_s$
are both affine or both triangular, so we replace F with
$F_s$
are both affine or both triangular, so we replace F with
![]() $(F_1)^g \circ F\circ F_1^{-1}$
. This replaces
$(F_1)^g \circ F\circ F_1^{-1}$
. This replaces
![]() $G_r=F^{g^{r-1}} \circ \cdots \circ F^{g} \circ F$
with
$G_r=F^{g^{r-1}} \circ \cdots \circ F^{g} \circ F$
with
![]() $\tilde {G}_r=(F_1)^{g^r}\circ G_r\circ F_1^{-1}$
. As
$\tilde {G}_r=(F_1)^{g^r}\circ G_r\circ F_1^{-1}$
. As
![]() $\deg ((F_1)^{g^r})=\deg (F_1)$
for each
$\deg ((F_1)^{g^r})=\deg (F_1)$
for each
![]() $r\ge 1$
, one has
$r\ge 1$
, one has
so this replacement does not change the value of
![]() $\unicode{x3bb} _2$
. As this decreases the value of s, we may assume that
$\unicode{x3bb} _2$
. As this decreases the value of s, we may assume that
![]() $F_1$
and
$F_1$
and
![]() $F_s$
are not both triangular or affine. Hence, for each
$F_s$
are not both triangular or affine. Hence, for each
![]() $r\ge 1$
,
$r\ge 1$
,
![]() $G_r$
is a product of
$G_r$
is a product of
![]() $rs$
elements that are affine or triangular, with no two consecutive in the same group. This gives
$rs$
elements that are affine or triangular, with no two consecutive in the same group. This gives
![]() $\deg (G_r)=\prod _{i=0}^{r-1} \prod _{j=1}^s \deg (F_j^{g^i})=\prod _{i=0}^{r-1} \prod _{j=1}^s \deg (F_j)=\deg (F)^r$
. Hence,
$\deg (G_r)=\prod _{i=0}^{r-1} \prod _{j=1}^s \deg (F_j^{g^i})=\prod _{i=0}^{r-1} \prod _{j=1}^s \deg (F_j)=\deg (F)^r$
. Hence,
![]() $\unicode{x3bb} _2=\deg (F)$
is an integer.
$\unicode{x3bb} _2=\deg (F)$
is an integer.
Corollary 2.4.3. The dynamical degree of any element of
![]() $\operatorname {\mathrm {Aut}}(\mathbb {A}^2)$
is an integer. Similarly, the dynamical degree of any element of
$\operatorname {\mathrm {Aut}}(\mathbb {A}^2)$
is an integer. Similarly, the dynamical degree of any element of
![]() $\operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
(respectively
$\operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
(respectively
![]() $\operatorname {\mathrm {Aut}}(\mathbb {A}^4)$
) which preserves the set of fibres of a linear projection
$\operatorname {\mathrm {Aut}}(\mathbb {A}^4)$
) which preserves the set of fibres of a linear projection
![]() $\mathbb {A}^3\to \mathbb {A}^1$
or
$\mathbb {A}^3\to \mathbb {A}^1$
or
![]() $\mathbb {A}^3\to \mathbb {A}^2$
(respectively
$\mathbb {A}^3\to \mathbb {A}^2$
(respectively
![]() $\mathbb {A}^4\to \mathbb {A}^2$
) is an integer.
$\mathbb {A}^4\to \mathbb {A}^2$
) is an integer.
Proof. The fact that the dynamical degree of any element of
![]() $\operatorname {\mathrm {Aut}}(\mathbb {A}^2)$
is an integer follows from Corollary 2.4.2 applied to
$\operatorname {\mathrm {Aut}}(\mathbb {A}^2)$
is an integer follows from Corollary 2.4.2 applied to
![]() $n=2$
. If
$n=2$
. If
![]() $f\in \operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
is an automorphism that preserves the set of fibres of a linear projection
$f\in \operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
is an automorphism that preserves the set of fibres of a linear projection
![]() $\mathbb {A}^3\to \mathbb {A}^1$
or
$\mathbb {A}^3\to \mathbb {A}^1$
or
![]() $\mathbb {A}^3\to \mathbb {A}^2$
, then one may conjugate by an element of
$\mathbb {A}^3\to \mathbb {A}^2$
, then one may conjugate by an element of
![]() $\operatorname {\mathrm {GL}}_3$
and obtain
$\operatorname {\mathrm {GL}}_3$
and obtain
![]() $f=(f_1,f_2,f_3)$
with either
$f=(f_1,f_2,f_3)$
with either
![]() $f_1\in \mathbf {k}[x_1]$
or
$f_1\in \mathbf {k}[x_1]$
or
![]() $f_1,f_2\in \mathbf {k}[x_1,x_2]$
. The fact that
$f_1,f_2\in \mathbf {k}[x_1,x_2]$
. The fact that
![]() $\unicode{x3bb} (f)$
is an integer follows then from Corollary 2.4.2 and Lemma 2.4.1, respectively (in the second case, one uses the fact that the dynamical degree of
$\unicode{x3bb} (f)$
is an integer follows then from Corollary 2.4.2 and Lemma 2.4.1, respectively (in the second case, one uses the fact that the dynamical degree of
![]() $(f_1, f_2) \in \operatorname {\mathrm {Aut}}({\mathbb A}^2)$
is an integer). Similarly, in the case of an automorphism of
$(f_1, f_2) \in \operatorname {\mathrm {Aut}}({\mathbb A}^2)$
is an integer). Similarly, in the case of an automorphism of
![]() $\mathbb {A}^4$
preserving a linear projection
$\mathbb {A}^4$
preserving a linear projection
![]() $\mathbb {A}^4\to \mathbb {A}^2$
, one restricts to the case
$\mathbb {A}^4\to \mathbb {A}^2$
, one restricts to the case
![]() $f=(f_1,\ldots ,f_4)\in \operatorname {\mathrm {Aut}}(\mathbb {A}^4)$
with
$f=(f_1,\ldots ,f_4)\in \operatorname {\mathrm {Aut}}(\mathbb {A}^4)$
with
![]() $f_1,f_2\in \mathbf {k}[x_1,x_2]$
, and applies Corollary 2.4.2.
$f_1,f_2\in \mathbf {k}[x_1,x_2]$
, and applies Corollary 2.4.2.
2.5 Homogeneous endomorphisms
Lemma 2.5.1. Let
![]() $h = (h_1, \ldots , h_n) \in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
, let
$h = (h_1, \ldots , h_n) \in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
, let
![]() $\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n\setminus \{0\}$
and let
$\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n\setminus \{0\}$
and let
![]() $\theta \in {\mathbb R}_{\ge 0}$
. The following conditions are equivalent.
$\theta \in {\mathbb R}_{\ge 0}$
. The following conditions are equivalent.
-
(1) The polynomial
 $h_i$
is
$h_i$
is
 $\mu $
-homogeneous of degree
$\mu $
-homogeneous of degree
 $\theta \mu _i$
for each
$\theta \mu _i$
for each
 $i\in \{1,\ldots ,n\}$
.
$i\in \{1,\ldots ,n\}$
. -
(2) For each
 $\mu $
-homogeneous polynomial p of degree
$\mu $
-homogeneous polynomial p of degree
 $\xi $
and each integer
$\xi $
and each integer
 $r\ge 1$
, the polynomial
$r\ge 1$
, the polynomial
 $p \circ h^r$
is
$p \circ h^r$
is
 $\mu $
-homogeneous of degree
$\mu $
-homogeneous of degree
 $\theta ^r \xi $
.
$\theta ^r \xi $
.
If additionally
![]() $h_i \neq 0$
for each
$h_i \neq 0$
for each
![]() $i \in \{1, \ldots , n\}$
, then conditions (1) and (2) are equivalent to the following.
$i \in \{1, \ldots , n\}$
, then conditions (1) and (2) are equivalent to the following.
-
(3) For each matrix M contained in h,
 $\mu $
is an eigenvector to the eigenvalue
$\mu $
is an eigenvector to the eigenvalue
 $\theta $
.
$\theta $
.
Proof. The implication condition (2)
![]() $\Rightarrow $
(1) is given by choosing
$\Rightarrow $
(1) is given by choosing
![]() $p=x_i$
for
$p=x_i$
for
![]() $i = 1, \ldots , n$
, so we may assume condition (1) and prove condition (2). It suffices to prove condition (2) for
$i = 1, \ldots , n$
, so we may assume condition (1) and prove condition (2). It suffices to prove condition (2) for
![]() $r=1$
, as the general result follows by induction.
$r=1$
, as the general result follows by induction.
If
![]() $p=0$
, then
$p=0$
, then
![]() $h(p)=0$
is
$h(p)=0$
is
![]() $\mu $
-homogeneous of any degree. It then suffices to do the case where p is a monomial: we write
$\mu $
-homogeneous of any degree. It then suffices to do the case where p is a monomial: we write
![]() $p=\zeta x_1^{a_1}x_2^{a_2}\cdots x_n^{a_n}$
with
$p=\zeta x_1^{a_1}x_2^{a_2}\cdots x_n^{a_n}$
with
![]() $\zeta \in \mathbf {k}^*$
,
$\zeta \in \mathbf {k}^*$
,
![]() $a_1,\ldots ,a_n\ge 0$
, which is
$a_1,\ldots ,a_n\ge 0$
, which is
![]() $\mu $
-homogeneous of degree
$\mu $
-homogeneous of degree
![]() $\deg _\mu (p)=\sum _{i=1}^n a_i\mu _i$
. As
$\deg _\mu (p)=\sum _{i=1}^n a_i\mu _i$
. As
![]() $h_i$
is
$h_i$
is
![]() $\mu $
-homogeneous of degree
$\mu $
-homogeneous of degree
![]() $\theta \mu _i$
, the polynomial
$\theta \mu _i$
, the polynomial
![]() $p\circ h=\zeta h_1^{a_1}h_2^{a_2}\cdots h_n^{a_n}$
is
$p\circ h=\zeta h_1^{a_1}h_2^{a_2}\cdots h_n^{a_n}$
is
![]() $\mu $
-homogeneous of degree
$\mu $
-homogeneous of degree
![]() $\sum _{i=1}^n a_i \theta \mu _i=\theta \deg _\mu (p)$
.
$\sum _{i=1}^n a_i \theta \mu _i=\theta \deg _\mu (p)$
.
Now, we assume additionally that
![]() $h_i \neq 0$
for each
$h_i \neq 0$
for each
![]() $i \in \{1, \ldots , n\}$
. The equivalence between conditions (1) and (3) follows immediately from the definition of the
$i \in \{1, \ldots , n\}$
. The equivalence between conditions (1) and (3) follows immediately from the definition of the
![]() $\mu $
-degree.
$\mu $
-degree.
Definition 2.5.2. Let
![]() $\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n\setminus \{0\}$
and let
$\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n\setminus \{0\}$
and let
![]() $\theta \in {\mathbb R}_{\ge 0}$
. We say that
$\theta \in {\mathbb R}_{\ge 0}$
. We say that
![]() $h \in \operatorname {\mathrm {End}}({\mathbb A}^n)$
is
$h \in \operatorname {\mathrm {End}}({\mathbb A}^n)$
is
![]() $\mu $
-homogeneous of degree
$\mu $
-homogeneous of degree
![]() $\theta $
if the conditions of Lemma 2.5.1 are satisfied.
$\theta $
if the conditions of Lemma 2.5.1 are satisfied.
Lemma 2.5.3. Let
![]() $\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n\setminus \{0\}$
. For each
$\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n\setminus \{0\}$
. For each
![]() $f=(f_1,\ldots ,f_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
and each
$f=(f_1,\ldots ,f_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
and each
![]() $\theta \in {\mathbb R}_{\ge 0}$
, the following are equivalent:
$\theta \in {\mathbb R}_{\ge 0}$
, the following are equivalent:
-
(1) we can write f as a finite sum
 $f=\sum _{0\le \xi \le \theta } g_\xi $
, where each
$f=\sum _{0\le \xi \le \theta } g_\xi $
, where each
 $g_\xi \in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
is
$g_\xi \in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
is
 $\mu $
-homogeneous of degree
$\mu $
-homogeneous of degree
 $\xi $
;
$\xi $
; -
(2)
 $\deg _\mu (f)\le \theta $
.
$\deg _\mu (f)\le \theta $
.
Proof. Condition (1)
![]() $\Rightarrow $
(2): For each
$\Rightarrow $
(2): For each
![]() $i\in \{1,\ldots ,n\}$
, the polynomial
$i\in \{1,\ldots ,n\}$
, the polynomial
![]() $f_i$
is the sum of the ith components of the endomorphisms
$f_i$
is the sum of the ith components of the endomorphisms
![]() $g_{\xi }$
. As each of these polynomials has degree
$g_{\xi }$
. As each of these polynomials has degree
![]() $\xi \mu _i\le \theta \mu _i$
, the polynomial
$\xi \mu _i\le \theta \mu _i$
, the polynomial
![]() $f_i$
is of
$f_i$
is of
![]() $\mu $
-degree
$\mu $
-degree
![]() $\deg _\mu (f_i)\le \theta \mu _i$
.
$\deg _\mu (f_i)\le \theta \mu _i$
.
Condition (2)
![]() $\Rightarrow $
(1): As in Remark 2.3.1(1), we write each
$\Rightarrow $
(1): As in Remark 2.3.1(1), we write each
![]() $f_i$
,
$f_i$
,
![]() $i\in \{1,\ldots ,n\}$
as
$i\in \{1,\ldots ,n\}$
as
![]() $f_i=\sum _{0\le \kappa \le \theta \mu _i} p_{i,\kappa }$
, where each
$f_i=\sum _{0\le \kappa \le \theta \mu _i} p_{i,\kappa }$
, where each
![]() $p_{i,\kappa }$
is
$p_{i,\kappa }$
is
![]() $\mu $
-homogeneous of degree
$\mu $
-homogeneous of degree
![]() $\kappa $
.
$\kappa $
.
We define
![]() $g_0=(p_{1,0},\ldots ,p_{n,0})\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
, which is
$g_0=(p_{1,0},\ldots ,p_{n,0})\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
, which is
![]() $\mu $
-homogeneous of degree
$\mu $
-homogeneous of degree
![]() $0$
.
$0$
.
For each
![]() $\xi \in {\mathbb R}$
with
$\xi \in {\mathbb R}$
with
![]() $0\le \xi \le \theta $
, we define the ith component
$0\le \xi \le \theta $
, we define the ith component
![]() $(g_\xi )_i$
of
$(g_\xi )_i$
of
![]() $g_\xi $
as follows: if
$g_\xi $
as follows: if
![]() $\mu _i=0$
and
$\mu _i=0$
and
![]() $\xi> 0$
, then
$\xi> 0$
, then
![]() $(g_\xi )_i=0$
and otherwise, we choose
$(g_\xi )_i=0$
and otherwise, we choose
![]() $(g_\xi )_i=p_{i,\xi \mu _i}$
. By construction,
$(g_\xi )_i=p_{i,\xi \mu _i}$
. By construction,
![]() $g_\xi $
is
$g_\xi $
is
![]() $\mu $
-homogeneous of degree
$\mu $
-homogeneous of degree
![]() $\xi $
.
$\xi $
.
Moreover,
![]() $f_i=\sum _{0\le \kappa \le \theta \mu _i} p_{i,\kappa }=\sum _{0\le \xi \le \theta } (g_{\xi })_i$
for each
$f_i=\sum _{0\le \kappa \le \theta \mu _i} p_{i,\kappa }=\sum _{0\le \xi \le \theta } (g_{\xi })_i$
for each
![]() $i\in \{1,\ldots ,n\}$
with
$i\in \{1,\ldots ,n\}$
with
![]() ${\mu _i>0}$
. If
${\mu _i>0}$
. If
![]() $\mu _i=0$
, then
$\mu _i=0$
, then
![]() $f_i=\sum _{0\le \kappa \le \theta \mu _i} p_{i,\kappa }=p_{i,0}=\sum _{0\le \xi \le \theta } (g_{\xi })_i$
. This yields
$f_i=\sum _{0\le \kappa \le \theta \mu _i} p_{i,\kappa }=p_{i,0}=\sum _{0\le \xi \le \theta } (g_{\xi })_i$
. This yields
![]() $f=\sum _{0\le \xi \le \theta } g_\xi $
.here
$f=\sum _{0\le \xi \le \theta } g_\xi $
.here
Remark 2.5.4. In the decomposition of Lemma 2.5.3(1), the ith component of each
![]() $g_{\xi }$
is unique if
$g_{\xi }$
is unique if
![]() $\mu _i>0$
, but is not unique if
$\mu _i>0$
, but is not unique if
![]() $\mu _i=0$
.
$\mu _i=0$
.
Example 2.5.5. We have
![]() $\deg _{(1,\ldots ,1)}(f)=\deg (f)$
and
$\deg _{(1,\ldots ,1)}(f)=\deg (f)$
and
![]() $\deg _\mu (\operatorname {\mathrm {id}}_{\mathbb {A}^n})=1$
for each
$\deg _\mu (\operatorname {\mathrm {id}}_{\mathbb {A}^n})=1$
for each
![]() $\mu \in (\mathbb {R}_{\ge 0})^n\setminus \{0\}$
. However,
$\mu \in (\mathbb {R}_{\ge 0})^n\setminus \{0\}$
. However,
![]() $\deg _{(2,3,0)}(x_1,x_2+x_1^2x_3,x_3)=\tfrac 43$
.
$\deg _{(2,3,0)}(x_1,x_2+x_1^2x_3,x_3)=\tfrac 43$
.
Lemma 2.5.6. Let
![]() $\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n\setminus \{0\}$
. For each
$\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n\setminus \{0\}$
. For each
![]() $f=(f_1,\ldots ,f_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
, the following are equivalent:
$f=(f_1,\ldots ,f_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
, the following are equivalent:
-
(1)
 $\deg _\mu (f)<\infty $
;
$\deg _\mu (f)<\infty $
; -
(2) for each
 $i\in \{1,\ldots ,n\}$
such that
$i\in \{1,\ldots ,n\}$
such that
 $\mu _i=0$
, the element
$\mu _i=0$
, the element
 $f_i$
is a polynomial in the variables
$f_i$
is a polynomial in the variables
 $\{x_j\mid j\in \{1,\ldots ,n\},\mu _j=0\}$
.
$\{x_j\mid j\in \{1,\ldots ,n\},\mu _j=0\}$
.
In particular, if
![]() $\mu \in (\mathbb {R}_{>0})^n$
, then the above conditions hold.
$\mu \in (\mathbb {R}_{>0})^n$
, then the above conditions hold.
Proof. Condition (1)
![]() $\Rightarrow $
(2): Suppose that
$\Rightarrow $
(2): Suppose that
![]() $\theta =\deg _\mu (f)<\infty $
. For each
$\theta =\deg _\mu (f)<\infty $
. For each
![]() $i\in \{1,\ldots ,n\}$
, we get
$i\in \{1,\ldots ,n\}$
, we get
![]() $\deg _\mu (f_i)\le \theta \mu _i$
(Definition 1.4.3). If
$\deg _\mu (f_i)\le \theta \mu _i$
(Definition 1.4.3). If
![]() $\mu _i=0$
, then
$\mu _i=0$
, then
![]() $\deg _\mu (f_i)=0$
, which means that
$\deg _\mu (f_i)=0$
, which means that
![]() $f_i$
is a polynomial in the variables
$f_i$
is a polynomial in the variables
![]() $\{x_j\mid j\in \{1,\ldots ,n\},\mu _j=0\}$
.
$\{x_j\mid j\in \{1,\ldots ,n\},\mu _j=0\}$
.
Condition (2)
![]() $\Rightarrow $
(1): It follows from condition (2) that
$\Rightarrow $
(1): It follows from condition (2) that
![]() $\deg _\mu (f_i) \leq 0$
for each
$\deg _\mu (f_i) \leq 0$
for each
![]() $i\in \{1,\ldots ,n\}$
such that
$i\in \{1,\ldots ,n\}$
such that
![]() $\mu _i=0$
. This gives
$\mu _i=0$
. This gives
![]() $\deg _\mu (f)=\max \{ \deg _\mu (f_i) / \mu _i \, | \, \mu _i>0 \}<\infty $
.
$\deg _\mu (f)=\max \{ \deg _\mu (f_i) / \mu _i \, | \, \mu _i>0 \}<\infty $
.
Lemma 2.5.7. Let
![]() $f=(f_1,\ldots ,f_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
be a dominant endomorphism. For each maximal eigenvector
$f=(f_1,\ldots ,f_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
be a dominant endomorphism. For each maximal eigenvector
![]() $\mu $
of f, the
$\mu $
of f, the
![]() $\mu $
-leading part
$\mu $
-leading part
![]() $g=(g_1, \ldots , g_n) \in \operatorname {\mathrm {End}}({\mathbb A}^n)$
of f has the following properties:
$g=(g_1, \ldots , g_n) \in \operatorname {\mathrm {End}}({\mathbb A}^n)$
of f has the following properties:
-
(1) the maximal eigenvalue
 $\theta $
of f is such that
$\theta $
of f is such that
 $\deg _\mu (g)=\deg _\mu (f)=\theta < \infty ;$
$\deg _\mu (g)=\deg _\mu (f)=\theta < \infty ;$
-
(2) for each
 $i\in \{1,\ldots ,n\}$
, the polynomial
$i\in \{1,\ldots ,n\}$
, the polynomial
 $g_i$
is non-constant.
$g_i$
is non-constant.
Proof. As
![]() $\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n$
is a maximal eigenvector of f, we have
$\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n$
is a maximal eigenvector of f, we have
![]() $\deg _\mu (f_i)= \theta \mu _i$
for each
$\deg _\mu (f_i)= \theta \mu _i$
for each
![]() $i\in \{1,\ldots ,n\}$
, where
$i\in \{1,\ldots ,n\}$
, where
![]() $\theta $
is the maximal eigenvalue of f. This gives
$\theta $
is the maximal eigenvalue of f. This gives
![]() $\deg _\mu (f)=\theta < \infty $
and therefore
$\deg _\mu (f)=\theta < \infty $
and therefore
![]() $\deg _\mu (g_i)=\theta \mu _i=\deg _\mu (f_i)$
for each
$\deg _\mu (g_i)=\theta \mu _i=\deg _\mu (f_i)$
for each
![]() $i\in \{1,\ldots ,n\}$
. Hence, we get property (1). In case
$i\in \{1,\ldots ,n\}$
. Hence, we get property (1). In case
![]() $\mu _i> 0$
, we have
$\mu _i> 0$
, we have
![]() $\deg _\mu (g_i) = \theta \mu _i> 0$
and thus
$\deg _\mu (g_i) = \theta \mu _i> 0$
and thus
![]() $g_i$
is non-constant. In case
$g_i$
is non-constant. In case
![]() $\mu _i = 0$
, we have
$\mu _i = 0$
, we have
![]() $\deg _\mu (f_i) = \theta \mu _i = 0$
and thus
$\deg _\mu (f_i) = \theta \mu _i = 0$
and thus
![]() $g_i = f_i$
. As f is dominant, the latter polynomial is non-constant. This shows property (2).
$g_i = f_i$
. As f is dominant, the latter polynomial is non-constant. This shows property (2).
2.6 Inequalities obtained by iterations
Lemma 2.6.1. Let
![]() $f=(f_1,\ldots ,f_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
be a dominant endomorphism. Suppose that
$f=(f_1,\ldots ,f_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
be a dominant endomorphism. Suppose that
![]() $\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n$
and that
$\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n$
and that
![]() $\theta = \deg _\mu (f) \in {\mathbb R}_{\geq 0}$
. Let
$\theta = \deg _\mu (f) \in {\mathbb R}_{\geq 0}$
. Let
![]() $g=(g_1,\ldots ,g_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
be the
$g=(g_1,\ldots ,g_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
be the
![]() $\mu $
-leading part of f. Then the following hold.
$\mu $
-leading part of f. Then the following hold.
-
(1) We can write f as a finite sum
 $f=g+\sum _{0\le \xi < \theta } g_\xi $
, where each
$f=g+\sum _{0\le \xi < \theta } g_\xi $
, where each
 $g_\xi \in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
is
$g_\xi \in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
is
 $\mu $
-homogeneous of degree
$\mu $
-homogeneous of degree
 $\xi $
.
$\xi $
. -
(2) The ith coordinate function
 $(g^r)_i$
of
$(g^r)_i$
of
 $g^r$
is the
$g^r$
is the
 $\mu $
-homogeneous part of degree
$\mu $
-homogeneous part of degree
 $\theta ^r \mu _i$
of
$\theta ^r \mu _i$
of
 $(f^r)_i$
for each
$(f^r)_i$
for each
 $i\in \{1,\ldots ,n\}$
and each
$i\in \{1,\ldots ,n\}$
and each
 $r\ge 1$
.
$r\ge 1$
. -
(3)
 $\deg _\mu (f^r)\le \theta ^r$
for each
$\deg _\mu (f^r)\le \theta ^r$
for each
 $r\ge 1$
.
$r\ge 1$
. -
(4) We have
 $$ \begin{align*} 1\le \lim\limits_{r\to\infty} \max\limits_{i\in \{1,\ldots,n\}} \deg_\mu ((f^r)_i)^{1/r} =\lim\limits_{r\to\infty}(\deg_\mu(f^r))^{1/r}\le \theta. \end{align*} $$
$$ \begin{align*} 1\le \lim\limits_{r\to\infty} \max\limits_{i\in \{1,\ldots,n\}} \deg_\mu ((f^r)_i)^{1/r} =\lim\limits_{r\to\infty}(\deg_\mu(f^r))^{1/r}\le \theta. \end{align*} $$
-
(5) If
 $\theta> 1$
, the following are equivalent:
$\theta> 1$
, the following are equivalent:-
(i)
 $\lim _{r\to \infty }(\deg _\mu (f^r))^{1/r} = \theta $
;
$\lim _{r\to \infty }(\deg _\mu (f^r))^{1/r} = \theta $
; -
(ii) f is
 $\mu $
-algebraically stable;
$\mu $
-algebraically stable; -
(iii) for each
 $r\ge 1$
, there is
$r\ge 1$
, there is
 $i\in \{1,\ldots ,n\}$
with
$i\in \{1,\ldots ,n\}$
with
 $\mu _i>0$
and
$\mu _i>0$
and
 $(g^r)_i\not =0$
.
$(g^r)_i\not =0$
.
-
Proof. As
![]() $\deg _\mu (f) = \theta $
, we have
$\deg _\mu (f) = \theta $
, we have
![]() $\deg _\mu (f_i)\le \theta \mu _i$
for each
$\deg _\mu (f_i)\le \theta \mu _i$
for each
![]() $i\in \{1,\ldots ,n\}$
. Moreover, as f is dominant and
$i\in \{1,\ldots ,n\}$
. Moreover, as f is dominant and
![]() $\mu \not =0$
, there are
$\mu \not =0$
, there are
![]() $i,j\in \{1,\ldots ,n\}$
such that
$i,j\in \{1,\ldots ,n\}$
such that
![]() $\mu _i>0$
and
$\mu _i>0$
and
![]() $\deg _{x_i}(f_j)\ge 1$
. This implies that
$\deg _{x_i}(f_j)\ge 1$
. This implies that
![]() $\deg _\mu (f_j)\ge \mu _i>0$
and thus
$\deg _\mu (f_j)\ge \mu _i>0$
and thus
We now observe that
![]() $\deg _\mu (f-g)<\theta $
. Indeed, for each
$\deg _\mu (f-g)<\theta $
. Indeed, for each
![]() $j\in \{1,\ldots ,n\}$
, the jth component
$j\in \{1,\ldots ,n\}$
, the jth component
![]() $g_j$
of g is the
$g_j$
of g is the
![]() $\mu $
-homogeneous part of
$\mu $
-homogeneous part of
![]() $f_j$
of degree
$f_j$
of degree
![]() $\theta \mu _j\ge \deg _\mu (f_j)$
. If
$\theta \mu _j\ge \deg _\mu (f_j)$
. If
![]() $\mu _j=0$
, then
$\mu _j=0$
, then
![]() $f_j=g_j$
, and if
$f_j=g_j$
, and if
![]() $\mu _j>0$
, then
$\mu _j>0$
, then
![]() $\deg _\mu (f_j-g_j)<\theta \mu _j$
.
$\deg _\mu (f_j-g_j)<\theta \mu _j$
.
By Lemma 2.5.3, we can write
![]() $f-g$
as a finite sum
$f-g$
as a finite sum
![]() $f-g=\sum _{0\le \xi <\theta } g_\xi $
, where each
$f-g=\sum _{0\le \xi <\theta } g_\xi $
, where each
![]() $g_\xi \in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
is
$g_\xi \in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
is
![]() $\mu $
-homogeneous of degree
$\mu $
-homogeneous of degree
![]() $\xi $
. This gives assertion (1).
$\xi $
. This gives assertion (1).
We now prove assertions (2)–(3) by induction on
![]() $r\ge 1$
. For
$r\ge 1$
. For
![]() $r=1$
, assertion (2) follows from the definition of g. Moreover, assertion (3) is given by hypothesis.
$r=1$
, assertion (2) follows from the definition of g. Moreover, assertion (3) is given by hypothesis.
We now assume assertions (2)–(3) for some integer
![]() $r\ge 1$
and prove them for
$r\ge 1$
and prove them for
![]() $r+1$
. For each
$r+1$
. For each
![]() $i\in \{1,\ldots ,r\}$
, we write
$i\in \{1,\ldots ,r\}$
, we write
![]() $(f^{r})_i=(g^{r})_i+s_i$
, where
$(f^{r})_i=(g^{r})_i+s_i$
, where
![]() $(g^{r})_i$
is
$(g^{r})_i$
is
![]() $\mu $
-homogeneous of degree
$\mu $
-homogeneous of degree
![]() $\theta ^r\mu _i$
and
$\theta ^r\mu _i$
and
![]() $\deg _\mu (s_i)<\theta ^r\mu _i$
. This gives
$\deg _\mu (s_i)<\theta ^r\mu _i$
. This gives
 $$ \begin{align*} (f^{r+1})_i&=((g^{r})_i+s_i) \circ f \\ &\stackrel{\scriptsize({1})}{=} (g^{r+1})_i +s_i \circ g +\displaystyle\sum\limits_{0\le \xi< \theta} ((g^{r})_i+s_i) \circ g_\xi . \end{align*} $$
$$ \begin{align*} (f^{r+1})_i&=((g^{r})_i+s_i) \circ f \\ &\stackrel{\scriptsize({1})}{=} (g^{r+1})_i +s_i \circ g +\displaystyle\sum\limits_{0\le \xi< \theta} ((g^{r})_i+s_i) \circ g_\xi . \end{align*} $$
As g is
![]() $\mu $
-homogeneous of degree
$\mu $
-homogeneous of degree
![]() $\theta $
, the polynomial
$\theta $
, the polynomial
![]() $(g^{r+1})_i$
is
$(g^{r+1})_i$
is
![]() $\mu $
-homogeneous of degree
$\mu $
-homogeneous of degree
![]() $\theta ^{r+1}\mu _i$
(Lemma 2.5.1). As
$\theta ^{r+1}\mu _i$
(Lemma 2.5.1). As
![]() $s_i$
is a sum of
$s_i$
is a sum of
![]() $\mu $
-homogeneous polynomials of degree
$\mu $
-homogeneous polynomials of degree
![]() $<\theta ^r\mu _i$
and
$<\theta ^r\mu _i$
and
![]() $g_\xi $
is
$g_\xi $
is
![]() $\mu $
-homogeneous of degree
$\mu $
-homogeneous of degree
![]() $\xi <\theta $
, we have
$\xi <\theta $
, we have
 $$ \begin{align*} \deg_\mu\bigg( s_i \circ g +\sum\limits_{0\le \xi< \theta} ((g^{r})_i+s_i) \circ g_\xi \bigg)< \theta^{r+1}\mu_i \end{align*} $$
$$ \begin{align*} \deg_\mu\bigg( s_i \circ g +\sum\limits_{0\le \xi< \theta} ((g^{r})_i+s_i) \circ g_\xi \bigg)< \theta^{r+1}\mu_i \end{align*} $$
(by using Lemma 2.5.1 again). This yields assertions (2)–(3) for
![]() $r+1$
.
$r+1$
.
We now prove assertion (4). We choose
![]() $i\in \{1,\ldots ,n\}$
such that
$i\in \{1,\ldots ,n\}$
such that
![]() $\mu _i=\max \{\mu _1,\ldots , \mu _n\}$
, and observe that for each
$\mu _i=\max \{\mu _1,\ldots , \mu _n\}$
, and observe that for each
![]() $r\ge 1$
, there is
$r\ge 1$
, there is
![]() $j\in \{1,\ldots ,n\}$
such that
$j\in \{1,\ldots ,n\}$
such that
![]() $\deg _{x_i}((f^r)_j)>0$
(as f is dominant), so
$\deg _{x_i}((f^r)_j)>0$
(as f is dominant), so
![]() $\deg _\mu ((f^r)_j) \ge \mu _i = \max \{\mu _1,\ldots ,\mu _n\}>0$
. This implies that
$\deg _\mu ((f^r)_j) \ge \mu _i = \max \{\mu _1,\ldots ,\mu _n\}>0$
. This implies that
(the limit exists by Remark 2.3.1(2)). Let us write
![]() $I_0=\{i\in \{1,\ldots ,n\}\mid \mu _i=0\}$
. For each
$I_0=\{i\in \{1,\ldots ,n\}\mid \mu _i=0\}$
. For each
![]() $i\in I_0$
, we have
$i\in I_0$
, we have
![]() $\deg _\mu (f_i)\le \theta \mu _i=0$
, so
$\deg _\mu (f_i)\le \theta \mu _i=0$
, so
![]() $f_i$
is a polynomial in the variables
$f_i$
is a polynomial in the variables
![]() $\{x_j\mid j\in I_0\}$
. This implies that the same holds for
$\{x_j\mid j\in I_0\}$
. This implies that the same holds for
![]() $(f^r)_i$
, for each integer
$(f^r)_i$
, for each integer
![]() $r\ge 1$
. Hence,
$r\ge 1$
. Hence,
![]() $\deg _\mu ((f^r)_i)=0$
for each
$\deg _\mu ((f^r)_i)=0$
for each
![]() $i\in I_0$
. Writing
$i\in I_0$
. Writing
![]() $I_{>0}=\{i\in \{1,\ldots ,n\}\mid \mu _i>0\}$
, we get for each
$I_{>0}=\{i\in \{1,\ldots ,n\}\mid \mu _i>0\}$
, we get for each
![]() $r\ge 1$
,
$r\ge 1$
,
 $$ \begin{align*} \deg_\mu(f^r)= \max\bigg\{\frac{\deg_\mu((f^r)_i)}{\mu_i} \bigg| i\in I_{>0}\bigg\}. \end{align*} $$
$$ \begin{align*} \deg_\mu(f^r)= \max\bigg\{\frac{\deg_\mu((f^r)_i)}{\mu_i} \bigg| i\in I_{>0}\bigg\}. \end{align*} $$
As
![]() $\deg _\mu (f^r)\le \theta ^r$
(assertion (3)), we obtain
$\deg _\mu (f^r)\le \theta ^r$
(assertion (3)), we obtain
It remains to prove assertion (5); for this, we assume that
![]() $\theta> 1$
. For each
$\theta> 1$
. For each
![]() $r\ge 1$
, assertion (3) gives
$r\ge 1$
, assertion (3) gives
![]() $\deg _\mu (f^r)\le \theta ^r$
, or equivalently
$\deg _\mu (f^r)\le \theta ^r$
, or equivalently
![]() $\deg _\mu ((f^r)_i)\le \theta ^r \mu _i$
for each
$\deg _\mu ((f^r)_i)\le \theta ^r \mu _i$
for each
![]() $i\in \{1,\ldots ,n\}$
. The equality
$i\in \{1,\ldots ,n\}$
. The equality
![]() $\deg _\mu (f^r) = \theta ^r$
holds if and only if there exists
$\deg _\mu (f^r) = \theta ^r$
holds if and only if there exists
![]() $i\in \{1,\ldots ,n\}$
such that
$i\in \{1,\ldots ,n\}$
such that
![]() $\mu _i>0$
and
$\mu _i>0$
and
![]() $\deg _\mu ((f^r)_i)= \theta ^r \mu _i$
. Because
$\deg _\mu ((f^r)_i)= \theta ^r \mu _i$
. Because
![]() $(g^r)_i$
is the
$(g^r)_i$
is the
![]() $\mu $
-homogeneous part of
$\mu $
-homogeneous part of
![]() $(f^r)_i$
of degree
$(f^r)_i$
of degree
![]() $\theta ^r \mu _i$
(follows from assertion (2)), this gives the equivalence between assertions (ii) and (iii). It remains then to prove assertion (5)
$\theta ^r \mu _i$
(follows from assertion (2)), this gives the equivalence between assertions (ii) and (iii). It remains then to prove assertion (5)
![]() $\Leftrightarrow $
(5).
$\Leftrightarrow $
(5).
‘Assertion (5)
![]() $\Rightarrow $
(5)’: Suppose that for each
$\Rightarrow $
(5)’: Suppose that for each
![]() $r\ge 1$
, there is
$r\ge 1$
, there is
![]() $i\in \{1,\ldots ,n\}$
such that
$i\in \{1,\ldots ,n\}$
such that
![]() $\mu _i>0$
and
$\mu _i>0$
and
![]() $(g^r)_i\not =0$
. There is then
$(g^r)_i\not =0$
. There is then
![]() $j\in \{1,\ldots ,n\}$
and an infinite set
$j\in \{1,\ldots ,n\}$
and an infinite set
![]() $I\subset \mathbb {N}$
such that
$I\subset \mathbb {N}$
such that
![]() $\mu _j>0$
and
$\mu _j>0$
and
![]() $(g^r)_j\not =0$
for each
$(g^r)_j\not =0$
for each
![]() $r\in I$
. Assertion (2) implies that
$r\in I$
. Assertion (2) implies that
![]() $\deg _\mu ((f^r)_j)\ge \theta ^r\mu _j$
, for each
$\deg _\mu ((f^r)_j)\ge \theta ^r\mu _j$
, for each
![]() $r\in I$
, which implies that
$r\in I$
, which implies that
This, together with assertion (4), gives
![]() $\lim _{r\to \infty }(\deg _\mu (f^r))^{1/r} = \theta $
.
$\lim _{r\to \infty }(\deg _\mu (f^r))^{1/r} = \theta $
.
‘Assertion (5)
![]() $\Rightarrow $
(5)’: Conversely, suppose that there exists
$\Rightarrow $
(5)’: Conversely, suppose that there exists
![]() $s\ge 1$
such that
$s\ge 1$
such that
![]() $(g^s)_i=0$
for each
$(g^s)_i=0$
for each
![]() $i\in \{1,\ldots ,n\}$
with
$i\in \{1,\ldots ,n\}$
with
![]() $\mu _i>0$
. For all such i, we obtain
$\mu _i>0$
. For all such i, we obtain
![]() $\deg _\mu ((f^s)_i)< \theta ^s \mu _i$
(by assertions (2) and (3)). As
$\deg _\mu ((f^s)_i)< \theta ^s \mu _i$
(by assertions (2) and (3)). As
![]() $\theta> 1$
, there exists then
$\theta> 1$
, there exists then
![]() $\theta '\in {\mathbb R}$
with
$\theta '\in {\mathbb R}$
with
![]() $1<\theta '< \theta $
such that
$1<\theta '< \theta $
such that
for each
![]() $i\in \{1,\ldots ,n\}$
. Applying the inequality of assertion (4) for
$i\in \{1,\ldots ,n\}$
. Applying the inequality of assertion (4) for
![]() $f^s$
, we obtain
$f^s$
, we obtain
which gives, by taking the sth root,
 $$ \begin{align*} \displaystyle\lim\limits_{r\to\infty}\Bigg(\max\limits_{i\in \{1,\ldots,n\}} (\deg_\mu (f^r)_i)^{1/r}\Bigg)\le \theta'<\theta.\\[-42pt] \end{align*} $$
$$ \begin{align*} \displaystyle\lim\limits_{r\to\infty}\Bigg(\max\limits_{i\in \{1,\ldots,n\}} (\deg_\mu (f^r)_i)^{1/r}\Bigg)\le \theta'<\theta.\\[-42pt] \end{align*} $$
Now we can give a short proof of Proposition A.
Proof of Proposition A
As
![]() $\mu \in (\mathbb {R}_{> 0})^n$
, we have
$\mu \in (\mathbb {R}_{> 0})^n$
, we have
![]() $\theta : = \deg _\mu (f) < \infty $
(Lemma 2.5.6).
$\theta : = \deg _\mu (f) < \infty $
(Lemma 2.5.6).
By definition, g is the
![]() $\mu $
-leading part of f. Now, Lemma 2.6.1(4) implies that
$\mu $
-leading part of f. Now, Lemma 2.6.1(4) implies that
![]() $1 \leq \unicode{x3bb} (f) \leq \theta $
. If
$1 \leq \unicode{x3bb} (f) \leq \theta $
. If
![]() $\theta> 1$
, we moreover obtain
$\theta> 1$
, we moreover obtain
Another consequence of Lemma 2.6.1 is the following result, that generalizes Proposition A to the case where some coordinates of
![]() $\mu $
are zero.
$\mu $
are zero.
Corollary 2.6.2. Let
![]() $f=(f_1,\ldots ,f_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
be a dominant endomorphism and let
$f=(f_1,\ldots ,f_n)\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
be a dominant endomorphism and let
![]() $\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n$
be such that
$\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n$
be such that
![]() $\theta = \deg _\mu (f) <\infty $
, and assume that
$\theta = \deg _\mu (f) <\infty $
, and assume that
![]() $m\in \{0,\ldots ,n\}$
exists, such that
$m\in \{0,\ldots ,n\}$
exists, such that
![]() $\mu _i=0$
for
$\mu _i=0$
for
![]() $i\in \{1,\ldots ,m\}$
and
$i\in \{1,\ldots ,m\}$
and
![]() $\mu _i>0$
for
$\mu _i>0$
for
![]() $i\in \{m+1,\ldots ,n\}$
(which can always be obtained by conjugating with a permutation). Then, the following hold.
$i\in \{m+1,\ldots ,n\}$
(which can always be obtained by conjugating with a permutation). Then, the following hold.
-
(1) For each
 $i\in \{1,\ldots ,m\}$
, we have
$i\in \{1,\ldots ,m\}$
, we have
 $f_i\in \mathbf {k}[x_1,\ldots ,x_m]$
. Hence, the element
$f_i\in \mathbf {k}[x_1,\ldots ,x_m]$
. Hence, the element
 $\hat {f}= (f_1,\ldots ,f_m)$
belongs to
$\hat {f}= (f_1,\ldots ,f_m)$
belongs to
 $\operatorname {\mathrm {End}}(\mathbb {A}^m)$
.
$\operatorname {\mathrm {End}}(\mathbb {A}^m)$
. -
(2) If
 $\unicode{x3bb} (\hat {f})=\theta $
, then
$\unicode{x3bb} (\hat {f})=\theta $
, then
 $\unicode{x3bb} (f)=\theta $
.
$\unicode{x3bb} (f)=\theta $
. -
(3) If
 $\unicode{x3bb} (\hat {f})<\theta $
, then
$\unicode{x3bb} (\hat {f})<\theta $
, then
 $\unicode{x3bb} (f)=\theta \Leftrightarrow f$
is
$\unicode{x3bb} (f)=\theta \Leftrightarrow f$
is
 $\mu $
-algebraically stable.
$\mu $
-algebraically stable.
Proof. Assertion (1) follows from the fact that
![]() $\deg _\mu (f)<\infty $
and the choice of m (Lemma 2.5.6(2)).
$\deg _\mu (f)<\infty $
and the choice of m (Lemma 2.5.6(2)).
Lemma 2.4.1 then gives
![]() $\unicode{x3bb} (f)=\max \{\unicode{x3bb} (\hat {f}), \lim _{r\to \infty }\deg _{x_{m+1},\ldots ,x_n}(f^r)^{1/r}\}$
. By using the equality
$\unicode{x3bb} (f)=\max \{\unicode{x3bb} (\hat {f}), \lim _{r\to \infty }\deg _{x_{m+1},\ldots ,x_n}(f^r)^{1/r}\}$
. By using the equality
![]() $\lim _{r\to \infty }\deg _{x_{m+1},\ldots ,x_n}(f^r)^{1/r}=\lim _{r\to \infty }\deg _{\mu }(f^r)^{1/r}$
(see Remark 2.3.1(2) and Lemma 2.6.1(4)), we obtain
$\lim _{r\to \infty }\deg _{x_{m+1},\ldots ,x_n}(f^r)^{1/r}=\lim _{r\to \infty }\deg _{\mu }(f^r)^{1/r}$
(see Remark 2.3.1(2) and Lemma 2.6.1(4)), we obtain
Moreover, Lemma 2.6.1(4) implies that
![]() $\lim _{r\to \infty }\deg _{\mu }(f^r)^{1/r}\le \deg _{\mu }(f)=\theta.$
This provides assertion (2). To show assertion (3), we assume that
$\lim _{r\to \infty }\deg _{\mu }(f^r)^{1/r}\le \deg _{\mu }(f)=\theta.$
This provides assertion (2). To show assertion (3), we assume that
![]() $\unicode{x3bb} (\hat {f})<\theta $
and obtain
$\unicode{x3bb} (\hat {f})<\theta $
and obtain
![]() $\unicode{x3bb} (f)=\theta \Leftrightarrow \lim _{r\to \infty }\deg _{\mu }(f^r)^{1/r} =\theta $
. This is equivalent to ask that
$\unicode{x3bb} (f)=\theta \Leftrightarrow \lim _{r\to \infty }\deg _{\mu }(f^r)^{1/r} =\theta $
. This is equivalent to ask that
![]() $ f$
is
$ f$
is
![]() $\mu $
-algebraically stable, by Lemma 2.6.1(5) (note that
$\mu $
-algebraically stable, by Lemma 2.6.1(5) (note that
![]() $1 \leq \unicode{x3bb} (\hat {f})$
, since f, and thus
$1 \leq \unicode{x3bb} (\hat {f})$
, since f, and thus
![]() $\hat {f}$
, is dominant).
$\hat {f}$
, is dominant).
We finish this section by the following simple observation.
Lemma 2.6.3. Let
![]() $f\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
be a dominant endomorphism. For each
$f\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
be a dominant endomorphism. For each
![]() $\mu \in ({\mathbb R}_{>0})^n$
such that
$\mu \in ({\mathbb R}_{>0})^n$
such that
![]() $\theta =\deg _\mu (f)\in {\mathbb R}_{>1}$
and each translation
$\theta =\deg _\mu (f)\in {\mathbb R}_{>1}$
and each translation
![]() $\tau =(x_1+c_1,\ldots ,x_n+c_n)\in \operatorname {\mathrm {Aut}}(\mathbb {A}^n)$
, where
$\tau =(x_1+c_1,\ldots ,x_n+c_n)\in \operatorname {\mathrm {Aut}}(\mathbb {A}^n)$
, where
![]() $c_1,\ldots ,c_n\in \mathbf {k}$
, the following holds:
$c_1,\ldots ,c_n\in \mathbf {k}$
, the following holds:
Proof. Denote by g the
![]() $\mu $
-leading part of f. As
$\mu $
-leading part of f. As
![]() $\mu \in ({\mathbb R}_{>0})^n$
, no component of g contains any constant. Hence, g is also the
$\mu \in ({\mathbb R}_{>0})^n$
, no component of g contains any constant. Hence, g is also the
![]() $\mu $
-leading part of
$\mu $
-leading part of
![]() $\tau \circ f$
. By Lemma 2.6.1(5), f (respectively
$\tau \circ f$
. By Lemma 2.6.1(5), f (respectively
![]() $\tau \circ f$
) is
$\tau \circ f$
) is
![]() $\mu $
-algebraically stable if and only if for each
$\mu $
-algebraically stable if and only if for each
![]() $r\ge 1$
, there is
$r\ge 1$
, there is
![]() $i\in \{1,\ldots ,n\}$
such that
$i\in \{1,\ldots ,n\}$
such that
![]() $(g^r)_i\not =0$
.
$(g^r)_i\not =0$
.
3 Matrices associated to endomorphisms and the proof of Proposition B
3.1 Spectral radii of N-uples of matrices
In the following, we fix the usual Euclidean norm on
![]() ${\mathbb R}^n$
, and on
${\mathbb R}^n$
, and on
![]() $n\times n$
-matrices.
$n\times n$
-matrices.
Definition 3.1.1. Let
![]() $n\ge 1$
.
$n\ge 1$
.
-
(1) We endow
 ${\mathbb R}^n$
with the usual norm:
${\mathbb R}^n$
with the usual norm:  $$ \begin{align*}\lVert x\rVert=\sqrt{\sum_{i=1}^n x_i^2}\quad\text{for each } x=(x_1, \ldots, x_n) \in {\mathbb R}^n.\end{align*} $$
$$ \begin{align*}\lVert x\rVert=\sqrt{\sum_{i=1}^n x_i^2}\quad\text{for each } x=(x_1, \ldots, x_n) \in {\mathbb R}^n.\end{align*} $$
-
(2) This endows the ring
 $ \mathrm {Mat}_n({\mathbb R})$
of
$ \mathrm {Mat}_n({\mathbb R})$
of
 $n\times n$
-real matrices with the norm
$n\times n$
-real matrices with the norm  $$ \begin{align*}\lVert M\rVert=\mathop{\mathrm{sup}}\limits \bigg\{\frac{\lVert Mv\rVert}{\lVert v\rVert} \bigg| v\in {\mathbb R}^n\setminus \{0\}\bigg\}\quad \text{for each }M\in \mathrm{Mat}_n({\mathbb R}).\end{align*} $$
$$ \begin{align*}\lVert M\rVert=\mathop{\mathrm{sup}}\limits \bigg\{\frac{\lVert Mv\rVert}{\lVert v\rVert} \bigg| v\in {\mathbb R}^n\setminus \{0\}\bigg\}\quad \text{for each }M\in \mathrm{Mat}_n({\mathbb R}).\end{align*} $$
-
(3) The spectrum of
 $M \in \mathrm {Mat}_n({\mathbb R})$
is the finite subset
$M \in \mathrm {Mat}_n({\mathbb R})$
is the finite subset
 $\sigma (M) \subset {\mathbb C}$
of eigenvalues of M.
$\sigma (M) \subset {\mathbb C}$
of eigenvalues of M. -
(4) The spectral radius of
 $M\in \mathrm {Mat}_n({\mathbb R})$
is defined by and satisfies
$M\in \mathrm {Mat}_n({\mathbb R})$
is defined by and satisfies $$ \begin{align*} \rho(M)=\max_{\unicode{x3bb} \in \sigma(M)} \lvert \unicode{x3bb} \rvert \end{align*} $$
If
$$ \begin{align*} \rho(M)=\max_{\unicode{x3bb} \in \sigma(M)} \lvert \unicode{x3bb} \rvert \end{align*} $$
If $$ \begin{align*} \rho(M)=\lim_{n\to \infty} \lVert M^n \rVert^{1/n}. \end{align*} $$
$$ \begin{align*} \rho(M)=\lim_{n\to \infty} \lVert M^n \rVert^{1/n}. \end{align*} $$
 $M = (m_{i, j})_{i, j = 1}^n$
and
$M = (m_{i, j})_{i, j = 1}^n$
and
 $N = (n_{i,j})_{i, j = 1}^n$
are matrices in
$N = (n_{i,j})_{i, j = 1}^n$
are matrices in
 $\mathrm {Mat}_n({\mathbb R})$
such that for each
$\mathrm {Mat}_n({\mathbb R})$
such that for each
 $(i, j)$
, we have
$(i, j)$
, we have
 $0 \leq m_{i, j} \leq n_{i, j}$
, then
$0 \leq m_{i, j} \leq n_{i, j}$
, then
 $\rho (M) \leq \rho (N)$
.
$\rho (M) \leq \rho (N)$
.
-
(5) We have a partial order on
 ${\mathbb R}^n$
given by where
${\mathbb R}^n$
given by where $$ \begin{align*} x \leq y \quad \text{if only if} \quad x_i \leq y_i\quad \text{for all}\ i = 1, \ldots, n, \end{align*} $$
$$ \begin{align*} x \leq y \quad \text{if only if} \quad x_i \leq y_i\quad \text{for all}\ i = 1, \ldots, n, \end{align*} $$
 $x = (x_1, \ldots , x_n)$
and
$x = (x_1, \ldots , x_n)$
and
 $y = (y_1, \ldots , y_n)$
. Note that for
$y = (y_1, \ldots , y_n)$
. Note that for
 $0 \leq x \leq y$
, we have
$0 \leq x \leq y$
, we have
 $\lVert x \rVert \leq \lVert y \rVert $
.
$\lVert x \rVert \leq \lVert y \rVert $
.
-
(6) For
 $M \in \mathrm {Mat}_n({\mathbb R})$
, we denote by
$M \in \mathrm {Mat}_n({\mathbb R})$
, we denote by
 $\chi _M$
the characteristic polynomial of M.
$\chi _M$
the characteristic polynomial of M.
3.2 The Perron–Frobenius theorem and its applications
The Perron–Frobenius theory was first established for matrices with positive coefficients, then generalized to irreducible matrices with non-negative coefficients and then to any matrices with non-negative coefficients. There are three equivalent definitions of reducible matrices (see [Reference GantmacherGan59, Vol. 2, Ch. XIII, §1, Definitions 2,2′,2″]). Let us recall one of them.
Definition 3.2.1. [Reference GantmacherGan59, Vol. 2, Ch. XIII, §1, Definition 2′]
For each
![]() $n\ge 1$
, a matrix
$n\ge 1$
, a matrix
![]() $M\in \mathrm {Mat}_n({\mathbb R}_{\ge 0})$
is called reducible if there is a permutation matrix
$M\in \mathrm {Mat}_n({\mathbb R}_{\ge 0})$
is called reducible if there is a permutation matrix
![]() $S\in \operatorname {\mathrm {GL}}_n(\mathbb {Z})$
such that the matrix
$S\in \operatorname {\mathrm {GL}}_n(\mathbb {Z})$
such that the matrix
![]() $SMS^{-1}\in \mathrm {Mat}_n({\mathbb R}_{\ge 0})$
is block-triangular, that is,
$SMS^{-1}\in \mathrm {Mat}_n({\mathbb R}_{\ge 0})$
is block-triangular, that is,
 $$ \begin{align*} SMS^{-1} = \begin{pmatrix} A & 0 \\ C & D \end{pmatrix}, \end{align*} $$
$$ \begin{align*} SMS^{-1} = \begin{pmatrix} A & 0 \\ C & D \end{pmatrix}, \end{align*} $$
where
![]() $A,D$
are square matrices, and where the zero matrix has positive dimensions.
$A,D$
are square matrices, and where the zero matrix has positive dimensions.
A matrix
![]() $M\in \mathrm {Mat}_n({\mathbb R}_{\ge 0})$
is called irreducible if it is not reducible.
$M\in \mathrm {Mat}_n({\mathbb R}_{\ge 0})$
is called irreducible if it is not reducible.
Lemma 3.2.2. [Reference GantmacherGan59, Vol. 2, Ch. XIII, §4]
For each reducible matrix
![]() $M\in \mathrm {Mat}_n({\mathbb R}_{\ge 0})$
, there is a permutation matrix
$M\in \mathrm {Mat}_n({\mathbb R}_{\ge 0})$
, there is a permutation matrix
![]() $S\in \operatorname {\mathrm {GL}}_n(\mathbb {Z})$
such that
$S\in \operatorname {\mathrm {GL}}_n(\mathbb {Z})$
such that
![]() $SMS^{-1}$
is a lower triangular block-matrix
$SMS^{-1}$
is a lower triangular block-matrix
 $$ \begin{align*}\begin{pmatrix} A_{1,1} & 0 & \cdots & 0 \\ A_{2,1} & A_{2,2} & \ddots & 0 \\ \vdots & \ddots & \ddots & 0 \\ A_{m,1} & \cdots & A_{m,m-1}& A_{m,m}\end{pmatrix},\end{align*} $$
$$ \begin{align*}\begin{pmatrix} A_{1,1} & 0 & \cdots & 0 \\ A_{2,1} & A_{2,2} & \ddots & 0 \\ \vdots & \ddots & \ddots & 0 \\ A_{m,1} & \cdots & A_{m,m-1}& A_{m,m}\end{pmatrix},\end{align*} $$
where
![]() $A_{1,1},\ldots ,A_{m,m}$
are irreducible matrices.
$A_{1,1},\ldots ,A_{m,m}$
are irreducible matrices.
Theorem 3.2.3. (Perron–Frobenius theorem [Reference GantmacherGan59, Vol. 2, Ch. XIII, §2 and §3, Theorems 2 and 3])
For each
![]() $M\in \mathrm {Mat}_n({\mathbb R}_{\ge 0})$
, there exists an eigenvector
$M\in \mathrm {Mat}_n({\mathbb R}_{\ge 0})$
, there exists an eigenvector
![]() $v\in ({\mathbb R}_{\ge 0})^n\setminus \{0\}$
to the eigenvalue
$v\in ({\mathbb R}_{\ge 0})^n\setminus \{0\}$
to the eigenvalue
![]() $\rho (M)$
. Moreover, if M is irreducible, we can choose v in
$\rho (M)$
. Moreover, if M is irreducible, we can choose v in
![]() $({\mathbb R}_{> 0})^n$
.
$({\mathbb R}_{> 0})^n$
.
Theorem 3.2.4. (Theorem of Lind on weak Perron numbers)
For each
![]() $\unicode{x3bb} \in {\mathbb R}$
, the following conditions are equivalent:
$\unicode{x3bb} \in {\mathbb R}$
, the following conditions are equivalent:
-
(1)
 $\unicode{x3bb} $
is a weak Perron number (see Definition 1.1.1);
$\unicode{x3bb} $
is a weak Perron number (see Definition 1.1.1); -
(2)
 $\unicode{x3bb} $
is the spectral radius of a non-zero square matrix with non-negative integral coefficients;
$\unicode{x3bb} $
is the spectral radius of a non-zero square matrix with non-negative integral coefficients; -
(3)
 $\unicode{x3bb} $
is the spectral radius of an irreducible square matrix with non-negative integral coefficients;
$\unicode{x3bb} $
is the spectral radius of an irreducible square matrix with non-negative integral coefficients; -
(4)
 $\unicode{x3bb}> 0$
and
$\unicode{x3bb}> 0$
and
 $\unicode{x3bb} ^m$
is a Perron number for some
$\unicode{x3bb} ^m$
is a Perron number for some
 $m\ge 1$
.
$m\ge 1$
.
Proof. The equivalence between conditions (1) and (3) follows from [Reference LindLin84, Theorem 3, p. 291], and the equivalence between conditions (2) and (3) follows from Lemma 3.2.2. The equivalence between conditions (1) and (4) can be found, for instance, in [Reference SchinzelSch97, Lemma 4] or [Reference BrunotteBru13, Theorem 2].
As a consequence of Corollary 2.6.2 and of the Perron–Frobenius theorem, we obtain the following result (which is classical, see for instance [Reference Favre and WulcanFW12, Reference LinLin12]).
Corollary 3.2.5. For each matrix
![]() $M=(m_{i,j})_{i,j=1}^n\in \mathrm {Mat}_n({\mathbb N})$
and for each
$M=(m_{i,j})_{i,j=1}^n\in \mathrm {Mat}_n({\mathbb N})$
and for each
![]() $(\alpha _1,\ldots ,\alpha _n) \in (\mathbf {k}^*)^n$
, the monomial endomorphism
$(\alpha _1,\ldots ,\alpha _n) \in (\mathbf {k}^*)^n$
, the monomial endomorphism
is dominant if and only if
![]() $\det (M)\not =0$
. In this case, the dynamical degree of
$\det (M)\not =0$
. In this case, the dynamical degree of
![]() $f_M$
is equal to the spectral radius of M:
$f_M$
is equal to the spectral radius of M:
Proof. Note that the endomorphism
![]() $f_M \in \operatorname {\mathrm {End}}({\mathbb A}^n)$
restricts to an endomorphism
$f_M \in \operatorname {\mathrm {End}}({\mathbb A}^n)$
restricts to an endomorphism
![]() $h_M \in \operatorname {\mathrm {End}}(({\mathbb A}^1 \setminus \{ 0 \})^n)$
.
$h_M \in \operatorname {\mathrm {End}}(({\mathbb A}^1 \setminus \{ 0 \})^n)$
.
If
![]() $\det (M)=0$
, any non-zero element of the kernel of the transpose of M gives rise to a non-constant element p in the Laurent polynomial ring
$\det (M)=0$
, any non-zero element of the kernel of the transpose of M gives rise to a non-constant element p in the Laurent polynomial ring
![]() $\mathbf {k}[x_1^{\pm }, \ldots , x_n^{\pm }]$
such that
$\mathbf {k}[x_1^{\pm }, \ldots , x_n^{\pm }]$
such that
![]() $p \circ h_M$
is constant, so
$p \circ h_M$
is constant, so
![]() $h_M$
, and thus
$h_M$
, and thus
![]() $f_M$
, is not dominant. We then assume that
$f_M$
, is not dominant. We then assume that
![]() $\det (M)\not =0$
. This implies that
$\det (M)\not =0$
. This implies that
![]() $h_M \in \operatorname {\mathrm {End}}(({\mathbb A}^1 \setminus \{0\})^n)$
is surjective on
$h_M \in \operatorname {\mathrm {End}}(({\mathbb A}^1 \setminus \{0\})^n)$
is surjective on
![]() $\overline {\mathbf {k}}$
-points and thus
$\overline {\mathbf {k}}$
-points and thus
![]() $f_M$
is dominant. In particular,
$f_M$
is dominant. In particular,
![]() $\unicode{x3bb} (f_M) \geq 1$
. Thus we only have to show that
$\unicode{x3bb} (f_M) \geq 1$
. Thus we only have to show that
![]() $\unicode{x3bb} (f_M)=\rho (M)$
. By the Perron–Frobenius theorem (Theorem 3.2.3), there exists an eigenvector
$\unicode{x3bb} (f_M)=\rho (M)$
. By the Perron–Frobenius theorem (Theorem 3.2.3), there exists an eigenvector
![]() $\mu \in (\mu _1,\ldots ,\mu _n)\in ({\mathbb R}_{\ge 0})^n$
of M to the eigenvalue
$\mu \in (\mu _1,\ldots ,\mu _n)\in ({\mathbb R}_{\ge 0})^n$
of M to the eigenvalue
![]() $\rho (M)$
. Because the spectral radius of M and the dynamical degree of
$\rho (M)$
. Because the spectral radius of M and the dynamical degree of
![]() $f_M$
do not change if we conjugate M with a permutation matrix, we may assume that there is
$f_M$
do not change if we conjugate M with a permutation matrix, we may assume that there is
![]() $m < n$
such that
$m < n$
such that
![]() $\mu _1 = \cdots = \mu _m = 0$
and
$\mu _1 = \cdots = \mu _m = 0$
and
![]() $\mu _i> 0$
for each
$\mu _i> 0$
for each
![]() $i \geq m+1$
. Because
$i \geq m+1$
. Because
![]() $(f_M)^r = f_{M^r}$
, we get for each
$(f_M)^r = f_{M^r}$
, we get for each
![]() $r \geq 1$
and each
$r \geq 1$
and each
![]() $i \in \{1, \ldots , n\}$
that
$i \in \{1, \ldots , n\}$
that
![]() $\deg _\mu (((f_M)^r)_i) = (M^r \mu )_i = \rho (M)^r \mu _i$
. This implies that
$\deg _\mu (((f_M)^r)_i) = (M^r \mu )_i = \rho (M)^r \mu _i$
. This implies that
![]() $\deg _\mu ((f_M)^r)=\rho (M)^r$
for each
$\deg _\mu ((f_M)^r)=\rho (M)^r$
for each
![]() $r \geq 1$
. Thus
$r \geq 1$
. Thus
![]() $f_M$
is
$f_M$
is
![]() $\mu $
-algebraically stable and
$\mu $
-algebraically stable and
![]() $\deg _\mu (f_M) = \rho (M) < \infty $
. By Corollary 2.6.2(1), we may write
$\deg _\mu (f_M) = \rho (M) < \infty $
. By Corollary 2.6.2(1), we may write
 $$ \begin{align*} M = \left( \begin{array}{c|c} \hat{M} & 0 \\ \hline \ast & \ast \end{array} \right), \end{align*} $$
$$ \begin{align*} M = \left( \begin{array}{c|c} \hat{M} & 0 \\ \hline \ast & \ast \end{array} \right), \end{align*} $$
where
![]() $\hat {M} \in \mathrm {Mat}_m({\mathbb N})$
with
$\hat {M} \in \mathrm {Mat}_m({\mathbb N})$
with
![]() $\det (\hat {M}) \neq 0$
. By induction, the endomorphism
$\det (\hat {M}) \neq 0$
. By induction, the endomorphism
![]() $f_{\hat {M}} \in \operatorname {\mathrm {End}}({\mathbb A}^m)$
satisfies
$f_{\hat {M}} \in \operatorname {\mathrm {End}}({\mathbb A}^m)$
satisfies
![]() $\unicode{x3bb} (f_{\hat {M}}) = \rho (\hat {M}) \leq \rho (M)$
. By Corollary 2.6.2(2), (3), we get then
$\unicode{x3bb} (f_{\hat {M}}) = \rho (\hat {M}) \leq \rho (M)$
. By Corollary 2.6.2(2), (3), we get then
![]() $\unicode{x3bb} (f_M) = \deg _\mu (f_M) = \rho (M)$
.
$\unicode{x3bb} (f_M) = \deg _\mu (f_M) = \rho (M)$
.
Corollary 3.2.6. For each endomorphism
![]() $f\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
and each matrix
$f\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
and each matrix
![]() $M\in \mathrm {Mat}_n({\mathbb N})$
that is contained in f, we have
$M\in \mathrm {Mat}_n({\mathbb N})$
that is contained in f, we have
![]() $ \rho (M)\le \deg (f)$
.
$ \rho (M)\le \deg (f)$
.
Proof. By the Perron–Frobenius theorem (Theorem 3.2.3), there exists an eigenvector
![]() $\mu =(\mu _1,\ldots ,\mu _n)\in ({\mathbb R}_{\ge 0})^n$
of M to the eigenvalue
$\mu =(\mu _1,\ldots ,\mu _n)\in ({\mathbb R}_{\ge 0})^n$
of M to the eigenvalue
![]() $\rho (M)$
. Hence,
$\rho (M)$
. Hence,
![]() $\sum _{j=1}^n m_{i,j}\mu _j=\rho (M)\mu _i$
for each
$\sum _{j=1}^n m_{i,j}\mu _j=\rho (M)\mu _i$
for each
![]() $i\in \{1,\ldots ,n\}$
. By choosing an integer
$i\in \{1,\ldots ,n\}$
. By choosing an integer
![]() $r\in \{1,\ldots ,n\}$
such that
$r\in \{1,\ldots ,n\}$
such that
![]() $\mu _r=\max \{\mu _1,\ldots ,\mu _n\}$
, we obtain
$\mu _r=\max \{\mu _1,\ldots ,\mu _n\}$
, we obtain
 $$ \begin{align*}\rho(M)\mu_r=\sum_{j=1}^n m_{r,j}\mu_j\le \mu_r\sum_{j=1}^n m_{r,j}.\end{align*} $$
$$ \begin{align*}\rho(M)\mu_r=\sum_{j=1}^n m_{r,j}\mu_j\le \mu_r\sum_{j=1}^n m_{r,j}.\end{align*} $$
The coefficient of the monomial
![]() $\prod _{j=1}^n x_j^{m_{r,j}}$
in
$\prod _{j=1}^n x_j^{m_{r,j}}$
in
![]() $f_r$
is non-zero (as M is contained in f, see Definition 1.4.8). This monomial has degree
$f_r$
is non-zero (as M is contained in f, see Definition 1.4.8). This monomial has degree
![]() $\sum _{j=1}^n m_{r,j}$
, so
$\sum _{j=1}^n m_{r,j}$
, so
![]() $\deg (f)\ge \sum _{j=1}^n m_{r,j}$
. As
$\deg (f)\ge \sum _{j=1}^n m_{r,j}$
. As
![]() $\mu _r>0$
, this gives
$\mu _r>0$
, this gives
![]() $\rho (M)\le \deg (f)$
.
$\rho (M)\le \deg (f)$
.
In the following, we will use the next basic property of Handelman numbers. It is a straightforward application of Descarte’s Rule of Signs, see e.g. [Reference StruikStr86, p. 91].
Lemma 3.2.7. (Basic property of Handelman numbers)
Let
![]() $n \geq 1$
. For each
$n \geq 1$
. For each
![]() $(a_0,\ldots , a_{n-1}) \in ({\mathbb R}_{\ge 0})^n\setminus \{0\}$
, the polynomial
$(a_0,\ldots , a_{n-1}) \in ({\mathbb R}_{\ge 0})^n\setminus \{0\}$
, the polynomial
![]() $x^n-\sum _{i=0}^{n-1} a_i x^i\in {\mathbb R}[x]$
has a unique positive real root. In particular, a Handelman number has no other positive real Galois conjugate.
$x^n-\sum _{i=0}^{n-1} a_i x^i\in {\mathbb R}[x]$
has a unique positive real root. In particular, a Handelman number has no other positive real Galois conjugate.
Corollary 3.2.8. Each Handelman number is a weak Perron number.
Proof. Let
![]() $\unicode{x3bb} \in {\mathbb R}_{> 0}$
be a Handelman number. There exists
$\unicode{x3bb} \in {\mathbb R}_{> 0}$
be a Handelman number. There exists
![]() $(a_0, \ldots , a_{n-1}) \in {\mathbb Z}^n \setminus \{ 0 \}$
such that
$(a_0, \ldots , a_{n-1}) \in {\mathbb Z}^n \setminus \{ 0 \}$
such that
![]() $\unicode{x3bb} $
is a root of
$\unicode{x3bb} $
is a root of
![]() $P(x) = x^n - \sum _{i=0}^{n-1} a_i x^i \in {\mathbb Z}[x]$
. By Lemma 3.2.7, all roots of P, except
$P(x) = x^n - \sum _{i=0}^{n-1} a_i x^i \in {\mathbb Z}[x]$
. By Lemma 3.2.7, all roots of P, except
![]() $\unicode{x3bb} $
, are either non-real or real and non-positive. Because P is the characteristic polynomial of the matrix
$\unicode{x3bb} $
, are either non-real or real and non-positive. Because P is the characteristic polynomial of the matrix
 $$ \begin{align*} A = \begin{pmatrix} a_{n-1} & \cdots & a_1 & a_0 \\ 1 & \cdots & 0 & 0 \\ \vdots & \ddots & \vdots & \vdots \\ 0 & \cdots & 1 & 0 \end{pmatrix} \in \mathrm{Mat}_n({\mathbb R}_{\geq 0}), \end{align*} $$
$$ \begin{align*} A = \begin{pmatrix} a_{n-1} & \cdots & a_1 & a_0 \\ 1 & \cdots & 0 & 0 \\ \vdots & \ddots & \vdots & \vdots \\ 0 & \cdots & 1 & 0 \end{pmatrix} \in \mathrm{Mat}_n({\mathbb R}_{\geq 0}), \end{align*} $$
it follows by the Perron-Frobenius theorem (Theorem 3.2.3) that the spectral radius of A is equal to
![]() $\unicode{x3bb} $
. This implies that
$\unicode{x3bb} $
. This implies that
![]() $\unicode{x3bb} $
is a weak Perron number (Theorem 3.2.4).
$\unicode{x3bb} $
is a weak Perron number (Theorem 3.2.4).
3.3 Sequences of matrices
To study endomorphisms of
![]() $\mathbb {A}^n$
, we will need to consider finite sets of elements of
$\mathbb {A}^n$
, we will need to consider finite sets of elements of
![]() $\mathrm {Mat}_n({\mathbb R})$
that have the property that we can exchange rows. To take the norm on such sets, we will have to see them ordered, and thus see these in
$\mathrm {Mat}_n({\mathbb R})$
that have the property that we can exchange rows. To take the norm on such sets, we will have to see them ordered, and thus see these in
![]() $\mathrm {Mat}_n({\mathbb R})^N$
for some
$\mathrm {Mat}_n({\mathbb R})^N$
for some
![]() $N\ge 1$
.
$N\ge 1$
.
Notation 3.3.1. Let
![]() $n,N\ge 1$
. We denote by
$n,N\ge 1$
. We denote by
![]() $\widehat {\mathcal {M}}_{n,N}\subset \mathrm {Mat}_n({\mathbb R})^N$
the
$\widehat {\mathcal {M}}_{n,N}\subset \mathrm {Mat}_n({\mathbb R})^N$
the
![]() ${\mathbb R}$
-vector subspace of N-tuples
${\mathbb R}$
-vector subspace of N-tuples
![]() $(M_1,\ldots ,M_N)$
that have the following property:
$(M_1,\ldots ,M_N)$
that have the following property:
For each
![]() $i,j\in \{1,\ldots ,N\}$
and each
$i,j\in \{1,\ldots ,N\}$
and each
![]() $l \in \{1,\ldots ,n\}$
, the replacement of the lth row of
$l \in \{1,\ldots ,n\}$
, the replacement of the lth row of
![]() $M_i$
with the lth row of
$M_i$
with the lth row of
![]() $M_j$
gives a matrix which lies in
$M_j$
gives a matrix which lies in
![]() $\{M_1,\ldots ,M_N\}$
.
$\{M_1,\ldots ,M_N\}$
.
We then denote by
![]() $\mathcal {M}_{n,N}\subset \widehat {\mathcal {M}}_{n,N}$
the subset that consists of the N-tuples
$\mathcal {M}_{n,N}\subset \widehat {\mathcal {M}}_{n,N}$
the subset that consists of the N-tuples
![]() $(M_1,\ldots ,M_N)$
, where
$(M_1,\ldots ,M_N)$
, where
![]() $M_1,\ldots ,M_N$
are N distinct matrices with non-negative coefficients.
$M_1,\ldots ,M_N$
are N distinct matrices with non-negative coefficients.
Remark 3.3.2. If
![]() $f\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
is an endomorphism, then there exists some integer
$f\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
is an endomorphism, then there exists some integer
![]() $N\ge 1$
and some N-tuple
$N\ge 1$
and some N-tuple
![]() $(S_1,\ldots ,S_N)\in \mathcal {M}_{n,N}$
such that
$(S_1,\ldots ,S_N)\in \mathcal {M}_{n,N}$
such that
![]() $\{S_1,\ldots ,S_N\}$
is the set of matrices that are contained in f (as in Definition 1.4.8).
$\{S_1,\ldots ,S_N\}$
is the set of matrices that are contained in f (as in Definition 1.4.8).
The following two lemmas build the key ingredients for proving the existence of maximal eigenvectors of endomorphisms of
![]() ${\mathbb A}^n$
in the next subsection (see Proposition 3.4.1). This eventually leads then to a proof of Proposition B.
${\mathbb A}^n$
in the next subsection (see Proposition 3.4.1). This eventually leads then to a proof of Proposition B.
Lemma 3.3.3. Let
![]() $n,N\ge 1$
. For each
$n,N\ge 1$
. For each
![]() $M=(M_1,\ldots ,M_N)\in \mathcal {M}_{n,N}$
, there exists a sequence
$M=(M_1,\ldots ,M_N)\in \mathcal {M}_{n,N}$
, there exists a sequence
![]() ${(D_t)}_{t\in \mathbb {N}}$
of elements
${(D_t)}_{t\in \mathbb {N}}$
of elements
![]() $D_t=(D_{t,1},\ldots ,D_{t,N})\in \mathcal {M}_{n,N}$
that converges towards
$D_t=(D_{t,1},\ldots ,D_{t,N})\in \mathcal {M}_{n,N}$
that converges towards
![]() $M$
(with respect to the topology of
$M$
(with respect to the topology of
![]() $\mathrm {Mat}_n({\mathbb R})^N$
that is given by the norm as in Definition 3.1.1) and such that for each
$\mathrm {Mat}_n({\mathbb R})^N$
that is given by the norm as in Definition 3.1.1) and such that for each
![]() $t\in \mathbb {N}$
, there is no complex number which is an eigenvalue of two elements of
$t\in \mathbb {N}$
, there is no complex number which is an eigenvalue of two elements of
![]() $D_{t,1},\ldots ,D_{t,N}$
.
$D_{t,1},\ldots ,D_{t,N}$
.
Proof. The result being trivially true for
![]() $N=1$
, we will assume
$N=1$
, we will assume
![]() $N\ge 2$
. For each
$N\ge 2$
. For each
![]() $i\in \{1,\ldots ,n\}$
, we denote by
$i\in \{1,\ldots ,n\}$
, we denote by
![]() $\Gamma _i \subset {\mathbb R}^n$
the finite set of ith rows of the matrices
$\Gamma _i \subset {\mathbb R}^n$
the finite set of ith rows of the matrices
![]() $M_1,\ldots ,M_N$
:
$M_1,\ldots ,M_N$
:
We then write
![]() $\Gamma _i=\{r_{i,1},\ldots ,r_{i,s_i}\}$
, where
$\Gamma _i=\{r_{i,1},\ldots ,r_{i,s_i}\}$
, where
![]() $s_i\ge 1$
is the cardinality of
$s_i\ge 1$
is the cardinality of
![]() $\Gamma _i$
.
$\Gamma _i$
.
As all matrices
![]() $M_1,\ldots ,M_N$
are pairwise distinct and as one can ‘exchange rows’ (see Notation 3.3.1), we have
$M_1,\ldots ,M_N$
are pairwise distinct and as one can ‘exchange rows’ (see Notation 3.3.1), we have
![]() $N=s_1\cdot \cdots s_n$
, and obtain a unique
$N=s_1\cdot \cdots s_n$
, and obtain a unique
![]() ${\mathbb R}$
-linear map
${\mathbb R}$
-linear map
 $$ \begin{align*} \varphi\colon \prod_{i=1}^n ({\mathbb R}^n)^{s_i}\to \widehat{\mathcal{M}}_{n,N} \end{align*} $$
$$ \begin{align*} \varphi\colon \prod_{i=1}^n ({\mathbb R}^n)^{s_i}\to \widehat{\mathcal{M}}_{n,N} \end{align*} $$
with the following properties.
-
(1) For each
 $k \in \{1, \ldots , N \}$
, the composition of
$k \in \{1, \ldots , N \}$
, the composition of
 $\varphi $
with the projection map
$\varphi $
with the projection map
 $\pi _k \colon \mathrm {Mat}_n({\mathbb R})^N\to \mathrm {Mat}_n({\mathbb R})$
onto the kth factor is of the form where
$\pi _k \colon \mathrm {Mat}_n({\mathbb R})^N\to \mathrm {Mat}_n({\mathbb R})$
onto the kth factor is of the form where $$ \begin{align*}\begin{array}{rccc} \pi_k\circ \varphi\colon& \prod_{i=1}^n ({\mathbb R}^n)^{s_i}&\to& \mathrm{Mat}_n({\mathbb R})\\ &(v_{i,j})_{1\le i\le n, 1\le j\le s_i} & \mapsto & \begin{pmatrix} v_{1, j_1} \\ \vdots \\ v_{n, j_n} \end{pmatrix}, \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{rccc} \pi_k\circ \varphi\colon& \prod_{i=1}^n ({\mathbb R}^n)^{s_i}&\to& \mathrm{Mat}_n({\mathbb R})\\ &(v_{i,j})_{1\le i\le n, 1\le j\le s_i} & \mapsto & \begin{pmatrix} v_{1, j_1} \\ \vdots \\ v_{n, j_n} \end{pmatrix}, \end{array}\end{align*} $$
 $j_i\in \{1,\ldots ,s_i\}$
for each
$j_i\in \{1,\ldots ,s_i\}$
for each
 $i\in \{1,\ldots ,n\}$
.
$i\in \{1,\ldots ,n\}$
.
-
(2)
 $(M_1,\ldots ,M_N)=\varphi ((r_{i,j})_{1\le i\le n, 1\le j\le s_i})$
.
$(M_1,\ldots ,M_N)=\varphi ((r_{i,j})_{1\le i\le n, 1\le j\le s_i})$
.
Indeed, the possibilities for maps
![]() $\pi _k \circ \varphi $
as in property
$\pi _k \circ \varphi $
as in property
![]() $(1)$
are parametrized by the N possible choices of
$(1)$
are parametrized by the N possible choices of
![]() $j_i\in \{1,\ldots ,s_i\}$
for each
$j_i\in \{1,\ldots ,s_i\}$
for each
![]() $i\in \{1,\ldots ,n\}$
, and by property
$i\in \{1,\ldots ,n\}$
, and by property
![]() $(2)$
, the image of
$(2)$
, the image of
![]() $(r_{i,j})_{1\le i\le n, 1\le j\le s_i}$
by the maps
$(r_{i,j})_{1\le i\le n, 1\le j\le s_i}$
by the maps
![]() $\pi _1 \circ \varphi , \ldots , \pi _N \circ \varphi $
give the matrices
$\pi _1 \circ \varphi , \ldots , \pi _N \circ \varphi $
give the matrices
![]() $M_1,\ldots ,M_N$
; this gives the existence and the unicity of
$M_1,\ldots ,M_N$
; this gives the existence and the unicity of
![]() $\varphi $
.
$\varphi $
.
We now identify
![]() $\prod _{i=1}^n ({\mathbb R}^n)^{s_i}$
with the real locus
$\prod _{i=1}^n ({\mathbb R}^n)^{s_i}$
with the real locus
![]() $X({\mathbb R})$
of the affine space
$X({\mathbb R})$
of the affine space
![]() $X=\mathbb {A}^{n\sum s_i}$
.
$X=\mathbb {A}^{n\sum s_i}$
.
For any two matrices
![]() $A,B\in \mathrm {Mat}_n({\mathbb R})$
, the resultant of the characteristic polynomials
$A,B\in \mathrm {Mat}_n({\mathbb R})$
, the resultant of the characteristic polynomials
![]() $\chi _A$
and
$\chi _A$
and
![]() $\chi _B$
is denoted by
$\chi _B$
is denoted by
![]() $r(A,B)$
. Recall that
$r(A,B)$
. Recall that
![]() $r(A, B) = 0$
if and only if A and B have a common eigenvalue. Hence, for any distinct
$r(A, B) = 0$
if and only if A and B have a common eigenvalue. Hence, for any distinct
![]() $a,b \in \{1,\ldots ,N\}$
, the set
$a,b \in \{1,\ldots ,N\}$
, the set
 $$ \begin{align*} Z_{a,b}=\bigg\{x\in \prod_{i=1}^n ({\mathbb R}^n)^{s_i} \bigg| \begin{array}{l}\text{the matrices }\pi_{a}(\varphi(x))\text{ and }\pi_{b}(\varphi(x))\\ \text{have a common eigenvalue}\end{array}\!\!\bigg\} \end{align*} $$
$$ \begin{align*} Z_{a,b}=\bigg\{x\in \prod_{i=1}^n ({\mathbb R}^n)^{s_i} \bigg| \begin{array}{l}\text{the matrices }\pi_{a}(\varphi(x))\text{ and }\pi_{b}(\varphi(x))\\ \text{have a common eigenvalue}\end{array}\!\!\bigg\} \end{align*} $$
corresponds to the elements of
![]() $X({\mathbb R})$
that satisfy one polynomial equation
$X({\mathbb R})$
that satisfy one polynomial equation
![]() $P_{a,b}\in {\mathbb R}[X]$
.
$P_{a,b}\in {\mathbb R}[X]$
.
We now prove that
![]() $P_{a,b}\not =0$
, or equivalently that
$P_{a,b}\not =0$
, or equivalently that
![]() $Z_{a,b}\not = X({\mathbb R})=\prod _{i=1}^n ({\mathbb R}^n)^{s_i}$
, by showing that
$Z_{a,b}\not = X({\mathbb R})=\prod _{i=1}^n ({\mathbb R}^n)^{s_i}$
, by showing that
![]() $\pi _{a}(\varphi (x))$
and
$\pi _{a}(\varphi (x))$
and
![]() $\pi _{b}(\varphi (x))$
have no common eigenvalue for at least one
$\pi _{b}(\varphi (x))$
have no common eigenvalue for at least one
![]() $x\in X({\mathbb R})$
. We consider
$x\in X({\mathbb R})$
. We consider
![]() $j_1,\ldots ,j_n$
and
$j_1,\ldots ,j_n$
and
![]() $j_1',\ldots ,j_n'$
so that
$j_1',\ldots ,j_n'$
so that
![]() $\pi _a\circ \varphi $
and
$\pi _a\circ \varphi $
and
![]() $\pi _b\circ \varphi $
are respectively given by
$\pi _b\circ \varphi $
are respectively given by
 $$ \begin{align*}\begin{array}{ccc} \prod_{i=1}^n ({\mathbb R}^n)^{s_i}&\to& \mathrm{Mat}_n({\mathbb R})\\ (v_{i,j})_{\scriptsize\begin{array}{l} 1\le i\le n\\ 1\le j\le s_i\end{array}} & \mapsto & \begin{pmatrix} v_{1, j_1} \\ \vdots \\ v_{n, j_n} \end{pmatrix} \end{array} \qquad \textrm{and} \qquad \begin{array}{ccc} \prod_{i=1}^n ({\mathbb R}^n)^{s_i}&\to& \mathrm{Mat}_n({\mathbb R})\\ (v_{i,j})_{\scriptsize\begin{array}{l} 1\le i\le n\\ 1\le j\le s_i\end{array}} & \mapsto & \begin{pmatrix} v_{1, j_1'} \\ \vdots \\ v_{n, j_n'} \end{pmatrix}. \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ccc} \prod_{i=1}^n ({\mathbb R}^n)^{s_i}&\to& \mathrm{Mat}_n({\mathbb R})\\ (v_{i,j})_{\scriptsize\begin{array}{l} 1\le i\le n\\ 1\le j\le s_i\end{array}} & \mapsto & \begin{pmatrix} v_{1, j_1} \\ \vdots \\ v_{n, j_n} \end{pmatrix} \end{array} \qquad \textrm{and} \qquad \begin{array}{ccc} \prod_{i=1}^n ({\mathbb R}^n)^{s_i}&\to& \mathrm{Mat}_n({\mathbb R})\\ (v_{i,j})_{\scriptsize\begin{array}{l} 1\le i\le n\\ 1\le j\le s_i\end{array}} & \mapsto & \begin{pmatrix} v_{1, j_1'} \\ \vdots \\ v_{n, j_n'} \end{pmatrix}. \end{array} \end{align*} $$
Because the matrices
![]() $M_a$
and
$M_a$
and
![]() $M_b$
are distinct, the linear maps
$M_b$
are distinct, the linear maps
![]() $\pi _a \circ \varphi $
and
$\pi _a \circ \varphi $
and
![]() $\pi _b\circ \varphi $
are also distinct. Thus, there is
$\pi _b\circ \varphi $
are also distinct. Thus, there is
![]() $l\in \{1,\ldots ,n\}$
such that
$l\in \{1,\ldots ,n\}$
such that
![]() $j_l\not =j_l'$
. Suppose first that
$j_l\not =j_l'$
. Suppose first that
![]() $l=1$
, that is,
$l=1$
, that is,
![]() $j_1\not =j_1'$
. We may choose
$j_1\not =j_1'$
. We may choose
![]() $x\in X({\mathbb R})$
such that
$x\in X({\mathbb R})$
such that
 $$ \begin{align*} \pi_{a}(\varphi(x))=\left(\begin{array}{c|c} 0 & 1 \\ \hline I_{n-1} & 0 \end{array}\right) \quad \textrm{and} \quad \pi_{b}(\varphi(x))=\left(\begin{array}{c|c} 0 & 0 \\ \hline I_{n-1} & 0 \end{array}\right)\!. \end{align*} $$
$$ \begin{align*} \pi_{a}(\varphi(x))=\left(\begin{array}{c|c} 0 & 1 \\ \hline I_{n-1} & 0 \end{array}\right) \quad \textrm{and} \quad \pi_{b}(\varphi(x))=\left(\begin{array}{c|c} 0 & 0 \\ \hline I_{n-1} & 0 \end{array}\right)\!. \end{align*} $$
These matrices have characteristic polynomials
![]() $t^n-1$
and
$t^n-1$
and
![]() $t^n$
, respectively. If
$t^n$
, respectively. If
![]() $l>1$
, we simply consider conjugation of the above matrices by permutations. In all cases, we find an
$l>1$
, we simply consider conjugation of the above matrices by permutations. In all cases, we find an
![]() $x\in X({\mathbb R})$
such that
$x\in X({\mathbb R})$
such that
![]() $\pi _{{a}}(\varphi (x))$
and
$\pi _{{a}}(\varphi (x))$
and
![]() $\pi _{{b}}(\varphi (x))$
are matrices without common eigenvalue in
$\pi _{{b}}(\varphi (x))$
are matrices without common eigenvalue in
![]() $\mathbb {C}$
. This shows that
$\mathbb {C}$
. This shows that
![]() $Z_{a,b} \neq X({\mathbb R})$
, that is,
$Z_{a,b} \neq X({\mathbb R})$
, that is,
![]() $P_{a,b} \neq 0$
.
$P_{a,b} \neq 0$
.
The product of all polynomials
![]() $P_{a,b}$
with distinct
$P_{a,b}$
with distinct
![]() $a,b \in \{1,\ldots ,n\}$
gives a non-zero polynomial
$a,b \in \{1,\ldots ,n\}$
gives a non-zero polynomial
![]() $P\in {\mathbb R}[X]$
. Thus we can take a real affine linear map
$P\in {\mathbb R}[X]$
. Thus we can take a real affine linear map
![]() $\ell \colon \mathbb {A}^1 \to X =\mathbb {A}^{n\sum s_i}$
such that
$\ell \colon \mathbb {A}^1 \to X =\mathbb {A}^{n\sum s_i}$
such that
![]() $\ell (0)=(r_{i,j})_{1\le i\le n, 1\le j\le s_i}$
, such that the coordinates of
$\ell (0)=(r_{i,j})_{1\le i\le n, 1\le j\le s_i}$
, such that the coordinates of
![]() $\ell ({\mathbb R}_{\ge 0})$
are non-negative and such that the restriction of P to
$\ell ({\mathbb R}_{\ge 0})$
are non-negative and such that the restriction of P to
![]() $\ell ({\mathbb R})$
is non-zero. We obtain that
$\ell ({\mathbb R})$
is non-zero. We obtain that
![]() $P(\ell ({1}/{n})) \neq 0$
for any sufficiently large positive integer n. It suffices then to fix a sufficiently large
$P(\ell ({1}/{n})) \neq 0$
for any sufficiently large positive integer n. It suffices then to fix a sufficiently large
![]() $c\ge 1$
and to define
$c\ge 1$
and to define
![]() $D_t=\varphi (\ell ({1}/(t+c)))$
for each integer
$D_t=\varphi (\ell ({1}/(t+c)))$
for each integer
![]() $t\ge 0$
.
$t\ge 0$
.
Lemma 3.3.4. Let
![]() $S = (S_1, \ldots , S_N) \in \mathcal {M}_{n,N}$
and let
$S = (S_1, \ldots , S_N) \in \mathcal {M}_{n,N}$
and let
![]() $v\geq 0$
be an eigenvector of
$v\geq 0$
be an eigenvector of
![]() $S_1$
to the eigenvalue
$S_1$
to the eigenvalue
![]() $\unicode{x3bb} \geq 0$
. Moreover, suppose that
$\unicode{x3bb} \geq 0$
. Moreover, suppose that
![]() $\unicode{x3bb}>\rho (S_i)$
for each
$\unicode{x3bb}>\rho (S_i)$
for each
![]() $i\in \{2,\ldots ,N\}$
. Then
$i\in \{2,\ldots ,N\}$
. Then
![]() $S_i v \leq \unicode{x3bb} v$
for each
$S_i v \leq \unicode{x3bb} v$
for each
![]() $i\in \{1,\ldots ,N\}$
.
$i\in \{1,\ldots ,N\}$
.
Proof. Assume for contradiction that there is
![]() $i\in \{2,\ldots ,N\}$
such that
$i\in \{2,\ldots ,N\}$
such that
![]() $S_i v \not \leq \unicode{x3bb} v$
. Denote by
$S_i v \not \leq \unicode{x3bb} v$
. Denote by
![]() $v_j$
the jth component of v for each
$v_j$
the jth component of v for each
![]() $j \in \{1, \ldots , n\}$
. Because we may replace each row
$j \in \{1, \ldots , n\}$
. Because we may replace each row
![]() $R_j$
in
$R_j$
in
![]() $S_i$
, such that
$S_i$
, such that
![]() $R_j v < \unicode{x3bb} v_j$
, with the jth row from
$R_j v < \unicode{x3bb} v_j$
, with the jth row from
![]() $S_1$
and still get an element in
$S_1$
and still get an element in
![]() $\{S_1, \ldots , S_N\}$
, we may assume that
$\{S_1, \ldots , S_N\}$
, we may assume that
![]() $S_i v \geq \unicode{x3bb} v \geq 0$
. As the coefficients of v and
$S_i v \geq \unicode{x3bb} v \geq 0$
. As the coefficients of v and
![]() $S_i$
are non-negative, we obtain by induction that
$S_i$
are non-negative, we obtain by induction that
![]() $(S_i)^r v \geq \unicode{x3bb} ^r v \geq 0$
for each
$(S_i)^r v \geq \unicode{x3bb} ^r v \geq 0$
for each
![]() $r\ge 1$
. In particular,
$r\ge 1$
. In particular,
and we obtain
![]() $\rho (S_i)=\lim _{r\to \infty } \lVert (S_i)^r \rVert ^{1/r} \geq \unicode{x3bb} $
. This contradicts the assumption that
$\rho (S_i)=\lim _{r\to \infty } \lVert (S_i)^r \rVert ^{1/r} \geq \unicode{x3bb} $
. This contradicts the assumption that
![]() $\unicode{x3bb}>\rho (S_i)$
.
$\unicode{x3bb}>\rho (S_i)$
.
3.4 Existence of maximal eigenvectors of endomorphisms of
 ${\mathbb A}^n$
${\mathbb A}^n$
Proposition 3.4.1. For each
![]() $n,N\ge 1$
and each
$n,N\ge 1$
and each
![]() $S=(S_1,\ldots ,S_N) \in \mathcal {M}_{n,N}$
, there exists
$S=(S_1,\ldots ,S_N) \in \mathcal {M}_{n,N}$
, there exists
![]() $j \in \{1,\ldots ,N\}$
and an eigenvector
$j \in \{1,\ldots ,N\}$
and an eigenvector
![]() $v \in ({\mathbb R}_{\geq 0})^n \setminus \{ 0 \}$
of
$v \in ({\mathbb R}_{\geq 0})^n \setminus \{ 0 \}$
of
![]() $S_{j}$
to the eigenvalue
$S_{j}$
to the eigenvalue
![]() $\unicode{x3bb} =\max \{\rho (S_1),\ldots ,\rho (S_N)\}$
such that for each
$\unicode{x3bb} =\max \{\rho (S_1),\ldots ,\rho (S_N)\}$
such that for each
![]() $i \in \{1,\ldots ,N\}$
, we have
$i \in \{1,\ldots ,N\}$
, we have
Proof. Let
![]() $S = (S_1, \ldots , S_N) \in \mathcal {M}_{n,N}$
. By Lemma 3.3.3, there exists a sequence
$S = (S_1, \ldots , S_N) \in \mathcal {M}_{n,N}$
. By Lemma 3.3.3, there exists a sequence
![]() ${(D_t)}_{t\in \mathbb {N}}$
of elements
${(D_t)}_{t\in \mathbb {N}}$
of elements
![]() $D_t=(D_{t,1},\ldots ,D_{t,N})\in \mathcal {M}_{n,N}$
that converges towards S and such that for each
$D_t=(D_{t,1},\ldots ,D_{t,N})\in \mathcal {M}_{n,N}$
that converges towards S and such that for each
![]() $t\in \mathbb {N}$
, there is no complex number which is an eigenvalue of two elements of
$t\in \mathbb {N}$
, there is no complex number which is an eigenvalue of two elements of
![]() $D_{t,1},\ldots ,D_{t,N}$
. In particular,
$D_{t,1},\ldots ,D_{t,N}$
. In particular,
![]() $\rho (D_{t, i}) \neq \rho (D_{t, j})$
for distinct
$\rho (D_{t, i}) \neq \rho (D_{t, j})$
for distinct
![]() $i, j$
by the Perron–Frobenius theorem (Theorem 3.2.3).
$i, j$
by the Perron–Frobenius theorem (Theorem 3.2.3).
By possibly replacing this sequence with a subsequence, we may assume that there is a
![]() $j\in \{1,\ldots ,N\}$
such that
$j\in \{1,\ldots ,N\}$
such that
![]() $\rho (D_{t, j})> \rho (D_{t, i})$
for all
$\rho (D_{t, j})> \rho (D_{t, i})$
for all
![]() $i \in \{1,\ldots ,N\}\setminus \{j\}$
and each
$i \in \{1,\ldots ,N\}\setminus \{j\}$
and each
![]() $t\in \mathbb {N}$
. After exchanging the ordering of
$t\in \mathbb {N}$
. After exchanging the ordering of
![]() $S_1,\ldots ,S_N$
, we may assume that
$S_1,\ldots ,S_N$
, we may assume that
![]() $j = 1$
. For each
$j = 1$
. For each
![]() $i\in \{1,\ldots ,N\}$
, the sequence
$i\in \{1,\ldots ,N\}$
, the sequence
![]() $(D_{t,i})_{t\in \mathbb {N}}$
converges towards
$(D_{t,i})_{t\in \mathbb {N}}$
converges towards
![]() $S_i$
, so
$S_i$
, so
![]() $(\rho (D_{t,i}))_{t\in \mathbb {N}}$
converges towards
$(\rho (D_{t,i}))_{t\in \mathbb {N}}$
converges towards
![]() $\rho (S_i)$
[Reference OstrowskiOst73, Theorem in Appendix A]. In particular,
$\rho (S_i)$
[Reference OstrowskiOst73, Theorem in Appendix A]. In particular,
![]() $\rho (S_1)=\unicode{x3bb} =\max \{\rho (S_1),\ldots ,\rho (S_n)\}$
. By the Perron–Frobenius theorem (Theorem 3.2.3), there is for each
$\rho (S_1)=\unicode{x3bb} =\max \{\rho (S_1),\ldots ,\rho (S_n)\}$
. By the Perron–Frobenius theorem (Theorem 3.2.3), there is for each
![]() $t\in \mathbb {N}$
an eigenvector
$t\in \mathbb {N}$
an eigenvector
![]() $v_t \geq 0$
of
$v_t \geq 0$
of
![]() $D_{t,1}$
to the eigenvalue
$D_{t,1}$
to the eigenvalue
![]() $\rho (D_{t,1})$
. Lemma 3.3.4 then gives for each
$\rho (D_{t,1})$
. Lemma 3.3.4 then gives for each
![]() $i\in \{1,\ldots ,N\}$
and each
$i\in \{1,\ldots ,N\}$
and each
![]() $t\in \mathbb {N}$
,
$t\in \mathbb {N}$
,
Now, we may assume that
![]() $\lVert v_t \rVert = 1$
for all t (after normalizing
$\lVert v_t \rVert = 1$
for all t (after normalizing
![]() $v_t$
). Let
$v_t$
). Let
Because
![]() $\mathbb {S}^{n-1}$
is compact (with respect to the Euclidean topology), we may take a subsequence and assume that
$\mathbb {S}^{n-1}$
is compact (with respect to the Euclidean topology), we may take a subsequence and assume that
![]() $(v_t)_{t\in \mathbb {N}}$
converges to a
$(v_t)_{t\in \mathbb {N}}$
converges to a
![]() $v \geq 0$
in
$v \geq 0$
in
![]() $\mathbb {S}^{n-1}$
. Thus we get
$\mathbb {S}^{n-1}$
. Thus we get
and for each
![]() $i\in \{1,\ldots ,N\}$
,
$i\in \{1,\ldots ,N\}$
,
This finishes the proof of the proposition.
Proof of Proposition B
By Remark 3.3.2, there exists
![]() $(S_1, \ldots , S_N) \in \mathcal {M}_{n, N}$
such that
$(S_1, \ldots , S_N) \in \mathcal {M}_{n, N}$
such that
![]() $\{ S_1, \ldots , S_N \}$
is the set of matrices contained in f. By Proposition 3.4.1, there exists
$\{ S_1, \ldots , S_N \}$
is the set of matrices contained in f. By Proposition 3.4.1, there exists
![]() $j \in \{1, \ldots , N\}$
and an eigenvector
$j \in \{1, \ldots , N\}$
and an eigenvector
![]() $\mu =(\mu _1,\ldots ,\mu _n) \in ({\mathbb R}_{\geq 0})^n \setminus \{ 0 \}$
of
$\mu =(\mu _1,\ldots ,\mu _n) \in ({\mathbb R}_{\geq 0})^n \setminus \{ 0 \}$
of
![]() $S_{j}$
to the eigenvalue
$S_{j}$
to the eigenvalue
![]() $\theta =\max \{\rho (S_1),\ldots ,\rho (S_N)\}$
such that
$\theta =\max \{\rho (S_1),\ldots ,\rho (S_N)\}$
such that
![]() $S_i \mu \leq S_{j} \mu = \theta \mu $
for each
$S_i \mu \leq S_{j} \mu = \theta \mu $
for each
![]() $i \in \{1,\ldots ,N\}$
. We now prove that this implies that
$i \in \{1,\ldots ,N\}$
. We now prove that this implies that
![]() $\deg _\mu (f_l) = \theta \mu _l$
for each
$\deg _\mu (f_l) = \theta \mu _l$
for each
![]() $l \in \{1, \ldots , n\}$
, which shows that
$l \in \{1, \ldots , n\}$
, which shows that
![]() $\mu =(\mu _1,\ldots ,\mu _n)$
is a maximal eigenvector of f, and thus proves assertion (1). For each monomial
$\mu =(\mu _1,\ldots ,\mu _n)$
is a maximal eigenvector of f, and thus proves assertion (1). For each monomial
![]() $m=\chi x_1^{r_1}\cdots x_n^{r_n}$
of
$m=\chi x_1^{r_1}\cdots x_n^{r_n}$
of
![]() $f_l$
with
$f_l$
with
![]() $\chi \in \mathbf {k}^*$
, there is a matrix
$\chi \in \mathbf {k}^*$
, there is a matrix
![]() $S_i$
with its lth line equal to
$S_i$
with its lth line equal to
![]() $(r_1\ r_2\ \cdots \ r_n)$
. The lth component of
$(r_1\ r_2\ \cdots \ r_n)$
. The lth component of
![]() $S_i \mu $
is equal to
$S_i \mu $
is equal to
![]() $r_1\mu _1+\cdots +r_n\mu _n=\deg _\mu (m)$
. The inequality
$r_1\mu _1+\cdots +r_n\mu _n=\deg _\mu (m)$
. The inequality
![]() $S_i\mu \le \theta \mu $
then yields
$S_i\mu \le \theta \mu $
then yields
![]() $\deg _\mu (m)\le \theta \mu _l$
. As this holds for each monomial of
$\deg _\mu (m)\le \theta \mu _l$
. As this holds for each monomial of
![]() $f_l$
, we obtain
$f_l$
, we obtain
![]() $\deg _\mu (f_l) \leq \theta \mu _l$
. The equality follows from
$\deg _\mu (f_l) \leq \theta \mu _l$
. The equality follows from
![]() $S_j\mu =\theta \mu $
, because the monomial m that corresponds to the lth row of
$S_j\mu =\theta \mu $
, because the monomial m that corresponds to the lth row of
![]() $S_j$
has
$S_j$
has
![]() $\mu $
-degree equal to
$\mu $
-degree equal to
![]() $\theta \mu _l$
.
$\theta \mu _l$
.
We now prove assertion (2). The dominance of f implies that
![]() $1\le \deg (f^r)$
for each r and this in turn gives
$1\le \deg (f^r)$
for each r and this in turn gives
![]() $1 \leq \unicode{x3bb} (f)$
. The inequality
$1 \leq \unicode{x3bb} (f)$
. The inequality
![]() $\theta \le \deg (f)$
follows from Corollary 3.2.6, so we only need to prove
$\theta \le \deg (f)$
follows from Corollary 3.2.6, so we only need to prove
![]() $\unicode{x3bb} (f)\le \theta $
. This is done by induction on n. If
$\unicode{x3bb} (f)\le \theta $
. This is done by induction on n. If
![]() $n = 1$
, then
$n = 1$
, then
![]() $\mu \in ({\mathbb R}_{>0})^1$
and the statement follows from Proposition A(2). Now, let
$\mu \in ({\mathbb R}_{>0})^1$
and the statement follows from Proposition A(2). Now, let
![]() $n> 1$
. We may assume (after a permutation of the coordinates) that
$n> 1$
. We may assume (after a permutation of the coordinates) that
![]() $\mu _1 \leq \mu _2 \leq \cdots \leq \mu _n$
. Now, let
$\mu _1 \leq \mu _2 \leq \cdots \leq \mu _n$
. Now, let
![]() $m \in \{0, \ldots , n-1\}$
with
$m \in \{0, \ldots , n-1\}$
with
![]() $\mu _i = 0$
for
$\mu _i = 0$
for
![]() $i \leq m$
and
$i \leq m$
and
![]() $\mu _i> 0$
for
$\mu _i> 0$
for
![]() $i> m$
. From Remark 2.3.1(2), we get
$i> m$
. From Remark 2.3.1(2), we get
From Lemma 2.5.6, we get that for each
![]() $i \in \{1, \ldots , m \}$
, the element
$i \in \{1, \ldots , m \}$
, the element
![]() $f_i$
is a polynomial in the variables
$f_i$
is a polynomial in the variables
![]() $\{x_1, \ldots , x_m \}$
. Thus we get from Lemma 2.4.1 that
$\{x_1, \ldots , x_m \}$
. Thus we get from Lemma 2.4.1 that
![]() $\unicode{x3bb} (f) = \max \{\unicode{x3bb} _1, \unicode{x3bb} _2 \}$
, where
$\unicode{x3bb} (f) = \max \{\unicode{x3bb} _1, \unicode{x3bb} _2 \}$
, where
Because
![]() $m \leq n-1$
, by induction hypothesis we have
$m \leq n-1$
, by induction hypothesis we have
Note that each eigenvalue of a matrix that is contained in
![]() $\hat {f}$
is an eigenvalue of a matrix that is contained in f. Thus we get
$\hat {f}$
is an eigenvalue of a matrix that is contained in f. Thus we get
![]() $\theta _1 \leq \theta $
. From Lemma 2.6.1(4), it follows that
$\theta _1 \leq \theta $
. From Lemma 2.6.1(4), it follows that
![]() $\unicode{x3bb} _2 \leq \theta $
. In summary, we proved that
$\unicode{x3bb} _2 \leq \theta $
. In summary, we proved that
![]() $\unicode{x3bb} (f) = \max \{\unicode{x3bb} _1, \unicode{x3bb} _2\} \leq \theta $
, that is, assertion (2) holds for n.
$\unicode{x3bb} (f) = \max \{\unicode{x3bb} _1, \unicode{x3bb} _2\} \leq \theta $
, that is, assertion (2) holds for n.
We now prove assertion (3). We take a maximal eigenvector
![]() $\mu $
of f. As
$\mu $
of f. As
![]() $\deg _\mu (f_i)= \theta \mu _i$
for each
$\deg _\mu (f_i)= \theta \mu _i$
for each
![]() $i\in \{1,\ldots ,n\}$
, we have
$i\in \{1,\ldots ,n\}$
, we have
![]() $\deg _\mu (f)=\theta $
. If
$\deg _\mu (f)=\theta $
. If
![]() $\theta =1$
, (i) follows from assertion (2) and (ii) is trivially true, so we may assume that
$\theta =1$
, (i) follows from assertion (2) and (ii) is trivially true, so we may assume that
![]() $\theta>1$
. If f is
$\theta>1$
. If f is
![]() $\mu $
-algebraically stable, then Lemma 2.6.1(5) gives
$\mu $
-algebraically stable, then Lemma 2.6.1(5) gives
![]() $\unicode{x3bb} _2 = \theta $
and thus
$\unicode{x3bb} _2 = \theta $
and thus
![]() $\unicode{x3bb} (f) = \theta $
, so (i) is proven. Conversely, if
$\unicode{x3bb} (f) = \theta $
, so (i) is proven. Conversely, if
![]() $\mu \in ({\mathbb R}_{>0})^n$
and
$\mu \in ({\mathbb R}_{>0})^n$
and
![]() $\unicode{x3bb} (f)=\theta>1$
, then f is
$\unicode{x3bb} (f)=\theta>1$
, then f is
![]() $\mu $
-algebraically stable by Proposition A(3). This achieves the proof of (3). As
$\mu $
-algebraically stable by Proposition A(3). This achieves the proof of (3). As
![]() $\theta = \deg _\mu (f) \in {\mathbb R}_{\geq 0}$
(that is, is not equal to
$\theta = \deg _\mu (f) \in {\mathbb R}_{\geq 0}$
(that is, is not equal to
![]() $+\infty $
), (3) is a direct consequence of Lemma 2.6.1(5).
$+\infty $
), (3) is a direct consequence of Lemma 2.6.1(5).
We now give an example that shows that the implication of Proposition B(3)(i) is not an equivalence.
Example 3.4.2. We consider the automorphism
As
![]() $\deg (f)=2$
, the maximal eigenvalue
$\deg (f)=2$
, the maximal eigenvalue
![]() $\theta $
of f (see Definition 1.4.8) satisfies
$\theta $
of f (see Definition 1.4.8) satisfies
![]() $\theta \le 2$
(Corollary 3.2.6). Moreover,
$\theta \le 2$
(Corollary 3.2.6). Moreover,
![]() $\theta =2$
, as the matrix
$\theta =2$
, as the matrix
 $$ \begin{align*} \begin{pmatrix} 2 & 0 & 0&0\\ 1 & 0 & 0&0\\ 0 & 0 &1&0\\ 0 & 0 & 0&1 \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} 2 & 0 & 0&0\\ 1 & 0 & 0&0\\ 0 & 0 &1&0\\ 0 & 0 & 0&1 \end{pmatrix} \end{align*} $$
is contained in f. When we choose
![]() $\mu =(0,0,1,1)$
, we get
$\mu =(0,0,1,1)$
, we get
![]() $\deg _\mu (f)=2$
, and we see that f is not
$\deg _\mu (f)=2$
, and we see that f is not
![]() $\mu $
-algebraically stable, as
$\mu $
-algebraically stable, as
![]() $\deg _\mu (f^2)=2<4$
. Moreover,
$\deg _\mu (f^2)=2<4$
. Moreover,
![]() $\deg _\mu (f_i) = 0$
for
$\deg _\mu (f_i) = 0$
for
![]() $i \in \{1, 2\}$
and
$i \in \{1, 2\}$
and
![]() $\deg _\mu (f_i) = 2$
for
$\deg _\mu (f_i) = 2$
for
![]() $i \in \{3, 4\}$
. Thus
$i \in \{3, 4\}$
. Thus
![]() $\mu $
is a maximal eigenvector of f (see Definition 1.4.8). However,
$\mu $
is a maximal eigenvector of f (see Definition 1.4.8). However,
![]() $\unicode{x3bb} (f)=\theta $
. Indeed,
$\unicode{x3bb} (f)=\theta $
. Indeed,
![]() $\unicode{x3bb} (f)\le \deg (f)=2$
, and
$\unicode{x3bb} (f)\le \deg (f)=2$
, and
![]() $((x_1)^2+x_2,x_1)$
is algebraically stable for the standard degree, as its homogeneous part of degree
$((x_1)^2+x_2,x_1)$
is algebraically stable for the standard degree, as its homogeneous part of degree
![]() $2$
is
$2$
is
![]() $((x_1)^2,0)$
, which satisfies
$((x_1)^2,0)$
, which satisfies
![]() $((x_1)^2,0)^r=((x_1)^{2^r},0)$
for each
$((x_1)^2,0)^r=((x_1)^{2^r},0)$
for each
![]() $r\ge 1$
(see Proposition A).
$r\ge 1$
(see Proposition A).
4 Explicit calculation of dynamical degrees of affine-triangular automorphisms
In this section, we apply Proposition B to compute the dynamical degrees of affine-triangular dominant endomorphisms of
![]() $\mathbb {A}^n$
. We prove Proposition 4.2.3, which implies Propositions 4.2.5 and C.
$\mathbb {A}^n$
. We prove Proposition 4.2.3, which implies Propositions 4.2.5 and C.
Notation 4.0.1. We denote by
![]() $\operatorname {\mathrm {TEnd}}(\mathbb {A}^n)$
and
$\operatorname {\mathrm {TEnd}}(\mathbb {A}^n)$
and
![]() $\operatorname {\mathrm {TAut}}(\mathbb {A}^n)$
(respectively
$\operatorname {\mathrm {TAut}}(\mathbb {A}^n)$
(respectively
![]() $\operatorname {\mathrm {EEnd}}(\mathbb {A}^n)$
and
$\operatorname {\mathrm {EEnd}}(\mathbb {A}^n)$
and
![]() $\operatorname {\mathrm {EAut}}(\mathbb {A}^n)$
) the monoid and group of triangular (respectively elementary) endomorphisms and automorphisms of
$\operatorname {\mathrm {EAut}}(\mathbb {A}^n)$
) the monoid and group of triangular (respectively elementary) endomorphisms and automorphisms of
![]() $\mathbb {A}^n$
. We denote by
$\mathbb {A}^n$
. We denote by
![]() $\operatorname {\mathrm {Aff}}(\mathbb {A}^n)$
the group of affine automorphisms of
$\operatorname {\mathrm {Aff}}(\mathbb {A}^n)$
the group of affine automorphisms of
![]() $\mathbb {A}^n$
and by
$\mathbb {A}^n$
and by
![]() $\operatorname {\mathrm {Sym}}(\mathbb {A}^n)\subset \operatorname {\mathrm {Aff}}(\mathbb {A}^n)$
the group of permutations of the coordinates.
$\operatorname {\mathrm {Sym}}(\mathbb {A}^n)\subset \operatorname {\mathrm {Aff}}(\mathbb {A}^n)$
the group of permutations of the coordinates.
4.1 From affine-triangular to permutation-triangular endomorphisms
We can restrict ourselves to permutation-triangular endomorphisms, as the next simple result shows.
Proposition 4.1.1. Each affine-triangular endomorphism of
![]() $\mathbb {A}^n$
is conjugate by an element of
$\mathbb {A}^n$
is conjugate by an element of
![]() $\operatorname {\mathrm {Aff}}(\mathbb {A}^n)$
to a permutation-triangular endomorphism.
$\operatorname {\mathrm {Aff}}(\mathbb {A}^n)$
to a permutation-triangular endomorphism.
Proof. We take
![]() $\alpha \in \operatorname {\mathrm {Aff}}(\mathbb {A}^n)$
and
$\alpha \in \operatorname {\mathrm {Aff}}(\mathbb {A}^n)$
and
![]() $\tau \in \operatorname {\mathrm {TEnd}}(\mathbb {A}^n)$
and show that we can conjugate
$\tau \in \operatorname {\mathrm {TEnd}}(\mathbb {A}^n)$
and show that we can conjugate
![]() $f=\alpha \circ \tau $
to a permutation-triangular endomorphism by an element of
$f=\alpha \circ \tau $
to a permutation-triangular endomorphism by an element of
![]() $\operatorname {\mathrm {Aff}}(\mathbb {A}^n)$
.
$\operatorname {\mathrm {Aff}}(\mathbb {A}^n)$
.
Let
![]() $p=(p_1,\ldots ,p_n)\in \mathbb {A}^n$
be the point such that
$p=(p_1,\ldots ,p_n)\in \mathbb {A}^n$
be the point such that
![]() $\alpha (p)=0$
and consider the translation
$\alpha (p)=0$
and consider the translation
![]() $\tau _p=(x_1+p_1,\ldots ,x_n+p_n) \in \operatorname {\mathrm {Aff}}(\mathbb {A}^n)\cap \operatorname {\mathrm {TAut}}(\mathbb {A}^n)$
. Then
$\tau _p=(x_1+p_1,\ldots ,x_n+p_n) \in \operatorname {\mathrm {Aff}}(\mathbb {A}^n)\cap \operatorname {\mathrm {TAut}}(\mathbb {A}^n)$
. Then
![]() $\alpha '=\alpha \circ \tau _p \in \operatorname {\mathrm {Aff}}(\mathbb {A}^n)$
fixes the origin
$\alpha '=\alpha \circ \tau _p \in \operatorname {\mathrm {Aff}}(\mathbb {A}^n)$
fixes the origin
![]() $(0,\ldots ,0)\in \mathbb {A}^n$
. We then replace
$(0,\ldots ,0)\in \mathbb {A}^n$
. We then replace
![]() $\alpha $
with
$\alpha $
with
![]() $\alpha '$
and
$\alpha '$
and
![]() $\tau $
with
$\tau $
with
![]() $\tau _p^{-1} \circ \tau $
, and may assume that
$\tau _p^{-1} \circ \tau $
, and may assume that
![]() $\alpha $
belongs to the subgroup
$\alpha $
belongs to the subgroup
![]() $\operatorname {\mathrm {GL}}_n=\operatorname {\mathrm {GL}}_n(\mathbf {k})\subset \operatorname {\mathrm {Aff}}(\mathbb {A}^n)$
of elements that fix the origin.
$\operatorname {\mathrm {GL}}_n=\operatorname {\mathrm {GL}}_n(\mathbf {k})\subset \operatorname {\mathrm {Aff}}(\mathbb {A}^n)$
of elements that fix the origin.
The group
![]() $B = \operatorname {\mathrm {TAut}}({\mathbb A}^n) \cap \operatorname {\mathrm {GL}}_n$
is a Borel subgroup of
$B = \operatorname {\mathrm {TAut}}({\mathbb A}^n) \cap \operatorname {\mathrm {GL}}_n$
is a Borel subgroup of
![]() $\operatorname {\mathrm {GL}}_n$
. It consists of all lower triangular matrices. The so-called Bruhat decomposition of
$\operatorname {\mathrm {GL}}_n$
. It consists of all lower triangular matrices. The so-called Bruhat decomposition of
![]() $\operatorname {\mathrm {GL}}_n$
:
$\operatorname {\mathrm {GL}}_n$
:
yields
![]() $\beta , \gamma \in B$
and
$\beta , \gamma \in B$
and
![]() $\sigma \in \operatorname {\mathrm {Sym}}(\mathbb {A}^n)$
such that
$\sigma \in \operatorname {\mathrm {Sym}}(\mathbb {A}^n)$
such that
![]() $\alpha = \beta \circ \sigma \circ \gamma $
. This gives
$\alpha = \beta \circ \sigma \circ \gamma $
. This gives
where
![]() $\gamma \circ \tau \circ \beta \in \operatorname {\mathrm {TEnd}}({\mathbb A}^n)$
. This achieves the proof.
$\gamma \circ \tau \circ \beta \in \operatorname {\mathrm {TEnd}}({\mathbb A}^n)$
. This achieves the proof.
4.2 Permutation-elementary automorphisms
Up to conjugation, each permutation-elementary automorphism has a particular form. This shows the following easy observation.
Lemma 4.2.1. Let
![]() $n\ge 1$
and let
$n\ge 1$
and let
![]() $h\in \operatorname {\mathrm {End}}(\mathbb {A}^{n+1})$
be a permutation-elementary automorphism. There is a permutation of the coordinates
$h\in \operatorname {\mathrm {End}}(\mathbb {A}^{n+1})$
be a permutation-elementary automorphism. There is a permutation of the coordinates
![]() $\alpha \in \operatorname {\mathrm {Sym}}(\mathbb {A}^{n+1})$
such that
$\alpha \in \operatorname {\mathrm {Sym}}(\mathbb {A}^{n+1})$
such that
where
![]() $0\le m\le n$
,
$0\le m\le n$
,
![]() $\{x_1,\ldots ,x_m\}=\{f_1,\ldots ,f_m\}$
,
$\{x_1,\ldots ,x_m\}=\{f_1,\ldots ,f_m\}$
,
![]() $\xi \in \mathbf {k}^*$
and
$\xi \in \mathbf {k}^*$
and
![]() $p\in \mathbf {k}[x_1,\ldots ,x_n]$
.
$p\in \mathbf {k}[x_1,\ldots ,x_n]$
.
Proof. We write
![]() $h=\sigma \circ \tau $
, where
$h=\sigma \circ \tau $
, where
![]() $\sigma \in \operatorname {\mathrm {Sym}}(\mathbb {A}^{n+1})$
and
$\sigma \in \operatorname {\mathrm {Sym}}(\mathbb {A}^{n+1})$
and
![]() $\tau \in \operatorname {\mathrm {EAut}}(\mathbb {A}^{n+1})$
. We may choose
$\tau \in \operatorname {\mathrm {EAut}}(\mathbb {A}^{n+1})$
. We may choose
![]() $\alpha = (\alpha _1, \ldots , \alpha _{n+1})\in \operatorname {\mathrm {Sym}}(\mathbb {A}^{n+1})$
such that
$\alpha = (\alpha _1, \ldots , \alpha _{n+1})\in \operatorname {\mathrm {Sym}}(\mathbb {A}^{n+1})$
such that
![]() $\alpha _{n+1} = x_{n+1}$
and
$\alpha _{n+1} = x_{n+1}$
and
![]() $\alpha \circ \sigma \circ \alpha ^{-1}$
induces the following cyclic permutation on the last coordinates
$\alpha \circ \sigma \circ \alpha ^{-1}$
induces the following cyclic permutation on the last coordinates
for some integer m with
![]() $0\le m\le n$
. This gives
$0\le m\le n$
. This gives
where
![]() $\{ x_1, \ldots , x_m \} = \{f_1, \ldots , f_m \}$
. As
$\{ x_1, \ldots , x_m \} = \{f_1, \ldots , f_m \}$
. As
![]() $\alpha _{n+1}=x_{n+1}$
, we obtain
$\alpha _{n+1}=x_{n+1}$
, we obtain
for some
![]() $\xi \in \mathbf {k}^\ast $
and
$\xi \in \mathbf {k}^\ast $
and
![]() $p \in \mathbf {k}[x_1, \ldots , x_n]$
. This implies that
$p \in \mathbf {k}[x_1, \ldots , x_n]$
. This implies that
![]() $\alpha \circ h \circ \alpha ^{-1}$
is equal to
$\alpha \circ h \circ \alpha ^{-1}$
is equal to
 $$ \begin{align*} &(\alpha \circ \sigma \circ \alpha^{-1}) \circ (\alpha \circ \tau \circ \alpha^{-1}) \\ &\qquad= (f_{1},\ldots,f_{m}, \xi x_{n+1}+p(x_1,\ldots,x_{n}),x_{m+1},\ldots,x_{n}). \\[-40pt] \end{align*} $$
$$ \begin{align*} &(\alpha \circ \sigma \circ \alpha^{-1}) \circ (\alpha \circ \tau \circ \alpha^{-1}) \\ &\qquad= (f_{1},\ldots,f_{m}, \xi x_{n+1}+p(x_1,\ldots,x_{n}),x_{m+1},\ldots,x_{n}). \\[-40pt] \end{align*} $$
We will need the following result to obtain Proposition 4.2.3. Proposition 4.2.3 will be the key ingredient to show Proposition 4.2.5 and Proposition C.
Lemma 4.2.2. Let
![]() $0\le m\le n$
, let
$0\le m\le n$
, let
![]() $\hat {f}=(f_{1},\ldots ,f_m)\in \operatorname {\mathrm {Aut}}(\mathbb {A}^m)$
and let
$\hat {f}=(f_{1},\ldots ,f_m)\in \operatorname {\mathrm {Aut}}(\mathbb {A}^m)$
and let
![]() $q\in \mathbf {k}[x_1,\ldots , x_{n+1}] \setminus \{0\}$
. For each
$q\in \mathbf {k}[x_1,\ldots , x_{n+1}] \setminus \{0\}$
. For each
![]() $r\ge 1$
, every component of
$r\ge 1$
, every component of
![]() $g^r$
is non-zero where
$g^r$
is non-zero where
Proof. For each
![]() $r\ge 1$
, we write
$r\ge 1$
, we write
![]() $g^r=((g^r)_1,\ldots ,(g^r)_{n+1})$
. The result is true by assumption when
$g^r=((g^r)_1,\ldots ,(g^r)_{n+1})$
. The result is true by assumption when
![]() $r=1$
. For each
$r=1$
. For each
![]() $r\ge 1$
and
$r\ge 1$
and
![]() $1 \leq i \leq m$
, we have
$1 \leq i \leq m$
, we have
![]() $(g^r)_i = (\hat {f}^r)_i \not =0$
.
$(g^r)_i = (\hat {f}^r)_i \not =0$
.
As
![]() $(f_1,\ldots ,f_m)\in \operatorname {\mathrm {Aut}}(\mathbb {A}^m)$
, we also have
$(f_1,\ldots ,f_m)\in \operatorname {\mathrm {Aut}}(\mathbb {A}^m)$
, we also have
![]() $(f_1,\ldots ,f_m,x_{m+1},\ldots ,x_{n})\in \operatorname {\mathrm {Aut}}(\mathbb {A}^{n})$
. In particular, g is dominant if
$(f_1,\ldots ,f_m,x_{m+1},\ldots ,x_{n})\in \operatorname {\mathrm {Aut}}(\mathbb {A}^{n})$
. In particular, g is dominant if
![]() $q\not \in \mathbf {k}[x_1,\ldots ,x_n]$
, that is, if
$q\not \in \mathbf {k}[x_1,\ldots ,x_n]$
, that is, if
![]() $\deg _{x_{n+1}}(q)\ge 1$
. Thus we assume that
$\deg _{x_{n+1}}(q)\ge 1$
. Thus we assume that
![]() $q \in \mathbf {k}[x_1, \ldots , x_n] \setminus \{0\}$
.
$q \in \mathbf {k}[x_1, \ldots , x_n] \setminus \{0\}$
.
Suppose first that
![]() $m=n$
, in which case
$m=n$
, in which case
![]() $g=(f_1,\ldots ,f_m,q)$
. For each
$g=(f_1,\ldots ,f_m,q)$
. For each
![]() $r\ge 2$
, we get
$r\ge 2$
, we get
![]() $g^r=((g^r)_1,\ldots ,(g^r)_{m},q((g^{r-1})_1,\ldots ,(g^{r-1})_{m}))$
. As
$g^r=((g^r)_1,\ldots ,(g^r)_{m},q((g^{r-1})_1,\ldots ,(g^{r-1})_{m}))$
. As
![]() $\hat {f}$
is dominant and q is not the zero polynomial, every component of
$\hat {f}$
is dominant and q is not the zero polynomial, every component of
![]() $g^r$
is not zero.
$g^r$
is not zero.
We then assume that
![]() $n>m$
and prove the result by induction on
$n>m$
and prove the result by induction on
![]() $n-m$
. As
$n-m$
. As
![]() $(f_1,\ldots ,f_m,x_{m+1},\ldots ,x_{n})\in \operatorname {\mathrm {Aut}}(\mathbb {A}^{n})$
, there is a polynomial
$(f_1,\ldots ,f_m,x_{m+1},\ldots ,x_{n})\in \operatorname {\mathrm {Aut}}(\mathbb {A}^{n})$
, there is a polynomial
![]() $h\in \mathbf {k}[x_1,\ldots ,x_n]$
such that
$h\in \mathbf {k}[x_1,\ldots ,x_n]$
such that
![]() $h(f_1,\ldots ,f_m,x_{m+1},\ldots ,x_n)=q$
, because
$h(f_1,\ldots ,f_m,x_{m+1},\ldots ,x_n)=q$
, because
![]() $q \in \mathbf {k}[x_1,\ldots ,x_n]$
. We denote by
$q \in \mathbf {k}[x_1,\ldots ,x_n]$
. We denote by
![]() $\phi \colon \mathbb {A}^n\hookrightarrow \mathbb {A}^{n+1}$
the closed embedding that is given by
$\phi \colon \mathbb {A}^n\hookrightarrow \mathbb {A}^{n+1}$
the closed embedding that is given by
and we write
![]() $\tau =(f_1,\ldots ,f_m,h,x_{m+1},\ldots ,x_{n-1})\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
. We now prove that
$\tau =(f_1,\ldots ,f_m,h,x_{m+1},\ldots ,x_{n-1})\in \operatorname {\mathrm {End}}(\mathbb {A}^n)$
. We now prove that
![]() $g\circ \phi =\phi \circ \tau $
:
$g\circ \phi =\phi \circ \tau $
:
 $$ \begin{align*} &g\circ \phi(x_1,\ldots,x_n) \\ &=(f_1,\ldots,f_m,q(x_1,\ldots,x_m,h,x_{m+1},\ldots,x_{n-1}),h,x_{m+1},\ldots,x_{n-1})\\ &=(f_1,\ldots,f_m,h(f_1,\ldots,f_m,h,x_{m+1},\ldots,x_{n-1}),h,x_{m+1},\ldots,x_{n-1})\\ &=\phi\circ \tau(x_1,\ldots,x_n). \end{align*} $$
$$ \begin{align*} &g\circ \phi(x_1,\ldots,x_n) \\ &=(f_1,\ldots,f_m,q(x_1,\ldots,x_m,h,x_{m+1},\ldots,x_{n-1}),h,x_{m+1},\ldots,x_{n-1})\\ &=(f_1,\ldots,f_m,h(f_1,\ldots,f_m,h,x_{m+1},\ldots,x_{n-1}),h,x_{m+1},\ldots,x_{n-1})\\ &=\phi\circ \tau(x_1,\ldots,x_n). \end{align*} $$
Hence,
![]() $g^r\circ \phi =\phi \circ \tau ^r$
for each
$g^r\circ \phi =\phi \circ \tau ^r$
for each
![]() $r\ge 1$
. By induction, every component of
$r\ge 1$
. By induction, every component of
![]() $\tau ^r$
is non-zero, so every component of
$\tau ^r$
is non-zero, so every component of
![]() $g^r$
is non-zero, except maybe the
$g^r$
is non-zero, except maybe the
![]() $(m+1)$
th component. However, if the
$(m+1)$
th component. However, if the
![]() $(m+1)$
th component of
$(m+1)$
th component of
![]() $g^r$
were zero, then the
$g^r$
were zero, then the
![]() $(m+2)$
th of
$(m+2)$
th of
![]() $g^{r+1}$
would be zero, which is impossible as the
$g^{r+1}$
would be zero, which is impossible as the
![]() $(m+2)$
th component of
$(m+2)$
th component of
![]() $g^{r+1}\circ \phi =\phi \circ \tau ^{r+1}$
is not equal to zero.
$g^{r+1}\circ \phi =\phi \circ \tau ^{r+1}$
is not equal to zero.
Proposition 4.2.3. Let
![]() $0\le m < n$
, let
$0\le m < n$
, let
![]() $\hat {f}=(f_{1},\ldots ,f_m)\in \operatorname {\mathrm {Aut}}(\mathbb {A}^m)$
,
$\hat {f}=(f_{1},\ldots ,f_m)\in \operatorname {\mathrm {Aut}}(\mathbb {A}^m)$
,
![]() $\xi \in \mathbf {k}^*$
and
$\xi \in \mathbf {k}^*$
and
![]() $p\in \mathbf {k}[x_1,\ldots ,x_n]$
. Denote by
$p\in \mathbf {k}[x_1,\ldots ,x_n]$
. Denote by
![]() $I\subset {\mathbb N}^n$
the finite subset of indices of the monomials of p, and define
$I\subset {\mathbb N}^n$
the finite subset of indices of the monomials of p, and define
 $$ \begin{align*} \theta =\max\bigg\{\unicode{x3bb}\in {\mathbb R}\mid\unicode{x3bb}^{n-m}= \sum_{j=m+1}^n i_j \unicode{x3bb}^{n-j} \text{ for some } (i_1,\ldots,i_n)\in I\bigg\}.\end{align*} $$
$$ \begin{align*} \theta =\max\bigg\{\unicode{x3bb}\in {\mathbb R}\mid\unicode{x3bb}^{n-m}= \sum_{j=m+1}^n i_j \unicode{x3bb}^{n-j} \text{ for some } (i_1,\ldots,i_n)\in I\bigg\}.\end{align*} $$
Then,
has the following properties.
-
(1) If
 $\deg _{x_{m+1},\ldots ,x_n}(p)\le 1$
, then
$\deg _{x_{m+1},\ldots ,x_n}(p)\le 1$
, then
 $\unicode{x3bb} (f)=\unicode{x3bb} (\hat {f})$
.
$\unicode{x3bb} (f)=\unicode{x3bb} (\hat {f})$
. -
(2) If
 $\deg _{x_{m+1},\ldots ,x_n}(p)\ge 2$
, define that is,
$\deg _{x_{m+1},\ldots ,x_n}(p)\ge 2$
, define that is, $$ \begin{align*} \mu &= (\mu_1, \ldots, \mu_{n+1}) = (0,\ldots,0,\theta^{n-m},\theta^{n-m-1},\ldots,\theta,1), \end{align*} $$
$$ \begin{align*} \mu &= (\mu_1, \ldots, \mu_{n+1}) = (0,\ldots,0,\theta^{n-m},\theta^{n-m-1},\ldots,\theta,1), \end{align*} $$
 $\mu _{j}=0$
for
$\mu _{j}=0$
for
 $j\le m$
and
$j\le m$
and
 $\mu _{j}=\theta ^{n+1-j}$
for
$\mu _{j}=\theta ^{n+1-j}$
for
 $j\ge m+1$
. Then we have
$j\ge m+1$
. Then we have
 $\theta>1$
,
$\theta>1$
,
 $\deg _\mu (f_{j}) = \theta \mu _{j}$
for each j (in particular
$\deg _\mu (f_{j}) = \theta \mu _{j}$
for each j (in particular
 $\deg _\mu (f)=\theta$
) and f is
$\deg _\mu (f)=\theta$
) and f is
 $\mu $
-algebraically stable. Moreover, if
$\mu $
-algebraically stable. Moreover, if
 $\unicode{x3bb} (\hat {f}) \leq \theta$
(in particular, if
$\unicode{x3bb} (\hat {f}) \leq \theta$
(in particular, if
 $m = 0$
), then
$m = 0$
), then
 $\unicode{x3bb} (f) = \theta $
.
$\unicode{x3bb} (f) = \theta $
.
-
(3) Assume
 $\{f_1, \ldots , f_m\} = \{x_1, \ldots , x_m\}$
. If
$\{f_1, \ldots , f_m\} = \{x_1, \ldots , x_m\}$
. If
 $\deg _{x_{m+1},\ldots ,x_n}(p)\le 1$
, then the maximal eigenvalue of f is equal to
$\deg _{x_{m+1},\ldots ,x_n}(p)\le 1$
, then the maximal eigenvalue of f is equal to
 $1$
and otherwise it is equal to
$1$
and otherwise it is equal to
 $\theta $
.
$\theta $
.
Remark 4.2.4. The case
![]() $m=n$
, not treated in Proposition 4.2.3, is rather trivial. We have
$m=n$
, not treated in Proposition 4.2.3, is rather trivial. We have
![]() $f=(f_1,\ldots ,f_n,\xi x_{n+1}+p(x_1,\ldots ,x_n))$
, where
$f=(f_1,\ldots ,f_n,\xi x_{n+1}+p(x_1,\ldots ,x_n))$
, where
![]() $\{f_1,\ldots ,f_n\}=\{x_1,\ldots ,x_n\}$
. Every matrix contained in f is then a block-matrix with a
$\{f_1,\ldots ,f_n\}=\{x_1,\ldots ,x_n\}$
. Every matrix contained in f is then a block-matrix with a
![]() $(n\times n)$
-permutation-matrix and a
$(n\times n)$
-permutation-matrix and a
![]() $(1\times 1)$
-matrix with a
$(1\times 1)$
-matrix with a
![]() $0$
or a
$0$
or a
![]() $1$
on the diagonal, so every eigenvalue is either
$1$
on the diagonal, so every eigenvalue is either
![]() $0$
or a root of unity. This implies that
$0$
or a root of unity. This implies that
![]() $\theta =1$
is the only possible maximal eigenvalue.
$\theta =1$
is the only possible maximal eigenvalue.
Proof of Proposition 4.2.3
(1) Because
![]() $\deg _{x_{m+1},\ldots ,x_n}(p)\le 1$
, Lemma 2.4.1 implies that
$\deg _{x_{m+1},\ldots ,x_n}(p)\le 1$
, Lemma 2.4.1 implies that
where, by convention,
![]() $\unicode{x3bb} (\hat {f}) = 1$
in case
$\unicode{x3bb} (\hat {f}) = 1$
in case
![]() $m = 0$
.
$m = 0$
.
(2) For each
![]() $i=(i_1,\ldots ,i_n)\in I$
, we set
$i=(i_1,\ldots ,i_n)\in I$
, we set
 $$ \begin{align*} p_i= \sum_{j=m+1}^n i_j x^{n-j} \in \mathbb{Z}[x] \end{align*} $$
$$ \begin{align*} p_i= \sum_{j=m+1}^n i_j x^{n-j} \in \mathbb{Z}[x] \end{align*} $$
and
![]() $q_i=x^{n-m}-p_i\in \mathbb {Z}[x]$
. Then
$q_i=x^{n-m}-p_i\in \mathbb {Z}[x]$
. Then
![]() $\theta $
is the biggest real root of one of the polynomials in
$\theta $
is the biggest real root of one of the polynomials in
![]() $\{q_i\mid i\in I\}$
. Note that
$\{q_i\mid i\in I\}$
. Note that
![]() $q_i$
is monic and of degree
$q_i$
is monic and of degree
![]() $n-m> 0$
. As
$n-m> 0$
. As
![]() $\deg _{x_{m+1},\ldots ,x_n}(p)\ge 2$
, there is
$\deg _{x_{m+1},\ldots ,x_n}(p)\ge 2$
, there is
![]() $i=(i_1,\ldots ,i_n)\in I$
such that
$i=(i_1,\ldots ,i_n)\in I$
such that
![]() $p_i(1)\ge 2$
. This implies that
$p_i(1)\ge 2$
. This implies that
![]() $q_i(1)=1-p_i(1)<0$
, so
$q_i(1)=1-p_i(1)<0$
, so
![]() $q_i$
has a real root that is bigger than
$q_i$
has a real root that is bigger than
![]() $1$
. This proves that
$1$
. This proves that
![]() $\theta>1$
. Moreover, for each
$\theta>1$
. Moreover, for each
![]() $i\in I$
, we have
$i\in I$
, we have
![]() $q_i(\theta )\ge 0$
, because
$q_i(\theta )\ge 0$
, because
![]() $q_i$
has no real root bigger than
$q_i$
has no real root bigger than
![]() $\theta $
. This gives
$\theta $
. This gives
![]() $\theta ^{n-m}\ge p_i(\theta )$
, with equality for at least one
$\theta ^{n-m}\ge p_i(\theta )$
, with equality for at least one
![]() $i \in I$
.
$i \in I$
.
We now prove that
![]() $\deg _\mu (f_{j})=\theta \mu _{j}$
for each
$\deg _\mu (f_{j})=\theta \mu _{j}$
for each
![]() $j\in \{1,\ldots ,n+1\}$
, where
$j\in \{1,\ldots ,n+1\}$
, where
![]() $f_j$
denotes the jth component of f. For each
$f_j$
denotes the jth component of f. For each
![]() $j \in \{1,\ldots ,m\}$
, we have
$j \in \{1,\ldots ,m\}$
, we have
![]() $\deg _\mu (f_{j})=0=\theta \mu _{j}$
and for each
$\deg _\mu (f_{j})=0=\theta \mu _{j}$
and for each
![]() $j \in \{m+2,\ldots ,n+1\}$
, we have
$j \in \{m+2,\ldots ,n+1\}$
, we have
![]() $\deg _\mu (f_{j})=\deg _\mu (x_{j-1})=\mu _{j-1}=\theta \mu _{j}$
. Moreover, we have
$\deg _\mu (f_{j})=\deg _\mu (x_{j-1})=\mu _{j-1}=\theta \mu _{j}$
. Moreover, we have
 $$ \begin{align*} \deg_{\mu}(f_{m+1})&= \max \bigg(\{\deg_\mu(x_{n+1})\}\cup \bigg\{\,\sum_{j=m+1}^{n} {i_j\mu_j} \ \bigg| \ (i_1,\ldots,i_n)\in {\mathbb N}^n\,\bigg\} \bigg) \\ &=\max(\{1\}\cup \{{\theta\cdot p_i(\theta)} \ | \ {i=(i_1,\ldots,i_n)\in {\mathbb N}^n}\} ) =\theta^{n-m+1}=\theta \mu_{m+1}. \end{align*} $$
$$ \begin{align*} \deg_{\mu}(f_{m+1})&= \max \bigg(\{\deg_\mu(x_{n+1})\}\cup \bigg\{\,\sum_{j=m+1}^{n} {i_j\mu_j} \ \bigg| \ (i_1,\ldots,i_n)\in {\mathbb N}^n\,\bigg\} \bigg) \\ &=\max(\{1\}\cup \{{\theta\cdot p_i(\theta)} \ | \ {i=(i_1,\ldots,i_n)\in {\mathbb N}^n}\} ) =\theta^{n-m+1}=\theta \mu_{m+1}. \end{align*} $$
This gives in particular
![]() $\theta = \deg _\mu (f)$
.
$\theta = \deg _\mu (f)$
.
It remains to prove that f is
![]() $\mu $
-algebraically stable, that is, that
$\mu $
-algebraically stable, that is, that
![]() $\deg _\mu (f^r)=\theta ^r$
for each
$\deg _\mu (f^r)=\theta ^r$
for each
![]() $r\ge 1$
; this will then give the result by Corollary 2.6.2.
$r\ge 1$
; this will then give the result by Corollary 2.6.2.
By Lemma 2.6.1(5), this corresponds to ask that for each
![]() $r\ge 1$
, there exists
$r\ge 1$
, there exists
![]() $j \in \{m+1,\ldots ,n\}$
such that
$j \in \{m+1,\ldots ,n\}$
such that
![]() $(g^r)_{j} \not =0$
, where
$(g^r)_{j} \not =0$
, where
![]() $g=(g_1,\ldots ,g_{n+1})\in \operatorname {\mathrm {End}}(\mathbb {A}^{n+1})$
is the
$g=(g_1,\ldots ,g_{n+1})\in \operatorname {\mathrm {End}}(\mathbb {A}^{n+1})$
is the
![]() $\mu $
-leading part of f and
$\mu $
-leading part of f and
![]() $(g^r)_{j}$
denotes the jth component of
$(g^r)_{j}$
denotes the jth component of
![]() $g^r$
. We observe that
$g^r$
. We observe that
where
![]() $g_{m+1}\in \mathbf {k}[x_1,\ldots ,x_{n+1}]\setminus \{0\}$
. The result then follows from Lemma 4.2.2
$g_{m+1}\in \mathbf {k}[x_1,\ldots ,x_{n+1}]\setminus \{0\}$
. The result then follows from Lemma 4.2.2
(3) The maximal eigenvalue of f is the biggest real number that is an eigenvalue of one of the matrices contained in f. Each such matrix is either contained in
![]() $(f_{1},\ldots ,f_{m}, \xi x_{n+1},x_{m+1},\ldots ,x_{n})$
, but then has spectral radius equal to
$(f_{1},\ldots ,f_{m}, \xi x_{n+1},x_{m+1},\ldots ,x_{n})$
, but then has spectral radius equal to
![]() $1$
, or is contained in
$1$
, or is contained in
![]() $(f_{1},\ldots ,f_{m}, \prod _{j=1}^n x_j^{i_j},x_{m+1},\ldots ,x_{n})$
for some
$(f_{1},\ldots ,f_{m}, \prod _{j=1}^n x_j^{i_j},x_{m+1},\ldots ,x_{n})$
for some
![]() $(i_1,\ldots ,i_n)\in I$
. In this latter case, the spectral radius is the one of the matrix
$(i_1,\ldots ,i_n)\in I$
. In this latter case, the spectral radius is the one of the matrix
 $$ \begin{align*} \begin{pmatrix} i_{m+1} & \cdots & i_n & 0 \\ 1 & \cdots & 0 & 0 \\ \vdots & \ddots & \vdots & \vdots \\ 0 & \cdots & 1 & 0 \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} i_{m+1} & \cdots & i_n & 0 \\ 1 & \cdots & 0 & 0 \\ \vdots & \ddots & \vdots & \vdots \\ 0 & \cdots & 1 & 0 \end{pmatrix} \end{align*} $$
and thus equal to the biggest real root of the polynomial
![]() $ x^{n-m}-\sum _{j=m+1}^{n} i_j x^{n-j}$
. If
$ x^{n-m}-\sum _{j=m+1}^{n} i_j x^{n-j}$
. If
![]() $\deg _{x_{m+1},\ldots ,x_n}(p)\le 1$
, the maximal eigenvalue is again equal to
$\deg _{x_{m+1},\ldots ,x_n}(p)\le 1$
, the maximal eigenvalue is again equal to
![]() $1$
, and if
$1$
, and if
![]() $\deg _{x_{m+1},\ldots ,x_n}(p)\ge 2$
, we get that
$\deg _{x_{m+1},\ldots ,x_n}(p)\ge 2$
, we get that
![]() $\theta $
is the maximal eigenvalue of f.
$\theta $
is the maximal eigenvalue of f.
As mentioned in the §1, the following result is attributed to Mattias Jonsson (unpublished).
Proposition 4.2.5. For each
![]() $n\ge 1$
and each polynomial
$n\ge 1$
and each polynomial
![]() $p\in \mathbf {k}[x_1,\ldots ,x_{n}]$
of degree
$p\in \mathbf {k}[x_1,\ldots ,x_{n}]$
of degree
![]() $\ge 2$
, let
$\ge 2$
, let
![]() $e_p\in \operatorname {\mathrm {Aut}}(\mathbb {A}^{n+1})$
be the automorphism
$e_p\in \operatorname {\mathrm {Aut}}(\mathbb {A}^{n+1})$
be the automorphism
Let
![]() $I\subset {\mathbb N}^n$
be the finite subset of indices of the monomials of p. We get
$I\subset {\mathbb N}^n$
be the finite subset of indices of the monomials of p. We get
 $$ \begin{align*} \unicode{x3bb}(e_p)=\max\bigg\{\unicode{x3bb}\in {\mathbb R}\mid \unicode{x3bb}^{n} = \sum_{j=1}^{n} i_j\unicode{x3bb}^{n-j} \text{ for some } (i_1,\ldots,i_n)\in I\bigg\}. \end{align*} $$
$$ \begin{align*} \unicode{x3bb}(e_p)=\max\bigg\{\unicode{x3bb}\in {\mathbb R}\mid \unicode{x3bb}^{n} = \sum_{j=1}^{n} i_j\unicode{x3bb}^{n-j} \text{ for some } (i_1,\ldots,i_n)\in I\bigg\}. \end{align*} $$
Proof of Proposition C
Let
![]() $h\in \operatorname {\mathrm {End}}(\mathbb {A}^{n+1})$
be a permutation-elementary automorphism. By Lemma 4.2.1, there is a permutation of the coordinates
$h\in \operatorname {\mathrm {End}}(\mathbb {A}^{n+1})$
be a permutation-elementary automorphism. By Lemma 4.2.1, there is a permutation of the coordinates
![]() $\alpha \in \operatorname {\mathrm {Sym}}(\mathbb {A}^{n+1})$
such that
$\alpha \in \operatorname {\mathrm {Sym}}(\mathbb {A}^{n+1})$
such that
where
![]() $0\le m\le n$
,
$0\le m\le n$
,
![]() $\{x_1,\ldots ,x_m\}=\{f_1,\ldots ,f_m\}$
,
$\{x_1,\ldots ,x_m\}=\{f_1,\ldots ,f_m\}$
,
![]() $\xi \in \mathbf {k}^*$
and
$\xi \in \mathbf {k}^*$
and
![]() $p\in \mathbf {k}[x_1,\ldots ,x_n]$
. In particular,
$p\in \mathbf {k}[x_1,\ldots ,x_n]$
. In particular,
![]() $\unicode{x3bb} (\hat {f}) = 1$
, where
$\unicode{x3bb} (\hat {f}) = 1$
, where
![]() $\hat {f} = (f_1, \ldots , f_m) \in \operatorname {\mathrm {Sym}}({\mathbb A}^m)$
.
$\hat {f} = (f_1, \ldots , f_m) \in \operatorname {\mathrm {Sym}}({\mathbb A}^m)$
.
As the maximal eigenvalue
![]() $\theta $
of f is bigger than
$\theta $
of f is bigger than
![]() $1$
, we have
$1$
, we have
![]() $m<n$
(see Remark 4.2.4). Moreover, Proposition 4.2.3(3) yields that
$m<n$
(see Remark 4.2.4). Moreover, Proposition 4.2.3(3) yields that
![]() $\deg _{x_{m+1,\ldots ,x_n}}(p)\ge 2$
. Then, Proposition 4.2.3(2), (3) give the existence of a maximal eigenvector
$\deg _{x_{m+1,\ldots ,x_n}}(p)\ge 2$
. Then, Proposition 4.2.3(2), (3) give the existence of a maximal eigenvector
![]() $\mu $
such that f is
$\mu $
such that f is
![]() $\mu $
-algebraically stable and prove that the dynamical degree
$\mu $
-algebraically stable and prove that the dynamical degree
![]() $\unicode{x3bb} (f)$
is equal to the maximal eigenvalue
$\unicode{x3bb} (f)$
is equal to the maximal eigenvalue
![]() $\theta $
of f (this latter fact also follows from Proposition B). Because
$\theta $
of f (this latter fact also follows from Proposition B). Because
![]() $\alpha \in \operatorname {\mathrm {Sym}}({\mathbb A}^{n+1})$
, we get that
$\alpha \in \operatorname {\mathrm {Sym}}({\mathbb A}^{n+1})$
, we get that
![]() $\alpha ^{-1}(\mu )$
is a maximal eigenvector of
$\alpha ^{-1}(\mu )$
is a maximal eigenvector of
![]() $h = \alpha ^{-1} \circ f \circ \alpha $
, h is
$h = \alpha ^{-1} \circ f \circ \alpha $
, h is
![]() $\alpha ^{-1}(\mu )$
-algebraically stable and
$\alpha ^{-1}(\mu )$
-algebraically stable and
![]() $\theta $
is the maximal eigenvalue of h. Moreover,
$\theta $
is the maximal eigenvalue of h. Moreover,
![]() $\unicode{x3bb} (h) = \unicode{x3bb} (f)$
. Proposition 4.2.3(2) shows that
$\unicode{x3bb} (h) = \unicode{x3bb} (f)$
. Proposition 4.2.3(2) shows that
![]() $\theta $
is the root of a monic integral polynomial where all coefficients (except the first one) are non-positive, so it is a Handelman number by definition.
$\theta $
is the root of a monic integral polynomial where all coefficients (except the first one) are non-positive, so it is a Handelman number by definition.
4.3 Affine-triangular automorphisms of
 $\mathbb {A}^3$
$\mathbb {A}^3$
In this section, we apply Proposition B to affine-triangular automorphisms
![]() $f\in \operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
and prove Proposition D and Theorem 1. By Proposition 4.1.1, we can reduce to the case of permutation-triangular automorphisms. If the maximal eigenvalue
$f\in \operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
and prove Proposition D and Theorem 1. By Proposition 4.1.1, we can reduce to the case of permutation-triangular automorphisms. If the maximal eigenvalue
![]() $\theta $
of f is equal to
$\theta $
of f is equal to
![]() $1$
, then Proposition B gives
$1$
, then Proposition B gives
![]() $\unicode{x3bb} (f)=\theta $
. If
$\unicode{x3bb} (f)=\theta $
. If
![]() $\theta>1$
, there is a maximal eigenvector
$\theta>1$
, there is a maximal eigenvector
![]() $\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n \setminus \{0\}$
of f, and if f is
$\mu =(\mu _1,\ldots ,\mu _n)\in (\mathbb {R}_{\ge 0})^n \setminus \{0\}$
of f, and if f is
![]() $\mu $
-algebraically stable, we obtain
$\mu $
-algebraically stable, we obtain
![]() $\unicode{x3bb} (f)=\theta $
(Proposition B(3)). We will then study the cases where f is not
$\unicode{x3bb} (f)=\theta $
(Proposition B(3)). We will then study the cases where f is not
![]() $\mu $
-algebraically stable. This implies that the
$\mu $
-algebraically stable. This implies that the
![]() $\mu $
-leading part g of f is such that one component of
$\mu $
-leading part g of f is such that one component of
![]() $g^r$
is equal to zero for some
$g^r$
is equal to zero for some
![]() $r\ge 1$
. The possibilities for such endomorphisms g are studied in Lemma 4.3.2 below. The following result is a simple observation, whose proof is left as an exercise.
$r\ge 1$
. The possibilities for such endomorphisms g are studied in Lemma 4.3.2 below. The following result is a simple observation, whose proof is left as an exercise.
Lemma 4.3.1. Let
![]() $n\ge 1$
and let
$n\ge 1$
and let
![]() $f=(f_1,\ldots ,f_n)\in \operatorname {\mathrm {TEnd}}(\mathbb {A}^n)$
be a triangular endomorphism. Then:
$f=(f_1,\ldots ,f_n)\in \operatorname {\mathrm {TEnd}}(\mathbb {A}^n)$
be a triangular endomorphism. Then:
-
(1) f is dominant if and only if
 $\deg _{x_i}(f_i)\ge 1$
for each
$\deg _{x_i}(f_i)\ge 1$
for each
 $i\in \{1,\ldots ,n\}$
; and
$i\in \{1,\ldots ,n\}$
; and -
(2) f is an automorphism if and only if
 $\deg _{x_i}(f_i) = 1$
for each
$\deg _{x_i}(f_i) = 1$
for each
 $i \in \{1, \ldots , n\}$
.
$i \in \{1, \ldots , n\}$
.
Lemma 4.3.2. Let
![]() $g=(g_1,g_2,g_3)=\sigma \circ \tau \in \operatorname {\mathrm {End}}(\mathbb {A}^3)$
, where
$g=(g_1,g_2,g_3)=\sigma \circ \tau \in \operatorname {\mathrm {End}}(\mathbb {A}^3)$
, where
![]() $\tau \in \operatorname {\mathrm {TEnd}}(\mathbb {A}^3)$
is a triangular endomorphism and
$\tau \in \operatorname {\mathrm {TEnd}}(\mathbb {A}^3)$
is a triangular endomorphism and
![]() $\sigma \in \operatorname {\mathrm {Sym}}(\mathbb {A}^3)$
is a permutation of the coordinates, where all
$\sigma \in \operatorname {\mathrm {Sym}}(\mathbb {A}^3)$
is a permutation of the coordinates, where all
![]() $g_i$
are non-constant and such that one of the components of
$g_i$
are non-constant and such that one of the components of
![]() $g^r$
is a constant for some
$g^r$
is a constant for some
![]() $r\ge 2$
. Then, one of the following holds:
$r\ge 2$
. Then, one of the following holds:
-
(1)
 $g_2,g_3\in \mathbf {k}[x_1]$
,
$g_2,g_3\in \mathbf {k}[x_1]$
,
 $g_1\in \mathbf {k}[x_1,x_2,x_3]\setminus (\mathbf {k}[x_1,x_2]\cup \mathbf {k}[x_1,x_3])$
and there exists
$g_1\in \mathbf {k}[x_1,x_2,x_3]\setminus (\mathbf {k}[x_1,x_2]\cup \mathbf {k}[x_1,x_3])$
and there exists
 $\zeta \in \mathbf {k}$
such that
$\zeta \in \mathbf {k}$
such that
 $g_1(t,g_2,g_3)=\zeta $
for each
$g_1(t,g_2,g_3)=\zeta $
for each
 $t\in \mathbf {k}$
;
$t\in \mathbf {k}$
; -
(2)
 $g_1,g_3\in \mathbf {k}[x_1]$
,
$g_1,g_3\in \mathbf {k}[x_1]$
,
 $g_2\in \mathbf {k}[x_1,x_3]\setminus \mathbf {k}[x_1]$
;
$g_2\in \mathbf {k}[x_1,x_3]\setminus \mathbf {k}[x_1]$
; -
(3)
 $g_1,g_2\in \mathbf {k}[x_1]$
,
$g_1,g_2\in \mathbf {k}[x_1]$
,
 $g_3\in \mathbf {k}[x_1,x_2]\setminus \mathbf {k}[x_1]$
; and
$g_3\in \mathbf {k}[x_1,x_2]\setminus \mathbf {k}[x_1]$
; and -
(4)
 $g_1,g_2\in \mathbf {k}[x_1,x_2]\setminus \mathbf {k}[x_1]$
,
$g_1,g_2\in \mathbf {k}[x_1,x_2]\setminus \mathbf {k}[x_1]$
,
 $g_3\in \mathbf {k}[x_1]$
and
$g_3\in \mathbf {k}[x_1]$
and
 $g_1(g_1,g_2)=\zeta _1$
,
$g_1(g_1,g_2)=\zeta _1$
,
 $g_2(g_1,g_2)=\zeta _2$
for some
$g_2(g_1,g_2)=\zeta _2$
for some
 $\zeta _1,\zeta _2\in \mathbf {k}$
.
$\zeta _1,\zeta _2\in \mathbf {k}$
.
Proof. We distinguish some cases, depending on which of the polynomials
![]() $g_1,g_2,g_3$
belong to
$g_1,g_2,g_3$
belong to
![]() $\mathbf {k}[x_1]$
.
$\mathbf {k}[x_1]$
.
We first observe that
![]() $g_1,g_2,g_3\in \mathbf {k}[x_1]$
is impossible, as each component of
$g_1,g_2,g_3\in \mathbf {k}[x_1]$
is impossible, as each component of
![]() $g^r$
, for each
$g^r$
, for each
![]() $r\ge 1$
, would then be obtained by composing dominant endomorphisms of
$r\ge 1$
, would then be obtained by composing dominant endomorphisms of
![]() $\mathbb {A}^1$
and thus would not be constant.
$\mathbb {A}^1$
and thus would not be constant.
-
• Suppose that
 $g_1,g_3\in \mathbf {k}[x_1]$
. By induction, we obtain
$g_1,g_3\in \mathbf {k}[x_1]$
. By induction, we obtain
 $(g^r)_1,(g^r)_3\in \mathbf {k}[x_1]\setminus \mathbf {k}$
for each
$(g^r)_1,(g^r)_3\in \mathbf {k}[x_1]\setminus \mathbf {k}$
for each
 $r\ge 1$
, so
$r\ge 1$
, so
 $(g^r)_2\in \mathbf {k}$
for some
$(g^r)_2\in \mathbf {k}$
for some
 $r\ge 2$
. If
$r\ge 2$
. If
 $g_2\in \mathbf {k}[x_1,x_3]$
, we obtain possibility (2). Otherwise,
$g_2\in \mathbf {k}[x_1,x_3]$
, we obtain possibility (2). Otherwise,
 $\deg _{x_2}(g_2)=d\ge 1$
and proceeding by induction, we obtain
$\deg _{x_2}(g_2)=d\ge 1$
and proceeding by induction, we obtain
 $\deg _{x_2}((g^r)_2)=d^r\ge 1$
for each
$\deg _{x_2}((g^r)_2)=d^r\ge 1$
for each
 $r\ge 1$
, impossible.
$r\ge 1$
, impossible. -
• If
 $g_1,g_2\in \mathbf {k}[x_1]$
, we do the same argument as before (by exchanging the roles of
$g_1,g_2\in \mathbf {k}[x_1]$
, we do the same argument as before (by exchanging the roles of
 $x_2$
and
$x_2$
and
 $x_3$
) and obtain possibility (3).
$x_3$
) and obtain possibility (3). -
• Suppose now that
 $g_2,g_3\in \mathbf {k}[x_1]$
. As
$g_2,g_3\in \mathbf {k}[x_1]$
. As
 $g_1\in \mathbf {k}[x_1,x_2,x_3]\setminus \mathbf {k}[x_1]$
, the closure of the image of
$g_1\in \mathbf {k}[x_1,x_2,x_3]\setminus \mathbf {k}[x_1]$
, the closure of the image of
 $g\in \operatorname {\mathrm {End}}(\mathbb {A}^3)$
is then equal to
$g\in \operatorname {\mathrm {End}}(\mathbb {A}^3)$
is then equal to
 $\mathbb {A}^1\times \Gamma $
, where
$\mathbb {A}^1\times \Gamma $
, where
 $\Gamma \subset \mathbb {A}^2$
is the irreducible curve that is the closure of the image of
$\Gamma \subset \mathbb {A}^2$
is the irreducible curve that is the closure of the image of
 $\mathbb {A}^1\to \mathbb {A}^2$
,
$\mathbb {A}^1\to \mathbb {A}^2$
,
 $x_1\mapsto (g_2(x_1),g_3(x_1))$
. The restriction of g gives an endomorphism
$x_1\mapsto (g_2(x_1),g_3(x_1))$
. The restriction of g gives an endomorphism
 $h=g|_{\mathbb {A}^1\times \Gamma }\in \operatorname {\mathrm {End}}(\mathbb {A}^1\times \Gamma )$
.
$h=g|_{\mathbb {A}^1\times \Gamma }\in \operatorname {\mathrm {End}}(\mathbb {A}^1\times \Gamma )$
.We now prove that h is not dominant. For each
 $r\ge 1$
and each
$r\ge 1$
and each
 $i\in \{1,2,3\}$
, the restriction of
$i\in \{1,2,3\}$
, the restriction of
 $(g^r)_{i}$
to
$(g^r)_{i}$
to
 $\mathbb {A}^1\times \Gamma $
is equal to
$\mathbb {A}^1\times \Gamma $
is equal to
 $\pi _i\circ h^r$
, where
$\pi _i\circ h^r$
, where
 $\pi _i\colon \mathbb {A}^1\times \Gamma \to \mathbb {A}^1$
is the ith projection. Choosing i and r such that
$\pi _i\colon \mathbb {A}^1\times \Gamma \to \mathbb {A}^1$
is the ith projection. Choosing i and r such that
 $(g^r)_i$
is constant, we find that
$(g^r)_i$
is constant, we find that
 $\pi _i\circ h^r$
is constant, so
$\pi _i\circ h^r$
is constant, so
 $h^r$
is not dominant, as
$h^r$
is not dominant, as
 $\pi _i$
is dominant. This proves that h is not dominant.
$\pi _i$
is dominant. This proves that h is not dominant.Denote by
 $\Gamma '\subset \mathbb {A}^1\times \Gamma $
the closure of
$\Gamma '\subset \mathbb {A}^1\times \Gamma $
the closure of
 $h(\mathbb {A}^1\times \Gamma )$
, which is an irreducible curve that contains
$h(\mathbb {A}^1\times \Gamma )$
, which is an irreducible curve that contains
 $\{{(g_1(x,g_2(y),g_3(y)),g_2(x),g_3(x)) } \ | \ {(x,y)\in \mathbb {A}^2}\}$
. This implies that the polynomial
$\{{(g_1(x,g_2(y),g_3(y)),g_2(x),g_3(x)) } \ | \ {(x,y)\in \mathbb {A}^2}\}$
. This implies that the polynomial
 $s=g_1(x,g_2(y),g_3(y))\in \mathbf {k}[x,y]$
is contained in
$s=g_1(x,g_2(y),g_3(y))\in \mathbf {k}[x,y]$
is contained in
 $\mathbf {k}[x]$
. Moreover, we observe that s is a constant. Indeed, otherwise the restriction of h to
$\mathbf {k}[x]$
. Moreover, we observe that s is a constant. Indeed, otherwise the restriction of h to
 $\Gamma '$
would be a dominant map
$\Gamma '$
would be a dominant map
 $\Gamma '\to \Gamma '$
and because
$\Gamma '\to \Gamma '$
and because
 $\pi _i |_{\Gamma '} \colon \Gamma ' \to {\mathbb A}^1$
is non-constant for each
$\pi _i |_{\Gamma '} \colon \Gamma ' \to {\mathbb A}^1$
is non-constant for each
 $i \in \{1, 2, 3\}$
, the restriction of
$i \in \{1, 2, 3\}$
, the restriction of
 $(g^r)_i$
to
$(g^r)_i$
to
 $\Gamma '$
would be non-constant for each
$\Gamma '$
would be non-constant for each
 $r\ge 1$
and each
$r\ge 1$
and each
 $i\in \{1,2,3\}$
, which is a contradiction. Hence,
$i\in \{1,2,3\}$
, which is a contradiction. Hence,
 $\pi _1\circ h=g_1|_{\mathbb {A}^1\times \Gamma }\colon \mathbb {A}^1\times \Gamma \to \mathbb {A}^1$
is equal to a constant
$\pi _1\circ h=g_1|_{\mathbb {A}^1\times \Gamma }\colon \mathbb {A}^1\times \Gamma \to \mathbb {A}^1$
is equal to a constant
 $\zeta \in \mathbf {k}$
. This yields
$\zeta \in \mathbf {k}$
. This yields
 $g_1(t,g_2,g_3)=\zeta $
for each
$g_1(t,g_2,g_3)=\zeta $
for each
 $t\in \mathbf {k}$
and implies that
$t\in \mathbf {k}$
and implies that
 $g_1\not \in \mathbf {k}[x_1,x_2]\cup \mathbf {k}[x_1,x_3]$
, because
$g_1\not \in \mathbf {k}[x_1,x_2]\cup \mathbf {k}[x_1,x_3]$
, because
 $g_1, g_2, g_3$
are non-constant, whence possibility (1).
$g_1, g_2, g_3$
are non-constant, whence possibility (1). -
• It remains to assume that, at most, one of the
 $g_i$
belongs to
$g_i$
belongs to
 $\mathbf {k}[x_1]$
. We write
$\mathbf {k}[x_1]$
. We write
 $\tau =(\tau _1,\tau _2,\tau _3)$
and observe that
$\tau =(\tau _1,\tau _2,\tau _3)$
and observe that
 $\{g_1,g_2,g_3\}=\{\tau _1,\tau _2,\tau _3\}$
. As
$\{g_1,g_2,g_3\}=\{\tau _1,\tau _2,\tau _3\}$
. As
 $\tau _1\in \mathbf {k}[x_1] \setminus \mathbf {k}$
, we get that exactly one of the
$\tau _1\in \mathbf {k}[x_1] \setminus \mathbf {k}$
, we get that exactly one of the
 $g_i$
belongs to
$g_i$
belongs to
 $\mathbf {k}[x_1]$
and that
$\mathbf {k}[x_1]$
and that
 $\tau _2\in \mathbf {k}[x_1,x_2]\setminus \mathbf {k}[x_1]$
. As g is not dominant, neither is
$\tau _2\in \mathbf {k}[x_1,x_2]\setminus \mathbf {k}[x_1]$
. As g is not dominant, neither is
 $\tau $
; Lemma 4.3.1 then implies that
$\tau $
; Lemma 4.3.1 then implies that
 $\tau _3\in \mathbf {k}[x_1,x_2]$
. So
$\tau _3\in \mathbf {k}[x_1,x_2]$
. So
 $g_1,g_2,g_3\in \mathbf {k}[x_1,x_2]$
and exactly one of the three belongs to
$g_1,g_2,g_3\in \mathbf {k}[x_1,x_2]$
and exactly one of the three belongs to
 $\mathbf {k}[x_1]$
. Note that the endomorphism
$\mathbf {k}[x_1]$
. Note that the endomorphism
 $h=(g_1,g_2)\in \operatorname {\mathrm {End}}(\mathbb {A}^2)$
is not dominant. Indeed, otherwise no component of
$h=(g_1,g_2)\in \operatorname {\mathrm {End}}(\mathbb {A}^2)$
is not dominant. Indeed, otherwise no component of
 $g^r$
is constant for each
$g^r$
is constant for each
 $r\ge 1$
, as
$r\ge 1$
, as
 $g_3\in \mathbf {k}[x_1,x_2]$
is non-constant. Thus it is impossible that
$g_3\in \mathbf {k}[x_1,x_2]$
is non-constant. Thus it is impossible that
 $g_1\in \mathbf {k}[x_1]$
or
$g_1\in \mathbf {k}[x_1]$
or
 $g_2\in \mathbf {k}[x_1]$
, as
$g_2\in \mathbf {k}[x_1]$
, as
 $(g_1,g_2)$
(respectively
$(g_1,g_2)$
(respectively
 $(g_2,g_1)$
) would be a dominant triangular endomorphism of
$(g_2,g_1)$
) would be a dominant triangular endomorphism of
 $\mathbb {A}^2$
(Lemma 4.3.1). Hence,
$\mathbb {A}^2$
(Lemma 4.3.1). Hence,
 $g_3\in \mathbf {k}[x_1] \setminus \mathbf {k}$
and
$g_3\in \mathbf {k}[x_1] \setminus \mathbf {k}$
and
 $g_1,g_2\in \mathbf {k}[x_1,x_2]\setminus \mathbf {k}[x_1]$
. As h is not dominant, the closure of
$g_1,g_2\in \mathbf {k}[x_1,x_2]\setminus \mathbf {k}[x_1]$
. As h is not dominant, the closure of
 $h(\mathbb {A}^2)$
is an irreducible curve
$h(\mathbb {A}^2)$
is an irreducible curve
 $\Gamma \subset \mathbb {A}^2$
.
$\Gamma \subset \mathbb {A}^2$
.If
 $g_j(\Gamma )$
is not a point for
$g_j(\Gamma )$
is not a point for
 $j=1$
or
$j=1$
or
 $j=2$
, then the restriction
$j=2$
, then the restriction
 $h |_\Gamma \colon \Gamma \to \Gamma $
would be dominant. As
$h |_\Gamma \colon \Gamma \to \Gamma $
would be dominant. As
 $g_3$
is not constant on
$g_3$
is not constant on
 $\Gamma $
(because
$\Gamma $
(because
 $g_3(g_1(x_1,x_2))$
is not constant), we get that
$g_3(g_1(x_1,x_2))$
is not constant), we get that
 $(g^r)_i$
is non-constant for each
$(g^r)_i$
is non-constant for each
 $r \geq 1$
and each
$r \geq 1$
and each
 $i \in \{1, 2, 3\}$
, which is a contradiction. Thus
$i \in \{1, 2, 3\}$
, which is a contradiction. Thus
 $g_i(\Gamma ) = \{\zeta _i\}$
for
$g_i(\Gamma ) = \{\zeta _i\}$
for
 $i=1,2$
, where
$i=1,2$
, where
 $\zeta _i \in \mathbf {k}$
. This gives possibility (4).
$\zeta _i \in \mathbf {k}$
. This gives possibility (4).
Lemma 4.3.3. Let
![]() $f=\sigma \circ \nu \in \operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
be a permutation-triangular automorphism, where
$f=\sigma \circ \nu \in \operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
be a permutation-triangular automorphism, where
![]() $\sigma \in \operatorname {\mathrm {Sym}}(\mathbb {A}^3)$
and
$\sigma \in \operatorname {\mathrm {Sym}}(\mathbb {A}^3)$
and
![]() $\nu \in \operatorname {\mathrm {TAut}}(\mathbb {A}^3)$
. Suppose that the maximal eigenvalue
$\nu \in \operatorname {\mathrm {TAut}}(\mathbb {A}^3)$
. Suppose that the maximal eigenvalue
![]() $\theta $
of f is bigger than
$\theta $
of f is bigger than
![]() $1$
and let
$1$
and let
![]() $\mu $
be a maximal eigenvector of f such that f is not
$\mu $
be a maximal eigenvector of f such that f is not
![]() $\mu $
-algebraically stable. Then, one of the following cases holds.
$\mu $
-algebraically stable. Then, one of the following cases holds.
-
(i)
 $f=(\xi _3 x_3+p_3(x_1,x_2),p_1(x_1),\xi _2 x_2+p_2(x_1))$
, where
$f=(\xi _3 x_3+p_3(x_1,x_2),p_1(x_1),\xi _2 x_2+p_2(x_1))$
, where
 $\xi _2,\xi _3\in \mathbf {k}^*$
,
$\xi _2,\xi _3\in \mathbf {k}^*$
,
 $p_1,p_2\in \mathbf {k}[x_1]$
,
$p_1,p_2\in \mathbf {k}[x_1]$
,
 $p_3\in \mathbf {k}[x_1,x_2]$
,
$p_3\in \mathbf {k}[x_1,x_2]$
,
 $\deg (p_1)=1$
, and
$\deg (p_1)=1$
, and
 $\deg (p_2)=\theta ^2>1$
. Moreover, there exists
$\deg (p_2)=\theta ^2>1$
. Moreover, there exists
 $s\in \mathbf {k}[x_2]$
such that the conjugation of f by
$s\in \mathbf {k}[x_2]$
such that the conjugation of f by
 $(x_1,x_2,x_3+s(x_2))$
does not increase the degree of
$(x_1,x_2,x_3+s(x_2))$
does not increase the degree of
 $p_3$
and (strictly) decreases the degree of
$p_3$
and (strictly) decreases the degree of
 $p_2$
.
$p_2$
. -
(ii)
 $f=(\xi _2 x_2+p_2(x_1),\xi _3 x_3+p_3(x_1,x_2),p_1(x_1))$
, where
$f=(\xi _2 x_2+p_2(x_1),\xi _3 x_3+p_3(x_1,x_2),p_1(x_1))$
, where
 $\xi _2,\xi _3\in \mathbf {k}^*$
,
$\xi _2,\xi _3\in \mathbf {k}^*$
,
 $p_1,p_2\in \mathbf {k}[x_1]$
,
$p_1,p_2\in \mathbf {k}[x_1]$
,
 $p_3\in \mathbf {k}[x_1,x_2]$
,
$p_3\in \mathbf {k}[x_1,x_2]$
,
 $\deg (p_1)=1$
and
$\deg (p_1)=1$
and
 $\deg (p_2)=\theta>1$
. Moreover, there exists
$\deg (p_2)=\theta>1$
. Moreover, there exists
 $s\in \mathbf {k}[x_1]$
such that the conjugation of f by
$s\in \mathbf {k}[x_1]$
such that the conjugation of f by
 $(x_1,x_2+s(x_1),x_3)$
(strictly) decreases the degrees of
$(x_1,x_2+s(x_1),x_3)$
(strictly) decreases the degrees of
 $p_2$
and
$p_2$
and
 $p_3$
.
$p_3$
.
Proof. Denote by
![]() $g=(g_1,g_2,g_3)$
the
$g=(g_1,g_2,g_3)$
the
![]() $\mu $
-leading part of f. As
$\mu $
-leading part of f. As
![]() $\mu =(\mu _1,\mu _2,\mu _3)\in ({\mathbb R}_{\ge 0})^3\setminus \{0\}$
is a maximal eigenvector of f,
$\mu =(\mu _1,\mu _2,\mu _3)\in ({\mathbb R}_{\ge 0})^3\setminus \{0\}$
is a maximal eigenvector of f,
![]() $g_i\not \in \mathbf {k}$
for each
$g_i\not \in \mathbf {k}$
for each
![]() $i\in \{1,2,3\}$
(Lemma 2.5.7). Moreover, as f is not
$i\in \{1,2,3\}$
(Lemma 2.5.7). Moreover, as f is not
![]() $\mu $
-algebraically stable, there is some
$\mu $
-algebraically stable, there is some
![]() $r\ge 1$
such that
$r\ge 1$
such that
![]() $(g^r)_i=0$
for all
$(g^r)_i=0$
for all
![]() $i\in \{1,2,3\}$
with
$i\in \{1,2,3\}$
with
![]() $\mu _i>0$
(Lemma 2.6.1(5)). We write
$\mu _i>0$
(Lemma 2.6.1(5)). We write
![]() $g=\sigma \circ \tau $
, where
$g=\sigma \circ \tau $
, where
![]() $\tau =(\tau _1,\tau _2,\tau _3)\in \operatorname {\mathrm {TEnd}}(\mathbb {A}^3)$
; Lemma 4.3.2 gives then four possibilities (1)–(4) for g, which we consider separately. We will show that cases (i) and (ii) occur in possibilities (1) and (4), respectively and that possibilities (2)–(3) do not occur.
$\tau =(\tau _1,\tau _2,\tau _3)\in \operatorname {\mathrm {TEnd}}(\mathbb {A}^3)$
; Lemma 4.3.2 gives then four possibilities (1)–(4) for g, which we consider separately. We will show that cases (i) and (ii) occur in possibilities (1) and (4), respectively and that possibilities (2)–(3) do not occur.
Possibilities (2)–(3): Let us first observe that possibility (2) (respectively (3)) of Lemma 4.3.2 does not occur. Indeed, otherwise the first and the last (respectively the first two) components of
![]() $g^r$
belong to
$g^r$
belong to
![]() $\mathbf {k}[x_1]\setminus \mathbf {k}$
for each
$\mathbf {k}[x_1]\setminus \mathbf {k}$
for each
![]() $r\ge 1$
, so
$r\ge 1$
, so
![]() $\mu =(0,\mu _2,0)$
(respectively
$\mu =(0,\mu _2,0)$
(respectively
![]() $\mu =(0,0,\mu _3)$
), because
$\mu =(0,0,\mu _3)$
), because
![]() $(g^r)_i = 0$
for each
$(g^r)_i = 0$
for each
![]() $i \in \{1, 2, 3\}$
with
$i \in \{1, 2, 3\}$
with
![]() $\mu _i> 0$
. This gives
$\mu _i> 0$
. This gives
![]() $\deg _\mu (g_i)=0$
for
$\deg _\mu (g_i)=0$
for
![]() $i=1,2,3$
, as
$i=1,2,3$
, as
![]() $g_1,g_2,g_3$
belong to
$g_1,g_2,g_3$
belong to
![]() $\mathbf {k}[x_1,x_3]$
(respectively
$\mathbf {k}[x_1,x_3]$
(respectively
![]() $\mathbf {k}[x_1,x_2]$
), which is impossible as
$\mathbf {k}[x_1,x_2]$
), which is impossible as
![]() $\deg _\mu (g)=\deg _\mu (f)=\theta>1$
(Lemma 2.5.7).
$\deg _\mu (g)=\deg _\mu (f)=\theta>1$
(Lemma 2.5.7).
Possibility (1): Suppose now that possibility (1) of Lemma 4.3.2 occurs. As
![]() $g_1\in \mathbf {k}[x_1,x_2,x_3]\setminus (\mathbf {k}[x_1,x_2]\cup \mathbf {k}[x_1,x_3])$
and because the monomials of
$g_1\in \mathbf {k}[x_1,x_2,x_3]\setminus (\mathbf {k}[x_1,x_2]\cup \mathbf {k}[x_1,x_3])$
and because the monomials of
![]() $g_1$
are some of those of
$g_1$
are some of those of
![]() $f_1$
, that is, one of the coordinates of the triangular automorphism
$f_1$
, that is, one of the coordinates of the triangular automorphism
![]() $\nu \in \operatorname {\mathrm {TAut}}(\mathbb {A}^3)$
, the polynomial
$\nu \in \operatorname {\mathrm {TAut}}(\mathbb {A}^3)$
, the polynomial
![]() $f_1$
is equal to the third coordinate of
$f_1$
is equal to the third coordinate of
![]() $\nu $
and
$\nu $
and
![]() $g_1$
is of the form
$g_1$
is of the form
![]() $g_1=\xi _3 x_3+q(x_1,x_2)$
for some
$g_1=\xi _3 x_3+q(x_1,x_2)$
for some
![]() $\xi _3\in \mathbf {k}^*$
and
$\xi _3\in \mathbf {k}^*$
and
![]() $q\in \mathbf {k}[x_1,x_2]\setminus \mathbf {k}[x_1]$
. Because
$q\in \mathbf {k}[x_1,x_2]\setminus \mathbf {k}[x_1]$
. Because
![]() $g_1(t,g_2,g_3)=\zeta \in \mathbf {k}$
for each
$g_1(t,g_2,g_3)=\zeta \in \mathbf {k}$
for each
![]() $t\in \mathbf {k}$
, we obtain
$t\in \mathbf {k}$
, we obtain
![]() $\xi _3 g_3+q(t,g_2)=\zeta $
for each
$\xi _3 g_3+q(t,g_2)=\zeta $
for each
![]() $t\in \mathbf {k}$
, so
$t\in \mathbf {k}$
, so
![]() $q\in \mathbf {k}[x_2]\setminus \mathbf {k}$
and
$q\in \mathbf {k}[x_2]\setminus \mathbf {k}$
and
where
![]() $g_2\in \mathbf {k}[x_1]$
. By definition (Definition 1.4.5),
$g_2\in \mathbf {k}[x_1]$
. By definition (Definition 1.4.5),
![]() $g_i$
is the
$g_i$
is the
![]() $\mu $
-homogeneous part of
$\mu $
-homogeneous part of
![]() $f_i$
of degree
$f_i$
of degree
![]() $\theta \mu _i$
, for each
$\theta \mu _i$
, for each
![]() $i\in \{1,2,3\}$
so each monomial of
$i\in \{1,2,3\}$
so each monomial of
![]() $g_i$
is of
$g_i$
is of
![]() $\mu $
-degree
$\mu $
-degree
![]() $\theta \mu _i$
. The explicit form of
$\theta \mu _i$
. The explicit form of
![]() $g_1,g_2,g_3$
directly gives
$g_1,g_2,g_3$
directly gives
In particular,
![]() $\mu _1,\mu _2,\mu _3\in {\mathbb R}_{>0}$
and
$\mu _1,\mu _2,\mu _3\in {\mathbb R}_{>0}$
and
![]() $\deg (g_3)=\deg (q)\deg (g_2)= \theta ^2>1$
. Because two monomials in the same variables have distinct
$\deg (g_3)=\deg (q)\deg (g_2)= \theta ^2>1$
. Because two monomials in the same variables have distinct
![]() $\mu $
-degrees, we find that q,
$\mu $
-degrees, we find that q,
![]() $g_2$
and
$g_2$
and
![]() $g_3$
are monomials, so
$g_3$
are monomials, so
![]() $\zeta =0$
.
$\zeta =0$
.
One component of f (and of
![]() $\tau $
) belongs to
$\tau $
) belongs to
![]() $\mathbf {k}[x_1]$
and is of degree
$\mathbf {k}[x_1]$
and is of degree
![]() $1$
. As
$1$
. As
![]() $g_1\not \in \mathbf {k}[x_1]$
and
$g_1\not \in \mathbf {k}[x_1]$
and
![]() $\deg (g_3)>1$
, we find that
$\deg (g_3)>1$
, we find that
![]() $f_2\in \mathbf {k}[x_1]$
is of degree
$f_2\in \mathbf {k}[x_1]$
is of degree
![]() $1$
. This yields
$1$
. This yields
![]() $\sigma =(x_3,x_1,x_2)$
and
$\sigma =(x_3,x_1,x_2)$
and
![]() $\deg (f_2)=\deg (g_2)=1$
, whence
$\deg (f_2)=\deg (g_2)=1$
, whence
![]() $\deg (q)=\deg (g_3)=\theta ^2>1$
. We obtain the form given in case (i): the automorphism f is equal to
$\deg (q)=\deg (g_3)=\theta ^2>1$
. We obtain the form given in case (i): the automorphism f is equal to
where
![]() $\xi _2,\xi _3\in \mathbf {k}^*$
,
$\xi _2,\xi _3\in \mathbf {k}^*$
,
![]() $p_1,p_2\in \mathbf {k}[x_1]$
,
$p_1,p_2\in \mathbf {k}[x_1]$
,
![]() $p_3\in \mathbf {k}[x_1,x_2]$
,
$p_3\in \mathbf {k}[x_1,x_2]$
,
![]() $\deg (p_1)=1$
. Moreover,
$\deg (p_1)=1$
. Moreover,
![]() $g_3=-q(g_2)/\xi _3\in \mathbf {k}[x_1]$
is the
$g_3=-q(g_2)/\xi _3\in \mathbf {k}[x_1]$
is the
![]() $\mu $
-leading part of
$\mu $
-leading part of
![]() $f_3=\xi _2 x_2+p_2(x_1)$
, so
$f_3=\xi _2 x_2+p_2(x_1)$
, so
![]() $g_3$
is only one monomial, of degree
$g_3$
is only one monomial, of degree
![]() $\theta ^2 = \deg (g_3)=\deg (p_2)$
.
$\theta ^2 = \deg (g_3)=\deg (p_2)$
.
To prove that we are indeed in case (i), it remains to show that the conjugation by
![]() $h=(x_1,x_2,x_3+\xi _3^{-1}q(x_2))$
does not increase the degree
$h=(x_1,x_2,x_3+\xi _3^{-1}q(x_2))$
does not increase the degree
![]() $p_3$
and strictly decreases the degree of
$p_3$
and strictly decreases the degree of
![]() $p_2$
. We calculate
$p_2$
. We calculate
As every monomial of
![]() $g_1=\xi _3 x_3+q(x_2)$
is contained in
$g_1=\xi _3 x_3+q(x_2)$
is contained in
![]() $f_1=\xi _3 x_3+p_3(x_1,x_2)$
, the degree of
$f_1=\xi _3 x_3+p_3(x_1,x_2)$
, the degree of
![]() $p_3(x_1,x_2)-q(x_2)$
is at most that of
$p_3(x_1,x_2)-q(x_2)$
is at most that of
![]() $p_3(x_1,x_2)$
. It remains to see that
$p_3(x_1,x_2)$
. It remains to see that
![]() $\deg (p_2+q(p_1)/\xi _3)<\deg (p_2)$
, which follows from the fact that
$\deg (p_2+q(p_1)/\xi _3)<\deg (p_2)$
, which follows from the fact that
![]() $g_3=-q(g_2)/\xi _3\in \mathbf {k}[x_1]$
is the
$g_3=-q(g_2)/\xi _3\in \mathbf {k}[x_1]$
is the
![]() $\mu $
-leading part of
$\mu $
-leading part of
![]() $f_3=\xi _2 x_2+p_2(x_1)$
, and that
$f_3=\xi _2 x_2+p_2(x_1)$
, and that
![]() $g_2$
is the leading monomial of
$g_2$
is the leading monomial of
![]() $p_1$
(of degree
$p_1$
(of degree
![]() $1$
).
$1$
).
Possibility (4): It remains to consider possibility (4) of Lemma 4.3.2. As
![]() $g_1,g_2\in \mathbf {k}[x_1,x_2]\setminus \mathbf {k}[x_1]$
, the only component of f which belongs to
$g_1,g_2\in \mathbf {k}[x_1,x_2]\setminus \mathbf {k}[x_1]$
, the only component of f which belongs to
![]() $\mathbf {k}[x_1]$
(and is of degree
$\mathbf {k}[x_1]$
(and is of degree
![]() $1$
) is
$1$
) is
![]() $f_3$
, so
$f_3$
, so
![]() $\sigma =(x_3,x_2,x_1)$
or
$\sigma =(x_3,x_2,x_1)$
or
![]() $\sigma =(x_2,x_3,x_1)$
. Let
$\sigma =(x_2,x_3,x_1)$
. Let
![]() $j\in \{1,2\}$
be such that
$j\in \{1,2\}$
be such that
![]() $f_j= \nu _2$
, where
$f_j= \nu _2$
, where
![]() $\nu = (\nu _1, \nu _2, \nu _3)$
. We then have
$\nu = (\nu _1, \nu _2, \nu _3)$
. We then have
![]() $f_j=\xi _2 x_2 +p_2(x_1)$
for some
$f_j=\xi _2 x_2 +p_2(x_1)$
for some
![]() $\xi _2\in \mathbf {k}^*$
and some
$\xi _2\in \mathbf {k}^*$
and some
![]() $p_2\in \mathbf {k}[x_1]$
. As
$p_2\in \mathbf {k}[x_1]$
. As
![]() $g_j\in \mathbf {k}[x_1,x_2]\setminus \mathbf {k}[x_1]$
, we get
$g_j\in \mathbf {k}[x_1,x_2]\setminus \mathbf {k}[x_1]$
, we get
![]() $g_j=\xi _2 x_2 +q(x_1)$
for some
$g_j=\xi _2 x_2 +q(x_1)$
for some
![]() $q\in \mathbf {k}[x_1]$
, which consists of some monomials of
$q\in \mathbf {k}[x_1]$
, which consists of some monomials of
![]() $p_2$
. Because
$p_2$
. Because
![]() $\zeta _j=g_j(g_1,g_2)$
, we obtain
$\zeta _j=g_j(g_1,g_2)$
, we obtain
![]() $\zeta _j=\xi _2 g_2+q(g_1)$
.
$\zeta _j=\xi _2 g_2+q(g_1)$
.
We now show that
![]() $j=2$
leads to a contradiction. It gives
$j=2$
leads to a contradiction. It gives
Because
![]() $\xi _2 x_2 +q(x_1)$
is irreducible, the polynomial
$\xi _2 x_2 +q(x_1)$
is irreducible, the polynomial
![]() $\zeta _2-q(g_1)$
is irreducible, and thus
$\zeta _2-q(g_1)$
is irreducible, and thus
![]() $\deg (q)=1$
, which in turn implies that
$\deg (q)=1$
, which in turn implies that
![]() $g_2$
and thus
$g_2$
and thus
![]() $g_1$
is of degree
$g_1$
is of degree
![]() $1$
. Hence,
$1$
. Hence,
![]() $g_1,g_2,g_3$
are of degree
$g_1,g_2,g_3$
are of degree
![]() $1$
, which is impossible, as
$1$
, which is impossible, as
![]() $\theta>1$
is the eigenvalue of a matrix that is contained in g (Lemma 2.5.1).
$\theta>1$
is the eigenvalue of a matrix that is contained in g (Lemma 2.5.1).
This contradiction proves that
![]() $j=1$
, so
$j=1$
, so
![]() $\sigma =(x_2,x_3,x_1)$
. This yields
$\sigma =(x_2,x_3,x_1)$
. This yields
where
![]() $\xi _2,\xi _3\in \mathbf {k}^*$
,
$\xi _2,\xi _3\in \mathbf {k}^*$
,
![]() $p_1,p_2\in \mathbf {k}[x_1]$
,
$p_1,p_2\in \mathbf {k}[x_1]$
,
![]() $p_3\in \mathbf {k}[x_1,x_2]$
and
$p_3\in \mathbf {k}[x_1,x_2]$
and
![]() $\deg (p_1)=1$
, as in case (ii).
$\deg (p_1)=1$
, as in case (ii).
We also have
![]() $g_1=\xi _2 x_2+q(x_1)$
and
$g_1=\xi _2 x_2+q(x_1)$
and
![]() $\zeta _1=\xi _2 g_2+q(g_1)$
, which yields
$\zeta _1=\xi _2 g_2+q(g_1)$
, which yields
![]() $g_2=(\zeta _1-q(g_1))/\xi _2=(\zeta _1-q(\xi _2 x_2 +q(x_1)))/\xi _2$
. As g is the
$g_2=(\zeta _1-q(g_1))/\xi _2=(\zeta _1-q(\xi _2 x_2 +q(x_1)))/\xi _2$
. As g is the
![]() $\mu $
-leading part of f, the polynomial
$\mu $
-leading part of f, the polynomial
![]() $g_2$
is not constant (Lemma 2.5.7), so
$g_2$
is not constant (Lemma 2.5.7), so
![]() $\deg (q)\ge 1$
. Recall that
$\deg (q)\ge 1$
. Recall that
![]() $g_i$
is the
$g_i$
is the
![]() $\mu $
-homogeneous part of
$\mu $
-homogeneous part of
![]() $f_i$
of degree
$f_i$
of degree
![]() $\theta \mu _i$
, for each
$\theta \mu _i$
, for each
![]() $i\in \{1,2,3\}$
(Definition 1.4.5) so each monomial of
$i\in \{1,2,3\}$
(Definition 1.4.5) so each monomial of
![]() $g_i$
is of
$g_i$
is of
![]() $\mu $
-degree
$\mu $
-degree
![]() $\theta \mu _i$
. We thus obtain
$\theta \mu _i$
. We thus obtain
This proves that
![]() $\mu _1,\mu _2,\mu _3\in {\mathbb R}_{>0}$
, that
$\mu _1,\mu _2,\mu _3\in {\mathbb R}_{>0}$
, that
![]() $\deg (q)=\theta>1$
and that
$\deg (q)=\theta>1$
and that
![]() $\mu =(\theta \mu _3,\theta ^2\mu _3,\mu _3)$
.
$\mu =(\theta \mu _3,\theta ^2\mu _3,\mu _3)$
.
Because two monomials in the same variables have distinct
![]() $\mu $
-degrees, we moreover find that q is a monomial, the leading monomial of
$\mu $
-degrees, we moreover find that q is a monomial, the leading monomial of
![]() $p_2$
, so
$p_2$
, so
![]() $\deg (p_2)=\deg (q)=\theta>1$
, as stated in case (ii).
$\deg (p_2)=\deg (q)=\theta>1$
, as stated in case (ii).
To prove that we are indeed in case (ii), it remains to show that the conjugation by
![]() $h=(x_1,x_2+q(x_1)/\xi _2,x_3)$
strictly decreases the degree of
$h=(x_1,x_2+q(x_1)/\xi _2,x_3)$
strictly decreases the degree of
![]() $p_2$
and
$p_2$
and
![]() $p_3$
. We calculate
$p_3$
. We calculate
where
 $$ \begin{align*} p_2'(x_1)&=p_2(x_1)-q(x_1),\\ p_3'(x_1,x_2)&=p_3(x_1,x_2-q(x_1)/\xi_2)+q(\xi_2 x_2+p_2'(x_1))/\xi_2. \end{align*} $$
$$ \begin{align*} p_2'(x_1)&=p_2(x_1)-q(x_1),\\ p_3'(x_1,x_2)&=p_3(x_1,x_2-q(x_1)/\xi_2)+q(\xi_2 x_2+p_2'(x_1))/\xi_2. \end{align*} $$
As q is the leading monomial of
![]() $p_2$
, this conjugation decreases the degree of
$p_2$
, this conjugation decreases the degree of
![]() $p_2$
, that is,
$p_2$
, that is,
![]() $\deg (p_2')<\deg (p_2)=\theta $
. It remains to see that
$\deg (p_2')<\deg (p_2)=\theta $
. It remains to see that
![]() $\deg (p_3')< \deg (p_3)$
. To simplify the calculations, we replace
$\deg (p_3')< \deg (p_3)$
. To simplify the calculations, we replace
![]() $\mu $
by a multiple of itself (this is still a maximal eigenvector) and may assume that
$\mu $
by a multiple of itself (this is still a maximal eigenvector) and may assume that
![]() $\mu =(1,\theta ,\theta ^{-1})$
. As
$\mu =(1,\theta ,\theta ^{-1})$
. As
![]() $g_2=(\zeta _1-q(\xi _2 x_2 +q(x_1)))/\xi _2$
is the
$g_2=(\zeta _1-q(\xi _2 x_2 +q(x_1)))/\xi _2$
is the
![]() $\mu $
-homogeneous part of
$\mu $
-homogeneous part of
![]() $f_2=\xi _3 x_3+p_3(x_1,x_2)$
of
$f_2=\xi _3 x_3+p_3(x_1,x_2)$
of
![]() $\mu $
-degree
$\mu $
-degree
![]() $\theta \mu _2=\theta ^2$
, the polynomial
$\theta \mu _2=\theta ^2$
, the polynomial
![]() $\Delta =p_3-g_2\in \mathbf {k}[x_1,x_2]$
is equal to
$\Delta =p_3-g_2\in \mathbf {k}[x_1,x_2]$
is equal to
 $$ \begin{align*} \Delta=\sum\limits_{i=0}^{\theta-1} x_2^i\Delta_i, \end{align*} $$
$$ \begin{align*} \Delta=\sum\limits_{i=0}^{\theta-1} x_2^i\Delta_i, \end{align*} $$
where each
![]() $\Delta _i\in \mathbf {k}[x_1]$
is such that
$\Delta _i\in \mathbf {k}[x_1]$
is such that
![]() $\deg (\Delta _i)+i\theta < \theta ^2$
. As
$\deg (\Delta _i)+i\theta < \theta ^2$
. As
![]() $\theta>1$
, this implies that
$\theta>1$
, this implies that
![]() $\deg (x_2^i\Delta _i)=i+\deg (\Delta _i)<\theta ^2$
for each i, so
$\deg (x_2^i\Delta _i)=i+\deg (\Delta _i)<\theta ^2$
for each i, so
![]() $\deg (\Delta )<\theta ^2$
, which implies that the degree of
$\deg (\Delta )<\theta ^2$
, which implies that the degree of
![]() $p_3=\Delta +g_2$
is equal to
$p_3=\Delta +g_2$
is equal to
![]() $\theta ^2$
, because
$\theta ^2$
, because
![]() $\deg (g_2)=\theta ^2$
. We then need to show that
$\deg (g_2)=\theta ^2$
. We then need to show that
![]() $\deg (p_3')< \theta ^2$
. Because
$\deg (p_3')< \theta ^2$
. Because
![]() $\deg (p_2')<\deg (q)=\theta $
, we have
$\deg (p_2')<\deg (q)=\theta $
, we have
![]() $\deg (q(\xi _2 x_2+p_2'(x_1))/\xi _2)<\theta ^2$
, so we only need to show that
$\deg (q(\xi _2 x_2+p_2'(x_1))/\xi _2)<\theta ^2$
, so we only need to show that
![]() $\deg (p_3(x_1,x_2-q(x_1)/\xi _2))<\theta ^2$
. This is given by
$\deg (p_3(x_1,x_2-q(x_1)/\xi _2))<\theta ^2$
. This is given by
 $$ \begin{align*} p_3(x_1,x_2-q(x_1)/\xi_2) &= \Delta(x_1,x_2-q(x_1)/\xi_2)+g_2(x_1,x_2-q(x_1)/\xi_2)\\ &= \displaystyle\sum\limits_{i=0}^{\theta-1} (x_2-q(x_1)/\xi_2)^i\Delta_i+(\zeta_1-q(\xi_2 x_2))/\xi_2 \end{align*} $$
$$ \begin{align*} p_3(x_1,x_2-q(x_1)/\xi_2) &= \Delta(x_1,x_2-q(x_1)/\xi_2)+g_2(x_1,x_2-q(x_1)/\xi_2)\\ &= \displaystyle\sum\limits_{i=0}^{\theta-1} (x_2-q(x_1)/\xi_2)^i\Delta_i+(\zeta_1-q(\xi_2 x_2))/\xi_2 \end{align*} $$
and by the fact that
![]() $\deg (\Delta _i)+i\theta < \theta ^2$
for each i.
$\deg (\Delta _i)+i\theta < \theta ^2$
for each i.
Example 4.3.4. We now give two distinct examples to show that cases (1) and (2) of Lemma 4.3.3 indeed occur.
-
(1) Let
 $n\ge 2$
, and let
$n\ge 2$
, and let
 $f=(x_3-x_2^n,x_1,x_2+x_1^n)\in \operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
. Because of the matrix contained in
$f=(x_3-x_2^n,x_1,x_2+x_1^n)\in \operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
. Because of the matrix contained in
 $(x_3,x_1,x_1^n)$
, the maximal eigenvalue satisfies
$(x_3,x_1,x_1^n)$
, the maximal eigenvalue satisfies
 $\theta \ge \sqrt {n}>1$
and as
$\theta \ge \sqrt {n}>1$
and as
 $f^2=(x_2,x_3-x_2^n,x_1+(x_3-x_2^n)^n)$
and
$f^2=(x_2,x_3-x_2^n,x_1+(x_3-x_2^n)^n)$
and
 $f^3=(x_1,x_2,x_3)$
, the map f is not
$f^3=(x_1,x_2,x_3)$
, the map f is not
 $\mu $
-algebraically stable for any maximal eigenvector
$\mu $
-algebraically stable for any maximal eigenvector
 $\mu $
of f. It has then to satisfy case (i) of Lemma 4.3.3, so
$\mu $
of f. It has then to satisfy case (i) of Lemma 4.3.3, so
 $\theta =\sqrt {n}$
.
$\theta =\sqrt {n}$
. -
(2) Let
 $n\ge 2$
and let
$n\ge 2$
and let
 $f=(x_2-x_1^n,x_3+(x_2-x_1^n)^n,x_1)\in \operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
. Because of the matrix contained in
$f=(x_2-x_1^n,x_3+(x_2-x_1^n)^n,x_1)\in \operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
. Because of the matrix contained in
 $(-x_1^n,x_3,x_1)$
, the maximal eigenvalue satisfies
$(-x_1^n,x_3,x_1)$
, the maximal eigenvalue satisfies
 $\theta \ge n>1$
and as
$\theta \ge n>1$
and as
 $f^2=(x_3,x_1+x_3^n,x_2-x_1^n)$
and
$f^2=(x_3,x_1+x_3^n,x_2-x_1^n)$
and
 $f^3=(x_1,x_2,x_3)$
, the element f is not
$f^3=(x_1,x_2,x_3)$
, the element f is not
 $\mu $
-algebraically stable for each maximal eigenvector
$\mu $
-algebraically stable for each maximal eigenvector
 $\mu $
of f. It has then to satisfy case (ii) of Lemma 4.3.3, so
$\mu $
of f. It has then to satisfy case (ii) of Lemma 4.3.3, so
 $\theta =n$
.
$\theta =n$
.
We now give examples of permutation-triangular automorphisms of
![]() $\mathbb {A}^3$
, which are
$\mathbb {A}^3$
, which are
![]() $\mu $
-algebraically stable. These will be useful in the proof of Theorem 1.
$\mu $
-algebraically stable. These will be useful in the proof of Theorem 1.
Lemma 4.3.5. For all
![]() $a,b,c\in {\mathbb N}$
such that
$a,b,c\in {\mathbb N}$
such that
![]() $\unicode{x3bb} =({a+\sqrt {a^2+4bc}})/{2}\not =0$
, the maximal eigenvalue and the dynamical degree of the automorphisms
$\unicode{x3bb} =({a+\sqrt {a^2+4bc}})/{2}\not =0$
, the maximal eigenvalue and the dynamical degree of the automorphisms
are equal to
![]() $\unicode{x3bb} $
. Both automorphisms are
$\unicode{x3bb} $
. Both automorphisms are
![]() $\mu $
-algebraic stable for each maximal eigenvector
$\mu $
-algebraic stable for each maximal eigenvector
![]() $\mu $
.
$\mu $
.
Proof. The matrices that are contained in f are
 $$ \begin{align*} \begin{pmatrix} a & b& 0\\ c & 0& 0\\ 1 & 0 &0 \end{pmatrix}, \begin{pmatrix} a & b& 0\\ 0 & 1& 0\\ 1 & 0 &0 \end{pmatrix}, \begin{pmatrix} 0 & 0& 1\\ c & 0& 0\\ 1 & 0 &0 \end{pmatrix} \text{ and } \begin{pmatrix} 0 & 0& 1\\ 0 & 1& 0\\ 1 & 0 &0 \end{pmatrix}, \end{align*} $$
$$ \begin{align*} \begin{pmatrix} a & b& 0\\ c & 0& 0\\ 1 & 0 &0 \end{pmatrix}, \begin{pmatrix} a & b& 0\\ 0 & 1& 0\\ 1 & 0 &0 \end{pmatrix}, \begin{pmatrix} 0 & 0& 1\\ c & 0& 0\\ 1 & 0 &0 \end{pmatrix} \text{ and } \begin{pmatrix} 0 & 0& 1\\ 0 & 1& 0\\ 1 & 0 &0 \end{pmatrix}, \end{align*} $$
whose characteristic polynomials are
![]() $x(x^2-ax-bc)$
,
$x(x^2-ax-bc)$
,
![]() $x(x-a)(x-1)$
,
$x(x-a)(x-1)$
,
![]() $x(x^2-1)$
and
$x(x^2-1)$
and
![]() $(x+1)(x^2-1)$
, respectively. The corresponding spectral radii are respectively
$(x+1)(x^2-1)$
, respectively. The corresponding spectral radii are respectively
![]() $\unicode{x3bb} $
, a,
$\unicode{x3bb} $
, a,
![]() $1$
and
$1$
and
![]() $1$
. Hence, the maximal eigenvalue of f is
$1$
. Hence, the maximal eigenvalue of f is
![]() $\unicode{x3bb} $
.
$\unicode{x3bb} $
.
Similarly, the matrices contained in
![]() $f'$
are
$f'$
are
 $$ \begin{align*} \begin{pmatrix} a & bc& 0\\ 1 & 0& 0\\ 0 & 1 &0 \end{pmatrix} \text{ and } \begin{pmatrix} 0 & 0& 1\\ 1 & 0& 0\\ 0 & 1 &0 \end{pmatrix}, \end{align*} $$
$$ \begin{align*} \begin{pmatrix} a & bc& 0\\ 1 & 0& 0\\ 0 & 1 &0 \end{pmatrix} \text{ and } \begin{pmatrix} 0 & 0& 1\\ 1 & 0& 0\\ 0 & 1 &0 \end{pmatrix}, \end{align*} $$
whose characteristic polynomials are
![]() $x(x^2-ax-bc)$
and
$x(x^2-ax-bc)$
and
![]() $x^3-1$
. The maximal eigenvalue of
$x^3-1$
. The maximal eigenvalue of
![]() $f'$
is then also
$f'$
is then also
![]() $\unicode{x3bb} $
.
$\unicode{x3bb} $
.
As neither f nor
![]() $f'$
satisfies any of the two cases (i) and (ii) of Lemma 4.3.3, both f and
$f'$
satisfies any of the two cases (i) and (ii) of Lemma 4.3.3, both f and
![]() $f'$
are
$f'$
are
![]() $\mu $
-algebraically stable for each maximal eigenvector
$\mu $
-algebraically stable for each maximal eigenvector
![]() $\mu $
(of f and
$\mu $
(of f and
![]() $f'$
, respectively). This gives then
$f'$
, respectively). This gives then
![]() $\unicode{x3bb} (f)=\unicode{x3bb} (f')=\unicode{x3bb} $
(Proposition B) and achieves the proof.
$\unicode{x3bb} (f)=\unicode{x3bb} (f')=\unicode{x3bb} $
(Proposition B) and achieves the proof.
Lemma 4.3.6. The maximal eigenvalue
![]() $\theta $
of a permutation-triangular automorphism
$\theta $
of a permutation-triangular automorphism
![]() $f\in \operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
of degree
$f\in \operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
of degree
![]() $d\ge 1$
is a non-zero number equal to
$d\ge 1$
is a non-zero number equal to
![]() $(a+\sqrt {a^2+4bc})/2$
for some
$(a+\sqrt {a^2+4bc})/2$
for some
![]() $(a,b,c)\in {\mathbb N}^3$
, where
$(a,b,c)\in {\mathbb N}^3$
, where
![]() $a+b\le d$
and
$a+b\le d$
and
![]() $c\le d$
. It is thus a positive integer or a quadratic integer and a Handelman number.
$c\le d$
. It is thus a positive integer or a quadratic integer and a Handelman number.
Proof. Each real number
![]() $\theta =({a+\sqrt {a^2+4bc}})/{2}\not =0$
, where
$\theta =({a+\sqrt {a^2+4bc}})/{2}\not =0$
, where
![]() $(a,b,c) \in {\mathbb N}^3$
is a root of the polynomial
$(a,b,c) \in {\mathbb N}^3$
is a root of the polynomial
![]() $P(x)=x^2-ax-bc$
, with
$P(x)=x^2-ax-bc$
, with
![]() $a,b,c\in {\mathbb N}^2\setminus \{0\}$
so it is a Handelman number. If P is irreducible, then
$a,b,c\in {\mathbb N}^2\setminus \{0\}$
so it is a Handelman number. If P is irreducible, then
![]() $\theta $
is a quadratic integer, and otherwise it is a positive integer. It remains to see that the maximal eigenvalue of every f is of the desired form.
$\theta $
is a quadratic integer, and otherwise it is a positive integer. It remains to see that the maximal eigenvalue of every f is of the desired form.
We write
![]() $f=\sigma \circ \tau $
, where
$f=\sigma \circ \tau $
, where
![]() $\sigma \in \operatorname {\mathrm {Sym}}(\mathbb {A}^3)$
and
$\sigma \in \operatorname {\mathrm {Sym}}(\mathbb {A}^3)$
and
![]() $\tau \in \operatorname {\mathrm {TAut}}(\mathbb {A}^3)$
is a triangular automorphism, which we write as
$\tau \in \operatorname {\mathrm {TAut}}(\mathbb {A}^3)$
is a triangular automorphism, which we write as
![]() $\tau =(\nu _1x_1+\epsilon ,\nu _2 x_2+p(x_1),\nu _3 x_3+q(x_1,x_2))$
, where
$\tau =(\nu _1x_1+\epsilon ,\nu _2 x_2+p(x_1),\nu _3 x_3+q(x_1,x_2))$
, where
![]() $\nu _1,\nu _2,\nu _3\in \mathbf {k}^*$
,
$\nu _1,\nu _2,\nu _3\in \mathbf {k}^*$
,
![]() $\epsilon \in \mathbf {k}$
,
$\epsilon \in \mathbf {k}$
,
![]() $p\in \mathbf {k}[x_1]$
and
$p\in \mathbf {k}[x_1]$
and
![]() $q\in \mathbf {k}[x_1,x_2]$
. The matrices contained in
$q\in \mathbf {k}[x_1,x_2]$
. The matrices contained in
![]() $\tau $
are all of the form
$\tau $
are all of the form
 $$ \begin{align*}\begin{pmatrix} m & 0 &0\\ 0 & 1 & 0\\ 0 & 0& 1 \end{pmatrix}, \begin{pmatrix} m & 0 &0\\ k & 0 & 0\\ 0 & 0& 1 \end{pmatrix},\begin{pmatrix} m & 0 &0\\ 0 & 1 & 0\\ i & j& 0 \end{pmatrix}, \begin{pmatrix} m & 0 &0\\ k & 0 & 0\\ i & j& 0 \end{pmatrix},\end{align*} $$
$$ \begin{align*}\begin{pmatrix} m & 0 &0\\ 0 & 1 & 0\\ 0 & 0& 1 \end{pmatrix}, \begin{pmatrix} m & 0 &0\\ k & 0 & 0\\ 0 & 0& 1 \end{pmatrix},\begin{pmatrix} m & 0 &0\\ 0 & 1 & 0\\ i & j& 0 \end{pmatrix}, \begin{pmatrix} m & 0 &0\\ k & 0 & 0\\ i & j& 0 \end{pmatrix},\end{align*} $$
where
![]() $m, k, i, j$
are non-negative integers and
$m, k, i, j$
are non-negative integers and
![]() $0 \leq m \leq 1$
,
$0 \leq m \leq 1$
,
![]() $k\le \deg (p)\le d$
and
$k\le \deg (p)\le d$
and
![]() $i+j\le \deg (q)\le d$
. Because the spectral radius is order-preserving on real square matrices with non-negative coefficients (see Definition 3.1.1(4)) and because
$i+j\le \deg (q)\le d$
. Because the spectral radius is order-preserving on real square matrices with non-negative coefficients (see Definition 3.1.1(4)) and because
![]() $\nu _1 \neq 0$
, the maximal eigenvalue is the spectral radius of a matrix where
$\nu _1 \neq 0$
, the maximal eigenvalue is the spectral radius of a matrix where
![]() $m=1$
. The matrices contained in f are obtained from one of the above four types by permuting the rows. Permuting the rows of the identity matrix only gives a spectral radius equal to
$m=1$
. The matrices contained in f are obtained from one of the above four types by permuting the rows. Permuting the rows of the identity matrix only gives a spectral radius equal to
![]() $1$
. In the second case, we conjugate by the permutation of the last two. In any case, we obtain that
$1$
. In the second case, we conjugate by the permutation of the last two. In any case, we obtain that
![]() $\theta $
is either equal to
$\theta $
is either equal to
![]() $1$
or is the spectral radius of a matrix
$1$
or is the spectral radius of a matrix
![]() $\sigma ' M$
, where
$\sigma ' M$
, where
![]() $\sigma '$
is a permutation matrix and M is of the form
$\sigma '$
is a permutation matrix and M is of the form
 $$ \begin{align*} \begin{pmatrix} 1 & 0 &0\\ 0 & 1& 0\\ k & 0 & 0 \end{pmatrix},\begin{pmatrix} 1 & 0 &0\\ 0 & 1 & 0\\ i & j& 0 \end{pmatrix}, \begin{pmatrix} 1 & 0 &0\\ k & 0 & 0\\ i & j& 0 \end{pmatrix},\end{align*} $$
$$ \begin{align*} \begin{pmatrix} 1 & 0 &0\\ 0 & 1& 0\\ k & 0 & 0 \end{pmatrix},\begin{pmatrix} 1 & 0 &0\\ 0 & 1 & 0\\ i & j& 0 \end{pmatrix}, \begin{pmatrix} 1 & 0 &0\\ k & 0 & 0\\ i & j& 0 \end{pmatrix},\end{align*} $$
where
![]() $k\le d$
and
$k\le d$
and
![]() $i+j\le d$
. We obtain
$i+j\le d$
. We obtain
 $$ \begin{align*}\sigma'M=\begin{pmatrix} m_{11} & m_{12} &0\\ m_{21} & m_{22} & 0\\ m_{31} & m_{32}& 0 \end{pmatrix}\end{align*} $$
$$ \begin{align*}\sigma'M=\begin{pmatrix} m_{11} & m_{12} &0\\ m_{21} & m_{22} & 0\\ m_{31} & m_{32}& 0 \end{pmatrix}\end{align*} $$
for some
![]() $m_{ij}\in {\mathbb N}$
, so
$m_{ij}\in {\mathbb N}$
, so
![]() $\theta $
is the spectral radius of the matrix
$\theta $
is the spectral radius of the matrix
 $$ \begin{align*} \begin{pmatrix} m_{11} & m_{12}\\ m_{21} & m_{22} \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} m_{11} & m_{12}\\ m_{21} & m_{22} \end{pmatrix}. \end{align*} $$
This last matrix is one of the following:
 $$ \begin{align*} \begin{pmatrix} r & 0\\ s & 0 \end{pmatrix}, \begin{pmatrix} r & 0\\ 0 & s \end{pmatrix}, \begin{pmatrix} r & 0\\ i & j \end{pmatrix}, \begin{pmatrix} i & j\\ 0 & 1 \end{pmatrix} \begin{pmatrix} i & j\\ r & 0 \end{pmatrix}, \begin{pmatrix} 0 & 1 \\ i & j \end{pmatrix}, \text{ or } \begin{pmatrix} 0 & r\\ s & 0 \end{pmatrix}, \end{align*} $$
$$ \begin{align*} \begin{pmatrix} r & 0\\ s & 0 \end{pmatrix}, \begin{pmatrix} r & 0\\ 0 & s \end{pmatrix}, \begin{pmatrix} r & 0\\ i & j \end{pmatrix}, \begin{pmatrix} i & j\\ 0 & 1 \end{pmatrix} \begin{pmatrix} i & j\\ r & 0 \end{pmatrix}, \begin{pmatrix} 0 & 1 \\ i & j \end{pmatrix}, \text{ or } \begin{pmatrix} 0 & r\\ s & 0 \end{pmatrix}, \end{align*} $$
where
![]() $r,s\in \{1,i,j,k\}$
. In the first four cases,
$r,s\in \{1,i,j,k\}$
. In the first four cases,
![]() $\theta $
is an integer in
$\theta $
is an integer in
![]() $\{1,\ldots ,d\}$
, so has the desired form, with
$\{1,\ldots ,d\}$
, so has the desired form, with
![]() $a=\theta $
, and
$a=\theta $
, and
![]() $b=c=0$
. In the fifth case, the characteristic polynomial is
$b=c=0$
. In the fifth case, the characteristic polynomial is
![]() $x^2-ix-jr$
. Choosing
$x^2-ix-jr$
. Choosing
![]() $a=i$
,
$a=i$
,
![]() $b=j$
and
$b=j$
and
![]() $c=r$
, we get
$c=r$
, we get
![]() $\theta =(a+\sqrt {a^2+4bc})/2$
. In the sixth case, the characteristic polynomial is
$\theta =(a+\sqrt {a^2+4bc})/2$
. In the sixth case, the characteristic polynomial is
![]() $x^2 - jx - i$
. When we choose
$x^2 - jx - i$
. When we choose
![]() $a = j$
,
$a = j$
,
![]() $b = i$
and
$b = i$
and
![]() $c = 1$
, we get again
$c = 1$
, we get again
![]() $\theta = (a+\sqrt {a^2+4bc})/2$
. In the last case, the characteristic polynomial is
$\theta = (a+\sqrt {a^2+4bc})/2$
. In the last case, the characteristic polynomial is
![]() $x^2-rs$
. We then choose
$x^2-rs$
. We then choose
![]() $a=0$
,
$a=0$
,
![]() $b=r$
and
$b=r$
and
![]() $c=s$
.
$c=s$
.
We can now give the proof of Proposition D.
Proof of Proposition D
We take an affine-triangular automorphism
![]() $f\in \operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
. By Proposition 4.1.1, there exists
$f\in \operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
. By Proposition 4.1.1, there exists
![]() $\alpha \in \operatorname {\mathrm {Aff}}(\mathbb {A}^3)$
such that
$\alpha \in \operatorname {\mathrm {Aff}}(\mathbb {A}^3)$
such that
![]() $f'=\alpha f \alpha ^{-1}$
is a permutation-triangular automorphism. We then have
$f'=\alpha f \alpha ^{-1}$
is a permutation-triangular automorphism. We then have
![]() $\deg (f')=\deg (f)$
. Moreover, Proposition B shows that there exists a maximal eigenvector of f. We denote by
$\deg (f')=\deg (f)$
. Moreover, Proposition B shows that there exists a maximal eigenvector of f. We denote by
![]() $\theta $
the maximal eigenvalue of
$\theta $
the maximal eigenvalue of
![]() $f'$
. If
$f'$
. If
![]() $\theta =1$
or if
$\theta =1$
or if
![]() $f'$
is
$f'$
is
![]() $\mu $
-algebraically stable for each maximal eigenvector
$\mu $
-algebraically stable for each maximal eigenvector
![]() $\mu $
, the dynamical degrees
$\mu $
, the dynamical degrees
![]() $\unicode{x3bb} (f)$
and
$\unicode{x3bb} (f)$
and
![]() $\unicode{x3bb} (f')$
are equal to the maximal eigenvalue
$\unicode{x3bb} (f')$
are equal to the maximal eigenvalue
![]() $\theta $
of
$\theta $
of
![]() $f'$
(Proposition B), which is a Handelman number (Lemma 4.3.6) so the result holds.
$f'$
(Proposition B), which is a Handelman number (Lemma 4.3.6) so the result holds.
Suppose now that
![]() $\theta>1$
and that
$\theta>1$
and that
![]() $f'$
is not
$f'$
is not
![]() $\mu $
-algebraically stable for some maximal eigenvector
$\mu $
-algebraically stable for some maximal eigenvector
![]() $\mu $
. Lemma 4.3.3 gives two possibilities for
$\mu $
. Lemma 4.3.3 gives two possibilities for
![]() $f'$
:
$f'$
:
 $$ \begin{align*} f' &=(\xi_3 x_3+p_3(x_1,x_2),p_1(x_1),\xi_2 x_2+p_2(x_1)) \quad \textrm{or} \\ f' &=(\xi_2 x_2+p_2(x_1),\xi_3 x_3+p_3(x_1,x_2),p_1(x_1)), \end{align*} $$
$$ \begin{align*} f' &=(\xi_3 x_3+p_3(x_1,x_2),p_1(x_1),\xi_2 x_2+p_2(x_1)) \quad \textrm{or} \\ f' &=(\xi_2 x_2+p_2(x_1),\xi_3 x_3+p_3(x_1,x_2),p_1(x_1)), \end{align*} $$
where
![]() $p_1, p_2 \in \mathbf {k}[x_1]$
,
$p_1, p_2 \in \mathbf {k}[x_1]$
,
![]() $p_3 \in \mathbf {k}[x_1, x_2]$
,
$p_3 \in \mathbf {k}[x_1, x_2]$
,
![]() $\xi _2, \xi _3 \in \mathbf {k}^\ast $
,
$\xi _2, \xi _3 \in \mathbf {k}^\ast $
,
![]() $\deg (p_1)=1$
and
$\deg (p_1)=1$
and
![]() $\deg (p_2)>1$
. In both cases, Lemma 4.3.3 shows that one can replace
$\deg (p_2)>1$
. In both cases, Lemma 4.3.3 shows that one can replace
![]() $f'$
by a conjugate, decrease the degree of
$f'$
by a conjugate, decrease the degree of
![]() $p_2$
and not increase the degree of
$p_2$
and not increase the degree of
![]() $f'$
. After finitely many steps, we obtain the desired case where
$f'$
. After finitely many steps, we obtain the desired case where
![]() $\theta =1$
or
$\theta =1$
or
![]() $f'$
is
$f'$
is
![]() $\mu $
-algebraically stable for each maximal eigenvector
$\mu $
-algebraically stable for each maximal eigenvector
![]() $\mu $
. Moreover, we still have
$\mu $
. Moreover, we still have
![]() $\deg (f')\le \deg (f)$
.
$\deg (f')\le \deg (f)$
.
Proof of Theorem 1
Let
![]() $f\in \operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
be an affine-triangular automorphism of
$f\in \operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
be an affine-triangular automorphism of
![]() $\mathbb {A}^3$
of degree d. Proposition D gives the existence of a permutation-triangular automorphism
$\mathbb {A}^3$
of degree d. Proposition D gives the existence of a permutation-triangular automorphism
![]() $f'\in \operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
such that
$f'\in \operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
such that
![]() $\deg (f')\le \deg (f)$
and such that either the maximal eigenvalue
$\deg (f')\le \deg (f)$
and such that either the maximal eigenvalue
![]() $\theta $
of
$\theta $
of
![]() $f'$
is equal to
$f'$
is equal to
![]() $1$
, or
$1$
, or
![]() $\theta>1$
and
$\theta>1$
and
![]() $f'$
is
$f'$
is
![]() $\mu $
-algebraically stable for each maximal eigenvector
$\mu $
-algebraically stable for each maximal eigenvector
![]() $\mu $
. In the first case, the dynamical degree
$\mu $
. In the first case, the dynamical degree
![]() $\unicode{x3bb} (f)$
is equal to
$\unicode{x3bb} (f)$
is equal to
![]() $\unicode{x3bb} (f')=1$
, by Proposition B(2). In the second case, we obtain
$\unicode{x3bb} (f')=1$
, by Proposition B(2). In the second case, we obtain
![]() $\unicode{x3bb} (f)=\unicode{x3bb} (f')=\theta $
, by Proposition B(3). Moreover, Lemma 4.3.6 proves that
$\unicode{x3bb} (f)=\unicode{x3bb} (f')=\theta $
, by Proposition B(3). Moreover, Lemma 4.3.6 proves that
![]() $\theta =({a+\sqrt {a^2+4bc}})/{2}$
for some
$\theta =({a+\sqrt {a^2+4bc}})/{2}$
for some
![]() $a,b,c\in {\mathbb N}$
with
$a,b,c\in {\mathbb N}$
with
![]() $a+b\le d, c\le d$
(and that
$a+b\le d, c\le d$
(and that
![]() $\theta \not =0$
).
$\theta \not =0$
).
Conversely, for all
![]() $a,b,c\in {\mathbb N}$
such that
$a,b,c\in {\mathbb N}$
such that
![]() $\theta =({a+\sqrt {a^2+4bc}})/{2}\not =0$
, the element
$\theta =({a+\sqrt {a^2+4bc}})/{2}\not =0$
, the element
![]() $\theta $
is the dynamical degree of
$\theta $
is the dynamical degree of
![]() $(x_1^ax_2^b+x_3,x_2+x_1^c,x_1)$
and
$(x_1^ax_2^b+x_3,x_2+x_1^c,x_1)$
and
![]() $(x_3+x_1^ax_2^{bc},x_1,x_2)$
(Lemma 4.3.5), and thus of a permutation-triangular automorphism of
$(x_3+x_1^ax_2^{bc},x_1,x_2)$
(Lemma 4.3.5), and thus of a permutation-triangular automorphism of
![]() $\mathbb {A}^3$
. This achieves the proof.
$\mathbb {A}^3$
. This achieves the proof.
Corollary 4.3.7. For each
![]() $d \ge 3$
, the set of all dynamical degrees of shift-like automorphisms of
$d \ge 3$
, the set of all dynamical degrees of shift-like automorphisms of
![]() $\mathbb {A}^3$
of degree d is strictly contained in the set of all dynamical degrees of affine-triangular automorphisms of degree d.
$\mathbb {A}^3$
of degree d is strictly contained in the set of all dynamical degrees of affine-triangular automorphisms of degree d.
Proof. As each shift-like automorphism is also an affine-triangular automorphism, we have an inclusion that we need to prove to be strict. From Proposition 4.2.5, it follows that the set of dynamical degrees of all shift-like automorphisms of
![]() $\mathbb {A}^3$
of degree d is equal to
$\mathbb {A}^3$
of degree d is equal to
From Theorem 1, it follows that
![]() $\unicode{x3bb} _d=(1 + \sqrt {1 + 4d})/2$
is the dynamical degree of the affine-triangular automorphism
$\unicode{x3bb} _d=(1 + \sqrt {1 + 4d})/2$
is the dynamical degree of the affine-triangular automorphism
![]() $(x_3 + x_1 x_2,x_2+x_1^d,x_1)$
. To show that
$(x_3 + x_1 x_2,x_2+x_1^d,x_1)$
. To show that
![]() $\unicode{x3bb} _d$
is not the dynamical degree of any shift-like automorphism of
$\unicode{x3bb} _d$
is not the dynamical degree of any shift-like automorphism of
![]() ${\mathbb A}^3$
of degree d, for each
${\mathbb A}^3$
of degree d, for each
![]() $d \geq 3$
, we only have to show that there exists no
$d \geq 3$
, we only have to show that there exists no
![]() $d \geq 3$
and no
$d \geq 3$
and no
![]() $a \in \{0, \ldots , d \}$
such that
$a \in \{0, \ldots , d \}$
such that
Indeed, if this would be the case, then
![]() $1 + 4d = (a-1)^2 + 2(a-1)\sqrt {a^2 + 4d-4a} + a^2 + 4d-4a$
, which yields
$1 + 4d = (a-1)^2 + 2(a-1)\sqrt {a^2 + 4d-4a} + a^2 + 4d-4a$
, which yields
This implies that
![]() $a \leq 3$
and
$a \leq 3$
and
![]() $a \not \in \{0, 1\}$
, that is,
$a \not \in \{0, 1\}$
, that is,
![]() $a = 2$
. However, in this case,
$a = 2$
. However, in this case,
![]() $d = 2$
.
$d = 2$
.
4.4 Automorphisms of affine spaces associated to weak Perron numbers
In this section, we construct some affine-triangular automorphisms associated to weak Perron numbers and prove Theorem 2.
Lemma 4.4.1. Let
![]() $n\ge 1$
and let
$n\ge 1$
and let
![]() $A=(a_{i,j})_{i,j=1}^n\in \mathrm {Mat}_n({\mathbb N})$
be an irreducible matrix with spectral radius
$A=(a_{i,j})_{i,j=1}^n\in \mathrm {Mat}_n({\mathbb N})$
be an irreducible matrix with spectral radius
![]() $\rho (A)>1$
. The automorphism
$\rho (A)>1$
. The automorphism
![]() $f \in \operatorname {\mathrm {Aut}}(\mathbb {A}^{2n})$
given by
$f \in \operatorname {\mathrm {Aut}}(\mathbb {A}^{2n})$
given by
 $$ \begin{align} \bigg(x_{n+1}+ \prod_{i=1}^n x_i^{a_{1,i}}, x_{n+2}+ \prod_{i=1}^n x_i^{a_{2,i}},\ldots,x_{2n}+ \prod_{i=1}^n x_i^{a_{n,i}}, x_1,\ldots,x_n\bigg) \end{align} $$
$$ \begin{align} \bigg(x_{n+1}+ \prod_{i=1}^n x_i^{a_{1,i}}, x_{n+2}+ \prod_{i=1}^n x_i^{a_{2,i}},\ldots,x_{2n}+ \prod_{i=1}^n x_i^{a_{n,i}}, x_1,\ldots,x_n\bigg) \end{align} $$
has dynamical degree
![]() $\unicode{x3bb} (f)=\rho (A)$
.
$\unicode{x3bb} (f)=\rho (A)$
.
Proof. Let us write
![]() $\theta =\rho (A)$
and choose an eigenvector
$\theta =\rho (A)$
and choose an eigenvector
![]() $v=(v_1,\ldots ,v_n)\in ({\mathbb R}_{>0})^n$
of A to the eigenvalue
$v=(v_1,\ldots ,v_n)\in ({\mathbb R}_{>0})^n$
of A to the eigenvalue
![]() $\theta $
(which exists by Theorem 3.2.3). We then choose
$\theta $
(which exists by Theorem 3.2.3). We then choose
![]() $\mu =(\theta v_1,\ldots ,\theta v_n,v_1,\ldots ,v_n)\in ({\mathbb R}_{>0})^{2n}$
. The matrix
$\mu =(\theta v_1,\ldots ,\theta v_n,v_1,\ldots ,v_n)\in ({\mathbb R}_{>0})^{2n}$
. The matrix
 $$ \begin{align*} M= \begin{pmatrix} A & 0 \\ I_n & 0 \end{pmatrix}\in \mathrm{Mat}_{2n}({\mathbb N}) \end{align*} $$
$$ \begin{align*} M= \begin{pmatrix} A & 0 \\ I_n & 0 \end{pmatrix}\in \mathrm{Mat}_{2n}({\mathbb N}) \end{align*} $$
is contained in f, its spectral radius is
![]() $\theta $
and
$\theta $
and
![]() $\mu $
is an eigenvector of M to the eigenvalue
$\mu $
is an eigenvector of M to the eigenvalue
![]() $\theta $
. Writing
$\theta $
. Writing
![]() $f=(f_1, \ldots , f_{2n})$
, we now prove that
$f=(f_1, \ldots , f_{2n})$
, we now prove that
![]() $\deg _\mu (f_j)= \theta \mu _j$
for each
$\deg _\mu (f_j)= \theta \mu _j$
for each
![]() $j\in \{1,\ldots ,2n\}$
, and compute the
$j\in \{1,\ldots ,2n\}$
, and compute the
![]() $\mu $
-homogeneous part
$\mu $
-homogeneous part
![]() $g_j$
of
$g_j$
of
![]() $f_j$
of degree
$f_j$
of degree
![]() $\theta \mu _j$
.
$\theta \mu _j$
.
-
(1) For each
 $j\in \{1,\ldots ,n\}$
, we have
$j\in \{1,\ldots ,n\}$
, we have
 $\deg _\mu (x_{n+j})=v_j$
and
$\deg _\mu (x_{n+j})=v_j$
and
 $\deg _\mu (\prod _{i=1}^n x_i^{a_{j,i}})=\sum _{i=1}^n \theta a_{j,i}v_i =\theta ^2 v_j$
, so
$\deg _\mu (\prod _{i=1}^n x_i^{a_{j,i}})=\sum _{i=1}^n \theta a_{j,i}v_i =\theta ^2 v_j$
, so
 $\deg _\mu (f_j)=\theta ^2 v_j=\theta \mu _j$
and
$\deg _\mu (f_j)=\theta ^2 v_j=\theta \mu _j$
and
 $g_j=\prod _{i=1}^n x_i^{a_{j,i}}$
.
$g_j=\prod _{i=1}^n x_i^{a_{j,i}}$
. -
(2) For each
 $j\in \{n+1,\ldots ,2n\}$
, we have
$j\in \{n+1,\ldots ,2n\}$
, we have
 $\deg _\mu (f_j)=\deg _\mu (x_{j-n})=\theta v_{j-n}=\theta \mu _j$
and
$\deg _\mu (f_j)=\deg _\mu (x_{j-n})=\theta v_{j-n}=\theta \mu _j$
and
 $g_j=f_j$
.
$g_j=f_j$
.
This implies that
![]() $\deg _\mu (f)=\theta $
. As the endomorphism
$\deg _\mu (f)=\theta $
. As the endomorphism
![]() $g=(g_1,\ldots ,g_{2n})\in \operatorname {\mathrm {End}}(\mathbb {A}^{2n})$
is monomial, it satisfies
$g=(g_1,\ldots ,g_{2n})\in \operatorname {\mathrm {End}}(\mathbb {A}^{2n})$
is monomial, it satisfies
![]() $g^r\not =0$
for each
$g^r\not =0$
for each
![]() $r\ge 1$
(and, moreover, each component of
$r\ge 1$
(and, moreover, each component of
![]() $g^r$
is not zero). This implies that f is
$g^r$
is not zero). This implies that f is
![]() $\mu $
-algebraically stable and that
$\mu $
-algebraically stable and that
![]() $\unicode{x3bb} (f)=\theta $
(see Proposition A).
$\unicode{x3bb} (f)=\theta $
(see Proposition A).
Proposition 4.4.2. Let
![]() $\unicode{x3bb} \in {\mathbb R}$
be a weak Perron number that is a quadratic integer and let
$\unicode{x3bb} \in {\mathbb R}$
be a weak Perron number that is a quadratic integer and let
![]() $x^2-ax-b$
be its minimal polynomial, with
$x^2-ax-b$
be its minimal polynomial, with
![]() $a,b\in \mathbb {Z}$
. We then have
$a,b\in \mathbb {Z}$
. We then have
![]() $a\ge 0$
and the following hold.
$a\ge 0$
and the following hold.
-
(1) If
 $b\ge 0$
, then
$b\ge 0$
, then
 $\unicode{x3bb} $
is the dynamical degree of the shift-like automorphism
$\unicode{x3bb} $
is the dynamical degree of the shift-like automorphism  $$ \begin{align*}(x_3+x_1^ax_2^b,x_1,x_2)\in \operatorname{\mathrm{Aut}}(\mathbb{A}^3).\end{align*} $$
$$ \begin{align*}(x_3+x_1^ax_2^b,x_1,x_2)\in \operatorname{\mathrm{Aut}}(\mathbb{A}^3).\end{align*} $$
-
(2) If
 $b<0$
, then
$b<0$
, then
 $\unicode{x3bb} $
is not the dynamical degree of an affine-triangular automorphism of
$\unicode{x3bb} $
is not the dynamical degree of an affine-triangular automorphism of
 $\mathbb {A}^3$
, but is the dynamical degree of a permutation-triangular automorphism of
$\mathbb {A}^3$
, but is the dynamical degree of a permutation-triangular automorphism of
 $\mathbb {A}^4$
of the form (*) in Lemma 4.4.1.
$\mathbb {A}^4$
of the form (*) in Lemma 4.4.1.
Proof. Let us write
![]() $x^2-ax-b=(x-\unicode{x3bb} )(x-\mu )$
for some
$x^2-ax-b=(x-\unicode{x3bb} )(x-\mu )$
for some
![]() $\mu \in {\mathbb R}$
. Note that
$\mu \in {\mathbb R}$
. Note that
![]() $\mu \not =\unicode{x3bb} $
, as otherwise
$\mu \not =\unicode{x3bb} $
, as otherwise
![]() $\unicode{x3bb} ^2\in \mathbb {Z}$
and
$\unicode{x3bb} ^2\in \mathbb {Z}$
and
![]() $2\unicode{x3bb} \in \mathbb {Z}$
would imply that
$2\unicode{x3bb} \in \mathbb {Z}$
would imply that
![]() $\unicode{x3bb} \in \mathbb {Z}$
, which is impossible as
$\unicode{x3bb} \in \mathbb {Z}$
, which is impossible as
![]() $\unicode{x3bb} $
is a quadratic integer. Because
$\unicode{x3bb} $
is a quadratic integer. Because
![]() $\unicode{x3bb} $
is a weak Perron number, we have
$\unicode{x3bb} $
is a weak Perron number, we have
![]() $\unicode{x3bb} \geq 1$
and
$\unicode{x3bb} \geq 1$
and
![]() $-\unicode{x3bb} \le \mu < \unicode{x3bb} $
. In particular,
$-\unicode{x3bb} \le \mu < \unicode{x3bb} $
. In particular,
![]() $a=\unicode{x3bb} +\mu \ge 0$
. As
$a=\unicode{x3bb} +\mu \ge 0$
. As
![]() $x^2 -ax -b$
is irreducible and has a real root by assumption, the discriminant is
$x^2 -ax -b$
is irreducible and has a real root by assumption, the discriminant is
![]() $a^2+4b \geq 1$
.
$a^2+4b \geq 1$
.
If
![]() $b\ge 0$
, assertion (1) follows from Lemma 4.3.5 (and also from Proposition 4.2.3).
$b\ge 0$
, assertion (1) follows from Lemma 4.3.5 (and also from Proposition 4.2.3).
Suppose now that
![]() $b< 0$
. As
$b< 0$
. As
![]() $\unicode{x3bb} \mu =-b$
, this implies that
$\unicode{x3bb} \mu =-b$
, this implies that
![]() $\mu>0$
, so
$\mu>0$
, so
![]() $\unicode{x3bb} $
is not a Handelman number (Lemma 3.2.7) and thus is not the dynamical degree of an affine-triangular automorphism of
$\unicode{x3bb} $
is not a Handelman number (Lemma 3.2.7) and thus is not the dynamical degree of an affine-triangular automorphism of
![]() $\mathbb {A}^3$
(Proposition D). It is now enough to show that
$\mathbb {A}^3$
(Proposition D). It is now enough to show that
is a permutation-triangular automorphism with dynamical degree
![]() $\unicode{x3bb} (f)=\unicode{x3bb} $
.
$\unicode{x3bb} (f)=\unicode{x3bb} $
.
First, we prove that f is a permutation-triangular automorphism of
![]() $\mathbb {A}^4$
by showing that the exponents are non-negative. As
$\mathbb {A}^4$
by showing that the exponents are non-negative. As
![]() $a\ge 0$
, the numbers
$a\ge 0$
, the numbers
![]() $\alpha = \lfloor a/2 \rfloor $
and
$\alpha = \lfloor a/2 \rfloor $
and
![]() $a-\alpha $
are non-negative integers, so we only need to see that
$a-\alpha $
are non-negative integers, so we only need to see that
![]() $\alpha (a-\alpha )+b\ge 0$
. Because
$\alpha (a-\alpha )+b\ge 0$
. Because
![]() ${a^2+4b \geq 1}$
, we get in case a is even, that
${a^2+4b \geq 1}$
, we get in case a is even, that
![]() $\alpha (a-\alpha )+b=\alpha ^2+b=(a^2+4b)/4>0$
and in case a is odd, that
$\alpha (a-\alpha )+b=\alpha ^2+b=(a^2+4b)/4>0$
and in case a is odd, that
![]() $\alpha =(a-1)/2$
, so
$\alpha =(a-1)/2$
, so
![]() $\alpha (a-\alpha )+b=((a-1)/2) \cdot ((a+1)/2)+b=(a^2+4b-1)/4 \ge ~0$
.
$\alpha (a-\alpha )+b=((a-1)/2) \cdot ((a+1)/2)+b=(a^2+4b-1)/4 \ge ~0$
.
Second, the matrix
 $$ \begin{align*} A=\begin{pmatrix} \alpha & 1 \\ \alpha(a-\alpha)+b & a-\alpha \end{pmatrix} \in \mathrm{Mat}_2({\mathbb N}) \end{align*} $$
$$ \begin{align*} A=\begin{pmatrix} \alpha & 1 \\ \alpha(a-\alpha)+b & a-\alpha \end{pmatrix} \in \mathrm{Mat}_2({\mathbb N}) \end{align*} $$
has characteristic polynomial
![]() $x^2-ax-b$
and thus spectral radius
$x^2-ax-b$
and thus spectral radius
![]() $\rho (A)=\unicode{x3bb} $
. As
$\rho (A)=\unicode{x3bb} $
. As
![]() $x^2-ax-b$
is irreducible by assumption, it follows that A is an irreducible matrix. Moreover, as
$x^2-ax-b$
is irreducible by assumption, it follows that A is an irreducible matrix. Moreover, as
![]() $b \leq -1$
and as
$b \leq -1$
and as
![]() $x^2 -ax -b$
has a real root, we get
$x^2 -ax -b$
has a real root, we get
![]() $a \neq 0$
and hence
$a \neq 0$
and hence
![]() $a \geq 1$
. Because
$a \geq 1$
. Because
![]() $a^2 + 4b \geq 1$
, we get
$a^2 + 4b \geq 1$
, we get
![]() $\unicode{x3bb} = (a + \sqrt {a^2 + 4b})/2 \geq 1$
. Now, if
$\unicode{x3bb} = (a + \sqrt {a^2 + 4b})/2 \geq 1$
. Now, if
![]() $\unicode{x3bb} = 1$
, then
$\unicode{x3bb} = 1$
, then
![]() $1 \le a \le 2$
and thus
$1 \le a \le 2$
and thus
![]() $a^2 + 4b \leq 0$
(as
$a^2 + 4b \leq 0$
(as
![]() $b \leq -1$
), which is a contradiction. Thus
$b \leq -1$
), which is a contradiction. Thus
![]() $\unicode{x3bb}> 1$
and we can apply Lemma 4.4.1 and get that the dynamical degree of f is
$\unicode{x3bb}> 1$
and we can apply Lemma 4.4.1 and get that the dynamical degree of f is
![]() $\unicode{x3bb} (f)=\rho (A)=\unicode{x3bb} $
.
$\unicode{x3bb} (f)=\rho (A)=\unicode{x3bb} $
.
Proof of Theorem 2
Let
![]() $\unicode{x3bb} \ge 1$
be a weak Perron number. By Theorem 3.2.4,
$\unicode{x3bb} \ge 1$
be a weak Perron number. By Theorem 3.2.4,
![]() $\unicode{x3bb} $
is the spectral radius of an irreducible square matrix with non-negative integral coefficients. Lemma 4.4.1 then shows that
$\unicode{x3bb} $
is the spectral radius of an irreducible square matrix with non-negative integral coefficients. Lemma 4.4.1 then shows that
![]() $\unicode{x3bb} $
is the dynamical degree of an affine-triangular automorphism of
$\unicode{x3bb} $
is the dynamical degree of an affine-triangular automorphism of
![]() $\mathbb {A}^{n}$
for some integer n. We denote by
$\mathbb {A}^{n}$
for some integer n. We denote by
![]() $n_0$
the least possible such n.
$n_0$
the least possible such n.
If
![]() $\unicode{x3bb} =1$
, then
$\unicode{x3bb} =1$
, then
![]() $n_0=1$
, by taking the identity.
$n_0=1$
, by taking the identity.
If
![]() $\unicode{x3bb}>1$
is an integer, then
$\unicode{x3bb}>1$
is an integer, then
![]() $n_0\ge 2$
, as every automorphism of
$n_0\ge 2$
, as every automorphism of
![]() $\mathbb {A}^1$
is affine and thus has dynamical degree
$\mathbb {A}^1$
is affine and thus has dynamical degree
![]() $1$
. Moreover,
$1$
. Moreover,
![]() $n_0=2$
as
$n_0=2$
as
![]() $f=(x_1^\unicode{x3bb} +x_2,x_1)$
has dynamical degree equal to
$f=(x_1^\unicode{x3bb} +x_2,x_1)$
has dynamical degree equal to
![]() $\unicode{x3bb} $
(f is
$\unicode{x3bb} $
(f is
![]() $\mu $
-algebraic stable for
$\mu $
-algebraic stable for
![]() $\mu =(1,0)$
and
$\mu =(1,0)$
and
![]() $\deg _{\mu }(f) = \unicode{x3bb} $
).
$\deg _{\mu }(f) = \unicode{x3bb} $
).
If
![]() $\unicode{x3bb} $
is not an integer, then
$\unicode{x3bb} $
is not an integer, then
![]() $n_0\ge 3$
, as the dynamical degree of every automorphism of
$n_0\ge 3$
, as the dynamical degree of every automorphism of
![]() $\mathbb {A}^2$
is an integer (Corollary 2.4.3). If
$\mathbb {A}^2$
is an integer (Corollary 2.4.3). If
![]() $\unicode{x3bb} $
is a quadratic integer, the minimal polynomial of
$\unicode{x3bb} $
is a quadratic integer, the minimal polynomial of
![]() $\unicode{x3bb} $
is equal to
$\unicode{x3bb} $
is equal to
![]() $x^2-ax-b$
with
$x^2-ax-b$
with
![]() $a\ge 0$
and
$a\ge 0$
and
![]() $b\in \mathbb {Z}$
(Proposition 4.4.2). If the conjugate of
$b\in \mathbb {Z}$
(Proposition 4.4.2). If the conjugate of
![]() $\unicode{x3bb} $
is negative, we have
$\unicode{x3bb} $
is negative, we have
![]() $b>0$
, so
$b>0$
, so
![]() $n_0=3$
by Proposition 4.4.2(1). If the conjugate of
$n_0=3$
by Proposition 4.4.2(1). If the conjugate of
![]() $\unicode{x3bb} $
is positive, we have
$\unicode{x3bb} $
is positive, we have
![]() $b<0$
, so
$b<0$
, so
![]() $n_0=4$
by Proposition 4.4.2(2).
$n_0=4$
by Proposition 4.4.2(2).
To complement Theorem 2, we now give a family of examples of quadratic integers that do not arise as dynamical degrees of affine-triangular automorphisms of
![]() $\operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
but which arise as dynamical degrees of some other automorphisms of
$\operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
but which arise as dynamical degrees of some other automorphisms of
![]() $\mathbb {A}^3$
.
$\mathbb {A}^3$
.
Lemma 4.4.3. For all integers
![]() $r, s, t\ge 1$
, the dynamical degree of the automorphism
$r, s, t\ge 1$
, the dynamical degree of the automorphism
is the biggest root of
![]() $x^2-ax+b\in {\mathbb R}[x]$
, with
$x^2-ax+b\in {\mathbb R}[x]$
, with
![]() $a=r+s+t$
,
$a=r+s+t$
,
![]() $b=rs$
and satisfies
$b=rs$
and satisfies
![]() $\unicode{x3bb} (f)>s+1$
. In particular, if
$\unicode{x3bb} (f)>s+1$
. In particular, if
![]() $\unicode{x3bb} (f)$
is not an integer, it is not the dynamical degree of an affine-triangular automorphism of
$\unicode{x3bb} (f)$
is not an integer, it is not the dynamical degree of an affine-triangular automorphism of
![]() $\mathbb {A}^3$
, so f is not conjugate to an affine-triangular automorphism of
$\mathbb {A}^3$
, so f is not conjugate to an affine-triangular automorphism of
![]() $\mathbb {A}^3$
.
$\mathbb {A}^3$
.
Proof. Let
![]() $\theta $
be the biggest root of
$\theta $
be the biggest root of
![]() $P(x)=x^2-ax+b =(x-r)(x-s)-tx\in {\mathbb R}[x]$
. As
$P(x)=x^2-ax+b =(x-r)(x-s)-tx\in {\mathbb R}[x]$
. As
![]() $P(s+1)=(s+1-r)-t(s+1)=(s+1)(1-t)-r<0$
, we find that
$P(s+1)=(s+1-r)-t(s+1)=(s+1)(1-t)-r<0$
, we find that
![]() $\theta>s+1$
. In particular,
$\theta>s+1$
. In particular,
![]() $\mu =(\theta -s,1,\theta )\in {\mathbb R}_{\ge 1}$
.
$\mu =(\theta -s,1,\theta )\in {\mathbb R}_{\ge 1}$
.
We compute
![]() $\deg _\mu (x^rz^{s+t})=r(\theta -s)+(s+t)\theta =(r+s+t)\theta -rs=\theta ^2$
and
$\deg _\mu (x^rz^{s+t})=r(\theta -s)+(s+t)\theta =(r+s+t)\theta -rs=\theta ^2$
and
![]() $\deg _\mu (x^rz^t)=\theta ^2-s\theta =\theta (\theta -s)$
. This gives
$\deg _\mu (x^rz^t)=\theta ^2-s\theta =\theta (\theta -s)$
. This gives
![]() $\deg _\mu (f)=\theta $
, with
$\deg _\mu (f)=\theta $
, with
![]() $\mu $
-leading part
$\mu $
-leading part
![]() $g=(x^rz^t,z,x^rz^{s+t})$
. Hence,
$g=(x^rz^t,z,x^rz^{s+t})$
. Hence,
![]() $\unicode{x3bb} (f)=\theta $
by Proposition A.
$\unicode{x3bb} (f)=\theta $
by Proposition A.
If
![]() $\theta $
is not an integer, the other root of
$\theta $
is not an integer, the other root of
![]() $P(x)$
is positive, so
$P(x)$
is positive, so
![]() $\theta $
is not the dynamical degree of an affine-triangular automorphism of
$\theta $
is not the dynamical degree of an affine-triangular automorphism of
![]() $\mathbb {A}^3$
(Theorem 2). This implies that f is not conjugate to an affine-triangular automorphism of
$\mathbb {A}^3$
(Theorem 2). This implies that f is not conjugate to an affine-triangular automorphism of
![]() $\mathbb {A}^3$
.
$\mathbb {A}^3$
.
Example 4.4.4. We now apply Lemma 4.4.3 to small values of
![]() $r,s,t$
, and find some examples of automorphisms
$r,s,t$
, and find some examples of automorphisms
![]() $f=(y+x^rz^t,z,x+z^s(y+x^rz^t))\in \operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
whose dynamical degree
$f=(y+x^rz^t,z,x+z^s(y+x^rz^t))\in \operatorname {\mathrm {Aut}}(\mathbb {A}^3)$
whose dynamical degree
![]() $\unicode{x3bb} (f)$
is not that of an affine-triangular automorphism of
$\unicode{x3bb} (f)$
is not that of an affine-triangular automorphism of
![]() $\mathbb {A}^3$
. We give in Table 2 all examples of
$\mathbb {A}^3$
. We give in Table 2 all examples of
![]() $\unicode{x3bb} (f)\le 5$
given by Lemma 4.4.3. Exchanging r and s does not change the value of
$\unicode{x3bb} (f)\le 5$
given by Lemma 4.4.3. Exchanging r and s does not change the value of
![]() $\unicode{x3bb} (f)$
, so we will assume that
$\unicode{x3bb} (f)$
, so we will assume that
![]() $r\le s\le 3$
.
$r\le s\le 3$
.
Table 2 Small dynamical degrees provided by Lemma 4.4.3.

Remark 4.4.5. Let
![]() $\unicode{x3bb} $
be a weak Perron number that is a quadratic integer.
$\unicode{x3bb} $
be a weak Perron number that is a quadratic integer.
By Theorem 2,
![]() $\unicode{x3bb} $
is the dynamical degree of an affine-triangular automorphism of
$\unicode{x3bb} $
is the dynamical degree of an affine-triangular automorphism of
![]() $\mathbb {A}^4$
but is the dynamical degree of an affine-triangular automorphism of
$\mathbb {A}^4$
but is the dynamical degree of an affine-triangular automorphism of
![]() $\mathbb {A}^3$
if and only if its conjugate
$\mathbb {A}^3$
if and only if its conjugate
![]() $\unicode{x3bb} '$
is negative. If
$\unicode{x3bb} '$
is negative. If
![]() $\unicode{x3bb} '>0$
, then one can ask if
$\unicode{x3bb} '>0$
, then one can ask if
![]() $\unicode{x3bb} $
is the dynamical degree of an automorphism of
$\unicode{x3bb} $
is the dynamical degree of an automorphism of
![]() $\mathbb {A}^3$
(which would then necessarily be not conjugate to an affine-triangular automorphism). Writing
$\mathbb {A}^3$
(which would then necessarily be not conjugate to an affine-triangular automorphism). Writing
![]() $x^2-ax+b$
the minimal polynomial of
$x^2-ax+b$
the minimal polynomial of
![]() $\unicode{x3bb} $
, with
$\unicode{x3bb} $
, with
![]() $a,b$
positive integers, Lemma 4.4.3 shows that this is indeed true if one can write
$a,b$
positive integers, Lemma 4.4.3 shows that this is indeed true if one can write
![]() $b=rs$
with
$b=rs$
with
![]() $r,s\ge 1$
and
$r,s\ge 1$
and
![]() $a>r+s$
. In particular, this holds if
$a>r+s$
. In particular, this holds if
![]() $b\le 4$
, as
$b\le 4$
, as
![]() $a^2-4b>0$
, so
$a^2-4b>0$
, so
![]() $a>2\sqrt {b}$
. If
$a>2\sqrt {b}$
. If
![]() $b=5$
, then
$b=5$
, then
![]() $a\ge 5$
(as
$a\ge 5$
(as
![]() $a> 2 \sqrt {b}$
), and Lemma 4.4.3 applies as soon as
$a> 2 \sqrt {b}$
), and Lemma 4.4.3 applies as soon as
![]() $a\ge 6$
. The case where
$a\ge 6$
. The case where
![]() $a=b=5$
corresponds to
$a=b=5$
corresponds to
![]() $\unicode{x3bb} =(5+\sqrt {5})/2$
, which is then the ‘simplest’ weak Perron quadratic integer that is not covered by Theorem 2 or Lemma 4.4.3.
$\unicode{x3bb} =(5+\sqrt {5})/2$
, which is then the ‘simplest’ weak Perron quadratic integer that is not covered by Theorem 2 or Lemma 4.4.3.
According to Remark 4.4.5, it seems natural to ask if every quadratic weak Perron number is the dynamical degree of an automorphism of
![]() $\mathbb {A}^3$
. A first intriguing case concerns the following question, which was in fact already asked to us by Jean-Philippe Furter and Pierre-Marie Poloni.
$\mathbb {A}^3$
. A first intriguing case concerns the following question, which was in fact already asked to us by Jean-Philippe Furter and Pierre-Marie Poloni.
Question 4.4.6. Is
![]() $(5+\sqrt {5})/2$
the dynamical degree of an automorphism of
$(5+\sqrt {5})/2$
the dynamical degree of an automorphism of
![]() $\mathbb {A}^3$
?
$\mathbb {A}^3$
?
Acknowledgements
The authors thank the referee for his careful reading and helpful suggestions. We thank Jean-Philippe Furter and Pierre-Marie Poloni for helpful discussions on dynamical degrees of automorphisms of
![]() $\mathbb {A}^3$
and Christian Urech for indicating to us the result of Mattias Jonsson (Proposition 4.2.5) that inspired our generalization.
$\mathbb {A}^3$
and Christian Urech for indicating to us the result of Mattias Jonsson (Proposition 4.2.5) that inspired our generalization.