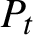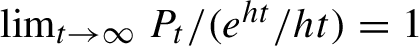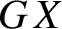1 Introduction
Given a locally geodesic space, it is natural to consider the number
$P_t$
of closed geodesics of length at most
$t> 0$
. In general,
$P_t$
may be infinite for all t above a certain threshold
$T \ge 0$
, but under certain geometric conditions one finds it is finite for all t and can obtain asymptotic information about the growth rate of
$P_t$
.
The classic example of this situation is a theorem of Margulis [Reference Margulis10]. If M is a closed, negatively curved Riemannian manifold, then
$\lim \nolimits _{t \to \infty } {P_t} / {(}{{e^{ht}}/{ht}}) = 1$
, where h is the entropy of the geodesic flow on the unit tangent bundle
$SM$
. Margulis also proved that the number
$Q_t$
of geodesic arcs of length less than or equal to t starting at
$x \in M$
and ending at
$y \in M$
satisfies
$\lim \nolimits _{t \to \infty } {Q_t} / {e^{ht}} = C$
, where C depends only on
$x,y$
.
In non-positive curvature (instead of strictly negative curvature), there are often parallel geodesics, which can make the number
$P_t$
as defined above infinite for large t. However, if one refines the definition of
$P_t$
to be the number of parallel classes of closed geodesics of length less than or equal to t, it becomes meaningful again in this case, while staying the same in the case of negative curvature. Knieper [Reference Knieper6] proved that when M is a closed, rank-one non-positively curved Riemannian manifold, there exists
$C> 0$
such that
${1}/{C} \le \liminf {P_t} / {({e^{ht}}/{ht})}$
and
$\limsup {P_t} / {e^{ht}} \le C$
. Knieper later improved his bounds [Reference Knieper7] to
${1}/{C} \le \liminf {P_t} / {({e^{ht}}/{ht})} \le \limsup {P_t} / {({e^{ht}}/{ht})} \le C$
. (This type of inequality occurs frequently enough in this paper that we will use the notation
${\widetilde {\lim }}$
when the inequality holds for both
$\liminf $
and
$\limsup $
. In this notation, the last inequalities become
${1}/{C} \le {\widetilde {\lim }} {P_t} / {({e^{ht}}/{ht})} \le C$
.) Knieper’s original bounds were recently proved by different means by Burns et al.f [Reference Burns, Climenhaga, Fisher and Thompson3]. A recent paper of Liu, Wang, and Wu [Reference Liu, Wang and Wu9] generalizes this beyond non-positive curvature to the case of closed Riemannian manifolds without focal points.
Another way to generalize the setting of Margulis’s theorem is to allow the spaces to admit singularities. In fact, locally
$\operatorname {\mathrm {CAT}}(-1)$
spaces are a generalization of negatively curved manifolds which allow branching and other singularities. They are locally geodesic spaces in which all sufficiently small geodesic triangles are ‘thinner’ than their respective comparison triangles in the hyperbolic plane
$\mathbb {H}^2$
. Roblin proved [Reference Roblin14] that if the Bowen–Margulis measure of a proper, locally
$\operatorname {\mathrm {CAT}}(-1)$
space is finite, then
$\lim \nolimits _{t \to \infty } {Q_t} / {e^{ht}} = C$
, where C depends only on
$x,y$
. A recent paper by Link [Reference Link8] generalizes this statement from
$\operatorname {\mathrm {CAT}}(-1)$
to rank-one
$\operatorname {\mathrm {CAT}}(0)$
. Locally
$\operatorname {\mathrm {CAT}}(0)$
spaces generalize non-positively curved manifolds by allowing singularities; the definition uses comparison triangles in the Euclidean plane
$\mathbb {R}^2$
instead of
$\mathbb {H}^2$
. Roblin also proved [Reference Roblin14] that if the Bowen–Margulis measure of a proper, locally
$\operatorname {\mathrm {CAT}}(-1)$
space X is finite and mixing, and X is geometrically finite, then
$\lim \nolimits _{t \to \infty } {P_t} / {({e^{ht}}/{ht})} = 1$
Footnote †.
In this paper, we focus on the case of proper, rank-one, locally
$\operatorname {\mathrm {CAT}}(0)$
spaces. We assume throughout the paper (with the exception of §3) that
$\Gamma $
is a group acting freely, properly discontinuously, non-elementarily, and by isometries on a proper, geodesically complete
$\operatorname {\mathrm {CAT}}(0)$
space X with rank-one axis. We also assume the geodesic flow is mixing and the Bowen–Margulis measure (constructed in [Reference Ricks12]) is finite and mixing under the geodesic flow. When
$\Gamma $
acts cocompactly, it is well known to also act non-elementarily unless X is isometric to the real line; in [Reference Ricks12] it was shown that cocompactness also implies the Bowen–Margulis measure is always finite and mixing unless X is homothetic to a tree with integer edge lengths. We prove the following theorem.
Theorem 1.1. Let
$\Gamma $
be a group acting freely, geometrically (that is, properly discontinuously, cocompactly, and by isometries) on a proper, geodesically complete
$\operatorname {\mathrm {CAT}}(0)$
space X with rank-one axis. Assume X is not homothetic to a tree with integer edge lengths. Let
$P_t$
be the number of parallel classes of oriented closed geodesics of length at most t in
$\Gamma \backslash X$
; then
$\lim \nolimits _{t \to \infty } P_t / ({e^{ht}}/{ht}) = 1$
, where h is the entropy of the geodesic flow on the space
$GX$
of parametrized unit-speed geodesics in X.
We remark that if X is homothetic to a tree with integer edge lengths, then the limit of
$P_t / ({e^{ht}}/{ht})$
does not exist. Also, the closed geodesics which bound a half flat in the universal cover (called the higher-rank geodesics) grow at a strictly smaller exponential rate; this statement is proved in Corollary 14.6 of this paper.
We note that a recent preprint of Gekhtman and Yang [Reference Gekhtman and Yang4] generalizes Knieper’s bounds
${1}/{C} \le {\widetilde {\lim }} {P_t} / {({e^{ht}}/{ht})} \le C$
to a class of group actions including the proper, rank-one, locally
$\operatorname {\mathrm {CAT}}(0)$
case. In our more restricted setting, we prove the exact limit. We also note that an unpublished paper from 2007 by Gunesch [Reference Gunesch5] claims our result for compact, rank-one, non-positively curved manifolds. Indeed, many of the ideas in Gunesch’s work are good and inspired the current paper.
We proceed as follows in the paper. First, after establishing notation and standard facts about rank-one
$\operatorname {\mathrm {CAT}}(0)$
spaces, we use Papasoglu and Swenson’s
$\pi $
-convergence theorem to prove a statement about local uniform expansion along unstable horospheres. Next, we construct product boxes (which behave better than standard flow boxes for measuring lengths of intersection for orbits), and use mixing to prove a result about the total measure of intersections under the flow for these product boxes. We use this to count the number of intersections coming from periodic orbits. Then we construct measures equally weighted along periodic orbits. We adapt Knieper’s proof of an equidistribution result to prove Theorem 1.1.
It may be of interest to the reader that Theorem 1.1 is the consequence of the more general Theorem 15.5, which we state as follows.
Theorem 1.2. Let
$\Gamma $
be a group acting freely, properly discontinuously, and by isometries on a proper, geodesically complete
$\operatorname {\mathrm {CAT}}(0)$
space X with rank-one axis. Assume
$m_\Gamma $
is finite and mixing. Also assume the closed geodesics of
$\Gamma \backslash X$
equidistribute onto
$m_\Gamma $
. Let
$U \subseteq GX$
contain an open neighborhood of some zero-width geodesic with both endpoints in the limit set of
$\Gamma $
. Let
$P_t(U)$
be the number of parallel classes of oriented closed geodesics of length at most t in
$\Gamma \backslash X$
; then
$\lim \nolimits _{t \to \infty } P_t(U) / ({e^{ht}}/{ht}) = 1$
, where h is the critical exponent
$\delta _\Gamma $
of the Poincaré series for
$\Gamma $
.
The main difficulty in applying Theorem 1.2 is the equidistribution hypothesis, which is shown in Theorem 14.7 for
$\Gamma \backslash X$
compact; Theorem 1.1 follows immediately.
We make one final remark. Although we assume throughout the paper that X is geodesically complete and
$\Gamma $
acts non-elementarily on X, these hypotheses do not play a role in the proofs of this paper except in guaranteeing that the Bowen–Margulis measure exists and has full support on the geodesics with both endpoints in the limit set of
$\Gamma $
, and that Proposition 5.2 and Theorem 5.3 hold.
2 Preliminaries
A geodesic in a metric space X is an isometric embedding of the real line
$\mathbb {R}$
into X. A geodesic segment is an isometric embedding of a compact interval, and a geodesic ray is an isometric embedding of
$[0, \infty )$
.
A metric space X is called uniquely geodesic if for every pair of distinct
$x,y \in X$
there is a unique geodesic segment
$u \colon [a,b] \to X$
such that
$u(a) = x$
and
$u(b) = y$
. The space X is geodesically complete (or X has the geodesic extension property) if every geodesic segment in X extends to a full geodesic in X.
A CAT
$(0)$
space is a uniquely geodesic space such that for every triple of distinct points
$x,y,z \in X$
, the geodesic triangle is no fatter than the corresponding comparison triangle in Euclidean
$\mathbb {R}^2$
(the triangle with the same edge lengths). A detailed account of
$\operatorname {\mathrm {CAT}}(0)$
spaces is found in [Reference Ballmann1] or [Reference Bridson and Haefliger2].
Every complete
$\operatorname {\mathrm {CAT}}(0)$
space X has an ideal boundary, written
$\partial X$
, obtained by taking equivalence classes of asymptotic geodesic rays. The compact-open topology on the set of rays induces a topology on
$\partial X$
, called the cone or visual topology. If X is proper (meaning all closed balls are compact), then both
$\partial X$
and
$\overline {X} = X \cup \partial X$
are compact metrizable spaces.
Standing hypothesis. From now on, X will always be a proper, geodesically complete
$\operatorname {\mathrm {CAT}}(0)$
space.
For
$\xi \in \partial X$
and
$p,q \in X$
, let
$b_{\xi } (p, q)$
be the Busemann cocycle
$$ \begin{align*}b_{\xi} (p, q) = \lim_{t \to \infty} [ d([q,\xi)(t), p) - t ].\end{align*} $$
These functions are continuous in all three variables and
$1$
-Lipschitz in p and q. They also satisfy the cocycle property
$b_{\xi } (x, y) + b_{\xi } (y, z) = b_{\xi } (x, z)$
. Furthermore,
$b_{\gamma \xi } (\gamma x, \gamma y) = b_{\xi } (x, y)$
for all
$\gamma \in \operatorname {\mathrm {Isom}} X$
.
Denote by
$GX$
the space of all geodesics
$\mathbb {R} \to X$
, where
$GX$
is endowed with the compact-open topology. Then
$GX$
is naturally a proper metric space, and there is a canonical footprint projection map
$\pi \colon GX \to X$
given by
$\pi (v) = v(0)$
; this map is proper. We will use the simple metric on
$GX$
given by
$$ \begin{align*} d_{GX}(v,w) = \mathop{\mathrm{sup}}\limits_{t \in \mathbb{R}} e^{-| t |}\,d_X(v(t), w(t)), \end{align*} $$
which makes
$\pi 1$
-Lipschitz. There is also a canonical endpoint projection map
$\operatorname {\mathrm {E}} \colon GX \to \partial X \times \partial X$
defined by
$\operatorname {\mathrm {E}}(v) = (v^-, v^+) := (\lim _{t \to -\infty } v(t), \lim _{t \to +\infty } v(t))$
. And
$w \in GX$
is parallel to
$v \in GX$
if and only if
$\operatorname {\mathrm {E}}(w) = \operatorname {\mathrm {E}}(v)$
.
The geodesic flow
$g^t$
on
$GX$
is defined by the formula
$(g^t v)(r) = v(t + r)$
.
Notice
$b_{v^-} (v(t), v(0)) = t$
and
$b_{v^+} (v(t), v(0)) = -t$
. Let
$\pi _p \colon GX \to \partial X \times \partial X \times \mathbb {R}$
be the continuous map
$$ \begin{align*}\pi_p(v) := (v^-, v^+, b_{v^-} (v(0), p)).\end{align*} $$
Define the cross-section of
$v \in GX$
to be
$CS(v) := \{w \in SX : \pi _p(w) = \pi _p(v)\}$
, and the width of a geodesic
$v \in GX$
to be
$\operatorname {\mathrm {width}}(v) := \operatorname {\mathrm {diam}} CS(v)$
. In fact, the set
$Par(v)$
of geodesics parallel to v splits isometrically as
$Par(v) = CS(v) \times \mathbb {R}$
, and so the width of v is actually the maximum width of a flat strip
$\mathbb {R} \times [0, R]$
in X parallel to v.
A geodesic v in X is called higher-rank if it can be extended to an isometric embedding of the half-flat
$\mathbb {R} \times [0, \infty ) \subseteq \mathbb {R}^2$
into X. A geodesic which is not higher-rank is called rank-one. Let
$\mathcal R \subseteq GX$
denote the set of rank-one geodesics. (Notice that
$v \in \mathcal R$
if and only if
$\operatorname {\mathrm {width}}(v)$
is finite.) The following lemma describes an important aspect of the geometry of rank-one geodesics in a
$\operatorname {\mathrm {CAT}}(0)$
space.
Lemma 2.1. [Reference Ballmann1, Lemma III.3.1]
Let
$w \colon \mathbb {R} \to X$
be a geodesic which does not bound a flat strip of width
$R> 0$
. Then there are neighborhoods U and V in
$\overline X$
of the endpoints of w such that for any
$\xi \in U$
and
$\eta \in V$
, there is a geodesic joining
$\xi $
to
$\eta $
. For any such geodesic v, we have
$d(v, w(0)) < R$
; in particular, v does not bound a flat strip of width
$2R$
.
Now let
$\Gamma $
be a group acting properly discontinuously, and by isometries on X. The
$\Gamma $
-action on X naturally induces an action by homeomorphisms on
$\overline {X}$
(and therefore on
$\partial X$
). The limit set of
$\Gamma $
is
$\Lambda = \overline {\Gamma x} \cap \partial X$
, for some
$x \in X$
. The limit set is closed and invariant, and it does not depend on choice of x. The action is called elementary if either
$\Lambda $
contains at most two points, or
$\Gamma $
fixes a point in
$\partial X$
.
The
$\Gamma $
-action on X also induces a properly discontinuous, isometric action on
$GX$
. Denote by
$g_\Gamma ^t$
the induced flow on the quotient
$\Gamma \backslash GX$
, and let
$\operatorname {\mathrm {pr}} \colon GX \to \Gamma \backslash GX$
be the canonical projection map.
A geodesic
$v \in GX$
is an axis of an isometry
$\gamma \in \operatorname {\mathrm {Isom}} X$
if
$\gamma $
translates along v, that is,
$\gamma v = g^t v$
for some
$t> 0$
. If some rank-one geodesic
$v \in \mathcal R$
is an axis for
$\gamma \in \operatorname {\mathrm {Isom}} X$
, we call
$\gamma $
rank-one. We call the
$\Gamma $
-action rank-one if some
$\gamma \in \Gamma $
is rank-one.
Standing hypothesis.
$\Gamma $
is a group acting properly discontinuously, and by isometries on X. Except in §3, we further assume the action is rank-one, non-elementary, and free (that is, no non-trivial
$\gamma \in \Gamma $
fixes a point of
$x \in X$
).
3 Locally uniform expansion along unstable horospheres
There is a topology on
$\partial X$
, finer than the visual topology, that comes from the Tits metric
${d_T}$
on
$\partial X$
. The Tits metric is complete
$\operatorname {\mathrm {CAT}}(1)$
, and measures the asymptotic angle between geodesic rays in X. In fact, a geodesic
$v \in GX$
is rank-one if and only if
${d_T}(v^-,v^+)> \pi $
. Write
${B_T} (\xi , r)$
for the open Tits ball of
${d_T}$
-radius r about
$\xi $
in
$\partial X$
and
$\overline {{B_T}} (\xi , r)$
for the closed ball.
Papasoglu and Swenson’s
$\pi $
-convergence result is stated as follows.
Theorem 3.1. [Reference Papasoglu and Swenson11, Lemma 18]
Let X be a proper
$\operatorname {\mathrm {CAT}}(0)$
space and G a group acting by isometries on X. Let
$x \in X$
,
$\theta \in [0,\pi ]$
, and
$(g_i) \subset G$
such that
$g_i (x) \to p \in \partial X$
and
$g_i^{-1} (x) \to n \in \partial X$
. For any compact set
$K \subset \partial X \backslash \overline {{B_T}} (n, \theta )$
,
$g_i (K) \to \overline {{B_T}} (p, \pi - \theta ),$
(in the sense that for any open
$U \supset \overline {{B_T}} (p, \pi - \theta ), g_i (K) \subset U$
for all i sufficiently large).
From Theorem 3.1 we prove that the geodesic flow expands unstable horospheres locally uniformly (Theorem 3.4).
Lemma 3.2. The evaluation map
$\mathrm {ev} \colon GX \times (-\infty , \infty ) \to X$
given by
$\mathrm {ev}(v,t) = v(t)$
extends continuously to a map
$GX \times [-\infty , \infty ] \to \overline {X}$
.
Lemma 3.3. Let
$\Gamma $
be a group acting properly discontinuously and by isometries on a proper
$\operatorname {\mathrm {CAT}}(0)$
space X. Let
$ \mathfrak {v} \subset GX$
be compact. Let
$ \mathfrak {v}^- = \{v^- : v \in \mathfrak {v}\}$
and
$ \mathfrak {v}^+ = \{v^+ : v \in \mathfrak {v}\}$
. Let
$(\gamma _i)$
be a sequence in
$\Gamma $
such that
$\gamma _i x \to \xi \in \partial X$
for some (hence any)
$x \in X$
and
$ \mathfrak {v} \cap \gamma _i g^{-t_i} \mathfrak {v} \neq \varnothing $
for some sequence
$(t_i)$
in
$[0, \infty )$
. Then
$\xi \in \mathfrak {v}^+$
. Let
$K \subset \partial X$
be compact such that
${d_T}( \mathfrak {v}^-, K)> \pi - c$
for some
$c \in [0,\pi ]$
. If
$U \subseteq \partial X$
is an open set such that
$\overline {{B_T}} (\xi , c) \subseteq U$
, then
$\gamma _i (K) \subseteq U$
for all i sufficiently large.
Proof First observe that the sets
$\pi (g^{[0,\infty ]} \mathfrak {v}) = \mathfrak {v}^+ \cup \{v(t) : v \in \mathfrak {v} \text { and } t \ge 0\}$
and
$\pi (g^{[-\infty ,0]} \mathfrak {v}) = \mathfrak {v}^- \cup \{v(t) : v \in \mathfrak {v} \text { and } t \le 0\}$
are closed in
$\overline {X}$
because
$ \mathfrak {v}$
is compact.
For each
$i \in \mathbb {N}$
, let
$v_i \in \mathfrak {v} \cap \gamma _i g^{-t_i} \mathfrak {v}$
. Passing to a subsequence if necessary, we may assume the sequence
$(v_i)$
converges to some
$v_0 \in \mathfrak {v}$
, and
$(\gamma _i^{-1} g^{t_i} v_i)$
converges to some
$w_0 \in \mathfrak {v}$
. Let
$x_0 = v_0(0)$
and
$y_0 = w_0(0)$
. Recall that
$\gamma _i y_0 \to \xi \in \partial X$
. We may assume the sequence
$(\gamma _i^{-1} x_0)$
converges to some
$\eta \in \partial X$
.
We know
$d(\gamma _i w_0, g^{t_i} v_i) \to 0$
, so
$d(\gamma _i y_0, v_i(t_i)) \to 0$
. Since
$\pi (g^{[0,\infty ]} \mathfrak {v})$
is closed, we may conclude
$\xi = \lim v_i(t_i) \in \mathfrak {v}^+$
. Now for each
$i \in \mathbb {N}$
let
$w_i = \gamma _i^{-1} g^{t_i} v_i$
. Then
$d(\gamma _i^{-1} v_0, g^{-t_i} w_i) = d(\gamma _i^{-1} v_0, \gamma _i^{-1} v_i) \to 0$
, and so
$d(\gamma _i^{-1} x_0, w_i(-t_i)) \to 0$
. Since each
$w_i \in \mathfrak {v}$
and
$\pi (g^{[-\infty ,0]} \mathfrak {v})$
is closed, we see that
$\eta = \lim w_i(-t_i) \in \mathfrak {v}^-$
.
Thus
$\gamma _i x_0 \to \xi \in \mathfrak {v}^+$
and
$\gamma _i^{-1} x_0 \to \eta \in \mathfrak {v}^-$
. Apply Theorem 3.1.
Theorem 3.4. Let
$\Gamma $
be a group acting properly discontinuously and by isometries on a proper
$\operatorname {\mathrm {CAT}}(0)$
space X. Let
$ \mathfrak {v} \subset GX$
be compact. Let
$ \mathfrak {v}^- = \{v^- : v \in \mathfrak {v}\}$
and
$ \mathfrak {v}^+ = \{v^+ : v \in \mathfrak {v}\}$
. Let
$c \in [0, \pi ]$
and let
$\{U_\lambda \}$
be an open cover of
$ \mathfrak {v}^+$
such that for every
$\xi \in \mathfrak {v}^+$
, there is some
$\lambda $
such that
$\overline {{B_T}} (\xi , c) \subseteq U_\lambda $
. For any compact set
$K \subset \partial X$
such that
${d_T} ( \mathfrak {v}^-, K)> \pi - c$
, there is some
$t_0 \ge 0$
such that for all
$t \ge t_0$
and
$\gamma \in \Gamma $
, if
$ \mathfrak {v} \cap \gamma g^{-t} \mathfrak {v} \neq \varnothing $
then
$\gamma K \subseteq U_\lambda $
for some
$\lambda $
.
Proof Suppose not. Then for each
$i \in \mathbb {N}$
there exist
$\gamma _i \in \Gamma $
and
$t_i \to \infty $
such that
$v_i \in \mathfrak {v} \cap \gamma _i g^{-t_i} \mathfrak {v}$
but
$\gamma _i \mathfrak {v}^+ \nsubseteq U_\lambda $
for all
$i, \lambda $
. Since
$(\gamma _i)$
escapes to infinity, we may assume
$\gamma _i x \to \xi \in \partial X$
for some
$\xi \in \partial X$
and
$x \in X$
. This contradicts Lemma 3.3. Therefore, the theorem must hold.
Putting
$c = 0$
into Theorem 3.4, we obtain the following corollary.
Corollary 3.5. Let
$\Gamma $
be a group acting properly discontinuously and by isometries on a proper
$\operatorname {\mathrm {CAT}}(0)$
space X. Let
$ \mathfrak {v} \subset GX$
be compact, let
$ \mathfrak {v}^- = \{v^- : v \in \mathfrak {v}\}$
and
$ \mathfrak {v}^+ = \{v^+ : v \in \mathfrak {v}\}$
, and let
$\{U_\lambda \}$
be an open cover of
$ \mathfrak {v}^+$
. For any compact set
$K \subset \partial X$
such that
${d_T} ( \mathfrak {v}^-, K)> \pi $
, there is some
$t_0 \ge 0$
such that for all
$t \ge t_0$
and
$\gamma \in \Gamma $
, if
$ \mathfrak {v} \cap \gamma g^{-t} \mathfrak {v} \neq \varnothing $
then
$\gamma K \subseteq U_\lambda $
for some
$\lambda $
.
4 Quasi-product neighborhoods
Fix a metric
$\rho $
on
$\partial X$
(with the cone topology). Let
$v_0 \in \mathcal R$
, let
$p = v_0(0)$
, and let
$\varepsilon \ge 0$
. For each
$\delta> 0$
, let
$$ \begin{align*} \mathfrak{v}(v_0, \varepsilon, \delta) = \pi_p^{-1} ( \overline{{B_{\rho}}}(v_0^-, \delta) \times \overline{{B_{\rho}}}(v_0^+, \delta) \times [0, \varepsilon] ).\end{align*} $$
We may abbreviate
$ \mathfrak {v}(v_0, \varepsilon , \delta ) = \mathfrak {v}_{\varepsilon ,\delta } = \mathfrak {v}_\delta = \mathfrak {v}$
. As it turns out, we will want to extend the sets
$ \mathfrak {v}_{\varepsilon ,\delta }$
slightly for some of our results, so we also define
$$ \begin{align*} \widetilde{\mathfrak{v}}_{\varepsilon,\delta} = g^{[-\varepsilon, \varepsilon]} \mathfrak{v}_{\varepsilon,\delta}.\end{align*} $$
Since
$v_0 \in \mathcal R$
, by Lemma 2.1 we know
$ \mathfrak {v}_\delta $
is always compact for
$\delta $
sufficiently small. In fact, we have the following lemma.
Lemma 4.1. Let
$v_0 \in \mathcal R$
. For all
$\varepsilon \ge 0$
we have
$\lim \nolimits _{\delta \to 0} \operatorname {\mathrm {diam}} \widetilde {\mathfrak {v}}_{\varepsilon ,\delta } \le 4\varepsilon + \operatorname {\mathrm {diam}} CS(v_0)$
.
Proof Suppose, by way of contradiction, there exist
$\alpha> 0$
and sequences of
$\delta _n> 0$
and
$v_n, w_n \in \widetilde {\mathfrak {v}}_{\varepsilon , \delta _n}$
such that
$\delta _n \to 0$
but
$d(v_n, w_n) \ge 4\varepsilon + \operatorname {\mathrm {diam}} CS(v_0) + \alpha $
for all n. For each n find
$s_n, t_n \in [-\varepsilon , 2\varepsilon ]$
such that
$g^{-s_n} v_n, g^{-t_n} w_n \in \mathfrak {v}_{0,\delta }$
. By the triangle inequality,
$d(g^{-s_n} v_n, g^{-t_n} w_n) \ge \operatorname {\mathrm {diam}} CS(v_0) + \alpha $
for all n. We may assume
$g^{-s_n} v_n \to v$
and
$g^{-t_n} w_n \to w$
for some
$v, w \in \bigcap _{\delta> 0} \mathfrak {v}_{0,\delta }$
. Thus
$v,w \in CS(v_0)$
, hence
$d(v, w) \le \operatorname {\mathrm {diam}} CS(v_0)$
, contradicting
$g^{-s_n} v_n \to v$
and
$g^{-t_n} w_n \to w$
. Therefore, the statement of the lemma must hold.
Let
$\varepsilon , \delta> 0$
. For each
$t \in \mathbb {R}$
and
$\gamma \in \Gamma $
, let
$$ \begin{align*} \mathfrak{w}^{\gamma}(v_0, \varepsilon, \delta, t) = \mathfrak{v}(v_0, \varepsilon, \delta) \cap \gamma g^{-t} \mathfrak{v}(v_0, \varepsilon, \delta).\end{align*} $$
We abbreviate
$ \mathfrak {w}^{\gamma }(v_0, \varepsilon , \delta , t) = \mathfrak {w}^{\gamma }_{\varepsilon , \delta , t} = \mathfrak {w}^{\gamma }_{\delta , t} = \mathfrak {w}^{\gamma }$
. Similarly, define
$\widetilde {\mathfrak {w}}^{\gamma } = \widetilde {\mathfrak {v}} \cap \gamma g^{-t} \widetilde {\mathfrak {v}}$
.
Lemma 4.2. Let
$v_0 \in \mathcal R$
have zero width. Assume
$\Gamma $
acts freely, properly discontinuously, and by isometries on X. There exist
$\varepsilon _0> 0$
and
$\delta _0> 0$
such that for all
$\varepsilon \in [0,\varepsilon _0]$
,
$\delta \in (0,\delta _0]$
, and
$t \in \mathbb {R}$
, the sets
$\operatorname {\mathrm {E}}(\widetilde {\mathfrak {w}}^{\gamma }) = \operatorname {\mathrm {E}}(\widetilde {\mathfrak {w}}^{\gamma }_{\varepsilon ,\delta ,t})$
are pairwise disjoint.
Proof Let
$p = v_0(0)$
. Because
$\Gamma $
acts freely and properly discontinuously on X, there is some
$r_0> 0$
such that
$d(p, \gamma p) \ge r_0$
for all non-trivial
$\gamma \in \Gamma $
. Let
$\varepsilon _0 = {r_0} / {30}$
, and let
$\delta _0> 0$
be small enough that
$\operatorname {\mathrm {diam}} \widetilde {\mathfrak {v}}_{3\varepsilon _0,\delta _0} < 15\varepsilon _0$
. This implies
$\widetilde {\mathfrak {v}}_{3\varepsilon _0,\delta _0} \cap \gamma \widetilde {\mathfrak {v}}_{3\varepsilon _0,\delta _0} = \varnothing $
for all
$\gamma \neq \operatorname {\mathrm {id}}$
by the triangle inequality.
Now let
$\varepsilon \in [0,\varepsilon _0]$
and
$\delta \in (0,\delta _0]$
. Let
$\gamma , \gamma ' \in \Gamma $
be such that
$\operatorname {\mathrm {E}}(\widetilde {\mathfrak {w}}^{\gamma }) \cap \operatorname {\mathrm {E}}(\widetilde {\mathfrak {w}}^{\gamma '})$
is non-empty. By definition of
$\widetilde {\mathfrak {v}}$
, there exist
$t' \in \mathbb {R}$
and
$w \in GX$
such that
$w \in g^{t} \widetilde {\mathfrak {w}}^{\gamma } \cap g^{t'} \widetilde {\mathfrak {w}}^{\gamma '}$
. Then
$$ \begin{align*} w &\in (g^{t} \widetilde{\mathfrak{v}} \cap \gamma \widetilde{\mathfrak{v}}) \cap (g^{t'} \widetilde{\mathfrak{v}} \cap \gamma' g^{t' - t} \widetilde{\mathfrak{v}})= (g^{t} \widetilde{\mathfrak{v}} \cap g^{t'} \widetilde{\mathfrak{v}}) \cap (\gamma \widetilde{\mathfrak{v}} \cap \gamma' g^{t' - t} \widetilde{\mathfrak{v}}). \end{align*} $$
So
$w \in g^{t} \widetilde {\mathfrak {v}} \cap g^{t'} \widetilde {\mathfrak {v}}$
, hence
$| t' - t | \le 3\varepsilon $
by definition of
$\widetilde {\mathfrak {v}}$
. Then also
$$ \begin{align*} \gamma^{-1} w &\in \widetilde{\mathfrak{v}}_{\varepsilon,\delta} \cap \gamma^{-1} \gamma' g^{t' - t} \widetilde{\mathfrak{v}}_{\varepsilon,\delta} \subset g^{-\varepsilon_0} \widetilde{\mathfrak{v}}_{3\varepsilon_0,\delta_0} \cap \gamma^{-1} \gamma' g^{-\varepsilon_0} \widetilde{\mathfrak{v}}_{3\varepsilon_0,\delta_0}, \end{align*} $$
which is empty by the previous paragraph unless
$\gamma ^{-1} \gamma ' = \operatorname {\mathrm {id}}$
. Therefore
$\gamma = \gamma '$
.
Corollary 4.3. All the
$\widetilde {\mathfrak {w}}^{\gamma }$
are disjoint.
Lemma 4.4. Fix a zero-width geodesic
$v_0 \in GX$
. Assume
$\Gamma $
acts freely, properly discontinuously, and by isometries on X. There exist
$\varepsilon _0> 0$
and
$\delta _0> 0$
such that for every
$\delta \in (0,\delta _0]$
and
$\varepsilon \in [0, \varepsilon _0]$
, the set
$ \mathfrak {v} = \mathfrak {v}(v_0, \varepsilon , \delta )$
satisfies all the following properties.
-
(1) If
$\varepsilon> 0$
then
$ \mathfrak {v}$
contains an open neighborhood of
$g^{{\varepsilon } / {2}} v_0$
in
$GX$
. -
(2)
$ \mathfrak {v}$
and
$\widetilde {\mathfrak {v}}$
are compact. -
(3) For all
$v \in \mathfrak {v}$
,
$g^t v \in \mathfrak {v}$
if and only if
$0 \le s(g^t v) \le \varepsilon $
. Similarly, for all
$v \in \widetilde {\mathfrak {v}}$
,
$g^t v \in \widetilde {\mathfrak {v}}$
if and only if
$-\varepsilon \le s(g^t v) \le 2\varepsilon $
. -
(4)
${d_T}(\widetilde {\mathfrak {v}}_{\delta }^-, \widetilde {\mathfrak {v}}_{\delta }^+) = {d_T}( \mathfrak {v}_{\delta }^-, \mathfrak {v}_{\delta }^+)> \pi $
. -
(5) The sets
$\operatorname {\mathrm {E}}(\widetilde {\mathfrak {w}}^{\gamma }) = \operatorname {\mathrm {E}}(\widetilde {\mathfrak {w}}^{\gamma }_{\varepsilon ,\delta ,t})$
are pairwise disjoint for all
$t \in \mathbb {R}$
.
Proof Property (1) follows from continuity of
$\pi _p$
, (2) and (4) from Lemma 2.1, (3) from the definitions, and (5) from Lemma 4.2.
Remark 4.5. Only property (5) requires
$v_0$
zero-width and
$\Gamma $
acting freely. The others require only
$v_0$
rank-one and
$\Gamma $
acting properly isometrically.
5 Mixing calculations
5.1 Measures
We recall the measures constructed in [Reference Ricks12].
The critical exponent
$\delta _\Gamma = \inf \{s \ge 0 : \sum _{\gamma \in \Gamma } e^{-s d(p, \gamma q)} < \infty \}$
of the Poincaré series for
$\Gamma $
does not depend on choice of p or q. We shall always assume
$\delta _\Gamma < \infty $
(which holds whenever
$\Gamma $
is finitely generated, for instance). Then Patterson’s construction yields a conformal density
$(\mu _p)_{p \in X}$
of dimension
$\delta _\Gamma $
on
$\partial X$
, called the Patterson–Sullivan measure.
Definition 5.1. A conformal density of dimension
$\delta $
is a family
$(\mu _p)_{p \in X}$
of equivalent finite Borel measures on
$\partial X$
, supported on
$\Lambda $
, such that for all
$p,q \in X$
and
$\gamma \in \Gamma $
:
-
(1) the pushforward
$\gamma _* \mu _p = \mu _{\gamma p}$
; and -
(2) the Radon–Nikodym derivative
$({d\mu _q}/{d\mu _p}) (\xi ) = e^{-\delta b_\xi (q, p)}$
.
Now fix
$p \in X$
. For
$(v^-,v^+) \in \operatorname {\mathrm {E}}(GX)$
, let
$\beta _p \colon \operatorname {\mathrm {E}}(GX) \to \mathbb {R}$
be
$\beta _p (v^-, v^+) = (b_{v^-} + b_{v^+}) (v(0), p)$
; this does not depend on choice of
$v \in \operatorname {\mathrm {E}}^{-1}(v^-,v^+)$
. The measure
$\mu $
on
$\partial X \times \partial X$
defined by
$$ \begin{align*}d\mu (\xi, \eta) = e^{-\delta_\Gamma \beta_p (\xi, \eta)}\,d\mu_p (\xi)\,d\mu_p (\eta)\end{align*} $$
is
$\Gamma $
-invariant and does not depend on choice of
$p \in X$
; it is called a geodesic current.
The Bowen–Margulis measure m, a Radon measure on
$GX$
that is invariant under both
$g^t$
and
$\Gamma $
, is constructed as follows [Reference Ricks12]. The measure
$\mu \times \lambda $
on
$\partial X \times \partial X \times \mathbb {R}$
(where
$\lambda $
is Lebesgue measure) is supported on
$\Lambda \times \Lambda \times \mathbb {R}$
. One shows the set
$\operatorname {\mathrm {E}}(\mathcal {Z}) \times \mathbb {R}$
has full measure, where
$\mathcal {Z} \subseteq GX$
is the set of zero-width geodesics in X. Recall from §2 the map
$\pi _p \colon GX \to \partial X \times \partial X \times \mathbb {R}$
given by
$\pi _p(v) = (v^-, v^+, b_{v^-} (v(0), p))$
. This map restricts to a homeomorphism from
$\mathcal {Z}$
to
$\operatorname {\mathrm {E}}(\mathcal {Z}) \times \mathbb {R}$
, hence
$m = \mu \times \lambda $
may be viewed as a Borel measure on
$GX$
.
Write
$G_{\Lambda } X = \operatorname {\mathrm {E}}^{-1}(\Lambda \times \Lambda ) \subseteq GX$
. Importantly, m has full support on
$G_{\Lambda } X$
—that is,
$m(U)> 0$
for every open neighborhood U of
$v \in G_{\Lambda } X$
in
$GX$
. In particular,
$m( \mathfrak {v}(v_0, \varepsilon , \delta ))> 0$
whenever
$v_0 \in G_{\Lambda } X$
. Moreover, we have the following proposition.
Proposition 5.2. [Reference Ricks12]
Let
$\Gamma $
be a group acting freely, non-elementarily, properly discontinuously, and by isometries on a proper, geodesically complete
$\operatorname {\mathrm {CAT}}(0)$
space X with rank-one axis. The zero-width geodesics of
$G_{\Lambda } X$
are dense in
$G_{\Lambda } X$
.
(However, the zero-width geodesics do not in general form an open set in
$GX$
, even in the cocompact case.)
The Bowen–Margulis measure m has a quotient measure
$m_\Gamma $
on
$\Gamma \backslash GX$
. Since we assume
$\Gamma $
acts freely on X (and therefore on
$GX$
),
$m_\Gamma $
can be described by saying that whenever
$A \subset GX$
is a Borel set on which
$\operatorname {\mathrm {pr}}$
is injective,
$m_\Gamma (\operatorname {\mathrm {pr}} A) = m(A)$
.
One can adapt the methods of Knieper’s proof [Reference Knieper6] that the Bowen–Margulis measure is the unique measure of maximal entropy to the locally
$\operatorname {\mathrm {CAT}}(0)$
case. One thus obtains the following theorem (see [Reference Ricks13] for details).
Theorem 5.3. [Reference Ricks13]
Let
$\Gamma $
be a group acting freely geometrically on a proper, geodesically complete
$\operatorname {\mathrm {CAT}}(0)$
space X with rank-one axis. The Bowen–Margulis measure
$m_\Gamma $
on
$\Gamma \backslash GX$
is the unique measure (up to rescaling) of maximal entropy for the geodesic flow, which has entropy
$h = \delta _\Gamma $
.
To simplify notation, we write
$h := \delta _\Gamma $
, even if
$\Gamma $
does not act cocompactly.
The
$\Gamma $
-action on X is said to have arithmetic length spectrum if the translation lengths of axes are all contained in some discrete subgroup
$c\mathbb {Z}$
of
$\mathbb {R}$
. In [Reference Ricks12], we showed that when
$\Lambda = \partial X$
, X is geodesically complete, and
$m_\Gamma $
is finite, the only examples of arithmetic length spectrum are when X is a tree with integer edge lengths, up to homothety. Moreover, when the
$\Gamma $
-action on X does not have arithmetic length spectrum, the measure
$m_\Gamma $
is mixing under the geodesic flow
$g_\Gamma ^t$
.
Standing hypothesis. We assume throughout that
$m_\Gamma $
is finite, and thus we may normalize the measure by assuming
$m_\Gamma (\Gamma \backslash GX) = 1$
. We also assume non-arithmetic length spectrum, so
$m_\Gamma $
is mixing.
5.2 Averaging
Fix a zero-width geodesic
$v_0 \in GX$
, and let
$p = v_0 (0)$
. Let
$\varepsilon \in (0, \varepsilon _0]$
and
$\delta \in (0, \delta _0]$
.
Our goal in this section is to prove Corollary 5.17, which describes the total measure of intersections
$ \mathfrak {v} \cap \Gamma g^t( \mathfrak {v})$
for large t. Let
$ \mathfrak {w} = \bigcup _{\gamma \in \Gamma } \mathfrak {w}^{\gamma }$
and
$\widetilde {\mathfrak {w}} = \bigcup _{\gamma \in \Gamma } \widetilde {\mathfrak {w}}^{\gamma }$
. It is easy to see by mixing that
$\lim _{t \to \infty } m( \mathfrak {w}) = m( \mathfrak {v})^2$
and
$\lim _{t \to \infty } m(\widetilde {\mathfrak {w}}) = m(\widetilde {\mathfrak {v}})^2$
. Less obvious, however, is that
$\lim _{t \to \infty } \mu (\operatorname {\mathrm {E}}( \mathfrak {w})) = ({2}/{\varepsilon }) m( \mathfrak {v})^2$
.
Definition 5.4. Define
$s \colon GX \to \mathbb {R}$
by
$s(v) = b_{v^-} (v(0), p)$
. And for each
$\gamma \in \Gamma $
, define
$\tau _{\gamma } \colon GX \to \mathbb {R}$
by
$\tau _{\gamma } (v) = b_{v^-} (\gamma p, p) - t$
.
Lemma 5.5.
$\tau _{\gamma } (v) = s(v) - s (\gamma ^{-1} g^t v)$
.
Proof We compute
$$ \begin{align*} s(v) - s(\gamma^{-1} g^t v) &= b_{v^-}(v(0), p) - b_{\gamma^{-1} v^-}(\gamma^{-1} v(t), p) \\ &= b_{v^-}(v(0), p) - [ b_{v^-}(v(0), \gamma p) + t ] \\ &= b_{v^-} (\gamma p, p) - t \\ &= \tau_{\gamma} (v).\\[-38pt] \end{align*} $$
Define
$\phi \colon \widetilde {\mathfrak {w}} \to \Gamma $
by putting
$\phi (v)$
equal to the unique
$\gamma \in \Gamma $
such that
$v \in \widetilde {\mathfrak {w}}^{\gamma }$
. Notice that for
$v \in \mathfrak {w}$
,
$\phi (v)$
is the unique
$\gamma \in \Gamma $
such that
$v \in \mathfrak {w}^{\gamma }$
.
Define
$\tau \colon \widetilde {\mathfrak {w}} \to \mathbb {R}$
by
$\tau (v) = \tau _{\phi (v)} (v)$
. Also define
$\ell \colon \widetilde {\mathfrak {w}} \to \mathbb {R}$
by
$\ell (v) = \varepsilon - | \tau (v) |$
, and let
$\widetilde {\ell }(v) = 2\varepsilon + \ell (v)$
.
Lemma 5.6. Let
$v \in \widetilde {\mathfrak {w}}$
. Then
$\widetilde {\ell }(v)$
is the length of the geodesic segment
$g^{\mathbb {R}}(v) \cap \widetilde {\mathfrak {w}}$
. Similarly, if
$v \in \mathfrak {w}$
then
$\ell (v)$
is the length of the geodesic segment
$g^{\mathbb {R}}(v) \cap \mathfrak {w}$
. Moreover,
$| \tau (v) | \le \varepsilon $
if and only if
$\operatorname {\mathrm {E}}(v) \in \operatorname {\mathrm {E}}( \mathfrak {w})$
. In other words,
$\widetilde {\ell }(v) \ge 2\varepsilon $
if and only if
$\operatorname {\mathrm {E}}(v) \in \operatorname {\mathrm {E}}( \mathfrak {w})$
.
Corollary 5.7. For all
$f \in L^1(\mu )$
,
$$ \begin{align*}\int_{\operatorname{\mathrm{E}}( \mathfrak{w})} f \; d\mu = \int_{ \mathfrak{w}} \frac{f \circ \operatorname{\mathrm{E}}}{\ell} \; dm = \int_{\operatorname{\mathrm{E}}(\widetilde{\mathfrak{w}}) \cap \left\{\widetilde{\ell} \ge 2\varepsilon\right\}} f \; d\mu = \int_{\widetilde{\mathfrak{w}} \cap \left\{\widetilde{\ell} \ge 2\varepsilon\right\}} \frac{f \circ \operatorname{\mathrm{E}}}{\widetilde{\ell}} \; dm.\end{align*} $$
By Lemma 4.4 (5), the map
$\phi \colon \widetilde {\mathfrak {w}} \to \Gamma $
factors as
$\phi = \hat \phi \circ \operatorname {\mathrm {E}}$
for some
$\hat \phi \colon \operatorname {\mathrm {E}}(\widetilde {\mathfrak {w}}) \to \Gamma $
. Similarly,
$\tau \colon \widetilde {\mathfrak {w}} \to \mathbb {R}$
factors as
$\tau = \hat \tau \circ \operatorname {\mathrm {E}}$
for some
$\hat \tau \colon \operatorname {\mathrm {E}}(\widetilde {\mathfrak {w}}) \to \mathbb {R}$
, and
$\ell = \hat \ell \circ \operatorname {\mathrm {E}}$
.
Corollary 5.8. If
$f \in L^1(\mathbb {R})$
vanishes outside
$[-\varepsilon , \varepsilon ]$
, then
$$ \begin{align*}\int_{\operatorname{\mathrm{E}}( \mathfrak{w})} f \circ \hat \tau \; d\mu = \int_{ \mathfrak{w}} \frac{f \circ \tau}{\ell} \; dm = \int_{\operatorname{\mathrm{E}}(\widetilde{\mathfrak{w}})} f \circ \hat \tau \; d\mu = \int_{\widetilde{\mathfrak{w}}} \frac{f \circ \tau}{\widetilde{\ell}} \; dm.\end{align*} $$
Define
$\sigma \colon \widetilde {\mathfrak {w}} \to \mathbb {R}$
by
$\sigma (v) = s (\phi (v)^{-1} g^t v)$
.
Lemma 5.9.
$\sigma $
is continuous.
Proof The restriction of
$\sigma $
to each
$\widetilde {\mathfrak {w}}^{\gamma }$
is
$s \circ \gamma ^{-1} \circ g^t$
, and
$\widetilde {\mathfrak {w}}$
is the disjoint union of finitely many (closed)
$\widetilde {\mathfrak {w}}^{\gamma }$
.
Fact 5.10.
$\tau = s - \sigma $
.
Fact 5.11. Both
$s(v), \sigma (v) \in [0, \varepsilon ]$
for all
$v \in \mathfrak {w}$
, and
$s(v), \sigma (v) \in [-\varepsilon , 2\varepsilon ]$
for
$v \in \widetilde {\mathfrak {w}}$
.
Recall the
$\Gamma $
-action on
$GX$
commutes with the geodesic flow
$g^t$
on
$GX$
, so we have a quotient flow
$g^t_\Gamma $
on
$\Gamma \backslash GX$
defined by
$g^t_\Gamma (\operatorname {\mathrm {pr}} v) = \operatorname {\mathrm {pr}}(g^t v)$
for all
$v,t$
.
Lemma 5.12. Let
$\psi \colon \Gamma \backslash GX \to \mathbb {R}$
be measurable, and let
$\psi _t = \psi \circ g^t_\Gamma $
. Then
$$ \begin{align*}\lim_{t \to \infty} ( \psi \times \psi_t )_* m_\Gamma (C \times D) = ( \psi_* m_\Gamma \times \psi_* m_\Gamma )(C \times D)\end{align*} $$
for every measurable
$C \times D \subseteq \mathbb {R}^2$
, where
$(\psi \times \psi _t)(\bar {v}) := (\psi (\bar {v}), \psi _t(\bar {v})) \in \mathbb {R}^2$
.
Proof By mixing,
${\lim \nolimits _{t \to \infty } m_\Gamma ( \psi ^{-1}(C) \cap \psi _t^{-1}(D) ) = m_\Gamma (\psi ^{-1} (C)) \cdot m_\Gamma (\psi ^{-1} (D))}.\\[-13pt] $
.
Lemma 5.13. If
$f \colon [0, \varepsilon ] \times [0, \varepsilon ] \to \mathbb {R}$
is Riemann integrable, then
$$ \begin{align*}\lim_{t \to \infty} \int_{ \mathfrak{w}} f( s(v), \sigma(v) ) \; dm(v) = \frac{m( \mathfrak{v})^2}{\varepsilon^2} \int_{0}^{\varepsilon} \int_{0}^{\varepsilon} f(x,y) \; dx \, dy.\end{align*} $$
Similarly, if
$f \colon [-\varepsilon , 2\varepsilon ] \times [-\varepsilon , 2\varepsilon ] \to \mathbb {R}$
is Riemann integrable, then
$$ \begin{align*}\lim_{t \to \infty} \int_{\widetilde{\mathfrak{w}}} f( s(v), \sigma(v) ) \; dm(v) = \frac{m( \mathfrak{v})^2}{\varepsilon^2} \int_{-\varepsilon}^{2\varepsilon} \int_{-\varepsilon}^{2\varepsilon} f(x,y) \; dx \, dy.\end{align*} $$
Thus
$(s \times \sigma )_* (m \vert _{ \mathfrak {w}})$
converges weakly to
${m( \mathfrak {v})^2}/{\varepsilon ^2}$
times Lebesgue measure on
$[0,\varepsilon ]^2$
, where
$m \vert _{ \mathfrak {w}}$
is the restriction of m to
$ \mathfrak {w}$
.
Proof Since
$s_* (m \vert _{ \mathfrak {v}})$
is
${m( \mathfrak {v})}/{\varepsilon }$
times Lebesgue measure on
$[0,\varepsilon ]$
, by Lemma 5.12 the conclusion of Lemma 5.13 holds whenever f is the characteristic function of a measurable product set
$C \times D \subseteq [0, \varepsilon ]^2$
. (Specifically, one can apply Lemma 5.12 to the well-defined measurable function
$\psi \colon \Gamma \backslash GX \to \mathbb {R}$
given by
$\psi (\operatorname {\mathrm {pr}} v) = s(v)$
for
$v \in \mathfrak {v}$
and
$\psi (\bar {v}) = -1$
if
$\bar {v} \notin \operatorname {\mathrm {pr}}( \mathfrak {v})$
. Then
$s_* (m \vert _{ \mathfrak {v}}) = (\psi _* m_\Gamma ) \vert _{[0,\varepsilon ]}$
, while
$(\psi \times \psi _t)(\bar {v}) \in [0,\varepsilon ]^2$
if and only if
$\bar {v} \in \operatorname {\mathrm {pr}}( \mathfrak {w})$
, hence
$(\psi \times \psi _t)_* (m_\Gamma \vert _{ \mathfrak {v}}) = ((\psi \times \psi _t)_* m_\Gamma ) \vert _{[0,\varepsilon ]^2}$
.) The conclusion of Lemma 5.13 then easily extends to all finite linear combinations of characteristic functions of measurable product sets.
Now if f is Riemann integrable, there exist step functions
$\varphi _n \le f \le \psi _n$
satisfying
$\lim _n \int _{0}^{\varepsilon } \! \int _{0}^{\varepsilon } \varphi _n = \int _{0}^{\varepsilon } \! \int _{0}^{\varepsilon } f = \lim _n \int _{0}^{\varepsilon } \! \int _{0}^{\varepsilon } \psi _n$
. Then
$$ \begin{align*} \int \varphi_n \; d(s \times \sigma)_* m \, \le \int f \; d(s \times \sigma)_* m \, \le \int \psi_n \; d(s \times \sigma)_* m, \end{align*} $$
and so letting
$t \to \infty $
, we obtain
$$ \begin{align*} \frac{m( \mathfrak{v})^2}{\varepsilon^2} \int_{0}^{\varepsilon} \! \int_{0}^{\varepsilon} \varphi_n \le \liminf_{t \to \infty} \int f \; d(s \times \sigma)_* m \end{align*} $$
and
$$ \begin{align*} \limsup_{t \to \infty} \int f \; d(s \times \sigma)_* m \le \frac{m( \mathfrak{v})^2}{\varepsilon^2} \int_{0}^{\varepsilon} \! \int_{0}^{\varepsilon} \psi_n. \end{align*} $$
Letting
$n \to \infty $
, we find
$$ \begin{align*} \lim_{t \to \infty} \int f \; d(s \times \sigma)_* m = \frac{m( \mathfrak{v})^2}{\varepsilon^2} \int_{0}^{\varepsilon} \! \int_{0}^{\varepsilon} f. \end{align*} $$
This proves the first part of the lemma.
In the same manner one obtains
$$ \begin{align*}\lim_{t \to \infty} \int_{\widetilde{\mathfrak{w}}} f( s(v), \sigma(v) ) \; dm(v) = \frac{m(\widetilde{\mathfrak{v}})^2}{9\varepsilon^2} \int_{-\varepsilon}^{2\varepsilon} \int_{-\varepsilon}^{2\varepsilon} f(x,y) \; dx \, dy,\end{align*} $$
and the second part of the lemma follows by observing that
$m(\widetilde {\mathfrak {v}}) = 3 m( \mathfrak {v})$
.
Lemma 5.14. If
$f \colon [-3\varepsilon , 3\varepsilon ] \to \mathbb {R}$
is Riemann integrable and supported on
$[-\varepsilon ,\varepsilon ]$
, then the function
$F \colon [-\varepsilon , 2\varepsilon ] \times [-\varepsilon , 2\varepsilon ] \to \mathbb {R}$
given by
$F (x,y) = ({1}/({3\varepsilon - | x - y |})) f(x - y)$
is Riemann integrable, and
$$ \begin{align*}\int_{-\varepsilon}^{2\varepsilon} \! \int_{-\varepsilon}^{2\varepsilon} F(x,y) \; dx \, dy = \int_{-\varepsilon}^{\varepsilon} f(z) \; dz.\end{align*} $$
Proof By change of variables (putting
$z = x - y$
and
$w = x + y - \varepsilon $
),
$$ \begin{align*}\int_{-\varepsilon}^{2\varepsilon} \! \int_{-\varepsilon}^{2\varepsilon} F(x,y) \; dx \, dy = \int_{-3\varepsilon}^{3\varepsilon} \frac{1}{2} \int_{-3\varepsilon + | z |}^{3\varepsilon - | z |} \frac{f(z)}{3\varepsilon - | z |} \; dw \, dz = \int_{-3\varepsilon}^{3\varepsilon} f(z) \; dz. \\[-43pt] \end{align*} $$
Remark 5.15. In the notation of Lemma 5.14,
$({f \circ \tau })/{\ell } = F \circ (s \times \sigma )$
.
Proposition 5.16. Let X be a proper
$\operatorname {\mathrm {CAT}}(0)$
space. Assume
$\Gamma $
acts freely, properly discontinuously, and by isometries on X, and that
$m_\Gamma $
is finite and mixing, and normalized so that
$\| m_\Gamma \| = 1$
. If
$f \colon [-\varepsilon , \varepsilon ] \to \mathbb {R}$
is Riemann integrable then
$$ \begin{align*}\lim_{t \to \infty} \int_{\operatorname{\mathrm{E}}( \mathfrak{w})} f \circ \hat \tau \; d\mu = \lim_{t \to \infty} \int_{ \mathfrak{w}} \frac{f \circ \tau}{\ell} \; dm = \frac{m( \mathfrak{v})^2}{\varepsilon^2} \int_{-\varepsilon}^{\varepsilon} f.\end{align*} $$
Proof Corollary 5.8 gives us the first equality. It also gives us
$\lim _{t \to \infty } \int _{ \mathfrak {w}} (({f \circ \tau })/{\ell }) \; dm\\ = \lim _{t \to \infty } \int _{\widetilde {\mathfrak {w}}} (({f \circ \tau })/{\widetilde {\ell }})\,dm$
. From Lemma 5.14 and Lemma 5.13 we obtain
$\lim \nolimits _{t \to \infty } \int _{\widetilde {\mathfrak {w}}}\\ (({f \circ \tau })/{\widetilde {\ell }})\,dm = ({m( \mathfrak {v})^2}/{\varepsilon ^2}) \int _{-\varepsilon }^{\varepsilon } f$
because
$ ({f \circ \tau })/{\ell } = F \circ (s \times \sigma )$
.
Corollary 5.17.
$\lim _{t \to \infty } \mu (\operatorname {\mathrm {E}}( \mathfrak {w})) = ({2}/{\varepsilon }) m( \mathfrak {v})^2= \lim _{t \to \infty } ({2}/{\varepsilon }) m( \mathfrak {w})$
.
Proof Putting
$f = 1$
in Proposition 5.16, we obtain
$\lim _{t \to \infty } \mu (\operatorname {\mathrm {E}}( \mathfrak {w})) = ({m( \mathfrak {v})^2}/{\varepsilon ^2}) \int _{-\varepsilon}^{\varepsilon}\\ 1 = ({2}/{\varepsilon }) m( \mathfrak {v})^2$
. Putting
$f = 1$
in Lemma 5.13, we find
$\lim _{t \to \infty } ({2}/{\varepsilon }) m( \mathfrak {w}) = ({2}/{\varepsilon }) m( \mathfrak {v})^2$
.
Remark 5.18. In terms of averages, we find
$ \lim _{t \to \infty } ({1}/{\mu (\operatorname {\mathrm {E}}( \mathfrak {w}))}) \int _{\operatorname {\mathrm {E}}( \mathfrak {w})} f \circ \hat \tau \; d\mu = ({1}/{2 \varepsilon }) \int _{-\varepsilon }^{\varepsilon } f $
. In particular,
$$ \begin{align*}\lim_{t \to \infty} \frac{1}{\mu(\operatorname{\mathrm{E}}( \mathfrak{w}))} \int_{\operatorname{\mathrm{E}}( \mathfrak{w})} \hat \ell \; d\mu = \frac{\varepsilon}{2} \quad \text{and} \quad \lim_{t \to \infty} \frac{1}{m( \mathfrak{w})} \int_{ \mathfrak{w}} \ell \; dm = \frac{2\varepsilon}{3}.\end{align*} $$
Thus the average length of intersection in
$ \mathfrak {w}$
is
${\varepsilon }/{2}$
if one averages by cross-sectional area, but
${2\varepsilon }/{3}$
if one averages by volume.
6 Product estimates
We recall our standing hypotheses, from §5.2 through the rest of the paper. The group
$\Gamma $
acts freely, non-elementarily, properly discontinuously, and by isometries on the proper, geodesically complete
$\operatorname {\mathrm {CAT}}(0)$
space X with rank-one axis. We also assume
$m_\Gamma $
is finite and mixing, and normalized so that
$\| m_\Gamma \| = 1$
.
For this section, fix
$v_0 \in GX$
and
$\varepsilon , \delta> 0$
, and let
$t \in \mathbb {R}$
.
6.1 Unclipped intersections
Definition 6.1. Let
$I = I(v_0, \varepsilon , \delta , t)$
be the set of non-trivial
$\gamma \in \Gamma $
such that
$ \mathfrak {w}^\gamma = \mathfrak {v} \cap g^{-t} \gamma \mathfrak {v}$
is not empty. Call
$\gamma \in I$
unclipped if
$\gamma \mathfrak {v}^+ \subseteq \mathfrak {v}^+$
and
$ \mathfrak {v}^- \subseteq \gamma \mathfrak {v}^-$
. Let
$ I^{\mathrm{unclipped}}$
be the set of unclipped
$\gamma \in I$
.
We would like to say that
$\gamma $
is unclipped if and only if
$\operatorname {\mathrm {E}}( \mathfrak {w}^\gamma ) = \mathfrak {v}^- \times \gamma \mathfrak {v}^+$
, but care requires us to pad the set
$ \mathfrak {v}$
slightly as follows. Define
$ \widehat {\mathfrak {v}}_{\varepsilon ,\delta } = \mathfrak {v}_{\widehat {\varepsilon }, \delta , t}$
, where
$\widehat {\varepsilon } = \varepsilon + 3\operatorname {\mathrm {diam}} \pi ( \mathfrak {v}_{0,\delta })$
. Write
$\widehat {\mathfrak {w}}^\gamma = \widehat {\mathfrak {v}} \cap g^{-t} \gamma \widehat {\mathfrak {v}}$
and
$\widehat {\mathfrak {w}} = \bigcup _{\gamma \in I} \widehat {\mathfrak {w}}^\gamma $
.
Lemma 6.2. Assume
$\operatorname {\mathrm {E}}(\widehat {\mathfrak {w}}^\gamma ) = \mathfrak {v}^- \times \gamma \mathfrak {v}^+$
. Then
$\gamma \mathfrak {v}^+ \subseteq \mathfrak {v}^+$
and
$ \mathfrak {v}^- \subseteq \gamma \mathfrak {v}^-$
.
Proof Notice that
$\operatorname {\mathrm {E}}(\widehat {\mathfrak {w}}^\gamma ) = \operatorname {\mathrm {E}}(\widehat {\mathfrak {v}} \cap g^{-t} \gamma \widehat {\mathfrak {v}}) \subseteq \operatorname {\mathrm {E}}(\widehat {\mathfrak {v}}) \cap \operatorname {\mathrm {E}}(g^{-t} \gamma \widehat {\mathfrak {v}}) = \operatorname {\mathrm {E}}( \mathfrak {v}) \cap \gamma \operatorname {\mathrm {E}}( \mathfrak {v}) = ( \mathfrak {v}^- \times \mathfrak {v}^+) \cap \gamma ( \mathfrak {v}^- \times \mathfrak {v}^+) = ( \mathfrak {v}^- \cap \gamma \mathfrak {v}^-) \times ( \mathfrak {v}^+ \cap \gamma \mathfrak {v}^+) $
. So by hypothesis,
$ \mathfrak {v}^- \times \gamma \mathfrak {v}^+ \subseteq ( \mathfrak {v}^- \cap \gamma \mathfrak {v}^-) \times ( \mathfrak {v}^+ \cap \gamma \mathfrak {v}^+)$
, that is,
$ \mathfrak {v}^- \subseteq \mathfrak {v}^- \cap \gamma \mathfrak {v}^-$
and
$\gamma \mathfrak {v}^+ \subseteq \mathfrak {v}^+ \cap \gamma \mathfrak {v}^+$
. But this implies
$ \mathfrak {v}^- \subseteq \gamma \mathfrak {v}^-$
and
$\gamma \mathfrak {v}^+ \subseteq \mathfrak {v}^+$
.
To prove the converse, we first bound
$\tau $
on
$ \mathfrak {v}$
.
Lemma 6.3. Let
$t \in \mathbb {R}$
and
$\gamma \in I_{0, \delta , t}$
(that is,
$\gamma $
is non-trivial and
$ \mathfrak {w}_{0, \delta , t}^{\gamma } = \mathfrak {v}_{0,\delta } \cap g^{-t} \gamma \mathfrak {v}_{0,\delta }$
is not empty). Then
$| b_{v^-}(\gamma p, p) - t | \le 3 \operatorname {\mathrm {diam}} \pi ( \mathfrak {v}_{0,\delta })$
for all
$v \in \mathfrak {v}_{\varepsilon ,\delta }$
.
Proof Let
$w \in \mathfrak {w}_{0, \delta , t}^{\gamma } = \mathfrak {v}_{0,\delta } \cap g^{-t} \gamma \mathfrak {v}_{0,\delta }$
and
$v \in \mathfrak {v}_{\varepsilon ,\delta }$
. Since
$\tau _\gamma (v)$
depends only on
$v^-$
, we may assume
$v^+ = w^+$
and
$v \in \mathfrak {v}_{0,\delta }$
. Then combine the bounds
$$ \begin{align*}| b_{v^-}(\gamma p, p) - b_{v^-}(\gamma \gamma^{-1} g^t w(0), v(0)) | \le 2 \operatorname{\mathrm{diam}} \pi( \mathfrak{v}_{0,\delta})\end{align*} $$
and
$$ \begin{align*} | b_{v^-}(w(t), v(0)) - t | &= | b_{v^-}(w(t), v(t)) | \\ &\le d(w(t), v(t)) \le d(w(0), v(0)) \le \operatorname{\mathrm{diam}} \pi( \mathfrak{v}_{0,\delta}) \end{align*} $$
to obtain the desired bound.
Our next bound on
$\tau $
is an easy consequence of Lemma 6.3.
Lemma 6.4. Let
$\gamma \in I_{\varepsilon ,\delta ,t}$
. Then
$| \tau _\gamma | \le \varepsilon + 3 \operatorname {\mathrm {diam}} \pi ( \mathfrak {v}_{0,\delta })$
on
$ \mathfrak {v}_{\varepsilon ,\delta }$
.
Proof By hypothesis, we may find
$v \in \mathfrak {v}_{\varepsilon ,\delta } \cap g^{-t} \gamma \mathfrak {v}_{\varepsilon ,\delta }$
. Then let
$w \in \mathfrak {v}_{\varepsilon ,\delta }$
. Since
$\tau _\gamma $
depends only on the backward endpoint, it suffices to prove the lemma when
$w^+ = v^+$
and
$s(w) = 0$
. So assume
$w^+ = v^+$
and
$s(w) = 0$
.
By choice of v, we know
$s(v), s(\gamma ^{-1} g^t v) \in [0, \varepsilon ]$
. Now
$s(\gamma ^{-1} g^t v) = s(v) - \tau _\gamma (v)$
, so
$g^{-s(v)} v \in \mathfrak {v}_{0,\delta }$
satisfies
$\gamma ^{-1} g^{t + \tau _\gamma (v)} g^{-s(v)} v = g^{- s(\gamma ^{-1} g^t v)} \gamma ^{-1} g^{t} v \in \mathfrak {v}_{0,\delta }$
. Thus by Lemma 6.3,
$$ \begin{align*}| \tau_\gamma(w) - \tau_\gamma(v) | = | b_{w^-}(\gamma p, p) - t - \tau_\gamma(v) | \le 3\operatorname{\mathrm{diam}} \pi( \mathfrak{v}_{0,\delta}).\end{align*} $$
Since
$\tau _\gamma (v) \in [-\varepsilon , \varepsilon ]$
, we see that
$| \tau _\gamma (w) | \le \varepsilon + 3 \operatorname {\mathrm {diam}} \pi ( \mathfrak {v}_{0,\delta })$
.
We can now state the relationship we wanted.
Lemma 6.5. Let
$\gamma \in I$
. Then
$\gamma $
is unclipped if and only if
$\operatorname {\mathrm {E}}(\widehat {\mathfrak {w}}^\gamma ) = \mathfrak {v}^- \times \gamma \mathfrak {v}^+$
.
Proof Lemma 6.2 proves the ‘backwards’ direction, so assume
$\gamma \mathfrak {v}^+ \subseteq \mathfrak {v}^+$
and
$ \mathfrak {v}^- \subseteq \gamma \mathfrak {v}^-$
. First observe that
$\operatorname {\mathrm {E}}(\widehat {\mathfrak {w}}^\gamma ) \subseteq \operatorname {\mathrm {E}}( \mathfrak {v}) \cap \gamma \operatorname {\mathrm {E}}( \mathfrak {v}) = ( \mathfrak {v}^- \cap \gamma \mathfrak {v}^-) \times ( \mathfrak {v}^+ \cap \gamma \mathfrak {v}^+) = \mathfrak {v}^- \times \gamma \mathfrak {v}^+$
by hypothesis on
$ \mathfrak {v}^-$
and
$ \mathfrak {v}^+$
. On the other hand, Lemma 6.4 implies
$(\xi , \eta ) \in \operatorname {\mathrm {E}}(\widehat {\mathfrak {w}}^\gamma )$
for all
$(\xi , \eta ) \in \operatorname {\mathrm {E}}( \mathfrak {v}) \cap \gamma \operatorname {\mathrm {E}}( \mathfrak {v})$
. This completes the proof.
We remark that if
$\gamma \in I$
is unclipped, then
$\operatorname {\mathrm {E}}( \mathfrak {w}^\gamma )$
is always non-empty (because
$\gamma \in I$
) and splits as a product
$\operatorname {\mathrm {E}}( \mathfrak {w}^\gamma ) = A \times \gamma \mathfrak {v}^+$
for some
$A \subseteq \mathfrak {v}^-$
(because whether
$v \in \mathfrak {v}$
lies in
$ \mathfrak {w}^\gamma $
depends only on
$\tau _\gamma (v)$
, which depends only on
$v^-$
).
6.2 Unclipped estimates
Here is a general statement about products of sets in the boundary.
Lemma 6.6. Let
$U,V \subseteq \partial X$
be Borel sets with
$\mu (U \times V)> 0$
, and let
$\gamma \in \Gamma $
. Assume
$\gamma V \subseteq V$
and
$| \beta _p | \le C$
on
$U \times V$
. Then
$$ \begin{align*} e^{-2hC} \le \frac {\int_{U \times \gamma V} f(\xi,\eta) \; d\mu(\xi,\eta)} {\int_{U \times V} f(\xi,\gamma \eta') \, e^{-h b_{\gamma \eta'} (p, \gamma p)} \; d\mu(\xi,\eta')} \le e^{2hC} \end{align*} $$
for any Borel function
$f \colon U \times \gamma V \to (0,\infty )$
.
Proof By the properties of conformal densities and the definition of
$\mu $
,
$$ \begin{align*} \int_{U \times \gamma V} f(\xi,\eta) \, d\mu(\xi,\eta) &= \int_{U \times \gamma V} f(\xi,\eta) \, e^{-h \beta_p(\xi,\eta)} \, d\mu_p(\xi) \, d\mu_p(\eta) \\ &= \int_{U \times V} f(\xi,\gamma \eta') \, e^{-h \beta_p(\xi,\gamma \eta')} \, d\mu_p(\xi) \, d\mu_{\gamma^{-1}p}(\eta') \\ &= \int_{U \times V} f(\xi,\gamma \eta') \, e^{-h \beta_p(\xi,\gamma \eta')} \, d\mu_p(\xi) \, e^{-h b_{\eta'} (\gamma^{-1} p, p)} \, d\mu_{p}(\eta') \\ &= \int_{U \times V} f(\xi,\gamma \eta') \, e^{-h b_{\gamma \eta'} (p, \gamma p)} e^{-h \beta_p(\xi,\gamma \eta')} \, d\mu_p(\xi) \, d\mu_{p}(\eta') \\ &= \int_{U \times V} f(\xi,\gamma \eta') \, e^{-h b_{\gamma \eta'} (p, \gamma p)} e^{-h [\beta_p(\xi,\gamma \eta') - \beta_p(\xi,\eta')]} \, d\mu(\xi,\eta'). \end{align*} $$
The conclusion of the lemma follows immediately.
We will use Lemma 6.6 with
$U \times V = \mathfrak {v}_\delta ^- \times \mathfrak {v}_\delta ^+$
. By Lemma 5.3 of [Reference Ricks12],
$\beta _p$
is continuous on
$\operatorname {\mathrm {E}}(\mathcal R)$
. Thus
$\lim \nolimits _{\delta \to 0} \max \nolimits _{v \in \mathfrak {v}_{\delta }} | \beta _p(v) | = 0$
. However, for simplicity we will just use the bound
$\max \nolimits _{v \in \mathfrak {v}_{\delta }} | \beta _p(v) | \le 2 \operatorname {\mathrm {diam}} \pi ( \mathfrak {v}_{0,\delta }) \le 2 \operatorname {\mathrm {diam}} ( \mathfrak {v}_{\varepsilon ,\delta })$
.
Lemma 6.7. Let
$\gamma \in \Gamma $
be unclipped. Then
$$ \begin{align*} e^{-6h \operatorname{\mathrm{diam}}( \mathfrak{v})} \le \frac {e^{ht} \int_{\operatorname{\mathrm{E}}(\widehat{\mathfrak{w}}^\gamma)} f(\xi,\eta) \; d\mu(\xi,\eta)} {\int_{\operatorname{\mathrm{E}}( \mathfrak{v})} f(\xi,\gamma \eta') \, d\mu(\xi,\eta')} \le e^{6h \operatorname{\mathrm{diam}}( \mathfrak{v})} \end{align*} $$
for any Borel function
$f \colon \operatorname {\mathrm {E}}( \mathfrak {v}) \to (0,\infty )$
.
Proof By Lemma 6.6,
$$ \begin{align*} e^{-4h \operatorname{\mathrm{diam}}( \mathfrak{v})} \le \frac {e^{ht} \int_{ \mathfrak{v}^- \times \gamma \mathfrak{v}^+} f(\xi,\eta) \; d\mu(\xi,\eta)} {\int_{ \mathfrak{v}^- \times \mathfrak{v}^+} f(\xi,\gamma \eta') \, e^{h[t - b_{\gamma \eta'} (p, \gamma p)]} \, d\mu(\xi,\eta')} \le e^{4h \operatorname{\mathrm{diam}}( \mathfrak{v})}. \end{align*} $$
If
$\eta ' \in \mathfrak {v}^+$
then
$\gamma \eta ' = w^+$
for some
$w \in \mathfrak {w}^\gamma $
because
$\gamma $
is unclipped. So both w and
$\gamma ^{-1} g^t w$
are in
$ \mathfrak {v}$
. Hence
$$ \begin{align*} | b_{\gamma \eta'} (p, \gamma p) - t | &= | b_{w^+} (p, \gamma p) - t | \\ &\le | b_{w^+} (w(0), \gamma \cdot \gamma^{-1} g^t w(0)) - t | + 2 \operatorname{\mathrm{diam}}(\pi( \mathfrak{v})) \\ &= 2 \operatorname{\mathrm{diam}} \pi( \mathfrak{v}) \le 2 \operatorname{\mathrm{diam}}( \mathfrak{v}). \end{align*} $$
Therefore,
$$ \begin{align*} e^{-6h \operatorname{\mathrm{diam}}( \mathfrak{v})} \le \frac {e^{ht} \int_{ \mathfrak{v}^- \times \gamma \mathfrak{v}^+} f(\xi,\eta) \; d\mu(\xi,\eta)} {\int_{ \mathfrak{v}^- \times \mathfrak{v}^+} f(\xi,\gamma \eta') \, d\mu(\xi,\eta')} \le e^{6h \operatorname{\mathrm{diam}}( \mathfrak{v})}.\\[-45pt] \end{align*} $$
Definition 6.8. To simplify future statements, we write
$ C_{\varepsilon ,\delta } = e^{6h \operatorname {\mathrm {diam}} ( \mathfrak {v}_{\varepsilon ,\delta })}$
.
Notice that for
$\varepsilon> 0$
fixed,
$ C_{\varepsilon ,\delta }$
is an upper semicontinuous increasing function of
$\delta $
. And for
$\delta> 0$
fixed,
$ C_{\varepsilon ,\delta }$
is a continuous increasing function of
$\varepsilon $
.
Corollary 6.9. Let
$\gamma \in I_{\varepsilon ,\delta ,t}^{\mathrm{unclipped}}$
. Then
$$ \begin{align*} \frac{1}{ C_{\varepsilon,\delta}} \le \frac{e^{ht}}{\mu(\operatorname{\mathrm{E}}( \mathfrak{v}))} \int_{\operatorname{\mathrm{E}}(\widehat{\mathfrak{w}}^\gamma)} d\mu \le C_{\varepsilon,\delta}. \end{align*} $$
7 Counting unclipped intersections
Fix a zero-width geodesic
$v_0 \in GX$
. Let
$N = N(v_0, \varepsilon , \delta , t) = \# {I(v_0, \varepsilon , \delta , t)}$
and
$ N^{\mathrm{unclipped}} = N^{\mathrm{unclipped}}(v_0, \varepsilon , \delta , t) = \# { I^{\mathrm{unclipped}}}(v_0, \varepsilon , \delta , t)$
.
Recall that
$ \mathfrak {w} = \bigcup _{\gamma \in \Gamma } \mathfrak {w}^{\gamma }$
. We also define
$ \mathfrak {w}^{\mathrm{unclipped}} = \bigcup _{\gamma \in I^{\mathrm{unclipped}}} \mathfrak {w}^{\gamma }$
. Similarly write
$\widehat {\mathfrak {w}} = \bigcup _{\gamma \in \Gamma } \widehat {\mathfrak {w}}^{\gamma }$
and
$ \widehat {\mathfrak {w}}^{\mathrm{unclipped}} = \bigcup _{\gamma \in I^{\mathrm{unclipped}}} \widehat {\mathfrak {w}}^{\gamma }$
.
Note that although
$\operatorname {\mathrm {E}}( \mathfrak {v}) = \operatorname {\mathrm {E}}(\widehat {\mathfrak {v}})$
, the inclusion
$\operatorname {\mathrm {E}}( \mathfrak {w}^{\gamma }) \subseteq \operatorname {\mathrm {E}}(\widehat {\mathfrak {w}}^{\gamma })$
may be strict.
Lemma 7.1. Assume
$\varepsilon \in (0, \varepsilon _0]$
and
$\delta \in (0, \delta _0]$
. Then
$$ \begin{align*} \frac{1}{ C_{\varepsilon,\delta}} \cdot \mu(\operatorname{\mathrm{E}}( \widehat{\mathfrak{w}}^{\mathrm{unclipped}})) \le e^{-ht} {\mu(\operatorname{\mathrm{E}}( \mathfrak{v}))} N^{\mathrm{unclipped}} \le C_{\varepsilon,\delta} \cdot \mu(\operatorname{\mathrm{E}}( \widehat{\mathfrak{w}}^{\mathrm{unclipped}})). \end{align*} $$
In particular, if
$\mu (\operatorname {\mathrm {E}}( \widehat {\mathfrak {w}}^{\mathrm{unclipped}}))> 0$
then we have
$$ \begin{align*} \frac{1}{ C_{\varepsilon,\delta}} \le e^{-ht} \frac{\mu(\operatorname{\mathrm{E}}( \mathfrak{v}))}{\mu(\operatorname{\mathrm{E}}( \widehat{\mathfrak{w}}^{\mathrm{unclipped}}))} N^{\mathrm{unclipped}} \le C_{\varepsilon,\delta}. \end{align*} $$
Proof Since
$m( \mathfrak {v}_{\varepsilon ,\delta })> 0$
, we have
$ N^{\mathrm{unclipped}} = 0$
if and only if
$\mu (\operatorname {\mathrm {E}}( \widehat {\mathfrak {w}}^{\mathrm{unclipped}})) = 0$
. Thus the lemma is trivial if
$\mu (\operatorname {\mathrm {E}}( \widehat {\mathfrak {w}}^{\mathrm{unclipped}})) = 0$
. So assume
$\mu (\operatorname {\mathrm {E}}( \widehat {\mathfrak {w}}^{\mathrm{unclipped}}))> 0$
. Start with the identity
$$ \begin{align*} N^{\mathrm{unclipped}} = \sum_{\gamma \in I^{\mathrm{unclipped}}} 1 = \sum_{\gamma \in I^{\mathrm{unclipped}}} \frac{1}{\mu(\operatorname{\mathrm{E}}(\widehat{\mathfrak{w}}^\gamma))} \int_{\operatorname{\mathrm{E}}(\widehat{\mathfrak{w}}^\gamma)}\, d\mu. \end{align*} $$
By Corollary 6.9,
$$ \begin{align*} \frac{1}{ C_{\varepsilon,\delta}} \le e^{-ht} \frac{\mu(\operatorname{\mathrm{E}}( \mathfrak{v}))}{\mu(\operatorname{\mathrm{E}}(\widehat{\mathfrak{w}}^\gamma))} \le C_{\varepsilon,\delta} \end{align*} $$
for
$\gamma $
unclipped, so
$$ \begin{align*} \frac{1}{ C_{\varepsilon,\delta}} \mu(\operatorname{\mathrm{E}}( \widehat{\mathfrak{w}}^{\mathrm{unclipped}})) &= \! \sum_{\gamma \in I^{\mathrm{unclipped}}} \frac{1}{ C_{\varepsilon,\delta}} \int_{\operatorname{\mathrm{E}}(\widehat{\mathfrak{w}}^\gamma)}\, d\mu \\ &\le e^{-ht} \mu(\operatorname{\mathrm{E}}( \mathfrak{v})) N^{\mathrm{unclipped}} \\ &\le \! \sum_{\gamma \in I^{\mathrm{unclipped}}} C_{\varepsilon,\delta} \int_{\operatorname{\mathrm{E}}(\widehat{\mathfrak{w}}^\gamma)}\, d\mu \\ &= C_{\varepsilon,\delta} \, \mu(\operatorname{\mathrm{E}}( \widehat{\mathfrak{w}}^{\mathrm{unclipped}})).\\[-37pt] \end{align*} $$
8 Jiggling near rank-one geodesics
Clearly the inclusions
$ I^{\mathrm{unclipped}}_{\delta , t} \subseteq I_{\delta , t}$
and
$ \mathfrak {w}^{\mathrm{unclipped}}_{\delta , t} \subseteq \mathfrak {w}_{\delta , t}$
always hold. We now prove inclusions when we allow
$\delta> 0$
to vary.
Lemma 8.1. Let
$v_0 \in \mathcal R$
and
$0 < r < \delta \le \delta _0$
. There exists
$t_0 \ge 0$
such that
$$ \begin{align*}I_{r, t} \subseteq I^{\mathrm{unclipped}}_{\delta, t} \subseteq I_{\delta, t}\end{align*} $$
for all
$t \ge t_0$
and
$\varepsilon \in (0, \varepsilon _0]$
.
Proof Let
$\alpha = \delta - r> 0$
. By Corollary 3.5, there exists
$t_1 \ge 0$
such that for all
$t \ge t_1$
and
$\gamma \in I_{r,t}$
(that is,
$ \mathfrak {v}_r \cap \gamma g^{-t} \mathfrak {v}_r \neq \varnothing $
),
$\gamma \mathfrak {v}_\delta ^+ \subseteq {B_{\rho }} ( \mathfrak {v}_r^+, \alpha ) = \mathfrak {v}_\delta ^+$
. Similarly, there exists
$t_2 \ge 0$
such that for all
$t \ge t_2$
and
$\gamma \in I_{r,t}$
(that is,
$ \mathfrak {v}_r \cap \gamma ^{-1} g^t \mathfrak {v}_r \neq \varnothing $
),
$\gamma ^{-1} \mathfrak {v}_\delta ^- \subseteq {B_{\rho }} ( \mathfrak {v}_r^-, \alpha ) = \mathfrak {v}_\delta ^-$
. So for all
$t \ge t_0 = \max \{t_1, t_2\}$
, if
$\gamma \in I_{r,t}$
then
$\gamma \in I^{\text {unclipped}}_{\delta ,t}$
.
Corollary 8.2. Let
$v_0 \in \mathcal R$
and
$0 < r < \delta \le \delta _0$
. There exists
$t_0 \ge 0$
such that
$$ \begin{align*} \mathfrak{w}_{r, t} \subseteq \mathfrak{w}^{\mathrm{unclipped}}_{\delta, t} \subseteq \mathfrak{w}_{\delta, t}\end{align*} $$
for all
$t \ge t_0$
and
$\varepsilon \in (0, \varepsilon _0]$
.
Since
$m( \mathfrak {v})> 0$
whenever
$v_0 \in G_{\Lambda } X$
, by Corollary 5.17 and Corollary 8.2 we see that
$m( \mathfrak {w}^{\mathrm{unclipped}}_{\delta , t})> 0$
for all
$v_0 \in G_{\Lambda } X \cap \mathcal R$
with small
$\delta , \varepsilon> 0$
and large
$t> 0$
.
In what follows, we shall often want to state things for both
$\liminf $
and
$\limsup $
. The following definition makes this more convenient. Write
$a \le {\widetilde {\lim }}_{t \to \infty } f(t) \le b$
if for every
$\varepsilon> 0$
there exists
$t_0 \in \mathbb {R}$
such that
$a - \varepsilon \le f(t) \le b + \varepsilon $
for all
$t \ge t_0$
. In other words,
$\liminf _{t \to \infty } f(t) \ge a$
and
$\limsup _{t \to \infty } f(t) \le b$
.
Lemma 8.3. Let
$v_0 \in G_{\Lambda } X$
be zero-width and
$\varepsilon \in (0, \varepsilon _0]$
. Let
$\delta \in (0, \delta _0]$
be a point of continuity of the non-decreasing function
$r \mapsto m( \mathfrak {v}_r)$
. Then
$$ \begin{align*} \frac{1}{ C_{\varepsilon,\delta}} \le {\widetilde{\lim_{t \to \infty}}} \frac{ N^{\mathrm{unclipped}}_{\delta,t}}{2 e^{ht} m( \mathfrak{v}_{\delta})} \le \frac{\widehat{\varepsilon}}{\varepsilon} C_{\varepsilon,\delta}. \end{align*} $$
Proof By Corollary 5.17,
$\lim _{t \to \infty } \mu (\operatorname {\mathrm {E}}( \mathfrak {w}_{r,t})) = ({2}/{\varepsilon }) m( \mathfrak {v}_r)^2$
for all
$r \in (0, \delta _0]$
. Hence
$\delta $
is a point of continuity of the function
$f(r) = \lim _{t \to \infty } \mu (\operatorname {\mathrm {E}}( \mathfrak {w}_{r,t}))$
. So by Corollary 8.2,
$$ \begin{align*} &\lim_{t \to \infty} \mu(\operatorname{\mathrm{E}}( \mathfrak{w}^{\mathrm{unclipped}}_{\delta,t})) = \lim_{t \to \infty} \mu(\operatorname{\mathrm{E}}( \mathfrak{w}_{\delta,t}))\\ &\quad= \frac{2}{\varepsilon} m( \mathfrak{v}_{\delta})^2 \le \lim_{t \to \infty} \mu(\operatorname{\mathrm{E}}( \widehat{\mathfrak{w}}^{\mathrm{unclipped}}_{\delta,t})) \le \lim_{t \to \infty} \mu(\operatorname{\mathrm{E}}(\widehat{\mathfrak{w}}_{\delta,t}))\\ &\quad= \frac{2}{\widehat{\varepsilon}} m(\widehat{\mathfrak{v}}_{\delta})^2 = \frac{2\widehat{\varepsilon}}{\varepsilon^2} m( \mathfrak{v}_{\delta})^2. \end{align*} $$
But now
$$ \begin{align*} \frac{1}{ C_{\varepsilon,\delta}} \le {\widetilde{\lim_{t \to \infty}}} \frac{ N^{\mathrm{unclipped}}_{\delta,t}}{2 e^{ht} m( \mathfrak{v}_{\delta})} \le \frac{\widehat{\varepsilon}}{\varepsilon} C_{\varepsilon,\delta} \end{align*} $$
by Lemma 7.1 because
$\mu (\operatorname {\mathrm {E}}( \mathfrak {v})) = {m( \mathfrak {v})}/{\varepsilon }$
.
Remark 8.4. The points of continuity of
$r \mapsto m( \mathfrak {v}_r) = \varepsilon \cdot \mu ( \mathfrak {v}_r^- \times \mathfrak {v}_r^+)$
do not depend on
$\varepsilon $
. Also, for such r we find that
$ \mathfrak {v}_r$
is a continuity set for m (that is, the topological frontier
$\partial \mathfrak {v}_r$
of
$ \mathfrak {v}_r$
has
$m(\partial \mathfrak {v}_r) = 0$
); this is easy to see because the projection
$GX \to \partial X \times \partial X \times \mathbb {R}$
is continuous, and therefore
$\partial \mathfrak {v}_r \subseteq \partial \operatorname {\mathrm {E}}( \mathfrak {v}_r) \times \{0,\varepsilon \}$
.
The remark above also applies to
$r \mapsto m(\widehat {\mathfrak {v}}_r) = \widehat {\varepsilon } \cdot \mu ( \mathfrak {v}_r^- \times \mathfrak {v}_r^+)$
, with
$\widehat {\varepsilon } = \varepsilon + 3\operatorname {\mathrm {diam}} \pi ( \mathfrak {v}_{0,\delta })$
. The points of continuity here are a subset of those above.
Lemma 8.5. Let
$v_0 \in G_{\Lambda } X$
be zero-width and
$\varepsilon \in (0, \varepsilon _0]$
. Let
$\delta \in (0, \delta _0)$
be a point of continuity of the non-decreasing function
$r \mapsto m( \mathfrak {v}_r)$
. Then
$$ \begin{align*} \frac{1}{ C_{\varepsilon,\delta}} \le {\widetilde{\lim_{t \to \infty}}} \frac{N_{\delta,t}}{2 e^{ht} m( \mathfrak{v}_{\delta})} \le \frac{\widehat{\varepsilon}}{\varepsilon} C_{\varepsilon,\delta}. \end{align*} $$
Proof Whenever
$\delta ' \in (\delta , \delta _0]$
, we find
$ N^{\mathrm{unclipped}}_{\delta ,t} \le N_{\delta ,t} \le N^{\mathrm{unclipped}}_{\delta '\!,t} \le N_{\delta '\!,t}$
for all t sufficiently large by Lemma 8.1, hence
$$ \begin{align*}\phi(r) = \limsup_{t \to \infty} e^{-ht} N^{\mathrm{unclipped}}_{r,t} \quad \text{and} \quad \psi(r) = \limsup_{t \to \infty} e^{-ht} N_{r,t}\end{align*} $$
satisfy
$\phi (\delta ) \le \psi (\delta ) \le \phi (\delta ') \le \psi (\delta ')$
. Taking a decreasing sequence
$\delta ^{\prime }_n \to \delta $
such that each
$\delta ^{\prime }_n> \delta $
is a point of continuity of
$r \mapsto m( \mathfrak {v}_r)$
, we find by Lemma 8.3 that
$$ \begin{align*}\frac{2 m( \mathfrak{v}_{\delta})}{ C_{\varepsilon,\delta}} \le \liminf_{t \to \infty} e^{-ht} N^{\mathrm{unclipped}}_{\delta,t} \le \liminf_{t \to \infty} e^{-ht} N_{\delta,t}\end{align*} $$
and
$$ \begin{align*}\psi(\delta) \le \liminf_{n \to \infty} \phi(\delta^{\prime}_n) \le \liminf_{n \to \infty} 2 m(\widehat{\mathfrak{v}}_{\delta^{\prime}_n}) C_{\varepsilon,\delta^{\prime}_n} = 2 m(\widehat{\mathfrak{v}}_{\delta}) C_{\varepsilon,\delta}. \\[-40pt] \end{align*} $$
9 Counting periodic intersections
Definition 9.1. Let
$v_0 \in \mathcal R$
and
$\varepsilon , \delta> 0$
. Define
$$ \begin{align*} I_{\varepsilon,\delta,t}^{\mathrm{periodic}} = \{\gamma \in I_{\varepsilon,\delta,t} : \gamma \text{ has an axis in } \mathfrak{v}_{\varepsilon,\delta}\}\end{align*} $$
and
$ N_{\varepsilon ,\delta ,t}^{\mathrm{periodic}} = \# { I_{\varepsilon ,\delta ,t}^{\mathrm{periodic}}}$
.
Clearly the inclusion
$ I_{\varepsilon ,\delta ,t}^{\mathrm{periodic}} \subseteq I_{\varepsilon ,\delta ,t}$
always holds.
Lemma 9.2. Let
$v_0 \in GX$
be zero-width, and let
$\varepsilon \in (0, \varepsilon _0]$
and
$\delta \in (0, \delta _0]$
. Then
$ I_{\varepsilon ,\delta ,t}^{\mathrm{unclipped}} \subseteq I_{\varepsilon ,\delta ,t}^{\mathrm{periodic}}$
for all
$t> 0$
.
Proof Let
$t> 0$
and
$\gamma \in I_{\varepsilon ,\delta ,t}^{\mathrm{unclipped}}$
. Since
$\gamma \mathfrak {v}^+ \subseteq \mathfrak {v}^+$
, the nested intersection
$\bigcap _{n \in \mathbb {N}} \gamma ^n \mathfrak {v}^+$
of compact sets must contain a point
$\xi \in \partial X$
. Similarly, the nested intersection
$\bigcap _{n \in \mathbb {N}} \gamma ^{-n} \mathfrak {v}^-$
must contain a point
$\eta \in \partial X$
. Since
$\operatorname {\mathrm {E}}( \mathfrak {v}) = \mathfrak {v}^- \times \mathfrak {v}^+$
, there is some geodesic
$v \in \mathfrak {v}$
with endpoints
$\operatorname {\mathrm {E}}(v) = (\eta , \xi )$
. We may assume v is the central geodesic in its parallel set—that is,
$v(0)$
is the circumcenter of
$CS(v)$
—so then
$\gamma $
must stabilize
$g^{\mathbb {R}} v$
(as a set). Thus
$\gamma $
must act on v by
$\gamma v = g^{t'} v$
for some
$t' \in \mathbb {R}$
. By Lemma 6.4,
$| t' - t | \le \varepsilon + 3\operatorname {\mathrm {diam}} \pi ( \mathfrak {v}_{0,\delta })$
. It follows from Lemma 4.2 that
$t'> 0$
. Thus
$ \mathfrak {v}$
contains an axis for
$\gamma $
.
Lemma 9.3. Let
$v_0 \in GX$
be zero-width,
$\varepsilon \in (0, \varepsilon _0]$
,
$\delta \in (0, \delta _0]$
, and
$t> 0$
. Then
where
.
Proof Let
$v \in \mathfrak {v}_{\varepsilon ,\delta }$
be an axis for
$\gamma \in \Gamma $
, that is,
$\gamma v = g^{| \gamma |} v$
, and observe that
$t + \tau _\gamma (v) = | \gamma |$
. By Lemma 6.4 we see that if
then
$\tau _\gamma (v) \in [-\varepsilon , \varepsilon ]$
; this proves the first inclusion. For the second, it suffices to show
$\tau _\gamma (v) \in [-\varepsilon , \varepsilon ]$
implies
$\gamma \in I_{\varepsilon ,\delta ,t}$
. So assume
$\tau _\gamma (v) \in [-\varepsilon , \varepsilon ]$
. We may also assume
$s(v) = 0$
. If
$\tau _{\gamma }(v) \in [-\varepsilon , 0]$
, then
$\gamma ^{-1} g^t v = g^{-\tau _{\gamma }(v)} v \in \mathfrak {v}_{\varepsilon ,\delta }$
, and therefore
$v \in \mathfrak {v} \cap g^{-t} \gamma \mathfrak {v}$
. If
$\tau _{\gamma }(v) \in [0, \varepsilon ]$
, then for
$w = g^{\tau _{\gamma }(v)} v \in \mathfrak {v}_{\varepsilon ,\delta }$
we find
$\gamma ^{-1} g^t w = g^{-\tau _{\gamma }(v)} w = v$
, and therefore
$w \in \mathfrak {v} \cap g^{-t} \gamma \mathfrak {v}$
. Thus in either case
$ \mathfrak {v} \cap g^{-t} \gamma \mathfrak {v}$
is not empty, hence
$\tau _{\gamma }(v) \in [-\varepsilon , \varepsilon ]$
implies
$\gamma \in I_{\varepsilon ,\delta ,t}$
.
Proposition 9.4. Let X be a proper
$\operatorname {\mathrm {CAT}}(0)$
space. Assume
$\Gamma $
acts freely, properly discontinuously, and by isometries on X, and that
$m_\Gamma $
is finite and mixing. Let
$v_0 \in G_{\Lambda } X$
be zero-width, and let
$\varepsilon \in (0, \varepsilon _0]$
. Let
$\delta \in (0, \delta _0)$
be a point of continuity of the non-decreasing function
$r \mapsto m( \mathfrak {v}_r)$
. Then
$$ \begin{align*} \frac{1}{ C_{\varepsilon,\delta}} \le {\widetilde{\lim_{t \to \infty}}} \frac{ N_{\varepsilon,\delta,t}^{\mathrm{periodic}}}{2e^{ht} m( \mathfrak{v}_{\varepsilon,\delta})} \le \frac{\widehat{\varepsilon}}{\varepsilon} C_{\varepsilon,\delta}. \end{align*} $$
Proof By Lemma 9.2,
$ N_{\varepsilon ,\delta ,t}^{\mathrm{unclipped}} \le N_{\varepsilon ,\delta ,t}^{\mathrm{periodic}} \le N_{\varepsilon ,\delta ,t}$
for all sufficiently large t, hence
$$ \begin{align*}\liminf_{t \to \infty} \frac{ N_{\varepsilon,\delta,t}^{\mathrm{unclipped}}}{2e^{ht} m( \mathfrak{v}_{\varepsilon,\delta})} \le {\widetilde{\lim_{t \to \infty}}} \frac{ N_{\varepsilon,\delta,t}^{\mathrm{periodic}}}{2e^{ht} m( \mathfrak{v}_{\varepsilon,\delta})} \le \limsup_{t \to \infty} \frac{ N_{\varepsilon,\delta,t}}{2e^{ht} m( \mathfrak{v}_{\varepsilon,\delta})}.\end{align*} $$
10 Conjugacy classes and intersection segments
We recall again our standing hypotheses, from §5.2 through the rest of the paper. The group
$\Gamma $
acts freely, non-elementarily, properly discontinuously, and by isometries on the proper, geodesically complete
$\operatorname {\mathrm {CAT}}(0)$
space X with rank-one axis. We also assume
$m_\Gamma $
is finite and mixing, and normalized so that
$\| m_\Gamma \| = 1$
.
A non-identity element
$\gamma \in \Gamma $
is called axial if it has an axis
$v \in GX$
. In other words,
$\gamma \neq \operatorname {\mathrm {id}}$
is axial if there exist
$v \in GX$
and
$t> 0$
such that
$\gamma v = g^t v$
.
10.1 Conjugacy classes
Let
$\mathfrak C(\Gamma )$
be the set of axial conjugacy classes
$[\gamma ]$
of
$\Gamma $
. Call a function
${\mathfrak a} \colon \mathfrak C(\Gamma ) \to GX$
a choice of axis if every
${\mathfrak a}[\gamma ]$
is an axis for some
$\gamma ' \in [\gamma ]$
. In other words, for every axial
$\gamma \in \Gamma $
there exists
$\phi \in \Gamma $
such that
$\phi {\mathfrak a}[\gamma ]$
is an axis for
$\gamma $
.
Call a conjugacy class
$[\gamma ] \in \mathfrak C(\Gamma )$
imprimitive if
$\gamma = \phi ^n$
for some
$\phi \in \Gamma $
and
$n> 1$
; note this does not depend on choice of representative
$\gamma $
for
$[\gamma ]$
. Note that by [Reference Bridson and Haefliger2, Theorem II.6.8(2)], if
$\gamma = \phi ^n$
with
$n> 1$
and
$\gamma $
is axial, then
$\phi $
is also axial. Let
$\mathfrak C^{\mathrm{prime}}(\Gamma ) \subset \mathfrak C(\Gamma )$
be the set of conjugacy classes which are not imprimitive.
For any subset
$U \subseteq GX$
, write
$\mathfrak C^{U}(\Gamma ) \subseteq \mathfrak C(\Gamma )$
for the set of conjugacy classes
$[\gamma ]$
such that
$\gamma $
has an axis parallel to some
$v \in \Gamma U$
; this also does not depend on choice of representative
$\gamma $
for
$[\gamma ]$
. Also define
$\mathfrak C^{{\mathrm{prime}}, U}(\Gamma ) = \mathfrak C^{\mathrm{prime}}(\Gamma ) \cap \mathfrak C^{U}(\Gamma )$
. We remark that
$\mathfrak C^{ \mathfrak {v}_{\varepsilon ,\delta }}(\Gamma ) = \{[\gamma ] \in \mathfrak C^{ \mathfrak {v}_{\varepsilon ,\delta }}(\Gamma ) : \gamma \text{ has an axis in } \Gamma \mathfrak {v}_{\varepsilon ,\delta }\}$
(that is, checking for parallel geodesics is unnecessary here by construction of
$ \mathfrak {v}_{\varepsilon ,\delta }$
).
For
$v \in GX$
, let
$| v |$
be the length of the smallest period under
$g^t_\Gamma $
of the projection
$\operatorname {\mathrm {pr}}(v) \in \Gamma \backslash GX$
, with
$| v | = \infty $
if
$\operatorname {\mathrm {pr}}(v)$
is not periodic.
For
$\gamma \in \Gamma $
, let
$| \gamma |$
be the translation length of
$\gamma $
. By
$\operatorname {\mathrm {CAT}}(0)$
geometry, if
$v \in GX$
is an axis for
$\gamma $
and
$\gamma $
is primitive (that is, not imprimitive) then
$| \gamma | = | v |$
.
For
$t \ge t' \ge 0$
, let
$\mathfrak C_\Gamma (t',t) = \{[\gamma ] \in \mathfrak C(\Gamma ) : t' \le | \gamma | \le t\}$
. Similarly define
$\mathfrak C_\Gamma ^{\mathrm{prime}} (t',t)$
,
$\mathfrak C_\Gamma ^{U} (t',t)$
, and
$\mathfrak C_\Gamma ^{{\mathrm{prime}}, U} (t',t)$
for
$U \subseteq GX$
. Let
${\mathrm{Conj}}_\Gamma (t',t) = \# {\mathfrak C_\Gamma (t',t)}$
, and similarly define
${\mathrm{Conj}}_\Gamma ^{\mathrm{prime}} (t',t)$
,
${\mathrm{Conj}}_\Gamma ^{U} (t',t)$
, and
${\mathrm{Conj}}_\Gamma ^{{\mathrm{prime}}, U} (t',t)$
.
10.2 Intersection segments
Let
$v_0 \in GX$
,
$\varepsilon \in (0,\varepsilon _0]$
, and
$\delta \in (0,\delta _0]$
.
For every
$v \in GX$
, the intersection of
$\Gamma \mathfrak {v}_{\varepsilon ,\delta }$
with
$g^{\mathbb {R}} v$
is the disjoint union of orbit segments of length
$\varepsilon $
. Call these segments intersection segments for v with
$ \mathfrak {v}_{\varepsilon ,\delta }$
; call two segments equivalent if there is an isometry
$\gamma \in \Gamma $
carrying one to the other.
Let
${\mathfrak S^{ \mathfrak {v}_{\varepsilon ,\delta }}}(v)$
be the collection of equivalence classes of intersection segments for v with
$ \mathfrak {v}_{\varepsilon ,\delta }$
, and let
$\operatorname {\mathrm {S}}^{ \mathfrak {v}_{\varepsilon ,\delta }}(v) = \# {{\mathfrak S^{ \mathfrak {v}_{\varepsilon ,\delta }}}(v)}$
. Notice that
${\mathfrak S^{ \mathfrak {v}_{\varepsilon ,\delta }}}(v)$
is in natural bijection with the collection of disjoint orbit segments (length
$\varepsilon $
) arising as intersections of
$ \mathfrak {v}_{\varepsilon ,\delta }$
with
$\Gamma g^{\mathbb {R}} v$
. Of course
${\mathfrak S^{ \mathfrak {v}_{\varepsilon ,\delta }}}(v)$
is infinite in general, but it is finite when v is an axis for some
$\gamma \in \Gamma $
. In fact, in this case, elements of
${\mathfrak S^{ \mathfrak {v}_{\varepsilon ,\delta }}}(v)$
correspond to those conjugacy classes of
$\gamma $
in
$\Gamma $
that have an axis in
$ \mathfrak {v}_{\varepsilon ,\delta }$
. We deduce the following lemma.
Lemma 10.1. For all U satisfying
$ \mathfrak {v}_{\varepsilon ,\delta } \subseteq U \subseteq GX$
, we have
Proof In the sum,
$\mathfrak C_\Gamma ^{U} (t - \varepsilon , t + \varepsilon )$
is the set of
$[\gamma ] \in \mathfrak C(\Gamma )$
such that
$\gamma $
has a conjugate with an axis parallel to some
$v \in U$
and
$| \gamma | \in [t - \varepsilon , t + \varepsilon ]$
, whereas
$\operatorname {\mathrm {S}}^{ \mathfrak {v}_{\varepsilon ,\delta }}({\mathfrak a}[\gamma ])$
is the number of conjugates of
$\gamma $
with an axis in
$ \mathfrak {v}_{\varepsilon ,\delta }$
. But by Lemma 9.3 we have
Lemma 10.2. Let
$v_0 \in G_{\Lambda } X$
be zero-width, and let
$\varepsilon \in (0, \varepsilon _0]$
. Let
$\delta \in (0, \delta _0)$
be a point of continuity of the non-decreasing function
$r \mapsto m( \mathfrak {v}_r)$
. Then
$$ \begin{align*} \limsup\limits_{t \to \infty} \frac{{\mathrm{Conj}}_\Gamma^{ \mathfrak{v}_{\varepsilon,\delta}} (t - \varepsilon, t + \varepsilon)}{2 e^{ht} m( \mathfrak{v}_{\varepsilon,\delta})} \le \frac{\widehat{\varepsilon}}{\varepsilon} C_{\varepsilon,\delta}. \end{align*} $$
Proof Since
$\operatorname {\mathrm {S}}^{ \mathfrak {v}_{\varepsilon ,\delta }}({\mathfrak a}[\gamma ]) \ge 1$
for all
$[\gamma ] \in \mathfrak C_\Gamma ^{ \mathfrak {v}_{\varepsilon ,\delta }}$
, we have
${\mathrm{Conj}}_\Gamma ^{ \mathfrak {v}_{\varepsilon ,\delta }}(t - \varepsilon , t + \varepsilon ) \le N_{\varepsilon ,\delta ,t}^{\mathrm{periodic}}$
by Lemma 10.1. Apply the upper bound from Proposition 9.4.
11 Measuring along periodic orbits
For each
$v \in GX$
, let
$\lambda ^{v}$
be Lebesgue measure on
$g^{\mathbb {R}}v$
. Notice the quotient measure
$\lambda _{\Gamma }^{v}$
on
$\Gamma \backslash GX$
has
$\| \lambda _{\Gamma }^{v} \| = | v |$
.
Lemma 11.1. Let
$v_0 \in GX$
,
$\varepsilon \in (0,\varepsilon _0]$
, and
$\delta \in (0,\delta _0]$
. For all
$v \in GX$
, there are
$({1}/{\varepsilon }) \lambda _{\Gamma }^{v} (\operatorname {\mathrm {pr}} \mathfrak {v}_{\varepsilon ,\delta })$
equivalence classes of intersection segments for v with
$ \mathfrak {v}_{\varepsilon ,\delta }$
; that is,
$$ \begin{align*}\operatorname{\mathrm{S}}^{ \mathfrak{v}_{\varepsilon,\delta}}(v) = \frac{1}{\varepsilon} \lambda_{\Gamma}^{v} (\operatorname{\mathrm{pr}} \mathfrak{v}_{\varepsilon,\delta}).\end{align*} $$
Proof The intersection segments for v with
$ \mathfrak {v}_{\varepsilon ,\delta }$
are each of length
$\varepsilon $
, and they are pairwise disjoint. Hence
$\lambda _{\Gamma }^{v} (\operatorname {\mathrm {pr}} \mathfrak {v}_{\varepsilon ,\delta }) = \varepsilon \cdot \operatorname {\mathrm {S}}^{ \mathfrak {v}_{\varepsilon ,\delta }}(v)$
.
For any
$U \subseteq GX$
and
$t \ge \alpha> 0$
, define
$$ \begin{align*} \lambda_{{\mathfrak a},t,\alpha}^{{\mathrm{mult}}, U} &= \frac{1}{{\mathrm{Conj}}_\Gamma^{U} (t - \alpha, t)} \sum_{[\gamma] \in \mathfrak C_\Gamma^{U} (t - \alpha, t)} \frac{1}{\| \lambda_{\Gamma}^{{\mathfrak a}[\gamma]} \|} \lambda_{\Gamma}^{{\mathfrak a}[\gamma]}, \\ \lambda_{{\mathfrak a},t,\alpha}^{{\mathrm{prime}}, U} &= \frac{1}{{\mathrm{Conj}}_\Gamma^{{\mathrm{prime}}, U} (t - \alpha, t)} \sum_{[\gamma] \in \mathfrak C_\Gamma^{{\mathrm{prime}}, U} (t - \alpha, t)} \frac{1}{\| \lambda_{\Gamma}^{{\mathfrak a}[\gamma]} \|} \lambda_{\Gamma}^{{\mathfrak a}[\gamma]}, \\ \tilde{\lambda}_{{\mathfrak a},t,\alpha}^{{\mathrm{mult}}, U} &= \frac{1}{t \cdot {\mathrm{Conj}}_\Gamma^{U} (t - \alpha, t + \alpha)} \sum_{[\gamma] \in \mathfrak C_\Gamma^{U} (t - \alpha, t + \alpha)} \lambda_{\Gamma}^{{\mathfrak a}[\gamma]}. \end{align*} $$
Note that by Proposition 9.4, if
$v_0 \in G_{\Lambda } X$
then for all
$\varepsilon , \delta> 0$
and sufficiently large
$t> 0$
, we have
$ N_{\varepsilon ,\delta ,t}^{\mathrm{periodic}}> 0$
, and thus we are not dividing by zero in the definition of the above measures, provided
$ \mathfrak {v}_{\varepsilon ,\delta } \subseteq U$
and
$t> 0$
is sufficiently large.
Lemma 11.2. For all U satisfying
$ \mathfrak {v}_{\varepsilon ,\delta } \subseteq U \subseteq GX$
, we have
Proof Lemma 11.1 gives us
$$ \begin{align*} \sum_{[\gamma] \in \mathfrak C_\Gamma^{U} (t - \varepsilon, t + \varepsilon)} \operatorname{\mathrm{S}}^{ \mathfrak{v}_{\varepsilon,\delta}}({\mathfrak a}[\gamma]) = \frac{t}{\varepsilon} {\mathrm{Conj}}_\Gamma^{U} (t - \varepsilon, t + \varepsilon) \tilde{\lambda}_{{\mathfrak a},t,\varepsilon}^{{\mathrm{mult}}, U} (\operatorname{\mathrm{pr}} \mathfrak{v}_{\varepsilon,\delta}), \end{align*} $$
and we apply Lemma 10.1.
Corollary 11.3. Let
$v_0 \in G_{\Lambda } X$
be zero-width, and let
$\varepsilon \in (0, \varepsilon _0]$
. Let
$\delta \in (0, \delta _0)$
be a point of continuity of the non-decreasing function
$r \mapsto m( \mathfrak {v}_r)$
. Then
whenever
$ \mathfrak {v}_{\varepsilon ,\delta } \subseteq U \subseteq GX$
.
The measures
$\tilde {\lambda }_{{\mathfrak a},t,\alpha }^{{\mathrm{mult}}, U}$
and
$\lambda _{{\mathfrak a}, t + \alpha , 2 \alpha }^{{\mathrm{mult}}, U}$
have the same weak limits. In fact, one easily checks the following result directly from the definitions.
Lemma 11.4. Let
$U \subseteq GX$
be such that
$ \mathfrak {v}_{\varepsilon ,\delta } \subseteq U$
. For any fixed
$\alpha> 0$
and choice of axis
${\mathfrak a}$
,
$\lim \nolimits _{t \to \infty } \| \tilde {\lambda }_{{\mathfrak a},t,\alpha }^{{\mathrm{mult}}, U} - \lambda _{{\mathfrak a}, t + \alpha , 2 \alpha }^{{\mathrm{mult}}, U} \| = 0$
.
Proof By definition,
$$ \begin{align*} \lambda_{{\mathfrak a}, t + \alpha, 2 \alpha}^{{\mathrm{mult}}, U} = \frac{1}{{\mathrm{Conj}}_\Gamma^{U} (t - \alpha, t + \alpha)} \sum_{[\gamma] \in \mathfrak C_\Gamma^{U} (t - \alpha, t + \alpha)} \frac{1}{| \lambda_{\Gamma}^{{\mathfrak a}[\gamma]} |} \lambda_{\Gamma}^{{\mathfrak a}[\gamma]} \end{align*} $$
and
$$ \begin{align*} \tilde{\lambda}_{{\mathfrak a},t,\alpha}^{{\mathrm{mult}}, U} = \frac{1}{{\mathrm{Conj}}_\Gamma^{U} (t - \alpha, t + \alpha)} \sum_{[\gamma] \in \mathfrak C_\Gamma^{U} (t - \alpha, t + \alpha)} \frac{1}{t} \lambda_{\Gamma}^{{\mathfrak a}[\gamma]}. \end{align*} $$
Since
$t - \alpha \le | \lambda _{\Gamma }^{{\mathfrak a}[\gamma ]} | \le t + \alpha $
for all
$\lambda _{\Gamma }^{{\mathfrak a}[\gamma ]} \in \mathfrak C_\Gamma ^{U} (t - \alpha , t + \alpha )$
, we see that for
$t> \alpha $
,
$$ \begin{align*} \frac{t}{t + \alpha} \tilde{\lambda}_{{\mathfrak a},t,\alpha}^{{\mathrm{mult}}, U} (V) \le \lambda_{{\mathfrak a}, t + \alpha, 2 \alpha}^{{\mathrm{mult}}, U} (V) \le \frac{t}{t - \alpha} \tilde{\lambda}_{{\mathfrak a},t,\alpha}^{{\mathrm{mult}}, U} (V) \end{align*} $$
for all Borel sets
$V \subseteq GX$
. The conclusion of the lemma follows.
Corollary 11.5. Let
$v_0 \in G_{\Lambda } X$
be zero-width, and let
$\varepsilon \in (0, \varepsilon _0]$
. Let
$\delta \in (0, \delta _0)$
be a point of continuity of the non-decreasing function
$r \mapsto m( \mathfrak {v}_r)$
. Then
Proof By Corollary 11.3 and Lemma 11.4,
The fact that
$\lambda _{{\mathfrak a}, t + \varepsilon , 2 \varepsilon }^{{\mathrm{mult}}, \mathfrak {v}_{\varepsilon ,\delta }}$
is a probability measure gives us the desired inequality.
Combining Lemma 10.2 and Corollary 11.5, we obtain the following result.
Proposition 11.6. Let X be a proper
$\operatorname {\mathrm {CAT}}(0)$
space. Assume
$\Gamma $
acts freely, properly discontinuously, and by isometries on X, and that
$m_\Gamma $
is finite and mixing. Let
$v_0 \in G_{\Lambda } X$
be zero-width, and let
$\varepsilon \in (0, \varepsilon _0]$
. Let
$\delta \in (0, \delta _0)$
be a point of continuity of the non-decreasing function
$r \mapsto m( \mathfrak {v}_r)$
. Then for every
$\alpha> 0$
there exists
$t_0> 0$
such that for all
$t \ge t_0$
,
We will not use Proposition 11.6 in what follows, but it gives an idea of the strength of result we can prove without adding additional hypotheses.
Lemma 11.7. Let
$U \subseteq GX$
and
$\alpha> 0$
. Assume there is an open set
$V \subseteq U$
such that
$V \cap G_{\Lambda } X$
is non-empty. There exist
$C> 0$
and
$t_0> 0$
such that for all
$t \ge t_0$
,
$$ \begin{align*}{\mathrm{Conj}}_\Gamma^{U} (t - \alpha, t + \alpha) \ge C \frac{e^{ht}}{t}.\end{align*} $$
Proof By Proposition 5.2, there is some zero-width
$v_0 \in V$
. By Lemma 2.1, there exist
$\delta> 0$
and
$\varepsilon> 0$
such that
$ \mathfrak {v}_{\varepsilon ,\delta } = \mathfrak {v}(v_0,\varepsilon ,\delta )$
is completely contained in
$\mathcal R \cap V$
. We may assume
$\varepsilon \le \min \{\alpha , \varepsilon _0\}$
and that
$\delta \in (0, \delta _0]$
is chosen such that
by Corollary 11.5. Thus there exist
$C> 0$
and
$t_0> 0$
such that for all
$t \ge t_0$
,
$$ \begin{align*}C \frac{e^{ht}}{t} \le {\mathrm{Conj}}_\Gamma^{ \mathfrak{v}_{\varepsilon,\delta}} (t - \varepsilon, t + \varepsilon) \le {\mathrm{Conj}}_\Gamma^{U} (t - \varepsilon, t + \varepsilon) \le {\mathrm{Conj}}_\Gamma^{U} (t - \alpha, t + \alpha).\\[-40pt] \end{align*} $$
It is easy to see that Lemma 11.7 is equivalent to the following statement, where we replace
${\mathrm{Conj}}_\Gamma ^{U} (t - \alpha , t + \alpha )$
by
${\mathrm{Conj}}_\Gamma ^{U} (t - \alpha , t)$
.
Corollary 11.8. Let
$U \subseteq GX$
and
$\alpha> 0$
. Assume U contains an open neighborhood about some
$v_0 \in G_{\Lambda } X$
. There exist
$C> 0$
and
$t_0> 0$
such that for all
$t \ge t_0$
,
$$ \begin{align*}{\mathrm{Conj}}_\Gamma^{U} (t - \alpha, t) \ge C \frac{e^{ht}}{t}.\end{align*} $$
Proof By Lemma 11.7, there exist
$C'> 0$
and
$t^{\prime }_0> 0$
such that for all
$t \ge t^{\prime }_0$
,
$$ \begin{align*}{\mathrm{Conj}}_\Gamma^{U} \bigg(t - \frac{\alpha}{2}, t + \frac{\alpha}{2}\bigg) \ge C' \cdot \frac{e^{ht}}{t}.\end{align*} $$
So let
$C = C' \cdot e^{{-h \alpha } / {2}}$
and
$t_0 = t^{\prime }_0 + {\alpha }/{2}$
. Then for all
$t \ge t_0$
,
$$ \begin{align*}{\mathrm{Conj}}_\Gamma^{U} (t - \alpha, t) \ge C' \cdot \frac{e^{h (t - {\alpha}/{2})}}{t - {\alpha}/{2}} = C \cdot \frac{t}{t - {\alpha}/{2}} \cdot \frac{e^{ht}}{t} \ge C \frac{e^{ht}}{t}. \\[-43pt] \end{align*} $$
12 Counting multiplicities
We start with a simple upper bound on the number of conjugacy classes, coming from the construction of the Patterson–Sullivan measures.
Lemma 12.1. If
$K \subset GX$
is compact, then
$\lim \nolimits _{t \to \infty } e^{-h't} {\mathrm{Conj}}_\Gamma ^{K} (0,t) = 0$
for all
$h'> h$
.
Proof Consider that for
$\gamma \in \Gamma $
with an axis in K, we know
$d(\gamma p, p) \le | \gamma | + 2 \operatorname {\mathrm {diam}} \pi (K)$
, and therefore for all
$h'> h$
,
$$ \begin{align*} \sum_{t> 0} e^{-h't} {\mathrm{Conj}}_\Gamma^{K}(t,t) &= \sum_{\substack{[\gamma] \in \mathfrak C(\Gamma) \\ \text{with an axis in }K}} e^{-h' | \gamma |} \le \sum_{\substack{\gamma \in \Gamma \\ \text{with an axis in }K}} e^{-h' | \gamma |} \\ &\le \sum_{\substack{\gamma \in \Gamma \\ \text{with an axis in }K}} e^{-h'\, d(\gamma p, p) + 2 h' \operatorname{\mathrm{diam}} \pi(K)} \\ &\le e^{2 h' \operatorname{\mathrm{diam}} \pi(K)} \sum_{\substack{\gamma \in \Gamma \\ \text{with an axis in }K}} e^{-h'\, d(\gamma p, p)} \end{align*} $$
converges because h is the critical exponent of the Poincaré series for Patterson’s construction. It follows that
$\lim _{t \to \infty } e^{-h't} {\mathrm{Conj}}_\Gamma ^{K} (0,t) = 0$
.
Lemma 12.2. Let
$U \subseteq GX$
contain an open neighborhood about some
$v_0 \in G_{\Lambda } X$
, and assume
$U \subseteq \Gamma K$
for some compact set
$K \subseteq GX$
. Then for every
$\alpha> 0$
,
$$ \begin{align*}\lim\limits_{t \to \infty} \frac{{\mathrm{Conj}}_\Gamma^{{\mathrm{prime}}, U} (t - \alpha, t)}{{\mathrm{Conj}}_\Gamma^{U} (t - \alpha, t)} = 1.\end{align*} $$
Remark 12.3. In particular, if
$\Gamma $
acts cocompactly on X, then
$\lim \nolimits _{t \to \infty } ({{\mathrm{Conj}}_\Gamma ^{\mathrm{prime}} (t - \alpha , t)}/\\ {{\mathrm{Conj}}_\Gamma (t - \alpha , t)}) = 1$
.
Proof Let
$\alpha> 0$
. By Corollary 11.8, there exist
$C> 0$
and
$t^{\prime }_0> 0$
such that
$$ \begin{align*}{\mathrm{Conj}}_\Gamma^{U} (t - \alpha, t) \ge C \frac{e^{ht}}{t}\end{align*} $$
for all
$t \ge t^{\prime }_0$
. Now by definition,
${\mathrm{Conj}}_\Gamma ^{K} (0,{t}/{2}) = {\mathrm{Conj}}_\Gamma ^{\Gamma K} (0,{t}/{2}) \ge {\mathrm{Conj}}_\Gamma ^{U} (0,{t}/{2})$
. Since
$\lim _{t \to \infty } 2t e^{-({3}/{2}) ht} {\mathrm{Conj}}_\Gamma ^{K} (0,t) = 0$
by Lemma 12.1, there exists
$t_0 \ge t^{\prime }_0$
such that
$$ \begin{align*}{\mathrm{Conj}}_\Gamma^{U} \bigg(0,\frac{t}{2}\bigg) \le {\mathrm{Conj}}_\Gamma^{K} \bigg(0,\frac{t}{2}\bigg) \le C \cdot \frac{e^{({3}/{4}) ht}}{t}\end{align*} $$
for all
$t \ge t_0$
. Since every imprimitive
$[\gamma ] \in \mathfrak C_\Gamma ^{U} (t - \alpha , t) ~\backslash~ \mathfrak C_\Gamma ^{{\mathrm{prime}}, U} (t - \alpha , t)$
is a multiple of some
$[\phi ] \in \mathfrak C_\Gamma ^{U} (0, {t}/{2})$
, we see that
$$ \begin{align*}0 \le {\mathrm{Conj}}_\Gamma^{U} (t - \alpha, t) - {\mathrm{Conj}}_\Gamma^{{\mathrm{prime}}, U} (t - \alpha, t) \le {\mathrm{Conj}}_\Gamma^{U} (0,{t}/{2}).\end{align*} $$
Thus
$$ \begin{align*}{\mathrm{Conj}}_\Gamma^{U} (t - \alpha, t) \ge {\mathrm{Conj}}_\Gamma^{{\mathrm{prime}}, U} (t - \alpha, t) \ge {\mathrm{Conj}}_\Gamma^{U} (t - \alpha, t) - {\mathrm{Conj}}_\Gamma^{U} (0,{t}/{2})\end{align*} $$
and therefore
$$ \begin{align*}1 \ge \frac{{\mathrm{Conj}}_\Gamma^{{\mathrm{prime}}, U} (t - \alpha, t)}{{\mathrm{Conj}}_\Gamma^{U} (t - \alpha, t)} \ge 1 - \frac{{\mathrm{Conj}}_\Gamma^{U} (0,{t}/{2})}{{\mathrm{Conj}}_\Gamma^{U} (t - \alpha, t)} \ge 1 - e^{-({1}/{4}) ht}. \\[-44pt] \end{align*} $$
Since
${\mathrm{Conj}}_\Gamma ^{U} (0,t)$
diverges, we obtain the following corollary.
Corollary 12.4. Under the hypotheses of Lemma 12.2,
$$ \begin{align*}\lim_{t \to \infty} \frac{{\mathrm{Conj}}_\Gamma^{{\mathrm{prime}}, U} (0, t)}{{\mathrm{Conj}}_\Gamma^{U} (0, t)} = 1.\end{align*} $$
It follows from Lemma 12.2 that the probability measures
$\lambda _{{\mathfrak a},t,\alpha }^{{\mathrm{prime}}, \mathfrak {v}_{\varepsilon ,\delta }}$
and
$\lambda _{{\mathfrak a},t,\alpha }^{{\mathrm{mult}}, \mathfrak {v}_{\varepsilon ,\delta }}$
have the same weak limits. In fact, we have the following lemma.
Lemma 12.5. Let
$U \subseteq GX$
contain an open neighborhood about some
$v_0 \in G_{\Lambda } X$
, and assume
$U \subseteq \Gamma K$
for some compact set
$K \subseteq GX$
. For any fixed
$\alpha> 0$
and choice of axis
${\mathfrak a}$
,
$$ \begin{align*} \lim\limits_{t \to \infty} \left\| \lambda_{{\mathfrak a},t,\alpha}^{{\mathrm{prime}}, U} - \lambda_{{\mathfrak a},t,\alpha}^{{\mathrm{mult}}, U} \right\| = 0. \end{align*} $$
Proof Let W be a Borel subset of
$GX$
. By the definitions,
$$ \begin{align*} \lambda_{{\mathfrak a},t,\alpha}^{{\mathrm{mult}}, GX}(W) = \frac{1}{{\mathrm{Conj}}_\Gamma^{U} (t - \alpha, t)} \sum_{[\gamma] \in \mathfrak C_\Gamma (t - \alpha, t)} \frac{1}{\| \lambda_{\Gamma}^{{\mathfrak a}[\gamma]} \|} \lambda_{\Gamma}^{{\mathfrak a}[\gamma]}(W) \end{align*} $$
and
$$ \begin{align*} \lambda_{{\mathfrak a},t,\alpha}^{{\mathrm{prime}}, GX}(W) = \frac{1}{{\mathrm{Conj}}_\Gamma^{{\mathrm{prime}}, U} (t - \alpha, t)} \sum_{[\gamma] \in \mathfrak C_\Gamma^{\mathrm{prime}} (t - \alpha, t)} \frac{1}{\| \lambda_{\Gamma}^{{\mathfrak a}[\gamma]} \|} \lambda_{\Gamma}^{{\mathfrak a}[\gamma]}(W). \end{align*} $$
The outside coefficients are asymptotically equal (and non-zero), and the difference in the sums is at most
${\mathrm{Conj}}_\Gamma ^{U} (t - \alpha , t) - {\mathrm{Conj}}_\Gamma ^{{\mathrm{prime}}, U} (t - \alpha , t)$
, which is asymptotically zero compared to
${\mathrm{Conj}}_\Gamma ^{U} (t - \alpha , t)$
by Lemma 12.2.
13 Limiting process
For a fixed interval
$[a,b] \subset \mathbb {R}$
and continuous function
$f \colon [a,b] \to \mathbb {R}$
, the Riemann sums
${\sum _{k = 1}^{n} 2\varepsilon _n f(x_n)}$
converge to
${\int _{a}^{b} f(x) \; dx}$
, for
$\varepsilon _n = ({b-a})/{2n}$
and
$x_n = (2k-1) \varepsilon _n$
. This also holds whenever f is Riemann integrable, for example, f is bounded and non-decreasing. For completeness, we give here a proof of a standard generalization of this fact to asymptotic intervals.
Lemma 13.1. Let
$F \colon \mathbb {R} \to \mathbb {R}$
be eventually positive and non-decreasing. Then
$$ \begin{align*} \frac{1}{C} \le {\widetilde{\lim_{t \to \infty}}} \frac {\int_{0}^{t} F(x) \; dx} {\sum_{k = 0}^{\lfloor {t}/{2\varepsilon} \rfloor} 2\varepsilon F(t - (2k+1) \varepsilon)} \le C, \end{align*} $$
where
$C = \limsup \nolimits _{x \to \infty } {F(x + \varepsilon )}/{F(x)}$
.
Proof For any fixed
$a \in \mathbb {R}$
and
$m \in \mathbb {Z}$
,
$$ \begin{align*} \lim\limits_{t \to \infty} \frac{\int_{0}^{t} F(x) \; dx}{\int_{a}^{t} F(x) \; dx} = 1 \qquad \text{and} \qquad \lim\limits_{t \to \infty} \frac{\sum_{k = 0}^{\lfloor {t}/{2\varepsilon} \rfloor} 2\varepsilon F(t - (2k+1) \varepsilon)} {\sum_{k = 0}^{\lfloor {t}/{2\varepsilon} \rfloor - m} 2\varepsilon F(t - (2k+1) \varepsilon)} = 1, \end{align*} $$
so without loss of generality we may assume F is positive and non-decreasing on
$[0, \infty )$
. We may similarly assume, for
$\alpha> 0$
fixed, that
$1 \le ({F(x + \varepsilon )}/{F(x)}) \le C + \alpha $
for all
$x> -2\varepsilon $
. Let
$t> 0$
and put
$n = \lfloor {t}/{2\varepsilon } \rfloor $
. For each
$k = 0, 1, 2, \dotsc , n$
, we have
$$ \begin{align*} \frac{1}{C + \alpha} F(t - (2k+1)\varepsilon) \le F(x) \le (C + \alpha) F(t - (2k+1)\varepsilon) \end{align*} $$
for all
$x \in [t - (2k+2)\varepsilon , t - 2k\varepsilon ]$
. Thus
$$ \begin{align*} \frac{1}{C + \alpha} 2\varepsilon F(t - (2k+1)\varepsilon) \le \int_{t - (2k+2)\varepsilon}^{t - 2k\varepsilon} F(x) \; dx \le (C + \alpha) 2\varepsilon F(t - (2k+1)\varepsilon) \end{align*} $$
for each
$k = 0, 1, 2, \dotsc , n$
, and therefore
$$ \begin{align*} \frac{1}{C + \alpha} \sum_{k = 0}^{n-1} 2\varepsilon F(t - (2k+1)\varepsilon) &\le \int_{2\varepsilon}^{t} F(x) \; dx \le \int_{0}^{t} F(x) \; dx \\ &\le \int_{-2\varepsilon}^{t} F(x) \; dx \le (C + \alpha) \sum_{k = 0}^{n} 2\varepsilon F(t - (2k+1)\varepsilon). \end{align*} $$
But
$$ \begin{align*} \lim_{t \to \infty} \frac {\sum_{k = 0}^{\lfloor {t}/{2\varepsilon} \rfloor} 2\varepsilon F(t - (2k+1)\varepsilon)} {\sum_{k = 0}^{\lfloor {t}/{2\varepsilon} \rfloor-1} 2\varepsilon F(t - (2k+1)\varepsilon)} = 1, \end{align*} $$
so
$$ \begin{align*} \frac{1}{C + \alpha} &\le {\widetilde{\lim_{t \to \infty}}} \frac {\int_{0}^{t} F(x) \; dx} {\sum_{k = 0}^{\lfloor {t}/{2\varepsilon} \rfloor} 2\varepsilon F(t - (2k+1)\varepsilon)} \le C + \alpha. \end{align*} $$
As
$\alpha> 0$
was arbitrary, we find
$$ \begin{align*} \frac{1}{C} \le {\widetilde{\lim_{t \to \infty}}} \frac{\int_{0}^{t} F(x) \; dx}{\sum_{k = 0}^{n} 2\varepsilon F(t - (2k+1)\varepsilon)} \le C. \\[-44pt] \end{align*} $$
The following is another standard calculation which we include for completeness.
Lemma 13.2. Let
$\varepsilon > 0$
. Then
$$ \begin{align*} \frac{1}{C} \le {\widetilde{\lim_{t \to \infty}}} \sum_{k = 0}^{\lfloor {t}/{2\varepsilon} \rfloor} 2\varepsilon \frac{{e^{h(t - (2k+1) \varepsilon)}}/({t - (2k+1) \varepsilon})}{{{e^{ht}}/{ht}}}\le C, \end{align*} $$
where
$C = e^{h \varepsilon }$
.
Proof It is a standard fact that for any fixed
$t_0> 0$
,
$$ \begin{align} \lim\limits_{t \to \infty} {\int_{t_0}^{t} \frac{e^{hx}}{x} \; dx} \bigg/ { }{\frac{e^{ht}}{ht}} = 1. \end{align} $$
This comes from the calculation
$$ \begin{align*} \int_{t_0}^{t} \frac{e^{hx}}{x} \; dx = \frac{e^{hx}}{hx} \bigg \vert_{t_0}^{t} + \int_{t_0}^{t} \frac{e^{hx}}{hx^2} \; dx = \frac{e^{ht}}{ht} - \frac{e^{h t_0}}{h t_0} + \int_{t_0}^{t} \frac{e^{hx}}{hx^2} \; dx; \end{align*} $$
the second term of the last expression tends to zero relative to
${e^{ht}} / {ht}$
because it is constant, the third because
$\lim \nolimits _{x \to \infty } {({e^{hx}}/{hx^2})} / {({e^{hx}}/{x})} = 0$
. On the other hand, for all
$\varepsilon> 0$
, Lemma 13.1 gives us
$$ \begin{align*} e^{-h \varepsilon} \le {\widetilde{\lim_{t \to \infty}}} {\sum_{k = 0}^{\lfloor {t}/{2\varepsilon} \rfloor} 2\varepsilon \frac{e^{h(t - (2k+1) \varepsilon)}}{t - (2k+1) \varepsilon}} \bigg/ { }{\int_{t_0}^{t} \frac{e^{hx}}{x} \; dx} \le e^{h \varepsilon} \end{align*} $$
and therefore
$$ \begin{align*} e^{-h \varepsilon} \le {\widetilde{\lim_{t \to \infty}}} {\sum_{k = 0}^{\lfloor {t}/{2\varepsilon} \rfloor} 2\varepsilon \frac{e^{h(t - (2k+1) \varepsilon)}}{t - (2k+1) \varepsilon}} \bigg/ { }{\frac{e^{ht}}{ht}} \le e^{h \varepsilon} \end{align*} $$
from (1).
14 Entropy and equidistribution
Knieper also proves an equidistribution result [Reference Knieper6, Proposition 6.4]; adapting his proof, we obtain a similar result. For clarity, we include a proof.
We first briefly recall the definition of measure-theoretic entropy (a good reference is [Reference Walters15]). Let
$\nu $
be a probability measure on a space Z. The entropy of a measurable partition
$\mathcal {A} = \{A_1, \dotsc , A_m\}$
of Z is
$$ \begin{align*}H_{\nu}(\mathcal{A}) = \sum_{i=1}^{m} -\nu(A_i) \log \nu(A_i).\end{align*} $$
Let
$\phi \colon Z \to Z$
be a measure-preserving transformation. For the partitions
$$ \begin{align*}\mathcal{A}_{\phi}^{(n)} := \{A_{j_1} \cap \phi^{-1} A_{j_2} \cap \dotsb \cap \phi^{-(n-1)} A_{j_{n-1}} : 1 \le j_1, j_2, \dotsc, j_{n-1} \le m\},\end{align*} $$
$n \mapsto ({1}/{n}) H_{\nu }(\mathcal {A}_\phi ^{(n)})$
is a subadditive function. Hence
$({1}/{n}) H_{\nu }(\mathcal {A}_\phi ^{(n)})$
decreases to a limit
$$ \begin{align*}h_{\nu}(\phi,\mathcal{A}) := \lim_{n \to \infty} \frac{1}{n} H_{\nu}(\mathcal{A}_\phi^{(n)}) = \inf_{n \in \mathbb{N}} \frac{1}{n} H_{\nu}(\mathcal{A}_\phi^{(n)}),\end{align*} $$
called the entropy of
$\phi $
with respect to
$\mathcal {A}$
. The measure-theoretic entropy of
$\phi $
is
$$ \begin{align*}h_{\nu}(\phi) := \mathop{\mathrm{sup}}\limits_{\mathcal{A}} h_{\nu}(\phi,\mathcal{A}).\end{align*} $$
The measure-theoretic entropy of a measure-preserving flow
$\phi = (\phi ^t)_{t \in \mathbb {R}}$
on Z is defined to be that of its time-one map
$\phi ^1$
, that is,
$h_{\nu }(\phi ) := h_{\nu }(\phi ^1)$
.
A significant portion of Knieper’s proof of his Proposition 6.4 is spent proving the following (unstated) general lemma.
Lemma 14.1. Let
$\phi $
be a measurable map of a measurable space to itself. Let
$(\mu _k)$
be a sequence of
$\phi $
-invariant probability measures, and let
${\mathcal A}$
be a measurable partition. Then
$$ \begin{align*}\limsup_{k \to \infty} \frac{H_{\mu_k} ({\mathcal A}_\phi^{(n_k)})}{n_k} \le \liminf_{k \to \infty} \frac{H_{\mu_k} ({\mathcal A}_\phi^{(q)})}{q}\end{align*} $$
for all integers
$q> 1$
and sequences
$(n_k)$
in
$\mathbb {N}$
such that
$n_k \to \infty $
.
We next define separated sets for
$g_\Gamma ^t$
. Recall the metric on
$GX$
is given by
$$ \begin{align*} d_{GX}(v,w) = \mathop{\mathrm{sup}}\limits_{t \in \mathbb{R}} e^{-| t |} d_X(v(t), w(t)). \end{align*} $$
The quotient metrics
$d_{\Gamma \backslash X}$
and
$d_{\Gamma \backslash GX}$
on
$\Gamma \backslash X$
and
$\Gamma \backslash GX$
, respectively, are
$$ \begin{align*}d_{\Gamma \backslash X}(\bar{x},\bar{y}) = \inf_{\gamma \in \Gamma} d_{X}(x,\gamma y) \quad \text{and} \quad d_{\Gamma \backslash GX}(\bar{v},\bar{w}) = \inf_{\gamma \in \Gamma} d_{GX}(v,\gamma w),\end{align*} $$
where
$x,y,v,w$
are arbitrary representatives of the equivalence classes
$\bar {x},\bar {y},\bar {v},\bar {w}$
, respectively. We will write d for all these metrics.
Now for
$n \in \mathbb {N}$
and
$\varepsilon> 0$
, call a set
$A \subset \Gamma \backslash GX (n, \varepsilon )$
-separated if for all distinct
$\bar {v},\bar {w} \in A$
, there is some integer k such that
$0 \le k \le n$
and
$d(g_\Gamma ^k(\bar {v}),g_\Gamma ^k(\bar {w}))> \varepsilon $
.
Write
$\operatorname {\mathrm {injrad}}(\Gamma \backslash X)$
for the injectivity radius of
$\Gamma \backslash X$
.
Lemma 14.2. Let
$\Gamma $
be a group acting freely, properly discontinuously, by and isometries on a proper
$\operatorname {\mathrm {CAT}}(0)$
space X. Let
$t_0> 0$
and let
$P \subset \mathfrak C_\Gamma (t_0 - \alpha , t_0)$
. If
$\alpha < e^{-{1}/{2}} \operatorname {\mathrm {injrad}}(\Gamma \backslash X)$
then
$\operatorname {\mathrm {pr}}({\mathfrak a}(P))$
is
$(\lceil t_0 \rceil ,\alpha )$
-separated for any choice of axis
${\mathfrak a}$
.
Proof Let
${\mathfrak a}$
be a choice of axis, and let
$0 < \alpha < e^{-{1}/{2}} \operatorname {\mathrm {injrad}}(\Gamma \backslash X)$
. Let
$\gamma _1, \gamma _2 \in \Gamma $
represent distinct conjugacy classes
$[\gamma _1], [\gamma _2] \in P$
. Let
$v = {\mathfrak a}[\gamma _1]$
and
$w = {\mathfrak a}[\gamma _2]$
, and write
$\bar v = \operatorname {\mathrm {pr}} v$
and
$\bar w = \operatorname {\mathrm {pr}} w$
. We may assume, replacing w by
$\gamma w$
and
$\gamma _2$
by
$\gamma \gamma _2 \gamma ^{-1}$
(for some
$\gamma \in \Gamma $
) if necessary, that
$d(\bar v, \bar w) = d(v,w)$
.
Write
$n = \lceil t_0 \rceil $
. Suppose, by way of contradiction, that
$d(g_\Gamma ^k \bar v, g_\Gamma ^k \bar w) \le \alpha $
for all
$k = 0, 1, 2, \dotsc , n$
. For each
$k \in \mathbb {Z}$
, let
$\varphi _k \in \Gamma $
satisfy
$d(g^k v, \varphi _k g^k w) = d(g_\Gamma ^k \bar v, g_\Gamma ^k \bar w)$
. (Note we assumed above that
$\varphi _0 = \operatorname {\mathrm {id}}$
.) Then
$$ \begin{align*}e^{-{1}/{2}} d(v(k \pm \tfrac{1}{2}), \varphi_k w(k \pm \tfrac{1}{2})) \le d(g^k v, \varphi_k g^k w) = d(g_\Gamma^k \bar{v}, g_\Gamma^k \bar{w}) \le \alpha\end{align*} $$
for all
$k = 0, 1, 2, \dotsc , n$
, hence
$d(v(k \pm \tfrac {1}{2}), \varphi _k w(k \pm \tfrac {1}{2})) \le e^{{1}/{2}} \alpha $
. So
$$ \begin{align*}d(\varphi_k w(k + \tfrac{1}{2}), \varphi_{k + 1} w(k + \tfrac{1}{2})) \le 2e^{{1}/{2}} \alpha < 2\operatorname{\mathrm{injrad}}(\Gamma \backslash X),\end{align*} $$
and therefore
$\varphi _n = \varphi _{n - 1} = \dotsb = \varphi _{0} = \operatorname {\mathrm {id}}$
. It follows that
$d(v(k), w(k)) = d(\bar v(k), \bar w(k)) \le \alpha $
for all
$k = 0, 1, 2, \dotsc , n$
. Thus
$d(v(t), w(t)) \le \alpha $
for all
$t \in [0,t_0]$
by convexity.
Find
$t_1, t_2 \in [t_0 - \alpha , t_0]$
such that
$\gamma _1 v = g^{t_1} v$
and
$\gamma _2 w = g^{t_2} w$
. Then
$$ \begin{align*}d(\gamma_2^{-1} \gamma_1 v(0), w(0)) = d(\gamma_2^{-1} v(t_1), \gamma_2^{-1} w(t_2)) = d(v(t_1), w(t_2)) \le 2\alpha.\end{align*} $$
Hence
$d(\gamma _2^{-1} \gamma _1 v(0), v(0)) \le 3\alpha < 2\operatorname {\mathrm {injrad}}(\Gamma \backslash X)$
, which is only possible if
$\gamma _2^{-1} \gamma _1$
is trivial. This contradicts our hypothesis that
$[\gamma _1]$
and
$[\gamma _2]$
are distinct. Therefore, there must be some
$k \in \{0, 1, 2, \dotsc , n\}$
such that
$d(g_\Gamma ^k \bar v, g_\Gamma ^k \bar w)> \alpha $
, and thus we see that
$\operatorname {\mathrm {pr}}({\mathfrak a}(P))$
is
$(n,\alpha )$
-separated.
Remark 14.3. The constant
$e^{-{1}/{2}}$
in the statement of Lemma 14.2 is an artifact of the metric we defined on
$GX$
. If we had used any constant
$b \in (1,\tfrac {9}{4})$
in place of e in defining
$d_{GX}$
, we could have used the constant
$\tfrac {2}{3}$
in place of
$e^{-{1}/{2}}$
in Lemma 14.2.
Definition 14.4. Let
$P \subset \mathfrak C_\Gamma $
be finite. Call a
$g^t$
-invariant probability measure
$\nu $
on
$\Gamma \backslash GX$
equal-weighted along
${\mathfrak a}(P)$
if
$\nu $
gives measure
${1}/{\# {P}}$
to the orbit of
$\operatorname {\mathrm {pr}}({\mathfrak a}[\gamma ])$
for each
$[\gamma ] \in P$
, where
$\operatorname {\mathrm {pr}} \colon GX \to \Gamma \backslash GX$
is the canonical projection map.
Proposition 14.5. Let
$\Gamma $
be a group acting freely geometrically on a proper, geodesically complete
$\operatorname {\mathrm {CAT}}(0)$
space X with rank-one axis. Let
$(\nu _k)$
be a sequence of
$g^t$
-invariant probability measures on
$\Gamma \backslash GX$
, and let
${\mathfrak a}$
be a choice of axis. Assume each
$\nu _k$
is equal-weighted along
${\mathfrak a}(P_k)$
for some subset
$P_k \subset \mathfrak C_\Gamma (t_k - \varepsilon , t_k)$
, where
$\varepsilon $
satisfies
$0 < \varepsilon < e^{-{1}/{2}} \operatorname {\mathrm {injrad}}(\Gamma \backslash X)$
and
$t_k \to \infty $
as
$k \to \infty $
. If
$$ \begin{align*}\lim_{k \to \infty} \frac{\log \# {P_k}}{t_k} = h\end{align*} $$
then
$\nu _k \to m_\Gamma $
weakly.
Proof By compactness of the space of
$g^t$
-invariant Borel probability measures on
$\Gamma \backslash GX$
under the weak* topology, every subsequence
$(\nu _{k_j})$
has at least one weak* accumulation point
$\nu $
of
$\{\nu _k\}$
. By uniqueness of the measure of maximal entropy, it suffices to prove that every such
$\nu $
is a measure of maximal entropy for
$g_\Gamma ^t$
.
Let
$\nu $
be a weak* accumulation point of
$\{\nu _k\}$
; passing to a subsequence if necessary, we may assume
$\nu _k \to \nu $
in the weak* topology. Fix a measurable partition
${\mathcal A} = \{A_1, \dotsc , A_m\}$
of
$\Gamma \backslash GX$
such that
$\delta := \operatorname {\mathrm {diam}} {\mathcal A} < \varepsilon $
and
$\nu (\partial A_i) = 0$
. Let
$n_k = \lceil t_k \rceil $
and
$\phi = g^1$
. Since the closed geodesics in
$\operatorname {\mathrm {pr}}({\mathfrak a}(P_k))$
are
$(n_k,\varepsilon )$
-separated by Lemma 14.2, they are also
$(n_k,\delta )$
-separated. But by construction, no two geodesics in any one
$\alpha \in {\mathcal A}_\phi ^{(n_k + 1)}$
are
$(n_k,\delta )$
-separated, hence each
$\alpha \in {\mathcal A}_\phi ^{(n_k + 1)}$
touches at most one geodesic from
$\operatorname {\mathrm {pr}}({\mathfrak a}(P_k))$
. But Lemma 14.2 holds for arbitrary choice of axis, including flowing each geodesic in
${\mathfrak a}(P_k)$
by a different amount; hence each
$\alpha \in {\mathcal A}_\phi ^{(n_k + 1)}$
touches at most one orbit from
$\operatorname {\mathrm {pr}}({\mathfrak a}(P_k))$
. Thus
$\nu _k(\alpha ) \le {1}/{\# {P_k}}$
. Therefore the entropy
$$ \begin{align*} H_{\nu_k}({\mathcal A}_\phi^{(n_k + 1)}) = \sum_{\alpha \in {\mathcal A}_\phi^{(n_k + 1)}} - \nu_k(\alpha) \log \nu_k(\alpha) \ge \sum_{\alpha \in {\mathcal A}_\phi^{(n_k + 1)}} \nu_k(\alpha) \log \# {P_k} = \log \# {P_k}. \end{align*} $$
Since
$\nu (\partial A_i) = 0$
for all
$A_i \in {\mathcal A}$
, we have
$H_{\nu _k}({\mathcal A}_\phi ^{(q)}) \to H_{\nu }({\mathcal A}_\phi ^{(q)})$
and thus
$$ \begin{align*} h_{\nu}(\phi) \ge h_{\nu}(\phi, {\mathcal A}) = \lim_{q \to \infty} \frac{H_{\nu} ({\mathcal A}_\phi^{(q)})}{q} = \lim_{q \to \infty} \lim_{k \to \infty} \frac{H_{\nu_k} ({\mathcal A}_\phi^{(q)})}{q}. \end{align*} $$
By Lemma 14.1 and the inequality
$H_{\nu _k}({\mathcal A}_\phi ^{(n_k + 1)}) \ge \log \# {P_k}$
from above,
$$ \begin{align*} \lim_{q \to \infty} \lim_{k \to \infty} \frac{H_{\nu_k} ({\mathcal A}_\phi^{(q)})}{q} \ge {\widetilde{\lim_{k \to \infty}}} \frac{H_{\nu_k} ({\mathcal A}_\phi^{(n_k + 1)})}{n_k} \ge \lim_{k \to \infty} \frac{\log \# {P_k}}{t_k} = h. \end{align*} $$
Therefore
$h_{\nu }(\phi ) \ge h$
, which shows that
$\nu $
is a measure of maximal entropy. Because
$m_\Gamma $
is the unique such probability measure by Proposition 5.3, we have
$\nu = m_\Gamma $
.
Corollary 14.6. Let
$\Gamma $
be a group acting freely geometrically on a proper, geodesically complete
$\operatorname {\mathrm {CAT}}(0)$
space X with rank-one axis. Then
$$ \begin{align*} \limsup_{t \to \infty} \frac{\log {\mathrm{Conj}}_\Gamma^{GX ~\backslash~ \mathcal R}(t-\varepsilon,t)}{t} < h \end{align*} $$
for all
$\varepsilon $
satisfying
$0 < \varepsilon < e^{-{1}/{2}} \operatorname {\mathrm {injrad}}(\Gamma \backslash GX))$
. In particular,
$$ \begin{align*} \limsup_{t \to \infty} \frac{\log {\mathrm{Conj}}_\Gamma^{GX ~\backslash~ \mathcal R}(0,t)}{t} < h \quad \text{and} \quad \limsup_{t \to \infty} \frac{\log {\mathrm{Conj}}_\Gamma^{GX ~\backslash~ \mathcal R}(0,t)}{\log {\mathrm{Conj}}_\Gamma^{\mathcal R}(0,t)} = 0. \end{align*} $$
Proof Suppose the first statement fails. Then we have
$\varepsilon \in (0, e^{-{1}/{2}} \operatorname {\mathrm {injrad}}(\Gamma \backslash GX))$
and
$t_k \to \infty $
such that the sets
$P_k := \mathfrak C_\Gamma ^{GX ~\backslash~ \mathcal R}(t_k - \varepsilon , t_k)$
satisfy
$\lim _{k \to \infty } ({\log \# {P_k}}/{t_k}) = h$
. Hence by Proposition 14.5,
$\lambda _{{\mathfrak a},t_k,\alpha }^{GX ~\backslash~ \mathcal R} \to m_\Gamma $
weakly. But
$GX ~\backslash~ \mathcal R$
is closed in
$GX$
, so
$m_\Gamma $
must be supported on
$\Gamma \backslash (GX ~\backslash~ \mathcal R)$
, which contradicts the fact that
$m_\Gamma $
is supported on
$\mathcal R$
. Therefore, the first statement must hold. Then there exist
$h' < h$
and
$t_0> 0$
such that
${\mathrm{Conj}}_\Gamma ^{GX ~\backslash~ \mathcal R}(t-\varepsilon ,t) \le e^{h' t}$
for all
$t \ge t_0$
, and thus
${\mathrm{Conj}}_\Gamma ^{GX ~\backslash~ \mathcal R}(0,t) \le C e^{h't}$
for some
$C> 0$
by Lemma 13.1; the second inequality follows directly and the final equality from Corollary 11.8.
Theorem 14.7. Let
$\Gamma $
be a group acting freely geometrically on a proper, geodesically complete
$\operatorname {\mathrm {CAT}}(0)$
space X with rank-one axis. Let
$U \subseteq GX$
contain a non-empty open set. For any fixed
$\alpha $
with
$0 < \alpha < e^{-{1}/{2}} \operatorname {\mathrm {injrad}}(\Gamma \backslash X)$
and choice of axis
${\mathfrak a}$
, the measures
$\lambda _{{\mathfrak a}, t + \alpha , 2 \alpha }^{{\mathrm{mult}}, U}$
,
$\lambda _{{\mathfrak a},t,\alpha }^{{\mathrm{prime}}, U}$
, and
$\tilde {\lambda }_{{\mathfrak a},t,\alpha }^{{\mathrm{mult}}, U}$
all converge weakly to
$m_\Gamma $
as
$t \to \infty $
.
Proof Let
$(t_k)$
be a sequence of positive real numbers such that
$t_k \to \infty $
. Let
$P_k = \mathfrak C_\Gamma ^{U}(t_k - \alpha , t_k)$
. By Corollary 11.8,
$\lim _{k \to \infty } ({\log \# {P_k}}/{t_k}) = h$
, and thus
$\lambda _{{\mathfrak a},t_k,\alpha }^{U} \to m_\Gamma $
weakly by Proposition 14.5. Since
$(t_k)$
was arbitrary, it follows that the measures
$\lambda _{{\mathfrak a},t,\alpha }^{{\mathrm{mult}}, U}$
converge weakly to
$m_\Gamma $
. By Lemma 12.5, so do the measures
$\lambda _{{\mathfrak a},t,\alpha }^{{\mathrm{mult}}, U}$
. It follows that
$\lambda _{{\mathfrak a}, t + \alpha , 2 \alpha }^{{\mathrm{mult}}, U} \to m_\Gamma $
weakly, and so
$\tilde {\lambda }_{{\mathfrak a},t,\alpha }^{{\mathrm{mult}}, U} \to m_\Gamma $
weakly by Lemma 11.4.
15 Using equidistribution
We recall again our standing hypotheses, from §5.2 through the rest of the paper. The group
$\Gamma $
acts freely, non-elementarily, properly discontinuously, and by isometries on the proper, geodesically complete
$\operatorname {\mathrm {CAT}}(0)$
space X with rank-one axis. We also assume
$m_\Gamma $
is finite and mixing, and normalized so that
$\| m_\Gamma \| = 1$
.
Lemma 15.1. Fix a zero-width geodesic
$v_0 \in G_{\Lambda } X$
. Let
$\varepsilon \in (0, \varepsilon _0]$
, and let
$\delta \in (0, \delta _0)$
be a point of continuity of the non-decreasing function
$r \mapsto m( \mathfrak {v}_r)$
. Let U satisfy
$ \mathfrak {v}_{\varepsilon ,\delta } \subseteq U \subseteq GX$
. Assume that, for some choice of axis
${\mathfrak a}$
, the measures
$\tilde {\lambda }_{{\mathfrak a},t,\varepsilon }^{{\mathrm{mult}}, U}$
converge weakly to
$m_\Gamma $
as
$t \to \infty $
. Then
Proof Since
$ \mathfrak {v}_{\varepsilon ,\delta }$
is a continuity set for m, we see that
$\lim _{t \to \infty } \tilde {\lambda }_{{\mathfrak a},t,\varepsilon }^{{\mathrm{mult}}, U} (\operatorname {\mathrm {pr}} \mathfrak {v}_{\varepsilon ,\delta }) = m_\Gamma (\operatorname {\mathrm {pr}} \mathfrak {v}_{\varepsilon ,\delta })$
by hypothesis on
$\tilde {\lambda }_{{\mathfrak a},t,\varepsilon }^{{\mathrm{mult}}, U}$
. By choice of
$\varepsilon _0, \delta _0> 0$
(Lemma 4.2), we find
$\operatorname {\mathrm {pr}}$
is injective on
$ \mathfrak {v}_{\varepsilon ,\delta }$
, and therefore
$m_\Gamma (\operatorname {\mathrm {pr}} \mathfrak {v}_{\varepsilon ,\delta }) = m( \mathfrak {v}_{\varepsilon ,\delta })$
. Apply Corollary 11.3.
Putting
$F(t) = e^{ht} / t$
in Lemma 13.1, by Lemma 15.1 we obtain our desired asymptotics for
${\mathrm{Conj}}_\Gamma ^{U}(0,t)$
. But to do so, we need to check the overlaps we get from counting the endpoints of closed intervals are asymptotically small.
We record first the following observation. If
$(a_k)$
and
$(b_k)$
are sequences in
$\mathbb {R}$
such that
$(b_k)$
is eventually positive and non-decreasing, and
${1}/{c} \le \mathop {\widetilde {\lim }}\nolimits _{k \to \infty } {a_k}/{b_k} \le c$
for some
$c \ge 1$
, then
${1}/{c} \le \mathop {\widetilde {\lim }}\nolimits _{n \to \infty } ({\sum \nolimits _{k=1}^{n} a_k}/{\sum \nolimits _{k=1}^{n} b_k}) \le c$
. The proof is straightforward: Since
$(b_k)$
is eventually positive and non-decreasing, the first finitely many terms of both sums are negligible. Thus for each
$\delta> 0$
, we may assume
${1}/{c} - \delta \le {a_k}/{b_k} \le c + \delta $
for all k, whence
${1}/{c} - \delta \le ({\sum _{k=1}^{n} a_k}/{\sum _{k=1}^{n} b_k}) \le c + \delta $
for all n, proving the claim. Essentially the same proof establishes the following result.
Lemma 15.2. Let
$f, g \colon \mathbb {R} \to \mathbb {R}$
, and assume g is eventually positive and non-decreasing. If
$a \le \mathop {\widetilde {\lim }}\nolimits _{t \to \infty } {f(t)}/{g(t)} \le b$
for some
$a,b> 0$
, then
$$ \begin{align*}a \le \mathop{\widetilde{\lim}}\limits_{t \to \infty} \frac {\sum_{k=0}^{\lfloor {t}/{2\varepsilon} \rfloor} f(t - (2k+1)\varepsilon)} {\sum_{k=0}^{\lfloor {t}/{2\varepsilon} \rfloor} g(t - (2k+1)\varepsilon)} \le b\end{align*} $$
for all
$\varepsilon> 0$
.
Proof Let
$\varepsilon> 0$
. By hypothesis on g, we may ignore finitely many terms from both sums. Thus for each
$\delta> 0$
, we may assume
$a - \delta \le {f(t)}/{g(t)} \le b + \delta $
for all
$t> 0$
, whence
$a - \delta \le ({\sum _{k=0}^{\lfloor {t}/{2\varepsilon } \rfloor } f(t - (2k+1)\varepsilon )})/({\sum _{k=0}^{\lfloor {t}/{2\varepsilon } \rfloor } g(t - (2k+1)\varepsilon )}) \le b + \delta $
for all
$t> 0$
. This proves the lemma.
Lemma 15.3. Fix a zero-width geodesic
$v_0 \in G_{\Lambda } X$
. Let
$\varepsilon \in (0, \varepsilon _0]$
, and let
$\delta \in (0, \delta _0)$
be a point of continuity of the non-decreasing function
$r \mapsto m( \mathfrak {v}_r)$
. Let U satisfy
$ \mathfrak {v}_{\varepsilon ,\delta } \subseteq U \subseteq GX$
. Assume that for every
$\alpha \in (0,\varepsilon ]$
there is a choice of axis
${\mathfrak a}$
such that the measures
$\tilde {\lambda }_{{\mathfrak a},t,\alpha }^{{\mathrm{mult}}, U}$
converge weakly to
$m_\Gamma $
as
$t \to \infty $
. Then
Proof By Lemma 15.1, for all
$\alpha \in (0, \varepsilon ]$
we have
and therefore by Lemma 15.2,
Since for all
$\alpha \in (0, \varepsilon )$
,
$$ \begin{align*} &\sum_{k = 0}^{\lfloor {t}/{2\varepsilon} \rfloor} {{\mathrm{Conj}}_\Gamma^{U} ( t - (2k+1)\varepsilon - \alpha, t - (2k+1)\varepsilon + \alpha )} \\ &\quad\le \, {\mathrm{Conj}}_\Gamma^{U}(0,t) \le \sum_{k = 0}^{\lfloor {t}/{2\varepsilon} \rfloor} {{\mathrm{Conj}}_\Gamma^{U} ( t - (2k+2)\varepsilon, t - 2k\varepsilon )}, \end{align*} $$
letting
$\alpha \to \varepsilon $
from below gives us
Thus by Lemma 13.2,
where
$C = e^{h \varepsilon }$
.
Remark 15.4. We do not actually need
$\tilde {\lambda }_{{\mathfrak a},t,\alpha }^{{\mathrm{mult}}, U} \to m_\Gamma $
weakly for all
$\alpha \in (0, \varepsilon ]$
. It suffices for this to hold for an increasing sequence
$\alpha _k \to \varepsilon $
, and for
$\varepsilon $
itself.
Theorem 15.5. Let
$\Gamma $
be a group acting freely, properly discontinuously, and by isometries on a proper, geodesically complete
$\operatorname {\mathrm {CAT}}(0)$
space X with rank-one axis. Let
$U \subseteq GX$
contain an open neighborhood of some zero-width geodesic
$v_0 \in G_{\Lambda } X$
. Assume
$m_\Gamma $
is finite and mixing, and also that for all sufficiently small
$\alpha> 0$
there is a choice of axis
${\mathfrak a}$
such that
$\tilde {\lambda }_{{\mathfrak a},t,\alpha }^{{\mathrm{mult}}, U} \to m_\Gamma $
weakly as
$t \to \infty $
. Then
$$ \begin{align*} \lim_{t \to \infty} \frac{{\mathrm{Conj}}_\Gamma^{U}(0,t)}{e^{ht}/ht} = 1. \end{align*} $$
Moreover, if
$U \subseteq \Gamma K$
for some compact set
$K \subseteq GX$
, then
$$ \begin{align*} \lim_{t \to \infty} \frac{{\mathrm{Conj}}_\Gamma^{{\mathrm{prime}}, U}(0,t)}{e^{ht}/ht} = \lim_{t \to \infty} \frac{{\mathrm{Conj}}_\Gamma^{U}(0,t)}{e^{ht}/ht} = 1. \end{align*} $$
Proof Choose decreasing sequences
$\varepsilon _k, \delta _k \to 0$
such that each
$\delta _k \in (0, \delta _0)$
is a point of continuity of the non-decreasing function
$r \mapsto m( \mathfrak {v}_{\varepsilon _k,r})$
. Since
$\lim _{\varepsilon ,\delta \to 0} C_{\varepsilon ,\delta } = 1$
, the first statement holds by Lemma 15.3. The second holds by Corollary 12.4.
Corollary 15.6. Let
$\Gamma $
be a group acting freely geometrically on a proper, geodesically complete
$\operatorname {\mathrm {CAT}}(0)$
space X with rank-one axis. Assume X is not homothetic to a tree with integer edge lengths. Let
$U \subseteq GX$
contain a non-empty open set. Then
$$ \begin{align*} \lim_{t \to \infty} \frac{{\mathrm{Conj}}_\Gamma^{{\mathrm{prime}}, U}(0,t)}{e^{ht}/ht} = \lim_{t \to \infty} \frac{{\mathrm{Conj}}_\Gamma^{U}(0,t)}{e^{ht}/ht} = 1. \end{align*} $$
Proof By [Reference Ricks12, Theorems 4 and 5],
$m_\Gamma $
is finite and mixing. By Theorem 14.7, for every
$\alpha> 0$
with
$\alpha < e^{-{1}/{2}} \operatorname {\mathrm {injrad}}(\Gamma \backslash X)$
and every choice of axis
${\mathfrak a}$
, we have
$\tilde {\lambda }_{{\mathfrak a},t,\alpha }^{{\mathrm{mult}}, U} \to m_\Gamma $
weakly as
$t \to \infty $
. Apply Theorem 15.5.
In particular, putting
$U = \mathcal R$
and
$U = GX$
in Corollary 15.6, we obtain
$$ \begin{align*} &\lim_{t \to \infty} \frac{{\mathrm{Conj}}_\Gamma^{{\mathrm{prime}}, \mathcal R}(0,t)}{e^{ht}/ht} = \lim_{t \to \infty} \frac{{\mathrm{Conj}}_\Gamma^{\mathcal R}(0,t)}{e^{ht}/ht}, \\ &\quad =\lim_{t \to \infty} \frac{{\mathrm{Conj}}_\Gamma^{\mathrm{prime}}(0,t)}{e^{ht}/ht} = \lim_{t \to \infty} \frac{{\mathrm{Conj}}_\Gamma(0,t)}{e^{ht}/ht} = 1. \end{align*} $$
This proves Theorem 1.1.
Acknowledgements
The author would like to thank the anonymous referee, who made helpful suggestions to improve the paper. Early work on this paper was supported by the National Science Foundation under Grant Number NSF 1045119.
