Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-11T07:05:33.432Z Has data issue: false hasContentIssue false
  • English
  • Français

Computable Følner monotilings and a theorem of Brudno

Part of: Ergodic theory Theory of computing

Published online by Cambridge University Press:  13 November 2020

NIKITA MORIAKOV
NIKITA MORIAKOV*
Affiliation:
Department of Imaging, Radboud University Medical Center, Geert Grooteplein 10, 6525 GANijmegen, The Netherlands Department of Radiation Oncology, Netherlands Cancer Institute, Plesmanlaan 121, 1066 CXAmsterdam, The Netherlands
*
e-mail: n.moriakov@nki.nl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A theorem of Brudno says that the Kolmogorov–Sinai entropy of an ergodic subshift over 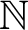$\mathbb {N}$ equals the asymptotic Kolmogorov complexity of almost every word in the subshift. The purpose of this paper is to extend this result to subshifts over computable groups that admit computable regular symmetric Følner monotilings, which we introduce in this work. For every 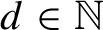$d \in \mathbb {N}$ , the groups 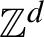$\mathbb {Z}^d$ and $\mathsf{UT}_{d+1}(\mathbb {Z})$ admit computable regular symmetric Følner monotilings for which the required computing algorithms are provided.

Keywords

entropyKolmogorov complexitymeasure-preserving dynamical systems

MSC classification

Primary: 37A35: Entropy and other invariants, isomorphism, classification 68Q30: Algorithmic information theory (Kolmogorov complexity, etc.)
Secondary: 37A15: General groups of measure-preserving transformations
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 11 , November 2021 , pp. 3389 - 3416
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

References

Alpeev, A.. Kolmogorov complexity and entropy of amenable group actions. Preprint, 2018, arXiv:1809.01634.Google Scholar
Brudno, A. A.. Topological entropy, and complexity in the sense of A. N. Kolmogorov. Uspehi Mat. Nauk 29(1974), 157–158.Google Scholar
Brudno, A. A.. Entropy and the complexity of the trajectories of a dynamic system. Tr. Mosk. Mat. Obs. 44(1982), 124–149.Google Scholar
Ceccherini-Silberstein, T. and Coornaert, M.. Cellular Automata and Groups (Springer Monographs in Mathematics, 44). Springer, Berlin, 2010.CrossRefGoogle Scholar
Glasner, E.. Ergodic Theory via Joinings ( Mathematical Surveys and Monographs , 101). American Mathematical Society, Providence, RI, 2003.CrossRefGoogle Scholar
Gromov, M.. Topological invariants of dynamical systems and spaces of holomorphic maps. I. Math. Phys. Anal. Geom. 2(4) (1999), 323–415.CrossRefGoogle Scholar
Golodets, V. Y. and Sinel'shchikov, S. D.. On the entropy theory of finitely-generated nilpotent group actions. Ergod. Th. & Dynam. Sys. 22(6) (2002), 1747–1771.CrossRefGoogle Scholar
Hedman, S.. A First Course in Logic ( Oxford Texts in Logic , 1). Oxford University Press, Oxford, 2004.CrossRefGoogle Scholar
Krieger, F.. Le lemme d’Ornstein-Weiss d’après Gromov. Dynamics, Ergodic Theory, and Geometry (Mathematical Sciences Research Institute Publications, 54). Cambridge University Press, Cambridge, 2007, pp. 99–111.10.1017/CBO9780511755187.004CrossRefGoogle Scholar
Lindenstrauss, E.. Pointwise theorems for amenable groups. Invent. Math. 146(2) (2001), 259–295.CrossRefGoogle Scholar
Lenz, D., Schwarzenberger, F., and Veselić, I.. A Banach space-valued ergodic theorem and the uniform approximation of the integrated density of states. Geom. Dedicata 150 (2011), 1–34.10.1007/s10711-010-9491-xCrossRefGoogle Scholar
Moriakov, N.. Computable Følner monotilings and a theorem of Brudno I. Preprint, 2015, arXiv:1509.07858.Google Scholar
Moriakov, N.. Computable Følner monotilings and a theorem of Brudno II. Preprint, 2015, arXiv:1311.0754v4.Google Scholar
Rabin, M. O.. Computable algebra, general theory and theory of computable fields. Trans. Amer. Math. Soc. 95(1960), 341–360.Google Scholar
Simpson, S. G.. Symbolic dynamics: entropy = dimension = complexity. Theory Comput. Syst. 56(3) (2015), 527–543.CrossRefGoogle Scholar
Weiss, B.. Monotileable amenable groups Topology, Ergodic Theory, Real Algebraic Geometry (American Mathematical Society Translations Series 2, 202). American Mathematical Society, Providence, RI, 2001, pp. 257–262.Google Scholar
Zorin-Kranich, P.. Return times theorem for amenable groups. Israel J. Math. 204(1) (2014), 85–96.CrossRefGoogle Scholar